problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
4. A4 (IRE) ${ }^{\mathrm{IMO} 5}$ Let $n$ be a positive integer and let $x_{1} \leq x_{2} \leq \cdots \leq x_{n}$ be real numbers. (a) Prove that $$ \left(\sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right|\right)^{2} \leq \frac{2\left(n^{2}-1\right)}{3} \sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2} $$ (b) Show that equality holds if and only if $x_{1}, \ldots, x_{n}$ is an arithmetic progession.
|
4. By the Cauchy-Schwarz inequality we have $$ \left(\sum_{i, j=1}^{n}(i-j)^{2}\right)\left(\sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2}\right) \geq\left(\sum_{i, j=1}^{n}|i-j| \cdot\left|x_{i}-x_{j}\right|\right)^{2} . $$ On the other hand, it is easy to prove (for example by induction) that $$ \sum_{i, j=1}^{n}(i-j)^{2}=(2 n-2) \cdot 1^{2}+(2 n-4) \cdot 2^{2}+\cdots+2 \cdot(n-1)^{2}=\frac{n^{2}\left(n^{2}-1\right)}{6} $$ and that $$ \sum_{i, j=1}^{n}|i-j| \cdot\left|x_{i}-x_{j}\right|=\frac{n}{2} \sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right| $$ Thus the inequality (1) becomes $$ \frac{n^{2}\left(n^{2}-1\right)}{6}\left(\sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2}\right) \geq \frac{n^{2}}{4}\left(\sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right|\right)^{2} $$ which is equivalent to the required one.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
4. A4 (IRE) ${ }^{\mathrm{IMO} 5}$ Let $n$ be a positive integer and let $x_{1} \leq x_{2} \leq \cdots \leq x_{n}$ be real numbers. (a) Prove that $$ \left(\sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right|\right)^{2} \leq \frac{2\left(n^{2}-1\right)}{3} \sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2} $$ (b) Show that equality holds if and only if $x_{1}, \ldots, x_{n}$ is an arithmetic progession.
|
4. By the Cauchy-Schwarz inequality we have $$ \left(\sum_{i, j=1}^{n}(i-j)^{2}\right)\left(\sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2}\right) \geq\left(\sum_{i, j=1}^{n}|i-j| \cdot\left|x_{i}-x_{j}\right|\right)^{2} . $$ On the other hand, it is easy to prove (for example by induction) that $$ \sum_{i, j=1}^{n}(i-j)^{2}=(2 n-2) \cdot 1^{2}+(2 n-4) \cdot 2^{2}+\cdots+2 \cdot(n-1)^{2}=\frac{n^{2}\left(n^{2}-1\right)}{6} $$ and that $$ \sum_{i, j=1}^{n}|i-j| \cdot\left|x_{i}-x_{j}\right|=\frac{n}{2} \sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right| $$ Thus the inequality (1) becomes $$ \frac{n^{2}\left(n^{2}-1\right)}{6}\left(\sum_{i, j=1}^{n}\left(x_{i}-x_{j}\right)^{2}\right) \geq \frac{n^{2}}{4}\left(\sum_{i, j=1}^{n}\left|x_{i}-x_{j}\right|\right)^{2} $$ which is equivalent to the required one.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a39a1520-9041-53e7-bd23-5c2b2a1de90a
| 25,156
|
6. A6 (USA) Let $n$ be a positive integer and let $\left(x_{1}, \ldots, x_{n}\right),\left(y_{1}, \ldots, y_{n}\right)$ be two sequences of positive real numbers. Suppose $\left(z_{2}, z_{3}, \ldots, z_{2 n}\right)$ is a sequence of positive real numbers such that $$ z_{i+j}^{2} \geq x_{i} y_{j} \quad \text { for all } 1 \leq i, j \leq n $$ Let $M=\max \left\{z_{2}, \ldots, z_{2 n}\right\}$. Prove that $$ \left(\frac{M+z_{2}+\cdots+z_{2 n}}{2 n}\right)^{2} \geq\left(\frac{x_{1}+\cdots+x_{n}}{n}\right)\left(\frac{y_{1}+\cdots+y_{n}}{n}\right) . $$
|
6. Set $X=\max \left\{x_{1}, \ldots, x_{n}\right\}$ and $Y=\max \left\{y_{1}, \ldots, y_{n}\right\}$. By replacing $x_{i}$ by $x_{i}^{\prime}=\frac{x_{i}}{X}, y_{i}$ by $y_{i}^{\prime}=\frac{y_{i}}{Y}$ and $z_{i}$ by $z_{i}^{\prime}=\frac{z_{i}}{\sqrt{X Y}}$, we may assume that $X=Y=1$. It is sufficient to prove that $$ M+z_{2}+\cdots+z_{2 n} \geq x_{1}+\cdots+x_{n}+y_{1}+\cdots+y_{n} $$ because this implies the result by the A-G mean inequality. To prove (1) it is enough to prove that for any $r$, the number of terms greater than $r$ on the left-hand side of (1) is at least that number on the right-hand side of (1). If $r \geq 1$, then there are no terms on the right-hand side greater than $r$. Suppose that $r<1$ and consider the sets $A=\left\{i \mid 1 \leq i \leq n, x_{i}>r\right\}$ and $B=\left\{i \mid 1 \leq i \leq n, y_{i}>r\right\}$. Set $a=|A|$ and $b=|B|$. If $x_{i}>r$ and $y_{j}>r$, then $z_{i+j} \geq \sqrt{x_{i} y_{j}}>r$; hence $$ C=\left\{k \mid 2 \leq k \leq 2 n, z_{k}>r\right\} \supseteq A+B=\{\alpha+\beta \mid \alpha \in A, \beta \in B\} $$ It is easy to verify that $|A+B| \geq|A|+|B|-1$. It follows that the number of $z_{k}$ 's greater than $r$ is $\geq a+b-1$. But in that case $M>r$, implying that at least $a+b$ elements of the left-hand side of (1) is greater than $r$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
6. A6 (USA) Let $n$ be a positive integer and let $\left(x_{1}, \ldots, x_{n}\right),\left(y_{1}, \ldots, y_{n}\right)$ be two sequences of positive real numbers. Suppose $\left(z_{2}, z_{3}, \ldots, z_{2 n}\right)$ is a sequence of positive real numbers such that $$ z_{i+j}^{2} \geq x_{i} y_{j} \quad \text { for all } 1 \leq i, j \leq n $$ Let $M=\max \left\{z_{2}, \ldots, z_{2 n}\right\}$. Prove that $$ \left(\frac{M+z_{2}+\cdots+z_{2 n}}{2 n}\right)^{2} \geq\left(\frac{x_{1}+\cdots+x_{n}}{n}\right)\left(\frac{y_{1}+\cdots+y_{n}}{n}\right) . $$
|
6. Set $X=\max \left\{x_{1}, \ldots, x_{n}\right\}$ and $Y=\max \left\{y_{1}, \ldots, y_{n}\right\}$. By replacing $x_{i}$ by $x_{i}^{\prime}=\frac{x_{i}}{X}, y_{i}$ by $y_{i}^{\prime}=\frac{y_{i}}{Y}$ and $z_{i}$ by $z_{i}^{\prime}=\frac{z_{i}}{\sqrt{X Y}}$, we may assume that $X=Y=1$. It is sufficient to prove that $$ M+z_{2}+\cdots+z_{2 n} \geq x_{1}+\cdots+x_{n}+y_{1}+\cdots+y_{n} $$ because this implies the result by the A-G mean inequality. To prove (1) it is enough to prove that for any $r$, the number of terms greater than $r$ on the left-hand side of (1) is at least that number on the right-hand side of (1). If $r \geq 1$, then there are no terms on the right-hand side greater than $r$. Suppose that $r<1$ and consider the sets $A=\left\{i \mid 1 \leq i \leq n, x_{i}>r\right\}$ and $B=\left\{i \mid 1 \leq i \leq n, y_{i}>r\right\}$. Set $a=|A|$ and $b=|B|$. If $x_{i}>r$ and $y_{j}>r$, then $z_{i+j} \geq \sqrt{x_{i} y_{j}}>r$; hence $$ C=\left\{k \mid 2 \leq k \leq 2 n, z_{k}>r\right\} \supseteq A+B=\{\alpha+\beta \mid \alpha \in A, \beta \in B\} $$ It is easy to verify that $|A+B| \geq|A|+|B|-1$. It follows that the number of $z_{k}$ 's greater than $r$ is $\geq a+b-1$. But in that case $M>r$, implying that at least $a+b$ elements of the left-hand side of (1) is greater than $r$, which completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1573aeae-7fcb-530c-815c-7dab493f2fde
| 25,158
|
7. C1 (BRA) ${ }^{\mathrm{IMO} 1}$ Let $A$ be a 101-element subset of the set $S=\{1,2, \ldots$, $1000000\}$. Prove that there exist numbers $t_{1}, t_{2}, \ldots, t_{100}$ in $S$ such that the sets $$ A_{j}=\left\{x+t_{j} \mid x \in A\right\}, \quad j=1,2, \ldots, 100 $$ are pairwise disjoint.
|
7. Consider the set $D=\{x-y \mid x, y \in A\}$. Obviously, the number of elements of the set $D$ is less than or equal to $101 \cdot 100+1$. The sets $A+t_{i}$ and $A+t_{j}$ are disjoint if and only if $t_{i}-t_{j} \notin D$. Now we shall choose inductively 100 elements $t_{1}, \ldots, t_{100}$. Let $t_{1}$ be any element of the set $S \backslash D$ (such an element exists, since the number of elements of $S$ is greater than the number of elements of $D$ ). Suppose now that we have chosen $k(k \leq 99)$ elements $t_{1}, \ldots, t_{k}$ from $D$ such that the difference of any two of the chosen elements does not belong to $D$. We can select $t_{k+1}$ to be an element of $S$ that does not belong to any of the sets $t_{1}+D, t_{2}+D, \ldots, t_{k}+D$ (this is possible to do, since each of the previous sets has at most $101 \cdot 100+1$ elements; hence their union has at most $99(101 \cdot 100+1)=999999<1000000$ elements $)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
7. C1 (BRA) ${ }^{\mathrm{IMO} 1}$ Let $A$ be a 101-element subset of the set $S=\{1,2, \ldots$, $1000000\}$. Prove that there exist numbers $t_{1}, t_{2}, \ldots, t_{100}$ in $S$ such that the sets $$ A_{j}=\left\{x+t_{j} \mid x \in A\right\}, \quad j=1,2, \ldots, 100 $$ are pairwise disjoint.
|
7. Consider the set $D=\{x-y \mid x, y \in A\}$. Obviously, the number of elements of the set $D$ is less than or equal to $101 \cdot 100+1$. The sets $A+t_{i}$ and $A+t_{j}$ are disjoint if and only if $t_{i}-t_{j} \notin D$. Now we shall choose inductively 100 elements $t_{1}, \ldots, t_{100}$. Let $t_{1}$ be any element of the set $S \backslash D$ (such an element exists, since the number of elements of $S$ is greater than the number of elements of $D$ ). Suppose now that we have chosen $k(k \leq 99)$ elements $t_{1}, \ldots, t_{k}$ from $D$ such that the difference of any two of the chosen elements does not belong to $D$. We can select $t_{k+1}$ to be an element of $S$ that does not belong to any of the sets $t_{1}+D, t_{2}+D, \ldots, t_{k}+D$ (this is possible to do, since each of the previous sets has at most $101 \cdot 100+1$ elements; hence their union has at most $99(101 \cdot 100+1)=999999<1000000$ elements $)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d0aa02b2-eafd-5f7a-b576-e8fcbf641104
| 25,159
|
1. A1 (KOR) ${ }^{\mathrm{IMO} 4}$ Let $n \geq 3$ be an integer and $t_{1}, t_{2}, \ldots, t_{n}$ positive real numbers such that $$ n^{2}+1>\left(t_{1}+t_{2}+\cdots+t_{n}\right)\left(\frac{1}{t_{1}}+\frac{1}{t_{2}}+\cdots+\frac{1}{t_{n}}\right) . $$ Show that $t_{i}, t_{j}, t_{k}$ are the side lengths of a triangle for all $i, j, k$ with $1 \leq i<j<k \leq n$.
|
1. By symmetry, it is enough to prove that $t_{1}+t_{2}>t_{3}$. We have $$ \left(\sum_{i=1}^{n} t_{i}\right)\left(\sum_{i=1}^{n} \frac{1}{t}_{i}\right)=n^{2}+\sum_{i<j}\left(\frac{t_{i}}{t_{j}}+\frac{t_{j}}{t_{i}}-2\right) . $$ All the summands on the RHS are positive, and therefore the RHS is not smaller than $n^{2}+T$, where $T=\left(t_{1} / t_{3}+t_{3} / t_{1}-2\right)+\left(t_{2} / t_{3}+t_{3} / t_{2}-2\right)$. We note that $T$ is increasing as a function in $t_{3}$ for $t_{3} \geq \max \left\{t_{1}, t_{2}\right\}$. If $t_{1}+t_{2}=t_{3}$, then $T=\left(t_{1}+t_{2}\right)\left(1 / t_{1}+1 / t_{2}\right)-1 \geq 3$ by the Cauchy-Schwarz inequality. Hence, if $t_{1}+t_{2} \leq t_{3}$, we have $T \geq 1$, and consequently the RHS in (1) is greater than or equal to $n^{2}+1$, a contradiction. Remark. In can be proved, for example using Lagrange multipliers, that if $n^{2}+1$ in the problem is replaced by $(n+\sqrt{10}-3)^{2}$, then the statement remains true. This estimate is the best possible.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
1. A1 (KOR) ${ }^{\mathrm{IMO} 4}$ Let $n \geq 3$ be an integer and $t_{1}, t_{2}, \ldots, t_{n}$ positive real numbers such that $$ n^{2}+1>\left(t_{1}+t_{2}+\cdots+t_{n}\right)\left(\frac{1}{t_{1}}+\frac{1}{t_{2}}+\cdots+\frac{1}{t_{n}}\right) . $$ Show that $t_{i}, t_{j}, t_{k}$ are the side lengths of a triangle for all $i, j, k$ with $1 \leq i<j<k \leq n$.
|
1. By symmetry, it is enough to prove that $t_{1}+t_{2}>t_{3}$. We have $$ \left(\sum_{i=1}^{n} t_{i}\right)\left(\sum_{i=1}^{n} \frac{1}{t}_{i}\right)=n^{2}+\sum_{i<j}\left(\frac{t_{i}}{t_{j}}+\frac{t_{j}}{t_{i}}-2\right) . $$ All the summands on the RHS are positive, and therefore the RHS is not smaller than $n^{2}+T$, where $T=\left(t_{1} / t_{3}+t_{3} / t_{1}-2\right)+\left(t_{2} / t_{3}+t_{3} / t_{2}-2\right)$. We note that $T$ is increasing as a function in $t_{3}$ for $t_{3} \geq \max \left\{t_{1}, t_{2}\right\}$. If $t_{1}+t_{2}=t_{3}$, then $T=\left(t_{1}+t_{2}\right)\left(1 / t_{1}+1 / t_{2}\right)-1 \geq 3$ by the Cauchy-Schwarz inequality. Hence, if $t_{1}+t_{2} \leq t_{3}$, we have $T \geq 1$, and consequently the RHS in (1) is greater than or equal to $n^{2}+1$, a contradiction. Remark. In can be proved, for example using Lagrange multipliers, that if $n^{2}+1$ in the problem is replaced by $(n+\sqrt{10}-3)^{2}$, then the statement remains true. This estimate is the best possible.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3c152912-8f10-586d-aa8e-a9d0e4bc2dc3
| 25,162
|
16. G1 (ROM) ${ }^{\mathrm{IMO} 1}$ Let $A B C$ be an acute-angled triangle with $A B \neq A C$. The circle with diameter $B C$ intersects the sides $A B$ and $A C$ at $M$ and $N$, respectively. Denote by $O$ the midpoint of $B C$. The bisectors of the angles $B A C$ and $M O N$ intersect at $R$. Prove that the circumcircles of the triangles $B M R$ and $C N R$ have a common point lying on the line segment $B C$.
|
16. Note that $\triangle A N M \sim \triangle A B C$ and consequently $A M \neq A N$. Since $O M=$ $O N$, it follows that $O R$ is a perpendicular bisector of $M N$. Thus, $R$ is the common point of the median of $M N$ and the bisector of $\angle M A N$. Then it follows from a well-known fact that $R$ lies on the circumcircle of $\triangle A M N$. Let $K$ be the intersection of $A R$ and $B C$. We then have $\angle M R A=$ $\angle M N A=\angle A B K$ and $\angle N R A=\angle N M A=\angle A C K$, from which we conclude that $R M B K$ and $R N C K$ are cyclic. Thus $K$ is the desired intersection of the circumcircles of $\triangle B M R$ and $\triangle C N R$ and it indeed lies on $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. G1 (ROM) ${ }^{\mathrm{IMO} 1}$ Let $A B C$ be an acute-angled triangle with $A B \neq A C$. The circle with diameter $B C$ intersects the sides $A B$ and $A C$ at $M$ and $N$, respectively. Denote by $O$ the midpoint of $B C$. The bisectors of the angles $B A C$ and $M O N$ intersect at $R$. Prove that the circumcircles of the triangles $B M R$ and $C N R$ have a common point lying on the line segment $B C$.
|
16. Note that $\triangle A N M \sim \triangle A B C$ and consequently $A M \neq A N$. Since $O M=$ $O N$, it follows that $O R$ is a perpendicular bisector of $M N$. Thus, $R$ is the common point of the median of $M N$ and the bisector of $\angle M A N$. Then it follows from a well-known fact that $R$ lies on the circumcircle of $\triangle A M N$. Let $K$ be the intersection of $A R$ and $B C$. We then have $\angle M R A=$ $\angle M N A=\angle A B K$ and $\angle N R A=\angle N M A=\angle A C K$, from which we conclude that $R M B K$ and $R N C K$ are cyclic. Thus $K$ is the desired intersection of the circumcircles of $\triangle B M R$ and $\triangle C N R$ and it indeed lies on $B C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
51c6ed1f-33c0-50ed-b59f-d694f6220bdc
| 25,169
|
17. G2 (KAZ) The circle $\Gamma$ and the line $\ell$ do not intersect. Let $A B$ be the diameter of $\Gamma$ perpendicular to $\ell$, with $B$ closer to $\ell$ than $A$. An arbitrary point $C \neq A, B$ is chosen on $\Gamma$. The line $A C$ intersects $\ell$ at $D$. The line $D E$ is tangent to $\Gamma$ at $E$, with $B$ and $E$ on the same side of $A C$. Let $B E$ intersect $\ell$ at $F$, and let $A F$ intersect $\Gamma$ at $G \neq A$. Prove that the reflection of $G$ in $A B$ lies on the line $C F$.
|
17. Let $H$ be the reflection of $G$ about $A B(G H \| \ell)$. Let $M$ be the intersection of $A B$ and $\ell$. Since $\angle F E A=\angle F M A=90^{\circ}$, it follows that $A E M F$ is cyclic and hence $\angle D F E=\angle B A E=\angle D E F$. The last equality holds because $D E$ is tangent to $\Gamma$. It follows that $D E=$ $D F$ and hence $D F^{2}=D E^{2}=$ 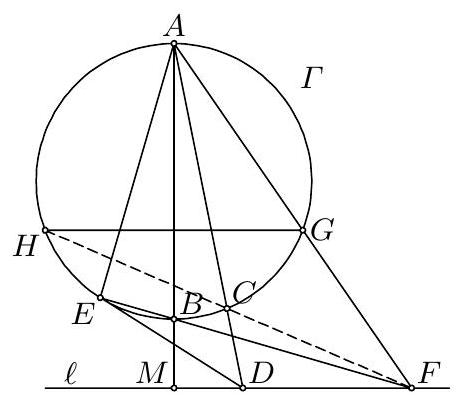 $D C \cdot D A$ (the power of $D$ with respect to $\Gamma$ ). It then follows that $\angle D C F=\angle D F A=\angle H G A=\angle H C A$. Thus it follows that $H$ lies on $C F$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
17. G2 (KAZ) The circle $\Gamma$ and the line $\ell$ do not intersect. Let $A B$ be the diameter of $\Gamma$ perpendicular to $\ell$, with $B$ closer to $\ell$ than $A$. An arbitrary point $C \neq A, B$ is chosen on $\Gamma$. The line $A C$ intersects $\ell$ at $D$. The line $D E$ is tangent to $\Gamma$ at $E$, with $B$ and $E$ on the same side of $A C$. Let $B E$ intersect $\ell$ at $F$, and let $A F$ intersect $\Gamma$ at $G \neq A$. Prove that the reflection of $G$ in $A B$ lies on the line $C F$.
|
17. Let $H$ be the reflection of $G$ about $A B(G H \| \ell)$. Let $M$ be the intersection of $A B$ and $\ell$. Since $\angle F E A=\angle F M A=90^{\circ}$, it follows that $A E M F$ is cyclic and hence $\angle D F E=\angle B A E=\angle D E F$. The last equality holds because $D E$ is tangent to $\Gamma$. It follows that $D E=$ $D F$ and hence $D F^{2}=D E^{2}=$  $D C \cdot D A$ (the power of $D$ with respect to $\Gamma$ ). It then follows that $\angle D C F=\angle D F A=\angle H G A=\angle H C A$. Thus it follows that $H$ lies on $C F$ as desired.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0fb153e2-4721-54bc-bca1-987e518fcf1d
| 25,170
|
18. G3 (KOR) Let $O$ be the circumcenter of an acute-angled triangle $A B C$ with $\angle B<\angle C$. The line $A O$ meets the side $B C$ at $D$. The circumcenters of the triangles $A B D$ and $A C D$ are $E$ and $F$, respectively. Extend the sides $B A$ and $C A$ beyond $A$, and choose on the respective extension points $G$ and $H$ such that $A G=A C$ and $A H=A B$. Prove that the quadrilateral $E F G H$ is a rectangle if and only if $\angle A C B-\angle A B C=60^{\circ}$.
|
18. It is important to note that since $\beta<\gamma, \angle A D C=90^{\circ}-\gamma+\beta$ is acute. It is elementary that $\angle C A O=90^{\circ}-\beta$. Let $X$ and $Y$ respectively be the intersections of $F E$ and $G H$ with $A D$. We trivially get $X \in E F \perp A D$ and $\triangle A G H \cong \triangle A C B$. Consequently, $\angle G A Y=\angle O A B=90^{\circ}-\gamma=$ $90^{\circ}-\angle A G Y$. Hence, $G H \perp A D$ and thus $G H \| F E$. That $E F G H$ is a rectangle is now equivalent to $F X=G Y$ and $E X=H Y$. We have that $G Y=A G \sin \gamma=A C \sin \gamma$ and $F X=A F \sin \gamma$ (since $\angle A F X=\gamma$ ). Thus, $$ F X=G Y \Leftrightarrow C F=A F=A C \Leftrightarrow \angle A F C=60^{\circ} \Leftrightarrow \angle A D C=30^{\circ} . $$ Since $\angle A D C=180^{\circ}-\angle D C A-\angle D A C=180^{\circ}-\gamma-\left(90^{\circ}-\beta\right)$, it immediately follows that $F X=G Y \Leftrightarrow \gamma-\beta=60^{\circ}$. We similarly obtain $E X=H Y \Leftrightarrow \gamma-\beta=60^{\circ}$, proving the statement of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
18. G3 (KOR) Let $O$ be the circumcenter of an acute-angled triangle $A B C$ with $\angle B<\angle C$. The line $A O$ meets the side $B C$ at $D$. The circumcenters of the triangles $A B D$ and $A C D$ are $E$ and $F$, respectively. Extend the sides $B A$ and $C A$ beyond $A$, and choose on the respective extension points $G$ and $H$ such that $A G=A C$ and $A H=A B$. Prove that the quadrilateral $E F G H$ is a rectangle if and only if $\angle A C B-\angle A B C=60^{\circ}$.
|
18. It is important to note that since $\beta<\gamma, \angle A D C=90^{\circ}-\gamma+\beta$ is acute. It is elementary that $\angle C A O=90^{\circ}-\beta$. Let $X$ and $Y$ respectively be the intersections of $F E$ and $G H$ with $A D$. We trivially get $X \in E F \perp A D$ and $\triangle A G H \cong \triangle A C B$. Consequently, $\angle G A Y=\angle O A B=90^{\circ}-\gamma=$ $90^{\circ}-\angle A G Y$. Hence, $G H \perp A D$ and thus $G H \| F E$. That $E F G H$ is a rectangle is now equivalent to $F X=G Y$ and $E X=H Y$. We have that $G Y=A G \sin \gamma=A C \sin \gamma$ and $F X=A F \sin \gamma$ (since $\angle A F X=\gamma$ ). Thus, $$ F X=G Y \Leftrightarrow C F=A F=A C \Leftrightarrow \angle A F C=60^{\circ} \Leftrightarrow \angle A D C=30^{\circ} . $$ Since $\angle A D C=180^{\circ}-\angle D C A-\angle D A C=180^{\circ}-\gamma-\left(90^{\circ}-\beta\right)$, it immediately follows that $F X=G Y \Leftrightarrow \gamma-\beta=60^{\circ}$. We similarly obtain $E X=H Y \Leftrightarrow \gamma-\beta=60^{\circ}$, proving the statement of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ede662be-cb7f-5caf-977b-6e8ee88baaa0
| 25,171
|
19. $\mathbf{G} 4 \mathbf{( P O L})^{\mathrm{IMO}}$ In a convex quadrilateral $A B C D$ the diagonal $B D$ does not bisect the angles $A B C$ and $C D A$. The point $P$ lies inside $A B C D$ and satisfies $$ \angle P B C=\angle D B A \quad \text { and } \quad \angle P D C=\angle B D A . $$ Prove that $A B C D$ is a cyclic quadrilateral if and only if $A P=C P$.
|
19. Assume first that the points $A, B, C, D$ are concyclic. Let the lines $B P$ and $D P$ meet the circumcircle of $A B C D$ again at $E$ and $F$, respectively. Then it follows from the given conditions that $\widehat{A B}=\widehat{C F}$ and $\widehat{A D}=\widehat{C E}$; hence $B F \| A C$ and $D E \| A C$. Therefore $B F E D$ and $B F A C$ are isosceles trapezoids and thus $P=B E \cap D F$ lies on the common bisector of segments $B F, E D, A C$. Hence $A P=C P$. Assume in turn that $A P=C P$. Let $P$ w.l.o.g. lie in the triangles $A C D$ and $B C D$. Let $B P$ and $D P$ meet $A C$ at $K$ and $L$, respectively. The points $A$ and $C$ are isogonal conjugates with respect to $\triangle B D P$, which implies that $\angle A P K=\angle C P L$. Since $A P=C P$, we infer that $K$ and $L$ are symmetric with respect to the perpendicular bisector $p$ of $A C$. Let $E$ be the reflection of $D$ in $p$. Then $E$ lies on the line $B P$, and the triangles $A P D$ and $C P E$ are congruent. Thus $\angle B D C=\angle A D P=\angle B E C$, which means that the points $B, C, E, D$ are concyclic. Moreover, $A, C, E, D$ are also concyclic. Hence, $A B C D$ is a cyclic quadrilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
19. $\mathbf{G} 4 \mathbf{( P O L})^{\mathrm{IMO}}$ In a convex quadrilateral $A B C D$ the diagonal $B D$ does not bisect the angles $A B C$ and $C D A$. The point $P$ lies inside $A B C D$ and satisfies $$ \angle P B C=\angle D B A \quad \text { and } \quad \angle P D C=\angle B D A . $$ Prove that $A B C D$ is a cyclic quadrilateral if and only if $A P=C P$.
|
19. Assume first that the points $A, B, C, D$ are concyclic. Let the lines $B P$ and $D P$ meet the circumcircle of $A B C D$ again at $E$ and $F$, respectively. Then it follows from the given conditions that $\widehat{A B}=\widehat{C F}$ and $\widehat{A D}=\widehat{C E}$; hence $B F \| A C$ and $D E \| A C$. Therefore $B F E D$ and $B F A C$ are isosceles trapezoids and thus $P=B E \cap D F$ lies on the common bisector of segments $B F, E D, A C$. Hence $A P=C P$. Assume in turn that $A P=C P$. Let $P$ w.l.o.g. lie in the triangles $A C D$ and $B C D$. Let $B P$ and $D P$ meet $A C$ at $K$ and $L$, respectively. The points $A$ and $C$ are isogonal conjugates with respect to $\triangle B D P$, which implies that $\angle A P K=\angle C P L$. Since $A P=C P$, we infer that $K$ and $L$ are symmetric with respect to the perpendicular bisector $p$ of $A C$. Let $E$ be the reflection of $D$ in $p$. Then $E$ lies on the line $B P$, and the triangles $A P D$ and $C P E$ are congruent. Thus $\angle B D C=\angle A D P=\angle B E C$, which means that the points $B, C, E, D$ are concyclic. Moreover, $A, C, E, D$ are also concyclic. Hence, $A B C D$ is a cyclic quadrilateral.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f1ce9651-dd80-5bda-a608-37e37814a1a0
| 25,172
|
2. A2 (ROM) An infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of real numbers satisfies the condition $$ a_{n}=\left|a_{n+1}-a_{n+2}\right| \text { for every } n \geq 0 $$ with $a_{0}$ and $a_{1}$ positive and distinct. Can this sequence be bounded?
|
2. We claim that the sequence $\left\{a_{n}\right\}$ must be unbounded. The condition of the sequence is equivalent to $a_{n}>0$ and $a_{n+1}=a_{n}+a_{n-1}$ or $a_{n}-a_{n-1}$. In particular, if $a_{n}<a_{n-1}$, then $a_{n+1}>\max \left\{a_{n}, a_{n-1}\right\}$. Let us remove all $a_{n}$ such that $a_{n}<a_{n-1}$. The obtained sequence $\left(b_{m}\right)_{m \in \mathbb{N}}$ is strictly increasing. Thus the statement of the problem will follow if we prove that $b_{m+1}-b_{m} \geq b_{m}-b_{m-1}$ for all $m \geq 2$. Let $b_{m+1}=a_{n+2}$ for some $n$. Then $a_{n+2}>a_{n+1}$. We distinguish two cases: (i) If $a_{n+1}>a_{n}$, we have $b_{m}=a_{n+1}$ and $b_{m-1} \geq a_{n-1}$ (since $b_{m-1}$ is either $a_{n-1}$ or $a_{n}$ ). Then $b_{m+1}-b_{m}=a_{n+2}-a_{n+1}=a_{n}=a_{n+1}-$ $a_{n-1}=b_{m}-a_{n-1} \geq b_{m}-b_{m-1}$. (ii) If $a_{n+1}<a_{n}$, we have $b_{m}=a_{n}$ and $b_{m-1} \geq a_{n-1}$. Consequently, $b_{m+1}-b_{m}=a_{n+2}-a_{n}=a_{n+1}=a_{n}-a_{n-1}=b_{m}-a_{n-1} \geq b_{m}-b_{m-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
2. A2 (ROM) An infinite sequence $a_{0}, a_{1}, a_{2}, \ldots$ of real numbers satisfies the condition $$ a_{n}=\left|a_{n+1}-a_{n+2}\right| \text { for every } n \geq 0 $$ with $a_{0}$ and $a_{1}$ positive and distinct. Can this sequence be bounded?
|
2. We claim that the sequence $\left\{a_{n}\right\}$ must be unbounded. The condition of the sequence is equivalent to $a_{n}>0$ and $a_{n+1}=a_{n}+a_{n-1}$ or $a_{n}-a_{n-1}$. In particular, if $a_{n}<a_{n-1}$, then $a_{n+1}>\max \left\{a_{n}, a_{n-1}\right\}$. Let us remove all $a_{n}$ such that $a_{n}<a_{n-1}$. The obtained sequence $\left(b_{m}\right)_{m \in \mathbb{N}}$ is strictly increasing. Thus the statement of the problem will follow if we prove that $b_{m+1}-b_{m} \geq b_{m}-b_{m-1}$ for all $m \geq 2$. Let $b_{m+1}=a_{n+2}$ for some $n$. Then $a_{n+2}>a_{n+1}$. We distinguish two cases: (i) If $a_{n+1}>a_{n}$, we have $b_{m}=a_{n+1}$ and $b_{m-1} \geq a_{n-1}$ (since $b_{m-1}$ is either $a_{n-1}$ or $a_{n}$ ). Then $b_{m+1}-b_{m}=a_{n+2}-a_{n+1}=a_{n}=a_{n+1}-$ $a_{n-1}=b_{m}-a_{n-1} \geq b_{m}-b_{m-1}$. (ii) If $a_{n+1}<a_{n}$, we have $b_{m}=a_{n}$ and $b_{m-1} \geq a_{n-1}$. Consequently, $b_{m+1}-b_{m}=a_{n+2}-a_{n}=a_{n+1}=a_{n}-a_{n-1}=b_{m}-a_{n-1} \geq b_{m}-b_{m-1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8e1340b7-786b-5f4f-94bb-21b3165d930c
| 25,173
|
21. G6 (GBR) Let $\mathcal{P}$ be a convex polygon. Prove that there is a convex hexagon that is contained in $\mathcal{P}$ and that occupies at least 75 percent of the area of $\mathcal{P}$.
|
21. Let $A B C$ be the triangle of maximum area $S$ contained in $\mathcal{P}$ (it exists because of compactness of $\mathcal{P}$ ). Draw parallels to $B C, C A, A B$ through $A, B, C$, respectively, and denote the triangle thus obtained by $A_{1} B_{1} C_{1}$ ( $A \in B_{1} C_{1}$, etc.). Since each triangle with vertices in $\mathcal{P}$ has area at most $S$, the entire polygon $\mathcal{P}$ is contained in $A_{1} B_{1} C_{1}$. Next, draw lines of support of $\mathcal{P}$ parallel to $B C, C A, A B$ and not intersecting the triangle $A B C$. They determine a convex hexagon $U_{a} V_{a} U_{b} V_{b} U_{c} V_{c}$ containing $\mathcal{P}$, with $V_{b}, U_{c} \in B_{1} C_{1}, V_{c}, U_{a} \in C_{1} A_{1}, V_{a}, U_{b} \in A_{1} B_{1}$. Each of the line segments $U_{a} V_{a}, U_{b} V_{b}, U_{c} V_{c}$ contains points of $\mathcal{P}$. Choose such points $A_{0}, B_{0}, C_{0}$ on $U_{a} V_{a}, U_{b} V_{b}, U_{c} V_{c}$, respectively. The convex hexagon $A C_{0} B A_{0} C B_{0}$ is contained in $\mathcal{P}$, because the latter is convex. We prove that $A C_{0} B A_{0} C B_{0}$ has area at least $3 / 4$ the area of $\mathcal{P}$. Let $x, y, z$ denote the areas of triangles $U_{a} B C, U_{b} C A$, and $U_{c} A B$. Then $S_{1}=S_{A C_{0} B A_{0} C B_{0}}=S+x+y+z$. On the other hand, the triangle $A_{1} U_{a} V_{a}$ is similar to $\triangle A_{1} B C$ with similitude $\tau=(S-x) / S$, and hence its area is $\tau^{2} S=(S-x)^{2} / S$. Thus the area of quadrilateral $U_{a} V_{a} C B$ is $S-(S-x)^{2} / S=2 z-z^{2} / S$. Analogous formulas hold for quadrilaterals $U_{b} V_{b} A C$ and $U_{c} V_{c} B A$. Therefore $$ \begin{aligned} S_{\mathcal{P}} & \leq S_{U_{a} V_{a} U_{b} V_{b} U_{c} V_{c}}=S+S_{U_{a} V_{a} C B}+S_{U_{b} V_{b} A C}+S_{U_{c} V_{c} B A} \\ & =S+2(x+y+z)-\frac{x^{2}+y^{2}+z^{2}}{S} \\ & \leq S+2(x+y+z)-\frac{(x+y+z)^{2}}{3 S} . \end{aligned} $$ Now $4 S_{1}-3 S_{\mathcal{P}} \geq=S-2(x+y+z)+(x+y+z)^{2} / S=(S-x-y-z)^{2} / S \geq 0$; i.e., $S_{1} \geq 3 S_{\mathcal{P}} / 4$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
21. G6 (GBR) Let $\mathcal{P}$ be a convex polygon. Prove that there is a convex hexagon that is contained in $\mathcal{P}$ and that occupies at least 75 percent of the area of $\mathcal{P}$.
|
21. Let $A B C$ be the triangle of maximum area $S$ contained in $\mathcal{P}$ (it exists because of compactness of $\mathcal{P}$ ). Draw parallels to $B C, C A, A B$ through $A, B, C$, respectively, and denote the triangle thus obtained by $A_{1} B_{1} C_{1}$ ( $A \in B_{1} C_{1}$, etc.). Since each triangle with vertices in $\mathcal{P}$ has area at most $S$, the entire polygon $\mathcal{P}$ is contained in $A_{1} B_{1} C_{1}$. Next, draw lines of support of $\mathcal{P}$ parallel to $B C, C A, A B$ and not intersecting the triangle $A B C$. They determine a convex hexagon $U_{a} V_{a} U_{b} V_{b} U_{c} V_{c}$ containing $\mathcal{P}$, with $V_{b}, U_{c} \in B_{1} C_{1}, V_{c}, U_{a} \in C_{1} A_{1}, V_{a}, U_{b} \in A_{1} B_{1}$. Each of the line segments $U_{a} V_{a}, U_{b} V_{b}, U_{c} V_{c}$ contains points of $\mathcal{P}$. Choose such points $A_{0}, B_{0}, C_{0}$ on $U_{a} V_{a}, U_{b} V_{b}, U_{c} V_{c}$, respectively. The convex hexagon $A C_{0} B A_{0} C B_{0}$ is contained in $\mathcal{P}$, because the latter is convex. We prove that $A C_{0} B A_{0} C B_{0}$ has area at least $3 / 4$ the area of $\mathcal{P}$. Let $x, y, z$ denote the areas of triangles $U_{a} B C, U_{b} C A$, and $U_{c} A B$. Then $S_{1}=S_{A C_{0} B A_{0} C B_{0}}=S+x+y+z$. On the other hand, the triangle $A_{1} U_{a} V_{a}$ is similar to $\triangle A_{1} B C$ with similitude $\tau=(S-x) / S$, and hence its area is $\tau^{2} S=(S-x)^{2} / S$. Thus the area of quadrilateral $U_{a} V_{a} C B$ is $S-(S-x)^{2} / S=2 z-z^{2} / S$. Analogous formulas hold for quadrilaterals $U_{b} V_{b} A C$ and $U_{c} V_{c} B A$. Therefore $$ \begin{aligned} S_{\mathcal{P}} & \leq S_{U_{a} V_{a} U_{b} V_{b} U_{c} V_{c}}=S+S_{U_{a} V_{a} C B}+S_{U_{b} V_{b} A C}+S_{U_{c} V_{c} B A} \\ & =S+2(x+y+z)-\frac{x^{2}+y^{2}+z^{2}}{S} \\ & \leq S+2(x+y+z)-\frac{(x+y+z)^{2}}{3 S} . \end{aligned} $$ Now $4 S_{1}-3 S_{\mathcal{P}} \geq=S-2(x+y+z)+(x+y+z)^{2} / S=(S-x-y-z)^{2} / S \geq 0$; i.e., $S_{1} \geq 3 S_{\mathcal{P}} / 4$, as claimed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
27486071-8779-5ba2-84ef-c5b47de4c220
| 25,175
|
22. G7 (RUS) For a given triangle $A B C$, let $X$ be a variable point on the line $B C$ such that $C$ lies between $B$ and $X$ and the incircles of the triangles $A B X$ and $A C X$ intersect at two distinct points $P$ and $Q$. Prove that the line $P Q$ passes through a point independent of $X$.
|
22. The proof uses the following observation: Lemma. In a triangle $A B C$, let $K, L$ be the midpoints of the sides $A C, A B$, respectively, and let the incircle of the triangle touch $B C, C A$ at $D, E$, respectively. Then the lines $K L$ and $D E$ intersect on the bisector of the angle $A B C$. Proof. Let the bisector $\ell_{b}$ of $\angle A B C$ meet $D E$ at $T$. One can assume that $A B \neq B C$, or else $T \equiv K \in K L$. Note that the incenter $I$ of $\triangle A B C$ is between $B$ and $T$, and also $T \neq E$. From the triangles $B D T$ and $D E C$ we obtain $\angle I T D=\alpha / 2=\angle I A E$, which implies that $A, I, T, E$ are concyclic. Then $\angle A T B=\angle A E I=90^{\circ}$. Thus $L$ is the circumcenter of $\triangle A T B$ from which $\angle L T B=\angle L B T=\angle T B C \Rightarrow L T \| B C \Rightarrow T \in$ $K L$, which is what we were supposed to prove. Let the incircles of $\triangle A B X$ and $\triangle A C X$ touch $B X$ at $D$ and $F$, respectively, and let them touch $A X$ at $E$ and $G$, respectively. Clearly, $D E$ and $F G$ are parallel. If the line $P Q$ intersects $B X$ and $A X$ at $M$ and $N$, respectively, then $M D^{2}=M P \cdot M Q=M F^{2}$, i.e., $M D=M F$ and analogously $N E=N G$. It follows that $P Q$ is parallel to $D E$ and $F G$ and equidistant from them. The midpoints of $A B, A C$, and $A X$ lie on the same line $m$, parallel to $B C$. Applying the lemma to $\triangle A B X$, we conclude that $D E$ passes through the common point $U$ of $m$ and the bisector of $\angle A B X$. Analogously, $F G$ passes through the common point $V$ of $m$ and the bisector of $\angle A C X$. Therefore $P Q$ passes through the midpoint $W$ of the line segment $U V$. Since $U, V$ do not depend on $X$, neither does $W$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
22. G7 (RUS) For a given triangle $A B C$, let $X$ be a variable point on the line $B C$ such that $C$ lies between $B$ and $X$ and the incircles of the triangles $A B X$ and $A C X$ intersect at two distinct points $P$ and $Q$. Prove that the line $P Q$ passes through a point independent of $X$.
|
22. The proof uses the following observation: Lemma. In a triangle $A B C$, let $K, L$ be the midpoints of the sides $A C, A B$, respectively, and let the incircle of the triangle touch $B C, C A$ at $D, E$, respectively. Then the lines $K L$ and $D E$ intersect on the bisector of the angle $A B C$. Proof. Let the bisector $\ell_{b}$ of $\angle A B C$ meet $D E$ at $T$. One can assume that $A B \neq B C$, or else $T \equiv K \in K L$. Note that the incenter $I$ of $\triangle A B C$ is between $B$ and $T$, and also $T \neq E$. From the triangles $B D T$ and $D E C$ we obtain $\angle I T D=\alpha / 2=\angle I A E$, which implies that $A, I, T, E$ are concyclic. Then $\angle A T B=\angle A E I=90^{\circ}$. Thus $L$ is the circumcenter of $\triangle A T B$ from which $\angle L T B=\angle L B T=\angle T B C \Rightarrow L T \| B C \Rightarrow T \in$ $K L$, which is what we were supposed to prove. Let the incircles of $\triangle A B X$ and $\triangle A C X$ touch $B X$ at $D$ and $F$, respectively, and let them touch $A X$ at $E$ and $G$, respectively. Clearly, $D E$ and $F G$ are parallel. If the line $P Q$ intersects $B X$ and $A X$ at $M$ and $N$, respectively, then $M D^{2}=M P \cdot M Q=M F^{2}$, i.e., $M D=M F$ and analogously $N E=N G$. It follows that $P Q$ is parallel to $D E$ and $F G$ and equidistant from them. The midpoints of $A B, A C$, and $A X$ lie on the same line $m$, parallel to $B C$. Applying the lemma to $\triangle A B X$, we conclude that $D E$ passes through the common point $U$ of $m$ and the bisector of $\angle A B X$. Analogously, $F G$ passes through the common point $V$ of $m$ and the bisector of $\angle A C X$. Therefore $P Q$ passes through the midpoint $W$ of the line segment $U V$. Since $U, V$ do not depend on $X$, neither does $W$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b1a13499-293b-5c1e-8c88-7ab1f4b1c52b
| 25,176
|
23. G8 (SMN) A cyclic quadrilateral $A B C D$ is given. The lines $A D$ and $B C$ intersect at $E$, with $C$ between $B$ and $E$; the diagonals $A C$ and $B D$ intersect at $F$. Let $M$ be the midpoint of the side $C D$, and let $N \neq M$ be a point on the circumcircle of the triangle $A B M$ such that $A N / B N=$ $A M / B M$. Prove that the points $E, F$, and $N$ are collinear.
|
23. To start with, note that point $N$ is uniquely determined by the imposed properties. Indeed, $f(X)=A X / B X$ is a monotone function on both arcs $A B$ of the circumcircle of $\triangle A B M$. Denote by $P$ and $Q$ respectively the second points of intersection of the line $E F$ with the circumcircles of $\triangle A B E$ and $\triangle A B F$. The problem is equivalent to showing that $N \in P Q$. In fact, we shall prove that $N$ coincides with the midpoint $\bar{N}$ of segment $P Q$. The cyclic quadrilaterals $A P B E$, $A Q B F$, and $A B C D$ yield $\angle A P Q=$ $180^{\circ}-\angle A P E=180^{\circ}-\angle A B E=$ $\angle A D C$ and $\angle A Q P=\angle A Q F=$ $\angle A B F=\angle A C D$. It follows that $\triangle A P Q \sim \triangle A D C$, and consequently $\triangle A \bar{N} P \sim \triangle A M D$. Analo-  gously $\triangle B \bar{N} P \sim \triangle B M C$. Therefore $A \bar{N} / A M=P Q / D C=B \bar{N} / B M$, i.e., $A \bar{N} / B \bar{N}=A M / B M$. Moreover, $\angle A \bar{N} B=\angle A \bar{N} P+\angle P \bar{N} B=$ $\angle A M D+\angle B M C=180^{\circ}-\angle A M B$, which means that point $\bar{N}$ lies on the circumcircle of $\triangle A M B$. By the uniqueness of $N$, we conclude that $\bar{N} \equiv N$, which completes the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
23. G8 (SMN) A cyclic quadrilateral $A B C D$ is given. The lines $A D$ and $B C$ intersect at $E$, with $C$ between $B$ and $E$; the diagonals $A C$ and $B D$ intersect at $F$. Let $M$ be the midpoint of the side $C D$, and let $N \neq M$ be a point on the circumcircle of the triangle $A B M$ such that $A N / B N=$ $A M / B M$. Prove that the points $E, F$, and $N$ are collinear.
|
23. To start with, note that point $N$ is uniquely determined by the imposed properties. Indeed, $f(X)=A X / B X$ is a monotone function on both arcs $A B$ of the circumcircle of $\triangle A B M$. Denote by $P$ and $Q$ respectively the second points of intersection of the line $E F$ with the circumcircles of $\triangle A B E$ and $\triangle A B F$. The problem is equivalent to showing that $N \in P Q$. In fact, we shall prove that $N$ coincides with the midpoint $\bar{N}$ of segment $P Q$. The cyclic quadrilaterals $A P B E$, $A Q B F$, and $A B C D$ yield $\angle A P Q=$ $180^{\circ}-\angle A P E=180^{\circ}-\angle A B E=$ $\angle A D C$ and $\angle A Q P=\angle A Q F=$ $\angle A B F=\angle A C D$. It follows that $\triangle A P Q \sim \triangle A D C$, and consequently $\triangle A \bar{N} P \sim \triangle A M D$. Analo-  gously $\triangle B \bar{N} P \sim \triangle B M C$. Therefore $A \bar{N} / A M=P Q / D C=B \bar{N} / B M$, i.e., $A \bar{N} / B \bar{N}=A M / B M$. Moreover, $\angle A \bar{N} B=\angle A \bar{N} P+\angle P \bar{N} B=$ $\angle A M D+\angle B M C=180^{\circ}-\angle A M B$, which means that point $\bar{N}$ lies on the circumcircle of $\triangle A M B$. By the uniqueness of $N$, we conclude that $\bar{N} \equiv N$, which completes the solution.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b9e28adf-0db5-58b2-be88-cfceb48511ed
| 25,177
|
24. N1 (BLR) Let $\tau(n)$ denote the number of positive divisors of the positive integer $n$. Prove that there exist infinitely many positive integers $a$ such that the equation $$ \tau(a n)=n $$ does not have a positive integer solution $n$.
|
24. Setting $m=a n$ we reduce the given equation to $m / \tau(m)=a$. Let us show that for $a=p^{p-1}$ the above equation has no solutions in $\mathbb{N}$ if $p>3$ is a prime. Assume to the contrary that $m \in \mathbb{N}$ is such that $m=p^{p-1} \tau(m)$. Then $p^{p-1} \mid m$, so we may set $m=p^{\alpha} k$, where $\alpha, k \in \mathbb{N}$, $\alpha \geq p-1$, and $p \nmid k$. Let $k=p_{1}^{\alpha_{1}} \cdots p_{r}^{\alpha_{r}}$ be the decomposition of $k$ into primes. Then $\tau(k)=\left(\alpha_{1}+1\right) \cdots\left(\alpha_{r}+1\right)$ and $\tau(m)=(\alpha+1) \tau(k)$. Our equation becomes $$ p^{\alpha-p+1} k=(\alpha+1) \tau(k) . $$ We observe that $\alpha \neq p-1$ : otherwise the RHS would be divisible by $p$ and the LHS would not be so. It follows that $\alpha \geq p$, which also easily implies that $p^{\alpha-p+1} \geq \frac{p}{p+1}(\alpha+1)$. Furthermore, since $\alpha+1$ cannot be divisible by $p^{\alpha-p+1}$ for any $\alpha \geq p$, it follows that $p \mid \tau(k)$. Thus if $p \mid \tau(k)$, then at least one $\alpha_{i}+1$ is divisible by $p$ and consequently $\alpha_{i} \geq p-1$ for some $i$. Hence $k \geq \frac{p_{i}^{\alpha_{i}}}{\alpha_{i}+1} \tau(k) \geq \frac{2^{p-1}}{p} \tau(k)$. But then we have $$ p^{\alpha-p+1} k \geq \frac{p}{p+1}(\alpha+1) \cdot \frac{2^{p-1}}{p} \tau(k)>(\alpha+1) \tau(k), $$ contradicting (1). Therefore (1) has no solutions in $\mathbb{N}$. Remark. There are many other values of $a$ for which the considered equation has no solutions in $\mathbb{N}$ : for example, $a=6 p$ for a prime $p \geq 5$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
24. N1 (BLR) Let $\tau(n)$ denote the number of positive divisors of the positive integer $n$. Prove that there exist infinitely many positive integers $a$ such that the equation $$ \tau(a n)=n $$ does not have a positive integer solution $n$.
|
24. Setting $m=a n$ we reduce the given equation to $m / \tau(m)=a$. Let us show that for $a=p^{p-1}$ the above equation has no solutions in $\mathbb{N}$ if $p>3$ is a prime. Assume to the contrary that $m \in \mathbb{N}$ is such that $m=p^{p-1} \tau(m)$. Then $p^{p-1} \mid m$, so we may set $m=p^{\alpha} k$, where $\alpha, k \in \mathbb{N}$, $\alpha \geq p-1$, and $p \nmid k$. Let $k=p_{1}^{\alpha_{1}} \cdots p_{r}^{\alpha_{r}}$ be the decomposition of $k$ into primes. Then $\tau(k)=\left(\alpha_{1}+1\right) \cdots\left(\alpha_{r}+1\right)$ and $\tau(m)=(\alpha+1) \tau(k)$. Our equation becomes $$ p^{\alpha-p+1} k=(\alpha+1) \tau(k) . $$ We observe that $\alpha \neq p-1$ : otherwise the RHS would be divisible by $p$ and the LHS would not be so. It follows that $\alpha \geq p$, which also easily implies that $p^{\alpha-p+1} \geq \frac{p}{p+1}(\alpha+1)$. Furthermore, since $\alpha+1$ cannot be divisible by $p^{\alpha-p+1}$ for any $\alpha \geq p$, it follows that $p \mid \tau(k)$. Thus if $p \mid \tau(k)$, then at least one $\alpha_{i}+1$ is divisible by $p$ and consequently $\alpha_{i} \geq p-1$ for some $i$. Hence $k \geq \frac{p_{i}^{\alpha_{i}}}{\alpha_{i}+1} \tau(k) \geq \frac{2^{p-1}}{p} \tau(k)$. But then we have $$ p^{\alpha-p+1} k \geq \frac{p}{p+1}(\alpha+1) \cdot \frac{2^{p-1}}{p} \tau(k)>(\alpha+1) \tau(k), $$ contradicting (1). Therefore (1) has no solutions in $\mathbb{N}$. Remark. There are many other values of $a$ for which the considered equation has no solutions in $\mathbb{N}$ : for example, $a=6 p$ for a prime $p \geq 5$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
67381ef5-9828-5e94-a381-15459cac240e
| 25,178
|
25. N2 (RUS) The function $\psi$ from the set $\mathbb{N}$ of positive integers into itself is defined by the equality $$ \psi(n)=\sum_{k=1}^{n}(k, n), \quad n \in \mathbb{N} $$ where $(k, n)$ denotes the greatest common divisor of $k$ and $n$. (a) Prove that $\psi(m n)=\psi(m) \psi(n)$ for every two relatively prime $m, n \in$ $\mathbb{N}$. (b) Prove that for each $a \in \mathbb{N}$ the equation $\psi(x)=a x$ has a solution. (c) Find all $a \in \mathbb{N}$ such that the equation $\psi(x)=a x$ has a unique solution.
|
25. Let $n$ be a natural number. For each $k=1,2, \ldots, n$, the number $(k, n)$ is a divisor of $n$. Consider any divisor $d$ of $n$. If $(k, n)=n / d$, then $k=n l / d$ for some $l \in \mathbb{N}$, and $(k, n)=(l, d) n / d$, which implies that $l$ is coprime to $d$ and $l \leq d$. It follows that $(k, n)$ is equal to $n / d$ for exactly $\varphi(d)$ natural numbers $k \leq n$. Therefore $$ \psi(n)=\sum_{k=1}^{n}(k, n)=\sum_{d \mid n} \varphi(d) \frac{n}{d}=n \sum_{d \mid n} \frac{\varphi(d)}{d} $$ (a) Let $n, m$ be coprime. Then each divisor $f$ of $m n$ can be uniquely expressed as $f=d e$, where $d \mid n$ and $e \mid m$. We now have by (1) $$ \begin{aligned} \psi(m n) & =m n \sum_{f \mid m n} \frac{\varphi(f)}{f}=m n \sum_{d|n, e| m} \frac{\varphi(d e)}{d e} \\ & =m n \sum_{d|n, e| m} \frac{\varphi(d)}{d} \frac{\varphi(e)}{e}=\left(n \sum_{d \mid n} \frac{\varphi(d)}{d}\right)\left(m \sum_{e \mid m} \frac{\varphi(e)}{e}\right) \\ & =\psi(m) \psi(n) . \end{aligned} $$ (b) Let $n=p^{k}$, where $p$ is a prime and $k$ a positive integer. According to (1), $$ \frac{\psi(n)}{n}=\sum_{i=0}^{k} \frac{\varphi\left(p^{i}\right)}{p^{i}}=1+\frac{k(p-1)}{p} $$ Setting $p=2$ and $k=2(a-1)$ we obtain $\psi(n)=a n$ for $n=2^{2(a-1)}$. (c) We note that $\psi\left(p^{p}\right)=p^{p+1}$ if $p$ is a prime. Hence, if $a$ has an odd prime factor $p$ and $a_{1}=a / p$, then $x=p^{p} 2^{2 a_{1}-2}$ is a solution of $\psi(x)=a x$ different from $x=2^{2 a-2}$. Now assume that $a=2^{k}$ for some $k \in \mathbb{N}$. Suppose $x=2^{\alpha} y$ is a positive integer such that $\psi(x)=2^{k} x$. Then $2^{\alpha+k} y=\psi(x)=\psi\left(2^{\alpha}\right) \psi(y)=$ $(\alpha+2) 2^{\alpha-1} \psi(y)$, i.e., $2^{k+1} y=(\alpha+2) \psi(y)$. We notice that for each odd $y, \psi(y)$ is (by definition) the sum of an odd number of odd summands and therefore odd. It follows that $\psi(y) \mid y$. On the other hand, $\psi(y)>$ $y$ for $y>1$, so we must have $y=1$. Consequently $\alpha=2^{k+1}-2=2 a-2$, giving us the unique solution $x=2^{2 a-2}$. Thus $\psi(x)=a x$ has a unique solution if and only if $a$ is a power of 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
25. N2 (RUS) The function $\psi$ from the set $\mathbb{N}$ of positive integers into itself is defined by the equality $$ \psi(n)=\sum_{k=1}^{n}(k, n), \quad n \in \mathbb{N} $$ where $(k, n)$ denotes the greatest common divisor of $k$ and $n$. (a) Prove that $\psi(m n)=\psi(m) \psi(n)$ for every two relatively prime $m, n \in$ $\mathbb{N}$. (b) Prove that for each $a \in \mathbb{N}$ the equation $\psi(x)=a x$ has a solution. (c) Find all $a \in \mathbb{N}$ such that the equation $\psi(x)=a x$ has a unique solution.
|
25. Let $n$ be a natural number. For each $k=1,2, \ldots, n$, the number $(k, n)$ is a divisor of $n$. Consider any divisor $d$ of $n$. If $(k, n)=n / d$, then $k=n l / d$ for some $l \in \mathbb{N}$, and $(k, n)=(l, d) n / d$, which implies that $l$ is coprime to $d$ and $l \leq d$. It follows that $(k, n)$ is equal to $n / d$ for exactly $\varphi(d)$ natural numbers $k \leq n$. Therefore $$ \psi(n)=\sum_{k=1}^{n}(k, n)=\sum_{d \mid n} \varphi(d) \frac{n}{d}=n \sum_{d \mid n} \frac{\varphi(d)}{d} $$ (a) Let $n, m$ be coprime. Then each divisor $f$ of $m n$ can be uniquely expressed as $f=d e$, where $d \mid n$ and $e \mid m$. We now have by (1) $$ \begin{aligned} \psi(m n) & =m n \sum_{f \mid m n} \frac{\varphi(f)}{f}=m n \sum_{d|n, e| m} \frac{\varphi(d e)}{d e} \\ & =m n \sum_{d|n, e| m} \frac{\varphi(d)}{d} \frac{\varphi(e)}{e}=\left(n \sum_{d \mid n} \frac{\varphi(d)}{d}\right)\left(m \sum_{e \mid m} \frac{\varphi(e)}{e}\right) \\ & =\psi(m) \psi(n) . \end{aligned} $$ (b) Let $n=p^{k}$, where $p$ is a prime and $k$ a positive integer. According to (1), $$ \frac{\psi(n)}{n}=\sum_{i=0}^{k} \frac{\varphi\left(p^{i}\right)}{p^{i}}=1+\frac{k(p-1)}{p} $$ Setting $p=2$ and $k=2(a-1)$ we obtain $\psi(n)=a n$ for $n=2^{2(a-1)}$. (c) We note that $\psi\left(p^{p}\right)=p^{p+1}$ if $p$ is a prime. Hence, if $a$ has an odd prime factor $p$ and $a_{1}=a / p$, then $x=p^{p} 2^{2 a_{1}-2}$ is a solution of $\psi(x)=a x$ different from $x=2^{2 a-2}$. Now assume that $a=2^{k}$ for some $k \in \mathbb{N}$. Suppose $x=2^{\alpha} y$ is a positive integer such that $\psi(x)=2^{k} x$. Then $2^{\alpha+k} y=\psi(x)=\psi\left(2^{\alpha}\right) \psi(y)=$ $(\alpha+2) 2^{\alpha-1} \psi(y)$, i.e., $2^{k+1} y=(\alpha+2) \psi(y)$. We notice that for each odd $y, \psi(y)$ is (by definition) the sum of an odd number of odd summands and therefore odd. It follows that $\psi(y) \mid y$. On the other hand, $\psi(y)>$ $y$ for $y>1$, so we must have $y=1$. Consequently $\alpha=2^{k+1}-2=2 a-2$, giving us the unique solution $x=2^{2 a-2}$. Thus $\psi(x)=a x$ has a unique solution if and only if $a$ is a power of 2 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6055ea42-4ad8-5dcb-a77c-d9d95a4d21ad
| 25,179
|
27. N4 (POL) Let $k$ be a fixed integer greater than 1 , and let $m=4 k^{2}-5$. Show that there exist positive integers $a$ and $b$ such that the sequence $\left(x_{n}\right)$ defined by $$ x_{0}=a, \quad x_{1}=b, \quad x_{n+2}=x_{n+1}+x_{n} \quad \text { for } \quad n=0,1,2, \ldots $$ has all of its terms relatively prime to $m$.
|
27. Set $a=1$ and assume that $b \in \mathbb{N}$ is such that $b^{2} \equiv b+1(\bmod m)$. An easy induction gives us $x_{n} \equiv b^{n}(\bmod m)$ for all $n \in \mathbb{N}_{0}$. Moreover, $b$ is obviously coprime to $m$, and hence each $x_{n}$ is coprime to $m$. It remains to show the existence of $b$. The congruence $b^{2} \equiv b+1(\bmod$ $m)$ is equivalent to $(2 b-1)^{2} \equiv 5(\bmod m)$. Taking $2 b-1 \equiv 2 k$, i.e., $b \equiv 2 k^{2}+k-2(\bmod m)$, does the job. Remark. A desired $b$ exists whenever 5 is a quadratic residue modulo $m$, in particular, when $m$ is a prime of the form $10 k \pm 1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
27. N4 (POL) Let $k$ be a fixed integer greater than 1 , and let $m=4 k^{2}-5$. Show that there exist positive integers $a$ and $b$ such that the sequence $\left(x_{n}\right)$ defined by $$ x_{0}=a, \quad x_{1}=b, \quad x_{n+2}=x_{n+1}+x_{n} \quad \text { for } \quad n=0,1,2, \ldots $$ has all of its terms relatively prime to $m$.
|
27. Set $a=1$ and assume that $b \in \mathbb{N}$ is such that $b^{2} \equiv b+1(\bmod m)$. An easy induction gives us $x_{n} \equiv b^{n}(\bmod m)$ for all $n \in \mathbb{N}_{0}$. Moreover, $b$ is obviously coprime to $m$, and hence each $x_{n}$ is coprime to $m$. It remains to show the existence of $b$. The congruence $b^{2} \equiv b+1(\bmod$ $m)$ is equivalent to $(2 b-1)^{2} \equiv 5(\bmod m)$. Taking $2 b-1 \equiv 2 k$, i.e., $b \equiv 2 k^{2}+k-2(\bmod m)$, does the job. Remark. A desired $b$ exists whenever 5 is a quadratic residue modulo $m$, in particular, when $m$ is a prime of the form $10 k \pm 1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cde14694-0c1c-56c1-8d37-31e16029b7a9
| 25,181
|
3. A3 (CAN) Does there exist a function $s: \mathbb{Q} \rightarrow\{-1,1\}$ such that if $x$ and $y$ are distinct rational numbers satisfying $x y=1$ or $x+y \in\{0,1\}$, then $s(x) s(y)=-1$ ? Justify your answer.
|
3. The answer is yes. Every rational number $x>0$ can be uniquely expressed as a continued fraction of the form $a_{0}+1 /\left(a_{1}+1 /\left(a_{2}+1 /\left(\cdots+1 / a_{n}\right)\right)\right)$ (where $a_{0} \in \mathbb{N}_{0}, a_{1}, \ldots, a_{n} \in \mathbb{N}$ ). Then we write $x=\left[a_{0} ; a_{1}, a_{2}, \ldots, a_{n}\right]$. Since $n$ depends only on $x$, the function $s(x)=(-1)^{n}$ is well-defined. For $x<0$ we define $s(x)=-s(-x)$, and set $s(0)=1$. We claim that this $s(x)$ satisfies the requirements of the problem. The equality $s(x) s(y)=-1$ trivially holds if $x+y=0$. Suppose that $x y=1$. We may assume w.l.o.g. that $x>y>0$. Then $x>1$, so if $x=\left[a_{0} ; a_{1}, a_{2}, \ldots, a_{n}\right]$, then $a_{0} \geq 1$ and $y=0+1 / x=$ $\left[0 ; a_{0}, a_{1}, a_{2}, \ldots, a_{n}\right]$. It follows that $s(x)=(-1)^{n}, s(y)=(-1)^{n+1}$, and hence $s(x) s(y)=-1$. Finally, suppose that $x+y=1$. We consider two cases: (i) Let $x, y>0$. We may assume w.l.o.g. that $x>1 / 2$. Then there exist natural numbers $a_{2}, \ldots, a_{n}$ such that $x=\left[0 ; 1, a_{2}, \ldots, a_{n}\right]=$ $1 /(1+1 / t)$, where $t=\left[a_{2}, \ldots, a_{n}\right]$. Since $y=1-x=1 /(1+t)=$ $\left[0 ; 1+a_{2}, a_{3}, \ldots, a_{n}\right]$, we have $s(x)=(-1)^{n}$ and $s(y)=(-1)^{n-1}$, giving us $s(x) s(y)=-1$. (ii) Let $x>0>y$. If $a_{0}, \ldots, a_{n} \in \mathbb{N}$ are such that $-y=\left[a_{0} ; a_{1}, \ldots, a_{n}\right]$, then $x=\left[1+a_{0} ; a_{1}, \ldots, a_{n}\right]$. Thus $s(y)=-s(-y)=-(-1)^{n}$ and $s(x)=(-1)^{n}$, so again $s(x) s(y)=-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
3. A3 (CAN) Does there exist a function $s: \mathbb{Q} \rightarrow\{-1,1\}$ such that if $x$ and $y$ are distinct rational numbers satisfying $x y=1$ or $x+y \in\{0,1\}$, then $s(x) s(y)=-1$ ? Justify your answer.
|
3. The answer is yes. Every rational number $x>0$ can be uniquely expressed as a continued fraction of the form $a_{0}+1 /\left(a_{1}+1 /\left(a_{2}+1 /\left(\cdots+1 / a_{n}\right)\right)\right)$ (where $a_{0} \in \mathbb{N}_{0}, a_{1}, \ldots, a_{n} \in \mathbb{N}$ ). Then we write $x=\left[a_{0} ; a_{1}, a_{2}, \ldots, a_{n}\right]$. Since $n$ depends only on $x$, the function $s(x)=(-1)^{n}$ is well-defined. For $x<0$ we define $s(x)=-s(-x)$, and set $s(0)=1$. We claim that this $s(x)$ satisfies the requirements of the problem. The equality $s(x) s(y)=-1$ trivially holds if $x+y=0$. Suppose that $x y=1$. We may assume w.l.o.g. that $x>y>0$. Then $x>1$, so if $x=\left[a_{0} ; a_{1}, a_{2}, \ldots, a_{n}\right]$, then $a_{0} \geq 1$ and $y=0+1 / x=$ $\left[0 ; a_{0}, a_{1}, a_{2}, \ldots, a_{n}\right]$. It follows that $s(x)=(-1)^{n}, s(y)=(-1)^{n+1}$, and hence $s(x) s(y)=-1$. Finally, suppose that $x+y=1$. We consider two cases: (i) Let $x, y>0$. We may assume w.l.o.g. that $x>1 / 2$. Then there exist natural numbers $a_{2}, \ldots, a_{n}$ such that $x=\left[0 ; 1, a_{2}, \ldots, a_{n}\right]=$ $1 /(1+1 / t)$, where $t=\left[a_{2}, \ldots, a_{n}\right]$. Since $y=1-x=1 /(1+t)=$ $\left[0 ; 1+a_{2}, a_{3}, \ldots, a_{n}\right]$, we have $s(x)=(-1)^{n}$ and $s(y)=(-1)^{n-1}$, giving us $s(x) s(y)=-1$. (ii) Let $x>0>y$. If $a_{0}, \ldots, a_{n} \in \mathbb{N}$ are such that $-y=\left[a_{0} ; a_{1}, \ldots, a_{n}\right]$, then $x=\left[1+a_{0} ; a_{1}, \ldots, a_{n}\right]$. Thus $s(y)=-s(-y)=-(-1)^{n}$ and $s(x)=(-1)^{n}$, so again $s(x) s(y)=-1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1bd04f89-5f23-5cc5-b8e3-8dcf28840df1
| 25,184
|
30. N7 (BUL) Let $p$ be an odd prime and $n$ a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length $p^{n}$. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by $p^{n+1}$.
|
30. We shall denote by $k$ the given circle with diameter $p^{n}$. Let $A, B$ be lattice points (i.e., points with integer coordinates). We shall denote by $\mu(A B)$ the exponent of the highest power of $p$ that divides the integer $A B^{2}$. We observe that if $S$ is the area of a triangle $A B C$ where $A, B, C$ are lattice points, then $2 S$ is an integer. According to Heron's formula and the formula for the circumradius, a triangle $A B C$ whose circumcenter has diameter $p^{n}$ satisfies $$ 2 A B^{2} B C^{2}+2 B C^{2} C A^{2}+2 C A^{2} A B^{2}-A B^{4}-B C^{4}-C A^{4}=16 S^{2} $$ and $$ A B^{2} \cdot B C^{2} \cdot C A^{2}=(2 S)^{2} p^{2 n} $$ Lemma 1. Let $A, B$, and $C$ be lattice points on $k$. If none of $A B^{2}, B C^{2}$, $C A^{2}$ is divisible by $p^{n+1}$, then $\mu(A B), \mu(B C), \mu(C A)$ are $0, n, n$ in some order. Proof. Let $k=\min \{\mu(A B), \mu(B C), \mu(C A)\}$. By (1), $(2 S)^{2}$ is divisible by $p^{2 k}$. Together with (2), this gives us $\mu(A B)+\mu(B C)+\mu(C A)=$ $2 k+2 n$. On the other hand, if none of $A B^{2}, B C^{2}, C A^{2}$ is divisible by $p^{n+1}$, then $\mu(A B)+\mu(B C)+\mu(C A) \leq k+2 n$. Therefore $k=0$ and the remaining two of $\mu(A B), \mu(B C), \mu(C A)$ are equal to $n$. Lemma 2. Among every four lattice points on $k$, there exist two, say $M, N$, such that $\mu(M N) \geq n+1$. Proof. Assume that this doesn't hold for some points $A, B, C, D$ on $k$. By Lemma $1, \mu$ for some of the segments $A B, A C, \ldots, C D$ is 0 , say $\mu(A C)=0$. It easily follows by Lemma 1 that then $\mu(B D)=0$ and $\mu(A B)=\mu(B C)=\mu(C D)=\mu(D A)=n$. Let $a, b, c, d, e, f \in \mathbb{N}$ be such that $A B^{2}=p^{n} a, B C^{2}=p^{n} b, C D^{2}=p^{n} c, D A^{2}=p^{n} d, A C^{2}=e$, $B D^{2}=f$. By Ptolemy's theorem we have $\sqrt{e f}=p^{n}(\sqrt{a c}+\sqrt{b d})$. Taking squares, we get that $\frac{e f}{p^{2 n}}=(\sqrt{a c}+\sqrt{b d})^{2}=a c+b d+2 \sqrt{a b c d}$ is rational and hence an integer. It follows that ef is divisible by $p^{2 n}$, a contradiction. Now we consider eight lattice points $A_{1}, A_{2}, \ldots, A_{8}$ on $k$. We color each segment $A_{i} A_{j}$ red if $\mu\left(A_{i} A_{j}\right)>n$ and black otherwise, and thus obtain a graph $G$. The degree of a point $X$ will be the number of red segments with an endpoint in $X$. We distinguish three cases: (i) There is a point, say $A_{8}$, whose degree is at most 1 . We may suppose w.l.o.g. that $A_{8} A_{7}$ is red and $A_{8} A_{1}, \ldots, A_{8} A_{6}$ black. By a well-known fact, the segments joining vertices $A_{1}, A_{2}, \ldots, A_{6}$ determine either a red triangle, in which case there is nothing to prove, or a black triangle, say $A_{1} A_{2} A_{3}$. But in the latter case the four points $A_{1}, A_{2}, A_{3}, A_{8}$ do not determine any red segment, a contradiction to Lemma 2 . (ii) All points have degree 2. Then the set of red segments partitions into cycles. If one of these cycles has length 3 , then the proof is complete. If all the cycles have length at least 4 , then we have two possibilities: two 4 -cycles, say $A_{1} A_{2} A_{3} A_{4}$ and $A_{5} A_{6} A_{7} A_{8}$, or one 8-cycle, $A_{1} A_{2} \ldots A_{8}$. In both cases, the four points $A_{1}, A_{3}, A_{5}, A_{7}$ do not determine any red segment, a contradiction. (iii) There is a point of degree at least 3 , say $A_{1}$. Suppose that $A_{1} A_{2}$, $A_{1} A_{3}$, and $A_{1} A_{4}$ are red. We claim that $A_{2}, A_{3}, A_{4}$ determine at least one red segment, which will complete the solution. If not, by Lemma $1, \mu\left(A_{2} A_{3}\right), \mu\left(A_{3} A_{4}\right), \mu\left(A_{4} A_{2}\right)$ are $n, n, 0$ in some order. Assuming w.l.o.g. that $\mu\left(A_{2} A_{3}\right)=0$, denote by $S$ the area of triangle $A_{1} A_{2} A_{3}$. Now by formula (1), $2 S$ is not divisible by $p$. On the other hand, since $\mu\left(A_{1} A_{2}\right) \geq n+1$ and $\mu\left(A_{1} A_{3}\right) \geq n+1$, it follows from (2) that $2 S$ is divisible by $p$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
30. N7 (BUL) Let $p$ be an odd prime and $n$ a positive integer. In the coordinate plane, eight distinct points with integer coordinates lie on a circle with diameter of length $p^{n}$. Prove that there exists a triangle with vertices at three of the given points such that the squares of its side lengths are integers divisible by $p^{n+1}$.
|
30. We shall denote by $k$ the given circle with diameter $p^{n}$. Let $A, B$ be lattice points (i.e., points with integer coordinates). We shall denote by $\mu(A B)$ the exponent of the highest power of $p$ that divides the integer $A B^{2}$. We observe that if $S$ is the area of a triangle $A B C$ where $A, B, C$ are lattice points, then $2 S$ is an integer. According to Heron's formula and the formula for the circumradius, a triangle $A B C$ whose circumcenter has diameter $p^{n}$ satisfies $$ 2 A B^{2} B C^{2}+2 B C^{2} C A^{2}+2 C A^{2} A B^{2}-A B^{4}-B C^{4}-C A^{4}=16 S^{2} $$ and $$ A B^{2} \cdot B C^{2} \cdot C A^{2}=(2 S)^{2} p^{2 n} $$ Lemma 1. Let $A, B$, and $C$ be lattice points on $k$. If none of $A B^{2}, B C^{2}$, $C A^{2}$ is divisible by $p^{n+1}$, then $\mu(A B), \mu(B C), \mu(C A)$ are $0, n, n$ in some order. Proof. Let $k=\min \{\mu(A B), \mu(B C), \mu(C A)\}$. By (1), $(2 S)^{2}$ is divisible by $p^{2 k}$. Together with (2), this gives us $\mu(A B)+\mu(B C)+\mu(C A)=$ $2 k+2 n$. On the other hand, if none of $A B^{2}, B C^{2}, C A^{2}$ is divisible by $p^{n+1}$, then $\mu(A B)+\mu(B C)+\mu(C A) \leq k+2 n$. Therefore $k=0$ and the remaining two of $\mu(A B), \mu(B C), \mu(C A)$ are equal to $n$. Lemma 2. Among every four lattice points on $k$, there exist two, say $M, N$, such that $\mu(M N) \geq n+1$. Proof. Assume that this doesn't hold for some points $A, B, C, D$ on $k$. By Lemma $1, \mu$ for some of the segments $A B, A C, \ldots, C D$ is 0 , say $\mu(A C)=0$. It easily follows by Lemma 1 that then $\mu(B D)=0$ and $\mu(A B)=\mu(B C)=\mu(C D)=\mu(D A)=n$. Let $a, b, c, d, e, f \in \mathbb{N}$ be such that $A B^{2}=p^{n} a, B C^{2}=p^{n} b, C D^{2}=p^{n} c, D A^{2}=p^{n} d, A C^{2}=e$, $B D^{2}=f$. By Ptolemy's theorem we have $\sqrt{e f}=p^{n}(\sqrt{a c}+\sqrt{b d})$. Taking squares, we get that $\frac{e f}{p^{2 n}}=(\sqrt{a c}+\sqrt{b d})^{2}=a c+b d+2 \sqrt{a b c d}$ is rational and hence an integer. It follows that ef is divisible by $p^{2 n}$, a contradiction. Now we consider eight lattice points $A_{1}, A_{2}, \ldots, A_{8}$ on $k$. We color each segment $A_{i} A_{j}$ red if $\mu\left(A_{i} A_{j}\right)>n$ and black otherwise, and thus obtain a graph $G$. The degree of a point $X$ will be the number of red segments with an endpoint in $X$. We distinguish three cases: (i) There is a point, say $A_{8}$, whose degree is at most 1 . We may suppose w.l.o.g. that $A_{8} A_{7}$ is red and $A_{8} A_{1}, \ldots, A_{8} A_{6}$ black. By a well-known fact, the segments joining vertices $A_{1}, A_{2}, \ldots, A_{6}$ determine either a red triangle, in which case there is nothing to prove, or a black triangle, say $A_{1} A_{2} A_{3}$. But in the latter case the four points $A_{1}, A_{2}, A_{3}, A_{8}$ do not determine any red segment, a contradiction to Lemma 2 . (ii) All points have degree 2. Then the set of red segments partitions into cycles. If one of these cycles has length 3 , then the proof is complete. If all the cycles have length at least 4 , then we have two possibilities: two 4 -cycles, say $A_{1} A_{2} A_{3} A_{4}$ and $A_{5} A_{6} A_{7} A_{8}$, or one 8-cycle, $A_{1} A_{2} \ldots A_{8}$. In both cases, the four points $A_{1}, A_{3}, A_{5}, A_{7}$ do not determine any red segment, a contradiction. (iii) There is a point of degree at least 3 , say $A_{1}$. Suppose that $A_{1} A_{2}$, $A_{1} A_{3}$, and $A_{1} A_{4}$ are red. We claim that $A_{2}, A_{3}, A_{4}$ determine at least one red segment, which will complete the solution. If not, by Lemma $1, \mu\left(A_{2} A_{3}\right), \mu\left(A_{3} A_{4}\right), \mu\left(A_{4} A_{2}\right)$ are $n, n, 0$ in some order. Assuming w.l.o.g. that $\mu\left(A_{2} A_{3}\right)=0$, denote by $S$ the area of triangle $A_{1} A_{2} A_{3}$. Now by formula (1), $2 S$ is not divisible by $p$. On the other hand, since $\mu\left(A_{1} A_{2}\right) \geq n+1$ and $\mu\left(A_{1} A_{3}\right) \geq n+1$, it follows from (2) that $2 S$ is divisible by $p$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
5b9293e4-5a8c-550e-b724-e446a7d444ce
| 25,185
|
5. A5 (THA) Let $a, b, c>0$ and $a b+b c+c a=1$. Prove the inequality $$ \sqrt[3]{\frac{1}{a}+6 b}+\sqrt[3]{\frac{1}{b}+6 c}+\sqrt[3]{\frac{1}{c}+6 a} \leq \frac{1}{a b c} $$
|
5. By the general mean inequality $\left(M_{1} \leq M_{3}\right)$, the LHS of the inequality to be proved does not exceed $$ E=\frac{3}{\sqrt[3]{3}} \sqrt[3]{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+6(a+b+c)} $$ From $a b+b c+c a=1$ we obtain that $3 a b c(a+b+c)=3(a b \cdot a c+$ $a b \cdot b c+a c \cdot b c) \leq(a b+a c+b c)^{2}=1$; hence $6(a+b+c) \leq \frac{2}{a b c}$. Since $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a b+b c+c a}{a b c}=\frac{1}{a b c}$, it follows that $$ E \leq \frac{3}{\sqrt[3]{3}} \sqrt[3]{\frac{3}{a b c}} \leq \frac{1}{a b c} $$ where the last inequality follows from the AM-GM inequality $1=a b+b c+$ $c a \geq 3 \sqrt[3]{(a b c)^{2}}$, i.e., $a b c \leq 1 /(3 \sqrt{3})$. The desired inequality now follows. Equality holds if and only if $a=b=c=1 / \sqrt{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
5. A5 (THA) Let $a, b, c>0$ and $a b+b c+c a=1$. Prove the inequality $$ \sqrt[3]{\frac{1}{a}+6 b}+\sqrt[3]{\frac{1}{b}+6 c}+\sqrt[3]{\frac{1}{c}+6 a} \leq \frac{1}{a b c} $$
|
5. By the general mean inequality $\left(M_{1} \leq M_{3}\right)$, the LHS of the inequality to be proved does not exceed $$ E=\frac{3}{\sqrt[3]{3}} \sqrt[3]{\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+6(a+b+c)} $$ From $a b+b c+c a=1$ we obtain that $3 a b c(a+b+c)=3(a b \cdot a c+$ $a b \cdot b c+a c \cdot b c) \leq(a b+a c+b c)^{2}=1$; hence $6(a+b+c) \leq \frac{2}{a b c}$. Since $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{a b+b c+c a}{a b c}=\frac{1}{a b c}$, it follows that $$ E \leq \frac{3}{\sqrt[3]{3}} \sqrt[3]{\frac{3}{a b c}} \leq \frac{1}{a b c} $$ where the last inequality follows from the AM-GM inequality $1=a b+b c+$ $c a \geq 3 \sqrt[3]{(a b c)^{2}}$, i.e., $a b c \leq 1 /(3 \sqrt{3})$. The desired inequality now follows. Equality holds if and only if $a=b=c=1 / \sqrt{3}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ce02777e-47ba-58b8-be19-268c44375176
| 25,187
|
7. A7 (IRE) Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, $n>1$. Denote by $g_{n}$ their geometric mean, and by $A_{1}, A_{2}, \ldots, A_{n}$ the sequence of arithmetic means defined by $A_{k}=\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}, k=1,2, \ldots, n$. Let $G_{n}$ be the geometric mean of $A_{1}, A_{2}, \ldots, A_{n}$. Prove the inequality $$ n \sqrt[n]{\frac{G_{n}}{A_{n}}}+\frac{g_{n}}{G_{n}} \leq n+1 $$ and establish the cases of equality.
|
7. Let us set $c_{k}=A_{k-1} / A_{k}$ for $k=1,2, \ldots, n$, where we define $A_{0}=0$. We observe that $a_{k} / A_{k}=\left(k A_{k}-(k-1) A_{k-1}\right) / A_{k}=k-(k-1) c_{k}$. Now we can write the LHS of the inequality to be proved in terms of $c_{k}$, as follows: $$ \sqrt[n]{\frac{G_{n}}{A_{n}}}=\sqrt[n^{2}]{c_{2} c_{3}^{2} \cdots c_{n}^{n-1}} \text { and } \frac{g_{n}}{G_{n}}=\sqrt[n]{\prod_{k=1}^{n}\left(k-(k-1) c_{k}\right)} $$ By the $A M-G M$ inequality we have $$ \begin{aligned} n \sqrt[n^{2}]{1^{n(n+1) / 2} c_{2} c_{3}^{2} \ldots c_{n}^{n-1}} & \leq \frac{1}{n}\left(\frac{n(n+1)}{2}+\sum_{k=2}^{n}(k-1) c_{k}\right) \\ & =\frac{n+1}{2}+\frac{1}{n} \sum_{k=1}^{n}(k-1) c_{k} . \end{aligned} $$ Also by the AM-GM inequality, we have $$ \sqrt[n]{\prod_{k=1}^{n}\left(k-(k-1) c_{k}\right)} \leq \frac{n+1}{2}-\frac{1}{n} \sum_{k=1}^{n}(k-1) c_{k} $$ Adding (1) and (2), we obtain the desired inequality. Equality holds if and only if $a_{1}=a_{2}=\cdots=a_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
7. A7 (IRE) Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers, $n>1$. Denote by $g_{n}$ their geometric mean, and by $A_{1}, A_{2}, \ldots, A_{n}$ the sequence of arithmetic means defined by $A_{k}=\frac{a_{1}+a_{2}+\cdots+a_{k}}{k}, k=1,2, \ldots, n$. Let $G_{n}$ be the geometric mean of $A_{1}, A_{2}, \ldots, A_{n}$. Prove the inequality $$ n \sqrt[n]{\frac{G_{n}}{A_{n}}}+\frac{g_{n}}{G_{n}} \leq n+1 $$ and establish the cases of equality.
|
7. Let us set $c_{k}=A_{k-1} / A_{k}$ for $k=1,2, \ldots, n$, where we define $A_{0}=0$. We observe that $a_{k} / A_{k}=\left(k A_{k}-(k-1) A_{k-1}\right) / A_{k}=k-(k-1) c_{k}$. Now we can write the LHS of the inequality to be proved in terms of $c_{k}$, as follows: $$ \sqrt[n]{\frac{G_{n}}{A_{n}}}=\sqrt[n^{2}]{c_{2} c_{3}^{2} \cdots c_{n}^{n-1}} \text { and } \frac{g_{n}}{G_{n}}=\sqrt[n]{\prod_{k=1}^{n}\left(k-(k-1) c_{k}\right)} $$ By the $A M-G M$ inequality we have $$ \begin{aligned} n \sqrt[n^{2}]{1^{n(n+1) / 2} c_{2} c_{3}^{2} \ldots c_{n}^{n-1}} & \leq \frac{1}{n}\left(\frac{n(n+1)}{2}+\sum_{k=2}^{n}(k-1) c_{k}\right) \\ & =\frac{n+1}{2}+\frac{1}{n} \sum_{k=1}^{n}(k-1) c_{k} . \end{aligned} $$ Also by the AM-GM inequality, we have $$ \sqrt[n]{\prod_{k=1}^{n}\left(k-(k-1) c_{k}\right)} \leq \frac{n+1}{2}-\frac{1}{n} \sum_{k=1}^{n}(k-1) c_{k} $$ Adding (1) and (2), we obtain the desired inequality. Equality holds if and only if $a_{1}=a_{2}=\cdots=a_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ce187ec1-812a-512e-977c-2433ba4f5732
| 25,189
|
The in-circle of triangle $A B C$ touches the sides $B C, C A$ and $A B$ in $K, L$ and $M$ respectively. The line through $A$ and parallel to $L K$ meets $M K$ in $P$ and the line through $A$ and parallel to $M K$ meets $L K$ in $Q$. Show that the line $P Q$ bisects the sides $A B$ and $A C$ of triangle $A B C$.
|
Let $A P, A Q$ produced meet $B C$ in $D, E$ respectively.
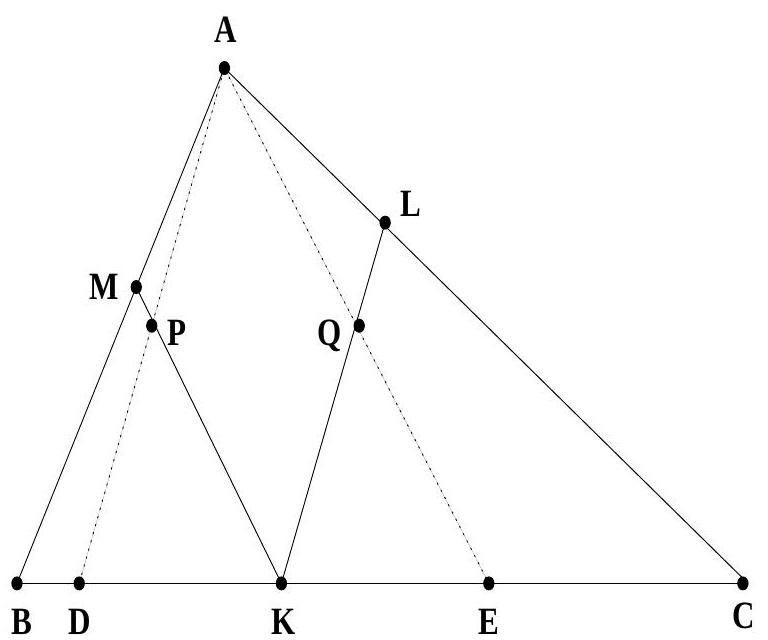
Since $M K$ is parallel to $A E$, we have $\angle A E K=\angle M K B$. Since $B K=B M$, both being tangents to the circle from $B, \angle M K B=\angle B M K$. This with the fact that $M K$ is parallel to $A E$ gives us $\angle A E K=\angle M A E$. This shows that $M A E K$ is an isosceles trapezoid. We conclude that $M A=K E$. Similarly, we can prove that $A L=D K$. But $A M=A L$. We get that $D K=K E$. Since $K P$ is parallel to $A E$, we get $D P=P A$ and similarly $E Q=Q A$. This implies that $P Q$ is parallel to $D E$ and hence bisects $A B, A C$ when produced.
[The same argument holds even if one or both of $P$ and $Q$ lie outside triangle $A B C$.]
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The in-circle of triangle $A B C$ touches the sides $B C, C A$ and $A B$ in $K, L$ and $M$ respectively. The line through $A$ and parallel to $L K$ meets $M K$ in $P$ and the line through $A$ and parallel to $M K$ meets $L K$ in $Q$. Show that the line $P Q$ bisects the sides $A B$ and $A C$ of triangle $A B C$.
|
Let $A P, A Q$ produced meet $B C$ in $D, E$ respectively.

Since $M K$ is parallel to $A E$, we have $\angle A E K=\angle M K B$. Since $B K=B M$, both being tangents to the circle from $B, \angle M K B=\angle B M K$. This with the fact that $M K$ is parallel to $A E$ gives us $\angle A E K=\angle M A E$. This shows that $M A E K$ is an isosceles trapezoid. We conclude that $M A=K E$. Similarly, we can prove that $A L=D K$. But $A M=A L$. We get that $D K=K E$. Since $K P$ is parallel to $A E$, we get $D P=P A$ and similarly $E Q=Q A$. This implies that $P Q$ is parallel to $D E$ and hence bisects $A B, A C$ when produced.
[The same argument holds even if one or both of $P$ and $Q$ lie outside triangle $A B C$.]
|
{
"resource_path": "INMO/segmented/en-2000.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution. :"
}
|
effd810d-1fec-5c76-8db0-4bfe8638f9a4
| 607,785
|
Let $a, b, c$ be three real numbers such that $1 \geq a \geq b \geq c \geq 0$. Prove that if $\lambda$ is a root of the cubic equation $x^{3}+a x^{2}+b x+c=0$ (real or complex), then $|\lambda| \leq 1$.
|
Since $\lambda$ is a root of the equation $x^{3}+a x^{2}+b x+c=0$, we have
$$
\lambda^{3}=-a \lambda^{2}-b \lambda-c
$$
This implies that
$$
\begin{aligned}
\lambda^{4} & =-a \lambda^{3}-b \lambda^{2}-c \lambda \\
& =(1-a) \lambda^{3}+(a-b) \lambda^{2}+(b-c) \lambda+c
\end{aligned}
$$
where we have used again
$$
-\lambda^{3}-a \lambda^{2}-b \lambda-c=0
$$
Suppose $|\lambda| \geq 1$. Then we obtain
$$
\begin{aligned}
|\lambda|^{4} & \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{2}+(b-c)|\lambda|+c \\
& \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{3}+(b-c)|\lambda|^{3}+c|\lambda|^{3} \\
& \leq|\lambda|^{3}
\end{aligned}
$$
This shows that $|\lambda| \leq 1$. Hence the only possibility in this case is $|\lambda|=1$. We conclude that $|\lambda| \leq 1$ is always true.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b, c$ be three real numbers such that $1 \geq a \geq b \geq c \geq 0$. Prove that if $\lambda$ is a root of the cubic equation $x^{3}+a x^{2}+b x+c=0$ (real or complex), then $|\lambda| \leq 1$.
|
Since $\lambda$ is a root of the equation $x^{3}+a x^{2}+b x+c=0$, we have
$$
\lambda^{3}=-a \lambda^{2}-b \lambda-c
$$
This implies that
$$
\begin{aligned}
\lambda^{4} & =-a \lambda^{3}-b \lambda^{2}-c \lambda \\
& =(1-a) \lambda^{3}+(a-b) \lambda^{2}+(b-c) \lambda+c
\end{aligned}
$$
where we have used again
$$
-\lambda^{3}-a \lambda^{2}-b \lambda-c=0
$$
Suppose $|\lambda| \geq 1$. Then we obtain
$$
\begin{aligned}
|\lambda|^{4} & \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{2}+(b-c)|\lambda|+c \\
& \leq(1-a)|\lambda|^{3}+(a-b)|\lambda|^{3}+(b-c)|\lambda|^{3}+c|\lambda|^{3} \\
& \leq|\lambda|^{3}
\end{aligned}
$$
This shows that $|\lambda| \leq 1$. Hence the only possibility in this case is $|\lambda|=1$. We conclude that $|\lambda| \leq 1$ is always true.
|
{
"resource_path": "INMO/segmented/en-2000.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSol. :"
}
|
e4f945e1-cdb4-57f6-882c-3e1430321cc5
| 607,789
|
For any natural number $n,(n \geq 3)$, let $f(n)$ denote the number of non-congruent integer-sided triangles with perimeter $n$ (e.g., $f(3)=1, f(4)=0, f(7)=2$ ). Show that
(a) $f(1999)>f(1996)$
(b) $f(2000)=f(1997)$.
|
(a) Let $a, b, c$ be the sides of a triangle with $a+b+c=1996$, and each being a positive integer. Then $a+1, b+1, c+1$ are also sides of a triangle with perimeter 1999 because
$$
a<b+c \quad \Longrightarrow \quad a+1<(b+1)+(c+1)
$$
and so on. Moreover $(999,999,1)$ form the sides of a triangle with perimeter 1999, which is not obtainable in the form $(a+1, b+1, c+1)$ where $a, b, c$ are the integers and the sides of a triangle with $a+b+c=1996$. We conclude that $f(1999)>f(1996)$.
(b) As in the case (a) we conclude that $f(2000) \geq f(1997)$. On the other hand, if $x, y, z$ are the integer sides of a triangle with $x+y+z=2000$, and say $x \geq y \geq z \geq 1$, then we cannot have $z=1$; for otherwise we would get $x+y=1999$ forcing $x, y$ to have opposite parity so that $x-y \geq 1=z$ violating triangle inequality for $x, y, z$. Hence $x \geq y \geq z>1$. This implies that $x-1 \geq y-1 \geq z-1>0$. We already have $x<y+z$. If $x \geq y+z-1$, then we see that $y+z-1 \leq x<y+z$, showing that $y+z-1=x$. Hence we obtain $2000=x+y+z=2 x+1$ which is impossible. We conclude that $x<y+z-1$. This shows that $x-1<(y-1)+(z-1)$ and hence $x-1, y-1, z-1$ are the sides of a triangle with perimeter 1997. This gives $f(2000) \leq f(1997)$. Thus we obtain the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any natural number $n,(n \geq 3)$, let $f(n)$ denote the number of non-congruent integer-sided triangles with perimeter $n$ (e.g., $f(3)=1, f(4)=0, f(7)=2$ ). Show that
(a) $f(1999)>f(1996)$
(b) $f(2000)=f(1997)$.
|
(a) Let $a, b, c$ be the sides of a triangle with $a+b+c=1996$, and each being a positive integer. Then $a+1, b+1, c+1$ are also sides of a triangle with perimeter 1999 because
$$
a<b+c \quad \Longrightarrow \quad a+1<(b+1)+(c+1)
$$
and so on. Moreover $(999,999,1)$ form the sides of a triangle with perimeter 1999, which is not obtainable in the form $(a+1, b+1, c+1)$ where $a, b, c$ are the integers and the sides of a triangle with $a+b+c=1996$. We conclude that $f(1999)>f(1996)$.
(b) As in the case (a) we conclude that $f(2000) \geq f(1997)$. On the other hand, if $x, y, z$ are the integer sides of a triangle with $x+y+z=2000$, and say $x \geq y \geq z \geq 1$, then we cannot have $z=1$; for otherwise we would get $x+y=1999$ forcing $x, y$ to have opposite parity so that $x-y \geq 1=z$ violating triangle inequality for $x, y, z$. Hence $x \geq y \geq z>1$. This implies that $x-1 \geq y-1 \geq z-1>0$. We already have $x<y+z$. If $x \geq y+z-1$, then we see that $y+z-1 \leq x<y+z$, showing that $y+z-1=x$. Hence we obtain $2000=x+y+z=2 x+1$ which is impossible. We conclude that $x<y+z-1$. This shows that $x-1<(y-1)+(z-1)$ and hence $x-1, y-1, z-1$ are the sides of a triangle with perimeter 1997. This gives $f(2000) \leq f(1997)$. Thus we obtain the desired result.
|
{
"resource_path": "INMO/segmented/en-2000.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSol. :"
}
|
8fa05009-7776-5519-a689-e20e4570d83c
| 607,790
|
Let $A B C$ be a triangle in which no angle is $90^{\circ}$. For any point $P$ in the plane of the triangle, let $A_{1}, B_{1}, C_{1}$ denote the reflections of $P$ in the sides $B C, C A, A B$ respectively. Prove the following statements:
(a) If $P$ is the incentre or an excentre of $A B C$, then $P$ is the circumcentre of $A_{1} B_{1} C_{1}$;
(b) If $P$ is the circumcentre of $A B C$, then $P$ is the orthocentre of $A_{1} B_{1} C_{1}$;
(c) If $P$ is the orthocentre of $A B C$, then $P$ is either the incentre or an excentre of $A_{1} B_{1} C_{1}$.
|
(a)
If $P=I$ is the incentre of triangle $A B C$, and $r$ its inradius, then it is clear that $A_{1} I=B_{1} I=C_{1} I=2 r$. It follows that $I$ is the circumcentre of $A_{1} B_{1} C_{1}$. On the otherhand if $P=I_{1}$ is the excentre of $A B C$ opposite $A$ and $r_{1}$ the corresponding exradius, then again we see that $A_{1} I_{1}=B_{1} I_{1}=C_{1} I_{1}=2 r_{1}$. Thus $I_{1}$ is the circumcentre of $A_{1} B_{1} C_{1}$.
(b)
Let $P=O$ be the circumcentre of $A B C$. By definition, it follows that $O A_{1}$ bisects and is bisected by $B C$ and so on. Let $D, E, F$ be the mid-points of $B C, C A, A B$ respectively. Then $F E$ is parallel to $B C$. But $E, F$ are also mid-points of $O B_{1}, O C_{1}$ and hence $F E$ is parallel to $B_{1} C_{1}$ as well. We conclude that $B C$ is parallel to $B_{1} C_{1}$. Since $O A_{1}$ is perpendicular to $B C$, it follows that $O A_{1}$ is perpendicular to $B_{1} C_{1}$. Similarly $O B_{1}$ is perpendicular to $C_{1} A_{1}$ and $O C_{1}$ is perpendicular to $A_{1} B_{1}$. These imply that $O$ is the orthocentre of $A_{1} B_{1} C_{1}$. (This applies whether $O$ is inside or outside $A B C$.)
(c)
let $P=H$, the orthocentre of $A B C$. We consider two possibilities; $H$ falls inside $A B C$ and $H$ falls outside $A B C$.
Suppose $H$ is inside $A B C$; this happens if $A B C$ is an acute triangle. It is known that $A_{1}, B_{1}, C_{1}$ lie on the circumcircle of $A B C$. Thus $\angle C_{1} A_{1} A=\angle C_{1} C A=90^{\circ}-A$. Similarly $\angle B_{1} A_{1} A=\angle B_{1} B A=90^{\circ}-A$. These show that $\angle C_{1} A_{1} A=\angle B_{1} A_{1} A$. Thus $A_{1} A$ is an internal bisector of $\angle C_{1} A_{1} B_{1}$. Similarly we can show that $B_{1}$ bisects $\angle A_{1} B_{1} C_{1}$ and $C_{1} C$ bisects $\angle B_{1} C_{1} A_{1}$. Since $A_{1} A, B_{1} B, C_{1} C$ concur at $H$, we conclude that $H$ is the incentre of $A_{1} B_{1} C_{1}$.
OR If $D, E, F$ are the feet of perpendiculars of $A, B, C$ to the sides $B C, C A, A B$ respectively, then we see that $E F, F D, D E$ are respectively parallel to $B_{1} C_{1}, C_{1} A_{1}$, $A_{1} B_{1}$. This implies that $\angle C_{1} A_{1} H=\angle F D H=\angle A B E=90^{\circ}-A$, as $B D H F$ is a cyclic quadrilateral. Similarly, we can show that $\angle B_{1} A_{1} H=90^{\circ}-A$. It follows that $A_{1} H$ is the internal bisector of $\angle C_{1} A_{1} B_{1}$. We can proceed as in the earlier case.
If $H$ is outside $A B C$, the same proofs go through again, except that two of $A_{1} H$, $B_{1} H, C_{1} H$ are external angle bisectors and one of these is an internal angle bisector. Thus $H$ becomes an excentre of triangle $A_{1} B_{1} C_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle in which no angle is $90^{\circ}$. For any point $P$ in the plane of the triangle, let $A_{1}, B_{1}, C_{1}$ denote the reflections of $P$ in the sides $B C, C A, A B$ respectively. Prove the following statements:
(a) If $P$ is the incentre or an excentre of $A B C$, then $P$ is the circumcentre of $A_{1} B_{1} C_{1}$;
(b) If $P$ is the circumcentre of $A B C$, then $P$ is the orthocentre of $A_{1} B_{1} C_{1}$;
(c) If $P$ is the orthocentre of $A B C$, then $P$ is either the incentre or an excentre of $A_{1} B_{1} C_{1}$.
|
(a)

If $P=I$ is the incentre of triangle $A B C$, and $r$ its inradius, then it is clear that $A_{1} I=B_{1} I=C_{1} I=2 r$. It follows that $I$ is the circumcentre of $A_{1} B_{1} C_{1}$. On the otherhand if $P=I_{1}$ is the excentre of $A B C$ opposite $A$ and $r_{1}$ the corresponding exradius, then again we see that $A_{1} I_{1}=B_{1} I_{1}=C_{1} I_{1}=2 r_{1}$. Thus $I_{1}$ is the circumcentre of $A_{1} B_{1} C_{1}$.

(b)
Let $P=O$ be the circumcentre of $A B C$. By definition, it follows that $O A_{1}$ bisects and is bisected by $B C$ and so on. Let $D, E, F$ be the mid-points of $B C, C A, A B$ respectively. Then $F E$ is parallel to $B C$. But $E, F$ are also mid-points of $O B_{1}, O C_{1}$ and hence $F E$ is parallel to $B_{1} C_{1}$ as well. We conclude that $B C$ is parallel to $B_{1} C_{1}$. Since $O A_{1}$ is perpendicular to $B C$, it follows that $O A_{1}$ is perpendicular to $B_{1} C_{1}$. Similarly $O B_{1}$ is perpendicular to $C_{1} A_{1}$ and $O C_{1}$ is perpendicular to $A_{1} B_{1}$. These imply that $O$ is the orthocentre of $A_{1} B_{1} C_{1}$. (This applies whether $O$ is inside or outside $A B C$.)
(c)
let $P=H$, the orthocentre of $A B C$. We consider two possibilities; $H$ falls inside $A B C$ and $H$ falls outside $A B C$.
Suppose $H$ is inside $A B C$; this happens if $A B C$ is an acute triangle. It is known that $A_{1}, B_{1}, C_{1}$ lie on the circumcircle of $A B C$. Thus $\angle C_{1} A_{1} A=\angle C_{1} C A=90^{\circ}-A$. Similarly $\angle B_{1} A_{1} A=\angle B_{1} B A=90^{\circ}-A$. These show that $\angle C_{1} A_{1} A=\angle B_{1} A_{1} A$. Thus $A_{1} A$ is an internal bisector of $\angle C_{1} A_{1} B_{1}$. Similarly we can show that $B_{1}$ bisects $\angle A_{1} B_{1} C_{1}$ and $C_{1} C$ bisects $\angle B_{1} C_{1} A_{1}$. Since $A_{1} A, B_{1} B, C_{1} C$ concur at $H$, we conclude that $H$ is the incentre of $A_{1} B_{1} C_{1}$.
OR If $D, E, F$ are the feet of perpendiculars of $A, B, C$ to the sides $B C, C A, A B$ respectively, then we see that $E F, F D, D E$ are respectively parallel to $B_{1} C_{1}, C_{1} A_{1}$, $A_{1} B_{1}$. This implies that $\angle C_{1} A_{1} H=\angle F D H=\angle A B E=90^{\circ}-A$, as $B D H F$ is a cyclic quadrilateral. Similarly, we can show that $\angle B_{1} A_{1} H=90^{\circ}-A$. It follows that $A_{1} H$ is the internal bisector of $\angle C_{1} A_{1} B_{1}$. We can proceed as in the earlier case.
If $H$ is outside $A B C$, the same proofs go through again, except that two of $A_{1} H$, $B_{1} H, C_{1} H$ are external angle bisectors and one of these is an internal angle bisector. Thus $H$ becomes an excentre of triangle $A_{1} B_{1} C_{1}$.
|
{
"resource_path": "INMO/segmented/en-2001.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
5f785437-32a9-5cdb-98f1-3a779786815c
| 607,791
|
Show that the equation
$$
x^{2}+y^{2}+z^{2}=(x-y)(y-z)(z-x)
$$
has infinitely many solutions in integers $x, y, z$.
|
We seek solutions $(x, y, z)$ which are in arithmetic progression. Let us put $y-x=z-y=d>0$ so that the equation reduces to the form
$$
3 y^{2}+2 d^{2}=2 d^{3}
$$
Thus we get $3 y^{2}=2(d-1) d^{2}$. We conclude that $2(d-1)$ is 3 times a square. This is satisfied if $d-1=6 n^{2}$ for some $n$. Thus $d=6 n^{2}+1$ and $3 y^{2}=d^{2} \cdot 2\left(6 n^{2}\right)$ giving us $y^{2}=4 d^{2} n^{2}$. Thus we can take $y=2 d n=2 n\left(6 n^{2}+1\right)$. From this we obtain $x=y-d=(2 n-1)\left(6 n^{2}+1\right), z=y+d=(2 n+1)\left(6 n^{2}+1\right)$. It is easily verified that
$$
(x, y, z)=\left((2 n-1)\left(6 n^{2}+1\right), 2 n\left(6 n^{2}+1\right),(2 n+1)\left(6 n^{2}+1\right)\right)
$$
is indeed a solution for a fixed $n$ and this gives an infinite set of solutions as $n$ varies over natural numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that the equation
$$
x^{2}+y^{2}+z^{2}=(x-y)(y-z)(z-x)
$$
has infinitely many solutions in integers $x, y, z$.
|
We seek solutions $(x, y, z)$ which are in arithmetic progression. Let us put $y-x=z-y=d>0$ so that the equation reduces to the form
$$
3 y^{2}+2 d^{2}=2 d^{3}
$$
Thus we get $3 y^{2}=2(d-1) d^{2}$. We conclude that $2(d-1)$ is 3 times a square. This is satisfied if $d-1=6 n^{2}$ for some $n$. Thus $d=6 n^{2}+1$ and $3 y^{2}=d^{2} \cdot 2\left(6 n^{2}\right)$ giving us $y^{2}=4 d^{2} n^{2}$. Thus we can take $y=2 d n=2 n\left(6 n^{2}+1\right)$. From this we obtain $x=y-d=(2 n-1)\left(6 n^{2}+1\right), z=y+d=(2 n+1)\left(6 n^{2}+1\right)$. It is easily verified that
$$
(x, y, z)=\left((2 n-1)\left(6 n^{2}+1\right), 2 n\left(6 n^{2}+1\right),(2 n+1)\left(6 n^{2}+1\right)\right)
$$
is indeed a solution for a fixed $n$ and this gives an infinite set of solutions as $n$ varies over natural numbers.
|
{
"resource_path": "INMO/segmented/en-2001.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
07fa5dad-9da4-5050-a391-5dc62457b970
| 607,792
|
If $a, b, c$ are positive real numbers such that $a b c=1$, prove that
$$
a^{b+c} b^{c+a} c^{a+b} \leq 1
$$
|
Note that the inequality is symmetric in $a, b, c$ so that we may assume that $a \geq b \geq c$. Since $a b c=1$, it follows that $a \geq 1$ and $c \leq 1$. Using $b=1 / a c$, we get
$$
a^{b+c} b^{c+a} c^{a+b}=\frac{a^{b+c} c^{a+b}}{a^{c+a} c^{c+a}}=\frac{c^{b-c}}{a^{a-b}} \leq 1
$$
because $c \leq 1, b \geq c, a \geq 1$ and $a \geq b$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $a, b, c$ are positive real numbers such that $a b c=1$, prove that
$$
a^{b+c} b^{c+a} c^{a+b} \leq 1
$$
|
Note that the inequality is symmetric in $a, b, c$ so that we may assume that $a \geq b \geq c$. Since $a b c=1$, it follows that $a \geq 1$ and $c \leq 1$. Using $b=1 / a c$, we get
$$
a^{b+c} b^{c+a} c^{a+b}=\frac{a^{b+c} c^{a+b}}{a^{c+a} c^{c+a}}=\frac{c^{b-c}}{a^{a-b}} \leq 1
$$
because $c \leq 1, b \geq c, a \geq 1$ and $a \geq b$.
|
{
"resource_path": "INMO/segmented/en-2001.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
3ab8f0e4-0aac-516f-8aab-0ebed8a34e0a
| 607,793
|
Given any nine integers show that it is possible to choose, from among them, four integers $a, b, c, d$ such that $a+b-c-d$ is divisible by 20 . Further show that such a selection is not possible if we start with eight integers instead of nine.
|
Suppose there are four numbers $a, b, c, d$ among the given nine numbers which leave the same remainder modulo 20 . Then $a+b \equiv c+d(\bmod 20)$ and we are done.
If not, there are two possibilities:
(1) We may have two disjoint pairs $\{a, c\}$ and $\{b, d\}$ obtained from the given nine numbers such that $a \equiv c(\bmod 20)$ and $b \equiv d(\bmod 20)$. In this case we get $a+b \equiv c+d$ $(\bmod 20)$.
(2) Or else there are at most three numbers having the same remainder modulo 20 and the remaining six numbers leave distinct remainders which are also different from the first remainder (i.e., the remainder of the three numbers). Thus there are at least 7 disinct remainders modulo 20 that can be obtained from the given set of nine numbers. These 7 remainders give rise to $\binom{7}{2}=21$ pairs of numbers. By pigeonhole principle, there must be two pairs $\left(r_{1}, r_{2}\right),\left(r_{3}, r_{4}\right)$ such that $r_{1}+r_{2} \equiv r_{3}+r_{4}(\bmod 20)$. Going back we get four numbers $a, b, c, d$ such that $a+b \equiv c+d(\bmod 20)$.
If we take the numbers $0,0,0,1,2,4,7,12$, we check that the result is not true for these eight numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Given any nine integers show that it is possible to choose, from among them, four integers $a, b, c, d$ such that $a+b-c-d$ is divisible by 20 . Further show that such a selection is not possible if we start with eight integers instead of nine.
|
Suppose there are four numbers $a, b, c, d$ among the given nine numbers which leave the same remainder modulo 20 . Then $a+b \equiv c+d(\bmod 20)$ and we are done.
If not, there are two possibilities:
(1) We may have two disjoint pairs $\{a, c\}$ and $\{b, d\}$ obtained from the given nine numbers such that $a \equiv c(\bmod 20)$ and $b \equiv d(\bmod 20)$. In this case we get $a+b \equiv c+d$ $(\bmod 20)$.
(2) Or else there are at most three numbers having the same remainder modulo 20 and the remaining six numbers leave distinct remainders which are also different from the first remainder (i.e., the remainder of the three numbers). Thus there are at least 7 disinct remainders modulo 20 that can be obtained from the given set of nine numbers. These 7 remainders give rise to $\binom{7}{2}=21$ pairs of numbers. By pigeonhole principle, there must be two pairs $\left(r_{1}, r_{2}\right),\left(r_{3}, r_{4}\right)$ such that $r_{1}+r_{2} \equiv r_{3}+r_{4}(\bmod 20)$. Going back we get four numbers $a, b, c, d$ such that $a+b \equiv c+d(\bmod 20)$.
If we take the numbers $0,0,0,1,2,4,7,12$, we check that the result is not true for these eight numbers.
|
{
"resource_path": "INMO/segmented/en-2001.jsonl",
"problem_match": "\n4.",
"solution_match": "## Solution:"
}
|
a02fdf03-7c0d-5bd8-8c9c-ed73992c66c4
| 607,794
|
Let $A B C$ be a triangle and $D$ be the mid-point of side $B C$. Suppose $\angle D A B=\angle B C A$ and $\angle D A C=15^{\circ}$. Show that $\angle A D C$ is obtuse. Further, if $O$ is the circumcentre of $A D C$, prove that triangle $A O D$ is equilateral.
|
Let $\alpha$ denote the equal angles $\angle B A D=\angle D C A$. Using sine rule in triangles $D A B$ and $D A C$, we get
$$
\frac{A D}{\sin B}=\frac{B D}{\sin \alpha}, \quad \frac{C D}{\sin 15^{\circ}}=\frac{A D}{\sin \alpha}
$$
Eliminating $\alpha$ (using $B D=D C$ and $2 \alpha+B+15^{\circ}=\pi$ ), we obtain $1+\cos \left(B+15^{\circ}\right)=$ $2 \sin B \sin 15^{\circ}$. But we know that $2 \sin B \sin 15^{\circ}=\cos \left(B-15^{\circ}\right)-\cos \left(B+15^{\circ}\right)$. Putting $\beta=B-15^{\circ}$, we get a relation $1+2 \cos (\beta+30)=\cos \beta$. We write this in the form
$$
(1-\sqrt{3}) \cos \beta+\sin \beta=1
$$
Since $\sin \beta \leq 1$, it follows that $(1-\sqrt{3}) \cos \beta \geq 0$. We conclude that $\cos \beta \leq 0$ and hence that $\beta$ is obtuse. So is angle $B$ and hence $\angle A D C$.
We have the relation $(1-\sqrt{3}) \cos \beta+\sin \beta=1$. If we set $x=\tan (\beta / 2)$, then we get, using $\cos \beta=\left(1-x^{2}\right) /\left(1+x^{2}\right), \sin \beta=2 x /\left(1+x^{2}\right)$,
$$
(\sqrt{3}-2) x^{2}+2 x-\sqrt{3}=0
$$
Solving for $x$, we obtain $x=1$ or $x=\sqrt{3}(2+\sqrt{3})$. If $x=\sqrt{3}(2+\sqrt{3})$, then $\tan (\beta / 2)>2+\sqrt{3}=\tan 75^{\circ}$ giving us $\beta>150^{\circ}$. This forces that $B>165^{\circ}$ and hence $B+A>165^{\circ}+15^{\circ}=180^{\circ}$, a contradiction. thus $x=1$ giving us $\beta=\pi / 2$. This gives $B=105^{\circ}$ and hence $\alpha=30^{\circ}$. Thus $\angle D A O=60^{\circ}$. Since $O A=O D$, the result follows.
## OR
Let $m_{a}$ denote the median $A D$. Then we can compute
$$
\cos \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{2 c m_{a}}, \quad \sin \alpha=\frac{2 \Delta}{c m_{a}}
$$
where $\Delta$ denotes the area of triangle $A B C$. These two expressions give
$$
\cot \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
$$
Similarly, we obtain
$$
\cot \angle C A D=\frac{b^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
$$
Thus we get
$$
\cot \alpha-\cot 15^{\circ}=\frac{c^{2}-a^{2}}{4 \Delta}
$$
Similarly we can also obtain
$$
\cot B-\cot \alpha=\frac{c^{2}-a^{2}}{4 \Delta}
$$
giving us the relation
$$
\cot B=2 \cot \alpha-\cot 15^{\circ}
$$
If $B$ is acute then $2 \cot \alpha>\cot 15^{\circ}=2+\sqrt{3}>2 \sqrt{3}$. It follows that $\cot \alpha>\sqrt{3}$. This implies that $\alpha<30^{\circ}$ and hence
$$
B=180^{\circ}-2 \alpha-15^{\circ}>105^{\circ}
$$
This contradiction forces that angle $B$ is obtuse and consequently $\angle A D C$ is obtuse.
Since $\angle B A D=\alpha=\angle A C D$, the line $A B$ is tangent to the circumcircle $\Gamma$ of $A D C$ at $A$. Hence $O A$ is perpendicular to $A B$. Draw $D E$ and $B F$ perpendicular to $A C$, and join $O D$. Since $\angle D A C=15^{\circ}$, we see that $\angle D O C=30^{\circ}$ and hence $D E=O D / 2$. But $D E$ is parallel to $B F$ and $B D=D C$ shows that $B F=2 D E$. We conclude that
$B F=D O$. But $D O=A O$, both being radii of $\Gamma$. Thus $B F=A O$. Using right triangles $B F O$ and $B A O$, we infer that $A B=O F$. We conclude that $A B F O$ is a rectangle. In particular $\angle A O F=90^{\circ}$. It follows that
$$
\angle A O D=90^{\circ}-\angle D O C=90^{\circ}-30^{\circ}=60^{\circ}
$$
Since $O A=O D$, we conclude that $A O D$ is equilateral.
OR
Note that triangles $A B D$ and $C B A$ are similar. Thus we have the ratios
$$
\frac{A B}{B D}=\frac{C B}{B A}
$$
This reduces to $a^{2}=2 c^{2}$ giving us $a=\sqrt{2} c$. This is equivalent to $\sin ^{2}\left(\alpha+15^{\circ}\right)=$ $2 \sin ^{2} \alpha$. We write this in the form
$$
\cos 15^{\circ}+\cot \alpha \sin 15^{\circ}=\sqrt{2}
$$
Solving for $\cot \alpha$, we get $\cot \alpha=\sqrt{3}$. We conclude that $\alpha=30^{\circ}$, and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and $D$ be the mid-point of side $B C$. Suppose $\angle D A B=\angle B C A$ and $\angle D A C=15^{\circ}$. Show that $\angle A D C$ is obtuse. Further, if $O$ is the circumcentre of $A D C$, prove that triangle $A O D$ is equilateral.
|

Let $\alpha$ denote the equal angles $\angle B A D=\angle D C A$. Using sine rule in triangles $D A B$ and $D A C$, we get
$$
\frac{A D}{\sin B}=\frac{B D}{\sin \alpha}, \quad \frac{C D}{\sin 15^{\circ}}=\frac{A D}{\sin \alpha}
$$
Eliminating $\alpha$ (using $B D=D C$ and $2 \alpha+B+15^{\circ}=\pi$ ), we obtain $1+\cos \left(B+15^{\circ}\right)=$ $2 \sin B \sin 15^{\circ}$. But we know that $2 \sin B \sin 15^{\circ}=\cos \left(B-15^{\circ}\right)-\cos \left(B+15^{\circ}\right)$. Putting $\beta=B-15^{\circ}$, we get a relation $1+2 \cos (\beta+30)=\cos \beta$. We write this in the form
$$
(1-\sqrt{3}) \cos \beta+\sin \beta=1
$$
Since $\sin \beta \leq 1$, it follows that $(1-\sqrt{3}) \cos \beta \geq 0$. We conclude that $\cos \beta \leq 0$ and hence that $\beta$ is obtuse. So is angle $B$ and hence $\angle A D C$.
We have the relation $(1-\sqrt{3}) \cos \beta+\sin \beta=1$. If we set $x=\tan (\beta / 2)$, then we get, using $\cos \beta=\left(1-x^{2}\right) /\left(1+x^{2}\right), \sin \beta=2 x /\left(1+x^{2}\right)$,
$$
(\sqrt{3}-2) x^{2}+2 x-\sqrt{3}=0
$$
Solving for $x$, we obtain $x=1$ or $x=\sqrt{3}(2+\sqrt{3})$. If $x=\sqrt{3}(2+\sqrt{3})$, then $\tan (\beta / 2)>2+\sqrt{3}=\tan 75^{\circ}$ giving us $\beta>150^{\circ}$. This forces that $B>165^{\circ}$ and hence $B+A>165^{\circ}+15^{\circ}=180^{\circ}$, a contradiction. thus $x=1$ giving us $\beta=\pi / 2$. This gives $B=105^{\circ}$ and hence $\alpha=30^{\circ}$. Thus $\angle D A O=60^{\circ}$. Since $O A=O D$, the result follows.
## OR
Let $m_{a}$ denote the median $A D$. Then we can compute
$$
\cos \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{2 c m_{a}}, \quad \sin \alpha=\frac{2 \Delta}{c m_{a}}
$$
where $\Delta$ denotes the area of triangle $A B C$. These two expressions give
$$
\cot \alpha=\frac{c^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
$$
Similarly, we obtain
$$
\cot \angle C A D=\frac{b^{2}+m_{a}^{2}-\left(a^{2} / 4\right)}{4 \Delta}
$$
Thus we get
$$
\cot \alpha-\cot 15^{\circ}=\frac{c^{2}-a^{2}}{4 \Delta}
$$
Similarly we can also obtain
$$
\cot B-\cot \alpha=\frac{c^{2}-a^{2}}{4 \Delta}
$$
giving us the relation
$$
\cot B=2 \cot \alpha-\cot 15^{\circ}
$$
If $B$ is acute then $2 \cot \alpha>\cot 15^{\circ}=2+\sqrt{3}>2 \sqrt{3}$. It follows that $\cot \alpha>\sqrt{3}$. This implies that $\alpha<30^{\circ}$ and hence
$$
B=180^{\circ}-2 \alpha-15^{\circ}>105^{\circ}
$$
This contradiction forces that angle $B$ is obtuse and consequently $\angle A D C$ is obtuse.
Since $\angle B A D=\alpha=\angle A C D$, the line $A B$ is tangent to the circumcircle $\Gamma$ of $A D C$ at $A$. Hence $O A$ is perpendicular to $A B$. Draw $D E$ and $B F$ perpendicular to $A C$, and join $O D$. Since $\angle D A C=15^{\circ}$, we see that $\angle D O C=30^{\circ}$ and hence $D E=O D / 2$. But $D E$ is parallel to $B F$ and $B D=D C$ shows that $B F=2 D E$. We conclude that
$B F=D O$. But $D O=A O$, both being radii of $\Gamma$. Thus $B F=A O$. Using right triangles $B F O$ and $B A O$, we infer that $A B=O F$. We conclude that $A B F O$ is a rectangle. In particular $\angle A O F=90^{\circ}$. It follows that
$$
\angle A O D=90^{\circ}-\angle D O C=90^{\circ}-30^{\circ}=60^{\circ}
$$
Since $O A=O D$, we conclude that $A O D$ is equilateral.
OR
Note that triangles $A B D$ and $C B A$ are similar. Thus we have the ratios
$$
\frac{A B}{B D}=\frac{C B}{B A}
$$
This reduces to $a^{2}=2 c^{2}$ giving us $a=\sqrt{2} c$. This is equivalent to $\sin ^{2}\left(\alpha+15^{\circ}\right)=$ $2 \sin ^{2} \alpha$. We write this in the form
$$
\cos 15^{\circ}+\cot \alpha \sin 15^{\circ}=\sqrt{2}
$$
Solving for $\cot \alpha$, we get $\cot \alpha=\sqrt{3}$. We conclude that $\alpha=30^{\circ}$, and the result follows.
|
{
"resource_path": "INMO/segmented/en-2001.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
e99978c4-f8da-5408-bde6-7feee22caa6d
| 607,795
|
For a convex hexagon $A B C D E F$ in which each pair of opposite sides is unequal, consider the following six statements:
$$
\begin{array}{ll}
\text { (a } \left.\mathrm{a}_{1}\right) A B \text { is parallel to } D E ; & \left(\mathrm{a}_{2}\right) A E=B D \\
\left(\mathrm{~b}_{1}\right) B C \text { is parallel to } E F ; & \left(\mathrm{b}_{2}\right) B F=C E \\
\text { (c } \left.\mathrm{c}_{1}\right) C D \text { is parallel to } F A ; & \left(\mathrm{c}_{2}\right) C A=D F
\end{array}
$$
(a) Show that if all the six statements are true, then the hexagon is cyclic(i.e., it can be inscribed in a circle).
(b) Prove that, in fact, any five of these six statements also imply that the hexagon is cyclic.
|
(a) Suppose all the six statements are true. Then $A B D E, B C E F, C D F A$ are isosceles trapeziums; if $K, L, M, P, Q, R$ are the mid-points of $A B, B C$, $C D, D E, E F, F A$ respectively, then we see that $K P \perp A B, E D ; L Q \perp$ $B C, E F$ and $M R \perp C D, F A$.
If $A D, B E, C F$ themselves concur at a point $O$, then $O A=O B=O C=$ $O D=O E=O F$. ( $O$ is on the perpendicular bisector of each of the sides.) Hence $A, B, C, D, E, F$ are concyclic and lie on a circle with centre $O$. Otherwise these lines $A D, B E, C F$ form a triangle, say $X Y Z$. (See Fig.) Then $K X, M Y, Q Z$, when extended, become the internal angle bisectors of the triangle $X Y Z$ and hence concur at the incentre $O^{\prime}$ of $X Y Z$. As earlier $O^{\prime}$ lies on the perpendicular bisector of each of the sides. Hence $O^{\prime} A=O^{\prime} B$ $=O^{\prime} C=O^{\prime} D=O^{\prime} E=O^{\prime} F$, giving the concyclicity of $A, B, C, D, E, F$.
(b) Suppose $\left(\mathrm{a}_{1}\right),\left(\mathrm{a}_{2}\right),\left(\mathrm{b}_{1}\right),\left(\mathrm{b}_{2}\right)$ are true. Then we see that $A D=B E=$ $C F$. Assume that ( $\mathrm{c}_{1}$ ) is true. Then $C D$ is parallel to $A F$. It follows that triangles $Y C D$ and $Y F A$ are similar. This gives
$$
\frac{F Y}{A Y}=\frac{Y C}{Y D}=\frac{F Y+Y C}{A Y+Y D}=\frac{F C}{A D}=1
$$
We obtain $F Y=A Y$ and $Y C=Y D$. This forces that triangles $C Y A$ and $D Y F$ are congruent. In particular $A C=D F$ so that ( $\mathrm{c}_{2}$ ) is true. The conclusion follows from (a). Now assume that ( $\mathrm{c}_{2}$ ) is true; i.e., $A C=F D$. We have seen that $A D=B E=C F$. It follows that triangles $F D C$ and $A C D$ are congruent. In particular $\angle A D C=\angle F C D$. Similarly, we can show that $\angle C F A=\angle D A F$. We conclude that $C D$ is parallel to $A F$ giving $\left(\mathrm{c}_{1}\right.$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
For a convex hexagon $A B C D E F$ in which each pair of opposite sides is unequal, consider the following six statements:
$$
\begin{array}{ll}
\text { (a } \left.\mathrm{a}_{1}\right) A B \text { is parallel to } D E ; & \left(\mathrm{a}_{2}\right) A E=B D \\
\left(\mathrm{~b}_{1}\right) B C \text { is parallel to } E F ; & \left(\mathrm{b}_{2}\right) B F=C E \\
\text { (c } \left.\mathrm{c}_{1}\right) C D \text { is parallel to } F A ; & \left(\mathrm{c}_{2}\right) C A=D F
\end{array}
$$
(a) Show that if all the six statements are true, then the hexagon is cyclic(i.e., it can be inscribed in a circle).
(b) Prove that, in fact, any five of these six statements also imply that the hexagon is cyclic.
|
(a) Suppose all the six statements are true. Then $A B D E, B C E F, C D F A$ are isosceles trapeziums; if $K, L, M, P, Q, R$ are the mid-points of $A B, B C$, $C D, D E, E F, F A$ respectively, then we see that $K P \perp A B, E D ; L Q \perp$ $B C, E F$ and $M R \perp C D, F A$.

If $A D, B E, C F$ themselves concur at a point $O$, then $O A=O B=O C=$ $O D=O E=O F$. ( $O$ is on the perpendicular bisector of each of the sides.) Hence $A, B, C, D, E, F$ are concyclic and lie on a circle with centre $O$. Otherwise these lines $A D, B E, C F$ form a triangle, say $X Y Z$. (See Fig.) Then $K X, M Y, Q Z$, when extended, become the internal angle bisectors of the triangle $X Y Z$ and hence concur at the incentre $O^{\prime}$ of $X Y Z$. As earlier $O^{\prime}$ lies on the perpendicular bisector of each of the sides. Hence $O^{\prime} A=O^{\prime} B$ $=O^{\prime} C=O^{\prime} D=O^{\prime} E=O^{\prime} F$, giving the concyclicity of $A, B, C, D, E, F$.
(b) Suppose $\left(\mathrm{a}_{1}\right),\left(\mathrm{a}_{2}\right),\left(\mathrm{b}_{1}\right),\left(\mathrm{b}_{2}\right)$ are true. Then we see that $A D=B E=$ $C F$. Assume that ( $\mathrm{c}_{1}$ ) is true. Then $C D$ is parallel to $A F$. It follows that triangles $Y C D$ and $Y F A$ are similar. This gives
$$
\frac{F Y}{A Y}=\frac{Y C}{Y D}=\frac{F Y+Y C}{A Y+Y D}=\frac{F C}{A D}=1
$$
We obtain $F Y=A Y$ and $Y C=Y D$. This forces that triangles $C Y A$ and $D Y F$ are congruent. In particular $A C=D F$ so that ( $\mathrm{c}_{2}$ ) is true. The conclusion follows from (a). Now assume that ( $\mathrm{c}_{2}$ ) is true; i.e., $A C=F D$. We have seen that $A D=B E=C F$. It follows that triangles $F D C$ and $A C D$ are congruent. In particular $\angle A D C=\angle F C D$. Similarly, we can show that $\angle C F A=\angle D A F$. We conclude that $C D$ is parallel to $A F$ giving $\left(\mathrm{c}_{1}\right.$ ).
|
{
"resource_path": "INMO/segmented/en-2002.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
abe2cbe9-caa1-5b4b-829e-8f5da921efab
| 607,797
|
Let $x, y$ be positive reals such that $x+y=2$. Prove that
$$
x^{3} y^{3}\left(x^{3}+y^{3}\right) \leq 2
$$
|
We have from the AM-GM inequality, that
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=1
$$
Thus we obtain $0<x y \leq 1$. We write
$$
\begin{aligned}
x^{3} y^{3}\left(x^{3}+y^{3}\right) & =(x y)^{3}(x+y)\left(x^{2}-x y+y^{2}\right) \\
& =2(x y)^{3}\left((x+y)^{2}-3 x y\right) \\
& =2(x y)^{3}(4-3 x y)
\end{aligned}
$$
Thus we need to prove that
$$
(x y)^{3}(4-3 x y) \leq 1
$$
Putting $z=x y$, this inequality reduces to
$$
z^{3}(4-3 z) \leq 1
$$
for $0<z \leq 1$. We can prove this in different ways. We can put the inequality in the form
$$
3 z^{4}-4 z^{3}+1 \geq 0
$$
Here the expression in the LHS factors to $(z-1)^{2}\left(3 z^{2}+2 z+1\right)$ and $\left(3 z^{2}+2 z+1\right)$ is positive since its discriminant $D=-8<0$. Or applying the AM-GM inequality to the positive reals $4-3 z, z, z, z$, we obtain
$$
z^{3}(4-3 z) \leq\left(\frac{4-3 z+3 z}{4}\right)^{4} \leq 1
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ be positive reals such that $x+y=2$. Prove that
$$
x^{3} y^{3}\left(x^{3}+y^{3}\right) \leq 2
$$
|
We have from the AM-GM inequality, that
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=1
$$
Thus we obtain $0<x y \leq 1$. We write
$$
\begin{aligned}
x^{3} y^{3}\left(x^{3}+y^{3}\right) & =(x y)^{3}(x+y)\left(x^{2}-x y+y^{2}\right) \\
& =2(x y)^{3}\left((x+y)^{2}-3 x y\right) \\
& =2(x y)^{3}(4-3 x y)
\end{aligned}
$$
Thus we need to prove that
$$
(x y)^{3}(4-3 x y) \leq 1
$$
Putting $z=x y$, this inequality reduces to
$$
z^{3}(4-3 z) \leq 1
$$
for $0<z \leq 1$. We can prove this in different ways. We can put the inequality in the form
$$
3 z^{4}-4 z^{3}+1 \geq 0
$$
Here the expression in the LHS factors to $(z-1)^{2}\left(3 z^{2}+2 z+1\right)$ and $\left(3 z^{2}+2 z+1\right)$ is positive since its discriminant $D=-8<0$. Or applying the AM-GM inequality to the positive reals $4-3 z, z, z, z$, we obtain
$$
z^{3}(4-3 z) \leq\left(\frac{4-3 z+3 z}{4}\right)^{4} \leq 1
$$
|
{
"resource_path": "INMO/segmented/en-2002.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
6b5cc7f3-8998-5d7c-b6c6-a25476bc56c7
| 607,799
|
Consider an acute triangle $A B C$ and let $P$ be an interior point of $A B C$. Suppose the lines $B P$ and $C P$, when produced, meet $A C$ and $A B$ in $E$ and $F$ respectively. Let $D$ be the point where $A P$ intersects the line segment $E F$ and $K$ be the foot of perpendicular from $D$ on to $B C$. Show that $D K$ bisects $\angle E K F$.
|
Produce $A P$ to meet $B C$ in $Q$. Join $K E$ and $K F$. Draw perpendiculars from $F$ and $E$ on to $B C$ to meet it in $M$ and $L$ respectively. Let us denote $\angle B K F$ by $\alpha$ and $\angle C K E$ by $\beta$. We show that $\alpha=\beta$ by proving $\tan \alpha=\tan \beta$. This implies that $\angle D K F=\angle D K E$.(See Figure below.)
Since the cevians $A Q, B E$ and $C F$ concur, we may write
$$
\frac{B Q}{Q C}=\frac{z}{y}, \frac{C E}{E A}=\frac{x}{z}, \frac{A F}{F B}=\frac{y}{x}
$$
We observe that
$$
\frac{F D}{D E}=\frac{[A F D]}{[A E D]}=\frac{[P F D]}{[P E D]}=\frac{[A F P]}{[A E P]}
$$
However standard computations involving bases give
$$
[A F P]=\frac{y}{y+x}[A B P], \quad[A E P]=\frac{z}{z+x}[A C P]
$$
and
$$
[A B P]=\frac{z}{x+y+z}[A B C], \quad[A C P]=\frac{y}{x+y+z}[A B C]
$$
Thus we obtain
$$
\frac{F D}{D E}=\frac{x+z}{x+y}
$$
On the other hand
$$
\tan \alpha=\frac{F M}{K M}=\frac{F B \sin B}{K M}, \tan \beta=\frac{E L}{K L}=\frac{E C \sin C}{K L}
$$
Using $F B=\left(\frac{x}{x+y}\right) A B, E C=\left(\frac{x}{x+z}\right) A C$ and $A B \sin B=A C \sin C$, we obtain
$$
\begin{aligned}
\frac{\tan \alpha}{\tan \beta} & =\left(\frac{x+z}{x+y}\right)\left(\frac{K L}{K M}\right) \\
& =\left(\frac{x+z}{x+y}\right)\left(\frac{D E}{F D}\right) \\
& =\left(\frac{x+z}{x+y}\right)\left(\frac{x+y}{x+z}\right)=1
\end{aligned}
$$
We conclude that $\alpha=\beta$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider an acute triangle $A B C$ and let $P$ be an interior point of $A B C$. Suppose the lines $B P$ and $C P$, when produced, meet $A C$ and $A B$ in $E$ and $F$ respectively. Let $D$ be the point where $A P$ intersects the line segment $E F$ and $K$ be the foot of perpendicular from $D$ on to $B C$. Show that $D K$ bisects $\angle E K F$.
|
Produce $A P$ to meet $B C$ in $Q$. Join $K E$ and $K F$. Draw perpendiculars from $F$ and $E$ on to $B C$ to meet it in $M$ and $L$ respectively. Let us denote $\angle B K F$ by $\alpha$ and $\angle C K E$ by $\beta$. We show that $\alpha=\beta$ by proving $\tan \alpha=\tan \beta$. This implies that $\angle D K F=\angle D K E$.(See Figure below.)

Since the cevians $A Q, B E$ and $C F$ concur, we may write
$$
\frac{B Q}{Q C}=\frac{z}{y}, \frac{C E}{E A}=\frac{x}{z}, \frac{A F}{F B}=\frac{y}{x}
$$
We observe that
$$
\frac{F D}{D E}=\frac{[A F D]}{[A E D]}=\frac{[P F D]}{[P E D]}=\frac{[A F P]}{[A E P]}
$$
However standard computations involving bases give
$$
[A F P]=\frac{y}{y+x}[A B P], \quad[A E P]=\frac{z}{z+x}[A C P]
$$
and
$$
[A B P]=\frac{z}{x+y+z}[A B C], \quad[A C P]=\frac{y}{x+y+z}[A B C]
$$
Thus we obtain
$$
\frac{F D}{D E}=\frac{x+z}{x+y}
$$
On the other hand
$$
\tan \alpha=\frac{F M}{K M}=\frac{F B \sin B}{K M}, \tan \beta=\frac{E L}{K L}=\frac{E C \sin C}{K L}
$$
Using $F B=\left(\frac{x}{x+y}\right) A B, E C=\left(\frac{x}{x+z}\right) A C$ and $A B \sin B=A C \sin C$, we obtain
$$
\begin{aligned}
\frac{\tan \alpha}{\tan \beta} & =\left(\frac{x+z}{x+y}\right)\left(\frac{K L}{K M}\right) \\
& =\left(\frac{x+z}{x+y}\right)\left(\frac{D E}{F D}\right) \\
& =\left(\frac{x+z}{x+y}\right)\left(\frac{x+y}{x+z}\right)=1
\end{aligned}
$$
We conclude that $\alpha=\beta$.
|
{
"resource_path": "INMO/segmented/en-2003.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
f7c513a5-fc1f-5996-b973-222e07c3bf0b
| 607,803
|
Let $A B C$ be a triangle with sides $a, b, c$. Consider a triangle $A_{1} B_{1} C_{1}$ with sides equal to $a+\frac{b}{2}, b+\frac{c}{2}, c+\frac{a}{2}$. Show that
$$
\left[A_{1} B_{1} C_{1}\right] \geq \frac{9}{4}[A B C]
$$
where $[X Y Z]$ denotes the area of the triangle $X Y Z$.
|
It is easy to observe that there is a triangle with sides $a+\frac{b}{2}$, $b+\frac{c}{2}, c+\frac{a}{2}$. Using Heron's formula, we get
$$
16[A B C]^{2}=(a+b+c)(a+b-c)(b+c-a)(c+a-b)
$$
and
$$
16\left[A_{1} B_{1} C_{1}\right]^{2}=\frac{3}{16}(a+b+c)(-a+b+3 c)(-b+c+3 a)(-c+a+3 b)
$$
Since $a, b, c$ are the sides of a triangle, there are positive real numbers $p, q, r$ such that $a=q+r, b=r+p, c=p+q$. Using these relations we obtain
$$
\frac{[A B C]^{2}}{\left[A_{1} B_{1} C_{1}\right]^{2}}=\frac{16 p q r}{3(2 p+q)(2 q+r)(2 r+p)}
$$
Thus it is sufficient to prove that
$$
(2 p+q)(2 q+r)(2 r+p) \geq 27 p q r
$$
for positive real numbers $p, q, r$. Using AM-GM inequality, we get
$$
2 p+q \geq 3\left(p^{2} q\right)^{1 / 3}, 2 q+r \geq 3\left(q^{2} r\right)^{1 / 3}, 2 r+p \geq 3\left(r^{2} p\right)^{1 / 3}
$$
Multiplying these, we obtain the desired result. We also observe that equality holds if and only if $p=q=r$. This is equivalent to the statement that $A B C$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with sides $a, b, c$. Consider a triangle $A_{1} B_{1} C_{1}$ with sides equal to $a+\frac{b}{2}, b+\frac{c}{2}, c+\frac{a}{2}$. Show that
$$
\left[A_{1} B_{1} C_{1}\right] \geq \frac{9}{4}[A B C]
$$
where $[X Y Z]$ denotes the area of the triangle $X Y Z$.
|
It is easy to observe that there is a triangle with sides $a+\frac{b}{2}$, $b+\frac{c}{2}, c+\frac{a}{2}$. Using Heron's formula, we get
$$
16[A B C]^{2}=(a+b+c)(a+b-c)(b+c-a)(c+a-b)
$$
and
$$
16\left[A_{1} B_{1} C_{1}\right]^{2}=\frac{3}{16}(a+b+c)(-a+b+3 c)(-b+c+3 a)(-c+a+3 b)
$$
Since $a, b, c$ are the sides of a triangle, there are positive real numbers $p, q, r$ such that $a=q+r, b=r+p, c=p+q$. Using these relations we obtain
$$
\frac{[A B C]^{2}}{\left[A_{1} B_{1} C_{1}\right]^{2}}=\frac{16 p q r}{3(2 p+q)(2 q+r)(2 r+p)}
$$
Thus it is sufficient to prove that
$$
(2 p+q)(2 q+r)(2 r+p) \geq 27 p q r
$$
for positive real numbers $p, q, r$. Using AM-GM inequality, we get
$$
2 p+q \geq 3\left(p^{2} q\right)^{1 / 3}, 2 q+r \geq 3\left(q^{2} r\right)^{1 / 3}, 2 r+p \geq 3\left(r^{2} p\right)^{1 / 3}
$$
Multiplying these, we obtain the desired result. We also observe that equality holds if and only if $p=q=r$. This is equivalent to the statement that $A B C$ is equilateral.
|
{
"resource_path": "INMO/segmented/en-2003.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
fbce4af6-9d0a-554c-9a08-a8d38021134f
| 607,807
|
Consider a convex quadrilateral $A B C D$, in which $K, L, M, N$ are the midpoints of the sides $A B$, $B C, C D, D A$ respectively. Suppose
(a) $B D$ bisects $K M$ at $Q$;
(b) $Q A=Q B=Q C=Q D$; and
(c) $L K / L M=C D / C B$.
Prove that $A B C D$ is a square.
|
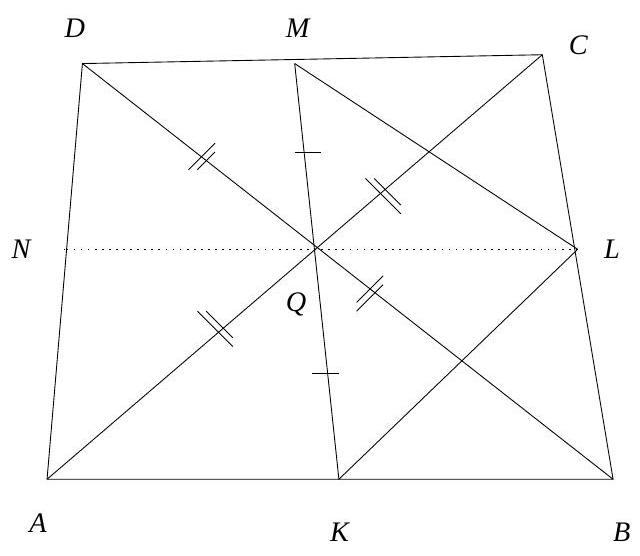
Fig. 1.
Observe that $K L M N$ is a paralellogram, $Q$ is the midpoint of $M K$ and hence $N L$ also passes through $Q$. Let $T$ be the point of intersection of $A C$ and $B D$; and let $S$ be the point of intersection of $B D$ and $M N$.
Consider the triangle $M N K$. Note that $S Q$ is parallel to $N K$ and $Q$ is the midpoint of $M K$. Hence $S$ is the mid-point of $M N$. Since $M N$ is parallel to $A C$, it follows that $T$ is the mid-point of $A C$. Now $Q$ is the circumcentre of $\triangle A B C$ and the median $B T$ passes through $Q$. Here there are two possibilities:
(i) $A B C$ is a right triangle with $\angle A B C=90^{\circ}$ and $T=Q$; and
(ii) $T \neq Q$ in which case $B T$ is perpendicular to $A C$.
Suppose $\angle A B C=90^{\circ}$ and $T=Q$. Observe that $Q$ is the circumcentre of the triangle $D C B$ and hence $\angle D C B=90^{\circ}$. Similarly $\angle D A B=90^{\circ}$. It follows that $\angle A D C=90^{\circ}$. and $A B C D$ is a rectangle. This implies that $K L M N$ is a rhombus. Hence $L K / L M=1$ and this gives $C D=C B$. Thus $A B C D$ is a square.
In the second case, observe that $B D$ is perpendicular to $A C, K L$ is parallel to $A C$ and $L M$ is parallel to $B D$. Hence it follows that $M L$ is perpendicular to $L K$. Similar reasoning shows that $K L M N$ is a rectangle.
Using $L K / L M=C D / C B$, we get that $C B D$ is similar to $L M K$. In particular, $\angle L M K=$ $\angle C B D=\alpha$ say. Since $L M$ is parallel to $D B$, we also get $\angle B Q K=\alpha$. Since $K L M N$ is a cyclic quadrilateral we also get $\angle L N K=\angle L M K=\alpha$. Using the fact that $B D$ is parallel to $N K$, we get $\angle L Q B=\angle L N K=\alpha$. Since $B D$ bisects $\angle C B A$, we also have $\angle K B Q=\alpha$. Thus
$$
Q K=K B=B L=L Q
$$
and $B L$ is parallel to $Q K$. This gives $Q M$ is parallel to $L C$ and
$$
Q M=Q L=B L=L C
$$
It follows that $Q L C M$ is a parallelogram. But $\angle L C M=90^{\circ}$. Hence $\angle M Q L=90^{\circ}$. This implies that $K L M N$ is a square. Also observe that $\angle L Q K=90^{\circ}$ and hence $\angle C B A=\angle L Q K=90^{\circ}$. This gives $\angle C D A=90^{\circ}$ and hence $A B C D$ is a rectangle. Since $B A=B C$, it follows that $A B C D$ is a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a convex quadrilateral $A B C D$, in which $K, L, M, N$ are the midpoints of the sides $A B$, $B C, C D, D A$ respectively. Suppose
(a) $B D$ bisects $K M$ at $Q$;
(b) $Q A=Q B=Q C=Q D$; and
(c) $L K / L M=C D / C B$.
Prove that $A B C D$ is a square.
|

Fig. 1.
Observe that $K L M N$ is a paralellogram, $Q$ is the midpoint of $M K$ and hence $N L$ also passes through $Q$. Let $T$ be the point of intersection of $A C$ and $B D$; and let $S$ be the point of intersection of $B D$ and $M N$.
Consider the triangle $M N K$. Note that $S Q$ is parallel to $N K$ and $Q$ is the midpoint of $M K$. Hence $S$ is the mid-point of $M N$. Since $M N$ is parallel to $A C$, it follows that $T$ is the mid-point of $A C$. Now $Q$ is the circumcentre of $\triangle A B C$ and the median $B T$ passes through $Q$. Here there are two possibilities:
(i) $A B C$ is a right triangle with $\angle A B C=90^{\circ}$ and $T=Q$; and
(ii) $T \neq Q$ in which case $B T$ is perpendicular to $A C$.
Suppose $\angle A B C=90^{\circ}$ and $T=Q$. Observe that $Q$ is the circumcentre of the triangle $D C B$ and hence $\angle D C B=90^{\circ}$. Similarly $\angle D A B=90^{\circ}$. It follows that $\angle A D C=90^{\circ}$. and $A B C D$ is a rectangle. This implies that $K L M N$ is a rhombus. Hence $L K / L M=1$ and this gives $C D=C B$. Thus $A B C D$ is a square.
In the second case, observe that $B D$ is perpendicular to $A C, K L$ is parallel to $A C$ and $L M$ is parallel to $B D$. Hence it follows that $M L$ is perpendicular to $L K$. Similar reasoning shows that $K L M N$ is a rectangle.
Using $L K / L M=C D / C B$, we get that $C B D$ is similar to $L M K$. In particular, $\angle L M K=$ $\angle C B D=\alpha$ say. Since $L M$ is parallel to $D B$, we also get $\angle B Q K=\alpha$. Since $K L M N$ is a cyclic quadrilateral we also get $\angle L N K=\angle L M K=\alpha$. Using the fact that $B D$ is parallel to $N K$, we get $\angle L Q B=\angle L N K=\alpha$. Since $B D$ bisects $\angle C B A$, we also have $\angle K B Q=\alpha$. Thus
$$
Q K=K B=B L=L Q
$$
and $B L$ is parallel to $Q K$. This gives $Q M$ is parallel to $L C$ and
$$
Q M=Q L=B L=L C
$$
It follows that $Q L C M$ is a parallelogram. But $\angle L C M=90^{\circ}$. Hence $\angle M Q L=90^{\circ}$. This implies that $K L M N$ is a square. Also observe that $\angle L Q K=90^{\circ}$ and hence $\angle C B A=\angle L Q K=90^{\circ}$. This gives $\angle C D A=90^{\circ}$ and hence $A B C D$ is a rectangle. Since $B A=B C$, it follows that $A B C D$ is a square.
|
{
"resource_path": "INMO/segmented/en-2004.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
fa59f4d3-93dc-5f6a-954d-442f38e8d0e7
| 607,809
|
Let $R$ denote the circumradius of a triangle $A B C ; a, b, c$ its sides $B C, C A, A B$; and $r_{a}, r_{b}, r_{c}$ its exradii opposite $A, B, C$. If $2 R \leq r_{a}$, prove that
(i) $a>b$ and $a>c$;
(ii) $2 R>r_{b}$ and $2 R>r_{c}$.
|
We know that $2 R=\frac{a b c}{2 \triangle}$ and $r_{a}=\frac{\triangle}{s-a}$, where $a, b, c$ are the sides of the triangle $A B C$, $s=\frac{a+b+c}{2}$ and $\triangle$ is the area of $A B C$. Thus the given condition $2 R \leq r_{a}$ translates to
$$
a b c \leq \frac{2 \triangle^{2}}{s-a}
$$
Putting $s-a=p, s-b=q, s-c=r$, we get $a=q+r, b=r+p, c=p+q$ and the condition now is
$$
p(p+q)(q+r)(r+p) \leq 2 \triangle^{2}
$$
But Heron's formula gives, $\triangle^{2}=s(s-a)(s-b)(s-c)=p q r(p+q+r)$. We obtain $(p+q)(q+$ $r)(r+p) \leq 2 q r(p+q+r)$. Expanding and effecting some cancellations, we get
$$
p^{2}(q+r)+p\left(q^{2}+r^{2}\right) \leq q r(q+r)
$$
Suppose $a \leq b$. This implies that $q+r \leq r+p$ and hence $q \leq p$. This implies that $q^{2} r \leq p^{2} r$ and $q r^{2} \leq p r^{2}$ giving $q r(q+r) \leq p^{2} r+p r^{2}<p^{2} r+p r^{2}+p^{2} q+p q^{2}=p^{2}(q+r)+p\left(q^{2}+r^{2}\right)$ which contradicts $(\star)$. Similarly, $a \leq c$ is also not possible. This proves (i).
Suppose $2 R \leq r_{b}$. As above this takes the form
$$
q^{2}(r+p)+q\left(r^{2}+p^{2}\right) \leq p r(p+r)
$$
Since $a>b$ and $a>c$, we have $q>p, r>p$. Thus $q^{2} r>p^{2} r$ and $q r^{2}>p r^{2}$. Hence
$$
q^{2}(r+p)+q\left(r^{2}+p^{2}\right)>q^{2} r+q r^{2}>p^{2} r+p r^{2}=p r(p+r)
$$
which contradicts ( $\star \star$ ). Hence $2 R>r_{b}$. Similarly, we can prove that $2 R>r_{c}$. This proves (ii)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $R$ denote the circumradius of a triangle $A B C ; a, b, c$ its sides $B C, C A, A B$; and $r_{a}, r_{b}, r_{c}$ its exradii opposite $A, B, C$. If $2 R \leq r_{a}$, prove that
(i) $a>b$ and $a>c$;
(ii) $2 R>r_{b}$ and $2 R>r_{c}$.
|
We know that $2 R=\frac{a b c}{2 \triangle}$ and $r_{a}=\frac{\triangle}{s-a}$, where $a, b, c$ are the sides of the triangle $A B C$, $s=\frac{a+b+c}{2}$ and $\triangle$ is the area of $A B C$. Thus the given condition $2 R \leq r_{a}$ translates to
$$
a b c \leq \frac{2 \triangle^{2}}{s-a}
$$
Putting $s-a=p, s-b=q, s-c=r$, we get $a=q+r, b=r+p, c=p+q$ and the condition now is
$$
p(p+q)(q+r)(r+p) \leq 2 \triangle^{2}
$$
But Heron's formula gives, $\triangle^{2}=s(s-a)(s-b)(s-c)=p q r(p+q+r)$. We obtain $(p+q)(q+$ $r)(r+p) \leq 2 q r(p+q+r)$. Expanding and effecting some cancellations, we get
$$
p^{2}(q+r)+p\left(q^{2}+r^{2}\right) \leq q r(q+r)
$$
Suppose $a \leq b$. This implies that $q+r \leq r+p$ and hence $q \leq p$. This implies that $q^{2} r \leq p^{2} r$ and $q r^{2} \leq p r^{2}$ giving $q r(q+r) \leq p^{2} r+p r^{2}<p^{2} r+p r^{2}+p^{2} q+p q^{2}=p^{2}(q+r)+p\left(q^{2}+r^{2}\right)$ which contradicts $(\star)$. Similarly, $a \leq c$ is also not possible. This proves (i).
Suppose $2 R \leq r_{b}$. As above this takes the form
$$
q^{2}(r+p)+q\left(r^{2}+p^{2}\right) \leq p r(p+r)
$$
Since $a>b$ and $a>c$, we have $q>p, r>p$. Thus $q^{2} r>p^{2} r$ and $q r^{2}>p r^{2}$. Hence
$$
q^{2}(r+p)+q\left(r^{2}+p^{2}\right)>q^{2} r+q r^{2}>p^{2} r+p r^{2}=p r(p+r)
$$
which contradicts ( $\star \star$ ). Hence $2 R>r_{b}$. Similarly, we can prove that $2 R>r_{c}$. This proves (ii)
|
{
"resource_path": "INMO/segmented/en-2004.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
c5a97e22-f6d9-5621-892f-d532eae191bd
| 607,812
|
Prove that the number of 5 -tuples of positive integers $(a, b, c, d, e)$ satisfying the equation
$$
a b c d e=5(b c d e+a c d e+a b d e+a b c e+a b c d)
$$
is an odd integer.
|
We write the equation in the form:
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}+\frac{1}{e}=\frac{1}{5}
$$
The number of five tuple ( $a, b, c, d, e)$ which satisfy the given relation and for which $a \neq b$ is even, because for if $(a, b, c, d, e)$ is a solution, then so is $(b, a, c, d, e)$ which is distinct from $(a, b, c, d, e)$. Similarly the number of five tuples which satisfy the equation and for which $c \neq d$ is also even. Hence it suffices to count only those five tuples $(a, b, c, d, e)$ for which $a=b, c=d$. Thus the equation reduces to
$$
\frac{2}{a}+\frac{2}{c}+\frac{1}{e}=\frac{1}{5}
$$
Here again the tuple ( $a, a, c, c, e)$ for which $a \neq c$ is even because we can associate different solution $(c, c, a, a, e)$ to this five tuple. Thus it suffices to consider the equation
$$
\frac{4}{a}+\frac{1}{e}=\frac{1}{5}
$$
and show that the number of pairs $(a, e)$ satisfying this equation is odd.
This reduces to
$$
a e=20 e+5 a
$$
or
$$
(a-20)(e-5)=100
$$
But observe that
$$
\begin{aligned}
& 100=1 \times 100=2 \times 50=4 \times 25=5 \times 20 \\
& \quad=10 \times 10=20 \times 5=25 \times 4=50 \times 2=100 \times 1
\end{aligned}
$$
Note that no factorisation of 100 as product of two negative numbers yield a positive tuple $(a, e)$. Hence we get these 9 solutions. This proves that the total number of five tuples $(a, b, c, d, e)$ satisfying the given equation is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that the number of 5 -tuples of positive integers $(a, b, c, d, e)$ satisfying the equation
$$
a b c d e=5(b c d e+a c d e+a b d e+a b c e+a b c d)
$$
is an odd integer.
|
We write the equation in the form:
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}+\frac{1}{e}=\frac{1}{5}
$$
The number of five tuple ( $a, b, c, d, e)$ which satisfy the given relation and for which $a \neq b$ is even, because for if $(a, b, c, d, e)$ is a solution, then so is $(b, a, c, d, e)$ which is distinct from $(a, b, c, d, e)$. Similarly the number of five tuples which satisfy the equation and for which $c \neq d$ is also even. Hence it suffices to count only those five tuples $(a, b, c, d, e)$ for which $a=b, c=d$. Thus the equation reduces to
$$
\frac{2}{a}+\frac{2}{c}+\frac{1}{e}=\frac{1}{5}
$$
Here again the tuple ( $a, a, c, c, e)$ for which $a \neq c$ is even because we can associate different solution $(c, c, a, a, e)$ to this five tuple. Thus it suffices to consider the equation
$$
\frac{4}{a}+\frac{1}{e}=\frac{1}{5}
$$
and show that the number of pairs $(a, e)$ satisfying this equation is odd.
This reduces to
$$
a e=20 e+5 a
$$
or
$$
(a-20)(e-5)=100
$$
But observe that
$$
\begin{aligned}
& 100=1 \times 100=2 \times 50=4 \times 25=5 \times 20 \\
& \quad=10 \times 10=20 \times 5=25 \times 4=50 \times 2=100 \times 1
\end{aligned}
$$
Note that no factorisation of 100 as product of two negative numbers yield a positive tuple $(a, e)$. Hence we get these 9 solutions. This proves that the total number of five tuples $(a, b, c, d, e)$ satisfying the given equation is odd.
|
{
"resource_path": "INMO/segmented/en-2004.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
796eb5a8-6931-501f-974a-fd998681371a
| 607,814
|
Let $p, q, r$ be positive real numbers, not all equal, such that some two of the equations
$$
p x^{2}+2 q x+r=0, \quad q x^{2}+2 r x+p=0, \quad r x^{2}+2 p x+q=0
$$
have a common root, say $\alpha$. Prove that
(a) $\alpha$ is real and negative; and
(b) the third equation has non-real roots.
|
Consider the discriminants of the three equations
$$
\begin{array}{r}
p x^{2}+q r+r=0 \\
q x^{2}+r x+p=0 \\
r x^{2}+p x+q=0
\end{array}
$$
Let us denote them by $D_{1}, D_{2}, D_{3}$ respectively. Then we have
$$
D_{1}=4\left(q^{2}-r p\right), D_{2}=4\left(r^{2}-p q\right), D_{3}=4\left(p^{2}-q r\right)
$$
We observe that
$$
\begin{aligned}
D_{1}+D_{2}+D_{3} & =4\left(p^{2}+q^{2}+r^{2}-p q-q r-r p\right) \\
& =2\left\{(p-q)^{2}+(q-r)^{2}+(r-p)^{2}\right\}>0
\end{aligned}
$$
since $p, q, r$ are not all equal. Hence at least one of $D_{1}, D_{2}, D_{3}$ must be positive. We may assume $D_{1}>0$.
Suppose $D_{2}<0$ and $D_{3}<0$. In this case both the equations (2) and (3) have only non-real roots and equation (1) has only real roots. Hence the common root $\alpha$ must be between (2) and (3). But then $\bar{\alpha}$ is the other root of both (2) and (3). Hence it follows that (2) and (3) have same set of roots. This implies that
$$
\frac{q}{r}=\frac{r}{p}=\frac{p}{q}
$$
Thus $p=q=r$ contradicting the given condition. Hence both $D_{2}$ and $D_{3}$ cannot be negative. We may assume $D_{2} \geq 0$. Thus we have
$$
q^{2}-r p>0, r^{2}-p q \geq 0
$$
These two give
$$
q^{2} r^{2}>p^{2} q r
$$
since $p, q, r$ are all positive. Hence we obtain $q r>p^{2}$ or $D_{3}<0$. We conclude that the common root must be between equations (1) and (2).
Thus
$$
\begin{aligned}
& p \alpha^{2}+q \alpha+r=0 \\
& q \alpha^{2}+r \alpha+p=0
\end{aligned}
$$
Eliminating $\alpha^{2}$, we obtain
$$
2\left(q^{2}-p r\right) \alpha=p^{2}-q r
$$
Since $q^{2}-p r>0$ and $p^{2}-q r<0$, we conclude that $\alpha<0$.
The condition $p^{2}-q r<0$ implies that the equation (3) has only non-real roots.
Alternately one can argue as follows. Suppose $\alpha$ is a common root of two equations, say, (1) and (2). If $\alpha$ is non-real, then $\bar{\alpha}$ is also a root of both (1) and (2). Hence The coefficients of (1) and (2) are proportional. This forces $p=q=r$, a contradiction. Hence the common root between any two equations cannot be non-real. Looking at the coefficients, we conclude that the common root $\alpha$ must be negative. If (1) and (2) have common root $\alpha$, then $q^{2} \geq r p$ and $r^{2} \geq p q$. Here at least one inequality is strict for $q^{2}=p r$ and $r^{2}=p q$ forces $p=q=r$. Hence $q^{2} r^{2}>p^{2} q r$. This gives $p^{2}<q r$ and hence (3) has nonreal roots.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p, q, r$ be positive real numbers, not all equal, such that some two of the equations
$$
p x^{2}+2 q x+r=0, \quad q x^{2}+2 r x+p=0, \quad r x^{2}+2 p x+q=0
$$
have a common root, say $\alpha$. Prove that
(a) $\alpha$ is real and negative; and
(b) the third equation has non-real roots.
|
Consider the discriminants of the three equations
$$
\begin{array}{r}
p x^{2}+q r+r=0 \\
q x^{2}+r x+p=0 \\
r x^{2}+p x+q=0
\end{array}
$$
Let us denote them by $D_{1}, D_{2}, D_{3}$ respectively. Then we have
$$
D_{1}=4\left(q^{2}-r p\right), D_{2}=4\left(r^{2}-p q\right), D_{3}=4\left(p^{2}-q r\right)
$$
We observe that
$$
\begin{aligned}
D_{1}+D_{2}+D_{3} & =4\left(p^{2}+q^{2}+r^{2}-p q-q r-r p\right) \\
& =2\left\{(p-q)^{2}+(q-r)^{2}+(r-p)^{2}\right\}>0
\end{aligned}
$$
since $p, q, r$ are not all equal. Hence at least one of $D_{1}, D_{2}, D_{3}$ must be positive. We may assume $D_{1}>0$.
Suppose $D_{2}<0$ and $D_{3}<0$. In this case both the equations (2) and (3) have only non-real roots and equation (1) has only real roots. Hence the common root $\alpha$ must be between (2) and (3). But then $\bar{\alpha}$ is the other root of both (2) and (3). Hence it follows that (2) and (3) have same set of roots. This implies that
$$
\frac{q}{r}=\frac{r}{p}=\frac{p}{q}
$$
Thus $p=q=r$ contradicting the given condition. Hence both $D_{2}$ and $D_{3}$ cannot be negative. We may assume $D_{2} \geq 0$. Thus we have
$$
q^{2}-r p>0, r^{2}-p q \geq 0
$$
These two give
$$
q^{2} r^{2}>p^{2} q r
$$
since $p, q, r$ are all positive. Hence we obtain $q r>p^{2}$ or $D_{3}<0$. We conclude that the common root must be between equations (1) and (2).
Thus
$$
\begin{aligned}
& p \alpha^{2}+q \alpha+r=0 \\
& q \alpha^{2}+r \alpha+p=0
\end{aligned}
$$
Eliminating $\alpha^{2}$, we obtain
$$
2\left(q^{2}-p r\right) \alpha=p^{2}-q r
$$
Since $q^{2}-p r>0$ and $p^{2}-q r<0$, we conclude that $\alpha<0$.
The condition $p^{2}-q r<0$ implies that the equation (3) has only non-real roots.
Alternately one can argue as follows. Suppose $\alpha$ is a common root of two equations, say, (1) and (2). If $\alpha$ is non-real, then $\bar{\alpha}$ is also a root of both (1) and (2). Hence The coefficients of (1) and (2) are proportional. This forces $p=q=r$, a contradiction. Hence the common root between any two equations cannot be non-real. Looking at the coefficients, we conclude that the common root $\alpha$ must be negative. If (1) and (2) have common root $\alpha$, then $q^{2} \geq r p$ and $r^{2} \geq p q$. Here at least one inequality is strict for $q^{2}=p r$ and $r^{2}=p q$ forces $p=q=r$. Hence $q^{2} r^{2}>p^{2} q r$. This gives $p^{2}<q r$ and hence (3) has nonreal roots.
|
{
"resource_path": "INMO/segmented/en-2005.jsonl",
"problem_match": "\n3.",
"solution_match": "## Solution:"
}
|
c8548108-a0b0-5fdc-bbbe-14d1088de691
| 607,817
|
Let $x_{1}$ be a given positive integer. A sequence $\left\langle x_{n}\right\rangle_{n=1}^{\infty}=\left\langle x_{1}, x_{2}, x_{3}, \cdots\right\rangle$ of positive integers is such that $x_{n}$, for $n \geq 2$, is obtained from $x_{n-1}$ by adding some nonzero digit of $x_{n-1}$. Prove that
(a) the sequence has an even number;
(b) the sequence has infinitely many even numbers.
|
(a) Let us assume that there are no even numbers in the sequence. This means that $x_{n+1}$ is obtained from $x_{n}$, by adding a nonzero even digit of $x_{n}$ to $x_{n}$, for each $n \geq 1$.
Let $E$ be the left most even digit in $x_{1}$ which may be taken in the form
$$
x_{1}=O_{1} O_{2} \cdots O_{k} E D_{1} D_{2} \cdots D_{l}
$$
where $O_{1}, O_{2}, \ldots, O_{k}$ are odd digits $(k \geq 0) ; D_{1}, D_{2}, \ldots, D_{l-1}$ are even or odd; and $D_{l}$ odd, $l \geq 1$.
Since each time we are adding at least 2 to a term of the sequence to get the next term, at some stage, we will have a term of the form
$$
x_{r}=O_{1} O_{2} \cdots O_{k} E 999 \cdots 9 F
$$
where $F=3,5,7$ or 9 . Now we are forced to add $E$ to $x_{r}$ to get $x_{r+1}$, as it is the only even digit available. After at most four steps of addition, we see that some next term is of the form
$$
x_{s}=O_{1} O_{2} \cdots O_{k} G 000 \cdots M
$$
where $G$ replaces $E$ of $x_{r}, G=E+1, M=1,3,5$, or 7 . But $x_{s}$ has no nonzero even digit contradicting our assumption. Hence the sequence has some even number as its term.
(b) If there are only finitely many even terms and $x_{t}$ is the last term, then the sequence $\left\langle x_{n}\right\rangle_{n=t+1}^{\infty}=$ $\left\langle x_{t+1}, x_{t+2}, \ldots\right\rangle$ is obtained in a similar manner and hence must have an even term by (a), a contradiction. Thus $\left\langle x_{n}\right\rangle_{n=1}^{\infty}$, has infinitely many even terms.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x_{1}$ be a given positive integer. A sequence $\left\langle x_{n}\right\rangle_{n=1}^{\infty}=\left\langle x_{1}, x_{2}, x_{3}, \cdots\right\rangle$ of positive integers is such that $x_{n}$, for $n \geq 2$, is obtained from $x_{n-1}$ by adding some nonzero digit of $x_{n-1}$. Prove that
(a) the sequence has an even number;
(b) the sequence has infinitely many even numbers.
|
(a) Let us assume that there are no even numbers in the sequence. This means that $x_{n+1}$ is obtained from $x_{n}$, by adding a nonzero even digit of $x_{n}$ to $x_{n}$, for each $n \geq 1$.
Let $E$ be the left most even digit in $x_{1}$ which may be taken in the form
$$
x_{1}=O_{1} O_{2} \cdots O_{k} E D_{1} D_{2} \cdots D_{l}
$$
where $O_{1}, O_{2}, \ldots, O_{k}$ are odd digits $(k \geq 0) ; D_{1}, D_{2}, \ldots, D_{l-1}$ are even or odd; and $D_{l}$ odd, $l \geq 1$.
Since each time we are adding at least 2 to a term of the sequence to get the next term, at some stage, we will have a term of the form
$$
x_{r}=O_{1} O_{2} \cdots O_{k} E 999 \cdots 9 F
$$
where $F=3,5,7$ or 9 . Now we are forced to add $E$ to $x_{r}$ to get $x_{r+1}$, as it is the only even digit available. After at most four steps of addition, we see that some next term is of the form
$$
x_{s}=O_{1} O_{2} \cdots O_{k} G 000 \cdots M
$$
where $G$ replaces $E$ of $x_{r}, G=E+1, M=1,3,5$, or 7 . But $x_{s}$ has no nonzero even digit contradicting our assumption. Hence the sequence has some even number as its term.
(b) If there are only finitely many even terms and $x_{t}$ is the last term, then the sequence $\left\langle x_{n}\right\rangle_{n=t+1}^{\infty}=$ $\left\langle x_{t+1}, x_{t+2}, \ldots\right\rangle$ is obtained in a similar manner and hence must have an even term by (a), a contradiction. Thus $\left\langle x_{n}\right\rangle_{n=1}^{\infty}$, has infinitely many even terms.
|
{
"resource_path": "INMO/segmented/en-2005.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
ac77e6f5-cbda-57de-b1b1-b75d93263a68
| 607,819
|
In a non-equilateral triangle $A B C$, the sides $a, b, c$ form an arithmetic progression. Let $I$ and $O$ denote the incentre and circumcentre of the triangle respectively.
(i) Prove that $I O$ is perpendicular to $B I$.
(ii) Suppose $B I$ extended meets $A C$ in $K$, and $D, E$ are the midpoints of $B C, B A$ respectively. Prove that $I$ is the circumcentre of triangle $D K E$.
|
(i) Extend $B I$ to meet the circumcircle in $F$. Then we know that $F A=F I=F C$. (See Figure)
Let $B I: I F=\lambda: \mu$. Applying Stewart's theorem to triangle $B A F$, we get
$$
\lambda A F^{2}+\mu A B^{2}=(\lambda+\mu)\left(A I^{2}+B I \cdot I F\right)
$$
Similarly, Stewart's theorem to triangle $B C F$ gives
$$
\lambda C F^{2}+\mu B C^{2}=(\lambda+\mu)\left(C I^{2}+B I \cdot I F\right)
$$
Since $C F=A F$, subtraction gives
$$
\mu\left(A B^{2}-B C^{2}\right)=(\lambda+\mu)\left(A I^{2}-C I^{2}\right)
$$
Using the standard notations $A B=c, B C=a, C A=b$ and $s=(a+b+c) / 2$, we get $A I^{2}=r^{2}+(s-a)^{2}$ and $C I^{2}=r^{2}+(s-c)^{2}$ where $r$ is the in-radius of $A B C$. Thus
$$
\mu\left(c^{2}-a^{2}\right)=(\lambda+\mu)\left((s-a)^{2}-(s-c)^{2}\right)=(\lambda+\mu)(c-a) b
$$
It follows that either $c=a$ or $\mu(c+a)=(\lambda+\mu) b$. But $c=a$ implies that $a=b=c$ since $a, b, c$ are in arithmetic progression. However, we have taken a non-equilateral triangle $A B C$. Thus $c \neq a$ and we have $\mu(c+a)=(\lambda+\mu) b$. But $c+a=2 b$ and we obtain
$2 b \mu=(\lambda+\mu) b$. We conclude that $\lambda=\mu$. This in turn tells that $I$ is the mid-point of $B F$. Since $O F=O B$, we conclude that $O I$ is perpendicular to $B F$.
## Alternatively
Applying Ptolemy's theorem to the cyclic quadrilateral $A B C F$, we get
$$
A B \cdot C F+A F \cdot B C=B F \cdot C A
$$
Since $C F=A F$, we get $C F(c+a)=B F \cdot b=B F(c+a) / 2$. This gives $B F=2 C F=2 I F$. Hence $I$ is the mid-point of $B F$ and as earlier we conclude that $O I$ is perpendicular to $B F$.
## Alternatively
Join $B O$. We have to prove that $\angle B I O=90^{\circ}$, which is equivalent to $B I^{2}+I O^{2}=B O^{2}$. Draw $I L$ perpendicular to $A B$. Let $R$ denote the circumradius of $A B C$ and let $\triangle$ denote its area. Observe that $B O=R, I O^{2}=R^{2}-2 R r$,
$$
B I=\frac{B L}{\cos (B / 2)}=(s-b) \sqrt{\frac{c a}{s(s-b)}}
$$
Thus we obtain
$$
B I^{2}=a c(s-b) / s=\frac{a c}{3}
$$
since $a, b, c$ are in arithmetic progression. Thus we need to prove that
$$
\frac{a c}{3}+R^{2}-2 R r=R^{2}
$$
This reduces to proving $2 R r=a c / 3$. But
$$
2 R r=2 \cdot \frac{a b c}{4 \Delta} \cdot \frac{\Delta}{s}=\frac{a b c}{2 s}=\frac{a b c}{a+b+c}=\frac{a c}{3}
$$
using $a+c=2 b$. This proves the claim.
(ii) Join $I D$. Note that $\angle B I O=\angle B D O=90^{\circ}$. Hence $B, D, I, O$ are concyclic and hence $\angle B I D=\angle B O D=A$. Since $\angle D B I=\angle K B A=B / 2$, it follows that triangles $B A K$ and $B I D$ are similar. This gives
$$
\frac{B A}{B I}=\frac{B K}{B D}=\frac{A K}{I D}
$$
However, we have seen earlier that $B I=a c / 3$. Moreover $A K=b c /(a+c)$. Thus we obtain
$$
B K=\frac{B A \cdot B D}{B I}=\frac{1}{2} \sqrt{3 a c}, \quad I D=\frac{A K \cdot B I}{B A}=\frac{1}{2} \sqrt{\frac{a c}{3}} .
$$
By symmetry, we must have $I E=\frac{1}{2} \sqrt{\frac{a c}{3}}$. Finally
$$
I K=\frac{b}{a+b+c} \cdot B K=\frac{1}{3} B K=\frac{1}{2} \sqrt{\frac{a c}{3}}
$$
Thus $I D=I E=I K$ and $I$ is the circumcentre of $D K E$.
## Alternatively
Observe that $A K=b c /(a+c)=c / 2=A E$. Since $A I$ bisects angle $A$, we see that $A I E$ is congruent to $A I K$. This gives $I E=I K$. Similarly $C I D$ is congruent to $C I K$ giving $I D=I K$. We conclude that $I D=I K=I E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a non-equilateral triangle $A B C$, the sides $a, b, c$ form an arithmetic progression. Let $I$ and $O$ denote the incentre and circumcentre of the triangle respectively.
(i) Prove that $I O$ is perpendicular to $B I$.
(ii) Suppose $B I$ extended meets $A C$ in $K$, and $D, E$ are the midpoints of $B C, B A$ respectively. Prove that $I$ is the circumcentre of triangle $D K E$.
|
(i) Extend $B I$ to meet the circumcircle in $F$. Then we know that $F A=F I=F C$. (See Figure)

Let $B I: I F=\lambda: \mu$. Applying Stewart's theorem to triangle $B A F$, we get
$$
\lambda A F^{2}+\mu A B^{2}=(\lambda+\mu)\left(A I^{2}+B I \cdot I F\right)
$$
Similarly, Stewart's theorem to triangle $B C F$ gives
$$
\lambda C F^{2}+\mu B C^{2}=(\lambda+\mu)\left(C I^{2}+B I \cdot I F\right)
$$
Since $C F=A F$, subtraction gives
$$
\mu\left(A B^{2}-B C^{2}\right)=(\lambda+\mu)\left(A I^{2}-C I^{2}\right)
$$
Using the standard notations $A B=c, B C=a, C A=b$ and $s=(a+b+c) / 2$, we get $A I^{2}=r^{2}+(s-a)^{2}$ and $C I^{2}=r^{2}+(s-c)^{2}$ where $r$ is the in-radius of $A B C$. Thus
$$
\mu\left(c^{2}-a^{2}\right)=(\lambda+\mu)\left((s-a)^{2}-(s-c)^{2}\right)=(\lambda+\mu)(c-a) b
$$
It follows that either $c=a$ or $\mu(c+a)=(\lambda+\mu) b$. But $c=a$ implies that $a=b=c$ since $a, b, c$ are in arithmetic progression. However, we have taken a non-equilateral triangle $A B C$. Thus $c \neq a$ and we have $\mu(c+a)=(\lambda+\mu) b$. But $c+a=2 b$ and we obtain
$2 b \mu=(\lambda+\mu) b$. We conclude that $\lambda=\mu$. This in turn tells that $I$ is the mid-point of $B F$. Since $O F=O B$, we conclude that $O I$ is perpendicular to $B F$.
## Alternatively
Applying Ptolemy's theorem to the cyclic quadrilateral $A B C F$, we get
$$
A B \cdot C F+A F \cdot B C=B F \cdot C A
$$
Since $C F=A F$, we get $C F(c+a)=B F \cdot b=B F(c+a) / 2$. This gives $B F=2 C F=2 I F$. Hence $I$ is the mid-point of $B F$ and as earlier we conclude that $O I$ is perpendicular to $B F$.
## Alternatively
Join $B O$. We have to prove that $\angle B I O=90^{\circ}$, which is equivalent to $B I^{2}+I O^{2}=B O^{2}$. Draw $I L$ perpendicular to $A B$. Let $R$ denote the circumradius of $A B C$ and let $\triangle$ denote its area. Observe that $B O=R, I O^{2}=R^{2}-2 R r$,
$$
B I=\frac{B L}{\cos (B / 2)}=(s-b) \sqrt{\frac{c a}{s(s-b)}}
$$
Thus we obtain
$$
B I^{2}=a c(s-b) / s=\frac{a c}{3}
$$
since $a, b, c$ are in arithmetic progression. Thus we need to prove that
$$
\frac{a c}{3}+R^{2}-2 R r=R^{2}
$$
This reduces to proving $2 R r=a c / 3$. But
$$
2 R r=2 \cdot \frac{a b c}{4 \Delta} \cdot \frac{\Delta}{s}=\frac{a b c}{2 s}=\frac{a b c}{a+b+c}=\frac{a c}{3}
$$
using $a+c=2 b$. This proves the claim.
(ii) Join $I D$. Note that $\angle B I O=\angle B D O=90^{\circ}$. Hence $B, D, I, O$ are concyclic and hence $\angle B I D=\angle B O D=A$. Since $\angle D B I=\angle K B A=B / 2$, it follows that triangles $B A K$ and $B I D$ are similar. This gives
$$
\frac{B A}{B I}=\frac{B K}{B D}=\frac{A K}{I D}
$$
However, we have seen earlier that $B I=a c / 3$. Moreover $A K=b c /(a+c)$. Thus we obtain
$$
B K=\frac{B A \cdot B D}{B I}=\frac{1}{2} \sqrt{3 a c}, \quad I D=\frac{A K \cdot B I}{B A}=\frac{1}{2} \sqrt{\frac{a c}{3}} .
$$
By symmetry, we must have $I E=\frac{1}{2} \sqrt{\frac{a c}{3}}$. Finally
$$
I K=\frac{b}{a+b+c} \cdot B K=\frac{1}{3} B K=\frac{1}{2} \sqrt{\frac{a c}{3}}
$$
Thus $I D=I E=I K$ and $I$ is the circumcentre of $D K E$.
## Alternatively
Observe that $A K=b c /(a+c)=c / 2=A E$. Since $A I$ bisects angle $A$, we see that $A I E$ is congruent to $A I K$. This gives $I E=I K$. Similarly $C I D$ is congruent to $C I K$ giving $I D=I K$. We conclude that $I D=I K=I E$.
|
{
"resource_path": "INMO/segmented/en-2006.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
96013b49-6ff3-50ac-930f-1ce10e55ee55
| 607,821
|
Prove that for every positive integer $n$ there exists a unique ordered pair $(a, b)$ of positive integers such that
$$
n=\frac{1}{2}(a+b-1)(a+b-2)+a
$$
|
We have to prove that $f: \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$ defined by
$$
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a, \quad \forall a, b \in \mathbb{N}
$$
is a bijection. (Note that the right side is a natural number.) To this end define
$$
T(n)=\frac{n(n+1)}{2}, \quad n \in \mathbb{N} \cup\{0\}
$$
An idea of the proof can be obtained by looking at the following table of values of $f(a, b)$ for some small values of $a, b$.
We observe that the $n$-th diagonal runs from $(1, n)$-th position to $(n, 1)$-th position and the entries are $n$ consecutive integers; the first entry in the $n$-th diagonal is one more than the last entry of the $(n-1)$-th diagonal. For example the first entry in 5 -th diagonal is 11 which is one more than the last entry of 4 -th diagonal which is 10 . Observe that 5 -th diagonal starts from 11 and ends with 15 which accounts for 5 consecutive natural numbers. Thus we see that $f(n-1,1)+1=f(1, n)$. We also observe that the first $n$ diagonals exhaust all the natural numbers from 1 to $T(n)$. (Thus a kind of visual bijection is already there. We formally prove the property.)
We first observe that
$$
f(a, b)-T(a+b-2)=a>0
$$
and
$$
T(a+b-1)-f(a, b)=\frac{(a+b-1)(a+b)}{2}-\frac{(a+b-1)(a+b-2)}{2}-a=b-1 \geq 0
$$
Thus we have
$$
T(a+b-2)<f(a, b)=\frac{(a+b-1)(a+b-2)}{2}+a \leq T(a+b-1)
$$
Suppose $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$. Then the previous observation shows that
$$
\begin{aligned}
& T\left(a_{1}+b_{1}-2\right)<f\left(a_{1}, b_{1}\right) \leq T\left(a_{1}+b_{1}-1\right) \\
& T\left(a_{2}+b_{2}-2\right)<f\left(a_{2}, b_{2}\right) \leq T\left(a_{2}+b_{2}-1\right)
\end{aligned}
$$
Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, it follows that $a_{1}+b_{1}=a_{2}+b_{2}$. But then the relation $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$ implies that $a_{1}=a_{2}$ and $b_{1}=b_{2}$. Hence $f$ is one-one.
Let $n$ be any natural number. Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, we can find a natural number $k$ such that
$$
T(k-1)<n \leq T(k)
$$
Equivalently,
$$
\frac{(k-1) k}{2}<n \leq \frac{k(k+1)}{2}
$$
Now set $a=n-\frac{k(k-1)}{2}$ and $b=k-a+1$. Observe that $a>0$. Now (1) shows that
$$
a=n-\frac{k(k-1)}{2} \leq \frac{k(k+1)}{2}-\frac{k(k-1)}{2}=k
$$
Hence $b=k-a+1 \geq 1$. Thus $a$ and $b$ are both positive integers and
$$
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a=\frac{k(k-1)}{2}+a=n
$$
This shows that every natural number is in the range of $f$. Thus $f$ is also onto. We conclude that $f$ is a bijection.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every positive integer $n$ there exists a unique ordered pair $(a, b)$ of positive integers such that
$$
n=\frac{1}{2}(a+b-1)(a+b-2)+a
$$
|
We have to prove that $f: \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$ defined by
$$
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a, \quad \forall a, b \in \mathbb{N}
$$
is a bijection. (Note that the right side is a natural number.) To this end define
$$
T(n)=\frac{n(n+1)}{2}, \quad n \in \mathbb{N} \cup\{0\}
$$
An idea of the proof can be obtained by looking at the following table of values of $f(a, b)$ for some small values of $a, b$.

We observe that the $n$-th diagonal runs from $(1, n)$-th position to $(n, 1)$-th position and the entries are $n$ consecutive integers; the first entry in the $n$-th diagonal is one more than the last entry of the $(n-1)$-th diagonal. For example the first entry in 5 -th diagonal is 11 which is one more than the last entry of 4 -th diagonal which is 10 . Observe that 5 -th diagonal starts from 11 and ends with 15 which accounts for 5 consecutive natural numbers. Thus we see that $f(n-1,1)+1=f(1, n)$. We also observe that the first $n$ diagonals exhaust all the natural numbers from 1 to $T(n)$. (Thus a kind of visual bijection is already there. We formally prove the property.)
We first observe that
$$
f(a, b)-T(a+b-2)=a>0
$$
and
$$
T(a+b-1)-f(a, b)=\frac{(a+b-1)(a+b)}{2}-\frac{(a+b-1)(a+b-2)}{2}-a=b-1 \geq 0
$$
Thus we have
$$
T(a+b-2)<f(a, b)=\frac{(a+b-1)(a+b-2)}{2}+a \leq T(a+b-1)
$$
Suppose $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$. Then the previous observation shows that
$$
\begin{aligned}
& T\left(a_{1}+b_{1}-2\right)<f\left(a_{1}, b_{1}\right) \leq T\left(a_{1}+b_{1}-1\right) \\
& T\left(a_{2}+b_{2}-2\right)<f\left(a_{2}, b_{2}\right) \leq T\left(a_{2}+b_{2}-1\right)
\end{aligned}
$$
Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, it follows that $a_{1}+b_{1}=a_{2}+b_{2}$. But then the relation $f\left(a_{1}, b_{1}\right)=f\left(a_{2}, b_{2}\right)$ implies that $a_{1}=a_{2}$ and $b_{1}=b_{2}$. Hence $f$ is one-one.
Let $n$ be any natural number. Since the sequence $\langle T(n)\rangle_{n=0}^{\infty}$ is strictly increasing, we can find a natural number $k$ such that
$$
T(k-1)<n \leq T(k)
$$
Equivalently,
$$
\frac{(k-1) k}{2}<n \leq \frac{k(k+1)}{2}
$$
Now set $a=n-\frac{k(k-1)}{2}$ and $b=k-a+1$. Observe that $a>0$. Now (1) shows that
$$
a=n-\frac{k(k-1)}{2} \leq \frac{k(k+1)}{2}-\frac{k(k-1)}{2}=k
$$
Hence $b=k-a+1 \geq 1$. Thus $a$ and $b$ are both positive integers and
$$
f(a, b)=\frac{1}{2}(a+b-1)(a+b-2)+a=\frac{k(k-1)}{2}+a=n
$$
This shows that every natural number is in the range of $f$. Thus $f$ is also onto. We conclude that $f$ is a bijection.
|
{
"resource_path": "INMO/segmented/en-2006.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
d4f205b8-eab7-5e04-ab34-dc8ccbf9808e
| 607,822
|
Some 46 squares are randomly chosen from a $9 \times 9$ chess board and are coloured red. Show that there exists a $2 \times 2$ block of 4 squares of which at least three are coloured red.
|
Consider a partition of $9 \times 9$ chess board using sixteen $2 \times 2$ block of 4 squares
| 1 | 2 | | |
| :---: | :---: | :---: | :---: |
| 7 | 6 | 5 | |
| 8 | 9 | | 10 |
| | | | |
| 10 | | | |
| | 1 | 1 | 13 |
each and remaining seventeen single squares as shown in the figure below.
If any one of these 16 big squares contain 3 red squares then we are done. On the contrary, each may contain at most 2 red squares and these account for at most $16 \cdot 2=32$ red squares. Then there are 17 single squares connected in zig-zag fashion. It looks as follows:
We split this again in to several mirror images of L-shaped figures as shown above. There are four such forks. If all the five unit squares of the first fork are red, then we can get a $2 \times 2$ square having three red squares. Hence there can be at most four unit squares having red colour. Similarly, there can be at most three red squares from each of the remaining three forks. Together we get $4+3 \cdot 3=13$ red squares. These together with 32 from the big squares account for only 45 red squares. But we know that 46 squares have red colour. The conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Some 46 squares are randomly chosen from a $9 \times 9$ chess board and are coloured red. Show that there exists a $2 \times 2$ block of 4 squares of which at least three are coloured red.
|
Consider a partition of $9 \times 9$ chess board using sixteen $2 \times 2$ block of 4 squares
| 1 | 2 | | |
| :---: | :---: | :---: | :---: |
| 7 | 6 | 5 | |
| 8 | 9 | | 10 |
| | | | |
| 10 | | | |
| | 1 | 1 | 13 |
each and remaining seventeen single squares as shown in the figure below.
If any one of these 16 big squares contain 3 red squares then we are done. On the contrary, each may contain at most 2 red squares and these account for at most $16 \cdot 2=32$ red squares. Then there are 17 single squares connected in zig-zag fashion. It looks as follows:

We split this again in to several mirror images of L-shaped figures as shown above. There are four such forks. If all the five unit squares of the first fork are red, then we can get a $2 \times 2$ square having three red squares. Hence there can be at most four unit squares having red colour. Similarly, there can be at most three red squares from each of the remaining three forks. Together we get $4+3 \cdot 3=13$ red squares. These together with 32 from the big squares account for only 45 red squares. But we know that 46 squares have red colour. The conclusion follows.
|
{
"resource_path": "INMO/segmented/en-2006.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
6784506d-6205-5653-9706-2faff429f98f
| 607,824
|
In a cyclic quadrilateral $A B C D, A B=a, B C=b, C D=c, \angle A B C=120^{\circ}$, and $\angle A B D=$ $30^{\circ}$. Prove that
(i) $c \geq a+b$;
(ii) $|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}$.
|
Applying cosine rule to triangle $A B C$, we get
$$
A C^{2}=a^{2}+b^{2}-2 a b \cos 120^{\circ}=a^{2}+b^{2}+a b
$$
Observe that $\angle D A C=\angle D B C=120^{\circ}-30^{\circ}=90^{\circ}$. Thus we get
$$
c^{2}=\frac{A C^{2}}{\cos ^{2} 30^{\circ}}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)
$$
So
$$
c^{2}-(a+b)^{2}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)-\left(a^{2}+b^{2}+2 a b\right)=\frac{(a-b)^{2}}{3} \geq 0
$$
This proves $c \geq a+b$ and thus (i) is true.
For proving (ii), consider the product
$$
Q=(\alpha+\beta+\gamma)(\alpha-\beta-\gamma)(\alpha+\beta-\gamma)(\alpha-\beta+\gamma)
$$
where $\alpha=\sqrt{c+a}, \beta=\sqrt{c+b}$ and $\gamma=\sqrt{c-a-b}$. Expanding the product, we get
$$
\begin{aligned}
Q & =(c+a)^{2}+(c+b)^{2}+(c-a-b)^{2}-2(c+a)(c+b)-2(c+a)(c-a-b)-2(c+b)(c-a-b) \\
& =-3 c^{2}+4 a^{2}+4 b^{2}+4 a b \\
& =0
\end{aligned}
$$
Thus at least one of the factors must be equal to 0 . Since $\alpha+\beta+\gamma>0$ and $\alpha+\beta-\gamma>0$, it follows that the product of the remaining two factors is 0 . This gives
$$
\sqrt{c+a}-\sqrt{c+b}=\sqrt{c-a-b} \text { or } \sqrt{c+a}-\sqrt{c+b}=-\sqrt{c-a-b}
$$
We conclude that
$$
|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a cyclic quadrilateral $A B C D, A B=a, B C=b, C D=c, \angle A B C=120^{\circ}$, and $\angle A B D=$ $30^{\circ}$. Prove that
(i) $c \geq a+b$;
(ii) $|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}$.
|
Applying cosine rule to triangle $A B C$, we get
$$
A C^{2}=a^{2}+b^{2}-2 a b \cos 120^{\circ}=a^{2}+b^{2}+a b
$$
Observe that $\angle D A C=\angle D B C=120^{\circ}-30^{\circ}=90^{\circ}$. Thus we get
$$
c^{2}=\frac{A C^{2}}{\cos ^{2} 30^{\circ}}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)
$$
So
$$
c^{2}-(a+b)^{2}=\frac{4}{3}\left(a^{2}+b^{2}+a b\right)-\left(a^{2}+b^{2}+2 a b\right)=\frac{(a-b)^{2}}{3} \geq 0
$$
This proves $c \geq a+b$ and thus (i) is true.

For proving (ii), consider the product
$$
Q=(\alpha+\beta+\gamma)(\alpha-\beta-\gamma)(\alpha+\beta-\gamma)(\alpha-\beta+\gamma)
$$
where $\alpha=\sqrt{c+a}, \beta=\sqrt{c+b}$ and $\gamma=\sqrt{c-a-b}$. Expanding the product, we get
$$
\begin{aligned}
Q & =(c+a)^{2}+(c+b)^{2}+(c-a-b)^{2}-2(c+a)(c+b)-2(c+a)(c-a-b)-2(c+b)(c-a-b) \\
& =-3 c^{2}+4 a^{2}+4 b^{2}+4 a b \\
& =0
\end{aligned}
$$
Thus at least one of the factors must be equal to 0 . Since $\alpha+\beta+\gamma>0$ and $\alpha+\beta-\gamma>0$, it follows that the product of the remaining two factors is 0 . This gives
$$
\sqrt{c+a}-\sqrt{c+b}=\sqrt{c-a-b} \text { or } \sqrt{c+a}-\sqrt{c+b}=-\sqrt{c-a-b}
$$
We conclude that
$$
|\sqrt{c+a}-\sqrt{c+b}|=\sqrt{c-a-b}
$$
|
{
"resource_path": "INMO/segmented/en-2006.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
2aed1a75-30ab-5f77-b3ca-6e9798f085f2
| 607,825
|
In a triangle $A B C$ right-angled at $C$, the median through $B$ bisects the angle between $B A$ and the bisector of $\angle B$. Prove that
$$
\frac{5}{2}<\frac{A B}{B C}<3
$$
|
Let us take $\angle B / 4=\theta$. Then $\angle E B C=\angle D B E=\theta$ and $\angle C B D=$ $2 \theta$.Using sine rule in triangles $B E A$ and $B E C$, we get
$$
\begin{aligned}
\frac{B E}{\sin A} & =\frac{A E}{\sin \theta} \\
\frac{B E}{\sin 90^{\circ}} & =\frac{C E}{\sin 3 \theta}
\end{aligned}
$$
Since $A E=C E$, we obtain $\sin 3 \theta \sin A=\sin \theta$. However $A=90^{\circ}-4 \theta$. Thus we get $\sin 3 \theta \cos 4 \theta=\sin \theta$. Note that
$$
\frac{c}{a}=\frac{1}{\cos 4 \theta}=\frac{\sin 3 \theta}{\sin \theta}=3-4 \sin ^{2} \theta
$$
This shows that $c / a<3$. Using $c / a=3-4 \sin ^{2} \theta$, it is easy to compute $\cos 2 \theta=((c / a)-1) / 2$. Hence
$$
\frac{a}{c}=\cos 4 \theta=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1
$$
Suppose $c / a \leq 5 / 2$. Then $((c / a)-1)^{2} \leq 9 / 4$ and $a / c \geq 2 / 5$. Thus
$$
\frac{2}{5} \leq \frac{a}{c}=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1 \leq \frac{9}{8}-1=\frac{1}{8}
$$
which is absurd. We conclude that $c / a>5 / 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$ right-angled at $C$, the median through $B$ bisects the angle between $B A$ and the bisector of $\angle B$. Prove that
$$
\frac{5}{2}<\frac{A B}{B C}<3
$$
|
Let us take $\angle B / 4=\theta$. Then $\angle E B C=\angle D B E=\theta$ and $\angle C B D=$ $2 \theta$.Using sine rule in triangles $B E A$ and $B E C$, we get
$$
\begin{aligned}
\frac{B E}{\sin A} & =\frac{A E}{\sin \theta} \\
\frac{B E}{\sin 90^{\circ}} & =\frac{C E}{\sin 3 \theta}
\end{aligned}
$$
Since $A E=C E$, we obtain $\sin 3 \theta \sin A=\sin \theta$. However $A=90^{\circ}-4 \theta$. Thus we get $\sin 3 \theta \cos 4 \theta=\sin \theta$. Note that
$$
\frac{c}{a}=\frac{1}{\cos 4 \theta}=\frac{\sin 3 \theta}{\sin \theta}=3-4 \sin ^{2} \theta
$$
This shows that $c / a<3$. Using $c / a=3-4 \sin ^{2} \theta$, it is easy to compute $\cos 2 \theta=((c / a)-1) / 2$. Hence
$$
\frac{a}{c}=\cos 4 \theta=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1
$$
Suppose $c / a \leq 5 / 2$. Then $((c / a)-1)^{2} \leq 9 / 4$ and $a / c \geq 2 / 5$. Thus
$$
\frac{2}{5} \leq \frac{a}{c}=\frac{1}{2}\left(\frac{c}{a}-1\right)^{2}-1 \leq \frac{9}{8}-1=\frac{1}{8}
$$
which is absurd. We conclude that $c / a>5 / 2$.
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution 2:"
}
|
c5e1bff3-2b66-50c1-9e6f-d1ad27a36b1c
| 607,827
|
Let $n$ be a natural number such that $n=a^{2}+b^{2}+c^{2}$, for some natural numbers $a, b, c$. Prove that
$$
9 n=\left(p_{1} a+q_{1} b+r_{1} c\right)^{2}+\left(p_{2} a+q_{2} b+r_{2} c\right)^{2}+\left(p_{3} a+q_{3} b+r_{3} c\right)^{2}
$$
where $p_{j}$ 's, $q_{j}$ 's, $r_{j}$ 's are all nonzero integers. Further, if 3 does not divide at least one of $a, b, c$, prove that $9 n$ can be expressed in the form $x^{2}+y^{2}+z^{2}$, where $x, y, z$ are natural numbers none of which is divisible by 3 .
|
It can be easily seen that
$$
9 n=(2 b+2 c-a)^{2}+(2 c+2 a-b)^{2}+(2 a+2 b-c)^{2}
$$
Thus we can take $p_{1}=p_{2}=p_{3}=2, q_{1}=q_{2}=q_{3}=2$ and $r_{1}=r_{2}=r_{3}=-1$. Suppose 3 does not divide $\operatorname{gcd}(a, b, c)$. Then 3 does divide at least one of $a, b, c$; say 3 does not divide $a$. Note that each of $2 b+2 c-a, 2 c+2 a-b$ and $2 a+2 b-c$ is either divisible by 3 or none of them is divisible by 3 , as the difference of any two sums is always divisible by 3 . If 3 does not divide $2 b+2 c-a$, then we have the required representation. If 3 divides $2 b+2 c-a$, then 3 does not divide $2 b+2 c+a$. On the other hand, we also note that
$$
9 n=(2 b+2 c+a)^{2}+(2 c-2 a-b)^{2}+(-2 a+2 b-c)^{2}=x^{2}+y^{2}+z^{2}
$$
where $x=2 b+2 c+a, y=2 c-2 a-b$ and $z=-2 a+2 b-c$. Since $x-y=3(b+a)$ and 3 does not divide $x$, it follows that 3 does not divide $y$ as well. Similarly, we conclude that 3 does not divide $z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a natural number such that $n=a^{2}+b^{2}+c^{2}$, for some natural numbers $a, b, c$. Prove that
$$
9 n=\left(p_{1} a+q_{1} b+r_{1} c\right)^{2}+\left(p_{2} a+q_{2} b+r_{2} c\right)^{2}+\left(p_{3} a+q_{3} b+r_{3} c\right)^{2}
$$
where $p_{j}$ 's, $q_{j}$ 's, $r_{j}$ 's are all nonzero integers. Further, if 3 does not divide at least one of $a, b, c$, prove that $9 n$ can be expressed in the form $x^{2}+y^{2}+z^{2}$, where $x, y, z$ are natural numbers none of which is divisible by 3 .
|
It can be easily seen that
$$
9 n=(2 b+2 c-a)^{2}+(2 c+2 a-b)^{2}+(2 a+2 b-c)^{2}
$$
Thus we can take $p_{1}=p_{2}=p_{3}=2, q_{1}=q_{2}=q_{3}=2$ and $r_{1}=r_{2}=r_{3}=-1$. Suppose 3 does not divide $\operatorname{gcd}(a, b, c)$. Then 3 does divide at least one of $a, b, c$; say 3 does not divide $a$. Note that each of $2 b+2 c-a, 2 c+2 a-b$ and $2 a+2 b-c$ is either divisible by 3 or none of them is divisible by 3 , as the difference of any two sums is always divisible by 3 . If 3 does not divide $2 b+2 c-a$, then we have the required representation. If 3 divides $2 b+2 c-a$, then 3 does not divide $2 b+2 c+a$. On the other hand, we also note that
$$
9 n=(2 b+2 c+a)^{2}+(2 c-2 a-b)^{2}+(-2 a+2 b-c)^{2}=x^{2}+y^{2}+z^{2}
$$
where $x=2 b+2 c+a, y=2 c-2 a-b$ and $z=-2 a+2 b-c$. Since $x-y=3(b+a)$ and 3 does not divide $x$, it follows that 3 does not divide $y$ as well. Similarly, we conclude that 3 does not divide $z$.
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
79e21e69-e3b9-5279-8142-03de13eddb48
| 607,828
|
Let $m$ and $n$ be positive integers such that the equation $x^{2}-m x+n=0$ has real roots $\alpha$ and $\beta$. Prove that $\alpha$ and $\beta$ are integers if and only if $[m \alpha]+[m \beta]$ is the square of an integer. (Here $[x]$ denotes the largest integer not exceeding $x$.)
|
If $\alpha$ and $\beta$ are both integers, then
$$
[m \alpha]+[m \beta]=m \alpha+m \beta=m(\alpha+\beta)=m^{2}
$$
This proves one implication.
Observe that $\alpha+\beta=m$ and $\alpha \beta=n$. We use the property of integer function: $x-1<[x] \leq x$ for any real number $x$. Thus
$m^{2}-2=m(\alpha+\beta)-2=m \alpha-1+m \beta-1<[m \alpha]+[m \beta] \leq m(\alpha+\beta)=m^{2}$.
Since $m$ and $n$ are positive integers, both $\alpha$ and $\beta$ must be positive. If $m \geq 2$, we observe that there is no square between $m^{2}-2$ and $m^{2}$. Hence, either $m=1$ or $[m \alpha]+[m \beta]=m^{2}$. If $m=1$, then $\alpha+\beta=1$ implies that both $\alpha$ and $\beta$ are positive reals smaller than 1 . Hence $n=\alpha \beta$ cannot be a positive integer. We conclude that $[m \alpha]+[m \beta]=m^{2}$. Putting $m=\alpha+\beta$ in this relation, we get
$$
\left[\alpha^{2}+n\right]+\left[\beta^{2}+n\right]=(\alpha+\beta)^{2}
$$
Using $[x+k]=[x]+k$ for any real number $x$ and integer $k$, this reduces to
$$
\left[\alpha^{2}\right]+\left[\beta^{2}\right]=\alpha^{2}+\beta^{2}
$$
This shows that $\alpha^{2}$ and $\beta^{2}$ are both integers. On the other hand,
$$
\alpha^{2}-\beta^{2}=(\alpha+\beta)(\alpha-\beta)=m(\alpha-\beta)
$$
Thus
$$
(\alpha-\beta)=\frac{\alpha^{2}-\beta^{2}}{m}
$$
is a rational number. Since $\alpha+\beta=m$ is a rational number, it follows that both $\alpha$ and $\beta$ are rational numbers. However, both $\alpha^{2}$ and $\beta^{2}$ are integers. Hence each of $\alpha$ and $\beta$ is an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $m$ and $n$ be positive integers such that the equation $x^{2}-m x+n=0$ has real roots $\alpha$ and $\beta$. Prove that $\alpha$ and $\beta$ are integers if and only if $[m \alpha]+[m \beta]$ is the square of an integer. (Here $[x]$ denotes the largest integer not exceeding $x$.)
|
If $\alpha$ and $\beta$ are both integers, then
$$
[m \alpha]+[m \beta]=m \alpha+m \beta=m(\alpha+\beta)=m^{2}
$$
This proves one implication.
Observe that $\alpha+\beta=m$ and $\alpha \beta=n$. We use the property of integer function: $x-1<[x] \leq x$ for any real number $x$. Thus
$m^{2}-2=m(\alpha+\beta)-2=m \alpha-1+m \beta-1<[m \alpha]+[m \beta] \leq m(\alpha+\beta)=m^{2}$.
Since $m$ and $n$ are positive integers, both $\alpha$ and $\beta$ must be positive. If $m \geq 2$, we observe that there is no square between $m^{2}-2$ and $m^{2}$. Hence, either $m=1$ or $[m \alpha]+[m \beta]=m^{2}$. If $m=1$, then $\alpha+\beta=1$ implies that both $\alpha$ and $\beta$ are positive reals smaller than 1 . Hence $n=\alpha \beta$ cannot be a positive integer. We conclude that $[m \alpha]+[m \beta]=m^{2}$. Putting $m=\alpha+\beta$ in this relation, we get
$$
\left[\alpha^{2}+n\right]+\left[\beta^{2}+n\right]=(\alpha+\beta)^{2}
$$
Using $[x+k]=[x]+k$ for any real number $x$ and integer $k$, this reduces to
$$
\left[\alpha^{2}\right]+\left[\beta^{2}\right]=\alpha^{2}+\beta^{2}
$$
This shows that $\alpha^{2}$ and $\beta^{2}$ are both integers. On the other hand,
$$
\alpha^{2}-\beta^{2}=(\alpha+\beta)(\alpha-\beta)=m(\alpha-\beta)
$$
Thus
$$
(\alpha-\beta)=\frac{\alpha^{2}-\beta^{2}}{m}
$$
is a rational number. Since $\alpha+\beta=m$ is a rational number, it follows that both $\alpha$ and $\beta$ are rational numbers. However, both $\alpha^{2}$ and $\beta^{2}$ are integers. Hence each of $\alpha$ and $\beta$ is an integer.
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
f46d782d-b119-5e23-a5ef-ffdc1f6d1dfb
| 607,829
|
Let $A B C$ be a triangle in which $A B=A C$. Let $D$ be the mid-point of $B C$ and $P$ be a point on $A D$. Suppose $E$ is the foot of perpendicular from $P$ on $A C$. If $\frac{A P}{P D}=\frac{B P}{P E}=\lambda, \frac{B D}{A D}=m$ and $z=m^{2}(1+\lambda)$, prove that
$$
z^{2}-\left(\lambda^{3}-\lambda^{2}-2\right) z+1=0
$$
Hence show that $\lambda \geq 2$ and $\lambda=2$ if and only if $A B C$ is equilateral.
|
Let $A D=h, P D=y$ and $B D=D C=a$. We
observe that $B P^{2}=a^{2}+y^{2}$. Moreover,
$P E=P A \sin \angle D A C=(h-y) \frac{D C}{A C}=\frac{a(h-y)}{b}$,
where $b=A C=A B$. Using $A P / P D=(h-$ $y) / y$, we obtain $y=h /(1+\lambda)$. Thus
$$
\lambda^{2}=\frac{B P^{2}}{P E^{2}}=\frac{\left(a^{2}+y^{2}\right) b^{2}}{(h-y)^{2} a^{2}}
$$
But $(h-y)=\lambda y=\lambda h /(1+\lambda)$ and $b^{2}=a^{2}+h^{2}$. Thus we obtain
$$
\lambda^{4}=\frac{\left(a^{2}(1+\lambda)^{2}+h^{2}\right)\left(a^{2}+h^{2}\right)}{a^{2} h^{2}}
$$
Using $m=a / h$ and $z=m^{2}(1+\lambda)$, this simplifies to
$$
z^{2}-z\left(\lambda^{3}-\lambda^{2}-2\right)+1=0
$$
Dividing by $z$, this gives
$$
z+\frac{1}{z}=\lambda^{3}-\lambda^{2}-2
$$
However $z+(1 / z) \geq 2$ for any positive real number $z$. Thus $\lambda^{3}-\lambda^{2}-4 \geq 0$. This may be written in the form $(\lambda-2)\left(\lambda^{2}+\lambda+2\right) \geq 0$. But $\lambda^{2}+\lambda+2>0$. (For example, one may check that its discriminant is negative.) Hence $\lambda \geq 2$. If $\lambda=2$, then $z+(1 / z)=2$ and hence $z=1$. This gives $m^{2}=1 / 3$ or $\tan (A / 2)=m=1 / \sqrt{3}$. Thus $A=60^{\circ}$ and hence $A B C$ is equilateral.
Conversely, if triangle $A B C$ is equilateral, then $m=\tan (A / 2)=1 / \sqrt{3}$ and hence $z=(1+\lambda) / 3$. Substituting this in the equation satisfied by $z$, we obtain
$$
(1+\lambda)^{2}-3(1+\lambda)\left(\lambda^{3}-\lambda^{2}-2\right)+9=0
$$
This may be written in the form $(\lambda-2)\left(3 \lambda^{3}+6 \lambda^{2}+8 \lambda+8\right)=0$. Here the second factor is positive because $\lambda>0$. We conclude that $\lambda=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle in which $A B=A C$. Let $D$ be the mid-point of $B C$ and $P$ be a point on $A D$. Suppose $E$ is the foot of perpendicular from $P$ on $A C$. If $\frac{A P}{P D}=\frac{B P}{P E}=\lambda, \frac{B D}{A D}=m$ and $z=m^{2}(1+\lambda)$, prove that
$$
z^{2}-\left(\lambda^{3}-\lambda^{2}-2\right) z+1=0
$$
Hence show that $\lambda \geq 2$ and $\lambda=2$ if and only if $A B C$ is equilateral.
|
Let $A D=h, P D=y$ and $B D=D C=a$. We

observe that $B P^{2}=a^{2}+y^{2}$. Moreover,
$P E=P A \sin \angle D A C=(h-y) \frac{D C}{A C}=\frac{a(h-y)}{b}$,
where $b=A C=A B$. Using $A P / P D=(h-$ $y) / y$, we obtain $y=h /(1+\lambda)$. Thus
$$
\lambda^{2}=\frac{B P^{2}}{P E^{2}}=\frac{\left(a^{2}+y^{2}\right) b^{2}}{(h-y)^{2} a^{2}}
$$
But $(h-y)=\lambda y=\lambda h /(1+\lambda)$ and $b^{2}=a^{2}+h^{2}$. Thus we obtain
$$
\lambda^{4}=\frac{\left(a^{2}(1+\lambda)^{2}+h^{2}\right)\left(a^{2}+h^{2}\right)}{a^{2} h^{2}}
$$
Using $m=a / h$ and $z=m^{2}(1+\lambda)$, this simplifies to
$$
z^{2}-z\left(\lambda^{3}-\lambda^{2}-2\right)+1=0
$$
Dividing by $z$, this gives
$$
z+\frac{1}{z}=\lambda^{3}-\lambda^{2}-2
$$
However $z+(1 / z) \geq 2$ for any positive real number $z$. Thus $\lambda^{3}-\lambda^{2}-4 \geq 0$. This may be written in the form $(\lambda-2)\left(\lambda^{2}+\lambda+2\right) \geq 0$. But $\lambda^{2}+\lambda+2>0$. (For example, one may check that its discriminant is negative.) Hence $\lambda \geq 2$. If $\lambda=2$, then $z+(1 / z)=2$ and hence $z=1$. This gives $m^{2}=1 / 3$ or $\tan (A / 2)=m=1 / \sqrt{3}$. Thus $A=60^{\circ}$ and hence $A B C$ is equilateral.
Conversely, if triangle $A B C$ is equilateral, then $m=\tan (A / 2)=1 / \sqrt{3}$ and hence $z=(1+\lambda) / 3$. Substituting this in the equation satisfied by $z$, we obtain
$$
(1+\lambda)^{2}-3(1+\lambda)\left(\lambda^{3}-\lambda^{2}-2\right)+9=0
$$
This may be written in the form $(\lambda-2)\left(3 \lambda^{3}+6 \lambda^{2}+8 \lambda+8\right)=0$. Here the second factor is positive because $\lambda>0$. We conclude that $\lambda=2$.
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
360edf9d-5e10-59f1-8a40-ca67315702d1
| 607,831
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
We begin with the observation that
$$
x^{2}+x y+y^{2}=\frac{3}{4}(x+y)^{2}+\frac{1}{4}(x-y)^{2} \geq \frac{3}{4}(x+y)^{2}
$$
and similar bounds for $y^{2}+y z+z^{2}, z^{2}+z x+x^{2}$. Thus
$$
3\left(x^{2}+x y+y^{2}\right)\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right) \geq \frac{81}{64}(x+y)^{2}(y+z)^{2}(z+x)^{2}
$$
Thus it is sufficient to prove that
$$
(x+y+z)(x y+y z+z x) \leq \frac{9}{8}(x+y)(y+z)(z+x)
$$
Equivalently, we need to prove that
$$
8(x+y+z)(x y+y z+z x) \leq 9(x+y)(y+z)(z+x)
$$
However, we note that
$$
(x+y)(y+z)(z+x)=(x+y+z)(y z+z x+x y)-x y z
$$
Thus the required inequality takes the form
$$
(x+y)(y+z)(z+x) \geq 8 x y z
$$
This follows from AM-GM inequalities;
$$
x+y \geq 2 \sqrt{x y}, \quad y+z \geq 2 \sqrt{y z}, \quad z+x \geq 2 \sqrt{z x}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
We begin with the observation that
$$
x^{2}+x y+y^{2}=\frac{3}{4}(x+y)^{2}+\frac{1}{4}(x-y)^{2} \geq \frac{3}{4}(x+y)^{2}
$$
and similar bounds for $y^{2}+y z+z^{2}, z^{2}+z x+x^{2}$. Thus
$$
3\left(x^{2}+x y+y^{2}\right)\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right) \geq \frac{81}{64}(x+y)^{2}(y+z)^{2}(z+x)^{2}
$$
Thus it is sufficient to prove that
$$
(x+y+z)(x y+y z+z x) \leq \frac{9}{8}(x+y)(y+z)(z+x)
$$
Equivalently, we need to prove that
$$
8(x+y+z)(x y+y z+z x) \leq 9(x+y)(y+z)(z+x)
$$
However, we note that
$$
(x+y)(y+z)(z+x)=(x+y+z)(y z+z x+x y)-x y z
$$
Thus the required inequality takes the form
$$
(x+y)(y+z)(z+x) \geq 8 x y z
$$
This follows from AM-GM inequalities;
$$
x+y \geq 2 \sqrt{x y}, \quad y+z \geq 2 \sqrt{y z}, \quad z+x \geq 2 \sqrt{z x}
$$
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 1:"
}
|
d960433c-90f2-5711-a3c1-c8442c9135b2
| 607,832
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
Let us introduce $x+y=c, y+z=a$ and $z+x=b$. Then $a, b, c$ are the sides of a triangle. If $s=(a+b+c) / 2$, then it is easy to calculate $x=s-a, y=s-b, z=s-c$ and $x+y+z=s$. We also observe that
$x^{2}+x y+y^{2}=(x+y)^{2}-x y=c^{2}-\frac{1}{4}(c+a-b)(c+b-a)=\frac{3}{4} c^{2}+\frac{1}{4}(a-b)^{2} \geq \frac{3}{4} c^{2}$.
Moreover, $x y+y z+z x=(s-a)(s-b)+(s-b)(s-c)+(s-c)(s-a)$. Thus it si sufficient to prove that
$$
s \sum(s-a)(s-b) \leq \frac{9}{8} a b c
$$
But, $\sum(s-a)(s-b)=r(4 R+r)$, where $r, R$ are respectively the in-radius, the circum-radius of the triangle whose sides are $a, b, c$, and $a b c=4 R r s$. Thus the inequality reduces to
$$
r(4 R+r) \leq \frac{9}{2} R r
$$
This is simply $2 r \leq R$. This follows from $I O^{2}=R(R-2 r)$, where $I$ is the incentre and $O$ the circumcentre.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
Let us introduce $x+y=c, y+z=a$ and $z+x=b$. Then $a, b, c$ are the sides of a triangle. If $s=(a+b+c) / 2$, then it is easy to calculate $x=s-a, y=s-b, z=s-c$ and $x+y+z=s$. We also observe that
$x^{2}+x y+y^{2}=(x+y)^{2}-x y=c^{2}-\frac{1}{4}(c+a-b)(c+b-a)=\frac{3}{4} c^{2}+\frac{1}{4}(a-b)^{2} \geq \frac{3}{4} c^{2}$.
Moreover, $x y+y z+z x=(s-a)(s-b)+(s-b)(s-c)+(s-c)(s-a)$. Thus it si sufficient to prove that
$$
s \sum(s-a)(s-b) \leq \frac{9}{8} a b c
$$
But, $\sum(s-a)(s-b)=r(4 R+r)$, where $r, R$ are respectively the in-radius, the circum-radius of the triangle whose sides are $a, b, c$, and $a b c=4 R r s$. Thus the inequality reduces to
$$
r(4 R+r) \leq \frac{9}{2} R r
$$
This is simply $2 r \leq R$. This follows from $I O^{2}=R(R-2 r)$, where $I$ is the incentre and $O$ the circumcentre.
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 2:"
}
|
d960433c-90f2-5711-a3c1-c8442c9135b2
| 607,832
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
If we set $x=\lambda a, y=\lambda b, z=\lambda c$, then the inequality changes to
$$
(a+b+c)^{2}(a b+b c+c a)^{2} \leq 3\left(a^{2}+a b+b^{2}\right)\left(b^{2}+b c+c^{2}\right)\left(c^{2}+c a+a^{2}\right)
$$
This shows that we may assume $x+y+z=1$. Let $\alpha=x y+y z+z x$. We see that
$$
\begin{aligned}
x^{2}+x y+y^{2} & =(x+y)^{2}-x y \\
& =(x+y)(1-z)-x y \\
& =x+y-\alpha=1-z-\alpha
\end{aligned}
$$
Thus
$$
\begin{aligned}
\prod\left(x^{2}+x y+y^{2}\right) & =(1-\alpha-z)(1-\alpha-x)(1-\alpha-y) \\
& =(1-\alpha)^{3}-(1-\alpha)^{2}+(1-\alpha) \alpha-x y z \\
& =\alpha^{2}-\alpha^{3}-x y z
\end{aligned}
$$
Thus we need to prove that $\alpha^{2} \leq 3\left(\alpha^{2}-\alpha^{3}-x y z\right)$. This reduces to
$$
3 x y z \leq \alpha^{2}(2-3 \alpha)
$$
However
$$
3 \alpha=3(x y+y z+z x) \leq(x+y+z)^{2}=1
$$
so that $2-3 \alpha \geq 1$. Thus it suffices to prove that $3 x y z \leq \alpha^{2}$. But
$$
\begin{aligned}
\alpha^{2}-3 x y z & =(x y+y z+z x)^{2}-3 x y z(x+y+z) \\
& =\sum_{\text {cyclic }} x^{2} y^{2}-x y z(x+y+z) \\
& =\frac{1}{2} \sum_{\text {cyclic }}(x y-y z)^{2} \geq 0
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
If $x, y, z$ are positive real numbers, prove that
$$
(x+y+z)^{2}(y z+z x+x y)^{2} \leq 3\left(y^{2}+y z+z^{2}\right)\left(z^{2}+z x+x^{2}\right)\left(x^{2}+x y+y^{2}\right)
$$
|
If we set $x=\lambda a, y=\lambda b, z=\lambda c$, then the inequality changes to
$$
(a+b+c)^{2}(a b+b c+c a)^{2} \leq 3\left(a^{2}+a b+b^{2}\right)\left(b^{2}+b c+c^{2}\right)\left(c^{2}+c a+a^{2}\right)
$$
This shows that we may assume $x+y+z=1$. Let $\alpha=x y+y z+z x$. We see that
$$
\begin{aligned}
x^{2}+x y+y^{2} & =(x+y)^{2}-x y \\
& =(x+y)(1-z)-x y \\
& =x+y-\alpha=1-z-\alpha
\end{aligned}
$$
Thus
$$
\begin{aligned}
\prod\left(x^{2}+x y+y^{2}\right) & =(1-\alpha-z)(1-\alpha-x)(1-\alpha-y) \\
& =(1-\alpha)^{3}-(1-\alpha)^{2}+(1-\alpha) \alpha-x y z \\
& =\alpha^{2}-\alpha^{3}-x y z
\end{aligned}
$$
Thus we need to prove that $\alpha^{2} \leq 3\left(\alpha^{2}-\alpha^{3}-x y z\right)$. This reduces to
$$
3 x y z \leq \alpha^{2}(2-3 \alpha)
$$
However
$$
3 \alpha=3(x y+y z+z x) \leq(x+y+z)^{2}=1
$$
so that $2-3 \alpha \geq 1$. Thus it suffices to prove that $3 x y z \leq \alpha^{2}$. But
$$
\begin{aligned}
\alpha^{2}-3 x y z & =(x y+y z+z x)^{2}-3 x y z(x+y+z) \\
& =\sum_{\text {cyclic }} x^{2} y^{2}-x y z(x+y+z) \\
& =\frac{1}{2} \sum_{\text {cyclic }}(x y-y z)^{2} \geq 0
\end{aligned}
$$
|
{
"resource_path": "INMO/segmented/en-2007.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution 3:"
}
|
d960433c-90f2-5711-a3c1-c8442c9135b2
| 607,832
|
Let $A B C$ be a triangle, $I$ its in-centre; $A_{1}, B_{1}, C_{1}$ be the reflections of $I$ in $B C, C A, A B$ respectively. Suppose the circum-circle of triangle $A_{1} B_{1} C_{1}$ passes through $A$. Prove that $B_{1}, C_{1}$, $I, I_{1}$ are concyclic, where $I_{1}$ is the in-centre of triangle $A_{1} B_{1} C_{1}$.
|
Note that $I A_{1}=I B_{1}=I C_{1}=2 r$, where $r$ is the in-radius of the triangle $A B C$. Hence $I$ is the circum-centre of the triangle $A_{1} B_{1} C_{1}$.
Let $K$ be the point of intersection of $I B_{1}$ and $A C$. Then $I K=r, I A=2 r$ and $\angle I K A=90^{\circ}$. It follows that $\angle I A K=30^{\circ}$ and hence $\angle I A B_{1}=60^{\circ}$. Thus $A I B_{1}$ is an equilateral triangle. Similarly triangle $A I C_{1}$ is also equilateral. We hence obtain $A B_{1}=A C_{1}=A I=I B_{1}=I C_{1}=2 r$.
We also observe that $\angle B_{1} I C_{1}=120^{\circ}$ and $I B_{1} A C_{1}$ is a rhombus. Thus $\angle B_{1} A C_{1}=120^{\circ}$ and by concyclicity $\angle A_{1}=60^{\circ}$. Since $A B_{1}=A C_{1}, A$ is the midpoint of the arc $B_{1} A C_{1}$. It follows that $A_{1} A$ bisects $\angle A_{1}$ and $I_{1}$ lies on the line $A_{1} A$. This implies that
$$
\angle B_{1} I_{1} C_{1}=90^{\circ}+\angle A_{1} / 2=90^{\circ}+30^{\circ}=120^{\circ}
$$
Since $\angle B_{1} I C_{1}=120^{\circ}$, we conclude that $B_{1}, I, I_{1}, C_{1}$ are concyclic. (Further $A$ is the centre.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, $I$ its in-centre; $A_{1}, B_{1}, C_{1}$ be the reflections of $I$ in $B C, C A, A B$ respectively. Suppose the circum-circle of triangle $A_{1} B_{1} C_{1}$ passes through $A$. Prove that $B_{1}, C_{1}$, $I, I_{1}$ are concyclic, where $I_{1}$ is the in-centre of triangle $A_{1} B_{1} C_{1}$.
|

Note that $I A_{1}=I B_{1}=I C_{1}=2 r$, where $r$ is the in-radius of the triangle $A B C$. Hence $I$ is the circum-centre of the triangle $A_{1} B_{1} C_{1}$.
Let $K$ be the point of intersection of $I B_{1}$ and $A C$. Then $I K=r, I A=2 r$ and $\angle I K A=90^{\circ}$. It follows that $\angle I A K=30^{\circ}$ and hence $\angle I A B_{1}=60^{\circ}$. Thus $A I B_{1}$ is an equilateral triangle. Similarly triangle $A I C_{1}$ is also equilateral. We hence obtain $A B_{1}=A C_{1}=A I=I B_{1}=I C_{1}=2 r$.
We also observe that $\angle B_{1} I C_{1}=120^{\circ}$ and $I B_{1} A C_{1}$ is a rhombus. Thus $\angle B_{1} A C_{1}=120^{\circ}$ and by concyclicity $\angle A_{1}=60^{\circ}$. Since $A B_{1}=A C_{1}, A$ is the midpoint of the arc $B_{1} A C_{1}$. It follows that $A_{1} A$ bisects $\angle A_{1}$ and $I_{1}$ lies on the line $A_{1} A$. This implies that
$$
\angle B_{1} I_{1} C_{1}=90^{\circ}+\angle A_{1} / 2=90^{\circ}+30^{\circ}=120^{\circ}
$$
Since $\angle B_{1} I C_{1}=120^{\circ}$, we conclude that $B_{1}, I, I_{1}, C_{1}$ are concyclic. (Further $A$ is the centre.)
|
{
"resource_path": "INMO/segmented/en-2008.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
aa4cd0b3-c6d6-5675-a8a0-c8897cf772f0
| 607,833
|
Let $A$ be a set of real numbers such that $A$ has at least four elements. Suppose $A$ has the property that $a^{2}+b c$ is a rational number for all distinct numbers $a, b, c$ in $A$. Prove that there exists a positive integer $M$ such that $a \sqrt{M}$ is a rational number for every $a$ in $A$.
|
Suppose $0 \in A$. Then $a^{2}=a^{2}+0 \times b$ is rational and $a b=0^{2}+a b$ is also rational for all $a, b$ in $A, a \neq 0, b \neq 0, a \neq b$. Hence $a=a_{1} \sqrt{M}$ for some rational $a_{1}$ and natural number $M$. For any $b \neq 0$, we have
$$
b \sqrt{M}=\frac{a b}{a_{1}}
$$
which is a rational number.
Hence we may assume 0 is not in $A$. If there is a number $a$ in $A$ such that $-a$ is also in $A$, then again we can get the conclusion as follows. Consider two other elements $c, d$ in $A$. Then $c^{2}+d a$ is rational and $c^{2}-d a$ is also rational. It follows that $c^{2}$ is rational and $d a$ is rational. Similarly, $d^{2}$ and $c a$ are also rationals. Thus $d / c=(d a) /(c a)$ is rational. Note that we can vary $d$ over $A$ with $d \neq c$ and $d \neq a$. Again $c^{2}$ is rational implies that $c=c_{1} \sqrt{M}$ for some rational $c_{1}$ and natural number $M$. We observe that $c \sqrt{M}=c_{1} M$ is rational, and
$$
a \sqrt{M}=\frac{c a}{c_{1}}
$$
so that $a \sqrt{M}$ is a rational number. Similarly is the case with $-a \sqrt{M}$. For any other element $d$,
$$
b \sqrt{M}=M c_{1} \frac{d}{c}
$$
is a rational number.
Thus we may now assume that 0 is not in $A$ and $a+b \neq 0$ for any $a, b$ in $A$. Let $a, b, c, d$ be four distinct elements of $A$. We may assume $|a|>\mid b$. Then $d^{2}+a b$ and $d^{2}+b c$ are rational numbers and so is their difference $a b-b c$. Writing $a^{2}+a b=a^{2}+b c+(a b-b c)$, and using the facts $a^{2}+b c$, $a b-b c$ are rationals, we conclude that $a^{2}+a b$ is also a rational number. Similarly, $b^{2}+a b$ is also a rational number.
Consider
$$
q=\frac{a}{b}=\frac{a^{2}+a b}{b^{2}+a b}
$$
Note that $a^{2}+a b>0$. Thus $q$ is a rational number and $a=b q$. This gives $a^{2}+a b=b^{2}\left(q^{2}+q\right)$. Let us take $b^{2}\left(q^{2}+q\right)=l$. Then
$$
|b|=\sqrt{\frac{l}{q^{2}+q}}=\sqrt{\frac{x}{y}}
$$
where $x$ and $y$ are natural numbers. Take $M=x y$. Then $|b| \sqrt{M}=x$ is a rational number. Finally, for any $c$ in $A$, we have
$$
c \sqrt{M}=b \sqrt{M} \frac{c}{b}
$$
is also a rational number.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $A$ be a set of real numbers such that $A$ has at least four elements. Suppose $A$ has the property that $a^{2}+b c$ is a rational number for all distinct numbers $a, b, c$ in $A$. Prove that there exists a positive integer $M$ such that $a \sqrt{M}$ is a rational number for every $a$ in $A$.
|
Suppose $0 \in A$. Then $a^{2}=a^{2}+0 \times b$ is rational and $a b=0^{2}+a b$ is also rational for all $a, b$ in $A, a \neq 0, b \neq 0, a \neq b$. Hence $a=a_{1} \sqrt{M}$ for some rational $a_{1}$ and natural number $M$. For any $b \neq 0$, we have
$$
b \sqrt{M}=\frac{a b}{a_{1}}
$$
which is a rational number.
Hence we may assume 0 is not in $A$. If there is a number $a$ in $A$ such that $-a$ is also in $A$, then again we can get the conclusion as follows. Consider two other elements $c, d$ in $A$. Then $c^{2}+d a$ is rational and $c^{2}-d a$ is also rational. It follows that $c^{2}$ is rational and $d a$ is rational. Similarly, $d^{2}$ and $c a$ are also rationals. Thus $d / c=(d a) /(c a)$ is rational. Note that we can vary $d$ over $A$ with $d \neq c$ and $d \neq a$. Again $c^{2}$ is rational implies that $c=c_{1} \sqrt{M}$ for some rational $c_{1}$ and natural number $M$. We observe that $c \sqrt{M}=c_{1} M$ is rational, and
$$
a \sqrt{M}=\frac{c a}{c_{1}}
$$
so that $a \sqrt{M}$ is a rational number. Similarly is the case with $-a \sqrt{M}$. For any other element $d$,
$$
b \sqrt{M}=M c_{1} \frac{d}{c}
$$
is a rational number.
Thus we may now assume that 0 is not in $A$ and $a+b \neq 0$ for any $a, b$ in $A$. Let $a, b, c, d$ be four distinct elements of $A$. We may assume $|a|>\mid b$. Then $d^{2}+a b$ and $d^{2}+b c$ are rational numbers and so is their difference $a b-b c$. Writing $a^{2}+a b=a^{2}+b c+(a b-b c)$, and using the facts $a^{2}+b c$, $a b-b c$ are rationals, we conclude that $a^{2}+a b$ is also a rational number. Similarly, $b^{2}+a b$ is also a rational number.
Consider
$$
q=\frac{a}{b}=\frac{a^{2}+a b}{b^{2}+a b}
$$
Note that $a^{2}+a b>0$. Thus $q$ is a rational number and $a=b q$. This gives $a^{2}+a b=b^{2}\left(q^{2}+q\right)$. Let us take $b^{2}\left(q^{2}+q\right)=l$. Then
$$
|b|=\sqrt{\frac{l}{q^{2}+q}}=\sqrt{\frac{x}{y}}
$$
where $x$ and $y$ are natural numbers. Take $M=x y$. Then $|b| \sqrt{M}=x$ is a rational number. Finally, for any $c$ in $A$, we have
$$
c \sqrt{M}=b \sqrt{M} \frac{c}{b}
$$
is also a rational number.
|
{
"resource_path": "INMO/segmented/en-2008.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
baeb7491-96a3-5a7b-8792-8a33f5412abd
| 607,835
|
All the points with integer coordinates in the $x y$-plane are coloured using three colours, red, blue and green, each colour being used at least once. It is known that the point $(0,0)$ is coloured red and the point $(0,1)$ is coloured blue. Prove that there exist three points with integer coordinates of distinct colours which form the vertices of a right-angled triangle.
|
Consider the lattice points(points with integer coordinates) on the lines $y=0$ and $y=1$, other than $(0,0)$ and $(0,1)$, If one of them, say $A=(p, 1)$, is coloured green, then we have a right-angled triangle with $(0,0),(0,1)$ and $A$ as vertices, all having different colours. (See Figures 1 and 2.)
If not, the lattice points on $y=0$ and $y=1$ are all red or blue. We consider three different cases.
Case 1. Suppose a point $B=(c, 0)$ is blue. Consider a green point $D=(p, q)$ in the plane. Suppose $p \neq 0$. If its projection $(p, 0)$ on the $x$-axis is red, then $(p, q),(p, 0)$ and $(c, 0)$ are the vertices of a required type of right-angled triangle. If $(p, 0)$ is blue, then we can consider the triangle whose vertices are $(0,0),(p, 0)$ and $(p, q)$. If $p=0$, then the points $D,(0,0)$ and $(c, 0)$ will work.(Figure 3.)
Case 2. A point $D=(c, 1)$, on the line $y=1$, is red. A similar argument works in this case.
Fig-4
Case 3. Suppose all the lattice points on the line $y=0$ are red and all on the line $y=1$ are blue points. Consider a green point $E=(p, q)$, where $q \neq 0$ and $q \neq 1$.(See Figure 4.) Consider an isosceles right-angled triangle $E K M$ with $\angle E=90^{\circ}$ such that the hypotenuse $K M$ is a part of the $x$-axis. Let $E M$ intersect $y=$ in $L$. Then $K$ is a red point and $L$ is a blue point. Hence $E K L$ is a desired triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
All the points with integer coordinates in the $x y$-plane are coloured using three colours, red, blue and green, each colour being used at least once. It is known that the point $(0,0)$ is coloured red and the point $(0,1)$ is coloured blue. Prove that there exist three points with integer coordinates of distinct colours which form the vertices of a right-angled triangle.
|
Consider the lattice points(points with integer coordinates) on the lines $y=0$ and $y=1$, other than $(0,0)$ and $(0,1)$, If one of them, say $A=(p, 1)$, is coloured green, then we have a right-angled triangle with $(0,0),(0,1)$ and $A$ as vertices, all having different colours. (See Figures 1 and 2.)

If not, the lattice points on $y=0$ and $y=1$ are all red or blue. We consider three different cases.
Case 1. Suppose a point $B=(c, 0)$ is blue. Consider a green point $D=(p, q)$ in the plane. Suppose $p \neq 0$. If its projection $(p, 0)$ on the $x$-axis is red, then $(p, q),(p, 0)$ and $(c, 0)$ are the vertices of a required type of right-angled triangle. If $(p, 0)$ is blue, then we can consider the triangle whose vertices are $(0,0),(p, 0)$ and $(p, q)$. If $p=0$, then the points $D,(0,0)$ and $(c, 0)$ will work.(Figure 3.)
Case 2. A point $D=(c, 1)$, on the line $y=1$, is red. A similar argument works in this case.

Fig-4
Case 3. Suppose all the lattice points on the line $y=0$ are red and all on the line $y=1$ are blue points. Consider a green point $E=(p, q)$, where $q \neq 0$ and $q \neq 1$.(See Figure 4.) Consider an isosceles right-angled triangle $E K M$ with $\angle E=90^{\circ}$ such that the hypotenuse $K M$ is a part of the $x$-axis. Let $E M$ intersect $y=$ in $L$. Then $K$ is a red point and $L$ is a blue point. Hence $E K L$ is a desired triangle.
|
{
"resource_path": "INMO/segmented/en-2008.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
862fa78f-0e1f-5f6d-abd9-3098b6e97b8b
| 607,836
|
Let $A B C$ be a triangle; $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ be three equal, disjoint circles inside $A B C$ such that $\Gamma_{A}$ touches $A B$ and $A C ; \Gamma_{B}$ touches $A B$; and $B C$, and $\Gamma_{C}$ touches $B C$ and $C A$. Let $\Gamma$ be a circle touching circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ externally. Prove that the line joining the circum-centre $O$ and the in-centre $I$ of triangle $A B C$ passes through the centre of $\Gamma$.
|
Let $O_{1}, O_{2}, O_{3}$ be the centres of the circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ respectively, and let $P$ be the circum-centre of the triangle $O_{1} O_{2} O_{3}$. Let $x$ denote the common radius of three circles $\Gamma_{A}, \Gamma_{B}$, $\Gamma_{C}$. Note that $P$ is also the centre of the circle $\Gamma$, as $O_{1} P, O_{2} P, O_{3} P$ each exceed the radius of $\Gamma$ by $x$. Let $D, X, K, L, M$ be respectively the projections of $I, P, O, O_{1}, O_{2}$ on $B C$.
From $\frac{B L}{B D}=\frac{L O_{2}}{D I}$, we get $B L=x(s-b) / r$, as $I D=r$ and $B D=(s-b)$. Similarly, $C M=$ $x(s-c) / r$. Therefore, $L M=a-\frac{x}{r}(s-b+s-c)=\frac{a}{r}(r-x)$. Since $O_{2} L M O_{3}$ is a rectangle and $P X$ is the perpendicular bisector of $\mathrm{O}_{2} \mathrm{O}_{3}$, it is perpendicular bisector of $L M$ as well. Thus
$$
\begin{aligned}
L X & =\frac{1}{2} L M=\frac{a}{2 r}(r-x) \\
B X & =B L+L X=\frac{x}{r}(s-b)+\frac{a}{2 r}(r-x)=\frac{a}{2}-\frac{x(b-c)}{2 r} \\
D K & =B K-B D=\frac{a}{2}-(s-b)=\frac{b-c}{2} \\
X K & =B K-B X=\frac{a}{2}-\frac{a}{2}+\frac{x(b-c)}{2 r}=\frac{x(b-c)}{2 r}
\end{aligned}
$$
Hence we get
$$
\frac{X K}{D K}=\frac{x}{r}
$$
We observe that the sides of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are
$$
O_{2} O_{3}=L M=\frac{a}{r}(r-x), \quad O_{3} O_{1}=\frac{b}{r}(r-x), \quad O_{1} O_{2}=\frac{c}{r}(r-x)
$$
Thus the sides of $O_{1} O_{2} O_{3}$ and those of $A B C$ are in the ratio $(r-x) / r$. Further, as the sides of $O_{1} O_{2} O_{3}$ are parallel to those of $A B C$, we see that $I$ is the in-centre of $O_{1} O_{2} O_{3}$ as well. This gives $I P / I O=(r-x) / r$, and hence $P O / I O=x / r$. Thus we obtain
$$
\frac{X K}{D K}=\frac{P O}{I O}
$$
It follows that $I, P, O$ are collinear.
Alternately, we also infer that $I$ is the centre of homothety which takes the figure $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ to $A B C$. Hence it takes $P$ to $O$. It follows that $I, P, O$ are collinear
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle; $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ be three equal, disjoint circles inside $A B C$ such that $\Gamma_{A}$ touches $A B$ and $A C ; \Gamma_{B}$ touches $A B$; and $B C$, and $\Gamma_{C}$ touches $B C$ and $C A$. Let $\Gamma$ be a circle touching circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ externally. Prove that the line joining the circum-centre $O$ and the in-centre $I$ of triangle $A B C$ passes through the centre of $\Gamma$.
|
Let $O_{1}, O_{2}, O_{3}$ be the centres of the circles $\Gamma_{A}, \Gamma_{B}, \Gamma_{C}$ respectively, and let $P$ be the circum-centre of the triangle $O_{1} O_{2} O_{3}$. Let $x$ denote the common radius of three circles $\Gamma_{A}, \Gamma_{B}$, $\Gamma_{C}$. Note that $P$ is also the centre of the circle $\Gamma$, as $O_{1} P, O_{2} P, O_{3} P$ each exceed the radius of $\Gamma$ by $x$. Let $D, X, K, L, M$ be respectively the projections of $I, P, O, O_{1}, O_{2}$ on $B C$.

From $\frac{B L}{B D}=\frac{L O_{2}}{D I}$, we get $B L=x(s-b) / r$, as $I D=r$ and $B D=(s-b)$. Similarly, $C M=$ $x(s-c) / r$. Therefore, $L M=a-\frac{x}{r}(s-b+s-c)=\frac{a}{r}(r-x)$. Since $O_{2} L M O_{3}$ is a rectangle and $P X$ is the perpendicular bisector of $\mathrm{O}_{2} \mathrm{O}_{3}$, it is perpendicular bisector of $L M$ as well. Thus
$$
\begin{aligned}
L X & =\frac{1}{2} L M=\frac{a}{2 r}(r-x) \\
B X & =B L+L X=\frac{x}{r}(s-b)+\frac{a}{2 r}(r-x)=\frac{a}{2}-\frac{x(b-c)}{2 r} \\
D K & =B K-B D=\frac{a}{2}-(s-b)=\frac{b-c}{2} \\
X K & =B K-B X=\frac{a}{2}-\frac{a}{2}+\frac{x(b-c)}{2 r}=\frac{x(b-c)}{2 r}
\end{aligned}
$$
Hence we get
$$
\frac{X K}{D K}=\frac{x}{r}
$$
We observe that the sides of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ are
$$
O_{2} O_{3}=L M=\frac{a}{r}(r-x), \quad O_{3} O_{1}=\frac{b}{r}(r-x), \quad O_{1} O_{2}=\frac{c}{r}(r-x)
$$
Thus the sides of $O_{1} O_{2} O_{3}$ and those of $A B C$ are in the ratio $(r-x) / r$. Further, as the sides of $O_{1} O_{2} O_{3}$ are parallel to those of $A B C$, we see that $I$ is the in-centre of $O_{1} O_{2} O_{3}$ as well. This gives $I P / I O=(r-x) / r$, and hence $P O / I O=x / r$. Thus we obtain
$$
\frac{X K}{D K}=\frac{P O}{I O}
$$
It follows that $I, P, O$ are collinear.
Alternately, we also infer that $I$ is the centre of homothety which takes the figure $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3}$ to $A B C$. Hence it takes $P$ to $O$. It follows that $I, P, O$ are collinear
|
{
"resource_path": "INMO/segmented/en-2008.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
3d672147-d8c1-5793-a99f-e500a4700775
| 607,837
|
Let $P(x)$ be a given polynomial with integer coefficients. Prove that there exist two polynomials $Q(x)$ and $R(x)$, again with integer coefficients, such that (i) $P(x) Q(x)$ is a polynomial in $x^{2}$; and (ii) $P(x) R(x)$ is a polynomial in $x^{3}$.
|
Let $P(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}$ be a polynomial with integer coefficients.
Part (i) We may write
$$
P(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots+x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
$$
Define
$$
Q(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots-x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
$$
Then $Q(x)$ is also a polynomial with integer coefficients and
$$
P(x) Q(x)=\left(a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots\right)^{2}-x^{2}\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)^{2}
$$
is a polynomial in $x^{2}$.
Part (ii) We write again
$$
P(x)=A(x)+x B(x)+x^{2} C(x)
$$
where
$$
\begin{aligned}
& A(x)=a_{0}+a_{3} x^{3}+a_{6} x^{6}+\cdots \\
& B(x)=a_{1}+a_{4} x^{3}+a_{7} x^{6}+\cdots \\
& C(x)=a_{2}+a_{5} x^{3}+a_{8} x^{6}+\cdots
\end{aligned}
$$
Note that $A(x), B(x)$ and $C(x)$ are polynomials with integer coefficients and each of these is a polynomial in $x^{3}$. We may introduce
$$
\begin{aligned}
& S(x)=A(x)+\omega x B(x)+\omega^{2} x^{2} C(x) \\
& T(x)=A(x)+\omega^{2} x B(x)+\omega x^{2} C(x)
\end{aligned}
$$
where $\omega$ is an imaginary cube-root of unity. Then
$$
\begin{aligned}
S(x) T(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} & \\
& -x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
\end{aligned}
$$
since $\omega^{3}=1$ and $\omega+\omega^{2}=-1$. Taking $R(x)=S(x) T(x)$, we obtain
$$
P(x) R(x)=(A(x))^{3}+x^{3}(B(x))^{3}+x^{6}(C(x))^{3}-3 x^{3} A(x) B(x) C(x)
$$
which is a polynomial in $x^{3}$. This follows from the identity
$$
(a+b+c)\left(a^{2}+b^{2}+c^{2}-a b-b c-c a\right)=a^{3}+b^{3}+c^{3}-3 a b c
$$
Alternately, $R(x)$ may be directly defined by
$$
\begin{aligned}
& R(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} \\
&-x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)$ be a given polynomial with integer coefficients. Prove that there exist two polynomials $Q(x)$ and $R(x)$, again with integer coefficients, such that (i) $P(x) Q(x)$ is a polynomial in $x^{2}$; and (ii) $P(x) R(x)$ is a polynomial in $x^{3}$.
|
Let $P(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}$ be a polynomial with integer coefficients.
Part (i) We may write
$$
P(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots+x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
$$
Define
$$
Q(x)=a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots-x\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)
$$
Then $Q(x)$ is also a polynomial with integer coefficients and
$$
P(x) Q(x)=\left(a_{0}+a_{2} x^{2}+a_{4} x^{4}+\cdots\right)^{2}-x^{2}\left(a_{1}+a_{3} x^{2}+a_{5} x^{5}+\cdots\right)^{2}
$$
is a polynomial in $x^{2}$.
Part (ii) We write again
$$
P(x)=A(x)+x B(x)+x^{2} C(x)
$$
where
$$
\begin{aligned}
& A(x)=a_{0}+a_{3} x^{3}+a_{6} x^{6}+\cdots \\
& B(x)=a_{1}+a_{4} x^{3}+a_{7} x^{6}+\cdots \\
& C(x)=a_{2}+a_{5} x^{3}+a_{8} x^{6}+\cdots
\end{aligned}
$$
Note that $A(x), B(x)$ and $C(x)$ are polynomials with integer coefficients and each of these is a polynomial in $x^{3}$. We may introduce
$$
\begin{aligned}
& S(x)=A(x)+\omega x B(x)+\omega^{2} x^{2} C(x) \\
& T(x)=A(x)+\omega^{2} x B(x)+\omega x^{2} C(x)
\end{aligned}
$$
where $\omega$ is an imaginary cube-root of unity. Then
$$
\begin{aligned}
S(x) T(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} & \\
& -x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
\end{aligned}
$$
since $\omega^{3}=1$ and $\omega+\omega^{2}=-1$. Taking $R(x)=S(x) T(x)$, we obtain
$$
P(x) R(x)=(A(x))^{3}+x^{3}(B(x))^{3}+x^{6}(C(x))^{3}-3 x^{3} A(x) B(x) C(x)
$$
which is a polynomial in $x^{3}$. This follows from the identity
$$
(a+b+c)\left(a^{2}+b^{2}+c^{2}-a b-b c-c a\right)=a^{3}+b^{3}+c^{3}-3 a b c
$$
Alternately, $R(x)$ may be directly defined by
$$
\begin{aligned}
& R(x)=(A(x))^{2}+x^{2}(B(x))^{2}+x^{4}(C(x))^{2} \\
&-x A(x) B(x)-x^{3} B(x) C(x)-x^{2} C(x) A(x)
\end{aligned}
$$
|
{
"resource_path": "INMO/segmented/en-2008.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
89ea6d5e-d442-5fe4-9725-a380347df5df
| 607,838
|
Let $A B C$ be a triangle and let $P$ be an interior point such that $\angle B P C=90^{\circ}, \angle B A P=$ $\angle B C P$. Let $M, N$ be the mid-points of $A C, B C$ respectively. Suppose $B P=2 P M$. Prove that $A, P, N$ are collinear.
|
Extend $C P$ to $D$ such that $C P=P D$. Let $\angle B C P=\alpha=\angle B A P$. Observe that $B P$ is the perpendicular bisector of $C D$. Hence $B C=B D$ and $B C D$ is an isosceles triangle. Thus $\angle B D P=\alpha$. But then $\angle B D P=$ $\alpha=\angle B A P$. This implies that $B, P, A, D$ all lie on a circle. In turn, we conclude that $\angle D A B=\angle D P B=90^{\circ}$. Since $P$ is the midpoint of $C P$ (by construction) and $M$ is the mid-point of $C A$ (given), it follows that $P M$ is parallel to $D A$ and $D A=2 P M=B P$. Thus $D B P A$ is an isosceles trapezium and $D B$ is parallel to $P A$.
We hence get
$$
\angle D P A=\angle B A P=\angle B C P=\angle N P C
$$
the last equality follows from the fact that $\angle B P C=90^{\circ}$, and $N$ is the mid-point of $C B$ so that $N P=N C=N B$ for the right-angled triangle $B P C$. It follows that $A, P, N$ are collinear.
## Alternate Solution:
We use coordinate geometry. Let us take $P=(0,0)$, and the coordinate axes along $P C$ and $P B$; We take $C=(c, 0)$ and $B=(0, b)$. Let $A=(u, v)$. We see that $N=(c / 2, b / 2)$ and $M=((u+c) / 2, v / 2)$. The condition $P B=2 P M$ translates to
$$
(u+c)^{2}+v^{2}=b^{2}
$$
We observe that the slope of $C P=0$; that of $C B$ is $-b / c$; that of $P A$ is $v / u$; and that of $B A$ is $(v-b) / u$. Taking proper signs, we can convert $\angle P C B=\angle P A B$, via tan function, to the following relation:
$$
u^{2}+v^{2}-v b=-c u
$$
Thus we obtain
$$
u(u+c)=v(b-v), \quad c(c+u)=b(b-v)
$$
It follows that $v / u=b / c$. But then we get that the slope of $A P$ and $P N$ are the same. We conclude that $A, P, N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle and let $P$ be an interior point such that $\angle B P C=90^{\circ}, \angle B A P=$ $\angle B C P$. Let $M, N$ be the mid-points of $A C, B C$ respectively. Suppose $B P=2 P M$. Prove that $A, P, N$ are collinear.
|
Extend $C P$ to $D$ such that $C P=P D$. Let $\angle B C P=\alpha=\angle B A P$. Observe that $B P$ is the perpendicular bisector of $C D$. Hence $B C=B D$ and $B C D$ is an isosceles triangle. Thus $\angle B D P=\alpha$. But then $\angle B D P=$ $\alpha=\angle B A P$. This implies that $B, P, A, D$ all lie on a circle. In turn, we conclude that $\angle D A B=\angle D P B=90^{\circ}$. Since $P$ is the midpoint of $C P$ (by construction) and $M$ is the mid-point of $C A$ (given), it follows that $P M$ is parallel to $D A$ and $D A=2 P M=B P$. Thus $D B P A$ is an isosceles trapezium and $D B$ is parallel to $P A$.

We hence get
$$
\angle D P A=\angle B A P=\angle B C P=\angle N P C
$$
the last equality follows from the fact that $\angle B P C=90^{\circ}$, and $N$ is the mid-point of $C B$ so that $N P=N C=N B$ for the right-angled triangle $B P C$. It follows that $A, P, N$ are collinear.
## Alternate Solution:
We use coordinate geometry. Let us take $P=(0,0)$, and the coordinate axes along $P C$ and $P B$; We take $C=(c, 0)$ and $B=(0, b)$. Let $A=(u, v)$. We see that $N=(c / 2, b / 2)$ and $M=((u+c) / 2, v / 2)$. The condition $P B=2 P M$ translates to
$$
(u+c)^{2}+v^{2}=b^{2}
$$
We observe that the slope of $C P=0$; that of $C B$ is $-b / c$; that of $P A$ is $v / u$; and that of $B A$ is $(v-b) / u$. Taking proper signs, we can convert $\angle P C B=\angle P A B$, via tan function, to the following relation:
$$
u^{2}+v^{2}-v b=-c u
$$
Thus we obtain
$$
u(u+c)=v(b-v), \quad c(c+u)=b(b-v)
$$
It follows that $v / u=b / c$. But then we get that the slope of $A P$ and $P N$ are the same. We conclude that $A, P, N$ are collinear.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution:"
}
|
c84a9d7b-9fc7-5308-99fd-99e90b594c55
| 607,839
|
Define a sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ as follows:
$$
a_{n}= \begin{cases}0, & \text { if the number of positive divisors of } n \text { is odd } \\ 1, & \text { if the number of positive divisors of } n \text { is even }\end{cases}
$$
(The positive divisors of $n$ include 1 as well as $n$.) Let $x=0 . a_{1} a_{2} a_{3} \ldots$ be the real number whose decimal expansion contains $a_{n}$ in the $n$-th place, $n \geq 1$. Determine, with proof, whether $x$ is rational or irrational.
|
We show that $x$ is irrational. Suppose that $x$ is rational. Then the sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ is periodic after some stage; there exist natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Choose $m$ such that $m l \geq k$ and $m l$ is a perfect square. Let
$$
m=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{r}^{\alpha_{r}}, \quad l=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \ldots p_{r}^{\beta_{r}}
$$
be the prime decompositions of $m, l$ so that $\alpha_{j}+\beta_{j}$ is even for $1 \leq j \leq r$. Now take a prime $p$ different from $p_{1}, p_{2}, \ldots, p_{r}$. Consider $m l$ and $p m l$. Since $p m l-m l$ is divisible by $l$, we have $a_{p m l}=a_{m l}$. Hence $d(p m l)$ and $d(m l)$ have same parity. But $d(p m l)=2 d(m l)$, since $\operatorname{gcd}(p, m l)=1$ and $p$ is a prime. Since $m l$ is a square, $d(m l)$ is odd. It follows that $d(p m l)$ is even and hence $a_{p m l} \neq a_{m l}$. This contradiction implies that $x$ is irrational.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Define a sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ as follows:
$$
a_{n}= \begin{cases}0, & \text { if the number of positive divisors of } n \text { is odd } \\ 1, & \text { if the number of positive divisors of } n \text { is even }\end{cases}
$$
(The positive divisors of $n$ include 1 as well as $n$.) Let $x=0 . a_{1} a_{2} a_{3} \ldots$ be the real number whose decimal expansion contains $a_{n}$ in the $n$-th place, $n \geq 1$. Determine, with proof, whether $x$ is rational or irrational.
|
We show that $x$ is irrational. Suppose that $x$ is rational. Then the sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ is periodic after some stage; there exist natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Choose $m$ such that $m l \geq k$ and $m l$ is a perfect square. Let
$$
m=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \ldots p_{r}^{\alpha_{r}}, \quad l=p_{1}^{\beta_{1}} p_{2}^{\beta_{2}} \ldots p_{r}^{\beta_{r}}
$$
be the prime decompositions of $m, l$ so that $\alpha_{j}+\beta_{j}$ is even for $1 \leq j \leq r$. Now take a prime $p$ different from $p_{1}, p_{2}, \ldots, p_{r}$. Consider $m l$ and $p m l$. Since $p m l-m l$ is divisible by $l$, we have $a_{p m l}=a_{m l}$. Hence $d(p m l)$ and $d(m l)$ have same parity. But $d(p m l)=2 d(m l)$, since $\operatorname{gcd}(p, m l)=1$ and $p$ is a prime. Since $m l$ is a square, $d(m l)$ is odd. It follows that $d(p m l)$ is even and hence $a_{p m l} \neq a_{m l}$. This contradiction implies that $x$ is irrational.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n2.",
"solution_match": "## Solution:"
}
|
31ba92f5-e13e-5144-af36-62e86b8371d9
| 607,840
|
Define a sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ as follows:
$$
a_{n}= \begin{cases}0, & \text { if the number of positive divisors of } n \text { is odd } \\ 1, & \text { if the number of positive divisors of } n \text { is even }\end{cases}
$$
(The positive divisors of $n$ include 1 as well as $n$.) Let $x=0 . a_{1} a_{2} a_{3} \ldots$ be the real number whose decimal expansion contains $a_{n}$ in the $n$-th place, $n \geq 1$. Determine, with proof, whether $x$ is rational or irrational.
|
As earlier, assume that $x$ is rational and choose natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Consider the numbers $a_{m+1}, a_{m+2}, \ldots, a_{m+l}$, where $m \geq k$ is any number. This must contain at least one 0 . Otherwise $a_{n}=1$ for all $n \geq k$. But $a_{r}=0$ if and only if $r$ is a square. Hence it follows that there are no squares for $n>k$, which is absurd. Thus every $l$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ must contain a 0 after certain stage. Let $t=\max \{k, l\}$, and consider $t^{2}$ and $(t+1)^{2}$. Since there are no squares between $t^{2}$ and $(t+1)^{2}$, we conclude that $a_{t^{2}+j}=1$ for $1 \leq j \leq 2 t$. But then, we have $2 t(>l)$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ which miss 0 , contradicting our earlier observation.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Define a sequence $\left\langle a_{n}\right\rangle_{n=1}^{\infty}$ as follows:
$$
a_{n}= \begin{cases}0, & \text { if the number of positive divisors of } n \text { is odd } \\ 1, & \text { if the number of positive divisors of } n \text { is even }\end{cases}
$$
(The positive divisors of $n$ include 1 as well as $n$.) Let $x=0 . a_{1} a_{2} a_{3} \ldots$ be the real number whose decimal expansion contains $a_{n}$ in the $n$-th place, $n \geq 1$. Determine, with proof, whether $x$ is rational or irrational.
|
As earlier, assume that $x$ is rational and choose natural numbers $k, l$ such that $a_{n}=a_{n+l}$ for all $n \geq k$. Consider the numbers $a_{m+1}, a_{m+2}, \ldots, a_{m+l}$, where $m \geq k$ is any number. This must contain at least one 0 . Otherwise $a_{n}=1$ for all $n \geq k$. But $a_{r}=0$ if and only if $r$ is a square. Hence it follows that there are no squares for $n>k$, which is absurd. Thus every $l$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ must contain a 0 after certain stage. Let $t=\max \{k, l\}$, and consider $t^{2}$ and $(t+1)^{2}$. Since there are no squares between $t^{2}$ and $(t+1)^{2}$, we conclude that $a_{t^{2}+j}=1$ for $1 \leq j \leq 2 t$. But then, we have $2 t(>l)$ consecutive terms of the sequence $\left\langle a_{n}\right\rangle$ which miss 0 , contradicting our earlier observation.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n2.",
"solution_match": "\nAlternative Solution:"
}
|
31ba92f5-e13e-5144-af36-62e86b8371d9
| 607,840
|
All the points in the plane are coloured using three colours. Prove that there exists a triangle with vertices having the same colour such that either it is isosceles or its angles are in geometric progression.
|
Consider a circle of positive radius in the plane and inscribe a regular heptagon $A B C D E F G$ in it. Since the seven vertices of this heptagon are coloured by three colours, some three vertices have the same colour, by pigeon-hole principle. Consider the triangle formed by these three vertices. Let us call the part of the circumference separated by any two consecutive vertices of the heptagon an arc. The three vertices of the same colour are separated by arcs of length $l, m, n$ as we move, say counter-clockwise, along the circle, starting from a fixed vertex among these three, where $l+m+n=7$. Since, the order of $l, m, n$ does not matter for a triangle, there are four possibilities: $1+1+5=7 ; 1+2+4=7 ; 1+3+3=7 ; 2+2+3=7$. In the first, third and fourth cases, we have isosceles triangles. In the second case, we have a triangle whose angles are in geometric progression. The four corresponding figures are shown below.
(i)
(ii)
(iii)
(iv)
In (i), $A B=B C$; in (iii), $A E=B E$; in (iv), $A C=C E$; and in (ii) we see that $\angle D=\pi / 7$, $\angle A=2 \pi / 7$ and $\angle B=4 \pi / 7$ which are in geometric progression.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
All the points in the plane are coloured using three colours. Prove that there exists a triangle with vertices having the same colour such that either it is isosceles or its angles are in geometric progression.
|
Consider a circle of positive radius in the plane and inscribe a regular heptagon $A B C D E F G$ in it. Since the seven vertices of this heptagon are coloured by three colours, some three vertices have the same colour, by pigeon-hole principle. Consider the triangle formed by these three vertices. Let us call the part of the circumference separated by any two consecutive vertices of the heptagon an arc. The three vertices of the same colour are separated by arcs of length $l, m, n$ as we move, say counter-clockwise, along the circle, starting from a fixed vertex among these three, where $l+m+n=7$. Since, the order of $l, m, n$ does not matter for a triangle, there are four possibilities: $1+1+5=7 ; 1+2+4=7 ; 1+3+3=7 ; 2+2+3=7$. In the first, third and fourth cases, we have isosceles triangles. In the second case, we have a triangle whose angles are in geometric progression. The four corresponding figures are shown below.

(i)

(ii)

(iii)

(iv)
In (i), $A B=B C$; in (iii), $A E=B E$; in (iv), $A C=C E$; and in (ii) we see that $\angle D=\pi / 7$, $\angle A=2 \pi / 7$ and $\angle B=4 \pi / 7$ which are in geometric progression.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n4.",
"solution_match": "## Solution:"
}
|
cf6b43ce-05e7-546b-9f9c-5dcc2b40e18f
| 607,842
|
Let $A B C$ be an acute-angled triangle and let $H$ be its ortho-centre. Let $h_{\text {max }}$ denote the largest altitude of the triangle $A B C$. Prove that
$$
A H+B H+C H \leq 2 h_{\max }
$$
|
Let $\angle C$ be the smallest angle, so that $C A \geq A B$ and $C B \geq A B$. In this case the altitude through $C$ is the longest one. Let the altitude through $C$ meet $A B$ in $D$ and let $H$ be the ortho-centre of $A B C$. Let $C D$ extended meet the circum-circle of $A B C$ in $K$. We have $C D=h_{\max }$ so that the inequality to be proved is
$$
A H+B H+C H \leq 2 C D
$$
Using $C D=C H+H D$, this reduces to $A H+B H \leq C D+H D$. However, we observe that $A H=A K, B H=B K$ and $H D=D K$.(For example $B H=B K$ and $D H=D K$ follow from the congruency of the right-angled triangles $D B K$ and $D B H$.)
Thus we need to prove that $A K+B K \leq C K$. Applying Ptolemy's theorem to the cyclic quadrilateral $B C A K$, we get
$$
A B \cdot C K=A C \cdot B K+B C \cdot A K \geq A B \cdot B K+A B \cdot A K
$$
This implies that $C K \geq A K+B K$, which is precisely what we are looking for.
There were other beautiful solutions given by students who participated in INMO-2009. We record them here.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle and let $H$ be its ortho-centre. Let $h_{\text {max }}$ denote the largest altitude of the triangle $A B C$. Prove that
$$
A H+B H+C H \leq 2 h_{\max }
$$
|

Let $\angle C$ be the smallest angle, so that $C A \geq A B$ and $C B \geq A B$. In this case the altitude through $C$ is the longest one. Let the altitude through $C$ meet $A B$ in $D$ and let $H$ be the ortho-centre of $A B C$. Let $C D$ extended meet the circum-circle of $A B C$ in $K$. We have $C D=h_{\max }$ so that the inequality to be proved is
$$
A H+B H+C H \leq 2 C D
$$
Using $C D=C H+H D$, this reduces to $A H+B H \leq C D+H D$. However, we observe that $A H=A K, B H=B K$ and $H D=D K$.(For example $B H=B K$ and $D H=D K$ follow from the congruency of the right-angled triangles $D B K$ and $D B H$.)
Thus we need to prove that $A K+B K \leq C K$. Applying Ptolemy's theorem to the cyclic quadrilateral $B C A K$, we get
$$
A B \cdot C K=A C \cdot B K+B C \cdot A K \geq A B \cdot B K+A B \cdot A K
$$
This implies that $C K \geq A K+B K$, which is precisely what we are looking for.
There were other beautiful solutions given by students who participated in INMO-2009. We record them here.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
c33a6239-0964-5cd7-9acf-d583cf125de5
| 607,843
|
Let $a, b, c$ be positive real numbers such that $a^{3}+b^{3}=c^{3}$. Prove that
$$
a^{2}+b^{2}-c^{2}>6(c-a)(c-b)
$$
|
The given inequality may be written in the form
$$
7 c^{2}-6(a+b) c-\left(a^{2}+b^{2}-6 a b\right)<0
$$
Putting $x=7 c^{2}, y=-6(a+b) c, z=-\left(a^{2}+b^{2}-6 a b\right)$, we have to prove that $x+y+z<0$. Observe that $x, y, z$ are not all equal $(x>0, y<0)$. Using the identity
$$
x^{3}+y^{3}+z^{3}-3 x y z=\frac{1}{2}(x+y+z)\left[(x-y)^{2}+(y-z)^{2}+(z-x)^{2}\right]
$$
we infer that it is sufficient to prove $x^{3}+y^{3}+z^{3}-3 x y z<0$. Substituting the values of $x, y, z$, we see that this is equivalent to
$$
343 c^{6}-216(a+b)^{3} c^{3}-\left(a^{2}+b^{2}-6 a b\right)^{3}-126 c^{3}(a+b)\left(a^{2}+b^{2}-6 a b\right)<0
$$
Using $c^{3}=a^{3}+b^{3}$, this reduces to
$343\left(a^{3}+b^{3}\right)^{2}-216(a+b)^{3}\left(a^{3}+b^{3}\right)-\left(a^{2}+b^{2}-6 a b\right)^{3}-126\left(\left(a^{3}+b^{3}\right)(a+b)\left(a^{2}+b^{2}-6 a b\right)<0\right.$.
This may be simplified (after some tedious calculations) to,
$$
-a^{2} b^{2}\left(129 a^{2}-254 a b+129 b^{2}\right)<0
$$
But $129 a^{2}-254 a b+129 b^{2}=129(a-b)^{2}+4 a b>0$. Hence the result follows.
Remark: The best constant $\theta$ in the inequality $a^{2}+b^{2}-c^{2} \geq \theta(c-a)(c-b)$, where $a, b, c$
are positive reals such that $a^{3}+b^{3}=c^{3}$, is $\theta=2\left(1+2^{1 / 3}+2^{-1 / 3}\right)$.
Here again, there were some beautiful solutions given by students.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a^{3}+b^{3}=c^{3}$. Prove that
$$
a^{2}+b^{2}-c^{2}>6(c-a)(c-b)
$$
|
The given inequality may be written in the form
$$
7 c^{2}-6(a+b) c-\left(a^{2}+b^{2}-6 a b\right)<0
$$
Putting $x=7 c^{2}, y=-6(a+b) c, z=-\left(a^{2}+b^{2}-6 a b\right)$, we have to prove that $x+y+z<0$. Observe that $x, y, z$ are not all equal $(x>0, y<0)$. Using the identity
$$
x^{3}+y^{3}+z^{3}-3 x y z=\frac{1}{2}(x+y+z)\left[(x-y)^{2}+(y-z)^{2}+(z-x)^{2}\right]
$$
we infer that it is sufficient to prove $x^{3}+y^{3}+z^{3}-3 x y z<0$. Substituting the values of $x, y, z$, we see that this is equivalent to
$$
343 c^{6}-216(a+b)^{3} c^{3}-\left(a^{2}+b^{2}-6 a b\right)^{3}-126 c^{3}(a+b)\left(a^{2}+b^{2}-6 a b\right)<0
$$
Using $c^{3}=a^{3}+b^{3}$, this reduces to
$343\left(a^{3}+b^{3}\right)^{2}-216(a+b)^{3}\left(a^{3}+b^{3}\right)-\left(a^{2}+b^{2}-6 a b\right)^{3}-126\left(\left(a^{3}+b^{3}\right)(a+b)\left(a^{2}+b^{2}-6 a b\right)<0\right.$.
This may be simplified (after some tedious calculations) to,
$$
-a^{2} b^{2}\left(129 a^{2}-254 a b+129 b^{2}\right)<0
$$
But $129 a^{2}-254 a b+129 b^{2}=129(a-b)^{2}+4 a b>0$. Hence the result follows.
Remark: The best constant $\theta$ in the inequality $a^{2}+b^{2}-c^{2} \geq \theta(c-a)(c-b)$, where $a, b, c$
are positive reals such that $a^{3}+b^{3}=c^{3}$, is $\theta=2\left(1+2^{1 / 3}+2^{-1 / 3}\right)$.
Here again, there were some beautiful solutions given by students.
|
{
"resource_path": "INMO/segmented/en-2009.jsonl",
"problem_match": "\n6.",
"solution_match": "## Solution:"
}
|
bb56b1fd-cbc3-55d1-aff2-0a7894d0a1be
| 607,844
|
Let $A B C$ be a triangle with circum-circle $\Gamma$. Let $M$ be a point in the interior of triangle $A B C$ which is also on the bisector of $\angle A$. Let $A M, B M, C M$ meet $\Gamma$ in $A_{1}, B_{1}, C_{1}$ respectively. Suppose $P$ is the point of intersection of $A_{1} C_{1}$ with $A B$; and $Q$ is the point of intersection of $A_{1} B_{1}$ with $A C$. Prove that $P Q$ is parallel to $B C$.
|
Let $A=2 \alpha$. Then $\angle A_{1} A C=\angle B A A_{1}=\alpha$. Thus
$$
\angle A_{1} B_{1} C=\alpha=\angle B B_{1} A_{1}=\angle A_{1} C_{1} C=\angle B C_{1} A_{1}
$$
We also have $\angle B_{1} C Q=\angle A A_{1} B_{1}=\beta$, say. It follows that triangles $M A_{1} B_{1}$ and $Q C B_{1}$ are similar and hence
$$
\frac{Q C}{M A_{1}}=\frac{B_{1} C}{B_{1} A_{1}}
$$
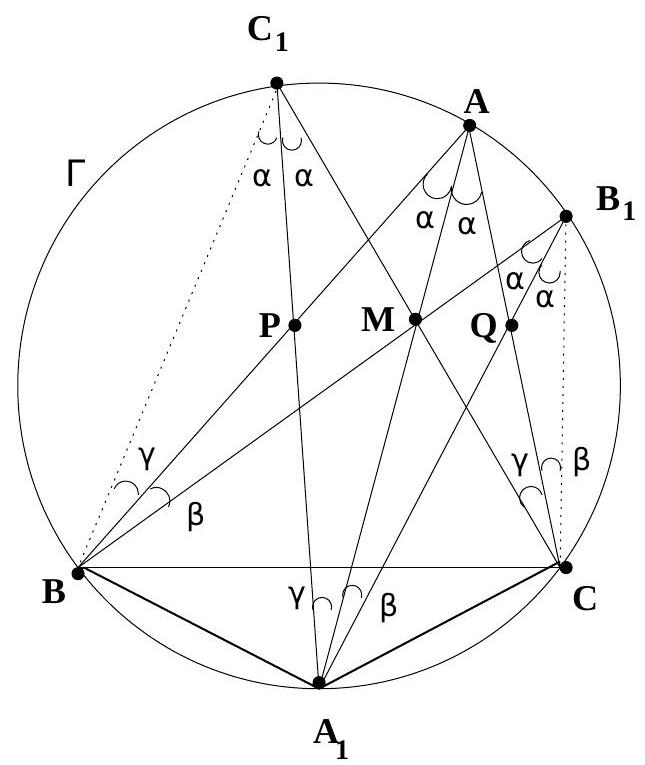
Similarly, triangles $A C M$ and $C_{1} A_{1} M$ are similar and we get
$$
\frac{A C}{A M}=\frac{C_{1} A_{1}}{C_{1} M}
$$
Using the point $P$, we get similar ratios:
$$
\frac{P B}{M A_{1}}=\frac{C_{1} B}{A_{1} C_{1}}, \quad \frac{A B}{A M}=\frac{A_{1} B_{1}}{M B_{1}}
$$
Thus,
$$
\frac{Q C}{P B}=\frac{A_{1} C_{1} \cdot B_{1} C}{C_{1} B \cdot B_{1} A_{1}}
$$
and
$$
\begin{aligned}
\frac{A C}{A B} & =\frac{M B_{1} \cdot C_{1} A_{1}}{A_{1} B_{1} \cdot C_{1} M} \\
& =\frac{M B_{1}}{C_{1} M} \frac{C_{1} A_{1}}{A_{1} B_{1}}=\frac{M B_{1}}{C_{1} M} \frac{C_{1} B \cdot Q C}{P B \cdot B_{1} C}
\end{aligned}
$$
However, triangles $C_{1} B M$ and $B_{1} C M$ are similar, which gives
$$
\frac{B_{1} C}{C_{1} B}=\frac{M B_{1}}{M C_{1}}
$$
Putting this in the last expression, we get
$$
\frac{A C}{A B}=\frac{Q C}{P B}
$$
We conclude that $P Q$ is parallel to $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circum-circle $\Gamma$. Let $M$ be a point in the interior of triangle $A B C$ which is also on the bisector of $\angle A$. Let $A M, B M, C M$ meet $\Gamma$ in $A_{1}, B_{1}, C_{1}$ respectively. Suppose $P$ is the point of intersection of $A_{1} C_{1}$ with $A B$; and $Q$ is the point of intersection of $A_{1} B_{1}$ with $A C$. Prove that $P Q$ is parallel to $B C$.
|
Let $A=2 \alpha$. Then $\angle A_{1} A C=\angle B A A_{1}=\alpha$. Thus
$$
\angle A_{1} B_{1} C=\alpha=\angle B B_{1} A_{1}=\angle A_{1} C_{1} C=\angle B C_{1} A_{1}
$$
We also have $\angle B_{1} C Q=\angle A A_{1} B_{1}=\beta$, say. It follows that triangles $M A_{1} B_{1}$ and $Q C B_{1}$ are similar and hence
$$
\frac{Q C}{M A_{1}}=\frac{B_{1} C}{B_{1} A_{1}}
$$

Similarly, triangles $A C M$ and $C_{1} A_{1} M$ are similar and we get
$$
\frac{A C}{A M}=\frac{C_{1} A_{1}}{C_{1} M}
$$
Using the point $P$, we get similar ratios:
$$
\frac{P B}{M A_{1}}=\frac{C_{1} B}{A_{1} C_{1}}, \quad \frac{A B}{A M}=\frac{A_{1} B_{1}}{M B_{1}}
$$
Thus,
$$
\frac{Q C}{P B}=\frac{A_{1} C_{1} \cdot B_{1} C}{C_{1} B \cdot B_{1} A_{1}}
$$
and
$$
\begin{aligned}
\frac{A C}{A B} & =\frac{M B_{1} \cdot C_{1} A_{1}}{A_{1} B_{1} \cdot C_{1} M} \\
& =\frac{M B_{1}}{C_{1} M} \frac{C_{1} A_{1}}{A_{1} B_{1}}=\frac{M B_{1}}{C_{1} M} \frac{C_{1} B \cdot Q C}{P B \cdot B_{1} C}
\end{aligned}
$$
However, triangles $C_{1} B M$ and $B_{1} C M$ are similar, which gives
$$
\frac{B_{1} C}{C_{1} B}=\frac{M B_{1}}{M C_{1}}
$$
Putting this in the last expression, we get
$$
\frac{A C}{A B}=\frac{Q C}{P B}
$$
We conclude that $P Q$ is parallel to $B C$.
|
{
"resource_path": "INMO/segmented/en-2010.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
ff587e37-226c-5387-8a98-d14deb8cc3bf
| 607,845
|
Let $A B C$ be an acute-angled triangle with altitude $A K$. Let $H$ be its ortho-centre and $O$ be its circum-centre. Suppose $K O H$ is an acute-angled triangle and $P$ its circum-centre. Let $Q$ be the reflection of $P$ in the line $H O$. Show that $Q$ lies on the line joining the mid-points of $A B$ and $A C$.
|
Let $D$ be the mid-point of $B C ; M$ that of $H K$; and $T$ that of $O H$. Then $P M$ is perpendicular to $H K$ and $P T$ is perpendicular to $O H$. Since $Q$ is the reflection of $P$ in $H O$, we observe that $P, T, Q$ are collinear, and $P T=T Q$. Let $Q L, T N$ and $O S$ be the perpendiculars drawn respectively from $Q, T$ and $O$ on to the altitude $A K$.(See the figure.)
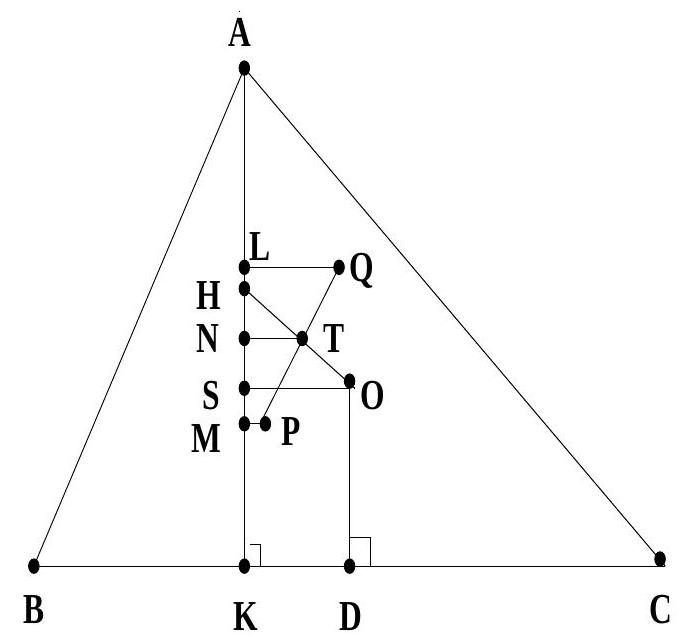
We have $L N=N M$, since $T$ is the mid-point of $Q P ; H N=N S$, since $T$ is the mid-point of $O H$; and $H M=M K$, as $P$ is the circum-centre of $K H O$. We obtain
$$
L H+H N=L N=N M=N S+S M
$$
which gives $L H=S M$. We know that $A H=2 O D$. Thus
$$
\begin{aligned}
A L=A H & -L H=2 O D-L H=2 S K-S M=S K+(S K-S M)=S K+M K \\
& =S K+H M=S K+H S+S M=S K+H S+L H=S K+L S=L K
\end{aligned}
$$
This shows that $L$ is the mid-point of $A K$ and hence lies on the line joining the midpoints of $A B$ and $A C$. We observe that the line joining the mid-points of $A B$ and $A C$ is also perpendicular to $A K$. Since $Q L$ is perpendicular to $A K$, we conclude that $Q$ also lies on the line joining the mid-points of $A B$ and $A C$.
Remark: It may happen that $H$ is above $L$ as in the adjoining figure, but the result remains true here as well. We have $H N=N S, L N=N M$, and $H M=$ $M K$ as earlier. Thus $H N=H L+L N$ and $N S=$ $S M+N M$ give $H L=S M$. Now $A L=A H+H L=$ $2 O D+S M=2 S K+S M=S K+(S K+S M)=$ $S K+M K=S K+H M=S K+H L+L M=S K+$ $S M+L M=L K$. The conclusion that $Q$ lies on the line joining the mid-points of $A B$ and $A C$ follows as earlier.
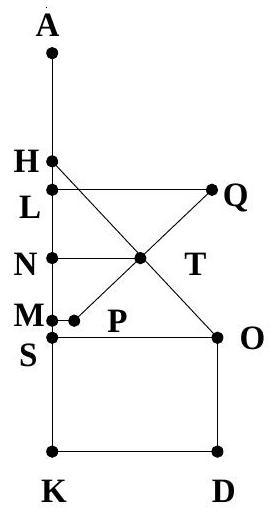
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with altitude $A K$. Let $H$ be its ortho-centre and $O$ be its circum-centre. Suppose $K O H$ is an acute-angled triangle and $P$ its circum-centre. Let $Q$ be the reflection of $P$ in the line $H O$. Show that $Q$ lies on the line joining the mid-points of $A B$ and $A C$.
|
Let $D$ be the mid-point of $B C ; M$ that of $H K$; and $T$ that of $O H$. Then $P M$ is perpendicular to $H K$ and $P T$ is perpendicular to $O H$. Since $Q$ is the reflection of $P$ in $H O$, we observe that $P, T, Q$ are collinear, and $P T=T Q$. Let $Q L, T N$ and $O S$ be the perpendiculars drawn respectively from $Q, T$ and $O$ on to the altitude $A K$.(See the figure.)

We have $L N=N M$, since $T$ is the mid-point of $Q P ; H N=N S$, since $T$ is the mid-point of $O H$; and $H M=M K$, as $P$ is the circum-centre of $K H O$. We obtain
$$
L H+H N=L N=N M=N S+S M
$$
which gives $L H=S M$. We know that $A H=2 O D$. Thus
$$
\begin{aligned}
A L=A H & -L H=2 O D-L H=2 S K-S M=S K+(S K-S M)=S K+M K \\
& =S K+H M=S K+H S+S M=S K+H S+L H=S K+L S=L K
\end{aligned}
$$
This shows that $L$ is the mid-point of $A K$ and hence lies on the line joining the midpoints of $A B$ and $A C$. We observe that the line joining the mid-points of $A B$ and $A C$ is also perpendicular to $A K$. Since $Q L$ is perpendicular to $A K$, we conclude that $Q$ also lies on the line joining the mid-points of $A B$ and $A C$.
Remark: It may happen that $H$ is above $L$ as in the adjoining figure, but the result remains true here as well. We have $H N=N S, L N=N M$, and $H M=$ $M K$ as earlier. Thus $H N=H L+L N$ and $N S=$ $S M+N M$ give $H L=S M$. Now $A L=A H+H L=$ $2 O D+S M=2 S K+S M=S K+(S K+S M)=$ $S K+M K=S K+H M=S K+H L+L M=S K+$ $S M+L M=L K$. The conclusion that $Q$ lies on the line joining the mid-points of $A B$ and $A C$ follows as earlier.

|
{
"resource_path": "INMO/segmented/en-2010.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
08e31e8d-1d68-51d2-8407-ab7135ef18d8
| 607,849
|
Define a sequence $\left\langle a_{n}\right\rangle_{n \geq 0}$ by $a_{0}=0, a_{1}=1$ and
$$
a_{n}=2 a_{n-1}+a_{n-2}
$$
for $n \geq 2$.
(a) For every $m>0$ and $0 \leq j \leq m$, prove that $2 a_{m}$ divides $a_{m+j}+(-1)^{j} a_{m-j}$.
(b) Suppose $2^{k}$ divides $n$ for some natural numbers $n$ and $k$. Prove that $2^{k}$ divides $a_{n}$.
|
(a) Consider $f(j)=a_{m+j}+(-1)^{j} a_{m-j}, 0 \leq j \leq m$, where $m$ is a natural number. We observe that $f(0)=2 a_{m}$ is divisible by $2 a_{m}$. Similarly,
$$
f(1)=a_{m+1}-a_{m-1}=2 a_{m}
$$
is also divisible by $2 a_{m}$. Assume that $2 a_{m}$ divides $f(j)$ for all $0 \leq j<l$, where $l \leq m$. We prove that $2 a_{m}$ divides $f(l)$. Observe
$$
\begin{aligned}
& f(l-1)=a_{m+l-1}+(-1)^{l-1} a_{m-l+1} \\
& f(l-2)=a_{m+l-2}+(-1)^{l-2} a_{m-l+2}
\end{aligned}
$$
Thus we have
$$
\begin{aligned}
a_{m+l} & =2 a_{m+l-1}+a_{m+l-2} \\
& =2 f(l-1)-2(-1)^{l-1} a_{m-l+1}+f(l-2)-(-1)^{l-2} a_{m-l+2} \\
& =2 f(l-1)+f(l-2)+(-1)^{l-1}\left(a_{m-l+2}-2 a_{m-l+1}\right) \\
& =2 f(l-1)+f(l-2)+(-1)^{l-1} a_{m-l}
\end{aligned}
$$
This gives
$$
f(l)=2 f(l-1)+f(l-2)
$$
By induction hypothesis $2 a_{m}$ divides $f(l-1)$ and $f(l-2)$. Hence $2 a_{m}$ divides $f(l)$. We conclude that $2 a_{m}$ divides $f(j)$ for $0 \leq j \leq m$.
(b) We see that $f(m)=a_{2 m}$. Hence $2 a_{m}$ divides $a_{2 m}$ for all natural numbers $m$. Let $n=2^{k} l$ for some $l \geq 1$. Taking $m=2^{k-1} l$, we see that $2 a_{m}$ divides $a_{n}$. Using an easy induction, we conclude that $2^{k} a_{l}$ divides $a_{n}$. In particular $2^{k}$ divides $a_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Define a sequence $\left\langle a_{n}\right\rangle_{n \geq 0}$ by $a_{0}=0, a_{1}=1$ and
$$
a_{n}=2 a_{n-1}+a_{n-2}
$$
for $n \geq 2$.
(a) For every $m>0$ and $0 \leq j \leq m$, prove that $2 a_{m}$ divides $a_{m+j}+(-1)^{j} a_{m-j}$.
(b) Suppose $2^{k}$ divides $n$ for some natural numbers $n$ and $k$. Prove that $2^{k}$ divides $a_{n}$.
|
(a) Consider $f(j)=a_{m+j}+(-1)^{j} a_{m-j}, 0 \leq j \leq m$, where $m$ is a natural number. We observe that $f(0)=2 a_{m}$ is divisible by $2 a_{m}$. Similarly,
$$
f(1)=a_{m+1}-a_{m-1}=2 a_{m}
$$
is also divisible by $2 a_{m}$. Assume that $2 a_{m}$ divides $f(j)$ for all $0 \leq j<l$, where $l \leq m$. We prove that $2 a_{m}$ divides $f(l)$. Observe
$$
\begin{aligned}
& f(l-1)=a_{m+l-1}+(-1)^{l-1} a_{m-l+1} \\
& f(l-2)=a_{m+l-2}+(-1)^{l-2} a_{m-l+2}
\end{aligned}
$$
Thus we have
$$
\begin{aligned}
a_{m+l} & =2 a_{m+l-1}+a_{m+l-2} \\
& =2 f(l-1)-2(-1)^{l-1} a_{m-l+1}+f(l-2)-(-1)^{l-2} a_{m-l+2} \\
& =2 f(l-1)+f(l-2)+(-1)^{l-1}\left(a_{m-l+2}-2 a_{m-l+1}\right) \\
& =2 f(l-1)+f(l-2)+(-1)^{l-1} a_{m-l}
\end{aligned}
$$
This gives
$$
f(l)=2 f(l-1)+f(l-2)
$$
By induction hypothesis $2 a_{m}$ divides $f(l-1)$ and $f(l-2)$. Hence $2 a_{m}$ divides $f(l)$. We conclude that $2 a_{m}$ divides $f(j)$ for $0 \leq j \leq m$.
(b) We see that $f(m)=a_{2 m}$. Hence $2 a_{m}$ divides $a_{2 m}$ for all natural numbers $m$. Let $n=2^{k} l$ for some $l \geq 1$. Taking $m=2^{k-1} l$, we see that $2 a_{m}$ divides $a_{n}$. Using an easy induction, we conclude that $2^{k} a_{l}$ divides $a_{n}$. In particular $2^{k}$ divides $a_{n}$.
|
{
"resource_path": "INMO/segmented/en-2010.jsonl",
"problem_match": "\n6.",
"solution_match": "## Solution:"
}
|
83d2ded2-3bb0-5a62-b531-2ad7941d0670
| 607,850
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
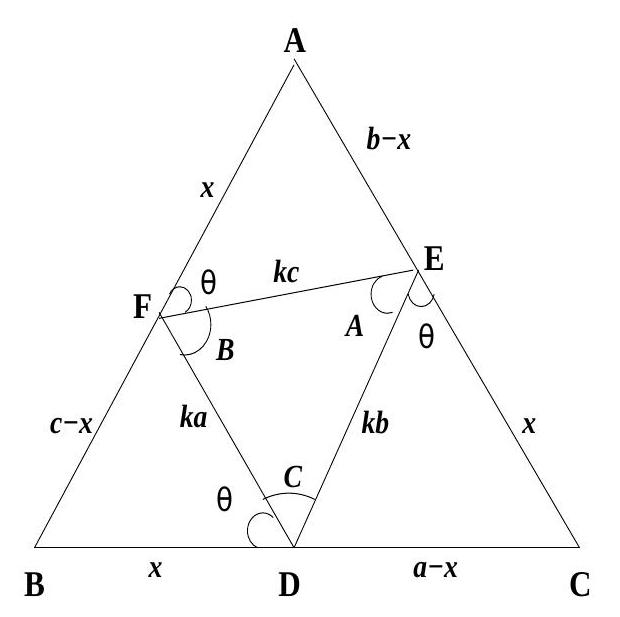
Let $B D=C E=A F=x ; \angle B D F=$ $\angle C E D=\angle A F E=\theta$. Note that $\angle A F D=$ $B+\theta$, and hence $\angle D F E=B$. Similarly, $\angle E D F=C$ and $\angle F E D=A$. Thus the triangle $E F D$ is similar to $A B C$. We may take $F D=k a, D E=k b$ and $E F=k c$, for some positive real constant $k$. Applying sine rule to triangle $B F D$, we obtain
$$
\frac{c-x}{\sin \theta}=\frac{k a}{\sin B}=\frac{2 R k a}{b}
$$
where $R$ is the circum-radius of $A B C$. Thus we get $2 R k \sin \theta=b(c-x) / a$. Similarly, we obtain $2 R k \sin \theta=c(a-x) / b$ and $2 R k \sin \theta=$ $a(b-x) / c$. We therefore get
$$
\frac{b(c-x)}{a}=\frac{c(a-x)}{b}=\frac{a(b-x)}{c}
$$
If some two sides are equal, say, $a=b$, then $a(c-x)=c(a-x)$ giving $a=c$; we get $a=b=c$ and $A B C$ is equilateral. Suppose no two sides of $A B C$ are equal. We may assume $a$ is the least. Since (1) is cyclic in $a, b, c$, we have to consider two cases: $a<b<c$ and $a<c<b$.
In this case $a<c$ and hence $b(c-x)<a(b-x)$, from (1). Since $b>a$ and $c-x>b-x$, we get $b(c-x)>a(b-x)$, which is a contradiction.
Case 2. $\underline{a<c<b}$.
We may write (1) in the form
$$
\frac{(c-x)}{a / b}=\frac{(a-x)}{b / c}=\frac{(b-x)}{c / a}
$$
Now $a<c$ gives $a-x<c-x$ so that $\frac{b}{c}<\frac{a}{b}$. This gives $b^{2}<a c$. But $b>a$ and $b>c$, so that $b^{2}>a c$, which again leads to a contradiction
Thus Case 1 and Case 2 cannot occur. We conclude that $a=b=c$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|

Let $B D=C E=A F=x ; \angle B D F=$ $\angle C E D=\angle A F E=\theta$. Note that $\angle A F D=$ $B+\theta$, and hence $\angle D F E=B$. Similarly, $\angle E D F=C$ and $\angle F E D=A$. Thus the triangle $E F D$ is similar to $A B C$. We may take $F D=k a, D E=k b$ and $E F=k c$, for some positive real constant $k$. Applying sine rule to triangle $B F D$, we obtain
$$
\frac{c-x}{\sin \theta}=\frac{k a}{\sin B}=\frac{2 R k a}{b}
$$
where $R$ is the circum-radius of $A B C$. Thus we get $2 R k \sin \theta=b(c-x) / a$. Similarly, we obtain $2 R k \sin \theta=c(a-x) / b$ and $2 R k \sin \theta=$ $a(b-x) / c$. We therefore get
$$
\frac{b(c-x)}{a}=\frac{c(a-x)}{b}=\frac{a(b-x)}{c}
$$
If some two sides are equal, say, $a=b$, then $a(c-x)=c(a-x)$ giving $a=c$; we get $a=b=c$ and $A B C$ is equilateral. Suppose no two sides of $A B C$ are equal. We may assume $a$ is the least. Since (1) is cyclic in $a, b, c$, we have to consider two cases: $a<b<c$ and $a<c<b$.
In this case $a<c$ and hence $b(c-x)<a(b-x)$, from (1). Since $b>a$ and $c-x>b-x$, we get $b(c-x)>a(b-x)$, which is a contradiction.
Case 2. $\underline{a<c<b}$.
We may write (1) in the form
$$
\frac{(c-x)}{a / b}=\frac{(a-x)}{b / c}=\frac{(b-x)}{c / a}
$$
Now $a<c$ gives $a-x<c-x$ so that $\frac{b}{c}<\frac{a}{b}$. This gives $b^{2}<a c$. But $b>a$ and $b>c$, so that $b^{2}>a c$, which again leads to a contradiction
Thus Case 1 and Case 2 cannot occur. We conclude that $a=b=c$.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n1.",
"solution_match": "## Solution 1:"
}
|
6d789d05-50ec-5549-ac39-b4fe3feff6cb
| 607,851
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
We write (1) in the form (2), and start from there. The case of two equal sides is dealt as in Solution 1. We assume no two sides are equal. Using ratio properties in (2), we obtain
$$
\frac{a-b}{\left(a b-c^{2}\right) / c a}=\frac{b-c}{\left(b c-a^{2}\right) / a b}
$$
This may be written as $c(a-b)\left(b c-a^{2}\right)=b(b-c)\left(a b-c^{2}\right)$. Further simplification gives $a b^{3}+b c^{3}+c a^{3}=a b c(a+b+c)$. This may be further written in the form
$$
a b^{2}(b-c)+b c^{2}(c-a)+c a^{2}(a-b)=0
$$
If $a<b<c$, we write (3) in the form
$$
0=a b^{2}(b-c)+b c^{2}(c-b+b-a)+c a^{2}(a-b)=b(c-b)\left(c^{2}-a b\right)+c(b-a)\left(b c-a^{2}\right)
$$
Since $c>b, c^{2}>a b, b>a$ and $b c>a^{2}$, this is impossible. If $a<c<b$, we write (3), as in previous case, in the form
$$
0=a(b-c)\left(b^{2}-c a\right)+c(c-a)\left(b c-a^{2}\right)
$$
which again is impossible.
One can also use inequalities: we can show that $a b^{3}+b c^{3}+c a^{3} \geq a b c(a+b+c)$, and equality holds if and only if $a=b=c$. Here are some ways of deriving it:
(i) We can write the inequality in the form
$$
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
$$
Adding $a+b+c$ both sides, this takes the form
$$
\frac{b^{2}}{c}+c+\frac{c^{2}}{a}+a+\frac{a^{2}}{b}+b \geq 2(a+b+c)
$$
But AM-GM inequality gives
$$
\frac{b^{2}}{c}+c \geq 2 b, \quad \frac{c^{2}}{a}+a \geq 2 a, \quad \frac{a^{2}}{b}+b \geq 2 a
$$
Hence the inequality follows and equality holds if and only if $a=b=c$.
(ii) Again we write the inequality in the form
$$
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
$$
We use $b / c$ with weight $b, c / a$ with weight $c$ and $a / b$ with weight $a$, and apply weighted AM-HM inequality:
$$
b \cdot \frac{b}{c}+c \cdot \frac{c}{a}+a \cdot \frac{a}{b} \geq \frac{(a+b+c)^{2}}{b \cdot \frac{c}{b}+c \cdot \frac{a}{c}+a \cdot \frac{b}{a}}
$$
which reduces to $a+b+c$. Again equality holds if and only if $a=b=c$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
We write (1) in the form (2), and start from there. The case of two equal sides is dealt as in Solution 1. We assume no two sides are equal. Using ratio properties in (2), we obtain
$$
\frac{a-b}{\left(a b-c^{2}\right) / c a}=\frac{b-c}{\left(b c-a^{2}\right) / a b}
$$
This may be written as $c(a-b)\left(b c-a^{2}\right)=b(b-c)\left(a b-c^{2}\right)$. Further simplification gives $a b^{3}+b c^{3}+c a^{3}=a b c(a+b+c)$. This may be further written in the form
$$
a b^{2}(b-c)+b c^{2}(c-a)+c a^{2}(a-b)=0
$$
If $a<b<c$, we write (3) in the form
$$
0=a b^{2}(b-c)+b c^{2}(c-b+b-a)+c a^{2}(a-b)=b(c-b)\left(c^{2}-a b\right)+c(b-a)\left(b c-a^{2}\right)
$$
Since $c>b, c^{2}>a b, b>a$ and $b c>a^{2}$, this is impossible. If $a<c<b$, we write (3), as in previous case, in the form
$$
0=a(b-c)\left(b^{2}-c a\right)+c(c-a)\left(b c-a^{2}\right)
$$
which again is impossible.
One can also use inequalities: we can show that $a b^{3}+b c^{3}+c a^{3} \geq a b c(a+b+c)$, and equality holds if and only if $a=b=c$. Here are some ways of deriving it:
(i) We can write the inequality in the form
$$
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
$$
Adding $a+b+c$ both sides, this takes the form
$$
\frac{b^{2}}{c}+c+\frac{c^{2}}{a}+a+\frac{a^{2}}{b}+b \geq 2(a+b+c)
$$
But AM-GM inequality gives
$$
\frac{b^{2}}{c}+c \geq 2 b, \quad \frac{c^{2}}{a}+a \geq 2 a, \quad \frac{a^{2}}{b}+b \geq 2 a
$$
Hence the inequality follows and equality holds if and only if $a=b=c$.
(ii) Again we write the inequality in the form
$$
\frac{b^{2}}{c}+\frac{c^{2}}{a}+\frac{a^{2}}{b} \geq a+b+c
$$
We use $b / c$ with weight $b, c / a$ with weight $c$ and $a / b$ with weight $a$, and apply weighted AM-HM inequality:
$$
b \cdot \frac{b}{c}+c \cdot \frac{c}{a}+a \cdot \frac{a}{b} \geq \frac{(a+b+c)^{2}}{b \cdot \frac{c}{b}+c \cdot \frac{a}{c}+a \cdot \frac{b}{a}}
$$
which reduces to $a+b+c$. Again equality holds if and only if $a=b=c$.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution 2."
}
|
6d789d05-50ec-5549-ac39-b4fe3feff6cb
| 607,851
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
Here is a pure geometric solution given by a student. Consider the triangle $B D F, C E D$ and $A F E$ with $B D, C E$ and $A F$ as bases. The sides $D F, E D$ and $F E$ make equal angles $\theta$ with the bases of respective triangles. If $B \geq C \geq A$, then it is easy to see that $F D \geq D E \geq E F$. Now using the triangle $F D E$, we see that $B \geq C \geq A$ gives $D E \geq E F \geq F D$. Combining, you get $F D=D E=E F$ and hence $A=B=\bar{C}=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D, E, F$ be points on the sides $B C, C A, A B$ respectively of a triangle $A B C$ such that $B D=C E=A F$ and $\angle B D F=\angle C E D=\angle A F E$. Prove that $A B C$ is equilateral.
|
Here is a pure geometric solution given by a student. Consider the triangle $B D F, C E D$ and $A F E$ with $B D, C E$ and $A F$ as bases. The sides $D F, E D$ and $F E$ make equal angles $\theta$ with the bases of respective triangles. If $B \geq C \geq A$, then it is easy to see that $F D \geq D E \geq E F$. Now using the triangle $F D E$, we see that $B \geq C \geq A$ gives $D E \geq E F \geq F D$. Combining, you get $F D=D E=E F$ and hence $A=B=\bar{C}=60^{\circ}$.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution 3."
}
|
6d789d05-50ec-5549-ac39-b4fe3feff6cb
| 607,851
|
Consider two polynomials $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ and $Q(x)=b_{n} x^{n}+$ $b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0}$ with integer coefficients such that $a_{n}-b_{n}$ is a prime, $a_{n-1}=b_{n-1}$ and $a_{n} b_{0}-a_{0} b_{n} \neq 0$. Suppose there exists a rational number $r$ such that $P(r)=Q(r)=0$. Prove that $r$ is an integer.
|
Let $r=u / v$ where $\operatorname{gcd}(u, v)=1$. Then we get
$$
\begin{array}{r}
a_{n} u^{n}+a_{n-1} u^{n-1} v+\cdots+a_{1} u v^{n-1}+a_{0} v^{n}=0 \\
b_{n} u^{n}+b_{n-1} u^{n-1} v+\cdots+b_{1} u v^{n-1}+b_{0} v^{n}=0
\end{array}
$$
Subtraction gives
$$
\left(a_{n}-b_{n}\right) u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v^{2}+\cdots+\left(a_{1}-b_{1}\right) u v^{n-1}+\left(a_{0}-b_{0}\right) v^{n}=0
$$
since $a_{n-1}=b_{n-1}$. This shows that $v$ divides $\left(a_{n}-b_{n}\right) u^{n}$ and hence it divides $a_{n}-b_{n}$. Since $a_{n}-b_{n}$ is a prime, either $v=1$ or $v=a_{n}-b_{n}$. Suppose the latter holds. The relation takes the form
$$
u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v+\cdots+\left(a_{1}-b_{1}\right) u v^{n-2}+\left(a_{0}-b_{0}\right) v^{n-1}=0
$$
(Here we have divided through-out by $v$.) If $n>1$, this forces $v \mid u$, which is impossible since $\operatorname{gcd}(v, u)=1\left(v>1\right.$ since it is equal to the prime $\left.a_{n}-b_{n}\right)$. If $n=1$, then we get two equations:
$$
\begin{aligned}
a_{1} u+a_{0} v & =0 \\
b_{1} u+b_{0} v & =0
\end{aligned}
$$
This forces $a_{1} b_{0}-a_{0} b_{1}=0$ contradicting $a_{n} b_{0}-a_{0} b_{n} \neq 0$. (Note: The condition $a_{n} b_{0}-a_{0} b_{n} \neq 0$ is extraneous. The condition $a_{n-1}=b_{n-1}$ forces that for $n=1$, we have $a_{0}=b_{0}$. Thus we obtain, after subtraction
$$
\left(a_{1}-b_{1}\right) u=0
$$
This implies that $u=0$ and hence $r=0$ is an integer.)
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Consider two polynomials $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$ and $Q(x)=b_{n} x^{n}+$ $b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0}$ with integer coefficients such that $a_{n}-b_{n}$ is a prime, $a_{n-1}=b_{n-1}$ and $a_{n} b_{0}-a_{0} b_{n} \neq 0$. Suppose there exists a rational number $r$ such that $P(r)=Q(r)=0$. Prove that $r$ is an integer.
|
Let $r=u / v$ where $\operatorname{gcd}(u, v)=1$. Then we get
$$
\begin{array}{r}
a_{n} u^{n}+a_{n-1} u^{n-1} v+\cdots+a_{1} u v^{n-1}+a_{0} v^{n}=0 \\
b_{n} u^{n}+b_{n-1} u^{n-1} v+\cdots+b_{1} u v^{n-1}+b_{0} v^{n}=0
\end{array}
$$
Subtraction gives
$$
\left(a_{n}-b_{n}\right) u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v^{2}+\cdots+\left(a_{1}-b_{1}\right) u v^{n-1}+\left(a_{0}-b_{0}\right) v^{n}=0
$$
since $a_{n-1}=b_{n-1}$. This shows that $v$ divides $\left(a_{n}-b_{n}\right) u^{n}$ and hence it divides $a_{n}-b_{n}$. Since $a_{n}-b_{n}$ is a prime, either $v=1$ or $v=a_{n}-b_{n}$. Suppose the latter holds. The relation takes the form
$$
u^{n}+\left(a_{n-2}-b_{n-2}\right) u^{n-2} v+\cdots+\left(a_{1}-b_{1}\right) u v^{n-2}+\left(a_{0}-b_{0}\right) v^{n-1}=0
$$
(Here we have divided through-out by $v$.) If $n>1$, this forces $v \mid u$, which is impossible since $\operatorname{gcd}(v, u)=1\left(v>1\right.$ since it is equal to the prime $\left.a_{n}-b_{n}\right)$. If $n=1$, then we get two equations:
$$
\begin{aligned}
a_{1} u+a_{0} v & =0 \\
b_{1} u+b_{0} v & =0
\end{aligned}
$$
This forces $a_{1} b_{0}-a_{0} b_{1}=0$ contradicting $a_{n} b_{0}-a_{0} b_{n} \neq 0$. (Note: The condition $a_{n} b_{0}-a_{0} b_{n} \neq 0$ is extraneous. The condition $a_{n-1}=b_{n-1}$ forces that for $n=1$, we have $a_{0}=b_{0}$. Thus we obtain, after subtraction
$$
\left(a_{1}-b_{1}\right) u=0
$$
This implies that $u=0$ and hence $r=0$ is an integer.)
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
1dfe56c7-b58f-5bed-974f-3e4b4ad242c9
| 607,853
|
Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
|
Suppose four distinct points $P, Q, R, S$ (in that order on the circle) among these five are such that $\widehat{P Q}=\widehat{R S}$. Then $P Q R S$ is an isosceles trapezium, with $P S \| Q R$. We use this in our argument.
- If four of the five points chosen are adjacent, then we are through as observed earlier. (In this case four points $A, B, C, D$ are such that $\widehat{A B}=\widehat{B C}=\widehat{C D}$.) See Fig 1 .
Fig 1.
Fig 2.
Fig 3.
- Suppose only three of the vertices are adjacent, say $A, B, C$ (see Fig 2.) Then the remaining two must be among $E, F, G, H$. If these two are adjacent vertices, we can pair them with $A, B$ or $B, C$ to get equal arcs. If they are not adjacent, then they must be either $E, G$ or $F, H$ or $E, H$. In the first two cases, we can pair them with $A, C$ to get equal arcs. In the last case, we observe that $\widehat{H A}=\widehat{C E}$ and $A H E C$ is an isosceles trapezium.
- Suppose only two among the five are adjacent, say $A, B$. Then the remaining three are among $D, E, F, G, H$. (See Fig 3.) If any two of these are adjacent, we can combine them with $A, B$ to get equal arcs. If no two among these three vertices are adjacent, then they must be $D, F, H$. In this case $\widehat{H A}=\widehat{B D}$ and $A H D B$ is an isosceles trapezium.
Finally, if we choose 5 among the 9 vertices of a regular nine-sided polygon, then some two must be adjacent. Thus any choice of 5 among 9 must fall in to one of the above three possibilities.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
|
Suppose four distinct points $P, Q, R, S$ (in that order on the circle) among these five are such that $\widehat{P Q}=\widehat{R S}$. Then $P Q R S$ is an isosceles trapezium, with $P S \| Q R$. We use this in our argument.
- If four of the five points chosen are adjacent, then we are through as observed earlier. (In this case four points $A, B, C, D$ are such that $\widehat{A B}=\widehat{B C}=\widehat{C D}$.) See Fig 1 .

Fig 1.

Fig 2.

Fig 3.
- Suppose only three of the vertices are adjacent, say $A, B, C$ (see Fig 2.) Then the remaining two must be among $E, F, G, H$. If these two are adjacent vertices, we can pair them with $A, B$ or $B, C$ to get equal arcs. If they are not adjacent, then they must be either $E, G$ or $F, H$ or $E, H$. In the first two cases, we can pair them with $A, C$ to get equal arcs. In the last case, we observe that $\widehat{H A}=\widehat{C E}$ and $A H E C$ is an isosceles trapezium.
- Suppose only two among the five are adjacent, say $A, B$. Then the remaining three are among $D, E, F, G, H$. (See Fig 3.) If any two of these are adjacent, we can combine them with $A, B$ to get equal arcs. If no two among these three vertices are adjacent, then they must be $D, F, H$. In this case $\widehat{H A}=\widehat{B D}$ and $A H D B$ is an isosceles trapezium.
Finally, if we choose 5 among the 9 vertices of a regular nine-sided polygon, then some two must be adjacent. Thus any choice of 5 among 9 must fall in to one of the above three possibilities.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution 1:"
}
|
0a334132-062b-5a3e-a339-1c5d58d975c6
| 87,318
|
Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
|
Here is another solution used by many students. Suppose you join the vertices of the nine-sided regular polygon. You get $\binom{9}{2}=36$ line segments. All these fall in to 9 sets of parallel lines. Now using any 5 points, you get $\binom{5}{2}=10$ line segments. By pigeon-hole principle, two of these must be parallel. But, these parallel lines determine a trapezium.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Suppose five of the nine vertices of a regular nine-sided polygon are arbitrarily chosen. Show that one can select four among these five such that they are the vertices of a trapezium.
|
Here is another solution used by many students. Suppose you join the vertices of the nine-sided regular polygon. You get $\binom{9}{2}=36$ line segments. All these fall in to 9 sets of parallel lines. Now using any 5 points, you get $\binom{5}{2}=10$ line segments. By pigeon-hole principle, two of these must be parallel. But, these parallel lines determine a trapezium.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution 2:"
}
|
0a334132-062b-5a3e-a339-1c5d58d975c6
| 87,318
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Gamma$. Let $E, F, G, H$ be the midpoints of the arcs $A B, B C, C D, D A$ of the circle $\Gamma$. Suppose $A C \cdot B D=E G \cdot F H$. Prove that $A C, B D$, $E G, F H$ are concurrent.
|
Let $R$ be the radius of the circle $\Gamma$. Observe that $\angle E D F=\frac{1}{2} \angle D$. Hence $E F=2 R \sin \frac{D}{2}$. Similarly, $H G=2 R \sin \frac{B}{2}$. But $\angle B=180^{\circ}-\angle D$. Thus $H G=2 R \cos \frac{D}{2}$. We hence get
$E F \cdot G H=4 R^{2} \sin \frac{D}{2} \cos \frac{D}{2}=2 R^{2} \sin D=R \cdot A C$.
Similarly, we obtain $E H \cdot F G=R \cdot B D$.
Therefore
$$
R(A C+B D)=E F \cdot G H+E H \cdot F G=E G \cdot F H
$$
by Ptolemy's theorem. By the given hypothesis, this gives $R(A C+B D)=A C \cdot B D$. Thus
$$
A C \cdot B D=R(A C+B D) \geq 2 R \sqrt{A C \cdot B D}
$$
using AM-GM inequality. This implies that $A C \cdot B D \geq 4 R^{2}$. But $A C$ and $B D$ are the chords of $\Gamma$, so that $A C \leq 2 R$ and $B D \leq 2 R$. We obtain $A C \cdot B D \leq 4 R^{2}$. It follows that $A C \cdot B D=4 R^{2}$, implying that $A C=B D=2 R$. Thus $A C$ and $B D$ are two diameters of $\Gamma$. Using $E G \cdot F H=A C \cdot B D$, we conclude that $E G$ and $F H$ are also two diameters of $\Gamma$. Hence $A C, B D, E G$ and $F H$ all pass through the centre of $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrilateral inscribed in a circle $\Gamma$. Let $E, F, G, H$ be the midpoints of the arcs $A B, B C, C D, D A$ of the circle $\Gamma$. Suppose $A C \cdot B D=E G \cdot F H$. Prove that $A C, B D$, $E G, F H$ are concurrent.
|

Let $R$ be the radius of the circle $\Gamma$. Observe that $\angle E D F=\frac{1}{2} \angle D$. Hence $E F=2 R \sin \frac{D}{2}$. Similarly, $H G=2 R \sin \frac{B}{2}$. But $\angle B=180^{\circ}-\angle D$. Thus $H G=2 R \cos \frac{D}{2}$. We hence get
$E F \cdot G H=4 R^{2} \sin \frac{D}{2} \cos \frac{D}{2}=2 R^{2} \sin D=R \cdot A C$.
Similarly, we obtain $E H \cdot F G=R \cdot B D$.
Therefore
$$
R(A C+B D)=E F \cdot G H+E H \cdot F G=E G \cdot F H
$$
by Ptolemy's theorem. By the given hypothesis, this gives $R(A C+B D)=A C \cdot B D$. Thus
$$
A C \cdot B D=R(A C+B D) \geq 2 R \sqrt{A C \cdot B D}
$$
using AM-GM inequality. This implies that $A C \cdot B D \geq 4 R^{2}$. But $A C$ and $B D$ are the chords of $\Gamma$, so that $A C \leq 2 R$ and $B D \leq 2 R$. We obtain $A C \cdot B D \leq 4 R^{2}$. It follows that $A C \cdot B D=4 R^{2}$, implying that $A C=B D=2 R$. Thus $A C$ and $B D$ are two diameters of $\Gamma$. Using $E G \cdot F H=A C \cdot B D$, we conclude that $E G$ and $F H$ are also two diameters of $\Gamma$. Hence $A C, B D, E G$ and $F H$ all pass through the centre of $\Gamma$.
|
{
"resource_path": "INMO/segmented/en-2011.jsonl",
"problem_match": "\n5.",
"solution_match": "## Solution:"
}
|
31444ff1-a75e-5545-8c5e-d6344f199a8e
| 607,854
|
Define a sequence $\left\langle f_{0}(x), f_{1}(x), f_{2}(x), \ldots\right\rangle$ of functions by
$$
f_{0}(x)=1, \quad f_{1}(x)=x, \quad\left(f_{n}(x)\right)^{2}-1=f_{n+1}(x) f_{n-1}(x), \text { for } n \geq 1
$$
Prove that each $f_{n}(x)$ is a polynomial with integer coefficients.
|
Observe that
$$
f_{n}^{2}(x)-f_{n-1}(x) f_{n+1}(x)=1=f_{n-1}^{2}(x)-f_{n-2}(x) f_{n}(x)
$$
This gives
$$
f_{n}(x)\left(f_{n}(x)+f_{n-2}(x)\right)=f_{n-1}\left(f_{n-1}(x)+f_{n+1}(x)\right)
$$
We write this as
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{n-2}(x)+f_{n}(x)}{f_{n-1}(x)}
$$
Using induction, we get
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{0}(x)+f_{2}(x)}{f_{1}(x)}
$$
Observe that
$$
f_{2}(x)=\frac{f_{1}^{2}(x)-1}{f_{0}(x)}=x^{2}-1
$$
Hence
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{1+\left(x^{2}-1\right)}{x}=x
$$
Thus we obtain
$$
f_{n+1}(x)=x f_{n}(x)-f_{n-1}(x)
$$
Since $f_{0}(x), f_{1}(x)$ and $f_{2}(x)$ are polynomials with integer coefficients, induction again shows that $f_{n}(x)$ is a polynomial with integer coefficients.
Note: We can get $f_{n}(x)$ explicitly:
$$
f_{n}(x)=x^{n}-\binom{n-1}{1} x^{n-2}+\binom{n-2}{2} x^{n-4}-\binom{n-3}{3} x^{n-6}+\cdots
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Define a sequence $\left\langle f_{0}(x), f_{1}(x), f_{2}(x), \ldots\right\rangle$ of functions by
$$
f_{0}(x)=1, \quad f_{1}(x)=x, \quad\left(f_{n}(x)\right)^{2}-1=f_{n+1}(x) f_{n-1}(x), \text { for } n \geq 1
$$
Prove that each $f_{n}(x)$ is a polynomial with integer coefficients.
|
Observe that
$$
f_{n}^{2}(x)-f_{n-1}(x) f_{n+1}(x)=1=f_{n-1}^{2}(x)-f_{n-2}(x) f_{n}(x)
$$
This gives
$$
f_{n}(x)\left(f_{n}(x)+f_{n-2}(x)\right)=f_{n-1}\left(f_{n-1}(x)+f_{n+1}(x)\right)
$$
We write this as
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{n-2}(x)+f_{n}(x)}{f_{n-1}(x)}
$$
Using induction, we get
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{f_{0}(x)+f_{2}(x)}{f_{1}(x)}
$$
Observe that
$$
f_{2}(x)=\frac{f_{1}^{2}(x)-1}{f_{0}(x)}=x^{2}-1
$$
Hence
$$
\frac{f_{n-1}(x)+f_{n+1}(x)}{f_{n}(x)}=\frac{1+\left(x^{2}-1\right)}{x}=x
$$
Thus we obtain
$$
f_{n+1}(x)=x f_{n}(x)-f_{n-1}(x)
$$
Since $f_{0}(x), f_{1}(x)$ and $f_{2}(x)$ are polynomials with integer coefficients, induction again shows that $f_{n}(x)$ is a polynomial with integer coefficients.
Note: We can get $f_{n}(x)$ explicitly:
$$
f_{n}(x)=x^{n}-\binom{n-1}{1} x^{n-2}+\binom{n-2}{2} x^{n-4}-\binom{n-3}{3} x^{n-6}+\cdots
$$
|
{
"resource_path": "INMO/segmented/en-2012.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
1710a0dc-ed76-5566-9b9a-ab37fb2b83d5
| 607,858
|
Let $A B C$ be an acute-angled triangle, and let $D, E, F$ be points on $B C$, $C A, A B$ respectively such that $A D$ is the median, $B E$ is the internal angle bisector and $C F$ is the altitude. Suppose $\angle F D E=\angle C, \angle D E F=$ $\angle A$ and $\angle E F D=\angle B$. Prove that $A B C$ is equilateral.
|
Since $\triangle B F C$ is right-angled at $F$, we have
$F D=B D=C D=a / 2$. Hence $\angle B F D=\angle B$. Since $\angle E F D=$ $\angle B$, we have $\angle A F E=\pi-2 \angle B$. Since $\angle D E F=\angle A$, we also get $\angle C E D=\pi-2 \angle B$. Applying sine rule in $\triangle D E F$, we have
$$
\frac{D F}{\sin A}=\frac{F E}{\sin C}=\frac{D E}{\sin B}
$$
Thus we get $F E=c / 2$ and $D E=b / 2$. Sine rule in $\triangle C E D$ gives
$$
\frac{D E}{\sin C}=\frac{C D}{\sin (\pi-2 B)}
$$
Thus $(b / \sin C)=(a / 2 \sin B \cos B)$. Solving for $\cos B$, we have
$$
\cos B=\frac{a \sin c}{2 b \sin B}=\frac{a c}{2 b^{2}}
$$
Similarly, sine rule in $\triangle A E F$ gives
$$
\frac{E F}{\sin A}=\frac{A E}{\sin (\pi-2 B)}
$$
This gives (since $A E=b c /(a+c)$ ), as earlier,
$$
\cos B=\frac{a}{a+c}
$$
Comparing the two values of $\cos B$, we get $2 b^{2}=c(a+c)$. We also have
$$
c^{2}+a^{2}-b^{2}=2 c a \cos B=\frac{2 a^{2} c}{a+c}
$$
Thus
$$
4 a^{2} c=(a+c)\left(2 c^{2}+2 a^{2}-2 b^{2}\right)=(a+c)\left(2 c^{2}+2 a^{2}-c(a+c)\right)
$$
This reduces to $2 a^{3}-3 a^{2} c+c^{3}=0$. Thus $(a-c)^{2}(2 a+c)=0$. We conclude that $a=c$. Finally
$$
2 b^{2}=c(a+c)=2 c^{2}
$$
We thus get $b=c$ and hence $a=c=b$. This shows that $\triangle A B C$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle, and let $D, E, F$ be points on $B C$, $C A, A B$ respectively such that $A D$ is the median, $B E$ is the internal angle bisector and $C F$ is the altitude. Suppose $\angle F D E=\angle C, \angle D E F=$ $\angle A$ and $\angle E F D=\angle B$. Prove that $A B C$ is equilateral.
|
Since $\triangle B F C$ is right-angled at $F$, we have

$F D=B D=C D=a / 2$. Hence $\angle B F D=\angle B$. Since $\angle E F D=$ $\angle B$, we have $\angle A F E=\pi-2 \angle B$. Since $\angle D E F=\angle A$, we also get $\angle C E D=\pi-2 \angle B$. Applying sine rule in $\triangle D E F$, we have
$$
\frac{D F}{\sin A}=\frac{F E}{\sin C}=\frac{D E}{\sin B}
$$
Thus we get $F E=c / 2$ and $D E=b / 2$. Sine rule in $\triangle C E D$ gives
$$
\frac{D E}{\sin C}=\frac{C D}{\sin (\pi-2 B)}
$$
Thus $(b / \sin C)=(a / 2 \sin B \cos B)$. Solving for $\cos B$, we have
$$
\cos B=\frac{a \sin c}{2 b \sin B}=\frac{a c}{2 b^{2}}
$$
Similarly, sine rule in $\triangle A E F$ gives
$$
\frac{E F}{\sin A}=\frac{A E}{\sin (\pi-2 B)}
$$
This gives (since $A E=b c /(a+c)$ ), as earlier,
$$
\cos B=\frac{a}{a+c}
$$
Comparing the two values of $\cos B$, we get $2 b^{2}=c(a+c)$. We also have
$$
c^{2}+a^{2}-b^{2}=2 c a \cos B=\frac{2 a^{2} c}{a+c}
$$
Thus
$$
4 a^{2} c=(a+c)\left(2 c^{2}+2 a^{2}-2 b^{2}\right)=(a+c)\left(2 c^{2}+2 a^{2}-c(a+c)\right)
$$
This reduces to $2 a^{3}-3 a^{2} c+c^{3}=0$. Thus $(a-c)^{2}(2 a+c)=0$. We conclude that $a=c$. Finally
$$
2 b^{2}=c(a+c)=2 c^{2}
$$
We thus get $b=c$ and hence $a=c=b$. This shows that $\triangle A B C$ is equilateral.
|
{
"resource_path": "INMO/segmented/en-2012.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
de9155ca-501f-575e-851a-ff2a67c57533
| 607,860
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
Consider the graph whose vertices are elements of $S$, with an edge between $x$ and $y$ if and only if $x y$ is a perfect square. We claim every connected component is a clique.
Indeed, take any two vertices corresponding to $x, y$ in $S$ in the same connected component. It suffices to show they are adjacent. By assumption, there is a path between them; so there is a sequence $x=a_{1}, a_{2}, \ldots, a_{n-1}, a_{n}=y$ so that $a_{i} a_{i+1}$ is a perfect square for $1 \leq i<n$. Therefore
$$
x y=a_{1} a_{n}=\frac{\left(a_{1} a_{2}\right)\left(a_{2} a_{3}\right) \cdots\left(a_{n-1} a_{n}\right)}{a_{2}^{2} \cdots a_{n-1}^{2}}
$$
is a perfect square as well. This proves our claim.
Now suppose first there are at most 3 connected components, with sizes $a, b, c$ (possibly zero). Note that for $(x, y) \in S \times S, x y$ is a perfect square if and only if $x, y$ are in the same component, which can be chosen is $a^{2}+b^{2}+c^{2}$ ways. Thus
$$
a^{2}+b^{2}+c^{2}=2023
$$
But since squares can only be 0,1 or $4 \bmod 8$, and 2023 is $7 \bmod 8$, the above equation is impossible. Thus our graph must have at least four components. Picking a number from each component, we can now satisfy the requirements of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
Consider the graph whose vertices are elements of $S$, with an edge between $x$ and $y$ if and only if $x y$ is a perfect square. We claim every connected component is a clique.
Indeed, take any two vertices corresponding to $x, y$ in $S$ in the same connected component. It suffices to show they are adjacent. By assumption, there is a path between them; so there is a sequence $x=a_{1}, a_{2}, \ldots, a_{n-1}, a_{n}=y$ so that $a_{i} a_{i+1}$ is a perfect square for $1 \leq i<n$. Therefore
$$
x y=a_{1} a_{n}=\frac{\left(a_{1} a_{2}\right)\left(a_{2} a_{3}\right) \cdots\left(a_{n-1} a_{n}\right)}{a_{2}^{2} \cdots a_{n-1}^{2}}
$$
is a perfect square as well. This proves our claim.
Now suppose first there are at most 3 connected components, with sizes $a, b, c$ (possibly zero). Note that for $(x, y) \in S \times S, x y$ is a perfect square if and only if $x, y$ are in the same component, which can be chosen is $a^{2}+b^{2}+c^{2}$ ways. Thus
$$
a^{2}+b^{2}+c^{2}=2023
$$
But since squares can only be 0,1 or $4 \bmod 8$, and 2023 is $7 \bmod 8$, the above equation is impossible. Thus our graph must have at least four components. Picking a number from each component, we can now satisfy the requirements of the problem.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 1."
}
|
93a9e825-60ff-5ec8-98b3-5ff0f8ca2166
| 607,862
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
For $a$ in $S$, let $S_{a}=\{x \in S \mid a x$ is a square $\}$. Let $a, b$ be elements of $S$. Suppose that $x$ is in $S_{a} \cap S_{b}$. Then $a x$ and $b x$ are squares and hence $a b=\frac{a x \cdot b x}{x^{2}}$ is a square. Then for any $y$ in $S$ such that $a y$ is a square it follows that by is a square, so $S_{a}=S_{b}$. Hence for two elements $a, b$ in $S$, either $S_{a}=S_{b}$ or $S_{a} \cap S_{b}=\emptyset$.
Now, $S=\cup S_{a}$ where the union runs over elements of $S$ (since $a \in S_{a}$ for any $a \in S$ ). Let $S=S_{a_{1}} \cup S_{a_{2}} \cup \cdots \cup S_{a_{n}}$ for some elements $a_{1}, a_{2}, \ldots, a_{n}$ of $S$ such that $S_{a_{i}} \cap S_{a_{j}}=\emptyset$ for $1 \leq i<j \leq n$. Then the number of distinct pairs $(x, y)$ of $S \times S$ such that $x y$ is a square is precisely $\left|S_{a_{1}}\right|^{2}+\left|S_{a_{2}}\right|^{2}+\cdots+\left|S_{a_{n}}\right|^{2}$. Since $2023 \equiv 7(\bmod 8)$ it follows that $n>3$ as in the previous solution. Thus we have four elements $a_{1}, a_{2}, a_{3}, a_{4}$ none of whose pairwise products is a square.
For those familiar with the language of linear algebra and finite fields, the above argument can be reformulated as follows:
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
For $a$ in $S$, let $S_{a}=\{x \in S \mid a x$ is a square $\}$. Let $a, b$ be elements of $S$. Suppose that $x$ is in $S_{a} \cap S_{b}$. Then $a x$ and $b x$ are squares and hence $a b=\frac{a x \cdot b x}{x^{2}}$ is a square. Then for any $y$ in $S$ such that $a y$ is a square it follows that by is a square, so $S_{a}=S_{b}$. Hence for two elements $a, b$ in $S$, either $S_{a}=S_{b}$ or $S_{a} \cap S_{b}=\emptyset$.
Now, $S=\cup S_{a}$ where the union runs over elements of $S$ (since $a \in S_{a}$ for any $a \in S$ ). Let $S=S_{a_{1}} \cup S_{a_{2}} \cup \cdots \cup S_{a_{n}}$ for some elements $a_{1}, a_{2}, \ldots, a_{n}$ of $S$ such that $S_{a_{i}} \cap S_{a_{j}}=\emptyset$ for $1 \leq i<j \leq n$. Then the number of distinct pairs $(x, y)$ of $S \times S$ such that $x y$ is a square is precisely $\left|S_{a_{1}}\right|^{2}+\left|S_{a_{2}}\right|^{2}+\cdots+\left|S_{a_{n}}\right|^{2}$. Since $2023 \equiv 7(\bmod 8)$ it follows that $n>3$ as in the previous solution. Thus we have four elements $a_{1}, a_{2}, a_{3}, a_{4}$ none of whose pairwise products is a square.
For those familiar with the language of linear algebra and finite fields, the above argument can be reformulated as follows:
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2."
}
|
93a9e825-60ff-5ec8-98b3-5ff0f8ca2166
| 607,862
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
Let $p_{1}<p_{2}<\ldots$ be the sequence of prime numbers. Denote by $\mathbb{F}_{2}^{\omega}$ the $\mathbb{F}_{2}$ vector space of all binary sequences $\left(a_{1}, a_{2}, \ldots\right)$ with entries in $\mathbb{F}_{2}$. Consider the set map $\Phi: \mathbb{N} \rightarrow \mathbb{F}_{2}^{\omega}$ defined by
$$
\Phi(n):=\left(v_{p_{i}}(n) \quad(\bmod 2)\right)_{i \geq 1}
$$
for all $n \in \mathbb{N}$. It is clear that for $x, y \in \mathbb{N}$, the product $x y$ is a perfect square if and only if $\Phi(x)=\Phi(y)$. So we want $|\Phi(S)| \geq 4$. Indeed, decompose $S$ as a union of fibres, $S=\cup_{a \in \Phi(S)} \Phi^{-1}(a)$. Each fibre with size $r$ accounts for $2\binom{r}{2}+r=r^{2}$ pairs towards the count, so if $\Phi(S)$ has at most three elements, then $a^{2}+b^{2}+c^{2}=2023$ has a solution in non-negative integers. This is a contradiction mod 8 , by simply checking that no triple formed using one of $\{0,1,4\}$ can add to $7 \bmod 8$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a finite set of positive integers. Assume that there are precisely 2023 ordered pairs $(x, y)$ in $S \times S$ so that the product $x y$ is a perfect square. Prove that one can find at least four distinct elements in $S$ so that none of their pairwise products is a perfect square.
Note: As an example, if $S=\{1,2,4\}$, there are exactly five such ordered pairs: $(1,1),(1,4)$, $(2,2),(4,1)$, and $(4,4)$.
|
Let $p_{1}<p_{2}<\ldots$ be the sequence of prime numbers. Denote by $\mathbb{F}_{2}^{\omega}$ the $\mathbb{F}_{2}$ vector space of all binary sequences $\left(a_{1}, a_{2}, \ldots\right)$ with entries in $\mathbb{F}_{2}$. Consider the set map $\Phi: \mathbb{N} \rightarrow \mathbb{F}_{2}^{\omega}$ defined by
$$
\Phi(n):=\left(v_{p_{i}}(n) \quad(\bmod 2)\right)_{i \geq 1}
$$
for all $n \in \mathbb{N}$. It is clear that for $x, y \in \mathbb{N}$, the product $x y$ is a perfect square if and only if $\Phi(x)=\Phi(y)$. So we want $|\Phi(S)| \geq 4$. Indeed, decompose $S$ as a union of fibres, $S=\cup_{a \in \Phi(S)} \Phi^{-1}(a)$. Each fibre with size $r$ accounts for $2\binom{r}{2}+r=r^{2}$ pairs towards the count, so if $\Phi(S)$ has at most three elements, then $a^{2}+b^{2}+c^{2}=2023$ has a solution in non-negative integers. This is a contradiction mod 8 , by simply checking that no triple formed using one of $\{0,1,4\}$ can add to $7 \bmod 8$.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 3."
}
|
93a9e825-60ff-5ec8-98b3-5ff0f8ca2166
| 607,862
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
Let $n=50$. For the sake of contradiction, assume that each of these polynomials has all real roots; these roots must be negative. Let
$$
-\alpha_{1, k},-\alpha_{2, k}, \ldots,-\alpha_{2 n, k}
$$
be the roots of the polynomial
$$
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+a_{2 n-2+k} x^{2 n-2}+a_{2 n-3+k} x^{2 n-3}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
Indices are taken modulo $2 n+1$, so $a_{2 n+k}=a_{k-1}$ and $a_{2 n-1+k}=a_{k-2}$. Then
$$
\sum_{j=1}^{2 n} \alpha_{j, k}=2 n \cdot\left(\frac{a_{k-2}}{a_{k-1}}\right) ; \prod_{j=1}^{2 n} \alpha_{j, k}=\frac{a_{k}}{a_{k-1}}
$$
Since the $\alpha_{j, k}$ 's are positive, AM-GM inequality can be applied and by virtue of it we are led to
$$
\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \frac{a_{k}}{a_{k-1}}
$$
for each $k$. As both sides of the inequalities are positive, multiplying them we obtain
$$
\prod_{k=0}^{2 n}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \prod_{k=0}^{2 n} \frac{a_{k}}{a_{k-1}}
$$
But both sides are equal to 1 . Therefore all the $2 n+1$ A.M-G.M inequalities are equalities implying that for each $k$,
$$
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
$$
Since $n \geq 2$, using Vieta's relations gives
$$
\frac{a_{k-3}}{a_{k-1}}=\sum_{1 \leq i<j \leq 2 n} \alpha_{i, k} \alpha_{j, k}=\binom{2 n}{2}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2}
$$
Simplifying leads
$$
\binom{2 n}{2} a_{k-2}^{2}=a_{k-1} a_{k-3}
$$
for each $k$. Multiplying all these equations yields
$$
\left(\binom{2 n}{2}^{2 n+1}-1\right)\left(\prod_{k=0}^{2 n} a_{k}\right)^{2}=0
$$
which shows that at least one $a_{k}=0$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
Let $n=50$. For the sake of contradiction, assume that each of these polynomials has all real roots; these roots must be negative. Let
$$
-\alpha_{1, k},-\alpha_{2, k}, \ldots,-\alpha_{2 n, k}
$$
be the roots of the polynomial
$$
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+a_{2 n-2+k} x^{2 n-2}+a_{2 n-3+k} x^{2 n-3}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
Indices are taken modulo $2 n+1$, so $a_{2 n+k}=a_{k-1}$ and $a_{2 n-1+k}=a_{k-2}$. Then
$$
\sum_{j=1}^{2 n} \alpha_{j, k}=2 n \cdot\left(\frac{a_{k-2}}{a_{k-1}}\right) ; \prod_{j=1}^{2 n} \alpha_{j, k}=\frac{a_{k}}{a_{k-1}}
$$
Since the $\alpha_{j, k}$ 's are positive, AM-GM inequality can be applied and by virtue of it we are led to
$$
\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \frac{a_{k}}{a_{k-1}}
$$
for each $k$. As both sides of the inequalities are positive, multiplying them we obtain
$$
\prod_{k=0}^{2 n}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n} \geq \prod_{k=0}^{2 n} \frac{a_{k}}{a_{k-1}}
$$
But both sides are equal to 1 . Therefore all the $2 n+1$ A.M-G.M inequalities are equalities implying that for each $k$,
$$
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
$$
Since $n \geq 2$, using Vieta's relations gives
$$
\frac{a_{k-3}}{a_{k-1}}=\sum_{1 \leq i<j \leq 2 n} \alpha_{i, k} \alpha_{j, k}=\binom{2 n}{2}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2}
$$
Simplifying leads
$$
\binom{2 n}{2} a_{k-2}^{2}=a_{k-1} a_{k-3}
$$
for each $k$. Multiplying all these equations yields
$$
\left(\binom{2 n}{2}^{2 n+1}-1\right)\left(\prod_{k=0}^{2 n} a_{k}\right)^{2}=0
$$
which shows that at least one $a_{k}=0$, a contradiction.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 1."
}
|
4748ca22-7eea-53a4-adcc-f61bd95d1501
| 607,863
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
As above, one proves that
$$
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
$$
This implies
$$
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+\cdots+a_{1+k} x+a_{k}=a_{2 n+k}\left(x+\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}
$$
For $n \geq 2$, comparing coefficients of $x^{0}$ and $x^{1}$, we see that
$$
a_{k}=a_{2 n+k}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}, \quad a_{k+1}=a_{2 n+k} \cdot 2 n\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n-1}
$$
whence we obtain
$$
\frac{a_{k+1}}{a_{k}}=2 n \cdot \frac{a_{k-1}}{a_{k-2}}
$$
This must hold for all $k$. However, if we pick $k$ is such that $\frac{a_{k+1}}{a_{k}}$ is minimal, we must necessarily have
$$
\frac{a_{k+1}}{a_{k}} \leq \frac{a_{k-1}}{a_{k-2}}<2 n \cdot \frac{a_{k-1}}{a_{k-2}}
$$
a contradiction.
Several other beautiful solutions were pointed out to us; we include a few of them.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
As above, one proves that
$$
\alpha_{1, k}=\alpha_{2, k}=\ldots=\alpha_{2 n, k}=\frac{a_{k-2}}{a_{k-1}}
$$
This implies
$$
a_{2 n+k} x^{2 n}+2 n a_{2 n-1+k} x^{2 n-1}+\cdots+a_{1+k} x+a_{k}=a_{2 n+k}\left(x+\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}
$$
For $n \geq 2$, comparing coefficients of $x^{0}$ and $x^{1}$, we see that
$$
a_{k}=a_{2 n+k}\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n}, \quad a_{k+1}=a_{2 n+k} \cdot 2 n\left(\frac{a_{k-2}}{a_{k-1}}\right)^{2 n-1}
$$
whence we obtain
$$
\frac{a_{k+1}}{a_{k}}=2 n \cdot \frac{a_{k-1}}{a_{k-2}}
$$
This must hold for all $k$. However, if we pick $k$ is such that $\frac{a_{k+1}}{a_{k}}$ is minimal, we must necessarily have
$$
\frac{a_{k+1}}{a_{k}} \leq \frac{a_{k-1}}{a_{k-2}}<2 n \cdot \frac{a_{k-1}}{a_{k-2}}
$$
a contradiction.
Several other beautiful solutions were pointed out to us; we include a few of them.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 2."
}
|
4748ca22-7eea-53a4-adcc-f61bd95d1501
| 607,863
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
As usual, assume all of these polynomials have all real roots. We consider the polynomial obtained by writing the coefficients of the given polynomials in reverse order:
$$
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
$$
This also has all its roots real: in fact, its roots are reciprocals of the original polynomial. By Rolle's theorem, its derivative must also have all roots real. Repeating this argument, we see that the polynomial obtained by differentiating this 98 times
$$
\frac{100!}{2!} a_{k} x^{2}+99!a_{k+1} x+98!a_{k+2}
$$
also have real roots. Therefore this must have nonnegative discriminant:
$$
99!^{2} a_{k+1}^{2} \geq 2 \cdot 98!\cdot 100!a_{k} a_{k+2}
$$
which simplifies to
$$
99 a_{k+1}^{2} \geq 200 a_{k} a_{k+2}
$$
This holds for all $k$, so multiplying these as $k$ varies, we obtain
$$
99^{101} \prod_{i=0}^{100} a_{i}^{2} \geq 200^{101} \prod_{i=0}^{100} a_{i}^{2}
$$
which is impossible since $99<200$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
As usual, assume all of these polynomials have all real roots. We consider the polynomial obtained by writing the coefficients of the given polynomials in reverse order:
$$
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
$$
This also has all its roots real: in fact, its roots are reciprocals of the original polynomial. By Rolle's theorem, its derivative must also have all roots real. Repeating this argument, we see that the polynomial obtained by differentiating this 98 times
$$
\frac{100!}{2!} a_{k} x^{2}+99!a_{k+1} x+98!a_{k+2}
$$
also have real roots. Therefore this must have nonnegative discriminant:
$$
99!^{2} a_{k+1}^{2} \geq 2 \cdot 98!\cdot 100!a_{k} a_{k+2}
$$
which simplifies to
$$
99 a_{k+1}^{2} \geq 200 a_{k} a_{k+2}
$$
This holds for all $k$, so multiplying these as $k$ varies, we obtain
$$
99^{101} \prod_{i=0}^{100} a_{i}^{2} \geq 200^{101} \prod_{i=0}^{100} a_{i}^{2}
$$
which is impossible since $99<200$.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 3."
}
|
4748ca22-7eea-53a4-adcc-f61bd95d1501
| 607,863
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
Choose $k$ so that $a_{k+1}$ is minimal. As before, consider the polynomial
$$
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
$$
and suppose its roots are $\beta_{1}, \cdots, \beta_{100}$. We have, by Vieta's relations,
$$
\sum_{i=1}^{100} \beta_{i}=-\frac{a_{k+1}}{a_{k}}, \quad \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}=\frac{a_{k+2}}{a_{k}}
$$
However, we note that
$$
\left(\sum_{i=1}^{100} \beta_{i}\right)^{2}=\sum_{i=1}^{100} \beta_{i}^{2}+2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j} \geq 2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}
$$
which yields
$$
\left(-\frac{a_{k+1}}{a_{k}}\right)^{2} \geq \frac{2 a_{k+2}}{a_{k}}
$$
This simplifies to $a_{k+1}^{2} \geq 2 a_{k} a_{k+2}$. However, by the choice of $k$, we have
$$
a_{k+1}^{2} \leq a_{k} a_{k+2}<2 a_{k} a_{k+2}
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose $a_{0}, \ldots, a_{100}$ are positive reals. Consider the following polynomial for each $k$ in $\{0,1, \ldots, 100\}$ :
$$
a_{100+k} x^{100}+100 a_{99+k} x^{99}+a_{98+k} x^{98}+a_{97+k} x^{97}+\cdots+a_{2+k} x^{2}+a_{1+k} x+a_{k}
$$
where indices are taken modulo 101, i.e., $a_{100+i}=a_{i-1}$ for any $i$ in $\{1,2, \ldots, 100\}$. Show that it is impossible that each of these 101 polynomials has all its roots real.
|
Choose $k$ so that $a_{k+1}$ is minimal. As before, consider the polynomial
$$
a_{k} x^{100}+a_{k+1} x^{99}+a_{k+2} x^{98}+\cdots+100 a_{k+99} x+a_{k+100}
$$
and suppose its roots are $\beta_{1}, \cdots, \beta_{100}$. We have, by Vieta's relations,
$$
\sum_{i=1}^{100} \beta_{i}=-\frac{a_{k+1}}{a_{k}}, \quad \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}=\frac{a_{k+2}}{a_{k}}
$$
However, we note that
$$
\left(\sum_{i=1}^{100} \beta_{i}\right)^{2}=\sum_{i=1}^{100} \beta_{i}^{2}+2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j} \geq 2 \sum_{1 \leq i<j \leq n} \beta_{i} \beta_{j}
$$
which yields
$$
\left(-\frac{a_{k+1}}{a_{k}}\right)^{2} \geq \frac{2 a_{k+2}}{a_{k}}
$$
This simplifies to $a_{k+1}^{2} \geq 2 a_{k} a_{k+2}$. However, by the choice of $k$, we have
$$
a_{k+1}^{2} \leq a_{k} a_{k+2}<2 a_{k} a_{k+2}
$$
a contradiction.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 2.",
"solution_match": "\nSolution 4."
}
|
4748ca22-7eea-53a4-adcc-f61bd95d1501
| 607,863
|
Euclid has a tool called cyclos which allows him to do the following:
- Given three non-collinear marked points, draw the circle passing through them.
- Given two marked points, draw the circle with them as endpoints of a diameter.
- Mark any intersection points of two drawn circles or mark a new point on a drawn circle.
Show that given two marked points, Euclid can draw a circle centered at one of them and passing through the other, using only the cyclos.
|
After deriving the first two lemmas in the previous solution, one can proceed as follows: Let $C$ denote the point such that $A$ is the midpoint of $C B$.
Choose a generic point $X$. We can get the midpoint $M$ of $B X$ and the foot of perpendicular $D$ from $X$ to $A B$. Draw the circle passing through $A, D$ and $M$. This is the nine-point of circle of triangle $C B X$. Intersect this circle with the circle whose diameter is $B X$. The intersection point other than $D$ is the foot of perpendicular $E$ from $B$ to $C X$. Note that $|A E|=|A B|$. Similarly, we can construct another point $F$ such that $|A F|=|A B|$. The circle through $B, E$ and $F$ is the required circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Euclid has a tool called cyclos which allows him to do the following:
- Given three non-collinear marked points, draw the circle passing through them.
- Given two marked points, draw the circle with them as endpoints of a diameter.
- Mark any intersection points of two drawn circles or mark a new point on a drawn circle.
Show that given two marked points, Euclid can draw a circle centered at one of them and passing through the other, using only the cyclos.
|
After deriving the first two lemmas in the previous solution, one can proceed as follows: Let $C$ denote the point such that $A$ is the midpoint of $C B$.
Choose a generic point $X$. We can get the midpoint $M$ of $B X$ and the foot of perpendicular $D$ from $X$ to $A B$. Draw the circle passing through $A, D$ and $M$. This is the nine-point of circle of triangle $C B X$. Intersect this circle with the circle whose diameter is $B X$. The intersection point other than $D$ is the foot of perpendicular $E$ from $B$ to $C X$. Note that $|A E|=|A B|$. Similarly, we can construct another point $F$ such that $|A F|=|A B|$. The circle through $B, E$ and $F$ is the required circle.
|
{
"resource_path": "INMO/segmented/en-2023.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution 2."
}
|
352f627d-c9ce-5d70-a865-082eeec48ea6
| 607,867
|
In triangle $A B C$ with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $F$ and $A B$ in $G$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
|
We have $F G=F A$ since $F G$ is parallel to $B C$. But also $\triangle G A E$ is a right angle triangle. Thus, if $F^{\prime}$ is the midpoint of $G E$, then $\angle G A F=\angle F G A=\angle F^{\prime} G A=\angle G A F^{\prime}$ which implies $F \equiv F^{\prime}$. Thus, $F$ is the midpoint of $G E$.
If $O$ is the circumcenter of $\triangle E B G$, then
$$
\angle F O E=\angle G B E=\angle A B E=\angle A C E=\angle F C E
$$
Thus, we get $\angle F O E=\angle F C E$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$ with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $F$ and $A B$ in $G$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
|

We have $F G=F A$ since $F G$ is parallel to $B C$. But also $\triangle G A E$ is a right angle triangle. Thus, if $F^{\prime}$ is the midpoint of $G E$, then $\angle G A F=\angle F G A=\angle F^{\prime} G A=\angle G A F^{\prime}$ which implies $F \equiv F^{\prime}$. Thus, $F$ is the midpoint of $G E$.
If $O$ is the circumcenter of $\triangle E B G$, then
$$
\angle F O E=\angle G B E=\angle A B E=\angle A C E=\angle F C E
$$
Thus, we get $\angle F O E=\angle F C E$ as desired.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "## Solution 1."
}
|
e7663d0f-a512-5149-93c8-a67cd37295da
| 607,872
|
In triangle $A B C$ with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $F$ and $A B$ in $G$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
|
( $\angle B C A$ acute case) Let $O_{1}$ be the circumcenter of $\triangle A B C, O$ be the circumcenter of $\triangle E B G$ and $\omega$ be the circumcircle of $\triangle E C F$.
First, show that $F$ is the midpoint of $E G$ as in Solution 1. Next, we show that $O_{1}$ lies on $\omega$. This follows from
$$
\angle E O_{1} C=2 \angle E B C=2 \angle O_{1} B C=2 \angle B C O_{1}=\angle B C A=\angle E F C
$$
Now, $O_{1}$ is the midpoint of $E B$ and $F$ is the midpoint of $E G$, therefore the homothety at $E$ with ratio $1 / 2$ takes $\triangle E G B$ to $\triangle E F O_{1}$. Thus, it takes $O$, the circumcenter of $\triangle E G B$, to the circumcenter of $\triangle E F O_{1}$, thus proving that the midpoint of $E O$ is the center of $\omega$. This immediately implies that $O$ lies on $\omega$.
## Remark.
- There are two configurations possible in the above problem, one for $C$ acute and one for obtuse. One may replace all the angles in the above solutions by directed angles to obtain a solution which remains invariant in all configurations.
- There is a direct solution by first proving that $O$ is on $B C$ by calculating $\angle E B O$ and then proving that $\angle O C F=\angle O E F$. However, this needs more care for handling both configurations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$ with $C A=C B$, point $E$ lies on the circumcircle of $A B C$ such that $\angle E C B=90^{\circ}$. The line through $E$ parallel to $C B$ intersects $C A$ in $F$ and $A B$ in $G$. Prove that the centre of the circumcircle of triangle $E G B$ lies on the circumcircle of triangle $E C F$.
|
( $\angle B C A$ acute case) Let $O_{1}$ be the circumcenter of $\triangle A B C, O$ be the circumcenter of $\triangle E B G$ and $\omega$ be the circumcircle of $\triangle E C F$.
First, show that $F$ is the midpoint of $E G$ as in Solution 1. Next, we show that $O_{1}$ lies on $\omega$. This follows from
$$
\angle E O_{1} C=2 \angle E B C=2 \angle O_{1} B C=2 \angle B C O_{1}=\angle B C A=\angle E F C
$$
Now, $O_{1}$ is the midpoint of $E B$ and $F$ is the midpoint of $E G$, therefore the homothety at $E$ with ratio $1 / 2$ takes $\triangle E G B$ to $\triangle E F O_{1}$. Thus, it takes $O$, the circumcenter of $\triangle E G B$, to the circumcenter of $\triangle E F O_{1}$, thus proving that the midpoint of $E O$ is the center of $\omega$. This immediately implies that $O$ lies on $\omega$.
## Remark.
- There are two configurations possible in the above problem, one for $C$ acute and one for obtuse. One may replace all the angles in the above solutions by directed angles to obtain a solution which remains invariant in all configurations.
- There is a direct solution by first proving that $O$ is on $B C$ by calculating $\angle E B O$ and then proving that $\angle O C F=\angle O E F$. However, this needs more care for handling both configurations.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution 2."
}
|
e7663d0f-a512-5149-93c8-a67cd37295da
| 607,872
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
Set $k=2023$. If one of $a, b, c$ is divisible by $p$, then all of them are. Indeed, for example, if $p \mid a$, then $p \mid a^{k}+b^{k}$ implies $p \mid b$, and then $p \mid b^{k+1}+c^{k+1}$ implies $p \mid c$. The other cases follow similarly.
So for the sake of contradiction assume none of $a, b, c$ is divisible by $p$. Then
$$
a^{k(k+2)} \equiv\left(a^{k}\right)^{k+2} \equiv\left(-b^{k}\right)^{k+2} \equiv-b^{k(k+2)} \quad(\bmod p)
$$
and
$$
a^{k(k+2)} \equiv\left(a^{k+2}\right)^{k}=\left(-c^{k+2}\right)^{k} \equiv-c^{k(k+2)} \quad(\bmod p)
$$
So $b^{k(k+2)} \equiv c^{k(k+2)}(\bmod p)$. But then
$$
c^{k(k+2)} \cdot c \equiv c^{(k+1)^{2}} \equiv\left(-b^{k+1}\right)^{k+1} \equiv b^{(k+1)^{2}} \equiv b^{k(k+2)} \cdot b \equiv c^{k(k+2)} \cdot b \quad(\bmod p)
$$
which forces $b \equiv c(\bmod p)$. Thus
$$
0 \equiv b^{k+1}+c^{k+1}=2 b^{k+1} \quad(\bmod p)
$$
implying $p \mid b$, a contradiction. Thus the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
Set $k=2023$. If one of $a, b, c$ is divisible by $p$, then all of them are. Indeed, for example, if $p \mid a$, then $p \mid a^{k}+b^{k}$ implies $p \mid b$, and then $p \mid b^{k+1}+c^{k+1}$ implies $p \mid c$. The other cases follow similarly.
So for the sake of contradiction assume none of $a, b, c$ is divisible by $p$. Then
$$
a^{k(k+2)} \equiv\left(a^{k}\right)^{k+2} \equiv\left(-b^{k}\right)^{k+2} \equiv-b^{k(k+2)} \quad(\bmod p)
$$
and
$$
a^{k(k+2)} \equiv\left(a^{k+2}\right)^{k}=\left(-c^{k+2}\right)^{k} \equiv-c^{k(k+2)} \quad(\bmod p)
$$
So $b^{k(k+2)} \equiv c^{k(k+2)}(\bmod p)$. But then
$$
c^{k(k+2)} \cdot c \equiv c^{(k+1)^{2}} \equiv\left(-b^{k+1}\right)^{k+1} \equiv b^{(k+1)^{2}} \equiv b^{k(k+2)} \cdot b \equiv c^{k(k+2)} \cdot b \quad(\bmod p)
$$
which forces $b \equiv c(\bmod p)$. Thus
$$
0 \equiv b^{k+1}+c^{k+1}=2 b^{k+1} \quad(\bmod p)
$$
implying $p \mid b$, a contradiction. Thus the proof is complete.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 1."
}
|
12908f67-47e7-5c53-abe2-6e327126b37d
| 607,874
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
As before, we may assume $p$ divides none of $a, b$, and $c$ and set $k=2023$. Then
$$
\begin{aligned}
a^{k} & \equiv-b^{k} \quad(\bmod p) \\
b^{k+1} & \equiv-c^{k+1} \quad(\bmod p) \\
c^{k+2} & \equiv-a^{k+2} \quad(\bmod p)
\end{aligned}
$$
and multiplying these three equations yields $a^{k} b^{k+1} c^{k+2} \equiv-b^{k} c^{k+1} a^{k+2}(\bmod p)$. By cancelling the factor $a^{k} b^{k} c^{k+1}$, we get $a^{2} \equiv-b c(\bmod p)$. Now
$$
p \mid a^{k}+b^{k} \Longrightarrow a^{4 k} \equiv b^{4 k} \quad(\bmod p) \Longrightarrow c^{2 k} \equiv b^{2 k} \quad(\bmod p)
$$
so
$$
p \mid b^{k+1}+c^{k+1} \Longrightarrow b^{2(k+1)} \equiv c^{2(k+1)} \quad(\bmod p) \Longrightarrow b^{2} \equiv c^{2} \quad(\bmod p)
$$
so either $b \equiv c(\bmod p)$ or $b \equiv-c(\bmod p)$. In the latter case, $a^{2} \equiv c^{2}(\bmod p)$ so $a \equiv c$ $(\bmod p)$ or $a \equiv-c(\bmod p)$. In any case, two out of $\{a, b, c\}$ are the same $\bmod p$, so one of the equations gives $p \mid 2 x^{y}$ where $x \in\{a, b, c\}$ and $y \in\{k, k+1, k+2\}$, hence $p$ odd implies $p \mid x$ so $p \mid a b c$, the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
As before, we may assume $p$ divides none of $a, b$, and $c$ and set $k=2023$. Then
$$
\begin{aligned}
a^{k} & \equiv-b^{k} \quad(\bmod p) \\
b^{k+1} & \equiv-c^{k+1} \quad(\bmod p) \\
c^{k+2} & \equiv-a^{k+2} \quad(\bmod p)
\end{aligned}
$$
and multiplying these three equations yields $a^{k} b^{k+1} c^{k+2} \equiv-b^{k} c^{k+1} a^{k+2}(\bmod p)$. By cancelling the factor $a^{k} b^{k} c^{k+1}$, we get $a^{2} \equiv-b c(\bmod p)$. Now
$$
p \mid a^{k}+b^{k} \Longrightarrow a^{4 k} \equiv b^{4 k} \quad(\bmod p) \Longrightarrow c^{2 k} \equiv b^{2 k} \quad(\bmod p)
$$
so
$$
p \mid b^{k+1}+c^{k+1} \Longrightarrow b^{2(k+1)} \equiv c^{2(k+1)} \quad(\bmod p) \Longrightarrow b^{2} \equiv c^{2} \quad(\bmod p)
$$
so either $b \equiv c(\bmod p)$ or $b \equiv-c(\bmod p)$. In the latter case, $a^{2} \equiv c^{2}(\bmod p)$ so $a \equiv c$ $(\bmod p)$ or $a \equiv-c(\bmod p)$. In any case, two out of $\{a, b, c\}$ are the same $\bmod p$, so one of the equations gives $p \mid 2 x^{y}$ where $x \in\{a, b, c\}$ and $y \in\{k, k+1, k+2\}$, hence $p$ odd implies $p \mid x$ so $p \mid a b c$, the desired contradiction.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 2."
}
|
12908f67-47e7-5c53-abe2-6e327126b37d
| 607,874
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
We have
$$
\begin{aligned}
a^{2023} & \equiv-b^{2023} \quad(\bmod p) \\
b^{2024} & \equiv-c^{2024} \quad(\bmod p) \\
c^{2025} & \equiv-a^{2025} \quad(\bmod p)
\end{aligned}
$$
Thus,
$$
\begin{aligned}
a^{2023 \cdot 2024 \cdot 2025} & \equiv b^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(1) \\
& \equiv-c^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(2) \\
& \equiv-a^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(3)
\end{aligned}
$$
Thus, $p \mid 2 \cdot a^{2023 \cdot 2024 \cdot 2025}$ and hence $p \mid a$ since $p$ is odd. Now, finish as before.
## Remark.
- Solution 3 is the shortest, and seems to crucially relies on 2024 being even but it can be modified to always work. In particular, instead of raising to power $k(k+1)(k+2)$, we raise it to $\operatorname{lcm}(k, k+1, k+2)$. This method even works if we have a longer chain of equations and more variables i.e. $p \mid a_{i}^{k+i}+a_{i+1}^{k+i}$ for all $i$ in $0, \cdots, n-1$ and $a_{n}=a_{0}$.
- There are other possible approaches: one using primitive roots and another using orders. These proceed by considering the highest power of 2 dividing the exponents of the primitive root or order of $a b^{-1} \bmod p$ respectively.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime number and $a, b, c$ be integers so that the integers
$$
a^{2023}+b^{2023}, \quad b^{2024}+c^{2024}, \quad c^{2025}+a^{2025}
$$
are all divisible by $p$. Prove that $p$ divides each of $a, b$, and $c$.
|
We have
$$
\begin{aligned}
a^{2023} & \equiv-b^{2023} \quad(\bmod p) \\
b^{2024} & \equiv-c^{2024} \quad(\bmod p) \\
c^{2025} & \equiv-a^{2025} \quad(\bmod p)
\end{aligned}
$$
Thus,
$$
\begin{aligned}
a^{2023 \cdot 2024 \cdot 2025} & \equiv b^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(1) \\
& \equiv-c^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(2) \\
& \equiv-a^{2023 \cdot 2024 \cdot 2025} \quad(\bmod p) \quad \text { by }(3)
\end{aligned}
$$
Thus, $p \mid 2 \cdot a^{2023 \cdot 2024 \cdot 2025}$ and hence $p \mid a$ since $p$ is odd. Now, finish as before.
## Remark.
- Solution 3 is the shortest, and seems to crucially relies on 2024 being even but it can be modified to always work. In particular, instead of raising to power $k(k+1)(k+2)$, we raise it to $\operatorname{lcm}(k, k+1, k+2)$. This method even works if we have a longer chain of equations and more variables i.e. $p \mid a_{i}^{k+i}+a_{i+1}^{k+i}$ for all $i$ in $0, \cdots, n-1$ and $a_{n}=a_{0}$.
- There are other possible approaches: one using primitive roots and another using orders. These proceed by considering the highest power of 2 dividing the exponents of the primitive root or order of $a b^{-1} \bmod p$ respectively.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution 3."
}
|
12908f67-47e7-5c53-abe2-6e327126b37d
| 607,874
|
Let points $A_{1}, A_{2}$, and $A_{3}$ lie on the circle $\Gamma$ in counter-clockwise order, and let $P$ be a point in the same plane. For $i \in\{1,2,3\}$, let $\tau_{i}$ denote the counter-clockwise rotation of the plane centred at $A_{i}$, where the angle of the rotation is equal to the angle at vertex $A_{i}$ in $\triangle A_{1} A_{2} A_{3}$. Further, define $P_{i}$ to be the point $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(P)\right)\right)$, where indices are taken modulo 3 (i.e., $\tau_{4}=\tau_{1}$ and $\tau_{5}=\tau_{2}$ ).
Prove that the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is at most the radius of $\Gamma$.
|
Fix an index $i \in\{1,2,3\}$. Let $D_{1}, D_{2}, D_{3}$ be the points of tangency of the incircle of triangle $\triangle A_{1} A_{2} A_{3}$ with its sides $A_{2} A_{3}, A_{3} A_{1}, A_{1} A_{2}$ respectively.
The key observation is that given a line $\ell$ in the plane, the image of $\ell$ under the mapping $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(\ell)\right)\right)$ is a line parallel to $\ell$. Indeed, $\ell$ is rotated thrice by angles equal to the angles of $\triangle A_{1} A_{2} A_{3}$, and the composition of these rotations induces a half-turn and translation on $\ell$ as the angles of $\triangle A_{1} A_{2} A_{3}$ add to $180^{\circ}$. Since $D_{i}$ is a fixed point of this transformation (by the chain of maps $D_{i} \xrightarrow{\tau_{i+1}} D_{i+2} \xrightarrow{\tau_{i}} D_{i+1} \xrightarrow{\tau_{i+2}} D_{i}$ ), we conclude that the line $\overline{P D_{i}}$ maps to the line $\overline{P_{i} D_{i}}$. But the two lines are parallel and both of them pass through $D_{i}$ hence they must coincide, so $D_{i}$ lies on $\overline{P P_{i}}$. Further, each rotation preserves distances, hence $P_{i}$ is the reflection of $P$ in $D_{i}$.
In other words, the triangle $P_{1} P_{2} P_{3}$ is obtained by applying a homothety with ratio 2 and center $P$ to the triangle $D_{1} D_{2} D_{3}$. Thus, the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is twice the radius of the circumcircle of $\triangle D_{1} D_{2} D_{3}$, i.e., twice the radius of the incircle of $\triangle A_{1} A_{2} A_{3}$, which is known to be at most the radius of the circumcircle $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let points $A_{1}, A_{2}$, and $A_{3}$ lie on the circle $\Gamma$ in counter-clockwise order, and let $P$ be a point in the same plane. For $i \in\{1,2,3\}$, let $\tau_{i}$ denote the counter-clockwise rotation of the plane centred at $A_{i}$, where the angle of the rotation is equal to the angle at vertex $A_{i}$ in $\triangle A_{1} A_{2} A_{3}$. Further, define $P_{i}$ to be the point $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(P)\right)\right)$, where indices are taken modulo 3 (i.e., $\tau_{4}=\tau_{1}$ and $\tau_{5}=\tau_{2}$ ).
Prove that the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is at most the radius of $\Gamma$.
|
Fix an index $i \in\{1,2,3\}$. Let $D_{1}, D_{2}, D_{3}$ be the points of tangency of the incircle of triangle $\triangle A_{1} A_{2} A_{3}$ with its sides $A_{2} A_{3}, A_{3} A_{1}, A_{1} A_{2}$ respectively.
The key observation is that given a line $\ell$ in the plane, the image of $\ell$ under the mapping $\tau_{i+2}\left(\tau_{i}\left(\tau_{i+1}(\ell)\right)\right)$ is a line parallel to $\ell$. Indeed, $\ell$ is rotated thrice by angles equal to the angles of $\triangle A_{1} A_{2} A_{3}$, and the composition of these rotations induces a half-turn and translation on $\ell$ as the angles of $\triangle A_{1} A_{2} A_{3}$ add to $180^{\circ}$. Since $D_{i}$ is a fixed point of this transformation (by the chain of maps $D_{i} \xrightarrow{\tau_{i+1}} D_{i+2} \xrightarrow{\tau_{i}} D_{i+1} \xrightarrow{\tau_{i+2}} D_{i}$ ), we conclude that the line $\overline{P D_{i}}$ maps to the line $\overline{P_{i} D_{i}}$. But the two lines are parallel and both of them pass through $D_{i}$ hence they must coincide, so $D_{i}$ lies on $\overline{P P_{i}}$. Further, each rotation preserves distances, hence $P_{i}$ is the reflection of $P$ in $D_{i}$.
In other words, the triangle $P_{1} P_{2} P_{3}$ is obtained by applying a homothety with ratio 2 and center $P$ to the triangle $D_{1} D_{2} D_{3}$. Thus, the radius of the circumcircle of $\triangle P_{1} P_{2} P_{3}$ is twice the radius of the circumcircle of $\triangle D_{1} D_{2} D_{3}$, i.e., twice the radius of the incircle of $\triangle A_{1} A_{2} A_{3}$, which is known to be at most the radius of the circumcircle $\Gamma$.
|
{
"resource_path": "INMO/segmented/en-INMO_2024_final_solutions.jsonl",
"problem_match": "\nProblem 5.",
"solution_match": "\nSolution 1."
}
|
8599b65a-40f7-559b-84da-66de4aeb2a0c
| 607,876
|
Let $A_{1} B_{1} C_{1} D_{1} E_{1}$ be a regular pentagon. For $2 \leq n \leq 11$,
let $A_{n} B_{n} C_{n} D_{n} E_{n}$ be the pentagon whose vertices are the midpoints of the sides of the pentagon $A_{n-1} B_{n-1} C_{n-1} D_{n-1} E_{n-1}$. All the 5 vertices of each of the 11 pentagons are arbitrarily coloured red or blue. Prove that four points among these 55 points have the same colour and form the vertices of a cyclic quadrilateral.
|
We first observe that all the eleven pentagons are regular. Moreover, there are 5 fixed directions and all the 55 sides are in one of these directions. If we consider any two sides which are parallel, they are the parallel sides of an isosceles trapezium, which is cyclic.
If we consider any pentagon, its two adjacent vertices have the same colour. Consider all such 11 sides whose end points are of the same colour. These are in 5 fixed directions. By pigeon-hole principle, there are 3 sides which are in the same directions and therefore parallel to each other. Among these three sides, two must have end points having one colour (again by $\mathrm{P}-\mathrm{H}$ principle). Thus there are two parallel sides among the 55 and the end points of these have one fixed colour. But these two sides are parallel sides of an isosceles trapezium. Hence the four end points are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $A_{1} B_{1} C_{1} D_{1} E_{1}$ be a regular pentagon. For $2 \leq n \leq 11$,
let $A_{n} B_{n} C_{n} D_{n} E_{n}$ be the pentagon whose vertices are the midpoints of the sides of the pentagon $A_{n-1} B_{n-1} C_{n-1} D_{n-1} E_{n-1}$. All the 5 vertices of each of the 11 pentagons are arbitrarily coloured red or blue. Prove that four points among these 55 points have the same colour and form the vertices of a cyclic quadrilateral.
|
We first observe that all the eleven pentagons are regular. Moreover, there are 5 fixed directions and all the 55 sides are in one of these directions. If we consider any two sides which are parallel, they are the parallel sides of an isosceles trapezium, which is cyclic.
If we consider any pentagon, its two adjacent vertices have the same colour. Consider all such 11 sides whose end points are of the same colour. These are in 5 fixed directions. By pigeon-hole principle, there are 3 sides which are in the same directions and therefore parallel to each other. Among these three sides, two must have end points having one colour (again by $\mathrm{P}-\mathrm{H}$ principle). Thus there are two parallel sides among the 55 and the end points of these have one fixed colour. But these two sides are parallel sides of an isosceles trapezium. Hence the four end points are concyclic.
|
{
"resource_path": "INMO/segmented/en-Inmo-2019-Solutions.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution:"
}
|
17ea00ca-5c1f-5c25-b2b0-b341b04613f6
| 607,879
|
Let $m, n$ be distinct positive integers. Prove that
$$
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, n+2) \leq 2|m-n|+1
$$
Further, determine when equality holds.
|
Observe that
$$
\operatorname{gcd}(m+j, n+j)=\operatorname{gcd}(m+j,|m-n|)
$$
for $j=0,1,2$. Hence we can find positive integers $a, b, c$ such that
$$
\operatorname{gcd}(m, n)=\frac{|m-n|}{a}, \quad \operatorname{gcd}(m+1, n+1)=\frac{|m-n|}{b}, \quad \operatorname{gcd}(m+2, n+2)=\frac{|m-n|}{c}
$$
It follows that $|m-n|$ divides $m a,(m+1) b$ and $(m+2) c$. Hence we can see that $|m-n|$ divides $a b$ and $b c$. We get $|m-n| \leq a b$ and $|m-n| \leq b c$. This leads to
$$
b \geq \frac{|m-n|}{a}, \quad b \geq \frac{|m-n|}{c}
$$
Thus
$$
\begin{aligned}
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, & n+2) \\
& =\frac{|m-n|}{a}+\frac{|m-n|}{b}+\frac{|m-n|}{c} \leq 2 b+\frac{|m-n|}{b}
\end{aligned}
$$
We have to prove that
$$
2 b+\frac{|m-n|}{b} \leq 2|m-n|+1
$$
Taking $|m-n|=K$, we have to show that $2 b^{2}+K \leq b(2 K+1)$. This reduces to $(b-K)(2 b-1) \leq 0$. However
$$
K=|m-n| \geq b \geq 1>\frac{1}{2}
$$
Equality holds only when $(m, n)=(k, k+1)$ or $(2 k, 2 k+2)$ or permutations of these for some $k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m, n$ be distinct positive integers. Prove that
$$
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, n+2) \leq 2|m-n|+1
$$
Further, determine when equality holds.
|
Observe that
$$
\operatorname{gcd}(m+j, n+j)=\operatorname{gcd}(m+j,|m-n|)
$$
for $j=0,1,2$. Hence we can find positive integers $a, b, c$ such that
$$
\operatorname{gcd}(m, n)=\frac{|m-n|}{a}, \quad \operatorname{gcd}(m+1, n+1)=\frac{|m-n|}{b}, \quad \operatorname{gcd}(m+2, n+2)=\frac{|m-n|}{c}
$$
It follows that $|m-n|$ divides $m a,(m+1) b$ and $(m+2) c$. Hence we can see that $|m-n|$ divides $a b$ and $b c$. We get $|m-n| \leq a b$ and $|m-n| \leq b c$. This leads to
$$
b \geq \frac{|m-n|}{a}, \quad b \geq \frac{|m-n|}{c}
$$
Thus
$$
\begin{aligned}
\operatorname{gcd}(m, n)+\operatorname{gcd}(m+1, n+1)+\operatorname{gcd}(m+2, & n+2) \\
& =\frac{|m-n|}{a}+\frac{|m-n|}{b}+\frac{|m-n|}{c} \leq 2 b+\frac{|m-n|}{b}
\end{aligned}
$$
We have to prove that
$$
2 b+\frac{|m-n|}{b} \leq 2|m-n|+1
$$
Taking $|m-n|=K$, we have to show that $2 b^{2}+K \leq b(2 K+1)$. This reduces to $(b-K)(2 b-1) \leq 0$. However
$$
K=|m-n| \geq b \geq 1>\frac{1}{2}
$$
Equality holds only when $(m, n)=(k, k+1)$ or $(2 k, 2 k+2)$ or permutations of these for some $k$.
|
{
"resource_path": "INMO/segmented/en-Inmo-2019-Solutions.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution:"
}
|
2e0a5957-cc6c-5793-a0c9-6deb81407b0a
| 607,880
|
Let $n$ and $M$ be positive integers such that $M>n^{n-1}$. Prove that there are $n$ distinct primes $p_{1}, p_{2}, p_{3}, \ldots, p_{n}$ such that $p_{j}$ divides $M+j$ for $1 \leq j \leq n$.
|
If some number $M+k, 1 \leq k \leq n$, has at least $n$ distinct prime factors, then we can associate a prime factor of $M+k$ with the number $M+k$ which is not associated with any of the remaining $n-1$ numbers.
Suppose $m+j$ has less than $n$ distinct prime factors. Write
$$
M+j=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{r}^{\alpha_{r}}, \quad r<n
$$
But $M+j>n^{n-1}$. Hence there exist $t, 1 \leq t \leq r$ such that $p_{t}^{\alpha_{t}}>n$. Associate $p_{t}$ with this $M+j$. Suppose $p_{t}$ is associated with some $M+l$. Let $p_{t}^{\beta_{t}}$ be the largest power of $p_{t}$ dividing $M+l$. Then $p_{t}^{\beta_{t}}>n$. Let $T=\operatorname{gcd}\left(p_{t}^{\alpha_{t}}, p_{t}^{\beta_{t}}\right)$. Then $T>n$. Since $T \mid(M+j)$ and $T \mid(M+l)$, it follows that $T \mid(|j-l|)$. But $|j-l|<n$ and $T>n$, and we get a contradiction. This shows that $p_{t}$ cannot be associated with any other $M+l$. Thus each $M+j$ is associated with different primes.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ and $M$ be positive integers such that $M>n^{n-1}$. Prove that there are $n$ distinct primes $p_{1}, p_{2}, p_{3}, \ldots, p_{n}$ such that $p_{j}$ divides $M+j$ for $1 \leq j \leq n$.
|
If some number $M+k, 1 \leq k \leq n$, has at least $n$ distinct prime factors, then we can associate a prime factor of $M+k$ with the number $M+k$ which is not associated with any of the remaining $n-1$ numbers.
Suppose $m+j$ has less than $n$ distinct prime factors. Write
$$
M+j=p_{1}^{\alpha_{1}} p_{2}^{\alpha_{2}} \cdots p_{r}^{\alpha_{r}}, \quad r<n
$$
But $M+j>n^{n-1}$. Hence there exist $t, 1 \leq t \leq r$ such that $p_{t}^{\alpha_{t}}>n$. Associate $p_{t}$ with this $M+j$. Suppose $p_{t}$ is associated with some $M+l$. Let $p_{t}^{\beta_{t}}$ be the largest power of $p_{t}$ dividing $M+l$. Then $p_{t}^{\beta_{t}}>n$. Let $T=\operatorname{gcd}\left(p_{t}^{\alpha_{t}}, p_{t}^{\beta_{t}}\right)$. Then $T>n$. Since $T \mid(M+j)$ and $T \mid(M+l)$, it follows that $T \mid(|j-l|)$. But $|j-l|<n$ and $T>n$, and we get a contradiction. This shows that $p_{t}$ cannot be associated with any other $M+l$. Thus each $M+j$ is associated with different primes.
|
{
"resource_path": "INMO/segmented/en-Inmo-2019-Solutions.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution:"
}
|
72422f76-adb8-5ba6-bc11-51f019b3b8db
| 607,881
|
Let $A B$ be a diameter of a circle $\Gamma$ and let $C$ be a point on $\Gamma$ different from $A$ and $B$. Let $D$ be the foot of perpendicular from $C$ on to $A B$. Let $K$ be a point of the segment $C D$ such that $A C$ is equal to the semiperimeter of the triangle $A D K$. Show that the excircle of triangle $A D K$ opposite $A$ is tangent to $\Gamma$.
|
Draw another diameter $P Q \perp A B$. Let $E$ be the point at which the excircle $\Gamma_{1}$ touches the line $A D$. Join $Q E$ and extend it to meet $\Gamma$ in $L$. Draw the diameter $E N$ of $\Gamma_{1}$ and draw $Q S \perp N E$ (extended). See the figure. We also observe that $D E=E M=E N / 2$.
Since $A E$ is equal to the semiperimeter of $\triangle A D K$, we have $A C=A E$. Hence $A E^{2}=A C^{2}=$ $A D \cdot A B$ (as $A C B$ is a right-angle triangle). Thus
$$
A D(A D+D E+E B)=(A D+D E)^{2}=A D^{2}+2 A D \cdot D E+D E^{2}
$$
Simplification gives
$$
\begin{aligned}
A D \cdot E B & =A D \cdot D E+D E^{2} \\
& =D E(A D+D E) \\
& =D E \cdot A E \\
& =D E(A B-B E)
\end{aligned}
$$
Therefore
$$
D E \cdot A B=E B(A D+D E)=E B \cdot A E
$$
But
$$
D E \cdot A B=D E \cdot P Q=2 D E \cdot O Q=E N \cdot E S
$$
and $E B \cdot A E=Q E \cdot E L$. Therefore we get
$$
Q E \cdot E L=E N \cdot E S
$$
It follows that $Q, S, L, N$ are concyclic. Since $\angle Q S E=90^{\circ}$, we get $\angle E L N=90^{\circ}$. Since $E N$ is a diameter, this implies that $L$ also lies on $\Gamma_{1}$. But $\angle Q L P=90^{\circ}$. Therefore $L, N, P$ are collinear. Since $N M \| P O$ and
$$
\frac{N M}{P O}=\frac{N E}{P Q}=\frac{L N}{L P}
$$
it follows that $L, M, O$ are collinear. Hence $\Gamma_{1}$ is tangent to $\Gamma$ at $L$.
Alternate solution: Let $R$ be the radius the circle $\Gamma$ and $r$ be that of the circle $\Gamma_{1}$. Let $O$ be the centre of $\Gamma$ and $M$ be that of the circle $\Gamma_{1}$. Let $E$ be the point of contact of $\Gamma_{1}$ with $A B$. Then $M E=D E=r$. Observe that $A E$ is the semiperimeter of $\triangle A D E$. We are given that $A C=A E$. Using that $\angle A C B=90^{\circ}$, we also get $A C^{2}=A D \cdot A B$. Hence $A E^{2}=A D \cdot A B$. We have to show that $R-r=O M$ for proving that $\Gamma_{1}$ is tangent to $\Gamma$. We have
$$
\begin{aligned}
& O M^{2}-(R-r)^{2}=O E^{2}+r^{2}-(R-r)^{2}=(A D+D E-A O)^{2}+r^{2}-(R-r)^{2} \\
&=(A D-(R-r))^{2}+r^{2}-(R-r)^{2}=A D^{2}-2 A D \cdot(R-r)+r^{2} \\
&=\left(A D^{2}+2 A D \cdot r+r^{2}\right)-2 A D \cdot R=(A D+r)^{2}-A D \cdot A B \\
&=(A D+D E)^{2}-A D \cdot A B=A E^{2}-A D \cdot A B=0
\end{aligned}
$$
Hence $O M=R-r$ and therefore $\Gamma_{1}$ is tangent to $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B$ be a diameter of a circle $\Gamma$ and let $C$ be a point on $\Gamma$ different from $A$ and $B$. Let $D$ be the foot of perpendicular from $C$ on to $A B$. Let $K$ be a point of the segment $C D$ such that $A C$ is equal to the semiperimeter of the triangle $A D K$. Show that the excircle of triangle $A D K$ opposite $A$ is tangent to $\Gamma$.
|
Draw another diameter $P Q \perp A B$. Let $E$ be the point at which the excircle $\Gamma_{1}$ touches the line $A D$. Join $Q E$ and extend it to meet $\Gamma$ in $L$. Draw the diameter $E N$ of $\Gamma_{1}$ and draw $Q S \perp N E$ (extended). See the figure. We also observe that $D E=E M=E N / 2$.

Since $A E$ is equal to the semiperimeter of $\triangle A D K$, we have $A C=A E$. Hence $A E^{2}=A C^{2}=$ $A D \cdot A B$ (as $A C B$ is a right-angle triangle). Thus
$$
A D(A D+D E+E B)=(A D+D E)^{2}=A D^{2}+2 A D \cdot D E+D E^{2}
$$
Simplification gives
$$
\begin{aligned}
A D \cdot E B & =A D \cdot D E+D E^{2} \\
& =D E(A D+D E) \\
& =D E \cdot A E \\
& =D E(A B-B E)
\end{aligned}
$$
Therefore
$$
D E \cdot A B=E B(A D+D E)=E B \cdot A E
$$
But
$$
D E \cdot A B=D E \cdot P Q=2 D E \cdot O Q=E N \cdot E S
$$
and $E B \cdot A E=Q E \cdot E L$. Therefore we get
$$
Q E \cdot E L=E N \cdot E S
$$
It follows that $Q, S, L, N$ are concyclic. Since $\angle Q S E=90^{\circ}$, we get $\angle E L N=90^{\circ}$. Since $E N$ is a diameter, this implies that $L$ also lies on $\Gamma_{1}$. But $\angle Q L P=90^{\circ}$. Therefore $L, N, P$ are collinear. Since $N M \| P O$ and
$$
\frac{N M}{P O}=\frac{N E}{P Q}=\frac{L N}{L P}
$$
it follows that $L, M, O$ are collinear. Hence $\Gamma_{1}$ is tangent to $\Gamma$ at $L$.
Alternate solution: Let $R$ be the radius the circle $\Gamma$ and $r$ be that of the circle $\Gamma_{1}$. Let $O$ be the centre of $\Gamma$ and $M$ be that of the circle $\Gamma_{1}$. Let $E$ be the point of contact of $\Gamma_{1}$ with $A B$. Then $M E=D E=r$. Observe that $A E$ is the semiperimeter of $\triangle A D E$. We are given that $A C=A E$. Using that $\angle A C B=90^{\circ}$, we also get $A C^{2}=A D \cdot A B$. Hence $A E^{2}=A D \cdot A B$. We have to show that $R-r=O M$ for proving that $\Gamma_{1}$ is tangent to $\Gamma$. We have
$$
\begin{aligned}
& O M^{2}-(R-r)^{2}=O E^{2}+r^{2}-(R-r)^{2}=(A D+D E-A O)^{2}+r^{2}-(R-r)^{2} \\
&=(A D-(R-r))^{2}+r^{2}-(R-r)^{2}=A D^{2}-2 A D \cdot(R-r)+r^{2} \\
&=\left(A D^{2}+2 A D \cdot r+r^{2}\right)-2 A D \cdot R=(A D+r)^{2}-A D \cdot A B \\
&=(A D+D E)^{2}-A D \cdot A B=A E^{2}-A D \cdot A B=0
\end{aligned}
$$
Hence $O M=R-r$ and therefore $\Gamma_{1}$ is tangent to $\Gamma$.
|
{
"resource_path": "INMO/segmented/en-Inmo-2019-Solutions.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution:"
}
|
ad1a59c8-c231-50cc-98d6-102d04b7d167
| 607,882
|
Let $f$ be function defined from the set $\{(x, y): x, y$ reals, $x y \neq 0\}$ in to the set of all positive real numbers such that
(i) $\quad f(x y, z)=f(x, z) f(y, z)$, for all $x, y \neq 0$;
(ii) $\quad f(x, y z)=f(x, y) f(x, z)$, for all $x, y \neq 0$;
(iii) $\quad f(x, 1-x)=1$, for all $x \neq 0,1$.
Prove that
(a) $\quad f(x, x)=f(x,-x)=1$, for all $x \neq 0$;
(b) $\quad f(x, y) f(y, x)=1$, for all $x, y \neq 0$.
|
(The condition (ii) was inadvertently left out in the paper. We give the solution with condition (ii).)
Taking $x=y=1$ in (ii), weget $f(1, z)^{2}=f(1, z)$ so that $f(1, z)=1$ for all $z \neq 0$. Similarly, $x=y=-1$ gives $f(-1, z)=1$ for all $z \neq 0$. Using the second condition, we also get $f(z, 1)=$ $f(z,-1)=1$ for all $z \neq 0$. Observe
$$
f\left(\frac{1}{x}, y\right) f(x, y)=f(1, y)=1=f(x, 1)=f\left(x, \frac{1}{y}\right) f(x, y)
$$
Therefore
$$
f\left(x, \frac{1}{y}\right)=f\left(\frac{1}{x}, y\right)=\frac{1}{f(x, y)}
$$
for all $x, y \neq 0$. Now for $x \neq 0,1$, condition (iii) gives
$$
1=f\left(\frac{1}{x}, 1-\frac{1}{x}\right)=f\left(x, \frac{1}{1-\frac{1}{x}}\right)
$$
Multiplying by $1=f(x, 1-x)$, we get
$$
1=f(x, 1-x) f\left(x, \frac{1}{1-\frac{1}{x}}\right)=f\left(x, \frac{1-x}{1-\frac{1}{x}}\right)=f(x,-x)
$$
for all $x \neq 0,1$. But $f(x,-1)=1$ for all $x \neq 0$ gives
$$
f(x, x)=f(x,-x) f(x,-1)=f(x,-x)=1
$$
for all $x \neq 0,1$. Observe $f(1,1)=f(1,-1)=1$. Hence
$$
f(x, x)=f(x,-x)=1
$$
for all $x \neq 0$, which proves (a).
We have
$$
1=f(x y, x y)=f(x, x y) f(y, x y)=f(x, x) f(x, y) f(y, x) f(y, y)=f(x, y) f(y, x)
$$
for all $x, y \neq 0$, which proves (b).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $f$ be function defined from the set $\{(x, y): x, y$ reals, $x y \neq 0\}$ in to the set of all positive real numbers such that
(i) $\quad f(x y, z)=f(x, z) f(y, z)$, for all $x, y \neq 0$;
(ii) $\quad f(x, y z)=f(x, y) f(x, z)$, for all $x, y \neq 0$;
(iii) $\quad f(x, 1-x)=1$, for all $x \neq 0,1$.
Prove that
(a) $\quad f(x, x)=f(x,-x)=1$, for all $x \neq 0$;
(b) $\quad f(x, y) f(y, x)=1$, for all $x, y \neq 0$.
|
(The condition (ii) was inadvertently left out in the paper. We give the solution with condition (ii).)
Taking $x=y=1$ in (ii), weget $f(1, z)^{2}=f(1, z)$ so that $f(1, z)=1$ for all $z \neq 0$. Similarly, $x=y=-1$ gives $f(-1, z)=1$ for all $z \neq 0$. Using the second condition, we also get $f(z, 1)=$ $f(z,-1)=1$ for all $z \neq 0$. Observe
$$
f\left(\frac{1}{x}, y\right) f(x, y)=f(1, y)=1=f(x, 1)=f\left(x, \frac{1}{y}\right) f(x, y)
$$
Therefore
$$
f\left(x, \frac{1}{y}\right)=f\left(\frac{1}{x}, y\right)=\frac{1}{f(x, y)}
$$
for all $x, y \neq 0$. Now for $x \neq 0,1$, condition (iii) gives
$$
1=f\left(\frac{1}{x}, 1-\frac{1}{x}\right)=f\left(x, \frac{1}{1-\frac{1}{x}}\right)
$$
Multiplying by $1=f(x, 1-x)$, we get
$$
1=f(x, 1-x) f\left(x, \frac{1}{1-\frac{1}{x}}\right)=f\left(x, \frac{1-x}{1-\frac{1}{x}}\right)=f(x,-x)
$$
for all $x \neq 0,1$. But $f(x,-1)=1$ for all $x \neq 0$ gives
$$
f(x, x)=f(x,-x) f(x,-1)=f(x,-x)=1
$$
for all $x \neq 0,1$. Observe $f(1,1)=f(1,-1)=1$. Hence
$$
f(x, x)=f(x,-x)=1
$$
for all $x \neq 0$, which proves (a).
We have
$$
1=f(x y, x y)=f(x, x y) f(y, x y)=f(x, x) f(x, y) f(y, x) f(y, y)=f(x, y) f(y, x)
$$
for all $x, y \neq 0$, which proves (b).
|
{
"resource_path": "INMO/segmented/en-Inmo-2019-Solutions.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution:"
}
|
e60335be-0e42-5b33-aaa3-c3934a55342c
| 607,883
|
Let $n$ be a natural number. Prove that
$$
\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n}]
$$
is even. (Here $[x]$ denotes the largest integer smaller than or equal to $x$.)
|
Let $f(n)$ denote the given equation. Then $f(1)=2$ which is even. Now suppose that $f(n)$ is even for some $n \geq 1$. Then
$$
\begin{aligned}
f(n+1) & =\left[\frac{n+1}{1}\right]+\left[\frac{n+1}{2}\right]+\left[\frac{n+1}{3}\right]+\cdots\left[\frac{n+1}{n+1}\right]+[\sqrt{n+1}] \\
& =\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n+1}]+\sigma(n+1)
\end{aligned}
$$
where $\sigma(n+1)$ denotes the number of positive divisors of $n+1$. This follows from $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]+1$ if $k$ divides $n+1$, and $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]$ otherwise. Note that $[\sqrt{n+1}]=[\sqrt{n}]$ unless $n+1$ is a square, in which case $[\sqrt{n+1}]=[\sqrt{n}]+1$. On the other hand $\sigma(n+1)$ is odd if and only if $n+1$ is a square. Therefore it follows that $f(n+1)=f(n)+2 l$ for some integer $l$. This proves that $f(n+1)$ is even.
Thus it follows by induction that $f(n)$ is even for all natural number $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a natural number. Prove that
$$
\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n}]
$$
is even. (Here $[x]$ denotes the largest integer smaller than or equal to $x$.)
|
Let $f(n)$ denote the given equation. Then $f(1)=2$ which is even. Now suppose that $f(n)$ is even for some $n \geq 1$. Then
$$
\begin{aligned}
f(n+1) & =\left[\frac{n+1}{1}\right]+\left[\frac{n+1}{2}\right]+\left[\frac{n+1}{3}\right]+\cdots\left[\frac{n+1}{n+1}\right]+[\sqrt{n+1}] \\
& =\left[\frac{n}{1}\right]+\left[\frac{n}{2}\right]+\left[\frac{n}{3}\right]+\cdots\left[\frac{n}{n}\right]+[\sqrt{n+1}]+\sigma(n+1)
\end{aligned}
$$
where $\sigma(n+1)$ denotes the number of positive divisors of $n+1$. This follows from $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]+1$ if $k$ divides $n+1$, and $\left[\frac{n+1}{k}\right]=\left[\frac{n}{k}\right]$ otherwise. Note that $[\sqrt{n+1}]=[\sqrt{n}]$ unless $n+1$ is a square, in which case $[\sqrt{n+1}]=[\sqrt{n}]+1$. On the other hand $\sigma(n+1)$ is odd if and only if $n+1$ is a square. Therefore it follows that $f(n+1)=f(n)+2 l$ for some integer $l$. This proves that $f(n+1)$ is even.
Thus it follows by induction that $f(n)$ is even for all natural number $n$.
|
{
"resource_path": "INMO/segmented/en-inmo-2014.jsonl",
"problem_match": "\n2.",
"solution_match": "\nSolution."
}
|
982ffec9-d92a-52c3-bc5b-544e8c51c210
| 607,885
|
Let $a, b$ be natural numbers with $a b>2$. Suppose that the sum of their greatest common divisor and least common multiple is divisible by $a+b$. Prove that the quotient is at most $(a+b) / 4$. When is this quotient exactly equal to $(a+b) / 4$ ?
|
Let $g$ and $l$ denote the greatest common divisor and the least common multiple, respectively, of $a$ and $b$. Then $g l=a b$. Therefore $g+l \leq a b+1$. Suppose that $(g+l) /(a+b)>(a+b) / 4$. Then we have $a b+1>(a+b)^{2} / 4$, so we get $(a-b)^{2}<4$. Assuming, $a \geq b$ we either have $a=b$ or $a=b+1$. In the former case, $g=l=a$ and the quotient is $(g+l) /(a+b)=1 \leq(a+b) / 4$. In the latter case, $g=1$ and $l=b(b+1)$ so we get that $2 b+1$ divides $b^{2}+b+1$. Therefore $2 b+1$ divides $4\left(b^{2}+b+1\right)-(2 b+1)^{2}=3$ which implies that $b=1$ and $a=2$, a contradiction to the given assumption that $a b>2$. This shows that $(g+l) /(a+b) \leq(a+b) / 4$. Note that for the equality to hold, we need that either $a=b=2$ or, $(a-b)^{2}=4$ and $g=1, l=a b$. The latter case happens if and only if $a$ and $b$ are two consecutive odd numbers. (If $a=2 k+1$ and $b=2 k-1$ then $a+b=4 k$ divides $a b+1=4 k^{2}$ and the quotient is precisely $(a+b) / 4$.)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a, b$ be natural numbers with $a b>2$. Suppose that the sum of their greatest common divisor and least common multiple is divisible by $a+b$. Prove that the quotient is at most $(a+b) / 4$. When is this quotient exactly equal to $(a+b) / 4$ ?
|
Let $g$ and $l$ denote the greatest common divisor and the least common multiple, respectively, of $a$ and $b$. Then $g l=a b$. Therefore $g+l \leq a b+1$. Suppose that $(g+l) /(a+b)>(a+b) / 4$. Then we have $a b+1>(a+b)^{2} / 4$, so we get $(a-b)^{2}<4$. Assuming, $a \geq b$ we either have $a=b$ or $a=b+1$. In the former case, $g=l=a$ and the quotient is $(g+l) /(a+b)=1 \leq(a+b) / 4$. In the latter case, $g=1$ and $l=b(b+1)$ so we get that $2 b+1$ divides $b^{2}+b+1$. Therefore $2 b+1$ divides $4\left(b^{2}+b+1\right)-(2 b+1)^{2}=3$ which implies that $b=1$ and $a=2$, a contradiction to the given assumption that $a b>2$. This shows that $(g+l) /(a+b) \leq(a+b) / 4$. Note that for the equality to hold, we need that either $a=b=2$ or, $(a-b)^{2}=4$ and $g=1, l=a b$. The latter case happens if and only if $a$ and $b$ are two consecutive odd numbers. (If $a=2 k+1$ and $b=2 k-1$ then $a+b=4 k$ divides $a b+1=4 k^{2}$ and the quotient is precisely $(a+b) / 4$.)
|
{
"resource_path": "INMO/segmented/en-inmo-2014.jsonl",
"problem_match": "\n3.",
"solution_match": "\nSolution."
}
|
c025d4a3-8307-5320-a54f-c4ac53874542
| 607,886
|
Written on a blackboard is the polynomial $x^{2}+x+2014$. Calvin and Hobbes take turns alternatively (starting with Calvin) in the following game. During his turn, Calvin should either increase or decrease the coefficient of $x$ by 1. And during his turn, Hobbes should either increase or decrease the constant coefficient by 1. Calvin wins if at any point of time the polynomial on the blackboard at that instant has integer roots. Prove that Calvin has a winning strategy.
|
For $i \geq 0$, let $f_{i}(x)$ denote the polynomial on the blackboard after Hobbes' $i$-th turn. We let Calvin decrease the coefficient of $x$ by 1 . Therefore $f_{i+1}(2)=f_{i}(2)-1$ or $f_{i+1}(2)=f_{i}(2)-3$ (depending on whether Hobbes increases or decreases the constant term). So for some $i$, we have $0 \leq f_{i}(2) \leq 2$. If $f_{i}(2)=0$ then Calvin has won the game. If $f_{i}(2)=2$ then Calvin wins the game by reducing the coefficient of $x$ by 1 . If $f_{i}(2)=1$ then $f_{i+1}(2)=0$ or $f_{i+1}(2)=-2$. In the former case, Calvin has won the game and in the latter case Calvin wins the game by increasing the coefficient of $x$ by 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Written on a blackboard is the polynomial $x^{2}+x+2014$. Calvin and Hobbes take turns alternatively (starting with Calvin) in the following game. During his turn, Calvin should either increase or decrease the coefficient of $x$ by 1. And during his turn, Hobbes should either increase or decrease the constant coefficient by 1. Calvin wins if at any point of time the polynomial on the blackboard at that instant has integer roots. Prove that Calvin has a winning strategy.
|
For $i \geq 0$, let $f_{i}(x)$ denote the polynomial on the blackboard after Hobbes' $i$-th turn. We let Calvin decrease the coefficient of $x$ by 1 . Therefore $f_{i+1}(2)=f_{i}(2)-1$ or $f_{i+1}(2)=f_{i}(2)-3$ (depending on whether Hobbes increases or decreases the constant term). So for some $i$, we have $0 \leq f_{i}(2) \leq 2$. If $f_{i}(2)=0$ then Calvin has won the game. If $f_{i}(2)=2$ then Calvin wins the game by reducing the coefficient of $x$ by 1 . If $f_{i}(2)=1$ then $f_{i+1}(2)=0$ or $f_{i+1}(2)=-2$. In the former case, Calvin has won the game and in the latter case Calvin wins the game by increasing the coefficient of $x$ by 1 .
|
{
"resource_path": "INMO/segmented/en-inmo-2014.jsonl",
"problem_match": "\n4.",
"solution_match": "\nSolution."
}
|
fdbb3b54-1a23-5c54-bb4a-d81042a1412d
| 607,887
|
In an acute-angled triangle $A B C$, a point $D$ lies on the segment $B C$. Let $O_{1}, O_{2}$ denote the circumcentres of triangles $A B D$ and $A C D$, respectively. Prove that the line joining the circumcentre of triangle $A B C$ and the orthocentre of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{D}$ is parallel to $B C$.
|
Without loss of generality assume that $\angle A D C \geq 90^{\circ}$. Let $O$ denote the circumcenter of triangle $A B C$ and $K$ the orthocentre of triangle $O_{1} O_{2} D$. We shall first show that the points $O$ and $K$ lie on the circumcircle of triangle $A O_{1} O_{2}$. Note that circumcircles of triangles $A B D$ and $A C D$ pass through the points $A$ and $D$, so $A D$ is perpendicular to $O_{1} O_{2}$ and, triangle $A O_{1} O_{2}$ is congruent to triangle $D O_{1} O_{2}$. In particular, $\angle A O_{1} O_{2}=\angle O_{2} O_{1} D=\angle B$ since $O_{2} O_{1}$ is the perpendicular bisector of $A D$. On the other hand since $O O_{2}$ is the perpendicular bisector of $A C$ it follows that $\angle A O O_{2}=\angle B$. This shows that $O$ lies on the circumcircle of triangle $A O_{1} O_{2}$. Note also that, since $A D$ is perpendicular to $O_{1} O_{2}$, we have $\angle O_{2} K A=90^{\circ}-\angle O_{1} O_{2} K=$ $\angle O_{2} O_{1} D=\angle B$. This proves that $K$ also lies on the circumcircle of triangle $A O_{1} O_{2}$.
Therefore $\angle A K O=180^{\circ}-\angle A O_{2} O=\angle A D C$ and hence $O K$ is parallel to $B C$.
Remark. The result is true even for an obtuse-angled triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In an acute-angled triangle $A B C$, a point $D$ lies on the segment $B C$. Let $O_{1}, O_{2}$ denote the circumcentres of triangles $A B D$ and $A C D$, respectively. Prove that the line joining the circumcentre of triangle $A B C$ and the orthocentre of triangle $\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{D}$ is parallel to $B C$.
|
Without loss of generality assume that $\angle A D C \geq 90^{\circ}$. Let $O$ denote the circumcenter of triangle $A B C$ and $K$ the orthocentre of triangle $O_{1} O_{2} D$. We shall first show that the points $O$ and $K$ lie on the circumcircle of triangle $A O_{1} O_{2}$. Note that circumcircles of triangles $A B D$ and $A C D$ pass through the points $A$ and $D$, so $A D$ is perpendicular to $O_{1} O_{2}$ and, triangle $A O_{1} O_{2}$ is congruent to triangle $D O_{1} O_{2}$. In particular, $\angle A O_{1} O_{2}=\angle O_{2} O_{1} D=\angle B$ since $O_{2} O_{1}$ is the perpendicular bisector of $A D$. On the other hand since $O O_{2}$ is the perpendicular bisector of $A C$ it follows that $\angle A O O_{2}=\angle B$. This shows that $O$ lies on the circumcircle of triangle $A O_{1} O_{2}$. Note also that, since $A D$ is perpendicular to $O_{1} O_{2}$, we have $\angle O_{2} K A=90^{\circ}-\angle O_{1} O_{2} K=$ $\angle O_{2} O_{1} D=\angle B$. This proves that $K$ also lies on the circumcircle of triangle $A O_{1} O_{2}$.
Therefore $\angle A K O=180^{\circ}-\angle A O_{2} O=\angle A D C$ and hence $O K$ is parallel to $B C$.
Remark. The result is true even for an obtuse-angled triangle.
|
{
"resource_path": "INMO/segmented/en-inmo-2014.jsonl",
"problem_match": "\n5.",
"solution_match": "\nSolution."
}
|
cb3156de-8a67-5925-8ea0-5cf4544227ed
| 607,888
|
Let $n$ be a natural number and $X=\{1,2, \ldots, n\}$. For subsets $A$ and $B$ of $X$ we define $A \Delta B$ to be the set of all those elements of $X$ which belong to exactly one of $A$ and $B$. Let $\mathcal{F}$ be a collection of subsets of $X$ such that for any two distinct elements $A$ and $B$ in $\mathcal{F}$ the set $A \Delta B$ has at least two elements. Show that $\mathcal{F}$ has at most $2^{n-1}$ elements. Find all such collections $\mathcal{F}$ with $2^{n-1}$ elements.
|
For each subset $A$ of $\{1,2, \ldots, n-1\}$, we pair it with $A \cup\{n\}$. Note that for any such pair $(A, B)$ not both $A$ and $B$ can be in $\mathcal{F}$. Since there are $2^{n-1}$ such pairs it follows that $\mathcal{F}$ can have at most $2^{n-1}$ elements.
We shall show by induction on $n$ that if $|\mathcal{F}|=2^{n-1}$ then $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets with even number of elements. The result is easy to see for $n=1$. Suppose that the result is true for $n=m-1$. We now consider the case $n=m$. Let $\mathcal{F}_{1}$ be the set of those elements in $\mathcal{F}$ which contain $m$ and $\mathcal{F}_{2}$ be the set of those elements which do not contain $m$. By induction, $\mathcal{F}_{2}$ can have at most $2^{m-2}$ elements. Further, for each element $A$ of $\mathcal{F}_{1}$ we consider $A \backslash\{m\}$. This new collection also satisfies the required property, so it follows that $\mathcal{F}_{1}$ has at most $2^{m-2}$ elements. Thus, if $|\mathcal{F}|=2^{m-1}$ then it follows that $\left|\mathcal{F}_{1}\right|=\left|\mathcal{F}_{2}\right|=2^{m-2}$. Further, by induction hypothesis, $\mathcal{F}_{2}$ contains all those subsets of $\{1,2, \ldots, m-1\}$ with (say) even number of elements. It then follows that $\mathcal{F}_{1}$ contains all those subsets of $\{1,2, \ldots, m\}$ which contain the element $m$ and which contains an even number of elements. This proves that $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets by even number of elements.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a natural number and $X=\{1,2, \ldots, n\}$. For subsets $A$ and $B$ of $X$ we define $A \Delta B$ to be the set of all those elements of $X$ which belong to exactly one of $A$ and $B$. Let $\mathcal{F}$ be a collection of subsets of $X$ such that for any two distinct elements $A$ and $B$ in $\mathcal{F}$ the set $A \Delta B$ has at least two elements. Show that $\mathcal{F}$ has at most $2^{n-1}$ elements. Find all such collections $\mathcal{F}$ with $2^{n-1}$ elements.
|
For each subset $A$ of $\{1,2, \ldots, n-1\}$, we pair it with $A \cup\{n\}$. Note that for any such pair $(A, B)$ not both $A$ and $B$ can be in $\mathcal{F}$. Since there are $2^{n-1}$ such pairs it follows that $\mathcal{F}$ can have at most $2^{n-1}$ elements.
We shall show by induction on $n$ that if $|\mathcal{F}|=2^{n-1}$ then $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets with even number of elements. The result is easy to see for $n=1$. Suppose that the result is true for $n=m-1$. We now consider the case $n=m$. Let $\mathcal{F}_{1}$ be the set of those elements in $\mathcal{F}$ which contain $m$ and $\mathcal{F}_{2}$ be the set of those elements which do not contain $m$. By induction, $\mathcal{F}_{2}$ can have at most $2^{m-2}$ elements. Further, for each element $A$ of $\mathcal{F}_{1}$ we consider $A \backslash\{m\}$. This new collection also satisfies the required property, so it follows that $\mathcal{F}_{1}$ has at most $2^{m-2}$ elements. Thus, if $|\mathcal{F}|=2^{m-1}$ then it follows that $\left|\mathcal{F}_{1}\right|=\left|\mathcal{F}_{2}\right|=2^{m-2}$. Further, by induction hypothesis, $\mathcal{F}_{2}$ contains all those subsets of $\{1,2, \ldots, m-1\}$ with (say) even number of elements. It then follows that $\mathcal{F}_{1}$ contains all those subsets of $\{1,2, \ldots, m\}$ which contain the element $m$ and which contains an even number of elements. This proves that $\mathcal{F}$ contains either all the subsets with odd number of elements or all the subsets by even number of elements.
|
{
"resource_path": "INMO/segmented/en-inmo-2014.jsonl",
"problem_match": "\n6.",
"solution_match": "\nSolution."
}
|
6be2d262-4ca0-5e33-ac6b-569dbb2ca262
| 607,889
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles touching each other externally at $R$. Let $l_{1}$ be a line which is tangent to $\Gamma_{2}$ at $P$ and passing through the center $O_{1}$ of $\Gamma_{1}$. Similarly, let $l_{2}$ be a line which is tangent to $\Gamma_{2}$ at $Q$ and passing through the center $O_{2}$ of $\Gamma_{2}$. Suppose $l_{1}$ and $l_{2}$ are not parallel and interesct at $K$. If $K P=K Q$, prove that the triangle $P Q R$ is equilateral.
|
Suppose that $P$ and $Q$ lie on the opposite sides of line joining $O_{1}$ and $O_{2}$. By symmetry we may assume that the configuration is as shown in the figure below. Then we have $K P>K O_{1}>K Q$ since $K O_{1}$ is the hypotenuse of triangle $K Q O_{1}$. This is a contradiction to the given assumption, and therefore $P$ and $Q$ lie on the same side of the line joining $O_{1}$ and $O_{2}$.
Since $K P=K Q$ it follows that $K$ lies on the radical axis of the given circles, which is the common tangent at $R$. Therefore $K P=K Q=K R$ and hence $K$ is the cirumcenter of $\triangle P Q R$.
On the other hand, $\triangle K Q O_{1}$ and $\triangle K R O_{1}$ are both right-angled triangles with $K Q=K R$ and $Q O_{1}=R O_{1}$, and hence the two triangles are congruent. Therefore $\widehat{Q K O_{1}}=\widehat{R K O_{1}}$, so $K O_{1}$, and hence $P K$ is perpendicular to $Q R$. Similarly, $Q K$ is perpendicular to $P R$, so it follows that $K$ is the orthocenter of $\triangle P Q R$. Hence we have that $\triangle P Q R$ is equilateral.
Alternate solution. We again rule out the possibility that $P$ and $Q$ are on the opposite side of the line joining $O_{1} O_{2}$, and assume that they are on the same side.
Observe that $\triangle K P O_{2}$ is congruent to $\triangle K Q O_{1}$ (since $K P=K Q$ ). Therefore $O_{1} P=O_{2} Q=r$ (say). In $\triangle O_{1} O_{2} Q$, we have $\widehat{O_{1} Q O_{2}}=\pi / 2$ and $R$ is the midpoint of the hypotenuse, so $R Q=$ $R O_{1}=r$. Therefore $\triangle O_{1} R Q$ is equilateral, so $\widehat{Q R O_{1}}=\pi / 3$. Similarly, $P R=r$ and $\widehat{P R O_{2}}=\pi / 3$, hence $\widehat{P R Q}=\pi / 3$. Since $P R=Q R$ it follows that $\triangle P Q R$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma_{1}$ and $\Gamma_{2}$ be two circles touching each other externally at $R$. Let $l_{1}$ be a line which is tangent to $\Gamma_{2}$ at $P$ and passing through the center $O_{1}$ of $\Gamma_{1}$. Similarly, let $l_{2}$ be a line which is tangent to $\Gamma_{2}$ at $Q$ and passing through the center $O_{2}$ of $\Gamma_{2}$. Suppose $l_{1}$ and $l_{2}$ are not parallel and interesct at $K$. If $K P=K Q$, prove that the triangle $P Q R$ is equilateral.
|
Suppose that $P$ and $Q$ lie on the opposite sides of line joining $O_{1}$ and $O_{2}$. By symmetry we may assume that the configuration is as shown in the figure below. Then we have $K P>K O_{1}>K Q$ since $K O_{1}$ is the hypotenuse of triangle $K Q O_{1}$. This is a contradiction to the given assumption, and therefore $P$ and $Q$ lie on the same side of the line joining $O_{1}$ and $O_{2}$.

Since $K P=K Q$ it follows that $K$ lies on the radical axis of the given circles, which is the common tangent at $R$. Therefore $K P=K Q=K R$ and hence $K$ is the cirumcenter of $\triangle P Q R$.

On the other hand, $\triangle K Q O_{1}$ and $\triangle K R O_{1}$ are both right-angled triangles with $K Q=K R$ and $Q O_{1}=R O_{1}$, and hence the two triangles are congruent. Therefore $\widehat{Q K O_{1}}=\widehat{R K O_{1}}$, so $K O_{1}$, and hence $P K$ is perpendicular to $Q R$. Similarly, $Q K$ is perpendicular to $P R$, so it follows that $K$ is the orthocenter of $\triangle P Q R$. Hence we have that $\triangle P Q R$ is equilateral.
Alternate solution. We again rule out the possibility that $P$ and $Q$ are on the opposite side of the line joining $O_{1} O_{2}$, and assume that they are on the same side.
Observe that $\triangle K P O_{2}$ is congruent to $\triangle K Q O_{1}$ (since $K P=K Q$ ). Therefore $O_{1} P=O_{2} Q=r$ (say). In $\triangle O_{1} O_{2} Q$, we have $\widehat{O_{1} Q O_{2}}=\pi / 2$ and $R$ is the midpoint of the hypotenuse, so $R Q=$ $R O_{1}=r$. Therefore $\triangle O_{1} R Q$ is equilateral, so $\widehat{Q R O_{1}}=\pi / 3$. Similarly, $P R=r$ and $\widehat{P R O_{2}}=\pi / 3$, hence $\widehat{P R Q}=\pi / 3$. Since $P R=Q R$ it follows that $\triangle P Q R$ is equilateral.
|
{
"resource_path": "INMO/segmented/en-inmo2013-solutions.jsonl",
"problem_match": "\nProblem 1.",
"solution_match": "\nSolution."
}
|
12f8370e-a5d6-58d3-887d-973f29033263
| 607,890
|
Let $a, b, c, d$ be positive integers such that $a \geq b \geq c \geq d$. Prove that the equation $x^{4}-a x^{3}-b x^{2}-c x-d=0$ has no integer solution.
|
Suppose that $m$ is an integer root of $x^{4}-a x^{3}-b x^{2}-c x-d=0$. As $d \neq 0$, we have $m \neq 0$. Suppose now that $m>0$. Then $m^{4}-a m^{3}=b m^{2}+c m+d>0$ and hence $m>a \geq d$. On the other hand $d=m\left(m^{3}-a m^{2}-b m-c\right)$ and hence $m$ divides $d$, so $m \leq d$, a contradiction. If $m<0$, then writing $n=-m>0$ we have $n^{4}+a n^{3}-b n^{2}+c n-d=n^{4}+n^{2}(a n-b)+(c n-d)>0$, a contradiction. This proves that the given polynomial has no integer roots.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b, c, d$ be positive integers such that $a \geq b \geq c \geq d$. Prove that the equation $x^{4}-a x^{3}-b x^{2}-c x-d=0$ has no integer solution.
|
Suppose that $m$ is an integer root of $x^{4}-a x^{3}-b x^{2}-c x-d=0$. As $d \neq 0$, we have $m \neq 0$. Suppose now that $m>0$. Then $m^{4}-a m^{3}=b m^{2}+c m+d>0$ and hence $m>a \geq d$. On the other hand $d=m\left(m^{3}-a m^{2}-b m-c\right)$ and hence $m$ divides $d$, so $m \leq d$, a contradiction. If $m<0$, then writing $n=-m>0$ we have $n^{4}+a n^{3}-b n^{2}+c n-d=n^{4}+n^{2}(a n-b)+(c n-d)>0$, a contradiction. This proves that the given polynomial has no integer roots.
|
{
"resource_path": "INMO/segmented/en-inmo2013-solutions.jsonl",
"problem_match": "\nProblem 3.",
"solution_match": "\nSolution."
}
|
e0c795d5-9db6-5a05-9834-5a023ec92ec1
| 607,892
|
Let $n$ be a positive integer. Call a nonempty subset $S$ of $\{1,2, \ldots, n\}$ good if the arithmetic mean of the elements of $S$ is also an integer. Further let $t_{n}$ denote the number of good subsets of $\{1,2, \ldots, n\}$. Prove that $t_{n}$ and $n$ are both odd or both even.
|
We show that $T_{n}-n$ is even. Note that the subsets $\{1\},\{2\}, \cdots,\{n\}$ are good. Among the other good subsets, let $A$ be the collection of subsets with an integer average which belongs to the subset, and let $B$ be the collection of subsets with an integer average which is not a member of the subset. Then there is a bijection between $A$ and $B$, because removing the average takes a member of $A$ to a member of $B$; and including the average in a member of $B$ takes it to its inverse. So $T_{n}-n=|A|+|B|$ is even.
Alternate solution. Let $S=\{1,2, \ldots, n\}$. For a subset $A$ of $S$, let $\bar{A}=\{n+1-a \mid a \in A\}$. We call a subset $A$ symmetric if $\bar{A}=A$. Note that the arithmetic mean of a symmetric subset is $(n+1) / 2$. Therefore, if $n$ is even, then there are no symmetric good subsets, while if $n$ is odd then every symmetric subset is good.
If $A$ is a proper good subset of $S$, then so is $\bar{A}$. Therefore, all the good subsets that are not symmetric can be paired. If $n$ is even then this proves that $t_{n}$ is even. If $n$ is odd, we have to show that there are odd number of symmetric subsets. For this, we note that a symmetric subset contains the element $(n+1) / 2$ if and only if it has odd number of elements. Therefore, for any natural number $k$, the number of symmetric subsets of size $2 k$ equals the number of symmetric subsets of size $2 k+1$. The result now follows since there is exactly one symmetric subset with only one element.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. Call a nonempty subset $S$ of $\{1,2, \ldots, n\}$ good if the arithmetic mean of the elements of $S$ is also an integer. Further let $t_{n}$ denote the number of good subsets of $\{1,2, \ldots, n\}$. Prove that $t_{n}$ and $n$ are both odd or both even.
|
We show that $T_{n}-n$ is even. Note that the subsets $\{1\},\{2\}, \cdots,\{n\}$ are good. Among the other good subsets, let $A$ be the collection of subsets with an integer average which belongs to the subset, and let $B$ be the collection of subsets with an integer average which is not a member of the subset. Then there is a bijection between $A$ and $B$, because removing the average takes a member of $A$ to a member of $B$; and including the average in a member of $B$ takes it to its inverse. So $T_{n}-n=|A|+|B|$ is even.
Alternate solution. Let $S=\{1,2, \ldots, n\}$. For a subset $A$ of $S$, let $\bar{A}=\{n+1-a \mid a \in A\}$. We call a subset $A$ symmetric if $\bar{A}=A$. Note that the arithmetic mean of a symmetric subset is $(n+1) / 2$. Therefore, if $n$ is even, then there are no symmetric good subsets, while if $n$ is odd then every symmetric subset is good.
If $A$ is a proper good subset of $S$, then so is $\bar{A}$. Therefore, all the good subsets that are not symmetric can be paired. If $n$ is even then this proves that $t_{n}$ is even. If $n$ is odd, we have to show that there are odd number of symmetric subsets. For this, we note that a symmetric subset contains the element $(n+1) / 2$ if and only if it has odd number of elements. Therefore, for any natural number $k$, the number of symmetric subsets of size $2 k$ equals the number of symmetric subsets of size $2 k+1$. The result now follows since there is exactly one symmetric subset with only one element.
|
{
"resource_path": "INMO/segmented/en-inmo2013-solutions.jsonl",
"problem_match": "\nProblem 4.",
"solution_match": "\nSolution."
}
|
c32c2833-feee-5bb7-912a-02c9908afbc0
| 607,893
|
Let $a, b, c, x, y, z$ be positive real numbers such that $a+b+c=x+y+z$ and abc $=x y z$. Further, suppose that $a \leq x<y<z \leq c$ and $a<b<c$. Prove that $a=x, b=y$ and $c=z$.
|
Let
$$
f(t)=(t-x)(t-y)(t-z)-(t-a)(t-b)(t-c)
$$
Then $f(t)=k t$ for some constant $k$. Note that $k a=f(a)=(a-x)(a-y)(a-z) \leq 0$ and hence $k \leq 0$. Similarly, $k c=f(c)=(c-x)(c-y)(c-z) \geq 0$ and hence $k \geq 0$. Combining the two, it follows that $k=0$ and that $f(a)=f(c)=0$. These equalities imply that $a=x$ and $c=z$, and then it also follows that $b=y$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a, b, c, x, y, z$ be positive real numbers such that $a+b+c=x+y+z$ and abc $=x y z$. Further, suppose that $a \leq x<y<z \leq c$ and $a<b<c$. Prove that $a=x, b=y$ and $c=z$.
|
Let
$$
f(t)=(t-x)(t-y)(t-z)-(t-a)(t-b)(t-c)
$$
Then $f(t)=k t$ for some constant $k$. Note that $k a=f(a)=(a-x)(a-y)(a-z) \leq 0$ and hence $k \leq 0$. Similarly, $k c=f(c)=(c-x)(c-y)(c-z) \geq 0$ and hence $k \geq 0$. Combining the two, it follows that $k=0$ and that $f(a)=f(c)=0$. These equalities imply that $a=x$ and $c=z$, and then it also follows that $b=y$.
|
{
"resource_path": "INMO/segmented/en-inmo2013-solutions.jsonl",
"problem_match": "\nProblem 6.",
"solution_match": "\nSolution."
}
|
8b9dd334-e756-5ce1-ac91-c087616ddb13
| 607,895
|
Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $B D$ be the altitude from $B$ on to $A C$. Let $P, Q$ and $I$ be the incentres of triangles $A B D, C B D$ and $A B C$ respectively. Show that the circumcentre of of the triangle $P I Q$ lies on the hypotenuse $A C$.
|
We begin with the following lemma:
Lemma: Let $X Y Z$ be a triangle with $\angle X Y Z=90+\alpha$. Construct an isosceles triangle $X E Z$, externally on the side $X Z$, with base angle $\alpha$. Then $E$ is the circumcentre of $\triangle X Y Z$.
Proof of the Lemma: Draw $E D \perp$ $X Z$. Then $D E$ is the perpendicular bisector of $X Z$. We also observe that $\angle X E D=\angle Z E D=90-\alpha$. Observe that $E$ is on the perpendicular bisector of $X Z$. Construct the circumcircle of $X Y Z$. Draw perpendicular bisector of $X Y$ and let it meet $D E$ in $F$. Then $F$ is the circumcentre of $\triangle X Y Z$. Join $X F$. Then $\angle X F D=90-\alpha$. But we know
that $\angle X E D=90-\alpha$. Hence $E=F$. Let $r_{1}, r_{2}$ and $r$ be the inradii of the triangles $A B D, C B D$ and $A B C$ respectively. Join $P D$ and $D Q$. Observe that $\angle P D Q=90^{\circ}$. Hence
$$
P Q^{2}=P D^{2}+D Q^{2}=2 r_{1}^{2}+2 r_{2}^{2}
$$
Let $s_{1}=(A B+B D+D A) / 2$. Observe that $B D=c a / b$ and $A D=$ $\sqrt{A B^{2}-B D^{2}}=\sqrt{c^{2}-\left(\frac{c a}{b}\right)^{2}}=c^{2} / b$. This gives $s_{1}=c s / b$. But $r_{1}=$ $s_{1}-c=(c / b)(s-b)=c r / b$. Similarly, $r_{2}=a r / b$. Hence
$$
P Q^{2}=2 r^{2}\left(\frac{c^{2}+a^{2}}{b^{2}}\right)=2 r^{2}
$$
Consider $\triangle P I Q$. Observe that $\angle P I Q=90+(B / 2)=135$. Hence $P Q$ subtends $90^{\circ}$ on the circumference of the circumcircle of $\triangle P I Q$. But we have seen that $\angle P D Q=90^{\circ}$. Now construct a circle with $P Q$ as diameter. Let it cut $A C$ again in $K$. It follows that $\angle P K Q=90^{\circ}$ and the points $P, D, K, Q$ are concyclic. We also notice $\angle K P Q=\angle K D Q=45^{\circ}$
and $\angle P Q K=\angle P D A=45^{\circ}$.
Thus $P K Q$ is an isosceles right-angled triangle with $K P=K Q$. Therfore $K P^{2}+K Q^{2}=P Q^{2}=2 r^{2}$ and hence $K P=K Q=r$.
Now $\angle P I Q=90+45$ and $\angle P K Q=2 \times 45^{\circ}=90^{\circ}$ with $K P=K Q=r$.
Hence $K$ is the circumcentre of $\triangle P I Q$.
(Incidentally, This also shows that $K I=r$ and hence $K$ is the point of contact of the incircle of $\triangle A B C$ with $A C$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $B D$ be the altitude from $B$ on to $A C$. Let $P, Q$ and $I$ be the incentres of triangles $A B D, C B D$ and $A B C$ respectively. Show that the circumcentre of of the triangle $P I Q$ lies on the hypotenuse $A C$.
|
We begin with the following lemma:
Lemma: Let $X Y Z$ be a triangle with $\angle X Y Z=90+\alpha$. Construct an isosceles triangle $X E Z$, externally on the side $X Z$, with base angle $\alpha$. Then $E$ is the circumcentre of $\triangle X Y Z$.
Proof of the Lemma: Draw $E D \perp$ $X Z$. Then $D E$ is the perpendicular bisector of $X Z$. We also observe that $\angle X E D=\angle Z E D=90-\alpha$. Observe that $E$ is on the perpendicular bisector of $X Z$. Construct the circumcircle of $X Y Z$. Draw perpendicular bisector of $X Y$ and let it meet $D E$ in $F$. Then $F$ is the circumcentre of $\triangle X Y Z$. Join $X F$. Then $\angle X F D=90-\alpha$. But we know

that $\angle X E D=90-\alpha$. Hence $E=F$. Let $r_{1}, r_{2}$ and $r$ be the inradii of the triangles $A B D, C B D$ and $A B C$ respectively. Join $P D$ and $D Q$. Observe that $\angle P D Q=90^{\circ}$. Hence
$$
P Q^{2}=P D^{2}+D Q^{2}=2 r_{1}^{2}+2 r_{2}^{2}
$$
Let $s_{1}=(A B+B D+D A) / 2$. Observe that $B D=c a / b$ and $A D=$ $\sqrt{A B^{2}-B D^{2}}=\sqrt{c^{2}-\left(\frac{c a}{b}\right)^{2}}=c^{2} / b$. This gives $s_{1}=c s / b$. But $r_{1}=$ $s_{1}-c=(c / b)(s-b)=c r / b$. Similarly, $r_{2}=a r / b$. Hence
$$
P Q^{2}=2 r^{2}\left(\frac{c^{2}+a^{2}}{b^{2}}\right)=2 r^{2}
$$
Consider $\triangle P I Q$. Observe that $\angle P I Q=90+(B / 2)=135$. Hence $P Q$ subtends $90^{\circ}$ on the circumference of the circumcircle of $\triangle P I Q$. But we have seen that $\angle P D Q=90^{\circ}$. Now construct a circle with $P Q$ as diameter. Let it cut $A C$ again in $K$. It follows that $\angle P K Q=90^{\circ}$ and the points $P, D, K, Q$ are concyclic. We also notice $\angle K P Q=\angle K D Q=45^{\circ}$

and $\angle P Q K=\angle P D A=45^{\circ}$.
Thus $P K Q$ is an isosceles right-angled triangle with $K P=K Q$. Therfore $K P^{2}+K Q^{2}=P Q^{2}=2 r^{2}$ and hence $K P=K Q=r$.
Now $\angle P I Q=90+45$ and $\angle P K Q=2 \times 45^{\circ}=90^{\circ}$ with $K P=K Q=r$.
Hence $K$ is the circumcentre of $\triangle P I Q$.
(Incidentally, This also shows that $K I=r$ and hence $K$ is the point of contact of the incircle of $\triangle A B C$ with $A C$.)
|
{
"resource_path": "INMO/segmented/en-inmosol-15.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution:"
}
|
861feddd-1f4f-5ec3-8f8a-976217d8f20b
| 607,896
|
Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $B D$ be the altitude from $B$ on to $A C$. Let $P, Q$ and $I$ be the incentres of triangles $A B D, C B D$ and $A B C$ respectively. Show that the circumcentre of of the triangle $P I Q$ lies on the hypotenuse $A C$.
|
Here we use computation to prove that the point of contact $K$ of the incircle with $A C$ is the circumcentre of $\triangle P I Q$. We show that $K P=K Q=r$. Let $r_{1}$ and $r_{2}$ be the inradii of triangles $A B D$ and $C B D$ respectively. Draw $P L \perp A C$ and $Q M \perp A C$. If $s_{1}$ is the semiperimeter of $\triangle A B D$, then $A L=s_{1}-B D$.
But
$$
s_{1}=\frac{A B+B D+D A}{2}, \quad B D=\frac{c a}{b}, \quad A D=\frac{c^{2}}{b}
$$
Hence $s_{1}=c s / b$. This gives $r_{1}=s_{1}-c=c r / b, A L=s_{1}-B D=c(s-a) / b$. Hence $K L=A K-A L=(s-a)-\frac{c(s-a)}{b}=\frac{(b-c)(s-a)}{b}$. We observe that $2 r^{2}=\frac{(c+a-b)^{2}}{2}=\frac{c^{2}+a^{2}+b^{2}-2 b c-2 a b+2 c a}{2}=\left(b^{2}-b a-b c+a c\right)=(b-c)(b-a)$.
This gives
$$
\begin{aligned}
(s-a)(b-c)=(s-b+b-a) & (b-c)=r(b-c)+(b-a)(b-c) \\
& =r(b-c)+2 r^{2}=r(b-c+c+a-b)=r a
\end{aligned}
$$
Thus $K L=r a / b$. Finally,
$$
K P^{2}=K L^{2}+L P^{2}=\frac{r^{2} a^{2}}{b^{2}}+\frac{r^{2}+c^{2}}{b^{2}}=r^{2}
$$
Thus $K P=r$. Similarly, $K Q=r$. This gives $K P=K I=K Q=r$ and therefore $K$ is the circumcentre of $\triangle K I Q$.
(Incidentally, this also shows that $K L=c a / b=r_{2}$ and $K M=r_{1}$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a right-angled triangle with $\angle B=90^{\circ}$. Let $B D$ be the altitude from $B$ on to $A C$. Let $P, Q$ and $I$ be the incentres of triangles $A B D, C B D$ and $A B C$ respectively. Show that the circumcentre of of the triangle $P I Q$ lies on the hypotenuse $A C$.
|
Here we use computation to prove that the point of contact $K$ of the incircle with $A C$ is the circumcentre of $\triangle P I Q$. We show that $K P=K Q=r$. Let $r_{1}$ and $r_{2}$ be the inradii of triangles $A B D$ and $C B D$ respectively. Draw $P L \perp A C$ and $Q M \perp A C$. If $s_{1}$ is the semiperimeter of $\triangle A B D$, then $A L=s_{1}-B D$.

But
$$
s_{1}=\frac{A B+B D+D A}{2}, \quad B D=\frac{c a}{b}, \quad A D=\frac{c^{2}}{b}
$$
Hence $s_{1}=c s / b$. This gives $r_{1}=s_{1}-c=c r / b, A L=s_{1}-B D=c(s-a) / b$. Hence $K L=A K-A L=(s-a)-\frac{c(s-a)}{b}=\frac{(b-c)(s-a)}{b}$. We observe that $2 r^{2}=\frac{(c+a-b)^{2}}{2}=\frac{c^{2}+a^{2}+b^{2}-2 b c-2 a b+2 c a}{2}=\left(b^{2}-b a-b c+a c\right)=(b-c)(b-a)$.
This gives
$$
\begin{aligned}
(s-a)(b-c)=(s-b+b-a) & (b-c)=r(b-c)+(b-a)(b-c) \\
& =r(b-c)+2 r^{2}=r(b-c+c+a-b)=r a
\end{aligned}
$$
Thus $K L=r a / b$. Finally,
$$
K P^{2}=K L^{2}+L P^{2}=\frac{r^{2} a^{2}}{b^{2}}+\frac{r^{2}+c^{2}}{b^{2}}=r^{2}
$$
Thus $K P=r$. Similarly, $K Q=r$. This gives $K P=K I=K Q=r$ and therefore $K$ is the circumcentre of $\triangle K I Q$.
(Incidentally, this also shows that $K L=c a / b=r_{2}$ and $K M=r_{1}$.)
|
{
"resource_path": "INMO/segmented/en-inmosol-15.jsonl",
"problem_match": "\n1.",
"solution_match": "\nSolution 2:"
}
|
861feddd-1f4f-5ec3-8f8a-976217d8f20b
| 607,896
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.