problem
stringlengths 54
2.23k
| solution
stringlengths 134
24.1k
| answer
stringclasses 1
value | problem_is_valid
stringclasses 1
value | solution_is_valid
stringclasses 1
value | question_type
stringclasses 1
value | problem_type
stringclasses 8
values | problem_raw
stringlengths 54
2.21k
| solution_raw
stringlengths 134
24.1k
| metadata
dict | uuid
stringlengths 36
36
| id
int64 23.5k
612k
|
|---|---|---|---|---|---|---|---|---|---|---|---|
24. (LIT) ${ }^{\mathrm{IMO} 6}$ For a positive integer $n$, let $f(n)$ denote the number of ways to represent $n$ as the sum of powers of 2 with nonnegative integer exponents. Representations that differ only in the ordering in their summands are not considered to be distinct. (For instance, $f(4)=4$ because the number 4 can be represented in the following four ways: $4 ; 2+2 ; 2+1+1 ; 1+1+1+1$.) Prove that the inequality $$ 2^{n^{2} / 4}<f\left(2^{n}\right)<2^{n^{2} / 2} $$ holds for any integer $n \geq 3$.
|
24. There is a bijective correspondence between representations in the given form of $2 k$ and $2 k+1$ for $k=0,1, \ldots$, since adding 1 to every representation of $2 k$, we obtain a representation of $2 k+1$, and conversely, every representation of $2 k+1$ contains at least one 1 , which can be removed. Hence, $f(2 k+1)=f(2 k)$. Consider all representations of $2 k$. The number of those that contain at least one 1 equals $f(2 k-1)=f(2 k-2)$, while the number of those not containing a 1 equals $f(k)$ (the correspondence is given by division of summands by 2). Therefore $$ f(2 k)=f(2 k-2)+f(k) . $$ Summing these equalities over $k=1, \ldots, n$, we obtain $$ f(2 n)=f(0)+f(1)+\cdots+f(n) $$ We first prove the right-hand inequality. Since $f$ is increasing, and $f(0)+$ $f(1)=f(2)$, (2) yields $f(2 n) \leq n f(n)$ for $n \geq 2$. Now $f\left(2^{3}\right)=f(0)+$ $\cdots+f(4)=10<2^{3^{2} / 2}$, and one can easily conclude by induction that $f\left(2^{n+1}\right) \leq 2^{n} f\left(2^{n}\right)<2^{n} \cdot 2^{n^{2} / 2}<2^{(n+1)^{2} / 2}$ for each $n \geq 3$. We now derive the lower estimate. It follows from (1) that $f(x+2)-f(x)$ is increasing. Consequently, for each $m$ and $k<m$ we have $f(2 m+2 k)-$ $f(2 m) \geq f(2 m+2 k-2)-f(2 m-2) \geq \cdots \geq f(2 m)-f(2 m-2 k)$, so $f(2 m+2 k)+f(2 m-2 k) \geq 2 f(2 m)$. Adding all these inequalities for $k=1,2, \ldots, m$, we obtain $f(0)+f(2)+\cdots+f(4 m) \geq(2 m+1) f(2 m)$. But since $f(2)=f(3), f(4)=f(5)$ etc., we also have $f(1)+f(3)+\cdots+$ $f(4 m-1)>(2 m-1) f(2 m)$, which together with the above inequality gives $$ f(8 m)=f(0)+f(1)+\cdots+f(4 m)>4 m f(2 m) . $$ Finally, we have that the inequality $f\left(2^{n}\right)>2^{n^{2} / 4}$ holds for $n=2$ and $n=3$, while for larger $n$ we have by induction $f\left(2^{n}\right)>2^{n-1} f\left(2^{n-2}\right)>$ $2^{n-1+(n-2)^{2} / 4}=2^{n^{2} / 4}$. This completes the proof. Remark. Despite the fact that the lower estimate is more difficult, it is much weaker than the upper estimate. It can be shown that $f\left(2^{n}\right)$ eventually (for large $n$ ) exceeds $2^{c n^{2}}$ for any $c<\frac{1}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
24. (LIT) ${ }^{\mathrm{IMO} 6}$ For a positive integer $n$, let $f(n)$ denote the number of ways to represent $n$ as the sum of powers of 2 with nonnegative integer exponents. Representations that differ only in the ordering in their summands are not considered to be distinct. (For instance, $f(4)=4$ because the number 4 can be represented in the following four ways: $4 ; 2+2 ; 2+1+1 ; 1+1+1+1$.) Prove that the inequality $$ 2^{n^{2} / 4}<f\left(2^{n}\right)<2^{n^{2} / 2} $$ holds for any integer $n \geq 3$.
|
24. There is a bijective correspondence between representations in the given form of $2 k$ and $2 k+1$ for $k=0,1, \ldots$, since adding 1 to every representation of $2 k$, we obtain a representation of $2 k+1$, and conversely, every representation of $2 k+1$ contains at least one 1 , which can be removed. Hence, $f(2 k+1)=f(2 k)$. Consider all representations of $2 k$. The number of those that contain at least one 1 equals $f(2 k-1)=f(2 k-2)$, while the number of those not containing a 1 equals $f(k)$ (the correspondence is given by division of summands by 2). Therefore $$ f(2 k)=f(2 k-2)+f(k) . $$ Summing these equalities over $k=1, \ldots, n$, we obtain $$ f(2 n)=f(0)+f(1)+\cdots+f(n) $$ We first prove the right-hand inequality. Since $f$ is increasing, and $f(0)+$ $f(1)=f(2)$, (2) yields $f(2 n) \leq n f(n)$ for $n \geq 2$. Now $f\left(2^{3}\right)=f(0)+$ $\cdots+f(4)=10<2^{3^{2} / 2}$, and one can easily conclude by induction that $f\left(2^{n+1}\right) \leq 2^{n} f\left(2^{n}\right)<2^{n} \cdot 2^{n^{2} / 2}<2^{(n+1)^{2} / 2}$ for each $n \geq 3$. We now derive the lower estimate. It follows from (1) that $f(x+2)-f(x)$ is increasing. Consequently, for each $m$ and $k<m$ we have $f(2 m+2 k)-$ $f(2 m) \geq f(2 m+2 k-2)-f(2 m-2) \geq \cdots \geq f(2 m)-f(2 m-2 k)$, so $f(2 m+2 k)+f(2 m-2 k) \geq 2 f(2 m)$. Adding all these inequalities for $k=1,2, \ldots, m$, we obtain $f(0)+f(2)+\cdots+f(4 m) \geq(2 m+1) f(2 m)$. But since $f(2)=f(3), f(4)=f(5)$ etc., we also have $f(1)+f(3)+\cdots+$ $f(4 m-1)>(2 m-1) f(2 m)$, which together with the above inequality gives $$ f(8 m)=f(0)+f(1)+\cdots+f(4 m)>4 m f(2 m) . $$ Finally, we have that the inequality $f\left(2^{n}\right)>2^{n^{2} / 4}$ holds for $n=2$ and $n=3$, while for larger $n$ we have by induction $f\left(2^{n}\right)>2^{n-1} f\left(2^{n-2}\right)>$ $2^{n-1+(n-2)^{2} / 4}=2^{n^{2} / 4}$. This completes the proof. Remark. Despite the fact that the lower estimate is more difficult, it is much weaker than the upper estimate. It can be shown that $f\left(2^{n}\right)$ eventually (for large $n$ ) exceeds $2^{c n^{2}}$ for any $c<\frac{1}{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cfd23377-c518-55df-9e5f-297ba67ab625
| 24,785
|
25. (POL) The bisectors of angles $A, B, C$ of a triangle $A B C$ meet its circumcircle again at the points $K, L, M$, respectively. Let $R$ be an internal point on the side $A B$. The points $P$ and $Q$ are defined by the following conditions: $R P$ is parallel to $A K$, and $B P$ is perpendicular to $B L ; R Q$ is parallel to $B L$, and $A Q$ is perpendicular to $A K$. Show that the lines $K P, L Q, M R$ have a point in common.
|
25. Let $M R$ meet the circumcircle of triangle $A B C$ again at a point $X$. We claim that $X$ is the common point of the lines $K P, L Q, M R$. By symmetry, it will be enough to show that $X$ lies on $K P$. It is easy to see that $X$ and $P$ lie on the same side of $A B$ as $K$. Let $I_{a}=A K \cap B P$ be the excenter of $\triangle A B C$ corresponding to $A$. It is easy to calculate that $\angle A I_{a} B=\gamma / 2$, from which we get $\angle R P B=\angle A I_{a} B=\angle M C B=\angle R X B$. Therefore $R, B, P, X$ are concyclic. Now if $P$ and $K$ are on distinct sides of $B X$ (the other case is similar), we have $\angle R X P=180^{\circ}-\angle R B P=90^{\circ}-$ $\beta / 2=\angle M A K=180^{\circ}-\angle R X K$, from which it follows that $K, X, P$ are collinear, as claimed. Remark. It is not essential for the statement of the problem that $R$ be an internal point of $A B$. Work with cases can be avoided using oriented 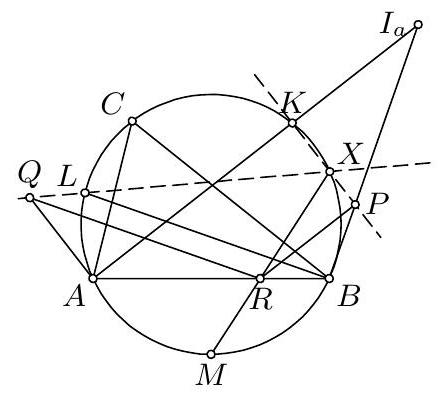 angles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
25. (POL) The bisectors of angles $A, B, C$ of a triangle $A B C$ meet its circumcircle again at the points $K, L, M$, respectively. Let $R$ be an internal point on the side $A B$. The points $P$ and $Q$ are defined by the following conditions: $R P$ is parallel to $A K$, and $B P$ is perpendicular to $B L ; R Q$ is parallel to $B L$, and $A Q$ is perpendicular to $A K$. Show that the lines $K P, L Q, M R$ have a point in common.
|
25. Let $M R$ meet the circumcircle of triangle $A B C$ again at a point $X$. We claim that $X$ is the common point of the lines $K P, L Q, M R$. By symmetry, it will be enough to show that $X$ lies on $K P$. It is easy to see that $X$ and $P$ lie on the same side of $A B$ as $K$. Let $I_{a}=A K \cap B P$ be the excenter of $\triangle A B C$ corresponding to $A$. It is easy to calculate that $\angle A I_{a} B=\gamma / 2$, from which we get $\angle R P B=\angle A I_{a} B=\angle M C B=\angle R X B$. Therefore $R, B, P, X$ are concyclic. Now if $P$ and $K$ are on distinct sides of $B X$ (the other case is similar), we have $\angle R X P=180^{\circ}-\angle R B P=90^{\circ}-$ $\beta / 2=\angle M A K=180^{\circ}-\angle R X K$, from which it follows that $K, X, P$ are collinear, as claimed. Remark. It is not essential for the statement of the problem that $R$ be an internal point of $A B$. Work with cases can be avoided using oriented  angles.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f0b65de7-151d-5faa-a8b5-a5b6d3aef7b9
| 24,788
|
3. (GER) For each finite set $U$ of nonzero vectors in the plane we define $l(U)$ to be the length of the vector that is the sum of all vectors in $U$. Given a finite set $V$ of nonzero vectors in the plane, a subset $B$ of $V$ is said to be maximal if $l(B)$ is greater than or equal to $l(A)$ for each nonempty subset $A$ of $V$. (a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively. (b) Show that for any set $V$ consisting of $n \geq 1$ vectors, the number of maximal subsets is less than or equal to $2 n$.
|
3. (a) For $n=4$, consider a convex quadrilateral $A B C D$ in which $A B=$ $B C=A C=B D$ and $A D=D C$, and take the vectors $\overrightarrow{A B}, \overrightarrow{B C}$, $\overrightarrow{C D}, \overrightarrow{D A}$. For $n=5$, take the vectors $\overrightarrow{A B}, \overrightarrow{B C}, \overrightarrow{C D}, \overrightarrow{D E}, \overrightarrow{E A}$ for any regular pentagon $A B C D E$. (b) Let us draw the vectors of $V$ as originated from the same point $O$. Consider any maximal subset $B \subset V$, and denote by $u$ the sum of all vectors from $B$. If $l$ is the line through $O$ perpendicular to $u$, then $B$ contains exactly those vectors from $V$ that lie on the same side of $l$ as $u$ does, and no others. Indeed, if any $v \notin B$ lies on the same side of $l$, then $|u+v| \geq|u|$; similarly, if some $v \in B$ lies on the other side of $l$, then $|u-v| \geq|u|$. Therefore every maximal subset is determined by some line $l$ as the set of vectors lying on the same side of $l$. It is obvious that in this way we get at most $2 n$ sets.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
3. (GER) For each finite set $U$ of nonzero vectors in the plane we define $l(U)$ to be the length of the vector that is the sum of all vectors in $U$. Given a finite set $V$ of nonzero vectors in the plane, a subset $B$ of $V$ is said to be maximal if $l(B)$ is greater than or equal to $l(A)$ for each nonempty subset $A$ of $V$. (a) Construct sets of 4 and 5 vectors that have 8 and 10 maximal subsets respectively. (b) Show that for any set $V$ consisting of $n \geq 1$ vectors, the number of maximal subsets is less than or equal to $2 n$.
|
3. (a) For $n=4$, consider a convex quadrilateral $A B C D$ in which $A B=$ $B C=A C=B D$ and $A D=D C$, and take the vectors $\overrightarrow{A B}, \overrightarrow{B C}$, $\overrightarrow{C D}, \overrightarrow{D A}$. For $n=5$, take the vectors $\overrightarrow{A B}, \overrightarrow{B C}, \overrightarrow{C D}, \overrightarrow{D E}, \overrightarrow{E A}$ for any regular pentagon $A B C D E$. (b) Let us draw the vectors of $V$ as originated from the same point $O$. Consider any maximal subset $B \subset V$, and denote by $u$ the sum of all vectors from $B$. If $l$ is the line through $O$ perpendicular to $u$, then $B$ contains exactly those vectors from $V$ that lie on the same side of $l$ as $u$ does, and no others. Indeed, if any $v \notin B$ lies on the same side of $l$, then $|u+v| \geq|u|$; similarly, if some $v \in B$ lies on the other side of $l$, then $|u-v| \geq|u|$. Therefore every maximal subset is determined by some line $l$ as the set of vectors lying on the same side of $l$. It is obvious that in this way we get at most $2 n$ sets.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
9e85fc21-7c94-577e-ad11-7d7e4fe83018
| 24,793
|
4. (IRN) ${ }^{\mathrm{IMO} 4} \mathrm{An} n \times n$ matrix with entries from $\{1,2, \ldots, 2 n-1\}$ is called a coveralls matrix if for each $i$ the union of the $i$ th row and the $i$ th column contains $2 n-1$ distinct entries. Show that: (a) There exist no coveralls matrices for $n=1997$. (b) Coveralls matrices exist for infinitely many values of $n$.
|
4. (a) Suppose that an $n \times n$ coveralls matrix $A$ exists for some $n>1$. Let $x \in\{1,2, \ldots, 2 n-1\}$ be a fixed number that does not appear on the fixed diagonal of $A$. Such an element must exist, since the diagonal can contain at most $n$ different numbers. Let us call the union of the $i$ th row and the $i$ th column the $i$ th cross. There are $n$ crosses, and each of them contains exactly one $x$. On the other hand, each entry $x$ of $A$ is contained in exactly two crosses. Hence $n$ must be even. However, 1997 is an odd number; hence no coveralls matrix exists for $n=1997$. (b) For $n=2, A_{2}=\left[\begin{array}{ll}1 & 2 \\ 3 & 1\end{array}\right]$ is a coveralls matrix. For $n=4$, one such matrix is, for example, $$ A_{4}=\left[\begin{array}{llll} 1 & 2 & 5 & 6 \\ 3 & 1 & 7 & 5 \\ 4 & 6 & 1 & 2 \\ 7 & 4 & 3 & 1 \end{array}\right] $$ This construction can be generalized. Suppose that we are given an $n \times n$ coveralls matrix $A_{n}$. Let $B_{n}$ be the matrix obtained from $A_{n}$ by adding $2 n$ to each entry, and $C_{n}$ the matrix obtained from $B_{n}$ by replacing each diagonal entry (equal to $2 n+1$ by induction) with $2 n$. Then the matrix $$ A_{2 n}=\left[\begin{array}{ll} A_{n} & B_{n} \\ C_{n} & A_{n} \end{array}\right] $$ is coveralls. To show this, suppose that $i \leq n$ (the case $i>n$ is similar). The $i$ th cross is composed of the $i$ th cross of $A_{n}$, the $i$ th row of $B_{n}$, and the $i$ th column of $C_{n}$. The $i$ th cross of $A_{i}$ covers $1,2, \ldots, 2 n-1$. The $i$ th row of $B_{n}$ covers all numbers of the form $2 n+j$, where $j$ is covered by the $i$ th row of $A_{n}$ (including $j=1$ ). Similarly, the $i$ th column of $C_{n}$ covers $2 n$ and all numbers of the form $2 n+k$, where $k>1$ is covered by the $i$ th column of $A_{n}$. Thus we see that all numbers are accounted for in the $i$ th cross of $A_{2 n}$, and hence $A_{2 n}$ is a desired coveralls matrix. It follows that we can find a coveralls matrix whenever $n$ is a power of 2 . Second solution for part $b$. We construct a coveralls matrix explicitly for $n=2^{k}$. We consider the coordinates/cells of the matrix elements modulo $n$ throughout the solution. We define the $i$-diagonal $(0 \leq i<$ $n$ ) to be the set of cells of the form $(j, j+i)$, for all $j$. We note that each cross contains exactly one cell from the 0 -diagonal (the main diagonal) and two cells from each $i$-diagonal. For two cells within an $i$ diagonal, $x$ and $y$, we define $x$ and $y$ to be related if there exists a cross containing both $x$ and $y$. Evidently, for every cell $x$ not on the 0 -diagonal there are exactly two other cells related to it. The relation thus breaks up each $i$-diagonal $(i>0)$ into cycles of length larger than 1 . Due to the diagonal translational symmetry (modulo $n$ ), all the cycles within a given $i$-diagonal must be of equal length and thus of an even length, since $n=2^{k}$. The construction of a coveralls matrix is now obvious. We select a number, say 1, to place on all the cells of the 0-diagonal. We pair up the remaining numbers and assign each pair to an $i$-diagonal, say $(2 i, 2 i+1)$. Going along each cycle within the $i$-diagonal we alternately assign values of $2 i$ and $2 i+1$. Since the cycle has an even length, a cell will be related only to a cell of a different number, and hence each cross will contain both $2 i$ and $2 i+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
4. (IRN) ${ }^{\mathrm{IMO} 4} \mathrm{An} n \times n$ matrix with entries from $\{1,2, \ldots, 2 n-1\}$ is called a coveralls matrix if for each $i$ the union of the $i$ th row and the $i$ th column contains $2 n-1$ distinct entries. Show that: (a) There exist no coveralls matrices for $n=1997$. (b) Coveralls matrices exist for infinitely many values of $n$.
|
4. (a) Suppose that an $n \times n$ coveralls matrix $A$ exists for some $n>1$. Let $x \in\{1,2, \ldots, 2 n-1\}$ be a fixed number that does not appear on the fixed diagonal of $A$. Such an element must exist, since the diagonal can contain at most $n$ different numbers. Let us call the union of the $i$ th row and the $i$ th column the $i$ th cross. There are $n$ crosses, and each of them contains exactly one $x$. On the other hand, each entry $x$ of $A$ is contained in exactly two crosses. Hence $n$ must be even. However, 1997 is an odd number; hence no coveralls matrix exists for $n=1997$. (b) For $n=2, A_{2}=\left[\begin{array}{ll}1 & 2 \\ 3 & 1\end{array}\right]$ is a coveralls matrix. For $n=4$, one such matrix is, for example, $$ A_{4}=\left[\begin{array}{llll} 1 & 2 & 5 & 6 \\ 3 & 1 & 7 & 5 \\ 4 & 6 & 1 & 2 \\ 7 & 4 & 3 & 1 \end{array}\right] $$ This construction can be generalized. Suppose that we are given an $n \times n$ coveralls matrix $A_{n}$. Let $B_{n}$ be the matrix obtained from $A_{n}$ by adding $2 n$ to each entry, and $C_{n}$ the matrix obtained from $B_{n}$ by replacing each diagonal entry (equal to $2 n+1$ by induction) with $2 n$. Then the matrix $$ A_{2 n}=\left[\begin{array}{ll} A_{n} & B_{n} \\ C_{n} & A_{n} \end{array}\right] $$ is coveralls. To show this, suppose that $i \leq n$ (the case $i>n$ is similar). The $i$ th cross is composed of the $i$ th cross of $A_{n}$, the $i$ th row of $B_{n}$, and the $i$ th column of $C_{n}$. The $i$ th cross of $A_{i}$ covers $1,2, \ldots, 2 n-1$. The $i$ th row of $B_{n}$ covers all numbers of the form $2 n+j$, where $j$ is covered by the $i$ th row of $A_{n}$ (including $j=1$ ). Similarly, the $i$ th column of $C_{n}$ covers $2 n$ and all numbers of the form $2 n+k$, where $k>1$ is covered by the $i$ th column of $A_{n}$. Thus we see that all numbers are accounted for in the $i$ th cross of $A_{2 n}$, and hence $A_{2 n}$ is a desired coveralls matrix. It follows that we can find a coveralls matrix whenever $n$ is a power of 2 . Second solution for part $b$. We construct a coveralls matrix explicitly for $n=2^{k}$. We consider the coordinates/cells of the matrix elements modulo $n$ throughout the solution. We define the $i$-diagonal $(0 \leq i<$ $n$ ) to be the set of cells of the form $(j, j+i)$, for all $j$. We note that each cross contains exactly one cell from the 0 -diagonal (the main diagonal) and two cells from each $i$-diagonal. For two cells within an $i$ diagonal, $x$ and $y$, we define $x$ and $y$ to be related if there exists a cross containing both $x$ and $y$. Evidently, for every cell $x$ not on the 0 -diagonal there are exactly two other cells related to it. The relation thus breaks up each $i$-diagonal $(i>0)$ into cycles of length larger than 1 . Due to the diagonal translational symmetry (modulo $n$ ), all the cycles within a given $i$-diagonal must be of equal length and thus of an even length, since $n=2^{k}$. The construction of a coveralls matrix is now obvious. We select a number, say 1, to place on all the cells of the 0-diagonal. We pair up the remaining numbers and assign each pair to an $i$-diagonal, say $(2 i, 2 i+1)$. Going along each cycle within the $i$-diagonal we alternately assign values of $2 i$ and $2 i+1$. Since the cycle has an even length, a cell will be related only to a cell of a different number, and hence each cross will contain both $2 i$ and $2 i+1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
98a5af96-fea7-59ba-a672-f7c4ab02779e
| 24,796
|
5. (ROM) Let $A B C D$ be a regular tetrahedron and $M, N$ distinct points in the planes $A B C$ and $A D C$ respectively. Show that the segments $M N, B N, M D$ are the sides of a triangle.
|
5. We shall prove first the 2-dimensional analogue: Lemma. Given an equilateral triangle $A B C$ and two points $M, N$ on the sides $A B$ and $A C$ respectively, there exists a triangle with sides $C M, B N, M N$. Proof. Consider a regular tetrahedron $A B C D$. Since $C M=D M$ and $B N=D N$, one such triangle is $D M N$. Now, to solve the problem for a regular tetrahedron $A B C D$, we consider a 4-dimensional polytope $A B C D E$ whose faces $A B C D, A B C E, A B D E$, $A C D E, B C D E$ are regular tetrahedra. We don't know what it looks like, but it yields a desired triangle: for $M \in A B C$ and $N \in A D C$, we have $D M=E M$ and $B N=E N$; hence the desired triangle is $E M N$. Remark. A solution that avoids embedding in $\mathbb{R}^{4}$ is possible, but no longer so short.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (ROM) Let $A B C D$ be a regular tetrahedron and $M, N$ distinct points in the planes $A B C$ and $A D C$ respectively. Show that the segments $M N, B N, M D$ are the sides of a triangle.
|
5. We shall prove first the 2-dimensional analogue: Lemma. Given an equilateral triangle $A B C$ and two points $M, N$ on the sides $A B$ and $A C$ respectively, there exists a triangle with sides $C M, B N, M N$. Proof. Consider a regular tetrahedron $A B C D$. Since $C M=D M$ and $B N=D N$, one such triangle is $D M N$. Now, to solve the problem for a regular tetrahedron $A B C D$, we consider a 4-dimensional polytope $A B C D E$ whose faces $A B C D, A B C E, A B D E$, $A C D E, B C D E$ are regular tetrahedra. We don't know what it looks like, but it yields a desired triangle: for $M \in A B C$ and $N \in A D C$, we have $D M=E M$ and $B N=E N$; hence the desired triangle is $E M N$. Remark. A solution that avoids embedding in $\mathbb{R}^{4}$ is possible, but no longer so short.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3badb301-a17a-51bb-889d-440a034b50ac
| 24,798
|
6. (IRE) (a) Let $n$ be a positive integer. Prove that there exist distinct positive integers $x, y, z$ such that $$ x^{n-1}+y^{n}=z^{n+1} . $$ (b) Let $a, b, c$ be positive integers such that $a$ and $b$ are relatively prime and $c$ is relatively prime either to $a$ or to $b$. Prove that there exist infinitely many triples $(x, y, z)$ of distinct positive integers $x, y, z$ such that $$ x^{a}+y^{b}=z^{c} . $$ Original formulation: Let $a, b, c, n$ be positive integers such that $n$ is odd and $a c$ is relatively prime to $2 b$. Prove that there exist distinct positive integers $x, y, z$ such that (i) $x^{a}+y^{b}=z^{c}$, and (ii) $x y z$ is relatively prime to $n$.
|
6. (a) One solution is $$ x=2^{n^{2}} 3^{n+1}, \quad y=2^{n^{2}-n} 3^{n}, \quad z=2^{n^{2}-2 n+2} 3^{n-1} . $$ (b) Suppose w.l.o.g. that $\operatorname{gcd}(c, a)=1$. We look for a solution of the form $$ x=p^{m}, \quad y=p^{n}, \quad z=q p^{r}, \quad p, q, m, n, r \in \mathbb{N} . $$ Then $x^{a}+y^{b}=p^{m a}+p^{n b}$ and $z^{c}=q^{c} p^{r c}$, and we see that it is enough to assume $m a-1=n b=r c$ (there are infinitely many such triples $(m, n, r))$ and $q^{c}=p+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
6. (IRE) (a) Let $n$ be a positive integer. Prove that there exist distinct positive integers $x, y, z$ such that $$ x^{n-1}+y^{n}=z^{n+1} . $$ (b) Let $a, b, c$ be positive integers such that $a$ and $b$ are relatively prime and $c$ is relatively prime either to $a$ or to $b$. Prove that there exist infinitely many triples $(x, y, z)$ of distinct positive integers $x, y, z$ such that $$ x^{a}+y^{b}=z^{c} . $$ Original formulation: Let $a, b, c, n$ be positive integers such that $n$ is odd and $a c$ is relatively prime to $2 b$. Prove that there exist distinct positive integers $x, y, z$ such that (i) $x^{a}+y^{b}=z^{c}$, and (ii) $x y z$ is relatively prime to $n$.
|
6. (a) One solution is $$ x=2^{n^{2}} 3^{n+1}, \quad y=2^{n^{2}-n} 3^{n}, \quad z=2^{n^{2}-2 n+2} 3^{n-1} . $$ (b) Suppose w.l.o.g. that $\operatorname{gcd}(c, a)=1$. We look for a solution of the form $$ x=p^{m}, \quad y=p^{n}, \quad z=q p^{r}, \quad p, q, m, n, r \in \mathbb{N} . $$ Then $x^{a}+y^{b}=p^{m a}+p^{n b}$ and $z^{c}=q^{c} p^{r c}$, and we see that it is enough to assume $m a-1=n b=r c$ (there are infinitely many such triples $(m, n, r))$ and $q^{c}=p+1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e4f6af0-4073-5784-8a4e-9e75e388e0d4
| 24,800
|
7. (RUS) Let $A B C D E F$ be a convex hexagon such that $A B=B C, C D=$ $D E, E F=F A$. Prove that $$ \frac{B C}{B E}+\frac{D E}{D A}+\frac{F A}{F C} \geq \frac{3}{2} $$ When does equality occur?
|
7. Let us set $A C=a, C E=b, E A=c$. Applying Ptolemy's inequality for the quadrilateral $A C E F$ we get $$ A C \cdot E F+C E \cdot A F \geq A E \cdot C F $$ Since $E F=A F$, this implies $\frac{F A}{F C} \geq \frac{c}{a+b}$. Similarly $\frac{B C}{B E} \geq \frac{a}{b+c}$ and $\frac{D E}{D A} \geq$ $\frac{b}{c+a}$. Now, $$ \frac{B C}{B E}+\frac{D E}{D A}+\frac{F A}{F C} \geq \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} $$ Hence it is enough to prove that $$ \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \geq \frac{3}{2} $$ If we now substitute $x=b+c, y=c+a, z=a+b$ and $S=a+b+c$ the inequality (1) becomes equivalent to $S(1 / x+1 / y+1 / y)-3 \geq 3 / 2$ which follows immediately form $1 / x+1 / y+1 / z \geq 9 /(x+y+z)=9 /(2 S)$. Equality occurs if it holds in Ptolemy's inequalities and also $a=b=c$. The former happens if and only if the hexagon is cyclic. Hence the only case of equality is when $A B C D E F$ is regular.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
7. (RUS) Let $A B C D E F$ be a convex hexagon such that $A B=B C, C D=$ $D E, E F=F A$. Prove that $$ \frac{B C}{B E}+\frac{D E}{D A}+\frac{F A}{F C} \geq \frac{3}{2} $$ When does equality occur?
|
7. Let us set $A C=a, C E=b, E A=c$. Applying Ptolemy's inequality for the quadrilateral $A C E F$ we get $$ A C \cdot E F+C E \cdot A F \geq A E \cdot C F $$ Since $E F=A F$, this implies $\frac{F A}{F C} \geq \frac{c}{a+b}$. Similarly $\frac{B C}{B E} \geq \frac{a}{b+c}$ and $\frac{D E}{D A} \geq$ $\frac{b}{c+a}$. Now, $$ \frac{B C}{B E}+\frac{D E}{D A}+\frac{F A}{F C} \geq \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} $$ Hence it is enough to prove that $$ \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \geq \frac{3}{2} $$ If we now substitute $x=b+c, y=c+a, z=a+b$ and $S=a+b+c$ the inequality (1) becomes equivalent to $S(1 / x+1 / y+1 / y)-3 \geq 3 / 2$ which follows immediately form $1 / x+1 / y+1 / z \geq 9 /(x+y+z)=9 /(2 S)$. Equality occurs if it holds in Ptolemy's inequalities and also $a=b=c$. The former happens if and only if the hexagon is cyclic. Hence the only case of equality is when $A B C D E F$ is regular.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1ef41373-9e98-54c3-8649-25d9d3396bca
| 24,802
|
8. (GBR) ${ }^{\mathrm{IMO} 2}$ Four different points $A, B, C, D$ are chosen on a circle $\Gamma$ such that the triangle $B C D$ is not right-angled. Prove that: (a) The perpendicular bisectors of $A B$ and $A C$ meet the line $A D$ at certain points $W$ and $V$, respectively, and that the lines $C V$ and $B W$ meet at a certain point $T$. (b) The length of one of the line segments $A D, B T$, and $C T$ is the sum of the lengths of the other two. Original formulation. In triangle $A B C$ the angle at $A$ is the smallest. A line through $A$ meets the circumcircle again at the point $U$ lying on the $\operatorname{arc} B C$ opposite to $A$. The perpendicular bisectors of $C A$ and $A B$ meet $A U$ at $V$ and $W$, respectively, and the lines $C V, B W$ meet at $T$. Show that $A U=T B+T C$.
|
8. (a) Denote by $b$ and $c$ the perpendicular bisectors of $A B$ and $A C$ respectively. If w.l.o.g. $b$ and $A D$ do not intersect (are parallel), then $\angle B C D=\angle B A D=90^{\circ}$, a contradiction. Hence $V, W$ are well-defined. Now, $\angle D W B=2 \angle D A B$ and $\angle D V C=2 \angle D A C$ as oriented angles, and therefore $\angle(W B, V C)=2(\angle D V C-\angle D W B)=2 \angle B A C=$ $2 \angle B C D$ is not equal to 0 . Consequently $C V$ and $B W$ meet at some $T$ with $\angle B T C=2 \angle B A C$. (b) Let $B^{\prime}$ be the second point of intersection of $B W$ with $\Gamma$. Clearly $A D=B B^{\prime}$. But we also have $\angle B T C=2 \angle B A C=2 \angle B B^{\prime} C$, which implies that $C T=T B^{\prime}$. It follows that $A D=B B^{\prime}=\left|B T \pm T B^{\prime}\right|=$ $|B T \pm C T|$. Remark. This problem is also solved easily using trigonometry.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. (GBR) ${ }^{\mathrm{IMO} 2}$ Four different points $A, B, C, D$ are chosen on a circle $\Gamma$ such that the triangle $B C D$ is not right-angled. Prove that: (a) The perpendicular bisectors of $A B$ and $A C$ meet the line $A D$ at certain points $W$ and $V$, respectively, and that the lines $C V$ and $B W$ meet at a certain point $T$. (b) The length of one of the line segments $A D, B T$, and $C T$ is the sum of the lengths of the other two. Original formulation. In triangle $A B C$ the angle at $A$ is the smallest. A line through $A$ meets the circumcircle again at the point $U$ lying on the $\operatorname{arc} B C$ opposite to $A$. The perpendicular bisectors of $C A$ and $A B$ meet $A U$ at $V$ and $W$, respectively, and the lines $C V, B W$ meet at $T$. Show that $A U=T B+T C$.
|
8. (a) Denote by $b$ and $c$ the perpendicular bisectors of $A B$ and $A C$ respectively. If w.l.o.g. $b$ and $A D$ do not intersect (are parallel), then $\angle B C D=\angle B A D=90^{\circ}$, a contradiction. Hence $V, W$ are well-defined. Now, $\angle D W B=2 \angle D A B$ and $\angle D V C=2 \angle D A C$ as oriented angles, and therefore $\angle(W B, V C)=2(\angle D V C-\angle D W B)=2 \angle B A C=$ $2 \angle B C D$ is not equal to 0 . Consequently $C V$ and $B W$ meet at some $T$ with $\angle B T C=2 \angle B A C$. (b) Let $B^{\prime}$ be the second point of intersection of $B W$ with $\Gamma$. Clearly $A D=B B^{\prime}$. But we also have $\angle B T C=2 \angle B A C=2 \angle B B^{\prime} C$, which implies that $C T=T B^{\prime}$. It follows that $A D=B B^{\prime}=\left|B T \pm T B^{\prime}\right|=$ $|B T \pm C T|$. Remark. This problem is also solved easily using trigonometry.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ca6d8ca-bed5-5d24-b84e-7e65ca2f586a
| 24,805
|
9. (USA) Let $A_{1} A_{2} A_{3}$ be a nonisosceles triangle with incenter $I$. Let $C_{i}$, $i=1,2,3$, be the smaller circle through $I$ tangent to $A_{i} A_{i+1}$ and $A_{i} A_{i+2}$ (the addition of indices being mod 3 ). Let $B_{i}, i=1,2,3$, be the second point of intersection of $C_{i+1}$ and $C_{i+2}$. Prove that the circumcenters of the triangles $A_{1} B_{1} I, A_{2} B_{2} I, A_{3} B_{3} I$ are collinear.
|
9. For $i=1,2,3$ (all indices in this problem will be modulo 3 ) we denote by $O_{i}$ the center of $C_{i}$ and by $M_{i}$ the midpoint of the $\operatorname{arc} A_{i+1} A_{i+2}$ that does not contain $A_{i}$. First we have that $O_{i+1} O_{i+2}$ is the perpendicular bisector of $I B_{i}$, and thus it contains the circumcenter $R_{i}$ of $A_{i} B_{i} I$. Additionally, it is easy to show that $T_{i+1} A_{i}=T_{i+1} I$ and $T_{i+2} A_{i}=$ $T_{i+2} I$, which implies that $R_{i}$ lies on the line $T_{i+1} T_{i+2}$. Therefore $R_{i}=$ $O_{i+1} O_{i+2} \cap T_{i+1} T_{i+2}$. 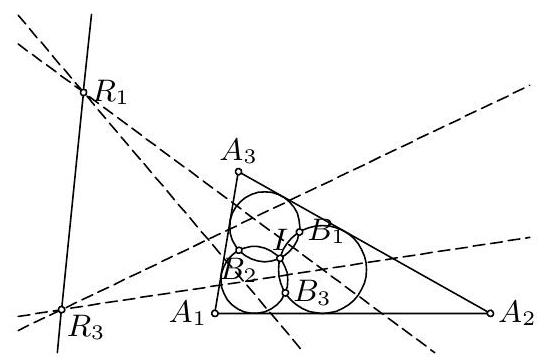 Now, the lines $T_{1} O_{1}, T_{2} O_{2}, T_{3} O_{3}$ are concurrent at $I$. By Desargues's theorem, the points of intersection of $O_{i+1} O_{i+2}$ and $T_{i+1} T_{i+2}$, i.e., the $R_{i}$ 's, lie on a line for $i=1,2,3$. Second solution. The centers of three circles passing through the same point $I$ and not touching each other are collinear if and only if they have another common point. Hence it is enough to show that the circles $A_{i} B_{i} I$ have a common point other than $I$. Now apply inversion at center $I$ and with an arbitrary power. We shall denote by $X^{\prime}$ the image of $X$ under this inversion. In our case, the image of the circle $C_{i}$ is the line $B_{i+1}^{\prime} B_{i+2}^{\prime}$ while the image of the line $A_{i+1} A_{i+2}$ is the circle $I A_{i+1}^{\prime} A_{i+2}^{\prime}$ that is tangent to $B_{i}^{\prime} B_{i+2}^{\prime}$, and $B_{i}^{\prime} B_{i+2}^{\prime}$. These three circles have equal radii, so their centers $P_{1}, P_{2}, P_{3}$ form a triangle also homothetic to $\triangle B_{1}^{\prime} B_{2}^{\prime} B_{3}^{\prime}$. Consequently, points $A_{1}^{\prime}, A_{2}^{\prime}, A_{3}^{\prime}$, that are the reflections of $I$ across the sides of $P_{1} P_{2} P_{3}$, are vertices of a triangle also homothetic to $B_{1}^{\prime} B_{2}^{\prime} B_{3}^{\prime}$. It follows that $A_{1}^{\prime} B_{1}^{\prime}, A_{2}^{\prime} B_{2}^{\prime}, A_{3}^{\prime} B_{3}^{\prime}$ are concurrent at some point $J^{\prime}$, i.e., that the circles $A_{i} B_{i} I$ all pass through $J$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
9. (USA) Let $A_{1} A_{2} A_{3}$ be a nonisosceles triangle with incenter $I$. Let $C_{i}$, $i=1,2,3$, be the smaller circle through $I$ tangent to $A_{i} A_{i+1}$ and $A_{i} A_{i+2}$ (the addition of indices being mod 3 ). Let $B_{i}, i=1,2,3$, be the second point of intersection of $C_{i+1}$ and $C_{i+2}$. Prove that the circumcenters of the triangles $A_{1} B_{1} I, A_{2} B_{2} I, A_{3} B_{3} I$ are collinear.
|
9. For $i=1,2,3$ (all indices in this problem will be modulo 3 ) we denote by $O_{i}$ the center of $C_{i}$ and by $M_{i}$ the midpoint of the $\operatorname{arc} A_{i+1} A_{i+2}$ that does not contain $A_{i}$. First we have that $O_{i+1} O_{i+2}$ is the perpendicular bisector of $I B_{i}$, and thus it contains the circumcenter $R_{i}$ of $A_{i} B_{i} I$. Additionally, it is easy to show that $T_{i+1} A_{i}=T_{i+1} I$ and $T_{i+2} A_{i}=$ $T_{i+2} I$, which implies that $R_{i}$ lies on the line $T_{i+1} T_{i+2}$. Therefore $R_{i}=$ $O_{i+1} O_{i+2} \cap T_{i+1} T_{i+2}$.  Now, the lines $T_{1} O_{1}, T_{2} O_{2}, T_{3} O_{3}$ are concurrent at $I$. By Desargues's theorem, the points of intersection of $O_{i+1} O_{i+2}$ and $T_{i+1} T_{i+2}$, i.e., the $R_{i}$ 's, lie on a line for $i=1,2,3$. Second solution. The centers of three circles passing through the same point $I$ and not touching each other are collinear if and only if they have another common point. Hence it is enough to show that the circles $A_{i} B_{i} I$ have a common point other than $I$. Now apply inversion at center $I$ and with an arbitrary power. We shall denote by $X^{\prime}$ the image of $X$ under this inversion. In our case, the image of the circle $C_{i}$ is the line $B_{i+1}^{\prime} B_{i+2}^{\prime}$ while the image of the line $A_{i+1} A_{i+2}$ is the circle $I A_{i+1}^{\prime} A_{i+2}^{\prime}$ that is tangent to $B_{i}^{\prime} B_{i+2}^{\prime}$, and $B_{i}^{\prime} B_{i+2}^{\prime}$. These three circles have equal radii, so their centers $P_{1}, P_{2}, P_{3}$ form a triangle also homothetic to $\triangle B_{1}^{\prime} B_{2}^{\prime} B_{3}^{\prime}$. Consequently, points $A_{1}^{\prime}, A_{2}^{\prime}, A_{3}^{\prime}$, that are the reflections of $I$ across the sides of $P_{1} P_{2} P_{3}$, are vertices of a triangle also homothetic to $B_{1}^{\prime} B_{2}^{\prime} B_{3}^{\prime}$. It follows that $A_{1}^{\prime} B_{1}^{\prime}, A_{2}^{\prime} B_{2}^{\prime}, A_{3}^{\prime} B_{3}^{\prime}$ are concurrent at some point $J^{\prime}$, i.e., that the circles $A_{i} B_{i} I$ all pass through $J$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d9482260-abab-5646-8a24-ca7a31eae85b
| 24,807
|
1. (LUX) ${ }^{\mathrm{IMO}} \mathrm{A}$ convex quadrilateral $A B C D$ has perpendicular diagonals. The perpendicular bisectors of $A B$ and $C D$ meet at a unique point $P$ inside $A B C D$. Prove that $A B C D$ is cyclic if and only if triangles $A B P$ and $C D P$ have equal areas.
|
1. We begin with the following observation: Suppose that $P$ lies in $\triangle A E B$, where $E$ is the intersection of $A C$ and $B D$ (the other cases are similar). Let $M, N$ be the feet of the perpendiculars from $P$ to $A C$ and $B D$ respectively. We have $S_{A B P}=S_{A B E}-S_{A E P}-S_{B E P}=\frac{1}{2}(A E \cdot B E-A E \cdot E N-B E$. $E M)=\frac{1}{2}(A M \cdot B N-E M \cdot E N)$. Similarly, $S_{C D P}=\frac{1}{2}(C M \cdot D N-E M$. $E N)$. Therefore, we obtain $$ S_{A B P}-S_{C D P}=\frac{A M \cdot B N-C M \cdot D N}{2} $$ Now suppose that $A B C D$ is cyclic. Then $P$ is the circumcenter of $A B C D$; hence $M$ and $N$ are the midpoints of $A C$ and $B D$. Hence $A M=C M$ and $B N=D N$; thus (1) gives us $S_{A B P}=S_{C D P}$. On the other hand, suppose that  $A B C D$ is not cyclic and let w.l.o.g. $P A=P B>P C=P D$. Then we must have $A M>C M$ and $B N>$ $D N$, and consequently by (1), $S_{A B P}>S_{C D P}$. This proves the other implication. Second solution. Let $F$ and $G$ denote the midpoints of $A B$ and $C D$, and assume that $P$ is on the same side of $F G$ as $B$ and $C$. Since $P F \perp A B$, $P G \perp C D$, and $\angle F E B=\angle A B E, \angle G E C=\angle D C E$, a direct computation yields $\angle F P G=\angle F E G=90^{\circ}+\angle A B E+\angle D C E$. Taking into account that $S_{A B P}=\frac{1}{2} A B \cdot F P=F E \cdot F P$, we note that $S_{A B P}=S_{C D P}$ is equivalent to $F E \cdot F P=G E \cdot G P$, i.e., to $F E / E G=$ $G P / P F$. But this last is equivalent to triangles $E F G$ and $P G F$ being similar, which holds if and only if $E F P G$ is a parallelogram. This last is equivalent to $\angle E F P=\angle E G P$, or $2 \angle A B E=2 \angle D C E$. Thus $S_{A B P}=$ $S_{C D P}$ is equivalent to $A B C D$ being cyclic. Remark. The problems also allows an analytic solution, for example putting the $x$ and $y$ axes along the diagonals $A C$ and $B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
1. (LUX) ${ }^{\mathrm{IMO}} \mathrm{A}$ convex quadrilateral $A B C D$ has perpendicular diagonals. The perpendicular bisectors of $A B$ and $C D$ meet at a unique point $P$ inside $A B C D$. Prove that $A B C D$ is cyclic if and only if triangles $A B P$ and $C D P$ have equal areas.
|
1. We begin with the following observation: Suppose that $P$ lies in $\triangle A E B$, where $E$ is the intersection of $A C$ and $B D$ (the other cases are similar). Let $M, N$ be the feet of the perpendiculars from $P$ to $A C$ and $B D$ respectively. We have $S_{A B P}=S_{A B E}-S_{A E P}-S_{B E P}=\frac{1}{2}(A E \cdot B E-A E \cdot E N-B E$. $E M)=\frac{1}{2}(A M \cdot B N-E M \cdot E N)$. Similarly, $S_{C D P}=\frac{1}{2}(C M \cdot D N-E M$. $E N)$. Therefore, we obtain $$ S_{A B P}-S_{C D P}=\frac{A M \cdot B N-C M \cdot D N}{2} $$ Now suppose that $A B C D$ is cyclic. Then $P$ is the circumcenter of $A B C D$; hence $M$ and $N$ are the midpoints of $A C$ and $B D$. Hence $A M=C M$ and $B N=D N$; thus (1) gives us $S_{A B P}=S_{C D P}$. On the other hand, suppose that  $A B C D$ is not cyclic and let w.l.o.g. $P A=P B>P C=P D$. Then we must have $A M>C M$ and $B N>$ $D N$, and consequently by (1), $S_{A B P}>S_{C D P}$. This proves the other implication. Second solution. Let $F$ and $G$ denote the midpoints of $A B$ and $C D$, and assume that $P$ is on the same side of $F G$ as $B$ and $C$. Since $P F \perp A B$, $P G \perp C D$, and $\angle F E B=\angle A B E, \angle G E C=\angle D C E$, a direct computation yields $\angle F P G=\angle F E G=90^{\circ}+\angle A B E+\angle D C E$. Taking into account that $S_{A B P}=\frac{1}{2} A B \cdot F P=F E \cdot F P$, we note that $S_{A B P}=S_{C D P}$ is equivalent to $F E \cdot F P=G E \cdot G P$, i.e., to $F E / E G=$ $G P / P F$. But this last is equivalent to triangles $E F G$ and $P G F$ being similar, which holds if and only if $E F P G$ is a parallelogram. This last is equivalent to $\angle E F P=\angle E G P$, or $2 \angle A B E=2 \angle D C E$. Thus $S_{A B P}=$ $S_{C D P}$ is equivalent to $A B C D$ being cyclic. Remark. The problems also allows an analytic solution, for example putting the $x$ and $y$ axes along the diagonals $A C$ and $B D$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8b631fc6-92e5-504b-88d7-ac149fdc2475
| 24,810
|
10. (AUS) Let $r_{1}, r_{2}, \ldots, r_{n}$ be real numbers greater than or equal to 1 . Prove that $$ \frac{1}{r_{1}+1}+\frac{1}{r_{2}+1}+\cdots+\frac{1}{r_{n}+1} \geq \frac{n}{\sqrt[n]{r_{1} r_{2} \cdots r_{n}}+1} $$
|
10. We shall first prove the inequality for $n$ of the form $2^{k}, k=0,1,2, \ldots$ The case $k=0$ is clear. For $k=1$, we have $$ \frac{1}{r_{1}+1}+\frac{1}{r_{2}+1}-\frac{2}{\sqrt{r_{1} r_{2}}+1}=\frac{\left(\sqrt{r_{1} r_{2}}-1\right)\left(\sqrt{r_{1}}-\sqrt{r_{2}}\right)^{2}}{\left(r_{1}+1\right)\left(r_{2}+1\right)\left(\sqrt{r_{1} r_{2}}+1\right)} \geq 0 $$ For the inductive step it suffices to show that the claim for $k$ and 2 implies that for $k+1$. Indeed, $$ \begin{aligned} \sum_{i=1}^{2^{k+1}} \frac{1}{r_{i}+1} & \geq \frac{2^{k}}{\sqrt[2^{k}]{r_{1} r_{2} \cdots r_{2^{k}}}+1}+\frac{2^{k}}{\sqrt[2^{k}]{r_{2^{k}+1^{\prime} r_{2^{k}}+2^{\cdots r_{2^{k+1}}}+1}}} \\ & \geq \frac{2^{k+1}}{\sqrt[2^{k+1}]{r_{1} r_{2} \cdots r_{2^{k+1}}}+1} \end{aligned} $$ and the induction is complete. We now show that if the statement holds for $2^{k}$, then it holds for every $n<2^{k}$ as well. Put $r_{n+1}=r_{n+2}=\cdots=r_{2^{k}}=\sqrt[n]{r_{1} r_{2} \ldots r_{n}}$. Then (1) becomes $$ \frac{1}{r_{1}+1}+\cdots+\frac{1}{r_{n}+1}+\frac{2^{k}-n}{\sqrt[n]{r_{1} \cdots r_{n}}+1} \geq \frac{2^{k}}{\sqrt[n]{r_{1} \cdots r_{n}}+1} $$ This proves the claim. Second solution. Define $r_{i}=e^{x_{i}}$, where $x_{i}>0$. The function $f(x)=\frac{1}{1+e^{x}}$ is convex for $x>0$ : indeed, $f^{\prime \prime}(x)=\frac{e^{x}\left(e^{x}-1\right)}{\left(e^{x}+1\right)^{3}}>0$. Thus by Jensen's inequality applied to $f\left(x_{1}\right), \ldots, f\left(x_{n}\right)$, we get $\frac{1}{r_{1}+1}+\cdots+\frac{1}{r_{n}+1} \geq \frac{n}{\sqrt[n]{r_{1} \cdots r_{n}}+1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
10. (AUS) Let $r_{1}, r_{2}, \ldots, r_{n}$ be real numbers greater than or equal to 1 . Prove that $$ \frac{1}{r_{1}+1}+\frac{1}{r_{2}+1}+\cdots+\frac{1}{r_{n}+1} \geq \frac{n}{\sqrt[n]{r_{1} r_{2} \cdots r_{n}}+1} $$
|
10. We shall first prove the inequality for $n$ of the form $2^{k}, k=0,1,2, \ldots$ The case $k=0$ is clear. For $k=1$, we have $$ \frac{1}{r_{1}+1}+\frac{1}{r_{2}+1}-\frac{2}{\sqrt{r_{1} r_{2}}+1}=\frac{\left(\sqrt{r_{1} r_{2}}-1\right)\left(\sqrt{r_{1}}-\sqrt{r_{2}}\right)^{2}}{\left(r_{1}+1\right)\left(r_{2}+1\right)\left(\sqrt{r_{1} r_{2}}+1\right)} \geq 0 $$ For the inductive step it suffices to show that the claim for $k$ and 2 implies that for $k+1$. Indeed, $$ \begin{aligned} \sum_{i=1}^{2^{k+1}} \frac{1}{r_{i}+1} & \geq \frac{2^{k}}{\sqrt[2^{k}]{r_{1} r_{2} \cdots r_{2^{k}}}+1}+\frac{2^{k}}{\sqrt[2^{k}]{r_{2^{k}+1^{\prime} r_{2^{k}}+2^{\cdots r_{2^{k+1}}}+1}}} \\ & \geq \frac{2^{k+1}}{\sqrt[2^{k+1}]{r_{1} r_{2} \cdots r_{2^{k+1}}}+1} \end{aligned} $$ and the induction is complete. We now show that if the statement holds for $2^{k}$, then it holds for every $n<2^{k}$ as well. Put $r_{n+1}=r_{n+2}=\cdots=r_{2^{k}}=\sqrt[n]{r_{1} r_{2} \ldots r_{n}}$. Then (1) becomes $$ \frac{1}{r_{1}+1}+\cdots+\frac{1}{r_{n}+1}+\frac{2^{k}-n}{\sqrt[n]{r_{1} \cdots r_{n}}+1} \geq \frac{2^{k}}{\sqrt[n]{r_{1} \cdots r_{n}}+1} $$ This proves the claim. Second solution. Define $r_{i}=e^{x_{i}}$, where $x_{i}>0$. The function $f(x)=\frac{1}{1+e^{x}}$ is convex for $x>0$ : indeed, $f^{\prime \prime}(x)=\frac{e^{x}\left(e^{x}-1\right)}{\left(e^{x}+1\right)^{3}}>0$. Thus by Jensen's inequality applied to $f\left(x_{1}\right), \ldots, f\left(x_{n}\right)$, we get $\frac{1}{r_{1}+1}+\cdots+\frac{1}{r_{n}+1} \geq \frac{n}{\sqrt[n]{r_{1} \cdots r_{n}}+1}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
db4913cf-4d39-5c04-9153-8d3cafb91673
| 24,812
|
11. (RUS) Let $x, y$, and $z$ be positive real numbers such that $x y z=1$. Prove that $$ \frac{x^{3}}{(1+y)(1+z)}+\frac{y^{3}}{(1+z)(1+x)}+\frac{z^{3}}{(1+x)(1+y)} \geq \frac{3}{4} $$
|
11. The given inequality is equivalent to $x^{3}(x+1)+y^{3}(y+1)+z^{3}(z+1) \geq$ $\frac{3}{4}(x+1)(y+1)(z+1)$. By the A-G mean inequality, it will be enough to prove a stronger inequality: $$ x^{4}+x^{3}+y^{4}+y^{3}+z^{4}+z^{3} \geq \frac{1}{4}\left[(x+1)^{3}+(y+1)^{3}+(z+1)^{3}\right] . $$ If we set $S_{k}=x^{k}+y^{k}+z^{k}$, (1) takes the form $S_{4}+S_{3} \geq \frac{1}{4} S_{3}+\frac{3}{4} S_{2}+\frac{3}{4} S_{1}+\frac{3}{4}$. Note that by the A-G mean inequality, $S_{1}=x+y+z \geq 3$. Thus it suffices to prove the following: $$ \text { If } S_{1} \geq 3 \text { and } m>n \text { are positive integers, then } S_{m} \geq S_{n} \text {. } $$ This can be shown in many ways. For example, by Hölder's inequality, $$ \left(x^{m}+y^{m}+z^{m}\right)^{n / m}(1+1+1)^{(m-n) / m} \geq x^{n}+y^{n}+z^{n} . $$ (Another way is using the Chebyshev inequality: if $x \geq y \geq z$ then $x^{k-1} \geq$ $y^{k-1} \geq z^{k-1}$; hence $S_{k}=x \cdot x^{k-1}+y \cdot y^{k-1}+z \cdot z^{k-1} \geq \frac{1}{3} S_{1} S_{k-1}$, and the claim follows by induction.) Second solution. Assume that $x \geq y \geq z$. Then also $\frac{1}{(y+1)(z+1)} \geq$ $\frac{1}{(x+1)(z+1)} \geq \frac{1}{(x+1)(y+1)}$. Hence Chebyshev's inequality gives that $$ \begin{aligned} & \frac{x^{3}}{(1+y)(1+z)}+\frac{y^{3}}{(1+x)(1+z)}+\frac{z^{3}}{(1+x)(1+y)} \\ \geq & \frac{1}{3} \frac{\left(x^{3}+y^{3}+z^{3}\right) \cdot(3+x+y+z)}{(1+x)(1+y)(1+z)} \end{aligned} $$ Now if we put $x+y+z=3 S$, we have $x^{3}+y^{3}+z^{3} \geq 3 S$ and $(1+$ $x)(1+y)(1+z) \leq(1+a)^{3}$ by the A-G mean inequality. Thus the needed inequality reduces to $\frac{6 S^{3}}{(1+S)^{3}} \geq \frac{3}{4}$, which is obviously true because $S \geq 1$. Remark. Both these solutions use only that $x+y+z \geq 3$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
11. (RUS) Let $x, y$, and $z$ be positive real numbers such that $x y z=1$. Prove that $$ \frac{x^{3}}{(1+y)(1+z)}+\frac{y^{3}}{(1+z)(1+x)}+\frac{z^{3}}{(1+x)(1+y)} \geq \frac{3}{4} $$
|
11. The given inequality is equivalent to $x^{3}(x+1)+y^{3}(y+1)+z^{3}(z+1) \geq$ $\frac{3}{4}(x+1)(y+1)(z+1)$. By the A-G mean inequality, it will be enough to prove a stronger inequality: $$ x^{4}+x^{3}+y^{4}+y^{3}+z^{4}+z^{3} \geq \frac{1}{4}\left[(x+1)^{3}+(y+1)^{3}+(z+1)^{3}\right] . $$ If we set $S_{k}=x^{k}+y^{k}+z^{k}$, (1) takes the form $S_{4}+S_{3} \geq \frac{1}{4} S_{3}+\frac{3}{4} S_{2}+\frac{3}{4} S_{1}+\frac{3}{4}$. Note that by the A-G mean inequality, $S_{1}=x+y+z \geq 3$. Thus it suffices to prove the following: $$ \text { If } S_{1} \geq 3 \text { and } m>n \text { are positive integers, then } S_{m} \geq S_{n} \text {. } $$ This can be shown in many ways. For example, by Hölder's inequality, $$ \left(x^{m}+y^{m}+z^{m}\right)^{n / m}(1+1+1)^{(m-n) / m} \geq x^{n}+y^{n}+z^{n} . $$ (Another way is using the Chebyshev inequality: if $x \geq y \geq z$ then $x^{k-1} \geq$ $y^{k-1} \geq z^{k-1}$; hence $S_{k}=x \cdot x^{k-1}+y \cdot y^{k-1}+z \cdot z^{k-1} \geq \frac{1}{3} S_{1} S_{k-1}$, and the claim follows by induction.) Second solution. Assume that $x \geq y \geq z$. Then also $\frac{1}{(y+1)(z+1)} \geq$ $\frac{1}{(x+1)(z+1)} \geq \frac{1}{(x+1)(y+1)}$. Hence Chebyshev's inequality gives that $$ \begin{aligned} & \frac{x^{3}}{(1+y)(1+z)}+\frac{y^{3}}{(1+x)(1+z)}+\frac{z^{3}}{(1+x)(1+y)} \\ \geq & \frac{1}{3} \frac{\left(x^{3}+y^{3}+z^{3}\right) \cdot(3+x+y+z)}{(1+x)(1+y)(1+z)} \end{aligned} $$ Now if we put $x+y+z=3 S$, we have $x^{3}+y^{3}+z^{3} \geq 3 S$ and $(1+$ $x)(1+y)(1+z) \leq(1+a)^{3}$ by the A-G mean inequality. Thus the needed inequality reduces to $\frac{6 S^{3}}{(1+S)^{3}} \geq \frac{3}{4}$, which is obviously true because $S \geq 1$. Remark. Both these solutions use only that $x+y+z \geq 3$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2b6c3db7-0089-526d-bdb6-ff62e2cbda55
| 24,815
|
12. (POL) Let $n \geq k \geq 0$ be integers. The numbers $c(n, k)$ are defined as follows: $$ \begin{aligned} c(n, 0) & =c(n, n)=1 & & \text { for all } n \geq 0 \\ c(n+1, k) & =2^{k} c(n, k)+c(n, k-1) & & \text { for } n \geq k \geq 1 \end{aligned} $$ Prove that $c(n, k)=c(n, n-k)$ for all $n \geq k \geq 0$.
|
12. The assertion is clear for $n=0$. We shall prove the general case by induction on $n$. Suppose that $c(m, i)=c(m, m-i)$ for all $i$ and $m \leq n$. Then by the induction hypothesis and the recurrence formula we have $c(n+1, k)=2^{k} c(n, k)+c(n, k-1)$ and $c(n+1, n+1-k)=$ $2^{n+1-k} c(n, n+1-k)+c(n, n-k)=2^{n+1-k} c(n, k-1)+c(n, k)$. Thus it remains only to show that $$ \left(2^{k}-1\right) c(n, k)=\left(2^{n+1-k}-1\right) c(n, k-1) $$ We prove this also by induction on $n$. By the induction hypothesis, $$ c(n-1, k)=\frac{2^{n-k}-1}{2^{k}-1} c(n-1, k-1) $$ and $$ c(n-1, k-2)=\frac{2^{k-1}-1}{2^{n+1-k}-1} c(n-1, k-1) $$ Using these formulas and the recurrence formula we obtain $\left(2^{k}-1\right) c(n, k)-$ $\left(2^{n+1-k}-1\right) c(n, k-1)=\left(2^{2 k}-2^{k}\right) c(n-1, k)-\left(2^{n}-3 \cdot 2^{k-1}+1\right) c(n-$ $1, k-1)-\left(2^{n+1-k}-1\right) c(n-1, k-2)=\left(2^{n}-2^{k}\right) c(n-1, k-1)-\left(2^{n}-\right.$ $\left.3 \cdot 2^{k-1}+1\right) c(n-1, k-1)-\left(2^{k-1}-1\right) c(n-1, k-1)=0$. This completes the proof. Second solution. The given recurrence formula resembles that of binomial coefficients, so it is natural to search for an explicit formula of the form $c(n, k)=\frac{F(n)}{F(k) F(n-k)}$, where $F(m)=f(1) f(2) \cdots f(m)($ with $F(0)=1$ ) and $f$ is a certain function from the natural numbers to the real numbers. If there is such an $f$, then $c(n, k)=c(n, n-k)$ follows immediately. After substitution of the above relation, the recurrence equivalently reduces to $f(n+1)=2^{k} f(n-k+1)+f(k)$. It is easy to see that $f(m)=2^{m}-1$ satisfies this relation. Remark. If we introduce the polynomial $P_{n}(x)=\sum_{k=0}^{n} c(n, k) x^{k}$, the recurrence relation gives $P_{0}(x)=1$ and $P_{n+1}(x)=x P_{n}(x)+P_{n}(2 x)$. As a consequence of the problem, all polynomials in this sequence are symmetric, i.e., $P_{n}(x)=x^{n} P_{n}\left(x^{-1}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. (POL) Let $n \geq k \geq 0$ be integers. The numbers $c(n, k)$ are defined as follows: $$ \begin{aligned} c(n, 0) & =c(n, n)=1 & & \text { for all } n \geq 0 \\ c(n+1, k) & =2^{k} c(n, k)+c(n, k-1) & & \text { for } n \geq k \geq 1 \end{aligned} $$ Prove that $c(n, k)=c(n, n-k)$ for all $n \geq k \geq 0$.
|
12. The assertion is clear for $n=0$. We shall prove the general case by induction on $n$. Suppose that $c(m, i)=c(m, m-i)$ for all $i$ and $m \leq n$. Then by the induction hypothesis and the recurrence formula we have $c(n+1, k)=2^{k} c(n, k)+c(n, k-1)$ and $c(n+1, n+1-k)=$ $2^{n+1-k} c(n, n+1-k)+c(n, n-k)=2^{n+1-k} c(n, k-1)+c(n, k)$. Thus it remains only to show that $$ \left(2^{k}-1\right) c(n, k)=\left(2^{n+1-k}-1\right) c(n, k-1) $$ We prove this also by induction on $n$. By the induction hypothesis, $$ c(n-1, k)=\frac{2^{n-k}-1}{2^{k}-1} c(n-1, k-1) $$ and $$ c(n-1, k-2)=\frac{2^{k-1}-1}{2^{n+1-k}-1} c(n-1, k-1) $$ Using these formulas and the recurrence formula we obtain $\left(2^{k}-1\right) c(n, k)-$ $\left(2^{n+1-k}-1\right) c(n, k-1)=\left(2^{2 k}-2^{k}\right) c(n-1, k)-\left(2^{n}-3 \cdot 2^{k-1}+1\right) c(n-$ $1, k-1)-\left(2^{n+1-k}-1\right) c(n-1, k-2)=\left(2^{n}-2^{k}\right) c(n-1, k-1)-\left(2^{n}-\right.$ $\left.3 \cdot 2^{k-1}+1\right) c(n-1, k-1)-\left(2^{k-1}-1\right) c(n-1, k-1)=0$. This completes the proof. Second solution. The given recurrence formula resembles that of binomial coefficients, so it is natural to search for an explicit formula of the form $c(n, k)=\frac{F(n)}{F(k) F(n-k)}$, where $F(m)=f(1) f(2) \cdots f(m)($ with $F(0)=1$ ) and $f$ is a certain function from the natural numbers to the real numbers. If there is such an $f$, then $c(n, k)=c(n, n-k)$ follows immediately. After substitution of the above relation, the recurrence equivalently reduces to $f(n+1)=2^{k} f(n-k+1)+f(k)$. It is easy to see that $f(m)=2^{m}-1$ satisfies this relation. Remark. If we introduce the polynomial $P_{n}(x)=\sum_{k=0}^{n} c(n, k) x^{k}$, the recurrence relation gives $P_{0}(x)=1$ and $P_{n+1}(x)=x P_{n}(x)+P_{n}(2 x)$. As a consequence of the problem, all polynomials in this sequence are symmetric, i.e., $P_{n}(x)=x^{n} P_{n}\left(x^{-1}\right)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a7cc9d67-16db-52c8-9b2b-01a4993d7c0b
| 24,817
|
2. (POL) Let $A B C D$ be a cyclic quadrilateral. Let $E$ and $F$ be variable points on the sides $A B$ and $C D$, respectively, such that $A E: E B=C F$ : $F D$. Let $P$ be the point on the segment $E F$ such that $P E: P F=A B$ : $C D$. Prove that the ratio between the areas of triangles $A P D$ and $B P C$ does not depend on the choice of $E$ and $F$.
|
2. If $A D$ and $B C$ are parallel, then $A B C D$ is an isosceles trapezoid with $A B=C D$, so $P$ is the midpoint of $E F$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$. Then $M N \| B C$, and the distance $d(E, M N)$ equals the distance $d(F, M N)$ because $B$ and $D$ are the same distance from $M N$ and $E M / B M=F N / D N$. It follows that the midpoint $P$ of $E F$ lies on $M N$, and consequently $S_{A P D}: S_{B P C}=A D: B C$. If $A D$ and $B C$ are not parallel, then they meet at some point $Q$. It is plain that $\triangle Q A B \sim \triangle Q C D$, and since $A E / A B=C F / C D$, we also deduce that $\triangle Q A E \sim \triangle Q C F$. Therefore $\angle A Q E=\angle C Q F$. Further, from these similarities we obtain $Q E / Q F=Q A / Q C=A B / C D=P E / P F$, which in turn means that $Q P$ is the internal bisector of $\angle E Q F$. But since $\angle A Q E=\angle C Q F$, this is also the internal bisector of $\angle A Q B$. Hence $P$ is at equal distances from $A D$ and $B C$, so again $S_{A P D}: S_{B P C}=A D: B C$. Remark. The part $A B \| C D$ could also be regarded as a limiting case of the other part. Second solution. Denote $\lambda=\frac{A E}{A B}, A B=a, B C=b, C D=c, D A=d$, $\angle D A B=\alpha, \angle A B C=\beta$. Since $d(P, A D)=\frac{c \cdot d(E, A D)+a \cdot d(F, A D)}{a+c}$, we have $S_{A P D}=\frac{c S_{E A D}+a S_{F A D}}{a+c}=\frac{\lambda c S_{A B D}+(1-\lambda) a S_{A C D}}{a+c}$. Since $S_{A B D}=\frac{1}{2} a d \sin \alpha$ and $S_{A C D}=\frac{1}{2} c d \sin \beta$, we are led to $S_{A P D}=\frac{a c d}{a+c}[\lambda \sin \alpha+(1-\lambda) \sin \beta]$, and analogously $S_{B P C}=\frac{a b c}{a+c}[\lambda \sin \alpha+(1-\lambda) \sin \beta]$. Thus we obtain $S_{A P D}: S_{B P C}=d: b$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
2. (POL) Let $A B C D$ be a cyclic quadrilateral. Let $E$ and $F$ be variable points on the sides $A B$ and $C D$, respectively, such that $A E: E B=C F$ : $F D$. Let $P$ be the point on the segment $E F$ such that $P E: P F=A B$ : $C D$. Prove that the ratio between the areas of triangles $A P D$ and $B P C$ does not depend on the choice of $E$ and $F$.
|
2. If $A D$ and $B C$ are parallel, then $A B C D$ is an isosceles trapezoid with $A B=C D$, so $P$ is the midpoint of $E F$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$. Then $M N \| B C$, and the distance $d(E, M N)$ equals the distance $d(F, M N)$ because $B$ and $D$ are the same distance from $M N$ and $E M / B M=F N / D N$. It follows that the midpoint $P$ of $E F$ lies on $M N$, and consequently $S_{A P D}: S_{B P C}=A D: B C$. If $A D$ and $B C$ are not parallel, then they meet at some point $Q$. It is plain that $\triangle Q A B \sim \triangle Q C D$, and since $A E / A B=C F / C D$, we also deduce that $\triangle Q A E \sim \triangle Q C F$. Therefore $\angle A Q E=\angle C Q F$. Further, from these similarities we obtain $Q E / Q F=Q A / Q C=A B / C D=P E / P F$, which in turn means that $Q P$ is the internal bisector of $\angle E Q F$. But since $\angle A Q E=\angle C Q F$, this is also the internal bisector of $\angle A Q B$. Hence $P$ is at equal distances from $A D$ and $B C$, so again $S_{A P D}: S_{B P C}=A D: B C$. Remark. The part $A B \| C D$ could also be regarded as a limiting case of the other part. Second solution. Denote $\lambda=\frac{A E}{A B}, A B=a, B C=b, C D=c, D A=d$, $\angle D A B=\alpha, \angle A B C=\beta$. Since $d(P, A D)=\frac{c \cdot d(E, A D)+a \cdot d(F, A D)}{a+c}$, we have $S_{A P D}=\frac{c S_{E A D}+a S_{F A D}}{a+c}=\frac{\lambda c S_{A B D}+(1-\lambda) a S_{A C D}}{a+c}$. Since $S_{A B D}=\frac{1}{2} a d \sin \alpha$ and $S_{A C D}=\frac{1}{2} c d \sin \beta$, we are led to $S_{A P D}=\frac{a c d}{a+c}[\lambda \sin \alpha+(1-\lambda) \sin \beta]$, and analogously $S_{B P C}=\frac{a b c}{a+c}[\lambda \sin \alpha+(1-\lambda) \sin \beta]$. Thus we obtain $S_{A P D}: S_{B P C}=d: b$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
195686b3-426c-59e5-bed2-3cecb1254d2d
| 24,839
|
20. (ARG) Prove that for each positive integer $n$, there exists a positive integer with the following properties: (i) It has exactly $n$ digits. (ii) None of the digits is 0 . (iii) It is divisible by the sum of its digits.
|
20. We first consider the special case $n=3^{r}$. Then the simplest choice $\frac{10^{n}-1}{9}=$ $11 \ldots 1$ ( $n$ digits) works. This can be shown by induction: it is true for $r=$ 1, while the inductive step follows from $10^{3^{r}}-1=\left(10^{3^{r-1}}-1\right)\left(10^{2 \cdot 3^{r-1}}+\right.$ $10^{3^{r-1}}+1$ ), because the second factor is divisible by 3 . In the general case, let $k \geq n / 2$ be a positive integer and $a_{1}, \ldots, a_{n-k}$ be nonzero digits. We have $$ \begin{aligned} A & =\left(10^{k}-1\right) \overline{a_{1} a_{2} \ldots a_{n-k}} \\ & =\overline{a_{1} a_{2} \ldots a_{n-k-1} a_{n-k}^{\prime} \underbrace{99 \ldots 99}_{2 k-n}} b_{1} b_{2} \ldots b_{n-k-1} b_{n-k}^{\prime} \end{aligned} $$ where $a_{n-k}^{\prime}=a_{n-k}-1, b_{i}=9-a_{i}$, and $b_{n-k}^{\prime}=9-a_{n-k}^{\prime}$. The sum of digits of $A$ equals $9 k$ independently of the choice of digits $a_{1}, \ldots, a_{n-k}$. Thus we need only choose $k \geq \frac{n}{2}$ and digits $a_{1}, \ldots, a_{n-k-1} \notin\{0,9\}$ and $a_{n-k} \in\{0,1\}$ in order for the conditions to be fulfilled. Let us choose $$ k=\left\{\begin{array}{l} 3^{r}, \quad \text { if } 3^{r}<n \leq 2 \cdot 3^{r} \text { for some } r \in \mathbb{Z} \\ 2 \cdot 3^{r}, \text { if } 2 \cdot 3^{r}<n \leq 3^{r+1} \text { for some } r \in \mathbb{Z} \end{array}\right. $$ and $\overline{a_{1} a_{2} \ldots a_{n-k}}=\overline{22 \ldots 2}$. The number $$ A=\overline{\underbrace{22 \ldots 2}_{n-k-1} 1 \underbrace{99 \ldots 99}_{2 k-n} \underbrace{77 \ldots 7}_{n-k-1} 8} $$ thus obtained is divisible by $2 \cdot\left(10^{k}-1\right)$, which is, as explained above, divisible by $18 \cdot 3^{r}$. Finally, the sum of digits of $A$ is either $9 \cdot 3^{r}$ or $18 \cdot 3^{r}$; thus $A$ has the desired properties.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
20. (ARG) Prove that for each positive integer $n$, there exists a positive integer with the following properties: (i) It has exactly $n$ digits. (ii) None of the digits is 0 . (iii) It is divisible by the sum of its digits.
|
20. We first consider the special case $n=3^{r}$. Then the simplest choice $\frac{10^{n}-1}{9}=$ $11 \ldots 1$ ( $n$ digits) works. This can be shown by induction: it is true for $r=$ 1, while the inductive step follows from $10^{3^{r}}-1=\left(10^{3^{r-1}}-1\right)\left(10^{2 \cdot 3^{r-1}}+\right.$ $10^{3^{r-1}}+1$ ), because the second factor is divisible by 3 . In the general case, let $k \geq n / 2$ be a positive integer and $a_{1}, \ldots, a_{n-k}$ be nonzero digits. We have $$ \begin{aligned} A & =\left(10^{k}-1\right) \overline{a_{1} a_{2} \ldots a_{n-k}} \\ & =\overline{a_{1} a_{2} \ldots a_{n-k-1} a_{n-k}^{\prime} \underbrace{99 \ldots 99}_{2 k-n}} b_{1} b_{2} \ldots b_{n-k-1} b_{n-k}^{\prime} \end{aligned} $$ where $a_{n-k}^{\prime}=a_{n-k}-1, b_{i}=9-a_{i}$, and $b_{n-k}^{\prime}=9-a_{n-k}^{\prime}$. The sum of digits of $A$ equals $9 k$ independently of the choice of digits $a_{1}, \ldots, a_{n-k}$. Thus we need only choose $k \geq \frac{n}{2}$ and digits $a_{1}, \ldots, a_{n-k-1} \notin\{0,9\}$ and $a_{n-k} \in\{0,1\}$ in order for the conditions to be fulfilled. Let us choose $$ k=\left\{\begin{array}{l} 3^{r}, \quad \text { if } 3^{r}<n \leq 2 \cdot 3^{r} \text { for some } r \in \mathbb{Z} \\ 2 \cdot 3^{r}, \text { if } 2 \cdot 3^{r}<n \leq 3^{r+1} \text { for some } r \in \mathbb{Z} \end{array}\right. $$ and $\overline{a_{1} a_{2} \ldots a_{n-k}}=\overline{22 \ldots 2}$. The number $$ A=\overline{\underbrace{22 \ldots 2}_{n-k-1} 1 \underbrace{99 \ldots 99}_{2 k-n} \underbrace{77 \ldots 7}_{n-k-1} 8} $$ thus obtained is divisible by $2 \cdot\left(10^{k}-1\right)$, which is, as explained above, divisible by $18 \cdot 3^{r}$. Finally, the sum of digits of $A$ is either $9 \cdot 3^{r}$ or $18 \cdot 3^{r}$; thus $A$ has the desired properties.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
760bead2-c71d-516e-95bc-4ed70cb7cdd4
| 24,842
|
22. (UKR) A rectangular array of numbers is given. In each row and each column, the sum of all numbers is an integer. Prove that each nonintegral number $x$ in the array can be changed into either $\lceil x\rceil$ or $\lfloor x\rfloor$ so that the row sums and column sums remain unchanged. (Note that $\lceil x\rceil$ is the least integer greater than or equal to $x$, while $\lfloor x\rfloor$ is the greatest integer less than or equal to $x$.)
|
22. We can obviously change each $x$ into $\lfloor x\rfloor$ or $\lceil x\rceil$ so that the column sums remain unchanged. However, this does not necessarily match the row sums as well, so let us consider the sum $S$ of the absolute values of the changes in the row sums. It is easily seen that $S$ is even, and we want it to be 0 . A row may have a higher or lower sum than desired. Let us mark a cell by - if its entry $x$ was changed to $\lfloor x\rfloor$, and by + if it was changed to $\lceil x\rceil$ instead. We call a row $R_{2}$ accessible from a row $R_{1}$ if there is a column $C$ such that $C \cap R_{1}$ is marked + and $C \cap R_{2}$ is marked - . Note that a column containing a + must contain a - as well, because column sums are unchanged. Hence from each row with a higher sum we can access another row. Assume that the row sum in $R_{1}$ is higher. If $R_{1}, R_{2}, \ldots, R_{k}$ is a sequence of rows such that $R_{i+1}$ is accessible from $R_{i}$ via some column $C_{i}$ and such that the row sum in $R_{k}$ is lower, then by changing the signs in $C_{i} \cap R_{i}$ and $C_{i} \cap R_{i+1}(i=1,2, \ldots, k-1)$ we decrease $S$ by 2 , leaving column sums unchanged. We claim that such a sequence of rows always exists. Let $\mathcal{R}$ be the union of all rows that are accessible from $R_{1}$, directly or indirectly; let $\overline{\mathcal{R}}$ be the union of the remaining rows. We show that for any column $C$, the sum in $\mathcal{R} \cap C$ is not higher. If $\mathcal{R} \cap C$ contains no +'s, then this is clear. If $\mathcal{R} \cap C$ contains a + , since the rows of $\overline{\mathcal{R}}$ are not accessible, the set $\overline{\mathcal{R}} \cap C$ contains no -'s. It follows that the sum in $\overline{\mathcal{R}} \cap C$ is not lower, and since column sums are unchanged, we again come to the same conclusion. Thus the total sum in $\mathcal{R}$ is not higher. Therefore, there is a row in $\mathcal{R}$ with too low a sum, justifying our claim.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
22. (UKR) A rectangular array of numbers is given. In each row and each column, the sum of all numbers is an integer. Prove that each nonintegral number $x$ in the array can be changed into either $\lceil x\rceil$ or $\lfloor x\rfloor$ so that the row sums and column sums remain unchanged. (Note that $\lceil x\rceil$ is the least integer greater than or equal to $x$, while $\lfloor x\rfloor$ is the greatest integer less than or equal to $x$.)
|
22. We can obviously change each $x$ into $\lfloor x\rfloor$ or $\lceil x\rceil$ so that the column sums remain unchanged. However, this does not necessarily match the row sums as well, so let us consider the sum $S$ of the absolute values of the changes in the row sums. It is easily seen that $S$ is even, and we want it to be 0 . A row may have a higher or lower sum than desired. Let us mark a cell by - if its entry $x$ was changed to $\lfloor x\rfloor$, and by + if it was changed to $\lceil x\rceil$ instead. We call a row $R_{2}$ accessible from a row $R_{1}$ if there is a column $C$ such that $C \cap R_{1}$ is marked + and $C \cap R_{2}$ is marked - . Note that a column containing a + must contain a - as well, because column sums are unchanged. Hence from each row with a higher sum we can access another row. Assume that the row sum in $R_{1}$ is higher. If $R_{1}, R_{2}, \ldots, R_{k}$ is a sequence of rows such that $R_{i+1}$ is accessible from $R_{i}$ via some column $C_{i}$ and such that the row sum in $R_{k}$ is lower, then by changing the signs in $C_{i} \cap R_{i}$ and $C_{i} \cap R_{i+1}(i=1,2, \ldots, k-1)$ we decrease $S$ by 2 , leaving column sums unchanged. We claim that such a sequence of rows always exists. Let $\mathcal{R}$ be the union of all rows that are accessible from $R_{1}$, directly or indirectly; let $\overline{\mathcal{R}}$ be the union of the remaining rows. We show that for any column $C$, the sum in $\mathcal{R} \cap C$ is not higher. If $\mathcal{R} \cap C$ contains no +'s, then this is clear. If $\mathcal{R} \cap C$ contains a + , since the rows of $\overline{\mathcal{R}}$ are not accessible, the set $\overline{\mathcal{R}} \cap C$ contains no -'s. It follows that the sum in $\overline{\mathcal{R}} \cap C$ is not lower, and since column sums are unchanged, we again come to the same conclusion. Thus the total sum in $\mathcal{R}$ is not higher. Therefore, there is a row in $\mathcal{R}$ with too low a sum, justifying our claim.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f8888995-f598-5b43-a933-5f273f0b14c8
| 24,848
|
23. (BLR) Let $n$ be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties: (i) The first operation is either addition or multiplication. (ii) Thereafter, additions and multiplications are used alternately. (iii) In each addition one can choose independently whether to add 2 or $n$. (iv) In each multiplication, one can choose independently whether to multiply by 2 or by $n$. A positive integer that cannot be so obtained is said to be unattainable. (a) Prove that if $n \geq 9$, there are infinitely many unattainable positive integers. (b) Prove that if $n=3$, all positive integers except 7 are attainable.
|
23. (a) If $n$ is even, then every odd integer is unattainable. Assume that $n \geq 9$ is odd. Let $a$ be obtained by addition from some $b$, and $b$ from $c$ by multiplication. Then $a$ is $2 c+2,2 c+n, n c+2$, or $n c+n$, and is in every case congruent to $2 c+2$ modulo $n-2$. In particular, if $a \equiv-2$ $(\bmod n-2)$, then also $b \equiv-4$ and $c \equiv-2(\bmod n-2)$. Now consider any $a=k n(n-2)-2$, where $k$ is odd. If it is attainable, but not divisible by 2 or $n$, it must have been obtained by addition. Thus all predecessors of $a$ are congruent to either -2 or $-4(\bmod$ $n-2$ ), and none of them equals 1 , a contradiction. (b) Call an attainable number addy if the last operation is addition, and multy if the last operation is multiplication. We prove the following claims by simultaneous induction on $k$ : (1) $n=6 k$ is both addy and multy; (2) $n=6 k+1$ is addy for $k \geq 2$; (3) $n=6 k+2$ is addy for $k \geq 1$; (4) $n=6 k+3$ is addy; (5) $n=6 k+4$ is multy for $k \geq 1$; (6) $n=6 k+5$ is addy. The cases $k \leq 1$ are easily verified. For $k \geq 2$, suppose all six statements hold up to $k-1$. Since $6 k-3$ is addy, $6 k$ is multy. Next, $6 k-2$ is multy, so both $6 k=(6 k-2)+2$ and $6 k+1=(6 k-2)+3$ are addy. Since $6 k$ is multy, both $6 k+2$ and $6 k+3$ are addy. Number $6 k+4=2 \cdot(3 k+2)$ is multy, because $3 k+2$ is addy (being either $6 l+2$ or $6 l+5)$. Finally, we have $6 k+5=3 \cdot(2 k+1)+2$. Since $2 k+1$ is $6 l+1,6 l+3$, or $6 l+5$, it is addy except for 7 . Hence $6 k+5$ is addy except possibly for 23 . But $23=((1 \cdot 2+2) \cdot 2+2) \cdot 2+3$ is also addy. This completes the induction. Now 1 is given and $2=1 \cdot 2,4=1+3$. It is easily checked that 7 is not attainable, and hence it is the only unattainable number.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
23. (BLR) Let $n$ be an integer greater than 2. A positive integer is said to be attainable if it is 1 or can be obtained from 1 by a sequence of operations with the following properties: (i) The first operation is either addition or multiplication. (ii) Thereafter, additions and multiplications are used alternately. (iii) In each addition one can choose independently whether to add 2 or $n$. (iv) In each multiplication, one can choose independently whether to multiply by 2 or by $n$. A positive integer that cannot be so obtained is said to be unattainable. (a) Prove that if $n \geq 9$, there are infinitely many unattainable positive integers. (b) Prove that if $n=3$, all positive integers except 7 are attainable.
|
23. (a) If $n$ is even, then every odd integer is unattainable. Assume that $n \geq 9$ is odd. Let $a$ be obtained by addition from some $b$, and $b$ from $c$ by multiplication. Then $a$ is $2 c+2,2 c+n, n c+2$, or $n c+n$, and is in every case congruent to $2 c+2$ modulo $n-2$. In particular, if $a \equiv-2$ $(\bmod n-2)$, then also $b \equiv-4$ and $c \equiv-2(\bmod n-2)$. Now consider any $a=k n(n-2)-2$, where $k$ is odd. If it is attainable, but not divisible by 2 or $n$, it must have been obtained by addition. Thus all predecessors of $a$ are congruent to either -2 or $-4(\bmod$ $n-2$ ), and none of them equals 1 , a contradiction. (b) Call an attainable number addy if the last operation is addition, and multy if the last operation is multiplication. We prove the following claims by simultaneous induction on $k$ : (1) $n=6 k$ is both addy and multy; (2) $n=6 k+1$ is addy for $k \geq 2$; (3) $n=6 k+2$ is addy for $k \geq 1$; (4) $n=6 k+3$ is addy; (5) $n=6 k+4$ is multy for $k \geq 1$; (6) $n=6 k+5$ is addy. The cases $k \leq 1$ are easily verified. For $k \geq 2$, suppose all six statements hold up to $k-1$. Since $6 k-3$ is addy, $6 k$ is multy. Next, $6 k-2$ is multy, so both $6 k=(6 k-2)+2$ and $6 k+1=(6 k-2)+3$ are addy. Since $6 k$ is multy, both $6 k+2$ and $6 k+3$ are addy. Number $6 k+4=2 \cdot(3 k+2)$ is multy, because $3 k+2$ is addy (being either $6 l+2$ or $6 l+5)$. Finally, we have $6 k+5=3 \cdot(2 k+1)+2$. Since $2 k+1$ is $6 l+1,6 l+3$, or $6 l+5$, it is addy except for 7 . Hence $6 k+5$ is addy except possibly for 23 . But $23=((1 \cdot 2+2) \cdot 2+2) \cdot 2+3$ is also addy. This completes the induction. Now 1 is given and $2=1 \cdot 2,4=1+3$. It is easily checked that 7 is not attainable, and hence it is the only unattainable number.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
876ab3ea-0799-5237-8bfd-7fb26cab7b44
| 24,851
|
24. (SWE) Cards numbered 1 to 9 are arranged at random in a row. In a move, one may choose any block of consecutive cards whose numbers are in ascending or descending order, and switch the block around. For example, $91 \underline{6532748}$ may be changed to $91 \underline{3562748}$. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
|
24. Let $f(n)$ be the minimum number of moves needed to monotonize any permutation of $n$ distinct numbers. Let us be given a permutation $\pi$ of $\{1,2, \ldots, n\}$, and let $k$ be the first element of $\pi$. In $f(n-1)$ moves, we can transform $\pi$ to either $(k, 1,2, \ldots, k-1, k+1, \ldots, n)$ or $(k, n, n-1, \ldots, k+$ $1, k-1, \ldots, 1)$. Now the former can be changed to $(k, k-1, \ldots, 2,1, k+$ $1, \ldots, n)$, which is then monotonized in the next move. Similarly, the latter also can be monotonized in two moves. It follows that $f(n) \leq f(n-1)+2$. Thus we shall be done if we show that $f(5) \leq 4$. First we note that $f(3)=1$. Consider a permutation of $\{1,2,3,4\}$. If either 1 or 4 is the first or the last element, we need one move to monotonize the other three elements, and at most one more to monotonize the whole permutation. Of the remaining four permutations, $(2,1,4,3)$ and $(3,4,1,2)$ can also be monotonized in two moves. The permutations $(2,4,1,3)$ and $(3,1,4,2)$ require 3 moves, but by this we can choose whether to change them into $(1,2,3,4)$ or $(4,3,2,1)$. We now consider a permutation of $\{1,2,3,4,5\}$. If either 1 or 5 is in the first or last position, we can monotonize the rest in 3 moves, but in such a way that the whole permutation can be monotonized in the next move. If this is not the case, then either 1 or 5 is in the second or fourth position. Then we simply switch it to the outside in one move and continue as in the former case. Hence $f(5)=4$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
24. (SWE) Cards numbered 1 to 9 are arranged at random in a row. In a move, one may choose any block of consecutive cards whose numbers are in ascending or descending order, and switch the block around. For example, $91 \underline{6532748}$ may be changed to $91 \underline{3562748}$. Prove that in at most 12 moves, one can arrange the 9 cards so that their numbers are in ascending or descending order.
|
24. Let $f(n)$ be the minimum number of moves needed to monotonize any permutation of $n$ distinct numbers. Let us be given a permutation $\pi$ of $\{1,2, \ldots, n\}$, and let $k$ be the first element of $\pi$. In $f(n-1)$ moves, we can transform $\pi$ to either $(k, 1,2, \ldots, k-1, k+1, \ldots, n)$ or $(k, n, n-1, \ldots, k+$ $1, k-1, \ldots, 1)$. Now the former can be changed to $(k, k-1, \ldots, 2,1, k+$ $1, \ldots, n)$, which is then monotonized in the next move. Similarly, the latter also can be monotonized in two moves. It follows that $f(n) \leq f(n-1)+2$. Thus we shall be done if we show that $f(5) \leq 4$. First we note that $f(3)=1$. Consider a permutation of $\{1,2,3,4\}$. If either 1 or 4 is the first or the last element, we need one move to monotonize the other three elements, and at most one more to monotonize the whole permutation. Of the remaining four permutations, $(2,1,4,3)$ and $(3,4,1,2)$ can also be monotonized in two moves. The permutations $(2,4,1,3)$ and $(3,1,4,2)$ require 3 moves, but by this we can choose whether to change them into $(1,2,3,4)$ or $(4,3,2,1)$. We now consider a permutation of $\{1,2,3,4,5\}$. If either 1 or 5 is in the first or last position, we can monotonize the rest in 3 moves, but in such a way that the whole permutation can be monotonized in the next move. If this is not the case, then either 1 or 5 is in the second or fourth position. Then we simply switch it to the outside in one move and continue as in the former case. Hence $f(5)=4$, as desired.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
62a48ce4-fba2-52b8-aa8f-3cd2e43bd877
| 24,854
|
25. (NZL) Let $U=\{1,2, \ldots, n\}$, where $n \geq 3$. A subset $S$ of $U$ is said to be split by an arrangement of the elements of $U$ if an element not in $S$ occurs in the arrangement somewhere between two elements of $S$. For example, 13542 splits $\{1,2,3\}$ but not $\{3,4,5\}$. Prove that for any $n-2$ subsets of $U$, each containing at least 2 and at most $n-1$ elements, there is an arrangement of the elements of $U$ that splits all of them.
|
25. We use induction on $n$. For $n=3$, we have a single two-element subset $\{i, j\}$ that is split by $(i, k, j)$ (where $k$ is the third element of $U$ ). Assume that the result holds for some $n \geq 3$, and consider a family $\mathcal{F}$ of $n-1$ proper subsets of $U=\{1,2, \ldots, n+1\}$, each with at least 2 elements. To continue the induction, we need an element $a \in U$ that is contained in all $n$-element subsets of $\mathcal{F}$, but in at most one of the two-element subsets. We claim that such an $a$ exists. Let $\mathcal{F}$ contain $k n$-element subsets and $m 2$-element subsets $(k+m \leq n-1)$. The intersection of the $n$-element subsets contains exactly $n+1-k \geq m+2$ elements. On the other hand, at most $m$ elements belong to more than one 2 -element subset, which justifies our claim. Now let $A$ be the 2-element subset that contains $a$, if it exists; otherwise, let $A$ be any subset from $\mathcal{F}$ containing $a$. Excluding $a$ from all the subsets from $\mathcal{F} \backslash\{A\}$, we get at most $n-2$ subsets of $U \backslash\{a\}$ with at least 2 and at most $n-1$ elements. By the inductive hypothesis, we can arrange $U \backslash\{a\}$ so that we split all the subsets of $\mathcal{F}$ except $A$. It remains to place $a$, and we shall make a desired arrangement if we put it anywhere away from $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
25. (NZL) Let $U=\{1,2, \ldots, n\}$, where $n \geq 3$. A subset $S$ of $U$ is said to be split by an arrangement of the elements of $U$ if an element not in $S$ occurs in the arrangement somewhere between two elements of $S$. For example, 13542 splits $\{1,2,3\}$ but not $\{3,4,5\}$. Prove that for any $n-2$ subsets of $U$, each containing at least 2 and at most $n-1$ elements, there is an arrangement of the elements of $U$ that splits all of them.
|
25. We use induction on $n$. For $n=3$, we have a single two-element subset $\{i, j\}$ that is split by $(i, k, j)$ (where $k$ is the third element of $U$ ). Assume that the result holds for some $n \geq 3$, and consider a family $\mathcal{F}$ of $n-1$ proper subsets of $U=\{1,2, \ldots, n+1\}$, each with at least 2 elements. To continue the induction, we need an element $a \in U$ that is contained in all $n$-element subsets of $\mathcal{F}$, but in at most one of the two-element subsets. We claim that such an $a$ exists. Let $\mathcal{F}$ contain $k n$-element subsets and $m 2$-element subsets $(k+m \leq n-1)$. The intersection of the $n$-element subsets contains exactly $n+1-k \geq m+2$ elements. On the other hand, at most $m$ elements belong to more than one 2 -element subset, which justifies our claim. Now let $A$ be the 2-element subset that contains $a$, if it exists; otherwise, let $A$ be any subset from $\mathcal{F}$ containing $a$. Excluding $a$ from all the subsets from $\mathcal{F} \backslash\{A\}$, we get at most $n-2$ subsets of $U \backslash\{a\}$ with at least 2 and at most $n-1$ elements. By the inductive hypothesis, we can arrange $U \backslash\{a\}$ so that we split all the subsets of $\mathcal{F}$ except $A$. It remains to place $a$, and we shall make a desired arrangement if we put it anywhere away from $A$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cfb7619b-6862-5f32-bfdc-67f9ee0d961c
| 24,856
|
3. (UKR) ${ }^{\mathrm{IMO}}$ Let $I$ be the incenter of triangle $A B C$. Let $K, L$, and $M$ be the points of tangency of the incircle of $A B C$ with $A B, B C$, and $C A$, respectively. The line $t$ passes through $B$ and is parallel to $K L$. The lines $M K$ and $M L$ intersect $t$ at the points $R$ and $S$. Prove that $\angle R I S$ is acute.
|
3. Lemma. If $U, W, V$ are three points on a line $l$ in this order, and $X$ a point in the plane with $X W \perp U V$, then $\angle U X V<90^{\circ}$ if and only if $X W^{2}>U W \cdot V W$. Proof. Let $X W^{2}>U W \cdot V W$, and let $X_{0}$ be a point on the segment $X W$ such that $X_{0} W^{2} \geq U W \cdot V W$. Then $X_{0} W / U W=V W / X_{0} W$, so that triangles $X_{0} W U$ and $V W X_{0}$ are similar. Thus $\angle U X_{0} V=\angle U X_{0} W+$ $\angle W U X_{0}=90^{\circ}$, which immediately implies that $\angle U X V<90^{\circ}$. Similarly, if $X W^{2} \leq U W \cdot V W$, then $\angle U X V \geq 90^{\circ}$. Since $B I \perp R S$, it will be enough by the lemma to show that $B I^{2}>$ $B R \cdot B S$. Note that $\triangle B K R \sim \triangle B S L$ : in fact, we have $\angle K B R=\angle S B L=$ $90^{\circ}-\beta / 2$ and $\angle B K R=\angle A K M=\angle K L M=\angle B S L=90^{\circ}-\alpha / 2$. In particular, we obtain $B R / B K=B L / B S=B K / B S$, so that $B R \cdot B S=$ $B K^{2}<B I^{2}$ 。 Second solution. Let $E, F$ be the midpoints of $K M$ and $L M$ respectively. The quadrilaterals $R B I E$ and $S B I F$ are inscribed in the circles with diameters $I R$ and $I S$. Now we have $\angle R I S=\angle R M S+\angle I R M+\angle I S M=$ $90^{\circ}-\beta / 2+\angle I B E+\angle I B F=90^{\circ}-\beta / 2+\angle E B F$. On the other hand, $B E$ and $B F$ are medians in $\triangle B K M$ and $\triangle B L M$ in which $B M>B K$ and $B M>B L$. We conclude that $\angle M B E<\frac{1}{2} \angle M B K$ and $\angle M B F<\frac{1}{2} \angle M B L$. Adding these two inequalities gives $\angle E B F<$ $\beta / 2$. Therefore $\angle R I S<90^{\circ}$. Remark. It can be shown (using vectors) that the statement remains true for an arbitrary line $t$ passing through $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
3. (UKR) ${ }^{\mathrm{IMO}}$ Let $I$ be the incenter of triangle $A B C$. Let $K, L$, and $M$ be the points of tangency of the incircle of $A B C$ with $A B, B C$, and $C A$, respectively. The line $t$ passes through $B$ and is parallel to $K L$. The lines $M K$ and $M L$ intersect $t$ at the points $R$ and $S$. Prove that $\angle R I S$ is acute.
|
3. Lemma. If $U, W, V$ are three points on a line $l$ in this order, and $X$ a point in the plane with $X W \perp U V$, then $\angle U X V<90^{\circ}$ if and only if $X W^{2}>U W \cdot V W$. Proof. Let $X W^{2}>U W \cdot V W$, and let $X_{0}$ be a point on the segment $X W$ such that $X_{0} W^{2} \geq U W \cdot V W$. Then $X_{0} W / U W=V W / X_{0} W$, so that triangles $X_{0} W U$ and $V W X_{0}$ are similar. Thus $\angle U X_{0} V=\angle U X_{0} W+$ $\angle W U X_{0}=90^{\circ}$, which immediately implies that $\angle U X V<90^{\circ}$. Similarly, if $X W^{2} \leq U W \cdot V W$, then $\angle U X V \geq 90^{\circ}$. Since $B I \perp R S$, it will be enough by the lemma to show that $B I^{2}>$ $B R \cdot B S$. Note that $\triangle B K R \sim \triangle B S L$ : in fact, we have $\angle K B R=\angle S B L=$ $90^{\circ}-\beta / 2$ and $\angle B K R=\angle A K M=\angle K L M=\angle B S L=90^{\circ}-\alpha / 2$. In particular, we obtain $B R / B K=B L / B S=B K / B S$, so that $B R \cdot B S=$ $B K^{2}<B I^{2}$ 。 Second solution. Let $E, F$ be the midpoints of $K M$ and $L M$ respectively. The quadrilaterals $R B I E$ and $S B I F$ are inscribed in the circles with diameters $I R$ and $I S$. Now we have $\angle R I S=\angle R M S+\angle I R M+\angle I S M=$ $90^{\circ}-\beta / 2+\angle I B E+\angle I B F=90^{\circ}-\beta / 2+\angle E B F$. On the other hand, $B E$ and $B F$ are medians in $\triangle B K M$ and $\triangle B L M$ in which $B M>B K$ and $B M>B L$. We conclude that $\angle M B E<\frac{1}{2} \angle M B K$ and $\angle M B F<\frac{1}{2} \angle M B L$. Adding these two inequalities gives $\angle E B F<$ $\beta / 2$. Therefore $\angle R I S<90^{\circ}$. Remark. It can be shown (using vectors) that the statement remains true for an arbitrary line $t$ passing through $B$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e5761c9a-66dd-5277-947b-e34bf2fd208f
| 24,868
|
4. (ARM) Let $M$ and $N$ be points inside triangle $A B C$ such that $$ \angle M A B=\angle N A C \quad \text { and } \quad \angle M B A=\angle N B C . $$ Prove that $$ \frac{A M \cdot A N}{A B \cdot A C}+\frac{B M \cdot B N}{B A \cdot B C}+\frac{C M \cdot C N}{C A \cdot C B}=1 $$
|
4. Let $K$ be the point on the ray $B N$ with $\angle B C K=\angle B M A$. Since $\angle K B C=\angle A B M$, we get $\triangle B C K \sim \triangle B M A$. It follows that $B C / B M=$ $B K / B A$, which implies that also $\triangle B A K \sim \triangle B M C$. The quadrilateral $A N C K$ is cyclic, because $\angle B K C=\angle B A M=\angle N A C$. Then by Ptolemy's theorem we obtain $$ A C \cdot B K=A C \cdot B N+A N \cdot C K+C N \cdot A K $$ On the other hand, from the similarities noted above we get $$ C K=\frac{B C \cdot A M}{B M}, A K=\frac{A B \cdot C M}{B M} \text { and } B K=\frac{A B \cdot B C}{B M} . $$ After substitution of these values, the equality (1) becomes $$ \frac{A B \cdot B C \cdot A C}{B M}=A C \cdot B N+\frac{B C \cdot A M \cdot A N}{B M}+\frac{A B \cdot C M \cdot C N}{B M}, $$ which is exactly the equality we must prove multiplied by $\frac{A B \cdot B C \cdot C A}{B M}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
4. (ARM) Let $M$ and $N$ be points inside triangle $A B C$ such that $$ \angle M A B=\angle N A C \quad \text { and } \quad \angle M B A=\angle N B C . $$ Prove that $$ \frac{A M \cdot A N}{A B \cdot A C}+\frac{B M \cdot B N}{B A \cdot B C}+\frac{C M \cdot C N}{C A \cdot C B}=1 $$
|
4. Let $K$ be the point on the ray $B N$ with $\angle B C K=\angle B M A$. Since $\angle K B C=\angle A B M$, we get $\triangle B C K \sim \triangle B M A$. It follows that $B C / B M=$ $B K / B A$, which implies that also $\triangle B A K \sim \triangle B M C$. The quadrilateral $A N C K$ is cyclic, because $\angle B K C=\angle B A M=\angle N A C$. Then by Ptolemy's theorem we obtain $$ A C \cdot B K=A C \cdot B N+A N \cdot C K+C N \cdot A K $$ On the other hand, from the similarities noted above we get $$ C K=\frac{B C \cdot A M}{B M}, A K=\frac{A B \cdot C M}{B M} \text { and } B K=\frac{A B \cdot B C}{B M} . $$ After substitution of these values, the equality (1) becomes $$ \frac{A B \cdot B C \cdot A C}{B M}=A C \cdot B N+\frac{B C \cdot A M \cdot A N}{B M}+\frac{A B \cdot C M \cdot C N}{B M}, $$ which is exactly the equality we must prove multiplied by $\frac{A B \cdot B C \cdot C A}{B M}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0e3cd4d4-8d80-51cc-98d5-68d56b7e5741
| 24,870
|
5. (FRA) Let $A B C$ be a triangle, $H$ its orthocenter, $O$ its circumcenter, and $R$ its circumradius. Let $D$ be the reflection of $A$ across $B C, E$ that of $B$ across $C A$, and $F$ that of $C$ across $A B$. Prove that $D, E$, and $F$ are collinear if and only if $O H=2 R$.
|
5. Let $G$ be the centroid of $\triangle A B C$ and $\mathcal{H}$ the homothety with center $G$ and ratio $-\frac{1}{2}$. It is well-known that $\mathcal{H}$ maps $H$ into $O$. For every other point $X$, let us denote by $X^{\prime}$ its image under $\mathcal{H}$. Also, let $A_{2} B_{2} C_{2}$ be the triangle in which $A, B, C$ are the midpoints of $B_{2} C_{2}, C_{2} A_{2}$, and $A_{2} B_{2}$, respectively. It is clear that $A^{\prime}, B^{\prime}, C^{\prime}$ are the midpoints of sides $B C, C A, A B$ respectively. Furthermore, $D^{\prime}$ is the reflection of $A^{\prime}$ across $B^{\prime} C^{\prime}$. Thus $D^{\prime}$ must lie on $B_{2} C_{2}$ and $A^{\prime} D^{\prime} \perp$  $B_{2} C_{2}$. However, it also holds that $O A^{\prime} \perp B_{2} C_{2}$, so we conclude that $O, D^{\prime}, A^{\prime}$ are collinear and $D^{\prime}$ is the projection of $O$ on $B_{2} C_{2}$. Analogously, $E^{\prime}, F^{\prime}$ are the projections of $O$ on $C_{2} A_{2}$ and $A_{2} B_{2}$. Now we apply Simson's theorem. It claims that $D^{\prime}, E^{\prime}, F^{\prime}$ are collinear (which is equivalent to $D, E, F$ being collinear) if and only if $O$ lies on the circumcircle of $A_{2} B_{2} C_{2}$. However, this circumcircle is centered at $H$ with radius $2 R$, so the last condition is equivalent to $H O=2 R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
5. (FRA) Let $A B C$ be a triangle, $H$ its orthocenter, $O$ its circumcenter, and $R$ its circumradius. Let $D$ be the reflection of $A$ across $B C, E$ that of $B$ across $C A$, and $F$ that of $C$ across $A B$. Prove that $D, E$, and $F$ are collinear if and only if $O H=2 R$.
|
5. Let $G$ be the centroid of $\triangle A B C$ and $\mathcal{H}$ the homothety with center $G$ and ratio $-\frac{1}{2}$. It is well-known that $\mathcal{H}$ maps $H$ into $O$. For every other point $X$, let us denote by $X^{\prime}$ its image under $\mathcal{H}$. Also, let $A_{2} B_{2} C_{2}$ be the triangle in which $A, B, C$ are the midpoints of $B_{2} C_{2}, C_{2} A_{2}$, and $A_{2} B_{2}$, respectively. It is clear that $A^{\prime}, B^{\prime}, C^{\prime}$ are the midpoints of sides $B C, C A, A B$ respectively. Furthermore, $D^{\prime}$ is the reflection of $A^{\prime}$ across $B^{\prime} C^{\prime}$. Thus $D^{\prime}$ must lie on $B_{2} C_{2}$ and $A^{\prime} D^{\prime} \perp$  $B_{2} C_{2}$. However, it also holds that $O A^{\prime} \perp B_{2} C_{2}$, so we conclude that $O, D^{\prime}, A^{\prime}$ are collinear and $D^{\prime}$ is the projection of $O$ on $B_{2} C_{2}$. Analogously, $E^{\prime}, F^{\prime}$ are the projections of $O$ on $C_{2} A_{2}$ and $A_{2} B_{2}$. Now we apply Simson's theorem. It claims that $D^{\prime}, E^{\prime}, F^{\prime}$ are collinear (which is equivalent to $D, E, F$ being collinear) if and only if $O$ lies on the circumcircle of $A_{2} B_{2} C_{2}$. However, this circumcircle is centered at $H$ with radius $2 R$, so the last condition is equivalent to $H O=2 R$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ad8506f4-abd4-5f8e-bf90-de1845bc28f1
| 24,873
|
6. (POL) Let $A B C D E F$ be a convex hexagon such that $\angle B+\angle D+\angle F=$ $360^{\circ}$ and $$ \frac{A B}{B C} \cdot \frac{C D}{D E} \cdot \frac{E F}{F A}=1 $$ Prove that $$ \frac{B C}{C A} \cdot \frac{A E}{E F} \cdot \frac{F D}{D B}=1 $$
|
6. Let $P$ be the point such that $\triangle C D P$ and $\triangle C B A$ are similar and equally oriented. Since then $\angle D C P=\angle B C A$ and $\frac{B C}{C A}=\frac{D C}{C P}$, it follows that $\angle A C P=\angle B C D$ and $\frac{A C}{C P}=\frac{B C}{C D}$, so $\triangle A C P \sim \triangle B C D$. In particular, $\frac{B C}{C A}=\frac{D B}{P A}$. Furthermore, by the conditions of the problem we have $\angle E D P=360^{\circ}-$ $\angle B-\angle D=\angle F$ and $\frac{P D}{D E}=\frac{P D}{C D} \cdot \frac{C D}{D E}=\frac{A B}{B C} \cdot \frac{C D}{D E}=\frac{A F}{F E}$. Therefore $\triangle E D P \sim \triangle E F A$ as well, so that similarly as above we conclude that $\triangle A E P \sim \triangle F E D$ and consequently $\frac{A E}{E F}=\frac{P A}{F D}$. Finally, $\frac{B C}{C A} \cdot \frac{A E}{E F} \cdot \frac{F D}{D B}=\frac{D B}{P A} \cdot \frac{P A}{F D} \cdot \frac{F D}{D B}=1$. Second solution. Let $a, b, c, d, e, f$ be the complex coordinates of $A, B$, $C, D, E, F$, respectively. The condition of the problem implies that $\frac{a-b}{b-c}$. $\frac{c-d}{d-e} \cdot \frac{e-f}{f-a}=-1$. On the other hand, since $(a-b)(c-d)(e-f)+(b-c)(d-e)(f-a)=$ $(b-c)(a-e)(f-d)+(c-a)(e-f)(d-b)$ holds identically, we immediately deduce that $\frac{b-c}{c-a} \cdot \frac{a-e}{e-f} \cdot \frac{f-d}{d-b}=-1$. Taking absolute values gives $\frac{B C}{C A} \cdot \frac{A E}{E F}$. $\frac{F D}{D B}=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
6. (POL) Let $A B C D E F$ be a convex hexagon such that $\angle B+\angle D+\angle F=$ $360^{\circ}$ and $$ \frac{A B}{B C} \cdot \frac{C D}{D E} \cdot \frac{E F}{F A}=1 $$ Prove that $$ \frac{B C}{C A} \cdot \frac{A E}{E F} \cdot \frac{F D}{D B}=1 $$
|
6. Let $P$ be the point such that $\triangle C D P$ and $\triangle C B A$ are similar and equally oriented. Since then $\angle D C P=\angle B C A$ and $\frac{B C}{C A}=\frac{D C}{C P}$, it follows that $\angle A C P=\angle B C D$ and $\frac{A C}{C P}=\frac{B C}{C D}$, so $\triangle A C P \sim \triangle B C D$. In particular, $\frac{B C}{C A}=\frac{D B}{P A}$. Furthermore, by the conditions of the problem we have $\angle E D P=360^{\circ}-$ $\angle B-\angle D=\angle F$ and $\frac{P D}{D E}=\frac{P D}{C D} \cdot \frac{C D}{D E}=\frac{A B}{B C} \cdot \frac{C D}{D E}=\frac{A F}{F E}$. Therefore $\triangle E D P \sim \triangle E F A$ as well, so that similarly as above we conclude that $\triangle A E P \sim \triangle F E D$ and consequently $\frac{A E}{E F}=\frac{P A}{F D}$. Finally, $\frac{B C}{C A} \cdot \frac{A E}{E F} \cdot \frac{F D}{D B}=\frac{D B}{P A} \cdot \frac{P A}{F D} \cdot \frac{F D}{D B}=1$. Second solution. Let $a, b, c, d, e, f$ be the complex coordinates of $A, B$, $C, D, E, F$, respectively. The condition of the problem implies that $\frac{a-b}{b-c}$. $\frac{c-d}{d-e} \cdot \frac{e-f}{f-a}=-1$. On the other hand, since $(a-b)(c-d)(e-f)+(b-c)(d-e)(f-a)=$ $(b-c)(a-e)(f-d)+(c-a)(e-f)(d-b)$ holds identically, we immediately deduce that $\frac{b-c}{c-a} \cdot \frac{a-e}{e-f} \cdot \frac{f-d}{d-b}=-1$. Taking absolute values gives $\frac{B C}{C A} \cdot \frac{A E}{E F}$. $\frac{F D}{D B}=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c826ebc7-d207-5895-8724-e7c76cf58c5b
| 24,875
|
7. (GBR) Let $A B C$ be a triangle such that $\angle A C B=2 \angle A B C$. Let $D$ be the point on the side $B C$ such that $C D=2 B D$. The segment $A D$ is extended to $E$ so that $A D=D E$. Prove that $$ \angle E C B+180^{\circ}=2 \angle E B C . $$
|
7. We shall use the following result. Lemma. In a triangle $A B C$ with $B C=a, C A=b$, and $A B=c$, i. $\angle C=2 \angle B$ if and only if $c^{2}=b^{2}+a b$; ii. $\angle C+180^{\circ}=2 \angle B$ if and only if $c^{2}=b^{2}-a b$. Proof. i. Take a point $D$ on the extension of $B C$ over $C$ such that $C D=b$. The condition $\angle C=2 \angle B$ is equivalent to $\angle A D C=\frac{1}{2} \angle C=\angle B$, and thus to $A D=A B=c$. This is further equivalent to triangles $C A D$ and $A B D$ being similar, so $C A / A D=A B / B D$, i.e., $c^{2}=$ $b(a+b)$. ii. Take a point $E$ on the ray $C B$ such that $C E=b$. As above, $\angle C+180^{\circ}=2 \angle B$ if and only if $\triangle C A E \sim \triangle A B E$, which is equivalent to $E B / B A=E A / A C$, or $c^{2}=b(b-a)$. Let $F, G$ be points on the ray $C B$ such that $C F=\frac{1}{3} a$ and $C G=\frac{4}{3} a$. Set $B C=a, C A=b, A B=c, E C=b_{1}$, and $E B=c_{1}$. By the lemma it follows that $c^{2}=b^{2}+a b$. Also $b_{1}=A G$ and $c_{1}=A F$, so Stewart's theorem gives us $c_{1}^{2}=\frac{2}{3} b^{2}+\frac{1}{3} c^{2}-\frac{2}{9} a^{2}=b^{2}+\frac{1}{3} a b-\frac{2}{9} a^{2}$ and $b_{1}^{2}=$ $-\frac{1}{3} b^{2}+\frac{4}{3} c^{2}+\frac{4}{9} a^{2}=b^{2}+\frac{4}{3} a b+\frac{4}{9} a^{2}$. It follows that $b_{1}=\frac{2}{3} a+b$ and $c_{1}^{2}=b_{1}^{2}-\left(a b+\frac{2}{3} a^{2}\right)=b_{1}^{2}-a b_{1}$. The statement of the problem follows immediately by the lemma.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. (GBR) Let $A B C$ be a triangle such that $\angle A C B=2 \angle A B C$. Let $D$ be the point on the side $B C$ such that $C D=2 B D$. The segment $A D$ is extended to $E$ so that $A D=D E$. Prove that $$ \angle E C B+180^{\circ}=2 \angle E B C . $$
|
7. We shall use the following result. Lemma. In a triangle $A B C$ with $B C=a, C A=b$, and $A B=c$, i. $\angle C=2 \angle B$ if and only if $c^{2}=b^{2}+a b$; ii. $\angle C+180^{\circ}=2 \angle B$ if and only if $c^{2}=b^{2}-a b$. Proof. i. Take a point $D$ on the extension of $B C$ over $C$ such that $C D=b$. The condition $\angle C=2 \angle B$ is equivalent to $\angle A D C=\frac{1}{2} \angle C=\angle B$, and thus to $A D=A B=c$. This is further equivalent to triangles $C A D$ and $A B D$ being similar, so $C A / A D=A B / B D$, i.e., $c^{2}=$ $b(a+b)$. ii. Take a point $E$ on the ray $C B$ such that $C E=b$. As above, $\angle C+180^{\circ}=2 \angle B$ if and only if $\triangle C A E \sim \triangle A B E$, which is equivalent to $E B / B A=E A / A C$, or $c^{2}=b(b-a)$. Let $F, G$ be points on the ray $C B$ such that $C F=\frac{1}{3} a$ and $C G=\frac{4}{3} a$. Set $B C=a, C A=b, A B=c, E C=b_{1}$, and $E B=c_{1}$. By the lemma it follows that $c^{2}=b^{2}+a b$. Also $b_{1}=A G$ and $c_{1}=A F$, so Stewart's theorem gives us $c_{1}^{2}=\frac{2}{3} b^{2}+\frac{1}{3} c^{2}-\frac{2}{9} a^{2}=b^{2}+\frac{1}{3} a b-\frac{2}{9} a^{2}$ and $b_{1}^{2}=$ $-\frac{1}{3} b^{2}+\frac{4}{3} c^{2}+\frac{4}{9} a^{2}=b^{2}+\frac{4}{3} a b+\frac{4}{9} a^{2}$. It follows that $b_{1}=\frac{2}{3} a+b$ and $c_{1}^{2}=b_{1}^{2}-\left(a b+\frac{2}{3} a^{2}\right)=b_{1}^{2}-a b_{1}$. The statement of the problem follows immediately by the lemma.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
d0e730a9-988b-5a10-b592-b16981eb4e16
| 24,878
|
8. (IND) Let $A B C$ be a triangle such that $\angle A=90^{\circ}$ and $\angle B<\angle C$. The tangent at $A$ to its circumcircle $\omega$ meets the line $B C$ at $D$. Let $E$ be the reflection of $A$ across $B C, X$ the foot of the perpendicular from $A$ to $B E$, and $Y$ the midpoint of $A X$. Let the line $B Y$ meet $\omega$ again at $Z$. Prove that the line $B D$ is tangent to the circumcircle of triangle $A D Z$.
|
8. Let $M$ be the point of intersection of $A E$ and $B C$, and let $N$ be the point on $\omega$ diametrically opposite $A$. Since $\angle B<\angle C$, points $N$ and $B$ are on the same side of $A E$. Furthermore, $\angle N A E=\angle B A X=$ $90^{\circ}-\angle A B E$; hence the triangles $N A E$ and $B A X$ are similar. Consequently, $\triangle B A Y$ and $\triangle N A M$ are also similar, since $M$ is the midpoint  of $A E$. Thus $\angle A N Z=\angle A B Z=\angle A B Y=\angle A N M$, implying that $N, M, Z$ are collinear. Now we have $\angle Z M D=90^{\circ}-\angle Z M A=\angle E A Z=$ $\angle Z E D$ (the last equality because $E D$ is tangent to $\omega$ ); hence $Z M E D$ is a cyclic quadrilateral. It follows that $\angle Z D M=\angle Z E A=\angle Z A D$, which is enough to conclude that $M D$ is tangent to the circumcircle of $A Z D$. Remark. The statement remains valid if $\angle B \geq \angle C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. (IND) Let $A B C$ be a triangle such that $\angle A=90^{\circ}$ and $\angle B<\angle C$. The tangent at $A$ to its circumcircle $\omega$ meets the line $B C$ at $D$. Let $E$ be the reflection of $A$ across $B C, X$ the foot of the perpendicular from $A$ to $B E$, and $Y$ the midpoint of $A X$. Let the line $B Y$ meet $\omega$ again at $Z$. Prove that the line $B D$ is tangent to the circumcircle of triangle $A D Z$.
|
8. Let $M$ be the point of intersection of $A E$ and $B C$, and let $N$ be the point on $\omega$ diametrically opposite $A$. Since $\angle B<\angle C$, points $N$ and $B$ are on the same side of $A E$. Furthermore, $\angle N A E=\angle B A X=$ $90^{\circ}-\angle A B E$; hence the triangles $N A E$ and $B A X$ are similar. Consequently, $\triangle B A Y$ and $\triangle N A M$ are also similar, since $M$ is the midpoint  of $A E$. Thus $\angle A N Z=\angle A B Z=\angle A B Y=\angle A N M$, implying that $N, M, Z$ are collinear. Now we have $\angle Z M D=90^{\circ}-\angle Z M A=\angle E A Z=$ $\angle Z E D$ (the last equality because $E D$ is tangent to $\omega$ ); hence $Z M E D$ is a cyclic quadrilateral. It follows that $\angle Z D M=\angle Z E A=\angle Z A D$, which is enough to conclude that $M D$ is tangent to the circumcircle of $A Z D$. Remark. The statement remains valid if $\angle B \geq \angle C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0dcf2465-406c-5397-9972-befa7ba59c76
| 24,881
|
9. (MON) Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+$ $\cdots+a_{n}<1$. Prove that $$ \frac{a_{1} a_{2} \cdots a_{n}\left[1-\left(a_{1}+a_{2}+\cdots+a_{n}\right)\right]}{\left(a_{1}+a_{2}+\cdots+a_{n}\right)\left(1-a_{1}\right)\left(1-a_{2}\right) \cdots\left(1-a_{n}\right)} \leq \frac{1}{n^{n+1}} . $$
|
9. Set $a_{n+1}=1-\left(a_{1}+\cdots+a_{n}\right)$. Then $a_{n+1}>0$, and the desired inequality becomes $$ \frac{a_{1} a_{2} \cdots a_{n+1}}{\left(1-a_{1}\right)\left(1-a_{2}\right) \cdots\left(1-a_{n+1}\right)} \leq \frac{1}{n^{n+1}} $$ To prove it, we observe that $1-a_{i}=a_{1}+\cdots+a_{i-1}+a_{i+1}+\cdots+a_{n+1} \geq n \sqrt[n]{a_{1} \cdots a_{i-1} a_{i+1} \cdots a_{n+1}}$. Multiplying these inequalities for $i=1,2, \ldots, n+1$, we get exactly the inequality we need.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
9. (MON) Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers such that $a_{1}+a_{2}+$ $\cdots+a_{n}<1$. Prove that $$ \frac{a_{1} a_{2} \cdots a_{n}\left[1-\left(a_{1}+a_{2}+\cdots+a_{n}\right)\right]}{\left(a_{1}+a_{2}+\cdots+a_{n}\right)\left(1-a_{1}\right)\left(1-a_{2}\right) \cdots\left(1-a_{n}\right)} \leq \frac{1}{n^{n+1}} . $$
|
9. Set $a_{n+1}=1-\left(a_{1}+\cdots+a_{n}\right)$. Then $a_{n+1}>0$, and the desired inequality becomes $$ \frac{a_{1} a_{2} \cdots a_{n+1}}{\left(1-a_{1}\right)\left(1-a_{2}\right) \cdots\left(1-a_{n+1}\right)} \leq \frac{1}{n^{n+1}} $$ To prove it, we observe that $1-a_{i}=a_{1}+\cdots+a_{i-1}+a_{i+1}+\cdots+a_{n+1} \geq n \sqrt[n]{a_{1} \cdots a_{i-1} a_{i+1} \cdots a_{n+1}}$. Multiplying these inequalities for $i=1,2, \ldots, n+1$, we get exactly the inequality we need.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ce4aaac-5587-5a45-ab5f-c5fecaafb8e0
| 24,884
|
11. G5 (FRA) Let $A B C$ be a triangle, $\Omega$ its incircle and $\Omega_{a}, \Omega_{b}, \Omega_{c}$ three circles three circles orthogonal to $\Omega$ passing through $B$ and $C, A$ and $C$, and $A$ and $B$ respectively. The circles $\Omega_{a}, \Omega_{b}$ meet again in $C^{\prime}$; in the same way we obtain the points $B^{\prime}$ and $A^{\prime}$. Prove that the radius of the circumcircle of $A^{\prime} B^{\prime} C^{\prime}$ is half the radius of $\Omega$.
|
11. Let $\Omega(I, r)$ be the incircle of $\triangle A B C$. Let $D, E$, and $F$ denote the points where $\Omega$ touches $B C, A C$, and $A B$, respectively. Let $P, Q$, and $R$ denote the midpoints of $E F, D F$, and $D E$ respectively. We prove that $\Omega_{a}$ passes through $Q$ and $R$. Since $\triangle I Q D \sim \triangle I D B$ and $\triangle I R D \sim \triangle I D C$, we obtain $I Q \cdot I B=I R \cdot I C=r^{2}$. We conclude that $B, C, Q$, and $R$ lie on a single circle $\Gamma_{a}$. Moreover, since the power of $I$ with respect to $\Gamma_{a}$ is $r^{2}$, it follows for a tangent $I X$ from $I$ to $\Gamma_{a}$ that $X$ lies on $\Omega$ and hence $\Omega$ is perpendicular to $\Gamma_{a}$. From the uniqueness of $\Omega_{a}$ it follows that $\Omega_{a}=\Gamma_{a}$. Thus $\Omega_{a}$ contains $Q$ and $R$. Similarly $\Omega_{b}$ contains $P$ and $R$ and $\Omega_{c}$ contains $P$ and $Q$. Hence, $A^{\prime}=P, B^{\prime}=Q$ and $C^{\prime}=R$. Therefore the radius of the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$ is half the radius of $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
11. G5 (FRA) Let $A B C$ be a triangle, $\Omega$ its incircle and $\Omega_{a}, \Omega_{b}, \Omega_{c}$ three circles three circles orthogonal to $\Omega$ passing through $B$ and $C, A$ and $C$, and $A$ and $B$ respectively. The circles $\Omega_{a}, \Omega_{b}$ meet again in $C^{\prime}$; in the same way we obtain the points $B^{\prime}$ and $A^{\prime}$. Prove that the radius of the circumcircle of $A^{\prime} B^{\prime} C^{\prime}$ is half the radius of $\Omega$.
|
11. Let $\Omega(I, r)$ be the incircle of $\triangle A B C$. Let $D, E$, and $F$ denote the points where $\Omega$ touches $B C, A C$, and $A B$, respectively. Let $P, Q$, and $R$ denote the midpoints of $E F, D F$, and $D E$ respectively. We prove that $\Omega_{a}$ passes through $Q$ and $R$. Since $\triangle I Q D \sim \triangle I D B$ and $\triangle I R D \sim \triangle I D C$, we obtain $I Q \cdot I B=I R \cdot I C=r^{2}$. We conclude that $B, C, Q$, and $R$ lie on a single circle $\Gamma_{a}$. Moreover, since the power of $I$ with respect to $\Gamma_{a}$ is $r^{2}$, it follows for a tangent $I X$ from $I$ to $\Gamma_{a}$ that $X$ lies on $\Omega$ and hence $\Omega$ is perpendicular to $\Gamma_{a}$. From the uniqueness of $\Omega_{a}$ it follows that $\Omega_{a}=\Gamma_{a}$. Thus $\Omega_{a}$ contains $Q$ and $R$. Similarly $\Omega_{b}$ contains $P$ and $R$ and $\Omega_{c}$ contains $P$ and $Q$. Hence, $A^{\prime}=P, B^{\prime}=Q$ and $C^{\prime}=R$. Therefore the radius of the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$ is half the radius of $\Omega$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c6f7fc0a-97a1-5dbb-ade3-863dbeddc00a
| 24,892
|
12. G6 (RUS) ${ }^{\mathrm{IMO} 5}$ Two circles $\Omega_{1}$ and $\Omega_{2}$ touch internally the circle $\Omega$ in $M$ and $N$, and the center of $\Omega_{2}$ is on $\Omega_{1}$. The common chord of the circles $\Omega_{1}$ and $\Omega_{2}$ intersects $\Omega$ in $A$ and $B . M A$ and $M B$ intersect $\Omega_{1}$ in $C$ and $D$. Prove that $\Omega_{2}$ is tangent to $C D$.
|
12. We first introduce the following lemmas. Lemma 1. Let $A B C$ be a triangle, $I$ its inenter and $I_{a}$ the center of the excircle touching $B C$. Let $A^{\prime}$ be the center of the arc $\widehat{B C}$ of the circumcircle not containing $A$. Then $A^{\prime} B=A^{\prime} C=A^{\prime} I=A^{\prime} I_{a}$. Proof. The result follows from a straightforward calculation of the relevant angles. Lemma 2. Let two circles $k_{1}$ and $k_{2}$ meet each other at points $X$ and $Y$ and touch a circle $k$ internally in points $M$ and $N$, respectively. Let $A$ be one of the intersections of the line $X Y$ with $k$. Let $A M$ and $A N$ intersect $k_{1}$ and $k_{2}$ respectively at $C$ and $E$. Then $C E$ is a common tangent of $k_{1}$ and $k_{2}$. Proof. Since $A C \cdot A M=A X \cdot A Y=A E \cdot A N$, the points $M, N, E, C$ lie on a circle. Let $M N$ meet $k_{1}$ again at $Z$. If $M^{\prime}$ is any point on the common tangent at $M$, then $\angle M C Z=\angle M^{\prime} M Z=\angle M^{\prime} M N=\angle M A N$ (as oriented angles), implying that $C Z \| A N$. It follows that $\angle A C E=$ $\angle A N M=\angle C Z M$. Hence $C E$ is tangent to $k_{1}$ and analogously to $k_{2}$. In the main problem, let us define $E$ and $F$ respectively as intersections of $N A$ and $N B$ with $\Omega_{2}$. Then applying Lemma 2 we get that $C E$ and $D F$ are the common tangents of $\Omega_{1}$ and $\Omega_{2}$. If the circles have the same radii, the result trivially holds. Otherwise, let $G$ be the intersection of $C E$ and $D F$. Let $O_{1}$ and $O_{2}$ be the centers of $\Omega_{1}$ and $\Omega_{2}$. Since $O_{1} D=O_{1} C$ and $\angle O_{1} D G=\angle O_{1} C G=90^{\circ}$, it follows that $O_{1}$ is the midpoint of the shorter arc of the circumcircle of $\triangle C D G$. The center $O_{2}$ is located on the bisector of $\angle C G D$, since $\Omega_{2}$  touches both $G C$ and $G D$. However, it also sits on $\Omega_{1}$, and using Lemma 1 we obtain that $O_{2}$ is either at the incenter or at the excenter of $\triangle C D G$ opposite $G$. Hence, $\Omega_{2}$ is either the incircle or the excircle of $C D G$ and thus in both cases touches $C D$. Second solution. Let $O$ be the center of $\Gamma$, and $r, r_{1}, r_{2}$ the radii of $\Gamma, \Gamma_{1}, \Gamma_{2}$. It suffices to show that the distance $d\left(O_{2}, C D\right)$ is equal to $r_{2}$. The homothety with center $M$ and ratio $r / r_{1}$ takes $\Gamma_{1}, C, D$ into $\Gamma, A, B$, respectively; hence $C D \| A B$ and $d(C, A B)=\frac{r-r_{1}}{r} d(M, A B)$. Let $O_{1} O_{2}$ meet $X Y$ at $R$. Then $d\left(O_{2}, C D\right)=O_{2} R+\frac{r-r_{1}}{r} d(M, A B)$, i.e., $$ d\left(O_{2}, C D\right)=O_{2} R+\frac{r-r_{1}}{r}\left[O_{1} O_{2}-O_{2} R+r_{1} \cos \angle O O_{1} O_{2}\right] $$ since $O, O_{1}$, and $M$ are collinear. We have $O_{1} X=O_{1} O_{2}=r_{1}, O O_{1}=$ $r-r_{1}, O O_{2}=r-r_{2}$, and $O_{2} X=r_{2}$. Using the cosine law in the triangles $O O_{1} O_{2}$ and $X O_{1} O_{2}$, we obtain that $\cos \angle O O_{1} O_{2}=\frac{2 r_{1}^{2}-2 r r_{1}+2 r r_{2}-r_{2}^{2}}{2 r_{1}\left(r-r_{1}\right)}$ and $O_{2} R=\frac{r_{2}^{2}}{2 r_{1}}$. Substituting these values in (1) we get $d\left(O_{2}, C D\right)=r_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
12. G6 (RUS) ${ }^{\mathrm{IMO} 5}$ Two circles $\Omega_{1}$ and $\Omega_{2}$ touch internally the circle $\Omega$ in $M$ and $N$, and the center of $\Omega_{2}$ is on $\Omega_{1}$. The common chord of the circles $\Omega_{1}$ and $\Omega_{2}$ intersects $\Omega$ in $A$ and $B . M A$ and $M B$ intersect $\Omega_{1}$ in $C$ and $D$. Prove that $\Omega_{2}$ is tangent to $C D$.
|
12. We first introduce the following lemmas. Lemma 1. Let $A B C$ be a triangle, $I$ its inenter and $I_{a}$ the center of the excircle touching $B C$. Let $A^{\prime}$ be the center of the arc $\widehat{B C}$ of the circumcircle not containing $A$. Then $A^{\prime} B=A^{\prime} C=A^{\prime} I=A^{\prime} I_{a}$. Proof. The result follows from a straightforward calculation of the relevant angles. Lemma 2. Let two circles $k_{1}$ and $k_{2}$ meet each other at points $X$ and $Y$ and touch a circle $k$ internally in points $M$ and $N$, respectively. Let $A$ be one of the intersections of the line $X Y$ with $k$. Let $A M$ and $A N$ intersect $k_{1}$ and $k_{2}$ respectively at $C$ and $E$. Then $C E$ is a common tangent of $k_{1}$ and $k_{2}$. Proof. Since $A C \cdot A M=A X \cdot A Y=A E \cdot A N$, the points $M, N, E, C$ lie on a circle. Let $M N$ meet $k_{1}$ again at $Z$. If $M^{\prime}$ is any point on the common tangent at $M$, then $\angle M C Z=\angle M^{\prime} M Z=\angle M^{\prime} M N=\angle M A N$ (as oriented angles), implying that $C Z \| A N$. It follows that $\angle A C E=$ $\angle A N M=\angle C Z M$. Hence $C E$ is tangent to $k_{1}$ and analogously to $k_{2}$. In the main problem, let us define $E$ and $F$ respectively as intersections of $N A$ and $N B$ with $\Omega_{2}$. Then applying Lemma 2 we get that $C E$ and $D F$ are the common tangents of $\Omega_{1}$ and $\Omega_{2}$. If the circles have the same radii, the result trivially holds. Otherwise, let $G$ be the intersection of $C E$ and $D F$. Let $O_{1}$ and $O_{2}$ be the centers of $\Omega_{1}$ and $\Omega_{2}$. Since $O_{1} D=O_{1} C$ and $\angle O_{1} D G=\angle O_{1} C G=90^{\circ}$, it follows that $O_{1}$ is the midpoint of the shorter arc of the circumcircle of $\triangle C D G$. The center $O_{2}$ is located on the bisector of $\angle C G D$, since $\Omega_{2}$  touches both $G C$ and $G D$. However, it also sits on $\Omega_{1}$, and using Lemma 1 we obtain that $O_{2}$ is either at the incenter or at the excenter of $\triangle C D G$ opposite $G$. Hence, $\Omega_{2}$ is either the incircle or the excircle of $C D G$ and thus in both cases touches $C D$. Second solution. Let $O$ be the center of $\Gamma$, and $r, r_{1}, r_{2}$ the radii of $\Gamma, \Gamma_{1}, \Gamma_{2}$. It suffices to show that the distance $d\left(O_{2}, C D\right)$ is equal to $r_{2}$. The homothety with center $M$ and ratio $r / r_{1}$ takes $\Gamma_{1}, C, D$ into $\Gamma, A, B$, respectively; hence $C D \| A B$ and $d(C, A B)=\frac{r-r_{1}}{r} d(M, A B)$. Let $O_{1} O_{2}$ meet $X Y$ at $R$. Then $d\left(O_{2}, C D\right)=O_{2} R+\frac{r-r_{1}}{r} d(M, A B)$, i.e., $$ d\left(O_{2}, C D\right)=O_{2} R+\frac{r-r_{1}}{r}\left[O_{1} O_{2}-O_{2} R+r_{1} \cos \angle O O_{1} O_{2}\right] $$ since $O, O_{1}$, and $M$ are collinear. We have $O_{1} X=O_{1} O_{2}=r_{1}, O O_{1}=$ $r-r_{1}, O O_{2}=r-r_{2}$, and $O_{2} X=r_{2}$. Using the cosine law in the triangles $O O_{1} O_{2}$ and $X O_{1} O_{2}$, we obtain that $\cos \angle O O_{1} O_{2}=\frac{2 r_{1}^{2}-2 r r_{1}+2 r r_{2}-r_{2}^{2}}{2 r_{1}\left(r-r_{1}\right)}$ and $O_{2} R=\frac{r_{2}^{2}}{2 r_{1}}$. Substituting these values in (1) we get $d\left(O_{2}, C D\right)=r_{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6e0aa8d6-f884-538e-b461-1058260910d5
| 24,895
|
13. G7 (ARM) The point $M$ inside the convex quadrilateral $A B C D$ is such that $M A=M C, \angle A M B=\angle M A D+\angle M C D, \angle C M D=\angle M C B+\angle M A B$. Prove that $A B \cdot C M=B C \cdot M D$ and $B M \cdot A D=M A \cdot C D$.
|
13. Let us construct a convex quadrilateral $P Q R S$ and an interior point $T$ such that $\triangle P T Q \cong \triangle A M B, \triangle Q T R \sim \triangle A M D$, and $\triangle P T S \sim \triangle C M D$. We then have $T S=\frac{M D \cdot P T}{M C}=M D$ and $\frac{T R}{T S}=\frac{T R \cdot T Q \cdot T P}{T Q \cdot T P \cdot T S}=\frac{M D \cdot M B \cdot M C}{M A \cdot M A \cdot M D}=$ $\frac{M B}{M C}$ (using $M A=M C$ ). We also have $\angle S T R=\angle B M C$ and therefore $\triangle R T S \sim \triangle B M C$. Now the relations between angles become $$ \angle T P S+\angle T Q R=\angle P T Q \quad \text { and } \quad \angle T P Q+\angle T S R=\angle P T S $$ implying that $P Q \| R S$ and $Q R \| P S$. Hence $P Q R S$ is a parallelogram and hence $A B=P Q=R S$ and $Q R=P S$. It follows that $\frac{B C}{M C}=\frac{R S}{T S}=$ $\frac{A B}{M D} \Rightarrow A B \cdot C M=B C \cdot M D$ and $\frac{A D \cdot B M}{A M}=\frac{A D \cdot Q T}{A M}=Q R=P S=$ $\frac{C D \cdot T S}{M D}=C D \Rightarrow B M \cdot A D=M A \cdot C D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. G7 (ARM) The point $M$ inside the convex quadrilateral $A B C D$ is such that $M A=M C, \angle A M B=\angle M A D+\angle M C D, \angle C M D=\angle M C B+\angle M A B$. Prove that $A B \cdot C M=B C \cdot M D$ and $B M \cdot A D=M A \cdot C D$.
|
13. Let us construct a convex quadrilateral $P Q R S$ and an interior point $T$ such that $\triangle P T Q \cong \triangle A M B, \triangle Q T R \sim \triangle A M D$, and $\triangle P T S \sim \triangle C M D$. We then have $T S=\frac{M D \cdot P T}{M C}=M D$ and $\frac{T R}{T S}=\frac{T R \cdot T Q \cdot T P}{T Q \cdot T P \cdot T S}=\frac{M D \cdot M B \cdot M C}{M A \cdot M A \cdot M D}=$ $\frac{M B}{M C}$ (using $M A=M C$ ). We also have $\angle S T R=\angle B M C$ and therefore $\triangle R T S \sim \triangle B M C$. Now the relations between angles become $$ \angle T P S+\angle T Q R=\angle P T Q \quad \text { and } \quad \angle T P Q+\angle T S R=\angle P T S $$ implying that $P Q \| R S$ and $Q R \| P S$. Hence $P Q R S$ is a parallelogram and hence $A B=P Q=R S$ and $Q R=P S$. It follows that $\frac{B C}{M C}=\frac{R S}{T S}=$ $\frac{A B}{M D} \Rightarrow A B \cdot C M=B C \cdot M D$ and $\frac{A D \cdot B M}{A M}=\frac{A D \cdot Q T}{A M}=Q R=P S=$ $\frac{C D \cdot T S}{M D}=C D \Rightarrow B M \cdot A D=M A \cdot C D$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6c6f2665-634e-5a0d-aa6a-6011a47bfe05
| 24,898
|
14. G8 (RUS) Points $A, B, C$ divide the circumcircle $\Omega$ of the triangle $A B C$ into three arcs. Let $X$ be a variable point on the $\operatorname{arc} A B$, and let $O_{1}, O_{2}$ be the incenters of the triangles $C A X$ and $C B X$. Prove that the circumcircle of the triangle $X O_{1} O_{2}$ intersects $\Omega$ in a fixed point.
|
14. We first introduce the same lemma as in problem 12 and state it here without proof. Lemma. Let $A B C$ be a triangle and $I$ the center of its incircle. Let $M$ be the center of the $\operatorname{arc} \widehat{B C}$ of the circumcircle not containing $A$. Then $M B=M C=M I$. Let the circle $X O_{1} O_{2}$ intersect the circle $\Omega$ again at point $T$. Let $M$ and $N$ be respectively the midpoints of $\operatorname{arcs} \widehat{B C}$ and $\widehat{A C}$, and let $P$ be the intersection of $\Omega$ and the line through $C$ parallel to $M N$. Then the lemma gives $M P=N C=N I=N O_{1}$ and $N P=M C=$ $M I=M O_{2}$. Since $O_{1}$ and $O_{2}$ lie on $X N$ and $X M$ respectively, we have $\angle N T M=\angle N X M=\angle O_{1} X O_{2}=\angle O_{1} T O_{2}$ and hence $\angle N T O_{1}=$ $\angle M T O_{2}$. Moreover, $\angle T N O_{1}=\angle T N X=\angle T M O_{2}$, from which it follows that $\triangle O_{1} N T \sim \triangle O_{2} M T$. Thus $\frac{N T}{M P}=\frac{N T}{N O_{1}}=\frac{M T}{M O_{2}}=\frac{M T}{N P} \Rightarrow$ $M P \cdot M T=N P \cdot N T \Rightarrow S_{M P T}=S_{N P T}$. It follows that $T P$ bisects the segment $M N$, and hence it passes through $I$. We conclude that $T$ belongs to the line $P I$ and does not depend on $X$. Remark. An alternative approach is to apply an inversion at point $C$. Points $O_{1}$ and $O_{2}$ become excenters of $\triangle A X C$ and $\triangle B X C$, and $T$ becomes the projection of $I_{c}$ onto $A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
14. G8 (RUS) Points $A, B, C$ divide the circumcircle $\Omega$ of the triangle $A B C$ into three arcs. Let $X$ be a variable point on the $\operatorname{arc} A B$, and let $O_{1}, O_{2}$ be the incenters of the triangles $C A X$ and $C B X$. Prove that the circumcircle of the triangle $X O_{1} O_{2}$ intersects $\Omega$ in a fixed point.
|
14. We first introduce the same lemma as in problem 12 and state it here without proof. Lemma. Let $A B C$ be a triangle and $I$ the center of its incircle. Let $M$ be the center of the $\operatorname{arc} \widehat{B C}$ of the circumcircle not containing $A$. Then $M B=M C=M I$. Let the circle $X O_{1} O_{2}$ intersect the circle $\Omega$ again at point $T$. Let $M$ and $N$ be respectively the midpoints of $\operatorname{arcs} \widehat{B C}$ and $\widehat{A C}$, and let $P$ be the intersection of $\Omega$ and the line through $C$ parallel to $M N$. Then the lemma gives $M P=N C=N I=N O_{1}$ and $N P=M C=$ $M I=M O_{2}$. Since $O_{1}$ and $O_{2}$ lie on $X N$ and $X M$ respectively, we have $\angle N T M=\angle N X M=\angle O_{1} X O_{2}=\angle O_{1} T O_{2}$ and hence $\angle N T O_{1}=$ $\angle M T O_{2}$. Moreover, $\angle T N O_{1}=\angle T N X=\angle T M O_{2}$, from which it follows that $\triangle O_{1} N T \sim \triangle O_{2} M T$. Thus $\frac{N T}{M P}=\frac{N T}{N O_{1}}=\frac{M T}{M O_{2}}=\frac{M T}{N P} \Rightarrow$ $M P \cdot M T=N P \cdot N T \Rightarrow S_{M P T}=S_{N P T}$. It follows that $T P$ bisects the segment $M N$, and hence it passes through $I$. We conclude that $T$ belongs to the line $P I$ and does not depend on $X$. Remark. An alternative approach is to apply an inversion at point $C$. Points $O_{1}$ and $O_{2}$ become excenters of $\triangle A X C$ and $\triangle B X C$, and $T$ becomes the projection of $I_{c}$ onto $A B$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
35c8fc95-8345-5db2-b922-aed233d2fde3
| 24,901
|
18. A4 (BLR) Prove that the set of positive integers cannot be partitioned into three nonempty subsets such that for any two integers $x, y$ taken from two different subsets, the number $x^{2}-x y+y^{2}$ belongs to the third subset.
|
18. Define $f(x, y)=x^{2}-x y+y^{2}$. Let us assume that three such sets $A, B$, and $C$ do exist and that w.l.o.g. $1, b$, and $c(c>b)$ are respectively their smallest elements. Lemma 1. Numbers $x, y$, and $x+y$ cannot belong to three different sets. Proof. The number $f(x, x+y)=f(y, x+y)$ must belong to both the set containing $y$ and the set containing $x$, a contradiction. Lemma 2. The subset $C$ contains a multiple of $b$. Moreover, if $k b$ is the smallest such multiple, then $(k-1) b \in B$ and $(k-1) b+1, k b+1 \in A$. Proof. Let $r$ be the residue of $c$ modulo $b$. If $r=0$, the first statement automatically holds. Let $0<r<b$. In that case $r \in A$, and $c-r$ is then not in $B$ according to Lemma 1. Hence $c-r \in A$ and since $b \mid c-r$, it follows that $b \mid f(c-r, b) \in C$, thus proving the first statement. It follows immediately from Lemma 1 that $(k-1) b \in B$. Now by Lemma $1,(k-1) b+1=k b-(b-1)$ must be in $A$; similarly, $k b+1=[(k-1) b+1]+b \in A$ as well. Let us show by induction that $(n k-1) b+1, n k b+1 \in A$ for all integers $n$. The inductive basis has been shown in Lemma 2. Assuming that [ $n-$ 1) $k-1] b+1 \in A$ and $(n-1) k b+1 \in A$, we get that $(n k-1) b+1=$ $((n-1) k b+1)+(k-1) b=[((n-1) k-1) b+1]+k b$ belongs to $A$ and $n k b+1=((n k-1) b+1)+b=((n-1) k b+1)+k b \Rightarrow n k b+1 \in A$. This finishes the inductive step. In particular, $f(k b, k b+1)=(k b+1) k b+1 \in A$. However, since $k b \in C, k b+1 \in A$, it follows that $f(k b, k b+1) \in B$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
18. A4 (BLR) Prove that the set of positive integers cannot be partitioned into three nonempty subsets such that for any two integers $x, y$ taken from two different subsets, the number $x^{2}-x y+y^{2}$ belongs to the third subset.
|
18. Define $f(x, y)=x^{2}-x y+y^{2}$. Let us assume that three such sets $A, B$, and $C$ do exist and that w.l.o.g. $1, b$, and $c(c>b)$ are respectively their smallest elements. Lemma 1. Numbers $x, y$, and $x+y$ cannot belong to three different sets. Proof. The number $f(x, x+y)=f(y, x+y)$ must belong to both the set containing $y$ and the set containing $x$, a contradiction. Lemma 2. The subset $C$ contains a multiple of $b$. Moreover, if $k b$ is the smallest such multiple, then $(k-1) b \in B$ and $(k-1) b+1, k b+1 \in A$. Proof. Let $r$ be the residue of $c$ modulo $b$. If $r=0$, the first statement automatically holds. Let $0<r<b$. In that case $r \in A$, and $c-r$ is then not in $B$ according to Lemma 1. Hence $c-r \in A$ and since $b \mid c-r$, it follows that $b \mid f(c-r, b) \in C$, thus proving the first statement. It follows immediately from Lemma 1 that $(k-1) b \in B$. Now by Lemma $1,(k-1) b+1=k b-(b-1)$ must be in $A$; similarly, $k b+1=[(k-1) b+1]+b \in A$ as well. Let us show by induction that $(n k-1) b+1, n k b+1 \in A$ for all integers $n$. The inductive basis has been shown in Lemma 2. Assuming that [ $n-$ 1) $k-1] b+1 \in A$ and $(n-1) k b+1 \in A$, we get that $(n k-1) b+1=$ $((n-1) k b+1)+(k-1) b=[((n-1) k-1) b+1]+k b$ belongs to $A$ and $n k b+1=((n k-1) b+1)+b=((n-1) k b+1)+k b \Rightarrow n k b+1 \in A$. This finishes the inductive step. In particular, $f(k b, k b+1)=(k b+1) k b+1 \in A$. However, since $k b \in C, k b+1 \in A$, it follows that $f(k b, k b+1) \in B$, which is a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cb3749e9-bb43-5420-b51b-baa8e593440b
| 24,912
|
2. N2 (ARM) Prove that every positive rational number can be represented in the form $\frac{a^{3}+b^{3}}{c^{3}+d^{3}}$, where $a, b, c, d$ are positive integers.
|
2. We first prove that every rational number in the interval $(1,2)$ can be represented in the form $\frac{a^{3}+b^{3}}{a^{3}+d^{3}}$. Taking $b, d$ such that $b \neq d$ and $a=b+d$, we get $a^{2}-a b+b^{2}=a^{2}-a d+d^{2}$ and $$ \frac{a^{3}+b^{3}}{a^{3}+d^{3}}=\frac{(a+b)\left(a^{2}-a b+b^{2}\right)}{(a+d)\left(a^{2}-a d+d^{2}\right)}=\frac{a+b}{a+d} . $$ For a given rational number $1<m / n<2$ we can select $a=m+n$ and $b=2 m-n$ such that along with $d=a-b$ we have $\frac{a+b}{a+d}=\frac{m}{n}$. This completes the proof of the first statement. For $m / n$ outside of the interval we can easily select a rational number $p / q$ such that $\sqrt[3]{\frac{n}{m}}<\frac{p}{q}<\sqrt[3]{\frac{2 n}{m}}$. In other words $1<\frac{p^{3} m}{q^{3} n}<2$. We now proceed to obtain $a, b$ and $d$ for $\frac{p^{3} m}{q^{3} n}$ as before, and we finally have $$ \frac{p^{3} m}{q^{3} n}=\frac{a^{3}+b^{3}}{a^{3}+d^{3}} \Rightarrow \frac{m}{n}=\frac{(a q)^{3}+(b q)^{3}}{(a p)^{3}+(d p)^{3}} . $$ Thus we have shown that all positive rational numbers can be expressed in the form $\frac{a^{3}+b^{3}}{c^{3}+d^{3}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
2. N2 (ARM) Prove that every positive rational number can be represented in the form $\frac{a^{3}+b^{3}}{c^{3}+d^{3}}$, where $a, b, c, d$ are positive integers.
|
2. We first prove that every rational number in the interval $(1,2)$ can be represented in the form $\frac{a^{3}+b^{3}}{a^{3}+d^{3}}$. Taking $b, d$ such that $b \neq d$ and $a=b+d$, we get $a^{2}-a b+b^{2}=a^{2}-a d+d^{2}$ and $$ \frac{a^{3}+b^{3}}{a^{3}+d^{3}}=\frac{(a+b)\left(a^{2}-a b+b^{2}\right)}{(a+d)\left(a^{2}-a d+d^{2}\right)}=\frac{a+b}{a+d} . $$ For a given rational number $1<m / n<2$ we can select $a=m+n$ and $b=2 m-n$ such that along with $d=a-b$ we have $\frac{a+b}{a+d}=\frac{m}{n}$. This completes the proof of the first statement. For $m / n$ outside of the interval we can easily select a rational number $p / q$ such that $\sqrt[3]{\frac{n}{m}}<\frac{p}{q}<\sqrt[3]{\frac{2 n}{m}}$. In other words $1<\frac{p^{3} m}{q^{3} n}<2$. We now proceed to obtain $a, b$ and $d$ for $\frac{p^{3} m}{q^{3} n}$ as before, and we finally have $$ \frac{p^{3} m}{q^{3} n}=\frac{a^{3}+b^{3}}{a^{3}+d^{3}} \Rightarrow \frac{m}{n}=\frac{(a q)^{3}+(b q)^{3}}{(a p)^{3}+(d p)^{3}} . $$ Thus we have shown that all positive rational numbers can be expressed in the form $\frac{a^{3}+b^{3}}{c^{3}+d^{3}}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
90d564e6-68b4-5400-bd0b-e660d711c603
| 24,918
|
20. A6 (SWE) For $n \geq 3$ and $a_{1} \leq a_{2} \leq \cdots \leq a_{n}$ given real numbers we have the following instructions: (1) place the numbers in some order in a circle; (2) delete one of the numbers from the circle; (3) if just two numbers are remaining in the circle, let $S$ be the sum of these two numbers. Otherwise, if there are more than two numbers in the circle, replace $\left(x_{1}, x_{2}, x_{3}, \ldots, x_{p-1}, x_{p}\right)$ with $\left(x_{1}+x_{2}, x_{2}+\right.$ $x_{3}, \ldots, x_{p-1}+x_{p}, x_{p}+x_{1}$ ). Afterwards, start again with step (2). Show that the largest sum $S$ that can result in this way is given by the formula $$ S_{\max }=\sum_{k=2}^{n}\binom{n-2}{\left[\frac{k}{2}\right]-1} a_{k} $$
|
20. We first introduce some useful notation. An arrangement around the circle will be denoted by $x=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$, where the elements are arranged clockwise and $x_{1}$ is fixed to be the smallest number. We will call an arrangement balanced if $x_{1} \leq x_{n} \leq x_{2} \leq x_{n-1} \leq x_{3} \leq x_{n-2} \leq \cdots$ (the string of inequalities continues until all the elements are accounted for). We will denote the permutation of $x=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ in ascending order by $x^{\prime}=\left\{x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{n}^{\prime}\right\}$. We will let $f_{i}(x)=\left\{f_{i}(x)_{1}, f_{i}(x)_{2}, \ldots, f_{i}(x)_{n-1}\right\}$ denote the arrangement after one iteration of the algorithm where $x_{i}$ was the deleted element. Lemma 1. If an arrangement $x$ is balanced, then $f_{1}(x)$ is also balanced. Proof. In one iteration we have $\left\{x_{1}, \ldots, x_{n}\right\} \rightarrow\left\{x_{n}+x_{2}, x_{2}+x_{3}, \ldots\right.$, $\left.x_{n-1}+x_{n}\right\}$. Since $x_{n} \leq x_{2} \leq x_{n-1} \leq x_{3} \leq x_{n-2} \leq \cdots$, it follows that $x_{n}+x_{2} \leq x_{n}+x_{n-1} \leq x_{2}+x_{3} \leq x_{n-1}+x_{n-2} \leq \cdots$, which means that $f_{1}(x)$ is balanced. We will first show by induction that $S_{\max }$ can be reached by using the balanced initial arrangement $\left\{a_{1}, a_{3}, a_{5}, \ldots, a_{6}, a_{4}, a_{2}\right\}$ and repeatedly deleting the smallest member. For $n=3$ we have $S_{3}=a_{2}+a_{3}$, in accordance with the formula. Assuming that the formula holds for a given $n$, we note that for an arrangement $x=\left\{a_{1}, a_{3}, a_{5}, \ldots, a_{6}, a_{4}, a_{2}\right\}$ the arrangement $f_{1}(x)$ is also balanced. We now apply the induction hypothesis and use that $\binom{n-2}{i}+\binom{n-2}{i-1}=\binom{n-1}{i}$ : $$ \begin{aligned} S(x) & =S\left(f_{1}(x)\right) \\ & =\sum_{k=2}^{n-1}\binom{n-2}{[k / 2]-1}\left(a_{k}+a_{k+2}\right)+\binom{n-2}{[n / 2]-1}\left(a_{n}+a_{n+1}\right)=S_{\max } \end{aligned} $$ We now prove that every other arrangement yields a smaller value. We shall write $\left\{x_{1}, \ldots, x_{n}\right\} \leq\left\{y_{1}, \ldots, y_{n}\right\}$ whenever $x_{n}^{\prime}+x_{n-1}^{\prime}+\cdots+x_{i}^{\prime} \leq$ $y_{n}^{\prime}+y_{n-1}^{\prime}+\cdots+y_{i}^{\prime}$ holds for all $1 \leq i \leq n$. Lemma 2. Let $x$ be an arbitrary arrangement and $y$ a balanced arrangement, both of $n$ elements, such that $x \leq y$. Then it follows that $f_{i}(x) \leq f_{1}(y)$, for all $i$. Proof. For any $1 \leq j \leq n-1$ there exists $k_{j}$ such that $f_{i}(x)_{j}=x_{k_{j}}+x_{k_{j}+1}$ (assuming $k_{j}+1=1$ if $k_{j}=n-1$ ). Then we have $$ \begin{aligned} f_{i}(x)_{n-1}+\cdots+f_{i}(x)_{n-j} & =\left(x_{k_{1}}+x_{k_{1}+1}\right)+\cdots+\left(x_{k_{j}}+x_{k_{j}+1}\right) \\ & \leq 2 x_{n}^{\prime}+\cdots+2 x_{n-i+1}^{\prime}+x_{n-i}^{\prime}+x_{n-i-1}^{\prime} \\ & =f_{1}(y)_{n-1}+\cdots+f_{1}(y)_{n-j} \end{aligned} $$ for all $j$, and hence $f_{i}(x) \leq f_{1}(y)$. An immediate consequence of Lemma 2 is $f^{n-2}(x) \leq f_{1}^{n-2}(y)$, implying $S=f^{n-2}(x)_{1}+f^{n-2}(x)_{2} \leq f_{1}^{n-2}(y)_{1}+f_{1}^{n-2}(y)_{2}=S_{\max }(y)$. Thus the proof is finished.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
20. A6 (SWE) For $n \geq 3$ and $a_{1} \leq a_{2} \leq \cdots \leq a_{n}$ given real numbers we have the following instructions: (1) place the numbers in some order in a circle; (2) delete one of the numbers from the circle; (3) if just two numbers are remaining in the circle, let $S$ be the sum of these two numbers. Otherwise, if there are more than two numbers in the circle, replace $\left(x_{1}, x_{2}, x_{3}, \ldots, x_{p-1}, x_{p}\right)$ with $\left(x_{1}+x_{2}, x_{2}+\right.$ $x_{3}, \ldots, x_{p-1}+x_{p}, x_{p}+x_{1}$ ). Afterwards, start again with step (2). Show that the largest sum $S$ that can result in this way is given by the formula $$ S_{\max }=\sum_{k=2}^{n}\binom{n-2}{\left[\frac{k}{2}\right]-1} a_{k} $$
|
20. We first introduce some useful notation. An arrangement around the circle will be denoted by $x=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$, where the elements are arranged clockwise and $x_{1}$ is fixed to be the smallest number. We will call an arrangement balanced if $x_{1} \leq x_{n} \leq x_{2} \leq x_{n-1} \leq x_{3} \leq x_{n-2} \leq \cdots$ (the string of inequalities continues until all the elements are accounted for). We will denote the permutation of $x=\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ in ascending order by $x^{\prime}=\left\{x_{1}^{\prime}, x_{2}^{\prime}, \ldots, x_{n}^{\prime}\right\}$. We will let $f_{i}(x)=\left\{f_{i}(x)_{1}, f_{i}(x)_{2}, \ldots, f_{i}(x)_{n-1}\right\}$ denote the arrangement after one iteration of the algorithm where $x_{i}$ was the deleted element. Lemma 1. If an arrangement $x$ is balanced, then $f_{1}(x)$ is also balanced. Proof. In one iteration we have $\left\{x_{1}, \ldots, x_{n}\right\} \rightarrow\left\{x_{n}+x_{2}, x_{2}+x_{3}, \ldots\right.$, $\left.x_{n-1}+x_{n}\right\}$. Since $x_{n} \leq x_{2} \leq x_{n-1} \leq x_{3} \leq x_{n-2} \leq \cdots$, it follows that $x_{n}+x_{2} \leq x_{n}+x_{n-1} \leq x_{2}+x_{3} \leq x_{n-1}+x_{n-2} \leq \cdots$, which means that $f_{1}(x)$ is balanced. We will first show by induction that $S_{\max }$ can be reached by using the balanced initial arrangement $\left\{a_{1}, a_{3}, a_{5}, \ldots, a_{6}, a_{4}, a_{2}\right\}$ and repeatedly deleting the smallest member. For $n=3$ we have $S_{3}=a_{2}+a_{3}$, in accordance with the formula. Assuming that the formula holds for a given $n$, we note that for an arrangement $x=\left\{a_{1}, a_{3}, a_{5}, \ldots, a_{6}, a_{4}, a_{2}\right\}$ the arrangement $f_{1}(x)$ is also balanced. We now apply the induction hypothesis and use that $\binom{n-2}{i}+\binom{n-2}{i-1}=\binom{n-1}{i}$ : $$ \begin{aligned} S(x) & =S\left(f_{1}(x)\right) \\ & =\sum_{k=2}^{n-1}\binom{n-2}{[k / 2]-1}\left(a_{k}+a_{k+2}\right)+\binom{n-2}{[n / 2]-1}\left(a_{n}+a_{n+1}\right)=S_{\max } \end{aligned} $$ We now prove that every other arrangement yields a smaller value. We shall write $\left\{x_{1}, \ldots, x_{n}\right\} \leq\left\{y_{1}, \ldots, y_{n}\right\}$ whenever $x_{n}^{\prime}+x_{n-1}^{\prime}+\cdots+x_{i}^{\prime} \leq$ $y_{n}^{\prime}+y_{n-1}^{\prime}+\cdots+y_{i}^{\prime}$ holds for all $1 \leq i \leq n$. Lemma 2. Let $x$ be an arbitrary arrangement and $y$ a balanced arrangement, both of $n$ elements, such that $x \leq y$. Then it follows that $f_{i}(x) \leq f_{1}(y)$, for all $i$. Proof. For any $1 \leq j \leq n-1$ there exists $k_{j}$ such that $f_{i}(x)_{j}=x_{k_{j}}+x_{k_{j}+1}$ (assuming $k_{j}+1=1$ if $k_{j}=n-1$ ). Then we have $$ \begin{aligned} f_{i}(x)_{n-1}+\cdots+f_{i}(x)_{n-j} & =\left(x_{k_{1}}+x_{k_{1}+1}\right)+\cdots+\left(x_{k_{j}}+x_{k_{j}+1}\right) \\ & \leq 2 x_{n}^{\prime}+\cdots+2 x_{n-i+1}^{\prime}+x_{n-i}^{\prime}+x_{n-i-1}^{\prime} \\ & =f_{1}(y)_{n-1}+\cdots+f_{1}(y)_{n-j} \end{aligned} $$ for all $j$, and hence $f_{i}(x) \leq f_{1}(y)$. An immediate consequence of Lemma 2 is $f^{n-2}(x) \leq f_{1}^{n-2}(y)$, implying $S=f^{n-2}(x)_{1}+f^{n-2}(x)_{2} \leq f_{1}^{n-2}(y)_{1}+f_{1}^{n-2}(y)_{2}=S_{\max }(y)$. Thus the proof is finished.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ed9a407f-dcab-5b2c-aa3d-9caa829b8415
| 24,921
|
21. C1 (IND) Let $n \geq 1$ be an integer. A path from $(0,0)$ to $(n, n)$ in the $x y$ plane is a chain of consecutive unit moves either to the right (move denoted by $E$ ) or upwards (move denoted by $N$ ), all the moves being made inside the half-plane $x \geq y$. A step in a path is the occurrence of two consecutive moves of the form $E N$. Show that the number of paths from $(0,0)$ to $(n, n)$ that contain exactly $s$ steps $(n \geq s \geq 1)$ is $$ \frac{1}{s}\binom{n-1}{s-1}\binom{n}{s-1} $$
|
21. Let us call $f(n, s)$ the number of paths from $(0,0)$ to $(n, n)$ that contain exactly $s$ steps. Evidently, for all $n$ we have $f(n, 1)=f(2,2)=1$, in accordance with the formula. Let us thus assume inductively for a given $n>2$ that for all $s$ we have $f(n, s)=\frac{1}{s}\binom{n-1}{s-1}\binom{n}{s-1}$. We shall prove that the given formula holds also for all $f(n+1, s)$, where $s \geq 2$. We say that an $(n+1, s)$ - or $(n+1, s+1)$-path is related to a given $(n, s)$ path if it is obtained from the given path by inserting a step $E N$ between two moves or at the beginning or the end of the path. We note that by inserting the step between two moves that form a step one obtains an $(n+1, s)$-path; in all other cases one obtains an $(n+1, s+1)$-path. For each $(n, s)$-path there are exactly $2 n+1-s$ related $(n+1, s+1)$-paths, and for each $(n, s+1)$-path there are $s+1$ related $(n+1, s+1)$-paths. Also, each $(n+1, s+1)$-path is related to exactly $s+1$ different $(n, s)$ - or $(n, s+1)$-paths. Thus: $$ \begin{aligned} (s+1) f(n+1, s+1) & =(2 n+1-s) f(n, s)+(s+1) f(n, s+1) \\ & =\frac{2 n+1-s}{s}\binom{n-1}{s-1}\binom{n}{s-1}+\binom{n-1}{s}\binom{n}{s} \\ & =\binom{n}{s}\binom{n+1}{s}, \end{aligned} $$ i.e., $f(n+1, s+1)=\frac{1}{s+1}\binom{n}{s}\binom{n+1}{s}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
21. C1 (IND) Let $n \geq 1$ be an integer. A path from $(0,0)$ to $(n, n)$ in the $x y$ plane is a chain of consecutive unit moves either to the right (move denoted by $E$ ) or upwards (move denoted by $N$ ), all the moves being made inside the half-plane $x \geq y$. A step in a path is the occurrence of two consecutive moves of the form $E N$. Show that the number of paths from $(0,0)$ to $(n, n)$ that contain exactly $s$ steps $(n \geq s \geq 1)$ is $$ \frac{1}{s}\binom{n-1}{s-1}\binom{n}{s-1} $$
|
21. Let us call $f(n, s)$ the number of paths from $(0,0)$ to $(n, n)$ that contain exactly $s$ steps. Evidently, for all $n$ we have $f(n, 1)=f(2,2)=1$, in accordance with the formula. Let us thus assume inductively for a given $n>2$ that for all $s$ we have $f(n, s)=\frac{1}{s}\binom{n-1}{s-1}\binom{n}{s-1}$. We shall prove that the given formula holds also for all $f(n+1, s)$, where $s \geq 2$. We say that an $(n+1, s)$ - or $(n+1, s+1)$-path is related to a given $(n, s)$ path if it is obtained from the given path by inserting a step $E N$ between two moves or at the beginning or the end of the path. We note that by inserting the step between two moves that form a step one obtains an $(n+1, s)$-path; in all other cases one obtains an $(n+1, s+1)$-path. For each $(n, s)$-path there are exactly $2 n+1-s$ related $(n+1, s+1)$-paths, and for each $(n, s+1)$-path there are $s+1$ related $(n+1, s+1)$-paths. Also, each $(n+1, s+1)$-path is related to exactly $s+1$ different $(n, s)$ - or $(n, s+1)$-paths. Thus: $$ \begin{aligned} (s+1) f(n+1, s+1) & =(2 n+1-s) f(n, s)+(s+1) f(n, s+1) \\ & =\frac{2 n+1-s}{s}\binom{n-1}{s-1}\binom{n}{s-1}+\binom{n-1}{s}\binom{n}{s} \\ & =\binom{n}{s}\binom{n+1}{s}, \end{aligned} $$ i.e., $f(n+1, s+1)=\frac{1}{s+1}\binom{n}{s}\binom{n+1}{s}$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
55424abb-7212-5009-9cc5-1aff57335409
| 24,923
|
22. C2 (CAN) (a) If a $5 \times n$ rectangle can be tiled using $n$ pieces like those shown in the diagram, prove that $n$ is even.  (b) Show that there are more than $2 \cdot 3^{k-1}$ ways to tile a fixed $5 \times 2 k$ rectangle ( $k \geq 3$ ) with $2 k$ pieces. (Symmetric constructions are considered to be different.)
|
22. (a) Color the first, third, and fifth row red, and the remaining squares white. There in total $n$ pieces and $3 n$ red squares. Since each piece can cover at most three red squares, it follows that each piece colors exactly three red squares. Then it follows that the two white squares it covers must be on the same row; otherwise, the piece has to cover at least three. Hence, each white row can be partitioned into pairs of squares belonging to the same piece. Thus it follows that the number of white squares in a row, which is $n$, must be even. (b) Let $a_{k}$ denote the number of different tilings of a $5 \times 2 k$ rectangle. Let $b_{k}$ be the number of tilings that cannot be partitioned into two smaller tilings along a vertical line (without cutting any pieces). It is easy to see that $a_{1}=b_{1}=2, b_{2}=2, a_{2}=6=2 \cdot 3, b_{3}=4$, and subsequently, by induction, $b_{3 k} \geq 4, b_{3 k+1} \geq 2$, and $b_{3 k+2} \geq 2$. We also have $a_{k}=b_{k}+\sum_{i=1}^{k-1} b_{i} a_{k-i}$. For $k \geq 3$ we now have inductively $$ a_{k}>2+\sum_{i=1}^{k-1} 2 a_{k-i} \geq 2 \cdot 3^{k-1}+2 a_{k-1} \geq 2 \cdot 3^{k} $$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
22. C2 (CAN) (a) If a $5 \times n$ rectangle can be tiled using $n$ pieces like those shown in the diagram, prove that $n$ is even.  (b) Show that there are more than $2 \cdot 3^{k-1}$ ways to tile a fixed $5 \times 2 k$ rectangle ( $k \geq 3$ ) with $2 k$ pieces. (Symmetric constructions are considered to be different.)
|
22. (a) Color the first, third, and fifth row red, and the remaining squares white. There in total $n$ pieces and $3 n$ red squares. Since each piece can cover at most three red squares, it follows that each piece colors exactly three red squares. Then it follows that the two white squares it covers must be on the same row; otherwise, the piece has to cover at least three. Hence, each white row can be partitioned into pairs of squares belonging to the same piece. Thus it follows that the number of white squares in a row, which is $n$, must be even. (b) Let $a_{k}$ denote the number of different tilings of a $5 \times 2 k$ rectangle. Let $b_{k}$ be the number of tilings that cannot be partitioned into two smaller tilings along a vertical line (without cutting any pieces). It is easy to see that $a_{1}=b_{1}=2, b_{2}=2, a_{2}=6=2 \cdot 3, b_{3}=4$, and subsequently, by induction, $b_{3 k} \geq 4, b_{3 k+1} \geq 2$, and $b_{3 k+2} \geq 2$. We also have $a_{k}=b_{k}+\sum_{i=1}^{k-1} b_{i} a_{k-i}$. For $k \geq 3$ we now have inductively $$ a_{k}>2+\sum_{i=1}^{k-1} 2 a_{k-i} \geq 2 \cdot 3^{k-1}+2 a_{k-1} \geq 2 \cdot 3^{k} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b0cbb1af-fbd8-5213-b29c-be7bd2ccc29d
| 24,926
|
24. C4 (GBR) Let $A$ be a set of $N$ residues $\left(\bmod N^{2}\right)$. Prove that there exists a set $B$ of $N$ residues $\left(\bmod N^{2}\right)$ such that the set $A+B=\{a+b \mid$ $a \in A, b \in B\}$ contains at least half of all residues $\left(\bmod N^{2}\right)$.
|
24. Let $S=\left\{0,1, \ldots, N^{2}-1\right\}$ be the group of residues (with respect to addition modulo $N^{2}$ ) and $A$ an $n$-element subset. We will use $|X|$ to denote the number of elements of a subset $X$ of $S$, and $\bar{X}$ to refer to the complement of $X$ in $S$. For $i \in S$ we also define $A_{i}=\{a+i \mid a \in A\}$. Our task is to select $0 \leq i_{1}<\cdots<i_{N} \leq N^{2}-1$ such that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq \frac{1}{2}|S|$. Each $x \in S$ appears in exactly $N$ sets $A_{i}$. We have $$ \begin{aligned} \sum_{i_{1}<\cdots<i_{N}}\left|\bigcap_{j=1}^{N} \bar{A}_{i_{j}}\right| & =\sum_{i_{1}<\cdots<i_{N}}\left|\left\{x \in S \mid x \notin A_{i_{1}}, \ldots, A_{i_{N}}\right\}\right| \\ & =\sum_{x \in S}\left|\left\{i_{1}<\cdots<i_{N} \mid x \notin A_{i_{1}}, \ldots, A_{i_{N}}\right\}\right| \\ & =\sum_{x \in S}\binom{N^{2}-N}{N}=\binom{N^{2}-N}{N}|S| . \end{aligned} $$ Hence $$ \begin{aligned} \sum_{i_{1}<\cdots<i_{N}}\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| & =\sum_{i_{1}<\cdots<i_{N}}\left(|S|-\left|\bigcap_{j=1}^{N} \bar{A}_{i_{j}}\right|\right) \\ & =\left(\binom{N^{2}}{N}-\binom{N^{2}-N}{N}\right)|S| . \end{aligned} $$ Thus, by the pigeonhole principle, one can choose $i_{1}<\cdots<i_{N}$ such that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq\left(1-\binom{N^{2}-N}{N} /\binom{N^{2}}{N}\right)|S|$. Since $\binom{N^{2}}{N} /\binom{N^{2}-N}{N} \geq\left(\frac{N^{2}}{N^{2}-N}\right)^{N}$ $=\left(1+\frac{1}{N-1}\right)^{N}>e>2$, it follows that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq \frac{1}{2}|S|$; hence the chosen $i_{1}<\cdots<i_{N}$ are indeed the elements of $B$ that satisfy the conditions of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
24. C4 (GBR) Let $A$ be a set of $N$ residues $\left(\bmod N^{2}\right)$. Prove that there exists a set $B$ of $N$ residues $\left(\bmod N^{2}\right)$ such that the set $A+B=\{a+b \mid$ $a \in A, b \in B\}$ contains at least half of all residues $\left(\bmod N^{2}\right)$.
|
24. Let $S=\left\{0,1, \ldots, N^{2}-1\right\}$ be the group of residues (with respect to addition modulo $N^{2}$ ) and $A$ an $n$-element subset. We will use $|X|$ to denote the number of elements of a subset $X$ of $S$, and $\bar{X}$ to refer to the complement of $X$ in $S$. For $i \in S$ we also define $A_{i}=\{a+i \mid a \in A\}$. Our task is to select $0 \leq i_{1}<\cdots<i_{N} \leq N^{2}-1$ such that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq \frac{1}{2}|S|$. Each $x \in S$ appears in exactly $N$ sets $A_{i}$. We have $$ \begin{aligned} \sum_{i_{1}<\cdots<i_{N}}\left|\bigcap_{j=1}^{N} \bar{A}_{i_{j}}\right| & =\sum_{i_{1}<\cdots<i_{N}}\left|\left\{x \in S \mid x \notin A_{i_{1}}, \ldots, A_{i_{N}}\right\}\right| \\ & =\sum_{x \in S}\left|\left\{i_{1}<\cdots<i_{N} \mid x \notin A_{i_{1}}, \ldots, A_{i_{N}}\right\}\right| \\ & =\sum_{x \in S}\binom{N^{2}-N}{N}=\binom{N^{2}-N}{N}|S| . \end{aligned} $$ Hence $$ \begin{aligned} \sum_{i_{1}<\cdots<i_{N}}\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| & =\sum_{i_{1}<\cdots<i_{N}}\left(|S|-\left|\bigcap_{j=1}^{N} \bar{A}_{i_{j}}\right|\right) \\ & =\left(\binom{N^{2}}{N}-\binom{N^{2}-N}{N}\right)|S| . \end{aligned} $$ Thus, by the pigeonhole principle, one can choose $i_{1}<\cdots<i_{N}$ such that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq\left(1-\binom{N^{2}-N}{N} /\binom{N^{2}}{N}\right)|S|$. Since $\binom{N^{2}}{N} /\binom{N^{2}-N}{N} \geq\left(\frac{N^{2}}{N^{2}-N}\right)^{N}$ $=\left(1+\frac{1}{N-1}\right)^{N}>e>2$, it follows that $\left|\bigcup_{j=1}^{N} A_{i_{j}}\right| \geq \frac{1}{2}|S|$; hence the chosen $i_{1}<\cdots<i_{N}$ are indeed the elements of $B$ that satisfy the conditions of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ad042c55-7f38-5d51-9b7d-7e48db42e8bb
| 24,931
|
26. C6 (GBR) Suppose that every integer has been given one of the colors red, blue, green, yellow. Let $x$ and $y$ be odd integers such that $|x| \neq|y|$. Show that there are two integers of the same color whose difference has one of the following values: $x, y, x+y, x-y$.
|
26. We denote colors by capital initial letters. Let us suppose that there exists a coloring $f: \mathbb{Z} \rightarrow\{R, G, B, Y\}$ such that for any $a \in \mathbb{Z}$ we have $f\{a, a+$ $x, a+y, a+x+y\}=\{R, G, B, Y\}$. We now define a coloring of an integer lattice $g: \mathbb{Z} \times \mathbb{Z} \rightarrow\{R, G, B, Y\}$ by the rule $g(i, j)=f(x i+y j)$. It follows that every unit square in $g$ must have its vertices colored by four different colors. If there is a row or column with period 2 , then applying the condition to adjacent unit squares, we get (by induction) that all rows or columns, respectively, have period 2 . On the other hand, taking a row to be not of period 2, i.e., containing a sequence of three distinct colors, for example $G R Y$, we get that the next row must contain in these columns $Y B G$, and the following $G R Y$, and so on. It would follow that a column in this case must have period 2. A similar conclusion holds if we start with an aperiodic column. Hence either all rows or all columns must have period 2. Let us assume w.l.o.g. that all rows have a period of 2. Assuming w.l.o.g. $\{g(0,0), g(1,0)\}=\{G, B\}$, we get that the even rows are painted with $\{G, B\}$ and odd with $\{Y, R\}$. Since $x$ is odd, it follows that $g(y, 0)$ and $g(0, x)$ are of different color. However, since $g(y, 0)=f(x y)=g(0, x)$, this is a contradiction. Hence the statement of the problem holds.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
26. C6 (GBR) Suppose that every integer has been given one of the colors red, blue, green, yellow. Let $x$ and $y$ be odd integers such that $|x| \neq|y|$. Show that there are two integers of the same color whose difference has one of the following values: $x, y, x+y, x-y$.
|
26. We denote colors by capital initial letters. Let us suppose that there exists a coloring $f: \mathbb{Z} \rightarrow\{R, G, B, Y\}$ such that for any $a \in \mathbb{Z}$ we have $f\{a, a+$ $x, a+y, a+x+y\}=\{R, G, B, Y\}$. We now define a coloring of an integer lattice $g: \mathbb{Z} \times \mathbb{Z} \rightarrow\{R, G, B, Y\}$ by the rule $g(i, j)=f(x i+y j)$. It follows that every unit square in $g$ must have its vertices colored by four different colors. If there is a row or column with period 2 , then applying the condition to adjacent unit squares, we get (by induction) that all rows or columns, respectively, have period 2 . On the other hand, taking a row to be not of period 2, i.e., containing a sequence of three distinct colors, for example $G R Y$, we get that the next row must contain in these columns $Y B G$, and the following $G R Y$, and so on. It would follow that a column in this case must have period 2. A similar conclusion holds if we start with an aperiodic column. Hence either all rows or all columns must have period 2. Let us assume w.l.o.g. that all rows have a period of 2. Assuming w.l.o.g. $\{g(0,0), g(1,0)\}=\{G, B\}$, we get that the even rows are painted with $\{G, B\}$ and odd with $\{Y, R\}$. Since $x$ is odd, it follows that $g(y, 0)$ and $g(0, x)$ are of different color. However, since $g(y, 0)=f(x y)=g(0, x)$, this is a contradiction. Hence the statement of the problem holds.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
38e9ae36-48f2-551e-9adb-10b21133d001
| 24,937
|
27. C7 (IRE) Let $p>3$ be a prime number. For each nonempty subset $T$ of $\{0,1,2,3, \ldots, p-1\}$ let $E(T)$ be the set of all $(p-1)$-tuples $\left(x_{1}, \ldots, x_{p-1}\right)$, where each $x_{i} \in T$ and $x_{1}+2 x_{2}+\cdots+(p-1) x_{p-1}$ is divisible by $p$ and let $|E(T)|$ denote the number of elements in $E(T)$. Prove that $$ |E(\{0,1,3\})| \geq|E(\{0,1,2\})|, $$ with equality if and only if $p=5$.
|
27. Denote $A=\{0,1,2\}$ and $B=\{0,1,3\}$. Let $f_{T}(x)=\sum_{a \in T} x^{a}$. Then define $F_{T}(x)=f_{T}(x) f_{T}\left(x^{2}\right) \cdots f_{T}\left(x^{p-1}\right)$. We can write $F_{T}(x)=\sum_{i=0}^{p(p-1)} a_{i} x^{i}$, where $a_{i}$ is the number of ways to select an array $\left\{x_{1}, \ldots, x_{p-1}\right\}$ where $x_{i} \in T$ for all $i$ and $x_{1}+2 x_{2}+\cdots+(p-1) x_{p-1}=i$. Let $w=\cos (2 \pi / p)+$ $i \sin (2 \pi / p)$, a $p$ th root of unity. Noting that $$ 1+w^{j}+w^{2 j}+\cdots+w^{(p-1) j}=\left\{\begin{array}{c} p, p \mid j, \\ 0, p \nmid j, \end{array}\right. $$ it follows that $F_{T}(1)+F_{T}(w)+\cdots+F_{T}\left(w^{p-1}\right)=p E(T)$. Since $|A|=|B|=3$, it follows that $F_{A}(1)=F_{B}(1)=3^{p-1}$. We also have for $p \nmid i, j$ that $F_{T}\left(w^{i}\right)=F_{T}(w)$. Finally, we have $$ F_{A}(w)=\prod_{i=1}^{p-1}\left(1+w^{i}+w^{2 i}\right)=\prod_{i=1}^{p-1} \frac{1-w^{3 i}}{1-w^{i}}=1 $$ Hence, combining these results, we obtain $$ E(A)=\frac{3^{p-1}+p-1}{p} \text { and } E(B)=\frac{3^{p-1}+(p-1) F_{B}(w)}{p} $$ It remains to demonstrate that $F_{B}(w) \geq 1$ for all $p$ and that equality holds only for $p=5$. Since $E(B)$ is an integer, it follows that $F_{B}(w)$ is an integer and $F_{B}(w) \equiv 1(\bmod p)$. Since $f_{B}\left(w^{p-i}\right)=\overline{f_{B}\left(w^{i}\right)}$, it follows that $F_{B}(w)=\left|f_{B}(w)\right|^{2}\left|f_{B}\left(w^{2}\right)\right|^{2} \cdots\left|f_{B}\left(w^{(p-1) / 2}\right)\right|^{2}>0$. Hence $F_{B}(w) \geq 1$. It remains to show that $F_{B}(w)=1$ if and only if $p=5$. We have the formula $(x-w)\left(x-w^{2}\right) \cdots\left(x-w^{p-1}\right)=x^{p-1}+x^{p-2}+\cdots+x+1=\frac{x^{p}-1}{x-1}$. Let $f_{B}(x)=x^{3}+x+1=(x-\lambda)(x-\mu)(x-\nu)$, where $\lambda$, $\mu$, and $\nu$ are the three zeros of the polynomial $f_{B}(x)$. It follows that $F_{B}(w)=\left(\frac{\lambda^{p}-1}{\lambda-1}\right)\left(\frac{\mu^{p}-1}{\mu-1}\right)\left(\frac{\nu^{p}-1}{\nu-1}\right)=-\frac{1}{3}\left(\lambda^{p}-1\right)\left(\mu^{p}-1\right)\left(\nu^{p}-1\right)$, since $(\lambda-1)(\mu-1)(\nu-1)=-f_{B}(1)=-3$. We also have $\lambda+\mu+\nu=0$, $\lambda \mu \nu=-1, \lambda \mu+\lambda \nu+\mu \nu=1$, and $\lambda^{2}+\mu^{2}+\nu^{2}=(\lambda+\mu+\nu)^{2}-2(\lambda \mu+$ $\lambda \nu+\mu \nu)=-2$. By induction (using that $\left(\lambda^{r}+\mu^{r}+\nu^{r}\right)+\left(\lambda^{r-2}+\mu^{r-2}+\right.$ $\left.\nu^{r-2}\right)+\left(\lambda^{r-3}+\mu^{r-3}+\nu^{r-3}\right)=0$ ), it follows that $\lambda^{r}+\mu^{r}+\nu^{r}$ is an integer for all $r \in \mathbb{N}$. Let us assume $F_{B}(x)=1$. It follows that $\left(\lambda^{p}-1\right)\left(\mu^{p}-1\right)\left(\nu^{p}-1\right)=-3$. Hence $\lambda^{p}, \mu^{p}, \nu^{p}$ are roots of the polynomial $p(x)=x^{3}-q x^{2}+(1+q) x+1$, where $q=\lambda^{p}+\mu^{p}+\nu^{p}$. Since $f_{B}(x)$ is an increasing function in real numbers, it follows that it has only one real root (w.l.o.g.) $\lambda$, the other two roots being complex conjugates. From $f_{B}(-1)<0<f_{B}(-1 / 2)$ it follows that $-1<\lambda<-1 / 2$. It also follows that $\lambda^{p}$ is the $x$ coordinate of the intersection of functions $y=x^{3}+x+1$ and $y=q\left(x^{2}-x\right)$. Since $\lambda<\lambda^{p}<0$, it follows that $q>0$; otherwise, $q\left(x^{2}-x\right)$ intersects $x^{3}+x+1$ at a value smaller than $\lambda$. Additionally, as $p$ increases, $\lambda^{p}$ approaches 0 , and hence $q$ must increase. For $p=5$ we have $1+w+w^{3}=-w^{2}\left(1+w^{2}\right)$ and hence $G(w)=\prod_{i=1}^{p-1}(1+$ $\left.w^{2 j}\right)=1$. For a zero of $f_{B}(x)$ we have $x^{5}=-x^{3}-x^{2}=-x^{2}+x+1$ and hence $q=\lambda^{5}+\mu^{5}+\nu^{5}=-\left(\lambda^{2}+\mu^{2}+\nu^{2}\right)+(\lambda+\mu+\nu)+3=5$. For $p>5$ we also have $q \geq 6$. Assuming again $F_{B}(x)=1$ and defining $p(x)$ as before, we have $p(-1)<0, p(0)>0, p(2)<0$, and $p(x)>0$ for a sufficiently large $x>2$. It follows that $p(x)$ must have three distinct real roots. However, since $\mu^{p}, \nu^{p} \in \mathbb{R} \Rightarrow \nu^{p}=\overline{\mu^{p}}=\mu^{p}$, it follows that $p(x)$ has at most two real roots, which is a contradiction. Hence, it follows that $F_{B}(x)>1$ for $p>5$ and thus $E(A) \leq E(B)$, where equality holds only for $p=5$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
27. C7 (IRE) Let $p>3$ be a prime number. For each nonempty subset $T$ of $\{0,1,2,3, \ldots, p-1\}$ let $E(T)$ be the set of all $(p-1)$-tuples $\left(x_{1}, \ldots, x_{p-1}\right)$, where each $x_{i} \in T$ and $x_{1}+2 x_{2}+\cdots+(p-1) x_{p-1}$ is divisible by $p$ and let $|E(T)|$ denote the number of elements in $E(T)$. Prove that $$ |E(\{0,1,3\})| \geq|E(\{0,1,2\})|, $$ with equality if and only if $p=5$.
|
27. Denote $A=\{0,1,2\}$ and $B=\{0,1,3\}$. Let $f_{T}(x)=\sum_{a \in T} x^{a}$. Then define $F_{T}(x)=f_{T}(x) f_{T}\left(x^{2}\right) \cdots f_{T}\left(x^{p-1}\right)$. We can write $F_{T}(x)=\sum_{i=0}^{p(p-1)} a_{i} x^{i}$, where $a_{i}$ is the number of ways to select an array $\left\{x_{1}, \ldots, x_{p-1}\right\}$ where $x_{i} \in T$ for all $i$ and $x_{1}+2 x_{2}+\cdots+(p-1) x_{p-1}=i$. Let $w=\cos (2 \pi / p)+$ $i \sin (2 \pi / p)$, a $p$ th root of unity. Noting that $$ 1+w^{j}+w^{2 j}+\cdots+w^{(p-1) j}=\left\{\begin{array}{c} p, p \mid j, \\ 0, p \nmid j, \end{array}\right. $$ it follows that $F_{T}(1)+F_{T}(w)+\cdots+F_{T}\left(w^{p-1}\right)=p E(T)$. Since $|A|=|B|=3$, it follows that $F_{A}(1)=F_{B}(1)=3^{p-1}$. We also have for $p \nmid i, j$ that $F_{T}\left(w^{i}\right)=F_{T}(w)$. Finally, we have $$ F_{A}(w)=\prod_{i=1}^{p-1}\left(1+w^{i}+w^{2 i}\right)=\prod_{i=1}^{p-1} \frac{1-w^{3 i}}{1-w^{i}}=1 $$ Hence, combining these results, we obtain $$ E(A)=\frac{3^{p-1}+p-1}{p} \text { and } E(B)=\frac{3^{p-1}+(p-1) F_{B}(w)}{p} $$ It remains to demonstrate that $F_{B}(w) \geq 1$ for all $p$ and that equality holds only for $p=5$. Since $E(B)$ is an integer, it follows that $F_{B}(w)$ is an integer and $F_{B}(w) \equiv 1(\bmod p)$. Since $f_{B}\left(w^{p-i}\right)=\overline{f_{B}\left(w^{i}\right)}$, it follows that $F_{B}(w)=\left|f_{B}(w)\right|^{2}\left|f_{B}\left(w^{2}\right)\right|^{2} \cdots\left|f_{B}\left(w^{(p-1) / 2}\right)\right|^{2}>0$. Hence $F_{B}(w) \geq 1$. It remains to show that $F_{B}(w)=1$ if and only if $p=5$. We have the formula $(x-w)\left(x-w^{2}\right) \cdots\left(x-w^{p-1}\right)=x^{p-1}+x^{p-2}+\cdots+x+1=\frac{x^{p}-1}{x-1}$. Let $f_{B}(x)=x^{3}+x+1=(x-\lambda)(x-\mu)(x-\nu)$, where $\lambda$, $\mu$, and $\nu$ are the three zeros of the polynomial $f_{B}(x)$. It follows that $F_{B}(w)=\left(\frac{\lambda^{p}-1}{\lambda-1}\right)\left(\frac{\mu^{p}-1}{\mu-1}\right)\left(\frac{\nu^{p}-1}{\nu-1}\right)=-\frac{1}{3}\left(\lambda^{p}-1\right)\left(\mu^{p}-1\right)\left(\nu^{p}-1\right)$, since $(\lambda-1)(\mu-1)(\nu-1)=-f_{B}(1)=-3$. We also have $\lambda+\mu+\nu=0$, $\lambda \mu \nu=-1, \lambda \mu+\lambda \nu+\mu \nu=1$, and $\lambda^{2}+\mu^{2}+\nu^{2}=(\lambda+\mu+\nu)^{2}-2(\lambda \mu+$ $\lambda \nu+\mu \nu)=-2$. By induction (using that $\left(\lambda^{r}+\mu^{r}+\nu^{r}\right)+\left(\lambda^{r-2}+\mu^{r-2}+\right.$ $\left.\nu^{r-2}\right)+\left(\lambda^{r-3}+\mu^{r-3}+\nu^{r-3}\right)=0$ ), it follows that $\lambda^{r}+\mu^{r}+\nu^{r}$ is an integer for all $r \in \mathbb{N}$. Let us assume $F_{B}(x)=1$. It follows that $\left(\lambda^{p}-1\right)\left(\mu^{p}-1\right)\left(\nu^{p}-1\right)=-3$. Hence $\lambda^{p}, \mu^{p}, \nu^{p}$ are roots of the polynomial $p(x)=x^{3}-q x^{2}+(1+q) x+1$, where $q=\lambda^{p}+\mu^{p}+\nu^{p}$. Since $f_{B}(x)$ is an increasing function in real numbers, it follows that it has only one real root (w.l.o.g.) $\lambda$, the other two roots being complex conjugates. From $f_{B}(-1)<0<f_{B}(-1 / 2)$ it follows that $-1<\lambda<-1 / 2$. It also follows that $\lambda^{p}$ is the $x$ coordinate of the intersection of functions $y=x^{3}+x+1$ and $y=q\left(x^{2}-x\right)$. Since $\lambda<\lambda^{p}<0$, it follows that $q>0$; otherwise, $q\left(x^{2}-x\right)$ intersects $x^{3}+x+1$ at a value smaller than $\lambda$. Additionally, as $p$ increases, $\lambda^{p}$ approaches 0 , and hence $q$ must increase. For $p=5$ we have $1+w+w^{3}=-w^{2}\left(1+w^{2}\right)$ and hence $G(w)=\prod_{i=1}^{p-1}(1+$ $\left.w^{2 j}\right)=1$. For a zero of $f_{B}(x)$ we have $x^{5}=-x^{3}-x^{2}=-x^{2}+x+1$ and hence $q=\lambda^{5}+\mu^{5}+\nu^{5}=-\left(\lambda^{2}+\mu^{2}+\nu^{2}\right)+(\lambda+\mu+\nu)+3=5$. For $p>5$ we also have $q \geq 6$. Assuming again $F_{B}(x)=1$ and defining $p(x)$ as before, we have $p(-1)<0, p(0)>0, p(2)<0$, and $p(x)>0$ for a sufficiently large $x>2$. It follows that $p(x)$ must have three distinct real roots. However, since $\mu^{p}, \nu^{p} \in \mathbb{R} \Rightarrow \nu^{p}=\overline{\mu^{p}}=\mu^{p}$, it follows that $p(x)$ has at most two real roots, which is a contradiction. Hence, it follows that $F_{B}(x)>1$ for $p>5$ and thus $E(A) \leq E(B)$, where equality holds only for $p=5$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1c18c375-c349-50c0-9ed1-75940a20e2d9
| 24,939
|
3. N3 (RUS) Prove that there exist two strictly increasing sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ such that $a_{n}\left(a_{n}+1\right)$ divides $b_{n}^{2}+1$ for every natural number $n$.
|
3. We first prove the following lemma. Lemma. For $d, c \in \mathbb{N}$ and $d^{2} \mid c^{2}+1$ there exists $b \in \mathbb{N}$ such that $d^{2}\left(d^{2}+1\right) \mid b^{2}+1$. Proof. It is enough to set $b=c+d^{2} c-d^{3}=c+d^{2}(c-d)$. Using the lemma it suffices to find increasing sequences $d_{n}$ and $c_{n}$ such that $c_{n}-d_{n}$ is an increasing sequence and $d_{n}^{2} \mid c_{n}^{2}+1$. We then obtain the desired sequences $a_{n}$ and $b_{n}$ from $a_{n}=d_{n}^{2}$ and $b_{n}=c_{n}+d_{n}^{2}\left(c_{n}-d_{n}\right)$. It is easy to check that $d_{n}=2^{2 n}+1$ and $c_{n}=2^{n d_{n}}$ satisfy the required conditions. Hence we have demonstrated the existence of increasing sequences $a_{n}$ and $b_{n}$ such that $a_{n}\left(a_{n}+1\right) \mid b_{n}^{2}+1$. Remark. There are many solutions to this problem. For example, it is sufficient to prove that the Pell-type equation $5 a_{n}\left(a_{n}+1\right)=b_{n}^{2}+1$ has an infinity of solutions in positive integers. Alternatively, one can show that $a_{n}\left(a_{n}+1\right)$ can be represented as a sum of two coprime squares for infinitely many $a_{n}$, which implies the existence of $b_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
3. N3 (RUS) Prove that there exist two strictly increasing sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ such that $a_{n}\left(a_{n}+1\right)$ divides $b_{n}^{2}+1$ for every natural number $n$.
|
3. We first prove the following lemma. Lemma. For $d, c \in \mathbb{N}$ and $d^{2} \mid c^{2}+1$ there exists $b \in \mathbb{N}$ such that $d^{2}\left(d^{2}+1\right) \mid b^{2}+1$. Proof. It is enough to set $b=c+d^{2} c-d^{3}=c+d^{2}(c-d)$. Using the lemma it suffices to find increasing sequences $d_{n}$ and $c_{n}$ such that $c_{n}-d_{n}$ is an increasing sequence and $d_{n}^{2} \mid c_{n}^{2}+1$. We then obtain the desired sequences $a_{n}$ and $b_{n}$ from $a_{n}=d_{n}^{2}$ and $b_{n}=c_{n}+d_{n}^{2}\left(c_{n}-d_{n}\right)$. It is easy to check that $d_{n}=2^{2 n}+1$ and $c_{n}=2^{n d_{n}}$ satisfy the required conditions. Hence we have demonstrated the existence of increasing sequences $a_{n}$ and $b_{n}$ such that $a_{n}\left(a_{n}+1\right) \mid b_{n}^{2}+1$. Remark. There are many solutions to this problem. For example, it is sufficient to prove that the Pell-type equation $5 a_{n}\left(a_{n}+1\right)=b_{n}^{2}+1$ has an infinity of solutions in positive integers. Alternatively, one can show that $a_{n}\left(a_{n}+1\right)$ can be represented as a sum of two coprime squares for infinitely many $a_{n}$, which implies the existence of $b_{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
70cf5474-3302-5a56-b6ba-60fa9c22fb74
| 24,942
|
5. N5 (ARM) Let $n, k$ be positive integers such that $n$ is not divisible by 3 and $k \geq n$. Prove that there exists a positive integer $m$ that is divisible by $n$ and the sum of whose digits in decimal representation is $k$.
|
5. Since one can arbitrarily add zeros at the end of $m$, which increases divisibility by 2 and 5 to an arbitrary exponent, it suffices to assume $2,5 \nmid n$. If $(n, 10)=1$, there exists an integer $w \geq 2$ such that $10^{w} \equiv 1(\bmod n)$. We also note that $10^{i w} \equiv 1(\bmod n)$ and $10^{j w+1} \equiv 10(\bmod n)$ for all integers $i$ and $j$. Let us assume that $m$ is of the form $m=\sum_{i=1}^{u} 10^{i w}+\sum_{j=1}^{v} 10^{j w+1}$ for integers $u, v \geq 0$ (where if $u$ or $v$ is 0 , the corresponding sum is 0 ). Obviously, the sum of the digits of $m$ is equal to $u+v$, and also $m \equiv u+10 v(\bmod n)$. Hence our problem reduces to finding integers $u, v \geq 0$ such that $u+v=k$ and $n \mid u+10 v=k+9 v$. Since $(n, 9)=1$, it follows that there exists some $v_{0}$ such that $0 \leq v_{0}<n \leq k$ and $9 v_{0} \equiv$ $-k(\bmod n) \Rightarrow n \mid k+9 v_{0}$. Taking this $v_{0}$ and setting $u_{0}=k-v_{0}$ we obtain the desired parameters for defining $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
5. N5 (ARM) Let $n, k$ be positive integers such that $n$ is not divisible by 3 and $k \geq n$. Prove that there exists a positive integer $m$ that is divisible by $n$ and the sum of whose digits in decimal representation is $k$.
|
5. Since one can arbitrarily add zeros at the end of $m$, which increases divisibility by 2 and 5 to an arbitrary exponent, it suffices to assume $2,5 \nmid n$. If $(n, 10)=1$, there exists an integer $w \geq 2$ such that $10^{w} \equiv 1(\bmod n)$. We also note that $10^{i w} \equiv 1(\bmod n)$ and $10^{j w+1} \equiv 10(\bmod n)$ for all integers $i$ and $j$. Let us assume that $m$ is of the form $m=\sum_{i=1}^{u} 10^{i w}+\sum_{j=1}^{v} 10^{j w+1}$ for integers $u, v \geq 0$ (where if $u$ or $v$ is 0 , the corresponding sum is 0 ). Obviously, the sum of the digits of $m$ is equal to $u+v$, and also $m \equiv u+10 v(\bmod n)$. Hence our problem reduces to finding integers $u, v \geq 0$ such that $u+v=k$ and $n \mid u+10 v=k+9 v$. Since $(n, 9)=1$, it follows that there exists some $v_{0}$ such that $0 \leq v_{0}<n \leq k$ and $9 v_{0} \equiv$ $-k(\bmod n) \Rightarrow n \mid k+9 v_{0}$. Taking this $v_{0}$ and setting $u_{0}=k-v_{0}$ we obtain the desired parameters for defining $m$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2c31e70a-f13c-56b7-a427-7b57d0ff42ca
| 24,947
|
6. N6 (BLR) Prove that for every real number $M$ there exists an infinite arithmetic progression such that: (i) each term is a positive integer and the common difference is not divisible by 10 ; (ii) the sum of the digits of each term (in decimal representation) exceeds $M$.
|
6. Let $N$ be the smallest integer greater than $M$. We take the difference of the numbers in the progression to be of the form $10^{m}+1, m \in \mathbb{N}$. Hence we can take $a_{n}=a_{0}+n\left(10^{m}+1\right)=\overline{b_{s} b_{s-1} \ldots b_{0}}$ where $a_{0}$ is the initial term in the progression and $\overline{b_{s} b_{s-1} \ldots b_{0}}$ is the decimal representation of $a_{n}$. Since $2 m$ is the smallest integer $x$ such that $10^{x} \equiv 1\left(\bmod 10^{m}+1\right)$, it follows that $10^{k} \equiv 10^{l}\left(\bmod 10^{m}+1\right) \Leftrightarrow k \equiv l(\bmod 2 m)$. Hence $$ a_{0} \equiv a_{n}=\overline{b_{s} b_{s-1} \ldots b_{0}} \equiv \sum_{i=0}^{2 m-1} c_{i} 10^{i}\left(\bmod 10^{m}+1\right), $$ where $c_{i}=b_{i}+b_{2 m+i}+b_{4 m+i}+\cdots \geq 0$ for $i=0,1, \ldots, 2 m-1$ (these $c_{i}$ also depend on $n$ ). We note that $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$ is invariant modulo $10^{m}+1$ for all $n$ and that $\sum_{i=0}^{2 m-1} c_{i}=\sum_{j=0}^{s} b_{j}$ for a given $n$. Hence we must choose $a_{0}$ and $m$ such that $a_{0}$ is not congruent to any number of the form $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$, where $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N\left(c_{0}, c_{1}, \ldots, c_{2 m-1} \geq 0\right)$. The number of ways to select the nonnegative integers $c_{0}, c_{1}, \ldots, c_{2 m-1}$ such that $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N$ is equal to the number of strictly increasing sequences $0 \leq c_{0}<c_{0}+c_{1}+1<c_{0}+c_{1}+c_{2}+2+\cdots<$ $c_{0}+c_{1}+\cdots+c_{2 m-1}+2 m-1 \leq N+2 m-1$, which is equal to the number of $2 m$-element subsets of $\{0,1,2, \ldots, N+2 m-1\}$, which is $\binom{N+2 m}{N}$. For sufficiently large $m$ we have $\binom{N+2 m}{N}<10^{m}$, and hence in this case one can select $a_{0}$ such that $a_{0}$ is not congruent to $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$ modulo $10^{m}+1$ for any set of integers $c_{0}, c_{1}, \ldots, c_{2 m-1}$ such that $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N$. Thus we have found the desired arithmetic progression.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
6. N6 (BLR) Prove that for every real number $M$ there exists an infinite arithmetic progression such that: (i) each term is a positive integer and the common difference is not divisible by 10 ; (ii) the sum of the digits of each term (in decimal representation) exceeds $M$.
|
6. Let $N$ be the smallest integer greater than $M$. We take the difference of the numbers in the progression to be of the form $10^{m}+1, m \in \mathbb{N}$. Hence we can take $a_{n}=a_{0}+n\left(10^{m}+1\right)=\overline{b_{s} b_{s-1} \ldots b_{0}}$ where $a_{0}$ is the initial term in the progression and $\overline{b_{s} b_{s-1} \ldots b_{0}}$ is the decimal representation of $a_{n}$. Since $2 m$ is the smallest integer $x$ such that $10^{x} \equiv 1\left(\bmod 10^{m}+1\right)$, it follows that $10^{k} \equiv 10^{l}\left(\bmod 10^{m}+1\right) \Leftrightarrow k \equiv l(\bmod 2 m)$. Hence $$ a_{0} \equiv a_{n}=\overline{b_{s} b_{s-1} \ldots b_{0}} \equiv \sum_{i=0}^{2 m-1} c_{i} 10^{i}\left(\bmod 10^{m}+1\right), $$ where $c_{i}=b_{i}+b_{2 m+i}+b_{4 m+i}+\cdots \geq 0$ for $i=0,1, \ldots, 2 m-1$ (these $c_{i}$ also depend on $n$ ). We note that $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$ is invariant modulo $10^{m}+1$ for all $n$ and that $\sum_{i=0}^{2 m-1} c_{i}=\sum_{j=0}^{s} b_{j}$ for a given $n$. Hence we must choose $a_{0}$ and $m$ such that $a_{0}$ is not congruent to any number of the form $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$, where $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N\left(c_{0}, c_{1}, \ldots, c_{2 m-1} \geq 0\right)$. The number of ways to select the nonnegative integers $c_{0}, c_{1}, \ldots, c_{2 m-1}$ such that $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N$ is equal to the number of strictly increasing sequences $0 \leq c_{0}<c_{0}+c_{1}+1<c_{0}+c_{1}+c_{2}+2+\cdots<$ $c_{0}+c_{1}+\cdots+c_{2 m-1}+2 m-1 \leq N+2 m-1$, which is equal to the number of $2 m$-element subsets of $\{0,1,2, \ldots, N+2 m-1\}$, which is $\binom{N+2 m}{N}$. For sufficiently large $m$ we have $\binom{N+2 m}{N}<10^{m}$, and hence in this case one can select $a_{0}$ such that $a_{0}$ is not congruent to $\sum_{i=0}^{2 m-1} c_{i} 10^{i}$ modulo $10^{m}+1$ for any set of integers $c_{0}, c_{1}, \ldots, c_{2 m-1}$ such that $c_{0}+c_{1}+\cdots+c_{2 m-1} \leq N$. Thus we have found the desired arithmetic progression.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
e9171a83-0f62-5f38-bb2b-8363a615ad75
| 24,950
|
7. G1 (ARM) Let $A B C$ be a triangle and $M$ an interior point. Prove that $$ \min \{M A, M B, M C\}+M A+M B+M C<A B+A C+B C . $$
|
7. We use the following simple lemma. Lemma. Suppose that $M$ is the interior point of a convex quadrilateral $A B C D$. Then it follows that $M A+M B<A D+D C+C B$. Proof. We repeatedly make use of the triangle inequality. The line $A M$, in addition to $A$, intersects the quadrilateral in a second point $N$. In that case $A M+M B<A N+N B<A D+D C+C B$. We now apply this lemma in the following way. Let $D, E$, and $F$ be median points of $B C, A C$, and $A B$. Any point $M$ in the interior of $\triangle A B C$ is contained in at least two of the three convex quadrilaterals $A B D E$, $B C E F$, and $C A F D$. Let us assume without loss of generality that $M$ is in the interior of $B C E F$ and $C A F D$. In that case we apply the lemma to obtain $A M+C M<A F+F D+D C$ and $B M+C M<C E+E F+F B$ to obtain $$ \begin{aligned} C M+A M+B M+C M & <A F+F D+D C+C E+E F+F B \\ & =A B+A C+B C \end{aligned} $$ from which the required conclusion immediately follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
7. G1 (ARM) Let $A B C$ be a triangle and $M$ an interior point. Prove that $$ \min \{M A, M B, M C\}+M A+M B+M C<A B+A C+B C . $$
|
7. We use the following simple lemma. Lemma. Suppose that $M$ is the interior point of a convex quadrilateral $A B C D$. Then it follows that $M A+M B<A D+D C+C B$. Proof. We repeatedly make use of the triangle inequality. The line $A M$, in addition to $A$, intersects the quadrilateral in a second point $N$. In that case $A M+M B<A N+N B<A D+D C+C B$. We now apply this lemma in the following way. Let $D, E$, and $F$ be median points of $B C, A C$, and $A B$. Any point $M$ in the interior of $\triangle A B C$ is contained in at least two of the three convex quadrilaterals $A B D E$, $B C E F$, and $C A F D$. Let us assume without loss of generality that $M$ is in the interior of $B C E F$ and $C A F D$. In that case we apply the lemma to obtain $A M+C M<A F+F D+D C$ and $B M+C M<C E+E F+F B$ to obtain $$ \begin{aligned} C M+A M+B M+C M & <A F+F D+D C+C E+E F+F B \\ & =A B+A C+B C \end{aligned} $$ from which the required conclusion immediately follows.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
cdeb8c40-7ae2-5069-9354-ba37db9b5943
| 24,953
|
8. G2 (JAP) A circle is called a separator for a set of five points in a plane if it passes through three of these points, it contains a fourth point in its interior, and the fifth point is outside the circle. Prove that every set of five points such that no three are collinear and no four are concyclic has exactly four separators.
|
8. Let $A, B, C$, and $D$ be inverses of four of the five points, with the fifth point being the pole of the inversion. A separator through the pole transforms into a line containing two of the remaining four points such that the remaining two points are on opposite sides of the line. A separator not containing the pole transforms into a circle through three of the points with the fourth point in its interior. Let $K$ be the convex hull of $A, B, C$, and $D$. We observe two cases: (i) $K$ is a quadrilateral, for example $A B C D$. In that case the four separators are the two diagonals and two circles $A B C$ and $A D C$ if $\angle A+\angle C<180^{\circ}$, or $B A D$ and $B C D$ otherwise. The remaining six viable circles and lines are clearly not separators. (ii) $K$ is a triangle, for example $A B C$ with $D$ in its interior. In that case the separators are lines $D A, D B, D C$ and the circle $A B C$. No other lines and circles qualify. We have thus shown that any set of five points satisfying the stated conditions will have exactly four separators.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. G2 (JAP) A circle is called a separator for a set of five points in a plane if it passes through three of these points, it contains a fourth point in its interior, and the fifth point is outside the circle. Prove that every set of five points such that no three are collinear and no four are concyclic has exactly four separators.
|
8. Let $A, B, C$, and $D$ be inverses of four of the five points, with the fifth point being the pole of the inversion. A separator through the pole transforms into a line containing two of the remaining four points such that the remaining two points are on opposite sides of the line. A separator not containing the pole transforms into a circle through three of the points with the fourth point in its interior. Let $K$ be the convex hull of $A, B, C$, and $D$. We observe two cases: (i) $K$ is a quadrilateral, for example $A B C D$. In that case the four separators are the two diagonals and two circles $A B C$ and $A D C$ if $\angle A+\angle C<180^{\circ}$, or $B A D$ and $B C D$ otherwise. The remaining six viable circles and lines are clearly not separators. (ii) $K$ is a triangle, for example $A B C$ with $D$ in its interior. In that case the separators are lines $D A, D B, D C$ and the circle $A B C$. No other lines and circles qualify. We have thus shown that any set of five points satisfying the stated conditions will have exactly four separators.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
92a7bf63-5c91-5585-8f21-c970c1f29e89
| 24,955
|
9. G3 (EST) ${ }^{\mathrm{IMO} 1}$ A set $S$ of points in space will be called completely symmetric if it has at least three elements and satisfies the following condition: For every two distinct points $A, B$ from $S$ the perpendicular bisector of the segment $A B$ is an axis of symmetry for $S$. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, a regular tetrahedron, or a regular octahedron.
|
9. Let $r_{P Q}$ denote a reflection about the planar bisector of $P Q$ with $P, Q \in S$. Let $G$ be the centroid of $S$. From $r_{P Q}(S)=S$ it follows that $r_{P Q}(G)=G$. Hence $G$ belongs to the perpendicular bisector of $P Q$ and thus $G P=G Q$. Consequently the whole of $S$ lies on a sphere $\Sigma$ centered at $G$. We note the following two cases: (a) $S$ is a subset of a plane $\pi$. In this case $S$ is included in a circle $k, G$ being its center. Hence its $n$ points form a convex polygon $A_{1} A_{2} \ldots A_{n}$. When applying $r_{A_{i} A_{i+2}}$ for some $0<i<n-1$ the point $A_{i+1}$ transforms into some point of $S$ lying on the same side of $A_{i} A_{i+1}$, which has to be $A_{i+1}$ itself. It thus follows that $A_{i} A_{i+1}=A_{i+1} A_{i+2}$ for all $0<i<n-1$ and hence $A_{1} A_{2} \ldots A_{n}$ is a regular $n$-gon. (b) The points in $S$ are not coplanar. It follows that $S$ is a polyhedron $P$ inscribed in a sphere $\Sigma$ centered at $G$. By applying the previous case to the faces of the polyhedron, it follows that all faces are regular $n$-gons. Let us take an arbitrary vertex $V$ and let $V V_{1}, V V_{2}$ and $V V_{3}$ be three consecutive edges stemming from $V\left(V, V_{1}, V_{2}\right.$, and $V_{3}$ defining two adjacent faces of $P$ ). We now look at $r_{V_{1} V_{3}}$. Since this transformation leaves the half-planes $\left[V_{1} V_{3}, V_{2}\right.$ and $\left[V_{1} V_{3}, V\right.$ invariant and since $V_{2}$ and $V$ are the only points of $P$ on the respective half-planes, it follows that $r_{V_{1} V_{3}}$ leaves $V$ and $V_{2}$ invariant. This transform also swaps $V_{1}$ and $V_{3}$. Hence, the face determined by $V V_{1} V_{2}$ is transformed by $r_{V_{1} V_{3}}$ into the face $V V_{3} V_{2}$, and thus the two faces sharing $V V_{2}$ are congruent. We conclude that all faces are congruent and similarly that vertices are endpoints of the same number of edges; hence $P$ is a regular polyhedron. Finally, we have to rule out $S$ being vertices of a cube, a dodecahedron, or an icosahedron. In all of these cases if we select two diametrically opposite points $P$ and $Q$, then $S \backslash\{P, Q\}$ is not symmetric with respect to the bisector of $P Q$, which prevents $r_{P Q}$ from being an invariant transformation of $S$. It thus follows that the only viable finite completely symmetric sets are vertices of regular $n$-gons, the tetrahedron, and the octahedron. It is not explicitly asked for, but it is easy to verify that all of these are indeed completely symmetric. Remark. On the IMO, a simpler version of this problem was adopted, adding the condition that $S$ belongs to a plane and thus eliminating the need for the second case altogether.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
9. G3 (EST) ${ }^{\mathrm{IMO} 1}$ A set $S$ of points in space will be called completely symmetric if it has at least three elements and satisfies the following condition: For every two distinct points $A, B$ from $S$ the perpendicular bisector of the segment $A B$ is an axis of symmetry for $S$. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, a regular tetrahedron, or a regular octahedron.
|
9. Let $r_{P Q}$ denote a reflection about the planar bisector of $P Q$ with $P, Q \in S$. Let $G$ be the centroid of $S$. From $r_{P Q}(S)=S$ it follows that $r_{P Q}(G)=G$. Hence $G$ belongs to the perpendicular bisector of $P Q$ and thus $G P=G Q$. Consequently the whole of $S$ lies on a sphere $\Sigma$ centered at $G$. We note the following two cases: (a) $S$ is a subset of a plane $\pi$. In this case $S$ is included in a circle $k, G$ being its center. Hence its $n$ points form a convex polygon $A_{1} A_{2} \ldots A_{n}$. When applying $r_{A_{i} A_{i+2}}$ for some $0<i<n-1$ the point $A_{i+1}$ transforms into some point of $S$ lying on the same side of $A_{i} A_{i+1}$, which has to be $A_{i+1}$ itself. It thus follows that $A_{i} A_{i+1}=A_{i+1} A_{i+2}$ for all $0<i<n-1$ and hence $A_{1} A_{2} \ldots A_{n}$ is a regular $n$-gon. (b) The points in $S$ are not coplanar. It follows that $S$ is a polyhedron $P$ inscribed in a sphere $\Sigma$ centered at $G$. By applying the previous case to the faces of the polyhedron, it follows that all faces are regular $n$-gons. Let us take an arbitrary vertex $V$ and let $V V_{1}, V V_{2}$ and $V V_{3}$ be three consecutive edges stemming from $V\left(V, V_{1}, V_{2}\right.$, and $V_{3}$ defining two adjacent faces of $P$ ). We now look at $r_{V_{1} V_{3}}$. Since this transformation leaves the half-planes $\left[V_{1} V_{3}, V_{2}\right.$ and $\left[V_{1} V_{3}, V\right.$ invariant and since $V_{2}$ and $V$ are the only points of $P$ on the respective half-planes, it follows that $r_{V_{1} V_{3}}$ leaves $V$ and $V_{2}$ invariant. This transform also swaps $V_{1}$ and $V_{3}$. Hence, the face determined by $V V_{1} V_{2}$ is transformed by $r_{V_{1} V_{3}}$ into the face $V V_{3} V_{2}$, and thus the two faces sharing $V V_{2}$ are congruent. We conclude that all faces are congruent and similarly that vertices are endpoints of the same number of edges; hence $P$ is a regular polyhedron. Finally, we have to rule out $S$ being vertices of a cube, a dodecahedron, or an icosahedron. In all of these cases if we select two diametrically opposite points $P$ and $Q$, then $S \backslash\{P, Q\}$ is not symmetric with respect to the bisector of $P Q$, which prevents $r_{P Q}$ from being an invariant transformation of $S$. It thus follows that the only viable finite completely symmetric sets are vertices of regular $n$-gons, the tetrahedron, and the octahedron. It is not explicitly asked for, but it is easy to verify that all of these are indeed completely symmetric. Remark. On the IMO, a simpler version of this problem was adopted, adding the condition that $S$ belongs to a plane and thus eliminating the need for the second case altogether.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
60a9f6f9-478c-593e-aa16-5b708cd11773
| 24,957
|
10. A4 (GBR) The function $F$ is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: For every $n \geq 0$, (i) $F(4 n)=F(2 n)+F(n)$; (ii) $F(4 n+2)=F(4 n)+1$; (iii) $F(2 n+1)=F(2 n)+1$. Prove that for each positive integer $m$, the number of integers $n$ with $0 \leq n<2^{m}$ and $F(4 n)=F(3 n)$ is $F\left(2^{m+1}\right)$.
|
10. Clearly $F(0)=0$ by (i). Moreover, it follows by induction from (i) that $F\left(2^{n}\right)=f_{n+1}$ where $f_{n}$ denotes the $n$th Fibonacci's number. In general, if $n=\epsilon_{k} 2^{k}+\epsilon_{k-1} 2^{k-1}+\cdots+\epsilon_{1} \cdot 2+\epsilon_{0}$ (where $\epsilon_{i} \in\{0,1\}$ ), it is straightforward to verify that $$ F(n)=\epsilon_{k} f_{k+1}+\epsilon_{k-1} f_{k}+\cdots+\epsilon_{1} f_{2}+\epsilon_{0} f_{1} $$ We observe that if the binary representation of $n$ contains no two adjacent ones, then $F(3 n)=F(4 n)$. Indeed, if $n=\epsilon_{k_{r}} 2^{k_{r}}+\cdots+\epsilon_{k_{0}} 2^{k_{0}}$, where $k_{i+1}-k_{i} \geq 2$ for all $i$, then $3 n=\epsilon_{k_{r}}\left(2^{k_{r}+1}+2^{k_{r}}\right)+\cdots+\epsilon_{k_{0}}\left(2^{k_{0}+1}+2^{k_{0}}\right)$. According to this, in computing $F(3 n)$ each $f_{i+1}$ in (1) is replaced by $f_{i+1}+f_{i+2}=f_{i+3}$, leading to the value of $F(4 n)$. We shall prove the converse: $F(3 n) \leq F(4 n)$ holds for all $n \geq 0$, with equality if and only if the binary representation of $n$ contains no two adjacent ones. We prove by induction on $m \geq 1$ that this holds for all $n$ satisfying $0 \leq n<$ $2^{m}$. The verification for the early values of $m$ is direct. Assume it is true for a certain $m$ and let $2^{m} \leq n \leq 2^{n+1}$. If $n=2^{m}+p, 0 \leq p<2^{m}$, then (1) implies $F(4 n)=F\left(2^{m+2}+4 p\right)=f_{m+3}+F(4 p)$. Now we distinguish three cases: (i) If $3 p<2^{m}$, then the binary representation of $3 p$ does not carry into that of $3 \cdot 2^{m}$. Then it follows from (1) and the induction hypothesis that $F(3 n)=F\left(3 \cdot 2^{m}\right)+F(3 p)=f_{m+3}+F(3 p) \leq f_{m+3}+F(4 p)=F(4 n)$. Equality holds if and only if $F(3 p)=F(4 p)$, i.e. $p$ has no two adjacent binary ones. (ii) If $2^{m} \leq 3 p<2^{m+1}$, then the binary representation of $3 p$ carries 1 into that of $3 \cdot 2^{m}$. Thus $F(3 n)=f_{m+3}+\left(F(3 p)-f_{m+1}\right)=f_{m+2}+F(3 p)<$ $f_{m+3}+F(4 p)=F(4 n)$. (iii) If $2^{m+1} \leq p<3 \cdot 2^{m}$, then the binary representation of $3 p$ caries 10 into that of $3 \cdot 2^{m}$, which implies $$ F(3 n)=f_{m+3}+f_{m+1}+\left(F(3 p)-f_{m+2}\right)=2 f_{m+1}+F(3 p)<F(4 n) . $$ It remains to compute the number of integers in $\left[0,2^{m}\right)$ with no two adjacent binary 1's. Denote their number by $u_{m}$. Among them there are $u_{m-1}$ less than $2^{m-1}$ and $u_{m-2}$ in the segment $\left[2^{m-1}, 2^{m}\right)$. Hence $u_{m}=u_{m-1}+u_{m-2}$ for $m \geq 3$. Since $u_{1}=2=f_{3}, u_{2}=3=f_{4}$, we conclude that $u_{m}=f_{m+2}=F\left(2^{m+1}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
10. A4 (GBR) The function $F$ is defined on the set of nonnegative integers and takes nonnegative integer values satisfying the following conditions: For every $n \geq 0$, (i) $F(4 n)=F(2 n)+F(n)$; (ii) $F(4 n+2)=F(4 n)+1$; (iii) $F(2 n+1)=F(2 n)+1$. Prove that for each positive integer $m$, the number of integers $n$ with $0 \leq n<2^{m}$ and $F(4 n)=F(3 n)$ is $F\left(2^{m+1}\right)$.
|
10. Clearly $F(0)=0$ by (i). Moreover, it follows by induction from (i) that $F\left(2^{n}\right)=f_{n+1}$ where $f_{n}$ denotes the $n$th Fibonacci's number. In general, if $n=\epsilon_{k} 2^{k}+\epsilon_{k-1} 2^{k-1}+\cdots+\epsilon_{1} \cdot 2+\epsilon_{0}$ (where $\epsilon_{i} \in\{0,1\}$ ), it is straightforward to verify that $$ F(n)=\epsilon_{k} f_{k+1}+\epsilon_{k-1} f_{k}+\cdots+\epsilon_{1} f_{2}+\epsilon_{0} f_{1} $$ We observe that if the binary representation of $n$ contains no two adjacent ones, then $F(3 n)=F(4 n)$. Indeed, if $n=\epsilon_{k_{r}} 2^{k_{r}}+\cdots+\epsilon_{k_{0}} 2^{k_{0}}$, where $k_{i+1}-k_{i} \geq 2$ for all $i$, then $3 n=\epsilon_{k_{r}}\left(2^{k_{r}+1}+2^{k_{r}}\right)+\cdots+\epsilon_{k_{0}}\left(2^{k_{0}+1}+2^{k_{0}}\right)$. According to this, in computing $F(3 n)$ each $f_{i+1}$ in (1) is replaced by $f_{i+1}+f_{i+2}=f_{i+3}$, leading to the value of $F(4 n)$. We shall prove the converse: $F(3 n) \leq F(4 n)$ holds for all $n \geq 0$, with equality if and only if the binary representation of $n$ contains no two adjacent ones. We prove by induction on $m \geq 1$ that this holds for all $n$ satisfying $0 \leq n<$ $2^{m}$. The verification for the early values of $m$ is direct. Assume it is true for a certain $m$ and let $2^{m} \leq n \leq 2^{n+1}$. If $n=2^{m}+p, 0 \leq p<2^{m}$, then (1) implies $F(4 n)=F\left(2^{m+2}+4 p\right)=f_{m+3}+F(4 p)$. Now we distinguish three cases: (i) If $3 p<2^{m}$, then the binary representation of $3 p$ does not carry into that of $3 \cdot 2^{m}$. Then it follows from (1) and the induction hypothesis that $F(3 n)=F\left(3 \cdot 2^{m}\right)+F(3 p)=f_{m+3}+F(3 p) \leq f_{m+3}+F(4 p)=F(4 n)$. Equality holds if and only if $F(3 p)=F(4 p)$, i.e. $p$ has no two adjacent binary ones. (ii) If $2^{m} \leq 3 p<2^{m+1}$, then the binary representation of $3 p$ carries 1 into that of $3 \cdot 2^{m}$. Thus $F(3 n)=f_{m+3}+\left(F(3 p)-f_{m+1}\right)=f_{m+2}+F(3 p)<$ $f_{m+3}+F(4 p)=F(4 n)$. (iii) If $2^{m+1} \leq p<3 \cdot 2^{m}$, then the binary representation of $3 p$ caries 10 into that of $3 \cdot 2^{m}$, which implies $$ F(3 n)=f_{m+3}+f_{m+1}+\left(F(3 p)-f_{m+2}\right)=2 f_{m+1}+F(3 p)<F(4 n) . $$ It remains to compute the number of integers in $\left[0,2^{m}\right)$ with no two adjacent binary 1's. Denote their number by $u_{m}$. Among them there are $u_{m-1}$ less than $2^{m-1}$ and $u_{m-2}$ in the segment $\left[2^{m-1}, 2^{m}\right)$. Hence $u_{m}=u_{m-1}+u_{m-2}$ for $m \geq 3$. Since $u_{1}=2=f_{3}, u_{2}=3=f_{4}$, we conclude that $u_{m}=f_{m+2}=F\left(2^{m+1}\right)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ac01acef-f671-591e-b84e-2be772d30268
| 24,963
|
11. A5 (BLR) ${ }^{\mathrm{IMO} 3}$ Let $n \geq 2$ be a positive integer and $\lambda$ a positive real number. Initially there are $n$ fleas on a horizontal line, not all at the same point. We define a move of choosing two fleas at some points $A$ and $B$, with $A$ to the left of $B$, and letting the flea from $A$ jump over the flea from $B$ to the point $C$ such that $B C / A B=\lambda$. Determine all values of $\lambda$ such that for any point $M$ on the line and for any initial position of the $n$ fleas, there exists a sequence of moves that will take them all to the position right of $M$.
|
11. We claim that for $\lambda \geq \frac{1}{n-1}$ we can take all fleas as far to the right as we want. In every turn we choose the leftmost flea and let it jump over the rightmost one. Let $d$ and $\delta$ denote the maximal and the minimal distances between two fleas at some moment. Clearly, $d \geq(n-1) \delta$. After the leftmost flea jumps over the rightmost one, the minimal distance does not decrease, because $\lambda d \geq \delta$. However, the position of the leftmost flea moved to the right by at least $\delta$, and consequently we can move the fleas arbitrarily far to the right after a finite number of moves. Suppose now that $\lambda<\frac{1}{n-1}$. Under this assumption we shall prove that there is a number $M$ that cannot be reached by any flea. Let us assign to each flea the coordinate on the real axis in which it is settled. Denote by $s_{k}$ the sum of all the numbers in the $k$ th step, and by $w_{k}$ the coordinate of the rightmost flea. Clearly, $s_{k} \leq n w_{k}$. We claim that the sequence $w_{k}$ is bounded. In the $(k+1)$ th move let a flea $A$ jump over $B$, landing at $C$, and let $a, b, c$ be their respective coordinates. We have $s_{k+1}-s_{k}=c-a$. Then by the given rule, $\lambda(b-a)=c-b=s_{k+1}-s_{k}+a-b$, which implies $s_{k+1}-s_{k}=$ $(1+\lambda)(b-a)=\frac{1+\lambda}{\lambda}(c-b)$. Hence $s_{k+1}-s_{k} \geq \frac{1+\lambda}{\lambda}\left(w_{k+1}-w_{k}\right)$. Summing up these inequalities for $k=0, \ldots, n-1$ yields $s_{n}-s_{0} \geq \frac{1+\lambda}{\lambda}\left(w_{n}-w_{0}\right)$. Now using $s_{n} \leq n w_{n}$ we conclude that $$ \left(\frac{1+\lambda}{\lambda}-n\right) w_{n} \leq \frac{1+\lambda}{\lambda} w_{0}-s_{0} . $$ Since $\frac{1+\lambda}{\lambda}-n>0$, this proves the result.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
11. A5 (BLR) ${ }^{\mathrm{IMO} 3}$ Let $n \geq 2$ be a positive integer and $\lambda$ a positive real number. Initially there are $n$ fleas on a horizontal line, not all at the same point. We define a move of choosing two fleas at some points $A$ and $B$, with $A$ to the left of $B$, and letting the flea from $A$ jump over the flea from $B$ to the point $C$ such that $B C / A B=\lambda$. Determine all values of $\lambda$ such that for any point $M$ on the line and for any initial position of the $n$ fleas, there exists a sequence of moves that will take them all to the position right of $M$.
|
11. We claim that for $\lambda \geq \frac{1}{n-1}$ we can take all fleas as far to the right as we want. In every turn we choose the leftmost flea and let it jump over the rightmost one. Let $d$ and $\delta$ denote the maximal and the minimal distances between two fleas at some moment. Clearly, $d \geq(n-1) \delta$. After the leftmost flea jumps over the rightmost one, the minimal distance does not decrease, because $\lambda d \geq \delta$. However, the position of the leftmost flea moved to the right by at least $\delta$, and consequently we can move the fleas arbitrarily far to the right after a finite number of moves. Suppose now that $\lambda<\frac{1}{n-1}$. Under this assumption we shall prove that there is a number $M$ that cannot be reached by any flea. Let us assign to each flea the coordinate on the real axis in which it is settled. Denote by $s_{k}$ the sum of all the numbers in the $k$ th step, and by $w_{k}$ the coordinate of the rightmost flea. Clearly, $s_{k} \leq n w_{k}$. We claim that the sequence $w_{k}$ is bounded. In the $(k+1)$ th move let a flea $A$ jump over $B$, landing at $C$, and let $a, b, c$ be their respective coordinates. We have $s_{k+1}-s_{k}=c-a$. Then by the given rule, $\lambda(b-a)=c-b=s_{k+1}-s_{k}+a-b$, which implies $s_{k+1}-s_{k}=$ $(1+\lambda)(b-a)=\frac{1+\lambda}{\lambda}(c-b)$. Hence $s_{k+1}-s_{k} \geq \frac{1+\lambda}{\lambda}\left(w_{k+1}-w_{k}\right)$. Summing up these inequalities for $k=0, \ldots, n-1$ yields $s_{n}-s_{0} \geq \frac{1+\lambda}{\lambda}\left(w_{n}-w_{0}\right)$. Now using $s_{n} \leq n w_{n}$ we conclude that $$ \left(\frac{1+\lambda}{\lambda}-n\right) w_{n} \leq \frac{1+\lambda}{\lambda} w_{0}-s_{0} . $$ Since $\frac{1+\lambda}{\lambda}-n>0$, this proves the result.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
98cda0eb-2d50-599c-9cc1-8fe229834589
| 24,966
|
12. A6 (IRE) A nonempty set $A$ of real numbers is called a $B_{3}$-set if the conditions $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6} \in A$ and $a_{1}+a_{2}+a_{3}=a_{4}+a_{5}+a_{6}$ imply that the sequences $\left(a_{1}, a_{2}, a_{3}\right)$ and $\left(a_{4}, a_{5}, a_{6}\right)$ are identical up to a permutation. Let $A=\left\{a_{0}=0<a_{1}<a_{2}<\cdots\right\}, B=\left\{b_{0}=0<b_{1}<b_{2}<\cdots\right\}$ be infinite sequences of real numbers with $D(A)=D(B)$, where, for a set $X$ of real numbers, $D(X)$ denotes the difference set $\{|x-y| \mid x, y \in X\}$. Prove that if $A$ is a $B_{3}$-set, then $A=B$.
|
12. Since $D(A)=D(B)$, we can define $f(i)>g(i) \geq 0$ that satisfy $b_{i}-b_{i-1}=$ $a_{f(i)}-a_{g(i)}$ for all $i$. The number $b_{i+1}-b_{i-1} \in D(B)=D(A)$ can be written in the form $a_{u}-a_{v}, u>v \geq 0$. Then $b_{i+1}-b_{i-1}=b_{i+1}-b_{i}+b_{i}-b_{i-1}$ implies $a_{f(i+1)}+a_{f(i)}+a_{v}=a_{g(i+1)}+a_{g(i)}+a_{u}$, so the $B_{3}$ property of $A$ implies that $(f(i+1), f(i), v)$ and $(g(i+1), g(i), u)$ coincide up to a permutation. It follows that either $f(i+1)=g(i)$ or $f(i)=g(i+1)$. Hence if we define $R=\left\{i \in \mathbb{N}_{0} \mid f(i+1)=g(i)\right\}$ and $S=\left\{i \in \mathbb{N}_{0} \mid f(i)=g(i+1)\right\}$ it holds that $R \cup S=\mathbb{N}_{0}$. Lemma. If $i \in R$, then also $i+1 \in R$. Proof. Suppose to the contrary that $i \in R$ and $i+1 \in S$, i.e., $g(i)=$ $f(i+1)=g(i+2)$. There are integers $x$ and $y$ such that $b_{i+2}-b_{i-1}=$ $a_{x}-a_{y}$. Then $a_{x}-a_{y}=a_{f(i+2)}-a_{g(i+2)}+a_{f(i+1)}-a_{g(i+1)}+a_{f(i)}-$ $a_{g(i)}=a_{f(i+2)}+a_{f(i)}-a_{g(i+1)}-a_{g(i)}$, so by the $B_{3}$ property $(x, g(i+$ $1), g(i))$ and $(y, f(i+2), f(i))$ coincide up to a permutation. But this is impossible, since $f(i+2), f(i)>g(i+2)=g(i)=f(i+1)>g(i+1)$. This proves the lemma. Therefore if $i \in R \neq \emptyset$, then it follows that every $j>i$ belongs to $R$. Consequently $g(i)=f(i+1)>g(i+1)=f(i+2)>g(i+2)=f(i+3)>$ $\cdots$ is an infinite decreasing sequence of nonnegative integers, which is impossible. Hence $S=\mathbb{N}_{0}$, i.e., $$ b_{i+1}-b_{i}=a_{f(i+1)}-a_{f(i)} \quad \text { for all } i \in \mathbb{N}_{0} $$ Thus $f(0)=g(1)<f(1)<f(2)<\cdots$, implying $f(i) \geq i$. On the other hand, for any $i$ there exist $j, k$ such that $a_{f(i)}-a_{i}=b_{j}-b_{k}=a_{f(j)}-a_{f(k)}$, so by the $B_{3}$ property $i \in\{f(i), f(k)\}$ is a value of $f$. Hence we must have $f(i)=i$ for all $i$, which finally gives $A=B$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
12. A6 (IRE) A nonempty set $A$ of real numbers is called a $B_{3}$-set if the conditions $a_{1}, a_{2}, a_{3}, a_{4}, a_{5}, a_{6} \in A$ and $a_{1}+a_{2}+a_{3}=a_{4}+a_{5}+a_{6}$ imply that the sequences $\left(a_{1}, a_{2}, a_{3}\right)$ and $\left(a_{4}, a_{5}, a_{6}\right)$ are identical up to a permutation. Let $A=\left\{a_{0}=0<a_{1}<a_{2}<\cdots\right\}, B=\left\{b_{0}=0<b_{1}<b_{2}<\cdots\right\}$ be infinite sequences of real numbers with $D(A)=D(B)$, where, for a set $X$ of real numbers, $D(X)$ denotes the difference set $\{|x-y| \mid x, y \in X\}$. Prove that if $A$ is a $B_{3}$-set, then $A=B$.
|
12. Since $D(A)=D(B)$, we can define $f(i)>g(i) \geq 0$ that satisfy $b_{i}-b_{i-1}=$ $a_{f(i)}-a_{g(i)}$ for all $i$. The number $b_{i+1}-b_{i-1} \in D(B)=D(A)$ can be written in the form $a_{u}-a_{v}, u>v \geq 0$. Then $b_{i+1}-b_{i-1}=b_{i+1}-b_{i}+b_{i}-b_{i-1}$ implies $a_{f(i+1)}+a_{f(i)}+a_{v}=a_{g(i+1)}+a_{g(i)}+a_{u}$, so the $B_{3}$ property of $A$ implies that $(f(i+1), f(i), v)$ and $(g(i+1), g(i), u)$ coincide up to a permutation. It follows that either $f(i+1)=g(i)$ or $f(i)=g(i+1)$. Hence if we define $R=\left\{i \in \mathbb{N}_{0} \mid f(i+1)=g(i)\right\}$ and $S=\left\{i \in \mathbb{N}_{0} \mid f(i)=g(i+1)\right\}$ it holds that $R \cup S=\mathbb{N}_{0}$. Lemma. If $i \in R$, then also $i+1 \in R$. Proof. Suppose to the contrary that $i \in R$ and $i+1 \in S$, i.e., $g(i)=$ $f(i+1)=g(i+2)$. There are integers $x$ and $y$ such that $b_{i+2}-b_{i-1}=$ $a_{x}-a_{y}$. Then $a_{x}-a_{y}=a_{f(i+2)}-a_{g(i+2)}+a_{f(i+1)}-a_{g(i+1)}+a_{f(i)}-$ $a_{g(i)}=a_{f(i+2)}+a_{f(i)}-a_{g(i+1)}-a_{g(i)}$, so by the $B_{3}$ property $(x, g(i+$ $1), g(i))$ and $(y, f(i+2), f(i))$ coincide up to a permutation. But this is impossible, since $f(i+2), f(i)>g(i+2)=g(i)=f(i+1)>g(i+1)$. This proves the lemma. Therefore if $i \in R \neq \emptyset$, then it follows that every $j>i$ belongs to $R$. Consequently $g(i)=f(i+1)>g(i+1)=f(i+2)>g(i+2)=f(i+3)>$ $\cdots$ is an infinite decreasing sequence of nonnegative integers, which is impossible. Hence $S=\mathbb{N}_{0}$, i.e., $$ b_{i+1}-b_{i}=a_{f(i+1)}-a_{f(i)} \quad \text { for all } i \in \mathbb{N}_{0} $$ Thus $f(0)=g(1)<f(1)<f(2)<\cdots$, implying $f(i) \geq i$. On the other hand, for any $i$ there exist $j, k$ such that $a_{f(i)}-a_{i}=b_{j}-b_{k}=a_{f(j)}-a_{f(k)}$, so by the $B_{3}$ property $i \in\{f(i), f(k)\}$ is a value of $f$. Hence we must have $f(i)=i$ for all $i$, which finally gives $A=B$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
867e2f04-33a5-5a13-8e02-1c5b9186315d
| 24,968
|
18. N5 (BUL) Prove that there exist infinitely many positive integers $n$ such that $p=n r$, where $p$ and $r$ are respectively the semiperimeter and the inradius of a triangle with integer side lengths.
|
18. It is known that the area of the triangle is $S=p r=p^{2} / n$ and $S=$ $\sqrt{p(p-a)(p-b)(p-c)}$. It follows that $p^{3}=n^{2}(p-a)(p-b)(p-c)$, which by putting $x=p-a, y=p-b$, and $z=p-c$ transforms into $$ (x+y+z)^{3}=n^{2} x y z . $$ We will be done if we show that (1) has a solution in positive integers for infinitely many natural numbers $n$. Let us assume that $z=k(x+y)$ for an integer $k>0$. Then (1) becomes $(k+1)^{3}(x+y)^{2}=k n^{2} x y$. Further, by setting $n=3(k+1)$ this equation reduces to $$ (k+1)(x+y)^{2}=9 k x y $$ Set $t=x / y$. Then (2) has solutions in positive integers if and only if $(k+$ 1) $(t+1)^{2}=9 k t$ has a rational solution, i.e., if and only if its discriminant $D=k(5 k-4)$ is a perfect square. Setting $k=u^{2}$, we are led to show that $5 u^{2}-4=v^{2}$ has infinitely many integer solutions. But this is a classic Pell-type equation, whose solution is every Fibonacci number $u=F_{2 i+1}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
18. N5 (BUL) Prove that there exist infinitely many positive integers $n$ such that $p=n r$, where $p$ and $r$ are respectively the semiperimeter and the inradius of a triangle with integer side lengths.
|
18. It is known that the area of the triangle is $S=p r=p^{2} / n$ and $S=$ $\sqrt{p(p-a)(p-b)(p-c)}$. It follows that $p^{3}=n^{2}(p-a)(p-b)(p-c)$, which by putting $x=p-a, y=p-b$, and $z=p-c$ transforms into $$ (x+y+z)^{3}=n^{2} x y z . $$ We will be done if we show that (1) has a solution in positive integers for infinitely many natural numbers $n$. Let us assume that $z=k(x+y)$ for an integer $k>0$. Then (1) becomes $(k+1)^{3}(x+y)^{2}=k n^{2} x y$. Further, by setting $n=3(k+1)$ this equation reduces to $$ (k+1)(x+y)^{2}=9 k x y $$ Set $t=x / y$. Then (2) has solutions in positive integers if and only if $(k+$ 1) $(t+1)^{2}=9 k t$ has a rational solution, i.e., if and only if its discriminant $D=k(5 k-4)$ is a perfect square. Setting $k=u^{2}$, we are led to show that $5 u^{2}-4=v^{2}$ has infinitely many integer solutions. But this is a classic Pell-type equation, whose solution is every Fibonacci number $u=F_{2 i+1}$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
dac665a2-cf10-5217-af5b-32f13231e6a3
| 24,984
|
19. N6 (ROM) Show that the set of positive integers that cannot be represented as a sum of distinct perfect squares is finite.
|
19. Suppose that a natural number $N$ satisfies $N=a_{1}^{2}+\cdots+a_{k}^{2}, 2 N=$ $b_{1}^{2}+\cdots+b_{l}^{2}$, where $a_{i}, b_{j}$ are natural numbers such that none of the ratios $a_{i} / a_{j}, b_{i} / b_{j}, a_{i} / b_{j}, b_{j} / a_{i}$ is a power of 2. We claim that every natural number $n>\sum_{i=0}^{4 N-2}(2 i N+1)^{2}$ can be represented as a sum of distinct squares. Suppose $n=4 q N+r, 0 \leq r<4 N$. Then $$ n=4 N s+\sum_{i=0}^{r-1}(2 i N+1)^{2} $$ for some positive integer $s$, so it is enough to show that $4 N s$ is a sum of distinct even squares. Let $s=\sum_{c=1}^{C} 2^{2 u_{c}}+\sum_{d=1}^{D} 2^{2 v_{d}+1}$ be the binary expansion of $s$. Then $$ 4 N s=\sum_{c=1}^{C} \sum_{i=1}^{k}\left(2^{u_{c}+1} a_{i}\right)^{2}+\sum_{d=1}^{D} \sum_{j=1}^{l}\left(2^{u_{d}+1} b_{j}\right)^{2} $$ where all the summands are distinct by the condition on $a_{i}, b_{j}$. It remains to choose an appropriate $N$ : for example $N=29$, because $29=5^{2}+2^{2}$ and $58=7^{2}+3^{2}$. Second solution. It can be directly checked that every odd integer $67<$ $n \leq 211$ can be represented as a sum of distinct squares. For any $n>211$ we can choose an integer $m$ such that $m^{2}>\frac{n}{2}$ and $n-m^{2}$ is odd and greater than 67 , and therefore by the induction hypothesis can be written as a sum of distinct squares. Hence $n$ is also a sum of distinct squares.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
19. N6 (ROM) Show that the set of positive integers that cannot be represented as a sum of distinct perfect squares is finite.
|
19. Suppose that a natural number $N$ satisfies $N=a_{1}^{2}+\cdots+a_{k}^{2}, 2 N=$ $b_{1}^{2}+\cdots+b_{l}^{2}$, where $a_{i}, b_{j}$ are natural numbers such that none of the ratios $a_{i} / a_{j}, b_{i} / b_{j}, a_{i} / b_{j}, b_{j} / a_{i}$ is a power of 2. We claim that every natural number $n>\sum_{i=0}^{4 N-2}(2 i N+1)^{2}$ can be represented as a sum of distinct squares. Suppose $n=4 q N+r, 0 \leq r<4 N$. Then $$ n=4 N s+\sum_{i=0}^{r-1}(2 i N+1)^{2} $$ for some positive integer $s$, so it is enough to show that $4 N s$ is a sum of distinct even squares. Let $s=\sum_{c=1}^{C} 2^{2 u_{c}}+\sum_{d=1}^{D} 2^{2 v_{d}+1}$ be the binary expansion of $s$. Then $$ 4 N s=\sum_{c=1}^{C} \sum_{i=1}^{k}\left(2^{u_{c}+1} a_{i}\right)^{2}+\sum_{d=1}^{D} \sum_{j=1}^{l}\left(2^{u_{d}+1} b_{j}\right)^{2} $$ where all the summands are distinct by the condition on $a_{i}, b_{j}$. It remains to choose an appropriate $N$ : for example $N=29$, because $29=5^{2}+2^{2}$ and $58=7^{2}+3^{2}$. Second solution. It can be directly checked that every odd integer $67<$ $n \leq 211$ can be represented as a sum of distinct squares. For any $n>211$ we can choose an integer $m$ such that $m^{2}>\frac{n}{2}$ and $n-m^{2}$ is odd and greater than 67 , and therefore by the induction hypothesis can be written as a sum of distinct squares. Hence $n$ is also a sum of distinct squares.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c406968e-8771-5142-bd5d-99f83df479ec
| 24,987
|
20. G1 (NET) In the plane we are given two circles intersecting at $X$ and $Y$. Prove that there exist four points $A, B, C, D$ with the following property: For every circle touching the two given circles at $A$ and $B$, and meeting the line $X Y$ at $C$ and $D$, each of the lines $A C, A D, B C, B D$ passes through one of these points.
|
20. Denote by $k_{1}, k_{2}$ the given circles and by $k_{3}$ the circle through $A, B, C, D$. We shall consider the case that $k_{3}$ is inside $k_{1}$ and $k_{2}$, since the other case is analogous. Let $A C$ and $A D$ meet $k_{1}$ at points $P$ and $R$, and $B C$ and $B D$ meet $k_{2}$ at $Q$ and $S$ respectively. We claim that $P Q$ and $R S$ are the common tangents to $k_{1}$ and $k_{2}$, and therefore $P, Q, R, S$ are the desired points. The circles $k_{1}$ and $k_{3}$ are tangent to each other, so we have $D C \| R P$. Since  $$ A C \cdot C P=X C \cdot C Y=B C \cdot C Q $$ the quadrilateral $A B Q P$ is cyclic, implying that $\angle A P Q=\angle A B Q=$ $\angle A D C=\angle A R P$. It follows that $P Q$ is tangent to $k_{1}$. Similarly, $P Q$ is tangent to $k_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
20. G1 (NET) In the plane we are given two circles intersecting at $X$ and $Y$. Prove that there exist four points $A, B, C, D$ with the following property: For every circle touching the two given circles at $A$ and $B$, and meeting the line $X Y$ at $C$ and $D$, each of the lines $A C, A D, B C, B D$ passes through one of these points.
|
20. Denote by $k_{1}, k_{2}$ the given circles and by $k_{3}$ the circle through $A, B, C, D$. We shall consider the case that $k_{3}$ is inside $k_{1}$ and $k_{2}$, since the other case is analogous. Let $A C$ and $A D$ meet $k_{1}$ at points $P$ and $R$, and $B C$ and $B D$ meet $k_{2}$ at $Q$ and $S$ respectively. We claim that $P Q$ and $R S$ are the common tangents to $k_{1}$ and $k_{2}$, and therefore $P, Q, R, S$ are the desired points. The circles $k_{1}$ and $k_{3}$ are tangent to each other, so we have $D C \| R P$. Since  $$ A C \cdot C P=X C \cdot C Y=B C \cdot C Q $$ the quadrilateral $A B Q P$ is cyclic, implying that $\angle A P Q=\angle A B Q=$ $\angle A D C=\angle A R P$. It follows that $P Q$ is tangent to $k_{1}$. Similarly, $P Q$ is tangent to $k_{2}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0515e4a-6846-5e18-a552-9721efc3c19d
| 24,992
|
21. G2 (RUS) ${ }^{\mathrm{IMO} 1}$ Two circles $G_{1}$ and $G_{2}$ intersect at $M$ and $N$. Let $A B$ be the line tangent to these circles at $A$ and $B$, respectively, such that $M$ lies closer to $A B$ than $N$. Let $C D$ be the line parallel to $A B$ and passing through $M$, with $C$ on $G_{1}$ and $D$ on $G_{2}$. Lines $A C$ and $B D$ meet at $E$; lines $A N$ and $C D$ meet at $P$; lines $B N$ and $C D$ meet at $Q$. Show that $E P=E Q$.
|
21. Let $K$ be the intersection point of the lines $M N$ and $A B$. Since $K A^{2}=K M \cdot K N=K B^{2}$, it follows that $K$ is the midpoint of the segment $A B$, and consequently $M$ is the midpoint of $A B$. Thus it will be enough to show that $E M \perp$ $P Q$, or equivalently that $E M \perp$ $A B$. However, since $A B$ is tangent to the circle $G_{1}$ we have $\angle B A M=$ 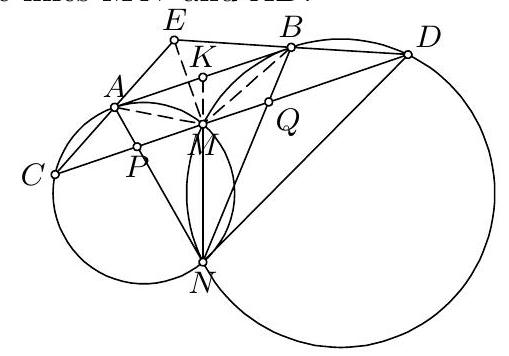 $\angle A C M=\angle E A B$, and similarly $\angle A B M=\angle E B A$. This implies that the triangles $E A B$ and $M A B$ are congruent. Hence $E$ and $M$ are symmetric with respect to $A B$; hence $E M \perp A B$. Remark. The proposer has suggested an alternative version of the problem: to prove that $E N$ bisects the angle $C N D$. This can be proved by noting that $E A N B$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
21. G2 (RUS) ${ }^{\mathrm{IMO} 1}$ Two circles $G_{1}$ and $G_{2}$ intersect at $M$ and $N$. Let $A B$ be the line tangent to these circles at $A$ and $B$, respectively, such that $M$ lies closer to $A B$ than $N$. Let $C D$ be the line parallel to $A B$ and passing through $M$, with $C$ on $G_{1}$ and $D$ on $G_{2}$. Lines $A C$ and $B D$ meet at $E$; lines $A N$ and $C D$ meet at $P$; lines $B N$ and $C D$ meet at $Q$. Show that $E P=E Q$.
|
21. Let $K$ be the intersection point of the lines $M N$ and $A B$. Since $K A^{2}=K M \cdot K N=K B^{2}$, it follows that $K$ is the midpoint of the segment $A B$, and consequently $M$ is the midpoint of $A B$. Thus it will be enough to show that $E M \perp$ $P Q$, or equivalently that $E M \perp$ $A B$. However, since $A B$ is tangent to the circle $G_{1}$ we have $\angle B A M=$  $\angle A C M=\angle E A B$, and similarly $\angle A B M=\angle E B A$. This implies that the triangles $E A B$ and $M A B$ are congruent. Hence $E$ and $M$ are symmetric with respect to $A B$; hence $E M \perp A B$. Remark. The proposer has suggested an alternative version of the problem: to prove that $E N$ bisects the angle $C N D$. This can be proved by noting that $E A N B$ is cyclic.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
273c0e04-9c6d-5392-8cf3-3c8879128403
| 24,995
|
22. G3 (IND) Let $O$ be the circumcenter and $H$ the orthocenter of an acute triangle $A B C$. Show that there exist points $D, E$, and $F$ on sides $B C$, $C A$, and $A B$ respectively such that $O D+D H=O E+E H=O F+F H$ and the lines $A D, B E$, and $C F$ are concurrent.
|
22. Let $L$ be the point symmetric to $H$ with respect to $B C$. It is well known that $L$ lies on the circumcircle $k$ of $\triangle A B C$. Let $D$ be the intersection point of $O L$ and $B C$. We similarly define $E$ and $F$. Then $$ O D+D H=O D+D L=O L=O E+E H=O F+F H $$ We shall prove that $A D, B E$, and $C F$ are concurrent. Let line $A O$ meet $B C$ at $D^{\prime}$. It is easy to see that $\angle O D^{\prime} D=\angle O D D^{\prime}$; hence the perpendicular bisector of $B C$ bisects $D D^{\prime}$ as well. Hence $B D=C D^{\prime}$. If we define $E^{\prime}$ and $F^{\prime}$ analogously, we have $C E=A E^{\prime}$ and $A F=B F^{\prime}$. Since the lines $A D^{\prime}, B E^{\prime}, C F^{\prime}$ meet at $O$, it follows that $\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B}=$ 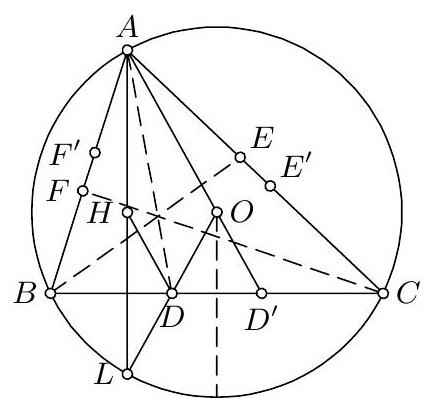 $\frac{B D^{\prime}}{D^{\prime} C} \cdot \frac{C E^{\prime}}{E^{\prime} A} \cdot \frac{A F^{\prime}}{F^{\prime} B}=1$. This proves our claim by Ceva's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
22. G3 (IND) Let $O$ be the circumcenter and $H$ the orthocenter of an acute triangle $A B C$. Show that there exist points $D, E$, and $F$ on sides $B C$, $C A$, and $A B$ respectively such that $O D+D H=O E+E H=O F+F H$ and the lines $A D, B E$, and $C F$ are concurrent.
|
22. Let $L$ be the point symmetric to $H$ with respect to $B C$. It is well known that $L$ lies on the circumcircle $k$ of $\triangle A B C$. Let $D$ be the intersection point of $O L$ and $B C$. We similarly define $E$ and $F$. Then $$ O D+D H=O D+D L=O L=O E+E H=O F+F H $$ We shall prove that $A D, B E$, and $C F$ are concurrent. Let line $A O$ meet $B C$ at $D^{\prime}$. It is easy to see that $\angle O D^{\prime} D=\angle O D D^{\prime}$; hence the perpendicular bisector of $B C$ bisects $D D^{\prime}$ as well. Hence $B D=C D^{\prime}$. If we define $E^{\prime}$ and $F^{\prime}$ analogously, we have $C E=A E^{\prime}$ and $A F=B F^{\prime}$. Since the lines $A D^{\prime}, B E^{\prime}, C F^{\prime}$ meet at $O$, it follows that $\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B}=$  $\frac{B D^{\prime}}{D^{\prime} C} \cdot \frac{C E^{\prime}}{E^{\prime} A} \cdot \frac{A F^{\prime}}{F^{\prime} B}=1$. This proves our claim by Ceva's theorem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
aa9d01cd-e7f8-5dec-a0d6-a1fc6421f97a
| 24,997
|
23. G4 (RUS) Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon, $n \geq 4$. Prove that $A_{1} A_{2} \ldots A_{n}$ is cyclic if and only if to each vertex $A_{j}$ one can assign a pair $\left(b_{j}, c_{j}\right)$ of real numbers, $j=1,2, \ldots n$, such that $$ A_{i} A_{j}=b_{j} c_{i}-b_{i} c_{j} \quad \text { for all } i, j \text { with } 1 \leq i \leq j \leq n $$
|
23. First, suppose that there are numbers $\left(b_{i}, c_{i}\right)$ assigned to the vertices of the polygon such that $$ A_{i} A_{j}=b_{j} c_{i}-b_{i} c_{j} \quad \text { for all } i, j \text { with } 1 \leq i \leq j \leq n $$ In order to show that the polygon is cyclic, it is enough to prove that $A_{1}, A_{2}, A_{3}, A_{i}$ lie on a circle for each $i, 4 \leq i \leq n$, or equivalently, by Ptolemy's theorem, that $A_{1} A_{2} \cdot A_{3} A_{i}+A_{2} A_{3} \cdot A_{i} A_{1}=A_{1} A_{3} \cdot A_{2} A_{i}$. But this is straightforward with regard to (1). Now suppose that $A_{1} A_{2} \ldots A_{n}$ is a cyclic quadrilateral. By Ptolemy's theorem we have $A_{i} A_{j}=A_{2} A_{j} \cdot \frac{A_{1} A_{i}}{A_{1} A_{2}}-A_{2} A_{i} \cdot \frac{A_{1} A_{j}}{A_{1} A_{2}}$ for all $i, j$. This suggests taking $b_{1}=-A_{1} A_{2}, b_{i}=A_{2} A_{i}$ for $i \geq 2$ and $c_{i}=\frac{A_{1} A_{i}}{A_{1} A_{2}}$ for all $i$. Indeed, using Ptolemy's theorem, one easily verifies (1).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
23. G4 (RUS) Let $A_{1} A_{2} \ldots A_{n}$ be a convex polygon, $n \geq 4$. Prove that $A_{1} A_{2} \ldots A_{n}$ is cyclic if and only if to each vertex $A_{j}$ one can assign a pair $\left(b_{j}, c_{j}\right)$ of real numbers, $j=1,2, \ldots n$, such that $$ A_{i} A_{j}=b_{j} c_{i}-b_{i} c_{j} \quad \text { for all } i, j \text { with } 1 \leq i \leq j \leq n $$
|
23. First, suppose that there are numbers $\left(b_{i}, c_{i}\right)$ assigned to the vertices of the polygon such that $$ A_{i} A_{j}=b_{j} c_{i}-b_{i} c_{j} \quad \text { for all } i, j \text { with } 1 \leq i \leq j \leq n $$ In order to show that the polygon is cyclic, it is enough to prove that $A_{1}, A_{2}, A_{3}, A_{i}$ lie on a circle for each $i, 4 \leq i \leq n$, or equivalently, by Ptolemy's theorem, that $A_{1} A_{2} \cdot A_{3} A_{i}+A_{2} A_{3} \cdot A_{i} A_{1}=A_{1} A_{3} \cdot A_{2} A_{i}$. But this is straightforward with regard to (1). Now suppose that $A_{1} A_{2} \ldots A_{n}$ is a cyclic quadrilateral. By Ptolemy's theorem we have $A_{i} A_{j}=A_{2} A_{j} \cdot \frac{A_{1} A_{i}}{A_{1} A_{2}}-A_{2} A_{i} \cdot \frac{A_{1} A_{j}}{A_{1} A_{2}}$ for all $i, j$. This suggests taking $b_{1}=-A_{1} A_{2}, b_{i}=A_{2} A_{i}$ for $i \geq 2$ and $c_{i}=\frac{A_{1} A_{i}}{A_{1} A_{2}}$ for all $i$. Indeed, using Ptolemy's theorem, one easily verifies (1).
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4dfe78be-87de-5210-b60b-a41a9f6f9dd6
| 25,000
|
25. G6 (ARG) Let $A B C D$ be a convex quadrilateral with $A B$ not parallel to $C D$, let $X$ be a point inside $A B C D$ such that $\measuredangle A D X=\measuredangle B C X<90^{\circ}$ and $\measuredangle D A X=\measuredangle C B X<90^{\circ}$. If $Y$ is the point of intersection of the perpendicular bisectors of $A B$ and $C D$, prove that $\measuredangle A Y B=2 \measuredangle A D X$.
|
25. By the condition of the problem, $\triangle A D X$ and $\triangle B C X$ are similar. Then there exist points $Y^{\prime}$ and $Z^{\prime}$ on the perpendicular bisector of $A B$ such that $\triangle A Y^{\prime} Z^{\prime}$ is similar and oriented the same as $\triangle A D X$, and $\triangle B Y^{\prime} Z^{\prime}$ is (being congruent to $\triangle A Y^{\prime} Z^{\prime}$ ) similar and oriented the same as $\triangle B C X$. Since then $A D / A Y^{\prime}=A X / A Z^{\prime}$ and $\angle D A Y^{\prime}=\angle X A Z^{\prime}, \triangle A D Y^{\prime}$ and $\triangle A X Z^{\prime}$ are also similar, implying $\frac{A D}{A X}=\frac{D Y^{\prime}}{X Z^{\prime}}$. Analogously, $\frac{B C}{B X}=\frac{C Y^{\prime}}{X Z^{\prime}}$. It follows from $\frac{A D}{A X}=\frac{B C}{B X}$ that $C Y^{\prime}=D Y^{\prime}$, which means that $Y^{\prime}$ lies on the perpendicular bisector of $C D$. Hence $Y^{\prime} \equiv Y$. Now $\angle A Y B=2 \angle A Y Z^{\prime}=2 \angle A D X$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
25. G6 (ARG) Let $A B C D$ be a convex quadrilateral with $A B$ not parallel to $C D$, let $X$ be a point inside $A B C D$ such that $\measuredangle A D X=\measuredangle B C X<90^{\circ}$ and $\measuredangle D A X=\measuredangle C B X<90^{\circ}$. If $Y$ is the point of intersection of the perpendicular bisectors of $A B$ and $C D$, prove that $\measuredangle A Y B=2 \measuredangle A D X$.
|
25. By the condition of the problem, $\triangle A D X$ and $\triangle B C X$ are similar. Then there exist points $Y^{\prime}$ and $Z^{\prime}$ on the perpendicular bisector of $A B$ such that $\triangle A Y^{\prime} Z^{\prime}$ is similar and oriented the same as $\triangle A D X$, and $\triangle B Y^{\prime} Z^{\prime}$ is (being congruent to $\triangle A Y^{\prime} Z^{\prime}$ ) similar and oriented the same as $\triangle B C X$. Since then $A D / A Y^{\prime}=A X / A Z^{\prime}$ and $\angle D A Y^{\prime}=\angle X A Z^{\prime}, \triangle A D Y^{\prime}$ and $\triangle A X Z^{\prime}$ are also similar, implying $\frac{A D}{A X}=\frac{D Y^{\prime}}{X Z^{\prime}}$. Analogously, $\frac{B C}{B X}=\frac{C Y^{\prime}}{X Z^{\prime}}$. It follows from $\frac{A D}{A X}=\frac{B C}{B X}$ that $C Y^{\prime}=D Y^{\prime}$, which means that $Y^{\prime}$ lies on the perpendicular bisector of $C D$. Hence $Y^{\prime} \equiv Y$. Now $\angle A Y B=2 \angle A Y Z^{\prime}=2 \angle A D X$, as desired.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
a0e934aa-9d91-5762-8501-8c18142d6d24
| 25,006
|
27. G8 (RUS) ${ }^{\mathrm{IMO}} A_{1} A_{2} A_{3}$ is an acute-angled triangle. The foot of the altitude from $A_{i}$ is $K_{i}$, and the incircle touches the side opposite $A_{i}$ at $L_{i}$. The line $K_{1} K_{2}$ is reflected in the line $L_{1} L_{2}$. Similarly, the line $K_{2} K_{3}$ is reflected in $L_{2} L_{3}$, and $K_{3} K_{1}$ is reflected in $L_{3} L_{1}$. Show that the three new lines form a triangle with vertices on the incircle.
|
27. Denote by $\alpha_{1}, \alpha_{2}, \alpha_{3}$ the angles of $\triangle A_{1} A_{2} A_{3}$ at vertices $A_{1}, A_{2}, A_{3}$ respectively. Let $T_{1}, T_{2}, T_{3}$ be the points symmetric to $L_{1}, L_{2}, L_{3}$ with respect to $A_{1} I, A_{2} I$, and $A_{3} I$ respectively. We claim that $T_{1} T_{2} T_{3}$ is the desired triangle. Denote by $S_{1}$ and $R_{1}$ the points symmetric to $K_{1}$ and $K_{3}$ with respect to $L_{1} L_{3}$. It is enough to show that $T_{1}$ and $T_{3}$ lie on the line $R_{1} S_{1}$. To prove this, we shall prove that $\angle K_{1} S_{1} T_{1}=\angle K^{\prime} K_{1} S_{1}$ for a point $K^{\prime}$ on the line $K_{1} K_{3}$ such that $K_{3}$ and $K^{\prime}$ lie on different sides of $K_{1}$. We show first that $S_{1} \in A_{1} I$. Let $X$ be the point of intersection of lines $A_{1} I$ and $L_{1} L_{3}$. We see from the triangle $A_{1} L_{3} X$ that $\angle L_{1} X I=$ $\alpha_{3} / 2=\angle L_{1} A_{3} I$, which implies that 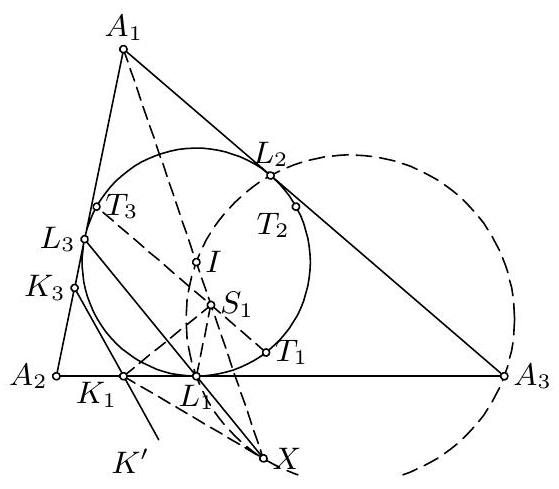 $L_{1} X A_{3} I$ is cyclic. We now have $\angle A_{1} X A_{3}=90^{\circ}=\angle A_{1} K_{1} A_{3}$; hence $A_{1} K_{1} X A_{3}$ is also cyclic. It follows that $\angle K_{1} X I=\angle K_{1} A_{3} A_{1}=\alpha_{3}=2 \angle L_{1} X I$; hence $X_{1} L_{1}$ bisects the angle $K_{1} X_{1} I$. Hence $S_{1} \in X I$ as claimed. Now we have $\angle K_{1} S_{1} T_{1}=\angle K_{1} S_{1} L_{1}+2 \angle L_{1} S_{1} X=\angle S_{1} K_{1} L_{1}+2 \angle L_{1} K_{1} X$. It remains to prove that $K_{1} X$ bisects $\angle A_{3} K_{1} K^{\prime}$. From the cyclic quadrilateral $A_{1} K_{1} X A_{3}$ we see that $\angle X K_{1} A_{3}=\alpha_{1} / 2$. Since $A_{1} K_{3} K_{1} A_{3}$ is cyclic, we also have $\angle K^{\prime} K_{1} A_{3}=\alpha_{1}=2 \angle X K_{1} A_{3}$, which proves the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
27. G8 (RUS) ${ }^{\mathrm{IMO}} A_{1} A_{2} A_{3}$ is an acute-angled triangle. The foot of the altitude from $A_{i}$ is $K_{i}$, and the incircle touches the side opposite $A_{i}$ at $L_{i}$. The line $K_{1} K_{2}$ is reflected in the line $L_{1} L_{2}$. Similarly, the line $K_{2} K_{3}$ is reflected in $L_{2} L_{3}$, and $K_{3} K_{1}$ is reflected in $L_{3} L_{1}$. Show that the three new lines form a triangle with vertices on the incircle.
|
27. Denote by $\alpha_{1}, \alpha_{2}, \alpha_{3}$ the angles of $\triangle A_{1} A_{2} A_{3}$ at vertices $A_{1}, A_{2}, A_{3}$ respectively. Let $T_{1}, T_{2}, T_{3}$ be the points symmetric to $L_{1}, L_{2}, L_{3}$ with respect to $A_{1} I, A_{2} I$, and $A_{3} I$ respectively. We claim that $T_{1} T_{2} T_{3}$ is the desired triangle. Denote by $S_{1}$ and $R_{1}$ the points symmetric to $K_{1}$ and $K_{3}$ with respect to $L_{1} L_{3}$. It is enough to show that $T_{1}$ and $T_{3}$ lie on the line $R_{1} S_{1}$. To prove this, we shall prove that $\angle K_{1} S_{1} T_{1}=\angle K^{\prime} K_{1} S_{1}$ for a point $K^{\prime}$ on the line $K_{1} K_{3}$ such that $K_{3}$ and $K^{\prime}$ lie on different sides of $K_{1}$. We show first that $S_{1} \in A_{1} I$. Let $X$ be the point of intersection of lines $A_{1} I$ and $L_{1} L_{3}$. We see from the triangle $A_{1} L_{3} X$ that $\angle L_{1} X I=$ $\alpha_{3} / 2=\angle L_{1} A_{3} I$, which implies that  $L_{1} X A_{3} I$ is cyclic. We now have $\angle A_{1} X A_{3}=90^{\circ}=\angle A_{1} K_{1} A_{3}$; hence $A_{1} K_{1} X A_{3}$ is also cyclic. It follows that $\angle K_{1} X I=\angle K_{1} A_{3} A_{1}=\alpha_{3}=2 \angle L_{1} X I$; hence $X_{1} L_{1}$ bisects the angle $K_{1} X_{1} I$. Hence $S_{1} \in X I$ as claimed. Now we have $\angle K_{1} S_{1} T_{1}=\angle K_{1} S_{1} L_{1}+2 \angle L_{1} S_{1} X=\angle S_{1} K_{1} L_{1}+2 \angle L_{1} K_{1} X$. It remains to prove that $K_{1} X$ bisects $\angle A_{3} K_{1} K^{\prime}$. From the cyclic quadrilateral $A_{1} K_{1} X A_{3}$ we see that $\angle X K_{1} A_{3}=\alpha_{1} / 2$. Since $A_{1} K_{3} K_{1} A_{3}$ is cyclic, we also have $\angle K^{\prime} K_{1} A_{3}=\alpha_{1}=2 \angle X K_{1} A_{3}$, which proves the claim.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8cb45b58-13b4-5b1b-90bb-9881ce113c97
| 25,012
|
7. A1 (USA) ${ }^{\mathrm{IMO} 2}$ Let $a, b, c$ be positive real numbers with product 1. Prove that $$ \left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right) \leq 1 . $$
|
7. Elementary computation gives $\left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)=a b-a+\frac{a}{c}-b+$ $1-\frac{1}{c}+1-\frac{1}{b}+\frac{1}{b c}$. Using $a b=\frac{1}{c}$ and $\frac{1}{b c}=a$ we obtain $$ \left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)=\frac{a}{c}-b-\frac{1}{b}+2 \leq \frac{a}{c} $$ since $b+\frac{1}{b} \geq 2$. Similarly we obtain $$ \left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right) \leq \frac{b}{a} \text { and }\left(c-1+\frac{1}{a}\right)\left(a-1+\frac{1}{b}\right) \leq \frac{c}{b} . $$ The desired inequality follows from the previous three inequalities. Equality holds if and only if $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
7. A1 (USA) ${ }^{\mathrm{IMO} 2}$ Let $a, b, c$ be positive real numbers with product 1. Prove that $$ \left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right) \leq 1 . $$
|
7. Elementary computation gives $\left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)=a b-a+\frac{a}{c}-b+$ $1-\frac{1}{c}+1-\frac{1}{b}+\frac{1}{b c}$. Using $a b=\frac{1}{c}$ and $\frac{1}{b c}=a$ we obtain $$ \left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)=\frac{a}{c}-b-\frac{1}{b}+2 \leq \frac{a}{c} $$ since $b+\frac{1}{b} \geq 2$. Similarly we obtain $$ \left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right) \leq \frac{b}{a} \text { and }\left(c-1+\frac{1}{a}\right)\left(a-1+\frac{1}{b}\right) \leq \frac{c}{b} . $$ The desired inequality follows from the previous three inequalities. Equality holds if and only if $a=b=c=1$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3844b0d4-3f37-5809-b70f-0f3581a8f88f
| 25,026
|
8. A2 (GBR) Let $a, b, c$ be positive integers satisfying the conditions $b>2 a$ and $c>2 b$. Show that there exists a real number $t$ with the property that all the three numbers $t a, t b, t c$ have their fractional parts lying in the interval (1/3,2/3].
|
8. We note that $\{t a\}$ lies in $\left(\frac{1}{3}, \frac{2}{3}\right]$ if and only if there is an integer $k$ such that $k+\frac{1}{3}<t a \leq k+\frac{2}{3}$, i.e., if and only if $t \in I_{k}=\left(\frac{k+1 / 3}{a}, \frac{k+2 / 3}{a}\right]$ for some $k$. Similarly, $t$ should belong to the sets $J_{m}=\left(\frac{m+1 / 3}{b}, \frac{m+2 / 3}{b}\right]$ and $K_{n}=\left(\frac{n+1 / 3}{c}, \frac{n+2 / 3}{c}\right]$ for some $m, n$. We have to show that $I_{k} \cap J_{m} \cap K_{n}$ is nonempty for some integers $k, m, n$. The intervals $K_{n}$ are separated by a distance $\frac{2}{3 c}$, and since $\frac{2}{3 c}<\frac{1}{3 b}$, each of the intervals $J_{m}$ intersects at least one of the $K_{n}$ 's. Hence it is enough to prove that $J_{m} \subset I_{k}$ for some $k, m$. Let $u_{m}$ and $v_{m}$ be the left and right endpoints of $J_{m}$. Since $a v_{m}=a u_{m}+$ $\frac{a}{3 b}<a u_{m}+\frac{1}{6}$, it will suffice to show that there is an integer $m$ such that the fractional part of $a u_{m}$ lies in $\left[\frac{1}{3}, \frac{1}{2}\right]$. Let $a=d \alpha, b=d \beta, \operatorname{gcd}(\alpha, \beta)=1$. Setting $m=d \mu$ we obtain that $a u_{m}=a \frac{m+1 / 3}{b}=\frac{\alpha m}{d \beta}+\frac{\alpha}{3 \beta}=\frac{\alpha \mu}{\beta}+\frac{\alpha}{3 \beta}$. Since $\alpha \mu$ gives all possible residues modulo $\beta$, every term of the arithmetic progression $\frac{j}{\beta}+\frac{\alpha}{3 \beta}(j \in \mathbb{Z})$ has its fractional part equal to the fractional part of some $a u_{m}$. Now for $\beta \geq 6$ the progression step is $\frac{1}{\beta} \leq \frac{1}{6}$, so at least one of the $a u_{m}$ has its fractional part in $[1 / 3,1 / 2]$. If otherwise $\beta \leq 5$, the only irreducible fractions $\frac{\alpha}{\beta}$ that satisfy $2 \alpha<\beta$ are $\frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{2}{5}$; hence one can take $m$ to be $1,1,2,3$ respectively. This justifies our claim.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
8. A2 (GBR) Let $a, b, c$ be positive integers satisfying the conditions $b>2 a$ and $c>2 b$. Show that there exists a real number $t$ with the property that all the three numbers $t a, t b, t c$ have their fractional parts lying in the interval (1/3,2/3].
|
8. We note that $\{t a\}$ lies in $\left(\frac{1}{3}, \frac{2}{3}\right]$ if and only if there is an integer $k$ such that $k+\frac{1}{3}<t a \leq k+\frac{2}{3}$, i.e., if and only if $t \in I_{k}=\left(\frac{k+1 / 3}{a}, \frac{k+2 / 3}{a}\right]$ for some $k$. Similarly, $t$ should belong to the sets $J_{m}=\left(\frac{m+1 / 3}{b}, \frac{m+2 / 3}{b}\right]$ and $K_{n}=\left(\frac{n+1 / 3}{c}, \frac{n+2 / 3}{c}\right]$ for some $m, n$. We have to show that $I_{k} \cap J_{m} \cap K_{n}$ is nonempty for some integers $k, m, n$. The intervals $K_{n}$ are separated by a distance $\frac{2}{3 c}$, and since $\frac{2}{3 c}<\frac{1}{3 b}$, each of the intervals $J_{m}$ intersects at least one of the $K_{n}$ 's. Hence it is enough to prove that $J_{m} \subset I_{k}$ for some $k, m$. Let $u_{m}$ and $v_{m}$ be the left and right endpoints of $J_{m}$. Since $a v_{m}=a u_{m}+$ $\frac{a}{3 b}<a u_{m}+\frac{1}{6}$, it will suffice to show that there is an integer $m$ such that the fractional part of $a u_{m}$ lies in $\left[\frac{1}{3}, \frac{1}{2}\right]$. Let $a=d \alpha, b=d \beta, \operatorname{gcd}(\alpha, \beta)=1$. Setting $m=d \mu$ we obtain that $a u_{m}=a \frac{m+1 / 3}{b}=\frac{\alpha m}{d \beta}+\frac{\alpha}{3 \beta}=\frac{\alpha \mu}{\beta}+\frac{\alpha}{3 \beta}$. Since $\alpha \mu$ gives all possible residues modulo $\beta$, every term of the arithmetic progression $\frac{j}{\beta}+\frac{\alpha}{3 \beta}(j \in \mathbb{Z})$ has its fractional part equal to the fractional part of some $a u_{m}$. Now for $\beta \geq 6$ the progression step is $\frac{1}{\beta} \leq \frac{1}{6}$, so at least one of the $a u_{m}$ has its fractional part in $[1 / 3,1 / 2]$. If otherwise $\beta \leq 5$, the only irreducible fractions $\frac{\alpha}{\beta}$ that satisfy $2 \alpha<\beta$ are $\frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{2}{5}$; hence one can take $m$ to be $1,1,2,3$ respectively. This justifies our claim.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
02c4fa8c-cb49-5ef8-a381-4e5e31fe3805
| 25,029
|
10. C4 (NZL) A set of three nonnegative integers $\{x, y, z\}$ with $x<y<z$ is called historic if $\{z-y, y-x\}=\{1776,2001\}$. Show that the set of all nonnegative integers can be written as the union of disjoint historic sets.
|
10. For convenience let us write $a=1776, b=2001,0<a<b$. There are two types of historic sets: $$ \text { (1) }\{x, x+a, x+a+b\} \quad \text { and } \quad \text { (2) }\{x, x+b, x+a+b\} \text {. } $$ We construct a sequence of historic sets $H_{1}, H_{2}, H_{3}, \ldots$ inductively as follows: (i) $H_{1}=\{0, a, a+b\}$, and (ii) Let $y_{n}$ be the least nonnegative integer not occurring in $U_{n}=H_{1} \cap$ $\cdots \cap H_{n}$. We take $H_{n+1}$ to be $\left\{y_{n}, y_{n}+a, y_{n}+a+b\right\}$ if $y_{n}+a \notin U_{n}$, and $\left\{y_{n}, y_{n}+b, y_{n}+a+b\right\}$ otherwise. It remains to show that this construction never fails. Suppose that it failed at the construction of $H_{n+1}$. The element $y_{n}+a+b$ is not contained in $U_{n}$, since by the construction the smallest elements of $H_{1}, \ldots, H_{n}$ are all less than $y_{n}$. Hence the reason for the failure must be the fact that both $y_{n}+a$ and $y_{n}+b$ are covered by $U_{n}$. Further, $y_{n}+b$ must have been the largest element of its set $H_{k}$, so the smallest element of $H_{k}$ equals $y_{n}-a$. But since $y_{n}$ is not covered, we conclude that $H_{k}$ is of type (2). This is a contradiction, because $y_{n}$ was free, so by the algorithm we had to choose for $H_{k}$ the set of type (1) (that is, $\left\{y_{n}-a, y_{n}, y_{n}+b\right\}$ ) first.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
10. C4 (NZL) A set of three nonnegative integers $\{x, y, z\}$ with $x<y<z$ is called historic if $\{z-y, y-x\}=\{1776,2001\}$. Show that the set of all nonnegative integers can be written as the union of disjoint historic sets.
|
10. For convenience let us write $a=1776, b=2001,0<a<b$. There are two types of historic sets: $$ \text { (1) }\{x, x+a, x+a+b\} \quad \text { and } \quad \text { (2) }\{x, x+b, x+a+b\} \text {. } $$ We construct a sequence of historic sets $H_{1}, H_{2}, H_{3}, \ldots$ inductively as follows: (i) $H_{1}=\{0, a, a+b\}$, and (ii) Let $y_{n}$ be the least nonnegative integer not occurring in $U_{n}=H_{1} \cap$ $\cdots \cap H_{n}$. We take $H_{n+1}$ to be $\left\{y_{n}, y_{n}+a, y_{n}+a+b\right\}$ if $y_{n}+a \notin U_{n}$, and $\left\{y_{n}, y_{n}+b, y_{n}+a+b\right\}$ otherwise. It remains to show that this construction never fails. Suppose that it failed at the construction of $H_{n+1}$. The element $y_{n}+a+b$ is not contained in $U_{n}$, since by the construction the smallest elements of $H_{1}, \ldots, H_{n}$ are all less than $y_{n}$. Hence the reason for the failure must be the fact that both $y_{n}+a$ and $y_{n}+b$ are covered by $U_{n}$. Further, $y_{n}+b$ must have been the largest element of its set $H_{k}$, so the smallest element of $H_{k}$ equals $y_{n}-a$. But since $y_{n}$ is not covered, we conclude that $H_{k}$ is of type (2). This is a contradiction, because $y_{n}$ was free, so by the algorithm we had to choose for $H_{k}$ the set of type (1) (that is, $\left\{y_{n}-a, y_{n}, y_{n}+b\right\}$ ) first.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c2848a19-5382-5399-8502-9e84050fb9f6
| 25,037
|
12. C6 (CAN) For a positive integer $n$ define a sequence of zeros and ones to be balanced if it contains $n$ zeros and $n$ ones. Two balanced sequences $a$ and $b$ are neighbors if you can move one of the $2 n$ symbols of $a$ to another position to form $b$. For instance, when $n=4$, the balanced sequences 01101001 and 00110101 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set $S$ of at most $\frac{1}{n+1}\binom{2 n}{n}$ balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in $S$.
|
12. For each balanced sequence $a=\left(a_{1}, a_{2}, \ldots, a_{2 n}\right)$ denote by $f(a)$ the sum of $j$ 's for which $a_{j}=1$ (for example, $f(100101)=1+4+6=11$ ). Partition the $\binom{2 n}{n}$ balanced sequences into $n+1$ classes according to the residue of $f$ modulo $n+1$. Now take $S$ to be a class of minimum size: obviously $|S| \leq \frac{1}{n+1}\binom{2 n}{n}$. We claim that every balanced sequence $a$ is either a member of $S$ or a neighbor of a member of $S$. We consider two cases. (i) Let $a_{1}$ be 1 . It is easy to see that moving this 1 just to the right of the $k$ th 0 , we obtain a neighboring balanced sequence $b$ with $f(b)=$ $f(a)+k$. Thus if $a \notin S$, taking a suitable $k \in\{1,2, \ldots, n\}$ we can achieve that $b \in S$. (ii) Let $a_{1}$ be 0 . Taking this 0 just to the right of the $k$ th 1 gives a neighbor $b$ with $f(b)=f(a)-k$, and the conclusion is similar to that of (i). This justifies our claim.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. C6 (CAN) For a positive integer $n$ define a sequence of zeros and ones to be balanced if it contains $n$ zeros and $n$ ones. Two balanced sequences $a$ and $b$ are neighbors if you can move one of the $2 n$ symbols of $a$ to another position to form $b$. For instance, when $n=4$, the balanced sequences 01101001 and 00110101 are neighbors because the third (or fourth) zero in the first sequence can be moved to the first or second position to form the second sequence. Prove that there is a set $S$ of at most $\frac{1}{n+1}\binom{2 n}{n}$ balanced sequences such that every balanced sequence is equal to or is a neighbor of at least one sequence in $S$.
|
12. For each balanced sequence $a=\left(a_{1}, a_{2}, \ldots, a_{2 n}\right)$ denote by $f(a)$ the sum of $j$ 's for which $a_{j}=1$ (for example, $f(100101)=1+4+6=11$ ). Partition the $\binom{2 n}{n}$ balanced sequences into $n+1$ classes according to the residue of $f$ modulo $n+1$. Now take $S$ to be a class of minimum size: obviously $|S| \leq \frac{1}{n+1}\binom{2 n}{n}$. We claim that every balanced sequence $a$ is either a member of $S$ or a neighbor of a member of $S$. We consider two cases. (i) Let $a_{1}$ be 1 . It is easy to see that moving this 1 just to the right of the $k$ th 0 , we obtain a neighboring balanced sequence $b$ with $f(b)=$ $f(a)+k$. Thus if $a \notin S$, taking a suitable $k \in\{1,2, \ldots, n\}$ we can achieve that $b \in S$. (ii) Let $a_{1}$ be 0 . Taking this 0 just to the right of the $k$ th 1 gives a neighbor $b$ with $f(b)=f(a)-k$, and the conclusion is similar to that of (i). This justifies our claim.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0c663798-5e4e-51e7-859a-ce85ed4e9954
| 25,042
|
13. C7 (FRA) A pile of $n$ pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column that contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each $n$, show that no matter what choices are made at each stage, the final configuration is unique. Describe that configuration in terms of $n$.
|
13. At any moment, let $p_{i}$ be the number of pebbles in the $i$ th column, $i=$ $1,2, \ldots$ The final configuration has obvious properties $p_{1} \geq p_{2} \geq \cdots$ and $p_{i+1} \in\left\{p_{i}, p_{i}-1\right\}$. We claim that $p_{i+1}=p_{i}>0$ is possible for at most one $i$. Assume the opposite. Then the final configuration has the property that for some $r$ and $s>r$ we have $p_{r+1}=p_{r}, p_{s+1}=p_{s}>0$ and $p_{r+k}=$ $p_{r+1}-k+1$ for all $k=1, \ldots, s-r$. Consider the earliest configuration, say $C$, with this property. What was the last move before $C$ ? The only possibilities are moving a pebble either from the $r$ th or from the $s$ th column; however, in both cases the configuration preceding this last move had the same property, contradicting the assumption that $C$ is the earliest. Therefore the final configuration looks as follows: $p_{1}=a \in \mathbb{N}$, and for some $r, p_{i}$ equals $a-(i-1)$ if $i \leq r$, and $a-(i-2)$ otherwise. It is easy to determine $a, r$ : since $n=p_{1}+p_{2}+\cdots=\frac{(a+1)(a+2)}{2}-r$, we get $\frac{a(a+1)}{2} \leq n<\frac{(a+1)(a+2)}{2}$, from which we uniquely find $a$ and then $r$ as well. The final configuration for $n=13$ : 
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
13. C7 (FRA) A pile of $n$ pebbles is placed in a vertical column. This configuration is modified according to the following rules. A pebble can be moved if it is at the top of a column that contains at least two more pebbles than the column immediately to its right. (If there are no pebbles to the right, think of this as a column with 0 pebbles.) At each stage, choose a pebble from among those that can be moved (if there are any) and place it at the top of the column to its right. If no pebbles can be moved, the configuration is called a final configuration. For each $n$, show that no matter what choices are made at each stage, the final configuration is unique. Describe that configuration in terms of $n$.
|
13. At any moment, let $p_{i}$ be the number of pebbles in the $i$ th column, $i=$ $1,2, \ldots$ The final configuration has obvious properties $p_{1} \geq p_{2} \geq \cdots$ and $p_{i+1} \in\left\{p_{i}, p_{i}-1\right\}$. We claim that $p_{i+1}=p_{i}>0$ is possible for at most one $i$. Assume the opposite. Then the final configuration has the property that for some $r$ and $s>r$ we have $p_{r+1}=p_{r}, p_{s+1}=p_{s}>0$ and $p_{r+k}=$ $p_{r+1}-k+1$ for all $k=1, \ldots, s-r$. Consider the earliest configuration, say $C$, with this property. What was the last move before $C$ ? The only possibilities are moving a pebble either from the $r$ th or from the $s$ th column; however, in both cases the configuration preceding this last move had the same property, contradicting the assumption that $C$ is the earliest. Therefore the final configuration looks as follows: $p_{1}=a \in \mathbb{N}$, and for some $r, p_{i}$ equals $a-(i-1)$ if $i \leq r$, and $a-(i-2)$ otherwise. It is easy to determine $a, r$ : since $n=p_{1}+p_{2}+\cdots=\frac{(a+1)(a+2)}{2}-r$, we get $\frac{a(a+1)}{2} \leq n<\frac{(a+1)(a+2)}{2}$, from which we uniquely find $a$ and then $r$ as well. The final configuration for $n=13$ : 
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
60c41242-3878-5360-a674-51ebbae8b6ab
| 25,044
|
14. C8 (GER) ${ }^{\mathrm{IMO} 3}$ Twenty-one girls and twenty-one boys took part in a mathematical competition. It turned out that (i) each contestant solved at most six problems, and (ii) for each pair of a girl and a boy, there was at least one problem that was solved by both the girl and the boy. Show that there is a problem that was solved by at least three girls and at least three boys.
|
14. We say that a problem is difficult for boys if at most two boys solved it, and difficult for girls if at most two girls solved it. Let us estimate the number of pairs boy-girl both of whom solved some problem difficult for boys. Consider any girl. By the condition (ii), among the six problems she solved, at least one was solved by at least 3 boys, and hence at most 5 were difficult for boys. Since each of these problems was solved by at most 2 boys and there are 21 girls, the considered number of pairs does not exceed $5 \cdot 2 \cdot 21=210$. Similarly, there are at most 210 pairs boy-girl both of whom solved some problem difficult for girls. On the other hand, there are $21^{2}>2 \cdot 210$ pairs boy-girl, and each of them solved one problem in common. Thus some problems were difficult neither for girls nor for boys, as claimed. Remark. The statement can be generalized: if $2(m-1)(n-1)+1$ boys and as many girls participated, and nobody solved more than $m$ problems, then some problem was solved by at least $n$ boys and $n$ girls.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
14. C8 (GER) ${ }^{\mathrm{IMO} 3}$ Twenty-one girls and twenty-one boys took part in a mathematical competition. It turned out that (i) each contestant solved at most six problems, and (ii) for each pair of a girl and a boy, there was at least one problem that was solved by both the girl and the boy. Show that there is a problem that was solved by at least three girls and at least three boys.
|
14. We say that a problem is difficult for boys if at most two boys solved it, and difficult for girls if at most two girls solved it. Let us estimate the number of pairs boy-girl both of whom solved some problem difficult for boys. Consider any girl. By the condition (ii), among the six problems she solved, at least one was solved by at least 3 boys, and hence at most 5 were difficult for boys. Since each of these problems was solved by at most 2 boys and there are 21 girls, the considered number of pairs does not exceed $5 \cdot 2 \cdot 21=210$. Similarly, there are at most 210 pairs boy-girl both of whom solved some problem difficult for girls. On the other hand, there are $21^{2}>2 \cdot 210$ pairs boy-girl, and each of them solved one problem in common. Thus some problems were difficult neither for girls nor for boys, as claimed. Remark. The statement can be generalized: if $2(m-1)(n-1)+1$ boys and as many girls participated, and nobody solved more than $m$ problems, then some problem was solved by at least $n$ boys and $n$ girls.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8d541a43-e122-5533-990c-14eeac236b2f
| 25,047
|
15. G1 (UKR) Let $A_{1}$ be the center of the square inscribed in acute triangle $A B C$ with two vertices of the square on side $B C$. Thus one of the two remaining vertices of the square is on side $A B$ and the other is on $A C$. Points $B_{1}, C_{1}$ are defined in a similar way for inscribed squares with two vertices on sides $A C$ and $A B$, respectively. Prove that lines $A A_{1}, B B_{1}, C C_{1}$ are concurrent.
|
15. Let $M N P Q$ be the square inscribed in $\triangle A B C$ with $M \in A B, N \in A C$, $P, Q \in B C$, and let $A A_{1}$ meet $M N, P Q$ at $K, X$ respectively. Put $M K=$ $P X=m, N K=Q X=n$, and $M N=d$. Then $$ \frac{B X}{X C}=\frac{m}{n}=\frac{B X+m}{X C+n}=\frac{B P}{C Q}=\frac{d \cot \beta+d}{d \cot \gamma+d}=\frac{\cot \beta+1}{\cot \gamma+1} . $$ Similarly, if $B B_{1}$ and $C C_{1}$ meet $A C$ and $B C$ at $Y, Z$ respectively then $\frac{C Y}{Y A}=\frac{\cot \gamma+1}{\cot \alpha+1}$ and $\frac{A Z}{Z B}=\frac{\cot \alpha+1}{\cot \beta+1}$. Therefore $\frac{B X}{X C} \frac{C Y}{Y A} \frac{A Z}{Z B}=1$, so by Ceva's theorem, $A X, B Y, C Z$ have a common point. Second solution. Let $A_{2}$ be the center of the square constructed over $B C$ outside $\triangle A B C$. Since this square and the inscribed square corresponding to the side $B C$ are homothetic, $A, A_{1}$, and $A_{2}$ are collinear. Points $B_{2}, C_{2}$ are analogously defined. Denote the angles $B A A_{2}, A_{2} A C, C B B_{2}$, $B_{2} B A, A C C_{2}, C_{2} C B$ by $\alpha_{1}, \alpha_{2}, \beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}$. By the law of sines we have $$ \frac{\sin \alpha_{1}}{\sin \alpha_{2}}=\frac{\sin \left(\beta+45^{\circ}\right)}{\sin \left(\gamma+45^{\circ}\right)}, \frac{\sin \beta_{1}}{\sin \beta_{2}}=\frac{\sin \left(\gamma+45^{\circ}\right)}{\sin \left(\alpha+45^{\circ}\right)}, \frac{\sin \gamma_{1}}{\sin \gamma_{2}}=\frac{\sin \left(\alpha+45^{\circ}\right)}{\sin \left(\beta+45^{\circ}\right)} $$ Since the product of these ratios is 1 , by the trigonometric Ceva's theorem $A A_{2}, B B_{2}, C C_{2}$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. G1 (UKR) Let $A_{1}$ be the center of the square inscribed in acute triangle $A B C$ with two vertices of the square on side $B C$. Thus one of the two remaining vertices of the square is on side $A B$ and the other is on $A C$. Points $B_{1}, C_{1}$ are defined in a similar way for inscribed squares with two vertices on sides $A C$ and $A B$, respectively. Prove that lines $A A_{1}, B B_{1}, C C_{1}$ are concurrent.
|
15. Let $M N P Q$ be the square inscribed in $\triangle A B C$ with $M \in A B, N \in A C$, $P, Q \in B C$, and let $A A_{1}$ meet $M N, P Q$ at $K, X$ respectively. Put $M K=$ $P X=m, N K=Q X=n$, and $M N=d$. Then $$ \frac{B X}{X C}=\frac{m}{n}=\frac{B X+m}{X C+n}=\frac{B P}{C Q}=\frac{d \cot \beta+d}{d \cot \gamma+d}=\frac{\cot \beta+1}{\cot \gamma+1} . $$ Similarly, if $B B_{1}$ and $C C_{1}$ meet $A C$ and $B C$ at $Y, Z$ respectively then $\frac{C Y}{Y A}=\frac{\cot \gamma+1}{\cot \alpha+1}$ and $\frac{A Z}{Z B}=\frac{\cot \alpha+1}{\cot \beta+1}$. Therefore $\frac{B X}{X C} \frac{C Y}{Y A} \frac{A Z}{Z B}=1$, so by Ceva's theorem, $A X, B Y, C Z$ have a common point. Second solution. Let $A_{2}$ be the center of the square constructed over $B C$ outside $\triangle A B C$. Since this square and the inscribed square corresponding to the side $B C$ are homothetic, $A, A_{1}$, and $A_{2}$ are collinear. Points $B_{2}, C_{2}$ are analogously defined. Denote the angles $B A A_{2}, A_{2} A C, C B B_{2}$, $B_{2} B A, A C C_{2}, C_{2} C B$ by $\alpha_{1}, \alpha_{2}, \beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}$. By the law of sines we have $$ \frac{\sin \alpha_{1}}{\sin \alpha_{2}}=\frac{\sin \left(\beta+45^{\circ}\right)}{\sin \left(\gamma+45^{\circ}\right)}, \frac{\sin \beta_{1}}{\sin \beta_{2}}=\frac{\sin \left(\gamma+45^{\circ}\right)}{\sin \left(\alpha+45^{\circ}\right)}, \frac{\sin \gamma_{1}}{\sin \gamma_{2}}=\frac{\sin \left(\alpha+45^{\circ}\right)}{\sin \left(\beta+45^{\circ}\right)} $$ Since the product of these ratios is 1 , by the trigonometric Ceva's theorem $A A_{2}, B B_{2}, C C_{2}$ are concurrent.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b9ef4a1d-aca3-5359-87a4-bfff01409b60
| 25,050
|
16. G2 (KOR) ${ }^{\mathrm{IMO} 1}$ In acute triangle $A B C$ with circumcenter $O$ and altitude $A P, \measuredangle C \geq \measuredangle B+30^{\circ}$. Prove that $\measuredangle A+\measuredangle C O P<90^{\circ}$.
|
16. Since $\angle O C P=90^{\circ}-\angle A$, we are led to showing that $\angle O C P>\angle C O P$, i.e., $O P>C P$. By the triangle inequality it suffices to prove $C P<\frac{1}{2} C O$. Let $C O=R$. The law of sines yields $C P=A C \cos \gamma=2 R \sin \beta \cos \gamma<$ $2 R \sin \beta \cos \left(\beta+30^{\circ}\right)$. Finally, we have $$ 2 \sin \beta \cos \left(\beta+30^{\circ}\right)=\sin \left(2 \beta+30^{\circ}\right)-\sin 30^{\circ} \leq \frac{1}{2} $$ which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. G2 (KOR) ${ }^{\mathrm{IMO} 1}$ In acute triangle $A B C$ with circumcenter $O$ and altitude $A P, \measuredangle C \geq \measuredangle B+30^{\circ}$. Prove that $\measuredangle A+\measuredangle C O P<90^{\circ}$.
|
16. Since $\angle O C P=90^{\circ}-\angle A$, we are led to showing that $\angle O C P>\angle C O P$, i.e., $O P>C P$. By the triangle inequality it suffices to prove $C P<\frac{1}{2} C O$. Let $C O=R$. The law of sines yields $C P=A C \cos \gamma=2 R \sin \beta \cos \gamma<$ $2 R \sin \beta \cos \left(\beta+30^{\circ}\right)$. Finally, we have $$ 2 \sin \beta \cos \left(\beta+30^{\circ}\right)=\sin \left(2 \beta+30^{\circ}\right)-\sin 30^{\circ} \leq \frac{1}{2} $$ which completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
0aca62fe-7a42-5f63-a425-55ed2910bc65
| 25,053
|
2. A2 (POL) Let $a_{0}, a_{1}, a_{2}, \ldots$ be an arbitrary infinite sequence of positive numbers. Show that the inequality $1+a_{n}>a_{n-1} \sqrt[n]{2}$ holds for infinitely many positive integers $n$.
|
2. It follows from Bernoulli's inequality that for each $n \in \mathbb{N},\left(1+\frac{1}{n}\right)^{n} \geq 2$, or $\sqrt[n]{2} \leq 1+\frac{1}{n}$. Consequently, it will be enough to show that $1+a_{n}>$ $\left(1+\frac{1}{n}\right) a_{n-1}$. Assume the opposite. Then there exists $N$ such that for each $n \geq N$, $$ 1+a_{n} \leq\left(1+\frac{1}{n}\right) a_{n-1}, \quad \text { i.e., } \quad \frac{1}{n+1}+\frac{a_{n}}{n+1} \leq \frac{a_{n-1}}{n} $$ Summing for $n=N, \ldots, m$ yields $\frac{a_{m}}{m+1} \leq \frac{a_{N-1}}{N}-\left(\frac{1}{N+1}+\cdots+\frac{1}{m+1}\right)$. However, it is well known that the sum $\frac{1}{N+1}+\cdots+\frac{1}{m+1}$ can be arbitrarily large for $m$ large enough, so that $\frac{a_{m}^{N+1}}{m+1}$ is eventually negative. This contradiction yields the result. Second solution. Suppose that $1+a_{n} \leq \sqrt[n]{2} a_{n-1}$ for all $n \geq N$. Set $b_{n}=2^{-(1+1 / 2+\cdots+1 / n)}$ and multiply both sides of the above inequality to obtain $b_{n}+b_{n} a_{n} \leq b_{n-1} a_{n-1}$. Thus $$ b_{N} a_{N}>b_{N} a_{N}-b_{n} a_{n} \geq b_{N}+b_{N+1}+\cdots+b_{n} $$ However, it can be shown that $\sum_{n>N} b_{N}$ diverges: in fact, since $1+\frac{1}{2}+$ $\cdots+\frac{1}{n}<1+\ln n$, we have $b_{n}>2^{-1-\ln n}=\frac{1}{2} n^{-\ln 2}>\frac{1}{2 n}$, and we already know that $\sum_{n>N} \frac{1}{2 n}$ diverges. Remark. As can be seen from both solutions, the value 2 in the problem can be increased to $e$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
2. A2 (POL) Let $a_{0}, a_{1}, a_{2}, \ldots$ be an arbitrary infinite sequence of positive numbers. Show that the inequality $1+a_{n}>a_{n-1} \sqrt[n]{2}$ holds for infinitely many positive integers $n$.
|
2. It follows from Bernoulli's inequality that for each $n \in \mathbb{N},\left(1+\frac{1}{n}\right)^{n} \geq 2$, or $\sqrt[n]{2} \leq 1+\frac{1}{n}$. Consequently, it will be enough to show that $1+a_{n}>$ $\left(1+\frac{1}{n}\right) a_{n-1}$. Assume the opposite. Then there exists $N$ such that for each $n \geq N$, $$ 1+a_{n} \leq\left(1+\frac{1}{n}\right) a_{n-1}, \quad \text { i.e., } \quad \frac{1}{n+1}+\frac{a_{n}}{n+1} \leq \frac{a_{n-1}}{n} $$ Summing for $n=N, \ldots, m$ yields $\frac{a_{m}}{m+1} \leq \frac{a_{N-1}}{N}-\left(\frac{1}{N+1}+\cdots+\frac{1}{m+1}\right)$. However, it is well known that the sum $\frac{1}{N+1}+\cdots+\frac{1}{m+1}$ can be arbitrarily large for $m$ large enough, so that $\frac{a_{m}^{N+1}}{m+1}$ is eventually negative. This contradiction yields the result. Second solution. Suppose that $1+a_{n} \leq \sqrt[n]{2} a_{n-1}$ for all $n \geq N$. Set $b_{n}=2^{-(1+1 / 2+\cdots+1 / n)}$ and multiply both sides of the above inequality to obtain $b_{n}+b_{n} a_{n} \leq b_{n-1} a_{n-1}$. Thus $$ b_{N} a_{N}>b_{N} a_{N}-b_{n} a_{n} \geq b_{N}+b_{N+1}+\cdots+b_{n} $$ However, it can be shown that $\sum_{n>N} b_{N}$ diverges: in fact, since $1+\frac{1}{2}+$ $\cdots+\frac{1}{n}<1+\ln n$, we have $b_{n}>2^{-1-\ln n}=\frac{1}{2} n^{-\ln 2}>\frac{1}{2 n}$, and we already know that $\sum_{n>N} \frac{1}{2 n}$ diverges. Remark. As can be seen from both solutions, the value 2 in the problem can be increased to $e$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
864e1d70-cbea-5b2b-a80d-15c4de86d383
| 25,063
|
20. G6 (IND) Let $A B C$ be a triangle and $P$ an exterior point in the plane of the triangle. Suppose $A P, B P, C P$ meet the sides $B C, C A, A B$ (or extensions thereof) in $D, E, F$, respectively. Suppose further that the areas of triangles $P B D, P C E, P A F$ are all equal. Prove that each of these areas is equal to the area of triangle $A B C$ itself.
|
20. By Ceva's theorem, we can choose real numbers $x, y, z$ such that $$ \frac{\overrightarrow{B D}}{\overrightarrow{D C}}=\frac{z}{y}, \frac{\overrightarrow{C E}}{\overrightarrow{E A}}=\frac{x}{z}, \text { and } \frac{\overrightarrow{A F}}{\overrightarrow{F B}}=\frac{y}{x} $$ The point $P$ lies outside the triangle $A B C$ if and only if $x, y, z$ are not all of the same sign. In what follows, $S_{X}$ will denote the signed area of a figure $X$. Let us assume that the area $S_{A B C}$ of $\triangle A B C$ is 1 . Since $S_{P B C}: S_{P C A}$ : $S_{P A B}=x: y: z$ and $S_{P B D}: S_{P D C}=z: y$, it follows that $S_{P B D}=\frac{z}{y+z} \frac{x}{x+y+z}$. Hence $S_{P B D}=\frac{1}{y(y+z)} \frac{x y z}{x+y+z}, S_{P C E}=\frac{1}{z(z+x)} \frac{x y z}{x+y+z}$, $S_{P A F}=\frac{1}{x(x+y)} \frac{x y z}{x+y+z}$. By the condition of the problem we have $\left|S_{P B D}\right|=$ $\left|S_{P C E}\right|=\left|S_{P A F}\right|$, or $$ |x(x+y)|=|y(y+z)|=|z(z+x)| . $$ Obviously $x, y, z$ are nonzero, so that we can put w.l.o.g. $z=1$. At least two of the numbers $x(x+y), y(y+1), 1(1+x)$ are equal, so we can assume that $x(x+y)=y(y+1)$. We distinguish two cases: (i) $x(x+y)=y(y+1)=1+x$. Then $x=y^{2}+y-1$, from which we obtain $\left(y^{2}+y-1\right)\left(y^{2}+2 y-1\right)=y(y+1)$. Simplification gives $y^{4}+3 y^{3}-y^{2}-4 y+1=0$, or $$ (y-1)\left(y^{3}+4 y^{2}+3 y-1\right)=0 $$ If $y=1$, then also $z=x=1$, so $P$ is the centroid of $\triangle A B C$, which is not an exterior point. Hence $y^{3}+4 y^{2}+3 y-1=0$. Now the signed area of each of the triangles $P B D, P C E, P A F$ equals $$ \begin{aligned} S_{P A F} & =\frac{y z}{(x+y)(x+y+z)} \\ & =\frac{y}{\left(y^{2}+2 y-1\right)\left(y^{2}+2 y\right)}=\frac{1}{y^{3}+4 y^{2}+3 y-2}=-1 . \end{aligned} $$ It is easy to check that not both of $x, y$ are positive, implying that $P$ is indeed outside $\triangle A B C$. This is the desired result. (ii) $x(x+y)=y(y+1)=-1-x$. In this case we are led to $$ f(y)=y^{4}+3 y^{3}+y^{2}-2 y+1=0 . $$ We claim that this equation has no real solutions. In fact, assume that $y_{0}$ is a real root of $f(y)$. We must have $y_{0}<0$, and hence $u=-y_{0}>0$ satisfies $3 u^{3}-u^{4}=(u+1)^{2}$. On the other hand, $$ \begin{aligned} 3 u^{3}-u^{4} & =u^{3}(3-u)=4 u\left(\frac{u}{2}\right)\left(\frac{u}{2}\right)(3-u) \\ & \leq 4 u\left(\frac{u / 2+u / 2+3-u}{3}\right)^{3}=4 u \\ & \leq(u+1)^{2} \end{aligned} $$ where at least one of the inequalities is strict, a contradiction. Remark. The official solution was incomplete, missing the case (ii).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
20. G6 (IND) Let $A B C$ be a triangle and $P$ an exterior point in the plane of the triangle. Suppose $A P, B P, C P$ meet the sides $B C, C A, A B$ (or extensions thereof) in $D, E, F$, respectively. Suppose further that the areas of triangles $P B D, P C E, P A F$ are all equal. Prove that each of these areas is equal to the area of triangle $A B C$ itself.
|
20. By Ceva's theorem, we can choose real numbers $x, y, z$ such that $$ \frac{\overrightarrow{B D}}{\overrightarrow{D C}}=\frac{z}{y}, \frac{\overrightarrow{C E}}{\overrightarrow{E A}}=\frac{x}{z}, \text { and } \frac{\overrightarrow{A F}}{\overrightarrow{F B}}=\frac{y}{x} $$ The point $P$ lies outside the triangle $A B C$ if and only if $x, y, z$ are not all of the same sign. In what follows, $S_{X}$ will denote the signed area of a figure $X$. Let us assume that the area $S_{A B C}$ of $\triangle A B C$ is 1 . Since $S_{P B C}: S_{P C A}$ : $S_{P A B}=x: y: z$ and $S_{P B D}: S_{P D C}=z: y$, it follows that $S_{P B D}=\frac{z}{y+z} \frac{x}{x+y+z}$. Hence $S_{P B D}=\frac{1}{y(y+z)} \frac{x y z}{x+y+z}, S_{P C E}=\frac{1}{z(z+x)} \frac{x y z}{x+y+z}$, $S_{P A F}=\frac{1}{x(x+y)} \frac{x y z}{x+y+z}$. By the condition of the problem we have $\left|S_{P B D}\right|=$ $\left|S_{P C E}\right|=\left|S_{P A F}\right|$, or $$ |x(x+y)|=|y(y+z)|=|z(z+x)| . $$ Obviously $x, y, z$ are nonzero, so that we can put w.l.o.g. $z=1$. At least two of the numbers $x(x+y), y(y+1), 1(1+x)$ are equal, so we can assume that $x(x+y)=y(y+1)$. We distinguish two cases: (i) $x(x+y)=y(y+1)=1+x$. Then $x=y^{2}+y-1$, from which we obtain $\left(y^{2}+y-1\right)\left(y^{2}+2 y-1\right)=y(y+1)$. Simplification gives $y^{4}+3 y^{3}-y^{2}-4 y+1=0$, or $$ (y-1)\left(y^{3}+4 y^{2}+3 y-1\right)=0 $$ If $y=1$, then also $z=x=1$, so $P$ is the centroid of $\triangle A B C$, which is not an exterior point. Hence $y^{3}+4 y^{2}+3 y-1=0$. Now the signed area of each of the triangles $P B D, P C E, P A F$ equals $$ \begin{aligned} S_{P A F} & =\frac{y z}{(x+y)(x+y+z)} \\ & =\frac{y}{\left(y^{2}+2 y-1\right)\left(y^{2}+2 y\right)}=\frac{1}{y^{3}+4 y^{2}+3 y-2}=-1 . \end{aligned} $$ It is easy to check that not both of $x, y$ are positive, implying that $P$ is indeed outside $\triangle A B C$. This is the desired result. (ii) $x(x+y)=y(y+1)=-1-x$. In this case we are led to $$ f(y)=y^{4}+3 y^{3}+y^{2}-2 y+1=0 . $$ We claim that this equation has no real solutions. In fact, assume that $y_{0}$ is a real root of $f(y)$. We must have $y_{0}<0$, and hence $u=-y_{0}>0$ satisfies $3 u^{3}-u^{4}=(u+1)^{2}$. On the other hand, $$ \begin{aligned} 3 u^{3}-u^{4} & =u^{3}(3-u)=4 u\left(\frac{u}{2}\right)\left(\frac{u}{2}\right)(3-u) \\ & \leq 4 u\left(\frac{u / 2+u / 2+3-u}{3}\right)^{3}=4 u \\ & \leq(u+1)^{2} \end{aligned} $$ where at least one of the inequalities is strict, a contradiction. Remark. The official solution was incomplete, missing the case (ii).
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
34365c03-d5ec-50a4-bb91-09340c3bc820
| 25,066
|
21. G7 (BUL) Let $O$ be an interior point of acute triangle $A B C$. Let $A_{1}$ lie on $B C$ with $O A_{1}$ perpendicular to $B C$. Define $B_{1}$ on $C A$ and $C_{1}$ on $A B$ similarly. Prove that $O$ is the circumcenter of $A B C$ if and only if the perimeter of $A_{1} B_{1} C_{1}$ is not less than any one of the perimeters of $A B_{1} C_{1}, B C_{1} A_{1}$, and $C A_{1} B_{1}$.
|
21. We denote by $p(X Y Z)$ the perimeter of a triangle $X Y Z$. If $O$ is the circumcenter of $\triangle A B C$, then $A_{1}, B_{1}, C_{1}$ are the midpoints of the corresponding sides of the triangle, and hence $p\left(A_{1} B_{1} C_{1}\right)=$ $p\left(A B_{1} C_{1}\right)=p\left(A_{1} B C_{1}\right)=p\left(A_{1} B_{1} C\right)$. Conversely, suppose that $p\left(A_{1} B_{1} C_{1}\right) \geq p\left(A B_{1} C_{1}\right), p\left(A_{1} B C_{1}\right), p\left(A_{1} B_{1} C\right)$. Let $\alpha_{1}, \alpha_{2}, \beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}$ denote $\angle B_{1} A_{1} C, \angle C_{1} A_{1} B, \angle C_{1} B_{1} A, \angle A_{1} B_{1} C$, $\angle A_{1} C_{1} B, \angle B_{1} C_{1} A$. Suppose that $\gamma_{1}, \beta_{2} \geq \alpha$. If $A_{2}$ is the fourth vertex of the parallelogram $B_{1} A C_{1} A_{2}$, then these conditions imply that $A_{1}$ is in the interior or on the border of $\triangle B_{1} C_{1} A_{2}$, and therefore $p\left(A_{1} B_{1} C_{1}\right) \leq p\left(A_{2} B_{1} C_{1}\right)=$ $p\left(A B_{1} C_{1}\right)$. Moreover, if one of the inequalities $\gamma_{1} \geq \alpha, \beta_{2} \geq \alpha$ is strict,  then $p\left(A_{1} B_{1} C_{1}\right)$ is strictly less than $p\left(A B_{1} C_{1}\right)$, contrary to the assumption. Hence $$ \begin{aligned} & \beta_{2} \geq \alpha \Longrightarrow \gamma_{1} \leq \alpha \\ & \gamma_{2} \geq \beta \Longrightarrow \alpha_{1} \leq \beta \\ & \alpha_{2} \geq \gamma \Longrightarrow \beta_{1} \leq \gamma \end{aligned} $$ the last two inequalities being obtained analogously to the first one. Because of the symmetry, there is no loss of generality in assuming that $\gamma_{1} \leq \alpha$. Then since $\gamma_{1}+\alpha_{2}=180^{\circ}-\beta=\alpha+\gamma$, it follows that $\alpha_{2} \geq \gamma$. From (1) we deduce $\beta_{1} \leq \gamma$, which further implies $\gamma_{2} \geq \beta$. Similarly, this leads to $\alpha_{1} \leq \beta$ and $\beta_{2} \geq \alpha$. To sum up, $$ \gamma_{1} \leq \alpha \leq \beta_{2}, \quad \alpha_{1} \leq \beta \leq \gamma_{2}, \quad \beta_{1} \leq \gamma \leq \alpha_{2} $$ Since $O A_{1} B C_{1}$ and $O B_{1} C A_{1}$ are cyclic, we have $\angle A_{1} O B=\gamma_{1}$ and $\angle A_{1} O C=\beta_{2}$. Hence $B O: C O=\cos \beta_{2}: \cos \gamma_{1}$, hence $B O \leq C O$. Analogously, $C O \leq A O$ and $A O \leq B O$. Therefore $A O=B O=C O$, i.e., $O$ is the circumcenter of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
21. G7 (BUL) Let $O$ be an interior point of acute triangle $A B C$. Let $A_{1}$ lie on $B C$ with $O A_{1}$ perpendicular to $B C$. Define $B_{1}$ on $C A$ and $C_{1}$ on $A B$ similarly. Prove that $O$ is the circumcenter of $A B C$ if and only if the perimeter of $A_{1} B_{1} C_{1}$ is not less than any one of the perimeters of $A B_{1} C_{1}, B C_{1} A_{1}$, and $C A_{1} B_{1}$.
|
21. We denote by $p(X Y Z)$ the perimeter of a triangle $X Y Z$. If $O$ is the circumcenter of $\triangle A B C$, then $A_{1}, B_{1}, C_{1}$ are the midpoints of the corresponding sides of the triangle, and hence $p\left(A_{1} B_{1} C_{1}\right)=$ $p\left(A B_{1} C_{1}\right)=p\left(A_{1} B C_{1}\right)=p\left(A_{1} B_{1} C\right)$. Conversely, suppose that $p\left(A_{1} B_{1} C_{1}\right) \geq p\left(A B_{1} C_{1}\right), p\left(A_{1} B C_{1}\right), p\left(A_{1} B_{1} C\right)$. Let $\alpha_{1}, \alpha_{2}, \beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}$ denote $\angle B_{1} A_{1} C, \angle C_{1} A_{1} B, \angle C_{1} B_{1} A, \angle A_{1} B_{1} C$, $\angle A_{1} C_{1} B, \angle B_{1} C_{1} A$. Suppose that $\gamma_{1}, \beta_{2} \geq \alpha$. If $A_{2}$ is the fourth vertex of the parallelogram $B_{1} A C_{1} A_{2}$, then these conditions imply that $A_{1}$ is in the interior or on the border of $\triangle B_{1} C_{1} A_{2}$, and therefore $p\left(A_{1} B_{1} C_{1}\right) \leq p\left(A_{2} B_{1} C_{1}\right)=$ $p\left(A B_{1} C_{1}\right)$. Moreover, if one of the inequalities $\gamma_{1} \geq \alpha, \beta_{2} \geq \alpha$ is strict,  then $p\left(A_{1} B_{1} C_{1}\right)$ is strictly less than $p\left(A B_{1} C_{1}\right)$, contrary to the assumption. Hence $$ \begin{aligned} & \beta_{2} \geq \alpha \Longrightarrow \gamma_{1} \leq \alpha \\ & \gamma_{2} \geq \beta \Longrightarrow \alpha_{1} \leq \beta \\ & \alpha_{2} \geq \gamma \Longrightarrow \beta_{1} \leq \gamma \end{aligned} $$ the last two inequalities being obtained analogously to the first one. Because of the symmetry, there is no loss of generality in assuming that $\gamma_{1} \leq \alpha$. Then since $\gamma_{1}+\alpha_{2}=180^{\circ}-\beta=\alpha+\gamma$, it follows that $\alpha_{2} \geq \gamma$. From (1) we deduce $\beta_{1} \leq \gamma$, which further implies $\gamma_{2} \geq \beta$. Similarly, this leads to $\alpha_{1} \leq \beta$ and $\beta_{2} \geq \alpha$. To sum up, $$ \gamma_{1} \leq \alpha \leq \beta_{2}, \quad \alpha_{1} \leq \beta \leq \gamma_{2}, \quad \beta_{1} \leq \gamma \leq \alpha_{2} $$ Since $O A_{1} B C_{1}$ and $O B_{1} C A_{1}$ are cyclic, we have $\angle A_{1} O B=\gamma_{1}$ and $\angle A_{1} O C=\beta_{2}$. Hence $B O: C O=\cos \beta_{2}: \cos \gamma_{1}$, hence $B O \leq C O$. Analogously, $C O \leq A O$ and $A O \leq B O$. Therefore $A O=B O=C O$, i.e., $O$ is the circumcenter of $A B C$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c0d07a5b-400b-538a-9a0e-bf93005f23a4
| 25,069
|
23. N1 (AUS) Prove that there is no positive integer $n$ such that for $k=$ $1,2, \ldots, 9$, the leftmost digit (in decimal notation) of $(n+k)$ ! equals $k$.
|
23. For each positive integer $x$, define $\alpha(x)=x / 10^{r}$ if $r$ is the positive integer satisfying $10^{r} \leq x<10^{r+1}$. Observe that if $\alpha(x) \alpha(y)<10$ for some $x, y \in \mathbb{N}$, then $\alpha(x y)=\alpha(x) \alpha(y)$. If, as usual, $[t]$ means the integer part of $t$, then $[\alpha(x)]$ is actually the leftmost digit of $x$. Now suppose that $n$ is a positive integer such that $k \leq \alpha((n+k)!)<k+1$ for $k=1,2, \ldots, 9$. We have $$ 1<\alpha(n+k)=\frac{\alpha((n+k)!)}{\alpha((n+k-1)!)}<\frac{k+1}{k-1} \leq 3 \quad \text { for } 2 \leq k \leq 9 $$ from which we obtain $\alpha(n+k+1)>\alpha(n+k)$ (the opposite can hold only if $\alpha(n+k) \geq 9)$. Therefore $$ 1<\alpha(n+2)<\cdots<\alpha(n+9) \leq \frac{5}{4} . $$ On the other hand, this implies that $\alpha((n+4)!)=\alpha((n+1)!) \alpha(n+2) \alpha(n+$ 3) $\alpha(n+4)<(5 / 4)^{3} \alpha((n+1)$ ! $)<4$, contradicting the assumption that the leftmost digit of $(n+4)$ ! is 4 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
23. N1 (AUS) Prove that there is no positive integer $n$ such that for $k=$ $1,2, \ldots, 9$, the leftmost digit (in decimal notation) of $(n+k)$ ! equals $k$.
|
23. For each positive integer $x$, define $\alpha(x)=x / 10^{r}$ if $r$ is the positive integer satisfying $10^{r} \leq x<10^{r+1}$. Observe that if $\alpha(x) \alpha(y)<10$ for some $x, y \in \mathbb{N}$, then $\alpha(x y)=\alpha(x) \alpha(y)$. If, as usual, $[t]$ means the integer part of $t$, then $[\alpha(x)]$ is actually the leftmost digit of $x$. Now suppose that $n$ is a positive integer such that $k \leq \alpha((n+k)!)<k+1$ for $k=1,2, \ldots, 9$. We have $$ 1<\alpha(n+k)=\frac{\alpha((n+k)!)}{\alpha((n+k-1)!)}<\frac{k+1}{k-1} \leq 3 \quad \text { for } 2 \leq k \leq 9 $$ from which we obtain $\alpha(n+k+1)>\alpha(n+k)$ (the opposite can hold only if $\alpha(n+k) \geq 9)$. Therefore $$ 1<\alpha(n+2)<\cdots<\alpha(n+9) \leq \frac{5}{4} . $$ On the other hand, this implies that $\alpha((n+4)!)=\alpha((n+1)!) \alpha(n+2) \alpha(n+$ 3) $\alpha(n+4)<(5 / 4)^{3} \alpha((n+1)$ ! $)<4$, contradicting the assumption that the leftmost digit of $(n+4)$ ! is 4 .
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
878a9232-ed3f-5f9b-a533-a797bfd06346
| 25,075
|
26. N4 (VIE) Let $p \geq 5$ be a prime number. Prove that there exists an integer $a$ with $1 \leq a \leq p-2$ such that neither $a^{p-1}-1$ nor $(a+1)^{p-1}-1$ is divisible by $p^{2}$.
|
26. Let $C$ be the set of those $a \in\{1,2, \ldots, p-1\}$ for which $a^{p-1} \equiv 1\left(\bmod p^{2}\right)$. At first, we observe that $a, p-a$ do not both belong to $C$, regardless of the value of $a$. Indeed, by the binomial formula, $$ (p-a)^{p-1}-a^{p-1} \equiv-(p-1) p a^{p-2} \not \equiv 0 \quad\left(\bmod p^{2}\right) $$ As a consequence we deduce that $|C| \leq \frac{p-1}{2}$. Further, we observe that $p-k \in C \Leftrightarrow k \equiv k(p-k)^{p-1}\left(\bmod p^{2}\right)$, i.e., $$ p-k \in C \Leftrightarrow k \equiv k\left(k^{p-1}-(p-1) p k^{p-2}\right) \equiv k^{p}+p\left(\bmod p^{2}\right) $$ Now assume the contrary to the claim, that for every $a=1, \ldots, p-2$ one of $a, a+1$ is in $C$. In this case it is not possible that $a, a+1$ are both in $C$, for then $p-a, p-a-1 \notin C$. Thus, since $1 \in C$, we inductively obtain that $2,4, \ldots, p-1 \notin C$ and $1,3,5, \ldots, p-2 \in C$. In particular, $p-2, p-4 \in C$, which is by $(1)$ equivalent to $2 \equiv 2^{p}+p$ and $4 \equiv 4^{p}+p\left(\bmod p^{2}\right)$. However, squaring the former equality and subtracting the latter, we obtain $2^{p+1} p \equiv p\left(\bmod p^{2}\right)$, or $4 \equiv 1(\bmod p)$, which is a contradiction unless $p=3$. This finishes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
26. N4 (VIE) Let $p \geq 5$ be a prime number. Prove that there exists an integer $a$ with $1 \leq a \leq p-2$ such that neither $a^{p-1}-1$ nor $(a+1)^{p-1}-1$ is divisible by $p^{2}$.
|
26. Let $C$ be the set of those $a \in\{1,2, \ldots, p-1\}$ for which $a^{p-1} \equiv 1\left(\bmod p^{2}\right)$. At first, we observe that $a, p-a$ do not both belong to $C$, regardless of the value of $a$. Indeed, by the binomial formula, $$ (p-a)^{p-1}-a^{p-1} \equiv-(p-1) p a^{p-2} \not \equiv 0 \quad\left(\bmod p^{2}\right) $$ As a consequence we deduce that $|C| \leq \frac{p-1}{2}$. Further, we observe that $p-k \in C \Leftrightarrow k \equiv k(p-k)^{p-1}\left(\bmod p^{2}\right)$, i.e., $$ p-k \in C \Leftrightarrow k \equiv k\left(k^{p-1}-(p-1) p k^{p-2}\right) \equiv k^{p}+p\left(\bmod p^{2}\right) $$ Now assume the contrary to the claim, that for every $a=1, \ldots, p-2$ one of $a, a+1$ is in $C$. In this case it is not possible that $a, a+1$ are both in $C$, for then $p-a, p-a-1 \notin C$. Thus, since $1 \in C$, we inductively obtain that $2,4, \ldots, p-1 \notin C$ and $1,3,5, \ldots, p-2 \in C$. In particular, $p-2, p-4 \in C$, which is by $(1)$ equivalent to $2 \equiv 2^{p}+p$ and $4 \equiv 4^{p}+p\left(\bmod p^{2}\right)$. However, squaring the former equality and subtracting the latter, we obtain $2^{p+1} p \equiv p\left(\bmod p^{2}\right)$, or $4 \equiv 1(\bmod p)$, which is a contradiction unless $p=3$. This finishes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
888aa0ab-cd06-52c6-a71b-9a48225ee29f
| 25,082
|
27. N5 (BUL) ${ }^{\mathrm{IMO} 6}$ Let $a>b>c>d$ be positive integers and suppose $$ a c+b d=(b+d+a-c)(b+d-a+c) . $$ Prove that $a b+c d$ is not prime.
|
27. The given equality is equivalent to $a^{2}-a c+c^{2}=b^{2}+b d+d^{2}$. Hence $(a b+c d)(a d+b c)=a c\left(b^{2}+b d+d^{2}\right)+b d\left(a^{2}-a c+c^{2}\right)$, or equivalently, $$ (a b+c d)(a d+b c)=(a c+b d)\left(a^{2}-a c+c^{2}\right) $$ Now suppose that $a b+c d$ is prime. It follows from $a>b>c>d$ that $$ a b+c d>a c+b d>a d+b c $$ hence $a c+b d$ is relatively prime with $a b+c d$. But then (1) implies that $a c+b d$ divides $a d+b c$, which is impossible by (2). Remark. Alternatively, (1) could be obtained by applying the law of cosines and Ptolemy's theorem on a quadrilateral $X Y Z T$ with $X Y=a$, $Y Z=c, Z T=b, T X=d$ and $\angle Y=60^{\circ}, \angle T=120^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
27. N5 (BUL) ${ }^{\mathrm{IMO} 6}$ Let $a>b>c>d$ be positive integers and suppose $$ a c+b d=(b+d+a-c)(b+d-a+c) . $$ Prove that $a b+c d$ is not prime.
|
27. The given equality is equivalent to $a^{2}-a c+c^{2}=b^{2}+b d+d^{2}$. Hence $(a b+c d)(a d+b c)=a c\left(b^{2}+b d+d^{2}\right)+b d\left(a^{2}-a c+c^{2}\right)$, or equivalently, $$ (a b+c d)(a d+b c)=(a c+b d)\left(a^{2}-a c+c^{2}\right) $$ Now suppose that $a b+c d$ is prime. It follows from $a>b>c>d$ that $$ a b+c d>a c+b d>a d+b c $$ hence $a c+b d$ is relatively prime with $a b+c d$. But then (1) implies that $a c+b d$ divides $a d+b c$, which is impossible by (2). Remark. Alternatively, (1) could be obtained by applying the law of cosines and Ptolemy's theorem on a quadrilateral $X Y Z T$ with $X Y=a$, $Y Z=c, Z T=b, T X=d$ and $\angle Y=60^{\circ}, \angle T=120^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
f9279bc0-25e1-5bfb-ad24-e30c365f1efa
| 25,084
|
3. A3 (ROM) Let $x_{1}, x_{2}, \ldots, x_{n}$ be arbitrary real numbers. Prove the inequality $$ \frac{x_{1}}{1+x_{1}^{2}}+\frac{x_{2}}{1+x_{1}^{2}+x_{2}^{2}}+\cdots+\frac{x_{n}}{1+x_{1}^{2}+\cdots+x_{n}^{2}}<\sqrt{n} $$
|
3. By the arithmetic-quadratic mean inequality, it suffices to prove that $$ \frac{x_{1}^{2}}{\left(1+x_{1}^{2}\right)^{2}}+\frac{x_{2}^{2}}{\left(1+x_{1}^{2}+x_{2}^{2}\right)^{2}}+\cdots+\frac{x_{n}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{n}^{2}\right)^{2}}<1 . $$ Observe that for $k \geq 2$ the following holds: $$ \begin{aligned} \frac{x_{k}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{k}^{2}\right)^{2}} & \leq \frac{x_{k}^{2}}{\left(1+\cdots+x_{k-1}^{2}\right)\left(1+\cdots+x_{k}^{2}\right)} \\ & =\frac{1}{1+x_{1}^{2}+\cdots+x_{k-1}^{2}}-\frac{1}{1+x_{1}^{2}+\cdots+x_{k}^{2}} \end{aligned} $$ For $k=1$ we have $\frac{x_{1}^{2}}{\left(1+x_{1}\right)^{2}} \leq 1-\frac{1}{1+x_{1}^{2}}$. Summing these inequalities, we obtain $$ \frac{x_{1}^{2}}{\left(1+x_{1}^{2}\right)^{2}}+\cdots+\frac{x_{n}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{n}^{2}\right)^{2}} \leq 1-\frac{1}{1+x_{1}^{2}+\cdots+x_{n}^{2}}<1 $$ Second solution. Let $a_{n}(k)=\sup \left(\frac{x_{1}}{k^{2}+x_{1}^{2}}+\cdots+\frac{x_{n}}{k^{2}+x_{1}^{2}+\cdots+x_{n}^{2}}\right)$ and $a_{n}=$ $a_{n}(1)$. We must show that $a_{n}<\sqrt{n}$. Replacing $x_{i}$ by $k x_{i}$ shows that $a_{n}(k)=a_{n} / k$. Hence $$ a_{n}=\sup _{x_{1}}\left(\frac{x_{1}}{1+x_{1}^{2}}+\frac{a_{n-1}}{\sqrt{1+x_{1}^{2}}}\right)=\sup _{\theta}\left(\sin \theta \cos \theta+a_{n-1} \cos \theta\right), $$ where $\tan \theta=x_{1}$. The above supremum can be computed explicitly: $$ a_{n}=\frac{1}{8 \sqrt{2}}\left(3 a_{n-1}+\sqrt{a_{n-1}^{2}+8}\right) \sqrt{4-a_{n-1}^{2}+a_{n-1} \sqrt{a_{n-1}^{2}+8}} . $$ However, the required inequality is weaker and can be proved more easily: if $a_{n-1}<\sqrt{n-1}$, then by (1) $a_{n}<\sin \theta+\sqrt{n-1} \cos \theta=\sqrt{n} \sin (\theta+\alpha) \leq$ $\sqrt{n}$, for $\alpha \in(0, \pi / 2)$ with $\tan \alpha=\sqrt{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
3. A3 (ROM) Let $x_{1}, x_{2}, \ldots, x_{n}$ be arbitrary real numbers. Prove the inequality $$ \frac{x_{1}}{1+x_{1}^{2}}+\frac{x_{2}}{1+x_{1}^{2}+x_{2}^{2}}+\cdots+\frac{x_{n}}{1+x_{1}^{2}+\cdots+x_{n}^{2}}<\sqrt{n} $$
|
3. By the arithmetic-quadratic mean inequality, it suffices to prove that $$ \frac{x_{1}^{2}}{\left(1+x_{1}^{2}\right)^{2}}+\frac{x_{2}^{2}}{\left(1+x_{1}^{2}+x_{2}^{2}\right)^{2}}+\cdots+\frac{x_{n}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{n}^{2}\right)^{2}}<1 . $$ Observe that for $k \geq 2$ the following holds: $$ \begin{aligned} \frac{x_{k}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{k}^{2}\right)^{2}} & \leq \frac{x_{k}^{2}}{\left(1+\cdots+x_{k-1}^{2}\right)\left(1+\cdots+x_{k}^{2}\right)} \\ & =\frac{1}{1+x_{1}^{2}+\cdots+x_{k-1}^{2}}-\frac{1}{1+x_{1}^{2}+\cdots+x_{k}^{2}} \end{aligned} $$ For $k=1$ we have $\frac{x_{1}^{2}}{\left(1+x_{1}\right)^{2}} \leq 1-\frac{1}{1+x_{1}^{2}}$. Summing these inequalities, we obtain $$ \frac{x_{1}^{2}}{\left(1+x_{1}^{2}\right)^{2}}+\cdots+\frac{x_{n}^{2}}{\left(1+x_{1}^{2}+\cdots+x_{n}^{2}\right)^{2}} \leq 1-\frac{1}{1+x_{1}^{2}+\cdots+x_{n}^{2}}<1 $$ Second solution. Let $a_{n}(k)=\sup \left(\frac{x_{1}}{k^{2}+x_{1}^{2}}+\cdots+\frac{x_{n}}{k^{2}+x_{1}^{2}+\cdots+x_{n}^{2}}\right)$ and $a_{n}=$ $a_{n}(1)$. We must show that $a_{n}<\sqrt{n}$. Replacing $x_{i}$ by $k x_{i}$ shows that $a_{n}(k)=a_{n} / k$. Hence $$ a_{n}=\sup _{x_{1}}\left(\frac{x_{1}}{1+x_{1}^{2}}+\frac{a_{n-1}}{\sqrt{1+x_{1}^{2}}}\right)=\sup _{\theta}\left(\sin \theta \cos \theta+a_{n-1} \cos \theta\right), $$ where $\tan \theta=x_{1}$. The above supremum can be computed explicitly: $$ a_{n}=\frac{1}{8 \sqrt{2}}\left(3 a_{n-1}+\sqrt{a_{n-1}^{2}+8}\right) \sqrt{4-a_{n-1}^{2}+a_{n-1} \sqrt{a_{n-1}^{2}+8}} . $$ However, the required inequality is weaker and can be proved more easily: if $a_{n-1}<\sqrt{n-1}$, then by (1) $a_{n}<\sin \theta+\sqrt{n-1} \cos \theta=\sqrt{n} \sin (\theta+\alpha) \leq$ $\sqrt{n}$, for $\alpha \in(0, \pi / 2)$ with $\tan \alpha=\sqrt{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6ece5606-9111-5aa7-bc9d-9a9f2d4bdae7
| 25,088
|
8. C2 (CAN) ${ }^{\mathrm{IMO} 4}$ Let $n$ be an odd integer greater than 1 and let $c_{1}, c_{2}, \ldots$, $c_{n}$ be integers. For each permutation $a=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of $\{1,2, \ldots, n\}$, define $S(a)=\sum_{i=1}^{n} c_{i} a_{i}$. Prove that there exist permutations $a \neq b$ of $\{1,2, \ldots, n\}$ such that $n$ ! is a divisor of $S(a)-S(b)$.
|
8. Suppose to the contrary that all the $S(a)$ 's are different modulo $n$ !. Then the sum of $S(a)$ 's over all permutations $a$ satisfies $\sum_{a} S(a) \equiv 0+1+\cdots+$ $(n!-1)=\frac{(n!-1) n!}{2} \equiv \frac{n!}{2}(\bmod n!)$. On the other hand, the coefficient of $c_{i}$ in $\sum_{a} S(a)$ is equal to $(n-1)!(1+2+\cdots+n)=\frac{n+1}{2} n!$ for all $i$, from which we obtain $$ \sum_{a} S(a) \equiv \frac{n+1}{2}\left(c_{1}+\cdots+c_{n}\right) n!\equiv 0(\bmod n!) $$ for odd $n$. This is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
8. C2 (CAN) ${ }^{\mathrm{IMO} 4}$ Let $n$ be an odd integer greater than 1 and let $c_{1}, c_{2}, \ldots$, $c_{n}$ be integers. For each permutation $a=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of $\{1,2, \ldots, n\}$, define $S(a)=\sum_{i=1}^{n} c_{i} a_{i}$. Prove that there exist permutations $a \neq b$ of $\{1,2, \ldots, n\}$ such that $n$ ! is a divisor of $S(a)-S(b)$.
|
8. Suppose to the contrary that all the $S(a)$ 's are different modulo $n$ !. Then the sum of $S(a)$ 's over all permutations $a$ satisfies $\sum_{a} S(a) \equiv 0+1+\cdots+$ $(n!-1)=\frac{(n!-1) n!}{2} \equiv \frac{n!}{2}(\bmod n!)$. On the other hand, the coefficient of $c_{i}$ in $\sum_{a} S(a)$ is equal to $(n-1)!(1+2+\cdots+n)=\frac{n+1}{2} n!$ for all $i$, from which we obtain $$ \sum_{a} S(a) \equiv \frac{n+1}{2}\left(c_{1}+\cdots+c_{n}\right) n!\equiv 0(\bmod n!) $$ for odd $n$. This is a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
59492ac3-4d4d-526e-9f4d-a5983f0a7a4b
| 25,098
|
9. C3 (RUS) Define a $k$-clique to be a set of $k$ people such that every pair of them are acquainted with each other. At a certain party, every pair of 3 -cliques has at least one person in common, and there are no 5 -cliques. Prove that there are two or fewer people at the party whose departure leaves no 3-clique remaining.
|
9. Consider one such party. The result is trivially true if there is only one 3 -clique, so suppose there exist at least two 3 -cliques $C_{1}$ and $C_{2}$. We distinguish two cases: (i) $C_{1}=\{a, b, c\}$ and $C_{2}=\{a, d, e\}$ for some distinct people $a, b, c, d, e$. If the departure of $a$ destroys all 3-cliques, then we are done. Otherwise, there is a third 3 -clique $C_{3}$, which has a person in common with each of $C_{1}, C_{2}$ and does not include $a$ : say, $C_{3}=\{b, d, f\}$ for some $f$. We thus obtain another 3 -clique $C_{4}=\{a, b, d\}$, which has two persons in common with $C_{3}$, and the case (ii) is applied. (ii) $C_{1}=\{a, b, c\}$ and $C_{2}=\{a, b, d\}$ for distinct people $a, b, c, d$. If the departure of $a, b$ leaves no 3-clique, then we are done. Otherwise, for some $e$ there is a clique $\{c, d, e\}$. We claim that then the departure of $c, d$ breaks all 3 -cliques. Suppose the opposite, that a 3 -clique $C$ remains. Since $C$ shares a person with each of the 3 -cliques $\{c, d, a\},\{c, d, b\},\{c, d, e\}$, it must be $C=\{a, b, e\}$. However, then $\{a, b, c, d, e\}$ is a 5 -clique, which is assumed to be impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
9. C3 (RUS) Define a $k$-clique to be a set of $k$ people such that every pair of them are acquainted with each other. At a certain party, every pair of 3 -cliques has at least one person in common, and there are no 5 -cliques. Prove that there are two or fewer people at the party whose departure leaves no 3-clique remaining.
|
9. Consider one such party. The result is trivially true if there is only one 3 -clique, so suppose there exist at least two 3 -cliques $C_{1}$ and $C_{2}$. We distinguish two cases: (i) $C_{1}=\{a, b, c\}$ and $C_{2}=\{a, d, e\}$ for some distinct people $a, b, c, d, e$. If the departure of $a$ destroys all 3-cliques, then we are done. Otherwise, there is a third 3 -clique $C_{3}$, which has a person in common with each of $C_{1}, C_{2}$ and does not include $a$ : say, $C_{3}=\{b, d, f\}$ for some $f$. We thus obtain another 3 -clique $C_{4}=\{a, b, d\}$, which has two persons in common with $C_{3}$, and the case (ii) is applied. (ii) $C_{1}=\{a, b, c\}$ and $C_{2}=\{a, b, d\}$ for distinct people $a, b, c, d$. If the departure of $a, b$ leaves no 3-clique, then we are done. Otherwise, for some $e$ there is a clique $\{c, d, e\}$. We claim that then the departure of $c, d$ breaks all 3 -cliques. Suppose the opposite, that a 3 -clique $C$ remains. Since $C$ shares a person with each of the 3 -cliques $\{c, d, a\},\{c, d, b\},\{c, d, e\}$, it must be $C=\{a, b, e\}$. However, then $\{a, b, c, d, e\}$ is a 5 -clique, which is assumed to be impossible.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3ee7ee76-2eb2-59a2-8b02-6a001ac1527b
| 25,100
|
10. G4 (RUS) Circles $S_{1}$ and $S_{2}$ intersect at points $P$ and $Q$. Distinct points $A_{1}$ and $B_{1}$ (not at $P$ or $Q$ ) are selected on $S_{1}$. The lines $A_{1} P$ and $B_{1} P$ meet $S_{2}$ again at $A_{2}$ and $B_{2}$ respectively, and the lines $A_{1} B_{1}$ and $A_{2} B_{2}$ meet at $C$. Prove that as $A_{1}$ and $B_{1}$ vary, the circumcenters of triangles $A_{1} A_{2} C$ all lie on one fixed circle.
|
10. Let $O$ be the circumcenter of $A_{1} A_{2} C$, and $O_{1}, O_{2}$ the centers of $S_{1}, S_{2}$ respectively. First, from $\angle A_{1} Q A_{2}=180^{\circ}-\angle P A_{1} Q-\angle Q A_{2} P=\frac{1}{2}\left(360^{\circ}-\angle P O_{1} Q-\right.$ $\left.\angle Q O_{2} P\right)=\angle O_{1} Q O_{2}$ we obtain $\angle A_{1} Q A_{2}=\angle B_{1} Q B_{2}=\angle O_{1} Q O_{2}$. Therefore $\angle A_{1} Q A_{2}=\angle B_{1} Q P+$ $\angle P Q B_{2}=\angle C A_{1} P+\angle C A_{2} P=$ $180^{\circ}-\angle A_{1} C A_{2}$, from which we conclude that $Q$ lies on the circumcircle of $\triangle A_{1} A_{2} C$. Hence $O A_{1}=$ $O Q$. However, we also have $O_{1} A_{2}=$ $O_{1} Q$. Consequently, $O, O_{1}$ both lie on the perpendicular bisector of $A_{1} Q$, so $O O_{1} \perp A_{1} Q$. Similarly, $O O_{2} \perp A_{2} Q$, leading to $\angle O_{2} O O_{1}=$  $180^{\circ}-\angle A_{1} Q A_{2}=180^{\circ}-\angle O_{1} Q O_{2}$. Hence, $O$ lies on the circle through $O_{1}, O_{2}, Q$, which is fixed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
10. G4 (RUS) Circles $S_{1}$ and $S_{2}$ intersect at points $P$ and $Q$. Distinct points $A_{1}$ and $B_{1}$ (not at $P$ or $Q$ ) are selected on $S_{1}$. The lines $A_{1} P$ and $B_{1} P$ meet $S_{2}$ again at $A_{2}$ and $B_{2}$ respectively, and the lines $A_{1} B_{1}$ and $A_{2} B_{2}$ meet at $C$. Prove that as $A_{1}$ and $B_{1}$ vary, the circumcenters of triangles $A_{1} A_{2} C$ all lie on one fixed circle.
|
10. Let $O$ be the circumcenter of $A_{1} A_{2} C$, and $O_{1}, O_{2}$ the centers of $S_{1}, S_{2}$ respectively. First, from $\angle A_{1} Q A_{2}=180^{\circ}-\angle P A_{1} Q-\angle Q A_{2} P=\frac{1}{2}\left(360^{\circ}-\angle P O_{1} Q-\right.$ $\left.\angle Q O_{2} P\right)=\angle O_{1} Q O_{2}$ we obtain $\angle A_{1} Q A_{2}=\angle B_{1} Q B_{2}=\angle O_{1} Q O_{2}$. Therefore $\angle A_{1} Q A_{2}=\angle B_{1} Q P+$ $\angle P Q B_{2}=\angle C A_{1} P+\angle C A_{2} P=$ $180^{\circ}-\angle A_{1} C A_{2}$, from which we conclude that $Q$ lies on the circumcircle of $\triangle A_{1} A_{2} C$. Hence $O A_{1}=$ $O Q$. However, we also have $O_{1} A_{2}=$ $O_{1} Q$. Consequently, $O, O_{1}$ both lie on the perpendicular bisector of $A_{1} Q$, so $O O_{1} \perp A_{1} Q$. Similarly, $O O_{2} \perp A_{2} Q$, leading to $\angle O_{2} O O_{1}=$  $180^{\circ}-\angle A_{1} Q A_{2}=180^{\circ}-\angle O_{1} Q O_{2}$. Hence, $O$ lies on the circle through $O_{1}, O_{2}, Q$, which is fixed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2776f468-c543-5e5a-a63b-546d57fa881b
| 25,104
|
13. G7 (BUL) The incircle $\Omega$ of the acute-angled triangle $A B C$ is tangent to $B C$ at $K$. Let $A D$ be an altitude of triangle $A B C$ and let $M$ be the midpoint of $A D$. If $N$ is the other common point of $\Omega$ and $K M$, prove that $\Omega$ and the circumcircle of triangle $B C N$ are tangent at $N$.
|
13. Let $k$ be the circle through $B, C$ that is tangent to the circle $\Omega$ at point $N^{\prime}$. We must prove that $K, M, N^{\prime}$ are collinear. Since the statement is trivial for $A B=A C$, we may assume that $A C>A B$. As usual, $R, r, \alpha, \beta, \gamma$ denote the circumradius and the inradius and the angles of $\triangle A B C$, respectively. We have $\tan \angle B K M=D M / D K$. Straightforward calculation gives $D M=\frac{1}{2} A D=R \sin \beta \sin \gamma$ and $D K=\frac{D C-D B}{2}-\frac{K C-K B}{2}=R \sin (\beta-$ $\gamma)-R(\sin \beta-\sin \gamma)=4 R \sin \frac{\beta-\gamma}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2}$, so we obtain $$ \tan \angle B K M=\frac{\sin \beta \sin \gamma}{4 \sin \frac{\beta-\gamma}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2}}=\frac{\cos \frac{\beta}{2} \cos \frac{\gamma}{2}}{\sin \frac{\beta-\gamma}{2}} $$ To calculate the angle $B K N^{\prime}$, we apply the inversion $\psi$ with center at $K$ and power $B K \cdot C K$. For each object $X$, we denote by $\widehat{X}$ its image under $\psi$. The incircle $\Omega$ maps to a  line $\widehat{\Omega}$ parallel to $\widehat{B} \widehat{C}$, at distance $\frac{B K \cdot C K}{2 r}$ from $\widehat{B} \widehat{C}$. Thus the point $\widehat{N^{\prime}}$ is the projection of the midpoint $\widehat{U}$ of $\widehat{B} \widehat{C}$ onto $\widehat{\Omega}$. Hence $$ \tan \angle B K N^{\prime}=\tan \angle \widehat{B} K \widehat{N^{\prime}}=\frac{\widehat{U} \widehat{N^{\prime}}}{\widehat{U} K}=\frac{B K \cdot C K}{r(C K-B K)} . $$ Again, one easily checks that $K B \cdot K C=b c \sin ^{2} \frac{\alpha}{2}$ and $r=4 R \sin \frac{\alpha}{2}$. $\sin \frac{\beta}{2} \cdot \sin \frac{\gamma}{2}$, which implies $$ \begin{aligned} \tan \angle B K N^{\prime} & =\frac{b c \sin ^{2} \frac{\alpha}{2}}{r(b-c)} \\ & =\frac{4 R^{2} \sin \beta \sin \gamma \sin ^{2} \frac{\alpha}{2}}{4 R \sin \frac{\alpha}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2} \cdot 2 R(\sin \beta-\sin \gamma)}=\frac{\cos \frac{\beta}{2} \cos \frac{\gamma}{2}}{\sin \frac{\beta-\gamma}{2}} . \end{aligned} $$ Hence $\angle B K M=\angle B K N^{\prime}$, which implies that $K, M, N^{\prime}$ are indeed collinear; thus $N^{\prime} \equiv N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. G7 (BUL) The incircle $\Omega$ of the acute-angled triangle $A B C$ is tangent to $B C$ at $K$. Let $A D$ be an altitude of triangle $A B C$ and let $M$ be the midpoint of $A D$. If $N$ is the other common point of $\Omega$ and $K M$, prove that $\Omega$ and the circumcircle of triangle $B C N$ are tangent at $N$.
|
13. Let $k$ be the circle through $B, C$ that is tangent to the circle $\Omega$ at point $N^{\prime}$. We must prove that $K, M, N^{\prime}$ are collinear. Since the statement is trivial for $A B=A C$, we may assume that $A C>A B$. As usual, $R, r, \alpha, \beta, \gamma$ denote the circumradius and the inradius and the angles of $\triangle A B C$, respectively. We have $\tan \angle B K M=D M / D K$. Straightforward calculation gives $D M=\frac{1}{2} A D=R \sin \beta \sin \gamma$ and $D K=\frac{D C-D B}{2}-\frac{K C-K B}{2}=R \sin (\beta-$ $\gamma)-R(\sin \beta-\sin \gamma)=4 R \sin \frac{\beta-\gamma}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2}$, so we obtain $$ \tan \angle B K M=\frac{\sin \beta \sin \gamma}{4 \sin \frac{\beta-\gamma}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2}}=\frac{\cos \frac{\beta}{2} \cos \frac{\gamma}{2}}{\sin \frac{\beta-\gamma}{2}} $$ To calculate the angle $B K N^{\prime}$, we apply the inversion $\psi$ with center at $K$ and power $B K \cdot C K$. For each object $X$, we denote by $\widehat{X}$ its image under $\psi$. The incircle $\Omega$ maps to a  line $\widehat{\Omega}$ parallel to $\widehat{B} \widehat{C}$, at distance $\frac{B K \cdot C K}{2 r}$ from $\widehat{B} \widehat{C}$. Thus the point $\widehat{N^{\prime}}$ is the projection of the midpoint $\widehat{U}$ of $\widehat{B} \widehat{C}$ onto $\widehat{\Omega}$. Hence $$ \tan \angle B K N^{\prime}=\tan \angle \widehat{B} K \widehat{N^{\prime}}=\frac{\widehat{U} \widehat{N^{\prime}}}{\widehat{U} K}=\frac{B K \cdot C K}{r(C K-B K)} . $$ Again, one easily checks that $K B \cdot K C=b c \sin ^{2} \frac{\alpha}{2}$ and $r=4 R \sin \frac{\alpha}{2}$. $\sin \frac{\beta}{2} \cdot \sin \frac{\gamma}{2}$, which implies $$ \begin{aligned} \tan \angle B K N^{\prime} & =\frac{b c \sin ^{2} \frac{\alpha}{2}}{r(b-c)} \\ & =\frac{4 R^{2} \sin \beta \sin \gamma \sin ^{2} \frac{\alpha}{2}}{4 R \sin \frac{\alpha}{2} \sin \frac{\beta}{2} \sin \frac{\gamma}{2} \cdot 2 R(\sin \beta-\sin \gamma)}=\frac{\cos \frac{\beta}{2} \cos \frac{\gamma}{2}}{\sin \frac{\beta-\gamma}{2}} . \end{aligned} $$ Hence $\angle B K M=\angle B K N^{\prime}$, which implies that $K, M, N^{\prime}$ are indeed collinear; thus $N^{\prime} \equiv N$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ca6a877d-2da7-5747-aed7-fe26d31e3def
| 25,110
|
14. G8 (ARM) Let $S_{1}$ and $S_{2}$ be circles meeting at the points $A$ and $B$. A line through $A$ meets $S_{1}$ at $C$ and $S_{2}$ at $D$. Points $M, N, K$ lie on the line segments $C D, B C, B D$ respectively, with $M N$ parallel to $B D$ and $M K$ parallel to $B C$. Let $E$ and $F$ be points on those $\operatorname{arcs} B C$ of $S_{1}$ and $B D$ of $S_{2}$ respectively that do not contain $A$. Given that $E N$ is perpendicular to $B C$ and $F K$ is perpendicular to $B D$, prove that $\measuredangle E M F=90^{\circ}$.
|
14. Let $G$ be the other point of intersection of the line $F K$ with the arc $B A D$. Since $B N / N C=D K / K B$ and $\angle C E B=\angle B G D$ the triangles $C E B$ and $B G D$ are similar. Thus $B N / N E=D K / K G=F K / K B$. From $B N=M K$ and $B K=$ $M N$ it follows that $M N / N E=$ $F K / K M$. But we also have that $\angle M N E=90^{\circ}+\angle M N B=90^{\circ}+$  $\angle M K B=\angle F K M$, and hence $\triangle M N E \sim \triangle F K M$. Now $\angle E M F=\angle N M K-\angle N M E-\angle K M F=\angle N M K-\angle N M E-$ $\angle N E M=\angle N M K-90^{\circ}+\angle B N M=90^{\circ}$ as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
14. G8 (ARM) Let $S_{1}$ and $S_{2}$ be circles meeting at the points $A$ and $B$. A line through $A$ meets $S_{1}$ at $C$ and $S_{2}$ at $D$. Points $M, N, K$ lie on the line segments $C D, B C, B D$ respectively, with $M N$ parallel to $B D$ and $M K$ parallel to $B C$. Let $E$ and $F$ be points on those $\operatorname{arcs} B C$ of $S_{1}$ and $B D$ of $S_{2}$ respectively that do not contain $A$. Given that $E N$ is perpendicular to $B C$ and $F K$ is perpendicular to $B D$, prove that $\measuredangle E M F=90^{\circ}$.
|
14. Let $G$ be the other point of intersection of the line $F K$ with the arc $B A D$. Since $B N / N C=D K / K B$ and $\angle C E B=\angle B G D$ the triangles $C E B$ and $B G D$ are similar. Thus $B N / N E=D K / K G=F K / K B$. From $B N=M K$ and $B K=$ $M N$ it follows that $M N / N E=$ $F K / K M$. But we also have that $\angle M N E=90^{\circ}+\angle M N B=90^{\circ}+$  $\angle M K B=\angle F K M$, and hence $\triangle M N E \sim \triangle F K M$. Now $\angle E M F=\angle N M K-\angle N M E-\angle K M F=\angle N M K-\angle N M E-$ $\angle N E M=\angle N M K-90^{\circ}+\angle B N M=90^{\circ}$ as claimed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
054c0506-932b-5450-bdb4-92e9f86cd4ab
| 25,112
|
17. A3 (POL) Let $P$ be a cubic polynomial given by $P(x)=a x^{3}+b x^{2}+c x+$ $d$, where $a, b, c, d$ are integers and $a \neq 0$. Suppose that $x P(x)=y P(y)$ for infinitely many pairs $x, y$ of integers with $x \neq y$. Prove that the equation $P(x)=0$ has an integer root.
|
17. Let $x, y$ be distinct integers satisfying $x P(x)=y P(y)$; this is equivalent to $a\left(x^{4}-y^{4}\right)+b\left(x^{3}-y^{3}\right)+c\left(x^{2}-y^{2}\right)+d(x-y)=0$. Dividing by $x-y$ we obtain $$ a\left(x^{3}+x^{2} y+x y^{2}+y^{3}\right)+b\left(x^{2}+x y+y^{2}\right)+c(x+y)+d=0 . $$ Putting $x+y=p, x^{2}+y^{2}=q$ leads to $x^{2}+x y+y^{2}=\frac{p^{2}+q}{2}$, so the above equality becomes $$ a p q+\frac{b}{2}\left(p^{2}+q\right)+c p+d=0, \quad \text { i.e. } \quad(2 a p+b) q=-\left(b p^{2}+2 c p+2 d\right) $$ Since $q \geq p^{2} / 2$, it follows that $p^{2}|2 a p+b| \leq 2\left|b p^{2}+2 c p+2 d\right|$, which is possible only for finitely many values of $p$, although there are infinitely many pairs $(x, y)$ with $x P(x)=y P(y)$. Hence there exists $p$ such that $x P(x)=(p-x) P(p-x)$ for infinitely many $x$, and therefore for all $x$. If $p \neq 0$, then $p$ is a root of $P(x)$. If $p=0$, the above relation gives $P(x)=-P(-x)$. This forces $b=d=0$, so $P(x)=x\left(a x^{2}+c\right)$. Thus 0 is a root of $P(x)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
17. A3 (POL) Let $P$ be a cubic polynomial given by $P(x)=a x^{3}+b x^{2}+c x+$ $d$, where $a, b, c, d$ are integers and $a \neq 0$. Suppose that $x P(x)=y P(y)$ for infinitely many pairs $x, y$ of integers with $x \neq y$. Prove that the equation $P(x)=0$ has an integer root.
|
17. Let $x, y$ be distinct integers satisfying $x P(x)=y P(y)$; this is equivalent to $a\left(x^{4}-y^{4}\right)+b\left(x^{3}-y^{3}\right)+c\left(x^{2}-y^{2}\right)+d(x-y)=0$. Dividing by $x-y$ we obtain $$ a\left(x^{3}+x^{2} y+x y^{2}+y^{3}\right)+b\left(x^{2}+x y+y^{2}\right)+c(x+y)+d=0 . $$ Putting $x+y=p, x^{2}+y^{2}=q$ leads to $x^{2}+x y+y^{2}=\frac{p^{2}+q}{2}$, so the above equality becomes $$ a p q+\frac{b}{2}\left(p^{2}+q\right)+c p+d=0, \quad \text { i.e. } \quad(2 a p+b) q=-\left(b p^{2}+2 c p+2 d\right) $$ Since $q \geq p^{2} / 2$, it follows that $p^{2}|2 a p+b| \leq 2\left|b p^{2}+2 c p+2 d\right|$, which is possible only for finitely many values of $p$, although there are infinitely many pairs $(x, y)$ with $x P(x)=y P(y)$. Hence there exists $p$ such that $x P(x)=(p-x) P(p-x)$ for infinitely many $x$, and therefore for all $x$. If $p \neq 0$, then $p$ is a root of $P(x)$. If $p=0$, the above relation gives $P(x)=-P(-x)$. This forces $b=d=0$, so $P(x)=x\left(a x^{2}+c\right)$. Thus 0 is a root of $P(x)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4db2ce9a-f6a2-59aa-a801-f7eef83d0b0f
| 25,116
|
19. A5 (IND) Let $n$ be a positive integer that is not a perfect cube. Define real numbers $a, b, c$ by $$ a=\sqrt[3]{n}, \quad b=\frac{1}{a-[a]}, \quad c=\frac{1}{b-[b]}, $$ where $[x]$ denotes the integer part of $x$. Prove that there are infinitely many such integers $n$ with the property that there exist integers $r, s, t$, not all zero, such that $r a+s b+t c=0$.
|
19. Write $m=[\sqrt[3]{n}]$. To simplify the calculation, we shall assume that $[b]=1$. Then $a=\sqrt[3]{n}, b=\frac{1}{\sqrt[3]{n}-m}=\frac{1}{n-m^{3}}\left(m^{2}+m \sqrt[3]{n}+\sqrt[3]{n^{2}}\right), c=\frac{1}{b-1}=$ $u+v \sqrt[3]{n}+w \sqrt[3]{n^{2}}$ for certain rational numbers $u, v, w$. Obviously, integers $r, s, t$ with $r a+s b+t c=0$ exist if (and only if) $u=m^{2} w$, i.e., if ( $b-$ 1) $\left(m^{2} w+v \sqrt[3]{n}+w \sqrt[3]{n^{2}}\right)=1$ for some rational $v, w$. When the last equality is expanded and simplified, comparing the coefficients at $1, \sqrt[3]{n}, \sqrt[3]{n^{2}}$ one obtains $$ \begin{array}{rlrl} 1: & v+\left(\left(m^{2}+m^{3}-n\right) m^{2}+m\right) w & =n-m^{3}, \\ \sqrt[3]{n}: & \left(m^{2}+m^{3}-n\right) v+ & \left(m^{3}+n\right) w & =0, \\ \sqrt[3]{n^{2}}: & m v+ & \left(2 m^{2}+m^{3}-n\right) w & =0 . \end{array} $$ In order for the system (1) to have a solution $v, w$, we must have $\left(2 m^{2}+\right.$ $\left.m^{3}-n\right)\left(m^{2}+m^{3}-n\right)=m\left(m^{3}+n\right)$. This quadratic equation has solutions $n=m^{3}$ and $n=m^{3}+3 m^{2}+m$. The former is not possible, but the latter gives $a-[a]>\frac{1}{2}$, so $[b]=1$, and the system (1) in $v, w$ is solvable. Hence every number $n=m^{3}+3 m^{2}+m, m \in \mathbb{N}$, satisfies the condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
19. A5 (IND) Let $n$ be a positive integer that is not a perfect cube. Define real numbers $a, b, c$ by $$ a=\sqrt[3]{n}, \quad b=\frac{1}{a-[a]}, \quad c=\frac{1}{b-[b]}, $$ where $[x]$ denotes the integer part of $x$. Prove that there are infinitely many such integers $n$ with the property that there exist integers $r, s, t$, not all zero, such that $r a+s b+t c=0$.
|
19. Write $m=[\sqrt[3]{n}]$. To simplify the calculation, we shall assume that $[b]=1$. Then $a=\sqrt[3]{n}, b=\frac{1}{\sqrt[3]{n}-m}=\frac{1}{n-m^{3}}\left(m^{2}+m \sqrt[3]{n}+\sqrt[3]{n^{2}}\right), c=\frac{1}{b-1}=$ $u+v \sqrt[3]{n}+w \sqrt[3]{n^{2}}$ for certain rational numbers $u, v, w$. Obviously, integers $r, s, t$ with $r a+s b+t c=0$ exist if (and only if) $u=m^{2} w$, i.e., if ( $b-$ 1) $\left(m^{2} w+v \sqrt[3]{n}+w \sqrt[3]{n^{2}}\right)=1$ for some rational $v, w$. When the last equality is expanded and simplified, comparing the coefficients at $1, \sqrt[3]{n}, \sqrt[3]{n^{2}}$ one obtains $$ \begin{array}{rlrl} 1: & v+\left(\left(m^{2}+m^{3}-n\right) m^{2}+m\right) w & =n-m^{3}, \\ \sqrt[3]{n}: & \left(m^{2}+m^{3}-n\right) v+ & \left(m^{3}+n\right) w & =0, \\ \sqrt[3]{n^{2}}: & m v+ & \left(2 m^{2}+m^{3}-n\right) w & =0 . \end{array} $$ In order for the system (1) to have a solution $v, w$, we must have $\left(2 m^{2}+\right.$ $\left.m^{3}-n\right)\left(m^{2}+m^{3}-n\right)=m\left(m^{3}+n\right)$. This quadratic equation has solutions $n=m^{3}$ and $n=m^{3}+3 m^{2}+m$. The former is not possible, but the latter gives $a-[a]>\frac{1}{2}$, so $[b]=1$, and the system (1) in $v, w$ is solvable. Hence every number $n=m^{3}+3 m^{2}+m, m \in \mathbb{N}$, satisfies the condition of the problem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
42eff7c3-cfbf-520d-8e75-615e69ff097f
| 25,118
|
2. N2 (ROM) ${ }^{\mathrm{IMO} 4}$ Let $n \geq 2$ be a positive integer, with divisors $1=d_{1}<$ $d_{2}<\cdots<d_{k}=n$. Prove that $d_{1} d_{2}+d_{2} d_{3}+\cdots+d_{k-1} d_{k}$ is always less than $n^{2}$, and determine when it is a divisor of $n^{2}$.
|
2. Set $S=d_{1} d_{2}+\cdots+d_{k-1} d_{k}$. Since $d_{i} / n=1 / d_{k+1-i}$, we have $\frac{S}{n^{2}}=$ $\frac{1}{d_{k} d_{k-1}}+\cdots+\frac{1}{d_{2} d_{1}}$. Hence $$ \frac{1}{d_{2} d_{1}} \leq \frac{S}{n^{2}} \leq\left(\frac{1}{d_{k-1}}-\frac{1}{d_{k}}\right)+\cdots+\left(\frac{1}{d_{1}}-\frac{1}{d_{2}}\right)=1-\frac{1}{d_{k}}<1 $$ or $\left(\right.$ since $\left.d_{1}=1\right) 1<\frac{n^{2}}{S} \leq d_{2}$. This shows that $S<n^{2}$. Also, if $S$ is a divisor of $n^{2}$, then $n^{2} / S$ is a nontrivial divisor of $n^{2}$ not exceeding $d_{2}$. But $d_{2}$ is obviously the least prime divisor of $n$ (and also of $n^{2}$ ), so we must have $n^{2} / S=d_{2}$, which holds if and only if $n$ is prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
2. N2 (ROM) ${ }^{\mathrm{IMO} 4}$ Let $n \geq 2$ be a positive integer, with divisors $1=d_{1}<$ $d_{2}<\cdots<d_{k}=n$. Prove that $d_{1} d_{2}+d_{2} d_{3}+\cdots+d_{k-1} d_{k}$ is always less than $n^{2}$, and determine when it is a divisor of $n^{2}$.
|
2. Set $S=d_{1} d_{2}+\cdots+d_{k-1} d_{k}$. Since $d_{i} / n=1 / d_{k+1-i}$, we have $\frac{S}{n^{2}}=$ $\frac{1}{d_{k} d_{k-1}}+\cdots+\frac{1}{d_{2} d_{1}}$. Hence $$ \frac{1}{d_{2} d_{1}} \leq \frac{S}{n^{2}} \leq\left(\frac{1}{d_{k-1}}-\frac{1}{d_{k}}\right)+\cdots+\left(\frac{1}{d_{1}}-\frac{1}{d_{2}}\right)=1-\frac{1}{d_{k}}<1 $$ or $\left(\right.$ since $\left.d_{1}=1\right) 1<\frac{n^{2}}{S} \leq d_{2}$. This shows that $S<n^{2}$. Also, if $S$ is a divisor of $n^{2}$, then $n^{2} / S$ is a nontrivial divisor of $n^{2}$ not exceeding $d_{2}$. But $d_{2}$ is obviously the least prime divisor of $n$ (and also of $n^{2}$ ), so we must have $n^{2} / S=d_{2}$, which holds if and only if $n$ is prime.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
8d1a0f40-652b-5fb5-88d1-ec150e3fb272
| 25,119
|
20. A6 (IRN) Let $A$ be a nonempty set of positive integers. Suppose that there are positive integers $b_{1}, \ldots, b_{n}$ and $c_{1}, \ldots, c_{n}$ such that (i) for each $i$ the set $b_{i} A+c_{i}=\left\{b_{i} a+c_{i} \mid a \in A\right\}$ is a subset of $A$, and (ii) the sets $b_{i} A+c_{i}$ and $b_{j} A+c_{j}$ are disjoint whenever $i \neq j$. Prove that $$ \frac{1}{b_{1}}+\cdots+\frac{1}{b_{n}} \leq 1 $$
|
20. Assume to the contrary that $\frac{1}{b_{1}}+\cdots+\frac{1}{b_{n}}>1$. Certainly $n \geq 2$ and $A$ is infinite. Define $f_{i}: A \rightarrow A$ as $f_{i}(x)=b_{i} x+c_{i}$ for each $i$. By condition (ii), $f_{i}(x)=f_{j}(y)$ implies $i=j$ and $x=y$; iterating this argument, we deduce that $f_{i_{1}}\left(\ldots f_{i_{m}}(x) \ldots\right)=f_{j_{1}}\left(\ldots f_{j_{m}}(x) \ldots\right)$ implies $i_{1}=j_{1}, \ldots, i_{m}=j_{m}$ and $x=y$. As an illustration, we shall consider the case $b_{1}=b_{2}=b_{3}=2$ first. If $a$ is large enough, then for any $i_{1}, \ldots, i_{m} \in\{1,2,3\}$ we have $f_{i_{1}} \circ \cdots \circ f_{i_{m}}(a) \leq$ $2.1^{m} a$. However, we obtain $3^{m}$ values in this way, so they cannot be all distinct if $m$ is sufficiently large, a contradiction. In the general case, let real numbers $d_{i}>b_{i}, i=1,2 \ldots, n$, be chosen such that $\frac{1}{d_{1}}+\cdots+\frac{1}{d_{n}}>1$ : for $a$ large enough, $f_{i}(x)<d_{i} a$ for each $x \geq a$. Also, let $k_{i}>0$ be arbitrary rational numbers with sum 1 ; denote by $N_{0}$ the least common multiple of their denominators. Let $N$ be a fixed multiple of $N_{0}$, so that each $k_{j} N$ is an integer. Consider all combinations $f_{i_{1}} \circ \cdots \circ f_{i_{N}}$ of $N$ functions, among which each $f_{i}$ appears exactly $k_{i} N$ times. There are $F_{N}=\frac{N!}{\left(k_{1} N\right)!\cdots\left(k_{n} N\right)!}$ such combinations, so they give $F_{N}$ distinct values when applied to $a$. On the other hand, $f_{i_{1}} \circ \cdots \circ f_{i_{N}}(a) \leq\left(d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}\right)^{N} a$. Therefore $$ \left(d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}\right)^{N} a \geq F_{N} \quad \text { for all } N, N_{0} \mid N $$ It remains to find a lower estimate for $F_{N}$. In fact, it is straightforward to verify that $F_{N+N_{0}} / F_{N}$ tends to $Q^{N_{0}}$, where $Q=1 /\left(k_{1}^{k_{1}} \cdots k_{n}^{k_{n}}\right)$. Consequently, for every $q<Q$ there exists $p>0$ such that $F_{N}>p q^{N}$. Then (1) implies that $$ \left(\frac{d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}}{q}\right)^{N}>\frac{p}{a} \text { for every multiple } N \text { of } N_{0} $$ and hence $d_{1}^{k_{1}} \cdots d_{n}^{k_{n}} / q \geq 1$. This must hold for every $q<Q$, and so we have $d_{1}^{k_{1}} \cdots d_{n}^{k_{n}} \geq Q$, i.e., $$ \left(k_{1} d_{1}\right)^{k_{1}} \cdots\left(k_{n} d_{n}\right)^{k_{n}} \geq 1 $$ However, if we choose $k_{1}, \ldots, k_{n}$ such that $k_{1} d_{1}=\cdots=k_{n} d_{n}=u$, then we must have $u \geq 1$. Therefore $\frac{1}{d_{1}}+\cdots+\frac{1}{d_{n}} \leq k_{1}+\cdots+k_{n}=1$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
20. A6 (IRN) Let $A$ be a nonempty set of positive integers. Suppose that there are positive integers $b_{1}, \ldots, b_{n}$ and $c_{1}, \ldots, c_{n}$ such that (i) for each $i$ the set $b_{i} A+c_{i}=\left\{b_{i} a+c_{i} \mid a \in A\right\}$ is a subset of $A$, and (ii) the sets $b_{i} A+c_{i}$ and $b_{j} A+c_{j}$ are disjoint whenever $i \neq j$. Prove that $$ \frac{1}{b_{1}}+\cdots+\frac{1}{b_{n}} \leq 1 $$
|
20. Assume to the contrary that $\frac{1}{b_{1}}+\cdots+\frac{1}{b_{n}}>1$. Certainly $n \geq 2$ and $A$ is infinite. Define $f_{i}: A \rightarrow A$ as $f_{i}(x)=b_{i} x+c_{i}$ for each $i$. By condition (ii), $f_{i}(x)=f_{j}(y)$ implies $i=j$ and $x=y$; iterating this argument, we deduce that $f_{i_{1}}\left(\ldots f_{i_{m}}(x) \ldots\right)=f_{j_{1}}\left(\ldots f_{j_{m}}(x) \ldots\right)$ implies $i_{1}=j_{1}, \ldots, i_{m}=j_{m}$ and $x=y$. As an illustration, we shall consider the case $b_{1}=b_{2}=b_{3}=2$ first. If $a$ is large enough, then for any $i_{1}, \ldots, i_{m} \in\{1,2,3\}$ we have $f_{i_{1}} \circ \cdots \circ f_{i_{m}}(a) \leq$ $2.1^{m} a$. However, we obtain $3^{m}$ values in this way, so they cannot be all distinct if $m$ is sufficiently large, a contradiction. In the general case, let real numbers $d_{i}>b_{i}, i=1,2 \ldots, n$, be chosen such that $\frac{1}{d_{1}}+\cdots+\frac{1}{d_{n}}>1$ : for $a$ large enough, $f_{i}(x)<d_{i} a$ for each $x \geq a$. Also, let $k_{i}>0$ be arbitrary rational numbers with sum 1 ; denote by $N_{0}$ the least common multiple of their denominators. Let $N$ be a fixed multiple of $N_{0}$, so that each $k_{j} N$ is an integer. Consider all combinations $f_{i_{1}} \circ \cdots \circ f_{i_{N}}$ of $N$ functions, among which each $f_{i}$ appears exactly $k_{i} N$ times. There are $F_{N}=\frac{N!}{\left(k_{1} N\right)!\cdots\left(k_{n} N\right)!}$ such combinations, so they give $F_{N}$ distinct values when applied to $a$. On the other hand, $f_{i_{1}} \circ \cdots \circ f_{i_{N}}(a) \leq\left(d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}\right)^{N} a$. Therefore $$ \left(d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}\right)^{N} a \geq F_{N} \quad \text { for all } N, N_{0} \mid N $$ It remains to find a lower estimate for $F_{N}$. In fact, it is straightforward to verify that $F_{N+N_{0}} / F_{N}$ tends to $Q^{N_{0}}$, where $Q=1 /\left(k_{1}^{k_{1}} \cdots k_{n}^{k_{n}}\right)$. Consequently, for every $q<Q$ there exists $p>0$ such that $F_{N}>p q^{N}$. Then (1) implies that $$ \left(\frac{d_{1}^{k_{1}} \cdots d_{n}^{k_{n}}}{q}\right)^{N}>\frac{p}{a} \text { for every multiple } N \text { of } N_{0} $$ and hence $d_{1}^{k_{1}} \cdots d_{n}^{k_{n}} / q \geq 1$. This must hold for every $q<Q$, and so we have $d_{1}^{k_{1}} \cdots d_{n}^{k_{n}} \geq Q$, i.e., $$ \left(k_{1} d_{1}\right)^{k_{1}} \cdots\left(k_{n} d_{n}\right)^{k_{n}} \geq 1 $$ However, if we choose $k_{1}, \ldots, k_{n}$ such that $k_{1} d_{1}=\cdots=k_{n} d_{n}=u$, then we must have $u \geq 1$. Therefore $\frac{1}{d_{1}}+\cdots+\frac{1}{d_{n}} \leq k_{1}+\cdots+k_{n}=1$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
3a6bfb3b-1729-52a0-ba18-33bdfc28e87b
| 25,120
|
21. $\mathbf{C 1}(\mathbf{C O L})^{\mathrm{IMO} 1}$ Let $n$ be a positive integer. Each point $(x, y)$ in the plane, where $x$ and $y$ are nonnegative integers with $x+y \leq n$, is colored red or blue, subject to the following condition: If a point $(x, y)$ is red, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ with $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Let $A$ be the number of ways to choose $n$ blue points with distinct $x$-coordinates, and let $B$ be the number of ways to choose $n$ blue points with distinct $y$-coordinates. Prove that $A=B$.
|
21. Let $a_{i}$ be the number of blue points with $x$-coordinate $i$, and $b_{i}$ the number of blue points with $y$-coordinate $i$. Our task is to show that $a_{0} a_{1} \cdots a_{n-1}=$ $b_{0} b_{1} \cdots b_{n-1}$. Moreover, we claim that $a_{0}, \ldots, a_{n-1}$ is a permutation of $b_{0}, \ldots, b_{n-1}$, and to show this we use induction on the number of red points. The result is trivial if all the points are blue. So, choose a red point $(x, y)$ with $x+y$ maximal: clearly $a_{x}=b_{y}=n-x-y-1$. If we change this point to blue, $a_{x}$ and $b_{y}$ will decrease by 1 . Then by the induction hypothesis, $a_{0}, \ldots, a_{n-1}$ with $a_{x}$ decreased by 1 is a permutation of $b_{0}, \ldots, b_{n-1}$ with $b_{y}$ decreased by 1 . However, $a_{x}=b_{y}$, and the claim follows. Remark. One can also use induction on $n$ : it is not more difficult.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
21. $\mathbf{C 1}(\mathbf{C O L})^{\mathrm{IMO} 1}$ Let $n$ be a positive integer. Each point $(x, y)$ in the plane, where $x$ and $y$ are nonnegative integers with $x+y \leq n$, is colored red or blue, subject to the following condition: If a point $(x, y)$ is red, then so are all points $\left(x^{\prime}, y^{\prime}\right)$ with $x^{\prime} \leq x$ and $y^{\prime} \leq y$. Let $A$ be the number of ways to choose $n$ blue points with distinct $x$-coordinates, and let $B$ be the number of ways to choose $n$ blue points with distinct $y$-coordinates. Prove that $A=B$.
|
21. Let $a_{i}$ be the number of blue points with $x$-coordinate $i$, and $b_{i}$ the number of blue points with $y$-coordinate $i$. Our task is to show that $a_{0} a_{1} \cdots a_{n-1}=$ $b_{0} b_{1} \cdots b_{n-1}$. Moreover, we claim that $a_{0}, \ldots, a_{n-1}$ is a permutation of $b_{0}, \ldots, b_{n-1}$, and to show this we use induction on the number of red points. The result is trivial if all the points are blue. So, choose a red point $(x, y)$ with $x+y$ maximal: clearly $a_{x}=b_{y}=n-x-y-1$. If we change this point to blue, $a_{x}$ and $b_{y}$ will decrease by 1 . Then by the induction hypothesis, $a_{0}, \ldots, a_{n-1}$ with $a_{x}$ decreased by 1 is a permutation of $b_{0}, \ldots, b_{n-1}$ with $b_{y}$ decreased by 1 . However, $a_{x}=b_{y}$, and the claim follows. Remark. One can also use induction on $n$ : it is not more difficult.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
52dca80b-e3b5-592d-a391-bb407198f1e1
| 25,121
|
25. C5 (BRA) Let $r \geq 2$ be a fixed positive integer, and let $\mathcal{F}$ be an infinite family of sets, each of size $r$, no two of which are disjoint. Prove that there exists a set of size $r-1$ that meets each set in $\mathcal{F}$.
|
25. Assume to the contrary that no set of size less than $r$ meets all sets in $\mathcal{F}$. Consider any set $A$ of size less than $r$ that is contained in infinitely many sets of $\mathcal{F}$. By the assumption, $A$ is disjoint from some set $B \in \mathcal{F}$. Then of the infinitely many sets that contain $A$, each must meet $B$, so some element $b$ of $B$ belongs to infinitely many of them. But then the set $A \cup\{b\}$ is contained in infinitely many sets of $\mathcal{F}$ as well. Such a set $A$ exists: for example, the empty set. Now taking for $A$ the largest such set we come to a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
25. C5 (BRA) Let $r \geq 2$ be a fixed positive integer, and let $\mathcal{F}$ be an infinite family of sets, each of size $r$, no two of which are disjoint. Prove that there exists a set of size $r-1$ that meets each set in $\mathcal{F}$.
|
25. Assume to the contrary that no set of size less than $r$ meets all sets in $\mathcal{F}$. Consider any set $A$ of size less than $r$ that is contained in infinitely many sets of $\mathcal{F}$. By the assumption, $A$ is disjoint from some set $B \in \mathcal{F}$. Then of the infinitely many sets that contain $A$, each must meet $B$, so some element $b$ of $B$ belongs to infinitely many of them. But then the set $A \cup\{b\}$ is contained in infinitely many sets of $\mathcal{F}$ as well. Such a set $A$ exists: for example, the empty set. Now taking for $A$ the largest such set we come to a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c696e2bd-1020-5241-9b61-cfa28f097264
| 25,125
|
26. C6 (POL) Let $n$ be an even positive integer. Show that there is a permutation $x_{1}, x_{2}, \ldots, x_{n}$ of $1,2, \ldots, n$ such that for every $1 \leq i \leq n$ the number $x_{i+1}$ is one of $2 x_{i}, 2 x_{i}-1,2 x_{i}-n, 2 x_{i}-n-1$ (where we take $x_{n+1}=x_{1}$ ).
|
26. Write $n=2 m$. We shall define a directed graph $G$ with vertices $1, \ldots, m$ and edges labelled $1,2, \ldots, 2 m$ in such a way that the edges issuing from $i$ are labelled $2 i-1$ and $2 i$, and those entering it are labelled $i$ and $i+m$. What we need is an Euler circuit in $G$, namely a closed path that passes each edge exactly once. Indeed, if $x_{i}$ is the $i$ th edge in such a circuit, then $x_{i}$ enters some vertex $j$ and $x_{i+1}$ leaves it, so $x_{i} \equiv j(\bmod m)$ and $x_{i+1}=2 j-1$ or $2 j$. Hence $2 x_{i} \equiv 2 j$ and $x_{i+1} \equiv 2 x_{i}$ or $2 x_{i}-1(\bmod n)$, as required. The graph $G$ is connected: by induction on $k$ there is a path from 1 to $k$, since 1 is connected to $j$ with $2 j=k$ or $2 j-1=k$, and there is an edge from $j$ to $k$. Also, the in-degree and out-degree of each vertex of $G$ are equal (to 2), and thus by a known result, $G$ contains an Euler circuit.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
26. C6 (POL) Let $n$ be an even positive integer. Show that there is a permutation $x_{1}, x_{2}, \ldots, x_{n}$ of $1,2, \ldots, n$ such that for every $1 \leq i \leq n$ the number $x_{i+1}$ is one of $2 x_{i}, 2 x_{i}-1,2 x_{i}-n, 2 x_{i}-n-1$ (where we take $x_{n+1}=x_{1}$ ).
|
26. Write $n=2 m$. We shall define a directed graph $G$ with vertices $1, \ldots, m$ and edges labelled $1,2, \ldots, 2 m$ in such a way that the edges issuing from $i$ are labelled $2 i-1$ and $2 i$, and those entering it are labelled $i$ and $i+m$. What we need is an Euler circuit in $G$, namely a closed path that passes each edge exactly once. Indeed, if $x_{i}$ is the $i$ th edge in such a circuit, then $x_{i}$ enters some vertex $j$ and $x_{i+1}$ leaves it, so $x_{i} \equiv j(\bmod m)$ and $x_{i+1}=2 j-1$ or $2 j$. Hence $2 x_{i} \equiv 2 j$ and $x_{i+1} \equiv 2 x_{i}$ or $2 x_{i}-1(\bmod n)$, as required. The graph $G$ is connected: by induction on $k$ there is a path from 1 to $k$, since 1 is connected to $j$ with $2 j=k$ or $2 j-1=k$, and there is an edge from $j$ to $k$. Also, the in-degree and out-degree of each vertex of $G$ are equal (to 2), and thus by a known result, $G$ contains an Euler circuit.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
135c1da1-6470-5d91-8ef0-54ca223e4564
| 25,126
|
3. N3 (MON) Let $p_{1}, p_{2}, \ldots, p_{n}$ be distinct primes greater than 3 . Show that $2^{p_{1} p_{2} \cdots p_{n}}+1$ has at least $4^{n}$ divisors.
|
3. We observe that if $a, b$ are coprime odd numbers, then $\operatorname{gcd}\left(2^{a}+1,2^{b}+1\right)=$ 3. In fact, this g.c.d. divides $\operatorname{gcd}\left(2^{2 a}-1,2^{2 b}-1\right)=2^{\operatorname{gcd}(2 a, 2 b)}-1=2^{2}-1=$ 3 , while 3 obviously divides both $2^{a}+1$ and $2^{b}+1$. In particular, if $3 \nmid b$, then $3^{2} \nmid 2^{b}+1$, so $2^{a}+1$ and $\left(2^{b}+1\right) / 3$ are coprime; consequently $2^{a b}+1$ (being divisible by $\left.2^{a}+1,2^{b}+1\right)$ is divisible by $\frac{\left(2^{a}+1\right)\left(2^{b}+1\right)}{3}$. Now we prove the desired result by induction on $n$. For $n=1,2^{p_{1}}+1$ is divisible by 3 and exceeds $3^{2}$, so it has at least 4 divisors. Assume that $2^{a}+1=2^{p_{1} \cdots p_{n-1}}+1$ has at least $4^{n-1}$ divisors and consider $N=2^{a b}+1=$ $2^{p_{1} \cdots p_{n}}+1\left(\right.$ where $\left.b=p_{n}\right)$. As above, $2^{a}+1$ and $\frac{2^{b}+1}{3}$ are coprime, and thus $Q=\left(2^{a}+1\right)\left(2^{b}+1\right) / 3$ has at least $2 \cdot 4^{n-1}$ divisors. Moreover, $N$ is divisible by $Q$ and is greater than $Q^{2}$ (indeed, $N>2^{a b}>2^{2 a} 2^{2 b}>Q^{2}$ if $a, b \geq 5$ ). Then $N$ has at least twice as many divisors as $Q$ (because for every $d \mid Q$ both $d$ and $N / d$ are divisors of $N$ ), which counts up to $4^{n}$ divisors, as required. Remark. With some knowledge of cyclotomic polynomials, one can show that $2^{p_{1} \cdots p_{n}}+1$ has at least $2^{2^{n-1}}$ divisors, far exceeding $4^{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
3. N3 (MON) Let $p_{1}, p_{2}, \ldots, p_{n}$ be distinct primes greater than 3 . Show that $2^{p_{1} p_{2} \cdots p_{n}}+1$ has at least $4^{n}$ divisors.
|
3. We observe that if $a, b$ are coprime odd numbers, then $\operatorname{gcd}\left(2^{a}+1,2^{b}+1\right)=$ 3. In fact, this g.c.d. divides $\operatorname{gcd}\left(2^{2 a}-1,2^{2 b}-1\right)=2^{\operatorname{gcd}(2 a, 2 b)}-1=2^{2}-1=$ 3 , while 3 obviously divides both $2^{a}+1$ and $2^{b}+1$. In particular, if $3 \nmid b$, then $3^{2} \nmid 2^{b}+1$, so $2^{a}+1$ and $\left(2^{b}+1\right) / 3$ are coprime; consequently $2^{a b}+1$ (being divisible by $\left.2^{a}+1,2^{b}+1\right)$ is divisible by $\frac{\left(2^{a}+1\right)\left(2^{b}+1\right)}{3}$. Now we prove the desired result by induction on $n$. For $n=1,2^{p_{1}}+1$ is divisible by 3 and exceeds $3^{2}$, so it has at least 4 divisors. Assume that $2^{a}+1=2^{p_{1} \cdots p_{n-1}}+1$ has at least $4^{n-1}$ divisors and consider $N=2^{a b}+1=$ $2^{p_{1} \cdots p_{n}}+1\left(\right.$ where $\left.b=p_{n}\right)$. As above, $2^{a}+1$ and $\frac{2^{b}+1}{3}$ are coprime, and thus $Q=\left(2^{a}+1\right)\left(2^{b}+1\right) / 3$ has at least $2 \cdot 4^{n-1}$ divisors. Moreover, $N$ is divisible by $Q$ and is greater than $Q^{2}$ (indeed, $N>2^{a b}>2^{2 a} 2^{2 b}>Q^{2}$ if $a, b \geq 5$ ). Then $N$ has at least twice as many divisors as $Q$ (because for every $d \mid Q$ both $d$ and $N / d$ are divisors of $N$ ), which counts up to $4^{n}$ divisors, as required. Remark. With some knowledge of cyclotomic polynomials, one can show that $2^{p_{1} \cdots p_{n}}+1$ has at least $2^{2^{n-1}}$ divisors, far exceeding $4^{n}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7fe645c2-ae59-5ff0-9c5e-c7c67282c69c
| 25,128
|
5. N5 (IRN) Let $m, n \geq 2$ be positive integers, and let $a_{1}, a_{2}, \ldots, a_{n}$ be integers, none of which is a multiple of $m^{n-1}$. Show that there exist integers $e_{1}, e_{2}, \ldots, e_{n}$, not all zero, with $\left|e_{i}\right|<m$ for all $i$, such that $e_{1} a_{1}+e_{2} a_{2}+\cdots+e_{n} a_{n}$ is a multiple of $m^{n}$.
|
5. Consider all possible sums $c_{1} a_{1}+c_{2} a_{2}+\cdots+c_{n} a_{n}$, where each $c_{i}$ is an integer with $0 \leq c_{i}<m$. There are $m^{n}$ such sums, and if any two of them give the same remainder modulo $m^{n}$, say $\sum c_{i} a_{i} \equiv \sum d_{i} a_{i}\left(\bmod m^{n}\right)$, then $\sum\left(c_{i}-d_{i}\right) a_{i}$ is divisible by $m^{n}$, and since $\left|c_{i}-d_{i}\right|<m$, we are done. We claim that two such sums must exist. Suppose to the contrary that the sums $\sum_{i} c_{i} a_{i}\left(0 \leq c_{i}<m\right)$ give all the different remainders modulo $m^{n}$. Consider the polynomial $$ P(x)=\sum x^{c_{1} a_{1}+\cdots+c_{n} a_{n}}, $$ where the sum is taken over all $\left(c_{1}, \ldots, c_{n}\right)$ with $0 \leq c_{i}<m$. If $\xi$ is a primitive $m^{n}$ th root of unity, then by the assumption we have $$ P(\xi)=1+\xi+\cdots+\xi^{m^{n}-1}=0 $$ On the other hand, $P(x)$ can be factored as $$ P(x)=\prod_{i=1}^{n}\left(1+x^{a_{i}}+\cdots+x^{(m-1) a_{i}}\right)=\prod_{i=1}^{n} \frac{1-x^{m a_{i}}}{1-x^{a_{i}}}, $$ so that none of its factors is zero at $x=\xi$ because $m a_{i}$ is not divisible by $m^{n}$. This is obviously a contradiction. Remark. The example $a_{i}=m^{i-1}$ for $i=1, \ldots, n$ shows that the condition that no $a_{i}$ is a multiple of $m^{n-1}$ cannot be removed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
5. N5 (IRN) Let $m, n \geq 2$ be positive integers, and let $a_{1}, a_{2}, \ldots, a_{n}$ be integers, none of which is a multiple of $m^{n-1}$. Show that there exist integers $e_{1}, e_{2}, \ldots, e_{n}$, not all zero, with $\left|e_{i}\right|<m$ for all $i$, such that $e_{1} a_{1}+e_{2} a_{2}+\cdots+e_{n} a_{n}$ is a multiple of $m^{n}$.
|
5. Consider all possible sums $c_{1} a_{1}+c_{2} a_{2}+\cdots+c_{n} a_{n}$, where each $c_{i}$ is an integer with $0 \leq c_{i}<m$. There are $m^{n}$ such sums, and if any two of them give the same remainder modulo $m^{n}$, say $\sum c_{i} a_{i} \equiv \sum d_{i} a_{i}\left(\bmod m^{n}\right)$, then $\sum\left(c_{i}-d_{i}\right) a_{i}$ is divisible by $m^{n}$, and since $\left|c_{i}-d_{i}\right|<m$, we are done. We claim that two such sums must exist. Suppose to the contrary that the sums $\sum_{i} c_{i} a_{i}\left(0 \leq c_{i}<m\right)$ give all the different remainders modulo $m^{n}$. Consider the polynomial $$ P(x)=\sum x^{c_{1} a_{1}+\cdots+c_{n} a_{n}}, $$ where the sum is taken over all $\left(c_{1}, \ldots, c_{n}\right)$ with $0 \leq c_{i}<m$. If $\xi$ is a primitive $m^{n}$ th root of unity, then by the assumption we have $$ P(\xi)=1+\xi+\cdots+\xi^{m^{n}-1}=0 $$ On the other hand, $P(x)$ can be factored as $$ P(x)=\prod_{i=1}^{n}\left(1+x^{a_{i}}+\cdots+x^{(m-1) a_{i}}\right)=\prod_{i=1}^{n} \frac{1-x^{m a_{i}}}{1-x^{a_{i}}}, $$ so that none of its factors is zero at $x=\xi$ because $m a_{i}$ is not divisible by $m^{n}$. This is obviously a contradiction. Remark. The example $a_{i}=m^{i-1}$ for $i=1, \ldots, n$ shows that the condition that no $a_{i}$ is a multiple of $m^{n-1}$ cannot be removed.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
ef9ad963-2ef4-524e-a087-033ff05c58e6
| 25,130
|
7. G1 (FRA) Let $B$ be a point on a circle $S_{1}$, and let $A$ be a point distinct from $B$ on the tangent at $B$ to $S_{1}$. Let $C$ be a point not on $S_{1}$ such that the line segment $A C$ meets $S_{1}$ at two distinct points. Let $S_{2}$ be the circle touching $A C$ at $C$ and touching $S_{1}$ at a point $D$ on the opposite side of $A C$ from $B$. Prove that the circumcenter of triangle $B C D$ lies on the circumcircle of triangle $A B C$.
|
7. To avoid working with cases, we use oriented angles modulo $180^{\circ}$. Let $K$ be the circumcenter of $\triangle B C D$, and $X$ any point on the common tangent to the circles at $D$. Since the tangents at the ends of a chord are equally inclined to the chord, we have $\angle B A C=\angle A B D+\angle B D C+\angle D C A=$ $\angle B D X+\angle B D C+\angle X D C=2 \angle B D C=\angle B K C$. It follows that $B, C, A, K$ are concyclic, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
7. G1 (FRA) Let $B$ be a point on a circle $S_{1}$, and let $A$ be a point distinct from $B$ on the tangent at $B$ to $S_{1}$. Let $C$ be a point not on $S_{1}$ such that the line segment $A C$ meets $S_{1}$ at two distinct points. Let $S_{2}$ be the circle touching $A C$ at $C$ and touching $S_{1}$ at a point $D$ on the opposite side of $A C$ from $B$. Prove that the circumcenter of triangle $B C D$ lies on the circumcircle of triangle $A B C$.
|
7. To avoid working with cases, we use oriented angles modulo $180^{\circ}$. Let $K$ be the circumcenter of $\triangle B C D$, and $X$ any point on the common tangent to the circles at $D$. Since the tangents at the ends of a chord are equally inclined to the chord, we have $\angle B A C=\angle A B D+\angle B D C+\angle D C A=$ $\angle B D X+\angle B D C+\angle X D C=2 \angle B D C=\angle B K C$. It follows that $B, C, A, K$ are concyclic, as required.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
53c32d53-0ab4-59cb-9042-471e60bd3405
| 25,132
|
8. G2 (KOR) Let $A B C$ be a triangle for which there exists an interior point $F$ such that $\angle A F B=\angle B F C=\angle C F A$. Let the lines $B F$ and $C F$ meet the sides $A C$ and $A B$ at $D$ and $E$ respectively. Prove that $$ A B+A C \geq 4 D E $$
|
8. Construct equilateral triangles $A C P$ and $A B Q$ outside the triangle $A B C$. Since $\angle A P C+\angle A F C=60^{\circ}+120^{\circ}=180^{\circ}$, the points $A, C, F, P$ lie on a circle; hence $\angle A F P=\angle A C P=60^{\circ}=\angle A F D$, so $D$ lies on the segment $F P$; similarly, $E$ lies on $F Q$. Further, note that $$ \frac{F P}{F D}=1+\frac{D P}{F D}=1+\frac{S_{A P C}}{S_{A F C}} \geq 4 $$ with equality if $F$ is the midpoint of the smaller $\operatorname{arc} A C$ : hence $F D \leq \frac{1}{4} F P$ and $F E \leq \frac{1}{4} F Q$. Then by the law of cosines, $$ \begin{aligned} D E & =\sqrt{F D^{2}+F E^{2}+F D \cdot F E} \\ & \leq \frac{1}{4} \sqrt{F P^{2}+F Q^{2}+F P \cdot F Q}=\frac{1}{4} P Q \leq A P+A Q=A B+A C . \end{aligned} $$ Equality holds if and only if $\triangle A B C$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
8. G2 (KOR) Let $A B C$ be a triangle for which there exists an interior point $F$ such that $\angle A F B=\angle B F C=\angle C F A$. Let the lines $B F$ and $C F$ meet the sides $A C$ and $A B$ at $D$ and $E$ respectively. Prove that $$ A B+A C \geq 4 D E $$
|
8. Construct equilateral triangles $A C P$ and $A B Q$ outside the triangle $A B C$. Since $\angle A P C+\angle A F C=60^{\circ}+120^{\circ}=180^{\circ}$, the points $A, C, F, P$ lie on a circle; hence $\angle A F P=\angle A C P=60^{\circ}=\angle A F D$, so $D$ lies on the segment $F P$; similarly, $E$ lies on $F Q$. Further, note that $$ \frac{F P}{F D}=1+\frac{D P}{F D}=1+\frac{S_{A P C}}{S_{A F C}} \geq 4 $$ with equality if $F$ is the midpoint of the smaller $\operatorname{arc} A C$ : hence $F D \leq \frac{1}{4} F P$ and $F E \leq \frac{1}{4} F Q$. Then by the law of cosines, $$ \begin{aligned} D E & =\sqrt{F D^{2}+F E^{2}+F D \cdot F E} \\ & \leq \frac{1}{4} \sqrt{F P^{2}+F Q^{2}+F P \cdot F Q}=\frac{1}{4} P Q \leq A P+A Q=A B+A C . \end{aligned} $$ Equality holds if and only if $\triangle A B C$ is equilateral.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
2b397b75-5e9d-5762-83a4-956728fbfd73
| 25,133
|
9. G3 (KOR) ${ }^{\mathrm{IMO} 2}$ The circle $S$ has center $O$, and $B C$ is a diameter of $S$. Let $A$ be a point of $S$ such that $\measuredangle A O B<120^{\circ}$. Let $D$ be the midpoint of the arc $A B$ that does not contain $C$. The line through $O$ parallel to $D A$ meets the line $A C$ at $I$. The perpendicular bisector of $O A$ meets $S$ at $E$ and at $F$. Prove that $I$ is the incenter of the triangle $C E F$.
|
9. Since $\angle B C A=\frac{1}{2} \angle B O A=\angle B O D$, the lines $C A$ and $O D$ are parallel, so that $O D A I$ is a parallelogram. It follows that $A I=O D=O E=A E=$ $A F$. Hence $\angle I F E=\angle I F A-\angle E F A=\angle A I F-\angle E C A=\angle A I F-\angle A C F=\angle C F I$. Also, from $A E=A F$ we get that $C I$ bisects $\angle E C F$. Therefore $I$ is the incenter of $\triangle C E F$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
9. G3 (KOR) ${ }^{\mathrm{IMO} 2}$ The circle $S$ has center $O$, and $B C$ is a diameter of $S$. Let $A$ be a point of $S$ such that $\measuredangle A O B<120^{\circ}$. Let $D$ be the midpoint of the arc $A B$ that does not contain $C$. The line through $O$ parallel to $D A$ meets the line $A C$ at $I$. The perpendicular bisector of $O A$ meets $S$ at $E$ and at $F$. Prove that $I$ is the incenter of the triangle $C E F$.
|
9. Since $\angle B C A=\frac{1}{2} \angle B O A=\angle B O D$, the lines $C A$ and $O D$ are parallel, so that $O D A I$ is a parallelogram. It follows that $A I=O D=O E=A E=$ $A F$. Hence $\angle I F E=\angle I F A-\angle E F A=\angle A I F-\angle E C A=\angle A I F-\angle A C F=\angle C F I$. Also, from $A E=A F$ we get that $C I$ bisects $\angle E C F$. Therefore $I$ is the incenter of $\triangle C E F$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
42d4b30e-cc05-535f-aa96-4687b7f00b72
| 25,134
|
1. A1 (USA) Let $a_{i j}, i=1,2,3, j=1,2,3$, be real numbers such that $a_{i j}$ is positive for $i=j$ and negative for $i \neq j$. Prove that there exist positive real numbers $c_{1}, c_{2}, c_{3}$ such that the numbers $$ a_{11} c_{1}+a_{12} c_{2}+a_{13} c_{3}, \quad a_{21} c_{1}+a_{22} c_{2}+a_{23} c_{3}, \quad a_{31} c_{1}+a_{32} c_{2}+a_{33} c_{3} $$ are all negative, all positive, or all zero.
|
1. Consider the points $O(0,0,0), P\left(a_{11}, a_{21}, a_{31}\right), Q\left(a_{12}, a_{22}, a_{32}\right), R\left(a_{13}, a_{23}\right.$, $\left.a_{33}\right)$ in three-dimensional Euclidean space. It is enough to find a point $U\left(u_{1}, u_{2}, u_{3}\right)$ in the interior of the triangle $P Q R$ whose coordinates are all positive, all negative, or all zero (indeed, then we have $\overrightarrow{O U}=c_{1} \overrightarrow{O P}+$ $c_{2} \overrightarrow{O Q}+c_{3} \overrightarrow{O R}$ for some $c_{1}, c_{2}, c_{3}>0$ with $\left.c_{1}+c_{2}+c_{3}=1\right)$. Let $P^{\prime}\left(a_{11}, a_{21}, 0\right), Q^{\prime}\left(a_{12}, a_{22}, 0\right)$, and $R^{\prime}\left(a_{13}, a_{23}, 0\right)$ be the projections of $P, Q$, and $R$ onto the $O x y$ plane. We see that $P^{\prime}, Q^{\prime}, R^{\prime}$ lie in the fourth, second, and third quadrants, respectively. We have the following two cases: (i) $O$ is in the exterior of $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Set $S^{\prime}=O R^{\prime} \cap P^{\prime} Q^{\prime}$ and let $S$ be the point of the segment $P Q$ that projects to $S^{\prime}$. The point $S$ has its $z$ coordinate negative (because the $z$ coordinates of $P$ and $Q$ are negative). Thus any point  of the segment $S R$ sufficiently close to $S$ has all coordinates negative. (ii) $O$ is in the interior or on the boundary of $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Let $T$ be the point in the plane $P Q R$ whose projection is $O$. If $T=O$, then all coordinates of $T$ are zero, and we are done. Otherwise $O$ is interior to $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Suppose that the $z$ coordinate of $T$ is positive (negative). Since $x$ and $y$ coordinates of $T$ are equal to 0 , there is a point $U$ inside $P Q R$ close to $T$ with both $x$ and $y$ coordinates positive (respectively negative), and this point $U$ has all coordinates of the same sign.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
1. A1 (USA) Let $a_{i j}, i=1,2,3, j=1,2,3$, be real numbers such that $a_{i j}$ is positive for $i=j$ and negative for $i \neq j$. Prove that there exist positive real numbers $c_{1}, c_{2}, c_{3}$ such that the numbers $$ a_{11} c_{1}+a_{12} c_{2}+a_{13} c_{3}, \quad a_{21} c_{1}+a_{22} c_{2}+a_{23} c_{3}, \quad a_{31} c_{1}+a_{32} c_{2}+a_{33} c_{3} $$ are all negative, all positive, or all zero.
|
1. Consider the points $O(0,0,0), P\left(a_{11}, a_{21}, a_{31}\right), Q\left(a_{12}, a_{22}, a_{32}\right), R\left(a_{13}, a_{23}\right.$, $\left.a_{33}\right)$ in three-dimensional Euclidean space. It is enough to find a point $U\left(u_{1}, u_{2}, u_{3}\right)$ in the interior of the triangle $P Q R$ whose coordinates are all positive, all negative, or all zero (indeed, then we have $\overrightarrow{O U}=c_{1} \overrightarrow{O P}+$ $c_{2} \overrightarrow{O Q}+c_{3} \overrightarrow{O R}$ for some $c_{1}, c_{2}, c_{3}>0$ with $\left.c_{1}+c_{2}+c_{3}=1\right)$. Let $P^{\prime}\left(a_{11}, a_{21}, 0\right), Q^{\prime}\left(a_{12}, a_{22}, 0\right)$, and $R^{\prime}\left(a_{13}, a_{23}, 0\right)$ be the projections of $P, Q$, and $R$ onto the $O x y$ plane. We see that $P^{\prime}, Q^{\prime}, R^{\prime}$ lie in the fourth, second, and third quadrants, respectively. We have the following two cases: (i) $O$ is in the exterior of $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Set $S^{\prime}=O R^{\prime} \cap P^{\prime} Q^{\prime}$ and let $S$ be the point of the segment $P Q$ that projects to $S^{\prime}$. The point $S$ has its $z$ coordinate negative (because the $z$ coordinates of $P$ and $Q$ are negative). Thus any point  of the segment $S R$ sufficiently close to $S$ has all coordinates negative. (ii) $O$ is in the interior or on the boundary of $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Let $T$ be the point in the plane $P Q R$ whose projection is $O$. If $T=O$, then all coordinates of $T$ are zero, and we are done. Otherwise $O$ is interior to $\triangle P^{\prime} Q^{\prime} R^{\prime}$. Suppose that the $z$ coordinate of $T$ is positive (negative). Since $x$ and $y$ coordinates of $T$ are equal to 0 , there is a point $U$ inside $P Q R$ close to $T$ with both $x$ and $y$ coordinates positive (respectively negative), and this point $U$ has all coordinates of the same sign.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b24e3cd6-144a-5d10-995d-74f153dc7820
| 25,135
|
10. C4 (IRN) Let $x_{1}, \ldots, x_{n}$ and $y_{1}, \ldots, y_{n}$ be real numbers. Let $A=$ $\left(a_{i j}\right)_{1 \leq i, j \leq n}$ be the matrix with entries $$ a_{i j}= \begin{cases}1, & \text { if } x_{i}+y_{j} \geq 0 \\ 0, & \text { if } x_{i}+y_{j}<0\end{cases} $$ Suppose that $B$ is an $n \times n$ matrix whose entries are 0,1 such that the sum of the elements in each row and each column of $B$ is equal to the corresponding sum for the matrix $A$. Prove that $A=B$.
|
10. Denote by $b_{i j}$ the entries of the matrix $B$. Suppose the contrary, i.e., that there is a pair $\left(i_{0}, j_{0}\right)$ such that $a_{i_{0}, j_{0}} \neq b_{i_{0}, j_{0}}$. We may assume without loss of generality that $a_{i_{0}, j_{0}}=0$ and $b_{i_{0}, j_{0}}=1$. Since the sums of elements in the $i_{0}$ th rows of the matrices $A$ and $B$ are equal, there is some $j_{1}$ for which $a_{i_{0}, j_{1}}=1$ and $b_{i_{0}, j_{1}}=0$. Similarly, from the fact that the sums in the $j_{1}$ th columns of the matrices $A$ and $B$ are equal, we conclude that there exists $i_{1}$ such that $a_{i_{1}, j_{1}}=0$ and $b_{i_{1}, j_{1}}=1$. Continuing this procedure, we construct two sequences $i_{k}, j_{k}$ such that $a_{i_{k}, j_{k}}=0, b_{i_{k}, j_{k}}=1, a_{i_{k}, j_{k+1}}=1, b_{i_{k}, j_{k+1}}=0$. Since the set of the pairs $\left(i_{k}, j_{k}\right)$ is finite, there are two different numbers $t, s$ such that $\left(i_{t}, j_{t}\right)=\left(i_{s}, j_{s}\right)$. From the given condition we have that $x_{i_{k}}+y_{i_{k}}<0$ and $x_{i_{k+1}}+y_{i_{k+1}} \geq 0$. But $j_{t}=j_{s}$, and hence $0 \leq \sum_{k=s}^{t-1}\left(x_{i_{k}}+y_{j_{k+1}}\right)=$ $\sum_{k=s}^{t-1}\left(x_{i_{k}}+y_{j_{k}}\right)<0$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
10. C4 (IRN) Let $x_{1}, \ldots, x_{n}$ and $y_{1}, \ldots, y_{n}$ be real numbers. Let $A=$ $\left(a_{i j}\right)_{1 \leq i, j \leq n}$ be the matrix with entries $$ a_{i j}= \begin{cases}1, & \text { if } x_{i}+y_{j} \geq 0 \\ 0, & \text { if } x_{i}+y_{j}<0\end{cases} $$ Suppose that $B$ is an $n \times n$ matrix whose entries are 0,1 such that the sum of the elements in each row and each column of $B$ is equal to the corresponding sum for the matrix $A$. Prove that $A=B$.
|
10. Denote by $b_{i j}$ the entries of the matrix $B$. Suppose the contrary, i.e., that there is a pair $\left(i_{0}, j_{0}\right)$ such that $a_{i_{0}, j_{0}} \neq b_{i_{0}, j_{0}}$. We may assume without loss of generality that $a_{i_{0}, j_{0}}=0$ and $b_{i_{0}, j_{0}}=1$. Since the sums of elements in the $i_{0}$ th rows of the matrices $A$ and $B$ are equal, there is some $j_{1}$ for which $a_{i_{0}, j_{1}}=1$ and $b_{i_{0}, j_{1}}=0$. Similarly, from the fact that the sums in the $j_{1}$ th columns of the matrices $A$ and $B$ are equal, we conclude that there exists $i_{1}$ such that $a_{i_{1}, j_{1}}=0$ and $b_{i_{1}, j_{1}}=1$. Continuing this procedure, we construct two sequences $i_{k}, j_{k}$ such that $a_{i_{k}, j_{k}}=0, b_{i_{k}, j_{k}}=1, a_{i_{k}, j_{k+1}}=1, b_{i_{k}, j_{k+1}}=0$. Since the set of the pairs $\left(i_{k}, j_{k}\right)$ is finite, there are two different numbers $t, s$ such that $\left(i_{t}, j_{t}\right)=\left(i_{s}, j_{s}\right)$. From the given condition we have that $x_{i_{k}}+y_{i_{k}}<0$ and $x_{i_{k+1}}+y_{i_{k+1}} \geq 0$. But $j_{t}=j_{s}$, and hence $0 \leq \sum_{k=s}^{t-1}\left(x_{i_{k}}+y_{j_{k+1}}\right)=$ $\sum_{k=s}^{t-1}\left(x_{i_{k}}+y_{j_{k}}\right)<0$, a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6318a1cf-c7b4-57c7-9aea-5fc415ad3806
| 25,136
|
11. C5 (ROM) Every point with integer coordinates in the plane is the center of a disk with radius $1 / 1000$. (a) Prove that there exists an equilateral triangle whose vertices lie in different disks. (b) Prove that every equilateral triangle with vertices in different disks has side length greater than 96.
|
11. (a) By the pigeonhole principle there are two different integers $x_{1}, x_{2}$, $x_{1}>x_{2}$, such that $\left|\left\{x_{1} \sqrt{3}\right\}-\left\{x_{2} \sqrt{3}\right\}\right|<0.001$. Set $a=x_{1}-x_{2}$. Consider the equilateral triangle with vertices $(0,0),(2 a, 0),(a, a \sqrt{3})$. The points $(0,0)$ and $(2 a, 0)$ are lattice points, and we claim that the point $(a, a \sqrt{3})$ is at distance less than 0.001 from a lattice point. Indeed, since $0.001>\left|\left\{x_{1} \sqrt{3}\right\}-\left\{x_{2} \sqrt{3}\right\}\right|=\left|a \sqrt{3}-\left(\left[x_{1} \sqrt{3}\right]-\left[x_{2} \sqrt{3}\right]\right)\right|$, we see that the distance between the points $(a, a \sqrt{3})$ and $\left(a,\left[x_{1} \sqrt{3}\right]-\right.$ $\left.\left[x_{2} \sqrt{3}\right]\right)$ is less than 0.001 , and the point $\left(a,\left[x_{1} \sqrt{3}\right]-\left[x_{2} \sqrt{3}\right]\right)$ is with integer coefficients. (b) Suppose that $P^{\prime} Q^{\prime} R^{\prime}$ is an equilateral triangle with side length $l \leq 96$ such that each of its vertices $P^{\prime}, Q^{\prime}, R^{\prime}$ lies in a disk of radius 0.001 centered at a lattice point. Denote by $P, Q, R$ the centers of these disks. Then we have $l-0.002 \leq P Q, Q R, R P \leq l+0.002$. Since $P Q R$ is not an equilateral triangle, two of its sides are different, say $P Q \neq Q R$. On the other hand, $P Q^{2}, Q R^{2}$ are integers, so we have $1 \leq\left|P Q^{2}-Q R^{2}\right|=(P Q+Q R)|P Q-Q R| \leq 0.004(P Q+Q R) \leq$ $(2 l+0.004) \cdot 0.004 \leq 2 \cdot 96.002 \cdot 0.004<1$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
11. C5 (ROM) Every point with integer coordinates in the plane is the center of a disk with radius $1 / 1000$. (a) Prove that there exists an equilateral triangle whose vertices lie in different disks. (b) Prove that every equilateral triangle with vertices in different disks has side length greater than 96.
|
11. (a) By the pigeonhole principle there are two different integers $x_{1}, x_{2}$, $x_{1}>x_{2}$, such that $\left|\left\{x_{1} \sqrt{3}\right\}-\left\{x_{2} \sqrt{3}\right\}\right|<0.001$. Set $a=x_{1}-x_{2}$. Consider the equilateral triangle with vertices $(0,0),(2 a, 0),(a, a \sqrt{3})$. The points $(0,0)$ and $(2 a, 0)$ are lattice points, and we claim that the point $(a, a \sqrt{3})$ is at distance less than 0.001 from a lattice point. Indeed, since $0.001>\left|\left\{x_{1} \sqrt{3}\right\}-\left\{x_{2} \sqrt{3}\right\}\right|=\left|a \sqrt{3}-\left(\left[x_{1} \sqrt{3}\right]-\left[x_{2} \sqrt{3}\right]\right)\right|$, we see that the distance between the points $(a, a \sqrt{3})$ and $\left(a,\left[x_{1} \sqrt{3}\right]-\right.$ $\left.\left[x_{2} \sqrt{3}\right]\right)$ is less than 0.001 , and the point $\left(a,\left[x_{1} \sqrt{3}\right]-\left[x_{2} \sqrt{3}\right]\right)$ is with integer coefficients. (b) Suppose that $P^{\prime} Q^{\prime} R^{\prime}$ is an equilateral triangle with side length $l \leq 96$ such that each of its vertices $P^{\prime}, Q^{\prime}, R^{\prime}$ lies in a disk of radius 0.001 centered at a lattice point. Denote by $P, Q, R$ the centers of these disks. Then we have $l-0.002 \leq P Q, Q R, R P \leq l+0.002$. Since $P Q R$ is not an equilateral triangle, two of its sides are different, say $P Q \neq Q R$. On the other hand, $P Q^{2}, Q R^{2}$ are integers, so we have $1 \leq\left|P Q^{2}-Q R^{2}\right|=(P Q+Q R)|P Q-Q R| \leq 0.004(P Q+Q R) \leq$ $(2 l+0.004) \cdot 0.004 \leq 2 \cdot 96.002 \cdot 0.004<1$, which is a contradiction.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7b917252-e589-5e9a-8f14-169f26b479a1
| 25,137
|
12. C6 (SAF) Let $f(k)$ be the number of integers $n$ that satisfy the following conditions: (i) $0 \leq n<10^{k}$, so $n$ has exactly $k$ digits (in decimal notation), with leading zeros allowed; (ii) the digits of $n$ can be permuted in such a way that they yield an integer divisible by 11 . Prove that $f(2 m)=10 f(2 m-1)$ for every positive integer $m$.
|
12. Denote by $\overline{a_{k-1} a_{k-2} \ldots a_{0}}$ the decimal representation of a number whose digits are $a_{k-1}, \ldots, a_{0}$. We will use the following well-known fact: $$ \overline{a_{k-1} a_{k-2} \ldots a_{0}} \equiv i(\bmod 11) \Longleftrightarrow \sum_{l=0}^{k-1}(-1)^{l} a_{l} \equiv i(\bmod 11) . $$ Let $m$ be a positive integer. Define $A$ as the set of integers $n(0 \leq n<$ $10^{2 m}$ ) whose right $2 m-1$ digits can be so permuted to yield an integer divisible by 11 , and $B$ as the set of integers $n\left(0 \leq n<10^{2 m-1}\right)$ whose digits can be permuted resulting in an integer divisible by 11. Suppose that $a=\overline{a_{2 m-1} \ldots a_{0}} \in A$. Then there that satisfies $$ \sum_{l=0}^{2 m-1}(-1)^{l} b_{l} \equiv 0(\bmod 11) $$ The $2 m$-tuple $\left(b_{2 m-1}, \ldots, b_{0}\right)$ satisfies (1) if and only if the $2 m$-tuple $\left(k b_{2 m-1}+l, \ldots, k b_{0}+l\right)$ satisfies ( 1 ), where $k, l \in \mathbb{Z}, 11 \nmid k$. Since $a_{0}+1 \not \equiv 0(\bmod 11)$, we can choose $k$ from the set $\{1, \ldots, 10\}$ such that $\left(a_{0}+1\right) k \equiv 1(\bmod 11)$. Thus there is a permutation of the $2 m$-tuple $\left(\left(a_{2 m-1}+1\right) k-1, \ldots,\left(a_{1}+1\right) k-1,0\right)$ satisfying (1). Interchanging odd and even positions if necessary, we may assume that this permutation keeps the 0 at the last position. Since $\left(a_{i}+1\right) k$ is not divisible by 11 for any $i$, there is a unique $b_{i} \in\{0,1, \ldots, 9\}$ such that $b_{i} \equiv\left(a_{i}+1\right) k-1(\bmod 11)$. Hence the number $\overline{b_{2 m-1} \ldots b_{1}}$ belongs to $B$. Thus for fixed $a_{0} \in\{0,1,2, \ldots, 9\}$, to each $a \in A$ such that the last digit of $a$ is $a_{0}$ we associate a unique $b \in B$. Conversely, having $a_{0} \in$ $\{0,1,2, \ldots, 9\}$ fixed, from any number $\overline{b_{2 m-1} \ldots b_{1}} \in B$ we can reconstruct $\overline{a_{2 m-1} \ldots a_{1} a_{0}} \in A$. Hence $|A|=10|B|$, i.e., $f(2 m)=10 f(2 m-1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
12. C6 (SAF) Let $f(k)$ be the number of integers $n$ that satisfy the following conditions: (i) $0 \leq n<10^{k}$, so $n$ has exactly $k$ digits (in decimal notation), with leading zeros allowed; (ii) the digits of $n$ can be permuted in such a way that they yield an integer divisible by 11 . Prove that $f(2 m)=10 f(2 m-1)$ for every positive integer $m$.
|
12. Denote by $\overline{a_{k-1} a_{k-2} \ldots a_{0}}$ the decimal representation of a number whose digits are $a_{k-1}, \ldots, a_{0}$. We will use the following well-known fact: $$ \overline{a_{k-1} a_{k-2} \ldots a_{0}} \equiv i(\bmod 11) \Longleftrightarrow \sum_{l=0}^{k-1}(-1)^{l} a_{l} \equiv i(\bmod 11) . $$ Let $m$ be a positive integer. Define $A$ as the set of integers $n(0 \leq n<$ $10^{2 m}$ ) whose right $2 m-1$ digits can be so permuted to yield an integer divisible by 11 , and $B$ as the set of integers $n\left(0 \leq n<10^{2 m-1}\right)$ whose digits can be permuted resulting in an integer divisible by 11. Suppose that $a=\overline{a_{2 m-1} \ldots a_{0}} \in A$. Then there that satisfies $$ \sum_{l=0}^{2 m-1}(-1)^{l} b_{l} \equiv 0(\bmod 11) $$ The $2 m$-tuple $\left(b_{2 m-1}, \ldots, b_{0}\right)$ satisfies (1) if and only if the $2 m$-tuple $\left(k b_{2 m-1}+l, \ldots, k b_{0}+l\right)$ satisfies ( 1 ), where $k, l \in \mathbb{Z}, 11 \nmid k$. Since $a_{0}+1 \not \equiv 0(\bmod 11)$, we can choose $k$ from the set $\{1, \ldots, 10\}$ such that $\left(a_{0}+1\right) k \equiv 1(\bmod 11)$. Thus there is a permutation of the $2 m$-tuple $\left(\left(a_{2 m-1}+1\right) k-1, \ldots,\left(a_{1}+1\right) k-1,0\right)$ satisfying (1). Interchanging odd and even positions if necessary, we may assume that this permutation keeps the 0 at the last position. Since $\left(a_{i}+1\right) k$ is not divisible by 11 for any $i$, there is a unique $b_{i} \in\{0,1, \ldots, 9\}$ such that $b_{i} \equiv\left(a_{i}+1\right) k-1(\bmod 11)$. Hence the number $\overline{b_{2 m-1} \ldots b_{1}}$ belongs to $B$. Thus for fixed $a_{0} \in\{0,1,2, \ldots, 9\}$, to each $a \in A$ such that the last digit of $a$ is $a_{0}$ we associate a unique $b \in B$. Conversely, having $a_{0} \in$ $\{0,1,2, \ldots, 9\}$ fixed, from any number $\overline{b_{2 m-1} \ldots b_{1}} \in B$ we can reconstruct $\overline{a_{2 m-1} \ldots a_{1} a_{0}} \in A$. Hence $|A|=10|B|$, i.e., $f(2 m)=10 f(2 m-1)$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
7631fd1c-833a-5112-9b42-6a2f804213ea
| 25,138
|
13. G1 (FIN) ${ }^{\mathrm{IMO} 4}$ Let $A B C D$ be a cyclic quadrilateral. Let $P, Q, R$ be the feet of the perpendiculars from $D$ to the lines $B C, C A, A B$, respectively. Show that $P Q=Q R$ if and only if the bisectors of $\angle A B C$ and $\angle A D C$ are concurrent with $A C$.
|
13. Denote by $K$ and $L$ the intersections of the bisectors of $\angle A B C$ and $\angle A D C$ with the line $A C$, respectively. Since $A B: B C=A K: K C$ and $A D: D C=A L: L C$, we have to prove that $$ P Q=Q R \Leftrightarrow \frac{A B}{B C}=\frac{A D}{D C} . $$ Since the quadrilaterals $A Q D R$ and $Q P C D$ are cyclic, we see that 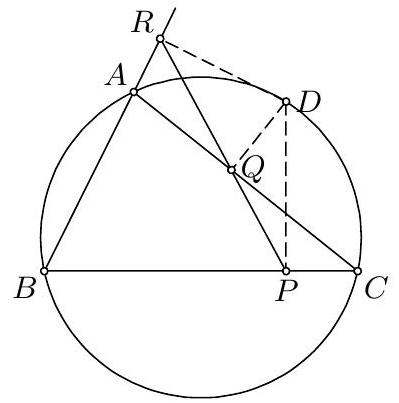 $\angle R D Q=\angle B A C$ and $\angle Q D P=\angle A C B$. By the law of sines it follows that $\frac{A B}{B C}=\frac{\sin (\angle A C B)}{\sin (\angle B A C)}$ and that $Q R=A D \sin (\angle R D Q), Q P=$ $C D \sin (\angle Q D P)$. Now we have $$ \frac{A B}{B C}=\frac{\sin (\angle A C B)}{\sin (\angle B A C)}=\frac{\sin (\angle Q D P)}{\sin (\angle R D Q)}=\frac{A D \cdot Q P}{Q R \cdot C D} $$ The statement (1) follows directly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
13. G1 (FIN) ${ }^{\mathrm{IMO} 4}$ Let $A B C D$ be a cyclic quadrilateral. Let $P, Q, R$ be the feet of the perpendiculars from $D$ to the lines $B C, C A, A B$, respectively. Show that $P Q=Q R$ if and only if the bisectors of $\angle A B C$ and $\angle A D C$ are concurrent with $A C$.
|
13. Denote by $K$ and $L$ the intersections of the bisectors of $\angle A B C$ and $\angle A D C$ with the line $A C$, respectively. Since $A B: B C=A K: K C$ and $A D: D C=A L: L C$, we have to prove that $$ P Q=Q R \Leftrightarrow \frac{A B}{B C}=\frac{A D}{D C} . $$ Since the quadrilaterals $A Q D R$ and $Q P C D$ are cyclic, we see that  $\angle R D Q=\angle B A C$ and $\angle Q D P=\angle A C B$. By the law of sines it follows that $\frac{A B}{B C}=\frac{\sin (\angle A C B)}{\sin (\angle B A C)}$ and that $Q R=A D \sin (\angle R D Q), Q P=$ $C D \sin (\angle Q D P)$. Now we have $$ \frac{A B}{B C}=\frac{\sin (\angle A C B)}{\sin (\angle B A C)}=\frac{\sin (\angle Q D P)}{\sin (\angle R D Q)}=\frac{A D \cdot Q P}{Q R \cdot C D} $$ The statement (1) follows directly.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
15c59ec4-419e-5634-81af-751c4c1d99ed
| 25,139
|
14. G2 (GRE) Three distinct points $A, B, C$ are fixed on a line in this order. Let $\Gamma$ be a circle passing through $A$ and $C$ whose center does not lie on the line $A C$. Denote by $P$ the intersection of the tangents to $\Gamma$ at $A$ and $C$. Suppose $\Gamma$ meets the segment $P B$ at $Q$. Prove that the intersection of the bisector of $\angle A Q C$ and the line $A C$ does not depend on the choice of $\Gamma$.
|
14. Denote by $R$ the intersection point of the bisector of $\angle A Q C$ and the line $A C$. From $\triangle A C Q$ we get $$ \frac{A R}{R C}=\frac{A Q}{Q C}=\frac{\sin \angle Q C A}{\sin \angle Q A C} $$ By the sine version of Ceva's theorem we have $\frac{\sin \angle A P B}{\sin \angle B P C} \cdot \frac{\sin \angle Q A C}{\sin \angle P A Q}$. $\frac{\sin \angle Q C P}{\sin \angle Q C A}=1$, which is equivalent to $$ \frac{\sin \angle A P B}{\sin \angle B P C}=\left(\frac{\sin \angle Q C A}{\sin \angle Q A C}\right)^{2} $$ because $\angle Q C A=\angle P A Q$ and $\angle Q A C=\angle Q C P$. Denote by $S(X Y Z)$ the area of a triangle $X Y Z$. Then $$ \frac{\sin \angle A P B}{\sin \angle B P C}=\frac{A P \cdot B P \cdot \sin \angle A P B}{B P \cdot C P \cdot \sin \angle B P C}=\frac{S(\Delta A B P)}{S(\Delta B C P)}=\frac{A B}{B C}, $$ which implies that $\left(\frac{A R}{R C}\right)^{2}=\frac{A B}{B C}$. Hence $R$ does not depend on $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
14. G2 (GRE) Three distinct points $A, B, C$ are fixed on a line in this order. Let $\Gamma$ be a circle passing through $A$ and $C$ whose center does not lie on the line $A C$. Denote by $P$ the intersection of the tangents to $\Gamma$ at $A$ and $C$. Suppose $\Gamma$ meets the segment $P B$ at $Q$. Prove that the intersection of the bisector of $\angle A Q C$ and the line $A C$ does not depend on the choice of $\Gamma$.
|
14. Denote by $R$ the intersection point of the bisector of $\angle A Q C$ and the line $A C$. From $\triangle A C Q$ we get $$ \frac{A R}{R C}=\frac{A Q}{Q C}=\frac{\sin \angle Q C A}{\sin \angle Q A C} $$ By the sine version of Ceva's theorem we have $\frac{\sin \angle A P B}{\sin \angle B P C} \cdot \frac{\sin \angle Q A C}{\sin \angle P A Q}$. $\frac{\sin \angle Q C P}{\sin \angle Q C A}=1$, which is equivalent to $$ \frac{\sin \angle A P B}{\sin \angle B P C}=\left(\frac{\sin \angle Q C A}{\sin \angle Q A C}\right)^{2} $$ because $\angle Q C A=\angle P A Q$ and $\angle Q A C=\angle Q C P$. Denote by $S(X Y Z)$ the area of a triangle $X Y Z$. Then $$ \frac{\sin \angle A P B}{\sin \angle B P C}=\frac{A P \cdot B P \cdot \sin \angle A P B}{B P \cdot C P \cdot \sin \angle B P C}=\frac{S(\Delta A B P)}{S(\Delta B C P)}=\frac{A B}{B C}, $$ which implies that $\left(\frac{A R}{R C}\right)^{2}=\frac{A B}{B C}$. Hence $R$ does not depend on $\Gamma$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
b3236015-8917-51d4-8b07-cb9f140d4a92
| 25,140
|
15. G3 (IND) Let $A B C$ be a triangle and let $P$ be a point in its interior. Denote by $D, E, F$ the feet of the perpendiculars from $P$ to the lines $B C$, $C A$, and $A B$, respectively. Suppose that $$ A P^{2}+P D^{2}=B P^{2}+P E^{2}=C P^{2}+P F^{2} $$ Denote by $I_{A}, I_{B}, I_{C}$ the excenters of the triangle $A B C$. Prove that $P$ is the circumcenter of the triangle $I_{A} I_{B} I_{C}$.
|
15. From the given equality we see that $0=\left(B P^{2}+P E^{2}\right)-\left(C P^{2}+P F^{2}\right)=$ $B F^{2}-C E^{2}$, so $B F=C E=x$ for some $x$. Similarly, there are $y$ and $z$ such that $C D=A F=y$ and $B D=A E=z$. It is easy to verify that $D$, $E$, and $F$ must lie on the segments $B C, C A, A B$. Denote by $a, b, c$ the length of the segments $B C, C A, A B$. It follows that $a=z+y, b=z+x, c=x+y$, so $D, E, F$ are the points where the excircles touch the sides of $\triangle A B C$. Hence $P, D$, and $I_{A}$ are collinear and $$ \angle P I_{A} C=\angle D I_{A} C=90^{\circ}-\frac{180^{\circ}-\angle A C B}{2}=\frac{\angle A C B}{2} $$ In the same way we obtain that $\angle P I_{B} C=\frac{\angle A C B}{2}$ and $P I_{B}=P I_{A}$. Analogously, we get $P I_{C}=P I_{B}$, which implies that $P$ is the circumcenter of the triangle $I_{A} I_{B} I_{C}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
15. G3 (IND) Let $A B C$ be a triangle and let $P$ be a point in its interior. Denote by $D, E, F$ the feet of the perpendiculars from $P$ to the lines $B C$, $C A$, and $A B$, respectively. Suppose that $$ A P^{2}+P D^{2}=B P^{2}+P E^{2}=C P^{2}+P F^{2} $$ Denote by $I_{A}, I_{B}, I_{C}$ the excenters of the triangle $A B C$. Prove that $P$ is the circumcenter of the triangle $I_{A} I_{B} I_{C}$.
|
15. From the given equality we see that $0=\left(B P^{2}+P E^{2}\right)-\left(C P^{2}+P F^{2}\right)=$ $B F^{2}-C E^{2}$, so $B F=C E=x$ for some $x$. Similarly, there are $y$ and $z$ such that $C D=A F=y$ and $B D=A E=z$. It is easy to verify that $D$, $E$, and $F$ must lie on the segments $B C, C A, A B$. Denote by $a, b, c$ the length of the segments $B C, C A, A B$. It follows that $a=z+y, b=z+x, c=x+y$, so $D, E, F$ are the points where the excircles touch the sides of $\triangle A B C$. Hence $P, D$, and $I_{A}$ are collinear and $$ \angle P I_{A} C=\angle D I_{A} C=90^{\circ}-\frac{180^{\circ}-\angle A C B}{2}=\frac{\angle A C B}{2} $$ In the same way we obtain that $\angle P I_{B} C=\frac{\angle A C B}{2}$ and $P I_{B}=P I_{A}$. Analogously, we get $P I_{C}=P I_{B}$, which implies that $P$ is the circumcenter of the triangle $I_{A} I_{B} I_{C}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
05b00397-c448-5d3c-a6be-5d87f485f673
| 25,141
|
16. G4 (ARM) Let $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}, \Gamma_{4}$ be distinct circles such that $\Gamma_{1}, \Gamma_{3}$ are externally tangent at $P$, and $\Gamma_{2}, \Gamma_{4}$ are externally tangent at the same point $P$. Suppose that $\Gamma_{1}$ and $\Gamma_{2} ; \Gamma_{2}$ and $\Gamma_{3} ; \Gamma_{3}$ and $\Gamma_{4} ; \Gamma_{4}$ and $\Gamma_{1}$ meet at $A, B, C, D$, respectively, and that all these points are different from $P$. Prove that $$ \frac{A B \cdot B C}{A D \cdot D C}=\frac{P B^{2}}{P D^{2}} $$
|
16. Apply an inversion with center at $P$ and radius $r$; let $\widehat{X}$ denote the image of $X$. The circles $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}, \Gamma_{4}$ are transformed into lines $\widehat{\Gamma_{1}}, \widehat{\Gamma_{2}}, \widehat{\Gamma_{3}}, \widehat{\Gamma}_{4}$, where $\widehat{\Gamma_{1}} \| \widehat{\Gamma_{3}}$ and $\widehat{\Gamma_{2}} \| \widehat{\Gamma_{4}}$, and therefore $\widehat{A} \widehat{B} \widehat{C} \widehat{D}$ is a parallelogram. Further, we have $A B=\frac{r^{2}}{P \widehat{A} \cdot P \widehat{B}} \widehat{A} \widehat{B}, B C=\frac{r^{2}}{P \widehat{B} \cdot P \widehat{C}} \widehat{B} \widehat{C}, C D=\frac{r^{2}}{P \widehat{C} \cdot P \widehat{D}} \widehat{C} \widehat{D}$, $D A=\frac{r^{2}}{P \widehat{D} \cdot P \widehat{A}} \widehat{D} \widehat{A}$ and $P B=\frac{r^{2}}{P \widehat{B}}, P D=\frac{r^{2}}{P \widehat{D}}$. The equality to be proven becomes $$ \frac{P \widehat{D}^{2}}{P \widehat{B}^{2}} \cdot \frac{\widehat{A} \widehat{B} \cdot \widehat{B} \widehat{C}}{\widehat{A} \cdot \widehat{D} \widehat{C}}=\frac{P \widehat{D}^{2}}{P \widehat{B}^{2}} $$ which holds because $\widehat{A} \widehat{B}=\widehat{C} \widehat{D}$ and $\widehat{B} \widehat{C}=\widehat{D} \widehat{A}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
16. G4 (ARM) Let $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}, \Gamma_{4}$ be distinct circles such that $\Gamma_{1}, \Gamma_{3}$ are externally tangent at $P$, and $\Gamma_{2}, \Gamma_{4}$ are externally tangent at the same point $P$. Suppose that $\Gamma_{1}$ and $\Gamma_{2} ; \Gamma_{2}$ and $\Gamma_{3} ; \Gamma_{3}$ and $\Gamma_{4} ; \Gamma_{4}$ and $\Gamma_{1}$ meet at $A, B, C, D$, respectively, and that all these points are different from $P$. Prove that $$ \frac{A B \cdot B C}{A D \cdot D C}=\frac{P B^{2}}{P D^{2}} $$
|
16. Apply an inversion with center at $P$ and radius $r$; let $\widehat{X}$ denote the image of $X$. The circles $\Gamma_{1}, \Gamma_{2}, \Gamma_{3}, \Gamma_{4}$ are transformed into lines $\widehat{\Gamma_{1}}, \widehat{\Gamma_{2}}, \widehat{\Gamma_{3}}, \widehat{\Gamma}_{4}$, where $\widehat{\Gamma_{1}} \| \widehat{\Gamma_{3}}$ and $\widehat{\Gamma_{2}} \| \widehat{\Gamma_{4}}$, and therefore $\widehat{A} \widehat{B} \widehat{C} \widehat{D}$ is a parallelogram. Further, we have $A B=\frac{r^{2}}{P \widehat{A} \cdot P \widehat{B}} \widehat{A} \widehat{B}, B C=\frac{r^{2}}{P \widehat{B} \cdot P \widehat{C}} \widehat{B} \widehat{C}, C D=\frac{r^{2}}{P \widehat{C} \cdot P \widehat{D}} \widehat{C} \widehat{D}$, $D A=\frac{r^{2}}{P \widehat{D} \cdot P \widehat{A}} \widehat{D} \widehat{A}$ and $P B=\frac{r^{2}}{P \widehat{B}}, P D=\frac{r^{2}}{P \widehat{D}}$. The equality to be proven becomes $$ \frac{P \widehat{D}^{2}}{P \widehat{B}^{2}} \cdot \frac{\widehat{A} \widehat{B} \cdot \widehat{B} \widehat{C}}{\widehat{A} \cdot \widehat{D} \widehat{C}}=\frac{P \widehat{D}^{2}}{P \widehat{B}^{2}} $$ which holds because $\widehat{A} \widehat{B}=\widehat{C} \widehat{D}$ and $\widehat{B} \widehat{C}=\widehat{D} \widehat{A}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4c75ce10-d871-57b1-82c9-05317c500cf2
| 25,142
|
17. G5 (KOR) Let $A B C$ be an isosceles triangle with $A C=B C$, whose incenter is $I$. Let $P$ be a point on the circumcircle of the triangle $A I B$ lying inside the triangle $A B C$. The lines through $P$ parallel to $C A$ and $C B$ meet $A B$ at $D$ and $E$, respectively. The line through $P$ parallel to $A B$ meets $C A$ and $C B$ at $F$ and $G$, respectively. Prove that the lines $D F$ and $E G$ intersect on the circumcircle of the triangle $A B C$.
|
17. The triangles $P D E$ and $C F G$ are homothetic; hence lines $F D, G E$, and $C P$ intersect at one point. Let $Q$ be the intersection point of the line $C P$ and the circumcircle of $\triangle A B C$. The required statement will follow if we show that $Q$ lies on the lines $G E$ and $F D$. Since $\angle C F G=\angle C B A=\angle C Q A$, the quadrilateral $A Q P F$ is cyclic. Analogously, $B Q P G$ is cyclic. However, the isosceles trapezoid $B D P G$ is also cyclic; it follows that $B, Q, D, P, G$ lie on a circle. Therefore we get $$ \angle P Q F=\angle P A C, \angle P Q D=\angle P B A . $$ Since $I$ is the incenter of $\triangle A B C$, we have $\angle C A I=\frac{1}{2} \angle C A B=$ $\frac{1}{2} \angle C B A=\angle I B A$; hence $C A$ is the tangent at $A$ to the circumcircle of $\triangle A B I$. This implies that $\angle P A C=$ $\angle P B A$, and it follows from (1) that $\angle P Q F=\angle P Q D$, i.e., that $F, D, Q$ are also collinear. Similarly, $G, E, Q$ are collinear and the claim is thus proved. 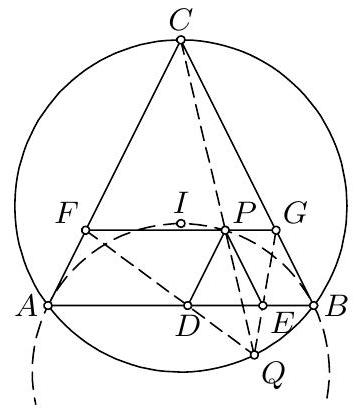
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
17. G5 (KOR) Let $A B C$ be an isosceles triangle with $A C=B C$, whose incenter is $I$. Let $P$ be a point on the circumcircle of the triangle $A I B$ lying inside the triangle $A B C$. The lines through $P$ parallel to $C A$ and $C B$ meet $A B$ at $D$ and $E$, respectively. The line through $P$ parallel to $A B$ meets $C A$ and $C B$ at $F$ and $G$, respectively. Prove that the lines $D F$ and $E G$ intersect on the circumcircle of the triangle $A B C$.
|
17. The triangles $P D E$ and $C F G$ are homothetic; hence lines $F D, G E$, and $C P$ intersect at one point. Let $Q$ be the intersection point of the line $C P$ and the circumcircle of $\triangle A B C$. The required statement will follow if we show that $Q$ lies on the lines $G E$ and $F D$. Since $\angle C F G=\angle C B A=\angle C Q A$, the quadrilateral $A Q P F$ is cyclic. Analogously, $B Q P G$ is cyclic. However, the isosceles trapezoid $B D P G$ is also cyclic; it follows that $B, Q, D, P, G$ lie on a circle. Therefore we get $$ \angle P Q F=\angle P A C, \angle P Q D=\angle P B A . $$ Since $I$ is the incenter of $\triangle A B C$, we have $\angle C A I=\frac{1}{2} \angle C A B=$ $\frac{1}{2} \angle C B A=\angle I B A$; hence $C A$ is the tangent at $A$ to the circumcircle of $\triangle A B I$. This implies that $\angle P A C=$ $\angle P B A$, and it follows from (1) that $\angle P Q F=\angle P Q D$, i.e., that $F, D, Q$ are also collinear. Similarly, $G, E, Q$ are collinear and the claim is thus proved. 
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
6c83c4b8-fdfd-5435-8715-fbfb44ea9755
| 25,143
|
18. G6 (POL) ${ }^{\mathrm{IMO} 3}$ Each pair of opposite sides of a convex hexagon has the following property: The distance between their midpoints is equal to $\sqrt{3} / 2$ times the sum of their lengths. Prove that all the angles of the hexagon are equal.
|
18. Let $A B C D E F$ be the given hexagon. We shall use the following lemma. Lemma. If $\angle X Z Y \geq 60^{\circ}$ and if $M$ is the midpoint of $X Y$, then $M Z \leq$ $\frac{\sqrt{3}}{2} X Y$, with equality if and only if $\triangle X Y Z$ is equilateral. Proof. Let $Z^{\prime}$ be the point such that $\triangle X Y Z^{\prime}$ is equilateral. Then $Z$ is inside the circle circumscribed about $\triangle X Y Z^{\prime}$. Consequently $M Z \leq$ $M Z^{\prime}=\frac{\sqrt{3}}{2} X Y$, with equality if and only if $Z=Z^{\prime}$. Set $A D \cap B E=P, B E \cap C F=Q$, and $C F \cap A D=R$. Suppose $\angle A P B=$ $\angle D P E>60^{\circ}$, and let $K, L$ be the midpoints of the segments $A B$ and $D E$ respectively. Then by the lemma, $$ \frac{\sqrt{3}}{2}(A B+D E)=K L \leq P K+P L<\frac{\sqrt{3}}{2}(A B+D E), $$ which is impossible. Therefore $\angle A P B \leq 60^{\circ}$ and similarly $\angle B Q C \leq 60^{\circ}$, $\angle C R D \leq 60^{\circ}$. But the sum of the angles $A P B, B Q C, C R D$ is $180^{\circ}$, from which we conclude that these angles are all equal to $60^{\circ}$, and moreover that the triangles $A P B, B Q C, C R D$ are equilateral. Thus $\angle A B C=\angle A B P+$ $\angle Q B C=120^{\circ}$, and in the same way all angles of the hexagon are equal to $120^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
18. G6 (POL) ${ }^{\mathrm{IMO} 3}$ Each pair of opposite sides of a convex hexagon has the following property: The distance between their midpoints is equal to $\sqrt{3} / 2$ times the sum of their lengths. Prove that all the angles of the hexagon are equal.
|
18. Let $A B C D E F$ be the given hexagon. We shall use the following lemma. Lemma. If $\angle X Z Y \geq 60^{\circ}$ and if $M$ is the midpoint of $X Y$, then $M Z \leq$ $\frac{\sqrt{3}}{2} X Y$, with equality if and only if $\triangle X Y Z$ is equilateral. Proof. Let $Z^{\prime}$ be the point such that $\triangle X Y Z^{\prime}$ is equilateral. Then $Z$ is inside the circle circumscribed about $\triangle X Y Z^{\prime}$. Consequently $M Z \leq$ $M Z^{\prime}=\frac{\sqrt{3}}{2} X Y$, with equality if and only if $Z=Z^{\prime}$. Set $A D \cap B E=P, B E \cap C F=Q$, and $C F \cap A D=R$. Suppose $\angle A P B=$ $\angle D P E>60^{\circ}$, and let $K, L$ be the midpoints of the segments $A B$ and $D E$ respectively. Then by the lemma, $$ \frac{\sqrt{3}}{2}(A B+D E)=K L \leq P K+P L<\frac{\sqrt{3}}{2}(A B+D E), $$ which is impossible. Therefore $\angle A P B \leq 60^{\circ}$ and similarly $\angle B Q C \leq 60^{\circ}$, $\angle C R D \leq 60^{\circ}$. But the sum of the angles $A P B, B Q C, C R D$ is $180^{\circ}$, from which we conclude that these angles are all equal to $60^{\circ}$, and moreover that the triangles $A P B, B Q C, C R D$ are equilateral. Thus $\angle A B C=\angle A B P+$ $\angle Q B C=120^{\circ}$, and in the same way all angles of the hexagon are equal to $120^{\circ}$.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
1d4e9119-4c93-5d1d-97cf-340ee346b786
| 25,144
|
19. G7 (SAF) Let $A B C$ be a triangle with semiperimeter $s$ and inradius $r$. The semicircles with diameters $B C, C A, A B$ are drawn outside of the triangle $A B C$. The circle tangent to all three semicircles has radius $t$. Prove that $$ \frac{s}{2}<t \leq \frac{s}{2}+\left(1-\frac{\sqrt{3}}{2}\right) r $$
|
19. Let $D, E, F$ be the midpoints of $B C, C A, A B$, respectively. We construct smaller semicircles $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$ inside $\triangle A B C$ with centers $D, E, F$ and radii $d=\frac{s-a}{2}, e=\frac{s-b}{2}, f=\frac{s-c}{2}$ respectively. Since $D E=d+e, D F=d+f$, and $E F=e+f$, we deduce that $\Gamma_{d}, \Gamma_{e}$, and $\Gamma_{f}$ touch each other at the points $D_{1}, E_{1}, F_{1}$ of tangency of the incircle $\gamma$ of $\triangle D E F$ with its sides ( $D_{1} \in E F$, etc.). Consider the circle $\Gamma_{g}$ with center $O$ and radius $g$ that lies inside $\triangle D E F$ and tangents $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$. Now let $O D, O E, O F$ meet the semicircles $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$ at $D^{\prime}, E^{\prime}, F^{\prime}$ respectively. We have $O D^{\prime}=O D+$ $D D^{\prime}=g+d+\frac{a}{2}=g+\frac{s}{2}$ and similarly $O E^{\prime}=O F^{\prime}=g+\frac{s}{2}$. It follows that the circle with center $O$ and radius $g+\frac{s}{2}$ touches all three semicircles, and consequently $t=$ $g+\frac{s}{2}>\frac{s}{2}$. Now set the coordinate system such that we have the points $D_{1}(0,0), E(-e, 0), F(f, 0)$ and such that the $y$ coordinate of $D$ is positive.  Apply the inversion with center $D_{1}$ and unit radius. This inversion maps the circles $\Gamma_{e}$ and $\Gamma_{f}$ to the lines $\widehat{\Gamma_{e}}\left[x=-\frac{1}{2 e}\right]$ and $\widehat{\Gamma_{e}}\left[x=\frac{1}{2 f}\right]$ respectively, and the circle $\gamma$ goes to the line $\widehat{\gamma}\left[y=\frac{1}{r}\right]$. The images $\widehat{\Gamma_{d}}$ and $\widehat{\Gamma_{g}}$ of $\Gamma_{d}, \Gamma_{g}$ are the circles that touch the lines $\widehat{\Gamma_{e}}$ and $\widehat{\Gamma_{f}}$. Since $\widehat{\Gamma_{d}}, \widehat{\Gamma_{g}}$ are perpendicular to $\gamma$, they have radii equal to $R=\frac{1}{4 e}+\frac{1}{4 f}$ and centers at $\left(-\frac{1}{4 e}+\frac{1}{4 f}, \frac{1}{r}\right)$ and $\left(-\frac{1}{4 e}+\frac{1}{4 f}, \frac{1}{r}+2 R\right)$ respectively. Let $p$ and $P$ be the distances from $D_{1}(0,0)$ to the centers of $\Gamma_{g}$ and $\widehat{\Gamma_{g}}$ respectively. We have that $P^{2}=\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}+\left(\frac{1}{r}+2 R\right)^{2}$, and that the circles $\Gamma_{g}$ and $\widehat{\Gamma_{g}}$ are homothetic with center of homothety $D_{1}$; hence $p / P=g / R$. On the other hand, $\widehat{\Gamma_{g}}$ is the image of $\Gamma_{g}$ under inversion; hence the product of the tangents from $D_{1}$ to these two circles is equal to 1 . In other words, we obtain $\sqrt{p^{2}-g^{2}} \cdot \sqrt{P^{2}-R^{2}}=1$. Using the relation $p / P=g / R$ we get $g=\frac{R}{P^{2}-R^{2}}$. The inequality we have to prove is equivalent to $(4+2 \sqrt{3}) g \leq r$. This can be proved as follows: $$ \begin{aligned} r-(4+2 \sqrt{3}) g & =\frac{r\left(P^{2}-R^{2}-(4+2 \sqrt{3}) R / r\right)}{P^{2}-R^{2}} \\ & =\frac{r\left(\left(\frac{1}{r}+2 R\right)^{2}+\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}-R^{2}-(4+2 \sqrt{3}) \frac{R}{r}\right)}{P^{2}-R^{2}} \\ & =\frac{r}{P^{2}-R^{2}}\left(\left(R \sqrt{3}-\frac{1}{r}\right)^{2}+\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}\right) \geq 0 \end{aligned} $$ Remark. One can obtain a symmetric formula for $g$ : $$ \frac{1}{2 g}=\frac{1}{s-a}+\frac{1}{s-b}+\frac{1}{s-c}+\frac{2}{r} $$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
19. G7 (SAF) Let $A B C$ be a triangle with semiperimeter $s$ and inradius $r$. The semicircles with diameters $B C, C A, A B$ are drawn outside of the triangle $A B C$. The circle tangent to all three semicircles has radius $t$. Prove that $$ \frac{s}{2}<t \leq \frac{s}{2}+\left(1-\frac{\sqrt{3}}{2}\right) r $$
|
19. Let $D, E, F$ be the midpoints of $B C, C A, A B$, respectively. We construct smaller semicircles $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$ inside $\triangle A B C$ with centers $D, E, F$ and radii $d=\frac{s-a}{2}, e=\frac{s-b}{2}, f=\frac{s-c}{2}$ respectively. Since $D E=d+e, D F=d+f$, and $E F=e+f$, we deduce that $\Gamma_{d}, \Gamma_{e}$, and $\Gamma_{f}$ touch each other at the points $D_{1}, E_{1}, F_{1}$ of tangency of the incircle $\gamma$ of $\triangle D E F$ with its sides ( $D_{1} \in E F$, etc.). Consider the circle $\Gamma_{g}$ with center $O$ and radius $g$ that lies inside $\triangle D E F$ and tangents $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$. Now let $O D, O E, O F$ meet the semicircles $\Gamma_{d}, \Gamma_{e}, \Gamma_{f}$ at $D^{\prime}, E^{\prime}, F^{\prime}$ respectively. We have $O D^{\prime}=O D+$ $D D^{\prime}=g+d+\frac{a}{2}=g+\frac{s}{2}$ and similarly $O E^{\prime}=O F^{\prime}=g+\frac{s}{2}$. It follows that the circle with center $O$ and radius $g+\frac{s}{2}$ touches all three semicircles, and consequently $t=$ $g+\frac{s}{2}>\frac{s}{2}$. Now set the coordinate system such that we have the points $D_{1}(0,0), E(-e, 0), F(f, 0)$ and such that the $y$ coordinate of $D$ is positive.  Apply the inversion with center $D_{1}$ and unit radius. This inversion maps the circles $\Gamma_{e}$ and $\Gamma_{f}$ to the lines $\widehat{\Gamma_{e}}\left[x=-\frac{1}{2 e}\right]$ and $\widehat{\Gamma_{e}}\left[x=\frac{1}{2 f}\right]$ respectively, and the circle $\gamma$ goes to the line $\widehat{\gamma}\left[y=\frac{1}{r}\right]$. The images $\widehat{\Gamma_{d}}$ and $\widehat{\Gamma_{g}}$ of $\Gamma_{d}, \Gamma_{g}$ are the circles that touch the lines $\widehat{\Gamma_{e}}$ and $\widehat{\Gamma_{f}}$. Since $\widehat{\Gamma_{d}}, \widehat{\Gamma_{g}}$ are perpendicular to $\gamma$, they have radii equal to $R=\frac{1}{4 e}+\frac{1}{4 f}$ and centers at $\left(-\frac{1}{4 e}+\frac{1}{4 f}, \frac{1}{r}\right)$ and $\left(-\frac{1}{4 e}+\frac{1}{4 f}, \frac{1}{r}+2 R\right)$ respectively. Let $p$ and $P$ be the distances from $D_{1}(0,0)$ to the centers of $\Gamma_{g}$ and $\widehat{\Gamma_{g}}$ respectively. We have that $P^{2}=\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}+\left(\frac{1}{r}+2 R\right)^{2}$, and that the circles $\Gamma_{g}$ and $\widehat{\Gamma_{g}}$ are homothetic with center of homothety $D_{1}$; hence $p / P=g / R$. On the other hand, $\widehat{\Gamma_{g}}$ is the image of $\Gamma_{g}$ under inversion; hence the product of the tangents from $D_{1}$ to these two circles is equal to 1 . In other words, we obtain $\sqrt{p^{2}-g^{2}} \cdot \sqrt{P^{2}-R^{2}}=1$. Using the relation $p / P=g / R$ we get $g=\frac{R}{P^{2}-R^{2}}$. The inequality we have to prove is equivalent to $(4+2 \sqrt{3}) g \leq r$. This can be proved as follows: $$ \begin{aligned} r-(4+2 \sqrt{3}) g & =\frac{r\left(P^{2}-R^{2}-(4+2 \sqrt{3}) R / r\right)}{P^{2}-R^{2}} \\ & =\frac{r\left(\left(\frac{1}{r}+2 R\right)^{2}+\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}-R^{2}-(4+2 \sqrt{3}) \frac{R}{r}\right)}{P^{2}-R^{2}} \\ & =\frac{r}{P^{2}-R^{2}}\left(\left(R \sqrt{3}-\frac{1}{r}\right)^{2}+\left(\frac{1}{4 e}-\frac{1}{4 f}\right)^{2}\right) \geq 0 \end{aligned} $$ Remark. One can obtain a symmetric formula for $g$ : $$ \frac{1}{2 g}=\frac{1}{s-a}+\frac{1}{s-b}+\frac{1}{s-c}+\frac{2}{r} $$
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
4a724885-c2d0-570f-8e6f-40ee9c350dea
| 25,145
|
25. N6 (FRA) ${ }^{\text {IMO6 }}$ Let $p$ be a prime number. Prove that there exists a prime number $q$ such that for every integer $n$, the number $n^{p}-p$ is not divisible by $q$.
|
25. Suppose that for every prime $q$, there exists an $n$ for which $n^{p} \equiv p(\bmod$ $q$ ). Assume that $q=k p+1$. By Fermat's theorem we deduce that $p^{k} \equiv$ $n^{k p}=n^{q-1} \equiv 1(\bmod q)$, so $q \mid p^{k}-1$. It is known that any prime $q$ such that $q \left\lvert\, \frac{p^{p}-1}{p-1}\right.$ must satisfy $q \equiv 1(\bmod$ $p$ ). Indeed, from $q \mid p^{q-1}-1$ it follows that $q \mid p^{\operatorname{gcd}(p, q-1)}-1$; but $q \nmid p-1$ because $\frac{p^{p}-1}{p-1} \equiv 1(\bmod p-1)$, so $\operatorname{gcd}(p, q-1) \neq 1$. Hence $\operatorname{gcd}(p, q-1)=p$. Now suppose $q$ is any prime divisor of $\frac{p^{p}-1}{p-1}$. Then $q \mid \operatorname{gcd}\left(p^{k}-1, p^{p}-1\right)=$ $p^{\operatorname{gcd}(p, k)}-1$, which implies that $\operatorname{gcd}(p, k)>1$, so $p \mid k$. Consequently $q \equiv 1$ $\left(\bmod p^{2}\right)$. However, the number $\frac{p^{p}-1}{p-1}=p^{p-1}+\cdots+p+1$ must have at least one prime divisor that is not congruent to 1 modulo $p^{2}$. Thus we arrived at a contradiction. Remark. Taking $q \equiv 1(\bmod p)$ is natural, because for every other $q, n^{p}$ takes all possible residues modulo $q$ (including $p$ too). Indeed, if $p \nmid q-1$, then there is an $r \in \mathbb{N}$ satisfying $p r \equiv 1(\bmod q-1)$; hence for any $a$ the congruence $n^{p} \equiv a(\bmod q)$ has the solution $n \equiv a^{r}(\bmod q)$. The statement of the problem itself is a special case of the Chebotarev's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
25. N6 (FRA) ${ }^{\text {IMO6 }}$ Let $p$ be a prime number. Prove that there exists a prime number $q$ such that for every integer $n$, the number $n^{p}-p$ is not divisible by $q$.
|
25. Suppose that for every prime $q$, there exists an $n$ for which $n^{p} \equiv p(\bmod$ $q$ ). Assume that $q=k p+1$. By Fermat's theorem we deduce that $p^{k} \equiv$ $n^{k p}=n^{q-1} \equiv 1(\bmod q)$, so $q \mid p^{k}-1$. It is known that any prime $q$ such that $q \left\lvert\, \frac{p^{p}-1}{p-1}\right.$ must satisfy $q \equiv 1(\bmod$ $p$ ). Indeed, from $q \mid p^{q-1}-1$ it follows that $q \mid p^{\operatorname{gcd}(p, q-1)}-1$; but $q \nmid p-1$ because $\frac{p^{p}-1}{p-1} \equiv 1(\bmod p-1)$, so $\operatorname{gcd}(p, q-1) \neq 1$. Hence $\operatorname{gcd}(p, q-1)=p$. Now suppose $q$ is any prime divisor of $\frac{p^{p}-1}{p-1}$. Then $q \mid \operatorname{gcd}\left(p^{k}-1, p^{p}-1\right)=$ $p^{\operatorname{gcd}(p, k)}-1$, which implies that $\operatorname{gcd}(p, k)>1$, so $p \mid k$. Consequently $q \equiv 1$ $\left(\bmod p^{2}\right)$. However, the number $\frac{p^{p}-1}{p-1}=p^{p-1}+\cdots+p+1$ must have at least one prime divisor that is not congruent to 1 modulo $p^{2}$. Thus we arrived at a contradiction. Remark. Taking $q \equiv 1(\bmod p)$ is natural, because for every other $q, n^{p}$ takes all possible residues modulo $q$ (including $p$ too). Indeed, if $p \nmid q-1$, then there is an $r \in \mathbb{N}$ satisfying $p r \equiv 1(\bmod q-1)$; hence for any $a$ the congruence $n^{p} \equiv a(\bmod q)$ has the solution $n \equiv a^{r}(\bmod q)$. The statement of the problem itself is a special case of the Chebotarev's theorem.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
529f9fd3-9a93-5696-839a-57e3907a4770
| 25,152
|
26. N7 (BRA) The sequence $a_{0}, a_{1}, a_{2}, \ldots$ is defined as follows: $$ a_{0}=2, \quad a_{k+1}=2 a_{k}^{2}-1 \quad \text { for } k \geq 0 $$ Prove that if an odd prime $p$ divides $a_{n}$, then $2^{n+3}$ divides $p^{2}-1$.
|
26. Define the sequence $x_{k}$ of positive reals by $a_{k}=\cosh x_{k}$ ( $\cosh$ is the hyperbolic cosine defined by $\left.\cosh t=\frac{e^{t}+e^{-t}}{2}\right)$. Since $\cosh \left(2 x_{k}\right)=2 a_{k}^{2}-1=$ $\cosh x_{k+1}$, it follows that $x_{k+1}=2 x_{k}$ and thus $x_{k}=\lambda \cdot 2^{k}$ for some $\lambda>0$. From the condition $a_{0}=2$ we obtain $\lambda=\log (2+\sqrt{3})$. Therefore $$ a_{n}=\frac{(2+\sqrt{3})^{2^{n}}+(2-\sqrt{3})^{2^{n}}}{2} $$ Let $p$ be a prime number such that $p \mid a_{n}$. We distinguish the following two cases: (i) There exists an $m \in \mathbb{Z}$ such that $m^{2} \equiv 3(\bmod p)$. Then we have $$ (2+m)^{2^{n}}+(2-m)^{2^{n}} \equiv 0(\bmod p) $$ Since $(2+m)(2-m)=4-m^{2} \equiv 1(\bmod p)$, multiplying both sides of $(1)$ by $(2+m)^{2^{n}}$ gives $(2+m)^{2^{n+1}} \equiv-1(\bmod p)$. It follows that the multiplicative order of $(2+m)$ modulo $p$ is $2^{n+2}$, or $2^{n+2} \mid p-1$, which implies that $2^{n+3} \mid(p-1)(p+1)=p^{2}-1$. (ii) $m^{2} \equiv 3(\bmod p)$ has no integer solutions. We will work in the algebraic extension $\mathbb{Z}_{p}(\sqrt{3})$ of the field $\mathbb{Z}_{p}$. In this field $\sqrt{3}$ plays the role of $m$, so as in the previous case we obtain $(2+\sqrt{3})^{2^{n+1}}=-1$; i.e., the order of $2+\sqrt{3}$ in the multiplicative group $\mathbb{Z}_{p}(\sqrt{3})^{*}$ is $2^{n+2}$. We cannot finish the proof as in the previous case: in fact, we would conclude only that $2^{n+2}$ divides the order $p^{2}-1$ of the group. However, it will be enough to find a $u \in \mathbb{Z}_{p}(\sqrt{3})$ such that $u^{2}=2+\sqrt{3}$, since then the order of $u$ is equal to $2^{n+3}$. Note that $(1+\sqrt{3})^{2}=2(2+\sqrt{3})$. Thus it is sufficient to prove that $\frac{1}{2}$ is a perfect square in $\mathbb{Z}_{p}(\sqrt{3})$. But we know that in this field $a_{n}=$ $0=2 a_{n-1}^{2}-1$, and hence $2 a_{n-1}^{2}=1$ which implies $\frac{1}{2}=a_{n-1}^{2}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
26. N7 (BRA) The sequence $a_{0}, a_{1}, a_{2}, \ldots$ is defined as follows: $$ a_{0}=2, \quad a_{k+1}=2 a_{k}^{2}-1 \quad \text { for } k \geq 0 $$ Prove that if an odd prime $p$ divides $a_{n}$, then $2^{n+3}$ divides $p^{2}-1$.
|
26. Define the sequence $x_{k}$ of positive reals by $a_{k}=\cosh x_{k}$ ( $\cosh$ is the hyperbolic cosine defined by $\left.\cosh t=\frac{e^{t}+e^{-t}}{2}\right)$. Since $\cosh \left(2 x_{k}\right)=2 a_{k}^{2}-1=$ $\cosh x_{k+1}$, it follows that $x_{k+1}=2 x_{k}$ and thus $x_{k}=\lambda \cdot 2^{k}$ for some $\lambda>0$. From the condition $a_{0}=2$ we obtain $\lambda=\log (2+\sqrt{3})$. Therefore $$ a_{n}=\frac{(2+\sqrt{3})^{2^{n}}+(2-\sqrt{3})^{2^{n}}}{2} $$ Let $p$ be a prime number such that $p \mid a_{n}$. We distinguish the following two cases: (i) There exists an $m \in \mathbb{Z}$ such that $m^{2} \equiv 3(\bmod p)$. Then we have $$ (2+m)^{2^{n}}+(2-m)^{2^{n}} \equiv 0(\bmod p) $$ Since $(2+m)(2-m)=4-m^{2} \equiv 1(\bmod p)$, multiplying both sides of $(1)$ by $(2+m)^{2^{n}}$ gives $(2+m)^{2^{n+1}} \equiv-1(\bmod p)$. It follows that the multiplicative order of $(2+m)$ modulo $p$ is $2^{n+2}$, or $2^{n+2} \mid p-1$, which implies that $2^{n+3} \mid(p-1)(p+1)=p^{2}-1$. (ii) $m^{2} \equiv 3(\bmod p)$ has no integer solutions. We will work in the algebraic extension $\mathbb{Z}_{p}(\sqrt{3})$ of the field $\mathbb{Z}_{p}$. In this field $\sqrt{3}$ plays the role of $m$, so as in the previous case we obtain $(2+\sqrt{3})^{2^{n+1}}=-1$; i.e., the order of $2+\sqrt{3}$ in the multiplicative group $\mathbb{Z}_{p}(\sqrt{3})^{*}$ is $2^{n+2}$. We cannot finish the proof as in the previous case: in fact, we would conclude only that $2^{n+2}$ divides the order $p^{2}-1$ of the group. However, it will be enough to find a $u \in \mathbb{Z}_{p}(\sqrt{3})$ such that $u^{2}=2+\sqrt{3}$, since then the order of $u$ is equal to $2^{n+3}$. Note that $(1+\sqrt{3})^{2}=2(2+\sqrt{3})$. Thus it is sufficient to prove that $\frac{1}{2}$ is a perfect square in $\mathbb{Z}_{p}(\sqrt{3})$. But we know that in this field $a_{n}=$ $0=2 a_{n-1}^{2}-1$, and hence $2 a_{n-1}^{2}=1$ which implies $\frac{1}{2}=a_{n-1}^{2}$. This completes the proof.
|
{
"resource_path": "IMO/segmented/en-compendium.jsonl",
"problem_match": null,
"solution_match": null
}
|
c00c299c-1ad7-5647-901a-5b3d76004fdb
| 25,153
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.