code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/BrunaKuntz/Python-Curso-em-Video/blob/main/Mundo02/Desafio038.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="xolHFjDi_Hj4"
#
#
#
# # **Desafio 038**
# **Python 3 - 2º Mundo**
#
# Descrição: Escreva um programa que leia dois números inteiros e compare-os. mostrando na tela uma mensagem:
# - O primeiro valor é maior
# - O segundo valor é maior
# - Não existe valor maior, os dois são iguais
#
# Link: https://www.youtube.com/watch?time_continue=12&v=iuPbB9uHczM&feature=emb_title
# + id="8Lylf4Su-6aB"
n1 = int(input('Digite um valor: '))
n2 = int(input('Digite outro valor: '))
if n1 > n2:
print(f'O primeiro número é maior. {n1} é maior que {n2}.')
elif n2 > n1:
print(f'O segundo número é maior. {n2} é maior que {n1}.')
else:
print(f'Não existe valor maior, {n1} e {n2} são iguais.')
|
Mundo02/Desafio038.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Investigating factors of WA highway crashes
# ### <NAME>, <NAME>, <NAME>, <NAME> (Group 5)
# #### CET 521 Inferential Data Analysis for Engineers
# + slideshow={"slide_type": "skip"}
from IPython.display import display, HTML
CSS = """
.output {
align-items: center;
}
"""
HTML('<style>{}</style>'.format(CSS))
# + slideshow={"slide_type": "skip"}
from notebook.services.config import ConfigManager
cm = ConfigManager()
cm.update('livereveal', {
'scroll': True,
})
# + [markdown] heading_collapsed=true slideshow={"slide_type": "skip"}
# ## set-ups
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# ### module
# + hidden=true slideshow={"slide_type": "skip"}
import os
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import matplotlib
import copy
plt.rc('text', usetex=True)
import warnings
warnings.filterwarnings('ignore')
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# ### functions
# + hidden=true slideshow={"slide_type": "skip"}
def detect_files(directory, keyword):
"""
detect files in specified directory with specified keyword
input
-----
directory : string
dir to search
keyword : string
keyword to look for
output
-----
sorted list of file names
test
-----
(1) if output has larger than length;
"""
file_list = []
for file in os.listdir(directory):
if not (keyword is None):
if keyword in file:
file_list.append(file)
else:
file_list.append(file)
return sorted(file_list)
def read_files(directory, keyword):
"""
read files with specified keyword
input
-----
directory : string
directory to read files from
keyword : string
keyword to search for
output
-----
output_dic : dic
dictionary of datasets
test
-----
(1) output_dic should have length 5, for 2013 - 2017;
(2) keyword should not be empty;
"""
output_dic = {}
file_list = detect_files(directory, keyword)
for yr in range(2013, 2018):
output_dic[yr] = pd.read_csv(os.path.join(directory, file_list[yr-2013]))
return output_dic
# Change color of each axis
def color_y_axis(ax, color):
"""Color your axes."""
for t in ax.get_yticklabels():
t.set_color(color)
def two_scales(ax1, time, data1, data2, data3, c1, c2, c3):
ax2 = ax1.twinx()
p1 = ax1.bar(time, data1, width=0.5, color=c1)
p2 = ax1.bar(time, data2, width=0.5, bottom=data1, color=c2)
ax1.set_xlabel('Year')
ax1.set_ylabel('Num. of cases')
ax1.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
p3 = ax2.plot(time, data3, color=c3, linewidth=3)
ax2.yaxis.set_major_locator(matplotlib.ticker.MaxNLocator(integer=True))
color_y_axis(ax2, 'b')
ax2.annotate("", xy=(2017.4, data3[-1]*0.98), xytext=(2017, data3[-1]*0.98),
arrowprops=dict(width=1, headwidth=8, headlength=8))
# ax2.set_ylabel('Fatal')
return ax1, ax2
def two_scales_with_legend(ax1, time, data1, data2, data3, c1, c2, c3):
ax2 = ax1.twinx()
p1 = ax1.bar(time, data1, width=0.5, color=c1, label='INJ')
p2 = ax1.bar(time, data2, width=0.5, bottom=data1, color=c2, label='PDO')
ax1.set_xlabel('Year')
ax1.set_ylabel('Num. of cases')
ax1.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
p3 = ax2.plot(time, data3, color=c3, linewidth=3, label='FAT')
ax2.yaxis.set_major_locator(matplotlib.ticker.MaxNLocator(integer=True))
color_y_axis(ax2, 'b')
ax2.annotate("", xy=(2017.4, data3[-1]*0.98), xytext=(2017, data3[-1]*0.98),
arrowprops=dict(width=1, headwidth=8, headlength=8))
# ax2.set_ylabel('Fatal')
return ax1, ax2
# + [markdown] heading_collapsed=true slideshow={"slide_type": "slide"}
# ## The problem
# + [markdown] hidden=true slideshow={"slide_type": "fragment"}
# ### What factors are associated with single vehicle accidents?
# # + Why and how are people getting themselves into trouble?
# + [markdown] heading_collapsed=true slideshow={"slide_type": "slide"}
# ## Exploratory analysis
# [HSIS data](https://www.hsisinfo.org/index.cfm)
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# $$e^x = \sum_{k=0}^{\infty} \frac{x^k}{k!}$$
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# <table>
# <tr>
# <td>
# \begin{eqnarray}
# \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\
# \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\
# \end{eqnarray}
# </td>
# <td>
# \begin{eqnarray}
# \nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\
# \nabla \cdot \vec{\mathbf{B}} & = 0
# \end{eqnarray}
# </td>
# </tr>
# </table>
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# Colons can be used to align columns.
#
# | Tables | Are | Cool |
# | ------------- |:-------------:| -----:|
# | col 3 is | right-aligned | 1600 |
# | col 2 is | centered | 12 |
# | zebra stripes | are neat | 1 |
#
# There must be at least 3 dashes separating each header cell.
# The outer pipes (|) are optional, and you don't need to make the
# raw Markdown line up prettily. You can also use inline Markdown.
#
# Markdown | Less | Pretty
# --- | --- | ---
# *Still* | `renders` | **nicely**
# 1 | 2 | 3
# + hidden=true slideshow={"slide_type": "skip"}
crash = read_files(".././hsis-csv", 'acc')
# + [markdown] hidden=true slideshow={"slide_type": "subslide"}
# ### Crash type
# + hidden=true slideshow={"slide_type": "skip"}
combine_map = {
1:11,
2:12,
3:13,
4:14,
5:15,
6:16,
7:17,
# other multi 29
27:29,
28:29,
71:77,# Peds and cyclist
72:77,
73:77,
74:77,
75:77,
76:77,
# single vehicle 99
32:99,
33:99,
34:99,
35:99,
40:99,
41:99,
50:99,
54:99,
60:99,
61:99,
62:99,
88:99,
98:99
}
# + hidden=true slideshow={"slide_type": "skip"}
acc_by_type = {}
for year in range(2013, 2018):
df = crash[year]
acc_by_type[year] = df.ACCTYPE.replace(combine_map).value_counts().sort_index().to_frame()
acc_by_type[year].columns = ['cnt']
df = df[['ACCTYPE', 'REPORT']]
df.ACCTYPE = df.ACCTYPE.replace(combine_map)
acc_by_type[year] = acc_by_type[year].merge(
df.groupby(['ACCTYPE', 'REPORT']).size().unstack().fillna(0).astype(int),
left_index=True, right_index=True)
columns = ['cnt', 'PDO', 'INJ', 'FAT']
acc_by_type[year].columns = columns
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# We group the **accident types** (**ACCTYPE**) into:
# # + Multi-vehicle;
# - Struck Head On;
# - Struck Left Side;
# - Struck Right Side;
# - Sideswiped Left Side;
# - Sideswiped Right Side;
# - Struck Rear End;
# - Struck Front End;
# - Other Multi;
# # + Peds & Cyclists related;
# # + Single-vehicle;
# + hidden=true slideshow={"slide_type": "skip"}
acc_type_list = [
r'Struck Head On', r'Struck Left Side', r'Struck Right Side',
r'Sideswiped Left Side', r'Sideswiped Right Side',
r'Struck Rear End', r'Struck Front End', r'Other Multi',
r'Peds \& Cyclists', r'Other Single'
]
# + hidden=true slideshow={"slide_type": "skip"}
width = 0.5
# + hidden=true slideshow={"slide_type": "skip"}
big_df = acc_by_type[2013] + acc_by_type[2014] + acc_by_type[2015] + acc_by_type[2016] + acc_by_type[2017]
fig, ax = plt.subplots(figsize=(10,8))
p1 = plt.bar(big_df.index, list(big_df.FAT), width)
p2 = plt.bar(big_df.index, list(big_df.INJ), width, bottom=list(big_df.FAT))
p3 = plt.bar(big_df.index, list(big_df.PDO), width, bottom=list(big_df.FAT+big_df.INJ))
plt.xticks([17, 77, 99], [r'Multi', r'Peds \& Cyclists', r'Single'],rotation=-25)
# big_df.index: [11, 12, 13, 14, 15, 16, 17, 29, 77, 99]
ax.set_xlabel(r'Type of accident', fontsize=18)
ax.set_ylabel(r'Num. of cases', fontsize=18)
ax.tick_params(labelsize=15)
plt.title(r'WA highway accidents for 2013 - 2017', fontsize=22)
ax.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.legend((p1[0], p2[0], p3[0]), ('Fatal', 'Injured', 'Property-damage Only'), fontsize=22)
plt.show()
# + hidden=true slideshow={"slide_type": "skip"}
big_df = acc_by_type[2013] + acc_by_type[2014] + acc_by_type[2015] + acc_by_type[2016] + acc_by_type[2017]
fig, ax = plt.subplots(figsize=(10,8))
p1 = plt.bar([11, 12, 13, 14, 15, 16, 17, 18, 20, 22], list(big_df.FAT), width)
p2 = plt.bar([11, 12, 13, 14, 15, 16, 17, 18, 20, 22], list(big_df.INJ), width, bottom=list(big_df.FAT))
p3 = plt.bar([11, 12, 13, 14, 15, 16, 17, 18, 20, 22], list(big_df.PDO), width, bottom=list(big_df.FAT+big_df.INJ))
plt.xticks([14,20,22], [r'Multi', r'Peds \& Cyclists', r'Single'], rotation=-45)
# big_df.index: [11, 12, 13, 14, 15, 16, 17, 29, 77, 99]
ax.set_xlabel(r'Type of accident', fontsize=18)
ax.set_ylabel(r'Num. of cases', fontsize=18)
ax.tick_params(labelsize=15)
plt.title(r'WA highway accidents for 2013 - 2017', fontsize=22)
ax.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.legend((p1[0], p2[0], p3[0]), ('Fatal', 'Injured', 'Property-damage Only'), fontsize=22, loc='best')
plt.show()
# + hidden=true slideshow={"slide_type": "skip"}
fig, ax = plt.subplots(figsize=(10,8))
labels = [r'Multi', r'Peds \& Cyclists', r'Single']
sizes = [big_df[big_df.index.isin([11,12,13,14,15,16,17, 29])].cnt.sum(),
big_df[big_df.index.isin([77])].cnt,
big_df[big_df.index.isin([99])].cnt]
#colors
colors = ['#ff9999','#66b3ff','#99ff99']
#explsion
explode = (0.06, 0.06, 0.06)
plt.pie(sizes, colors = colors, labels=labels, autopct='%1.1f%%',
startangle=90, pctdistance=0.8, explode = explode, textprops={'fontsize': 18})
#draw circle
centre_circle = plt.Circle((0,0),0.70,fc='white')
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax.axis('equal')
ax.set_title(r'Percentages of crash types', fontsize=22)
plt.tight_layout()
plt.show()
# + hidden=true slideshow={"slide_type": "subslide"}
fig
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# #### Zoom in on the bars for multi-vehicle
# + hidden=true slideshow={"slide_type": "skip"}
fig, ax = plt.subplots(figsize=(10,8))
p1 = plt.bar(big_df.index, list(big_df.FAT), width)
p2 = plt.bar(big_df.index, list(big_df.INJ), width, bottom=list(big_df.FAT))
p3 = plt.bar(big_df.index, list(big_df.PDO), width, bottom=list(big_df.FAT+big_df.INJ))
plt.xticks(big_df.index, acc_type_list,rotation=-45)
plt.xlim(10,18)
# plt.ylim(0,20000)
ax.set_xlabel(r'Type of accident (multi-veh zoom-in)', fontsize=18)
ax.set_ylabel(r'Num. of cases', fontsize=18)
ax.tick_params(labelsize=15)
plt.title(r'WA highway accidents for 2013 - 2017 (multi-veh zoom-in)', fontsize=22)
ax.get_yaxis().set_major_formatter(matplotlib.ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
plt.legend((p1[0], p2[0], p3[0]), ('Fatal', 'Injured', 'Property-damage Only'), fontsize=22)
plt.show()
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# ### We can conclude from the plots:
# # + Single vehicle accidents are a significant group, among the three;
# # + Rear-end strikes dominate the multi-vehicle accidents;
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# ### Break down the single-vehicle accidents
# # + Why and how are people getting themselves into trouble?
# # + Other parties, besides the vehicles, are lake, ditches, trains, self-caught fires in single-vehicle accidents;
# # + These accidents only involve **half or even less** human factors as in multi-vehicle or vehicle-peds/ cyclists accidents;
# # + This reduces uncertainty for modelling;
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# #### What are the types and how many are there?
# + hidden=true slideshow={"slide_type": "skip"}
crash = read_files(".././hsis-csv", 'acc')
combine_map = {
71:77,# Peds and cyclist
72:77,
73:77,
74:77,
75:77,
76:77
}
acc_by_type = {}
for year in range(2013, 2018):
df = crash[year]
acc_by_type[year] = df.ACCTYPE.replace(combine_map).value_counts().sort_index().to_frame()
acc_by_type[year].columns = ['cnt']
df = df[['ACCTYPE', 'REPORT']]
df.ACCTYPE = df.ACCTYPE.replace(combine_map)
acc_by_type[year] = acc_by_type[year].merge(
df.groupby(['ACCTYPE', 'REPORT']).size().unstack().fillna(0).astype(int),
left_index=True, right_index=True)
columns = ['cnt', 'PDO', 'INJ', 'FAT']
acc_by_type[year].columns = columns
# + hidden=true slideshow={"slide_type": "skip"}
acc_type_list = [
r'Strikes Animal or Bird', r'Strikes Appurtenance', r'Strikes Other Object', r'Strikes or Was Struck by Working Object',
r'Strikes Railroad Train', r'Was Struck by Railroad Train', r'Vehicle Overturned', r'Non-Collision Fire',
r'Ran into Roadway Ditch', r'Ran into River, Lake, etc.', r'Ran over Embankment – No Guardrail Present', r'Peds \& Cyclists',
r'Pushed Vehicle Struck by Pushing Vehicle', r'Jackknife Trailer', r'Other'
]
acc_type_index_list = [32, 33, 34, 35, 40, 41, 50, 54, 60, 61, 62, 77, 88, 98, 99]
width = 0.5
fat = [acc_by_type[year].FAT for year in range(2013, 2018)]
inj = [acc_by_type[year].INJ for year in range(2013, 2018)]
pdo = [acc_by_type[year].PDO for year in range(2013, 2018)]
# + hidden=true slideshow={"slide_type": "skip"}
for item in acc_type_index_list:
for df in fat:
if item not in df.index:
df.at[item] = 0
for df in inj:
if item not in df.index:
df.at[item] = 0
for df in pdo:
if item not in df.index:
df.at[item] = 0
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# #### single vehicle accidents sub-categories into two histogram
# + hidden=true slideshow={"slide_type": "skip"}
fig1, axes = plt.subplots(3,3, figsize=(18,15))
nyear = 5
t = range(2013, 2013 + nyear)
for ind in range(8):
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales(axes[ind//3][ind%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
ind += 1
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales_with_legend(axes[ind//3][ind%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
fig1.legend(
# loc="upper center", # Position of legend
borderaxespad=0.3, # Small spacing around legend box
ncol=4,
bbox_to_anchor=(0.65,1.07),
title="Severity level", # Title for the legend
fontsize="xx-large",title_fontsize="xx-large"
)
plt.tight_layout()
plt.show()
# + hidden=true slideshow={"slide_type": "skip"}
fig1
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# **Weird**<br>
# the scroll does not work with the big graph, but works with two sub-plots
# + hidden=true slideshow={"slide_type": "skip"}
fig2, axes = plt.subplots(2,3, figsize=(18,10))
nyear = 5
t = range(2013, 2013 + nyear)
for ind in range(9, len(acc_type_list) - 1):
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales(axes[(ind-9)//3][(ind-9)%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
ind += 1
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales_with_legend(axes[(ind-9)//3][(ind-9)%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
fig2.legend(
# loc="upper center", # Position of legend
borderaxespad=0.3, # Small spacing around legend box
ncol=4,
bbox_to_anchor=(0.65,1.1),
title="Severity level", # Title for the legend
fontsize="xx-large",title_fontsize="xx-large"
)
plt.tight_layout()
plt.show()
# + hidden=true slideshow={"slide_type": "skip"}
fig2
# + [markdown] heading_collapsed=true hidden=true slideshow={"slide_type": "skip"}
# #### combined for single-veh
# + hidden=true slideshow={"slide_type": "skip"}
fig1, axes = plt.subplots(5,3, figsize=(18,21))
nyear = 5
t = range(2013, 2013 + nyear)
for ind in range(len(acc_type_list) - 1):
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales(axes[ind//3][ind%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
ind += 1
s1 = [inj[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s2 = [pdo[year][acc_type_index_list[ind]] for year in range(0, nyear)]
s3 = [fat[year][acc_type_index_list[ind]] for year in range(0, nyear)]
ax1, _ = two_scales_with_legend(axes[ind//3][ind%3], t, s1, s2, s3, 'coral', 'mediumspringgreen', 'steelblue')
ax1.set_title('{}'.format(acc_type_list[ind]))
fig1.legend(
# loc="upper center", # Position of legend
borderaxespad=0.3, # Small spacing around legend box
ncol=4,
bbox_to_anchor=(0.65,1.05),
title="Severity level", # Title for the legend
fontsize="xx-large",title_fontsize="xx-large"
)
plt.tight_layout()
plt.show()
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# ### What we can tell from the plots?
# # + Subgroups occur
# - High occurrence, high deaths: **Strikes Appurtenance**, **Strikes Other Object**, **Vehicles OVerturned**;
# - High occurrence, low deaths: **Strikes Animal or Bird**;
# - Low occurrence, high deaths: **Peds & Cyclists**;
# - Low occurrence, low deaths: others;
# + [markdown] hidden=true slideshow={"slide_type": "skip"}
# # + Different groups have different trends
# - Generally increasing;
# - Staying at the same level, fluctuating;
# + [markdown] hidden=true slideshow={"slide_type": "subslide"}
# ### We picked a type...
# #### Strikes Appurtenance
# #### It's coded as *type 33* in HSIS databases. As per [TRB](http://onlinepubs.trb.org/Onlinepubs/trr/1981/796/796.pdf) and [NCHRP](http://onlinepubs.trb.org/Onlinepubs/nchrp/nchrp_rpt_230.pdf):
# Appurtenances covered by these procedures are<br>
# # + longitudinal barriers such as bridge rails, guardrails, median barriers, transitions, and terminals;
# # + crash cushions;
# # + breakaway or yielding supports for signs anci iuminaires.
# + [markdown] hidden=true slideshow={"slide_type": "slide"}
# ### Our model
# # + Response variable: severity level (PDO/ INJ/ FAT);
# # + Independent variable:
# - Driver and vehicle: driver sex, driver age, intoxication, vehicle year, vehicle type;
# - Roadway: curvature, grade, segment length, road surface material, shoulder and median material and width;
# - Accident-specific: time, location, weather, light, road surface condition when accident took place;
#
# + [markdown] hidden=true slideshow={"slide_type": "subslide"}
# | Variable | Description | possible values |
# | :---: | :--- | :--- |
# | <font color='red'>Weekday</font> | <font color='red'>Day of week when the accident occurred. <br>Further transformed into an indicator function.</font> | <font color='red'>1: Yes, 0: No</font> |
# | <font color='red'>Peak-hour</font> | <font color='red'>If accident took place in peak hours,<br>i.e. 7-10am, 5-8pm</font> | <font color='red'>1: Yes, 0: No</font> |
# | <font color='red'>Light</font> | <font color='red'>The type/level of light that existed<br>at the time of the crash</font> | <font color='red'>1: Daylight<br>2: Dawn<br>3: Dusk<br>4: Dark<br></font> |
# | <font color='red'>Roadway surface<br>condition</font> | <font color='red'>The condition of the road surface<br>where the crash occurred</font> | <font color='red'>1:Dry<br>2:Wet<br>3:Snow/Slush<br>4:Ice<br>5:Other<br></font> |
# | <font color='steelblue'>driver sex</font> | <font color='steelblue'>Driver sex</font> | <font color='steelblue'>1: Female<br>0: Male or unknown</font> |
# | <font color='steelblue'>young driver</font> | <font color='steelblue'>If driver is younger than 25 years old</font> | <font color='steelblue'>1: Yes, 0: No</font> |
# | <font color='steelblue'>old driver</font> | <font color='steelblue'>If driver is older than 65 years old</font> | <font color='steelblue'>1: Yes, 0: No</font> |
# | <font color='steelblue'>drunk driver</font> | <font color='steelblue'>If driver had been drinking <br>and ability had been impaird</font> | <font color='steelblue'>1: Yes, 0: No</font> |
# | <font color='LimeGreen'>Truck</font> | <font color='LimeGreen'>If the involved vehicle is truck</font> | <font color='LimeGreen'>1: Yes, 0: No</font> |
# | <font color='LimeGreen'>Old car</font> | <font color='LimeGreen'>If the involved vehicle was <br>more than 15 years old at the time of crash</font> | <font color='LimeGreen'>1: Yes, 0: No</font> |
# | <font color='DeepPink'>Rural/ Urban</font> | <font color='DeepPink'>Rural/ Urban indicator</font> | <font color='DeepPink'>R: Rural, U: Urban</font> |
# | <font color='DeepPink'>Rd surface material</font> | <font color='DeepPink'>Surface material type</font> | <font color='DeepPink'>A: Asphalt<br>B: Bituminous<br>G: Gravel<br>O: Other<br>P: Portland Concrete Cem<br>S: Soil</font> |
# | <font color='DeepPink'>lane width</font> | <font color='DeepPink'>Calculate lane width,<br> dividing total roadway width by num of lanes</font> | <font color='DeepPink'>continuous, in ft</font> |
# | <font color='DeepPink'>Roadway width</font> | <font color='DeepPink'>Total roadway width for the roadway segment</font> | <font color='DeepPink'>continuous</font> |
# | <font color='DeepPink'>degree of curvature</font> | <font color='DeepPink'>Degree of curvature for the curve,<br>calculated from curve radius</font> | <font color='DeepPink'>continuous, in ft</font> |
# | <font color='DeepPink'>grade percentage</font> | <font color='DeepPink'>Percent grade for this roadway segment</font> | <font color='DeepPink'>continuous, in %</font> |
# | <font color='DeepPink'>AADT</font> | <font color='DeepPink'>Calculated Annual average daily traffic (AADT)</font> | <font color='DeepPink'>integer</font> |
# | <font color='DeepPink'>Truck percentage in traffic</font> | <font color='DeepPink'>Truck percentage for the roadway segment</font> | <font color='DeepPink'>continuous, in %</font> |
# | <font color='DeepPink'>mvmt</font> | <font color='DeepPink'>Million vehicle miles traveled on road segment.</font> | <font color='DeepPink'>continuous, in veh-mile</font> |
# + [markdown] slideshow={"slide_type": "slide"}
# ## Data manipulation
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Initial steps
# # + Summarize and regroup categorical variables;
# # + Select possibly relevant variables from a original long list and drop those with too many missing values;
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Balance dataset
# Two-ends balance with middle (add a percentage plot & table).
#
# # + **Property damage only (PDO)** -> **Injury (INJ)**: Random sampling;
# # + **Fatality (FAT)** -> **Injury (INJ)**: SMOTE Algorithm (oversampling by generating synthetic data);
#
# Balanced dataset has size $$n_{\textrm{INJ}}\times3=4843\times3=14,529$$
# + slideshow={"slide_type": "skip"}
# before SMOTE [15809, 4843, 135]
# df = pd.read_csv('.././merged/final_type_correct.csv')
# df.REPORT.value_counts()
# before SMOTE [4843, 4843, 4843]
#df = pd.read_csv('.././merged/final_smote.csv')
# df.REPORT.value_counts()
fig, ax = plt.subplots(1,2, figsize=(12,8))
#colors
colors = ['#ff9999','#66b3ff','#99ff99']
#explsion
explode = (0.06, 0.06, 0.06)
labels = [r'PDO', r'INJ', r'FAT']
sizes = [[15809, 4843, 135], [4843, 4843, 4843]]
titles = [r'Imbalanced dataset from preprocessing (\%)', r'SMOTE balanced dataset (\%)']
for i in range(2):
ax[i].pie(sizes[i], colors = colors, labels=labels, autopct='%1.1f%%',
startangle=90, pctdistance=0.65, explode = explode, textprops={'fontsize': 18})
centre_circle = plt.Circle((0,0),0.70,fc='white')
# fig = plt.gcf()
# fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax[i].axis('equal')
ax[i].set_title(titles[i], fontsize=22)
plt.tight_layout()
plt.show()
# + slideshow={"slide_type": "subslide"}
fig
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Dataset fed into models
# See the first 5 observations to have a general idea.
# + slideshow={"slide_type": "skip"}
df_pre = pd.read_csv('.././merged/final_smote.csv')
df_pre = df_pre.drop(columns=['MEDWID', 'LSHLDWID', 'LSHL_WD2', 'RSHLDWID', 'RSHL_WD2', ])
# + slideshow={"slide_type": "skip"}
df_pre.columns = ['Weekday', 'Roadway Surface Condition', 'Light',
'Weather', 'Rural/Urban', 'Rd Surface Material',
'Func Class', 'driver sex', 'young driver', 'old driver',
'drunk driver', 'Truck', 'Old car', 'Peak-hour',
'Lane width', 'Roadway width', 'degree of curvature',
'grade percentage', 'AADT', 'Truck percentage in traffic',
'mvmt', 'Severity'
]
df_pre = df_pre[['Severity',
'driver sex', 'young driver', 'old driver', 'drunk driver',
'Truck', 'Old car',
'Rural/Urban', 'Lane width', 'Roadway width','degree of curvature','grade percentage',
'AADT', 'Truck percentage in traffic', 'mvmt',
'Weekday', 'Peak-hour', 'Light', 'Roadway Surface Condition', 'Rd Surface Material'
]]
# + slideshow={"slide_type": "skip"}
df_pre.shape
# + slideshow={"slide_type": "fragment"}
df_pre.head()
# + [markdown] slideshow={"slide_type": "slide"}
# ## Modeling and Results
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Multinomial
# # + Added interaction terms, e.g. **drunk \* young**;
# # + Removed several variables that might be too micro: material and widths of shoulder and medium;
# # + Response variable reference is **Fatality (FAT)**, category 3;
# + [markdown] slideshow={"slide_type": "fragment"}
# Accident severity level: (*PDO/INJ/FAT*) ~
# # + *driver sex + young driver + old driver + drunk driver + drunk driver* \* *young driver* + <br>
# # + *truck + old car* + <br>
# # + *rural/ urban + lane width + roadway width + degree of curvature + grade percentage + AADT + truck percentage in traffic + mvmt* + <br>
# # + *weekday + peak-hour + light conditinos + road surface condition* \* *roadway surface material*
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Some of our hypotheses:
#
# # + Driver sobriety (**drunk**): drivers who had been drinking and especially who had impaired ability are more likely to be involved in more severe crashes;
# # + Vehicle type (**truck**): strikes on appurtenance by trucks must be a lot more severe than passenger vehicles, because trucks have greater momentums;
# # + Light condition (**LIGHT**): more severe crashes are more likely to take place in darker conditions;
# # + Rural/ Urban roads (**RURURB**): rural roads in general have worse protection, and thus are more likely to have more severe crashes;
# # + Road surface condition (**RDSURF**): The more slippery it is, the more severe the accident is likely to be;
# # + Interaction of **drunk** and **young driver** (**drunk \* young**): young drivers who had been drinking are red alerts for severe crashes. Lack of experience is magnified by impaired abilities;
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Model results
# AIC(multinomial) = 24,211
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Driver
# # + Female driver are more likely to be involved in less severe crashes;
# # + *Young* drivers (< 25 years of age), compared to others, are more likely to see less severe crashes;
# # + *Old* drivers (> 65 years of age), compared to others, are more likely to see less severe crashes;
# # + That said, the people in the middle (25 < age < 65) are likely to see more severe crashes;
# # + *Drunk* drivers are more likely to see more severe crahes, like fatal;
# # + *Drunk* *young drivers* are more likely to see less severe crashes;
#
# | Variables | Coefficients | p-value |
# | ------------- |:-------------:| -----:|
# | **driver sex** *Female*:1 | 1.303e+00 | < 2e-16 ***|
# | **driver sex** *Female*:2 | 1.738e+00 | < 2e-16 *** |
# |**young driver** *True*:1 | 1.783e+00 | < 2e-16 *** |
# |**young driver** *True*:2 | 1.763e+00 | < 2e-16 *** |
# |**old driver** *True*:1 | 9.616e-01 | 2.89e-15 *** |
# |**old driver** *True*:2 | 1.196e+00 | < 2e-16 *** |
# |<font color='red'>**drunk driver** *True*:1 | <font color='red'>-6.914e-01| <font color='red'>2.52e-16 ***|
# |<font color='red'>**drunk driver** *True*:2 | <font color='red'> -2.285e-01 | <font color='red'>0.003188 ** |
# |<font color='red'>**young driver** *True* : **drunk** *True*:1 | <font color='red'>2.514e+00 |<font color='red'> 1.05e-08 ***|
# |<font color='red'>**young driver** *True* : **drunk** *True*:2 | <font color='red'>2.609e+00 | <font color='red'>1.92e-09 ***|
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Vehicle
# # + *Trucks* are more likely to see more severe crashes;
# # + *Old cars* tend to witness less severe crahes;
#
# | Variables | Coefficients | p-value |
# | ------------- |:-------------:| -----:|
# |<font color='red'>**Truck** *True*:1 | <font color='red'> -9.207e-01 | <font color='red'> < 2e-16 *** |
# |<font color='red'>**Truck** *True*:2 | <font color='red'> -2.947e-01 | <font color='red'>0.000159 ***|
# |**Old car** *True*:1 | 3.208e-01 | 1.39e-08 *** |
# |**Old car** *True*:2 | 4.326e-01 | 6.05e-15 *** |
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Road
# # + *Urban* roads are more likely to have less severe crashes, or equivalently, rural roads are more dangerous;
# # + The wider the lanes are, the more likely a crash would be less severe;
# # + Ohter roadway features are not contributing much;
#
# | Variables | Coefficients | p-value |
# | ------------- |:-------------:| -----:|
# |<font color='red'>**Rural/ Urban** *Urban*:1 | <font color='red'> 9.073e-01 | <font color='red'> < 2e-16 *** |
# |<font color='red'>**Rural/ Urban** *Urban*:2 | <font color='red'> 7.809e-01 | <font color='red'> < 2e-16 *** |
# |**Lane width**:1 | 1.006e-01 | 8.82e-09 *** |
# |**Lane width**:2 | 1.206e-01 | 3.04e-12 *** |
# |**Roadway width**:1 | 3.608e-04 | 0.869429 |
# |**Roadway width**:2 | -1.784e-03 | 0.411822 |
# |**degree of curvature**:1 | 1.189e-02 | 0.025466 * |
# |**degree of curvature**:2 | 2.029e-02 | 3.03e-05 *** |
# |**grade percentage**:1 | 6.779e-04 | 0.057607 . |
# |**grade percentage**:2 | 8.743e-04 | 0.014120 * |
# |**AADT**:1 | 2.301e-07 | 0.790135 |
# |**AADT**:2 | 3.054e-06 | 0.000311 *** |
# |**Truck percentage in traffic**:1 | 8.624e-03 | 0.049706 * |
# |**Truck percentage in traffic**:2 | 3.396e-03 | 0.435586 |
# |**mvmt**:1 | 1.439e-02 | 0.000970 *** |
# |**mvmt**:2 | 6.747e-03 | 0.122623 |
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Environmental conditions
# # + Crashes on *weekday* (vs. weekends) are more likely to be more severe;
# # + Crashes in *peak-hour* are in general less severe;
# # + Some light will help, as in *daylihgt*, *dawn*, *dusk*, crashes are more likely to be less severe, while *dark* is more likely to witness severe fatal crashes;
# # + All road conditions, including *wet*, *snow* and *ice*, are likely to have less severe crashes. However, *Portland Concrete Cemt* when *wet* sees particularly less severe crashes, compared to fatal;
#
# | Variables | Coefficients | p-value |
# | ------------- |:-------------:| -----:|
# | **Weekday** *True*:1 | -5.565e-01 | < 2e-16 ***|
# | **Weekday** *True*:2 | -6.472e-01 | < 2e-16 *** |
# | **Peak-hour** *True*:1 | 1.371e+00 | < 2e-16 *** |
# | **Peak-hour** *True*:2 | 1.299e+00 | < 2e-16 *** |
# |<font color='red'>**Light** *Dawn*:1 | <font color='red'> 3.698e+00 | <font color='red'> 3.90e-07 ***|
# |<font color='red'>**Light** *Dawn*:2 | <font color='red'> 3.717e+00 | <font color='red'> 3.32e-07 ***|
# |<font color='red'>**Light** *Dusk*:1 | <font color='red'> 3.586e+00 |<font color='red'> 3.92e-09 ***|
# |<font color='red'>**Light** *Dusk*:2 | <font color='red'> 3.464e+00 | <font color='red'> 1.21e-08 ***|
# |<font color='red'>**Light** *Dark*:1 | <font color='red'> -4.870e-01 | <font color='red'> < 2e-16 ***|
# |<font color='red'>**Light** *Dark*:2 | <font color='red'> -5.184e-01 | <font color='red'> < 2e-16 ***|
# |<font color='red'>**Roadway Surface Condition** *Wet*:1 | <font color='red'> 1.953e+00 | <font color='red'>< 2e-16 ***|
# |<font color='red'>**Roadway Surface Condition** *Wet*:2 | <font color='red'> 1.714e+00 | <font color='red'> < 2e-16 ***|
# |<font color='red'>**Roadway Surface Condition** *Snow/Slush*:1 | <font color='red'> 6.662e+00 | <font color='red'>3.44e-11 ***|
# |<font color='red'>**Roadway Surface Condition** *Snow/Slush*:2 | <font color='red'> 5.901e+00 |<font color='red'> 4.67e-09 ***|
# |<font color='red'>**Roadway Surface Condition** *Ice*:1 | <font color='red'> 5.652e+00 | <font color='red'>3.38e-15 ***|
# |<font color='red'>**Roadway Surface Condition** *Ice*:2 | <font color='red'> 5.145e+00 | <font color='red'>8.79e-13 **|
# |**Roadway Surface Condition** *Wet* : <br>**Rd Surface Material** *Portland Cem*:1 | 8.983e-01 | 2.28e-05 ***|
# |**Roadway Surface Condition** *Wet* : <br>**Rd Surface Material** *Portland Cem*:2 | 8.824e-01 2| 3.15e-05 ***|
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Did that validate our guesses?
# # + Almost everything is what we expected. Except **the following two**;
# # + Road surface at the crash scene is not very informative. It says *Wet*, *Snow/Slush* and *Ice* conditions are more likely to witness less severe crashes;
# # + **Drunk \* young** interaction term is not warning us against the danger of drunk young driver;
# + [markdown] slideshow={"slide_type": "skip"}
# # + Explanations:
# - ***Road surface condition*** appears weird:
# * **road surface conditions** themselves are simply not enough. We are looking at the problem from too high a level that details are overlooked. Think of how cooking time contribute to the quality of dishes. If we have more soups in our menu, then running a general model will tell us the longer we cook the better. However, this does not hold across the entire dataset.
# - ***Drunk * young*** interaction:
# * could be the *young drivers* effect offsettting the effect from *drunk* drivers. Remeber, even if young drivers are often associated with traffic accidents, they are not necessarily associated with severe accidents, e.g. fatal crashes. Being young is giving rise to the possibility of creating an accident, but not to that of a severe one.
# + [markdown] slideshow={"slide_type": "subslide"}
# ##### Why?
# + [markdown] slideshow={"slide_type": "subslide"}
# # + Complex interactions:
# - Compared to more inclusive models, we know interactions are missing;
# * Diffrent road surface materials may have different behaviors under different conditions. It's very likely that when **wet** (instead of **standing water**), some materials produce better friction. This is what we observed for *Portland Concrete Cemt*;
# # + Insufficient data:
# - Some important info is impossible to collect;
# * For example, speed of vehicle before crash is an important factor. Since we may acquire flow speed from sensors, how much faster the vehicle is travelling can largely impact the severity. However, it was almost impossible to collect such data;
# - When recorded as categorical, attributes lose the level of detail to be modeled by more complex link functions;
# # + Data quality control:
# - In general the dataset is well maintained. However, some problems still exist. Variables can take values not specified in the guidebook, the most common being *10* often coded as *.* (period). Another problem is the coding of **vehicle type**, where the WA file is not explicitly writing out the codings. Yet another is absence of data for some variables: nothing returned even the guidebook says the variables are recorded.
# - Considering these issues, the quality of dataset can be further enhanced. Maybe that can answer some of our confusions from the multinomial modeling.
# + [markdown] slideshow={"slide_type": "skip"}
# #### Ordinal
# AIC(Ordinal) is way higher than **multinomial**'s. We focus on multinomial then.
# + [markdown] slideshow={"slide_type": "skip"}
# #### prediction power
# Is our model robust in predicting for unseen data?
# + slideshow={"slide_type": "skip"}
cm_smote = np.array([[1114, 98, 149],
[ 320, 607, 435],
[ 298, 428, 632]])
# + slideshow={"slide_type": "skip"}
fig = plt.figure(figsize=(10,10))
# fig.set_size_inches(14, 12, forward=True)
# fig.align_labels()
# fig.subplots_adjust(left=0.0, right=1.0, bottom=0.0, top=1.0)
cm = cm_smote
normalize = True
classes = ['PDO','INJ','FAT']
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 2.5)
plt.xticks([0,1,2], classes, fontsize=15)
plt.yticks([0,1,2], classes, fontsize=15)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black",
fontsize=20
)
# plt.tight_layout()
plt.ylabel('True label', fontsize=18)
plt.xlabel('Predicted label', fontsize=18)
plt.title('Confusion matrix of multinomial logistic modelling', fontsize=22)
plt.show()
# + slideshow={"slide_type": "skip"}
fig
# + [markdown] slideshow={"slide_type": "skip"}
# ##### Class_weight balancing
# + [markdown] slideshow={"slide_type": "skip"}
# **LogisticRegression** from **sklearn.linear_model**<br>
# Overall accuracy is 49.65%.
# + slideshow={"slide_type": "skip"}
from sklearn.linear_model import LogisticRegression
# + slideshow={"slide_type": "skip"}
df = pd.read_csv('.././merged/final_type_correct.csv')
df = df.drop(columns=['FUNC_CLS'])
df_log = pd.get_dummies(df, columns=['WEEKDAY', 'RDSURF', 'LIGHT', 'RURURB', 'SURF_TYP'])
# + slideshow={"slide_type": "skip"}
y = df_log['REPORT']
X = df_log.drop(columns=['REPORT', 'ACCTYPE'])
msk = np.random.rand(len(df)) < 0.8
X_train = X[msk]
X_test = X[~msk]
y_train = y[msk]
y_test = y[~msk]
# + slideshow={"slide_type": "skip"}
clf = LogisticRegression(multi_class='multinomial',class_weight='balanced',
solver='newton-cg',penalty='none'
).fit(X_train, y_train)
prediction = clf.predict(X_test)
# + slideshow={"slide_type": "skip"}
clf.score(X_train, y_train)
# + slideshow={"slide_type": "skip"}
cnf_matrix
# + slideshow={"slide_type": "skip"}
from sklearn.metrics import confusion_matrix
import itertools
cnf_matrix = confusion_matrix(y_test, prediction)
fig = plt.figure(figsize=(10,10))
# fig.set_size_inches(14, 12, forward=True)
# fig.align_labels()
# fig.subplots_adjust(left=0.0, right=1.0, bottom=0.0, top=1.0)
cm = cnf_matrix
normalize = True
classes = ['PDO','INJ','FAT']
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.xlim(-0.5, 2.5)
plt.ylim(-0.5, 2.5)
plt.xticks([0,1,2], classes, fontsize=15)
plt.yticks([0,1,2], classes, fontsize=15)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black",
fontsize=20
)
# plt.tight_layout()
plt.ylabel('True label', fontsize=18)
plt.xlabel('Predicted label', fontsize=18)
plt.title('Confusion matrix of multinomial logistic modelling', fontsize=22)
plt.show()
# + slideshow={"slide_type": "skip"}
fig
# + [markdown] slideshow={"slide_type": "slide"}
# ## Conclusions
# WA highway crashes are complex interplays of many variables. It's hard to model completely using multinomial logit regression. Among the available and applied variables, we summarize influences of some for each category into single sentences.
# # + Driver:
# - Male, aged 25 - 65, drunk drivers are more likely to see more severe accidents;
# # + Vehicle:
# - New vehicle and trucks are more likely to be involved in more severe crashes;
# # + Roadway:
# - Rural roadway segments with narrower lanes and less traffic are more likely to witness more severe crashes;
# # + Accident specific:
# - Weekdays at non peak-hour and especially when it's dark but not slippery on road surfaces are more likely to have more severe crashes;
# + [markdown] slideshow={"slide_type": "slide"}
# ### Limitations
#
# # + Lack important variables (e.g. speed at crash);
# # + Some potential underlying interaction effects not included;
# # + Highly imbalanced dataset;
# + [markdown] slideshow={"slide_type": "slide"}
# ## Q&A
# Thank you for your attention!
|
presentation/presentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/EMC23/DeepLearningForAudioWithPython/blob/master/Copy_of_Disco_Diffusion_v4_1_%5Bw_Video_Inits%2C_Recovery_%26_DDIM_Sharpen%5D.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="1YwMUyt9LHG1"
# # Disco Diffusion v4.1 - Now with Video Inits, Recovery, DDIM Sharpen and improved UI
#
# For issues, message [@Somnai_dreams](https://twitter.com/Somnai_dreams) or Somnai#6855
#
# Credits & Changelog.
#
# + [markdown] id="wX5omb9C7Bjz"
# Original notebook by <NAME> (https://github.com/crowsonkb, https://twitter.com/RiversHaveWings). It uses either OpenAI's 256x256 unconditional ImageNet or Katherine Crowson's fine-tuned 512x512 diffusion model (https://github.com/openai/guided-diffusion), together with CLIP (https://github.com/openai/CLIP) to connect text prompts with images.
#
# Modified by <NAME> (https://github.com/russelldc, https://twitter.com/danielrussruss) to include (hopefully) optimal params for quick generations in 15-100 timesteps rather than 1000, as well as more robust augmentations.
#
# Further improvements from Dango233 and nsheppard helped improve the quality of diffusion in general, and especially so for shorter runs like this notebook aims to achieve.
#
# Vark added code to load in multiple Clip models at once, which all prompts are evaluated against, which may greatly improve accuracy.
#
# The latest zoom, pan, rotation, and keyframes features were taken from Chigo<NAME>'s VQGAN Zoom Notebook (https://github.com/chigozienri, https://twitter.com/chigozienri)
#
# Advanced DangoCutn Cutout method is also from Dango223.
#
# --
#
# I, Somnai (https://twitter.com/Somnai_dreams), have added Diffusion Animation techniques, QoL improvements and various implementations of tech and techniques, mostly listed in the changelog below.
# + cellView="form" id="wDSYhyjqZQI9"
# @title Licensed under the MIT License
# Copyright (c) 2021 <NAME>
# Permission is hereby granted, free of charge, to any person obtaining a copy
# of this software and associated documentation files (the "Software"), to deal
# in the Software without restriction, including without limitation the rights
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
# copies of the Software, and to permit persons to whom the Software is
# furnished to do so, subject to the following conditions:
# The above copyright notice and this permission notice shall be included in
# all copies or substantial portions of the Software.
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN
# THE SOFTWARE.
# + cellView="form" id="qFB3nwLSQI8X"
#@title <- View Changelog
skip_for_run_all = True #@param {type: 'boolean'}
if skip_for_run_all == False:
print(
'''
v1 Update: Oct 29th 2021
QoL improvements added by Somnai (@somnai_dreams), including user friendly UI, settings+prompt saving and improved google drive folder organization.
v1.1 Update: Nov 13th 2021
Now includes sizing options, intermediate saves and fixed image prompts and perlin inits. unexposed batch option since it doesn't work
v2 Update: Nov 22nd 2021
Initial addition of <NAME>'s Secondary Model Method (https://colab.research.google.com/drive/1mpkrhOjoyzPeSWy2r7T8EYRaU7amYOOi#scrollTo=X5gODNAMEUCR)
Noticed settings were saving with the wrong name so corrected it. Let me know if you preferred the old scheme.
v3 Update: Dec 24th 2021
Implemented Dango's advanced cutout method
Added SLIP models, thanks to NeuralDivergent
Fixed issue with NaNs resulting in black images, with massive help and testing from @Softology
Perlin now changes properly within batches (not sure where this perlin_regen code came from originally, but thank you)
v4 Update: Jan 2021
Implemented Diffusion Zooming
Added Chigozie keyframing
Made a bunch of edits to processes
v4.1 Update: Jan 14th 2021
Added video input mode
Added license that somehow went missing
Added improved prompt keyframing, fixed image_prompts and multiple prompts
Improved UI
Significant under the hood cleanup and improvement
Refined defaults for each mode
Added latent-diffusion SuperRes for sharpening
Added resume run mode
'''
)
# + [markdown] id="XTu6AjLyFQUq"
# #Tutorial
# + [markdown] id="YR806W0wi3He"
# **Diffusion settings**
# ---
#
# This section is outdated as of v2
#
# Setting | Description | Default
# --- | --- | ---
# **Your vision:**
# `text_prompts` | A description of what you'd like the machine to generate. Think of it like writing the caption below your image on a website. | N/A
# `image_prompts` | Think of these images more as a description of their contents. | N/A
# **Image quality:**
# `clip_guidance_scale` | Controls how much the image should look like the prompt. | 1000
# `tv_scale` | Controls the smoothness of the final output. | 150
# `range_scale` | Controls how far out of range RGB values are allowed to be. | 150
# `sat_scale` | Controls how much saturation is allowed. From nshepperd's JAX notebook. | 0
# `cutn` | Controls how many crops to take from the image. | 16
# `cutn_batches` | Accumulate CLIP gradient from multiple batches of cuts | 2
# **Init settings:**
# `init_image` | URL or local path | None
# `init_scale` | This enhances the effect of the init image, a good value is 1000 | 0
# `skip_steps Controls the starting point along the diffusion timesteps | 0
# `perlin_init` | Option to start with random perlin noise | False
# `perlin_mode` | ('gray', 'color') | 'mixed'
# **Advanced:**
# `skip_augs` |Controls whether to skip torchvision augmentations | False
# `randomize_class` |Controls whether the imagenet class is randomly changed each iteration | True
# `clip_denoised` |Determines whether CLIP discriminates a noisy or denoised image | False
# `clamp_grad` |Experimental: Using adaptive clip grad in the cond_fn | True
# `seed` | Choose a random seed and print it at end of run for reproduction | random_seed
# `fuzzy_prompt` | Controls whether to add multiple noisy prompts to the prompt losses | False
# `rand_mag` |Controls the magnitude of the random noise | 0.1
# `eta` | DDIM hyperparameter | 0.5
#
# ..
#
# **Model settings**
# ---
#
# Setting | Description | Default
# --- | --- | ---
# **Diffusion:**
# `timestep_respacing` | Modify this value to decrease the number of timesteps. | ddim100
# `diffusion_steps` || 1000
# **Diffusion:**
# `clip_models` | Models of CLIP to load. Typically the more, the better but they all come at a hefty VRAM cost. | ViT-B/32, ViT-B/16, RN50x4
# + [markdown] id="_9Eg9Kf5FlfK"
# # 1. Set Up
# + id="qZ3rNuAWAewx" cellView="form"
#@title 1.1 Check GPU Status
# !nvidia-smi -L
# + id="yZsjzwS0YGo6" cellView="form"
from google.colab import drive
#@title 1.2 Prepare Folders
#@markdown If you connect your Google Drive, you can save the final image of each run on your drive.
google_drive = True #@param {type:"boolean"}
#@markdown Click here if you'd like to save the diffusion model checkpoint file to (and/or load from) your Google Drive:
yes_please = True #@param {type:"boolean"}
if google_drive is True:
drive.mount('/content/drive')
root_path = '/content/drive/MyDrive/AI/Disco_Diffusion'
else:
root_path = '/content'
import os
from os import path
#Simple create paths taken with modifications from Datamosh's Batch VQGAN+CLIP notebook
def createPath(filepath):
if path.exists(filepath) == False:
os.makedirs(filepath)
print(f'Made {filepath}')
else:
print(f'filepath {filepath} exists.')
initDirPath = f'{root_path}/init_images'
createPath(initDirPath)
outDirPath = f'{root_path}/images_out'
createPath(outDirPath)
if google_drive and not yes_please or not google_drive:
model_path = '/content/models'
createPath(model_path)
if google_drive and yes_please:
model_path = f'{root_path}/models'
createPath(model_path)
# libraries = f'{root_path}/libraries'
# createPath(libraries)
# + id="JmbrcrhpBPC6" cellView="form"
#@title ### 2.1 Install and import dependencies
if google_drive is not True:
root_path = f'/content'
model_path = '/content/models'
model_256_downloaded = False
model_512_downloaded = False
model_secondary_downloaded = False
# !git clone https://github.com/openai/CLIP
# # !git clone https://github.com/facebookresearch/SLIP.git
# !git clone https://github.com/crowsonkb/guided-diffusion
# !git clone https://github.com/assafshocher/ResizeRight.git
# !pip install -e ./CLIP
# !pip install -e ./guided-diffusion
# !pip install lpips datetime timm
# !apt install imagemagick
import sys
# sys.path.append('./SLIP')
sys.path.append('./ResizeRight')
from dataclasses import dataclass
from functools import partial
import cv2
import pandas as pd
import gc
import io
import math
import timm
from IPython import display
import lpips
from PIL import Image, ImageOps
import requests
from glob import glob
import json
from types import SimpleNamespace
import torch
from torch import nn
from torch.nn import functional as F
import torchvision.transforms as T
import torchvision.transforms.functional as TF
from tqdm.notebook import tqdm
sys.path.append('./CLIP')
sys.path.append('./guided-diffusion')
import clip
from resize_right import resize
# from models import SLIP_VITB16, SLIP, SLIP_VITL16
from guided_diffusion.script_util import create_model_and_diffusion, model_and_diffusion_defaults
from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt
import random
from ipywidgets import Output
import hashlib
#SuperRes
# !git clone https://github.com/CompVis/latent-diffusion.git
# !git clone https://github.com/CompVis/taming-transformers
# !pip install -e ./taming-transformers
# !pip install ipywidgets omegaconf>=2.0.0 pytorch-lightning>=1.0.8 torch-fidelity einops wandb
#SuperRes
import ipywidgets as widgets
import os
sys.path.append(".")
sys.path.append('./taming-transformers')
from taming.models import vqgan # checking correct import from taming
from torchvision.datasets.utils import download_url
# %cd '/content/latent-diffusion'
from functools import partial
from ldm.util import instantiate_from_config
from ldm.modules.diffusionmodules.util import make_ddim_sampling_parameters, make_ddim_timesteps, noise_like
# from ldm.models.diffusion.ddim import DDIMSampler
from ldm.util import ismap
# %cd '/content'
from google.colab import files
from IPython.display import Image as ipyimg
from numpy import asarray
from einops import rearrange, repeat
import torch, torchvision
import time
from omegaconf import OmegaConf
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
import torch
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print('Using device:', device)
if torch.cuda.get_device_capability(device) == (8,0): ## A100 fix thanks to Emad
print('Disabling CUDNN for A100 gpu', file=sys.stderr)
torch.backends.cudnn.enabled = False
# + id="FpZczxnOnPIU" cellView="form"
#@title 2.2 Define necessary functions
# https://gist.github.com/adefossez/0646dbe9ed4005480a2407c62aac8869
def interp(t):
return 3 * t**2 - 2 * t ** 3
def perlin(width, height, scale=10, device=None):
gx, gy = torch.randn(2, width + 1, height + 1, 1, 1, device=device)
xs = torch.linspace(0, 1, scale + 1)[:-1, None].to(device)
ys = torch.linspace(0, 1, scale + 1)[None, :-1].to(device)
wx = 1 - interp(xs)
wy = 1 - interp(ys)
dots = 0
dots += wx * wy * (gx[:-1, :-1] * xs + gy[:-1, :-1] * ys)
dots += (1 - wx) * wy * (-gx[1:, :-1] * (1 - xs) + gy[1:, :-1] * ys)
dots += wx * (1 - wy) * (gx[:-1, 1:] * xs - gy[:-1, 1:] * (1 - ys))
dots += (1 - wx) * (1 - wy) * (-gx[1:, 1:] * (1 - xs) - gy[1:, 1:] * (1 - ys))
return dots.permute(0, 2, 1, 3).contiguous().view(width * scale, height * scale)
def perlin_ms(octaves, width, height, grayscale, device=device):
out_array = [0.5] if grayscale else [0.5, 0.5, 0.5]
# out_array = [0.0] if grayscale else [0.0, 0.0, 0.0]
for i in range(1 if grayscale else 3):
scale = 2 ** len(octaves)
oct_width = width
oct_height = height
for oct in octaves:
p = perlin(oct_width, oct_height, scale, device)
out_array[i] += p * oct
scale //= 2
oct_width *= 2
oct_height *= 2
return torch.cat(out_array)
def create_perlin_noise(octaves=[1, 1, 1, 1], width=2, height=2, grayscale=True):
out = perlin_ms(octaves, width, height, grayscale)
if grayscale:
out = TF.resize(size=(side_y, side_x), img=out.unsqueeze(0))
out = TF.to_pil_image(out.clamp(0, 1)).convert('RGB')
else:
out = out.reshape(-1, 3, out.shape[0]//3, out.shape[1])
out = TF.resize(size=(side_y, side_x), img=out)
out = TF.to_pil_image(out.clamp(0, 1).squeeze())
out = ImageOps.autocontrast(out)
return out
def regen_perlin():
if perlin_mode == 'color':
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, False)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, False)
elif perlin_mode == 'gray':
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, True)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, True)
else:
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, False)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, True)
init = TF.to_tensor(init).add(TF.to_tensor(init2)).div(2).to(device).unsqueeze(0).mul(2).sub(1)
del init2
return init.expand(batch_size, -1, -1, -1)
def fetch(url_or_path):
if str(url_or_path).startswith('http://') or str(url_or_path).startswith('https://'):
r = requests.get(url_or_path)
r.raise_for_status()
fd = io.BytesIO()
fd.write(r.content)
fd.seek(0)
return fd
return open(url_or_path, 'rb')
def read_image_workaround(path):
"""OpenCV reads images as BGR, Pillow saves them as RGB. Work around
this incompatibility to avoid colour inversions."""
im_tmp = cv2.imread(path)
return cv2.cvtColor(im_tmp, cv2.COLOR_BGR2RGB)
def parse_prompt(prompt):
if prompt.startswith('http://') or prompt.startswith('https://'):
vals = prompt.rsplit(':', 2)
vals = [vals[0] + ':' + vals[1], *vals[2:]]
else:
vals = prompt.rsplit(':', 1)
vals = vals + ['', '1'][len(vals):]
return vals[0], float(vals[1])
def sinc(x):
return torch.where(x != 0, torch.sin(math.pi * x) / (math.pi * x), x.new_ones([]))
def lanczos(x, a):
cond = torch.logical_and(-a < x, x < a)
out = torch.where(cond, sinc(x) * sinc(x/a), x.new_zeros([]))
return out / out.sum()
def ramp(ratio, width):
n = math.ceil(width / ratio + 1)
out = torch.empty([n])
cur = 0
for i in range(out.shape[0]):
out[i] = cur
cur += ratio
return torch.cat([-out[1:].flip([0]), out])[1:-1]
def resample(input, size, align_corners=True):
n, c, h, w = input.shape
dh, dw = size
input = input.reshape([n * c, 1, h, w])
if dh < h:
kernel_h = lanczos(ramp(dh / h, 2), 2).to(input.device, input.dtype)
pad_h = (kernel_h.shape[0] - 1) // 2
input = F.pad(input, (0, 0, pad_h, pad_h), 'reflect')
input = F.conv2d(input, kernel_h[None, None, :, None])
if dw < w:
kernel_w = lanczos(ramp(dw / w, 2), 2).to(input.device, input.dtype)
pad_w = (kernel_w.shape[0] - 1) // 2
input = F.pad(input, (pad_w, pad_w, 0, 0), 'reflect')
input = F.conv2d(input, kernel_w[None, None, None, :])
input = input.reshape([n, c, h, w])
return F.interpolate(input, size, mode='bicubic', align_corners=align_corners)
class MakeCutouts(nn.Module):
def __init__(self, cut_size, cutn, skip_augs=False):
super().__init__()
self.cut_size = cut_size
self.cutn = cutn
self.skip_augs = skip_augs
self.augs = T.Compose([
T.RandomHorizontalFlip(p=0.5),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomAffine(degrees=15, translate=(0.1, 0.1)),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomPerspective(distortion_scale=0.4, p=0.7),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomGrayscale(p=0.15),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
# T.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1),
])
def forward(self, input):
input = T.Pad(input.shape[2]//4, fill=0)(input)
sideY, sideX = input.shape[2:4]
max_size = min(sideX, sideY)
cutouts = []
for ch in range(self.cutn):
if ch > self.cutn - self.cutn//4:
cutout = input.clone()
else:
size = int(max_size * torch.zeros(1,).normal_(mean=.8, std=.3).clip(float(self.cut_size/max_size), 1.))
offsetx = torch.randint(0, abs(sideX - size + 1), ())
offsety = torch.randint(0, abs(sideY - size + 1), ())
cutout = input[:, :, offsety:offsety + size, offsetx:offsetx + size]
if not self.skip_augs:
cutout = self.augs(cutout)
cutouts.append(resample(cutout, (self.cut_size, self.cut_size)))
del cutout
cutouts = torch.cat(cutouts, dim=0)
return cutouts
cutout_debug = False
padargs = {}
class MakeCutoutsDango(nn.Module):
def __init__(self, cut_size,
Overview=4,
InnerCrop = 0, IC_Size_Pow=0.5, IC_Grey_P = 0.2
):
super().__init__()
self.cut_size = cut_size
self.Overview = Overview
self.InnerCrop = InnerCrop
self.IC_Size_Pow = IC_Size_Pow
self.IC_Grey_P = IC_Grey_P
if args.animation_mode == 'None':
self.augs = T.Compose([
T.RandomHorizontalFlip(p=0.5),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomAffine(degrees=10, translate=(0.05, 0.05), interpolation = T.InterpolationMode.BILINEAR),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomGrayscale(p=0.1),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1),
])
elif args.animation_mode == 'Video Input':
self.augs = T.Compose([
T.RandomHorizontalFlip(p=0.5),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomAffine(degrees=15, translate=(0.1, 0.1)),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomPerspective(distortion_scale=0.4, p=0.7),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomGrayscale(p=0.15),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
# T.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1),
])
elif args.animation_mode == '2D':
self.augs = T.Compose([
T.RandomHorizontalFlip(p=0.4),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomAffine(degrees=10, translate=(0.05, 0.05), interpolation = T.InterpolationMode.BILINEAR),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.RandomGrayscale(p=0.1),
T.Lambda(lambda x: x + torch.randn_like(x) * 0.01),
T.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.3),
])
def forward(self, input):
cutouts = []
gray = T.Grayscale(3)
sideY, sideX = input.shape[2:4]
max_size = min(sideX, sideY)
min_size = min(sideX, sideY, self.cut_size)
l_size = max(sideX, sideY)
output_shape = [1,3,self.cut_size,self.cut_size]
output_shape_2 = [1,3,self.cut_size+2,self.cut_size+2]
pad_input = F.pad(input,((sideY-max_size)//2,(sideY-max_size)//2,(sideX-max_size)//2,(sideX-max_size)//2), **padargs)
cutout = resize(pad_input, out_shape=output_shape)
if self.Overview>0:
if self.Overview<=4:
if self.Overview>=1:
cutouts.append(cutout)
if self.Overview>=2:
cutouts.append(gray(cutout))
if self.Overview>=3:
cutouts.append(TF.hflip(cutout))
if self.Overview==4:
cutouts.append(gray(TF.hflip(cutout)))
else:
cutout = resize(pad_input, out_shape=output_shape)
for _ in range(self.Overview):
cutouts.append(cutout)
if cutout_debug:
TF.to_pil_image(cutouts[0].clamp(0, 1).squeeze(0)).save("/content/cutout_overview0.jpg",quality=99)
if self.InnerCrop >0:
for i in range(self.InnerCrop):
size = int(torch.rand([])**self.IC_Size_Pow * (max_size - min_size) + min_size)
offsetx = torch.randint(0, sideX - size + 1, ())
offsety = torch.randint(0, sideY - size + 1, ())
cutout = input[:, :, offsety:offsety + size, offsetx:offsetx + size]
if i <= int(self.IC_Grey_P * self.InnerCrop):
cutout = gray(cutout)
cutout = resize(cutout, out_shape=output_shape)
cutouts.append(cutout)
if cutout_debug:
TF.to_pil_image(cutouts[-1].clamp(0, 1).squeeze(0)).save("/content/cutout_InnerCrop.jpg",quality=99)
cutouts = torch.cat(cutouts)
if skip_augs is not True: cutouts=self.augs(cutouts)
return cutouts
def spherical_dist_loss(x, y):
x = F.normalize(x, dim=-1)
y = F.normalize(y, dim=-1)
return (x - y).norm(dim=-1).div(2).arcsin().pow(2).mul(2)
def tv_loss(input):
"""L2 total variation loss, as in Mahendran et al."""
input = F.pad(input, (0, 1, 0, 1), 'replicate')
x_diff = input[..., :-1, 1:] - input[..., :-1, :-1]
y_diff = input[..., 1:, :-1] - input[..., :-1, :-1]
return (x_diff**2 + y_diff**2).mean([1, 2, 3])
def range_loss(input):
return (input - input.clamp(-1, 1)).pow(2).mean([1, 2, 3])
stop_on_next_loop = False # Make sure GPU memory doesn't get corrupted from cancelling the run mid-way through, allow a full frame to complete
def do_run():
seed = args.seed
print(range(args.start_frame, args.max_frames))
for frame_num in range(args.start_frame, args.max_frames):
if stop_on_next_loop:
break
display.clear_output(wait=True)
# Print Frame progress if animation mode is on
if args.animation_mode != "None":
batchBar = tqdm(range(args.max_frames), desc ="Frames")
batchBar.n = frame_num
batchBar.refresh()
# Inits if not video frames
if args.animation_mode != "Video Input":
if args.init_image == '':
init_image = None
else:
init_image = args.init_image
init_scale = args.init_scale
skip_steps = args.skip_steps
if args.animation_mode == "2D":
if args.key_frames:
angle = args.angle_series[frame_num]
zoom = args.zoom_series[frame_num]
translation_x = args.translation_x_series[frame_num]
translation_y = args.translation_y_series[frame_num]
print(
f'angle: {angle}',
f'zoom: {zoom}',
f'translation_x: {translation_x}',
f'translation_y: {translation_y}',
)
if frame_num > 0:
seed = seed + 1
if resume_run and frame_num == start_frame:
img_0 = cv2.imread(batchFolder+f"/{batch_name}({batchNum})_{start_frame-1:04}.png")
else:
img_0 = cv2.imread('prevFrame.png')
center = (1*img_0.shape[1]//2, 1*img_0.shape[0]//2)
trans_mat = np.float32(
[[1, 0, translation_x],
[0, 1, translation_y]]
)
rot_mat = cv2.getRotationMatrix2D( center, angle, zoom )
trans_mat = np.vstack([trans_mat, [0,0,1]])
rot_mat = np.vstack([rot_mat, [0,0,1]])
transformation_matrix = np.matmul(rot_mat, trans_mat)
img_0 = cv2.warpPerspective(
img_0,
transformation_matrix,
(img_0.shape[1], img_0.shape[0]),
borderMode=cv2.BORDER_WRAP
)
cv2.imwrite('prevFrameScaled.png', img_0)
init_image = 'prevFrameScaled.png'
init_scale = args.frames_scale
skip_steps = args.calc_frames_skip_steps
if args.animation_mode == "Video Input":
seed = seed + 1
init_image = f'{videoFramesFolder}/{frame_num+1:04}.jpg'
init_scale = args.frames_scale
skip_steps = args.calc_frames_skip_steps
loss_values = []
if seed is not None:
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.backends.cudnn.deterministic = True
target_embeds, weights = [], []
if args.prompts_series is not None and frame_num >= len(args.prompts_series):
frame_prompt = args.prompts_series[-1]
elif args.prompts_series is not None:
frame_prompt = args.prompts_series[frame_num]
else:
frame_prompt = []
print(args.image_prompts_series)
if args.image_prompts_series is not None and frame_num >= len(args.image_prompts_series):
image_prompt = args.image_prompts_series[-1]
elif args.image_prompts_series is not None:
image_prompt = args.image_prompts_series[frame_num]
else:
image_prompt = []
print(f'Frame Prompt: {frame_prompt}')
model_stats = []
for clip_model in clip_models:
cutn = 16
model_stat = {"clip_model":None,"target_embeds":[],"make_cutouts":None,"weights":[]}
model_stat["clip_model"] = clip_model
for prompt in frame_prompt:
txt, weight = parse_prompt(prompt)
txt = clip_model.encode_text(clip.tokenize(prompt).to(device)).float()
if args.fuzzy_prompt:
for i in range(25):
model_stat["target_embeds"].append((txt + torch.randn(txt.shape).cuda() * args.rand_mag).clamp(0,1))
model_stat["weights"].append(weight)
else:
model_stat["target_embeds"].append(txt)
model_stat["weights"].append(weight)
if image_prompt:
model_stat["make_cutouts"] = MakeCutouts(clip_model.visual.input_resolution, cutn, skip_augs=skip_augs)
for prompt in image_prompt:
path, weight = parse_prompt(prompt)
img = Image.open(fetch(path)).convert('RGB')
img = TF.resize(img, min(side_x, side_y, *img.size), T.InterpolationMode.LANCZOS)
batch = model_stat["make_cutouts"](TF.to_tensor(img).to(device).unsqueeze(0).mul(2).sub(1))
embed = clip_model.encode_image(normalize(batch)).float()
if fuzzy_prompt:
for i in range(25):
model_stat["target_embeds"].append((embed + torch.randn(embed.shape).cuda() * rand_mag).clamp(0,1))
weights.extend([weight / cutn] * cutn)
else:
model_stat["target_embeds"].append(embed)
model_stat["weights"].extend([weight / cutn] * cutn)
model_stat["target_embeds"] = torch.cat(model_stat["target_embeds"])
model_stat["weights"] = torch.tensor(model_stat["weights"], device=device)
if model_stat["weights"].sum().abs() < 1e-3:
raise RuntimeError('The weights must not sum to 0.')
model_stat["weights"] /= model_stat["weights"].sum().abs()
model_stats.append(model_stat)
init = None
if init_image is not None:
init = Image.open(fetch(init_image)).convert('RGB')
init = init.resize((args.side_x, args.side_y), Image.LANCZOS)
init = TF.to_tensor(init).to(device).unsqueeze(0).mul(2).sub(1)
if args.perlin_init:
if args.perlin_mode == 'color':
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, False)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, False)
elif args.perlin_mode == 'gray':
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, True)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, True)
else:
init = create_perlin_noise([1.5**-i*0.5 for i in range(12)], 1, 1, False)
init2 = create_perlin_noise([1.5**-i*0.5 for i in range(8)], 4, 4, True)
# init = TF.to_tensor(init).add(TF.to_tensor(init2)).div(2).to(device)
init = TF.to_tensor(init).add(TF.to_tensor(init2)).div(2).to(device).unsqueeze(0).mul(2).sub(1)
del init2
cur_t = None
def cond_fn(x, t, y=None):
with torch.enable_grad():
x_is_NaN = False
x = x.detach().requires_grad_()
n = x.shape[0]
if use_secondary_model is True:
alpha = torch.tensor(diffusion.sqrt_alphas_cumprod[cur_t], device=device, dtype=torch.float32)
sigma = torch.tensor(diffusion.sqrt_one_minus_alphas_cumprod[cur_t], device=device, dtype=torch.float32)
cosine_t = alpha_sigma_to_t(alpha, sigma)
out = secondary_model(x, cosine_t[None].repeat([n])).pred
fac = diffusion.sqrt_one_minus_alphas_cumprod[cur_t]
x_in = out * fac + x * (1 - fac)
x_in_grad = torch.zeros_like(x_in)
else:
my_t = torch.ones([n], device=device, dtype=torch.long) * cur_t
out = diffusion.p_mean_variance(model, x, my_t, clip_denoised=False, model_kwargs={'y': y})
fac = diffusion.sqrt_one_minus_alphas_cumprod[cur_t]
x_in = out['pred_xstart'] * fac + x * (1 - fac)
x_in_grad = torch.zeros_like(x_in)
for model_stat in model_stats:
for i in range(args.cutn_batches):
t_int = int(t.item())+1 #errors on last step without +1, need to find source
#when using SLIP Base model the dimensions need to be hard coded to avoid AttributeError: 'VisionTransformer' object has no attribute 'input_resolution'
try:
input_resolution=model_stat["clip_model"].visual.input_resolution
except:
input_resolution=224
cuts = MakeCutoutsDango(input_resolution,
Overview= args.cut_overview[1000-t_int],
InnerCrop = args.cut_innercut[1000-t_int], IC_Size_Pow=args.cut_ic_pow, IC_Grey_P = args.cut_icgray_p[1000-t_int]
)
clip_in = normalize(cuts(x_in.add(1).div(2)))
image_embeds = model_stat["clip_model"].encode_image(clip_in).float()
dists = spherical_dist_loss(image_embeds.unsqueeze(1), model_stat["target_embeds"].unsqueeze(0))
dists = dists.view([args.cut_overview[1000-t_int]+args.cut_innercut[1000-t_int], n, -1])
losses = dists.mul(model_stat["weights"]).sum(2).mean(0)
loss_values.append(losses.sum().item()) # log loss, probably shouldn't do per cutn_batch
x_in_grad += torch.autograd.grad(losses.sum() * clip_guidance_scale, x_in)[0] / cutn_batches
tv_losses = tv_loss(x_in)
if use_secondary_model is True:
range_losses = range_loss(out)
else:
range_losses = range_loss(out['pred_xstart'])
sat_losses = torch.abs(x_in - x_in.clamp(min=-1,max=1)).mean()
loss = tv_losses.sum() * tv_scale + range_losses.sum() * range_scale + sat_losses.sum() * sat_scale
if init is not None and args.init_scale:
init_losses = lpips_model(x_in, init)
loss = loss + init_losses.sum() * args.init_scale
x_in_grad += torch.autograd.grad(loss, x_in)[0]
if torch.isnan(x_in_grad).any()==False:
grad = -torch.autograd.grad(x_in, x, x_in_grad)[0]
else:
# print("NaN'd")
x_is_NaN = True
grad = torch.zeros_like(x)
if args.clamp_grad and x_is_NaN == False:
magnitude = grad.square().mean().sqrt()
return grad * magnitude.clamp(max=args.clamp_max) / magnitude #min=-0.02, min=-clamp_max,
return grad
if model_config['timestep_respacing'].startswith('ddim'):
sample_fn = diffusion.ddim_sample_loop_progressive
else:
sample_fn = diffusion.p_sample_loop_progressive
image_display = Output()
for i in range(args.n_batches):
if args.animation_mode == 'None':
display.clear_output(wait=True)
batchBar = tqdm(range(args.n_batches), desc ="Batches")
batchBar.n = i
batchBar.refresh()
print('')
display.display(image_display)
gc.collect()
torch.cuda.empty_cache()
cur_t = diffusion.num_timesteps - skip_steps - 1
total_steps = cur_t
if perlin_init:
init = regen_perlin()
if model_config['timestep_respacing'].startswith('ddim'):
samples = sample_fn(
model,
(batch_size, 3, args.side_y, args.side_x),
clip_denoised=clip_denoised,
model_kwargs={},
cond_fn=cond_fn,
progress=True,
skip_timesteps=skip_steps,
init_image=init,
randomize_class=randomize_class,
eta=eta,
)
else:
samples = sample_fn(
model,
(batch_size, 3, args.side_y, args.side_x),
clip_denoised=clip_denoised,
model_kwargs={},
cond_fn=cond_fn,
progress=True,
skip_timesteps=skip_steps,
init_image=init,
randomize_class=randomize_class,
)
# with run_display:
# display.clear_output(wait=True)
imgToSharpen = None
for j, sample in enumerate(samples):
cur_t -= 1
intermediateStep = False
if args.steps_per_checkpoint is not None:
if j % steps_per_checkpoint == 0 and j > 0:
intermediateStep = True
elif j in args.intermediate_saves:
intermediateStep = True
with image_display:
if j % args.display_rate == 0 or cur_t == -1 or intermediateStep == True:
for k, image in enumerate(sample['pred_xstart']):
# tqdm.write(f'Batch {i}, step {j}, output {k}:')
current_time = datetime.now().strftime('%y%m%d-%H%M%S_%f')
percent = math.ceil(j/total_steps*100)
if args.n_batches > 0:
#if intermediates are saved to the subfolder, don't append a step or percentage to the name
if cur_t == -1 and args.intermediates_in_subfolder is True:
save_num = f'{frame_num:04}' if animation_mode != "None" else i
filename = f'{args.batch_name}({args.batchNum})_{save_num}.png'
else:
#If we're working with percentages, append it
if args.steps_per_checkpoint is not None:
filename = f'{args.batch_name}({args.batchNum})_{i:04}-{percent:02}%.png'
# Or else, iIf we're working with specific steps, append those
else:
filename = f'{args.batch_name}({args.batchNum})_{i:04}-{j:03}.png'
image = TF.to_pil_image(image.add(1).div(2).clamp(0, 1))
if j % args.display_rate == 0 or cur_t == -1:
image.save('progress.png')
display.clear_output(wait=True)
display.display(display.Image('progress.png'))
if args.steps_per_checkpoint is not None:
if j % args.steps_per_checkpoint == 0 and j > 0:
if args.intermediates_in_subfolder is True:
image.save(f'{partialFolder}/{filename}')
else:
image.save(f'{batchFolder}/{filename}')
else:
if j in args.intermediate_saves:
if args.intermediates_in_subfolder is True:
image.save(f'{partialFolder}/{filename}')
else:
image.save(f'{batchFolder}/{filename}')
if cur_t == -1:
if frame_num == 0:
save_settings()
if args.animation_mode != "None":
image.save('prevFrame.png')
if args.sharpen_preset != "Off" and animation_mode == "None":
imgToSharpen = image
if args.keep_unsharp is True:
image.save(f'{unsharpenFolder}/{filename}')
else:
image.save(f'{batchFolder}/{filename}')
# if frame_num != args.max_frames-1:
# display.clear_output()
with image_display:
if args.sharpen_preset != "Off" and animation_mode == "None":
print('Starting Diffusion Sharpening...')
do_superres(imgToSharpen, f'{batchFolder}/{filename}')
display.clear_output()
plt.plot(np.array(loss_values), 'r')
def save_settings():
setting_list = {
'text_prompts': text_prompts,
'image_prompts': image_prompts,
'clip_guidance_scale': clip_guidance_scale,
'tv_scale': tv_scale,
'range_scale': range_scale,
'sat_scale': sat_scale,
# 'cutn': cutn,
'cutn_batches': cutn_batches,
'max_frames': max_frames,
'interp_spline': interp_spline,
# 'rotation_per_frame': rotation_per_frame,
'init_image': init_image,
'init_scale': init_scale,
'skip_steps': skip_steps,
# 'zoom_per_frame': zoom_per_frame,
'frames_scale': frames_scale,
'frames_skip_steps': frames_skip_steps,
'perlin_init': perlin_init,
'perlin_mode': perlin_mode,
'skip_augs': skip_augs,
'randomize_class': randomize_class,
'clip_denoised': clip_denoised,
'clamp_grad': clamp_grad,
'clamp_max': clamp_max,
'seed': seed,
'fuzzy_prompt': fuzzy_prompt,
'rand_mag': rand_mag,
'eta': eta,
'width': width_height[0],
'height': width_height[1],
'diffusion_model': diffusion_model,
'use_secondary_model': use_secondary_model,
'steps': steps,
'diffusion_steps': diffusion_steps,
'ViTB32': ViTB32,
'ViTB16': ViTB16,
'RN101': RN101,
'RN50': RN50,
'RN50x4': RN50x4,
'RN50x16': RN50x16,
'cut_overview': str(cut_overview),
'cut_innercut': str(cut_innercut),
'cut_ic_pow': cut_ic_pow,
'cut_icgray_p': str(cut_icgray_p),
'key_frames': key_frames,
'max_frames': max_frames,
'angle': angle,
'zoom': zoom,
'translation_x': translation_x,
'translation_y': translation_y,
'video_init_path':video_init_path,
'extract_nth_frame':extract_nth_frame,
}
# print('Settings:', setting_list)
with open(f"{batchFolder}/{batch_name}({batchNum})_settings.txt", "w+") as f: #save settings
json.dump(setting_list, f, ensure_ascii=False, indent=4)
# + cellView="form" id="TI4oAu0N4ksZ"
#@title 2.3 Define the secondary diffusion model
def append_dims(x, n):
return x[(Ellipsis, *(None,) * (n - x.ndim))]
def expand_to_planes(x, shape):
return append_dims(x, len(shape)).repeat([1, 1, *shape[2:]])
def alpha_sigma_to_t(alpha, sigma):
return torch.atan2(sigma, alpha) * 2 / math.pi
def t_to_alpha_sigma(t):
return torch.cos(t * math.pi / 2), torch.sin(t * math.pi / 2)
@dataclass
class DiffusionOutput:
v: torch.Tensor
pred: torch.Tensor
eps: torch.Tensor
class ConvBlock(nn.Sequential):
def __init__(self, c_in, c_out):
super().__init__(
nn.Conv2d(c_in, c_out, 3, padding=1),
nn.ReLU(inplace=True),
)
class SkipBlock(nn.Module):
def __init__(self, main, skip=None):
super().__init__()
self.main = nn.Sequential(*main)
self.skip = skip if skip else nn.Identity()
def forward(self, input):
return torch.cat([self.main(input), self.skip(input)], dim=1)
class FourierFeatures(nn.Module):
def __init__(self, in_features, out_features, std=1.):
super().__init__()
assert out_features % 2 == 0
self.weight = nn.Parameter(torch.randn([out_features // 2, in_features]) * std)
def forward(self, input):
f = 2 * math.pi * input @ self.weight.T
return torch.cat([f.cos(), f.sin()], dim=-1)
class SecondaryDiffusionImageNet(nn.Module):
def __init__(self):
super().__init__()
c = 64 # The base channel count
self.timestep_embed = FourierFeatures(1, 16)
self.net = nn.Sequential(
ConvBlock(3 + 16, c),
ConvBlock(c, c),
SkipBlock([
nn.AvgPool2d(2),
ConvBlock(c, c * 2),
ConvBlock(c * 2, c * 2),
SkipBlock([
nn.AvgPool2d(2),
ConvBlock(c * 2, c * 4),
ConvBlock(c * 4, c * 4),
SkipBlock([
nn.AvgPool2d(2),
ConvBlock(c * 4, c * 8),
ConvBlock(c * 8, c * 4),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]),
ConvBlock(c * 8, c * 4),
ConvBlock(c * 4, c * 2),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]),
ConvBlock(c * 4, c * 2),
ConvBlock(c * 2, c),
nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False),
]),
ConvBlock(c * 2, c),
nn.Conv2d(c, 3, 3, padding=1),
)
def forward(self, input, t):
timestep_embed = expand_to_planes(self.timestep_embed(t[:, None]), input.shape)
v = self.net(torch.cat([input, timestep_embed], dim=1))
alphas, sigmas = map(partial(append_dims, n=v.ndim), t_to_alpha_sigma(t))
pred = input * alphas - v * sigmas
eps = input * sigmas + v * alphas
return DiffusionOutput(v, pred, eps)
class SecondaryDiffusionImageNet2(nn.Module):
def __init__(self):
super().__init__()
c = 64 # The base channel count
cs = [c, c * 2, c * 2, c * 4, c * 4, c * 8]
self.timestep_embed = FourierFeatures(1, 16)
self.down = nn.AvgPool2d(2)
self.up = nn.Upsample(scale_factor=2, mode='bilinear', align_corners=False)
self.net = nn.Sequential(
ConvBlock(3 + 16, cs[0]),
ConvBlock(cs[0], cs[0]),
SkipBlock([
self.down,
ConvBlock(cs[0], cs[1]),
ConvBlock(cs[1], cs[1]),
SkipBlock([
self.down,
ConvBlock(cs[1], cs[2]),
ConvBlock(cs[2], cs[2]),
SkipBlock([
self.down,
ConvBlock(cs[2], cs[3]),
ConvBlock(cs[3], cs[3]),
SkipBlock([
self.down,
ConvBlock(cs[3], cs[4]),
ConvBlock(cs[4], cs[4]),
SkipBlock([
self.down,
ConvBlock(cs[4], cs[5]),
ConvBlock(cs[5], cs[5]),
ConvBlock(cs[5], cs[5]),
ConvBlock(cs[5], cs[4]),
self.up,
]),
ConvBlock(cs[4] * 2, cs[4]),
ConvBlock(cs[4], cs[3]),
self.up,
]),
ConvBlock(cs[3] * 2, cs[3]),
ConvBlock(cs[3], cs[2]),
self.up,
]),
ConvBlock(cs[2] * 2, cs[2]),
ConvBlock(cs[2], cs[1]),
self.up,
]),
ConvBlock(cs[1] * 2, cs[1]),
ConvBlock(cs[1], cs[0]),
self.up,
]),
ConvBlock(cs[0] * 2, cs[0]),
nn.Conv2d(cs[0], 3, 3, padding=1),
)
def forward(self, input, t):
timestep_embed = expand_to_planes(self.timestep_embed(t[:, None]), input.shape)
v = self.net(torch.cat([input, timestep_embed], dim=1))
alphas, sigmas = map(partial(append_dims, n=v.ndim), t_to_alpha_sigma(t))
pred = input * alphas - v * sigmas
eps = input * sigmas + v * alphas
return DiffusionOutput(v, pred, eps)
# + cellView="form" id="NJS2AUAnvn-D"
#@title 2.4 SuperRes Define
class DDIMSampler(object):
def __init__(self, model, schedule="linear", **kwargs):
super().__init__()
self.model = model
self.ddpm_num_timesteps = model.num_timesteps
self.schedule = schedule
def register_buffer(self, name, attr):
if type(attr) == torch.Tensor:
if attr.device != torch.device("cuda"):
attr = attr.to(torch.device("cuda"))
setattr(self, name, attr)
def make_schedule(self, ddim_num_steps, ddim_discretize="uniform", ddim_eta=0., verbose=True):
self.ddim_timesteps = make_ddim_timesteps(ddim_discr_method=ddim_discretize, num_ddim_timesteps=ddim_num_steps,
num_ddpm_timesteps=self.ddpm_num_timesteps,verbose=verbose)
alphas_cumprod = self.model.alphas_cumprod
assert alphas_cumprod.shape[0] == self.ddpm_num_timesteps, 'alphas have to be defined for each timestep'
to_torch = lambda x: x.clone().detach().to(torch.float32).to(self.model.device)
self.register_buffer('betas', to_torch(self.model.betas))
self.register_buffer('alphas_cumprod', to_torch(alphas_cumprod))
self.register_buffer('alphas_cumprod_prev', to_torch(self.model.alphas_cumprod_prev))
# calculations for diffusion q(x_t | x_{t-1}) and others
self.register_buffer('sqrt_alphas_cumprod', to_torch(np.sqrt(alphas_cumprod.cpu())))
self.register_buffer('sqrt_one_minus_alphas_cumprod', to_torch(np.sqrt(1. - alphas_cumprod.cpu())))
self.register_buffer('log_one_minus_alphas_cumprod', to_torch(np.log(1. - alphas_cumprod.cpu())))
self.register_buffer('sqrt_recip_alphas_cumprod', to_torch(np.sqrt(1. / alphas_cumprod.cpu())))
self.register_buffer('sqrt_recipm1_alphas_cumprod', to_torch(np.sqrt(1. / alphas_cumprod.cpu() - 1)))
# ddim sampling parameters
ddim_sigmas, ddim_alphas, ddim_alphas_prev = make_ddim_sampling_parameters(alphacums=alphas_cumprod.cpu(),
ddim_timesteps=self.ddim_timesteps,
eta=ddim_eta,verbose=verbose)
self.register_buffer('ddim_sigmas', ddim_sigmas)
self.register_buffer('ddim_alphas', ddim_alphas)
self.register_buffer('ddim_alphas_prev', ddim_alphas_prev)
self.register_buffer('ddim_sqrt_one_minus_alphas', np.sqrt(1. - ddim_alphas))
sigmas_for_original_sampling_steps = ddim_eta * torch.sqrt(
(1 - self.alphas_cumprod_prev) / (1 - self.alphas_cumprod) * (
1 - self.alphas_cumprod / self.alphas_cumprod_prev))
self.register_buffer('ddim_sigmas_for_original_num_steps', sigmas_for_original_sampling_steps)
@torch.no_grad()
def sample(self,
S,
batch_size,
shape,
conditioning=None,
callback=None,
normals_sequence=None,
img_callback=None,
quantize_x0=False,
eta=0.,
mask=None,
x0=None,
temperature=1.,
noise_dropout=0.,
score_corrector=None,
corrector_kwargs=None,
verbose=True,
x_T=None,
log_every_t=100,
**kwargs
):
if conditioning is not None:
if isinstance(conditioning, dict):
cbs = conditioning[list(conditioning.keys())[0]].shape[0]
if cbs != batch_size:
print(f"Warning: Got {cbs} conditionings but batch-size is {batch_size}")
else:
if conditioning.shape[0] != batch_size:
print(f"Warning: Got {conditioning.shape[0]} conditionings but batch-size is {batch_size}")
self.make_schedule(ddim_num_steps=S, ddim_eta=eta, verbose=verbose)
# sampling
C, H, W = shape
size = (batch_size, C, H, W)
# print(f'Data shape for DDIM sampling is {size}, eta {eta}')
samples, intermediates = self.ddim_sampling(conditioning, size,
callback=callback,
img_callback=img_callback,
quantize_denoised=quantize_x0,
mask=mask, x0=x0,
ddim_use_original_steps=False,
noise_dropout=noise_dropout,
temperature=temperature,
score_corrector=score_corrector,
corrector_kwargs=corrector_kwargs,
x_T=x_T,
log_every_t=log_every_t
)
return samples, intermediates
@torch.no_grad()
def ddim_sampling(self, cond, shape,
x_T=None, ddim_use_original_steps=False,
callback=None, timesteps=None, quantize_denoised=False,
mask=None, x0=None, img_callback=None, log_every_t=100,
temperature=1., noise_dropout=0., score_corrector=None, corrector_kwargs=None):
device = self.model.betas.device
b = shape[0]
if x_T is None:
img = torch.randn(shape, device=device)
else:
img = x_T
if timesteps is None:
timesteps = self.ddpm_num_timesteps if ddim_use_original_steps else self.ddim_timesteps
elif timesteps is not None and not ddim_use_original_steps:
subset_end = int(min(timesteps / self.ddim_timesteps.shape[0], 1) * self.ddim_timesteps.shape[0]) - 1
timesteps = self.ddim_timesteps[:subset_end]
intermediates = {'x_inter': [img], 'pred_x0': [img]}
time_range = reversed(range(0,timesteps)) if ddim_use_original_steps else np.flip(timesteps)
total_steps = timesteps if ddim_use_original_steps else timesteps.shape[0]
print(f"Running DDIM Sharpening with {total_steps} timesteps")
iterator = tqdm(time_range, desc='DDIM Sharpening', total=total_steps)
for i, step in enumerate(iterator):
index = total_steps - i - 1
ts = torch.full((b,), step, device=device, dtype=torch.long)
if mask is not None:
assert x0 is not None
img_orig = self.model.q_sample(x0, ts) # TODO: deterministic forward pass?
img = img_orig * mask + (1. - mask) * img
outs = self.p_sample_ddim(img, cond, ts, index=index, use_original_steps=ddim_use_original_steps,
quantize_denoised=quantize_denoised, temperature=temperature,
noise_dropout=noise_dropout, score_corrector=score_corrector,
corrector_kwargs=corrector_kwargs)
img, pred_x0 = outs
if callback: callback(i)
if img_callback: img_callback(pred_x0, i)
if index % log_every_t == 0 or index == total_steps - 1:
intermediates['x_inter'].append(img)
intermediates['pred_x0'].append(pred_x0)
return img, intermediates
@torch.no_grad()
def p_sample_ddim(self, x, c, t, index, repeat_noise=False, use_original_steps=False, quantize_denoised=False,
temperature=1., noise_dropout=0., score_corrector=None, corrector_kwargs=None):
b, *_, device = *x.shape, x.device
e_t = self.model.apply_model(x, t, c)
if score_corrector is not None:
assert self.model.parameterization == "eps"
e_t = score_corrector.modify_score(self.model, e_t, x, t, c, **corrector_kwargs)
alphas = self.model.alphas_cumprod if use_original_steps else self.ddim_alphas
alphas_prev = self.model.alphas_cumprod_prev if use_original_steps else self.ddim_alphas_prev
sqrt_one_minus_alphas = self.model.sqrt_one_minus_alphas_cumprod if use_original_steps else self.ddim_sqrt_one_minus_alphas
sigmas = self.model.ddim_sigmas_for_original_num_steps if use_original_steps else self.ddim_sigmas
# select parameters corresponding to the currently considered timestep
a_t = torch.full((b, 1, 1, 1), alphas[index], device=device)
a_prev = torch.full((b, 1, 1, 1), alphas_prev[index], device=device)
sigma_t = torch.full((b, 1, 1, 1), sigmas[index], device=device)
sqrt_one_minus_at = torch.full((b, 1, 1, 1), sqrt_one_minus_alphas[index],device=device)
# current prediction for x_0
pred_x0 = (x - sqrt_one_minus_at * e_t) / a_t.sqrt()
if quantize_denoised:
pred_x0, _, *_ = self.model.first_stage_model.quantize(pred_x0)
# direction pointing to x_t
dir_xt = (1. - a_prev - sigma_t**2).sqrt() * e_t
noise = sigma_t * noise_like(x.shape, device, repeat_noise) * temperature
if noise_dropout > 0.:
noise = torch.nn.functional.dropout(noise, p=noise_dropout)
x_prev = a_prev.sqrt() * pred_x0 + dir_xt + noise
return x_prev, pred_x0
def download_models(mode):
if mode == "superresolution":
# this is the small bsr light model
url_conf = 'https://heibox.uni-heidelberg.de/f/31a76b13ea27482981b4/?dl=1'
url_ckpt = 'https://heibox.uni-heidelberg.de/f/578df07c8fc04ffbadf3/?dl=1'
path_conf = f'{model_path}/superres/project.yaml'
path_ckpt = f'{model_path}/superres/last.ckpt'
download_url(url_conf, path_conf)
download_url(url_ckpt, path_ckpt)
path_conf = path_conf + '/?dl=1' # fix it
path_ckpt = path_ckpt + '/?dl=1' # fix it
return path_conf, path_ckpt
else:
raise NotImplementedError
def load_model_from_config(config, ckpt):
print(f"Loading model from {ckpt}")
pl_sd = torch.load(ckpt, map_location="cpu")
global_step = pl_sd["global_step"]
sd = pl_sd["state_dict"]
model = instantiate_from_config(config.model)
m, u = model.load_state_dict(sd, strict=False)
model.cuda()
model.eval()
return {"model": model}, global_step
def get_model(mode):
path_conf, path_ckpt = download_models(mode)
config = OmegaConf.load(path_conf)
model, step = load_model_from_config(config, path_ckpt)
return model
def get_custom_cond(mode):
dest = "data/example_conditioning"
if mode == "superresolution":
uploaded_img = files.upload()
filename = next(iter(uploaded_img))
name, filetype = filename.split(".") # todo assumes just one dot in name !
os.rename(f"{filename}", f"{dest}/{mode}/custom_{name}.{filetype}")
elif mode == "text_conditional":
w = widgets.Text(value='A cake with cream!', disabled=True)
display.display(w)
with open(f"{dest}/{mode}/custom_{w.value[:20]}.txt", 'w') as f:
f.write(w.value)
elif mode == "class_conditional":
w = widgets.IntSlider(min=0, max=1000)
display.display(w)
with open(f"{dest}/{mode}/custom.txt", 'w') as f:
f.write(w.value)
else:
raise NotImplementedError(f"cond not implemented for mode{mode}")
def get_cond_options(mode):
path = "data/example_conditioning"
path = os.path.join(path, mode)
onlyfiles = [f for f in sorted(os.listdir(path))]
return path, onlyfiles
def select_cond_path(mode):
path = "data/example_conditioning" # todo
path = os.path.join(path, mode)
onlyfiles = [f for f in sorted(os.listdir(path))]
selected = widgets.RadioButtons(
options=onlyfiles,
description='Select conditioning:',
disabled=False
)
display.display(selected)
selected_path = os.path.join(path, selected.value)
return selected_path
def get_cond(mode, img):
example = dict()
if mode == "superresolution":
up_f = 4
# visualize_cond_img(selected_path)
c = img
c = torch.unsqueeze(torchvision.transforms.ToTensor()(c), 0)
c_up = torchvision.transforms.functional.resize(c, size=[up_f * c.shape[2], up_f * c.shape[3]], antialias=True)
c_up = rearrange(c_up, '1 c h w -> 1 h w c')
c = rearrange(c, '1 c h w -> 1 h w c')
c = 2. * c - 1.
c = c.to(torch.device("cuda"))
example["LR_image"] = c
example["image"] = c_up
return example
def visualize_cond_img(path):
display.display(ipyimg(filename=path))
def sr_run(model, img, task, custom_steps, eta, resize_enabled=False, classifier_ckpt=None, global_step=None):
# global stride
example = get_cond(task, img)
save_intermediate_vid = False
n_runs = 1
masked = False
guider = None
ckwargs = None
mode = 'ddim'
ddim_use_x0_pred = False
temperature = 1.
eta = eta
make_progrow = True
custom_shape = None
height, width = example["image"].shape[1:3]
split_input = height >= 128 and width >= 128
if split_input:
ks = 128
stride = 64
vqf = 4 #
model.split_input_params = {"ks": (ks, ks), "stride": (stride, stride),
"vqf": vqf,
"patch_distributed_vq": True,
"tie_braker": False,
"clip_max_weight": 0.5,
"clip_min_weight": 0.01,
"clip_max_tie_weight": 0.5,
"clip_min_tie_weight": 0.01}
else:
if hasattr(model, "split_input_params"):
delattr(model, "split_input_params")
invert_mask = False
x_T = None
for n in range(n_runs):
if custom_shape is not None:
x_T = torch.randn(1, custom_shape[1], custom_shape[2], custom_shape[3]).to(model.device)
x_T = repeat(x_T, '1 c h w -> b c h w', b=custom_shape[0])
logs = make_convolutional_sample(example, model,
mode=mode, custom_steps=custom_steps,
eta=eta, swap_mode=False , masked=masked,
invert_mask=invert_mask, quantize_x0=False,
custom_schedule=None, decode_interval=10,
resize_enabled=resize_enabled, custom_shape=custom_shape,
temperature=temperature, noise_dropout=0.,
corrector=guider, corrector_kwargs=ckwargs, x_T=x_T, save_intermediate_vid=save_intermediate_vid,
make_progrow=make_progrow,ddim_use_x0_pred=ddim_use_x0_pred
)
return logs
@torch.no_grad()
def convsample_ddim(model, cond, steps, shape, eta=1.0, callback=None, normals_sequence=None,
mask=None, x0=None, quantize_x0=False, img_callback=None,
temperature=1., noise_dropout=0., score_corrector=None,
corrector_kwargs=None, x_T=None, log_every_t=None
):
ddim = DDIMSampler(model)
bs = shape[0] # dont know where this comes from but wayne
shape = shape[1:] # cut batch dim
# print(f"Sampling with eta = {eta}; steps: {steps}")
samples, intermediates = ddim.sample(steps, batch_size=bs, shape=shape, conditioning=cond, callback=callback,
normals_sequence=normals_sequence, quantize_x0=quantize_x0, eta=eta,
mask=mask, x0=x0, temperature=temperature, verbose=False,
score_corrector=score_corrector,
corrector_kwargs=corrector_kwargs, x_T=x_T)
return samples, intermediates
@torch.no_grad()
def make_convolutional_sample(batch, model, mode="vanilla", custom_steps=None, eta=1.0, swap_mode=False, masked=False,
invert_mask=True, quantize_x0=False, custom_schedule=None, decode_interval=1000,
resize_enabled=False, custom_shape=None, temperature=1., noise_dropout=0., corrector=None,
corrector_kwargs=None, x_T=None, save_intermediate_vid=False, make_progrow=True,ddim_use_x0_pred=False):
log = dict()
z, c, x, xrec, xc = model.get_input(batch, model.first_stage_key,
return_first_stage_outputs=True,
force_c_encode=not (hasattr(model, 'split_input_params')
and model.cond_stage_key == 'coordinates_bbox'),
return_original_cond=True)
log_every_t = 1 if save_intermediate_vid else None
if custom_shape is not None:
z = torch.randn(custom_shape)
# print(f"Generating {custom_shape[0]} samples of shape {custom_shape[1:]}")
z0 = None
log["input"] = x
log["reconstruction"] = xrec
if ismap(xc):
log["original_conditioning"] = model.to_rgb(xc)
if hasattr(model, 'cond_stage_key'):
log[model.cond_stage_key] = model.to_rgb(xc)
else:
log["original_conditioning"] = xc if xc is not None else torch.zeros_like(x)
if model.cond_stage_model:
log[model.cond_stage_key] = xc if xc is not None else torch.zeros_like(x)
if model.cond_stage_key =='class_label':
log[model.cond_stage_key] = xc[model.cond_stage_key]
with model.ema_scope("Plotting"):
t0 = time.time()
img_cb = None
sample, intermediates = convsample_ddim(model, c, steps=custom_steps, shape=z.shape,
eta=eta,
quantize_x0=quantize_x0, img_callback=img_cb, mask=None, x0=z0,
temperature=temperature, noise_dropout=noise_dropout,
score_corrector=corrector, corrector_kwargs=corrector_kwargs,
x_T=x_T, log_every_t=log_every_t)
t1 = time.time()
if ddim_use_x0_pred:
sample = intermediates['pred_x0'][-1]
x_sample = model.decode_first_stage(sample)
try:
x_sample_noquant = model.decode_first_stage(sample, force_not_quantize=True)
log["sample_noquant"] = x_sample_noquant
log["sample_diff"] = torch.abs(x_sample_noquant - x_sample)
except:
pass
log["sample"] = x_sample
log["time"] = t1 - t0
return log
sr_diffMode = 'superresolution'
sr_model = get_model('superresolution')
def do_superres(img, filepath):
if args.sharpen_preset == 'Faster':
sr_diffusion_steps = "25"
sr_pre_downsample = '1/2'
if args.sharpen_preset == 'Fast':
sr_diffusion_steps = "100"
sr_pre_downsample = '1/2'
if args.sharpen_preset == 'Slow':
sr_diffusion_steps = "25"
sr_pre_downsample = 'None'
if args.sharpen_preset == 'Very Slow':
sr_diffusion_steps = "100"
sr_pre_downsample = 'None'
sr_post_downsample = 'Original Size'
sr_diffusion_steps = int(sr_diffusion_steps)
sr_eta = 1.0
sr_downsample_method = 'Lanczos'
gc.collect()
torch.cuda.empty_cache()
im_og = img
width_og, height_og = im_og.size
#Downsample Pre
if sr_pre_downsample == '1/2':
downsample_rate = 2
elif sr_pre_downsample == '1/4':
downsample_rate = 4
else:
downsample_rate = 1
width_downsampled_pre = width_og//downsample_rate
height_downsampled_pre = height_og//downsample_rate
if downsample_rate != 1:
# print(f'Downsampling from [{width_og}, {height_og}] to [{width_downsampled_pre}, {height_downsampled_pre}]')
im_og = im_og.resize((width_downsampled_pre, height_downsampled_pre), Image.LANCZOS)
# im_og.save('/content/temp.png')
# filepath = '/content/temp.png'
logs = sr_run(sr_model["model"], im_og, sr_diffMode, sr_diffusion_steps, sr_eta)
sample = logs["sample"]
sample = sample.detach().cpu()
sample = torch.clamp(sample, -1., 1.)
sample = (sample + 1.) / 2. * 255
sample = sample.numpy().astype(np.uint8)
sample = np.transpose(sample, (0, 2, 3, 1))
a = Image.fromarray(sample[0])
#Downsample Post
if sr_post_downsample == '1/2':
downsample_rate = 2
elif sr_post_downsample == '1/4':
downsample_rate = 4
else:
downsample_rate = 1
width, height = a.size
width_downsampled_post = width//downsample_rate
height_downsampled_post = height//downsample_rate
if sr_downsample_method == 'Lanczos':
aliasing = Image.LANCZOS
else:
aliasing = Image.NEAREST
if downsample_rate != 1:
# print(f'Downsampling from [{width}, {height}] to [{width_downsampled_post}, {height_downsampled_post}]')
a = a.resize((width_downsampled_post, height_downsampled_post), aliasing)
elif sr_post_downsample == 'Original Size':
# print(f'Downsampling from [{width}, {height}] to Original Size [{width_og}, {height_og}]')
a = a.resize((width_og, height_og), aliasing)
display.display(a)
a.save(filepath)
return
print(f'Processing finished!')
# + [markdown] id="CQVtY1Ixnqx4"
# # 3. Diffusion and CLIP model settings
# + id="Fpbody2NCR7w" cellView="form"
#@markdown ####**Models Settings:**
diffusion_model = "512x512_diffusion_uncond_finetune_008100" #@param ["256x256_diffusion_uncond", "512x512_diffusion_uncond_finetune_008100"]
use_secondary_model = True #@param {type: 'boolean'}
timestep_respacing = '50' # param ['25','50','100','150','250','500','1000','ddim25','ddim50', 'ddim75', 'ddim100','ddim150','ddim250','ddim500','ddim1000']
diffusion_steps = 1000 # param {type: 'number'}
use_checkpoint = True #@param {type: 'boolean'}
ViTB32 = True #@param{type:"boolean"}
ViTB16 = True #@param{type:"boolean"}
RN101 = False #@param{type:"boolean"}
RN50 = True #@param{type:"boolean"}
RN50x4 = False #@param{type:"boolean"}
RN50x16 = False #@param{type:"boolean"}
SLIPB16 = False # param{type:"boolean"}
SLIPL16 = False # param{type:"boolean"}
#@markdown If you're having issues with model downloads, check this to compare SHA's:
check_model_SHA = False #@param{type:"boolean"}
model_256_SHA = '983e3de6f95c88c81b2ca7ebb2c217933be1973b1ff058776b970f901584613a'
model_512_SHA = '9c111ab89e214862b76e1fa6a1b3f1d329b1a88281885943d2cdbe357ad57648'
model_secondary_SHA = '983e3de6f95c88c81b2ca7ebb2c217933be1973b1ff058776b970f901584613a'
model_256_link = 'https://openaipublic.blob.core.windows.net/diffusion/jul-2021/256x256_diffusion_uncond.pt'
model_512_link = 'http://batbot.tv/ai/models/guided-diffusion/512x512_diffusion_uncond_finetune_008100.pt'
model_secondary_link = 'https://v-diffusion.s3.us-west-2.amazonaws.com/secondary_model_imagenet_2.pth'
model_256_path = f'{model_path}/256x256_diffusion_uncond.pt'
model_512_path = f'{model_path}/512x512_diffusion_uncond_finetune_008100.pt'
model_secondary_path = f'{model_path}/secondary_model_imagenet_2.pth'
# Download the diffusion model
if diffusion_model == '256x256_diffusion_uncond':
if os.path.exists(model_256_path) and check_model_SHA:
print('Checking 256 Diffusion File')
with open(model_256_path,"rb") as f:
bytes = f.read()
hash = hashlib.sha256(bytes).hexdigest();
if hash == model_256_SHA:
print('256 Model SHA matches')
model_256_downloaded = True
else:
print("256 Model SHA doesn't match, redownloading...")
# !wget --continue {model_256_link} -P {model_path}
model_256_downloaded = True
elif os.path.exists(model_256_path) and not check_model_SHA or model_256_downloaded == True:
print('256 Model already downloaded, check check_model_SHA if the file is corrupt')
else:
# !wget --continue {model_256_link} -P {model_path}
model_256_downloaded = True
elif diffusion_model == '512x512_diffusion_uncond_finetune_008100':
if os.path.exists(model_512_path) and check_model_SHA:
print('Checking 512 Diffusion File')
with open(model_512_path,"rb") as f:
bytes = f.read()
hash = hashlib.sha256(bytes).hexdigest();
if hash == model_512_SHA:
print('512 Model SHA matches')
model_512_downloaded = True
else:
print("512 Model SHA doesn't match, redownloading...")
# !wget --continue {model_512_link} -P {model_path}
model_512_downloaded = True
elif os.path.exists(model_512_path) and not check_model_SHA or model_512_downloaded == True:
print('512 Model already downloaded, check check_model_SHA if the file is corrupt')
else:
# !wget --continue {model_512_link} -P {model_path}
model_512_downloaded = True
# Download the secondary diffusion model v2
if use_secondary_model == True:
if os.path.exists(model_secondary_path) and check_model_SHA:
print('Checking Secondary Diffusion File')
with open(model_secondary_path,"rb") as f:
bytes = f.read()
hash = hashlib.sha256(bytes).hexdigest();
if hash == model_secondary_SHA:
print('Secondary Model SHA matches')
model_secondary_downloaded = True
else:
print("Secondary Model SHA doesn't match, redownloading...")
# !wget --continue {model_secondary_link} -P {model_path}
model_secondary_downloaded = True
elif os.path.exists(model_secondary_path) and not check_model_SHA or model_secondary_downloaded == True:
print('Secondary Model already downloaded, check check_model_SHA if the file is corrupt')
else:
# !wget --continue {model_secondary_link} -P {model_path}
model_secondary_downloaded = True
model_config = model_and_diffusion_defaults()
if diffusion_model == '512x512_diffusion_uncond_finetune_008100':
model_config.update({
'attention_resolutions': '32, 16, 8',
'class_cond': False,
'diffusion_steps': diffusion_steps,
'rescale_timesteps': True,
'timestep_respacing': timestep_respacing,
'image_size': 512,
'learn_sigma': True,
'noise_schedule': 'linear',
'num_channels': 256,
'num_head_channels': 64,
'num_res_blocks': 2,
'resblock_updown': True,
'use_checkpoint': use_checkpoint,
'use_fp16': True,
'use_scale_shift_norm': True,
})
elif diffusion_model == '256x256_diffusion_uncond':
model_config.update({
'attention_resolutions': '32, 16, 8',
'class_cond': False,
'diffusion_steps': diffusion_steps,
'rescale_timesteps': True,
'timestep_respacing': timestep_respacing,
'image_size': 256,
'learn_sigma': True,
'noise_schedule': 'linear',
'num_channels': 256,
'num_head_channels': 64,
'num_res_blocks': 2,
'resblock_updown': True,
'use_checkpoint': use_checkpoint,
'use_fp16': True,
'use_scale_shift_norm': True,
})
secondary_model_ver = 2
model_default = model_config['image_size']
if secondary_model_ver == 2:
secondary_model = SecondaryDiffusionImageNet2()
secondary_model.load_state_dict(torch.load(f'{model_path}/secondary_model_imagenet_2.pth', map_location='cpu'))
secondary_model.eval().requires_grad_(False).to(device)
clip_models = []
if ViTB32 is True: clip_models.append(clip.load('ViT-B/32', jit=False)[0].eval().requires_grad_(False).to(device))
if ViTB16 is True: clip_models.append(clip.load('ViT-B/16', jit=False)[0].eval().requires_grad_(False).to(device) )
if RN50 is True: clip_models.append(clip.load('RN50', jit=False)[0].eval().requires_grad_(False).to(device))
if RN50x4 is True: clip_models.append(clip.load('RN50x4', jit=False)[0].eval().requires_grad_(False).to(device))
if RN50x16 is True: clip_models.append(clip.load('RN50x16', jit=False)[0].eval().requires_grad_(False).to(device))
if RN101 is True: clip_models.append(clip.load('RN101', jit=False)[0].eval().requires_grad_(False).to(device))
if SLIPB16:
SLIPB16model = SLIP_VITB16(ssl_mlp_dim=4096, ssl_emb_dim=256)
if not os.path.exists(f'{model_path}/slip_base_100ep.pt'):
# !wget https://dl.fbaipublicfiles.com/slip/slip_base_100ep.pt -P {model_path}
sd = torch.load(f'{model_path}/slip_base_100ep.pt')
real_sd = {}
for k, v in sd['state_dict'].items():
real_sd['.'.join(k.split('.')[1:])] = v
del sd
SLIPB16model.load_state_dict(real_sd)
SLIPB16model.requires_grad_(False).eval().to(device)
clip_models.append(SLIPB16model)
if SLIPL16:
SLIPL16model = SLIP_VITL16(ssl_mlp_dim=4096, ssl_emb_dim=256)
if not os.path.exists(f'{model_path}/slip_large_100ep.pt'):
# !wget https://dl.fbaipublicfiles.com/slip/slip_large_100ep.pt -P {model_path}
sd = torch.load(f'{model_path}/slip_large_100ep.pt')
real_sd = {}
for k, v in sd['state_dict'].items():
real_sd['.'.join(k.split('.')[1:])] = v
del sd
SLIPL16model.load_state_dict(real_sd)
SLIPL16model.requires_grad_(False).eval().to(device)
clip_models.append(SLIPL16model)
normalize = T.Normalize(mean=[0.48145466, 0.4578275, 0.40821073], std=[0.26862954, 0.26130258, 0.27577711])
lpips_model = lpips.LPIPS(net='vgg').to(device)
# + [markdown] id="kjtsXaszn-bB"
# # 4. Settings
# + id="U0PwzFZbLfcy" cellView="form"
#@markdown ####**Basic Settings:**
batch_name = 'TimeToDisco' #@param{type: 'string'}
steps = 250 #@param [25,50,100,150,250,500,1000]{type: 'raw', allow-input: true}
width_height = [1280, 768]#@param{type: 'raw'}
clip_guidance_scale = 5000 #@param{type: 'number'}
tv_scale = 0#@param{type: 'number'}
range_scale = 150#@param{type: 'number'}
sat_scale = 0#@param{type: 'number'}
cutn_batches = 4 #@param{type: 'number'}
skip_augs = False#@param{type: 'boolean'}
#@markdown ---
#@markdown ####**Init Settings:**
init_image = None #@param{type: 'string'}
init_scale = 1000 #@param{type: 'integer'}
skip_steps = 0 #@param{type: 'integer'}
#Get corrected sizes
side_x = (width_height[0]//64)*64;
side_y = (width_height[1]//64)*64;
if side_x != width_height[0] or side_y != width_height[1]:
print(f'Changing output size to {side_x}x{side_y}. Dimensions must by multiples of 64.')
#Update Model Settings
timestep_respacing = f'ddim{steps}'
diffusion_steps = (1000//steps)*steps if steps < 1000 else steps
model_config.update({
'timestep_respacing': timestep_respacing,
'diffusion_steps': diffusion_steps,
})
#Make folder for batch
batchFolder = f'{outDirPath}/{batch_name}'
createPath(batchFolder)
# + [markdown] id="CnkTNXJAPzL2"
# ###Animation Settings
# + cellView="form" id="djPY2_4kHgV2"
#@markdown ####**Animation Mode:**
animation_mode = "None" #@param['None', '2D', 'Video Input']
#@markdown *For animation, you probably want to turn `cutn_batches` to 1 to make it quicker.*
#@markdown ---
#@markdown ####**Video Input Settings:**
video_init_path = "/content/training.mp4" #@param {type: 'string'}
extract_nth_frame = 2 #@param {type:"number"}
if animation_mode == "Video Input":
videoFramesFolder = f'/content/videoFrames'
createPath(videoFramesFolder)
print(f"Exporting Video Frames (1 every {extract_nth_frame})...")
try:
# !rm {videoFramesFolder}/*.jpg
except:
print('')
vf = f'"select=not(mod(n\,{extract_nth_frame}))"'
# !ffmpeg -i {video_init_path} -vf {vf} -vsync vfr -q:v 2 -loglevel error -stats {videoFramesFolder}/%04d.jpg
#@markdown ---
#@markdown ####**2D Animation Settings:**
#@markdown `zoom` is a multiplier of dimensions, 1 is no zoom.
key_frames = True #@param {type:"boolean"}
max_frames = 10000#@param {type:"number"}
if animation_mode == "Video Input":
max_frames = len(glob(f'{videoFramesFolder}/*.jpg'))
interp_spline = 'Linear' #Do not change, currently will not look good. param ['Linear','Quadratic','Cubic']{type:"string"}
angle = "0:(0)"#@param {type:"string"}
zoom = "0: (1), 10: (1.05)"#@param {type:"string"}
translation_x = "0: (0)"#@param {type:"string"}
translation_y = "0: (0)"#@param {type:"string"}
#@markdown ---
#@markdown ####**Coherency Settings:**
#@markdown `frame_scale` tries to guide the new frame to looking like the old one. A good default is 1500.
frames_scale = 1500 #@param{type: 'integer'}
#@markdown `frame_skip_steps` will blur the previous frame - higher values will flicker less but struggle to add enough new detail to zoom into.
frames_skip_steps = '60%' #@param ['40%', '50%', '60%', '70%', '80%'] {type: 'string'}
def parse_key_frames(string, prompt_parser=None):
"""Given a string representing frame numbers paired with parameter values at that frame,
return a dictionary with the frame numbers as keys and the parameter values as the values.
Parameters
----------
string: string
Frame numbers paired with parameter values at that frame number, in the format
'framenumber1: (parametervalues1), framenumber2: (parametervalues2), ...'
prompt_parser: function or None, optional
If provided, prompt_parser will be applied to each string of parameter values.
Returns
-------
dict
Frame numbers as keys, parameter values at that frame number as values
Raises
------
RuntimeError
If the input string does not match the expected format.
Examples
--------
>>> parse_key_frames("10:(Apple: 1| Orange: 0), 20: (Apple: 0| Orange: 1| Peach: 1)")
{10: 'Apple: 1| Orange: 0', 20: 'Apple: 0| Orange: 1| Peach: 1'}
>>> parse_key_frames("10:(Apple: 1| Orange: 0), 20: (Apple: 0| Orange: 1| Peach: 1)", prompt_parser=lambda x: x.lower()))
{10: 'apple: 1| orange: 0', 20: 'apple: 0| orange: 1| peach: 1'}
"""
import re
pattern = r'((?P<frame>[0-9]+):[\s]*[\(](?P<param>[\S\s]*?)[\)])'
frames = dict()
for match_object in re.finditer(pattern, string):
frame = int(match_object.groupdict()['frame'])
param = match_object.groupdict()['param']
if prompt_parser:
frames[frame] = prompt_parser(param)
else:
frames[frame] = param
if frames == {} and len(string) != 0:
raise RuntimeError('Key Frame string not correctly formatted')
return frames
def get_inbetweens(key_frames, integer=False):
"""Given a dict with frame numbers as keys and a parameter value as values,
return a pandas Series containing the value of the parameter at every frame from 0 to max_frames.
Any values not provided in the input dict are calculated by linear interpolation between
the values of the previous and next provided frames. If there is no previous provided frame, then
the value is equal to the value of the next provided frame, or if there is no next provided frame,
then the value is equal to the value of the previous provided frame. If no frames are provided,
all frame values are NaN.
Parameters
----------
key_frames: dict
A dict with integer frame numbers as keys and numerical values of a particular parameter as values.
integer: Bool, optional
If True, the values of the output series are converted to integers.
Otherwise, the values are floats.
Returns
-------
pd.Series
A Series with length max_frames representing the parameter values for each frame.
Examples
--------
>>> max_frames = 5
>>> get_inbetweens({1: 5, 3: 6})
0 5.0
1 5.0
2 5.5
3 6.0
4 6.0
dtype: float64
>>> get_inbetweens({1: 5, 3: 6}, integer=True)
0 5
1 5
2 5
3 6
4 6
dtype: int64
"""
key_frame_series = pd.Series([np.nan for a in range(max_frames)])
for i, value in key_frames.items():
key_frame_series[i] = value
key_frame_series = key_frame_series.astype(float)
interp_method = interp_spline
if interp_method == 'Cubic' and len(key_frames.items()) <=3:
interp_method = 'Quadratic'
if interp_method == 'Quadratic' and len(key_frames.items()) <= 2:
interp_method = 'Linear'
key_frame_series[0] = key_frame_series[key_frame_series.first_valid_index()]
key_frame_series[max_frames-1] = key_frame_series[key_frame_series.last_valid_index()]
# key_frame_series = key_frame_series.interpolate(method=intrp_method,order=1, limit_direction='both')
key_frame_series = key_frame_series.interpolate(method=interp_method.lower(),limit_direction='both')
if integer:
return key_frame_series.astype(int)
return key_frame_series
def split_prompts(prompts):
prompt_series = pd.Series([np.nan for a in range(max_frames)])
for i, prompt in prompts.items():
prompt_series[i] = prompt
# prompt_series = prompt_series.astype(str)
prompt_series = prompt_series.ffill().bfill()
return prompt_series
if key_frames:
try:
angle_series = get_inbetweens(parse_key_frames(angle))
except RuntimeError as e:
print(
"WARNING: You have selected to use key frames, but you have not "
"formatted `angle` correctly for key frames.\n"
"Attempting to interpret `angle` as "
f'"0: ({angle})"\n'
"Please read the instructions to find out how to use key frames "
"correctly.\n"
)
angle = f"0: ({angle})"
angle_series = get_inbetweens(parse_key_frames(angle))
try:
zoom_series = get_inbetweens(parse_key_frames(zoom))
except RuntimeError as e:
print(
"WARNING: You have selected to use key frames, but you have not "
"formatted `zoom` correctly for key frames.\n"
"Attempting to interpret `zoom` as "
f'"0: ({zoom})"\n'
"Please read the instructions to find out how to use key frames "
"correctly.\n"
)
zoom = f"0: ({zoom})"
zoom_series = get_inbetweens(parse_key_frames(zoom))
try:
translation_x_series = get_inbetweens(parse_key_frames(translation_x))
except RuntimeError as e:
print(
"WARNING: You have selected to use key frames, but you have not "
"formatted `translation_x` correctly for key frames.\n"
"Attempting to interpret `translation_x` as "
f'"0: ({translation_x})"\n'
"Please read the instructions to find out how to use key frames "
"correctly.\n"
)
translation_x = f"0: ({translation_x})"
translation_x_series = get_inbetweens(parse_key_frames(translation_x))
try:
translation_y_series = get_inbetweens(parse_key_frames(translation_y))
except RuntimeError as e:
print(
"WARNING: You have selected to use key frames, but you have not "
"formatted `translation_y` correctly for key frames.\n"
"Attempting to interpret `translation_y` as "
f'"0: ({translation_y})"\n'
"Please read the instructions to find out how to use key frames "
"correctly.\n"
)
translation_y = f"0: ({translation_y})"
translation_y_series = get_inbetweens(parse_key_frames(translation_y))
else:
angle = float(angle)
zoom = float(zoom)
translation_x = float(translation_x)
translation_y = float(translation_y)
# + [markdown] id="u1VHzHvNx5fd"
# ### Extra Settings
# Partial Saves, Diffusion Sharpening, Advanced Settings, Cutn Scheduling
# + id="lCLMxtILyAHA" cellView="form"
#@markdown ####**Saving:**
intermediate_saves = 0#@param{type: 'raw'}
intermediates_in_subfolder = True #@param{type: 'boolean'}
#@markdown Intermediate steps will save a copy at your specified intervals. You can either format it as a single integer or a list of specific steps
#@markdown A value of `2` will save a copy at 33% and 66%. 0 will save none.
#@markdown A value of `[5, 9, 34, 45]` will save at steps 5, 9, 34, and 45. (Make sure to include the brackets)
if type(intermediate_saves) is not list:
if intermediate_saves:
steps_per_checkpoint = math.floor((steps - skip_steps - 1) // (intermediate_saves+1))
steps_per_checkpoint = steps_per_checkpoint if steps_per_checkpoint > 0 else 1
print(f'Will save every {steps_per_checkpoint} steps')
else:
steps_per_checkpoint = steps+10
else:
steps_per_checkpoint = None
if intermediate_saves and intermediates_in_subfolder is True:
partialFolder = f'{batchFolder}/partials'
createPath(partialFolder)
#@markdown ---
#@markdown ####**SuperRes Sharpening:**
#@markdown *Sharpen each image using latent-diffusion. Does not run in animation mode. `keep_unsharp` will save both versions.*
sharpen_preset = 'Off' #@param ['Off', 'Faster', 'Fast', 'Slow', 'Very Slow']
keep_unsharp = True #@param{type: 'boolean'}
if sharpen_preset != 'Off' and keep_unsharp is True:
unsharpenFolder = f'{batchFolder}/unsharpened'
createPath(unsharpenFolder)
#@markdown ---
#@markdown ####**Advanced Settings:**
#@markdown *There are a few extra advanced settings available if you double click this cell.*
#@markdown *Perlin init will replace your init, so uncheck if using one.*
perlin_init = False #@param{type: 'boolean'}
perlin_mode = 'mixed' #@param ['mixed', 'color', 'gray']
set_seed = 'random_seed' #@param{type: 'string'}
eta = 0.8#@param{type: 'number'}
clamp_grad = True #@param{type: 'boolean'}
clamp_max = 0.05 #@param{type: 'number'}
### EXTRA ADVANCED SETTINGS:
randomize_class = True
clip_denoised = False
fuzzy_prompt = False
rand_mag = 0.05
#@markdown ---
#@markdown ####**Cutn Scheduling:**
#@markdown Format: `[40]*400+[20]*600` = 40 cuts for the first 400 /1000 steps, then 20 for the last 600/1000
#@markdown cut_overview and cut_innercut are cumulative for total cutn on any given step. Overview cuts see the entire image and are good for early structure, innercuts are your standard cutn.
cut_overview = "[12]*400+[4]*600" #@param {type: 'string'}
cut_innercut ="[4]*400+[12]*600"#@param {type: 'string'}
cut_ic_pow = 1#@param {type: 'number'}
cut_icgray_p = "[0.2]*400+[0]*600"#@param {type: 'string'}
# + [markdown] id="XIwh5RvNpk4K"
# ###Prompts
# `animation_mode: None` will only use the first set. `animation_mode: 2D / Video` will run through them per the set frames and hold on the last one.
# + id="BGBzhk3dpcGO"
text_prompts = {
0: ["A beautiful painting of a singular lighthouse, shining its light across a tumultuous sea of blood by <NAME> and thomas kinkade, Trending on artstation."],
# 100: ["This set of prompts start at frame 100", "This prompt has weight five:5"],
}
image_prompts = {
# 0:['ImagePromptsWorkButArentVeryGood.png:2',],
}
# + [markdown] id="Nf9hTc8YLoLx"
# # 5. Diffuse!
# + id="LHLiO56OfwgD" cellView="form"
#@title Do the Run!
#@markdown `n_batches` ignored with animation modes.
display_rate = 50 #@param{type: 'number'}
n_batches = 1 #@param{type: 'number'}
batch_size = 1
#@markdown ---
resume_run = False #@param{type: 'boolean'}
run_to_resume = 'latest' #@param{type: 'string'}
resume_from_frame = 'latest' #@param{type: 'string'}
retain_overwritten_frames = False #@param{type: 'boolean'}
if retain_overwritten_frames is True:
retainFolder = f'{batchFolder}/retained'
createPath(retainFolder)
skip_step_ratio = int(frames_skip_steps.rstrip("%")) / 100
calc_frames_skip_steps = math.floor(steps * skip_step_ratio)
if steps <= calc_frames_skip_steps:
sys.exit("ERROR: You can't skip more steps than your total steps")
if resume_run:
if run_to_resume == 'latest':
try:
batchNum
except:
batchNum = len(glob(f"{batchFolder}/{batch_name}(*)_settings.txt"))-1
else:
batchNum = int(run_to_resume)
if resume_from_frame == 'latest':
start_frame = len(glob(batchFolder+f"/{batch_name}({batchNum})_*.png"))
else:
start_frame = int(resume_from_frame)+1
if retain_overwritten_frames is True:
existing_frames = len(glob(batchFolder+f"/{batch_name}({batchNum})_*.png"))
frames_to_save = existing_frames - start_frame
print(f'Moving {frames_to_save} frames to the Retained folder')
move_files(start_frame, existing_frames, batchFolder, retainFolder)
else:
start_frame = 0
batchNum = len(glob(batchFolder+"/*.txt"))
while path.isfile(f"{batchFolder}/{batch_name}({batchNum})_settings.txt") is True or path.isfile(f"{batchFolder}/{batch_name}-{batchNum}_settings.txt") is True:
batchNum += 1
print(f'Starting Run: {batch_name}({batchNum}) at frame {start_frame}')
if set_seed == 'random_seed':
random.seed()
seed = random.randint(0, 2**32)
# print(f'Using seed: {seed}')
else:
seed = int(set_seed)
args = {
'batchNum': batchNum,
'prompts_series':split_prompts(text_prompts) if text_prompts else None,
'image_prompts_series':split_prompts(image_prompts) if image_prompts else None,
'seed': seed,
'display_rate':display_rate,
'n_batches':n_batches if animation_mode == 'None' else 1,
'batch_size':batch_size,
'batch_name': batch_name,
'steps': steps,
'width_height': width_height,
'clip_guidance_scale': clip_guidance_scale,
'tv_scale': tv_scale,
'range_scale': range_scale,
'sat_scale': sat_scale,
'cutn_batches': cutn_batches,
'init_image': init_image,
'init_scale': init_scale,
'skip_steps': skip_steps,
'sharpen_preset': sharpen_preset,
'keep_unsharp': keep_unsharp,
'side_x': side_x,
'side_y': side_y,
'timestep_respacing': timestep_respacing,
'diffusion_steps': diffusion_steps,
'animation_mode': animation_mode,
'video_init_path': video_init_path,
'extract_nth_frame': extract_nth_frame,
'key_frames': key_frames,
'max_frames': max_frames if animation_mode != "None" else 1,
'interp_spline': interp_spline,
'start_frame': start_frame,
'angle': angle,
'zoom': zoom,
'translation_x': translation_x,
'translation_y': translation_y,
'angle_series':angle_series,
'zoom_series':zoom_series,
'translation_x_series':translation_x_series,
'translation_y_series':translation_y_series,
'frames_scale': frames_scale,
'calc_frames_skip_steps': calc_frames_skip_steps,
'skip_step_ratio': skip_step_ratio,
'calc_frames_skip_steps': calc_frames_skip_steps,
'text_prompts': text_prompts,
'image_prompts': image_prompts,
'cut_overview': eval(cut_overview),
'cut_innercut': eval(cut_innercut),
'cut_ic_pow': cut_ic_pow,
'cut_icgray_p': eval(cut_icgray_p),
'intermediate_saves': intermediate_saves,
'intermediates_in_subfolder': intermediates_in_subfolder,
'steps_per_checkpoint': steps_per_checkpoint,
'perlin_init': perlin_init,
'perlin_mode': perlin_mode,
'set_seed': set_seed,
'eta': eta,
'clamp_grad': clamp_grad,
'clamp_max': clamp_max,
'skip_augs': skip_augs,
'randomize_class': randomize_class,
'clip_denoised': clip_denoised,
'fuzzy_prompt': fuzzy_prompt,
'rand_mag': rand_mag,
}
args = SimpleNamespace(**args)
print('Prepping model...')
model, diffusion = create_model_and_diffusion(**model_config)
model.load_state_dict(torch.load(f'{model_path}/{diffusion_model}.pt', map_location='cpu'))
model.requires_grad_(False).eval().to(device)
for name, param in model.named_parameters():
if 'qkv' in name or 'norm' in name or 'proj' in name:
param.requires_grad_()
if model_config['use_fp16']:
model.convert_to_fp16()
gc.collect()
torch.cuda.empty_cache()
try:
do_run()
except KeyboardInterrupt:
pass
finally:
print('Seed used:', seed)
gc.collect()
torch.cuda.empty_cache()
# + [markdown] id="EZUg3bfzazgW"
# # 6. Create the video
# + cellView="form" id="HV54fuU3pMzJ"
# @title ### **Create video**
#@markdown Video file will save in the same folder as your images.
skip_video_for_run_all = True #@param {type: 'boolean'}
if skip_video_for_run_all == False:
# import subprocess in case this cell is run without the above cells
import subprocess
from base64 import b64encode
latest_run = batchNum
folder = batch_name #@param
run = latest_run #@param
final_frame = 'final_frame'
init_frame = 1#@param {type:"number"} This is the frame where the video will start
last_frame = final_frame#@param {type:"number"} You can change i to the number of the last frame you want to generate. It will raise an error if that number of frames does not exist.
fps = 12#@param {type:"number"}
view_video_in_cell = False #@param {type: 'boolean'}
frames = []
# tqdm.write('Generating video...')
if last_frame == 'final_frame':
last_frame = len(glob(batchFolder+f"/{folder}({run})_*.png"))
print(f'Total frames: {last_frame}')
image_path = f"{outDirPath}/{folder}/{folder}({run})_%04d.png"
filepath = f"{outDirPath}/{folder}/{folder}({run}).mp4"
cmd = [
'ffmpeg',
'-y',
'-vcodec',
'png',
'-r',
str(fps),
'-start_number',
str(init_frame),
'-i',
image_path,
'-frames:v',
str(last_frame+1),
'-c:v',
'libx264',
'-vf',
f'fps={fps}',
'-pix_fmt',
'yuv420p',
'-crf',
'17',
'-preset',
'veryslow',
filepath
]
process = subprocess.Popen(cmd, cwd=f'{batchFolder}', stdout=subprocess.PIPE, stderr=subprocess.PIPE)
stdout, stderr = process.communicate()
if process.returncode != 0:
print(stderr)
raise RuntimeError(stderr)
else:
print("The video is ready")
if view_video_in_cell:
mp4 = open(filepath,'rb').read()
data_url = "data:video/mp4;base64," + b64encode(mp4).decode()
display.HTML("""
<video width=400 controls>
<source src="%s" type="video/mp4">
</video>
""" % data_url)
|
Copy_of_Disco_Diffusion_v4_1_[w_Video_Inits,_Recovery_&_DDIM_Sharpen].ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import time
import csv
import numpy as np
import torch
import torch.nn.parallel
import torch.optim
import models
import utils
from PIL import Image
import matplotlib.pyplot as plt
# -
checkpoint = torch.load('./mobilenet-nnconv5dw-skipadd-pruned.pth.tar',map_location=torch.device('cpu'))
if type(checkpoint) is dict:
start_epoch = checkpoint['epoch']
best_result = checkpoint['best_result']
model = checkpoint['model']
else:
start_epoch = 0
model = checkpoint
def loadimg(filepath):
img = Image.open(filepath).convert('RGB').resize((224,224),Image.NEAREST)
img = np.asarray(img).astype('float')
img /= 255.0
img = np.expand_dims(img,axis=0)
img = np.transpose(img, (0,3, 1, 2))
return torch.from_numpy(img).float().to('cpu')
img = loadimg('./examples/IMG_2148.png')
with torch.no_grad():
pred = model(img)
pred[0][0]
result = pred[0][0].numpy()
np.min(result)
# +
from mpl_toolkits.mplot3d import Axes3D
# generate some sample data
import scipy.misc
# create the x and y coordinate arrays (here we just use pixel indices)
xx, yy = np.mgrid[0:result.shape[0], 0:result.shape[1]]
# create the figure
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot_surface(xx, yy, result ,rstride=1, cstride=1, cmap=plt.cm.gray,
linewidth=0)
# show it
plt.show()
# -
|
fastdepth.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''base'': conda)'
# language: python
# name: python3
# ---
# +
# This notebook is responsible for analysing the data collected from the spotify users's playlists and producing insights.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import spotipy
# +
# Read audio features data from csv file
audio_features = pd.read_csv('data/tracks.csv')
# Drop unnecessary columns
audio_features = audio_features.drop(columns=['uri', 'track_href', 'analysis_url', 'type', 'time_signature'])
# +
# Generate audio feature density by genre plots
sns.set(style="whitegrid")
sns.set(font_scale=1.5)
sns.displot(data=audio_features, x='danceability', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='energy', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='valence', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='instrumentalness', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='speechiness', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='acousticness', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='liveness', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='tempo', hue='genre_playlist', palette='Set2', kind='kde')
sns.displot(data=audio_features, x='duration_ms', hue='genre_playlist', palette='Set2', kind='kde')
# -
sns.heatmap(audio_features.corr())
|
MLApproach/analyser.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # How heterogeneously is the pandemic hitting the US right now?
#
# After the last post (see [here](https://dangeles.github.io/jupyter/room_safety.html#How-safe-is-95%?)), multiple people commented on the fact that the pandemic has been characterized by its enormous heterogeneity throughout the US at the state and county and probably even neighborhood level. While I'm not particularly invested in getting data down to the county level, I thought it would be useful to see how safety profiles vary if I meet, say, $n = 3$ people every day since the pandemic started$*$ among the different states.
#
# Here's the punchline: As the pandemic has progressed, it has behaved differently among the various states. When this code was first written, on November 23 2020, I would have been very safe in Vermont if I met 3 *new* people every day until this date. However, in South Dakota, despite the lateness with which the pandemic hit, by November if I had met 3 people a day from inception to November 23 2020, there is an 80% chance I bumped into at least 1 COVID positive person throughout the year. **Not good**.
#
# Note: This post only talks about the behavior of ONE individual. If everyone behaved according to the probabilities seen here, then the situation would change rapidly and the virus would spread more. In essence, this blogpost is talking about the worst-case scenario where I **have** to meet individuals every day. My safety is a function of the degree of social distancing that others are doing in addition to other factors (how early the pandemic hit, conditions on the ground, etc...). This blogpost is *not* an endorsement for not socially distancing in some states, while socially distancing in others.
#
# What this notebook shows is how different communities react differently to a virus. Some communities can *choose* to socially distance and thus maintain themselves safer for longer. Others do not have that privilege, while yet others may choose to forego it (for example, because they don't believe the virus is real). More than anything, I think this exercise shows the enormous impact that socioeconomics has on epidemiology.
#
# Finally, please bear in mind that here I am using tests to estimate the probability of encountering a COVID(+) individual at any one time. As the pandemic changes, this may or may not be a good proxy. For example, we know that the first wave in NY, around March / April 2020, was likely 10x bigger than shown by tests. So these numbers should be taken with a grain of salt. The only thing I would trust at this time is the rough rank-ordering of states, assuming their positive test rates remain more-or-less constant, a likely terribly assumption!
#
# $*$ here, the start of the pandemic is defined as normalized cases reaching $10^{-6}$
# +
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc
rc('text', usetex=True)
rc('text.latex', preamble=r'\usepackage{cmbright}')
rc('font', **{'family': 'sans-serif', 'sans-serif': ['Helvetica']})
# %matplotlib inline
# This enables SVG graphics inline.
# %config InlineBackend.figure_formats = {'png', 'retina'}
# JB's favorite Seaborn settings for notebooks
rc = {'lines.linewidth': 2,
'axes.labelsize': 18,
'axes.titlesize': 18,
'axes.facecolor': 'DFDFE5'}
sns.set_context('notebook', rc=rc)
sns.set_style("dark")
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['legend.fontsize'] = 14
# -
# ## Set up our safety function as in the previous post:
# +
n = 2
def safety(p_covid, N=n):
"""Log of probability nobody has COVID in a room full of N people"""
p = np.exp(N * np.log(1 - p_covid))
if type(p) is not float:
p[p >= 1] = 1
return p
else:
if p <= 1:
return p
else:
return 1
# -
# ## Load the NYT data and run calculations
# +
# load into a dataframe:
pop = pd.read_excel('../data/nst-est2019-01.xlsx', comment='#', header=1)
# fetch NYT data:
url = 'https://raw.githubusercontent.com/nytimes/covid-19-data/master/us-states.csv'
df = pd.read_csv(url, usecols=[0, 1, 3, 4], parse_dates=['date'], squeeze=True)
pop.columns = np.append(np.array(['state']), pop.columns[1:].values)
pop.state = pop.state.str.strip('.')
# merge dfs:
df = df.merge(pop, left_on='state', right_on='state')
# calculate per population numbers:
df['normedPopCases'] = df.cases/ df[2019]
# drop days where normalized cases aren't high enough:
df = df[df.normedPopCases > 10 ** -6]
# generate smoothed prob of encountering a COVID + individual on any one day:
probs = df.groupby('state').normedPopCases.rolling(window=7, win_type='gaussian',
center=False).mean(std=2).diff(
).rolling(10).agg(np.sum
).reset_index().rename(
columns={'normedPopCases': 'pCOVID'})
# get our safety function:
probs['safety'] = probs.groupby('state').pCOVID.apply(safety)
# get cumulative safety to date:
probs['cumprob'] = probs.groupby('state').safety.cumprod()
# find best and worst states:
worst = probs[probs.cumprob == probs.groupby('state').apply(np.min).cumprob.min()].state.values[0]
best = probs[probs.cumprob == probs.groupby('state').apply(np.min).cumprob.max()].state.values[0]
# get cases assuming US is homogeneous:
cases = df.groupby('date').agg(np.sum).cases.rolling(window=7, win_type='gaussian',
center=False).mean(std=2).diff(
).rolling(10).agg(np.sum) / pop[pop.state == 'United States'].Census.values[0]
total = safety(cases.values, n)
# -
# # Plot daily safety levels:
# +
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(total, lw=4, color='black', label='Uniform US probability', zorder=np.inf)
for s, g in probs.groupby('state'):
if s not in ['Massachusetts', worst, best]:
plt.plot(g.safety.values, alpha=0.1, color='black', zorder=0)
else:
plt.plot(g.safety.values, alpha=1, label=s, lw=5)
plt.legend()
plt.xlabel('Days since start of pandemic (per state)')
_ = plt.ylabel('Daily Safety')
# -
# ## Plot cumulative safety levels to date:
#
# (Notice the log-y-scale)
# +
fig, ax = plt.subplots(figsize=(12, 6))
plt.plot(np.cumprod(total[~np.isnan(total)]), lw=4, color='black', label='Uniform US probability', zorder=np.inf)
for s, g in probs.groupby('state'):
if s not in ['Massachusetts', worst, best]:
plt.plot(g.cumprob.values, alpha=0.1, color='black', zorder=0)
else:
plt.plot(g.cumprob.values, alpha=1, label=s, lw=5)
plt.ylim(probs.cumprob.min() * .95, 1.05)
plt.yscale('log')
plt.legend()
plt.xlabel('Days since start of pandemic (per state)')
_ = plt.ylabel('Safety to Date')
# -
# ## Plot cumulative safety to date levels per state:
todate = probs.groupby('state').cumprob.apply(np.min).reset_index(
).rename({'cumprob': 'SafetyToDate'}, axis=1).sort_values('SafetyToDate')
fig, ax = plt.subplots(figsize=(8, 12.5))
sns.stripplot(x='SafetyToDate', y='state', data=todate)
plt.xlim(todate.SafetyToDate.min() * .8, 1)
plt.xscale('log')
_ = plt.title('Cumulative Prob of COVID contact\nmeeting {0} people / day to date'.format(n))
# Point of the story: Be aware of what communities you inhabit. Different communities, different safety profiles. Be proactively safe!
|
jupyter/social_distancing_by_state.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Conditionals Exercises
# +
number = int(input("Enter a number: "))
print("The number you entered is",number)
if number < 10:
print("This is a small number")
print("The square of this number is", number * number)
# -
# Write a program that reads in a name. If the name has more than 5 letters shortened it to 5 letters. Print out a personalised message using the shortened name if necessary.
# +
exam = int(input("what mark did you get in the exam?"))
if exam < 40:
print("You failed", end = " ")
else:
print("You passed", end = " ")
print("the exams")
# -
# Write a program that reads in a number and prints out if it is odd or even.
#
# *hint: num%2 divides num by 2 and returns the remainder*
# +
exam = int(input("Enter a temperature?"))
print("The water turned to ", end = "")
if temp > 100:
print("steam")
elif temp <= 0:
print("ice")
else:
print("liquid")
# -
# Change the program above to input a student's exam result and print out what grade they got (A,B,C,D,fail).
# Write a program that takes in a number and adds the correct suffix. For example...
#
# for 1 add st except 11 add th
# for 2 add nd except 12 add th
# for 3 add rd except 13 add th
# everythig else add th.
# Write a program to input a student's name. If the name starts with the letter 'M' and ends with the letter 'a', tell them they will be studying computing. If the name starts with a 'D' or 'T' they will be studing maths. Otherwise there is no course for them.
|
conditionals_exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="NidqB07kxzgW"
from fastai.vision.all import *
from fastai.vision.widgets import *
# + id="bhysZr6pgtzN"
# #!jupyter serverextension enable voila --user
# #!jupyter serverextension enable voila --sys-prefix
# + [markdown] id="WwsRqMnYNxmO"
# # **Application for Yoga Pose Classification**
# #### This is a project created to detect your Yoga Pose, It can classify total 10 Poses and you can know which asana you are doing.
#
# + id="DCIkndfxyh1P"
path = Path()
learn_inf = load_learner(path/'export.pkl',cpu=True)
btn_upload = widgets.FileUpload()
out_pl = widgets.Output()
lbl_pred = widgets.Label()
# + id="cODFq2mQyn2u"
def on_click(change):
img = PILImage.create(btn_upload.data[-1])
out_pl.clear_output()
with out_pl: display(img.to_thumb(128,128))
pred,pred_idx,probs = learn_inf.predict(img)
lbl_pred.value = f'Prediction: {pred}; Probability: {probs[pred_idx]:.04f}'
# + id="Bktja4bA0psW"
btn_upload.observe(on_click, names=['data'])
# + colab={"base_uri": "https://localhost:8080/", "height": 113, "referenced_widgets": ["18e48ac84fd147e386f0638124784d1f", "<KEY>", "ffa522e2ed1d4f6ca7a1c8056f3ffa32", "c5337cc135874e4b89fea7c78803dd2b", "<KEY>", "2bf3115f62b949e6896a25d53077e592", "64e62115b82e4f9f88b920cbe538c3da", "<KEY>", "<KEY>", "60ba0656c17c449c8260789772083cf9", "<KEY>", "<KEY>", "<KEY>"]} id="ivPtOdlIy80Z" outputId="bbb58ddf-9b5b-4d92-fa3b-fffae7e5a6d2"
display(VBox([widgets.Label('Upload an image of your Yoga Pose to know the asana'), btn_upload,out_pl, lbl_pred]))
# + id="cmKSUBHbap8h"
# #!pip install voila
# #!jupyter serverextension enable --sys-prefix voila
# -
|
yoga_pose_class.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.4 64-bit (''base'': conda)'
# language: python
# name: python37464bitbaseconda799c418b928447f7ab2d0aebc8459150
# ---
# + tags=[]
# %masearchotlib inline
import seaborn as sns
import matplotlib as mpl
import numpy as np
import pandas as pd
import matplotlib.ticker
import matplotlib.pyplot as plt
import pyreadr
from itca import itca, GreedySearch, bidict, compute_y_dist
from sklearn.metrics import pairwise_distances, accuracy_score
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.manifold import SpectralEmbedding
from sklearn.cluster import KMeans
from aesthetics import params
mpl.rcParams.update(params)
# + tags=[]
#========================================= Help functions ==================================================
def compute_class_centers(X, y):
num_classes = len(np.unique(y))
centers = []
for i in range(num_classes):
centers.append(np.mean(X[y==i, :], axis=0))
return centers
def compute_cluster_wise_dist(X, y, method="single", class_type="ordinal"):
"""
Compute ordinal cluster-wise distance.
"""
labels = np.unique(y)
n_classes = len(labels)
pdist_res = []
funcs = {"single": np.min, "average": np.mean, "complete": np.max}
if class_type == "ordinal":
for ind in range(n_classes - 1):
pdist = pairwise_distances(X[y==ind, :], X[y==ind + 1, :])
pdist_res.append(((ind, ind+1), funcs[method](pdist)))
elif class_type == "nominal":
for ind_i, ind_j in itertools.combinations(labels, 2):
pdist = pairwise_distances(X[y==ind_i, :], X[y==ind_j, :])
pdist_res.append(((ind_i, ind_j), funcs[method](pdist)))
return dict(pdist_res)
def combine_i_j(i, j, mapping):
"""
Combine (merged) class labels i and j in mapping.
Parameters
----------
i: int
j: int
Return
------
next_mapping: bidict
mapping that combines the class i and j
Example
-------
>>mapping = bidict({0:0, 1:1, 2:2})
>>self.combine_i_j(0, 1, mapping)
{0:0, 1:0, 2:1}
"""
next_mapping = dict()
for key in mapping.inverse:
if key < j:
next_mapping.update({e: key for e in mapping.inverse[key]})
elif key > j:
next_mapping.update({e: key - 1 for e in mapping.inverse[key]})
else:
next_mapping.update({e: i for e in mapping.inverse[key]})
return bidict(next_mapping)
def herichical_clustering(X, y, k, method="single", class_type="nominal"):
num_classes = len(np.unique(y))
path = []
y_obs = y
cur_mapping = bidict({i:i for i in range(num_classes)})
while num_classes > k:
pdist_res = compute_cluster_wise_dist(X, y_obs, class_type=class_type, method=method)
i, j = min(pdist_res, key=pdist_res.get)
cur_mapping = combine_i_j(i, j, cur_mapping)
num_classes = len(cur_mapping.inverse)
y_obs = cur_mapping.map(y)
path.append(cur_mapping)
return path
def compute_embedding(X, k):
embedding = SpectralEmbedding(n_components=k)
X_transformed = embedding.fit_transform(X)
return X_transformed
def benchmark(X, y, k):
centers = compute_class_centers(X, y)
kmeans = KMeans(n_clusters=k, random_state=0).fit(np.array(centers))
embedding = compute_embedding(X, k)
sc_centers = compute_class_centers(embedding, y)
sc = KMeans(n_clusters=k, random_state=0).fit(np.array(sc_centers))
return {"kmeans": kmeans.labels_,
"spectral": sc.labels_}
def labels_to_mapping(labels_):
return bidict({i: labels_[i] for i in range(len(labels_))})
def compute_accuracy_cv(X, y, clf, kfold=5, compute_itca = False):
kf = StratifiedKFold(n_splits=kfold, shuffle=True, random_state=42)
kf_split = kf.split(X, y)
a = []
b = []
y_dist = compute_y_dist(y)
id_mapping = bidict({i : i for i in range(np.max(y) + 1)})
for train_index, test_index in kf_split:
X_train, X_test = X[train_index], X[test_index]
y_train, y_test = y[train_index], y[test_index]
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
a.append(accuracy_score(y_test, y_pred))
if compute_itca:
b.append(itca(y_test, y_pred, id_mapping, y_dist=y_dist))
if compute_itca:
return a, b
else:
return a
def compute_best_guess(y):
y_dist = compute_y_dist(y)
return y_dist[max(y_dist, key=y_dist.get)]
# + tags=[]
## ================================ load data =================================
X = pyreadr.read_r('../data/application1/cov_casacolina.rds')[None]
Y = pyreadr.read_r('../data/application1/response_tot_casacolina.rds')[None]
X = X.drop(columns=["ComatoseAtAdmit", "DeleriousAtAdmit"])
features = pd.get_dummies(X)
features_name = list(features.columns)
response_names = list(Y.columns)
# Convert to numpy array
X = np.array(features)
labels = np.array(Y) - 1
ind_list = [0, 2, 3, 5, 9, 10, 12, 16]
for ind in ind_list:
print(response_names[ind])
# + tags=[]
def list_to_bidict(l):
k = len(l)
d = dict()
key = 0
for i in range(k):
if isinstance(l[i], tuple) :
for e in l[i]:
d[key] = i
key += 1
else:
d[key] = i
key += 1
return bidict(d)
expert_mapping = list_to_bidict([1, (2, 3, 4), 5, 6, 7])
# + tags=[]
# It takes ~20 minutes
rf = RandomForestClassifier(n_estimators = 1000, random_state = 2021, n_jobs=10)
kmeans_acc_mean = []
spectral_acc_mean = []
single_acc_mean = []
guess_v = {"itca": [], "expert": [], "single": [], "complete": [], "average": []}
acc_v = {"itca": [], #[0.5250, 0.4994, 0.5010, 0.4974, 0.5127, 0.5042, 0.5643, 0.5533],
"expert": [], #[0.5533, 0.5244, 0.6218, 0.5845, 0.5718, 0.5861, 0.5880, 0.6004],
"single": [], "complete": [], "average": []}
acc_std = {"itca": [], #[0.5250, 0.4994, 0.5010, 0.4974, 0.5127, 0.5042, 0.5643, 0.5533],
"expert": [], #[0.5533, 0.5244, 0.6218, 0.5845, 0.5718, 0.5861, 0.5880, 0.6004],
"single": [], "complete": [], "average": []}
itca_v = {"itca": [], #[0.5250, 0.4994, 0.5010, 0.4974, 0.5127, 0.5042, 0.5643, 0.5533],
"expert": [], #[0.5533, 0.5244, 0.6218, 0.5845, 0.5718, 0.5861, 0.5880, 0.6004],
"single": [], "complete": [], "average": []}
itca_std = {"itca": [], #[0.5250, 0.4994, 0.5010, 0.4974, 0.5127, 0.5042, 0.5643, 0.5533],
"expert": [], #[0.5533, 0.5244, 0.6218, 0.5845, 0.5718, 0.5861, 0.5880, 0.6004],
"single": [], "complete": [], "average": []}
itca_mappings = []
for ind in range(len(ind_list)):
y = labels[:, ind_list[ind]]
print(response_names[ind_list[ind]])
# itca
gs = GreedySearch(class_type="ordinal")
gs.search(X, y, rf, early_stop=True)
y_itca = gs.selected.mapping.map(y)
acc, it = compute_accuracy_cv(X, y_itca, rf, compute_itca=True)
acc_v["itca"].append(np.mean(acc))
acc_std["itca"].append(np.std(acc))
itca_v["itca"].append(np.mean(it))
itca_std["itca"].append(np.std(it))
guess_v["itca"].append(compute_best_guess(y_itca))
itca_mappings.append(gs.selected.mapping)
# expert
y_expert = expert_mapping.map(y)
guess_v["expert"].append(compute_best_guess(y_expert))
acc, it = compute_accuracy_cv(X, y_expert, rf, compute_itca=True)
acc_v["expert"].append(np.mean(acc))
acc_std["expert"].append(np.std(acc))
itca_v["expert"].append(np.mean(it))
itca_std["expert"].append(np.std(it))
for method in ["average"]: # single complete
method_mapping = herichical_clustering(X, y, 5, method=method, class_type="ordinal")[-1]
method_y = method_mapping.map(y)
acc = compute_accuracy_cv(X, method_y, rf)
acc_v[method].append(np.mean(acc))
acc_std[method].append(np.std(acc))
itca_v[method].append(np.mean(it))
itca_std[method].append(np.std(it))
guess_v[method].append(compute_best_guess(method_y))
# -
# ## Figure 5 Greedy-search-based and exhaustive-search-based multilayer frameworks for predicting the Toileting activity in the Casa Colina dataset.
# + tags=[]
# The figure is plotted with powerpoint.
rf = RandomForestClassifier(n_estimators = 1000, random_state=2021, n_jobs=10)
y = labels[:, ind_list[ind]]
print(response_names[ind_list[0]])
gs = GreedySearch(class_type="ordinal")
gs.search(X, y, rf, early_stop=True)
# + tags=[]
print("Greedy search selected class combination: ", gs.selected.mapping.inverse)
# -
# ## Figure 6: Prediction accuracy for the optimal level combination indicated by ITCA
# + tags=[]
# ================ plot figure ==================================
#The text is anotated by powerpoint.
nrows = 2
ncols = 4
fig, axes = plt.subplots(nrows, ncols, sharex=True, sharey=True)
ind_expert = 24
marker_size = 20
xl, yl = .15, .15
xu, yu = .85, .85
hide_text = (0, 1, 6)
names = ["itca", "expert", "average"] #["itca", "expert", "single", "complete", "average"]
#["optimal", "experts", "hierachical single", "hierachical complete", "hierachical average"]
marker_labels = ["s-ITCA", "experts", "hierachical average"]
colors = ["#d7191c", "#fdae61", '#66c2a4'] # ,'#66c2a4','#66c2a4']
marker_types = ["*", "d", "^"]
for ind in range(nrows * ncols):
ax = axes[ind // ncols, ind % ncols]
ax.set_xlim([xl, xu])
ax.set_ylim([yl, yu])
if ind >= 10:
ax.axis("off")
continue
ax.plot([xl, xu], [yl, yu], 'k--')
for inner_ind in range(len(names)):
ax.scatter(guess_v[names[inner_ind]][ind], acc_v[names[inner_ind]][ind],
marker= marker_types[inner_ind], s=marker_size, c=colors[inner_ind],
label=marker_labels[inner_ind])
ax.plot([guess_v[names[inner_ind]][ind], guess_v[names[inner_ind]][ind]],
[guess_v[names[inner_ind]][ind], acc_v[names[inner_ind]][ind]],
linestyle="-.", color="#d7191c")
# ax.errorbar(guess_v[names[inner_ind]][ind], acc_v[names[inner_ind]][ind],
# yerr=acc_std[names[inner_ind]][ind], barsabove=True, capsize=2, ecolor=colors[inner_ind])
if names[inner_ind] in ("itca", "expert", "average") and ind in hide_text:
pass
# else:
# ax.text(guess_v[names[inner_ind]][ind] - 0.04,
# (guess_v[names[inner_ind]][ind] + acc_v[names[inner_ind]][ind])/2,
# "{:.3f}".format( acc_v[names[inner_ind]][ind] - guess_v[names[inner_ind]][ind]),
# bbox=dict(facecolor='white', edgecolor='none', alpha=0.5))
ax.set_title(response_names[ind_list[ind]][8:])
if ind == 0:
ax.legend(loc="lower right")
if ind >= 4:
ax.set_xlabel("ACC (best guess)")
if ind == 0 or ind == 4:
ax.set_ylabel("ACC (RF)")
fig.set_size_inches(8.5, 4.5)
plt.tight_layout()
|
notebooks/application1_prognosis_of_TBI.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: SageMath 8.9
# language: sage
# name: sagemath
# ---
# # Eigenvectors and Eigenvalues
import numpy as np
import scipy as sp
A = np.array([[0,1,0],[0,0,1],[4,-17,8]])
eigenValues, eigenVectors =np.linalg.eig(A)
eigenValues
eigenVectors
np.poly(A)
eigenValues[0]
# +
lambdas = eigenValues * np.eye(3)
sp.linalg.null(lambdas[2]-A)
# -
|
code/eigenvalues_eigenvectors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
s = pd.Series(['a', 'd', 'a', 'a', 'b', 'b'])
s.value_counts()
s = pd.Series([1, 2, None])
s.fillna(-1)
s.dropna()
arr = np.array([5, 0, 2])
indexer = arr.argsort() # organize the values, ordred by the index they appear in
arr[indexer] # sort using indexer
|
classwork/05_03_2021/05_03_2021.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 1: Auto Correct
#
# Welcome to the first assignment of Course 2. This assignment will give you a chance to brush up on your python and probability skills. In doing so, you will implement an auto-correct system that is very effective and useful.
# ## Outline
# - [0. Overview](#0)
# - [0.1 Edit Distance](#0-1)
# - [1. Data Preprocessing](#1)
# - [1.1 Exercise 1](#ex-1)
# - [1.2 Exercise 2](#ex-2)
# - [1.3 Exercise 3](#ex-3)
# - [2. String Manipulation](#2)
# - [2.1 Exercise 4](#ex-4)
# - [2.2 Exercise 5](#ex-5)
# - [2.3 Exercise 6](#ex-6)
# - [2.4 Exercise 7](#ex-7)
# - [3. Combining the edits](#3)
# - [3.1 Exercise 8](#ex-8)
# - [3.2 Exercise 9](#ex-9)
# - [3.3 Exercise 10](#ex-10)
# - [4. Minimum Edit Distance](#4)
# - [4.1 Exercise 11](#ex-11)
# - [5. Backtrace (Optional)](#5)
# <a name='0'></a>
# ## 0. Overview
#
# You use autocorrect every day on your cell phone and computer. In this assignment, you will explore what really goes on behind the scenes. Of course, the model you are about to implement is not identical to the one used in your phone, but it is still quite good.
#
# By completing this assignment you will learn how to:
#
# - Get a word count given a corpus
# - Get a word probability in the corpus
# - Manipulate strings
# - Filter strings
# - Implement Minimum edit distance to compare strings and to help find the optimal path for the edits.
# - Understand how dynamic programming works
#
#
# Similar systems are used everywhere.
# - For example, if you type in the word **"I am lerningg"**, chances are very high that you meant to write **"learning"**, as shown in **Figure 1**.
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/auto-correct.png' alt="alternate text" width="width" height="height" style="width:300px;height:250px;" /> Figure 1 </div>
# <a name='0-1'></a>
# #### 0.1 Edit Distance
#
# In this assignment, you will implement models that correct words that are 1 and 2 edit distances away.
# - We say two words are n edit distance away from each other when we need n edits to change one word into another.
#
# An edit could consist of one of the following options:
#
# - Delete (remove a letter): ‘hat’ => ‘at, ha, ht’
# - Switch (swap 2 adjacent letters): ‘eta’ => ‘eat, tea,...’
# - Replace (change 1 letter to another): ‘jat’ => ‘hat, rat, cat, mat, ...’
# - Insert (add a letter): ‘te’ => ‘the, ten, ate, ...’
#
# You will be using the four methods above to implement an Auto-correct.
# - To do so, you will need to compute probabilities that a certain word is correct given an input.
#
# This auto-correct you are about to implement was first created by [<NAME>](https://en.wikipedia.org/wiki/Peter_Norvig) in 2007.
# - His [original article](https://norvig.com/spell-correct.html) may be a useful reference for this assignment.
#
# The goal of our spell check model is to compute the following probability:
#
# $$P(c|w) = \frac{P(w|c)\times P(c)}{P(w)} \tag{Eqn-1}$$
#
# The equation above is [Bayes Rule](https://en.wikipedia.org/wiki/Bayes%27_theorem).
# - Equation 1 says that the probability of a word being correct $P(c|w) $is equal to the probability of having a certain word $w$, given that it is correct $P(w|c)$, multiplied by the probability of being correct in general $P(C)$ divided by the probability of that word $w$ appearing $P(w)$ in general.
# - To compute equation 1, you will first import a data set and then create all the probabilities that you need using that data set.
# <a name='1'></a>
# # Part 1: Data Preprocessing
import re
from collections import Counter
import numpy as np
import pandas as pd
# As in any other machine learning task, the first thing you have to do is process your data set.
# - Many courses load in pre-processed data for you.
# - However, in the real world, when you build these NLP systems, you load the datasets and process them.
# - So let's get some real world practice in pre-processing the data!
#
# Your first task is to read in a file called **'shakespeare.txt'** which is found in your file directory. To look at this file you can go to `File ==> Open `.
# <a name='ex-1'></a>
# ### Exercise 1
# Implement the function `process_data` which
#
# 1) Reads in a corpus (text file)
#
# 2) Changes everything to lowercase
#
# 3) Returns a list of words.
# #### Options and Hints
# - If you would like more of a real-life practice, don't open the 'Hints' below (yet) and try searching the web to derive your answer.
# - If you want a little help, click on the green "General Hints" section by clicking on it with your mouse.
# - If you get stuck or are not getting the expected results, click on the green 'Detailed Hints' section to get hints for each step that you'll take to complete this function.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>General Hints</b></font>
# </summary>
# <p>
#
# General Hints to get started
# <ul>
# <li>Python <a href="https://docs.python.org/3/tutorial/inputoutput.html">input and output<a></li>
# <li>Python <a href="https://docs.python.org/3/library/re.html" >'re' documentation </a> </li>
# </ul>
# </p>
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Detailed Hints</b></font>
# </summary>
# <p>
# Detailed hints if you're stuck
# <ul>
# <li>Use 'with' syntax to read a file</li>
# <li>Decide whether to use 'read()' or 'readline(). What's the difference?</li>
# <li>Choose whether to use either str.lower() or str.lowercase(). What is the difference?</li>
# <li>Use re.findall(pattern, string)</li>
# <li>Look for the "Raw String Notation" section in the Python 're' documentation to understand the difference between r'\W', r'\W' and '\\W'. </li>
# <li>For the pattern, decide between using '\s', '\w', '\s+' or '\w+'. What do you think are the differences?</li>
# </ul>
# </p>
#
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: process_data
def process_data(file_name):
"""
Input:
A file_name which is found in your current directory. You just have to read it in.
Output:
words: a list containing all the words in the corpus (text file you read) in lower case.
"""
words = [] # return this variable correctly
### START CODE HERE ###
with open(file_name, 'r') as f:
lines = f.readlines()
for line in lines:
words.extend(re.findall(r'\w+', line.lower()))
### END CODE HERE ###
return words
# Note, in the following cell, 'words' is converted to a python `set`. This eliminates any duplicate entries.
#DO NOT MODIFY THIS CELL
word_l = process_data('shakespeare.txt')
vocab = set(word_l) # this will be your new vocabulary
print(f"The first ten words in the text are: \n{word_l[0:10]}")
print(f"There are {len(vocab)} unique words in the vocabulary.")
# #### Expected Output
# ```Python
# The first ten words in the text are:
# ['o', 'for', 'a', 'muse', 'of', 'fire', 'that', 'would', 'ascend', 'the']
# There are 6116 unique words in the vocabulary.
# ```
# <a name='ex-2'></a>
# ### Exercise 2
#
# Implement a `get_count` function that returns a dictionary
# - The dictionary's keys are words
# - The value for each word is the number of times that word appears in the corpus.
#
# For example, given the following sentence: **"I am happy because I am learning"**, your dictionary should return the following:
# <table style="width:20%">
#
# <tr>
# <td> <b>Key </b> </td>
# <td> <b>Value </b> </td>
#
#
# </tr>
# <tr>
# <td> I </td>
# <td> 2</td>
#
# </tr>
#
# <tr>
# <td>am</td>
# <td>2</td>
# </tr>
#
# <tr>
# <td>happy</td>
# <td>1</td>
# </tr>
#
# <tr>
# <td>because</td>
# <td>1</td>
# </tr>
#
# <tr>
# <td>learning</td>
# <td>1</td>
# </tr>
# </table>
#
#
# **Instructions**:
# Implement a `get_count` which returns a dictionary where the key is a word and the value is the number of times the word appears in the list.
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>Try implementing this using a for loop and a regular dictionary. This may be good practice for similar coding interview questions</li>
# <li>You can also use defaultdict instead of a regualr dictionary, along with the for loop</li>
# <li>Otherwise, to skip using a for loop, you can use Python's <a href="https://docs.python.org/3.7/library/collections.html#collections.Counter" > Counter class</a> </li>
# </ul>
# </p>
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: get_count
def get_count(word_l):
'''
Input:
word_l: a set of words representing the corpus.
Output:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
'''
word_count_dict = {} # fill this with word counts
### START CODE HERE
word_count_dict = Counter(word_l)
### END CODE HERE ###
return word_count_dict
#DO NOT MODIFY THIS CELL
word_count_dict = get_count(word_l)
print(f"There are {len(word_count_dict)} key values pairs")
print(f"The count for the word 'thee' is {word_count_dict.get('thee',0)}")
#
# #### Expected Output
# ```Python
# There are 6116 key values pairs
# The count for the word 'thee' is 240
# ```
# <a name='ex-3'></a>
# ### Exercise 3
# Given the dictionary of word counts, compute the probability that each word will appear if randomly selected from the corpus of words.
#
# $$P(w_i) = \frac{C(w_i)}{M} \tag{Eqn-2}$$
# where
#
# $C(w_i)$ is the total number of times $w_i$ appears in the corpus.
#
# $M$ is the total number of words in the corpus.
#
# For example, the probability of the word 'am' in the sentence **'I am happy because I am learning'** is:
#
# $$P(am) = \frac{C(w_i)}{M} = \frac {2}{7} \tag{Eqn-3}.$$
#
# **Instructions:** Implement `get_probs` function which gives you the probability
# that a word occurs in a sample. This returns a dictionary where the keys are words, and the value for each word is its probability in the corpus of words.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# General advice
# <ul>
# <li> Use dictionary.values() </li>
# <li> Use sum() </li>
# <li> The cardinality (number of words in the corpus should be equal to len(word_l). You will calculate this same number, but using the word count dictionary.</li>
# </ul>
#
# If you're using a for loop:
# <ul>
# <li> Use dictionary.keys() </li>
# </ul>
#
# If you're using a dictionary comprehension:
# <ul>
# <li>Use dictionary.items() </li>
# </ul>
# </p>
#
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: get_probs
def get_probs(word_count_dict):
'''
Input:
word_count_dict: The wordcount dictionary where key is the word and value is its frequency.
Output:
probs: A dictionary where keys are the words and the values are the probability that a word will occur.
'''
probs = {} # return this variable correctly
M = sum(word_count_dict.values())
### START CODE HERE ###
for word, count in word_count_dict.items():
probs[word] = count / M
### END CODE HERE ###
return probs
#DO NOT MODIFY THIS CELL
probs = get_probs(word_count_dict)
print(f"Length of probs is {len(probs)}")
print(f"P('thee') is {probs['thee']:.4f}")
# #### Expected Output
#
# ```Python
# Length of probs is 6116
# P('thee') is 0.0045
# ```
# <a name='2'></a>
# # Part 2: String Manipulations
#
# Now, that you have computed $P(w_i)$ for all the words in the corpus, you will write a few functions to manipulate strings so that you can edit the erroneous strings and return the right spellings of the words. In this section, you will implement four functions:
#
# * `delete_letter`: given a word, it returns all the possible strings that have **one character removed**.
# * `switch_letter`: given a word, it returns all the possible strings that have **two adjacent letters switched**.
# * `replace_letter`: given a word, it returns all the possible strings that have **one character replaced by another different letter**.
# * `insert_letter`: given a word, it returns all the possible strings that have an **additional character inserted**.
#
# #### List comprehensions
#
# String and list manipulation in python will often make use of a python feature called [list comprehensions](https://docs.python.org/3/tutorial/datastructures.html#list-comprehensions). The routines below will be described as using list comprehensions, but if you would rather implement them in another way, you are free to do so as long as the result is the same. Further, the following section will provide detailed instructions on how to use list comprehensions and how to implement the desired functions. If you are a python expert, feel free to skip the python hints and move to implementing the routines directly.
# Python List Comprehensions embed a looping structure inside of a list declaration, collapsing many lines of code into a single line. If you are not familiar with them, they seem slightly out of order relative to for loops.
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/GenericListComp3.PNG' alt="alternate text" width="width" height="height" style="width:800px;height:400px;"/> Figure 2 </div>
# The diagram above shows that the components of a list comprehension are the same components you would find in a typical for loop that appends to a list, but in a different order. With that in mind, we'll continue the specifics of this assignment. We will be very descriptive for the first function, `deletes()`, and less so in later functions as you become familiar with list comprehensions.
# <a name='ex-4'></a>
# ### Exercise 4
#
# **Instructions for delete_letter():** Implement a `delete_letter()` function that, given a word, returns a list of strings with one character deleted.
#
# For example, given the word **nice**, it would return the set: {'ice', 'nce', 'nic', 'nie'}.
#
# **Step 1:** Create a list of 'splits'. This is all the ways you can split a word into Left and Right: For example,
# 'nice is split into : `[('', 'nice'), ('n', 'ice'), ('ni', 'ce'), ('nic', 'e'), ('nice', '')]`
# This is common to all four functions (delete, replace, switch, insert).
#
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/Splits1.PNG' alt="alternate text" width="width" height="height" style="width:650px;height:200px;" /> Figure 3 </div>
# **Step 2:** This is specific to `delete_letter`. Here, we are generating all words that result from deleting one character.
# This can be done in a single line with a list comprehension. You can make use of this type of syntax:
# `[f(a,b) for a, b in splits if condition]`
#
# For our 'nice' example you get:
# ['ice', 'nce', 'nie', 'nic']
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/ListComp2.PNG' alt="alternate text" width="width" height="height" style="width:550px;height:300px;" /> Figure 4 </div>
# #### Levels of assistance
#
# Try this exercise with these levels of assistance.
# - We hope that this will make it both a meaningful experience but also not a frustrating experience.
# - Start with level 1, then move onto level 2, and 3 as needed.
#
# - Level 1. Try to think this through and implement this yourself.
# - Level 2. Click on the "Level 2 Hints" section for some hints to get started.
# - Level 3. If you would prefer more guidance, please click on the "Level 3 Hints" cell for step by step instructions.
#
# - If you are still stuck, look at the images in the "list comprehensions" section above.
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Level 2 Hints</b></font>
# </summary>
# <p>
# <ul>
# <li><a href="" > Use array slicing like my_string[0:2] </a> </li>
# <li><a href="" > Use list comprehensions or for loops </a> </li>
# </ul>
# </p>
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Level 3 Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>splits: Use array slicing, like my_str[0:2], to separate a string into two pieces.</li>
# <li>Do this in a loop or list comprehension, so that you have a list of tuples.
# <li> For example, "cake" can get split into "ca" and "ke". They're stored in a tuple ("ca","ke"), and the tuple is appended to a list. We'll refer to these as L and R, so the tuple is (L,R)</li>
# <li>When choosing the range for your loop, if you input the word "cans" and generate the tuple ('cans',''), make sure to include an if statement to check the length of that right-side string (R) in the tuple (L,R) </li>
# <li>deletes: Go through the list of tuples and combine the two strings together. You can use the + operator to combine two strings</li>
# <li>When combining the tuples, make sure that you leave out a middle character.</li>
# <li>Use array slicing to leave out the first character of the right substring.</li>
# </ul>
# </p>
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: deletes
def delete_letter(word, verbose=False):
'''
Input:
word: the string/word for which you will generate all possible words
in the vocabulary which have 1 missing character
Output:
delete_l: a list of all possible strings obtained by deleting 1 character from word
'''
delete_l = []
split_l = []
### START CODE HERE ###
split_l = [(word[:i], word[i:]) for i in range(len(word) + 1)]
delete_l = [L + R[1:] for L, R in split_l if R]
### END CODE HERE ###
if verbose: print(f"input word {word}, \nsplit_l = {split_l}, \ndelete_l = {delete_l}")
return delete_l
delete_word_l = delete_letter(word="cans",
verbose=True)
# #### Expected Output
# ```CPP
# Note: You might get a slightly different result with split_l
#
# input word cans,
# split_l = [('', 'cans'), ('c', 'ans'), ('ca', 'ns'), ('can', 's')],
# delete_l = ['ans', 'cns', 'cas', 'can']
# ```
# #### Note 1
# - Notice how it has the extra tuple `('cans', '')`.
# - This will be fine as long as you have checked the size of the right-side substring in tuple (L,R).
# - Can you explain why this will give you the same result for the list of deletion strings (delete_l)?
#
# ```CPP
# input word cans,
# split_l = [('', 'cans'), ('c', 'ans'), ('ca', 'ns'), ('can', 's'), ('cans', '')],
# delete_l = ['ans', 'cns', 'cas', 'can']
# ```
# #### Note 2
# If you end up getting the same word as your input word, like this:
#
# ```Python
# input word cans,
# split_l = [('', 'cans'), ('c', 'ans'), ('ca', 'ns'), ('can', 's'), ('cans', '')],
# delete_l = ['ans', 'cns', 'cas', 'can', 'cans']
# ```
#
# - Check how you set the `range`.
# - See if you check the length of the string on the right-side of the split.
# test # 2
print(f"Number of outputs of delete_letter('at') is {len(delete_letter('at'))}")
# #### Expected output
#
# ```CPP
# Number of outputs of delete_letter('at') is 2
# ```
# <a name='ex-5'></a>
# ### Exercise 5
#
# **Instructions for switch_letter()**: Now implement a function that switches two letters in a word. It takes in a word and returns a list of all the possible switches of two letters **that are adjacent to each other**.
# - For example, given the word 'eta', it returns {'eat', 'tea'}, but does not return 'ate'.
#
# **Step 1:** is the same as in delete_letter()
# **Step 2:** A list comprehension or for loop which forms strings by swapping adjacent letters. This is of the form:
# `[f(L,R) for L, R in splits if condition]` where 'condition' will test the length of R in a given iteration. See below.
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/Switches1.PNG' alt="alternate text" width="width" height="height" style="width:600px;height:200px;"/> Figure 5 </div>
# #### Levels of difficulty
#
# Try this exercise with these levels of difficulty.
# - Level 1. Try to think this through and implement this yourself.
# - Level 2. Click on the "Level 2 Hints" section for some hints to get started.
# - Level 3. If you would prefer more guidance, please click on the "Level 3 Hints" cell for step by step instructions.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Level 2 Hints</b></font>
# </summary>
# <p>
# <ul>
# <li><a href="" > Use array slicing like my_string[0:2] </a> </li>
# <li><a href="" > Use list comprehensions or for loops </a> </li>
# <li>To do a switch, think of the whole word as divided into 4 distinct parts. Write out 'cupcakes' on a piece of paper and see how you can split it into ('cupc', 'k', 'a', 'es')</li>
# </ul>
# </p>
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Level 3 Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>splits: Use array slicing, like my_str[0:2], to separate a string into two pieces.</li>
# <li>Splitting is the same as for delete_letter</li>
# <li>To perform the switch, go through the list of tuples and combine four strings together. You can use the + operator to combine strings</li>
# <li>The four strings will be the left substring from the split tuple, followed by the first (index 1) character of the right substring, then the zero-th character (index 0) of the right substring, and then the remaining part of the right substring.</li>
# <li>Unlike delete_letter, you will want to check that your right substring is at least a minimum length. To see why, review the previous hint bullet point (directly before this one).</li>
# </ul>
# </p>
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: switches
def switch_letter(word, verbose=False):
'''
Input:
word: input string
Output:
switches: a list of all possible strings with one adjacent charater switched
'''
switch_l = []
split_l = []
### START CODE HERE ###
split_l = [(word[:i], word[i:]) for i in range(len(word) + 1)]
switch_l = [L + R[1] + R[0] + R[2:] for L, R in split_l if len(R)>1]
### END CODE HERE ###
if verbose: print(f"Input word = {word} \nsplit_l = {split_l} \nswitch_l = {switch_l}")
return switch_l
switch_word_l = switch_letter(word="eta",
verbose=True)
# #### Expected output
#
# ```Python
# Input word = eta
# split_l = [('', 'eta'), ('e', 'ta'), ('et', 'a')]
# switch_l = ['tea', 'eat']
# ```
# #### Note 1
#
# You may get this:
# ```Python
# Input word = eta
# split_l = [('', 'eta'), ('e', 'ta'), ('et', 'a'), ('eta', '')]
# switch_l = ['tea', 'eat']
# ```
# - Notice how it has the extra tuple `('eta', '')`.
# - This is also correct.
# - Can you think of why this is the case?
# #### Note 2
#
# If you get an error
# ```Python
# IndexError: string index out of range
# ```
# - Please see if you have checked the length of the strings when switching characters.
# test # 2
print(f"Number of outputs of switch_letter('at') is {len(switch_letter('at'))}")
# #### Expected output
#
# ```CPP
# Number of outputs of switch_letter('at') is 1
# ```
# <a name='ex-6'></a>
# ### Exercise 6
# **Instructions for replace_letter()**: Now implement a function that takes in a word and returns a list of strings with one **replaced letter** from the original word.
#
# **Step 1:** is the same as in `delete_letter()`
#
# **Step 2:** A list comprehension or for loop which form strings by replacing letters. This can be of the form:
# `[f(a,b,c) for a, b in splits if condition for c in string]` Note the use of the second for loop.
# It is expected in this routine that one or more of the replacements will include the original word. For example, replacing the first letter of 'ear' with 'e' will return 'ear'.
#
# **Step 3:** Remove the original input letter from the output.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>To remove a word from a list, first store its contents inside a set()</li>
# <li>Use set.discard('the_word') to remove a word in a set (if the word does not exist in the set, then it will not throw a KeyError. Using set.remove('the_word') throws a KeyError if the word does not exist in the set. </li>
# </ul>
# </p>
#
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: replaces
def replace_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
replaces: a list of all possible strings where we replaced one letter from the original word.
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
replace_l = []
split_l = []
### START CODE HERE ###
split_l = [(word[:i], word[i:]) for i in range(len(word) + 1)]
replace_l = [L + c + R[1:] for L, R in split_l if R for c in letters]
replace_set = set(replace_l)
### END CODE HERE ###
# turn the set back into a list and sort it, for easier viewing
replace_l = sorted(list(replace_set))
if verbose: print(f"Input word = {word} \nsplit_l = {split_l} \nreplace_l {replace_l}")
return replace_l
replace_l = replace_letter(word='can',
verbose=True)
# #### Expected Output**:
# ```Python
# Input word = can
# split_l = [('', 'can'), ('c', 'an'), ('ca', 'n')]
# replace_l ['aan', 'ban', 'caa', 'cab', 'cac', 'cad', 'cae', 'caf', 'cag', 'cah', 'cai', 'caj', 'cak', 'cal', 'cam', 'cao', 'cap', 'caq', 'car', 'cas', 'cat', 'cau', 'cav', 'caw', 'cax', 'cay', 'caz', 'cbn', 'ccn', 'cdn', 'cen', 'cfn', 'cgn', 'chn', 'cin', 'cjn', 'ckn', 'cln', 'cmn', 'cnn', 'con', 'cpn', 'cqn', 'crn', 'csn', 'ctn', 'cun', 'cvn', 'cwn', 'cxn', 'cyn', 'czn', 'dan', 'ean', 'fan', 'gan', 'han', 'ian', 'jan', 'kan', 'lan', 'man', 'nan', 'oan', 'pan', 'qan', 'ran', 'san', 'tan', 'uan', 'van', 'wan', 'xan', 'yan', 'zan']
# ```
# - Note how the input word 'can' should not be one of the output words.
# #### Note 1
# If you get something like this:
#
# ```Python
# Input word = can
# split_l = [('', 'can'), ('c', 'an'), ('ca', 'n'), ('can', '')]
# replace_l ['aan', 'ban', 'caa', 'cab', 'cac', 'cad', 'cae', 'caf', 'cag', 'cah', 'cai', 'caj', 'cak', 'cal', 'cam', 'cao', 'cap', 'caq', 'car', 'cas', 'cat', 'cau', 'cav', 'caw', 'cax', 'cay', 'caz', 'cbn', 'ccn', 'cdn', 'cen', 'cfn', 'cgn', 'chn', 'cin', 'cjn', 'ckn', 'cln', 'cmn', 'cnn', 'con', 'cpn', 'cqn', 'crn', 'csn', 'ctn', 'cun', 'cvn', 'cwn', 'cxn', 'cyn', 'czn', 'dan', 'ean', 'fan', 'gan', 'han', 'ian', 'jan', 'kan', 'lan', 'man', 'nan', 'oan', 'pan', 'qan', 'ran', 'san', 'tan', 'uan', 'van', 'wan', 'xan', 'yan', 'zan']
# ```
# - Notice how split_l has an extra tuple `('can', '')`, but the output is still the same, so this is okay.
# #### Note 2
# If you get something like this:
# ```Python
# Input word = can
# split_l = [('', 'can'), ('c', 'an'), ('ca', 'n'), ('can', '')]
# replace_l ['aan', 'ban', 'caa', 'cab', 'cac', 'cad', 'cae', 'caf', 'cag', 'cah', 'cai', 'caj', 'cak', 'cal', 'cam', 'cana', 'canb', 'canc', 'cand', 'cane', 'canf', 'cang', 'canh', 'cani', 'canj', 'cank', 'canl', 'canm', 'cann', 'cano', 'canp', 'canq', 'canr', 'cans', 'cant', 'canu', 'canv', 'canw', 'canx', 'cany', 'canz', 'cao', 'cap', 'caq', 'car', 'cas', 'cat', 'cau', 'cav', 'caw', 'cax', 'cay', 'caz', 'cbn', 'ccn', 'cdn', 'cen', 'cfn', 'cgn', 'chn', 'cin', 'cjn', 'ckn', 'cln', 'cmn', 'cnn', 'con', 'cpn', 'cqn', 'crn', 'csn', 'ctn', 'cun', 'cvn', 'cwn', 'cxn', 'cyn', 'czn', 'dan', 'ean', 'fan', 'gan', 'han', 'ian', 'jan', 'kan', 'lan', 'man', 'nan', 'oan', 'pan', 'qan', 'ran', 'san', 'tan', 'uan', 'van', 'wan', 'xan', 'yan', 'zan']
# ```
# - Notice how there are strings that are 1 letter longer than the original word, such as `cana`.
# - Please check for the case when there is an empty string `''`, and if so, do not use that empty string when setting replace_l.
# test # 2
print(f"Number of outputs of switch_letter('at') is {len(switch_letter('at'))}")
# #### Expected output
# ```CPP
# Number of outputs of switch_letter('at') is 1
# ```
# <a name='ex-7'></a>
# ### Exercise 7
#
# **Instructions for insert_letter()**: Now implement a function that takes in a word and returns a list with a letter inserted at every offset.
#
# **Step 1:** is the same as in `delete_letter()`
#
# **Step 2:** This can be a list comprehension of the form:
# `[f(a,b,c) for a, b in splits if condition for c in string]`
# UNQ_C7 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: inserts
def insert_letter(word, verbose=False):
'''
Input:
word: the input string/word
Output:
inserts: a set of all possible strings with one new letter inserted at every offset
'''
letters = 'abcdefghijklmnopqrstuvwxyz'
insert_l = []
split_l = []
### START CODE HERE ###
split_l = [(word[:i], word[i:]) for i in range(len(word) + 1)]
insert_l = [L + c + R for L, R in split_l for c in letters]
### END CODE HERE ###
if verbose: print(f"Input word {word} \nsplit_l = {split_l} \ninsert_l = {insert_l}")
return insert_l
insert_l = insert_letter('at', True)
print(f"Number of strings output by insert_letter('at') is {len(insert_l)}")
# #### Expected output
#
# ```Python
# Input word at
# split_l = [('', 'at'), ('a', 't'), ('at', '')]
# insert_l = ['aat', 'bat', 'cat', 'dat', 'eat', 'fat', 'gat', 'hat', 'iat', 'jat', 'kat', 'lat', 'mat', 'nat', 'oat', 'pat', 'qat', 'rat', 'sat', 'tat', 'uat', 'vat', 'wat', 'xat', 'yat', 'zat', 'aat', 'abt', 'act', 'adt', 'aet', 'aft', 'agt', 'aht', 'ait', 'ajt', 'akt', 'alt', 'amt', 'ant', 'aot', 'apt', 'aqt', 'art', 'ast', 'att', 'aut', 'avt', 'awt', 'axt', 'ayt', 'azt', 'ata', 'atb', 'atc', 'atd', 'ate', 'atf', 'atg', 'ath', 'ati', 'atj', 'atk', 'atl', 'atm', 'atn', 'ato', 'atp', 'atq', 'atr', 'ats', 'att', 'atu', 'atv', 'atw', 'atx', 'aty', 'atz']
# Number of strings output by insert_letter('at') is 78
# ```
# #### Note 1
#
# If you get a split_l like this:
# ```Python
# Input word at
# split_l = [('', 'at'), ('a', 't')]
# insert_l = ['aat', 'bat', 'cat', 'dat', 'eat', 'fat', 'gat', 'hat', 'iat', 'jat', 'kat', 'lat', 'mat', 'nat', 'oat', 'pat', 'qat', 'rat', 'sat', 'tat', 'uat', 'vat', 'wat', 'xat', 'yat', 'zat', 'aat', 'abt', 'act', 'adt', 'aet', 'aft', 'agt', 'aht', 'ait', 'ajt', 'akt', 'alt', 'amt', 'ant', 'aot', 'apt', 'aqt', 'art', 'ast', 'att', 'aut', 'avt', 'awt', 'axt', 'ayt', 'azt']
# Number of strings output by insert_letter('at') is 52
# ```
# - Notice that split_l is missing the extra tuple ('at', ''). For insertion, we actually **WANT** this tuple.
# - The function is not creating all the desired output strings.
# - Check the range that you use for the for loop.
# #### Note 2
# If you see this:
# ```Python
# Input word at
# split_l = [('', 'at'), ('a', 't'), ('at', '')]
# insert_l = ['aat', 'bat', 'cat', 'dat', 'eat', 'fat', 'gat', 'hat', 'iat', 'jat', 'kat', 'lat', 'mat', 'nat', 'oat', 'pat', 'qat', 'rat', 'sat', 'tat', 'uat', 'vat', 'wat', 'xat', 'yat', 'zat', 'aat', 'abt', 'act', 'adt', 'aet', 'aft', 'agt', 'aht', 'ait', 'ajt', 'akt', 'alt', 'amt', 'ant', 'aot', 'apt', 'aqt', 'art', 'ast', 'att', 'aut', 'avt', 'awt', 'axt', 'ayt', 'azt']
# Number of strings output by insert_letter('at') is 52
# ```
#
# - Even though you may have fixed the split_l so that it contains the tuple `('at', '')`, notice that you're still missing some output strings.
# - Notice that it's missing strings such as 'ata', 'atb', 'atc' all the way to 'atz'.
# - To fix this, make sure that when you set insert_l, you allow the use of the empty string `''`.
# test # 2
print(f"Number of outputs of insert_letter('at') is {len(insert_letter('at'))}")
# #### Expected output
#
# ```CPP
# Number of outputs of insert_letter('at') is 78
# ```
# <a name='3'></a>
#
# # Part 3: Combining the edits
#
# Now that you have implemented the string manipulations, you will create two functions that, given a string, will return all the possible single and double edits on that string. These will be `edit_one_letter()` and `edit_two_letters()`.
# <a name='3-1'></a>
# ## 3.1 Edit one letter
#
# <a name='ex-8'></a>
# ### Exercise 8
#
# **Instructions**: Implement the `edit_one_letter` function to get all the possible edits that are one edit away from a word. The edits consist of the replace, insert, delete, and optionally the switch operation. You should use the previous functions you have already implemented to complete this function. The 'switch' function is a less common edit function, so its use will be selected by an "allow_switches" input argument.
#
# Note that those functions return *lists* while this function should return a *python set*. Utilizing a set eliminates any duplicate entries.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li> Each of the functions returns a list. You can combine lists using the `+` operator. </li>
# <li> To get unique strings (avoid duplicates), you can use the set() function. </li>
# </ul>
# </p>
#
# UNQ_C8 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: edit_one_letter
def edit_one_letter(word, allow_switches = True):
"""
Input:
word: the string/word for which we will generate all possible wordsthat are one edit away.
Output:
edit_one_set: a set of words with one possible edit. Please return a set. and not a list.
"""
edit_one_set = set()
### START CODE HERE ###
if allow_switches:
edit_one_set = set(replace_letter(word) + insert_letter(word) + delete_letter(word) + switch_letter(word))
else:
edit_one_set = set(replace_letter(word) + insert_letter(word) + delete_letter(word))
### END CODE HERE ###
return edit_one_set
# +
tmp_word = "at"
tmp_edit_one_set = edit_one_letter(tmp_word)
# turn this into a list to sort it, in order to view it
tmp_edit_one_l = sorted(list(tmp_edit_one_set))
print(f"input word {tmp_word} \nedit_one_l \n{tmp_edit_one_l}\n")
print(f"The type of the returned object should be a set {type(tmp_edit_one_set)}")
print(f"Number of outputs from edit_one_letter('at') is {len(edit_one_letter('at'))-1}")
# -
# #### Expected Output
# ```CPP
# input word at
# edit_one_l
# ['a', 'aa', 'aat', 'ab', 'abt', 'ac', 'act', 'ad', 'adt', 'ae', 'aet', 'af', 'aft', 'ag', 'agt', 'ah', 'aht', 'ai', 'ait', 'aj', 'ajt', 'ak', 'akt', 'al', 'alt', 'am', 'amt', 'an', 'ant', 'ao', 'aot', 'ap', 'apt', 'aq', 'aqt', 'ar', 'art', 'as', 'ast', 'ata', 'atb', 'atc', 'atd', 'ate', 'atf', 'atg', 'ath', 'ati', 'atj', 'atk', 'atl', 'atm', 'atn', 'ato', 'atp', 'atq', 'atr', 'ats', 'att', 'atu', 'atv', 'atw', 'atx', 'aty', 'atz', 'au', 'aut', 'av', 'avt', 'aw', 'awt', 'ax', 'axt', 'ay', 'ayt', 'az', 'azt', 'bat', 'bt', 'cat', 'ct', 'dat', 'dt', 'eat', 'et', 'fat', 'ft', 'gat', 'gt', 'hat', 'ht', 'iat', 'it', 'jat', 'jt', 'kat', 'kt', 'lat', 'lt', 'mat', 'mt', 'nat', 'nt', 'oat', 'ot', 'pat', 'pt', 'qat', 'qt', 'rat', 'rt', 'sat', 'st', 't', 'ta', 'tat', 'tt', 'uat', 'ut', 'vat', 'vt', 'wat', 'wt', 'xat', 'xt', 'yat', 'yt', 'zat', 'zt']
#
# The type of the returned object should be a set <class 'set'>
# Number of outputs from edit_one_letter('at') is 129
# ```
# <a name='3-2'></a>
# ## Part 3.2 Edit two letters
#
# <a name='ex-9'></a>
# ### Exercise 9
#
# Now you can generalize this to implement to get two edits on a word. To do so, you would have to get all the possible edits on a single word and then for each modified word, you would have to modify it again.
#
# **Instructions**: Implement the `edit_two_letters` function that returns a set of words that are two edits away. Note that creating additional edits based on the `edit_one_letter` function may 'restore' some one_edits to zero or one edits. That is allowed here. This accounted for in get_corrections.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>You will likely want to take the union of two sets.</li>
# <li>You can either use set.union() or use the '|' (or operator) to union two sets</li>
# <li>See the documentation <a href="https://docs.python.org/2/library/sets.html" > Python sets </a> for examples of using operators or functions of the Python set.</li>
# </ul>
# </p>
#
# UNQ_C9 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: edit_two_letters
def edit_two_letters(word, allow_switches = True):
'''
Input:
word: the input string/word
Output:
edit_two_set: a set of strings with all possible two edits
'''
edit_two_set = set()
### START CODE HERE ###
edit_two_set = set(edit2 for edit1 in edit_one_letter(word) for edit2 in edit_one_letter(edit1))
### END CODE HERE ###
return edit_two_set
tmp_edit_two_set = edit_two_letters("a")
tmp_edit_two_l = sorted(list(tmp_edit_two_set))
print(f"Number of strings with edit distance of two: {len(tmp_edit_two_l)}")
print(f"First 10 strings {tmp_edit_two_l[:10]}")
print(f"Last 10 strings {tmp_edit_two_l[-10:]}")
print(f"The data type of the returned object should be a set {type(tmp_edit_two_set)}")
print(f"Number of strings that are 2 edit distances from 'at' is {len(edit_two_letters('at'))}")
# #### Expected Output
#
# ```CPP
# Number of strings with edit distance of two: 2654
# First 10 strings ['', 'a', 'aa', 'aaa', 'aab', 'aac', 'aad', 'aae', 'aaf', 'aag']
# Last 10 strings ['zv', 'zva', 'zw', 'zwa', 'zx', 'zxa', 'zy', 'zya', 'zz', 'zza']
# The data type of the returned object should be a set <class 'set'>
# Number of strings that are 2 edit distances from 'at' is 7154
# ```
# <a name='3-3'></a>
# ## Part 3-3: suggest spelling suggestions
#
# Now you will use your `edit_two_letters` function to get a set of all the possible 2 edits on your word. You will then use those strings to get the most probable word you meant to type aka your typing suggestion.
#
# <a name='ex-10'></a>
# ### Exercise 10
# **Instructions**: Implement `get_corrections`, which returns a list of zero to n possible suggestion tuples of the form (word, probability_of_word).
#
# **Step 1:** Generate suggestions for a supplied word: You'll use the edit functions you have developed. The 'suggestion algorithm' should follow this logic:
# * If the word is in the vocabulary, suggest the word.
# * Otherwise, if there are suggestions from `edit_one_letter` that are in the vocabulary, use those.
# * Otherwise, if there are suggestions from `edit_two_letters` that are in the vocabulary, use those.
# * Otherwise, suggest the input word.*
# * The idea is that words generated from fewer edits are more likely than words with more edits.
#
#
# Note:
# - Edits of one or two letters may 'restore' strings to either zero or one edit. This algorithm accounts for this by preferentially selecting lower distance edits first.
# #### Short circuit
# In Python, logical operations such as `and` and `or` have two useful properties. They can operate on lists and they have ['short-circuit' behavior](https://docs.python.org/3/library/stdtypes.html). Try these:
# example of logical operation on lists or sets
print( [] and ["a","b"] )
print( [] or ["a","b"] )
#example of Short circuit behavior
val1 = ["Most","Likely"] or ["Less","so"] or ["least","of","all"] # selects first, does not evalute remainder
print(val1)
val2 = [] or [] or ["least","of","all"] # continues evaluation until there is a non-empty list
print(val2)
# The logical `or` could be used to implement the suggestion algorithm very compactly. Alternately, if/then constructs could be used.
#
# **Step 2**: Create a 'best_words' dictionary where the 'key' is a suggestion and the 'value' is the probability of that word in your vocabulary. If the word is not in the vocabulary, assign it a probability of 0.
#
# **Step 3**: Select the n best suggestions. There may be fewer than n.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>edit_one_letter and edit_two_letters return *python sets*. </li>
# <li> Sets have a handy <a href="https://docs.python.org/2/library/sets.html" > set.intersection </a> feature</li>
# <li>To find the keys that have the highest values in a dictionary, you can use the Counter dictionary to create a Counter object from a regular dictionary. Then you can use Counter.most_common(n) to get the n most common keys.
# </li>
# <li>To find the intersection of two sets, you can use set.intersection or the & operator.</li>
# <li>If you are not as familiar with short circuit syntax (as shown above), feel free to use if else statements instead.</li>
# <li>To use an if statement to check of a set is empty, use 'if not x:' syntax </li>
# </ul>
# </p>
#
# +
# UNQ_C10 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# UNIT TEST COMMENT: Candidate for Table Driven Tests
# GRADED FUNCTION: get_corrections
def get_corrections(word, probs, vocab, n=2, verbose = False):
'''
Input:
word: a user entered string to check for suggestions
probs: a dictionary that maps each word to its probability in the corpus
vocab: a set containing all the vocabulary
n: number of possible word corrections you want returned in the dictionary
Output:
n_best: a list of tuples with the most probable n corrected words and their probabilities.
'''
suggestions = []
n_best = []
### START CODE HERE ###
suggestions = known([word]) or known(edit_one_letter(word)) or known(edit_two_letter(word)) or [word]
n_best = sorted([(suggestion, probs.get(suggestion, 0)) for suggestion in suggestions], key=lambda tup: tup[1], reverse=True)
### END CODE HERE ###
if verbose: print("entered word = ", word, "\nsuggestions = ", suggestions)
return n_best
def known(words):
return set(w for w in words if w in vocab)
# +
# Test your implementation - feel free to try other words in my word
my_word = 'dys'
tmp_corrections = get_corrections(my_word, probs, vocab, 2, verbose=True) # keep verbose=True
for i, word_prob in enumerate(tmp_corrections):
print(f"word {i}: {word_prob[0]}, probability {word_prob[1]:.6f}")
# CODE REVIEW COMMENT: using "tmp_corrections" insteads of "cors". "cors" is not defined
print(f"data type of corrections {type(tmp_corrections)}")
# -
# #### Expected Output
# - Note: This expected output is for `my_word = 'dys'`. Also, keep `verbose=True`
# ```CPP
# entered word = dys
# suggestions = {'days', 'dye'}
# word 0: days, probability 0.000410
# word 1: dye, probability 0.000019
# data type of corrections <class 'list'>
# ```
# <a name='4'></a>
# # Part 4: Minimum Edit distance
#
# Now that you have implemented your auto-correct, how do you evaluate the similarity between two strings? For example: 'waht' and 'what'
#
# Also how do you efficiently find the shortest path to go from the word, 'waht' to the word 'what'?
#
# You will implement a dynamic programming system that will tell you the minimum number of edits required to convert a string into another string.
# <a name='4-1'></a>
# ### Part 4.1 Dynamic Programming
#
# Dynamic Programming breaks a problem down into subproblems which can be combined to form the final solution. Here, given a string source[0..i] and a string target[0..j], we will compute all the combinations of substrings[i, j] and calculate their edit distance. To do this efficiently, we will use a table to maintain the previously computed substrings and use those to calculate larger substrings.
#
# You have to create a matrix and update each element in the matrix as follows:
# $$\text{Initialization}$$
#
# \begin{align}
# D[0,0] &= 0 \\
# D[i,0] &= D[i-1,0] + del\_cost(source[i]) \tag{4}\\
# D[0,j] &= D[0,j-1] + ins\_cost(target[j]) \\
# \end{align}
#
# $$\text{Per Cell Operations}$$
# \begin{align}
# \\
# D[i,j] =min
# \begin{cases}
# D[i-1,j] + del\_cost\\
# D[i,j-1] + ins\_cost\\
# D[i-1,j-1] + \left\{\begin{matrix}
# rep\_cost; & if src[i]\neq tar[j]\\
# 0 ; & if src[i]=tar[j]
# \end{matrix}\right.
# \end{cases}
# \tag{5}
# \end{align}
# So converting the source word **play** to the target word **stay**, using an input cost of one, a delete cost of 1, and replace cost of 2 would give you the following table:
# <table style="width:20%">
#
# <tr>
# <td> <b> </b> </td>
# <td> <b># </b> </td>
# <td> <b>s </b> </td>
# <td> <b>t </b> </td>
# <td> <b>a </b> </td>
# <td> <b>y </b> </td>
# </tr>
# <tr>
# <td> <b> # </b></td>
# <td> 0</td>
# <td> 1</td>
# <td> 2</td>
# <td> 3</td>
# <td> 4</td>
#
# </tr>
# <tr>
# <td> <b> p </b></td>
# <td> 1</td>
# <td> 2</td>
# <td> 3</td>
# <td> 4</td>
# <td> 5</td>
# </tr>
#
# <tr>
# <td> <b> l </b></td>
# <td>2</td>
# <td>3</td>
# <td>4</td>
# <td>5</td>
# <td>6</td>
# </tr>
#
# <tr>
# <td> <b> a </b></td>
# <td>3</td>
# <td>4</td>
# <td>5</td>
# <td>4</td>
# <td>5</td>
# </tr>
#
# <tr>
# <td> <b> y </b></td>
# <td>4</td>
# <td>5</td>
# <td>6</td>
# <td>5</td>
# <td>4</td>
# </tr>
#
#
# </table>
#
#
# The operations used in this algorithm are 'insert', 'delete', and 'replace'. These correspond to the functions that you defined earlier: insert_letter(), delete_letter() and replace_letter(). switch_letter() is not used here.
# The diagram below describes how to initialize the table. Each entry in D[i,j] represents the minimum cost of converting string source[0:i] to string target[0:j]. The first column is initialized to represent the cumulative cost of deleting the source characters to convert string "EER" to "". The first row is initialized to represent the cumulative cost of inserting the target characters to convert from "" to "NEAR".
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/EditDistInit4.PNG' alt="alternate text" width="width" height="height" style="width:1000px;height:400px;"/> Figure 6 Initializing Distance Matrix</div>
# Filling in the remainder of the table utilizes the 'Per Cell Operations' in the equation (5) above. Note, the diagram below includes in the table some of the 3 sub-calculations shown in light grey. Only 'min' of those operations is stored in the table in the `min_edit_distance()` function.
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/EditDistFill2.PNG' alt="alternate text" width="width" height="height" style="width:800px;height:400px;"/> Figure 7 Filling Distance Matrix</div>
# Note that the formula for $D[i,j]$ shown in the image is equivalent to:
#
# \begin{align}
# \\
# D[i,j] =min
# \begin{cases}
# D[i-1,j] + del\_cost\\
# D[i,j-1] + ins\_cost\\
# D[i-1,j-1] + \left\{\begin{matrix}
# rep\_cost; & if src[i]\neq tar[j]\\
# 0 ; & if src[i]=tar[j]
# \end{matrix}\right.
# \end{cases}
# \tag{5}
# \end{align}
#
# The variable `sub_cost` (for substitution cost) is the same as `rep_cost`; replacement cost. We will stick with the term "replace" whenever possible.
# Below are some examples of cells where replacement is used. This also shows the minimum path from the lower right final position where "EER" has been replaced by "NEAR" back to the start. This provides a starting point for the optional 'backtrace' algorithm below.
# <div style="width:image width px; font-size:100%; text-align:center;"><img src='res/EditDistExample1.PNG' alt="alternate text" width="width" height="height" style="width:1200px;height:400px;"/> Figure 8 Examples Distance Matrix</div>
# <a name='ex-11'></a>
# ### Exercise 11
#
# Again, the word "substitution" appears in the figure, but think of this as "replacement".
# **Instructions**: Implement the function below to get the minimum amount of edits required given a source string and a target string.
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>The range(start, stop, step) function excludes 'stop' from its output</li>
# <li><a href="" > words </a> </li>
# </ul>
# </p>
#
# UNQ_C11 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: min_edit_distance
def min_edit_distance(source, target, ins_cost = 1, del_cost = 1, rep_cost = 2):
'''
Input:
source: a string corresponding to the string you are starting with
target: a string corresponding to the string you want to end with
ins_cost: an integer setting the insert cost
del_cost: an integer setting the delete cost
rep_cost: an integer setting the replace cost
Output:
D: a matrix of len(source)+1 by len(target)+1 containing minimum edit distances
med: the minimum edit distance (med) required to convert the source string to the target
'''
# use deletion and insert cost as 1
m = len(source)
n = len(target)
#initialize cost matrix with zeros and dimensions (m+1,n+1)
D = np.zeros((m+1, n+1), dtype=int)
### START CODE HERE (Replace instances of 'None' with your code) ###
# Fill in column 0, from row 1 to row m, both inclusive
for row in range(1,m+1): # Replace None with the proper range
D[row,0] = row
# Fill in row 0, for all columns from 1 to n, both inclusive
for col in range(1,n+1): # Replace None with the proper range
D[0,col] = col
# Loop through row 1 to row m, both inclusive
for row in range(1,m+1):
# Loop through column 1 to column n, both inclusive
for col in range(1,n+1):
# Intialize r_cost to the 'replace' cost that is passed into this function
r_cost = rep_cost
# Check to see if source character at the previous row
# matches the target character at the previous column,
if source[row-1] == target[col-1]:
# Update the replacement cost to 0 if source and target are the same
r_cost = 0
# Update the cost at row, col based on previous entries in the cost matrix
# Refer to the equation calculate for D[i,j] (the minimum of three calculated costs)
D[row,col] = min((D[row-1, col] + del_cost), (D[row, col-1] + ins_cost), (D[row-1, col-1] + r_cost))
# Set the minimum edit distance with the cost found at row m, column n
med = D[-1, -1]
### END CODE HERE ###
return D, med
#DO NOT MODIFY THIS CELL
# testing your implementation
source = 'play'
target = 'stay'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list('#' + source)
cols = list('#' + target)
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
# **Expected Results:**
#
# ```CPP
# minimum edits: 4
#
# # s t a y
# # 0 1 2 3 4
# p 1 2 3 4 5
# l 2 3 4 5 6
# a 3 4 5 4 5
# y 4 5 6 5 4
# ```
#DO NOT MODIFY THIS CELL
# testing your implementation
source = 'eer'
target = 'near'
matrix, min_edits = min_edit_distance(source, target)
print("minimum edits: ",min_edits, "\n")
idx = list(source)
idx.insert(0, '#')
cols = list(target)
cols.insert(0, '#')
df = pd.DataFrame(matrix, index=idx, columns= cols)
print(df)
# **Expected Results**
# ```CPP
# minimum edits: 3
#
# # n e a r
# # 0 1 2 3 4
# e 1 2 1 2 3
# e 2 3 2 3 4
# r 3 4 3 4 3
# ```
# We can now test several of our routines at once:
source = "eer"
targets = edit_one_letter(source,allow_switches = False) #disable switches since min_edit_distance does not include them
for t in targets:
_, min_edits = min_edit_distance(source, t,1,1,1) # set ins, del, sub costs all to one
if min_edits > 1: print(source, t, min_edits)
# **Expected Results**
# ```CPP
# (empty)
# ```
#
# The 'replace()' routine utilizes all letters a-z one of which returns the original word.
source = "eer"
targets = edit_two_letters(source,allow_switches = False) #disable switches since min_edit_distance does not include them
for t in targets:
_, min_edits = min_edit_distance(source, t,1,1,1) # set ins, del, sub costs all to one
if min_edits < 2 and min_edits != 1: print(source, t, min_edits)
# **Expected Results**
# ```CPP
# eer eer 0
# ```
#
# We have to allow single edits here because some two_edits will restore a single edit.
# # Submission
# Make sure you submit your assignment before you modify anything below
#
# <a name='5'></a>
#
# # Part 5: Optional - Backtrace
#
#
# Once you have computed your matrix using minimum edit distance, how would find the shortest path from the top left corner to the bottom right corner?
#
# Note that you could use backtrace algorithm. Try to find the shortest path given the matrix that your `min_edit_distance` function returned.
#
# You can use these [lecture slides on minimum edit distance](https://web.stanford.edu/class/cs124/lec/med.pdf) by <NAME> to learn about the algorithm for backtrace.
# +
# Experiment with back trace - insert your code here
# -
# #### References
# - <NAME> - Speech and Language Processing - Textbook
# - This auto-correct explanation was first done by <NAME> in 2007
|
Natural Language Processing Specialization/autocorrect_and_minimum_edit_distance/.ipynb_checkpoints/C2_W1_Assignment-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### The Data Analysis Framework
#
# 1. Look at the information in the data
# 2. Decide on the analysis objective(s)
# 3. What are the different questions that come to mind when looking at the data?
# 4. Select the questions that are in line with the objective(s)
# 5. Look for answers to these questions in the data
# 6. Summarise the findings
#
# ### Let's see how to use this in a data analysis setting with a simple example
# We would be using the gender-weight-height-bmi dataset downloaded from Kaggle and apply the above framework on it to generate some insights
## loading required packages
import numpy as np
import pandas as pd
import seaborn as sns
## Loading the gender-weight-height dataset
df = pd.read_csv('500_Person_Gender_Height_Weight_Index.csv')
print('data shape:',df.shape)
df.head()
# #### Step 1: Look at the information in the data
#
# Our data contains the gender, weight, height and body mass index (BMI) information of 500 distinct people. The fields - Height & Weight are numeric, while Gender & Index are categorical in nature. There are no missing values in the data.
#
# Below is the decsription of fields in the data:
#
# Gender : Male / Female
#
# Height : Number (cm)
#
# Weight : Number (Kg)
#
# Index :
# 0 - Extremely Weak,
# 1 - Weak,
# 2 - Normal,
# 3 - Overweight,
# 4 - Obesity,
# 5 - Extreme Obesity
# #### Step 2: Decide on the analysis objective(s)
#
# Let's try to look at the impact of gender on weight and height
# #### Step 3 & 4:
#
# We can combine step 3 & 4 in the framework and jot down some questions that we would try to answer further in the exercise
#
# Q1: Average height of male vs female? <br>
# Q2: Min height of male vs female? <br>
# Q3: Max height of male vs female?
#
# Q4: Average weight of male vs female? <br>
# Q5: Min weight of male vs female? <br>
# Q6: Max weight of male vs female? <br>
# #### Step 5: Try answering the questions using the data
# +
## Average Height
avg_height = df.groupby('Gender')['Height'].mean()
## Minimum Height
min_height = df.groupby('Gender')['Height'].min()
## Maximum Height
max_height = df.groupby('Gender')['Height'].max()
## Average Weight
avg_weight = df.groupby('Gender')['Weight'].mean()
## Minimum Weight
min_weight = df.groupby('Gender')['Weight'].min()
## Maximum Weight
max_weight = df.groupby('Gender')['Weight'].max()
print('### Height Metrics ###')
print('Avg_Height:', avg_height.round(1))
print('Min_Height:', min_height)
print('Max_Height:', max_height)
print('\n')
print('\n')
print('### Weight Metrics ###')
print('Avg_Weight:', avg_weight.round(1))
print('Min_Weight:', min_weight)
print('Max_Weight:', max_weight)
# -
# #### Step 6: Summarising the findings
#
# Our analysis on our dataset shows no impact of gender on height or weight.
|
Section-1-Introduction-to-the-course/Data_Analysis_Framework_in_action.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# import numpy as np
import os
import datetime
# import pandas as pd
# import pywt
# from scipy.stats import skew
import sys
WORKING_DIR_PATH = globals()['_dh'][0]
WORKING_DIR_PARENT_PATH = os.path.dirname(os.path.dirname(WORKING_DIR_PATH))
sys.path.insert(1, WORKING_DIR_PARENT_PATH)
from custom_module.utilities import *
SAMPLE_FILE= '/Users/macbookretina/blues.00042.wav'
SAMPLE_FILE= '/Users/macbookretina/073192.mp3'
print(datetime.datetime.now())
extract_audio_features(dataframe, SAMPLE_FILE, 'hiphop', 'fma')
print(datetime.datetime.now())
type(SAMPLE_FILE) == str
|
feature_extraction_deep_learning/notebooks/rough/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Support Vector Machine (SVM)
# Importing the libraries
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
import seaborn as sns
# -
# Importing the dataset
dataset = pd.read_csv('heart.csv')
dataset.head(10)
X = dataset.iloc[:, :-1]
y = dataset.iloc[:, -1]
# Splitting the dataset into the Training set and Test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30, random_state=20, shuffle=True)
# +
# Feature Scaling
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# -
# Fitting SVM to the Training set
classifier = SVC(kernel='rbf', random_state=20, degree=3, gamma='auto', max_iter=500, C=1.0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
print(y_pred)
print('SVCModel Train Score is : ' , classifier.score(X_train, y_train))
print('SVCModel Test Score is : ' , classifier.score(X_test, y_test))
cm = confusion_matrix(y_test, y_pred)
print(cm)
sns.heatmap(cm, center=True)
plt.show()
|
Sklearn/SVR & SVC/.ipynb_checkpoints/SVC 2.5.4-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import siibra
siibra.logger.setLevel('INFO')
# # Assignment of an MNI coordinate to Julich-Brain probabilistic cytoarchitectonic maps
# `siibra` can use the probabilistic maps of the Julich-Brain cytorachitectonic atlas to make a probabilistic assignment of a coordinate with error radius (modelled as a Gaussian) to brain regions.
# +
# some coordinates in MNI space, e.g. from an EEG contact
xyz_mni = [
(31.0, -89.6, -6.475), # a real sEEG contact point
(27.75, -32.0, 63.725) # this should be in PostCG, right hemisphere
]
# a confidence radius for the coordinate, i.e. the expected localization error.
radius_mm = 5
# -
# We instantiate the human atlas with the Julich-brain probabilistic cytoarchitectonic maps, and then ask it to assign regions. It will return a sorted list of probabilities with the corresponding regions.
atlas = siibra.atlases.MULTILEVEL_HUMAN_ATLAS
atlas.select_parcellation(
siibra.parcellations.JULICH_BRAIN_CYTOARCHITECTONIC_MAPS_2_5)
assignments = atlas.assign_regions(
siibra.spaces.MNI152_2009C_NONL_ASYM,xyz_mni,radius_mm)
# Just out of curiosity, we look at the three best fitting maps at the first requested location.
from nilearn import plotting
for region,prob in assignments[0][:3]:
plotting.plot_stat_map(
region.get_regional_map(siibra.spaces.MNI152_2009C_NONL_ASYM),
cut_coords=xyz_mni[0],
title="{} ({}%)".format(region.name,prob))
# # Connectivity profiles of the most probable brain region
#
# `siibra`'s key feature is access to regional data features, including connectivity profiles from different projects. This can be used to check the connection strengh of the most likely region assignment to the MNI coordinate.
# get profiles for the top assigned region
closest_region,_ = assignments[0][0]
atlas.select_region(closest_region)
profiles = atlas.get_features(
siibra.modalities.ConnectivityProfile)
# We will create plots of the connection strength to the 20 most strongly connected regions, for each of the returned profiles. Note that the profiles come from different connectivity datasets. The `src_info` and `src_name` attributes tell us more about each dataset.
#
# First, we decode the profiles with the parcellation object. This will convert the column names of the connectivity profile to explicit brain region objects, helping to disambiguiate region names.
siibra.logger.setLevel("ERROR") # ignore warnings
decoded_profiles = [p.decode(atlas.selected_parcellation)
for p in profiles]
siibra.logger.setLevel("INFO")
p = decoded_profiles[0]
target_regions = [region for strength,region in p[:20]]
target_regions
# We build a plotting function for the decoded profiles, which takes the N most strongly connected regions of the first profile, and then plots the connection strengths of all found profiles for those N target regions.
# +
import matplotlib.pyplot as plt
# %matplotlib inline
# a function to create a nice plot of multiple profiles from different
# data sources
def plot_connectivity_profiles(profiles,target_regions):
# Let's plot the so obtained regions and their strenghts
N = len(target_regions)
xticks = range(N)
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.set_xticks(xticks)
ax1.set_xticklabels([r.name for r in target_regions],
rotation=45,fontsize=10,ha='right')
for p in profiles:
probs = {region:prob for prob,region in p}
y = [probs[r] if r in probs else 0
for r in target_regions ]
strengths = []
ax1.plot(xticks,y,'.-',lw=1)
ax1.grid(True)
return fig
# -
fig = plot_connectivity_profiles(decoded_profiles,target_regions)
fig.legend([p.src_name for p in profiles],
loc='upper left', bbox_to_anchor=(1.05, 1.0),
prop={'size': 9})
fig.gca().set_title(f"Connection strengths from area {atlas.selected_region}")
plt.show()
|
examples/Probabilistic_assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Setup
#
# This script isolates coastal profiles from the World Ocean Database.
# +
# import packages
# %run ../../global_packages.py
# get the global parameters
# %run ../../global_pars.py
# import your local functions
sys.path.insert(1, '../../')
from global_functions import *
# make sure the figures plot inline rather than at the end
# %matplotlib inline
# -
# # Parameters and Paths
outfn = 'IO_coastal_mask.nc'
# # Get Data
ds_WOD = xr.open_dataset('../0_WOD/wod_processed.nc')
ds_WOD
ds_mask = xr.open_dataset('dist2coast_1deg_indian_ocean.nc')
ds_mask
ds_L17 = xr.open_dataset('Laruelle_2017_coastal_ocean_mask.nc')
ds_L17
# # Interpolate to 1/4 degree
# +
# do this because to intensive to use full 0.1 degree data
mask_o = np.array(ds_mask.dist)
lon = np.array(ds_mask.lon)
lat = np.array(ds_mask.lat)
xx,yy = np.meshgrid(lon,lat)
# use my global function latlonbin
mask,bincounts,latbins,lonbins = latlonbin(mask_o.flatten(),yy.flatten(),xx.flatten(), bounds = cm_bounds)
# -
# ## Wide Shelf (later used for eAS and eBoB) using ~300km from coast from Laruelle et al 2017
# +
maskw_L17 = ds_L17.mask_coastal2
lat_slice = slice(lat_bounds[0], lat_bounds[1])
lon_slice = slice(lon_bounds[0], lon_bounds[1])
#subset gridded data
maskw_L17 = maskw_L17.sel(latitude = lat_slice, longitude = lon_slice)
# +
lat_L17 = np.array(maskw_L17.latitude)
lon_L17 = np.array(maskw_L17.longitude)
maskw_L17 = np.array(maskw_L17).astype(int).T
xx_L17,yy_L17 = np.meshgrid(lon_L17,lat_L17)
# remove nicobar islands
maskw_L17 = np.where(~((yy_L17>7) & (yy_L17<13.75) & (xx_L17>92) & (xx_L17<94)),maskw_L17,False)
# -
plt.pcolor(lon_L17,lat_L17,maskw_L17)
plt.colorbar()
plt.title('Wide Shelf Mask, 300km from Coast')
# ## Narrow Shelf (later used for wAS and wBoB) 150km from coast using from distance from coast dataset.
maskn = np.array(mask)
maskn[maskn > 150] = np.nan
plt.pcolor(lonbins,latbins,maskn)
plt.colorbar()
plt.title('Narrow Shelf, 150km from Coast')
# +
ds_out=xr.Dataset()
# add plain masks to dataset
ds_out['maskw'] = xr.DataArray(maskw_L17,dims = ['latw','lonw'],coords =[lat_L17,lon_L17])
ds_out['maskn'] = xr.DataArray(maskn,dims = ['latn','lonn'],coords =[latbins,lonbins])
ds_out
# -
# # Apply to WOD
# +
inlat = ds_WOD.lat
inlon = ds_WOD.lon
maskw_wod = mask_coast(inlat,inlon,ds_out.maskw,ds_out.latw,ds_out.lonw)
maskn_wod = mask_coast(inlat,inlon,ds_out.maskn,ds_out.latn,ds_out.lonn)
ds_out['maskw_wod'] = xr.DataArray(maskw_wod,dims = ['loc_wod'],coords =[np.arange(len(maskw_wod))])
ds_out['maskn_wod'] = xr.DataArray(maskn_wod,dims = ['loc_wod'],coords =[np.arange(len(maskw_wod))])
# -
plt.scatter(inlon,inlat,c = ds_WOD.temp_50_200, s = 1)
plt.title('Orignal Temperature Profile Locations')
tmp = np.array(ds_WOD.temp_50_200)
plt.scatter(inlon[maskw_wod],inlat[maskw_wod],c = tmp[maskw_wod], s = 1)
plt.title('Wide Mask Temperature Profile Locations')
plt.scatter(inlon[maskn_wod],inlat[maskn_wod],c = tmp[maskn_wod], s = 1)
plt.title('Narrow Mask Temperature Profile Locations')
# # SAVE
# +
# delete if already present
if os.path.isfile(outfn):
os.remove(outfn)
ds_out.to_netcdf(outfn,mode='w',format = "NETCDF4")
# -
ds_out
|
data_processing/1_WOD_Coastal/0_make_coastal_mask.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py36]
# language: python
# name: conda-env-py36-py
# ---
# # Simulating a random variable
#
# The objective of this notebook is to give a feeling of what a random variable is. We will do this by the mean of simulations.
# First we will simulate the experiment of tossing a coin. Then we will simulate the rolling of a die.
# We will build *histograms* using the outcome of these two experiments. This will lead us to the notion of *probability distribution function* in the case of a discrete random variable.
#
# Finnaly, we will code a function allowing to simulate values comming from a discrete random variable with an arbitrary *probability distribution*.
#
# +
import random, bisect
import matplotlib.pyplot as plt
% matplotlib inline
# +
# Some useful functions
def flipCoin(n):
# Simulates n flips of a fair coin
values = []
for i in range(n):
s = random.random()
if s < 0.5:
values.append(0)
else:
values.append(1)
return(values)
def rollDie(n):
# Simulates n rolls of a fair die
values = []
for i in range(n):
s = random.random()
if s < 1./6:
values.append(1)
elif s < 2./6:
values.append(2)
elif s < 3./6:
values.append(3)
elif s < 4./6:
values.append(4)
elif s < 5./6:
values.append(5)
else:
values.append(6)
return(values)
def simulateRV(probVect, n):
# Simulates a Random Variable using a probability vector
values = []
if (min(probVect) < 0) or (sum(probVect) != 1):
print("No valid probability vector")
return([])
p = [probVect[0]]
for i in range(1, len(probVect)):
p.append(p[-1] + probVect[i])
for i in range(n):
s = random.random()
values.append(bisect.bisect(p, s))
return(values)
# -
# # Tossing a coin
n = 10000
values = flipCoin(n)
print(values)
# Let's count how many times we have each value
#
nb0 = values.count(0)
nb1 = values.count(1)
print(nb0, nb1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(values, bins=[-0.5, 0.5, 1.5], histtype='bar', ec='black')
ax.set_xticks([0, 1])
ax.tick_params(labelsize=15)
plt.show()
dValues = rollDie(n)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(dValues, bins=[0.5, 1.5, 2.5, 3.5, 4.5, 5.5, 6.5], histtype='bar', ec='black')
ax.set_xticks([1, 2, 3, 4, 5, 6])
ax.tick_params(labelsize=15)
plt.show()
# To do
# ------
# * Write a function that produce a histogram from a set of values
# * Use the function *simulateRV* to simulate discrete random values with any given distribution. Then, verify that the data follow the given distribution by making the corresponding histogram
# * Write functions to simulate values comming from other discrete random variables: Bernoulli, Binomial
# * Write a function to simulate values comming from a Poisson distribution
#
|
Notebooks/randomVariableSimulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Task04分享 - 文字图例尽眉目
#
# 学习内容:https://github.com/datawhalechina/fantastic-matplotlib
#
# 本节主要分为文字部分和图例部分。
import numpy as np
import matplotlib.pyplot as plt
# ## 文字部分
#
# 我们最熟悉的文字应用就是标题和标签了。
#
# + 为子图设置标题
#
# `Axes.set_title(self, label, fontdict=None, loc=None, pad=None, *, y=None, **kwargs)`
#
# + 为主图设置标题
#
# `Figure.suptitle(self, t, **kwargs)`
#
# + 为子图设定x轴标签
#
# `Axes.set_xlabel(self, xlabel, fontdict=None, labelpad=None, *, loc=None, **kwargs)`
#
# + 为子图设定y轴标签
#
# `Axes.set_ylabel(self, ylabel, fontdict=None, labelpad=None,*, loc=None, **kwargs)`
#
#
# (注:还有一些通过绝对定位的文本API,例如`Axes.text()`和`Axes.annotate()`等。这些用法偏底层,导出用PhotoShop实现会更方便,这里就将它们忽略啦)
# 通过观察上述的方法签名,我们可以总结出适用于大多数文本设定的参数。
#
# 除去self,第一个参数通常是文本的内容,`str`类型。
# ### fontdict参数
#
# `dict`类型,控制字体样式。通常来说,看见这种参数就和`**kwargs`一样,一定要查阅官方文档。
#
# 下面简单演示一下。
fig, axes = plt.subplots(figsize=(4, 1))
axes.set_title('abc123', fontdict={'family': 'serif', 'size': 24, 'color': 'blue'})
# 当你查阅[官方文档](https://matplotlib.org/api/text_api.html#matplotlib.text.Text)以后,就会发现fontdict的参数其实也可以放在`kwargs`里面。
#
# 我们看下另一种写法。
fig, axes = plt.subplots(figsize=(4, 1))
axes.set_title('abc123', family='Calibri', size=24, color='green')
# 没有什么特别的嘛,大家可以根据自己喜好来。比如我喜欢都放在`kwargs`里。
#
# 有的同学可能认为这样不方便复用,比如希望切换多套样式啥的。`kwargs`参数是支持字典解构的,像下面这样写就可以了。
d = {'family': 'serif', 'size': 24, 'color': 'blue'}
axes.set_title('abc123', **d)
# `FontProperties`对象也可以用于设置属性,但只能设置部分属性,例如字体颜色就不行。
#
# 个人感觉,样式管理部分matplotlib的接口比较乱,设置方法不统一。官方原本可能是想把字体本身样式的设置和附加样式的设置区分开,但用户通常意识不到这种界限,导致不知道哪个设置该用哪个接口。
#
# 建议还是`kwargs`,自己维护字典吧!
# ### loc参数
#
# `str`类型,用于设定对齐方式,默认为`center`。还可以是`left`或者`right`。
fig, axes = plt.subplots(figsize=(4, 1))
axes.set_title('abc123', loc='left', family='Calibri', size=24)
# ### pad参数
#
# `float`类型,设定一个相对距离。在不同的情景下意义略有区别,在标签那里叫`labelpad`。
#
# 如下所示,在子图标题中,`pad`是控制字体到图上边框的距离。
#
# 默认的pad数量基本够用,有特殊需求时可以手动调到合适值。
fig, axes = plt.subplots(figsize=(4, 1))
axes.set_title('abc123', pad=32, family='Calibri', size=24)
# ## Tick上的文本
#
# 以x为例,主要涉及`Axes.set_xticks()`和`Axes.set_xticklabels()`两个方法。
#
# 前者是一个实数构成的数组,指示哪些位置应放置标度,后者给出每个标度对应的标签。二者长度是要相等的。
x = np.linspace(0.0, 6.0, 100)
y = np.cos(2 * np.pi * x) * np.exp(-x)
fig, axes = plt.subplots(1, 1, figsize=(6, 2), tight_layout=True)
axes.set_xticks(list(range(7)))
axes.set_xticklabels('{:.4f}'.format(i) for i in range(7))
axes.plot(x, y)
# 还有其他方法来设置Tick文本,例如Tick Locators和Formatters。它们只是对直接设置的一种封装。
#
# 具体情景中还是建议用上述直接设置的方法,加以处理即可达到想要的效果。
# ## 图例部分
#
# 首先图例(legend)是什么?
#
# 图例用来说明图中的各个对象有什么含义。比如我现在画两条曲线,$y=x$和$y=x^2$,如下图。
#
x = np.arange(-1, 1, 0.01)
plt.plot(x, x, label='$y=x$', c='blue')
plt.plot(x, x**2, label='$y=x^2$', c='green')
plt.legend()
plt.show()
# 右下角这个小框就是图例,它清晰的表明蓝色曲线是$y=x$,而绿色曲线是$y=x^2$。
#
# 通常来说,显示图例调用`.legend()`就可以了,不需要带参数。matplotlib会自动显示需要显示的。
#
# 我们对图例的自定义操作主要是改变它的样式。比如修改边框颜色,加大字号等。
plt.plot(x, x, label='$y=x$', c='blue')
plt.plot(x, x**2, label='$y=x^2$', c='green')
lgd = plt.legend(
prop={'size': 20}, # 设置字号
facecolor='white', # 纯白背景
edgecolor='black', # 纯黑边框
shadow=False, # 关闭阴影
fancybox=False # 不要圆角矩形
)
plt.scatter(np.random.uniform(0, 1, 50), np.random.uniform(0, 1, 50),
label='$U(0, 1)$', c='blue', alpha=0.75)
plt.scatter(np.random.normal(0, 1, 50), np.random.normal(0, 1, 50),
label='$N(0, 1)$', c='green', alpha=0.75)
lgd = plt.legend(
prop={'size': 16}, # 设置字号
facecolor='cyan', # 浅蓝色背景
edgecolor='black', # 纯黑边框
framealpha=1.0, # 不透明的边框
shadow=False, # 关闭阴影
fancybox=False, # 不要圆角矩形
markerscale=2 # 图例圆点为普通点两倍
)
# 最后,复现一个论文里的图作为作业吧。目标:
#
# 
# 数据随便生成啦,不保证完全一样哦。
# +
# 创建图
fig, axes = plt.subplots()
# 伪造数据
r_data = np.random.normal(12, 2, 900)
g_data = np.random.exponential(8, 900)
# 生成伪造的图像
axes.hist(r_data, bins=np.linspace(0, 25, 25), color='r', alpha=0.5, label='regular examples')
axes.hist(g_data, bins=np.linspace(0, 25, 25), color='g', alpha=0.5, label='noisy examples')
# 设置x轴范围
axes.set_xlim(0, 25)
# 设置x轴和y轴标签
axes.set_xlabel('number of forgetting events', size=12)
axes.set_ylabel('fraction of corresponding samples', size=12, )
# 设置x轴标度和字号
axes.set_xticklabels(list(range(0, 26, 5)), fontsize=12)
# 设置y轴标度和字号
axes.set_yticklabels(['{:.3f}'.format(i / 100.0) for i in range(0, 225, 25)], fontsize=12)
# 开启图例
axes.legend(fontsize=11)
# 开启虚线网格
axes.grid(True, linestyle='--')
# -
|
backup/Task04.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.12 ('nlp')
# language: python
# name: python3
# ---
# + [markdown] id="YKaFSjvWbuhs"
# <a href="https://colab.research.google.com/github/Zumo09/Feedback-Prize/blob/main/training.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="w7GdsD-0R82W" outputId="83ed8593-092a-45d2-cbae-2b6928911183"
# Clone the entire repo.
# !git clone -l -s git://github.com/Zumo09/Feedback-Prize.git cloned-repo
# %cd cloned-repo
# !ls
# + id="2tL2VLdonI2u" outputId="de903734-db10-469f-9893-6bca8ac4b457" colab={"base_uri": "https://localhost:8080/"}
# !pip install transformers
from transformers import LEDTokenizerFast
import pandas as pd
import numpy as np
from tqdm.notebook import tqdm
# + id="RDbNnqjrbuh4" outputId="cd04a558-5e3d-424e-be12-4e0f762267f9" colab={"base_uri": "https://localhost:8080/", "height": 177, "referenced_widgets": ["fa88bc2036cd4d37b3f09e485213c515", "<KEY>", "<KEY>", "a63dbef366df4a8588b1d6f3f4319ec4", "<KEY>", "<KEY>", "da6a4d1aa7664d93b65ab4c8476af8f0", "<KEY>", "2c680016de914adb8a4f8a6c2f183958", "<KEY>", "<KEY>", "2abd35ced4b24d6a81ac279251aca887", "101cc3e982204e17bc3a73d12d2d5aa0", "<KEY>", "41a4f2205beb408e8bff841fce7745ca", "<KEY>", "<KEY>", "b93e665dc5c743168f1daba7bb69adc3", "0b0d1e9cae504edab187e84ad1d67546", "<KEY>", "cf3eda6f63b64894993bad768bce0b54", "8548bc7529f94fa0ad4dd4a28dd114f2", "a878d0ccffd54f3bbe5b6eb0b7e355b9", "fff76fb1848e477db0fb853d5e1d5a01", "<KEY>", "b4a9c09366c6445790a0b5135afc31d8", "c5c5b51a86b848699e17188936d8f5e7", "<KEY>", "7cc4ee696127435d82a66aa08b1947d7", "<KEY>", "4fcb00e7a43749dc95ddd3ed62305803", "023a9447caf648cda741f315d840ac22", "<KEY>", "be5a090b899e4f21aca77d8f5acaa63b", "<KEY>", "488a2e3f92074961a62ac007950e0a9f", "<KEY>", "af55d28a19294c97aea400304c3ab0e4", "<KEY>", "24fb92271af046d5af902a45ec1617e0", "fc24428d0ea34ed0b74ee47f33c5f0d0", "3de8fa287b69400f978d3a48def9f644", "2b52603efd6a4071a86d7bdd27455e82", "7deb280e85c6425bbe3a7975dd7856f5", "<KEY>", "<KEY>", "0832381b20344150ac6630493c03c298", "<KEY>", "610c814fa9b54979ac2c9d595788e4e8", "d03c2462eaac405cb21be3a6ae3a10f0", "<KEY>", "761b9e1607cf4926986eb6d4925429cc", "<KEY>", "0a207bf4ea0b44c2a3a09d2c1ec2c17e", "72f3ae0ba804484c80bf9d91e8db0e85"]}
tokenizer = LEDTokenizerFast.from_pretrained("allenai/led-base-16384")
df = pd.read_csv('./input/feedback-prize-2021/train.csv')
df["token_prediction"] = None
# + id="ueMmUYhEyCAa" outputId="c6e9083d-02a3-480c-c146-76e18b624f2f" colab={"base_uri": "https://localhost:8080/", "height": 852}
df
# + id="07yHh794n709" outputId="1e691302-425e-4d4f-a635-63c1ef1b1a24" colab={"base_uri": "https://localhost:8080/", "height": 49, "referenced_widgets": ["7dc6f79bbf8d4d87ac7de72ae23caa62", "70e1ddf040a34d99a811e173b33411a1", "96ed4fdc6aa540aba815138f4ed1cf33", "0dc07ad83f80486e90cf76d677c30b6d", "f5ed2b53be6b47ba89fb9a7737a19a0d", "5f4eef8e27fe4c51a758ffa368e33cf4", "e956baae3d8d4d95864da5429ea9d8f1", "78c14e0738934ad5adf9e47d3827ddf4", "b8328be6300149eb91b3844fe889dc75", "7bb5ff0f3a7e47e7a6ddbea692dcfb07", "<KEY>"]}
for i in tqdm(range(len(df))):
id = df.iloc[i]["id"]
discourse_start = int(df.iloc[0]["discourse_start"])
discourse_end = int(df.iloc[0]["discourse_end"])
with open(f'./input/feedback-prize-2021/train/{id}.txt', 'r') as f:
text = f.read()
char_array = np.zeros( (len(text)) )
char_array[discourse_start : discourse_end] = 1
encoding = tokenizer(text, padding='max_length',
truncation=True, return_offsets_mapping=True)
map_token_to_char = encoding['offset_mapping']
token_array = np.zeros(len(map_token_to_char))
for k in range(len(token_array)):
token_array[k] = char_array[ map_token_to_char[k][0] - 1]
df.at[i, "token_prediction"] = " ".join(token_array.nonzero()[0].astype(str)).strip()
# + id="FWOmLK0JsU7X" outputId="a8c45caa-664a-4c1d-d10e-fe659d5090d8" colab={"base_uri": "https://localhost:8080/", "height": 852}
df
# + id="KNTFc_QyyjSd" outputId="83a3f4c2-0687-4524-d449-eccfdb2adb6e" colab={"base_uri": "https://localhost:8080/"}
np.any(df["token_prediction"] == None)
# + id="qjeKhLew-xNC"
df.to_csv("train.csv")
# + id="Maw-6x8s_B59"
|
input/feedback-prize-2021/add_token_prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from fastai import * # Quick accesss to most common functionality
from fastai.tabular import * # Quick accesss to tabular functionality
from fastai.docs import * # Access to example data provided with fastai
# # Tabular example
# Tabular data should be in a Pandas `DataFrame`.
df = get_adult()
train_df, valid_df = df[:-2000].copy(),df[-2000:].copy()
train_df.head()
# Convert your `DataFrame` in to a `DataBunch` suitable for modeling by calling `tabular_data_from_df`.
dep_var = '>=50k'
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race', 'sex', 'native-country']
data = tabular_data_from_df(ADULT_PATH, train_df, valid_df, dep_var, tfms=[FillMissing, Categorify], cat_names=cat_names)
# Now you can create a `Learner` with `gen_tabular_dta`, and fit your model
learn = get_tabular_learner(data, layers=[200,100], metrics=accuracy)
learn.fit(1, 1e-2)
|
examples/tabular.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# Sanity Check: when model behaviours should overlap
# --
# *<NAME> and <NAME>, 2016*
#
# Many of the model classes in GPflow have overlapping behaviour in special cases. In this section, we fit some approximations to a model with a Gaussian likelihood, and make sure they're all the same.
#
# The models are:
# - `GPR` full Gaussian process regression
#
# - `VGP` a Gaussian approximation with Variational Bayes
# (approximating a Gaussian posterior with a Gaussian should be exact)
#
# - `SVGP` a sparse GP, with a Gaussian approximation. The inducing points are set to be at the data points, so again, should be exact.
#
# - `SVGP` (with whitened representation) As above, but with a rotation applied to whiten the representation of the process
#
# - `SGPR` A sparse GP with a *collapsed* posterior (Titsias 2009). Again, the inducing points are fixed to the data points.
#
# - `GPRFITC` The FITC approximation, again, the inducing points are fixed to the data points.
#
# In all cases the parameters are estimated by the method using maximum likelihood (or approximate maximum likelihood, as appropriate). The parameter estimates should all be the same.
# + deletable=true editable=true
import gpflow
import numpy as np
import matplotlib
# %matplotlib inline
matplotlib.rcParams['figure.figsize'] = (12, 6)
plt = matplotlib.pyplot
# + deletable=true editable=true
np.random.seed(0)
X = np.random.rand(20,1)*10
Y = np.sin(X) + 0.9 * np.cos(X*1.6) + np.random.randn(*X.shape)* 0.4
Xtest = np.random.rand(10,1)*10
plt.plot(X, Y, 'kx', mew=2)
# + deletable=true editable=true
m1 = gpflow.models.GPR(X, Y, kern=gpflow.kernels.RBF(1))
m2 = gpflow.models.VGP(X, Y, gpflow.kernels.RBF(1), likelihood=gpflow.likelihoods.Gaussian())
m3 = gpflow.models.SVGP(X, Y, gpflow.kernels.RBF(1),
likelihood=gpflow.likelihoods.Gaussian(),
Z=X.copy(), q_diag=False)
m3.feature.set_trainable(False)
m4 = gpflow.models.SVGP(X, Y, gpflow.kernels.RBF(1),
likelihood=gpflow.likelihoods.Gaussian(),
Z=X.copy(), q_diag=False, whiten=True)
m4.feature.set_trainable(False)
m5 = gpflow.models.SGPR(X, Y, gpflow.kernels.RBF(1), Z=X.copy())
m5.feature.set_trainable(False)
m6 = gpflow.models.GPRFITC(X, Y, gpflow.kernels.RBF(1), Z=X.copy())
m6.feature.set_trainable(False)
models = [m1, m2, m3, m4, m5, m6]
# + [markdown] deletable=true editable=true
# Now optimize the models. For GPR, SVGP and GPFITC this simply optimizes the hyper-parameters (since the inducing points are fixed). For the variational models, this jointly maximises the ELBO with respect to the variational parameters and the kernel parameters.
# + deletable=true editable=true
o = gpflow.train.ScipyOptimizer(method='BFGS')
_ = [o.minimize(m, maxiter=100) for m in models]
# + [markdown] deletable=true editable=true
# If everything worked as planned, the models should have the same
#
# - prediction functions
# - log (marginal) likelihood
# - kernel parameters
#
# For the variational models, where we use a ELBO in place of the likelihood, the ELBO should be tight to the likelihood in the cases studied here.
# + deletable=true editable=true
def plot(m, color, ax):
xx = np.linspace(-1, 11, 100)[:,None]
mu, var = m.predict_y(xx)
ax.plot(xx, mu, color, lw=2)
ax.fill_between(xx[:,0], mu[:,0] - 2*np.sqrt(var[:,0]), mu[:,0] + 2*np.sqrt(var[:,0]), color=color, alpha=0.2)
ax.plot(X, Y, 'kx', mew=2)
ax.set_xlim(-1, 11)
f, ax = plt.subplots(3,2,sharex=True, sharey=True, figsize=(12,9))
plot(m1, 'C0', ax[0,0])
plot(m2, 'C1', ax[1,0])
plot(m3, 'C2', ax[0,1])
plot(m4, 'C3', ax[1,1])
plot(m5, 'C4', ax[2,0])
plot(m6, 'C5', ax[2,1])
# + [markdown] deletable=true editable=true
# Here are the kernels and likelihoods, which show the fitted kernel parameters and noise variance:
# + deletable=true editable=true
from IPython import display
#_ = [display.display(m.kern, m.likelihood) for m in models]
[print(m.kern, '\n\n', m.likelihood, '\n\n----\n') for m in models];
# + [markdown] deletable=true editable=true
# Here are the likelihoods (or ELBOs)
# + deletable=true editable=true
print(np.array([m.compute_log_likelihood() for m in models]))
|
doc/source/notebooks/Sanity_check.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center>Utilize the dataset that is provided to make a NBA predicition</center>
import pandas as pd
import math
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from xgboost import XGBClassifier
import random
Info2018_2019 = pd.read_csv('./data/Year_2018_2019.csv')
# **Create the target, HomeWin. Create at least three new features from your dataset. Quantize all relevant features. Insert as many code and text cells as you need.**
# Firstly, I fond more information to be features of each team from [this link](https://www.basketball-reference.com/). And I saved them as .csv file. Then I load them as features. A helper function is defined.
# +
# read csv file and build information matrix
def initialize_data(Mstat, Ostat, Tstat):
new_Mstat = Mstat.drop(['Rk', 'Arena'], axis=1)
new_Ostat = Ostat.drop(['Rk', 'G', 'MP'], axis=1)
new_Tstat = Tstat.drop(['Rk', 'G', 'MP'], axis=1)
team_stats1 = pd.merge(new_Mstat, new_Ostat, how='left', on='Team')
team_stats1 = pd.merge(team_stats1, new_Tstat, how='left', on='Team')
# print(team_stats1.info())
return team_stats1.set_index('Team', inplace=False, drop=True)
Mstat = pd.read_csv('./data/18-19Miscellaneous_Stat.csv')
Ostat = pd.read_csv('./data/18-19Opponent_Per_Game_Stat.csv')
Tstat = pd.read_csv('./data/18-19Team_Per_Game_Stat.csv')
team_stats = initialize_data(Mstat, Ostat, Tstat)
# -
# The match information is storaged in `Year_2018_2019.csv` file. Then load the match results needed with some helper functions. `X` denotes the features and `y` denotes the labels, which value of 1 means the winner team is Home team, otherwise the winner team is Visitor team.
# +
base_elo = 1600
team_elos = {}
X = []
y = []
# calculate Elo score
def calc_elo(win_team, lose_team):
winner_rank = get_elo(win_team)
loser_rank = get_elo(lose_team)
rank_diff = winner_rank - loser_rank
exp = (rank_diff * -1) / 400
odds = 1 / (1 + math.pow(10, exp))
if winner_rank < 2100:
k = 32
elif 2100 <= winner_rank < 2400:
k = 24
else:
k = 16
new_winner_rank = round(winner_rank + (k * (1 - odds)))
new_rank_diff = new_winner_rank - winner_rank
new_loser_rank = loser_rank - new_rank_diff
return new_winner_rank, new_loser_rank
def get_elo(team):
try:
return team_elos[team]
except:
# if not, init elo score as base_elo
team_elos[team] = base_elo
return team_elos[team]
def build_dataSet(all_data):
# print("Building data set..")
for index, row in all_data.iterrows():
WLoc = ''
if float(row['PTS']) > float(row['PTS.1']):
Wteam = row['Visitor/Neutral']
Lteam = row['Home/Neutral']
WLoc = 'V'
else:
Wteam = row['Home/Neutral']
Lteam = row['Visitor/Neutral']
WLoc = 'H'
team1_elo = get_elo(Wteam)
team2_elo = get_elo(Lteam)
if WLoc == 'H':
team1_elo += 100
else:
team2_elo += 100
team1_features = [team1_elo]
team2_features = [team2_elo]
for key, value in team_stats.loc[Wteam].iteritems():
team1_features.append(value)
for key, value in team_stats.loc[Lteam].iteritems():
team2_features.append(value)
if WLoc=='H':
X.append(team1_features + team2_features)
y.append(1)
else:
X.append(team2_features + team1_features)
y.append(0)
new_winner_rank, new_loser_rank = calc_elo(Wteam, Lteam)
team_elos[Wteam] = new_winner_rank
team_elos[Lteam] = new_loser_rank
return np.nan_to_num(X), np.array(y)
X, y = build_dataSet(Info2018_2019)
# -
# **Explore dataset. Show relevant statistics, tables, graphs, visualizations. Try to find relationships between your features and the target. Insert as many code and text cells as you need.**
# Let's take a look inside of features.
print('X.shape=',X.shape)
print('Which means there are {} samples, and each sample has {} features.'.format(X.shape[0],X.shape[1]))
print('such as:Feature')
print(pd.DataFrame(X).head(10))
print('lables:(1 denotes HomeWin, 0 denotes VisitorWin)')
print(pd.DataFrame(y).head(10))
# Plot the features. There is no significant feature only on when plot them.
import matplotlib.pyplot as plt
f1=X[0,:]
f2=X[2,:]
plt.plot(f1)
plt.plot(f2)
plt.legend(['feature of HomeWin match','feature of HomeLose match'])
plt.show()
# **Create the following ML models and report the training and testing accuracy of each:**
#
# **Decision Tree Random Forest XGBoost Logistic Regression Naive Bayes (Gaussian) Use 80% of your data for training, and the remainder for testing. Use appropriate pruning and parameter tuning. Insert as many code and text cells as you need.**
# And normally in machine learning, data sets should be shuffled.
per = np.random.permutation(len(y))
X = X[per, :]
y = y[per]
# Split data sets to training set and test set. 80% of data should be for training, and remainder for testing.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
print('sample of trainning set:{},sample of test set:{}'.format(len(y_train), len(y_test)))
# Build and train **LogisticRegression** model
lr = LogisticRegression(penalty='l2', tol=0.00001, C=0.5, solver='liblinear')
lr.fit(X_train, y_train)
score_lr = lr.score(X_test, y_test)
score_lr_train = lr.score(X_train, y_train)
print('score of Logistic Regression model in test set is {:.4f} (score of training set:{:.4f})'.format(score_lr,score_lr_train))
# Build and train **GaussianNB** model.
# more setting:https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html
gnb = GaussianNB(var_smoothing=1e-09)
gnb.fit(X_train, y_train)
score_gnb = gnb.score(X_test, y_test)
score_gnb_train = gnb.score(X_train, y_train)
print('score of Naive Bayes (Gaussian) model in test set is {:.4f} (score of training set:{:.4f})'.format(score_gnb,score_gnb_train))
# Build and train **Random Forest** model.
# more setting:https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html
rf = RandomForestClassifier()
rf.fit(X_train, y_train)
score_rf = rf.score(X_test, y_test)
score_rf_train = rf.score(X_train, y_train)
print('score of Random Forest model in test set is {:.4f} (score of training set:{:.4f})'.format(score_rf,score_rf_train))
# Build and train **Decision Tree** model.
# more setting: https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html
dt = DecisionTreeClassifier()
dt.fit(X_train, y_train)
score_dt = dt.score(X_test, y_test)
score_dt_train = dt.score(X_train, y_train)
print('score of Decision Tree model in test set is {:.4f} (score of training set:{:.4f})'.format(score_dt,score_dt_train))
# Build and train **XGBoost** model.
# more setting: https://dask-ml.readthedocs.io/en/stable/modules/generated/dask_ml.xgboost.XGBClassifier.html
xgb = XGBClassifier(learning_rate=0.01, max_depth=5)
xgb.fit(X_train, y_train)
score_xgb = xgb.score(X_test, y_test)
score_xgb_train = xgb.score(X_train, y_train)
print('score of XGBoost model in test set is {:.4f} (score of training set:{:.4f})'.format(score_xgb,score_xgb_train))
# For summery info:
print('score of Logistic Regression model in test set is {:.4f} (score of training set:{:.4f})'.format(score_lr,score_lr_train))
print('score of Naive Bayes (Gaussian) model in test set is {:.4f} (score of training set:{:.4f})'.format(score_gnb,score_gnb_train))
print('score of Random Forest model in test set is {:.4f} (score of training set:{:.4f})'.format(score_rf,score_rf_train))
print('score of Decision Tree model in test set is {:.4f} (score of training set:{:.4f})'.format(score_dt,score_dt_train))
print('score of XGBoost model in test set is {:.4f} (score of training set:{:.4f})'.format(score_xgb,score_xgb_train))
# **Analyze the models created from above question. Which ones were the best and why? Which ones were the worst? What made sense and what didn't? Insert as many code and text cells as you need. Explain your top two ML models with visualizations and words.**
# since there are some random process in above functions, different trial will get different result. In one trial, result showed like:
#
# **score of Logistic Regression model in test set is 0.6350 (score of training set:0.7140)**
#
# **score of Naive Bayes (Gaussian) model in test set is 0.6274 (score of training set:0.6835)**
#
# **score of Random Forest model in test set is 0.6008 (score of training set:0.9752)**
#
# **score of Decision Tree model in test set is 0.6236 (score of training set:1.0000)**
#
# **score of XGBoost model in test set is 0.6312 (score of training set:0.8036)**
#
# In trainning set, decision tree is the best, but not in test test. Naive Bayes (Gaussian) performed worst with score of 0.6835. In the test set, Logistic Regression performed best(score of 0.6350) and Random Forest performed worst(score of 0.6008), The second best model is XGBoost model with score of 0.6312.
plt.plot(['LR','GNB','RF','DT','XGB'],[score_lr,score_gnb,score_rf,score_dt,score_xgb])
plt.plot(['LR','GNB','RF','DT','XGB'],[score_lr_train,score_gnb_train,score_rf_train,score_dt_train,score_xgb_train])
plt.legend(['score on test set','score on training set'])
# **Test each ML model from Question 4 on the current partial year, 2019-2020, and report the accuracies for each. Insert as many code and text cells as you need. Was your best model still the best? Analyze and discuss the results.**
# for this part, an .csv file named `Year_2019_2020.csv` should be storaged in `data` subpath. Re-load match info with code as below.
#
# **Note:** if you do not have `Year_2019_2020.csv`, you will get an error as **FileNotFoundError: File b'data/Year_2019_2020.csv' does not exist**
result_data = pd.read_csv('./data/Year_2019_2020.csv')
X_2019, y_2019 = build_dataSet(team_stats, result_data)
score_lr = lr.score(X_2019, y_2019)
score_gnb = gnb.score(X_2019, y_2019)
score_rf = rf.score(X_2019, y_2019)
score_dt = dt.score(X_2019, y_2019)
score_xgb = xgb.score(X_2019, y_2019)
print('score of Logistic Regression model in test set is {:.4f}'.format(score_lr))
print('score of Naive Bayes (Gaussian) model in test set is {:.4f}'.format(score_gnb))
print('score of Random Forest model in test set is {:.4f}'.format(score_rf))
print('score of Decision Tree model in test set is {:.4f}'.format(score_dt))
print('score of XGBoost model in test set is {:.4f}'.format(score_xgb))
# **Do at least two things that you think will improve your model's prediction capabilities for 2019-2020 (ie incorporate more data, engineer another feature, use a new ML model, normalize your data, etc). Insert as many code and text cells as you need.**
# If pruning model needed, the websites are listed above for more parameter setting. For example, we create GaussianNB model with one line code `gnb = GaussianNB(var_smoothing=1e-09)`, if the [link](https://scikit-learn.org/stable/modules/generated/sklearn.naive_bayes.GaussianNB.html) is checked, two parameter(priors,var_smoothing) can be set. Please feel free to modify one or two parameter(s). That will be interesting if you implyment this part by yourself. examples:
#
# xgb = XGBClassifier(learning_rate=0.01, max_depth=3)
#
# lr = LogisticRegression(C=0.5, solver='liblinear')
# **Re-evaluate: did it improve your model? Give relevant results and visualizations.**
# This part result depends on your 2019-2020 schedule and match result. I think some report should finish by yourself.
|
colab_like.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7 (tensorflow)
# language: python
# name: tensorflow
# ---
# <a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_02_3_pandas_grouping.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# # T81-558: Applications of Deep Neural Networks
# **Module 2: Python for Machine Learning**
# * Instructor: [<NAME>](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
# * For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# # Module 2 Material
#
# Main video lecture:
#
# * Part 2.1: Introduction to Pandas [[Video]](https://www.youtube.com/watch?v=bN4UuCBdpZc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_1_python_pandas.ipynb)
# * Part 2.2: Categorical Values [[Video]](https://www.youtube.com/watch?v=4a1odDpG0Ho&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_2_pandas_cat.ipynb)
# * **Part 2.3: Grouping, Sorting, and Shuffling in Python Pandas** [[Video]](https://www.youtube.com/watch?v=YS4wm5gD8DM&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_3_pandas_grouping.ipynb)
# * Part 2.4: Using Apply and Map in Pandas for Keras [[Video]](https://www.youtube.com/watch?v=XNCEZ4WaPBY&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_4_pandas_functional.ipynb)
# * Part 2.5: Feature Engineering in Pandas for Deep Learning in Keras [[Video]](https://www.youtube.com/watch?v=BWPTj4_Mi9E&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](t81_558_class_02_5_pandas_features.ipynb)
# # Google CoLab Instructions
#
# The following code ensures that Google CoLab is running the correct version of TensorFlow.
try:
# %tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
# # Part 2.3: Grouping, Sorting, and Shuffling
#
# Now we will take a look at a few ways to affect an entire Pandas data frame. These techniques will allow us to group, sort, and shuffle data sets. These are all essential operations for both data preprocessing and evaluation.
#
# ### Shuffling a Dataset
# There may be information lurking in the order of the rows of your dataset. Unless you are dealing with time-series data, the order of the rows should not be significant. Consider if your training set included employees in a company. Perhaps this dataset is ordered by the number of years that the employees were with the company. It is okay to have an individual column that specifies years of service. However, having the data in this order might be problematic.
#
# Consider if you were to split the data into training and validation. You could end up with your validation set having only the newer employees and the training set longer-term employees. Separating the data into a k-fold cross validation could have similar problems. Because of these issues, it is important to shuffle the data set.
#
# Often shuffling and reindexing are both performed together. Shuffling randomizes the order of the data set. However, it does not change the Pandas row numbers. The following code demonstrates a reshuffle. Notice that the first column, the row indexes, has not been reset. Generally, this will not cause any issues and allows trace back to the original order of the data. However, I usually prefer to reset this index. I reason that I typically do not care about the initial position, and there are a few instances where this unordered index can cause issues.
# +
import os
import pandas as pd
import numpy as np
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
#np.random.seed(42) # Uncomment this line to get the same shuffle each time
df = df.reindex(np.random.permutation(df.index))
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
display(df)
# -
# The following code demonstrates a reindex. Notice how the reindex orders the row indexes.
# +
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 0)
df.reset_index(inplace=True, drop=True)
display(df[0:10])
# -
# ### Sorting a Data Set
#
# While it is always a good idea to shuffle a data set before training, during training and preprocessing, you may also wish to sort the data set. Sorting the data set allows you to order the rows in either ascending or descending order for one or more columns. The following code sorts the MPG dataset by name and displays the first car.
# +
import os
import pandas as pd
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
df = df.sort_values(by='name', ascending=True)
idx = 0
for name in df['name']:
print(f"The number {idx + 1} car is: {df['name'].iloc[idx]}")
idx += 1
# print(f"The first car is: {df['name'].iloc[0]}")
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 0)
display(df)
# -
# ### Grouping a Data Set
#
# Grouping is a typical operation on data sets. Structured Query Language (SQL) calls this operation a "GROUP BY." Programmers use grouping to summarize data. Because of this, the summarization row count will usually shrink, and you cannot undo the grouping. Because of this loss of information, it is essential to keep your original data before the grouping.
#
# The Auto MPG dataset is used to demonstrate grouping.
# +
import os
import pandas as pd
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/auto-mpg.csv",
na_values=['NA', '?'])
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
display(df)
# -
# The above data set can be used with the group to perform summaries. For example, the following code will group cylinders by the average (mean). This code will provide the grouping. In addition to **mean**, you can use other aggregating functions, such as **sum** or **count**.
g = df.groupby('cylinders')['mpg'].std()
g
# It might be useful to have these **mean** values as a dictionary.
d = g.to_dict()
d
# A dictionary allows you to access an individual element quickly. For example, you could quickly look up the mean for six-cylinder cars. You will see that target encoding, introduced later in this module, makes use of this technique.
d[6]
# The code below shows how to count the number of rows that match each cylinder count.
df.groupby('cylinders')['mpg'].count().to_dict()
|
t81_558_class_02_3_pandas_grouping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
get_ipython().magic('matplotlib notebook')
# get_ipython().magic('matplotlib inline')
get_ipython().magic('load_ext autoreload')
get_ipython().magic('autoreload 2')
#___________________________________________________________________________________________________________________
import os
import tripyview as tpv
import shapefile as shp
import numpy as np
import xarray as xr
# + tags=["parameters"]
# Parameters
# mesh_path ='/work/ollie/projects/clidyn/FESOM2/meshes/core2/'
mesh_path = '/work/ollie/pscholz/mesh_fesom2.0/core2_srt_dep@node/'
save_path = None #'~/figures/test_papermill/'
save_fname= None
#_____________________________________________________________________________________
which_cycl= 6
which_mode= 'dmoc'
#_____________________________________________________________________________________
input_paths= list()
input_paths.append('/home/ollie/pscholz/results/trr181_tke_ctrl_ck0.1/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke_ctrl_ck0.3/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke+idemix_orig_ck0.1/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke+idemix_jayne09_ck0.1/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke+idemix_nycander05_ck0.1/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke+idemix_stormtide2_ck0.1/')
# input_paths.append('/home/ollie/pscholz/results/trr181_tke+idemix_jayne09_ck0.3/')
# input_paths.append('/home/ollie/pscholz/results/old_trr181_tke+idemix_nycander05_ck0.3/')
# input_paths.append('/home/ollie/pscholz/results/old_trr181_tke+idemix_stormtide2_ck0.3/')
input_names= list()
input_names.append('TKE, ck=0.1')
# input_names.append('TKE, ck=0.3')
# input_names.append('TKE+IDEMIX, ck=0.1, jayne (old param)')
# input_names.append('TKE+IDEMIX, ck=0.1, jayne (new param)')
# input_names.append('TKE+IDEMIX, ck=0.1, nycander (new param)')
# input_names.append('TKE+IDEMIX, ck=0.1, stormtide (new param)')
# input_names.append('TKE+IDEMIX, ck=0.3, jayne (new param)')
# input_names.append('TKE+IDEMIX, ck=0.3, nycander (new param)')
# input_names.append('TKE+IDEMIX, ck=0.3, stormtide (new param)')
vname = 'dflux'
year = [1979,2019]
mon, day, record, box, depth = None, None, None, None, None
#_____________________________________________________________________________________
# do anomaly plots in case ref_path is not None
ref_path = None #'/home/ollie/pscholz/results/trr181_tke_ctrl_ck0.1/' # None
ref_name = None # 'TKE, ck=0.1' # None
ref_year = None # [2009,2019]
ref_mon, ref_day, ref_record = None, None, None
#_____________________________________________________________________________________
cstr = 'blue2red'
cnum = 20
cref = 0
crange, cmin, cmax, cfac, climit = None, None, None, None, None
chist, ctresh = True, 0.995
#_____________________________________________________________________________________
ncolumn = 1 # 3
which_dpi = 300
do_rescale= None #'log10'
proj = 'pc'
do_contour= True
which_isopyc = 36.72
# +
#___LOAD FESOM2 MESH___________________________________________________________________________________
mesh=tpv.load_mesh_fesom2(mesh_path, do_rot='None', focus=0, do_info=True, do_pickle=True,
do_earea=True, do_narea=True, do_eresol=[True,'mean'], do_nresol=[True,'eresol'])
#______________________________________________________________________________________________________
if which_cycl is not None:
for ii,ipath in enumerate(input_paths):
input_paths[ii] = os.path.join(ipath,'{:d}/'.format(which_cycl))
print(ii, input_paths[ii])
if ref_path is not None:
ref_path = os.path.join(ref_path,'{:d}/'.format(which_cycl))
print('R', ref_path)
#______________________________________________________________________________________________________
cinfo=dict({'cstr':cstr, 'cnum':cnum})
if crange is not None: cinfo['crange']=crange
if cmin is not None: cinfo['cmin' ]=cmin
if cmax is not None: cinfo['cmax' ]=cmax
if cref is not None: cinfo['cref' ]=cref
if cfac is not None: cinfo['cfac' ]=cfac
if climit is not None: cinfo['climit']=climit
if chist is not None: cinfo['chist' ]=chist
if ctresh is not None: cinfo['ctresh']=ctresh
if ref_path is not None: cinfo['cref' ]=0.0
#______________________________________________________________________________________________________
# in case of diff plots
if ref_path is not None:
if ref_year is None: ref_year = year
if ref_mon is None: ref_mon = mon
if ref_record is None: ref_record = record
#______________________________________________________________________________________________________
# define density levels
# original dima
# std_dens=[0.0000, 30.00000, 30.55556, 31.11111, 31.36000, 31.66667, 31.91000, 32.22222, 32.46000,
# 32.77778, 33.01000, 33.33333, 33.56000, 33.88889, 34.11000, 34.44444, 34.62000, 35.00000,
# 35.05000, 35.10622, 35.20319, 35.29239, 35.37498, 35.41300, 35.45187, 35.52380, 35.59136,
# 35.65506, 35.71531, 35.77247, 35.82685, 35.87869, 35.92823, 35.97566, 35.98000, 36.02115,
# 36.06487, 36.10692, 36.14746, 36.18656, 36.22434, 36.26089, 36.29626, 36.33056, 36.36383,
# 36.39613, 36.42753, 36.45806, 36.48778, 36.51674, 36.54495, 36.57246, 36.59500, 36.59932,
# 36.62555, 36.65117, 36.67621, 36.68000, 36.70071, 36.72467, 36.74813, 36.75200, 36.77111,
# 36.79363, 36.81570, 36.83733, 36.85857, 36.87500, 36.87940, 36.89985, 36.91993, 36.93965,
# 36.95904, 36.97808, 36.99682, 37.01524, 37.03336, 37.05119, 37.06874, 37.08602, 37.10303,
# 37.11979, 37.13630, 37.15257, 37.16861, 37.18441, 37.50000, 37.75000, 40.00000]
# my density layers 2nd try
std_dens=[ 0.00000, 29.50000, 30.00000, 30.55556, 31.11111, 31.36000, 31.66667, 31.91000, 32.22222, 32.46000,
32.77778, 33.01000, 33.33333, 33.56000, 33.78170, 33.79659, 33.81331, 33.83206, 33.85258, 33.87502,
33.88889, 33.90019, 33.92843, 33.96012, 33.99567, 34.03267, 34.07050, 34.11295, 34.16058, 34.21400,
34.27274, 34.33865, 34.41114, 34.47728, 34.55149, 34.62872, 34.71458, 34.81014, 34.91325, 35.02337,
35.13865, 35.25518, 35.37026, 35.48624, 35.58763, 35.67886, 35.76112, 35.82097, 35.87630, 35.92691,
35.97247, 36.02033, 36.06813, 36.11950, 36.17459, 36.23291, 36.29566, 36.36239, 36.43058, 36.50178,
36.57474, 36.64730, 36.71590, 36.77414, 36.82096, 36.85908, 36.89139, 36.91962, 36.94532, 36.96900,
36.98623, 37.00269, 37.01746, 37.03056, 37.04018, 37.05134, 37.06372, 37.07111, 37.10000, 37.25556,
37.41111, 37.56667, 37.72222, 37.87778, 38.03333, 38.18889, 38.34444, 38.50000, 40.00000]
# +
#___LOAD FESOM2 REFERENCE DATA________________________________________________________________________
# load divergence of density class
if ref_path is not None:
print(ref_path, ref_name)
data_DFLX_ref = tpv.load_dmoc_data(mesh, ref_path, ref_name, year, 'srf', std_dens, do_dflx=True, do_info=False)
#___LOAD FESOM2 DATA___________________________________________________________________________________
# load divergence of density class
data_DFLX_list = list()
for datapath, descript in zip(input_paths, input_names):
print(datapath, descript)
data_DFLX_list.append( tpv.load_dmoc_data(mesh, datapath, descript, year, 'srf', std_dens, do_dflx=True, do_info=False) )
# +
#___COMPUTE DIAPYCNAL VERTICAL VELOCITY________________________________________________________________
# finds closest index of isopycnal class
ndens = len(std_dens)
idx_isopycn = np.argmin(np.abs(np.array(std_dens)-which_isopyc))
print(' sigma_2 = {:5.2f} kg/m^3'.format(std_dens[idx_isopycn]))
# integrate (xr.sum) divergence over all density classes below idx_isopycn
if ref_path is not None:
dflux_ref = -data_DFLX_ref.isel(ndens=idx_isopycn).rename({'std_dens_flux':'dflux'})
dflux_ref[list(dflux_ref.keys())[0]] = dflux_ref[list(dflux_ref.keys())[0]].assign_attrs({'description':'surface buoyancy forced transformations',
'long_name' :'surface buoyancy forced transformationsx',
'units' :'m/s',
'str_ldep' :', $\sigma_{{2}}$={:5.2f}kg/m³'.format(std_dens[idx_isopycn])})
# integrate (xr.sum) divergence over all density classes below idx_isopycn
dflux_list = list()
for data in data_DFLX_list:
dflux = -data.isel(ndens=idx_isopycn).rename({'std_dens_flux':'dflux'})
dflux[list(dflux.keys())[0]] = dflux[list(dflux.keys())[0]].assign_attrs({'description':'surface buoyancy forced transformations',
'long_name' :'surface buoyancy forced transformations',
'units' :'m/s',
'str_ldep' :', $\sigma_{{2}}$={:5.2f}kg/m³'.format(std_dens[idx_isopycn])})
if ref_path is not None: dflux_list.append( tpv.do_anomaly(dflux, dflux_ref) )
else: dflux_list.append( dflux )
# -
#___PLOT FESOM2 DATA___________________________________________________________________________________
spath = save_path
sname = list(dflux_list[0].keys())[0] #vname
slabel = dflux_list[0][sname].attrs['str_lsave']
if spath is not None: spath = os.path.join(spath,'{}_{}_{}.png'.format(which_mode, sname, slabel))
ncolumn= np.min([ncolumn,len(dflux_list)])
nrow = np.ceil(len(dflux_list)/ncolumn).astype('int')
if save_fname is not None: spath = save_fname
pos_gap = [0.005, 0.04]
if proj in ['nps, sps']:pos_gap = [0.005, 0.035]
# cinfo = dict({'cstr':'blue2red', 'crange':[-1.5e-5, 1.5e-5, 0.0] })
fig, ax, cbar = tpv.plot_hslice(mesh, dflux_list, cinfo=cinfo, box=box, n_rc=[nrow, ncolumn],
figsize=[ncolumn*7, nrow*3.5], proj = proj, do_plot='tpc',
do_lsmask='fesom', do_rescale=do_rescale, title='descript',
pos_gap=pos_gap, pos_extend=[0.03, 0.03, 0.905, 0.975],
do_save=spath, save_dpi=which_dpi)
mesh.e_pbnd_a
|
templates_notebooks/template_dmoc_srfcbflx.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
70
30
# ## Sum(+)
70 + 30
round(3.565544 + 4.345356, 2)
# ## Sub(-)
70 - 30
round(5.565544 - 4.345356, 2)
# ## Mul(*)
70 * 30
3.565544 * 4.345356
# ## Div(/)
45/30
4.5/2.0
# ## Div(//) | Coeff
45//30
4.5//2.5
# ## Mod(%)
45%30
4.5 % 2
# ## Pow(**)
5**5
2.1**5
2**5
1.01**365
1**3650
|
Week - 1/Arithmetic Operations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py38_pyhdx_pn011]
# language: python
# name: conda-env-py38_pyhdx_pn011-py
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # PyHDX basics
# + pycharm={"name": "#%%\n"}
from pyhdx import PeptideMasterTable, read_dynamx, HDXMeasurement
from pyhdx.plot import peptide_coverage
import matplotlib.pyplot as plt
import proplot as pplt
from pathlib import Path
# + [markdown] pycharm={"name": "#%% md\n"}
# We can use the ``read_dynamx`` function to read the input DynamX state file. Exposure times in the .csv files are in the
# field exposure, and we specify the unit with the `time_unit` keyword argument. The exposure time units are converted to
# seconds.
#
# This function returns a ``numpy`` structured array where each entry corresponds to one peptide, in this example 567 peptides.
# + pycharm={"name": "#%%\n"}
fpath = Path() / '..' / '..' / 'tests' / 'test_data' / 'input' / 'ecSecB_apo.csv'
data = read_dynamx(fpath, time_unit='min')
data.size
# + [markdown] pycharm={"name": "#%% md\n"}
# This array is loaded into the ``PeptideMasterTable`` class, which is the main data entry class. The parameter ``drop_first``
# determines how many N-terminal residues are considered to be fully back-exchanged, and therefore is subtracted from the
# total amount of exchangable D per peptide. The parameter ``ignore_prolines`` is controls whether the number of Prolines
# residues in the peptide should be subtracted from the total amount of exchangable and should generally be set to ``True``.
#
# The final number of exchangable residues is found in the 'ex_residues' field.
# + pycharm={"name": "#%%\n"}
master_table = PeptideMasterTable(data, drop_first=1, ignore_prolines=True)
master_table.data['ex_residues'][:50]
# + [markdown] pycharm={"name": "#%% md\n"}
# This master table allows us to control how the deuterium uptake content is determined. The method ``set_control`` can be
# used to choose which set of peptides is used as the fully deuterated (FD) control. This adds a new field called 'uptake'
# which is the normalized (to 100%) deuterium uptake of each peptide, with respect to the total amount of exchanging residues.
# + pycharm={"name": "#%%\n"}
master_table.set_control(('Full deuteration control', 0.167*60))
master_table.data['uptake'][:50]
# + [markdown] pycharm={"name": "#%% md\n"}
# Next we'll select our state of interest from the master Table. The available states are listed in `master_table.states`.
# Using `get_state` allows us to select all entries which belong to this state.
# + pycharm={"name": "#%%\n"}
master_table.states
state_data = master_table.get_state('SecB WT apo')
state_data.size
# -
# This `data` array can now be used to create an ``HDXMeasurement`` object, the main data object in PyHDX.
# Experimental metadata such as labelling pH and temperature can be specified. These quantities are required for calculating
# intrinsic exchange rates and ΔG values. The pH values are uncorrected values are measured by the pH meter (ie p(H, D)
# values)
# + pycharm={"name": "#%%\n"}
hdxm = HDXMeasurement(state_data, temperature=303.15, pH=8., name='My HDX measurement')
type(hdxm), len(hdxm), hdxm.timepoints, hdxm.name, hdxm.state
# + [markdown] pycharm={"name": "#%% md\n"}
# Iterating over a ``HDXMeasurement`` object returns a set of ``HDXTimepoint`` each with their own attributes describing
# the topology of the coverage. When creating the object, peptides which are not present in all timepoints are removed, such
# that all timepoints and ``HDXTimepoint`` have identical coverage.
#
# Note that the internal time units in PyHDX are seconds.
# + pycharm={"name": "#%%\n"}
fig, ax = pplt.subplots(figsize=(10, 5))
i = 0
peptide_coverage(ax, hdxm[i].data, 20, cbar=True)
t = ax.set_title(f'Peptides t = {hdxm.timepoints[i]}')
l = ax.set_xlabel('Residue number')
# + pycharm={"name": "#%%\n"}
fig, ax = pplt.subplots(figsize=(10, 5))
i = 3
peptide_coverage(ax, hdxm[i].data, 20, cbar=True)
t = ax.set_title(f'Peptides t = {hdxm.timepoints[i]}')
l = ax.set_xlabel('Residue number')
# + [markdown] pycharm={"name": "#%% md\n"}
# The data in an ``HDXMeasurement`` object can be saved to and reloaded from disk (with associated metadata)
# in .csv format.
# + pycharm={"name": "#%%\n"}
from pyhdx.fileIO import csv_to_hdxm
hdxm.to_file('My_HDX_file.csv')
hdx_load = csv_to_hdxm('My_HDX_file.csv')
# + pycharm={"name": "#%%\n"}
|
docs/examples/01_basic_usage.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### Author: <NAME>
# # Arrays
# ## What is an Array?
# * Array is a data structure used to store homogeneous elements at contiguous locations.
# * One memory block is allocated for the entire array to hold the elements of the array. The array elements can be accessed in constant time by using the index of the parliculnr element as the subscript.
# ## Properties of Arrays:
# * Arrays stores similar data types. That is, array can hold data of same data type values. This is one of the limitations of arrays compared to other data structures.
#
# * Each value stored, in an array, is known as an element and all elements are indexed. The first element added, by default, gets 0 index. That is, the 5th element added gets an index number of 4.
#
# * Elements can be retrieved by their index number. (__random access__)
#
# * Array elements are stored in contiguous (continuous) memory locations.
#
# * One array name can represent multiple values. Array is the easiest way to store a large quantity of data of same data types. For example, to store the salary of 100 employees, it is required to declare 100 variables. But with arrays, with one array name all the 100 employees salaries can be stored.
#
# * At the time of creation itself, array size should be declared (array initialization does not require size).
# ## Arrays in Python:
# Python does not have a native support for arrays, but has a more generic data structure called LIST. List provides all the options as array with more functionality.
# But with few tweaks we can implement Array data structure in Python.
# We will be seeing how to do this.
# ### Creating an array:
# +
class Array(object):
''' sizeOfArray: denotes the total size of the array to be initialized
arrayType: denotes the data type of the array(as all the elements of the array have same data type)
arrayItems: values at each position of array
'''
def __init__(self, sizeOfArray, arrayType = int):
self.sizeOfArray = len(list(map(arrayType, range(sizeOfArray))))
self.arrayItems =[arrayType(0)] * sizeOfArray # initialize array with zeroes
def __str__(self):
return ' '.join([str(i) for i in self.arrayItems])
# function for search
def search(self, keyToSearch):
for i in range(self.sizeOfArray):
if (self.arrayItems[i] == keyToSearch): # brute-forcing
return i # index at which element/ key was found
return -1 # if key not found, return -1
# function for inserting an element
def insert(self, keyToInsert, position):
if(self.sizeOfArray > position):
for i in range(self.sizeOfArray - 2, position - 1, -1):
self.arrayItems[i + 1] = self.arrayItems[i]
self.arrayItems[position] = keyToInsert
else:
print('Array size is:', self.sizeOfArray)
# function to delete an element
def delete(self, keyToDelete, position):
if(self.sizeOfArray > position):
for i in range(position, self.sizeOfArray - 1):
self.arrayItems[i] = self.arrayItems[i + 1]
else:
print('Array size is:', self.sizeOfArray)
a = Array(10, int)
print(a)
# -
# ### Common array operations:
# * Search
# * Insert
# * Delete
#
# __Time complexity__:
#
# * Search: O(n)
# * Insert: O(n)
# * Delete: O(n)
# * Indexing: O(1)
# ### Search Operation on Array:
a = Array(10, int)
index = a.search(0)
print('Element found at:', index)
# ### Insert Operation:
a = Array(10, int)
a.insert(1, 2)
a.insert(2,3)
a.insert(3,4)
print(a)
# ### Delete Operation:
a = Array(10, int)
a.insert(1, 2)
a.insert(2,3)
a.insert(3,4)
a.delete(3, 4)
print(a)
index = a.search(1)
print('Element found at:',index)
# #### These were the basics of how to implement Array using Python. Now we will see how to use Python built-in module 'array'.
#
#
# Syntax: array(dataType, valueList)
# +
# importing 'array' module
import array
# initializing array
arr = array.array('i', [1, 2, 3, 4, 5]) # initialize array with integers ('i')
# printing original array
print ("The new created array is : ",end="")
for i in range (0, 5):
print (arr[i], end=" ")
# using append() to insert new value at end
arr.append(6);
# printing appended array
print ("\nThe appended array is : ", end="")
for i in range (0, 6):
print (arr[i], end=" ")
# using insert() to insert value at specific position
# inserts 5 at 2nd position
arr.insert(2, 5)
# printing array after insertion
print ("\nThe array after insertion is : ", end="")
for i in range (0, 7):
print (arr[i], end=" ")
arr.remove(1)
# deleting a value from array
print ("\nThe array after deletion is : ", end="")
for i in range (0, 6):
print (arr[i], end=" ")
# -
# ### Disadvantages of Array
# * __Fixed size__: The size of the array is static (specify the array size before using it, this can be overcome using Dynamic Arrays).
# * __One block allocation__: To allocate the array itself at the beginning, sometimes it may not be possible to get the memory for the complete array (if the array size is big).
# * __Complex position-based insertion__: To insert an element at a given position, we may need to shift the existing elements. This will create a position for us to insert the new element at the desired position. If the position at which we want to add an element is at the beginning, then the shifting operation is more expensive .
|
Not My Work just references/Data-Structures-using-Python-master/Arrays/Arrays.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# <font size=3 color="midnightblue" face="arial">
# <h1 align="center">Escuela de Ciencias Básicas, Tecnología e Ingeniería</h1>
# </font>
#
# <font size=3 color="navy" face="arial">
# <h1 align="center">ECBTI</h1>
# </font>
#
# <font size=2 color="darkorange" face="arial">
# <h1 align="center">Curso: Métodos Numéricos</h1>
# </font>
#
# <font size=2 color="midnightblue" face="arial">
# <h1 align="center">Unidad 1: Error</h1>
# </font>
#
# <font size=1 color="darkorange" face="arial">
# <h1 align="center">Febrero 28 de 2020</h1>
# </font>
#
# ***
#
# > **Tutor:** <NAME>, I.C. D.Sc.
#
# > **skype:** carlos.alberto.alvarez.henao
#
# > **Herramienta:** [Jupyter](http://jupyter.org/)
#
# > **Kernel:** Python 3.7
#
#
# ***
# ***Comentario:*** estas notas están basadas en el curso del profesor [<NAME>](https://github.com/mandli/intro-numerical-methods) (en inglés)
# # Fuentes de error
#
# Los cálculos numéricos, que involucran el uso de máquinas (análogas o digitales) presentan una serie de errores que provienen de diferentes fuentes:
#
# - del Modelo
# - de los datos
# - de truncamiento
# - de representación de los números (punto flotante)
# - $\ldots$
#
# ***Meta:*** Categorizar y entender cada tipo de error y explorar algunas aproximaciones simples para analizarlas.
# # Error en el modelo y los datos
#
# Errores en la formulación fundamental
#
# - Error en los datos: imprecisiones en las mediciones o incertezas en los parámetros
#
# Infortunadamente no tenemos control de los errores en los datos y el modelo de forma directa pero podemos usar métodos que pueden ser más robustos en la presencia de estos tipos de errores.
# # Error de truncamiento
#
# Los errores surgen de la expansión de funciones con una función simple, por ejemplo, $sin(x) \approx x$ para $|x|\approx0$.
# # Error de representación de punto fotante
#
# Los errores surgen de aproximar números reales con la representación en precisión finita de números en el computador.
# # Definiciones básicas
#
# Dado un valor verdadero de una función $f$ y una solución aproximada $F$, se define:
#
# - Error absoluto
#
# $$e_a=|f-F|$$
#
# - Error relativo
#
# $$e_r = \frac{e_a}{|f|}=\frac{|f-F|}{|f|}$$
#
#
# # Notación $\text{Big}-\mathcal{O}$
#
# sea $$f(x)= \mathcal{O}(g(x)) \text{ cuando } x \rightarrow a$$
#
# si y solo si
#
# $$|f(x)|\leq M|g(x)| \text{ cuando } |x-a| < \delta \text{ donde } M, a > 0$$
#
#
# En la práctica, usamos la notación $\text{Big}-\mathcal{O}$ para decir algo sobre cómo se pueden comportar los términos que podemos haber dejado fuera de una serie. Veamos el siguiente ejemplo de la aproximación de la serie de Taylor:
# ***Ejemplo:***
#
# sea $f(x) = \sin x$ con $x_0 = 0$ entonces
#
# $$T_N(x) = \sum^N_{n=0} (-1)^{n} \frac{x^{2n+1}}{(2n+1)!}$$
#
# Podemos escribir $f(x)$ como
#
# $$f(x) = x - \frac{x^3}{6} + \frac{x^5}{120} + \mathcal{O}(x^7)$$
#
# Esto se vuelve más útil cuando lo vemos como lo hicimos antes con $\Delta x$:
#
# $$f(x) = \Delta x - \frac{\Delta x^3}{6} + \frac{\Delta x^5}{120} + \mathcal{O}(\Delta x^7)$$
# # Reglas para el error de propagación basado en la notación $\text{Big}-\mathcal{O}$
#
# En general, existen dos teoremas que no necesitan prueba y se mantienen cuando el valor de $x$ es grande:
#
# Sea
#
# $$\begin{aligned}
# f(x) &= p(x) + \mathcal{O}(x^n) \\
# g(x) &= q(x) + \mathcal{O}(x^m) \\
# k &= \max(n, m)
# \end{aligned}$$
#
# Entonces
#
# $$
# f+g = p + q + \mathcal{O}(x^k)
# $$
#
# y
#
# \begin{align}
# f \cdot g &= p \cdot q + p \mathcal{O}(x^m) + q \mathcal{O}(x^n) + O(x^{n + m}) \\
# &= p \cdot q + \mathcal{O}(x^{n+m})
# \end{align}
# De otra forma, si estamos interesados en valores pequeños de $x$, $\Delta x$, la expresión puede ser modificada como sigue:
#
# \begin{align}
# f(\Delta x) &= p(\Delta x) + \mathcal{O}(\Delta x^n) \\
# g(\Delta x) &= q(\Delta x) + \mathcal{O}(\Delta x^m) \\
# r &= \min(n, m)
# \end{align}
#
# entonces
#
# $$
# f+g = p + q + O(\Delta x^r)
# $$
#
# y
#
# \begin{align}
# f \cdot g &= p \cdot q + p \cdot \mathcal{O}(\Delta x^m) + q \cdot \mathcal{O}(\Delta x^n) + \mathcal{O}(\Delta x^{n+m}) \\
# &= p \cdot q + \mathcal{O}(\Delta x^r)
# \end{align}
# ***Nota:*** En este caso, supongamos que al menos el polinomio con $k=max(n,m)$ tiene la siguiente forma:
#
# $$
# p(\Delta x) = 1 + p_1 \Delta x + p_2 \Delta x^2 + \ldots
# $$
#
# o
#
# $$
# q(\Delta x) = 1 + q_1 \Delta x + q_2 \Delta x^2 + \ldots
# $$
#
# para que $\mathcal{O}(1)$
#
#
# de modo que hay un término $\mathcal{O}(1)$ que garantiza la existencia de $\mathcal{O}(\Delta x^r)$ en el producto final.
# Para tener una idea de por qué importa más la potencia en $\Delta x$ al considerar la convergencia, la siguiente figura muestra cómo las diferentes potencias en la tasa de convergencia pueden afectar la rapidez con la que converge nuestra solución. Tenga en cuenta que aquí estamos dibujando los mismos datos de dos maneras diferentes. Graficar el error como una función de $\Delta x$ es una forma común de mostrar que un método numérico está haciendo lo que esperamos y muestra el comportamiento de convergencia correcto. Dado que los errores pueden reducirse rápidamente, es muy común trazar este tipo de gráficos en una escala log-log para visualizar fácilmente los resultados. Tenga en cuenta que si un método fuera realmente del orden $n$, será una función lineal en el espacio log-log con pendiente $n$.
import numpy as np
import matplotlib.pyplot as plt
# +
dx = np.linspace(1.0, 1e-4, 100)
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 2.0)
axes = []
axes.append(fig.add_subplot(1, 2, 1))
axes.append(fig.add_subplot(1, 2, 2))
for n in range(1, 5):
axes[0].plot(dx, dx**n, label="$\Delta x^%s$" % n)
axes[1].loglog(dx, dx**n, label="$\Delta x^%s$" % n)
axes[0].legend(loc=2)
axes[1].set_xticks([10.0**(-n) for n in range(5)])
axes[1].set_yticks([10.0**(-n) for n in range(16)])
axes[1].legend(loc=4)
for n in range(2):
axes[n].set_title("Crecimiento del Error vs. $\Delta x^n$")
axes[n].set_xlabel("$\Delta x$")
axes[n].set_ylabel("Error Estimado")
axes[n].set_title("Crecimiento de las diferencias")
axes[n].set_xlabel("$\Delta x$")
axes[n].set_ylabel("Error Estimado")
plt.show()
# -
# # Error de truncamiento
#
# ***Teorema de Taylor:*** Sea $f(x) \in C^{m+1}[a,b]$ y $x_0 \in [a,b]$, para todo $x \in (a,b)$ existe un número $c = c(x)$ que se encuentra entre $x_0$ y $x$ tal que
#
# $$ f(x) = T_N(x) + R_N(x)$$
#
# donde $T_N(x)$ es la aproximación del polinomio de Taylor
#
# $$T_N(x) = \sum^N_{n=0} \frac{f^{(n)}(x_0)\times(x-x_0)^n}{n!}$$
#
# y $R_N(x)$ es el residuo (la parte de la serie que obviamos)
#
# $$R_N(x) = \frac{f^{(n+1)}(c) \times (x - x_0)^{n+1}}{(n+1)!}$$
# Otra forma de pensar acerca de estos resultados consiste en reemplazar $x - x_0$ con $\Delta x$. La idea principal es que el residuo $R_N(x)$ se vuelve mas pequeño cuando $\Delta x \rightarrow 0$.
#
# $$T_N(x) = \sum^N_{n=0} \frac{f^{(n)}(x_0)\times \Delta x^n}{n!}$$
#
# y $R_N(x)$ es el residuo (la parte de la serie que obviamos)
#
# $$ R_N(x) = \frac{f^{(n+1)}(c) \times \Delta x^{n+1}}{(n+1)!} \leq M \Delta x^{n+1}$$
# ***Ejemplo 1:***
#
# $f(x) = e^x$ con $x_0 = 0$
#
# Usando esto podemos encontrar expresiones para el error relativo y absoluto en función de $x$ asumiendo $N=2$.
# Derivadas:
# $$\begin{aligned}
# f'(x) &= e^x \\
# f''(x) &= e^x \\
# f^{(n)}(x) &= e^x
# \end{aligned}$$
#
# Polinomio de Taylor:
# $$\begin{aligned}
# T_N(x) &= \sum^N_{n=0} e^0 \frac{x^n}{n!} \Rightarrow \\
# T_2(x) &= 1 + x + \frac{x^2}{2}
# \end{aligned}$$
#
# Restos:
# $$\begin{aligned}
# R_N(x) &= e^c \frac{x^{n+1}}{(n+1)!} = e^c \times \frac{x^3}{6} \quad \Rightarrow \\
# R_2(x) &\leq \frac{e^1}{6} \approx 0.5
# \end{aligned}$$
#
# Precisión:
# $$
# e^1 = 2.718\ldots \\
# T_2(1) = 2.5 \Rightarrow e \approx 0.2 ~~ r \approx 0.1
# $$
# ¡También podemos usar el paquete `sympy` que tiene la capacidad de calcular el polinomio de *Taylor* integrado!
# +
import sympy
x = sympy.symbols('x')
f = sympy.symbols('f', cls=sympy.Function)
f = sympy.exp(x)
f.series(x0=0, n=5)
# -
# Graficando
# +
x = np.linspace(-1, 1, 100)
T_N = 1.0 + x + x**2 / 2.0
R_N = np.exp(1) * x**3 / 6.0
plt.plot(x, T_N, 'r', x, np.exp(x), 'k', x, R_N, 'b')
plt.plot(0.0, 1.0, 'o', markersize=10)
plt.grid(True)
plt.xlabel("x")
plt.ylabel("$f(x)$, $T_N(x)$, $R_N(x)$")
plt.legend(["$T_N(x)$", "$f(x)$", "$R_N(x)$"], loc=2)
plt.show()
# -
# ***Ejemplo 2:***
#
# Aproximar
#
# $$ f(x) = \frac{1}{x} \quad x_0 = 1,$$
#
# usando $x_0 = 1$ para el tercer termino de la serie de Taylor.
# $$\begin{aligned}
# f'(x) &= -\frac{1}{x^2} \\
# f''(x) &= \frac{2}{x^3} \\
# f^{(n)}(x) &= \frac{(-1)^n n!}{x^{n+1}}
# \end{aligned}$$
#
# $$\begin{aligned}
# T_N(x) &= \sum^N_{n=0} (-1)^n (x-1)^n \Rightarrow \\
# T_2(x) &= 1 - (x - 1) + (x - 1)^2
# \end{aligned}$$
#
# $$\begin{aligned}
# R_N(x) &= \frac{(-1)^{n+1}(x - 1)^{n+1}}{c^{n+2}} \Rightarrow \\
# R_2(x) &= \frac{-(x - 1)^{3}}{c^{4}}
# \end{aligned}$$
# +
x = np.linspace(0.8, 2, 100)
T_N = 1.0 - (x-1) + (x-1)**2
R_N = -(x-1.0)**3 / (1.1**4)
plt.plot(x, T_N, 'r', x, 1.0 / x, 'k', x, R_N, 'b')
plt.plot(1.0, 1.0, 'o', markersize=10)
plt.grid(True)
plt.xlabel("x")
plt.ylabel("$f(x)$, $T_N(x)$, $R_N(x)$")
plt.legend(["$T_N(x)$", "$f(x)$", "$R_N(x)$"], loc=8)
plt.show()
# -
# # En esta celda haz tus comentarios
#
#
# Esta cosa con esta vaina quizas tal vez-.-.--
#
#
#
#
#
#
#
#
# ## Error de punto flotante
#
# Errores surgen de aproximar números reales con números de precisión finita
#
# $$\pi \approx 3.14$$
#
# o $\frac{1}{3} \approx 0.333333333$ en decimal, los resultados forman un número finito de registros para representar cada número.
# ### Sistemas de punto flotante
#
# Los números en sistemas de punto flotante se representan como una serie de bits que representan diferentes partes de un número. En los sistemas de punto flotante normalizados, existen algunas convenciones estándar para el uso de estos bits. En general, los números se almacenan dividiéndolos en la forma
#
# $$F = \pm d_1 . d_2 d_3 d_4 \ldots d_p \times \beta^E$$
# donde
#
# 1. $\pm$ es un bit único y representa el signo del número.
#
#
# 2. $d_1 . d_2 d_3 d_4 \ldots d_p$ es la *mantisa*. observe que, técnicamente, el decimal se puede mover, pero en general, utilizando la notación científica, el decimal siempre se puede colocar en esta ubicación. Los digitos $d_2 d_3 d_4 \ldots d_p$ son llamados la *fracción* con $p$ digitos de precisión. Los sistemas normalizados específicamente ponen el punto decimal en el frente y asume $d_1 \neq 0$ a menos que el número sea exactamente $0$.
#
#
# 3. $\beta$ es la *base*. Para el sistema binario $\beta = 2$, para decimal $\beta = 10$, etc.
#
#
# 4. $E$ es el *exponente*, un entero en el rango $[E_{\min}, E_{\max}]$
# Los puntos importantes en cualquier sistema de punto flotante es
#
# 1. Existe un conjunto discreto y finito de números representables.
#
#
# 2. Estos números representables no están distribuidos uniformemente en la línea real
#
#
# 3. La aritmética en sistemas de punto flotante produce resultados diferentes de la aritmética de precisión infinita (es decir, matemática "real")
# ### Propiedades de los sistemas de punto flotante
#
# Todos los sistemas de punto flotante se caracterizan por varios números importantes
#
# - Número normalizado reducido (underflow si está por debajo, relacionado con números sub-normales alrededor de cero)
#
#
# - Número normalizado más grande (overflow)
#
#
# - Cero
#
#
# - $\epsilon$ o $\epsilon_{mach}$
#
#
# - `Inf` y `nan`
# ***Ejemplo: Sistema de juguete***
#
# Considere el sistema decimal de 2 digitos de precisión (normalizado)
#
# $$f = \pm d_1 . d_2 \times 10^E$$
#
# con $E \in [-2, 0]$.
#
# **Numero y distribución de números**
#
#
# 1. Cuántos números pueden representarse con este sistema?
#
#
# 2. Cuál es la distribución en la línea real?
#
#
# 3. Cuáles son los límites underflow y overflow?
# Cuántos números pueden representarse con este sistema?
#
# $$f = \pm d_1 . d_2 \times 10^E ~~~ \text{with} E \in [-2, 0]$$
#
# $$2 \times 9 \times 10 \times 3 + 1 = 541$$
# Cuál es la distribución en la línea real?
# +
d_1_values = [1, 2, 3, 4, 5, 6, 7, 8, 9]
d_2_values = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
E_values = [0, -1, -2]
fig = plt.figure(figsize=(10.0, 1.0))
axes = fig.add_subplot(1, 1, 1)
for E in E_values:
for d1 in d_1_values:
for d2 in d_2_values:
axes.plot( (d1 + d2 * 0.1) * 10**E, 0.0, 'r+', markersize=20)
axes.plot(-(d1 + d2 * 0.1) * 10**E, 0.0, 'r+', markersize=20)
axes.plot(0.0, 0.0, '+', markersize=20)
axes.plot([-10.0, 10.0], [0.0, 0.0], 'k')
axes.set_title("Distribución de Valores")
axes.set_yticks([])
axes.set_xlabel("x")
axes.set_ylabel("")
axes.set_xlim([-0.1, 0.1])
plt.show()
# -
# Cuáles son los límites superior (overflow) e inferior (underflow)?
#
# - El menor número que puede ser representado (underflow) es: $1.0 \times 10^{-2} = 0.01$
#
#
#
# - El mayor número que puede ser representado (overflow) es: $9.9 \times 10^0 = 9.9$
# ### Sistema Binario
#
# Considere el sistema en base 2 de 2 dígitos de precisión
#
# $$f=\pm d_1 . d_2 \times 2^E \quad \text{with} \quad E \in [-1, 1]$$
#
#
# #### Numero y distribución de números**
#
#
# 1. Cuántos números pueden representarse con este sistema?
#
#
# 2. Cuál es la distribución en la línea real?
#
#
# 3. Cuáles son los límites underflow y overflow?
# Cuántos números pueden representarse en este sistema?
#
#
# $$f=\pm d_1 . d_2 \times 2^E ~~~~ \text{con} ~~~~ E \in [-1, 1]$$
#
# $$ 2 \times 1 \times 2 \times 3 + 1 = 13$$
# Cuál es la distribución en la línea real?
# +
d_1_values = [1]
d_2_values = [0, 1]
E_values = [1, 0, -1]
fig = plt.figure(figsize=(10.0, 1.0))
axes = fig.add_subplot(1, 1, 1)
for E in E_values:
for d1 in d_1_values:
for d2 in d_2_values:
axes.plot( (d1 + d2 * 0.5) * 2**E, 0.0, 'r+', markersize=20)
axes.plot(-(d1 + d2 * 0.5) * 2**E, 0.0, 'r+', markersize=20)
axes.plot(0.0, 0.0, 'r+', markersize=20)
axes.plot([-4.5, 4.5], [0.0, 0.0], 'k')
axes.set_title("Distribución de Valores")
axes.set_yticks([])
axes.set_xlabel("x")
axes.set_ylabel("")
axes.set_xlim([-3.5, 3.5])
plt.show()
# -
# Cuáles son los límites superior (*overflow*) e inferior (*underflow*)?
#
# - El menor número que puede ser representado (*underflow*) es: $1.0 \times 2^{-1} = 0.5$
#
#
#
#
# - El mayor número que puede ser representado (*overflow*) es: $1.1 \times 2^1 = 3$
#
# Observe que estos números son en sistema binario.
#
# Una rápida regla de oro:
#
# $$2^3 2^2 2^1 2^0 . 2^{-1} 2^{-2} 2^{-3}$$
#
# corresponde a
#
# 8s, 4s, 2s, 1s . mitades, cuartos, octavos, $\ldots$
# ### Sistema real - IEEE 754 sistema binario de punto flotante
#
# #### Precisión simple
#
# - Almacenamiento total es de 32 bits
#
#
# - Exponente de 8 bits $\Rightarrow E \in [-126, 127]$
#
#
# - Fracción 23 bits ($p = 24$)
#
#
# ```
# s EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF
# 0 1 8 9 31
# ```
#
# Overflow $= 2^{127} \approx 3.4 \times 10^{38}$
#
# Underflow $= 2^{-126} \approx 1.2 \times 10^{-38}$
#
# $\epsilon_{\text{machine}} = 2^{-23} \approx 1.2 \times 10^{-7}$
#
# #### Precisión doble
#
# - Almacenamiento total asignado es 64 bits
#
# - Exponenete de 11 bits $\Rightarrow E \in [-1022, 1024]$
#
# - Fracción de 52 bits ($p = 53$)
#
# ```
# s EEEEEEEEEE FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FFFFFFFFFF FF
# 0 1 11 12 63
# ```
# Overflow $= 2^{1024} \approx 1.8 \times 10^{308}$
#
# Underflow $= 2^{-1022} \approx 2.2 \times 10^{-308}$
#
# $\epsilon_{\text{machine}} = 2^{-52} \approx 2.2 \times 10^{-16}$
# ### Acceso de Python a números de la IEEE
#
# Accede a muchos parámetros importantes, como el epsilon de la máquina
#
# ```python
# import numpy
# numpy.finfo(float).eps
# ```
# +
import numpy
numpy.finfo(float).eps
print(numpy.finfo(numpy.float16))
print(numpy.finfo(numpy.float32))
print(numpy.finfo(float))
print(numpy.finfo(numpy.float128))
# -
# ## Por qué debería importarnos esto?
#
# - Aritmética de punto flotante no es conmutativa o asociativa
#
#
# - Errores de punto flotante compuestos, No asuma que la precisión doble es suficiente
#
#
# - Mezclar precisión es muy peligroso
# ### Ejemplo 1: Aritmética simple
#
# Aritmética simple $\delta < \epsilon_{\text{machine}}$
#
# $$(1+\delta) - 1 = 1 - 1 = 0$$
#
# $$1 - 1 + \delta = \delta$$
# ### Ejemplo 2: Cancelación catastrófica
#
# Miremos qué sucede cuando sumamos dos números $x$ y $y$ cuando $x+y \neq 0$. De hecho, podemos estimar estos límites haciendo un análisis de error. Aquí necesitamos presentar la idea de que cada operación de punto flotante introduce un error tal que
#
# $$
# \text{fl}(x ~\text{op}~ y) = (x ~\text{op}~ y) (1 + \delta)
# $$
#
# donde $\text{fl}(\cdot)$ es una función que devuelve la representación de punto flotante de la expresión encerrada, $\text{op}$ es alguna operación (ex. $+, -, \times, /$), y $\delta$ es el error de punto flotante debido a $\text{op}$.
# De vuelta a nuestro problema en cuestión. El error de coma flotante debido a la suma es
#
# $$\text{fl}(x + y) = (x + y) (1 + \delta).$$
#
#
# Comparando esto con la solución verdadera usando un error relativo tenemos
#
# $$\begin{aligned}
# \frac{(x + y) - \text{fl}(x + y)}{x + y} &= \frac{(x + y) - (x + y) (1 + \delta)}{x + y} = \delta.
# \end{aligned}$$
#
# entonces si $\delta = \mathcal{O}(\epsilon_{\text{machine}})$ no estaremos muy preocupados.
# Que pasa si consideramos un error de punto flotante en la representación de $x$ y $y$, $x \neq y$, y decimos que $\delta_x$ y $\delta_y$ son la magnitud de los errores en su representación. Asumiremos que esto constituye el error de punto flotante en lugar de estar asociado con la operación en sí.
#
# Dado todo esto, tendríamos
#
# $$\begin{aligned}
# \text{fl}(x + y) &= x (1 + \delta_x) + y (1 + \delta_y) \\
# &= x + y + x \delta_x + y \delta_y \\
# &= (x + y) \left(1 + \frac{x \delta_x + y \delta_y}{x + y}\right)
# \end{aligned}$$
# Calculando nuevamente el error relativo, tendremos
#
# $$\begin{aligned}
# \frac{x + y - (x + y) \left(1 + \frac{x \delta_x + y \delta_y}{x + y}\right)}{x + y} &= 1 - \left(1 + \frac{x \delta_x + y \delta_y}{x + y}\right) \\
# &= \frac{x}{x + y} \delta_x + \frac{y}{x + y} \delta_y \\
# &= \frac{1}{x + y} (x \delta_x + y \delta_y)
# \end{aligned}$$
#
# Lo importante aquí es que ahora el error depende de los valores de $x$ y $y$, y más importante aún, su suma. De particular preocupación es el tamaño relativo de $x + y$. A medida que se acerca a cero en relación con las magnitudes de $x$ y $y$, el error podría ser arbitrariamente grande. Esto se conoce como ***cancelación catastrófica***.
# +
dx = numpy.array([10**(-n) for n in range(1, 16)])
x = 1.0 + dx
y = -numpy.ones(x.shape)
error = numpy.abs(x + y - dx) / (dx)
fig = plt.figure()
fig.set_figwidth(fig.get_figwidth() * 2)
axes = fig.add_subplot(1, 2, 1)
axes.loglog(dx, x + y, 'o-')
axes.set_xlabel("$\Delta x$")
axes.set_ylabel("$x + y$")
axes.set_title("$\Delta x$ vs. $x+y$")
axes = fig.add_subplot(1, 2, 2)
axes.loglog(dx, error, 'o-')
axes.set_xlabel("$\Delta x$")
axes.set_ylabel("$|x + y - \Delta x| / \Delta x$")
axes.set_title("Diferencia entre $x$ y $y$ vs. Error relativo")
plt.show()
# -
# ### Ejemplo 3: Evaluación de una función
#
# Considere la función
#
# $$
# f(x) = \frac{1 - \cos x}{x^2}
# $$
#
# con $x\in[-10^{-4}, 10^{-4}]$.
#
# Tomando el límite cuando $x \rightarrow 0$ podemos ver qué comportamiento esperaríamos ver al evaluar esta función:
#
# $$
# \lim_{x \rightarrow 0} \frac{1 - \cos x}{x^2} = \lim_{x \rightarrow 0} \frac{\sin x}{2 x} = \lim_{x \rightarrow 0} \frac{\cos x}{2} = \frac{1}{2}.
# $$
#
# ¿Qué hace la representación de punto flotante?
# +
x = numpy.linspace(-1e-3, 1e-3, 100, dtype=numpy.float32)
error = (0.5 - (1.0 - numpy.cos(x)) / x**2) / 0.5
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, error, 'o')
axes.set_xlabel("x")
axes.set_ylabel("Error Relativo")
# -
# ### Ejemplo 4: Evaluación de un Polinomio
#
# $$f(x) = x^7 - 7x^6 + 21 x^5 - 35 x^4 + 35x^3-21x^2 + 7x - 1$$
# +
x = numpy.linspace(0.988, 1.012, 1000, dtype=numpy.float16)
y = x**7 - 7.0 * x**6 + 21.0 * x**5 - 35.0 * x**4 + 35.0 * x**3 - 21.0 * x**2 + 7.0 * x - 1.0
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, y, 'r')
axes.set_xlabel("x")
axes.set_ylabel("y")
axes.set_ylim((-0.1, 0.1))
axes.set_xlim((x[0], x[-1]))
plt.show()
# -
# ### Ejemplo 5: Evaluación de una función racional
#
# Calcule $f(x) = x + 1$ por la función $$F(x) = \frac{x^2 - 1}{x - 1}$$
#
# ¿Cuál comportamiento esperarías encontrar?
# +
x = numpy.linspace(0.5, 1.5, 101, dtype=numpy.float16)
f_hat = (x**2 - 1.0) / (x - 1.0)
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, numpy.abs(f_hat - (x + 1.0)))
axes.set_xlabel("$x$")
axes.set_ylabel("Error Absoluto")
plt.show()
# -
# ## Combinación de error
#
# En general, nos debemos ocupar de la combinación de error de truncamiento con el error de punto flotante.
#
# - Error de Truncamiento: errores que surgen de la aproximación de una función, truncamiento de una serie.
#
# $$\sin x \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} + O(x^7)$$
#
#
# - Error de punto flotante: errores derivados de la aproximación de números reales con números de precisión finita
#
# $$\pi \approx 3.14$$
#
# o $\frac{1}{3} \approx 0.333333333$ en decimal, los resultados forman un número finito de registros para representar cada número.
# ### Ejemplo 1:
#
# Considere la aproximación de diferencias finitas donde $f(x) = e^x$ y estamos evaluando en $x=1$
#
# $$f'(x) \approx \frac{f(x + \Delta x) - f(x)}{\Delta x}$$
#
# Compare el error entre disminuir $\Delta x$ y la verdadera solucion $f'(1) = e$
# +
delta_x = numpy.linspace(1e-20, 5.0, 100)
delta_x = numpy.array([2.0**(-n) for n in range(1, 60)])
x = 1.0
f_hat_1 = (numpy.exp(x + delta_x) - numpy.exp(x)) / (delta_x)
f_hat_2 = (numpy.exp(x + delta_x) - numpy.exp(x - delta_x)) / (2.0 * delta_x)
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.loglog(delta_x, numpy.abs(f_hat_1 - numpy.exp(1)), 'o-', label="Unilateral")
axes.loglog(delta_x, numpy.abs(f_hat_2 - numpy.exp(1)), 's-', label="Centrado")
axes.legend(loc=3)
axes.set_xlabel("$\Delta x$")
axes.set_ylabel("Error Absoluto")
plt.show()
# -
# ### Ejemplo 2:
#
# Evalúe $e^x$ con la serie de *Taylor*
#
# $$e^x = \sum^\infty_{n=0} \frac{x^n}{n!}$$
#
# podemos elegir $n< \infty$ que puede aproximarse $e^x$ en un rango dado $x \in [a,b]$ tal que el error relativo $E$ satisfaga $E<8 \cdot \varepsilon_{\text{machine}}$?
#
# ¿Cuál podría ser una mejor manera de simplemente evaluar el polinomio de Taylor directamente por varios $N$?
# +
import scipy.special
def my_exp(x, N=10):
value = 0.0
for n in range(N + 1):
value += x**n / scipy.special.factorial(n)
return value
x = numpy.linspace(-2, 2, 100, dtype=numpy.float32)
for N in range(1, 50):
error = numpy.abs((numpy.exp(x) - my_exp(x, N=N)) / numpy.exp(x))
if numpy.all(error < 8.0 * numpy.finfo(float).eps):
break
print(N)
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.plot(x, error)
axes.set_xlabel("x")
axes.set_ylabel("Error Relativo")
plt.show()
# -
# ### Ejemplo 3: Error relativo
#
# Digamos que queremos calcular el error relativo de dos valores $x$ y $y$ usando $x$ como valor de normalización
#
# $$
# E = \frac{x - y}{x}
# $$
# y
# $$
# E = 1 - \frac{y}{x}
# $$
#
# son equivalentes. En precisión finita, ¿qué forma pidría esperarse que sea más precisa y por qué?
#
# Ejemplo tomado de [blog](https://nickhigham.wordpress.com/2017/08/14/how-and-how-not-to-compute-a-relative-error/) posteado por <NAME>*
# Usando este modelo, la definición original contiene dos operaciones de punto flotante de manera que
#
# $$\begin{aligned}
# E_1 = \text{fl}\left(\frac{x - y}{x}\right) &= \text{fl}(\text{fl}(x - y) / x) \\
# &= \left[ \frac{(x - y) (1 + \delta_+)}{x} \right ] (1 + \delta_/) \\
# &= \frac{x - y}{x} (1 + \delta_+) (1 + \delta_/)
# \end{aligned}$$
# Para la otra formulación tenemos
#
# $$\begin{aligned}
# E_2 = \text{fl}\left( 1 - \frac{y}{x} \right ) &= \text{fl}\left(1 - \text{fl}\left(\frac{y}{x}\right) \right) \\
# &= \left(1 - \frac{y}{x} (1 + \delta_/) \right) (1 + \delta_-)
# \end{aligned}$$
# Si suponemos que todos las $\text{op}$s tienen magnitudes de error similares, entonces podemos simplificar las cosas dejando que
#
# $$
# |\delta_\ast| \le \epsilon.
# $$
#
# Para comparar las dos formulaciones, nuevamente usamos el error relativo entre el error relativo verdadero $e_i$ y nuestras versiones calculadas $E_i$
# Definición original
#
# $$\begin{aligned}
# \frac{e - E_1}{e} &= \frac{\frac{x - y}{x} - \frac{x - y}{x} (1 + \delta_+) (1 + \delta_/)}{\frac{x - y}{x}} \\
# &\le 1 - (1 + \epsilon) (1 + \epsilon) = 2 \epsilon + \epsilon^2
# \end{aligned}$$
# Definición manipulada:
#
# $$\begin{aligned}
# \frac{e - E_2}{e} &= \frac{e - \left[1 - \frac{y}{x}(1 + \delta_/) \right] (1 + \delta_-)}{e} \\
# &= \frac{e - \left[e - \frac{y}{x} \delta_/) \right] (1 + \delta_-)}{e} \\
# &= \frac{e - \left[e + e\delta_- - \frac{y}{x} \delta_/ - \frac{y}{x} \delta_/ \delta_-)) \right] }{e} \\
# &= - \delta_- + \frac{1}{e} \frac{y}{x} \left(\delta_/ + \delta_/ \delta_- \right) \\
# &= - \delta_- + \frac{1 -e}{e} \left(\delta_/ + \delta_/ \delta_- \right) \\
# &\le \epsilon + \left |\frac{1 - e}{e}\right | (\epsilon + \epsilon^2)
# \end{aligned}$$
#
# Vemos entonces que nuestro error de punto flotante dependerá de la magnitud relativa de $e$
# +
# Based on the code by <NAME>
# https://gist.github.com/higham/6f2ce1cdde0aae83697bca8577d22a6e
# Compares relative error formulations using single precision and compared to double precision
N = 501 # Note: Use 501 instead of 500 to avoid the zero value
d = numpy.finfo(numpy.float32).eps * 1e4
a = 3.0
x = a * numpy.ones(N, dtype=numpy.float32)
y = [x[i] + numpy.multiply((i - numpy.divide(N, 2.0, dtype=numpy.float32)), d, dtype=numpy.float32) for i in range(N)]
# Compute errors and "true" error
relative_error = numpy.empty((2, N), dtype=numpy.float32)
relative_error[0, :] = numpy.abs(x - y) / x
relative_error[1, :] = numpy.abs(1.0 - y / x)
exact = numpy.abs( (numpy.float64(x) - numpy.float64(y)) / numpy.float64(x))
# Compute differences between error calculations
error = numpy.empty((2, N))
for i in range(2):
error[i, :] = numpy.abs((relative_error[i, :] - exact) / numpy.abs(exact))
fig = plt.figure()
axes = fig.add_subplot(1, 1, 1)
axes.semilogy(y, error[0, :], '.', markersize=10, label="$|x-y|/|x|$")
axes.semilogy(y, error[1, :], '.', markersize=10, label="$|1-y/x|$")
axes.grid(True)
axes.set_xlabel("y")
axes.set_ylabel("Error Relativo")
axes.set_xlim((numpy.min(y), numpy.max(y)))
axes.set_ylim((5e-9, numpy.max(error[1, :])))
axes.set_title("Comparasión Error Relativo")
axes.legend()
plt.show()
# -
# Algunos enlaces de utilidad con respecto al punto flotante IEEE:
#
# - [What Every Computer Scientist Should Know About Floating-Point Arithmetic](http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html)
#
#
# - [IEEE 754 Floating Point Calculator](http://babbage.cs.qc.edu/courses/cs341/IEEE-754.html)
#
#
# - [Numerical Computing with IEEE Floating Point Arithmetic](http://epubs.siam.org/doi/book/10.1137/1.9780898718072)
# ## Operaciones de conteo
#
# - ***Error de truncamiento:*** *¿Por qué no usar más términos en la serie de Taylor?*
#
#
# - ***Error de punto flotante:*** *¿Por qué no utilizar la mayor precisión posible?*
# ### Ejemplo 1: Multiplicación matriz - vector
#
# Sea $A, B \in \mathbb{R}^{N \times N}$ y $x \in \mathbb{R}^N$.
#
# 1. Cuenta el número aproximado de operaciones que tomará para calcular $Ax$
#
# 2. Hacer lo mismo para $AB$
# ***Producto Matriz-vector:*** Definiendo $[A]_i$ como la $i$-ésima fila de $A$ y $A_{ij}$ como la $i$,$j$-ésima entrada entonces
#
# $$
# A x = \sum^N_{i=1} [A]_i \cdot x = \sum^N_{i=1} \sum^N_{j=1} A_{ij} x_j
# $$
#
# Tomando un caso en particular, siendo $N=3$, entonces la operación de conteo es
#
# $$
# A x = [A]_1 \cdot v + [A]_2 \cdot v + [A]_3 \cdot v = \begin{bmatrix}
# A_{11} \times v_1 + A_{12} \times v_2 + A_{13} \times v_3 \\
# A_{21} \times v_1 + A_{22} \times v_2 + A_{23} \times v_3 \\
# A_{31} \times v_1 + A_{32} \times v_2 + A_{33} \times v_3
# \end{bmatrix}
# $$
#
# Esto son 15 operaciones (6 sumas y 9 multiplicaciones)
# Tomando otro caso, siendo $N=4$, entonces el conteo de operaciones es:
#
# $$
# A x = [A]_1 \cdot v + [A]_2 \cdot v + [A]_3 \cdot v = \begin{bmatrix}
# A_{11} \times v_1 + A_{12} \times v_2 + A_{13} \times v_3 + A_{14} \times v_4 \\
# A_{21} \times v_1 + A_{22} \times v_2 + A_{23} \times v_3 + A_{24} \times v_4 \\
# A_{31} \times v_1 + A_{32} \times v_2 + A_{33} \times v_3 + A_{34} \times v_4 \\
# A_{41} \times v_1 + A_{42} \times v_2 + A_{43} \times v_3 + A_{44} \times v_4 \\
# \end{bmatrix}
# $$
#
# Esto lleva a 28 operaciones (12 sumas y 16 multiplicaciones).
#
# Generalizando, hay $N^2$ mutiplicaciones y $N(N-1)$ sumas para un total de
#
# $$
# \text{operaciones} = N (N - 1) + N^2 = \mathcal{O}(N^2).
# $$
# ***Producto Matriz-Matriz ($AB$):*** Definiendo $[B]_j$ como la $j$-ésima columna de $B$ entonces
#
# $$
# (A B)_{ij} = \sum^N_{i=1} \sum^N_{j=1} [A]_i \cdot [B]_j
# $$
#
# El producto interno de dos vectores es representado por
#
# $$
# a \cdot b = \sum^N_{i=1} a_i b_i
# $$
#
# conduce a $\mathcal{O}(3N)$ operaciones. Como hay $N^2$ entradas en la matriz resultante, tendríamos $\mathcal{O}(N^3)$ operaciones
# Existen métodos para realizar la multiplicación matriz - matriz más rápido. En la siguiente figura vemos una colección de algoritmos a lo largo del tiempo que han podido limitar el número de operaciones en ciertas circunstancias
# $$
# \mathcal{O}(N^\omega)
# $$
# 
# ### Ejemplo 2: Método de Horner para evaluar polinomios
#
# Dado
#
# $$P_N(x) = a_0 + a_1 x + a_2 x^2 + \ldots + a_N x^N$$
#
# o
#
#
# $$P_N(x) = p_1 x^N + p_2 x^{N-1} + p_3 x^{N-2} + \ldots + p_{N+1}$$
#
# queremos encontrar la mejor vía para evaluar $P_N(x)$
# Primero considere dos vías para escribir $P_3$
#
# $$ P_3(x) = p_1 x^3 + p_2 x^2 + p_3 x + p_4$$
#
# y usando multiplicación anidada
#
# $$ P_3(x) = ((p_1 x + p_2) x + p_3) x + p_4$$
# Considere cuántas operaciones se necesitan para cada...
#
# $$ P_3(x) = p_1 x^3 + p_2 x^2 + p_3 x + p_4$$
#
# $$P_3(x) = \overbrace{p_1 \cdot x \cdot x \cdot x}^3 + \overbrace{p_2 \cdot x \cdot x}^2 + \overbrace{p_3 \cdot x}^1 + p_4$$
# Sumando todas las operaciones, en general podemos pensar en esto como una pirámide
#
# 
#
# podemos estimar de esta manera que el algoritmo escrito de esta manera tomará aproximadamente $\mathcal{O}(N^2/2)$ operaciones para completar.
# Mirando nuetros otros medios de evaluación
#
# $$ P_3(x) = ((p_1 x + p_2) x + p_3) x + p_4$$
#
# Aquí encontramos que el método es $\mathcal{O}(N)$ (el 2 generalmente se ignora en estos casos). Lo importante es que la primera evaluación es $\mathcal{O}(N^2)$ y la segunda $\mathcal{O}(N)$!
# ### Algoritmo
#
#
# Complete la función e implemente el método de *Horner*
#
# ```python
# def eval_poly(p, x):
# """Evaluates polynomial given coefficients p at x
#
# Function to evaluate a polynomial in order N operations. The polynomial is defined as
#
# P(x) = p[0] x**n + p[1] x**(n-1) + ... + p[n-1] x + p[n]
#
# The value x should be a float.
# """
# pass
# ```
def eval_poly(p, x):
"""Evaluates polynomial given coefficients p at x
Function to evaluate a polynomial in order N operations. The polynomial is defined as
P(x) = p[0] x**n + p[1] x**(n-1) + ... + p[n-1] x + p[n]
The value x should be a float.
"""
### ADD CODE HERE
pass
# +
# Scalar version
def eval_poly(p, x):
"""Evaluates polynomial given coefficients p at x
Function to evaluate a polynomial in order N operations. The polynomial is defined as
P(x) = p[0] x**n + p[1] x**(n-1) + ... + p[n-1] x + p[n]
The value x should be a float.
"""
y = p[0]
for coefficient in p[1:]:
y = y * x + coefficient
return y
# Vectorized version
def eval_poly(p, x):
"""Evaluates polynomial given coefficients p at x
Function to evaluate a polynomial in order N operations. The polynomial is defined as
P(x) = p[0] x**n + p[1] x**(n-1) + ... + p[n-1] x + p[n]
The value x can by a NumPy ndarray.
"""
y = numpy.ones(x.shape) * p[0]
for coefficient in p[1:]:
y = y * x + coefficient
return y
p = [1, -3, 10, 4, 5, 5]
x = numpy.linspace(-10, 10, 100)
plt.plot(x, eval_poly(p, x))
plt.show()
# -
|
Cap_01_Error.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8 - AzureML
# language: python
# name: python38-azureml
# ---
# # Train a basic neural network with distributed MPI on the MNIST dataset using Horovod
#
# **Requirements** - In order to benefit from this tutorial, you will need:
# - A basic understanding of Machine Learning
# - An Azure account with an active subscription. [Create an account for free](https://azure.microsoft.com/free/?WT.mc_id=A261C142F)
# - An Azure ML workspace with computer cluster - [Configure workspace](../../../configuration.ipynb)
#
# - A python environment
# - Installed Azure Machine Learning Python SDK v2 - [install instructions](../../../../README.md) - check the getting started section
#
# **Learning Objectives** - By the end of this tutorial, you should be able to:
# - Connect to your AML workspace from the Python SDK
# - Create and run a **distributed** `Command` which executes a Python command
# - Use a local file as an `input` to the Command
#
# **Motivations** - This notebook explains how to setup and run a Command. The Command is a fundamental construct of Azure Machine Learning. It can be used to run a task on a specified compute (either local or on the cloud). The Command accepts `environment` and `compute` to setup required infrastructure. You can define a `command` to run on this infrastructure with `inputs`.
# # 1. Connect to Azure Machine Learning Workspace
#
# The [workspace](https://docs.microsoft.com/en-us/azure/machine-learning/concept-workspace) is the top-level resource for Azure Machine Learning, providing a centralized place to work with all the artifacts you create when you use Azure Machine Learning. In this section we will connect to the workspace in which the job will be run.
#
# ## 1.1. Import the required libraries
# import required libraries
from azure.ai.ml import MLClient
from azure.ai.ml import command, MpiDistribution
from azure.identity import DefaultAzureCredential
# ## 1.2. Configure workspace details and get a handle to the workspace
#
# To connect to a workspace, we need identifier parameters - a subscription, resource group and workspace name. We will use these details in the `MLClient` from `azure.ai.ml` to get a handle to the required Azure Machine Learning workspace. We use the default [default azure authentication](https://docs.microsoft.com/en-us/python/api/azure-identity/azure.identity.defaultazurecredential?view=azure-python) for this tutorial. Check the [configuration notebook](../../../configuration.ipynb) for more details on how to configure credentials and connect to a workspace.
# Enter details of your AML workspace
subscription_id = "<SUBSCRIPTION_ID>"
resource_group = "<RESOURCE_GROUP>"
workspace = "<AML_WORKSPACE_NAME>"
# get a handle to the workspace
ml_client = MLClient(
DefaultAzureCredential(), subscription_id, resource_group, workspace
)
# # 2. Configure and run the Command
# In this section we will configure and run a standalone job using the `command` class. The `command` class can be used to run standalone jobs and can also be used as a function inside pipelines.
#
# ## 2.1 Configure the Command
# The `command` allows user to configure the following key aspects.
# - `code` - This is the path where the code to run the command is located
# - `command` - This is the command that needs to be run
# - `inputs` - This is the dictionary of inputs using name value pairs to the command. The key is a name for the input within the context of the job and the value is the input value. Inputs can be referenced in the `command` using the `${{inputs.<input_name>}}` expression. To use files or folders as inputs, we can use the `Input` class. The `Input` class supports three parameters:
# - `type` - The type of input. This can be a `uri_file` or `uri_folder`. The default is `uri_folder`.
# - `path` - The path to the file or folder. These can be local or remote files or folders. For remote files - http/https, wasb are supported.
# - Azure ML `data`/`dataset` or `datastore` are of type `uri_folder`. To use `data`/`dataset` as input, you can use registered dataset in the workspace using the format '<data_name>:<version>'. For e.g Input(type='uri_folder', path='my_dataset:1')
# - `mode` - Mode of how the data should be delivered to the compute target. Allowed values are `ro_mount`, `rw_mount` and `download`. Default is `ro_mount`
# - `environment` - This is the environment needed for the command to run. Curated or custom environments from the workspace can be used. Or a custom environment can be created and used as well. Check out the [environment](../../../../assets/environment/environment.ipynb) notebook for more examples.
# - `compute` - The compute on which the command will run. In this example we are using a compute called `cpu-cluster` present in the workspace. You can replace it any other compute in the workspace. You can run it on the local machine by using `local` for the compute. This will run the command on the local machine and all the run details and output of the job will be uploaded to the Azure ML workspace.
# - `distribution` - Distribution configuration for distributed training scenarios. Azure Machine Learning supports PyTorch, TensorFlow, and MPI-based distributed training. The allowed values are `PyTorch`, `TensorFlow` or `Mpi`.
# - `display_name` - The display name of the Job
# - `description` - The description of the experiment
#
# In this example we will use `MPI` for distribution.
job = command(
code="./src", # local path where the code is stored
command="python train.py --epochs ${{inputs.epochs}}",
inputs={"epochs": 1},
environment="AzureML-tensorflow-2.4-ubuntu18.04-py37-cuda11-gpu@latest",
compute="gpu-cluster",
instance_count=2,
distribution=MpiDistribution(process_count_per_instance=2),
display_name="tensorflow-mnist-distributed-horovod-example"
# experiment_name: tensorflow-mnist-distributed-horovod-example
# description: Train a basic neural network with TensorFlow on the MNIST dataset, distributed via Horovod.
)
# ## 2.2 Run the Command
# Using the `MLClient` created earlier, we will now run this Command as a job in the workspace.
# submit the command
returned_job = ml_client.create_or_update(job)
# # Next Steps
# You can see further examples of running a job [here](../../../single-step/)
#
|
sdk/jobs/single-step/tensorflow/mnist-distributed-horovod/tensorflow-mnist-distributed-horovod.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.6.12 64-bit (''azure_automl'': conda)'
# name: python3612jvsc74a57bd03fec2c5a411dce07235ef28c8752b6cecf1f94423de7e7c24e62fc38b1bc47de
# ---
# # ESML - accelerator
#
# ## PROJECT + DATA CONCEPTS + ENTERPRISE Datalake Design + DEV->PROD MLOps
# - `1)ESML Project`: The ONLY thing you need to remember is your `Project number` (and `BRONZE, SILVER, GOLD` concept )
# - ProjectNo=4 have a list of all your datasets as ESMLDatasets. (Well you need to provide names for them also: "mydata01", "mydata02" - but thats it)
# - `2)AutoLake - lakedesign & Roles`: Bronze, silver, gold + IN and date folders
# - Benefits: Physical datalake design! onnected to Azure ML Workspace, with autoregistration of `Azure ML Datasets`
# - `Role 1`: `Data ingestion team` only need to care about 1 thing - onboard data to `IN-folder`, in .CSV format
# - `Auto parquet-conversion` from `IN` folder (.CSV) to `OUT`/BRONZE/bronze.PARQUET
# - `Role 2`: `Data scientists` only need to care about 3 things (R/W): `BRONZE, SILVER, GOLD` datasets, all in .PARQUET format
# - How? The ESML project will `Automap` and `Autoregister` Azure ML Datasets - `IN, SILVER, BRONZE, GOLD`
# - `2a) R&D VS Production phase`: "Latest data" VS versioning on Datasets and datefolders
# - Benefits "R&D mode": Faster RnD phase to onboard and refresh data easy. Also fast "flip-switch" to production
# - How? `ESMLDataset is context self aware` - knows when it is used in TRAIN or INFERENCE pipeline
# - `2b) TRAIN vs INFERENCE` versions</u> `Reuse (Bronze->Silver->Gold) pipepline`, for both TRAIN preprocessing, and INFERENCE
# - Benefits: Inference with different MODEL version, on data from the same day/time, (to compare scoring etc)
# - How? ESMLDataset have context self awareness, and `knows WHERE and HOW to load/save data`
# - `2c) BATCH CONFIG`: Turn on/off features on ALL datasets
# - Accelerate setup: `Datadrift, Time series traits, Smart noise, etc`
# - Share refined data back to its "origin/non-projectbased structure" easy:
# - ESMLProject.ShareBack(ds.Silver)
# - How? ESMProject controls all ESMDatasets, in a uniform way
# ## ENTERPRISE Deployment of Models & Governance - MLOps at scale
# - `3) DEV->TEST-PROD` (configs, compute, performance)
# - ESML has config for 3 environemnts: Easy DEPLOY model across subscriptions and Azure ML Studio workspaces
# - Save costs & time:
# - `DEV` has cheaper compute performance for TRAIN and INFERENCE (batch, AKS)
# - `DEV` has Quick-debug ML training (fast training...VS good scoring in TEST and PROD)
# - How? ESML `AutoMLFactory` and `ComputeFactory`
#
#
# ### Q&A:
# - Q: Is ESML Machine learning specific? If I only want to refine some data...for integration, or report?
# - A: You can use this for just data refinement also: `Bronze->Silver->Gold` refinement.
# - Benefits: Enterprise security, Read/write to datalake, easy to share refined data.
# - Benefits: The tooling "glued togehter": Azure datafactory + Azure Databricks (and Azure ML Studio pipelines if needed)
#
#
# # Datalake design - convention
#
# ## Train model
# 1)Data ingestion team: Lands raw in-data, and transform to .parquet in bronze. (Not included in MLOps. Use "Azure data factory / Biztalk / Logic apps".
# - master/1_projects/project002/03_diabetes_model_reg/`train`/ds01_diabetes/`in`/`dev`/2020/01/01/
#
# 2) `Bronze->Silver->Gold`
# - master/1_projects/project002/03_diabetes_model_reg/`train`/ds01_diabetes/out/bronze/`dev`/
# - master/1_projects/project002/03_diabetes_model_reg/`train`/ds01_diabetes/out/silver/`dev`/
# - master/1_projects/project002/03_diabetes_model_reg/`train`/gold/dev/
#
# ## Inference: Batch scoring
# 1) Data ingestion
# - master/1_projects/project002/03_diabetes_model_reg/`inference/1/`ds01_diabetes/in/`dev`/2020/01/01/
#
# 2) `Bronze->Silver->Gold`
# - master/1_projects/project002/03_diabetes_model_reg/`inference/1/`ds01_diabetes/out/bronze/`dev`/
# - master/1_projects/project002/03_diabetes_model_reg/`inference/1/`ds01_diabetes/out/silver/`dev`/
# - master/1_projects/project002/03_diabetes_model_reg/`inference/1/`gold/`dev`/
#
# Notes: Inference ONLINE scoring (AKS)
# - `inference/1/` = Model version
# - inference/1/ds01_diabetes/in/`dev`/2020/01/01/`17/30/58/00` Can be used for Online AKS scenario - save scoring history on blob storage, down to `millisecond` (ms)
# - Save individual calls as Guid.parquet in `17/30/58/00` folder
# - Pipeline logic `Bronze->Silver->Gold` = Can be used for Online AKS scenario to process raw input before calling `model.predict()` in the [run(raw_data)] method
#
# Q: `dev`, `test`,`prod` folders at the end?
# - A: We have these folders at the end, for customers that wants a slim solution/low-maintenance, with just 1 datalake instance, and not 3 storage accounts.
# - If you have 3 storage accounts, only 1 of these folders (dev in dev storage account) will have data at each storage account.
# - Pro's:
# - This alternative is more cost flexible. Example: You can have lower cost replication-settings on DEV storage account.
# - Con's:
# - A bit more work to share data between projects.
# - A bit more work to update datalake design.
# - Below all says `dev` folder. But `dev`can also be `test`,`prod`
#
# Q2: Why not `dev`, `test`,`prod` folders at the the top, e.g. on root-folder or container?
# - A: Separation of access RBAC. Granularity: project-based AND environment-based. And "optimizeing the tree" same as keeping datetimefolders at the end..where it can grow massively if fast frequency
# - Each project/models, should have access to only THEIR dev,test,prod data...not all projects goes to production either.
#
# ## 1) ESMLProject - Project number gives you "lake area"
# - Config? settings/project_specific/`lake_settings.json`, or `overwrite with constructor`
# - `folderDate, ProjectNumber, inferenceModelVersion,`modelAlias`, *datasetFolderNames`
# - `folderDate` needs to be types DATETIME hence not in set in `lake_settings.json`
# - `modelAlias` can be iteration-based `M03`, and/or tied to a user-alias `M01_joakim`.
# - Purpose: UI info in Azure ML Studio to easily see which datasets belong to WHAT model (if multi-model approach in project)
# - `R&D phase vs Production`: Set on `ESMLProject.rnd=True` to avoid versioning
# - Tran VS Inference?
# - ESMLProject and ESMLDatasets are `context self aware` and will figure this out
# - Benefits:
# - ESMLProject `Automaps` + `Autoregister` Azure ML Datasets as: `IN, SILVER, BRONZE, GOLD`
# - `ESMLDatasets` are `context aware`, will write to TRAIN or INFERERENCE structure, and `inferenceModelVersion` is involved here.
#
# ### TIP: How to know your ProjectNumber? Dataset names? Date folder?
# - You need to provide projectnumber, and dataset folder names
# - Tip: same names you gave data ingestion team, the folder-names for datasets in lake
# - TRAIN: Choose data onboarding date-folder?
# - Tip: Ask data ingestion team about datefolders "2020-01-01" under IN folder, and what environment you want your data to land (dev,test,prod)
# # 1A) Connect to TEST - using Authentication (SP's needed in TEST Azure ML workspace keyvault)
# +
import sys, os
import pandas as pd
from azureml.core import Workspace
sys.path.append(os.path.abspath("../azure-enterprise-scale-ml/esml/common/")) # NOQA: E402
from esml import ESMLDataset, ESMLProject
from azureml.core.authentication import InteractiveLoginAuthentication
p = ESMLProject() # 1) self-aware about its config sources, p.dev_test_prod = "dev" # active environment (override config)
p.dev_test_prod = "test"
auth = InteractiveLoginAuthentication(tenant_id = p.tenant)
ws, config_name = p.authenticate_workspace_and_write_config(auth)
print(ws.name)
p.init(ws) # Init TEST
# Feture engineering: Bronze 2 Gold - working with Azure ML Datasets with Bronze, Silver, Gold concept
ds = p.DatasetByName("ds01_diabetes") #
df = ds.Silver.to_pandas_dataframe()
df_filtered = df[df.AGE > 0.015]
gold_train = p.save_gold(df_filtered)
# -
# # 1B) Connect to TEST - via DEV workspae (prereq: datastore for TEST is needed)
# +
import sys, os
import pandas as pd
from azureml.core import Workspace
sys.path.append(os.path.abspath("../azure-enterprise-scale-ml/esml/common/")) # NOQA: E402
from esml import ESMLDataset, ESMLProject
from azureml.core.authentication import InteractiveLoginAuthentication
p = ESMLProject() # 1) self-aware about its config sources, p.dev_test_prod = "dev" # active environment (override config)
print(p.dev_test_prod) # DEV
p.ws = p.get_workspace_from_config() #2) Get DEV. Then Load TEST via DEV
print(p.ws.name)
#p.dev_test_prod = "test" # does this work? Yes
test_ws = p.get_other_workspace("test") # Get TEST via DEV workspace/keyvault via Service Principle
p.dev_test_prod = "test" # Works
p.init(test_ws) # Automapping from datalake to Azure ML datasets, prints status)
p.describe()
# Feture engineering: Bronze 2 Gold - working with Azure ML Datasets with Bronze, Silver, Gold concept
ds = p.DatasetByName("ds01_diabetes") #
df = ds.Silver.to_pandas_dataframe()
df_filtered = df[df.AGE > 0.015]
gold_train = p.save_gold(df_filtered)
# -
# ## Alt 1) Empty constructor - auto-read config (for debugging here)
# +
import datetime
sys.path.append(os.path.abspath("../azure-enterprise-scale-ml/esml/common/")) # NOQA: E402
from esml import ESMLDataset, ESMLProject
p = ESMLProject() # self-aware about its config sources
p.describe()
# -
# ### Alt 2) Overwrite COMFIG via ESMLProject constructor - parameters:
# - Either only `folderDate`, or set all parameters below:
# - `folderDate, ProjectNumber, inferenceModelVersion,modelAlias, *datasetFolderNames`
# +
import os,sys,json, datetime
sys.path.append(os.path.abspath("../azure-enterprise-scale-ml/esml/common/")) # NOQA: E402
from esml import ESMLDataset, ESMLProject
## TRAIN - ESMLProject
train_dt = '2020-01-01 15:35:01.243860'
train_in_date = datetime.datetime.strptime(train_dt, '%Y-%m-%d %H:%M:%S.%f')
model_short_alias = "M03"
p = ESMLProject(train_in_date,2,0,model_short_alias,"ds01_diabetes","ds02_other")
p.rnd=True
p.describe()
## INFERENCE -ESMLProject
inf_dt = '2021-01-01 15:35:01.243860'
inf_in_date = datetime.datetime.strptime(inf_dt, '%Y-%m-%d %H:%M:%S.%f')
p2 = ESMLProject(inf_in_date,2,4,model_short_alias, "ds01_name","ds02_other", "ds03_yet_another")
p2.describe()
# -
# ## Alt 3) Inject 2 config objects from JSON - copy settings folder to your root
# - `../../../settings` instead of `../settings`
#
# +
import json
sys.path.append(os.path.abspath("../azure-enterprise-scale-ml/esml/common/")) # NOQA: E402
from esml import ESMLDataset, ESMLProject
# These and the other configs for TRAIN and AutoML are self-booting from ESMLProject
# ESML will search in ROOT for your copied SETTINGS folder '../../../settings', but if forced to "DEMO", it will use the TEMPLATE path '../settings'
try:
#with open("../../../settings/enterprise_specific/dev_test_prod_settings.json") as f: # Read from YOUR Settings
# env_settings = json.load(f)
with open("../settings/enterprise_specific/dev_test_prod_settings.json") as f: # Reads from TEMPLATE settings
env_settings = json.load(f)
with open("../settings/project_specific/model/lake_settings.json") as f:
esml_settings = json.load(f)
with open("../settings/project_specific/security_config.json") as f2: # Project service principles, etc
security_config = json.load(f2)
except Exception as e:
raise Exception("Could not open config.json or storage_config.json - could not load experimentname, or access storage") from e
# -
p = ESMLProject(esml_settings,env_settings,security_config) # read from config
p.describe()
# # Great! Thats your ESML datalake area & environements (string generation from config)
# ## Now - involve Azure dependency: Automatically generate Datastore and Datasets
# +
#### NB! This is needed only 1st time
from azureml.core import Workspace
from azureml.core.authentication import InteractiveLoginAuthentication
auth = InteractiveLoginAuthentication(tenant_id = p.tenant)
ws, config_name = p.authenticate_workspace_and_write_config(auth)
#### After that, you can use 'ws = p.get_workspace_from_config()'
# -
# # 2) ESML will Automap and Autoregister Azure ML Datasets - IN, SILVER, BRONZE, GOLD
# - `Automap` and `Autoregister` Azure ML Datasets as: `IN, SILVER, BRONZE, GOLD`
from azureml.core import Workspace
ws = p.get_workspace_from_config()
ws.name
datastore = p.automap_and_register_aml_datasets(ws)# p.init()
ds_other = p.Datasets[1]
ds_other = p.DatasetByName("ds02_other")
print(ds_other.InData.name)
print(ds_other.Bronze.name)
print(ds_other.Silver.name)
#print(p.Gold.name) # No data yet
# # 3) IN->`BRONZE->SILVER`->Gold
# - Create dataset from PANDAS - Save to SILVER
import pandas as pd
ds = p.DatasetByName("ds01_diabetes")
df = ds.Bronze.to_pandas_dataframe()
df.head()
# ## 3) BRONZE-SILVER (EDIT rows & SAVE)
# - Test change rows, same structure = new version (and new file added)
# - Note: not earlier files in folder are removed. They are needed for other "versions".
# - Expected: For 3 files: New version, 997 rows: 2 older files=627 + 1 new file=370
# - Expected (if we delete OLD files): New version, with less rows. 370 instead of 997
df_filtered = df[df.AGE > 0.015]
print(df.shape[0], df_filtered.shape[0])
# ## 3a) Save `SILVER` ds01_diabetes
aml_silver = p.save_silver(p.DatasetByName("ds01_diabetes"),df_filtered)
aml_silver.name
# ### COMPARE `BRONZE vs SILVER`
# - Compare and validate the feature engineering
# +
ds01 = p.DatasetByName("ds01_diabetes")
bronze_rows = ds01.Bronze.to_pandas_dataframe().shape[0]
silver_rows = ds01.Silver.to_pandas_dataframe().shape[0]
print("Bronze: {}".format(bronze_rows)) # Expected 442 rows
print("Silver: {}".format(silver_rows)) # Expected 185 rows (filtered)
assert bronze_rows == 442,"BRONZE Should have 442 rows to start with, but is {}".format(bronze_rows)
assert silver_rows == 185,"SILVER should have 185 after filtering, but is {}".format(silver_rows)
# -
# ## 3b) Save `BRONZE → SILVER` ds02_other
df_edited = p.DatasetByName("ds02_other").Silver.to_pandas_dataframe()
ds02_silver = p.save_silver(p.DatasetByName("ds02_other"),df_edited)
ds02_silver.name
# ## 3c) Merge all `SILVERS -> SAVE to GOLD`
# https://stackoverflow.com/questions/40468069/merge-two-dataframes-by-index
# - pd.JOIN is a column-wise `left join`
# - df1.join(df2)
# - pd.MERGE is a column-wise `inner join`
# - When to use: concatenating by `custom fields / indexes`
# - pd.merge(df1, df2, left_index=True, right_index=True)
# - `join by: df1.col1 == df2.index`
# - pd.merge(df1, df2, left_on='col1' right_index=True)
# - `join by _common_ columns`: `col1`, `col3`
# - pd.merge(df1, df2, on=['col1','col3'])
# - pd.CONCAT is a `ROW`-wise `outer join`
# - When to use? To contact 2-M dataframes `aligned by index`
# - pd.concat([df1, df2], axis=1)
# +
df_01 = ds01.Silver.to_pandas_dataframe()
df_02 = ds02_silver.to_pandas_dataframe()
# 1) LEFT join
df_gold1_join = df_01.join(df_02) # left join -> NULL on df_02
# Alternative JOINS:
# 2) outer join -> NULL on both sides
df_gold2_concat = pd.concat([df_01, df_02], axis=1) # outer join -> NULL on both sides
# 3) # inner join -> no nulls
df_gold3_merged = df_01.merge(df_02,how="left", left_on="Y", right_on="Age", indicator="indicator_column")
df_gold4_mergd = df_01.merge(df_02, left_index=True, right_index=True) # inner join -> no nulls
# -
print("Diabetes shape: ", df_01.shape)
print(df_gold1_join.shape)
print(df_gold2_concat.shape)
print(df_gold3_merged.shape)
print(df_gold4_mergd.shape)
# # Save `GOLD` v1
print(p.rnd)
p.rnd=False
ds_gold_v1 = p.save_gold(df_gold1_join)
# ### 3c) Ops! "faulty" GOLD - too many features
print(p.Gold.to_pandas_dataframe().shape)
print("Are we in RnD phase? Or do we have 'versioning on datasets=ON'")
print("RnD phase = {}".format(p.rnd))
# # Save `GOLD` v2
# Lets just go with features from ds01
ds_gold_v1 = p.save_gold(df_01)
# # Split `GOLD` into 3 - `train, validate, test`
#
label = "Y"
train_6, validate_set_2, test_set_2 = p.split_gold_3(0.6, label)
print(" - Q:Why add LABEL info when splitting for TRAIN? For future sake...VALIDATE, TEST")
print("...This is why:")
X_test, y_test, tags = p.get_gold_validate_Xy() # Version is default latest
print(tags)
# # Get `GOLD` by version
gold_1 = p.get_gold_version(1)
gold_1.to_pandas_dataframe().shape # (185, 19)
gold_2 = p.get_gold_version(2)
gold_2.to_pandas_dataframe().shape # (185, 11)
p.Gold.to_pandas_dataframe().shape # Latest version (185, 11)
new_project = ESMLProject()
new_project.init(ws)
# +
gold_1 = new_project.get_gold_version(1)
print(gold_1.to_pandas_dataframe().shape) # (185, 19)
gold_2 = new_project.get_gold_version(2)
print(gold_2.to_pandas_dataframe().shape) # (185, 11)
print(new_project.Gold.to_pandas_dataframe().shape) # Latest(185, 11)
# -
gold_2
p.rnd = True
ds_gold_v1 = p.save_gold(df_01)
ds_gold_v1 = p.save_gold(df_01)
ds_gold_v1 = p.save_gold(df_gold1_join)
p.rnd = False
ds_gold_v1 = p.save_gold_pandas_as_azure_dataset(df_gold1_join) # v2
ds_gold_v1 = p.save_gold_pandas_as_azure_dataset(df_01)
ds_gold_v1 = p.save_gold_pandas_as_azure_dataset(df_gold1_join)
# # Slice `ROWS` and create filtered version
df_01_filtered = df_01[df_01.AGE > 0.03807]
ds_gold_v1 = p.save_gold(df_01_filtered)
# # Look at ds_02 - Titanic
df_02.head()
import seaborn as sns
corr = df_02.corr() # print(corr)
sns.heatmap(corr, xticklabels=corr.columns, yticklabels=corr.columns)
|
notebook_demos/esml_howto_5_datasets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import csv
with open('PyBank_Resources.csv') as csv_file:
csv_reader = csv.reader(csv_file,delimiter=',')
csv_header = next(csv_reader)
print(csv_header)
csv_reader_1 = list(csv_reader)
num_rows = 0
profit_sum = 0
Month_list =[]
profit_n_loss_list =[]
Diff_list =[]
for row in csv_reader_1:
print(row)
num_rows += 1
profit_sum += int((row[1]))
months = row[0]
Month_list.append(months)
profit_n_loss = row[1]
profit_n_loss_list.append(float(profit_n_loss))
Diff = [profit_n_loss_list[i+1] - profit_n_loss_list[i] for i in range(len(profit_n_loss_list)-1)]
Avg_Diff = round(sum(Diff) / len(Diff), 2)
Max_value= max(Diff)
Max_month_num = Diff.index(Max_value)+1
Month_list[Max_month_num]
Min_value= min(Diff)
Min_month_num = Diff.index(Min_value)+1
a =f"Total No of Months: {num_rows}\n"
b =f"Total Profit/Loss: {profit_sum}\n"
d =f"Average_Difference: {Avg_Diff}\n"
e =f"Greatest Increase in Profits:{Month_list[Max_month_num]} {max(Diff)}\n"
f =f"Greatest Decrease in Profits:{Month_list[Min_month_num]} {min(Diff)}\n"
output_list =[a,b,d,e,f]
# +
output_file = "PyBank.txt"
with open (output_file, "w") as csv_file:
csv_file.writelines(output_list)
#csv_writer = csv.writer(csv_file, delimiter=',')
# -
|
Py_bank/Resources/PyBank.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Determining the Most Frequently Occuring Items in a Sequence ###
#
# #### Problem: In a sequence of items, we want to determine the most frequently occuring items in the sequence.
#
# #### Solution:
# The `collections.Counter` class helps solve such problems.
# - It has a `most_common()` method that helps arrive at the solution.
# - Example:
words = [
'look', 'into', 'my', 'eyes', 'look', 'into', 'my', 'eyes',
'the', 'eyes', 'the', 'eyes', 'the', 'eyes', 'not', 'around', 'the',
'eyes', "don't", 'look', 'around', 'the', 'eyes', 'look', 'into',
'my', 'eyes', "you're", 'under'
]
# +
from collections import Counter
word_counts = Counter(words)
top_three = word_counts.most_common(3)
print(top_three)
# -
# The `Counter` objects can be fed any sequence of hashable input items.
# - the `Counter` is a dictionary that maps the items to the number of occurrences.
# - Example:
word_counts['not']
word_counts['eyes']
# We can increment the count manually,
morewords = ['why','are','you','not','looking','in','my','eyes']
for word in morewords:
word_counts[word]+= 1
word_counts['eyes']
# Alternatively, `update()` can also be used.
word_counts.update(morewords)
# `Counter` instances can be combined using various math operations.
# - Example:
a = Counter(words)
b = Counter(morewords)
a
b
# Combine counts
c = a + b
c
# Subtract counts
d = a - b
d
|
data structures & algorithms/12.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Thread
# 프로그램을 실행하면서 시간이 걸린다면 대부분 아래 두가지중 한가지의 이유이다
#
# - I/O 바운드 : 대부분의 경우 (data Input/Output)
# - CPU 바운드 : 계산량이 굉장히 많을 경우
# Synchronous (동기)
# - 한가지가 끝나야 다음 작업을 수행한다.
#
# Asynchronous (비동기)
# - 작업이 독립적으로 수행된다.
import threading
# +
ls1 = []
ls2 = []
def threading_func_1(number=1000):
for idx in range(number):
ls1.append(idx)
if idx % 100 == 0:
print("ls1:",idx)
def threading_func_2(number=1000):
for idx in range(number):
ls2.append(idx)
if idx % 100 == 0:
print("ls2:",idx)
# +
th1 = threading.Thread(target=threading_func_1, args=(2000,))
th1.start()
th2 = threading.Thread(target=threading_func_2, args=(3000,))
th2.start()
# -
len(ls1), len(ls2)
# - I/O 바운드 문제 : thread 사용
# - CPU 바운드 문제 : process 사용
|
programming/10_thread.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="X0z2OscejN1o"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# + id="YNfGQB90jZQZ"
path="https://raw.githubusercontent.com/sristhimohanty1/18cse095/main/car_onehot.csv"
# + id="lWPiJURTjioC"
import pandas as pd
data=pd.read_csv(path)
# + colab={"base_uri": "https://localhost:8080/", "height": 435} id="tE-LZI3QjwrO" outputId="3592b6ec-db51-4d82-d62b-bda176f09a0f"
data
# + colab={"base_uri": "https://localhost:8080/", "height": 222} id="PzRpOYQWj_xb" outputId="16207663-9a49-4323-fa3c-39be01b8ac61"
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 222} id="pYbYJZoTqNn7" outputId="9402a692-61e6-4d4a-baed-78f827d77c4d"
data.tail()
# + id="rEb18fBBqcOS"
data.dropna(axis=0,inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="NWsaT_S0qjXN" outputId="2067c259-3deb-41f1-ffb2-b26379734395"
data.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 222} id="ZkrpycF1ql0c" outputId="510d17d3-a824-41ec-a533-00b2d87c17f4"
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 285} id="A8YWvP28qt_g" outputId="50d56726-78e1-466a-8a49-0449602049b5"
plt.scatter(data['buying_high'],data['buying_low'],c='red')
plt.xlabel('buying_high')
plt.ylabel('buying_low')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 268} id="sx8MBgl6ruKt" outputId="77e99f03-7ebb-477c-9889-9426994a48b2"
plt.hist(data['buying_vhigh'])
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 337} id="yMopl7SBr9Ai" outputId="73ce9f95-4935-41f5-ce82-4007fe99b257"
plt.hist(data['buying_vhigh'])
# + colab={"base_uri": "https://localhost:8080/", "height": 285} id="cINhzTSssFDP" outputId="352a2750-e5a5-4de0-ffee-95ed3f9c27e6"
plt.hist(data['buying_vhigh'],color='orange',edgecolor='white',bins=5)
plt.title=("histogram of veryhigh buying")
plt.xlabel("rate")
plt.ylabel("buying_vhigh")
plt.show()
# + id="zGc0XhZWZvj7"
import seaborn as sns
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="9wQIn-ZtZ2kz" outputId="cafc2417-a8c6-48ec-eb42-0bead39c7e1a"
sns.set(style='darkgrid')
sns.regplot(x=data['buying_high'],y=data['buying_low'])
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="kz0lMCgXb2ev" outputId="f0682846-c0ff-4ded-abd9-6e1b32617297"
sns.set(style='darkgrid')
sns.regplot(x=data['buying_high'],y=data['buying_low'],marker='*',fit_reg=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="GU39q3OYcJ9U" outputId="309ebaa1-e287-4921-f37e-270242614c26"
sns.distplot(data['buying_high'])
# + colab={"base_uri": "https://localhost:8080/", "height": 383} id="Ut9sS_7UcSeE" outputId="3d8484d1-9385-4e9e-a282-62dd3b018966"
sns.displot(data['buying_high'],kde=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="cYqGZvvFdFX8" outputId="c0d85db9-2ddd-4261-a4b6-8ff4111f5472"
sns.distplot(data['buying_high'],kde=False,bins=5)
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="QiHUcnrGdVdr" outputId="a8a3d916-ccb0-4aed-e20a-2704c50390b7"
sns.countplot(x="maint_high",data=data)
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="X4pCV6YPgeCe" outputId="efbc5eea-8d94-43ac-b62f-e630e638e5f2"
sns.countplot(x="maint_high",data=data,hue='maint_vhigh')
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="6GvGw35OhUBd" outputId="de38f884-b5ba-4350-8925-ef4b6a394b10"
sns.boxplot(y=data['buying_low'])
# + colab={"base_uri": "https://localhost:8080/", "height": 303} id="RIPwy2NghiZ2" outputId="2df38891-d494-487d-bc6d-95f7ad29b7b2"
sns.boxplot(x=data['buying_high'],y=data['buying_low'],data=data,hue='maint_vhigh')
|
Visualization_using_python1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.7 64-bit ('venv')
# metadata:
# interpreter:
# hash: 0ccd6c582c9a76e057095d94821e135e22982a469d4000f0b42c2f79ec6ee6ee
# name: Python 3.7.7 64-bit ('venv')
# ---
import os
import sys
import csv
import h5py
import numpy as np
import pandas as pd
import pickle
# python.dataSciense.textOutputLimit = 0
_5000_batch_raw ="D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/5000_batch_raw.csv"
batch_298_result = "D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/Batch_2980374_batch_results.csv"
extreme_sentiment = "D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/extreme_sentiment_results.csv"
mosi_pom_output = "D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/mosi_pom_output.csv"
mturk_extra_v2 = "D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/mturk_extra_v2.csv"
pom_extra_sqa_mono_result = "D:/Software/reluu_extra_space/CMU_MOSEI/Raw/Labels/pom_extra_sqa_mono_results.csv"
pd.set_option('display.max_rows', 20)
pd.set_option('display.max_columns', None)
class ShowData:
def __init__(self, data_set_path):
self.data_frame = pd.DataFrame()
self.data_frame = pd.read_csv(data_set_path)
def __call__(self):
return self.data_frame.head()
def any(self, column, value):
return self.data_frame.loc[(self.data_frame[column]==value)]
_pom_extra_sqa_mono_result = ShowData(pom_extra_sqa_mono_result)
_pom_extra_sqa_mono_result()
# _pom_extra_sqa_mono_result.any("Input.VIDEO_ID", "pom_extra/257277")
_pom_extra_sqa_mono_result.any("Input.VIDEO_ID", "sqa_mosi/eE8Qr9fOvVA")
# _pom_extra_sqa_mono_result.any("Answer.anger", 3)
_5000_batch_raw_ = ShowData(_5000_batch_raw)
_5000_batch_raw_()
_batch_298_result = ShowData(batch_298_result)
_batch_298_result()
_extreme_sentiment = ShowData(extreme_sentiment)
_extreme_sentiment()
_mosi_pom_output = ShowData(mosi_pom_output)
_mosi_pom_output()
_mturk_extra_v2= ShowData(mturk_extra_v2)
_mturk_extra_v2()
from scipy.io import loadmat
x = loadmat('../CMU_MOSEI/Raw/Audio/Full/COVAREP/_0efYOjQYRc.mat')
print(x['names'])
|
parse_dataset_labels/parse_CMU_video.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.7.1
# language: julia
# name: julia-1.7
# ---
versioninfo()
# # DiracNotation.jl sample
#
#
# By using this package, matrix representation is changed into Dirac notation.
#
# ## Basic usage
#
# In order to change display style, all you have to do is import this package.
using DiracNotation, LinearAlgebra, Random; Random.seed!(0);
ket = normalize(rand(Complex{Float64}, 4)); bra = ket';
dirac(ket)
dirac(bra)
dirac(ket)
op = rand(2,2);
dirac(op)
# ## Qudit system and Operator
# 7 dimensional state
#
# $| \psi \rangle \in \mathbb{C}^7$
dim = 7
ket = normalize(rand(dim))
dirac(ket, [dim])
# qubit-qutrit
#
# $| \psi \rangle \in \mathbb{C}^2 \otimes \mathbb{C}^3$
dims = [2,3]
ket = normalize(randn(prod(dims)))
dirac(ket, dims)
# Operator
#
# $A: V \rightarrow W$ where $V = \mathbb{C}^2$ and $W = \mathbb{C}^3$
A = rand(3,2)
dirac(A, [3], [2])
# ## Precision
DiracNotation.set_properties(precision=2)
op = rand(2,3);
leftdims = [2];
rightdims = [3];
dirac(op, leftdims, rightdims)
# ## Disable mathjax
DiracNotation.set_properties(islatex=false)
op = rand(2,3);
leftdims = [2];
rightdims = [3];
dirac(op, leftdims, rightdims)
|
examples/example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import platform
import numpy as np
import pycuda
from pycuda import autoinit # set up the PyCUDA runtime
print("Platform == " + platform.platform() + ' ' + platform.machine())
print("Python version == " + platform.python_version())
print("NumPy version == " + np.__version__)
print("PyCUDA version == " + pycuda.VERSION_TEXT)
# -
# # Background
#
# ## Autotuning
#
# Autotuning is the idea of letting programs find the best parameters to an algorithm and generate the algorithm according to these parameters. It is a widely used technique in numerical computation software such as [ATLAS](http://math-atlas.sourceforge.net/) and [FFTW](http://www.fftw.org/).
#
# The use of autotuning for GPU kernels has become a hot research topic in the recent years. Two major approaches to autotuning are model-based tuning (which creates a computation model *a priori* based on the algorithm and architecture) and empirical tuning (which measures the performance as if the kernel is a black box). The latter is used for the `autotuner` package for the specific problem of GPU dense matrix multiplication.
#
# ## Matrix Multiplication
#
# Dense matrix multiplication is one of the most studied GPU applications. Although highly tuned implementations can be found with relative ease, an autotuner for matrix multiplication still has its benefits. This is because hand-tuned implementations for one device may not run as well on another device, while autotuners can be ported easily to new architectures with good performance. In addition, matrix multiplication kernels are relatively simple and serves as a good introduction to autotuner design.
#
# ## PyCUDA and GPU metaprogramming
#
# [PyCUDA](https://mathema.tician.de/software/pycuda/) is a Python library for accessing Nvidia’s CUDA parallel computation API. One of the main strengths of PyCUDA is its ability to perform **just-in-time compilation (JIT)** of CUDA C source code. A programmer can create some kernels, compile and run them on the GPU, and then modify the existing kernels dynamically based on the results without leaving the Python interpreter. This process, when done in a program-controlled manner, enables **GPU metaprogramming**, which is crucial to the development of autotuners.
# # Using `autotuner.py`
#
# When invoked as a Python script on the command line, `autotuner.py` parses the arguments and initiates a profiling session to find the optimal parameters for the matmul kernel (this is the autotuning part). After profiling is done, the source code for the optimal kernel is written out as a `.cu` file which can later be used either with PyCUDA or just as input to `nvcc`.
run autotuner.py -h
# A sample session using `autotuner.py` looks like the following:
run autotuner.py 2000 single -o kernel.cu
with open('kernel.cu', 'r') as f:
print(f.read())
# # A closer look at the internals
#
# The base building block of each kernel is the template file `template.cu`
with open('template.cu', 'r') as f:
print(f.read())
# The template is meant to be passed to `str.format` to convert to a functioning CUDA C kernel (thus the existence of all the double curly braces, which escape to single curly braces in the `str.format` specification). It is a fairly straightforward tiled matrix multiplication kernel, the tile width `{TW}` being one of the parameters. The `{loop}` section is meant to both represent a full or unrolled version of the inner loop, which the user can also specify.
#
# The textual convertion is handled by the class `MatMulKernel` defined in `matmul.py`, which also serves to interface with the PyCUDA runtime. We can construct a kernel for double precision matmul with 16 tile width and non-unrolled loops as:
from matmul import MatMulKernel
k1 = MatMulKernel(dtype=np.float64, tile_width=16, loop_unroll=False)
# Under the hood, the constructor calls the `gen_source` method to retrieve the template and perform textual transformation. The generated source code is then compiled by `nvcc` via the `compile` method and loaded onto the GPU. Alternatively, we can skip the compilation explicitly by:
k1_uncompiled = MatMulKernel(dtype=np.float64, tile_width=16, loop_unroll=False, compile=False)
# The `matmul` method of `MatMulKernel` provides a convenient interface to compute matrix multiplication using the compiled kernel. It determines the block and grid size automatically and launches CDUA kernels using PyCUDA's APIs. It also includes code to track execution time, which is used by the profiler to determine the relative performance of different kernels.
n = 2000
# Construct test matrices
M = np.random.randn(n, n)
N = np.random.randn(n, n)
P = M.dot(N) # sequential result
P_gpu = k1.matmul(M, N) # GPU result using our kernel
# P_gpu, milisecs = k1.matmul(M, N, timed=True)
err = np.max(np.abs((P - P_gpu) / P))
print("Error between CPU and GPU result: {:e}".format(err))
# The profiling is done by the `tune_kernels` function defined in `autotuner.py`. `tune_kernels` accepts a matrix width `n` and data type `dtype` (can be `numpy.float32` or `numpy.float64`) and finds the best kernel for which n*n `dtype` matrix multiplication is fastest on the current CUDA device. It does this by constructing different `MatMulKernel` instances, generating two randomly constructed matrices and timing the execution of all `MatMulKernel` on these two matrices. Since GPU execution time may differ drastically between runs, a third parameter, `num_trials`, is used to determine how many trials to average. After profiling data is gathered, the parameter set with the least execution time is returned.
from autotuner import tune_kernels
n = 2000
dtype = np.float64
tw, unroll = tune_kernels(n, dtype) # invoke the autotuner
# And you can construct the optimal kernel using the returned parameter set to use in subsequent calculations (this is essentially what the script interface does):
k_optimal = MatMulKernel(dtype, tw, unroll)
print(k_optimal.src)
# Do something with k_optimal
|
autotuner/autotuner-demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="x8COawULBVgm" colab_type="code" colab={}
import random
import numpy as np
import os
import torch
from torch import nn
from torch.distributions import Normal
from torch.nn import functional as F
SEED = 423 # 627, 8, 11
def make_reproducible(seed, make_cuda_reproducible):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if make_cuda_reproducible:
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
make_reproducible(SEED, make_cuda_reproducible=False)
def transform_state(state):
return torch.tensor(state).float().to(DEVICE)
class Actor(nn.Module):
def __init__(self, hidden=400, in_dim=3, out_dim=1):
super().__init__()
self.fc = nn.Linear(in_dim, hidden)
self.mu = nn.Linear(hidden, out_dim)
self.sigma = nn.Parameter(torch.full((1,), np.log(0.6)), requires_grad=True)
def forward(self, x):
z2 = F.relu(self.fc(x))
mu = 2 * F.tanh(self.mu(z2))
sigma = self.sigma.expand_as(mu).exp()
return mu, sigma
class Agent:
def __init__(self):
self.actor = Agent.generate_model()
self.actor.load_state_dict(torch.load(__file__[:-8] + "/agent.pkl"))
self.actor.to(torch.device("cpu"))
self.actor.eval()
@staticmethod
def generate_model():
return Actor()
def act(self, state):
state = transform_state(state)
out = self.actor(state)
return np.array([Normal(out[0], out[1]).sample().item()])
def reset(self):
pass
# + id="9Eb_Z9XaBXmq" colab_type="code" colab={}
import time
from collections import deque
from copy import deepcopy
from gym import make
import numpy as np
import torch
import random
from torch.nn import functional as F
from torch import nn
from torch.distributions import Normal
from torch.optim import Adam
N_STEP = 1
GAMMA = 0.9
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu")
UPDATE_LENGTH = 10
ENTROPY = 0.01
TARGET_UPDATE = 800
EPOSIODE_LEN = 200
class Critic(nn.Module):
def __init__(self, hidden=400, in_dim=3, out_dim=1):
super().__init__()
self.fc2 = nn.Linear(in_dim, hidden)
self.valNet = nn.Linear(hidden, 1)
def forward(self, x):
z = F.relu(self.fc2(x))
val = self.valNet(z)
return val
class A2C:
def __init__(self, state_dim, action_dim):
self.gamma = GAMMA ** N_STEP
self.actor = Agent.generate_model().to(DEVICE) # Torch model
self.critic = Critic().to(DEVICE) # Torch model
self.actor_optimizer = Adam(self.actor.parameters(), lr=0.0001)
self.critic_optimizer = Adam(self.critic.parameters(), lr=0.001)
self.states = []
self.actions = []
self.next_states = []
self.rewards = []
self.log_probs = []
self.entropies = []
self.critic_values = []
self.target_values = []
self.update_steps = 0
self.distribution = None
self.target = deepcopy(self.critic)
def optimizer_step(self, log_probs, entropies, returns, critic_values):
self.actor_optimizer.zero_grad()
self.critic_optimizer.zero_grad()
adv = (returns - critic_values).detach()
policy_loss = -(log_probs * adv).mean()
entropy_loss = -entropies.mean() * ENTROPY
value_loss = ((critic_values - returns) ** 2 / 2).mean()
total_loss = value_loss + entropy_loss + policy_loss
total_loss.backward()
self.actor_optimizer.step()
self.critic_optimizer.step()
def update(self, transition):
self.update_steps += 1
if self.update_steps % TARGET_UPDATE == 0:
self.target = deepcopy(self.critic)
state, action, next_state, reward, done = transition
action = torch.tensor(action)
self.states.append(transform_state(state))
self.actions.append(action)
self.next_states.append(transform_state(next_state))
self.rewards.append((reward + 8.1) / 8.1)
self.log_probs.append(self.distribution.log_prob(action))
self.entropies.append(self.distribution.entropy())
self.critic_values.append(self.critic(transform_state(state)))
self.target_values.append(self.target(transform_state(state)))
if done or len(self.states) == UPDATE_LENGTH:
next_target = torch.zeros(1) if done else self.target(self.next_states[-1])
if len(self.target_values) > 1:
returns = torch.tensor(self.rewards).view(-1, 1) + \
self.gamma * torch.cat((torch.cat(self.target_values[1:]), next_target)).view(-1, 1).detach()
else:
self.states = []
self.actions = []
self.next_states = []
self.rewards = []
self.log_probs = []
self.entropies = []
self.critic_values = []
self.target_values = []
return
self.optimizer_step(
torch.cat(self.log_probs).view(-1, 1),
torch.cat(self.entropies).view(-1, 1),
returns,
torch.cat(self.critic_values).view(-1, 1)
)
self.states = []
self.actions = []
self.next_states = []
self.rewards = []
self.log_probs = []
self.entropies = []
self.critic_values = []
self.target_values = []
def act(self, state):
# Remember: agent is not deterministic, sample actions from distribution (e.g. Gaussian)
state = transform_state(state)
out = self.actor(state)
self.distribution = Normal(out[0], out[1])
return np.array([self.distribution.sample().item()])
def save(self, i):
torch.save(self.actor.state_dict(), f'agent_{i}.pkl')
# + id="bnRWCN3wBejp" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 781} outputId="402e11c6-4a86-49ea-9727-9c110da9b5ee"
env = make("Pendulum-v0")
a2c = A2C(state_dim=3, action_dim=1)
episodes = 10000
scores = []
best_score = -10000.0
best_score_25 = -10000.0
total_steps = 0
start = time.time()
for i in range(episodes):
state = env.reset()
total_reward = 0
steps = 0
done = False
reward_buffer = deque(maxlen=N_STEP)
state_buffer = deque(maxlen=N_STEP)
action_buffer = deque(maxlen=N_STEP)
while not done:
if steps == EPOSIODE_LEN:
break
total_steps += 1
action = a2c.act(state)
next_state, reward, done, _ = env.step(action)
next_state = next_state
total_reward += reward
steps += 1
reward_buffer.append(reward)
state_buffer.append(state)
action_buffer.append(action)
if len(reward_buffer) == N_STEP:
a2c.update((state_buffer[0], action_buffer[0], next_state, sum([(GAMMA ** i) * r for i, r in enumerate(reward_buffer)]), done))
state = next_state
#env.render()
scores.append(total_reward)
if len(reward_buffer) == N_STEP:
rb = list(reward_buffer)
for k in range(1, N_STEP):
a2c.update((state_buffer[k], action_buffer[k], next_state, sum([(GAMMA ** i) * r for i, r in enumerate(rb[k:])]), done))
if (i + 1) % 75 == 0:
current_score = np.mean(scores)
print(f'Current score: {current_score}')
scores = []
if current_score > best_score:
best_score = current_score
a2c.save(75)
print(f'Best model saved with score: {best_score}')
end = time.time()
elapsed = end - start
start = end
print(f'Elapsed time: {elapsed}')
#elif (i + 1) % 25 == 0:
# current_score_25 = np.mean(scores[-25:])
# print(f'Intermediate score: {current_score_25}')
# if current_score_25 > best_score_25:
# best_score_25 = current_score_25
# a2c.save(25)
# print(f'Best 25 model saved with score: {best_score_25}')
# + id="GtuIjQ6LB8Uw" colab_type="code" colab={}
|
HW03/RL_HW03(1).ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python3
# name: python3
# ---
# # Weekly exercise 6: Simple NumPy exercises
#
# In this task you are practicing using NumPy in several applications.
# ## Task 1. Power of a matrix
#
# Write a function that would take in a matrix and a non-negative integer,
# check for that matrix is square, and return the power of the matrix computed through
# successive multiplication.
# + hide-output=false
import numpy as np
def matrix_power(mtrx,n=1):
# Write your code here
pass
A = np.array([[1,2,0],[0,2,3],[1,1,5]])
print(matrix_power(A))
# -
# Here are the tests to pass for your code (which are referred to as *unit tests*)
# + hide-output=false
# Test the code above
A = np.array([[1,2,0],[0,2,3],[1,1,5]])
B = [[355,614,1806],[903,1565,4533],[1210,2113,6098]]
eq=np.equal(matrix_power(A,5),B)
if eq.all():
print('Test 1 passed')
else:
print('Test 1 FAIL')
A = [[1,2,0],[0,2,3],[1,1,5]]
B = [[355,614,1806],[903,1565,4533],[1210,2113,6098]]
eq=np.equal(matrix_power(A,5),B)
if eq.all():
print('Test 2 passed')
else:
print('Test 2 FAIL')
try:
matrix_power([1],4.5)
except TypeError:
print('Test 3 passed')
except:
print('Test 3 FAIL')
else:
print('Test 3 FAIL')
try:
matrix_power([1],-5)
except ValueError:
print('Test 4 passed')
except:
print('Test 4 FAIL')
else:
print('Test 4 FAIL')
# -
# ## Task 2. Autoregressive model in matrix form
#
# Consider the AR(1) model
#
# $$
# y_t = a y_{t-1} + \varepsilon, \; \varepsilon \sim N(0, 1).
# $$
#
# We can represent it in the form
#
# $$
# Ay = \varepsilon \quad \quad \varepsilon \sim N(0, 1)
# $$
#
# where $ A $ is
#
# $$
# A = \begin{bmatrix} 1 & 0 & \cdots & 0 & 0 \cr
# -a & 1 & \cdots & 0 & 0 \cr
# \vdots & \vdots & \cdots & \vdots & \vdots \cr
# \vdots & \vdots & \cdots & 1 & 0 \cr
# 0 & 0 & \cdots & -a & 1 \end{bmatrix}
# $$
#
# and $ y $ and $ \varepsilon $ are $ (T x 1) $ vectors
#
# Generate an AR(1) series with $ T=500 $ and $ \alpha = 0.9 $
# using matrix algebra, and make a plot of $ y_t $.
#
# Hint: use NumPy.eye() with additional arguments.
# + hide-output=false
# replace @@@ by your code
import numpy as np
T = @@@
α = @@@
ɛ = np.random.randn(T)
A = @@@
y = @@@
import matplotlib.pyplot as plt
@@@
|
exercise06.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import argparse
import sys
import time
import pandas as pd
from sklearn import metrics
import numpy as np
from pylib.tlsh_lib import *
import warnings
warnings.filterwarnings("ignore")
# -
# List of Function
def getResult(hashType, clusterType, labelList, clusterNumber):
data = tlist2cdata(hashList)
d = {word: key for key, word in enumerate(set(labelList))}
labelList_id = [d[word] for word in labelList]
outlierRemoveLabel = []
outlierRemoveID = []
outlierRemoveData = []
for i in range(len(clusterNumber)):
if clusterNumber[i] >= 0:
outlierRemoveLabel.append(clusterNumber[i])
outlierRemoveID.append(labelList_id[i])
outlierRemoveData.append(data[i])
#print("labelList_id=", labelList_id)
#print("cluster labels=",clusterNumber)
#print("outlierRemoveLabel =", outlierRemoveLabel)
#print("outlierRemoveData =", outlierRemoveData)
# Number of decimal place for score
dp = 4
homo = round(metrics.homogeneity_score(outlierRemoveID, outlierRemoveLabel), dp)
silh1 = round(metrics.silhouette_score(data, clusterNumber, metric=sim), dp)
silh2 = round(metrics.silhouette_score(outlierRemoveData, outlierRemoveLabel, metric=sim), dp)
#cali = round(metrics.calinski_harabasz_score(outlierRemoveData, outlierRemoveLabel), dp)
#dav = round(metrics.davies_bouldin_score(outlierRemoveData, outlierRemoveLabel), dp)
print(clusterType + " ran in " + str(end) + " seconds")
print("Homogeneity score =",homo)
print("Silhouette score =",silh1)
print("Silhouette score with Outlier Remove =",silh2)
#print("Calinski harabasz score =",cali)
#print("Davies bouldin score =",dav)
#print(metrics.silhouette_samples(outlierRemoveData, outlierRemoveLabel, metric=sim))
print()
result = {"nSample": int(len(tlist)),
"Hash": str(hashType),
"Cluster": str(clusterType),
"nLabel": int(nlabel),
"nCluster": int(max(clusterNumber)),
"Time(s)": float(end),
"Homogeneity": float(homo),
"Silhouette": float(silh2)
#"Cal.": float(cali),
#"Dav.": float(dav)
}
return result
# +
datafile = "dataDir/mb_10000.csv" #<-----Change this file size
if (datafile == ""):
print("you must provide a datafile name (-f)\n")
sys.exit()
tic = time.perf_counter() # experiment time counter
df = pd.DataFrame() #Result Table
(path, file) = datafile.split("/") # save file path
(filename, filetype) = file.split(".") # save file type
(tlist, [labelList, dateList, slist]) = tlsh_csvfile(datafile) # return (tlshList, [labelList, dateList, ssdeepList])
hashList = tlist
print("Number of samples is " + str(len(hashList)))
print("Number of Unique Label is " + str(len(set(labelList))))
print("Example hash: " + str(hashList[0]))
nlabel = len(set(labelList))
nClusters = [nlabel]
# +
# Agglomerative Clustering
try:
start = time.perf_counter()
res = assignCluster(hashList, nlabel)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "ac", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("Agglomerative Clustering didn't work.")
print(e)
# +
# DBSCAN
from pylib.hac_lib import *
try:
resetDistCalc()
start = time.perf_counter()
res = runDBSCAN(hashList, eps=30, min_samples=2, algorithm='auto')
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "dbscan", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
nclusters = max(res.labels_)
nDistCalc = lookupDistCalc()
#print("nclusters is " + str(nclusters))
#print("nDistCalc is " + str(nDistCalc))
nClusters.append(nclusters)
#outfile = path + "/output/" + filename + "_dbscan_out.txt"
#outputClusters(outfile, hashList, res.labels_, labelList, quiet=True)
except Exception as e:
print("DBSCAN didn't work.")
print(e)
# +
# HAC-T
from pylib.hac_lib import *
try:
hac_resetDistCalc()
start = time.perf_counter()
res = HAC_T(datafile, CDist=30, step3=0, outfname="tmp.txt", cenfname="tmp2.txt")
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "hac-t", labelList, res)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
nclusters = max(res)
nDistCalc = hac_lookupDistCalc()
#print("nclusters is " + str(nclusters))
#print("nDistCalc is " + str(nDistCalc))
nClusters.append(nclusters)
#outfile = path + "/output/" + filename + "_hac-t_out.txt"
#outputClusters(outfile, hashList, res, labelList, quiet=True)
except Exception as e:
print("HAC-T didn't work.")
print(e)
# +
# OPTICS
try:
start = time.perf_counter()
res = runOPTICS(hashList, min_samples=2)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "optics", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("OPTICS didn't work.")
print(e)
# -
"""
# KMeans
for i in nClusters:
try:
start = time.perf_counter()
res = runKMean(hashList, n_clusters=i)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "kmeans", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("KMeans didn't work.")
print(e)
"""
"""
# BIRCH
for i in nClusters:
try:
start = time.perf_counter()
res = runBIRCH(hashList, n_clusters=i)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "birch", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("BIRCH didn't work.")
print(e)
"""
"""
# Affinity Propagation
try:
start = time.perf_counter()
res = runAffinityPropagation(hashList, random_state=5)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "ap", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("Affinity Propagation didn't work.")
print(e)
"""
"""
# Mean Shift
try:
start = time.perf_counter()
res = runMeanShift(hashList, bandwidth=5)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "ms", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("Mean Shift didn't work.")
print(e)
"""
"""
# Spectral Clustering
try:
start = time.perf_counter()
res = runSpectral(hashList, n_clusters=nlabel)
end = round(time.perf_counter() - start, 4)
dict = getResult("tlsh", "sp", labelList, res.labels_)
df = pd.concat((df, pd.DataFrame([dict])), ignore_index=True)
except Exception as e:
print("Spectral Clustering didn't work.")
print(e)
"""
# +
# Output
outfile = path + "/output/" + filename + "_Tlsh_result.csv"
df.to_csv(outfile, index=False)
toc = round(time.perf_counter() - tic, 4)
print("All code ran in " + str(toc) + " seconds")
df
# -
|
.ipynb_checkpoints/Evaluation Result_10K-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction - Using COSINE Metric
#
# In this notebook we demonstrate the use of **LSI (Latent Semantic Indexing)** technique of Information Retrieval context to make trace link recovery between Test Cases and Bug Reports.
#
# We model our study as follows:
#
# * Each bug report title, summary and description compose a single query.
# * We use each use case content as an entire document that must be returned to the query made
# # Import Libraries
# %load_ext autoreload
# %autoreload 2
# +
from mod_finder_util import mod_finder_util
mod_finder_util.add_modules_origin_search_path()
import pandas as pd
from modules.models_runner.tc_br_models_runner import TC_BR_Runner
from modules.models_runner.tc_br_models_runner import TC_BR_Models_Hyperp
from modules.utils import aux_functions
from modules.utils import firefox_dataset_p2 as fd
import modules.utils.tokenizers as tok
from modules.models.lsi import LSI
from IPython.display import display
import warnings; warnings.simplefilter('ignore')
# -
# # Load Datasets
tcs = [x for x in range(37,59)]
orc = fd.Tc_BR_Oracles.read_oracle_expert_df()
orc_subset = orc[orc.index.isin(tcs)]
#aux_functions.highlight_df(orc_subset)
# +
tcs = [13,37,60,155]
brs = [1292566,1267501]
testcases = fd.Datasets.read_testcases_df()
testcases = testcases[testcases.TC_Number.isin(tcs)]
bugreports = fd.Datasets.read_selected_bugreports_df()
bugreports = bugreports[bugreports.Bug_Number.isin(brs)]
print('tc.shape: {}'.format(testcases.shape))
print('br.shape: {}'.format(bugreports.shape))
# -
print(bugreports.iloc[0,:].Summary)
bugreports
testcases
# # Running LSI Model
# +
corpus = testcases.tc_desc
query = bugreports.br_desc
test_cases_names = testcases.tc_name
bug_reports_names = bugreports.br_name
lsi_hyperp = TC_BR_Models_Hyperp.get_lsi_model_hyperp()
lsi_model = LSI(**lsi_hyperp)
lsi_model.set_name('LSI_Model_TC_BR')
lsi_model.recover_links(corpus, query, test_cases_names, bug_reports_names)
# -
lsi_model.get_sim_matrix().shape
sim_matrix = lsi_model.get_sim_matrix()
aux_functions.highlight_df(sim_matrix)
# ### TF-IDF Application
print(bugreports.Summary.values[0])
print(bugreports.First_Comment_Text.values[0])
# +
q = query.values[0]
tok = lsi_model.vectorizer.tokenizer
words_list = tok.__call__(q)
from collections import Counter
wordcount = Counter(words_list).most_common()
df = pd.DataFrame(columns=['term','tf',''])
print(wordcount)
# -
lsi_model.get_svd_matrix().shape
svd_matrix = pd.DataFrame(lsi_model.get_svd_matrix())
#svd_matrix.index = test_cases_names
aux_functions.highlight_df(svd_matrix)
len(lsi_model.vectorizer.get_feature_names())
# +
import modules.utils.tokenizers as tok
tokenizer = tok.WordNetBased_LemmaTokenizer()
tokens = [tokenizer.__call__(doc) for doc in bugreports.br_desc]
final_tokens = set()
for token_list in tokens:
for t in token_list:
final_tokens.add(t)
#final_tokens = final_tokens.intersection(set())
final_tokens = sorted(list(final_tokens))
print(final_tokens)
dff = pd.DataFrame(final_tokens)
print(dff.shape)
#display(dff)
# + jupyter={"outputs_hidden": true} tags=[]
X = lsi_model.vectorizer.transform(bugreports.br_desc)
df1 = pd.DataFrame(X.T.toarray())
df1.index = lsi_model.vectorizer.get_feature_names()
df1.rename(columns={0:'BR_1267501_SRC',1:'BR_1292566_SRC'}, inplace=True)
print(df1.shape)
aux_functions.highlight_df(df1)
# -
query_vec = lsi_model._query_vector
query_vec = pd.DataFrame(query_vec)
query_vec.index = bug_reports_names
query_vec
from sklearn.metrics import pairwise
results = pd.DataFrame(pairwise.cosine_similarity(X=svd_matrix, Y=query_vec))
results.index = test_cases_names
results.rename(columns={0:bug_reports_names.values[0],
1:bug_reports_names.values[1]}, inplace=True)
aux_functions.highlight_df(results)
# +
import numpy as np
tokenizer = tok.WordNetBased_LemmaTokenizer()
tokens = [tokenizer.__call__(doc) for doc in testcases.tc_desc]
final_tokens = []
for token_list in tokens:
for t in token_list:
final_tokens.append(t)
print(np.unique(final_tokens))
print(len(np.unique(final_tokens)))
# -
# Term-by-Document Matrix - SVD Matrix
# + jupyter={"outputs_hidden": true} tags=[]
df = pd.DataFrame(lsi_model.svd_model.components_.T)
df.index = lsi_model.vectorizer.get_feature_names()
df.rename(columns={0:'TC_13_TRG',1:'TC_37_TRG',2:'TC_60_TRG',3:'TC_155_TRG'}, inplace=True)
print(df.shape)
aux_functions.highlight_df(df)
# -
lsi_model.docs_feats_df
|
notebooks/firefox_p2/tc_br_tracing/lsi-model-cosine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="9brUxyTpYZHy"
# Se importar los datos en formato .zip, y se extraen en la maquina virtual
# + id="PLy3pthUS0D2" executionInfo={"status": "ok", "timestamp": 1621715768626, "user_tz": 300, "elapsed": 446, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
import os
import zipfile
local_zip = 'Data_T2.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp')
zip_ref.close()
# + [markdown] id="o-qUPyfO7Qr8"
# Aqui se define, los directorios de donde se sacara la data de la imagen.
# + id="MLZKVtE0dSfk" executionInfo={"status": "ok", "timestamp": 1621715774680, "user_tz": 300, "elapsed": 11, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
base_dir = '/tmp/Data_T2'
train_leo_dir = os.path.join(base_dir, 'Leopardo2')
train_lince_dir = os.path.join(base_dir, '<NAME>')
train_ocelote_dir = os.path.join(base_dir, 'Ocelote')
train_guepardo_dir = os.path.join(base_dir, 'Guepardo')
train_serval_dir = os.path.join(base_dir, 'Serval')
# + [markdown] id="8Pc014Svbn6n"
# # Sección nueva
# + [markdown] id="LuBYtA_Zd8_T"
# Aqui no mas se muestran el nombre de los archivos,
# + colab={"base_uri": "https://localhost:8080/"} id="4PIP1rkmeAYS" executionInfo={"status": "ok", "timestamp": 1621715776915, "user_tz": 300, "elapsed": 210, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="d26e356e-55f7-4e32-8606-7d7d051862ec"
train_leo_fnames = os.listdir( train_leo_dir )
train_lince_fnames = os.listdir( train_lince_dir )
train_ocelote_fnames = os.listdir(train_ocelote_dir)
train_guepardo_fnames = os.listdir(train_guepardo_dir)
train_serval_fnames = os.listdir(train_serval_dir)
print(train_leo_fnames[:10])
print(train_lince_fnames[:10])
print(train_ocelote_fnames[:10])
print(train_guepardo_fnames[:10])
print(train_serval_fnames[:10])
# + [markdown] id="HlqN5KbafhLI"
# Aqui vemos el total de imagenes en que hay en los directorios de leopardos y linces.
# + colab={"base_uri": "https://localhost:8080/"} id="H4XHh2xSfgie" executionInfo={"status": "ok", "timestamp": 1621715778709, "user_tz": 300, "elapsed": 233, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="206ad8ac-8ec3-49a3-f56b-ddaeaa4bcb99"
print('total training leo images :', len(os.listdir(train_leo_dir ) ))
print('total training lince images :', len(os.listdir( train_lince_dir ) ))
print('total training ocelote images :', len(os.listdir( train_ocelote_dir ) ))
print('total training guepardo images :', len(os.listdir( train_guepardo_dir ) ))
print('total training serval images :', len(os.listdir( train_serval_dir ) ))
# + [markdown] id="C3WZABE9eX-8"
# las siguientes lineas de codigo son para enseñar una pequeña muestra de loas imagenes en los directorios.
# + id="b2_Q0-_5UAv-" executionInfo={"status": "ok", "timestamp": 1621715780305, "user_tz": 300, "elapsed": 315, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
# %matplotlib inline
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
nrows = 20
ncols = 4
pic_index = 0
# + colab={"base_uri": "https://localhost:8080/", "height": 1000, "output_embedded_package_id": "1hy7hm4kGTu42X1fb06UTR58em1Ondbas"} id="Wpr8GxjOU8in" executionInfo={"status": "ok", "timestamp": 1621715788448, "user_tz": 300, "elapsed": 6775, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="bbfb16b5-bcfe-45c7-c689-1f9a517833e9"
fig = plt.gcf()
fig.set_size_inches(ncols*4, nrows*4)
pic_index+=8
next_leo_pix = [os.path.join(train_leo_dir, fname)
for fname in train_leo_fnames[ pic_index-8:pic_index]
]
next_lince_pix = [os.path.join(train_lince_dir, fname)
for fname in train_lince_fnames[ pic_index-8:pic_index]
]
next_ocelote_pix = [os.path.join(train_ocelote_dir, fname)
for fname in train_ocelote_fnames[ pic_index-8:pic_index]
]
next_guepardo_pix = [os.path.join(train_guepardo_dir, fname)
for fname in train_guepardo_fnames[ pic_index-8:pic_index]
]
next_serval_pix = [os.path.join(train_serval_dir, fname)
for fname in train_serval_fnames[ pic_index-8:pic_index]
]
for i, img_path in enumerate(next_leo_pix+next_lince_pix+next_ocelote_pix+next_guepardo_pix+next_serval_pix ):
sp = plt.subplot(nrows, ncols, i + 1)
sp.axis('Off')
img = mpimg.imread(img_path)
plt.imshow(img)
plt.show()
# + [markdown] id="5oqBkNBJmtUv"
# # Construyendo el Modelo
# + id="qvfZg3LQbD-5" executionInfo={"status": "ok", "timestamp": 1621715820776, "user_tz": 300, "elapsed": 221, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
import tensorflow as tf
# + [markdown] id="BnhYCP4tdqjC"
# La siguiente secuencia de codigo es el "core" de nuestra red nueronal, donde estan definidas, las capas de convulucion, la densidad de la red entre otros parametros.
# + id="PixZ2s5QbYQ3" executionInfo={"status": "ok", "timestamp": 1621715828950, "user_tz": 300, "elapsed": 5729, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
data_augmetntation=tf.keras.Sequential(
[
tf.keras.layers.experimental.preprocessing.Resizing(height=400,width=400),
tf.keras.layers.experimental.preprocessing.RandomFlip(mode='vertical'),
tf.keras.layers.experimental.preprocessing.RandomRotation(factor=0.4),
tf.keras.layers.experimental.preprocessing.RandomContrast(factor=0.4),
tf.keras.layers.experimental.preprocessing.RandomZoom(height_factor=0.4,width_factor=0.4)
]
)
initializer=tf.keras.initializers.RandomNormal(mean=0.3, stddev=1.)
model = tf.keras.models.Sequential([
tf.keras.Input((400, 400, 3)),
#data_augmetntation,
tf.keras.layers.Conv2D(16, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(128,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(256,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(512,(3,3),activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(16,kernel_initializer=initializer,activation='relu'),
tf.keras.layers.Dense(32,activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(128,activation='relu'),
tf.keras.layers.Dropout(0.4),
tf.keras.layers.Dense(256,activation='relu'),
tf.keras.layers.Dropout(0.8),
tf.keras.layers.Dense(1024, activation='relu'),
tf.keras.layers.Dense(5, activation='softmax')
])
# + [markdown] id="s9EaFDP5srBa"
# aqui podemos ver la constidad de parametros en cada, "capa de la red", y tambien se evidenca el decrecimiento de la imagen en cada cada capa
#
#
# + id="7ZKj8392nbgP" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1621715828956, "user_tz": 300, "elapsed": 25, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="8f264c45-6985-4f07-931b-1c6dcccaf91b"
model.summary()
# + [markdown] id="PEkKSpZlvJXA"
# Aqui se va definen las funciones de perdida y el optimizador, que ayudaran al modelo a aprender.
# + id="8DHWhFP_uhq3" executionInfo={"status": "ok", "timestamp": 1621715832377, "user_tz": 300, "elapsed": 215, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}}
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.optimizers import RMSprop
model.compile(optimizer=RMSprop(lr=0.0003,rho=0.92),
loss='categorical_crossentropy',
metrics = ['accuracy'])
# + [markdown] id="Sn9m9D3UimHM"
# Aqui se rescalan las imagenes, para que la red trabaje con valores entre 0 y 1, tambien crearemos un "split", que nos servira para la validacion de datos.
# + id="ClebU9NJg99G" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1621715834300, "user_tz": 300, "elapsed": 397, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="d7155f90-3299-4b16-b2ca-2fab96cb301c"
from tensorflow.keras.preprocessing.image import ImageDataGenerator
#todas las imagenes sera resscaldad a 1/255
train_datagen = ImageDataGenerator( rescale = 1.0/255. ,validation_split=0.15)
# --------------------
# Imágenes de entrenamiento en lotes de 20 usando el generador train_datagen
# --------------------
train_generator = train_datagen.flow_from_directory(base_dir,
batch_size=80,
class_mode='categorical',
target_size=(400,400),
subset='training')
# --------------------
# imagenes de validadcion en lotes de 5 usando el generador test_datagen generator
# --------------------
test_generator = train_datagen.flow_from_directory(base_dir,
batch_size=5,
class_mode='categorical',
target_size=(400, 400),
subset='validation')
# + [markdown] id="mu3Jdwkjwax4"
# Por ultimo para entrenar la red, se le dieron 5 epocas, y se le especifico cuales era los datos de validacion y de entrenamiento.
#
# + id="Fb1_lgobv81m" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1621717089596, "user_tz": 300, "elapsed": 1235832, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="081f0ff8-7492-4f17-c9df-8e6aafedb7ee"
#augmentation=data_augmetntation.compile(train_generator)
history = model.fit(train_generator,
validation_data=test_generator,
epochs=150,
verbose=1)
# + id="O5oKlNxq_AnA"
# Guardar el Modelo
model.save('path_to_my_modelv2.h5')
#model = tf.keras.models.load_model('path_to_my_modelv1.h5')
# Recrea exactamente el mismo modelo solo desde el archivo
#new_model = keras.models.load_model('path_to_my_model.h5')
# + [markdown] id="o6vSHzPR2ghH"
# El siguiente codigo, nos permitira ingresar imagenes de nuestro computador para mostraselas a nuestra red nueronal y las clasifique entre linces y leopardos
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 1000} id="4fWLIs900YXO" executionInfo={"status": "ok", "timestamp": 1621717137328, "user_tz": 300, "elapsed": 39124, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="9dbfe290-0e5e-44ac-cf1b-ecfaf9525034"
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded = files.upload()
for fn in uploaded.keys():
# predicting images
path = fn
img = image.load_img(path, target_size=(400, 400))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(fn)
print(classes)
# + id="DoWp43WxJDNT" colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 347} executionInfo={"status": "ok", "timestamp": 1614009668660, "user_tz": 300, "elapsed": 12634, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="726b2378-eed3-4dce-9825-9218d3514a58"
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded=files.upload()
for fn in uploaded.keys():
# predicting images
path='/content/' + fn
img=image.load_img(path, target_size=(100, 100))
x=image.img_to_array(img)
x=np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(classes[0])
if classes[0]>0:
print(fn + " es un Lince")
else:
print(fn + " es un leopardo")
# + [markdown] id="-8EHQyWGDvWz"
# Podmeos observar el recorrido de una imagen en nuestra red neuronal
# + id="-5tES8rXFjux" colab={"base_uri": "https://localhost:8080/", "height": 732} executionInfo={"status": "error", "timestamp": 1618092737039, "user_tz": 300, "elapsed": 1267, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="c3274e97-ea32-481e-bf22-7df3b727db3d"
import numpy as np
import random
from tensorflow.keras.preprocessing.image import img_to_array, load_img
# Definamos un nuevo modelo que tomará una imagen como entrada y generará
# representaciones intermedias para todas las capas en el modelo anterior después de la primera.
successive_outputs = [layer.output for layer in model.layers[1:]]
#visualization_model = Model(img_input, successive_outputs)
visualization_model = tf.keras.models.Model(inputs = model.input, outputs = successive_outputs)
# Preparemos una imagen de entrada aleatoria de un leopardo o un lince del conjunto de entrenamiento.
leo_img_files = [os.path.join(train_leo_dir, f) for f in train_leo_fnames]
lince_img_files = [os.path.join(train_lince_dir, f) for f in train_lince_fnames]
img_path = random.choice(leo_img_files + lince_img_files)
img = load_img(img_path, target_size=(100, 100)) # esta es uan imagen de tipo PIL
x = img_to_array(img) # Numpy array con la forma (150, 150, 3)
x = x.reshape((1,) + x.shape) # Numpy array con la forma (1, 150, 150, 3)
# Rescale by 1/255
x /= 255.0
# Ejecutamos nuestra imagen a través de nuestra red, obteniendo así todas las representaciones intermedias para esta imagen.
successive_feature_maps = visualization_model.predict(x)
# Estos son los nombres de las capas, por lo que podemos tenerlos como parte de nuestra trama.
layer_names = [layer.name for layer in model.layers]
# -----------------------------------------------------------------------
# ahora vamos a mostrar nuestras representaciones
# -----------------------------------------------------------------------
for layer_name, feature_map in zip(layer_names, successive_feature_maps):
if len(feature_map.shape) == 4:
#-------------------------------------------
n_features = feature_map.shape[-1] # numero caracteristicas en el mapa de caracteristicas
size = feature_map.shape[ 1] # forma del mapa de caracteristicas (1, tamaño, tmaño, n_caracteristicas)
# se colaca las imágenes en mosaico en esta matriz.
display_grid = np.zeros((size, size * n_features))
#-------------------------------------------------
# Procesamiento de la funcion
#-------------------------------------------------
for i in range(n_features):
x = feature_map[0, :, :, i]
x -= x.mean()
x /= x.std ()
x *= 64
x += 128
x = np.clip(x, 0, 255).astype('uint8')
display_grid[:, i * size : (i + 1) * size] = x # Coloca en mosaico cada filtro en una cuadrícula horizontal
#-----------------
# mostrar la figura
#-----------------
scale = 20. / n_features
plt.figure( figsize=(scale * n_features, scale) )
plt.axis( 'off' )
plt.title ( layer_name )
plt.grid ( False )
plt.imshow( display_grid, aspect='auto', cmap='viridis')
# + [markdown] id="Q5Vulban4ZrD"
# Se puede observa la perdida y la exactitud, tanto en los datos de entreanmiento y los de perdida.
# + id="0oj0gTIy4k60" colab={"base_uri": "https://localhost:8080/", "height": 911} executionInfo={"status": "ok", "timestamp": 1618111524502, "user_tz": 300, "elapsed": 1438, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="6dfa5731-ace5-4964-dff9-ced8d48f55bc"
acc = history.history[ 'accuracy' ]
val_acc = history.history[ 'val_accuracy' ]
loss = history.history[ 'loss' ]
val_loss = history.history['val_loss' ]
epochs = range(len(acc)) # Get number of epochs
#------------------------------------------------
# Pplotear precicios del entranamiento y al valuidacion por epoca
#------------------------------------------------
plt.figure(figsize=(30,10))
plt.plot ( epochs, acc, label='entrenamiento' )
plt.plot ( epochs, val_acc, label='Validacion' )
plt.title ('Training and validation accuracy')
plt.grid()
plt.legend(loc=4)
plt.figure()
#------------------------------------------------
# plotear perdida en el entranamiento y la validacion por epoca
#------------------------------------------------
plt.figure(figsize=(30,10))
plt.plot ( epochs, loss, label='Entrenamiento' )
plt.plot ( epochs, val_loss,label= 'validacion')
plt.title ('Training and validation loss' )
plt.grid()
plt.legend(loc=2)
# + colab={"base_uri": "https://localhost:8080/", "height": 958} id="IBnBFFXMs26-" executionInfo={"status": "ok", "timestamp": 1621717348132, "user_tz": 300, "elapsed": 1047, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="301d8c53-7651-4f89-d316-f14548a2440d"
acc = history.history[ 'accuracy' ]
val_acc = history.history[ 'val_accuracy' ]
loss = history.history[ 'loss' ]
val_loss = history.history['val_loss' ]
epochs = range(len(acc)) # Get number of epochs
#------------------------------------------------
# Pplotear precicios del entranamiento y al valuidacion por epoca
#------------------------------------------------
parameters = {'xtick.labelsize': 17,
'ytick.labelsize': 17}
plt.rcParams.update(parameters)
plt.figure(figsize=(13,7))
plt.plot ( epochs, acc, label='entrenamiento')
plt.plot ( epochs, val_acc, label='Validacion' )
plt.title ('Training and validation accuracy (Modelo con factores acendentes)',fontsize=20)
plt.xlabel("Epoca",fontsize=18) # Configuramos la etiqueta del eje X
plt.ylabel("Exactitud",fontsize=18)
plt.grid()
plt.show()
#------------------------------------------------
# plotear perdida en el entranamiento y la validacion por epoca
#------------------------------------------------
fig2=plt.figure(figsize=(13,7))
plt.plot ( epochs, loss, label='Entrenamiento' )
plt.plot ( epochs, val_loss,label= 'validacion')
plt.title ('Training and validation loss (Modelo con factores acendentes)' ,fontsize=20 )
plt.xlabel("Epoca", fontsize=18) # Configuramos la etiqueta del eje X
plt.ylabel("Perdida",fontsize=18)
plt.grid()
plt.legend(loc=2,fontsize=13)
# + colab={"base_uri": "https://localhost:8080/"} id="GYFEJmsqPaLu" executionInfo={"status": "ok", "timestamp": 1615767743846, "user_tz": 300, "elapsed": 5307, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="2a283ed9-453b-4631-bfea-3cf592dadda6"
from numpy import exp
# softmax activation function
def softmax(x):
return exp(x) / exp(x).sum()
# define input data
inputs = [1.0, 3.0, 2.0]
print(exp(inputs))
print(exp(inputs).sum())
# calculate outputs
outputs = softmax(inputs)
# report the probabilities
print(outputs)
# report the sum of the probabilities
print(outputs.sum())
# + [markdown] id="mt037H8VdWJw"
# Referencia:
#
# Auotores de Tensorflow: Course_2_Part_2_Lesson_2_Notebook
# + id="iV7R_bNY0fbi" colab={"base_uri": "https://localhost:8080/", "height": 409} executionInfo={"status": "error", "timestamp": 1619391980097, "user_tz": 300, "elapsed": 1846, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjZfvANqTAhHQmepK9lFJm7bmfTfJUSLYWRO8ug=s64", "userId": "17667841987185628598"}} outputId="1bcb111a-c388-4a01-aeef-cf52342cab30"
import numpy as np
np.set_printoptions(linewidth=200,precision=None)
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import plot_confusion_matrix
import seaborn as sns
import pandas as pd
preds = model.predict(test_generator)
label_preds=np.argmax(preds,axis=1)
#(train_genartor, training_labels), (test_generator, test_labels) = base_dir
base_dir = '/tmp/Data_T2'
data=train_generator, test_generator
#(train_generator, training_labels), (test_generator, test_labels)=data
print('Confusion Matrix:\n')
c_m=confusion_matrix(b, label_preds)
#print(c_m)
figure = plt.figure(figsize=(5, 5))
sns.heatmap(c_m, annot=True,cmap=plt.cm.Blues,fmt="d")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()
print(classification_report(test_labels, label_preds))
|
Notebook/Pruebas_DP/Prueba DP1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Analyse public Solvency 2 data of Dutch insurance undertakings
# Welcome! In this tutorial we will use the public Solvency 2 data of all Dutch insurance undertakings and present it in one large DataFrame. In doing so, we are able to use some easy but powerful machine learning algorithms to analyze the data.
#
# Solvency 2 data of individual insurance undertakings are published yearly by the Statistics department of DNB. The data represents the financial and solvency situation of each insurance undertaking at the end of each year. Because Solvency 2 came into effect in 2016, we currently have three years of data: ultimo 2016, ultimo 2017 and ultimo 2018.
#
# The publication of the data is in the form of an Excel file with a number of worksheets containing the aggregated data and the individual data. In this tutorial we will use the individual data.
# +
import pandas as pd
import networkx as nx
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
from sklearn.neighbors import NearestNeighbors
from sklearn.manifold import TSNE
from sklearn.cluster import KMeans
from src.data.make_dataframe import get_sheet
# -
# We use the data published on the DNB website in an Excel file
#
# https://statistiek.dnb.nl/en/downloads/index.aspx#/?statistics_type=toezichtdata&theme=verzekeraars
xls = pd.ExcelFile("../data/Data individual insurers (year).xlsx")
# The Excel file contains several worksheets with data. We want to combine all the data together in one DataFrame. To do that we need some data preparation and data cleaning for each worksheet. This is done by the following function.
# ## Creating one large vector per insurance undertaking
# With the function above we can read a part of the Excel file and store it in a Pandas DataFrame. The following worksheets are contained in the Excel file published by DNB.
#
# * Worksheet 14: balance sheet
# * Worksheet 15: premiums - life
# * Worksheet 16: premiums - nonlife
# * Worksheet 17: technical provisions - 1
# * Worksheet 18: technical provisions - 2
# * Worksheet 19: transition and adjustments
# * Worksheet 20: own funds
# * Worksheet 21: solvency capital requirements - 1
# * Worksheet 22: solvency capital requirements - 2
# * Worksheet 23: minimum capital requirements
# * Worksheet 24: additional information life
# * Worksheet 25: additional information non-life
# * Worksheet 26: additional information reinsurance
# Let’s read the first worksheet with data and then append the other sheets to it. We shall not read the last three worksheets, because these contain the country specific reports.
df = get_sheet(xls, 14)
for l in range(15, 24):
df_temp = get_sheet(xls, l)
df = df.join(df_temp, rsuffix = "_"+ str(l))
# We take the data from the year 2018, and select all columns that have floating numbers in them.
df_18 = df.xs(datetime(2018,12,31), axis = 0, level = 1, drop_level = True)
df_18 = df_18[[df_18.columns[c] for c in range(len(df_18.columns)) if df_18.dtypes[c] == 'float64']]
df_18.fillna(0, inplace = True)
# ## Data analysis solvency ratio
# We only consider insurance undertakings with the same book year and insurance undertakings that have reported every year.
df = df.drop(['Bos Fruit Aardappelen Onderlinge verzekeringen BFAO U.A.'], level='relatienaam')
years = df.index.get_level_values(1).unique()
names = df.index.get_level_values(0).unique()
for i in names:
if (((i,years[0]) in df.index) & ((i,years[1]) in df.index) & ((i,years[2]) in df.index)) == False:
df = df.drop(i,level='relatienaam')
# We calculate the solvency ratio for each insurance undertaking in each year. Under Solvency 2, the solvency ratio is
# the ratio of eligible own funds to required own funds. Required own funds, also referred to as the solvency capital
# requirement (SCR), constitute a risk-based buffer, based on the actual risks on the balance sheet.
SCR = pd.DataFrame(index = df.index)
SCR['assets'] = df['assets|total assets , solvency ii value']
SCR['ratio'] = (df['excess of assets over liabilities , solvency ii value'])/df['scr']
SCR['weight']=0
years = df.index.get_level_values(1).unique()
names = df.index.get_level_values(0).unique()
for i in names:
for j in years:
SCR.loc[(i,j),'weight'] = SCR.loc[(i,j),'assets']/sum(SCR.xs(j, level = 'periode')['assets'])
# Besides the solvency ratio for each insurance undertaking we also calculate the weighted average solvency ratio of the whole insurance sector for each year.
ratio_t = pd.DataFrame(index=years)
ratio_t['ratio'] = 0
for j in years:
ratio_t.loc[j,'ratio'] = sum(SCR.xs(j,level = 'periode')['ratio']*SCR.xs(j,level = 'periode')['weight'])
# We are interested in the development of the solvency ratio over time. We plot the solvency ratio of an individual insurance undertaking - in this case AEGON Levensverzekering - and the weighted average solvency ratio.
plt.plot(years.year, SCR.xs('AEGON Levensverzekering N.V.',level = 'relatienaam')['ratio'], color = 'blue',label = 'Aegon')
plt.plot(years.year,ratio_t['ratio'], color = 'red', label = 'average sector')
plt.xticks(np.arange(min(years.year), max(years.year)+1, 1))
plt.legend()
plt.title('Solvency ratio over time')
plt.xlabel('year')
plt.ylabel('solvency ratio')
plt.show()
# ## Finding the most similar insurance undertaking
# Now let’s apply some algorithms to this data set. Suppose we want to know what insurance undertakings are similar with respect to their financial and solvency structure. To do that we can calculate the distances between all the data points of each insurance undertakings. An insurance undertaking with a low distance to another insurance undertaking might be similar to that undertaking.
#
# If we divide each row by the total assets we do as if all insurance undertakings have equal size, and then the distances indicate similarity in financial and solvency structure (and not similarity in size).
X = df_18.div(df_18['assets|total assets , solvency ii value'], axis = 0)
# The scikit-learn package provides numerous algorithms to do calculations with distances. Below we apply the NearestNeighbors algorithm to find the neighbors of each insurance undertaking. Then we get the distances and the indices of the data set and store them.
# +
nbrs = NearestNeighbors(n_neighbors = 2, algorithm = 'brute').fit(X.values)
distances, indices = nbrs.kneighbors(X)
# -
# What are the nearest neighbors of the first ten insurance undertakings in the list?
for i in indices[0:10]:
print(X.index[i[0]] + " --> " + X.index[i[1]])
# And with the shortest distance between two insurance undertakings we can find the two insurance undertakings that have the highest similarity in their structure.
# +
min_list = np.where(distances[:,1] == distances[:,1].min())
list(X.index[min_list])
# -
# To find clusters of insurance undertakings who are similar to each other we increase the number of nearest neighbors and plot the results in a network diagram. The nodes represent the individual insurance undertakings and an edge between two insurance undertakings implies that they are nearest neigbors.
# +
#Create adjacency matrix
G = nx.from_numpy_matrix(nbrs.kneighbors_graph(X.values, 3, mode='connectivity').toarray())
#Coordinates of insurance nodes
pos = nx.spring_layout(G,seed=4)
plt.figure(1,figsize=(10,10))
#Create network
nx.draw(G, pos = pos, random_state = 0, node_size = 60)
#Print the names of some individual insurance undertakings
pos2 = {0: pos[5], 1: pos[26], 2: pos[28], 3: pos[112]}
labels2 = {0: X.index[5][:14], 1: X.index[26][:11], 2: X.index[28][:16], 3: X.index[112][:11]}
nx.draw_networkx_labels(G, pos2, labels = labels2, font_size = 12, font_color = 'red', font_family = 'sans-serif')
plt.show()
# -
# There is a small cluster with Univé entities. Moreover, there are two clear clusters of life insurance undertakings. Finally, health insurance undertakings are connected to each other.
# If you want to understand the financial performance it is of course handy to know which insurance undertakings are similar. A more general approach when comparing insurance undertakings is to cluster them into a small number of peer groups.
# ## Clustering of insurance undertakings
# Can we cluster the insurance undertakings based on the 1272-dimensional data? To do this we apply the t-sne algorithm.
Y = TSNE(n_components = 2, perplexity = 5, verbose = 0, random_state = 0).fit_transform(X.values)
# Subsequently, we plot the results.
# +
plt.figure(figsize = (7, 7))
plt.scatter(x = Y[:, 0],
y = Y[:, 1],
s = 7)
kmeans = KMeans(n_clusters = 3, random_state = 0, n_init = 10).fit(Y)
#Give the clusters a different colour
for i in range(len(Y)):
if kmeans.labels_[i] == 0:
plt.scatter(x = Y[i,0], y = Y[i,1], s = 5, c = 'red')
elif kmeans.labels_[i] == 1:
plt.scatter(x = Y[i,0], y = Y[i,1], s = 5, c = 'green')
elif kmeans.labels_[i] == 2:
plt.scatter(x = Y[i,0], y = Y[i,1], s = 5, c = 'blue')
#Print the names of some individual insurance undertakings
plt.text(Y[1,0]+1, Y[1,1]+1, X.index.get_level_values(0)[1], fontsize=9)
plt.text(Y[2,0]+1, Y[2,1]+1, X.index.get_level_values(0)[2], fontsize=9)
plt.text(Y[6,0]+1, Y[6,1]+1, X.index.get_level_values(0)[6], fontsize=9)
plt.text(Y[7,0]+1, Y[7,1]+1, X.index.get_level_values(0)[7], fontsize=9)
plt.show()
# -
# Depending on how you zoom in you see different clusters in this picture. The green cluster represents the health insurance undertakings (with more clusters within that set: those offering basic health insurance and other offering additional health insurances, or both). The blue cluster consists of (mostly) non-life insurance undertakings, and the red cluster consists of (mostly) life insurance undertakings. And both clusters can be divided into several more sub clusters. These clusters can be used in further analysis. For example, you could use these as peer groups of similar insurance undertakings.
# ## Clustering of features
# Given that we have a 1272-dimensional vector of each insurance undertaking we might wish somehow to cluster the features in the data set. That is, we want to know which columns belong to each other and what columns are different.
#
# An initial form of clustering were the different worksheets in the original Excel file. The data was clustered around the balance sheet, premiums, technical provisions, etc. But can we also find clusters within the total vector without any prior knowledge of the different worksheets?
#
# A simple and effective way is to transpose the data matrix and feed it into the t-sne algorithm. That is, instead of assuming that each feature provides additional information about an insurance undertaking, we assume that each insurance undertaking provides additional information about a feature.
#
# Let’s do this for only the balance sheet. In a balance sheet it is not immediately straightforward how the left side is related to the right side of the balance sheet, i.e. which assets are related to which liabilities. If you cluster all the data of the balance sheet then related items are clustered (irrespective of whether they are assets or liabilities).
df = get_sheet(xls, 14)
# Instead of the scaled values we now take whether or not a data point was reported or not, and then transpose the matrix.
# scale data
X = (df != 0).T
# Then we apply the t-sne algorithm. In this case with a lower perplexity.
Y = TSNE(n_components = 2,
perplexity = 1.0,
verbose = 0,
random_state = 0,
learning_rate = 20,
n_iter = 10000).fit_transform(X.values)
# We plot the result with 15 identified clusters.
# +
plt.figure(figsize = (7, 7))
plt.scatter(x = Y[:, 0],
y = Y[:, 1],
s = 5)
kmeans = KMeans(n_clusters = 15, random_state = 0, n_init = 10).fit(Y)
for i in range(len(kmeans.cluster_centers_)):
plt.scatter(x = kmeans.cluster_centers_[i,0],
y = kmeans.cluster_centers_[i,1],
s = 1,
c = 'yellow')
plt.annotate(str(i),
xy = (kmeans.cluster_centers_[i, 0], kmeans.cluster_centers_[i, 1]),
size = 13)
plt.show()
# -
# We see are large number of different clusters.
#
# In a balance sheet it is not immediately straightforward how the left side is related to the right side of the balance sheet, i.e. which assets are related to which liabilities. If you cluster all the data of the balance sheet then related items are clustered (irrespective of whether they are assets or liabilities).
for i in df.T.loc[kmeans.labels_ == 6].index:
print(i)
# So the assets held for index-linked and unit-linked contracts are in the same cluster as the technical provisions for index-linked and unit-linked items (and some other related items are found).
#
# Besides clustering based on whether a data point was reported or not we now cluster the data related in their changes over time. We only consider insurance undertakings which report with the same book year and have reported every year.
df = get_sheet(xls, 14)
df = df.drop(['Bos Fruit Aardappelen Onderlinge verzekeringen BFAO U.A.'], level = 'relatienaam')
years = df.index.get_level_values(1).unique()
names = df.index.get_level_values(0).unique()
for name in names:
if (((name,years[0]) in df.index) & ((name,years[1]) in df.index) & ((name,years[2]) in df.index)) == False:
df = df.drop(name, level = 'relatienaam')
X = df.T
# Subsequently, we create a new DataFrame which consists of the changes over time and remove NaN too large numbers.
a = pd.DataFrame((X.loc[:,pd.IndexSlice[:,years[1]]]-X.loc[:,pd.IndexSlice[:,years[0]]].values)/X.loc[:,pd.IndexSlice[:,years[0]]].values).rename(columns = {years[1]:'change1617'})
b = pd.DataFrame((X.loc[:,pd.IndexSlice[:,years[2]]]-X.loc[:,pd.IndexSlice[:,years[1]]].values)/X.loc[:,pd.IndexSlice[:,years[1]]].values).rename(columns = {years[2]:'change1718'})
X2 = a.join(b).sort_index(axis = 1)
X2.fillna(0, inplace = True)
X2[X2 >= np.finfo(np.float64).max]= 1000
X2[X2 == float('-inf')] = -1000
X2[X2 == float('+inf')] = 1000
# Then we apply the t-sne algorithm.
Y = TSNE(n_components = 2,
perplexity = 1.0,
verbose = 0,
random_state = 0,
learning_rate = 20,
n_iter = 10000).fit_transform(X2.values)
# We plot the results with 7 identified clusters
# +
plt.figure(figsize = (7, 7))
plt.scatter(x = Y[:, 0],
y = Y[:, 1],
s = 5)
kmeans = KMeans(n_clusters = 7, random_state = 0, n_init = 10).fit(Y)
for i in range(len(kmeans.cluster_centers_)):
#Plot center of each cluster
plt.scatter(x = kmeans.cluster_centers_[i,0],
y = kmeans.cluster_centers_[i,1],
s = 1,
c = 'yellow')
#Give number to each cluster
plt.annotate(str(i),
xy = (kmeans.cluster_centers_[i, 0], kmeans.cluster_centers_[i, 1]),
size = 13)
plt.show()
# -
# Unfortunately, this does not yield very clear clusters. This is presumable because we do not have enough data since we only have two yearly differences available. Cluster 1 consists of
for i in df.T.loc[kmeans.labels_ == 5].index:
print(i)
# This cluster contains index-linked and unit-linked assets and liabilities.
for i in df.T.loc[kmeans.labels_ == 6].index:
print(i)
# This cluster contains reinsurance recoverables.
|
notebooks/Tutorial Solvency 2 data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ODE solver
#
# In this notebook, we show some examples of solving an ODE model. For the purposes of this example, we use the Scipy solver, but the syntax remains the same for other solvers
# +
# Setup
# %pip install pybamm -q # install PyBaMM if it is not installed
import pybamm
import tests
import numpy as np
import os
import matplotlib.pyplot as plt
from pprint import pprint
os.chdir(pybamm.__path__[0]+'/..')
# Create solver
ode_solver = pybamm.ScipySolver()
# -
# ## Integrating ODEs
# In PyBaMM, a model is solved by calling a solver with `solve`. This sets up the model to be solved, and then calls the method `_integrate`, which is specific to each solver. We begin by setting up and discretising a model
# +
# Create model
model = pybamm.BaseModel()
u = pybamm.Variable("u")
v = pybamm.Variable("v")
model.rhs = {u: -v, v: u}
model.initial_conditions = {u: 2, v: 1}
model.variables = {"u": u, "v": v}
# Discretise using default discretisation
disc = pybamm.Discretisation()
disc.process_model(model);
# -
# Now the model can be solved by calling `solver.solve` with a specific time vector at which to evaluate the solution
# +
# Solve ########################
t_eval = np.linspace(0, 5, 30)
solution = ode_solver.solve(model, t_eval)
################################
# Extract u and v
t_sol = solution.t
u = solution["u"]
v = solution["v"]
# Plot
t_fine = np.linspace(0,t_eval[-1],1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))
ax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), "o")
ax1.set_xlabel("t")
ax1.legend(["2*cos(t) - sin(t)", "u"], loc="best")
ax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), "o")
ax2.set_xlabel("t")
ax2.legend(["2*sin(t) + cos(t)", "v"], loc="best")
plt.tight_layout()
plt.show()
# -
# Note that, where possible, the solver makes use of the mass matrix and jacobian for the model. However, the discretisation or solver will have created the mass matrix and jacobian algorithmically, using the expression tree, so we do not need to calculate and input these manually.
# The solution terminates at the final simulation time:
solution.termination
# ### Events
#
# It is possible to specify events at which a solution should terminate. This is done by adding events to the `model.events` dictionary. In the following example, we solve the same model as before but add a termination event when `v=-2`.
# +
# Create model
model = pybamm.BaseModel()
u = pybamm.Variable("u")
v = pybamm.Variable("v")
model.rhs = {u: -v, v: u}
model.initial_conditions = {u: 2, v: 1}
model.events.append(pybamm.Event('v=-2', v + 2)) # New termination event
model.variables = {"u": u, "v": v}
# Discretise using default discretisation
disc = pybamm.Discretisation()
disc.process_model(model)
# Solve ########################
t_eval = np.linspace(0, 5, 30)
solution = ode_solver.solve(model, t_eval)
################################
# Extract u and v
t_sol = solution.t
u = solution["u"]
v = solution["v"]
# Plot
t_fine = np.linspace(0,t_eval[-1],1000)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(13,4))
ax1.plot(t_fine, 2 * np.cos(t_fine) - np.sin(t_fine), t_sol, u(t_sol), "o")
ax1.set_xlabel("t")
ax1.legend(["2*cos(t) - sin(t)", "u"], loc="best")
ax2.plot(t_fine, 2 * np.sin(t_fine) + np.cos(t_fine), t_sol, v(t_sol), "o", t_fine, -2 * np.ones_like(t_fine), "k")
ax2.set_xlabel("t")
ax2.legend(["2*sin(t) + cos(t)", "v", "v = -2"], loc="best")
plt.tight_layout()
plt.show()
# -
# Now the solution terminates because the event has been reached
solution.termination
print("event time: ", solution.t_event, "\nevent state", solution.y_event.flatten())
|
examples/notebooks/solvers/ode-solver.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Kepler's orbits
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from convert_kepler_data import read_kepler_data
kepler_data = read_kepler_data('kepler11data.txt')
kepler_data
kepler_data['ecc']
# use another function to convert this dataset into initial conditions
# that the hermite solver is used to
from convert_kepler_data import convert_kepler_data
star_mass, \
planet_mass, \
planet_initial_position, \
planet_initial_velocity, ecc = convert_kepler_data(kepler_data)
star_mass
planet_mass
planet_initial_position
planet_initial_velocity
# use hermite solver to solve these
from hermite_library import do_hermite
r_h, v_h, t_h, E_h = do_hermite(star_mass,
planet_mass,
planet_initial_position,
planet_initial_velocity,
tfinal=1e7, Nsteps=5000)
r_h.shape
# +
# we'll plot this
fig, ax = plt.subplots(1, 2, figsize=(10*2, 10))
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]):
ax[0].plot(r_h[i,0,:], r_h[i, 1, :])
# energy plot
ax[1].plot(t_h, E_h)
plt.show()
# -
# # practice saving stuff
from hermite_library import save_hermite_solution_to_file
save_hermite_solution_to_file('myPlanetSystem_kepler11_solution1.txt',
t_h, E_h, r_h, v_h)
from hermite_library import read_hermite_solution_from_file
t_h2, E_h2, r_h2, v_h2 = read_hermite_solution_from_file('myPlanetSystem_kepler101_solution1.txt')
r_h2
# ### Exercise
# Re-do with Kepler-11 dataset.
# # INTO 3D FINALLY! Hurray.
# First doing this "by hand":
# +
star_mass = 1.0 # Msun
planet_mass = np.array([1.0, 0.5]) # in Mjupiter
# initial positions in 3D
planet_initial_position = np.array([[1.0, 0.0, 1.0],
[1.0, 0.0, 0.0]])
# velocities in 3D
planet_initial_velocity = np.array([[0.0, 35, 0],
[35.0, 0, 0]])
# star is assumed to be at the center with zero velocity
# -
r_h, v_h, t_h, E_h = do_hermite(star_mass,
planet_mass,
planet_initial_position,
planet_initial_velocity,
tfinal=1e10, Nsteps=5000,
threeDee=True)
# +
# we'll plot this
fig, ax = plt.subplots(1, 4, figsize=(10*4, 10))
# my X vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]):
ax[0].plot(r_h[i,0,:], r_h[i, 1, :])
# label my axis
ax[0].set_xlabel('x in AU')
ax[0].set_ylabel('y in AU')
# my Z vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[1].plot(r_h[i,0,:], r_h[i, 2, :])
# label my axis
ax[1].set_xlabel('x in AU')
ax[1].set_ylabel('z in AU')
# my Y vs. Z plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[2].plot(r_h[i,2,:], r_h[i, 1, :])
# label my axis
ax[2].set_xlabel('z in AU')
ax[2].set_ylabel('y in AU')
# energy plot
ax[3].plot(t_h, E_h)
plt.show()
# -
# # Kepler in 3D
#
star_mass, \
planet_mass, \
planet_initial_position, \
planet_initial_velocity, ecc = convert_kepler_data(kepler_data, use_inclination_3d=True)
planet_initial_position
planet_initial_velocity
r_h, v_h, t_h, E_h = do_hermite(star_mass,
planet_mass,
planet_initial_position,
planet_initial_velocity,
tfinal=1e8, Nsteps=5000,
threeDee=True)
# +
# we'll plot this
fig, ax = plt.subplots(1, 4, figsize=(10*4, 10))
# my X vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]):
ax[0].plot(r_h[i,0,:], r_h[i, 1, :])
# label my axis
ax[0].set_xlabel('x in AU')
ax[0].set_ylabel('y in AU')
# my Z vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[1].plot(r_h[i,0,:], r_h[i, 2, :])
# label my axis
ax[1].set_xlabel('x in AU')
ax[1].set_ylabel('z in AU')
# my Y vs. Z plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[2].plot(r_h[i,2,:], r_h[i, 1, :])
# label my axis
ax[2].set_xlabel('z in AU')
ax[2].set_ylabel('y in AU')
# energy plot
ax[3].plot(t_h, E_h)
plt.show()
# -
planet_mass
planet_mass2 = np.append(planet_mass, 1.0) # adding in a jupiter
planet_mass2, planet_mass
planet_initial_position
planet_initial_position2 = np.append(planet_initial_position, [[0.5, 0, 0]], axis=0)
planet_initial_position2, planet_initial_position
planet_initial_velocity2 = np.append(planet_initial_velocity, [[0.0, 0.5, 0]], axis=0)
planet_initial_velocity2, planet_initial_velocity
r_h2, v_h2, t_h2, E_h2 = do_hermite(star_mass,
planet_mass2,
planet_initial_position2,
planet_initial_velocity2,
tfinal=1e8, Nsteps=5000,
threeDee=True)
# +
# we'll plot this
fig, ax = plt.subplots(1, 4, figsize=(10*4, 10))
# my X vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h2.shape[0]):
ax[0].plot(r_h2[i,0,:], r_h2[i, 1, :])
# label my axis
ax[0].set_xlabel('x in AU')
ax[0].set_ylabel('y in AU')
# my Z vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h2.shape[0]): # looping over number of planets
ax[1].plot(r_h2[i,0,:], r_h2[i, 2, :])
# label my axis
ax[1].set_xlabel('x in AU')
ax[1].set_ylabel('z in AU')
# my Y vs. Z plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h2.shape[0]): # looping over number of planets
ax[2].plot(r_h2[i,2,:], r_h2[i, 1, :])
# label my axis
ax[2].set_xlabel('z in AU')
ax[2].set_ylabel('y in AU')
# energy plot
ax[3].plot(t_h2, E_h2)
plt.show()
# -
# # reading data back in
from hermite_library import read_hermite_solution_from_file
t_h, E_h, r_h, v_h = read_hermite_solution_from_file('myPlanetarySystem2.txt')
# +
# we'll plot this
fig, ax = plt.subplots(1, 4, figsize=(10*4, 10))
# my X vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]):
ax[0].plot(r_h[i,0,:], r_h[i, 1, :])
# label my axis
ax[0].set_xlabel('x in AU')
ax[0].set_ylabel('y in AU')
# my Z vs. Y plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[1].plot(r_h[i,0,:], r_h[i, 2, :])
# label my axis
ax[1].set_xlabel('x in AU')
ax[1].set_ylabel('z in AU')
# my Y vs. Z plot
# loop over the number of particles in this sim
# coordinate plot
for i in range(r_h.shape[0]): # looping over number of planets
ax[2].plot(r_h[i,2,:], r_h[i, 1, :])
# label my axis
ax[2].set_xlabel('z in AU')
ax[2].set_ylabel('y in AU')
# energy plot
ax[3].plot(t_h, E_h)
plt.show()
# -
|
lesson05/inClass_lesson05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] formulas={"_eq_1": {"meaning": "The quantum state is a function of both the input data and the parameters, equivalent to the encoding applied on the ground state then the parameterized circuit applied."}, "_map_1": {"meaning": "This means f is a function that takes a bit string of length n, and returns a single bit."}} gloss={"adhoc-dataset": {"text": "A dataset just created as needed.", "title": "Adhoc dataset"}, "barren-plateaus": {"text": "A \u2018plateau\u2019 is a flat, high area of land. \u2018Barren\u2019 means empty, or bleak. The barren plateau problem is where the loss landscape becomes increasingly flat (and thus hard to determine the direction to the minimum).", "title": "Barren plateau"}, "classifier": {"text": "Classification is the problem of working out which class a datapoint belongs to, e.g. working out whether or not a photo contains a tortoise.", "title": "Classifier"}, "eigensolver": {"text": "An eigensolver is an algorithm that finds eigenvectors, eigenvalues of an operator.", "title": "Eigensolver"}, "global-minimum": {"text": "A global minimum is <i>the</i> lowest point, anywhere in our function (i.e. for any value of \u03b8).", "title": "Global minimum"}, "local-minimum": {"text": "A local minimum is the lowest point of the function, for a small range of values of \u03b8.", "title": "Local minimum"}, "near-term-algorithm": {"text": "For the next few years, quantum computers will be very noisy, and have limited qubit counts. \u201cNear-term\u201d algorithms are more resiliant to noise, and require less qubits, so are more likely to be useful on these machines.", "title": "Near-term algorithm"}, "parity-function": {"text": "A parity function returns True if the input bit string has an odd number of 1s, and returns False otherwise.", "title": "Parity function"}}
# # Variational classification
#
# In this page, we introduce variational algorithms, then describe and implement variational quantum [classifier](gloss:classifier) and discuss variational training.
# -
# ## Variational algorithms
#
# Variational algorithms were introduced in 2014, with the variational [eigensolver](gloss:eigensolver) in Reference 1 and the quantum approximate optimization algorithm in Reference 2. They are [near-term algorithm](gloss:near-term-algorithm)s, that can be executed on current quantum computers in concert with classical computers.
#
# Using a parameterized quantum circuit, or ansatz, $U(\theta)$, we prepare a state $|\psi(\theta) \rangle = U(\theta) |0 \rangle$, and measure the expectation value using a quantum computer. We define a cost function $C(\theta)$, that determines how good $\theta$ is for the problem we are trying to solve. We then use a classical computer to calculate the cost function and provide updated circuit parameters using an optimization algorithm. The goal of the algorithm is to find the circuit parameters $\theta$ for the parameterized quantum circuit $U(\theta)$ that minimizes the cost function $C(\theta)$.
#
# 
# ## The variational quantum classifier
#
# The variational quantum classifier is a variational algorithm where the measured expectation value is interpreted as the output of a classifier, introduced by multiple groups in 2018. For a binary classification problem, with input data vectors $\vec{x}_i$ and binary output labels $y_i = \{0,1\}$; for each input data vector, we build a parameterized quantum circuit that outputs the quantum state:
# $$ \cssId{_eq_1}{|\psi(\vec{x}_i;\vec{\theta}) \rangle = U_{W(\vec{\theta})}U_{\phi(\vec{x}_i)}|0 \rangle}$$
# where $U_{W(\vec{\theta})}$ corresponds to the variational circuit unitary and $U_{\phi(\vec{x}_i)}$ corresponds to the data encoding circuit unitary. After creating and measuring the circuit of $n$ qubits, we're left with a $n$ length bitstring from which we must derive the binary output which will be our classification result. This is done with the help of a boolean function $ \cssId{_map_1}{ f: \{0, 1\}^{n} \rightarrow \{0, 1\} }$. The [parity function](gloss:parity-function) is a popular choice for this.
#
# 
#
# In the training phase, we're trying to find the values for $\vec{\theta}$ that give us the best predictions. The classical computer compares the predicted labels $\hat{y_i}$, to the provided labels $y_i$, and we calculate the success of our predictions using a cost function. Based on this cost, the classical computer chooses another value for $\vec{\theta}$ using a classical optimization algorithm. This new $\vec{\theta}$ is then used to run a new circuit, and the process is repeated until the cost function stabilizes.
# ### Full implementation
#
# Let's implement all the separate components of the variational quantum classifer, and classify the `adhoc` dataset, as described in Reference 3, following [this implementation](https://github.com/0x6f736f646f/variational-quantum-classifier-on-heartattack/blob/main/Src/Notebooks/02-qiskit.ipynb) from [<NAME>](https://medium.com/qiskit/building-a-quantum-variational-classifier-using-real-world-data-809c59eb17c2).
#
# 1. We create 20 training datapoints and 5 testing datapoints of 2 features from each class.
# +
from qiskit.utils import algorithm_globals
algorithm_globals.random_seed = 3142
import numpy as np
np.random.seed(algorithm_globals.random_seed)
from qiskit_machine_learning.datasets import ad_hoc_data
train_data, train_labels, test_data, test_labels= (
ad_hoc_data(training_size=20, test_size=5, n=2, gap=0.3, one_hot=False))
# -
# 2. We prepare the classification circuit, using the Qiskit `ZZFeatureMap` as the data encoding circuit, and the Qiskit `TwoLocal` circuit with $Y$ and $Z$ rotations and controlled-phase gates, as the variational circuit, as per Reference 3.
# +
from qiskit.circuit.library import ZZFeatureMap, TwoLocal
adhoc_feature_map = ZZFeatureMap(feature_dimension=2, reps=2)
adhoc_var_form = TwoLocal(2, ['ry', 'rz'], 'cz', reps=2)
adhoc_circuit = adhoc_feature_map.compose(adhoc_var_form)
adhoc_circuit.measure_all()
adhoc_circuit.decompose().draw()
# -
# 3. We create a function that associates the data to the feature map and the variational parameters to the variational circuit. This is to ensure that the right parameters in the circuit are associated with the right quantities.
def circuit_parameters(data, variational):
parameters = {}
for i, p in enumerate(adhoc_feature_map.ordered_parameters):
parameters[p] = data[i]
for i, p in enumerate(adhoc_var_form.ordered_parameters):
parameters[p] = variational[i]
return parameters
# 4. We create a class assignment function to calculate the parity of the given bitstring. If the parity is even, it returns a $1$ label, and if the parity is odd it returns a $0$ label, as per Reference 3.
def assign_label(bitstring):
hamming_weight = sum([int(k) for k in list(bitstring)])
odd = hamming_weight & 1
if odd:
return 0
else:
return 1
# 5. We create a function that returns the probability distribution over the label classes, given experimental counts from running the quantum circuit multiple times.
def label_probability(results):
shots = sum(results.values())
probabilities = {0: 0, 1: 0}
for bitstring, counts in results.items():
label = assign_label(bitstring)
probabilities[label] += counts / shots
return probabilities
# 6. We create a function that classifies our data. It takes in data and parameters. For every data point in the dataset, we assign the parameters to the feature map and the parameters to the variational circuit. We then evolve our system and store the quantum circuit, so as to run the circuits at once at the end. We measure each circuit and return the probabilities based on the bit string and class labels.
# +
from qiskit import BasicAer, execute
def classification_probability(data, variational):
circuits = [adhoc_circuit.assign_parameters(
circuit_parameters(d,variational)) for d in data]
backend = BasicAer.get_backend('qasm_simulator')
results = execute(circuits, backend).result()
classification = [label_probability(results.get_counts(c)) for c in circuits]
return classification
# -
# 7. For training, we create the loss and cost functions.
# +
def cross_entropy_loss(predictions, expected):
p = predictions.get(expected)
return -(expected*np.log(p)+(1-expected)*np.log(1-p))
def cost_function(data, labels, variational):
classifications = classification_probability(data, variational)
cost = 0
for i, classification in enumerate(classifications):
cost += cross_entropy_loss(classification, labels[i])
cost /= len(data)
return cost
# -
# 8. We set up our classical optimizer, using [`SPSA`](https://qiskit.org/documentation/stubs/qiskit.algorithms.optimizers.SPSA.html) (as per Reference 3), initialize our variational circuit parameters for reproducibility, and optimize our cost function modifying the variational circuit parameters, using our 40 training datapoints. Note that the optimization will take a while to run.
# +
# Callback function for optimiser for plotting purposes
def store_intermediate_result(evaluation, parameter, cost,
stepsize, accept):
evaluations.append(evaluation)
parameters.append(parameter)
costs.append(cost)
# Set up the optimization
from qiskit.algorithms.optimizers import SPSA
parameters = []
costs = []
evaluations = []
optimizer = SPSA(maxiter=100, callback=store_intermediate_result)
#initial_point = np.random.random(adhoc_var_form.num_parameters)
initial_point = np.array([3.28559355, 5.48514978, 5.13099949,
0.88372228, 4.08885928, 2.45568528,
4.92364593, 5.59032015, 3.66837805,
4.84632313, 3.60713748, 2.43546])
objective_function = lambda variational: cost_function(train_data,
train_labels,
variational)
# Run the optimization
opt_var, opt_value, _ = optimizer.optimize(len(initial_point), objective_function, initial_point=initial_point)
import matplotlib.pyplot as plt
fig = plt.figure()
plt.plot(evaluations, costs)
plt.xlabel('Steps')
plt.ylabel('Cost')
plt.show()
# -
# Plotting the cost function with respect to optimization step, we can see it converges to a minimum.
#
# 9. We implement a function to score our variational quantum classifier, using the classification function we created earlier, and use it to test our trained classifer on our 10 test datapoints.
# +
def score_classifier(data, labels, variational):
probability = classification_probability(data, variational)
prediction = [0 if p[0] >= p[1] else 1 for p in probability]
accuracy = 0
for i, p in enumerate(probability):
if (p[0] >= p[1]) and (labels[i] == 0):
accuracy += 1
elif (p[1]) >= p[0] and (labels[i] == 1):
accuracy += 1
accuracy /= len(labels)
return accuracy, prediction
accuracy, prediction = score_classifier(test_data, test_labels, opt_var)
accuracy
# +
from matplotlib.lines import Line2D
plt.figure(figsize=(9, 6))
for feature, label in zip(train_data, train_labels):
marker = 'o'
color = 'C0' if label == 0 else 'C1'
plt.scatter(feature[0], feature[1],
marker=marker, s=100, color=color)
for feature, label, pred in zip(test_data, test_labels, prediction):
marker = 's'
color = 'C0' if pred == 0 else 'C1'
plt.scatter(feature[0], feature[1],
marker=marker, s=100, color=color)
if label != pred: # mark wrongly classified
plt.scatter(feature[0], feature[1], marker='o', s=500,
linewidths=2.5, facecolor='none', edgecolor='C3')
legend_elements = [
Line2D([0], [0], marker='o', c='w', mfc='C0', label='A', ms=10),
Line2D([0], [0], marker='o', c='w', mfc='C0', label='B', ms=10),
Line2D([0], [0], marker='s', c='w', mfc='C1', label='predict A',
ms=10),
Line2D([0], [0], marker='s', c='w', mfc='C0', label='predict B',
ms=10),
Line2D([0], [0], marker='o', c='w', mfc='none', mec='C3',
label='wrongly classified', mew=2, ms=15)
]
plt.legend(handles=legend_elements, bbox_to_anchor=(1, 1),
loc='upper left')
plt.title('Training & Test Data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# -
# We see that the performance of the trained classifier is not great on the test data. The training optimization probably found a [local minimum](gloss:local-minimum), rather than the [global minimum](gloss:global-minimum).
# ### Qiskit implementation
#
# Qiskit has an implementation of the variational quantum classifer in the [`VQC`](https://qiskit.org/documentation/machine-learning/stubs/qiskit_machine_learning.algorithms.VQC.html) class. Let's use it on the same dataset.
#
# First, we need to one hot encode our labels, as required by the algorithm.
# +
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
train_labels_oh = encoder.fit_transform(train_labels.reshape(-1, 1)).toarray()
test_labels_oh = encoder.fit_transform(test_labels.reshape(-1, 1)).toarray()
# -
# Next, we set up and run the `VQC` algorithm, setting initial variational circuit parameters for reproducibility and using the callback function we created earlier to plot the results, then plot the results.
# +
parameters = []
costs = []
evaluations = []
#initial_point = np.random.random(adhoc_var_form.num_parameters)
initial_point = np.array([0.3200227 , 0.6503638 , 0.55995053,
0.96566328, 0.38243769, 0.90403094,
0.82271449, 0.26810137, 0.61076489,
0.82301609, 0.11789148, 0.29667125])
from qiskit_machine_learning.algorithms.classifiers import VQC
vqc = VQC(feature_map=adhoc_feature_map,
ansatz=adhoc_var_form,
loss='cross_entropy',
optimizer=SPSA(callback=store_intermediate_result),
initial_point=initial_point,
quantum_instance=BasicAer.get_backend('qasm_simulator'))
vqc.fit(train_data, train_labels_oh)
# -
fig = plt.figure()
plt.plot(evaluations, costs)
plt.xlabel('Steps')
plt.ylabel('Cost')
plt.show()
# Third, we test the trained classifier on the test data.
vqc.score(test_data, test_labels_oh)
# +
from matplotlib.lines import Line2D
plt.figure(figsize=(9, 6))
for feature, label in zip(train_data, train_labels_oh):
color = 'C1' if label[0] == 0 else 'C0'
plt.scatter(feature[0], feature[1], marker='o', s=100,
color=color)
for feature, label, pred in zip(test_data, test_labels_oh,
vqc.predict(test_data)):
color = 'C1' if pred[0] == 0 else 'C0'
plt.scatter(feature[0], feature[1], marker='s', s=100, color=color)
if not np.array_equal(label,pred): # mark wrongly classified
plt.scatter(feature[0], feature[1], marker='o', s=500,
linewidths=2.5, facecolor='none', edgecolor='C3')
legend_elements = [
Line2D([0], [0], marker='o', c='w', mfc='C1', label='A', ms=10),
Line2D([0], [0], marker='o', c='w', mfc='C0', label='B', ms=10),
Line2D([0], [0], marker='s', c='w', mfc='C1', label='predict A',
ms=10),
Line2D([0], [0], marker='s', c='w', mfc='C0', label='predict B',
ms=10),
Line2D([0], [0], marker='o', c='w', mfc='none', mec='C3',
label='wrongly classified', mew=2, ms=15)
]
plt.legend(handles=legend_elements, bbox_to_anchor=(1, 1),
loc='upper left')
plt.title('Training & Test Data')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
# -
# We see that the performance of the trained classifier is pretty good on the test data. The training optimization probably found the global minimum.
#
# ## Variational training
#
# As with all variational algorithms, finding the optimal parameters of the variational circuit takes most of the processing time, and is dependent on the optimization method used, as discussed in the [training page](./training-quantum-circuits).
#
# 
#
# Our optimal circuit parameters, $\vec{\theta}^*$ are found when we find the minimum of the loss function, $f(\vec{\theta})$. However, there isn't a simple relationship between the loss function and the circuit parameters. In fact, the loss landscape can be quite complicated, as shown in hills and valleys of the example below. The optimization method navigates us around the loss landscape, searching for the minimum, as shown by the black points and lines. we can see that two of the three searches end up in a local landscape minimum, rather than a global one.
#
# 
#
# Generally the optimization methods can be categorised into two groups: gradient-based and gradient-free methods. To determine an optimal solution, gradient-based methods identify an extreme point at which the gradient is equal to zero. A search direction is selected and the searching direction is determined by the derivative of the loss function. The main disadvantages of this type of optimization are the convergence speed can be very slow and there is no guarantee to achieve the optimal solution.
#
# When derivative information is unavailable or impractical to obtain (e.g. when the loss function is expensive to evaluate or somewhat noisy), gradient-free methods can be very useful. Such optimisation techniques are robust to find the global optima, while the gradient-based methods tend to converge into local optima. However, gradient-free methods require higher computational capacities, especially for the problems with high-dimensional search spaces.
#
# 
#
# Despite what type of optimization method is used, if the loss landscape is fairly flat, it can be difficult for the method to determine which direction to search. This situation is called a _[barren plateau](gloss:barren-plateaus),_ and was studied in Reference 4, where it was hown that show that for a wide class of reasonable parameterized quantum circuits, the probability that the gradient along any reasonable direction is non-zero to some fixed precision is exponentially small as a function of the number of qubits.
#
# One approach to overcome this problem is to use structured initial guesses, such as those adopted in quantum simulation. Another possibility is to consider the full quantum circuit as a sequence of shallow blocks, selecting some parameters randomly and choosing the rest of the parameters such that all shallow blocks implement the identity to restrict the effective depth. This is an area of current investigation.
# ## References
#
# 1. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME> and <NAME>, *A variational eigenvalue solver on a quantum processor*, Nature Communications, 5:4213 (2014), [doi.org:10.1038/ncomms5213](https://doi.org/10.1038/ncomms5213), [arXiv:1304.3061](https://arxiv.org/abs/1304.3061).
# 1. <NAME>, <NAME> and <NAME>, *A Quantum Approximate Optimization Algorithm* (2014), [arXiv:1411.4028](https://arxiv.org/abs/1411.4028).
# 1. <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME> and <NAME>, *Supervised learning with quantum enhanced feature spaces*, Nature 567, 209-212 (2019), [doi.org:10.1038/s41586-019-0980-2](https://doi.org/10.1038/s41586-019-0980-2), [arXiv:1803.07128](https://arxiv.org/abs/1803.07128).
# 1. <NAME>, <NAME>, <NAME>, <NAME> and <NAME>, *Barren plateaus in quantum neural network training landscapes*, Nature Communications volume 9, Article number: 4812 (2018), [doi.org:10.1038/s41467-018-07090-4](https://www.nature.com/articles/s41467-018-07090-4) [arXiv:1803.1117](https://arxiv.org/abs/1803.11173)
import qiskit.tools.jupyter
# %qiskit_version_table
|
notebooks/quantum-machine-learning/vqc.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:geospatial]
# language: python
# name: conda-env-geospatial-py
# ---
# + [markdown] id="MYe-1iFbo3dQ"
# # Evaluating Semantic Segmentation Models
# > A guide for understanding the performance of semantic segmentation for land use / land cover in satellite imagery.
# + [markdown] id="zYmAYTogOkpd"
# After we have trained a model for segmenting images according to a set of classes it's time to evaluate how well it has performed. With any supervised machine learning model, we are typically interested in minimizing false positives or false negatives, with a preference for one or the other.
#
# Additionally, are also interested in making sure our model generalizes beyond the training dataset to new data it was not trained on. Finally, we'd like our model to make high confidence, correct predictions, and for higher confidence thresholds to not result in many more false negatives.
#
# For semantic segmentation, our evaluation unit is an individual pixel, which can be one of four categories:
# * true positive: the pixel was classified correctly as a class of interest.
# * true negative: the pixel was classified correctly as the background class.
# * false positive: the pixel was incorrectly assigned a class of interest
# * false negative: the pixel was incorrectly assigned the background class or a different class
#
# The most in depth and succinct summary we can produce is a confusion matrix. It summarrizes the counts of pixels that fall into each of these categories for each of our classes of interest and the background class.
#
#
# 
#
# In this tutorial we will using data from two reference datasets, Imaflora and Para, and our U-Net predictions from Planet NICFI monthly imagery to compute a confusion matrix to assess our model performance. As we go through this exercise, you'll notice that our reference datasets do not always correspond to the imagery, so take this lesson as a demonstration of how to carry out an experiment, not as an evaluation of a model that will be used in production. The next episode will cover how to deal with innacurate or limited reference data.
#
# ## Specific concepts that will be covered
# In the process, we will build practical experience and develop intuition around the following concepts:
# * **[sci-kit learn](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html)** - we will use sci-kit learn to compute a confusion matrix and discuss how supplying different values to the `normalize `argument can help us interpret our data.
# * **Metrics** - We will cover useful summary metrics that capture much of the information in the confusion matrix, including precision, recall, and F1 Score.
#
#
# **Audience:** This post is geared towards intermediate users who are comfortable with basic machine learning concepts.
#
# **Time Estimated**: 60-120 min
#
#
# + [markdown] id="8wLP8n9tvVwD"
# ## Setup Notebook
# + id="lYMOkBeaeuoV"
# install required libraries
# !pip install -q rasterio==1.2.10
# !pip install -q geopandas==0.10.2
# !pip install -q git+https://github.com/tensorflow/examples.git
# !pip install -q -U tfds-nightly
# !pip install -q focal-loss
# !pip install -q tensorflow-addons==0.8.3
# #!pip install -q matplotlib==3.5 # UNCOMMENT if running on LOCAL
# !pip install -q scikit-learn==1.0.1
# !pip install -q scikit-image==0.18.3
# + id="X-hVmWq9Okpl"
# import required libraries
import os, glob, functools, fnmatch
from zipfile import ZipFile
from itertools import product
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['axes.grid'] = False
mpl.rcParams['figure.figsize'] = (12,12)
import matplotlib.image as mpimg
import pandas as pd
from PIL import Image
import geopandas as gpd
from IPython.display import clear_output
from time import sleep
import skimage.io as skio # lighter dependency than tensorflow for working with our tensors/arrays
from sklearn.metrics import confusion_matrix, f1_score
# + [markdown] id="uVQOf_jbw5fN"
# ### Getting set up with the data
#
# ```{important}
# Create drive shortcuts of the tiled imagery to your own My Drive Folder by Right-Clicking on the Shared folder `servir-tf-devseed`. Then, this folder will be available at the following path that is accessible with the google.colab `drive` module: `'/content/gdrive/My Drive/servir-tf-devseed/'`
# ```
#
# We'll be working witht he following folders in the `servir-tf-devseed` folder:
# ```
# servir-tf-devseed/
# ├── images/
# ├── images_bright/
# ├── indices/
# ├── indices_800/
# ├── labels/
# ├── labels_800/
# ├── background_list_train.txt
# ├── train_list_clean.txt
# └── terrabio_classes.csv
# ```
# + colab={"base_uri": "https://localhost:8080/"} id="Y_UgojhBOkpe" outputId="4551ccba-1f97-4fa5-a4d6-b0dd25f35945"
# set your root directory and tiled data folders
if 'google.colab' in str(get_ipython()):
# mount google drive
from google.colab import drive
drive.mount('/content/gdrive')
root_dir = '/content/gdrive/My Drive/servir-tf-devseed/'
workshop_dir = '/content/gdrive/My Drive/servir-tf-devseed-workshop'
print('Running on Colab')
else:
root_dir = os.path.abspath("./data/servir-tf-devseed")
workshop_dir = os.path.abspath('./servir-tf-devseed-workshop')
print(f'Not running on Colab, data needs to be downloaded locally at {os.path.abspath(root_dir)}')
img_dir = os.path.join(root_dir,'indices/') # or os.path.join(root_dir,'images_bright/') if using the optical tiles
label_dir = os.path.join(root_dir,'labels/')
# + colab={"base_uri": "https://localhost:8080/"} id="LEmJkl8AlE1r" outputId="bc158aa4-6697-4a7f-d80f-4453664da82c"
# go to root directory
# %cd $root_dir
# + [markdown] id="ldG5RFPFNgOo"
# ### Check out the labels
# We'll use these labels to label our confusion matrix and table with class specific metrics.
# + colab={"base_uri": "https://localhost:8080/"} id="jAbEMB8i87FL" outputId="8c50c8d9-2a5c-46d1-b171-8f547e46f3f2"
# Read the classes
class_index = pd.read_csv(os.path.join(root_dir,'terrabio_classes.csv'))
class_names = class_index.class_name.unique()
print(class_index)
# + [markdown] id="zI4907uiOkqN"
# ### Getting image, prediction, and label filenames
#
# Before creating our confusion matrix, we need to associate labels, images, and prediction files together so that we know what to compare. We'll use our standard python for this.
# + [markdown] id="dYbvmkUXCsrL"
# ### Evaluate Model
#
# Compute confusion matrix from all predicted images and their ground truth label masks.
# -
# First we need to read in our prediction masks that we saved out in the last notebook. To do this, we can use scikit image, and then we can use scikit learn to compute our confusion matrix. No tensorflow needed for this part!
path_df = pd.read_csv(os.path.join(root_dir, "test_file_paths.csv"))
pd.set_option('display.max_colwidth', None)
path_df
# reading in preds
label_arr_lst = path_df["label_names"].apply(skio.imread)
pred_arr_lst = path_df["pred_names"].apply(skio.imread)
# One of our labels has an image dimension that doesn't match the prediction dimension! It's possible this image was corrupted. We can skip it and the corresponding prediction when computing our metrics.
pred_arr_lst_valid = []
label_arr_lst_valid = []
for i in range(0, len(pred_arr_lst)):
if pred_arr_lst[i].shape != label_arr_lst[i].shape:
print(f"The {i}th label has an incorrect dimension, skipping.")
print(pred_arr_lst[i])
print(label_arr_lst[i])
print(pred_arr_lst[i].shape)
print(label_arr_lst[i].shape)
else:
pred_arr_lst_valid.append(pred_arr_lst[i])
label_arr_lst_valid.append(label_arr_lst[i])
# With our predictions and labels in lists of tiled arrays, we can then flatten these so that we instead have lists of pixels for predictions and labels. This is the format expected by scikit-learn's `confusion_matrix` function.
# + id="wI2LV_U5Okrb"
# flatten our tensors and use scikit-learn to create a confusion matrix
flat_preds = np.concatenate(pred_arr_lst_valid).flatten()
flat_truth = np.concatenate(label_arr_lst_valid).flatten()
OUTPUT_CHANNELS = 9
cm = confusion_matrix(flat_truth, flat_preds, labels=list(range(OUTPUT_CHANNELS)))
# -
# Finally, we can plot the confusion matrix. We can either use the built-in method from scikit-learn...
# +
from sklearn.metrics import ConfusionMatrixDisplay
ConfusionMatrixDisplay.from_predictions(flat_truth, flat_preds, normalize='true')
# -
# ... or matplotlib, which allows us to more easily customize all aspects of our plot.
# + colab={"base_uri": "https://localhost:8080/", "height": 727} id="1wlhiog_Okre" outputId="4372c319-50af-4e91-e315-d7838dc5dad4"
classes = [0,1,2,3,4,5,6,7,8]
# %matplotlib inline
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
fig, ax = plt.subplots(figsize=(10, 10))
im = ax.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=list(range(OUTPUT_CHANNELS)), yticklabels=list(range(OUTPUT_CHANNELS)),
title='Normalized Confusion Matrix',
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' #'d' # if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout(pad=2.0, h_pad=2.0, w_pad=2.0)
ax.set_ylim(len(classes)-0.5, -0.5)
# + [markdown] id="pmFmZ45aI95a"
# Now let's compute the f1 score
#
# F1 = 2 * (precision * recall) / (precision + recall)
#
# -
# You can view the documentation for a python function in a jupyter notebook with "??". scikit-learn docs usually come with detaile descriptions of each argument and examples of usage.
# +
# f1_score??
# + colab={"base_uri": "https://localhost:8080/"} id="MSdwTssgI7MF" outputId="a1569699-ae88-48ed-95a0-6958209e4d3c"
# compute f1 score
f1_score(flat_truth, flat_preds, average='macro')
# + id="N5vOIKFXOkrh"
|
ds_book/docs/Lesson4_evaluation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# Welcome to the ***AMUSE binary release***. This release contains a working version of AMUSE with some small substractions and additions. Most notable addition is the current web-page you are viewing. This is the [IPython Notebook web-application](http://ipython.org/ipython-doc/dev/interactive/htmlnotebook.html "IPython Notebook documentation"). With this application you can create, edit and run python scripts on your local computer. We will be using it for these AMUSE tutorials, but you can use it for all your interactive explorations of Python and it's many libraries, scripts and applications.
# Using the notebook interface is not very difficult, but you''ll need to get acquainted with some keyboard shortcuts.
# To perform a simple Python expression, type it inside a ***code*** cell and press 'Shift-Enter':
6.6738e-11 * 5.972e24 / 6378.1**2
# The application also supports _keyboard completion_. If you know the first letters of a function or a class, IPython can lookup the rest. For example type 'pri' and press the 'Tab' key:
pri
# This also works for modules, just enter an import statement and press tab on the module name:
from amuse import l
# The 'Tab' key can also be used to get documentation for a function. The documentation will be shown when you press the 'Tab' key just after a open parenthesis '('. For example type 'sort(' and press the 'Tab' key:
sort(
# There are a few more keyboard shortcuts. To find out which, you can press 'ctrl-m h' or navigate to the 'Keyboard Shortcuts' item in the Help menu.
# Here, and also in normal AMUSE scripts, matplotlib and numpy are often used for plotting and numerical operations, these are enabled by the following imports. The inline statement includes the plots into the notebook:
# +
# %matplotlib inline
from matplotlib import pyplot
import numpy
pyplot.plot(numpy.arange(10))
|
doc/interactive_tutorial/00-Welcome.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Dueling Deep Reinforcement Learning with Praoritized replay
# ## setup the enviroment
# +
# GFootball environment.
# !pip install kaggle_environments
# !apt-get update -y
# !apt-get install -y libsdl2-gfx-dev libsdl2-ttf-dev
# !git clone -b v2.3 https://github.com/google-research/football.git
# !mkdir -p football/third_party/gfootball_engine/lib
# !wget https://storage.googleapis.com/gfootball/prebuilt_gameplayfootball_v2.3.so -O football/third_party/gfootball_engine/lib/prebuilt_gameplayfootball.so
# !cd football && GFOOTBALL_USE_PREBUILT_SO=1 pip3 install .
# Some helper code
# !git clone https://github.com/garethjns/kaggle-football.git
# !pip install reinforcement_learning_keras==0.6.0
# +
import collections
from typing import Union, Callable, List, Tuple, Iterable, Any, Dict
from dataclasses import dataclass
from tqdm import tqdm
import matplotlib.pyplot as plt
import numpy as np
from tensorflow import keras
import tensorflow as tf
import seaborn as sns
import gym
import gfootball
import glob
import imageio
import pathlib
import zlib
import pickle
import tempfile
import os
import sys
from IPython.display import Image, display
from gfootball.env import observation_preprocessing
sns.set()
from __future__ import division
from __future__ import print_function
import itertools as it
from random import sample, randint, random
from time import time, sleep
import numpy as np
import skimage.color, skimage.transform
import tensorflow as tf
from tqdm import trange
from argparse import ArgumentParser
sys.path.append("/kaggle/working/kaggle-football/")
# -
# ## Define the SumTree Structure for the Data buffer
# +
import numpy
# SumTree
# a binary tree data structure where the parent’s value is the sum of its children
class SumTree:
write = 0
def __init__(self, capacity):
self.capacity = capacity
self.tree = numpy.zeros(2 * capacity - 1)
self.data = numpy.zeros(capacity, dtype=object)
self.n_entries = 0
# update to the root node
def _propagate(self, idx, change):
parent = (idx - 1) // 2
self.tree[parent] += change
if parent != 0:
self._propagate(parent, change)
# find sample on leaf node
def _retrieve(self, idx, s):
left = 2 * idx + 1
right = left + 1
if left >= len(self.tree):
return idx
if s <= self.tree[left]:
return self._retrieve(left, s)
else:
return self._retrieve(right, s - self.tree[left])
def total(self):
return self.tree[0]
# store priority and sample
def add(self, p, data):
idx = self.write + self.capacity - 1
self.data[self.write] = data
self.update(idx, p)
self.write += 1
if self.write >= self.capacity:
self.write = 0
if self.n_entries < self.capacity:
self.n_entries += 1
# update priority
def update(self, idx, p):
change = p - self.tree[idx]
self.tree[idx] = p
self._propagate(idx, change)
# get priority and sample
def get(self, s):
idx = self._retrieve(0, s)
dataIdx = idx - self.capacity + 1
return (idx, self.tree[idx], self.data[dataIdx])
# -
# ## Define the prioritized memory buffer
# +
import random
import numpy as np
class ReplayBuffer : # stored as ( s, a, r, s_ ) in SumTree
e = 0.01
a = 0.6
beta = 0.4
beta_increment_per_sampling = 0.001
def __init__(self, capacity):
self.tree = SumTree(capacity)
self.capacity = capacity
self.experience = namedtuple('Experience' , field_names=['state','action','reward','next_state','done'])
def _get_priority(self, error):
return (np.abs(error) + self.e) ** self.a
def add(self, error, state , action , reward , next_state , done):
p = self._get_priority(error)
experience = self.experience(state , action , reward , next_state , done)
self.tree.add(p, experience)
def sample(self, n):
try:
batch = []
idxs = []
segment = self.tree.total() / n
priorities = []
self.beta = np.min([1., self.beta + self.beta_increment_per_sampling])
for i in range(n):
a = segment * i
b = segment * (i + 1)
s = random.uniform(a, b)
(idx, p, data) = self.tree.get(s)
priorities.append(p)
batch.append(data)
idxs.append(idx)
states = torch.from_numpy( np.stack([ e.state.reshape(8,72,96) for e in batch if e is not None ],axis=0) ).float().to(device)
action = torch.from_numpy( np.stack([ (e.action).reshape(1,) for e in batch if e is not None] , axis=0) ).long().to(device)
reward = torch.from_numpy( np.stack([ np.array((e.reward)).reshape(1,) for e in batch if e is not None] , axis=0) ).float().to(device)
next_state = torch.from_numpy( np.stack([ e.next_state.reshape(8,72,96) for e in batch if e is not None ] , axis=0) ).float().to(device)
done = torch.from_numpy( np.stack([ np.array((e.done)).reshape(1,) for e in batch if e is not None], axis=0).astype(np.uint8) ).float().to(device)
sampling_probabilities = priorities / self.tree.total()
is_weight = np.power(self.tree.n_entries * sampling_probabilities, -self.beta)
is_weight /= is_weight.max()
return (states , action , reward , next_state , done) , idxs, is_weight
except :
print(batch)
def update(self, idx, error):
p = self._get_priority(error)
self.tree.update(idx, p)
def __len__(self):
return self.tree.n_entries
# +
BATCH_SIZE = 16
UPDATE_EVERY = 4
SEED= 1244
BUFFER_SIZE=int(1e2)
GAMMA= 0.99
TAU = 1e-3 # for soft update of target parameters
LR = 5e-4 # learning rate
device = 'cuda:0' if torch.cuda.is_available() else 'cpu'
class Agent :
def __init__(self,state_size , action_size , seed):
self.state_size = state_size
self.action_size = action_size
self.seed = random.seed(seed)
self.train_loss = deque(maxlen=500)
self.q_local = MyQNet(self.state_size , self.action_size , seed).to(device)
self.q_target = MyQNet(self.state_size , self.action_size , seed).to(device)
self.optimizer = optim.Adam(self.q_local.parameters() , lr=LR)
self.replay_buffer = ReplayBuffer(BUFFER_SIZE)
self.t_step = 0 # for determine the update instances
def step(self,state , action , reward , next_state , done , fill_buffer=False):
# need to calculate the error for the each sample
self.q_local.eval()
self.q_target.eval()
with torch.no_grad():
target = self.q_local(Variable(torch.FloatTensor(state).unsqueeze(0).to(device) )).data
old_val = target[0][action]
target_val = self.q_target(Variable(torch.FloatTensor(next_state).unsqueeze(0).to(device) )).data
if done:
target[0][action] = reward
else:
target[0][action] = reward + GAMMA * torch.max(target_val)
error = abs(old_val - target[0][action])
error = error.detach().to('cpu').numpy()
self.q_local.train()
self.q_target.train()
self.replay_buffer.add(error,state , action , reward , next_state , done)
self.t_step = (self.t_step + 1)%UPDATE_EVERY
if( not fill_buffer):
if(self.t_step == 0):
if(len(self.replay_buffer) > BATCH_SIZE):
#get the training batch from the tree structuer raply buffer
train_sample , idxs, is_weight = self.replay_buffer.sample(BATCH_SIZE)
self.learn(train_sample , idxs , is_weight , GAMMA)
def learn(self , train_sample ,idxs , is_weights , GAMMA) :
state , action , reward , next_state , done = train_sample
"""
1 --> infernce the local model with state and take the Q values for actions associated
2 --> indernce the target model and get the maximum Q value
3 --> obtain the q target with ( reward + GAMMA * max(Q_target_model(next_state))*(1-dones))
4 --> MSELoss(Q_local , Q_target)
5 --> optimize the model
"""
Q_expected = self.q_local(state).gather(1,action)
Q_target = self.q_target(next_state).detach().max(1)[0].unsqueeze(1)
Q_target = reward + GAMMA*(Q_target*(1-done))
#calculate errors for the tree update
errors = torch.abs(Q_expected - Q_target).data
errors = errors.detach().to('cpu').numpy()
# update priority
for i in range(BATCH_SIZE):
idx = idxs[i]
self.replay_buffer.update(idx, errors[i])
q_loss = (torch.FloatTensor(is_weights).to(device) * F.mse_loss(Q_expected, Q_target)).mean()
self.train_loss.append(q_loss.to('cpu').detach().item())
# reset the optimizer
self.optimizer.zero_grad()
q_loss.backward()
self.optimizer.step()
#update the weights of target model weights
self.soft_update(self.q_target , self.q_local ,TAU)
def act(self , state , eps=0.):
"""
expand the dim 0 of the state tensor
base on eps either select max action or a random action
"""
state_tensor = torch.from_numpy(state).float().unsqueeze(0).to(device)
self.q_local.eval()
with torch.no_grad():
action_tensor = self.q_local(state_tensor)
self.q_local.train()
# if the random.random > eps --> select a random action else select greedy action
if(random.random() > eps ):
return np.argmax(action_tensor.to('cpu').detach().numpy())
else :
return random.choice(np.arange(self.action_size))
def soft_update(self , target_model , local_model , tau) :
for target_param , local_param in zip(target_model.parameters() , local_model.parameters()):
target_param.data.copy_(tau*local_param.data + (1.-tau)*target_param.data)
# -
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
# ## Dueling Deep Q Network
# 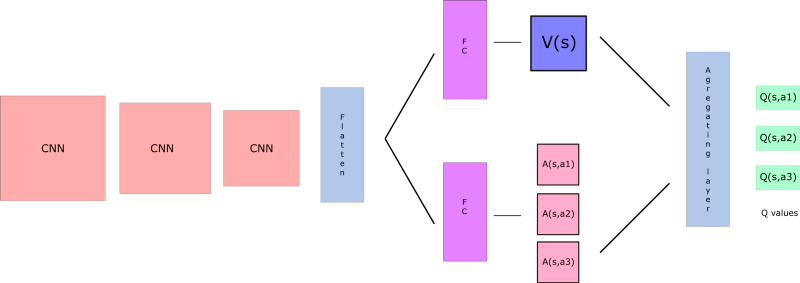
# +
def conv_block(in_channels , out_channles , kernel_size =3 , stride=1 , padding=1 , batch_norm=True , maxpool=False ):
layers =[]
conv_layer = nn.Conv2d(in_channels ,out_channles , kernel_size=kernel_size ,stride=stride , padding=padding)
layers.append(conv_layer)
if(batch_norm):
bn = nn.BatchNorm2d(out_channles)
layers.append(bn)
layers.append(nn.ReLU())
if(maxpool):
max_layer = nn.MaxPool2d(kernel_size=4, stride=2 , padding=1)
layers.append(max_layer)
return nn.Sequential(*layers)
class MyQNet(nn.Module):
def __init__(self,stack_size , action_size , seed):
super(DeepQNet , self).__init__()
"""
define a simple model with some conv layers and later with fully connected layers
"""
self.in_size = stack_size
self.out_size = action_size
self.seed = torch.manual_seed(seed)
# 224 * 224 * 4 --> 224 * 224 * 32
self.conv_block1 = conv_block(self.in_size , 32 , maxpool=True)
# 224 * 224 * 32 --> 112 * 112 * 64
self.conv_block2 = conv_block(32 , 64 , maxpool=True)
#112 * 112 * 64 --> 112 * 112 * 128
self.conv_block3 = conv_block(64 , 128 , maxpool=True)
self.flatten_size = 128*9*12
#state value stream
self.fc_value = nn.Linear(self.flatten_size , 512)
self.fc_value_bn = nn.BatchNorm1d(512)
self.fc_value_out = nn.Linear(512 , 1 )
#advantage stream
self.fc_advantage = nn.Linear(self.flatten_size , 512)
self.fc_advantage_bn = nn.BatchNorm1d(512)
self.fc_advantage_out = nn.Linear(512 , self.out_size)
def forward(self, x):
x = self.conv_block1(x)
x = self.conv_block2(x)
x = self.conv_block3(x)
x = x.view(-1,self.flatten_size)
#state value stream
state_value = F.dropout(F.relu(self.fc_value_bn(self.fc_value(x))) ,p=0.4 )
state_value = self.fc_value_out(state_value)
#state advantage stream
advantage_value = F.dropout(F.relu(self.fc_advantage_bn(self.fc_advantage(x))) , p=0.4 )
advantage_value = self.fc_advantage_out(advantage_value)
output = state_value + torch.sub(advantage_value , torch.mean(advantage_value , dim=1 , keepdim=True))
return output
# -
agent = Agent(state_size=8, action_size=19, seed=1243)
agent.q_local.load_state_dict(torch.load('../input/doom-rl/local_model.pth'))
agent.q_target.load_state_dict(torch.load('../input/doom-rl/target_model.pth'))
# ## Fill the memory buffer with rndom samples
# +
import random # Handling random number generation
import time # Handling time calculation
from skimage import transform# Help us to preprocess the frames
from collections import deque# Ordered collection with ends
from collections import namedtuple
import torch
import torch.optim as optim
import numpy as np
stacked_size = 2
class DataPreprocess():
def __init__(self , stack_size ):
self.stack_size = stack_size
self.stacked_frames = deque([ np.zeros([4,72,96] ,dtype=int) for i_dx in range(stacked_size) ] , maxlen=self.stack_size)
def preprocess(self , frame):
"""
screen frames are in grayscale format defalut
1.normalize the images
2. apply some transformations
"""
frame = frame / 255.0
frame = transform.resize(frame ,[4,72,96])
return frame
def reset(self ):
self.stacked_frames = deque([ np.zeros([4,72,96] ,dtype=int) for i_dx in range(stacked_size) ] , maxlen=self.stack_size)
def stack_frames(self , frame , new_episode=False):
"""
stack multiple frames with each other to idenitify the temporal movemnts of the objects
1. preprocess the new frame
"""
processed_frame = self.preprocess(frame)
if(new_episode):
#for initial step after new episode add same frame to all the stacked frames
self.reset()
self.stacked_frames.append(processed_frame)
self.stacked_frames.append(processed_frame)
stack_states = np.concatenate(self.stacked_frames , axis=0)
return stack_states
else:
self.stacked_frames.append(processed_frame)
stack_states = np.concatenate(self.stacked_frames , axis=0)
return stack_states
# +
env = gym.make("GFootball-11_vs_11_kaggle-SMM-v0")
print(smm_env.reset().shape)
possible_actions = np.arange(19)
data_processor = DataPreprocess(stack_size=2)
state = smm_env.reset()
# Remember that stack frame function also call our preprocess function.
state = data_buffer.stack_frames(state , new_episode=True)
step =0
max_lenght=int(1e2)
while step < max_lenght:
step += 1
# Predict the action to take and take it
action = random.choice(possible_actions)
#step the agent
next_state , reward, done, info = env.step(action)
# If the game is finished
if done:
# the episode ends so no next state
next_state = np.zeros((72,96,4), dtype=np.int)
next_state = data_buffer.stack_frames( next_state, False)
# Set step = max_steps to end the episode
step = max_lenght
# Get the total reward of the episode
total_reward = np.sum(episode_rewards)
if(episode%1==0):
print('Episode: {}'.format(episode),
'Total reward: {}'.format(total_reward),
'Training loss: {:.4f}'.format(np.mean(agent.train_loss)),
'Explore P: {:.4f}'.format(explore_probability))
agent.step(state, action, reward, next_state, done)
else:
# Stack the frame of the next_state
next_state = data_buffer.stack_frames( next_state, False)
# Add experience to memory
agent.step(state, action, reward, next_state, done)
# st+1 is now our current state
state = next_state
# +
# Init the game
explore_probability = 1.0
explore_probability_end=0.01
eps_decay = 0.98
max_steps = 1000
total_episodes = 150
for episode in range(total_episodes):
# Set step to 0
step = 0
# Initialize the rewards of the episode
episode_rewards = []
# Make a new episode and observe the first state
state = env.reset()
# Remember that stack frame function also call our preprocess function.
state = data_buffer.stack_frames(state , new_episode=True)
while step < max_steps:
step += 1
# Predict the action to take and take it
action = agent.act(state , eps=explore_probability)
# Do the action
next_state , reward, done, info = env.step(action)
# Add the reward to total reward
episode_rewards.append(reward)
# If the game is finished
if done:
# the episode ends so no next state
next_state = np.zeros((72,96,4), dtype=np.int)
next_state = data_buffer.stack_frames( next_state, False)
# Set step = max_steps to end the episode
step = max_steps
# Get the total reward of the episode
total_reward = np.sum(episode_rewards)
if(episode%1==0):
print('Episode: {}'.format(episode),
'Total reward: {}'.format(total_reward),
'Training loss: {:.4f}'.format(np.mean(agent.train_loss)),
'Explore P: {:.4f}'.format(explore_probability))
agent.step(state, action, reward, next_state, done)
else:
# Stack the frame of the next_state
next_state = data_processor.stack_frames( next_state, False)
# Add experience to memory
agent.step(state, action, reward, next_state, done)
# st+1 is now our current state
state = next_state
explore_probability = max(explore_probability_end, explore_probability*eps_decay)
if(episode%2==0):
print('Episode: {}'.format(episode),
'Total reward: {}'.format(np.sum(episode_rewards)),
'Training loss: {:.4f}'.format(np.mean(agent.train_loss)),
'Explore P: {:.4f}'.format(explore_probability))
# -
torch.save(agent.q_local.state_dict(),'local_model.pth')
torch.save(agent.q_target.state_dict(),'target_model.pth')
# +
# %%writefile main.py
#from kaggle_environments.envs.football.helpers import *
# @human_readable_agent wrapper modifies raw observations
# provided by the environment:
# https://github.com/google-research/football/blob/master/gfootball/doc/observation.md#raw-observations
# into a form easier to work with by humans.
# Following modifications are applied:
# - Action, PlayerRole and GameMode enums are introduced.
# - 'sticky_actions' are turned into a set of active actions (Action enum)
# see usage example below.
# - 'game_mode' is turned into GameMode enum.
# - 'designated' field is removed, as it always equals to 'active'
# when a single player is controlled on the team.
# - 'left_team_roles'/'right_team_roles' are turned into PlayerRole enums.
# - Action enum is to be returned by the agent function.
import collections
import pickle
import zlib
from typing import Tuple, Dict, Any, Union, Callable, List
import torch.nn as nn
import torch.nn.functional as F
import gym
import numpy as np
import tensorflow as tf
from gfootball.env import observation_preprocessing
from tensorflow import keras
import random # Handling random number generation
import time # Handling time calculation
from skimage import transform# Help us to preprocess the frames
from collections import deque# Ordered collection with ends
from collections import namedtuple
import torch
import torch.optim as optim
import numpy as np
class Data_Module():
def __init__(self , stack_size ):
self.stack_size = stack_size
self.stacked_frames = deque([ np.zeros([4,72,96] ,dtype=int) for i_dx in range(stacked_size) ] , maxlen=self.stack_size)
def preprocess(self , frame):
"""
screen frames are in grayscale format defalut
1.normalize the images
2. apply some transformations
"""
frame = frame / 255.0
frame = transform.resize(frame ,[4,72,96])
return frame
def reset(self ):
self.stacked_frames = deque([ np.zeros([4,72,96] ,dtype=int) for i_dx in range(stacked_size) ] , maxlen=self.stack_size)
def stack_frames(self , frame , new_episode=False):
"""
stack multiple frames with each other to idenitify the temporal movemnts of the objects
1. preprocess the new frame
"""
processed_frame = self.preprocess(frame)
if(new_episode):
#for initial step after new episode add same frame to all the stacked frames
self.reset()
self.stacked_frames.append(processed_frame)
self.stacked_frames.append(processed_frame)
stack_states = np.concatenate(self.stacked_frames , axis=0)
return stack_states
else:
self.stacked_frames.append(processed_frame)
stack_states = np.concatenate(self.stacked_frames , axis=0)
return stack_states
#----------------------------------- Model ------------------------------------------------------------
def conv_block(in_channels , out_channles , kernel_size =3 , stride=1 , padding=1 , batch_norm=True , maxpool=False ):
layers =[]
conv_layer = nn.Conv2d(in_channels ,out_channles , kernel_size=kernel_size ,stride=stride , padding=padding)
layers.append(conv_layer)
if(batch_norm):
bn = nn.BatchNorm2d(out_channles)
layers.append(bn)
layers.append(nn.ReLU())
if(maxpool):
max_layer = nn.MaxPool2d(kernel_size=4, stride=2 , padding=1)
layers.append(max_layer)
return nn.Sequential(*layers)
class DuelingDQNet(nn.Module):
def __init__(self,stack_size , action_size , seed):
super(DeepQNet , self).__init__()
"""
define a simple model with some conv layers and later with fully connected layers
"""
self.in_size = stack_size
self.out_size = action_size
self.seed = torch.manual_seed(seed)
# 224 * 224 * 4 --> 224 * 224 * 32
self.conv_block1 = conv_block(self.in_size , 32 , maxpool=True)
# 224 * 224 * 32 --> 112 * 112 * 64
self.conv_block2 = conv_block(32 , 64 , maxpool=True)
#112 * 112 * 64 --> 112 * 112 * 128
self.conv_block3 = conv_block(64 , 128 , maxpool=True)
self.flatten_size = 128*9*12
#state value stream
self.fc_value = nn.Linear(self.flatten_size , 512)
self.fc_value_bn = nn.BatchNorm1d(512)
self.fc_value_out = nn.Linear(512 , 1 )
#advantage stream
self.fc_advantage = nn.Linear(self.flatten_size , 512)
self.fc_advantage_bn = nn.BatchNorm1d(512)
self.fc_advantage_out = nn.Linear(512 , self.out_size)
def forward(self, x):
x = self.conv_block1(x)
x = self.conv_block2(x)
x = self.conv_block3(x)
x = x.view(-1,self.flatten_size)
#state value stream
state_value = F.dropout(F.relu(self.fc_value_bn(self.fc_value(x))) ,p=0.4 )
state_value = self.fc_value_out(state_value)
#state advantage stream
advantage_value = F.dropout(F.relu(self.fc_advantage_bn(self.fc_advantage(x))) , p=0.4 )
advantage_value = self.fc_advantage_out(advantage_value)
output = state_value + torch.sub(advantage_value , torch.mean(advantage_value , dim=1 , keepdim=True))
return output
ddq_model = DuelingDQNet(8,19,2333)
try:
ddq_model.load_state_dict(torch.load("/kaggle_simulations/agent/local_model.pth" , map_location="cpu"))
except (FileNotFoundError, ValueError):
ddq_model.load_state_dict(torch.load("local_model.pth" , map_location="cpu"))
model.eval()
data_collection = Data_Module(stack_size=2)
#@human_readable_agent
def agent(obs):
# Get the raw observations return by the environment
obs = obs['players_raw'][0]
# Convert these to the same output as the SMMWrapper we used in training
obs = observation_preprocessing.generate_smm([obs]).squeeze()
ddq_state = data_collection.stack_frames(obs ,False)
ddq_state_tensor = torch.from_numpy(ddq_state).float().unsqueeze(0).to(device)
#inference the model
action_tensor = model.forward(ddq_state_tensor)
# Use the SMMFrameProcessWrapper to do the buffering, but not enviroment
# stepping or anything related to the Gym API.
action = np.argmax(action_tensor.to('cpu').detach().numpy())
return [int(action)]
# +
from typing import Tuple, Dict, List, Any
from kaggle_environments import make
env = make("football", debug=True,configuration={"save_video": True,
"scenario_name": "11_vs_11_kaggle"})
# Define players
left_player = "/kaggle/working/main.py" # A custom agent, eg. random_agent.py or example_agent.py
right_player = "run_right" # eg. A built in 'AI' agent or the agent again
output: List[Tuple[Dict[str, Any], Dict[str, Any]]] = env.run([left_player, right_player])
#print(f"Final score: {sum([r['reward'] for r in output[0]])} : {sum([r['reward'] for r in output[1]])}")
env.render(mode="human", width=800, height=600)
# -
# !tar -czvf submission.tar.gz ./main.py* ./local_model.pth*
|
rl-football-dueling-dqnet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Transfer Learning
#
# Most of the time you won't want to train a whole convolutional network yourself. Modern ConvNets training on huge datasets like ImageNet take weeks on multiple GPUs.
# > Instead, most people use a pretrained network either as a fixed feature extractor, or as an initial network to fine tune.
#
# In this notebook, you'll be using [VGGNet](https://arxiv.org/pdf/1409.1556.pdf) trained on the [ImageNet dataset](http://www.image-net.org/) as a feature extractor. Below is a diagram of the VGGNet architecture, with a series of convolutional and maxpooling layers, then three fully-connected layers at the end that classify the 1000 classes found in the ImageNet database.
#
# <img src="notebook_ims/vgg_16_architecture.png" width=700px>
#
# VGGNet is great because it's simple and has great performance, coming in second in the ImageNet competition. The idea here is that we keep all the convolutional layers, but **replace the final fully-connected layer** with our own classifier. This way we can use VGGNet as a _fixed feature extractor_ for our images then easily train a simple classifier on top of that.
# * Use all but the last fully-connected layer as a fixed feature extractor.
# * Define a new, final classification layer and apply it to a task of our choice!
#
# You can read more about transfer learning from [the CS231n Stanford course notes](http://cs231n.github.io/transfer-learning/).
#
# ---
# ## Flower power
#
# Here we'll be using VGGNet to classify images of flowers. We'll start, as usual, by importing our usual resources. And checking if we can train our model on GPU.
#
# ### Download Data
#
# Download the flower data from [this link](https://s3.amazonaws.com/video.udacity-data.com/topher/2018/September/5baa60a0_flower-photos/flower-photos.zip), save it in the home directory of this notebook and extract the zip file to get the directory `flower_photos/`. **Make sure the directory has this exact name for accessing data: flower_photos**.
# +
import os
import numpy as np
import torch
import torchvision
from torchvision import datasets, models, transforms
import matplotlib.pyplot as plt
# %matplotlib inline
# +
# check if CUDA is available
train_on_gpu = torch.cuda.is_available()
if not train_on_gpu:
print('CUDA is not available. Training on CPU ...')
else:
print('CUDA is available! Training on GPU ...')
# -
# ## Load and Transform our Data
#
# We'll be using PyTorch's [ImageFolder](https://pytorch.org/docs/stable/torchvision/datasets.html#imagefolder) class which makes it very easy to load data from a directory. For example, the training images are all stored in a directory path that looks like this:
# ```
# root/class_1/xxx.png
# root/class_1/xxy.png
# root/class_1/xxz.png
#
# root/class_2/123.png
# root/class_2/nsdf3.png
# root/class_2/asd932_.png
# ```
#
# Where, in this case, the root folder for training is `flower_photos/train/` and the classes are the names of flower types.
# +
# define training and test data directories
data_dir = 'flower_photos/'
train_dir = os.path.join(data_dir, 'train/')
test_dir = os.path.join(data_dir, 'test/')
# classes are folders in each directory with these names
classes = ['daisy', 'dandelion', 'roses', 'sunflowers', 'tulips']
# -
# ### Transforming the Data
#
# When we perform transfer learning, we have to shape our input data into the shape that the pre-trained model expects. VGG16 expects `224`-dim square images as input and so, we resize each flower image to fit this mold.
# +
# load and transform data using ImageFolder
# VGG-16 Takes 224x224 images as input, so we resize all of them
data_transform = transforms.Compose([transforms.RandomResizedCrop(224),
transforms.ToTensor()])
train_data = datasets.ImageFolder(train_dir, transform=data_transform)
test_data = datasets.ImageFolder(test_dir, transform=data_transform)
# print out some data stats
print('Num training images: ', len(train_data))
print('Num test images: ', len(test_data))
# -
# ### DataLoaders and Data Visualization
# +
# define dataloader parameters
batch_size = 20
num_workers=0
# prepare data loaders
train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size,
num_workers=num_workers, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size,
num_workers=num_workers, shuffle=True)
# +
# Visualize some sample data
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy() # convert images to numpy for display
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
plt.imshow(np.transpose(images[idx], (1, 2, 0)))
ax.set_title(classes[labels[idx]])
# -
# ---
# ## Define the Model
#
# To define a model for training we'll follow these steps:
# 1. Load in a pre-trained VGG16 model
# 2. "Freeze" all the parameters, so the net acts as a fixed feature extractor
# 3. Remove the last layer
# 4. Replace the last layer with a linear classifier of our own
#
# **Freezing simply means that the parameters in the pre-trained model will *not* change during training.**
# +
# Load the pretrained model from pytorch
vgg16 = models.vgg16(pretrained=True)
# print out the model structure
print(vgg16)
# -
print(vgg16.classifier[6].in_features)
print(vgg16.classifier[6].out_features)
# Freeze training for all "features" layers
for param in vgg16.features.parameters():
param.requires_grad = False
# ---
# ### Final Classifier Layer
#
# Once you have the pre-trained feature extractor, you just need to modify and/or add to the final, fully-connected classifier layers. In this case, we suggest that you repace the last layer in the vgg classifier group of layers.
# > This layer should see as input the number of features produced by the portion of the network that you are not changing, and produce an appropriate number of outputs for the flower classification task.
#
# You can access any layer in a pretrained network by name and (sometimes) number, i.e. `vgg16.classifier[6]` is the sixth layer in a group of layers named "classifier".
#
# #### TODO: Replace the last fully-connected layer with one that produces the appropriate number of class scores.
# +
import torch.nn as nn## TODO: add a last linear layer that maps n_inputs -> 5 flower classes
## new layers automatically have requires_grad = True
n_input = vgg16.classifier[6].in_features
n_output = len(classes)
vgg16.classifier[6] = nn.Linear(n_input, n_output)
# after completing your model, if GPU is available, move the model to GPU
if train_on_gpu:
vgg16.cuda()
# -
# ### Specify [Loss Function](http://pytorch.org/docs/stable/nn.html#loss-functions) and [Optimizer](http://pytorch.org/docs/stable/optim.html)
#
# Below we'll use cross-entropy loss and stochastic gradient descent with a small learning rate. Note that the optimizer accepts as input _only_ the trainable parameters `vgg.classifier.parameters()`.
# +
import torch.optim as optim
# specify loss function (categorical cross-entropy)
criterion = nn.CrossEntropyLoss()
# specify optimizer (stochastic gradient descent) and learning rate = 0.001
optimizer = optim.SGD(vgg16.classifier.parameters(), lr=0.001)
# -
# ---
# ## Training
#
# Here, we'll train the network.
#
# > **Exercise:** So far we've been providing the training code for you. Here, I'm going to give you a bit more of a challenge and have you write the code to train the network. Of course, you'll be able to see my solution if you need help.
# +
# number of epochs to train the model
n_epochs = 2
## TODO complete epoch and training batch loops
## These loops should update the classifier-weights of this model
## And track (and print out) the training loss over time
for epoch in range(n_epochs):
running_loss = 0.0
for i, data in enumerate(train_loader, 0):
inputs, labels = data
# zero the parameter gradients
optimizer.zero_grad()
# forward + backward + optimize
outputs = vgg16(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# print statistics
running_loss += loss.item()
if i % 20 == 19: # print every 20 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, i + 1, running_loss / 20))
running_loss = 0.0
# -
# ---
# ## Testing
#
# Below you see the test accuracy for each flower class.
# +
# track test loss
# over 5 flower classes
test_loss = 0.0
class_correct = list(0. for i in range(5))
class_total = list(0. for i in range(5))
vgg16.eval() # eval mode
# iterate over test data
for data, target in test_loader:
# move tensors to GPU if CUDA is available
if train_on_gpu:
data, target = data.cuda(), target.cuda()
# forward pass: compute predicted outputs by passing inputs to the model
output = vgg16(data)
# calculate the batch loss
loss = criterion(output, target)
# update test loss
test_loss += loss.item()*data.size(0)
# convert output probabilities to predicted class
_, pred = torch.max(output, 1)
# compare predictions to true label
correct_tensor = pred.eq(target.data.view_as(pred))
correct = np.squeeze(correct_tensor.numpy()) if not train_on_gpu else np.squeeze(correct_tensor.cpu().numpy())
# calculate test accuracy for each object class
for i in range(batch_size):
label = target.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
# calculate avg test loss
test_loss = test_loss/len(test_loader.dataset)
print('Test Loss: {:.6f}\n'.format(test_loss))
for i in range(5):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
classes[i], 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
# -
# ### Visualize Sample Test Results
# +
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
images.numpy()
# move model inputs to cuda, if GPU available
if train_on_gpu:
images = images.cuda()
# get sample outputs
output = vgg16(images)
# convert output probabilities to predicted class
_, preds_tensor = torch.max(output, 1)
preds = np.squeeze(preds_tensor.numpy()) if not train_on_gpu else np.squeeze(preds_tensor.cpu().numpy())
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(20):
ax = fig.add_subplot(2, 20/2, idx+1, xticks=[], yticks=[])
plt.imshow(np.transpose(images[idx], (1, 2, 0)))
ax.set_title("{} ({})".format(classes[preds[idx]], classes[labels[idx]]),
color=("green" if preds[idx]==labels[idx].item() else "red"))
# -
|
transfer-learning/Transfer_Learning_Exercise.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Common Techniques and issues
#
# Note that array question and string questions are often interchangable.
#
# ## Hash Tables
#
# If the number of collisions in a hash table are very high, the worst case runtime for searching for an item in a has table is O(n), where n is the number of keys. However, we generally assume a good implementation that keeps collisions to a minimum, in which case the lookup time is O(1).
#
# ## Dyanmic Arrays
# The amortized insertion runtime is O(1). Suppose you have an array of size N. We can work backwards to compute how many elements were copied at each capacity increase. Observe that when you increase the array to K elements, the array was perviously have that size. Therefore we had to copy over k/2 elements. Therefore, the total number of copies to insert N elements is roughly N/2 + N/4 + N/8 + ... + 2 + 1 , which is just less than N. This is similar to if oyu had a mile long walk to the store and you walk 0.5 miles, then 0.25, then 0.125 and so on. You will never exceed one mile although you get very close to it.
#
# Therefore, inserting N elements takes o(N) work total. Each insertion is o(1) on average, even though some insertions take O(n) time in the worst case
#
# # String Builder
#
# if you had to continually concatentate a letter to a string, on each concatenation, a new copy of the string is created, and the two strings are copied over, character by character. The first iteration requires us to copy x characters. The second iteration requires copying 2x characters. The third iteration requires 3x and so on. The total time therefore is 0(x + 2x + ... + nx) which reduces down to O(xn^2)
#
# It is better to use an array to hold the characters and then join them, copying them back to a string only when necessary
#
# ---
# # QUESTIONS
import unittest
# # Is Unique
#
# Implement an algorithm to determine if a string has all unique characters. WHat if you cannot use additional data structures?
# **General Idea**
# The optimal approach would be to either use a list or a dictionary to act as a record if we have seen a letter before. This way, in the worst case scenario, we would have to go through the list once, leading to a time complexity of O(n).
#
# **Improvements**
# We could also ask whether the string is either ASCII or Unicode. There are far greater # of characters in Unicode vs ASCII (less than 200 for regular ascii and 256 for exte4nded ascii vs in the hundred thousands). Then we can then add a clause in the beginning of our function that checks if our string is greater than that number and immediatley return false.
#
#
string1 = "qwertyu" # has no repeating characters
string2 = "qwertbq" # does have 1 repeating character
# using a dictionary
def is_unique(string):
dictionary = {}
for i in list(string):
if i in dictionary:
return False
else:
dictionary[i] = 1
return True
is_unique(string2)
# +
# leveraging the fact that there is a number associated with the characters and using a list
def is_unique(string):
store = [None] * 256
for i in list(string):
if store[ord(i)] is not None:
return False
else:
store[ord(i)] = 1
return True
# -
is_unique(string1)
# If we could not use additional data structures, there are two approaches we could take with their different benefits and setbacks.
#
# The most straightforward solution would be to check every letter against every other letter, which would lead to a big O(n^2). This saves on memory but takes more time.
#
# The other approach would be to first sort the string and then compare every letter to the one that comes after. This would be faster with O(n log n) and then searching through with O(n). This would require some memory to sort but would be faster. Both implementations are below.
# O(n^2)
def is_unique(string):
for i,j in enumerate(string):
for x in range(i + 1,len(string)):
if string[x] == j:
return False
return True
is_unique(string2)
# sorting
def is_unique(string):
sorted_string = sorted(string)
for i,j in enumerate(sorted_string[:-1]):
if j == sorted_string[i + 1]:
return False
return True
is_unique(string1)
# ---
# # Check Permutation
#
# Given two strings, write a method to decide if one is a permutation of the other
#
# There are two approaches that come to mind, depending on how you think of permutation. One way to think of permutation is the ordering of characters and the other way to think of it would be the number of each character.
#
# The order approach has a higher big o, but the code is simpler
# +
s1 = 'abcdefghijklmnopqrstuvwxyz' # all of the letters of the alphabet
s2 = 'qwertyuiopasdfghjklzxcvbnm' # all of the letters in a different order
s3 = 'qwertyuioqasdfghjklzxcvbnm' # repeated q
s4 = '<KEY>' # all of the letters
# +
# Order approach
def check_permutation(s1, s2):
return sorted(s1) == sorted(s2)
print(check_permutation(s1,s2)) # should be true
print(check_permutation(s3,s4)) # should be false
# +
# number approach
def check_permutation(s1, s2):
s1_dict = {}
s2_dict = {}
for i in s1:
if i in s1_dict:
s1_dict[i] += 1
else:
s1_dict[i] = 1
for i in s2:
if i in s2_dict:
s2_dict[i] += 1
else:
s2_dict[i] = 1
return s1_dict == s2_dict
print(check_permutation(s1,s2)) # should be true
print(check_permutation(s3,s4)) # should be false
# -
# # Palindrome Permutation
# Given a string, write a function to check if it is a permutation of a palindrome. A palindrome is a word or phrase that is the same forwards and backwards. A permutation is a rearrangement of letters. This palindrome does not need to be limited to just dictionary words
#
# We should use a hash table to count how many times a character appears. Then, we iterate through the hash table and ensure that no more than one character has an odd count
should_be_true = "tact coa"
should_be_false = "this is not a palindrome permutation"
def pal_perm(string):
holder = {}
tracker = 0
for i in string:
if i.isalpha():
if i.lower() in holder:
holder[i.lower()] += 1
else:
holder[i.lower()] = 1
tracker += 1
# now need to go through the holder
odd_trigger = tracker % 2
for j in holder.values():
if odd_trigger and (j % 2 == 1):
odd_trigger -= 1
elif j % 2 == 1:
return False
return True
pal_perm("abba")
pal_perm(should_be_false)
# # One Away
#
# There are 3 types of edits that can be perfomed on the two given strings:
# * Insert a character
# * Remove a character
# * Replace a character
#
# Given two strings, write a function to check if they are one (or zero) edits away
#
# ex) pale ,ple -> True \
# pales, pale -> True \
# pale, bale -> True \
# pale, bake -> False
#
# First we check if the strings are the same, then we dont have to do any work and just return true. Then we have to realize that checking whether a string is missing a character can check both removing and inserting, depending on how we view it. Finally, if the characters are the same size, then we can run through both and make sure that there is at most one discrepency.
# +
def one_away(s1, s2):
# checking if the strings are the same
if s1 == s2:
return True
# determining the lengths of the strings so we can decide which function to call
s1_len = len(s1)
s2_len = len(s2)
if s1_len == s2_len:
return equal_length(s1, s2)
if abs(s1_len - s2_len) > 1:
return False
if s1_len > s2_len:
return diff_length(s1, s2)
if s2_len > s1_len:
return diff_length(s2, s1)
def equal_length(s1, s2):
ALLOWANCE = 1
for i, j in enumerate(s1):
if j != s2[i]:
if ALLOWANCE == 0:
return False
else:
ALLOWANCE -= 1
return True
def diff_length(longer, shorter):
counter = 0
for i in shorter:
if i != longer[counter]:
counter += 1
if i != longer[counter]:
return False
else:
counter += 1
return True
# -
one_away('pale', 'bake')
# # String Compression
#
# Implement a method to perform basic string compression using the counts of repeated characters. If the "compressed" string would not become smaller than the original string, your method should return hte original string. You can assume the string has onle uppercase and lowercase letters
#
# ex) aabcccccaaa -> a2b1c5a3
#
# The implementation seems fairly straighforward. We iterate through the string, copying the characters to a new string and counting the repeats. At each iteration, check if the current character is the same as the next character. if not, add its compressed version to the result. This works but remember **when building a string that you will need to repeatedly append to, it is better to use a list and then join**. String join is significantly faster then concatenation because Strings are immutable and can't be changed in place. To alter one, a new representation needs to be created (a concatenation of the two) String concatenation operates in O(n^2). This would mean that the runtime would be O(p + k^2) where p is the size of the original string and k is the number of character sequences.
#
#
# We can avoid this by using a string builder
def string_compression(string):
compressed = []
holder = ""
count = 0
for i in string:
if i != holder:
if holder != "":
compressed.append(holder)
if count != 0:
compressed.append(str(count))
holder = i
count = 1
else:
count += 1
compressed.append(holder)
compressed.append(str(count))
if len(string) > len(compressed):
return "".join(compressed)
else:
return string
string_compression('aabcccccaaa')
# # Rotate Matrix
#
# Given an image represented by an NxN matrix, write a method to rotate the image by 90 degrees. Can you do this in place?
#
# If you had no memory constraints and did not have to do this in place, all you had to do is copy the rows into the correct collumns and the matrix would be rotated. Given that the question is asking you to do this in place is where things get difficult.
#
# Since the matrix will be NxN, we can think of the matrix as having an outer layer and then inner layers. We would shift around each cell to the corresponding position at a time. We can do this by holding a temporary variable with the value of the top left cell, move the value of the bottom left to the top left. The bottom right to the bottom left, top right to the bottom right, and finall the temp into the top right.
#
# We then shift over by one until and repeat the process until we get to N -1 since the very last cell would have been rotated.
#
# Since the matrix is NxN, we can have a left and right variable that keeps track of the outermost layer, which would also keep track of the top and bottom as well.
#
# Once we sort out the outer layer, all we have to do is increase our left (bottom) and right (top) variables to get to the inner layer. You would do this until the right equlas the left, then you know you are done
#
# **This one was hard to wrap my head around. Will need to revisit later**
import pandas as pd
from copy import deepcopy
x = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]]
df = pd.DataFrame(x)
df
# +
def rotate_matrix(matrix):
n = len(matrix)
L = 0
R = n-1
while R >= L:
for i in range(R-L):
# top left corner temp
temp = matrix[L][L+i]
# moving bottom left to top left
matrix[L][L+i] = matrix[R-i][L]
# moving bottom left to top left
matrix[R-i][L] = matrix[R][R-i]
# moving right column to bottom
matrix[R][R-i] = matrix[L+i][R]
# moving temp to right column
matrix[L+i][R] = temp
R -= 1
L += 1
# -
rotate_matrix(x)
pd.DataFrame(x)
# # Zero Matrix
#
# Write an algorithm such that if an element in an MxN matrix is 0, its entire row and column are set to 0.
#
# My initial approach would have been to just go through all of the items in the matrix and put in a list the coordinates that are 0. Then can zero out rows and columns that way.
#
# If you wanted to approach the problem without having to create another data structure, you could use the first row and first column as holders for the zero instead of a list. But if you were to take this approach, then you would need to first take note if there were any zeros in them to begin with because then those would need to be overwritten with zeroes as well
def zero_matrix(matrix):
n_rows = len(matrix)
n_columns = len(matrix[0])
row_zero = False
column_zero = False
# Going through and checking if there are any zeros in the first column and row
for i in matrix[0]:
if i == 0:
row_zero = True
for i in matrix:
if i[0] == 0:
column_zero = True
# bulk of the zeroes get identified here
for i in range(1, n_rows):
for j in range(1, n_columns):
if matrix[i][j] == 0:
matrix[0][j] = 0
matrix[i][0] = 0
# converting columns
for i, j in enumerate(matrix[0]):
if j == 0:
for x in range(n_rows):
matrix[x][i] = 0
# converting rows
for i, j in enumerate(matrix):
if j[0] == 0:
for x in range(n_columns):
matrix[i][x] = 0
# converting the top row and first column if necessary
if row_zero:
for i in range(n_columns):
matrix[0][i] = 0
if column_zero:
for i in range(n_rows):
matrix[i][0] = 0
# # String rotation
#
# Assume you have a method is_substring which checks if one word is a substring of another. Given two strigs, s1 and s2, write code to check if s2 is a rotation of s1 using only one call to is_substring
#
# ex) waterbottle is a rotation of erbottlewat
#
# This one is really easy once you know the trick. you have to realize that there is a pivot point within the string where it rotates. all you have to do is put the string twice to complete the word at some point within the combined string
def string_rotation(s1, s2):
return is_substring(s1+s1, s2)
|
Interview Questions/Arrays and Strings/Arrays and Strings.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction
#
#
# In this notebook, we will load the data that we generated using [RandomDataGenerator](https://github.com/abulbasar/RandomDataGenerator) script before. Create the schema in Cassandra using [this script](https://github.com/abulbasar/pyspark-examples/blob/master/kafka-clients/cassandra_schema.cql). After loading the data into Cassandra tables, we will also write a few queries to generate the behavioural characteristics. In this notebook, we will find the avg spent and standard deviation by each customer and based those we define a threshold. We will use threshold to see what transactions are anomalous. We can apply the anomaly detetection in the batch process and streaming application as well.
# Create a spark session.
# +
import sys, glob, os
SPARK_HOME=os.environ['SPARK_HOME']
sys.path.append(SPARK_HOME + "/python")
sys.path.append(glob.glob(SPARK_HOME + "/python/lib/py4j*.zip")[0])
from pyspark.sql import SparkSession
from pyspark.conf import SparkConf
cassandra_host = "localhost"
spark_conf = (SparkConf()
.setAppName("BatchJob - Data loader")
.setIfMissing("spark.master", "local")
.set("spark.cassandra.connection.host", cassandra_host)
.set("spark.cassandra.connection.port", 9042)
.set("spark.sql.shuffle.partitions", 10)
.set("", 10)
)
# Create spark session
spark = (SparkSession
.builder
.config(conf = spark_conf)
.getOrCreate()
)
sc = spark.sparkContext
sql = spark.sql
print(sc.uiWebUrl)
# -
# Import libraries for Spark SQL
from pyspark.sql import Row
from pyspark.sql import functions as F
# In the base path output of the data generator are saved.
base_path = "file:///home/cloudera/notebooks/RandomDataGenerator-master/target/"
# Load customers.json into customers table in Cassandra. Remember to include cassandra driver for spark. Otherwise, spark will not be able to interact with Cassandra
customers = spark.read.options(inferSchena = True).json(base_path + "customers.json")
customers.show()
customers.printSchema()
(customers
.drop("address")
.write
.mode("overwrite")
.format("org.apache.spark.sql.cassandra")
.options(table = "customer", keyspace = "cc")
.save())
# Create a utility function to return a dataframe based on a cassandra table.
def cass_table(table_name):
return (spark
.read
.format("org.apache.spark.sql.cassandra")
.options(table = table_name, keyspace = "cc")
.load())
cass_table("customer").show()
# Load merchants.json to merchants table in cassandra.
merchants = spark.read.options(inferSchena = True).json(base_path + "merchants.json")
merchants.show()
merchants.printSchema()
(merchants
.write
.mode("overwrite")
.format("org.apache.spark.sql.cassandra")
.options(table = "merchant", keyspace = "cc")
.save())
cass_table("merchant").show()
# Upload transactions.json to transactions table. Here we are doing some basic transformation for the time timestamp column.
transactions = (spark
.read
.options(inferSchena = True)
.json(base_path + "transactions.json")
.withColumn("timestamp"
, F.expr("from_unixtime(cast(timestamp/pow(10, 9) as bigint))"))
)
transactions.show()
transactions.printSchema()
(transactions
.write
.mode("overwrite")
.format("org.apache.spark.sql.cassandra")
.options(table = "transactions", keyspace = "cc")
.save())
cass_table("transactions").limit(5).toPandas()
# Find Standard deviation and avg amount of transactions for each customers and define the amount thresholds.
# +
agg = (transactions
.groupBy("customer_id")
.agg(F.avg("amount").alias("amount_avg"), F.stddev("amount").alias("amount_std"))
.withColumn("amount_upper_threshold", F.expr("amount_avg + amount_std"))
.withColumn("amount_lower_threshold", F.expr("amount_avg - amount_std"))
)
agg.show()
# -
# Update customer profile with threshold values.
(agg
.select("customer_id", "amount_upper_threshold", "amount_lower_threshold")
.withColumnRenamed("customer_id", "id")
.write
.mode("append")
.format("org.apache.spark.sql.cassandra")
.options(table = "customer", keyspace = "cc")
.save())
cass_table("customer").show()
# Work with Cassandra table directly with python. We will use this technique from streaming application.
from cassandra.cluster import Cluster
cluster = Cluster(["localhost"])
cass = cluster.connect("cc")
cass.execute("select amount_lower_threshold from customer where id = %s", ('800000009260',)).one()
# +
rdd = sc.parallelize(['800000009260', '800000001652', '800000005063'])
def detect_anomalies(tnx):
cluster = Cluster(["localhost"])
cass = cluster.connect("cc")
result = []
for r in tnx:
rec = cass.execute("select id, amount_lower_threshold from customer where id = %s"
, (r,)).one()
result.append((rec.id, rec.amount_lower_threshold))
cass.shutdown()
cluster.shutdown()
return result
rdd.mapPartitions(detect_anomalies).collect()
# -
|
kafka-clients/Load to Cassandra.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Functions
# Functions are like methods but are independent of a specific class. Any objects that they act on must be passed in as arguments. Let's break down the anatomy of a function.
#
# ```Python
# def funcname(arg1, arg2):
# """Docstring"""
# # Do stuff here
# return output
# ```
#
# All functions start with a `def` or **define** statement, followed by the name of the function and a list of arguments in parentheses.
#
# Below the `def` statement is the **docstring** in triple quotes `""" """`. Docstrings are important for humans (including you) who need to read / use your code. The docstring explains what the function does, what arguments the function needs to work properly, and can even suggest example usage. The docsting is what is shown when you call `help(funcname)` on your function.
#
# As we saw with the if blocks, Python uses indentation to organize code. All code indented in the function definition will be run when the function is called.
#
# Finally, if your function produces an output, it must be **returned** with a `return` statement. This signals the end of the function. Python will pick up where it left off before running the function.
#
# Let's work through an example. Say we encounter the following function `stuff()`. We may not know what it does initially if we don't know where it is defined. Let's try calling `help()`.
def stuff(a):
return a**2
help(stuff)
# Hmm. Not very descriptive. And the name of the function is not exactly helpful. I guess we need to try some examples to figure it out.
stuff('hello?')
# Well it didn't like the `str`, so let's try an `int` instead.
stuff(1)
# Now we're getting somewhere, maybe `stuff` returns the number it is given!
stuff(2)
# There goes that idea. But this looks like it could be pattern.
print(stuff(1),stuff(2),stuff(3),stuff(4),stuff(5))
# Cool it looks like `stuff` takes the square of the number it is given! Now to do the same trial and error with the function `allxsonthelistorunderbutnotboth(x1, x2, x3, x4, x5, x6, list1, list2)`. Uhh...
#
# That was an example of writing a function with poor *style*. The function worked as intended, but was frustrating to use if you didn't remember what `stuff()` did. I hope this highlights the importance of readable code. Python comes built-in with features like the **docstring** to avoid situations like the one above. Python won't force you to use docstrings, but it is highly encouraged to get into the habit, especially if you are working with others. And if not for others, do it for future you who won't remember what `stuff()` is in 6 months.
#
# So how do we improve our `stuff()` function for squaring numbers? The first step is giving it a self-evident name, e.g. `square(num)`. Next, we can add a docstring with a description `"""Return the square of num"""`. Finally, we can describe the parameters, return values and provide a couple examples of how to use it. Altogether, it might look like this.
def square(num):
"""Return the square of num.
Parameters
----------
num: int, float
The number to square.
Returns
-------
int, float
The square of num.
Examples
--------
>>> square(2)
4
>>> square(2.5)
6.25
"""
return num**2
# Say we encounter `square()` in the wild and want to know how to use it. Now we can call `help(square)` and see a nicely formatted docstring.
help(square)
# We can even try the examples it provides to ensure the function is working properly.
print(square(2), square(2.5))
# Much less frustrating!
#
# *Style* is an aspect of writing code that is often overlooked in sciences. Just like writing good `git commit` messages, it is very important to write code in a way that future you and future collaborators will be able to read and use.
#
# Another aspect of style is knowing when to break your code down into functions that perform small tasks. This is one of the hardest, but most useful programming skills to master. If you can define function(s) for complex / repetitive code and give those functions good names and good docstrings, you are on your way to writing readable, re-usable code!
#
# Your turn!
# ## Breaking code down into functions
# The following example is long and repetitive. See if you can define functions to shorten and simplify the code, and get the same result.
#
# In this example, we want to see if 3 people like apples, oranges, and are above the age of 20. The data is formatted as such:
#
# person = 'likesapples likesoranges age'
# ```Python
# person1 = 'yes yes 13'
# person2 = 'yes nah 21'
# person3 = 'nah nah 80'
# ```
#
# We want to `print('It's a match!')` if all 3 people like apples and oranges and are older than 20. Otherwise, `print('It's not a match!')`.
# +
person1 = 'yes yes 42'
person2 = 'yes yes 64'
person3 = 'yes yes 80'
# Uncomment these three for an example of not a match
# person1 = 'yes yes 13'
# person2 = 'yes nah 21'
# person3 = 'nah nah 80'
if person1[0:3] == 'yes' and person1[4:7] == 'yes' and int(person1[8:]) > 20:
if person2[0:3] == 'yes' and person2[4:7] == 'yes' and int(person2[8:]) > 20:
if person3[0:3] == 'yes' and person3[4:7] == 'yes' and int(person3[8:]) > 20:
print("It's a match!")
else:
print("It's not a match!")
else:
print("It's not a match!")
else:
print("It's not a match!")
# +
# Put your function version of the above code here
# Don't forget the docstrings!
# -
# There are many possible ways to break up code into functions. How specific you make your functions depends on your particular use case. If you want to see my solution, you can copy and paste it from [here](https://github.com/cjtu/sci_coding/tree/master/lessons/lesson3/data/function_solution.py) and compare with yours!
#
#
# Great job! You made it to the end of the crash course on objects, methods and functions (oh my). Next, we will be working with `Lists and Tuples`.
|
spirl/python_functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Single Particle Model (SPM)
# ## Model Equations
# The SPM consists of two spherically symmetric diffusion equations: one within a representative negative particle ($\text{k}=\text{n}$) and one within a representative positive particle ($\text{k}=\text{p}$). In the centre of the particle the standard no-flux condition is imposed. Since the SPM assumes that all particles in an electrode behave in exactly the same way, the flux on the surface of a particle is simply the current $I$ divided by the thickness of the electrode $L_{\text{k}}$. The concentration of lithium in electrode $\text{k}$ is denoted $c_{\text{k}}$ and the current is denoted by $I$. All parameters in the model stated here are dimensionless and are given in terms of dimensional parameters at the end of this notebook. The model equations for the SPM are then:
# \begin{align}
# \mathcal{C}_{\text{k}} \frac{\partial c_{\text{s,k}}}{\partial t} &= -\frac{1}{r_{\text{k}}^2} \frac{\partial}{\partial r_{\text{k}}} \left(r_{\text{k}}^2 N_{\text{s,k}}\right), \\
# N_{\text{s,k}} &= -D_{\text{s,k}}(c_{\text{s,k}}) \frac{\partial c_{\text{s,k}}}{\partial r_{\text{k}}}, \quad \text{k} \in \text{n, p}, \end{align}
# $$
# N_{\text{s,k}}\big|_{r_{\text{k}}=0} = 0, \quad \text{k} \in \text{n, p}, \quad \ \ - \frac{a_{R, \text{k}}\gamma_{\text{k}}}{\mathcal{C}_{\text{k}}} N_{\text{s,k}}\big|_{r_{\text{k}}=1} =
# \begin{cases}
# \frac{I}{L_{\text{n}}}, \quad &\text{k}=\text{n}, \\
# -\frac{I}{L_{\text{p}}}, \quad &\text{k}=\text{p},
# \end{cases} \\
# c_{\text{s,k}}(r_{\text{k}},0) = c_{\text{s,k,0}}, \quad \text{k} \in \text{n, p},$$
# where $D_{\text{s,k}}$ is the diffusion coefficient in the solid, $N_{\text{s,k}}$ denotes the flux of lithium ions in the solid particle within the region $\text{k}$, and $r_{\text{k}} \in[0,1]$ is the radial coordinate of the particle in electrode $\text{k}$.
#
# ### Voltage Expression
# The terminal voltage is obtained from the expression:
# $$
# V = U_{\text{p}}(c_{\text{p}})\big|_{r_{\text{p}}=1} - U_{\text{n}}(c_{\text{n}})\big|_{r_{\text{n}}=1} -2\sinh^{-1}\left(\frac{I}{j_{\text{0,p}} L_{\text{p}}}\right) - 2\sinh^{-1}\left(\frac{I}{j_{\text{0,n}} L_{\text{n}}}\right)
# $$
# with the exchange current densities given by
# $$j_{\text{0,k}} = \frac{\gamma_{\text{k}}}{\mathcal{C}_{\text{r,k}}}(c_{\text{k}})^{1/2}(1-c_{\text{k}})^{1/2} $$
#
# More details can be found in [[3]](#References).
# ## Example solving SPM using PyBaMM
#
# Below we show how to solve the Single Particle Model, using the default geometry, mesh, parameters, discretisation and solver provided with PyBaMM. In this notebook we explicitly handle all the stages of setting up, processing and solving the model in order to explain them in detail. However, it is often simpler in practice to use the `Simulation` class, which handles many of the stages automatically, as shown [here](../simulation-class.ipynb).
#
# First we need to import `pybamm`, and then change our working directory to the root of the pybamm folder.
# %pip install pybamm -q # install PyBaMM if it is not installed
import pybamm
import numpy as np
import os
import matplotlib.pyplot as plt
os.chdir(pybamm.__path__[0]+'/..')
# We then create an instance of the SPM:
model = pybamm.lithium_ion.SPM()
# The model object is a subtype of [`pybamm.BaseModel`](https://pybamm.readthedocs.io/en/latest/source/models/base_models/base_model.html), and contains all the equations that define this particular model. For example, the `rhs` dict contained in `model` has a dictionary mapping variables such as $c_n$ to the equation representing its rate of change with time (i.e. $\partial{c_n}/\partial{t}$). We can see this explicitly by visualising this entry in the `rhs` dict:
variable = next(iter(model.rhs.keys()))
equation = next(iter(model.rhs.values()))
print('rhs equation for variable \'',variable,'\' is:')
path = 'examples/notebooks/models/'
equation.visualise(path+'spm1.png')
# 
# We need a geometry in which to define our model equations. In pybamm this is represented by the [`pybamm.Geometry`](https://pybamm.readthedocs.io/en/latest/source/geometry/geometry.html) class. In this case we use the default geometry object defined by the model
geometry = model.default_geometry
# This geometry object defines a number of domains, each with its own name, spatial variables and min/max limits (the latter are represented as equations similar to the rhs equation shown above). For instance, the SPM has the following domains:
print('SPM domains:')
for i, (k, v) in enumerate(geometry.items()):
print(str(i+1)+'.',k,'with variables:')
for var, rng in v.items():
if 'min' in rng:
print(' -(',rng['min'],') <=',var,'<= (',rng['max'],')')
else:
print(var, '=', rng['position'])
# Both the model equations and the geometry include parameters, such as $\gamma_p$ or $L_p$. We can substitute these symbolic parameters in the model with values by using the [`pybamm.ParameterValues`](https://pybamm.readthedocs.io/en/latest/source/parameters/parameter_values.html) class, which takes either a python dictionary or CSV file with the mapping between parameter names and values. Rather than create our own instance of `pybamm.ParameterValues`, we will use the default parameter set included in the model
param = model.default_parameter_values
# We can then apply this parameter set to the model and geometry
param.process_model(model)
param.process_geometry(geometry)
# The next step is to mesh the input geometry. We can do this using the [`pybamm.Mesh`](https://pybamm.readthedocs.io/en/latest/source/meshes/meshes.html) class. This class takes in the geometry of the problem, and also two dictionaries containing the type of mesh to use within each domain of the geometry (i.e. within the positive or negative electrode domains), and the number of mesh points.
#
# The default mesh types and the default number of points to use in each variable for the SPM are:
for k, t in model.default_submesh_types.items():
print(k,'is of type',t.__repr__())
for var, npts in model.default_var_pts.items():
print(var,'has',npts,'mesh points')
# With these defaults, we can then create our mesh of the given geometry:
mesh = pybamm.Mesh(geometry, model.default_submesh_types, model.default_var_pts)
# The next step is to discretise the model equations using this mesh. We do this using the [`pybamm.Discretisation`](https://pybamm.readthedocs.io/en/latest/source/spatial_methods/discretisation.html) class, which takes both the mesh we have already created, and a dictionary of spatial methods to use for each geometry domain. For the case of the SPM, we use the following defaults for the spatial discretisation methods:
for k, method in model.default_spatial_methods.items():
print(k,'is discretised using',method.__class__.__name__,'method')
# We then create the `pybamm.Discretisation` object, and use this to discretise the model equations
disc = pybamm.Discretisation(mesh, model.default_spatial_methods)
disc.process_model(model);
# After this stage, all of the variables in `model` have been discretised into `pybamm.StateVector` objects, and spatial operators have been replaced by matrix-vector multiplications, ready to be evaluated within a time-stepping algorithm of a given solver. For example, the rhs expression for $\partial{c_n}/\partial{t}$ that we visualised above is now represented by:
model.concatenated_rhs.children[0].visualise(path+'spm2.png')
# 
#
# Now we are ready to run the time-stepping routine to solve the model. Once again we use the default ODE solver.
# Solve the model at the given time points (in seconds)
solver = model.default_solver
n = 250
t_eval = np.linspace(0, 3600, n)
print('Solving using',type(solver).__name__,'solver...')
solution = solver.solve(model, t_eval)
print('Finished.')
# Each model in pybamm has a list of relevant variables defined in the model, for use in visualising the model solution or for comparison with other models. The SPM defines the following variables:
print('SPM model variables:')
for v in model.variables.keys():
print('\t-',v)
# To help visualise the results, pybamm provides the `pybamm.ProcessedVariable` class, which takes the output of a solver and a variable, and allows the user to evaluate the value of that variable at any given time or $x$ value. These processed variables are automatically created by the solution dictionary.
voltage = solution['Terminal voltage [V]']
c_s_n_surf = solution['Negative particle surface concentration']
c_s_p_surf = solution['Positive particle surface concentration']
# One we have these variables in hand, we can begin generating plots using a library such as Matplotlib. Below we plot the terminal voltage and surface particle concentrations versus time
# +
t = solution["Time [s]"].entries
x = solution["x [m]"].entries[:, 0]
f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(13,4))
ax1.plot(t, voltage(t))
ax1.set_xlabel(r'$Time [s]$')
ax1.set_ylabel('Terminal voltage [V]')
ax2.plot(t, c_s_n_surf(t=t, x=x[0])) # can evaluate at arbitrary x (single representative particle)
ax2.set_xlabel(r'$Time [s]$')
ax2.set_ylabel('Negative particle surface concentration')
ax3.plot(t, c_s_p_surf(t=t, x=x[-1])) # can evaluate at arbitrary x (single representative particle)
ax3.set_xlabel(r'$Time [s]$')
ax3.set_ylabel('Positive particle surface concentration')
plt.tight_layout()
plt.show()
# -
# Some of the output variables are defined over space as well as time. Once option to visualise these variables is to use the `interact` slider widget. Below we plot the negative/positive particle concentration over $r$, using a slider to change the current time point
c_s_n = solution['Negative particle concentration']
c_s_p = solution['Positive particle concentration']
r_n = solution["r_n [m]"].entries[:, 0]
r_p = solution["r_p [m]"].entries[:, 0]
# +
c_s_n = solution['Negative particle concentration']
c_s_p = solution['Positive particle concentration']
r_n = solution["r_n [m]"].entries[:, 0, 0]
r_p = solution["r_p [m]"].entries[:, 0, 0]
def plot_concentrations(t):
f, (ax1, ax2) = plt.subplots(1, 2 ,figsize=(10,5))
plot_c_n, = ax1.plot(r_n, c_s_n(r=r_n,t=t,x=x[0])) # can evaluate at arbitrary x (single representative particle)
plot_c_p, = ax2.plot(r_p, c_s_p(r=r_p,t=t,x=x[-1])) # can evaluate at arbitrary x (single representative particle)
ax1.set_ylabel('Negative particle concentration')
ax2.set_ylabel('Positive particle concentration')
ax1.set_xlabel(r'$r_n$ [m]')
ax2.set_xlabel(r'$r_p$ [m]')
ax1.set_ylim(0, 1)
ax2.set_ylim(0, 1)
plt.show()
import ipywidgets as widgets
widgets.interact(plot_concentrations, t=widgets.FloatSlider(min=0,max=3600,step=10,value=0));
# -
# The QuickPlot class can be used to plot the common set of useful outputs which should give you a good initial overview of the model. The method `Quickplot.dynamic_plot` employs the slider widget.
quick_plot = pybamm.QuickPlot(solution)
quick_plot.dynamic_plot();
# ## Dimensionless Parameters
# In the table below, we provide the dimensionless parameters in the SPM in terms of the dimensional parameters in LCO.csv. We use a superscript * to indicate dimensional quantities.
#
# | Parameter | Expression |Interpretation |
# |:--------------------------|:----------------------------------------|:------------------------------------------|
# | $L_{\text{k}}$ | $L_{\text{k}}^*/L^*$ | Ratio of region thickness to cell thickness|
# |$\mathcal{C}_{\text{k}}$ | $\tau_{\text{k}}^*/\tau_{\text{d}}^*$ | Ratio of solid diffusion and discharge timescales |
# |$\mathcal{C}_{\text{r,k}}$ |$\tau_{\text{r,k}}^*/\tau_{\text{d}}^*$ |Ratio of reaction and discharge timescales|
# |$a_{R, \text{k}}$ |$a_{\text{k}}^* R_{\text{k}}^*$ | Product of particle radius and surface area to volume ratio|
# |$\gamma_{\text{k}}$ |$c_{\text{k,max}}^*/c_{\text{n,max}}^*$ |Ratio of maximum lithium concentrations in solid|
# ## References
#
# The relevant papers for this notebook are:
pybamm.print_citations()
|
examples/notebooks/models/SPM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/quickgrid/CodeLab/blob/master/code-lab/computer_vision/MediaPipe_Face_Mesh_TFLite_Direct_Inference_Intermediate_Layer_Output.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="AVxoAhueGtkZ"
# ### References,
#
# https://github.com/shortcipher3/stackoverflow/blob/master/mediapipe_iris_2d_landmarks.ipynb
#
# ### Model card,
#
# https://drive.google.com/file/d/1QvwWNfFoweGVjsXF3DXzcrCnz-mx-Lha/view
# + [markdown] id="_i4o8yjZGwXk"
# # Details,
#
# Input to model is 192x192, so image should be resized the same. Image should be a crop of a face with 25% more area all around.
# + colab={"base_uri": "https://localhost:8080/"} id="XUfMiNZ5GGEL" outputId="ebf76023-e1d1-4da8-d427-f9db6c5ae723"
# !wget "https://github.com/google/mediapipe/raw/master/mediapipe/modules/face_landmark/face_landmark.tflite"
# + id="HmHbk4MOG9hz"
import tensorflow as tf
import numpy as np
# + colab={"base_uri": "https://localhost:8080/"} id="Q-zDPTQFIXjm" outputId="20bc1fb3-be35-439e-ebbe-b78d00d08cc3"
print(tf.__version__)
# + colab={"base_uri": "https://localhost:8080/"} id="Qmy7x4xHHMxO" outputId="eb07c350-015b-44a3-efd0-302256de7187"
model_file = '/content/face_landmark.tflite'
interpreter = tf.lite.Interpreter(
model_path=model_file)
interpreter.allocate_tensors()
input_details = interpreter.get_input_details()
output_details = interpreter.get_output_details()
print(f'input_details {input_details}')
print(f'output_details {output_details}')
# check the type of the input tensor
floating_model = input_details[0]['dtype'] == np.float32
print(f'is floating model: {floating_model}')
# NxHxWxC, H:1, W:2
height = input_details[0]['shape'][1]
width = input_details[0]['shape'][2]
# + [markdown] id="cCpljK59qKXx"
# # Print intermediate layers
# + colab={"base_uri": "https://localhost:8080/"} id="AiZZ8NwXqIep" outputId="d5ec0c00-2161-40db-e553-bb6837581c8a"
intermediate_layers = interpreter.get_tensor_details()
selected_layer = 'conv2d_20'
selected_layer_dict = {}
for layer in intermediate_layers:
print(layer)
if layer['name'] == selected_layer:
selected_layer_dict = layer
# + colab={"base_uri": "https://localhost:8080/"} id="dOWB7J6_qkU5" outputId="cca5b1eb-2662-4842-f565-19eb4db86f61"
print(selected_layer_dict)
# + colab={"base_uri": "https://localhost:8080/"} id="H_nZDExKrTQY" outputId="1170568c-0abc-4bb9-ff28-229eae4d34ab"
print(selected_layer_dict['index'])
# + [markdown] id="saRJ7uhzsa0A"
# **Zero since image was not passed yet.**
# + colab={"base_uri": "https://localhost:8080/"} id="hwyPBYGprvUn" outputId="d55667b4-19c7-46c0-d998-b53353102314"
print(interpreter.get_tensor(selected_layer_dict['index'])[0])
# + [markdown] id="HDe9cQgkWoBY"
# ## Test on sample image
# + id="PXgEw9_vHoJg"
import cv2
import matplotlib.pyplot as plt
# + colab={"base_uri": "https://localhost:8080/"} id="wKtmS8vnVztZ" outputId="cd663b9e-749c-4e72-cd22-ff59a583c6d2"
# !wget "https://peoplepill.com/media/people/thumbs/G/geoffrey-hinton.jpg" -O "hinton.jpg"
# + id="FM0kdzX2U58X"
image = cv2.imread('hinton.jpg')
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="eqksLdFAQFfE" outputId="789699aa-40f6-402b-b0cb-2437230a7755"
plt.imshow(image[:,:,::-1])
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="rDQ2CMlXQJNs" outputId="f7b67b39-8c23-4f5f-b33f-15cbe330d63f"
image_cropped = image[:image.shape[0], :image.shape[0], ::-1] # crop to avoid letterboxing step
plt.imshow(image_cropped)
# + id="44acHnZ5QLqo"
img = cv2.resize(image_cropped, (192, 192))[np.newaxis, :, :, :]
img = (np.float32(img) - 0.0) / 255.0 # normalization (specified in tflite_converter_calculator, not in model card)
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="3N2Xg7H5UZcF" outputId="6216fbdc-e529-4e73-b37b-f1dc2040cfd8"
plt.imshow(img.squeeze())
# + id="mh9QGd4RQOGa"
interpreter.set_tensor(input_details[0]['index'], img)
interpreter.invoke()
output_face_landmarks = interpreter.get_tensor(output_details[0]['index'])[0]
output_face_flag = interpreter.get_tensor(output_details[1]['index'])[0] # Most likely this is the face flag as written in model card
# + [markdown] id="23u_AD0qsh6u"
# **This time there is output after passing the image.**
# + colab={"base_uri": "https://localhost:8080/"} id="rvv0gQ7csVu2" outputId="a8592d25-08b4-40de-f569-93740a1d3460"
print(interpreter.get_tensor(selected_layer_dict['index']).shape)
print(interpreter.get_tensor(selected_layer_dict['index']))
# + colab={"base_uri": "https://localhost:8080/"} id="kgpRMdG3RkW7" outputId="9f25eadd-c83f-4512-e7e2-172bc6ea975e"
print(output_face_flag)
# + colab={"base_uri": "https://localhost:8080/"} id="tCuqjG_rQwlS" outputId="472a88e6-3851-45a1-beee-9f405abfed4f"
print(output_face_landmarks.squeeze()[0:9])
print(output_face_landmarks.squeeze().shape)
output_face_landmarks = tf.reshape(tensor=output_face_landmarks, shape=(468,3))
print(output_face_landmarks)
#print(output_face_landmarks[:, 0:1])
face_landmark_x = output_face_landmarks[:, 0:1]
face_landmark_y = output_face_landmarks[:, 1:2]
#face_landmark_z = output_face_landmarks[:, 2:3]
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="uxDme-ehQXvF" outputId="dddd6360-205c-47f1-fd96-1bd690fb3b0e"
# cropped image
plt.imshow(image_cropped)
plt.plot(face_landmark_x/192.0*image_cropped.shape[0], (face_landmark_y/192.0)*image_cropped.shape[1], '*')
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="qwEysmFUQbKe" outputId="9758feac-1a9e-4249-a297-b701f21c25d5"
# original image
plt.imshow(image[:,:,::-1])
plt.plot(face_landmark_x/192.0*image_cropped.shape[0], (face_landmark_y/192.0)*image_cropped.shape[1], '*')
# + id="8vNeatULRWI-"
|
computer_vision/MediaPipe_Face_Mesh_TFLite_Direct_Inference_Intermediate_Layer_Output.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] nbsphinx="hidden"
# # Quantization of Signals
#
# *This jupyter notebook is part of a [collection of notebooks](../index.ipynb) on various topics of Digital Signal Processing. Please direct questions and suggestions to [<EMAIL>](mailto:<EMAIL>).*
# -
# ## Introduction
#
# [Digital signal processors](https://en.wikipedia.org/wiki/Digital_signal_processor) and general purpose processors can only perform arithmetic operations within a limited number range. So far we considered discrete signals with continuous amplitude values. These cannot be handled by processors in a straightforward manner. [Quantization](https://en.wikipedia.org/wiki/Quantization_%28signal_processing%29) is the process of mapping a continuous amplitude to a countable set of amplitude values. This refers also to the *requantization* of a signal from a large set of countable amplitude values to a smaller set. Scalar quantization is an instantaneous and memoryless operation. It can be applied to the continuous amplitude signal, also referred to as *analog signal* or to the (time-)discrete signal. The quantized discrete signal is termed as *digital signal*. The connections between the different domains are illustrated in the following.
#
# 
# ### Model of the Quantization Process
#
# In order to discuss the effects of quantizing a continuous amplitude signal, a mathematical model of the quantization process is required. We restrict our considerations to a discrete real-valued signal $x[k]$. The following mapping is used in order to quantize the continuous amplitude signal $x[k]$
#
# \begin{equation}
# x_Q[k] = g( \; \lfloor \, f(x[k]) \, \rfloor \; )
# \end{equation}
#
# where $g(\cdot)$ and $f(\cdot)$ denote real-valued mapping functions, and $\lfloor \cdot \rfloor$ a rounding operation. The quantization process can be split into two stages
#
# 1. **Forward quantization**
# The mapping $f(x[k])$ maps the signal $x[k]$ such that it is suitable for the rounding operation. This may be a scaling of the signal or a non-linear mapping. The result of the rounding operation is an integer number $\lfloor \, f(x[k]) \, \rfloor \in \mathbb{Z}$, which is termed as *quantization index*.
#
# 2. **Inverse quantization**
# The mapping $g(\cdot)$, maps the quantization index to the quantized value $x_Q[k]$ such that it constitutes an approximation of $x[k]$. This may be a simple scaling or non-linear operation.
#
# The quantization error (quantization noise) $e[k]$ is defined as
#
# \begin{equation}
# e[k] = x_Q[k] - x[k]
# \end{equation}
#
# Rearranging yields that the quantization process can be modeled by adding the quantization error to the discrete signal
#
# 
# #### Example - Quantization of a sine signal
#
# In order to illustrate the introduced model, the quantization of one period of a sine signal is considered
#
# \begin{equation}
# x[k] = \sin[\Omega_0 k]
# \end{equation}
#
# using
#
# \begin{align}
# f(x[k]) &= 3 \cdot x[k] \\
# i &= \lfloor \, f(x[k]) \, \rfloor \\
# g(i) &= \frac{1}{3} \cdot i
# \end{align}
#
# where $\lfloor \cdot \rfloor$ denotes the [nearest integer function](https://en.wikipedia.org/wiki/Nearest_integer_function) and $i$ the quantization index. The quantized signal is then given as
#
# \begin{equation}
# x_Q[k] = \frac{1}{3} \cdot \lfloor \, 3 \cdot \sin[\Omega_0 k] \, \rfloor
# \end{equation}
#
# The discrete signals are not shown by stem plots for ease of illustration.
# +
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
N = 1024 # length of signal
# generate signal
x = np.sin(2*np.pi/N * np.arange(N))
# quantize signal
xi = np.round(3 * x)
xQ = 1/3 * xi
e = xQ - x
# plot (quantized) signals
fig, ax1 = plt.subplots(figsize=(10,4))
ax2 = ax1.twinx()
ax1.plot(x, 'r', label=r'signal $x[k]$')
ax1.plot(xQ, 'b', label=r'quantized signal $x_Q[k]$')
ax1.plot(e, 'g', label=r'quantization error $e[k]$')
ax1.set_xlabel('k')
ax1.set_ylabel(r'$x[k]$, $x_Q[k]$, $e[k]$')
ax1.axis([0, N, -1.2, 1.2])
ax1.legend()
ax2.set_ylim([-3.6, 3.6])
ax2.set_ylabel('quantization index')
ax2.grid()
# -
# **Exercise**
#
# * Investigate the quantization error $e[k]$. Is its amplitude bounded?
# * If you would represent the quantization index (shown on the right side) by a binary number, how much bits would you need?
# * Try out other rounding operations like `np.floor()` and `np.ceil()` instead of `np.round()`. What changes?
#
# Solution: It can be concluded from the illustration that the quantization error is bounded as $|e[k]| < \frac{1}{3}$. There are in total 7 quantization indexes needing 3 bits in a binary representation. The properties of the quantization error are different for different rounding operations.
# ### Properties
#
# Without knowledge of the quantization error $e[k]$, the signal $x[k]$ cannot be reconstructed exactly from its quantization index or quantized representation $x_Q[k]$. The quantization error $e[k]$ itself depends on the signal $x[k]$. Therefore, quantization is in general an irreversible process. The mapping from $x[k]$ to $x_Q[k]$ is furthermore non-linear, since the superposition principle does not hold in general. Summarizing, quantization is an inherently irreversible and non-linear process. It potentially removes information from the signal.
# ### Applications
#
# Quantization has widespread applications in Digital Signal Processing. For instance
#
# * [Analog-to-Digital conversion](https://en.wikipedia.org/wiki/Analog-to-digital_converter)
# * [Lossy compression](https://en.wikipedia.org/wiki/Lossy_compression) of signals (speech, music, video, ...)
# * Storage and transmission ([Pulse-Code Modulation](https://en.wikipedia.org/wiki/Pulse-code_modulation), ...)
# + [markdown] nbsphinx="hidden"
# **Copyright**
#
# This notebook is provided as [Open Educational Resource](https://en.wikipedia.org/wiki/Open_educational_resources). Feel free to use the notebook for your own purposes. The text is licensed under [Creative Commons Attribution 4.0](https://creativecommons.org/licenses/by/4.0/), the code of the IPython examples under the [MIT license](https://opensource.org/licenses/MIT). Please attribute the work as follows: *<NAME>, Digital Signal Processing - Lecture notes featuring computational examples, 2016-2018*.
|
quantization/introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial for loading Final Testing competition data
#
# To start with this competition, you will need to download the data for the two tasks, sleep cassette and motor imagery (MI). You could either handle them yourself, downloading them from here:
# - Sleep final test data :
# https://figshare.com/articles/dataset/finalSleep/16586225
#
# There are 5 example subjects with labels of this age group in ‘sleep_target’ folder for convenience of transfer learning.
#
# - MI final test data :
# https://figshare.com/articles/dataset/finalMI/16586213
#
# There are some example trials with labels in ‘training’ folder of each subject for convenience of transfer learning.
#
#
# APIs for auto downloading the final testing data will be also available in the next update of [package](https://github.com/sylvchev/beetl-competition), currently you could directly use upper links for downloading.
#
# You are allowed to use the Sleep/MI data in the leaderboard phase in this final testing phase, while we will not provide true labels of data in leaderboard phase.
#
# We will test run code from top ranking teams in the final stage of the competition. Please fix your random seed or so to make sure the experiemnts are reproducible.
#
# ## Sleep stage task
#
#
# **Data information**
#
# | Type | Value |
# | :- | :-: |
# | Sampling rate | 100 Hz |
# | Trial window | 30s |
# | Nb of channels | 2 bipolar (Fpz-Cz, Pz-Oz) |
# | Highpass filter | 0.5 Hz |
# | Lowpass filter | 100.Hz |
#
# The sleep stage labels to predict are:
#
# | Sleep stage | label |
# | :- | :-: |
# | W | 0 |
# | stage 1 | 1 |
# | stage 2| 2 |
# | stage 3 | 3 |
# | stage 4 | 4 |
# | REM | 5 |
#
#
# ## Motor imagery task
#
# The source datasets are available on the url indicated above or from MOABB, as `BNCI2014001`, `Cho2017` and `PhysionetMI` datasets.
#
# **Data information for dataset A (subject 1 , 2 & 3)**
#
# | Type | Value |
# | :- | :-: |
# | Sampling rate | 500 Hz |
# | Trial window | 4s |
# | Nb of channels | 63 EEG |
# | Highpass filter | 1 Hz |
# | Lowpass filter | 100.Hz |
# | Notch filter | 50 Hz |
#
# The name of the channels are:
# 'Fp1', 'Fz', 'F3', 'F7', 'FT9', 'FC5', 'FC1', 'C3', 'T7',
# 'TP9', 'CP5', 'CP1', 'Pz', 'P3', 'P7', 'O1', 'Oz',
# 'O2', 'P4', 'P8', 'TP10', 'CP6', 'CP2', 'C4', 'T8',
# 'FT10', 'FC6', 'FC2', 'F4', 'F8', 'Fp2', 'AF7', 'AF3',
# 'AFz', 'F1', 'F5', 'FT7', 'FC3', 'FCz', 'C1', 'C5',
# 'TP7', 'CP3', 'P1', 'P5', 'PO7', 'PO3', 'POz', 'PO4',
# 'PO8', 'P6', 'P2', 'CPz', 'CP4', 'TP8', 'C6', 'C2',
# 'FC4', 'FT8', 'F6', 'F2', 'AF4', 'AF8'.
#
# **Data information for dataset B (subject 4, 5)**
#
# | Type | Value |
# | :- | :-: |
# | Sampling rate | 200 Hz |
# | Trial window | 4s |
# | Nb of channels | 32 EEG |
# | Highpass filter | 1 Hz |
# | Lowpass filter | 100.Hz |
#
# The name of the channels are:
# 'Fp1', 'Fp2', 'F3', 'Fz', 'F4', 'FC5', 'FC1', 'FC2','FC6', 'C5', 'C3',
# 'C1', 'Cz', 'C2', 'C4', 'C6', 'CP5', 'CP3', 'CP1',
# 'CPz', 'CP2', 'CP4', 'CP6', 'P7', 'P5', 'P3', 'P1', 'Pz',
# 'P2', 'P4', 'P6', 'P8'
#
# In both datasets, the motor imagery labels to predict are:
#
# | MI task | label |
# | :- | :-: |
# | Lefthand | 0 |
# | Righthand | 1 |
# | Feet | 2 |
# | Rest | 3 |
#
# **However, in task 2, there will be only three catergorties to predict as output labels - Lefthand (0), Righthand (1) and other (2)**
# # Loading data manually
#
# When you have downloaded the competition data, you could load your data as shown below. You just need to specify the path where you store the data
#
# ## Sleep task
import numpy as np
import pickle
# +
savebase = 'D:\\beetl_testingData\\finalSleep\\testing\\'
X_sleep_test = []
#starts from s5 in final set
for subj in range(5, 14):
for session in range(1, 3):
# "testing_s{}r{}X.npy", replacing "leaderboard_s{}r{}X.npy" before
with open(savebase + "testing_s{}r{}X.npy".format(subj, session), 'rb') as f:
X_sleep_test.append(pickle.load(f))
X_sleep_test = np.concatenate(X_sleep_test)
print ("There are {} trials with {} electrodes and {} time samples".format(*X_sleep_test.shape))
# -
# ## Motor imagery dataset A (S1, S2, S3)
# +
import os.path as osp
path = 'D:\\beetl_testingData\\finalMI\\'
#3 subjects in data set A in final set
X_MIA_test = []
for subj in range(1, 4):
savebase = osp.join(path, "S{}".format(subj), "testing")
for i in range(6, 16):
with open(osp.join(savebase, "race{}_padsData.npy".format(i)), 'rb') as f:
X_MIA_test.append(pickle.load(f))
X_MIA_test = np.concatenate(X_MIA_test)
print ("There are {} trials with {} electrodes and {} time samples".format(*X_MIA_test.shape))
# -
# ## Motor imagery dataset B (S4, S5)
# +
path = 'D:\\beetl_testingData\\finalMI\\'
# path = '/Users/sylchev/mne_data/MNE-beetlmileaderboard-data/'
# path = '/home/sylchev/mne_data/MNE-beetlmileaderboard-data/'
# 2 subjects from data set B in final set
X_MIB_test = []
for subj in range(4, 6):
savebase = osp.join(path, "S{}".format(subj), "testing")
with open(osp.join(savebase, "testing_s{}X.npy".format(subj)), 'rb') as f:
X_MIB_test.append(pickle.load(f))
X_MIB_test = np.concatenate(X_MIB_test)
print ("There are {} trials with {} electrodes and {} time samples".format(*X_MIB_test.shape))
# -
|
start_kits/5.FinalTestingDataGuide.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Creating a polygon from a list of points
#
# For many of those working with geo data it is a common task being asked to create a polygon from a list of points. More specific, to create a polygon that wraps around those points in a meaningful manner. So, there are several sources in the web explaining how to create the shape (see sources at end of document). This example notebook is the application of those solutions to folium maps.
# ## Helpers
# +
# Imports
import random
import folium
from scipy.spatial import ConvexHull
# Function to create a list of some random points
def randome_points(amount, LON_min, LON_max, LAT_min, LAT_max):
points = []
for _ in range(amount):
points.append(
(random.uniform(LON_min, LON_max), random.uniform(LAT_min, LAT_max))
)
return points
# Function to draw points in the map
def draw_points(map_object, list_of_points, layer_name, line_color, fill_color, text):
fg = folium.FeatureGroup(name=layer_name)
for point in list_of_points:
fg.add_child(
folium.CircleMarker(
point,
radius=1,
color=line_color,
fill_color=fill_color,
popup=(folium.Popup(text)),
)
)
map_object.add_child(fg)
# -
# ## Convex hull
#
# The convex hull is probably the most common approach - its goal is to create the smallest polygon that contains all points from a given list. The scipy.spatial package provides this algorithm (https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.spatial.ConvexHull.html, accessed 29.12.2018).
# +
# Function that takes a map and a list of points (LON,LAT tupels) and
# returns a map with the convex hull polygon from the points as a new layer
def create_convexhull_polygon(
map_object, list_of_points, layer_name, line_color, fill_color, weight, text
):
# Since it is pointless to draw a convex hull polygon around less than 3 points check len of input
if len(list_of_points) < 3:
return
# Create the convex hull using scipy.spatial
form = [list_of_points[i] for i in ConvexHull(list_of_points).vertices]
# Create feature group, add the polygon and add the feature group to the map
fg = folium.FeatureGroup(name=layer_name)
fg.add_child(
folium.vector_layers.Polygon(
locations=form,
color=line_color,
fill_color=fill_color,
weight=weight,
popup=(folium.Popup(text)),
)
)
map_object.add_child(fg)
return map_object
# +
# Initialize map
my_convexhull_map = folium.Map(location=[48.5, 9.5], zoom_start=8)
# Create a convex hull polygon that contains some points
list_of_points = randome_points(
amount=10, LON_min=48, LON_max=49, LAT_min=9, LAT_max=10
)
create_convexhull_polygon(
my_convexhull_map,
list_of_points,
layer_name="Example convex hull",
line_color="lightblue",
fill_color="lightskyblue",
weight=5,
text="Example convex hull",
)
draw_points(
my_convexhull_map,
list_of_points,
layer_name="Example points for convex hull",
line_color="royalblue",
fill_color="royalblue",
text="Example point for convex hull",
)
# Add layer control and show map
folium.LayerControl(collapsed=False).add_to(my_convexhull_map)
my_convexhull_map
# -
# ## Envelope
#
# The envelope is another interesting approach - its goal is to create a box that contains all points from a given list.
def create_envelope_polygon(
map_object, list_of_points, layer_name, line_color, fill_color, weight, text
):
# Since it is pointless to draw a box around less than 2 points check len of input
if len(list_of_points) < 2:
return
# Find the edges of box
from operator import itemgetter
list_of_points = sorted(list_of_points, key=itemgetter(0))
x_min = list_of_points[0]
x_max = list_of_points[len(list_of_points) - 1]
list_of_points = sorted(list_of_points, key=itemgetter(1))
y_min = list_of_points[0]
y_max = list_of_points[len(list_of_points) - 1]
upper_left = (x_min[0], y_max[1])
upper_right = (x_max[0], y_max[1])
lower_right = (x_max[0], y_min[1])
lower_left = (x_min[0], y_min[1])
edges = [upper_left, upper_right, lower_right, lower_left]
# Create feature group, add the polygon and add the feature group to the map
fg = folium.FeatureGroup(name=layer_name)
fg.add_child(
folium.vector_layers.Polygon(
locations=edges,
color=line_color,
fill_color=fill_color,
weight=weight,
popup=(folium.Popup(text)),
)
)
map_object.add_child(fg)
return map_object
# +
# Initialize map
my_envelope_map = folium.Map(location=[49.5, 8.5], zoom_start=8)
# Create an envelope polygon that contains some points
list_of_points = randome_points(
amount=10, LON_min=49.1, LON_max=50, LAT_min=8, LAT_max=9
)
create_envelope_polygon(
my_envelope_map,
list_of_points,
layer_name="Example envelope",
line_color="indianred",
fill_color="red",
weight=5,
text="Example envelope",
)
draw_points(
my_envelope_map,
list_of_points,
layer_name="Example points for envelope",
line_color="darkred",
fill_color="darkred",
text="Example point for envelope",
)
# Add layer control and show map
folium.LayerControl(collapsed=False).add_to(my_envelope_map)
my_envelope_map
# -
# ## Concave hull (alpha shape)
# In some cases the convex hull does not yield good results - this is when the shape of the polygon should be concave instead of convex. The solution is a concave hull that is also called alpha shape. Yet, there is no ready to go, off the shelve solution for this but there are great resources (see: http://blog.thehumangeo.com/2014/05/12/drawing-boundaries-in-python/, accessed 04.01.2019 or https://towardsdatascience.com/the-concave-hull-c649795c0f0f, accessed 29.12.2018).
# ## Main code
# Just putting it all together...
# +
# Initialize map
my_map_global = folium.Map(location=[48.2460683, 9.26764125], zoom_start=7)
# Create a convex hull polygon that contains some points
list_of_points = randome_points(
amount=10, LON_min=48, LON_max=49, LAT_min=9, LAT_max=10
)
create_convexhull_polygon(
my_map_global,
list_of_points,
layer_name="Example convex hull",
line_color="lightblue",
fill_color="lightskyblue",
weight=5,
text="Example convex hull",
)
draw_points(
my_map_global,
list_of_points,
layer_name="Example points for convex hull",
line_color="royalblue",
fill_color="royalblue",
text="Example point for convex hull",
)
# Create an envelope polygon that contains some points
list_of_points = randome_points(
amount=10, LON_min=49.1, LON_max=50, LAT_min=8, LAT_max=9
)
create_envelope_polygon(
my_map_global,
list_of_points,
layer_name="Example envelope",
line_color="indianred",
fill_color="red",
weight=5,
text="Example envelope",
)
draw_points(
my_map_global,
list_of_points,
layer_name="Example points for envelope",
line_color="darkred",
fill_color="darkred",
text="Example point for envelope",
)
# Add layer control and show map
folium.LayerControl(collapsed=False).add_to(my_map_global)
my_map_global
# -
# ## Sources:
#
# * http://blog.yhat.com/posts/interactive-geospatial-analysis.html, accessed 28.12.2018
#
# * https://docs.scipy.org/doc/scipy-0.19.0/reference/generated/scipy.spatial.ConvexHull.html, accessed 29.12.2018
#
# * https://www.oreilly.com/ideas/an-elegant-solution-to-the-convex-hull-problem, accessed 29.12.2018
#
# * https://medium.com/@vworri/simple-geospacial-mapping-with-geopandas-and-the-usual-suspects-77f46d40e807, accessed 29.12.2018
#
# * https://towardsdatascience.com/the-concave-hull-c649795c0f0f, accessed 29.12.2018
#
# * http://blog.thehumangeo.com/2014/05/12/drawing-boundaries-in-python/, accessed 04.01.2019
#
|
examples/Polygons_from_list_of_points.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Copyright (c) 2017-2019 [Serpent-Tools developer team](https://github.com/CORE-GATECH-GROUP/serpent-tools/graphs/contributors), GTRC
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
# Data files are not included with the python package, but can be downloaded from the [GitHub repository](https://github.com/CORE-GATECH-GROUP/serpent-tools). For this tutorial, the files are placed in the directory identified with the ``SERPENT_TOOLS_DATA`` environment variable.
import os
branchFile = os.path.join(
os.environ["SERPENT_TOOLS_DATA"],
"demo.coe",
)
# # Branching Reader
# ## Basic Operation
# This notebook demonstrates the capability of the [`serpentTools`](https://github.com/CORE-GATECH-GROUP/serpent-tools) package to read branching coefficient files. The format of these files is structured to iterate over:
#
# 1. Branch states, e.g. burnup, material properties
# 1. Homogenized universes
# 1. Group constant data
#
# The output files are described in more detail on the [SERPENT Wiki](http://serpent.vtt.fi/mediawiki/index.php/Automated_burnup_sequence#Output_format)
# **Note**
#
# Without modifying the settings, the [`BranchingReader`](http://serpent-tools.readthedocs.io/en/latest/api/branching.html#serpentTools.parsers.branching.BranchingReader) assumes that all group constant data is presented without the associated uncertainties. See below for examples on the various ways to adjust the UserSettings
# %matplotlib inline
import serpentTools
r0 = serpentTools.read(branchFile)
# The branches are stored in custom dictionary-like [`BranchContainer`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.BranchContainer) objects in the `branches` dictionary
r0.branches.keys()
# Here, the keys are tuples of strings indicating what perturbations/branch states were applied for each `SERPENT` solution. Examining a particular case
b0 = r0.branches['B1000', 'FT600']
print(b0)
# `SERPENT` allows the user to define variables for each branch through:
#
# `
# var V1_name V1_value
# `
#
# cards. These are stored in the `stateData` attribute
b0.stateData
# The keys `'DATE'`, `'TIME'`, and `'VERSION'` are included by default in the output, while the `'BOR'` and `'TFU'` have been defined for this branch.
# ### Group Constant Data
# **Note**: Group constants are converted from `SERPENT_STYLE` to `mixedCase` to fit the overall style of the project.
# The [`BranchContainer`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.BranchContainer) stores group constant data in [`HomogUniv`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv) objects as a dictionary.
for key in b0:
print(key)
# The keys here are `UnivTuple` instances indicating the universe ID and point in burnup schedule.
# These universes can be obtained by indexing into the `BranchContainer`, or by using the [`getUniv`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.BranchContainer.getUniv) method.
univ0 = b0['0', 1, 1, None]
univ0
univ0.name, univ0.bu, univ0.step, univ0.day
univ1 = b0.getUniv('0', burnup=1)
univ2 = b0.getUniv('0', index=1)
assert univ0 is univ1 is univ2
# Group constant data is spread out across sub-dictionaries:
#
# 1. [`infExp`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.infExp): Expected values for infinite medium group constants
# 1. [`infUnc`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.infUnc): Relative uncertainties for infinite medium group constants
# 1. [`b1Exp`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.b1Exp): Expected values for leakge-corrected group constants
# 1. [`b1Unc`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.b1Unc): Relative uncertainties for leakge-corrected group constants
# 1. [`gc`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.gc): Group constant data that does not match the `INF` nor `B1` scheme
# 1. [`gcUnc`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.gcUnc): Relative uncertainties for data in [`gc`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.gc)
# For this problem, only expected values for infinite and critical spectrum (B1) group constants are returned, so only the `infExp` and `b1Exp` dictionaries contain data
univ0.infExp
univ0.infUnc
univ0.b1Exp
univ0.gc
univ0.gcUnc
# Group constants and their associated uncertainties can be obtained using the [`get`](http://serpent-tools.readthedocs.io/en/latest/api/containers.html#serpentTools.objects.containers.HomogUniv.get) method.
univ0.get('infFiss')
try:
univ0.get('infS0', uncertainty=True)
except KeyError as ke: # no uncertainties here
print(str(ke))
# ## Plotting Universe Data
#
# `HomogUniv` objects are capable of plotting homogenized data using the `plot` method. This method is tuned to plot group constants, such as cross sections, for a known group structure. This is reflected in the default axis scaling, but can be adjusted on a per case basis. If the group structure is not known, then the data is plotted simply against bin-index.
univ0.plot('infFiss')
univ0.plot(['infFiss', 'b1Tot'], loglog=False);
# The [`ResultsReader` example](http://serpent-tools.readthedocs.io/en/latest/examples/ResultsReader.html#plotting-universes) has a more thorough example of this `plot` method, including formatting the line labels.
# ## Iteration
# The branching reader has a `iterBranches` method that works to yield branch names and their associated `BranchContainer` objects. This can be used to efficiently iterate over all the branches presented in the file.
for names, branch in r0.iterBranches():
print(names, branch)
# ## User Control
# The `SERPENT` [`set coefpara`](http://serpent.vtt.fi/mediawiki/index.php/Input_syntax_manual#set_coefpara) card already restricts the data present in the coeffient file to user control, and the `BranchingReader` includes similar control.
# Below are the various settings that the `BranchingReader` uses to read and process coefficient files.
# * [`branching.floatVariables`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#branching-floatvariables)
# * [`branching.intVariables`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#branching-intvariables)
# * [`xs.getB1XS`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-getb1xs)
# * [`xs.getInfXS`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-getinfxs)
# * [`xs.reshapeScatter`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-reshapescatter)
# * [`xs.variableExtras`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-variableextras)
# * [`xs.variableGroups`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-variablegroups)
# In our example above, the `BOR` and `TFU` variables represented boron concentration and fuel temperature, and can easily be cast into numeric values using the [`branching.floatVariables`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#branching-floatvariables) and [`branching.intVariables`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#branching-intvariables) settings. From the previous example, we see that the default action is to store all state data variables as strings.
assert isinstance(b0.stateData['BOR'], str)
# As demonstrated in the [Settings example](https://github.com/CORE-GATECH-GROUP/serpent-tools/blob/master/examples/Settings.ipynb), use of [`xs.variableExtras`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-variableextras) [`xs.variableGroups`](http://serpent-tools.readthedocs.io/en/latest/settingsTop.html#xs-variablegroups)controls what data is stored on the `HomogUniv` objects. By default, all variables present in the coefficient file are stored.
from serpentTools.settings import rc
rc['branching.floatVariables'] = ['BOR']
rc['branching.intVariables'] = ['TFU']
rc['xs.getB1XS'] = False
rc['xs.variableExtras'] = ['INF_TOT', 'INF_SCATT0']
r1 = serpentTools.read(branchFile)
b1 = r1.branches['B1000', 'FT600']
b1.stateData
assert isinstance(b1.stateData['BOR'], float)
assert isinstance(b1.stateData['TFU'], int)
# Inspecting the data stored on the homogenized universes reveals only the variables explicitly requested are present
univ4 = b1.getUniv('0', 0)
univ4.infExp
univ4.b1Exp
# ## Conclusion
# The `BranchingReader` is capable of reading coefficient files created by the `SERPENT` automated branching process. The data is stored according to the branch parameters, universe information, and burnup. This reader also supports user control of the processing by selecting what state parameters should be converted from strings to numeric types, and further down-selection of data.
|
examples/Branching.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercise Set 2 - Content
# #### 1. Run the following code to download the dataset:
#
# - French Colleges: https://opendata.arcgis.com/datasets/e51c463be0234a86afa5d243e085cc03_12.zip
# - Traffic Accidents: https://opendata.arcgis.com/datasets/da2cb32e8c0a4007aca8b3c339408665_0.gdb
#
import requests, os
urls = [(r'./data/frenchshapefile.zip', 'https://opendata.arcgis.com/datasets/e51c463be0234a86afa5d243e085cc03_12.zip'),
(r'./data/fgdb.zip', 'https://opendata.arcgis.com/datasets/da2cb32e8c0a4007aca8b3c339408665_0.gdb')]
for fname, url in urls:
resp = requests.get(url, allow_redirects=True)
if os.path.isfile(fname):
os.remove(fname)
with open(fname, 'wb') as writer:
writer.write(resp.content)
shapefile_data = urls[0][0]
fgdb_data = urls[1][0]
# #### 2. Publish each dataset to your organization.
#
# - For the accidents item, set the thumbnail to `./data/car_accidents.png`
# insert add and publish code here for the two files
from arcgis.gis import GIS
gis = GIS(profile='your_online_profile')
for f in ['frenchshapefile.zip', 'fgdb.zip']:
items = gis.content.search(f)
print(items)
if len(items) > 0:
print(items[0].delete())
college__item = (gis
.content
.add({'title' : "French_Colleges",
'type' : 'Shapefile',
'tags' : "College, University"},
data=shapefile_data))
college__item__published = college__item.publish(publish_parameters={'name' : "FrenchColleges"})
college__item__published
traffic_published_item = (gis
.content
.add({'title' : "Traffic_Incidents",
'type' : 'File Geodatabase',
'tags' : "Traffic, Crash"},
data=fgdb_data,
thumbnail="./data/car_accidents.png")
.publish()
)
traffic_published_item
# #### 3. Create a Group and share the items with that group
#
# - Call the Group: `EuropeanDevTutorial`
# - Add 10 members to the group
# - share the published item from question `2` to the group
#
#
try:
gis.groups.search("EuropeanDevTutorial")[0].delete()
except: pass
# insert code here
grp = gis.groups.create(title='EuropeanDevTutorial',
tags='erase, me',
description="European DevSummit Demo Group",)
grp
traffic_published_item.share(groups=[grp])
college__item__published.share(groups=[grp])
grp.add_users(gis.content.search("*")[:10])
# #### 4. Create a Web Map and add the two layers to the map.
#
# - Set the extent to: `-30498.37428577314,5490739.271321731,2376350.772357217,6469133.233371727`
# - Ensure the extent is 3857
# - use a dictionary data structure to do this
#
# - Once added, turn on the legend.
#
# - Change the `basemap` to light gray
#
#
#
#
# +
from arcgis.gis import GIS
gis = GIS()
m = gis.map()
# m.add_layer?
# -
m.extent = {'spatialReference': {'latestWkid': 3857, 'wkid': 102100},
'xmin': -30498.37428577314,
'ymin': 5490739.271321731,
'xmax': 2376350.772357217,
'ymax': 6469133.233371727}
m.legend = True
m.basemap = 'gray'
m
m.add_layer(traffic_published_item)
# #### 5. How can we update the symbology on the layer?
# type answer here (this is a discussion question)
|
02. Managing Your Content/student_exercise/exercise_questions-answers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from statsmodels.tsa.vector_ar.var_model import VAR
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# set datetime index
resampled_data = pd.read_csv("Sprint_Resampled Data.csv")
resampled_data['Date'] = resampled_data['Date'].apply(pd.to_datetime)
resampled_data = resampled_data.set_index('Date')
# +
# handling missing value
test = resampled_data['1991-3': '2019-5'].dropna(axis=1)
train = test[:int(0.95*(len(test)))]
valid = test[int(0.95*(len(test))):]
# resampled_data
# model = VAR(endog=train)
# model_fit = model.fit()
# prediction = model_fit.forecast(model_fit.y, steps=len(valid))
# +
model = VAR(endog=test)
model_fit = model.fit()
true = model_fit.forecast(model_fit.y, steps=(len(valid)+3))
prediction = true
# -
len(valid)
# remove seasonality
test['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'].diff(12).plot()
test['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'].plot()
# +
pred = pd.DataFrame(index=range(0,len(prediction)),columns=[test.columns])
pred = pred.set_index(pd.date_range("2019-5","2021-1",freq = "M"))
for j in range(0,18):
for i in range(0, len(prediction)):
pred.iloc[i][j] = prediction[i][j]
# for i in test.columns:
# print('rmse value for', i, 'is : ', np.sqrt(mean_squared_error(pred[i], valid[i])))
# -
fig, ax = plt.subplots(figsize=(5, 3))
l1 = plt.plot(pred['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'])
l2 = plt.plot(valid['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'])
temp = pred["Cushing, OK WTI Spot Price FOB (Dollars per Barrel)"]["2020"]
temp
np.mean(temp)
# + active=""
#
# +
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(pred['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'], color = "red",label="Prediction")
ax.plot(valid['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'], color = "blue",label="Actual")
plt.legend()
plt.grid()
plt.tight_layout()
# +
# feature selection
from sklearn.ensemble import ExtraTreesClassifier
import matplotlib.pyplot as plt
import seaborn as sns
model = ExtraTreesClassifier()
X = test.iloc[:,1:28]
y = test.iloc[:,0]
corrmat = test.corr()
top_corr_features = corrmat.index
plt.figure(figsize=(20,20))
#plot heat map
g=sns.heatmap(test[top_corr_features].corr(),annot=True,cmap="RdYlGn")
# -
test.shape
# +
# choosing parameters based on their corr
matrix = test[top_corr_features].corr()
threshold = 0.7
chosen = matrix["Cushing, OK WTI Spot Price FOB (Dollars per Barrel)"][np.absolute(matrix["Cushing, OK WTI Spot Price FOB (Dollars per Barrel)"])> threshold]
chosenCol = chosen.index
chosen
# +
test = test[chosenCol]
test = resampled_data['1991-3': '2019-5'].dropna(axis=1)
train = test[:int(0.95*(len(test)))]
valid = test[int(0.95*(len(test))):]
model = VAR(endog=train)
model_fit = model.fit()
prediction = model_fit.forecast(model_fit.y, steps=len(valid))
# -
valid.index
# +
pred = pd.DataFrame(index=range(0,len(prediction)),columns=[test.columns])
pred = pred.set_index(valid.index)
for j in range(0,29):
for i in range(0, len(prediction)):
pred.iloc[i][j] = prediction[i][j]
# -
pred
# +
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.plot(pred['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'], color = "red",label="Prediction")
ax.plot(valid['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)'],color = "blue", label="Actual")
plt.legend()
plt.grid()
plt.tight_layout()
# +
a = pred['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)']
b = valid['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)']
df = pd.concat([a,b], axis=1, ignore_index=True)
df.reset_index(inplace=True)
df.drop("Date",axis = 1, inplace = True)
df.corr()
corrmat = df.corr()
top_corr_features = corrmat.index
plt.figure(figsize=(20,20))
#plot heat map
g=sns.heatmap(df[top_corr_features].corr(),annot=True,cmap="RdYlGn")
# +
# # detrend and remove seasonality
# from sta,tsmodels.tsa.seasonal import seasonal_decompose
# series = test['Cushing, OK WTI Spot Price FOB (Dollars per Barrel)']
# result = seasonal_decompose(series, model='additive')
# result.plot()
# plt.show()
# +
# from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# fig, ax = plt.subplots(2, figsize=(12,6))
# ax[0] = plot_acf(result.Residual, ax=ax[0], lags=20)
# ax[1] = plot_pacf(series, ax=ax[1], lags=20)
# +
# for col in chosenCol:
# result = seasonal_decompose(test[col],model = 'additive')
# result.plot()
# -
# +
# # VARMAX example
# from statsmodels.tsa.statespace.varmax import VARMAX
# from random import random
# # contrived dataset with dependency
# vary = train.iloc[:,0]
# varx = train.iloc[:,1:]
# # fit model
# model = VARMAX(endog=vary, order=(1, 0))
# model_fit = model.fit(disp=False)
# # make prediction
# data_exog2 = [[100]]
# yhat = model_fit.forecast(ex='Cushing, OK WTI Spot Price FOB (Dollars per Barrel)')
# print(yhat)
# +
# # HWES example
# from statsmodels.tsa.holtwinters import ExponentialSmoothing
# # contrived dataset
# # fit model
# # model = ExponentialSmoothing(test)
# model_fit = model.fit()
# # make prediction
# yhat = model_fit.predict(len(valid), len(valid))
# print(yhat)
# +
# from sklearn.feature_selection import SelectKBest
# from sklearn.feature_selection import chi2
# X = test.iloc[:,1:10]
# y = test.iloc[:,0]
# #apply SelectKBest class to extract top 10 best features
# bestfeatures = SelectKBest(score_func=chi2, k=4)
# fit = bestfeatures.fit(X,y)
# dfscores = pd.DataFrame(fit.scores_)
# dfcolumns = pd.DataFrame(X.columns)
# #concat two dataframes for better visualization
# featureScores = pd.concat([dfcolumns,dfscores],axis=1)
# featureScores.columns = ['Specs','Score'] #naming the dataframe columns
# print(featureScores.nlargest(10,'Score')) #print 10 best features
# +
# from sklearn.ensemble import RandomForestClassifier
# X = test.iloc[:,1:28]
# y = test.iloc[:,0]
# clf = RandomForestClassifier()
# clf.fit(X, y)
# importance = pd.Series(clf.feature_importances_)
# importance.sort_values(ascending=False)
# print(importance)
# -
|
VAR model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Predicting NBA players positions using Keras #
# In this notebook we will build a neural net to predict the positions of NBA players using the [Keras](https://keras.io) library.
# %load_ext autoreload
# %autoreload 2
# +
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelBinarizer, StandardScaler
from keras.models import Sequential
from keras.layers import Dense, Activation, Dropout
# -
# ## Data preparation ##
#
# We will use the Kaggle dataset ["NBA Players stats since 1950"](https://www.kaggle.com/drgilermo/nba-players-stats), with stats for all players since 1950. We will take special interest in how the pass of time affects to the position of each player, and the definition of the positions themselves (a Small Forward, for example, was absolutely different in the 60's than now)
stats = pd.read_csv(r'data/Seasons_Stats.csv', index_col=0)
# The file ```Seasons_Stats.csv``` contains the statics of all players since 1950. First, we drop a couple of blank columns, and the "Tm" column, that contains the team.
stats = pd.read_csv(r'data/Seasons_Stats.csv', index_col=0)
stats_clean = stats.drop(['blanl', 'blank2', 'Tm'], axis=1)
stats_clean.head()
# A second file, ```players.csv```, contains static information for each player, as height, weight, etc.
players = pd.read_csv(r'data/players.csv', index_col=0)
players.head(10)
# We merge both tables, and do some data cleaning:
#
# * Keep only players with more than 400 minutes for each season (with a 82 games regular season, thats around 5 minutes per game. Players with less than that will be only anecdotical, and will distort the analysis).
# * Replace the \* sign in some of the names
# * For the stats that represent total values (others, as TS%, represent percentages), we will take the values per 36 minutes. The reason is to judge every player according to his characteristics, not the time he was on the floor.
# +
data = pd.merge(stats_clean, players[['Player', 'height', 'weight']], left_on='Player', right_on='Player', right_index=False,
how='left', sort=False).fillna(value=0)
data = data[~(data['Pos']==0) & (data['MP'] > 200)]
data.reset_index(inplace=True, drop=True)
data['Player'] = data['Player'].str.replace('*','')
totals = ['PER', 'OWS', 'DWS', 'WS', 'OBPM', 'DBPM', 'BPM', 'VORP', 'FG', 'FGA', '3P', '3PA', '2P', '2PA', 'FT', 'FTA',
'ORB', 'DRB', 'TRB', 'AST', 'STL', 'BLK', 'TOV', 'PF', 'PTS']
for col in totals:
data[col] = 36 * data[col] / data['MP']
# -
data.tail()
# We will train a neural network with this data, to try to predict the position of each player.
#
# A way we didn't follow was to transform the positions into numbers from 1 to 5 (1 for a PG, 2 for a SG, 1.5 for a PG-SG, and so on, until 5 for a C), and use the network for regression instead of classification. But we wanted to see if the network was able to predict labels as "SG-PF", so we decided to work with the categorical labels. Another reason is that this makes this study more easily portable to other areas.
# We convert our DataFrame into a matrix X with the inputs, and a vector y with the labels. We scale the inputs and encode the outputs into dummy variables using the corresponding ```sklearn``` utilities.
#
# Instead of a stochastic partition, we decided to use the 2017 season as our test data, and all the previous as the train set.
# +
X = data.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = data['Pos'].as_matrix()
encoder = LabelBinarizer()
y_cat = encoder.fit_transform(y)
nlabels = len(encoder.classes_)
scaler =StandardScaler()
Xnorm = scaler.fit_transform(X)
stats2017 = (data['Year'] == 2017)
X_train = Xnorm[~stats2017]
y_train = y_cat[~stats2017]
X_test = Xnorm[stats2017]
y_test = y_cat[stats2017]
# -
# ## Neural network training ##
#
# We build using Keras (with Tensorflow as beckend) a neural network with two hidden layers. We will use relu activations, except for the last one, where we use a softmax to properly obtain the label probability. We will use a 20% of the data as a validation set, to make sure we are not overfitting.
model = Sequential()
model.add(Dense(40, activation='relu', input_dim=46))
model.add(Dropout(0.5))
model.add(Dense(30, activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(nlabels, activation='softmax'))
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
# x_train and y_train are Numpy arrays --just like in the Scikit-Learn API.
model.fit(X_train, y_train, epochs=200, batch_size=128, validation_split=0.2, verbose=1)
model.test_on_batch(X_test, y_test, sample_weight=None)
# The model performs well both for the validation and the test sets (65% might not seem a lot, but it is satisfying enough for our problem, where all the labels are very subjective (Was Larry Bird a "SM-PF" or a "PF-SF"? Nobody can tell).
#
# Now we train again the model, using all the training data (we will still reserve the 2017 season out of the training).
# Production model, using all data
model.fit(X_train, y_train, epochs=200, batch_size=128, validation_split=0, verbose=1)
# ## Predicting the positions of the First NBA Team of 2017 ##
#
# As a first test of the model, we will predict the positions of the player in the First NBA Team of 2017
first_team_members = ['<NAME>', '<NAME>', '<NAME>', '<NAME>', '<NAME>']
first_team_stats = data[[((x[1]['Player'] in first_team_members) & (x[1]['Year']==2017)) for x in data.iterrows()]]
first_team_stats
pd.DataFrame(index=first_team_stats.loc[:, 'Player'].values, data={'Real': first_team_stats.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm[first_team_stats.index, :]))})
# The model gets right four of the five. It's even more interesting that the one that gets wrong, <NAME>, can play in both PF and C positions, and that in the last season, he played more as a Power Forward than as a Center, as the model predicts:
#
# [New Orleans Pelicans Depth Chart - 2016-17](http://www.espn.com/nba/team/depth/_/name/no/new-orleans-pelicans).
# ## Predicting the positions of the NBA MVP ##
# We will use now the model to predict the positions of all the NBA MVP since the creation of the award, in 1956.
mvp = [(1956, '<NAME>'), (1957, '<NAME>'), (1958, '<NAME>'), (1959, '<NAME>'),
(1960, '<NAME>'), (1961, '<NAME>'), (1962, '<NAME>'), (1963, '<NAME>'),
(1964, '<NAME>'), (1965, '<NAME>'), (1966, '<NAME>'), (1967, '<NAME>'),
(1968, '<NAME>'), (1969, '<NAME>'), (1970, '<NAME>'), (1971, '<NAME>'),
(1972, '<NAME>'), (1973, '<NAME>'), (19704, '<NAME>'), (1975, '<NAME>'),
(1976, '<NAME>'), (1977, '<NAME>'), (1978, '<NAME>'), (1979, '<NAME>'),
(1980, '<NAME>'), (1981, '<NAME>'), (1982, '<NAME>'), (1983, '<NAME>'),
(1984, '<NAME>'), (1985, '<NAME>'), (1986, '<NAME>'), (1987, '<NAME>'),
(1988, '<NAME>'), (1989, '<NAME>'), (1990, '<NAME>'), (1991, '<NAME>'),
(1992, '<NAME>'), (1993, '<NAME>'), (1994, '<NAME>'), (1995, '<NAME>'),
(1996, '<NAME>'), (1997, '<NAME>'), (1998, '<NAME>'), (1999, '<NAME>'),
(2000, '<NAME>'), (2001, '<NAME>'), (2002, '<NAME>'), (2003, '<NAME>'),
(2004, '<NAME>'), (2005, '<NAME>'), (2006, '<NAME>'), (2007, '<NAME>'),
(2008, '<NAME>'), (2009, '<NAME>'), (2010, '<NAME>'), (2011, '<NAME>'),
(2012, '<NAME>'), (2013, '<NAME>'), (2014, '<NAME>'), (2015, '<NAME>'),
(2016, '<NAME>')]
mvp_stats = pd.concat([data[(data['Player'] == x[1]) & (data['Year']==x[0])] for x in mvp], axis=0)
mvp_stats
mvp_pred = pd.DataFrame(index=mvp_stats.loc[:, 'Player'].values, data={'Real': mvp_stats.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm[mvp_stats.index, :]))})
mvp_pred
# The model gets right most of the players, and the errors are always for a contiguous position (it is interesting that the model does it without having been provided with any information about the distances between the labels.)
# # Does year metter? #
#
# The definition of what a forward, or a center are always changing (in the very recent years, there is, for example, a trend towards having scoring point guards (as <NAME>) and forwards that direct the game instead of the guard (as <NAME>).
# Also, the physical requirements are increasing, and a height that in the 50's could characterize you as a center you will be a forward today.
#
# We will follow the first and last MVP's, <NAME> and <NAME>, and see where our model will put them in different years in the NBA history.
curry2017 = data[(data['Player'] == '<NAME>') & (data['Year']==2017)]
pettit1956 = data[(data['Player'] == '<NAME>') & (data['Year']==1956)]
# +
time_travel_curry = pd.concat([curry2017 for year in range(1956, 2018)], axis=0)
time_travel_curry['Year'] = range(1956, 2018)
X = time_travel_curry.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = time_travel_curry['Pos'].as_matrix()
y_cat = encoder.transform(y)
Xnorm = scaler.transform(X)
time_travel_curry_pred = pd.DataFrame(index=time_travel_curry.loc[:, 'Year'].values,
data={'Real': time_travel_curry.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm))})
time_travel_pettit = pd.concat([pettit1956 for year in range(1956, 2018)], axis=0)
time_travel_pettit['Year'] = range(1956, 2018)
X = time_travel_pettit.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = time_travel_pettit['Pos'].as_matrix()
y_cat = encoder.transform(y)
Xnorm = scaler.transform(X)
time_travel_pettit_pred = pd.DataFrame(index=time_travel_pettit.loc[:, 'Year'].values,
data={'Real': time_travel_pettit.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm))})
# -
pd.concat([time_travel_curry_pred,time_travel_pettit_pred],axis=1,keys=['<NAME>','<NAME>'])
# Curry is labeled as a point guards (his real position) from 1973 until today, and as a shooting guard before that. Perhaps because of his heigh (191cm), or perhaps because he is too much of a scorer. <NAME> is labeled as a center until 1967, and as a power forward after that (he played both roles, but nowadays he would have difficulties to play as a center, and would be for sure a forwards, perhaps even a small forward).
# # Changing positions #
#
# Many players go towards more interior roles with age, as they lose velocity. We will follow two cases, <NAME>, and <NAME>. Both of the retire, and return years later with more interior roles.
magic = data[(data['Player'] == '<NAME>')]
jordan = data[(data['Player'] == '<NAME>')]
# +
# Magic
X = magic.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = magic['Pos'].as_matrix()
y_cat = encoder.transform(y)
Xnorm = scaler.transform(X)
magic_pred = pd.DataFrame(index=magic.loc[:, 'Age'].values,
data={'Real': magic.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm))})
# Jordan
X = jordan.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = jordan['Pos'].as_matrix()
y_cat = encoder.transform(y)
Xnorm = scaler.transform(X)
jordan_pred = pd.DataFrame(index=jordan.loc[:, 'Age'].values,
data={'Real': jordan.loc[:, 'Pos'].values,
'Predicted':encoder.inverse_transform(model.predict(Xnorm))})
# -
pd.concat([magic_pred,jordan_pred],axis=1,keys=['<NAME>','<NAME>'])
# The model is able to detect the conversion of Jordan into a forward at the end of his career, but not the return of Magic as a power forward. Also, in his rookie season, he is classified as a small forward instead of as a shooting guard (Magic was clearly and outlier in the data, a 205cm point guard who could easily play in the five position. It is even surprised that is properly labelled as a point guard during most of his career)
# # How important are height and weight? #
# A concern we have before training the model was that the model would use the height and weight as the main classifiers, and that would labelled incorrectly players as <NAME> (a 205 cm point guard), or <NAME> (a 196cm power forward). Almost surprisingly, it works properly on this two players.
#
# We will use again the 2017 First NBA Team and play with the heights and weights of the players. Keeping constant all other statistics, we will change the height and weight and observe how the predicted positions change.
first_team_stats
# +
multiplier = np.arange(0.8,1.2,0.02)
growing_predicted = []
for p in first_team_stats.iterrows():
growing = pd.concat([p[1].to_frame().T for x in multiplier], axis=0)
growing['height'] = growing['height'] * multiplier
growing['weight'] = growing['weight'] * (multiplier ** 3)
X = growing.drop(['Player', 'Pos', 'G', 'GS', 'MP'], axis=1).as_matrix()
y = growing['Pos'].as_matrix()
y_cat = encoder.transform(y)
Xnorm = scaler.transform(X)
growing_predicted.append(pd.DataFrame(index=multiplier, data={'height': growing.loc[:, 'height'].values,
'Real': growing.loc[:, 'Pos'].values, 'Predicted':encoder.inverse_transform(model.predict(Xnorm))}))
# -
pd.concat(growing_predicted,axis=1,keys=first_team_stats['Player'])
# As we can see height matters, but it's not enough. Any player can be classified as a center if he is tall enough (very tall: Kawhi Leonard would need to be 221cm tall to be considered a center), but being short it's not enough to be considered a guard: a 165cm <NAME> would be still considered a power forward.
|
NBA_Keras/.ipynb_checkpoints/Predicting NBA players positions using Keras-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <small><i>This notebook was put together by [<NAME>](http://www.vanderplas.com). Source and license info is on [GitHub](https://github.com/jakevdp/sklearn_tutorial/).</i></small>
# # Introduction to Scikit-Learn: Machine Learning with Python
#
# This session will cover the basics of Scikit-Learn, a popular package containing a collection of tools for machine learning written in Python. See more at http://scikit-learn.org.
# ## Outline
#
# **Main Goal:** To introduce the central concepts of machine learning, and how they can be applied in Python using the Scikit-learn Package.
#
# - Definition of machine learning
# - Data representation in scikit-learn
# - Introduction to the Scikit-learn API
# ## About Scikit-Learn
#
# [Scikit-Learn](http://github.com/scikit-learn/scikit-learn) is a Python package designed to give access to **well-known** machine learning algorithms within Python code, through a **clean, well-thought-out API**. It has been built by hundreds of contributors from around the world, and is used across industry and academia.
#
# Scikit-Learn is built upon Python's [NumPy (Numerical Python)](http://numpy.org) and [SciPy (Scientific Python)](http://scipy.org) libraries, which enable efficient in-core numerical and scientific computation within Python. As such, scikit-learn is not specifically designed for extremely large datasets, though there is [some work](https://github.com/ogrisel/parallel_ml_tutorial) in this area.
#
# For this short introduction, I'm going to stick to questions of in-core processing of small to medium datasets with Scikit-learn.
# ## What is Machine Learning?
#
# In this section we will begin to explore the basic principles of machine learning.
# Machine Learning is about building programs with **tunable parameters** (typically an
# array of floating point values) that are adjusted automatically so as to improve
# their behavior by **adapting to previously seen data.**
#
# Machine Learning can be considered a subfield of **Artificial Intelligence** since those
# algorithms can be seen as building blocks to make computers learn to behave more
# intelligently by somehow **generalizing** rather that just storing and retrieving data items
# like a database system would do.
#
# We'll take a look at two very simple machine learning tasks here.
# The first is a **classification** task: the figure shows a
# collection of two-dimensional data, colored according to two different class
# labels. A classification algorithm may be used to draw a dividing boundary
# between the two clusters of points:
# +
# %matplotlib inline
# set seaborn plot defaults.
# This can be safely commented out
import seaborn; seaborn.set()
# -
# Import the example plot from the figures directory
from fig_code import plot_sgd_separator
plot_sgd_separator()
# This may seem like a trivial task, but it is a simple version of a very important concept.
# By drawing this separating line, we have learned a model which can **generalize** to new
# data: if you were to drop another point onto the plane which is unlabeled, this algorithm
# could now **predict** whether it's a blue or a red point.
#
# If you'd like to see the source code used to generate this, you can either open the
# code in the `figures` directory, or you can load the code using the `%load` magic command:
# The next simple task we'll look at is a **regression** task: a simple best-fit line
# to a set of data:
from fig_code import plot_linear_regression
plot_linear_regression()
# Again, this is an example of fitting a model to data, such that the model can make
# generalizations about new data. The model has been **learned** from the training
# data, and can be used to predict the result of test data:
# here, we might be given an x-value, and the model would
# allow us to predict the y value. Again, this might seem like a trivial problem,
# but it is a basic example of a type of operation that is fundamental to
# machine learning tasks.
# ## Representation of Data in Scikit-learn
#
# Machine learning is about creating models from data: for that reason, we'll start by
# discussing how data can be represented in order to be understood by the computer. Along
# with this, we'll build on our matplotlib examples from the previous section and show some
# examples of how to visualize data.
# Most machine learning algorithms implemented in scikit-learn expect data to be stored in a
# **two-dimensional array or matrix**. The arrays can be
# either ``numpy`` arrays, or in some cases ``scipy.sparse`` matrices.
# The size of the array is expected to be `[n_samples, n_features]`
#
# - **n_samples:** The number of samples: each sample is an item to process (e.g. classify).
# A sample can be a document, a picture, a sound, a video, an astronomical object,
# a row in database or CSV file,
# or whatever you can describe with a fixed set of quantitative traits.
# - **n_features:** The number of features or distinct traits that can be used to describe each
# item in a quantitative manner. Features are generally real-valued, but may be boolean or
# discrete-valued in some cases.
#
# The number of features must be fixed in advance. However it can be very high dimensional
# (e.g. millions of features) with most of them being zeros for a given sample. This is a case
# where `scipy.sparse` matrices can be useful, in that they are
# much more memory-efficient than numpy arrays.
# 
#
# (Figure from the [Python Data Science Handbook](https://github.com/jakevdp/PythonDataScienceHandbook))
# ## A Simple Example: the Iris Dataset
#
# As an example of a simple dataset, we're going to take a look at the
# iris data stored by scikit-learn.
# The data consists of measurements of three different species of irises.
# There are three species of iris in the dataset, which we can picture here:
# +
from IPython.core.display import Image, display
display(Image(filename='images/iris_setosa.jpg'))
print("Iris Setosa\n")
display(Image(filename='images/iris_versicolor.jpg'))
print("Iris Versicolor\n")
display(Image(filename='images/iris_virginica.jpg'))
print("Iris Virginica")
# -
# ### Quick Question:
#
# **If we want to design an algorithm to recognize iris species, what might the data be?**
#
# Remember: we need a 2D array of size `[n_samples x n_features]`.
#
# - What would the `n_samples` refer to?
#
# - What might the `n_features` refer to?
#
# Remember that there must be a **fixed** number of features for each sample, and feature
# number ``i`` must be a similar kind of quantity for each sample.
# ### Loading the Iris Data with Scikit-Learn
#
# Scikit-learn has a very straightforward set of data on these iris species. The data consist of
# the following:
#
# - Features in the Iris dataset:
#
# 1. sepal length in cm
# 2. sepal width in cm
# 3. petal length in cm
# 4. petal width in cm
#
# - Target classes to predict:
#
# 1. Iris Setosa
# 2. Iris Versicolour
# 3. Iris Virginica
#
# ``scikit-learn`` embeds a copy of the iris CSV file along with a helper function to load it into numpy arrays:
from sklearn.datasets import load_iris
iris = load_iris()
iris.keys()
n_samples, n_features = iris.data.shape
print((n_samples, n_features))
print(iris.data[0])
print(iris.data.shape)
print(iris.target.shape)
print(iris.target)
print(iris.target_names)
# This data is four dimensional, but we can visualize two of the dimensions
# at a time using a simple scatter-plot:
# +
import numpy as np
import matplotlib.pyplot as plt
x_index = 0
y_index = 1
# this formatter will label the colorbar with the correct target names
formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])
plt.scatter(iris.data[:, x_index], iris.data[:, y_index],
c=iris.target, cmap=plt.cm.get_cmap('RdYlBu', 3))
plt.colorbar(ticks=[0, 1, 2], format=formatter)
plt.clim(-0.5, 2.5)
plt.xlabel(iris.feature_names[x_index])
plt.ylabel(iris.feature_names[y_index]);
# -
# ### Quick Exercise:
#
# **Change** `x_index` **and** `y_index` **in the above script
# and find a combination of two parameters
# which maximally separate the three classes.**
#
# This exercise is a preview of **dimensionality reduction**, which we'll see later.
# ## Other Available Data
# They come in three flavors:
#
# - **Packaged Data:** these small datasets are packaged with the scikit-learn installation,
# and can be downloaded using the tools in ``sklearn.datasets.load_*``
# - **Downloadable Data:** these larger datasets are available for download, and scikit-learn
# includes tools which streamline this process. These tools can be found in
# ``sklearn.datasets.fetch_*``
# - **Generated Data:** there are several datasets which are generated from models based on a
# random seed. These are available in the ``sklearn.datasets.make_*``
#
# You can explore the available dataset loaders, fetchers, and generators using IPython's
# tab-completion functionality. After importing the ``datasets`` submodule from ``sklearn``,
# type
#
# datasets.load_ + TAB
#
# or
#
# datasets.fetch_ + TAB
#
# or
#
# datasets.make_ + TAB
#
# to see a list of available functions.
from sklearn import datasets
# +
# Type datasets.fetch_<TAB> or datasets.load_<TAB> in IPython to see all possibilities
# datasets.fetch_
# +
# datasets.load_
# -
# In the next section, we'll use some of these datasets and take a look at the basic principles of machine learning.
|
notebooks/02.1-Machine-Learning-Intro.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import declus
import pygslib
# # test with arbitrary gslib files
parameters = {
'datafl' : '../pygslib/data/cluster.dat', # path to file, or none (to use '_xxx_.in') or numpy array (with columns [x,y])
'icolx' : 1, # -columns for X, Y, Z and variable
'icoly' : 2,
'icolz' : 0,
'icolvr' : 3,
'tmin' : -1.0e21, # trimming limits min and max (raws out of this range will be ignored)
'tmax' : 1.0e21,
'sumfl' : None, # path to the output summary file or None (to use '_xxs_.out')
'outfl' : None, # path to the output file or None (to use '_xxx_.out')
'anisy': 1.0, # Y and Z cell anisotropies (Ysize=size*Yanis)
'anisz': 1.0,
'minmax' : 0, # 0=look for minimum declustered mean (1=max)
'ncell' : 24, # number of cell sizes, min size, max size
'cmin' : 1.0,
'cmax' : 25.,
'noff' : 5} # number of origin offsets
result, sumary =declus.declus(parameters)
result.head()
sumary.plot(x='Cell Size', y = 'Declustered Mean')
parameters['ncell'] = 1
parameters['cmin'] = 5
parameters['cmax'] = 5
parameters['noff'] = 8
result, sumary =declus.declus(parameters)
result.head()
# # test with numpy array
#
result['Zlocation']=0
parameters = {
'datafl' : result[['Xlocation','Ylocation','Zlocation','Primary']].values,
'tmin' : -1.0e21,
'tmax' : 1.0e21,
'sumfl' : None,
'outfl' : None,
'anisy': 1.0,
'anisz': 1.0,
'minmax' : 0,
'ncell' : 24,
'cmin' : 1.0,
'cmax' : 25.,
'noff' : 5}
result, sumary =declus.declus(parameters)
result.head()
sumary.plot(x='Cell Size', y = 'Declustered Mean')
|
sandbox/declus from gslib exe.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This notebook was prepared by [<NAME>](http://donnemartin.com). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# # Solution Notebook
# ## Problem: Maximizing XOR
#
# See the [HackerRank problem page](https://www.hackerrank.com/challenges/maximizing-xor).
#
# * [Constraints](#Constraints)
# * [Test Cases](#Test-Cases)
# * [Algorithm](#Algorithm)
# * [Code](#Code)
# * [Unit Test](#Unit-Test)
# ## Constraints
#
# See the [HackerRank problem page](https://www.hackerrank.com/challenges/maximizing-xor).
# ## Test Cases
#
# See the [HackerRank problem page](https://www.hackerrank.com/challenges/maximizing-xor).
# ## Algorithm
#
# * Set max to 0
# * For i in the range (lower, upper) inclusive
# * For j in the range (lower, upper) inclusive
# * Compare i ^ j with max, update max if needed
# * return max
#
# Complexity:
# * Time: O(n^2) - See note below
# * Space: O(1)
#
# Note:
# * TODO: Add more optimal solutions such as those discussed [here](https://www.hackerrank.com/challenges/maximizing-xor/editorial).
# ## Code
class Solution(object):
def max_xor(self, lower, upper):
result = 0
for l in range(lower, upper + 1):
for u in range(lower, upper + 1):
curr = l ^ u
if result < curr:
result = curr
return result
# ## Unit Test
#
#
# +
# %%writefile test_maximizing_xor.py
from nose.tools import assert_equal
class TestMaximizingXor(object):
def test_maximizing_xor(self):
solution = Solution()
assert_equal(solution.max_xor(10, 15), 7)
print('Success: test_maximizing_xor')
def main():
test = TestMaximizingXor()
test.test_maximizing_xor()
if __name__ == '__main__':
main()
# -
# %run -i test_maximizing_xor.py
|
online_judges/maximizing_xor/maximizing_xor_solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Buidling the first model
# +
# imports
from dataclasses import dataclass
from typing import Any
import pandas as pd
import numpy as np
from sklearn.preprocessing import Normalizer
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_percentage_error
from sklearn.model_selection import train_test_split
# scikit learn later
# %matplotlib inline
# -
# # Load dataset
# load dataset
dataset_1 = "../data/input_dataset-1.parquet"
dataset_2 = "../data/input_dataset-2.parquet"
bolt_pretension_file = "../data/bolt_pretension.csv"
prediction_input_file = "../data/prediction_input.parquet"
validation = pd.read_parquet(prediction_input_file)
validation.head()
features = list(validation.columns)
features
train_main = pd.read_parquet(dataset_2)
train_main.head()
train_main_features = train_main[features]
train_main_features.head()
# +
target_vars = ["Bolt_1_Tensile", "Bolt_2_Tensile", "Bolt_3_Tensile", "Bolt_4_Tensile", "Bolt_5_Tensile", "Bolt_6_Tensile"]
targets_df = train_main[target_vars]
targets_df
# -
for target_var in target_vars:
targets[target_var] = train_main[target_var]
targets
# # Preprocessing and feature engineering
#
def copy_df(df:pd.DataFrame):
return df.copy()
def mode_to_numerical(df: pd.DataFrame):
df.loc[:, "mode"] = (df["mode"]=="operation").astype(float)
return df
def drop_na(df: pd.DataFrame):
return df.dropna(axis=0)
train_main_features_prep = (
train_main_features.pipe(copy_df)
.pipe(mode_to_numerical)
.pipe(drop_na)
)
train_main_features_prep.head()
validation_prep = (
validation.pipe(copy_df)
.pipe(mode_to_numerical)
.pipe(drop_na)
)
validation_prep.head()
print(validation.shape)
print(validation_prep.shape)
# ## Normalize data
# ## Training data
# +
normalizer = Normalizer().fit(train_main_features_prep)
train_main_features_prep_norm = normalizer.transform(train_main_features_prep)
train_main_features_prep_norm
# -
# ### validation data
validation_prep_norm = normalizer.transform(validation_prep)
# ## Preprocess targets:
# drop nas
def drop_target_nans(targets_df, train_raw_df):
is_nan_row = train_raw_df.isna().any(axis=1)
targets_df = targets_df[~is_nan_row]
return targets_df
targets_df_prep = (
targets_df.pipe(copy_df)
.pipe(drop_target_nans,train_main_features )
)
targets_df_prep.head()
# ## Varify that data has the same shaep
targets_df_prep.shape
train_main_features_prep_norm.shape
# # build model
@dataclass
class ModelResponse:
model: Any
train_mape: float
test_mape: float
def train_bolts_models(train_df, targets_df, model_name="linear"):
if model_name == "linear":
model = LinearRegression
else:
raise ValueError()
res = {}
for target_name, target_data in targets_df.iteritems():
X_train, X_test, y_train, y_test = train_test_split(train_df, target_data, test_size = 0.8, shuffle=True)
m = model()
m.fit(X_train, y_train)
y_pred_train = m.predict(X_train)
y_pred_test = m.predict(X_test)
train_mape = mean_absolute_percentage_error(y_train, y_pred_train)
test_mape = mean_absolute_percentage_error(y_test, y_pred_test)
res[target_name] = ModelResponse(model = m, train_mape=train_mape, test_mape=test_mape)
return res
model_responses = train_bolts_models(train_main_features_prep_norm, targets_df_prep)
model_responses
|
machine-learning-notebooks/model_rev_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#After predicting disordered residues with iupred,
#each string of contiguous disordered residues was
#saved an item in a dictionary. Likewise, there is
#a dictionary for all ordered domains and a
#dictionary that contains the entirety of every
#proteins sequence proteome-wide. These dictionaries
#were then exported as a pickle bundle which this
#bit of code unpacks and converts to a dictinary.
import pickle as pkl
disorderdictionary = open('UP000000803DisorderDict.pkl', 'rb')
ProteomeDisorderDict = pkl.load(disorderdictionary)
orderdictionary = open('UP000000803OrderDict.pkl', 'rb')
ProteomeOrderDict = pkl.load(orderdictionary)
proteomedictionary = open('UP000000803ProteomeDict.pkl', 'rb')
ProteomeDict = pkl.load(proteomedictionary)
# +
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import numpy as np
def residue_distance(protein_dictionary, residue_list):
#finds the average distance between residues specified in the residue_list in amino acids
average = {}
for protein in protein_dictionary:
distance = 0
sequence = protein_dictionary[protein]
values = []
if len(sequence) > 100:
while sequence:
if sequence[0] in residue_list:
values.append(distance)
distance = 0
sequence = sequence[1:]
else:
distance += 1
sequence = sequence[1:]
if len(values) <= 2:
average[protein] = 0
else:
average[protein] = (sum(values) - values[0] - values[-1]) / (len(values) - 2)
return average
def nested_residue_distance(nested_dict, residue_list):
#takes in a nested dictionary of many sequences and finds the average of each sequence
nested_average = {}
for protein in nested_dict:
subseq_dictionary_average = residue_distance(nested_dict[protein], residue_list)
nested_average[protein] = subseq_dictionary_average
return nested_average
def dictionary_to_list(dict):
data_points = []
for key in dict:
data_points.append(dict[key])
return data_points
def nested_dictionary_to_list(nested_dict):
data_points = []
for key in nested_dict:
nested_list = dictionary_to_list(nested_dict[key])
data_points.extend(nested_list)
return data_points
# +
def fraction_composition(sequence, aa_list):
#takes in sequence and finds percent composition of the given amino acids
total = 0
length = len(sequence)
while sequence:
if sequence[0] in aa_list:
total += 1
sequence = sequence[1:]
else:
sequence = sequence[1:]
return total / length
dmcdt1 = 'MAQPSVAAFFTNRKRAALDDAISIKNRRLVEPAETVSPASAPSQLPAGDQDADLDTLKAAATGMRTRSGRTARLIVTAAQESKKKTPAAAKMEPHIKQPKLVQFIKKGTLSPRKQAQSSKLDEEELQQSSAISEHTPKVNFTITSQQNADNVQRGLRTPTKQILKDASPIKADLRRQLTFDEVKTKVSRSAKLQELKAVLALKAALEQKRKEQEERNRKLRDAGPSPSKSKMSVQLKEFDTIELEVLISPLKTFKTPTKIPPPTPDKHELMSPRHTDVSKRLLFSPAKNGSPVKLVE'
fly_bulky_hydrophobics = fraction_composition(dmcdt1, ['L', 'I', 'V', 'F', 'Y', 'W'])
fly_positive = fraction_composition(dmcdt1, ['K', 'R'])
fly_proline = fraction_composition(dmcdt1, ['P'])
print(fly_bulky_hydrophobics, fly_positive, fly_proline)
def dictionary_composition_filter(dict, percent, aa_list):
#takes in a percent composition and creates a new dictionary with proteins that match the composition
percent_comp_dict = {}
for key in dict:
if fraction_composition(dict[key], aa_list) >= percent - (percent * 0.05) and fraction_composition(dict[key], aa_list) <= percent + (percent * 0.05):
percent_comp_dict[key] = dict[key]
return percent_comp_dict
def nested_dictionary_composition_filter(nested_dict, percent, aa_list):
#takes in nested dictionaries
nested_percent_comp_dict = {}
for protein in nested_dict:
subseq_dictionary_average = dictionary_composition_filter(nested_dict[protein], percent, aa_list)
nested_percent_comp_dict[protein] = subseq_dictionary_average
return nested_percent_comp_dict
# +
filtered_proteome_positive = dictionary_composition_filter(ProteomeDict, fly_positive, ['R', 'K'])
filtered_ordered_proteome_positive = nested_dictionary_composition_filter(ProteomeOrderDict, fly_positive, ['R', 'K'])
filtered_disordered_proteome_positive = nested_dictionary_composition_filter(ProteomeDisorderDict, fly_positive, ['R', 'K'])
drosophila_proteome_positive_average = residue_distance(filtered_proteome_positive, ['R', 'K'])
drosophila_ordered_proteome_positive_average = nested_residue_distance(filtered_ordered_proteome_positive, ['R', 'K'])
drosophila_disordered_proteome_positive_average = nested_residue_distance(filtered_disordered_proteome_positive, ['R', 'K'])
positive_data_points = dictionary_to_list(drosophila_proteome_positive_average)
ordered_positive_average = nested_dictionary_to_list(drosophila_ordered_proteome_positive_average)
disordered_positive_average = nested_dictionary_to_list(drosophila_disordered_proteome_positive_average)
print(len(positive_data_points))
data_to_plot = [positive_data_points, ordered_positive_average, disordered_positive_average]
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
bp = ax.violinplot(data_to_plot, vert=False)
ax.set_yticklabels(['', 'Entire Proteome', '', 'Ordered Proteome', '', 'Disordered Proteome'])
#DmCdt1 line
plt.axvline(x=4.188679245283019, color='r')
plt.xlabel('Distance')
plt.title('Distances Between Positive Amino Acids')
plt.show()
#plt.savefig('Drosophila Proteome Positive Distance Violin Plot.png', bbox_inches='tight')
# +
filtered_proteome_hydrophobic = dictionary_composition_filter(ProteomeDict, fly_bulky_hydrophobics, ['L', 'I', 'F', 'Y', 'W'])
filtered_ordered_proteome_hydrophobic = nested_dictionary_composition_filter(ProteomeOrderDict, fly_bulky_hydrophobics, ['L', 'I', 'F', 'Y', 'W'])
filtered_disordered_proteome_hydrophobic = nested_dictionary_composition_filter(ProteomeDisorderDict, fly_bulky_hydrophobics, ['L', 'I', 'F', 'Y', 'W'])
drosophila_proteome_hydrophobic_average = residue_distance(filtered_proteome_hydrophobic, ['L', 'I', 'F', 'Y', 'W'])
drosophila_ordered_proteome_hydrophobic_average = nested_residue_distance(filtered_ordered_proteome_hydrophobic, ['L', 'I', 'F', 'Y', 'W'])
drosophila_disordered_proteome_hydrophobic_average = nested_residue_distance(filtered_disordered_proteome_hydrophobic, ['L', 'I', 'F', 'Y', 'W'])
hydrophobic_data_points = dictionary_to_list(drosophila_proteome_hydrophobic_average)
ordered_hydrophobic_average = nested_dictionary_to_list(drosophila_ordered_proteome_hydrophobic_average)
disordered_hydrophobic_average = nested_dictionary_to_list(drosophila_disordered_proteome_hydrophobic_average)
data_to_plot = [hydrophobic_data_points, ordered_hydrophobic_average, disordered_hydrophobic_average]
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
bp = ax.violinplot(data_to_plot, vert=False)
ax.set_yticklabels(['', 'Entire Proteome', '', 'Ordered Proteome', '', 'Disordered Proteome'])
#DmCdt1 line
plt.axvline(x=3.737704918032787, color='r')
plt.xlabel('Distance')
plt.title('Distances Between Large Hydrophobic Amino Acids')
plt.show()
#plt.savefig('Drosophila Proteome Large Hydrophobics Distance Violin Plot.png', bbox_inches='tight')
# +
filtered_proteome_proline = dictionary_composition_filter(ProteomeDict, fly_proline, ['P'])
filtered_ordered_proteome_proline = nested_dictionary_composition_filter(ProteomeOrderDict, fly_proline, ['P'])
filtered_disordered_proteome_proline = nested_dictionary_composition_filter(ProteomeDisorderDict, fly_proline, ['P'])
drosophila_proteome_proline_average = residue_distance(filtered_proteome_proline, ['P'])
drosophila_ordered_proteome_proline_average = nested_residue_distance(filtered_ordered_proteome_proline, ['P'])
drosophila_disordered_proteome_proline_average = nested_residue_distance(filtered_disordered_proteome_proline, ['P'])
proline_data_points = dictionary_to_list(drosophila_proteome_proline_average)
ordered_proline_average = nested_dictionary_to_list(drosophila_ordered_proteome_proline_average)
disordered_proline_average = nested_dictionary_to_list(drosophila_disordered_proteome_proline_average)
data_to_plot = [proline_data_points, ordered_proline_average, disordered_proline_average]
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
bp = ax.violinplot(data_to_plot, vert=False)
ax.set_yticklabels(['', 'Entire Proteome', '', 'Ordered Proteome', '', 'Disordered Proteome'])
#DmCdt1 line
plt.axvline(x=12.090909090909092, color='r')
plt.xlabel('Distance')
plt.title('Distances Between Prolines')
plt.show()
#plt.savefig('Drosophila Proteome Proline Distance Violin Plot.png', bbox_inches='tight')
# +
positive_dataframe = pd.DataFrame({'Values': positive_data_points})
order_positive_dataframe = pd.DataFrame({'Values': ordered_positive_average})
disorder_positive_dataframe = pd.DataFrame({'Values': disordered_positive_average})
positive_dataframe['Proteome Section'] = 'Whole Protein'
order_positive_dataframe['Proteome Section'] = 'Ordered Region'
disorder_positive_dataframe['Proteome Section'] = 'Disordered Region'
positive_combined_dataframe = positive_dataframe.append([order_positive_dataframe, disorder_positive_dataframe])
sns.violinplot(x='Proteome Section', y='Values', data=positive_combined_dataframe, color='white')
plt.axhline(y=4.188679245283019, color='r')
# +
hydrophobic_dataframe = pd.DataFrame({'Values': hydrophobic_data_points})
order_hydrophobic_dataframe = pd.DataFrame({'Values': ordered_hydrophobic_average})
disorder_hydrophobic_dataframe = pd.DataFrame({'Values': disordered_hydrophobic_average})
hydrophobic_dataframe['Proteome Section'] = 'Whole Protein'
order_hydrophobic_dataframe['Proteome Section'] = 'Ordered Region'
disorder_hydrophobic_dataframe['Proteome Section'] = 'Disordered Region'
hydrophobic_combined_dataframe = hydrophobic_dataframe.append([order_hydrophobic_dataframe, disorder_hydrophobic_dataframe])
sns.violinplot(x='Proteome Section', y='Values', data=hydrophobic_combined_dataframe, color='white')
plt.axhline(y=3.737704918032787, color='r')
# +
proline_dataframe = pd.DataFrame({'Values': proline_data_points})
order_proline_dataframe = pd.DataFrame({'Values': ordered_proline_average})
disorder_proline_dataframe = pd.DataFrame({'Values': disordered_proline_average})
proline_dataframe['Proteome Section'] = 'Whole Protein'
order_proline_dataframe['Proteome Section'] = 'Ordered Region'
disorder_proline_dataframe['Proteome Section'] = 'Disordered Region'
proline_combined_dataframe = proline_dataframe.append([order_proline_dataframe, disorder_proline_dataframe])
sns.violinplot(x='Proteome Section', y='Values', data=proline_combined_dataframe, color='white')
plt.axhline(y=12.090909090909092, color='r')
# -
|
Drosophila Proteome Percent Content Controlled Violin Plots.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Machine Learning - Formação Cientista de dados
# ### Regras de associação e associação com eclat
# +
#pacote para regras de associação
#install.packages("arules")
# -
library(arules)
transacoes = read.transactions(file.choose(), format = "basket", sep=",") #leitura do arquivo transactions
transacoes
inspect(transacoes)
image(transacoes)
#chamada da função apriori para associação de mineração
??apriori
regras = apriori(transacoes, parameter = list(supp=0.5,conf=0.5))
regras
inspect(regras)
install.packages("arulesViz")
library("arulesViz")
plot(regras)
plot(regras, method="graph", control=list(type="items"))
# ### Associação com eclat
# +
#library(arules)
# -
transacoes = read.transactions(file.choose(), format = "basket", sep=",") #leitura da transação, arquivo transactions2.txt
image(transacoes) #imagem da transação
regras = eclat(transacoes, parameter = list(supp = 0.1, maxlen = 15)) #
inspect(regras) #inspeção da variável
# +
#library(arulesViz)
# -
plot(regras, method = "graph", control = list(type = "items")) #plotagem das regras de associação
# ## FIM
|
Notebooks/ML_Regras_Associacao.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
a =
if a>= 21:
print ("vote and poker")
elif a>= 19 and a <= 21:
print("vote, don´t poker")
else:
print("don´t vote, don`t poker")
# +
age = 23
#
if age <= 10:
print('Listen, learn, and have fun.')
elif age <= 19:
print('Go fearlessly forward.')
elif age <= 29:
print('Seize the day.')
elif age <= 39:
print('Go for what you want.')
elif age <= 59:
print('Stay physically fit and healthy.')
elif age <= 69:
print('retire and enjoy your hard work')
#if none of the above is true, than the else sentence is being printed
else:
print('Each day is magical.')
# +
#LOOPS (start, end, and increment between number in the loop)
x = 5
while x<= 20:
print(x)
x += 5
# -
|
01_Workshop-master/Chapter01/Activity03/Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Computer Vision, Lab 01: OpenCV and Octave
#
# Today we'll learn how to perform some useful computer
# vision tasks with OpenCV (C++ and Python) and Octave.
#
# ## Install OpenCV
#
# In this lab, we give you multiple options for installing
# OpenCV and a C++/Python IDE.
#
# Different projects will typically use different versions
# of OpenCV. On Ubuntu, you will therefore generally want to install
# each version you use in <tt>/usr/local</tt> and pick
# the precise version you need for a specific project
# at build time. I'm not sure what you should do to maintain
# different versions on Windows!
#
# If you haven't already, go ahead and install OpenCV
# 4.5.2 according to the instructions below. It will take 20
# minutes plus. If you're on Windows, skip to the Windows
# intructions, where you'll have a choice between Visual Studio Community
# and Visual Studio Code.
# ### Apple Mac people!
#
# We don't provide instructions here.
# Please see the instructions [here](https://thecodinginterface.com/blog/opencv-cpp-vscode/).
# ### Linux
#
# #### Dependencies for Ubuntu 20.04
#
# I'm not sure these are all the dependencies you will need. Let me know if some are missing!
#
# $ sudo apt-get install cmake build-essential git unzip python3 libjpeg-dev libpng-dev \
# python3-pip wget libtbb2 libtbb-dev libtiff-dev libqt5opengl5-dev libqt5gui5 libqwt-qt5-dev \
# libqt5test5 libqt5concurrent5 libopenblas-dev libopenblas64-dev liblapack-dev liblapack64-dev \
# liblapacke-dev libeigen3-dev libavfilter-dev libvtk6-dev libwebp-dev libopenexr-dev libgdal-dev \
# libavutil-dev libavcodec-dev libavformat-dev libswscale-dev libavresample-dev libavdevice-dev \
# libatlas-base-dev libvtk7-dev libv4l-dev libeigen3-dev libatlas-base-dev libatlas-cpp-0.6-dev \
# libgstreamer1.0-dev gstreamer1.0-plugins-{base,good,bad,ugly}
#
# #### Download
#
# The current stable version of OpenCV is 4.5.2. Download the source from
# [the OpenCV GitHub page](https://github.com/opencv/opencv/archive/4.5.2.zip) and unpack it somewhere:
#
# $ cd ~/Desktop
# $ wget https://github.com/opencv/opencv/archive/4.5.2.zip
# $ unzip 4.5.2.zip
# $ rm 4.5.2.zip
# $ wget https://github.com/opencv/opencv_contrib/archive/4.5.2.zip
# $ unzip 4.5.2.zip
# $ rm 4.5.2.zip
# $ cd opencv-4.5.2
# $ mkdir build
# $ cd build
#
# #### Build
#
# I like to build and install the library in such a way that each project can point to its preferred version of the library. I use the following build definitions:
#
# $ cmake -Wno-dev \
# -DCMAKE_BUILD_TYPE=RELEASE \
# -DOPENCV_EXTRA_MODULES_PATH=$HOME/Desktop/opencv_contrib-4.5.2/modules \
# -DCMAKE_INSTALL_PREFIX=/usr/local/opencv-4.5.2 \
# -DBUILD_opencv_java=OFF -DWITH_OPENGL=ON \
# -DWITH_OPENCL=ON -DWITH_IPP=OFF -DFORCE_VTK=ON \
# -DWITH_GDAL=ON -DWITH_XINE=ON \
# -DENABLE_PRECOMPILED_HEADERS=OFF \
# -DENABLE_AVX=ON -DWITH_TBB=ON -DWITH_EIGEN=ON \
# -DWITH_V4L=ON -DWITH_LAPACK=ON -DWITH_QT=ON \
# -DWITH_FFMPEG=ON -DBUILD_TESTS=OFF \
# -DBUILD_PERF_TESTS=OFF -DOPENCV_ENABLE_NONFREE=ON ..
# $ # Check that the dependencies you want are found by cmake
# $ make -j8
# $ sudo make install
#
# This gives us QT windows with OpenGL support, as well as non-free modules like SIFT. You'll have
# to do more work to get CUDA support (if you have an Nvidia graphics card).
#
# Sit back and relax while it compiles. You can install VSCode while OpenCV is building (see below).
# ### Windows Method 1 (Visual Studio C++)
#
# These instructions were written by <NAME>.
#
# In Windows, we have many options for how to install. Here we give some pointers for Visual Studio Community on Windows, for C++ and Python.
# Later, we'll give instructions for Visual Studio Code on Windows.
#
# Here are some references:
#
# - https://demystifymachinelearning.wordpress.com/2018/08/30/installing-opencv-on-windows-using-anaconda/
# - https://cv-tricks.com/how-to/installation-of-opencv-4-1-0-in-windows-10-from-source/
# - https://docs.opencv.org/master/d5/de5/tutorial_py_setup_in_windows.html
# - https://medium.com/@kswalawage/install-python-and-jupyter-notebook-to-windows-10-64-bit-66db782e1d02
# - https://cuda-chen.github.io/programming/image%20processing/2020/01/21/vscode-with-opencv-cpp-on-windows10-explained.html
# - https://www.pranav.ai/cplusplus-for-jupyter
# - https://learnopencv.com/tag/xeus-cling/
# - https://sourceforge.net/projects/opencvlibrary/files/opencv-win/
# - https://www.youtube.com/watch?v=FCzMpHWUUKg
#
# 1. Download latest OpenCV release from __[OpenCV site](https://opencv.org/releases/)__ site
# - Click on the **Windows** of the latest version on openCV.
# - Extract it to the desire location: In this step, I choose <code>C:\opencv</code>
# 2. Clone OpenCV-Contribute at __[GitHub](https://github.com/opencv/opencv_contrib.git)__, and extract it at the same location.
#
# <img src="img/lab01-1.PNG" width="400"/>
#
# 3. Install Visual Studio Community from __[here](https://visualstudio.microsoft.com/vs/community/)__
# 4. While setting up visual studio installation, select 2 workloads as below:
# - Python Development
# - Desktop Development with C++
#
# <img src="img/lab01-2.PNG" width="800"/>
#
# 5. Go to System Properties $\rightarrow$ *Environment Variables*
#
# **Note**: In Windows10, you can go type "Environment Variables" to search System Properties
# - At the User variables $\rightarrow$ Path tab select $\rightarrow$ *Edit..*
# - Press *New* and input
# - Variable value: <code>C:\opencv\opencv\build\x64\vc15\bin</code> (Your location)
#
# <img src="img/lab01-3.PNG" width="600"/>
#
# 7. After installation done, the Visual Studio require restart. After restart, open Visual studio
# 8. Create a new project as **Console App** (C++)
#
# <img src="img/lab01-4.PNG" width="800"/>
#
# #### Setting up OpenCV in Visual Studio C++
#
# 1. Set platform target to x64
#
# <img src="img/lab01-5.PNG" width="200"/>
#
# 2. Go to *Project* $\rightarrow$ \[project name\] Properties
#
# <img src="img/lab01-6.PNG" width="300"/>
#
# 3. At VC++ Directories tab $\rightarrow$ Include Directories $\rightarrow$ click Edit and add opencv/include path
#
# <img src="img/lab01-7.PNG" width="600"/>
#
# <img src="img/lab01-8.PNG" width="400"/>
#
# 4. At VC++ Directories tab $\rightarrow$ Library Directories $\rightarrow$ click Edit and add opencv/lib path
#
# <img src="img/lab01-9.PNG" width="600"/>
#
# <img src="img/lab01-10.PNG" width="400"/>
#
# 5. At Linker/Input tab $\rightarrow$ Additional Dependencies $\rightarrow$ click Edit and add <code>opencv_worldxxxd.lib</code> file
#
# **Note**: You can see the library file name in <code>C:\opencv\opencv\build\x64\vc15\lib</code>
#
# <img src="img/lab01-11.PNG" width="600"/>
#
# <img src="img/lab01-12.PNG" width="400"/>
#
# 6. Try to write the code as below.
#
# **Note**: To run as debug, press F5. To run without debugging, press Ctrl+F5
#
# #### Set up OpenCV Python in Visual Studio
#
# 1. Create a python project in Visual studio
# 2. At the solution explorer, right click at **Python 3.x** $\rightarrow$ Manage Python package
#
# <img src="img/lab01-15.PNG" width="400"/>
#
# 3. Select Package PyPI $\rightarrow$ type **opencv-python** $\rightarrow$ double click at *install opencv-python*
#
# <img src="img/lab01-16.PNG" width="400"/>
#
# 4. Go to **Tools** $\rightarrow$ **Python** $\rightarrow$ *Python Interactive Wimdow*
# 5. Try to type anything of opencv code
#
# <img src="img/lab01-17.PNG" width="400"/>
#
# You can check your version of OpenCV with code like this:
#
# import cv2
# print(cv2.__version__)
#
# Try to write the Python code below in a .py file and verify you get the same result as in C++.
# +
import cv2
import numpy as np
print(cv2.__version__)
size = 300, 600, 3
image = np.zeros(size, dtype=np.uint8)
cv2.circle(image, (250,150), 100, (0,255,128), -100)
cv2.circle(image, (350,150), 100, (255,255,255), -100)
cv2.imshow("", image)
cv2.waitKey(0)
# -
# ### Windows Method 2 (Visual Studio Code)
#
# #### Python
#
# First, the Python installation:
#
# 1. Download Python from Microsoft Store (***Recommend***:by type **python** in command line) or __[Python website](https://www.python.org/downloads/)__ and install it.
# 2. Set **PythonXX** path and **PythonXX/Scripts** path to environment variable (No need for microsoft store install)
# - **PythonXX** path - <code>C:\Users\\[username\]\AppData\Local\Programs\Python\Python39</code>
# - **PythonXX/Scripts** path - <code>C:\Users\\[username\]\AppData\Local\Programs\Python\Python39\Scripts</code>
# 3. Download Visual Studio Code from __[here](https://code.visualstudio.com/download)__ and install it.
# 4. Open command line:
# - Check python version <code>python --version</code>
# - Install virtual environment <code>pip install virtualenv</code>
# - Create a virtual environment called opencv <code>python -m virtualenv opencv</code>
# - Go to opencv environment, activate the virtual environment.
# - <code>cd opencv/Scripts</code>
# - <code>activate.bat</code>
# - Install numpy <code>pip install numpy</code>
# - Install MatPlotLib <code>pip install matplotlib</code>
# - Install OpenCV <code>pip install opencv-python</code>
# - Install Jupyter <code>python -m pip install jupyter</code>
# - Try to open Jupyter Notebook <code>jupyter notebook</code>
# - Cancel Jupyter notebook using Ctrl-C
# 5. Open Visual Studio Code and select Python interpreter (at left bottom of the screen).
#
# <img src="img/lab01-18.PNG" width="800"/>
#
# 6. Try to create a jupyter program or python program.
#
# # For jupyter notebook, you cannot use imshow directly. Please use pyplot to show image.
#
# import cv2
# import numpy as np
# import matplotlib.pyplot as plt
#
# print(cv2.__version__)
# size = 300, 600, 3
# image = np.zeros(size, dtype=np.uint8)
# cv2.circle(image, (250,150), 100, (0,255,128), -100)
# cv2.circle(image, (350,150), 100, (255,255,255), -100)
#
# def imshow(image):
# img2 = image[:,:,::-1] #change color from BGR color to RGB color
# plt.imshow(img2)
# plt.title('image')
# plt.show()
#
# imshow(image)
#
# #### C++
#
# 1. After install VS code, Install VS Code C/C++ extensions (ms-vscode.cpptools)
#
# <img src="img/lab01-19.PNG" width="800"/>
#
# 2. Download and install MinGW-w64 from __[here](https://sourceforge.net/projects/mingw-w64/files/Toolchains%20targetting%20Win32/Personal%20Builds/mingw-builds/installer/mingw-w64-install.exe/download)__. Setting while install as:
# - Version 8.1.0
# - Architecture x86-64
# - posix
# - Exception seh
# - Build revision 0
# - Set path of compiler as: <code>C:\mingw-w64\x86_64-8.1.0-posix-seh-rt_v6-rev0</code>
#
# <img src="img/lab01-20.PNG" width="600"/>
#
# 3. Download __[OpenCV MinGW](https://github.com/huihut/OpenCV-MinGW-Build)__ in zip file. unzip it and put into <code>C:\opencv\OpenCV-MinGW-Build-OpenCV-4.5.2-x64</code>
#
# 4. Go to System Properties $\rightarrow$ *Environment Variables*
#
# **Note**: In Windows10, you can go type "Environment Variables" to search System Properties
# - At the User variables $\rightarrow$ Path tab select $\rightarrow$ *Edit..*
# - Press *New* and input
# - Binaries OpenCV path: <code>C:\opencv\OpenCV-MinGW-Build-OpenCV-4.5.2-x64\x64\mingw\bin</code>
# - Binaries MinGW path: <code>C:\mingw-w64\x86_64-8.1.0-posix-seh-rt_v6-rev0\mingw64\bin</code>
#
# <img src="img/lab01-21.PNG" width="600"/>
#
# **Note**: If you don't do this step, you will find *gdb* error in last step
#
# 5. Configure file in vscode
#
# 5.1. Create a workspace in vs code.
#
# 5.2. Create a main.cpp and try to run it.
#
# 5.3. in folder .vscode, you will see <code>tasks.json</code>, <code>launch.json</code>, and <code>c_cpp_properties.json</code>. The code will be looked like __[repo](https://github.com/Cuda-Chen/opencv-config-with-vscode)__
#
# <img src="img/lab01-22.PNG" width="480"/>
#
# 5.4. Modify all 3 files as below (You can copy)
#
# ##### tasks.json
#
# <code>
# {
# "tasks": [
# {
# "type": "cppbuild",
# "label": "C/C++: g++.exe build active file",
# "command": "C:\\mingw-w64\\x86_64-8.1.0-posix-seh-rt_v6-rev0\\mingw64\\bin\\g++.exe",
# "args": [
# "-g",
# "${file}",
# "-o",
# "${fileDirname}\\${fileBasenameNoExtension}.exe",
# "-I","C:\\opencv\\OpenCV-MinGW-Build-OpenCV-4.5.2-x64\\include",
# "-L","C:\\opencv\\OpenCV-MinGW-Build-OpenCV-4.5.2-x64\\x64\\mingw\\bin",
# "-l","libopencv_calib3d452",
# "-l","libopencv_core452",
# "-l","libopencv_dnn452",
# "-l","libopencv_features2d452",
# "-l","libopencv_flann452",
# "-l","libopencv_highgui452",
# "-l","libopencv_imgcodecs452",
# "-l","libopencv_imgproc452",
# "-l","libopencv_ml452",
# "-l","libopencv_objdetect452",
# "-l","libopencv_photo452",
# "-l","libopencv_stitching452",
# "-l","libopencv_video452",
# "-l","libopencv_videoio452"
# ],
# "options": {
# "cwd": "C:\\mingw-w64\\x86_64-8.1.0-posix-seh-rt_v6-rev0\\mingw64\\bin"
# },
# "problemMatcher": [
# "$gcc"
# ],
# "group": {
# "kind": "build",
# "isDefault": true
# },
# "detail": "Task generated by Debugger."
# }
# ],
# "version": "2.0.0"
# }
# </code>
#
# ##### launch.json
#
# <code>
# {
# // Use IntelliSense to learn about possible attributes.
# // Hover to view descriptions of existing attributes.
# // For more information, visit: https://go.microsoft.com/fwlink/?linkid=830387
# "version": "0.2.0",
# "configurations": [
# {
# "name": "g++.exe - Build and debug active file",
# "type": "cppdbg",
# "request": "launch",
# "program": "${fileDirname}\\${fileBasenameNoExtension}.exe",
# "args": [],
# "stopAtEntry": true,
# "cwd": "C:\\mingw-w64\\x86_64-8.1.0-posix-seh-rt_v6-rev0\\mingw64\\bin",
# "environment": [],
# "externalConsole": false,
# "MIMode": "gdb",
# "miDebuggerPath": "C:\\mingw-w64\\x86_64-8.1.0-posix-seh-rt_v6-rev0\\mingw64\\bin\\gdb.exe",
# "setupCommands": [
# {
# "description": "Enable pretty-printing for gdb",
# "text": "-enable-pretty-printing",
# "ignoreFailures": true
# }
# ],
# "preLaunchTask": "C/C++: g++.exe build active file"
# }
# ]
# }
# </code>
#
# ##### c_cpp_properties.json
# <code>
# {
# "configurations": [
# {
# "name": "Win32",
# "includePath": [
# "${workspaceFolder}/**",
# "C:\\opencv\\OpenCV-MinGW-Build-OpenCV-4.5.2-x64\\include"
# ],
# "defines": [
# "_DEBUG",
# "UNICODE",
# "_UNICODE"
# ],
# "compilerPath": "C:\\mingw-w64\\x86_64-8.1.0-posix-seh-rt_v6-rev0\\mingw64\\bin\\gcc.exe",
# "cStandard": "c11",
# "cppStandard": "c++17",
# "intelliSenseMode": "clang-x64"
# }
# ],
# "version": 4
# }
# </code>
#
# 6. Write some code to test:
#
# <code>
# #include <iostream>
#
# #include <opencv2/opencv.hpp>
#
# using namespace cv;
#
# int main( int argc, char** argv )
# {
# std::cout << "aa" << std::endl;
#
# Mat image = Mat::zeros(300, 600, CV_8UC3);
# circle(image, Point(250, 150), 100, Scalar(0, 255, 128), -100);
# circle(image, Point(350, 150), 100, Scalar(255, 255, 255), -100);
# imshow("Display Window", image);
# waitKey(0);
# std::cout << "bb" << std::endl;
#
# // In case of load image file
# std::string img = "C:\\Users\\alisa\\OneDrive\\Documents\\CPPVSCODE\\lenna.jpg";
# Mat srcImage = imread(img);
# if (!srcImage.data) {
# return 1;
# }
# imshow("srcImage", srcImage);
# waitKey(0);
#
# Mat greyMat;
# cv::cvtColor(srcImage, greyMat, COLOR_BGR2GRAY);
# imshow("greyImage", greyMat);
# waitKey(0);
#
# return 0;
# }
# </code>
#
# #### Additional OpenCV C++ setup for Windows VS code
#
# 1. After setting OpenCV Python completed, open VS code.
# 2. Create a workspace, then go to **.vscode** folder create a file named **c_cpp_properties.json**
#
# <img src="img/lab01-27.PNG" width="400"/>
#
# 3. input data as below
# <code>
# {
# "configurations": [
# {
# "name": "Win32",
# "includePath": [
# "${workspaceFolder}/**",
# "/home/alisa/anaconda3/include/opencv4/**" <<< Your opencv4 path
# ],
# "defines": [
# "_DEBUG",
# "UNICODE",
# "_UNICODE"
# ],
# "compilerPath": "/usr/bin/g++",
# "cStandard": "c11",
# "cppStandard": "c++17",
# "intelliSenseMode": "clang-x64"
# }
# ],
# "version": 4
# }
# </code>
#
# <img src="img/lab01-29.PNG" width="400"/>
#
# 4. At line <code>"/home/alisa/anaconda3/include/opencv4/**"</code>, search the path yourself, and modify it.
# 5. Create a cpp file which has opencv code.
# 6. Create **Makefile** which has detail below.
#
# <img src="img/lab01-30.PNG" width="400"/>
#
# <code>
# // make file
#
# CC = "g++"
# PROJECT = CVLab // your project name
# SRC = testcpp01.cpp // cpp file
#
# LIBS = `pkg-config opencv4 --cflags --libs`
#
# /$(PROJECT) : /$(SRC)
# \$(CC) \$(SRC) -o \$(PROJECT) \$(LIBS)
# </code>
#
# 7. Open terminal, run <code>make</code>
# 8. Enable library path: <code> export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:/usr/local/lib/</code>
# 9. Run application project file <code>./CVLab</code>
#
# <img src="img/lab01-28.PNG" width="600"/>
#
# ### Alternative method for installing OpenCV on Ubuntu 20.04 with VS Code
#
# I like the custom build of OpenCV for my C++ development as described
# in the beginning. If you aren't
# too picky, though, you can skip the custom build of OpenCV and just
# go with the libraries that come with Python and use VSCode for your
# dev environment, similar to Windows:
#
# 1. Download VS code from __[here](https://code.visualstudio.com/download)__ and install it.
# 2. Open terminal and do step:
# - Update and Refresh Repository lists:
# - <code>sudo apt-get update</code>
# - <code>sudo apt-get upgrade</code>
# - Install Python: <code>sudo apt-get install build-essential cmake python3-numpy python3-dev python3-tk libavcodec-dev libavformat-dev libavutil-dev libswscale-dev libavresample-dev libdc1394-dev libeigen3-dev libgtk-3-dev libvtk7-qt-dev</code>
# - Upgrade pip: <code>sudo -H pip3 install --upgrade pip</code>
# - Install virtual environment: <code>sudo -H pip3 install virtualenv</code>
# - Create virtual environment: <code>virtualenv opencv</code>
# - Activate virtual environment: <code>source opencv/bin/activate</code>
# - Install Jupyter: <code>pip install jupyter</code>
# - Install OpenCV: <code>sudo apt-get install python3-opencv</code>
# - Install OpenCV-dev: <code>sudo apt-get install libopencv-dev</code> (for C++ use)
# - Run Jupyter Notebook: <code>jupyter notebook</code>
# 3. Open Visual Studio Code and select Python interpreter (at left bottom of the screen).
# 4. Try to code OpenCV for check the error.
# ## Start an OpenCV C++ project (no IDE, for Linux)
#
# If you're on Windows, you've followed the instructions above and can already compile and run C++ programs. Right?
#
# If you're on Linux, let's start our first project. In some directory
# on your file system, create files <tt>main.cpp</tt>
# and <tt>CMakeLists.txt</tt>.
#
# For <tt>main.cpp</tt>, start out with a "Hello World!"
# message:
#
# #include <iostream>
# using namespace std;
#
# int main(void)
# {
# cout << "Hello, World!" << endl;
# return 0;
# }
#
# In <tt>CMakeLists.txt</tt>, add some minimal definitions
# to generate the <tt>Makefile</tt>:
#
# cmake_minimum_required(VERSION 3.12)
#
# project(hello)
# set(CMAKE_CXX_STANDARD 14)
#
# add_executable(hello main.cpp)
#
# To build, make a build directory, run <tt>cmake</tt>,
# then run <tt>make</tt>:
#
# $ cd /home/$USER/CV/hello
# $ mkdir build-debug
# $ cd build-debug
# $ cmake -DCMAKE_BUILD_TYPE=Debug ..
# $ make
# $ ./hello
#
# Note that here we're asking <tt>cmake</tt>
# to build a "debug" executable. To run the program in the
# debugger and step through it:
#
# $ sudo apt-get install gdb
# $ gdb ./hello
# (gdb) break main
# Breakpoint 1 at 0x11a9: file /home/mdailey/CV/hello/main.cpp, line 5.
# (gdb) run
# Starting program: /home/mdailey/CV/hello/build-debug/hello
# (gdb) list
# 1
# 2 #include <iostream>
# 3 using namespace std;
# 4
# 5 int main() {
# 6 cout << "Hello, World!" << endl;
# 7 return 0;
# 8 }
# (gdb) next
# 6 cout << "Hello, World!" << endl;
# (gdb) next
# Hello, World!
# 7 return 0;
# (gdb) next
#
# If you want your code to run as fast as possible
# with optimization, you have to use "release" mode for
# the build:
#
# $ cd /home/$USER/CV/hello
# $ mkdir build-release
# $ cd build-release
# $ cmake -DCMAKE_BUILD_TYPE=Release ..
# $ make
# $ ./hello
#
# You can still run the executable in the debugger,
# but you'll only see the assembly language instructions
# instead of the original source code.
#
# OK, but what about OpenCV? Let's do something that
# uses the library. Add necessary definitions to your
# <tt>CMakeLists.txt</tt>:
#
# find_package(OpenCV 4.5.2 REQUIRED)
# target_include_directories(hello PUBLIC ${OpenCV_INCLUDE_DIRS})
# target_link_libraries(hello ${OpenCV_LIBS})
#
# If all goes well, when you run <tt>cmake</tt>, now
# you should see a message like
#
# -- Found OpenCV: /usr/local/opencv-4.5.2 (found suitable version "4.5.2", minimum required is "4.5.2")
#
# If you don't see "Found OpenCV: ..." or have some other error, you have probably
# installed OpenCV in a place that cmake can't find it. Try giving it a hint:
#
# find_package(OpenCV 4.5.2 REQUIRED PATHS /home/$USER/wherever/opencv/is)
#
# In our simple program, let's get the singular value
# decomposition of a matrix. You'll need to include
# OpenCV's core functionality:
#
# #include <opencv2/core.hpp>
#
# then, in the <tt>main()</tt> function:
#
# double adData[] = { 3, 2, 4, 8, 4, 2, 1, 3, 2 };
# cv::Mat matA( 3, 3, CV_64F, adData );
# cout << "A:" << endl << matA << endl;
# cv::SVD svdA( matA, cv::SVD::FULL_UV );
# cout << "U:" << endl << svdA.u << endl;
# cout << "W:" << endl << svdA.w << endl;
# cout << "Vt:" << endl << svdA.vt << endl;
#
# Try it! To verify correctness of the result,
# we'll use Octave in the next part below.
#
# While we're here, though, let's try another program that uses some graphics:
#
# #include <opencv2/core/core.hpp>
# #include <opencv2/highgui/highgui.hpp>
# #include <opencv2/imgproc.hpp>
# #include <iostream>
#
# using namespace cv;
# using namespace std;
#
# int main()
# {
# Mat image = Mat::zeros(300, 600, CV_8UC3);
# circle(image, Point(250, 150), 100, Scalar(0, 255, 128), -100);
# circle(image, Point(350, 150), 100, Scalar(255, 255, 255), -100);
# imshow("Display Window", image);
# waitKey(0);
# return 0;
# }
#
# Do you get a result like this?
#
# <img src="img/lab01-14.PNG" width="400"/>
#
# **Windows tip if it does not work**
#
# If you found this error:
#
# <img src="img/lab01-13.PNG" width="400"/>
#
# The easiest way to solve the problem is copy <code>opencv_world452d.dll</code> from <code>C:\opencv\opencv\build\x64\vc15\bin</code> into <code>\[your project path\]/x64/Debug</code>
#
# ## Python OpenCV Programs
#
# Regardless of how you installed, you should be able to run a Python program using OpenCV.
#
# **Note:** if you've compiled OpenCV from source and want Python to use the version you've compiled rather than the default
# version from pip, you need to set the `PYTHONPATH` either in your environment setup file (`$HOME/.bashrc` in Ubuntu) or at the command line:
#
# $ cat > myprog.py
# import cv2
# print(cv2.__version__)
# $ python3 myprog.py
# 4.3.0
# $ export PYTHONPATH=/usr/local/opencv-4.5.2/lib/python3.8/dist-packages
# $ python3 myprog.py
# 4.5.2
#
# +
# Python SVD example
import numpy as np
import cv2
matA = np.array([[3.0,2.0,4.0],[8.0,4.0,2.0],[1.0,3.0,2.0]])
w, u, vt = cv2.SVDecomp(matA)
print("A:")
print(matA)
print("U:")
print(u)
print("W:")
print(w)
print("Vt:")
print(vt)
# -
# ### IDE or no IDE?
#
# Some experienced programmers say that IDEs are bad for
# you, because they get between you and your code.
#
# My view is that it's important to understand how to do
# things without an IDE, so that you don't depend on it.
# Then, if you use an IDE, you should take care to
# understand precisely what it is doing for you and how.
#
# That's the beauty of development on Linux. Since everything
# is open and nothing is hidden from you, you have
# full control over everything you're doing, and you
# can go as deep as you want to to understand what your
# system is doing. IDEs that work well in Linux are just
# wrappers around the same ordinary tools that we would
# use from the command line.
#
# So I don't think it's harmful to use a good IDE for
# C++ development on Linux. One of the best I've seen
# is CLion by JetBrains. Since JetBrains gives educational
# licenses for all of its IDEs, we can use it freely,
# and once you have a real job, you can convince your
# boss to buy licenses.
#
# Note, however, that CLion can be heavy and with all
# the indexing and code completion it's doing, you'll
# burn through your battery charge on your laptop pretty
# quick! You'll probably
# have to plug in or use the PowerSave mode.
#
# If you want to, go ahead and download CLion from
# [the JetBrains CLion download
# page](https://www.jetbrains.com/clion/download/#section=linux)
# and set it up. Repeat the <tt>CMakeLists.txt</tt> and
# <tt>main.cpp</tt> setup from the first part of the
# lab, and get your OpenCV program running at the console
# and in the debugger.
#
# Alternatively, we can use Visual Studio Code, which is not quite
# as capable as CLion, especially when it comes to automatically
# refactoring code, but is more lightweight and lets you move around
# between Python and C++ and other languages very easily. It also
# supports remote development over a SSH connection.
# If you want to use VSCode, go to [the VSCode home page](https://code.visualstudio.com/)
# and download the package for your OS (64-bit .deb if you're on Ubuntu).
# ## Octave
#
# Developing OpenCV code in C++ can be tedious sometimes,
# especially when the program is not quite working and
# you're not sure where the mistake in your calculations
# is.
#
# One way to develop more quickly would be to use Python
# instead of C++ for the development. This may be more
# productive, but you won't learn as much about the
# OpenCV core, internals will be more mysterious, and
# your code won't (usually) be as fast as it could be.
#
# An even better way to develop _algorithms_, however,
# is to code them in a much higher level language such
# as Matlab or Octave, verify correctness, then port
# the algorithm to OpenCV, either in C++ or Python.
#
# OK, so let's install Octave:
#
# $ sudo apt-get install octave
#
# I am old fashioned and don't really care for Octave's
# GUI, so I run like this:
#
# $ octave --no-gui
# GNU Octave, version 5.2.0
# ...
# octave:1> A = [ 3, 2, 4; 8, 4, 2; 1, 3, 2 ]
# A =
#
# 3 2 4
# 8 4 2
# 1 3 2
#
# octave:2> [U, W, Vt] = svd(A)
# U =
#
# -0.455849 0.637848 -0.620767
# -0.844431 -0.530370 0.075129
# -0.281315 0.558442 0.780387
#
# W =
#
# Diagonal Matrix
#
# 10.6578 0 0
# 0 3.2594 0
# 0 0 1.6696
#
# Vt =
#
# -0.78856 -0.54334 -0.28802
# -0.48165 0.25451 0.83859
# -0.38234 0.80000 -0.46240
#
# octave:3>
#
# Now you can verify whether the OpenCV code and the Octave
# code give the same result. First, you will probably see
# differences in the sign of the basis vectors in U and
# Vt but that's not important. More importantly, however,
# notice that the result for the third matrix is transposed.
#
# This can be confusing. The SVD factors a matrix A
# as a product of two orthogonal matrices and a diagonal
# matrix. We usually write the svd as U W V' = A. But
# some libraries will give you V, and some will give you
# V transposed.
#
# It is easy to check which is which in Octave:
#
# octave:3> U * W * Vt
# ans =
#
# 3.22601 2.33969 3.62198
# 7.88153 4.55033 1.08442
# 0.98938 3.13467 1.78744
#
# Since we didn't get our original A back, we would
# hypothesize that Octave is giving us V, not V transposed:
#
# octave:4> U * W * Vt'
# ans =
#
# 3.00000 2.00000 4.00000
# 8.00000 4.00000 2.00000
# 1.00000 3.00000 2.00000
#
# So now we know that our Octave code should have
# read
#
# octave:5> [U, W, V] = svd(A);
# octave:6> U*W*V'
# ans =
#
# 3.00000 2.00000 4.00000
# 8.00000 4.00000 2.00000
# 1.00000 3.00000 2.00000
#
# and we can also check the result in the C++ code:
#
# cout << "Reconstruction of A from its SVD:" << endl << svdA.u * cv::Mat::diag(svdA.w) * svdA.vt << endl;
#
# ## Octave Online?
#
# If you don't want to install Octave on your machine, you may want to try it online.
#
# 1. Go to https://octave-online.net/ for run octave online (Need internet)
#
# <img src="img/lab01-23.PNG" width="600"/>
#
# 2. Click at ***Menu*** $\rightarrow$ Sign in with google $\rightarrow$ Use youre e-mail
# 3. You can use it as Matlab or octave.
# 4. At the left side, you can create m-files for do your homework.
# 5. Here's the same SVD example:
#
# <code language="octave">
# octave:1> A = [ 3, 2, 4; 8, 4, 2; 1, 3, 2 ]
# A =
#
# 3 2 4
# 8 4 2
# 1 3 2
#
# octave:2> [U, W, Vt] = svd(A)
# U =
#
# -0.455849 0.637848 -0.620767
# -0.844431 -0.530370 0.075129
# -0.281315 0.558442 0.780387
#
# W =
#
# Diagonal Matrix
#
# 10.6578 0 0
# 0 3.2594 0
# 0 0 1.6696
#
# Vt =
#
# -0.78856 -0.54334 -0.28802
# -0.48165 0.25451 0.83859
# -0.38234 0.80000 -0.46240
#
# octave:3> U * W * Vt
# ans =
#
# 3.22601 2.33969 3.62198
# 7.88153 4.55033 1.08442
# 0.98938 3.13467 1.78744
#
# octave:4> U * W * Vt'
# ans =
#
# 3.00000 2.00000 4.00000
# 8.00000 4.00000 2.00000
# 1.00000 3.00000 2.00000
#
# octave:5> [U, W, V] = svd(A);
# octave:6> U * W * V'
# ans =
#
# 3.00000 2.00000 4.00000
# 8.00000 4.00000 2.00000
# 1.00000 3.00000 2.00000
#
# </code>
#
# <img src="img/lab01-24.PNG" width="480"/>
#
# <img src="img/lab01-25.PNG" width="480"/>
# ## Exercises to do in lab
#
# 1. Write OpenCV C++, OpenCV Python, and Octave code to test which, if any,
# of the homogeneous 2D points (2, 4, 2),
# (6, 3, 3), (1, 2, 0.5), and
# (16, 8, 4) are on the homogeneous 2D line
# (8, -4, 0). Output the inhomogeneous representations
# of the points that are on the line.
#
# 2. Figure out how to plot the 2D line (8, -4, 0) and the
# four homogeneous 2D points from exercise 1 above in
# Octave (you will need to install gnuplot).
#
# ## Exercises to do on your own
#
# Here's a very basic mobile robot I built with scrap metal, two DC motors from cordless drills, 3D
# printed motor mounts, miscellaneous hardware and caster wheels,
# hobby RC brushed motor speed controllers and radio receiver, and an Arduino for Nano for control.
#
# <img alt="matt-robot" src="http://www.cs.ait.ac.th/~mdailey/class/vision/20200529_061126.jpg" width="640">
#
# For vision, I added an
# [NVIDIA Jetson Nano Development Kit](https://th.rs-online.com/web/p/processor-development-tools/1999831/?cm_mmc=TH-PLA-DS3A-_-google-_-PLA_TH_THB_Fallback-_-All+Products-_-1999831&matchtype=&aud-827186183886:pla-293946777986&gclid=Cj0KCQjw--GFBhDeARIsACH_kdbBNFCyMXmHOx-PvOxQZwIi09Re8pic9SLaIQWj3FbCVZr0hEwK-FgaArvUEALw_wcB&gclsrc=aw.ds)
# and an [8MP camera for the Jetson Nano](https://www.lazada.co.th/products/8mp-imx219-jetson-nano-200-fov-3280x246415-i2298839807-s7747540313.html?spm=a2o4m.searchlist.list.1.547e4cc8uIGag2&search=1&freeshipping=1).
#
# You may
# want to make something similar (maybe smaller)
# to play with this semester to experiment with
# autonomous control using computer vision!
#
# Download [this video acquired from the mobile robot](https://drive.google.com/file/d/1K2EjcMJifDUOkSP_amlg8wcHmv_jh44V/view?usp=sharing).
#
# 1. Figure out how to read and display the video
# in an OpenCV window (using C++!). You may find the [<tt>VideoCapture</tt> tutorial](https://docs.opencv.org/4.5.2/d8/dfe/classcv_1_1VideoCapture.html) useful.
#
# 1. Do the same thing using OpenCV from Python.
#
# 1. Get the sparse optical flow example from
# [the OpenCV optical flow tutorial page](https://docs.opencv.org/4.5.2/d4/dee/tutorial_optical_flow.html)
# working on this video. Try both C++ and Python.
#
# ### The report
#
# Turn in a brief report in PDF format
# describing your experience
# in the lab and the results of the
# two sets of exercises using Google Classroom before the next lab.
#
|
Labs/01-Install-OpenCV/01-Install-OpenCV.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import brfss
import thinkplot
from thinkbayes2 import *
import numpy as np
from matplotlib import pyplot as plt
# +
nrows = None
resp = brfss.ReadBrfss(nrows=nrows).dropna(subset=['sex', 'htm3'])
groups = resp.groupby('sex')
d = {}
for name, group in groups:
d[name] = group.htm3.values
labels = {1:'male', 2:'female'}
# -
|
code/0ABC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import keras
keras.__version__
# # 이미지 생성
#
# 이 노트북은 [케라스 창시자에게 배우는 딥러닝](https://tensorflow.blog/%EC%BC%80%EB%9D%BC%EC%8A%A4-%EB%94%A5%EB%9F%AC%EB%8B%9D/) 책의 8장 4절의 코드 예제입니다. 책에는 더 많은 내용과 그림이 있습니다. 이 노트북에는 소스 코드에 관련된 설명만 포함합니다.
#
# ---
#
# ## 변이형 오토인코더
#
# 2013년 12월 킹마와 웰링 그리고 2014년 1월 르젠드, 무함마드, 위스트라가 동시에 발견한 변이형 오토인코더는 생성 모델의 한 종류로 개념 벡터를 사용해 이미지를 변형하는데 아주 적절합니다. 오토인코더는 입력을 저차원 잠재 공간으로 인코딩한 다음 디코딩하여 복원하는 네트워크입니다. 변이형 오토인코더는 딥러닝과 베이즈 추론의 아이디어를 혼합한 오토인코더의 최신 버전입니다.
#
# 고전적인 오토인코더는 이미지를 입력받아 인코더 모듈을 사용해 잠재 벡터 공간으로 매핑합니다. 그다음 디코더 모듈을 사용해 원본 이미지와 동일한 차원으로 복원하여 출력합니다. 오토인코더는 입력 이미지와 동일한 이미지를 타깃 데이터로 사용하여 훈련합니다. 다시 말해 오토인코더는 원본 입력을 재구성하는 방법을 학습합니다. 코딩(인코더의 출력)에 여러 제약을 가하면 오토인코더가 더 흥미로운 혹은 덜 흥미로운 잠재 공간의 표현을 학습합니다. 일반적으로 코딩이 저차원이고 희소(0이 많은)하도록 제약을 가합니다. 이런 경우 인코더는 입력 데이터의 정보를 적은 수의 비트에 압축하기 위해 노력합니다.
# 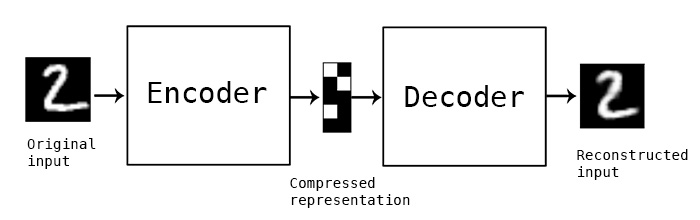
# 현실적으로 이런 전통적인 오토인코더는 특별히 유용하거나 구조화가 잘 된 잠재 공간을 만들지 못합니다. 압축도 아주 뛰어나지 않습니다. 이런 이유 때문에 시대의 흐름에서 대부분 멀어졌습니다. VAE는 오토인코더에 약간의 통계 기법을 추가하여 연속적이고 구조적인 잠재 공간을 학습하도록 만들었습니다. 결국 이미지 생성을 위한 강력한 도구로 탈바꿈되었습니다.
#
# 입력 이미지를 잠재 공간의 고정된 코딩으로 압축하는 대신 VAE는 이미지를 어떤 통계 분포의 파라미터로 변환합니다. 이는 입력 이미지가 통계적 과정을 통해서 생성되었다고 가정하여 인코딩과 디코딩하는 동안 무작위성이 필요하다는 것을 의미합입니다. VAE는 평균과 분산 파라미터를 사용해 이 분포에서 무작위로 하나의 샘플을 추출합니다. 이 샘플을 디코딩하여 원본 입력으로 복원합니다(그림 8-13 참조). 이런 무작위한 과정은 안정성을 향상하고 잠재 공간 어디서든 의미있는 표현을 인코딩하도록 만듭니다. 즉 잠재 공간에서 샘플링한 모든 포인트는 유효한 출력으로 디코딩됩니다.
# 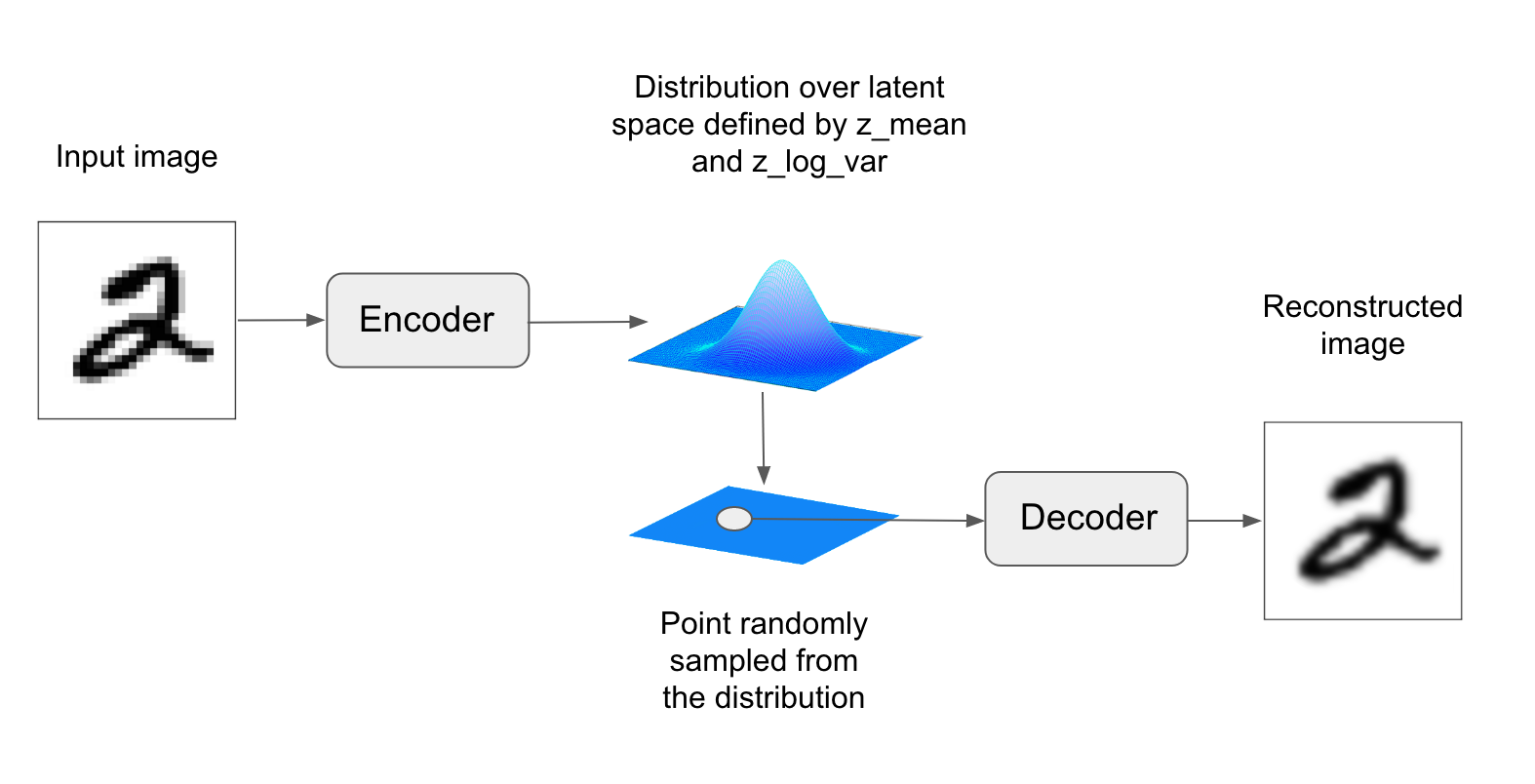
# 기술적으로 보면 VAE는 다음과 같이 작동합니다. 먼저 인코더 모듈이 입력 샘플 `imput_img`을 잠재 공간의 두 파라미터 `z_mean`과 `z_log_variance`로 변환합니다. 그다음 입력 이미지가 생성되었다고 가정한 잠재 공간의 정규 분포에서 포인트 `z`를 `z = z_mean + exp(0.5 * z_log_variance) * epsilon`와 같이 무작위로 샘플링합니다. `epsilon`는 작은 값을 가진 랜덤 텐서입니다. 마지막으로 디코더 모듈은 잠재 공간의 이 포인트를 원본 입력 이미지로 매핑하여 복원합니다. `epsilon`이 무작위로 만들어지기 때문에 `input_img`를 인코딩한 잠재 공간의 위치(`z_mean`)에 가까운 포인트는 `input_img`와 비슷한 이미지로 디코딩될 것입니다. 이는 잠재 공간을 연속적이고 의미 있는 공간으로 만들어 줍니다. 잠재 공간에서 가까운 두 개의 포인트는 아주 비슷한 이미지로 디코딩될 것입니다. 잠재 공간의 이런 저차원 연속성은 잠재 공간에서 모든 방향이 의미있는 데이터 변화의 축을 인코딩하도록 만듭니다. 결국 잠재 공간은 매우 구조적이고 개념 벡터로 다루기에 매우 적합해집니다.
#
# VAE의 파라미터는 두 개의 손실 함수로 훈련합니다. 디코딩된 샘플이 원본 입력과 동일하도록 만드는 재구성 손실과 잠재 공간을 잘 형성하고 훈련 데이터에 과대적합을 줄이는 규제 손실입니다.
#
# 케라스의 VAE 구현을 간단히 살펴보겠습니다. 개략적으로 보면 다음과 같습니다:
# ```python
# # 입력을 평균과 분산 파라미터로 인코딩합니다
# z_mean, z_log_variance = encoder(input_img)
#
# # 무작위로 선택한 작은 epsilon 값을 사용해 잠재 공간의 포인트를 뽑습니다
# z = z_mean + exp(z_log_variance) * epsilon
#
# # z를 이미지로 디코딩합니다
# reconstructed_img = decoder(z)
#
# # 모델 객체를 만듭니다
# model = Model(input_img, reconstructed_img)
#
# # 입력 이미지와 재구성 이미지를 매핑한 오토인코더 모델을 훈련합니다.
# ```
# 다음 코드는 이미지를 잠재 공간 상의 확률 분포 파라미터로 매핑하는 인코더 네트워크입니다. 입력 이미지 `x`를 두 벡터 `z_mean`과 `z_log_var`로 매핑하는 간단한 컨브넷입니다.
# +
import keras
from keras import layers
from keras import backend as K
from keras.models import Model
import numpy as np
img_shape = (28, 28, 1)
batch_size = 16
latent_dim = 2 # 잠재 공간의 차원: 2D 평면
input_img = keras.Input(shape=img_shape)
x = layers.Conv2D(32, 3,
padding='same', activation='relu')(input_img)
x = layers.Conv2D(64, 3,
padding='same', activation='relu',
strides=(2, 2))(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
x = layers.Conv2D(64, 3,
padding='same', activation='relu')(x)
shape_before_flattening = K.int_shape(x)
x = layers.Flatten()(x)
x = layers.Dense(32, activation='relu')(x)
z_mean = layers.Dense(latent_dim)(x)
z_log_var = layers.Dense(latent_dim)(x)
# -
# 다음은 `z_mean`과 `z_log_var`를 사용하는 코드입니다. 이 두 파라미터가 `input_img`를 생성한 통계 분포의 파라미터라고 가정하고 잠재 공간 포인트 `z`를 생성합니다. 여기에서 (케라스의 백엔드 기능으로 만든) 일련의 코드를 `Lambda` 층으로 감쌉니다. 케라스에서는 모든 것이 층이므로 기본 층을 사용하지 않은 코드는 `Lambda`로 (또는 직접 만든 층으로) 감싸야 합니다.
# +
def sampling(args):
z_mean, z_log_var = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean=0., stddev=1.)
return z_mean + K.exp(z_log_var) * epsilon
z = layers.Lambda(sampling)([z_mean, z_log_var])
# -
# 다음 코드는 디코더 구현입니다. 벡터 `z`를 이전 특성 맵 차원으로 크기를 바꾸고 몇 개의 합성곱 층을 사용해 최종 출력 이미지를 만듭니다. 최종 이미지는 원본 `input_img`와 차원이 같습니다.
# +
# Input에 z를 주입합니다
decoder_input = layers.Input(K.int_shape(z)[1:])
# 입력을 업샘플링합니다
x = layers.Dense(np.prod(shape_before_flattening[1:]),
activation='relu')(decoder_input)
# 인코더 모델의 마지막 Flatten 층 직전의 특성 맵과 같은 크기를 가진 특성 맵으로 z의 크기를 바꿉니다
x = layers.Reshape(shape_before_flattening[1:])(x)
# Conv2DTranspose 층과 Conv2D 층을 사용해 z를 원본 입력 이미지와 같은 크기의 특성 맵으로 디코딩합니다
x = layers.Conv2DTranspose(32, 3,
padding='same', activation='relu',
strides=(2, 2))(x)
x = layers.Conv2D(1, 3,
padding='same', activation='sigmoid')(x)
# 특성 맵의 크기가 원본 입력과 같아집니다
# 디코더 모델 객체를 만듭니다
decoder = Model(decoder_input, x)
# 모델에 z를 주입하면 디코딩된 z를 출력합니다
z_decoded = decoder(z)
# -
# 일반적인 샘플 기준의 함수인 `loss(y_true, y_pred)` 형태는 VAE의 이중 손실에 맞지 않습니다. `add_loss` 내장 메서드를 사용하는 층을 직접 만들어 임의의 손실을 정의하겠습니다.
# +
class CustomVariationalLayer(keras.layers.Layer):
def vae_loss(self, x, z_decoded):
x = K.flatten(x)
z_decoded = K.flatten(z_decoded)
xent_loss = keras.metrics.binary_crossentropy(x, z_decoded)
kl_loss = -5e-4 * K.mean(
1 + z_log_var - K.square(z_mean) - K.exp(z_log_var), axis=-1)
return K.mean(xent_loss + kl_loss)
def call(self, inputs):
x = inputs[0]
z_decoded = inputs[1]
loss = self.vae_loss(x, z_decoded)
self.add_loss(loss, inputs=inputs)
# 출력 값을 사용하지 않습니다
return x
# 입력과 디코딩된 출력으로 이 층을 호출하여 모델의 최종 출력을 얻습니다
y = CustomVariationalLayer()([input_img, z_decoded])
# -
# 이제 모델 객체를 만들고 훈련할 준비가 되었습니다. 층에서 손실을 직접 다루기 때문에 `compile` 메서드에서 손실을 지정하지 않습니다(`loss=None`). 그 결과 훈련하는 동안 타깃 데이터를 전달하지 않아도 됩니다(다음 코드처럼 모델의 `fit` 메서드에 `x_train`만 전달합니다).
# +
from keras.datasets import mnist
vae = Model(input_img, y)
vae.compile(optimizer='rmsprop', loss=None)
vae.summary()
# MNIST 숫자 이미지에서 VAE를 훈련합니다
(x_train, _), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_train = x_train.reshape(x_train.shape + (1,))
x_test = x_test.astype('float32') / 255.
x_test = x_test.reshape(x_test.shape + (1,))
vae.fit(x=x_train, y=None,
shuffle=True,
epochs=10,
batch_size=batch_size,
validation_data=(x_test, None))
# -
# MNIST 데이터셋으로 모델의 훈련을 마치면 디코더 네트워크를 사용하여 잠재 공간의 임의의 벡터를 이미지로 변환할 수 있습니다:
import matplotlib.pyplot as plt
# +
from scipy.stats import norm
# Display a 2D manifold of the digits
n = 15 # 15 × 15 숫자의 그리드를 출력합니다
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# 싸이파이 ppf 함수를 사용하여 일정하게 떨어진 간격마다 잠재 변수 z의 값을 만듭니다
# 잠재 공간의 사전 확률은 가우시안입니다
grid_x = norm.ppf(np.linspace(0.05, 0.95, n))
grid_y = norm.ppf(np.linspace(0.05, 0.95, n))
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]])
z_sample = np.tile(z_sample, batch_size).reshape(batch_size, 2)
x_decoded = decoder.predict(z_sample, batch_size=batch_size)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure, cmap='Greys_r')
plt.show()
# -
# 샘플링된 숫자의 그리드는 다른 숫자 클래스 사이에서 완벽하게 연속된 분포를 보여줍니다. 잠재 공간의 한 경로를 따라서 한 숫자가 다른 숫자로 자연스럽게 바뀝니다. 이 공간의 특정 방향은 어떤 의미를 가집니다. 예를 들어 '6으로 가는 방향', '9로 가는 방향' 등입니다.
|
8.4-generating-images-with-vaes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: data_mining
# language: python
# name: data_mining
# ---
# + [markdown] id="UnTZE3HF8f05"
# # 13장. 나이브 베이즈 (NaiveBayes) 과제
# + [markdown] id="dYJxWp6j8npp"
# ## 1. 데이터 읽기
# -
# ### 1.1 SpamAssassin 데이터셋 다운 로드
# + id="lbb41k9n9QAE"
from io import BytesIO
import requests
import tarfile
import os
from scratch.machine_learning import split_data
BASE_URL = "https://spamassassin.apache.org/old/publiccorpus/"
FILES = ["20021010_easy_ham.tar.bz2",
"20021010_hard_ham.tar.bz2",
"20021010_spam.tar.bz2"]
OUTPUT_DIR = 'spam_data'
if os.path.exists(OUTPUT_DIR) is False:
for filename in FILES:
content = requests.get(f"{BASE_URL}/{filename}").content
fin = BytesIO(content)
with tarfile.open(fileobj=fin, mode='r:bz2') as tf:
tf.extractall(OUTPUT_DIR)
# -
# ### 1.2 메세지 클래스 정의
# + id="QiuEkgoAVCyT"
from typing import NamedTuple
class Message(NamedTuple):
text: str
is_spam: bool
# -
# ### 1.3 이메일 본문 디코딩
# +
from email.parser import Parser
def decode_email(msg_str):
p = Parser()
message = p.parsestr(msg_str)
decoded_message = ''
for part in message.walk():
if part.get_content_type() not in ('text/plain', 'text/html'): continue
charset = part.get_content_charset()
part_str = part.get_payload(decode=1)
try:
decoded_message += part_str.decode(charset)
except:
decoded_message += str(part_str)
return decoded_message
# -
# ### 1.3 이메일 텍스트 읽기 (Q)
# 이메일의 제목과 본문 텍스트를 읽어서 Message 타입을 만들고 데이터 리스트를 생성하시오.
# + id="dIrBCKg3Wnl7"
import glob
import email
from typing import List
def read_emails(include_body : bool = False) -> List[Message]:
# modify the path to wherever you've put the files
path = 'spam_data/*/*'
data: List[Message] = []
# glob.glob returns every filename that matches the wildcarded path
for filename in glob.glob(path):
is_spam = "ham" not in filename
# There are some garbage characters in the emails, the errors='ignore'
# skips them instead of raising an exception.
with open(filename, errors='ignore') as email_file:
raw_email = email_file.read()
# your code
msgobj = email.message_from_string(raw_email)
body = decode_email(raw_email)
message = msgobj['Subject'] or ""
message = message + " " + body
data.append(Message(message, is_spam))
return data
# -
include_body = True
data = read_emails(include_body= True)
print("읽은 email 개수 :", len(data))
# ## 2. NLTK 설치 및 테스트
# ### 2.1 NLTK설치 및 리소스 다운로드
# ! pip install nltk
import nltk
nltk.download()
# ### 2.1 단어 토큰화 및 어간 추출 테스트
# #### 단어 토큰화
from nltk.tokenize import TreebankWordTokenizer
text="This was not the map we found in Billy Bones's chest, but an accurate copy, complete in all things--names and heights and soundings--with the single exception of the red crosses and the written notes."
tokenizer=TreebankWordTokenizer()
words = tokenizer.tokenize(text)
print("tokens : ", words)
# #### 불용어
from nltk.corpus import stopwords
stopwords_set = set(stopwords.words('english'))
print("stopwords : ", stopwords_set)
# #### 어간 추출
from nltk.stem import PorterStemmer
s = PorterStemmer()
stem_words = [s.stem(w) for w in words]
print("stem tokens : ", len(stem_words), stem_words)
print("")
stem_words_wo_stopwords = [s.stem(w) for w in words if w not in stopwords_set]
print("stem tokens without stopwords: ",
len(stem_words_wo_stopwords),
stem_words_wo_stopwords)
# ### 2.3 토큰화 함수 (Q)
# Treebank Tokenizer를 사용해서 어간 추출 및 불용어 제거를 해보자.
# + id="Ny6lEE8S7o7w"
from nltk.tokenize import TreebankWordTokenizer
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
from typing import Set
def tokenize(text: str) -> Set[str]:
# your code
tokenizer = TreebankWordTokenizer()
words = tokenizer.tokenize(text)
stopwords_set = set(stopwords.words('english'))
s = PorterStemmer()
words = [s.stem(w) for w in words if w not in stopwords_set]
return set(words) # remove duplicates.
# -
# ## 3. 나이브 베이즈 분류기
# + [markdown] id="AfyIAKvLUzGl"
# ### 3.1 NaiveBayesClassifier (Q)
# 단어의 최소 빈도수를 설정해서 그 이하로 나오는 단어는 무시하도록 _thresholding_tokens 함수 작성하시오
# + id="XrYMT3FEU2mP"
from typing import List, Tuple, Dict, Iterable
import math
from collections import defaultdict
import matplotlib.pyplot as plt
class NaiveBayesClassifier:
def __init__(self, k: float = 0.5) -> None:
self.k = k # smoothing factor
self.tokens: Set[str] = set()
self.token_spam_counts: Dict[str, int] = defaultdict(int)
self.token_ham_counts: Dict[str, int] = defaultdict(int)
self.spam_messages = self.ham_messages = 0
def train(self,
messages: Iterable[Message],
threshold: int = 0,
verbos : bool = True) -> None:
self._count_tokens(messages)
del_spam_count, del_ham_count = self._thresholding_tokens(messages, threshold)
if verbos :
print(del_spam_count, "tokens are deleted in spams ")
print(del_ham_count, "tokens are deleted in hams ")
print("spam ", self.spam_messages)
print("ham ", self.ham_messages)
print("token", len(self.tokens))
print("spam token", len(self.token_spam_counts))
print("ham token", len(self.token_ham_counts))
print("======= token probabilities ======= ")
self.print_token_probilities()
def _count_tokens(self, messages: Iterable[Message]) -> None:
for message in messages:
# Increment message counts
if message.is_spam:
self.spam_messages += 1
else:
self.ham_messages += 1
# Increment word counts
for token in tokenize(message.text):
if message.is_spam:
self.token_spam_counts[token] += 1
else:
self.token_ham_counts[token] += 1
def _thresholding_tokens(self,
messages: Iterable[Message],
threshold: int = 0) -> Tuple[int, int]:
del_spam_count = 0
del_ham_count = 0
# your code
for message in messages:
for token in tokenize(message.text):
if(self.token_spam_counts[token]<= threshold):
#del self.token_spam_counts[token]
#del_spam_count += 1
self.token_spam_counts.pop(token)
del_spam_count += 1
else:
self.tokens.add(token)
if(self.token_ham_counts[token]<=threshold):
#del self.token_ham_counts[token]
#del_ham_count += 1
self.token_ham_counts.pop(token)
del_ham_count += 1
else:
self.tokens.add(token)
return del_spam_count, del_ham_count
def print_token_probilities(self, count=10):
for token in self.tokens:
p_token_spam, p_token_ham = self._probabilities(token)
print(token, "(spam:", p_token_spam, "ham:", p_token_ham, ")")
count -= 1
if count == 0 : return
def token_histogram(self):
plt.figure(figsize=(15,8))
plt.subplot(2, 1, 1)
n, bins, patches = plt.hist(self.token_spam_counts.values(),
200,
facecolor="#2E495E",
edgecolor=(0, 0, 0))
plt.title("Spam words")
plt.xlabel("")
plt.ylabel("Word Count")
plt.subplot(2, 1, 2)
n, bins, patches = plt.hist(self.token_ham_counts.values(),
200,
facecolor="#2E495E",
edgecolor=(0, 0, 0))
plt.title("Ham words")
plt.xlabel("")
plt.ylabel("Word Count")
plt.show()
def _probabilities(self, token: str) -> Tuple[float, float]:
"""returns P(token | spam) and P(token | not spam)"""
spam = self.token_spam_counts[token]
ham = self.token_ham_counts[token]
p_token_spam = (spam + self.k) / (self.spam_messages + 2 * self.k)
p_token_ham = (ham + self.k) / (self.ham_messages + 2 * self.k)
return p_token_spam, p_token_ham
def token_histogram(self):
plt.figure(figsize=(15,8))
plt.subplot(2, 1, 1)
n, bins, patches = plt.hist(self.token_spam_counts.values(),
200,
facecolor="#2E495E",
edgecolor=(0, 0, 0))
plt.title("Spam words")
plt.xlabel("")
plt.ylabel("Word Count")
plt.subplot(2, 1, 2)
n, bins, patches = plt.hist(self.token_ham_counts.values(),
200,
facecolor="#2E495E",
edgecolor=(0, 0, 0))
plt.title("Ham words")
plt.xlabel("")
plt.ylabel("Word Count")
plt.show()
def predict(self, text: str) -> float:
text_tokens = tokenize(text)
log_prob_if_spam = log_prob_if_ham = 0.0
# Iterate through each word in our vocabulary.
for token in self.tokens:
prob_if_spam, prob_if_ham = self._probabilities(token)
# If *token* appears in the message,
# add the log probability of seeing it;
if token in text_tokens:
log_prob_if_spam += math.log(prob_if_spam)
log_prob_if_ham += math.log(prob_if_ham)
# otherwise add the log probability of _not_ seeing it
# which is log(1 - probability of seeing it)
else:
log_prob_if_spam += math.log(1.0 - prob_if_spam)
log_prob_if_ham += math.log(1.0 - prob_if_ham)
prob_if_spam = math.exp(log_prob_if_spam)
prob_if_ham = math.exp(log_prob_if_ham)
try :
posterior = prob_if_spam / (prob_if_spam + prob_if_ham)
except ZeroDivisionError:
posterior = 0
return posterior
# + [markdown] id="nLcGR34JWsq-"
# ### 3.2 모델 훈련
# + id="QgNxx5sM7v7Z"
import random
from scratch.machine_learning import split_data
random.seed(0) # just so you get the same answers as me
train_messages, test_messages = split_data(data, 0.75)
model = NaiveBayesClassifier()
model.train(train_messages, 15)
model.token_histogram()
# + [markdown] id="SEfBwdtiW0jl"
# ### 3.3 예측 및 성능 평가
# -
# #### 예측
# + colab={"base_uri": "https://localhost:8080/"} id="zD1zHTB6WwwN" outputId="d36cafe4-5447-4d40-e65d-abfed6a77832"
from collections import Counter
predictions = [(message, model.predict(message.text))
for message in test_messages]
# -
# #### 혼동 행렬
# +
# Assume that spam_probability > 0.5 corresponds to spam prediction
# and count the combinations of (actual is_spam, predicted is_spam)
confusion_matrix = Counter((message.is_spam, spam_probability > 0.5)
for message, spam_probability in predictions)
print(confusion_matrix)
# -
# #### 정확도, 정밀도, 재현율 F1점수 (Q)
# 혼동 행렬 결과를 이용해서 정확도, 정밀도, 재현율 F1점수를 계산해 보시오.
# +
from scratch.machine_learning import accuracy, precision, recall, f1_score
# your code
tp = confusion_matrix.get((True, True))
tn = confusion_matrix.get((False, False))
fp = confusion_matrix.get((True, False))
fn = confusion_matrix.get((False, True))
a = accuracy(tp,fp,fn,tn)
p = precision(tp,fp,fn,tn)
r = recall(tp,fp,fn,tn)
f = f1_score(tp,fp,fn,tn)
print("accuracy: ", a)
print("precision: ", p)
print("recall: ", r)
print("f1_score: ", f)
#print(list(confusion_matrix))
# + [markdown] id="fCQ-lqiiW4D0"
# ### 3.4 스팸과 햄을 대표하는 단어 확인
# + colab={"base_uri": "https://localhost:8080/"} id="oTBcHk7RXCEE" outputId="8791d3be-72d5-4945-83c5-ee3bf9cd0261"
def p_spam_given_token(token: str, model: NaiveBayesClassifier) -> float:
# We probably shouldn't call private methods, but it's for a good cause.
prob_if_spam, prob_if_ham = model._probabilities(token)
return prob_if_spam / (prob_if_spam + prob_if_ham)
words = sorted(model.tokens, key=lambda t: p_spam_given_token(t, model))
print("spammiest_words", words[-10:])
print("hammiest_words", words[:10])
|
13. NaiveBayes_Homework_Student.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cpp
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: C++17
// language: C++17
// name: xcpp17
// ---
// # CS1 Review: Basic concepts & C++ fundamentals
// - Note: use your installed C++ compiler or online compilers in case C++ kernel crashes on this notebook or doesn't work in some cases:
// - [https://repl.it/](https://repl.it/)
// - [https://coliru.stacked-crooked.com/](https://coliru.stacked-crooked.com/)
// - [http://cpp.sh](http://cpp.sh/)
//
//
// ## Table of Contents
//
// - [Fundamental concepts](#concepts)
// - [Fundamental types](#types)
// - [Variables](#variables)
// - [Type casting](#casting)
// - [Input/Output](#io)
// - [Output formatting](#format)
// - [Functions](#functions)
// - [Unit test](#unittest)
// - [String data](#string)
// - [Escape sequences](#escape)
// - [Operators](#operators)
// - [Unary operators](#unary)
// - [Binary operators](#binary)
// - [Bitwise operators](#bitwise)
// - [Ternary operator](#ternary)
// - [Other operators](#other)
// - [Math functions](#math)
// - [Conditionals](#conditionals)
// - [One-way selector](#oneway)
// - [Two-way selector](#twoway)
// - [Multi-way selector](#multiway)
// - [Switch statement](#switch)
// - [Loops](#loop)
// - [for loop](#for)
// - [range-based for loop](#range)
// - [while loop](#while)
// - [do while loop](#dowhile)
// - [Arrays](#arrays)
// - [2D Arrays](#2darrays)
// <a id="concepts"></a>
// ## Fundamental concepts/building blocks
// - Data types and variables
// - Input/Output
// - Math operations
// - Decision/Conditionals
// - Loops
// ## Headers and helper functions
// - run include headers and helper function cells right below if Kernel crashes or is restarted
// +
// headers and namespace required in this notebook demo codes
#include <iostream> //cin, cout
#include <cstdio> //printf
#include <cstring> // funciton to work with cstring
#include <string> // string functions
#include <fstream> // file io
#include <iomanip> // output formatting
using namespace std;
// -
// <a id="types"></a>
// ## fundamental data types
// https://en.cppreference.com/w/cpp/language/types
// - void : type with an empty set of values
// - bool : true or false
// - int : integer/whole number
// - signed int : signed (positive and negative) representation - default
// - unsigned int : unsigned (only positive) representation
// - short : target type will have width of atleast 16 bits
// - long : width of at least 32 bits
// - long long : width of at least 64 bits
// - size_t : unsigned int type
// - int32_t : signed int 32
// - int64_t : signed int 64
// - char : signed char representation
// - float : single precision float (32 bit)
// - double : double precision (64 bit)
// - long double: extended precision floating point type
//
// - No fundadamental type available to work with string data (array of characters or buffer)
// <a id='variables'></a>
// + [markdown] heading_collapsed=true
// ## variables
// - identifier or named memory location that allows us to store data
// - syntax to declare a variable:
// ```c++
// type varName;
// ```
// - know the rules of naming identifiers
// + hidden=true
// declaring variables
int x, y, z;
string buffer;
float test1, test2, test3;
// + hidden=true
// variable declaration and initialization
// = assignment operator;
bool a = true;
char b = 'Z';
short c = 100;
int d = -2000000000;
unsigned int dd = 23232; // must be positive value only!
long e = 2000000000;
long long f = 123456789;
size_t g = 111; //same as unsigned long
int64_t h = 2345;
float i = 123.1234567;
double j = 1234.123456789;
long double k = 12112.1212121211121;
string l = "some string";
// + hidden=true
cout << "sizeof(bool) = " << 8*sizeof(bool) << " bits." << endl;
// printf("sizeof(b) = %lu\n", sizeof(b)*8); doesn't work!
cout << "sizeof(b) = " << 8*sizeof(b) << " bits." << endl;
cout << "sizeof(short) = " << 8*sizeof(short) << " bits." << endl;
cout << "sizeof(int) = " << 8*sizeof(int) << " bits." << endl;
cout << "sizeof(unsigned int) = " << 8*sizeof(unsigned int) << " bits." << endl;
cout << "sizeof(long) = " << 8*sizeof(long) << " bits." << endl;
cout << "sizeof(long long) = " << 8*sizeof(long long) << " bits." << endl;
cout << "sizeof(size_t) = " << 8*sizeof(size_t) << " bits." << endl;
cout << "sizeof(int32_t) = " << 8*sizeof(int32_t) << " bits." << endl;
cout << "sizeof(int64_t) = " << 8*sizeof(int64_t) << " bits." << endl;
cout << "sizeof(float) = " << 8*sizeof(float) << " bits." << endl;
cout << "sizeof(double) = " << 8*sizeof(double) << " bits." << endl;
cout << "sizeof(long double) = " << 8*sizeof(long double) << " bits." << endl;
cout << "sizeof(string) = " << 8*sizeof(string) << " bits." << endl;
// + [markdown] hidden=true
// <a id='casting'></a>
// + [markdown] heading_collapsed=true
// ## type casting
// https://en.cppreference.com/w/cpp/string/basic_string
// - converting one type into another if possible
// - stoi(), stol(), stoll() : converts a string to a signed int
// - stoul(), stoull() : converts a string to unsigned int
// - stof(), stod(), stold() : converts a string to float
// - to_string() : converts an int or float to string
// + hidden=true
int id = stoi("111");
float PI = stof("3.1416");
string strNum = to_string(1000.99);
// + hidden=true
int num = stoi("1234");
cout << num+10;
// + hidden=true
float price = stof("10.99");
cout << price*10;
// + hidden=true
strNum = to_string(100.99);
cout << strNum + "99" << endl;
// + [markdown] hidden=true
// <a id='io'></a>
// + [markdown] heading_collapsed=true
// ## input/output
// - standard input/output
// - iostream: cin, cout
// - getline - read the whole line (including \\n) into a string
// - \\n is read and discarded
// - cstdio: printf, scanf
//
// - file input/output
// - fstream, ifstream, ofstream
// - steps working with files:
// 1. declare file handlers
// 2. open file
// 3. check if file opened successfully
// 4. read from or write to file
// 5. close file
// + hidden=true
int fileio() {
ifstream fin;
string line;
fin.open("README.md");
if (!fin)
cout << "file couldn't be opened!" << endl;
else {
while(!fin.eof()) {
getline(fin, line);
cout << line << endl;
}
}
return 0;
}
// + hidden=true
fileio();
// + [markdown] hidden=true
// <a href="format"></a>
// + [markdown] heading_collapsed=true
// ## output formatting
// - iomanip - https://en.cppreference.com/w/cpp/header/iomanip
// - hex, oct, fixed and scientific formats to display float values
// - showpoints
// + hidden=true
cout << fixed << setprecision(2) << 19.19999 << endl;
cout << hex << showbase << "hex 16 = " << 16 << " oct 8 = " << oct << 8 << endl << dec;
cout << setfill('*') << setw(10) << right << "hi " << left << setw(15) << "there!" << endl;
// + [markdown] hidden=true
// <a id='functions'></a>
// -
// ## functions
// - sub-routine/sub-program/procedure
// - burrowed from math/algebra concept: $y = f(x) = 2x^2 + 3x +10$
// - block of code identified by a single identifier
// - two steps:
// 1. define function
// 2. call function
// - defination syntax:
//
// ```c++
// type functionName(type1 para1, type2& para2, ...) {
// /* block of code */
// return;
// }
// ```
// - call syntax:
// ```c++
// functionName(arg1, arg2, ...);
// ```
// - helps break problems into sub-problems
// - helps code reuse and code abstraction (hiding implementation details)
// - function can call many other functions
// - two ways to pass data to a function: by value and by reference
// - fruitful function can return answer/value from function
// - fruitful functions can be automatically tested
// - void functions do not return a value; values printed are usually manually tested
int add(int a, int b) {
return a+b;
}
int num1 = 100;
int num2 = -50;
cout << add(num1, num2) << endl;
// <a id='unittest'></a>
// ## unittest
// https://en.cppreference.com/w/cpp/error/assert
// - automatic testing of functions
// - use assert function defined in assert.h or cassert header file
#include <cassert>
//#include <assert.h>
assert(add(99, 1) == 100);
assert(add(100, 200) == 400); // this should give assertion error but doesn't work here...
// try it here: https://coliru.stacked-crooked.com/
// <a id='string'></a>
// + [markdown] heading_collapsed=true
// ## string data
// https://en.cppreference.com/w/cpp/string/basic_string
// - two ways to work with string:
// 1. C string - array of char type
// 2. C++ string - Abstract Data Type (ADT);
// + [markdown] hidden=true
// <a id="cstring"></a>
// + [markdown] hidden=true
// ### C string
// - array of characters
// - must be \\0 (null terminated) to prevent from buffer-overrun
// - many limitations while manipulating c string
// - must learn to mitigate buffer overflow vulnerabiliy
// ```c++
// char name[size];
// ```
// + hidden=true
#include <cstring>
// + hidden=true
// declare c-string
char name[20];
// + hidden=true
strncpy(name, "John\0", 5);
cout << name << endl;
cout << strlen(name) << endl;
// + hidden=true
// declare and initialize c-string
char word[] = "Hello";
// + hidden=true
cout << word << endl;
cout << "len of word = " << strlen(word) << endl;
// + [markdown] hidden=true
// <a id="cppstring"></a>
// + [markdown] hidden=true
// ### C++ string
// - must include string header file
// - not fundamental type; but ADT (Abstract Data Type); user-defined type that's part of library
// ```c++
// string varName;
// ```
// + hidden=true
string phrase;
// + hidden=true
phrase = "There may be a needle in the stack of stack of haystacks!";
// + hidden=true
cout << phrase.length() << endl;
cout << phrase[0] << endl;
// cout << phrase.find("needle", 0);
// https://en.cppreference.com/w/cpp/string/basic_string/find
// + hidden=true
// loop throuch each char at a time
for (auto c: phrase)
cout << c << " ";
// + hidden=true
// declare and initialize
string phrase1 = "Another phrase!"
// + [markdown] hidden=true
// <a href="escape"></a>
// -
// ## escape sequences
// https://en.cppreference.com/w/cpp/language/escape
// - used to represent certain special characters within string literals
//
// | character | description
// | --- | --- |
// | \\ | backslash
// | \\' | single quote
// | \\" | double quote
// | \\n | new line - line feed
// | \\r | carriage return
// | \t | horizontal tab
// | \\v | vertical tab
// | \\b | backspace
//
char q = '\'';
cout << q;
string sent = "\"Oh no!\", exclaimed Jill. \"Jack broke my bike!\"";
cout << sent;
// <a id="operators"></a>
// ## Operators
// - operators and precedence rule: https://en.cppreference.com/w/cpp/language/operator_precedence
//
// - arithmetic operators: https://en.cppreference.com/w/cpp/language/operator_arithmetic
// <a id="unary"></a>
// ## unary operators
//
// | Operator | Symbol | Syntax | Operation |
// |--- | --- | --- | --- |
// | positive | + | +100 | positive 100 (default) |
// | negative | - | -23.45 | negative 23.45 |
// <a id="binary"></a>
// ## binary operators
// - take two operands
// - follows PEMDAS rule of precedence
//
// | Operator | Symbol | Syntax | Operation |
// |--- | --- | --- | --- |
// | add | + | x + y | add the value of y with the value of x
// | subtract | - | x - y | subtract y from x |
// | multiply | * | x * y | multiply x by y |
// | divide | / | x / y | divide x by y (int division if x and y are both ints) |
// | modulo | % | x % y | remainder when
// <a id="bitwise"></a>
// ## binary bitwise operators
// - https://www.learncpp.com/cpp-tutorial/38-bitwise-operators/
//
// | Operator | Symbol | Syntax | Operation |
// |------| ------ | ---- | ---- |
// |bitwise left shift | << | x << y | all bits in x shifted left y bits; multiplication by 2
// |bitwise right shift | >> | x >> y | all bits in x shifted right y bits; division by 2
// bitwise NOT | ~ | ~x | all bits in x flipped
// |bitwise AND | & | x & y | each bit in x AND each bit in y
// |bitwise OR | \| | x \| y | each bit in x OR each bit in y
// bitwise XOR | ^ | x ^ y | each bit in x XOR each bit in y
cout << " bitwise and &" << endl;
cout << (1 & 1) << endl;
cout << (1 & 0) << endl;
cout << (0 & 1) << endl;
cout << (0 & 0) << endl;
cout << "bitwise or | " << endl;
cout << (1 | 1) << endl;
cout << (1 | 0) << endl;
cout << (0 | 1) << endl;
cout << (0 | 0) << endl;
cout << "bitwise not ~" << endl;
cout << ~(1|1) << endl;
cout << ~0 << endl;
cout << "bitwise xor ^" << endl;
cout << (1 ^ 1) << endl;
cout << (1 ^ 0) << endl;
cout << (0 ^ 1) << endl;
cout << (0 ^ 0) << endl;
cout << (1 << 10); // pow(2, 10)
cout << (1024 >> 10);
// <a id="ternary"></a>
// ## Ternary conditional operator (? :)
// - syntax:
// ```c++
// (condition) ? TrueValue : FalseValue;
// ```
int number1, number2, larger;
number1 = 10;
number2 = 20;
larger = (number1 > number2) ? number1 : number2;
cout << "larger = " << larger << endl;
// <a id="other"></a>
// ## Other operators
// - scope resolution operator: ::
// - std::string, std::cin
// - can create your own namespace : http://www.cplusplus.com/doc/tutorial/namespaces/
// - increment/decrement (pre and post): ++, --
// - compound assignments: +=, -=, *=, /-, %=, <<=, >>=, &=, ^=, |=
// <a id="math"></a>
// ## Math functions
// - cmath library for advanced math operations: https://en.cppreference.com/w/cpp/header/cmath
// - ceil, floor, round, sqrt, pow, abs, log, sin, cos, tan
// <a id='conditionals'></a>
// ## conditionals - control flow
// - select a block of code to execute based on some condition
// - add logic to the code as if your code is thinking and making a decision
// - use boolean expression that evaluates to true or false
// - use comparision operators ( == , != , <=, >= ) to compare values/expressions that will provide true or false or (yes or no) result
// - use logical operators (&&, ||) to formulate compound logical expression
// - three types:
// 1. one-way selector
// 2. two-way selector
// 3. multi-way selector
// - one selector type can be nested inside another!
// <a id='oneway'></a>
// + [markdown] heading_collapsed=true
// ### one way selector
//
// ```c++
// if (expression == true) {
// /* execute code... */
// }
// ```
// + hidden=true
// one way selector
bool execute = false;
if (execute)
cout << "this block executed!" << endl;
cout << "done!"
// + [markdown] hidden=true
// <a id='twoway'></a>
// + [markdown] heading_collapsed=true
// ### two way selector
//
// ```c++
// if (expression == true) {
// /* execute this block */
// }
// else {
// /* otherwise, execute this block */
// }
// ```
// + hidden=true
// two way selector
// test if a given number is even or odd
bool isEven(int n) {
if (n%2 == 0)
return true;
else
return false;
}
// + hidden=true
int someNum;
// + hidden=true
someNum = 11;
if (isEven(someNum))
cout << someNum << " is even!";
else
cout << someNum << " is odd!";
// + [markdown] hidden=true
// <a id='multiway'></a>
// + [markdown] heading_collapsed=true
// ### multi-way selector
//
// ```c++
// if (expression1 == true) {
// /* execute this block and continue after else block */
// }
// else if (expression2 == true) {
// /* execute this block and continue after else block */
// }
// else if (expression3 == true) {
// /* execute this block and continue after else block*/
// }
// ...
// else {
// /* if no condition is evaluated true, by default execute
// this block
// */
// }
// ```
// + hidden=true
int day;
// + hidden=true
// multiway selector
day = 0;
if (day == 0) {
cout << "Sunday" << endl;
cout << "Yay!! it's a weekend!\n";
}
else if (day == 1)
cout << "Monday";
else if (day == 2)
cout << "Tuesday";
else if (day == 3)
cout << "Wednesday";
else if (day == 4)
cout << "Thursday";
else if (day == 5) {
cout << "Friday";
cout << "Almost weekend!";
}
else {
cout << "Saturday" << endl;
cout << "Yay!! it's a weekend!\n";
}
cout << "done..." << endl;
// + [markdown] hidden=true
// <a id='switch'></a>
// -
// ### swtich statment
// https://en.cppreference.com/w/cpp/language/switch
// - works on integral data/expression to compare its value with many cases
// - similar to multi-way selector are more efficient and adds readability
//
// ```c++
// switch (expression) {
// case value1:
// //...
// break;
// case value2:
// case value3:
// //...
// break;
// default:
// //...
// }
// ```
enum Colors
{
COLOR_BLACK,
COLOR_WHITE,
COLOR_RED,
COLOR_GREEN,
COLOR_BLUE
};
void printColor(Colors color) {
switch (color) {
case COLOR_BLACK:
std::cout << "Black";
break;
case COLOR_WHITE:
std::cout << "White";
break;
case COLOR_RED:
std::cout << "Red";
break;
case COLOR_GREEN:
std::cout << "Green";
break;
case COLOR_BLUE:
std::cout << "Blue";
break;
default:
std::cout << "Unknown";
break;
}
}
Colors favColor;
favColor = COLOR_BLACK;
printColor(favColor);
// <a id='loop'></a>
// ## loops - control flows
// - repeatedly execute a block of code over-again with a different result
// - be careful of infinite loop!
// - `break` and `continue` keywords can be used inside loop
// - `break` : breaks the loop immidiately ignoring all the trailing codes and execution continues after loop body
// - `continue` : continues to the next iteration ignoring all the trailing codes inside loop
// - four types of loop structures
// 1. for loop
// 2. range based for loop
// 3. while loop
// 4. do while
// <a id='for'></a>
// ### for loop
// https://en.cppreference.com/w/cpp/language/for
// ```c++
// for(init; condition; update) {
// // statements
// }
// ```
// - order of execution:
// 1. init; only one
// 2. condition
// 3. statements
// 4. update
// 5. repeat from step 2
for (int i=1; i<=20; i++) {
if (i%2 == 0)
cout << i << " ";
}
// <a id='range'></a>
// ### range-based for loop
// https://en.cppreference.com/w/cpp/language/range-for
// ```c++
// for(range_declaraion: range_expression) {
// // statements
// }
// ```
for (auto num: {1, 2, 3, 4, 100})
cout << num << " ";
string hello = "Hello World";
for (char ch: hello)
cout << ch << "-";
// <a id='while'></a>
// ### while loop
// https://en.cppreference.com/w/cpp/language/while
// - Executes statement(s) repeatedly, until the value of condition becomes false.
// - The test takes place before each iteration.
//
// ```c++
// while (condition) {
// // statements
// }
// ```
int k;
k = 0;
while (k <= 20) {
if (k%2 == 0)
cout << k << " ";
k += 1; // DO NOT FORGET TO UPDATE LOOP VARIABLE TO AVOID INFINITE LOOP!!!
}
// <a id='dowhile'></a>
// + [markdown] heading_collapsed=true
// ### do while loop
// https://en.cppreference.com/w/cpp/language/do
// - executes statement(s) repeatedly, until the value of condition becomes false.
// - the test takes place after each iteration.
//
// ```c++
// do {
// // statements
// } while (condition);
// ```
// + hidden=true
int MAX_TIMES;
int times;
// + hidden=true
times = 0;
MAX_TIMES = 20;
do {
cout << times << " ";
times ++; // DO NOT FORGET TO UPDATE LOOP VARIABLE TO AVOID INFINITE LOOP!!!
break;
} while(times <= MAX_TIMES);
// + [markdown] hidden=true
// <a id='arrays'></a>
// + [markdown] heading_collapsed=true
// ## arrays
// - container that stores 1 or more similar data called elements
// - use array when you need to store large number of data values as declaring individual variable for each variable is not desireable or not even possible!
// - size of the array has to be known and is fixed
// - use 0-based index to access each element stored in array
// - array is passed by reference ONLY to a function
// - array can't be returned from a function
// - aggregate operations such as IO, assignment, comparision are not allowed
// - syntax:
// ```c++
// type arrayName[const_size];
// ```
// + hidden=true
int tests[10];
float prices[] = {1, 2, 3, 100.99};
string names[2] = {"John", "James"};
// + hidden=true
tests
// + hidden=true
prices
// + hidden=true
names
// + hidden=true
tests[0] = 100;
tests[9] = 75;
tests
// + hidden=true
prices = {2, 3, 4, 5}
// + hidden=true
cout << prices[10] << endl;
// + [markdown] hidden=true
// <a id='2darrays'></a>
// + [markdown] heading_collapsed=true
// ## 2-D arrays
// - row-major 2-d arrays
// - syntax:
// ```c++
// type name[rowSize][colSize];
// ```
// + hidden=true
int matrix[4][4] = {{1, 2, 3, 4}, {10, 20, 30, 40}, {100, 200, 300, 400}, {1, 1, 1, 1}};
// + hidden=true
matrix
// + hidden=true
matrix[0][0] = matrix[2][0]*matrix[3][0]
// + hidden=true
matrix
// + hidden=true
for(int i=0; i<4; i++) {
cout << "[ ";
for(int j=0; j< 4; j++) {
cout << matrix[i][j] << ", ";
}
cout << "]" << endl;
}
// + hidden=true
|
CS1-Review.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# +
data = pd.read_csv('C:\\Users\\RAM\\Downloads\\03. Pandas\\Datasets/employee.csv')
print(data.shape)
# -
pd.set_option('max_Columns', 35)
#pd.set_option('max_rows', 10000) -> to set maximum number of rows(10000 is the number of rows we set)
data.head()
data.columns
# ## Groupby
data[['Age','Department']].groupby(['Department']).agg(['min','max','mean'])
data[['Department','Age']].groupby(by = ['Department']).agg(['mean'])
data[['Department','Age']].groupby(by = ['Department']).agg(['max'])
data[['Department','Age']].groupby(by = ['Department']).agg(['min'])
data[['Department','EducationField',
'MonthlyRate']].groupby(by= ['Department','EducationField']).agg('mean')
data[['EducationField',
'Department','MonthlyRate']].groupby(by = ['EducationField',
'Department']).agg('mean')
# ## Pivot table
# +
# let's make a pivot table for the department and their mean ages
data.pivot_table(values ='Age', index = 'Department', aggfunc = 'mean')
# -
data.pivot_table(values ='Age', index = 'Department', aggfunc = ['mean', 'min', 'max'])
data.pivot_table(values = ['MonthlyRate','DailyRate'],
index = ['Department','EducationField'],
aggfunc = ['max','min','count'])
data[['MonthlyRate',
'Department']].groupby(['Department']).agg('mean').sort_values(by =
'MonthlyRate',ascending = False)
# ## Crosstab
x = pd.crosstab(data['Department'], data['EducationField'])
x = pd.DataFrame(x)
x
|
Groupby, Pivot table and crosstab.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import ccxt
import datetime
from backtesting import Strategy
from backtesting.lib import crossover
# +
# Example OHLC daily data for Google Inc.
from backtesting.test import GOOG
GOOG.tail()
# +
exchange = ccxt.kraken()
BTCUSD = exchange.fetch_ohlcv("BTC/USD")
BTCUSD = pd.DataFrame(BTCUSD)
BTCUSD.columns = (["Date Time", "Open", "High", "Low", "Close", "Volume"])
def parse_dates(ts):
return datetime.datetime.fromtimestamp(ts/1000.0)
BTCUSD["Date Time"] = BTCUSD["Date Time"].apply(parse_dates)
BTCUSD = BTCUSD.set_index('Date Time')
BTCUSD.head()
# -
def SMA(values, n):
"""
Return simple moving average of `values`, at
each step taking into account `n` previous values.
"""
return pd.Series(values).rolling(n).mean()
def SmoothedHeikinAshi(df):
pd.DataFrame(df)
df['HA_Close']=(df.Open + df.High + df.Low +df.Close )/4
idx = df.index.name
df.reset_index(inplace=True)
for i in range(0, len(df)):
if i == 0:
df.set_value(i, 'HA_Open', ((df.get_value(i, 'Open') + df.get_value(i, 'Close')) / 2))
else:
df.set_value(i, 'HA_Open', ((df.get_value(i - 1, 'HA_Open') + df.get_value(i - 1, 'HA_Close')) / 2))
if idx:
df.set_index(idx, inplace=True)
df['HA_High']=df[['HA_Open','HA_Close','High']].max(axis=1)
df['HA_Low']=df[['HA_Open','HA_Close','Low']].min(axis=1)
return df
# +
from backtesting.lib import crossover
class SmaCross(Strategy):
# Define the two MA lags as *class variables*
# for later optimization
length = 10
length2 = 10
def init(self):
# Precompute the two moving averages
self.ha = self.I(SmoothedHeikinAshi, self.data)
self.sma = self.I(SMA, self.data.Close, self.length)
def next(self):
# If sma1 crosses above sma2, close any existing
# short trades, and buy the asset
if crossover(self.ha, self.sma):
self.position.close()
self.buy()
# Else, if sma1 crosses below sma2, close any existing
# long trades, and sell the asset
elif crossover(self.sma, self.ha):
self.position.close()
self.sell()
# -
def next(self):
if (self.sma[-2] < self.ha[-2] and
self.sma[-1] > self.ha[-1]):
self.position.close()
self.buy()
elif (self.sma[-2] > self.ha[-2] and # Ugh!
self.sma[-1] < self.ha[-1]):
self.position.close()
self.sell()
# +
from backtesting import Backtest
bt = Backtest(BTCUSD, SmaCross, cash=100_000, commission=.002)
stats = bt.run()
stats
# -
bt.plot()
stats = bt.optimize(n1=range(5, 30, 5),
n2=range(10, 70, 5),
maximize='Equity Final [$]',
constraint=lambda param: param.n1 < param.n2)
stats
stats._strategy
bt.plot(plot_volume=False, plot_pl=False)
stats.tail()
stats['_equity_curve']
stats['_trades']
|
.ipynb_checkpoints/Backtest.py-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="bSg5U4D5I35S"
# [](https://colab.research.google.com/github/JorisRoels/deep-learning-biology/blob/main/exercises/solutions/2020-dlb-1-neural-networks-solution.ipynb)
#
# # Exercise 1: Neural Networks
#
# In this notebook, we will be using neural networks to identify enzyme sequences from protein sequences.
#
# The structure of these exercises is as follows:
#
# 1. [Import libraries and download data](#scrollTo=ScagUEMTMjlK)
# 2. [Data pre-processing](#scrollTo=ohZHyOTnI35b)
# 3. [Building a neural network with PyTorch](#scrollTo=kIry8iFZI35y)
# 4. [Training & validating the network](#scrollTo=uXrEb0rTI35-)
# 5. [Improving the model](#scrollTo=o76Hxj7-Mst5)
# 6. [Understanding the model](#scrollTo=Ult7CTpCMxTi)
#
# This notebook is largely based on the research published in:
#
# <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., <NAME>., & <NAME>. (2018). DEEPre: Sequence-based enzyme EC number prediction by deep learning. Bioinformatics, 34(5), 760–769. https://doi.org/10.1093/bioinformatics/btx680
# + [markdown] id="ScagUEMTMjlK"
# ## 1. Import libraries and download data
# Let's start with importing the necessary libraries.
# + executionInfo={"elapsed": 1152, "status": "ok", "timestamp": 1607183794439, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="S1oGi88ZU8eN"
import pickle
import numpy as np
import random
import os
import matplotlib.pyplot as plt
plt.rcdefaults()
import pandas as pd
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.manifold import TSNE
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from progressbar import ProgressBar, Percentage, Bar, ETA, FileTransferSpeed
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.utils.data as data
from torch.utils.data import DataLoader
from torchvision import datasets
import gdown
import zipfile
import os
# + [markdown] id="yIPng9wbV-Zs"
# As you will notice, Colab environments come with quite a large library pre-installed. If you need to import a module that is not yet specified, you can add it in the previous cell (make sure to run it again). If the module is not installed, you can install it with `pip`.
#
# To make your work reproducible, it is advised to initialize all modules with stochastic functionality with a fixed seed. Re-running this script should give the same results as long as the seed is fixed.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 1463, "status": "ok", "timestamp": 1607183794755, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="8OOFPFLiV-mh" outputId="664cfd92-aed4-46c4-9cde-0d5a8c699082"
# make sure the results are reproducible
seed = 0
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# run all computations on the GPU if available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print('Running computations with %s' % torch.device(device))
if torch.cuda.is_available():
print(torch.cuda.get_device_properties(device))
# + [markdown] id="PjfnM2ffU9G0"
# We will now download the required data from a public Google Drive repository. The data is stored as a zip archive and automatically extracted to the `data` directory in the current directory.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 3144, "status": "ok", "timestamp": 1607183796442, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="4Ilt9ZM3I35T" outputId="95afa272-c1e8-4bbb-e2cf-9b2ae73215ba"
# fields
url = 'http://data.bits.vib.be/pub/trainingen/DeepLearning/data-1.zip'
cmp_data_path = 'data.zip'
# download the compressed data
gdown.download(url, cmp_data_path, quiet=False)
# extract the data
zip = zipfile.ZipFile(cmp_data_path)
zip.extractall('')
# remove the compressed data
os.remove(cmp_data_path)
# + [markdown] id="ohZHyOTnI35b"
# ## 2. Data pre-processing
#
# The data are protein sequences and stored in binary format as pickle files. However, we encode the data to a binary matrix $X$ where the value at position $(i,j)$ represents the absence or presence of the protein $i$ in the sequence $j$:
#
# $$
# X_{i,j}=\left\{
# \begin{array}{ll}
# 1 \text{ (protein } i \text{ is present in sequence } j \text{)}\\
# 0 \text{ (protein } i \text{ is not present in sequence } j \text{)}
# \end{array}
# \right.
# $$
#
# The corresponding labels $y$ are also binary, they separate the enzyme from the non-enzyme sequences:
#
# $$
# y_{j}=\left\{
# \begin{array}{ll}
# 1 \text{ (sequence } j \text{ is an enzyme)}\\
# 0 \text{ (sequence } j \text{ is not an enzyme)}
# \end{array}
# \right.
# $$
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 21358, "status": "ok", "timestamp": 1607183814660, "user": {"displayName": "Jor<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="4hJjZQEGI35f" outputId="7fa7a1ec-50d6-43ac-864f-e9daf73c45cb"
def encode_data(f_name_list, proteins):
with open(f_name_list,'rb') as f:
name_list = pickle.load(f)
encoding = []
widgets = ['Encoding data: ', Percentage(), ' ', Bar(), ' ', ETA()]
pbar = ProgressBar(widgets=widgets, maxval=len(name_list))
pbar.start()
for i in range(len(name_list)):
single_encoding = np.zeros(len(proteins))
if name_list[i] != []:
for protein_name in name_list[i]:
single_encoding[proteins.index(protein_name)] = 1
encoding.append(single_encoding)
pbar.update(i)
pbar.finish()
return np.asarray(encoding, dtype='int8')
# specify where the data is stored
data_dir = 'data-1'
f_name_list_enzymes = os.path.join(data_dir, 'Pfam_name_list_new_data.pickle')
f_name_list_nonenzyme = os.path.join(data_dir, 'Pfam_name_list_non_enzyme.pickle')
f_protein_names = os.path.join(data_dir, 'Pfam_model_names_list.pickle')
# load the different proteins
with open(f_protein_names,'rb') as f:
proteins = pickle.load(f)
num_proteins = len(proteins)
# encode the sequences to a binary matrix
enzymes = encode_data(f_name_list_enzymes, proteins)
non_enzymes = encode_data(f_name_list_nonenzyme, proteins)
# concatenate everything together
X = np.concatenate([enzymes, non_enzymes], axis=0)
# the labels are binary (1 for enzymes, 0 for non-enzymes) and are one-hot encoded
y = np.concatenate([np.ones([22168,1]), np.zeros([22168,1])], axis=0).flatten()
# print a few statistics
print('There are %d sequences with %d protein measurements' % (X.shape[0], X.shape[1]))
print('There are %d enzyme and %d non-enzyme sequences' % (enzymes.shape[0], non_enzymes.shape[0]))
# + [markdown] id="VChZ6dD9I35l"
# Here is a quick glimpse in the data. For a random selection of proteins, we plot the amount of times it was counted in the enzyme and non-enzyme sequences.
# + colab={"base_uri": "https://localhost:8080/", "height": 279} executionInfo={"elapsed": 22475, "status": "ok", "timestamp": 1607183815783, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="8alfRhgtI35n" outputId="85863012-c7f8-4dfd-f2ee-92474f530365"
# selection of indices for the proteins
inds = np.random.randint(num_proteins, size=20)
proteins_subset = [proteins[i] for i in inds]
# compute the sum over the sequences
enzymes_sum = np.sum(enzymes, axis=1)
non_enzymes_sum = np.sum(non_enzymes, axis=1)
# plot the counts on the subset of proteins
df = pd.DataFrame({'Enzyme': enzymes_sum[inds], 'Non-enzyme': non_enzymes_sum[inds]}, index=proteins_subset)
df.plot.barh()
plt.xlabel('Counts')
plt.ylabel('Protein')
plt.show()
# + [markdown] id="jMI8G95EI35r"
# To evaluate our approaches properly, we will split the data in a training and testing set. We will use the training set to train our algorithms and the testing set as a separate set of unseen data to evaluate the performance of our models.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 22476, "status": "ok", "timestamp": 1607183815787, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="h_t-j1gWI35s" outputId="88e75116-25f8-4c96-a556-c0d79db7ab77"
test_ratio = 0.5 # we will use 50% of the data for testing
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=test_ratio, random_state=seed)
print('%d sequences for training and %d for testing' % (x_train.shape[0], x_test.shape[0]))
# + [markdown] id="kIry8iFZI35y"
# ## 3. Building a neural network with PyTorch
#
# Now, we have to implement the neural network and train it. For this, we will use the high-level deep learning library [PyTorch](https://pytorch.org/). PyTorch is a well-known, open-source, machine learning framework that has a comprehensive set of tools and libraries and accelerates research prototyping. It also supports transparant training of machine learning models on GPU devices, which can benefit runtimes significantly. The full documentation can be found [here](https://pytorch.org/docs/stable/index.html).
#
# Let's start by defining the architecture of neural network.
#
# **Exercise**: build a network with a single hidden layer with PyTorch:
# - The first layer will be a [fully connected layer](https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear) with [relu](https://pytorch.org/docs/stable/nn.functional.html?highlight=relu#torch.nn.functional.relu) activation that transforms the input features to a 512 dimensional (hidden) feature vector representation.
# - The output layer is another [fully connected layer](https://pytorch.org/docs/stable/generated/torch.nn.Linear.html#torch.nn.Linear) that transforms the hidden representation to a class probability distribution.
# - Print the network architecture to validate your architecture.
# - Run the network on a random batch of samples. Note that you have to transfer the numpy ndarray type inputs to floating point [PyTorch tensors](https://pytorch.org/docs/stable/tensors.html).
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 22474, "status": "ok", "timestamp": 1607183815789, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="dhB6nbkXI35z" outputId="8933194b-fe5e-40cf-f9dd-4dc4491b67ed"
# define the number of classes
num_classes = 2
# The network will inherit the Module class
class Net(nn.Module):
def __init__(self, n_features=512):
super(Net, self).__init__()
# first (input) layer
self.hidden = nn.Linear(num_proteins, n_features)
# final layer that generates the output
self.output = nn.Linear(n_features, num_classes)
def forward(self, x):
# forward propagation of the network, we only use relu activation in the first two layers
x = F.relu(self.hidden(x))
x = self.output(x)
return x
# initialize the network and print the architecture
n_features = 512
net = Net(n_features=n_features)
print(net)
# run the network on a batch of samples
# note that we have to transfer the numpy ndarray type inputs to float torch tensors
inputs = torch.from_numpy(x_test[:4]).float()
outputs = F.softmax(net(inputs), dim=1)
print(outputs.detach().numpy())
# + [markdown] id="WRgIWPOwI354"
# The summary gives an overview of the network architecture. Note that the network is also randomly initialized and therefore returns random outputs for a set of inputs, i.e. there is a 50% chance that a sequence is (non-)enzyme.
#
# **Exercise**: manually compute the amount of parameters in this network and verify this with PyTorch.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 22470, "status": "ok", "timestamp": 1607183815790, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="n8l0jAmOI356" outputId="cd3acbbe-89e9-4fc0-9f86-e08337da8786"
n_params = sum(p.numel() for p in net.parameters() if p.requires_grad)
print('There are %d trainable parameters in the network' % n_params)
# + [markdown] id="uXrEb0rTI35-"
# ## 4. Training and validating the network
#
# To train this network, we still need two things: a loss function and an optimizer. For the loss function, we will use the commonly used cross entropy loss for classification. For the optimizer, we will use stochastic gradient descent (SGD) with a learning rate of 0.1.
# + executionInfo={"elapsed": 22468, "status": "ok", "timestamp": 1607183815792, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="8H8AJGfjI35_"
learning_rate = 0.1
loss_fn = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=learning_rate)
# + [markdown] id="Bz8b8lTkI36C"
# Great. Now it's time to train our model and implement backpropagation. Fortunately, PyTorch makes this relatively easy. A single optimization iteration consists of the following steps:
# 1. Sample a batch from the training data: we use the convenient [data loading](https://pytorch.org/tutorials/beginner/data_loading_tutorial.html) system provided by PyTorch. You can simply enumerate over the `DataLoader` objects.
# 2. Set all gradients equal to zero. You can use the [`zero_grad()`](https://pytorch.org/docs/stable/generated/torch.nn.Module.html?highlight=zero_grad#torch.nn.Module.zero_grad) function.
# 3. Feed the batch to the network and compute the outputs.
# 4. Compare the outputs to the labels with the loss function. Note that the loss function itself is a `Module` object as well and thus can be treated in a similar fashion as the network for computing outputs.
# 5. Backpropagate the gradients w.r.t. the computed loss. You can use the [`backward()`](https://pytorch.org/docs/stable/autograd.html?highlight=backward#torch.autograd.backward) function for this.
# 6. Apply one step in the optimization (e.g. gradient descent). For this, you will need the optimizer's [`step()`](https://pytorch.org/docs/stable/optim.html#torch.optim.Optimizer.step) function.
#
# **Exercise**: train the model with the following settings:
# - Train the network for 50 epochs
# - Use a mini batch size of 1024
# - Track the performance of the classifier by additionally providing the test data. We have already provided a validation function that tracks the accuracy. This function expects a network module, a binary matrix $X$ of sequences, their corresponding labels $y$ and the batch size (for efficiency reasons) as inputs.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 176286, "status": "ok", "timestamp": 1607183969613, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="jkpn9G8AI36D" outputId="d09b905a-ab30-4b54-a18c-610ded4d27b7"
# dataset useful for sampling (and many other things)
class ProteinSeqDataset(data.Dataset):
def __init__(self, data, labels):
self.data = data
self.labels = labels
def __getitem__(self, i):
return self.data[i], self.labels[i]
def __len__(self):
return len(self.data)
def validate_accuracy(net, X, y, batch_size=1024):
# evaluation mode
net.eval()
# save predictions
y_preds = np.zeros((len(y)))
for b in range(len(y) // batch_size):
# sample a batch
inputs = X[b*batch_size: (b+1)*batch_size]
# transform to tensors
inputs = torch.from_numpy(inputs).float().to(device)
# forward call
y_pred = net(inputs)
y_pred = F.softmax(y_pred, dim=1)[:, 1] > 0.5
# save predictions
y_preds[b*batch_size: (b+1)*batch_size] = y_pred.detach().cpu().numpy()
# remaining batch
b = len(y) // batch_size
inputs = torch.from_numpy(X[b*batch_size:]).float().to(device)
y_pred = net(inputs)
y_pred = F.softmax(y_pred, dim=1)[:, 1] > 0.5
y_preds[b*batch_size:] = y_pred.detach().cpu().numpy()
# compute accuracy
acc = accuracy_score(y, y_preds)
return acc
# implementation of a single training epoch
def train_epoch(net, loader, loss_fn, optimizer):
# set the network in training mode
net.train()
# keep track of the loss
loss_cum = 0
cnt = 0
for i, data in enumerate(loader):
# sample data
x, y = data
x = x.float().to(device)
y = y.long().to(device)
# set all gradients equal to zero
net.zero_grad()
# feed the batch to the network and compute the outputs
y_pred = net(x)
# compare the outputs to the labels with the loss function
loss = loss_fn(y_pred, y)
loss_cum += loss.data.cpu().numpy()
cnt += 1
# backpropagate the gradients w.r.t. computed loss
loss.backward()
# apply one step in the optimization
optimizer.step()
# compute the average loss
loss_avg = loss_cum / cnt
return loss_avg
# implementation of a single testing epoch
def test_epoch(net, loader, loss_fn):
# set the network in training mode
net.eval()
# keep track of the loss
loss_cum = 0
cnt = 0
for i, data in enumerate(loader):
# sample data
x, y = data
x = x.float().to(device)
y = y.long().to(device)
# feed the batch to the network and compute the outputs
y_pred = net(x)
# compare the outputs to the labels with the loss function
loss = loss_fn(y_pred, y)
loss_cum += loss.data.cpu().numpy()
cnt += 1
# compute the average loss
loss_avg = loss_cum / cnt
return loss_avg
def train_net(net, train_loader, test_loader, loss_fn, optimizer, epochs):
# transfer the network to the GPU
net = net.cuda()
train_loss = np.zeros((epochs))
test_loss = np.zeros((epochs))
train_acc = np.zeros((epochs))
test_acc = np.zeros((epochs))
for epoch in range(epochs):
# training
train_loss[epoch] = train_epoch(net, train_loader, loss_fn, optimizer)
train_acc[epoch] = validate_accuracy(net, x_train, y_train)
# testing
test_loss[epoch] = test_epoch(net, test_loader, loss_fn)
test_acc[epoch] = validate_accuracy(net, x_test, y_test)
print('Epoch %5d - Train loss: %.6f - Train accuracy: %.6f - Test loss: %.6f - Test accuracy: %.6f'
% (epoch, train_loss[epoch], train_acc[epoch], test_loss[epoch], test_acc[epoch]))
return train_loss, test_loss, train_acc, test_acc
# parameters
n_epochs = 50
batch_size = 1024
# build a training and testing dataloader that handles batch sampling
train_data = ProteinSeqDataset(x_train, y_train)
train_loader = DataLoader(train_data, batch_size=batch_size)
test_data = ProteinSeqDataset(x_test, y_test)
test_loader = DataLoader(test_data, batch_size=batch_size)
# start training
train_loss, test_loss, train_acc, test_acc = train_net(net, train_loader, test_loader, loss_fn, optimizer, n_epochs)
# + [markdown] id="tK7oPH6TI36P"
# Clearly, this is the time intensive part, and it becomes more challenging with larger networks or larger datasets. GPU acceleration is therefore a crucial part.
#
# The code below visualizes the learning curves: these curves illustrate how the loss on the train and test set decays over time. Additionally, we also report a similar curve for the train and test accuracy. The final accuracy is also reported.
# + colab={"base_uri": "https://localhost:8080/", "height": 298} executionInfo={"elapsed": 176284, "status": "ok", "timestamp": 1607183969616, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcRE<KEY>", "userId": "00181780506485155029"}, "user_tz": -60} id="W6fR4aCwI36Q" outputId="572c383a-53a8-4e85-835c-6089afc4476e"
def plot_learning_curves(train_loss, test_loss, train_acc, test_acc):
plt.figure(figsize=(11, 4))
plt.subplot(1, 2, 1)
plt.plot(train_loss)
plt.plot(test_loss)
plt.xlabel('epochs')
plt.ylabel('loss')
plt.legend(('Train', 'Test'))
plt.subplot(1, 2, 2)
plt.plot(train_acc)
plt.plot(test_acc)
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend(('Train', 'Test'))
plt.show()
# plot the learning curves (i.e. train/test loss and accuracy)
plot_learning_curves(train_loss, test_loss, train_acc, test_acc)
# report final accuracy
print('The model obtains an accuracy of %.2f%%' % (100*test_acc[-1]))
# + [markdown] id="xWtU0CXgI36U"
# You should achieve over 80% accuracy. There are two things we can conclude from the learning curves:
#
# - Training still requires a long time, especially if you would compare this to alternative classifiers such as random forests or support vector machines.
# - The testing curve has reached a plateau, whereas the training curve can still improve. You could increase the amount of epochs and train for a longer period, but this will not improve the test performance that much. Even worse, the performance on the test set would likely become worse! This is called overfitting: the optimization aims to maximize the performance on the training set, focuses on details in the training set and fails to generalize to new data. This is one of the biggest challenges in machine learning.
# + [markdown] id="o76Hxj7-Mst5"
# ## 5. Improving the model
#
# We will try to improve the model by improving the training time and mitigating the overfitting to some extent.
#
# **Exercise**: Improve the model by implementing the following adjustments:
# - Train the network based on [`Adam`](https://pytorch.org/docs/stable/optim.html#torch.optim.Adam) optimization instead of stochastic gradient descent. The Adam optimizer adapts its learning rate over time and therefore improves convergence significantly. For more details on the algorithm, we refer to the [original published paper](https://arxiv.org/pdf/1412.6980.pdf). You can significantly reduce the learning rate (e.g. 0.0001) and number of training epochs (e.g. 20).
# - The first adjustment to avoid overfitting is reduce the size of the network. At first sight this may seem strange because this reduces the capacity of the network. However, large networks are more likely to focus on details in the training data because of the redundant number of neurons in the hidden layer. Experiment with smaller hidden representations (e.g. 32 or 16).
# - The second adjustment to mitigate overfitting is [Dropout](https://pytorch.org/docs/stable/generated/torch.nn.Dropout.html). During training, Dropout layers randomly switch off neurons (i.e. their value is temporarily set to zero). This forces the network to use the other neurons to make an appropriate decision. At test time, the dropout layers are obviously ignored and no neurons are switched off. The amount of neurons that are switched off during training is called the dropout factor (e.g. 0.50). For more details, we refer to the [original published paper](https://jmlr.org/papers/volume15/srivastava14a/srivastava14a.pdf).
# + colab={"base_uri": "https://localhost:8080/", "height": 835} executionInfo={"elapsed": 248869, "status": "ok", "timestamp": 1607184042206, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="FtkzDTniI36V" outputId="ff51e78c-2029-4f69-c670-086f96dc78df"
# The network will inherit the Module class
class ImprovedNet(nn.Module):
def __init__(self, n_features=512, p=0.5):
super(ImprovedNet, self).__init__()
# first (input) layer
self.hidden = nn.Linear(num_proteins, n_features)
self.dropout = nn.Dropout(p=p)
# final layer that generates the output
self.output = nn.Linear(n_features, num_classes)
def forward(self, x):
# forward propagation of the network, we only use relu activation in the first two layers
x = self.dropout(F.relu(self.hidden(x)))
x = self.output(x)
return x
# initialize the network and print the architecture
n_features = 64
p = 0.75 # dropout factor
improved_net = ImprovedNet(n_features=n_features, p=p)
print(improved_net)
# reduce the learning rate
learning_rate = 0.001
n_epochs = 25
# Adam optimization
optimizer = optim.Adam(improved_net.parameters(), lr=learning_rate)
# start training
train_loss, test_loss, train_acc, test_acc = train_net(improved_net, train_loader, test_loader, loss_fn, optimizer, n_epochs)
# plot the learning curves (i.e. train/test loss and accuracy)
plot_learning_curves(train_loss, test_loss, train_acc, test_acc)
# report final accuracy
print('The model obtains an accuracy of %.2f%%' % (100*test_acc[-1]))
# + [markdown] id="R115UJfUI36Z"
# Great, that looks much better! You should achieve over 93% accuracy in significantly less training time.
#
# Of course, there are much more ways of trying to improve the model: e.g. batch normalization, regularization, increase the amount of hidden layers, etc. In what follows, we will study the most frequently used techniques. We will provide guidelines on how to use these techniques, however, it is not always guaranteed that they will improve the model.
# + [markdown] id="Ult7CTpCMxTi"
# ## 6. Understanding the model
#
# To gain more insight in the network, it can be useful to take a look to the hidden representations of the network. To do this, you have to propagate a number of samples through the first hidden layer of the network and visualize them using dimensionality reduction techniques.
#
# **Exercise**: Visualize the hidden representations of a batch of samples in 2D to gain more insight in the network's decision process:
# - Compute the hidden representation of a batch of samples. To do this, you will have to select a batch, transform this in a torch Tensor and apply the hidden and relu layer of the network on the inputs. Since these are also modules, you can use them in a similar fashion as the original network.
# - Extract the outputs of the networks as a numpy array and apply dimensionality reduction. A common dimensionality reducing method is the t-SNE algorithm.
# + colab={"base_uri": "https://localhost:8080/", "height": 265} executionInfo={"elapsed": 252025, "status": "ok", "timestamp": 1607184045368, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="Tt7F9fwZI36a" outputId="89992cf7-fd48-4454-9f09-c038f30146ef"
# select a batch of samples
n = 512
batch = x_test[:n]
batch_labels = y_test[:n]
batch = torch.from_numpy(batch).float().cuda()
# compute the hidden representation of the batch
h = F.relu(improved_net.hidden(batch))
h = h.data.cpu().numpy()
# reduce the dimensionality of the hidden representations
h_red = TSNE(n_components=2, random_state=seed).fit_transform(h)
# visualize the reduced representations and label each sample
scatter = plt.scatter(h_red[:, 0], h_red[:, 1], c=batch_labels)
plt.legend(handles=scatter.legend_elements()[0], labels=('Non-enzyme', 'Enzyme'))
plt.show()
# + [markdown] id="sN6UbAXdI36f"
# We can clearly identify two clusters that correspond to the two classes that we would like to predict. The network has optimized its neurons in order to separate these two classes as good as possible. Nevertheless, there also seem to be some positive samples located in the negative cluster and vice versa. These samples probably correspond to false positives and false negatives and are worth investigating further.
#
# Another way to analyze the network is by checking which proteins cause the highest hidden activations in enzyme and non-enzyme samples. These features are discriminative for predicting the classes.
# + colab={"base_uri": "https://localhost:8080/"} executionInfo={"elapsed": 252024, "status": "ok", "timestamp": 1607184045370, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO17HAi3vdM28rwcREixXOvi5CItNho4sxx-YCwkU=s64", "userId": "00181780506485155029"}, "user_tz": -60} id="zP1nUqHmxHyJ" outputId="56f7b903-8026-412c-9a1e-e3d28ed50e59"
# isolate the positive and negative samples
h_pos = h[batch_labels == 1]
h_neg = h[batch_labels == 0]
# compute the mean activation
h_pos_mean = h_pos.mean(axis=0)
h_neg_mean = h_neg.mean(axis=0)
# sort the mean activations
i_pos = np.argsort(h_pos_mean)
i_neg = np.argsort(h_neg_mean)
# select the highest activations
n = 5
i_pos = i_pos[-n:][::-1]
i_neg = i_neg[-n:][::-1]
print('Discriminative features that result in high activation for enzyme prediction: ')
for i in i_pos:
print(' - %s (mean activation value: %.3f)' % (proteins[i], h_pos_mean[i]))
print('Discriminative features that result in high activation for non-enzyme prediction: ')
for i in i_neg:
print(' - %s (mean activation value: %.3f)' % (proteins[i], h_neg_mean[i]))
# + [markdown] id="he0PuLhL4X_x"
# Let's hope these proteins have an interesting meaning w.r.t. enzymes from a biological point of view!
#
# Understanding how neural networks make decisions is up to this day still an unresolved problem. Especially as the amount of layers increases, the extracted features tend to become more abstract and more challenging to study. If you are interested in this domain, feel free to dig a little deeper in the Explainable AI research domain. For example, [this blogpost](https://medium.com/@shagunm1210/the-explainable-neural-network-8f95256dcddb) might be a good starting point!
|
exercises/solutions/2020-dlb-1-neural-networks-solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.12 ('py39')
# language: python
# name: python3
# ---
# +
import logging
import sys
import os
import pandas as pd
from pandas import Timestamp
# pylint: disable=import-error disable=wrong-import-position
sys.path.append(os.path.dirname(os.path.dirname(os.path.abspath("__file__"))))
print(os.path.dirname(os.path.abspath("__file__")))
import pydit
logger = pydit.setup_logging_info()
logger.info("Started")
fm= pydit.FileManager.getInstance()
fm.input_path="./demo_data/"
fm.output_path="./demo_data/"
fm.temp_path="./demo_data/"
# -
df = pd.DataFrame([
[1, 'INV-220001', Timestamp('2022-01-01 00:00:00'), 'OPEN', 35.94,''],
[2, 'INV-220002', Timestamp('2022-01-02 00:00:00'), 'OPEN', 99.99,'-5'],
[3, 'INV-220003', Timestamp('2022-01-03 00:00:00'), 'CANCELLED', 13.0,'reinbursed 10.5'],
[4, 'INV-220003', Timestamp('2022-01-04 00:00:00'), 'OPEN', float('nan'),''],
[5, 'INV-220005', Timestamp('2022-01-04 00:00:00'), 'OPEN', 204.2,''],
[6, 'INV-220006', Timestamp('2022-01-15 00:00:00'), 'OPEN', -4.2,'discount'],
[7, float('nan'), Timestamp('2022-01-06 00:00:00'), float('nan'), 0.0,'Unknown error'],
[8, 'INV-220007', Timestamp('2022-01-15 00:00:00'), 'PENDING', 50.4,''],
[9, '', pd.NaT, 'ERROR', 0.0,'Timeout Error'],
[10, 'INV-220007', Timestamp('2022-01-15 00:00:00'), 'PENDING', 50.4,'']],
columns=['id', 'ref', 'date_trans', 'status', 'amount','notes'])
df
pydit.profile_dataframe(df)
# +
pydit.check_blanks(df)
# -
# +
"""Function for performing coalesce."""
import logging
from typing import Optional, Union
import pandas as pd
logger = logging.getLogger(__name__)
def coalesce_columns(
df: pd.DataFrame,
*column_names,
target_column_name: Optional[str] = None,
default_value: Optional[Union[int, float, str]] = None,
operation=None
) -> pd.DataFrame:
if not column_names:
return df
print(column_names)
if len(column_names) < 2:
if isinstance(column_names[0],list) and len(column_names[0])>1:
column_names=column_names[0]
else:
raise ValueError("The number of columns to coalesce should be a minimum of 2.")
if isinstance(column_names, list) or isinstance(column_names, tuple):
wrong_columns = [x for x in column_names if x not in df.columns]
if wrong_columns:
raise ValueError("Columns not in the dataframe:" + " ".join(wrong_columns))
else:
raise TypeError("Please provide a list of columns")
if target_column_name:
check_types("target_column_name", target_column_name, [str])
if default_value:
check_types("default_value", default_value, [int, float, str])
if target_column_name is None:
target_column_name = column_names[0]
print("Target column name:", target_column_name)
# bfill/ffill combo is faster than combine_first
if operation is None:
outcome = (
df.filter(column_names).bfill(axis="columns").ffill(axis="columns").iloc[:, 0]
)
elif operation="concatenate":
if outcome.hasnans and (default_value is not None):
outcome = outcome.fillna(default_value)
return df.assign(**{target_column_name: outcome})
coalesce_columns(df,["status","notes"])
# -
|
examples/demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## **Task-2: Supervised Machine Learning with Python and Scikit Learn**
# Supervised Machine Learning is one of types of Machine Learning Algorithams in which we have labeled data i.e. we have the output labels,based on these output labels we try to predict the output for unknown inputs.
#
# We deal with two kind of problems in supervised learning 1)Regression and 2)Classification.
#
# In Regression problems, we have the continous values as output while in classification, we have classes as our output('good' or 'bad' etc).
#
# There are many supervised regression as well as classification algorithams out there.
#
# Here,in this section we are going to see how linear regression algorithm works in regression problem using scikit_learn library for Machine Learning.
#
# ## Linear Regression ##
# Our task is to visualise the relationship between hours fo study and percentage scores obtained.And then to predict the score where study hour is 93.5 hour.This is a simple linear regression task with two variables.
# linear regression uses the equation: Y=MX+C, where x is our feature and y is our target variable.
## importing libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
df = pd.read_csv('Hours_Scores.csv')
print('Importing data')
## taking a glance at data
df.head()
## checking the shape
df.shape
# Plotting the distribution of scores with respect to hours
df.plot(x='Hours', y='Scores', style='o')
plt.title('Hours vs Percentage_Scores')
plt.xlabel('No. of Hours Studied')
plt.ylabel('Percentage Score')
plt.show()
sns.pairplot(df)
# Here the hours and scores have linear relationship between them.
## checking the distribution of scores weather it is guassian or not
sns.distplot(df['Scores'])
# The distribution of our scores is not perfect guassian.But as we have less data it will not affect our performance much.Hence, no applying normalization or scaling.
# ## Preparing the data
# The data contains two variables one is our dependent variable(Hour) and other is independent variable or label(Scores). So we will assign them as their designation.
## getting location of feature values and target
X = df.iloc[:,:-1].values ##all the rows of all columns except the last column as that is our label
y = df.iloc[:,1].values ##the label column with all of its rows
# Now that we have our attributes and labels, the next step is to split this data into training and test sets.
# We'll do this by using Scikit-Learn's built-in train_test_split() method:
## splitting the data into train and test for checking our model
from sklearn.model_selection import train_test_split
x_train, x_valid, y_train, y_valid = train_test_split(X, y,
test_size=0.2, random_state=0)
# ## creating and training our model
# We have data for training and testing. Now we will first train our linear regression model on train dataset then will test on test dataset.
##importing our model and fitting to the training dataset
from sklearn.linear_model import LinearRegression
lgr = LinearRegression()
lgr.fit(x_train,y_train)
print('Training Completed')
# +
# Plotting the regression line
line = lgr.coef_*X+lgr.intercept_
# Plotting for the test data
plt.scatter(X, y)
plt.plot(X, line);
plt.show()
# -
# ## Making prediction
#
# We have trained our model using training dataset. Now we will predict the outputs on test dataset using the trained model.
##testing the model by making prediction on our test dataset
y_prediction = lgr.predict(x_valid)
# ## Performance Evaluating
# We have predicted the outputs on our test dataset. Now is the time to evaluate the performance of our model using r2_score, mean_squared_error and mean_absolute_error.
# We will import these metrices from scikit_learn library.
# +
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
score = r2_score(y_prediction,y_valid)
mse = mean_squared_error(y_prediction,y_valid)
mae = mean_absolute_error(y_prediction,y_valid)
print('r2_score: {}'.format(score))
print('mean_squared_error: {}'.format(mse))
print('Mean Absolute Error:',mae)
# -
# We have got the quite good performance using this simple linear regression model.
# Comparing Actual vs Predicted after combining them into a dataframe
df_label = pd.DataFrame({'Actual': y_valid, 'Predicted': y_prediction})
df_label
# Plotting the prediction with actual values
df_label.plot(x='Actual', y='Predicted',kind = 'bar')
plt.title('Actual vs predicted')
plt.xlabel('Actual scores')
plt.ylabel('Predicted Scores')
plt.show()
# We can also visualize comparison result as a bar graph
df1 = df_label.head()
df1.plot(kind='bar',figsize=(15,8))
plt.grid(which='major', linestyle='-', linewidth='0.4', color='black')
plt.grid(which='minor', linestyle=':', linewidth='0.4', color='black')
plt.show()
df_label.plot()
# ## Predicting score
#
# Now we will be predicting the scores with respect to 9.25 hours of study using our trained model.
hour = [[9.25]]
pred_score = lgr.predict(hour)
print('hour_studied: {}'.format(hour))
print('Score_prediced: {}'.format(pred_score))
# Finally, our hard work paid off! We have studied for 9.25 hours daily and got a good score of 93.69%.
# ## Lasso Regularization Model
## Training lasso regularization model
from sklearn.linear_model import Lasso
lsr = Lasso()
lsr.fit(x_train, y_train)
# making prediction using lasso
lsr_preds = lsr.predict(x_valid)
## Evaluating performance of lasso
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
r2 = r2_score(lsr_preds, y_valid)
mae_lsr = mean_absolute_error(lsr_preds, y_valid)
r2, mae_lsr
# making final prediction using lasso
hour = [[9.25]]
pred_score_lsr = lsr.predict(hour)
print('hour_studied: {}'.format(hour))
print('Score_prediced: {}'.format(pred_score_lsr))
## Comparing result with actual
check=pd.DataFrame({'Actual':y_valid,'Predicted':lsr_preds})
check.reset_index(drop=True,inplace=True)
check['Deviation']=abs(check['Actual']-check['Predicted'])
check
## Visualiazing deviation between actual vs predicted values
plt.figure(figsize=(8,5))
sns.regplot('Predicted','Actual',data=check,line_kws={'color':'green'},scatter_kws={'color':'red'},marker='*')
plt.title('Deviation In Actual v/s Predicted Values(Lasso)')
# ## Ridge Regularization Model
# +
## training ridge regularization
from sklearn.linear_model import Ridge
rgr=Ridge(alpha = 10)
rgr.fit(x_train,y_train)
# -
## making predictions using ridge
rgr_preds = rgr.predict(x_valid)
## evaluating ridge
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
r2_rgr = r2_score(rgr_preds, y_valid)
mae_rgr = mean_absolute_error(rgr_preds, y_valid)
r2_rgr, mae_rgr
## comparing ridge results with actual label
check=pd.DataFrame({'Actual':y_valid,'Predicted':rgr_preds})
check.reset_index(drop=True,inplace=True)
check['Deviation']=abs(check['Actual']-check['Predicted'])
check
## visualizing daviation betwwn actual vs predicted labels
plt.figure(figsize=(8,5))
sns.regplot('Predicted','Actual',data=check,line_kws={'color':'black'},scatter_kws={'color':'blue'},marker='*')
plt.title('Deviation In Actual v/s Predicted Values(Ridge)')
# ## Using ElasticNet Model
## Training elastic net model
from sklearn.linear_model import ElasticNet
els_net=ElasticNet(alpha=1)
els_net.fit(x_train,y_train)
## making prediction using elasticnet
els_preds = els_net.predict(x_valid)
## evaluating elastic_net
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
r2_els = r2_score(els_preds, y_valid)
mae_els = mean_absolute_error(els_preds, y_valid)
r2_els, mae_els
## comapring elastic_net predictions with actual labels
check=pd.DataFrame({'Actual':y_valid,'Predicted':els_preds})
check['Deviation']=abs(check['Actual']-check['Predicted'])
check
## visualizinng daviation between actual and predicted labels
plt.figure(figsize=(8,5))
sns.regplot('Predicted','Actual',data=check,line_kws={'color':'blue'},scatter_kws={'color':'red'},marker='*')
plt.title('Deviation In Actual v/s Predicted Values(ElasticNet)')
# ## Comparing All Models
## Comparing all the models prediction altogether with actual outputs
final=pd.DataFrame()
errs=[mae_lsr, mae_rgr, mae_els]
final['Valid']=y_valid
final['LinearRegression']=y_prediction
final['Lasso']=lsr_preds
final['Ridge']=rgr_preds
final['ElasticNet']=els_preds
# +
## plotting all the model's results to see best fitted model
N=np.arange(5)
plt.bar(N+0.35,y_valid,width=0.35,label='Actual',color='red')
plt.bar(N,y_prediction,width=0.35,label='Linear Regression',color='blue')
plt.ylabel('Scores')
plt.title('Variation In Prediction & Actual Values(Linear Regression Model)\nMAE: {}\nR2_SCORE: {}'.format(mae.round(2),score.round(2)))
plt.legend(loc='best')
plt.show()
plt.bar(N+0.35,y_valid,width=0.35,label='Actual',color='orange')
plt.bar(N,lsr_preds,width=0.35,label='Lasso',color='blue')
plt.title('Variation In Prediction & Actual(Lasso)\nMAE: {}\nR2_SCORE: {}'.format(mae_lsr.round(2),r2.round(2)))
plt.ylabel('Scores')
plt.legend(loc='best')
plt.show()
plt.bar(N+0.35,y_valid,width=0.35,label='Actual',color='red')
plt.bar(N,rgr_preds,width=0.35,label='Ridge', color = 'black')
plt.ylabel('Scores')
plt.title('Variation In Prediction & Actual Values(Ridge)\nMAE: {}\nR2_Score: {}'.format(mae_rgr.round(2),r2_rgr.round(2)))
plt.legend(loc='best')
plt.show()
plt.bar(N+0.35,y_valid,width=0.35,label='Actual',color='red')
plt.bar(N,els_preds,width=0.35,label='ElasticNet',color='yellow')
plt.ylabel('Scores')
plt.title('Variation In Prediction & Actual Values(ElasticNet)\nMAE: {}\nR2_SCORE: {}'.format(mae_els.round(2),r2_els.round(2)))
plt.legend(loc='best')
plt.show()
# -
#
# Clearly, Elastic net model is giving the relatively most accurate output with least mean_absolute error. So, We Finalize Model 4!
#
#
# ## Making Prediction Using Finalized Model
n=float(input())
result=els_net.predict([[n]])
print("After studying for {} hours, The Expected Score Should be {}".format(n,result.round(2)))
# ## Saving the model for future predictions
# +
import pickle
# Saving model to disk
pickle.dump(els_net, open('model.pkl','wb')) ## writting as model.pkl
# -
# Loading model to compare the results
model = pickle.load(open('model.pkl','rb'))
print(model.predict([[9.25]])) ## making prediction using saved model
# We have got a decent percentage score after going through diferent-different models.
# # THANKS!
|
Task_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # CORN MLP for predicting cement strength (cement_strength)
# This tutorial explains how to train a deep neural network (here: multilayer perceptron) with the CORN loss function for ordinal regression.
# ## 0 -- Obtaining and preparing the cement_strength dataset
# We will be using the cement_strength dataset from [https://github.com/gagolews/ordinal_regression_data/blob/master/cement_strength.csv](https://github.com/gagolews/ordinal_regression_data/blob/master/cement_strength.csv).
#
# First, we are going to download and prepare the and save it as CSV files locally. This is a general procedure that is not specific to CORN.
#
# This dataset has 5 ordinal labels (1, 2, 3, 4, and 5). Note that CORN requires labels to be starting at 0, which is why we subtract "1" from the label column.
# +
import pandas as pd
import numpy as np
data_df = pd.read_csv("https://raw.githubusercontent.com/gagolews/ordinal_regression_data/master/cement_strength.csv")
data_df["response"] = data_df["response"]-1 # labels should start at 0
data_labels = data_df["response"]
data_features = data_df.loc[:, ["V1", "V2", "V3", "V4", "V5", "V6", "V7", "V8"]]
print('Number of features:', data_features.shape[1])
print('Number of examples:', data_features.shape[0])
print('Labels:', np.unique(data_labels.values))
# + [markdown] tags=[]
# ### Split into training and test data
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
data_features.values,
data_labels.values,
test_size=0.2,
random_state=1,
stratify=data_labels.values)
# -
# ### Standardize features
# +
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# -
# ## 1 -- Setting up the dataset and dataloader
# In this section, we set up the data set and data loaders. This is a general procedure that is not specific to CORN.
# +
import torch
##########################
### SETTINGS
##########################
# Hyperparameters
random_seed = 1
learning_rate = 0.001
num_epochs = 20
batch_size = 128
# Architecture
NUM_CLASSES = 5
# Other
DEVICE = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print('Training on', DEVICE)
# +
from torch.utils.data import Dataset
class MyDataset(Dataset):
def __init__(self, feature_array, label_array, dtype=np.float32):
self.features = feature_array.astype(np.float32)
self.labels = label_array
def __getitem__(self, index):
inputs = self.features[index]
label = self.labels[index]
return inputs, label
def __len__(self):
return self.labels.shape[0]
# +
import torch
from torch.utils.data import DataLoader
# Note transforms.ToTensor() scales input images
# to 0-1 range
train_dataset = MyDataset(X_train_std, y_train)
test_dataset = MyDataset(X_test_std, y_test)
train_loader = DataLoader(dataset=train_dataset,
batch_size=batch_size,
shuffle=True, # want to shuffle the dataset
num_workers=0) # number processes/CPUs to use
test_loader = DataLoader(dataset=test_dataset,
batch_size=batch_size,
shuffle=False,
num_workers=0)
# Checking the dataset
for inputs, labels in train_loader:
print('Input batch dimensions:', inputs.shape)
print('Input label dimensions:', labels.shape)
break
# -
# ## 2 - Equipping MLP with a CORN layer
# In this section, we are implementing a simple MLP for ordinal regression with CORN. Note that the only specific modification required is setting the number of output of the last layer (a fully connected layer) to the number of classes - 1 (these correspond to the binary tasks used in the extended binary classification as described in the paper).
# +
class MLP(torch.nn.Module):
def __init__(self, in_features, num_classes, num_hidden_1=300, num_hidden_2=300):
super().__init__()
self.my_network = torch.nn.Sequential(
# 1st hidden layer
torch.nn.Linear(in_features, num_hidden_1, bias=False),
torch.nn.LeakyReLU(),
torch.nn.Dropout(0.2),
torch.nn.BatchNorm1d(num_hidden_1),
# 2nd hidden layer
torch.nn.Linear(num_hidden_1, num_hidden_2, bias=False),
torch.nn.LeakyReLU(),
torch.nn.Dropout(0.2),
torch.nn.BatchNorm1d(num_hidden_2),
### Specify CORN layer
torch.nn.Linear(num_hidden_2, (num_classes-1))
###--------------------------------------------------------------------###
)
def forward(self, x):
logits = self.my_network(x)
return logits
torch.manual_seed(random_seed)
model = MLP(in_features=8, num_classes=NUM_CLASSES)
model.to(DEVICE)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# -
# ## 3 - Using the CORN loss for model training
# During training, all you need to do is to use the `corn_loss` provided via `coral_pytorch`. The loss function will take care of the conditional training set processing and modeling the conditional probabilities used in the chain rule (aka general product rule).
# +
from coral_pytorch.losses import corn_loss
for epoch in range(num_epochs):
model = model.train()
for batch_idx, (features, class_labels) in enumerate(train_loader):
class_labels = class_labels.to(DEVICE)
features = features.to(DEVICE)
logits = model(features)
#### CORN loss
loss = corn_loss(logits, class_labels, NUM_CLASSES)
###--------------------------------------------------------------------###
optimizer.zero_grad()
loss.backward()
optimizer.step()
### LOGGING
if not batch_idx % 200:
print ('Epoch: %03d/%03d | Batch %03d/%03d | Cost: %.4f'
%(epoch+1, num_epochs, batch_idx,
len(train_loader), loss))
# -
# ## 4 -- Evaluate model
#
# Finally, after model training, we can evaluate the performance of the model. For example, via the mean absolute error and mean squared error measures.
#
# For this, we are going to use the `corn_label_from_logits` utility function from `coral_pytorch` to convert the probabilities back to the orginal label.
#
# +
from coral_pytorch.dataset import corn_label_from_logits
def compute_mae_and_mse(model, data_loader, device):
with torch.no_grad():
mae, mse, acc, num_examples = 0., 0., 0., 0
for i, (features, targets) in enumerate(data_loader):
features = features.to(device)
targets = targets.float().to(device)
logits = model(features)
predicted_labels = corn_label_from_logits(logits).float()
num_examples += targets.size(0)
mae += torch.sum(torch.abs(predicted_labels - targets))
mse += torch.sum((predicted_labels - targets)**2)
mae = mae / num_examples
mse = mse / num_examples
return mae, mse
# -
train_mae, train_mse = compute_mae_and_mse(model, train_loader, DEVICE)
test_mae, test_mse = compute_mae_and_mse(model, test_loader, DEVICE)
print(f'Mean absolute error (train/test): {train_mae:.2f} | {test_mae:.2f}')
print(f'Mean squared error (train/test): {train_mse:.2f} | {test_mse:.2f}')
# Note that MNIST is not an ordinal dataset (there is no order between the image categories), so computing the MAE or MSE doesn't really make sense but we use it anyways for demonstration purposes.
# ## 5 -- Rank probabilities from logits
# To obtain the rank probabilities from the logits, you can use the sigmoid function to get the conditional probabilities for each task and then compute the task probabilities via the chain rule for probabilities. Note that this is also done internally by the `corn_label_from_logits` we used above.
# +
logits = model(features)
with torch.no_grad():
probas = torch.sigmoid(logits)
probas = torch.cumprod(probas, dim=1)
print(probas)
# -
|
docs/tutorials/pure_pytorch/CORN_cement.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
#
# <a href='http://www.pieriandata.com'> <img src='../Pierian_Data_Logo.png' /></a>
# ___
# # Sentiment Analysis
# Now that we've seen word vectors we can start to investigate sentiment analysis. The goal is to find commonalities between documents, with the understanding that similarly *combined* vectors should correspond to similar sentiments.
#
# While the scope of sentiment analysis is very broad, we will focus our work in two ways.
#
# ### 1. Polarity classification
# We won't try to determine if a sentence is objective or subjective, fact or opinion. Rather, we care only if the text expresses a *positive*, *negative* or *neutral* opinion.
# ### 2. Document level scope
# We'll also try to aggregate all of the sentences in a document or paragraph, to arrive at an overall opinion.
# ### 3. Coarse analysis
# We won't try to perform a fine-grained analysis that would determine the degree of positivity/negativity. That is, we're not trying to guess how many stars a reviewer awarded, just whether the review was positive or negative.
# ## Broad Steps:
# * First, consider the text being analyzed. A model trained on paragraph-long movie reviews might not be effective on tweets. Make sure to use an appropriate model for the task at hand.
# * Next, decide the type of analysis to perform. In the previous section on text classification we used a bag-of-words technique that considered only single tokens, or *unigrams*. Some rudimentary sentiment analysis models go one step further, and consider two-word combinations, or *bigrams*. In this section, we'd like to work with complete sentences, and for this we're going to import a trained NLTK lexicon called *VADER*.
# ## NLTK's VADER module
# VADER is an NLTK module that provides sentiment scores based on words used ("completely" boosts a score, while "slightly" reduces it), on capitalization & punctuation ("GREAT!!!" is stronger than "great."), and negations (words like "isn't" and "doesn't" affect the outcome).
# <br>To view the source code visit https://www.nltk.org/_modules/nltk/sentiment/vader.html
# **Download the VADER lexicon.** You only need to do this once.
import nltk
nltk.download('vader_lexicon')
# <div class="alert alert-danger">NOTE: At the time of this writing there's a <a href='https://github.com/nltk/nltk/issues/2053'>known issue</a> with SentimentIntensityAnalyzer that raises a harmless warning on loading<br>
# <tt><font color=black> UserWarning: The twython library has not been installed.<br> Some functionality from the twitter package will not be available.</tt>
#
# This is due to be fixed in an upcoming NLTK release. For now, if you want to avoid it you can (optionally) install the NLTK twitter library with<br>
# <tt><font color=black> conda install nltk[twitter]</tt><br>or<br>
# <tt><font color=black> pip3 install -U nltk[twitter]</tt></div>
# +
from nltk.sentiment.vader import SentimentIntensityAnalyzer
sid = SentimentIntensityAnalyzer()
# -
# VADER's `SentimentIntensityAnalyzer()` takes in a string and returns a dictionary of scores in each of four categories:
# * negative
# * neutral
# * positive
# * compound *(computed by normalizing the scores above)*
a = 'This was a good movie.'
sid.polarity_scores(a)
a = 'This was the best, most awesome movie EVER MADE!!!'
sid.polarity_scores(a)
a = 'This was the worst film to ever disgrace the screen.'
sid.polarity_scores(a)
# ## Use VADER to analyze Amazon Reviews
# For this exercise we're going to apply `SentimentIntensityAnalyzer` to a dataset of 10,000 Amazon reviews. Like our movie reviews datasets, these are labeled as either "pos" or "neg". At the end we'll determine the accuracy of our sentiment analysis with VADER.
# +
import numpy as np
import pandas as pd
df = pd.read_csv('../TextFiles/amazonreviews.tsv', sep='\t')
df.head()
# -
df['label'].value_counts()
# ### Clean the data (optional):
# Recall that our moviereviews.tsv file contained empty records. Let's check to see if any exist in amazonreviews.tsv.
# +
# REMOVE NaN VALUES AND EMPTY STRINGS:
df.dropna(inplace=True)
blanks = [] # start with an empty list
for i,lb,rv in df.itertuples(): # iterate over the DataFrame
if type(rv)==str: # avoid NaN values
if rv.isspace(): # test 'review' for whitespace
blanks.append(i) # add matching index numbers to the list
df.drop(blanks, inplace=True)
# -
df['label'].value_counts()
# In this case there were no empty records. Good!
# ## Let's run the first review through VADER
sid.polarity_scores(df.loc[0]['review'])
df.loc[0]['label']
# Great! Our first review was labeled "positive", and earned a positive compound score.
# ## Adding Scores and Labels to the DataFrame
# In this next section we'll add columns to the original DataFrame to store polarity_score dictionaries, extracted compound scores, and new "pos/neg" labels derived from the compound score. We'll use this last column to perform an accuracy test.
# +
df['scores'] = df['review'].apply(lambda review: sid.polarity_scores(review))
df.head()
# +
df['compound'] = df['scores'].apply(lambda score_dict: score_dict['compound'])
df.head()
# +
df['comp_score'] = df['compound'].apply(lambda c: 'pos' if c >=0 else 'neg')
df.head()
# -
# ## Report on Accuracy
# Finally, we'll use scikit-learn to determine how close VADER came to our original 10,000 labels.
from sklearn.metrics import accuracy_score,classification_report,confusion_matrix
accuracy_score(df['label'],df['comp_score'])
print(classification_report(df['label'],df['comp_score']))
print(confusion_matrix(df['label'],df['comp_score']))
# This tells us that VADER correctly identified an Amazon review as "positive" or "negative" roughly 71% of the time.
# ## Up Next: Sentiment Analysis Project
|
NLP_COURSE/04-Semantics-and-Sentiment-Analysis/01-Sentiment-Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cv2
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import scipy.misc
'''
출처
https://github.com/inyl/my_notebook/blob/master/open_cv/image_color_cluster.ipynb
https://www.pyimagesearch.com/2014/05/26/opencv-python-k-means-color-clustering/
'''
def plot_colors(hist, centroids):
'''
initialize the bar chart representing the relative frequency of each of the colors
각 색의 빈도를 나타내는 바 차트를 초기화
'''
bar = np.zeros((50, 300, 3), dtype="uint8")
startX = 0
# loop over the percentage of each cluster and the color of each cluster
for (percent, color) in zip(hist, centroids):
# plot the relative percentage of each cluster
endX = startX + (percent * 300)
cv2.rectangle(bar, (int(startX), 0), (int(endX), 50),
color.astype("uint8").tolist(), -1)
startX = endX
# return the bar chart
return bar
def centroid_histogram(clt):
'''
# grab the number of different clusters and create a histogram
히스토그램 형식으로 색을 반환
based on the number of pixels assigned to each cluster
각 클러스터의 픽셀의 숫자를 기반으로 함
'''
numLabels = np.arange(0, len(np.unique(clt.labels_)) + 1)
(hist, _) = np.histogram(clt.labels_, bins=numLabels)
# normalize the histogram, such that it sums to one
hist = hist.astype("float")
hist /= hist.sum() # hist = hist/hist.sum()
# return the histogram
return hist
def image_color_cluster(image_path, k = 5):
image = cv2.imread(image_path)
# image의 shape을 찍어보면, height, width, channel 순으로 나옴
# channel은 RGB를 말함
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
# cv에서는 RGB가 아닌 BGR 순으로 나오기 때문에 순서를 RGB로 전환
image = image.reshape((image.shape[0] * image.shape[1], 3))
# shape의 0,1번째 즉, height와 width를 통합시킴
clt = KMeans(n_clusters = k) # 평균 알고리즘 KMeans
clt.fit(image)
hist = centroid_histogram(clt)
bar = plot_colors(hist, clt.cluster_centers_)
return bar
def dec_to_hex(color):
if color < 16:
return '0' + str(hex(int(color)).split('x')[1])
else:
return str(hex(int(color)).split('x')[1])
def read_real_color(filename):
image = cv2.imread(filename, cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
image_list = [str(list(image[i][k])) for i in range(len(image)) for k in range(len(image[0]))]
image_unique = {}
for d in image_list:
if d not in image_unique:
image_unique[d] = 1
else:
image_unique[d] += 1
import operator
icon_color_list = max(image_unique.items(), key=operator.itemgetter(1))[0]
color_R = int(icon_color_list.split('[')[1].split(']')[0].split(', ')[0])
color_G = int(icon_color_list.split('[')[1].split(']')[0].split(', ')[1])
color_B = int(icon_color_list.split('[')[1].split(']')[0].split(', ')[2])
color_R = dec_to_hex(color_R)
color_G = dec_to_hex(color_G)
color_B = dec_to_hex(color_B)
return str(color_R + color_G + color_B)
'''
이거슨 매우 위험한 코드입니다. 잘못하면 컴퓨터 터질지경
for index in range(len(path_list)):
result = image_color_cluster('./cafe_image/'+path_list[index])
scipy.misc.imsave('./cafe_color_result/'+path_list[index], result)
'''
df_cafe = pd.read_csv('final_cafe_info_with_path.csv')
# df_cafe.head()
df_cafe = df_cafe.drop('Unnamed: 0', axis=1)
df_cafe.head()
# color_list = [read_real_color(png) for n in df_cafe.index png = './cafe_color_result/' + df_cafe['파일명'][n]]
color_list = []
for n in df_cafe.index:
png = './cafe_color_result/' + df_cafe['파일명'][n]
color_list.append(read_real_color(png))
df_cafe['대표색'] = color_list
df_cafe.head()
# +
# df_cafe['대표색'].astype(hex)
# df_cafe.hist['대표색']
# -
length = [len(df_cafe['대표색'][i]) for i in df_cafe.index]
df_cafe['RGB길이'] = length
df_cafe.loc[df_cafe['RGB길이'] != 6]
df_location = pd.DataFrame()
df_location['위도'] = df_cafe['위도'].copy(deep=True)
df_location['경도'] = df_cafe['경도'].copy(deep=True)
df_location['색'] = df_cafe['대표색'].copy(deep=True)
df_location.head()
# +
from plotnine import *
(ggplot(df_location)
+ aes(x='위도', y='경도')
+ geom_point(size=5, alpha=0.6, color='#'+df_location['색'])
# + ggtitle('서울시 카페 지도')
)
# -
import googlemaps
gmaps_key = '<KEY>' # 자신의 key를 사용합니다.
gmaps = googlemaps.Client(key=gmaps_key)
# +
# help(folium.Icon)
# +
import base64
import folium
map = folium.Map(location=[df_cafe['위도'].mean(), df_cafe['경도'].mean()], zoom_start=13)
for n in df_cafe.index:
png = './cafe_color_result/' + df_cafe['파일명'][n]
encoded = base64.b64encode(open(png, 'rb').read()).decode('utf-8')
cafe_name = df_cafe['카페명'][n] + ' - ' + df_cafe['주소'][n]
html = f'<p>{cafe_name}</p> <img src="data:image/png;base64,{encoded}">'
iframe = folium.IFrame(html, width=700, height=130)
popup = folium.Popup(iframe, max_width=300)
color = '#' + df_cafe['대표색'][n]
icon = folium.Icon(icon_color=color, color='white')
folium.Marker([df_cafe['위도'][n], df_cafe['경도'][n]], popup=popup, icon=icon).add_to(map)
map
# -
|
image_cluster/.ipynb_checkpoints/code_ggplot_soryeong_ver01-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Playing with Regression
#
# This notebook will help us with testing different regression techniques, and demonstrate the diagnostic class which can be used to find the optimal parameters for COBRA.
#
# So for now we will generate a random data-set and try some of the popular regression techniques on it, after it has been loaded to COBRA.
#
# #### Imports
from pycobra.cobra import Cobra
from pycobra.diagnostics import Diagnostics
import numpy as np
# %matplotlib inline
# #### Setting up data set
# +
# setting up our random data-set
rng = np.random.RandomState(1)
# D1 = train machines; D2 = create COBRA; D3 = calibrate epsilon, alpha; D4 = testing
n_features = 20
D1, D2, D3, D4 = 200, 200, 200, 200
D = D1 + D2 + D3 + D4
X = rng.uniform(-1, 1, D * n_features).reshape(D, n_features)
Y = np.power(X[:,1], 2) + np.power(X[:,3], 3) + np.exp(X[:,10])
# Y = np.power(X[:,0], 2) + np.power(X[:,1], 3)
# training data-set
X_train = X[:D1 + D2]
X_test = X[D1 + D2 + D3:D1 + D2 + D3 + D4]
X_eps = X[D1 + D2:D1 + D2 + D3]
# for testing
Y_train = Y[:D1 + D2]
Y_test = Y[D1 + D2 + D3:D1 + D2 + D3 + D4]
Y_eps = Y[D1 + D2:D1 + D2 + D3]
# -
# ### Setting up COBRA
#
# Let's up our COBRA machine with the data.
cobra = Cobra(random_state=0, epsilon=0.5)
cobra.fit(X_train, Y_train, default=False)
# When we are fitting, we initialise COBRA with an epsilon value of $0.5$ - this is because we are aware of the distribution and 0.5 is a fair guess of what would be a "good" epsilon value, because the data varies from $-1$ to $1$.
#
# If we do not pass the $\epsilon$ parameter, we perform a CV on the training data for an optimised epsilon.
#
# It can be noticed that the `default` parameter is set as false: this is so we can walk you through what happens when COBRA is set-up, instead of the deafult settings being used.
# We're now going to split our dataset into two parts, and shuffle data points.
cobra.split_data(D1, D1 + D2, shuffle_data=True)
# Let's load the default machines to COBRA.
cobra.load_default()
# We note here that further machines can be loaded using either the `loadMachine()` and `loadSKMachine()` methods. The only prerequisite is that the machine has a valid `predict()` method.
# ## Using COBRA's machines
#
# We've created our random dataset and now we're going to use the default sci-kit machines to see what the results look like.
query = X_test[9].reshape(1, -1)
cobra.machines_
cobra.machines_['lasso'].predict(query)
cobra.machines_['tree'].predict(query)
cobra.machines_['ridge'].predict(query)
cobra.machines_['random_forest'].predict(query)
# ## Aggregate!
#
# By using the aggregate function we can combine our predictors.
# You can read about the aggregation procedure either in the original COBRA paper or look around in the source code for the algorithm.
#
# We start by loading each machine's predictions now.
cobra.load_machine_predictions()
cobra.predict(query)
Y_test[9]
# ### Optimizing COBRA
#
# To squeeze the best out of COBRA we make use of the COBRA diagnostics class. With a grid based approach to optimizing hyperparameters, we can find out the best epsilon value, number of machines (alpha value), and combination of machines.
# Let's check the MSE for each of COBRAs machines:
cobra_diagnostics = Diagnostics(cobra, X_test, Y_test, load_MSE=True)
cobra_diagnostics.machine_MSE
# This error is bound by the value $C\mathscr{l}^{\frac{-2}{M + 2}}$ upto a constant $C$, which is problem dependant. For more details, we refer the user to the original [paper](http://www.sciencedirect.com/science/article/pii/S0047259X15000950).
cobra_diagnostics.error_bound
# ### Playing with Data-Splitting
#
# When we initially started to set up COBRA, we split our training data into two further parts - $D_k$, and $D_l$.
# This split was done 50-50, but it is upto us how we wish to do this.
# The following section will compare 20-80, 60-40, 50-50, 40-60, 80-20 and check for which case we get the best MSE values, for a fixed Epsilon (or use a grid).
cobra_diagnostics.optimal_split(X_eps, Y_eps)
# What we saw was the default result, with the optimal split ratio and the corresponding MSE. We can do a further analysis here by enabling the info and graph options, and using more values to split on.
split = [(0.05, 0.95), (0.10, 0.90), (0.20, 0.80), (0.40, 0.60), (0.50, 0.50), (0.60, 0.40), (0.80, 0.20), (0.90, 0.10), (0.95, 0.05)]
cobra_diagnostics.optimal_split(X_eps, Y_eps, split=split, info=True, graph=True)
# ### Alpha, Epsilon and Machines
#
# The following are methods to idetify the optimal epislon values, alpha values, and combination of machines.
# The grid methods allow for us to predict for a single point the optimal alpha/machines and epsilon combination.
#
# #### Epsilon
#
# The epsilon paramter controls how "strict" cobra should behave while choosing the points to aggregate.
cobra_diagnostics.optimal_epsilon(X_eps, Y_eps, line_points=100)
# #### Alpha
#
# The alpha parameter decides how many machines must a point be picked up by before being added to an aggregate. The default value is 4.
cobra_diagnostics.optimal_alpha(X_eps, Y_eps, info=True)
# In this particular case, the best performance is obtained by seeking consensus over all 4 machines.
# #### Machines
#
# Decide which subset of machines to select for the aggregate.
cobra_diagnostics.optimal_machines(X_eps, Y_eps, info=True)
cobra_diagnostics.optimal_alpha_grid(X_eps[0], Y_eps[0], line_points=100)
cobra_diagnostics.optimal_machines_grid(X_eps[0], Y_eps[0], line_points=100)
# Increasing the number of line points helps in finding a better optimal value. These are the results for the same point. The MSEs are to the second value of the tuple.
#
# With 10:
# ((('ridge', 'random_forest', 'lasso'), 1.1063905961135443), 0.96254542159345469)
#
# With 20:
# ((('tree', 'random_forest'), 0.87346626008964035), 0.53850941611803993)
#
# With 50:
# ((('ridge', 'tree'), 0.94833479666875231), 0.48256303899450931)
#
# With 100:
# ((('ridge', 'tree', 'random_forest'), 0.10058096328304948), 0.30285776885759158)
#
# With 200:
# ((('ridge', 'tree', 'lasso'), 0.10007553130675276), 0.30285776885759158)
# pycobra is Licensed under the MIT License - https://opensource.org/licenses/MIT
|
docs/notebooks/regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ##### Algorithms implemented in Python from the book "Discrete Mathematics" by Dossey, Otto, Spence and Eynden
#
import numpy as np
import random
from sympy import *
# ### Chapter 1
# #### Algorithm for evaluating $x^n$
# +
def eval(x, n):
P=x
k=1
while k<n:
P*=x
k+=1
return P
eval(3, 4)
# -
# #### Polynomial Evaluation Algorithm: computes $P(x)=a_nx^n + a_{n-1}x^{n-1} +...+ a_0$, given the non-negative integer $n$ and real numbers $x$, $a_0$, $a_1$, ..., $a_n$
def P(x, a):
# a is the list of the constants: a0, a1, ..., an
S=a[0]
k=1
n=len(a)-1
while k<=n:
S+=a[k]*x**k
k+=1
return S
P(2, [4, 3, -2, 5])
# #### Horner's Polynomial Evaluation Algorithm
def HP(x, a):
n=len(a)-1
S=a[n]
k=1
while k<=n:
S=x*S+a[n-k]
k+=1
return S
HP(2, [4, 3, -2, 5])
# #### Next Subset Algorithm
def NS(a):
"""a is a string of 0s and 1s corresponding to a subset of n elements"""
n=len(a)
a=list(a)
k=n-1
while k>=0 and a[k]=='1':
k-=1
if k>=0:
a[k]='1'
for j in range(k+1, n):
a[j]='0'
return ''.join(a)
else: return 'The string contains all 1s'
NS('110')
# #### Bubble Sort Algorithm
# +
def BS(a):
"""A is a list of unsorted real numbers"""
n=len(a)-1
for j in range(n):
for k in range(n-1, j-1, -1):
if a[k+1]<a[k]:
t=a[k+1]
a[k+1]=a[k]
a[k]=t
return a
BS([1.2, 3.2, 9.0, 3.2, 0.5, 0.43, 8.44])
# -
# #### Revised Polynomial Evaluation Algorithm
def RP(x, a):
S=a[0]
y=1
k=1
n=len(a)-1
while k<=n:
y=x*y
S+=y*a[k]
k+=1
return S
RP(2, [4, 3, -2, 5])
# ### Chapter 3
# #### The Euclidean Algorithm
# +
def gcd(m, n):
"""m and n are both non-negative integers"""
while n!=0:
m, n = n, m%n
return m
gcd(427, 154)
# -
# #### The Extended Euclidean Algorithm
def exgcd(m, n):
r=[m, n]
x=[1, 0]
y=[0, 1]
i=1
while r[i]!=0:
i+=1
q=r[i-2]//r[i-1]
x+=[x[i-2]-q*x[i-1],]
y+=[y[i-2]-q*y[i-1],]
r+=[r[i-2]%r[i-1],]
return (r[i-1], x[i-1], y[i-1])
exgcd(101, 1120)
# #### The Modular Exponentiation Algorithm: Given positive integers P, E and n, this algorithm computes the remainder when $P^E$ is divided by $n$.
# +
def ME(P, E, n):
r2=1
p=P
e=E
while e!=0:
Q=e//2
R=e%2
r1=p**2%n
if R==1: r2=(r2*p)%n
p=r1
e=Q
return r2
ME(582, 621,1189)
# -
# #### Check Matrix Row Decoding Algorithm
# +
def CMRD(codeword, generatorMatrix):
A=generatorMatrix
w=codeword
k=len(A)
n=len(A[0])
J=np.copy(A[:, k:])
A_star=np.append(J, np.eye(len(J[0]), dtype=int), axis=0)
print(A_star)
s=(w.dot(A_star))%2
print(s)
if sum(s)==0: return w[:k]
if list(s) in A_star.tolist():
i=np.where(np.all(A_star==s,axis=1))
w[i]=(w[i]+1)%2
return w[:k]
if list(s) not in A_star.tolist(): return "unknown"
A=np.array(([1, 0, 0, 1, 0, 1, 0], [0, 1, 0, 1, 1, 0, 1], [0, 0, 1, 0, 1, 1, 1]))
w1=np.array([0, 0, 1, 0, 1, 1, 1])
w2=np.array([1, 0, 1, 1, 1, 0, 0])
w3=np.array([0, 1, 1, 1, 0, 1, 0])
w4=np.array([1, 0, 0, 0, 1, 1, 1])
w5=np.array([1, 1, 0, 0, 0, 1, 0])
#CMRD(w5, A)
#ex 3.6, 29
B=np.array(([1, 0, 1, 1, 0], [0, 1, 0, 1, 1])) # Generator matrix
c=np.array([1, 0, 1, 1, 0]) # received word
CMRD(c, B)
# -
# ### Chapter 4
# #### Euler circuit Algorithm
# +
V=['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'J']
Ed={'a':['A', 'B'], 'c':['B', 'E'], 'f':['E', 'D'], 'b':['D', 'A'], 'd':['E', 'C'], 'e':['C', 'F'], 'g':['F', 'E'], 'h':['E', 'G'], 'k':['H', 'G'], 'm':['H', 'J'], 'l':['J', 'H'], 'j':['H', 'E']}
def EulerCircuit(V, Ed):
E1=list(Ed.keys())
E2=[Ed[i] for i in Ed]
U=random.choice(V)
R=[i for i in E2 if U in i]
#print(R)
st=random.choice(R)
ind=E2.index(st)
C={}
#print(C)
if st[0]!=U: st=st[::-1]
C[E1[ind]]=st
del E1[ind]
del E2[ind]
#print(E1)
#print(E2)
while st[1]!=U:
u=st[1]
R=[i for i in E2 if u in i]
st=random.choice(R)
ind=E2.index(st)
if st[0]!=u: st=st[::-1]
C[E1[ind]]=st
del E1[ind]
del E2[ind]
while len(E1)!=0 and len(E2)!=0:
E21=sympy.flatten(E2)
E3=list(C.keys())
E4=[C[i] for i in C]
E41=sympy.flatten(E4)
L=[] # store the vertices whose edges are not listed in C
L=list(set([i for i in E41 if E21.count(i)>0]))
#print(L)
u= random.choice(L)
R=[i for i in E2 if u in i]
st=random.choice(R)
ind=E2.index(st)
P={}
if st[0]!=u: st=st[::-1]
P[E1[ind]]=st
del E1[ind]
del E2[ind]
while st[1]!=u:
u1=st[1]
R=[i for i in E2 if u1 in i]
st=random.choice(R)
ind=E2.index(st)
if st[0]!=u1: st=st[::-1]
P[E1[ind]]=st
del E1[ind]
del E2[ind]
x=list(P.keys())
y=[P[i] for i in P]
z=[i for i in E4 if i[1]==u]
#print(E3)
#print(E4)
#print(x, y, z)
ra=random.choice(z)
k1=E4.index(ra)
E3[k1+1:k1+1]=x
E4[k1+1:k1+1]=y
C={}
for i in range(len(E3)): C[E3[i]]=E4[i]
#print(P)
return C
#EulerCircuit(V, Ed)
Ed={'a':['U', 'V'], 'b':['U', 'V'], 'c':['U', 'A'], 'd':['A', 'V'], 'e':['U', 'V']}
V=['A', 'U', 'V']
print(Ed)
EulerCircuit(V, Ed)
# -
# #### Breadth-First Search Algorithm
# +
#Ed=[['S', 'A'], ['S', 'B'], ['A', 'E'], ['E', 'C'], ['A', 'C'], ['C', 'B'], ['F', 'E'], ['F', 'H'], ['C', 'H'], ['H', 'I'], ['I', 'J'], ['J', 'G'], ['G', 'D'], ['D', 'B']]
#V=['S', 'A', 'B', 'E', 'F', 'H', 'I', 'J', 'G', 'D', 'B', 'C']
#start='S'
#end='I'
Ed=[['S', 'A'], ['S', 'D'], ['D', 'B'], ['G', 'D'], ['B', 'G'], ['E', 'C'], ['E', 'F'], ['C', 'F'], ['E', 'G'], ['G', 'H'], ['F', 'H'], ['F', 'T'], ['H', 'I'], ['T', 'I']]
V=['S', 'A', 'D', 'B', 'G', 'E', 'C', 'F', 'G', 'H', 'I', 'T']
start='S'
end='T'
def BFSA(Ed, V, start, end):
st=[start]
L={st[0]:[0, '-']}
k=0
while len(V)>1:
k+=1
st1=[]
for s in st:
del V[V.index(s)]
I=[j for j in Ed if (j[0]==s or j[1]==s)]
for i in I:
del Ed[Ed.index(i)]
I1=[i[::-1] if i[1]==s else i for i in I]
I2=[i for i in I1 if (i[0] in st and i[1] not in st) or (i[0] not in st and i[1] in st) ]
for [i, j] in I2:
L[j]=[k, s]
st1+=[j, ]
st=list(set(st1))
print(L)
path=end
pr=L[end][1]
while pr!='-':
path+=pr
pr=L[pr][1]
return path[::-1]
BFSA(Ed, V, start, end)
# -
# #### Dijkstra's Algorithm
# +
#Ed=[['S', 'A', 3], ['S', 'B', 1], ['C', 'A', 2], ['C', 'B', 3], ['D', 'B', 5], ['A', 'B', 1], ['C', 'E', 3], ['D', 'C', 1], ['D','E', 1]]
#V=['A', 'S', 'B', 'D', 'C', 'E']
#st='S'
#end='E'
##Ex 4.3, 6
#Ed=[['S', 'C', 2], ['S', 'E', 4], ['E', 'C', 1], ['C', 'F', 3], ['C', 'D', 5], ['F', 'E', 1], ['F', 'G', 2], ['D', 'F', 3], ['D', 'G', 1], ['D', 'H',1], ['G', 'H', 3], ['A', 'H', 3], ['E', 'J', 2], ['G', 'J', 3]]
#V=['S', 'C', 'D', 'E', 'F', 'G', 'H', 'A', 'J']
#st='S'
#end='A'
##Ex 4.3, 7
Ed=[['S', 'C', 3], ['S', 'E', 2], ['S', 'H', 1], ['C', 'E', 1], ['E', 'H', 1], ['F', 'C', 3], ['F', 'H', 2], ['F', 'D', 2], ['C', 'D', 2], ['F', 'B', 3], ['B', 'H', 5], ['G', 'D', 1], ['G', 'B', 1], ['G', 'A', 2], ['A', 'D', 5], ['A', 'B', 4]]
V=['S', 'C', 'E', 'H', 'D', 'F', 'G', 'B', 'A']
st='S'
end='A'
def DA(Ed, V, st, end):
"""Each of the entries in Ed has form: ['vertex1', 'vertex2', weight of the edge joining vertex1 and vertex2]"""
E1=[]
E2=[]
for i in Ed:
E1+=[[i[0], i[1]], ]
E2+=[i[2], ]
P={st:[0, '-']}
V1=V[:]
del V1[V1.index(st)]
temp={}
I=[]
for i in V1:
if [i, st] in E1:
ind=E1.index([i, st])
temp[i]=[E2[ind], st]
I+=[ind,]
elif [st, i] in E1:
ind=E1.index([st, i])
temp[i]=[E2[ind], st]
I+=[ind,]
elif (not [i, st] in E1) or (not [st, i] in E1):
temp[i]=[oo, st]
for ind in sorted(I, reverse=True):
del E1[ind]
del E2[ind]
t1=list(temp.keys())
t2=[temp[i] for i in temp]
while len(t2)!=0:
temp1={}
I=[]
Min=min(t2)
Ind=t2.index(Min)
st_old=st
st=t1[Ind]
label_st=Min
P[st]=label_st
del V1[V1.index(st)]
for i in V1:
if [i, st] in E1:
old_label=temp[i]
o1=old_label[0]
o2=old_label[1]
ind=E1.index([i, st])
if o1<=label_st[0]+E2[ind]: temp1[i]=old_label
else:
Minimum=min([o1, label_st[0]+E2[ind]])
temp1[i]=[Minimum, st]
I+=[ind,]
elif [st, i] in E1:
old_label=temp[i]
o1=old_label[0]
o2=old_label[1]
ind=E1.index([st, i])
if o1<=label_st[0]+E2[ind]: temp1[i]=old_label
else:
Minimum=min([o1, label_st[0]+E2[ind]])
temp1[i]=[Minimum, st]
I+=[ind,]
elif (not [i, st] in E1) or (not [st, i] in E1):
temp1[i]=temp[i]
for ind in sorted(I, reverse=True):
del E1[ind]
del E2[ind]
temp=temp1
t1=list(temp.keys())
t2=[temp[i] for i in temp]
path=end
pr=P[end][1]
if P[end][0]==oo: return 'No shortest path exists'
while pr!='-':
path+=pr
pr=P[pr][1]
print(P)
return path[::-1]
DA(Ed, V, st, end)
|
discrete math.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="zmwWs4S9cRIn"
# # ECE 570 Assignment 6 Exercise
#
#
#
#
#
#
# Your Name: <NAME>
# + [markdown] id="Zz2T0QYYpwVR"
# ## Exercise 1: Creating an image denoiser using a CNN autoencoder. (30 points)
# In this exercise you are trying to build a autoencoder with CNN layers that can denoise images.
#
# ### Task 1: Create additive noise transform
# 1. Add code to `AddGaussianNoise` transform class that will:
# * Add additive Gaussian noise to the batch of input images (i.e add noise with gaussian distribution on each pixel). The noise for every pixel should have mean value 0 and standard deviation of 0.3, i.e $ \epsilon \sim N(0, 0.3)$.
# * Clip the values to be between 0 and 1 again as they may be outside the range for pixel values after adding Gaussian noise.
# 2. Plot the first 3 training images and their noisy counterparts in a 2x3 subplot with appropriate titles, figure size, label, etc.
#
# In this task, we concatenate the original dataset and noisy dataset and get a single dataloader. You should be careful with what you load at each iteration. In a more general case, there are many ways of dealing with multiple datasets. For example, you can create separate dataloaders and use ``zip`` to load samples from them. Here is a post discussing how to use ``zip`` [https://discuss.pytorch.org/t/two-dataloaders-from-two-different-datasets-within-the-same-loop/87766/1](https://discuss.pytorch.org/t/two-dataloaders-from-two-different-datasets-within-the-same-loop/87766/1).
# + id="wTo6hwMo-6Ai"
# Import and load MNIST data
import torchvision
import numpy as np
import torch
import matplotlib.pyplot as plt
class AddGaussianNoise(object):
########################### <YOUR CODE> ############################
def __init__(self, mean, std):
self.mean = mean
self.std = std
def __call__(self, tensor):
tn_size = tensor.size()
image_noise = tensor + self.mean+ torch.randn(tn_size) * self.std
y = torch.clamp(image_noise,min=0,max = 1)
return y
######################### <END YOUR CODE> ############################
transform_noisy = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), AddGaussianNoise(0.,0.3)])
transform_original = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
train_dataset_noisy = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform_noisy)
train_dataset_original = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform_original)
test_dataset_noisy = torchvision.datasets.MNIST('data', train=False, download=True, transform=transform_noisy)
test_dataset_original = torchvision.datasets.MNIST('data', train=False, download=True, transform=transform_original)
print(torch.max(train_dataset_noisy.__getitem__(0)[0]).item())
print(torch.min(train_dataset_noisy.__getitem__(0)[0]).item())
# -
device = 'cuda' if torch.cuda.is_available()==True else 'cpu'
device = torch.device(device)
print(f'We are using device name "{device}"')
print(f'Device name {torch.cuda.get_device_name(0)}')
# + id="aVGreIhv8WKh"
class ConcatDataset(torch.utils.data.Dataset):
def __init__(self, *datasets):
self.datasets = datasets
def __getitem__(self, i):
return tuple(d[i] for d in self.datasets)
def __len__(self):
return min(len(d) for d in self.datasets)
batch_size_train, batch_size_test = 64, 1000
train_loader = torch.utils.data.DataLoader(ConcatDataset(train_dataset_noisy, train_dataset_original),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(ConcatDataset(test_dataset_noisy, test_dataset_original),
batch_size=batch_size_test, shuffle=False)
########################### <YOUR CODE> ############################
# Plot the first 3 training images with corresponding noisy images
batch_idx, (images, _) = next(enumerate(test_loader))
#images = images.to(device).cpu().detach()
#images = images.cpu()
#print(images.size(), output.size())
fig, ax = plt.subplots(2,3)
fig.set_size_inches(12,8)
for idx in range(3):
ax[0,idx].imshow(images[0][idx][0], cmap='gray')
ax[0,idx].set_title(f'Noisy img label: {images[1][idx]}')
ax[1,idx].imshow(_[0][idx][0], cmap='gray')
ax[1,idx].set_title(f'Original img label: {_[1][idx]}')
fig.show()
######################### <END YOUR CODE> ############################
# + [markdown] id="DFKqew7r-E-q"
# ### Task 2: Create and train a denoising autoencoder
# 1. Build an autoencoder neural network structure with encoders and decoders that is a little more complicated than in the instructions. You can also create the network to have convolutional or transpose convolutional layers. (You can follow the instructions code skeleton with a key difference of using convolutional layers).
# 2. Move your model to GPU so that you can train your model with GPU. (This step can be simultaneously implemented in the above step)
# 3. Train your denoising autoencoder model with appropriate optimizer and **MSE** loss function. The loss function should be computed between the output of the noisy images and the clean images, i.e., $L(x, g(f(\tilde{x})))$, where $\tilde{x} = x + \epsilon$ is the noisy image and $\epsilon$ is the Gaussian niose. You should train your model with enough epochs so that your loss reaches a relatively steady value. **Note: Your loss on the test data should be lower than 20.** You may have to experiment with various model architectures to achieve this test loss.
# 4. Visualize your result with a 3 x 3 grid of subplots. You should show 3 test images, 3 test images with noise added, and 3 test images reconstructed after passing your noisy test images through the DAE.
# -
batch_size_train, batch_size_test = 64, 1000
train_loader = torch.utils.data.DataLoader(ConcatDataset(train_dataset_noisy, train_dataset_original),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(ConcatDataset(test_dataset_noisy, test_dataset_original),
batch_size=batch_size_test, shuffle=False)
# +
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
latent_feature = 16
class our_AE(nn.Module):
def __init__(self):
super(our_AE, self).__init__()
# encoder
self.en_fc1 = nn.Linear(in_features=784, out_features=512)
self.en_fc2 = nn.Linear(in_features=512, out_features=latent_feature)
# decoder
self.de_fc1 = nn.Linear(in_features=latent_feature, out_features=512)
self.de_fc2 = nn.Linear(in_features=512, out_features=784)
def forward(self, x):
# encoding layers
x = x.view(-1, 784)
x = F.relu(self.en_fc1(x))
x = F.relu(self.en_fc2(x))
# decoding layers
x = F.relu(self.de_fc1(x))
x = torch.sigmoid(self.de_fc2(x))
x = x.view(-1, 1, 28, 28)
return x
AE = our_AE().to(device)
optimizer = optim.Adam(AE.parameters(), lr=1e-4)
loss_fn = nn.MSELoss(reduction='sum')
# + id="FIVO5T4JgA_N"
########################### <YOUR CODE> ############################
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
latent_feature = 16
class our_AE(nn.Module):
def __init__(self):
super(our_AE, self).__init__()
self.en_fc1 = nn.Linear(in_features=288, out_features=128)
self.en_fc2 = nn.Linear(in_features=128, out_features=16)
self.de_fc1 = nn.Linear(in_features=latent_feature, out_features=128)
self.de_fc2 = nn.Linear(in_features=128, out_features=288)
self.en1 = nn.Conv2d(1, 8, 3, stride=2, padding=1)
self.en2 = nn.Conv2d(8, 16, 3, stride=2, padding=1)
self.en3 = nn.Conv2d(16, 32, 3, stride=2, padding=0)
self.batch = nn.BatchNorm2d(latent_feature)
self.flat = nn.Flatten(start_dim=1)
self.deflat = nn.Unflatten(dim=1, unflattened_size=(32, 3, 3))
self.de1 = nn.ConvTranspose2d(32 , latent_feature, 3, stride=2, output_padding=0)
self.batch1 = nn.BatchNorm2d(latent_feature)
self.de2 = nn.ConvTranspose2d(16, 8, 3, stride=2, padding=1, output_padding=1)
self.batch2 = nn.BatchNorm2d(8)
self.de3 = nn.ConvTranspose2d(8, 1, 3, stride=2, padding=1, output_padding=1)
# encoder
#self.en_fc1 = nn.Linear(in_features=288, out_features=128)
#self.en_fc2 = nn.Linear(in_features=128, out_features=latent_feature)
#self.batch = nn.BatchNorm2d(latent_feature)
#self.en1 = nn.Conv2d(1,8,3,stride = 2, padding = 1)
#self.en2 = nn.Conv2d(8,16,3,stride = 2, padding = 1)
#self.en3 = nn.Conv2d(16,32,3,stride = 2, padding = 1)
#self.flat = nn.Flatten(start_dim=1)
# decoder
#self.de_fc1 = nn.Linear(in_features=latent_feature, out_features=128)
#self.de_fc2 = nn.Linear(in_features=128, out_features=288)
#self.de1 = nn.ConvTranspose2d(32,16,3,padding = 1,stride = 2, output_padding = 0)
#self.de2 = nn.ConvTranspose2d(16,8,3,padding = 1,stride = 2, output_padding = 1)
#self.de3 = nn.ConvTranspose2d(8,1,3,padding = 1,stride = 2, output_padding = 1)
#self.debatch1 = nn.BatchNorm2d(latent_feature)
#self.debatch2 = nn.BatchNorm2d(8)
#self.deflat = nn.Unflatten(dim =1, unflattened_size=(32,3,3))
#self.en_fc1 = nn.Linear(in_features=288, out_features=128)
#self.en_fc2 = nn.Linear(in_features=128, out_features=latent_feature)
#self.en1 = nn.Conv2d(1, 8, 3, stride=2, padding=1)
#self.en2 = nn.Conv2d(8, 16, 3, stride=2, padding=1)
#self.en3 = nn.Conv2d(16, 32, 3, stride=2, padding=0)
# self.batch = nn.BatchNorm2d(latent_feature)
#self.en1 = nn.Conv2d(1, 8, 3, padding=1, stride=2)
#self.en2 = nn.Conv2d(8, 16, 3, padding=1, stride=2)
#self.en3 = nn.Conv2d(16, 32, 3, stride=2, padding=0)
#self.en_fc1 = nn.Linear(in_features=288, out_features=128)
#self.en_fc2 = nn.Linear(in_features=128, out_features=latent_feature)
#self.flat = nn.Flatten(start_dim=1)
#self.en_batch = nn.BatchNorm2d(latent_feature)
#self.de_fc1 = nn.Linear(in_features=16, out_features=128)
#self.de_fc2 = nn.Linear(in_features=128, out_features=288)
#self.debatch1 = nn.BatchNorm2d(latent_feature)
#self.debatch2 = nn.BatchNorm2d(8)
#self.deflat = nn.Unflatten(dim=1, unflattened_size=(32, 3, 3))
#self.de1 = nn.ConvTranspose2d(32 , 16, 3, stride=2, output_padding=0)
#self.de2 = nn.ConvTranspose2d(16, 8, 3, stride=2, padding=1, output_padding=1)
#self.de3 = nn.ConvTranspose2d(8, 1, 3, stride=2, padding=1, output_padding=1)
#self.de_fc1 = nn.Linear(in_features=latent_feature, out_features=128)
#self.de_fc2 = nn.Linear(in_features=128, out_features=288)
#self.de1 = nn.ConvTranspose2d(32 , 16, 3, stride=2, output_padding=1)
#self.debatch1 = nn.BatchNorm2d(latent_feature)
#self.de2 = nn.ConvTranspose2d(16, 8, 3, stride=2, padding=1, output_padding=1)
#self.deflat = nn.Unflatten(dim=1, unflattened_size=(16, 3, 3))
#self.debatch2 = nn.BatchNorm2d(8)
# self.de3 = nn.ConvTranspose2d(8, 1, 3, stride=2, padding=1, output_padding=1)
def forward(self, x):
x = F.relu(self.en1(x))
x = F.relu(self.batch(self.en2(x)))
x = F.relu(self.en3(x))
x = self.flat(x)
x = F.relu(self.en_fc1(x))
x = self.en_fc2(x)
x = F.relu(self.de_fc1(x))
x = F.relu(self.de_fc2(x))
x = self.deflat(x)
x = F.relu(self.batch1(self.de1(x)))
x = F.relu(self.batch2(self.de2(x)))
x = self.de3(x)
x = torch.sigmoid(x)
#x = F.relu(self.en1(x))
#x = F.relu(self.batch(self.en2(x)))
#x = F.relu(self.en3(x))
#x = x.view(-1, 288)
#x = F.relu(self.en_fc1(x))
#x = self.en_fc2(x)
#x = F.relu(self.en1(x))
#x = self.en2(x)
#print(x.size())
#x = F.relu(self.en_batch(x))
#print(x.size())
#x = F.relu(self.en3(x))
##print(x.size())
#x = x.view(-1, 288)
#print(x.size())
#x = F.relu(self.en_fc1(x))
#print(x.size())
#x = F.relu(self.en_fc2(x))
#print(x.size())
# encoding layers
#x = F.relu(self.en1(x))
#x = F.relu(self.batch(self.en2(x)))
#x = F.relu(self.en3(x))
#x = x.view(-1,32768)
#x = x.view(-1, 784)
#x = F.relu(self.en_fc1(x))
#x = self.en_fc2(x)
# decoding layers
#x = F.relu(self.de_fc1(x))
#x = F.relu(self.de_fc2(x))
#x = self.deflat(x)
#x = self.de1(x)
#x = F.relu(self.debatch1(self.de1(x)))
#x = self.de2(x)
#x = F.relu(self.debatch2(self.de2(x)))
#x = self.de3(x)
#x = torch.sigmoid((x))
#x = torch.sigmoid(self.de_fc2(x))
#x = x.view(-1, 1, 28, 28)
#x = F.relu(self.de1(x))
#x = F.relu(x)
#x = F.relu(self.de2(x))
#x = self.deflat(x)
#x = self.de_conv1(x)
#x = F.relu(self.debatch1(x))
#x = F.relu(self.debatch2(self.de_conv2(x)))
#x = self.de_conv3(x)
#x = F.relu(self.de_fc1(x))
#x = F.relu(self.de_fc2(x))
#x = self.deflat(x)
#x = F.relu(self.debatch1(self.de1(x)))
#x = F.relu(self.debatch2(self.de2(x)))
# x = F.relu(self.de3(x))
# x = torch.sigmoid(x)
return x
AE = our_AE().to(device)
optimizer = optim.Adam(AE.parameters(), lr=1e-4)
loss_fn = nn.MSELoss(reduction='sum')
######################### <END YOUR CODE> ############################
# +
def train(epoch, device):
AE.train()
for batch_idx, (images, _) in enumerate(train_loader):
images,orig = images[0], _[0]
optimizer.zero_grad()
images,orig = images.float(), orig.float()
images = images.to(device)
orig = orig.to(device)
output = AE(images)
loss = loss_fn(output,orig)
loss.backward()
optimizer.step()
if batch_idx % 10 == 0:
train_losses.append(loss.item()/batch_size_train)
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
if batch_idx % 100 == 0:
print(f'Epoch {epoch}: [{batch_idx*len(images)}/{len(train_loader.dataset)}] Loss: {loss.item()/batch_size_train}')
def test(epoch, device):
AE.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for images, _ in test_loader:
images = images[0]
_ = _[0].float()
images = images.to(device)
_ = _.to(device)
output = AE(images)
test_loss += loss_fn(output, _).item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
test_counter.append(len(train_loader.dataset)*epoch)
print(f'Test result on epoch {epoch}: Avg loss is {test_loss}')
# -
# +
train_losses = []
train_counter = []
test_losses = []
test_counter = []
max_epoch = 10
for epoch in range(1, max_epoch+1):
train(epoch, device=device)
test(epoch, device=device)
# +
batch_idx, (images, _) = next(enumerate(test_loader))
images = images[0].to(device)
output = AE(images).cpu().detach()
images = images.cpu()
print(images.size(), output.size())
fig, ax = plt.subplots(3,3)
fig.set_size_inches(12,12)
#batch_idx, (images, _) = next(enumerate(test_loader))
for idx in range(3):
ax[0,idx].imshow(images[idx][0], cmap='gray')
ax[0,idx].set_title(f'Noisy img label: {_[1][idx]}')
ax[1,idx].imshow(output[idx][0], cmap='gray')
ax[1,idx].set_title(f'reconstruct img label: {_[1][idx]}')
ax[2,idx].imshow(_[0][idx][0], cmap='gray')
ax[2,idx].set_title(f'Normal img label: {_[1][idx]}')
fig.show()
# + [markdown] id="290mOBEHgEXr"
# ## Exercise 2: Build a variational autoencoder(VAE) that can generate MNIST images (70 points)
#
# ### Task 0: Setup
# 1. Import necessary packages
# 2. Load the MNIST data as above.
# 3. Specify the device.
# + id="xd8vWof8nIHw"
########################### <YOUR CODE> ############################
import torchvision
import torch
import torch.optim as optim
transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor()]) # Images already in [0,1]
train_dataset = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform)
test_dataset = torchvision.datasets.MNIST('data', train=False, download=True, transform=transform)
device = 'cuda' if torch.cuda.is_available()==True else 'cpu'
device = torch.device(device)
print(f'We are using device name "{device}"')
print(f'Device name {torch.cuda.get_device_name(0)}')
######################### <END YOUR CODE> ############################
# +
transform = torchvision.transforms.Compose([torchvision.transforms.ToTensor()])
batch_size_train, batch_size_test = 64, 1000
train_dataset = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform)
test_dataset = torchvision.datasets.MNIST('data', train=False, download=True, transform=transform)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size_test, shuffle=False)
# + [markdown] id="oYskA84daTnl"
# ### Task 1: VAE Loss function
# Construct your loss function. The loss function for VAE is a little bit difficult:
# $$
# \begin{aligned}
# \textbf{NegativeELBO}(x, g, f) &= \mathbb{E}_{q_f}[-\log p_g(x|z)] + KL(q_f(z|x), p_g(z))\\
# &= \text{ReconstructionLoss} + \text{Regularizer}
# \end{aligned}
# $$
# In this exercise, you will build the VAE (variational autoencoder) model satisfying following conditions which simplifies the computation of loss function:
# 1. $p_g(z)$ is a standard normal distribution.
# 2. $q_f(z|x)$ is a multivariate Gaussian with trainable mean and variance along each dimension.
# 3. The output distribution of the decoder is an independent Bernoulli distribution for every pixel value since the values are between 0 and 1.
#
# While we discussed the Gaussian distribution in class, here we assume the output distribution of the decoder is an independent Bernoulli distribution for every pixel value since the values are between 0 and 1.
# The value of the pixel corresponds to the average of the Bernoulli distribution.
# This loss can be seen in Appendix C.1 of the original VAE paper: https://arxiv.org/pdf/1312.6114.pdf.
# With such assumpition, the reconstruction loss can be calculated using the binary-cross-entropy loss between the original images and the output of the VAE.
# See [torch.nn.functional.binary_cross_entropy](https://pytorch.org/docs/stable/nn.functional.html#binary-cross-entropy).
# You should use the sum reduction of the loss to sum the loss over all the pixels.
#
# The second part is the KL-Divergence between your model's approximate posterier $q_f(z|x)$ and the model prior $p_g(z)$.
# If we assume $p_g(z)$ is a standard normal distribution and $q_f(z|x)$ is a Gaussian with unknown mean and variance, then this KL divergence can be computed in closed form (see Appendix B of original VAE paper above):
# $KL(q_f(z|x), p_g(z)) = -\frac{1}{2}\sum_{j=1}^d(1+\log(\sigma_j^2)-\mu_j^2-\sigma_j^2)$.
#
#
# Your task here is to write a function `vae_loss` that takes the value of your model's output, the original images, mu, and log_var (i.e., the $\log(\sigma_j^2)$ term), and returns the the reconstruction loss and the KL loss terms **separately** (i.e., the function should return two loss arrays). To visualize these losses separately in a later task, you will need the reconstruction loss and KL loss separated.
#
# + id="oHShuMq5dJOE"
def vae_loss(output, mu, log_var, images):
########################### <YOUR CODE> ############################
regu = 1 + log_var - mu.pow(2) - log_var.exp()
regu_sum = -0.5 * torch.sum(regu)
Loss_reco = F.binary_cross_entropy(input=output.view(-1, 28*28), target=images.view(-1, 28*28), reduction='sum')
return Loss_reco, regu_sum
######################### <END YOUR CODE> ############################
# + [markdown] id="KtRaZjtp-pEM"
# ### Task 2: VAE model
# Build the VAE (variational autoencoder) model based on the instructions given below and in the comments.
# * Inside the `reparameterize` function you job is to output a latent vector. You should first calculate the standard deviation `std` from the log variance variable `log_var` (i.e., compute $\sigma$ from $\log (\sigma^2)$, then generate the vector in Gaussian distribution with `mu` and `std`. **Importantly**, this should use the reparametrization trick so that we can backpropagate through this random step.
#
# * Inside the `forward` function you should extract the `mu` and `log_var` from the latent representation after the encoder. The output of encoder should be in the dimension ` [batch_size x 2 x latent_feature]`, which includes a mean and log variance for each latent feature and for each instance in the batch. Remember that in VAEs, the encoder outputs the parameters of the latent distribution. Note that the second dimension has value 2, so you need to split this tensor into two components, one called `mu` and the other called `log_var`---which will be fed into reparameterize.
#
#
# + id="I-BxB-qYBWQv"
import torch.nn as nn
import torch.nn.functional as F
class our_VAE(nn.Module):
def __init__(self, latent_feature = 16): # you can use any number of latent features you want in the training
super(our_VAE, self).__init__()
self.latent_feature = latent_feature
self.en_input1 = nn.Linear(in_features=784, out_features=500)
self.en_hidden1 = nn.Linear(in_features=500, out_features=latent_feature)
self.en_hidden2 = nn.Linear(in_features=500, out_features=latent_feature)
# self.en_hidden2 = nn.Linear(in_features=500, out_features=latent_feature)
self.de_hidden = nn.Linear(in_features=500, out_features=784)
self.de_latent = nn.Linear(in_features=latent_feature, out_features=500)
def reparameterize(self, mu, log_var):
sample = torch.randn_like(torch.exp(log_var/2))*torch.exp(log_var/2) + mu # mean + std+E
return sample
def encoder(self, x):
#forword
x = x.view(-1, 784)
x = self.en_input1(x)
x = F.relu(x)
mu = self.en_hidden1(x)
log_var = self.en_hidden2(x)
z = self.reparameterize(mu,log_var)
return mu, log_var, z
def decoder(self, z):
#forword
z = self.de_latent(z)
x = F.relu(z)
x = torch.sigmoid((self.de_hidden(x)))
return x
def forward(self, x):
mu = self.encoder(x)[0]
log_var = self.encoder(x)[1]
z = self.encoder(x)[2]
#decode
x = self.decoder(z)
return x, mu, log_var
# + [markdown] id="vvSUZtwcd4jx"
# ### Task 3: Train and visualize output
# 1. Train your model with an appropriate optimizer and the above loss function. You should train your model with enough epochs so that your loss reaches a relatively steady value.
#
# 2. Visualize your result. You should **show three pairs of images** where each pair consists of an original test image and its VAE reconstructed version.
#
# 3. Keep track of the loss. You should save the negative ELBO, Reconstruction Loss and KL Divergence Loss after every 10 batches in the trainining and **create a plot with three curves** using [matplotlib.pyplot.plot](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html). Each curve should correpond to one of the losses. The x-axis will be the number of batches divided by 10 and the y-axis will be the loss. **Make sure you clearly specify the legend, x-label and y-label.**
#
# **Note:** It is always a good idea to keep track of the loss in the process of training to help you understand what is happening during training.
# + id="oKHOYLYldYC7"
########################### <YOUR CODE> ############################
device = 'cuda' if torch.cuda.is_available()==True else 'cpu'
device = torch.device(device)
learning_rate = 0.0001
batch_size_train, batch_size_test = 64, 1000
epochs = 1
VAE = our_VAE().to(device)
optimizer = optim.Adam(params=VAE.parameters(), lr=learning_rate)
######################### <END YOUR CODE> ###########################
# +
elbo_n = []
loss_rec = []
KL_loss = []
epochs = 29
for epoch in range(epochs):
batch_count = 0
for idx, (images,_) in enumerate(train_loader, 0):
_ = _.to(device)
images = images.to(device)
reconstructions, mu, log_var = VAE(images)
ReconstructionLoss, Regularizer = vae_loss(reconstructions, mu, log_var, images)
loss = ReconstructionLoss + Regularizer
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (idx % 10) == 0:
elbo_n.append(loss.item()/batch_size_train)
loss_rec.append(ReconstructionLoss/batch_size_train)
KL_loss.append(Regularizer/batch_size_train)
if (idx % 100) == 0:
print(f'Epoch {epoch+1}: [{idx*len(images)}/{len(train_loader.dataset)}] Loss: {loss.item()/batch_size_train}')
# +
import random
with torch.no_grad():
data = random.sample(list(test_loader), 1)
for (images, label) in random.sample(list(test_loader), 1):
images = images.to(device)
images_0 = np.transpose(imgs[0].cpu().numpy(), [1,2,0])
images_1 = np.transpose(imgs[1].cpu().numpy(), [1,2,0])
images_2 = np.transpose(imgs[2].cpu().numpy(), [1,2,0])
out0 = out[0]
img1 = out0.cpu().reshape(28,28)
out1 = out[1]
img2 = out1.cpu().reshape(28,28)
out2 = out[2]
img3 = out2.cpu().reshape(28,28)
#fig, ax = plt.subplots(2,3)
#fig.set_size_inches(12,8)
fig,ax = plt.subplots(2,3)
fig.set_size_inches(12,8)
ax[0,0].imshow(np.squeeze(img_1),cmap='gray')
ax[0,0].set_title(f'original img label: {label[1]}')
ax[1,0].imshow(img2, cmap='gray')
ax[1,0].set_title(f'reconstructed img label: {label[1]}')
ax[0,1].imshow(np.squeeze(img_0),cmap='gray')
ax[0,1].set_title(f'original img label: {label[0]}')
ax[1,1].imshow(img1, cmap='gray')
ax[1,1].set_title(f'reconstructed img label: {label[0]}')
ax[0,2].imshow(np.squeeze(img_2),cmap='gray')
ax[0,2].set_title(f'original img label: {label[2]}')
ax[1,2].imshow(img3, cmap='gray')
ax[1,2].set_title(f'reconstructed img label: {label[2]}')
fig.show()
i = 0
VAE.eval()
# +
losses = plt.figure(2)
#fig, ax = plt.subplots(1,3)
#fig.set_size_inches(12,8)
plt.plot(np.arange(len(elbo_n))/10, elbo_n, 'b')
plt.plot(np.arange(len(loss_rec))/10, loss_rec,'k')
plt.plot(np.arange(len(KL_loss))/10, KL_loss,'r')
plt. title ('Testing Loss at Different Batches')
plt. ylabel ('Loss (distance function)')
plt.xlabel ('Batches (10x)')
legend1 = ['Neg ELBO', 'reconstruct Loss', 'KLdivergence loss']
plt. legend(legend1)
plt.show()
# -
# + [markdown] id="uzgIFsux2wu3"
# ### Task 4.1: Latent space of VAE
# + [markdown] id="ojuYyCpvVjeV"
# The latent space will change over time during training as the networks learn which features of the input are most important. In the beginning, the reconstruction error will be poor and the latent space will be mixed up (i.e., it has not identified good features for dimensionality reduction and then reconstruction). However, as it continues to train, the space will begin to show some structure (similar to in PCA) as it finds features that enable good reconstruction even after adding a little noise. Therefore, to get some intuition about this process, in this task, you will visualize how latent space changes in the process of training with the given function ``plot_latent``.
#
# 1. For better visualization, create a VAE with ``latent_features=2``.
# 2. Similar to task 3, train the VAE for a few epochs. But you will need to plot the latent distribution using the provided ``plot_latent`` function below at initialization (so you can see what the latent space looks like at initialization) AND after **each** epoch. You should use the **test** data for plotting this visualization task.
#
# + id="Mojv6PtOVwKy"
def plot_latent(vae, data_loader, num_batches=2):
with torch.no_grad():
for ibx, (images,label) in enumerate(data_loader):
_,_,z = vae.encoder(images.to(device))
z = z.to('cpu').detach().numpy()
plt.scatter(z[:, 0], z[:, 1], c=label, cmap='tab10',s=1)
if ibx > num_batches:
break
plt.colorbar()
plt.show()
# -
########################### <YOUR CODE> ############################
class our_VAE2(nn.Module):
def __init__(self, latent_feature = 2): # you can use any number of latent features you want in the training
super(our_VAE2, self).__init__()
self.latent_feature = latent_feature
# define the transformations for your encoder and decoder
self.en_input1 = nn.Linear(in_features=784, out_features=500)
self.en_hidden1 = nn.Linear(in_features=500, out_features=latent_feature)
self.en_hidden2 = nn.Linear(in_features=500, out_features=latent_feature)
# self.en_hidden2 = nn.Linear(in_features=500, out_features=latent_feature)
self.de_hidden = nn.Linear(in_features=500, out_features=784)
self.de_latent = nn.Linear(in_features=latent_feature, out_features=500)
def reparameterize(self, mu, log_var):
sample = torch.randn_like(torch.exp(log_var/2))*torch.exp(log_var/2) + mu # mean + std+E
return sample
def encoder(self, x):
#forword
x = x.view(-1, 784)
x = self.en_input1(x)
x = F.relu(x)
mu = self.en_hidden1(x)
log_var = self.en_hidden2(x)
z = self.reparameterize(mu,log_var)
return mu, log_var, z
def decoder(self, z):
#forword
z = self.de_latent(z)
x = F.relu(z)
x = torch.sigmoid((self.de_hidden(x)))
return x
def forward(self, x):
mu = self.encoder(x)[0]
log_var = self.encoder(x)[1]
z = self.encoder(x)[2]
#decode
x = self.decoder(z)
return x, mu, log_var
# +
device = 'cuda' if torch.cuda.is_available()==True else 'cpu'
device = torch.device(device)
learning_rate = 0.0001
batch_size_train, batch_size_test = 64, 1000
epochs = 1
VAE = our_VAE2().to(device)
optimizer = optim.Adam(params=VAE.parameters(), lr=learning_rate)
# +
def train(epoch, device):
VAE.train()
for batch_idx, (images, orig) in enumerate(train_loader):
optimizer.zero_grad()
images = images.to(device)
orig = orig.to(device)
output, mu, log_var = VAE(images)
loss, KLD = vae_loss(output, mu, log_var, images)
elbo = loss + KLD
elbo.backward()
optimizer.step()
if batch_idx % 10 == 0:
train_elbo.append(elbo.item()/batch_size_train)
train_loss.append(loss.item()/batch_size_train)
train_kld.append(KLD.item()/batch_size_train)
train_idx.append(batch_idx / 10)
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
if batch_idx % 100 == 0:
print(f'Epoch {epoch}: [{batch_idx*len(images)}/{len(train_loader.dataset)}] Loss: {elbo.item()/batch_size_train}')
def test(epoch, device):
VAE.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for images, orig in test_loader:
#images = images.()
images = images.to(device)
orig = orig.to(device)
output, mu, log_var = VAE(images)
loss, kld = vae_loss(output, mu, log_var, images)
elbo = loss + kld
test_loss += elbo
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
test_counter.append(len(train_loader.dataset)*epoch)
print(f'Test result on epoch {epoch}: Avg loss is {test_loss}')
# +
train_losses = []
train_counter = []
test_losses = []
test_counter = []
train_elbo = []
train_loss = []
train_kld = []
train_idx = []
train_counter = []
max_epoch = 5
for epoch in range(1, max_epoch+1):
train(epoch, device=device)
test(epoch, device=device)
plot_latent(VAE, test_loader, num_batches=2)
# -
# + [markdown] id="6t8USlTaWuyH"
# ### Task 4.2 Interpolation of latent space
#
# Interpolation can be quite useful for autoencoder models. For example, by linearly interpolating (or mixing) codes in latent space and decoding the result, the autoencoder can produce a more **semantically meaningful**
# combination of the corresponding datapoints than linear interpolation in the raw pixel space.
# Besides, in some cases, interpolation experiments can show that the model has learned a latent space with a particular structure. Specifically, if interpolation between points in the latent space shows a smooth semantic warping in the original image space, then the visualization may suggest that similar points are semantically clustered in the latent space.
#
# In this task, you will do a simple experiment to see the difference between linear interpolation in the latent space and the original data space (raw pixels).
# 1. With a trained model and test data, sample one $z\sim q(z|x)$ corresponding to label 0 and 1 separately (two samples in total); this can be done by passing test samples (with labels 0 and 1 respectively) through the encoder. These two latent samples will be denoted $z_0$ and $z_1$ respectively.
#
# 2. Compute the linear interpolation of $x_0$ and $x_1$ in the following way: $x'=\alpha x_1 + (1-\alpha)x_0$ where $\alpha = 0, 0.1, 0.2, \dots, 0.9, 1.0$. **Plot** all $x'$ images you get in a 1x11 grid.
#
# 3. Compute the latent linear interpolation of $z_0$ and $z_1$ to get $z'$ in a similar way. Then, reconstruct the $x'$ corresponding to each $z'$ using the decoder. **Plot** all $x'$ images you get in a 1x11 grid.
# + id="hYIIEV24PcP3"
########################### <YOUR CODE> ############################
######################### <END YOUR CODE> ###########################
# + id="Ftjmg7smZ-ut"
|
Assignment6/Assignment_06_Exercise.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from __future__ import print_function
import os
import pandas as pd
from statsmodels.tsa import stattools
# %matplotlib inline
from matplotlib import pyplot as plt
#Start by setting the current directory and henceforth working relative to it
os.chdir('D:/Practical Time Series')
#read the data from into a pandas.DataFrame
air_miles = pd.read_csv('datasets/us-airlines-monthly-aircraft-miles-flown.csv')
air_miles.index = air_miles.Month
#Let's find out the shape of the DataFrame
print('Shape of the DataFrame:', air_miles.shape)
#Let's see first 10 rows of it
air_miles.head(10)
#Let's rename the 2nd column
air_miles.rename(columns={'U.S. airlines: monthly aircraft miles flown (Millions) 1963 -1970':\
'Air miles flown'
},
inplace=True
)
#Check for missing values and remove the row
missing = pd.isnull(air_miles['Air miles flown'])
print('Number of missing values found:', missing.sum())
air_miles = air_miles.loc[~missing, :]
#Plot the time series of air miles flown
fig = plt.figure(figsize=(5.5, 5.5))
ax = fig.add_subplot(1,1,1)
air_miles['Air miles flown'].plot(ax=ax)
ax.set_title('Monthly air miles flown during 1963 - 1970')
plt.savefig('plots/ch2/B07887_02_13.png', format='png', dpi=300)
adf_result = stattools.adfuller(air_miles['Air miles flown'], autolag='AIC')
print('p-val of the ADF test in air miles flown:', adf_result[1])
|
Chapter02/Chapter_2_Augmented_Dickey_Fuller_Test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PythonData
# language: python
# name: pythondata
# ---
# ## COVID Data
# Dependencies and Setup
import json
import os
import pandas as pd
import urllib.request
import requests
# from config import db_pwd, db_user
from sqlalchemy import create_engine
csv_file = "covid_states.csv"
covid = pd.read_csv(csv_file)
covid.head()
# Sort the data by state
covid_state = covid.sort_values(['date'])
covid_state
# Cut the data by date - same start and end date as Google Mobility Data 2020-02-15 : 2020-08-04
start_date = '2020-02-14'
end_date = '2020-08-04'
mask = (covid_state ['date'] > start_date) & (covid_state ['date'] <= end_date)
covid_states = covid_state.loc[mask]
covid_states
# Grouping by date, so we can get all the data for all states into one date
# skipnabool, default is True, and all NA/null values are excluded, when computing the result.
data_by_date_VA_df = pd.DataFrame(google_mob_VA.groupby("dates").mean())
data_by_date_VA_df.reset_index(inplace = True)
data_by_date_VA_df.head()
# Sort the data by date - Test date filter is correct
covid_st_date = covid_states.sort_values(['date'])
covid_st_date
# Export the cleaned data as a csv file
covid_states.to_csv("covid_us_states.csv")
|
COMPLETE/COVID Cases & Deaths/COVID Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.4 64-bit ('pydatk')
# metadata:
# interpreter:
# hash: 191f923cb66d773162629997b180780ff6671a6d24890c003180089c1fb45d90
# name: python3
# ---
# +
import pandas as pd
df = pd.read_csv("./housing.csv")
df.head()
# +
# need to create test dataset
# +
import os.path
import sys
sys.path.append(os.path.abspath(os.path.join(os.path.abspath(''),os.path.pardir)))
from datk.model import ModelTrainer
# +
ModelTrainer(cmd='fit',data_path="./housing.csv",yaml_path="./model_regression.yaml")
# +
eval_params = {
'cmd':'evaluate',
'data_path': './examples/train_titanic.csv'
}
ModelTrainer(**eval_params)
# -
# # XGBClassifier Test
# +
import os.path
import sys
sys.path.append(os.path.abspath(os.path.join(os.path.abspath(''),os.path.pardir)))
from datk.model import ModelTrainer
# +
m = ModelTrainer(cmd='fit',data_path="./housing.csv",yaml_path="./xgb_model_regression.yaml",results_path="./xgb_regression/model_results")
# -
m._load_model()
m.model.feature_importances_
m.model.get_booster().feature_names
|
examples/example_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### This Notebook shows how to use the Camera_Calibration_API to calibrate the camera using symmetrical circular grid pattern
import sys
sys.path.append("../../")
from camera_calibration import Camera_Calibration_API
import glob
import matplotlib.pyplot as plt
# %matplotlib inline
import os
import cv2
test_img = cv2.imread("../example_images/symmetric_grid/Image__2018-02-14__10-12-45.png",0)
print(test_img.shape)
plt.imshow(test_img,cmap="gray")
plt.title("One of the calibration images")
plt.show()
symmetric_circles = Camera_Calibration_API(pattern_type="symmetric_circles",
pattern_rows=6,
pattern_columns=5,
distance_in_world_units = 10,
debug_dir=None)
# %%time
results = symmetric_circles.calibrate_camera(glob.glob("../example_images/symmetric_grid/*.png"))
symmetric_circles.calibration_df
symmetric_circles.visualize_calibration_boards(20,10)
|
examples/example_notebooks/symmertric_grid_calibration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # StarGAN [with celebA dataset]
#
# * `Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks`, [arXiv:1703.10593](https://arxiv.org/abs/1703.10593)
# * <NAME>, <NAME>, <NAME>, <NAME>
#
# * This code is available to tensorflow version 2.0
# * Implemented by [`tf.keras.layers`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/layers) [`tf.losses`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/losses)
# ## Import modules
# +
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
from __future__ import unicode_literals
import os
import sys
import time
import glob
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import PIL
import imageio
from IPython import display
import urllib.request
import zipfile
import tensorflow as tf
from tensorflow.keras import layers
sys.path.append(os.path.dirname(os.path.abspath('.')))
from utils.image_utils import *
from utils.ops import *
os.environ["CUDA_VISIBLE_DEVICES"]="0"
# -
tf.__version__
# ## Setting hyperparameters
# +
# Training Flags (hyperparameter configuration)
model_name = 'stargan'
train_dir = os.path.join('train', model_name, 'exp1')
dataset_name = 'celebA'
assert dataset_name in ['celebA']
constant_lr_epochs = 10
decay_lr_epochs = 10
max_epochs = constant_lr_epochs + decay_lr_epochs
save_model_epochs = 2
print_steps = 10
save_images_epochs = 1
batch_size = 16
learning_rate_D = 1e-4
learning_rate_G = 1e-4
k = 1 # the number of step of learning D before learning G
num_examples_to_generate = 1
BUFFER_SIZE = 10000
IMG_SIZE = 128
num_domain = 5
LAMBDA_class = 1
LAMBDA_reconstruction = 10
gp_lambda = 10
# -
# ## Load the dataset
#
# You can download celebA dataset from [here](https://people.eecs.berkeley.edu/~taesung_park/CycleGAN/datasets/).
#
# As mentioned in the [paper](https://arxiv.org/abs/1703.10593) we apply random jittering and mirroring to the training dataset.
# * In random jittering, the image is resized to 286 x 286 and then randomly cropped to 256 x 256
# * In random mirroring, the image is randomly flipped horizontally i.e left to right.
# #### Actually create random data
# +
N = 2000
train_images = np.random.uniform(low=-1., high=1., size=[N, IMG_SIZE, IMG_SIZE, 3]).astype(np.float32)
train_labels = np.random.uniform(low=0, high=num_domain, size=[N]).astype(np.int32)
test_images = np.random.uniform(low=-1., high=1., size=[N, IMG_SIZE, IMG_SIZE, 3]).astype(np.float32)
test_labels = np.random.uniform(low=0, high=num_domain, size=[N]).astype(np.int32)
# -
# ## Set up dataset with `tf.data`
# ### Use tf.data to create batches, map(do preprocessing) and shuffle the dataset
def preprocessing(image, label):
one_hot_label = tf.one_hot(label, depth=num_domain)
return image, one_hot_label
train_dataset = tf.data.Dataset.from_tensor_slices((train_images, train_labels))
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.map(preprocessing)
train_dataset = train_dataset.batch(batch_size, drop_remainder=True)
test_dataset = tf.data.Dataset.from_tensor_slices((test_images, test_labels))
test_dataset = test_dataset.shuffle(BUFFER_SIZE)
test_dataset = test_dataset.map(preprocessing)
test_dataset = test_dataset.batch(num_examples_to_generate, drop_remainder=True)
# ## Write the generator and discriminator models
#
# ### Generator
#
# * The architecture of generator is similiar to [Johnson's architecture](https://arxiv.org/abs/1603.08155).
# * Conv block in the generator is (Conv -> InstanceNorm -> ReLU)
# * Res block in the generator is (Conv -> IN -> ReLU -> Conv -> IN -> add X -> ReLU)
# * ConvTranspose block in the generator is (Transposed Conv -> IN -> ReLU) (except last layer: tanh)
class InstanceNormalization(layers.Layer):
"""InstanceNormalization for only 4-rank Tensor (image data)
"""
def __init__(self, epsilon=1e-5):
super(InstanceNormalization, self).__init__()
self.epsilon = epsilon
def build(self, input_shape):
shape = tf.TensorShape(input_shape)
param_shape = shape[-1]
# Create a trainable weight variable for this layer.
self.gamma = self.add_weight(name='gamma',
shape=param_shape,
initializer='ones',
trainable=True)
self.beta = self.add_weight(name='beta',
shape=param_shape,
initializer='zeros',
trainable=True)
# Make sure to call the `build` method at the end
super(InstanceNormalization, self).build(input_shape)
def call(self, inputs):
# Compute the axes along which to reduce the mean / variance
input_shape = inputs.get_shape()
reduction_axes = [1, 2] # only shape index
mean, variance = tf.nn.moments(inputs, reduction_axes, keepdims=True)
normalized = (inputs - mean) / tf.sqrt(variance + self.epsilon)
return self.gamma * normalized + self.beta
class Conv(tf.keras.Model):
def __init__(self, filters, size, strides=1, padding='same',
activation='relu', apply_norm='instance'):
super(Conv, self).__init__()
assert apply_norm in ['instance', 'none']
self.apply_norm = apply_norm
assert activation in ['relu', 'tanh', 'leaky_relu', 'none']
self.activation = activation
if self.apply_norm == 'none':
use_bias = True
else:
use_bias = False
self.conv = layers.Conv2D(filters=filters,
kernel_size=(size, size),
strides=strides,
padding=padding,
kernel_initializer=tf.random_normal_initializer(0., 0.02),
use_bias=use_bias)
if self.apply_norm == 'instance':
self.instancenorm = InstanceNormalization()
def call(self, x):
# convolution
x = self.conv(x)
# normalization
if self.apply_norm == 'instance':
x = self.instancenorm(x)
# activation
if self.activation == 'relu':
x = tf.nn.relu(x)
elif self.activation == 'tanh':
x = tf.nn.tanh(x)
elif self.activation == 'leaky_relu':
x = tf.nn.leaky_relu(x, alpha=0.01)
else:
pass
return x
class ResBlock(tf.keras.Model):
def __init__(self, filters, size):
super(ResBlock, self).__init__()
self.conv1 = Conv(filters, size, activation='relu')
self.conv2 = Conv(filters, size, activation='none')
def call(self, x):
conv = self.conv1(x)
conv = self.conv2(conv)
x = tf.nn.relu(x + conv)
return x
class ConvTranspose(tf.keras.Model):
def __init__(self, filters, size, apply_norm='instance'):
super(ConvTranspose, self).__init__()
assert apply_norm in ['instance', 'none']
self.apply_norm = apply_norm
self.up_conv = layers.Conv2DTranspose(filters=filters,
kernel_size=(size, size),
strides=2,
padding='same',
kernel_initializer=tf.random_normal_initializer(0., 0.02),
use_bias=False)
if self.apply_norm == 'instance':
self.instancenorm = InstanceNormalization()
def call(self, x):
x = self.up_conv(x)
if self.apply_norm == 'instance':
x = self.instancenorm(x)
x = tf.nn.relu(x)
return x
class Generator(tf.keras.Model):
def __init__(self):
super(Generator, self).__init__()
self.down1 = Conv(64, 7)
self.down2 = Conv(128, 4, 2)
self.down3 = Conv(256, 4, 2)
self.res1 = ResBlock(256, 3)
self.res2 = ResBlock(256, 3)
self.res3 = ResBlock(256, 3)
self.res4 = ResBlock(256, 3)
self.res5 = ResBlock(256, 3)
self.res6 = ResBlock(256, 3)
self.up1 = ConvTranspose(128, 4)
self.up2 = ConvTranspose(64, 3)
self.last = Conv(3, 7, activation='tanh')
def call(self, images, labels):
# images shape: (bs, 128, 128, 3)
# labels shape: (bs, num_domain) -> (bs, 128, 128, num_domain)
# x shape: (bs, 128, 128, 3 + num_domain)
labels = tf.expand_dims(tf.expand_dims(labels, axis=1), axis=2)
x = tf.concat([images,
labels * tf.ones([images.shape[0],
IMG_SIZE, IMG_SIZE, num_domain])], axis=3)
x1 = self.down1(x) # x1 shape: (bs, 128, 128, 32)
x2 = self.down2(x1) # x2 shape: (bs, 64, 64, 64)
x3 = self.down3(x2) # x3 shape: (bs, 32, 32, 128)
x4 = self.res1(x3) # x4 shape: (bs, 32, 32, 128)
x5 = self.res2(x4) # x5 shape: (bs, 32, 32, 128)
x6 = self.res3(x5) # x6 shape: (bs, 32, 32, 128)
x7 = self.res4(x6) # x7 shape: (bs, 32, 32, 128)
x8 = self.res5(x7) # x8 shape: (bs, 32, 32, 128)
x9 = self.res6(x8) # x8 shape: (bs, 32, 32, 128)
x10 = self.up1(x9) # x10 shape: (bs, 64, 64, 64)
x11 = self.up2(x10) # x11 shape: (bs, 128, 128, 32)
generated_images = self.last(x11) # generated_images shape: (bs, 128, 128, 3)
return generated_images
for images, labels in train_dataset.take(1):
pass
# +
# Create and test a generators
generator = Generator()
#gen_output = generator(images[tf.newaxis, ...], training=False)
gen_output = generator(images, labels)
plt.imshow(gen_output[0, ...])
# -
# ### Discriminator
#
# * The Discriminator is a variation of PatchGAN.
# * Each block in the discriminator is (Conv -> Leaky ReLU), **NO** normalization
# * The shape of the output after the last layer is (batch_size, 2, 2, 1)
#
# To learn more about the architecture and the hyperparameters you can refer the [paper](https://arxiv.org/abs/1711.09020).
class Discriminator(tf.keras.Model):
def __init__(self):
super(Discriminator, self).__init__()
self.down1 = Conv(64, 4, 2, activation='leaky_relu', apply_norm='none')
self.down2 = Conv(128, 4, 2, activation='leaky_relu', apply_norm='none')
self.down3 = Conv(256, 4, 2, activation='leaky_relu', apply_norm='none')
self.down4 = Conv(512, 4, 2, activation='leaky_relu', apply_norm='none')
self.down5 = Conv(1024, 4, 2, activation='leaky_relu', apply_norm='none')
self.down6 = Conv(2048, 4, 2, activation='leaky_relu', apply_norm='none')
self.source = Conv(1, 3, activation='none', apply_norm='none')
self.classification = Conv(5, 2, padding='valid', activation='none', apply_norm='none')
@tf.function
def call(self, x):
# x shape == (bs, 128, 128, 3)
x = self.down1(x) # (bs, 64, 64, 64)
x = self.down2(x) # (bs, 32, 32, 128)
x = self.down3(x) # (bs, 16, 16, 256)
x = self.down4(x) # (bs, 8, 8, 512)
x = self.down5(x) # (bs, 4, 4, 1024)
x = self.down6(x) # (bs, 2, 2, 2048)
disc_logits = self.source(x) # (bs, 2, 2, 1)
classification_logits = self.classification(x) # (bs, 1, 1, 5)
classification_logits = tf.squeeze(classification_logits, axis=[1, 2])
return disc_logits, classification_logits
# +
# Create and test a discriminator
discriminator = Discriminator()
#disc_out = discriminator(images[tf.newaxis,...], training=False)
disc_out1, disc_out2 = discriminator(images)
print(disc_out2[0])
plt.imshow(disc_out1[0,...,-1], vmin=-20, vmax=20, cmap='RdBu_r')
plt.colorbar()
# -
# ## Model summary
generator.summary()
discriminator.summary()
# ## Define the loss functions and the optimizer
#
# * **Discriminator loss**
# * The discriminator loss function takes 2 inputs; real images, generated images
# * real_loss is a sigmoid cross entropy loss of the real images and an array of ones(since these are the real images)
# * generated_loss is a sigmoid cross entropy loss of the generated images and an array of zeros(since these are the fake images)
# * Then the total_loss is the sum of real_loss and the generated_loss
# * **Generator loss**
# * It is a sigmoid cross entropy loss of the generated images and an array of ones.
# * The paper also includes L1 loss which is MAE (mean absolute error) between the generated image and the target image.
# * This allows the generated image to become structurally similar to the target image.
# * The formula to calculate the total generator loss = gan_loss + LAMBDA * l1_loss, where LAMBDA = 100. This value was decided by the authors of the paper.
bce_object = tf.losses.BinaryCrossentropy(from_logits=True)
mse_object = tf.losses.MeanSquaredError()
mae_object = tf.losses.MeanAbsoluteError()
def GANLoss(logits, is_real=True, use_lsgan=True):
"""Computes standard GAN or LSGAN loss between `logits` and `labels`.
Args:
logits (`2-rank Tensor`): logits.
is_real (`bool`): True means `1` labeling, False means `0` labeling.
use_lsgan (`bool`): True means LSGAN loss, False means standard GAN loss.
Returns:
loss (`0-rank Tensor`): the standard GAN or LSGAN loss value. (binary_cross_entropy or mean_squared_error)
"""
if is_real:
labels = tf.ones_like(logits)
else:
labels = tf.zeros_like(logits)
if use_lsgan:
loss = mse_object(y_true=labels, y_pred=tf.nn.sigmoid(logits))
else:
loss = bce_object(y_true=labels, y_pred=logits)
return loss
def WGANLoss(logits, is_real=True):
"""Computes Wasserstain GAN loss
Args:
logits (`2-rank Tensor`): logits
is_real (`bool`): boolean, Treu means `-` sign, False means `+` sign.
Returns:
loss (`0-rank Tensor`): the WGAN loss value.
"""
loss = tf.reduce_mean(logits)
if is_real:
loss = -loss
return loss
def discriminator_loss(real_logits, fake_logits, real_class_logits, original_labels):
# losses of real with label "1"
real_loss = WGANLoss(logits=real_logits, is_real=True)
# losses of fake with label "0"
fake_loss = WGANLoss(logits=fake_logits, is_real=False)
# domain classification loss
domain_class_loss = bce_object(real_class_logits, original_labels)
return real_loss + fake_loss + (LAMBDA_class * domain_class_loss)
def cycle_consistency_loss(X, X2Y2X):
cycle_loss = mae_object(y_true=X, y_pred=X2Y2X) # L1 loss
#cycle_loss = mse_object(y_true=X, y_pred=X2Y2X) # L2 loss
return cycle_loss
def generator_loss(fake_logits, fake_class_logits, target_domain, input_images, generated_images_o2t2o):
# losses of Generator with label "1" that used to fool the Discriminator
gan_loss = WGANLoss(logits=fake_logits, is_real=True)
# domain classification loss
domain_class_loss = bce_object(fake_class_logits, target_domain)
# mean absolute error
cycle_loss = cycle_consistency_loss(input_images, generated_images_o2t2o)
return gan_loss + (LAMBDA_class * domain_class_loss) + (LAMBDA_reconstruction * cycle_loss)
# ### Define learning rate decay functions
global_step = tf.Variable(0, trainable=False)
lr_D = learning_rate_D
def get_lr_D(global_step):
global lr_D
num_steps_per_epoch = int(N / batch_size)
if global_step.numpy() > num_steps_per_epoch * constant_lr_epochs:
decay_step = num_steps_per_epoch * decay_lr_epochs
lr_D = lr_D - (learning_rate_D * 1. / decay_step) # tf.train.polynomial_decay (linear decay)
return lr_D
else:
return lr_D
lr_G = learning_rate_G
def get_lr_G(global_step):
global lr_G
num_steps_per_epoch = int(N / batch_size)
if global_step.numpy() > num_steps_per_epoch * constant_lr_epochs:
decay_step = num_steps_per_epoch * decay_lr_epochs
lr_G = lr_G - (learning_rate_G * 1. / decay_step) # tf.train.polynomial_decay (linear decay)
return lr_G
else:
return lr_G
discriminator_optimizer = tf.keras.optimizers.Adam(get_lr_D(global_step), beta_1=0.5)
generator_optimizer = tf.keras.optimizers.Adam(get_lr_G(global_step), beta_1=0.5)
# ## Checkpoints (Object-based saving)
checkpoint_dir = train_dir
if not tf.io.gfile.exists(checkpoint_dir):
tf.io.gfile.makedirs(checkpoint_dir)
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
# ## Define generate_and_print_or_save functions
def generate_and_print_or_save(inputs, lables, target_domain=None,
is_save=False, epoch=None, checkpoint_dir=checkpoint_dir):
n = inputs.shape[0]
if target_domain is None:
target_domain = tf.random.uniform(shape=[n], minval=0, maxval=num_domain, dtype=tf.int32)
target_domain = tf.one_hot(target_domain, depth=num_domain)
assert n == target_domain.shape[0]
generated_images_o2t = generator(inputs, target_domain)
generated_images_o2t2o = generator(generated_images_o2t, lables)
print_or_save_sample_images_pix2pix(const_test_inputs, generated_images_o2t, generated_images_o2t2o,
model_name='stargan', name=None,
is_save=is_save, epoch=epoch, checkpoint_dir=checkpoint_dir)
# +
# keeping the constant test input for generation (prediction) so
# it will be easier to see the improvement of the pix2pix.
for inputs, labels in test_dataset.take(1):
const_test_inputs = inputs
const_test_labels = labels
const_target_domains = tf.random.uniform(shape=[const_test_inputs.shape[0]], minval=0, maxval=num_domain, dtype=tf.int32)
const_target_domains = tf.one_hot(const_target_domains, depth=num_domain)
# -
# Check for test data X -> Y -> X
generate_and_print_or_save(const_test_inputs, const_test_labels, const_target_domains)
# ## Training
# ### Define training one step function
@tf.function()
def discriminator_train_step(input_images, labels):
# generating target domain
target_domain = tf.random.uniform(shape=[batch_size], minval=0, maxval=num_domain, dtype=tf.int32)
target_domain = tf.one_hot(target_domain, depth=num_domain)
with tf.GradientTape() as disc_tape:
# Image generation from original domain to target domain
generated_images_o2t = generator(input_images, target_domain)
# Image generation from target domain to original domain
generated_images_o2t2o = generator(generated_images_o2t, labels)
real_logits, real_class_logits = discriminator(input_images)
fake_logits, fake_class_logits = discriminator(generated_images_o2t)
# interpolation of x hat for gradient penalty : epsilon * real image + (1 - epsilon) * generated image
epsilon = tf.random.uniform([batch_size])
epsilon = tf.expand_dims(tf.stack([tf.stack([epsilon]*IMG_SIZE, axis=1)]*IMG_SIZE, axis=1), axis=3)
interpolated_images_4gp = epsilon * images + (1. - epsilon) * generated_images_o2t
with tf.GradientTape() as gp_tape:
gp_tape.watch(interpolated_images_4gp)
interpolated_images_logits, _ = discriminator(interpolated_images_4gp)
gradients_of_interpolated_images = gp_tape.gradient(interpolated_images_logits, interpolated_images_4gp)
norm_grads = tf.sqrt(tf.reduce_sum(tf.square(gradients_of_interpolated_images), axis=[1, 2, 3]))
gradient_penalty_loss = tf.reduce_mean(tf.square(norm_grads - 1.))
disc_loss = discriminator_loss(real_logits, fake_logits, real_class_logits, labels) + \
gp_lambda * gradient_penalty_loss
gen_loss = generator_loss(fake_logits, fake_class_logits, target_domain, input_images, generated_images_o2t2o)
gradients_of_discriminator = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
discriminator_optimizer.apply_gradients(zip(gradients_of_discriminator, discriminator.trainable_variables))
return gen_loss, disc_loss
@tf.function()
def generator_train_step(input_images, labels):
# generating target domain
target_domain = tf.random.uniform(shape=[batch_size], minval=0, maxval=num_domain, dtype=tf.int32)
target_domain = tf.one_hot(target_domain, depth=num_domain)
with tf.GradientTape() as gen_tape:
# Image generation from original domain to target domain
generated_images_o2t = generator(input_images, target_domain)
# Image generation from target domain to original domain
generated_images_o2t2o = generator(generated_images_o2t, labels)
real_logits, real_class_logits = discriminator(input_images)
fake_logits, fake_class_logits = discriminator(generated_images_o2t)
gen_loss = generator_loss(fake_logits, fake_class_logits, target_domain, input_images, generated_images_o2t2o)
gradients_of_generator = gen_tape.gradient(gen_loss, generator.trainable_variables)
generator_optimizer.apply_gradients(zip(gradients_of_generator, generator.trainable_variables))
# ### Training until max_epochs
# +
print('Start Training.')
num_batches_per_epoch = int(N / batch_size)
num_learning_critic = 0
for epoch in range(max_epochs):
for step, (images, labels) in enumerate(train_dataset):
start_time = time.time()
if num_learning_critic < k:
gen_loss, disc_loss = discriminator_train_step(images, labels)
num_learning_critic += 1
global_step.assign_add(1)
else:
generator_train_step(images, labels)
num_learning_critic = 0
# print the result images every print_steps
if global_step.numpy() % print_steps == 0:
epochs = epoch + step / float(num_batches_per_epoch)
duration = time.time() - start_time
examples_per_sec = batch_size / float(duration)
display.clear_output(wait=True)
print("Epochs: {:.2f} lr: {:.3g}, {:.3g}, global_step: {} loss_D: {:.3g} loss_G: {:.3g} ({:.2f} examples/sec; {:.3f} sec/batch)".format(
epochs, generator_optimizer.lr.numpy(), discriminator_optimizer.lr.numpy(), global_step.numpy(), disc_loss, gen_loss, examples_per_sec, duration))
# generate image to target domain for test_dataset
for test_inputs, test_labels in test_dataset.take(1):
generate_and_print_or_save(test_inputs, test_labels)
# saving the result image files every save_images_epochs
if (epoch + 1) % save_images_epochs == 0:
display.clear_output(wait=True)
print("This images are saved at {} epoch".format(epoch+1))
generate_and_print_or_save(const_test_inputs, const_test_labels, const_target_domains,
is_save=True, epoch=epoch+1, checkpoint_dir=checkpoint_dir)
# saving (checkpoint) the model every save_epochs
if (epoch + 1) % save_model_epochs == 0:
checkpoint.save(file_prefix=checkpoint_prefix)
print('Training Done.')
# -
# generating after the final epoch
display.clear_output(wait=True)
generate_and_print_or_save(const_test_inputs, const_test_labels, const_target_domains)
# ## Restore the latest checkpoint
# restoring the latest checkpoint in checkpoint_dir
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
# ## Display an image using the epoch number
display_image(max_epochs, checkpoint_dir=checkpoint_dir)
# ## Generate a GIF of all the saved images.
filename = model_name + '_' + dataset_name + '.gif'
generate_gif(filename, checkpoint_dir)
display.Image(filename=filename + '.png')
|
gans/stargan.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tensorflow_gpuenv
# language: python
# name: tensorflow_gpuenv
# ---
# +
#
from __future__ import print_function
import numpy as np
import sklearn.metrics as metrics
from keras.models import Model
from keras.layers import Input, Add, Activation, Dropout, Flatten, Dense
from keras.layers.convolutional import Convolution2D, MaxPooling2D, AveragePooling2D
from keras.layers.normalization import BatchNormalization
from keras.regularizers import l2
from keras import backend as K
#import wide_residual_network as wrn
from keras.datasets import cifar10
import keras.callbacks as callbacks
import keras.utils.np_utils as kutils
from keras.preprocessing.image import ImageDataGenerator
from keras.utils import plot_model
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras.datasets import cifar10
from keras.callbacks import LearningRateScheduler
import numpy as np
from keras import optimizers
weight_decay = 0.0005
def initial_conv(input):
x = Convolution2D(16, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(input)
channel_axis = 1 if K.image_data_format() == "channels_first" else -1
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
return x
def expand_conv(init, base, k, strides=(1, 1)):
x = Convolution2D(base * k, (3, 3), padding='same', strides=strides, kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(init)
channel_axis = 1 if K.image_data_format() == "channels_first" else -1
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = Convolution2D(base * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
skip = Convolution2D(base * k, (1, 1), padding='same', strides=strides, kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(init)
m = Add()([x, skip])
return m
def conv1_block(input, k=1, dropout=0.0):
init = input
channel_axis = 1 if K.image_data_format() == "channels_first" else -1
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(input)
x = Activation('relu')(x)
x = Convolution2D(16 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
if dropout > 0.0: x = Dropout(dropout)(x)
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = Convolution2D(16 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
m = Add()([init, x])
return m
def conv2_block(input, k=1, dropout=0.0):
init = input
#channel_axis = 1 if K.image_dim_ordering() == "th" else -1
channel_axis = -1
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(input)
x = Activation('relu')(x)
x = Convolution2D(32 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
if dropout > 0.0: x = Dropout(dropout)(x)
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = Convolution2D(32 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
m = Add()([init, x])
return m
def conv3_block(input, k=1, dropout=0.0):
init = input
#channel_axis = 1 if K.image_dim_ordering() == "th" else -1
channel_axis = -1
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(input)
x = Activation('relu')(x)
x = Convolution2D(64 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
if dropout > 0.0: x = Dropout(dropout)(x)
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = Convolution2D(64 * k, (3, 3), padding='same', kernel_initializer='he_normal',
W_regularizer=l2(weight_decay),
use_bias=False)(x)
m = Add()([init, x])
return m
def create_wide_residual_network(input_dim, nb_classes=100, N=2, k=1, dropout=0.0, verbose=1):
"""
Creates a Wide Residual Network with specified parameters
:param input: Input Keras object
:param nb_classes: Number of output classes
:param N: Depth of the network. Compute N = (n - 4) / 6.
Example : For a depth of 16, n = 16, N = (16 - 4) / 6 = 2
Example2: For a depth of 28, n = 28, N = (28 - 4) / 6 = 4
Example3: For a depth of 40, n = 40, N = (40 - 4) / 6 = 6
:param k: Width of the network.
:param dropout: Adds dropout if value is greater than 0.0
:param verbose: Debug info to describe created WRN
:return:
"""
channel_axis = 1 if K.image_data_format() == "channels_first" else -1
ip = Input(shape=input_dim)
x = initial_conv(ip)
nb_conv = 4
x = expand_conv(x, 16, k)
nb_conv += 2
for i in range(N - 1):
x = conv1_block(x, k, dropout)
nb_conv += 2
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = expand_conv(x, 32, k, strides=(2, 2))
nb_conv += 2
for i in range(N - 1):
x = conv2_block(x, k, dropout)
nb_conv += 2
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = expand_conv(x, 64, k, strides=(2, 2))
nb_conv += 2
for i in range(N - 1):
x = conv3_block(x, k, dropout)
nb_conv += 2
x = BatchNormalization(axis=channel_axis, momentum=0.1, epsilon=1e-5, gamma_initializer='uniform')(x)
x = Activation('relu')(x)
x = AveragePooling2D((8, 8))(x)
x = Flatten()(x)
x = Dense(nb_classes, W_regularizer=l2(weight_decay), activation='softmax')(x)
model = Model(ip, x)
if verbose: print("Wide Residual Network-%d-%d created." % (nb_conv, k))
return model
def lr_schedule(epoch):
lrate = 0.1
if epoch > 60:
lrate = 0.02
if epoch > 120:
lrate = 0.004
if epoch > 160:
lrate = 0.0008
return lrate
batch_size = 128
num_classes = 10
epochs = 200
# input image dimensions
img_rows, img_cols = 32, 32
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 3, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 3, img_rows, img_cols)
input_shape = (3, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 3)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 3)
input_shape = (img_rows, img_cols, 3)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
#old normalization
#x_train /= 255
#x_test /= 255
# new normalization with z-score
mean = np.mean(x_train,axis=(0,1,2,3))
std = np.std(x_train,axis=(0,1,2,3))
x_train = (x_train-mean)/(std+1e-7)
x_test = (x_test-mean)/(std+1e-7)
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
#model definition
# For WRN-16-8 put N = 2, k = 8
# For WRN-28-10 put N = 4, k = 10
# For WRN-40-4 put N = 6, k = 4
model = create_wide_residual_network(input_shape, nb_classes=10, N=2, k=2, dropout=0.00)
model.summary()
plot_model(model, "WRN-16-2.png", show_shapes=False)
# define optimizer
sgd = optimizers.SGD(lr=0.1, decay=5e-4, momentum=0.9)
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=sgd,
metrics=['accuracy'])
model.fit(x_train, y_train,
batch_size=batch_size,
epochs=epochs,
verbose=2,
validation_data=(x_test, y_test),
callbacks=[LearningRateScheduler(lr_schedule)])
#save to disk
model_json = model.to_json()
with open('model-16-2.json', 'w') as json_file:
json_file.write(model_json)
model.save_weights('model-16-2.h5')
# final evaluation on test
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# +
# load the model we just trained
# if i use the last for CIFAR10
from __future__ import print_function
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras import backend as K
from keras.datasets import cifar10
from keras.callbacks import LearningRateScheduler
from keras.models import model_from_json
from keras.models import load_model
import numpy as np
batch_size = 128
num_classes = 10
epochs = 6
# input image dimensions
img_rows, img_cols = 32, 32
# the data, split between train and test sets
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
if K.image_data_format() == 'channels_first':
x_train = x_train.reshape(x_train.shape[0], 3, img_rows, img_cols)
x_test = x_test.reshape(x_test.shape[0], 3, img_rows, img_cols)
input_shape = (3, img_rows, img_cols)
else:
x_train = x_train.reshape(x_train.shape[0], img_rows, img_cols, 3)
x_test = x_test.reshape(x_test.shape[0], img_rows, img_cols, 3)
input_shape = (img_rows, img_cols, 3)
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
#old normalization
#x_train /= 255
#x_test /= 255
# new normalization with z-score
mean = np.mean(x_train,axis=(0,1,2,3))
std = np.std(x_train,axis=(0,1,2,3))
x_train = (x_train-mean)/(std+1e-7)
x_test = (x_test-mean)/(std+1e-7)
print('x_train shape:', x_train.shape)
print(x_train.shape[0], 'train samples')
print(x_test.shape[0], 'test samples')
# convert class vectors to binary class matrices
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
# Model reconstruction from JSON file
with open('model.json', 'r') as f:
model = model_from_json(f.read())
# Load weights into the new model
model.load_weights('model.h5')
# define optimizer
opt_rms = keras.optimizers.rmsprop(lr=0.001,decay=1e-6)
model.compile(loss=keras.losses.categorical_crossentropy,
optimizer=opt_rms,
metrics=['accuracy'])
# final evaluation on test
score = model.evaluate(x_test, y_test, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
# -
|
Our_code/Keras(not working)/older failed tests/.ipynb_checkpoints/old_train_teacher2-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 1: Pixel Regression.
#
# Can we recover an image by learning a deep regression map from pixels $(x,y)$ to colors $(r,g,b)$?
#
# Our target image will be Mona Lisa:
# +
import matplotlib.image as mpimg
import matplotlib.pylab as plt
import numpy as np
# %matplotlib inline
im = mpimg.imread("data/monalisa.jpg")
plt.imshow(im)
plt.show()
im.shape
# -
# Ourt training dataset will be composed of pixels locations and input and pixel values as output:
# +
X_train = []
Y_train = []
for i in range(im.shape[0]):
for j in range(im.shape[1]):
X_train.append([float(i),float(j)])
Y_train.append(im[i][j])
X_train = np.array(X_train)
Y_train = np.array(Y_train)
print('Samples:', X_train.shape[0])
print('(x,y):', X_train[1230],'->', '(r,g,b):',Y_train[0])
# -
# Our objective is to train a deep MLP that is able to reconstruct the image:
#
# 
#
# +
import keras
from keras.models import Sequential
from keras.layers.core import Dense, Activation, Dropout
# your model here
# hints: k*10^2 neurons per layer + good initialization + deep network (>2 layers)
# +
# use this cell to find the best model architecture
model.fit(X_train, Y_train, nb_epoch=1, shuffle=True, verbose=1, batch_size=10)
Y = model.predict(X_train, batch_size=10000)
k = 0
im_out = im[:]
for i in range(im.shape[0]):
for j in range(im.shape[1]):
im_out[i,j]= Y[k]
k += 1
plt.imshow(im_out)
plt.show()
|
Assignment 1. Pixel regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Setup
# +
# Python 3 compatability
from __future__ import division, print_function
# system functions that are always useful to have
import time, sys, os
# basic numeric setup
import numpy as np
import math
from numpy import linalg
import scipy
from scipy import stats
# plotting
import matplotlib
from matplotlib import pyplot as plt
# fits data
from astropy.io import fits
# inline plotting
# %matplotlib inline
# -
# re-defining plotting defaults
from matplotlib import rcParams
rcParams.update({'xtick.major.pad': '7.0'})
rcParams.update({'xtick.major.size': '7.5'})
rcParams.update({'xtick.major.width': '1.5'})
rcParams.update({'xtick.minor.pad': '7.0'})
rcParams.update({'xtick.minor.size': '3.5'})
rcParams.update({'xtick.minor.width': '1.0'})
rcParams.update({'ytick.major.pad': '7.0'})
rcParams.update({'ytick.major.size': '7.5'})
rcParams.update({'ytick.major.width': '1.5'})
rcParams.update({'ytick.minor.pad': '7.0'})
rcParams.update({'ytick.minor.size': '3.5'})
rcParams.update({'ytick.minor.width': '1.0'})
rcParams.update({'axes.titlepad': '15.0'})
rcParams.update({'axes.labelpad': '15.0'})
rcParams.update({'font.size': 30})
# # Star with 2 Bands: Joint Photometry
# Load data.
# +
nruns, ncolors, ntrials = 9, 4, 100000
sigclip = 5.
# effective area
psfwidth, noise = 2., 1.
aeff = 4. * np.pi * psfwidth**2
err = np.sqrt(aeff * noise**2)
# true values
f, f2, ferr, ftrials = np.zeros((4, nruns, ncolors))
# extract data
flux, fluxerr, x, y = np.zeros((4, nruns, ncolors, ntrials))
flux2, fluxerr2 = np.zeros((2, nruns, ncolors, ntrials))
for i in range(nruns):
for j in range(ncolors):
fname = 'data/sim_fit/run{0}.fits'.format(i * ncolors + j) # run
if os.path.isfile(fname):
hdul = fits.open(fname)
# grab true values
f[i, j] = hdul[0].header['TRUEFLUX'] # true flux
f2[i, j] = f[i, j] * hdul[0].header['TRUECOLR'] # second true flux
psfwidth = hdul[0].header['PSFWIDTH'] # Gaussian PSF width
noise = hdul[0].header['NOISE'] # iid Gaussian noise
aeff = 4. * np.pi * psfwidth**2 # effective area
ferr[i, j] = np.sqrt(aeff * noise**2) # true error
# grab trials
data = hdul[1].data
flux[i, j] = data['Flux'] # fluxes
fluxerr[i, j] = data['Fluxerr'] # flux errors
x[i, j], y[i, j] = data['X'], data['Y'] # positions
flux2[i, j] = data['Flux2'] # fluxes
fluxerr2[i, j] = data['Flux2Err'] # errors
# clip suspicious trials
pos = np.c_[x[i, j], y[i, j]]
cinv = np.linalg.inv(np.cov(pos, rowvar=False)) # inv-cov
sqdist = np.array([np.dot(np.dot(p, cinv), p)
for p in pos]) # normalized distance
sel = (sqdist <= sigclip**2) & (flux[i, j] / fluxerr[i, j] > 0.2) # clip outliers
flux[i, j, ~sel], fluxerr[i, j, ~sel] = np.nan, np.nan
x[i, j, ~sel], y[i, j, ~sel] = np.nan, np.nan
flux2[i, j, ~sel], fluxerr2[i, j, ~sel] = np.nan, np.nan
ftrials[i, j] = len(sel)
else:
print(fname + ' not found.')
# +
# define relevant quantities
snr = f / ferr # true SNR (band 1)
favg, fstd = np.nanmean(flux, axis=2), np.nanstd(flux, axis=2)
fbias_avg = (favg - f) / f # fractional bias
fbias_err = fstd / f / np.sqrt(ftrials) # uncertainty
snr2 = f2 / ferr # true SNR (band 2)
favg2, fstd2 = np.nanmean(flux2, axis=2), np.nanstd(flux2, axis=2)
fbias_avg2 = (favg2 - f2) / f2 # fractional bias
fbias_err2 = fstd2 / f2 / np.sqrt(ftrials) # uncertainty
snr_eff = np.sqrt(snr**2 + snr2**2)
cbias_avg = np.nanmedian(-2.5 * np.log10(flux / flux2), axis=2) + 2.5 * np.log10(f / f2)
cbias_sel = np.isnan(-2.5 * np.log10(flux / flux2)).sum(axis=2) < 0.02 * ntrials
cbias_std = np.nanstd(-2.5 * np.log10(flux / flux2), axis=2) / np.sqrt(ftrials)
# +
snr_grid = np.linspace(np.nanmin(snr_eff), np.nanmax(snr_eff), 1000)
# plot flux bias + variance
plt.figure(figsize=(36, 10))
plt.suptitle('Star: Joint Photometry', y=1.02)
# flux (band 1)
plt.subplot(1, 3, 1)
plt.errorbar(snr_eff.flatten(),
fbias_avg.flatten() * 100.,
yerr=fbias_err.flatten() * 100.,
marker='o', color='black',
linestyle='none', markersize=8,
elinewidth=2) # avg fractional bias
plt.plot(snr_grid, snr_grid**-2 * 100.,
linestyle='-', color='red',
label='1st-order', lw=3) # 1st-order correction
plt.plot(snr_grid, (snr_grid**-2 + snr_grid**-4) * 100.,
linestyle='-', color='dodgerblue',
label='2nd-order', lw=3) # 2nd-order correction
# label
plt.text(5.5, 1.7, 'First-order\ncorrection',
horizontalalignment='center', verticalalignment='center',
color='red')
plt.text(6, 5.5, 'Second-order\ncorrection',
horizontalalignment='center', verticalalignment='center',
color='dodgerblue')
# prettify
plt.text(12.2, 6.3, 'Overestimated',
horizontalalignment='center', verticalalignment='center',
color='black', alpha=0.8)
plt.text(10.5, 4.0, 'Brighter Band', weight='bold', fontsize='large',
horizontalalignment='center', verticalalignment='center',
color='black')
plt.xlabel(r'Effective SNR over All Bands', labelpad=10)
plt.ylabel(r'Flux Bias [%]', labelpad=10)
plt.xlim(np.nanmin(snr_eff) / 1.05, np.nanmax(snr_eff) * 1.05)
plt.ylim([0.2, 6.8])
plt.tight_layout()
# flux (band 2)
plt.subplot(1, 3, 2)
plt.errorbar(snr_eff.flatten(), fbias_avg2.flatten() * 100.,
yerr=fbias_err2.flatten() * 100.,
marker='o', color='black',
linestyle='none', markersize=12,
elinewidth=2) # avg fractional bias
plt.plot(snr_grid, snr_grid**-2 * 100.,
linestyle='-', color='red',
label='1st-order', lw=3) # 1st-order correction
plt.plot(snr_grid, (snr_grid**-2 + snr_grid**-4) * 100.,
linestyle='-', color='dodgerblue',
label='2nd-order', lw=3) # 2nd-order correction
# prettify
plt.text(12.2, 6.3, 'Overestimated',
horizontalalignment='center', verticalalignment='center',
color='black', alpha=0.8)
plt.text(10.5, 4.0, 'Fainter Band', weight='bold', fontsize='large',
horizontalalignment='center', verticalalignment='center',
color='black')
plt.xlabel(r'Effective SNR over All Bands', labelpad=10)
plt.ylabel(r'Flux Bias [%]', labelpad=10)
plt.xlim(np.nanmin(snr_eff) / 1.05, np.nanmax(snr_eff) * 1.05)
plt.ylim([0.2, 6.8])
plt.tight_layout()
# color (band 1 - band 2)
plt.subplot(1, 3, 3)
plt.errorbar((snr_eff)[cbias_sel], cbias_avg[cbias_sel],
yerr=cbias_std[cbias_sel],
marker='o', color='black',
linestyle='none', markersize=12,
elinewidth=2) # avg fractional bias
plt.plot(snr_grid, np.zeros_like(snr_grid),
linestyle='-', color='red',
label='1st-order', lw=3) # 1st-order correction
# prettify
plt.text(12.7, 0.0315, 'Unbiased',
horizontalalignment='center', verticalalignment='center',
color='black', alpha=0.8)
plt.text(10.5, 0.016, 'Measured Color', weight='bold', fontsize='large',
horizontalalignment='center', verticalalignment='center',
color='black')
plt.xlabel(r'Effective SNR over All Bands', labelpad=10)
plt.ylabel(r'Color Bias [mag]', labelpad=10)
plt.xlim(np.nanmin(snr_eff) / 1.05, np.nanmax(snr_eff) * 1.05)
plt.ylim([-0.01, 0.035])
plt.tight_layout()
# save figure
plt.savefig('plots/star_joint.png', bbox_inches='tight')
# -
|
plot_star_multi_joint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="MeEN6dXxgWn5" colab_type="text"
# # Time Series Forecasting with Convolutional Neural Networks
# The core part of this notebook was digested from https://github.com/JEddy92/TimeSeries_Seq2Seq/blob/master/notebooks/TS_Seq2Seq_Conv_Full_Exog.ipynb.
#
# I mainly added
#
# **0. Utilities**
#
# **1. Loading Data**
#
# **4. Saving Model with weights**
# + [markdown] id="SX9wumcOlv-Z" colab_type="text"
# ## 0. Utilities
# + id="DwC97OUMfn6T" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
sns.set()
# + id="vbcvDPPR0jcx" colab_type="code" colab={}
from google.colab import files
import os
import os.path
from os import path
# + [markdown] id="03vG8zspoCCn" colab_type="text"
# Please check the **real file name** after uploading.
# There is no bug, but this upload solution is not perfect.
# + id="zazYkvKbhZ3R" colab_type="code" colab={}
def upload_1_file():
uploaded = files.upload()
for fn in uploaded.keys():
print('User uploaded file "{name}" with length {length} bytes'.format(
name=fn, length=len(uploaded[fn])))
return fn
return ""
# + id="WbVwi1u1dpRA" colab_type="code" cellView="both" colab={}
def download_1_file(http_path):
import requests
import shutil
response = requests.get(http_path, stream=True)
import tempfile
fname = tempfile.mkstemp()[1]
#print(fname)
with open(fname, 'wb') as fin:
shutil.copyfileobj(response.raw, fin)
return fname # Works!
# + id="sH51WPU6jjb1" colab_type="code" colab={}
def download_or_upload_1_file(http_or_file_path):
if (path.exists(http_or_file_path) and (path.isfile(http_or_file_path))):
return http_or_file_path
if (http_or_file_path==""):
encoder_input_file=upload_1_file()
return encoder_input_file
else:
print(http_or_file_path)
return download_1_file(http_or_file_path)
# + [markdown] id="Jbl1FmmQg8E_" colab_type="text"
# ## 1. Loading Data
#
#
# + [markdown] id="jztCPS8ShyIv" colab_type="text"
# For convinence, I uploaded the cleaned data to the following web path.
# + id="9QojLKy_hkgu" colab_type="code" colab={}
encoder_input_web_or_local="https://MrYingLee.Github.io/Seq2Seq/encoder_input.npy"
decoder_target_web_or_local="https://MrYingLee.Github.io/Seq2Seq/decoder_target.npy"
# + [markdown] id="9Jd__n9T1a4s" colab_type="text"
# ### Encoder File
# + id="_A9UKELx90i5" colab_type="code" outputId="00e4a7b3-06de-4d83-a3af-b7b163f4acdd" colab={"base_uri": "https://localhost:8080/", "height": 34}
file1=download_or_upload_1_file(encoder_input_web_or_local)
encoder_input_data=np.load(file1)
# + id="FIXhePOz2wbJ" colab_type="code" outputId="d9c0b0e7-f3f0-458f-808a-56e65f622620" colab={"base_uri": "https://localhost:8080/", "height": 34}
encoder_input_data.shape
# + [markdown] id="szQhe5dF1j8_" colab_type="text"
# ### Decoder File
#
# Please check the **real file name** after uploading.
# + id="IX-J_URT-aoo" colab_type="code" outputId="ced70151-692d-4792-dafb-be9aa8431f8b" colab={"base_uri": "https://localhost:8080/", "height": 34}
file2=download_or_upload_1_file(decoder_target_web_or_local)
decoder_target_data=np.load(file2)
# + id="H1wf5IEbhawE" colab_type="code" outputId="fe5e1998-7a0c-4110-ec2c-618227bd4bc4" colab={"base_uri": "https://localhost:8080/", "height": 34}
decoder_target_data.shape
# + [markdown] id="P_QO46Q_gWpX" colab_type="text"
# ## 2. Building the Model - Architecture
#
# This convolutional architecture is a full-fledged version of the [WaveNet model](https://deepmind.com/blog/wavenet-generative-model-raw-audio/), designed as a generative model for audio (in particular, for text-to-speech applications). The wavenet model can be abstracted beyond audio to apply to any time series forecasting problem, providing a nice structure for capturing long-term dependencies without an excessive number of learned weights. Exogenous features can be integrated into WaveNet simply by extending the 3rd dimension (feature dimension) of the tensors that we feed to the model.
#
# The core of the wavenet model can be described as a **stack of residual blocks** that utilize **dilated causal convolutions**, visualized by the two diagrams from the wavenet paper below. I've gone into detailed discussion of these model components in the two previous notebooks of this series ([part 1](https://github.com/JEddy92/TimeSeries_Seq2Seq/blob/master/notebooks/TS_Seq2Seq_Conv_Intro.ipynb), [part 2](https://github.com/JEddy92/TimeSeries_Seq2Seq/blob/master/notebooks/TS_Seq2Seq_Conv_Full.ipynb)), so I'd recommend checking those out if you want to build familiarity.
#
# 
#
# 
#
#
# ### **Our Architecture**
#
# With all of our components now laid out, here's what we'll use:
#
# * 16 dilated causal convolutional blocks
# * Preprocessing and postprocessing (time distributed) fully connected layers (convolutions with filter width 1): 32 output units
# * 32 filters of width 2 per block
# * Exponentially increasing dilation rate with a reset (1, 2, 4, 8, ..., 128, 1, 2, ..., 128)
# * Gated activations
# * Residual and skip connections
# * 2 (time distributed) fully connected layers to map sum of skip outputs to final output
#
# Note that the only change in architecture from the previous notebook (without exogenous features) is an increase in units from 16 to 32 for the pre and postprocessing layers. This increase lets us better handle the larger number of input features (before we only used 1 feature!).
#
# As in the previous notebook, we'll extract the last 60 steps from the output sequence as our predicted output for training. We'll also use teacher forcing again during training, and write a separate function for iterative inference (section 5).
# + id="T-rvzIWKgWpY" colab_type="code" colab={}
def create_conv_model(input_last_length):
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.FATAL) # suppress unhelpful tf warnings
from keras.models import Model
from keras.layers import Input, Conv1D, Dense, Activation, Dropout, Lambda, Multiply, Add, Concatenate
# convolutional operation parameters
n_filters = 32 # 32
filter_width = 2
dilation_rates = [2**i for i in range(8)] * 2
# define an input history series and pass it through a stack of dilated causal convolution blocks.
# Note the feature input dimension corresponds to the raw series and all exogenous features
history_seq = Input(shape=(None, input_last_length))
x = history_seq
skips = []
for dilation_rate in dilation_rates:
# preprocessing - equivalent to time-distributed dense
x = Conv1D(32, 1, padding='same', activation='relu')(x)
# filter convolution
x_f = Conv1D(filters=n_filters,
kernel_size=filter_width,
padding='causal',
dilation_rate=dilation_rate)(x)
# gating convolution
x_g = Conv1D(filters=n_filters,
kernel_size=filter_width,
padding='causal',
dilation_rate=dilation_rate)(x)
# multiply filter and gating branches
z = Multiply()([Activation('tanh')(x_f),
Activation('sigmoid')(x_g)])
# postprocessing - equivalent to time-distributed dense
z = Conv1D(32, 1, padding='same', activation='relu')(z)
# residual connection
x = Add()([x, z])
# collect skip connections
skips.append(z)
# add all skip connection outputs
out = Activation('relu')(Add()(skips))
# final time-distributed dense layers
out = Conv1D(128, 1, padding='same')(out)
out = Activation('relu')(out)
out = Dropout(.2)(out)
out = Conv1D(1, 1, padding='same')(out)
# extract the last 60 time steps as the training target
def slice(x, seq_length):
return x[:,-seq_length:,:]
pred_seq_train = Lambda(slice, arguments={'seq_length':60})(out)
model = Model(history_seq, pred_seq_train)
return model
# + id="qXcUg5IYk_iP" colab_type="code" outputId="554eb031-0a56-4b56-ca1d-e7ad6ad86976" colab={"base_uri": "https://localhost:8080/", "height": 79}
from keras.optimizers import Adam
conv_model=create_conv_model(encoder_input_data.shape[-1])
# + id="SSZ3v7VRgWpc" colab_type="code" outputId="143f60d9-29d4-4aaa-b0f8-dd3ebefd12c3" colab={"base_uri": "https://localhost:8080/", "height": 1000}
conv_model.summary()
# + [markdown] id="_46ZBYBcgWpf" colab_type="text"
# With our training architecture defined, we're ready to train the model! We'll leverage the transformer utility functions we defined earlier, and train using mean absolute error loss.
#
# For this expansion of the full-fledged model, once again we end up more than doubling the total number of trainable parameters and incur the cost of slower training time. These additional parameters are due to the increase in filters for the pre/postprocessing layers. Training a model at this scale will take quite a while if you're not running fancy hardware - I'd recommend using a GPU. When constructing this notebook, I used an AWS EC2 instance with a GPU (p2.xlarge) and the Amazon Deep Learning AMI, and training took about an hour.
#
# This time around, we'll go ahead and use all of the series in the dataset for training, and train for 15 epochs to give this more complex model more time to try to reach its full potential.
#
# This is only a starting point, and I would encourage you to play around with this pipeline to see if you can get even better results! You could try selecting/engineering different exogenous features, adjusting the model architecture/hyperparameters, tuning the learning rate and number of epochs, etc.
# + [markdown] id="OCh0enP8WdXu" colab_type="text"
# ## 3. Trainging Model
# + id="2JWJZSWRgWph" colab_type="code" outputId="44e46c13-3bd8-4020-ab4b-ecda963dcad5" colab={"base_uri": "https://localhost:8080/", "height": 521}
batch_size = 2**10
epochs = 15
conv_model.compile(Adam(), loss='mean_absolute_error')
conv_history = conv_model.fit(encoder_input_data, decoder_target_data,
batch_size=batch_size,
epochs=epochs)
# + [markdown] id="hISZY_kpreHz" colab_type="text"
# ## 4. Saving Model with weights
# + id="j74up-dCrdgo" colab_type="code" colab={}
from keras.models import load_model
model_file='conv_model.h5'
conv_model.save(model_file)
from google.colab import files
files.download(model_file)
|
Seq2Seq/2_Seq2Seq_Conv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Consensus Motif Search
#
# [](https://mybinder.org/v2/gh/TDAmeritrade/stumpy/main?filepath=notebooks/Tutorial_Consensus_Motif.ipynb)
#
# This tutorial utilizes the main takeaways from the [Matrix Profile XV paper](https://www.cs.ucr.edu/~eamonn/consensus_Motif_ICDM_Long_version.pdf).
#
# [Matrix profiles](https://stumpy.readthedocs.io/en/latest/Tutorial_The_Matrix_Profile.html) can be used to [find conserved patterns within a single time series](https://stumpy.readthedocs.io/en/latest/Tutorial_STUMPY_Basics.html) (self-join) and [across two time series](https://stumpy.readthedocs.io/en/latest/Tutorial_AB_Joins.html) (AB-join). In both cases these conserved patterns are often called "motifs". And, when considering a set of three or more time series, one common trick for identifying a conserved motif across the entire set is to:
#
# 1. Append a `np.nan` to the end of each time series. This is used to identify the boundary between neighboring time series and ensures that any identified motif will not straddle multiple time series.
# 2. Concatenate all of the time series into a single long time series
# 3. Compute the matrix profile (self-join) on the aforementioned concatenated time series
#
# However, this is not guaranteed to find patterns that are conserved across *all* of the time series within the set. This idea of a finding a conserved motif that is common to all of the time series in a set is referred to as a "consensus motif". In this tutorial we will introduce the "Ostinato" algorithm, which is an efficient way to find the consensus motif amongst a set of time series.
# ## Getting started
#
# Let’s import the packages that we’ll need to load, analyze, and plot the data.
# +
# %matplotlib inline
import stumpy
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from itertools import cycle, combinations
from matplotlib.patches import Rectangle
from scipy.cluster.hierarchy import linkage, dendrogram
from scipy.special import comb
plt.style.use('stumpy.mplstyle')
# -
# ## Loading the Eye-tracking (EOG) Dataset
#
# In the following dataset, a volunteer was asked to "spell" out different Japanese sentences by performing eye movements that represented writing strokes of individual Japanese characters. Their eye movements were recorded by an electrooculograph (EOG) and they were given one second to "visually trace" each Japanese character. For our purposes we're only using the vertical eye positions and, conceptually, this basic example reproduced Figure 1 and Figure 2 of the [Matrix Profile XV](https://www.cs.ucr.edu/~eamonn/consensus_Motif_ICDM_Long_version.pdf) paper.
# +
sentence_idx = [6, 7, 9, 10, 16, 24]
Ts = [None] * len(sentence_idx)
fs = 50 # eog signal was downsampled to 50 Hz
for i, s in enumerate(sentence_idx):
Ts[i] = pd.read_csv(f'https://zenodo.org/record/4288978/files/EOG_001_01_{s:03d}.csv?download=1').iloc[:, 0].values
# the literal sentences
sentences = pd.read_csv(f'https://zenodo.org/record/4288978/files/test_sent.jp.csv?download=1', index_col=0)
# -
# ## Visualizing the EOG Dataset
#
# Below, we plotted six time series that each represent the vertical eye position while a person "wrote" Japanese sentences using their eyes. As you can see, some of the Japanese sentences are longer and contain more words while others are shorter. However, there is one common Japanese word (i.e., a "common motif") that is contained in all six examples. Can you spot the one second long pattern that is common across these six time series?
# +
def plot_vertical_eog():
fig, ax = plt.subplots(6, sharex=True, sharey=True)
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = cycle(prop_cycle.by_key()['color'])
for i, e in enumerate(Ts):
ax[i].plot(np.arange(0, len(e)) / fs, e, color=next(colors))
ax[i].set_ylim((-330, 1900))
plt.subplots_adjust(hspace=0)
plt.xlabel('Time (s)')
return ax
plot_vertical_eog()
plt.suptitle('Vertical Eye Position While Writing Different Japanese Sentences', fontsize=14)
plt.show()
# -
# ## Consensus Motif Search
#
# To find out, we can use the `stumpy.ostinato` function to help us discover the "consensus motif" by passing in the list of time series, `Ts`, along with the subsequence window size, `m`:
m = fs
radius, Ts_idx, subseq_idx = stumpy.ostinato(Ts, m)
print(f'Found Best Radius {np.round(radius, 2)} in time series {Ts_idx} starting at subsequence index location {subseq_idx}.')
# Now, Let's plot the individual subsequences from each time series that correspond to the matching consensus motif:
seed_motif = Ts[Ts_idx][subseq_idx : subseq_idx + m]
x = np.linspace(0,1,50)
nn = np.zeros(len(Ts), dtype=np.int64)
nn[Ts_idx] = subseq_idx
for i, e in enumerate(Ts):
if i != Ts_idx:
nn[i] = np.argmin(stumpy.core.mass(seed_motif, e))
lw = 1
label = None
else:
lw = 4
label = 'Seed Motif'
plt.plot(x, e[nn[i]:nn[i]+m], lw=lw, label=label)
plt.title('The Consensus Motif')
plt.xlabel('Time (s)')
plt.legend()
plt.show()
# There is a striking similarity between the subsequences. The most central "seed motif" is plotted with a thicker purple line.
#
# When we highlight the above subsequences in their original context (light blue boxes below), we can see that they occur at different times:
ax = plot_vertical_eog()
for i in range(len(Ts)):
y = ax[i].get_ylim()
r = Rectangle((nn[i] / fs, y[0]), 1, y[1]-y[0], alpha=0.3)
ax[i].add_patch(r)
plt.suptitle('Vertical Eye Position While Writing Different Japanese Sentences', fontsize=14)
plt.show()
# The discovered conserved motif (light blue boxes) correspond to writing the Japanese character `ア`, which occurs at different times in the different example sentences.
# ## Phylogeny Using Mitochondrial DNA (mtDNA)
# In this next example, we'll reproduce Figure 9 from the [Matrix Profile XV](https://www.cs.ucr.edu/~eamonn/consensus_Motif_ICDM_Long_version.pdf) paper.
#
# [Mitochondrial DNA (mtDNA)](https://en.wikipedia.org/wiki/Mitochondrial_DNA) has been successfully used to determine evolutionary relationships between organisms (phylogeny). Since DNAs are essentially ordered sequences of letters, we can loosely treat them as time series and use all of the available time series tools.
# ## Loading the mtDNA Dataset
# +
animals = ['python', 'hippo', 'red_flying_fox', 'alpaca']
data = {}
for animal in animals:
data[animal] = pd.read_csv(f"https://zenodo.org/record/4289120/files/{animal}.csv?download=1").iloc[:,0].values
colors = {'python': 'tab:blue', 'hippo': 'tab:green', 'red_flying_fox': 'tab:purple', 'alpaca': 'tab:red'}
# -
# ## Clustering Using Large mtDNA Sequences
#
# Naively, using `scipy.cluster.hierarchy` we can cluster the mtDNAs based on the majority of the sequences. A correct clustering would place the two "artiodactyla", hippo and alpaca, closest and, together with the red flying fox, we would expect them to form a cluster of "mammals". Finally, the python, a "reptile", should be furthest away from all of the "mammals".
# +
fig, ax = plt.subplots(ncols=2)
# sequences in Fig 9 left
truncate = 15000
for k, v in data.items():
ax[0].plot(v[:truncate], label=k, color=colors[k])
ax[0].legend()
ax[0].set_xlabel('Number of mtDNA Base Pairs')
ax[0].set_title('mtDNA Sequences')
# clustering in Fig 9 left
truncate = 16000
dp = np.zeros(int(comb(4, 2)))
for i, a_c in enumerate(combinations(data.keys(), 2)):
dp[i] = stumpy.core.mass(data[a_c[0]][:truncate], data[a_c[1]][:truncate])
Z = linkage(dp, optimal_ordering=True)
dendrogram(Z, labels=[k for k in data.keys()], ax=ax[1])
ax[1].set_ylabel('Z-Normalized Euclidean Distance')
ax[1].set_title('Clustering')
plt.show()
# -
# Uh oh, the clustering is clearly wrong! Amongst other problems, the alpaca (a mammal) should not be most closely related to the python (a reptile).
#
# ## Consensus Motif Search
#
# In order to obtain the correct relationships, we need to identify and then compare the parts of the mtDNA that is the most conserved across the mtDNA sequences. In other words, we need to cluster based on their consensus motif. Let's limit the subsequence window size to 1,000 base pairs and identify the consensus motif again using the `stumpy.ostinato` function:
m = 1000
bsf_radius, bsf_Ts_idx, bsf_subseq_idx = stumpy.ostinato(list(data.values()), m)
print(f'Found best radius {np.round(bsf_radius, 2)} in time series {bsf_Ts_idx} starting at subsequence index location {bsf_subseq_idx}.')
# ## Clustering Using the Consensus mtDNA Motif
# Now, let's perform the clustering again but, this time, using the consensus motif:
# +
consensus_motifs = {}
best_motif = list(data.items())[bsf_Ts_idx][1][bsf_subseq_idx : bsf_subseq_idx + m]
for i, (k, v) in enumerate(data.items()):
if i == bsf_Ts_idx:
consensus_motifs[k] = best_motif
else:
idx = np.argmin(stumpy.core.mass(best_motif, v))
consensus_motifs[k] = v[idx : idx + m]
fig, ax = plt.subplots(ncols=2)
# plot the consensus motifs
for animal, motif in consensus_motifs.items():
ax[0].plot(motif, label=animal, color=colors[animal])
ax[0].legend()
# cluster consensus motifs
dp = np.zeros(int(comb(4, 2)))
for i, motif in enumerate(combinations(list(consensus_motifs.values()), 2)):
dp[i] = stumpy.core.mass(motif[0], motif[1])
Z = linkage(dp, optimal_ordering=True)
dendrogram(Z, labels=[k for k in consensus_motifs.keys()])
ax[0].set_title('Consensus mtDNA Motifs')
ax[0].set_xlabel('Number of mtDNA Base Pairs')
ax[1].set_title('Clustering Using the Consensus Motifs')
ax[1].set_ylabel('Z-normalized Euclidean Distance')
plt.show()
# -
# Now this looks much better! Hierarchically, the python is "far away" from the other mammals and, amongst the mammalia, the red flying fox (a bat) is less related to both the alpaca and the hippo which are the closest evolutionary relatives in this set of animals.
# ## Summary
#
# And that’s it! You have now learned how to search for a consensus motif amongst a set of times series using the awesome `stumpy.ostinato` function. You can now import this package and use it in your own projects. Happy coding!
# ## Resources
#
# [Matrix Profile XV](https://www.cs.ucr.edu/~eamonn/consensus_Motif_ICDM_Long_version.pdf)
#
# [STUMPY Documentation](https://stumpy.readthedocs.io/en/latest/)
#
# [STUMPY Matrix Profile Github Code Repository](https://github.com/TDAmeritrade/stumpy)
|
docs/Tutorial_Consensus_Motif.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Best Practices for Scientific Computing
# + [markdown] slideshow={"slide_type": "subslide"}
# Summary of Best Practices, according to [[1]](http://dx.doi.org/10.1371/journal.pbio.1001745):
#
# 1. Write programs for people, not computers.
# 1. Let the computer do the work.
# 1. Make incremental changes.
# 1. Don't repeat yourself (or others).
# 1. Plan for mistakes.
# 1. Optimize software only after it works correctly.
# 1. Document design and purpose, not mechanics.
# 1. Collaborate.
# -
# [1]: *Best Practices for Scientific Computing*
#
# <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>.
#
# PLOS, http://dx.doi.org/10.1371/journal.pbio.1001745
# + [markdown] slideshow={"slide_type": "slide"}
# # 1. Code Readability
# + [markdown] slideshow={"slide_type": "subslide"}
# ## The Zen of Python
#
# - Beautiful is better than ugly.
# - Explicit is better than implicit.
# - Simple is better than complex.
# - Complex is better than complicated.
# - Flat is better than nested.
# - Sparse is better than dense.
# - **Readability counts.**
# - Special cases aren't special enough to break the rules.
# - Although practicality beats purity.
# - Errors should never pass silently.
# - Unless explicitly silenced.
# - In the face of ambiguity, refuse the temptation to guess.
# - There should be one-- and preferably only one --obvious way to do it.
# - Although that way may not be obvious at first unless you're Dutch.
# - Now is better than never.
# - Although never is often better than *right* now.
# - If the implementation is hard to explain, it's a bad idea.
# - If the implementation is easy to explain, it may be a good idea.
# - Namespaces are one honking great idea -- let's do more of those!
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Variable/function names
#
# Scientists often just translate their equations into code:
#
# Bad:
# ```python
# p0 = 3.5
# p = p0 * np.cos(0.4 * x - 13.2 * t)
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# Better:
# ```python
# # Constants:
# base_pressure = 3.5 # Pa
# wave_length = 15.7 # m
# wave_number = 2 * np.pi / wave_length # m-1
# angular_frequency = 13.2 # Hz
#
# # Calculate:
# pressure = base_pressure * np.cos(wave_number * x - angular_frequency * t)
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# *If you have to sacrifice readability for performance reasons, make sure you add comments to explain the code.*
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Coding style.
#
# This will vary from project to project, but a recommendation for a "default" style exists for Python, the [PEP 8](https://www.python.org/dev/peps/pep-0008/) (PEP = Python Enchancement Proposal). Several editors have functionality to give you hints for improving your style.
# + [markdown] slideshow={"slide_type": "slide"}
# # 3. Use version control
# + [markdown] slideshow={"slide_type": "-"}
# Avoid this:
#
# mycode.py
# mycode_v2.py
# mycode_v2_conference.py
# mycode_v3_BROKEN.py
# mycode_v3_FIXED.py
# mycode_v2+v3.py
# -
# Instead use a version control system (VCS). There exist many alternatives, but the most common is to use *git* in combination with [github](github.com).
# + [markdown] slideshow={"slide_type": "subslide"}
# ## What is version control?
# -
# - A system to store history of files/folders.
# - Typically when you want to store a new version of your files, you make a *commit*.
# - A folder under version control is normally called a *repository*.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Why use version control?
# -
# * Backups:
# * Manage changes of files such as scripts, source code, documents, etc
# * Store copy of git repository on an external platform (e.g. github)
# * Organization:
# * Retrieve old versions of files.
# * Print history of changes.
# * Collaboration:
# * Useful for programming or writing in teams.
# * Programmers work on *copies* of repository files and upload the changes to the official repository.
# * Non-conflicting modifications by different team members are merged automatically.
# * Conflicting modifications are detected and must be resolved manually.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## How does it work?
# -
# - A simple repository will normally be a linear series of commits.
# - However, changes can also branch off, and be merged together.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Commit flow
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Branch flow
#
# 
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Non-software use
#
# Version control can be used for more than just making software!
# -
from IPython.display import YouTubeVideo
YouTubeVideo('kM9zcfRtOqo')
# + [markdown] slideshow={"slide_type": "subslide"}
# ## How do I use it?
#
# If you want to use git, the base program is terminal based, and to unlock the most powerful features of git you will have to use it in this way. However, if you are just starting out, it might be a good idea to start out with a graphical interface, at least until you get the hang of the git flow.
# -
# Suggested graphical UIs:
# - Windows/Mac: [GitHub Desktop](https://desktop.github.com/)
# - Linux: [SmartGit](https://www.syntevo.com/smartgit/), [Git-cola](https://git-cola.github.io/) or [Gitg](https://wiki.gnome.org/Apps/Gitg/)
# + [markdown] slideshow={"slide_type": "slide"}
# # 5. Use tools to automate testing
# + [markdown] slideshow={"slide_type": "fragment"}
# You will make mistakes when programming! Everyone does. The trick is in spotting the mistakes early and efficiently (after release/publication is normally undesirable).
# -
# Best tool available: Unit tests
# + [markdown] slideshow={"slide_type": "subslide"}
# ## How to write unit tests
# -
# 1. Identify a *unit* in your program that should have a well defined behavior given a certain input. A unit can be a:
# - function
# - module
# - entire program
# 1. Write a test function that calls this input and checks that the output/behavior is as expected
# 1. The more the better! Preferably on several levels (function/module/program).
# + [markdown] slideshow={"slide_type": "subslide"}
# ## How to write unit tests in Python
# -
# Use a test framework like [py.test](http://docs.pytest.org/en/latest/) or [nose](https://nose.readthedocs.io/en/latest/). Several other frameworks exist as well.
# ```bash
# $ pip install pytest
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# Make a file `test_<unit or module name>.py`, preferably in a folder called `tests`.
# + [markdown] slideshow={"slide_type": "fragment"}
# Import the code to be tested.
# + [markdown] slideshow={"slide_type": "fragment"}
# Add a function `def test_<test name>():`, and have it check for the correct behavior given a certain input
# + slideshow={"slide_type": "subslide"}
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from mandlebrot import mandelbrot
x = np.linspace(-2.25, 0.75, 500)
y = np.linspace(-1.25, 1.25, 500)
output = mandelbrot(x, y, 200, False)
plt.imshow(output)
# + slideshow={"slide_type": "subslide"}
import numpy as np
from mandlebrot import mandelbrot
def test_mandelbrot_small():
x = np.linspace(-2.25, 0.75, 10)
y = np.linspace(-1.25, 1.25, 10)
output = mandelbrot(x, y, 100, False)
assert output.shape == (10, 10)
def test_mandelbrot_zero_outside():
# The Mandelbrot set should be zero outside the "active" area
x = np.linspace(1.5, 2.0, 10)
y = np.linspace(1.5, 2.0, 10)
output = mandelbrot(x, y, 100, False)
assert np.all(output == 0.0)
def test_mandelbrot_incorrect_test():
x = np.linspace(-1.5, -2.0, 10)
y = np.linspace(-1.25, 1.25, 10)
output = mandelbrot(x, y, 100, False)
assert np.all(output == 0.0)
# + slideshow={"slide_type": "subslide"}
test_mandelbrot_small()
# -
test_mandelbrot_zero_outside()
test_mandelbrot_incorrect_test()
# + [markdown] slideshow={"slide_type": "subslide"}
# ## How to run tests
# -
# Call `py.test` or `nosetests` in the folder containing your project. The tools will look for anything that looks like a test (e.g. `test_*()` functions in `test_*.py` files) in your project.
# !py.test
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Utilities to express expected behavior
# -
# While `assert` and comparisons operators like `==`, `>` etc. should be able to express most expected behaviors, there are a few utilities that can greatly simplify tests, a few of these include:
# + [markdown] slideshow={"slide_type": "-"}
# ### Numpy tests
# -
small_noise = 1e-6 * np.random.rand(10, 10)
np.testing.assert_almost_equal(small_noise, 0.0, decimal=5) # OK
np.testing.assert_almost_equal(small_noise, 0.0, decimal=7) # Will likely fail
# + [markdown] slideshow={"slide_type": "slide"}
# # Python modules
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Local modules
# -
# - Previously, we have only written code to scripts or cells in Notebooks.
# - All python files can also be treated as modules, i.e. they can be imported in other Python files / Notebooks.
# - However, compared to scripts, modules typically only contain definitions (functions/classes/constants) meant to be imported somewhere else
# + [markdown] slideshow={"slide_type": "subslide"}
# Given a file `mymodule.py` with a function `my_function()`:
# +
# %%writefile mymodule.py
def my_function():
return "Surprise!"
# -
# The function can then be imported in another file or a Notebook:
# +
from mymodule import my_function
my_function()
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Packages
# -
# Modules and scripts can be organized into packages. These can then easily be distributed and imported by name. A set of built-in packages are included in Python, like:
# * **sys** System specific functionality
# * **os** Operating system specific functionality
# Other packages can be downloaded and installed, e.g.
# * **scipy** Scientific Python (www.scipy.org)
# * **numpy** Numerical Python
# * **ipython** Interactive Python
# * **matplotlib** Plotting
# * **pandas** Data analsyis
#
# *Several useful packages are included in Python distributions like Anaconda*
# + [markdown] slideshow={"slide_type": "subslide"}
# ## The Python Package Index (PyPI) collects a large number of modules
#
# Official webpage https://pypi.python.org/pypi
#
# Search the Python index with
# ```bash
# pip search KEYWORD
# ```
# Install any new package with
# ```bash
# pip install PACKAGENAME --user
# ````
# + [markdown] slideshow={"slide_type": "slide"}
# # Final points
# -
# - Before publishing/release: Get your code to run on another computer! Preferably on another platform.
# - When unit tests and version control is combined you can have tests be run automatically each time changes are pushed to the repository. This is called *continuous integration*.
# + [markdown] slideshow={"slide_type": "slide"}
# # Challenges
# -
# - Take your code from the previous heat equation diffusion task and make it into a module.
# - Put the reference implementation in one submodule, and the plotting code in a script that can be called.
# - Add it to a git repository.
# - Add unit tests that checks that the diffusion algorthim behaves as expected. Commit it to the repository.
# - Replace the Python code with the vectorized version, and commit that to the repository. Check that the vectorized version passes the test!
# - [Bonus] Turn your module into a package, and expose the callable script as a console entry point.
|
notebooks/0_best_practices.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Assignment 2 | Programming Logic
#
# Reminder: in all of the assignments this semester, the answer is not the only consideration, but also how you get to it. It's OK (suggested even!) to use the internet for help. But you _should_ be able to answer all of these questions using only the programming techniques you have learned in class and from the readings.
#
# A few keys for success:
# - Avoid manual data entry
# - Emphasize logic and clarity
# - Use comments, docstrings, and descriptive variable names
# - In general, less code is better. But if more lines of code makes your program easier to read or understand what its doing, then go for it.
# ## Problem 1
# Write a Python program to count the number of even and odd numbers from a list of numbers. Test your code by running it on a list of integers from 1 to 9. No need to make this a function unless you want to.
#creates a list from 1-9
test_list = [1,2,3,4,5,6,7,8,9]
#have even and odd count start at 0
even_num, odd_num = 0,0
# +
for i in test_list:
if i % 2 == 0: #no remainder therefore even number
even_num += 1 #if true, assigns value as even and adds one number to the number that ran through function
else:
odd_num += 1 #other values are assigned odd and adds one number to the number that ran through function
print("Even count: ", even_num)
print("Odd count: ",odd_num)
# -
# ## Problem 2
# Write a Python function that takes a list of numbers and returns a list containing only the even numbers from the original list. Test your function by running it on a list of integers from 1 to 9.
# +
def get_even(number): #create new function
even_number=[] #create empty list
for x in (number):
if x % 2 == 0: #if returns no remainder then its even and append to even number list
even_number.append(x)
return even_number #return list
get_even(test_list) #test function
# -
# ## Problem 3
#
# 1. Create a function that accepts a list of integers as an argument and returns a list of floats which equals each number as a fraction of the sum of all the items in the original list.
#
# 2. Next, create a second function which is the same as the first, but limit each number in the output list to two decimals.
#
# 3. Create another function which builds on the previous one by allowing a "user" pass in an argument that defines the number of decimal places to use in the output list.
#
# 4. Test each of these functions with a list of integers
# ### P3 Part 1
# +
#Create a function that accepts a list of integers as an argument and returns a list of floats which equals each
#number as a fraction of the sum of all the items in the original list.
new_list = [1,2,3,4,5] #creates list
sum_list = sum(new_list) #create new list which sums all items in new list
fraction = [] #create empty fraction list
def frac_func(x): #define a function called frac_func
for x in new_list:
fraction.append(x / sum_list) #divide each item in new list by sum list and append to the fraction list
print(fraction)
frac_func(1)
# -
# ### P3 Part 2
# +
#Next, create a second function which is the same as the first,
#but limit each number in the output list to two decimals.
fraction = [] #create empty fraction list
def frac_func(x): #define a function called frac_func
for x in new_list:
fraction.append(x / sum_list) #divide each item in new list by sum list and append to the fraction list
two_dec = [ '%.2f' % x for x in fraction]
print(two_dec)
frac_func(1)
# -
# ### P3 Part 3
import numpy as np
# +
#Create another function which builds on the previous one by allowing a "user" pass in an argument that defines the
#number of decimal places to use in the output list. galaxy prompt
fraction = [] #create empty fraction list
def frac_func(x): #define a function called frac_func
user = 3 #allow user to change how many decimals are shown just by changing user variable
for x in new_list:
fraction.append(x / sum_list) #divide each item in new list by sum list and append to the fraction list
fraction_array = np.array(fraction)
fraction_array2 = np.round(fraction_array,user)
print(fraction_array2)
frac_func(1)
# -
# ## Problem 4
# A prime number is any whole number greater than 1 that has no positive divisors besides 1 and itself. In other words, a prime number must be:
# 1. an integer
# 2. greater than 1
# 3. divisible only by 1 and itself.
#
# Write a function is_prime(n) that accepts an argument `n` and returns `True` (boolean) if `n` is a prime number and `False` if n is not prime. For example, `is_prime(11)` should return `True` and `is_prime(12)` should return `False`.
#
# +
def is_prime(n):
if n <= 1: #n is not prime if less than or equal to 1
return False #return that its not prime
for i in range(2,n): # for all numbers i in the range running from 2 to n, do the following
if n % i ==0: # if number i divides n evenly, then it is false
return False #return false boolean
return True #for everything else, it must be true
#is_prime(24) #checking a non-prime and it works!
is_prime(23) #checking a prime and it works also!
# -
# ## Problem 5
# 1. Create a class called `Housing`, and add the following attributes to it:
# - type
# - area
# - number of bedrooms
# - value (price)
# - year built.
# 2. Create two instances of your class and populate their attributes (make 'em up)
# 3. Create a method called `rent()` that calculates the estimated monthly rent for each house (assume that monthly rent is 0.4% of the value of the house)
# 4. Print the rent for both instances.
# ### P5 Part 1
# +
#create class called housing
class Housing: #creates class called housing
def __init__(self, type_house, area, number_bedrooms, value, year_built):
self.type_house = type_house #add the attributes
self.area = area
self.number_bedrooms = number_bedrooms
self.value = value
self.year_built = year_built
# -
# ### P5 Part 2
# +
#Create two instances of your class and populate their attributes
unit_1 = Housing('Apartment', 2300, 3, 500000, 1995) #assign these values to each of the five attributes
unit_2 = Housing('Duplex', 4500, 4, 950000, 2009)
print("The {0} is {1} square feet, {2} bedrooms, ${3} to buy, and was built in {4}".format(unit_1.type_house, unit_1.area, unit_1.number_bedrooms, unit_1.value, unit_1.year_built)) #test to see if attribute prints
# -
# ### P5 Part 3
# +
#Create a method called rent() that calculates the estimated monthly rent for each house
class Housing: #creates class called housing
def __init__(self, type_house, area, number_bedrooms, value, year_built):
self.type_house = type_house #add the attributes
self.area = area
self.number_bedrooms = number_bedrooms
self.value = value
self.year_built = year_built
def rent(self, price_rent = 0.004): #create method that takes value and multiplies by specified percent of price of property
return round (self.value * price_rent)
# -
unit_1 = Housing('Apartment', 2300, 3, 500000, 1995) #assign these values to each of the five attributes
unit_2 = Housing('Duplex', 4500, 4, 950000, 2009)
# ### P5 Part 4
#print rent
print(unit_1.rent())
print(unit_2.rent())
|
assignments/assignment_2/assignment_2_sydneymaves.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="pc5-mbsX9PZC"
# # AlphaFold Colab
#
# This Colab notebook allows you to easily predict the structure of a protein using a slightly simplified version of [AlphaFold v2.0](https://doi.org/10.1038/s41586-021-03819-2).
#
# **Differences to AlphaFold v2.0**
#
# In comparison to AlphaFold v2.0, this Colab notebook uses **no templates (homologous structures)** and a selected portion of the [BFD database](https://bfd.mmseqs.com/). We have validated these changes on several thousand recent PDB structures. While accuracy will be near-identical to the full AlphaFold system on many targets, a small fraction have a large drop in accuracy due to the smaller MSA and lack of templates. For best reliability, we recommend instead using the [full open source AlphaFold](https://github.com/deepmind/alphafold/), or the [AlphaFold Protein Structure Database](https://alphafold.ebi.ac.uk/).
#
# Please note that this Colab notebook is provided as an early-access prototype and is not a finished product. It is provided for theoretical modelling only and caution should be exercised in its use.
#
# **Citing this work**
#
# Any publication that discloses findings arising from using this notebook should [cite](https://github.com/deepmind/alphafold/#citing-this-work) the [AlphaFold paper](https://doi.org/10.1038/s41586-021-03819-2).
#
# **Licenses**
#
# This Colab uses the [AlphaFold model parameters](https://github.com/deepmind/alphafold/#model-parameters-license) and its outputs are thus for non-commercial use only, under the Creative Commons Attribution-NonCommercial 4.0 International ([CC BY-NC 4.0](https://creativecommons.org/licenses/by-nc/4.0/legalcode)) license. The Colab itself is provided under the [Apache 2.0 license](https://www.apache.org/licenses/LICENSE-2.0). See the full license statement below.
#
# **More information**
#
# You can find more information about how AlphaFold works in our two Nature papers:
#
# * [AlphaFold methods paper](https://www.nature.com/articles/s41586-021-03819-2)
# * [AlphaFold predictions of the human proteome paper](https://www.nature.com/articles/s41586-021-03828-1)
#
# FAQ on how to interpret AlphaFold predictions are [here](https://alphafold.ebi.ac.uk/faq).
# + [markdown] id="W4JpOs6oA-QS"
# ## Making a prediction
#
# Please paste the sequence of your protein in the text box below, then run the remaining cells via _Runtime_ > _Run after_. You can also run the cells individually by pressing the _Play_ button on the left.
#
# Note that the search against databases and the actual prediction can take some time, from minutes to hours, depending on the length of the protein and what type of GPU you are allocated by Colab (see FAQ below).
# + cellView="form" id="rowN0bVYLe9n"
#@title Enter the amino acid sequence to fold ⬇️
sequence = 'MAAHKGAEHHHKAAEHHEQAAKHHHAAAEHHEKGEHEQAAHHADTAYAHHKHAEEHAAQAAKHDAEHHAPKPH' #@param {type:"string"}
MIN_SEQUENCE_LENGTH = 16
MAX_SEQUENCE_LENGTH = 2500
# Remove all whitespaces, tabs and end lines; upper-case
sequence = sequence.translate(str.maketrans('', '', ' \n\t')).upper()
aatypes = set('ACDEFGHIKLMNPQRSTVWY') # 20 standard aatypes
if not set(sequence).issubset(aatypes):
raise Exception(f'Input sequence contains non-amino acid letters: {set(sequence) - aatypes}. AlphaFold only supports 20 standard amino acids as inputs.')
if len(sequence) < MIN_SEQUENCE_LENGTH:
raise Exception(f'Input sequence is too short: {len(sequence)} amino acids, while the minimum is {MIN_SEQUENCE_LENGTH}')
if len(sequence) > MAX_SEQUENCE_LENGTH:
raise Exception(f'Input sequence is too long: {len(sequence)} amino acids, while the maximum is {MAX_SEQUENCE_LENGTH}. Please use the full AlphaFold system for long sequences.')
# -
TQDM_BAR_FORMAT
# + cellView="form" id="2tTeTTsLKPjB"
#@title Search against genetic databases
#@markdown Once this cell has been executed, you will see
#@markdown statistics about the multiple sequence alignment
#@markdown (MSA) that will be used by AlphaFold. In particular,
#@markdown you’ll see how well each residue is covered by similar
#@markdown sequences in the MSA.
# --- Python imports ---
import sys
sys.path.append('/opt/conda/lib/python3.7/site-packages')
import os
os.environ['TF_FORCE_UNIFIED_MEMORY'] = '1'
os.environ['XLA_PYTHON_CLIENT_MEM_FRACTION'] = '2.0'
from urllib import request
from concurrent import futures
from google.colab import files
import json
from matplotlib import gridspec
import matplotlib.pyplot as plt
import numpy as np
import py3Dmol
from alphafold.model import model
from alphafold.model import config
from alphafold.model import data
from alphafold.data import parsers
from alphafold.data import pipeline
from alphafold.data.tools import jackhmmer
from alphafold.common import protein
from alphafold.relax import relax
from alphafold.relax import utils
from IPython import display
from ipywidgets import GridspecLayout
from ipywidgets import Output
# Color bands for visualizing plddt
PLDDT_BANDS = [(0, 50, '#FF7D45'),
(50, 70, '#FFDB13'),
(70, 90, '#65CBF3'),
(90, 100, '#0053D6')]
# --- Find the closest source ---
test_url_pattern = 'https://storage.googleapis.com/alphafold-colab{:s}/latest/uniref90_2021_03.fasta.1'
ex = futures.ThreadPoolExecutor(3)
def fetch(source):
request.urlretrieve(test_url_pattern.format(source))
return source
fs = [ex.submit(fetch, source) for source in ['', '-europe', '-asia']]
source = None
for f in futures.as_completed(fs):
source = f.result()
ex.shutdown()
break
# --- Search against genetic databases ---
with open('target.fasta', 'wt') as f:
f.write(f'>query\n{sequence}')
# Run the search against chunks of genetic databases (since the genetic
# databases don't fit in Colab ramdisk).
jackhmmer_binary_path = '/usr/bin/jackhmmer'
dbs = []
num_jackhmmer_chunks = {'uniref90': 59, 'smallbfd': 17, 'mgnify': 71}
total_jackhmmer_chunks = sum(num_jackhmmer_chunks.values())
with tqdm.notebook.tqdm(total=total_jackhmmer_chunks, bar_format=TQDM_BAR_FORMAT) as pbar:
def jackhmmer_chunk_callback(i):
pbar.update(n=1)
pbar.set_description('Searching uniref90')
jackhmmer_uniref90_runner = jackhmmer.Jackhmmer(
binary_path=jackhmmer_binary_path,
database_path=f'https://storage.googleapis.com/alphafold-colab{source}/latest/uniref90_2021_03.fasta',
get_tblout=True,
num_streamed_chunks=num_jackhmmer_chunks['uniref90'],
streaming_callback=jackhmmer_chunk_callback,
z_value=135301051)
dbs.append(('uniref90', jackhmmer_uniref90_runner.query('target.fasta')))
pbar.set_description('Searching smallbfd')
jackhmmer_smallbfd_runner = jackhmmer.Jackhmmer(
binary_path=jackhmmer_binary_path,
database_path=f'https://storage.googleapis.com/alphafold-colab{source}/latest/bfd-first_non_consensus_sequences.fasta',
get_tblout=True,
num_streamed_chunks=num_jackhmmer_chunks['smallbfd'],
streaming_callback=jackhmmer_chunk_callback,
z_value=65984053)
dbs.append(('smallbfd', jackhmmer_smallbfd_runner.query('target.fasta')))
pbar.set_description('Searching mgnify')
jackhmmer_mgnify_runner = jackhmmer.Jackhmmer(
binary_path=jackhmmer_binary_path,
database_path=f'https://storage.googleapis.com/alphafold-colab{source}/latest/mgy_clusters_2019_05.fasta',
get_tblout=True,
num_streamed_chunks=num_jackhmmer_chunks['mgnify'],
streaming_callback=jackhmmer_chunk_callback,
z_value=304820129)
dbs.append(('mgnify', jackhmmer_mgnify_runner.query('target.fasta')))
# --- Extract the MSAs and visualize ---
# Extract the MSAs from the Stockholm files.
# NB: deduplication happens later in pipeline.make_msa_features.
mgnify_max_hits = 501
msas = []
deletion_matrices = []
full_msa = []
for db_name, db_results in dbs:
unsorted_results = []
for i, result in enumerate(db_results):
msa, deletion_matrix, target_names = parsers.parse_stockholm(result['sto'])
e_values_dict = parsers.parse_e_values_from_tblout(result['tbl'])
e_values = [e_values_dict[t.split('/')[0]] for t in target_names]
zipped_results = zip(msa, deletion_matrix, target_names, e_values)
if i != 0:
# Only take query from the first chunk
zipped_results = [x for x in zipped_results if x[2] != 'query']
unsorted_results.extend(zipped_results)
sorted_by_evalue = sorted(unsorted_results, key=lambda x: x[3])
db_msas, db_deletion_matrices, _, _ = zip(*sorted_by_evalue)
if db_msas:
if db_name == 'mgnify':
db_msas = db_msas[:mgnify_max_hits]
db_deletion_matrices = db_deletion_matrices[:mgnify_max_hits]
full_msa.extend(db_msas)
msas.append(db_msas)
deletion_matrices.append(db_deletion_matrices)
msa_size = len(set(db_msas))
print(f'{msa_size} Sequences Found in {db_name}')
deduped_full_msa = list(dict.fromkeys(full_msa))
total_msa_size = len(deduped_full_msa)
print(f'\n{total_msa_size} Sequences Found in Total\n')
aa_map = {restype: i for i, restype in enumerate('ABCDEFGHIJKLMNOPQRSTUVWXYZ-')}
msa_arr = np.array([[aa_map[aa] for aa in seq] for seq in deduped_full_msa])
num_alignments, num_res = msa_arr.shape
fig = plt.figure(figsize=(12, 3))
plt.title('Per-Residue Count of Non-Gap Amino Acids in the MSA')
plt.plot(np.sum(msa_arr != aa_map['-'], axis=0), color='black')
plt.ylabel('Non-Gap Count')
plt.yticks(range(0, num_alignments + 1, max(1, int(num_alignments / 3))))
plt.show()
# + cellView="form" id="XUo6foMQxwS2"
#@title Run AlphaFold and download prediction
#@markdown Once this cell has been executed, a zip-archive with
#@markdown the obtained prediction will be automatically downloaded
#@markdown to your computer.
# --- Run the model ---
model_names = ['model_1', 'model_2', 'model_3', 'model_4', 'model_5', 'model_2_ptm']
def _placeholder_template_feats(num_templates_, num_res_):
return {
'template_aatype': np.zeros([num_templates_, num_res_, 22], np.float32),
'template_all_atom_masks': np.zeros([num_templates_, num_res_, 37, 3], np.float32),
'template_all_atom_positions': np.zeros([num_templates_, num_res_, 37], np.float32),
'template_domain_names': np.zeros([num_templates_], np.float32),
'template_sum_probs': np.zeros([num_templates_], np.float32),
}
output_dir = 'prediction'
os.makedirs(output_dir, exist_ok=True)
plddts = {}
pae_outputs = {}
unrelaxed_proteins = {}
with tqdm.notebook.tqdm(total=len(model_names) + 1, bar_format=TQDM_BAR_FORMAT) as pbar:
for model_name in model_names:
pbar.set_description(f'Running {model_name}')
num_templates = 0
num_res = len(sequence)
feature_dict = {}
feature_dict.update(pipeline.make_sequence_features(sequence, 'test', num_res))
feature_dict.update(pipeline.make_msa_features(msas, deletion_matrices=deletion_matrices))
feature_dict.update(_placeholder_template_feats(num_templates, num_res))
cfg = config.model_config(model_name)
params = data.get_model_haiku_params(model_name, './alphafold/data')
model_runner = model.RunModel(cfg, params)
processed_feature_dict = model_runner.process_features(feature_dict,
random_seed=0)
prediction_result = model_runner.predict(processed_feature_dict)
mean_plddt = prediction_result['plddt'].mean()
if 'predicted_aligned_error' in prediction_result:
pae_outputs[model_name] = (
prediction_result['predicted_aligned_error'],
prediction_result['max_predicted_aligned_error']
)
else:
# Get the pLDDT confidence metrics. Do not put pTM models here as they
# should never get selected.
plddts[model_name] = prediction_result['plddt']
# Set the b-factors to the per-residue plddt.
final_atom_mask = prediction_result['structure_module']['final_atom_mask']
b_factors = prediction_result['plddt'][:, None] * final_atom_mask
unrelaxed_protein = protein.from_prediction(processed_feature_dict,
prediction_result,
b_factors=b_factors)
unrelaxed_proteins[model_name] = unrelaxed_protein
# Delete unused outputs to save memory.
del model_runner
del params
del prediction_result
pbar.update(n=1)
# --- AMBER relax the best model ---
pbar.set_description(f'AMBER relaxation')
amber_relaxer = relax.AmberRelaxation(
max_iterations=0,
tolerance=2.39,
stiffness=10.0,
exclude_residues=[],
max_outer_iterations=20)
# Find the best model according to the mean pLDDT.
best_model_name = max(plddts.keys(), key=lambda x: plddts[x].mean())
relaxed_pdb, _, _ = amber_relaxer.process(
prot=unrelaxed_proteins[best_model_name])
pbar.update(n=1) # Finished AMBER relax.
# Construct multiclass b-factors to indicate confidence bands
# 0=very low, 1=low, 2=confident, 3=very high
banded_b_factors = []
for plddt in plddts[best_model_name]:
for idx, (min_val, max_val, _) in enumerate(PLDDT_BANDS):
if plddt >= min_val and plddt <= max_val:
banded_b_factors.append(idx)
break
banded_b_factors = np.array(banded_b_factors)[:, None] * final_atom_mask
to_visualize_pdb = utils.overwrite_b_factors(relaxed_pdb, banded_b_factors)
# Write out the prediction
pred_output_path = os.path.join(output_dir, 'selected_prediction.pdb')
with open(pred_output_path, 'w') as f:
f.write(relaxed_pdb)
# --- Visualise the prediction & confidence ---
show_sidechains = True
def plot_plddt_legend():
"""Plots the legend for pLDDT."""
thresh = [
'Very low (pLDDT < 50)',
'Low (70 > pLDDT > 50)',
'Confident (90 > pLDDT > 70)',
'Very high (pLDDT > 90)']
colors = [x[2] for x in PLDDT_BANDS]
plt.figure(figsize=(2, 2))
for c in colors:
plt.bar(0, 0, color=c)
plt.legend(thresh, frameon=False, loc='center', fontsize=20)
plt.xticks([])
plt.yticks([])
ax = plt.gca()
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
plt.title('Model Confidence', fontsize=20, pad=20)
return plt
# Color the structure by per-residue pLDDT
color_map = {i: bands[2] for i, bands in enumerate(PLDDT_BANDS)}
view = py3Dmol.view(width=800, height=600)
view.addModelsAsFrames(to_visualize_pdb)
style = {'cartoon': {
'colorscheme': {
'prop': 'b',
'map': color_map}
}}
if show_sidechains:
style['stick'] = {}
view.setStyle({'model': -1}, style)
view.zoomTo()
grid = GridspecLayout(1, 2)
out = Output()
with out:
view.show()
grid[0, 0] = out
out = Output()
with out:
plot_plddt_legend().show()
grid[0, 1] = out
display.display(grid)
# Display pLDDT and predicted aligned error (if output by the model).
if pae_outputs:
num_plots = 2
else:
num_plots = 1
plt.figure(figsize=[8 * num_plots, 6])
plt.subplot(1, num_plots, 1)
plt.plot(plddts[best_model_name])
plt.title('Predicted LDDT')
plt.xlabel('Residue')
plt.ylabel('pLDDT')
if num_plots == 2:
plt.subplot(1, 2, 2)
pae, max_pae = list(pae_outputs.values())[0]
plt.imshow(pae, vmin=0., vmax=max_pae, cmap='Greens_r')
plt.colorbar(fraction=0.046, pad=0.04)
plt.title('Predicted Aligned Error')
plt.xlabel('Scored residue')
plt.ylabel('Aligned residue')
# Save pLDDT and predicted aligned error (if it exists)
pae_output_path = os.path.join(output_dir, 'predicted_aligned_error.json')
if pae_outputs:
# Save predicted aligned error in the same format as the AF EMBL DB
rounded_errors = np.round(pae.astype(np.float64), decimals=1)
indices = np.indices((len(rounded_errors), len(rounded_errors))) + 1
indices_1 = indices[0].flatten().tolist()
indices_2 = indices[1].flatten().tolist()
pae_data = json.dumps([{
'residue1': indices_1,
'residue2': indices_2,
'distance': rounded_errors.flatten().tolist(),
'max_predicted_aligned_error': max_pae.item()
}],
indent=None,
separators=(',', ':'))
with open(pae_output_path, 'w') as f:
f.write(pae_data)
# --- Download the predictions ---
# !zip -q -r {output_dir}.zip {output_dir}
files.download(f'{output_dir}.zip')
# + [markdown] id="lUQAn5LYC5n4"
# ### Interpreting the prediction
#
# Please see the [AlphaFold methods paper](https://www.nature.com/articles/s41586-021-03819-2) and the [AlphaFold predictions of the human proteome paper](https://www.nature.com/articles/s41586-021-03828-1), as well as [our FAQ](https://alphafold.ebi.ac.uk/faq) on how to interpret AlphaFold predictions.
# + [markdown] id="<KEY>"
# ## FAQ & Troubleshooting
#
#
# * How do I get a predicted protein structure for my protein?
# * Click on the _Connect_ button on the top right to get started.
# * Paste the amino acid sequence of your protein (without any headers) into the “Enter the amino acid sequence to fold”.
# * Run all cells in the Colab, either by running them individually (with the play button on the left side) or via _Runtime_ > _Run all._
# * The predicted protein structure will be downloaded once all cells have been executed. Note: This can take minutes to hours - see below.
# * How long will this take?
# * Downloading the AlphaFold source code can take up to a few minutes.
# * Downloading and installing the third-party software can take up to a few minutes.
# * The search against genetic databases can take minutes to hours.
# * Running AlphaFold and generating the prediction can take minutes to hours, depending on the length of your protein and on which GPU-type Colab has assigned you.
# * My Colab no longer seems to be doing anything, what should I do?
# * Some steps may take minutes to hours to complete.
# * If nothing happens or if you receive an error message, try restarting your Colab runtime via _Runtime_ > _Restart runtime_.
# * If this doesn’t help, try resetting your Colab runtime via _Runtime_ > _Factory reset runtime_.
# * How does this compare to the open-source version of AlphaFold?
# * This Colab version of AlphaFold searches a selected portion of the BFD dataset and currently doesn’t use templates, so its accuracy is reduced in comparison to the full version of AlphaFold that is described in the [AlphaFold paper](https://doi.org/10.1038/s41586-021-03819-2) and [Github repo](https://github.com/deepmind/alphafold/) (the full version is available via the inference script).
# * What is a Colab?
# * See the [Colab FAQ](https://research.google.com/colaboratory/faq.html).
# * I received a warning “Notebook requires high RAM”, what do I do?
# * The resources allocated to your Colab vary. See the [Colab FAQ](https://research.google.com/colaboratory/faq.html) for more details.
# * You can execute the Colab nonetheless.
# * I received an error “Colab CPU runtime not supported” or “No GPU/TPU found”, what do I do?
# * Colab CPU runtime is not supported. Try changing your runtime via _Runtime_ > _Change runtime type_ > _Hardware accelerator_ > _GPU_.
# * The type of GPU allocated to your Colab varies. See the [Colab FAQ](https://research.google.com/colaboratory/faq.html) for more details.
# * If you receive “Cannot connect to GPU backend”, you can try again later to see if Colab allocates you a GPU.
# * [Colab Pro](https://colab.research.google.com/signup) offers priority access to GPUs.
# * Does this tool install anything on my computer?
# * No, everything happens in the cloud on Google Colab.
# * At the end of the Colab execution a zip-archive with the obtained prediction will be automatically downloaded to your computer.
# * How should I share feedback and bug reports?
# * Please share any feedback and bug reports as an [issue](https://github.com/deepmind/alphafold/issues) on Github.
#
#
# ## Related work
#
# Take a look at these Colab notebooks provided by the community (please note that these notebooks may vary from our validated AlphaFold system and we cannot guarantee their accuracy):
#
# * The [ColabFold AlphaFold2 notebook](https://colab.research.google.com/github/sokrypton/ColabFold/blob/main/AlphaFold2.ipynb) by <NAME>, <NAME> and <NAME>, which uses an API hosted at the Södinglab based on the MMseqs2 server ([Mirdita et al. 2019, Bioinformatics](https://academic.oup.com/bioinformatics/article/35/16/2856/5280135)) for the multiple sequence alignment creation.
#
# + [markdown] id="YfPhvYgKC81B"
# # License and Disclaimer
#
# This is not an officially-supported Google product.
#
# This Colab notebook and other information provided is for theoretical modelling only, caution should be exercised in its use. It is provided ‘as-is’ without any warranty of any kind, whether expressed or implied. Information is not intended to be a substitute for professional medical advice, diagnosis, or treatment, and does not constitute medical or other professional advice.
#
# Copyright 2021 DeepMind Technologies Limited.
#
#
# ## AlphaFold Code License
#
# Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at https://www.apache.org/licenses/LICENSE-2.0.
#
# Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
#
# ## Model Parameters License
#
# The AlphaFold parameters are made available for non-commercial use only, under the terms of the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) license. You can find details at: https://creativecommons.org/licenses/by-nc/4.0/legalcode
#
#
# ## Third-party software
#
# Use of the third-party software, libraries or code referred to in the [Acknowledgements section](https://github.com/deepmind/alphafold/#acknowledgements) in the AlphaFold README may be governed by separate terms and conditions or license provisions. Your use of the third-party software, libraries or code is subject to any such terms and you should check that you can comply with any applicable restrictions or terms and conditions before use.
#
#
# ## Mirrored Databases
#
# The following databases have been mirrored by DeepMind, and are available with reference to the following:
# * UniRef90: v2021\_03 (unmodified), by The UniProt Consortium, available under a [Creative Commons Attribution-NoDerivatives 4.0 International License](http://creativecommons.org/licenses/by-nd/4.0/).
# * MGnify: v2019\_05 (unmodified), by <NAME> al., available free of all copyright restrictions and made fully and freely available for both non-commercial and commercial use under [CC0 1.0 Universal (CC0 1.0) Public Domain Dedication](https://creativecommons.org/publicdomain/zero/1.0/).
# * BFD: (modified), by <NAME>. and <NAME>., modified by DeepMind, available under a [Creative Commons Attribution-ShareAlike 4.0 International License](https://creativecommons.org/licenses/by/4.0/). See the Methods section of the [AlphaFold proteome paper](https://www.nature.com/articles/s41586-021-03828-1) for details.
|
AlphaFold.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/JenFaith/DS-Unit-2-Linear-Models/blob/master/faith_module1-regression-1/LS_DS_211_assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="i4UK2xy84dEm"
# Lambda School Data Science
#
# *Unit 2, Sprint 1, Module 1*
#
# ---
# + [markdown] id="7IXUfiQ2UKj6"
# # Regression 1
#
# ## Assignment
#
# You'll use another **New York City** real estate dataset.
#
# But now you'll **predict how much it costs to rent an apartment**, instead of how much it costs to buy a condo.
#
# The data comes from renthop.com, an apartment listing website.
#
# - [ ] Look at the data. Choose a feature, and plot its relationship with the target.
# - [ ] Use scikit-learn for linear regression with one feature. You can follow the [5-step process from Jake VanderPlas](https://jakevdp.github.io/PythonDataScienceHandbook/05.02-introducing-scikit-learn.html#Basics-of-the-API).
# - [ ] Define a function to make new predictions and explain the model coefficient.
# - [ ] Organize and comment your code.
#
# > [Do Not Copy-Paste.](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit) You must type each of these exercises in, manually. If you copy and paste, you might as well not even do them. The point of these exercises is to train your hands, your brain, and your mind in how to read, write, and see code. If you copy-paste, you are cheating yourself out of the effectiveness of the lessons.
#
# If your **Plotly** visualizations aren't working:
# - You must have JavaScript enabled in your browser
# - You probably want to use Chrome or Firefox
# - You may need to turn off ad blockers
# - [If you're using Jupyter Lab locally, you need to install some "extensions"](https://plot.ly/python/getting-started/#jupyterlab-support-python-35)
#
# ## Stretch Goals
# - [ ] Do linear regression with two or more features.
# - [ ] Read [The Discovery of Statistical Regression](https://priceonomics.com/the-discovery-of-statistical-regression/)
# - [ ] Read [_An Introduction to Statistical Learning_](http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf), Chapter 2.1: What Is Statistical Learning?
# + id="o9eSnDYhUGD7"
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
# If you're working locally:
else:
DATA_PATH = '../data/'
# Ignore this Numpy warning when using Plotly Express:
# FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
# + id="4S2wXSrFV_g4"
# Read New York City apartment rental listing data
import pandas as pd
df = pd.read_csv(DATA_PATH+'apartments/renthop-nyc.csv')
assert df.shape == (49352, 34)
# + id="yEg0H7XI4dEn"
# Remove outliers:
# the most extreme 1% prices,
# the most extreme .1% latitudes, &
# the most extreme .1% longitudes
df = df[(df['price'] >= 1375) & (df['price'] <= 15500) &
(df['latitude'] >=40.57) & (df['latitude'] < 40.99) &
(df['longitude'] >= -74.1) & (df['longitude'] <= -73.38)]
# + id="KGz7VVH3904t" outputId="436bb8a3-1023-4cd4-cc29-72e2a5706e58" colab={"base_uri": "https://localhost:8080/"}
df.shape
# + id="-etxzqVFBHfF" outputId="f361865e-138c-459c-af27-b4f421f39172" colab={"base_uri": "https://localhost:8080/", "height": 513}
df.head()
# + id="4RA3McBZ_y6t" outputId="c68a9ac9-6a80-4c76-eecf-fe6894282dbb" colab={"base_uri": "https://localhost:8080/"}
df.info()
# + [markdown] id="Z-abHjVT8NpT"
# # Predict how much it costs to rent an apartment
# + [markdown] id="qK7qKjZe8kAp"
# ## 1. Chose a class of model
# + id="-RqSOyG_8jU_"
from sklearn.linear_model import LinearRegression
# + [markdown] id="K7iY0RK_B_XF"
# ##2. Chose Model Hyperameters
# + id="wXocQ-hfC5D0"
model = LinearRegression()
# + [markdown] id="W5jdSaqMCCwY"
# ###3. Arrange Data into Feature Matrixes and Target Vectors
# + id="n821TaieAGWk" outputId="cf2a686c-a84e-4e3c-e948-dace7bcc9a0e" colab={"base_uri": "https://localhost:8080/"}
#Target Vector Y
target = 'price'
y = df[target]
#Feature Matrix X
X = df[['latitude']]
X.shape
# + [markdown] id="QjuA9zZyCLlq"
# ##4. Fit the Model to Data
# + id="B52cxljQC9J0" outputId="803e2dff-591c-46c2-8fd9-2b94d7040d1b" colab={"base_uri": "https://localhost:8080/"}
model.fit(X,y)
# + id="ycDl-0BjDX3f" outputId="3193c6d5-ec12-42ad-f587-acda2c33cc1e" colab={"base_uri": "https://localhost:8080/"}
model.coef_
# + id="x_QUUK7KDbxb" outputId="80b7e627-08d9-4838-872b-9f7d0657ec79" colab={"base_uri": "https://localhost:8080/"}
model.intercept_
# + id="bJLuKzRYDtpa" outputId="4c8d86dd-cc19-4e09-e061-b6e502ab9071" colab={"base_uri": "https://localhost:8080/", "height": 35}
f'Price = {model.intercept_} + {model.coef_[0]} * latitude'
# + [markdown] id="OE7ftUspDk33"
# ##Visualization
# + id="oujM5dhEDkTS" outputId="0307acbc-8ab3-46d2-b4c9-dd463081947d" colab={"base_uri": "https://localhost:8080/"}
from sklearn.metrics import mean_absolute_error
#Establishing Basic Baseline
y_mean = y.mean()
y_basic = [y_mean]*len(y)
print('Baseline Mean Absolute Error:', mean_absolute_error(y, y_basic))
#Establishing Linear Regression Error
print('Linear Regression Mean Absolute Error:', mean_absolute_error(y, model.predict(X)))
# + id="s6bmQJ5eJ-bm" outputId="3cdb7e42-95fb-49f3-f8d4-642c40a76173" colab={"base_uri": "https://localhost:8080/", "height": 266}
import matplotlib.pyplot as plt
plt.scatter(X,y)
plt.plot(X, model.predict(X),
label = 'Linear Regression Model',
color = 'red');
# + [markdown] id="9gh5VbO1cJE2"
# ##Predictive Function
# + id="rCf7fYtJcs0W" outputId="b5dc7630-75e5-4513-f8b6-627e5db74fca" colab={"base_uri": "https://localhost:8080/"}
latitude = 40.7145
def predict(latitude):
y_pred = model.predict([[latitude]])
estimate = y_pred[0]
print (int(estimate), 'is our estimated price for an apartment with latitude', int(latitude), 'in New York CIty.')
predict(40.7145)
|
faith_module1-regression-1/LS_DS_211_assignment.ipynb
|