code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Constrained optimization using scipy
#
# **<NAME>, PhD**
#
# This demo is based on the original Matlab demo accompanying the <a href="https://mitpress.mit.edu/books/applied-computational-economics-and-finance">Computational Economics and Finance</a> 2001 textbook by <NAME> and <NAME>.
#
# Original (Matlab) CompEcon file: **demopt08.m**
#
# Running this file requires the Python version of CompEcon. This can be installed with pip by running
#
# # !pip install compecon --upgrade
#
# <i>Last updated: 2021-Oct-01</i>
# <hr>
# ## About
#
# The problem is
#
# \begin{equation*}
# \max\{-x_0^2 - (x_1-1)^2 - 3x_0 + 2\}
# \end{equation*}
#
# subject to
#
# \begin{align*}
# 4x_0 + x_1 &\leq 0.5\\
# x_0^2 + x_0x_1 &\leq 2.0\\
# x_0 &\geq 0 \\
# x_1 &\geq 0
# \end{align*}
# ## Using scipy
#
# The **scipy.optimize.minimize** function minimizes functions subject to equality constraints, inequality constraints, and bounds on the choice variables.
# +
import numpy as np
from scipy.optimize import minimize
np.set_printoptions(precision=4,suppress=True)
# -
# * First, we define the objective function, changing its sign so we can minimize it
def f(x):
return x[0]**2 + (x[1]-1)**2 + 3*x[0] - 2
# * Second, we specify the inequality constraints using a tuple of two dictionaries (one per constraint), writing each of them in the form $g_i(x) \geq 0$, that is
# \begin{align*}
# 0.5 - 4x_0 - x_1 &\geq 0\\
# 2.0 - x_0^2 - x_0x_1 &\geq 0
# \end{align*}
cons = ({'type': 'ineq', 'fun': lambda x: 0.5 - 4*x[0] - x[1]},
{'type': 'ineq', 'fun': lambda x: 2.0 - x[0]**2 - x[0]*x[1]})
# * Third, we specify the bounds on $x$:
# \begin{align*}
# 0 &\leq x_0 \leq \infty\\
# 0 &\leq x_1 \leq \infty
# \end{align*}
bnds = ((0, None), (0, None))
# * Finally, we minimize the problem, using the SLSQP method, starting from $x=[0,1]$
x0 = [0.0, 1.0]
res = minimize(f, x0, method='SLSQP', bounds=bnds, constraints=cons)
print(res)
|
_build/jupyter_execute/notebooks/opt/08 Constrained optimization using scipy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.6.12 64-bit (''mash'': conda)'
# language: python
# name: python3
# ---
# # t-SNE
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
X = pd.read_csv('checkpoints/visual_test2/latent_space.tsv',sep='\t', header=0, index_col=0)
labels = pd.read_csv('data/labels.tsv', sep='\t',header=0, index_col=0)
n_classes = 34 #no of classes to visualize
labels = labels[labels['sample_type.samples'].isin(range(n_classes))]
X = X.reset_index()
labels = labels.reset_index()
X = X.rename(columns={'index': 'sample'})
df = pd.merge(X, labels, on='sample', how='inner', sort=False)[['sample','sample_type.samples']]
X = X[X['sample'].isin(df['sample'])]
plt.scatter(X_embedded[:, 0], X_embedded[:, 1], c=df.loc[:,'sample_type.samples'], s=0.5)
# +
import math
import numpy as np
from matplotlib.colors import ListedColormap
from matplotlib.cm import hsv
def generate_colormap(number_of_distinct_colors: int = 80):
if number_of_distinct_colors == 0:
number_of_distinct_colors = 80
number_of_shades = 7
number_of_distinct_colors_with_multiply_of_shades = int(math.ceil(number_of_distinct_colors / number_of_shades) * number_of_shades)
# Create an array with uniformly drawn floats taken from <0, 1) partition
linearly_distributed_nums = np.arange(number_of_distinct_colors_with_multiply_of_shades) / number_of_distinct_colors_with_multiply_of_shades
# We are going to reorganise monotonically growing numbers in such way that there will be single array with saw-like pattern
# but each saw tooth is slightly higher than the one before
# First divide linearly_distributed_nums into number_of_shades sub-arrays containing linearly distributed numbers
arr_by_shade_rows = linearly_distributed_nums.reshape(number_of_shades, number_of_distinct_colors_with_multiply_of_shades // number_of_shades)
# Transpose the above matrix (columns become rows) - as a result each row contains saw tooth with values slightly higher than row above
arr_by_shade_columns = arr_by_shade_rows.T
# Keep number of saw teeth for later
number_of_partitions = arr_by_shade_columns.shape[0]
# Flatten the above matrix - join each row into single array
nums_distributed_like_rising_saw = arr_by_shade_columns.reshape(-1)
# HSV colour map is cyclic (https://matplotlib.org/tutorials/colors/colormaps.html#cyclic), we'll use this property
initial_cm = hsv(nums_distributed_like_rising_saw)
lower_partitions_half = number_of_partitions // 2
upper_partitions_half = number_of_partitions - lower_partitions_half
# Modify lower half in such way that colours towards beginning of partition are darker
# First colours are affected more, colours closer to the middle are affected less
lower_half = lower_partitions_half * number_of_shades
for i in range(3):
initial_cm[0:lower_half, i] *= np.arange(0.2, 1, 0.8/lower_half)
# Modify second half in such way that colours towards end of partition are less intense and brighter
# Colours closer to the middle are affected less, colours closer to the end are affected more
for i in range(3):
for j in range(upper_partitions_half):
modifier = np.ones(number_of_shades) - initial_cm[lower_half + j * number_of_shades: lower_half + (j + 1) * number_of_shades, i]
modifier = j * modifier / upper_partitions_half
initial_cm[lower_half + j * number_of_shades: lower_half + (j + 1) * number_of_shades, i] += modifier
return ListedColormap(initial_cm)
# -
import matplotlib
cm = generate_colormap(n_classes)
colors = []
for i in range(n_classes):
rgba = cm(i)
# rgb2hex accepts rgb or rgba
colors.append(matplotlib.colors.rgb2hex(rgba))
tumors = ['LUAD','BRCA', 'UCEC','OV','LUSC','HNSC','KIRC','CESC','normal','PRAD','GBM','PAAD','BLCA','SARC',
'THCA','KIRP','UVM','LIHC','SKCM','ACC','LGG','STAD','PCPG','TGCT','COAD','THYM','LAML','KICH','ESCA','UCS',
'READ','MESO','DLBC','CHOL']
from tsnecuda import TSNE
X_embedded = TSNE(n_components=2, perplexity=15, learning_rate=30).fit_transform(X.iloc[:,1:])
# +
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import numpy as np
x = X_embedded[:, 0]
y = X_embedded[:, 1]
categories = df.loc[:,'sample_type.samples'].to_numpy()
colormap = np.array(colors)
plt.scatter(x, y, s=1, c=colormap[categories])
pop_a = mpatches.Patch(color='#0b559f', label='Population A')
pop_b = mpatches.Patch(color='#89bedc', label='Population B')
handles = []
for t, c in zip(tumors, colors):
handles.append(mpatches.Patch(color=c, label=t))
plt.legend(loc='upper center', bbox_to_anchor=(1.4, 1.05), handles=handles,
ncol=3, fancybox=True, shadow=True)
plt.title('Visualization using t-SNE')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.savefig('images/tsne.png')
plt.show()
# -
# # Log
# ## Train log
path = "./checkpoints/omics_mode/ABC/ABC_inter/train_log.txt"
with open(path) as f:
lines = f.readlines()
l = lines[-2]
sp = l.split(']')[1].split(': ')
int(sp[2].strip().split(' ')[0])
def process_train_log(lines):
recon_A, recon_B, recon_C, kl, classifier, accuracy = [], [], [], [], [], []
for l in lines:
if l.startswith("[TRAIN]"):
# print(l)
sp = l.split(']')[2].split(': ')
spl = l.split(']')[1].split(': ')
epoch = int(spl[2].strip().split(' ')[0])
if(epoch==7166):
recon_A.append(float(sp[1].split(' ')[0]))
recon_B.append(float(sp[2].split(' ')[0]))
recon_C.append(float(sp[3].split(' ')[0]))
kl.append(float(sp[4].split(' ')[0]))
classifier.append(float(sp[5].split(' ')[0]))
accuracy.append(float(sp[6].split(' ')[0]))
# print(recon_A, recon_B, recon_C, kl, classifier, accuracy)
return recon_A, recon_B, recon_C, kl, classifier, accuracy
recon_A, recon_B, recon_C, kl, classifier, accuracy = process_train_log(lines)
plt.plot(recon_A)
plt.plot(recon_B)
plt.plot(recon_C)
plt.plot(accuracy)
plt.xlabel('No of epochs')
plt.ylabel('Train accuracy')
plt.title('Cancer type classification with multi-omics data')
# ## Test log
path = "./checkpoints/omics_mode/ABC/ABC_inter2/test_log.txt"
with open(path) as f:
lines = f.readlines()
l = lines[-2]
spl = l.split(']')[1].split(': ')
int(spl[2].strip().split(' ')[0])
print(l)
def process_test_log(lines):
recon_A, recon_B, recon_C, kl, classifier, accuracy = [], [], [], [], [], []
for l in lines:
if l.startswith("[TEST]"):
# print(l)
sp = l.split(']')[2].split(': ')
spl = l.split(']')[1].split(': ')
epoch = int(spl[2].strip().split(' ')[0])
if(epoch==1792):
recon_A.append(float(sp[1].split(' ')[0]))
recon_B.append(float(sp[2].split(' ')[0]))
recon_C.append(float(sp[3].split(' ')[0]))
kl.append(float(sp[4].split(' ')[0]))
classifier.append(float(sp[5].split(' ')[0]))
accuracy.append(float(sp[6].split(' ')[0]))
# print(recon_A, recon_B, recon_C, kl, classifier, accuracy)
return recon_A, recon_B, recon_C, kl, classifier, accuracy
recon_A, recon_B, recon_C, kl, classifier, accuracy = process_test_log(lines)
plt.plot(accuracy)
|
Visualisation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Betfair predictions for the 2019 vote
#
# 
#
# [Betfair](https://www.betfair.com/exchange/plus/politics) is a betting exchange, where punters can gamble
# on sports and other events including the UK election. There is no bookmaker — it's just punters gambling against each other — so it embodies the [_wisdom of the crowd_](https://en.wikipedia.org/wiki/Wisdom_of_the_crowd).
# It's also a real-time data exchange, so we can get real-time snapshots of opinion, not lagged like conventional polling.
#
# In this analysis, we look at Betfairs predictions for each constituency. We plot it on a three-way map, plotting each point according to how the 2017 vote split between Labour / Conservative / LibDem. Constituencies in the bottom right went Conservative, those in the top right went Labour, and those on the left went LibDem
# (and other constituencies are plotted according to their vote share between these three parties).
#
# The points to look at are the constituencies on the border. For example, if there's a blue point above the line, it means a constituency which went Labour in 2017, but is likely to go Conservative in 2019.
# ## Preamble
import numpy as np
import pandas
import matplotlib.pyplot as plt
import json
# +
# To read an Excel file from within Python, install this package.
# (If you're unable to install it on your system, then open the Excel file
# from the House of Commons Library in Excel, save as CSV, then use
# pandas.read_csv.)
# !pip install --user xlrd
# -
# # Data import
# There are many useful statistics at https://commonslibrary.parliament.uk/local-data/constituency-dashboard/. Here I'm just using data about the 2017 election.
url = 'https://data.parliament.uk/resources/constituencystatistics/Current-Parliament-Election-Results.xlsx'
vote2017 = pandas.read_excel(url, sheet_name='DATA')
# At [Betfair Exchange](https://www.betfair.com/exchange/plus/politics), users make bets for and against outcomes ("back" and "lay"). A crude summary of how to read it:
#
# * if there is an open offer to back a candidate at odds $q$, then the market believes that the probability of this candidate's winning is $\leq 1/q$
#
# * if there is an open offer to lay a candidate at odds $q$, then the market believes that the probability of this candidate's winning is $\geq 1/q$.
#
#
# I have used the Betfair json api to fetch the latest betting data.
# The code for fetching it is at the bottom -- but you need to sign up
# with betfair to use their api. To save the bother, I have assembled the
# betting data into a single json file. The format is a list with one item per constituency,
# ```
# [(market, (runners,), (prices,)), ...]
# ```
# where
#
# * `market` comes from [listMarketCatalogue](https://docs.developer.betfair.com/display/1smk3cen4v3lu3yomq5qye0ni/listMarketCatalogue)
# and lists the COMPETITION and EVENT details for a constituency
# * `runners` comes from [listMarketCatalogue](https://docs.developer.betfair.com/display/1smk3cen4v3lu3yomq5qye0ni/listMarketCatalogue) and lists the RUNNER_DESCRIPTION for each candidate in the constituency
# * `prices` comes from [listMarketBook](https://docs.developer.betfair.com/display/1smk3cen4v3lu3yomq5qye0ni/listMarketBook) and lists the current odds for each candidate
#
# +
with open('data/betfair_20191209.json') as f:
res = json.load(f)
prices = []
runners = []
for m,(r,),(p,) in iter(res.values()):
for pr in p['runners']:
layed = max([b['price'] for b in pr['ex']['availableToBack']], default=np.nan)
backed = min([b['price'] for b in pr['ex']['availableToLay']], default=np.nan)
prices.append([p['marketId'], pr['selectionId'], layed, backed])
for rr in r['runners']:
runners.append([m['marketId'], m['marketName'], rr['selectionId'], rr['runnerName']])
prices = pandas.DataFrame.from_records(prices, columns=['marketId','runnerId','layed','backed'])
runners = pandas.DataFrame.from_records(runners, columns=['marketId','marketName','runnerId','runnerName'])
odds = prices.merge(runners, how='outer', on=['marketId','runnerId']).reset_index()
# -
# The Betfair data labels each constituency by `marketId`. UK sources usually label by `ONSconstID`, an id from the Office for National Statistics. I have assembled a mapping file between them.
# +
# Bothersomely, Betfair marketId is a string but it looks like a floating point number. To stop pandas from
# converting it (and thereby truncating or losing trailing zeros), we have to tell it explicitly what type to use.
const_ids = pandas.read_csv('data/constituency_id_map.csv', dtype={'betfair_id':np.str})
# -
# # Data preparation
# It's overwhelming to plot all parties (including the "Space Navies Party" etc.)
# so we'll restrict attention to the most common parties.
# This tabulation lists the parties, ordered by the number of candidates they stood in 2017. This lets us see how the popular parties were named, so we can filter out the others.
vote2017.groupby('PartyShortName').apply(len) \
.sort_values(ascending=False) \
.iloc[:10]
# The `vote2017` dataframe has one row per constituency:candidate. We'll cut it down to one row per constituency, and put the candidates (for major parties) in columns. This will be easier for the plots we want to do next.
#
# There are also some extra per-constituency fields, such as constituency name and turnout, which we'll merge in.
# +
constituencies = \
vote2017.loc[np.isin(vote2017.PartyShortName, ['Con','Lab','LD','Green','SNP','PC'])] \
.groupby(['ONSconstID','PartyShortName'])['Votes'].apply(sum) \
.unstack(fill_value=0).reset_index() \
.rename_axis(None, axis=1)
df = vote2017.drop_duplicates('ONSconstID') \
[['ONSconstID','ConstituencyName','RegionName','Turnout','Electorate']]
constituencies = constituencies.merge(df, on='ONSconstID')
# -
# Next, align the 2017 vote data with the Betfair predictions. There are many interesting things in the Betfair data, but all we'll pull out is its prediction for the most likely winning party in each constituency.
#
# There are many candidates that no one wants to bet on. This could either be because the candidate is a sure-fire winner, or a sure-fire loser. For the purposes of plotting, I'll only use candidates where there is an actual betting market.
# +
# As described above, the offered odds tell us about the probability of winning
df = odds.copy()
df['pmin'] = 1 / df.backed
df['pmax'] = 1 / df.layed
df['p'] = (df.pmin + df.pmax) / 2
bfwin = df.loc[~pandas.isna(df.p)] \
.sort_values('p', ascending=False) \
.groupby('marketId')['runnerName'].apply(lambda x: x.iloc[0]) \
.reset_index(name='predwin')
# see also .topk, .nlargest, .head
# Look up the official ONS id for each constituency.
# Relabel the columns, and keep only the ones we'll use for plotting.
bfwin = bfwin.merge(const_ids, left_on='marketId', right_on='betfair_id', how='outer')
bfwin = pandas.DataFrame({'ONSconstID': bfwin.id, 'predwin': bfwin.predwin})
# -
# # Plotting code
# +
party_style = {
'Con': (np.cos(2*np.pi/6), -np.sin(2*np.pi/6), 2),
'Lab': (np.cos(2*np.pi/6), np.sin(2*np.pi/6), 2),
'LD': (-1,0, 4)
}
df = constituencies.merge(bfwin, on='ONSconstID')
df['x'] = 0
df['y'] = 0
for party,(dx,dy,__) in party_style.items():
df['x'] += np.log(np.maximum(df[party],1)) * dx
df['y'] += np.log(np.maximum(df[party],1)) * dy
# -
# First attempt at a plot ...
fig,ax = plt.subplots()
ax.scatter(df.x, df.y)
plt.show()
# Final plot, after iteratively fiddling with the layout, the colours, the legend, etc.
# +
# We'll specify colours for the main parties, and leave the others on a
# standard colour palette.
parties = np.unique(df.predwin[~pandas.isna(df.predwin)])
def col(i):
cols = {'Labour': (217,55,63),
'Conservative': (0,100,157),
'Liberal Democrat': (235,179,45),
'SNP': (252,238,92),
'Green': (0,128,0)}
cols2 = plt.get_cmap('Set2', len(parties))
if i in cols:
return np.array(cols[i])/255
elif pandas.isna(i):
return '0.7'
else:
return cols2(np.where(parties==i)[0])
# Set up the plot
with plt.rc_context({'figure.figsize': (8,6)}):
fig,ax = plt.subplots()
# Scatter plot, for each constituency, colour-coded by predicted winner
i = pandas.isna(df.predwin)
ax.scatter(df.x[i], df.y[i], label='no bet', alpha=.6, color=col(np.nan))
for p in parties:
i = df.predwin==p
ax.scatter(df.x[i], df.y[i], label=p, alpha=.6, color=col(p))
# Annotate with text (and trim some points that are out of bounds --
# ax.text doesn't respect xlim and ylim)
for i in np.arange(len(df)):
if df.x[i]<4.5 and df.y[i]>-2:
ax.text(df.x[i], df.y[i], df.ConstituencyName[i], fontsize=1)
# Grid lines, to lay out the axes showing which seats went which way in 2017
for (dx,dy,m) in party_style.values():
ax.plot([0,-m*dx],[0,-m*dy], color='black', linestyle='dashed')
# Configure the scales
ax.set_xlim([-2,4.5])
ax.set_ylim([-2,2.5])
ax.set_xticks([])
ax.set_yticks([])
ax.legend(title='Betfair prediction', loc='upper left', bbox_to_anchor=(1,1,0,0))
# Save as pdf, so we can zoom and search the text labels
plt.savefig('predictions.pdf', transparent=True, bbox_inches='tight', pad_inches=0)
plt.show()
# -
# # Appendix: code to fetch data from Betfair
# To use the Betfair api, you need to create a Betfair account, and then an application key at https://docs.developer.betfair.com/visualisers/api-ng-account-operations/.
#
# +
import requests
import json
from IPython.display import clear_output
import time
import pathlib
import pandas
import numpy as np
endpoint = "https://api.betfair.com/exchange/betting/rest/v1.0/"
# +
# Login
# I don't like to store sensitive data in a version-controlled Juputer notebook.
# Instead, I store credentials in a json file, not under version control.
# I have two-factor authentication turned on, so Betfair tells me to append
# an auth_code (from an Authenticator app on my phone) to the password field.
CREDENTIALS_FILE = 'betfair_creds.json'
with open(CREDENTIALS_FILE) as f:
creds = json.loads(f.read())
auth_code = input()
conn = requests.Session()
conn.headers['Accept'] = 'application/json'
conn.headers['X-Application'] = creds['app_key']
r = conn.post('https://identitysso.betfair.com/api/login',
data = {'username': creds['username'], 'password': creds['password'] + str(auth_code)}
)
r.raise_for_status()
r = r.json()
assert r['status'] == 'SUCCESS'
conn.headers['X-Authentication'] = r['token']
# +
# Get a list of all constituencies
politics = conn.post(endpoint+'listEventTypes/',
json = {'filter': {'textQuery':'Politics'}})
politics = politics.json()[0]['eventType']['id']
events = conn.post(endpoint+'listEvents/',
json = {'filter' :{'eventTypeIds': [politics], 'textQuery':'Constituencies'}})
events = [int(e['event']['id']) for e in events.json()]
competitions = conn.post(endpoint+'listCompetitions/',
json = {'filter': {'eventIds': events}})
competitions = [int(c['competition']['id']) for c in competitions.json()]
markets = conn.post(endpoint+'listMarketCatalogue/',
json = {'filter': {'competitionIds': competitions},
'marketProjection': ['EVENT','COMPETITION'],
'maxResults': 1000})
markets = markets.json()
print(f"{len(markets)} markets")
# +
# Get current prices for all constituencies
res = {}
for i,market in enumerate(markets):
m = market['marketId']
if m in res: continue
clear_output(wait=True)
print(f'{i+1} / {len(markets)}')
print(market)
r = conn.post(endpoint+'listMarketCatalogue/',
json = {'filter': {'marketIds': [m]},
'marketProjection': ['RUNNER_DESCRIPTION'],
'maxResults': 1000})
b = conn.post(endpoint+'listMarketBook/',
json = {'marketIds': [m],
'priceProjection': {
'priceData': ["EX_BEST_OFFERS", "EX_TRADED"],
'virtualise': True
}
})
res[m] = (market, r.json(), b.json())
time.sleep(3)
with open('betfair_data.json', 'w') as f:
json.dump(res, f)
|
scicomp-master/vote2019/analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (scivis-plankton)
# language: python
# name: scivis-plankton
# ---
# # Random Forest Classifier - Label 3
#
# Classify plankton species (keeping detritus) using random forests.
# delete variables in memory
# %reset
# Import libraries
import pandas as pd
import numpy as np
from sklearn.preprocessing import LabelEncoder
from sklearn.ensemble import RandomForestClassifier
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
import pickle
# Load he data which have been preprocessed in R.
# +
train = pd.read_csv("../../../data/processed/labelled-features/labelled-features-train.csv")
train = train.set_index('index')
test = pd.read_csv("../../../data/processed/labelled-features/labelled-features-test.csv")
test = test.set_index('index')
# -
print(train["label3"].unique())
print( len( train["label3"].unique() ) )
for col in train.columns:
print(col)
# These are the columns we are retaining in the features matrix (X)
cols_retain = [ col for col in train.columns if col not in ['filename', 'label1', 'label2', 'label3',
'img_file_name', 'img_rank'] ]
for col in cols_retain:
print(col)
# Encode target labels with value between 0 and n_classes-1.
# Encode taget labels with value between 0 and n_classes-1
LE = LabelEncoder()
LE.fit( train['label3'] ) # fit label encoder
y_train = LE.transform( train['label3'] ) # transform labels to normalized encoding
y_test = LE.transform( test['label3'] ) # transform labels to normalized encoding
LE.classes_
X_train = train[cols_retain] # Features
X_test = test[cols_retain] # Features
# Apply random forest classifier using default settings and make prediction
# Create a Gaussian Classifier
clf=RandomForestClassifier(n_estimators=100) # this is the default number of trees in the forest
# +
import time
tic = time.perf_counter()
clf.fit(X_train,y_train) # Train the model using the training sets
toc = time.perf_counter()
print("Time to train model: %.4f seconds" % (toc-tic))
# -
#Make prediction using features in test set
y_pred=clf.predict(X_test)
y_pred
# Calculate metrics on the random forest model
print('Mean Absolute Error:', metrics.mean_absolute_error(y_test, y_pred))
print('Mean Squared Error:', metrics.mean_squared_error(y_test, y_pred))
print('Root Mean Squared Error:', np.sqrt(metrics.mean_squared_error(y_test, y_pred)))
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
print(metrics.classification_report(y_test,y_pred, target_names=LE.classes_))
plt.rcParams['figure.figsize'] = [12, 8]
plt.rcParams['figure.dpi'] = 100
metrics.plot_confusion_matrix(clf, X_test, y_test)
plt.show()
# Find important features for classification
feature_names = X_train.columns
feature_imp = pd.Series(clf.feature_importances_,index=feature_names).sort_values(ascending=False)
print(feature_imp)
# Creating a bar plot
sns.barplot(x=feature_imp, y=feature_imp.index)
# Add labels to your graph
plt.rcParams['figure.figsize'] = [12, 8]
plt.rcParams['figure.dpi'] = 100
plt.xlabel('Feature Importance Score')
plt.ylabel('Features')
plt.title("Visualizing Important Features")
plt.show()
# The following calculates precision, recall, accuracy and f1 using the pre-computed confusion matrix
confusion_matrix = metrics.confusion_matrix(y_test, y_pred)
from evaluate_model import model_metrics
accuracy, precision, recall, f1 = model_metrics(confusion_matrix)
print("precision = %.3f" % precision)
print("recall = %.3f" % recall)
print("accuracy = %.3f" % accuracy)
print("f1 = %.3f" % f1)
# Export pre-trained model as pkl file so that it can later be used in scivision
with open('/output/models/randomforest/rf-label3.pkl','wb') as f:
pickle.dump(clf,f)
|
notebooks/python/dsg2021/random_forest_label3_with_detritus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="XqhnaAncBm3Y" outputId="376d4295-9af0-4930-b2e9-7fa1a69127c6"
import tensorflow as tf
from tensorflow import keras
tf.__version__
# + id="HVfCcR6HCUsu"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# + colab={"base_uri": "https://localhost:8080/"} id="mTepy9G6CZej" outputId="6f7548ea-f483-44f3-d844-17f478f04fd6"
# loading the MNIST dataset
mnist = tf.keras.datasets.mnist
(X_train, y_train), (X_test, y_test)=mnist.load_data()
# + colab={"base_uri": "https://localhost:8080/", "height": 446} id="vc1OR4-2CwOX" outputId="fb3bec18-aa9c-4c0d-ad4e-47fe02f2c7a0"
plt.figure(figsize = (7,7))
plt.imshow(X_train[0], cmap = 'binary')
# + id="gYXa5tvaDH46"
# Normalizing the data and dividing the training data into train and validation set/
X_valid, X_train = X_train[:5000]/255, X_train[5000:]/255
X_test = X_test/255
y_valid, y_train = y_train[:5000], y_train[5000:]
# + id="iu0u7LA3EGj6"
# in this cell we are defining the layers architecture for our model
LAYERS = [
keras.layers.Flatten(input_shape = [28,28], name = 'inputLayer'),
keras.layers.Dense(300, activation = 'relu'),
keras.layers.Dense(100, activation = 'relu'),
keras.layers.Dense(10, activation = 'softmax')
]
# + colab={"base_uri": "https://localhost:8080/"} id="jacQ2mjU3RyL" outputId="c0237521-3d85-44fe-ad1c-3793a9fa4ada"
model_classifier = keras.models.Sequential(LAYERS)
model_classifier.layers
# + colab={"base_uri": "https://localhost:8080/"} id="tXMG9YoT3iZ7" outputId="3c4b5cf7-fc9c-458e-9016-0700ea38c3b4"
model_classifier.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="yYmM-tiO3q_4" outputId="83b57849-9d23-4e23-9ada-aa0c5b324fba"
weights, biases = model_classifier.layers[1].get_weights()
weights.shape
# + [markdown] id="0xjMKMuI7cku"
# ### If you imagine above cell output, it is from every input is connected to 300 other neurons, so there are 784 inputs and then they go into 300 neurons of next layer, that is how we get this (784,300) shape.
# + id="Hc_MVzUf6LIY"
LOSS_FUNCTION = "sparse_categorical_crossentropy"
OPTIMIZER = "SGD"
METRICS = ["ACCURACY"]
EPOCHS = 10
VALIDATION = (X_valid, y_valid)
# + id="VXffD0zt7d73"
model_classifier.compile(loss= LOSS_FUNCTION, optimizer = OPTIMIZER, metrics = METRICS)
# + colab={"base_uri": "https://localhost:8080/"} id="VLw8cLxd8dLh" outputId="6a935f00-e5d8-4e7c-acb8-aca29332d085"
model_classifier.fit(X_train, y_train, epochs = EPOCHS, validation_data= VALIDATION, batch_size = 32)
# + [markdown] id="l7r9qWvgS492"
# ## 1719 is number of iterations and in every epoch model will see all 55000 points but in 1719 forward and backward passes.
#
# 1719 as if we divide 55000/32(which is batch size 32).
# + colab={"base_uri": "https://localhost:8080/", "height": 284} id="b_Qgb2ds83Zx" outputId="e03559a5-4d4f-4214-f7a0-a221d1e3b7d0"
pd.DataFrame(model_classifier.history.history).plot()
# + colab={"base_uri": "https://localhost:8080/"} id="KwSLdzZz-_iN" outputId="94707586-a780-4972-ee27-c6999b63dc2b"
# it will print loss and accuracy score
model_classifier.evaluate(X_test, y_test)
# + colab={"base_uri": "https://localhost:8080/"} id="uF958D28TrjT" outputId="c1d24fe4-b67a-4f37-9974-497683d36bc7"
model_classifier.predict(X_test[:5])
# + colab={"base_uri": "https://localhost:8080/"} id="8JMJ5mjAU9my" outputId="da791439-94cd-4c34-d880-695b9b468afa"
model_classifier.predict(X_test[:5]).round(3)
# + colab={"base_uri": "https://localhost:8080/"} id="QCodo5IZVA6u" outputId="042bde69-ebc3-4096-aed3-fbe3fa02080e"
np.argmax(model_classifier.predict(X_test[:5]), axis = 1)
# + colab={"base_uri": "https://localhost:8080/"} id="GMa00KqJVPtY" outputId="1d2b7acf-2a34-4776-b581-ca64a4a4d462"
y_test[:5]
# + id="w2vpWm1PVfoD"
|
ANN_Implimentation_Demo - 26th Sep/ANN_Implimentation_Demo - 26th Sep.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
os.environ['CUDA_VISIBLE_DEVICES'] = ''
from glob import glob
goemotions = glob('goemotions_*.csv')
goemotions
import malaya
import pandas as pd
df = pd.read_csv(goemotions[0])
df.head()
transformer = malaya.translation.en_ms.transformer()
preprocessing = malaya.preprocessing.preprocessing(normalize = [],
annotate = [],
lowercase = [],
expand_english_contractions = True)
texts = df['text'].tolist()
# +
from tqdm import tqdm
translate_nmt, translate_replace = [], []
for i in tqdm(range(len(texts))):
s = texts[i]
r_nmt = None
r_replace = None
try:
r_nmt = transformer.greedy_decoder([s])[0]
except:
pass
try:
r_replace = ' '.join(preprocessing.process(s))
except:
pass
translate_nmt.append(r_nmt)
translate_replace.append(r_replace)
# -
df['translate_nmt'] = translate_nmt
df['translate_replace'] = translate_replace
df.to_csv('goemotions_2.translated.csv', index = False)
|
corpus/goemotions/translate-geomotions-part2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Creating a simple visualization.
# In this exercise, we will create our first simple plot using Matplotlib.
# #### Import statements
# Import the necessary modules and enable plotting within a jupyter notebook.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# #### Creating a figure
# Explicitly create a figure and set the dpi to 200.
plt.figure(dpi=200)
# #### Plotting data pairs
# Plot the following data pairs (x, y) as circles, which are connected via line segments: (1, 1), (2, 3), (4, 4), (5, 3). Visualize the plot.
plt.plot([1, 2, 4, 5], [1, 3, 4, 3], '-o')
plt.show()
|
Lesson03/Exercise03/exercise03_solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import warnings
warnings.filterwarnings('ignore')
df = pd.read_csv('student-por.csv')
df.head()
df = pd.read_csv('student-por.csv', sep=';')
df.head()
df.isnull().sum()
df.fillna(-99.0, inplace=True)
df[df.isna().any(axis=1)]
df['age'] = df['age'].fillna(df['age'].median())
df['sex'] = df['sex'].fillna(df['sex'].mode())
df['guardian'] = df['guardian'].fillna(df['guardian'].mode())
df.head()
categorical_columns = df.columns[df.dtypes==object].tolist()
from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder()
hot = ohe.fit_transform(df[categorical_columns])
hot_df = pd.DataFrame(hot.toarray())
hot_df.head()
print(hot)
hot
cold_df = df.select_dtypes(exclude=["object"])
cold_df.head()
# +
from scipy.sparse import csr_matrix
cold = csr_matrix(cold_df)
from scipy.sparse import hstack
final_sparse_matrix = hstack((hot, cold))
final_df = pd.DataFrame(final_sparse_matrix.toarray())
final_df.head()
# -
from sklearn.base import TransformerMixin
class NullValueImputer(TransformerMixin):
def __init__(self):
None
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
for column in X.columns.tolist():
if column in X.columns[X.dtypes==object].tolist():
X[column] = X[column].fillna(X[column].mode())
else:
X[column]=X[column].fillna(X[column].median())
return X
df = pd.read_csv('student-por.csv', sep=';')
nvi = NullValueImputer().fit_transform(df)
nvi.head()
class SparseMatrix(TransformerMixin):
def __init__(self):
None
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
categorical_columns= X.columns[X.dtypes==object].tolist()
ohe = OneHotEncoder()
hot = ohe.fit_transform(X[categorical_columns])
cold_df = X.select_dtypes(exclude=["object"])
cold = csr_matrix(cold_df)
final_sparse_matrix = hstack((hot, cold))
final_csr_matrix = final_sparse_matrix.tocsr()
return final_csr_matrix
sm = SparseMatrix().fit_transform(nvi)
print(sm)
sm_df = pd.DataFrame(sm.toarray())
sm_df.head()
df = pd.read_csv('student-por.csv', sep=';')
y = df.iloc[:, -1]
X = df.iloc[:, :-3]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=2)
from sklearn.pipeline import Pipeline
data_pipeline = Pipeline([('null_imputer', NullValueImputer()), ('sparse', SparseMatrix())])
X_train_transformed = data_pipeline.fit_transform(X_train)
import numpy as np
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score, KFold
from sklearn.metrics import mean_squared_error as MSE
from xgboost import XGBRegressor
y_train.value_counts()
kfold = KFold(n_splits=5, shuffle=True, random_state=2)
def cross_val(model):
scores = cross_val_score(model, X_train_transformed, y_train, scoring='neg_root_mean_squared_error', cv=kfold)
rmse = (-scores.mean())
return rmse
cross_val(XGBRegressor(objective='reg:squarederror', missing='unknown'))
X_train_2, X_test_2, y_train_2, y_test_2 = train_test_split(X_train_transformed, y_train, random_state=2)
def n_estimators(model):
eval_set = [(X_test_2, y_test_2)]
eval_metric="rmse"
model.fit(X_train_2, y_train_2, eval_metric=eval_metric, eval_set=eval_set, early_stopping_rounds=100)
y_pred = model.predict(X_test_2)
rmse = MSE(y_test_2, y_pred)**0.5
return rmse
n_estimators(XGBRegressor(n_estimators=5000))
def grid_search(params, reg=XGBRegressor(objective='reg:squarederror')):
grid_reg = GridSearchCV(reg, params, scoring='neg_mean_squared_error', cv=kfold)
grid_reg.fit(X_train_transformed, y_train)
best_params = grid_reg.best_params_
print("Best params:", best_params)
best_score = np.sqrt(-grid_reg.best_score_)
print("Best score:", best_score)
grid_search(params={'max_depth':[1, 2, 3, 4, 6, 7, 8],
'n_estimators':[31]})
grid_search(params={'max_depth':[1, 2],
'min_child_weight':[1,2,3,4,5],
'n_estimators':[31]})
grid_search(params={'max_depth':[1],
'min_child_weight':[2,3],
'subsample':[0.5, 0.6, 0.7, 0.8, 0.9],
'n_estimators':[31, 50]})
grid_search(params={'max_depth':[1],
'min_child_weight':[1, 2, 3],
'subsample':[0.8, 0.9, 1],
'colsample_bytree':[0.5, 0.6, 0.7, 0.8, 0.9, 1],
'n_estimators':[50]})
grid_search(params={'max_depth':[1],
'min_child_weight':[3],
'subsample':[.8],
'colsample_bytree':[0.9],
'colsample_bylevel':[0.6, 0.7, 0.8, 0.9, 1],
'colsample_bynode':[0.6, 0.7, 0.8, 0.9, 1],
'n_estimators':[50]})
cross_val(XGBRegressor(max_depth=1,
min_child_weight=3,
subsample=0.8,
colsample_bytree=0.9,
colsample_bylevel=0.9,
colsample_bynode=0.8,
objective='reg:squarederror',
booster='dart',
one_drop=True))
X_test_transformed = data_pipeline.fit_transform(X_test)
type(y_train)
model = XGBRegressor(max_depth=1,
min_child_weight=3,
subsample=0.8,
colsample_bytree=0.9,
colsample_bylevel=0.9,
colsample_bynode=0.8,
n_estimators=50,
objective='reg:squarederror')
model.fit(X_train_transformed, y_train)
y_pred = model.predict(X_test_transformed)
rmse = MSE(y_pred, y_test)**0.5
rmse
model = XGBRegressor(max_depth=1,
min_child_weight=5,
subsample=0.6,
colsample_bytree=0.9,
colsample_bylevel=0.9,
colsample_bynode=0.8,
n_estimators=50,
objective='reg:squarederror')
model.fit(X_train_transformed, y_train)
y_pred = model.predict(X_test_transformed)
rmse = MSE(y_pred, y_test)**0.5
rmse
full_pipeline = Pipeline([('null_imputer', NullValueImputer()),
('sparse', SparseMatrix()),
('xgb', XGBRegressor(max_depth=1,
min_child_weight=5,
subsample=0.6,
colsample_bytree=0.9,
colsample_bylevel=0.9,
colsample_bynode=0.8,
objective='reg:squarederror'))])
full_pipeline.fit(X, y)
new_data = X_test
full_pipeline.predict(new_data)
np.round(full_pipeline.predict(new_data))
new_df = pd.read_csv('student-por.csv')
new_X = df.iloc[:, :-3]
new_y = df.iloc[:, -1]
new_model = full_pipeline.fit(new_X, new_y)
more_new_data = X_test[:25]
np.round(new_model.predict(more_new_data))
single_row = X_test[:1]
single_row_plus = pd.concat([single_row, X_test[:25]])
print(np.round(new_model.predict(single_row_plus))[:1])
|
Chapter10/XGBoost_Model_Deployment-Copy1.ipynb
|
# ---
#
# jupyter:
# jupytext:
# formats: ipynb,md
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
#
# + language="bash"
#
# + language="bash"
#
# + language="bash"
#
# -
# ```
# ```
#
# ---
# title: "Loops"
# teaching: 40
# exercises: 10
# questions:
# - "How can I perform the same actions on many different files?"
# objectives:
# - "Write a loop that applies one or more commands separately to each file in a set of files."
# - "Trace the values taken on by a loop variable during execution of the loop."
# - "Explain the difference between a variable's name and its value."
# - "Explain why spaces and some punctuation characters shouldn't be used in file names."
# - "Demonstrate how to see what commands have recently been executed."
# - "Re-run recently executed commands without retyping them."
# keypoints:
# - "A `for` loop repeats commands once for every thing in a list."
# - "Every `for` loop needs a variable to refer to the thing it is currently operating on."
# - "Use `$name` to expand a variable (i.e., get its value). `${name}` can also be used."
# - "Do not use spaces, quotes, or wildcard characters such as '*' or '?' in filenames, as it complicates variable expansion."
# - "Give files consistent names that are easy to match with wildcard patterns to make it easy to select them for looping."
# - "Use the up-arrow key to scroll up through previous commands to edit and repeat them."
# - "Use <kbd>Ctrl</kbd>+<kbd>R</kbd> to search through the previously entered commands."
# - "Use `history` to display recent commands, and `![number]` to repeat a command by number."
# ---
# **Loops** are a programming construct which allow us to repeat a command or set of commands
# for each item in a list.
# As such they are key to productivity improvements through automation.
# Similar to wildcards and tab completion, using loops also reduces the
# amount of typing required (and hence reduces the number of typing mistakes).
# Suppose we have several hundred genome data files named `basilisk.dat`, `minotaur.dat`, and
# `unicorn.dat`.
# For this example, we'll use the `creatures` directory which only has three example files,
# but the principles can be applied to many many more files at once.
# The structure of these files is the same: the common name, classification, and updated date are
# presented on the first three lines, with DNA sequences on the following lines.
# Let's look at the files:
# ```
# $ head -n 5 basilisk.dat minotaur.dat unicorn.dat
# ```
# {: .language-bash}
# We would like to print out the classification for each species, which is given on the second
# line of each file.
# For each file, we would need to execute the command `head -n 2` and pipe this to `tail -n 1`.
# We’ll use a loop to solve this problem, but first let’s look at the general form of a loop:
# ```
# for thing in list_of_things
# do
# operation_using $thing # Indentation within the loop is not required, but aids legibility
# done
# ```
# {: .language-bash}
# and we can apply this to our example like this:
# ```
# $ for filename in basilisk.dat minotaur.dat unicorn.dat
# > do
# > head -n 2 $filename | tail -n 1
# > done
# ```
# {: .language-bash}
# ```
# CLASSIFICATION: basiliscus vulgaris
# CLASSIFICATION: bos hominus
# CLASSIFICATION: equus monoceros
# ```
# {: .output}
# > ## Follow the Prompt
# >
# > The shell prompt changes from `$` to `>` and back again as we were
# > typing in our loop. The second prompt, `>`, is different to remind
# > us that we haven't finished typing a complete command yet. A semicolon, `;`,
# > can be used to separate two commands written on a single line.
# {: .callout}
# When the shell sees the keyword `for`,
# it knows to repeat a command (or group of commands) once for each item in a list.
# Each time the loop runs (called an iteration), an item in the list is assigned in sequence to
# the **variable**, and the commands inside the loop are executed, before moving on to
# the next item in the list.
# Inside the loop,
# we call for the variable's value by putting `$` in front of it.
# The `$` tells the shell interpreter to treat
# the variable as a variable name and substitute its value in its place,
# rather than treat it as text or an external command.
# In this example, the list is three filenames: `basilisk.dat`, `minotaur.dat`, and `unicorn.dat`.
# Each time the loop iterates, it will assign a file name to the variable `filename`
# and run the `head` command.
# The first time through the loop,
# `$filename` is `basilisk.dat`.
# The interpreter runs the command `head` on `basilisk.dat`
# and pipes the first two lines to the `tail` command,
# which then prints the second line of `basilisk.dat`.
# For the second iteration, `$filename` becomes
# `minotaur.dat`. This time, the shell runs `head` on `minotaur.dat`
# and pipes the first two lines to the `tail` command,
# which then prints the second line of `minotaur.dat`.
# For the third iteration, `$filename` becomes
# `unicorn.dat`, so the shell runs the `head` command on that file,
# and `tail` on the output of that.
# Since the list was only three items, the shell exits the `for` loop.
# > ## Same Symbols, Different Meanings
# >
# > Here we see `>` being used as a shell prompt, whereas `>` is also
# > used to redirect output.
# > Similarly, `$` is used as a shell prompt, but, as we saw earlier,
# > it is also used to ask the shell to get the value of a variable.
# >
# > If the *shell* prints `>` or `$` then it expects you to type something,
# > and the symbol is a prompt.
# >
# > If *you* type `>` or `$` yourself, it is an instruction from you that
# > the shell should redirect output or get the value of a variable.
# {: .callout}
# When using variables it is also
# possible to put the names into curly braces to clearly delimit the variable
# name: `$filename` is equivalent to `${filename}`, but is different from
# `${file}name`. You may find this notation in other people's programs.
# We have called the variable in this loop `filename`
# in order to make its purpose clearer to human readers.
# The shell itself doesn't care what the variable is called;
# if we wrote this loop as:
# + language="bash"
# $ for x in basilisk.dat minotaur.dat unicorn.dat
# > do
# > head -n 2 $x | tail -n 1
# > done
# -
# ```
# ```
#
# {: .language-bash}
# or:
# + language="bash"
# $ for temperature in basilisk.dat minotaur.dat unicorn.dat
# > do
# > head -n 2 $temperature | tail -n 1
# > done
# -
# ```
# ```
#
# {: .language-bash}
# it would work exactly the same way.
# *Don't do this.*
# Programs are only useful if people can understand them,
# so meaningless names (like `x`) or misleading names (like `temperature`)
# increase the odds that the program won't do what its readers think it does.
# > ## Variables in Loops
# >
# > This exercise refers to the `shell-lesson-data/molecules` directory.
# > `ls` gives the following output:
# >
#
# ```
# > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# ```
#
# > {: .output}
# >
# > What is the output of the following code?
# >
# + language="bash"
# > $ for datafile in *.pdb
# > > do
# > > ls *.pdb
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > Now, what is the output of the following code?
# >
# + language="bash"
# > $ for datafile in *.pdb
# > > do
# > > ls $datafile
# > > done
# + language="bash"
#
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > Why do these two loops give different outputs?
# >
# > > ## Solution
# > > The first code block gives the same output on each iteration through
# > > the loop.
# > > Bash expands the wildcard `*.pdb` within the loop body (as well as
# > > before the loop starts) to match all files ending in `.pdb`
# > > and then lists them using `ls`.
# > > The expanded loop would look like this:
# > > ```
# > > $ for datafile in cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > > do
# > > > ls cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > > done
# > > ```
# > > {: .language-bash}
# > >
# > > ```
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > cubane.pdb ethane.pdb methane.pdb octane.pdb pentane.pdb propane.pdb
# > > ```
# > > {: .output}
# > >
# > > The second code block lists a different file on each loop iteration.
# > > The value of the `datafile` variable is evaluated using `$datafile`,
# > > and then listed using `ls`.
# > >
# > > ```
# > > cubane.pdb
# > > ethane.pdb
# > > methane.pdb
# > > octane.pdb
# > > pentane.pdb
# > > propane.pdb
# > > ```
# > > {: .output}
# > {: .solution}
# {: .challenge}
# > ## Limiting Sets of Files
# >
# > What would be the output of running the following loop in the
# > `shell-lesson-data/molecules` directory?
# >
# + language="bash"
# > $ for filename in c*
# > > do
# > > ls $filename
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > 1. No files are listed.
# > 2. All files are listed.
# > 3. Only `cubane.pdb`, `octane.pdb` and `pentane.pdb` are listed.
# > 4. Only `cubane.pdb` is listed.
# >
# > > ## Solution
# > > 4 is the correct answer. `*` matches zero or more characters, so any file name starting with
# > > the letter c, followed by zero or more other characters will be matched.
# > {: .solution}
# >
# > How would the output differ from using this command instead?
# >
# + language="bash"
# > $ for filename in *c*
# > > do
# > > ls $filename
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > 1. The same files would be listed.
# > 2. All the files are listed this time.
# > 3. No files are listed this time.
# > 4. The files `cubane.pdb` and `octane.pdb` will be listed.
# > 5. Only the file `octane.pdb` will be listed.
# >
# > > ## Solution
# > > 4 is the correct answer. `*` matches zero or more characters, so a file name with zero or more
# > > characters before a letter c and zero or more characters after the letter c will be matched.
# > {: .solution}
# {: .challenge}
# > ## Saving to a File in a Loop - Part One
# >
# > In the `shell-lesson-data/molecules` directory, what is the effect of this loop?
# >
# + language="bash"
# > for alkanes in *.pdb
# > do
# > echo $alkanes
# > cat $alkanes > alkanes.pdb
# > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > 1. Prints `cubane.pdb`, `ethane.pdb`, `methane.pdb`, `octane.pdb`, `pentane.pdb` and
# > `propane.pdb`, and the text from `propane.pdb` will be saved to a file called `alkanes.pdb`.
# > 2. Prints `cubane.pdb`, `ethane.pdb`, and `methane.pdb`, and the text from all three files
# > would be concatenated and saved to a file called `alkanes.pdb`.
# > 3. Prints `cubane.pdb`, `ethane.pdb`, `methane.pdb`, `octane.pdb`, and `pentane.pdb`,
# > and the text from `propane.pdb` will be saved to a file called `alkanes.pdb`.
# > 4. None of the above.
# >
# > > ## Solution
# > > 1. The text from each file in turn gets written to the `alkanes.pdb` file.
# > > However, the file gets overwritten on each loop iteration, so the final content of `alkanes.pdb`
# > > is the text from the `propane.pdb` file.
# > {: .solution}
# {: .challenge}
# > ## Saving to a File in a Loop - Part Two
# >
# > Also in the `shell-lesson-data/molecules` directory,
# > what would be the output of the following loop?
# >
# + language="bash"
# > for datafile in *.pdb
# > do
# > cat $datafile >> all.pdb
# > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > 1. All of the text from `cubane.pdb`, `ethane.pdb`, `methane.pdb`, `octane.pdb`, and
# > `pentane.pdb` would be concatenated and saved to a file called `all.pdb`.
# > 2. The text from `ethane.pdb` will be saved to a file called `all.pdb`.
# > 3. All of the text from `cubane.pdb`, `ethane.pdb`, `methane.pdb`, `octane.pdb`, `pentane.pdb`
# > and `propane.pdb` would be concatenated and saved to a file called `all.pdb`.
# > 4. All of the text from `cubane.pdb`, `ethane.pdb`, `methane.pdb`, `octane.pdb`, `pentane.pdb`
# > and `propane.pdb` would be printed to the screen and saved to a file called `all.pdb`.
# >
# > > ## Solution
# > > 3 is the correct answer. `>>` appends to a file, rather than overwriting it with the redirected
# > > output from a command.
# > > Given the output from the `cat` command has been redirected, nothing is printed to the screen.
# > {: .solution}
# {: .challenge}
# Let's continue with our example in the `shell-lesson-data/creatures` directory.
# Here's a slightly more complicated loop:
# + language="bash"
# $ for filename in *.dat
# > do
# > echo $filename
# > head -n 100 $filename | tail -n 20
# > done
# -
# ```
# ```
#
# {: .language-bash}
# The shell starts by expanding `*.dat` to create the list of files it will process.
# The **loop body**
# then executes two commands for each of those files.
# The first command, `echo`, prints its command-line arguments to standard output.
# For example:
# + language="bash"
# $ echo hello there
# -
# ```
# ```
#
# {: .language-bash}
# prints:
#
# ```
# hello there
# ```
#
# {: .output}
# In this case,
# since the shell expands `$filename` to be the name of a file,
# `echo $filename` prints the name of the file.
# Note that we can't write this as:
# + language="bash"
# $ for filename in *.dat
# > do
# > $filename
# > head -n 100 $filename | tail -n 20
# > done
# -
# ```
# ```
#
# {: .language-bash}
# because then the first time through the loop,
# when `$filename` expanded to `basilisk.dat`, the shell would try to run `basilisk.dat` as a program.
# Finally,
# the `head` and `tail` combination selects lines 81-100
# from whatever file is being processed
# (assuming the file has at least 100 lines).
# > ## Spaces in Names
# >
# > Spaces are used to separate the elements of the list
# > that we are going to loop over. If one of those elements
# > contains a space character, we need to surround it with
# > quotes, and do the same thing to our loop variable.
# > Suppose our data files are named:
# >
#
# ```
# > red dragon.dat
# > purple unicorn.dat
# ```
#
# > {: .source}
# >
# > To loop over these files, we would need to add double quotes like so:
# >
# + language="bash"
# > $ for filename in "red dragon.dat" "purple unicorn.dat"
# > > do
# > > head -n 100 "$filename" | tail -n 20
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > It is simpler to avoid using spaces (or other special characters) in filenames.
# >
# > The files above don't exist, so if we run the above code, the `head` command will be unable
# > to find them, however the error message returned will show the name of the files it is
# > expecting:
# >
#
# ```
# > head: cannot open ‘red dragon.dat’ for reading: No such file or directory
# > head: cannot open ‘purple unicorn.dat’ for reading: No such file or directory
# ```
#
# > {: .output}
# >
# > Try removing the quotes around `$filename` in the loop above to see the effect of the quote
# > marks on spaces. Note that we get a result from the loop command for unicorn.dat
# > when we run this code in the `creatures` directory:
# >
#
# ```
# > head: cannot open ‘red’ for reading: No such file or directory
# > head: cannot open ‘dragon.dat’ for reading: No such file or directory
# > head: cannot open ‘purple’ for reading: No such file or directory
# > CGGTACCGAA
# > AAGGGTCGCG
# > CAAGTGTTCC
# > ...
# ```
#
# > {: .output}
# {: .callout}
# We would like to modify each of the files in `shell-lesson-data/creatures`, but also save a version
# of the original files, naming the copies `original-basilisk.dat` and `original-unicorn.dat`.
# We can't use:
# + language="bash"
# $ cp *.dat original-*.dat
# -
# ```
# ```
#
# {: .language-bash}
# because that would expand to:
# + language="bash"
# $ cp basilisk.dat minotaur.dat unicorn.dat original-*.dat
# -
# ```
# ```
#
# {: .language-bash}
# This wouldn't back up our files, instead we get an error:
#
# ```
# cp: target `original-*.dat' is not a directory
# ```
#
# {: .error}
# This problem arises when `cp` receives more than two inputs. When this happens, it
# expects the last input to be a directory where it can copy all the files it was passed.
# Since there is no directory named `original-*.dat` in the `creatures` directory we get an
# error.
# Instead, we can use a loop:
# + language="bash"
# $ for filename in *.dat
# > do
# > cp $filename original-$filename
# > done
# -
# ```
# ```
#
# {: .language-bash}
# This loop runs the `cp` command once for each filename.
# The first time,
# when `$filename` expands to `basilisk.dat`,
# the shell executes:
# + language="bash"
# cp basilisk.dat original-basilisk.dat
# -
# ```
# ```
#
# {: .language-bash}
# The second time, the command is:
# + language="bash"
# cp minotaur.dat original-minotaur.dat
# -
# ```
# ```
#
# {: .language-bash}
# The third and last time, the command is:
# + language="bash"
# cp unicorn.dat original-unicorn.dat
# -
# ```
# ```
#
# {: .language-bash}
# Since the `cp` command does not normally produce any output, it's hard to check
# that the loop is doing the correct thing.
# However, we learned earlier how to print strings using `echo`, and we can modify the loop
# to use `echo` to print our commands without actually executing them.
# As such we can check what commands *would be* run in the unmodified loop.
# The following diagram
# shows what happens when the modified loop is executed, and demonstrates how the
# judicious use of `echo` is a good debugging technique.
# 
# ## Nelle's Pipeline: Processing Files
# Nelle is now ready to process her data files using `goostats.sh` ---
# a shell script written by her supervisor.
# This calculates some statistics from a protein sample file, and takes two arguments:
# 1. an input file (containing the raw data)
# 2. an output file (to store the calculated statistics)
# Since she's still learning how to use the shell,
# she decides to build up the required commands in stages.
# Her first step is to make sure that she can select the right input files --- remember,
# these are ones whose names end in 'A' or 'B', rather than 'Z'.
# Starting from her home directory, Nelle types:
# + language="bash"
# $ cd north-pacific-gyre/2012-07-03
# $ for datafile in NENE*A.txt NENE*B.txt
# > do
# > echo $datafile
# > done
# -
# {: .language-bash}
#
# ```
# NENE01729A.txt
# NENE01729B.txt
# NENE01736A.txt
# ...
# NENE02043A.txt
# NENE02043B.txt
# ```
#
# {: .output}
# Her next step is to decide
# what to call the files that the `goostats.sh` analysis program will create.
# Prefixing each input file's name with 'stats' seems simple,
# so she modifies her loop to do that:
# + language="bash"
# $ for datafile in NENE*A.txt NENE*B.txt
# > do
# > echo $datafile stats-$datafile
# > done
# -
# {: .language-bash}
#
# ```
# NENE01729A.txt stats-NENE01729A.txt
# NENE01729B.txt stats-NENE01729B.txt
# NENE01736A.txt stats-NENE01736A.txt
# ...
# NENE02043A.txt stats-NENE02043A.txt
# NENE02043B.txt stats-NENE02043B.txt
# ```
#
# {: .output}
# She hasn't actually run `goostats.sh` yet,
# but now she's sure she can select the right files and generate the right output filenames.
# Typing in commands over and over again is becoming tedious,
# though,
# and Nelle is worried about making mistakes,
# so instead of re-entering her loop,
# she presses <kbd>↑</kbd>.
# In response,
# the shell redisplays the whole loop on one line
# (using semi-colons to separate the pieces):
# + language="bash"
# $ for datafile in NENE*A.txt NENE*B.txt; do echo $datafile stats-$datafile; done
# -
# ```
# ```
#
# {: .language-bash}
# Using the left arrow key,
# Nelle backs up and changes the command `echo` to `bash goostats.sh`:
# + language="bash"
# $ for datafile in NENE*A.txt NENE*B.txt; do bash goostats.sh $datafile stats-$datafile; done
# -
# ```
# ```
#
# {: .language-bash}
# When she presses <kbd>Enter</kbd>,
# the shell runs the modified command.
# However, nothing appears to happen --- there is no output.
# After a moment, Nelle realizes that since her script doesn't print anything to the screen
# any longer, she has no idea whether it is running, much less how quickly.
# She kills the running command by typing <kbd>Ctrl</kbd>+<kbd>C</kbd>,
# uses <kbd>↑</kbd> to repeat the command,
# and edits it to read:
# + language="bash"
# $ for datafile in NENE*A.txt NENE*B.txt; do echo $datafile;
# bash goostats.sh $datafile stats-$datafile; done
# -
# ```
# ```
#
# {: .language-bash}
# > ## Beginning and End
# >
# > We can move to the beginning of a line in the shell by typing <kbd>Ctrl</kbd>+<kbd>A</kbd>
# > and to the end using <kbd>Ctrl</kbd>+<kbd>E</kbd>.
# {: .callout}
# When she runs her program now,
# it produces one line of output every five seconds or so:
#
# ```
# NENE01729A.txt
# NENE01729B.txt
# NENE01736A.txt
# ...
# ```
#
# {: .output}
# 1518 times 5 seconds,
# divided by 60,
# tells her that her script will take about two hours to run.
# As a final check,
# she opens another terminal window,
# goes into `north-pacific-gyre/2012-07-03`,
# and uses `cat stats-NENE01729B.txt`
# to examine one of the output files.
# It looks good,
# so she decides to get some coffee and catch up on her reading.
# > ## Those Who Know History Can Choose to Repeat It
# >
# > Another way to repeat previous work is to use the `history` command to
# > get a list of the last few hundred commands that have been executed, and
# > then to use `!123` (where '123' is replaced by the command number) to
# > repeat one of those commands. For example, if Nelle types this:
# >
# + language="bash"
# > $ history | tail -n 5
# -
# > {: .language-bash}
#
# ```
# > 456 ls -l NENE0*.txt
# > 457 rm stats-NENE01729B.txt.txt
# > 458 bash goostats.sh NENE01729B.txt stats-NENE01729B.txt
# > 459 ls -l NENE0*.txt
# > 460 history
# ```
#
# > {: .output}
# >
# > then she can re-run `goostats.sh` on `NENE01729B.txt` simply by typing
# > `!458`.
# {: .callout}
# > ## Other History Commands
# >
# > There are a number of other shortcut commands for getting at the history.
# >
# > - <kbd>Ctrl</kbd>+<kbd>R</kbd> enters a history search mode 'reverse-i-search' and finds the
# > most recent command in your history that matches the text you enter next.
# > Press <kbd>Ctrl</kbd>+<kbd>R</kbd> one or more additional times to search for earlier matches.
# > You can then use the left and right arrow keys to choose that line and edit
# > it then hit <kbd>Return</kbd> to run the command.
# > - `!!` retrieves the immediately preceding command
# > (you may or may not find this more convenient than using <kbd>↑</kbd>)
# > - `!$` retrieves the last word of the last command.
# > That's useful more often than you might expect: after
# > `bash goostats.sh NENE01729B.txt stats-NENE01729B.txt`, you can type
# > `less !$` to look at the file `stats-NENE01729B.txt`, which is
# > quicker than doing <kbd>↑</kbd> and editing the command-line.
# {: .callout}
# > ## Doing a Dry Run
# >
# > A loop is a way to do many things at once --- or to make many mistakes at
# > once if it does the wrong thing. One way to check what a loop *would* do
# > is to `echo` the commands it would run instead of actually running them.
# >
# > Suppose we want to preview the commands the following loop will execute
# > without actually running those commands:
# >
# + language="bash"
# > $ for datafile in *.pdb
# > > do
# > > cat $datafile >> all.pdb
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > What is the difference between the two loops below, and which one would we
# > want to run?
# >
# + language="bash"
# > # Version 1
# > $ for datafile in *.pdb
# > > do
# > > echo cat $datafile >> all.pdb
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# + language="bash"
# > # Version 2
# > $ for datafile in *.pdb
# > > do
# > > echo "cat $datafile >> all.pdb"
# > > done
# -
# ```
# ```
#
# > {: .language-bash}
# >
# > > ## Solution
# > > The second version is the one we want to run.
# > > This prints to screen everything enclosed in the quote marks, expanding the
# > > loop variable name because we have prefixed it with a dollar sign.
# > > It also *does not* modify nor create the file `all.pdb`, as the `>>`
# > > is treated literally as part of a string rather than as a
# > > redirection instruction.
# > >
# > > The first version appends the output from the command `echo cat $datafile`
# > > to the file, `all.pdb`. This file will just contain the list;
# > > `cat cubane.pdb`, `cat ethane.pdb`, `cat methane.pdb` etc.
# > >
# > > Try both versions for yourself to see the output! Be sure to open the
# > > `all.pdb` file to view its contents.
# > {: .solution}
# {: .challenge}
# > ## Nested Loops
# >
# > Suppose we want to set up a directory structure to organize
# > some experiments measuring reaction rate constants with different compounds
# > *and* different temperatures. What would be the
# > result of the following code:
# >
# + language="bash"
# > $ for species in cubane ethane methane
# > > do
# > > for temperature in 25 30 37 40
# > > do
# > > mkdir $species-$temperature
# > > done
# > > done
# -
#
|
_episodes/05-loop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: drlnd
# language: python
# name: drlnd
# ---
# # Collaboration and Competition
#
# ---
#
# In this notebook, you will learn how to use the Unity ML-Agents environment for the third project of the [Deep Reinforcement Learning Nanodegree](https://www.udacity.com/course/deep-reinforcement-learning-nanodegree--nd893) program.
#
# ### 1. Start the Environment
#
# We begin by importing the necessary packages. If the code cell below returns an error, please revisit the project instructions to double-check that you have installed [Unity ML-Agents](https://github.com/Unity-Technologies/ml-agents/blob/master/docs/Installation.md) and [NumPy](http://www.numpy.org/).
from IPython.core.display import display, HTML
display(HTML(
'<style>'
'#notebook { padding-top:0px !important; } '
'.container { width:95% !important; } '
'.end_space { min-height:0px !important; } '
'</style>'
))
from unityagents import UnityEnvironment
import numpy as np
# Next, we will start the environment! **_Before running the code cell below_**, change the `file_name` parameter to match the location of the Unity environment that you downloaded.
#
# - **Mac**: `"path/to/Tennis.app"`
# - **Windows** (x86): `"path/to/Tennis_Windows_x86/Tennis.exe"`
# - **Windows** (x86_64): `"path/to/Tennis_Windows_x86_64/Tennis.exe"`
# - **Linux** (x86): `"path/to/Tennis_Linux/Tennis.x86"`
# - **Linux** (x86_64): `"path/to/Tennis_Linux/Tennis.x86_64"`
# - **Linux** (x86, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86"`
# - **Linux** (x86_64, headless): `"path/to/Tennis_Linux_NoVis/Tennis.x86_64"`
#
# For instance, if you are using a Mac, then you downloaded `Tennis.app`. If this file is in the same folder as the notebook, then the line below should appear as follows:
# ```
# env = UnityEnvironment(file_name="Tennis.app")
# ```
#env = UnityEnvironment(file_name="Tennis_Linux/Tennis.x86_64")
env = UnityEnvironment(file_name="Tennis_Windows_x86_64/Tennis.exe")
# Environments contain **_brains_** which are responsible for deciding the actions of their associated agents. Here we check for the first brain available, and set it as the default brain we will be controlling from Python.
# get the default brain
brain_name = env.brain_names[0]
brain = env.brains[brain_name]
# ### 2. Examine the State and Action Spaces
#
# In this environment, two agents control rackets to bounce a ball over a net. If an agent hits the ball over the net, it receives a reward of +0.1. If an agent lets a ball hit the ground or hits the ball out of bounds, it receives a reward of -0.01. Thus, the goal of each agent is to keep the ball in play.
#
# The observation space consists of 8 variables corresponding to the position and velocity of the ball and racket. Two continuous actions are available, corresponding to movement toward (or away from) the net, and jumping.
#
# Run the code cell below to print some information about the environment.
# +
# reset the environment
env_info = env.reset(train_mode=True)[brain_name]
# number of agents
num_agents = len(env_info.agents)
print('Number of agents:', num_agents)
# size of each action
action_size = brain.vector_action_space_size
print('Size of each action:', action_size)
# examine the state space
states = env_info.vector_observations
state_size = states.shape[1]
print('There are {} agents. Each observes a state with length: {}'.format(states.shape[0], state_size))
print('The state for the first agent looks like:', states[0])
# -
# When finished, you can close the environment.
# ### 4. It's Your Turn!
#
# Now it's your turn to train your own agent to solve the environment! When training the environment, set `train_mode=True`, so that the line for resetting the environment looks like the following:
# ```python
# env_info = env.reset(train_mode=True)[brain_name]
# ```
# +
#from buffer import ReplayBuffer
from common.Memory import ReplayMemory
from maddpg import MADDPG
import torch
import numpy as np
from tensorboardX import SummaryWriter
import os
from utilities import transpose_list, transpose_to_tensor
from collections import deque
# keep training awake
#from workspace_utils import keep_awake
# for saving gif
#import imageio
# %load_ext autoreload
# %autoreload 2
# +
seed = 0
np.random.seed(seed)
torch.manual_seed(seed)
# number of training episodes.
# change this to higher number to experiment. say 30000.
number_of_episodes = 60000
episode_length = 200
batchsize = 256
# how many episodes to save policy and gif
save_interval = 200
# +
# amplitude of OU noise
# this slowly decreases to 0
#noise = 2
#noise_reduction = 0.999
log_path = os.getcwd()+"/log"
model_dir= os.getcwd()+"/model_dir"
os.makedirs(model_dir, exist_ok=True)
# keep 5000 episodes worth of replay
buffer = ReplayMemory(int(1e5))
# initialize policy and critic
in_actor = state_size
hidden_in_actor = 256
hidden_out_actor = 128
out_actor = 2
# critic input = obs from both agents + actions from both agents
in_critic = 2*state_size + 2*action_size
hidden_in_critic = 256
hidden_out_critic = 128
maddpg = MADDPG(in_actor, hidden_in_actor, hidden_out_actor,
out_actor, in_critic, hidden_in_critic, hidden_out_critic,
lr_actor=1.0e-4, lr_critic=1.0e-3, discount_factor=0.99, tau=1.0e-3)
logger = SummaryWriter(log_dir=log_path)
# +
# how many episodes before update
steps_per_update = 1
num_updates = 4
random_actions = 8000
update_start = 8000
agent0_reward = []
agent1_reward = []
average_score_log = []
# +
# training loop
# show progressbar
#import progressbar as pb
#widget = ['episode: ', pb.Counter(),'/',str(number_of_episodes),' ',
# pb.Percentage(), ' ', pb.ETA(), ' ', pb.Bar(marker=pb.RotatingMarker()), ' ' ]
#timer = pb.ProgressBar(widgets=widget, maxval=number_of_episodes).start()
scores_deque = deque(np.zeros(100))
ep_len_deque = deque(np.zeros(100))
#rand = 1.0
t = 0
for episode in range(1, number_of_episodes+1):
#timer.update(episode)
reward_this_episode = np.zeros(num_agents)
env_info = env.reset(train_mode=True)[brain_name]
obs = env_info.vector_observations
ep_len = 0
#for calculating rewards for this particular episode - addition of all time steps
# save info or not
save_info = ((episode) % save_interval == 0 or episode==number_of_episodes)
#frames = []
maddpg.reset()
#for episode_t in range(episode_length):
while True:
if t > random_actions:
rand = 1.0
else:
rand = 0.0
t += 1
ep_len += 1
# explore = only explore for a certain number of episodes
# action input needs to be transposed
actions = maddpg.act(torch.tensor(obs, dtype=torch.float), rand=rand, add_noise=True)
#noise *= noise_reduction
actions = torch.stack(actions).detach().numpy()
# step forward one frame
env_info = env.step(actions)[brain_name]
next_obs = env_info.vector_observations # get next state (for each agent)
rewards = env_info.rewards # get reward (for each agent)
dones = env_info.local_done # see if episode finished
# add data to buffer
transition = (obs, actions, rewards, next_obs, dones)
buffer.push(*transition)
# update once after every episode_per_update
if t > update_start and t % steps_per_update == 0:
for _ in range(steps_per_update * num_updates): # train for x times per update
samples = buffer.sample(batchsize)
for a_i in range(num_agents):
#samples = buffer.sample(batchsize)
maddpg.update(samples, a_i, logger)
maddpg.update_targets() #soft update the target network towards the actual networks
reward_this_episode += rewards
obs = next_obs
if np.any(dones):
break
ep_len_deque.append(ep_len)
avg_ep_len = np.mean(ep_len_deque)
score = np.max(reward_this_episode)
scores_deque.append(score)
average_score = np.mean(scores_deque)
average_score_log.append(average_score)
'''
# update once after every episode_per_update
if len(buffer) > batchsize and episode % episode_per_update == 0:
for _ in range(5): # train for 5 times
samples = buffer.sample(batchsize)
for a_i in range(num_agents):
#samples = buffer.sample(batchsize)
maddpg.update(samples, a_i, logger)
maddpg.update_targets() #soft update the target network towards the actual networks
'''
agent0_reward.append(reward_this_episode[0])
agent1_reward.append(reward_this_episode[1])
if episode % 100 == 0 or episode == number_of_episodes-1:
avg_rewards = [np.mean(agent0_reward), np.mean(agent1_reward)]
agent0_reward = []
agent1_reward = []
for a_i, avg_rew in enumerate(avg_rewards):
logger.add_scalar('agent%i/mean_episode_rewards' % a_i, avg_rew, episode)
print('\rEpisode {}\tAverage Score: {:.4f}\tScore: {:.4f}\tAvg Ep Len: {:.2f}'.format(episode, average_score, score, avg_ep_len), end="")
if episode % 100 == 0:
print('\rEpisode {}\tAverage Score: {:.4f}\tScore: {:.4f}\tAvg Ep Len: {:.2f}'.format(episode, average_score, score, avg_ep_len))
if average_score >= 0.5:
print('\nEnvironment solved in {:d} episodes!\tAverage Score: {:.4f}'.format(episode, average_score))
break
'''
if episode %100 == 0:
print('last 100 avg reward for episode ending {} is {}'.format(episode, np.mean(scores_deque)))
'''
#saving model
if save_info:
save_dict_list =[]
for i in range(2):
save_dict = {'actor_params' : maddpg.maddpg_agent[i].actor.state_dict(),
'actor_optim_params': maddpg.maddpg_agent[i].actor_optimizer.state_dict(),
'critic_params' : maddpg.maddpg_agent[i].critic.state_dict(),
'critic_optim_params' : maddpg.maddpg_agent[i].critic_optimizer.state_dict()}
save_dict_list.append(save_dict)
torch.save(save_dict_list, os.path.join(model_dir, 'episode-{}.pt'.format(episode)))
#timer.finish()
# -
# +
import torch
import torch.nn.functional as F
import torch.nn as nn
import torch.optim as optim
from unityagents import UnityEnvironment
import numpy as np
import random
import copy
from collections import namedtuple, deque
import os
import time
import sys
import matplotlib.pyplot as plt
device = torch.device("cpu")
# -
class Buffer:
"""Fixed-size buffer to store experience tuples."""
def __init__(self, buffer_size, batch_size, seed):
"""Initialize a ReplayBuffer object.
Params
======
action_size (int): dimension of each action
buffer_size (int): maximum size of buffer
batch_size (int): size of each training batch
seed (int): seed
"""
self.memory = deque(maxlen=buffer_size) # internal memory (deque)
self.batch_size = batch_size
self.seed = seed
self.experience = namedtuple("Experience", field_names=[
"observation", "action", "reward", "next_observation", "done"])
def add(self, observation, action, reward, next_observation, done):
"""Add a new experience to memory."""
# Join a sequence of agents's states, next states and actions along columns
e = self.experience(observation, action, reward, next_observation, done)
self.memory.append(e)
def sample(self):
"""Randomly sample a batch of experiences from memory."""
experiences = random.sample(self.memory, k=self.batch_size)
observations = torch.from_numpy(np.vstack([e.observation for e in experiences if e is not None])).float().to(device)
actions = torch.from_numpy(np.vstack([e.action for e in experiences if e is not None])).float().to(device)
rewards = torch.from_numpy(np.vstack([e.reward for e in experiences if e is not None])).float().to(device)
next_observations = torch.from_numpy(np.vstack([e.next_observation for e in experiences if e is not None])).float().to(device)
dones = torch.from_numpy(np.vstack([e.done for e in experiences if e is not None]).astype(np.uint8)).float().to(device)
return (observations, actions, rewards, next_observations, dones)
def __len__(self):
"""Return the current size of internal memory."""
return len(self.memory)
# +
class RNoise:
"""uniformly distributed random noise process"""
def __init__(self, shape, amplitude):
"""Initialize parameters and noise process
Params
======
shape (int): dimension of each action
buffer_size (int): maximum size of buffer
amplitude (int): size of each training batch
"""
self.amplitude = amplitude
self.shape = shape
self.state = np.zeros(self.shape)
def reset(self):
"""Reset the internal state (= noise) to zero."""
self.state = np.zeros(self.shape)
def sample(self):
"""Return a noise sample."""
self.state = self.amplitude*(2.*np.random.rand(self.shape) - 1.)
return self.state
class OUNoise:
"""Ornstein-Uhlenbeck process."""
def __init__(self, size, seed, mu=0., theta=0.15, sigma=0.2):
"""Initialize parameters and noise process."""
self.mu = mu * np.ones(size)
self.theta = theta
self.sigma = sigma
np.random.seed(seed)
self.seed = np.random.randint(0,100)
self.size = size
self.reset()
def reset(self):
"""Reset the internal state (= noise) to mean (mu)."""
self.state = copy.copy(self.mu)
def sample(self):
"""Update internal state and return it as a noise sample."""
x = self.state
dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(self.size)
self.state = x + dx
return self.state
# +
import torch.nn as nn
def hidden_init(layer):
fan_in = layer.weight.data.size()[0]
lim = 1. / np.sqrt(fan_in)
return (-lim, lim)
class Actor(nn.Module):
"""Actor (Policy) Model."""
def __init__(self, state_size, action_size, seed, fc1_units=256, fc2_units=128, percent_dropout = 0.1):
"""Initialize parameters and build model.
Params
======
state_size (int): Dimension of each state
action_size (int): Dimension of each action
seed (int): seed
fc1_units (int): Number of nodes in first hidden layer
fc2_units (int): Number of nodes in second hidden layer
percent_dropout (float): percentage of nodes being dropped out.
"""
super(Actor, self).__init__()
self.seed = torch.manual_seed(seed)
self.layer_1 = nn.Sequential(nn.Linear(state_size, fc1_units),
nn.ReLU(),
nn.Dropout(percent_dropout))
self.layer_2 = nn.Sequential(nn.Linear(fc1_units, fc2_units),
nn.ReLU(),
nn.Dropout(percent_dropout))
self.layer_3 = nn.Linear(fc2_units, action_size)
self.reset_parameters()
def reset_parameters(self):
# Apply to layers the specified weight initialization
self.layer_1[0].weight.data.uniform_(*hidden_init(self.layer_1[0]))
self.layer_2[0].weight.data.uniform_(*hidden_init(self.layer_2[0]))
self.layer_3.weight.data.uniform_(-3e-3, 3e-3)
def forward(self, state):
"""Build an actor (policy) network that maps states -> actions."""
x = self.layer_1(state)
x = self.layer_2(x)
x = self.layer_3(x)
return torch.tanh(x)
class Critic(nn.Module):
"""Critic (Value) Model."""
def __init__(self, state_size, action_size, seed, fc1_units=256, fc2_units=128, percent_dropout = 0.1):
"""Initialize parameters and build model.
Params
======
state_size (int): Dimension of each state
action_size (int): Dimension of each action
seed (int): seed
num_agents (int): Total number of agents
fc1_units (int): Number of nodes in the first hidden layer
fc2_units (int): Number of nodes in the second hidden layer
"""
super(Critic, self).__init__()
self.seed = torch.manual_seed(seed)
self.layer_1 = nn.Sequential(nn.Linear(state_size * NUM_AGENTS + action_size * NUM_AGENTS, fc1_units),
nn.ReLU(),
nn.Dropout(percent_dropout))
self.layer_2 = nn.Sequential(nn.Linear(fc1_units, fc2_units),
nn.ReLU(),
nn.Dropout(percent_dropout))
self.layer_3 = nn.Linear(fc2_units, 1)
self.reset_parameters()
def reset_parameters(self):
# Apply to layers the specified weight initialization
self.layer_1[0].weight.data.uniform_(*hidden_init(self.layer_1[0]))
self.layer_2[0].weight.data.uniform_(*hidden_init(self.layer_2[0]))
self.layer_3.weight.data.uniform_(-3e-3, 3e-3)
def forward(self, state, action):
"""Build a critic (value) network that maps (state, action) pairs -> Q-value."""
xs = torch.cat((state, action), dim = 1)
x = self.layer_1(xs)
x = self.layer_2(x)
return self.layer_3(x)
# +
class DDPG_Agent():
"""Interacts with and learns from the environment."""
def __init__(self, agent_name, state_size, action_size, random_seed):
"""Initialize an Agent object.
Params
======
agent_name (str): name of the agent
state_size (int): dimension of each state
action_size (int): dimension of each action
random_seed (int): random seed
"""
self.state_size = state_size
self.action_size = action_size
self.seed = random_seed
self.agent_name = agent_name
# Actor Network (w/ Target Network)
self.actor_local = Actor(state_size, action_size, self.seed).to(device)
self.actor_target = Actor(state_size, action_size, self.seed).to(device)
self.actor_optimizer = optim.Adam(self.actor_local.parameters(), lr=LR_ACTOR)
# Critic Network (w/ Target Network)
self.critic_local = Critic(state_size, action_size, self.seed).to(device)
self.critic_target = Critic(state_size, action_size, self.seed).to(device)
self.critic_optimizer = optim.Adam(self.critic_local.parameters(), lr=LR_CRITIC, weight_decay=WEIGHT_DECAY)
self.epsilon = 1.
self.epsilon_decay_rate = 0.999
self.epsilon_min = 0.2
# Noise process
# self.noise = OUNoise(action_size, random_seed)
self.noise = RNoise(action_size, 0.5)
def epsilon_decay(self):
self.epsilon = max(self.epsilon_decay_rate*self.epsilon, self.epsilon_min)
def act(self, state, add_noise=True):
"""Returns actions for given state as per current policy."""
if (type(state) != torch.Tensor):
state = torch.from_numpy(state).float().to(device)
self.actor_local.eval()
with torch.no_grad():
action = self.actor_local(state).cpu().data.numpy()
self.actor_local.train()
if add_noise:
action += self.epsilon * self.noise.sample()
return np.clip(action, -1, 1)
def reset(self):
self.noise.reset()
# def learn(self, agent_name, experiences, gamma):
def learn(self, agent_name, my_next_observation, other_next_action, next_observations,
actions, observations, self_observation, other_pred_action, my_reward, my_done, gamma):
"""Update policy and value parameters using given batch of experience tuples.
Q_targets = r + γ * critic_target(next_state, actor_target(next_state))
where:
actor_target(state) -> action
critic_target(state, action) -> Q-value
Params
======
agent_name (str): name of the agent
my_next_observation (torch.Tensor): current agent's own next observation
other_next_action (torch.Tensor): other agents' actions **
next_observations (torch.Tensor): god-view next observation
actions (torch.Tensor): god-view observations
observations (torch.Tensor): god-view observations
self_observation (torch.Tensor): current agent's own observation
other_pred_action (torch.Tensor): other agents' predicted actions
gamma (float): discount factor
"""
# ---------------------------- update critic ---------------------------- #
# Get predicted next-state actions and Q values from target models
next_action = self.actor_target(my_next_observation)
if agent_name == 'agent_0':
next_actions = torch.cat(
[next_action, other_next_action],
1).to(device)
else:
next_actions = torch.cat(
[other_next_action, next_action],
1).to(device)
Q_targets_next = self.critic_target(next_observations, next_actions)
# Compute Q targets for current states (y_i)
Q_targets = my_reward + (gamma * Q_targets_next * (1 - my_done))
# Compute critic loss
Q_expected = self.critic_local(observations, actions)
critic_loss = F.mse_loss(Q_expected, Q_targets)
# Minimize the loss
self.critic_optimizer.zero_grad()
critic_loss.backward()
self.critic_optimizer.step()
# ---------------------------- update actor ---------------------------- #
# Compute actor loss
pred_action = self.actor_local(self_observation)
if agent_name == 'agent_0':
pred_actions = torch.cat(
[pred_action, other_pred_action],
1).to(device)
else:
pred_actions = torch.cat(
[other_pred_action, pred_action],
1).to(device)
actor_loss = -self.critic_local(observations, pred_actions).mean()
# Minimize the loss
self.actor_optimizer.zero_grad()
actor_loss.backward()
self.actor_optimizer.step()
# ----------------------- update target networks ----------------------- #
self.soft_update(self.critic_local, self.critic_target, TAU)
self.soft_update(self.actor_local, self.actor_target, TAU)
def soft_update(self, local_model, target_model, tau):
"""Soft update model parameters.
θ_target = τ*θ_local + (1 - τ)*θ_target
Params
======
local_model: PyTorch model (weights will be copied from)
target_model: PyTorch model (weights will be copied to)
tau (float): interpolation parameter
"""
for target_param, local_param in zip(target_model.parameters(), local_model.parameters()):
target_param.data.copy_(tau*local_param.data + (1.0-tau)*target_param.data)
# -
class MADDPG_Agent:
def __init__(self, state_size, action_size, num_agents, random_seed = 0):
"""Initialize an Agent object.
Params
======
state_size (int): dimension of each state
action_size (int): dimension of each action
num_agents (int): how many agents to be trained
random_seed (int): random seed
"""
self.state_size = state_size
self.action_size = action_size
self.num_agents = num_agents
self.seed = random_seed
self.memory = Buffer(BUFFER_SIZE, BATCH_SIZE, self.seed)
self.agent_names = []
for i in range(num_agents):
self.agent_names.append( 'agent_' + str(i) )
self.agents = dict()
for agent_name in self.agent_names:
self.agents[agent_name] = DDPG_Agent(agent_name, state_size, action_size, self.seed)
def act(self, observations, add_noise = True):
'''get actions for both agents
Params
======
observations (np.array): current observation
add_noise (bool): add noise or not
'''
actions = []
for i, agent_name in enumerate(self.agent_names):
actions.append(self.agents[agent_name].act(observations[i], add_noise))
return np.array(actions)
def reset(self):
'''reset the noise class'''
for agent_name in self.agent_names:
self.agents[agent_name].reset()
def epsilon_decay(self):
'''Decay the noise amplitude if required'''
for agent_name in self.agent_names:
self.agents[agent_name].epsilon_decay()
def step(self, observation, action, reward, next_observation, done, step):
"""Learning process, get past experience tuple in the replay buffer,
Params
======
observation (torch.Tensor): all agents' observations
action (torch.Tensor): all agents' observations
next_observations (torch.Tensor): all agents' next observation
observations (torch.Tensor): all agents' observations
done (torch.Tensor): all agents' dones
step (int): current training step, use it for noise decay
"""
self.memory.add(observation, action, reward, next_observation, done)
if (len(self.memory) > BATCH_SIZE) and (step % TRAIN_EVERY) == 0:
for _ in range(NUM_TRAINS) :
experiences = self.memory.sample()
observations, actions, rewards, next_observations, dones = experiences
my_observation = torch.chunk(observations, NUM_AGENTS, dim = 1)
my_next_observation = torch.chunk(next_observations, NUM_AGENTS, dim = 1)
my_reward = torch.chunk(rewards, NUM_AGENTS, dim = 1)
my_done = torch.chunk(dones, NUM_AGENTS, dim = 1)
other_next_actions = []
other_pred_actions = []
# prepare next step actions for actor learning process. The date will be fed in critic_local
for num_agent, agent_name in enumerate(self.agent_names):
other_next_actions.append( torch.Tensor(self.agents[agent_name].act(my_next_observation[num_agent])) )
other_pred_actions.append( torch.Tensor(self.agents[agent_name].act(my_observation[num_agent])) )
self.agents['agent_0'].learn('agent_0', my_next_observation[0], other_next_actions[1], next_observations,
actions, observations, my_observation[0], other_pred_actions[1], my_reward[0], my_done[0], gamma = GAMMA)
self.agents['agent_1'].learn('agent_1', my_next_observation[1], other_next_actions[0], next_observations,
actions, observations, my_observation[1], other_pred_actions[0], my_reward[1], my_done[1], gamma = GAMMA)
# +
SEED = 0
BUFFER_SIZE = int(1e5) # replay buffer size
BATCH_SIZE = 256 # minibatch size
GAMMA = 0.99 # discount factor
TAU = 1e-3 # for soft update of target parameters
LR_ACTOR = 1e-4 # learning rate of the actor
LR_CRITIC = 1e-3 # learning rate of the critic
NUM_AGENTS = 2 # number of agents
WEIGHT_DECAY = 0. # L2 weight decay
TRAIN_EVERY = 1 # how often to train the network
NUM_TRAINS = 5 # number of trains per each train step
agent = MADDPG_Agent(state_size, action_size, num_agents, random_seed = SEED)
# +
def maddpg(n_episodes=5000, score_lenth = 100 ):
"""Multi-Agent Deep Deterministic Policy Gradient for N agents
Params
======
n_episodes (int): maximum number of training episodes
"""
scores_deque = deque(maxlen=score_lenth)
scores = []
average_scores = []
for i_episode in range(1, n_episodes+1):
env_info = env.reset(train_mode=True)[brain_name]
states = env_info.vector_observations
observation = states.reshape(1,NUM_AGENTS*state_size).squeeze(0) # merge both agents' states as an observation
score = np.zeros(num_agents)
agent.reset()
step = 0
while True:
step += 1
actions = agent.act(states)
action = actions.reshape(1,NUM_AGENTS*action_size).squeeze(0) # merge both agents' actions as an action
env_info = env.step(actions)[brain_name]
next_states = env_info.vector_observations
next_observation = next_states.reshape(1,NUM_AGENTS*state_size).squeeze(0) # merge both agents' next states as the next observation
rewards = env_info.rewards
dones = env_info.local_done
agent.step(observation, action, rewards, next_observation, dones, step)
states = next_states
observation = next_observation
score += rewards
if any(dones):
break
# agent.epsilon_decay()
score = np.max(score)
scores.append(score)
scores_deque.append(score)
average_score = np.mean(scores_deque)
average_scores.append(average_score)
print('\rEpisode {}\tAverage Score: {:.4f}\tScore: {:.4f}'.format(i_episode, average_score, score), end="")
if i_episode % 100 == 0:
print('\rEpisode {}\tAverage score: {:.4f}'.format(i_episode , average_score))
if average_score >= 0.5:
print('\nEnvironment solved in {:d} episodes!\tAverage Score: {:.4f}'.format(i_episode, average_score))
break
torch.save(agent.agents['agent_0'].actor_local.state_dict(), 'agent_one_checkpoint_actor.pth')
torch.save(agent.agents['agent_0'].critic_local.state_dict(), 'agent_one_checkpoint_critic.pth')
torch.save(agent.agents['agent_1'].actor_local.state_dict(), 'agent_two_checkpoint_actor.pth')
torch.save(agent.agents['agent_1'].critic_local.state_dict(), 'agent_two_checkpoint_critic.pth')
return scores, average_scores
scores, average_scores = maddpg()
# -
agent0_rewards = np.random.randn(300)
agent1_rewards = np.random.randn(300)
scores = np.max(np.stack((agent0_rewards, agent1_rewards)), axis=0)
scores[-1]
scores[299]
scores[:100]
len(average_scores)
|
p3_collab-compet/MADDPG/Tennis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from itertools import product
import time
import pandas as pd
import arxiv
# -
# # Define Classes to Be Aggregated
material_classes = ['ceramic','polymer','semiconductor','metal','organometallic']
experiment_classes = ['experiment','simulation']
material_base = ["material"]
all_classes = material_classes + experiment_classes
class_combinations = list(product(material_classes, experiment_classes, material_base))
class_combinations
# # Define Helper Functions
# +
def clean_results(r):
return r.get('summary').replace('\n', ' ')
def get_arxiv_results(query, start, max_results):
res = arxiv.query(' AND '.join(c),
start = start,
max_results = max_results)
return [clean_results(r) for r in res]
# -
# # Fetch Results from ArXiv
# +
total_results = 100
max_results = 20
query_wait = 0.1
results = []
for c in all_classes:
print(c)
n_results = 0
tmp_array = []
while n_results < total_results:
r = get_arxiv_results(' AND '.join(c),
start = n_results,
max_results = max_results)
if len(r) == 0: break
n_results = n_results + len(r)
tmp_array = tmp_array + r
time.sleep(query_wait)
results.append({"label":c, "data":tmp_array})
# -
# # Build DataFrame and Output to File
# +
output_file = "./data/arxiv_results.pkl"
df = pd.DataFrame(results)
# One-hot encoded columns
for c in all_classes:
df[c] = df['label'].apply(lambda x: 1 if c in x else 0)
df.drop('labels', axis=0)
df.to_pickle(output_file)
df
# -
# # Add One-hot Encoded Columns
# +
df
# -
# # Load Previous Results
input_file = "./data/arxiv_results.pkl"
df = pd.read_pickle(input_file)
df
|
arxiv_pull.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import tensorflow as tf
# What we really want to do is building a *custom estimator* which will simplify our life for results tracking and data visualization. Further improvements might include a distributed Cloud version of it to overcome the important computational cost it requires.
# +
# loading datasets and phreshing folds for evaluations and testing
train_ds, test_ds = np.load("train.npz"), np.load("test.npz")
partition, x_train, y_train = train_ds["partition"], train_ds["X_train"], train_ds["y_train"]
x_test, y_test = test_ds['X_test'], test_ds['y_test']
# -
# First attempt, _without_ cross validation
# This is the actual training phase:
#
# for cross validation, we train the data on 4 different models by splitting the dataset in 4 subsets.
# +
feature_columns = [tf.feature_column.numeric_column("X", shape=(1000, 20))]
num_hidden_units = [512, 256, 128]
model = tf.estimator.DDN(feature_columns=feature_columns,
n_classes=10,
model_dir="./checkpoints_tutorial17-1/")
# -
# giving an error, but at least we've fixed it
for i in range(1,5):
x_part, y_part, x_val, y_val = x_train[np.where(partition != i)], y_train[np.where(partition != i)], x_train[np.where(partition == i)], y_train[np.where(partition == i)]
train_input_fn = tf.estimator.inputs.numpy_input_fn(x={'X':x_part},
y=y_part,
num_epochs=1,
batch_size=128,
shuffle=False)
model.train(input_fn=train_input_fn, steps=10)
final_test_input_fn = tf.estimator.inputs.numpy_input_fn(x={'X':x_test},
y=y_test,
num_epochs=20,
batch_size=128,
shuffle=False)
# +
# the model function
def cnn_clocator(inputs, classes, mode):
conv1 = tf.layers.conv2d(inputs=inputs, filters=50, kernel_size=3,
padding="same", activation=tf.nn.relu)
conv2 = tf.layers.conv2d(inputs=conv1, filters=80, kernel_size=5,
padding="same", activation=tf.nn.relu)
pool = tf.layers.max_pooling2d(inputs=conv2, pool_size=[2, 2], strides=2)
pool_flat = tf.layers.flatten(pool)
# -
len(x_train[np.where(partition == 1)]
# +
train_input_fn = tf.estimator.inputs.numpy_input_fn(x={'X':x_train[np.where(partition == 1)]},
y=y_train[np.where(partition == 1)],
num_epochs=1,
shuffle=False)
model.train(input_fn=train_input_fn, steps=10)
# -
|
depr/Cell Maps.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# # !/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on 20180410
@author: zhangji
"""
# %pylab inline
pylab.rcParams['figure.figsize'] = (18.5, 10.5)
fontsize = 40
import os
import importlib
import numpy as np
import scipy as sp
import pandas as pd
import re
from scanf import scanf
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import axes3d, Axes3D
from scipy.interpolate import interp1d
from IPython.display import display, HTML
from scipy import interpolate, integrate, optimize
from codeStore import support_fun as spf
from src import slenderBodyTheory as slb
from src import stokesletsInPipe as stlpp
from tqdm.notebook import tqdm as tqdm_notebook
PWD = os.getcwd()
np.set_printoptions(linewidth=130, precision=5)
# -
greenFun = stlpp.detail_light(threshold=100)
greenFun.solve_prepare_light()
greenFun.set_b(b=0.1)
greenFun.solve_prepare_b()
mij = greenFun.solve_u_light(0.2, 0.2, 0.2)
t1 = np.random.sample(3)
# %timeit greenFun.solve_u_light(*t1)
|
src/stokesletsInPipe.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction
#
# 
# ***The process of Neural Machine Translation was widely infulenced from the innovations done by Britishers during World War 2 in breaking the Enigma code. Later this process was adopted by US agencies to keep a track of Russian innovations through translation of their published papers***
# # What is Machine Translation?
# **Machine translation is the task of automatically converting source text in one language to text in another language.**
#
# ***In a machine translation task, the input already consists of a sequence of symbols in some language, and the computer program must convert this into a sequence of symbols in another language.***
#
#
# **Given a sequence of text in a source language, there is no one single best translation of that text to another language. This is because of the natural ambiguity and flexibility of human language. This makes the challenge of automatic machine translation difficult, perhaps one of the most difficult in artificial intelligence:**
#
# ***The fact is that accurate translation requires background knowledge in order to resolve ambiguity and establish the content of the sentence.***
#
# **Classical machine translation methods often involve rules for converting text in the source language to the target language. The rules are often developed by linguists and may operate at the lexical, syntactic, or semantic level. This focus on rules gives the name to this area of study: Rule-based Machine Translation, or RBMT.**
#
# ***RBMT is characterized with the explicit use and manual creation of linguistically informed rules and representations.***
#
# **The key limitations of the classical machine translation approaches are both the expertise required to develop the rules, and the vast number of rules and exceptions required.**
#
# **For more details refer [here](https://machinelearningmastery.com/introduction-neural-machine-translation/)**
# **For Implementation simplicity I'll be refereing to [keras](https://github.com/keras-team/keras/blob/master/examples/lstm_seq2seq.py) documentation for this**
#
# **Happy Learning**
# **To get started watch this video of <NAME> on Machine Translation!!**
#
# **bon<NAME>**
# +
from IPython.display import YouTubeVideo
YouTubeVideo('nRBnh4qbPHI',width=800, height=450)
# -
# # Loading Libraries
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python Docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
# Input data files are available in the read-only "../input/" directory
# For example, running this (by clicking run or pressing Shift+Enter) will list all files under the input directory
import os
from keras.models import Model
from keras.layers import Input, LSTM, Dense, GRU
import matplotlib.pyplot as plt
import seaborn as sns
# You can write up to 5GB to the current directory (/kaggle/working/) that gets preserved as output when you create a version using "Save & Run All"
# You can also write temporary files to /kaggle/temp/, but they won't be saved outside of the current session
# -
# # Loading Dataset
data_dir = '../input/frenchenglish/'
os.listdir(data_dir)
path = '../input/frenchenglish/fra.txt'
batch_size = 128
epochs=100
latent_dim=256
num_samples=10000
# +
# Vectorize the data.
input_texts = []
target_texts = []
input_characters = set()
target_characters = set()
with open(path, 'r', encoding='utf-8') as f:
lines = f.read().split('\n')
for line in lines[: min(num_samples, len(lines) - 1)]:
input_text, target_text, _ = line.split('\t')
# We use "tab" as the "start sequence" character
# for the targets, and "\n" as "end sequence" character.
target_text = '\t' + target_text + '\n'
input_texts.append(input_text)
target_texts.append(target_text)
for char in input_text:
if char not in input_characters:
input_characters.add(char)
for char in target_text:
if char not in target_characters:
target_characters.add(char)
# +
input_characters = sorted(list(input_characters))
target_characters = sorted(list(target_characters))
num_encoder_tokens = len(input_characters)
num_decoder_tokens = len(target_characters)
max_encoder_seq_length = max([len(txt) for txt in input_texts])
max_decoder_seq_length = max([len(txt) for txt in target_texts])
# +
print('Number of samples:', len(input_texts))
print('Number of unique input tokens:', num_encoder_tokens)
print('Number of unique output tokens:', num_decoder_tokens)
print('Max sequence length for inputs:', max_encoder_seq_length)
print('Max sequence length for outputs:', max_decoder_seq_length)
# +
input_token_index = dict(
[(char, i) for i, char in enumerate(input_characters)])
target_token_index = dict(
[(char, i) for i, char in enumerate(target_characters)])
encoder_input_data = np.zeros(
(len(input_texts), max_encoder_seq_length, num_encoder_tokens),
dtype='float32')
decoder_input_data = np.zeros(
(len(input_texts), max_decoder_seq_length, num_decoder_tokens),
dtype='float32')
decoder_target_data = np.zeros(
(len(input_texts), max_decoder_seq_length, num_decoder_tokens),
dtype='float32')
# -
for i, (input_text, target_text) in enumerate(zip(input_texts, target_texts)):
for t, char in enumerate(input_text):
encoder_input_data[i, t, input_token_index[char]] = 1.
encoder_input_data[i, t + 1:, input_token_index[' ']] = 1.
for t, char in enumerate(target_text):
# decoder_target_data is ahead of decoder_input_data by one timestep
decoder_input_data[i, t, target_token_index[char]] = 1.
if t > 0:
'''
decoder_target_data will be ahead by one timestep
and will not include the start character.
'''
decoder_target_data[i, t - 1, target_token_index[char]] = 1.
decoder_input_data[i, t + 1:, target_token_index[' ']] = 1.
decoder_target_data[i, t:, target_token_index[' ']] = 1.
# # Model Developement
#
# **We start by defining Encoder and Decoder, Encoder will recieve words in english while Decoder will play the role of translator to the words**
#Encoder
encoder_inputs = Input(shape=(None, num_encoder_tokens))
encoder = LSTM(latent_dim, return_state=True)
encoder_outputs, state_h, state_c = encoder(encoder_inputs)
# We discard `encoder_outputs` and only keep the states.
encoder_states = [state_h, state_c]
#Decoder
decoder_inputs = Input(shape=(None, num_decoder_tokens))
# We set up our decoder to return full output sequences,
# and to return internal states as well. We don't use the
# return states in the training model, but we will use them in inference.
decoder_lstm = LSTM(latent_dim, return_sequences=True, return_state=True)
decoder_outputs, _, _ = decoder_lstm(decoder_inputs,
initial_state=encoder_states)
decoder_dense = Dense(num_decoder_tokens, activation='softmax')
decoder_outputs = decoder_dense(decoder_outputs)
model = Model([encoder_inputs, decoder_inputs], decoder_outputs)
# Run training
model.compile(optimizer='rmsprop', loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit([encoder_input_data, decoder_input_data], decoder_target_data,
batch_size=batch_size,
epochs=epochs,
validation_split=0.2)
# # Save Model
model.save('s2s.h5')
# # Inference stage
# **Now we begin with Inference mode or sampling mode, The process can be summarized below**
# 1. **Encode input and retrieve initial decoder state**
# 2. **Run one step of decoder with this initial state and a "start of sequence" token as target. Output will be the next target token**
# 3. **Repeat with the current target token and current states**
# +
encoder_model = Model(encoder_inputs, encoder_states)
decoder_state_input_h = Input(shape=(latent_dim,))
decoder_state_input_c = Input(shape=(latent_dim,))
decoder_states_inputs = [decoder_state_input_h, decoder_state_input_c]
decoder_outputs, state_h, state_c = decoder_lstm(
decoder_inputs, initial_state=decoder_states_inputs)
decoder_states = [state_h, state_c]
decoder_outputs = decoder_dense(decoder_outputs)
decoder_model = Model(
[decoder_inputs] + decoder_states_inputs,
[decoder_outputs] + decoder_states)
# -
# Reverse-lookup token index to decode sequences back to
# something readable.
reverse_input_char_index = dict(
(i, char) for char, i in input_token_index.items())
reverse_target_char_index = dict(
(i, char) for char, i in target_token_index.items())
def decode_sequence(input_seq):
# Encode the input as state vectors.
states_value = encoder_model.predict(input_seq)
# Generate empty target sequence of length 1.
target_seq = np.zeros((1, 1, num_decoder_tokens))
# Populate the first character of target sequence with the start character.
target_seq[0, 0, target_token_index['\t']] = 1.
# Sampling loop for a batch of sequences
# (to simplify, here we assume a batch of size 1).
stop_condition = False
decoded_sentence = ''
while not stop_condition:
output_tokens, h, c = decoder_model.predict(
[target_seq] + states_value)
# Sample a token
sampled_token_index = np.argmax(output_tokens[0, -1, :])
sampled_char = reverse_target_char_index[sampled_token_index]
decoded_sentence += sampled_char
# Exit condition: either hit max length
# or find stop character.
if (sampled_char == '\n' or
len(decoded_sentence) > max_decoder_seq_length):
stop_condition = True
# Update the target sequence (of length 1).
target_seq = np.zeros((1, 1, num_decoder_tokens))
target_seq[0, 0, sampled_token_index] = 1.
# Update states
states_value = [h, c]
return decoded_sentence
# # Prédiction
for seq_index in range(100):
# Take one sequence (part of the training set)
# for trying out decoding.
input_seq = encoder_input_data[seq_index: seq_index + 1]
decoded_sentence = decode_sequence(input_seq)
print('-')
print('Input sentence:', input_texts[seq_index])
print('Decoded sentence:', decoded_sentence)
|
neural-machine-translation-de-l-anglais-vers-le-f.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# +
# Copyright 2021 Google LLC
# Use of this source code is governed by an MIT-style
# license that can be found in the LICENSE file or at
# https://opensource.org/licenses/MIT.
# Notebook authors: <NAME> (<EMAIL>)
# and <NAME> (<EMAIL>)
# This notebook reproduces figures for chapter 23 from the book
# "Probabilistic Machine Learning: An Introduction"
# by <NAME> (MIT Press, 2021).
# Book pdf is available from http://probml.ai
# -
# <a href="https://opensource.org/licenses/MIT" target="_parent"><img src="https://img.shields.io/github/license/probml/pyprobml"/></a>
# <a href="https://colab.research.google.com/github/probml/pyprobml/blob/master/book1/figures/chapter23_graph_embeddings_figures.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# ## Figure 23.1:<a name='23.1'></a> <a name='non_euclidean_vs_euclidean'></a>
#
# An illustration of Euclidean vs. non-Euclidean graphs. Used with permission from \cite chami2020machine .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.1_A.pdf")
show_image("/pyprobml/book1/figures/images/Figure_23.1_B.pdf")
# ## Figure 23.2:<a name='23.2'></a> <a name='enc-dec'></a>
#
# Illustration of the \textsc GraphEDM framework from \citet chami2020machine . Based on the supervision available, methods will use some or all of the branches. In particular, unsupervised methods do not leverage label decoding for training and only optimize the similarity decoder (lower branch). On the other hand, semi-supervised and supervised methods leverage the additional supervision to learn models' parameters (upper branch). Used with permission.\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
# ## Figure 23.3:<a name='23.3'></a> <a name='shallow'></a>
#
# Shallow embedding methods. The encoder is a simple embedding look-up and the graph structure is only used in the loss function. Reprinted with permission from \cite chami2020machine .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
# ## Figure 23.4:<a name='23.4'></a> <a name='walk'></a>
#
# An overview of the pipeline for random-walk graph embedding methods. Reprinted with permission from <a href='#godec_2018'>[Pri18]</a> .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.4.png")
# ## Figure 23.5:<a name='23.5'></a> <a name='graphSage'></a>
#
# Illustration of the GraphSAGE model. Reprinted with permission from <a href='#hamilton2017inductive'>[WZJ17]</a> .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.5.png")
# ## Figure 23.6:<a name='23.6'></a> <a name='hgcn_viz'></a>
#
# Euclidean (left) and hyperbolic (right) embeddings of a tree graph. Hyperbolic embeddings learn natural hierarchies in the embedding space (depth indicated by color). Reprinted with permission from <a href='#chami2019hyperbolic'>[Ine+19]</a> .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.6_A.pdf")
show_image("/pyprobml/book1/figures/images/Figure_23.6_B.pdf")
# ## Figure 23.7:<a name='23.7'></a> <a name='agg_unsup'></a>
#
# Unsupervised graph neural networks. Graph structure and input features are mapped to low-dimensional embeddings using a graph neural network encoder. Embeddings are then decoded to compute a graph regularization loss (unsupervised). Reprinted with permission from \cite chami2020machine .\relax
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
# ## Figure 23.8:<a name='23.8'></a> <a name='fraudGraph'></a>
#
# A graph representation of some financial transactions. Adapted from http://pgql-lang.org/spec/1.2/ .
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.8.png")
# ## Figure 23.9:<a name='23.9'></a> <a name='smell'></a>
#
# Structurally similar molecules do not necessarily have similar odor descriptors. (A) Lyral, the reference molecule. (B) Molecules with similar structure can share similar odor descriptors. (C) However, a small structural change can render the molecule odorless. (D) Further, large structural changes can leave the odor of the molecule largely unchanged. From Figure 1 of <a href='#SanchezLengeling2019'>[Ben+19]</a> , originally from <a href='#Ohloff2012'>[GWP12]</a> . Used with kind permission of <NAME>.
#@title Click me to run setup { display-mode: "form" }
try:
if PYPROBML_SETUP_ALREADY_RUN:
print('skipping setup')
except:
PYPROBML_SETUP_ALREADY_RUN = True
print('running setup...')
# !git clone https://github.com/probml/pyprobml /pyprobml &> /dev/null
# %cd -q /pyprobml/scripts
import pyprobml_utils as pml
import colab_utils
import os
os.environ["PYPROBML"] = ".." # one above current scripts directory
import google.colab
from google.colab.patches import cv2_imshow
# %reload_ext autoreload
# %autoreload 2
def show_image(img_path,size=None,ratio=None):
img = colab_utils.image_resize(img_path, size)
cv2_imshow(img)
print('finished!')
show_image("/pyprobml/book1/figures/images/Figure_23.9.png")
# ## References:
# <a name='SanchezLengeling2019'>[Ben+19]</a> <NAME>, <NAME>, <NAME>, <NAME>, <NAME> and <NAME>. "Machine Learning for Scent: Learning GeneralizablePerceptual Representations of Small Molecules". abs/1910.10685 (2019). arXiv: 1910.10685
#
# <a name='Ohloff2012'>[GWP12]</a> O. Gunther, <NAME> and <NAME>. "Scent and Chemistry". (2012).
#
# <a name='chami2019hyperbolic'>[Ine+19]</a> <NAME>, <NAME>, <NAME> and <NAME>. "Hyperbolic graph convolutional neural networks". (2019).
#
# <a name='godec_2018'>[Pri18]</a> <NAME> "". (2018).
#
# <a name='hamilton2017inductive'>[WZJ17]</a> <NAME>, <NAME> and <NAME>. "Inductive representation learning on large graphs". (2017).
#
#
|
book1/figures/chapter23_graph_embeddings_figures.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: ML100
# language: python
# name: ml100
# ---
# # 作業目標:
# 寫出 ReLU & dReLU 一階導數
# 並列印
#
# # 作業重點
#
# # Rectified Linear Unit- Relu
#
# f(x)=max(0,x)
#
# +
import numpy as np
from numpy import *
import matplotlib.pylab as plt
# %matplotlib inline
'''
作業:
寫出 ReLU & dReLU 一階導數
並列印
'''
# +
import numpy as np
from numpy import *
import matplotlib.pylab as plt
# %matplotlib inline
#RelU 數學函數表示方式
#RelU = lambda x: 1 / (1 + np.exp(-x))
def RelU(x):
posMask = x > 0
return posMask * x + (1 - posMask) * 0
# linespace generate an array from start and stop value
# with requested number of elements. Example 10 elements or 100 elements.
x = plt.linspace(-10,10,100)
# prepare the plot, associate the color r(ed) or b(lue) and the label
plt.plot(x, RelU(x), 'b', label='linspace(-10,10,10)')
# Draw the grid line in background.
plt.grid()
# 顯現圖示的Title
plt.title('ReLU Function')
#resize the X and Y axes
plt.gca().xaxis.set_major_locator(plt.MultipleLocator(1))
plt.gca().yaxis.set_major_locator(plt.MultipleLocator(1))
# create the graph
plt.show()
# +
#Relu 微分
def dRelU(x):
posMask = x > 0
return posMask * 1 + (1 - posMask) * 0
# prepare the plot, associate the color r(ed) or b(lue) and the label
plt.plot(x, dRelU(x), 'b', label='linspace(-10,10,10)')
# Draw the grid line in background.
plt.grid()
# 顯現圖示的Title
plt.title('dReLU Function')
#resize the X and Y axes
plt.gca().xaxis.set_major_locator(plt.MultipleLocator(1))
plt.gca().yaxis.set_major_locator(plt.MultipleLocator(0.1))
# create the graph
plt.show()
# -
|
2nd-ML100Days/homework/D-072/Day72-Activation_function_HW.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.10.0 64-bit (''.venv'': venv)'
# name: python3
# ---
# # Dynamic Programming
#
# Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.
#
# FAn optimization problem can be solved using dynamic programming if the problem has the following properties:
#
# 1. Overlapping Subproblems
# 2. Optimal Substructure
#
# ## Overlapping Subproblems
#
# Like Divide and Conquer, **Dynamic Programming** combines solutions to sub-problems. Dynamic Programming is mainly used when *solutions of same subproblems are needed again and again*. In dynamic programming, *computed solutions to subproblems are stored in a table so that these don’t have to be recomputed*. So Dynamic Programming is not useful when there are no common (overlapping) subproblems because there is no point storing the solutions if they are not needed again.
#
# **Example**
#
# Recursive program for Fibonacci Numbers, there are many subproblems which are solved again and again.
#
# ```
# fib(5)
# / \
# fib(4) fib(3)
# / \ / \
# fib(3) fib(2) fib(2) fib(1)
# / \ / \ / \
# fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
# / \
# fib(1) fib(0)
# ```
#
# ## Optimal Substructure
#
# A given problems has Optimal Substructure Property if optimal solution of the given problem can be obtained by using optimal solutions of its subproblems.
#
# **Example**
#
# The Shortest Path problem has following optimal substructure property:
#
# If a node x lies in the shortest path from a source node u to destination node v then
# shortest path from u to v is combination of shortest path from u to x and shortest path from x to v.
#
# The standard All Pair Shortest Path algorithms like Floyd–Warshall and Bellman–Ford are typical examples of **Dynamic Programming**.
#
# ## Tabulation vs Memoization
#
# There are following two different ways to store the values so that the values of a sub-problem can be reused. Here, will discuss two patterns of solving DP problem:
#
# 1. Tabulation (Bottom Up)
# 2. Memoization (Top Down)
#
# ### Tabulation Method (Bottom Up Dynamic Programming)
#
# As the name itself suggests starting from the bottom and cumulating answers to the top. Let’s discuss in terms of state transition.
#
# Let’s describe a state for our DP problem to be **`dp[x]`** with **`dp[0]` as base state** and **`dp[n]` as our destination state**. So, we need to find the value of destination state i.e `dp[n]`.
#
# If we start our transition from our base state i.e `dp[0]` and follow our state transition relation to reach our destination state `dp[n]`, we call it **Bottom Up** approach as it is quite clear that we started our transition from the **bottom base state** and reached the **top most desired state**.
#
# ### Memoization Method (Top Down Dynamic Programming)
#
# Let’s describe it in terms of state transition. If we need to find the value for some state say `dp[n]` and instead of starting from the base state that i.e `dp[0]` we ask our answer from the states that can reach the destination state `dp[n]` following the state transition relation, then it is the top-down fashion of DP.
#
# Here, we start our journey from the **top most destination state** and compute its answer by taking in count the values of states that can reach the **destination state**, till we reach the **bottom most base state**.
#
#
# | | Tabulation (Bottom Up) | Memoization (Top Down ) |
# | :---------------------- | :---------------------------------------------: | :----------------------------------------: |
# | **State** | State transition relation is difficult to think | State transition relation is easy to think |
# | **Code** | Code is complicated with a lot conditions | Code is easy and less complicated |
# | **Speed** | Fast | Slow |
# | **Sub-Problem Solving** | All sub-problems are solved | Solves only required sub-problems |
# | **Table Entries** | All entries are filled. | Entries are filled on demand |
#
# +
fibonacci_table = [0, 1]
def fibonacci_tabulation(n):
for i in range(2, n + 1):
fib_num = fibonacci_table[i - 1] + fibonacci_table[i - 2]
fibonacci_table.append(fib_num)
return fibonacci_table[-1]
fibonacci_lookups = {}
def fibonacci_memoization(n):
if n in fibonacci_lookups:
return fibonacci_lookups[n]
if n < 2: # base case
fibonacci_lookups[n] = n
return fibonacci_lookups[n]
fibonacci_lookups[n] = fibonacci_memoization(n - 1) + fibonacci_memoization(n - 2)
return fibonacci_lookups[n]
n = 500
print(fibonacci_tabulation(n))
print(fibonacci_memoization(n))
# -
|
algorithms/dynamic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 228} colab_type="code" id="lIYdn1woOS1n" outputId="a30c21d5-b7cc-4ea6-a0d3-f9f1392ee04a"
import torch
import torch.nn as nn
import torch.optim as optim
import torchtext
import torchtext.experimental
import torchtext.experimental.vectors
from torchtext.experimental.datasets.raw.text_classification import RawTextIterableDataset
from torchtext.experimental.datasets.text_classification import TextClassificationDataset
from torchtext.experimental.functional import sequential_transforms, vocab_func, totensor
import collections
import random
import time
# + colab={} colab_type="code" id="II-XIfhSkZS-"
seed = 1234
torch.manual_seed(seed)
random.seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
# + colab={} colab_type="code" id="kIkeEy2mkcT6"
raw_train_data, raw_test_data = torchtext.experimental.datasets.raw.IMDB()
# + colab={} colab_type="code" id="_a5ucP1ZkeDv"
def get_train_valid_split(raw_train_data, split_ratio = 0.7):
raw_train_data = list(raw_train_data)
random.shuffle(raw_train_data)
n_train_examples = int(len(raw_train_data) * split_ratio)
train_data = raw_train_data[:n_train_examples]
valid_data = raw_train_data[n_train_examples:]
train_data = RawTextIterableDataset(train_data)
valid_data = RawTextIterableDataset(valid_data)
return train_data, valid_data
# + colab={} colab_type="code" id="1WP4nz-_kf_0"
raw_train_data, raw_valid_data = get_train_valid_split(raw_train_data)
# + colab={} colab_type="code" id="pPvrMZlWkicJ"
class Tokenizer:
def __init__(self, tokenize_fn = 'basic_english', lower = True, max_length = None):
self.tokenize_fn = torchtext.data.utils.get_tokenizer(tokenize_fn)
self.lower = lower
self.max_length = max_length
def tokenize(self, s):
tokens = self.tokenize_fn(s)
if self.lower:
tokens = [token.lower() for token in tokens]
if self.max_length is not None:
tokens = tokens[:self.max_length]
return tokens
# + colab={} colab_type="code" id="SMsMQSuSkkt3"
max_length = 500
tokenizer = Tokenizer(max_length = max_length)
# + colab={} colab_type="code" id="Yie7TKWKkmeK"
def build_vocab_from_data(raw_data, tokenizer, **vocab_kwargs):
token_freqs = collections.Counter()
for label, text in raw_data:
tokens = tokenizer.tokenize(text)
token_freqs.update(tokens)
vocab = torchtext.vocab.Vocab(token_freqs, **vocab_kwargs)
return vocab
# + colab={} colab_type="code" id="9jW7Ci7WkoSn"
max_size = 25_000
vocab = build_vocab_from_data(raw_train_data, tokenizer, max_size = max_size)
# + colab={} colab_type="code" id="cvSZt_iFkqkt"
def process_raw_data(raw_data, tokenizer, vocab):
raw_data = [(label, text) for (label, text) in raw_data]
text_transform = sequential_transforms(tokenizer.tokenize,
vocab_func(vocab),
totensor(dtype=torch.long))
label_transform = sequential_transforms(totensor(dtype=torch.long))
transforms = (label_transform, text_transform)
dataset = TextClassificationDataset(raw_data,
vocab,
transforms)
return dataset
# + colab={} colab_type="code" id="bwsSiBdkktRk"
train_data = process_raw_data(raw_train_data, tokenizer, vocab)
valid_data = process_raw_data(raw_valid_data, tokenizer, vocab)
test_data = process_raw_data(raw_test_data, tokenizer, vocab)
# + colab={} colab_type="code" id="5m3xRusSk8v3"
class Collator:
def __init__(self, pad_idx):
self.pad_idx = pad_idx
def collate(self, batch):
labels, text = zip(*batch)
labels = torch.LongTensor(labels)
lengths = torch.LongTensor([len(x) for x in text])
text = nn.utils.rnn.pad_sequence(text, padding_value = self.pad_idx)
return labels, text, lengths
# + colab={} colab_type="code" id="1ZMuZqZxk8-p"
pad_token = '<pad>'
pad_idx = vocab[pad_token]
collator = Collator(pad_idx)
# + colab={} colab_type="code" id="mxG97Si9lAI2"
batch_size = 256
train_iterator = torch.utils.data.DataLoader(train_data,
batch_size,
shuffle = True,
collate_fn = collator.collate)
valid_iterator = torch.utils.data.DataLoader(valid_data,
batch_size,
shuffle = False,
collate_fn = collator.collate)
test_iterator = torch.utils.data.DataLoader(test_data,
batch_size,
shuffle = False,
collate_fn = collator.collate)
# + colab={} colab_type="code" id="ty3NbheMlPYs"
class BiLSTM(nn.Module):
def __init__(self, input_dim, emb_dim, hid_dim, output_dim, n_layers, dropout, pad_idx):
super().__init__()
self.embedding = nn.Embedding(input_dim, emb_dim, padding_idx = pad_idx)
self.lstm = nn.LSTM(emb_dim, hid_dim, num_layers = n_layers, bidirectional = True, dropout = dropout)
self.fc = nn.Linear(2 * hid_dim, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, text, lengths):
# text = [seq len, batch size]
# lengths = [batch size]
embedded = self.dropout(self.embedding(text))
# embedded = [seq len, batch size, emb dim]
packed_embedded = nn.utils.rnn.pack_padded_sequence(embedded, lengths, enforce_sorted = False)
packed_output, (hidden, cell) = self.lstm(packed_embedded)
output, _ = nn.utils.rnn.pad_packed_sequence(packed_output)
# outputs = [seq_len, batch size, n directions * hid dim]
# hidden = [n layers * n directions, batch size, hid dim]
hidden_fwd = hidden[-2]
hidden_bck = hidden[-1]
# hidden_fwd/bck = [batch size, hid dim]
hidden = torch.cat((hidden_fwd, hidden_bck), dim = 1)
# hidden = [batch size, hid dim * 2]
prediction = self.fc(self.dropout(hidden))
# prediction = [batch size, output dim]
return prediction
# + colab={} colab_type="code" id="trg6yTjBqOLZ"
input_dim = len(vocab)
emb_dim = 100
hid_dim = 256
output_dim = 2
n_layers = 2
dropout = 0.5
model = BiLSTM(input_dim, emb_dim, hid_dim, output_dim, n_layers, dropout, pad_idx)
# + colab={} colab_type="code" id="9dgdCRsqqQoD"
def count_parameters(model):
return sum(p.numel() for p in model.parameters() if p.requires_grad)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="bfiGzjvnqV-s" outputId="168a3662-b95a-48de-d722-c76264e8c8ab"
print(f'The model has {count_parameters(model):,} trainable parameters')
# -
for n, p in model.named_parameters():
print(f'name: {n}, shape: {p.shape}')
def initialize_parameters(m):
if isinstance(m, nn.Embedding):
nn.init.uniform_(m.weight, -0.05, 0.05)
elif isinstance(m, nn.LSTM):
for n, p in m.named_parameters():
if 'weight_ih' in n:
i, f, g, o = p.chunk(4)
nn.init.xavier_uniform_(i)
nn.init.xavier_uniform_(f)
nn.init.xavier_uniform_(g)
nn.init.xavier_uniform_(o)
elif 'weight_hh' in n:
i, f, g, o = p.chunk(4)
nn.init.orthogonal_(i)
nn.init.orthogonal_(f)
nn.init.orthogonal_(g)
nn.init.orthogonal_(o)
elif 'bias' in n:
i, f, g, o = p.chunk(4)
nn.init.zeros_(i)
nn.init.ones_(f)
nn.init.zeros_(g)
nn.init.zeros_(o)
elif isinstance(m, nn.Linear):
nn.init.xavier_uniform_(m.weight)
nn.init.zeros_(m.bias)
model.apply(initialize_parameters)
# + colab={} colab_type="code" id="Sah17A41qW5d"
glove = torchtext.experimental.vectors.GloVe(name = '6B',
dim = emb_dim)
# + colab={} colab_type="code" id="S1Dfcn2Nqabo"
def get_pretrained_embedding(initial_embedding, pretrained_vectors, vocab, unk_token):
pretrained_embedding = torch.FloatTensor(initial_embedding.weight.clone()).detach()
pretrained_vocab = pretrained_vectors.vectors.get_stoi()
unk_tokens = []
for idx, token in enumerate(vocab.itos):
if token in pretrained_vocab:
pretrained_vector = pretrained_vectors[token]
pretrained_embedding[idx] = pretrained_vector
else:
unk_tokens.append(token)
return pretrained_embedding, unk_tokens
# + colab={} colab_type="code" id="sGyV94f7qvdr"
unk_token = '<unk>'
pretrained_embedding, unk_tokens = get_pretrained_embedding(model.embedding, glove, vocab, unk_token)
# + colab={"base_uri": "https://localhost:8080/", "height": 139} colab_type="code" id="KYnGxbVisUsk" outputId="e1a88c1c-0f3e-48c6-afcf-9d791fd54bb9"
model.embedding.weight.data.copy_(pretrained_embedding)
# -
model.embedding.weight.data[pad_idx] = torch.zeros(emb_dim)
# + colab={} colab_type="code" id="DTwNU41WseMS"
optimizer = optim.Adam(model.parameters())
# + colab={} colab_type="code" id="Rxlx7a72s1ze"
criterion = nn.CrossEntropyLoss()
# + colab={} colab_type="code" id="1CLimBxus2yX"
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# + colab={} colab_type="code" id="108fm55ftBgO"
model = model.to(device)
criterion = criterion.to(device)
# + colab={} colab_type="code" id="IYCxbvXUvE5v"
def calculate_accuracy(predictions, labels):
top_predictions = predictions.argmax(1, keepdim = True)
correct = top_predictions.eq(labels.view_as(top_predictions)).sum()
accuracy = correct.float() / labels.shape[0]
return accuracy
# + colab={} colab_type="code" id="Ik2JQo6TvGml"
def train(model, iterator, optimizer, criterion, device):
epoch_loss = 0
epoch_acc = 0
model.train()
for labels, text, lengths in iterator:
labels = labels.to(device)
text = text.to(device)
optimizer.zero_grad()
predictions = model(text, lengths)
loss = criterion(predictions, labels)
acc = calculate_accuracy(predictions, labels)
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + colab={} colab_type="code" id="aGy1Zk6jvIf8"
def evaluate(model, iterator, criterion, device):
epoch_loss = 0
epoch_acc = 0
model.eval()
with torch.no_grad():
for labels, text, lengths in iterator:
labels = labels.to(device)
text = text.to(device)
predictions = model(text, lengths)
loss = criterion(predictions, labels)
acc = calculate_accuracy(predictions, labels)
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
# + colab={} colab_type="code" id="9MyMRRzbvKPx"
def epoch_time(start_time, end_time):
elapsed_time = end_time - start_time
elapsed_mins = int(elapsed_time / 60)
elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
return elapsed_mins, elapsed_secs
# + colab={"base_uri": "https://localhost:8080/", "height": 537} colab_type="code" id="dRKwD51WvMa3" outputId="79389e66-c1bf-45c9-a919-63ee787ad660"
n_epochs = 10
best_valid_loss = float('inf')
for epoch in range(n_epochs):
start_time = time.monotonic()
train_loss, train_acc = train(model, train_iterator, optimizer, criterion, device)
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion, device)
end_time = time.monotonic()
epoch_mins, epoch_secs = epoch_time(start_time, end_time)
if valid_loss < best_valid_loss:
best_valid_loss = valid_loss
torch.save(model.state_dict(), 'bilstm-model.pt')
print(f'Epoch: {epoch+1:02} | Epoch Time: {epoch_mins}m {epoch_secs}s')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc*100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc*100:.2f}%')
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="hKOg4oARvPHJ" outputId="7cfe4b85-de2f-47f3-8437-45589c32ceca"
model.load_state_dict(torch.load('bilstm-model.pt'))
test_loss, test_acc = evaluate(model, test_iterator, criterion, device)
print(f'Test Loss: {test_loss:.3f} | Test Acc: {test_acc*100:.2f}%')
# + colab={} colab_type="code" id="tQ4Jsf_vvWgB"
def predict_sentiment(tokenizer, vocab, model, device, sentence):
model.eval()
tokens = tokenizer.tokenize(sentence)
length = torch.LongTensor([len(tokens)]).to(device)
indexes = [vocab.stoi[token] for token in tokens]
tensor = torch.LongTensor(indexes).unsqueeze(-1).to(device)
prediction = model(tensor, length)
probabilities = nn.functional.softmax(prediction, dim = -1)
pos_probability = probabilities.squeeze()[-1].item()
return pos_probability
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="Yy7_6rhovZTE" outputId="78860852-39ea-4a7b-eb33-9a1a077fb9e0"
sentence = 'the absolute worst movie of all time.'
predict_sentiment(tokenizer, vocab, model, device, sentence)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="L3LmQxrgvau9" outputId="0204aa17-0bc1-45f2-9be1-c014798af120"
sentence = 'one of the greatest films i have ever seen in my life.'
predict_sentiment(tokenizer, vocab, model, device, sentence)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="t7Qoy21Bvb7v" outputId="6094a141-4f37-4110-edc7-aa14b9a3c667"
sentence = "i thought it was going to be one of the greatest films i have ever seen in my life, \
but it was actually the absolute worst movie of all time."
predict_sentiment(tokenizer, vocab, model, device, sentence)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="EPGXBr18vdQT" outputId="e5b3d210-0254-4d5f-bdbe-609c0b7d6a8a"
sentence = "i thought it was going to be the absolute worst movie of all time, \
but it was actually one of the greatest films i have ever seen in my life."
predict_sentiment(tokenizer, vocab, model, device, sentence)
|
experimental/3_rnn_bilstm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Pandas for Data Science ##
# [Pandas Documentation](https://pandas.pydata.org/)
import pandas as pd
print(pd)
df = pd.read_csv('/home/martin/datasets/flights.csv')
df.head()
df.describe()
df.isnull()
df.isnull().sum()
df = df.drop(['year', 'month', 'day', 'dep_time', 'arr_time', 'flight', 'tailnum', 'air_time',
'distance', 'hour', 'minute', 'time_hour'], axis=1)
df.head()
pd.value_counts(df['carrier'])
pd.value_counts(df['carrier']).plot.bar()
df.groupby('carrier').mean()
df.groupby('carrier').mean()['dep_delay']
# This will cause an error
df.groupby('carrier').mean()['dep_delay', 'arr_delay']
df.groupby('carrier').mean()[['dep_delay', 'arr_delay']]
df.groupby('carrier').mean()[['dep_delay', 'arr_delay']].plot.bar()
df['route'] = df['origin'] + ' - ' + df['dest']
df.head()
df['schedule_flight_time'] = df['sched_arr_time'] - df['sched_dep_time']
df.head()
df.groupby(['route', 'carrier']).mean()
df.groupby(['route', 'carrier']).mean()[:50]
df.sort_values('dep_delay')
df.dropna(subset=['dep_delay']).sort_values('dep_delay')
df.dropna(subset=['dep_delay']).sort_values('dep_delay', ascending=False)
df.dropna(subset=['dep_delay']).sort_values(['carrier', 'dep_delay'])
|
02 The Basics/pandas_for_data_science.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="bIRn7Id03kis"
# # Mounting Google Drive
# + [markdown] id="GSNu5sZi3nxI"
# First add the data to your google drive using the following link:
#
# https://drive.google.com/drive/u/1/folders/17SpWmNSl9dcbyqUFpdvnYlHj1EYXwHju
# + colab={"base_uri": "https://localhost:8080/"} id="CHnLvRu7pQWI" outputId="ef436652-d8db-44d5-d69b-cc8cbb0ed953"
from google.colab import drive
drive.mount('/content/drive')
# + [markdown] id="X91RRwh2H3NU"
# # Installing Required Libraries
#
# + id="cJEEQWrHr_XX" colab={"base_uri": "https://localhost:8080/"} outputId="dec31b65-ca6c-4fb7-f1f0-fa77313f6e10"
# !pip3 install transformers
# !pip3 install unidecode
# + id="FH6kE3WDpXXc" colab={"base_uri": "https://localhost:8080/"} outputId="ed4d2705-3f7c-445a-8718-95d467b8600e"
# memory footprint support libraries/code
# !ln -sf /opt/bin/nvidia-smi /usr/bin/nvidia-smi
# !pip install gputil
# !pip install psutil
# !pip install humanize
import psutil
import humanize
import os
import GPUtil as GPU
GPUs = GPU.getGPUs()
# XXX: only one GPU on Colab and isn’t guaranteed
gpu = GPUs[0]
def printm():
process = psutil.Process(os.getpid())
print("Gen RAM Free: " + humanize.naturalsize(psutil.virtual_memory().available), " | Proc size: " + humanize.naturalsize(process.memory_info().rss))
print("GPU RAM Free: {0:.0f}MB | Used: {1:.0f}MB | Util {2:3.0f}% | Total {3:.0f}MB".format(gpu.memoryFree, gpu.memoryUsed, gpu.memoryUtil*100, gpu.memoryTotal))
printm()
# + id="CxgcFw4yqHrb"
import numpy as np
import pandas as pd
import os
from os import listdir
from os.path import join
import unidecode
import re
import logging
from tqdm.notebook import tnrange
import glob
import json
#For ploting results
import matplotlib.pyplot as plt
# DL Libraries
from transformers import BertModel, AdamW, BertTokenizer, BertConfig, RobertaTokenizer, RobertaModel
from keras.preprocessing.sequence import pad_sequences
import torch
import torch.nn as nn
from torch.utils.data import (DataLoader, RandomSampler, SequentialSampler, TensorDataset)
from sklearn.metrics import classification_report, accuracy_score
from sklearn.model_selection import train_test_split
from scipy.stats import pearsonr
from sklearn.utils import shuffle
from sklearn.metrics import mean_squared_error
# + colab={"base_uri": "https://localhost:8080/"} id="qsvm8PnwsPJr" outputId="9f18c024-185b-4de6-e910-1cd783779b46"
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
n_gpu = torch.cuda.device_count()
print("device: {} n_gpu: {}".format(device, n_gpu))
# + id="hqr28wmZsPXE" colab={"base_uri": "https://localhost:8080/"} outputId="354e242f-65cf-4c4b-d282-1fa1e2a55029"
logging.basicConfig(format = '%(asctime)s - %(levelname)s - %(name)s - %(message)s',
datefmt = '%m/%d/%Y %H:%M:%S',
level = logging.INFO)
logger = logging.getLogger(__name__)
print(logger)
# + [markdown] id="GSfkrPfcH_F-"
# # Loading the data
#
# + id="8T9YIozF2I_X"
data_df= pd.read_csv('/content/drive/MyDrive/NLP/openBook_QA.csv')
train_df, test_df= train_test_split(data_df, test_size=0.2)
# + [markdown] id="y6I0Iar-ISEc"
# # Training the model
#
# + id="LHMuExjH9xSI"
def create_dataloader(tokenizer, df):
input_ids= list()
attention_masks= list()
print("Shape: {}".format(df.shape))
special_sentences_1 = [sentence for i, sentence in enumerate(df.question)]
special_sentences_2 = [" [SEP] " + str(sentence) for i, sentence in enumerate(df.sentence)]
special_sentences = [i + j for i, j in zip(special_sentences_1, special_sentences_2)]
for sentence in special_sentences:
encoded_text = tokenizer.encode_plus(sentence, max_length=512, add_special_tokens=True, return_token_type_ids=False,
padding='max_length', return_attention_mask=True, truncation=True)
input_ids.append(encoded_text['input_ids'])
attention_masks.append(encoded_text['attention_mask'])
inputs = torch.tensor(input_ids).to(device)
masks = torch.tensor(attention_masks).to(device)
gold_labels = torch.tensor(df.sia_score.tolist()).to(device)
data = TensorDataset(inputs, masks, gold_labels)
sampler = RandomSampler(data)
dataloader = DataLoader(data, sampler=sampler, batch_size=4)
return dataloader
# + colab={"base_uri": "https://localhost:8080/", "height": 237, "referenced_widgets": ["95eb97093ca748b0b70a78a0ae43b474", "749c3e18ad71441782fa240520b26aef", "<KEY>", "81e758fb28984c6094ec669db975441e", "<KEY>", "62d2f3b8ec2542c69a68ac756eb1d1b1", "2d994c21a2b349289d5d3a056ba5ce61", "5de0d2ca193547f7b805c88864a6e5e5", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "b26c73367a344f0f92d8747859551683", "4e53468ab3f3480db7dfb2a8edf9b2ba", "<KEY>", "<KEY>"]} id="keU3hNF19hgK" outputId="a05583a7-2308-4cf7-c02c-e5da700d7973"
#Dataloaders
tokenizer = RobertaTokenizer.from_pretrained('roberta-base')
train_dataloader= create_dataloader(tokenizer, train_df)
test_dataloader= create_dataloader(tokenizer, test_df)
# + id="47UOUdBt-fBO"
#Class for Regression
class Regressor(nn.Module):
def __init__(self):
super(Regressor, self).__init__()
self.bert = RobertaModel.from_pretrained('roberta-base')
self.out = nn.Linear(self.bert.config.hidden_size, 1)
def forward(self, input_ids, attention_mask):
output, pooler_out = self.bert(input_ids=input_ids, attention_mask=attention_mask)
score= self.out(pooler_out)
return score
# + id="mvYjtCsm9q2W"
epochs = 10
#Load Model
model= Regressor()
model.to(device)
# Prepare optimizer
optimizer = AdamW(model.parameters(),lr=2e-5)
#Loss Function
mse_loss= nn.MSELoss().to(device)
# + id="jyBLulkT-Y7J"
output_dir= '/content/drive/My Drive/NLP/sia_experiment/SIA_OpenBookQA'
output_result= '/content/drive/My Drive/NLP/sia_experiment/results_OpenBookQA'
if not os.path.exists(output_dir):
os.makedirs(output_dir)
if not os.path.exists(output_result):
os.makedirs(output_result)
# + colab={"base_uri": "https://localhost:8080/", "height": 542, "referenced_widgets": ["4f50389077bb495f9c9f17e6dd55627e", "49314041a89e4501b21201b66b2723ee", "<KEY>", "b653e1059dbc41afaf9dd363d5ca13f7", "fc9873de1459433b8b71bb4c97e89da3", "5f3b1a2de85c4ac8acf9199d3f682987", "b3c35924d71e4459bb647bfe5847a6df", "bde5fa1720254d5aa450cb097699e2d8"]} id="VL8fTr1W-Yvt" outputId="2985d057-7de2-4d81-995c-59c89d04e2cd"
for iteration in tnrange(epochs, desc='Epochs'):
model.train()
logger.info("Running for iteration: {}".format(iteration+1))
training_loss, training_steps = 0,0
true_labels, predicted_labels = list(), list()
for step, batch in enumerate(train_dataloader):
batch = tuple(t.to(device) for t in batch)
ip_ids, masks, gold_labels= batch
score = model(ip_ids, attention_mask=masks)
score = score.squeeze(1)
loss= mse_loss(score, gold_labels.float())
loss.backward()
optimizer.step()
optimizer.zero_grad()
training_loss+=loss.item()
training_steps+=1
if (step+1)%10000 == 0:
print(step+1)
true_labels.extend(gold_labels.cpu().numpy())
predicted_labels.extend(score.detach().cpu().numpy())
training_loss_for_epoch= training_loss/training_steps
pcc= pearsonr(true_labels, predicted_labels)
rmse= mean_squared_error(true_labels, predicted_labels, squared=False)
result = {'loss': training_loss_for_epoch, 'PCC': pcc[0], 'RMSE':rmse}
print(result)
model_to_save = model.bert.module if hasattr(model.bert, 'module') else model.bert
model_to_save.save_pretrained(output_dir)
torch.save(model.out.state_dict(), join(output_dir, 'model_state.bin'))
#Testing
print("Running evaluation for epoch: {}".format(iteration+1))
true_labels, predicted_labels= list(), list()
model.eval()
with torch.no_grad():
for step, batch in enumerate(test_dataloader):
batch = tuple(t.to(device) for t in batch)
ip_ids, masks, gold_labels= batch
score = model(ip_ids, attention_mask=masks)
score = score.squeeze(1)
true_labels.extend(gold_labels.cpu().numpy())
predicted_labels.extend(score.detach().cpu().numpy())
pcc= pearsonr(true_labels, predicted_labels)
rmse= mean_squared_error(true_labels, predicted_labels, squared=False)
test_report= {'PCC': pcc[0], 'RMSE':str(rmse)}
print(test_report)
with open(join(output_result, 'result_'+str(iteration+1)+'.json'), 'w') as fp:
json.dump(test_report, fp)
# + id="YHcFMgFe-nNB" colab={"base_uri": "https://localhost:8080/"} outputId="5618afbf-7771-4f2e-a9bb-c8b56f3331cf"
filepaths= glob.glob(join(output_result,'*.json'))
pcc, rmse= list(), list()
for path in filepaths:
print(path)
f = open(path,'r')
data = json.load(f)
pcc.append(data['PCC'])
rmse.append(float(data['RMSE']))
# + id="rZzjy6wJ-npx" colab={"base_uri": "https://localhost:8080/", "height": 545} outputId="ea7a1c7e-a9b9-4722-9186-30740ed8a99b"
#plot rmse
plt.plot(rmse)
plt.ylabel('RMSE')
plt.xticks(range(1, 11))
plt.xlabel('Epochs')
plt.savefig(join(output_result, 'rmse.png'))
plt.show()
#plot
plt.plot(pcc)
plt.ylabel('PCC')
plt.xticks(range(1, 11))
plt.ylim(0, 1)
plt.xlabel('Epochs')
plt.savefig(join(output_result, 'pcc.png'))
plt.show()
|
OPENBOOKQA_Rajasree/SIA_Model_Training_with_Roberta.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # scikit-learn-pca
# Credits: Forked from [PyCon 2015 Scikit-learn Tutorial](https://github.com/jakevdp/sklearn_pycon2015) by <NAME>
# ## Dimensionality Reduction: PCA
# +
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn;
from sklearn import neighbors, datasets
import pylab as pl
seaborn.set()
iris = datasets.load_iris()
X, y = iris.data, iris.target
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
X_reduced = pca.transform(X)
print("Reduced dataset shape:", X_reduced.shape)
import pylab as pl
pl.scatter(X_reduced[:, 0], X_reduced[:, 1], c=y,
cmap='RdYlBu')
print("Meaning of the 2 components:")
for component in pca.components_:
print(" + ".join("%.3f x %s" % (value, name)
for value, name in zip(component,
iris.feature_names)))
# -
# # Dimensionality Reduction: Principal Component Analysis in-depth
#
# Here we'll explore **Principal Component Analysis**, which is an extremely useful linear dimensionality reduction technique. Principal Component Analysis is a very powerful unsupervised method for *dimensionality reduction* in data. Look for directions in the data with the most variance.
#
# Useful to explore data, visualize data and relationships.
#
# It's easiest to visualize by looking at a two-dimensional dataset:
np.random.seed(1)
X = np.dot(np.random.random(size=(2, 2)), np.random.normal(size=(2, 200))).T
plt.plot(X[:, 0], X[:, 1], 'o')
plt.axis('equal');
# We can see that there is a definite trend in the data. What PCA seeks to do is to find the **Principal Axes** in the data, and explain how important those axes are in describing the data distribution:
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
print(pca.explained_variance_)
print(pca.components_)
plt.plot(X[:, 0], X[:, 1], 'o', alpha=0.5)
for length, vector in zip(pca.explained_variance_ratio_, pca.components_):
v = vector * 3 * np.sqrt(length)
plt.plot([0, v[0]], [0, v[1]], '-k', lw=3)
plt.axis('equal');
# Notice that one vector is longer than the other. In a sense, this tells us that that direction in the data is somehow more "important" than the other direction.
# The explained variance quantifies this measure of "importance" in direction.
#
# Another way to think of it is that the second principal component could be **completely ignored** without much loss of information! Let's see what our data look like if we only keep 95% of the variance:
clf = PCA(0.95) # keep 95% of variance
X_trans = clf.fit_transform(X)
print(X.shape)
print(X_trans.shape)
# Isomap: manifold learning, good when PCA doesn't work like in a loop. Large number of datasets, can use randomized PCA.
# By specifying that we want to throw away 5% of the variance, the data is now compressed by a factor of 50%! Let's see what the data look like after this compression:
X_new = clf.inverse_transform(X_trans)
plt.plot(X[:, 0], X[:, 1], 'o', alpha=0.2)
plt.plot(X_new[:, 0], X_new[:, 1], 'ob', alpha=0.8)
plt.axis('equal');
# The light points are the original data, while the dark points are the projected version. We see that after truncating 5% of the variance of this dataset and then reprojecting it, the "most important" features of the data are maintained, and we've compressed the data by 50%!
#
# This is the sense in which "dimensionality reduction" works: if you can approximate a data set in a lower dimension, you can often have an easier time visualizing it or fitting complicated models to the data.
testing complete; Gopal
|
tests/python-scientific/scikit-learn-pca.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:tensorflow2]
# language: python
# name: conda-env-tensorflow2-py
# ---
# +
from ingredient_phrase_tagger.training.cli import Cli
from ingredient_phrase_tagger.training.cli import utils as ingred_utils
import pandas as pd
import numpy as np
import os
import re
import pickle
import random
import string
import math
from nltk.stem.wordnet import WordNetLemmatizer
from keras.preprocessing.text import text_to_word_sequence
# Model libraries
from tagger_model import *
# Recommendation Model
import gensim
from sklearn.metrics.pairwise import pairwise_distances, cosine_similarity, euclidean_distances, manhattan_distances
from sklearn.preprocessing import MinMaxScaler, StandardScaler
from IPython.core.debugger import set_trace
# -
# Objects for later use
dataPath = '../data/'
ingred_mod_save_name = 'ingredient_model_clean_tags_crf_wordOnly'
ingred_crf_mod = True
# +
# Read in raw data
json_files = [os.path.join(dataPath, file) for file in os.listdir(dataPath) if
file.endswith('.json')]
raw = pd.concat([pd.read_json(file) for file in json_files])
raw.reset_index(inplace=True)
# -
# ## Pre-process Ingredients
# Ingredient Model to Apply Named-Entity-Recognition to Ingredients to be able to pull out the actual ingredients
# +
def parse_ingredients(recipes_ingredients):
return [[ingred_utils.tokenize(ingredient) for ingredient in recipe]
for recipe in recipes_ingredients]
def reshape_ingredients(row):
"""Reformat so that instead of each row being one recipe with several
ingredients, each row will be one ingredient"""
index = [row.name] * len(row['token_ingred'])
return pd.Series(row['token_ingred'], index = index)
def predict_ingred_ner(raw):
"""Predict NER ingredients"""
# Tokenize the ingredients
raw['token_ingred'] = parse_ingredients(raw.ingredients)
# Reshape ingredients for tagging
ingreds = []
for i in range(raw.shape[0]):
ingreds.append(reshape_ingredients(raw.iloc[i]))
ingred_data = pd.concat(ingreds)
# Load ingredient tagger lexicon
ingred_lexicon = lexiconTransformer(words_min_freq=2, unknown_tag_token='OTHER', saveNamePrefix='Ingred_mod')
ingred_lexicon.load_lexicon()
# Convert Ingredients from words to tokens for modeling
indx_ingred, _ = ingred_lexicon.transform(ingred_data, [])
indx_ingred = pd.Series(indx_ingred, index=ingred_data.index)
# Combine sentences and tokens into a DataFrame
ingred_final = pd.concat([ingred_data, indx_ingred], axis=1)
ingred_final.columns = ['sents', 'sent_indx']
# Ingredient parameters
n_word_embedding_nodes=300
n_tag_embedding_nodes=150
n_RNN_nodes=400
n_dense_nodes=200
ingred_mod = create_test_model(ingred_mod_save_name, ingred_lexicon, crf=ingred_crf_mod,
n_word_embedding_nodes=n_word_embedding_nodes,
n_tag_embedding_nodes=n_tag_embedding_nodes,
n_RNN_nodes=n_RNN_nodes,
n_dense_nodes=n_dense_nodes)
ingred_preds = predict_new_tag(ingred_mod, ingred_final, ingred_lexicon)
ingred_final['tags'] = pd.Series(ingred_preds, index=ingred_final.index)
return ingred_final
# ingred_res = pd.concat([ingred_preds, ingred_preds], axis=1)
# ingred_res.columns = ['sents', 'sent_indx', 'predictions']
# return ingred_res
# +
# Predict tags of ingredients
# ingred_preds = predict_ingred_ner(raw)
# Save model output so don't need to re-run each time
# ingred_preds.to_pickle(os.path.join(dataPath, 'ingred_predictions.pkl'))
# Load model output
ingred_preds = pd.read_pickle(os.path.join(dataPath, 'ingred_predictions.pkl'))
# +
table = str.maketrans({key: None for key in string.punctuation})
def get_ingred(row, table=table):
"""Find the ingredients tagged by the model.
If no ingredients are tagged, randomly select
one as long as it isn't a number.
"""
tagList = [ingred for ingred, tag in zip(row['sents'], row['tags']) if tag == 'NAME']
if tagList == []:
noNums = [token for token in row['sents'] if not re.search(r'\d', token)]
if noNums == []:
return ''
asSent = random.choice(noNums)
else:
asSent = ' '.join(tagList)
removeNums = re.sub(r'\d+', '', asSent)
removePunct = removeNums.translate(table)
# removePunct = re.sub(r'{}'.format(string.punctuation), '', removeNums)
removeExtraSpaces = re.sub(r'\s+', ' ', removePunct)
removeBegSpace = re.sub(r'^\s', '', removeExtraSpaces)
return removeBegSpace
# -
# Pull out the ingredients and then recombine all ingredients for
# one recipe back into a list on one row
ingredients = ingred_preds.apply(get_ingred, axis=1)
ingredients = ingredients.groupby(ingredients.index).apply(lambda x: [y for y in set(x.tolist()) if y != ''])
ingredients.name = 'clean_ingredients'
# +
with_ingreds = raw.join(ingredients)
# Remove those recipes that don't have ingredients
with_ingreds = with_ingreds[~with_ingreds.ingredients.apply(lambda x: x == [] or x is None)]
# -
max_ingred_len = get_max_seq_len(with_ingreds['clean_ingredients'])
ingred_w2v = gensim.models.Word2Vec(with_ingreds['clean_ingredients'],
size=50, min_count=1, workers=-1,
window=max_ingred_len)
def convert_word_mat_to_mean_embed(word_mat, w2v):
"""Finds the average embedding for a list of words"""
dim = ingred_w2v.layer1_size
return [np.mean([w2v.wv.word_vec(w) for w in words if w in w2v.wv.vocab.keys()]
or [np.zeros(dim)], axis=0)
for words in word_mat]
with_ingreds['avg_ingred_embedding'] = convert_word_mat_to_mean_embed(with_ingreds.clean_ingredients, ingred_w2v)
# ## Pre-process directions
# +
wordnet = WordNetLemmatizer()
def clean_and_tokenize_directions(directions, wordnet=wordnet):
"""Clean up directions for a recipe by:
1. Removing 'Photograph by... statements since these wasted text
2. Joining all steps into one string
3. Removing numbers since only interested in cooking verbs
4. Remove C. and F. which are Celsius and Farenheit indicators
5. Removing extra white space.
"""
directions = [wordnet.lemmatize(x.lower()) for x in directions if not re.search(r'^Photograph', x, re.IGNORECASE)]
oneText = ' '.join(directions)
noNumbers = re.sub(r'(\d+)\s?x\s?\d+', '', oneText)
noNumbers = re.sub(r'\d+', '', noNumbers)
noDegrees = re.sub(r' (f|c)\.?\b', '', noNumbers)
clean_directions = re.sub(r'\s+', ' ', noDegrees)
tokenized_directions = text_to_word_sequence(clean_directions)
return tokenized_directions
# -
with_ingreds['clean_directions'] = with_ingreds['directions'].apply(clean_and_tokenize_directions)
dir_w2v = gensim.models.Word2Vec(with_ingreds['clean_directions'],
size=250, min_count=4, workers=-1,
window=3)
cooking_verbs = ['puree', 'cover', 'crumble', 'roll', 'layer', 'saute', 'rotat',
'bak', 'heat', 'blend', 'dress', 'melt', 'stir', 'trim', 'soak',
'microwave', 'cook', 'wrap', 'steam', 'scrape', 'gather',
'quarter', 'spray', 'reduce', 'char', 'pour', 'juice', 'crush',
'wash', 'sift', 'pound', 'marinat', 'spread', 'mix', 'shred',
'dice', 'brush', 'stem', 'cut', 'boil', 'grate', 'slice', 'whisk',
'heat', 'grill', 'fry', 'freeze', 'stuff', 'top', 'toss', 'stew',
'beat', 'swirl', 'warm', 'garnish', 'grease', 'squeeze', 'flour',
'place', 'press', 'whip', 'chill', 'combine', 'add', 'use',
'thread', 'arrange', 'measure', 'select', 'grind']
def pull_out_cooking_verbs(directions, cooking_verbs=cooking_verbs):
return re.findall(r'{}'.format('|'.join(cooking_verbs)), ' '.join(directions))
# return [token for token in directions if token in cooking_verbs]
# +
with_ingreds['direction_verbs'] = with_ingreds['clean_directions'].apply(pull_out_cooking_verbs)
# Filter out those without any directions
with_ingreds = with_ingreds.loc[~with_ingreds['direction_verbs'].apply(lambda x: x == [])]
with_ingreds['avg_directions_embedded'] = convert_word_mat_to_mean_embed(with_ingreds['direction_verbs'], dir_w2v)
# -
# ## Clean other Columns
# Make sure recipe names are unique so that each name is a key.
# +
def clean_recipe_names(names):
"""Replace recipe names if the names already exist"""
counts = dict()
newNames = []
for name in names:
counts[name] = counts.get(name, 0) + 1
newNames.append('{} {}'.format(name, str(counts[name])))
return pd.Series(newNames, index=names.index)
with_ingreds['unique_name'] = clean_recipe_names(with_ingreds.name)
# -
# Clean total time column for use in recommendation model
# +
timeDict = {'hr': 60, 'min': 1, 'day': 1440}
def calc_time(timeText, timeDict=timeDict):
"""Calculate time in minutes based on text"""
num, time = re.search(r'(\d+)\s+(\w+)', timeText).groups()
return timeDict[time] * int(num)
def find_calc_and_sum_all_time(timeInfo):
if isinstance(timeInfo, list):
if timeInfo == []:
return np.NaN
timeInfo = timeInfo[0]
if not timeInfo:
return np.NaN
matches = re.findall(r'(\d+\s+\w+)', timeInfo)
if matches:
return sum([calc_time(time) for time in matches])
return 0
# -
with_ingreds['cleaned_total_time'] = with_ingreds.totalTime.apply(find_calc_and_sum_all_time)
# Count the number of recipes that will be deleted if total Time is missing
with_ingreds['cleaned_total_time'].loc[(with_ingreds['cleaned_total_time'].isnull())].shape
# Count the number of recipes that will be deleted if total Time is missing
with_ingreds['cleaned_total_time'].loc[(with_ingreds['cleaned_total_time'].isnull()) |
(with_ingreds['cleaned_total_time'] > 2880)].shape
# Scale time
def scale_time_to_embeddings(totalTime):
"""Scale the Total Time column so that it has the
same Min/Max as the emeddings so that it doesn't
dominate the recommendations.
Will make sure the time is logged since some recipes call
for days which greatly skews the recipe.
"""
minNum = min(min(with_ingreds.avg_ingred_embedding.apply(min)),
min(with_ingreds.avg_directions_embedded.apply(min)))
maxNum = max(max(with_ingreds.avg_ingred_embedding.apply(max)),
max(with_ingreds.avg_directions_embedded.apply(max)))
scaler = MinMaxScaler(feature_range=(minNum, maxNum))
return scaler.fit_transform(totalTime)
# Delete off rows with missing data and recipes longer than 2 days
finalData = with_ingreds.loc[(with_ingreds['cleaned_total_time'].notnull()) |
(with_ingreds['cleaned_total_time'] < 2880)]
finalData['logged_total_time'] = finalData['cleaned_total_time'].apply(math.log)
finalData['scaled_total_time'] = scale_time_to_embeddings(finalData['logged_total_time'].reshape(-1, 1))
# Save for later use
finalData.to_pickle(os.path.join(dataPath, 'final_data.pkl'))
# Create final data for model
def create_model_data(finalData):
"""Prepare an array to be used for recommendation model.
Will pull out the correct columns, turn the embedding columns
from one column to several columns, scale all columns to put
them in the same feature space.
"""
modelVars = ['avg_ingred_embedding', 'avg_directions_embedded', 'scaled_total_time']
tmpData = finalData.loc[:, modelVars]
avgIngredCols = ['AvgIngredEmbed{}'.format(i) for i in range(len(tmpData['avg_ingred_embedding'][0]))]
avgDirCols = ['AvgDirEmbed{}'.format(i) for i in range(len(tmpData['avg_directions_embedded'][0]))]
modelData = pd.concat([pd.DataFrame.from_records(tmpData['avg_ingred_embedding'],
columns=avgIngredCols),
pd.DataFrame.from_records(tmpData['avg_directions_embedded'],
columns=avgDirCols),
pd.DataFrame(tmpData['scaled_total_time'].tolist())], axis=1, ignore_index=True)
modelData.index = tmpData.index
return modelData
modelData = create_model_data(finalData)
modelData = modelData.dropna()
# Save for later use
modelData.to_pickle(os.path.join(dataPath, 'model_data.pkl'))
|
model/preprocessing_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.10 64-bit (''multalign_graph'': conda)'
# name: python3
# ---
import torch, sys
sys.path.insert(0, '../')
from my_utils import gpu_utils
import importlib, gc
from my_utils.alignment_features import *
import my_utils.alignment_features as afeatures
importlib.reload(afeatures)
import gnn_utils.graph_utils as gutils
# +
# # !pip install torch-geometric
# # !pip install tensorboardX
# # !wget https://bin.equinox.io/c/4VmDzA7iaHb/ngrok-stable-linux-amd64.zip
# # !unzip ngrok-stable-linux-amd64.zip
# print(torch.version.cuda)
# print(torch.__version__)
dev = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# + tags=[]
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch_geometric.nn as pyg_nn
import torch_geometric.utils as pyg_utils
import time
from datetime import datetime
import networkx as nx
import numpy as np
import torch
import torch.optim as optim
from torch_geometric.datasets import TUDataset
from torch_geometric.datasets import Planetoid
from torch_geometric.data import DataLoader
import torch_geometric.transforms as T
from tensorboardX import SummaryWriter
from sklearn.manifold import TSNE
# import matplotlib.pyplot as plt
# + tags=[]
from my_utils import align_utils as autils, utils
import argparse
from multiprocessing import Pool
import random
# set random seed
config_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc-ui-demo/config_pbc.ini"
utils.setup(config_file)
params = argparse.Namespace()
params.gold_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-grc-fin-gold-alignments_train.txt"
pros, surs = autils.load_gold(params.gold_file)
all_verses = list(pros.keys())
params.gold_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-heb-fin-gold-alignments_train.txt"
pros, surs = autils.load_gold(params.gold_file)
all_verses.extend(list(pros.keys()))
all_verses = list(set(all_verses))
print(len(all_verses))
params.editions_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi_lang_list.txt"
editions, langs = autils.load_simalign_editions(params.editions_file)
current_editions = [editions[lang] for lang in langs]
def get_pruned_verse_alignments(args):
verse, current_editions = args
verse_aligns_inter = autils.get_verse_alignments(verse)
verse_aligns_gdfa = autils.get_verse_alignments(verse, gdfa=True)
autils.prune_non_necessary_alignments(verse_aligns_inter, current_editions)
autils.prune_non_necessary_alignments(verse_aligns_gdfa, current_editions)
gc.collect()
return verse_aligns_inter, verse_aligns_gdfa
verse_alignments_inter = {}
verse_alignments_gdfa = {}
args = []
for i,verse in enumerate(all_verses):
args.append((verse, current_editions[:]))
#print('going to get alignments')
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(all_verses):
# verse_aligns_inter, verse_aligns_gdfa = all_res[i]
#verse_alignments_inter[verse] = verse_aligns_inter
#verse_alignments_gdfa[verse] = verse_aligns_gdfa
#utils.LOG.info("done reading alignments")
#torch.save(verse_alignments_inter, "/mounts/work/ayyoob/models/gnn/pruned_alignments_train_inter.pickle")
#torch.save(verse_alignments_gdfa, "/mounts/work/ayyoob/models/gnn/pruned_alignments_train_gdfa.pickle")
#utils.LOG.info('done saving pruned alignments')
print('reading inter verse alignments')
verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_train_inter_8000.pickle")
gc.collect()
print('done reading inter verse alignments')
# -
class Discriminator(torch.nn.Module):
def __init__(self, in_channels, hidden_channels, out_channels):
super(Discriminator, self).__init__()
self.lin1 = torch.nn.Linear(in_channels, hidden_channels)
self.lin2 = torch.nn.Linear(hidden_channels, hidden_channels)
self.lin3 = torch.nn.Linear(hidden_channels, out_channels)
def forward(self, x):
x = F.relu(self.lin1(x))
x = F.relu(self.lin2(x))
x = self.lin3(x)
return x
# +
#importlib.reload(afeatures)
class Encoder2(torch.nn.Module):
def __init__(self, in_channels, out_channels):
super(Encoder2, self).__init__()
self.conv1 = pyg_nn.GATConv(in_channels, 2*out_channels)
self.conv2 = pyg_nn.GATConv(2 * out_channels , out_channels)
def forward(self, x, edge_index):
x = F.elu(self.conv1(x, edge_index, ))
return self.conv2(x, edge_index)
class Encoder(torch.nn.Module):
def __init__(self, in_channels, out_channels, features, n_head = 2, edge_feature_dim = 0,):
super(Encoder, self).__init__()
#self.lin = nn.Linear(in_channels, out_channels)
self.conv1 = pyg_nn.GATConv(in_channels, 2*out_channels, heads= n_head)
self.conv2 = pyg_nn.GATConv(2 * n_head * out_channels , out_channels, heads= 1)
#self.conv3 = pyg_nn.GATConv(2 * n_head * out_channels , out_channels, heads= n_head)
#self.f_embedding = nn.Linear(in_channels, in_channels)
self.fin_lin = nn.Linear(out_channels, out_channels)
self.feature_encoder = afeatures.FeatureEncoding(features, word_vectors)
#self.already_inited = False
#self.prev_edge_index = None
#self.prev_edge_attr = None
def forward(self, x, edge_index):
x = self.feature_encoder(x, dev)
#x = F.relu(self.f_embedding(x))
#if not self.already_inited or self.prev_edge_index.data_ptr() != edge_index.data_ptr():
# edge_index_np = edge_index.cpu().numpy()
# val_indices = x_edge_np[edge_index_np[0, :], edge_index_np[1, :]]
# vals = x_edge_vals[val_indices, :]
# vals = vals.reshape((vals.shape[1], vals.shape[2]))
# self.prev_edge_attr = vals.to(dev)
# self.prev_edge_index = edge_index
# self.already_inited = True
#x = self.lin(x)
x = F.elu(self.conv1(x, edge_index, ))
#x = self.conv_gin(x, edge_index)
x = F.elu(self.conv2(x, edge_index))
return F.relu(self.fin_lin(x))#, self.conv3(x, edge_index)
# +
def clean_memory():
gc.collect()
with torch.no_grad():
torch.cuda.empty_cache()
def train(epoch):
global optimizer
total_loss = 0
cluster_loss = 0
model.train()
#for i in tqdm(range(int(train_pos_edge_index_permed.shape[1]/batch_size)+1)):
for i,batch_ in enumerate(tqdm(data_loader)):
for verse in batch_:
if verse in masked_verses:
continue
batch = batch_[verse]
optimizer.zero_grad()
x = batch['x'].to(dev)
edge_index = batch['edge_index'].to(dev)
if torch.max(edge_index) >= x.shape[0]:
print(torch.max(edge_index), x.shape)
print(batch)
break
try:
z = model.encode(x, edge_index)
except Exception as e:
global sag, khar, gav
sag, khar, gav = (i, batch_, verse)
print(e)
1/0
#z1 = encoder2(z, torch.tensor(batch['intra_sent_edges'], dtype=torch.long).to(dev))
#z = torch.cat((z,z1), dim=1)
#for j in range(5):
# discriminator_optimizer.zero_grad()
# discriminator_loss = model.discriminator_loss(z) / (int(train_pos_edge_index_permed.shape[1]/batch_size)+1)
# discriminator_loss.backward()
# discriminator_optimizer.step()
pos = torch.tensor(batch['pos'], dtype=torch.long).to(dev)
neg = torch.tensor(batch['neg'], dtype=torch.long).to(dev)
#nodes = torch.tensor(list(batch['nodes']), dtype=torch.long).to(dev)
loss1 = model.recon_loss( z, pos, neg) #TODO try providing better neg edges
#ortho_loss, mincut_loss, entropy_loss = model.decoder.clustering_loss(z, nodes, batch['adjacency'])
loss = loss1 * pos.shape[1] #+ ortho_loss + mincut_loss #+ 0.05 * entropy_loss #* pos.shape[1]/train_neg_edge_index.shape[1] #+ model.reg_loss(z)/(int(train_pos_edge_index_permed.shape[1]/batch_size)+1)# + (1 / x.shape[0]) * model.kl_loss()
loss.backward()
optimizer.step()
total_loss += loss.item()
cluster_loss += loss1
if i % 10000 == 9999:
#alignment_test(epoch, test_dataset.edge_index, editf1, editf2, test_verses, test_nodes_map,
# dev, model, x_test, pros, surs, verse_alignments_inter, verse_alignments_gdfa, writer, gnn_dataset.verse_info)
clean_memory()
eval_utils.alignment_test(epoch, grc_test_dataset.edge_index, editf_fin, editf_grc, grc_test_verses[:], grc_test_dataset.nodes_map,
dev, model, grc_test_dataset.x, pros_grc, surs_grc, grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa, writer, gnn_dataset_grc.verse_info)
eval_utils.alignment_test(epoch, heb_test_dataset.edge_index, editf_fin, editf_heb, heb_test_verses[:], heb_test_dataset.nodes_map,
dev, model, heb_test_dataset.x, pros_heb, surs_heb, heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa, writer, gnn_dataset_heb.verse_info)
eval_utils.alignment_test(epoch, blinker_test_dataset.edge_index, editf12, editf22, blinker_verses, blinker_test_dataset.nodes_map,
dev, model, blinker_test_dataset.x, pros_blinker, surs_blinker, blinker_verse_alignments_inter, blinker_verse_alignments_gdfa, writer, gnn_dataset_blinker.verse_info)
clean_memory()
# decoder.set_objective('sequence_prediction')
# auc, ap = test(edge_index_seq_sent, edge_index_seq_sent_neg, epoch)
# print('Epoch: {:03d}, AUC: {:.4f}, AP: {:.4f}'.format(epoch, auc, ap))
# if epoch > 4:
# decoder.set_objective('link_prediction')
model.train()
#if (i+1)*batch_size > train_pos_edge_index.shape[1]:
# break
#if i % 51 == 0:
# clean_memory
writer.add_scalar("loss", total_loss, epoch)
print(f"train loss: {total_loss}")
print(f"cluster loss: {cluster_loss}")
def test(pos_edge_index, neg_edge_index, epoch):
model.eval()
tot_auc = tot_ap = 0
with torch.no_grad():
z = model.encode(x_test, torch.cat((train_pos_edge_index, neg_edge_index), dim=1).to(dev))
neg_pos_coeff = neg_edge_index.shape[1]/ pos_edge_index.shape[1]
for i in (range(int(pos_edge_index.shape[1]/batch_size)+1)):
auc,ap = model.test(z, pos_edge_index[:, i*batch_size:(i+1)*batch_size].to(dev),
neg_edge_index[:, int(i*batch_size*neg_pos_coeff):int((i+1)*batch_size*neg_pos_coeff)].to(dev))
tot_auc += auc * pos_edge_index[:, i*batch_size:(i+1)*batch_size].shape[1]
tot_ap += ap * pos_edge_index[:, i*batch_size:(i+1)*batch_size].shape[1]
return tot_auc/pos_edge_index.shape[1], tot_ap/pos_edge_index.shape[1]
# +
EPS = 1e-15
def _diag(x):
eye = torch.eye(x.size(0)).type_as(x)
out = eye * x.unsqueeze(1).expand(x.size(0), x.size(0))
return out
class Decoder(nn.Module):
def __init__(self, input_size, hidden_size, edge_features, n_cluster=32):
super(Decoder, self).__init__()
#self.feature_encoder = afeatures.FeatureEncoding(edge_features)
self.features_size = sum([x.out_dim for x in edge_features])
self.representataion_size = (input_size - self.features_size)
self.transfer = nn.Sequential(nn.Linear(input_size, hidden_size*2), nn.ReLU(), nn.Dropout(drop_out),
#nn.Linear(hidden_size*2, hidden_size), nn.ReLU(), nn.Dropout(drop_out),
nn.Linear(hidden_size*2, 1))
#self.transfer = nn.Sequential(nn.ELU(), nn.Linear(n_cluster*2, 1), nn.ELU())
#self.n_cluster = n_cluster
#self.cluster = nn.Sequential(nn.Linear(int((input_size - len(edge_features))/2), hidden_size*2), nn.ELU(), nn.Linear(hidden_size*2, 2*n_cluster))
#self.actual_cluster = nn.Linear(2*n_cluster, n_cluster)
#self.cos = nn.CosineSimilarity(dim=1)
#self.dist = nn.PairwiseDistance()
#self.gnn_transform = nn.Sequential(nn.Linear(self.representataion_size, hidden_size), nn.ReLU(), nn.Dropout(drop_out))
self.counter = 0
self.objective = 'link_prediction'
def forward(self, z, edge_index, sigmoid = True):
if self.features_size > 0:
if self.objective == 'link_prediction':
edge_index_np = edge_index.cpu().numpy()
val_indices = x_edge_np[edge_index_np[0, :], edge_index_np[1, :]]
val_indices = np.squeeze(np.asarray(val_indices))
vals = x_edge_vals2[val_indices, :]
elif self.objective == 'sequence_prediction':
vals = torch.zeros((edge_index.shape[1], self.features_size)).to(dev)
features = self.feature_encoder(vals.to(dev), dev)
#features = vals.to(dev)
h1 = z[edge_index[0, :]]
h2 = z[edge_index[1, :]]
self.counter += 1
#rep = self.gnn_transform(torch.cat((h1, h2), dim=1))
res = self.transfer(torch.cat((self.cluster(h1), self.cluster(h2), features), dim=1))
#res = self.transfer(features)
else:
h1 = z[edge_index[0, :]]
h2 = z[edge_index[1, :]]
res = self.transfer(torch.cat((h1, h2), dim=-1))
#res = self.transfer(torch.cat((self.cluster(h1), self.cluster(h2)), dim=1))
#res = torch.sum(torch.pow(F.softmax(self.cluster(h1)/1, dim=1) - F.softmax(self.cluster(h2)/1, dim=1), 2), dim=1)
#res = self.cos(self.cluster(h1), self.cluster(h2))
#res = - self.dist(self.cluster(h1), self.cluster(h2))
#print(res)
res = torch.sigmoid(res) if sigmoid else res
return res
def set_objective(self, objective):
self.objective = objective
def clustering_loss(self, z, nodes, adjacency):
s = self.actual_cluster(torch.relu(self.cluster(z[nodes])))
s = torch.softmax(s, dim=-1)
entropy_loss = (-s * torch.log(s + EPS)).sum(dim=-1).mean()
ss = torch.matmul(s.transpose(0, 1), s)
i_s = torch.eye(self.n_cluster).type_as(ss)
ortho_loss = torch.norm(
ss / torch.norm(ss, dim=(-1, -2), keepdim=True) -
i_s / torch.norm(i_s), dim=(-1, -2))
ortho_loss = torch.mean(ortho_loss)
adjacency = adjacency.to(dev).float()
out_adj = torch.matmul(s.transpose(0, 1),torch.sparse.mm(adjacency, s))
# MinCUT regularization.
mincut_num = torch.trace(out_adj)
#d_flat = torch.einsum('ij->i', adjacency) # FIXME since I don't consider the whole adjacency matrix this could be a source of problem
d_flat = torch.sparse.sum(adjacency, dim=1).to_dense()
d = _diag(d_flat)
mincut_den = torch.trace(
torch.matmul(torch.matmul(s.transpose(0, 1), d), s))
mincut_loss = -(mincut_num / mincut_den)
mincut_loss = torch.mean(mincut_loss)
return ortho_loss, mincut_loss, entropy_loss
def get_alignments(self, z, edge_index):
h1 = z[edge_index[0, :]]
h2 = z[edge_index[1, :]]
h1 = torch.softmax(self.cluster(h1), dim=1)
h2 = torch.softmax(self.cluster(h2), dim=1)
h1_max = torch.argmax(h1, dim=1)
h2_max = torch.argmax(h2, dim=1)
h1_cluster = torch.zeros(*h1.shape)
h2_cluster = torch.zeros(*h2.shape)
h1_cluster[range(h1.size(0)), h1_max] = 1
h2_cluster[range(h2.size(0)), h2_max] = 1
res = torch.max(h1_cluster * h2_cluster, dim=1).values
#res = h1 * h2
#res = torch.sum(res, dim = 1)
return torch.unsqueeze(res, dim=1)
# + tags=[]
import pickle
train_verses = all_verses[:]
test_verses = all_verses[:]
editf1 = 'fin-x-bible-helfi'
editf2 = "heb-x-bible-helfi"
if 'jpn-x-bible-newworld' in current_editions[:]:
current_editions.remove('jpn-x-bible-newworld')
if 'grc-x-bible-unaccented' in current_editions[:]:
current_editions.remove('grc-x-bible-unaccented')
train_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_helfi_train_community_word_8000.pickle", map_location=torch.device('cpu'))
#train_dataset, train_nodes_map = create_dataset(train_verses, verse_alignments_inter, small_editions)
features = train_dataset.features
train_nodes_map = train_dataset.nodes_map
#edge_index_intra_sent = train_dataset.edge_index_intra_sent
#test_edge_index_intra_sent = edge_index_intra_sent
# test_dataset, test_nodes_map = create_dataset(test_verses, verse_alignments_inter, small_editions)
test_dataset, test_nodes_map = train_dataset, train_nodes_map
test_verses = train_verses
print(train_dataset.x.shape)
# gutils.augment_features(test_dataset)
# x_edge, features_edge = gutils.create_edge_attribs(train_nodes_map, train_verses, small_editions, verse_alignments_inter, train_dataset.x.shape[0])
# with open("./dataset.pickle", 'wb') as of:
# pickle.dump(train_dataset, of)
gc.collect()
# +
from gensim.models import Word2Vec
w2v_model = Word2Vec.load("/mounts/work/ayyoob/models/w2v/word2vec_helfi_langs_15e.model")
print(w2v_model.wv.vectors.shape)
word_vectors = torch.from_numpy(w2v_model.wv.vectors).float()
print(word_vectors.shape)
# + tags=[]
# edges_intra_sent, edges_seq_sent = get_inter_sentence_connections(train_dataset.nodes_map)
# edge_index_seq_sent = torch.tensor(edges_seq_sent, dtype=torch.long)
# train_dataset.edge_index_seq_sent = edge_index_seq_sent
# torch.cuda.set_device(int(free_gpu1))
# edge_index_intra_sent = torch.tensor(edges_intra_sent, dtype=torch.long).to(dev)
# train_dataset.edge_index_intra_sent = edge_index_intra_sent
# test_edge_index_intra_sent = train_dataset.edge_index_intra_sent
# print(train_dataset.edge_index_intra_sent.shape)
# + tags=[]
import pickle
import torch
## with open("./features_edge.pickle", 'wb') as of:
## pickle.dump(features_edge, of)
## print('done first')
## with open("/mounts/work/ayyoob/models/gnn//x_edge.pickle", 'wb') as of:
## pickle.dump(x_edge, of)
#with open("./features_edge.pickle", 'rb') as inf:
# features_edge = pickle.load(inf)
## indices = [[],[]]
## values = []
## print('going to create sparse matrix representation')
## for i in range(len(ss)):
## print(i)
## for j in range(len(ss)):
## if ss[i][j] != None and ss[i][j] != []:
## indices[0].append(i)
## indices[1].append(j)
## values.append(ss[i][j])
## with open("./edge_attribs_sparse_indices.pickle", 'wb') as of:
## pickle.dump(indices, of)
## with open("./edge_attribs_sparse_values.pickle", 'wb') as of:
## pickle.dump(values, of)
## print('loading indices')
## with open("./edge_attribs_sparse_indices.pickle", 'rb') as inf:
## indices = pickle.load(inf)
## print('loading values')
## with open("./edge_attribs_sparse_values.pickle", 'rb') as inf:
## values = pickle.load(inf)
## print('creating sparse tensor')
## s = torch.sparse_coo_tensor(indices, values, (67800, 67800, len(ff)), dtype=torch.float16)
## print('saving sparse matrix')
## torch.save(s, "/mounts/work/ayyoob/models/gnn/edge_attribs_tensor16.pickle")
#print('loading sparse matrix')
#x_edge = torch.load("/mounts/work/ayyoob/models/gnn/edge_attribs_tensor.pickle")
#train_dataset.features_edge = features_edge
# +
from scipy.sparse import csr_matrix
import numpy as np
#x_edge = x_edge.coalesce()
#torch.cuda.set_device(1)
#x_edge_vals = x_edge.values()
#indices_np = x_edge.indices().numpy()
#print(indices_np.shape)
#x_edge_np = csr_matrix((np.arange(indices_np.shape[1]), (indices_np[0, :], indices_np[1,:])), shape=(67800, 67800))
##x_edge_vals = x_edge_vals.cpu()
##maxes = torch.max(x_edge_vals,0)
##mins = torch.min(x_edge_vals,0)
##x_edge_vals_d = torch.div(x_edge_vals, maxes.values)
#print('creating targets')
#targets = torch.zeros(indices_np.shape[1], dtype=torch.int64)
#pos_indices = x_edge_np[train_dataset.edge_index.cpu().numpy()[0,:], train_dataset.edge_index.cpu().numpy()[1,:]]
#pos_indices = np.squeeze(np.asarray(pos_indices))
#targets[pos_indices] = 1
#print("done")
# +
# run on delta, extract w2v features
#sys.path.insert(0, '../')
#import pickle
#from gensim.models import Word2Vec
#from app.document_retrieval import DocumentRetriever
#from my_utils import utils
#config_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc-ui-demo/config_pbc.ini"
#utils.setup(config_file)
#import torch
#import my_utils.alignment_features as feat_utils
#doc_retriever = DocumentRetriever()
#model_w2v = Word2Vec.load("word2vec_83langs_15epoch.model")
#train_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_en_fr_full.pickle")
#nodes_map = train_dataset.nodes_map
#x = [[] for i in range(train_dataset.x.shape[0])]
#for edition_f in nodes_map:
# utils.LOG.info(f"processing edition {edition_f}")
# for verse in nodes_map[edition_f]: #toknom nodecount
# line = doc_retriever.retrieve_document(f'{verse}@{edition_f}')
# line = line.strip().split()
# for tok in nodes_map[edition_f][verse]:
# w_emb = model_w2v.wv[f'{edition_f[:3]}:{line[tok]}']
# x[nodes_map[edition_f][verse][tok]].extend(w_emb)
#x = torch.tensor(x, dtype=torch.float)
#train_dataset.x = torch.cat((train_dataset.x, x), dim=1)
#train_dataset.features.append(feat_utils.ForwardFeature(50, 100, 'W2v'))
#print(x.shape, train_dataset.x.shape, len(train_dataset.features))
#torch.save(train_dataset, "/mounts/work/ayyoob/models/gnn/dataset_en_fr_full.pickle")
# +
## Add node embedding features
#importlib.reload(gutils)
#x_,features_ = gutils.get_embedding_node_features(train_dataset.nodes_map, train_verses, small_editions, verse_alignments_inter, x_edge_np, x_edge_vals.cpu().numpy())
#train_dataset.x = torch.cat((train_dataset.x,x_), dim=1)
#train_dataset.features.extend(features_)
# +
blinker_test_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_blinker_full_community_word.pickle", map_location=torch.device('cpu'))
editf12 = "eng-x-bible-mixed"
editf22 = 'fra-x-bible-louissegond'
test_gold_eng_fra = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/eng_fra_pbc/eng-fra.gold"
pros_blinker, surs_blinker = autils.load_gold(test_gold_eng_fra)
blinker_verses = list(pros_blinker.keys())
#blinker_verse_alignments_inter = {}
#blinker_verse_alignments_gdfa = {}
#args = []
#for i,verse in enumerate(blinker_verses):
# args.append((verse, current_editions))
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(blinker_verses):
# verse_aligns_inter, verse_aligns_gdfa = all_res[i]
# blinker_verse_alignments_inter[verse] = verse_aligns_inter
# blinker_verse_alignments_gdfa[verse] = verse_aligns_gdfa
utils.LOG.info("done reading alignments")
#torch.save(blinker_verse_alignments_inter, "/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_inter.pickle")
#torch.save(blinker_verse_alignments_gdfa, "/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_gdfa.pickle")
utils.LOG.info('done saving pruned alignments')
print('reading inter verse alignments')
blinker_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_inter.pickle")
blinker_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_gdfa.pickle")
gc.collect()
print('done reading inter verse alignments')
verses_map = {}
for edit in blinker_test_dataset.nodes_map:
for verse in blinker_test_dataset.nodes_map[edit]:
if verse not in verses_map:
for tok in blinker_test_dataset.nodes_map[edit][verse]:
verses_map[verse] = blinker_test_dataset.nodes_map[edit][verse][tok]
break
sorted_verses = sorted(verses_map.items(), key = lambda x: x[1])
blinker_verses = [item[0] for item in sorted_verses]
# +
helfi_heb_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_helfi_heb_test_community_word.pickle", map_location=torch.device('cpu'))
editf_fin = "fin-x-bible-helfi"
editf_heb = 'heb-x-bible-helfi'
test_gold_helfi_heb = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-heb-fin-gold-alignments_test.txt"
pros_heb, surs_heb = autils.load_gold(test_gold_helfi_heb)
heb_verses = list(pros_blinker.keys())
#blinker_verse_alignments_inter = {}
#blinker_verse_alignments_gdfa = {}
#args = []
#for i,verse in enumerate(blinker_verses):
# args.append((verse, current_editions))
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(blinker_verses):
# verse_aligns_inter, verse_aligns_gdfa = all_res[i]
# blinker_verse_alignments_inter[verse] = verse_aligns_inter
# blinker_verse_alignments_gdfa[verse] = verse_aligns_gdfa
utils.LOG.info("done reading alignments")
#torch.save(blinker_verse_alignments_inter, "/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_inter.pickle")
#torch.save(blinker_verse_alignments_gdfa, "/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_gdfa.pickle")
utils.LOG.info('done saving pruned alignments')
print('reading inter verse alignments')
blinker_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_inter.pickle")
blinker_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_gdfa.pickle")
gc.collect()
print('done reading inter verse alignments')
verses_map = {}
for edit in blinker_test_dataset.nodes_map:
for verse in blinker_test_dataset.nodes_map[edit]:
if verse not in verses_map:
for tok in blinker_test_dataset.nodes_map[edit][verse]:
verses_map[verse] = blinker_test_dataset.nodes_map[edit][verse][tok]
break
sorted_verses = sorted(verses_map.items(), key = lambda x: x[1])
blinker_verses = [item[0] for item in sorted_verses]
# +
#importlib.reload(afeatures)
grc_test_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_helfi_grc_test_community_word.pickle", map_location=torch.device('cpu'))
editf_fin = "fin-x-bible-helfi"
editf_grc = 'grc-x-bible-helfi'
test_gold_grc = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-grc-fin-gold-alignments_test.txt"
pros_grc, surs_grc = autils.load_gold(test_gold_grc)
grc_verses = list(pros_grc.keys())
grc_test_verse_alignments_inter = {}
grc_test_verse_alignments_gdfa = {}
gc.collect()
#args = []
#for i,verse in enumerate(grc_verses):
# args.append((verse, current_editions))
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(grc_verses):
# verse_aligns_inter, verse_aligns_gdfa = all_res[i]
# grc_test_verse_alignments_inter[verse] = verse_aligns_inter
# grc_test_verse_alignments_gdfa[verse] = verse_aligns_gdfa
utils.LOG.info("done reading alignments")
#torch.save(grc_test_verse_alignments_inter, "/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_inter.pickle")
#torch.save(grc_test_verse_alignments_gdfa, "/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_gdfa.pickle")
utils.LOG.info('done saving pruned alignments')
print('reading inter verse alignments')
grc_test_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_inter.pickle")
grc_test_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_gdfa.pickle")
gc.collect()
print('done reading inter verse alignments')
verses_map = {}
for edit in grc_test_dataset.nodes_map:
for verse in grc_test_dataset.nodes_map[edit]:
if verse not in verses_map:
for tok in grc_test_dataset.nodes_map[edit][verse]:
verses_map[verse] = grc_test_dataset.nodes_map[edit][verse][tok]
break
sorted_verses = sorted(verses_map.items(), key = lambda x: x[1])
grc_test_verses = [item[0] for item in sorted_verses]
gc.collect()
# +
heb_test_dataset = torch.load("/mounts/work/ayyoob/models/gnn/dataset_helfi_heb_test_community_word.pickle", map_location=torch.device('cpu'))
editf_fin = "fin-x-bible-helfi"
editf_heb = 'heb-x-bible-helfi'
test_gold_heb = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-heb-fin-gold-alignments_test.txt"
pros_heb, surs_heb = autils.load_gold(test_gold_heb)
heb_verses = list(pros_heb.keys())
heb_test_verse_alignments_inter = {}
heb_test_verse_alignments_gdfa = {}
#args = []
#for i,verse in enumerate(heb_verses):
# args.append((verse, current_editions))
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(heb_verses):
# verse_aligns_inter, verse_aligns_gdfa = all_res[i]
# heb_test_verse_alignments_inter[verse] = verse_aligns_inter
# heb_test_verse_alignments_gdfa[verse] = verse_aligns_gdfa
#utils.LOG.info("done reading alignments")
#torch.save(heb_test_verse_alignments_inter, "/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_inter.pickle")
#torch.save(heb_test_verse_alignments_gdfa, "/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_gdfa.pickle")
#utils.LOG.info('done saving pruned alignments')
print('reading inter verse alignments')
heb_test_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_inter.pickle")
heb_test_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_gdfa.pickle")
gc.collect()
print('done reading inter verse alignments')
verses_map = {}
for edit in heb_test_dataset.nodes_map:
for verse in heb_test_dataset.nodes_map[edit]:
if verse not in verses_map:
for tok in heb_test_dataset.nodes_map[edit][verse]:
verses_map[verse] = heb_test_dataset.nodes_map[edit][verse][tok]
break
sorted_verses = sorted(verses_map.items(), key = lambda x: x[1])
heb_test_verses = [item[0] for item in sorted_verses]
gc.collect()
# +
verses_map = {}
for edit in train_dataset.nodes_map:
for verse in train_dataset.nodes_map[edit]:
if verse not in verses_map:
for tok in train_dataset.nodes_map[edit][verse]:
verses_map[verse] = train_dataset.nodes_map[edit][verse][tok]
break
sorted_verses = sorted(verses_map.items(), key = lambda x: x[1])
all_verses = [item[0] for item in sorted_verses]
long_verses = set()
for edit in train_dataset.nodes_map.keys():
for verse in train_dataset.nodes_map[edit]:
to_print = False
for tok in train_dataset.nodes_map[edit][verse]:
if tok > 150:
to_print = True
if to_print == True:
long_verses.add(verse)
train_verses = all_verses[:]
masked_verses = list(long_verses)
masked_verses.extend(blinker_verses)
# +
from tqdm import tqdm
from torch.utils.data import Dataset, DataLoader
import random
class GNNDataset(Dataset):
def __init__(self, dataset, verses, edit_files, alignments, group_size = 360):
self.verses = list(verses)
self.edit_files = list(edit_files)
self.nodes_map = dataset.nodes_map
self.items = self.calculate_size(self.nodes_map, self.verses, self.edit_files, group_size)
self.alignments = alignments
self.verse_info = {}
self.calculate_verse_stats(verses, edit_files, alignments, dataset)
def calculate_size(self, nodes_map, verses, edit_files, group_size):
res = []
item = []
self.not_presented = []
for verse in verses:
if len(item) > 0:
res.append(item)
item = []
for i,editf1 in enumerate(edit_files):
if editf1 not in nodes_map:
self.not_presented.append(editf1)
continue
if verse in nodes_map[editf1]:
for editf2 in edit_files[i+1:]:
if editf2 not in nodes_map:
self.not_presented.append(editf2)
continue
if verse in nodes_map[editf2]:
item.append((verse, editf1, editf2))
if len(item) >= group_size:
res.append(item)
item = []
if len(item)>0:
res.append(item)
print(f"not presented: {set(self.not_presented)}")
return res
def calculate_verse_stats(self,verses, edition_files, alignments, dataset):
min_edge = 0
for verse in tqdm(verses):
min_nodes = 99999999999999
max_nodes = 0
#utils.LOG.info(f"adding {verse}")
edges_tmp = [[],[]]
x_tmp = []
features = []
for i,editf1 in enumerate(edition_files):
for j,editf2 in enumerate(edition_files[i+1:]):
aligns = autils.get_aligns(editf1, editf2, alignments[verse])
if aligns != None:
for align in aligns:
try:
n1,_ = gutils.node_nom(verse, editf1, align[0], None, dataset.nodes_map, x_tmp, edition_files, features)
n2,_ = gutils.node_nom(verse, editf2, align[1], None, dataset.nodes_map, x_tmp, edition_files, features)
edges_tmp[0].extend([n1, n2])
max_nodes = max(n1, n2, max_nodes)
min_nodes = min(n1, n2, min_nodes)
except Exception as e:
print(editf1, editf2, verse)
raise(e)
self.verse_info[verse] = {}
self.verse_info[verse]['padding'] = min_nodes
self.verse_info[verse]['x'] = dataset.x[min_nodes:max_nodes+1,:]
self.verse_info[verse]['edge_index'] = dataset.edge_index[:, min_edge : min_edge + len(edges_tmp[0])] - min_nodes
if torch.min(self.verse_info[verse]['edge_index']) != 0:
print(verse, min_nodes, max_nodes, min_edge, len(edges_tmp[0]))
print(torch.min(self.verse_info[verse]['edge_index']))
if self.verse_info[verse]['x'].shape[0] != torch.max(self.verse_info[verse]['edge_index']) + 1 :
print(verse, min_nodes, max_nodes, min_edge, len(edges_tmp[0]))
print(torch.min(self.verse_info[verse]['edge_index']))
min_edge = min_edge + len(edges_tmp[0])
def __len__(self):
#return self.length
return len(self.items)
def __getitem__(self, idx):
if torch.is_tensor(idx):
idx = idx.tolist()
item = self.items[idx]
res_pos = [[],[]]
res_neg = [[],[]]
nodes = set()
for instance in item:
verse, editf1, editf2 = instance
aligns = autils.get_aligns(editf1, editf2, self.alignments[verse])
if aligns != None:
for align in aligns:
p1, p2 = align
n1 = self.nodes_map[editf1][verse][p1] - self.verse_info[verse]['padding']
n2 = self.nodes_map[editf2][verse][p2] - self.verse_info[verse]['padding']
res_pos[0].extend([n1,n2])
res_pos[1].extend([n2,n1])
n2_ = random.choice( list(self.nodes_map[editf2][verse].values()) ) - self.verse_info[verse]['padding']
n1_ = random.choice( list(self.nodes_map[editf1][verse].values()) ) - self.verse_info[verse]['padding']
if n2_ != n2:
res_neg[0].extend([n1, n2_])
res_neg[1].extend([n2_, n1])
if n1_ != n1:
res_neg[0].extend([n1_, n2])
res_neg[1].extend([n2, n1_])
#nodes.update([n1, n2, n1_, n2_])
return {'pos':res_pos, 'neg':res_neg, 'nodes':nodes, 'verse':verse, 'editf1':editf1, 'editf2':editf2}
def collate_fun(input):
res = {}
#all_edits = {}
for item in input:
verse = item['verse']
if verse not in res:
res[verse] = {'pos': [[],[]], 'neg' : [[],[]],
'x':gnn_dataset.verse_info[verse]['x'], 'edge_index':gnn_dataset.verse_info[verse]['edge_index']
,'intra_sent_edges':[[],[]]}
res[verse]['pos'][0].extend(item['pos'][0])
res[verse]['pos'][1].extend(item['pos'][1])
res[verse]['neg'][0].extend(item['neg'][0])
res[verse]['neg'][1].extend(item['neg'][1])
#if verse not in all_edits:
# all_edits[verse] = []
#if item['editf1'] not in all_edits[verse]:
# e = eval_utils.get_all_edges(verse, item['editf1'], train_dataset.nodes_map, gnn_dataset.verse_info)
# res[verse]['intra_sent_edges'][0].extend(e[0])
# res[verse]['intra_sent_edges'][1].extend(e[1])
#if item['editf2'] not in all_edits[verse]:
# e = eval_utils.get_all_edges(verse, item['editf2'], train_dataset.nodes_map, gnn_dataset.verse_info)
# res[verse]['intra_sent_edges'][0].extend(e[0])
# res[verse]['intra_sent_edges'][1].extend(e[1])
#nodes = list(nodes)
#mapping = {node:pos for pos, node in enumerate(nodes)}
##indices = [[i for i in range(len(res_pos[0]))],[i for i in range(len(res_pos[1]))]]
#indices = [[],[]]
##adjacency = torch.zeros((len(nodes), len(nodes)), dtype=torch.float)
#for i in range(len(res_pos[0])):
## adjacency[mapping[res_pos[0][i]], mapping[res_pos[1][i]]] = 1
# indices[0].append(mapping[res_pos[0][i]])
# indices[1].append(mapping[res_pos[1][i]])
#adjacency = torch.sparse_coo_tensor(indices, [1 for i in range(len(res_pos[0]))], (len(nodes), len(nodes)))
return res
gnn_dataset_train = GNNDataset(train_dataset, train_verses, current_editions, verse_alignments_inter)
gnn_dataset_blinker = GNNDataset(blinker_test_dataset, blinker_verses, current_editions, blinker_verse_alignments_inter)
gnn_dataset_heb = GNNDataset(heb_test_dataset, heb_test_verses, current_editions, heb_test_verse_alignments_inter)
gnn_dataset_grc = GNNDataset(grc_test_dataset, grc_test_verses, current_editions, grc_test_verse_alignments_inter)
len(gnn_dataset_train)
gc.collect()
# +
from gnn_utils import eval_utils
train_dataset.train_mask = train_dataset.val_mask = train_dataset.test_mask = train_dataset.y = None
test_dataset.train_mask = test_dataset.val_mask = test_dataset.test_mask = test_dataset.y = None
torch.cuda.set_device(0)
features = train_dataset.features
# -
def save_model(model):
model.encoder.feature_encoder.feature_types[0] = afeatures.OneHotFeature(20, 83, 'editf')
model.encoder.feature_encoder.feature_types[1] = afeatures.OneHotFeature(32, 150, 'position')
model.encoder.feature_encoder.feature_types[2] = afeatures.FloatFeature(4, 'degree_centrality')
model.encoder.feature_encoder.feature_types[3] = afeatures.FloatFeature(4, 'closeness_centrality')
model.encoder.feature_encoder.feature_types[4] = afeatures.FloatFeature(4, 'betweenness_centrality')
model.encoder.feature_encoder.feature_types[5] = afeatures.FloatFeature(4, 'load_centrality')
model.encoder.feature_encoder.feature_types[6] = afeatures.FloatFeature(4, 'harmonic_centrality')
model.encoder.feature_encoder.feature_types[7] = afeatures.OneHotFeature(32, 250, 'greedy_modularity_community')
model.encoder.feature_encoder.feature_types[8] = afeatures.OneHotFeature(32, 250, 'community_2')
model.encoder.feature_encoder.feature_types[9] = afeatures.MappingFeature(100, 'word')
torch.save(model, '/mounts/work/ayyoob/models/gnn/checkpoint/gnn_256_flggll_word_halfTrain_nofeatlinear_encoderlineear_decoderonelayer' + datetime.now().strftime("%Y%m%d-%H%M%S-") + '.pickle')
# + tags=[]
from tqdm import tqdm
features_edge = [] #TODO remove me
#features_edge = train_dataset.features_edge[:]
#x_edge_vals2 = x_edge_vals[:, :]
#features = train_dataset.features
gnn_dataset = gnn_dataset_train
data_loader = DataLoader(gnn_dataset_train, batch_size=1, collate_fn=collate_fun, shuffle=True)
gc.collect()
with torch.no_grad():
torch.cuda.empty_cache()
drop_out = 0
pos_noise = 0.0
neg_noise = 0.0
n_head = 1
batch_size = 100
channels = 256
in_dim = sum(t.out_dim for t in features)
decoder_in_dim = n_head * channels * 2 + sum(t.out_dim for t in features_edge)
print('edge features size: ', sum(t.out_dim for t in features_edge))
#discriminator = Discriminator(channels*n_head, channels * (n_head+1), channels*n_head)
#discriminator_optimizer = torch.optim.AdamW(discriminator.parameters(), lr=0.0007)
#encoder2 = Encoder2(channels, int(channels/2)).to(dev)
decoder = Decoder(decoder_in_dim, int(decoder_in_dim/2), features_edge, n_cluster=64)
model = pyg_nn.GAE(Encoder(in_dim, channels, features, n_head, edge_feature_dim=len(features_edge)), decoder).to(dev)
#model.encoder2 = encoder2
#model = pyg_nn.GAE(DeeperGCN(in_dim, len(features_edge), channels, 10, features), decoder=decoder).to(dev)
#model = pyg_nn.GAE(Encoder(in_dim, channels, features, n_head)).to(dev)
print("sending input to gpu")
optimizer = torch.optim.AdamW(model.parameters(), lr=0.001)
optimizer.add_param_group({'params': word_vectors})
writer = SummaryWriter("./log/" + datetime.now().strftime("%Y%m%d-%H%M%S-") + f"samett-{channels}chs-feat{train_dataset.num_node_features}-")
torch.set_printoptions(edgeitems=5)
print("model params - decoder params - conv1", sum(p.numel() for p in model.parameters()), sum(p.numel() for p in decoder.parameters()))
for epoch in range(1, 2):
print(f"\n----------------epoch {epoch} ---------------")
#if epoch % 1 == 0:
# train_neg_edge_index = gutils.get_negative_edges(train_verses, small_editions, train_dataset.nodes_map, verse_alignments_inter).to(dev)
#edge_index_seq_sent_neg = get_negative_edges_seq(train_dataset.nodes_map).to(dev)
train(epoch)
save_model(model)
clean_memory()
if epoch % 1 == 0:
#alignment_test(epoch, test_dataset.edge_index, editf1, editf2, test_verses[:30], test_nodes_map,
# dev, model, x_test, pros, surs, verse_alignments_inter, verse_alignments_gdfa, writer, gnn_dataset.verse_info)
#eval_utils.alignment_test(epoch, test_dataset.edge_index, editf1, editf2, test_verses[:], test_nodes_map,
# dev, model, x_test, pros, surs, verse_alignments_inter, verse_alignments_gdfa, writer, gnn_dataset.verse_info)
eval_utils.alignment_test(epoch, grc_test_dataset.edge_index, editf_fin, editf_grc, grc_test_verses[:], grc_test_dataset.nodes_map,
dev, model, grc_test_dataset.x, pros_grc, surs_grc, grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa, writer, gnn_dataset_grc.verse_info)
eval_utils.alignment_test(epoch, heb_test_dataset.edge_index, editf_fin, editf_heb, heb_test_verses[:], heb_test_dataset.nodes_map,
dev, model, heb_test_dataset.x, pros_heb, surs_heb, heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa, writer, gnn_dataset_heb.verse_info)
eval_utils.alignment_test(epoch, blinker_test_dataset.edge_index, editf12, editf22, blinker_verses, blinker_test_dataset.nodes_map,
dev, model, blinker_test_dataset.x, pros_blinker, surs_blinker, blinker_verse_alignments_inter, blinker_verse_alignments_gdfa, writer, gnn_dataset_blinker.verse_info)
# auc, ap = test(edge_index_seq_sent, edge_index_seq_sent_neg, epoch)
# print('Epoch: {:03d}, AUC: {:.4f}, AP: {:.4f}'.format(epoch, auc, ap))
clean_memory()
# +
i = sag
batch = khar
verse = gav
print(i, verse)
keys = list(gnn_dataset.verse_info.keys())
gnn_dataset.verse_info[verse]
# +
data_loader_blinker = DataLoader(gnn_dataset_blinker, batch_size=1, collate_fn=collate_fun, shuffle=True)
data_loader_heb = DataLoader(gnn_dataset_heb, batch_size=1, collate_fn=collate_fun, shuffle=True)
data_loader_grc = DataLoader(gnn_dataset_grc, batch_size=1, collate_fn=collate_fun, shuffle=True)
clean_memory()
data_loader = data_loader_blinker
gnn_dataset = gnn_dataset_blinker
train(1)
clean_memory()
eval_utils.alignment_test(epoch, blinker_test_dataset.edge_index, editf12, editf22, blinker_verses[:], blinker_test_dataset.nodes_map,
dev, model, blinker_test_dataset.x, pros_blinker, surs_blinker, blinker_verse_alignments_inter, blinker_verse_alignments_gdfa, writer, gnn_dataset_blinker.verse_info)
clean_memory()
data_loader = data_loader_grc
gnn_dataset = gnn_dataset_grc
train(1)
clean_memory()
eval_utils.alignment_test(epoch, grc_test_dataset.edge_index, editf_fin, editf_grc, grc_test_verses[:], grc_test_dataset.nodes_map,
dev, model, grc_test_dataset.x, pros_grc, surs_grc, grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa, writer, gnn_dataset_grc.verse_info)
clean_memory()
data_loader = data_loader_heb
gnn_dataset = gnn_dataset_heb
train(1)
clean_memory()
eval_utils.alignment_test(epoch, heb_test_dataset.edge_index, editf_fin, editf_heb, heb_test_verses[:], heb_test_dataset.nodes_map,
dev, model, heb_test_dataset.x, pros_heb, surs_heb, heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa, writer, gnn_dataset_heb.verse_info)
clean_memory()
# +
from gnn_utils import eval_utils
importlib.reload(eval_utils)
clean_memory()
eval_utils.alignment_test(epoch, heb_test_dataset.edge_index, editf_fin, editf_heb, heb_test_verses, heb_test_dataset.nodes_map,
dev, model, heb_test_dataset.x, pros_heb, surs_heb, heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa, writer, gnn_dataset_heb.verse_info)
eval_utils.alignment_test(epoch, grc_test_dataset.edge_index, editf_fin, editf_grc, grc_test_verses, grc_test_dataset.nodes_map,
dev, model, grc_test_dataset.x, pros_grc, surs_grc, grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa, writer, gnn_dataset_grc.verse_info)
eval_utils.alignment_test(epoch, blinker_test_dataset.edge_index, editf12, editf22, blinker_verses, blinker_test_dataset.nodes_map,
dev, model, blinker_test_dataset.x, pros_blinker, surs_blinker, blinker_verse_alignments_inter, blinker_verse_alignments_gdfa, writer, gnn_dataset_blinker.verse_info)
clean_memory()
# +
# produce for uruba
importlib.reload(eval_utils)
editf_yor = 'yor-x-bible-2010'
editf_others = ['eng-x-bible-mixed', 'deu-x-bible-newworld', 'ces-x-bible-newworld', 'fra-x-bible-louissegond', 'hin-x-bible-newworld',
'ita-x-bible-2009', 'prs-x-bible-goodnews', 'ron-x-bible-2006', 'spa-x-bible-newworld']
#def get_pruned_verse_alignments(args):
# verse, current_editions = args
# #verse_aligns_inter = autils.get_verse_alignments(verse)
# verse_aligns_gdfa = autils.get_verse_alignments(verse, gdfa=True)
# #autils.prune_non_necessary_alignments(verse_aligns_inter, current_editions)
# autils.prune_non_necessary_alignments(verse_aligns_gdfa, current_editions)
# gc.collect()
# return verse_aligns_gdfa
#verse_alignments_gdfa = {}
#args = []
#editfs = editf_others[:]
#editfs.append(editf_yor)
#for i,verse in enumerate(train_verses):
# args.append((verse, editfs))
#print('going to get alignments')
#with Pool(20) as p:
# all_res = p.map(get_pruned_verse_alignments, args)
#for i,verse in enumerate(all_verses):
# verse_aligns_gdfa = all_res[i]
# verse_alignments_gdfa[verse] = verse_aligns_gdfa
for verse in train_dataset.nodes_map[editf_yor]:
if verse not in surs :
surs[verse] = set()
pros[verse] = set()
#verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_train_gdfa_yoruba.pickle")
for eidtf_t in editf_others:
res = {}
print('going to align heb ')
if eidtf_t in heb_test_dataset.nodes_map:
verses = set(heb_test_dataset.nodes_map[editf_yor].keys()).intersection(heb_test_dataset.nodes_map[eidtf_t].keys())
res_ = eval_utils.alignment_test(epoch, heb_test_dataset.edge_index, editf_yor, eidtf_t, list(verses), heb_test_dataset.nodes_map,
dev, model, heb_test_dataset.x, pros_heb, surs_heb, heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa,
writer, gnn_dataset_heb.verse_info, calc_numbers=False)
clean_memory()
res.update(res_)
print('going to align train ')
verses = set(train_dataset.nodes_map[editf_yor].keys()).intersection(train_dataset.nodes_map[eidtf_t].keys())
res_ = eval_utils.alignment_test(epoch, train_dataset.edge_index, editf_yor, eidtf_t, list(verses - set(masked_verses)), train_dataset.nodes_map,
dev, model, train_dataset.x, pros, surs, verse_alignments_inter, verse_alignments_gdfa, writer, gnn_dataset_train.verse_info, calc_numbers=False)
clean_memory()
res.update(res_)
print('going to align blinker ')
verses = set(blinker_test_dataset.nodes_map[editf_yor].keys()).intersection(blinker_test_dataset.nodes_map[eidtf_t].keys())
res_ = eval_utils.alignment_test(epoch, blinker_test_dataset.edge_index, editf_yor, eidtf_t, list(verses), blinker_test_dataset.nodes_map,
dev, model, blinker_test_dataset.x, pros_blinker, surs_blinker, blinker_verse_alignments_inter, blinker_verse_alignments_gdfa,
writer, gnn_dataset_blinker.verse_info, calc_numbers=False)
clean_memory()
res.update(res_)
print('going to align grc ')
verses = set(grc_test_dataset.nodes_map[editf_yor].keys()).intersection(grc_test_dataset.nodes_map[eidtf_t].keys())
res_ = eval_utils.alignment_test(epoch, grc_test_dataset.edge_index, editf_yor, eidtf_t, list(verses), grc_test_dataset.nodes_map,
dev, model, grc_test_dataset.x, pros_grc, surs_grc, grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa,
writer, gnn_dataset_grc.verse_info, calc_numbers=False)
clean_memory()
res.update(res_)
print(f'going save alignments for {eidtf_t}')
torch.save(res, f'/mounts/work/ayyoob/results/gnn_align/yoruba/{eidtf_t}_alignments.bin')
# +
global model, decoder
#1/0
decoder = None
model = None
gc.collect()
with torch.no_grad():
torch.cuda.empty_cache()
# +
features = blinker_test_dataset.features[:]
#features_edge = train_dataset.features_edge[:]
from pprint import pprint
#print('indim',in_dim)
#features[-1].out_dim = 50
for i in features:
#if i.type==3:
# i.out_dim=4
print(vars(i))
sum(p.out_dim for p in features)
#train_dataset.features.pop()
#train_dataset.features[0] = afeatures.OneHotFeature(20, 83, 'editf')
#train_dataset.features[1] = afeatures.OneHotFeature(32, 150, 'position')
#train_dataset.features[2] = afeatures.FloatFeature(4, 'degree_centrality')
#train_dataset.features[3] = afeatures.FloatFeature(4, 'closeness_centrality')
#train_dataset.features[4] = afeatures.FloatFeature(4, 'betweenness_centrality')
#train_dataset.features[5] = afeatures.FloatFeature(4, 'load_centrality')
#train_dataset.features[6] = afeatures.FloatFeature(4, 'harmonic_centrality')
#train_dataset.features[7] = afeatures.OneHotFeature(32, 250, 'greedy_modularity_community')
##train_dataset.features.append(afeatures.MappingFeature(100, 'word'))
#torch.save(train_dataset, "/mounts/work/ayyoob/models/gnn/dataset_helfi_train_community_word.pickle")
#torch.save(train_dataset.features[-3], "./features.tmp")
# +
# count number of deleted edges by each community detection method
# from networkx.algorithms.community import greedy_modularity_communities, asyn_lpa_communities, label_propagation_communities, asyn_fluidc
# tmp_verses = [all_verses[2]]
# tmp_editions = small_editions[:10]
# tmp_dataset, tmp_nodes_map = create_dataset(tmp_verses, verse_alignments_inter, tmp_editions)
# tmp_g = pyg_utils.convert.to_networkx(tmp_dataset, to_undirected=True)
def count_deleted_edges(tmp_dataset, c):
deleted_edges = 0
for i in range(0, len(tmp_dataset.edge_index[0]), 2):
for comp in c:
if tmp_dataset.edge_index[0][i].item() in comp and tmp_dataset.edge_index[1][i].item() not in comp:
deleted_edges += 1
return deleted_edges
# print("eng token count: ", tmp_nodes_map['eng-x-bible-mixed'][tmp_verses[0]])
# print("original connected components",nx.number_connected_components(tmp_g))
# c = list(greedy_modularity_communities(tmp_g))
# print("new connected_components", len(c))
# print("deleted edges: ", count_deleted_edges(tmp_dataset, c))
# c = list(asyn_lpa_communities(tmp_g))
# print("asyn_lpa_communities number of components", len(c))
# print("deleted edges: ", count_deleted_edges(tmp_dataset, c))
# c = list(label_propagation_communities(tmp_g))
# print("label_propagation_communities number of components", len(c))
# print("deleted edges: ", count_deleted_edges(tmp_dataset, c))
# cents = nx.edge_betweenness_centrality(tmp_g)
# vals = sorted(list(cents.values()))
# print(vals[0], vals[10], vals[100], vals[1000], vals[2000], vals[3000], vals[10000])
# print(vals[-1], vals[-10], vals[-100], vals[-1000], vals[-2000], vals[-3000], vals[-10000])
# +
# measure different community detection algorithms
# from networkx.algorithms.community import greedy_modularity_communities, asyn_lpa_communities, label_propagation_communities, asyn_fluidc
# def remove_bad_community_edges(nodes_map, verses, edition_files, alignments):
# edges_tmp = [[],[]]
# res_edges = [[],[]]
# for verse in verses:
# utils.LOG.info(f"extracting edge features for {verse}")
# for i,editf1 in enumerate(edition_files):
# for j,editf2 in enumerate(edition_files[i+1:]):
# aligns = autils.get_aligns(editf1, editf2, alignments[verse])
# if aligns != None:
# for align in aligns:
# n1, node_count = node_nom(verse, editf1, align[0], 0, nodes_map, None, None)
# n2, node_count = node_nom(verse, editf2, align[1], 0, nodes_map, None, None)
# edges_tmp[0].extend([n1, n2])
# edges_tmp[1].extend([n2, n1])
# gnx = convert_to_netx(edges_tmp)
# print('detecting communities')
# coms = greedy_modularity_communities(gnx)
# print('finding good edges')
# for i in range(0, len(edges_tmp[0]), 2):
# for c in coms:
# if edges_tmp[0][i] in c and edges_tmp[0][i+1] in c:
# res_edges[0].extend([edges_tmp[0][i], edges_tmp[0][i+1]])
# res_edges[1].extend([edges_tmp[0][i+1], edges_tmp[0][i]])
# edges_tmp = [[],[]]
# print('to keep edges:', len(res_edges[0]))
# return torch.tensor(res_edges, dtype=torch.long)
# # old_edge_index = train_dataset.edge_index
# # new_edge_index = remove_bad_community_edges(train_dataset.nodes_map, train_verses, small_editions, verse_alignments_inter)
# # train_dataset.edge_index = new_edge_index
# # with open("./dataset_greedy_modularity_communities.pickle", 'rb') as inf:
# # train_dataset = pickle.load(inf)
# test_dataset = train_dataset
# print('orig edge count', old_edge_index.shape)
# print('new edge count', train_dataset.edge_index.shape)
# print("done")
# -
nodes_map = train_dataset.nodes_map
bad_edition_files = []
for edit in nodes_map:
bad_count = 0
for verse in nodes_map[edit]:
if len(nodes_map[edit][verse].keys()) < 2:
bad_count += 1
if bad_count > 1:
bad_edition_files.append(edit)
break
print(bad_edition_files)
# +
all_japanese_nodes = set()
nodes_map = train_dataset.nodes_map
for bad_editionf in bad_edition_files:
for verse in nodes_map[bad_editionf]:
for item in nodes_map[bad_editionf][verse].items():
all_japanese_nodes.add(item[1])
print(" all japansese nodes: ", len(all_japanese_nodes))
edge_index = train_dataset.edge_index.to('cpu')
remaining_edges_index = []
for i in tqdm(range(0, edge_index.shape[1], 2)):
if edge_index[0, i].item() not in all_japanese_nodes and edge_index[0, i+1].item() not in all_japanese_nodes:
remaining_edges_index.extend([i, i+1])
print('original total edges count', edge_index.shape)
print('remaining edge count', len(remaining_edges_index))
train_dataset.edge_index = edge_index[:, remaining_edges_index]
train_dataset.edge_index.shape
# +
print("################# you have to run first three cells first ###################")
from networkx.algorithms.community import greedy_modularity_communities, asyn_lpa_communities, label_propagation_communities, asyn_fluidc
from my_utils import align_utils as autils, utils
from torch_geometric.data import Data
def node_nom(verse, editf, tok_nom, node_count, nodes_map, x=None, edit_fs=None, features = None):
utils.setup_dict_entry(nodes_map, editf, {})
utils.setup_dict_entry(nodes_map[editf], verse, {})
if not tok_nom in nodes_map[editf][verse]:
nodes_map[editf][verse][tok_nom] = node_count
x.append([edit_fs.index(editf), tok_nom]) # TODO we should have better representation
node_count += 1
return nodes_map[editf][verse][tok_nom], node_count
def create_dataset(verse, alignments, edition_files):
node_count = 0
edges = [[],[]]
x = []
nodes_map = {}
features = []
for i,editf1 in enumerate(edition_files):
for j,editf2 in enumerate(edition_files[i+1:]):
aligns = autils.get_aligns(editf1, editf2, alignments[verse])
if aligns != None:
for align in aligns:
n1, node_count = node_nom(verse, editf1, align[0], node_count, nodes_map, x, edition_files, features)
n2, node_count = node_nom(verse, editf2, align[1], node_count, nodes_map, x, edition_files, features)
edges[0].extend([n1, n2])
edges[1].extend([n2, n1])
edge_index = torch.tensor(edges, dtype=torch.long)
x = torch.tensor(x, dtype=torch.float)
res = Data(x=x, edge_index=edge_index)
res.nodes_map = nodes_map
res.features = features
return res, nodes_map
# +
blinker_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_inter.pickle")
blinker_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_blinker_gdfa.pickle")
heb_test_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_inter.pickle")
heb_test_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_heb_gdfa.pickle")
grc_test_verse_alignments_inter = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_inter.pickle")
grc_test_verse_alignments_gdfa = torch.load("/mounts/work/ayyoob/models/gnn/pruned_alignments_grc_gdfa.pickle")
editions_file = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi_lang_list.txt"
editions, langs = autils.load_simalign_editions(editions_file)
current_editions = [editions[lang] for lang in langs]
if 'jpn-x-bible-newworld' in current_editions[:]:
current_editions.remove('jpn-x-bible-newworld')
if 'grc-x-bible-unaccented' in current_editions[:]:
current_editions.remove('grc-x-bible-unaccented')
test_gold_eng_fra = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/eng_fra_pbc/eng-fra.gold"
pros_blinker, surs_blinker = autils.load_gold(test_gold_eng_fra)
test_gold_helfi_heb = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-heb-fin-gold-alignments_test.txt"
pros_heb, surs_heb = autils.load_gold(test_gold_helfi_heb)
test_gold_grc = "/mounts/Users/student/ayyoob/Dokumente/code/pbc_utils/data/helfi/splits/helfi-grc-fin-gold-alignments_test.txt"
pros_grc, surs_grc = autils.load_gold(test_gold_grc)
# +
def get_community_edges(c, verse):
res = []
edges = []
for n1 in all_nodes_map[editf1][verse].items():
for n2 in all_nodes_map[editf2][verse].items():
for com in c:
if n1[1] in com and n2[1] in com:
res.append((n1[0], n2[0]))
edges.append((n1[1], n2[1]))
return res, edges
def intersect(e1, e2):
res = set()
for item in e1:
if item in e2:
res.add(item)
return res
datasets = {'blinker' : [blinker_verse_alignments_inter, blinker_verse_alignments_gdfa, 'eng-x-bible-mixed', 'fra-x-bible-louissegond', pros_blinker, surs_blinker],
'heb': [heb_test_verse_alignments_inter, heb_test_verse_alignments_gdfa, 'fin-x-bible-helfi', 'heb-x-bible-helfi', pros_heb, surs_heb],
'grc': [grc_test_verse_alignments_inter, grc_test_verse_alignments_gdfa, 'fin-x-bible-helfi', 'grc-x-bible-helfi', pros_grc, surs_grc]}
for dataset in datasets:
print('community for ', dataset)
test_verses = list(datasets[dataset][0].keys())[:]
verse_alignments_inter = datasets[dataset][0]
verse_alignments_gdfa = datasets[dataset][1]
editf1, editf2 = datasets[dataset][2], datasets[dataset][3]
pros, surs = datasets[dataset][4], datasets[dataset][5]
measures = {}
measures['intersection']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
measures['gdfa']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
measures['c1_all']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
measures['c1_inter']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
measures['c3_all']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
measures['c3_inter']= {"p_hit_count": 0, "s_hit_count": 0, "total_hit_count": 0, "gold_s_hit_count": 0, "prec": 0, "rec": 0, "f1": 0, "aer": 0}
no_c_sum = 0
c1_sum = 0
c3_sum = 0
nodes = 0
total_edges = 0
removed_edges1 = 0
removed_edges2 = 0
for verse in test_verses:
inter_edges = autils.get_aligns(editf1, editf2, verse_alignments_inter[verse])
all_dataset, all_nodes_map = create_dataset(verse, verse_alignments_inter, current_editions)
nodes += all_dataset.x.shape[0] / len(all_nodes_map)
g = pyg_utils.convert.to_networkx(all_dataset, to_undirected=True)
c1 = list(greedy_modularity_communities(g))
c3 = list(label_propagation_communities(g))
c1_edges, graph_edges1 = get_community_edges(c1, verse)
c3_edges, graph_edges2 = get_community_edges(c3, verse)
no_c_sum += nx.number_connected_components(g)
c1_sum += len(c1)
c3_sum += len(c3)
total_edges += len(g.edges)
removed_edges1 += count_deleted_edges(all_dataset, c1)
removed_edges2 += count_deleted_edges(all_dataset, c3)
print(1, removed_edges1/ total_edges)
print(2, removed_edges2/ total_edges)
#autils.calc_and_update_alignment_score(inter_edges, pros[verse], surs[verse], measures['intersection'])
#autils.calc_and_update_alignment_score(autils.get_aligns(editf1, editf2, verse_alignments_gdfa[verse]), pros[verse], surs[verse], measures['gdfa'])
#autils.calc_and_update_alignment_score(c1_edges, pros[verse], surs[verse], measures['c1_all'])
#autils.calc_and_update_alignment_score(c3_edges, pros[verse], surs[verse], measures['c3_all'])
#autils.calc_and_update_alignment_score(intersect(c1_edges, inter_edges), pros[verse], surs[verse], measures['c1_inter'])
#autils.calc_and_update_alignment_score(intersect(c3_edges, inter_edges), pros[verse], surs[verse], measures['c3_inter'])
#print('avg sentence len', nodes/len(test_verses))
#print('communities counts:' )
#print('\t\t\ttotal\t\t average')
#print(f'original:\t{no_c_sum}\t\t{no_c_sum/len(test_verses)}')
#print(f'original:\t{c1_sum}\t\t{c1_sum/len(test_verses)}')
#print(f'original:\t{c3_sum}\t\t{c3_sum/len(test_verses)}')
#for item in measures:
# print(item, measures[item])
print('gmc', removed_edges1/total_edges)
print('lpc', removed_edges2/total_edges)
|
app/gnn_multalign_full_dataset_word_community.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Car Decor Sales Forecasting - LeatherSeatCovers
# + active=""
# Summary of the Code below :
# 1. Establish MySQL Connection and load data
# 2. Data Preprocessing (Typecasting and Resampling daily data to monthly)
# 3. Visualizing Rolling statistics to observe variation in mean and standard deviation for selected Feature.
# 4. Checking for Data Stationarity using Augmented Dickey-Fuller Test for the feature
# 5. Hyper-parameter Tuning using ACF and PACF plots for building SARIMA Model (this process takes little time)
# 6. Models
# (a) SARIMA
# (b) HoltWinters Exponential Smoothing with Additive Seasonality & Additive Trend
# (c) FB Prophet
# (d) Auto Time Series
# 7. Evaluation of the Models
# 8. Saving the model with least MAPE
# 9. Loading saved model (.pkl) to predict sales for 12 months.
# 10. Closing MySQL Connection
# -
# ###### Importing Libraries
# +
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# %matplotlib inline
from sklearn.metrics import mean_squared_error
from math import sqrt
# Connecting Python to MySQL for fetching data
import mysql.connector
import warnings
from statsmodels.tools.sm_exceptions import ConvergenceWarning
warnings.simplefilter('ignore', ConvergenceWarning)
# -
# ###### MySQL Connection to fetch data
# +
try:
connection = mysql.connector.connect(host='localhost',
database='car_decors',
user='root',
password='***********')
sql_select_Query = "SELECT * FROM decorsales"
cursor = connection.cursor()
cursor.execute(sql_select_Query)
columns = len(cursor.description)
columns = [i[0] for i in cursor.description]
print(columns)
# get all records
records = cursor.fetchall()
print("Total number of rows in table: ", cursor.rowcount)
except mysql.connector.Error as e:
print("Error reading data from MySQL table", e)
# -
# ### Data Cleaning and Exploratory Data Analysis
# ###### Converting fetched records to Pandas dataframe
records = np.array(records)
records = records[:,0:25]
decor_sales=pd.DataFrame(records,columns=columns)
# ###### Type Casting Date and other features
decor_sales.dtypes
decor_sales.Date = pd.to_datetime(decor_sales.Date)
decor_sales.iloc[:,1:] = decor_sales.iloc[:,1:].astype("int32")
decor_sales.dtypes
# ###### Creating Subset of Decor Sales Dataset and resampling Monthly Time Series
df = decor_sales
df = df.set_index('Date')
df = df.resample("MS").sum()
# + active=""
# Note : Time period options when resampling a time series # MS - Monthly ; W - Weekly ; QS - Quarterly ; YS - Yearly
# -
# ###### Data Visualization
plt.rc("figure", figsize=(16,8))
sns.set_style('darkgrid')
# ###### Rolling statistics to observe variation in mean and standard deviation.
timeseries = df ['LeatherSeatCovers']
timeseries.rolling(12).mean().plot(label='12 Month Rolling Mean', marker='.')
timeseries.rolling(12).std().plot(label='12 Month Rolling Std', marker='.')
timeseries.plot(marker='.')
plt.title('Rolling Statistics to observe variation in Mean and Standard Deviation', fontsize = 18, fontweight = 'bold')
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend()
# + active=""
# # The plot shows, there is nearly a constant mean and standard deviation except noise in Qtr 2 - 2020 (Lockdown period)
# -
# ###### Checking Seasonalty and Trend components for the feature
from statsmodels.tsa.seasonal import seasonal_decompose
add = seasonal_decompose(df["LeatherSeatCovers"],model="additive",period=12)
add.plot();
# + active=""
# # Decomposition plot shows constant trend with noise in Qtr 2 - 2020 and seasonality is additive in nature.
# # The data is seasonal and follows constant trend.
# # Also, the average value or the mean of the residuals seem to be zero which holds our assumption.
# -
# ##### Checking for Data Stationarity using Augmented Dickey-Fuller Test
# +
from statsmodels.tsa.stattools import adfuller
def check_adf(time_series):
test_result = adfuller(df['LeatherSeatCovers'])
print ('ADF Test:')
labels = ['ADF Statistic','p-value','No. of Lags Used','Number of Observations Used']
for value,label in zip(test_result,labels):
print (label+': '+str(value)+str("\n"))
if test_result [1] <= 0.05:
print ("Reject null hypothesis; Data is stationary")
else:
print ("Fail to reject H0; Data is non-stationary")
# + active=""
# If the data is non-stationary so we need to apply differencing to make our data stationary.
# df ['LeatherSeatCovers'] = df ['LeatherSeatCovers'] - df ['LeatherSeatCovers']. shift (1)
# adf_check(df['LeatherSeatCovers'].dropna())
# If again data is non-stationary we need to differencing with subsequent shifts.
# -
check_adf(df['LeatherSeatCovers'])
# # Adfuller test Results for all variables
# +
from statsmodels.tsa.stattools import adfuller
def adfuller_parameter(x):
P = []
columns = []
used_lag = []
for i in x.columns:
test_stats,p,used_lags,nobs,critical_value,ic_best = adfuller(x[i])
columns.append(i)
P.append(p)
used_lag.append(used_lags)
return pd.DataFrame({"COLUMNS":columns,"P_VALUE":P,"MAX_USED_LAG":used_lag})
adfuller_parameter(df)
# + active=""
# By looking at adfuller test result we conclude that we need differencing by 0 shifts to make our data stationary for android headunits.
# -
# ##### Hyper-parameter Tuning # Autocorrelation Function (ACF) and Partial Autocorrelation Function (PACF) plots
# + active=""
# # By looking at ACF pot and PACF plot we decide the value p(Auto regressive) and q(Moving average)
# # p = sudden shuts off in pacf plot.
# # q = Exponential drop in acf plot.
# # d = degree of differencing/shift by adfuller test
#
# #Auto Regressive (p)
# # Identification of an AR model is often best done with the PACF.
# # For an AR model, the theoretical PACF “shuts off” past the order of the model.
# # The phrase “shuts off” means that in theory the partial autocorrelations are equal to 0 beyond that point.
# # Put another way, the number of non-zero partial autocorrelations gives the order of the AR model.
# # By the “order of the model” we mean the most extreme lag of x that is used as a predictor.
#
# # Integration (d)
# # Integration paramter is choosen through how much value you have differentiated from original
# # For a stationary data its either be 0 or 1
#
# # Moving Average (q)
# # the theoretical PACF does not shut off, but instead tapers or exponetially decrease toward 0 in some manner.
# # A clearer pattern for an MA model is in the ACF.
# # The ACF will have non-zero autocorrelations only at lags involved in the model.
# +
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
import statsmodels.api as sm
fig, ax = plt.subplots(1,2, figsize=(15,5))
sm.graphics.tsa.plot_acf(df["LeatherSeatCovers"], lags=12, title = 'ACF Plot', ax=ax[0])
sm.graphics.tsa.plot_pacf(df["LeatherSeatCovers"], lags=12, title = 'PACF Plot',ax=ax[1])
plt.show()
# -
# ### Model Building - SARIMA Model ( Seasonal ARIMA Model )
# ###### Train Test Split
# +
train_df = df["LeatherSeatCovers"].iloc[0:int(len(df)*.95)] #train model with approx 95% data
test_df = df["LeatherSeatCovers"].iloc[int(len(train_df)):] #test model with 5% data
print("Train_df : ",len(train_df))
print("Test_df : ",len(test_df))
# -
# ###### User Defined Function to calculate the MAPE value
def mape(y_true, y_pred):
y_true, y_pred = np.array(y_true), np.array(y_pred)
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
# ###### Automated Hyperparameter tuning
# +
import itertools as i
p = range(0,3)
d = range(0,2)
q = range(0,3)
pdq_combo = list(i.product(p,d,q)) #this will all combination of p,d,q throgh a tuple
error = []
aic_sarima = []
order_arima = []
order_sarima = []
seasonality = 12
for pdq in pdq_combo:
for PDQ in pdq_combo:
try:
SEASONAL_ORDER = list(PDQ)
SEASONAL_ORDER.append(seasonality)
model = sm.tsa.SARIMAX(train_df,order=(pdq),seasonal_order=tuple(SEASONAL_ORDER))
result = model.fit(disp=0)
pred = result.predict(start=len(train_df),end=len(df)-1)
eror = mape(test_df,pred)
aic_sarima.append(result.aic)
order_arima.append(pdq)
order_sarima.append(tuple(SEASONAL_ORDER))
error.append(eror)
except:
continue
# -
# Creating a dataframe of seasonality orders and errors
df_error = pd.DataFrame({"arima_order":order_arima,"sarima_order": order_sarima,"error":error,"aic":aic_sarima})
df_error = df_error.sort_values(by="error",ascending = True)
df_error.reset_index(inplace=True,drop=True)
## best parameter selection
p_d_q = df_error.iloc[0,0] #choosing best parameter for arima order
P_D_Q = df_error.iloc[0,1] #choosing best parameter for seasonal order
## best parameter selection
print("Best p_d_q parameter : ", p_d_q)
print("Best P_D_Q parameter : ", P_D_Q)
# ###### Model with best parameter
sarima_model = sm.tsa.SARIMAX(train_df, order=(p_d_q), seasonal_order=(P_D_Q))
sarima_results = sarima_model.fit(disp = 0)
sarima_pred = sarima_results.predict(start=test_df.index[0],end=test_df.index[-1])
sarima_pred_large = sarima_results.predict(start=75,end=86,dynamic=True)
print(sarima_results.summary())
sarima_diagnostics = sarima_results.plot_diagnostics(figsize=(16,8))
# + active=""
# # Insights from these diagnostic plot :
# # 1.The top left plot shows the residuals over time.
# # The plot shows our residuals are fluctuating around mean 0 there is uniform deviation over time
# # except some noise in second quarter of 2021 due to lockdown imposed by government with effect of COVID-19 pandemic.
#
# # 2.In the top-right plot,
# # We see that the KDE follows closely with the N(0,1) line to indicate that the residuals are normally distributed.
# # This line is the standard notation for a normal distribution with a mean of 0 and a standard deviation of 1.
# # In our plot residuals are normally distributed.
#
# # 3.In the bottom left qq-plot,
# # We see the ordered distribution of residuals(blue dots) following the linear trend(red line)
# # of the samples taken from a standard normal distribution with N(0, 1).
#
# # 4.The autocorrelation visual (called a “correlogram”) on the bottom right shows that-
# # The time series residuals have a low correlation with the lagged versions of itself
# # (that is, the majority of dots fall into the blue shaded area).
# -
# Predicted values
# Point estimation
sarima_prediction = sarima_results.get_prediction(start = test_df.index[0], end = test_df.index[-1], dynamic = True, full_results = True)
sarima_point_estimation = sarima_prediction.predicted_mean
sarima_point_estimation
#Checking MAPE
mape(test_df, sarima_point_estimation)
# At 95% confidence interval
sarima_pred_range = sarima_prediction.conf_int(alpha = 0.05)
sarima_pred_range
# Ploting Sarima Prediction
plt.plot(train_df,color="g",label="Train Data", marker='.')
plt.plot(test_df,color="b",label="Test Data", marker='.')
plt.plot(sarima_point_estimation,color="r",label="Forecast (Test Data)", marker='.')
plt.figtext(0.13, 0.15, '\nMAPE : {} \nSARIMA : {},{} \nAIC : {}'.format(mape(test_df, sarima_point_estimation), p_d_q, P_D_Q, sarima_results.aic, fontsize = 11))
plt.fill_between(sarima_pred_range.index,sarima_pred_range.iloc[:,0],sarima_pred_range.iloc[:,1],color='b',alpha=.2)
plt.legend(loc="upper right")
# + active=""
# ############################################################################################################################
# -
# ### Holt Winters Exponential Smoothing with Additive Seasonality and Additive Trend
# +
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.holtwinters import ExponentialSmoothing #
hwe_model_add_add = ExponentialSmoothing(train_df, seasonal ="add", trend = "add", seasonal_periods = 12).fit()
pred_hwe_add_add = hwe_model_add_add.predict(start = test_df.index[0], end = test_df.index[-1])
# -
pred_hwe_add_add
# ###### Plotting Holt Winters Model
plt.plot(train_df,color="g",label="Train Data")
plt.plot(test_df,color="b",label="Test Data")
plt.plot(pred_hwe_add_add,color="r",label="Forecast (Test Data)")
plt.suptitle('Model : Holt Winters', fontsize = 12, fontweight = 'bold')
plt.title('Car Decors - ANDROID HEAD UNITS', fontsize = 18, fontweight = 'bold')
plt.figtext(0.13, 0.14, '\nMAPE : {} \nAIC : {}'.format(mape(test_df, pred_hwe_add_add), hwe_model_add_add.aic))
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend(loc="best")
mape(test_df, pred_hwe_add_add)
# + active=""
# ############################################################################################################################
# -
# ### FB Prophet Model
# +
# Loading Libraries
from fbprophet import Prophet
from fbprophet.plot import plot_plotly
df1 = decor_sales
df1 = df1.set_index('Date')
df1 = df1.resample("MS").sum()
df1.reset_index(inplace=True)
# +
train_df1 = df1[["Date","LeatherSeatCovers"]].iloc[0:int(len(df1)*.95)] #train model with approx 95% data
test_df1 = df1[["Date","LeatherSeatCovers"]].iloc[int(len(train_df1)):] #test model with 5% data
print("Train : ",len(train_df1))
print("Test : ",len(test_df1))
# -
train_df1.columns = ["ds","y"]
test_df1.columns = ["ds","y"]
# Fitting the Model
prophet_model = Prophet().fit(train_df1)
# Define the period for which we want a prediction
future = list()
for i in range(1, 5):
date = '2021-%02d' % i
future.append([date])
future = pd.DataFrame(future)
future.columns = ['ds']
future['ds']= pd.to_datetime(future['ds'])
future
forecast = prophet_model.predict(future)
print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']])
test_df1=test_df1.set_index("ds")
train_df1 = train_df1.set_index("ds")
forecast=forecast.set_index("ds")
plt.style.use("ggplot")
plt.plot(train_df1['y'],color="r",label="Train Data")
plt.plot(test_df1['y'],color="b",label="Test Data")
plt.plot(forecast["yhat"],color="g",label="Forecast (Test Data)")
plt.grid( linestyle='-', linewidth=2)
plt.legend(loc="best")
# MAPE
mape(test_df1['y'], forecast['yhat'])
#RMSE
sqrt(mean_squared_error(test_df1['y'], forecast['yhat'].tail(4)))
# + active=""
# ############################################################################################################################
# -
# ### Auto Time Series Model
from auto_ts import auto_timeseries
train_df2 = train_df1
test_df2 = test_df1
ts_model = auto_timeseries( score_type='rmse', time_interval='MS', non_seasonal_pdq=(12,12,12), seasonality=True, seasonal_period=12, model_type="best", verbose=2)
ts_model.fit(traindata= train_df2, ts_column="ds", target="y")
ts_model.get_leaderboard()
ts_model.plot_cv_scores()
future_predictions = ts_model.predict(test_df2, model='best')
future_predictions
# define the period for which we want a prediction
ts_future = list()
for i in range(1, 5):
date = '2021-%02d' % i
ts_future.append([date])
ts_future = pd.DataFrame(ts_future)
ts_future.columns = ['ds']
ts_future['ds']= pd.to_datetime(ts_future['ds'])
ts_model.predict(ts_future)
mape(test_df2["y"],future_predictions["yhat"])
# + active=""
# ############################################################################################################################
# -
# ### Models Evaluation
from sklearn.metrics import mean_squared_error as mse
print("\nSARIMA Trend : ", p_d_q)
print("SARIMA Seasonal Order : ", P_D_Q)
print("SARIMA AIC : ", sarima_results.aic)
print("SARIMA RMSE : ", np.sqrt(mse(test_df,sarima_point_estimation)))
print("SARIMA MAPE : ", mape(test_df, sarima_point_estimation))
print("\nHolt Winters AIC : ", hwe_model_add_add.aic)
print("Holt Winters RMSE : ", np.sqrt(mse(test_df,pred_hwe_add_add)))
print("Holt Winters MAPE : ", mape(test_df, pred_hwe_add_add))
print("\nFB Prophet RMSE : ", sqrt(mean_squared_error(test_df1['y'], forecast['yhat'])))
print("FB Prophet MAPE : ", mape(test_df1['y'], forecast['yhat']))
print("\nAuto Time Series: \n ", ts_model.get_leaderboard())
print("Auto Time Series MAPE : ", mape(test_df2["y"],future_predictions["yhat"]))
# +
sarima = mape(test_df, sarima_point_estimation)
hwinters = mape(test_df, pred_hwe_add_add)
fbprophet = mape(test_df1['y'], forecast['yhat'])
autots = mape(test_df2["y"],future_predictions["yhat"])
mape_data = {'models':['SARIMA','HOLTWINTERS','FB_PROPHET','AUTO_TS'], 'name':['sarima_model', 'hwe_model_add_add','prophet_model','ts_model'],'mape':[sarima, hwinters, fbprophet, autots]}
mape_error = pd.DataFrame(mape_data)
mape_error = mape_error.sort_values(by="mape",ascending = True)
mape_error.reset_index(inplace=True,drop=True)
#best_model = mape_error.iloc[0,0]
print('\033[1m'+"Best Model with lowest MAPE : ", mape_error.iloc[0,0] + " ( " + mape_error.iloc[0,1] + " ) " + '\033[0m')
print("\nMAPE ERRORS :\n\n", mape_error)
# + active=""
# ############################################################################################################################
# -
# ##### Saving Model
import pickle
filename = 'sarima_LeatherSeatCover.pkl'
pickle.dump(sarima_model, open(filename, 'wb'))
# ###### Testing saved Model for prediction
# +
####### Model summary and diagnstics plot #######
with open(filename, "rb") as file:
load_model = pickle.load(file)
result = load_model.fit()
#print(result.summary())
#diagnostics = result.plot_diagnostics(figsize=(16,8))
# +
pred = result.get_prediction(start = 76, end = 87, dynamic = False)
# Point estimation
prediction = pred.predicted_mean
prediction = round(prediction)
prediction
# -
# Ploting final Sarima Prediction
plt.plot(df['LeatherSeatCovers'],color="g",label="Actual", marker='.')
plt.plot(prediction,color="r",label="Forecast", marker='.')
plt.suptitle('Model : SARIMA', fontsize = 12, fontweight = 'bold')
plt.title('Car Decors - Leather Seat Covers', fontsize = 18, fontweight = 'bold')
plt.figtext(0.13, 0.14, '\nMAPE : {} \nAIC : {}'.format(mape(test_df, sarima_point_estimation), sarima_results.aic))
plt.xlabel('Year', fontsize = 14)
plt.ylabel('Sales (Number of Units)', fontsize = 14)
plt.legend(loc="best")
# ### Closing connection to MySQL and clearing variables from memory.
# +
#if connection.is_connected():
# connection.close()
# cursor.close()
# print("MySQL connection is closed")
# Clear all variables from memory
#globals().clear()
#####################################################################
|
Model Buidling/Models_LeatherSeatCovers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.3 64-bit (''msc_project'': conda)'
# language: python
# name: python38364bitmscprojectconda1b7ed98db8104d919ac5b59276832f86
# ---
# # Notebook_14: Rewrite for Linear Model
#
# Over the course of this project, the primary focus has changed from predictive accuracy to real world interpretability. It is clear from the initial model experimentation than Linear Models still have good accuracy on this data, and the additional interpretability they provide will be very useful for the linking to theory, a key component of the project.
# +
import altair as alt
import altair_data_server
from altair_saver import save
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# %matplotlib inline
sns.set(style='white', context='notebook')
# %config InlineBackend.figure_format = 'retina'
alt.data_transformers.enable('data_server')
# -
from sklearn.linear_model import LinearRegression, RidgeCV
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from src.config import FINAL_DATA, FIGURES
from src.models.model_metrics import score_model
al_df = pd.read_csv(FINAL_DATA/'al_data_final.csv')
abs_df = pd.read_csv(FINAL_DATA/'abs_data_final.csv')
al_df
abs_df
# ## Training Linear Models
# Let's just start with the aluminium data for now
# +
X = al_df.drop('tc_act', axis = 1)
y = al_df['tc_act']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, shuffle = True)
# +
al_reg = LinearRegression()
al_reg.fit(X_train, y_train)
# + tags=[]
score_model(al_reg, X_train, y_train)
# -
al_reg.coef_
feats = ['x', 'temp', 'nf_hz', 'amp_mm']
act_coefs = list(al_reg.coef_)
# + tags=[]
X = abs_df.drop('tc_act', axis = 1)
y = abs_df['tc_act']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, shuffle = True)
abs_nonscaled_reg = LinearRegression()
abs_nonscaled_reg.fit(X, y)
score_model(abs_nonscaled_reg, X_train, y_train)
# -
abs_nonscaled_reg.coef_
# +
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# + tags=[]
scaled_al_reg = RidgeCV()
scaled_al_reg.fit(X_train_scaled, y_train)
score_model(scaled_al_reg, X_train_scaled, y_train)
# -
scaled_al_reg.coef_
# Getting scaled coefs because it's a good proxy for feature_importance
scaled_coefs = list(scaled_al_reg.coef_)
scaled_coefs
coef_dict = {feat: abs(coef) for (feat, coef) in zip(feats, scaled_coefs)}
coef_dict
df_dict = {'features': ['Crack Position', 'Temperature', 'Natural Frequency', 'Amplitude'], 'coefficients': [abs(coef) for coef in scaled_coefs]}
df_dict
coef_df = pd.DataFrame(data = df_dict)
coef_df
alt.Chart(coef_df).mark_bar().encode(
x = alt.X('features:N', title = 'Features', sort = '-y', axis = alt.Axis(labelAngle=-45)),
y = alt.Y('coefficients:Q', title = 'Absolute Magnitude of Coefficient')
).properties(
width = 600,
height = 400,
title = "Ridge Regression Feature Importance (Aluminium)"
)
# ## Let's add the ABS data
# + tags=[]
X_abs = abs_df.drop('tc_act', axis = 1)
y_abs = abs_df['tc_act']
X_train_abs, X_test_abs, y_train_abs, y_test_abs = train_test_split(X_abs, y_abs, test_size = 0.2, shuffle = True)
abs_reg = RidgeCV()
abs_scaler = StandardScaler()
X_train_abs_scaled = abs_scaler.fit_transform(X_train_abs)
X_test_abs_scaled = abs_scaler.transform(X_test_abs)
abs_reg.fit(X_train_abs_scaled, y_train_abs)
score_model(abs_reg, X_train_abs_scaled, y_train_abs)
# -
abs_dict = {'features': ['Crack Position', 'Temperature', 'Natural Frequency', 'Amplitude'], 'coefficients': [abs(coef) for coef in list(abs_reg.coef_)]}
abs_df = pd.DataFrame(data = abs_dict)
abs_df
coef_df
coef_df['Material'] = ['Aluminium', 'Aluminium', 'Aluminium', 'Aluminium']
abs_df['Material'] = ['ABS', 'ABS', 'ABS', 'ABS']
coef_df
full_df = coef_df.append(abs_df, ignore_index = True)
full_df
alt.Chart(full_df).mark_bar(opacity = 0.6).encode(
x = alt.X('features:N', title = 'Features', sort = '-y', axis = alt.Axis(labelAngle=-45)),
y = alt.Y('coefficients:Q', title = 'Relative Importance', stack = None),
color = alt.Color('Material:N', title = 'Material')
).properties(
width = 600,
height = 400,
title = "Relative Importance in Crack Depth Prediction"
)
# +
fig, ax = plt.subplots(figsize = (12, 6), dpi = 300)
sns.barplot(x = 'features', y = 'coefficients', data = full_df, hue = 'Material', ax = ax, order = ['Natural Frequency', 'Temperature', 'Amplitude', 'Crack Position'])
sns.despine()
ax.set_title('Relative Importance in Crack Depth Prediction')
ax.set_ylabel('Relative Importance')
ax.set_xlabel('Features')
plt.savefig(FIGURES.joinpath("relative_importance_in_crack_depth_prediction.png"))
# -
# ## Recreating some of the Original Plots for ABS
al_df = pd.read_csv(FINAL_DATA/'al_data_final.csv')
abs_df = pd.read_csv(FINAL_DATA/'abs_data_final.csv')
abs_df
al_df
# Combine the two for ease of analysis
abs_df['material'] = 'ABS'
al_df['material'] = 'Aluminium'
abs_df
both_df = pd.concat([al_df, abs_df])
both_df['temp'].replace({23: 22}, inplace = True)
# + tags=[]
fig1 = alt.Chart(both_df).mark_circle(opacity = 0.5).encode(
x = alt.X('nf_hz:Q', title = 'Natural Frequency (Hz)'),
y = alt.Y('amp_mm:Q', title = 'Amplitude (mm)', scale = alt.Scale(domain=(0, 22))),
color = alt.Color('material:N', title = 'Material'),
size = alt.Size('temp:O', title = 'Temperature (Celsius)')
).properties(
width = 800,
height = 400,
title = 'Dynamic Response by Material'
).configure_axis(labelFontSize = 14).configure_legend(labelFontSize = 14)
save(fig1, fp = str(FIGURES/'dynamic_response_by_material.png'), fmt = 'png', method = 'selenium', scale_factor = 6.0)
# -
fig1
# +
fig2 = alt.Chart(both_df).mark_circle(opacity = 0.5).encode(
x = alt.X('tc_act:Q', title = 'Measured Crack Depth (mm)'),
y = alt.Y('nf_hz:Q', title = 'Natural Frequency (Hz)'),
color = alt.Color('material:N', title = 'Material'),
size = alt.Size('temp:O', title = 'Temperature (C)')
).properties(
width = 800,
height = 400,
title = "Frequency Response to Crack Depth"
).configure_axis(labelFontSize = 14).configure_legend(labelFontSize = 14)
save(fig2, fp = str(FIGURES/'frequency_response_to_crack_depth.png'), fmt = 'png', method = 'selenium', scale_factor = 6.0)
# -
fig2
# +
fig3 = alt.Chart(both_df).mark_circle(opacity = 0.5).encode(
x = alt.X('tc_act:Q', title = 'Measured Crack Depth (mm)'),
y = alt.Y('amp_mm:Q', title = 'Amplitude (mm)'),
color = alt.Color('material:N', title = 'Material'),
size = alt.Size('temp:O', title = 'Temperature (C)')
).properties(
width = 800,
height = 400,
title = "Amplitude Response to Crack Depth"
).configure_axis(labelFontSize = 14).configure_legend(labelFontSize = 14)
save(fig3, fp = str(FIGURES/'amplitude_response_to_crack_depth.png'), fmt = 'png', method = 'selenium', scale_factor = 6.0)
# -
fig3
# ### Raw Values of the Coefficients
scaled_al_reg.coef_
abs_reg.coef_
al_coef_dict = {'features': ['Crack Position', 'Temperature', 'Natural Frequency', 'Amplitude'], 'coefficients': [coef for coef in list(scaled_al_reg.coef_)]}
al_coef_dict
al_coef_df = pd.DataFrame(al_coef_dict)
al_coef_df
abs_coef_dict = {'features': ['Crack Position', 'Temperature', 'Natural Frequency', 'Amplitude'], 'coefficients': [coef for coef in list(abs_reg.coef_)]}
abs_coef_df = pd.DataFrame(abs_coef_dict)
abs_coef_df
al_coef_df['Material'] = ['Aluminium', 'Aluminium', 'Aluminium', 'Aluminium']
abs_coef_df['Material'] = ['ABS', 'ABS', 'ABS', 'ABS']
all_coefs = pd.concat([al_coef_df, abs_coef_df], ignore_index = True)
all_coefs
all_coefs['coefficients_rounded'] = np.round(all_coefs['coefficients'], 3)
all_coefs
alt.Chart(all_coefs).mark_bar().encode(
x = alt.X('features:N', title = 'Feature'),
y = alt.Y('coefficients:Q', title = 'Model Coefficient'),
color = alt.Color('Material:N', title = 'Material'),
).properties(
width = 800,
height = 400,
title = 'Model Coefficients'
)
# +
fig, ax = plt.subplots(figsize = (12, 6), dpi = 300)
sns.barplot(x = 'features', y = 'coefficients', data = all_coefs, hue = 'Material', ax = ax, order = ['Natural Frequency', 'Temperature', 'Amplitude', 'Crack Position'])
ax.set_title('Model Coefficients')
ax.set_ylabel('Coefficient Value')
ax.set_xlabel('Features')
sns.despine()
plt.savefig(FIGURES.joinpath("model_coefficients_seaborn.png"))
# -
|
Notebooks/Notebook_14 Linear Rewrite.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#
# +
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# -
# get historical daily price
symbol = 'ZM'
tick = yf.Ticker(symbol)
history = tick.history(period="max")
# +
df=pd.DataFrame()
df['price'] = history.Close
df['pct_chg'] = df.price.pct_change()
# log return computation
df['log_ret'] = np.log(df.price) - np.log(df.price.shift(1))
df['ret_mean'] = df.log_ret.rolling(21).mean()
# https://en.wikipedia.org/wiki/Volatility_(finance) "annualized vol" but looking back only 21 days
df['hist_volatility'] = df.log_ret.rolling(21).std()*np.sqrt(252)*100
df = df.dropna()
# -
the_vol_mean = df.hist_volatility.mean()
the_vol_std = df.hist_volatility.std()
print(f'mean of hist_volatility {the_vol_mean:1.5f}')
the_ret_mean = df.ret_mean.mean()
the_ret_tsd = df.ret_mean.std()
print(f'mean of rolling mean {the_ret_mean:1.5f}')
# +
ind = -252*13
plt.figure(0,figsize=(10,10))
plt.subplot(311)
plt.plot(df.iloc[ind:].price)
plt.title(f'{symbol} price, volatility, rolling price return mean plot n={np.abs(ind)}')
plt.xlabel('time')
plt.ylabel('price')
plt.grid(True)
plt.subplot(312)
plt.plot(df.iloc[ind:].hist_volatility)
plt.axhline(the_vol_mean,color='red')
plt.axhline(the_vol_mean-2*the_vol_std,color='green')
plt.axhline(the_vol_mean+2*the_vol_std,color='green')
plt.xlabel('time')
plt.ylabel('historical volatiility')
plt.grid(True)
plt.subplot(313)
plt.plot(df.iloc[ind:].ret_mean)
plt.axhline(the_ret_mean,color='red')
plt.axhline(the_ret_mean-2*the_ret_tsd,color='green')
plt.axhline(the_ret_mean+2*the_ret_tsd,color='green')
plt.grid(True)
plt.xlabel('time')
plt.ylabel('rolling mean of daily price return')
# +
ind = -200
plt.figure(0,figsize=(10,10))
print(df.iloc[-1,:])
plt.subplot(311)
plt.plot(df.iloc[ind:].price)
plt.title(f'{symbol} price, volatility, rolling price return mean plot n={np.abs(ind)}')
plt.xlabel('time')
plt.ylabel('price')
plt.grid(True)
plt.subplot(312)
plt.plot(df.iloc[ind:].hist_volatility)
plt.axhline(the_vol_mean,color='red')
plt.axhline(the_vol_mean-2*the_vol_std,color='green')
plt.axhline(the_vol_mean+2*the_vol_std,color='green')
plt.xlabel('time')
plt.ylabel('historical volatiility')
plt.grid(True)
plt.subplot(313)
plt.plot(df.iloc[ind:].ret_mean)
plt.axhline(the_ret_mean,color='red')
plt.axhline(the_ret_mean-2*the_ret_tsd,color='green')
plt.axhline(the_ret_mean+2*the_ret_tsd,color='green')
plt.grid(True)
plt.xlabel('time')
plt.ylabel('rolling mean of daily price return')
# -
# https://stackoverflow.com/questions/2369492/generate-a-heatmap-in-matplotlib-using-a-scatter-data-set
from matplotlib.colors import LogNorm
heatmap, xedges, yedges = np.histogram2d(df.ret_mean,df.hist_volatility, bins=10)
extent = [xedges[0], xedges[-1], yedges[0], yedges[-1]]
aspect = (xedges[-1]-xedges[0])/(yedges[-1]-yedges[0])
plt.figure(figsize=(10,10))
cmap = 'viridis' #viridis hot
plt.imshow(heatmap.T, extent=extent, origin='lower', aspect=aspect,norm=LogNorm(),cmap=cmap)
plt.grid(True)
plt.colorbar()
plt.xlabel('rolling mean of daily price return')
plt.ylabel('historical volatility')
|
finance/basics/mean-reversion-2020-11-12-ZM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# +
import numpy as np
import time
import torch
import scipy.stats as stats
from scipy.special import gammaln
import train_2D_rt as tr
# -
# # Testing the Timing of exact CME vs. NN prediction
#
#
# First, generate some number of parameters to use in timing. I'll start with 15 but maybe increase this?
#
#
# +
set_size = 1
num_files = 15
N = num_files*set_size
params = tr.generate_param_vectors(N)
# -
# -----
#
#
# ## Timing for exact CME
#
# Now, define the calculate exact CME function and get_moments. Get moments now accepts a multiple of sigma over which to calculate the solution.
# +
def get_moments(p,N):
b,beta,gamma=p
r = torch.tensor([1/beta, 1/gamma])
MU = b*r
VAR = MU*torch.tensor([1+b,1+b*beta/(beta+gamma)])
STD = torch.sqrt(VAR)
xmax = torch.ceil(MU)
xmax = torch.ceil(xmax + N*STD)
xmax = torch.clip(xmax,30,np.inf).int()
return MU, VAR, STD, xmax
def calculate_exact_cme(p,method,N):
'''Given parameter vector p, calculate the exact probabilites using CME integrator.'''
p1 = torch.from_numpy(p).float()
p1 = 10**p1
MU, VAR, STD, xmaxc = get_moments(p1,N)
xmaxc = np.array([int(xmaxc[0]),int(xmaxc[1])])
y = tr.cme_integrator(np.array(p1),xmaxc+1,method=method)
return(xmaxc[0]*xmaxc[1])
# -
# ----
#
# ## Increasing the State Space of Each Grid (multiple sigmas)
#
#
# ### Quad_vec
# +
P = 15
sigmas = [1,2,3,5,10,15,25,50]
state_spaces = []
time_sigmas_fixedquad = []
for sig in sigmas:
print(sig)
t1 = time.time()
state_spaces_ = np.zeros(P)
for i in range(P):
s_ = calculate_exact_cme(params[i], method = 'fixed_quad',N=sig)
state_spaces_[i] = s_
state_spaces.append(state_spaces_)
t2 = time.time()
time_sigmas_fixedquad.append(t2-t1)
# +
P = 15
sigmas = [1,2,3,5,10,15,25,50]
state_spaces = []
time_sigmas_quadvec = []
for sig in sigmas:
print(sig)
t1 = time.time()
state_spaces_ = np.zeros(P)
for i in range(P):
s_ = calculate_exact_cme(params[i], method = 'quad_vec',N=sig)
state_spaces_[i] = s_
state_spaces.append(state_spaces_)
t2 = time.time()
time_sigmas_quadvec.append(t2-t1)
# -
# ------
# # Increasing the Number of P vectors
# +
P = 15
p_vecs = [1,2,3,5,10,15,25]
time_repeatP_fixedquad = []
for p in p_vecs:
print(p)
param_list = list(params)
params_ = np.array(p*list(params))
t1 = time.time()
for i in range(P*p):
s_ = calculate_exact_cme(params_[i], method = 'fixed_quad',N=1)
t2 = time.time()
time_repeatP_fixedquad.append(t2-t1)
# +
P = 15
p_vecs = [1,2,3,5,10,15,25]
time_repeatP_quadvec = []
for p in p_vecs:
print(p)
param_list = list(params)
params_ = np.array(p*list(params))
t1 = time.time()
for i in range(P*p):
s_ = calculate_exact_cme(params_[i], method = 'quad_vec',N=1)
t2 = time.time()
time_repeatP_quadvec.append(t2-t1)
# -
# ### Nice.
#
#
# Great, we now have the timings for 1) increasing the grid size over which we integrate the exact CME and 2) increasing the number of parameters we use (kinda the same as increasing grid sizes, just in chunks? i think?) for 1) fixed_quad and 2) quad_vec.
#
#
# Let's do the same timing tests for the NN, with several different generating basis functions.
# ------
# # Timing for NN
#
# First, I'll define the grid and get_ypred_at_RT functions!
# +
def generate_grid(npdf,VAR,MU,quantiles=None):
if quantiles=='PRESET':
logstd = torch.sqrt(np.log((VAR/MU**2)+1))
logmean = torch.log(MU**2/np.sqrt(VAR+MU**2))
translin_0 = torch.exp(logmean[0]+logstd[0]*NORM_nas)
translin_1 = torch.exp(logmean[1]+logstd[1]*NORM_mat)
return translin_0,translin_1
return(translin)
def get_ypred_at_RT(p,npdf,w,N,hyp=2.4,quantiles='PRESET',
first_special=False,special_std='tail_prob'):
p = 10**p
MU, VAR, STD, xmax = get_moments(p,N)
#two separate variables. a bit ugly and leaves room for error.
grid_nas,grid_mat = generate_grid(npdf,VAR,MU,quantiles=quantiles)
# no zs implementation yet. not sure i want to implement it.
s_nas = torch.zeros(npdf[0])
s_mat = torch.zeros(npdf[1])
spec = 0 if first_special else -1
if first_special:
s_nas[1:] = torch.diff(grid_nas)
s_mat[1:] = torch.diff(grid_mat)
else: #last special... for now
s_nas[:-1] = torch.diff(grid_nas)
s_mat[:-1] = torch.diff(grid_mat)
if special_std == 'mean':
s_nas[spec] = grid_nas[spec]
s_mat[spec] = grid_mat[spec]
elif special_std == 'neighbor': #assign_neighbor_to_special
s_nas[spec] = s_nas[1] if first_special else s_nas[-2]
s_mat[spec] = s_mat[1] if first_special else s_mat[-2]
elif special_std == 'tail_prob':
if first_special:
print('If you are using this setting, you are doing something wrong.')
t_max = torch.log(p[1]/p[2])/(p[1] - p[2])
f = (torch.exp(-p[2]*t_max) - torch.exp(-p[1]*t_max)) * p[1]/(p[1] - p[2]) * p[0]
tailratio = 1/(1+1/f) #the mature tail ratio
s_mat[spec] = torch.sqrt(grid_mat[spec] / (1-tailratio))
tailratio = p[0]/(1+p[0]) #the nascent tail ratio
s_nas[spec] = torch.sqrt(grid_nas[spec] / (1-tailratio))
else:
print('did not specify a standard deviation convention!')
s_nas *= hyp
s_mat *= hyp
v_nas = s_nas**2
v_mat = s_mat**2
r_nas = grid_nas**2/(v_nas-grid_nas)
p_nas = 1-grid_nas/v_nas
r_mat = grid_mat**2/(v_mat-grid_mat)
p_mat = 1-grid_mat/v_mat
xgrid_nas = torch.arange(xmax[0]+1)
xgrid_mat = torch.arange(xmax[1]+1)
gammaln_xgrid_nas = lnfactorial[1:(xmax[0]+2)]
gammaln_xgrid_mat = lnfactorial[1:(xmax[1]+2)]
Y = torch.zeros((xmax[0]+1,xmax[1]+1))
for i in range(npdf[0]):
lnas = -grid_nas[i] + xgrid_nas * torch.log(grid_nas[i]) - gammaln_xgrid_nas
if p_nas[i] > 1e-10:
lnas += torch.special.gammaln(xgrid_nas+r_nas[i]) - torch.special.gammaln(r_nas[i]) \
- xgrid_nas*torch.log(r_nas[i] + grid_nas[i]) + grid_nas[i] \
+ r_nas[i]*torch.log(1-p_nas[i])
for j in range(npdf[1]):
lmat = - grid_mat[j] + xgrid_mat * torch.log(grid_mat[j]) - gammaln_xgrid_mat
if p_mat[j] > 1e-10:
lmat += torch.special.gammaln(xgrid_mat+r_mat[j]) - torch.special.gammaln(r_mat[j]) \
- xgrid_mat*torch.log(r_mat[j] + grid_mat[j]) + grid_mat[j] \
+ r_mat[j]*torch.log(1-p_mat[j]) #wasteful: we're recomputing a lot of stuff.
Y += w[i*npdf[1] + j] * torch.exp(lnas[:,None] + lmat[None,:])
#note convention change. Y = the predicted PMF is now returned in the same shape as the original histogram.
#this is fine bc Y is flattened anyway later on down the line.
return Y
# +
# define NORM and YPRED_FUN
def NORM_function(npdf):
if npdf[0] == npdf[1]:
n = np.arange(npdf[0])
q = np.flip((np.cos((2*(n+1)-1)/(2*npdf)*np.pi)+1)/2)
NORM = stats.norm.ppf(q)
NORM_nas = torch.tensor(NORM)
NORM_mat = NORM_nas
else:
n = np.arange(npdf[0])
q = np.flip((np.cos((2*(n+1)-1)/(2*npdf[0])*np.pi)+1)/2)
#print(q)
NORM_nas = torch.tensor(stats.norm.ppf(q))
n = np.arange(npdf[1])
q = np.flip((np.cos((2*(n+1)-1)/(2*npdf[1])*np.pi)+1)/2)
#print(q)
NORM_mat = torch.tensor(stats.norm.ppf(q))
n_n = np.linspace(0,1,npdf[0]+2)[1:-1]
n_m = np.linspace(0,1,npdf[1]+2)[1:-1]
NORM_nas = stats.norm.ppf(n_n)
NORM_mat = stats.norm.ppf(n_m)
#print(NORM_nas)
return(NORM_nas,NORM_mat)
lnfactorial = torch.special.gammaln(torch.arange(10000000))
YPRED_FUN = lambda p, npdf, w, N: get_ypred_at_RT(p=p,npdf=npdf,w=w,N=N,hyp=2.4,
quantiles='PRESET')
# -
def get_predicted_PMF(p_list,npdf,N,position,model,get_ypred_at_RT):
'''Returns predicted histogram for p given current state of model.'''
model.eval()
p1 = p_list[position:position+1]
w_p1 = model(p1)[0]
p1 = p1[0]
predicted_y1 = get_ypred_at_RT(p1,npdf,w_p1,N)
return(predicted_y1)
# The next thing to do is load in the models. :)
#
#
# I'll try for models with the following number of basis functions:
# 1. [10,11]
# 2. [20,21]
# 3. [30,31]
# 4. [50,51]
npdf = [10,11]
model_10 = tr.my_MLP1(3,npdf[0]*npdf[1])
model_10.load_state_dict(torch.load('./quadvec_models/10npdf_256params_qlin_MODEL'))
model_10.eval();
npdf = [20,21]
# pre-loaded model
model_20 = tr.my_MLP1(3,npdf[0]*npdf[1])
model_20.load_state_dict(torch.load('./quadvec_models/07032022_20npdf_1train_qlin_15epochs_MODEL'))
model_20.eval();
npdf = [30,31]
# pre-loaded model
model_30 = tr.my_MLP1(3,npdf[0]*npdf[1])
model_30.load_state_dict(torch.load('./quadvec_models/30npdf_256params_qlin_MODEL'))
model_30.eval();
npdf = [50,51]
# pre-loaded model
model_50 = tr.my_MLP1(3,npdf[0]*npdf[1])
model_50.load_state_dict(torch.load('./quadvec_models/50npdf_256params_qlin_MODEL'))
model_50.eval();
npdf = [30,31]
# pre-loaded model
model_30 = tr.my_MLP1(3,npdf[0]*npdf[1])
model_30.load_state_dict(torch.load('./quadvec_models/30npdf_256params_qlin_MODEL'))
model_30.eval();
# # Increasing Sigma (grid size)
# +
# need to work with tensors now!
params_tensor = torch.from_numpy(params).float()
# +
# def get_predicted_PMF(p_list,npdf,position,model,get_ypred_at_RT)
P = 15
sigmas = [1,2,3,5,10,15,25,50]
npdf = [10,11]
time_sigmas_NN_10 = []
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for sig in sigmas:
print(sig)
t1 = time.time()
for i in range(P):
s_ = get_predicted_PMF(params_tensor[i:i+1],npdf,sig,0,model_10,
YPRED_FUN)
t2 = time.time()
time_sigmas_NN_10.append(t2-t1)
# +
P = 15
sigmas = [1,2,3,5,10,15,25,50]
npdf = [20,21]
time_sigmas_NN_20 = []
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for sig in sigmas:
print(sig)
t1 = time.time()
for i in range(P):
s_ = get_predicted_PMF(params_tensor[i:i+1],npdf,sig,0,model_20,
YPRED_FUN)
t2 = time.time()
time_sigmas_NN_20.append(t2-t1)
# +
P = 15
sigmas = [1,2,3,5,10,15,25,50]
npdf = [30,31]
time_sigmas_NN_30 = []
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for sig in sigmas:
print(sig)
t1 = time.time()
for i in range(P):
s_ = get_predicted_PMF(params_tensor[i:i+1],npdf,sig,0,model_30,
YPRED_FUN)
t2 = time.time()
time_sigmas_NN_30.append(t2-t1)
# -
# -----
#
# # Calculating with increasing P vectors
# +
time_repeatP_NN_10 = []
npdf = [10,11]
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for p in p_vecs:
print(p)
param_list = list(params)
params_ = np.array(p*list(params))
params_ = torch.from_numpy(params_).float()
t1 = time.time()
for i in range(P*p):
ss_ = get_predicted_PMF(params_[i:i+1],npdf,sig,0,model_10,
YPRED_FUN)
t2 = time.time()
time_repeatP_NN_10.append(t2-t1)
# +
time_repeatP_NN_20 = []
npdf = [20,21]
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for p in p_vecs:
print(p)
param_list = list(params)
params_ = p*list(params)
params_ = torch.from_numpy(params_).float()
t1 = time.time()
for i in range(P*p):
ss_ = get_predicted_PMF(params_[i:i+1],npdf,sig,0,model_20,
YPRED_FUN)
t2 = time.time()
time_repeatP_NN_20.append(t2-t1)
# +
time_repeatP_NN_30 = []
npdf = [30,31]
NORM_nas,NORM_mat = NORM_function(np.array(npdf))
for p in p_vecs:
print(p)
param_list = list(params)
params_ = p*list(params)
params_ = torch.from_numpy(params_).float()
t1 = time.time()
for i in range(P*p):
ss_ = get_predicted_PMF(params_[i:i+1],npdf,sig,0,model_30,
YPRED_FUN)
t2 = time.time()
time_repeatP_NN_30.append(t2-t1)
# -
# Amaxing! We now have the timing for various state spaces and generating methods.
#
# Let's see how the timing looks.
#
# This should be fairly interesting.
#
#
# ----
#
# # Plotting
#
# ## Increasing Sigma
# +
sigma_state_space = [np.sum(a) for a in state_spaces]
plt.plot(sigma_state_space,time_sigmas_quadvec,c='red',label='Quad Vec')
plt.plot(sigma_state_space,time_sigmas_fixedquad,c='green',label='Fixed Quad')
plt.plot(sigma_state_space,time_sigmas_NN_10,c='turquoise',label='NN, 10 basis')
plt.plot(sigma_state_space,time_sigmas_NN_20,c='teal',label='NN, 10 basis')
plt.plot(sigma_state_space,time_sigmas_NN_30,c='blue',label='NN, 10 basis')
plt.xlabel('State Space')
plt.ylabel('Generating Time')
plt.legend()
# -
|
2D/Testing_Time.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# %matplotlib inline
import numpy as np
from misc import *
import matplotlib.pyplot as plt
solar_mass_in_seconds = 4.92686088e-6
# -
# # Brief summary
# In this example we will generate a reduced basis set for a simple two-parameter oscillating function - which corresponds to a simple (gravitational) waveform. The idea of a writing a function in terms of an orthonormal basis will be familiar. Perhaps the most common example is the Fourier series.
#
# For many applications a Fourier series is a very conveinent representation. However, for certain applications the Fourier series might be very cumbersome: the number of terms in the series might be very large for the desired accuracy, or the series might not converge, for example. In such cases it would be useful to have a way of computing some kind of "well adapted" basis for the specific problem of interest. A common approach to this sort of problem is to use a singular value decomposition, or principle component analysis, to represent the space of functions. In these cases, the bases generated by the SVD or PCA can lead to very compact and accurate representations of a space of functions. However, such approaches are not guaranteed to be gobally optimal, and hence the repersentations may be more accurate in some parts of the function space than others. To generate a globally optimal basis (that is, where the representation errors are minimized everywhere over the function space) we will consider yet another approach, known as the 'reduced basis method'.
#
# Before proceeding, I'll give a short sumamry of how the method works. Essentially we want to find a highly accurate, compact representation of the space of waveforms - in practice we will construct the basis so that the reduced basis representation suffers from essentially no loss in precision. Not only does this method produce highly accurate bases, but the algorithm used to generate them converges exponentially, which is a neat feature. It is also totally application specific, so the bases produced are very well adapted to particular problems.
#
# The space of waveforms is parameterized by two parameters; a mass and frequency. The reduced basis method works by first constructing a dense space of waveforms, distributed on the mass parameter, and discretely sampled in frequency. This "training space" is used in a greedy algorithm, which will select waveforms in this space to make up the basis: unlike SVD, Fourier, PCA etc..., the bases used in the reduced basis method are directly related to the functions we're trying to represent, and are therefore somewhat less abstract. In this case the bases will be an orthonormalized set of waveforms.
#
# The greedy algorithm selects the basis elements iteratively, and works as follows. On the zeroth iteration, one selects an arbitrary seed waveform: at this iteration, the reduced basis consists of one waveform - the seed waveform. For the first iteration, one then computes the projection error of this basis element with every waveform in the training space. The waveform in the training space which has the worst projection error with the basis is then added to the basis, and the basis is orthonormalized. On the second iteration, one computes the projection error of the two basis elements with every waveform in the training space, finds the waveform with the worst projection error, adds it to the basis and orthonormalizes. And so on for the third, fourth....iteraions. The algorithm is terminated once once the projection error of the $n^{th}$ iteration reaches some user-defined threshold.
#
# The input to the algorithm is a training space of m waveforms $\{h_j(M_c;f)\}_{j=1}^{m}$. The output is an orthonormal basis $\{e(f)_i\}_{i=1}^{n}$. The result is that we will be able to write the waveform as an expansion $h(Mc;f) = \sum_{i=1}^{n} \langle h(M_c;f), e_i(f) \rangle\,e_i(f)$. The coeffieicnts $\langle h(M_c;f), e_i(f) \rangle$ are the inner product of $h$ with the basis elements $e_i$.
#
# In this note, I'll show how to build the reduced basis in practice. The waveform is shown in the cell directly below. It corresponds to a post-Newtonian gravitational waveform, but it's not important and I want to stress the generality of the approach: it can be applied to any parameterized function.
# +
def phase(f, Mc):
phase = -np.pi/4. + ( 3./( 128. * pow(Mc*np.pi*f, 5./3.) ) )
return phase
def htilde(f, Mc):
Mc *= solar_mass_in_seconds
htilde = pow(f, -7./6.) * pow(Mc,5./6.) * np.exp(1j*phase(f,Mc))
return htilde
# -
# The parameters (f, Mc) are frequency and chirp mass. Before we generate the basis we need to decide on the range in parameter space that we will work in. The chirp mass range I'll work in will be $1.5 \leq M_c \leq 3$. I won't explain the exact choice of these values,
Mc_min = 1.5
Mc_max = 3
# Next I'll define the upper and lower frequencies of the waveforms: $f_{min} =40Hz$ and $f_{max} = 1024Hz$. Rather than have a uniformly sampled waveforms in this range, I've opted to create a frequency series at the Chebyshev-Gauss-Lobatto nodes in the frequency interval. The only reason for doing this is to make the greedy more efficient, but don't dwell on this as it will probably just obscure the main point of the example.
fmin = 40.
fmax = 1024.
fseries, df = chebyshev_gauss_lobatto_nodes_and_weights(fmin, fmax, 5000)
np.savetxt("fseries.dat", np.matrix(fseries))
np.savetxt("df.dat", np.matrix(df))
# Next I'll define the parameters for the training space. I'll make a training space with 2000 waveforms. Rather than distribute the waveforms uniformly between $Mc_{min}$ and $Mc_{max}$, I'll distribute them uniformly between $Mc_{min}^{5/3}$ and $Mc_{max}^{5/3}$. This is because $Mc^{5/3}$ appears in the phase, and it will turn out to be a much more judicious way to make the training space. In particular, it will make this script run much faster on your laptop.
TS_size = 2000 # training space of TS_size number of waveforms
Mcs_5_over_3 = np.linspace(Mc_min**(5./3.), Mc_max**(5./3.), TS_size)
Mcs = Mcs_5_over_3**(3./5.)
# Now I'll actually make the training space. For storage purposes I'll allocate it as a matrix whose rows correspond to waveforms distributed on $M_c$. The columns of the matrix are the frequency samples of the waveforms. In addition, I'll normalize all the waveforms: You don't have to do this last step, but it makes computing the projection errors in the next step more simple.
# +
#### allocate memory for training space ####
TS = np.zeros(TS_size*len(fseries), dtype=complex).reshape(TS_size, len(fseries)) # store training space in TS_size X len(fseries) array
for i in range(TS_size):
TS[i] = htilde(fseries, Mcs[i])
# normalize
TS[i] /= np.sqrt(abs(dot_product(df, TS[i], TS[i])))
plt.plot(fseries, TS[0], 'b', fseries, TS[345], 'r', fseries, TS[999], 'k')
plt.show()
# -
# The projection operation and the projection errors are defined as follows.
#
# $\textbf{Projection}$: for a basis set $\{e_i\}_{i=1}^{n}$, the projection of $h$ onto the basis is defined as $\mathcal{P}h = \sum_{i=1}^{n}\langle h,e_i \rangle e_i$, where $\langle a, b \rangle$ is an inner product.
#
# $\textbf{Projection coefficient}$: the coefficients $\langle h,e_i \rangle$ are the projection coefficients.
#
# $\textbf{Projection error}$: the projection error $\sigma$ is the inner product of the residual of $h$ and it's projection: $\sigma = \langle (h - \mathcal{P}h), (h - \mathcal{P}h) \rangle.$
#
# The stuff below is just some convenient storage for all the projections and projection coefficients.
# +
#### Set up stuff for greedy####
# Allocate storage for projection coefficients of training space waveforms onto the reduced basis elements
proj_coefficients = np.zeros(TS_size*TS_size, dtype=complex).reshape(TS_size, TS_size)
# Allocate matrix to store the projection of training space waveforms onto the reduced basis
projections = np.zeros(TS_size*len(fseries), dtype=complex).reshape(TS_size, len(fseries))
rb_errors = []
# -
# Now we will start the greedy algorithm to find the bases. We start by seeding the algorithm with the first basis element, chosen arbitrarily as the first waveform in the training set. This is stored in RB_matrix. For this example, I've set tolerance = 1e-12, which will be the target error of the complete basis to represent the training spcae, i.e., the waveforms written as an expansion in terms of the bases should be accurate to one part in $10^{12}$. The greedy algorithm will terminate once the maximum projection error - of the waveforms in the training space onto the basis - is less than or equal to the tolerance.
#
# Once the algorithm is done, the real and imaginary parts of the basis are stored in basis_re.dat and basis_im.dat respectively.
# +
#### Begin greedy: see Field et al. arXiv:1308.3565v2 ####
tolerance = 10e-12 # set maximum RB projection error
sigma = 1 # (2) of Algorithm 1. (projection error at 0th iteration)
rb_errors.append(sigma)
RB_matrix = [TS[0]] # (3) of Algorithm 1. (seed greedy algorithm (arbitrary))
iter = 0
while sigma >= tolerance: # (5) of Algorithm 1.
# project the whole training set onto the reduced basis set
projections = project_onto_basis(df, RB_matrix, TS, projections, proj_coefficients, iter)
residual = TS - projections
# Find projection errors
projection_errors = [dot_product(df, residual[i], residual[i]) for i in range(len(residual))]
sigma = abs(max(projection_errors)) # (7) of Algorithm 1. (Find largest projection error)
print sigma, iter
index = np.argmax(projection_errors) # Find Training-space index of waveform with largest proj. error
rb_errors.append(sigma)
#Gram-Schmidt to get the next basis and normalize
next_basis = TS[index] - projections[index] # (9) of Algorithm 1. (Gram-Schmidt)
next_basis /= np.sqrt(abs(dot_product(df, next_basis, next_basis))) #(10) of Alg 1. (normalize)
RB_matrix.append(next_basis) # (11) of Algorithm 1. (append reduced basis set)
iter += 1
np.savetxt("basis_re.dat", np.matrix(RB_matrix).real)
np.savetxt("basis_im.dat", np.matrix(RB_matrix).imag)
# -
plt.plot(rb_errors)
plt.yscale('log')
plt.xlabel('greedy iteration')
plt.ylabel('projection error')
plt.show()
# The above plot shows the projection error as a function of the greedy iteration. Notice that the errors hover around 1 for most of the algorithm and at some point decrease rapidly in only a few iterations. This feature is common, and corresponds to the exponential convergence promised earlier.
# We should now check that the basis is as good as we hope: while the basis is already accurate to the 1e-12 level for approximating the training set, we should also check that it's accurate at describing waveforms which are in the Mc interval we considered, but which were not in the training space. To do this, I'll generate a new random training space in the Mc interval, and look at the projection errors of the reduced basis on the random training space.
# +
#### Error check ####
TS_rand_size = 2000
TS_rand = np.zeros(TS_rand_size*len(fseries), dtype=complex).reshape(TS_rand_size, len(fseries)) # Allocate random training space
Mcs_5_over_3_rand = Mc_min**(5./3.) + np.random.rand(TS_rand_size) * ( Mc_max**(5./3.) - Mc_min**(5./3.) )
Mcs_rand = pow(Mcs_5_over_3_rand, 3./5.)
for i in range(TS_rand_size):
TS_rand[i] = htilde(fseries, Mcs_rand[i])
# normalize
TS_rand[i] /= np.sqrt(abs(dot_product(df, TS_rand[i], TS_rand[i])))
### find projection errors ###
iter = 0
proj_rand = np.zeros(len(fseries), dtype=complex)
proj_error = []
for h in TS_rand:
while iter < len(RB_matrix):
proj_coefficients_rand = dot_product(df, RB_matrix[iter], h)
proj_rand += proj_coefficients_rand*RB_matrix[iter]
iter += 1
residual = h - proj_rand
projection_errors = abs(dot_product(df, residual, residual))
proj_error.append(projection_errors)
proj_rand = np.zeros(len(fseries), dtype=complex)
iter = 0
plt.scatter(np.linspace(0, len(proj_error), len(proj_error)), np.log10(proj_error))
plt.ylabel('log10 projection error')
plt.show()
# -
# and you can see that the projection errors are all less than or around 1e-12, as we wanted!
|
ROQ/Reduced Basis generation for a simple function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/vdnew/Sentiment-Analysis-on-tweet/blob/main/Sentiment_Analysis_Gradient_Boosting_Score.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="5iapzfg-KbJx"
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# + id="OqD1Kyp4KzAJ" colab={"base_uri": "https://localhost:8080/"} outputId="fdf587e9-3d35-4813-dbc5-f3c5d3746c0d"
import nltk
import nltk.corpus
from nltk.corpus import stopwords
from nltk.tokenize import BlanklineTokenizer
from nltk.tokenize import TweetTokenizer
nltk.download('punkt')
nltk.download('wordnet')
nltk.download('stopwords')
from nltk.stem import WordNetLemmatizer
import string
# + id="dEJ9CJvCK-ql"
import re
from nltk.tokenize import word_tokenize
import gensim
from keras.preprocessing.text import Tokenizer
# + id="4lE11theLG6f"
from nltk.stem import PorterStemmer
from wordcloud import WordCloud
from sklearn.model_selection import train_test_split
# + id="RbsZx1-OLOJV"
dataset = pd.read_csv('/content/Tweets.csv')
# + id="nHL6vPYLLep7" colab={"base_uri": "https://localhost:8080/", "height": 452} outputId="81933979-27d5-45c2-bcc5-120904290f2f"
dataset.head()
# + id="-IwocnoMLf13" colab={"base_uri": "https://localhost:8080/"} outputId="d209965e-8a17-45a5-ff96-de6443464956"
dataset.shape
# + id="54I0WJXjLidb" colab={"base_uri": "https://localhost:8080/"} outputId="ed78cca7-bb5e-4101-b5f3-850c9f1daedf"
dataset.airline_sentiment.value_counts()
# + id="TZMhbpyBL0TC"
#notre objectif est de prédicter la valeur de la colonne "airlaine_sentiment"
# + id="GsnoCvsTL_EL" colab={"base_uri": "https://localhost:8080/"} outputId="9f5f8ed8-5366-4a12-b3c7-7066e8d5425f"
dataset.info()
# + id="I23_bdgjMG30"
# les colonnes "airline_sentiment_gold " et "negativereason_gold" ont trop peu de valeurs non nulles
#donc on va les supprimer
# + id="K9EdRCSOMbO8"
dataset.drop(['airline_sentiment_gold','negativereason_gold'],axis=1,inplace=True)
# + id="1F2rQ2u6MmIO" colab={"base_uri": "https://localhost:8080/"} outputId="57fb3d07-dc58-4486-ddd8-4c4cf4242ed4"
dataset.tweet_coord.nunique()
# + id="aWboGq7BM9i2"
#parmi 1019 valeurs non nulles du colonne 'tweet_coord' ilya 832 valeurs uniques
#donc c'est une colonne peu important
# + id="AKaaWdaKNWtM"
dataset.drop(['tweet_coord'],axis=1,inplace=True)
# + id="9YX1bzDcN29T" colab={"base_uri": "https://localhost:8080/"} outputId="742dd353-4ed6-4064-d23c-79235c2a950e"
dataset.info()
# + id="5q3HyZ49N_xm" colab={"base_uri": "https://localhost:8080/"} outputId="9533799f-21eb-4a7d-f4a8-ae1d47ce46be"
dataset.negativereason.value_counts()
# + id="frzEWEiAOEq0" colab={"base_uri": "https://localhost:8080/"} outputId="a2f587f8-9f63-47a8-82e5-6c1865fe944f"
dataset.negativereason.nunique()
# + id="pkzJxmxyOOVL"
#trés bien il ya que 10 valeurs uniques
# + id="mdKsBNZyOSks" colab={"base_uri": "https://localhost:8080/"} outputId="6626bf82-671c-48e9-d9a5-0491de991d20"
nr = dataset.negativereason.unique()
nr
# + id="fPc9tMvTOZK7" colab={"base_uri": "https://localhost:8080/"} outputId="afcfa02f-5241-4695-8942-fcffa01349df"
nr.reshape(1,11)
# + id="Oebf8JNHOg8u" colab={"base_uri": "https://localhost:8080/"} outputId="58904ca9-df9d-4781-a07f-630fc12e40a6"
nr[0]
# + id="SufImvwAOqzF" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="e7e7f89e-d1f5-4132-b2aa-9ca0287e4f76"
nr[5]
# + id="39GI_GOsOsjv" colab={"base_uri": "https://localhost:8080/"} outputId="bafd8d04-4bd8-4eb1-99d6-1880c9932dbc"
dataset.negativereason.iloc[0] = 'Bad Flight'
# + id="BAdPMGT0PfO4" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="e2a982bc-a407-4bab-e321-844dba04c159"
dataset.negativereason.iloc[0]
# + id="4A6qcI_nQX18" colab={"base_uri": "https://localhost:8080/"} outputId="960eee9f-3ba8-4411-e2e2-56a1999190f7"
dataset.negativereason.iloc[1] is np.NaN
# + id="FXrzxRrtPso9" colab={"base_uri": "https://localhost:8080/"} outputId="6a2afe2e-098a-4ded-96a5-266f0ff7aeba"
import random
for k in range (dataset.shape[0]):
if dataset.negativereason.iloc[k] is np.NaN:
p = random.randint(1, 10)
dataset.negativereason.iloc[k] = nr[p]
# + id="tFx9yORpRMpq" colab={"base_uri": "https://localhost:8080/"} outputId="21b97929-217c-4fae-8657-9b3f3a9b8ac2"
dataset.info()
# + id="2jAhK3uARPAW" colab={"base_uri": "https://localhost:8080/"} outputId="5d2f5820-8e46-4e95-b6fd-5d65b4e97965"
#on va vérifier le résultat
dataset.negativereason.value_counts()
# + id="f00vFz-jRgMA"
#trés bien
# + id="KSTq01R_RiXB" colab={"base_uri": "https://localhost:8080/"} outputId="73e0445e-2e34-479c-9429-02e30a7bb240"
dataset.negativereason_confidence.nunique()
# + id="cgxQ8pElR35m" colab={"base_uri": "https://localhost:8080/"} outputId="d797defa-da2d-473f-b4df-3a3c73f8ecbe"
#1410 valeurs se répétent dans 10522 lignes donc on va les utiliser pour remplacer les valeurs 'NaN'
nr = dataset.negativereason_confidence.unique()
len(nr)
# + id="FOaL-NFWUW-T" colab={"base_uri": "https://localhost:8080/"} outputId="014c9b66-3659-4f20-e350-d5cf2e92ba3f"
nr.reshape(1,1411)
# + id="4fHH4rDEUzG9"
dataset.negativereason_confidence = dataset.negativereason_confidence.astype('object')
# + id="gJeBIkTmU8tX" colab={"base_uri": "https://localhost:8080/"} outputId="fc7c2374-41ca-4261-ff98-889c4f01091d"
dataset.info()
# + id="jp6Pjrl9Sa-4"
for k in range (dataset.shape[0]):
if dataset.negativereason_confidence.iloc[k] is np.NaN:
p = random.randint(1, 1411)
dataset.negativereason_confidence.iloc[k] = nr[p]
# + id="i7rGic_EUeu3" colab={"base_uri": "https://localhost:8080/"} outputId="2792580d-c092-4106-867b-f60aad684968"
dataset.info()
# + id="mXMmRLK9SyY_" colab={"base_uri": "https://localhost:8080/"} outputId="a703fd9f-0670-41fd-d010-526b4e40a6f4"
dataset.user_timezone.nunique()
# + id="lWyUMWiaS8sG"
#trés bien juste 85 uniques valeurs qui se répétent dans plus de 9000 lignes
# + id="AjADBRAGTEj6" colab={"base_uri": "https://localhost:8080/"} outputId="51b36be4-fb06-4138-f9de-5e7ccb44d81d"
nr = dataset.user_timezone.unique()
nr.reshape(1,86)
# + id="cSWcQfU_TS1G" colab={"base_uri": "https://localhost:8080/"} outputId="2d4c0623-732b-4844-8a54-9995ff3143d5"
for k in range (dataset.shape[0]):
if dataset.user_timezone.iloc[k] is np.NaN:
p = random.randint(1, 85)
dataset.user_timezone.iloc[k] = nr[p]
# + id="-cM6sbKgTdcG" colab={"base_uri": "https://localhost:8080/"} outputId="438e9117-a5e0-4103-cebc-6a924f46d805"
dataset.info()
# + id="1C395R9GTi0Y" colab={"base_uri": "https://localhost:8080/"} outputId="20383bf3-bf44-454a-d1ea-fc7d58525ada"
dataset.tweet_location.nunique()
# + id="5wEO53NPVe-_" colab={"base_uri": "https://localhost:8080/"} outputId="7f32beee-2885-4539-9698-632f5192d015"
nr = dataset.tweet_location.unique()
nr.shape
# + id="rYHdU9RJVk16" colab={"base_uri": "https://localhost:8080/"} outputId="95e3d868-d53e-4081-f2c8-cac22cbfa872"
nr.reshape(1,3082)
# + id="o3mQo3uDTz99" colab={"base_uri": "https://localhost:8080/"} outputId="79b85f8b-96cd-4ba5-b85b-8e11fc41f650"
for k in range (dataset.shape[0]):
if dataset.tweet_location.iloc[k] is np.NaN:
p = random.randint(1, 3081)
dataset.tweet_location.iloc[k] = nr[p]
# + id="RXjeXgAeVvsV" colab={"base_uri": "https://localhost:8080/"} outputId="f714fcdd-ef27-4620-f547-2a4b8e430c47"
dataset.info()
# + id="yOhSS5tjVzpC"
#ilya un probléme avec la colonne 'negativereason_confidence'
# + id="HNCcOXUeWdFD" colab={"base_uri": "https://localhost:8080/", "height": 452} outputId="b61be2ba-67d1-4887-9c5d-1b0e29b7f2cf"
dataset.head()
# + id="9LiUvaWoWnOA" colab={"base_uri": "https://localhost:8080/"} outputId="6dc02201-b73e-42dd-99c3-b4e30ba2e679"
dataset.negativereason_confidence.iloc[0] in range(0,2)
# + id="nthpG3cTXWVM" colab={"base_uri": "https://localhost:8080/"} outputId="3da44baa-2cb3-42df-e84a-19c4d879547e"
dataset.negativereason_confidence.iloc[0] = 1
# + id="Sre7UMcmXUVk" colab={"base_uri": "https://localhost:8080/"} outputId="b8ac8880-fdd8-4101-a3ef-476951d3cc91"
dataset.negativereason_confidence.iloc[0]
# + id="us7edCqZXcy9"
nr = dataset.negativereason_confidence.unique()
# + id="nGdZwKubXhLe" colab={"base_uri": "https://localhost:8080/"} outputId="9b3d84ff-b843-4a65-9985-237b83c6bf9b"
nr.shape
# + id="0Inhh0l1XjM1" colab={"base_uri": "https://localhost:8080/"} outputId="824cb0d9-94e1-402f-950c-15dfcbf162d2"
nr.reshape(1,1411)
# + id="HDiOH9H6XjLl"
nr[2] = 0.644
# + id="ATu1nwV6YCy_" colab={"base_uri": "https://localhost:8080/"} outputId="9c7bb554-850b-47d4-acba-69e7a725afdb"
nr
# + id="F3Nb7tTzWsu5" colab={"base_uri": "https://localhost:8080/"} outputId="0366126c-21d8-4d53-8ba8-27c664d683fa"
for k in range (dataset.shape[0]):
if dataset.negativereason_confidence.iloc[k] not in range(0,2):
p = random.randint(0,1410)
dataset.negativereason_confidence.iloc[k] = nr[p]
# + id="IwPLhhnXYXrC" colab={"base_uri": "https://localhost:8080/"} outputId="f8ebe16f-85dd-49e9-e23f-248f2137ce5a"
dataset.info()
# + id="w2u42rgwYhBo"
#trés bien
# + id="p7tXPapxonKO" colab={"base_uri": "https://localhost:8080/", "height": 452} outputId="918df8ce-2c31-4018-ba56-0b642e876c27"
dataset.head()
# + id="mEQj5t__optg"
dataset.drop(['tweet_id'],axis=1,inplace=True)
# + id="JP0AsOhXoxjp" colab={"base_uri": "https://localhost:8080/"} outputId="038ce2e3-7f8f-4e70-a412-551ff5be6780"
dataset.name.nunique()
# + id="SlkZKDFEo89Z"
X = dataset.drop(['airline_sentiment'],axis=1)
y = dataset.airline_sentiment
# + id="9pso9DIbpVF6"
y = y.replace({'negative' : 0 , 'neutral' : 1 , 'positive' : 2})
# + id="p2AIEGzjpp0i"
#on va traiter la colonne "tweet_created"
# + id="eOHwsyfsqEJJ"
X['year'] = pd.to_datetime(X.tweet_created).dt.year
X['day'] = pd.to_datetime(X.tweet_created).dt.day
X['month'] = pd.to_datetime(X.tweet_created).dt.month
X['hour'] = pd.to_datetime(X.tweet_created).dt.hour
X['minute'] = pd.to_datetime(X.tweet_created).dt.minute
X['second'] = pd.to_datetime(X.tweet_created).dt.second
# + id="GYJ25kZFrE86" colab={"base_uri": "https://localhost:8080/", "height": 452} outputId="9a68289b-2d69-4daa-d3d2-1b5fa76cc513"
X.head()
# + id="Li5Ttj2jrHG4"
X.drop(['tweet_created'],axis=1,inplace=True)
# + id="BJ8YuedusAET"
X.drop(['name'],axis=1,inplace=True)
# + id="Hva3fIi1rQKX"
from sklearn.preprocessing import LabelEncoder
# + id="thN5iSM0r4z9"
X.negativereason = X.negativereason.astype('str')
X.airline = X.airline.astype('str')
X.tweet_location = X.tweet_location.astype('str')
X.user_timezone = X.user_timezone.astype('str')
columns_to_Encode = ["negativereason","airline","tweet_location","user_timezone"]
le = LabelEncoder()
for each in columns_to_Encode:
X[each] = le.fit_transform(X[each])
# + id="N8ZUhuEcsfsu" colab={"base_uri": "https://localhost:8080/", "height": 452} outputId="5eb268ab-d510-4674-ad8e-09bc79df9ffd"
X.head()
# + id="kCaZIlO2tzzI"
#Etape suivante : traiter la colonne "text"
# + id="Vzssx5RSt81T" colab={"base_uri": "https://localhost:8080/", "height": 486} outputId="f241ca09-99c4-432a-a3e7-1daa987692e2"
X.tail()
# + id="xb11exNqvfry"
X['len_text'] = X['text'].apply(len)
# + id="tDee1Hhswtho" colab={"base_uri": "https://localhost:8080/", "height": 427} outputId="7fab1de4-9b0f-41e7-9b7e-015dd771bc33"
plt.style.use('seaborn-darkgrid')
plt.figure(figsize=(10,5))
sns.distplot(X['len_text'],kde=False,color='red',hist=True)
plt.xlabel("text Length",size=15)
plt.ylabel("Frequency",size=15)
plt.title("Length Histogram",size=15)
# + id="UOv2vu4Qw_Va"
from nltk.stem.porter import PorterStemmer
# + id="bNCcjPQ9xF9B"
ps = PorterStemmer() #pour "text preprocessing"
message = []
for i in range(0, X.shape[0]):
#accepter que les mots alphabétiques
review = re.sub('[^a-zA-Z]', ' ', X['text'][i])
#convertir tous minuscule
review = review.lower()
#splitter chaque ligne
review = review.split()
#
review = [ps.stem(word) for word in review if not word in stopwords.words('english')]
#construire de nouveau la ligne
review = ' '.join(review)
message.append(review)
# + id="CU08XXJPxToo" colab={"base_uri": "https://localhost:8080/", "height": 656} outputId="95c7d3e7-51f1-4be7-e0ee-9683b8cd204f"
X['clean_text']=np.empty((len(message),1))
for i in range(len(message)):
X['clean_text'][i]=message[i]
X['clean_text_len']=X['clean_text'].apply(len)
X.head()
# + id="hH2-GTQRxiiz"
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features=15000)
X1 = cv.fit_transform(message).toarray()
# + id="QMC0CZUvyC7a" colab={"base_uri": "https://localhost:8080/"} outputId="06d72859-68d0-4d09-d5ff-01826b01898d"
X1.shape
# + id="QCWYQDAayYLq"
X2 = X.copy()
# + id="KLW8u4k2yoXp"
X2.drop(['text','clean_text'],axis=1,inplace=True)
# + id="EbIe-FYwzCAn"
X3 = pd.DataFrame(data=X1)
# + id="aWWN2GVv0aWN" colab={"base_uri": "https://localhost:8080/"} outputId="db6c4419-a292-4413-e50d-7f00cb34c855"
X3.shape
# + id="_cbXdNF_0cHO"
X4 = pd.concat([X2,X3],axis=1)
# + id="spjHeeOQ1QDS" colab={"base_uri": "https://localhost:8080/"} outputId="9bf9f9cc-29bf-46b9-cfc7-5129e76cb0ce"
X4.shape
# + id="YvsvIcZO1StF"
x_train,x_test,y_train,y_test = train_test_split(X4,y,test_size=0.2,random_state=42)
# + id="7sb2pL7R2Bav"
from sklearn.ensemble import GradientBoostingClassifier
gbk = GradientBoostingClassifier(random_state=42, n_estimators=100,min_samples_split=100)
gbk.fit(x_train, y_train)
gbk_predict = gbk.predict(x_test)
# + id="T3XcdM_l38gj" colab={"base_uri": "https://localhost:8080/"} outputId="07447970-9f28-40c6-967e-56e3b1cef7fe"
from sklearn.metrics import accuracy_score
print("Gradient Boosting Score :",accuracy_score(y_test,gbk_predict ))
# + id="j8BVvLQvOD0j"
|
Sentiment_Analysis_Gradient_Boosting_Score.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to loading data <img align="right" src="../Supplementary_data/dea_logo.jpg">
#
# * **Acknowledgement**: This notebook was originally created by [Digital Eath Australia (DEA)](https://www.ga.gov.au/about/projects/geographic/digital-earth-australia) and has been modified for use in the EY Data Science Program
# * **Products used:**
# [ga_s2a_ard_nbar_granule](https://explorer.sandbox.dea.ga.gov.au/ga_s2a_ard_nbar_granule),
# [ga_s2b_ard_nbar_granule](https://explorer.sandbox.dea.ga.gov.au/ga_s2b_ard_nbar_granule)
# * **Prerequisites:** Users of this notebook should have a basic understanding of:
# * How to run a [Jupyter notebook](01_Jupyter_notebooks.ipynb)
# * The basic structure of the DEA [satellite datasets](02_DEA.ipynb)
# * Inspecting available [DEA products and measurements](03_Products_and_measurements.ipynb)
#
# ## Background
# Loading data from the [Digital Earth Australia (DEA)](https://www.ga.gov.au/dea) instance of the [Open Data Cube](https://www.opendatacube.org/) requires the construction of a data query that specifies the what, where, and when of the data request.
# Each query returns a [multi-dimensional xarray object](http://xarray.pydata.org/en/stable/) containing the contents of your query.
# It is essential to understand the `xarray` data structures as they are fundamental to the structure of data loaded from the datacube.
# Manipulations, transformations and visualisation of `xarray` objects provide datacube users with the ability to explore and analyse DEA datasets, as well as pose and answer scientific questions.
# ## Description
# This notebook will introduce how to load data from the DEA datacube through the construction of a query and use of the `dc.load()` function.
# Topics covered include:
#
# 1. Loading data using `dc.load()`
# 2. Interpreting the resulting `xarray.Dataset` object
# * Inspecting an individual `xarray.DataArray`
# 3. Customising parameters passed to the `dc.load()` function
# * Loading specific measurements
# * Loading data for coordinates in a custom coordinate reference system (CRS)
# * Projecting data to a new CRS and spatial resolution
# * Specifying a specific spatial resampling method
# 4. Loading data using a reusable dictionary query
# 5. Loading matching data from multiple products using `like`
# 6. Adding a progress bar to the data load
#
# ***
# ## Getting started
# To run this introduction to loading data from DEA, run all the cells in the notebook starting with the "Load packages" cell. For help with running notebook cells, refer back to the [Jupyter Notebooks notebook](01_Jupyter_notebooks.ipynb).
# ### Load packages
# The `datacube` package is required to query the datacube database and load some data.
# The `with_ui_cbk` function from `odc.ui` enables a progress bar when loading large amounts of data.
import datacube
from odc.ui import with_ui_cbk
# ### Connect to the datacube
# The next step is to connect to the datacube database.
# The resulting `dc` datacube object can then be used to load data.
# The `app` parameter is a unique name used to identify the notebook that does not have any effect on the analysis.
dc = datacube.Datacube(app="04_Loading_data")
# ## Loading data using `dc.load()`
#
# Loading data from the datacube uses the [dc.load()](https://datacube-core.readthedocs.io/en/latest/dev/api/generate/datacube.Datacube.load.html) function.
#
# The function requires the following minimum arguments:
#
# * `product`: The data product to load (to revise DEA products, see the [Products and measurements](03_Products_and_measurements.ipynb) notebook).
# * `x`: The spatial region in the *x* dimension.
# * `y`: The spatial region in the *y* dimension. The dimensions ``longitude``/``latitude`` and ``x``/``y`` can be used interchangeably.
# * `crs`: The geographical Cooridinate Reference System (CRS) that the *x* and *y* arguments are in.
# * `time`: The temporal extent. The time dimension can be specified using a tuple of datetime objects or strings in the "YYYY", "YYYY-MM" or "YYYY-MM-DD" format.
# * `output_crs`: The CRS to return the data in.
# * `resolution`: The resolution to return the data in. The units are set by the output_crs argument.
#
# For example, to load the first week of January 2018 data from the [Sentinel-2A Analysis Ready Data NBAR product](https://explorer.sandbox.dea.ga.gov.au/ga_s2a_ard_nbar_granule) for Western Port Bay near Phillip Island in southern Victoria, use the following parameters:
#
# * `product`: `ga_s2a_ard_nbar_granule`
# * `x`: `(145.1, 145.2)`
# * `y`: `(-38.4, -38.5)`
# * `time`: `("2018-01-01", "2018-01-07")`
# * `crs`: `"epsg:4326"`
# * `output_crs`: `"epsg:4326"`
# * `resolution`: `(-0.01, 0.01)`
#
# Run the following cell to load all datasets from the `ga_s2a_ard_nbar_granule` product that match this spatial and temporal extent:
# +
ds = dc.load(product="ga_s2a_ard_nbar_granule",
x=(145.1, 145.2),
y=(-38.4, -38.5),
time=("2018-01-01", "2018-01-07"),
crs="epsg:4326",
output_crs="epsg:4326",
resolution=(-0.01, 0.01))
print(ds)
# -
# ### Interpreting the resulting `xarray.Dataset`
# The variable `ds` has returned an `xarray.Dataset` containing all data that matched the spatial and temporal query parameters inputted into `dc.load`.
#
# *Dimensions*
#
# * This header identifies the number of timesteps returned in the search (`time: 1`) as well as the number of pixels in the `latitude` and `longitude` directions of the data query.
#
# *Coordinates*
#
# * `time` identifies the date attributed to each returned timestep.
# * `latitude` and `longitude` are the coordinates for each pixel within the spatial bounds of the query.
#
# *Data variables*
#
# * These are the measurements available for the nominated product.
# For every date (`time`) returned by the query, the measured value at each pixel (`latitude`, `longitude`) is returned as an array for each measurement.
# Each data variable is itself an `xarray.DataArray` object ([see below](#Inspecting-an-individual-xarray.DataArray)).
#
# *Attributes*
#
# * `crs` identifies the coordinate reference system (CRS) of the loaded data.
# ### Inspecting an individual `xarray.DataArray`
# The `xarray.Dataset` loaded above is itself a collection of individual `xarray.DataArray` objects that hold the actual data for each data variable/measurement.
# For example, all measurements listed under _Data variables_ above (e.g. `nbar_blue`, `nbar_green`, `nbar_red`, `nbar_nir_1`, `nbar_nir_2`, `nbar_swir_1`) are `xarray.DataArray` objects.
#
# These `xarray.DataArray` objects can be inspected or interacted with by using either of the following syntaxes:
# ```
# ds["measurement_name"]
# ```
# or
# ```
# ds.measurement_name
# ```
#
# The ability to access individual variables means that these can be directly viewed, or further manipulated to create new variables.
# For example, run the following cell to access data from the near infra-red satellite band (i.e. `nbar_nir_1`):
print(ds.nbar_nir_1)
# Note that the object header informs us that it is an `xarray.DataArray` containing data for the `nir` satellite band.
#
# Like an `xarray.Dataset`, the array also includes information about the data's **dimensions** (i.e. `(time: 1, latitude: 10, longitude: 10)`), **coordinates** and **attributes**.
# This particular data variable/measurement contains some additional information that is specific to the `nbar_nir_1` band, including details of array's nodata value (i.e. `nodata: -999`).
#
# > For a more in-depth introduction to `xarray` data structures, refer to the [official xarray documentation](http://xarray.pydata.org/en/stable/data-structures.html)
# ## Customising the `dc.load()` function
#
# The `dc.load()` function can be tailored to refine a query.
#
# Customisation options include:
#
# * `measurements:` This argument is used to provide a list of measurement names to load, as listed in `dc.list_measurements()`.
# For satellite datasets, measurements contain data for each individual satellite band (e.g. near infrared).
# If not provided, all measurements for the product will be returned.
# * `crs:` The coordinate reference system (CRS) of the query's `x` and `y` coordinates is assumed to be `WGS84`/`EPSG:4326` unless the `crs` field is supplied, even if the stored data is in another projection or the `output_crs` is specified.
# The `crs` parameter is required if the query's coordinates are in any other CRS.
# * `group_by:` Satellite datasets based around scenes can have multiple observations per day with slightly different time stamps as the satellite collects data along its path.
# These observations can be combined by reducing the `time` dimension to the day level using `group_by=solar_day`.
# * `output_crs` and `resolution`: To reproject or change the resolution the data, supply the `output_crs` and `resolution` fields.
# * `resampling`: This argument allows you to specify a custom spatial resampling method to use when data is reprojected into a different CRS.
#
# Example syntax on the use of these options follows in the cells below.
#
# > For help or more customisation options, run `help(dc.load)` in an empty cell or visit the function's [documentation page](https://datacube-core.readthedocs.io/en/latest/dev/api/generate/datacube.Datacube.load.html)
#
# ### Specifying measurements
# By default, `dc.load()` will load *all* measurements in a product.
#
# To load data from the `red`, `green` and `blue` satellite bands only, add `measurements=["nbar_red", "nbar_green", "nbar_blue"]` to the query:
# +
# Note the optional inclusion of the measurements list
ds_rgb = dc.load(product="ga_s2a_ard_nbar_granule",
measurements=["nbar_red", "nbar_green", "nbar_blue"],
x=(145.1, 145.2),
y=(-38.4, -38.5),
time=("2018-01-01", "2018-01-07"),
crs="epsg:4326",
output_crs="epsg:4326",
resolution=(-0.01, 0.01))
print(ds_rgb)
# -
# Note that the **Data variables** component of the `xarray.Dataset` now includes only the measurements specified in the query (i.e. the `nbar_red`, `nbar_green` and `nbar_blue` satellite bands).
# ### Loading data for coordinates in any CRS
# By default, `dc.load()` assumes that the queried `x` and `y` coordinates are in the `WGS84`/`EPSG:4326` CRS.
# If these coordinates are in a different coordinate system, specify this using the `crs` parameter.
#
# The example cell below loads data for a set of `x` and `y` coordinates defined in GDA94 / MGA zone 55 (`EPSG:28355`), ensuring that the `dc.load()` function accounts for this by including `crs="EPSG:28355"`:
# +
# Note the new `x` and `y` coordinates and `crs` parameter
ds_custom_crs = dc.load(product="ga_s2a_ard_nbar_granule",
measurements=["nbar_red", "nbar_green", "nbar_blue"],
time=("2018-01-01", "2018-01-07"),
x=(356895, 333715),
y=(5729345, 5744446),
output_crs="EPSG:28355",
crs="EPSG:28355",
resolution=(-250, 250))
print(ds_custom_crs)
# -
# Note that the `crs` attribute in the **Attributes** section has changed to `EPSG:28355`.
# ### Spatial resampling methods
# When a product is re-projected to a different CRS and/or resolution, the new pixel grid may differ from the original input pixels by size, number and alignment.
# It is therefore necessary to apply a spatial "resampling" rule that allocates input pixel values into the new pixel grid.
#
# By default, `dc.load()` resamples pixel values using "nearest neighbour" resampling, which allocates each new pixel with the value of the closest input pixel.
# Depending on the type of data and the analysis being run, this may not be the most appropriate choice (e.g. for continuous data).
#
# The `resampling` parameter in `dc.load()` allows you to choose a custom resampling method from the following options:
#
# ```
# "nearest", "cubic", "bilinear", "cubic_spline", "lanczos",
# "average", "mode", "gauss", "max", "min", "med", "q1", "q3"
# ```
#
# The example cell below requests that all loaded data is resampled using "average" resampling:
# +
# Note the additional `resampling` parameter
ds_averageresampling = dc.load(product="ga_s2a_ard_nbar_granule",
measurements=["nbar_red", "nbar_green", "nbar_blue"],
time=("2018-01-01", "2018-01-07"),
x=(356895, 333715),
y=(5729345, 5744446),
output_crs="EPSG:28355",
crs="EPSG:28355",
resolution=(-250, 250))
print(ds_averageresampling)
# -
# Python dictionaries can be used to request different sampling methods for different measurements.
# This can be particularly useful when some measurements contain contain categorical data which require resampling methods such as "nearest" or "mode" that do not modify the input pixel values.
#
# The example cell below specifies `resampling={"nbar_red": "nearest", "*": "average"}`, which implements "nearest" neighbour resampling for the `nbar_red` satellite band only. `"*": "average"` will apply "average" resampling for all other satellite bands:
#
# +
ds_customresampling = dc.load(product="ga_s2a_ard_nbar_granule",
measurements=["nbar_red", "nbar_green", "nbar_blue"],
time=("2018-01-01", "2018-01-07"),
x=(356895, 333715),
y=(5729345, 5744446),
output_crs="EPSG:28355",
crs="EPSG:28355",
resolution=(-250, 250),
resampling={"nbar_red": "nearest", "*": "average"})
print(ds_customresampling)
# -
# > For more information about spatial resampling methods, see the [following guide](https://rasterio.readthedocs.io/en/stable/topics/resampling.html)
# ## Loading data using the query dictionary syntax
# It is often useful to re-use a set of query parameters to load data from multiple products.
# To achieve this, load data using the "query dictionary" syntax.
# This involves placing the query parameters inside a Python dictionary object which can be re-used for multiple data loads:
query = {"x": (145.1, 145.2),
"y": (-38.4, -38.5),
"time": ("2018-01-01", "2018-01-07"),
"crs": "epsg:4326",
"output_crs": "epsg:4326",
"resolution": (-0.01, 0.01),
"measurements": ["nbar_red", "nbar_green", "nbar_blue"]}
# The query dictionary object can be added as an input to `dc.load()`.
#
# > The `**` syntax below is Python's "keyword argument unpacking" operator.
# This operator takes the named query parameters listed in the query dictionary (e.g. `"x": (145.1, 145.2)`), and "unpacks" them into the `dc.load()` function as new arguments.
# For more information about unpacking operators, refer to the [Python documentation](https://docs.python.org/3/tutorial/controlflow.html#unpacking-argument-lists)
# +
ds = dc.load(product="ga_s2a_ard_nbar_granule",
**query)
print(ds)
# -
# After specifying the reusable query, it can be easily used to load data from a different product.
# The example cell below loads Sentinel-2B data for the same extent, time, output CRS and resolution as the previously loaded Sentinel-2A data:
# +
ds_s2b = dc.load(product="ga_s2b_ard_nbar_granule",
**query)
print(ds_s2b)
# -
# ## Other helpful tricks
# ### Adding a progress bar
# When loading large amounts of data, it can be useful to view the progress of the data load.
# The `progress_cbk` parameter in `dc.load()` adds a progress bar that indicates how the load is progressing:
#
# 
#
# The example cell below loads a full month of data (December 2017) from the `ga_s2a_ard_nbar_granule` product with a progress bar:
# +
query = {"x": (356895, 333715),
"y": (5729345, 5744446),
"time": ("2017-12"),
"crs": "epsg:28355",
"output_crs": "epsg:28355",
"resolution": (-250, 250)}
ds_progress = dc.load(product="ga_s2a_ard_nbar_granule",
measurements=["nbar_red", "nbar_green", "nbar_blue"],
progress_cbk=with_ui_cbk(),
**query)
print(ds_progress)
# -
# ## Recommended next steps
#
# To continue working through the notebooks in this beginner's guide, the following notebooks are designed to be worked through in the following order:
#
# 1. [Jupyter Notebooks](01_Jupyter_notebooks.ipynb)
# 2. [Digital Earth Australia](02_DEA.ipynb)
# 3. [Products and measurements](03_Products_and_measurements.ipynb)
# 4. **Loading data (this notebook)**
# 5. [Plotting](05_Plotting.ipynb)
# 6. [Performing a basic analysis](06_Basic_analysis.ipynb)
# 7. [Introduction to Numpy](07_Intro_to_numpy.ipynb)
# 8. [Introduction to Xarray](08_Intro_to_xarray.ipynb)
# 9. [Parallel processing with Dask](09_Parallel_processing_with_dask.ipynb)
# ***
# ## Additional information
#
# **License:** The code in this notebook is licensed under the [Apache License, Version 2.0](https://www.apache.org/licenses/LICENSE-2.0).
# Digital Earth Australia data is licensed under the [Creative Commons by Attribution 4.0](https://creativecommons.org/licenses/by/4.0/) license.
#
# **Contact:** If you need assistance, please review the FAQ section and support options on the [EY Data Science platform](https://datascience.ey.com/).
|
notebooks/01_Beginners_guide/04_Loading_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# +
library(caret, quiet = TRUE)
library(base64enc)
library(httr, quiet = TRUE)
library(mlbench)
# -
# # Build a Model
# +
# a character vector specifying the type of processing.
# Possible values are
# "BoxCox", "YeoJohnson", "expoTrans", "center", "scale", "range",
# "knnImpute", "bagImpute", "medianImpute", "pca", "ica", "spatialSign",
# "corr", "zv", "nzv", and "conditionalX"
data(BostonHousing)
BostonHousing$chas = as.numeric(BostonHousing$chas)
set.seed(1960)
BostonHousing$crim <- ifelse(BostonHousing$crim > 0.5, NA, BostonHousing$crim)
BostonHousing$age <- ifelse(BostonHousing$age > 93, NA, BostonHousing$age)
dataset = BostonHousing[, -14]
create_model = function() {
model <- train(medv ~ ., data = BostonHousing, method = "rpart",
na.action = na.pass,
preProcess=c("medianImpute"))
return(model)
}
# -
summary(BostonHousing)
model = create_model()
# cat(model$feature_names)
# print(model)
pred_labels <- predict(model, BostonHousing[, -14] , type="raw", na.action = na.pass)
df = data.frame(BostonHousing[,14])
names(df) = c("medv")
df$Estimator = pred_labels
df$Error = df$Estimator - df$medv
MAPE = mean(abs(df$Error / df$medv))
summary(df)
MAPE
# # SQL Code Generation
# +
test_ws_sql_gen = function(mod) {
WS_URL = "https://sklearn2sql.herokuapp.com/model"
WS_URL = "http://localhost:1888/model"
model_serialized <- serialize(mod, NULL)
b64_data = base64encode(model_serialized)
data = list(Name = "xgboost_test_model", SerializedModel = b64_data , SQLDialect = "postgresql" , Mode="caret")
r = POST(WS_URL, body = data, encode = "json")
# print(r)
content = content(r)
# print(content)
lSQL = content$model$SQLGenrationResult[[1]]$SQL # content["model"]["SQLGenrationResult"][0]["SQL"]
return(lSQL);
}
# -
lModelSQL = test_ws_sql_gen(model)
cat(lModelSQL)
# # Execute the SQL Code
library(RODBC)
conn = odbcConnect("pgsql", uid="db", pwd="db", case="nochange")
odbcSetAutoCommit(conn , autoCommit = TRUE)
# +
df_sql = dataset
names(df_sql) = sprintf("Feature_%d",0:(ncol(df_sql)-1))
df_sql$KEY = seq.int(nrow(dataset))
sqlDrop(conn , "INPUT_DATA" , errors = FALSE)
sqlSave(conn, df_sql, tablename = "INPUT_DATA", verbose = FALSE)
# df_sql
# -
colnames(df_sql)
# odbcGetInfo(conn)
# sqlTables(conn)
df_sql_out = sqlQuery(conn, lModelSQL)
head(df_sql_out[order(df_sql_out$KEY),])
# +
#df_sql_out
# -
# # R RPART Output
# +
estimator = predict(model, dataset, type = "raw", na.action = na.pass)
df_r_out = data.frame(estimator)
names(df_r_out) = c("Estimator")
df_r_out$KEY = seq.int(nrow(dataset))
head(df_r_out)
# -
# # Compare R and SQL output
df_merge = merge(x = df_r_out, y = df_sql_out, by = "KEY", all = TRUE, , suffixes = c("_1","_2"))
head(df_merge)
df_merge$Error = df_merge$Estimator_1 - df_merge$Estimator_2
df_merge$AbsError = abs(df_merge$Error)
head(df_merge)
df_merge_largest_errors = df_merge[df_merge$AbsError > 0.0001,]
df_merge_largest_errors
stopifnot(nrow(df_merge_largest_errors) == 0)
summary(df_sql_out)
summary(df_r_out)
summary(df_merge)
model$finalModel
prep = model$preProcess
model
prep$method
prep$median
|
doc/preprocess/Impute/caret2sql-medianImpute-rpart-boston.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Input to Chempy
# *Chempy* was developed with the intention to flexibly test all the assumptions going into chemical evolution modeling. Here we give a range of input parameters that can be played around with in *Chempy*
# %pylab inline
from Chempy.parameter import ModelParameters
a = ModelParameters()
# ## Star formation rate (SFR)
# Determines how many stars a formed at a specific time of the simulation
# +
# We load the SFR class
from Chempy.sfr import SFR
# Its initialised with t_0, t_end, and number of time-steps
basic_sfr = SFR(0,13.5,136)
# Then we load it with its default parameters
getattr(basic_sfr, a.basic_sfr_name)(S0 = a.S_0 * a.mass_factor,a_parameter = a.a_parameter, loc = a.sfr_beginning, scale = a.sfr_scale)
# +
# Here a list of already implemented SFR functions
print('these SFR functions are already implemented, see source/sfr.py')
print(a.basic_sfr_name_list)
# The SFR should always sum to 1 if you want to make your own SFR function
print('the sfr sums to 1')
# Plot the default SFR function (gamma function) with different SFR_peak parameters
for sfr_scale in [2.0,3.5,5.0]:
basic_sfr = SFR(a.start,a.end,136)
getattr(basic_sfr, 'gamma_function')(S0 = a.S_0 * a.mass_factor,a_parameter = a.a_parameter, loc = a.sfr_beginning, scale = sfr_scale)
plt.plot(basic_sfr.t,basic_sfr.sfr, label = 'SFR peak at %.1f' %(sfr_scale))
print(sum(basic_sfr.sfr)*basic_sfr.dt)
plt.legend()
plt.xlabel('time in Gyr')
# -
# ## Infall
# infall of gas from the corona into the ISM (usually diluting the ISM gas).
# In *Chempy* the infall can also be prescribed (you will need to make sure that always enough gas for star formation is available), or you can relate the infall to the star formation, e.g. via the Kennicut-Schmidt law.
# +
# Initialising the infall
from Chempy.infall import INFALL
basic_infall = INFALL(np.copy(basic_sfr.t),np.copy(basic_sfr.sfr))
getattr(basic_infall, 'sfr_related')()
# +
# SFR_related infall will be calculated during the Chempy run according to the needed gas mass
basic_infall.infall
# +
# But the infall can also be prescribed here we use the exponential infall:
basic_infall = INFALL(np.copy(basic_sfr.t),np.copy(basic_sfr.sfr))
getattr(basic_infall, 'exponential')((-0.15,0.,0.9))
# And compare it to the SFR
print(sum(basic_infall.sfr)*basic_sfr.dt)
print(sum(basic_infall.infall)*basic_sfr.dt)
plt.plot(basic_infall.t,basic_infall.sfr, label = 'SFR')
plt.plot(basic_infall.t,basic_infall.infall, label = 'Infall')
plt.legend()
# -
# ## stellar initial mass function (IMF)
# defines the distribution of stellar masses formed in a starburst.
# +
# We initialise the IMF class and plot it for different IMFs
from Chempy.imf import IMF
basic_imf = IMF(a.mmin,a.mmax,a.mass_steps)
getattr(basic_imf, a.imf_type_name)((a.chabrier_para1,a.chabrier_para2,a.high_mass_slope))
plt.plot(basic_imf.x,basic_imf.dn, label ='Chabrier')
basic_imf = IMF(a.mmin,a.mmax,a.mass_steps)
getattr(basic_imf, 'salpeter')((2.35))
plt.plot(basic_imf.x,basic_imf.dn, label = 'Salpeter')
basic_imf = IMF(a.mmin,a.mmax,a.mass_steps)
getattr(basic_imf, 'normed_3slope')((-1.3,-2.2,-2.7,0.5,1.0))
plt.plot(basic_imf.x,basic_imf.dn, label = 'Kroupa')
plt.yscale('log')
plt.xscale('log')
plt.xlim((0.07,110))
plt.legend()
# -
# ### Mass range of exploding CC-SNe
# The Kroupa IMF only has 8% of stars exploding as CC-SNe whereas Salpeter has 12%.
#
# +
# We calculate the Kroupa IMF mass fractions
print(basic_imf.imf_mass_fraction(8.,100.))
print(basic_imf.imf_mass_fraction(1.,8.))
print(basic_imf.imf_mass_fraction(0.08,1.))
# +
# And compare the mass fraction exploding as CC-SN to the Salpeter IMF
basic_imf = IMF(a.mmin,a.mmax,a.mass_steps)
getattr(basic_imf, 'salpeter')((2.35))
print(basic_imf.imf_mass_fraction(8.,100.))
# -
# IMF sampling
# ---------------
# The IMF can also be realized *stochastically*. Albeit each reaslization is new and it takes more time than the analytic version.
# +
# We sample the Chabrier IMF for 3 different masses:
for item in [1e1,1e3,1e5]:
basic_imf = IMF(a.mmin,a.mmax,a.mass_steps)
getattr(basic_imf, a.imf_type_name)((a.chabrier_para1,a.chabrier_para2,a.high_mass_slope))
basic_imf.stochastic_sampling(item)
plt.plot(basic_imf.x,basic_imf.dn, label ='SSP with %dMsun' %(item))
plt.title('Chabrier IMF realized for different SSP masses')
plt.yscale('log')
plt.xscale('log')
plt.xlim((0.07,200))
plt.ylabel('dn/dm')
plt.xlabel('Mass in Msun')
plt.legend()
# This looks a bit weired in v 0.2. needs checking
# -
# ## Stellar lifetimes
# in order to calculate when a star is dying and returns its newly produced elements into the ISM. The lifetimes are to zeroth order *mass* dependent and to first order *metallicity* dependent
# +
# Here we show the difference of Lifetime calculations
from Chempy.weighted_yield import lifetime_Argast, lifetime_Raiteri
metallicity = 0.015
plt.plot(basic_imf.x,lifetime_Argast(basic_imf.x,metallicity), label = 'Argast')
plt.plot(basic_imf.x,lifetime_Raiteri(basic_imf.x,metallicity), label = 'Raiteri')
plt.yscale('log')
plt.xscale('log')
plt.ylabel('Age in Gyr')
plt.xlabel('Mass in Msun')
plt.xlim((0.07,200))
plt.legend()
# +
# And here the difference of the lifetimes with metallicity
for metallicity in [0.00015,0.0015,0.015]:
plt.plot(basic_imf.x,lifetime_Argast(basic_imf.x,metallicity), label = 'Argast Z=%f' %(metallicity))
plt.yscale('log')
plt.xscale('log')
plt.ylabel('Age in Gyr')
plt.xlabel('Mass in Msun')
plt.xlim((0.07,200))
plt.legend()
# -
|
tutorials/3-Chempy_inputs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
os.environ['CHURN_DB']='churn'
os.environ['CHURN_DB_USER']='user'
os.environ['CHURN_DB_PASS']='<PASSWORD>'
run run_churn_listing.py --chapter 2 --listing 1
|
listings/py/run_churn_listing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib notebook
# Import modules
import math
import numpy as np
import matplotlib.pyplot
from matplotlib.ticker import FormatStrFormatter
import csv
from pyne import serpent
from pyne import nucname
from scipy.stats.stats import pearsonr
import scipy.integrate as inte
dir_pre='/home/andrei2/Desktop/git/publications/2020-rykhl-dissertation/data/spectrum/'
det0 = serpent.parse_det(dir_pre+'bol/tap_spectrum.serpent_det0.m')
#det0 = serpent.parse_det(dir_pre+'bol/scale_grid/tap_spectrum.serpent_det0.m')
det10 = serpent.parse_det(dir_pre+'eol/tap_spectrum_eol_ben.serpent_det0.m')
#det10 = serpent.parse_det('/home/andrei2/Desktop/git/msr-neutronics/RobertsonMSBR/neutronics_paper/reproc/eoc/core_det0.m')
energy_grid = det0['DETavrgE']
spectrum_grid = det0['DETavrg']
spectrum_grid2 = det10['DETavrg']
energy = energy_grid[:,2]
energy2 = det10['DETavrgE'][:,2]
flux_spectrum = spectrum_grid[:,10]
lat_v = 2*155*2*155*2*180
flux_bol = 1e-13*spectrum_grid[:,10]/lat_v #1.490277013
#flux_bol = spectrum_grid[:,10]/inte.trapz(spectrum_grid[:,10],energy) #1.490277013
flux_eol = 1e-13*spectrum_grid2[:,10]/lat_v
#flux_eol = spectrum_grid2[:,10]/inte.trapz(spectrum_grid2[:,10], energy2)
print(len(flux_bol), len(flux_eol))
# -
# # Read data fron Ben's paper digitized
# +
fben_bol = dir_pre + 'bol/ben_full_BOL.csv'
#fben_bol = dir_pre + 'bol/ben_shift_unit_bol.csv'
fben_eol = dir_pre + 'eol/ben_full_EOL.csv'
ene_grid_bol = []
ben_flux_bol = []
ene_grid_eol = []
ben_flux_eol = []
with open(fben_bol, 'r') as file:
reader = csv.reader(file)
for row in reader:
ene_grid_bol.append(float(row[0]))
ben_flux_bol.append(1e-13*float(row[1]))
with open(fben_eol, 'r') as file:
reader = csv.reader(file)
for row in reader:
ene_grid_eol.append(float(row[0]))
ben_flux_eol.append(1e-13*float(row[1]))
# +
# Initialize figure
fig_1 = matplotlib.pyplot.figure(1, figsize=[6,5])
ax1 = fig_1.add_subplot(111)
ax1.grid(True)
ax1.set_xlabel('Energy [MeV]', fontsize=12)
ax1.set_ylabel(r'flux per unit lethargy [$\times 10^{13}$ n/cm$^2\cdot s$]', fontsize=12)
ax1.tick_params('y', labelsize=12)
ax1.yaxis.set_major_formatter(FormatStrFormatter('%.1f'))
ax1.tick_params('x', labelsize=12)
#ax1.set_ylim(0,7.0)
ax1.set_xlim(1e-8,10)
ax1.semilogx(energy, flux_bol, '-', label='BOL (current work)',
color='#ff8100', linewidth=1.1, alpha=0.7)
#ax1.semilogx(energy2, 1.490277013*spectrum_grid2[:,10]/lat_v, '-', label='EOL (current work)',
# color='b', linewidth=1.3)
ax1.semilogx(ene_grid_bol, ben_flux_bol, '-', label='BOL (Betzler et al. 2017)',
color='blue', linewidth=1.1, alpha=0.7)
#ax1.semilogx(ene_grid_eol, ben_flux_eol, ':', label='EOL (Betzler et al. 2017)',
# color='g', linewidth=0.9)
ax1.legend(loc=0, fontsize=12)
#ax2=ax1.twinx()
#ax2.loglog(energy_grid_xe, xe_capture_xs, 'o-',markevery=[100,210],fillstyle='none',color='r',label='Xe135')
#ax2.loglog(energy_grid_i, i_capture_xs, '*--',markevery=[92,125],fillstyle='none',color='r',label='I135')
#ax2.set_ylabel('Capture cross-section [b]', color='r', fontsize=14)
#ax2.tick_params('y', colors='r', labelsize=12)
#ax2.set_xlim(1e-9,12)
#ax2.legend(loc=7, fontsize=12)
#ax1.set_title('Neutron spectrum normalized per unit lethargy for \n PWR/TAP vs posions capture cross-section\n')
fig_1.show()
#fig_1.savefig('/home/andrei2/Desktop/git/publications/2020-rykhl-dissertation/dissertation/figures/ch4/ben_spec_bol.png',bbox_inches='tight', dpi=900)
print(np.amax(1e-13*spectrum_grid[:,10]/lat_v))
print ("Correlation between neutron Betzler and current work is "
+ str(pearsonr(flux_bol,ben_flux_bol[:-1]) ) )
delta = 100*abs(inte.trapz(flux_bol,energy)-inte.trapz(ben_flux_bol,ene_grid_bol))/inte.trapz(ben_flux_bol,ene_grid_bol)
print('Relative difference in total flux between Betzler and current work %f %%' %delta)
# +
# Initialize figure
fig_2 = matplotlib.pyplot.figure(2, figsize=[6,5])
ax1 = fig_2.add_subplot(111)
ax1.grid(True)
ax1.set_xlabel('Energy [MeV]', fontsize=12)
ax1.set_ylabel(r'flux per unit lethargy [$\times 10^{13}$ n/cm$^2\cdot s$]', fontsize=12)
ax1.tick_params('y', labelsize=12)
ax1.tick_params('x', labelsize=12)
#ax1.set_ylim(0,4e+13)
ax1.set_xlim(1e-8,10)
ax1.semilogx(energy2, flux_eol, '-', label='EOL (current work)',
color='#ff8100', linewidth=1.1, alpha=0.7)
ax1.semilogx(ene_grid_eol, ben_flux_eol, '-', label='EOL (Betzler et al. 2017)',
color='blue', linewidth=1.1, alpha=0.6)
ax1.legend(loc=0, fontsize=12)
#ax2=ax1.twinx()
#ax2.loglog(energy_grid_xe, xe_capture_xs, 'o-',markevery=[100,210],fillstyle='none',color='r',label='Xe135')
#ax2.loglog(energy_grid_i, i_capture_xs, '*--',markevery=[92,125],fillstyle='none',color='r',label='I135')
#ax2.set_ylabel('Capture cross-section [b]', color='r', fontsize=14)
#ax2.tick_params('y', colors='r', labelsize=12)
#ax2.set_xlim(1e-9,12)
#ax2.legend(loc=7, fontsize=12)
#ax1.set_title('Neutron spectrum normalized per unit lethargy for \n PWR/TAP vs posions capture cross-section\n')
fig_2.show()
#fig_2.savefig('/home/andrei2/Desktop/git/publications/2020-rykhl-dissertation/dissertation/figures/ch4/ben_spec_eol.png',bbox_inches='tight', dpi=900)
#print ("Correlation between neutron Betzler and current work is "
# + str(pearsonr(flux_eol,ben_flux_eol[:-1]) ) )
delta_eol = 100*abs(inte.trapz(flux_eol,energy2)-inte.trapz(ben_flux_eol,ene_grid_eol))/inte.trapz(ben_flux_eol,ene_grid_eol)
print('Relative difference in total flux between Betzler and current work %f %%' %delta_eol)
|
data/scripts/safety_analysis/spectrum_compare_with_ben_newt_mulitgroup.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Built-in read/write functions
# create our text file to read
with open('textfile.txt', mode='w') as f:
f.writelines(['This is a text file.\n', 'Now you can read it!'])
# open a file and read the contents
file = open(file='textfile.txt', mode='r')
text = file.readlines()
text # remember if our last line is a variable, jupyter notebook will print out that variable
# this is the file object
file
# the file is 'open' until we close it.
file.close()
# +
# the 'with' context will automatically close the file once we are out of the 'with' section
with open(file='textfile.txt', mode='r') as f:
text = f.readlines()
text
# +
# the read function reads the entire file at once
with open(file='textfile.txt', mode='r') as f:
text = f.read()
print(text)
# -
# remember we can take a subset of strings like this
text[:10]
# writing to a file
# open the file in a text editor to see the results, or read it with Python
with open(file='writetest.txt', mode='w') as f:
f.write('testing writing out')
# writing a list of text to a file
# open the file in a text editor or read it through Python to see the results
text_lines = ['This is text for testing writing.', 'Now you can write to a file!']
with open(file='writetest2.txt', mode='w') as f:
f.writelines(text_lines)
# ## JSON
import json
data_dictionary = {'books': 12, 'articles': 100, 'subjects': ['math', 'programming', 'data science']}
json_string = json.dumps(data_dictionary)
json_string
data_dict = json.loads(json_string)
data_dict
with open('reading.json', 'w') as f:
json.dump(data_dictionary, f)
with open('reading.json') as f:
loaded_data = json.load(f)
loaded_data
# ## Credentials in a .py file
import credentials as creds
print(f'username: {creds.username}\npassword: {creds.password}')
# ## The pickle library
# pickle can be used for saving and loading raw Python objects.
# +
import pickle as pk
data_dictionary = {'books': 12, 'articles': 100, 'subjects': ['math', 'programming', 'data science']}
with open('readings.pk', 'wb') as f:
pk.dump(data_dictionary, f)
# +
with open('readings.pk', 'rb') as f:
data = pk.load(f)
print(data)
# -
# ## The joblib library
# We can also save and load data with joblib. First be sure to install it with `conda install -c conda-forge joblib -y` if you don't already have it installed. Joblib has extra features beyond pickle, such as compression, automatic opening and closing of files, and features to make saving/loading specific data (numpy arrays) faster. Pickle is often faster than joblib, except in special situations (which is why we didn't cover it in the book). This extra section is for your extra knowledge.
# +
import joblib
joblib.dump(value=data_dictionary, filename='readings.job', compress=True)
# -
data = joblib.load(filename='readings.job')
data
# We can time how long something takes with the magic command `%%timeit` in Jupyter Notebooks. Note that pickle is faster for saving and reading this dictionary.
# %%timeit
joblib.dump(value=data_dictionary, filename='readings.job', compress=True)
# %%timeit
with open('readings.pk', 'wb') as f:
pk.dump(data_dictionary, f)
# %%timeit
data = joblib.load(filename='readings.job')
# %%timeit
with open('readings.pk', 'rb') as f:
data = pk.load(f)
# We can see that for normal dictionaries, pickle is much faster for saving and loading than joblib.
# ## sqlite3
# When we install Python, we also install SQLite3. We can use it from within Python, but also from the command line. If we open a terminal and type `sqlite3`, it takes us to the SQLite shell. From the shell, we can run any SQLite command. For example, if we are in the directory with the chinook.db file from this GitHub repo (within the same folder that contains this notebook), we can type `.open chinook.db` to load the database. Then we can see the tables within the database with `.tables`. We can also connect to the database through Python and run commands as show below.
import sqlite3
connection = sqlite3.connect('chinook.db')
cursor = connection.cursor()
# list out tables -- .table does not work from Python sqlite3
cursor.execute("SELECT name FROM sqlite_master WHERE type='table';")
cursor.fetchall()
# get table information (column names, types, settings)
cursor.execute('PRAGMA table_info(artists);')
cursor.fetchall()
# SELECT the first 5 rows of artists
cursor.execute('SELECT * FROM artists LIMIT 5;')
cursor.fetchall()
# especially for longer queries, it helps to format them like this, with each SQL command on a separate line
query = """
SELECT *
FROM artists
LIMIT 5;
"""
cursor.execute(query)
cursor.fetchall()
# get table information (column names, types, settings)
cursor.execute('PRAGMA table_info(invoices);')
cursor.fetchall()
# save table column names in a list
cursor.execute('PRAGMA table_info(invoices);')
results = cursor.fetchall()
column_names = [r[1] for r in results]
column_names
cursor.execute('SELECT * FROM invoices LIMIT 5;')
cursor.fetchall()
# ORDER BY
cursor.execute('SELECT Total, InvoiceDate from invoices ORDER BY Total DESC LIMIT 5;')
cursor.fetchall()
# WHERE statement
cursor.execute('SELECT Total, BillingCountry from invoices WHERE BillingCountry == "Canada" LIMIT 5;')
cursor.fetchall()
# WHERE using an inserted argument
cursor.execute('SELECT Total, BillingCountry from invoices WHERE BillingCountry == ? LIMIT 5;', ('Canada',))
cursor.fetchall()
# LIKE command
cursor.execute('SELECT Total, BillingCountry from invoices WHERE BillingCountry LIKE "%can%" LIMIT 5;')
cursor.fetchall()
# GROUP BY statement
cursor.execute('SELECT SUM(Total), BillingCountry from invoices GROUP BY BillingCountry ORDER BY SUM(Total) DESC LIMIT 5;')
cursor.fetchall()
# examine column names for invoice_items table
cursor.execute('PRAGMA table_info(invoice_items);')
cursor.fetchall()
# examine a sample of the data
cursor.execute('SELECT * FROM invoice_items LIMIT 5;')
cursor.fetchall()
# aliases can be used to rename columns and tables
# according to some SQL style guides, it's not best practice to alias a table
cursor.execute('SELECT i.TrackID as tid, i.UnitPrice as up FROM invoice_items as i LIMIT 5;')
cursor.fetchall()
# DISTINCT
cursor.execute('SELECT DISTINCT UnitPrice FROM invoice_items;')
cursor.fetchall()
# JOIN
# get tracks that were purchased and combine with the country
query = """
SELECT invoices.BillingCountry, invoice_items.TrackId
FROM invoices
JOIN invoice_items
ON invoices.InvoiceId = invoice_items.InvoiceId
LIMIT 5;
"""
cursor.execute(query)
cursor.fetchall()
# get number of purchased tracks for each track by country, sorted by the top-most purchased
query = """
SELECT invoice_items.TrackId, COUNT(invoice_items.TrackId), invoices.BillingCountry
FROM invoices
JOIN invoice_items
ON invoices.InvoiceId = invoice_items.InvoiceId
GROUP BY invoices.BillingCountry
ORDER BY COUNT(invoice_items.TrackId) DESC
LIMIT 5;
"""
cursor.execute(query)
cursor.fetchall()
# multiple JOINs
query = """
SELECT tracks.Name, COUNT(invoice_items.TrackId), invoices.BillingCountry
FROM invoices
JOIN invoice_items
ON invoices.InvoiceId = invoice_items.InvoiceId
JOIN tracks
ON tracks.TrackId = invoice_items.TrackId
GROUP BY invoices.BillingCountry
ORDER BY COUNT(invoice_items.TrackId) DESC
LIMIT 5;
"""
cursor.execute(query)
cursor.fetchall()
# this same command as above can also be done with a subquery like this, but is easier with multiple joins
query = """
SELECT tracks.Name, invoice_merged.track_count, invoice_merged.BillingCountry
FROM
(SELECT ii.TrackId, COUNT(ii.TrackId) as track_count, i.BillingCountry
FROM invoices as i
JOIN invoice_items as ii
ON i.InvoiceId = ii.InvoiceId
GROUP BY BillingCountry) as invoice_merged
JOIN tracks
ON tracks.TrackId = invoice_merged.TrackId
ORDER BY track_count DESC
LIMIT 5;
"""
cursor.execute(query)
cursor.fetchall()
# be sure to close the connection when done
connection.close()
# ### Storing data in a sqlite3 database
# hypothetical book sales data
book_data = [('12-1-2020', 'Practical Data Science With Python', 19.99, 1),
('12-15-2020', 'Python Machine Learning', 27.99, 1),
('12-17-2020', 'Machine Learning For Algorithmic Trading', 34.99, 1)]
# CREATE and INSERT
connection = sqlite3.connect('book_sales.db')
cursor = connection.cursor()
# Create table
cursor.execute('''CREATE TABLE IF NOT EXISTS book_sales
(date text, book_title text, price real, quantity real)''')
# the table is now there
cursor.execute("SELECT name FROM sqlite_master WHERE type='table';")
cursor.fetchall()
# Insert a row of data
cursor.execute("INSERT INTO book_sales VALUES (?, ?, ?, ?)", book_data[0])
cursor.execute('SELECT * FROM book_sales ;')
cursor.fetchall()
# Save the changes with .commit()
# Without this line, the inserted data will not be saved in the database after we close the connection
connection.commit()
# insert several records at a time
cursor.executemany('INSERT INTO book_sales VALUES (?, ?, ?, ?)', book_data[1:])
# don't forget to save the changes
connection.commit()
cursor.execute('SELECT * FROM book_sales;')
cursor.fetchall()
connection.close()
# ## SQLAlchemy
from sqlalchemy import create_engine
engine = create_engine('sqlite:///book_sales.db')
connection = engine.connect()
result = connection.execute("select * from book_sales")
result
list(result)
for row in result:
print(row['date'])
result = connection.execute("select * from book_sales")
for row in result:
print(row['date'])
# be sure to close the connection when finished
connection.close()
# we can also use the with clause to automatically close the connection
with engine.connect() as connection:
result = connection.execute("select * from book_sales")
for row in result:
print(row)
connection.closed
# the connection is closed from the 'with' statement, so we can't use it
# notice in the middle and at the bottom of the error, it says 'This Connection is closed'
result = connection.execute("select * from book_sales")
# +
from sqlalchemy import MetaData, Table
metadata = MetaData(engine)
book_sales = Table('book_sales', metadata, autoload=True)
conn = engine.connect()
# -
res = conn.execute(book_sales.select())
for r in res:
print(r)
ins = book_sales.insert().values(book_title='machine learining', price='10.99')
conn.execute(ins)
res = conn.execute(book_sales.select())
for r in res:
print(r)
|
3-Chapter-3/Chapter_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
df = pd.read_pickle('parking_eda.pkle')
df['total'] = 1
df.head()
df.ticket_issue_datetime.sort_values()
violation_state_df = df.groupby(['violation_code', 'rp_plate_state']).holiday.count().reset_index()
# +
# violation_state_df.sort_values('holiday', ascending=False)
# -
# http://opendata.dc.gov/datasets/aa514416aaf74fdc94748f1e56e7cc8a_0.csv
dc_address_df = pd.read_csv('../data/dc_address_id.csv', encoding="utf-8-sig")
dc_address_df.columns = [col.lower() for col in dc_address_df.columns]
dc_address_df
dc_address_df_selected = dc_address_df[['address_id', 'x', 'y', 'fulladdress']]
# +
# +
fines_df = pd.read_csv('../cleaned_data/fine.csv', encoding="utf-8-sig")
fines_df.columns = [col.lower() for col in fines_df.columns]
fines_df.drop('shortdesc', axis=1, inplace=True)
fines_df.rename(columns={'code': 'violation_code'}, inplace=True)
fines_df.head(1)
# -
# pd.groupby(b,by=[b.index.month,b.index.year])
df_address_id = df.groupby(['address_id']).total.count().reset_index()
df_address_id = df_address_id.sort_values('total', ascending=False).reset_index(drop=True)
df_address_id = df_address_id.merge(dc_address_df_selected, on='address_id')
df_address_id.to_csv('../cleaned_data/most_tickets_by_address_id_all_loaded_data.tsv', sep='\t', index=False)
df_address_id
# +
# vehicle versus everything else
# -
violation_code_by_state_df = df.groupby(['violation_code', 'rp_plate_state']).total.count().reset_index()
violation_code_by_state_df = violation_code_by_state_df.sort_values('total', ascending=False).reset_index(drop=True)
violation_code_by_state_df = violation_code_by_state_df.merge(fines_df, on='violation_code')
violation_code_by_state_df['estimated_fine_total'] = violation_code_by_state_df.total * violation_code_by_state_df.fine
violation_code_by_state_df.to_csv('../cleaned_data/violation_code_by_state_play_with_fine_info.tsv', sep='\t', index=False)
holiday_df = df[df.holiday==True]
# +
holiday_df_violation_code = holiday_df.groupby(['violation_code', 'rp_plate_state']).total.count().reset_index()
holiday_df_violation_code = holiday_df_violation_code.sort_values('total', ascending=False).reset_index(drop=True)
holiday_df_violation_code = holiday_df_violation_code.merge(fines_df, on='violation_code')
holiday_df_violation_code['estimated_fine_total'] = holiday_df_violation_code.total * holiday_df_violation_code.fine
holiday_df_violation_code.to_csv('../cleaned_data/on_holiday_violation_code_by_state_play_with_fine_info.tsv', sep='\t', index=False)
# +
# -
# +
body_style_df_violation_code = df.groupby(['violation_code', 'body_style']).total.count().reset_index()
body_style_df_violation_code = body_style_df_violation_code.sort_values('total', ascending=False).reset_index(drop=True)
body_style_df_violation_code = body_style_df_violation_code.merge(fines_df, on='violation_code')
body_style_df_violation_code['estimated_fine_total'] = body_style_df_violation_code.total * body_style_df_violation_code.fine
body_style_df_violation_code.to_csv('../cleaned_data/body_style_violation_code_with_fine_info.tsv', sep='\t', index=False)
# -
# +
violation_code_df = df.groupby(['violation_code']).total.count().reset_index()
violation_code_df = violation_code_df.sort_values('total', ascending=False).reset_index(drop=True)
violation_code_df = violation_code_df.merge(fines_df, on='violation_code')
violation_code_df['estimated_fine_total'] = violation_code_df.total * violation_code_df.fine
# violation_code_df
violation_code_df.to_csv('../cleaned_data/violation_code_with_fine_info.tsv', sep='\t', index=False)
# -
|
notebooks/old/Parking Violations EDA with Address_id and fine data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Task 14 - Parameter Study Optimisation
#
# The previous task sampled from the available parameters and aimed to cover the parameter space efficiently. This task uses Scikit-opt Gaussian Processing to home-in on the optimal solution. Optimisation is even more efficient as it removes the need to sample the entire parameter space and, instead, focuses on the area of interest.
#
# In optimisation algorithms it is common to see a combination of exploration and exploitation to find the optimal value.
# +
# Install dependencies
import json
import numpy as np
import pandas as pd
import adaptive
import holoviews
import ipywidgets
import nest_asyncio
import plotly.graph_objects as go
from tqdm import tqdm
from pathlib import Path
from skopt import gp_minimize
from skopt.utils import dump, load
from scipy.interpolate import griddata
from openmc_model import objective
adaptive.notebook_extension()
nest_asyncio.apply()
# method for saving results in json file
def output_result(filepath, result):
filename = filepath
Path(filename).parent.mkdir(parents=True, exist_ok=True)
with open(filename, mode="w", encoding="utf-8") as f:
json.dump(result, f, indent=4)
# -
# The following codes run neutronics simulations using a simple pre-defined model. We will compare optimised simulations with simple parameter sweeps.
# ## 1D Optimisation
#
# The code below runs a simple parameter sweep to obtain TBR as a function of breeder to multiplier ratio in a 1D parameter sweep. These results are the 'true' TBR values across the parameter space that we will compare our optimised results with.
# +
# get_true_values_1D
tbr_values = []
for breeder_percent_in_breeder_plus_multiplier in tqdm(np.linspace(0, 100, 101)):
tbr_values.append({'breeder_percent_in_breeder_plus_multiplier':breeder_percent_in_breeder_plus_multiplier,
'tbr':-objective([breeder_percent_in_breeder_plus_multiplier])})
# results saved in json file
output_result("outputs/1d_tbr_values.json", tbr_values)
# -
# The next code block runs an optimised simulation using the same model, but will search the parameter space for where TBR is maximum. It does this by sampling the parameter space, fitting the results using Gaussian Processing and running a new simulation at the point where TBR is maximum according to the fitted data. If this process is iterated sufficiently, the simulations performed get closer and closer to the point across the parameter space where TBR is maximum.
# +
# get_optimised_values_1d
learner = adaptive.SKOptLearner(objective,
dimensions=[(0., 100.)],
base_estimator="GP",
acq_func="gp_hedge",
acq_optimizer="lbfgs",
)
runner = adaptive.Runner(learner, ntasks=1, goal=lambda l: l.npoints > 30)
runner.live_info()
runner.ioloop.run_until_complete(runner.task)
# results saved in json file
output_result("outputs/1d_optimised_values.json", dict(learner.data))
# -
# The next code block plots the 'true' simulation data and optimisation data on the same graph. This allows us to see how close the optimisation got to the true maximum TBR across the parameter space.
# +
# 1_plot_1d_optimisation
# Note, optimisation functions tend to minimise the value therefore there are a few negative signs in these scripts
# Loads true data for comparison
data = pd.read_json('outputs/1d_tbr_values.json')
x_data=data['breeder_percent_in_breeder_plus_multiplier']
fx=-data['tbr']
# Load optimisation data
with open('outputs/1d_optimised_values.json', 'r') as f: data = json.load(f).items()
x_vals = [i[0] for i in data]
tbr_vals = [-i[1] for i in data]
# Print max TBR from optimisation data
print('Maximum TBR of ', tbr_vals[-1], 'found with a breeder percent in breeder plus multiplier of ', x_vals[-1])
fig = go.Figure()
# Plot samples from optimsation points
fig.add_trace(go.Scatter(x = x_vals,
y = tbr_vals,
name="Samples from optimisation",
mode='markers',
marker=dict(color='red', size=10)
)
)
# Plot true function.
fig.add_trace(go.Scatter(name="True value (unknown)",
x = x_data,
y = [-i for i in fx],
mode='lines',
line = {'shape': 'spline'},
marker=dict(color='green')
)
)
fig.update_layout(title='Optimal breeder percent in breeder plus multiplier',
xaxis={'title': 'breeder percent in breeder plus multiplier', 'range': [0, 100]},
yaxis={'title': 'TBR', 'range': [0.1, 2]}
)
fig.show()
# -
# As shown, the optimisation samples are spread across the parameter space but are more dense towards the true TBR maximum . This shows how the optimisation homes-in on this point by repeatedly simulating and fitting data.
#
# To reach the true maximum TBR value, sufficient simulations must be performed so that the data trend across the parameter space evaluated to a sufficient accuracy. However, optimisation achieved this using fewer samples than the sweep of the entire parameter space as it focused on sampling the important areas of the space (101 sweep samples vs 30 optimised samples).
#
# This was a 1D problem, however, the same techniques can be applied to N-dimension problems but the number of simulations required increases. The next example is a 2D dimensional problem where the optimal breeder to multiplier ratio and enrichment are being found.
# ## 2D Optimisation
#
# The code below runs a simple parameter sweep to obtain TBR as a function of breeder to multiplier ratio and enrichment in a 2D parameter sweep. These results are the 'true' TBR values across the parameter space that we will compare our optimised results with.
# +
# get_true_values_2D
tbr_values = []
for breeder_percent_in_breeder_plus_multiplier in tqdm(np.linspace(0, 100, 20)):
for blanket_breeder_li6_enrichment in np.linspace(0, 100, 20):
tbr_values.append({'breeder_percent_in_breeder_plus_multiplier': breeder_percent_in_breeder_plus_multiplier,
'blanket_breeder_li6_enrichment': blanket_breeder_li6_enrichment,
'tbr': -objective([breeder_percent_in_breeder_plus_multiplier,
blanket_breeder_li6_enrichment])
})
# results saved in json file
output_result("outputs/2d_tbr_values.json", tbr_values)
# -
# The next code block runs an optimised simulation but searches the 2D parameter space for where TBR is maximum.
# +
# get_optimised_values_2d
# Uses adaptive sampling methods from task X to obtain starting points for the optimiser
learner = adaptive.Learner2D(objective, bounds=[(0, 100), (0, 100)])
runner = adaptive.Runner(learner, ntasks=1, goal=lambda l: l.npoints > 40)
runner.live_info()
runner.ioloop.run_until_complete(runner.task)
# Gaussian Processes based optimisation that returns an SciPy optimisation object
res = gp_minimize(objective, # the function to minimize
dimensions=[(0., 100.), (0., 100.)], # the bounds on each dimension of x
n_calls=40, # the number of evaluations of f
n_random_starts=0, # the number of random initialization points
verbose=True,
x0=[i for i in list(learner.data.keys())], # initial data from the adaptive sampling method
y0=list(learner.data.values()) # initial data from the adaptive sampling method
)
# saves 2d optimisation results in .dat file
dump(res, "outputs/2d_optimised_values.dat")
# -
# The next code block plots the true results and optimised results on the same 2D scatter graph.
# +
# 2d_plot_2d_optimisation_scatter.py
# load true data for comparison
data = pd.read_json('outputs/2d_tbr_values.json')
x=data['breeder_percent_in_breeder_plus_multiplier']
y=data['blanket_breeder_li6_enrichment']
z=data['tbr']
# Print max TBR from optimisation data
print('Optimal breeder_percent_in_breeder_plus_multiplier_ratio = ', res.x[0])
print('Optimal Li6 enrichment = ', res.x[1])
print('Maximum TBR = ', -res.fun)
fig = go.Figure()
fig.add_trace(go.Scatter3d(name='TBR values found during optimisation',
x=[x[0] for x in res.x_iters],
y=[x[1] for x in res.x_iters],
z=-res.func_vals,
mode='markers',
marker=dict(size=7)
)
)
fig.add_trace(go.Scatter3d(name='True values',
x=x,
y=y,
z=z,
mode='markers',
marker=dict(size=7)
)
)
fig.add_trace(go.Scatter3d(name='Maximum TBR value found',
x=[res.x[0]],
y=[res.x[1]],
z=[-res.fun],
mode='markers',
marker=dict(size=7)
)
)
fig.update_layout(title='Optimal Li6 enrichment and breeder percent in breeder plus multiplier',
scene={'yaxis': {'title': 'Li6 enrichment percent'},
'zaxis': {'title': 'breeder percent in breeder plus multiplier'},
'zaxis': {'title': 'TBR'}
}
)
fig.show()
# -
# As shown, the optimisation samples are spread across the parameter space but are more dense towards the true TBR maximum . This shows how the optimisation homes-in on this point by repeatedly simulating and fitting data. In this case, this is a 2D fitting.
#
# We can also produce a contour graph to show similar results.
# +
# 2_plot_2d_optimisation_contour
# Print max TBR from optimisation data
print('Optimal Li6 enrichment = ', res.x[0])
print('Optimal breeder percent in breeder plus multiplier = ', res.x[1])
print('Maximum TBR = ', -res.fun)
# creates a grid and interploates values on it
xi = np.linspace(0, 100, 100)
yi = np.linspace(0, 100, 100)
zi = griddata((x, y), z, (xi[None,:], yi[:,None]), method='linear')
fig = go.Figure()
# plots interpolated values as colour map plot
fig.add_trace(trace = go.Contour(
z=zi,
x=yi,
y=xi,
colorscale="Viridis",
opacity=0.9,
line=dict(width=0, smoothing=0.85),
contours=dict(
showlines=False,
showlabels=False,
size=0,
labelfont=dict(size=15,),
),
))
fig.add_trace(go.Scatter(name='TBR values found during optimisation',
x=[x[0] for x in res.x_iters],
y=[x[1] for x in res.x_iters],
hovertext=-res.func_vals,
hoverinfo="text",
marker={"size": 8},
mode='markers'
)
)
# This add the final optimal value found during the optimisation as a seperate scatter point on the graph
fig.add_trace(go.Scatter(name='Maximum TBR value found',
x=[res.x[0]],
y=[res.x[1]],
hovertext=[-res.fun],
hoverinfo="text",
marker={"size": 8},
mode='markers'
)
)
fig.update_layout(title='',
xaxis={'title': 'breeder percent in breeder plus multiplier', 'range':(-1, 101)},
yaxis={'title': 'blanket breeder li6 enrichment', 'range':(-1, 101)},
legend_orientation="h"
)
fig.show()
# -
# As show, the number of optimised simulations required to reach the area of parameter space where TBR is maximum is much lower than the number run in the sweep of the entire parameter space (400 sweep samples vs 40 optimised samples). Optimised simulations are, therefore, more efficient than sweeping the entire parameter space but a sufficiently high number are still needed to find the true maximum (or minimum) across the parameter space.
#
# **Learning Outcomes for Task 14:**
#
# - Introduction to methods of optimising neutronics results in 1D and 2D.
# - Appreciation that for high dimensional space approaches to reduce the amount of sampling are needed.
# - Understand that there are several factors that can be changed to increase TBR.
|
tasks/task_14_parameter_study_optimisation/parameter_study_optimisation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Advanced Lists
#
# In this series of lectures we will be diving a little deeper into all the methods available in a list object. These aren't officially "advanced" features, just methods that you wouldn't typically encounter without some additional exploring. It's pretty likely that you've already encountered some of these yourself!
#
# Let's begin!
list1 = [1,2,3]
# ## append
# You will definitely have used this method by now, which merely appends an element to the end of a list:
# +
list1.append(4)
list1
# -
# ## count
# We discussed this during the methods lectures, but here it is again. <code>count()</code> takes in an element and returns the number of times it occurs in your list:
list1.count(10)
list1.count(2)
# ## extend
# Many times people find the difference between extend and append to be unclear. So note:
#
# **append: appends whole object at end:**
x = [1, 2, 3]
x.append([4, 5])
print(x)
# **extend: extends list by appending elements from the iterable:**
x = [1, 2, 3]
x.extend([4, 5])
print(x)
# Note how <code>extend()</code> appends each element from the passed-in list. That is the key difference.
# ## index
# <code>index()</code> will return the index of whatever element is placed as an argument. Note: If the the element is not in the list an error is raised.
list1.index(2)
list1.index(12)
# ## insert
# <code>insert()</code> takes in two arguments: <code>insert(index,object)</code> This method places the object at the index supplied. For example:
list1
# Place a letter at the index 2
list1.insert(2,'inserted')
list1
# ## pop
# You most likely have already seen <code>pop()</code>, which allows us to "pop" off the last element of a list. However, by passing an index position you can remove and return a specific element.
ele = list1.pop(1) # pop the second element
list1
ele
# ## remove
# The <code>remove()</code> method removes the first occurrence of a value. For example:
list1
list1.remove('inserted')
list1
list2 = [1,2,3,4,3]
list2.remove(3)
list2
# ## reverse
# As you might have guessed, <code>reverse()</code> reverses a list. Note this occurs in place! Meaning it affects your list permanently.
list2.reverse()
list2
# ## sort
# The <code>sort()</code> method will sort your list in place:
list2
list2.sort()
list2
# The <code>sort()</code> method takes an optional argument for reverse sorting. Note this is different than simply reversing the order of items.
list2.sort(reverse=True)
list2
# ## Be Careful With Assignment!
# A common programming mistake is to assume you can assign a modified list to a new variable. While this typically works with immutable objects like strings and tuples:
x = 'hello world'
y = x.upper()
print(y)
# This will NOT work the same way with lists:
x = [1,2,3]
y = x.append(4)
print(y)
# What happened? In this case, since list methods like <code>append()</code> affect the list *in-place*, the operation returns a None value. This is what was passed to **y**. In order to retain **x** you would have to assign a *copy* of **x** to **y**, and then modify **y**:
x = [1,2,3]
y = x.copy()
y.append(4)
print(x)
print(y)
# Great! You should now have an understanding of all the methods available for a list in Python!
|
14-Advanced Python Objects and Data Structures/05-Advanced Lists.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import scipy.optimize as sco
import typing
import warnings
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import math as m
import scipy as sp
import pandas_datareader as pd_data
# -
# ### Need to define inputs (type: pd.Dataframe):
# 1. expRtns: "LIBOR rates & forecasted returns"
# 2. cov: "covariance based on historical data"
# 3. mu_f: "US treasury yield"
def Portfolio_stats(weights: "porportions of capital",
expRtns: "LIBOR rates & forecasted returns",
cov: "covariance based on historical data",
mu_f: "US treasury yield") -> "portfolio returns,variance,volatility,sharpe_ratio":
varP = np.dot(weights.T, np.dot(cov,weights))
volP = np.sqrt(varP)
rtnP = np.sum(weights*expRtns)
sharpeP = (rtnP-mu_f)/volP
return rtnP, varP, volP, sharpeP
def negative_sharpe(weights):
return -Portfolio_stats(weights,expRtns,cov,mu_f)[3]
# +
def returns_from_prices(prices, log_returns=False):
"""
Calculate the returns given prices.
:param prices: adjusted (daily) closing prices of the asset, each row is a
date and each column is a ticker/id.
:type prices: pd.DataFrame
:param log_returns: whether to compute using log returns
:type log_returns: bool, defaults to False
:return: (daily) returns
:rtype: pd.DataFrame
"""
if log_returns:
return np.log(prices).diff().dropna(how="all")
else:
return prices.pct_change().dropna(how="all")
def _pair_exp_cov(X, Y, span=180):
"""
Calculate the exponential covariance between two timeseries of returns.
:param X: first time series of returns
:type X: pd.Series
:param Y: second time series of returns
:type Y: pd.Series
:param span: the span of the exponential weighting function, defaults to 180
:type span: int, optional
:return: the exponential covariance between X and Y
:rtype: float
"""
covariation = (X - X.mean()) * (Y - Y.mean())
# Exponentially weight the covariation and take the mean
if span < 10:
warnings.warn("it is recommended to use a higher span, e.g 30 days")
return covariation.ewm(span=span).mean().iloc[-1]
def exp_cov(prices, returns_data=False, span=180, frequency=252, **kwargs):
"""
Estimate the exponentially-weighted covariance matrix, which gives
greater weight to more recent data.
:param prices: adjusted closing prices of the asset, each row is a date
and each column is a ticker/id.
:type prices: pd.DataFrame
:param returns_data: if true, the first argument is returns instead of prices.
:type returns_data: bool, defaults to False.
:param span: the span of the exponential weighting function, defaults to 180
:type span: int, optional
:param frequency: number of time periods in a year, defaults to 252 (the number
of trading days in a year)
:type frequency: int, optional
:return: annualised estimate of exponential covariance matrix
:rtype: pd.DataFrame
"""
if not isinstance(prices, pd.DataFrame):
warnings.warn("data is not in a dataframe", RuntimeWarning)
prices = pd.DataFrame(prices)
assets = prices.columns
if returns_data:
returns = prices
else:
returns = returns_from_prices(prices)
N = len(assets)
# Loop over matrix, filling entries with the pairwise exp cov
S = np.zeros((N, N))
for i in range(N):
for j in range(i, N):
S[i, j] = S[j, i] = _pair_exp_cov(
returns.iloc[:, i], returns.iloc[:, j], span
)
cov = pd.DataFrame(S * frequency, columns=assets, index=assets)
return cov
# +
start_date = '2015-09-01'
end_date = '2016-09-01' # hypothetically the current time
ahead_date = '2017-09-01'
symbols = ['AAPL', 'GS', 'GC=F', 'GE']
# historical data: to be used to compute variance
df = pd_data.DataReader(symbols,'yahoo',start_date,end_date)['Adj Close']
df = df.dropna()
# one-year-ahead data: to be used as the (fake) forecasted return
df2 = pd_data.DataReader(symbols,'yahoo',end_date,ahead_date)['Adj Close']
df2 = df2.dropna()
# -
# import LIBOR rates data
LIBOR_rates = pd.read_csv("LIBOR_USD.csv")
LIBOR_rates
# convert to datetime
LIBOR_rates['Date'] = pd.to_datetime(LIBOR_rates['Date'],format="%d.%m.%Y")
# LIBOR rates between start date & end date
Rates = LIBOR_rates.loc[ (LIBOR_rates['Date'] >= start_date) & (LIBOR_rates['Date'] <= end_date) ]
Rates.sort_values(by='Date',ascending=True,inplace=True)
Rates.set_index('Date', inplace=True)
Rates
# ### LIBOR rates are quoted as <ins>annual</ins> interest rates (in %).
# ##### To get <ins>daily</ins> percentage change, need to divide by 252 (#trading days in a year).
# ## Compute covariance (historical data)
df_all = df.copy()
df_all['Cash'] = Rates['ON']/100/252 # short-term interest rates (OverNight LIBOR)
df_all = df_all.dropna()
dfrtn_all = df_all.pct_change().dropna() # the percentage (not log) returns of stocks
cov = exp_cov(dfrtn_all, returns_data = True) #covariance of percentage returns
cov
# ## Compute expected returns (one-year-ahead data)
# expected returns: current short-term rate for cash, and (heuristically) the one-year-ahead average percentage returns for stocks
expRtns = df2.pct_change().mean(axis=0)
expRtns['Cash'] = Rates['ON'][end_date]/100/252
expRtns
# ## Use LIBOR rate for short-term risk-free rate
# ### => for daily expected return of cash
# ##### Tenor of rate = rebalancing period
# ## Use Treasury yield for long-term risk-free rate
# ### => for performance measure, Sharpe ratio, etc.
# ##### Tenor of rate = portfolio holding period
TreasuryYields = pd.read_csv('USTREASURY_YIELD.csv')
TreasuryYields
TreasuryYields['Date']= pd.to_datetime(TreasuryYields['Date'],format="%Y-%m-%d")
TreasuryYields
# Treasury yield at current time
# assuming portfolio holding period = 3 years
mu_f = TreasuryYields.loc[TreasuryYields['Date']==end_date]['3 YR'].values[0]/100/252
mu_f
# ## Compute optimal weights
# +
# total number of stocks (+cash)
nn = len(expRtns)
# Initialise weights
w0 = [1.0/nn for i in range(nn)]
w0 = np.array(w0)
# Constraints on weights
cons = ({'type':'eq','fun': lambda x: np.sum(x)-1}) #add up to 1
bnds = tuple((0,1) for x in range(nn)) #only between 0 and 1, i.e. no short-selling
# Maximise sharpes ratio
opts = sco.minimize(negative_sharpe, w0 , method = 'SLSQP', bounds= bnds, constraints = cons)
# Optimal weights
w_opt = opts['x'].round(3)
w_opt
# -
# # Things to do:
# 1. #units of stocks (compute based on optimal weights)
# 2. Performance on portfolio (plots, P&L, max. draw-down, turn-over rate, risk measures, compare with S&P index)
|
Backtesting - Max Sharpe Strategy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Using Earth Engine and geemap for mapping surface water dynamics
#
# **Steps to create Landsat timeseries:**
#
# 1. Pan and zoom to your area of interest, and click on the map to select a polygon.
# 2. Adjust the parameters (e.g., band combination, threshold, color) if needed.
# 3. Click the `Submit` button to create timeseries of Landsat imagery and normalized difference indices.
#
# **Web Apps:** https://gishub.org/water-app, https://gishub.org/water-ngrok
#
# **Contact:** Dr. <NAME> ([Website](https://wetlands.io/), [LinkedIn](https://www.linkedin.com/in/qiushengwu), [Twitter](https://twitter.com/giswqs), [YouTube](https://www.youtube.com/c/QiushengWu))
# +
# Check geemap installation
import subprocess
try:
import geemap
except ImportError:
print('geemap package is not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# -
# Import libraries
import os
import ee
import geemap
import ipywidgets as widgets
from bqplot import pyplot as plt
from ipyleaflet import WidgetControl
# +
# Create an interactive map
Map = geemap.Map(center=[37.71, 105.47], zoom=4, add_google_map=False)
Map.add_basemap('HYBRID')
Map.add_basemap('ROADMAP')
# Add Earth Engine data
fc = ee.FeatureCollection('users/giswqs/public/chn_admin_level2')
Map.addLayer(fc, {}, '二级行政区')
Map
# +
# Designe interactive widgets
style = {'description_width': 'initial'}
output_widget = widgets.Output(layout={'border': '1px solid black'})
output_control = WidgetControl(widget=output_widget, position='bottomright')
Map.add_control(output_control)
admin1_widget = widgets.Text(
description='一级行政区:',
value='广东省',
width=200,
style=style
)
admin2_widget = widgets.Text(
description='二级行政区:',
value='广州市',
width=300,
style=style
)
band_combo = widgets.Dropdown(
description='显示影像波段组合:',
options=['Red/Green/Blue', 'NIR/Red/Green', 'SWIR2/SWIR1/NIR', 'NIR/SWIR1/Red','SWIR2/NIR/Red',
'SWIR2/SWIR1/Red', 'SWIR1/NIR/Blue', 'NIR/SWIR1/Blue', 'SWIR2/NIR/Green', 'SWIR1/NIR/Red'],
value='NIR/Red/Green',
style=style
)
year_widget = widgets.IntSlider(min=1984, max=2020, value=2010, description='显示指定年份数据:', width=400, style=style)
fmask_widget = widgets.Checkbox(
value=True,
description='应用fmask(去除云, 阴影, 雪)',
style=style
)
# Normalized Satellite Indices: https://www.usna.edu/Users/oceano/pguth/md_help/html/norm_sat.htm
nd_options = ['Vegetation Index (NDVI)',
'Water Index (NDWI)',
'Modified Water Index (MNDWI)',
'Snow Index (NDSI)',
'Soil Index (NDSI)',
'Burn Ratio (NBR)',
'Customized']
nd_indices = widgets.Dropdown(options=nd_options, value='Modified Water Index (MNDWI)', description='归一化指数:', style=style)
first_band = widgets.Dropdown(
description='波段1:',
options=['Blue', 'Green','Red','NIR', 'SWIR1', 'SWIR2'],
value='Green',
style=style
)
second_band = widgets.Dropdown(
description='波段2:',
options=['Blue', 'Green','Red','NIR', 'SWIR1', 'SWIR2'],
value='SWIR1',
style=style
)
nd_threshold = widgets.FloatSlider(
value=0,
min=-1,
max=1,
step=0.01,
description='阈值:',
orientation='horizontal',
style=style
)
nd_color = widgets.ColorPicker(
concise=False,
description='颜色:',
value='blue',
style=style
)
def nd_index_change(change):
if nd_indices.value == 'Vegetation Index (NDVI)':
first_band.value = 'NIR'
second_band.value = 'Red'
elif nd_indices.value == 'Water Index (NDWI)':
first_band.value = 'NIR'
second_band.value = 'SWIR1'
elif nd_indices.value == 'Modified Water Index (MNDWI)':
first_band.value = 'Green'
second_band.value = 'SWIR1'
elif nd_indices.value == 'Snow Index (NDSI)':
first_band.value = 'Green'
second_band.value = 'SWIR1'
elif nd_indices.value == 'Soil Index (NDSI)':
first_band.value = 'SWIR1'
second_band.value = 'NIR'
elif nd_indices.value == 'Burn Ratio (NBR)':
first_band.value = 'NIR'
second_band.value = 'SWIR2'
elif nd_indices.value == 'Customized':
first_band.value = None
second_band.value = None
nd_indices.observe(nd_index_change, names='value')
submit = widgets.Button(
description='Submit',
button_style='primary',
tooltip='Click me',
style=style
)
full_widget = widgets.VBox([
widgets.HBox([admin1_widget, admin2_widget]),
widgets.HBox([band_combo, year_widget, fmask_widget]),
widgets.HBox([nd_indices, first_band, second_band, nd_threshold, nd_color]),
submit
])
full_widget
# +
# Capture user interaction with the map
def handle_interaction(**kwargs):
latlon = kwargs.get('coordinates')
if kwargs.get('type') == 'click':
Map.default_style = {'cursor': 'wait'}
xy = ee.Geometry.Point(latlon[::-1])
selected_fc = fc.filterBounds(xy)
with output_widget:
output_widget.clear_output()
try:
admin1_id = selected_fc.first().get('ADM1_ZH').getInfo()
admin2_id = selected_fc.first().get('ADM2_ZH').getInfo()
admin1_widget.value = admin1_id
admin2_widget.value = admin2_id
Map.layers = Map.layers[:4]
geom = selected_fc.geometry()
layer_name = admin1_id + '-' + admin2_id
Map.addLayer(ee.Image().paint(geom, 0, 2), {'palette': 'red'}, layer_name)
print(layer_name)
except:
print('找不到相关行政区')
Map.layers = Map.layers[:4]
Map.default_style = {'cursor': 'pointer'}
Map.on_interaction(handle_interaction)
# +
# Click event handler
def submit_clicked(b):
with output_widget:
output_widget.clear_output()
print('Computing...')
Map.default_style = {'cursor': 'wait'}
try:
admin1_id = admin1_widget.value
admin2_id = admin2_widget.value
band1 = first_band.value
band2 = second_band.value
selected_year = year_widget.value
threshold = nd_threshold.value
bands = band_combo.value.split('/')
apply_fmask = fmask_widget.value
palette = nd_color.value
roi = fc.filter(ee.Filter.And(ee.Filter.eq('ADM1_ZH', admin1_id), ee.Filter.eq('ADM2_ZH', admin2_id)))
Map.layers = Map.layers[:4]
geom = roi.geometry()
layer_name = admin1_id + '-' + admin2_id
Map.addLayer(ee.Image().paint(geom, 0, 2), {'palette': 'red'}, layer_name)
images = geemap.landsat_timeseries(roi=roi, start_year=1984, end_year=2020, start_date='01-01', end_date='12-31', apply_fmask=apply_fmask)
nd_images = images.map(lambda img: img.normalizedDifference([band1, band2]))
result_images = nd_images.map(lambda img: img.gt(threshold))
selected_image = ee.Image(images.toList(images.size()).get(selected_year - 1984))
selected_result_image = ee.Image(result_images.toList(result_images.size()).get(selected_year - 1984)).selfMask()
vis_params = {
'bands': bands,
'min': 0,
'max': 3000
}
Map.addLayer(selected_image, vis_params, 'Landsat ' + str(selected_year))
Map.addLayer(selected_result_image, {'palette': palette}, 'Result ' + str(selected_year))
def cal_area(img):
pixel_area = img.multiply(ee.Image.pixelArea()).divide(1e6)
img_area = pixel_area.reduceRegion(**{
'geometry': roi.geometry(),
'reducer': ee.Reducer.sum(),
'scale': 1000,
'maxPixels': 1e12,
'bestEffort': True
})
return img.set({'area': img_area})
areas = result_images.map(cal_area)
stats = areas.aggregate_array('area').getInfo()
x = list(range(1984, 2021))
y = [item.get('nd') for item in stats]
fig = plt.figure(1)
fig.layout.height = '270px'
plt.clear()
plt.plot(x, y)
plt.title('Temporal trend (1984-2020)')
plt.xlabel('Year')
plt.ylabel('Area (km2)')
output_widget.clear_output()
plt.show()
except Exception as e:
print(e)
print('An error occurred during computation.')
Map.default_style = {'cursor': 'default'}
submit.on_click(submit_clicked)
|
notebooks/chn_water_app.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import cv2
import PIL
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from PIL import Image, ImageDraw, ImageFont
import os
import glob
from datetime import datetime, timezone, timedelta
# For movie processing
from moviepy.editor import VideoFileClip
from IPython.display import HTML
# built-in modules
import itertools as it
# %matplotlib inline
# Various globals
img = []; images = []; imgid = 0
imgfmt = "rgb"
imgname = ""
meth = 0; methch = 0
thresh = [(40,100), (170,240)]
winname = 'fit line'
invcnt = 0
model_left_fit = []; model_right_fit = []
pipeline_lbls = ["_pp_Undistort", "_pp_Threshold", "_pp_Warp", "_pp_LaneFind", "_pp_Unwarp", "_pp_Final"]
lcrad = 0; rcrad = 0; carpos = []
output_dir = "output_images/"
# ###############################################################
#
# ############ VARIOUS VISUALIZATION AND PRINT ROUTINES
#
def plot_corners(img, chlay, corners):
cv2.drawChessboardCorners(img, chlay, corners, True)
cv2.imshow(img)
def weighted_img(img, initial_img, α=0.8, β=1., γ=0.):
# `img` is the output of the hough_lines(), An image with lines drawn on it.
# Should be a blank image (all black) with lines drawn on it.
# `initial_img` should be the image before any processing.
# The result image is computed as follows:
# initial_img * α + img * β + γ
# NOTE: initial_img and img must be the same shape!
return cv2.addWeighted(initial_img, α, img, β, γ)
# Plot 2 images side by side
def visualize_imgs(img1, img2, tit1, tit2):
# Visualize before and after images
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(20,10))
ax1.imshow(img1); ax1.set_title(tit1, fontsize=30)
ax2.imshow(img2); ax2.set_title(tit2, fontsize=30)
def toint(p):
return tuple(map(int, p))
# Given a list of points, plot them
def plot_pts(img, lnpts, color=[255,255,255], sz=1):
for p in lnpts:
# print (type(p), p.ndim, p.shape, type(p[0]), type(p[1]))
# if ((p[0] > 700 and p[0] < 900) and (p[1] > 400 and p[1] < 550)):
cv2.circle(img, toint(p), sz, color, -1)
# Put a string on an image
def draw_str(img, target, s):
x, y = target
cv2.putText(img, s, (x+1, y+1), cv2.FONT_HERSHEY_PLAIN, 1.0, (0, 0, 0), thickness = 2, lineType=cv2.LINE_AA)
cv2.putText(img, s, (x, y), cv2.FONT_HERSHEY_PLAIN, 1.0, (255, 255, 255), lineType=cv2.LINE_AA)
# Given an array of points plot them on a blank image
# This is used to plot the "fitting" polygonal envelope representing the lane regions
#
# Returns a 3-D image
def draw_fit_polygon(imgdim0, imgdim1, left_fitx, right_fitx, ploty, margin, color=[0,255,0]):
# Generate a polygon to illustrate the search window area
# And recast the x and y points into usable format for cv2.fillPoly()
left_line_window1 = np.array([np.transpose(np.vstack([left_fitx-margin, ploty]))])
left_line_window2 = np.array([np.flipud(np.transpose(np.vstack([left_fitx+margin, ploty])))])
left_line_pts = np.hstack((left_line_window1, left_line_window2))
right_line_window1 = np.array([np.transpose(np.vstack([right_fitx-margin, ploty]))])
right_line_window2 = np.array([np.flipud(np.transpose(np.vstack([right_fitx+margin, ploty])))])
right_line_pts = np.hstack((right_line_window1, right_line_window2))
# Draw the lane onto the warped blank image
window_img = np.zeros((imgdim0,imgdim1,3), dtype=np.uint8)
cv2.fillPoly(window_img, np.int_([left_line_pts]), color)
cv2.fillPoly(window_img, np.int_([right_line_pts]), color)
return window_img
# Draw an image overlaid with name of image
def draw_img(imgname, img):
global winname
if imgfmt == "bgr" and img.ndim == 3:
imgcopy = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
else:
imgcopy = np.copy(img)
draw_str(imgcopy, (40, 20), imgname)
# hpos = int(imgdim[1]*0.60)
# draw_str(img, (hpos, 20), "( " + str(tmin) + ", " + str(tmax) + " )")
# cv2.imshow(winname, imgcopy)
plt.imshow(imgcopy)
# Print the timings for the various stages of the pipeline. Used to evaluate performance
def print_times(tvals, inv=-1):
labels = [ " NONE ", " THR: ", ". PERS: ", ". LANE: ", ". XPER: ", ". FIN: " ]
ostr = "" if inv < 0 else str(inv)+">> "
tms = tvals[0]
for t in range(1, len(tvals)):
tmt = tvals[t]
ostr += labels[t] + str((tmt-tms).microseconds // 1000)
print (ostr)
# ############################################
#
# ###### CAMERA CALIBRATION
#
def calib_camera():
# for each chessboard pattern
#. read_img
#. convert to gray
#. findChessCorners
#. append corners to imgpoints
# call calibrateCamera
chlay = (9,6)
i,nowtest = 0,-1
retcorn = []
objpts = []; imgpts = []
savecorners = False
cfiles = glob.glob("camera_cal/cal*.jpg")
for i, cfile in enumerate(cfiles):
# calibration1 is a 9x5, cal*4 is a 7x4, cal*5 is a 7x6.
if (cfile == "camera_cal/calibration1.jpg"):
chlay = (9,5)
savecorners = True
elif (cfile == "camera_cal/calibration4.jpg"):
chlay = (7,4)
elif (cfile == "camera_cal/calibration5.jpg"):
chlay = (7,6)
else:
chlay = (9,6)
# print ("Attempting " + cfile)
if (nowtest == -1 or i == nowtest):
img = cv2.imread(cfile)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
ret, corners = cv2.findChessboardCorners(gray, chlay, None)
if (ret):
imgpts.append(corners)
if (savecorners):
retcorn = corners
# print("Found the corners to be ", corners)
savecorners = False
ccoord = np.zeros((chlay[0]*chlay[1],3), np.float32)
ccoord[:,:2] = np.mgrid[:chlay[0], :chlay[1]].T.reshape(-1,2)
objpts.append(ccoord)
# plot_corners(img, chlay, corners)
else:
print("Failed to find the corners for ", cfile)
if (len(imgpts) > 0):
imgsz = (img.shape[1], img.shape[0])
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpts, imgpts, imgsz, None,None)
print ("Calibration ", "successful" if ret else "failed", ". Obtained ", len(imgpts), " calibrations from ", (i+1), " files")
return ret, mtx, dist
return (False, None, None)
# ########################
#
# THRESHOLDING / FILTERING OPERATIONS
#
def apply_colorfilter(img):
global imgfmt
# Lanes are typically yellow (strong R/G) and white (strong R/G/B)
# So filter out any that are below. This should take out the blacks / blues / darker colors
rthresh, gthresh = (210, 210)
ridx = 0 if imgfmt == "rbg" else 2
gidx = 1
rfiltered = (img[:,:,ridx] <= rthresh)
gfiltered = (img[:,:,gidx] <= gthresh)
rgfiltered = rfiltered | gfiltered
colfilt = np.copy(img)
colfilt [ rgfiltered ] = [ 0, 0, 0 ]
# colfilt = np.zeros_like(img)
# for i in range(rfiltered.shape[0]):
# for j in range(rfiltered.shape[1]):
# if (rfiltered[i][j] and gfiltered[i][j]):
# colfilt[i][j] = img[i][j]
# colfilt[:,:, = np.where(rfiltered & gfiltered, img, np.zeros_like(img) )
return colfilt
# Apply the Sobel transformation and filter out "weak" pixels to help isolate lanes
# Returns a binary image
def apply_sobel(img, tmin, tmax):
global imgfmt, globcfg
wimg = apply_colorfilter(img) if globcfg["colfilt"] else img
cxform = cv2.COLOR_RGB2GRAY if (imgfmt == "rgb") else cv2.COLOR_BGR2GRAY
gray = cv2.cvtColor(wimg, cxform)
# Sobel x
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0) # Take the derivative in x
abs_sobelx = np.absolute(sobelx) # Absolute x derivative to accentuate lines away from horizontal
scaled_sobel = np.uint8(255*abs_sobelx/np.max(abs_sobelx))
sxbinary = np.zeros_like(scaled_sobel)
sxbinary[(scaled_sobel >= tmin) & (scaled_sobel <= tmax)] = 255
return sxbinary
# Filter image based on the saturation of the pixels
# Returns a binary image
def apply_satthresh(img, tmin, tmax):
global imgfmt
wimg = img
cxform = cv2.COLOR_RGB2HLS if (imgfmt == "rgb") else cv2.COLOR_BGR2HLS
hls = cv2.cvtColor(wimg, cxform)
s_channel = hls[:,:,2]
# Threshold color channel
s_binary = np.zeros_like(s_channel)
s_binary[(s_channel >= tmin) & (s_channel <= tmax) ] = 255
return s_binary
# An indirection routine
# Not very helpful right now, but could be useful when applying multiple levels of HLS filteration
def apply_hlsthresh(img, tmin, tmax):
return apply_satthresh(img, tmin, tmax)
# The thresholding stage of the pipeline
# Applies sobel and sat filtration and masks out portions of image not of interest (typically the top half and some sides)
# Returns a binary image
def thresholding(img):
global thresh, winname
# Apply Sobel
tmin, tmax = thresh[0]
# print ("Sobel - applying thresholds: ", tmin, tmax)
oimg_c = apply_sobel(img, tmin, tmax)
tmin, tmax = thresh[1]
# print ("Satn - applying thresholds: ", tmin, tmax)
oimg_s = apply_hlsthresh(img, tmin, tmax)
# Combined binary from the 2 thresholdings
oimg = np.zeros_like(oimg_c)
oimg[(oimg_c == 255) | (oimg_s == 255)] = 255
# print ("Sobel: ", np.sum(oimg_c), " L/S: ", np.sum(oimg_s), " Final: ", np.sum(oimg))
oimg = apply_region_of_interest(oimg, 't')
return oimg
# #####################
#
# MASKING
#
# Given an image and a set of vertices defining a polygon, retains image within the polygon
def region_of_interest(img, vertices):
# Applies an image mask.
# Only keeps the region of the image defined by the polygon
# formed from `vertices`. The rest of the image is set to black.
# `vertices` should be a numpy array of integer points.
#defining a blank mask to start with
mask = np.zeros_like(img)
# defining a 3 channel or 1 channel color to fill the mask with depending on the input image
if len(img.shape) > 2:
channel_count = img.shape[2] # i.e. 3 or 4 depending on your image
ignore_mask_color = (255,) * channel_count
else:
ignore_mask_color = 255
#filling pixels inside the polygon defined by \"vertices\" with the fill color \n",
cv2.fillPoly(mask, vertices, ignore_mask_color)
#returning the image only where mask pixels are nonzero
masked_image = cv2.bitwise_and(img, mask)
return masked_image
# Mask out portions of an image
# Determines the boundaries of the mask by type of masking desired: 'r' - rectangular, or 't' - trapezoidal
# Returns a masked image of the same shape as the input
def apply_region_of_interest(img, type='t'):
xlmt = img.shape[1]
ylmt = img.shape[0]
if (type == 't'):
if (xlmt & 0x1): xlmt -= 1
xtopmrg = int(xlmt/10); xbotmrg = xtopmrg
xbotmrg = 0
xtopmrg = 0
tlt = [int(xlmt/2-xtopmrg),int(ylmt//2)]
trt = [int(xlmt/2+xtopmrg),int(ylmt//2)]
blt = [xbotmrg, ylmt]
brt = [xlmt,ylmt]
elif (type == 'r'):
tlt = [0,int(ylmt/2)]
blt = [0, ylmt]
trt = [xlmt,int(ylmt/2)]
brt = [xlmt,ylmt]
intpoly = np.array([[blt,tlt,trt,brt]])
return region_of_interest(img, intpoly)
# #####################
#
# PERSPECTIVE
#
#
# Given a set of src and dst points, determine the perspective transform matrix and apply it to the input img
#
# Returns a "warped" image of the same shape as the input
def apply_pers_chg(img, src, dst, dir=1):
# Grab the image shape
xlmt = img.shape[1]
ylmt = img.shape[0]
img_size = (xlmt, ylmt)
if dir == 1:
# Given src and dst points, calculate the perspective transform matrix
# print ("Using src as ", src); print ("Using dst as ", dst)
M = cv2.getPerspectiveTransform(src, dst)
# Warp the image using OpenCV warpPerspective()
warped = cv2.warpPerspective(img, M, img_size, flags=cv2.INTER_LINEAR)
else:
M = cv2.getPerspectiveTransform(dst, src)
# Warp the image using OpenCV warpPerspective()
warped = cv2.warpPerspective(img, M, img_size, flags=cv2.INTER_LINEAR)
return warped
def topt(x):
return (int(x[0]), int(x[1])) if (x.shape[0] == 2) else (0,0)
# Apply a perspective transform
# Uses a fixed set of points (manually determined) for the perspective transform
#
# Returns a "warped" image
def chg_perspective(img, dir=1):
src = np.float32([(450, 450), (900, 450), (300, 630), (1100, 630) ])
dst = np.float32([(170, 210), (1180, 210), (500, 680), (900, 680) ])
warped = apply_pers_chg(img, src, dst, dir)
return warped
# Imprint img with the curvature and car position details
def imprint_curvature(img):
global lcrad, rcrad, carpos
lx = carpos[0]; rx = carpos[1];
px2m = (rx-lx)/3.7 ; # Given lanes are 3.7m wide
carpxpos = int(((lx + rx)//2) - (img.shape[1]//2))
lcradstr = str(round(lcrad / px2m, 1)); rcradstr = str(round(rcrad / px2m, 1))
curvestr = "LtCurve Rad: " + lcradstr + "m RtCurve Rad: " + rcradstr + "m carpxpos: " + str(round(carpxpos/px2m, 2)) + "m"
curvestr = curvestr + (" left" if (carpxpos < 0) else " right")
draw_str(img, (20, 20), curvestr)
return img
# Given a set of points, find the curvature
def measure_curvature_pixels(ploty, left_fit, right_fit):
global lcrad, rcrad, carpos
'''
Calculates the curvature of polynomial functions in pixels.
'''
# Define y-value where we want radius of curvature
# We'll choose the maximum y-value, corresponding to the bottom of the image
y_eval = np.max(ploty)
# Calculate the curvatures for the left and the right fits
l_A = left_fit[0]; l_B = left_fit[1]
lcrad = int(( (1 + (2*l_A * y_eval + l_B)**2)**(3/2)) / abs(2 * l_A))
r_A = right_fit[0]; r_B = right_fit[1]
rcrad = int(( (1 + (2*r_A * y_eval + r_B)**2)**(3/2)) / abs(2 * r_A))
# Determine the car position as the center of the lanes
lx = left_fit[0]*y_eval**2 + left_fit[1]*y_eval + left_fit[2]
rx = right_fit[0]*y_eval**2 + right_fit[1]*y_eval + right_fit[2]
carpos = [lx, rx]
return lcrad, rcrad, carpos
# #####################
#
# LANE FINDING - Polynomial Fit/Histogram routines
#
#
# Given a histogram, find the region of the histogram that has the maximum strength
# Frames with solid shadows can result in histogram peaks and sometimes these peaks were stronger than
# the lane peaks. However, lane peaks showed wider strength than the shadow peaks
# Used this function to convolve and find regions of maximum strength
def get_convolved_histpeaks(lbl, histogram):
window_width = 40
window = np.ones(window_width) # Create our window template that we will use for convolutions
pk = np.int(np.argmax(np.convolve(window,histogram)) - window_width/2)
pk = 0 if (pk < 0) else pk
# print (lbl + " alt peak ", pk)
return pk
# Given an image, estimate lane positions by determining the histogram peaks
def get_histpeaks(binary_warped):
# Consider the bottom third of the window
histht = (2*binary_warped.shape[0])//3
# Take a histogram of the bottom half of the image
histogram = np.sum(binary_warped[histht:,:], axis=0)
# Find the peak of the left and right halves of the histogram
# These will be the starting point for the left and right lines
midp = np.int(histogram.shape[0]//2)
leftx_base = np.argmax(histogram[:midp])
rightx_base = np.argmax(histogram[midp:]) + midp
leftx_base = get_convolved_histpeaks("Left", histogram[:midp])
rightx_base = get_convolved_histpeaks("right", histogram[midp:]) + midp
# print ("Found Histogram Peaks at ", leftx_base, "(", histogram[leftx_base], ") ", rightx_base, "(", histogram[rightx_base], ")")
# print ("Could also use", alt_lb, alt_rb, type(alt_lb), type(alt_rb))
# print (histogram[:midp])
return (leftx_base, rightx_base)
# Given the current window centers, determine the window centers for the next strip
# Typically, the next centers are the average of the current window's x-pos provided the current window has enough pixels
# else use the last known polygon fit to determine the x-pos
def get_next_win_centers(nonzerox, inds, curr, lastfit, yhi, ylo):
# Set minimum number of pixels found to recenter window
minpix = 50
### If found > minpix pixels, recenter next window ###
### (`rightx_current` or `leftx_current`) on their mean position ###
if (len(inds) > 0 and (inds.shape[0] > minpix)):
curr = int(np.average(nonzerox[inds]))
else:
if len(lastfit) > 0 and ylo > 0:
xhi = lastfit[0]*yhi**2 + lastfit[1]*yhi + lastfit[2]
xlo = lastfit[0]*ylo**2 + lastfit[1]*ylo + lastfit[2]
# print ("Curr ", curr, " Would have returned: ", (xhi+xlo)//2, " for ", xhi, " @ ", yhi, " and ", xlo, " for lo @ ", ylo)
# Make sure the vlaue determined is within range of the last value
# 200 - empirically determined
if (abs(xhi-curr) <= 200):
curr = np.int(xhi)
return curr
# Use a sliding window to determine all the pixels that represent the left and right lanes
# Find centers of feasible lane positions at the bottom of the image
# centers may be found using histogram or the last known polynomial fitting the image
# Find possible lane pixels in a box around the centers
# Using the pixels found in the current box, determine the box position in the strip above
# Do so for the entire image
#
# Returns arrays containing the X and Y coordinates of pixesl that form the left and right lanes
# Additionally, returns a 3-D image with the windows and the pixels drawn if requested
def find_lane_pixels_bywin(binary_warped, leftx_base, rightx_base, nonzero, nonzerox, nonzeroy):
global model_left_fit, model_right_fit, globcfg
# out_img = np.dstack((binary_warped, binary_warped, binary_warped))
out_img = np.zeros((binary_warped.shape[0], binary_warped.shape[1], 3), dtype=np.uint8)
# HYPERPARAMETERS
# Choose the number of sliding windows and thus the height of each slice
nwindows = 9
window_height = np.int(binary_warped.shape[0]//nwindows)
# Set the width of the windows +/- margin
margin = 50
# Current positions to be updated later for each window in nwindows
leftx_current = leftx_base
rightx_current = rightx_base
# Create empty lists to receive left and right lane pixel indices
left_lane_inds = []
right_lane_inds = []
# Step through the windows one by one
for window in range(nwindows):
# Identify window boundaries in x and y (and right and left)
win_y_low = binary_warped.shape[0] - (window+1)*window_height
win_y_high = binary_warped.shape[0] - window*window_height
### Find the four below boundaries of the window ###
win_xl_lo = leftx_current-margin
win_xl_hi = leftx_current+margin
win_xr_lo = rightx_current-margin
win_xr_hi = rightx_current+margin
# Draw the windows on the visualization image
if (globcfg["drawrect"]):
cv2.rectangle(out_img,(win_xl_lo,win_y_low), (win_xl_hi,win_y_high),(0,255,0), 2)
cv2.rectangle(out_img,(win_xr_lo,win_y_low), (win_xr_hi,win_y_high),(0,255,0), 2)
# Truth matrix of pixels that are within the Y margins of the current window
yon = np.logical_and(nonzeroy >= win_y_low, nonzeroy < win_y_high)
# Find X indices of "ON" pixels that are within the Left Window
xon = np.logical_and(nonzerox >= win_xl_lo, nonzerox < win_xl_hi)
xyon = xon & yon
if xyon.any():
good_left_inds = np.where(xon & yon)[0]
left_lane_inds.append(good_left_inds)
else:
good_left_inds = np.array(())
# Find X indices of "ON" pixels that are within the Right Window
xon = np.logical_and(nonzerox >= win_xr_lo, nonzerox < win_xr_hi)
xyon = xon & yon
if xyon.any():
good_right_inds = np.where(xon & yon)[0]
right_lane_inds.append(good_right_inds)
else:
good_right_inds = np.array(())
# print (" Win#", window, " Adding L coords: ", len(good_left_inds), " FIT: ", " curr ", leftx_current)
# print (" Win#", window, " Adding R coords: ", len(good_right_inds), " FIT: ", " curr ", rightx_current)
# print ("Window: ", window, " Adding R coords: ", nonzerox[good_right_inds[:10]], " ", nonzeroy[good_right_inds[:10]])
# Get New "current" X coordinates to center the next window around
leftx_current = get_next_win_centers(nonzerox, good_left_inds, leftx_current, model_left_fit, win_y_low, (win_y_low-window_height))
rightx_current = get_next_win_centers(nonzerox, good_right_inds, rightx_current, model_right_fit, win_y_low, (win_y_low-window_height))
# Concatenate the arrays of indices (previously was a list of arrays of pixels)
# print ("LEFT: ", len(left_lane_inds), "RIGHT: ", len(right_lane_inds))
if len(left_lane_inds) > 0:
left_lane_inds = np.concatenate(left_lane_inds)
if len(right_lane_inds) > 0:
right_lane_inds = np.concatenate(right_lane_inds)
# Extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
return leftx, lefty, rightx, righty, out_img
# #######
#
# Given a set of X and Y points, finds a fitting polynomial
# and then runs ploty to obtain the matching X
#
def enumerate_poly(img_shape, left_fit, right_fit):
# Generate x and y values for plotting
ploty = np.linspace(0, img_shape[0]-1, img_shape[0])
had_except = False
### Calc both polynomials using ploty, left_fit and right_fit ###
try:
left_fitx = left_fit[0]*(ploty**2) + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*(ploty**2) + right_fit[1]*ploty + right_fit[2]
except TypeError:
# Avoids an error if `left` and `right_fit` are still none or incorrect
print('The function failed to fit a line!')
left_fitx = 1*ploty**2 + 1*ploty
right_fitx = 1*ploty**2 + 1*ploty
had_except = True
return (left_fitx, right_fitx, ploty, had_except)
# Given a fitting polygon, find lanes based on the polygonal value
def find_lane_pixels_byfit(binary_warped, model_left_fit, model_right_fit, nonzero, nonzerox, nonzeroy):
global invcnt
# HYPERPARAMETER
# Choose the width of the margin around the previous polynomial to search
# The quiz grader expects 100 here, but feel free to tune on your own!
margin = 20
xlmt = binary_warped.shape[1] - 1
ylmt = binary_warped.shape[0] - 1
#DBG print (invcnt, "-- Zy ", len(nonzeroy), " Zx ", len(nonzerox), " Ml ", model_left_fit, " Mr ", model_right_fit)
### TO-DO: Set the area of search based on activated x-values ###
### within the +/- margin of our polynomial function ###
### Hint: consider the window areas for the similarly named variables ###
### in the previous quiz, but change the windows to our new search area ###
left_fitx = model_left_fit[0]*(nonzeroy**2) + model_left_fit[1]*nonzeroy + model_left_fit[2]
left_lane_inds = ((nonzerox > (left_fitx - margin)) & (nonzerox < (left_fitx + margin)))
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
right_fitx = model_right_fit[0]*(nonzeroy**2) + model_right_fit[1]*nonzeroy + model_right_fit[2]
right_lane_inds = ((nonzerox > (right_fitx - margin)) & (nonzerox < (right_fitx + margin)))
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# Fit new polynomials and find plotting X,Y
had_except = False
try:
left_fit = np.polyfit(lefty, leftx, 2)
except:
left_fit = [0,0,0]
had_except = True
try:
right_fit = np.polyfit(righty, rightx, 2)
except:
right_fit = [0,0,0]
had_except = True
if (not had_except):
left_basex = np.int(left_fit[0]*(ylmt**2) + left_fit[1]*ylmt + left_fit[2])
right_basex = np.int(right_fit[0]*(ylmt**2) + right_fit[1]*ylmt + right_fit[2])
if (not (0 <= left_basex <= xlmt) or not (0 <= right_basex <= xlmt)):
left_basex = 0; right_basex = 0
else:
left_basex = 0; right_basex = 0
# This is the area that will be searched
left_fitx, right_fitx, ploty, had_except = enumerate_poly(binary_warped.shape, left_fit, right_fit)
fit_img = draw_fit_polygon(binary_warped.shape[0], binary_warped.shape[1], left_fitx, right_fitx, ploty, margin, [0,0,255])
## End visualization steps ##
return left_basex, right_basex, fit_img
# Given two sets of lane positions, determines the better fit and returns it
# "Better" is determined by assuming that lanes are approximately 300 pixels apart
def resolve_hist_fit_peaks(leftx_byfit, rightx_byfit, leftx_byhist, rightx_byhist):
global invcnt, globcfg
width_byhist = (rightx_byhist - leftx_byhist) if (rightx_byhist or leftx_byhist) else 9999
width_byfit = (rightx_byfit - leftx_byfit) if (rightx_byfit or leftx_byfit) else 9999
# ASSUMPTION WARNING: in the "project_video" and test_images, lanes seem to be about 300 pixels in width
# The following uses this to determine which of the two peaks - determined by fit of the existing polynomial
# or by using histogram gives a closer fit
# While the lane widths are hard-coded, this can easily be computed at the beginning and set up to dynamically
# adjust to road conditions. For example, any time a turn is taken, the new lane dimensions can be computed
# Alternately, lane widths presumanly must be standard for types of roads, and thus can be obtained from a map as well
# The 'globcfg["fitpref"]' is used to allow an easy switch between the two to determine which one works better
#
if globcfg["fitpref"]:
if (250 <= width_byfit <= 350):
use='f'
elif (250 <= width_byhist <= 350):
use='h'
else:
if (abs(width_byfit - 300) <= abs(width_byhist-300)):
use='f'
else:
use='h'
else:
if (250 <= width_byhist <= 350):
use='h'
elif (250 <= width_byfit <= 350):
use='f'
else:
if (abs(width_byfit - 300) <= abs(width_byhist-300)):
use='f'
else:
use='h'
if (use == 'h'):
leftx_base, rightx_base = leftx_byhist, rightx_byhist
#DBG print(invcnt, ": Using histogram peaks at ", leftx_base, rightx_base, ". Fit Peaks: ", leftx_byfit, rightx_byfit)
else:
leftx_base, rightx_base = leftx_byfit, rightx_byfit
#DBG print(invcnt, ": Using fit peaks at ", leftx_base, rightx_base, ". Hist Peaks: ", leftx_byhist, rightx_byhist)
return leftx_base, rightx_base
def get_fitpeaks(binary_warped, model_left_fit, model_right_fit, nonzero, nonzerox, nonzeroy):
if ( (len(model_left_fit) > 0 and model_left_fit[0] != 0) and (len(model_right_fit) > 0 and model_right_fit[0] != 0) ):
leftx_byfit, rightx_byfit, fit_img = find_lane_pixels_byfit(binary_warped, model_left_fit, model_right_fit, nonzero, nonzerox, nonzeroy)
else:
#DBG print (invcnt, ": Skipped fitting by form")
leftx_byfit = 0; rightx_byfit = 0
fit_img = None
return (leftx_byfit, rightx_byfit, fit_img)
# #####
#
# fit_polynomial
#
# Invokes find_by_window or find_by_fit to find the lane pixels, and then finds a fitting polynomial
#
# Returns: an image with the lanes marked along with the poygonal fit envelopes
#
def fit_polynomial(binary_warped):
global invcnt, globcfg, model_left_fit, model_right_fit
# Identify the x and y positions of all nonzero pixels in the image
nonzero = binary_warped.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# Find our lane pixels first
#
# If a model fit is available (typically the last frame's polygon fit), then use it to determine where the lanes might exist
# Also obtain the lane positions using the histogram methodology
# Then compare which of the two results provide a suitable match.
# Suitability is determined by evaluating the lane-width by each method and finding the one closest to "normal",
# assumed to be 300 pix for this project (empirical determination)
# Potential lane positions by model fit
leftx_byfit, rightx_byfit, fit_img = get_fitpeaks(binary_warped, model_left_fit, model_right_fit, nonzero, nonzerox, nonzeroy)
# Potential lane positions using the histogram method
leftx_byhist, rightx_byhist = get_histpeaks(binary_warped)
# Determine which of the two solutions return a better fit
leftx_base, rightx_base = resolve_hist_fit_peaks(leftx_byfit, rightx_byfit, leftx_byhist, rightx_byhist)
# Having found the lane marketers, find the lane pixels
leftx, lefty, rightx, righty, out_img = find_lane_pixels_bywin(binary_warped, leftx_base, rightx_base, nonzero, nonzerox, nonzeroy)
if (fit_img is not None):
out_img = weighted_img(fit_img, out_img, 0.8, 0.2)
# Fit a second order polynomial to each using `np.polyfit` ###
left_fit = []
right_fit = []
had_except = False
try:
left_fit = np.polyfit(lefty, leftx, 2)
except np.linalg.LinAlgError:
left_fit = model_left_fit
had_except = True
print (invcnt, ": Failed to find left polyfit")
try:
right_fit = np.polyfit(righty, rightx, 2)
except np.linalg.LinAlgError:
right_fit = model_right_fit
had_except = True
print (invcnt, ": Failed to find left polyfit")
if not had_except and globcfg["savefit"]:
#DBG print ("Saving FIT FUNCTIONS: ", left_fit, right_fit)
model_left_fit = left_fit
model_right_fit = right_fit
left_fitx, right_fitx, ploty, had_except = enumerate_poly(binary_warped.shape, left_fit, right_fit)
# Colors in the left and right lane regions
if not had_except:
fit_img = draw_fit_polygon(binary_warped.shape[0], binary_warped.shape[1], left_fitx, right_fitx, ploty, 20)
out_img = weighted_img(fit_img, out_img, 0.8, 0.2)
# Color in the pixels used to find the fitting polynomial
# Also, plot the pixels derived using the polynomial
out_img[lefty, leftx] = [255, 0, 0] if imgfmt == "rgb" else [0,0,255]
out_img[righty, rightx] = [0, 0, 255] if imgfmt == "rgb" else [255,0,0]
plot_pts(out_img, np.vstack((left_fitx, ploty)).T, [255,255,0])
plot_pts(out_img, np.vstack((right_fitx, ploty)).T, [255,255,0])
# plt.plot(left_fitx, ploty, color='yellow')
# plt.plot(right_fitx, ploty, color='yellow')
# Determine the radius of curvature and the position of the vehicle
measure_curvature_pixels(ploty, left_fit, right_fit)
return out_img
def save_img(img, imgname, lbl):
global imgfmt, output_dir
if (imgfmt == "rgb"):
plt.imsave(output_dir + imgname + lbl + ".jpg", img)
else:
cv2.imwrite(output_dir + imgname + lbl + ".jpg", img)
def tstamp_img(sts, img, lbl=""):
global globcfg, imgfmt, imgname
tdur = (datetime.now() - sts)
if lbl != "" and globcfg["savepipe"]:
save_img(img, imgname, lbl)
return tdur
# ###
#
# PIPELINE - processes the different stages of lane finding
#
# Can be used to save images (useful when processing a video stream for debugging)
# as well as takes timestamps
def timed_pipeline(img, lbls=["", "", "", "", "", ""], toplot=False, tvals=False):
global globcfg, invcnt, imgname, imgfmt
global mtx, dist
if globcfg["saveclips"]:
save_img(img, imgname, ("_clip_" + str(invcnt)))
tms = datetime.now()
# Run undistort if we are inspecting the pipeline
if globcfg["savepipe"]:
uimg = cv2.undistort(img, mtx, dist, None, mtx); tmt = tstamp_img(tms, uimg, lbls[0])
else:
uimg = img
timg = thresholding(uimg); tmt = tstamp_img(tms, timg, lbls[1])
wimg = chg_perspective(timg); tmw = tstamp_img(tmt, wimg, lbls[2])
oimg = fit_polynomial(wimg); tmo = tstamp_img(tmw, oimg, lbls[3])
vimg = chg_perspective(oimg, -1); tmv = tstamp_img(tmo, vimg, lbls[4])
fimg = weighted_img(vimg, img); tmf = tstamp_img(tmv, fimg, lbls[5])
fimg = imprint_curvature(fimg)
if (toplot):
f, axes = plt.subplots(3, 2, figsize=(12,16))
(ax0, ax1, ax2, ax3, ax4, ax5) = axes.flatten()
ax0.imshow(img); ax0.set_title("Original", fontsize=8)
ax1.imshow(uimg); ax1.set_title("Undistorted", fontsize=8)
ax2.imshow(timg, cmap='gray'); ax2.set_title("Thresholded", fontsize=8)
ax3.imshow(wimg, cmap='gray'); ax3.set_title("Warped", fontsize=8)
ax4.imshow(oimg, cmap='gray'); ax4.set_title("Fitted", fontsize=8)
ax5.imshow(fimg); ax5.set_title("Final", fontsize=8)
if globcfg["saveclips"]:
save_img(img, imgname, "_out_clip_" + str(invcnt))
invcnt += 1
if (tvals):
print_times((tms, tmt, tmw, tmo, tmv, tmf))
return fimg
# Print the configuration in use. Primarily used to match output to the configuration used
def print_globcfg():
global globcfg
print (datetime.now())
print ("Global configurations: ")
for k,v in globcfg.items(): print (k,v)
return
# Set up some basic parameters
def basic_setup():
global mtx, dist
# Calibrate camera
ret, mtx, dist = calib_camera()
if (not ret):
print ("Failed to calibrate the camera")
return False
print_globcfg()
return True
# ###
#
# The following routine allows to interactively test the different stages of the pipeline on individual images
# to determine effect and understand what stage is going wrong
# images are set up in the routine
#
def test_sandbox(imglist):
global img, imgfmt, thresh, meth, methch, imgname
global imgs, imgid
global model_left_fit, model_right_fit
global mtx, dist
# Read-in the images
imgs = []
for i, imgname in enumerate(imglist):
imgs.append(plt.imread(imgname))
imgfmt = "rgb"
imgname = imglist[0]
img = imgs[0]
draw_img(imgname, img)
# cv2.createTrackbar('outlier %', 'fit line', 30, 100, update)
while True:
ch = cv2.waitKey(0)
if ch >= ord('1') and ch <= ord('9'):
imgid = ch-ord('1')
if (imgid >= len(imglist)):
print ("Invalid index: ", imgid)
imgid = 0
imgname = imglist[imgid]; print ("Using: ", imgname)
img = imgs[imgid]
draw_img(imgname, img)
elif ch == ord('j') or ch == ord('k'):
dir = 1 if ch == ord('k') else -1
imgid += dir
if imgid < 0 or imgid >= len(imglist): imgid = 0
imgname = imglist[imgid]; print ("Using: ", imgname)
img = imgs[imgid]
draw_img(imgname, img)
elif ch == ord('o'):
meth = 2
draw_img(imgname, img)
elif ch == ord('f'):
uimg = cv2.undistort(img, mtx, dist, None, mtx);
timg = thresholding(uimg)
draw_img(imgname, timg)
elif ch == ord('d'):
oimg = timed_pipeline(img, True, True)
draw_img(imgname, oimg)
plt.show()
elif ch == ord('p'):
oimg = timed_pipeline(img, False, True)
draw_img(imgname, oimg)
# plt.show()
elif ch == ord('w'):
# oimg = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# oimg = timed_pipeline(img, True, True)
oimg = thresholding(img)
oimg = chg_perspective(oimg)
draw_img(imgname, oimg)
elif ch == ord('u'):
model_left_fit = []
model_right_fit = []
if ch == 27 or ch == ord('q'):
cv2.destroyWindow(winname)
cv2.waitKey(1000)
break
# ##
#
# Encapsulates all tests that need to be run. A test can be run by invoking this function w/ the test-id
#
# 1: Run through the test_images and save the final annotated images
# 2: Run through the project video and save the final annotated video
# 3: Run the pipeline for one test image saving output of each stage of the pipeline
# 4: Calibration test
# 5: Perspective Transformation test
# 6/7: Internal tests used during development
#
def test_harness(runtest):
global img, imgfmt, imgname, winname
global invcnt, pipeline_lbls
if runtest == 1: # Run the pipeline on individual images
imglist = glob.glob("test_images/*.jpg")
for tfname in imglist:
print ("Processing ", tfname)
img = plt.imread(tfname)
imgfmt = "rgb"
imgname = os.path.splitext(os.path.basename(tfname))[0]
fimg = timed_pipeline(img)
save_img(fimg, imgname, "_out")
# plt.imshow(fimg)
if runtest == 2: # Run the pipeline on a video stream
vfile = "harder_challenge_video.mp4"
# vfile = "challenge_video.mp4"
vfile = "project_video.mp4"
imgname = os.path.splitext(os.path.basename(vfile))[0]
extname = os.path.splitext(vfile)[-1]
# Save the fitting polynomial parameters at end of each frame to be used for next frame
globcfg["savefit"] = True
print_globcfg()
# vclip = VideoFileClip(vfile, audio=False).subclip(1,t_end=3)
# vclip = VideoFileClip(vfile, audio=False).subclip(3,8)
# vclip = VideoFileClip(vfile, audio=False).subclip(20,29)
# vclip = VideoFileClip(vfile, audio=False).subclip(39,44)
vclip = VideoFileClip(vfile, audio=False) # .subclip(t_end=10)
tms = datetime.now()
oclip = vclip.fl_image(timed_pipeline)
oclip.write_videofile(imgname + "_out" + extname)
tme = datetime.now()
# print ("Clip Processing time: ", (tme-tms), ". Invocations: ", invcnt)
if runtest == 3: # Run the pipeline for a single test image saving output after each stage
tfname = "video_clips/project_video_clip_884.jpg"
# tfname = "test_images/test2.jpg"
print ("Processing ", tfname)
imgname = os.path.splitext(os.path.basename(tfname))[0]
img = plt.imread(tfname)
imgfmt = "rgb"
spcfg = globcfg["savepipe"]
globcfg["savepipe"] = True
fimg = timed_pipeline(img, pipeline_lbls, toplot=True)
globcfg["savepipe"] = spcfg
plt.show()
if runtest == 4: # Run camera calibration and gather undistorted image
tfname = "camera_cal/calibration1.jpg"
print ("Processing ", tfname)
imgname = os.path.splitext(os.path.basename(tfname))[0]
tms = datetime.now()
spcfg = globcfg["savepipe"]
globcfg["savepipe"] = True
# Read the file
img = plt.imread(tfname)
imgfmt = "rgb"
# Run undistort on the image. Note that camera calibration was already run as part of basic_setup
uimg = cv2.undistort(img, mtx, dist, None, mtx)
tstamp_img(tms, img, "_cal_Original")
tstamp_img(tms, uimg, "_cal_Undistorted")
globcfg["savepipe"] = spcfg
visualize_imgs(img, uimg, "Original", "Undistorted")
plt.show()
if runtest == 5: # Run perspective warping on an image and show before/after results
tms, tmt, tmw, tmo, tmv, tmf = (0,0,0,0,0,0)
tfname = "test_images/straight_lines1.jpg"
imgname = os.path.splitext(os.path.basename(tfname))[0]
tms = datetime.now()
spcfg = globcfg["savepipe"]
globcfg["savepipe"] = True
# Read the file
img = plt.imread(tfname)
imgfmt = "rgb"
# The following coordinates draw a lane-aligned trapezoid for test-image straight_lines1.jpg
cv2.line(img, (590,456), (686,456), [255,0,0])
cv2.line(img, (337,636), (968,636), [255,0,0])
cv2.line(img, (590,456), (337,636), [255,0,0])
cv2.line(img, (686,456), (968,636), [255,0,0])
# Apply the perspective transform
wimg = chg_perspective(img, 1)
tstamp_img(tms, img, "_persp_Original")
tstamp_img(tms, wimg, "_persp_Warped")
globcfg["savepipe"] = spcfg
visualize_imgs(img, wimg, "Original", "Warped")
plt.show()
# The following is just a kitchen sink area to allow running of various routines
# with different levels of debug controls
if runtest == 6:
# imglist = [ "video_clips_3944/project_video_28.jpg" ]
imglist = ["video_clips/challenge_video_0.jpg"]
imglist = []
for i in range(20,48):
imglist.append("video_clips/challenge_video_" + str(i) + ".jpg")
imglist = glob.glob("test_images/*.jpg")
imglist = glob.glob("test_images/straight_lines1.jpg")
# create_filt_trackers()
# create_pers_trackers()
test_sandbox(imglist)
# Process an image with fine-grained control for each stage of pipeline
if runtest == 7:
tms, tmt, tmw, tmo, tmv, tmf = (0,0,0,0,0,0)
imglist = ["video_clips/project_video_28.jpg"]
imglist = ["video_clips/challenge_video_0.jpg"]
imglist = ["video_clips_conv_nowin/project_video_884.jpg"]
imglist = ["test_images/straight_lines1.jpg"]
for item in imglist:
print ("Processing ", item)
img = plt.imread(item)
imgfmt = "rgb"
imgname = os.path.splitext(os.path.basename(item))[0]
tms = datetime.now()
if True:
f, axes = plt.subplots(5, 1, figsize=(4,14))
(ax0, ax1, ax2, ax3, ax4) = axes.flatten()
ax0.imshow(img); ax0.set_title("Original", fontsize=8)
timg = thresholding(img)
tmt = datetime.now()
ax1.imshow(timg); ax1.set_title("Thresholded", fontsize=8)
wimg = chg_perspective(timg)
tmw = datetime.now()
ax2.imshow(wimg, cmap='gray'); ax2.set_title("Warped", fontsize=8)
oimg = fit_polynomial(wimg)
tmo = datetime.now()
ax3.imshow(oimg); ax3.set_title("Fitted", fontsize=8)
if False:
vimg = chg_perspective(oimg, -1)
tmv = datetime.now()
fimg = weighted_img(vimg, img)
tmf = datetime.now()
ax4.imshow(fimg); ax4.set_title("Final", fontsize=8)
else:
fimg = wimg
# cv2.imshow(winname, fimg)
# print_times((tms, tmt, tmw, tmo, tmv, tmf))
plt.show()
ch = cv2.waitKey(0)
if ch == 27 or ch == ord('q'):
cv2.destroyWindow(winname)
break
# cv2.destroyWindow(winname)
# plt.close()
# ###
# Global controls
#
# colfilt - Apply the color filter
# fitpref - Prefer lane positions determined by previous fit over lane positions determined by histogram on current frame
# saveclips - Save before and after images of the pipeline. Used when storing of frames of a video is required (for debugging)
# savepipe - Save images from each stage of a pipeline
# savefit - Save the polynomial results of the current frame. Useful when processing a video
#
globcfg = { "colfilt":True, "fitpref":True, "saveclips":False, "drawrect":False, "savepipe":False, "savefit":False }
# Set up some environment variables
r = basic_setup()
if not r:
runtest=99
# +
# Run the calibration and undistortion test
test_harness(4)
oimglist = glob.glob("output_images/*_cal_*.jpg")
print ("Output Images: ", oimglist)
# +
# Show the perspective transformation
test_harness(5)
oimglist = glob.glob("output_images/*_persp_*.jpg")
print ("Output Images: ", oimglist)
# +
# Run the pipeline against a single test image and show each stage's output
test_harness(3)
oimglist = glob.glob("video_clips/*_clip_884*.jpg")
print ("Input Images: ", oimglist)
oimglist = glob.glob("output_images/*884_pp_*.jpg")
print ("Output Images: ", oimglist)
# +
# Run the pipeline against each of the test_images
test_harness(1)
oimglist = glob.glob("output_images/*_out.jpg")
print ("Output Images: ")
for x in oimglist: print (" ", x)
# +
# Run the pipeline against the project video stream
test_harness(2)
oimglist = glob.glob("*_out.mp4")
print ("Output Images: ", oimglist)
# +
# Let us take a look at the video output
HTML("""
<video width="800" height="450" controls>
<source src="{0}">
</video>
""".format("project_video_out.mp4"))
# -
#
|
.ipynb_checkpoints/AdvLaneFind-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tarea de clase # 1
# **Programación I**
# ## Ejercicio 1
#
# * Asigne valores para ``A`` y ``B``.
# * Para cada operador (``+``,``-``,``*``,``/``,``/``/,``%``,``**``) haga un ejemplo con los valores asignados previamente.
# * Utilizando el comando ``print()`` Muestre los valores a operar, la operación y el resultado.
#
# **Asigne valores para A y B**
A = 5
B = 10
# **Para cada operador (``+``,``-``,``*``,``/``,``/``/,``%``,``**``) haga un ejemplo con los valores asignados previamente.**
# ## Ejercicio 2
#
# * Asigne ``A='Aa'`` y ``B='aa'``
# * Verifique las siguientes expresiones:
# - ``A<B``
# - ``A<B``
# * Explique el resultado de las expresiones anteriores. ¿Por qué no son iguales?
# ## Ejercicio 3
#
# 1. Escriba un programa que calcule la hipotenusa e imprima el resultado dado dos catetos.
# 2. Reescriba el ejemplo anterior para que los puntos sean bidimensionales.
# 3. Escriba un programa que, dados tres puntos bidimensionales, imprima si son colineales o no. (No emplee la estructura ``if else``, solamente operadores).
#
# ## Ejercicio 4
#
# Traduzca las siguientes expresiones lógicas y verifique su resultado, siendo ``A=0`` y ``B=1``.
#
# 1. $A \implies B$
# 2. $A \iff B$
|
ejercicios-tareas-proyectos/tareas/1_tarea.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# +
#https://github.com/Azure-Samples/storage-blobs-python-quickstart/blob/master/example.py
# +
import os, uuid, sys
from azure.storage.blob import BlockBlobService, PublicAccess
import time
import urllib.request
import os
import shutil
train_file = 'noun-curatedTrain-df.csv'
validation_file = 'noun-curatedValidation-df.csv'
def download_data_vm():
ip_file = open(train_file, 'r+')
old_ctg = ''
image_dict = {}
for l in ip_file.readlines()[1:]:
l_split = l.split('\t')
ctg, img_link = l_split[1], l_split[2].rstrip()
if ctg in image_dict:
if len(image_dict[ctg]) > 2000:
continue
image_dict[ctg].append(img_link)
else:
image_dict[ctg] = [img_link]
if len(image_dict) == 400:
break
# data_folder = os.path.join(os.getcwd(), 'validation_data')
# test_data_folder = os.path.join(os.getcwd(), 'test_data')
train_data_folder = os.path.join(os.getcwd(), 'train_data')
# if os.path.exists(data_folder):
# shutil.rmtree(data_folder)
# if os.path.exists(test_data_folder):
# shutil.rmtree(test_data_folder)
if os.path.exists(train_data_folder):
shutil.rmtree(train_data_folder)
# os.makedirs(data_folder, exist_ok=True)
# os.makedirs(test_data_folder, exist_ok=True)
os.makedirs(train_data_folder, exist_ok=True)
for k, v in image_dict.items():
# val_cat_data_folder = os.path.join(data_folder, k)
# os.makedirs(val_cat_data_folder, exist_ok=True)
# test_cat_data_folder = os.path.join(test_data_folder, k)
# os.makedirs(test_cat_data_folder, exist_ok=True)
train_cat_data_folder = os.path.join(train_data_folder, k)
os.makedirs(train_cat_data_folder, exist_ok=True)
for counter,url in enumerate(v):
# if counter < 499:
# download_folder = val_cat_data_folder
# else:
# download_folder = test_cat_data_folder
download_folder = train_cat_data_folder
try:
#urllib.request.urlretrieve(url, filename=os.path.join(download_folder, url.rsplit('/', 1)[-1]))
open_save(url,os.path.join(download_folder, url.rsplit('/', 1)[-1]))
except:
pass
def download_val_test_data_vm():
ip_file = open(validation_file, 'r+')
old_ctg = ''
image_dict = {}
for l in ip_file.readlines()[1:]:
l_split = l.split('\t')
ctg, img_link = l_split[1], l_split[2].rstrip()
if ctg in image_dict:
if len(image_dict[ctg]) > 1000:
continue
image_dict[ctg].append(img_link)
else:
image_dict[ctg] = [img_link]
if len(image_dict) == 400:
break
data_folder = os.path.join(os.getcwd(), 'validation_data')
test_data_folder = os.path.join(os.getcwd(), 'test_data')
if os.path.exists(data_folder):
shutil.rmtree(data_folder)
if os.path.exists(test_data_folder):
shutil.rmtree(test_data_folder)
os.makedirs(data_folder, exist_ok=True)
os.makedirs(test_data_folder, exist_ok=True)
for k, v in image_dict.items():
val_cat_data_folder = os.path.join(data_folder, k)
os.makedirs(val_cat_data_folder, exist_ok=True)
test_cat_data_folder = os.path.join(test_data_folder, k)
os.makedirs(test_cat_data_folder, exist_ok=True)
for counter,url in enumerate(v):
if counter < 499:
download_folder = val_cat_data_folder
else:
download_folder = test_cat_data_folder
try:
open_save(url,os.path.join(download_folder, url.rsplit('/', 1)[-1]))
except:
pass
def open_save(url,path):
request_ = urllib.request.urlopen(url, timeout=10)
with open(path+'.jpg', 'wb') as f:
try:
f.write(request_.read())
f.flush()
except:
pass
# Main method.
if __name__ == '__main__':
download_data_vm()
download_val_test_data_vm()
# + active=""
# from azureml.core import Workspace
# # load workspace configuration from the config.json file in the current folder.
# ws = Workspace.from_config()
# print(ws.name, ws.location, ws.resource_group, ws.location, sep='\t')
#
# train_data_folder = os.path.join(os.getcwd(), 'train_data')
# test_data_folder = os.path.join(os.getcwd(), 'test_data')
# validation_data_folder = os.path.join(os.getcwd(), 'validation_data')
#
# ds = ws.get_default_datastore()
# print(ds.datastore_type, ds.account_name, ds.container_name)
#
# ds.upload(src_dir=train_data_folder, target_path='guessingobject_context_train', overwrite=True, show_progress=False)
# ds.upload(src_dir=test_data_folder, target_path='guessingobject_context_test', overwrite=True, show_progress=False)
# ds.upload(src_dir=validation_data_folder, target_path='guessingobject_context_validation', overwrite=True, show_progress=False)
# -
|
azure_code/upload_data_blobstore.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
org_data = pd.read_csv('C:/Users/<NAME>/Desktop/NMT Project/dataset/datalist_modified.csv')
org_data.head()
striped_eng = []
for line in org_data["English"]:
striped_eng.append(line.strip(" "))
striped_kor = []
for line in org_data["Korean"]:
striped_kor.append(line.strip(" "))
org_data["Korean"] = striped_kor
org_data["English"] = striped_eng
kor_word_cnt = []
eng_word_cnt = []
for i in range(len(org_data)):
kor_word_cnt.append(len(org_data['Korean'][i].split(" ")))
eng_word_cnt.append(len(org_data['English'][i].split(" ")))
org_data["Korean_word_count"] = kor_word_cnt
org_data["English_word_count"] = eng_word_cnt
eng_sorted = org_data.sort_values(by=['English_word_count'], axis=0, ascending=False)
eng_sorted.head()
len(eng_sorted["English"][1416839].split(" "))
eng_sorted["English"][1416839]
eng_sorted["Korean"][1416839]
kor_sorted = org_data.sort_values(by=['Korean_word_count'], axis=0, ascending=False)
kor_sorted.head()
org_data.head()
del org_data["Korean_word_count"]
del org_data["English_word_count"]
# +
#org_data.to_csv("C:/Users/<NAME>/Desktop/NMT Project/dataset/datalist_striped.csv", encoding = 'utf-8-sig', index = False, mode = "w")
|
data_codes/Strip Blank Space.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/zihangdai/xlnet/blob/master/notebooks/colab_imdb_gpu.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="fnOHnctkG6kW"
# # XLNet IMDB movie review classification project
#
# This notebook is for classifying the [imdb sentiment dataset](https://ai.stanford.edu/~amaas/data/sentiment/). It will be easy to edit this notebook in order to run all of the classification tasks referenced in the [XLNet paper](https://arxiv.org/abs/1906.08237). Whilst you cannot expect to obtain the state-of-the-art results in the paper on a GPU, this model will still score very highly.
# + [markdown] colab_type="text" id="2mBzLdrdzodb"
# ## Setup
# Install dependencies
# + colab={} colab_type="code" id="hRHRPImGUth7"
# ! pip install sentencepiece
# + [markdown] colab_type="text" id="jy8gUsPuJNyw"
# Download the pretrained XLNet model and unzip
# + colab={} colab_type="code" id="HfPDGsUtHKG0"
# only needs to be done once
# ! wget https://storage.googleapis.com/xlnet/released_models/cased_L-24_H-1024_A-16.zip
# ! unzip cased_L-24_H-1024_A-16.zip
# + [markdown] colab_type="text" id="4uUwjq3BJRbu"
# Download extract the imdb dataset - surpessing output
# + colab={} colab_type="code" id="QOGRICbOIsU8"
# ! wget http://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
# ! tar zxf aclImdb_v1.tar.gz
# + [markdown] colab_type="text" id="yGY_ggUUMrwU"
# Git clone XLNet repo for access to run_classifier and the rest of the xlnet module
# + colab={} colab_type="code" id="-r190eYVMpiG"
# ! git clone https://github.com/ricklentz/xlnet.git
# + [markdown] colab_type="text" id="jDP-IaVuPC-z"
# ## Define Variables
# Define all the dirs: data, xlnet scripts & pretrained model.
# If you would like to save models then you can authenticate a GCP account and use that for the OUTPUT_DIR & CHECKPOINT_DIR - you will need a large amount storage to fix these models.
#
# Alternatively it is easy to integrate a google drive account, checkout this guide for [I/O in colab](https://colab.research.google.com/notebooks/io.ipynb) but rememeber these will take up a large amount of storage.
#
# + colab={} colab_type="code" id="y7N_xVwavQlV"
SCRIPTS_DIR = 'xlnet' #@param {type:"string"}
DATA_DIR = 'aclImdb' #@param {type:"string"}
OUTPUT_DIR = 'proc_data/imdb' #@param {type:"string"}
PRETRAINED_MODEL_DIR = 'xlnet_cased_L-24_H-1024_A-16' #@param {type:"string"}
CHECKPOINT_DIR = 'exp/imdb' #@param {type:"string"}
# -
# + [markdown] colab_type="text" id="<KEY>"
# ## Run Model
# This will set off the fine tuning of XLNet. There are a few things to note here:
#
#
# 1. This script will train and evaluate the model
# 2. This will store the results locally on colab and will be lost when you are disconnected from the runtime
# 3. This uses the large version of the model (base not released presently)
# 4. We are using a max seq length of 128 with a batch size of 8 please refer to the [README](https://github.com/zihangdai/xlnet#memory-issue-during-finetuning) for why this is.
# 5. This will take approx 4hrs to run on GPU.
#
#
# + colab={} colab_type="code" id="CEMuT6LU0avg"
train_command = "python xlnet/run_classifier.py \
--do_train=True \
--do_eval=True \
--eval_all_ckpt=True \
--task_name=imdb \
--data_dir="+DATA_DIR+" \
--output_dir="+OUTPUT_DIR+" \
--model_dir="+CHECKPOINT_DIR+" \
--uncased=False \
--spiece_model_file="+PRETRAINED_MODEL_DIR+"/spiece.model \
--model_config_path="+PRETRAINED_MODEL_DIR+"/xlnet_config.json \
--init_checkpoint="+PRETRAINED_MODEL_DIR+"/xlnet_model.ckpt \
--max_seq_length=128 \
--train_batch_size=8 \
--eval_batch_size=8 \
--num_hosts=1 \
--num_core_per_host=2 \
--learning_rate=2e-5 \
--train_steps=4000 \
--warmup_steps=500 \
--save_steps=500 \
--iterations=500"
# ! {train_command}
# + [markdown] colab_type="text" id="VvhqD-sO0Kyh"
# ## Running & Results
# These are the results that I got from running this experiment
# ### Params
# * --max_seq_length=128 \
# * --train_batch_size= 8
#
# ### Times
# * Training: 1hr 11mins
# * Evaluation: 2.5hr
#
# ### Results
# * Most accurate model on final step
# * Accuracy: 0.92416, eval_loss: 0.31708
#
# + [markdown] colab_type="text" id="XUW2avFM_fi_"
# ### Model
#
# * The trained model checkpoints can be found in 'exp/imdb'
#
#
|
notebooks/colab_imdb_gpu.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=false editable=false
# # <img style="float: left; padding-right: 10px; width: 45px" src="https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/iacs.png"> CS109B Data Science 2: Advanced Topics in Data Science
#
# ## Homework 8: Reinforcement Learning [100 pts]
#
#
# **Harvard University**<br/>
# **Spring 2020**<br/>
# **Instructors**: <NAME>, <NAME> and <NAME><br/>
#
# **DISCLAIMER**: No public reproduction of this homework nor its solution is allowed without the explicit consent of their authors.
#
#
#
# <hr style="height:2pt">
#
# ---
# + deletable=false editable=false
#PLEASE RUN THIS CELL
import requests
from IPython.core.display import HTML
styles = requests.get("https://raw.githubusercontent.com/Harvard-IACS/2018-CS109A/master/content/styles/cs109.css").text
HTML(styles)
# + [markdown] deletable=false editable=false
# ### INSTRUCTIONS
#
# - To submit your assignment follow the instructions given in Canvas.
# - Restart the kernel and run the whole notebook again before you submit.
# - Do not submit a notebook that is excessively long because output was not suppressed or otherwise limited.
# + deletable=false editable=false
# Numpy and plotting libraries
import numpy as np
import matplotlib.pyplot as plt
import time
# %matplotlib inline
# + [markdown] deletable=false editable=false
# # Overview
# + [markdown] deletable=false editable=false
# The objective of this homework assignment is to get a taste of implementing a planning algorithm in a very simple setting.
# + [markdown] deletable=false editable=false
# <div class='exercise'><b> Markov Decision Process [100 points] </b></div>
#
#
# We have a hallway consisting of 5 blocks (states 0-4). There are two actions, which deterministically move the agent to the left or the right. More explicitly: Performing action “left” in state 0 keeps you in state 0, moves you from state 1 to state 0, from state 2 to state 1, state 3 to state 2, and state 4 to state 3. Performing action “right” in state 4 keeps you in state 4, moves you from state 3 to state 4, from state 2 to state 3, from state 1 to state 2, and from state 0 to state 1. The agent receives a reward of -1.0 if it starts any iteration in state 0, state 1, state 2, or state 3. The agent receives a reward of +10.0 if it starts in state 4. Let the discount factor γ = 0.75.
#
# We provide class MDP that instantiates an object representing a Markov decision process and verifies shapes.
#
# **1.1** MDP proble [10 pts]: Build an MDP representing the hallway setting described above, by completing the function `build_hallway_mdp()`. You need to specify the array T that encodes the transitions from state and actions into next states; and a reward vector R that specifies the reward for being at a certain state.
#
# **1.2** Policy Evaluation [20 pts]: Initialize a policy “left” for every state (a 1D numpy array). Implement policy evaluation as described in lecture (also in Chapter 4 of [Sutton and Barto](http://incompleteideas.net/book/RLbook2018.pdf)). That is, for each possible starting state, what is the expected sum of future rewards for this policy? Using an iterative approach, how many iterations did it take for the value of the policy to converge to a precision of 10−5?
#
# **1.3** Q-function Computation [20 pts]: Compute the Q-function for the `always_left` policy above. Do you see any opportunties for policy improvement?
#
# **1.4** Policy Iteration [20 pts]: Using your solutions to questions 1.2 and 1.3 above, implement policy iteration. Report the sequence of policies you find starting with the policy “left” in every state. How many rounds of policy iteration are required to converge to the optimal policy?
#
# **1.5** [10 pts] What are the effects of different choices of the discount factor on the convergence of policy evaluation? Run policy evaluation for discount factor $\gamma \in [ 10^{-12}, 10^{-3}, 0.1, 0.33, 0.67, 0.9, 0.95, 0.99]$.
#
# **1.6** [20 pts] What happens if the transitions are stochastic? Recode the MDP with probability of switching to the opposite action of 0.1. What are now the values when following the optimal policy?
# + deletable=false editable=false
class MDP(object):
"""Wrapper for a discrete Markov decision process that makes shape checks"""
def __init__(self, T, R, discount):
"""Initialize the Markov Decision Process.
- `T` should be a 3D array whose dimensions represent initial states,
actions, and next states, respectively, and whose values represent
transition probabilities.
- `R` should be a 1D array describing rewards for beginning each
timestep in a particular state (or a 3D array like `T`). It will be
transformed into the appropriate 3D shape.
- `discount` should be a value in [0,1) controlling the decay of future
rewards."""
Ds, Da, _ = T.shape
if T.shape not in [(Ds, Da, Ds)]:
raise ValueError("T should be in R^|S|x|A|x|S|")
if R.shape not in [(Ds, Da, Ds), (Ds,)]:
raise ValueError("R should be in R^|S| or like T")
if discount < 0 or discount >= 1:
raise ValueError("discount should be in [0,1)")
if R.shape == (Ds,): # Expand R if necessary
R = np.array([[[R[s1] for s2 in range(Ds)] for a in range(Da)] for s1 in range(Ds)])
self.T = T
self.R = R
self.discount = discount
self.num_states = Ds
self.num_actions = Da
self.states = np.arange(Ds)
self.actions = np.arange(Da)
# + [markdown] autograde="1.1" deletable=false editable=false
# **1.1** MDP proble [10 pts]: Build an MDP representing the hallway setting described above, by completing the function `build_hallway_mdp()`. You need to specify the array T that encodes the transitions from state and actions into next states; and a reward vector R that specifies the reward for being at a certain state.
#
# + deletable=false
def build_hallway_mdp():
"""Build an MDP representing the hallway setting described."""
# your code here
T = np.array([[[1,0,0,0,0],[0,1,0,0,0]],
[[1,0,0,0,0],[0,0,1,0,0]],
[[0,1,0,0,0],[0,0,0,1,0]],
[[0,0,1,0,0],[0,0,0,0,1]],
[[0,0,0,1,0],[0,0,0,0,1]]])
R = np.array([-1,-1,-1,-1,10])
# end of your code here
return MDP(T, R, 0.75)
# + deletable=false editable=false
# Run for sanity check
mdp = build_hallway_mdp()
plt.figure(figsize=(5,2))
plt.subplot(121, title='Left transitions')
plt.imshow(mdp.T[:,0,:])
plt.ylabel("Initial state"); plt.xlabel('Next state')
plt.subplot(122, title='Right transitions')
plt.imshow(mdp.T[:,1,:])
plt.ylabel("Initial state"); plt.xlabel('Next state')
plt.show()
# + [markdown] autograde="1.2" deletable=false editable=false
# **1.2** Policy Evaluation [20 pts]: Initialize a policy “left” for every state (a 1D numpy array). Implement policy evaluation as described in lecture (also in Chapter 4 of [Sutton and Barto](http://incompleteideas.net/book/RLbook2018.pdf)). That is, for each possible starting state, what is the expected sum of future rewards for this policy? Using an iterative approach, how many iterations did it take for the value of the policy to converge to a precision of 10−5?
#
# + deletable=false
def build_always_left_policy():
"""Build a policy representing the action "left" in every state."""
# your code here
actions = [0,0,0,0,0]
return actions
# + deletable=false
def iterative_value_estimation(mdp, policy, tol=1e-5):
"""Value estimation algorithm from page 75, Sutton and Barto. Returns an
estimate of the value of a given policy under the MDP (with the number of
iterations required to reach specified tolerance)."""
V = np.zeros(mdp.num_states)
num_iters = 0
delta = float("inf")
while delta>tol:
V_old = V.copy()
num_iters+=1
for s in mdp.states:
action = policy[s]
V[s] = mdp.T[s,action,:]@(mdp.R[s,action,:]+mdp.discount*V_old)
delta = sum(abs(V_old-V))
# your code here
# end of your code here
return V, num_iters
# + deletable=false editable=false
# Run for sanity check
always_left = build_always_left_policy()
values, iters = iterative_value_estimation(mdp, always_left)
print('Policy value was:')
print(values.round(4))
tols = np.logspace(0,-8,9)
iters = [iterative_value_estimation(mdp, always_left, tol=tol)[1] for tol in tols]
plt.plot(tols, iters, marker='o')
plt.xscale('log')
plt.xlabel("Tolerance")
plt.ylabel("Iterations to converge to within tolerance")
plt.show()
# -
# The policy value was: [-4. -4. -4. -4. 7.]. It takes 46 iteration to reach a precision of 10-5.
# + [markdown] autograde="1.3" deletable=false editable=false
# **1.3** Q-function Computation [20 pts]: Compute the Q-function for the `always_left` policy above. Do you see any opportunties for policy improvement?
#
# + deletable=false
# 1.3
def Q_function(mdp, policy, tol=1e-5):
"""Q function from Equation 4.6, Sutton and Barto. For each state and
action, returns the value of performing the action at that state, then
following the policy thereafter."""
# your code here
V,_ = iterative_value_estimation(mdp, policy, tol=1e-5)
Q = np.zeros((mdp.num_states,mdp.num_actions))
for s in mdp.states:
for a in mdp.actions:
Q[s,a] = mdp.T[s,a,:]@(mdp.R[s,a,:]+mdp.discount*V)
# end of your code here
assert Q.shape == (mdp.num_states, mdp.num_actions)
return Q
# + deletable=false editable=false
# Run for sanity check
Q = Q_function(mdp, always_left)
print('Q function was:')
print(Q.round(4))
# + [markdown] deletable=false
# *Your answer here*
#
# Yes, for state 3 and 4, we should go right as Q value is larger than the policy values in those two states.
# + [markdown] autograde="1.4" deletable=false editable=false
# **1.4** Policy Iteration [20 pts]: Using your solutions to questions 1.2 and 1.3 above, implement policy iteration. Report the sequence of policies you find starting with the policy “left” in every state. How many rounds of policy iteration are required to converge to the optimal policy?
#
# + deletable=false
# 1.4
def policy_iteration(mdp, init_policy=None, tol=1e-5):
"""Policy iteration algorithm from page 80, Sutton and Barto.
Iteratively transform the initial policy to become optimal.
Return the full path."""
# your code here
policy = init_policy.copy()
policy_stable = False
max_iter = 5000
n_iter = 0
policies = []
while n_iter < max_iter and (not policy_stable):
old_policy = policy.copy()
policies.append(old_policy)
n_iter+=1
V,_ = iterative_value_estimation(mdp, policy, tol=1e-5)
Q = Q_function(mdp, policy)
policy_stable = True
for s in mdp.states:
old_action = policy[s]
policy[s] = np.argmax(Q[s,:])
if old_action != policy[s]:
policy_stable = False
# end of your code here
return policies
# + deletable=false editable=false
# Sanity check
policy_iters = policy_iteration(mdp, always_left)
policy_iters
# + [markdown] deletable=false
# *Your answer here*
#
# Please see the evolution of policy above. 5 policy iteration required to find the optimal policy.
# + [markdown] autograde="1.5" deletable=false editable=false
# **1.5** [10 pts] What are the effects of different choices of the discount factor on the convergence of policy evaluation? Run policy evaluation for discount factor $\gamma \in [ 10^{-12}, 10^{-3}, 0.1, 0.33, 0.67, 0.9, 0.95, 0.99]$.
#
# + deletable=false
# 1.5
# your code here
discount_factors = [.1**12,.1**3,0.1,0.33,0.67,0.9,0.95,0.99]
iters_by_factor = []
for gamma in discount_factors:
mdp.discount = gamma
n_iterations = iterative_value_estimation(mdp, always_left)[1]
iters_by_factor.append(n_iterations)
# + deletable=false editable=false
plt.plot(discount_factors, iters_by_factor, marker='o')
plt.xlabel('Discount factor $\gamma$')
plt.ylabel('Iterations for value estimate to converge')
plt.title("Convergence of value estimate by $\gamma$")
plt.show()
# + [markdown] deletable=false
# *Your answer here*
#
# The smaller discount fatcor is, the smaller weight put for the reward from next states, therefore the policy evaluation converges faster as the model care less about the reward from next action. If the discount increases, the number of iteration needed for convergence grows exponential because for each state, the reward from all previous states are taken into consideration (as the discount factor is close to one), which leads the complexity grows exponentially.
# + [markdown] autograde="1.6" deletable=false editable=false
# **1.6** [20 pts] What happens if the transitions are stochastic? Recode the MDP with probability of switching to the opposite action of 0.1. What are now the values when following the optimal policy?
# + deletable=false
# 1.6
# your code here
mdp = build_hallway_mdp()
policy_iters_static = policy_iteration(mdp, always_left)
best_policy_static = policy_iters_static[-1]
best_values_static = iterative_value_estimation(mdp, best_policy_static)
print("The values for optimal policy %s for the original mdp is: %s"%(best_policy_static,best_values_static))
# +
def build_stochastic_mdp():
"""Build an MDP representing the hallway setting described."""
# your code here
T = np.array([[[0.9,0.1,0,0,0],[0.1,0.9,0,0,0]],
[[0.9,0,0.1,0,0],[0.1,0,0.9,0,0]],
[[0,0.9,0,0.1,0],[0,0.1,0,0.9,0]],
[[0,0,0.9,0,0.1],[0,0,0.1,0,0.9]],
[[0,0,0,0.9,0.1],[0,0,0,0.1,0.9]]])
R = np.array([-1,-1,-1,-1,10])
# end of your code here
return MDP(T, R, 0.75)
mdp_stochatsic = build_stochastic_mdp()
plt.figure(figsize=(5,2))
plt.subplot(121, title='Left transitions')
plt.imshow(mdp_stochatsic.T[:,0,:])
plt.ylabel("Initial state"); plt.xlabel('Next state')
plt.subplot(122, title='Right transitions')
plt.imshow(mdp_stochatsic.T[:,1,:])
plt.ylabel("Initial state"); plt.xlabel('Next state')
plt.show()
# -
policy_iters = policy_iteration(mdp_stochatsic, always_left)
best_policy = policy_iters[-1]
best_values = iterative_value_estimation(mdp_stochatsic, best_policy)
print("The values for optimal policy %s for stochastic mdp is: %s"%(best_policy,best_values))
# + [markdown] deletable=false
# *Your answer here*
#
# From the output above we can see the optimal policies are the same but the value of the optimal policy becomes smaller. This makes sense as there is a small probability that the best going right policy would go left, resulting in negative reward, which decreases the expectation of the best policy.
# -
|
content/homeworks/hw08/notebook/cs109b_hw8_to_submit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Self-Driving Car Engineer Nanodegree
#
#
# ## Project: **Finding Lane Lines on the Road**
# ***
# In this project, you will use the tools you learned about in the lesson to identify lane lines on the road. You can develop your pipeline on a series of individual images, and later apply the result to a video stream (really just a series of images). Check out the video clip "raw-lines-example.mp4" (also contained in this repository) to see what the output should look like after using the helper functions below.
#
# Once you have a result that looks roughly like "raw-lines-example.mp4", you'll need to get creative and try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4". Ultimately, you would like to draw just one line for the left side of the lane, and one for the right.
#
# In addition to implementing code, there is a brief writeup to complete. The writeup should be completed in a separate file, which can be either a markdown file or a pdf document. There is a [write up template](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) that can be used to guide the writing process. Completing both the code in the Ipython notebook and the writeup template will cover all of the [rubric points](https://review.udacity.com/#!/rubrics/322/view) for this project.
#
# ---
# Let's have a look at our first image called 'test_images/solidWhiteRight.jpg'. Run the 2 cells below (hit Shift-Enter or the "play" button above) to display the image.
#
# **Note: If, at any point, you encounter frozen display windows or other confounding issues, you can always start again with a clean slate by going to the "Kernel" menu above and selecting "Restart & Clear Output".**
#
# ---
# **The tools you have are color selection, region of interest selection, grayscaling, Gaussian smoothing, Canny Edge Detection and Hough Tranform line detection. You are also free to explore and try other techniques that were not presented in the lesson. Your goal is piece together a pipeline to detect the line segments in the image, then average/extrapolate them and draw them onto the image for display (as below). Once you have a working pipeline, try it out on the video stream below.**
#
# ---
#
# <figure>
# <img src="examples/line-segments-example.jpg" width="380" alt="Combined Image" />
# <figcaption>
# <p></p>
# <p style="text-align: center;"> Your output should look something like this (above) after detecting line segments using the helper functions below </p>
# </figcaption>
# </figure>
# <p></p>
# <figure>
# <img src="examples/laneLines_thirdPass.jpg" width="380" alt="Combined Image" />
# <figcaption>
# <p></p>
# <p style="text-align: center;"> Your goal is to connect/average/extrapolate line segments to get output like this</p>
# </figcaption>
# </figure>
# **Run the cell below to import some packages. If you get an `import error` for a package you've already installed, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
# ## Import Packages
# +
# importing some useful packages
import cv2
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import numpy as np
% matplotlib inline
% load_ext autoreload
% autoreload 2
# -
# ## Read in an Image
# +
# reading in an image
image = mpimg.imread('test_images/solidWhiteRight.jpg')
# printing out some stats and plotting
print('This image is:', type(image), 'with dimensions:', image.shape)
y, x, _ = image.shape
# if you wanted to show a single color channel image called 'gray',
# for example, call as plt.imshow(gray, cmap='gray')
plt.imshow(image)
# -
# ## Ideas for Lane Detection Pipeline
# **Some OpenCV functions (beyond those introduced in the lesson) that might be useful for this project are:**
#
# `cv2.inRange()` for color selection
# `cv2.fillPoly()` for regions selection
# `cv2.line()` to draw lines on an image given endpoints
# `cv2.addWeighted()` to coadd / overlay two images
# `cv2.cvtColor()` to grayscale or change color
# `cv2.imwrite()` to output images to file
# `cv2.bitwise_and()` to apply a mask to an image
#
# **Check out the OpenCV documentation to learn about these and discover even more awesome functionality!**
# ### Helper Functions
from utils import grayscale, gaussian_blur, canny, hough_lines, region_of_interest, weighted_img, draw_quadrilateral
# ## Test Images
#
# Build your pipeline to work on the images in the directory "test_images"
# **You should make sure your pipeline works well on these images before you try the videos.**
import os
test_image_names = os.listdir("test_images/")
print(test_image_names)
# ## Build a Lane Finding Pipeline
#
#
# Build the pipeline and run your solution on all test_images. Make copies into the `test_images_output` directory, and you can use the images in your writeup report.
#
# Try tuning the various parameters, especially the low and high Canny thresholds as well as the Hough lines parameters.
# <a href="https://docs.opencv.org/3.0-beta/modules/imgcodecs/doc/reading_and_writing_images.html#cv2.imread" target="new">
# imread
# </a>
#
# <a href="https://docs.opencv.org/3.0-beta/modules/imgproc/doc/drawing_functions.html?highlight=fillpoly#cv2.fillPoly" target="new">
# fillPoly
# </a>
#
# <a href="https://docs.opencv.org/3.0-beta/modules/core/doc/operations_on_arrays.html#addweighted" target="new">
# addweighted
# </a>
#
# +
# Numbers obtained by kruler ubuntu app
p1 = (int(0.13 * x), y)
p2 = (int(0.43 * x), int(0.61 * y))
p3 = (int(0.55 * x), int(0.59 * y))
p4 = (int(0.93 * x), y)
roi = [p1, p2, p3, p4]
# +
# Pipeline that will draw lane lines on the test_images then save them to the test_images_output directory.
save_intermediate_images = False
for i, t_img_name in enumerate(test_image_names):
base_img = cv2.imread("test_images/" + t_img_name)
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_00_color{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), base_img)
out_img = grayscale(base_img, format="BGR")
# img = np.copy(base_img)
# img = draw_quadrilateral(img, roi)
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_01_gray{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), out_img)
"""
The next operation is going to be edge detection,
before edge detection a good preprocessing step is smooothining
the image so that strong gradients are left in the image blurring
operation is analogous to that of low pass filter
"""
out_img = gaussian_blur(out_img, kernel_size=5)
"""
Find out edges in the image using canny edge detection
Canny recommended to use low_thres/high_thres ratio of 1:2 or 1:3
as image here is grayscale the range of gradient is [0, 255]
since we are interested in lanes which are visually disticnt entitites
their gradient threshold should be higher
"""
out_img = canny(out_img, low_threshold=50, high_threshold=150)
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_02_edge{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), out_img)
"""
np.int32 is crucial
https://stackoverflow.com/questions/17241830/
opencv-polylines-function-in-python-throws-exception/18817152#18817152
"""
out_img = region_of_interest(out_img, np.int32([roi]))
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_03_roi{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), out_img)
out_img = hough_lines(out_img,
rho=1,
theta=2 * np.pi / 180,
threshold=35,
min_line_len=15,
max_line_gap=6,
draw_hough_lines=True,
clip=35)
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_04_lanes{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), out_img)
out_img = weighted_img(out_img, base_img, α=0.8, β=1.0, γ=0.0)
if save_intermediate_images:
cv2.imwrite("output_images/intermediate_images/{}_{}_05_weight{}"
.format(i, t_img_name[:-4], t_img_name[-4:]), out_img)
# print("\n")
# break
# -
# ## Test on Videos
#
# You know what's cooler than drawing lanes over images? Drawing lanes over video!
#
# We can test our solution on two provided videos:
#
# `solidWhiteRight.mp4`
#
# `solidYellowLeft.mp4`
#
# **Note: if you get an import error when you run the next cell, try changing your kernel (select the Kernel menu above --> Change Kernel). Still have problems? Try relaunching Jupyter Notebook from the terminal prompt. Also, consult the forums for more troubleshooting tips.**
#
# **If you get an error that looks like this:**
# ```
# NeedDownloadError: Need ffmpeg exe.
# You can download it by calling:
# imageio.plugins.ffmpeg.download()
# ```
# **Follow the instructions in the error message and check out [this forum post](https://discussions.udacity.com/t/project-error-of-test-on-videos/274082) for more troubleshooting tips across operating systems.**
# +
# Import everything needed to edit/save/watch video clips
from IPython.display import HTML
from moviepy.editor import VideoFileClip
# +
img_counter = 0
def process_image(base_img):
global img_counter
imgs = []
try:
out_img = grayscale(base_img)
imgs.append(out_img)
out_img = gaussian_blur(out_img, kernel_size=5)
out_img = canny(out_img, low_threshold=50, high_threshold=150)
imgs.append(out_img)
# np.int32 is crucial
out_img = region_of_interest(out_img, np.int32([roi]))
imgs.append(out_img)
out_img = hough_lines(out_img,
rho=1,
theta=2 * np.pi / 180,
threshold=35,
min_line_len=15,
max_line_gap=6,
draw_hough_lines=False,
clip=35)
imgs.append(out_img)
out_img = weighted_img(out_img, base_img, α=0.8, β=1.0, γ=0.0)
imgs.append(out_img)
img_counter += 1
return out_img
except Exception:
for i, img in enumerate(imgs):
cv2.imwrite("output_images/error/{}.jpg".format(i), img)
raise Exception("process_image(...)")
# -
# Let's try the one with the solid white lane on the right first ...
# To speed up the testing process you may want to try your pipeline on a shorter subclip of the video To do so add .subclip(start_second,end_second) to the end of the line below Where start_second and end_second are integer values representing the start and end of the subclip You may also uncomment the following line for a subclip of the first 5 seconds
#
# clip3 = VideoFileClip('test_videos/challenge.mp4').subclip(0,5)
# +
white_output = 'test_videos_output/solidWhiteRight.mp4'
clip1 = VideoFileClip("test_videos/solidWhiteRight.mp4")
# NOTE: this function expects color images!!
white_clip = clip1.fl_image(process_image)
% time white_clip.write_videofile(white_output, audio=False)
# -
# Play the video inline, or if you prefer find the video in your filesystem (should be in the same directory) and play it in your video player of choice.
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(white_output))
# ## Improve the draw_lines() function
#
# **At this point, if you were successful with making the pipeline and tuning parameters, you probably have the Hough line segments drawn onto the road, but what about identifying the full extent of the lane and marking it clearly as in the example video (P1_example.mp4)? Think about defining a line to run the full length of the visible lane based on the line segments you identified with the Hough Transform. As mentioned previously, try to average and/or extrapolate the line segments you've detected to map out the full extent of the lane lines. You can see an example of the result you're going for in the video "P1_example.mp4".**
#
# **Go back and modify your draw_lines function accordingly and try re-running your pipeline. The new output should draw a single, solid line over the left lane line and a single, solid line over the right lane line. The lines should start from the bottom of the image and extend out to the top of the region of interest.**
# To speed up the testing process you may want to try your pipeline on a shorter subclip of the video, to do so add .subclip(start_second,end_second) to the end of the line below where start_second and end_second are integer values representing the start and end of the subclip you may also uncomment the following line for a subclip of the first 5 seconds
#
# clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4').subclip(0,5)
# Now for the one with the solid yellow lane on the left. This one's more tricky!
# +
yellow_output = 'test_videos_output/solidYellowLeft.mp4'
clip2 = VideoFileClip('test_videos/solidYellowLeft.mp4')
yellow_clip = clip2.fl_image(process_image)
% time yellow_clip.write_videofile(yellow_output, audio=False)
# -
HTML("""
<video width="960" height="540" controls>
<source src="{0}">
</video>
""".format(yellow_output))
# ## Writeup and Submission
#
# If you're satisfied with your video outputs, it's time to make the report writeup in a pdf or markdown file. Once you have this Ipython notebook ready along with the writeup, it's time to submit for review! Here is a [link](https://github.com/udacity/CarND-LaneLines-P1/blob/master/writeup_template.md) to the writeup template file.
#
|
Lane_Lines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CuSignal API Guide in Greenflow
#
# The convolution examples are taken from [cusignal convolution notebook](https://github.com/rapidsai/cusignal/blob/branch-21.08/notebooks/api_guide/convolution_examples.ipynb). The examples below showing output were run on Volta GPU V100.
import cupy.testing as cptest
from greenflow.dataframe_flow import (TaskGraph, TaskSpecSchema)
# ## Correlate
tgraph_corr = TaskGraph.load_taskgraph('./taskgraphs/correlate.gq.yaml')
tgraph_corr.draw(show='ipynb', show_ports=True, pydot_options={'rankdir': 'LR'})
# If you would like to run via GreenflowLab follow the instructions in the next cell. Running via GreenflowLab will appear as shown in the image below. The output values might differ, because of the random signal generator.
#
# 
# + active=""
# # To run via GreenflowLab convert this cell from raw, add an output collector, and run.
# tgraph_corr.draw()
# -
# The code to generate signals for correlation is included in the "sig_task" via "pycode" parameter. Feel free to tinker with the "pycode" via GreenflowLab to test other types of signals. Start by drawing the graph `tgraph_corr.draw()` and then click on the nodes to edit their parameters.
tgraph_corr.build()
gensig_code = tgraph_corr['sig_task'].conf.get('pycode')
print('# PyCode to generate output for sig_task\n{}'.format(gensig_code))
(corr_gpu, sig_noise, sig_corr) = tgraph_corr.run(
['correlate_task.correlate', 'sig_task.out1', 'sig_task.out2'])
# The "sig_task" is a place holder to be able to load a signal programmatically. We can use the replace spec to specify "load" and corresponding output ports for the "sig_task". This will avoid re-running "sig_task", and keep the signals consistent for comparison between CPU and GPU. Also, the configuration of the "correlate_task" is changed to "use_cpu" for the CPU runs. This pattern is repeated throughout the notebook.
# + tags=[]
replace_gpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': sig_noise,
'out2': sig_corr
}
}
}
conf_cpu = tgraph_corr['correlate_task'].conf.copy()
conf_cpu.update({'use_cpu': True})
replace_cpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': sig_noise.get(),
'out2': sig_corr.get()
}
},
'correlate_task': {
TaskSpecSchema.conf: conf_cpu
}
}
# -
(corr_cpu,) = tgraph_corr.run(['correlate_task.correlate'], replace=replace_cpu)
print('CORR GPU: {}\nCORR CPU: {}'.format(corr_gpu, corr_cpu))
cptest.assert_array_almost_equal(corr_gpu, corr_cpu)
# gpu_time = %timeit -o (corr_gpu,) = tgraph_corr.run(['correlate_task.correlate'], replace=replace_gpu)
# cpu_time = %timeit -o (corr_cpu,) = tgraph_corr.run(['correlate_task.correlate'], replace=replace_cpu)
print('SPEEDUP: {}x'.format(round(cpu_time.average / gpu_time.average, 1)))
# ## Convolve
tgraph_conv = TaskGraph.load_taskgraph('./taskgraphs/convolve.gq.yaml')
tgraph_conv.draw(show='ipynb', show_ports=True, pydot_options={'rankdir': 'LR'})
tgraph_conv.build()
gensig_code = tgraph_conv['sig_task'].conf.get('pycode')
print('# PyCode to generate output for sig_task\n{}'.format(gensig_code))
(conv_gpu, sig) = tgraph_conv.run(['convolve_task.convolve', 'sig_task.out1'])
# +
replace_gpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': sig
}
}
}
conf_cpu = {
'convolve_task': tgraph_conv['convolve_task'].conf.copy(),
'win_hann': tgraph_conv['win_hann'].conf.copy()
}
conf_cpu['convolve_task'].update({'use_cpu': True})
conf_cpu['win_hann'].update({'use_cpu': True})
replace_cpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': sig.get()
}
},
'win_hann': {
TaskSpecSchema.conf: conf_cpu['win_hann']
},
'convolve_task': {
TaskSpecSchema.conf: conf_cpu['convolve_task']
}
}
# -
(conv_cpu,) = tgraph_conv.run(['convolve_task.convolve'], replace=replace_cpu)
print('CONV GPU: {}\nCONV CPU: {}'.format(conv_gpu, conv_cpu))
cptest.assert_array_almost_equal(conv_gpu, conv_cpu)
# gpu_time = %timeit -o (conv_gpu,) = tgraph_conv.run(['convolve_task.convolve'], replace=replace_gpu)
# cpu_time = %timeit -o (conv_cpu,) = tgraph_conv.run(['convolve_task.convolve'], replace=replace_cpu)
print('SPEEDUP: {}x'.format(round(cpu_time.average / gpu_time.average, 1)))
# ## Convolution using the FFT Method
tgraph_fftconv = TaskGraph.load_taskgraph('./taskgraphs/fftconvolve.gq.yaml')
tgraph_fftconv.draw(show='ipynb', show_ports=True, pydot_options={'rankdir': 'LR'})
# + tags=[]
tgraph_fftconv.build()
gensig_code = tgraph_fftconv['sig_task'].conf.get('pycode')
print('# PyCode to generate output for sig_task\n{}'.format(gensig_code))
# -
(gautocorr, gsig, gsig_reverse) = tgraph_fftconv.run(
['fftconvolve_task.fftconvolve', 'sig_task.out1', 'sig_task.out2'])
# +
replace_gpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': gsig,
'out2': gsig_reverse
}
}
}
conf_cpu = tgraph_fftconv['fftconvolve_task'].conf.copy()
conf_cpu.update({'use_cpu': True})
replace_cpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': gsig.get(),
'out2': gsig_reverse.get()
}
},
'fftconvolve_task': {
TaskSpecSchema.conf: conf_cpu
}
}
# -
(cautocorr,) = tgraph_fftconv.run(['fftconvolve_task.fftconvolve'], replace=replace_cpu)
print('AUTOCORR GPU: {}\nAUTOCORR CPU: {}'.format(gautocorr, cautocorr))
cptest.assert_array_almost_equal(gautocorr, cautocorr)
# +
# Clean up memory. FFTconvolve seems to use a lot of GPU memory.
import gc
try:
del corr_gpu
except Exception:
pass
try:
del conv_gpu
except Exception:
pass
try:
del gautocorr
except Exception:
pass
gc.collect()
# -
# gpu_time = %timeit -o (gautocorr,) = tgraph_fftconv.run(['fftconvolve_task.fftconvolve'], replace=replace_gpu)
# cpu_time = %timeit -o (cautocorr,) = tgraph_fftconv.run(['fftconvolve_task.fftconvolve'], replace=replace_cpu)
print('SPEEDUP: {}x'.format(round(cpu_time.average / gpu_time.average, 1)))
# ## Perform 2-D Convolution and Correlation
# ### Convolve2d
tgraph_conv2d = TaskGraph.load_taskgraph('./taskgraphs/convolve2d.gq.yaml')
tgraph_conv2d.draw(show='ipynb', show_ports=True, pydot_options={'rankdir': 'LR'})
tgraph_conv2d.build()
gensig_code = tgraph_conv2d['sig_task'].conf.get('pycode')
print('# PyCode to generate output for sig_task\n{}'.format(gensig_code))
(ggrad, gsig, gfilt) = tgraph_conv2d.run(
['convolve2d_task.convolve2d', 'sig_task.out1', 'sig_task.out2'])
# +
replace_gpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': gsig,
'out2': gfilt
}
}
}
conf_cpu = tgraph_conv2d['convolve2d_task'].conf.copy()
conf_cpu.update({'use_cpu': True})
replace_cpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': gsig.get(),
'out2': gfilt.get()
}
},
'convolve2d_task': {
TaskSpecSchema.conf: conf_cpu
}
}
# -
(cgrad,) = tgraph_conv2d.run(['convolve2d_task.convolve2d'], replace=replace_cpu)
print('CONV GRAD GPU: {}\nCONV GRAD CPU: {}'.format(ggrad, cgrad))
cptest.assert_array_almost_equal(ggrad, cgrad)
# gpu_time = %timeit -o (ggrad,) = tgraph_conv2d.run(['convolve2d_task.convolve2d'], replace=replace_gpu)
# cpu_time = %timeit -o (cgrad,) = tgraph_conv2d.run(['convolve2d_task.convolve2d'], replace=replace_cpu)
print('SPEEDUP: {}x'.format(round(cpu_time.average / gpu_time.average, 1)))
# ### Correlate2d
tgraph_corr2d = TaskGraph.load_taskgraph('./taskgraphs/correlate2d.gq.yaml')
tgraph_corr2d.draw(show='ipynb', show_ports=True, pydot_options={'rankdir': 'LR'})
# re-using gsig and gfilt from above convolve2d.
# But need to update configuration for correlate2d_task
tgraph_corr2d.build()
conf_cpu = tgraph_corr2d['correlate2d_task'].conf.copy()
conf_cpu.update({'use_cpu': True})
replace_cpu = {
'sig_task': {
TaskSpecSchema.load: {
'out1': gsig.get(),
'out2': gfilt.get()
}
},
'correlate2d_task': {
TaskSpecSchema.conf: conf_cpu
}
}
(ggrad_corr,) = tgraph_corr2d.run(['correlate2d_task.correlate2d'], replace=replace_gpu)
(cgrad_corr,) = tgraph_corr2d.run(['correlate2d_task.correlate2d'], replace=replace_cpu)
print('CORR GRAD GPU: {}\nCORR GRAD CPU: {}'.format(ggrad_corr, cgrad_corr))
cptest.assert_array_almost_equal(ggrad_corr, cgrad_corr)
# gpu_time = %timeit -o (ggrad_corr, ) = tgraph_corr2d.run(['correlate2d_task.correlate2d'], replace=replace_gpu)
# cpu_time = %timeit -o (cgrad_corr, ) = tgraph_corr2d.run(['correlate2d_task.correlate2d'], replace=replace_cpu)
print('SPEEDUP: {}x'.format(round(cpu_time.average / gpu_time.average, 1)))
|
gQuant/plugins/cusignal_plugin/notebooks/convolution_examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Feed Forward Loops
#
# We're now going to use some of these tools to look at a class of network motifs, called Feed Forward Loops (FFLs), found in signaling and regulatory networks. FFLs involve interactions between three components, with the basic topology illustrated below. Depending on the signs of the edges (whether activating or repressing) we can classify FFLs as "coherent" or "incoherent." We'll take a look at an example of each class.
# ## A Coherent FFL
#
# The most common type of coherent FFL is illustrated in the figure below. In this system $X$ is an activator of $Y$ and both $X$ and $Y$ regulate the production of $Z$ with AND logic (i.e. both $X$ and $Y$ must be above particular thresholds in order to trigger the production of $Z$).
#
# 
#
# Using our logic approximation framework we will model the coherent FFL network illustrated above as follows.
#
# #### Gene Y:
#
# \begin{eqnarray*}
# Y = f(X) = \beta_y\ \Theta(X > K_{xy})
# \\
# \\
# \frac{dY}{dt} = \beta_y\ \Theta(X > K_{xy}) - \alpha_{y}Y
# \end{eqnarray*}
#
#
#
# #### Gene Z:
#
# \begin{eqnarray*}
# Z = g(X,Y) = \beta_z\ \Theta(X > K_{xz})\Theta(Y > K_{yz})
# \\
# \\
# \frac{dZ}{dt} = \beta_z\ \Theta(X > K_{xz})\Theta(Y > K_{yz}) - \alpha_{z}Z
# \end{eqnarray*}
# import statements to make numeric and plotting functions available
# %matplotlib inline
from numpy import *
from matplotlib.pyplot import *
# +
## We'll specify the behavior of X as a series of pulse of different length
## so we'll define a function to generate pulses
def pulse(ontime, offtime, ntimes, onval=1):
if ontime >= offtime:
raise Exception("Invalid on/off times.")
signal = np.zeros(ntimes)
signal[ontime:offtime] = onval
return signal
# +
nsteps = 150
short_pulse = pulse(20, 23, nsteps) # 5 sec pulse
long_pulse = pulse(50, 100, nsteps) # 50 sec pulse
X = short_pulse + long_pulse # we can then add the pulses to create
# a single time trace
plot(X, color='black')
xlabel('Time units')
ylabel('Amount of Gene Product')
ylim(0, 1.5)
pass
# -
# ### Define Python functions for dY/dt and dZ/dt
#
# Recall from above that
#
# \begin{eqnarray*}
# \frac{dY}{dt} & = & \beta_y\ \Theta(X > K_{xy}) - \alpha_{y}Y \\ \\
# \frac{dZ}{dt} & = & \beta_z\ \Theta(X > K_{xz})\Theta(Y > K_{yz}) - \alpha_{z}Z
# \end{eqnarray*}
# +
## Write Python functions for dY/dt and dZ/dt
def dY(B,K,a,X,Y):
pass ## replace this line with your function definition
def dZ(B,Kx,Ky,a,X,Y,Z):
pass ## replace this line with your function definition
def dY(B,K,a,X,Y):
if X > K:
theta = 1
else:
theta = 0
return B * theta - a * Y
def dZ(B,Kx,Ky,a,X,Y,Z):
theta = 0
if (X > Kx) and (Y > Ky):
theta = 1
return B * theta - a * Z
# +
## Plot X, Y, and Z on the same time scale
nsteps = 150
short_pulse = pulse(20, 23, nsteps) # 5 sec pulse
long_pulse = pulse(50, 100, nsteps) # 50 sec pulse
X = short_pulse + long_pulse
# setup parameters for Y and Z
Y = [0]
betay, alphay = 0.2, 0.1
Kxy = 0.5
Z = [0]
betaz, alphaz = 0.2, 0.1
Kxz = 0.5
Kyz = 1
for i in range(nsteps):
xnow = X[i]
ynow, znow = Y[-1], Z[-1]
ynew = ynow + dY(betay, Kxy, alphay, xnow, ynow)
znew = znow + dZ(betaz, Kxz, Kyz, alphaz, xnow, ynow, znow)
Y.append(ynew)
Z.append(znew)
plot(X, 'k--', label='X', linewidth=1.5)
plot(Y, 'b', label='Y')
plot(Z, 'r', label='Z')
ylim(-0.1, 2.5)
xlabel("Time")
ylabel("Concentration")
legend()
pass
# -
# <h3> <font color='firebrick'>Questions</font> </h3>
#
# 1. How do the dynamics of $Y$ and $Z$ differ in the simulation above?
#
# 2. Try varying the length of the first (short) pulse? How does changing the length of the pulse affect the dynamics of $Y$ and $Z$?
# # Performance of the Coherent FFL under noisy inputs
#
# Let's further explore the behavior of the coherent FFL defined given noisy inputs. As before we're going to define an input signal, $X$, that has a short and long pulse, but now we're going to pollute $X$ with random noise.
# +
nsteps = 150
p1start = 10
p1duration = 5
p2start = 50
p2duration = 50
short_pulse = pulse(p1start, p1start + p1duration, nsteps) # short pulse
long_pulse = pulse(p2start, p2start + p2duration, nsteps) # long pulse
X = short_pulse + long_pulse
# change this `scale` argument to increase/decrease noise
noise = np.random.normal(loc=0, scale=0.2, size=nsteps) # mean=0, sd=0.2
X = X + noise
# setup parameters for Y and Z
Y = [0]
betay, alphay = 0.2, 0.1
Kxy = 0.5
Z = [0]
betaz, alphaz = 0.2, 0.1
Kxz = 0.5
Kyz = 1
for i in range(nsteps):
xnow = X[i]
ynow, znow = Y[-1], Z[-1]
ynew = ynow + dY(betay, Kxy, alphay, xnow, ynow)
znew = znow + dZ(betaz, Kxz, Kyz, alphaz, xnow, ynow, znow)
Y.append(ynew)
Z.append(znew)
# draw each trace as a subfigure
# subfigures stacked in a vertical grid
subplot2grid((3,1),(0,0))
plot(X, 'k', label='X', linewidth=1)
legend()
subplot2grid((3,1),(1,0))
plot(Y, 'b', label='Y', linewidth=2)
legend()
subplot2grid((3,1),(2,0))
plot(Z, 'r', label='Z', linewidth=2)
vlines(p1start, min(Z),max(Z)*1.1,color='black',linestyle='dashed')
annotate("pulse 1 on", xy=(p1start,1),xytext=(40,20),
textcoords='offset points',
horizontalalignment="center",
verticalalignment="bottom",
arrowprops=dict(arrowstyle="->",color='black',
connectionstyle='arc3,rad=0.5',
linewidth=1))
vlines(p2start, min(Z),max(Z)*1.1,color='black',linestyle='dashed')
annotate("pulse 2 on", xy=(p2start,1),xytext=(-40,0),
textcoords='offset points',
horizontalalignment="center",
verticalalignment="bottom",
arrowprops=dict(arrowstyle="->",color='black',
connectionstyle='arc3,rad=0.5',
linewidth=1))
legend()
pass
# -
# ### To Explore
#
# In the code cell above, try changing the duration of the first pulse and the `scale` of the noise (see comments in code) to get a sense of how good a filter the FFL is. Is there a bias to the filtering with respect to turn on versus turn of?
#
# ### OPTIONAL: Dynamics of Y and Z in the Coherent FFL
#
# As before we can solve for Y as a function of time and calculate what its steady state value will be:
#
# $$
# Y(t) = Y_{st}(1-e^{-\alpha_{y}t})
# $$
#
# and
#
# $$
# Y_{st}=\frac{\beta_y}{\alpha_y}
# $$
#
# #### How about $Z$?
#
# Since $Z$ is governed by an AND function it needs both $X$ and $Y$ to be above their respective thresholds, $K_{xz}$ and $K_{yz}$. For the sake of simplicity let's assume that both $Y$ and $Z$ have the same threshold with respect to $X$, i.e. $K_{xy} = K_{xz}$. This allows us just to consider how long it takes for $Y$ to reach the threshold value $K_{yz}$. Given this we can calculate the delay before $Z$ turns on, $T_{\mathrm{on}}$ as follows.
#
# $$
# Y(T_{\mathrm{on}}) = Y_{st}(1-e^{-\alpha_y T_{\mathrm{on}}}) = K_{yz}
# $$
#
# and solving for $T_{\mathrm{on}}$ we find:
#
# $$
# T_{\mathrm{on}} = \frac{1}{\alpha_y} \log\left[\frac{1}{(1-K_{yz}/Y_{st})}\right]
# $$
#
# Thus we see that the delay before $Z$ turns on is a function of the degradation rate of $Y$ and the ratio between $Y_{st}$ and $K_{yz}$.
#
# #### Exploring the Parameter space of $Z$'s turn-on time
#
# From the above formula, we see that there are two parameters that affect the turn-on time of $Z$ -- $\alpha_y$ (the scaling factor for the decay rate of $Y$) and the compound parameter $K_{yz}/Y_{st}$ (the threshold concentration where $Y$ activate $Z$ relative to the steady state of $Y$). To explore the two-dimensional parameter space of $Z's$ $T_on$ we can create a contour plot.
# +
def Ton(alpha, KYratio):
return (1.0/alpha) * log(1.0/(1.0-KYratio))
## Create a contour plot for a range of alpha and Kyz/Yst
x = alpha = linspace(0.01, 0.2, 100)
y = KYratio = linspace(0.01, 0.99, 100)
X,Y = meshgrid(x, y)
Z = Ton(X,Y)
levels = MaxNLocator(nbins=20).tick_values(Z.min(), Z.max())
im = contourf(X,Y,Z, cmap=cm.inferno_r, levels=levels)
contour(X, Y, Z, levels,
colors=('k',),
linewidths=(0.5,))
colorbar(im)
xlabel('alpha')
ylabel("Kyz/Yst")
pass
# -
# ### Type 1 Coherent FFLs can act as a Sign-Sensitive Delays
#
# As discussed in the article by Shen-Orr et al. a feed forward loop of the type we've just discussed can act as a type of filter -- a sign-sensitive delay that keeps $Z$ from firing in response to transient noisy signals from $X$, but shuts down $Z$ immediately once the signal from $X$ is removed.
# # An Incoherent FFL
#
# Consider the FFL illustrated in the figure below.
#
# 
#
# In this incoherent FFL, the logic function that regulates $Z$ is "X AND NOT Y". That is $Z$ turns on once $X$ is above a given threshold, but only stays on fully as long as $Y$ is below another threshold. Again for simplicity we assume $K_{xy} = K_{yz}$.
# ### Dynamics of Y
#
# As before, the dynamics of $Y$ are described by:
#
# $$
# \frac{dY}{dt} = \beta_y\ \Theta(X > K_{xy}) - \alpha_{y}Y
# $$
#
# and
#
# $$
# Y(t) = Y_{st}(1-e^{-\alpha_{y}t})
# $$
#
#
# ### Dynamics of Z
#
# To describe $Z$ we consider two phases - 1) while $Y < K_{yz}$ and 2) while $Y > K_{yz}$.
#
# #### Z, Phase 1
#
# For the first phase:
#
# $$
# \frac{dZ}{dt} = \beta_z\ \Theta(X > K_{xz}) - \alpha_{z}Z
# $$
#
# and
#
# $$
# Z(t) = Z_{m}(1-e^{-\alpha_{z}t})
# $$
#
# As we did in the case of the coherent FFL, we can calculate the time until $Y$ reaches the treshold $K_{yz}$. We'll call this $T_{\mathrm{rep}}$ and it is the same formula we found for $T_{\mathrm{on}}$ previously.
#
# $$
# T_{\mathrm{rep}} = \frac{1}{\alpha_y \log[\frac{1}{1-K_{yz}/Y_{st}}]}
# $$
#
# #### Z, Phase 2
#
# After a delay, $T_{\mathrm{rep}}$, $Y$ starts to repress the transcription of $Z$ and $Z$ decays to a new lower steady state, $Z_{st} = \beta_{z}^{'}/\alpha$. The value of $\beta_{z}^{'}$ depends on how leaky the repression of $Z$ is by $Y$.
#
#
# The dynamics of $Z$ in Phase 2 is given by:
#
# $$
# Z(t) = Z_{st} + (Z_0 - Z_{st})e^{-\alpha_{z}(t-T_{\mathrm{rep}})}
# $$
#
# where
# $$
# Z_0 = Z_{m}(1-e^{-\alpha_{z}T_{\mathrm{rep}}})
# $$
#
# ### Combining the two phases of Z
#
# We can combine the two phases of $Z$ into a single function:
#
# $$
# f(X,Y) = \beta_z\Theta(X > K_{xz} \land Y < K_{yz}) + \beta_{z}^{'}\Theta(Y \geq K_{yz}) - \alpha_z Z
# $$
# +
## Write a Python function that represents dZ/dt for the Incoherent FFL
## our dY function previously defined stays the same
def dZ_incoh(B1,B2,Kx,Ky,a,X,Y,Z):
pass # define the function here
def dZ_incoh(B1,B2,Kx,Ky,a,X,Y,Z):
theta = 0
B = 0
if (X > Kx) and (Y < Ky):
theta = 1
B = B1
elif (X > Kx) and (Y >= Ky):
theta = 1
B = B2
return B * theta - a * Z
# +
## Write your simulation here
nsteps = 150
short_pulse = pulse(20, 25, nsteps) # 5 sec pulse
long_pulse = pulse(50, 100, nsteps) # 50 sec pulse
X = short_pulse + long_pulse
# setup parameters for Y and Z
Y = [0]
betay, alphay = 0.2, 0.1
Kxy = 0.5
Z = [0]
betaz1, betaz2 = 0.2, 0.001
alphaz = 0.1
Kxz = 0.5
Kyz = 0.5
for i in range(nsteps):
xnow = X[i]
ynow, znow = Y[-1], Z[-1]
ynew = ynow + dY(betay, Kxy, alphay, xnow, ynow)
znew = znow + dZ_incoh(betaz1, betaz2, Kxz, Kyz, alphaz, xnow, ynow, znow)
Y.append(ynew)
Z.append(znew)
# draw each trace as a subfigure
# subfigures stacked in a vertical grid
subplot2grid((3,1),(0,0))
plot(X, 'k', label='X', linewidth=1)
legend()
ylim(0,1.1)
subplot2grid((3,1),(1,0))
plot(Y, 'b', label='Y', linewidth=2)
legend()
ylim(0,2.1)
subplot2grid((3,1),(2,0))
plot(Z, 'r', label='Z', linewidth=2)
legend()
ylim(0,0.7)
pass
# -
# ### Dynamics of the Incoherent FFL
#
# Note that the stimulus amount of $Z$ in the system initially increases, but then decreases to a lower steady even when the initial stimulus persists. This system thus generates **pulse-like dynamics to a persistent signal**. How pulse-like the signal is depends on the ratio of $\beta_z$ to $\beta_{z}^{'}$. We define the repression factor, $F$, as follows:
#
# $$
# F = \frac{\beta_z}{\beta_{z}^{'}} = \frac{Z_m}{Z_{st}}
# $$
#
# <h1> <font color='firebrick'> Modeling Challenge </font> </h1>
#
# See if you can come up with a reasonably small set of coupled ODEs for one of the signaling or regulatory networks you've learned about in this mini-term.
#
|
ode-modeling2-instructor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import json
import pickle
import random
from collections import defaultdict, Counter
from indra.literature.adeft_tools import universal_extract_text
from indra.databases.hgnc_client import get_hgnc_name, get_hgnc_id
from adeft.discover import AdeftMiner
from adeft.gui import ground_with_gui
from adeft.modeling.label import AdeftLabeler
from adeft.modeling.classify import AdeftClassifier
from adeft.disambiguate import AdeftDisambiguator, load_disambiguator
from adeft_indra.ground.ground import AdeftGrounder
from adeft_indra.model_building.s3 import model_to_s3
from adeft_indra.model_building.escape import escape_filename
from adeft_indra.db.content import get_pmids_for_agent_text, get_pmids_for_entity, \
get_plaintexts_for_pmids
# -
adeft_grounder = AdeftGrounder()
shortforms = ['RAS']
model_name = ':'.join(sorted(escape_filename(shortform) for shortform in shortforms))
results_path = os.path.abspath(os.path.join('../..', 'results', model_name))
# +
miners = dict()
all_texts = {}
for shortform in shortforms:
pmids = get_pmids_for_agent_text(shortform)
if len(pmids) > 10000:
pmids = random.choices(pmids, k=10000)
text_dict = get_plaintexts_for_pmids(pmids, contains=shortforms)
text_dict = {pmid: text for pmid, text in text_dict.items() if len(text) > 5}
miners[shortform] = AdeftMiner(shortform)
miners[shortform].process_texts(text_dict.values())
all_texts.update(text_dict)
longform_dict = {}
for shortform in shortforms:
longforms = miners[shortform].get_longforms()
longforms = [(longform, count, score) for longform, count, score in longforms
if count*score > 2]
longform_dict[shortform] = longforms
combined_longforms = Counter()
for longform_rows in longform_dict.values():
combined_longforms.update({longform: count for longform, count, score
in longform_rows})
grounding_map = {}
names = {}
for longform in combined_longforms:
groundings = adeft_grounder.ground(longform)
if groundings:
grounding = groundings[0]['grounding']
grounding_map[longform] = grounding
names[grounding] = groundings[0]['name']
longforms, counts = zip(*combined_longforms.most_common())
pos_labels = []
# -
list(zip(longforms, counts))
grounding_map, names, pos_labels = ground_with_gui(longforms, counts,
grounding_map=grounding_map,
names=names, pos_labels=pos_labels, no_browser=True, port=8890)
result = [grounding_map, names, pos_labels]
result
grounding_map, names, pos_labels = ({'radial artery spasm': 'ungrounded',
'radiation attenuated plasmodium sporozoites': 'MESH:D034101',
'radiation attenuated sporozoites': 'MESH:D034101',
'radix angelica sinensis': 'MESH:D029971',
'ras': 'FPLX:RAS',
'ras alone': 'FPLX:RAS',
'ras g12v': 'FPLX:RAS',
'rasv12': 'FPLX:RAS',
'rat sarcoma': 'FPLX:RAS',
'rat sarcoma oncogene': 'FPLX:RAS',
'rat sarcoma viral oncogene': 'FPLX:RAS',
'rat sarcoma virus': 'FPLX:RAS',
'recirculating aquaculture system': 'ungrounded',
'recurrent aphthous stomatitis': 'MESH:D013281',
'reflectance anisotropy spectroscopy': 'ungrounded',
'regulatory activation score': 'ungrounded',
'related allele signaling': 'ungrounded',
'renal artery stenosis': 'ungrounded',
'renin ang system': 'MESH:D012084',
'renin angiotensin': 'MESH:D012084',
'renin angiotensin aldosterone': 'MESH:D012084',
'renin angiotensin aldosterone system': 'MESH:D012084',
'renin angiotensin ang system': 'MESH:D012084',
'renin angiotensin system': 'MESH:D012084',
'renin angiotensin system inhibitors': 'ungrounded',
'renin angiotensinsystem': 'MESH:D012084',
'renin − angiotensin system': 'MESH:D012084',
'reninangiotensin system': 'MESH:D012084',
'rennin angiotensin system': 'MESH:D012084',
'resistance associated substitution': 'ungrounded',
'restrictive allograft syndrome': 'ungrounded',
'reticular activation system': 'ungrounded',
'retinoic acid syndrome': 'ungrounded',
'retroviruses associated dna sequences': 'ungrounded',
'rhythmic auditory stimulation': 'MESH:D000161',
'ribi adjuvant system': 'ungrounded',
'robot assisted surgery': 'ungrounded'},
{'MESH:D034101': 'Sporozoites',
'MESH:D029971': 'Angelica sinensis',
'FPLX:RAS': 'RAS',
'MESH:D013281': 'Stomatitis, Aphthous',
'MESH:D012084': 'Renin-Angiotensin System',
'MESH:D000161': 'Acoustic Stimulation'},
['FPLX:RAS',
'MESH:D000161',
'MESH:D012084',
'MESH:D013281',
'MESH:D029971',
'MESH:D034101'])
excluded_longforms = []
grounding_dict = {shortform: {longform: grounding_map[longform]
for longform, _, _ in longforms if longform in grounding_map
and longform not in excluded_longforms}
for shortform, longforms in longform_dict.items()}
result = [grounding_dict, names, pos_labels]
if not os.path.exists(results_path):
os.mkdir(results_path)
with open(os.path.join(results_path, f'{model_name}_preliminary_grounding_info.json'), 'w') as f:
json.dump(result, f)
additional_entities = {}
unambiguous_agent_texts = {}
# +
labeler = AdeftLabeler(grounding_dict)
corpus = labeler.build_from_texts((text, pmid) for pmid, text in all_texts.items())
agent_text_pmid_map = defaultdict(list)
for text, label, id_ in corpus:
agent_text_pmid_map[label].append(id_)
entity_pmid_map = {entity: set(get_pmids_for_entity(*entity.split(':', maxsplit=1),
major_topic=True))for entity in additional_entities}
# -
intersection1 = []
for entity1, pmids1 in entity_pmid_map.items():
for entity2, pmids2 in entity_pmid_map.items():
intersection1.append((entity1, entity2, len(pmids1 & pmids2)))
intersection2 = []
for entity1, pmids1 in agent_text_pmid_map.items():
for entity2, pmids2 in entity_pmid_map.items():
intersection2.append((entity1, entity2, len(set(pmids1) & pmids2)))
intersection1
intersection2
# +
all_used_pmids = set()
for entity, agent_texts in unambiguous_agent_texts.items():
used_pmids = set()
for agent_text in agent_texts[1]:
pmids = set(get_pmids_for_agent_text(agent_text))
new_pmids = list(pmids - all_texts.keys() - used_pmids)
text_dict = get_plaintexts_for_pmids(new_pmids, contains=agent_texts)
corpus.extend([(text, entity, pmid) for pmid, text in text_dict.items() if len(text) >= 5])
used_pmids.update(new_pmids)
all_used_pmids.update(used_pmids)
for entity, pmids in entity_pmid_map.items():
new_pmids = list(set(pmids) - all_texts.keys() - all_used_pmids)
if len(new_pmids) > 10000:
new_pmids = random.choices(new_pmids, k=10000)
_, contains = additional_entities[entity]
text_dict = get_plaintexts_for_pmids(new_pmids, contains=contains)
corpus.extend([(text, entity, pmid) for pmid, text in text_dict.items() if len(text) >= 5])
# -
names.update({key: value[0] for key, value in additional_entities.items()})
names.update({key: value[0] for key, value in unambiguous_agent_texts.items()})
pos_labels = list(set(pos_labels) | additional_entities.keys() |
unambiguous_agent_texts.keys())
# +
# %%capture
classifier = AdeftClassifier(shortforms, pos_labels=pos_labels, random_state=1729)
param_grid = {'C': [100.0], 'max_features': [10000]}
texts, labels, pmids = zip(*corpus)
classifier.cv(texts, labels, param_grid, cv=5, n_jobs=5)
# -
classifier.stats
disamb = AdeftDisambiguator(classifier, grounding_dict, names)
disamb.dump(model_name, results_path)
print(disamb.info())
model_to_s3(disamb)
|
model_notebooks/RAS/model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: python(oed)
# language: python
# name: oed
# ---
# # Explore Models
# Refer to the script of Explore models written by Baihua
# Model: MW_BASE_RC8_UpperROCONNEL.rsproj
# Created by: <NAME>
# Date created: 3/11/18
# Try to find structures about Source by veneer-py:
# 0 What are the constituents in the model?
# 1 What functional units in this URO catchment?
# 2 Does each funtional unit have its own model and parameters?
# 3 What are the input data for each submodel/function? How to change the values?
# +
import veneer
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# import geopandas as gpd
import re
from SALib.util import read_param_file
from SALib.plotting.morris import horizontal_bar_plot, covariance_plot, \
sample_histograms
import matplotlib.pyplot as plt
# %matplotlib inline
## Open Source project file, then enable Veneer (Tools->Web Server Monitoring->Allow scripts)
v = veneer.Veneer(port=9876)
# +
#### Run this to improve model performance, mainly through parallel computing. These can also be modified through Source UI
def configure_options(self,options):
lines = ["# Generated Script","from Dynamic_SedNet.PluginSetup import DSScenarioDetails"]
lines += ["DSScenarioDetails.%s = %s"%(k,v) for (k,v) in options.items()]
script = '\n'.join(lines)
#print(script)
res = self.model._safe_run(script)
configure_options(v,{'RunNetworksInParallel':True,'PreRunCatchments':True,'ParallelFlowPhase':True})
v.model.sourceScenarioOptions("PerformanceConfiguration","ProcessCatchmentsInParallel",True)
# -
#### Run this to turn off dsednet reporting window
configure_options(v,{'ShowResultsAfterRun':False,'OverwriteResults':True})
# ## Run the model with script codes
from veneer.manage import start, create_command_line, kill_all_now
import veneer
import pandas as pd
import gc
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d
from subprocess import Popen, PIPE
import subprocess
import shutil
import os
import re
# +
parent_dir = os.getcwd()
job_name = 'work'
pst_file = '126001A.pst'
catchment_project= parent_dir + '\\pest_source\\MW_BASE_RC10.rsproj'
pest_path= parent_dir + '\\pest_source'
print('pest path ',pest_path)
python_path = 'C:\\UserData\\Qian\\anaconda'
os.environ['PATH'] = os.environ['PATH']+';'+pest_path
os.environ['PATH'] = os.environ['PATH']+';'+python_path
print(os.environ['PATH'])
# Setup Veneer
# define paths to veneer command and the catchment project
veneer_path = 'pest_source\\vcmd45\\FlowMatters.Source.VeneerCmd.exe'
# Number of instances to open
num_copies=1 # Important - set this to be a number ~ the number of CPU cores in your system!
first_port=15000
#Now, go ahead and start source
processes,ports = start(catchment_project,
n_instances=num_copies,
ports=first_port,
debug=True,
veneer_exe=veneer_path,
remote=False,
overwrite_plugins=True)
# -
# # find sub-catchments upstream
v = veneer.Veneer(port=ports[0])
# filter gauges to use
gauge_names = ['gauge_126001A_SandyCkHomebush',
]#'Outlet Node24'
# find links and upstream subcatchments for the whole Sandy Creek Catchment
gauges_ID = [a[6:13] for a in gauge_names]
links_ID = [161]#, 101
the_network = v.network()
the_links = the_network['features'].find_by_feature_type('link')
ct_gauges = {ga: None for ga in gauges_ID}
for i in range(len(links_ID)):
ct_temp = []
link_all = []
link_find = []
ini_link = the_links[links_ID[i]]
link_temp = the_network.upstream_links(ini_link)
link_temp
while len(link_temp)>0:
link_find = []
for lt in link_temp:
link_all.append(lt)
ele = the_network.upstream_links(lt)
if lt['properties']['name'] == 'downstream_MultiFarm_gauge1260092':
ct_temp.append('SC #112')
else:
sc_start = re.search(r'SC', lt['properties']['name']).start()
ct_temp.append(lt['properties']['name'][sc_start:])
if len(ele)>0:
for e in ele:
link_find.append(e)
link_temp = link_find
ct_gauges[gauges_ID[i]] = ct_temp
#find catchments
# +
# the_network.upstream_links?
# -
# find the catchment area
catchment_area = {}
area_list = []
for cat in ct_gauges[' Node24']:
area_temp = v.model.catchment.get_areas(catchments=cat)
catchment_area[cat] = area_temp
area_list.append(area_temp)
catchment_area_df = pd.DataFrame.from_dict(catchment_area)
# ## End of finding catchments upstream
## Identify list of constituents
const = v.model.get_constituents()
const_df = pd.DataFrame(const)
# const_df
#Identify the list of function units
fun_units = set(v.model.catchment.get_functional_unit_types())
fun_units_df = pd.DataFrame(list(fun_units))
# fun_units_df
for ct in ct_temp:
for i in range(len(fun_units_df)):
fu = fun_units_df.iloc[i].values[0]
area_fus = v.model.catchment.get_functional_unit_areas(fus=fu, catchments=ct)
fun_units_df.loc[i, ct] = np.sum(area_fus)
# reset index for the dataframe
fun_units_df.set_index([0], inplace=True)
fun_units_df.index.name = 'fun_units'
fun_units_df
cmt_names = ct_temp
ct_area = []
for ct in cmt_names:
ct_area.append(v.model.catchment.get_areas(catchments=ct)[0])
ct_area_total = np.sum(ct_area)
for fu in fun_units_df.index:
fun_units_df.loc[fu,'proportion'] = fun_units_df.loc[fu, :].sum() / ct_area_total
# fun_units_df.to_csv('E:/cloudStor/PhDocs/pce_fixing/func_units_area.csv')
# +
# List of generation models
gen_models = set(v.model.catchment.generation.get_models(constituents = 'N_DIN'))
gen_models
# Parameters and value ranges of each generation model
model_params = {}
for ele in gen_models:
params = v.model.find_parameters(ele) #Get parameters of a certain model
param_values = {}
for param in params:
param_value = v.model.catchment.generation.get_param_values(param)
param_values[param] = [min(param_value), max(param_value), len(param_value), set(param_value)] #get min, max and lenth of a parameter
model_params[ele] = param_values
model_params
# + jupyter={"outputs_hidden": true}
dwc_init = v.model.catchment.generation.get_param_values('DWC', fus=['Sugarcane'])
dwc_init
# -
v.model.catchment.generation.set_param_values('DWC', [0.5], fus=['Sugarcane'], fromList=True)
v.model.catchment.generation.get_param_values('DWC', fus=['Sugarcane'])
# + jupyter={"outputs_hidden": true}
v.model.catchment.generation.set_param_values('DWC', dwc_init, fus=['Sugarcane'], fromList=True)
v.model.catchment.generation.get_param_values('DWC', fus=['Sugarcane'])
# -
for ct in ct_temp:
param_value = v.model.catchment.generation.get_param_values('DWC', fus=['Sugarcane'], catchments=ct)
print(f'{ct}: {param_value}')
param_value
a = np.array([1, 0, 0, 1])
a = np.where(a>0, 0.1, 0)
a
#find models of specific catchment and constituents
gen_models = set(v.model.catchment.generation.get_models(constituents = 'N_DIN'))
gen_models
pd.set_option('max_colwidth',200) #set length of dataframe outputs
gen_model_names = model_params.keys()
pd.DataFrame(list(gen_model_names))
# Use the information and in Source UI-> SedNet Utilities -> Constituent Generation Model Matrix Viewer
#
# Generation models related to fine sediment:
# RiverSystem.Catchments.Models.ContaminantGenerationModels.NilConstituent for Water
# RiverSystem.Catchments.Models.ContaminantGenerationModels.EmcDwcCGModel for Conservation, Forestry, Horticulture, Urban, Other
# Dynamic_SedNet.Models.SedNet_Sediment_Generation for Grazing Forested, Grazing Open
# GBR_DynSed_Extension.Models.GBR_CropSed_Wrap_Model for Sugarcane, Dryland Cropping, Irrigated Cropping
#
# +
## To find the parameters:
param_emcdwc = v.model.find_parameters('RiverSystem.Catchments.Models.ContaminantGenerationModels.NilConstituent')
print(param_emcdwc)
for p in param_emcdwc:
param_val = v.model.catchment.generation.get_param_values(p)
print(p, ' values: ', set(param_val))
# -
# transport models
transport_models = v.model.link.constituents.get_models(constituents = 'Sediment - Fine')
set(transport_models)
#find parameters for sediment transport model
transport_models = v.model.find_parameters('Dynamic_SedNet.Models.SedNet_InStream_Fine_Sediment_Model')
pd.DataFrame(transport_models)
# Use the above information and Source UI -> SetNet Model Setup -> Edit Routing and Instream Models
# Transport models for fine sediment:
# 'Dynamic_SedNet.Models.SedNet_InStream_Fine_Sediment_Model'
#get node models
set(v.model.node.get_models())
#get parameters for node model
v.model.find_parameters('RiverSystem.Nodes.Confluence.ConfluenceNodeModel')
# ## Find Parameters used for fine sediment
gen_models
# +
#get all models for sediment generation and transport in this project
sed_gen_models = ['Dynamic_SedNet.Models.SedNet_Sediment_Generation','GBR_DynSed_Extension.Models.GBR_CropSed_Wrap_Model',
'RiverSystem.Catchments.Models.ContaminantGenerationModels.EmcDwcCGModel']
sed_trp_models = ['Dynamic_SedNet.Models.SedNet_InStream_Fine_Sediment_Model']
sed_gen_params = []
for model in sed_gen_models:
sed_gen_param = v.model.find_parameters(model)
sed_gen_params = sed_gen_params + sed_gen_param
sed_trp_params = v.model.find_parameters(sed_trp_models)
#sed_gen_params
print('These are %d parameters for sediment generation models\n' % len(sed_gen_params))
print(pd.DataFrame(sed_gen_params))
print('\nThese are %d parameters for sediment transport models\n' % len(sed_trp_params))
print(pd.DataFrame(sed_trp_params))
# + jupyter={"outputs_hidden": true}
# Overview of parameters for fine sediment, such as the count of the parameter values, and unique values (e.g. are they constant/binary/vary, numeric/string)
for param in sed_gen_params:
param_value = v.model.catchment.generation.get_param_values(param)
param_value_len = len(param_value)
param_value_set = set(param_value) #get uni
print(param, param_value_len, param_value_set)
# -
# Overview of parameters for fine sediment, such as the count of the parameter values, and unique values (e.g. are they constant/binary/vary, numeric/string)
for param_trp in sed_trp_params:
param_value = v.model.link.constituents.get_param_values(param_trp)
param_value_len = len(param_value)
param_value_set = set(param_value) #get uni
print(param_trp, param_value_len, param_value_set)
# ## Change parameter values
# +
#place all parameters (for both sediment generation and transport) together
myparam_sed_gen = ['DeliveryRatioSeepage','DeliveryRatioSurface','Gully_Management_Practice_Factor','Gully_SDR_Fine','HillslopeCoarseSDR','HillslopeFineSDR','USLE_HSDR_Fine','Max_Conc']
# either using selected testing parameters (myparam_sedidin_gen) or all parameters (params_seddin_gen)
for i in myparam_sed_gen:
param = v.model.catchment.generation.get_param_values(i)
paraml = len(param) ## Count of the parameter values
param_set = set(param) ## unique values
print(i, paraml, param_set)
# +
myparam_sed_trp = ['bankErosionCoeff','propBankHeightForFineDep','fineSedSettVelocity','fineSedReMobVelocity','RiparianVegPercent','UptakeVelocity']
# either using testing parameters (myparam_seddin_trp) or all parameters (params_seddin_trp)
for i in myparam_sed_trp:
param = v.model.link.constituents.get_param_values(i)
paraml = len(param) ## Count of the parameter values
param_set = set(param) ## unique values
print(i, paraml, param_set)
# -
myparameters = myparam_sed_gen + myparam_sed_trp
myparameters
sedigen_bounds = [[0, 2.5],
[0.5, 1],
[0, 2],
[0, 1.4],
[0, 1],
[0, 3],
[0, 2],
[0.1, 1]]
seditrp_bounds = [[0, 10],
[0.1, 2.5],
[0, 10],
[0, 3],
[0.1, 1.3],
[0.1, 10]]
mybounds = sedigen_bounds + seditrp_bounds
mybounds
# Define the model inputs
problem = {
'num_vars': len(myparameters),
'names': myparameters,
'bounds': mybounds,
'groups': None
}
problem
# +
# %%time
## Generate samples (Morris)
N = 10
morris_level = 50
morris_grid = 2
optim_trj = False ## False or a int, >2 and <N, but generallly <=6
Loc_opt = False ## True or False.
samples_morris = sample(problem, N, num_levels=morris_level, grid_jump=morris_grid, optimal_trajectories = optim_trj, local_optimization=Loc_opt)
samples_morris
samples_morris.shape
# -
## Record initial parameter values. These values will be restored after each run.
initial_params = {}
for param_i, param_n in enumerate(problem['names']):
param_gen = v.model.catchment.generation.get_param_values(param_n)
param_trp = v.model.link.constituents.get_param_values(param_n)
param_v = param_gen + param_trp
initial_params[param_n] = param_v
print(initial_params)
# +
# %%time
## Run model iteratively
v.drop_all_runs()
for index,item in enumerate(samples_morris):
print(index)
## Update parameter values
for param_i, param_n in enumerate(problem['names']):
#print(param_i, param_n)
#print(samples_morris[n,param_i])
param_new = [x * samples_morris[index,param_i] for x in initial_params[param_n]]
#print(initial_params[param_n], param_new)
if param_n in myparam_sed_gen:
assert v.model.catchment.generation.set_param_values(param_n,param_new, fromList=True)
if param_n in myparam_sed_trp:
assert v.model.link.constituents.set_param_values(param_n,param_new,fromList=True)
## Run model
v.run_model(start='01/07/2000',end='30/06/2002')
## Return default parameter value
for param_i, param_n in enumerate(problem['names']):
if param_n in myparam_sed_gen:
v.model.catchment.generation.set_param_values(param_n,initial_params[param_n], fromList=True)
if param_n in myparam_sed_trp:
v.model.link.constituents.set_param_values(param_n,initial_params[param_n], fromList=True)
# print(temp,samples_morris[n,param_i])
# -
help(v.retrieve_multiple_time_series)
# +
## Retrieve results
allruns = v.retrieve_runs()
result_sed=[]
for index, item in enumerate(allruns):
run_name = allruns[index]['RunUrl']
run_index = v.retrieve_run(run_name)
finesediment = v.retrieve_multiple_time_series(run = run_name, run_data=run_index, criteria={'NetworkElement':'Outlet Node17','RecordingVariable':'Constituents@Sediment - Fine@Downstream Flow Mass'})
result_sed.append(finesediment.mean()[0]) ## use [0] to extract value data only
# -
# ## find constituents, models, parameters for sediment
# + jupyter={"outputs_hidden": true}
#obtain data sources
data_source = v.data_sources()
data_source.as_dataframe()
# -
set(v.model.catchment.get_functional_unit_types())
# + jupyter={"outputs_hidden": true}
constituents = v.model.get_constituents()
set(constituents)
# -
models = v.model.catchment.generation.get_models(constituents = 'N_DIN' )
models_set = set(models)
models_set
#get parameter values of sed
gen_params = []
for model in models_set:
param_sed = v.model.find_parameters(model)
gen_params += [{model: param_sed}]
gen_params
for model in models_set:
print(model,v.model.find_inputs(model))
# + jupyter={"outputs_hidden": true}
v.model.catchment.generation.get_param_values('dissConst_DWC ', fus='Horticulture', catchments=ct_gauges[' Node24'])
# -
v.model.catchment.generation.get_param_values('dissConst_EMC', fus='Grazing Forested', catchments=['SC #103'])
# + jupyter={"outputs_hidden": true}
variables = v.variables()
variables.as_dataframe()
# -
v.model.find_model_type('Times')
v.model.find_parameters('Dynamic_SedNet.Models.SedNet_TimeSeries_Load_Model')
v.model.catchment.generation.get_param_values('Load_Conversion_Factor')
# %matplotlib notebook
# Input variables
f_dir = 'rainfall_0101/'
f_name = 'rainfall_ave.csv'
rain = pd.read_csv('{}{}'.format(f_dir, f_name)).set_index('Unnamed: 0')
rain.index.name = 'Year'
rain.plot(figsize=(10, 8))
# # obtain inputs from APSIM
data_sources=v.data_sources()
data_sources.as_dataframe()
cropping = data_sources[15]['Items'][0]
# Obtain the name of DIN data for catchments in Sandy Creek area
cropping_input = [ii['Name'] for ii in cropping['Details'] if (('N_DIN' in ii['Name']) & (ii['Name'].split('$')[2] in ct_temp))]
forcing = v.data_source('Cropping Data')
forcing
|
src/Explore Models_wq.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Problems in numerical earthquake modeling
#
# Last updated Sept 9th, 2021.
#
# There are many many interesting problems to work on in the world of earthquake modeling and simulation. This page is intended to explain some of the interesting topics to software and numerics experts outside the field and is intended to be continually updated. Currently, it is mostly unfinished with some sections completely blank and it is too light on literature review.
#
# At the moment, the tooling is a major limitation for the field. Improving both the algorithms and the software would be a very productive contribution.
#
# In particular, boundary integral equation (BIE) methods are very promising for a set of problems where the object under study is itself a boundary! So, let's focus on boundary integral (and element) methods. At the moment, the standard methodology is to use constant basis function boundary elements for [which](okada) [analytical](tdes) [solutions](qdyn) have been derived. Generally, these elements are used to represent the fault in either a fullspace or halfspace. There are some efforts to move beyond these simple methods but those efforts have not yet panned out. The main barrier is lack of software and knowledge of appropriate algorithms. I think QBX-based integration combined with FMM or H-matrix acceleration would be very powerful.
#
# ## Target capabilities
# So, what would that hypothetical BIE software look like? Let's start by just listing the types of applications that would be nice to tackle, starting with "absolutely critical" down to "nice to have".
#
# * linear elasticity
# * complex realistic geometries
# * faults
# * topography
# * material interfaces
# * fault roughness
# * large models (large enough that $O(n^2)$ methods won't work)
# * high performance
# * earthquake rupture modeling
# * linear and nonlinear viscoelastic behavior
# * elastic-plastic behavior
# * seismic waves
#
# This list is probably biased to my personal preferences and the things I've worked on so far, but also covers a huge range of problems. Solving even two or three of these bullet points would be a huge contribution!
#
# ## A starting point!
#
# As an initial application of QBX/FMM methodology, I would propose working on a 2D antiplane earthquake rupture problem. A useful starting reference would be "Quasi‐dynamic versus fully dynamic simulations of earthquakes and aseismic slip with and without enhanced coseismic weakening" by Thomas and others. I'd especially recommend sections 2.1 and 2.2.
#
# The basic model that has been used in the past here is that of a horizontally infinite half-space free surface above a out-of-plane infinite strike slip fault. Bear with me if these words aren't making sense. In this "antiplane shear" setting, the Navier equations of elasticity reduce to the Poisson equation. Combining this with fault frictional ODEs into a DAE system, we get an exciting but fairly simple time dependent model of earthquakes.
#
# Let's dig more into the details of the geometry. There are two main surfaces:
# - The free surface. We assume that the atmosphere applies negligible force on the surface of the Earth. As a result, the traction on the surface is zero. Or in Poisson-speak, the potential gradient is zero. The infinite free surface, is of course problematic in a numerical setting and must be made finite.
# - One approach is to just truncate the flat surface. However that introduces some problems because the domain is no longer closed.
# - Another approach is to adopt a more realistic geometry and simply use an Earth-sized circle for the free surface. That also introduces problems because the length-scale of the Earth is much much larger than that of most fault systems.
# - A third approach is to truncate the domain with some physically-justifiable far-field vertical and basal boundary conditions - basically replace the half-space with a box. This is probably the best approach in many situations, but it does require being very careful about those far-field boundary conditions. Also, doing this in a naive way will introduce some numerically annoying corners from the corners of the box. Smoothing out those corners makes the numerics easier!
# - The fault. Here, we will be updating some ODEs in order to compute the slip rate. Slip on a fault is an earthquake science term for crack displacement. See below in the "Background" section for an explanation of how to deal with cracks in a BIE approach to elasticity. Ultimately, the jump in displacement requires using a hypersingular integral equation.
# +
"""
A simple analytical solution for constant slip on a fault underneath a free surface.
See "Earthquake and Volcano Deformation", Segall chapter 2.
"""
import matplotlib.pyplot as plt
# %config InlineBackend.figure_format='retina'
N = 100
xs = np.linspace(-1, 1, N)
ys = np.linspace(-2, 0, N)
X, Y = np.meshgrid(xs, ys)
# We need to account for the fault tip and it's image across the free surface
# in order to impose zero traction on the free surface.
fault_term = np.arctan((Y - 1) / X)
image_term = np.arctan((Y + 1) / X)
u3 = -1 / (2 * np.pi) * (fault_term - image_term)
plt.plot([-10, 10], [0,0], linewidth = 3)
plt.plot([0, 0], [0, -1], 'r-', linewidth = 3)
plt.contourf(X, Y, u3, levels = np.linspace(-0.5, 0.5, 11))
plt.axis('equal')
plt.xlim([-1, 1])
plt.ylim([-1, 0])
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
cbar = plt.colorbar()
cbar.set_label('displacement')
plt.title('displacement resulting from unit slip on a fault beneath a free surface')
plt.show()
# -
# For many methods, the fault introduces a lot of difficulties because of the need to integrate a hypersingular kernel. QBX-based integration has none of those problems. However, there is a critical problem, *What do we do about the fault-surface intersection?* This seems closely related with corner-handling in parametrized curves. However, it actually seems a bit easier because there is no singular physical behavior.
#
# Let's return to those ODEs that we are integrating on the fault. [I wrote an accessible introduction to a common form of fault friction here](https://tbenthompson.com/post/block_slider/) This type of *rate and state friction* is a common framework for frictional earthquake modeling. For more info, "Laboratory-Derived Friction Laws and Their Application to Seismic Faulting" by <NAME> is a useful review that covers a lot of the study of fault friction. However, going into too much depth is probably not necessary initially.
#
# Ultimately, in pseudocode, an earthquake simulation will often look something like this, alternating between solving the PDEs for elasticity and solving the fault-frictional equations:
# ```
# while not done:
# slip += velocity * dt
# fault_traction = elastic_solver(slip)
# velocity = friction_solver(fault_traction)
# ```
#
# #### Test problems
# I don't know of any analytical solutions for this type of earthquake simulation, but there are several useful testing avenues:
# - The elastic solver can be thoroughly tested. There are a wide variety of idealized elasticity solutions.
# - The analytical solutions for the displacement from a constant amount of slip on a line segment, triangle or rectangular are available. These are called "dislocation solutions" and are common building blocks for boudnary element methods. For line segments, see sections 2.1 and 2.2 of "Earthquake and Volcano Deformation" by <NAME>. In 3D with constant slip on a triangle, see [the software here](https://github.com/tbenthompson/cutde) and the paper referenced there.
# - The solution for slip on a line segment in a 2D model is particularly useful. I replicated [it using QBX-based BIE methods here](https://tbenthompson.com/book/c1qbx/part3_topo_solver.html). One specific solution that is very useful is exactly
# - Another useful solution is that of a compressed sphere. Solutions for this problem and other similar "elementary elasticity" problems can be found in "Theory of Elasticity" by <NAME> Goodier. That book is a treasure trove of useful analytical test problems.
# - Several extensions of the elastic solver can be tested in special cases, for example, if the deeper regions are visco-elastic instead of elastic.
# - There is a project, "The SCEC Sequences of Earthquakes and Aseismic Slip Project" that is a community to benchmark earthquake simulation software solutions against each other. While that doesn't prove that any particular piece of software is correct, it does help to identify errors.
# - I've been working on an implementation of body force handling which would enable *method of manufactured solutions* testing.
# ## Example past applications
# ## A couple potential future applications
#
# The space of possibilities is huge, but I think the most exciting potential research is in geometrically realistic modeling of actual fault systems. Simulating the interaction of many faults at once would be a powerful demonstration of methodological capabilities and also have real scientific value. It would also provide a foundation for connecting a lot more empirical and observational evidence into theoretical models.
#
# Another area of personal interest is evaluating Lyapunov time scales for chaotic behavior in an earthquake system as a function of different parameters and physics. This would be foundational work in the study of whether earthquakes are predictable or not.
# # Notes and more details
#
# ## Linear elasticity
#
# Let's focus on elasticity as it appears in a BIE method. If you need a more basic introduction to linear elasticity, there's a lot out there. Some terms to search are "elastostatics", "elastodynamics", "solid mechanics". (Link to some books and documents http://www.cns.gatech.edu/~predrag/GTcourses/PHYS-4421-04/lautrup/2.8/solids.pdf)
#
# For someone coming from an applied math or numerics background, relating the concepts here to the Poisson equation can be helpful. We can extend the concept of a scalar potential into the analogous vector displacement. And extend the vector potential gradient into the tensor stress.
#
# ### Differential form
#
# In differential form, the equations for (static, isotropic, homogeneous) linear elasticity are:
#
# \begin{align}
# \nabla \cdot \sigma &= f\\
# \epsilon &= (\nabla u) + (\nabla u)^T\\
# \sigma &= \lambda \delta_{ij} \epsilon_{kk} + 2\mu\epsilon_{ij}
# \end{align}
#
# where $\sigma$ is the stress tensor, $f$ is the vector body force, $\epsilon$ is the strain tensor, $u$ is the displacement vector, $\lambda$ is the Lamé parameter, $\mu$ is the shear modulus and $\delta_{ij}$ is the Kronecker delta. The first equation is a differential statement of Newton's law. The second and third statements together are a statement of infinitesimal strain linear elasticity. These equations are sometimes called the Navier equations or the Navier-Cauchy equations (not to be mistaken for the Navier-Stokes equations!!).
# ### Integral form
#
# The Somigliana identity is an integral representation of the displacements in an elastic body in terms of the displacements and stresses on the boundary of that body. We can write the Somigliana identity cleanly by adopting index notation:
#
# \begin{equation}
# u_{k}(\mathbf{x}) + \int_{S} T^{*}_{kj}(\mathbf{x},\mathbf{y}) u_j(\mathbf{y}) d\mathbf{y} = \int_{S} U^*_{kj}(\mathbf{x},\mathbf{y}) t_j(\mathbf{y}) d\mathbf{y} ~~~~~ \forall \mathbf{x} \in V
# \label{somigliana}
# \end{equation}
#
# where $S = \partial V$ (the boundary of $V$), $u_k(\textbf{x})$ is $k$-th component the displacement field at $\mathbf{x}$, $t_k(\textbf{x})$ is $k$-th component of the traction field (note: $t_k = \sigma_{kj} n_j$ -- the traction is "stress applied to a surface") and
#
# \begin{equation}
# U^*_{kj}(\mathbf{x},\mathbf{y}) = \frac{1}{16\pi\mu(1 - \nu)r}\big[(3 - 4\nu)\delta_{kj} + r_{,k}r_{,j}\big]
# \end{equation}
# \begin{equation}
# T^*_{kj}(\mathbf{x},\mathbf{y}) = \frac{-1}{8\pi(1-\nu)r^2}\big[ \{(1-2\nu)\delta_{kj} + 3r_{,k}r_{,j} \}\frac{\partial r}{\partial \mathbf{n}} - (1 - 2\nu)\{n_jr_{,k} - n_kr_{,j}\}\big]
# \end{equation}
#
# are the fundamental elastic and traction Green's functions of elasticity,
# with $\delta_{ij}$ is the Kronecker delta, $\mu$ as the elastic shear modulus, $\nu$ as the poisson ratio, $\mathbf{n}$ is the normal vector to $S$ at $y$, $r = \|\mathbf{x} - \mathbf{y}\|$ and $r_{,i} = \partial r/\partial x_i$.
#
# If traction, $t$, is known on the surface, we have Neumann problem. If displacement $u$ is known, we have a Dirichlet problem.
# ### Cracks
#
# So far, we've ignored cracks or faults in the elastic body. However, for earthquake science, these are the most important surfaces in the problem. The standard approach to treat cracks is to separate the crack into two infinitesimally separated surfaces, $C^+$ and $C^-$. Then, introducing the displacement discontinuity $\Delta u = u^+ - u^-$, enforcing force balance across the crack, $t^+ + t^- = 0$, the $U^*$ integrals cancel each other out and we get:
# \begin{equation}
# \begin{split}
# u_{k}(\mathbf{x}) = -\int_{F} T^{*}_{kj}(\mathbf{x},\mathbf{y}) \Delta u_j(\mathbf{y}) d\mathbf{y}
# \end{split}
# \label{somigliana_crack}
# \end{equation}
# where $F$ is the crack surface. Note that the $U^*$ integral over $F$ on the right hand side has dropped out to the force balance assumption.
#
# For folks who've seen some potential theory, this is starting to look a lot like the double layer potential.
# ### Traction BIE
#
# Critically, the traction on the fault surface does not appear in equation (\ref{somigliana_crack}). Solving for traction given fault slip is a critical step in many earthquake simulation problems. To solve this issue, another integral equation can be derived from the Somigliana identity by taking gradients and applying the elastic constitutive equations:
# \begin{equation}
# \sigma_{lk}(\mathbf{x}) - \int_{S} A^*_{lkj}(\mathbf{x},\mathbf{y}) t_j(\mathbf{y}) d\mathbf{y} = -\int_{S} H^{*}_{lkj}(\mathbf{x},\mathbf{y}) u_j(\mathbf{y}) d\mathbf{y} ~~~~~ \forall \mathbf{x} \in V
# \label{tractionbie}
# \end{equation}
# with
# \begin{equation}
# A^*_{lkj}(\mathbf{x},\mathbf{y}) = \frac{1}{8\pi(1 - \nu)r^2}\big[(1 - 2\nu)\{\delta_{lj}r_{,k} + \delta{kj}r_{,l} - \delta_{lk}r_{,j}\} + 3r_{,l}r_{,k}r_{,j}\big]
# \end{equation}
# \begin{equation}
# \begin{split}
# H^*_{lkj}(\mathbf{x},\mathbf{y}) = \frac{\mu}{4\pi(1 \nu)r^3}\big[&3\frac{\partial r}{\partial \mathbf{n}}(\{1 - 2\nu\}\delta_{lk}r_{,j} + \nu(\delta_{kj}r_{,l} + \delta_{lj}r_{,k}) - 5r_{,l}r_{,k}r_{,j})\\
# &+ (1 - 2\nu)(3n_jr_{,l}r_{,k} + n_k\delta{lj} + n_l\delta_{kj})\\
# &+ 3\nu(n_lr_{,k}r_{,j} + n_kr_{,l}r_{,j})\\
# &- (1 - 4\nu)n_m\delta_{lk} \big]
# \end{split}
# \end{equation}
#
# This equation is often called the traction boundary integral equation, because in contrast to equation (\ref{somigliana}), given the boundary conditions, we calculate the traction at any interior point instead of the displacement.
#
# Just like the displacement boundary integral equation, we can treat cracks as two infinitesimally separated surfaces with a jump in displacement and balanced tractions. The resulting integral equation is:
#
# \begin{equation}
# \begin{split}
# \sigma_{lk}(\mathbf{x}) = \int_{F} H^{*}_{lkj}(\mathbf{x},\mathbf{y}) \Delta u_j(\mathbf{y}) d\mathbf{y}~~~~~ \forall \mathbf{x} \in V
# \end{split}
# \label{tractionbie_crack}
# \end{equation}
#
# While the fault traction still does not appear within any surface integrals, the point $\mathbf{x}$ can be chosen to lie on the surface $F$, giving us the stress and traction on the fault surface. As a result, in contrast to the displacement boundary integral equation, this integral equation can be used to solve for fault stress and traction and will be a fundamental component of earthquake simulation methods.
#
# ### Displacement discontinuity method
#
# We can solve Somigliana's identity as described above directly for displacement and traction is at least one or the other is known at any point on $S$. However, it's often easier to use a double layer potential approach to represent the solution in terms of an only-sometimes-meaningful vector density $\phi(\mathbf{y})$. Given $u$ for some subset $S_u$ and $t$ for some subset $S_t$, we solve:
#
# \begin{equation}
# u_{k}(\mathbf{x}) = -\int_{F} T^{*}_{kj}(\mathbf{x},\mathbf{y}) \phi(\mathbf{y}) d\mathbf{y}
# \end{equation}
# \begin{equation}
# t_{k}(\mathbf{x}) = \int_{F} H^{*}_{lkj}(\mathbf{x},\mathbf{y}) n_l \phi(\mathbf{y}) d\mathbf{y}
# \end{equation}
#
# Given that these equations are exactly the ones that we derived above for a crack, $\phi$ matches exactly with the displacement discontinuity (aka "slip") $\Delta u$ when $S$ is a crack surface. For any other surface, we can interpret $\phi$ as a sort of fictitious slip or fictitious displacement discontinuity. Then, if we want to compute displacement or traction, we can compute the result using the above integrals of $\phi$. This approach is called the "Displacement discontinuity method". It is exactly analogous to solving a Poisson or Laplace equation problem using a double layer potential.
# ## Complex geometries, large models and high performance
#
# There's a lot of data on the Earth. Put a cool 3D figure here.
#
# ### Fault roughness
#
# Fault roughness is a particularly fascinating topic because it introduces a small scale geometrical nonlinearity into the model.
#
# ## Quasidynamic rupture modeling
#
# ###
# TODO: Put a link to youtube video here
#
# Quasidynamic earthquake simulation is a powerful tool for investigating the frictional behavior of faults over many earthquake cycles without having to invest the numerical resources required for fully dynamic rupture modeling \citep{rice1993spatio, liu2005aseismic, thomas2014quasi}.
#
# The quasidynamic approximation is a first order approximation of inertial wave effects with a "radiation damping" term. The quasidynamic shear stress on the fault surface is
# \begin{equation}
# \tau_{\mathrm{qd}} = \tau_{\mathrm{static}} - \frac{\mu}{2c_s} V
# \end{equation}
# where $\mu$ is the shear modulus, $c_s$ is the shear wave speed, and $V$ is the local fault slip velocity. The advantage of this approximation is that the shear stress can be calculated using static elastic numerical methods and then adjusted by the slip velocity.
#
# To complete the system, we need to a friction law that relates shear stress to slip velocity. A common framework is rate-state friction where the strength of friction is related to both the rate of slip and a state variable the evolves during fault slip. The state variable evolution law can take various forms. Here, we present the aging law. Then, rate-state friction takes the form
# \begin{align}
# \tau_{\mathrm{qd}} = a\sigma_n \sinh^{-1}\left(\frac{V}{2V_0}e^{\Psi / a}\right)\label{ratestate}\\
# \frac{d\Psi}{dt} = \frac{bV_0}{D_c}\left(e^{(f_0 - \Psi) / b} - \frac{V}{V_0}\right)\label{stateevolution}
# \end{align}
# where $\sigma_n$ is the normal stress, $\Psi$ is the state variable, $f_0$ is a the friction coefficient at a steady state slip velocity of $V_0$, $a$ and $b$ are dimensionless parameters determining the strength of velocity and state changes respectively on the evolution of friction and $D_c$ is the state evolution length scale. In our implementation, fault slip is always parallel to the shear stress vector and can be in any direction on the fault plane.
#
# Several approaches have been used for quasidynamic earthquake cycle simulation. Fourier domain convolution methods are extremely efficient for planar faults with a uniform discretization \citep{rice1993spatio, lapusta2000elastodynamic}. However, these methods break down in the face of any non-planarity. Boundary element methods using rectangular or triangular dislocations \citep{liu2005aseismic, segall2012slow} have the aforementioned stress singularity issues, especially on nonplanar faults. Both Fourier and dislocation approaches struggle with rheologies beyond linear elasticity. In comparison, finite difference methods or finite element methods can successfully model a much wider range of rheologies including non-uniform material properties \citep{erickson2014efficient} or viscoplasticity \citep{allison2018earthquake}. However, finite difference methods still have difficulty with complex nonplanar fault geometries. In comparison, our boundary element methods can model arbitrary nonplanar fault geometries.
#
# We build a quasidynamic earthquake cycle simulator on top of Tectosaur. We track the current slip deficit and state variable at every degree of freedom on the fault surface. Then, at each time step, we calculate the traction on the fault surface from the slip deficit field using Tectosaur to solve the static elastic equations. The friction equations are then solved for the current slip velocity using Equation (\ref{ratestate}). The state derivatives are calculated using Equation (\ref{stateevolution}). Finally, having both the slip deficit derivatives and state derivatives, we integrate in time. The algorithm is flexible to the particular time integration method. A popular method has been to use a time step dependent on the fastest slip velocity on the fault \citep{lapusta2009three}. We follow \citet{erickson2014efficient} in using an adaptive Runge-Kutta algorithm.
#
# ## Viscoelastic behavior and elasto-plastic behavior
#
# The Earth is not purely elastic and there are many settings.
#
# DEFINE A MAXWELL RHEOLOGY
#
# DEFINE A SIMPLE PLASTIC RHEOLOGY
#
# Change the fundamental material behavior seems like it would require a new set of basic equations, but given the mild perturbation away from elasticity, it's also possible to push the extra physics into the "body force" term.
#
# ## Seismic waves
#
# ## Fully dynamic rupture modeling
|
tutorials/overview/problem_description.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import pickle
import torch
import numpy as np
from math import ceil
from model_vc import Generator
def pad_seq(x, base=32):
len_out = int(base * ceil(float(x.shape[0])/base))
len_pad = len_out - x.shape[0]
assert len_pad >= 0
return np.pad(x, ((0,len_pad),(0,0)), 'constant'), len_pad
device = 'cuda:0'
G = Generator(32,256,512,32).eval().to(device)
g_checkpoint = torch.load('autovc.ckpt', map_location="cuda:0")
G.load_state_dict(g_checkpoint['model'])
metadata = pickle.load(open('metadata.pkl', "rb"))
spect_vc = []
for sbmt_i in metadata:
x_org = sbmt_i[2]
x_org, len_pad = pad_seq(x_org)
uttr_org = torch.from_numpy(x_org[np.newaxis, :, :]).to(device)
emb_org = torch.from_numpy(sbmt_i[1][np.newaxis, :]).to(device)
for sbmt_j in metadata:
emb_trg = torch.from_numpy(sbmt_j[1][np.newaxis, :]).to(device)
with torch.no_grad():
_, x_identic_psnt, _ = G(uttr_org, emb_org, emb_trg)
if len_pad == 0:
uttr_trg = x_identic_psnt[0, 0, :, :].cpu().numpy()
else:
uttr_trg = x_identic_psnt[0, 0, :-len_pad, :].cpu().numpy()
spect_vc.append( ('{}x{}'.format(sbmt_i[0], sbmt_j[0]), uttr_trg) )
with open('results.pkl', 'wb') as handle:
pickle.dump(spect_vc, handle)
# -
|
.ipynb_checkpoints/conversion-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/richardtml/riiaa-19-dmtl/blob/master/notebooks/1_mlp.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# -
# # Perceptrón multicapa
#
# #### <div style="text-align: right"> <NAME> </div>
#
# En este ejemplo veremos como implementar un perceptrón multicapa para la tarea de clasificación de imágenes. Emplearemos un conjunto referencia llamado [MNIST](http://yann.lecun.com/exdb/mnist/) recolectado por [Yann LeCun](http://yann.lecun.com). Tiene imágenes en escala de grises de 28 × 28 píxeles que contienen dígitos entre 0 y 9 escritos a mano. El conjunto cuenta con 60,000 imágenes de entrenamiento y 10,000 de prueba.
#
# 
# ## 1 Carga de datos
# ### 1.1 Importando bibliotecas
# +
# para cargar Tensorflow 2 en Colab
try:
# %tensorflow_version 2.x
except Exception:
pass
# graficación
import matplotlib.pyplot as plt
# arreglos multidimensionales
import numpy as np
# redes neuronales
import tensorflow as tf
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras import Model
# fijamos una semilla para reproducibilidad
tf.random.set_seed(2019)
# -
# ### 1.2 Descarga de los datos
# Comenzaremos descargando y leyendo el conjunto de datos. Aprovecharemos que Tensorflow cuenta con utilerias en el paquete [`tf.keras.datasets`](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/datasets) para descargar algunos conjuntos de datos de referencia preprocesados.
# alias
mnist = tf.keras.datasets.mnist
# descarga
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# ### 1.3 Visualización
plt.figure(figsize=(5, 6))
for i in range(1, 10):
plt.subplot(330 + i)
plt.xticks([])
plt.yticks([])
plt.imshow(x_train[5 * i], cmap='Greys')
# ### 1.4 Normalización
x_train, x_test = x_train / 255.0, x_test / 255.0
y_train = y_train[..., tf.newaxis]
y_test = y_test[..., tf.newaxis]
# ### 1.5 Tuberia de datos
#
# 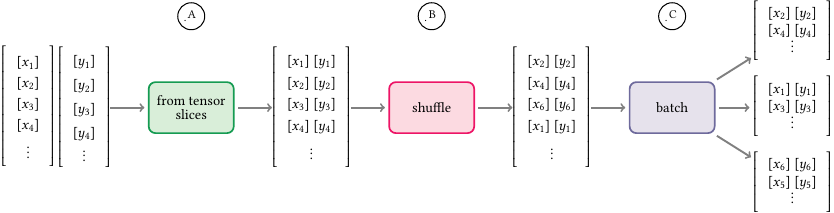
# +
batch_size = 64
# Cargamor en un Dataset
ds = tf.data.Dataset.from_tensor_slices((x_train, y_train))
# lo barajeamos
ds = ds.shuffle(60000)
# empaquetamos los lotes
ds = ds.batch(batch_size)
# exploremos
for x, y_true in ds:
print('x.shape={}'.format(x.shape))
print('x={}'.format(x.numpy().flatten()))
print('y_true.shape={}'.format(y_true.shape))
print('y={}'.format(y_true.numpy().flatten()))
break
# -
# ### Quiz 1
#
# ¿Cúal es la función de activación adecuada para la capa de salida de una red neuronal para clasificación multiclase?
# ## 2 Definición del modelo
# ### 2.1 implementación
# se define una clase que hereda de tensorflow.keras.Moldel
class MLP(Model):
#se define el inicializador
def __init__(self):
# se llama al inicializador de la clase padre
super(MLP, self).__init__()
# importante: se definen las capas como atributos de la clase
# Flatten aplana tensores
self.flatten = Flatten()
# Dense es un capa completamente conectada donde
# units es el número de neuronas y
# activation es la función de activación
self.fc1 = Dense(units=128, activation=tf.nn.relu)
self.fc2 = Dense(units=10, activation=tf.nn.softmax)
# se realiza inferencia y definición de arquitectura al vuelo
def call(self, x):
# (N, 28, 28) =>
# (N, 28*28)
o = self.flatten(x)
# (N, 28*28) =>
# (N, 128)
o = self.fc1(o)
# (N, 128) =>
# (N, 10)
o = self.fc2(o)
return o
# ### Quiz 2
#
# Si las clases fueran 100 en vez de 10 y quisera utilizar la misma arquitectura anterior ¿qué modificación tendría que realizar?
# ### 2.2 Definición de pérdida y optimizador
loss_fn = tf.keras.losses.SparseCategoricalCrossentropy()
optimizer = tf.keras.optimizers.SGD(learning_rate=1e-3)
# ### 2.3 Definición de métricas
#
# Las clases dentro de `tf.keras.metrics` están diseñadas para mantener un histórico de una métrica a lo largo de los pasas de entrenamiento y agregarlo (con el promedio por ejemplo) para obtener el desempeño de la métrica a nivel epoca.
# +
# historiales a nivel época
loss_epoch = tf.keras.metrics.SparseCategoricalCrossentropy()
acc_epoch = tf.keras.metrics.SparseCategoricalAccuracy()
# historiales a nivel entrenamiento
loss_history = []
acc_history = []
# -
# ## 3 Entrenamiento
# ### 3.1 Ciclo de entrenamiento
# +
# instanciamos nuestro modelo
model = MLP()
epochs = 25
# épocas de entrenamiento
for epoch in range(epochs):
# pasos de entrenamiento
for x, y_true in ds:
# registramos el flujo del cómputo en GradientTape
with tf.GradientTape() as tape:
# realizamos inferencia con el lote
y_pred = model(x)
# realizamos inferencia con el lote
loss = loss_fn(y_true, y_pred)
# computamos los gradientes de los parámetros del modelo
gradients = tape.gradient(loss, model.trainable_variables)
# aplicamos los gradientes
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
# calculamos las métricas y agramos al historial de la época
loss_epoch(y_true, y_pred)
acc_epoch(y_true, y_pred)
# guardamos las métricas de la época
loss_res = loss_epoch.result().numpy() * 100
acc_res = acc_epoch.result().numpy() * 100
# reiniciamos los historiales de las épocas
loss_epoch.reset_states()
acc_epoch.reset_states()
# agreagmos a los historiales nivel entrenamiento
loss_history.append(loss_res)
acc_history.append(acc_res)
# imprimimos métricas
print('{:3d} loss={:6.2f}, acc={:6.2f}'.format(epoch, loss_res, acc_res))
# -
# ### 3.2 Gráfica de la pérdida
plt.plot(np.arange(len(loss_history)), loss_history, color='red')
plt.xlabel('iteraciones')
plt.ylabel('entropía cruzada categorica')
plt.show()
# ### 3.3 Gráfica la exactitud
plt.plot(np.arange(len(acc_history)), acc_history, color='blue')
plt.xlabel('iteraciones')
plt.ylabel('exactitud')
plt.show()
# ## 4 Validación
# ### 4.1 Exactitud
y_pred_test = model(x_test)
print(acc_epoch(y_test, y_pred_test).numpy() * 100)
# ### 4.2 Inferencia
plt.figure(figsize=(5, 6))
for i in range(1, 10):
plt.subplot(330 + i)
plt.xticks([])
plt.yticks([])
plt.imshow(x_test[5*i], cmap='Greys')
plt.title(y_pred_test[5*i].numpy().argmax())
|
notebooks/1_mlp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/sid779/Deep_learning_with_pytorch/blob/master/intro-to-pytorch/Part%207%20-%20Loading%20Image%20Data%20(Exercises).ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="u2FR3fOfscQn" colab_type="text"
# # Loading Image Data
#
# So far we've been working with fairly artificial datasets that you wouldn't typically be using in real projects. Instead, you'll likely be dealing with full-sized images like you'd get from smart phone cameras. In this notebook, we'll look at how to load images and use them to train neural networks.
#
# We'll be using a [dataset of cat and dog photos](https://www.kaggle.com/c/dogs-vs-cats) available from Kaggle. Here are a couple example images:
#
# <img src='https://github.com/sid779/Deep_learning_with_pytorch/blob/master/intro-to-pytorch/assets/dog_cat.png?raw=1'>
#
# We'll use this dataset to train a neural network that can differentiate between cats and dogs. These days it doesn't seem like a big accomplishment, but five years ago it was a serious challenge for computer vision systems.
# + id="Slo13PjBscQ0" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 202} outputId="26c73dae-5abf-432a-dfae-2bfd2e750261"
# %matplotlib inline
# %config InlineBackend.figure_format = 'retina'
import matplotlib.pyplot as plt
# http://pytorch.org/
from os.path import exists
from wheel.pep425tags import get_abbr_impl, get_impl_ver, get_abi_tag
platform = '{}{}-{}'.format(get_abbr_impl(), get_impl_ver(), get_abi_tag())
# cuda_output = !ldconfig -p|grep cudart.so|sed -e 's/.*\.\([0-9]*\)\.\([0-9]*\)$/cu\1\2/'
accelerator = cuda_output[0] if exists('/dev/nvidia0') else 'cpu'
# !pip install -q http://download.pytorch.org/whl/{accelerator}/torch-0.4.1-{platform}-linux_x86_64.whl torchvision
import torch
import torch
from torchvision import datasets, transforms
# !wget -c https://raw.githubusercontent.com/udacity/deep-learning-v2-pytorch/master/intro-to-pytorch/helper.py
import helper
# + id="lmJGeIhBs9hD" colab_type="code" colab={}
# + [markdown] id="ChzXrIAYscRD" colab_type="text"
# The easiest way to load image data is with `datasets.ImageFolder` from `torchvision` ([documentation](http://pytorch.org/docs/master/torchvision/datasets.html#imagefolder)). In general you'll use `ImageFolder` like so:
#
# ```python
# dataset = datasets.ImageFolder('path/to/data', transform=transform)
# ```
#
# where `'path/to/data'` is the file path to the data directory and `transform` is a list of processing steps built with the [`transforms`](http://pytorch.org/docs/master/torchvision/transforms.html) module from `torchvision`. ImageFolder expects the files and directories to be constructed like so:
# ```
# root/dog/xxx.png
# root/dog/xxy.png
# root/dog/xxz.png
#
# root/cat/123.png
# root/cat/nsdf3.png
# root/cat/asd932_.png
# ```
#
# where each class has it's own directory (`cat` and `dog`) for the images. The images are then labeled with the class taken from the directory name. So here, the image `123.png` would be loaded with the class label `cat`. You can download the dataset already structured like this [from here](https://s3.amazonaws.com/content.udacity-data.com/nd089/Cat_Dog_data.zip). I've also split it into a training set and test set.
#
# ### Transforms
#
# When you load in the data with `ImageFolder`, you'll need to define some transforms. For example, the images are different sizes but we'll need them to all be the same size for training. You can either resize them with `transforms.Resize()` or crop with `transforms.CenterCrop()`, `transforms.RandomResizedCrop()`, etc. We'll also need to convert the images to PyTorch tensors with `transforms.ToTensor()`. Typically you'll combine these transforms into a pipeline with `transforms.Compose()`, which accepts a list of transforms and runs them in sequence. It looks something like this to scale, then crop, then convert to a tensor:
#
# ```python
# transform = transforms.Compose([transforms.Resize(255),
# transforms.CenterCrop(224),
# transforms.ToTensor()])
#
# ```
#
# There are plenty of transforms available, I'll cover more in a bit and you can read through the [documentation](http://pytorch.org/docs/master/torchvision/transforms.html).
#
# ### Data Loaders
#
# With the `ImageFolder` loaded, you have to pass it to a [`DataLoader`](http://pytorch.org/docs/master/data.html#torch.utils.data.DataLoader). The `DataLoader` takes a dataset (such as you would get from `ImageFolder`) and returns batches of images and the corresponding labels. You can set various parameters like the batch size and if the data is shuffled after each epoch.
#
# ```python
# dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# ```
#
# Here `dataloader` is a [generator](https://jeffknupp.com/blog/2013/04/07/improve-your-python-yield-and-generators-explained/). To get data out of it, you need to loop through it or convert it to an iterator and call `next()`.
#
# ```python
# # Looping through it, get a batch on each loop
# for images, labels in dataloader:
# pass
#
# # Get one batch
# images, labels = next(iter(dataloader))
# ```
#
# >**Exercise:** Load images from the `Cat_Dog_data/train` folder, define a few transforms, then build the dataloader.
# + id="NpBBsqquscRI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 585} outputId="ee9a886c-7f97-4eea-b1eb-9db0ed422137"
data_dir = 'Cat_Dog_data/train'
transform = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
dataset = datasets.ImageFolder(data_dir, transform=transform)
dataloader = torch.utils.data.DataLoader(dataset, batch_size=32, shuffle=True)
# + id="yRvAATFCscRT" colab_type="code" colab={}
# Run this to test your data loader
images, labels = next(iter(dataloader))
helper.imshow(images[0], normalize=False)
# + [markdown] id="hkzEuPQascRe" colab_type="text"
# If you loaded the data correctly, you should see something like this (your image will be different):
#
# <img src='https://github.com/sid779/Deep_learning_with_pytorch/blob/master/intro-to-pytorch/assets/cat_cropped.png?raw=1' width=244>
# + [markdown] id="JSpFsCQwscRi" colab_type="text"
# ## Data Augmentation
#
# A common strategy for training neural networks is to introduce randomness in the input data itself. For example, you can randomly rotate, mirror, scale, and/or crop your images during training. This will help your network generalize as it's seeing the same images but in different locations, with different sizes, in different orientations, etc.
#
# To randomly rotate, scale and crop, then flip your images you would define your transforms like this:
#
# ```python
# train_transforms = transforms.Compose([transforms.RandomRotation(30),
# transforms.RandomResizedCrop(224),
# transforms.RandomHorizontalFlip(),
# transforms.ToTensor(),
# transforms.Normalize([0.5, 0.5, 0.5],
# [0.5, 0.5, 0.5])])
# ```
#
# You'll also typically want to normalize images with `transforms.Normalize`. You pass in a list of means and list of standard deviations, then the color channels are normalized like so
#
# ```input[channel] = (input[channel] - mean[channel]) / std[channel]```
#
# Subtracting `mean` centers the data around zero and dividing by `std` squishes the values to be between -1 and 1. Normalizing helps keep the network work weights near zero which in turn makes backpropagation more stable. Without normalization, networks will tend to fail to learn.
#
# You can find a list of all [the available transforms here](http://pytorch.org/docs/0.3.0/torchvision/transforms.html). When you're testing however, you'll want to use images that aren't altered (except you'll need to normalize the same way). So, for validation/test images, you'll typically just resize and crop.
#
# >**Exercise:** Define transforms for training data and testing data below.
# + id="6-0O7kF4scRm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 585} outputId="86a08474-1cf1-465d-974b-51f5818bb76c"
data_dir = 'Cat_Dog_data'
# TODO: Define transforms for the training data and testing data
train_transforms = transforms.Compose([transforms.RandomRotation(30),
transforms.RandomResizedCrop(224),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()])
test_transforms = transforms.Compose([transforms.Resize(255),
transforms.CenterCrop(224),
transforms.ToTensor()])
# Pass transforms in here, then run the next cell to see how the transforms look
train_data = datasets.ImageFolder(data_dir + '/train', transform=train_transforms)
test_data = datasets.ImageFolder(data_dir + '/test', transform=test_transforms)
trainloader = torch.utils.data.DataLoader(train_data, batch_size=32)
testloader = torch.utils.data.DataLoader(test_data, batch_size=32)
# + id="C9ye0WM2scRu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 229} outputId="cff82391-3627-411e-ff9e-baa015e22702"
# change this to the trainloader or testloader
data_iter = iter(testloader)
images, labels = next(data_iter)
fig, axes = plt.subplots(figsize=(10,4), ncols=4)
for ii in range(4):
ax = axes[ii]
helper.imshow(images[ii], ax=ax, normalize=False)
# + [markdown] id="jYoAWZ3lscR0" colab_type="text"
# Your transformed images should look something like this.
#
# <center>Training examples:</center>
# <img src='https://github.com/sid779/Deep_learning_with_pytorch/blob/master/intro-to-pytorch/assets/train_examples.png?raw=1' width=500px>
#
# <center>Testing examples:</center>
# <img src='https://github.com/sid779/Deep_learning_with_pytorch/blob/master/intro-to-pytorch/assets/test_examples.png?raw=1' width=500px>
# + [markdown] id="yv4AYQ8DscR2" colab_type="text"
# At this point you should be able to load data for training and testing. Now, you should try building a network that can classify cats vs dogs. This is quite a bit more complicated than before with the MNIST and Fashion-MNIST datasets. To be honest, you probably won't get it to work with a fully-connected network, no matter how deep. These images have three color channels and at a higher resolution (so far you've seen 28x28 images which are tiny).
#
# In the next part, I'll show you how to use a pre-trained network to build a model that can actually solve this problem.
# + id="NxnXn5iRscR5" colab_type="code" colab={}
# Optional TODO: Attempt to build a network to classify cats vs dogs from this dataset
|
intro-to-pytorch/Part 7 - Loading Image Data (Exercises).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Simple Quantum Algorithms (part 1)
#
# <div class="youtube-wrapper">
# <iframe src="https://www.youtube.com/embed/WYAUh-4K5E0" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# </div>
#
#
# Elisa covers the basics of qubits, Dirac notations, basic gate operations (e.g. Hadamard gate, NOT gate, Controlled-NOT gate, etc.), and the Bloch sphere representation of a qubit. Elisa then introduces few basic quantum algorithms to show how quantum computers work, and to show certain advantages over the classical system.
#
# Elisa introduces oracle operators, and we want to work out their properties using the fewest queries possible. We can build a phase oracle from a classical oracle for use in the Deutsch-Jozsa algorithm. Deutsch-Jozsa algorithm determines whether a given function is constant (i.e. output will be always 0 or always 1) or balanced (i.e output is 0 for half the inputs and 1 for the rest). Elisa gives the intuition of this algorithm and follows through the mathematics step-by-step.
#
# ### Suggested links
#
# - Download the lecturer's notes [here](/content/summer-school/2021/resources/lecture-notes/Lecture2.1.pdf)
#
# - Read Microsoft on [Quantum Computing for Computer Scientists](https://www.microsoft.com/en-us/research/video/quantum-computing-computer-scientists/)
# - Read Classical Computation on a Quantum Computer [Description: Understanding reversible in computer science (and also quantum computing being reversible is usefull).](/course/ch-gates/classical-computation-on-a-quantum-computer)
# - Read about Quantum Oracle Functions [Description: Understanding of Quantum Oracle Function and implementation of an Oracle function in Qiskit](https://docs.microsoft.com/en-us/azure/quantum/concepts-oracles)
# - Read about the Deutsch-Jozsa Algorithm [Description: Understanding of Quantum Oracle Function](/course/ch-algorithms/deutsch-jozsa-algorithm)
#
# <!-- ::: q-block.reminder -->
#
# ### FAQ
#
# <details>
# <summary>What is an oracle?</summary>
# It’s just a black-box like device, that performs implementation in a function as a unitary operator.
#
# In other words, an oracle is like a 'black box'. It gets an input and creates an output that one can measure but actually cannot see inside the black box, which means one doesn't know its property (in this case, one doesn't know if the function is constant or balanced). The goal is to find the property of the oracle.
# </details>
#
# <details>
# <summary>Due to Superposition, we have to run quantum computers once. This is a huge speed advantage over classical systems. However, to measure a probability, we must run the quantum algorithm many times to get the meaningful probability given real-life noise. How does this speed factor vary between classical and quantum?</summary>
# It depends on a lot of noise. In the example of the Deutsch-Jozsa Algorithm, users can quickly determine whether the function is balanced or constant. Because you can only get one output from the circuit and the rest of the combinations are zero, the probability distribution is also based on it. Then you can a few shots at the same time, do the measurements, and get a higher chance (above 90%) to get the correct output.
# </details>
#
# <details>
# <summary>What are Balanced Function and Constant Function in the Oracle?</summary>
# If a function with n-qubits input gives n number of 0s (all 0s) or n number of 1s (all 1s) regardless of the input, then that function is known as Constant Function whereas, If a function with n-qubits gives half-of the n numbers of 0s and another half as 1s, then the function is balanced.
#
# In another way, we can mention that a function ‘f’ is called balanced if it is equal to 1 for exactly half of all the possible x, and 0 for the other half.
# </details>
#
# <details>
# <summary>For the Quantum solution of the algorithms, how to determine the number of qubits need to use in this algorithm?</summary>
# It depends on the function on which this algorithm is implemented.
# </details>
#
# <!-- ::: -->
#
# ### Other resources
#
# - Read by <NAME> and <NAME> on [Quantum Computation and Quantum Information Textbook](https://www.amazon.com/Quantum-Computation-Information-10th-Anniversary/dp/1107002176)
# - Read IBM on [Qiskit textbook](https://qiskit.org/textbook/preface.html)
#
#
|
notebooks/summer-school/2021/lec2.1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.image as image
# %matplotlib inline
plt.xkcd()
start='20130428'
end='20181207'
def plotter(currency,i,c='orange',st='2012-12-20',last='2017'):
dfs=pd.read_html('https://coinmarketcap.com/currencies/'+currency+'/historical-data/?start='+start+'&end='+end)
df=dfs[0]
df=df[['Date','Close**']]
df.columns=['Date','.']
df['Date']=pd.to_datetime(df['Date'])
fig,ax=plt.subplots(figsize=(13,6))
df[(last>df['Date'])&(df['Date']>'2013')].set_index('Date').plot(ax=ax,c='grey')
ax2=ax.twiny()
ax2=ax2.twinx()
dz=df[df['Date']>'2017'].set_index('Date')
dz.columns=[u'Before and after the last bubble\n2013-2016 (bottom + left axis)']
dz.plot(ax=ax2,c='grey')
dz.columns=[currency.capitalize()+u' price in $ since 2017 (top + right axis)']
dz.plot(ax=ax2,c=c)
ax.set_xlim(st,pd.to_datetime(st)+pd.to_timedelta(3, unit='Y'))
ax2.set_xlim('2017','2020')
ax.set_xlabel('')
ax2.legend()
im = image.imread('https://s2.coinmarketcap.com/static/img/coins/32x32/'+str(i)+'.png')
ax3 = fig.add_axes([0.12, 0.74, 0.07, 0.07])
ax3.axis('off')
ax3.imshow(im)
ax3.set_title(str(int(max(df[df['Date']>'2017']['.'])/max(df[df['Date']<'2017']['.'])))+'x',color=c,)
plt.savefig(currency)
plotter('bitcoin',1,'orange')
plotter('litecoin',2,'lightgrey')
plotter('ripple',52,'black','2012-11-30')
plotter('dash',131,'dodgerblue','2013-06-07')
plotter('namecoin',3,'lightsteelblue','2012-11-18')
plotter('dogecoin',74,'darkkhaki','2013-01-22')
plotter('bytecoin-bcn',372,'deeppink','2013-02-15')
plotter('nxt',66,'deepskyblue','2013-06-15')
plotter('nem',873,'mediumturquoise','2015-06-25','2017-02')
plotter('peercoin',5,'limegreen')
plotter('feathercoin',8,'black','2012-11-20')
|
hodlon/.ipynb_checkpoints/binance-nov-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Reshaping data: Portland housing developments
#
# In this notebook, we're going to work with some data on Portland (Oregon) housing developments since 2014. Right now, the data are scattered across a jillion spreadsheets. Our goal is to parse them all into one clean CSV. (Thanks to [<NAME> of the Portland Mercury](https://twitter.com/Kelly_Kenoyer) for donating this data.)
#
# The spreadsheets, a mixture of `xls` and `xlsx` files, live in `../data/portland/`. A few things to note:
# - Some of the spreadsheets have extra columns
# - Some of the spreadsheets have other worksheets in addition to the data worksheet (pivot tables, mostly) -- but these are not always in the same position
# - Some of the spreadsheets have columns of mostly blank data that the city once used to manually aggregate data by category -- we don't want these columns
# - Some of the spreadsheets have blank rows
#
# Our strategy:
# - Get a list of Excel files in that directory using the [`glob`](https://docs.python.org/3/library/glob.html) module
# - Create an empty pandas data frame
# - Loop over the list of spreadsheet files and ...
# - Read in the file to a data frame
# - Find the correct worksheet
# - Drop empty columns and rows
# - Append to the main data frame
#
# First, we'll import `glob` and pandas.
# import glob and pandas
# Next, we'll use `glob` to get a list of the files we're going to loop over. We'll use the asterisk `*`, which means "match everything."
# use glob to find everything in the `../data/portland/` directory
# print that list to make sure we have what we think we have
# Now we'll create an empty data frame. This will be the container we stuff the data into as we loop over the files.
# create an empty data frame
# Let's take a look at what we're dealing with. We're going to loop over the spreadsheet, and for each one, we're going to look at:
# - The names of the worksheets in that spreadsheet
# - The columns in each worksheet
#
# This will help us decide, later, which worksheets we need to target.
#
# We're going to take advantage of the fact, [according to the `read_excel()` documentation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_excel.html), that you can pass `None` as the `sheet_names` argument and pandas will read in _all_ of the sheets as a big dictionary -- the keys are the names of the worksheets, the values are the associated data frames.
#
# Later, our logic will go like this:
# - Read in every worksheet as a data frame
# - Target the worksheet whose name matches the pattern for the data we need
#
# 👉 For a refresher on _for loops_ and dictionaries, [check out this notebook](../reference/Python%20data%20types%20and%20basic%20syntax.ipynb#for-loops).
# +
# loop over the excel file paths
# load the file into a data frame
# specifying `None` as the sheet name
# print the name of the file
# print the worksheet names
# -- the .keys() in the dictionary
# print a divider to make scanning easier
# and an empty line
# -
# OK. So it looks like our target sheets are called a few different things: `nrs`, `04_2016 New Res Units'`, `'2018 04 New Residential Units'`, etc.
#
# Can we come up with a list of patterns to match all of them? I think we can.
# the items in this list are lowercased,
# because we're gonna match on .lower()'d versions of the sheet names
target_sheet_name_fragments = ['new res', 'nrs', 'lus stats']
# So now, we need to write some logic that says: Pick the worksheet that has one of our `target_sheet_name_fragments` in the name. A nested pair of _for loops_ will do the trick for us.
# +
# loop over the excel file paths
# load the file into a data frame
# specifying `None` as the sheet name
# start off with no match -- None
# loop over the worksheet names
# loop over the word fragments
# if this fragment exists in the lowercased worksheet name
# we've got a winner
# if, when we get to the end of this, `match` is still None
# print something to let us know about it
# and the names of the sheets
# and break out of the loop
# otherwise, grab a handle to the worksheet we want
# print a status message to let us know what's up
# -
# Scanning through that list, I feel comfortable that we're grabbing the correct data. Let's take a look at the columns in each worksheet we'll be parsing.
# +
# loop over the excel file paths
# load the file into a data frame
# specifying `None` as the sheet name
# start off with no match - None
# loop over the worksheet names
# loop over the word fragments
# if this fragment exists in the lowercased worksheet name
# we've got a winner
# if, when we get to the end of this, `match` is still None
# print something to let us know about it
# and the names of the sheets
# and break out of the loop
# otherwise, grab a handle to the worksheet we want
# print a status message to let us know what's up
# print a sorted list of column names
# print a divider to make scanning our results easier
# print an empty line
# -
# I notice that some columns are, e.g. `Unnamed: 4`. That means there's no column header. Let's take a look at one of those:
test = pd.read_excel('../data/portland/08_2014 New Res Units.xls', sheet_name='08_2014 New Res Units')
test.head(20)
# Looks like they're using those columns to total up the valuations for groups of housing types. I'm noticing, too, that there are some blank rows -- probably used as dividers between groups -- so we'll want to drop those as well.
#
# We'll keep that in mind as we roll through these sheets.
#
# Here's the pandas documentation on the methods we'll be using here:
# - [`append()`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.append.html)
# - [`drop()`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.drop.html)
# - [`dropna()`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.dropna.html)
# +
# loop over the excel file paths
# load the file into a data frame
# specifying `None` as the sheet name
# start off with no match
# loop over the worksheet names
# loop over the word fragments
# if this fragment exists in the lowercased worksheet name
# we've got a winner
# if, when we get to the end of this, `match` is still None
# print something to let us know about it
# and the names of the sheets
# and break out of the loop
# otherwise, grab a handle to the worksheet we want
# print a status message to let us know what's up
# get a list of columns we want to drop
# drop those bad boys
# drop empty rows in place, but only if _all_ of the values are nulls
# append to our `housing` data frame
# -
# check it out with head()
# check the len()
# check dtypes
# One last thing I'd do, before writing out to file, is parse the date columns as dates:
# +
# convert "indate" column to datetime
# convert "indate" column to datetime
# -
# check it out with head()
# Now we can use the `to_csv()` method to write out to a new file:
# write out to 'portland-developments.csv'
# specify no index
|
workshop/11. Reshaping data => Portland housing developments - working copy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Criando um banco de dados SQLite em Python
#
# Documentação SQLite: https://www.sqlite.org/docs.html
#
# ### Acessando banco de dados com Python
# +
# Remove o arquivo com o banco de dados SQLite (caso exista)
import os
os.remove('escola.db') if os.path.exists('escola.db') else None
# +
# Importando o módulo de acaesso ao SQLite
import sqlite3
# Cria uma conexão com o banco de dados. Se o banco de dados não existir, ele é criado neste momento
con = sqlite3.connect('escola.db')
type(con)
# +
# Criando um cursor (um crusor permite percoerrer todos os registros em um conjunto de dados)
cur = con.cursor()
type(cur)
# -
# ### Criando um banco de dados SQL utilizando o comando DDL `create table`
# +
# Criar uma instrução sql. Para criar uma tabela utiliza-se o comando DDL criate table. O nome da tabela, cursos, vem logo após
# o comando create table. Em seguida, são adicionadas as colunas da tabela 'cursos': id, título e categoria. O tipo da coluna
# (ex: integer, varchar, float) é informado após seu título e a chave primária (PK) é identificada. A primeira coluna não pode
# ter valores repetido por se tratar de uma chave primária. varchar(100) = variável do tipo caracter com até 100 posições;
# varhar(140) = até 140 posições
sql_create = 'create table cursos '\
'(id integer primary key, '\
'titulo varchar(100), '\
'categoria varchar(140))'
# +
# Executando a instrução sql no cursor. Aqui é onde a tabela é de fato criada
cur.execute(sql_create)
# -
# ### Inserindo registros no banco SQL utilizando o comando DML `insert into`
# +
# Criando outra sentença SQL para inserir registros. Para inserir registros na tabela usiliza-se o comando DML `insert into`,
# em seguida o nome da tabela. o comando `values` é utilizado para indicar os valores dos registros que serão incluídos
sql_insert = 'insert into cursos values (?, ?, ?)'
# +
# Dados. recset = recrod setting, ou conjunto de registros. Esse será o conjunto de registros adicionado a tabela 'cursos'
recset = [(1000, 'Ciência de Dados', 'Data Science'),
(1001, 'Big Data Fundamentos', 'Big Data'),
(1002, 'Python Fundamentos', 'Análise de Dados')]
# +
# Inserindo os registros. Para cada registro rec em recset o cursor executará o comando de inclusão de registro na tabela
for rec in recset:
cur.execute(sql_insert, rec)
# -
# ### Gravando os novos registros que foram inseridos no banco de dados utilizando o comando `commit`
# +
# Grava a transação
con.commit()
# +
# Criando outra sentença SQL para selecionar registros
sql_select = 'select * from cursos'
# -
# ### Selecionando registros no banco SQL utilizando o comando `select`
# +
# Criando outra sentença SQL para selecionar registros
sql_select = 'select * from cursos'
# +
# Seleciona todos os registros e recupera os registros
cur.execute(sql_select) # cur é o cursor, a conexão com o banco de dados
dados = cur.fetchall() # pega os registros e salva em dados
# +
# Mostra os registros selecionados
for linha in dados:
print('Curso Id: {}, Título : {}, Categoria: {} \n'.format(linha[0], linha[1], linha[2]))
# -
# ### Gerando novos resgistros, inserindo e gravando
# +
# Gerando outros registros
recset = [(1003, 'Gestão de Dados com MongoDB', 'Big Data'),
(1004, 'R Fundamentos', 'Análise de Dados')]
# Inserindo os novos registros
for rec in recset:
cur.execute(sql_insert, rec)
# Gravando os novos registros
con.commit()
# -
# ### Selecionando todos os registros
# +
# selecionando todos os registros
cur.execute('select * from cursos') # utilizando o comando SQL `select` diretamente no cursor
# Recupera os resultados
recset = cur.fetchall()
# Mostra os registros
for rec in recset:
print('Curos Id: {}, Título: {}, Categoria: {}\n'.format(rec[0], rec[1], rec[2]))
# +
# Fecha a conexão
con.close()
# -
# ## Fim
|
Cap06/Notebooks/.ipynb_checkpoints/Criando um banco de dados SQLite-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # 语言模型
#
# 语言模型(language model)是自然语言处理的重要技术。自然语言处理中最常见的数据是文本数据。我们可以把一段自然语言文本看作一段离散的时间序列。假设一段长度为$T$的文本中的词依次为$w_1, w_2, \ldots, w_T$,那么在离散的时间序列中,$w_t$($1 \leq t \leq T$)可看作在时间步(time step)$t$的输出或标签。给定一个长度为$T$的词的序列$w_1, w_2, \ldots, w_T$,语言模型将计算该序列的概率:
#
# $$P(w_1, w_2, \ldots, w_T).$$
#
#
# 语言模型可用于提升语音识别和机器翻译的性能。例如,在语音识别中,给定一段“厨房里食油用完了”的语音,有可能会输出“厨房里食油用完了”和“厨房里石油用完了”这两个读音完全一样的文本序列。如果语言模型判断出前者的概率大于后者的概率,我们就可以根据相同读音的语音输出“厨房里食油用完了”的文本序列。在机器翻译中,如果对英文“you go first”逐词翻译成中文的话,可能得到“你走先”“你先走”等排列方式的文本序列。如果语言模型判断出“你先走”的概率大于其他排列方式的文本序列的概率,我们就可以把“you go first”翻译成“你先走”。
#
#
# ## 语言模型的计算
#
#
# 既然语言模型很有用,那该如何计算它呢?假设序列$w_1, w_2, \ldots, w_T$中的每个词是依次生成的,我们有
#
# $$P(w_1, w_2, \ldots, w_T) = \prod_{t=1}^T P(w_t \mid w_1, \ldots, w_{t-1}).$$
#
# 例如,一段含有4个词的文本序列的概率
#
# $$P(w_1, w_2, w_3, w_4) = P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_1, w_2, w_3).$$
#
# 为了计算语言模型,我们需要计算词的概率,以及一个词在给定前几个词的情况下的条件概率,即语言模型参数。设训练数据集为一个大型文本语料库,如维基百科的所有条目。词的概率可以通过该词在训练数据集中的相对词频来计算。例如,$P(w_1)$可以计算为$w_1$在训练数据集中的词频(词出现的次数)与训练数据集的总词数之比。因此,根据条件概率定义,一个词在给定前几个词的情况下的条件概率也可以通过训练数据集中的相对词频计算。例如,$P(w_2 \mid w_1)$可以计算为$w_1, w_2$两词相邻的频率与$w_1$词频的比值,因为该比值即$P(w_1, w_2)$与$P(w_1)$之比;而$P(w_3 \mid w_1, w_2)$同理可以计算为$w_1$、$w_2$和$w_3$三词相邻的频率与$w_1$和$w_2$两词相邻的频率的比值。以此类推。
#
#
# ## $n$元语法
#
# 当序列长度增加时,计算和存储多个词共同出现的概率的复杂度会呈指数级增加。$n$元语法通过马尔可夫假设(虽然并不一定成立)简化了语言模型的计算。这里的马尔可夫假设是指一个词的出现只与前面$n$个词相关,即$n$阶马尔可夫链(Markov chain of order $n$)。如果$n=1$,那么有$P(w_3 \mid w_1, w_2) = P(w_3 \mid w_2)$。如果基于$n-1$阶马尔可夫链,我们可以将语言模型改写为
#
# $$P(w_1, w_2, \ldots, w_T) \approx \prod_{t=1}^T P(w_t \mid w_{t-(n-1)}, \ldots, w_{t-1}) .$$
#
#
# 以上也叫$n$元语法($n$-grams)。它是基于$n - 1$阶马尔可夫链的概率语言模型。当$n$分别为1、2和3时,我们将其分别称作一元语法(unigram)、二元语法(bigram)和三元语法(trigram)。例如,长度为4的序列$w_1, w_2, w_3, w_4$在一元语法、二元语法和三元语法中的概率分别为
#
# $$
# \begin{aligned}
# P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2) P(w_3) P(w_4) ,\\
# P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_2) P(w_4 \mid w_3) ,\\
# P(w_1, w_2, w_3, w_4) &= P(w_1) P(w_2 \mid w_1) P(w_3 \mid w_1, w_2) P(w_4 \mid w_2, w_3) .
# \end{aligned}
# $$
#
# 当$n$较小时,$n$元语法往往并不准确。例如,在一元语法中,由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而,当$n$较大时,$n$元语法需要计算并存储大量的词频和多词相邻频率。
#
# 那么,有没有方法在语言模型中更好地平衡以上这两点呢?我们将在本章探究这样的方法。
#
# ## 小结
#
# * 语言模型是自然语言处理的重要技术。
# * $N$元语法是基于$n-1$阶马尔可夫链的概率语言模型,其中$n$权衡了计算复杂度和模型准确性。
#
#
# ## 练习
#
# * 假设训练数据集中有10万个词,四元语法需要存储多少词频和多词相邻频率?
# * 你还能想到哪些语言模型的应用?
#
#
#
#
# ## 扫码直达[讨论区](https://discuss.gluon.ai/t/topic/6650)
#
# 
|
chapter_recurrent-neural-networks/lang-model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="cZCM65CBt1CJ"
# ##### Copyright 2019 The TensorFlow Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# + cellView="form" id="JOgMcEajtkmg"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="rCSP-dbMw88x"
# # Image segmentation
# + [markdown] id="NEWs8JXRuGex"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/tutorials/images/segmentation">
# <img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
# View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/images/segmentation.ipynb">
# <img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
# Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/images/segmentation.ipynb">
# <img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
# View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/images/segmentation.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="sMP7mglMuGT2"
# This tutorial focuses on the task of image segmentation, using a modified <a href="https://lmb.informatik.uni-freiburg.de/people/ronneber/u-net/" class="external">U-Net</a>.
#
# ## What is image segmentation?
# So far you have seen image classification, where the task of the network is to assign a label or class to an input image. However, suppose you want to know where an object is located in the image, the shape of that object, which pixel belongs to which object, etc. In this case you will want to segment the image, i.e., each pixel of the image is given a label. Thus, the task of image segmentation is to train a neural network to output a pixel-wise mask of the image. This helps in understanding the image at a much lower level, i.e., the pixel level. Image segmentation has many applications in medical imaging, self-driving cars and satellite imaging to name a few.
#
# The dataset that will be used for this tutorial is the [Oxford-IIIT Pet Dataset](https://www.robots.ox.ac.uk/~vgg/data/pets/), created by Parkhi *et al*. The dataset consists of images, their corresponding labels, and pixel-wise masks. The masks are basically labels for each pixel. Each pixel is given one of three categories :
#
# * Class 1 : Pixel belonging to the pet.
# * Class 2 : Pixel bordering the pet.
# * Class 3 : None of the above/ Surrounding pixel.
# + id="MQmKthrSBCld"
# !pip install git+https://github.com/tensorflow/examples.git
# + id="YQX7R4bhZy5h"
import tensorflow as tf
# + id="g87--n2AtyO_"
from tensorflow_examples.models.pix2pix import pix2pix
import tensorflow_datasets as tfds
from IPython.display import clear_output
import matplotlib.pyplot as plt
# + [markdown] id="oWe0_rQM4JbC"
# ## Download the Oxford-IIIT Pets dataset
#
# The dataset is already included in TensorFlow datasets, all that is needed to do is download it. The segmentation masks are included in version 3+.
# + id="40ITeStwDwZb"
dataset, info = tfds.load('oxford_iiit_pet:3.*.*', with_info=True)
# + [markdown] id="rJcVdj_U4vzf"
# The following code performs a simple augmentation of flipping an image. In addition, image is normalized to [0,1]. Finally, as mentioned above the pixels in the segmentation mask are labeled either {1, 2, 3}. For the sake of convenience, let's subtract 1 from the segmentation mask, resulting in labels that are : {0, 1, 2}.
# + id="FD60EbcAQqov"
def normalize(input_image, input_mask):
input_image = tf.cast(input_image, tf.float32) / 255.0
input_mask -= 1
return input_image, input_mask
# + id="2NPlCnBXQwb1"
@tf.function
def load_image_train(datapoint):
input_image = tf.image.resize(datapoint['image'], (128, 128))
input_mask = tf.image.resize(datapoint['segmentation_mask'], (128, 128))
if tf.random.uniform(()) > 0.5:
input_image = tf.image.flip_left_right(input_image)
input_mask = tf.image.flip_left_right(input_mask)
input_image, input_mask = normalize(input_image, input_mask)
return input_image, input_mask
# + id="Zf0S67hJRp3D"
def load_image_test(datapoint):
input_image = tf.image.resize(datapoint['image'], (128, 128))
input_mask = tf.image.resize(datapoint['segmentation_mask'], (128, 128))
input_image, input_mask = normalize(input_image, input_mask)
return input_image, input_mask
# + [markdown] id="65-qHTjX5VZh"
# The dataset already contains the required splits of test and train and so let's continue to use the same split.
# + id="yHwj2-8SaQli"
TRAIN_LENGTH = info.splits['train'].num_examples
BATCH_SIZE = 64
BUFFER_SIZE = 1000
STEPS_PER_EPOCH = TRAIN_LENGTH // BATCH_SIZE
# + id="39fYScNz9lmo"
train = dataset['train'].map(load_image_train, num_parallel_calls=tf.data.AUTOTUNE)
test = dataset['test'].map(load_image_test)
# + id="DeFwFDN6EVoI"
train_dataset = train.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
train_dataset = train_dataset.prefetch(buffer_size=tf.data.AUTOTUNE)
test_dataset = test.batch(BATCH_SIZE)
# + [markdown] id="Xa3gMAE_9qNa"
# Let's take a look at an image example and it's correponding mask from the dataset.
# + id="3N2RPAAW9q4W"
def display(display_list):
plt.figure(figsize=(15, 15))
title = ['Input Image', 'True Mask', 'Predicted Mask']
for i in range(len(display_list)):
plt.subplot(1, len(display_list), i+1)
plt.title(title[i])
plt.imshow(tf.keras.preprocessing.image.array_to_img(display_list[i]))
plt.axis('off')
plt.show()
# + id="a6u_Rblkteqb"
for image, mask in train.take(1):
sample_image, sample_mask = image, mask
display([sample_image, sample_mask])
# + [markdown] id="FAOe93FRMk3w"
# ## Define the model
# The model being used here is a modified U-Net. A U-Net consists of an encoder (downsampler) and decoder (upsampler). In-order to learn robust features, and reduce the number of trainable parameters, a pretrained model can be used as the encoder. Thus, the encoder for this task will be a pretrained MobileNetV2 model, whose intermediate outputs will be used, and the decoder will be the upsample block already implemented in TensorFlow Examples in the [Pix2pix tutorial](https://github.com/tensorflow/examples/blob/master/tensorflow_examples/models/pix2pix/pix2pix.py).
#
# The reason to output three channels is because there are three possible labels for each pixel. Think of this as multi-classification where each pixel is being classified into three classes.
# + id="c6iB4iMvMkX9"
OUTPUT_CHANNELS = 3
# + [markdown] id="W4mQle3lthit"
# As mentioned, the encoder will be a pretrained MobileNetV2 model which is prepared and ready to use in [tf.keras.applications](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/keras/applications). The encoder consists of specific outputs from intermediate layers in the model. Note that the encoder will not be trained during the training process.
# + id="liCeLH0ctjq7"
base_model = tf.keras.applications.MobileNetV2(input_shape=[128, 128, 3], include_top=False)
# Use the activations of these layers
layer_names = [
'block_1_expand_relu', # 64x64
'block_3_expand_relu', # 32x32
'block_6_expand_relu', # 16x16
'block_13_expand_relu', # 8x8
'block_16_project', # 4x4
]
layers = [base_model.get_layer(name).output for name in layer_names]
# Create the feature extraction model
down_stack = tf.keras.Model(inputs=base_model.input, outputs=layers)
down_stack.trainable = False
# + [markdown] id="KPw8Lzra5_T9"
# The decoder/upsampler is simply a series of upsample blocks implemented in TensorFlow examples.
# + id="p0ZbfywEbZpJ"
up_stack = [
pix2pix.upsample(512, 3), # 4x4 -> 8x8
pix2pix.upsample(256, 3), # 8x8 -> 16x16
pix2pix.upsample(128, 3), # 16x16 -> 32x32
pix2pix.upsample(64, 3), # 32x32 -> 64x64
]
# + id="45HByxpVtrPF"
def unet_model(output_channels):
inputs = tf.keras.layers.Input(shape=[128, 128, 3])
x = inputs
# Downsampling through the model
skips = down_stack(x)
x = skips[-1]
skips = reversed(skips[:-1])
# Upsampling and establishing the skip connections
for up, skip in zip(up_stack, skips):
x = up(x)
concat = tf.keras.layers.Concatenate()
x = concat([x, skip])
# This is the last layer of the model
last = tf.keras.layers.Conv2DTranspose(
output_channels, 3, strides=2,
padding='same') #64x64 -> 128x128
x = last(x)
return tf.keras.Model(inputs=inputs, outputs=x)
# + [markdown] id="j0DGH_4T0VYn"
# ## Train the model
# Now, all that is left to do is to compile and train the model. The loss being used here is `losses.SparseCategoricalCrossentropy(from_logits=True)`. The reason to use this loss function is because the network is trying to assign each pixel a label, just like multi-class prediction. In the true segmentation mask, each pixel has either a {0,1,2}. The network here is outputting three channels. Essentially, each channel is trying to learn to predict a class, and `losses.SparseCategoricalCrossentropy(from_logits=True)` is the recommended loss for
# such a scenario. Using the output of the network, the label assigned to the pixel is the channel with the highest value. This is what the create_mask function is doing.
# + id="6he36HK5uKAc"
model = unet_model(OUTPUT_CHANNELS)
model.compile(optimizer='adam',
loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=['accuracy'])
# + [markdown] id="xVMzbIZLcyEF"
# Have a quick look at the resulting model architecture:
# + id="sw82qF1Gcovr"
tf.keras.utils.plot_model(model, show_shapes=True)
# + [markdown] id="Tc3MiEO2twLS"
# Let's try out the model to see what it predicts before training.
# + id="UwvIKLZPtxV_"
def create_mask(pred_mask):
pred_mask = tf.argmax(pred_mask, axis=-1)
pred_mask = pred_mask[..., tf.newaxis]
return pred_mask[0]
# + id="YLNsrynNtx4d"
def show_predictions(dataset=None, num=1):
if dataset:
for image, mask in dataset.take(num):
pred_mask = model.predict(image)
display([image[0], mask[0], create_mask(pred_mask)])
else:
display([sample_image, sample_mask,
create_mask(model.predict(sample_image[tf.newaxis, ...]))])
# + id="X_1CC0T4dho3"
show_predictions()
# + [markdown] id="22AyVYWQdkgk"
# Let's observe how the model improves while it is training. To accomplish this task, a callback function is defined below.
# + id="wHrHsqijdmL6"
class DisplayCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs=None):
clear_output(wait=True)
show_predictions()
print ('\nSample Prediction after epoch {}\n'.format(epoch+1))
# + id="StKDH_B9t4SD"
EPOCHS = 20
VAL_SUBSPLITS = 5
VALIDATION_STEPS = info.splits['test'].num_examples//BATCH_SIZE//VAL_SUBSPLITS
model_history = model.fit(train_dataset, epochs=EPOCHS,
steps_per_epoch=STEPS_PER_EPOCH,
validation_steps=VALIDATION_STEPS,
validation_data=test_dataset,
callbacks=[DisplayCallback()])
# + id="P_mu0SAbt40Q"
loss = model_history.history['loss']
val_loss = model_history.history['val_loss']
epochs = range(EPOCHS)
plt.figure()
plt.plot(epochs, loss, 'r', label='Training loss')
plt.plot(epochs, val_loss, 'bo', label='Validation loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss Value')
plt.ylim([0, 1])
plt.legend()
plt.show()
# + [markdown] id="unP3cnxo_N72"
# ## Make predictions
# + [markdown] id="7BVXldSo-0mW"
# Let's make some predictions. In the interest of saving time, the number of epochs was kept small, but you may set this higher to achieve more accurate results.
# + id="ikrzoG24qwf5"
show_predictions(test_dataset, 3)
# + [markdown] id="R24tahEqmSCk"
# ## Next steps
# Now that you have an understanding of what image segmentation is and how it works, you can try this tutorial out with different intermediate layer outputs, or even different pretrained model. You may also challenge yourself by trying out the [Carvana](https://www.kaggle.com/c/carvana-image-masking-challenge/overview) image masking challenge hosted on Kaggle.
#
# You may also want to see the [Tensorflow Object Detection API](https://github.com/tensorflow/models/tree/master/research/object_detection) for another model you can retrain on your own data.
|
site/en/tutorials/images/segmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.3 64-bit (''base'': conda)'
# language: python
# name: python373jvsc74a57bd0210f9608a45c0278a93c9e0b10db32a427986ab48cfc0d20c139811eb78c4bbc
# ---
from torchvision.models import *
import wandb
from sklearn.model_selection import train_test_split
import os,cv2
import numpy as np
import matplotlib.pyplot as plt
from torch.nn import *
import torch,torchvision
from tqdm import tqdm
device = 'cuda'
PROJECT_NAME = 'Chest-X-ray-Images'
def load_data():
data = []
labels = {}
labels_r = {}
idx = -1
for folder in tqdm(os.listdir('./data/')):
idx += 1
for file in os.listdir(f'./data/{folder}/')[:1250]:
img = cv2.imread(f'./data/{folder}/{file}')
img = cv2.resize(img,(112,112))
img = img / 255.0
data.append([img,idx])
X = []
y = []
for d in data:
X.append(d[0])
y.append(d[1])
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.125,shuffle=False)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.25,shuffle=False)
X_train = torch.from_numpy(np.array(X_train)).to(device).view(-1,3,56,56).float()
y_train = torch.from_numpy(np.array(y_train)).to(device).float()
X_test = torch.from_numpy(np.array(X_test)).to(device).view(-1,3,56,56).float()
y_test = torch.from_numpy(np.array(y_test)).to(device).float()
return X,y,X_train,X_test,y_train,y_test,labels,labels_r,idx,data
X,y,X_train,X_test,y_train,y_test,labels,labels_r,idx,data = load_data()
torch.save(X_train,'X_train.pt')
torch.save(y_train,'y_train.pt')
torch.save(X_test,'X_test.pt')
torch.save(y_test,'y_test.pt')
torch.save(labels_r,'labels_r.pt')
torch.save(labels,'labels.pt')
torch.save(X_train,'X_train.pth')
torch.save(y_train,'y_train.pth')
torch.save(X_test,'X_test.pth')
torch.save(y_test,'y_test.pth')
torch.save(labels_r,'labels_r.pth')
torch.save(labels,'labels.pth')
len(X)
def get_loss(model,X,y,criterion):
preds = model(X)
loss = criterion(preds,y)
return loss.item()
def get_accuracy(model,X,y):
correct = 1
total = 1
preds = model(X)
for pred,yb in tqdm(zip(preds,y)):
pred = int(torch.round(pred))
yb = int(torch.round(yb))
if pred == yb:
correct += 1
total += 1
acc = round(correct/total,3)*100
return acc
model = shufflenet_v2_x0_5().to(device)
model.fc = Linear(512,1)
criterion = MSELoss()
optimizer = torch.optim.Adam(model.parameters(),lr=0.001)
batch_size = 32
epochs = 100
# +
# wandb.init(project=PROJECT_NAME,name='baseline')
# for _ in tqdm(range(epochs)):
# for i in tqdm(range(0,len(X_train),batch_size)):
# try:
# X_batch = X_train[i:i+batch_size].to(device)
# y_batch = y_train[i:i+batch_size].to(device)
# model.to(device)
# preds = model(X_batch)
# loss = criterion(preds,y_batch)
# optimizer.zero_grad()
# loss.backward()
# optimizer.step()
# except:
# pass
# model.eval()
# torch.cuda.empty_cache()
# wandb.log({'Loss':(get_loss(model,X_train,y_train,criterion)+get_loss(model,X_batch,y_batch,criterion))/2})
# torch.cuda.empty_cache()
# wandb.log({'Val Loss':get_loss(model,X_test,y_test,criterion)})
# torch.cuda.empty_cache()
# wandb.log({'Acc':(get_accuracy(model,X_train,y_train)+get_accuracy(model,X_batch,y_batch))/2})
# torch.cuda.empty_cache()
# wandb.log({'Val ACC':get_accuracy(model,X_test,y_test)})
# torch.cuda.empty_cache()
# model.train()
# wandb.finish()
# -
torch.save(model,'model-resnet18.pt')
torch.save(model,'model-resnet18.pth')
torch.save(model.state_dict(),'model-sd-resnet18.pt')
torch.save(model.state_dict(),'model-sd-resnet18.pth')
class Model(Module):
def __init__(self):
super().__init__()
self.max_pool2d = MaxPool2d((2,2),(2,2))
self.activation = ReLU()
self.conv1 = Conv2d(3,7,(5,5))
self.conv2 = Conv2d(7,14,(5,5))
self.conv2bn = BatchNorm2d(14)
self.conv3 = Conv2d(14,21,(5,5))
self.linear1 = Linear(21*3*3,256)
self.linear2 = Linear(256,512)
self.linear2bn = BatchNorm1d(512)
self.linear3 = Linear(512,256)
self.output = Linear(256,len(labels))
def forward(self,X):
preds = self.max_pool2d(self.activation(self.conv1(X)))
preds = self.max_pool2d(self.activation(self.conv2bn(self.conv2(preds))))
preds = self.max_pool2d(self.activation(self.conv3(preds)))
print(preds.shape)
preds = preds.view(-1,21*3*3)
preds = self.activation(self.linear1(preds))
preds = self.activation(self.linear2bn(self.linear2(preds)))
preds = self.activation(self.linear3(preds))
preds = self.output(preds)
return preds
model = Model().to(device)
criterion = MSELoss()
optimizer = torch.optim.Adam(model.parameters(),lr=0.001)
# +
# wandb.init(project=PROJECT_NAME,name='baseline')
# for _ in tqdm(range(epochs)):
# for i in range(0,len(X_train),batch_size):
# X_batch = X_train[i:i+batch_size]
# y_batch = y_train[i:i+batch_size]
# model.to(device)
# preds = model(X_batch)
# loss = criterion(preds.view(-1,1),y_batch.view(-1,1))
# optimizer.zero_grad()
# loss.backward()
# optimizer.step()
# model.eval()
# torch.cuda.empty_cache()
# wandb.log({'Loss':(get_loss(model,X_train,y_train,criterion)+get_loss(model,X_batch,y_batch,criterion))/2})
# torch.cuda.empty_cache()
# wandb.log({'Val Loss':get_loss(model,X_test,y_test,criterion)})
# torch.cuda.empty_cache()
# wandb.log({'Acc':(get_accuracy(model,X_train,y_train)+get_accuracy(model,X_batch,y_batch))/2})
# torch.cuda.empty_cache()
# wandb.log({'Val ACC':get_accuracy(model,X_test,y_test)})
# torch.cuda.empty_cache()
# model.train()
# wandb.finish()
# -
torch.save(model,'model-CNN.pt')
torch.save(model,'model-CNN.pth')
torch.save(model.state_dict(),'model-sd-CNN.pt')
torch.save(model.state_dict(),'model-sd-CNN.pth')
|
00.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 368} colab_type="code" executionInfo={"elapsed": 499, "status": "error", "timestamp": 1553714879572, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "09403825919811439227"}, "user_tz": 300} id="PHeY3vEBn0no" outputId="b3d734a6-0ca4-455f-a9e2-dc7a541e56c5"
# Imports
import skfuzzy as fuzz
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from skfuzzy import control as ctrl
# + colab={} colab_type="code" id="F0K7PDuRn0ns"
# %matplotlib notebook
# + colab={} colab_type="code" id="qnriAPfdn0nu"
# Define Variables Range
humidity = ctrl.Antecedent(np.linspace(0,100, num=100), 'humidity')
temperature = ctrl.Antecedent(np.linspace(14,30, num=100), 'temperature')
score = ctrl.Consequent(np.linspace(0,100, num=100), 'score')
# + colab={} colab_type="code" id="BSYAJZKYn0nw"
# Define Variables Terms
names = ['low','moderate','high']
humidity.automf(names=names)
temperature.automf(names=names)
score.automf(names=names)
# + colab={} colab_type="code" id="4jHmp3Jmn0nx"
#Define Varibles Fuzzy Sets
#Humidity
humidity['low'] = fuzz.trimf(humidity.universe, [-39.7, 0.265, 40])
humidity['moderate'] = fuzz.trimf(humidity.universe, [0, 50, 100])
humidity['high'] = fuzz.trimf(humidity.universe, [59.9206349206349, 99.7, 140])
#Temperature
temperature['low'] = fuzz.trimf(temperature.universe,[7.64, 14, 20.1])
temperature['moderate'] = fuzz.trimf(temperature.universe,[18, 22, 26])
temperature['high'] = fuzz.trimf(temperature.universe,[23.968253968254, 30, 36.4])
#Score
score['low'] = fuzz.trimf(score.universe,[-40, 0, 39.8148148148148])
score['moderate'] = fuzz.trimf(score.universe,[20, 50, 80.026455026455])
score['high'] = fuzz.trimf(score.universe,[60, 100, 140])
# + colab={} colab_type="code" id="IRphsuUmn0nz"
#Define Fuzzy Rules
rule1 = ctrl.Rule(humidity['low'] & temperature['low'], score['low'])
rule2 = ctrl.Rule(humidity['low'] & temperature['moderate'], score['low'])
rule3 = ctrl.Rule(humidity['low'] & temperature['high'], score['low'])
rule4 = ctrl.Rule(humidity['moderate'] & temperature['low'], score['high'])
rule5 = ctrl.Rule(humidity['moderate'] & temperature['moderate'], score['moderate'])
rule6 = ctrl.Rule(humidity['moderate'] & temperature['high'], score['moderate'])
rule7 = ctrl.Rule(humidity['high'] & temperature['low'], score['high'])
rule8 = ctrl.Rule(humidity['high'] & temperature['moderate'], score['high'])
rule9 = ctrl.Rule(humidity['high'] & temperature['high'], score['moderate'])
# + colab={} colab_type="code" id="3djLf7Ejn0n1"
#Create Control System
score_ctrl = ctrl.ControlSystem(rules=[rule1, rule2, rule3, rule4, rule5, rule6, rule7, rule8, rule9])
score_simulation = ctrl.ControlSystemSimulation(score_ctrl)
# + colab={} colab_type="code" id="WunjCztfn0n3"
def generate_surface(sim, size, plot=False):
# We can simulate at higher resolution with full accuracy
x, y = np.meshgrid(np.linspace(0, 100, size), np.linspace(14, 30, size))
z = np.zeros_like(x)
# Loop through the system to collect the control surface
for i in range(size):
for j in range(size):
sim.input['humidity'] = x[i, j]
sim.input['temperature'] = y[i, j]
sim.compute()
z[i, j] = sim.output['score']
if plot:
# Plot the result in pretty 3D with alpha blending
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='viridis',
linewidth=0.4, antialiased=True)
ax.view_init(30, 200)
return x, y, z
# + colab={} colab_type="code" id="6oLrngYUn0n6"
#x, y, z_sim = generate_surface(score_simulation, 15, plot=True)
# + colab={} colab_type="code" id="sazUR2DAn0n7"
# Load sensor data
temp_data = pd.read_csv('input/temperature.csv')
hum_data = pd.read_csv('input/humidity.csv')
# Create empty score variable
score_sim = pd.DataFrame(columns=hum_data.columns)
# +
sample = pd.read_csv('input/sample.csv')
hum_data['Monday'] = sample['z']
# + colab={} colab_type="code" id="45Rq0myGn0n9"
# Generate scores for each day
for col in hum_data.columns:
score_simulation.input['humidity'] = hum_data[col].values
score_simulation.input['temperature'] = temp_data[col].values
score_simulation.compute()
score_sim.loc[:,col] = score_simulation.output['score']
# -
df = pd.DataFrame(columns=["Humidity","Temperature","Score"])
for col in hum_data.columns:
temporal_df = pd.DataFrame([hum_data[col], temp_data[col], score_sim[col]]).T
temporal_df.columns = ["Humidity","Temperature","Score"]
df = df.append(temporal_df, ignore_index=True, sort=False)
df.to_csv('matlab_files/ANFIS/data_for_anfis.csv')
# + colab={} colab_type="code" id="zF003bbJn0n_"
# Save data for dashboard
temp_dash = pd.DataFrame(temp_data.values.reshape(4,16,7).mean(axis=1), index=['Cuadrante 3','Cuadrante 2','Cuadrante 4','Cuadrante 1'], columns=hum_data.columns)
temp_dash = temp_dash.sort_index()
temp_dash.to_csv('temp_cuadrantes_x_dia.csv')
# + colab={} colab_type="code" id="zF003bbJn0n_"
score_dash = pd.DataFrame(score_sim.values.reshape(4,16,7).mean(axis=1), index=['Cuadrante 3','Cuadrante 2','Cuadrante 4','Cuadrante 1'], columns=hum_data.columns)
# -
score_dash= score_dash.sort_index()
# + colab={} colab_type="code" id="zF003bbJn0n_"
score_dash.to_csv('score_cuadrantes_x_dia.csv')
# -
|
FIS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: DeepLearning Python
# language: python
# name: dl
# ---
# <font size="+5">#04. Why Neural Networks Deeply Learn a Mathematical Formula?</font>
# - Book + Private Lessons [Here ↗](https://sotastica.com/reservar)
# - Subscribe to my [Blog ↗](https://blog.pythonassembly.com/)
# - Let's keep in touch on [LinkedIn ↗](www.linkedin.com/in/jsulopz) 😄
# # Discipline to Search Solutions in Google
# > Apply the following steps when **looking for solutions in Google**:
# >
# > 1. **Necesity**: How to load an Excel in Python?
# > 2. **Search in Google**: by keywords
# > - `load excel python`
# > - ~~how to load excel in python~~
# > 3. **Solution**: What's the `function()` that loads an Excel in Python?
# > - A Function to Programming is what the Atom to Phisics.
# > - Every time you want to do something in programming
# > - **You will need a `function()`** to make it
# > - Theferore, you must **detect parenthesis `()`**
# > - Out of all the words that you see in a website
# > - Because they indicate the presence of a `function()`.
# + [markdown] tags=[]
# # Machine Learning, what does it mean?
# -
# > - The Machine Learns...
# >
# > But, **what does it learn?**
# %%HTML
<blockquote class="twitter-tweet" data-lang="en"><p lang="en" dir="ltr">Machine Learning, what does it mean? ⏯<br><br>· The machine learns...<br><br>Ha ha, not funny! 🤨 What does it learn?<br><br>· A mathematical equation. For example: <a href="https://t.co/sjtq9F2pq7">pic.twitter.com/sjtq9F2pq7</a></p>— <NAME> (@sotastica) <a href="https://twitter.com/sotastica/status/1449735653328031745?ref_src=twsrc%5Etfw">October 17, 2021</a></blockquote> <script async src="https://platform.twitter.com/widgets.js" charset="utf-8"></script>
# # How does the Machine Learn?
# ## In a Linear Regression
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/Ht3rYS-JilE" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# ## In a Neural Network
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/IHZwWFHWa-w?start=329" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# A Practical Example → [Tesla Autopilot](https://www.tesla.com/AI)
# An Example where It Fails → [Tesla Confuses Moon with Semaphore](https://twitter.com/Carnage4Life/status/1418920100086784000?s=20)
# # Load the Data
# > - Simply execute the following lines of code to load the data.
# > - This dataset contains **statistics about Car Accidents** (columns)
# > - In each one of **USA States** (rows)
# https://www.kaggle.com/fivethirtyeight/fivethirtyeight-bad-drivers-dataset/
# +
import seaborn as sns
df = sns.load_dataset(name='car_crashes', index_col='abbrev')
df.sample(5)
# -
# ## Fit a Neural Network Model in Python
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(12, input_dim=6, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
# ### Initialize the `weights` to start in 0
#
# > - `kernel_initializer='zeros'` on second `Dense` layer
model = Sequential()
model.add(Dense(12, input_dim=6, activation='relu', kernel_initializer='zeros'))
model.add(Dense(1, activation='sigmoid'))
# ### Make a Prediction
model.predict()
X = df.drop(columns='total')
y = df.total
AL = X[:1].copy()
df[:1]
AL
model.predict(x=AL)
# ### Predict for All USA States
y_pred = model.predict(x=X)
dfsel = df[['total']].copy()
dfsel['initial_pred'] = y_pred
dfsel.head()
# > - [ ] Why are these predictions so far away from reality?
# ### Fit the Mathematical Equation of the Model
# $$
# accidents = speeding \cdot w_1 + alcohol \cdot w_2 \ + ... + \ ins\_losses \cdot w_7
# $$
# > In other words: calculate the `best numbers` for the `weights`
model.fit(X, y, epochs=500)
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X, y, epochs=500)
# #### Predictions vs Reality **After `fit()`**
y_pred = model.predict(X)
dfsel['pred_after_fit'] = y_pred
dfsel.head()
# #### Observe the numbers for the `weights`
#
# > - Have they changed?
model.get_weights()
# #### Loss
# > - They are synonyms:
# > - Cost | Error | Loss
# > - https://keras.io/api/losses/
# #### `binary_crossentropy`
# #### `sparse_categorical_crossentropy`
# #### `mean_absolute_error`
# #### `mean_squared_error`
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/IHZwWFHWa-w?start=206" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# #### Change the `loss` accordingly to your Data
model = Sequential()
model.add(Dense(12, input_dim=6, activation='relu', kernel_initializer='zeros'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='mse', optimizer='adam', metrics=['mse'])
model.fit(X, y, epochs=500)
# > - [ ] Why is the model not improving as it iterates (**deep**ly **learn**s)?
# > - [ ] How can we solve this problem?
# ## Play with the Activation Function
# > - https://keras.io/api/layers/activations/
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/IHZwWFHWa-w?start=29" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/IHZwWFHWa-w?start=182" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# + [markdown] tags=[]
# ### Configure `linear` activation in last layer
# -
model = Sequential()
model.add(Dense(12, input_dim=6, activation='relu', kernel_initializer='zeros'))
model.add(Dense(1, activation='linear'))
# #### Observe the `weights` (numbers) on the Mathematical Equation
# $$
# accidents = speeding \cdot w_1 + alcohol \cdot w_2 \ + ... + \ ins\_losses \cdot w_7
# $$
model.get_weights()
# #### Predictions vs Reality
# > 1. Calculate the Predicted Accidents and
y_pred = model.predict(X)
# > 2. Compare it with the Real Total Accidents
dfsel = df[['total']].copy()
dfsel['pred_initial'] = y_pred
dfsel.head()
# ### `compile()` the Model
model.compile(loss='mse', optimizer='adam', metrics=['mse'])
# + [markdown] tags=[]
# #### `fit()` the Model
# -
model.fit(X, y, epochs=500, verbose=2)
# #### Predictions vs Reality **After fit()**
y_pred = model.predict(X)
dfsel['pred_after_fit'] = y_pred
dfsel.head()
# #### Observe the numbers for the `weights`
#
# > - Have they changed?
model.get_weights()
# ### Use `relu` activation in last layer
# ### Use `tanh` activation in last layer
# ### How are the predictions changing? Why?
# ## Initializing the `Weights`
# > - https://keras.io/api/layers/initializers/
# ### How to `kernel_initializer` the weights?
# $$
# accidents = speeding \cdot (w_1) + alcohol \cdot (w_2) \ + ... + \ ins\_losses \cdot (w_7) \\
# accidents = speeding \cdot (0) + alcohol \cdot (0) \ + ... + \ ins\_losses \cdot (0) \\
# accidents = speeding \cdot (1) + alcohol \cdot (1) \ + ... + \ ins\_losses \cdot (1) \\
# $$
# ### How to `kernel_initializer` the weights to 1?
# ### How to `kernel_initializer` the weights to `glorot_uniform` (default)?
# ## Optimizer
# > - https://keras.io/api/optimizers/#available-optimizers
# %%HTML
<iframe width="560" height="315" src="https://www.youtube.com/embed/IHZwWFHWa-w?start=324" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
# Optimizers comparison in GIF → https://mlfromscratch.com/optimizers-explained/#adam
# Tesla's Neural Network Models is composed of 48 models trainned in 70.000 hours of GPU → https://tesla.com/ai
# 1 Year with a 8 GPU Computer → https://twitter.com/thirdrowtesla/status/1252723358342377472
# ### Use Gradient Descent `SGD`
from keras.models import Sequential
from keras.layers import Input, Dense
model = Sequential()
model.add(layer=Input(shape=(6,)))
model.add(layer=Dense(units=3, kernel_initializer='glorot_uniform'))
model.add(layer=Dense(units=1, activation='linear'))
# + [markdown] tags=[]
# #### `compile()` the model
# -
model.compile(optimizer='sgd', loss='mse', metrics=['mse'])
# #### `fit()` the Model
history = model.fit(X, y, epochs=500, verbose=0, validation_split=0.3)
#
# #### View History
import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'val'], loc='upper left')
plt.show()
# ### Use `ADAM`
# ### Use `RMSPROP`
# ### Does it take different times to get the best accuracy? Why?
# ## In the end, what should be a feasible configuration of the Neural Network for this data?
# # Common Errors
# ## The `kernel_initializer` Matters
# ## The `activation` Function Matters
# ## The `optimizer` Matters
# ## The Number of `epochs` Matters
# ## The `loss` Function Matters
# ## The Number of `epochs` Matters
# # Neural Network's importance to find **Non-Linear Patterns** in the Data
#
# > - The number of Neurons & Hidden Layers
# https://towardsdatascience.com/beginners-ask-how-many-hidden-layers-neurons-to-use-in-artificial-neural-networks-51466afa0d3e
# https://playground.tensorflow.org/#activation=tanh&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=4,2&seed=0.87287&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false
# ## Summary
#
# - Mathematical Formula
# - Weights / Kernel Initializer
# - Loss Function
# - Activation Function
# - Optimizers
# ## What cannot you change arbitrarily of a Neural Network?
#
# - Input Neurons
# - Output Neurons
# - Loss Functions
# - Activation Functions
|
II Machine Learning & Deep Learning/01_Why Neural Networks Deeply Learn a Mathematical Formula/.ipynb_checkpoints/01session_why-neural-networks-deeply-learn-a-mathematical-formula-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 3. Data Pre-processing
# Data pre-processing techniques generally refer to the addition, deletion, or transformation of training set data. Different models have different sensitivities to the type of predictors in the model; *how* the predictors enter the model is also important.
#
# The need for data pre-processing is determined by the type of model being used. Some procedures, such as tree-based models, are notably insensitive to the characteristics of the predictor data. Others, like linear regression, are not. In this chapter, a wide array of possible methodologies are discussed.
#
# How the predictors are encoded, called *feature engineering*, can have a significant impact on model performance. Often the most effective encoding of the data is informed by the modeler's understanding of the problem and thus is not derived from any mathematical techniques.
# ## 3.1 Case Study: Cell Segmentation in High-Content Screening
# Check if data exists.
# !ls -l ../datasets/segmentationOriginal/
# This dataset is from Hill et al. (2007) that consists of 2019 cells. Of these cells, 1300 were judged to be poorly segmented (PS) and 719 were well segmented (WS); 1009 cells were reserved for the training set.
# +
import numpy as np
import pandas as pd
cell_segmentation = pd.read_csv("../datasets/segmentationOriginal/segmentationOriginal.csv")
# -
cell_segmentation.shape
# A first look at the dataset.
cell_segmentation.head(5)
# This chapter will use the training set samples to demonstrate data pre-processing techniques.
cell_segmentation.groupby('Case').count()
# +
# separate training and test data
cell_train = cell_segmentation.ix[cell_segmentation['Case'] == 'Train']
cell_test = cell_segmentation.ix[cell_segmentation['Case'] == 'Test']
cell_train.head(5)
# -
# ## 3.2 Data Transformation for Individual Predictors
# Transformations of predictor variables may be needed for several reasons. Some modeling techniques may have strict requirements, such as the predictors having a commom scale. In other cases, creating a good model may be difficult due to specific characteristics of the data (e.g., outliers).
# ### Centering and Scaling
# To center a predictor variable, the average predictor value is substracted from all the values. As a result of centering, the predictor has a zero mean. Similarly, to scale the data, each value of the predictor variable is divided by its standard deviation. Scaling the data coerce the values to have a common standard deviation of one. These manipulations are generally used to improve the numerical stability of some calculations, such as PLS. The only real downside to these transformation is a loss of interpretability of the individual values.
# ### Transformations to Resolve Skewness
# An un-skewed distribution is one that is roughly symmetric. A rule of thumb to consider is that skewed data whose ratio of the highest value to the lowest value is greater than 20 have significant skewness. The sample skewness statistic is defined $$\text{skewness} = {\sum (x_i - \bar{x})^3 \over (n - 1) v^{3/2}},$$ where $$v = {\sum (x_i - \bar{x})^2 \over (n - 1)}.$$ Note that the skewness for a normal distribution is zero.
# The cell segmentation data contain a predictor that measures the standard deviation of the intensity of the pixels in the actin filaments.
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# Some nice default configuration for plots
plt.rcParams['figure.figsize'] = 10, 7.5
plt.rcParams['axes.grid'] = True
plt.gray()
# +
fig, (ax1, ax2, ax3) = plt.subplots(1, 3)
ax1.hist(cell_train['VarIntenCh3'].values, bins=20)
ax1.set_xlabel('Natural Units')
ax1.set_ylabel('Count')
ax2.hist(np.log(cell_train['VarIntenCh3'].values), bins=20)
ax2.set_xlabel('Log Units')
ax3.hist(np.sqrt(cell_train['VarIntenCh3'].values), bins=20)
ax3.set_xlabel('Square Root Units')
# -
# The histogram shows a strong right skewness. The log transformation seems to work well for this dataset. The ratio of the smallest to largest value and the sample skewness statistic all agree with the histogram under natural units.
# +
from scipy.stats import skew
r = np.max(cell_train['VarIntenCh3'].values)/np.min(cell_train['VarIntenCh3'].values)
skewness = skew(cell_train['VarIntenCh3'].values)
print 'Ratio of the smallest to largest value is {0} \nSample skewness statistic is {1}'.format(r, skewness)
# -
# Alternatively, statistical models can be used to empirically identify an appropriate transformation. One of the most famous transformations is the Box-Cox family, i.e.
# \begin{equation}
# x^* = \begin{cases} {x^{\lambda}-1 \over \lambda} & \text{if} \ \lambda \neq 0 \\ log(x) & \text{if} \ \lambda = 0 \end{cases}
# \end{equation}
# This family covers the log ($\lambda = 0$), square ($\lambda = 2$), square root ($\lambda = 0.5$), inverse ($\lambda = -1$), and others in-between. Using the training data, $\lambda$ can be estimated using maximum likelihood estimation (MLE). This procedure would be applied independently to each predictor data that contain values **greater than 0**.
# The boxcox() in *scipy.stats* finds the estimated lambda and performs the transformation at the same time.
# +
from scipy.stats import boxcox
print 'Estimated lambda is {0}'.format(boxcox(cell_train['VarIntenCh3'].values)[1])
# -
# Take another predictor for example.
# +
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.hist(cell_train['PerimCh1'].values, bins=20)
ax1.set_xlabel('Natural Units')
ax1.set_ylabel('Count')
ax2.hist(boxcox(cell_train['PerimCh1'].values)[0], bins=20)
ax2.set_xlabel('Transformed Data (lambda = {:1.4f})'.format(boxcox(cell_train['PerimCh1'].values)[1]))
# -
# ## 3.3 Data Transformations for Multiple Predictors
# These transformations act on groups of predictors, typically the entire set under consideration. Of primary importance are methods to resolve outliers and reducce the dimension of the data.
# ### Transformations to Resolve Outliers
# We generally define outliers as samples that are exceptionally far from the mainstream of the data. Even with a thorough understanding of the data, outliers can be hard to define. However, we can often identify an unusual value by looking at a figure. When one or more samples are suspected to be outliers, the first step is to make sure that the values are scientifically valid and that no data recording errors have occured. Great care should be taken not to hastily remove or change values, especially if the sample size is small. With small sample sizes, apparent outliers might be a result of a skewed distribution where there are not yet enough data to see the skewness. Also, the outlying data may be an indication of a special part of the population under study that is just starting to be sampled. Depending on how the data were collected, a "cluster" of valid points that reside outside the mainstream of the data might belong to a different population than the other samples, e.g. *extrapolation* and *applicability domain*.
# There are several predictive models that are resistant to outliers, e.g.
# - Tree based classification models: creat splits of the training set.
# - Support Vector Machines (SVM) for classification: disregard a portion if tge training set that may be far away from the decision boundary.
# If a model is considered to be sensitive to outliers, one data transformation that can minimize the problem is the *spatial sign*. Mathematically, each sample is divided by its squared norm: $$x_{ij}^* = {x_{ij} \over \sqrt{\sum_{j=1}^p x_{ij}^2}}.$$ Since the denominator is intended to measure the squared distance to the center of the predictor's distribution, it is **important** to center and scale the predictor data prior to using this transformation. Note that, unlike centering and scaling, this manipulation of the predictors transform them as a group. Removing predictor variables after applying the spatial sign transformation may be problematic.
# +
# toy example
beta0 = -2.3 # intercept
beta1 = 0.8 # slope
n = 1000
x1_true = np.random.normal(4, 2, n)
x2_true = np.zeros(n)
# generate a random sample
for i in xrange(n):
x2_true[i] = beta0 + beta1*x1_true[i] + np.random.normal(size = 1)
# generate outliers
x1_outliers = np.random.uniform(-4, -3, 8)
x2_outliers = np.zeros(8)
for i in xrange(8):
x2_outliers[i] = x1_outliers[i] + np.random.normal(size = 1)
plt.scatter(x1_true, x2_true)
plt.plot(x1_outliers, x2_outliers, 'ro', markersize=8)
# +
from sklearn.preprocessing import scale
x1 = scale(np.concatenate([x1_true, x1_outliers]))
x2 = scale(np.concatenate([x2_true, x2_outliers]))
x = np.array(zip(x1, x2))
# spatial sign
dist = x[:, 0]**2 + x[:, 1]**2
x1 = x[:, 0]/np.sqrt(dist)
x2 = x[:, 1]/np.sqrt(dist)
plt.scatter(x1[:-8], x2[:-8])
plt.plot(x1[-7:], x2[-7:], 'ro', markersize=8)
# -
# The *spatial sign* transformation brings the outliers towards the majority of the data.
# ### Data Reduction and Feature Extraction
# These methods reduce the data by generating a smaller set of predictors that seek to capture a majority of the information in the original variables. For most data reduction techniques, the new predictors are functions of the original predictors; therefore, all the original predictors are still needed to create the surrogate variables. This class of methods is often called *signal extraction* or *feature extraction* techniques.
# Principal component analysis (PCA) seeks to find linear combinations of the predictors, known as principal components (PCs), which capture the most possible variance. The first PC is defined as the linear combination of the predictors that captures the most variability of all possible linear combinations. Then, subsequent PCs are derived such that these linear combinations capture the most remaining variability while also being uncorrelated with all previous PCs. Mathematically,
# $$\text{PC}_j = (a_{j1} \times \text{Predictor 1}) + \cdots + (a_{jP} \times \text{Predictor P}).$$
# P is the number of predictors. The coefficients $a_{j1}, \cdots, a_{jP}$ are called component weights and help us understand which predictors are most important to each PC.
# Let us look at an example from the previous dataset.
cell_train_subset = cell_train[['Class', 'FiberWidthCh1', 'EntropyIntenCh1']]
# +
colors = ['b', 'r']
markers = ['s', 'o']
c = ['PS', 'WS']
for k, m in enumerate(colors):
i = (cell_train_subset['Class'] == c[k])
if k == 0:
plt.scatter(cell_train_subset['FiberWidthCh1'][i], cell_train_subset['EntropyIntenCh1'][i],
c=m, marker=markers[k], alpha=0.4, s=26, label='PS')
else:
plt.scatter(cell_train_subset['FiberWidthCh1'][i], cell_train_subset['EntropyIntenCh1'][i],
c=m, marker=markers[k], alpha=0.4, s=26, label='WS')
plt.title('Original Data')
plt.xlabel('Channel 1 Fiber Width')
plt.ylabel('Entropy intensity of Channel 1')
plt.legend(loc='upper right')
plt.show()
# -
# Calculate PCs
# +
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(cell_train_subset[['FiberWidthCh1', 'EntropyIntenCh1']])
print 'variance explained by PCs {0}'.format(pca.explained_variance_ratio_)
# -
# The first PC summarizes 97% of the original variability, while the second summarizes 3%. Hence, it is reasonable to use only the first PC for modeling since it accounts for the majority of the information in the data.
# +
cell_train_subset_pca = pca.transform(cell_train_subset[['FiberWidthCh1', 'EntropyIntenCh1']])
colors = ['b', 'r']
markers = ['s', 'o']
c = ['PS', 'WS']
for k, m in enumerate(colors):
i = np.where(cell_train_subset['Class'] == c[k])[0]
if k == 0:
plt.scatter(cell_train_subset_pca[i, 0], cell_train_subset_pca[i, 1],
c=m, marker=markers[k], alpha=0.4, s=26, label='PS')
else:
plt.scatter(cell_train_subset_pca[i, 0], cell_train_subset_pca[i, 1],
c=m, marker=markers[k], alpha=0.4, s=26, label='WS')
plt.title('Transformed')
plt.xlabel('Principal Component #1')
plt.ylabel('Principal Component #2')
plt.legend(loc='upper right')
plt.show()
# -
# The primary advantage of PCA is that it creates components that are uncorrelated. PCA preprocessing creates new predictors with desirable characteristics for models that prefer predictors to be uncorrelated.
# While PCA delivers new predictors with desirable characteristics, it must be used with understanding and care. PCA seeks predictor-set variation without regard to any further understanding of the predictors (i.e. measurement scales or distributions) or to knowledge of the modeling objectives (i.e. response variable). Hence, without proper guidance, PCA can generate components that summarize characteristics of the data that are irrelevant to the underlying structure of the data and also to the ultimate modeling objectives.
# PCA was applied to the entire set of segmentation data predictors.
cell_train.head(5)
cell_train_feature = cell_train.iloc[:, 4:]
cell_train_feature.head(5)
# Because PCA seeks linear combinations of predictors that maximize variability, it will naturally first be drawn to summarizing predictors that have more variation. If the original predictors are on measurement scales that differ in orders of magnitude or have skewed distributions, PCA will be focusing its efforts on identifying the data structure based on measurement scales and distributional difference rather than based on the important relationships within the data for the current problem. Hence, it is best to first transform skewed predictors and then center and scale the predictors prior to performing PCA.
# +
# Box-Cox transformation on positive predictors
# separate positive and non-positive predictors
pos_indx = np.where(cell_train_feature.apply(lambda x: np.all(x > 0)))[0]
cell_train_feature_pos = cell_train_feature.iloc[:, pos_indx]
print "# of positive features is {0}".format(pos_indx.shape[0])
cell_train_feature_nonpos = cell_train_feature.drop(cell_train_feature.columns[pos_indx], axis=1, inplace=False)
print "# of npn-positive features is {0}".format(cell_train_feature.shape[1] - pos_indx.shape[0])
cell_train_feature_pos_tr = cell_train_feature_pos.apply(lambda x: boxcox(x)[0])
cell_train_feature_tr = np.c_[cell_train_feature_pos_tr, cell_train_feature_nonpos]
print "The shape before/after transformation is {0} and {1}".format(cell_train_feature.shape, cell_train_feature_tr.shape)
# +
# scale and center predictors
from sklearn.preprocessing import scale
cell_train_feature_tr = scale(cell_train_feature_tr, with_mean=True, with_std=True)
# -
# The second caveat of PCA is that it does not consider the modeling obejective or response variable when summarizing variability -- it is an *unsupervised technique*. If the predictive relationship between the predictors and response is not connected to the predictors' variability, then the derived PCs will not provide a suitable relationship with the response. In this case, a *supervised technique*, like PLS will derive components while simultaneously considering the corresponding response.
# To decide how many components to retain after PCA, a heuristic approach is to create a scree plot, which contains the ordered component number (x-axis) and the ammount of summarized variability (y-axis). Generally, the component number prior to the tapering off of variation is the maximal component that is retained. In an automated model building process, the optimal number of components can be determined by cross-validation.
# +
# conduct PCA to transformed predictors
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(cell_train_feature_tr)
# generate scree plot
plt.plot(pca.explained_variance_ratio_)
plt.xlabel('Percent of Total Variance')
plt.ylabel('Component')
# -
print "The first four components account for {0} of the total variance".format(pca.explained_variance_ratio_[:4])
print "All together they account for {0} of the total variance".format(np.sum(pca.explained_variance_ratio_[:4]))
# Visually examining the principal components is a critical step for assessing data quality and gaining intuition for the problem. To do this, the first few PCs can be plotted against each other and the plot symbols can be colored by the relevant characteristics, such as the class labels. If PCA has captured a sufficient amount of the information in the data, this type of plot can demonstrate clusters of samples or outliers that may prompt a closer examination of the individual data points. Note that the scale of the components tend to become smaller as they account for less and less variation in the data. If axes are displayed on separate scales, there is the potential to over-interpret any patterns that might be seen for components that account for small amounts of variation.
# look at the first 3 PCs
pca = PCA(n_components=3)
cell_train_feature_pca = pca.fit_transform(cell_train_feature_tr)
# +
colors = ['b', 'r']
markers = ['s', 'o']
c = ['PS', 'WS']
fig, axarr = plt.subplots(3, 3, sharex=True, sharey=True)
# PC1 vs PC3
for k, m in enumerate(colors):
i = np.where(cell_train['Class'] == c[k])[0]
if k == 0:
line1= axarr[0,0].scatter(cell_train_feature_pca[i, 0], cell_train_feature_pca[i, 2],
c=m, marker=markers[k], alpha=0.4, s=26, label='PS')
else:
line2= axarr[0,0].scatter(cell_train_feature_pca[i, 0], cell_train_feature_pca[i, 2],
c=m, marker=markers[k], alpha=0.4, s=26, label='WS')
# PC2 vs PC3
for k, m in enumerate(colors):
i = np.where(cell_train['Class'] == c[k])[0]
if k == 0:
axarr[0,1].scatter(cell_train_feature_pca[i, 1], cell_train_feature_pca[i, 2],
c=m, marker=markers[k], alpha=0.4, s=26, label='PS')
else:
axarr[0,1].scatter(cell_train_feature_pca[i, 1], cell_train_feature_pca[i, 2],
c=m, marker=markers[k], alpha=0.4, s=26, label='WS')
# PC1 vs PC2
for k, m in enumerate(colors):
i = np.where(cell_train['Class'] == c[k])[0]
if k == 0:
axarr[1,0].scatter(cell_train_feature_pca[i, 0], cell_train_feature_pca[i, 1],
c=m, marker=markers[k], alpha=0.4, s=26, label='PS')
else:
axarr[1,0].scatter(cell_train_feature_pca[i, 0], cell_train_feature_pca[i, 1],
c=m, marker=markers[k], alpha=0.4, s=26, label='WS')
axarr[2,0].text(0.5, -1.0, 'PC1', ha='center', va='center', fontsize=24)
axarr[1,1].text(0.5, -1.0, 'PC2', ha='center', va='center', fontsize=24)
axarr[0,2].text(0.5, -1.0, 'PC3', ha='center', va='center', fontsize=24)
fig.legend([line1, line2], ('PS', 'WS'), loc='upper center', ncol=2, frameon=False)
fig.subplots_adjust(hspace=0.12, wspace=0.1)
fig.text(0.5, 0.06, 'Scatter Plot Matrix', ha='center', va='center', fontsize=18)
# -
# Since the percentages of variation explained are not large for the first three components, it is important not to over-interpret the resulting image. From this plot, there appears to be some separation between the classes when plotting the first and second components. However, the distribution of the well-segmented cells is roughly contained within the distribution of the poorly identified cells. One conclusion is that the cell types are not easily separated.
# Another exploratory use of PCA is characterizing which predictors are associated with each component. Recall that each component is a linear combination of the predictors and the coefficient for each predictor is called the loading. Loadings close to zero indicate that the predictor variable did not contribute much to that component.
# loadings
pca.components_.shape
# ## 3.4 Dealing with Missing Values
# In many cases, some predictors have no values for a given sample. It is important to understand *why* the values are missing. First and foremost, it is important to know if the pattern of missing data is related to the outcome. This is called *informative missingness* since the missing data pattern is instructional on its own. Informative missingness can induce significant bias in the model.
# Missing data should not be confused with *censored* data where the exact value is missing but something is known about its value. When building traditional statistical models focused on interpretation or inference, the censoring is usually taken in to account in a formal manner by making assumptions about the censoring mechanism. For predictive models, it is more common to treat these data as simple missing data or use the censored value as the observed value.
# Missing values are more often related to predictive variables than the sample. Because of this, amount of missing data may be concentrated in a subset of predictors rather than occuring randomly across all the predictors. In some cases, the percentage of missing data is substantial enough to remove this predictor from subsequent modeling activities.
# There are cases where the missing values might be concentrated in specific samples. For large datasets, removal of samples based on missing values is not a problem, assuming that the missingness is not informative. In smaller datasets, there is a steep price in removing samples; some of alternative approaches described below may be more appropriate.
# If we do not remove the missing data, there are two general approaches. First, a few predictive models, especially tree-based techniques, can specifically account for missing data. Alternatively, missing data can be imputed. In this case, we can use information in the training set predictors to, in essence, estimate the values of other predictors.
# Imputation is just another layer of modeling where we try to estimate values of the predictor variables based on other predictor variables. The most relevant scheme for accomplishing this is to use the training set to built an imputation model for each predictor in the daa set. Prior to model training or the prediction of new samples, missing values are filled in using imputation. Note that this extra layer of models adds uncertainty. If we are using resampling to select tuning parameter values or to estimate performance, the imputation should be incorporated within the resampling. This will increase the computational time for building models, but it will also provide honest estimates of model performance.
# If the number of predictors affected by missing values is small, an exploratory analysis of the relationships between the preditors is a good idea. For example, visulization or methods like PCA can be used to determine if there are strong relationships between the predictors. If a variable with missing values is highly correlated with another predictor that has few missing values, a focused model can often be effective for imputation.
# One popular technique for imputation is a $K$-nearest neighbor model. A new sample is imputed by finding the samples in the training set "closest" to it and averages these nearby points to fill in the value. One advantage of this approach is that the imputed data are confined to be within the range of the training set values. One disadvantage is that the entire training set is required every time a missing value needs to be imputed. Also, the number of neighbors is a tuning parameter, as is the method for determining "closeness" of two points. However, Troyanskaya et al. (2001) found the nearest neighbor approach to be fairly robust to the tuning parameters, as well as the amount of missing data.
# +
# randomly sample 50 test set
import random
cell_test_subset = cell_test.iloc[np.sort(random.sample(range(cell_test.shape[0]), 50))]
# separate features
cell_test_subset_f = cell_test_subset.iloc[:, 4:].drop('VarIntenCh3', 1)
cell_test_subset_v = cell_test_subset.iloc[:, 4:]['VarIntenCh3']
cell_train_f = cell_train_feature.drop('VarIntenCh3', 1)
cell_train_v = cell_train_feature['VarIntenCh3']
# +
# scale and center before imputation
from sklearn.preprocessing import StandardScaler
# standardize based on training set
sc_f = StandardScaler()
cell_train_f_sc = sc_f.fit_transform(cell_train_f)
cell_test_subset_f_sc = sc_f.transform(cell_test_subset_f)
sc_v = StandardScaler()
cell_train_v_sc = sc_v.fit_transform(cell_train_v)
cell_test_subset_v_sc = sc_v.transform(cell_test_subset_v)
# +
# use 5-nearest neighbor
from sklearn.neighbors import NearestNeighbors
nbrs = NearestNeighbors(n_neighbors = 5)
nbrs.fit(cell_train_f_sc) # based on training set
distance, indices = nbrs.kneighbors(cell_test_subset_f_sc) # neighbors for test set
# imputation
cell_test_subset_v_pred_knn = np.empty(50)
for idx, i in enumerate(indices):
cell_test_subset_v_pred_knn[idx] = np.mean(cell_train_v_sc[i[1:]])
# -
# Find the predictor with highest correlation.
# +
from scipy.stats.stats import pearsonr
print "corr('VarIntenCh3', 'DiffIntenDensityCh3') is {0}".format(pearsonr(cell_train_v, cell_train_f['DiffIntenDensityCh3'])[0])
# +
# use linear model
from sklearn.linear_model import LinearRegression
lm = LinearRegression()
lm.fit(cell_train_f_sc[:, cell_train_f.columns.get_loc('DiffIntenDensityCh3')][:, np.newaxis],
cell_train_v_sc[:, np.newaxis]) # find the predictor with highest correlation
cell_test_subset_v_pred_lm = \
lm.predict(cell_test_subset_f_sc[:, cell_train_f.columns.get_loc('DiffIntenDensityCh3')][:, np.newaxis])
# -
# Correlation between the real and imputed values
print "kNN: {0}".format(pearsonr(cell_test_subset_v_sc, cell_test_subset_v_pred_knn)[0])
print "Linear Model: {0}".format(pearsonr(cell_test_subset_v_sc[:, np.newaxis], cell_test_subset_v_pred_lm)[0][0])
# Note that the better performance of linear model is because of the high correlation (0.895) between these two predictors. kNN is generally more robust since it takes all predictors into consideration.
# +
fig, (ax1, ax2) = plt.subplots(1, 2)
ax1.scatter(cell_test_subset_v_sc, cell_test_subset_v_pred_knn)
ax1.set(xlim=(-1.5, 3), ylim=(-1.5, 3))
ax1.plot(ax1.get_xlim(), ax1.get_ylim(), ls="--", c=".3")
ax1.set_title('5NN')
ax2.scatter(cell_test_subset_v_sc, cell_test_subset_v_pred_lm)
ax2.set(xlim=(-1.5, 3), ylim=(-1.5, 3))
ax2.plot(ax2.get_xlim(), ax2.get_ylim(), ls="--", c=".3")
ax2.set_title('Linear Model')
fig.text(0.5, 0.04, 'Original Value (centered and scaled)', ha='center', va='center')
fig.text(0.06, 0.5, 'Imputed', ha='center', va='center', rotation='vertical')
# -
# ## 3.5 Removing Predictors
# There are potential advantages to removing predictors prior to modeling. First, fewer predictors means decreased computational time and complexity. Second, if two predictors are highly correlated, this implies that they are measuring the same underlying information. Removing one should not compromise the performance of the model and might lead to a more parsimonious and interpretable model. Third, some models can be crippled by predictors with degenerate distributions, e.g. near-zero variance predictors. In these cases, there can be a significant improvement in model performance and/or stability without the problematic variables.
# A rule of thumb for detecting near-zero variance predictors:
# - The fraction of unique values over the sample size is low (say 10%)
# - The ratio of the frequency of the most prevalent value to the frequency of the second most prevalent value is large (say around 20)
#
# If both of these criteria are true and the model in question is susceptible to this type of predictor, it may be advantageous to remove the variable from the model.
# ### Between-Predictor Correlations
# *Collinearity* is the technical term for the situation where a pair of predictor variables have a substantial correlation with each other. It is also possible to have relationships between multiple predictors at once (called *multicollinearity*).
# A direct visualization of the correlation matrix from the training set.
# +
# calculate the correlation matrix
corr_dataframe = cell_train_feature.corr()
# compute hierarchical cluster on both rows and columns for correlation matrix and plot heatmap
def corr_heatmap(corr_dataframe):
import scipy.cluster.hierarchy as sch
corr_matrix = np.array(corr_dataframe)
col_names = corr_dataframe.columns
Y = sch.linkage(corr_matrix, 'single', 'correlation')
Z = sch.dendrogram(Y, color_threshold=0, no_plot=True)['leaves']
corr_matrix = corr_matrix[Z, :]
corr_matrix = corr_matrix[:, Z]
col_names = col_names[Z]
im = plt.imshow(corr_matrix, interpolation='nearest', aspect='auto', cmap='bwr')
plt.colorbar()
plt.xticks(range(corr_matrix.shape[0]), col_names, rotation='vertical', fontsize=4)
plt.yticks(range(corr_matrix.shape[0]), col_names[::-1], fontsize=4)
# plot
corr_heatmap(corr_dataframe)
# -
# Note that the predictor variables have been grouped using a clustering technique so that collinear groups of predictors are adjacent to one another.
# When the data set consists of too many predictors to examine visually, techniques such as PCA can be used to characterize the magnitude of the problem. For example, if the first principal component accounts for a large percentage of the variance, this implies that there is at least one group of predictors that represent the same information. The PCA loadings can be used to understand which predictors are associated with each component to tease out this relationship.
# In general, there are good reasons to avoid data with highly correlated predictors. First, redundant predictors frequently add more complexity to the model than information they provide to the model. In situations where obtaining the predictor data is costly, fewer variables is obviously better. Using highly correlated predictors in techniques like linear regression can result in highly unstable models, numerical values, and degraded predictive performances.
# Classical regression analysis has several tools to diagnose multicollinearity for linear regression. A statistic called the variance inflation factor (VIF) can be used to identify predictors that are impacted. A common rule of thumb is that if VIF > 5, then multicollinearity is high. Note that this method is developed for linear models, it requires more samples than predictor variables and it does not determine which should be removed to resolve the problem
# A more heuristic approach is to remove the minimum number of predictors to ensure that all pairwise correlation are below a certain threshold. The algorithm is as follows:
# - Calculate the correlation matrix of the predictors.
# - Determine the two predictors associated with the largest absolute pairwise correlation (A and B).
# - Determine the average absolute correlation between A and the other variables. Do the same for predictor B.
# - If A has a larger average correlation, remove it; otherwise, remove predictor B.
# - Repeat Steps 2-4 until no absolute correlations are above the threshold.
#
# Suppose we wanted to use a model that is particularly sensitive to between predictor correlations, we might apply a threshold of 0.75.
# As previously mentioned, feature extraction methods (e.g., principal components) are another technique for mitigating the effect of strong correlations between predictors. However, these techniques make the connection between the predictors and the outcome more complex. Additionally, since signal extraction methods are usually unsupervised, there is no guarantee that the resulting surrogate preditors have any relationship with the outcome.
# ## 3.6 Adding Predictors
# When a predictor is categorical, it is common to decompose the predictor into a set of more specific variables.
# Look at the following example for the credit scoring data.
# !ls -l ../datasets/GermanCredit/
credit_data = pd.read_csv("../datasets/GermanCredit/GermanCredit.csv")
credit_data.head(5)
credit_data.shape
# The predictor based on how much money was in the applicant's saving account is categorical coded into dummy variables.
credit_data_saving = credit_data[['SavingsAccountBonds.lt.100', 'SavingsAccountBonds.100.to.500',
'SavingsAccountBonds.500.to.1000', 'SavingsAccountBonds.gt.1000',
'SavingsAccountBonds.Unknown']]
credit_data_saving.head(10)
credit_data_saving.apply(np.sum)
# | Value | n | <100 | 100-500 | 500-1000 | >1000 | Unknown |
# |:---------|:----:|:----:|:-------:|:--------:|:-----:|:-------:|
# | < 100 | 603 | 1 | 0 | 0 | 0 | 0 |
# | 100-500 | 100 | 0 | 1 | 0 | 0 | 0 |
# | 500-1000 | 63 | 0 | 0 | 1 | 0 | 0 |
# | >1000 | 48 | 0 | 0 | 0 | 1 | 0 |
# | Unknown | 183 | 0 | 0 | 0 | 0 | 1 |
#
# Usually, each category gets its own dummy variable that is a zero/one indicator for that group. Only four dummy variables are needed here, the fifth can be inferred. However, the decision to include all of the dummy variables can depend on the choice of the model. Models that include an intercept term, such as simple linear model, would have numerical issues if each dummy variable was included in the model. The reason is that, for each sample, these variables all add up to one and this would provide the same information as the intercept. If the model is insensitive to this type of issue, using the complete set of dummy variables would help improve interpretation of the model.
# Many of the advanced models automatically generate highly complex, nonlinear relationships between the predictors and the outcome. More simplistic models do not unless the user manually specifices which predictors should be nonlinear and in what way. Another technique to augment the prediction data for classification model is through the "*class centroids*", which are the centers of the predictor data for each class. For each predictor, the distance to each class centroid can be calculated and these distances can be added to the model.
# ## 3.7 Binning Predictors (to avoid)
# There are many issues with the manual binning of continuous data. First, there can be a significant loss of performance in the model. Second, there is a loss of precision in the predictions when the predictors are categorized. Unfortunately, the predictive models that are most powerful are usually the least interpretable. The bottom line is that the perceived improvement in interpretability gained by manual categorization is usually offset by a significant loss in performance.
# Note that the argument here is related to the *manual* categorization of predictors prior to model building. There are several models, such as classification/regression trees and multivariate adaptive regression splines, that estimate cut points in the process of model building. The difference between these methodologies and manual binning is that the models ues all the predictors to derive bins based on a single objective (such as maximizing accuracy). They evaluate many variable simultaneously and are usually based on statistically sound methodologies.
|
notebooks/Chapter 3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="vXmCbC6j8Mew"
# # Run predictions with shifting data distributions
# ## Clone code and prepare data
# + id="5As7ePLH7E1J"
# !git clone https://github.com/dsikar/sdsandbox
# %cd sdsandbox/src/
# !tar xvf examples/logs_Wed_Nov_25_23_39_22_2020.tar.gz
# + id="0XyFugpaXQVY"
def GetJSONSteeringAngles(filemask):
"""
Get steering angles stored as 'user/angle' attributes in .json files
Inputs:
filemask: string, path and mask
Outputs
svals: list, steering values
"""
filemask = os.path.expanduser(filemask)
path, mask = os.path.split(filemask)
matches = []
for root, dirnames, filenames in os.walk(path):
for filename in fnmatch.filter(filenames, mask):
matches.append(os.path.join(root, filename))
# sort by create date
# matches = sorted(matches, key=os.path.getmtime)
# sort by filename prefix
matches = sort_sdsandbox_files(matches)
# steering values
svals = []
for fullpath in matches:
# print(fullpath)
frame_number = os.path.basename(fullpath).split("_")[0]
json_filename = os.path.join(os.path.dirname(fullpath), "record_" + frame_number + ".json")
jobj = load_json(json_filename)
svals.append(jobj['user/angle'])
return svals
def load_json(filepath):
"""
Load a json file
Inputs
filepath: string, path to file
Outputs
data: dictionary, json key, value pairs
Example
path = "~/git/msc-data/unity/roboRacingLeague/log/logs_Sat_Nov_14_12_36_16_2020/record_11640.json"
js = load_json(path)
"""
with open(filepath, "rt") as fp:
data = json.load(fp)
return data
def sort_sdsandbox_files(matches):
"""
Sort sdsandbox files in format e.g. 'logs_Wed_Nov_25_23_39_22_2020/1339_cam-image_array_.jpg'
This is to emulate a sort-by-date feature, once files have been copied and datetime stamp is lost
Parameters
-------
matches: list of strings, image filepaths
Output
-------
sorted_matches: list of strings, sorted list
Example
-------
matches = sort_sdsandbox_files(matches)
for match in matches:
print(match)
"""
filenums = {}
sorted_matches = []
for match in matches:
# match ~ 'logs_Wed_Nov_25_23_39_22_2020/1339_cam-image_array_.jpg'
# match.split('/')[-1].split('_')[0] ~ 1339
filenums[int(match.split('/')[-1].split('_')[0])] = match
filenums = sorted(filenums.items(), key=lambda filenums: filenums[0])
for key in filenums:
sorted_matches.append(key[1])
return sorted_matches
def GetPredictions(filemask, modelpath, datashift = 0, modelname = 'nvidia2'):
"""
Get predictions of a given model
Parameters
-------
filemask: string, path of the images to generate steering angle predictions
modelpath: string, path of the trained model
datashift: integer, RGB intensity mean shift to left (negative) or right (positive) or
input image RGB intensity mean
modelname: string, model name refering to input geometry to use
Output
-------
predictions: numpy array of floats, steering angle predictons
Example:
filemask = '../../../../Downloads/dataset/unity/genTrack/genTrackOneLap/logs_Wed_Nov_25_23_39_22_2020/*.jpg'
modelpath = '../../../../Downloads/trained_models/nvidia2/20201207192948_nvidia2.h5'
datashift = -10
filename = 'nvidia2'
p = GetPredictions(filemask, modelpath, datashift)
"""
import os
from tensorflow.python.keras.models import load_model
import cv2
import Augment_cls
import fnmatch
from PIL import Image
import numpy as np
import sys # for exception handling
ag = Augment_cls.Augment_cls(modelname)
model = load_model(modelpath)
model.compile("sgd", "mse")
filemask = os.path.expanduser(filemask)
path, mask = os.path.split(filemask)
matches = []
for root, dirnames, filenames in os.walk(path):
for filename in fnmatch.filter(filenames, mask):
matches.append(os.path.join(root, filename))
# sort by create date
matches = sorted(matches, key=os.path.getmtime)
# sort by filename prefix
matches = sort_sdsandbox_files(matches)
# steering values
svals = []
for fullpath in matches:
try:
image = Image.open(fullpath)
#PIL Image as a numpy array
image = np.array(image, dtype=np.float32)
# shift distribution
image, rgbmean, rgbstd, rgbvar = shiftRGBValues(image, datashift, datashift, datashift)
# keep data type for prediction model
image = np.array(image, dtype=np.float32)
image = ag.preprocess(image)
image = image.reshape((1,) + image.shape)
mod_pred = model.predict(image)
svals.append(mod_pred)
except:
print("Error ", sys.exc_info()[0], " occurred processing image ", fullpath, ", skipping")
pass
preds = []
# only return steering angles
for i in range(0, len(svals)):
preds.append(svals[i][0][0])
return preds
# change rgb values
# https://stackoverflow.com/questions/59320564/how-to-access-and-change-color-channels-using-pil
def shiftRGBValues(img, rv=0, gv=0, bv=0):
"""
Shift RGB values using PIL, and return mean and standard deviations
Parameters
-------
img: uint8 numpy image array
rv: integer, value to be added to red channel
gv: integer, value to be added to green channel
bv, integer, value to be added to blue channel
Output
-------
myimg: uint8 numpy image array
rgbmean: float, rgb mean
rgbstd: float, rgb standard deviation
rgbvar: float, rgb variance
Example
-------
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
img = mpimg.imread('steph.jpeg')
myimg, rgbmean, rgbstd, rgbvar = changeRGB(img, 60, 0, 0)
plt.imshow(myimg)
"""
from PIL import Image
import numpy as np
im = Image.fromarray(np.uint8(img))
# Split into 3 channels
r, g, b = im.split()
# Red
r = r.point(lambda i: i + rv)
# Green
g = g.point(lambda i: i + gv)
# Blue
b = b.point(lambda i: i + bv)
# Recombine back to RGB image
result = Image.merge('RGB', (r, g, b))
rgbmean = np.mean(result)
rgbstd = np.std(result)
rgbvar = np.var(result)
# Convert to uint8 numpy array
myimg = np.asarray(result)
return myimg, rgbmean, rgbstd, rgbvar
# TODO Rename gos steer_error, Steering Error, average error over a set of predictions in degrees
def gos(p, g, n):
"""
Calculate the goodness-of-steer between a prediction and a ground truth array.
Inputs
p: array of floats, steering angle prediction
g: array of floats, steering angle ground truth.
n: float, normalization constant
Output
gos: float, average of absolute difference between ground truth and prediction arrays
"""
# todo add type assertion
assert len(p) == len(g), "Arrays must be of equal length"
return sum(abs(p - g)) / len(p) * n
# print("Goodness of steer: {:.2f}".format(steer))
# + colab={"base_uri": "https://localhost:8080/"} id="q7xaEwC3qYbu" outputId="5c6ce064-42da-4e67-8f89-07b6fd71138c"
# runtime 1 minute, 1.4k predictions
filemask = 'logs_Wed_Nov_25_23_39_22_2020/*.jpg'
modelpath = 'examples/20201207192948_nvidia2.h5'
modelname = 'nvidia2'
datashift = 120
# p = GetPredictions(filemask, modelpath, datashift, modelname)
# pPlus80 = GetPredictions(filemask, modelpath, datashift, modelname)
pPlus120 = GetPredictions(filemask, modelpath, datashift, modelname)
# Error with path: logs_Wed_Nov_25_23_39_22_2020/0_cam-image_array_.jpg
# + [markdown] id="GniJcPYITZQG"
# # Generate data
# + colab={"base_uri": "https://localhost:8080/"} id="JBl6FjP-Dakp" outputId="dc2c7b0d-c009-4ab4-8bf3-11b068450828"
from datetime import datetime
now = datetime.now()
date_time = now.strftime("%m/%d/%Y, %H:%M:%S")
print("******************")
print("Start time:",date_time)
filemask = 'logs_Wed_Nov_25_23_39_22_2020/*.jpg'
modelpath = 'examples/20201207192948_nvidia2.h5'
modelname = 'nvidia2'
# datashift values to test
pMinus120 = 0
pMinus80 = 1
pMinus40 = 2
pMinus0 = 3
pPlus40 = 4
pPlus80 = 5
pPlus120 = 6
datashifts = [-120,-80,-40,0,40,80,120]
results = []
for val in datashifts:
print("Processing shift: {}".format(str(val)))
res = GetPredictions(filemask, modelpath, val, modelname)
results.append(res)
now = datetime.now()
date_time = now.strftime("%m/%d/%Y, %H:%M:%S")
print("******************")
print("End time:",date_time)
# + [markdown] id="KspvmeCddkUx"
# # Cleanup
# To avoid error when computing steering errors
# + colab={"base_uri": "https://localhost:8080/"} id="wkDQ-UJwdpUv" outputId="6d5e8249-7a80-4c13-dfda-831bc2a80643"
# !rm logs_Wed_Nov_25_23_39_22_2020/0_cam-image_array_.jpg
# + [markdown] id="COnjz90UUGaU"
# # Convert to Numpy arrays
# + id="_sW6EXNsUF48"
import numpy as np
for i in range (0, len(results)):
results[i] = np.array(results[i])
# + [markdown] id="XxAcTkgkpzOt"
# # Data shift steering error average
# + colab={"base_uri": "https://localhost:8080/"} id="eTgiLTmPp4eO" outputId="78a3491c-93c6-49c2-fc2d-5c4f0710b50c"
sterr = []
for i in range (0, len(results)):
steer_err = gos(results[i],g,nc)
sterr.append(steer_err)
strline = "Steering error average for data shift = {}: {}".format(str(datashifts[i]), str(steer_err))
print(strline)
# + [markdown] id="mtDs3g5yTV4t"
# # Plot graphs
# ## Negative 120, 80, 40 and 0
# + colab={"base_uri": "https://localhost:8080/", "height": 241} id="7R8Ow8IPXGC4" outputId="b583dd5f-a709-4760-87e4-253af1be7da7"
import os
import fnmatch
import json
import matplotlib.pyplot as plt
# plot ground truth steering angles for
# filemask = 'logs_Wed_Nov_25_23_39_22_2020/*.jpg'
nc = 25 # norm. constant, maximum steering angle in degrees
g = GetJSONSteeringAngles(filemask)
g = np.asarray(g)
plt.rcParams["figure.figsize"] = (18,3)
plt.plot(g*nc, label='Ground truth')
res = "{:.2f}".format(sterr[pMinus0])
plt.plot(results[pMinus0]*nc, label='RGB shift | st. err: 0 | ' + res)
res = "{:.2f}".format(sterr[pMinus40])
plt.plot(results[pMinus40]*nc, label='RGB shift | st. err: -40 | ' + res)
res = "{:.2f}".format(sterr[pMinus80])
plt.plot(results[pMinus80]*nc, label='RGB shift | st. err: -80 | ' + res)
res = "{:.2f}".format(sterr[pMinus120])
plt.plot(results[pMinus120]*nc, label='RGB shift | st. err: -120 | ' + res)
plt.ylabel('Steering angle')
plt.xlabel('Frame number')
# Set a title of the current axes.
modelstr = modelname + ' (' + modelpath + ')'
#pMinus120 = 0
#pMinus80 = 1
#pMinus40 = 2
#pMinus0 = 3
#pPlus40 = 4
#pPlus80 = 5
#pPlus120 = 6
#datashifts = [-120,-80,-40,0,40,80,120]
#results
mytitle = 'Ground truth and steering predictions for shifted data, from model ' + modelstr + ', ' + 'for logs_Wed_Nov_25_23_39_22_2020'
plt.title(mytitle)
plt.grid(axis='y')
# set limit
plt.xlim([-5,len(g)+5])
plt.gca().invert_yaxis()
plt.legend(loc='lower right')
plt.show()
# + [markdown] id="CYjEaYCAX8zT"
# ## Positive 40, 80, 120
# + colab={"base_uri": "https://localhost:8080/", "height": 241} id="0XaWeUgzXrZ5" outputId="f56a60c6-5af1-4765-c516-e1fb5b46e9ea"
plt.rcParams["figure.figsize"] = (18,3)
plt.plot(g*nc, label='Ground truth')
#plt.plot(results[pMinus0]*nc, label='RGB shift: 0')
res = "{:.2f}".format(sterr[pPlus40])
plt.plot(results[pPlus40]*nc, label='RGB shift | st. err: 40 | ' + res)
res = "{:.2f}".format(sterr[pPlus80])
plt.plot(results[pPlus80]*nc, label='RGB shift | st. err: 80 | ' + res)
res = "{:.2f}".format(sterr[pPlus120])
plt.plot(results[pPlus120]*nc, label='RGB shift | st. err: 120 | ' + res)
plt.ylabel('Steering angle')
plt.xlabel('Frame number')
# Set a title of the current axes.
modelstr = modelname + ' (' + modelpath + ')'
#pMinus120 = 0
#pMinus80 = 1
#pMinus40 = 2
#pMinus0 = 3
#pPlus40 = 4
#pPlus80 = 5
#pPlus120 = 6
#datashifts = [-120,-80,-40,0,40,80,120]
#results
mytitle = 'Ground truth and steering predictions for shifted data, from model ' + modelstr + ', ' + 'for logs_Wed_Nov_25_23_39_22_2020'
plt.title(mytitle)
plt.grid(axis='y')
# set limit
plt.xlim([-5,len(g)+5])
plt.gca().invert_yaxis()
plt.legend(loc='lower right')
plt.show()
# + [markdown] id="bTw_7z4gca4A"
# # Data shift steering error average
# + colab={"base_uri": "https://localhost:8080/"} id="HktYUA-OcLym" outputId="d23d14b0-349c-403e-e1e2-41ef6acede78"
sterr = []
for i in range (0, len(results)):
steer_err = gos(results[i],g,nc)
sterr.append(steer_err)
strline = "Steering error average for data shift = {}: {}".format(str(datashifts[i]), str(steer_err))
print(strline)
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="fuNdmP7w8hYL" outputId="d1b9251d-6a2c-4591-b56a-dbb99fa41073"
def listSteeringBins(svals, pname="output", save=True, nc=25, rmout=0):
"""
Plot a steering values' histogram
Inputs
svals: list, array of normalized steering values
pname: string, output plot name
save: boolean, save plot to disk
nc: int, normalization constant, used in the simulator to put angles in range
-1, 1. Default is 25.
rmout: integer, outlier range to remove
Outputs
none
"""
svalscp = [element * nc for element in svals]
values = len(svals)
# remove outliers
if(rmout>0):
#my_iterator = filter(lambda svalscp: svalscp <= rmout and svalscp >= (-1 * rmout), svalscp)
#svalsrmout = list(my_iterator)
#svalscp = svalsrmout
#values = len(svalsrmout)
#print("Removed {} records".format(len(svals) - len(svalsrmout)))
#svals = svalsrmout
svals = removeOutliers(svalscp, rmout, nc)
values = len(svals)
mean = ("%.2f" % statistics.mean(svalscp))
std = ("%.2f" % statistics.stdev(svalscp))
plt.title=(pname)
# NB Plotted as normalized histogram
sns.distplot(svalscp, bins=nc*2, kde=False, norm_hist=True,
axlabel= pname + ' steer. degs. norm. hist. ' + str(values) + ' values, mean = ' + mean + ' std = ' + std)
#if(save):
# sns.save("output.png")
if(save):
plt.savefig(pname + '.png')
plt.show()
listSteeringBins(preds)
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="ldVjfNZK_rDV" outputId="d01c0914-3ffe-48f9-d098-445e8ad1998f"
listSteeringBins(preds)
# + [markdown] id="LNYppkSJCNud"
# # Positive steering angle example, labelled dataset
# + colab={"base_uri": "https://localhost:8080/"} id="pfBO4PG-CMME" outputId="b4ba6f48-2a40-4e67-ab3b-32ea47049c78"
# 1105_cam-image_array_.jpg
# #!ls logs_Wed_Nov_25_23_39_22_2020/1105_cam-image_array_.jpg
# # !ls logs_Wed_Nov_25_23_39_22_2020/*1105*
# !cat logs_Wed_Nov_25_23_39_22_2020/record_1105.json
# {"cam/image_array":"1105_cam-image_array_.jpg","user/throttle":0.0,"user/angle":0.31525176763534548,"user/mode":"user","track/lap":0,"track/loc":21}
# 0.31525176763534548 * 25 = 7.88129419088 ~ 7.9 degrees
# + colab={"base_uri": "https://localhost:8080/", "height": 430} id="K80nALow0DbX" outputId="342f9b18-c575-42ae-ca48-2772a404bcce"
from utils.utils import plot_img_hist # need utils.py
from PIL import Image
import matplotlib.image as mpimg
import cv2
from google.colab.patches import cv2_imshow
imgpath = 'logs_Wed_Nov_25_23_39_22_2020/1105_cam-image_array_.jpg'
image = Image.open(imgpath)
plt.imshow(image)
myfig = plot_img_hist(image)
myplot = mpimg.imread('temp_plot.jpg')
# correct channels
b,g,r = cv2.split(myplot)
myplot = cv2.merge([r,g,b])
cv2_imshow(myplot)
# + [markdown] id="XP1nT8cE3Z7S"
# # Shift and plot
# + colab={"base_uri": "https://localhost:8080/", "height": 232} id="ebtJLQ9h3b-Q" outputId="3fa8ec07-abda-4750-e4df-94d7b8ea5779"
# image = Image.open(imgpath)
datashift = 120
imageshifted, rgbmean, rgbstd, rgbvar = shiftRGBValues(image, datashift, datashift, datashift)
plt.imshow(imageshifted)
|
src/notebooks/RGBShiftPredict.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from datetime import date
from gs_quant.common import PayReceive, Currency
from gs_quant.instrument import IRSwap
from gs_quant.session import Environment, GsSession
# external users should substitute their client id and secret; please skip this step if using internal jupyterhub
GsSession.use(Environment.PROD, client_id=None, client_secret=None, scopes=('run_analytics',))
swap = IRSwap(PayReceive.Receive, date(2025, 1, 15), Currency.EUR)
print(swap.price())
|
gs_quant/examples/01_pricing_and_risk/00_rates/010002_calc_swap_price.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# import necessary libraries - Monir
import pandas as pd
import os
import glob
import numpy as np
# +
# assign dataset names - Monir
PUBLIC_DISPATCHSCADA_list_of_files = []
#read all dataset names with starting PUBLIC_DISPATCHSCADA - Monir
PUBLIC_DISPATCHSCADA_list_of_files = glob.glob('PUBLIC_DISPATCHSCADA*.csv')
# +
# create empty list
dataframes_list = []
list_of_names = PUBLIC_DISPATCHSCADA_list_of_files
# -
# append datasets into teh list
for i in range(len(list_of_names)):
temp_df = pd.read_csv(list_of_names[i], skiprows = 1, skipfooter = 1)
#dataframes_list[i]=temp_df
dataframes_list.append(temp_df)
dataframes_list[0].head()
dataframes_list[0].tail()
dataframes_list[0].shape
len(dataframes_list)
dataframes_list[8890].tail()
# multiple DataFrames are be merged (Concatenate pandas objects) - Monir
PUBLIC_DISPATCHSCADA_df = pd.concat(dataframes_list)
PUBLIC_DISPATCHSCADA_df.shape
# set a specific column of DataFrame as index - Monir
PUBLIC_DISPATCHSCADA_df.set_index('DUID')
PUBLIC_DISPATCHSCADA_df.dtypes
PUBLIC_DISPATCHSCADA_df.info()
# Export Pandas DataFrame to CSV - Monir
PUBLIC_DISPATCHSCADA_df.to_csv('PUBLIC_DISPATCHSCADA_df.csv', index=False)
|
code-for-fetching-data/PUBLIC_DISPATCHSCADA_DATA-monir.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/cltl/python-for-text-analysis/blob/colab/Assignments-colab/ASSIGNMENT_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="t-VUo0H7MlkI"
# %%capture
# !wget https://github.com/cltl/python-for-text-analysis/raw/master/zips/Data.zip
# !wget https://github.com/cltl/python-for-text-analysis/raw/master/zips/images.zip
# !wget https://github.com/cltl/python-for-text-analysis/raw/master/zips/Extra_Material.zip
# !unzip Data.zip -d ../
# !unzip images.zip -d ./
# !unzip Extra_Material.zip -d ../
# !rm Data.zip
# !rm Extra_Material.zip
# !rm images.zip
# + [markdown] id="8JfKD8CZMlCh"
# # Assignment 1: Calculation, Strings, Boolean Expressions and Conditions
#
# **Deadline: Friday, September 9, 2021 before 3pm (submit via Canvas: Block I/Assignment 1)**
#
#
# This assignment is **not graded**, but it is mandatory to submit a version that shows you have given it a serious try. We will check your assignments to monitor the progress and get an impression of how the course is going so far. You will receive feedback and solutions on Monday September 13. **Please note that the material taught in this block is essential for all subsequent blocks.**
#
# - Please name your notebook with the following naming convention: ASSIGNMENT_1_FIRSTNAME_LASTNAME.ipynb
# - If you have **questions** about this topic, please contact **<EMAIL>**.
#
#
# In this block, we covered the following chapters:
#
# - Chapter 1 - Getting Started with Variables and Values
# - Chapter 2 - Basic Data Types (Integers and Floats)
# - Chapter 3 - Strings
# - Chapter 4 - Boolean Expressions and Conditions
#
# In this assignment, you will be asked to show what you have learned from the topics above!
#
# **Looking things up**
#
# Don't worry - you do not have to know things by heart yet - feel free to have all Chapters of block 1 open while you work on this. This also goes for all future assignments.
#
# **Finding solutions online**
#
# Very often, you can find good solutions online. We encourage you to use online resources when you get stuck. However, please always try to understand the code you find and indicate that it is not your own. Use the following format to mark code written by someone else:
#
# ###Taken from [link] [date]
#
# [code]
#
# \###
#
# Please use a similar format to indicate that you have worked with a classmate (e.g. mention the name instead of the link).
#
# *Indicating online resources and collaboration is mandatory! Please stick to this strategy for all course assignments.*
#
# **Being stuck and getting help**
#
# It is very normal to get stuck every now and then. Sometimes you find what is wrong within minutes, sometimes this takes longer. If you get stuck, please apply the strategies described in the readme. If none of them work, please contact us (<EMAIL>).
# + [markdown] id="WkONFxvnMlCl"
# ## Exercise 1: Calculation
#
# + [markdown] id="l4kqGzI_MlCl"
# #### 1a. Average
# Define three variables `var1`, `var2` and `var3`. Calculate the average of these variables and assign it to the variable `average`. Print the outcome of your program as follows (use casting or an f-string):
#
# `The average of [...], [...] and [...] is: [...]`
# + id="EQbNol6eMlCm"
# average code
# + [markdown] id="JhqS1z6sMlCn"
# #### 1b. Book prices
#
#
# Calculate book prices for the following scenarios:
#
# Suppose the price of a book is 24.95 EUR, but if the book is bought by a bookstore, they get a 30 percent discount (as opposed to customers buying from an online stores). Shipping costs 3 EUR for the first copy and 75 cents for each additional copy. Shipping costs always apply (the books also have to be shipped to the bookstore).
#
# Write a program that can calculate the total costs for any number of copies for both bookstores and other customers. Use variables with clear names for your calculations and print the result using a full sentence.
#
# The program should use variables which indicate whether the customer is a bookstore or not and how many books are bought. You can simply assign values to the variables in you code or use the input function (both is accepted).
#
#
# **Tip**
#
# Start small and add things in steps. For instance, start by calculating the price minus the discount. Then add the additional steps. Also, it helps to a start by simply assuming a specific number of books (start with 1 and make sure it works with any other number). Do not forget to test your program!
# + colab={"base_uri": "https://localhost:8080/", "height": 130} id="y6hiv-dDMlCo" outputId="9da36c64-516f-431c-d201-d0b0400a9a50"
# complete the code below
n_books =
customer_is_bookstore =
# you bookprice calculations here
# + [markdown] id="twOCOyWBMlCo"
# #### 1c. The modulus operator
#
# There is one operator (like the ones for multiplication and subtraction) that we did not discuss yet, namely the modulus operator %. Could you figure out by yourself what it does when you place it between two numbers (e.g. 113 % 9)? (PS: Try to figure it out by yourself first, by trying multiple combinations of numbers. If you do not manage, it's OK to use online resources...)
#
# You don't need this operator all that often, but when you do, it comes in really handy! Also, it is important to learn how to figure out what operators/methods/functions you have never seen before do by playing with code, googling or reading documentation.
#
# + id="Xg-Z58VDMlCp"
# try out the modulus operator!
# + [markdown] id="fL5Scyj4MlCp"
# **Help the cashier**
#
# Can you use the modulus operator you just learned about to solve the following task? Imagine you want to help cashiers to return the change in a convenient way. This means you do not want to return hands full of small coins, but rather use bills and as few coins as possible.
#
# Write code that classifies a given amount of money into smaller monetary units. Given a specific amout of dollars, your program should report the maximum number of dollar bills, quarters, dimes, nickels, and pennies.
#
# Set the amount variable to 11.67. You code should output a report listing the monetary equivalent in dollars, quarters, dimes, nickels, and pennies (one quarter is equivalent to 25 cents; one dime to 10 cents; one nickle to 5 cents and a pennie to 1 cent). Your program should report the maximum number of dollars, then the number of quarters, dimes, nickels, and pennies, in this order, to result in the minimum number of coins. Here are the steps in developing the program:
#
# 1. Convert the amount (11.67) into cents (1167).
# 2. First get the amount of cents that you would get after subtracting the maximum amount of dollars (100 cents) using the modulus operator (67 cents).
# 3. Then subtract the remainder (67 cents) from the total amount of cents (1167 cents) and divide this by 100 to find the number of dollars.
# 4. Use the modulus operator again to find out the remainder after subtracting the maximum amount of quarters (17 cents).
# 5. Subtract this remainder (17 cents) from the previous remainder (67 cents) and divide this by 25 to find out the number of quarters.
# 6. Follow the same steps for the dimes, nickels and pennies.
# 7. Display the result for your cashier! (the amount of dollars, quarters, dimes, nickels and pennies that (s)he would have to give back)`
# + id="Z4VsgSmIMlCq"
# cashier code
# + [markdown] id="rd4qszFfMlCq"
# ## Exercise 2: Printing and user input
#
# + [markdown] id="1_Jtib9tMlCr"
# #### 2a. Difference between "," and "+"
#
# What is the difference between using **+** and **,** in a print statement? Illustrate by using both in each of the following:
#
# * calling the `print()` fuction with multiple strings
# * printing combinations of strings and integers
# * concatenating multiple strings and assign to one single variable
# * concatenating strings and integers and assign to one single variable
# + id="LBKtLk2tMlCr"
# + id="0rx547-jMlCr"
# + id="IivJxD-PMlCr"
# + id="OZfHpqEaMlCs"
# + [markdown] id="eLdRMOkiMlCs"
# #### 2b. Small Talk
# Write a program to have a little conversation with someone. First ask them for their name and their age, and then say something about your own age compared to theirs. Your code should result in a conversation following this example:
#
# > `Hello there! What is your name?`
#
# > -- Emily.
#
# > `Nice to meet you, Emily. How old are you?`
#
# > -- 23
#
# > `I'm 25 years old, so I'm 2 years older than you.`
#
# Also account for situations where the other person is older or the same age. You will need to use `if-else`-statements!
# + colab={"base_uri": "https://localhost:8080/"} id="4c28G3M-MlCs" outputId="85698836-539b-41af-ca71-4e8ce243282e"
name = input("Hello there! What is your name? ")
# finish this code
# + [markdown] id="dbR7zxIWMlCs"
# ## Exercise 3: String Art
# + [markdown] id="I7LyvUtvMlCs"
# #### 3a. Drawing figures
# We start with some repetition of the theory about strings:
# + [markdown] id="LvfW3H01MlCt"
# | Topic | Explanation |
# |-----------|--------|
# | `quotes` | A string is delimited by single quotes ('...') or double quotes ("...") |
# | `special characters` | Certain special characters can be used, such as "\n" (for newline) and "\t" (for a tab) |
# | `printing special characters` | To print the special characters, they must be preceded by a backslash (\\) |
# | `continue on next line` | A backslash (\\) at the end of a line is used to continue a string on the next line |
# | `multi-line strings` | A multi-line print statement should be enclosed by three double or three single quotes ("""...""" of '''...''') |
# + [markdown] id="ZsVZkETDMlCt"
# Please run the code snippet below and observe what happens:
# + colab={"base_uri": "https://localhost:8080/"} id="pWbC_UCHMlCt" outputId="ce48c77a-be83-43bd-d43d-abbea63aded2"
print('hello\n')
print('To print a newline use \\n')
print('She said: \'hello\'')
print('\tThis is indented')
print('This is a very, very, very, very, very, very \
long print statement')
print('''
This is a multi-line print statement
First line
Second line
''')
# + [markdown] id="F3eCBwV-MlCt"
# Now write a Python script that prints the following figure using **only one line of code**! (so don't use triple quotes)
#
# | | |
# @ @
# u
# |"""|
#
# + id="yUceT5baMlCt"
# your code here
# + [markdown] id="OZNArc1rMlCu"
# #### 3b. Colors
# We start again with some repetition of the theory:
# + [markdown] id="lWcmR1AVMlCu"
# | Topic | Explanation |
# |-----------|--------|
# | a = b + c | if b and c are strings: concatenate b and c to form a new string a|
# | a = b * c | if b is an integer and c is a string: c is repeated b times to form a new string a |
# | a[0] | the first character of string a |
# | len(a) | the number of characters in string a |
# | min(a) | the smallest element in string a (alphabetically first) |
# | max(a) | the largest element in string a (alphabetically last) |
# + [markdown] id="jPKx3HlcMlCu"
# Please run the code snippet below and observe what happens:
# + colab={"base_uri": "https://localhost:8080/"} id="Ew8GiEhGMlCu" outputId="289cf80f-7a10-418f-d3bd-e713c9270b0d"
b = 'the'
c = 'cat'
d = ' is on the mat'
a = b + ' ' + c + d
print(a)
a = b * 5
print(a)
print('The first character of', c, 'is' , c[0])
print('The word c has,', len(c) ,'characters')
# + [markdown] id="0G5vPKNsMlCu"
# Now write a program that asks users for their favorite color. Create the following output (assuming "red" is the chosen color). Use "+" and "\*".
# It should work with any color name though.
#
# ```xml
# red red red red red red red red red red
# red red
# red red
# red red red red red red red red red red
# ```
# + colab={"base_uri": "https://localhost:8080/"} id="KXrVdCjQMlCu" outputId="3465ffdf-5cc2-43d2-96bc-de1cdb8ed113"
color = input('what is your favorite color? ')
print(color)
print(color)
print(color)
print(color)
# + [markdown] id="36wDrvkMMlCv"
# ## Exercise 4: String methods
#
# Remember that you can see all methods of the class `str` by using `dir()`. You can ignore all methods that start with one or two underscores.
# + colab={"base_uri": "https://localhost:8080/"} id="U8973UUnMlCv" outputId="16796e37-bfa9-4a90-cf65-3680438127ee"
dir(str)
# + [markdown] id="AtZJaDDzMlCv"
# To see the explanation for a method of this class, you can use `help(str.method)`. For example:
# + colab={"base_uri": "https://localhost:8080/"} id="4JBUqnfDMlCv" outputId="61d9244b-bc54-48c9-88c2-aea1d5f52d87"
help(str.upper)
# + [markdown] id="zSGgIM_qMlCv"
# #### 4a. Counting vowels
# Count how many of each vowel (a,e,i,o,u) there are in the text string in the next cell. Print the count for each vowel with a single formatted string. Remember that vowels can be both lower and uppercase.
# + id="tzl6uSWyMlCv"
text = """But I must explain to you how all this mistaken idea of denouncing pleasure and praising pain was born
and I will give you a complete account of the system, and expound the actual teachings of the great explorer of the
truth, the master-builder of human happiness. No one rejects, dislikes, or avoids pleasure itself, because it is
pleasure, but because those who do not know how to pursue pleasure rationally encounter consequences that are
extremely painful. Nor again is there anyone who loves or pursues or desires to obtain pain of itself, because it is
pain, but because occasionally circumstances occur in which toil and pain can procure him some great pleasure.
To take a trivial example, which of us ever undertakes laborious physical exercise, except to obtain some advantage
from it? But who has any right to find fault with a man who chooses to enjoy a pleasure that has no annoying
consequences, or one who avoids a pain that produces no resultant pleasure? On the other hand, we denounce with
righteous indignation and dislike men who are so beguiled and demoralized by the charms of pleasure of the moment,
so blinded by desire, that they cannot foresee the pain and trouble that are bound to ensue; and equal blame belongs
to those who fail in their duty through weakness of will, which is the same as saying through shrinking from toil
and pain."""
# your code here
# + [markdown] id="XcnH44h-MlCv"
# #### 4b. Printing the lexicon
# Have a good look at the internal representation of the string below. Use a combination of string methods (you will need at least 3 different ones and some will have to be used multiple times) in the correct order to remove punctuation and redundant whitespaces, and print each word in lowercase characters on a new line. The result should look like:
#
# `the
# quick
# brown
# fox
# jumps
# etc.`
# + colab={"base_uri": "https://localhost:8080/"} id="o_gzK0kiMlCw" outputId="cf9a6465-20d6-44e9-a0b2-931ff534f45e"
text = """ The quick, brown fox jumps over a lazy dog.\tDJs flock by when MTV ax quiz prog.
Junk MTV quiz graced by fox whelps.\tBawds jog, flick quartz, vex nymphs.
Waltz, bad nymph, for quick jigs vex!\tFox nymphs grab quick-jived waltz.
Brick quiz whangs jumpy veldt fox. """
print(text)
print()
print(repr(text))
# + colab={"base_uri": "https://localhost:8080/", "height": 130} id="QpBgInepMlCw" outputId="60172249-51c3-4356-f535-04a36fb5a0cc"
text = # your code here
print(text)
# + [markdown] id="JnyPM7DOMlCw"
# #### 4c. Passwords
#
# Write a program that asks a user for a password and checks some simple requirements of a password. If necessary, print out the following warnings (use if-statements):
#
# 1. Your password should contain at least 6 characters.
# 2. Your password should contain no more than 12 characters.
# 3. Your password only contains alphabetic characters! Please also use digits and/or special characters.
# 4. Your password only contains digits! Please also use alphabetic and/or special characters.
# 5. Your password should contain at least one special character.
# 6. Your password contains only lowercase letters! Please also use uppercase letters.
# 7. Your password contains only uppercase letters! Please also use lowercase letters.
# + id="dFuvGQEYMlCw"
# your code here
# + [markdown] id="2gaH49ikMlCw"
# ## Exercise 5: Boolean Logic and Conditions
# + [markdown] id="Fy28pQJoMlCw"
# #### 5a. Speeding
#
# Write code to solve the following scenario:
#
# You are driving a little too fast, and a police officer stops you. Write code to compute and print the result, encoded as a string: 'no ticket', 'small ticket', 'big ticket'. If speed is 60 or less, the result is 'no ticket'. If speed is between 61 and 80 inclusive, the result is 'small ticket'. If speed is 81 or more, the result is 'big ticket'. Unless it is your birthday -- on that day, your speed can be 5 higher in all cases.
#
# + id="FK1gaWkXMlCw"
# your code here
# + [markdown] id="FjczqqvWMlCx"
# #### 5b. Alarm clock
#
# Write code to set you alarm clock! Given the day of the week and information about whether you are currently on vacation or not, your code should print the time you want to be woken up following these constraints:
#
# Weekdays, the alarm should be "7:00" and on the weekend it should be "10:00". Unless we are on vacation -- then on weekdays it should be "10:00" and weekends it should be "off".
#
#
# Encode the weeks days as ints in the following way: 0=Sun, 1=Mon, 2=Tue, ...6=Sat. Encode the vacation infromation as boolean. Your code should assign the correct time to a variable as a string (following this format: "7:00") and print it.
#
# Note: Encoding the days as an integer helps you with defining conditions. You can check whether the week day is in a certain interval (instead of writing code for every single day).
# + id="Eig-ZRn9MlCx"
# your code here
# + [markdown] id="bh7QfeWhMlCx"
# #### 5c. Parcel delivery
# The required postage for an international parcel delivery service is calculated based on item weight and country of destination:
#
#
# | Tariff zone | 0 - 2 kg | 2 - 5 kg | 5 - 10 kg | 10 - 20 kg | 20 - 30 kg |
# |-------------|----------|----------|-----------|------------|------------|
# |EUR 1 | € 13.00 | € 19.50 | € 25.00 | € 34.00 | € 45.00 |
# |EUR 2 | € 18.50 | € 25.00 | € 31.00 | € 40.00 | € 55.00 |
# |World | € 24.30 | € 34.30 | € 58.30 | € 105.30 | - |
#
# Ask a user for the `weight` and `zone`. Use (nested) `if`-statements to find the required postage based on these variables. Assign the result to a variable `postage` and print the result using a full sentence:
#
# `The price of sending a [...] kg parcel to the [...] zone is € [...].`
# + id="4tPcHe5NMlCx"
# your code here
# + id="ZwEcNwspMlCx"
|
Assignments-colab/ASSIGNMENT_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ISM Benchmark
#
# Benchmark NaiveISM and fastISM.
# +
import sys
sys.path.append("../")
import fastISM
from fastISM.models.basset import basset_model
from fastISM.models.factorized_basset import factorized_basset_model
from fastISM.models.bpnet import bpnet_model
import tensorflow as tf
import numpy as np
from importlib import reload
import time
# -
tf.__version__
# !nvidia-smi
# !nvidia-smi -L
# !nvcc --version
print("Num GPUs Available: ", len(tf.config.experimental.list_physical_devices('GPU')))
device = 'GPU:0' if tf.config.experimental.list_physical_devices('GPU') else '/device:CPU:0'
device
seqs = np.load("test.seq.npy")
seqs.shape
# ## Benchmark
#
# Best practice would be to restart kernel after benchmarking each model!
def time_ism(ism_model, batch_sizes, seqlen):
times = []
per_100 = []
for b in batch_sizes:
# dry run -- required as first batch slower for setting up
# and variable batch sizes (due to varying number
# of seqs that need to be mutated at a position)
# also slows down first call
# x = np.random.random((b,seqlen,4))
x = seqs[:b, :seqlen]
x = tf.constant(x, dtype=ism_model.model.inputs[0].dtype)
o = ism_model(x, [0,0,0,1])
t = time.time()
x = tf.constant(x, dtype=ism_model.model.inputs[0].dtype)
# NOTE: computations are only performed at those positions
# at which the existing base != replace_with
o = ism_model(x, replace_with=[0,0,0,1])
o = ism_model(x, replace_with=[0,0,1,0])
o = ism_model(x, replace_with=[0,1,0,0])
o = ism_model(x, replace_with=[1,0,0,0])
times.append(time.time()-t)
per_100.append((times[-1]/b)*100)
print("BATCH: {}\tTIME: {:.2f}\tPER 100: {:.2f}".format(b, times[-1], (times[-1]/b)*100))
print("BEST PER 100: {:.2f}".format(min(per_100)))
# ### Basset (1000)
model = basset_model(seqlen=1000, num_outputs=1)
model_fism = fastISM.FastISM(model, test_correctness=False)
time_ism(model_fism, [64, 256, 2048, 3096, 4096], 1000)
model_nism = fastISM.NaiveISM(model)
time_ism(model_nism, [128, 256, 512, 1024, 2048], 1000)
# ### Basset (2000)
model = basset_model(seqlen=2000, num_outputs=1)
model_fism = fastISM.FastISM(model, test_correctness=False)
time_ism(model_fism, [128, 1024, 2048], 2000)
model_nism = fastISM.NaiveISM(model)
time_ism(model_nism, [64, 128, 256, 512, 1024], 2000)
time_ism(model_nism, [2048], 2000)
# ### Factorized Basset (1000)
model = factorized_basset_model(seqlen=1000, num_outputs=1)
model_fism = fastISM.FastISM(model, test_correctness=False)
time_ism(model_fism, [64, 256, 2048, 3072], 1000)
model_nism = fastISM.NaiveISM(model)
time_ism(model_nism, [64, 128, 256, 512, 1024], 1000)
time_ism(model_nism, [2048], 1000)
# ### Factorized Basset (2000)
model = factorized_basset_model(seqlen=2000, num_outputs=1)
model_fism = fastISM.FastISM(model, test_correctness=False)
time_ism(model_fism, [128, 512, 1024], 2000)
time_ism(model_fism, [1280], 2000)
model_nism = fastISM.NaiveISM(model)
# FINAL
time_ism(model_nism, [64, 128, 256, 512], 2000)
# ### BPNet (1000)
model = bpnet_model(seqlen=1000, num_dilated_convs=9)
model_fism = fastISM.FastISM(model, test_correctness=False)
# FINAL
time_ism(model_fism, [64, 512, 1280], 1000)
model_nism = fastISM.NaiveISM(model)
# FINAL
time_ism(model_nism, [128, 256, 512, 1024], 1000)
# ### BPNet (2000)
model = bpnet_model(seqlen=2000, num_dilated_convs=9)
model_fism = fastISM.FastISM(model, test_correctness=False)
# FINAL
time_ism(model_fism, [64,512,768], 2000)
model_nism = fastISM.NaiveISM(model)
# FINAL
time_ism(model_nism, [64, 128, 256, 512], 2000)
|
notebooks/ISMBenchmark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py37]
# language: python
# name: conda-env-py37-py
# ---
# ### netcdf example for PMEL tools - Drifters and Alamo Floats (2018) - multifloat x-section
#
# __pyversion__==3.7
# __author__==S.Bell
# + slideshow={"slide_type": "slide"}
import xarray as xa
import pandas as pd
import numpy as np
import cmocean
from geopy.distance import great_circle
# -
import datetime
print("Last run {0}".format(datetime.datetime.now()))
# +
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
import cmoceans
# + slideshow={"slide_type": "subslide"}
### specify primary bulk figure parameters
fontsize = 10
labelsize = 10
#plotstyle = 'seaborn'
#max_xticks = 10
plt.style.use('seaborn-ticks')
mpl.rcParams['svg.fonttype'] = 'none'
mpl.rcParams['ps.fonttype'] = 42 #truetype/type2 fonts instead of type3
mpl.rcParams['pdf.fonttype'] = 42 #truetype/type2 fonts instead of type3
mpl.rcParams['axes.grid'] = False
mpl.rcParams['axes.edgecolor'] = 'black'
mpl.rcParams['axes.linewidth'] = 1.5
mpl.rcParams['axes.labelcolor'] = 'black'
mpl.rcParams['grid.linestyle'] = '--'
mpl.rcParams['grid.linestyle'] = '--'
mpl.rcParams['xtick.major.size'] = 4
mpl.rcParams['xtick.minor.size'] = 2
mpl.rcParams['xtick.major.width'] = 2
mpl.rcParams['xtick.minor.width'] = 0.5
mpl.rcParams['ytick.major.size'] = 4
mpl.rcParams['ytick.minor.size'] = 2
mpl.rcParams['ytick.major.width'] = 2
mpl.rcParams['ytick.minor.width'] = 0.5
mpl.rcParams['ytick.direction'] = 'out'
mpl.rcParams['xtick.direction'] = 'out'
mpl.rcParams['ytick.color'] = 'black'
mpl.rcParams['xtick.color'] = 'black'
mpl.rcParams['contour.negative_linestyle'] = 'solid'
# + [markdown] slideshow={"slide_type": "slide"}
# Load data from NetCDF Archive
# + slideshow={"slide_type": "fragment"}
archive_path = '/Volumes/Archive/ecoraid/NonEcoFOCI_ProjectData/ArcticHeat/ALAMO/netcdf/'
AlamoID=['11012','11013','11015','11016','11018']
CycleNum=['0001','0001','0001','0001','0001']
dataxa = {}
initial_location = ()
distance = []
for ind,alamo in enumerate(AlamoID):
dataxa.update({alamo: xa.open_dataset(archive_path + alamo + '/R' + alamo + '_' + CycleNum[ind] + '.nc')})
### Using geopy, use great circle calculator to get distance between profiles
if ind == 0:
initial_location = (dataxa[alamo].LATITUDE.values[0],dataxa[alamo].LONGITUDE.values[0])
distance = distance + [0]
else:
### test the direction increasing eastward, decreasing westward
if (dataxa[alamo].LONGITUDE.values[0] > initial_location[1]):
sign = -1
else:
sign = 1
distance = distance + [sign * great_circle(initial_location,
(dataxa[alamo].LATITUDE.values[0],dataxa[alamo].LONGITUDE.values[0])).kilometers]
# -
#
distance
|
Arctic Heat/ALAMO Analysis/NetCDF_ALAMO-Xsection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Regular Expressions
# - Definition
# - Match Vs Search
# - Substitute substrings
# - Meta Vs Literal characters
# - Various identifiers
# - Back referencing example
# - Exercise
import re
# # match
a = "This is Learnbay class1"
mObj = re.match("This",a)
# mObj = re.match("Learnbay",a)
if mObj:
print(mObj.group())
a = "This is Learnbay class1"
# mObj = re.match("This",a)
mObj = re.match("Learnbay",a)
if mObj:
print(mObj.group())
# # Search
a = "This is Learnbay class1"
sObj = re.search("Learnbay",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
# # grouping
a = "This is Learnbay class1"
sObj = re.search("(Learnbay) (class)",a)
if sObj:
print(sObj.group())
print(sObj.group(1))
print(sObj.groups())
# # Substitute
a = "This is Learnbay class1"
op = re.sub("Learnbay","LEARNBAY",a)
print(op)
a = "This is Learnbay class1 class1 class1 class1 class1"
op = re.sub("class","CLASS",a)
print(op)
a = "This is Learnbay class1 class1 class1 class1 class1"
op = re.sub("class","CLASS",a,count=2)
print(op)
# # Findall
a = "This is Learnbay class1 class1 cLaSS1 cLASS1 CLAss1"
op = re.findall("class",a)
print(op)
# # using flags
a = "This is Learnbay class1 class1 cLaSS1 cLASS1 CLAss1"
op = re.findall("class",a,re.I)
print(op)
print(len(op))
a = "ABCDE123@#$ABC^@#123"
sObj = re.search("\w+",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "ABCDE123@#$ABC^@#123"
sObj = re.search("\d+",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "ABCDE123@#$ABC^@#123"
sObj = re.search("(\w+)(\W+)(\w+)",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
print(sObj.groups())
a = "1111111111"
sObj = re.search("\d\d\d\d",a)
# sObj = re.search("\d{4}",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "22 33356 1111111111 111 2"
sObj = re.search("\d{4,}",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "1111111111"
sObj = re.search("\d{4,6}",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "1111111111"
sObj = re.search("[0-9]{4,6}",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "111 2222 22 333"
# sObj = re.search("2{3,}",a)
# sObj = re.search("2{2,}",a)
sObj = re.search("2{2,6}",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "This is LEAR\nbay"
sObj = re.search("lear.bay",a,re.I|re.S)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "This is leaRnbay"
sObj = re.search("(learnbay|LEARNBAY|leaRnbay)",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "This is leaRnbay"
sObj = re.search("([a-z]eaRnbay)",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
a = "This is 2eaRnbay"
sObj = re.search("([^aA-zZ]eaRnbay)",a)
if sObj:
print(sObj.group())
# print(sObj.group(1))
# print(sObj.groups())
# # ?
a = "This is learnbay"
sObj = re.search("l?earnbay",a)
if sObj:
print(sObj.group())
# # *
a = "This is learnbayyyz456"
sObj = re.search("learnbay+.",a)
if sObj:
print(sObj.group())
# # Back referencing
a = "111 111 111 111 "
sObj = re.search("(111 )(111 )",a)
if sObj:
print(sObj.group())
a = "111 111 111 111 "
sObj = re.search("(111 )(\\1)\\2\\2",a)
if sObj:
print(sObj.group())
a = "111 111 111 111 "
sObj = re.search("(111 ){2}",a)
if sObj:
print(sObj.group())
a = "111 111 111 111 "
sObj = re.search("(111 )(.)",a)
if sObj:
print(sObj.group())
print(sObj.group(2))
|
14_RegularExpression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/AI4Finance-Foundation/FinRL/blob/master/FinRL_StockTrading_NeurIPS_2018.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="gXaoZs2lh1hi"
# # Deep Reinforcement Learning for Stock Trading from Scratch: Multiple Stock Trading
#
# * **Pytorch Version**
#
#
# + [markdown] id="lGunVt8oLCVS"
# # Content
# + [markdown] id="HOzAKQ-SLGX6"
# * [1. Problem Definition](#0)
# * [2. Getting Started - Load Python packages](#1)
# * [2.1. Install Packages](#1.1)
# * [2.2. Check Additional Packages](#1.2)
# * [2.3. Import Packages](#1.3)
# * [2.4. Create Folders](#1.4)
# * [3. Download Data](#2)
# * [4. Preprocess Data](#3)
# * [4.1. Technical Indicators](#3.1)
# * [4.2. Perform Feature Engineering](#3.2)
# * [5.Build Environment](#4)
# * [5.1. Training & Trade Data Split](#4.1)
# * [5.2. User-defined Environment](#4.2)
# * [5.3. Initialize Environment](#4.3)
# * [6.Implement DRL Algorithms](#5)
# * [7.Backtesting Performance](#6)
# * [7.1. BackTestStats](#6.1)
# * [7.2. BackTestPlot](#6.2)
# * [7.3. Baseline Stats](#6.3)
# * [7.3. Compare to Stock Market Index](#6.4)
# * [RLlib Section](#7)
# + [markdown] id="sApkDlD9LIZv"
# <a id='0'></a>
# # Part 1. Problem Definition
# + [markdown] id="HjLD2TZSLKZ-"
# This problem is to design an automated trading solution for single stock trading. We model the stock trading process as a Markov Decision Process (MDP). We then formulate our trading goal as a maximization problem.
#
# The algorithm is trained using Deep Reinforcement Learning (DRL) algorithms and the components of the reinforcement learning environment are:
#
#
# * Action: The action space describes the allowed actions that the agent interacts with the
# environment. Normally, a ∈ A includes three actions: a ∈ {−1, 0, 1}, where −1, 0, 1 represent
# selling, holding, and buying one stock. Also, an action can be carried upon multiple shares. We use
# an action space {−k, ..., −1, 0, 1, ..., k}, where k denotes the number of shares. For example, "Buy
# 10 shares of AAPL" or "Sell 10 shares of AAPL" are 10 or −10, respectively
#
# * Reward function: r(s, a, s′) is the incentive mechanism for an agent to learn a better action. The change of the portfolio value when action a is taken at state s and arriving at new state s', i.e., r(s, a, s′) = v′ − v, where v′ and v represent the portfolio
# values at state s′ and s, respectively
#
# * State: The state space describes the observations that the agent receives from the environment. Just as a human trader needs to analyze various information before executing a trade, so
# our trading agent observes many different features to better learn in an interactive environment.
#
# * Environment: Dow 30 consituents
#
#
# The data of the single stock that we will be using for this case study is obtained from Yahoo Finance API. The data contains Open-High-Low-Close price and volume.
#
# + [markdown] id="Ffsre789LY08"
# <a id='1'></a>
# # Part 2. Getting Started- Load Python Packages
# + [markdown] id="Uy5_PTmOh1hj"
# <a id='1.1'></a>
# ## 2.1. Install all the packages through FinRL library
#
# + colab={"base_uri": "https://localhost:8080/"} id="mPT0ipYE28wL" outputId="ef0ba8d0-f57a-4c74-bb0b-46737762677d"
## install finrl library
# !pip install git+https://github.com/AI4Finance-LLC/FinRL-Library.git
# + id="w9A8CN5R5PuZ"
from finrl.apps import config
import os
if not os.path.exists("./" + config.DATA_SAVE_DIR):
os.makedirs("./" + config.DATA_SAVE_DIR)
if not os.path.exists("./" + config.TRAINED_MODEL_DIR):
os.makedirs("./" + config.TRAINED_MODEL_DIR)
if not os.path.exists("./" + config.TENSORBOARD_LOG_DIR):
os.makedirs("./" + config.TENSORBOARD_LOG_DIR)
if not os.path.exists("./" + config.RESULTS_DIR):
os.makedirs("./" + config.RESULTS_DIR)
# + [markdown] id="osBHhVysOEzi"
#
# <a id='1.2'></a>
# ## 2.2. Check if the additional packages needed are present, if not install them.
# * Yahoo Finance API
# * pandas
# * numpy
# * matplotlib
# * stockstats
# * OpenAI gym
# * stable-baselines
# * tensorflow
# * pyfolio
# + [markdown] id="nGv01K8Sh1hn"
# <a id='1.3'></a>
# ## 2.3. Import Packages
# + colab={"base_uri": "https://localhost:8080/"} id="lPqeTTwoh1hn" outputId="10b08480-3a0c-4826-8e51-f94ce97ab84a"
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
# matplotlib.use('Agg')
import datetime
# %matplotlib inline
from finrl.finrl_meta.preprocessor.yahoodownloader import YahooDownloader
from finrl.finrl_meta.preprocessor.preprocessors import FeatureEngineer, data_split
from finrl.finrl_meta.env_stock_trading.env_stocktrading import StockTradingEnv
from finrl.drl_agents.stablebaselines3.models import DRLAgent
from finrl.finrl_meta.data_processor import DataProcessor
from finrl.plot import backtest_stats, backtest_plot, get_daily_return, get_baseline
from pprint import pprint
import sys
sys.path.append("../FinRL-Library")
import itertools
# + [markdown] id="T2owTj985RW4"
# <a id='1.4'></a>
# ## 2.4. Create Folders
# + [markdown] id="A289rQWMh1hq"
# <a id='2'></a>
# # Part 3. Download Data
# Yahoo Finance is a website that provides stock data, financial news, financial reports, etc. All the data provided by Yahoo Finance is free.
# * FinRL uses a class **YahooDownloader** to fetch data from Yahoo Finance API
# * Call Limit: Using the Public API (without authentication), you are limited to 2,000 requests per hour per IP (or up to a total of 48,000 requests a day).
#
# + [markdown] id="NPeQ7iS-LoMm"
#
#
# -----
# class YahooDownloader:
# Provides methods for retrieving daily stock data from
# Yahoo Finance API
#
# Attributes
# ----------
# start_date : str
# start date of the data (modified from config.py)
# end_date : str
# end date of the data (modified from config.py)
# ticker_list : list
# a list of stock tickers (modified from config.py)
#
# Methods
# -------
# fetch_data()
# Fetches data from yahoo API
#
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="h3XJnvrbLp-C" outputId="5302d7c0-1c68-4c6e-b30e-b1395bdc109e"
# from config.py start_date is a string
config.START_DATE
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="FUnY8WEfLq3C" outputId="35dd8c5b-d58f-49b8-e4df-ae7e122448cd"
# from config.py end_date is a string
config.END_DATE
# + colab={"base_uri": "https://localhost:8080/"} id="yCKm4om-s9kE" outputId="83c7f894-3757-473b-8afb-a904e6caabda"
df = YahooDownloader(start_date = '2009-01-01',
end_date = '2021-10-31',
ticker_list = config.DOW_30_TICKER).fetch_data()
# + colab={"base_uri": "https://localhost:8080/"} id="JzqRRTOX6aFu" outputId="7a991dfe-f39c-40db-ec44-7c416cdce7dc"
print(config.DOW_30_TICKER)
# + colab={"base_uri": "https://localhost:8080/"} id="CV3HrZHLh1hy" outputId="5267773c-399c-4ec9-d4d5-13ab1e4cced0"
df.shape
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="4hYkeaPiICHS" outputId="210fade5-e912-40df-be99-4ad00bdb9d2f"
df.sort_values(['date','tic'],ignore_index=True).head()
# + [markdown] id="uqC6c40Zh1iH"
# # Part 4: Preprocess Data
# Data preprocessing is a crucial step for training a high quality machine learning model. We need to check for missing data and do feature engineering in order to convert the data into a model-ready state.
# * Add technical indicators. In practical trading, various information needs to be taken into account, for example the historical stock prices, current holding shares, technical indicators, etc. In this article, we demonstrate two trend-following technical indicators: MACD and RSI.
# * Add turbulence index. Risk-aversion reflects whether an investor will choose to preserve the capital. It also influences one's trading strategy when facing different market volatility level. To control the risk in a worst-case scenario, such as financial crisis of 2007–2008, FinRL employs the financial turbulence index that measures extreme asset price fluctuation.
# + colab={"base_uri": "https://localhost:8080/"} id="PmKP-1ii3RLS" outputId="0708badb-77ef-4c86-f77c-6525f0e8934d" pycharm={"name": "#%%\n"}
fe = FeatureEngineer(
use_technical_indicator=True,
tech_indicator_list = config.TECHNICAL_INDICATORS_LIST,
use_vix=True,
use_turbulence=True,
user_defined_feature = False)
processed = fe.preprocess_data(df)
# + id="Kixon2tR3RLT"
list_ticker = processed["tic"].unique().tolist()
list_date = list(pd.date_range(processed['date'].min(),processed['date'].max()).astype(str))
combination = list(itertools.product(list_date,list_ticker))
processed_full = pd.DataFrame(combination,columns=["date","tic"]).merge(processed,on=["date","tic"],how="left")
processed_full = processed_full[processed_full['date'].isin(processed['date'])]
processed_full = processed_full.sort_values(['date','tic'])
processed_full = processed_full.fillna(0)
# + colab={"base_uri": "https://localhost:8080/", "height": 600} id="grvhGJJII3Xn" outputId="733758c3-3552-4aa5-e1f9-789bd4ce0c92"
processed_full.sort_values(['date','tic'],ignore_index=True).head(10)
# + [markdown] id="-QsYaY0Dh1iw"
# <a id='4'></a>
# # Part 5. Design Environment
# Considering the stochastic and interactive nature of the automated stock trading tasks, a financial task is modeled as a **Markov Decision Process (MDP)** problem. The training process involves observing stock price change, taking an action and reward's calculation to have the agent adjusting its strategy accordingly. By interacting with the environment, the trading agent will derive a trading strategy with the maximized rewards as time proceeds.
#
# Our trading environments, based on OpenAI Gym framework, simulate live stock markets with real market data according to the principle of time-driven simulation.
#
# The action space describes the allowed actions that the agent interacts with the environment. Normally, action a includes three actions: {-1, 0, 1}, where -1, 0, 1 represent selling, holding, and buying one share. Also, an action can be carried upon multiple shares. We use an action space {-k,…,-1, 0, 1, …, k}, where k denotes the number of shares to buy and -k denotes the number of shares to sell. For example, "Buy 10 shares of AAPL" or "Sell 10 shares of AAPL" are 10 or -10, respectively. The continuous action space needs to be normalized to [-1, 1], since the policy is defined on a Gaussian distribution, which needs to be normalized and symmetric.
# + [markdown] id="5TOhcryx44bb"
# ## Training data split: 2009-01-01 to 2020-07-01
# ## Trade data split: 2020-07-01 to 2021-10-31
# + colab={"base_uri": "https://localhost:8080/"} id="W0qaVGjLtgbI" outputId="ca8d1a43-ffc3-4fc3-efa9-4de9a9065842"
train = data_split(processed_full, '2009-01-01','2020-07-01')
trade = data_split(processed_full, '2020-07-01','2021-10-31')
print(len(train))
print(len(trade))
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="p52zNCOhTtLR" outputId="b3ad3e10-376f-4186-f875-0331708c5e14"
train.tail()
# + colab={"base_uri": "https://localhost:8080/", "height": 357} id="k9zU9YaTTvFq" outputId="72213585-39a3-4bff-c031-874ec0ca06f9"
trade.head()
# + colab={"base_uri": "https://localhost:8080/"} id="zYN573SOHhxG" outputId="7f228183-abe3-4477-f574-3c9b25c62cd8"
config.TECHNICAL_INDICATORS_LIST
# + colab={"base_uri": "https://localhost:8080/"} id="Q2zqII8rMIqn" outputId="1f54d044-e2d3-4a34-c041-e913d686654e"
stock_dimension = len(train.tic.unique())
state_space = 1 + 2*stock_dimension + len(config.TECHNICAL_INDICATORS_LIST)*stock_dimension
print(f"Stock Dimension: {stock_dimension}, State Space: {state_space}")
# + id="AWyp84Ltto19"
env_kwargs = {
"hmax": 100,
"initial_amount": 1000000,
"buy_cost_pct": 0.001,
"sell_cost_pct": 0.001,
"state_space": state_space,
"stock_dim": stock_dimension,
"tech_indicator_list": config.TECHNICAL_INDICATORS_LIST,
"action_space": stock_dimension,
"reward_scaling": 1e-4
}
e_train_gym = StockTradingEnv(df = train, **env_kwargs)
# + [markdown] id="64EoqOrQjiVf"
# ## Environment for Training
#
#
# + colab={"base_uri": "https://localhost:8080/"} id="xwSvvPjutpqS" outputId="deeaef07-afda-4ca1-fea8-99384224c7cf"
env_train, _ = e_train_gym.get_sb_env()
print(type(env_train))
# + [markdown] id="HMNR5nHjh1iz"
# <a id='5'></a>
# # Part 6: Implement DRL Algorithms
# * The implementation of the DRL algorithms are based on **OpenAI Baselines** and **Stable Baselines**. Stable Baselines is a fork of OpenAI Baselines, with a major structural refactoring, and code cleanups.
# * FinRL library includes fine-tuned standard DRL algorithms, such as DQN, DDPG,
# Multi-Agent DDPG, PPO, SAC, A2C and TD3. We also allow users to
# design their own DRL algorithms by adapting these DRL algorithms.
# + id="364PsqckttcQ"
agent = DRLAgent(env = env_train)
# + [markdown] id="YDmqOyF9h1iz"
# ### Model Training: 5 models, A2C DDPG, PPO, TD3, SAC
#
# + [markdown] id="uijiWgkuh1jB"
# ### Model 1: A2C
#
# + colab={"base_uri": "https://localhost:8080/"} id="GUCnkn-HIbmj" outputId="a90a7a60-21a5-47e1-b683-1f7cbb4b8bc0"
agent = DRLAgent(env = env_train)
model_a2c = agent.get_model("a2c")
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="0GVpkWGqH4-D" outputId="570d540f-abe9-402b-e0cc-f9b007228e8e"
trained_a2c = agent.train_model(model=model_a2c,
tb_log_name='a2c',
total_timesteps=50000)
# + [markdown] id="MRiOtrywfAo1"
# ### Model 2: DDPG
# + id="M2YadjfnLwgt"
agent = DRLAgent(env = env_train)
model_ddpg = agent.get_model("ddpg")
# + id="tCDa78rqfO_a" jupyter={"outputs_hidden": true}
trained_ddpg = agent.train_model(model=model_ddpg,
tb_log_name='ddpg',
total_timesteps=50000)
# + [markdown] id="_gDkU-j-fCmZ"
# ### Model 3: PPO
# + id="y5D5PFUhMzSV"
agent = DRLAgent(env = env_train)
PPO_PARAMS = {
"n_steps": 2048,
"ent_coef": 0.01,
"learning_rate": 0.00025,
"batch_size": 128,
}
model_ppo = agent.get_model("ppo",model_kwargs = PPO_PARAMS)
# + id="Gt8eIQKYM4G3" jupyter={"outputs_hidden": true}
trained_ppo = agent.train_model(model=model_ppo,
tb_log_name='ppo',
total_timesteps=50000)
# + [markdown] id="3Zpv4S0-fDBv"
# ### Model 4: TD3
# + id="JSAHhV4Xc-bh"
agent = DRLAgent(env = env_train)
TD3_PARAMS = {"batch_size": 100,
"buffer_size": 1000000,
"learning_rate": 0.001}
model_td3 = agent.get_model("td3",model_kwargs = TD3_PARAMS)
# + id="OSRxNYAxdKpU"
trained_td3 = agent.train_model(model=model_td3,
tb_log_name='td3',
total_timesteps=30000)
# + [markdown] id="Dr49PotrfG01"
# ### Model 5: SAC
# + id="xwOhVjqRkCdM"
agent = DRLAgent(env = env_train)
SAC_PARAMS = {
"batch_size": 128,
"buffer_size": 1000000,
"learning_rate": 0.0001,
"learning_starts": 100,
"ent_coef": "auto_0.1",
}
model_sac = agent.get_model("sac",model_kwargs = SAC_PARAMS)
# + id="K8RSdKCckJyH"
trained_sac = agent.train_model(model=model_sac,
tb_log_name='sac',
total_timesteps=60000)
# + [markdown] id="f2wZgkQXh1jE"
# ## Trading
# Assume that we have $1,000,000 initial capital at 2020-07-01. We use the DDPG model to trade Dow jones 30 stocks.
# + [markdown] id="bEv5KGC8h1jE"
# ### Set turbulence threshold
# Set the turbulence threshold to be greater than the maximum of insample turbulence data, if current turbulence index is greater than the threshold, then we assume that the current market is volatile
# + id="efwBi84ch1jE"
data_risk_indicator = processed_full[(processed_full.date<'2020-07-01') & (processed_full.date>='2009-01-01')]
insample_risk_indicator = data_risk_indicator.drop_duplicates(subset=['date'])
# + id="VHZMBpSqh1jG"
insample_risk_indicator.vix.describe()
# + id="BDkszkMloRWT"
insample_risk_indicator.vix.quantile(0.996)
# + id="AL7hs7svnNWT"
insample_risk_indicator.turbulence.describe()
# + id="N78hfHckoqJ9"
insample_risk_indicator.turbulence.quantile(0.996)
# + [markdown] id="U5mmgQF_h1jQ"
# ### Trade
#
# DRL model needs to update periodically in order to take full advantage of the data, ideally we need to retrain our model yearly, quarterly, or monthly. We also need to tune the parameters along the way, in this notebook I only use the in-sample data from 2009-01 to 2020-07 to tune the parameters once, so there is some alpha decay here as the length of trade date extends.
#
# Numerous hyperparameters – e.g. the learning rate, the total number of samples to train on – influence the learning process and are usually determined by testing some variations.
# + id="cIqoV0GSI52v"
#trade = data_split(processed_full, '2020-07-01','2021-10-31')
e_trade_gym = StockTradingEnv(df = trade, turbulence_threshold = 70,risk_indicator_col='vix', **env_kwargs)
# env_trade, obs_trade = e_trade_gym.get_sb_env()
# + id="W_XNgGsBMeVw"
trade.head()
# + id="eLOnL5eYh1jR"
df_account_value, df_actions = DRLAgent.DRL_prediction(
model=trained_sac,
environment = e_trade_gym)
# + id="ERxw3KqLkcP4"
df_account_value.shape
# + id="2yRkNguY5yvp"
df_account_value.tail()
# + id="nFlK5hNbWVFk"
df_actions.head()
# + [markdown] id="W6vvNSC6h1jZ"
# <a id='6'></a>
# # Part 7: Backtest Our Strategy
# Backtesting plays a key role in evaluating the performance of a trading strategy. Automated backtesting tool is preferred because it reduces the human error. We usually use the Quantopian pyfolio package to backtest our trading strategies. It is easy to use and consists of various individual plots that provide a comprehensive image of the performance of a trading strategy.
# + [markdown] id="Lr2zX7ZxNyFQ"
# <a id='6.1'></a>
# ## 7.1 BackTestStats
# pass in df_account_value, this information is stored in env class
#
# + id="Nzkr9yv-AdV_"
print("==============Get Backtest Results===========")
now = datetime.datetime.now().strftime('%Y%m%d-%Hh%M')
perf_stats_all = backtest_stats(account_value=df_account_value)
perf_stats_all = pd.DataFrame(perf_stats_all)
perf_stats_all.to_csv("./"+config.RESULTS_DIR+"/perf_stats_all_"+now+'.csv')
# + id="QkV-LB66iwhD"
#baseline stats
print("==============Get Baseline Stats===========")
baseline_df = get_baseline(
ticker="^DJI",
start = df_account_value.loc[0,'date'],
end = df_account_value.loc[len(df_account_value)-1,'date'])
stats = backtest_stats(baseline_df, value_col_name = 'close')
# + id="qg1kvfemrrQH"
df_account_value.loc[0,'date']
# + id="tt1bzL5OrsTa"
df_account_value.loc[len(df_account_value)-1,'date']
# + [markdown] id="9U6Suru3h1jc"
# <a id='6.2'></a>
# ## 7.2 BackTestPlot
# + id="lKRGftSS7pNM"
print("==============Compare to DJIA===========")
# %matplotlib inline
# S&P 500: ^GSPC
# Dow Jones Index: ^DJI
# NASDAQ 100: ^NDX
backtest_plot(df_account_value,
baseline_ticker = '^DJI',
baseline_start = df_account_value.loc[0,'date'],
baseline_end = df_account_value.loc[len(df_account_value)-1,'date'])
# + id="BzBaE63H3RLc"
# + id="ZYeOjax-7H_5"
|
FinRL_StockTrading_NeurIPS_2018.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <div style='background-image: url("../share/images/header.svg") ; padding: 0px ; background-size: cover ; border-radius: 5px ; height: 250px'>
# <div style="float: right ; margin: 50px ; padding: 20px ; background: rgba(255 , 255 , 255 , 0.7) ; width: 50% ; height: 150px">
# <div style="position: relative ; top: 50% ; transform: translatey(-50%)">
# <div style="font-size: xx-large ; font-weight: 900 ; color: rgba(0 , 0 , 0 , 0.8) ; line-height: 100%">ORFEUS Workshop - Lisbon 2017</div>
# <div style="font-size: large ; padding-top: 20px ; color: rgba(0 , 0 , 0 , 0.5)">ORFEUS EIDA Webservices</div>
# </div>
# </div>
# </div>
# Seismo-Live: http://seismo-live.org
#
# ##### Authors:
# * <NAME> ([@jollyfant](https://github.com/jollyfant))
#
# ---
# ## 1 Basic Webservice Usage
# ## 1.1 Introduction
# EIDA webservices are designed to provide programmatic access to waveform data and instrument metadata from EIDA. FDSN standerdised webservices are running since 2015 and are scheduled to replace Arclink and other deprecated procotols in the near future. Because webservices requests are URLs It is possible to communicate directly with the webservice APIs in a browser, command-line tools (e.g. curl; wget) or through abstracted clients (e.g. [ObsPy](http://obspy.org), [fdsnws-fetch](https://github.com/andres-h/fdsnws_scripts/blob/master/fdsnws_fetch.py)).
#
# Webservices are identified by the service domain (URL) that is data center specific, a label that identifies the service (e.g. dataselect; station) and a list of request options (e.g. stream identifiers or time window) included in its query string. In this initial exercise we will introduce five webservices:
#
# * 1.2 FDSNWS-Dataselect - Raw waveform service
# * 1.3 FDSNWS-Station - Station metadata and instrument specifics
# * 1.4 EIDAWS-Routing - Service routing within EIDA
# * 1.5 EIDAWS-WFCatalog - Waveform metadata
# * 1.6 EIDA Mediator - Automatically federated requests across EIDA
#
# In this notebook we will practise direct communication with the webservice APIs in addition to recommended and more convenient workflows using ObsPy.
# ## 1.2 FDSNWS-Dataselect
# ### 1.2.1 Interacting with the API
# The following example makes a request to the FDSNWS-Dataselect API hosted at ORFEUS Data Center (http://orfeus-eu.org). We will request a 10-minute window of miniSEED data from a single station. The data will be read and plotted using ObsPy. Alternatively, we could save the data to disk. The service label for FDSNWS-Dataselect is:
#
# > fdsnws/dataselect/1/query
# +
# %matplotlib inline
# Import the read module from ObsPy
from obspy import read
# The URL that points to the dataselect service
# The label that identifies the service
SERVICE_DOMAIN = "http://www.orfeus-eu.org"
LABEL = "fdsnws/dataselect/1/query"
# The 10-minute time window tuple
starttime, endtime = ("2016-01-01T00:00:00", "2016-01-01T00:10:00")
# Get the SEED codes, we will use wildcards for location, channel
network, station, location, channel = "NL", "HGN", "*", "*"
# Create a query string
queryString = "&".join([
"network=%s" % network,
"station=%s" % station,
"location=%s" % location,
"channel=%s" % channel,
"starttime=%s" % starttime,
"endtime=%s" % endtime
])
# The URL that we are requesting data from
# Try visiting this URL in your browser:
# http://www.orfeus-eu.org/fdsnws/dataselect/1/query?network=NL&station=HGN&location=*&channel=*&starttime=2016-01-01T00:00:00&endtime=2016-01-01T00:10:00
st = read("%s/%s?%s" % (SERVICE_DOMAIN, LABEL, queryString))
# Plot the data returned by the webservice
st.plot();
# -
# ### 1.2.2 Waveforms through ObsPy (recommended usage)
# Alternatively we can use the ObsPy library to communicate with the API through an abstracted client. All we need to do is call an ObsPy function with our time window constraint and SEED identifiers. This function will do all the work of the previous exercise for us internally and make the result available for use within ObsPy.
#
# **Note:** Instead of building the URL yourself in the previous exercise, when working with ObsPy it is recommended that the client class is used.
# +
# Include the Client class from ObsPy
from obspy.clients.fdsn import Client
# Create an ObsPy Client that points to ODC (http://www.orfeus-eu.org)
client = Client("ODC")
# Get the waveforms for the same trace identifiers and time window
st = client.get_waveforms(network, station, location, channel, starttime, endtime)
# Plot identical result
st.plot();
# -
# ## 1.3 FDSNWS-Station
# ### 1.3.1 Interacting with the API
# The fdsnws-station service works similar to the fdsnws-dataselect but has a service different label (*station* instead of *dataselect*). The response of this webservice is StationXML by default. In the following example we will however request the output formatted as text for clarity. The label for this webservice is:
#
# > fdsnws/station/1/query
# +
# Import a library to make a HTTP request to the webservice
import requests
# The URL that points to the station service
SERVICE_DOMAIN = "http://www.orfeus-eu.org"
LABEL = "fdsnws/station/1/query"
# Get the SEED codes for the entire NL network
network, station, location, channel = "NL", "*", "*", "*"
# The query string includes our seed identifiers
# and we request output format text
queryString = "&".join([
"network=%s" % network,
"station=%s" % station,
"location=%s" % location,
"channel=%s" % channel,
"format=text",
"level=station"
])
# The URL that we are requesing
# Try this in your browser:
# http://www.orfeus-eu.org/fdsnws/station/1/query?network=NL&station=*&location=*&channel=*&format=text
r = requests.get("%s/%s?%s" % (SERVICE_DOMAIN, LABEL, queryString))
# This will print station information for all stations in network NL
print(r.text)
# -
# Practically, the data would be requested in StatonXML format and saved to file, to be further used during data processing. In the following exercise we will read the data directly into ObsPy. Note again that when working with ObsPy, using the client class is the best solution.
# ### 1.3.2 Station Metadata through ObsPy (recommended usage)
# Alternatively, we use an ObsPy client to be able to directly manipulate the data in ObsPy. In the following example we request the instrument response for a single channel and print the response information. In combination with the raw waveform data returned from dataselect service we can deconvolve the frequency response for this sensor.
# +
# We will request instrument metadata for a single trace
network, station, location, channel = "NL", "HGN", "02", "BH*"
# We pass level=response to request instrument response metadata
inv = client.get_stations(
network=network,
station=station,
location=location,
channel=channel,
level="response"
)
# This object now has response information for the selected trace (NL.HGN.02.BHZ)
for network in inv:
for station in network:
for channel in station:
print(channel.response)
# Deconvolve instrument response
st.remove_response(inventory=inv)
# Plot the data (output units = velocity)
st.plot();
# -
# ## 1.4 EIDAWS-Routing
# The seismic archive of EIDA is distributed across 11 different data centers, called EIDA Nodes. EIDAWS-routing helps you to find data within this federated data archive. If you don't know which EIDA node holds your data of interest the routing service will provide you with the appropriate EIDA node and corresponding webservice URL to be queried.
#
# In this example we will request the "get" format (i.e. URLs that hold the data) for four networks. We are asking for all routes to the station webservice. The label for this service is:
#
# > eidaws/routing/1/query
#
# **Note:** routing and communication with all EIDA nodes individually can be omitted by using the EIDA Mediator in federated mode (see section 1.6).
# +
# The URL that points to the routing service (notice the different eidaws label)
SERVICE_DOMAIN = "http://www.orfeus-eu.org"
LABEL = "eidaws/routing/1/query"
# Network codes must be comma delimited
network = ",".join(["HL", "GE", "NL", "KO"])
# The query string includes our network codes and our output format must is set as URLs (get)
# We specify the service as fdsnws-station (change this to dataselect)
queryString = "&".join([
"network=%s" % network,
"format=get",
"service=station"
])
# The URL that we are requesing
# Try this in your browser:
# http://www.orfeus-eu.org/eidaws/routing/1/query?network=HL,GE,NL,KO&format=get
r = requests.get("%s/%s?%s" % (SERVICE_DOMAIN, LABEL, queryString))
# Should print four routes to different data centers
# Here we can find station metadata for these four networks respectively
# We make a request to all returned routes (status 200 indicates success!)
for line in r.text.split("\n"):
r = requests.get(line)
print("[%i] %s" % (r.status_code, line))
# -
# ## 1.5 EIDAWS-WFCatalog
# The WFCatalog is a catalogue of seismic waveform metadata. This is not to be confused with station metadata but contains purely metadata describing the waveforms. These metadata include availability information (e.g. gaps), sample metrics (e.g. mean, standard deviations, median values) and miniSEED header flags.
#
# The EIDAWS-WFCatalog webservice returns quality metrics from raw waveform data. The WFCatalog can serve as a powerful waveform index for data discovery by appending filters (e.g. lt, ge) to the query string. This can help identify waveforms with metric values below or above a certain threshold. The label for this service is:
#
# > eidaws/wfcatalog/1/query
# +
# The URL that points to the routing service (notice the different eidaws label)
SERVICE_DOMAIN = "http://www.orfeus-eu.org"
LABEL = "eidaws/wfcatalog/1/query"
# The start and end date for the metrics
# Feel free to change the window
starttime, endtime = ("2010-11-01", "2010-11-07")
# Network codes must be comma delimited
network, station, location, channel = "NL.HGN.02.BHZ".split(".")
# The query string includes our seed identifiers, temporal constraints, we ask for sample metrics to be included
# include can be either (default, sample, header, all)
# We request metrics for daily waveforms with an availability over 50%
# Try changing the percent_availability to 100 - less documents will be returned
queryString = "&".join([
"network=%s" % network,
"station=%s" % station,
"location=%s" % location,
"channel=%s" % channel,
"starttime=%s" % starttime,
"endtime=%s" % endtime,
"include=sample",
"percent_availability_ge=50"
])
# Try this in your browser:
# http://www.orfeus-eu.org/eidaws/wfcatalog/1/query?network=NL&station=HGN&location=02&channel=BHZ&start=2010-11-01&end=2010-11-07&include=sample
r = requests.get("%s/%s?%s" % (SERVICE_DOMAIN, LABEL, queryString))
# Should print JSON response of quality metrics for three days.
r.json()
# -
# ## 1.6 EIDA Mediator
# The EIDA mediator (beta) can automatically route and retrieve requests federated between EIDA nodes. This prevents using from having to query the routing service before making data requests. There is a single entry poiny to the entire archive available within EIDA as demonstrated below. Currently there is supported for federated mode between **station** and **dataselect**. Federation of **WFCatalog** requests will be supported in the future.
# +
# The URL that points to the routing service (the EIDA mediator is hosted by ETHZ)
SERVICE_DOMAIN = "http://mediator-devel.ethz.ch"
LABEL = "fdsnws/station/1/query"
# Network codes must be comma delimited
# Networks are federated across 4 different EIDA nodes
network = ",".join(["HL", "GE", "NL", "KO"])
# Creathe queyr string and append all networks
# We ask for level=network to limit the amount of data returned for clarity
queryString = "&".join([
"network=%s" % network,
"level=network"
])
# Try this in your browser:
# http://mediator-devel.ethz.ch/fdsnws/station/1/query?network=HL,GE,NL&level=network
##### This currently does not seem to work.
# r = requests.get("%s/%s?%s" %(SERVICE_DOMAIN, LABEL, queryString))
# StationXML for all four networks
# print(r.text)
# -
# ## Graphical user interfaces
# The following tools are available on orfeus-eu.org and are built on top of the discussed webservices. Please note that these interfaces currently only work for data archived at ORFEUS Data Center.
#
# > http://www.orfeus-eu.org/data/odc/quality
# # 2 Advanced Example - Webservices pipeline
# ## 2.1 Introduction
# This example demonstrates the use of FDSN webservices in a processing pipeline. The goal of this exercise is to download raw waveform data from stations surrounding an earthquake. This pipeline is based on functionality provided with ObsPy.
# +
# Define the module imports
import requests
import math
from obspy.taup import TauPyModel
from obspy.geodetics import locations2degrees
from obspy import read, UTCDateTime
import datetime
import dateutil.parser
# -
# ## 2.2 FDSNWS-Event
#
# We define a function that collects event information from fdsnws-event. We pass an event identifier to the webservice, parse the response and return an Event class that has **location**, **origin time**, and **depth** attributes. The event data is requested from the seismicportal webservice provided by the EMSC.
def getEvent(identifier):
# Try in your browser:
# http://www.seismicportal.eu/fdsnws/event/1/query?eventid=20170720_0000091&format=text
# Service address
FDSN_EVENT = "http://www.seismicportal.eu/fdsnws/event/1/query"
# Define class for Events
class Event():
def __init__(self, line):
self.id, self.time, self.latitude, self.longitude, self.depth = line.split("|")[:5]
self.latitude = float(self.latitude)
self.longitude = float(self.longitude)
self.depth = float(self.depth)
# We query for a single event identifier and request a text format return
queryString = "&".join([
"eventid=%s" % identifier,
"format=text"
])
# Create the query for an event identifier
r = requests.get("%s?%s" % (FDSN_EVENT, queryString))
# Split by lines and remove head & tail
lines = r.text.split("\n")[1:-1]
# Return Event classes for each entry
return list(map(Event, lines))[0]
# Should print a single Event instance
print(getEvent("20170720_0000091"))
# ## 2.3 FDSNWS-Station
#
# Define a function that can find the stations around an event. We pass the Event instance to the function and call the station webservice to return stations within 20 degrees arc-distance of this event location. We parse the response and return a map of station instances with attributes network, station, and location.
def getStations(event):
# Try it in your browser:
# http://orfeus-eu.org/fdsnws/station/1/query?latitude=30&longitude=30&maxradius=20&format=text
# Service address
FDSN_STATION = "http://orfeus-eu.org/fdsnws/station/1/query"
MAX_RADIUS = 20
# Define a Station class
class Station():
def __init__(self, line):
self.network, self.station, self.latitude, self.longitude = line.split("|")[:4]
self.latitude = float(self.latitude)
self.longitude = float(self.longitude)
# We query with the event location and a maximum radius around the event
queryString = "&".join([
"latitude=%s" % event.latitude,
"longitude=%s" % event.longitude,
"maxradius=%s" % MAX_RADIUS,
"format=text"
])
# Request from webservice
r = requests.get("%s?%s" % (FDSN_STATION, queryString))
# Split by lines and remove head & tail
lines = r.text.split("\n")[1:-1]
# Return Event classes for each entry
return map(Station, lines)
# Should print a map (array) of Station instances
print(getStations(getEvent("20170720_0000091")))
# ## 2.4 Theoretical Arrival Times
#
# Define a function that calculates the theoretical P arrival time at a station location using the TauP module in ObsPy. The function takes an Event and Station instance. The arc-distance in degrees between the source and receiver is calculated using the *haversine function* (see below).
# +
# We use the iasp91 reference model
TAUP_MODEL = TauPyModel(model="iasp91")
def getPArrival(event, station):
# Determine the arc distance using the haversine formula
arcDistanceDegrees = locations2degrees(
event.latitude,
station.latitude,
event.longitude,
station.longitude
)
# Calculate the theoretical P-arrival time
arrivals = TAUP_MODEL.get_travel_times(
source_depth_in_km=1E-3 * event.depth,
distance_in_degree=arcDistanceDegrees,
phase_list=["P"]
)
# Add the theorical P-arrival delta to the event time
return UTCDateTime(event.time) + arrivals[0].time
# -
# Definition of the havesine function, we pass two latitudes and longitudes and return the arc-distance in degrees. This is a supplementary function.
# ## 2.5 FDSNWS-Dataselect
#
# The main body of the script that collects an event with event identifier 20170720_0000091. We loop over all the stations returned by the getStations function within 20 degrees arc-distance of the event. In each iteration, we make a call to fdsnws-dataselect to collect the waveform data for all stations between 300 seconds before, and 1200 seconds after the theoretical P-arrival time.
#
# This data (channel BH?) is loaded in to ObsPy using the read function, filtered and plotted. After the first iteration the loop is broken. Alternatively, all data can be saved to disk.
#
# +
FDSN_DATASELECT = "http://orfeus-eu.org/fdsnws/dataselect/1/query"
EVENT_IDENTIFIER = "20170720_0000091"
# Get the event
event = getEvent(EVENT_IDENTIFIER)
# Go over all stations returned in the radius
for station in getStations(event):
# Get the theoretical (TauP) pArrval from event to station
stationArrivalTime = getPArrival(event, station)
# Create the query for fdsn-dataselect
# between 300 seconds before & 1200 seconds after the theoretical P-arrival
queryString = "&".join([
"network=%s" % station.network,
"station=%s" % station.station,
"starttime=%s" % (stationArrivalTime - 300).isoformat(),
"endtime=%s" % (stationArrivalTime + 1200).isoformat(),
"channel=BH?"
])
# Get the waveform data and read to ObsPy Stream
# Empty responses are skipped
try:
st = read("%s?%s" % (FDSN_DATASELECT, queryString))
except Exception:
continue
# Use with ObsPy and apply a filter, then plot
# Alternatively, we would save the data to a file
st.filter("lowpass", freq=0.5)
st.plot()
# Break after the first result
break
# -
# ## Acknowledgements
# Thanks to <NAME> and Seismo-Live for hosting this notebook.
|
notebooks/Workshops/ORFEUS_lisbon_2017_EIDA_webservices.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Coronavirus 2020 - effectiveness of measures taken - Germany
# See http://fangohr.github.io/coronavirus/index-germany.html for the corresponding plots for each Landkreis in Germany.
# +
# %config InlineBackend.figure_formats = ['svg']
# %matplotlib inline
# Alternative plotting backend for interative data exploration
# # %matplotlib notebook
from coronavirus import overview, fetch_data_germany, germany_get_region
# If you want to edit the source in the notebook, try "%load coronavirus.py"
# and comment out the import statement above.
# -
overview("Germany");
# # Hamburg
c, d, axes = overview("Germany", region="Hamburg");
# # <NAME>, Pinneberg
overview("Germany", subregion="LK Pinneberg");
# # Heinsberg
c, d, axes = overview("Germany", subregion="LK Heinsberg");
# # All Bundesländer in alphabetical order
# +
germany = fetch_data_germany()
laender = germany['Bundesland'].drop_duplicates().sort_values()
for land in laender:
overview('Germany', region=land)
# -
# - Acknowledgements:
# - great tutorials from https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
# - Open Source and scientific computing community for the data tools, github for hosting repository
# - Robert Koch Institute provides data for within Germany
# - Johns Hopkins University provides data for countries
# - If you want to execute this notebook, press SHIFT+RETURN to advance code cell to code cell.
# - Acknowledgements:
# - great tutorials from https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw
# - Open Source and scientific computing community for the data tools, github for hosting repository
# - Robert Koch Institute provides data for within Germany
# - Johns Hopkins University provides data for countries
#
import coronavirus
# download dates, data in Germany
print(f"Download of Johns Hopkins cases at {coronavirus.fetch_cases_last_execution()} and "
f"deaths at {coronavirus.fetch_deaths_last_execution()}.")
print(f"Download of data from Robert Koch Institute at {coronavirus.fetch_data_germany_last_execution()}.")
|
notebooks/germany.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: U4-S2-NNF-DS10
# language: python
# name: u4-s2-nnf-ds10
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/mudesir/DS-Unit-4-Sprint-3-Deep-Learning/blob/main/Copy_of_LS_DS_432_Convolution_Neural_Networks_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="fc4yMj7mtCAZ" colab_type="text"
# <img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
# <br></br>
# <br></br>
#
# ## *Data Science Unit 4 Sprint 3 Assignment 2*
# # Convolutional Neural Networks (CNNs)
# + [markdown] colab_type="text" id="0lfZdD_cp1t5"
# # Assignment
#
# - <a href="#p1">Part 1:</a> Pre-Trained Model
# - <a href="#p2">Part 2:</a> Custom CNN Model
# - <a href="#p3">Part 3:</a> CNN with Data Augmentation
#
#
# You will apply three different CNN models to a binary image classification model using Keras. Classify images of Mountains (`./data/train/mountain/*`) and images of forests (`./data/train/forest/*`). Treat mountains as the positive class (1) and the forest images as the negative (zero).
#
# |Mountain (+)|Forest (-)|
# |---|---|
# |||
#
# The problem is relatively difficult given that the sample is tiny: there are about 350 observations per class. This sample size might be something that you can expect with prototyping an image classification problem/solution at work. Get accustomed to evaluating several different possible models.
# + [markdown] colab_type="text" id="1eawBP-otCAb"
# # Pre - Trained Model
# <a id="p1"></a>
#
# Load a pretrained network from Keras, [ResNet50](https://tfhub.dev/google/imagenet/resnet_v1_50/classification/1) - a 50 layer deep network trained to recognize [1000 objects](https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt). Starting usage:
#
# ```python
# import numpy as np
#
# from tensorflow.keras.applications.resnet50 import ResNet50
# from tensorflow.keras.preprocessing import image
# from tensorflow.keras.applications.resnet50 import preprocess_input, decode_predictions
#
# from tensorflow.keras.layers import Dense, GlobalAveragePooling2D
# from tensorflow.keras.models import Model # This is the functional API
#
# resnet = ResNet50(weights='imagenet', include_top=False)
#
# ```
#
# The `include_top` parameter in `ResNet50` will remove the full connected layers from the ResNet model. The next step is to turn off the training of the ResNet layers. We want to use the learned parameters without updating them in future training passes.
#
# ```python
# for layer in resnet.layers:
# layer.trainable = False
# ```
#
# Using the Keras functional API, we will need to additional additional full connected layers to our model. We we removed the top layers, we removed all preivous fully connected layers. In other words, we kept only the feature processing portions of our network. You can expert with additional layers beyond what's listed here. The `GlobalAveragePooling2D` layer functions as a really fancy flatten function by taking the average of each of the last convolutional layer outputs (which is two dimensional still).
#
# ```python
# x = resnet.output
# x = GlobalAveragePooling2D()(x) # This layer is a really fancy flatten
# x = Dense(1024, activation='relu')(x)
# predictions = Dense(1, activation='sigmoid')(x)
# model = Model(resnet.input, predictions)
# ```
#
# Your assignment is to apply the transfer learning above to classify images of Mountains (`./data/train/mountain/*`) and images of forests (`./data/train/forest/*`). Treat mountains as the positive class (1) and the forest images as the negative (zero).
#
# Steps to complete assignment:
# 1. Load in Image Data into numpy arrays (`X`)
# 2. Create a `y` for the labels
# 3. Train your model with pre-trained layers from resnet
# 4. Report your model's accuracy
# + [markdown] id="CLdGdXCatCAb" colab_type="text"
# ## Load in Data
#
# This surprisingly more difficult than it seems, because you are working with directories of images instead of a single file. This boiler plate will help you download a zipped version of the directory of images. The directory is organized into "train" and "validation" which you can use inside an `ImageGenerator` class to stream batches of images thru your model.
#
# + [markdown] id="moRVuHUqtCAc" colab_type="text"
# ### Download & Summarize the Data
#
# This step is completed for you. Just run the cells and review the results.
# + id="AR66H8o9tCAc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 50} outputId="5205ec08-c8e0-4412-d85d-a23a43a51afd"
import tensorflow as tf
import os
_URL = 'https://github.com/LambdaSchool/DS-Unit-4-Sprint-3-Deep-Learning/blob/main/module2-convolutional-neural-networks/data.zip?raw=true'
path_to_zip = tf.keras.utils.get_file('./data.zip', origin=_URL, extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), 'data')
# + id="MNFsIu_KtCAg" colab_type="code" colab={}
train_dir = os.path.join(PATH, 'train')
validation_dir = os.path.join(PATH, 'validation')
# + id="PrKeWLiKo4cg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="7e785608-f8a6-4b8c-ed59-4718561ec359"
train_dir.shape
# + id="OsI9BQLotCAj" colab_type="code" colab={}
train_mountain_dir = os.path.join(train_dir, 'mountain') # directory with our training cat pictures
train_forest_dir = os.path.join(train_dir, 'forest') # directory with our training dog pictures
validation_mountain_dir = os.path.join(validation_dir, 'mountain') # directory with our validation cat pictures
validation_forest_dir = os.path.join(validation_dir, 'forest') # directory with our validation dog pictures
# + id="NUs1e5-XtCAl" colab_type="code" colab={}
num_mountain_tr = len(os.listdir(train_mountain_dir))
num_forest_tr = len(os.listdir(train_forest_dir))
num_mountain_val = len(os.listdir(validation_mountain_dir))
num_forest_val = len(os.listdir(validation_forest_dir))
total_train = num_mountain_tr + num_forest_tr
total_val = num_mountain_val + num_forest_val
# + id="ycI0lv0S8hdb" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b39cf07b-7126-4b74-91ad-26156fcb5a1e"
# ? validation_steps
# + id="ZmklbgSMtCAn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 134} outputId="0fb8191f-81b2-442e-e933-d58bcceb2402"
print('total training mountain images:', num_mountain_tr)
print('total training forest images:', num_forest_tr)
print('total validation mountain images:', num_mountain_val)
print('total validation forest images:', num_forest_val)
print("--")
print("Total training images:", total_train)
print("Total validation images:", total_val)
# + [markdown] id="dQ4ag4ultCAq" colab_type="text"
# ### Keras `ImageGenerator` to Process the Data
#
# This step is completed for you, but please review the code. The `ImageGenerator` class reads in batches of data from a directory and pass them to the model one batch at a time. Just like large text files, this method is advantageous, because it stifles the need to load a bunch of images into memory.
#
# Check out the documentation for this class method: [Keras `ImageGenerator` Class](https://keras.io/preprocessing/image/#imagedatagenerator-class). You'll expand it's use in the third assignment objective.
# + id="67i9IW49tCAq" colab_type="code" colab={}
batch_size = 16
epochs = 50
IMG_HEIGHT = 224
IMG_WIDTH = 224
# + id="B1wNKMo1tCAt" colab_type="code" colab={}
from tensorflow.keras.preprocessing.image import ImageDataGenerator
train_image_generator = ImageDataGenerator(rescale=1./255) # Generator for our training data
validation_image_generator = ImageDataGenerator(rescale=1./255) # Generator for our validation data
# + id="ndsuM4L9tCAv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="8586f0f1-ad1e-4b5d-c491-7ad59d5237a4"
train_data_gen = train_image_generator.flow_from_directory(batch_size=batch_size,
directory=train_dir,
shuffle=True,
target_size=(IMG_HEIGHT, IMG_WIDTH),
class_mode='binary')
# + id="9kxlk3optCAy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="86d2e17e-205f-4226-acff-4edbd0387e03"
val_data_gen = validation_image_generator.flow_from_directory(batch_size=batch_size,
directory=validation_dir,
target_size=(IMG_HEIGHT, IMG_WIDTH),
class_mode='binary')
# + [markdown] id="2l7ue6NutCA0" colab_type="text"
# ## Instatiate Model
# + id="mKNIYOEItCA0" colab_type="code" colab={}
from tensorflow.keras import datasets
from tensorflow.keras.models import Sequential, Model
from tensorflow.keras.layers import Dense, Conv2D, MaxPooling2D, Flatten, Dropout
# + id="ajKnlblqEIsk" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="2b4101f7-1ff7-49bc-e6c1-1955440ab470"
train_data_gen
# + id="2Qb-Z05W7pXJ" colab_type="code" colab={}
import imageio
import matplotlib.pyplot as plt
from skimage import color, io
from skimage.exposure import rescale_intensity
# + id="HbKHRvas5xBr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 139} outputId="7bd321f8-1bb9-44b3-967f-72f259ad1279"
class_names = ['mountain', 'forest', 'mountain', 'forest',
'mountain', 'forest', 'mountain', 'forest', 'mountain', 'forest']
plt.figure(figsize=(10,10))
for i in range(2):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_dir[i], cmap=plt.cm.binary)
# The CIFAR labels happen to be arrays,
# which is why you need the extra index
plt.xlabel(class_names[train_labels[i][0]])
plt.show()
# + id="YC3zzpnz8Ukn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="0126b323-8447-4157-e2ce-572a4f843686"
total_train/16
# + [markdown] id="BVPBWYG7tCA2" colab_type="text"
# ## Fit Model
# + id="H4XdvWA5tCA3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 454} outputId="9ea1d502-033d-4860-f33a-ea47a27d750f"
history = model.fit(
train_data_gen,
steps_per_epoch=33,
epochs=epochs,
validation_data=val_data_gen,
validation_steps=11
)
# + [markdown] id="UPzsgS94tCA5" colab_type="text"
# # Custom CNN Model
#
# In this step, write and train your own convolutional neural network using Keras. You can use any architecture that suits you as long as it has at least one convolutional and one pooling layer at the beginning of the network - you can add more if you want.
# + id="hnbJJie3tCA5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 420} outputId="4a26f9cd-3329-47be-d81f-015ba9b2774b"
# Define the Model
model = Sequential()
model.add(Conv2D(32, (3,3), activation='relu', input_shape=(32,32,3)))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3,3), activation='relu'))
model.add(MaxPooling2D((2,2)))
model.add(Conv2D(64, (3,3), activation='relu'))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(10, activation='softmax'))
model.summary()
# + id="1P_mRtoutCA9" colab_type="code" colab={}
# Compile Model
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# + id="CwM4GsaetCA_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 370} outputId="6293708d-5572-415b-87f9-037babffcd87"
# Fit Model
model.fit(train_dir, train_labels, epochs=10, validation_data=(validation_dir, validation_labels))
# + id="ceT3GrIq3r9I" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="fe90ae34-fe42-4c4d-b45b-7b0f2bdc7064"
# Evaluate Model
validation_loss, validation_acc = model.evaluate(validation_dir, validation_labels, verbose=2)
# + [markdown] id="FNTHjUddtCBB" colab_type="text"
# # Custom CNN Model with Image Manipulations
#
# To simulate an increase in a sample of image, you can apply image manipulation techniques: cropping, rotation, stretching, etc. Luckily Keras has some handy functions for us to apply these techniques to our mountain and forest example. Simply, you should be able to modify our image generator for the problem. Check out these resources to help you get started:
#
# 1. [Keras `ImageGenerator` Class](https://keras.io/preprocessing/image/#imagedatagenerator-class)
# 2. [Building a powerful image classifier with very little data](https://blog.keras.io/building-powerful-image-classification-models-using-very-little-data.html)
#
# + id="XKioBv3WtCBB" colab_type="code" colab={}
# + [markdown] colab_type="text" id="uT3UV3gap9H6"
# # Resources and Stretch Goals
#
# Stretch goals
# - Enhance your code to use classes/functions and accept terms to search and classes to look for in recognizing the downloaded images (e.g. download images of parties, recognize all that contain balloons)
# - Check out [other available pretrained networks](https://tfhub.dev), try some and compare
# - Image recognition/classification is somewhat solved, but *relationships* between entities and describing an image is not - check out some of the extended resources (e.g. [Visual Genome](https://visualgenome.org/)) on the topic
# - Transfer learning - using images you source yourself, [retrain a classifier](https://www.tensorflow.org/hub/tutorials/image_retraining) with a new category
# - (Not CNN related) Use [piexif](https://pypi.org/project/piexif/) to check out the metadata of images passed in to your system - see if they're from a national park! (Note - many images lack GPS metadata, so this won't work in most cases, but still cool)
#
# Resources
# - [Deep Residual Learning for Image Recognition](https://arxiv.org/abs/1512.03385) - influential paper (introduced ResNet)
# - [YOLO: Real-Time Object Detection](https://pjreddie.com/darknet/yolo/) - an influential convolution based object detection system, focused on inference speed (for applications to e.g. self driving vehicles)
# - [R-CNN, Fast R-CNN, Faster R-CNN, YOLO](https://towardsdatascience.com/r-cnn-fast-r-cnn-faster-r-cnn-yolo-object-detection-algorithms-36d53571365e) - comparison of object detection systems
# - [Common Objects in Context](http://cocodataset.org/) - a large-scale object detection, segmentation, and captioning dataset
# - [Visual Genome](https://visualgenome.org/) - a dataset, a knowledge base, an ongoing effort to connect structured image concepts to language
|
Copy_of_LS_DS_432_Convolution_Neural_Networks_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## This is a custom section
#
# This is part of a functional test for `rsmtool`(or `rsmeval`) on including custom sections in reports.
#
# Below we have some random stuff.
import warnings
# ## A header
warnings.warn("This is a deprecation warning", DeprecationWarning)
# ### A subheader
warnings.warn("This is a syntax warning", SyntaxWarning)
x = 5
warnings.warn("This is a unicode warning", UnicodeWarning)
|
tests/data/experiments/lr-with-warnings/custom1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _cell_guid="f2ef93cd-2bc2-4681-bc6e-9a9395b25691" _uuid="ebd8119d-fb40-454f-a46f-940e80e7f8ce"
# # Overview
#
# It only takes one toxic comment to sour an online discussion. The Conversation AI team, a research initiative founded by [Jigsaw](https://jigsaw.google.com/) and Google, builds technology to protect voices in conversation. A main area of focus is machine learning models that can identify toxicity in online conversations, where toxicity is defined as anything *rude, disrespectful or otherwise likely to make someone leave a discussion*. Our API, [Perspective](http://perspectiveapi.com/), serves these models and others in a growing set of languages (see our [documentation](https://github.com/conversationai/perspectiveapi/blob/master/2-api/models.md#all-attribute-types) for the full list). If these toxic contributions can be identified, we could have a safer, more collaborative internet.
#
# In this competition, we'll explore how models for recognizing toxicity in online conversations might generalize across different languages. Specifically, in this notebook, we'll demonstrate this with a multilingual BERT (m-BERT) model. Multilingual BERT is pretrained on monolingual data in a variety of languages, and through this learns multilingual representations of text. These multilingual representations enable *zero-shot cross-lingual transfer*, that is, by fine-tuning on a task in one language, m-BERT can learn to perform that same task in another language (for some examples, see e.g. [How multilingual is Multilingual BERT?](https://arxiv.org/abs/1906.01502)).
#
# We'll study this zero-shot transfer in the context of toxicity in online conversations, similar to past competitions we've hosted ([[1]](https://www.kaggle.com/c/jigsaw-unintended-bias-in-toxicity-classification), [[2]](https://www.kaggle.com/c/jigsaw-toxic-comment-classification-challenge)). But rather than analyzing toxicity in English as in those competitions, here we'll ask you to do it in several different languages. For training, we're including the (English) datasets from our earlier competitions, as well as a small amount of new toxicity data in other languages.
# + _cell_guid="593619be-8090-4dad-a462-e883e560ec1c" _uuid="cba509cb-708d-4fd0-8e2a-e5c1c7a0982d"
import os, time, logging
import tensorflow as tf
import tensorflow_hub as hub
from matplotlib import pyplot as plt
print(tf.version.VERSION)
tf.get_logger().setLevel(logging.ERROR)
# + [markdown] _cell_guid="ae9fd8d4-bb00-4b3d-8452-0ec605f6ebba" _uuid="add2f478-e634-42db-b3c6-732ebd484ce3"
# # TPU or GPU detection
# + _cell_guid="f5ccaf08-c532-4fde-9306-b897c890d0f8" _uuid="bc97f110-17eb-44dd-a792-d66c27a0b3a6"
# Detect hardware, return appropriate distribution strategy
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
except ValueError:
tpu = None
if tpu:
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
strategy = tf.distribute.experimental.TPUStrategy(tpu)
else:
strategy = tf.distribute.MirroredStrategy() # works on GPU and multi-GPU
policy = tf.keras.mixed_precision.experimental.Policy('mixed_float16')
tf.config.optimizer.set_jit(True) # XLA compilation
tf.keras.mixed_precision.experimental.set_policy(policy)
print('Mixed precision enabled')
print("REPLICAS: ", strategy.num_replicas_in_sync)
# mixed precision
# On TPU, bfloat16/float32 mixed precision is automatically used in TPU computations.
# Enabling it in Keras also stores relevant variables in bfloat16 format (memory optimization).
# This additional optimization was not used for TPUs in this sample.
# On GPU, specifically V100, mixed precision must be enabled for hardware TensorCores to be used.
# XLA compilation must be enabled for this to work. (On TPU, XLA compilation is the default and cannot be turned off)
# + [markdown] _cell_guid="c55830a8-39e7-4607-9691-cd0848a092f7" _uuid="b1188d07-d23d-4d04-b9f5-125d16b982ed"
# # Configuration
# Set maximum sequence length and path variables.
# + _cell_guid="7acc953d-b1f6-4d29-a006-69af6839f7a9" _uuid="7d8d39c7-1fd2-4af7-a88a-9ca1242a6277"
SEQUENCE_LENGTH = 128
# Copy of the TF Hub model at https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/1
BERT_GCS_PATH = 'gs://bert_multilingual_public/bert_multi_cased_L-12_H-768_A-12_2/'
EPOCHS = 6
# select the GCS bucket closest to your accelerator
GCS_PATH = 'gs://jigsaw_multilingual_toxic_comments_public/data' # US
#GCS_PATH = 'gs://jigsaw_multilingual_toxic_comments_public_euwest/data' # eu-west4
if tpu:
BATCH_SIZE = 128 * strategy.num_replicas_in_sync
else:
BATCH_SIZE = 64 * strategy.num_replicas_in_sync
TRAIN_DATA = GCS_PATH + "/jigsaw-toxic-comment-train-processed-seqlen{}.csv".format(SEQUENCE_LENGTH)
TRAIN_DATA_LENGTH = 223549 # rows
VALID_DATA = GCS_PATH + "/validation-processed-seqlen{}.csv".format(SEQUENCE_LENGTH)
STEPS_PER_EPOCH = TRAIN_DATA_LENGTH // BATCH_SIZE
LR_MAX = 0.001 * strategy.num_replicas_in_sync
LR_EXP_DECAY = .9
LR_MIN = 0.0001
@tf.function
def lr_fn(epoch):
lr = (LR_MAX - LR_MIN) * LR_EXP_DECAY**(epoch) + LR_MIN
return lr
print("Learning rate schedule:")
rng = [i for i in range(EPOCHS)]
y = [lr_fn(x) for x in rng]
plt.plot(rng, [lr_fn(x) for x in rng])
plt.show()
# -
# # Model
#
# Define the model. We convert m-BERT's output to a final probabilty estimate. We're using an [m-BERT model from TensorFlow Hub](https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/1).
# + _cell_guid="fcd2093b-0774-4adf-9e4c-e9096f156d32" _uuid="1392a5e0-c8e4-46ea-b45d-0d9289682e09"
def multilingual_bert_model(max_seq_length=SEQUENCE_LENGTH):
"""Build and return a multilingual BERT model and tokenizer."""
input_word_ids = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="input_word_ids")
input_mask = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="input_mask")
segment_ids = tf.keras.layers.Input(
shape=(max_seq_length,), dtype=tf.int32, name="all_segment_id")
bert_layer = tf.saved_model.load(BERT_GCS_PATH) # copy of TF Hub model 'https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/1'
bert_layer = hub.KerasLayer(bert_layer, trainable=True)
pooled_output, _ = bert_layer([input_word_ids, input_mask, segment_ids])
output = tf.keras.layers.Dense(32, activation='relu')(pooled_output)
output = tf.keras.layers.Dense(1, activation='sigmoid', name='labels', dtype=tf.float32)(output)
return tf.keras.Model(inputs={'input_word_ids': input_word_ids,
'input_mask': input_mask,
'all_segment_id': segment_ids},
outputs=output)
# + [markdown] _cell_guid="48479a32-25c1-40c9-bd1c-d076eb39d86e" _uuid="b24c47ad-a156-41f2-97b8-f5618181382c"
# # Dataset
# Load the preprocessed dataset. See the demo notebook for sample code for performing this preprocessing.
# +
def parse_string_list_into_ints(strlist):
s = tf.strings.strip(strlist)
s = tf.strings.substr(
strlist, 1, tf.strings.length(s) - 2) # Remove parentheses around list
s = tf.strings.split(s, ',', maxsplit=SEQUENCE_LENGTH)
s = tf.strings.to_number(s, tf.int32)
s = tf.reshape(s, [SEQUENCE_LENGTH]) # Force shape here needed for XLA compilation (TPU)
return s
def format_sentences(data, label='toxic', remove_language=False):
labels = {'labels': data.pop(label)}
if remove_language:
languages = {'language': data.pop('lang')}
# The remaining three items in the dict parsed from the CSV are lists of integers
for k,v in data.items(): # "input_word_ids", "input_mask", "all_segment_id"
data[k] = parse_string_list_into_ints(v)
return data, labels
def make_sentence_dataset_from_csv(filename, label='toxic', language_to_filter=None):
# This assumes the column order label, input_word_ids, input_mask, segment_ids
SELECTED_COLUMNS = [label, "input_word_ids", "input_mask", "all_segment_id"]
label_default = tf.int32 if label == 'id' else tf.float32
COLUMN_DEFAULTS = [label_default, tf.string, tf.string, tf.string]
if language_to_filter:
insert_pos = 0 if label != 'id' else 1
SELECTED_COLUMNS.insert(insert_pos, 'lang')
COLUMN_DEFAULTS.insert(insert_pos, tf.string)
preprocessed_sentences_dataset = tf.data.experimental.make_csv_dataset(
filename, column_defaults=COLUMN_DEFAULTS, select_columns=SELECTED_COLUMNS,
batch_size=1, num_epochs=1, shuffle=False) # We'll do repeating and shuffling ourselves
# make_csv_dataset required a batch size, but we want to batch later
preprocessed_sentences_dataset = preprocessed_sentences_dataset.unbatch()
if language_to_filter:
preprocessed_sentences_dataset = preprocessed_sentences_dataset.filter(
lambda data: tf.math.equal(data['lang'], tf.constant(language_to_filter)))
#preprocessed_sentences.pop('lang')
preprocessed_sentences_dataset = preprocessed_sentences_dataset.map(
lambda data: format_sentences(data, label=label,
remove_language=language_to_filter))
return preprocessed_sentences_dataset
# + [markdown] _cell_guid="e006f30f-6350-45d5-b452-338c4bc78cc5" _uuid="10ff216a-2248-4104-858c-2b2461b42fba"
# Set up our data pipelines for training and evaluation.
# + _cell_guid="b17b24d7-1b0f-442b-bfd2-c42748bcd067" _uuid="864f31ac-8285-442b-93cf-dcae11d7fe62"
def make_dataset_pipeline(dataset, repeat_and_shuffle=True):
"""Set up the pipeline for the given dataset.
Caches, repeats, shuffles, and sets the pipeline up to prefetch batches."""
cached_dataset = dataset.cache()
if repeat_and_shuffle:
cached_dataset = cached_dataset.repeat().shuffle(2048)
cached_dataset = cached_dataset.batch(BATCH_SIZE, drop_remainder=True) # no remainder on repeated dataset
else:
cached_dataset = cached_dataset.batch(BATCH_SIZE)
cached_dataset = cached_dataset.prefetch(tf.data.experimental.AUTOTUNE)
return cached_dataset
# Load the preprocessed English dataframe.
preprocessed_en_filename = TRAIN_DATA
# Set up the dataset and pipeline.
english_train_dataset = make_dataset_pipeline(
make_sentence_dataset_from_csv(preprocessed_en_filename))
# Process the new datasets by language.
preprocessed_val_filename = VALID_DATA
nonenglish_val_datasets = {}
for language_name, language_label in [('Spanish', 'es'), ('Italian', 'it'),
('Turkish', 'tr')]:
nonenglish_val_datasets[language_name] = make_sentence_dataset_from_csv(
preprocessed_val_filename, language_to_filter=language_label)
nonenglish_val_datasets[language_name] = make_dataset_pipeline(
nonenglish_val_datasets[language_name], repeat_and_shuffle=False)
nonenglish_val_datasets['Combined'] = make_sentence_dataset_from_csv(preprocessed_val_filename)
nonenglish_val_datasets['Combined'] = make_dataset_pipeline(nonenglish_val_datasets['Combined'], repeat_and_shuffle=False)
# + [markdown] _cell_guid="ffd5c9ef-a806-4ae6-a1c5-8723ed822232" _uuid="0779be08-0502-47c0-b284-5f3d851de2e1"
# # Instantiate the model
#
# Compile our model. We will fine-tune the multilingual model on one of our English datasets, and then evaluate its performance on the new multilingual toxicity data. As our metric, we'll use the [AUC](https://www.tensorflow.org/api_docs/python/tf/keras/metrics/AUC).
# + _cell_guid="422a984e-e571-4898-9667-b95d38416ddd" _uuid="e3d569ca-0bf4-4bde-aa69-95a46908f65a"
with strategy.scope():
multilingual_bert = multilingual_bert_model()
# Compile the model. Optimize using stochastic gradient descent.
multilingual_bert.compile(
loss=tf.keras.losses.BinaryCrossentropy(),
optimizer=tf.keras.optimizers.SGD(learning_rate=0.001*strategy.num_replicas_in_sync),
metrics=[tf.keras.metrics.AUC()])
multilingual_bert.summary()
# + _cell_guid="f477d7f4-20ec-4858-87d6-c041313ad276" _uuid="730e2b4b-6e7c-43f3-912e-3cbea3db62c2"
# %%time
# Train on English Wikipedia comment data.
lr_callback = tf.keras.callbacks.LearningRateScheduler(lr_fn)
history = multilingual_bert.fit(
english_train_dataset, steps_per_epoch=STEPS_PER_EPOCH, epochs=EPOCHS,
#validation_data=nonenglish_val_datasets['Combined'],
callbacks=[lr_callback])
# -
# Performance on non-English comments after training.
for language in nonenglish_val_datasets:
results = multilingual_bert.evaluate(nonenglish_val_datasets[language], verbose=0)
print('{} loss, AUC after training:'.format(language), results)
# # License
# Copyright 2020 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#
#
# ---
#
#
# This is not an official Google product but sample code provided for an educational purpose
#
|
courses/fast-and-lean-data-science/benchmark_keras_multilingual_bert.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import csv
import os
from slugify import slugify
with open("bus_by_networks.csv", 'r') as in_file:
tt = csv.DictReader(in_file)
all_lines= list(tt)
#all_lines
all_networks = list(set([elem['agency_name'] for elem in all_lines]))
len(all_networks)
# +
def create_settings_content(network_name, folder_name):
content = """
#!/bin/bash
#
# set variales for analysis of network
#
PREFIX="{}"
OVERPASS_QUERY="http://overpass-api.de/api/interpreter?data=area[wikidata=Q13917][type=boundary];(rel(area)[route~'bus'];rel(br);rel[type='route'](r);)->.routes;(.routes;<<;rel(r.routes);way(r.routes);node(r.routes););out;"
NETWORK_LONG=""
NETWORK_SHORT="{}"
ANALYSIS_PAGE=""
ANALYSIS_TALK=""
#
# Routes data is in GitHub only, not in OSM-Wiki
#
WIKI_ROUTES_PAGE=""
ANALYSIS_OPTIONS="--check-access --check-bus-stop --check-name --check-osm-separator --check-sequence --check-stop-position --check-version --coloured-sketchline --check-motorway-link --max-error=10 --multiple-ref-type-entries=analyze --positive-notes"
# --language=en
# --check-bus-stop
# --expect-network-short
# --expect-network-long
# --expect-network-short-for=
# --expect-network-long-for=
# --relaxed-begin-end-for=
""".format(folder_name, network_name)
return content
def create_lines_list(network_name, line_list):
content = """
#
# This data is *not* stored in the OSM Wiki but in GitHub
#
# Format: format is like in the OSM Wiki
#
# Links: [[...|...]] are interne link like in the OSM Wiki
# [... ...] are external links
#
# Headers start with '=', '==', '===', '====', ... at the beginning of a line
#
# Simple text starts with '-' at the beginning of a line.
# A single '-' at the beginning of a line, followed by nothing:
# - if there was simple text before, it creates a line feed (i.e. encloses the text in a paragraph <p> ... </p>)
# - if there was no simple text before or a line feed, it creates an empty line (i.e. <p>&nbsp;</p>)
#
# !!!Text yellow background!!! in simple text or headers
# '''''Text mit bold and italics''''' in simple text or headers
# '''Text with bold chars''' in simple text or headers
# ''Text with italic chars'' in simple text or headers
#
# Comments start with '#' at the beginning of a line. '#' inside text is not recognized as the start of a comment, i.e.. '#' may occur inside of text.
#
# Format of the file: UTF-8
#
#
# Contents in CSV-Format - if ';' is part of the field, then enclose that field in "..."
#
# ref;type;comment;from;to;operator
#
# - ref == tag 'ref' of route or route_master
# 250 defines that routes with 'ref'='250' are expected
# 250|250a|250b defines that routes with 'ref'='250' or 'ref'='250a' or 'ref'='250b' are expected - independent of whether this is allowed according to PTv1/PTv2
# - type == contents of tags 'route' respectively 'route_master'
# - comment == can include comments like; Bus, Expressbus, ... will not be analyzed, but simply be printed out
# !Text with yellow background! in comment (surrounded by single !)
# - from == if there is more than one entry with "ref;type" and "operator" is the same, then 'from' and 'to are also used to distinguish between same line number in different cities/villages
# - to == if there is more than one entry with "ref;type" and "operator" is the same, then 'from' and 'to are also used to distinguish between same line number in different cities/villages
# - operator == if there is more than one entry with "ref;type", then "operator" is used to distinguish between same line number in different cities/villages
#
= Overview on '''{}''' Public Transport Lines
-
- '''!!!This summary is a list of what has been published in open data by Île-de-France Mobilités and found in OSM!!!'''
-
- Feel free to modify the list on github
-
#
#ref;type;comment;from;to;operator
== Lines""".format(network_name)
sorted_line_list = sorted(line_list, key=lambda k: k['route_short_name'])
for a_line in sorted_line_list:
content += "\n{};{};;;;".format(a_line['route_short_name'], a_line['osm_transport_mode'])
return content
# -
for a_network in all_networks:
if a_network in ['RATP', 'SNCF', 'SNCF/RATP']:
continue
lines = [elem for elem in all_lines if elem['agency_name'] == a_network]
if len(lines) >= 10:
print(a_network)
folder_name = "FR-IDF-{}".format(slugify(a_network))
folder_path = os.path.join(os.getcwd(),folder_name)
os.makedirs(folder_path)
content = create_settings_content(a_network, folder_name)
with open(os.path.join(folder_path,"settings.sh"),"w") as setting_file:
setting_file.write(content)
content = create_lines_list(a_network, lines)
file_name = "{}-Routes.txt".format(folder_name)
with open(os.path.join(folder_path,file_name),"w") as route_file:
route_file.write(content)
|
ptna_idf/ptna_generate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Chapter 18 – Reinforcement Learning**
# _This notebook contains all the sample code in chapter 18_.
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/ageron/handson-ml2/blob/master/18_reinforcement_learning.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# </td>
# <td>
# <a target="_blank" href="https://kaggle.com/kernels/welcome?src=https://github.com/ageron/handson-ml2/blob/add-kaggle-badge/18_reinforcement_learning.ipynb"><img src="https://kaggle.com/static/images/open-in-kaggle.svg" /></a>
# </td>
# </table>
# # Cài đặt
# Đầu tiên hãy nhập một vài mô-đun thông dụng, đảm bảo rằng Matplotlib sẽ vẽ đồ thị ngay trong notebook, và chuẩn bị một hàm để lưu đồ thị. Ta cũng kiểm tra xem Python phiên bản từ 3.5 trở lên đã được cài đặt hay chưa (mặc dù Python 2.x vẫn có thể hoạt động, phiên bản này đã bị deprecated nên chúng tôi rất khuyến khích việc sử dụng Python 3), cũng như Scikit-Learn ≥ 0.20.
# +
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Is this notebook running on Colab or Kaggle?
IS_COLAB = "google.colab" in sys.modules
IS_KAGGLE = "kaggle_secrets" in sys.modules
if IS_COLAB or IS_KAGGLE:
# !apt update && apt install -y libpq-dev libsdl2-dev swig xorg-dev xvfb
# !pip install -q -U tf-agents pyvirtualdisplay gym[atari,box2d]
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# TensorFlow ≥2.0 is required
import tensorflow as tf
from tensorflow import keras
assert tf.__version__ >= "2.0"
if not tf.config.list_physical_devices('GPU'):
print("No GPU was detected. CNNs can be very slow without a GPU.")
if IS_COLAB:
print("Go to Runtime > Change runtime and select a GPU hardware accelerator.")
if IS_KAGGLE:
print("Go to Settings > Accelerator and select GPU.")
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
tf.random.set_seed(42)
# To plot pretty figures
# %matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
# To get smooth animations
import matplotlib.animation as animation
mpl.rc('animation', html='jshtml')
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "rl"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
# -
# # Introduction to OpenAI gym
# In this notebook we will be using [OpenAI gym](https://gym.openai.com/), a great toolkit for developing and comparing Reinforcement Learning algorithms. It provides many environments for your learning *agents* to interact with. Let's start by importing `gym`:
import gym
# Let's list all the available environments:
gym.envs.registry.all()
# The Cart-Pole is a very simple environment composed of a cart that can move left or right, and pole placed vertically on top of it. The agent must move the cart left or right to keep the pole upright.
env = gym.make('CartPole-v1')
# Let's initialize the environment by calling is `reset()` method. This returns an observation:
env.seed(42)
obs = env.reset()
# Observations vary depending on the environment. In this case it is a 1D NumPy array composed of 4 floats: they represent the cart's horizontal position, its velocity, the angle of the pole (0 = vertical), and the angular velocity.
obs
# An environment can be visualized by calling its `render()` method, and you can pick the rendering mode (the rendering options depend on the environment).
# **Warning**: some environments (including the Cart-Pole) require access to your display, which opens up a separate window, even if you specify `mode="rgb_array"`. In general you can safely ignore that window. However, if Jupyter is running on a headless server (ie. without a screen) it will raise an exception. One way to avoid this is to install a fake X server like [Xvfb](http://en.wikipedia.org/wiki/Xvfb). On Debian or Ubuntu:
#
# ```bash
# $ apt update
# $ apt install -y xvfb
# ```
#
# You can then start Jupyter using the `xvfb-run` command:
#
# ```bash
# $ xvfb-run -s "-screen 0 1400x900x24" jupyter notebook
# ```
#
# Alternatively, you can install the [pyvirtualdisplay](https://github.com/ponty/pyvirtualdisplay) Python library which wraps Xvfb:
#
# ```bash
# python3 -m pip install -U pyvirtualdisplay
# ```
#
# And run the following code:
try:
import pyvirtualdisplay
display = pyvirtualdisplay.Display(visible=0, size=(1400, 900)).start()
except ImportError:
pass
env.render()
# In this example we will set `mode="rgb_array"` to get an image of the environment as a NumPy array:
img = env.render(mode="rgb_array")
img.shape
def plot_environment(env, figsize=(5,4)):
plt.figure(figsize=figsize)
img = env.render(mode="rgb_array")
plt.imshow(img)
plt.axis("off")
return img
plot_environment(env)
plt.show()
# Let's see how to interact with an environment. Your agent will need to select an action from an "action space" (the set of possible actions). Let's see what this environment's action space looks like:
env.action_space
# Yep, just two possible actions: accelerate towards the left or towards the right.
# Since the pole is leaning toward the right (`obs[2] > 0`), let's accelerate the cart toward the right:
action = 1 # accelerate right
obs, reward, done, info = env.step(action)
obs
# Notice that the cart is now moving toward the right (`obs[1] > 0`). The pole is still tilted toward the right (`obs[2] > 0`), but its angular velocity is now negative (`obs[3] < 0`), so it will likely be tilted toward the left after the next step.
plot_environment(env)
save_fig("cart_pole_plot")
# Looks like it's doing what we're telling it to do!
# The environment also tells the agent how much reward it got during the last step:
reward
# When the game is over, the environment returns `done=True`:
done
# Finally, `info` is an environment-specific dictionary that can provide some extra information that you may find useful for debugging or for training. For example, in some games it may indicate how many lives the agent has.
info
# The sequence of steps between the moment the environment is reset until it is done is called an "episode". At the end of an episode (i.e., when `step()` returns `done=True`), you should reset the environment before you continue to use it.
if done:
obs = env.reset()
# Now how can we make the poll remain upright? We will need to define a _policy_ for that. This is the strategy that the agent will use to select an action at each step. It can use all the past actions and observations to decide what to do.
# # A simple hard-coded policy
# Let's hard code a simple strategy: if the pole is tilting to the left, then push the cart to the left, and _vice versa_. Let's see if that works:
# +
env.seed(42)
def basic_policy(obs):
angle = obs[2]
return 0 if angle < 0 else 1
totals = []
for episode in range(500):
episode_rewards = 0
obs = env.reset()
for step in range(200):
action = basic_policy(obs)
obs, reward, done, info = env.step(action)
episode_rewards += reward
if done:
break
totals.append(episode_rewards)
# -
np.mean(totals), np.std(totals), np.min(totals), np.max(totals)
# Well, as expected, this strategy is a bit too basic: the best it did was to keep the poll up for only 68 steps. This environment is considered solved when the agent keeps the poll up for 200 steps.
# Let's visualize one episode:
# +
env.seed(42)
frames = []
obs = env.reset()
for step in range(200):
img = env.render(mode="rgb_array")
frames.append(img)
action = basic_policy(obs)
obs, reward, done, info = env.step(action)
if done:
break
# -
# Now show the animation:
# +
def update_scene(num, frames, patch):
patch.set_data(frames[num])
return patch,
def plot_animation(frames, repeat=False, interval=40):
fig = plt.figure()
patch = plt.imshow(frames[0])
plt.axis('off')
anim = animation.FuncAnimation(
fig, update_scene, fargs=(frames, patch),
frames=len(frames), repeat=repeat, interval=interval)
plt.close()
return anim
# -
plot_animation(frames)
# Clearly the system is unstable and after just a few wobbles, the pole ends up too tilted: game over. We will need to be smarter than that!
# # Neural Network Policies
# Let's create a neural network that will take observations as inputs, and output the probabilities of actions to take for each observation. To choose an action, the network will estimate a probability for each action, then we will select an action randomly according to the estimated probabilities. In the case of the Cart-Pole environment, there are just two possible actions (left or right), so we only need one output neuron: it will output the probability `p` of the action 0 (left), and of course the probability of action 1 (right) will be `1 - p`.
# +
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
n_inputs = 4 # == env.observation_space.shape[0]
model = keras.models.Sequential([
keras.layers.Dense(5, activation="elu", input_shape=[n_inputs]),
keras.layers.Dense(1, activation="sigmoid"),
])
# -
# In this particular environment, the past actions and observations can safely be ignored, since each observation contains the environment's full state. If there were some hidden state then you may need to consider past actions and observations in order to try to infer the hidden state of the environment. For example, if the environment only revealed the position of the cart but not its velocity, you would have to consider not only the current observation but also the previous observation in order to estimate the current velocity. Another example is if the observations are noisy: you may want to use the past few observations to estimate the most likely current state. Our problem is thus as simple as can be: the current observation is noise-free and contains the environment's full state.
# You may wonder why we plan to pick a random action based on the probability given by the policy network, rather than just picking the action with the highest probability. This approach lets the agent find the right balance between _exploring_ new actions and _exploiting_ the actions that are known to work well. Here's an analogy: suppose you go to a restaurant for the first time, and all the dishes look equally appealing so you randomly pick one. If it turns out to be good, you can increase the probability to order it next time, but you shouldn't increase that probability to 100%, or else you will never try out the other dishes, some of which may be even better than the one you tried.
# Let's write a small function that will run the model to play one episode, and return the frames so we can display an animation:
def render_policy_net(model, n_max_steps=200, seed=42):
frames = []
env = gym.make("CartPole-v1")
env.seed(seed)
np.random.seed(seed)
obs = env.reset()
for step in range(n_max_steps):
frames.append(env.render(mode="rgb_array"))
left_proba = model.predict(obs.reshape(1, -1))
action = int(np.random.rand() > left_proba)
obs, reward, done, info = env.step(action)
if done:
break
env.close()
return frames
# Now let's look at how well this randomly initialized policy network performs:
frames = render_policy_net(model)
plot_animation(frames)
# Yeah... pretty bad. The neural network will have to learn to do better. First let's see if it is capable of learning the basic policy we used earlier: go left if the pole is tilting left, and go right if it is tilting right.
# We can make the same net play in 50 different environments in parallel (this will give us a diverse training batch at each step), and train for 5000 iterations. We also reset environments when they are done. We train the model using a custom training loop so we can easily use the predictions at each training step to advance the environments.
# +
n_environments = 50
n_iterations = 5000
envs = [gym.make("CartPole-v1") for _ in range(n_environments)]
for index, env in enumerate(envs):
env.seed(index)
np.random.seed(42)
observations = [env.reset() for env in envs]
optimizer = keras.optimizers.RMSprop()
loss_fn = keras.losses.binary_crossentropy
for iteration in range(n_iterations):
# if angle < 0, we want proba(left) = 1., or else proba(left) = 0.
target_probas = np.array([([1.] if obs[2] < 0 else [0.])
for obs in observations])
with tf.GradientTape() as tape:
left_probas = model(np.array(observations))
loss = tf.reduce_mean(loss_fn(target_probas, left_probas))
print("\rIteration: {}, Loss: {:.3f}".format(iteration, loss.numpy()), end="")
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
actions = (np.random.rand(n_environments, 1) > left_probas.numpy()).astype(np.int32)
for env_index, env in enumerate(envs):
obs, reward, done, info = env.step(actions[env_index][0])
observations[env_index] = obs if not done else env.reset()
for env in envs:
env.close()
# -
frames = render_policy_net(model)
plot_animation(frames)
# Looks like it learned the policy correctly. Now let's see if it can learn a better policy on its own. One that does not wobble as much.
# # Policy Gradients
# To train this neural network we will need to define the target probabilities `y`. If an action is good we should increase its probability, and conversely if it is bad we should reduce it. But how do we know whether an action is good or bad? The problem is that most actions have delayed effects, so when you win or lose points in an episode, it is not clear which actions contributed to this result: was it just the last action? Or the last 10? Or just one action 50 steps earlier? This is called the _credit assignment problem_.
#
# The _Policy Gradients_ algorithm tackles this problem by first playing multiple episodes, then making the actions in good episodes slightly more likely, while actions in bad episodes are made slightly less likely. First we play, then we go back and think about what we did.
# Let's start by creating a function to play a single step using the model. We will also pretend for now that whatever action it takes is the right one, so we can compute the loss and its gradients (we will just save these gradients for now, and modify them later depending on how good or bad the action turned out to be):
def play_one_step(env, obs, model, loss_fn):
with tf.GradientTape() as tape:
left_proba = model(obs[np.newaxis])
action = (tf.random.uniform([1, 1]) > left_proba)
y_target = tf.constant([[1.]]) - tf.cast(action, tf.float32)
loss = tf.reduce_mean(loss_fn(y_target, left_proba))
grads = tape.gradient(loss, model.trainable_variables)
obs, reward, done, info = env.step(int(action[0, 0].numpy()))
return obs, reward, done, grads
# If `left_proba` is high, then `action` will most likely be `False` (since a random number uniformally sampled between 0 and 1 will probably not be greater than `left_proba`). And `False` means 0 when you cast it to a number, so `y_target` would be equal to 1 - 0 = 1. In other words, we set the target to 1, meaning we pretend that the probability of going left should have been 100% (so we took the right action).
# Now let's create another function that will rely on the `play_one_step()` function to play multiple episodes, returning all the rewards and gradients, for each episode and each step:
def play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
all_rewards = []
all_grads = []
for episode in range(n_episodes):
current_rewards = []
current_grads = []
obs = env.reset()
for step in range(n_max_steps):
obs, reward, done, grads = play_one_step(env, obs, model, loss_fn)
current_rewards.append(reward)
current_grads.append(grads)
if done:
break
all_rewards.append(current_rewards)
all_grads.append(current_grads)
return all_rewards, all_grads
# The Policy Gradients algorithm uses the model to play the episode several times (e.g., 10 times), then it goes back and looks at all the rewards, discounts them and normalizes them. So let's create couple functions for that: the first will compute discounted rewards; the second will normalize the discounted rewards across many episodes.
# +
def discount_rewards(rewards, discount_rate):
discounted = np.array(rewards)
for step in range(len(rewards) - 2, -1, -1):
discounted[step] += discounted[step + 1] * discount_rate
return discounted
def discount_and_normalize_rewards(all_rewards, discount_rate):
all_discounted_rewards = [discount_rewards(rewards, discount_rate)
for rewards in all_rewards]
flat_rewards = np.concatenate(all_discounted_rewards)
reward_mean = flat_rewards.mean()
reward_std = flat_rewards.std()
return [(discounted_rewards - reward_mean) / reward_std
for discounted_rewards in all_discounted_rewards]
# -
# Say there were 3 actions, and after each action there was a reward: first 10, then 0, then -50. If we use a discount factor of 80%, then the 3rd action will get -50 (full credit for the last reward), but the 2nd action will only get -40 (80% credit for the last reward), and the 1st action will get 80% of -40 (-32) plus full credit for the first reward (+10), which leads to a discounted reward of -22:
discount_rewards([10, 0, -50], discount_rate=0.8)
# To normalize all discounted rewards across all episodes, we compute the mean and standard deviation of all the discounted rewards, and we subtract the mean from each discounted reward, and divide by the standard deviation:
discount_and_normalize_rewards([[10, 0, -50], [10, 20]], discount_rate=0.8)
n_iterations = 150
n_episodes_per_update = 10
n_max_steps = 200
discount_rate = 0.95
optimizer = keras.optimizers.Adam(lr=0.01)
loss_fn = keras.losses.binary_crossentropy
# +
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
model = keras.models.Sequential([
keras.layers.Dense(5, activation="elu", input_shape=[4]),
keras.layers.Dense(1, activation="sigmoid"),
])
# +
env = gym.make("CartPole-v1")
env.seed(42);
for iteration in range(n_iterations):
all_rewards, all_grads = play_multiple_episodes(
env, n_episodes_per_update, n_max_steps, model, loss_fn)
total_rewards = sum(map(sum, all_rewards)) # Not shown in the book
print("\rIteration: {}, mean rewards: {:.1f}".format( # Not shown
iteration, total_rewards / n_episodes_per_update), end="") # Not shown
all_final_rewards = discount_and_normalize_rewards(all_rewards,
discount_rate)
all_mean_grads = []
for var_index in range(len(model.trainable_variables)):
mean_grads = tf.reduce_mean(
[final_reward * all_grads[episode_index][step][var_index]
for episode_index, final_rewards in enumerate(all_final_rewards)
for step, final_reward in enumerate(final_rewards)], axis=0)
all_mean_grads.append(mean_grads)
optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))
env.close()
# -
frames = render_policy_net(model)
plot_animation(frames)
# # Markov Chains
# +
np.random.seed(42)
transition_probabilities = [ # shape=[s, s']
[0.7, 0.2, 0.0, 0.1], # from s0 to s0, s1, s2, s3
[0.0, 0.0, 0.9, 0.1], # from s1 to ...
[0.0, 1.0, 0.0, 0.0], # from s2 to ...
[0.0, 0.0, 0.0, 1.0]] # from s3 to ...
n_max_steps = 50
def print_sequence():
current_state = 0
print("States:", end=" ")
for step in range(n_max_steps):
print(current_state, end=" ")
if current_state == 3:
break
current_state = np.random.choice(range(4), p=transition_probabilities[current_state])
else:
print("...", end="")
print()
for _ in range(10):
print_sequence()
# -
# # Markov Decision Process
# Let's define some transition probabilities, rewards and possible actions. For example, in state s0, if action a0 is chosen then with proba 0.7 we will go to state s0 with reward +10, with probability 0.3 we will go to state s1 with no reward, and with never go to state s2 (so the transition probabilities are `[0.7, 0.3, 0.0]`, and the rewards are `[+10, 0, 0]`):
transition_probabilities = [ # shape=[s, a, s']
[[0.7, 0.3, 0.0], [1.0, 0.0, 0.0], [0.8, 0.2, 0.0]],
[[0.0, 1.0, 0.0], None, [0.0, 0.0, 1.0]],
[None, [0.8, 0.1, 0.1], None]]
rewards = [ # shape=[s, a, s']
[[+10, 0, 0], [0, 0, 0], [0, 0, 0]],
[[0, 0, 0], [0, 0, 0], [0, 0, -50]],
[[0, 0, 0], [+40, 0, 0], [0, 0, 0]]]
possible_actions = [[0, 1, 2], [0, 2], [1]]
# # Q-Value Iteration
Q_values = np.full((3, 3), -np.inf) # -np.inf for impossible actions
for state, actions in enumerate(possible_actions):
Q_values[state, actions] = 0.0 # for all possible actions
# +
gamma = 0.90 # the discount factor
history1 = [] # Not shown in the book (for the figure below)
for iteration in range(50):
Q_prev = Q_values.copy()
history1.append(Q_prev) # Not shown
for s in range(3):
for a in possible_actions[s]:
Q_values[s, a] = np.sum([
transition_probabilities[s][a][sp]
* (rewards[s][a][sp] + gamma * np.max(Q_prev[sp]))
for sp in range(3)])
history1 = np.array(history1) # Not shown
# -
Q_values
np.argmax(Q_values, axis=1)
# The optimal policy for this MDP, when using a discount factor of 0.90, is to choose action a0 when in state s0, and choose action a0 when in state s1, and finally choose action a1 (the only possible action) when in state s2.
# Let's try again with a discount factor of 0.95:
Q_values = np.full((3, 3), -np.inf) # -np.inf for impossible actions
for state, actions in enumerate(possible_actions):
Q_values[state, actions] = 0.0 # for all possible actions
# +
gamma = 0.95 # the discount factor
for iteration in range(50):
Q_prev = Q_values.copy()
for s in range(3):
for a in possible_actions[s]:
Q_values[s, a] = np.sum([
transition_probabilities[s][a][sp]
* (rewards[s][a][sp] + gamma * np.max(Q_prev[sp]))
for sp in range(3)])
# -
Q_values
np.argmax(Q_values, axis=1)
# Now the policy has changed! In state s1, we now prefer to go through the fire (choose action a2). This is because the discount factor is larger so the agent values the future more, and it is therefore ready to pay an immediate penalty in order to get more future rewards.
# # Q-Learning
# Q-Learning works by watching an agent play (e.g., randomly) and gradually improving its estimates of the Q-Values. Once it has accurate Q-Value estimates (or close enough), then the optimal policy consists in choosing the action that has the highest Q-Value (i.e., the greedy policy).
# We will need to simulate an agent moving around in the environment, so let's define a function to perform some action and get the new state and a reward:
def step(state, action):
probas = transition_probabilities[state][action]
next_state = np.random.choice([0, 1, 2], p=probas)
reward = rewards[state][action][next_state]
return next_state, reward
# We also need an exploration policy, which can be any policy, as long as it visits every possible state many times. We will just use a random policy, since the state space is very small:
def exploration_policy(state):
return np.random.choice(possible_actions[state])
# Now let's initialize the Q-Values like earlier, and run the Q-Learning algorithm:
# +
np.random.seed(42)
Q_values = np.full((3, 3), -np.inf)
for state, actions in enumerate(possible_actions):
Q_values[state][actions] = 0
alpha0 = 0.05 # initial learning rate
decay = 0.005 # learning rate decay
gamma = 0.90 # discount factor
state = 0 # initial state
history2 = [] # Not shown in the book
for iteration in range(10000):
history2.append(Q_values.copy()) # Not shown
action = exploration_policy(state)
next_state, reward = step(state, action)
next_value = np.max(Q_values[next_state]) # greedy policy at the next step
alpha = alpha0 / (1 + iteration * decay)
Q_values[state, action] *= 1 - alpha
Q_values[state, action] += alpha * (reward + gamma * next_value)
state = next_state
history2 = np.array(history2) # Not shown
# -
Q_values
np.argmax(Q_values, axis=1) # optimal action for each state
# +
true_Q_value = history1[-1, 0, 0]
fig, axes = plt.subplots(1, 2, figsize=(10, 4), sharey=True)
axes[0].set_ylabel("Q-Value$(s_0, a_0)$", fontsize=14)
axes[0].set_title("Q-Value Iteration", fontsize=14)
axes[1].set_title("Q-Learning", fontsize=14)
for ax, width, history in zip(axes, (50, 10000), (history1, history2)):
ax.plot([0, width], [true_Q_value, true_Q_value], "k--")
ax.plot(np.arange(width), history[:, 0, 0], "b-", linewidth=2)
ax.set_xlabel("Iterations", fontsize=14)
ax.axis([0, width, 0, 24])
save_fig("q_value_plot")
# -
# # Deep Q-Network
# Let's build the DQN. Given a state, it will estimate, for each possible action, the sum of discounted future rewards it can expect after it plays that action (but before it sees its outcome):
# +
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
env = gym.make("CartPole-v1")
input_shape = [4] # == env.observation_space.shape
n_outputs = 2 # == env.action_space.n
model = keras.models.Sequential([
keras.layers.Dense(32, activation="elu", input_shape=input_shape),
keras.layers.Dense(32, activation="elu"),
keras.layers.Dense(n_outputs)
])
# -
# To select an action using this DQN, we just pick the action with the largest predicted Q-value. However, to ensure that the agent explores the environment, we choose a random action with probability `epsilon`.
def epsilon_greedy_policy(state, epsilon=0):
if np.random.rand() < epsilon:
return np.random.randint(n_outputs)
else:
Q_values = model.predict(state[np.newaxis])
return np.argmax(Q_values[0])
# We will also need a replay memory. It will contain the agent's experiences, in the form of tuples: `(obs, action, reward, next_obs, done)`. We can use the `deque` class for that (but make sure to check out DeepMind's excellent [Reverb library](https://github.com/deepmind/reverb) for a much more robust implementation of experience replay):
# +
from collections import deque
replay_memory = deque(maxlen=2000)
# -
# And let's create a function to sample experiences from the replay memory. It will return 5 NumPy arrays: `[obs, actions, rewards, next_obs, dones]`.
def sample_experiences(batch_size):
indices = np.random.randint(len(replay_memory), size=batch_size)
batch = [replay_memory[index] for index in indices]
states, actions, rewards, next_states, dones = [
np.array([experience[field_index] for experience in batch])
for field_index in range(5)]
return states, actions, rewards, next_states, dones
# Now we can create a function that will use the DQN to play one step, and record its experience in the replay memory:
def play_one_step(env, state, epsilon):
action = epsilon_greedy_policy(state, epsilon)
next_state, reward, done, info = env.step(action)
replay_memory.append((state, action, reward, next_state, done))
return next_state, reward, done, info
# Lastly, let's create a function that will sample some experiences from the replay memory and perform a training step:
#
# **Notes**:
# * The first 3 releases of the 2nd edition were missing the `reshape()` operation which converts `target_Q_values` to a column vector (this is required by the `loss_fn()`).
# * The book uses a learning rate of 1e-3, but in the code below I use 1e-2, as it significantly improves training. I also tuned the learning rates of the DQN variants below.
# +
batch_size = 32
discount_rate = 0.95
optimizer = keras.optimizers.Adam(lr=1e-2)
loss_fn = keras.losses.mean_squared_error
def training_step(batch_size):
experiences = sample_experiences(batch_size)
states, actions, rewards, next_states, dones = experiences
next_Q_values = model.predict(next_states)
max_next_Q_values = np.max(next_Q_values, axis=1)
target_Q_values = (rewards +
(1 - dones) * discount_rate * max_next_Q_values)
target_Q_values = target_Q_values.reshape(-1, 1)
mask = tf.one_hot(actions, n_outputs)
with tf.GradientTape() as tape:
all_Q_values = model(states)
Q_values = tf.reduce_sum(all_Q_values * mask, axis=1, keepdims=True)
loss = tf.reduce_mean(loss_fn(target_Q_values, Q_values))
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# -
# And now, let's train the model!
# +
env.seed(42)
np.random.seed(42)
tf.random.set_seed(42)
rewards = []
best_score = 0
# +
for episode in range(600):
obs = env.reset()
for step in range(200):
epsilon = max(1 - episode / 500, 0.01)
obs, reward, done, info = play_one_step(env, obs, epsilon)
if done:
break
rewards.append(step) # Not shown in the book
if step >= best_score: # Not shown
best_weights = model.get_weights() # Not shown
best_score = step # Not shown
print("\rEpisode: {}, Steps: {}, eps: {:.3f}".format(episode, step + 1, epsilon), end="") # Not shown
if episode > 50:
training_step(batch_size)
model.set_weights(best_weights)
# -
plt.figure(figsize=(8, 4))
plt.plot(rewards)
plt.xlabel("Episode", fontsize=14)
plt.ylabel("Sum of rewards", fontsize=14)
save_fig("dqn_rewards_plot")
plt.show()
# +
env.seed(42)
state = env.reset()
frames = []
for step in range(200):
action = epsilon_greedy_policy(state)
state, reward, done, info = env.step(action)
if done:
break
img = env.render(mode="rgb_array")
frames.append(img)
plot_animation(frames)
# -
# Not bad at all! 😀
# ## Double DQN
# +
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
model = keras.models.Sequential([
keras.layers.Dense(32, activation="elu", input_shape=[4]),
keras.layers.Dense(32, activation="elu"),
keras.layers.Dense(n_outputs)
])
target = keras.models.clone_model(model)
target.set_weights(model.get_weights())
# +
batch_size = 32
discount_rate = 0.95
optimizer = keras.optimizers.Adam(lr=6e-3)
loss_fn = keras.losses.Huber()
def training_step(batch_size):
experiences = sample_experiences(batch_size)
states, actions, rewards, next_states, dones = experiences
next_Q_values = model.predict(next_states)
best_next_actions = np.argmax(next_Q_values, axis=1)
next_mask = tf.one_hot(best_next_actions, n_outputs).numpy()
next_best_Q_values = (target.predict(next_states) * next_mask).sum(axis=1)
target_Q_values = (rewards +
(1 - dones) * discount_rate * next_best_Q_values)
target_Q_values = target_Q_values.reshape(-1, 1)
mask = tf.one_hot(actions, n_outputs)
with tf.GradientTape() as tape:
all_Q_values = model(states)
Q_values = tf.reduce_sum(all_Q_values * mask, axis=1, keepdims=True)
loss = tf.reduce_mean(loss_fn(target_Q_values, Q_values))
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# -
replay_memory = deque(maxlen=2000)
# +
env.seed(42)
np.random.seed(42)
tf.random.set_seed(42)
rewards = []
best_score = 0
for episode in range(600):
obs = env.reset()
for step in range(200):
epsilon = max(1 - episode / 500, 0.01)
obs, reward, done, info = play_one_step(env, obs, epsilon)
if done:
break
rewards.append(step)
if step >= best_score:
best_weights = model.get_weights()
best_score = step
print("\rEpisode: {}, Steps: {}, eps: {:.3f}".format(episode, step + 1, epsilon), end="")
if episode >= 50:
training_step(batch_size)
if episode % 50 == 0:
target.set_weights(model.get_weights())
# Alternatively, you can do soft updates at each step:
#if episode >= 50:
#target_weights = target.get_weights()
#online_weights = model.get_weights()
#for index in range(len(target_weights)):
# target_weights[index] = 0.99 * target_weights[index] + 0.01 * online_weights[index]
#target.set_weights(target_weights)
model.set_weights(best_weights)
# -
plt.figure(figsize=(8, 4))
plt.plot(rewards)
plt.xlabel("Episode", fontsize=14)
plt.ylabel("Sum of rewards", fontsize=14)
save_fig("double_dqn_rewards_plot")
plt.show()
# +
env.seed(43)
state = env.reset()
frames = []
for step in range(200):
action = epsilon_greedy_policy(state)
state, reward, done, info = env.step(action)
if done:
break
img = env.render(mode="rgb_array")
frames.append(img)
plot_animation(frames)
# -
# # Dueling Double DQN
# +
keras.backend.clear_session()
tf.random.set_seed(42)
np.random.seed(42)
K = keras.backend
input_states = keras.layers.Input(shape=[4])
hidden1 = keras.layers.Dense(32, activation="elu")(input_states)
hidden2 = keras.layers.Dense(32, activation="elu")(hidden1)
state_values = keras.layers.Dense(1)(hidden2)
raw_advantages = keras.layers.Dense(n_outputs)(hidden2)
advantages = raw_advantages - K.max(raw_advantages, axis=1, keepdims=True)
Q_values = state_values + advantages
model = keras.models.Model(inputs=[input_states], outputs=[Q_values])
target = keras.models.clone_model(model)
target.set_weights(model.get_weights())
# +
batch_size = 32
discount_rate = 0.95
optimizer = keras.optimizers.Adam(lr=7.5e-3)
loss_fn = keras.losses.Huber()
def training_step(batch_size):
experiences = sample_experiences(batch_size)
states, actions, rewards, next_states, dones = experiences
next_Q_values = model.predict(next_states)
best_next_actions = np.argmax(next_Q_values, axis=1)
next_mask = tf.one_hot(best_next_actions, n_outputs).numpy()
next_best_Q_values = (target.predict(next_states) * next_mask).sum(axis=1)
target_Q_values = (rewards +
(1 - dones) * discount_rate * next_best_Q_values)
target_Q_values = target_Q_values.reshape(-1, 1)
mask = tf.one_hot(actions, n_outputs)
with tf.GradientTape() as tape:
all_Q_values = model(states)
Q_values = tf.reduce_sum(all_Q_values * mask, axis=1, keepdims=True)
loss = tf.reduce_mean(loss_fn(target_Q_values, Q_values))
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# -
replay_memory = deque(maxlen=2000)
# +
env.seed(42)
np.random.seed(42)
tf.random.set_seed(42)
rewards = []
best_score = 0
for episode in range(600):
obs = env.reset()
for step in range(200):
epsilon = max(1 - episode / 500, 0.01)
obs, reward, done, info = play_one_step(env, obs, epsilon)
if done:
break
rewards.append(step)
if step >= best_score:
best_weights = model.get_weights()
best_score = step
print("\rEpisode: {}, Steps: {}, eps: {:.3f}".format(episode, step + 1, epsilon), end="")
if episode >= 50:
training_step(batch_size)
if episode % 50 == 0:
target.set_weights(model.get_weights())
model.set_weights(best_weights)
# -
plt.plot(rewards)
plt.xlabel("Episode")
plt.ylabel("Sum of rewards")
plt.show()
# +
env.seed(42)
state = env.reset()
frames = []
for step in range(200):
action = epsilon_greedy_policy(state)
state, reward, done, info = env.step(action)
if done:
break
img = env.render(mode="rgb_array")
frames.append(img)
plot_animation(frames)
# -
# This looks like a pretty robust agent!
env.close()
# # Using TF-Agents to Beat Breakout
# Let's use TF-Agents to create an agent that will learn to play Breakout. We will use the Deep Q-Learning algorithm, so you can easily compare the components with the previous implementation, but TF-Agents implements many other (and more sophisticated) algorithms!
# ## TF-Agents Environments
tf.random.set_seed(42)
np.random.seed(42)
# +
from tf_agents.environments import suite_gym
env = suite_gym.load("Breakout-v4")
env
# -
env.gym
env.seed(42)
env.reset()
env.step(1) # Fire
# +
img = env.render(mode="rgb_array")
plt.figure(figsize=(6, 8))
plt.imshow(img)
plt.axis("off")
save_fig("breakout_plot")
plt.show()
# -
env.current_time_step()
# ## Environment Specifications
env.observation_spec()
env.action_spec()
env.time_step_spec()
# ## Environment Wrappers
# You can wrap a TF-Agents environments in a TF-Agents wrapper:
# +
from tf_agents.environments.wrappers import ActionRepeat
repeating_env = ActionRepeat(env, times=4)
repeating_env
# -
repeating_env.unwrapped
# Here is the list of available wrappers:
# +
import tf_agents.environments.wrappers
for name in dir(tf_agents.environments.wrappers):
obj = getattr(tf_agents.environments.wrappers, name)
if hasattr(obj, "__base__") and issubclass(obj, tf_agents.environments.wrappers.PyEnvironmentBaseWrapper):
print("{:27s} {}".format(name, obj.__doc__.split("\n")[0]))
# -
# The `suite_gym.load()` function can create an env and wrap it for you, both with TF-Agents environment wrappers and Gym environment wrappers (the latter are applied first).
# +
from functools import partial
from gym.wrappers import TimeLimit
limited_repeating_env = suite_gym.load(
"Breakout-v4",
gym_env_wrappers=[partial(TimeLimit, max_episode_steps=10000)],
env_wrappers=[partial(ActionRepeat, times=4)],
)
# -
limited_repeating_env
limited_repeating_env.unwrapped
# Create an Atari Breakout environment, and wrap it to apply the default Atari preprocessing steps:
# **Warning**: Breakout requires the player to press the FIRE button at the start of the game and after each life lost. The agent may take a very long time learning this because at first it seems that pressing FIRE just means losing faster. To speed up training considerably, we create and use a subclass of the `AtariPreprocessing` wrapper class called `AtariPreprocessingWithAutoFire` which presses FIRE (i.e., plays action 1) automatically at the start of the game and after each life lost. This is different from the book which uses the regular `AtariPreprocessing` wrapper.
# +
from tf_agents.environments import suite_atari
from tf_agents.environments.atari_preprocessing import AtariPreprocessing
from tf_agents.environments.atari_wrappers import FrameStack4
max_episode_steps = 27000 # <=> 108k ALE frames since 1 step = 4 frames
environment_name = "BreakoutNoFrameskip-v4"
class AtariPreprocessingWithAutoFire(AtariPreprocessing):
def reset(self, **kwargs):
obs = super().reset(**kwargs)
super().step(1) # FIRE to start
return obs
def step(self, action):
lives_before_action = self.ale.lives()
obs, rewards, done, info = super().step(action)
if self.ale.lives() < lives_before_action and not done:
super().step(1) # FIRE to start after life lost
return obs, rewards, done, info
env = suite_atari.load(
environment_name,
max_episode_steps=max_episode_steps,
gym_env_wrappers=[AtariPreprocessingWithAutoFire, FrameStack4])
# -
env
# Play a few steps just to see what happens:
env.seed(42)
env.reset()
for _ in range(4):
time_step = env.step(3) # LEFT
def plot_observation(obs):
# Since there are only 3 color channels, you cannot display 4 frames
# with one primary color per frame. So this code computes the delta between
# the current frame and the mean of the other frames, and it adds this delta
# to the red and blue channels to get a pink color for the current frame.
obs = obs.astype(np.float32)
img = obs[..., :3]
current_frame_delta = np.maximum(obs[..., 3] - obs[..., :3].mean(axis=-1), 0.)
img[..., 0] += current_frame_delta
img[..., 2] += current_frame_delta
img = np.clip(img / 150, 0, 1)
plt.imshow(img)
plt.axis("off")
plt.figure(figsize=(6, 6))
plot_observation(time_step.observation)
save_fig("preprocessed_breakout_plot")
plt.show()
# Convert the Python environment to a TF environment:
# +
from tf_agents.environments.tf_py_environment import TFPyEnvironment
tf_env = TFPyEnvironment(env)
# -
# ## Creating the DQN
# Create a small class to normalize the observations. Images are stored using bytes from 0 to 255 to use less RAM, but we want to pass floats from 0.0 to 1.0 to the neural network:
# Create the Q-Network:
# +
from tf_agents.networks.q_network import QNetwork
preprocessing_layer = keras.layers.Lambda(
lambda obs: tf.cast(obs, np.float32) / 255.)
conv_layer_params=[(32, (8, 8), 4), (64, (4, 4), 2), (64, (3, 3), 1)]
fc_layer_params=[512]
q_net = QNetwork(
tf_env.observation_spec(),
tf_env.action_spec(),
preprocessing_layers=preprocessing_layer,
conv_layer_params=conv_layer_params,
fc_layer_params=fc_layer_params)
# -
# Create the DQN Agent:
# +
from tf_agents.agents.dqn.dqn_agent import DqnAgent
train_step = tf.Variable(0)
update_period = 4 # run a training step every 4 collect steps
optimizer = keras.optimizers.RMSprop(lr=2.5e-4, rho=0.95, momentum=0.0,
epsilon=0.00001, centered=True)
epsilon_fn = keras.optimizers.schedules.PolynomialDecay(
initial_learning_rate=1.0, # initial ε
decay_steps=250000 // update_period, # <=> 1,000,000 ALE frames
end_learning_rate=0.01) # final ε
agent = DqnAgent(tf_env.time_step_spec(),
tf_env.action_spec(),
q_network=q_net,
optimizer=optimizer,
target_update_period=2000, # <=> 32,000 ALE frames
td_errors_loss_fn=keras.losses.Huber(reduction="none"),
gamma=0.99, # discount factor
train_step_counter=train_step,
epsilon_greedy=lambda: epsilon_fn(train_step))
agent.initialize()
# -
# Create the replay buffer (this will use a lot of RAM, so please reduce the buffer size if you get an out-of-memory error):
# **Warning**: we use a replay buffer of size 100,000 instead of 1,000,000 (as used in the book) since many people were getting OOM (Out-Of-Memory) errors.
# +
from tf_agents.replay_buffers import tf_uniform_replay_buffer
replay_buffer = tf_uniform_replay_buffer.TFUniformReplayBuffer(
data_spec=agent.collect_data_spec,
batch_size=tf_env.batch_size,
max_length=100000) # reduce if OOM error
replay_buffer_observer = replay_buffer.add_batch
# -
# Create a simple custom observer that counts and displays the number of times it is called (except when it is passed a trajectory that represents the boundary between two episodes, as this does not count as a step):
class ShowProgress:
def __init__(self, total):
self.counter = 0
self.total = total
def __call__(self, trajectory):
if not trajectory.is_boundary():
self.counter += 1
if self.counter % 100 == 0:
print("\r{}/{}".format(self.counter, self.total), end="")
# Let's add some training metrics:
# +
from tf_agents.metrics import tf_metrics
train_metrics = [
tf_metrics.NumberOfEpisodes(),
tf_metrics.EnvironmentSteps(),
tf_metrics.AverageReturnMetric(),
tf_metrics.AverageEpisodeLengthMetric(),
]
# -
train_metrics[0].result()
from tf_agents.eval.metric_utils import log_metrics
import logging
logging.getLogger().setLevel(logging.INFO)
log_metrics(train_metrics)
# Create the collect driver:
# +
from tf_agents.drivers.dynamic_step_driver import DynamicStepDriver
collect_driver = DynamicStepDriver(
tf_env,
agent.collect_policy,
observers=[replay_buffer_observer] + train_metrics,
num_steps=update_period) # collect 4 steps for each training iteration
# -
# Collect the initial experiences, before training:
# +
from tf_agents.policies.random_tf_policy import RandomTFPolicy
initial_collect_policy = RandomTFPolicy(tf_env.time_step_spec(),
tf_env.action_spec())
init_driver = DynamicStepDriver(
tf_env,
initial_collect_policy,
observers=[replay_buffer.add_batch, ShowProgress(20000)],
num_steps=20000) # <=> 80,000 ALE frames
final_time_step, final_policy_state = init_driver.run()
# -
# Let's sample 2 sub-episodes, with 3 time steps each and display them:
# **Note**: `replay_buffer.get_next()` is deprecated. We must use `replay_buffer.as_dataset(..., single_deterministic_pass=False)` instead.
# +
tf.random.set_seed(9) # chosen to show an example of trajectory at the end of an episode
#trajectories, buffer_info = replay_buffer.get_next( # get_next() is deprecated
# sample_batch_size=2, num_steps=3)
trajectories, buffer_info = next(iter(replay_buffer.as_dataset(
sample_batch_size=2,
num_steps=3,
single_deterministic_pass=False)))
# -
trajectories._fields
trajectories.observation.shape
# +
from tf_agents.trajectories.trajectory import to_transition
time_steps, action_steps, next_time_steps = to_transition(trajectories)
time_steps.observation.shape
# -
trajectories.step_type.numpy()
plt.figure(figsize=(10, 6.8))
for row in range(2):
for col in range(3):
plt.subplot(2, 3, row * 3 + col + 1)
plot_observation(trajectories.observation[row, col].numpy())
plt.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0, wspace=0.02)
save_fig("sub_episodes_plot")
plt.show()
# Now let's create the dataset:
dataset = replay_buffer.as_dataset(
sample_batch_size=64,
num_steps=2,
num_parallel_calls=3).prefetch(3)
# Convert the main functions to TF Functions for better performance:
# +
from tf_agents.utils.common import function
collect_driver.run = function(collect_driver.run)
agent.train = function(agent.train)
# -
# And now we are ready to run the main loop!
def train_agent(n_iterations):
time_step = None
policy_state = agent.collect_policy.get_initial_state(tf_env.batch_size)
iterator = iter(dataset)
for iteration in range(n_iterations):
time_step, policy_state = collect_driver.run(time_step, policy_state)
trajectories, buffer_info = next(iterator)
train_loss = agent.train(trajectories)
print("\r{} loss:{:.5f}".format(
iteration, train_loss.loss.numpy()), end="")
if iteration % 1000 == 0:
log_metrics(train_metrics)
# Run the next cell to train the agent for 50,000 steps. Then look at its behavior by running the following cell. You can run these two cells as many times as you wish. The agent will keep improving! It will likely take over 200,000 iterations for the agent to become reasonably good.
train_agent(n_iterations=50000)
# +
frames = []
def save_frames(trajectory):
global frames
frames.append(tf_env.pyenv.envs[0].render(mode="rgb_array"))
watch_driver = DynamicStepDriver(
tf_env,
agent.policy,
observers=[save_frames, ShowProgress(1000)],
num_steps=1000)
final_time_step, final_policy_state = watch_driver.run()
plot_animation(frames)
# -
# If you want to save an animated GIF to show off your agent to your friends, here's one way to do it:
# +
import PIL
image_path = os.path.join("images", "rl", "breakout.gif")
frame_images = [PIL.Image.fromarray(frame) for frame in frames[:150]]
frame_images[0].save(image_path, format='GIF',
append_images=frame_images[1:],
save_all=True,
duration=30,
loop=0)
# + language="html"
# <img src="images/rl/breakout.gif" />
# -
# # Extra material
# ## Deque vs Rotating List
# The `deque` class offers fast append, but fairly slow random access (for large replay memories):
# +
from collections import deque
np.random.seed(42)
mem = deque(maxlen=1000000)
for i in range(1000000):
mem.append(i)
[mem[i] for i in np.random.randint(1000000, size=5)]
# -
# %timeit mem.append(1)
# %timeit [mem[i] for i in np.random.randint(1000000, size=5)]
# Alternatively, you could use a rotating list like this `ReplayMemory` class. This would make random access faster for large replay memories:
class ReplayMemory:
def __init__(self, max_size):
self.buffer = np.empty(max_size, dtype=np.object)
self.max_size = max_size
self.index = 0
self.size = 0
def append(self, obj):
self.buffer[self.index] = obj
self.size = min(self.size + 1, self.max_size)
self.index = (self.index + 1) % self.max_size
def sample(self, batch_size):
indices = np.random.randint(self.size, size=batch_size)
return self.buffer[indices]
mem = ReplayMemory(max_size=1000000)
for i in range(1000000):
mem.append(i)
mem.sample(5)
# %timeit mem.append(1)
# %timeit mem.sample(5)
# ## Creating a Custom TF-Agents Environment
# To create a custom TF-Agent environment, you just need to write a class that inherits from the `PyEnvironment` class and implements a few methods. For example, the following minimal environment represents a simple 4x4 grid. The agent starts in one corner (0,0) and must move to the opposite corner (3,3). The episode is done if the agent reaches the goal (it gets a +10 reward) or if the agent goes out of bounds (-1 reward). The actions are up (0), down (1), left (2) and right (3).
class MyEnvironment(tf_agents.environments.py_environment.PyEnvironment):
def __init__(self, discount=1.0):
super().__init__()
self._action_spec = tf_agents.specs.BoundedArraySpec(
shape=(), dtype=np.int32, name="action", minimum=0, maximum=3)
self._observation_spec = tf_agents.specs.BoundedArraySpec(
shape=(4, 4), dtype=np.int32, name="observation", minimum=0, maximum=1)
self.discount = discount
def action_spec(self):
return self._action_spec
def observation_spec(self):
return self._observation_spec
def _reset(self):
self._state = np.zeros(2, dtype=np.int32)
obs = np.zeros((4, 4), dtype=np.int32)
obs[self._state[0], self._state[1]] = 1
return tf_agents.trajectories.time_step.restart(obs)
def _step(self, action):
self._state += [(-1, 0), (+1, 0), (0, -1), (0, +1)][action]
reward = 0
obs = np.zeros((4, 4), dtype=np.int32)
done = (self._state.min() < 0 or self._state.max() > 3)
if not done:
obs[self._state[0], self._state[1]] = 1
if done or np.all(self._state == np.array([3, 3])):
reward = -1 if done else +10
return tf_agents.trajectories.time_step.termination(obs, reward)
else:
return tf_agents.trajectories.time_step.transition(obs, reward,
self.discount)
# The action and observation specs will generally be instances of the `ArraySpec` or `BoundedArraySpec` classes from the `tf_agents.specs` package (check out the other specs in this package as well). Optionally, you can also define a `render()` method, a `close()` method to free resources, as well as a `time_step_spec()` method if you don't want the `reward` and `discount` to be 32-bit float scalars. Note that the base class takes care of keeping track of the current time step, which is why we must implement `_reset()` and `_step()` rather than `reset()` and `step()`.
#
my_env = MyEnvironment()
time_step = my_env.reset()
time_step
time_step = my_env.step(1)
time_step
# # Exercise Solutions
# ## 1. to 7.
#
# See Appendix A.
# ## 8.
# _Exercise: Use policy gradients to solve OpenAI Gym's LunarLander-v2 environment. You will need to install the Box2D dependencies (`python3 -m pip install -U gym[box2d]`)._
# Let's start by creating a LunarLander-v2 environment:
env = gym.make("LunarLander-v2")
# The inputs are 8-dimensional:
env.observation_space
env.seed(42)
obs = env.reset()
obs
# From the [source code](https://github.com/openai/gym/blob/master/gym/envs/box2d/lunar_lander.py), we can see that these each 8D observation (x, y, h, v, a, w, l, r) correspond to:
# * x,y: the coordinates of the spaceship. It starts at a random location near (0, 1.4) and must land near the target at (0, 0).
# * h,v: the horizontal and vertical speed of the spaceship. It starts with a small random speed.
# * a,w: the spaceship's angle and angular velocity.
# * l,r: whether the left or right leg touches the ground (1.0) or not (0.0).
# The action space is discrete, with 4 possible actions:
env.action_space
# Looking at the [LunarLander-v2's description](https://gym.openai.com/envs/LunarLander-v2/), these actions are:
# * do nothing
# * fire left orientation engine
# * fire main engine
# * fire right orientation engine
# Let's create a simple policy network with 4 output neurons (one per possible action):
# +
keras.backend.clear_session()
np.random.seed(42)
tf.random.set_seed(42)
n_inputs = env.observation_space.shape[0]
n_outputs = env.action_space.n
model = keras.models.Sequential([
keras.layers.Dense(32, activation="relu", input_shape=[n_inputs]),
keras.layers.Dense(32, activation="relu"),
keras.layers.Dense(n_outputs, activation="softmax"),
])
# -
# Note that we're using the softmax activation function in the output layer, instead of the sigmoid activation function
# like we did for the CartPole-v1 environment. This is because we only had two possible actions for the CartPole-v1 environment, so a binary classification model worked fine. However, since we now how more than two possible actions, we need a multiclass classification model.
# Next, let's reuse the `play_one_step()` and `play_multiple_episodes()` functions we defined for the CartPole-v1 Policy Gradient code above, but we'll just tweak the `play_one_step()` function to account for the fact that the model is now a multiclass classification model rather than a binary classification model. We'll also tweak the `play_multiple_episodes()` function to call our tweaked `play_one_step()` function rather than the original one, and we add a big penalty if the spaceship does not land (or crash) before a maximum number of steps.
# +
def lander_play_one_step(env, obs, model, loss_fn):
with tf.GradientTape() as tape:
probas = model(obs[np.newaxis])
logits = tf.math.log(probas + keras.backend.epsilon())
action = tf.random.categorical(logits, num_samples=1)
loss = tf.reduce_mean(loss_fn(action, probas))
grads = tape.gradient(loss, model.trainable_variables)
obs, reward, done, info = env.step(action[0, 0].numpy())
return obs, reward, done, grads
def lander_play_multiple_episodes(env, n_episodes, n_max_steps, model, loss_fn):
all_rewards = []
all_grads = []
for episode in range(n_episodes):
current_rewards = []
current_grads = []
obs = env.reset()
for step in range(n_max_steps):
obs, reward, done, grads = lander_play_one_step(env, obs, model, loss_fn)
current_rewards.append(reward)
current_grads.append(grads)
if done:
break
all_rewards.append(current_rewards)
all_grads.append(current_grads)
return all_rewards, all_grads
# -
# We'll keep exactly the same `discount_rewards()` and `discount_and_normalize_rewards()` functions as earlier:
# +
def discount_rewards(rewards, discount_rate):
discounted = np.array(rewards)
for step in range(len(rewards) - 2, -1, -1):
discounted[step] += discounted[step + 1] * discount_rate
return discounted
def discount_and_normalize_rewards(all_rewards, discount_rate):
all_discounted_rewards = [discount_rewards(rewards, discount_rate)
for rewards in all_rewards]
flat_rewards = np.concatenate(all_discounted_rewards)
reward_mean = flat_rewards.mean()
reward_std = flat_rewards.std()
return [(discounted_rewards - reward_mean) / reward_std
for discounted_rewards in all_discounted_rewards]
# -
# Now let's define some hyperparameters:
n_iterations = 200
n_episodes_per_update = 16
n_max_steps = 1000
discount_rate = 0.99
# Again, since the model is a multiclass classification model, we must use the categorical cross-entropy rather than the binary cross-entropy. Moreover, since the `lander_play_one_step()` function sets the targets as class indices rather than class probabilities, we must use the `sparse_categorical_crossentropy()` loss function:
optimizer = keras.optimizers.Nadam(lr=0.005)
loss_fn = keras.losses.sparse_categorical_crossentropy
# We're ready to train the model. Let's go!
# +
env.seed(42)
mean_rewards = []
for iteration in range(n_iterations):
all_rewards, all_grads = lander_play_multiple_episodes(
env, n_episodes_per_update, n_max_steps, model, loss_fn)
mean_reward = sum(map(sum, all_rewards)) / n_episodes_per_update
print("\rIteration: {}/{}, mean reward: {:.1f} ".format(
iteration + 1, n_iterations, mean_reward), end="")
mean_rewards.append(mean_reward)
all_final_rewards = discount_and_normalize_rewards(all_rewards,
discount_rate)
all_mean_grads = []
for var_index in range(len(model.trainable_variables)):
mean_grads = tf.reduce_mean(
[final_reward * all_grads[episode_index][step][var_index]
for episode_index, final_rewards in enumerate(all_final_rewards)
for step, final_reward in enumerate(final_rewards)], axis=0)
all_mean_grads.append(mean_grads)
optimizer.apply_gradients(zip(all_mean_grads, model.trainable_variables))
# -
# Let's look at the learning curve:
# +
import matplotlib.pyplot as plt
plt.plot(mean_rewards)
plt.xlabel("Episode")
plt.ylabel("Mean reward")
plt.grid()
plt.show()
# -
# Now let's look at the result!
def lander_render_policy_net(model, n_max_steps=500, seed=42):
frames = []
env = gym.make("LunarLander-v2")
env.seed(seed)
tf.random.set_seed(seed)
np.random.seed(seed)
obs = env.reset()
for step in range(n_max_steps):
frames.append(env.render(mode="rgb_array"))
probas = model(obs[np.newaxis])
logits = tf.math.log(probas + keras.backend.epsilon())
action = tf.random.categorical(logits, num_samples=1)
obs, reward, done, info = env.step(action[0, 0].numpy())
if done:
break
env.close()
return frames
frames = lander_render_policy_net(model, seed=42)
plot_animation(frames)
# That's pretty good. You can try training it for longer and/or tweaking the hyperparameters to see if you can get it to go over 200.
# ## 9.
# _Exercise: Use TF-Agents to train an agent that can achieve a superhuman level at SpaceInvaders-v4 using any of the available algorithms._
# Please follow the steps in the [Using TF-Agents to Beat Breakout](http://localhost:8888/notebooks/18_reinforcement_learning.ipynb#Using-TF-Agents-to-Beat-Breakout) section above, replacing `"Breakout-v4"` with `"SpaceInvaders-v4"`. There will be a few things to tweak, however. For example, the Space Invaders game does not require the user to press FIRE to begin the game. Instead, the player's laser cannon blinks for a few seconds then the game starts automatically. For better performance, you may want to skip this blinking phase (which lasts about 40 steps) at the beginning of each episode and after each life lost. Indeed, it's impossible to do anything at all during this phase, and nothing moves. One way to do this is to use the following custom environment wrapper, instead of the `AtariPreprocessingWithAutoFire` wrapper:
class AtariPreprocessingWithSkipStart(AtariPreprocessing):
def skip_frames(self, num_skip):
for _ in range(num_skip):
super().step(0) # NOOP for num_skip steps
def reset(self, **kwargs):
obs = super().reset(**kwargs)
self.skip_frames(40)
return obs
def step(self, action):
lives_before_action = self.ale.lives()
obs, rewards, done, info = super().step(action)
if self.ale.lives() < lives_before_action and not done:
self.skip_frames(40)
return obs, rewards, done, info
# Moreover, you should always ensure that the preprocessed images contain enough information to play the game. For example, the blasts from the laser cannon and from the aliens should still be visible despite the limited resolution. In this particular case, the preprocessing we did for Breakout still works fine for Space Invaders, but that's something you should always check if you want try other games. To do this, you can let the agent play randomly for a while, and record the preprocessed frames, then play the animation and ensure the game still looks playable.
#
# You will also need to let the agent train for quite a long time to get good performance. Sadly, the DQN algorithm is not able to reach superhuman level on Space Invaders, likely because humans are able to learn efficient long term strategies in this game, whereas DQN can only master fairly short strategies. But there has been a lot of progress over the past few years, and now many other RL algorithms are able to surpass human experts at this game. Check out the [State-of-the-Art for Space Invaders on paperswithcode.com](https://paperswithcode.com/sota/atari-games-on-atari-2600-space-invaders).
# ## 10.
# _Exercise: If you have about $100 to spare, you can purchase a Raspberry Pi 3 plus some cheap robotics components, install TensorFlow on the Pi, and go wild! For an example, check out this [fun post](https://homl.info/2) by <NAME>, or take a look at GoPiGo or BrickPi. Start with simple goals, like making the robot turn around to find the brightest angle (if it has a light sensor) or the closest object (if it has a sonar sensor), and move in that direction. Then you can start using Deep Learning: for example, if the robot has a camera, you can try to implement an object detection algorithm so it detects people and moves toward them. You can also try to use RL to make the agent learn on its own how to use the motors to achieve that goal. Have fun!_
# It's your turn now: go crazy, be creative, but most of all, be patient and move forward step by step, you can do it!
|
18_reinforcement_learning.ipynb
|
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Welcome to nbdev
# > Create delightful python projects using Jupyter Notebooks
#
# - image:images/nbdev_source.gif
# `nbdev` is a library that allows you to develop a python library in [Jupyter Notebooks](https://jupyter.org/), putting all your code, tests and documentation in one place. That is: you now have a true [literate programming](https://en.wikipedia.org/wiki/Literate_programming) environment, as envisioned by <NAME> back in 1983!
#
# `nbdev` makes debugging and refactoring your code much easier relative to traditional programming environments. Furthermore, using nbdev promotes software engineering best practices because tests and documentation are first class citizens.
#
# The developers use this regularly on macOS and Linux. We have not tested it on Windows and not all features may work correctly.
# ## Features of Nbdev
#
# `nbdev` provides the following tools for developers:
#
# - **Automatically generate docs** from Jupyter notebooks. These docs are searchable and automatically hyperlinked to appropriate documentation pages by introspecting keywords you surround in backticks.
# - Utilities to **automate the publishing of pypi and conda packages** including version number management.
# - A robust, **two-way sync between notebooks and source code**, which allow you to use your IDE for code navigation or quick edits if desired.
# - **Fine-grained control on hiding/showing cells**: you can choose to hide entire cells, just the output, or just the input. Furthermore, you can embed cells in collapsible elements that are open or closed by default.
# - Ability to **write tests directly in notebooks** without having to learn special APIs. These tests get executed in parallel with a single CLI command. You can even define certain groups of tests such that you don't have to always run long-running tests.
# - Tools for **merge/conflict resolution** with notebooks in a **human readable format**.
# - **Continuous integration (CI) comes setup for you with [GitHub Actions](https://github.com/features/actions)** out of the box, that will run tests automatically for you. Even if you are not familiar with CI or GitHub Actions, this starts working right away for you without any manual intervention.
# - **Integration With GitHub Pages for docs hosting**: nbdev allows you to easily host your documentation for free, using GitHub pages.
# - Create Python modules, following **best practices such as automatically defining `__all__`** ([more details](http://xion.io/post/code/python-all-wild-imports.html)) with your exported functions, classes, and variables.
# - **Math equation support** with LaTeX.
# - ... and much more! See the [Getting Started](https://nbdev.fast.ai/#Getting-Started) section below for more information.
# ## A Motivating Example
#
# For example, lets define a class that represents a playing card, with associated docs and tests in a Jupyter Notebook:
#
# 
#
# In the above screenshot, we have code, tests and documentation in one context! `nbdev` renders this into searchable docs (which are optionally hosted for free on GitHub Pages). Below is an annotated screenshot of the generated docs for further explanation:
#
# 
#
# The above illustration is a subset of [this nbdev tutorial with a minimal example](https://nbdev.fast.ai/example.html), which uses code from [Think Python 2](https://github.com/AllenDowney/ThinkPython2) by <NAME>.
#
# ### Explanation of annotations:
#
# 1. The heading **Card** corresponds to the first `H1` heading in a notebook with a note block _API Details_ as the summary.
# 2. `nbdev` automatically renders a Table of Contents for you.
# 3. `nbdev` automatically renders the signature of your class or function as a heading.
# 4. The cells where your code is defined will be hidden and replaced by standardized documentation of your function, showing its name, arguments, docstring, and link to the source code on github.
# 5. This part of docs is rendered automatically from the docstring.
# 6. The rest of the notebook is rendered as usual. You can hide entire cells, hide only cell input or hide only output by using the [flags described on this page](https://nbdev.fast.ai/export2html.html).
# 7. nbdev supports special block quotes that render as colored boxes in the documentation. You can read more about them [here](https://nbdev.fast.ai/export2html.html#add_jekyll_notes). In this specific example, we are using the `Note` block quote.
# 8. Words you surround in backticks will be automatically hyperlinked to the associated documentation where appropriate. This is a trivial case where `Card` class is defined immediately above, however this works across pages and modules. We will see another example of this in later steps.
# ## Installing
# nbdev is on PyPI and conda so you can just run `pip install nbdev` or `conda install -c fastai nbdev`.
#
# For an [editable install](https://stackoverflow.com/questions/35064426/when-would-the-e-editable-option-be-useful-with-pip-install), use the following:
# ```
# git clone https://github.com/fastai/nbdev
# pip install -e nbdev
# ```
#
# nbdev is tested to work on Ubuntu, Macos and Windows, for the versions tagged with the `-latest` suffix in [these docs](https://docs.github.com/en/actions/reference/specifications-for-github-hosted-runners#supported-runners-and-hardware-resources).
#
# _Note that `nbdev` must be installed into the same python environment that you use for both your Jupyter Server and your workspace._
# ## Getting Started
#
# The following are helpful resources for getting started with nbdev:
#
# - The [tutorial](https://nbdev.fast.ai/tutorial.html).
# - A [minimal, end-to-end example](https://nbdev.fast.ai/example.html) of using nbdev. We suggest replicating this example after reading through the tutorial to solidify your understanding.
# - The [docs](https://nbdev.fast.ai/).
# - [release notes](https://github.com/fastai/nbdev/blob/master/CHANGELOG.md).
#
#
# ## If Someone Tells You Should Not Use Notebooks For Software Development
#
# [Watch this video](https://youtu.be/9Q6sLbz37gk).
# ## Contributing
# If you want to contribute to `nbdev`, be sure to review the [contributions guidelines](https://github.com/fastai/nbdev/blob/master/CONTRIBUTING.md). This project adheres to fastai`s [code of conduct](https://github.com/fastai/nbdev/blob/master/CODE-OF-CONDUCT.md). By participating, you are expected to uphold this code. In general, the fastai project strives to abide by generally accepted best practices in open-source software development.
#
# Make sure you have the git hooks we use installed by running
# ```
# nbdev_install_git_hooks
# ```
# in the cloned repository folder.
# ## Copyright
# Copyright 2019 onwards, fast.ai, Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this project's files except in compliance with the License. A copy of the License is provided in the LICENSE file in this repository.
# ## Appendix
#
# ### nbdev and fastai
# `nbdev` has been used to build innovative software used by many developers, such as [fastai](https://docs.fast.ai/), a deep learning library which implements a [unique layered api and callback system](https://arxiv.org/abs/2002.04688), and [fastcore](https://fastcore.fast.ai/), an extension to the Python programming language. Furthermore, `nbdev` allows a very small number of developers to maintain and grow a [large ecosystem](https://github.com/fastai) of software engineering, data science, machine learning and devops tools.
#
# Here, for instance, is how `combined_cos` is defined and documented in the `fastai` library:
# <img alt="Exporting from nbdev" width="700" caption="An example of a function defined in one cell (marked with the export flag) and explained, along with a visual example, in the following cells" src="images/export_example.png" />
|
nbs/index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
torcs_kill = 'killall torcs-bin'
torcs_cmd = 'torcs -nofuel -nodamage -t 500000 -r %s '
driver_cmd = 'java -jar torcs.jar'
race_xml = 'quickrace.xml'
trackTemplate = '<section name="%%IDX%%"><attstr name="name" val="%%TRACK_NAME%%"/><attstr name="category" val="%%TRACK_TYPE%%"/></section>'
tracks = [("dirt-1","dirt"),("dirt-2","dirt"),("dirt-3","dirt"),("dirt-4","dirt"),("dirt-5","dirt"),("dirt-6","dirt"),("mixed-1","dirt"),
("mixed-2","dirt"),("b-speedway","oval"),("c-speedway","oval"),("d-speedway","oval"),("e-speedway","oval"),("e-track-5","oval"),("f-speedway", "oval"),("g-speedway","oval"),("michigan","oval"),("aalborg","road"),
("brondehach","road"),("g-track-1","road"),("ole-road-1","road"),("e-track-4","road"),("street-1","road"),("alpine-1","road"),
("corkscrew","road"),("e-track-2","road"),("e-track-6","road"),("g-track-2","road"),
("ruudskogen","road"),("wheel-1","road"),("alpine-2","road"),("eroad","road"),
("e-track-3","road"),("forza","road"),("g-track-3","road"),("wheel-2","road"),("spring","road")]
# +
def getTrackCmd(i, trackName, trackType):
return trackTemplate.replace("%%TRACK_NAME%%", trackName).replace("%%TRACK_TYPE%%", trackType).replace('%%IDX%%', str(i+1))
def generateXML():
path = "./track.xml.tmpl"
tracks_xml = ''
picks = np.random.choice(range(len(tracks)), 5, replace=False)
for i,t in enumerate(picks):
tracks_xml += getTrackCmd(i, tracks[t][0], tracks[t][1]) + '\n'
with open(path, "r") as f:
content = f.read()
f.close()
content = content.replace('%%TRACK%%', tracks_xml)
with open(race_xml, "w") as f:
f.write(content)
f.close()
# -
generateXML()
def start_torcs():
Popen(["torcs", "-d -nofuel -nodamage -t 100000", "-r", os.path.join(os.getcwd(),race_xml)])
def start_evaluation():
generateXML()
start_torcs()
results = []
port, proc = (3002, Popen([driver_cmd], stdout=PIPE, stderr=PIPE))
notComplete = True
while driver_proc:
retcode = proc.poll()
if retcode is not None:
notComplete = False
else:
time.sleep(.1)
if retcode != 0 and retcode is not None:
#raise RuntimeError(proc.stderr.read())
print(proc.stderr.read())
if retcode == 0:
results.append(proc.stdout.read())
usefulres = []
for res in results:
if 'laptime' in res:
print res
usefulres.append(res)
return usefulres
# +
# Runs driver and torcs and reads from cmd
|
src/python/Evaluator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Batch Classify a Group of Pieces to ONE output file
#
# from crim_intervals import *
from intervals.main_objs import *
import pandas as pd
import ast
import matplotlib
from itertools import tee, combinations
import numpy as np
from fractions import Fraction
import re
from tqdm import tqdm
# +
# Set Basic Parameters
min_exact_matches = 2
min_close_matches = 3
close_distance = 1
vector_size = 4
increment_size = 4
forward_gap_limit = 40
backward_gap_limit = 40
min_sum_durations = 10
max_sum_durations = 30
offset_difference_limit = 500
duration_type = "real"
interval_type = "generic"
match_type = "close"
# +
crim = 'https://raw.githubusercontent.com/CRIM-Project/CRIM-online/master/crim/static/mei/MEI_3.0/'
git = 'https://raw.githubusercontent.com/RichardFreedman/CRIM_additional_works/main/'
def batch_classify(corpus_titles, duration_type="real", interval_type="generic", match_type="close"):
for title in titles:
path = f"{crim}{title}"
clean_title = re.search("[a-zA-Z_\d]+", title).group()
corpus = CorpusBase([path])
# corpus = CorpusBase(corpus_titles)
if duration_type == "real":
vectors = IntervalBase(corpus.note_list)
elif duration_type == "incremental":
vectors = IntervalBase(corpus.note_list_incremental_offset(increment_size))
if interval_type == "generic":
patterns = into_patterns([vectors.generic_intervals], vector_size)
elif interval_type == "semitone":
patterns = into_patterns([vectors.semitone_intervals], vector_size)
if match_type == "exact":
exact_matches = find_exact_matches(patterns, min_exact_matches)
output_exact = export_pandas(exact_matches)
df = output_exact
pd.set_option("display.max_rows", None, "display.max_columns", None)
df["note_durations"] = df["note_durations"].map(lambda x: pd.eval(x))
df["start_offset"] = df["start_offset"].map(lambda x: pd.eval(x))
df["end_offset"] = df["end_offset"].map(lambda x: pd.eval(x))
df["pattern_generating_match"] = df["pattern_generating_match"].apply(tuple)
df["pattern_matched"] = df["pattern_matched"].apply(tuple)
df["sum_durs"] = df.note_durations.apply(sum)
df = df.round(2)
elif match_type == "close":
close_matches = find_close_matches(patterns, min_close_matches, close_distance)
output_close = export_pandas(close_matches)
output_close["pattern_generating_match"] = output_close["pattern_generating_match"].apply(tuple)
df = output_close
pd.set_option("display.max_rows", None, "display.max_columns", None)
df["note_durations"] = df["note_durations"].map(lambda x: pd.eval(x))
df["start_offset"] = df["start_offset"].map(lambda x: pd.eval(x))
df["end_offset"] = df["end_offset"].map(lambda x: pd.eval(x))
df["pattern_generating_match"] = df["pattern_generating_match"].apply(tuple)
df["pattern_matched"] = df["pattern_matched"].apply(tuple)
df["sum_durs"] = df.note_durations.apply(sum)
df = df.round(2)
df2 = df
# Make Groups, Sort By Group and Offset, then and Add Previous/Next
df2["group_number"] = df2.groupby('pattern_matched').ngroup()
df2 = df2.sort_values(['group_number', 'start_offset'])
df2["prev_entry_off"] = df2["start_offset"].shift(1)
df2["next_entry_off"] = df2["start_offset"].shift(-1)
first_of_group = df2.drop_duplicates(subset=["pattern_matched"], keep='first').index
df2["is_first"] = df2.index.isin(first_of_group)
last_of_group = df2.drop_duplicates(subset=["pattern_matched"], keep='last').index
df2["is_last"] = df2.index.isin(last_of_group)
# Check Differences between Next and Last Offset
df2["last_off_diff"] = df2["start_offset"] - df2["prev_entry_off"]
df2["next_off_diff"] = df2["next_entry_off"] - df2["start_offset"]
# Find Parallel Entries
df2["parallel"] = df2["last_off_diff"] == 0
# Set Gap Limits and Check Gaps Forward and Back
df2["forward_gapped"] = df2["next_off_diff"] >= forward_gap_limit
df2["back_gapped"] = df2["last_off_diff"] >= backward_gap_limit
# Find Singletons and Split Groups with Gaps
df2["singleton"] = ((df2['forward_gapped'] == True) & (df2['back_gapped'] == True) | (df2['back_gapped'] == True) & (df2["is_last"]))
df2["split_group"] = (df2['forward_gapped'] == False) & (df2['back_gapped'] == True)
#Mask Out Parallels and Singletons
df2 = df2[df2["parallel"] != True]
df2 = df2[df2["singleton"] != True]
df2["next_off_diff"] = df2["next_off_diff"].abs()
df2["last_off_diff"] = df2["last_off_diff"].abs()
# Find Final Groups
df2["combined_group"] = (df2.split_group | df2.is_first)
df2.loc[(df2["combined_group"]), "sub_group_id"] = range(df2.combined_group.sum())
df2["sub_group_id"] = df2["sub_group_id"].ffill()
###
### FILTER SHORT OR LONG ENTRIES
###
df2 = df2[df2["sum_durs"] >= min_sum_durations]
df2 = df2[df2["sum_durs"] <= max_sum_durations]
classified2 = df2.applymap(lists_to_tuples).groupby("sub_group_id").apply(predict_type)
# OPTIONAL: drop the new singletons
classified2.drop(classified2[classified2['predicted_type'] == "Singleton"].index, inplace = True)
# OPTIONAL: select only certain presentation types
# classified2 = classified2[classified2["predicted_type"] == "PEN"]
classified2["start"] = classified2["start_measure"].astype(str) +"/"+ classified2["start_beat"].astype(str)
classified2.drop(columns=['start_measure', 'start_beat','offset_diffs'], inplace=True)
# put things back in order by offset and group them again
classified2.sort_values(by = ["start_offset"], inplace=True)
# Now transform as Pivot Table
pivot = classified2.pivot_table(index=["piece_title", "pattern_generating_match", "pattern_matched", "predicted_type", "sub_group_id"],
columns="entry_number",
values=["part", "start_offset", "start", "sum_durs"],
aggfunc=lambda x: x)
pivot_sort = pivot.sort_values(by = [("start_offset", 1)])
pivot_sort = pivot_sort.fillna("-")
pivot_sort.reset_index(inplace=True)
pivot_sort = pivot_sort.drop(columns=['start_offset', "sub_group_id"], level=0)
# group by patterns and minimum of two pieces
# pivot_sort["pattern_matched"] = pivot_sort.pattern_matched.apply(pd.eval).apply(tuple)
# pivot_sort["unique_titles_for_pattern"] = pivot_sort.groupby("pattern_matched").piece_title.transform(lambda group: group.nunique())
# p2 = pivot_sort[pivot_sort.unique_titles_for_pattern > 1]
# p3 = p2.sort_values("pattern_matched")
#
# p3.to_csv("corpus_classified.csv")
#
pivot_sort.to_csv(f"{clean_title}_{interval_type}_{match_type}_{duration_type}.csv")
# return pivot_sort
# Converts lists to tuples
def lists_to_tuples(el):
if isinstance(el, list):
return tuple(el)
else:
return el
# Filters for the length of the Presentation Type in the Classifier
def limit_offset_size(array, limit):
under_limit = np.cumsum(array) <= limit
return array[: sum(under_limit)]
# Gets the the list of offset differences for each group
def get_offset_difference_list(group):
# if we do sort values as part of the func call, then we don't need this first line
group = group.sort_values("start_offset")
group["next_offset"] = group.start_offset.shift(-1)
offset_difference_list = (group.next_offset - group.start_offset).dropna().tolist()
return offset_difference_list
# The classifications are done here
# be sure to have the offset difference limit set here and matched in gap check below 80 = ten bars
def classify_offsets(offset_difference_list):
"""
Put logic for classifying an offset list here
"""
#
offset_difference_list = limit_offset_size(offset_difference_list, offset_difference_limit)
alt_list = offset_difference_list[::2]
if len(set(offset_difference_list)) == 1 and len(offset_difference_list) > 1:
return ("PEN", offset_difference_list)
# elif (len(offset_difference_list) %2 != 0) and (len(set(alt_list)) == 1):
elif (len(offset_difference_list) %2 != 0) and (len(set(alt_list)) == 1) and (len(offset_difference_list) >= 3):
return ("ID", offset_difference_list)
elif len(offset_difference_list) >= 1:
return ("Fuga", offset_difference_list)
else:
return ("Singleton", offset_difference_list)
# adds predicted type, offsets and entry numbers to the results
def predict_type(group):
offset_differences = get_offset_difference_list(group)
predicted_type, offsets = classify_offsets(offset_differences)
group["predicted_type"] = [predicted_type for i in range(len(group))]
group["offset_diffs"] = [offsets for i in range(len(group))]
group["entry_number"] = [i + 1 for i in range(len(group))]
return group
# +
# titles = ['CRIM_Mass_0015_2.mei']
titles = ['CRIM_Model_0025.mei', 'CRIM_Mass_0021_1.mei',
'CRIM_Mass_0021_2.mei', 'CRIM_Mass_0021_3.mei', 'CRIM_Mass_0021_4.mei', 'CRIM_Mass_0021_5.mei']
# titles = ['Riquet_Missa_Susanne_1.mei_msg.mei',
# 'Riquet_Missa_Susanne_2.mei_msg.mei',
# 'Riquet_Missa_Susanne_3.mei_msg.mei',
# 'Riquet_Missa_Susanne_4.mei_msg.mei',
# 'Riquet_Missa_Susanne_5.mei_msg.mei']
batch_classify(titles)
# -
|
.ipynb_checkpoints/CRIM_Classify_Corpus-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Übung: Canary Deployments
# -----------------
#
# In dieser Übung führen wir einen Canary Deployment durch.
#
# Dazu wird ein weiteres Deployment mit der neuen (Canary) Version vom BPMN Frontend erstellt. Der Service hat **keinen** Selector für die Version und steuert so beide Versionen an.
#
# Aus Einfachheitsgründen, verwenden wir die Blue/Green YAML Dateien mit einer neuen Service Datei.
#
# Das passiert in einer eigenen Namespace um die Resultate gezielt Darstellen zu können:
# ! kubectl create namespace canary
# Deployment und Services wurde in einzelne Dateien aufgeteilt. Die Ingress Ressource, aus Einfachheitsgründen weggelassen.
#
# Nur die Labels des Deploymments und natürlich das Image wurde um eine Version erweitert:
#
# apiVersion: v1
# kind: Service
# metadata:
# name: bpmn-frontend
# labels:
# app: bpmn-frontend
# spec:
# ...
# selector:
# app: bpmn-frontend
#
# - - -
#
# apiVersion: apps/v1
# kind: Deployment
# metadata:
# name: bpmn-frontend-green
# version: 0.2
# ...
# spec:
# containers:
# - name: bpmn-frontend
# image: misegr/bpmn-frontend:v0.2
# imagePullPolicy: IfNotPresent
#
# - - -
#
# apiVersion: apps/v1
# kind: Deployment
# metadata:
# name: bpmn-frontend-blue
# version: 1.0
# ...
# spec:
# containers:
# - name: bpmn-frontend
# image: misegr/bpmn-frontend:V1.0
# imagePullPolicy: IfNotPresent
#
# Die Anzahl Pods pro Deployment steuern wir Ausnahmsweise mittels `kubectl`.
# +
# ! kubectl apply -f 09-4-Deployment/bpmn-frontend-deployment-green.yaml --namespace canary
# ! kubectl apply -f 09-4-Deployment/bpmn-frontend-deployment-blue.yaml --namespace canary
# ! kubectl scale --replicas=4 deployment/bpmn-frontend-green --namespace canary
# ! kubectl scale --replicas=1 deployment/bpmn-frontend-blue --namespace canary
# ! kubectl apply -f 09-4-Deployment/bpmn-frontend-service-canary.yaml --namespace canary
# -
# Als Ergebnis haben wir zwei Deployments mit fünf Pods. Vier mit der Version 0.2 und einer mit der Version 1.
#
# Der Service steuert mit einem Verhältnis von 80/20 % auf die fünf Pods zu.
# ! kubectl get all --namespace canary
# ! echo "\n\nBPMN Frontend: "$(kubectl config view -o=jsonpath='{ .clusters[0].cluster.server }' | sed -e 's/https:/http:/' -e "s/6443/$(kubectl get service --namespace canary bpmn-frontend -o=jsonpath='{ .spec.ports[0].nodePort }')/")"/frontend/index.html"
# - - -
#
# Aufräumen
# ! kubectl delete namespace canary
|
data/jupyter/09-4-Deployment-Canary.ipynb
|
;; -*- coding: utf-8 -*-
;; ---
;; jupyter:
;; jupytext:
;; text_representation:
;; extension: .scm
;; format_name: light
;; format_version: '1.5'
;; jupytext_version: 1.14.4
;; kernelspec:
;; display_name: Calysto Scheme 3
;; language: scheme
;; name: calysto_scheme
;; ---
;; ### 練習問題2.43
;; Louis Reasonerは練習問題2.42を解くのにだいぶ苦労している。
;; 彼が書いたqueens⼿続きは動いてはいるようだが、
;; ⾮常に遅いのだ(6×6の場合でも、Louisは待ちきれなくなっ てしまう)。
;; LouisがEva Lu Atorに⾒てくれるよう頼むと、
;; 彼⼥はLouisがflatmap内のマップのネストの順番を次のように逆にしてしまっていることを指摘した。
;;
;; (flatmap (lambda (new-row)
;; (map (lambda (rest-of-queens)
;; (adjoin-position new-row k rest-of-queens))
;; (queen-cols (- k 1)))
;; )
;; (enumerate-interval 1 board-size)
;; )
;;
;; 逆にするとなぜプログラムの実⾏が遅くなるのか説明せよ。
;; 練習問題2.42のプログラムが8クイーンパズルを解く時間をTとして、
;; Louisのプログラムがパズルを解くのにかかる時間を⾒積もれ。
;; Louisのプログラムの時間の見積もりの回答については割愛する。
;;
;; Louisのプログラムは、
;;
;; - queen-cols手続き
;; - enumerate-interval手続き
;;
;; の呼び出しが逆になっていることから、
;; (enumerate-interval 1 board-size)で繰り返す箇所で
;; queen-cols手続きを呼び出すことで無駄なループになっており、これが実行時間が遅くなることが伺える。
;; Louisのプログラムは実行時間が遅いが、
;; 動作確認してみると、
;;
;; - 正しい組み合わせが出力される
;; - 重複した組み合わせが出力されることはない
;;
;; ということから、
;; プロセス図を記述してみて、どのような動作になっているかについては考えてみる価値はあるかと思われる。
;; 練習問題2.42のプログラムのプロセス図と、
;; Louisのプログラムのプロセス図については、
;; [練習問題2.42 8クイーンパズルのプロセス図](../exercises/2.43.xlsx)
;; を参照。
;; 練習問題2.42のプロセス図は、
;; バックトラックアルゴリズムにより、k<board-size(k:処理対象の列番号)のときに、
;; safe?手続きにより、NGのものはそれ以降組み合わせを考えることがなく、無駄な試行がないことが分かる。
;; それに対し、練習問題2.43(Louisのプログラム)のプロセス図は、
;; k=board-sizeの動作は無駄がないが、
;; k<board-sizeのときは1度チェックした組み合わせについても
;; safe?手続きを再起呼び出しすることが何度も(指数関数的)に呼び出しているのが分かる。
;; k<board-sizeのときは、同じ組み合わせを何度もチェックはするが、
;; k=board-sizeまで含めると異なる組み合わせとなっているので重複した回答になることはない。
;; k<board-sizeの場合は、
;; 全組み合わせを列挙しているわけではないが、
;; それに近いステップ数の増加オーダーであることが考えられる。
;; +
; 練習問題2.42の回答
; 問題文のqueens手続き
; 以下の定義が必要
; ・empty-board
; ・safe?手続き
; ・adjoin-position手続き
(define (queens board-size)
(define (queen-cols k)
(if (= k 0) (list empty-board)
(filter
(lambda (positions) (safe? k positions))
(flatmap (lambda (rest-of-queens)
(map (lambda (new-row) (adjoin-position new-row k rest-of-queens))
(enumerate-interval 1 board-size))
)
(queen-cols (- k 1))
)
)
)
)
(queen-cols board-size)
)
(define (flatmap proc seq)
(accumulate append '() (map proc seq)))
; 整数列の列挙
(define (enumerate-interval low high)
(if (> low high) '()
(cons low (enumerate-interval (+ low 1) high))))
; 集積
(define (accumulate op initial sequence)
(if (null? sequence) initial
(op (car sequence) (accumulate op initial (cdr sequence)))))
; フィルタリング
(define (filter predicate sequence)
(cond ((null? sequence) '())
((predicate (car sequence))(cons (car sequence) (filter predicate (cdr sequence))))
(else (filter predicate (cdr sequence))))
)
; 回答1
(define empty-board '())
; 回答2
; adjoin-position手続きの呼び出し方が決まっているため、
; この回答しかないはず。
; 列ごとの位置(Y座標)をリストで表す。
(define (adjoin-position new-row k rest-of-queens)
(append rest-of-queens (list new-row))
)
; k列目の位置のy座標を返す
(define (get-k-y k positions)
(define (iter count pos)
(if (>= count k) (car pos)
(iter (+ count 1) (cdr pos))
)
)
(iter 1 positions)
)
; 位置情報のダンプ
(define (print-pos positions)
(if (null? positions) ()
(begin
(display (car positions))
(display " ")
(print-pos (cdr positions))
)
)
)
; 回答3
(define (safe? k positions)
(begin
;(display "'")
;(print-pos positions)
(display positions)
(newline)
(let ((k-y-pos (get-k-y k positions)))
(define (iter count pos)
(if (>= count k) #t
(if (null? pos) #t
(let (
(y (car pos))
)
(let ((y-upper (- y (- k count)))
(y-lower (+ y (- k count))))
; y座標が同じか、対角線上にあればFalseを返す。
; それ以外はチェックを継続する。
(if (or (= k-y-pos y) (= k-y-pos y-upper) (= k-y-pos y-lower)) #f
(iter (+ count 1) (cdr pos))
)
)
)
)
)
)
(iter 1 positions)
)
)
)
;; -
(queens 3)
(queens 4)
; Louisのプログラム(間違った実装)
; ダンプ処理付き
(define (queens-ng board-size)
(define (queen-cols k)
(if (= k 0) (list empty-board)
(filter
(lambda (positions) (safe? k positions))
;(flatmap (lambda (rest-of-queens)
; (map (lambda (new-row) (adjoin-position new-row k rest-of-queens))
; (enumerate-interval 1 board-size))
; )
; (queen-cols (- k 1))
;)
(flatmap (lambda (new-row)
(map (lambda (rest-of-queens)
(adjoin-position new-row k rest-of-queens))
(queen-cols (- k 1)))
)
(enumerate-interval 1 board-size)
)
)
)
)
(queen-cols board-size)
)
(queens-ng 3)
(queens-ng 4)
|
exercises/2.43.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from tensorflow.keras.datasets import reuters
(train_data,train_labels),(test_data,test_labels)=reuters.load_data(num_words=10000)
import numpy as np
def vectorize_sequences(sequences,dimensions=10000):
results=np.zeros((len(sequences),dimensions))
for i,sequence in enumerate(sequences):
results[i,sequence]=1.
return results
x_train=vectorize_sequences(train_data)
x_test=vectorize_sequences(test_data)
#ahora aplicaremos el procesamiento de datos para los datos de salida
from tensorflow.keras.utils import to_categorical
y_train=to_categorical(train_labels)
y_test=to_categorical(test_labels)
#ahora comenzaremos a preparar la estrutie para nuestra red neuronal
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.utils import plot_model
def generate_model():
"""
para este modelo de deep learning recomendamos usar capas de 64 neuronas cada una
"""
model=Sequential()
model.add(Dense(64,activation='relu',input_shape=(10000,)))
model.add(Dense(64,activation='relu'))
model.add(Dense(46,activation='softmax'))
#ahora agregamos la configuracion de compilacion
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy']
)
return model
model=generate_model()
model.summary()
plot_model(model,show_shapes=True)
# +
#separamos los datos en entrenamiento y validacion
x_val=x_train[:1000]
y_val=y_train[:1000]
x_train=x_train[1000:]
y_train=y_train[1000:]
# -
#entrenamos el modelo por primera vez
history=model.fit(x_train,y_train,epochs=20,batch_size=512,validation_data=(x_val,y_val))
history.history.keys()
# +
# %matplotlib inline
import matplotlib.pyplot as plt
#ahora veamos el rendimiento del modelo
train_loss=history.history['loss']
validation_loss=history.history['val_loss']
#para la funcion de puntaje en este caso accuracy
train_acc=history.history['accuracy']
validation_acc=history.history['val_accuracy']
epochs=range(1,len(history.history['accuracy'])+1)
#funcion de perdida
def plot_perdida(train_loss,validation_loss,epochs):
plt.plot(epochs,train_loss,'go-',label='train loss')
plt.plot(epochs,validation_loss,'ro-',label='validation loss')
plt.xlabel('epochs')
plt.ylabel('loss function')
plt.legend(loc='best')
plt.show()
# -
def plot_accuracy(train_acc,validation_acc,epochs):
plt.plot(epochs,train_acc,'go-',label='train accuracy')
plt.plot(epochs,validation_acc,'ro-',label='validation accuracy')
plt.xlabel('epochs')
plt.ylabel('accuracy')
plt.legend(loc='best')
plt.show()
#mostramos las graficas
plot_perdida(train_loss,validation_loss,epochs)
plot_accuracy(train_acc,validation_acc,epochs)
model.evaluate(x_test,y_test)
#obtuvimos un puntaje de 78.76%, ahora trataremos
# de ejecutar el modelo con menos epochs o iteraciones sobre los dtos de entrenamiento, en este caso 10
model=generate_model()
history=model.fit(x_train,y_train,epochs=9,batch_size=512,validation_data=(x_val,y_val))
# +
train_loss=history.history['loss']
validation_loss=history.history['val_loss']
#para la funcion de puntaje en este caso accuracy
train_acc=history.history['accuracy']
validation_acc=history.history['val_accuracy']
epochs=range(1,len(history.history['accuracy'])+1)
# -
plot_perdida(train_loss,validation_loss,epochs)
plot_accuracy(train_acc,validation_acc,epochs)
model.evaluate(x_test,y_test)
y_pred=model.predict(x_test)
y_pred=np.argmax(y_pred,axis=1)
y_test1=np.argmax(y_test,axis=1)
#ahora elaboraremos un reporte de clasificacion con librerias de machine lasrning de python
from sklearn.metrics import classification_report
result=classification_report(y_test1,y_pred)
print(result)
#ahora probaremos una matriz de confusion para estos dastos de clasificacion multietiqueta
from sklearn.metrics import confusion_matrix
import seaborn as sns; sns.set()
mat=confusion_matrix(y_test1,y_pred)
sns.heatmap(mat,annot=True,fmt='.2f',square=True)
|
Classificacion Multiple.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import quantiacsToolbox
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import linear_model
from sklearn.preprocessing import PolynomialFeatures
# %matplotlib inline
class myStrategy(object):
def myTradingSystem(self, DATE, OPEN, HIGH, LOW, CLOSE, VOL, OI, P, R, RINFO, exposure, equity, settings):
""" This system uses linear regression to allocate capital into the desired equities"""
# Get parameters from setting
nMarkets = len(settings['markets'])
lookback = settings['lookback']
dimension = settings['dimension']
threshold = settings['threshold']
pos = np.zeros(nMarkets, dtype=np.float)
poly = PolynomialFeatures(degree=dimension)
for market in range(nMarkets):
reg = linear_model.LinearRegression()
try:
#predicting volume
reg.fit(poly.fit_transform(np.arange(lookback).reshape(-1,1)), VOL[:,market])
vol_predict = reg.predict(poly.fit_transform(np.array([[lookback]])))
#predicting open price
reg.fit(poly.fit_transform(np.arange(lookback).reshape(-1,1)), OPEN[:,market])
open_predict = reg.predict(poly.fit_transform(np.array([[lookback]])))
#predicting close price
X = np.append(VOL[:,market], OPEN[:,market], axis=1)
reg.fit(X,CLOSE[:,market])
x = np.append(vol_predict,open_predict,axis=1)
close_predict = reg.predict(x)
trend = (close_predict - CLOSE[-1, market]) / CLOSE[-1, market]
if abs(trend[0]) < threshold:
trend[0] = 0
pos[market] = np.sign(trend)
# for NaN data set position to 0
except ValueError:
pos[market] = .0
return pos, settings
def mySettings(self):
""" Define your trading system settings here """
settings = {}
Futures Contracts
settings['markets'] = ['CASH', 'F_AD', 'F_BO', 'F_BP', 'F_C', 'F_CC', 'F_CD',
'F_CL', 'F_CT', 'F_DX', 'F_EC', 'F_ED', 'F_ES', 'F_FC', 'F_FV', 'F_GC',
'F_HG', 'F_HO', 'F_JY', 'F_KC', 'F_LB', 'F_LC', 'F_LN', 'F_MD', 'F_MP',
'F_NG', 'F_NQ', 'F_NR', 'F_O', 'F_OJ', 'F_PA', 'F_PL', 'F_RB', 'F_RU',
'F_S', 'F_SB', 'F_SF', 'F_SI', 'F_SM', 'F_TU', 'F_TY', 'F_US', 'F_W', 'F_XX',
'F_YM']
#settings['markets'] = ['CASH', 'F_S', 'F_AD']
settings['lookback'] = 252
settings['budget'] = 10 ** 6
settings['slippage'] = 0.05
settings['threshold'] = 0.05
settings['dimension'] = 3
return settings
result = quantiacsToolbox.runts(myStrategy)
|
Windows_folder/Python Notebooks/Quantiacs_LR_v1.1.1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Let's look at the distribution of a markov chain with two states and see if we can predict the equilibrium distribution before it actually converges.
#
# Here we are not concerned with a single markov chain but learning from the aggregate dynamics of the chains.
#
# $A$ is a transition matrix and we start with an initial distribution of $[1,0]$ which means that 100% of samples are in state 1. The matrix $A$ is column stochastic.
#
# $$ A = \begin{bmatrix} \alpha & 1 - \beta \\ 1 - \alpha & \beta\end{bmatrix}$$
#
# As $k$ increases, $A^{k} v_0$ will converge for most reasonable values of $\alpha$ and $\beta$. We can figure out what it converges to by just observing the first two distributions.
#
# At the first step the distribution will be $[\alpha, 1 - \alpha]$ and if we know what these values are, we can figure out $\alpha$.
# At the second step the distribution will be $[\alpha^2 + (1 - \alpha)(1 - \beta), \alpha (1 -\alpha) + \beta (1 - \alpha) ]$. If we know this value and we know the value of $\alpha$ from step 1 we can figure out what $\beta$ is. Once we have recovered $\alpha$ and $\beta$ we can recover the transition matrix. The eigenvector of the transition matrix $A$ corresponding to the eigenvalue $1$ will give us the equilibrium distribution.
import numpy as np
A = np.array([[0.8, 0.2], [0.4, 0.6]]).transpose()
A
# +
# initial vector
v_0 = np.array([1,0]).transpose()
# time steps for iteration
steps = np.arange(0, 20)
# -
# Evaluate state in each round
state_1_frac = np.array([(np.linalg.matrix_power(A, x) @ v_0)[0] for x in steps])
state_2_frac = 1 - state_1_frac
# Use round 1 and round 2 data to recover alpha and beta
alpha = state_1_frac[1]
beta = 1 - (state_1_frac[2] - alpha * alpha) / (1 - alpha)
print("alpha={0:.2f}, beta={1:.2f}".format(alpha, beta))
# now find the eignvalues of the transition matrix
A_pred = np.array([[alpha, 1 - alpha], [1 - beta, beta]]).transpose()
evals, evecs = np.linalg.eig(A_pred)
predicted_states = evecs[:,0] / evecs[:, 0].sum()
print("Equilibrium States = ", predicted_states)
# +
# %matplotlib inline
import matplotlib.pyplot as plt
# now plot the markov chain distributions
plt.figure(figsize=(12, 6))
plt.plot(steps, state_1_frac, '-ob', markersize=3, label="state_1 percentage")
plt.ylim(0, 1)
plt.xlabel("Rounds")
plt.ylabel("Percentage of state in distribution")
plt.xticks(steps)
plt.axhline(predicted_states[0], linestyle="--", color='b', alpha=0.3, label="state_1 predicted equilibrium")
plt.plot(steps, state_2_frac, '-or', markersize=3, label="state_2 percentage")
plt.axhline(predicted_states[1], linestyle="--", color='r', alpha=0.3, label="state_2 predicted equilibrium")
plt.grid()
plt.legend(bbox_to_anchor=(1.15, 1.0))
plt.axvline(2, linestyle='--', color="black", alpha=0.6)
bbox_props = dict(boxstyle="larrow,pad=0.3", fc="wheat", ec="black", lw=1, alpha=0.8)
plt.text(2.3, 0.9, 'Equilibrium Prediction done here',
horizontalalignment='left', verticalalignment='center', bbox=bbox_props
)
plt.title("Showing that we can predict the equilibrium distribution after just two rounds")
plt.savefig("assets/Distribution Dynamics Each Round 2x2.png", transparent=False, dpi=600)
# -
# ### General $n \times n$ case <a id="generalcase"></a>
#
# We can generalize this to the $n\times n $ case by solving the recurrence relations.
# $$A v_{k} = v_{k+1} \hspace{.2in} \forall \hspace{.2in} 0 \leq k \leq n-1.$$ If we have $n$ rounds then we can recover $A$ with a system of linear equations. We also need to ensure that
# 1. The entries of $A$ are positive (or atleast non-negative)
# 2. The the columns of $A$ sum up to one.
#
# We can add both these conditions as constraints and find an optimal solution with the method of Lagrange Multipliers. However if we have fewer than $n$ rounds of evolution then our solution would not be unique. We would need another constraint.
# 1. Minimize the norm of $A$. This should give us a unique solution.
# 2. Put in a biologically motivated prior for the transition matrix. The Maximum a posteriori estimate will be the solution.
|
projects/PCA_to_DCA/notebooks/Markov_chain_distributions_2x2_case.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Multirotor validator eCalc
# +
import ipywidgets as widgets
from ipywidgets import interact, Dropdown, HBox
import ipyvuetify as v
import math
from math import pi, sqrt
from IPython.display import clear_output
from ipywidgets import interactive, AppLayout, HTML, Layout
import pandas as pd
path='./Motors/'
df_mot = pd.read_csv(path+'Motors_Data.csv', sep=';')
path='./Propeller/'
df_pro = pd.read_csv(path+'Propeller_Data.csv', sep=';')
path='./Batteries/'
df_bat = pd.read_csv(path+'Batteries_Data.csv', sep=';')
path='./ESC/'
df_esc = pd.read_csv(path+'ESC_data.csv', sep=';')
style = {'description_width': '150pt'}
layout = {'width': '500pt'}
label_layout = widgets.Layout(width='50px')
Motmodel =widgets.HTML(value = f"<b><font color='red'>{'Motor parameters'}</b>")
Mot= Dropdown(
options= df_mot['Model'].values,
description='Motor model:',
disabled=False,
)
df_motfilter=df_mot[df_mot['Model']== Mot.value] #filter data containing such values
Kt_DC= Dropdown(
options=df_motfilter['Kt_Nm_A'].values,
description='K_T:(Nm/A)',
disabled=True,
)
Tmot_DC= Dropdown(
options=df_motfilter['Tnom_Nm'].values,
description='Nominal torque(N.m)',
disabled=True,
)
Propmodel =widgets.HTML(value = f"<b><font color='red'>{'Propeller parameters'}</b>")
Dia_DC= Dropdown(
options= sorted(df_pro['DIAMETER'].unique().tolist()),
description='Propeller diameter:',
disabled=False,
)
df_profilter=df_pro[df_pro['DIAMETER']== Dia_DC.value] #filter data containing such values
Pitch_DC= Dropdown(
options= sorted(df_profilter['BETA'].unique().tolist()),
description='Pitch/diameter:',
disabled=False,)
Batmodel =widgets.HTML(value = f"<b><font color='red'>{'Battery parameters'}</b>")
Cbat_DC= Dropdown(
options= sorted(df_bat['Capacity_mAh'].unique().tolist()),
description='Capacity (mAh):',
disabled=False,)
df_batfilter=df_bat[df_bat['Capacity_mAh']== Cbat_DC.value] #filter data containing such values
Ubat_DC= Dropdown(
options= sorted(df_batfilter['Voltage_V'].unique().tolist()),
description='Voltage (V):',
disabled=False,)
df_batfilter_model=df_bat[(df_bat['Capacity_mAh']==Cbat_DC.value) & (df_bat['Voltage_V']==Ubat_DC.value)] #filter data containing such values
Modelbat= Dropdown(
options=sorted(df_batfilter_model['Model'].unique().tolist()),
description='Model battery',
disabled=False,
)
ESCmodel =widgets.HTML(value = f"<b><font color='red'>{'ESC parameters'}</b>")
Pesc_DC= Dropdown(
options= sorted(df_esc['Pmax.in[W]'].unique().tolist()),
description='Power ESC:',
disabled=False,)
df_escfilter=df_esc[df_esc['Pmax.in[W]']== Pesc_DC.value] #filter data containing such values
Vesc_DC= Dropdown(
options= sorted(df_escfilter['Vmax.in[V]'].unique().tolist()),
description='Voltage ESC (V):',
disabled=False,)
df_escfilter_model=df_esc[(df_esc['Pmax.in[W]']==Pesc_DC.value) & (df_esc['Vmax.in[V]']==Vesc_DC.value)] #filter data containing such values
Modelesc= Dropdown(
options=sorted(df_escfilter_model['Model'].unique().tolist()),
description='Model ESC',
disabled=False,
)
archit = widgets.HTML(value = f"<b><font color='red'>{'Architecture'}</b>")
Narm_slider_DC = widgets.FloatSlider(
value=8,
min=3,
max=12,
step=1,
description='Number of arms [-]',
readout_format='.0f', style=style, layout=layout
)
Narm_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Narm_slider_DC, 'value'), (Narm_tex_DC, 'value'))
D_ratio_slider_DC = widgets.FloatSlider(
value=0.8,
min=0.01,
max=0.99,
step=1,
description='Ratio inner / outer diameter [-]',
readout_format='.0f', style=style, layout=layout
)
D_ratio_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((D_ratio_slider_DC, 'value'), (D_ratio_tex_DC, 'value'))
Narm_DC=widgets.HBox([Narm_slider_DC,Narm_tex_DC,D_ratio_slider_DC,D_ratio_tex_DC])
Np_arm_DC=widgets.ToggleButtons(options=['Single rotor setup', 'Coaxial setup'],
description='Number of propellers per arm:',
disabled=False,style=style)
Mod_DC=widgets.ToggleButtons(options=['Direct Drive', 'Gear Drive'],
description='Motor configuration:',
tooltips=['No speed reductor', 'Motor with reduction'],style=style)
# A_top_slider = widgets.FloatSlider(
# value=0.09,
# min=0.01,
# max=1,
# step=0.01,
# description='Top surface [m^2]',
# readout_format='.2f', style=style, layout=layout
# )
# A_top_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
# widgets.link((A_top_slider, 'value'), (A_top_tex, 'value'))
# A_top_DC = widgets.HBox([A_top_slider,A_top_tex])
arc=widgets.HBox([Np_arm_DC,Mod_DC])
perf = widgets.HTML(value = f"<b><font color='red'>{'Performance'}</b>")
k_maxthrust_slider_DC = widgets.FloatSlider(
value=3,
min=1.1,
max=4,
step=.1,
description='Ratio max thrust-hover [-]',
readout_format='.1f', style=style, layout=layout
)
k_maxthrust_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((k_maxthrust_slider_DC, 'value'), (k_maxthrust_tex_DC, 'value'))
k_maxthrust_DC=widgets.HBox([k_maxthrust_slider_DC,k_maxthrust_tex_DC])
V_cl_slider_DC = widgets.FloatSlider(
value=8,
min=1,
max=10,
step=1,
description='Rate of climb [m/s]',
readout_format='.0f', style=style, layout=layout
)
V_cl_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((V_cl_slider_DC, 'value'), (V_cl_tex_DC, 'value'))
V_cl_DC = widgets.HBox([V_cl_slider_DC,V_cl_tex_DC])
Nred_slider_DC = widgets.FloatSlider(
value=1,
min=1,
max=3,
step=1,
description='Geat ratio',
readout_format='.2f', style=style, layout=layout
)
Nred_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Nred_slider_DC, 'value'), (Nred_tex_DC, 'value'))
Nred_DC = widgets.HBox([Nred_slider_DC,Nred_tex_DC])
Ncel_slider_DC = widgets.FloatSlider(
value=1,
min=1,
max=30,
step=1,
description='Cell numbers',
readout_format='.0f'
)
Ncel_tex_DC = widgets.FloatText(description="", continuous_update=False)
widgets.link((Ncel_slider_DC, 'value'), (Ncel_tex_DC, 'value'))
Ncel_DC = widgets.HBox([Ncel_slider_DC,Ncel_tex_DC])
M_pay_DC = widgets.FloatSlider(
value=4.,
min=1,
max=100.0,
step=.1,
description='Load mass [kg]:',
readout_format='.1f', style=style, layout=layout
)
M_load_tex_DC = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((M_pay_DC, 'value'), (M_load_tex_DC, 'value'))
M_load_DC=widgets.HBox([M_pay_DC,M_load_tex_DC])
NDmax_slider = widgets.FloatSlider(
value=105000/60*0.0254,
min=0.1,
max=100,
step=1,
description='Max Rotational Speed [Hz*m]',
readout_format='.2f', style=style, layout=layout
)
NDmax_tex = widgets.FloatText(description="", readout_format='.2f', continuous_update=False,layout=label_layout)
widgets.link((NDmax_slider, 'value'), (NDmax_tex, 'value'))
NDmax_w = widgets.HBox([NDmax_slider,NDmax_tex])
rho_air_slider = widgets.FloatSlider(
value=1.2,
min=1,
max=1.3,
step=0.01,
description='Air density [kg/m^3]',
readout_format='.2f', style=style, layout=layout
)
rho_air_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((rho_air_slider, 'value'), (rho_air_tex, 'value'))
rho_air_w = widgets.HBox([rho_air_slider,rho_air_tex])
C_D_slider = widgets.FloatSlider(
value=1.18,
min=1,
max=3,
step=0.1,
description='Drag coefficient [-]',
readout_format='.1f', style=style, layout=layout
)
C_D_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((C_D_slider, 'value'), (C_D_tex, 'value'))
C_D_w = widgets.HBox([C_D_slider,C_D_tex])
Dpro_ref_slider = widgets.FloatSlider(
value=11*.0254,
min=0,
max=50*0.0254,
step=0.1,
description='Propeller diameter of reference [m]',
readout_format='.1f', style=style, layout=layout
)
Dpro_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Dpro_ref_slider, 'value'), (Dpro_ref_tex, 'value'))
Dpro_ref_w= widgets.HBox([Dpro_ref_slider,Dpro_ref_tex])
Mpro_ref_slider = widgets.FloatSlider(
value=0.53*0.0283,
min=0,
max=5,
step=0.1,
description='Propeller mass of reference [kg]',
readout_format='.1f', style=style, layout=layout
)
Mpro_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Mpro_ref_slider, 'value'), (Mpro_ref_tex, 'value'))
Mpro_ref_w= widgets.HBox([Mpro_ref_slider,Mpro_ref_tex])
Tmot_ref_slider = widgets.FloatSlider(
value=2.32,
min=0,
max=15,
step=0.1,
description='Motor torque of reference [N.m]',
readout_format='.1f', style=style, layout=layout
)
Tmot_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Tmot_ref_slider, 'value'), (Tmot_ref_tex, 'value'))
Tmot_ref_w= widgets.HBox([Tmot_ref_slider,Tmot_ref_tex])
Rmot_ref_slider = widgets.FloatSlider(
value=0.03,
min=0,
max=1,
step=0.01,
description='Motor resistance of reference [Ohm]',
readout_format='.1f', style=style, layout=layout
)
Rmot_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Rmot_ref_slider, 'value'), (Rmot_ref_tex, 'value'))
Rmot_ref_w= widgets.HBox([Rmot_ref_slider,Rmot_ref_tex])
Mmot_ref_slider = widgets.FloatSlider(
value=0.575,
min=0,
max=10,
step=0.01,
description='Motor mass of reference [kg]',
readout_format='.1f', style=style, layout=layout
)
Mmot_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Mmot_ref_slider, 'value'), (Mmot_ref_tex, 'value'))
Mmot_ref_w= widgets.HBox([Mmot_ref_slider,Mmot_ref_tex])
Ktmot_ref_slider = widgets.FloatSlider(
value=0.03,
min=0,
max=1,
step=0.01,
description='Torque coefficient of reference [N.m/A]',
readout_format='.1f', style=style, layout=layout
)
Ktmot_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Ktmot_ref_slider, 'value'), (Ktmot_ref_tex, 'value'))
Ktmot_ref_w= widgets.HBox([Ktmot_ref_slider,Ktmot_ref_tex])
Tfmot_ref_slider = widgets.FloatSlider(
value=0.03,
min=0,
max=1,
step=0.01,
description='Friction torque of reference [N.m/A]',
readout_format='.1f', style=style, layout=layout
)
Tfmot_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Tfmot_ref_slider, 'value'), (Tfmot_ref_tex, 'value'))
Tfmot_ref_w= widgets.HBox([Ktmot_ref_slider,Ktmot_ref_tex])
Mbat_ref_slider = widgets.FloatSlider(
value=0.329,
min=0,
max=40,
step=0.01,
description='Battery mass of reference [N.m/A]',
readout_format='.2f', style=style, layout=layout
)
Mbat_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Mbat_ref_slider, 'value'), (Mbat_ref_tex, 'value'))
Mbat_ref_w= widgets.HBox([Mbat_ref_slider,Mbat_ref_tex])
Cbat_ref_slider = widgets.FloatSlider(
value=3.400*3600,
min=0,
max=340*3600,
step=0.01,
description='Battery capacity of reference [A.s]',
readout_format='.2f', style=style, layout=layout
)
Cbat_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Cbat_ref_slider, 'value'), (Cbat_ref_tex, 'value'))
Cbat_ref_w= widgets.HBox([Cbat_ref_slider,Cbat_ref_tex])
Vbat_ref_slider = widgets.FloatSlider(
value=4*3.7,
min=3.7,
max=20*3.7,
step=0.01,
description='Battery voltage of reference [V]',
readout_format='.2f', style=style, layout=layout
)
Vbat_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Vbat_ref_slider, 'value'), (Vbat_ref_tex, 'value'))
Vbat_ref_w= widgets.HBox([Vbat_ref_slider,Vbat_ref_tex])
Imax_ref_slider = widgets.FloatSlider(
value=170,
min=0,
max=400,
step=0.01,
description='Max current of reference [A]',
readout_format='.2f', style=style, layout=layout
)
Imax_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Imax_ref_slider, 'value'), (Imax_ref_tex, 'value'))
Imax_ref_w= widgets.HBox([Imax_ref_slider,Imax_ref_tex])
Pesc_ref_slider = widgets.FloatSlider(
value=3108,
min=0,
max=6000,
step=0.01,
description='ESC power of reference [W]',
readout_format='.0f', style=style, layout=layout
)
Pesc_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Pesc_ref_slider, 'value'), (Pesc_ref_tex, 'value'))
Pesc_ref_w= widgets.HBox([Pesc_ref_slider,Pesc_ref_tex])
Vesc_ref_slider = widgets.FloatSlider(
value=44.4,
min=0,
max=100,
step=0.01,
description='ESC voltage of reference [W]',
readout_format='.1f', style=style, layout=layout
)
Vesc_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Vesc_ref_slider, 'value'), (Vesc_ref_tex, 'value'))
Vesc_ref_w= widgets.HBox([Vesc_ref_slider,Vesc_ref_tex])
Mesc_ref_slider = widgets.FloatSlider(
value=.115,
min=0,
max=1,
step=0.01,
description='ESC power of reference [W]',
readout_format='.3f', style=style, layout=layout
)
Mesc_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Mesc_ref_slider, 'value'), (Mesc_ref_tex, 'value'))
Mesc_ref_w= widgets.HBox([Mesc_ref_slider,Mesc_ref_tex])
Mfra_ref_slider = widgets.FloatSlider(
value=.347,
min=0,
max=1,
step=0.01,
description='Frame mass of reference [kg]',
readout_format='.3f', style=style, layout=layout
)
Mfra_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Mfra_ref_slider, 'value'), (Mfra_ref_tex, 'value'))
Mfra_ref_w= widgets.HBox([Mfra_ref_slider,Mfra_ref_tex])
Marm_ref_slider = widgets.FloatSlider(
value=.14,
min=0,
max=1,
step=0.1,
description='Arms mass of reference [kg]',
readout_format='.3f', style=style, layout=layout
)
Marm_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Marm_ref_slider, 'value'), (Marm_ref_tex, 'value'))
Marm_ref_w= widgets.HBox([Marm_ref_slider,Marm_ref_tex])
Sigma_max_ref_slider = widgets.FloatSlider(
value=280e6/4,
min=0,
max=1e8,
step=10e6,
description='Arms mass of reference [kg]',
readout_format='.0f', style=style, layout=layout
)
Sigma_max_ref_tex = widgets.FloatText(description="", continuous_update=False,layout=label_layout)
widgets.link((Sigma_max_ref_slider, 'value'), (Sigma_max_ref_tex, 'value'))
Sigma_max_ref_w= widgets.HBox([Sigma_max_ref_slider,Sigma_max_ref_tex])
w2=v.Tabs(_metadata={'mount_id': 'content-main'}, children=[
v.Tab(children=['Specs.']),
v.Tab(children=['References']),
v.TabItem(children=[Motmodel,HBox([Mot,Kt_DC,Tmot_DC]), Propmodel,HBox([Dia_DC,Pitch_DC]), Batmodel, HBox([Cbat_DC,Ubat_DC,Modelbat]), Ncel_DC,ESCmodel, HBox([Pesc_DC,Vesc_DC, Modelesc]),archit, Narm_DC,arc, perf, k_maxthrust_DC,V_cl_DC,Nred_DC,M_load_DC]),
v.TabItem(children=[rho_air_w,NDmax_w,C_D_w,Dpro_ref_w,Mpro_ref_w,Tmot_ref_w,Rmot_ref_w,Mmot_ref_w,Ktmot_ref_w,Tfmot_ref_w,Mbat_ref_w,
Cbat_ref_w,Vbat_ref_w,Imax_ref_w,Pesc_ref_w,Vesc_ref_w,Mesc_ref_w,Mfra_ref_w,Marm_ref_w,Sigma_max_ref_w]),
]
)
display(w2)
def change_event(x):
clear_output()
df_motfilter=df_mot[df_mot['Model']== Mot.value] #filter data containing such values
df_profilter=df_pro[df_pro['DIAMETER']== Dia_DC.value] #filter data containing such values
df_batfilter=df_bat[df_bat['Capacity_mAh']== Cbat_DC.value] #filter data containing such values
df_batfilter_model=df_bat[(df_bat['Capacity_mAh']==Cbat_DC.value) & (df_bat['Voltage_V']==Ubat_DC.value)] #filter data containing such values
df_escfilter= df_esc[df_esc['Pmax.in[W]']== Pesc_DC.value] #filter data containing such values
df_escfilter_model=df_esc[(df_esc['Pmax.in[W]']==Pesc_DC.value) & (df_esc['Vmax.in[V]']==Vesc_DC.value)] #filter data containing such values
Kt_DC.options = df_motfilter['Kt_Nm_A'].values
Tmot_DC.options = df_motfilter['Tnom_Nm'].values
Ubat_DC.options= sorted(df_batfilter['Voltage_V'].unique().tolist())
Modelbat.options=sorted(df_batfilter_model['Model'].unique().tolist())
Vesc_DC.options= sorted(df_escfilter['Vmax.in[V]'].unique().tolist())
Modelesc.options= sorted(df_escfilter_model['Model'].unique().tolist())
Pitch_DC.options = sorted(df_profilter['BETA'].unique().tolist())
display(w2)
Dia_DC.observe(change_event)
Mot.observe(change_event)
Cbat_DC.observe(change_event)
Ubat_DC.observe(change_event)
Vesc_DC.observe(change_event)
Pesc_DC.observe(change_event)
# +
# Calculation
# Data values:
Ktmot=Kt_DC.value
Tmot=Tmot_DC.value
Dpro=Dia_DC.value*0.0254
beta=Pitch_DC.value
Cbat=Cbat_DC.value/1000*3600#[As] Capacity battery As
Ncel=Ncel_slider_DC.value
Ubat=Ubat_DC.value*Ncel
P_esc=Pesc_DC.value
Vesc=Vesc_DC.value
Narm=Narm_slider_DC.value
D_ratio=D_ratio_slider_DC.value
Np_arm=Np_arm_DC.value
Mod=Mod_DC.value
k_maxthrust=k_maxthrust_slider_DC.value
V_cl=V_cl_slider_DC.value
Nred=Nred_slider_DC.value
M_load=M_pay_DC.value
#Ref. values:
rho_air=rho_air_tex.value
NDmax=NDmax_tex.value
C_D=C_D_tex.value
Dpro_ref=Dpro_ref_tex.value
Mpro_ref=Mpro_ref_tex.value
Tmot_ref=Tmot_ref_tex.value
Rmot_ref=Rmot_ref_tex.value
Mmot_ref=Mmot_ref_tex.value
Ktmot_ref=Ktmot_ref_tex.value
Tfmot_ref=Tfmot_ref_tex.value
Mbat_ref=Mbat_ref_tex.value
Cbat_ref=Cbat_ref_tex.value
Vbat_ref=Vbat_ref_tex.value
Imax_ref=Imax_ref_tex.value
Pesc_ref=Pesc_ref_tex.value
Vesc_ref=Vesc_ref_tex.value
Mesc_ref=Mesc_ref_tex.value
Mfra_ref=Mfra_ref_tex.value
Marm_ref=Marm_ref_tex.value
Sigma_max_ref=Sigma_max_ref_tex.value
# -
Mpro=Mpro_ref*(Dpro/Dpro_ref)**3 # [kg] Propeller mass
Mpro
def Calculator():
#Propeller number:
if Np_arm=='Gear Drive':
Npro=1*(Narm) # [-] Propellers number
else:
Npro=2*(Narm) # [-] Propellers number
#Propeller models
C_t_sta=4.27e-02 + 1.44e-01 * beta # Thrust coef with T=C_T.rho.n^2.D^4
C_p_sta=-1.48e-03 + 9.72e-02 * beta # Power coef with P=C_p.rho.n^3.D^5
n_pro_to=NDmax/Dpro #[Hz] max rotational speed
F_pro_to=C_t_sta*(rho_air)*Dpro**4*n_pro_to**2# [N] max propeller thrust
# Frame parameters
Lbra=Dpro/2/(math.sin(pi/(Narm))) #[m] length of the arm
Dout=(F_pro_to*Lbra*32/(pi*Sigma_max_ref*(1-D_ratio**4)))**(1/3) # [m] outer diameter of the beam
#Total mass:
Mpro=Mpro_ref*(Dpro/Dpro_ref)**3 # [kg] Propeller mass
Mmot=Mmot_ref*(Tmot/Tmot_ref)**(3/3.5) # [kg] Motor mass
Mesc = Mesc_ref*(P_esc/Pesc_ref) # [kg] Mass ESC
Mbat=Mbat_ref*(Cbat/Cbat_ref)*(Ubat/Vbat_ref) # Battery mass
Marm=pi/4*(Dout**2-(D_ratio*Dout)**2)*Lbra*1700*(Narm) # [kg] mass of the arms
Mfra=Mfra_ref*(Marm/Marm_ref)# [kg] mass of the frame
#Gear box model
if Mod=='Gear Drive':
mg1=0.0309*Nred**2+0.1944*Nred+0.6389 # Ratio input pinion to mating gear
WF=1+1/mg1+mg1+mg1**2+Nred**2/mg1+Nred**2 # Weight Factor (ƩFd2/C) [-]
k_sd=1000 # Surface durability factor [lb/in]
C=2*8.85*Tmot_hover/k_sd # Coefficient (C=2T/K) [in3]
Fd2=WF*C # Solid rotor volume [in3]
Mgear=Fd2*0.3*0.4535 # Mass reducer [kg] (0.3 is a coefficient evaluated for aircraft application and 0.4535 to pass from lb to kg)
Fdp2=C*(Nred+1)/Nred # Solid rotor pinion volume [in3]
dp=(Fdp2/0.7)**(1/3)*0.0254 # Pinion diameter [m] (0.0254 to pass from in to m)
dg=Nred*dp # Gear diameter [m]
di=mg1*dp # Inler diameter [m]
# Propeller numbers:
# Total mass:
if Mod=='Direct Drive':
Mtotal = (Mesc+Mpro+Mmot)*Npro+(M_load)+Mbat+Mfra+Marm #total mass without reducer
else:
Mtotal = (Mesc+Mpro+Mmot+Mgear)*Npro+(M_load)+Mbat+Mfra+Marm #total mass with reducer
#Propeller thrust
F_pro_hov=Mtotal*(9.81)/Npro # [N] Thrust per propeller for hover
# Propeller selection with take-off scenario
pitch=beta*Dpro # [m] Propeller pitch
# Propeller selection with take-off scenario
Wpro_to=n_pro_to*2*3.14 # [rad/s] Propeller speed
Ppro_to=C_p_sta*(rho_air)*n_pro_to**3*Dpro**5# [W] Power per propeller
Qpro_to=Ppro_to/Wpro_to # [N.m] Propeller torque
# Propeller torque& speed for hover
n_pro_hover=sqrt(F_pro_hov/(C_t_sta*(rho_air)*Dpro**4)) # [Hz] hover speed
Wpro_hover=n_pro_hover*2*3.14 # [rad/s] Propeller speed
Ppro_hover=C_p_sta*(rho_air)*n_pro_hover**3*Dpro**5# [W] Power per propeller
Qpro_hover=Ppro_hover/Wpro_hover # [N.m] Propeller torque
#---------------------------------
# Motor
# Motor selection & scaling laws
# ---
# Motor reference sized from max thrust
# Ref : AXI 5325/16 GOLD LINE
Tmot_max_ref=85/70*Tmot_ref # [N.m] max torque
#Motor speeds:
if Mod=='Gear Drive':
W_hover_motor=Wpro_hover*Nred # [rad/s] Nominal motor speed with reduction
W_to_motor=Wpro_to*Nred # [rad/s] Motor take-off speed with reduction
else:
W_hover_motor=Wpro_hover # [rad/s] Nominal motor speed
W_to_motor=Wpro_to # [rad/s] Motor take-off speed
#Motor torque:
if Mod=='Gear Drive':
Tmot_hover=Qpro_hover/Nred # [N.m] motor nominal torque with reduction
Tmot_to=Qpro_to/Nred # [N.m] motor take-off torque with reduction
else:
Tmot_hover=Qpro_hover# [N.m] motor take-off torque
Tmot_to=Qpro_to # [N.m] motor take-off torque
Tmot_max=Tmot_max_ref*(Tmot/Tmot_ref)**(1) # [N.m] max torque
# Selection with take-off speed
Rmot=Rmot_ref*(Tmot/Tmot_ref)**(-5/3.5)*(Ktmot/Ktmot_ref)**(2) # [Ohm] motor resistance
Tfmot=Tfmot_ref*(Tmot/Tmot_ref)**(3/3.5) # [N.m] Friction torque
# Hover current and voltage
Imot_hover = (Tmot_hover+Tfmot)/Ktmot # [I] Current of the motor per propeller
Umot_hover = Rmot*Imot_hover + W_hover_motor*Ktmot # [V] Voltage of the motor per propeller
P_el_hover = Umot_hover*Imot_hover # [W] Hover : output electrical power
# Take-Off current and voltage
Imot_to = (Tmot_to+Tfmot)/Ktmot # [I] Current of the motor per propeller
Umot_to = Rmot*Imot_to + W_to_motor*Ktmot # [V] Voltage of the motor per propeller
P_el_to = Umot_to*Imot_to # [W] Takeoff : output electrical power
#----------------
#Battery
I_bat = (P_el_hover*Npro)/.95/Ubat # [I] Current of the battery
t_hf = .8*Cbat/I_bat/60 # [min] Hover time
Imax=Imax_ref*Cbat/Cbat_ref # [A] max current battery
col_names = ['Type', 'Name', 'Value', 'Unit', 'Comment']
#print
df = pd.DataFrame()
df = df.append([{'Type': 'Constraints', 'Name': 'Const 0', 'Value': (Tmot_max-Tmot_to)/Tmot_max, 'Max': '-', 'Unit': '[-]', 'Comment': '(Tmot_max-Tmot_to)/Tmot_max'}])[col_names]
df = df.append([{'Type': 'Constraints', 'Name': 'Const 1', 'Value': (Tmot-Qpro_hover)/Tmot, 'Max': '-', 'Unit': '[-]', 'Comment': '(Tmot-Qpro_hover)/Tmot'}])[col_names]
df = df.append([{'Type': 'Constraints', 'Name': 'Const 2', 'Value': (Ubat-Umot_to)/Ubat, 'Max': '-', 'Unit': '[-]', 'Comment': '(V_bat-Umot_takeoff)/V_bat)'}])[col_names]
df = df.append([{'Type': 'Constraints', 'Name': 'Const 3', 'Value': (Ubat-Vesc)/Ubat, 'Max': '-', 'Unit': '[-]', 'Comment': '(V_bat-Vesc)/V_bat'}])[col_names]
df = df.append([{'Type': 'Constraints', 'Name': 'Const 4', 'Value': (Ubat*Imax-Umot_to*Imot_to*Npro/0.95)/(Ubat*I_bat), 'Max': '-', 'Unit': '[-]', 'Comment': '(V_bat*Imax-Umot_takeoff*Imot_takeoffr*Npro/0.95)/(V_bat*I_bat'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'F_pro_to', 'Value': F_pro_to, 'Unit': '[N]', 'Comment': 'Thrust for 1 propeller during Take Off'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'F_pro_hov', 'Value': F_pro_hov, 'Unit': '[N]', 'Comment': 'Thrust for 1 propeller during Hover'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'rho_air', 'Value': (rho_air), 'Unit': '[kg/m^3]', 'Comment': 'Air density'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'ND_max', 'Value': (NDmax), 'Unit': '[Hz.m]', 'Comment': 'Max speed limit (N.D max)'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'Dpro_ref', 'Value': Dpro_ref, 'Unit': '[m]', 'Comment': 'Reference propeller diameter'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'M_pro_ref', 'Value': Mpro_ref, 'Unit': '[kg]', 'Comment': 'Reference propeller mass'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'C_t_sta', 'Value': C_t_sta, 'Unit': '[-]', 'Comment': 'Static thrust coefficient of the propeller'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'C_p_sta', 'Value': C_p_sta, 'Unit': '[-]', 'Comment': 'Static power coefficient of the propeller'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'D_pro', 'Value': Dpro, 'Unit': '[m]', 'Comment': 'Diameter of the propeller'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'n_pro_to', 'Value': n_pro_to, 'Unit': '[Hz]', 'Comment': 'Rev speed of the propeller during takeoff'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'n_pro_hov', 'Value': n_pro_hover, 'Unit': '[Hz]', 'Comment': 'Rev speed of the propeller during hover'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'P_pro_to', 'Value': Ppro_to, 'Unit': '[W]', 'Comment': 'Power on the mechanical shaft of the propeller during takeoff'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'P_pro_hov', 'Value': Ppro_hover, 'Unit': '[W]', 'Comment': 'Power on the mechanical shaft of the propeller during hover'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'M_pro', 'Value': Mpro, 'Unit': '[kg]', 'Comment': 'Mass of the propeller'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'Omega_pro_to', 'Value': Wpro_to, 'Unit': '[rad/s]', 'Comment': 'Rev speed of the propeller during takeoff'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'Omega_pro_hov', 'Value': Wpro_hover, 'Unit': '[rad/s]', 'Comment': 'Rev speed of the propeller during hover'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'T_pro_hov', 'Value': Qpro_hover, 'Unit': '[N.m]', 'Comment': 'Torque on the mechanical shaft of the propeller during hover'}])[col_names]
df = df.append([{'Type': 'Propeller', 'Name': 'T_pro_to', 'Value': Qpro_to, 'Unit': '[N.m]', 'Comment': 'Torque on the mechanical shaft of the propeller during takeoff'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_max_mot_ref', 'Value': Tmot_max_ref, 'Unit': '[N.m]', 'Comment': 'Max torque'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'R_mot_ref', 'Value': Rmot_ref, 'Unit': '[Ohm]', 'Comment': 'Resistance'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'M_mot_ref', 'Value': Mmot_ref, 'Unit': '[kg]', 'Comment': 'Reference motor mass'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'K_mot_ref', 'Value': Ktmot_ref, 'Unit': '[N.m/A]', 'Comment': 'Torque coefficient'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_mot_fr_ref', 'Value': Tfmot_ref, 'Unit': '[N.m]', 'Comment': 'Friction torque (zero load, nominal speed)'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_nom_mot', 'Value': Tmot_hover, 'Unit': '[N.m]', 'Comment': 'Continuous of the selected motor torque'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_mot_to', 'Value': Tmot_to, 'Unit': '[N.m]', 'Comment': 'Transient torque possible for takeoff'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_max_mot', 'Value': Tmot_max, 'Unit': '[N.m]', 'Comment': 'Transient torque possible for climbing'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'R_mot', 'Value': Rmot, 'Unit': '[Ohm]', 'Comment': 'Resistance'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'M_mot', 'Value': Mmot, 'Unit': '[kg]', 'Comment': 'Motor mass'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'K_mot', 'Value': Ktmot, 'Unit': '[N.m/A', 'Comment': 'Torque constant of the selected motor'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'T_mot_fr', 'Value': Tfmot, 'Unit': '[N.m]', 'Comment': 'Friction torque of the selected motor'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'I_mot_hov', 'Value': Imot_hover, 'Unit': '[A]', 'Comment': 'Motor current for hover'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'I_mot_to', 'Value': Imot_to, 'Unit': '[A]', 'Comment': 'Motor current for takeoff'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'U_mot_cl', 'Value': Umot_hover, 'Unit': '[V]', 'Comment': 'Motor voltage for climbing'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'U_mot_to', 'Value': Umot_to, 'Unit': '[V]', 'Comment': 'Motor voltage for takeoff'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'U_mot', 'Value': Umot_hover, 'Unit': '[V]', 'Comment': 'Nominal voltage '}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'P_el_mot_to', 'Value': P_el_to, 'Unit': '[W]', 'Comment': 'Motor electrical power for takeoff'}])[col_names]
df = df.append([{'Type': 'Motor', 'Name': 'P_el_mot_hov', 'Value': P_el_hover, 'Unit': '[W]', 'Comment': 'Motor electrical power for hover'}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'M_bat_ref', 'Value': Mbat_ref, 'Unit': '[kg]', 'Comment': 'Mass of the reference battery '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'M_esc_ref', 'Value': Mesc_ref, 'Unit': '[kg]', 'Comment': 'Reference ESC mass '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'P_esc_ref', 'Value': Pesc_ref, 'Unit': '[W]', 'Comment': 'Reference ESC power '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'U_bat', 'Value': Ubat, 'Unit': '[V]', 'Comment': 'Battery voltage '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'M_bat', 'Value': Mbat, 'Unit': '[kg]', 'Comment': 'Battery mass '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'C_bat', 'Value': Cbat, 'Unit': '[A.s]', 'Comment': 'Battery capacity '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'I_bat', 'Value': I_bat, 'Unit': '[A]', 'Comment': 'Battery current '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 't_hf', 'Value': t_hf, 'Unit': '[min]', 'Comment': 'Hovering time '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'P_esc', 'Value': P_esc, 'Unit': '[W]', 'Comment': 'Power electronic power (corner power or apparent power) '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'M_esc', 'Value': Mesc, 'Unit': '[kg]', 'Comment': 'ESC mass '}])[col_names]
df = df.append([{'Type': 'Battery & ESC', 'Name': 'V_esc', 'Value': Vesc, 'Unit': '[V]', 'Comment': 'ESC voltage '}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'N_arm', 'Value': (Narm), 'Unit': '[-]', 'Comment': 'Number of arms '}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'N_pro_arm', 'Value': (Np_arm), 'Unit': '[-]', 'Comment': 'Number of propellers per arm '}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'sigma_max', 'Value': Sigma_max_ref, 'Unit': '[Pa]', 'Comment': 'Max admisible stress'}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'L_arm', 'Value': Lbra, 'Unit': '[m]', 'Comment': 'Length of the arm'}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'D_out', 'Value': Dout, 'Unit': '[m]', 'Comment': 'Outer diameter of the arm (tube)'}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'Marm', 'Value': Marm, 'Unit': '[kg]', 'Comment': '1 Arm mass'}])[col_names]
df = df.append([{'Type': 'Frame', 'Name': 'M_frame', 'Value': Mfra, 'Unit': '[kg]', 'Comment': 'Frame mass'}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 'M_load', 'Value': (M_load), 'Unit': '[kg]', 'Comment': 'Payload mass'}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 't_hf', 'Value': (t_hf), 'Unit': '[min]', 'Comment': 'Hovering time '}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 'k_maxthrust', 'Value': (k_maxthrust), 'Unit': '[-]', 'Comment': 'Ratio max thrust'}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 'N_arm', 'Value': (Narm), 'Unit': '[-]', 'Comment': 'Number of arms '}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 'N_pro_arm', 'Value': (Np_arm), 'Unit': '[-]', 'Comment': 'Number of propellers per arm '}])[col_names]
df = df.append([{'Type': 'Specifications', 'Name': 'CD', 'Value': C_D, 'Unit': '[-]', 'Comment': 'Drag coefficient'}])[col_names]
df = df.append([{'Type': 'Objective', 'Name': 'Objective','Value': Mtotal, 'Unit': '[kg]', 'Comment': 'Total mass'}])[col_names]
items = sorted(df['Type'].unique().tolist())+['Optimization']
if (Tmot_max-Tmot_to)/Tmot_max<0:
print('Insufficient motor torque. Choose a larger motor.')
if (Ubat-Umot_to)/Ubat<0 or (Ubat-Vesc)/Ubat<0 or (Ubat*Imax-Umot_to*Imot_to*Npro/0.95)/(Ubat*I_bat)<0:
print('Insufficient battery power. Choose a larger battery')
return df
# +
from IPython.display import display, clear_output
from ipywidgets import widgets
button = widgets.Button(description="Calculate")
display(button)
output = widgets.Output()
@output.capture()
def on_button_clicked(b):
clear_output()
print("-----------------------------------------------")
print("Final characteristics after calculation :")
data=Calculator()
pd.options.display.float_format = '{:,.3f}'.format
def view(x=''):
display(data[data['Type']==x])
items = sorted(data['Type'].unique().tolist())
w = widgets.Select(options=items)
return display(interactive(view, x=w))
# display(data)
button.on_click(on_button_clicked)
display(output)
# -
|
notebooks/.ipynb_checkpoints/12-Multicopter_Validator_eCalc-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Neural Network to predict success of Kickstarter campaigns in 2017
#
# A two layer ANN is trained and evaluated for a regression task on a preprocessed version of the Kickstarter dataset found on: https://www.kaggle.com/kemical/kickstarter-projects
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
import seaborn as sns
# +
# %matplotlib inline
# basic settings
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:,.2f}'.format
plt.rcParams['figure.figsize'] = (5, 5)
sns.set_palette('husl')
# +
def bmplot(yt, xt, X):
''' Function plots matrix X as image with lines separating fields. '''
plt.imshow(X,interpolation='none',cmap='bone')
plt.xticks(range(0,len(xt)), xt)
plt.yticks(range(0,len(yt)), yt)
for i in range(0,len(yt)):
plt.axhline(i-0.5, color='black')
for i in range(0,len(xt)):
plt.axvline(i-0.5, color='black')
def feature_selector_lr(X,y,cvf=10,features_record=None,loss_record=None,display=''):
''' Function performs feature selection for linear regression model using
'cvf'-fold cross validation. The process starts with empty set of
features, and in every recurrent step one feature is added to the set
(the feature that minimized loss function in cross-validation.)
Parameters:
X training data set
y vector of values
cvf number of crossvalidation folds
Returns:
selected_features indices of optimal set of features
features_record boolean matrix where columns correspond to features
selected in subsequent steps
loss_record vector with cv errors in subsequent steps
Example:
selected_features, features_record, loss_record = ...
feature_selector_lr(X_train, y_train, cvf=10)
'''
y = y.squeeze()
# first iteration error corresponds to no-feature estimator
if loss_record is None:
loss_record = np.array([np.square(y-y.mean()).sum()/y.shape[0]])
if features_record is None:
features_record = np.zeros((X.shape[1],1))
# Add one feature at a time to find the most significant one.
# Include only features not added before.
selected_features = features_record[:,-1].nonzero()[0]
min_loss = loss_record[-1]
if display is 'verbose':
print(min_loss)
best_feature = False
for feature in range(0,X.shape[1]):
if np.where(selected_features==feature)[0].size==0:
trial_selected = np.concatenate((selected_features,np.array([feature])),0).astype(int)
# validate selected features with linear regression and cross-validation:
trial_loss = glm_validate(X[:,trial_selected],y,cvf)
if display is 'verbose':
print(trial_loss)
if trial_loss<min_loss:
min_loss = trial_loss
best_feature = feature
# If adding extra feature decreased the loss function, update records
# and go to the next recursive step
if best_feature is not False:
features_record = np.concatenate((features_record, np.array([features_record[:,-1]]).T), 1)
features_record[best_feature,-1]=1
loss_record = np.concatenate((loss_record,np.array([min_loss])),0)
selected_features, features_record, loss_record = feature_selector_lr(X,y,cvf,features_record,loss_record)
# Return current records and terminate procedure
return selected_features, features_record, loss_record
def glm_validate(X,y,cvf=10):
''' Validate linear regression model using 'cvf'-fold cross validation.
The loss function computed as mean squared error on validation set (MSE).
Function returns MSE averaged over 'cvf' folds.
Parameters:
X training data set
y vector of values
cvf number of crossvalidation folds
'''
y = y.squeeze()
CV = model_selection.KFold(n_splits=cvf, shuffle=True)
validation_error=np.empty(cvf)
f=0
for train_index, test_index in CV.split(X):
X_train = X[train_index]
y_train = y[train_index]
X_test = X[test_index]
y_test = y[test_index]
m = linear_model.LinearRegression(fit_intercept=True).fit(X_train, y_train)
validation_error[f] = np.square(y_test-m.predict(X_test)).sum()/y_test.shape[0]
f=f+1
return validation_error.mean()
# -
# ### Artificial neural network
#
# An artificial neural network model is fitted to the data. The number of hidden neurons [10, 20 and 30] is chosen as a complexity-controlling parameter and a two-level cross-validation to both optimize the parameter and estimate the generalization error is applied.
# ### Load, preprocess and visualize dataset
# +
data=pd.read_csv('kickstarter-projects-cleaned_data.csv')
attributes = list(data.columns.values)
# Create index of unwanted attributes
A = np.array([0])
B = np.arange(5,164)
C = np.arange(195,206)
D = np.array([193])
index = list(np.concatenate([A,B,C,D]))
mask = [attributes[i] for i in index]
# Cut down data set to only 2017 data
df17 = data[data.yearlaunched_2017 == 1]
# Remove unwanted attributes
df17 = df17.drop(mask,axis = 1)
df17['backers_log']=np.log10(df17['backers']+1)
df17['backers_log_squared']=np.power(np.log10(df17['backers']+1),2)
df17['usd_goal_real_log']=np.log10(df17['usd_goal_real']+1)
df17['usd_pledged_real']=np.log10(df17['usd_pledged_real']+1)
# Visualize Correlation Matrix
corr = df17.corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
plt.figure(figsize=(9,8))
sns.heatmap(corr, mask=mask, cmap='PiYG', vmin=-0.25, vmax=0.25);
# -
# ### Selecting relevant features and splitting the data
#
# Creating a training- and a testing subset of the dataframe. Given the amount of data, a train-test-ratio of 4:1 is chosen (eg. 80% training, 20% testing).
# The features that were included the most in the feedforward selection shown above were chosen as inputs for the neural network.
# +
my_color=np.where(abs(corr['usd_pledged_real']) > 0.05, 'orange', 'lightgray')
f, ax = plt.subplots(figsize=(5,2))
ax.bar(np.arange(len(corr['usd_pledged_real'])), corr['usd_pledged_real'],
color=my_color, label='Selected features\n(correlation > 5%)')
ax.set(ylabel='Correlation', xlabel='Number of available attributes');
plt.legend();
plt.savefig('ANN_feature_selection.png', dpi = 300)
# -
# features that correlate to the target by more than 5% are selected
significant_features = list(df17.columns[abs(corr['usd_pledged_real']) > 0.05])
df = df17[significant_features]
df.describe()
# Convert a Pandas dataframe to the x,y inputs that TensorFlow needs
def to_xy(df, target):
result = []
for x in df.columns:
if x != target:
result.append(x)
# find out the type of the target column. Is it really this hard? :(
target_type = df[target].dtypes
target_type = target_type[0] if hasattr(target_type, '__iter__') else target_type
# Encode to int for classification, float otherwise. TensorFlow likes 32 bits.
if target_type in (np.int64, np.int32):
# Classification
dummies = pd.get_dummies(df[target])
return df.as_matrix(result).astype(np.float32), dummies.as_matrix().astype(np.float32)
else:
# Regression
return df.as_matrix(result).astype(np.float32), df.as_matrix([target]).astype(np.float32)
# df_red[['usd_pledged_real']].values.astype(np.float32)
df17.drop('usd_goal_real', axis=1)
# +
from sklearn.model_selection import KFold, train_test_split
from sklearn import metrics
from scipy.stats import zscore
import os
import io
import requests
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras import optimizers, regularizers
from keras.callbacks import EarlyStopping, ModelCheckpoint, History
from keras.layers.core import Dense, Activation, Dropout
history = History()
# +
dfr = df[0:6000] # reduced dataframe for faster training
x,y = to_xy(dfr, 'usd_pledged_real')
# Split into train/test
x_train, x_test, y_train, y_test = train_test_split(
x, y, test_size=0.20, random_state=42)
model = Sequential()
model.add(Dense(50, input_dim=x.shape[1], activation='relu'))
model.add(Dense(20, activation='relu'))
model.add(Dropout(0.01))
model.add(Dense(1))
adam = optimizers.Adam(lr=0.02, beta_1=0.9,
beta_2=0.999, epsilon=1e-08, decay=0.0)
model.compile(loss='mean_squared_error', optimizer= adam)
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=5, verbose=1, mode='auto')
# checkpointer = ModelCheckpoint(filepath="best_weights.hdf5", verbose=0, save_best_only=True) # save best model
model.fit(x_train,y_train,validation_data=(x_test,y_test),callbacks=[monitor],verbose=2,epochs=1000)
# -
# ### Error measurement
#
# $ \text{MSE} = \frac{1}{n} \sum_{i=1}^n \left(\hat{y}_i - y_i\right)^2 $
#
# $ \text{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^n \left(\hat{y}_i - y_i\right)^2} $
#
# Keep in mind, that the target is the __base-10 logarithm__ of money pledged in USD.
# Regression chart.
def chart_regression(pred,y,sort=True):
t = pd.DataFrame({'pred' : pred, 'y' : y.flatten()})
if sort:
t.sort_values(by=['y'],inplace=True)
a = plt.plot(t['y'].tolist(),label='expected')
b = plt.plot(t['pred'].tolist(),label='prediction', alpha=0.5)
plt.ylabel('output')
plt.legend()
plt.show()
# +
# Predict
pred = model.predict(x_test)
# Measure RMSE error. RMSE is common for regression.
score = metrics.mean_squared_error(pred,y_test)
print("Final score \n(MSE): {}".format(score))
print("(RMSE): {}".format(np.sqrt(score)))
chart_regression(pred.flatten(),y_test)
# -
# ## 5-fold crossvalidation for generalization error estimation
# +
# CROSS VALIDATION
dfr = df[0:6000] # reduced dataframe for faster training
# Shuffle
np.random.seed(42)
dfr = dfr.reindex(np.random.permutation(dfr.index))
dfr.reset_index(inplace=True, drop=True)
# Encode to a 2D matrix for training
x,y = to_xy(dfr, 'usd_pledged_real')
# Cross-Validate
kf = KFold(5)
oos_y = []
oos_pred = []
fold = 0
# generalization error estimation
for train, test in kf.split(x):
fold+=1
print("Fold #{}".format(fold))
x_train = x[train]
y_train = y[train]
x_test = x[test]
y_test = y[test]
model = Sequential()
model.add(Dense(30, input_dim=x.shape[1], activation='relu',
bias_regularizer=regularizers.l2(0.02)))
model.add(Dense(20, activation='relu'))
model.add(Dropout(0.01))
model.add(Dense(1))
adam = optimizers.Adam(lr=0.01, beta_1=0.9,
beta_2=0.999, epsilon=1e-08, decay=0.0)
model.compile(loss='mean_squared_error', optimizer= adam)
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=5, verbose=1, mode='auto')
# checkpointer = ModelCheckpoint(filepath="best_weights.hdf5", verbose=0, save_best_only=True) # save best model
model.fit(x_train,y_train,validation_data=(x_test,y_test),callbacks=[monitor],verbose=0,epochs=1000)
pred = model.predict(x_test)
oos_y.append(y_test)
oos_pred.append(pred)
# Measure this fold's RMSE
score = metrics.mean_squared_error(pred,y_test)
print("Fold score (MSE): {0:.2f}".format(score))
chart_regression(pred.flatten(),y_test)
# Build the oos prediction list and calculate the error.
oos_y = np.concatenate(oos_y)
oos_pred = np.concatenate(oos_pred)
score = metrics.mean_squared_error(oos_pred,oos_y)
print("Final, out of sample score (MSE): {0:.2f}".format(score))
# Write the cross-validated prediction
# oos_y = pd.DataFrame(oos_y)
# oos_pred = pd.DataFrame(oos_pred)
# oosDF = pd.concat( [dfr, oos_y, oos_pred],axis=1 )
# oosDF.to_csv(filename_write,index=False)
# -
# ## Two layer crossvalidation for model selection and generalization error estimation
# +
dfr = df
# K-fold crossvalidation
K = 10
CV = model_selection.KFold(n_splits=K,shuffle=True,random_state=1)
K_in = 4
CV_in = model_selection.KFold(n_splits=K_in,shuffle=True,random_state=2)
# Set up emtpy vector to gather test errors
test_errors_ann = np.empty((K,1))
# Encode to a 2D matrix for training
x,y = to_xy(dfr, 'usd_pledged_real')
# complexity controlling parameter:
n_neurons = np.array([10, 20, 30])
S = len(n_neurons)
oos_y = []
oos_pred = []
fold = 0
#Initialize k for k'th split
k = 0
# ------ OUTER LAYER ------
# Create splits, begin loop
for train_index, test_index in CV.split(x):
# Extract training and test set for the current outer fold
X_train, y_train = x[train_index,:], y[train_index]
X_test, y_test = x[test_index,:], y[test_index]
# Print progress
print('Begin outer fold {0}'.format(k+1))
# ------ INNER LAYER ------
# Empty vector for validation errors
val_errors_ann = np.empty((K_in, S))
k_in = 0
for train_index, test_index in CV_in.split(X_train):
# Extract training and test set for the current inner fold
X_train_in, y_train_in = X_train[train_index,:], y_train[train_index]
X_test_in, y_test_in = X_train[test_index,:], y_train[test_index]
# Print progress
current_inner_fold = k_in+1
print(' - Current fold: {0}.{1}'.format(k+1, current_inner_fold))
# Train, test, and save the error of model s
for i in range(S):
print('Number of neurons in hidden layer: ', n_neurons[i])
# Fit neural net
model = Sequential()
model.add(Dense(n_neurons[i], input_dim=x.shape[1], activation='relu',
bias_regularizer=regularizers.l2(0.02)))
model.add(Dense(20, activation='relu'))
model.add(Dropout(0.01))
model.add(Dense(1))
adam = optimizers.Adam(lr=0.01, beta_1=0.9,
beta_2=0.999, epsilon=1e-08, decay=0.0)
model.compile(loss='mean_squared_error', optimizer= adam)
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=5, verbose=1, mode='auto')
# checkpointer = ModelCheckpoint(filepath="best_weights.hdf5", verbose=0, save_best_only=True) # save best model
model.fit(X_train_in, y_train_in, validation_data=(X_test_in, y_test_in),
callbacks=[monitor],verbose=0,epochs=100)
pred = model.predict(X_test_in)
oos_y.append(y_test_in)
oos_pred.append(pred)
# Measure this fold's RMSE
score = np.sqrt(metrics.mean_squared_error(pred, y_test_in))
print("Fold score (RMSE): {0:.2f}".format(score))
val_er_ann = sum(np.abs(pred - y_test_in)) / float(len(pred))
val_errors_ann[k_in, i] = val_er_ann
# Move to next inner split
k_in+=1
# Build the oos prediction list and calculate the error.
# oos_y = np.concatenate(oos_y)
# oos_pred = np.concatenate(oos_pred)
# score = np.sqrt(metrics.mean_squared_error(oos_pred, oos_y))
# print("Final, out of sample score (RMSE): {0:.2f}".format(score))
# Evaluate gen. error for model s
gen_errors_s = np.average(val_errors_ann,axis=0)
print('Generalization errors:\n', gen_errors_s)
# Find s* (model with the lowest est. gen. error)
s_star = int(n_neurons[gen_errors_s == min(gen_errors_s)])
print('s* = ', s_star)
# Train the Ms* on the current outer split
M_star = Sequential()
M_star.add(Dense(s_star, input_dim=x.shape[1], activation='relu',
bias_regularizer=regularizers.l2(0.02)))
M_star.add(Dense(20, activation='relu'))
M_star.add(Dropout(0.01))
M_star.add(Dense(1))
adam = optimizers.Adam(lr=0.01, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0)
M_star.compile(loss='mean_squared_error', optimizer= adam)
monitor = EarlyStopping(monitor='val_loss', min_delta=1e-3, patience=5, verbose=1, mode='auto')
M_star.fit(X_train, y_train, validation_data=(X_test, y_test),
callbacks=[monitor],verbose=0,epochs=100)
# Find and save the test error on the current outer split
y_est_test = M_star.predict(X_test)
test_err_k = sum(np.abs(y_est_test - y_test)) / float(len(y_est_test))
test_errors_ann[k] = test_err_k
print('Test errors: ', test_errors_ann)
# Move to next outer split
k+=1
print('\nDone training, believe it or not.')
# -
gen_errs = np.array([[0.30640358, 0.5165964, 0.2918906 ],
[0.29552126, 0.32290896, 0.36205496],
[0.29468293, 0.32881419, 0.28683154],
[0.32307399, 0.30109809, 0.30190605],
[0.32334641, 0.33401129, 0.33029597],
[0.32744938, 0.29884046, 0.31428399],
[0.33579167, 0.55123852, 0.64945341],
[0.2968639, 0.28989638, 0.30702102],
[0.56041283, 0.30725306, 0.30106330],
[0.30072655, 0.30294626, 0.28507698]])
# +
# validation errors
SE_flat = np.ndarray.flatten(gen_errs**2)
nn10 = SE_flat[::3]
nn20 = SE_flat[1::3]
nn30 = SE_flat[2::3]
#test errors
MSE = test_errors_ann**2
# +
# Results of 2-layer CV on neural net
width = 0.2
x_ = np.arange(1, K+1)
fig, ax = plt.subplots(figsize=(9,4))
ax.bar(x_-width, nn10, width, label='Val. error 10 neurons')
ax.bar(x_, nn20, width, label='Val. error 20 neurons')
ax.bar(x_+width, nn30, width, label='Val. error 30 neurons')
ax.bar(x_, list(MSE_flat), width*5, edgecolor='k',
alpha = 0.1, label='Test error on selected model')
ax.axhline(MSE.mean(), alpha = 0.6, label='Estimated generalization error = '\
+str(round(MSE.mean(), 3)))
ax.set(#title='ANN 2-layer cross-validation \n(inner folds: 4)',
xlabel='Outer Fold', xticks=x_, ylabel='Mean squared error');
plt.legend();
plt.savefig('2-layer_CV_ANN_results.png', dpi = 300)
# -
# ### Evaluate performance against a base case
#
# Base case: guessing the mean value of 'usd_pledged_real'
# +
# baseline performance
pledged_mean = df['usd_pledged_real'].mean()
base_error = ((pledged_mean - df['usd_pledged_real'])**2).sum()/len(df['usd_pledged_real'])
print('Guessing the mean value of "usd_pledged_real" (', np.round(pledged_mean, 3), \
') \nresults in a baseline mean squared error of: ', np.round(base_error, 3))
# -
# With the ANN having an __estimated generalization error of 0.147__ this baseline is outperformed by an order of magnitude.
|
Neural_Net_Kickstarter_success_2017.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from astrometry.util.fits import *
# %matplotlib inline
import pylab as plt
import numpy as np
import json
from astrometry.util.util import Tan, Sip, fit_sip_wcs_py
from astrometry.util.starutil_numpy import radectoxyz, arcsec_between
from scipy.interpolate import InterpolatedUnivariateSpline
import fitsio
# +
from mappings import *
guide_loc = 8
petal_id = petal_loc_to_id[guide_loc]
gfa_num = petal_id_to_gfa_num[petal_id]
print('Petal id', petal_id)
print('GFA#', gfa_num)
fn = 'data/sip-petal%i.fits' % petal_id
print('Reading', fn)
labwcs = Sip(fn)
hdr = fitsio.read_header(fn)
# -
petal_loc_to_id
prefix = '32840-10-GUIDE%i' % guide_loc
skywcs = Tan(prefix + '.wcs')
xy = fits_table(prefix + '.axy')
rd = fits_table(prefix + '.rdls')
img = fitsio.read(prefix + '.fits')
corr = fits_table(prefix + '.corr')
print(skywcs)
skycd = np.array(skywcs.cd).reshape((2,2))
#thsky = np.arctan2(skycd[0,1], skycd[0,0])
# x axis
#thsky = np.arctan2(skycd[1,0], skycd[0,0])
thsky = np.arctan2(skycd[1,0]+skycd[1,1], skycd[0,0]+skycd[0,1])
thsky
labcd = np.array(labwcs.wcstan.cd).reshape((2,2))
#thlab = np.arctan2(labcd[0,1], labcd[0,0])
# x axis
#thlab = np.arctan2(labcd[1,0], labcd[0,0])
# avg of x,y axes
thlab = np.arctan2(labcd[1,0]+labcd[1,1], labcd[0,0]+labcd[0,1])
thlab
labcd
skycd
dth = thsky - thlab
R = np.array([[np.cos(dth), -np.sin(dth)],[np.sin(dth), np.cos(dth)]])
newcd = np.dot(R, labcd)
newcd
np.rad2deg(dth)
# +
plt.plot([0, skycd[0,0]], [0, skycd[1,0]], 'b-')
plt.plot([0, skycd[0,1]], [0, skycd[1,1]], 'c-')
plt.plot([0, newcd[0,0]], [0, newcd[1,0]], 'r-')
plt.plot([0, newcd[0,1]], [0, newcd[1,1]], 'm-')
plt.plot([0, labcd[0,0]], [0, labcd[1,0]], 'g-')
plt.plot([0, labcd[0,1]], [0, labcd[1,1]], 'k-')
plt.axis('equal');
# -
fitwcs = Sip(labwcs)
fitwcs.wcstan.set_cd(*newcd.ravel())
fitwcs.wcstan.set_crval(*skywcs.crval)
print(fitwcs)
# +
plt.figure(figsize=(12,6))
#refra = rd.ra
#refdec = rd.dec
refra = corr.index_ra
refdec = corr.index_dec
ok,tx,ty = fitwcs.radec2pixelxy(refra, refdec)
mn,mx = np.percentile(img.ravel(), [50,99])
plt.imshow(np.minimum(img,mx), interpolation='nearest', origin='lower', vmin=mn, vmax=mx*1.2, cmap='gray');
ax = plt.axis()
plt.plot(tx-1, ty-1, 'o', mec='r', mfc='none',ms=10, mew=2)
imx = corr.field_x/1.1
imy = corr.field_y
plt.plot(imx-1, imy-1, '+', mec='c', mfc='none', ms=15, mew=2);
#plt.axis(ax)
# +
# Undo SIP distortion for pixel locations of stars
# Re-fit to reference stars for the TAN terms (with CRPIX=center)
# +
# SIP_pixelxy2radec: sip_distortion -> tan_pixelxy2radec
# xy2radec: xy2iwc, iwc2xyz, xyz2rd
# Re-fit: CRVAL, CD rotation. Scale?
# -
dixy = np.array([fitwcs.get_distortion(xi,yi) for xi,yi in zip(imx, imy)])
dix = dixy[:,0]
diy = dixy[:,1]
plt.figure(figsize=(12,6))
plt.imshow(np.minimum(img,mx), interpolation='nearest', origin='lower', vmin=mn, vmax=mx*1.2, cmap='gray');
ax = plt.axis()
plt.plot(imx-1, imy-1, '+', mec='r', mfc='none', ms=15, mew=2);
plt.plot(dix-1, diy-1, '+', mec='c', mfc='none', ms=15, mew=2);
# +
fittan = Tan(fitwcs.wcstan)
def move_tan_1(intan, dr, dd, rot):
otan = Tan(intan)
cra,cdec = otan.crval
cd = np.array(otan.cd).reshape((2,2))
otan.set_crval(*(cra+dr, cdec+dd))
R = np.array([[np.cos(rot), -np.sin(rot)],[np.sin(rot), np.cos(rot)]])
rcd = np.dot(R, cd)
otan.set_cd(*rcd.ravel())
return otan
def objective_1(params):
dr,dd,rot = params
otan = move_tan_1(fittan, dr, dd, rot)
ok,xx,yy = otan.radec2pixelxy(refra, refdec)
return np.sum(np.hypot(xx - dix, yy - diy))
# +
def move_tan_2(intan, dr, dd, rot, scale):
otan = Tan(intan)
cra,cdec = otan.crval
cd = np.array(otan.cd).reshape((2,2))
otan.set_crval(*(cra+dr, cdec+dd))
R = np.array([[np.cos(rot), -np.sin(rot)],[np.sin(rot), np.cos(rot)]])
rcd = np.dot(R, cd)
otan.set_cd(*((1.+scale) * rcd.ravel()))
return otan
def objective_2(params):
dr,dd,rot, scale = params
otan = move_tan_2(fittan, dr, dd, rot, scale)
ok,xx,yy = otan.radec2pixelxy(refra, refdec)
return np.sum(np.hypot(xx - dix, yy - diy))
# -
from scipy.optimize import minimize
res1 = minimize(objective_1, np.array([0,0,0]))
res1
res2 = minimize(objective_2, np.array([0.,0.,0.,0.]))
res2
opttan = move_tan_1(fittan, *res1.x)
optsip = Sip(fitwcs)
optsip.wcstan = opttan
opttan2 = move_tan_2(fittan, *res2.x)
optsip2 = Sip(fitwcs)
optsip2.wcstan = opttan2
print(fittan)
print(opttan)
print(optsip)
print(optsip2)
plt.figure(figsize=(12,6))
plt.imshow(np.minimum(img,mx), interpolation='nearest', origin='lower', vmin=mn, vmax=mx*1.2, cmap='gray');
ax = plt.axis()
plt.plot(imx-1, imy-1, '+', mec='c', mfc='none', ms=15, mew=2);
ok,tx,ty = optsip.radec2pixelxy(refra, refdec)
plt.plot(tx-1, ty-1, 'o', mec='r', mfc='none',ms=10, mew=2);
plt.figure(figsize=(12,6))
plt.imshow(np.minimum(img,mx), interpolation='nearest', origin='lower', vmin=mn, vmax=mx*1.2, cmap='gray');
ax = plt.axis()
plt.plot(imx-1, imy-1, '+', mec='c', mfc='none', ms=15, mew=2);
ok,tx,ty = optsip2.radec2pixelxy(refra, refdec)
plt.plot(tx-1, ty-1, 'o', mec='r', mfc='none',ms=10, mew=2);
gif1xy = np.array([(hdr['GIF1X%i'%i], hdr['GIF1Y%i'%i]) for i in range(1,5)])
gif2xy = np.array([(hdr['GIF2X%i'%i], hdr['GIF2Y%i'%i]) for i in range(1,5)])
plt.figure(figsize=(12,6))
plt.imshow(np.minimum(img,mx), interpolation='nearest', origin='lower', vmin=mn, vmax=mx*1.2, cmap='gray');
ax = plt.axis()
plt.plot(imx-1, imy-1, '+', mec='c', mfc='none', ms=15, mew=2);
ok,tx,ty = optsip2.radec2pixelxy(refra, refdec)
plt.plot(tx-1, ty-1, 'o', mec='r', mfc='none',ms=10, mew=2);
plt.plot(gif1xy[:,0], gif1xy[:,1], 'r.')
plt.plot(gif2xy[:,0], gif2xy[:,1], 'b.');
gif1ra,gif1dec = optsip.pixelxy2radec(gif1xy[:,0], gif1xy[:,1])
gif2ra,gif2dec = optsip.pixelxy2radec(gif2xy[:,0], gif2xy[:,1])
# +
h,w = 1032,2048
ccdbx,ccdby = [1,w,w,1,1], [1,1,h,h,1]
ccdra,ccddec = optsip.pixelxy2radec(ccdbx, ccdby)
#sra,sdec = skywcs.pixelxy2radec(ccdbx, ccdby)
#plt.plot(sra, sdec, 'g-');
#plt.plot(sra[0], sdec[0], 'go');
plt.plot(ccdra, ccddec, 'k-');
plt.plot(ccdra[0], ccddec[0], 'ko');
plt.plot(refra, refdec, 'b+');
plt.plot(gif1ra, gif1dec, 'r.')
plt.plot(gif2ra, gif2dec, 'b.')
plt.axis('equal')
xl,xh = plt.xlim()
plt.xlim(xh,xl);
# -
for g in [0,2,3,5,7]:#,8]:
fn = 'gfa-28205-GUIDE%i.wcs' % g
wcs = Tan(fn)
ra,dec = wcs.pixelxy2radec(ccdbx, ccdby)
plt.plot(ra, dec, 'k-')
plt.plot(ra[0], dec[0], 'ko')
plt.text(np.mean(ra), np.mean(dec), 'GUIDE%i'%g)
xl,xh = plt.xlim()
plt.xlim(xh,xl)
plt.xlabel('RA (deg)')
plt.ylabel('Dec (deg)')
|
where-gifs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: distillation
# language: python
# name: distillation
# ---
# +
#default_exp nbdev_tests.multiple
# -
# # Test if we can re-define the same function on different notebooks
# +
#export
def defined_in_multiple_nbs():
print("This function was defined on notebook 02")
# -
|
nbs/test_nbdev_define_in_subfolder/02 define in multiple nbs 2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## PCA GPU Acceleration Demo
# *Principal component analysis (PCA)* is a technique used for identification of a smaller number of uncorrelated variables known as principal components from a larger set of data. The technique is widely used to emphasize variation and capture strong patterns in a data set.
#
# Principal component analysis is considered a useful statistical method and used in fields such as image compression, face recognition, neuroscience and computer graphics.
#
#
#
# source : https://www.techopedia.com/definition/32509/principal-component-analysis-pca
# ## Why do we use PCA ?
# Large number of features in the dataset is one of the factors that affect both the training time as well as accuracy of machine learning models. You have different **options to deal with huge number of features in a dataset**.
#
# 1. Try to train the models on original number of features, which take days or weeks if the number of features is too high.
# 2. Reduce the number of variables by merging correlated variables.
# 3. Extract the most important features from the dataset that are responsible for maximum variance in the output. Different statistical techniques are used for this purpose e.g. linear discriminant analysis, factor analysis, and principal component analysis.
#
# Principal component analysis, or PCA, is a statistical technique to **convert high dimensional data to low dimensional data** by selecting the most important features that capture maximum information about the dataset.
#
# The features are selected on the basis of variance that they cause in the output. The feature that causes highest variance is the *first principal component*. The feature that is responsible for second highest variance is considered the *second principal component*, and so on. It is important to mention that principal components do not have any correlation with each other.
#
# source: https://stackabuse.com/implementing-pca-in-python-with-scikit-learn/
# ## Setup
# Let's check out our hardware setup by runing the `nvidia-smi` command:
# !nvidia-smi
# ## CUDA Version
#
# Next, let's see what CUDA version we have.
# !nvcc --version
# ## Basic Example using Iris Dataset
# ### Importing libraries
# At first, we are going to import basic python libraries needed to run a very simple exaple to explain the above mentioned algorithm
# !pip install matplotlib
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA as skPCA
import os
# -
# ### Import IRIS Dataset
# https://archive.ics.uci.edu/ml/datasets/iris
#
# The dataset consists of 150 records of Iris plant with **four features**: 'sepal-length', 'sepal-width', 'petal-length', and 'petal-width'. All of the features are numeric. The records have been classified into one of the **three classes** i.e. 'Iris-setosa', 'Iris-versicolor', or 'Iris-verginica'.
# ### Dataset Overview
from sklearn.datasets import load_iris
iris = load_iris()
# +
#source : https://towardsdatascience.com/pca-using-python-scikit-learn-e653f8989e60
# The indices of the features that we are plotting
x_index = 0
y_index = 1
# this formatter will label the colorbar with the correct target names
formatter = plt.FuncFormatter(lambda i, *args: iris.target_names[int(i)])
plt.figure(figsize=(5, 4))
plt.scatter(iris.data[:, x_index], iris.data[:, y_index], c=iris.target)
plt.colorbar(ticks=[0, 1, 2], format=formatter)
plt.xlabel(iris.feature_names[x_index])
plt.ylabel(iris.feature_names[y_index])
plt.tight_layout()
plt.show()
# -
print(iris.data.shape) ## number of rows/columns
print(iris.feature_names) ## feature names
print(iris.target_names) ## categories
# ### Basic cleaning of the data
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']
df = pd.read_csv(url, names=names)
df.head()
#divide the dataset into a feature set and corresponding labels.
X = df.drop('Class', 1)
y = df['Class']
# +
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# +
#PCA performs best with a normalized feature set. We will perform standard scalar normalization to normalize our feature set.
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# -
# ### Applying PCA
# Performing PCA using Scikit-Learn is a two-step process:
#
# 1. **Initialize the PCA class** by passing the number of components to the constructor.
# 2. **Call the *fit* and then *transform* methods** by passing the feature set to these methods. The *transform* method returns the specified number of principal components.
pca = skPCA()
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
# The PCA class contains `explained_variance_ratio_` which returns the variance caused by each of the principal components.
explained_variance = pca.explained_variance_ratio_
print(explained_variance)
# It can be seen that first principal component is responsible for 72.22% variance. Similarly, the second principal component causes 23.9% variance in the dataset. Collectively we can say that (72.22 + 23.9) 96.21% percent of the classification information contained in the feature set is captured by the first two principal components.
pca = skPCA(n_components=1)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
# ### Training and Making Predictions
# In this case we'll use random forest classification for making the predictions.
# +
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(max_depth=2, random_state=0)
classifier.fit(X_train, y_train)
# Predicting the Test set results
y_pred = classifier.predict(X_test)
# +
#Performance Evaluation
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
print( accuracy_score(y_test, y_pred))
# -
# it can be seen from the output that with only one feature, the random forest algorithm is able to correctly predict 28 out of 30 instances, resulting in 93.33% accuracy.
# ## PCA on larger dataset and CPU vs GPU comparisson
# We will first import some helper functions
# +
# measure the execution time
from timeit import default_timer
class Timer(object): #Class for timing execution speed of small code snippets.
def __init__(self):
self._timer = default_timer
def __enter__(self):
self.start()
return self
def __exit__(self, *args):
self.stop()
def start(self):
"""Start the timer."""
self.start = self._timer()
def stop(self):
"""Stop the timer. Calculate the interval in seconds."""
self.end = self._timer()
self.interval = self.end - self.start
# +
def load_data(nrows, ncols, ):
print('use random data')
X = np.random.rand(nrows,ncols)
df = pd.DataFrame({'fea%d'%i:X[:,i] for i in range(X.shape[1])})
return df
# +
from sklearn.metrics import mean_squared_error
def array_equal(a,b,threshold=2e-3,with_sign=True):
a = to_nparray(a)
b = to_nparray(b)
if with_sign == False:
a,b = np.abs(a),np.abs(b)
error = mean_squared_error(a,b)
res = error<threshold
return res
def to_nparray(x):
if isinstance(x,np.ndarray) or isinstance(x,pd.DataFrame):
return np.array(x)
elif isinstance(x,np.float64):
return np.array([x])
elif isinstance(x,cudf.DataFrame) or isinstance(x,cudf.Series):
return x.to_pandas().values
return x
# -
# ### Run some tests using random data
#
# Let's use the larger dataset with more features
# +
# %%time
## here, we will load the random data with 1M rows and 400 columns. Feel free to experiment with a different dataset sizes.
nrows = 1000000
ncols = 400
X = load_data(nrows,ncols)
print('data',X.shape)
# -
# Let's take a look into all possible parameters that we can use when applying PCA :http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
#
# We will start here with the following :
#
# - **n_components : int, float, None or string** <br>
# Number of components to keep. if `n_components` is not set all components are kept
# - **whiten : bool, optional (default False)** <br>
# When `True` (`False` by default) the `components_` vectors are multiplied by the square root of `n_samples` and then divided by the singular values to ensure uncorrelated outputs with unit component-wise variances.<br/>Whitening will remove some information from the transformed signal (the relative variance scales of the components) but can sometime improve the predictive accuracy of the downstream estimators by making their data respect some hard-wired assumptions
#
# - **random_state : int, RandomState instance or None, optional (default None)** <br>
# If int, `random_state` is the seed used by the random number generator
#
# - **svd_solver : string {‘auto’, ‘full’, ‘arpack’, ‘randomized’}** <br>
# If `"full"` :run exact full SVD calling the standard LAPACK solver via scipy.linalg.svd and select the components by postprocessing
# +
n_components = 10
whiten = False
random_state = 42
svd_solver="full"
# -
# Let's check the time needed to execute PCA function using standard *sklearn* library. Note: this algorithm runs on CPU only.
import multiprocessing
print(multiprocessing.cpu_count()) # Return the number of CPUs in the system.
# +
# %%time
from sklearn.decomposition import PCA as skPCA
pca_sk = skPCA(n_components=n_components,svd_solver=svd_solver,
whiten=whiten, random_state=random_state)
result_sk = pca_sk.fit_transform(X)
# -
# Now, before we execute PCA function using RAPIDS *cuml* library we will first read the data in GPU data format using *cudf* :
# - cudf - GPU DataFrame manipulation library https://github.com/rapidsai/cudf
# - cuml - suite of libraries that implements a machine learning algorithms within the RAPIDS data science ecosystem https://github.com/rapidsai/cuml
# +
# %%time
import cudf
import cuml #documentaton can be found here https://cuml.readthedocs.io/en/latest/
from cuml import PCA as cumlPCA
X = cudf.DataFrame.from_pandas(X)
# -
# Next, we will execute the PCA function using cuml and check the performance
# %%time
pca_cuml = cumlPCA(n_components=n_components,svd_solver=svd_solver,
whiten=whiten, random_state=random_state)
result_cuml = pca_cuml.fit_transform(X)
# We see that for dataset of size 1000000 rows and 400 columns it takes around 8X less time to execute the PCA algorithm using RAPIDS cuml library.
#
# Block of the code below compares the attributes and results of two libraries : *sklearn* PCA and *cuml* PCA. Here, we see that results and attributes are exacty the same and that user will not see any difference in the existing workflow.
for attr in ['singular_values_','components_','explained_variance_',
'explained_variance_ratio_']:
passed = array_equal(getattr(pca_sk,attr),getattr(pca_cuml,attr))
message = 'compare pca: cuml vs sklearn {:>25} {}'.format(attr,'equal' if passed else 'NOT equal')
print(message)
passed = array_equal(result_sk,result_cuml)
message = 'compare pca: cuml vs sklearn transformed results %s'%('equal'if passed else 'NOT equal')
print(message)
|
2-CuML/2. PCA_Demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit (conda)
# language: python
# name: python3
# ---
from nrs import NRS_Model, Element, NRS_Revision, NRS_Observer_E # классы НРС
from nrs import NRS_Data as nd # Табличные данные НРС
from nrs import q_out_simple, q_out_nozzle # модели расчета параметров
import matplotlib.pyplot as plt # библиотеки для отрисовки получаемых данных
# ## Простая модель от одного насоса к одному стволу
# 
#
#
# Схема НРС состоит из:
# * 1 источника в виде насоса ПА
# * 1 рабочей рукавной линии
# * 1 прибора подачи воды
# Вычисляем проводимость насадка для ствола Б
p_nozzleB = NRS_Revision.calc_p(3.7, 40)
p_nozzleB
# +
# Создаем элементы НРС
pump = Element('Насос', e_type=0, H_add=20) # Стартовый напор на насосе = 20м
hoseW1 = Element('РРЛ 1', e_type=1, s=nd.ss["51"], n=10) # Рукава 51мм, кол-во рукавов=10
nozzle1 = Element('Ствол 1', e_type=2, p=p_nozzleB, q_out = q_out_nozzle) # Для ствола указываем проводимость расчитанную ранее (p_nozzleB) и метод расчета q_out_nozzle
# Соединяем элементы друг с другом Насос->Рукавная линия->Ствол
pump.append(hoseW1).append(nozzle1)
# Добавляем наблюдателей
watcher_pump = NRS_Observer_E(pump, ['q', 'H_add']) # Для насоса. Наблюдаем изменения расхода и дополнительного напора (создаваемого насосом)
watcher_nozzle1 = NRS_Observer_E(nozzle1, ['q', 'H_in']) # Для ствола. Наблюдаем изменения расхода и напора на входе
# Строим модель и инициируем обозревателей
model = NRS_Model('Простая модель от одного насоса к одному стволу')
model.build(pump, interpretate=True).observersInit()
# -
# Печатаем состав модели
NRS_Revision.print_model_elements(model)
# Печать предыдущего элемента для ствола nozzle1
NRS_Revision.print_previous_elements(nozzle1)
# Рассчет
model.calc(accuracy=0.05)
print(model.summaryQ())
# +
# Рассчитываем (для 10 итераций)
# model.calc(iters=10)
# -
# Получаем текущий суммарный расход НРС
print(model.summaryQ())
# +
# Выведем графики
fig, axs = plt.subplots(2, 1, figsize=(12, 6))
axs[0].plot(watcher_nozzle1.history()['q'], label=nozzle1.name)
axs[0].set_title('Проиводительность НРС:')
axs[0].set_ylabel('Q, л/с')
axs[0].legend(fontsize=10)
axs[1].plot(watcher_nozzle1.history()['H_in'], label=nozzle1.name)
axs[1].plot(watcher_pump.history()['H_add'], label=pump.name, )
axs[1].set_title('Напоры:')
axs[1].set_xlabel('итерации')
axs[1].set_ylabel('Н, м')
axs[1].legend(fontsize=10)
plt.show()
# -
# Постепенно повысим напоры на насосе. Сначала до 40м, затем до 80м. Для каждого повышения проведем расчет на 10 итерациях.
pump.set_H_add(40)
model.calc(10)
print(model.summaryQ())
pump.set_H_add(80)
model.calc(10)
print(model.summaryQ())
# +
# Выведем графики
fig, axs = plt.subplots(2, 1, figsize=(12, 6))
axs[0].plot(watcher_nozzle1.history()['q'], label=nozzle1.name)
axs[0].set_title('Проиводительность НРС:')
axs[0].set_ylabel('Q, л/с')
axs[0].legend(fontsize=10)
axs[1].plot(watcher_nozzle1.history()['H_in'], label=nozzle1.name)
axs[1].plot(watcher_pump.history()['H_add'], label=pump.name, )
axs[1].set_title('Напоры:')
axs[1].set_xlabel('итерации')
axs[1].set_ylabel('Н, м')
axs[1].legend(fontsize=10)
plt.show()
# -
# ## Расчет до достижения необходимой точности
# +
# Сбрасываем историю расчета
# model.observersInit()
# Устанавливаем напор на насосе
pump.set_H_add(40)
# Рассчитываем для точности 0.005л/с
_, iters_count = model.calc(accuracy=0.005)
print("Итоговый расход: {} л/с".format(model.summaryQ()))
print("Потребовалось итераций: {}".format(iters_count))
# +
# Выведем графики
fig, axs = plt.subplots(2, 1, figsize=(12, 6))
axs[0].plot(watcher_nozzle1.history()['q'], label=nozzle1.name)
axs[0].set_title('Проиводительность НРС:')
axs[0].set_ylabel('Q, л/с')
axs[0].legend(fontsize=10)
axs[1].plot(watcher_nozzle1.history()['H_in'], label=nozzle1.name)
axs[1].plot(watcher_pump.history()['H_add'], label=pump.name, )
axs[1].set_title('Напоры:')
axs[1].set_xlabel('итерации')
axs[1].set_ylabel('Н, м')
axs[1].legend(fontsize=10)
plt.show()
|
workFolder/simple_NRS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Tce3stUlHN0L"
# ##### Copyright 2020 The TensorFlow Authors.
# + cellView="form" id="tuOe1ymfHZPu"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="23R0Z9RojXYW"
# # Standalone Model Card Toolkit Demo
#
# This "standalone" notebook demonstrates using the Model Card Toolkit without the TFX/MLMD context. To learn how to use Model Card Toolkit with TFX/MLMD, please check [MLMD Model Card Toolkit Demo](./MLMD_Model_Card_Toolkit_Demo.ipynb).
# + [markdown] id="MfBg1C5NB3X0"
# <table class="tfo-notebook-buttons" align="left">
# <!-- TODO(b/157683787) uncomment when MCT tutorial is shown in tf site.
# <td>
# <a target="_blank" href="https://www.tensorflow.org/responsible_ai"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# -->
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/documentation/examples/Standalone_Model_Card_Toolkit_Demo.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/documentation/examples/Standalone_Model_Card_Toolkit_Demo.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View on GitHub</a>
# </td>
# <!-- TODO(b/157683787) uncomment when MCT tutorial is uploaded to tf docs.
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/tools/templates/notebook.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# -->
# </table>
# + [markdown] id="sfSQ-kX-MLEr"
# ## Objective
#
# This notebook demonstrates how to generate a Model Card using the Model Card Toolkit in a Jupyter/Colab environment. You can learn more about model cards at https://modelcards.withgoogle.com/about.
#
# We are using a Keras model in this demo. But the logic below also applies to other ML frameworks in general.
#
#
# + [markdown] id="2GivNBNYjb3b"
# ## Setup
# We first need to a) install and import the necessary packages, and b) download the data.
# + [markdown] id="Fmgi8ZvQkScg"
# ### Upgrade to Pip 20.2 and install the Model Card Toolkit
# + id="as4OTe2ukSqm"
try:
import colab
# !pip install --upgrade pip==20.2
except:
pass
# !pip install 'model-card-toolkit>=0.1.1,<0.2'
# !pip install 'tensorflow>=2.3.1,<2.4'
# + [markdown] id="EwT0nov5QO1M"
# #### Did you restart the runtime?
#
# If you are using Google Colab, the first time that you run the cell above, you must restart the runtime (Runtime > Restart runtime ...). This is because of the way that Colab loads packages.
# + [markdown] id="7-JNjw8eUdrL"
# ### Imports
# + id="Nx4sE8cUUhF-"
import tensorflow as tf
import numpy as np
from model_card_toolkit import ModelCardToolkit
from model_card_toolkit.documentation.examples import cats_vs_dogs
from model_card_toolkit.utils.graphics import figure_to_base64str
import tempfile
import matplotlib.pyplot as plt
from IPython import display
import requests
import os
import zipfile
# + [markdown] id="jzNHy94JjfEJ"
# ## Model
# + [markdown] id="u7UTf5FqXeQd"
# We will use a pretrained model with architecture based off [MobileNetV2](https://arxiv.org/abs/1801.04381), a popular 16-layer image classification model. Our model has been trained to distinguish between betweens cats and dogs using the [Cats vs Dogs](https://www.tensorflow.org/datasets/catalog/cats_vs_dogs) dataset. The model training was based on the [TensorFlow transfer learning tutorial](https://www.tensorflow.org/tutorials/images/transfer_learning).
# + id="TJzHu_ZQCJ_z"
URL = 'https://storage.googleapis.com/cats_vs_dogs_model/cats_vs_dogs_model.zip'
BASE_PATH = tempfile.mkdtemp()
ZIP_PATH = os.path.join(BASE_PATH, 'cats_vs_dogs_model.zip')
MODEL_PATH = os.path.join(BASE_PATH,'cats_vs_dogs_model')
r = requests.get(URL, allow_redirects=True)
open(ZIP_PATH, 'wb').write(r.content)
with zipfile.ZipFile(ZIP_PATH, 'r') as zip_ref:
zip_ref.extractall(BASE_PATH)
model = tf.keras.models.load_model(MODEL_PATH)
# + [markdown] id="7SUMYXTM3Cch"
# ## Dataset
# + [markdown] id="5ABTI039kuEn"
# In the cats-vs-dogs dataset, label=0 corresponds to cats while label=1 corresponds to dogs.
# + id="qxzLef3Z6c4c"
def compute_accuracy(data):
x = np.stack(data['examples'])
y = np.asarray(data['labels'])
_, metric = model.evaluate(x, y)
return metric
# + id="CZpI3nR-NRza"
examples = cats_vs_dogs.get_data()
print('num validation examples:', len(examples['combined']['examples']))
print('num cat examples:', len(examples['cat']['examples']))
print('num dog examples:', len(examples['dog']['examples']))
# + id="1pra-P9ZkZ1N"
accuracy = compute_accuracy(examples['combined'])
cat_accuracy = compute_accuracy(examples['cat'])
dog_accuracy = compute_accuracy(examples['dog'])
# + [markdown] id="sYM7Tnrf7Ffr"
# ## Use the Model Card Toolkit
# + [markdown] id="nFZ4VJ2HR8BH"
# ### Initialize the Model Card Toolkit
#
# The first step is to initialize a `ModelCardToolkit` object, which maintains assets including a [model card JSON file](https://github.com/tensorflow/model-card-toolkit/tree/master/model_card_toolkit/schema/) and [model card document](https://github.com/tensorflow/model-card-toolkit/tree/master/model_card_toolkit/template). Call `ModelCardToolkit.scaffold_assets()` to generate these assets and return a `ModelCard` object.
# + id="Lw5Xcn4xnNQB"
# https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/model_card_toolkit.py
model_card_dir = tempfile.mkdtemp()
mct = ModelCardToolkit(model_card_dir)
# https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/model_card.py
model_card = mct.scaffold_assets()
# + [markdown] id="FrnPOUcAOStf"
# ### Annotate the Model Card
#
# The `ModelCard` object returned by `scaffold_assets()` has many fields that can be directly modified. These fields are rendered in the final generated Model Card document. For a comprehensive list, see [model_card.py](https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/model_card.py). See [the documentation](https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/documentation/concepts.md) for more details.
#
# + [markdown] id="x5eg7xbISa4g"
# #### Text Fields
# + [markdown] id="3cO1srgD2EHw"
# ##### Model Details
#
# `model_card.model_details` contains many basic metadata fields such as `name`, `owners`, and `version`. You can provide a description for your model in the `overview` field.
# + id="RvFUltDAB3O5"
model_card.model_details.name = 'Fine-tuned MobileNetV2 Model for Cats vs. Dogs'
model_card.model_details.overview = (
'This model distinguishes cat and dog images. It uses the MobileNetV2 '
'architecture (https://arxiv.org/abs/1801.04381) and is trained on the '
'Cats vs Dogs dataset '
'(https://www.tensorflow.org/datasets/catalog/cats_vs_dogs). This model '
'performed with high accuracy on both Cat and Dog images.'
)
model_card.model_details.owners = [
{'name': 'Model Cards Team', 'contact': '<EMAIL>'}
]
model_card.model_details.version = {'name': 'v1.0', 'date': '08/28/2020'}
model_card.model_details.references = [
'https://www.tensorflow.org/guide/keras/transfer_learning',
'https://arxiv.org/abs/1801.04381',
]
model_card.model_details.license = 'Apache-2.0'
model_card.model_details.citation = 'https://github.com/tensorflow/model-card-toolkit/blob/master/model_card_toolkit/documentation/examples/Standalone_Model_Card_Toolkit_Demo.ipynb'
# + [markdown] id="yoxXI5-P7JQC"
# ##### Quantitative Analysis
#
# `model_card.quantitative_analysis` contains information about a model's performance metrics.
#
# Below, we create some synthetic performance metric values for a hypothetical model built on our dataset.
# + id="rtd9Y7yN7ITg"
model_card.quantitative_analysis.performance_metrics = [
{'type': 'accuracy', 'value': accuracy},
{'type': 'accuracy', 'value': cat_accuracy, 'slice': 'cat'},
{'type': 'accuracy', 'value': dog_accuracy, 'slice': 'Dog'},
]
# + [markdown] id="zRhj7rQX3gS4"
# ##### Considerations
#
# `model_card.considerations` contains qualifying information about your model - what are the appropriate use cases, what are limitations that users should keep in mind, what are the ethical considerations of application, etc.
# + id="-b12rEyq7QXG"
model_card.considerations.use_cases = [
'This model classifies images of cats and dogs.'
]
model_card.considerations.limitations = [
'This model is not able to classify images of other classes.'
]
model_card.considerations.ethical_considerations = [{
'name':
'While distinguishing between cats and dogs is generally agreed to be '
'a benign application of machine learning, harmful results can occur '
'when the model attempts to classify images that don’t contain cats or '
'dogs.',
'mitigation_strategy':
'Avoid application on non-dog and non-cat images.'
}]
# + [markdown] id="Zo9xHyAcVl6h"
# #### Graph Fields
#
# It's often best practice for a report to provide information on a model's training data, and its performance across evaluation data. Model Card Toolkit allows users to encode this information in visualizations, rendered in the Model Card.
#
# `model_card` has three sections for graphs -- `model_card.model_parameters.data.train.graphics` for training dataset statistics, `model_card.model_parameters.data.eval.graphics` for evaluation dataset statistics, and `model_card.quantitative_analysis.graphics` for quantitative analysis of model performance.
#
# Graphs are stored as [base64 strings](https://en.wikipedia.org/wiki/Base64). If you have a [matplotlib](https://pypi.org/project/matplotlib/) figure, you can convert it to a base64 string with `model_card_toolkit.utils.graphics.figure_to_base64str()`.
# + id="ZMis4kzXdeqy"
# Validation Set Size Bar Chart
fig, ax = plt.subplots()
width = 0.75
rects0 = ax.bar(0, len(examples['combined']['examples']), width, label='Overall')
rects1 = ax.bar(1, len(examples['cat']['examples']), width, label='Cat')
rects2 = ax.bar(2, len(examples['dog']['examples']), width, label='Dog')
ax.set_xticks(np.arange(3))
ax.set_xticklabels(['Overall', 'Cat', 'Dog'])
ax.set_ylabel('Validation Set Size')
ax.set_xlabel('Slices')
ax.set_title('Validation Set Size for Slices')
validation_set_size_barchart = figure_to_base64str(fig)
# + id="UPY-j2RG9Wtr"
# Acuracy Bar Chart
fig, ax = plt.subplots()
width = 0.75
rects0 = ax.bar(0, accuracy, width, label='Overall')
rects1 = ax.bar(1, cat_accuracy, width, label='Cat')
rects2 = ax.bar(2, dog_accuracy, width, label='Dog')
ax.set_xticks(np.arange(3))
ax.set_xticklabels(['Overall', 'Cat', 'Dog'])
ax.set_ylabel('Accuracy')
ax.set_xlabel('Slices')
ax.set_title('Accuracy on Slices')
accuracy_barchart = figure_to_base64str(fig)
# + [markdown] id="Z7NmkfuAsPV1"
# Now we can add them to our `ModelCard`.
# + id="By8Qcr9usRZh"
model_card.model_parameters.data.eval.graphics.collection = [
{'name': 'Validation Set Size', 'image': validation_set_size_barchart},
]
model_card.quantitative_analysis.graphics.collection = [
{'name': 'Accuracy', 'image': accuracy_barchart},
]
# + [markdown] id="SOYofSZKOMZx"
# ### Generate the Model Card
# Let's generate the Model Card document. Available formats are stored at [model_card_toolkit/template](https://github.com/tensorflow/model-card-toolkit/tree/master/model_card_toolkit/template). Here, we will demonstrate the HTML and Markdown formats.
#
# First, we need to update the `ModelCardToolkit` with the latest `ModelCard`.
# + id="X7V0pJLB8jqJ"
mct.update_model_card_json(model_card)
# + [markdown] id="Fe4dya_26fJc"
# Now, the `ModelCardToolkit` can generate a Model Card document with `ModelCardToolkit.export_format()`.
# + id="Sd68Ih928vr9"
# Generate a model card document in HTML (default)
html_doc = mct.export_format()
# Display the model card document in HTML
display.display(display.HTML(html_doc))
# + [markdown] id="Vtl8lZG3Amr5"
# You can also output a Model Card in other formats, like Markdown.
# + id="uncQA2NfAnIS"
# Generate a model card document in Markdown
md_path = os.path.join(model_card_dir, 'template/md/default_template.md.jinja')
md_doc = mct.export_format(md_path, 'model_card.md')
# Display the model card document in Markdown
display.display(display.Markdown(md_doc))
|
model_card_toolkit/documentation/examples/Standalone_Model_Card_Toolkit_Demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Create input for DeCiFer
#
# This notebook provides an exemplary script for generating the input for DeCiFer from multiple bulk tumour samples and matched normal sample when using:
# - HATCHet for inferring allele-specific copy numbers
# - Varscan for inverring somatic single-nucleotide variants (SNVs)
# - BCFtools for counting sequencing reads for all SNVs across all tumour samples
#
# ## 1. Required inputs
#
# There are three required inputs that should be provided in the related variables below.
#
# 1. **`CNAs`**: `best.seg.ucn` file with HATCHet's inferred allele-specific copy numbers.
# 2. **`SNVs`**: Varscan output TSV file with somatic SNVs (mandatory fields include `chrom`, `position`, `ref`, and `var`) called for every sample independently.
# 3. **`MPIs`**: BCFtools files of read counts generated for every tumour sample independently and for all genomic positions of all SNVs present across all `${SNVs}`. Specifically, each file `${SAMPLE}.mpileup.tsv` should be generated with a command equivalent to the follow for every sample `${SAM}`, with reference genome `${REF}`, SNV files `${SNV1} ... ${SNVN}` from 2. above, and when `chrom` and `position` are the first two columns of the files in 2. (otherwise change `-f1,2` to match):
# ```shell
# bcftools mpileup ${SAM} -f ${REF} -T <(cat ${SNV1} ... ${SNVN} | cut -f1,2 | sort -k2,2 -k1,1 | uniq | grep -v position) -a INFO/AD -Ou | bcftools query -f'%CHROM\t%POS\t%REF,%ALT\t%AD\n' > ${SAMPLE}.mpileup.tsv
# ```
# +
## Please specify the required inputs in the three related variables with the suggested format
CNAs = '/path/to/best.seg.ucn'
SNVs = {
'SAMPLE1' : '/path/to/SAMPLE1.varscan.tsv',
'SAMPLE2' : '/path/to/SAMPLE2.varscan.tsv',
}
MPIs = {
'SAMPLE1' : '/path/to/SAMPLE1.mpileup.tsv',
'SAMPLE2' : '/path/to/SAMPLE2.mpileup.tsv',
}
## Also, please specify the name or full path of the two generated input files for DeCiFer
INPUT_SNVs = 'decifer.input.tsv'
INPUT_PURITY = 'decifer.purity.tsv'
## Finally, the following parameters are used for variant filtering
PVALUE = 1e-03 # Maximum threshold for Varscan pvalue score, choose 1 if you want to disable it.
MINREADS = 30 # Minimum total number of reads per SNV across all samples
MAXREADS = 10000 # Maximum total number of reads per SNV across all samples
# -
# ## 2. Execute the script for creating DeCiFer's input
#
# After succesfully setting up the required inputs, the following steps can be executed directly through this python notebook (or as a python script) to create DeCiFer input. When using this jupyter notebook, simply run all the cells below
# + tags=[]
import sys, os
import glob
import pandas as pd
from collections import defaultdict
from collections import Counter
# + tags=[]
## SNVs data and read counts are properly combined and formatted
snv_df = {}
for sam, f in SNVs.items():
snv_df[sam] = pd.read_csv(f, sep='\t')
snv_df[sam] = snv_df[sam][snv_df[sam]['somatic_p_value'] < PVALUE]
snv_df[sam]['snv_id'] = snv_df[sam].apply(lambda line: ".".join(map(str, [line['chrom'], line['position'], line['ref'], line['var']])), axis=1)
mpi = {}
form = (lambda p : ((p[0], int(p[1])), Counter(dict(filter(lambda v : '*' not in v[0], zip(p[2].split(','), map(int, p[3].split(','))))))))
for sam, f in MPIs.items():
mpi[sam] = defaultdict(lambda : Counter({'A' : 0, 'C' : 0, 'G' : 0, 'T' : 0}))
with open(f, 'r') as i:
for l in i:
g, u = form(l.strip().split())
mpi[sam][g].update(u)
mpi[sam] = dict(mpi[sam])
refvar = defaultdict(lambda : (Counter({'A' : 0, 'C' : 0, 'G' : 0, 'T' : 0}), Counter({'A' : 0, 'C' : 0, 'G' : 0, 'T' : 0})))
for sam in snv_df:
for i, r in snv_df[sam].iterrows():
g = (str(r['chrom']), r['position'])
refvar[g][0].update(Counter({r['ref'] : mpi[sam][g][r['ref']]}))
refvar[g][1].update(Counter({r['var'] : mpi[sam][g][r['var']]}))
refvar = {g : refvar[g] for g in refvar if sum(refvar[g][0].values()) > 0 and sum(refvar[g][1].values()) > 0 and MINREADS <= (sum(refvar[g][0].values()) + sum(refvar[g][1].values())) <= MAXREADS}
argmax = (lambda D : max(D.keys(), key=(lambda x : D[x])))
refvar = {g : tuple(map(argmax, refvar[g])) for g in refvar}
assert all(refvar[g][0] != refvar[g][1] for g in refvar)
gid = (lambda g : '.'.join(map(str, [g[0], g[1], refvar[g][0], refvar[g][1]])))
form = (lambda s, g : {'snv_id' : gid(g), 'Sample' : s, 'chrom' : g[0], 'position' : g[1], 'tumor_reads1' : mpi[s][g][refvar[g][0]], 'tumor_reads2' : mpi[s][g][refvar[g][1]]})
default = (lambda s, g : {'snv_id' : gid(g), 'Sample' : s, 'chrom' : g[0], 'position' : g[1], 'tumor_reads1' : 1, 'tumor_reads2' : 0})
snv_df = pd.DataFrame([form(s, g) if g in mpi[s] else default(s, g) for s in mpi for g in refvar])
selected_ids = snv_df['snv_id'].unique()
print('Number of selected SNVs: {}'.format(len(selected_ids)))
sample_index = {v:i for i, v in enumerate(snv_df['Sample'].unique())}
character_index = {v:i for i, v in enumerate(selected_ids)}
# + tags=[]
## Read CNAs data and generate purity input
cna_df = pd.read_csv(CNAs, sep = '\t')
cna_df['purity'] = 1.0 - cna_df['u_normal']
purities = dict({(r['SAMPLE'], r['purity']) for i, r in cna_df.iterrows()})
with open(INPUT_PURITY, 'w') as o:
for s in purities:
o.write("{}\t{}\n".format(sample_index[s], purities[s]))
# +
## Combine SNVs and CNAs data
discarded = 0
input_data = []
for i, snv in enumerate(selected_ids):
highcn = False
buff = []
char_idx = character_index[snv]
char_label = snv
if i % 500 == 0: print("{} {}".format(i, len(character_index)))
for sample in snv_df['Sample'].unique():
sample_idx = sample_index[sample]
snv_line = snv_df[(snv_df['snv_id'] == snv) & (snv_df['Sample'] == sample)].iloc[0]
try:
chrom = int(snv_line['chrom'])
except ValueError:
continue
pos = int(snv_line['position'])
ref = snv_line['tumor_reads1']
var = snv_line['tumor_reads2']
intervals = cna_df[(cna_df['#CHR'] == chrom) & (cna_df['START'] <= pos) & (cna_df['END'] > pos) & (cna_df['SAMPLE'] == sample)]
if len(intervals) == 0:
discarded += 1
continue
try:
cn_dict = {}
for idx in ['normal', 'clone1', 'clone2', 'clone3', 'clone4', 'clone5', 'clone6', 'clone7', 'clone8', 'clone9', 'clone10']:
try:
cn = intervals.iloc[0]['cn_{}'.format(idx)]
mu = intervals.iloc[0]['u_{}'.format(idx)]
except:
continue
try:
cn_dict[cn] += mu
except:
cn_dict[cn] = mu
except IndexError:
continue
line = [sample_idx, sample, char_idx, char_label, ref, var]
states6 = set()
for cn in sorted(cn_dict):
c1a = cn.split('|')[0]
c1b = cn.split('|')[1]
mu1 = cn_dict[cn]
line += [c1a, c1b, mu1]
highcn = highcn or (int(c1a) + int(c1b)) > 6
if (int(c1a) + int(c1b)) == 6:
states6.add((c1a, c1b))
highcn = highcn or len(states6) > 1
buff.append(line)
if not highcn:
input_data.extend(buff)
else:
discarded += 1
print('Discarded {}'.format(discarded))
# + tags=[]
## Generate the SNV input for DeCiFer with CNAs
with open(INPUT_SNVs, 'w') as out:
out.write('{} #characters\n'.format(len(selected_ids)))
out.write('{} #samples\n'.format(len(purities)))
out.write("#sample_index sample_label character_index character_label ref var\n")
for line in input_data:
out.write("\t".join(map(str, line))+"\n")
|
scripts/input_from_varscan/create_input.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jereyel/LinearAlgebra/blob/main/Assignment6_DelosReyes.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="fi2yRG-jEpde"
# #<NAME>
#
# ---
# LINEAR ALGEBRA FOR ELECTRONICS ENGINEERING LAB 1800-2100 Wed
#
# + [markdown] id="omP0HgKtFTP0"
# ##Objectives
# + [markdown] id="DwDiPdREFTLD"
# # ++ To be familiarized with the fundamentals of matricex operations.
#
# # ++ Apply the operations to solve intermediate equations.
#
# # ++ Apply matrix algebra in engineering solutions.
# + [markdown] id="HPzTNKseFAl0"
# ###Discussion
# + id="-U4MGZp2H2et"
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] id="aJKnuDWIITM7"
# ###Transposition
# + [markdown] id="SEymu14EKdlL"
# $$
# A = \begin{bmatrix} 1 & 2 & 5\\5 & -1 &0 \\ 0 & -3 & 3\end{bmatrix} $$
# $A^T$
# + id="PQwkm9lHJIz_" colab={"base_uri": "https://localhost:8080/"} outputId="ba7702ca-182d-480a-af92-303d98941236"
A = np.array([
[1,2,5],
[5,-1,0],
[0,-3,3]
])
A
# + colab={"base_uri": "https://localhost:8080/"} id="5FftyoZxKibe" outputId="4d227d99-ea3a-4740-bcbb-19fff0fcf801"
AT1 = np.transpose(A)
AT1
# + colab={"base_uri": "https://localhost:8080/"} id="ttzpJo8LKotQ" outputId="7ae95ca4-2310-46f0-b709-b4581ff407f0"
AT2 = A.T
AT2
# + colab={"base_uri": "https://localhost:8080/"} id="1OcdoBPxKruk" outputId="b4f41e08-bebb-489f-8d3e-5400290e4580"
np.array_equiv(AT1,AT2)
# + colab={"base_uri": "https://localhost:8080/"} id="Ib5XIrAmKzJx" outputId="6eb7ca5d-6efc-4f69-f9f8-0aa9c7f58413"
B = np.array([
[1,2,3,4],
[1,0,2,1],
])
B.shape
# + colab={"base_uri": "https://localhost:8080/"} id="-_bsR6KgK5j4" outputId="8f4bc751-7bdb-444f-eadd-9737cd03952e"
np.transpose(B).shape
# + colab={"base_uri": "https://localhost:8080/"} id="tCW0XX9kLNFd" outputId="488b4daf-220a-4207-dce8-9c3064ebb6a0"
B.T.shape
# + colab={"base_uri": "https://localhost:8080/"} id="AAmhkbnQLfeO" outputId="9d6c916b-3cac-412e-9459-7c1546062274"
C = np.array([
[1,3,7],
[2,4,6]
])
C.shape
# + colab={"base_uri": "https://localhost:8080/"} id="u6Xv2MX6Lri4" outputId="7e561b91-2cbc-4926-bfaa-eef84adbaef0"
np.transpose(C).shape
# + colab={"base_uri": "https://localhost:8080/"} id="u12v9axiLzO5" outputId="9b69602d-5182-46a5-caf3-5deec5f16e68"
C.T.shape
# + [markdown] id="PPpp3W4zI_1S"
# ###Dot Product / Inner Product
# + id="l2Hvhn2rOJOU"
X = np.array([
[1,2],
[0,1]
])
Y = np.array([
[-1,0],
[2,2]
])
# + colab={"base_uri": "https://localhost:8080/"} id="o6E7uZBDOeu2" outputId="d240be9d-ee0c-40f3-99d7-7b3a5461aea1"
X.dot(Y)
# + colab={"base_uri": "https://localhost:8080/"} id="L8I4Y4b9Og8I" outputId="7f31212f-85cc-4a32-a741-b64fa95765cc"
X @ Y
# + colab={"base_uri": "https://localhost:8080/"} id="uN0cpkv-Oi6I" outputId="8b690223-db20-4bd2-9e51-ea4110516944"
np.matmul(X,Y)
# + id="Injm1HNEOsBs"
J = np.array([
[1,2,3],
[5,7,9],
[4,6,8]
])
N = np.array([
[1,3,7],
[5,6,9],
[2,4,8]
])
# + colab={"base_uri": "https://localhost:8080/"} id="LBOp6rFfO0PB" outputId="b3bb8ecd-1365-4de1-893a-1b812ae92a63"
J.dot(N)
# + colab={"base_uri": "https://localhost:8080/"} id="x3rwZ3LHPGlU" outputId="67f96762-4e95-4d96-8712-6cfee8d875ba"
J @ N
# + colab={"base_uri": "https://localhost:8080/"} id="jC-ft4MjPJWu" outputId="2514bb4b-a36e-4d1c-b91e-69a514fdce51"
np.matmul(J,N)
# + colab={"base_uri": "https://localhost:8080/"} id="ieHHMwqARQhK" outputId="a75e8550-d763-495b-f2d0-cdfbe3aa5e40"
A = np.array([
[2,4,4],
[5,-2,7],
[0,1,1]
])
B = np.array([
[1,1,8],
[3,3,3],
[-1,-2,8]
])
C = np.array([
[9,1,1],
[1,1,2],
[1,2,3]
])
print(A.shape)
print(B.shape)
print(C.shape)
# + id="MHN8pkfgQWBD"
A5 = A @ B
# + id="bR6QydaYQa_6"
A6 = B @ A
# + colab={"base_uri": "https://localhost:8080/"} id="aehMvcEYQg2Q" outputId="7df3378d-b4ed-4f70-d1de-a8fbde0fc4e6"
np.array_equal(A5, A6)
# + id="Dam0SOrkQmkb"
A7 = A @ (B @ C)
# + id="m6CZkCtgQ3GO"
A8 = (A @ B) @ C
# + colab={"base_uri": "https://localhost:8080/"} id="jVfhCau_Q70_" outputId="832979b0-2114-48ae-b4f8-76f6250ceab1"
np.array_equal(A7, A8)
# + id="gyKrCSSqORD3"
A1 = A @ (B + C)
# + id="QwpNE8qIOUhe"
A2 = (A @ B) + (A @ C)
# + colab={"base_uri": "https://localhost:8080/"} id="wyB5JzjVObO1" outputId="63cd0fc1-cfc0-4727-c740-7caed9284c04"
np.array_equal(A1, A2)
# + id="fCz4oux2O_7X"
A3 = (B + C) @ A
# + id="N24dVHlqPmTg"
A4 = (B @ A) + (C @ A)
# + colab={"base_uri": "https://localhost:8080/"} id="nz3qHCptP1uc" outputId="0d9ffeb8-3658-4793-efce-85e5d1034813"
np.array_equiv(A1, A2)
# + colab={"base_uri": "https://localhost:8080/"} id="RGIRcmO_SYxY" outputId="e0969b16-5f18-43a3-d756-14f7c8020624"
X = np.array([
[1,2,3,0]
])
Y = np.array([
[1,0,4,-1]
])
print(X.shape)
print(Y.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="i6HXHt6USka3" outputId="c5f45227-2e17-4e60-a16d-0e895a84b33c"
Y.T @ X
# + colab={"base_uri": "https://localhost:8080/"} id="XgQ8OtoxSiGR" outputId="fdf0db5c-fa8a-4d14-d73e-c7bc40bdc9d8"
X @ Y.T
# + [markdown] id="-Y2iJL0bKCpt"
# ###Determinant
# + colab={"base_uri": "https://localhost:8080/"} id="lm8otsCPY43C" outputId="60292c88-2cb1-4e5b-e9ae-9ac59fbdee77"
A = np.array([
[1,4],
[0,3]
])
np.linalg.det(A)
# + colab={"base_uri": "https://localhost:8080/"} id="l0yRwMvSZZ-b" outputId="c552e901-aca9-4884-92cc-dd46a66fd8c3"
B = np.array([
[1,5,2],
[3,-1,-1],
[0,-2,1]
])
np.linalg.det(B)
# + [markdown] id="3WrlGTDvK07u"
# ###Inverse
# + colab={"base_uri": "https://localhost:8080/"} id="fuqZhsPEafR-" outputId="4627f175-98cf-4e29-8842-c57120c524e5"
M = np.array([
[1,7],
[-3,5]
])
np.array(M @ np.linalg.inv(M), dtype=int)
# + id="KZmf5F5La5_8"
P = np.array([
[6,9,0],
[4,2,-1],
[3,6,7]
])
Q = np.linalg.inv(P)
# + colab={"base_uri": "https://localhost:8080/"} id="IHuJymSUbOyk" outputId="bbce7d19-6f28-4f99-bd31-63bf620ef390"
P @ Q
# + colab={"base_uri": "https://localhost:8080/"} id="fTwkAPneC49r" outputId="860e6deb-1bc0-4c12-8ff2-c80dec0d70b5"
np.array (P @ Q, dtype=int)
# + [markdown] id="jJRxBk8cHplo"
# ##Conclusion
#
# + [markdown] id="IPhKOWmBTXuK"
# Matrix can be difficult. A different system can be equipped by the
# application of matrices such as circuit, electronics, image processing, computer graphics and so on. As matrices do things to vectors, for this lesson, matrices can be boring for some but with the use of application and with google Collab it can be easier or hard for other. With the help of google Collab and python programming language it will be easier to understand the working principles of matrices and its corners how does an equation is being solved.
|
Assignment6_DelosReyes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
# <script>
# window.dataLayer = window.dataLayer || [];
# function gtag(){dataLayer.push(arguments);}
# gtag('js', new Date());
#
# gtag('config', 'UA-59152712-8');
# </script>
#
# # IDScalarWaveNRPy: An Einstein Toolkit Initial Data Thorn for the Scalar Wave Equation
#
# ## Author: <NAME> & <NAME>
# ### Formatting improvements courtesy <NAME>
#
# [comment]: <> (Abstract: TODO)
#
# [comment]: <> (Notebook Status and Validation Notes: TODO)
#
# ### NRPy+ Source Code for this module: [ScalarWave/InitialData.py](../edit/ScalarWave/InitialData.py) [\[**tutorial**\]](Tutorial-ScalarWave.ipynb) Contructs the SymPy expressions for spherical gaussian and plane-wave initial data
#
# ## Introduction:
# In this part of the tutorial, we will construct an Einstein Toolkit (ETK) thorn (module) that will set up *initial data* for the scalar wave initial value problem. In a [previous tutorial notebook](Tutorial-ScalarWave.ipynb), we used NRPy+ to contruct the SymPy expressions for either spherical gaussian or plane-wave initial data. This thorn is largely based on and should function similarly to the $\text{IDScalarWaveC}$ thorn included in the Einstein Toolkit (ETK) $\text{CactusWave}$ arrangement.
#
# We will construct this thorn in two steps.
#
# 1. Call on NRPy+ to convert the SymPy expressions for the initial data into one C-code kernel.
# 1. Write the C code and linkages to the Einstein Toolkit infrastructure (i.e., the .ccl files) to complete this Einstein Toolkit module.
# <a id='toc'></a>
#
# # Table of Contents
# $$\label{toc}$$
#
# This notebook is organized as follows
#
# 1. [Step 1](#initializenrpy): Call on NRPy+ to convert the SymPy expression for the scalar wave initial data into a C-code kernel
# 1. [Step 2](#einstein): Interfacing with the Einstein Toolkit
# 1. [Step 2.a](#einstein_c): Constructing the Einstein Toolkit C-code calling functions that include the C code kernels
# 1. [Step 2.b](#einstein_ccl): CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure
# 1. [Step 2.c](#einstein_list): Add the C code to the Einstein Toolkit compilation list
# 1. [Step 3](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
# <a id='initializenrpy'></a>
#
# # Step 1: Initialize needed Python/NRPy+ modules \[Back to [top](#toc)\]
#
# $$\label{initializenrpy}$$
# +
# Step 1: Import needed core NRPy+ modules
from outputC import lhrh # NRPy+: Core C code output module
import finite_difference as fin # NRPy+: Finite difference C code generation module
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import loop as lp # NRPy+: Generate C code loops
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
import os, sys # Standard Python modules for multiplatform OS-level functions
import time # Standard Python module; useful for benchmarking
# Step 1a: Create directories for the thorn if they don't exist.
# Create directory for WaveToyNRPy thorn & subdirectories in case they don't exist.
outrootdir = "IDScalarWaveNRPy/"
cmd.mkdir(os.path.join(outrootdir))
outdir = os.path.join(outrootdir,"src") # Main C code output directory
cmd.mkdir(outdir)
# Step 1b: This is an Einstein Toolkit (ETK) thorn. Here we
# tell NRPy+ that gridfunction memory access will
# therefore be in the "ETK" style.
par.set_parval_from_str("grid::GridFuncMemAccess","ETK")
# -
# <a id='einstein'></a>
#
# # Step 2: Interfacing with the Einstein Toolkit \[Back to [top](#toc)\]
# $$\label{einstein}$$
#
# <a id='einstein_c'></a>
#
# ## Step 2.a: Constructing the Einstein Toolkit C-code calling functions that include the C code kernels \[Back to [top](#toc)\]
# $$\label{einstein_c}$$
#
# Using sympy, we construct the exact expressions for all scalar wave initial data currently supported in NRPy, documented in [Tutorial-ScalarWave.ipynb](Tutorial-ScalarWave.ipynb). We write the generated C codes into different C files, corresponding to the type of initial data the may want to choose at run time. Note that the code below can be easily extensible to include other types of initial data.
# +
# Step 1c: Call the InitialData() function from within the
# ScalarWave/InitialData.py module.
import ScalarWave.InitialData as swid
# Step 1e: Call the InitialData() function to set up initial data.
# Options include:
# "PlaneWave": monochromatic (single frequency/wavelength) plane wave
# "SphericalGaussian": spherically symmetric Gaussian, with default stdev=3
ID_options = ["PlaneWave", "SphericalGaussian"]
for ID in ID_options:
gri.glb_gridfcs_list = []
# Within the ETK, the 3D gridfunctions x, y, and z store the
# Cartesian grid coordinates. Setting the gri.xx[] arrays
# to point to these gridfunctions forces NRPy+ to treat
# the Cartesian coordinate gridfunctions properly --
# reading them from memory as needed.
x,y,z = gri.register_gridfunctions("AUX",["x","y","z"])
rfm.xx[0] = x
rfm.xx[1] = y
rfm.xx[2] = z
swid.InitialData(Type=ID,
default_sigma=0.25,
default_k0=1.0,
default_k1=0.,
default_k2=0.)
# Step 1f: Register uu and vv gridfunctions so they can be written to by NRPy.
uu,vv = gri.register_gridfunctions("EVOL",["uu","vv"])
# Step 1g: Set the uu and vv gridfunctions to the uu_ID & vv_ID variables
# defined by InitialData_PlaneWave().
uu = swid.uu_ID
vv = swid.vv_ID
# Step 1h: Create the C code output kernel.
ScalarWave_ID_SymbExpressions = [\
lhrh(lhs=gri.gfaccess("out_gfs","uu"),rhs=uu),\
lhrh(lhs=gri.gfaccess("out_gfs","vv"),rhs=vv),]
ScalarWave_ID_CcodeKernel = fin.FD_outputC("returnstring",ScalarWave_ID_SymbExpressions)
ScalarWave_ID_looped = lp.loop(["i2","i1","i0"],["0","0","0"],["cctk_lsh[2]","cctk_lsh[1]","cctk_lsh[0]"],\
["1","1","1"],["#pragma omp parallel for","",""],"",\
ScalarWave_ID_CcodeKernel.replace("time","cctk_time"))
# Write the C code kernel to file.
with open(os.path.join(outdir,"ScalarWave_"+ID+"ID.h"), "w") as file:
file.write(str(ScalarWave_ID_looped))
# -
# <a id='einstein_ccl'></a>
#
# ## Step 2. b: CCL files - Define how this module interacts and interfaces with the larger Einstein Toolkit infrastructure \[Back to [top](#toc)\]
# $$\label{einstein_ccl}$$
#
# Writing a module ("thorn") within the Einstein Toolkit requires that three "ccl" files be constructed, all in the root directory of the thorn:
#
# 1. `interface.ccl`: defines the gridfunction groups needed, and provides keywords denoting what this thorn provides and what it should inherit from other thorns. Specifically, this file governs the interaction between this thorn and others; more information can be found in the [official Einstein Toolkit documentation](https://einsteintoolkit.org/usersguide/UsersGuide.html#x1-179000D2.2).
# With "implements", we give our thorn its unique name. By "inheriting" other thorns, we tell the Toolkit that we will rely on variables that exist and are declared "public" within those functions.
# +
evol_gfs_list = []
for i in range(len(gri.glb_gridfcs_list)):
if gri.glb_gridfcs_list[i].gftype == "EVOL":
evol_gfs_list.append( gri.glb_gridfcs_list[i].name+"GF")
# NRPy+'s finite-difference code generator assumes gridfunctions
# are alphabetized; not sorting may result in unnecessary
# cache misses.
evol_gfs_list.sort()
with open(os.path.join(outrootdir,"interface.ccl"), "w") as file:
file.write("""
# With "implements", we give our thorn its unique name.
implements: IDScalarWaveNRPy
# By "inheriting" other thorns, we tell the Toolkit that we
# will rely on variables/function that exist within those
# functions.
inherits: WaveToyNRPy grid
""")
# -
# 2. `param.ccl`: specifies free parameters within the thorn, enabling them to be set at runtime. It is required to provide allowed ranges and default values for each parameter. More information on this file's syntax can be found in the [official Einstein Toolkit documentation](https://einsteintoolkit.org/usersguide/UsersGuide.html#x1-184000D2.3).
# +
def keep_param__return_type(paramtuple):
keep_param = True # We'll not set some parameters in param.ccl;
# e.g., those that should be #define'd like M_PI.
typestring = ""
# Separate thorns within the ETK take care of grid/coordinate parameters;
# thus we ignore NRPy+ grid/coordinate parameters:
if paramtuple.module == "grid" or paramtuple.module == "reference_metric" or paramtuple.parname == "wavespeed":
keep_param = False
partype = paramtuple.type
if partype == "bool":
typestring += "BOOLEAN "
elif partype == "REAL":
if paramtuple.defaultval != 1e300: # 1e300 is a magic value indicating that the C parameter should be mutable
typestring += "CCTK_REAL "
else:
keep_param = False
elif partype == "int":
typestring += "CCTK_INT "
elif partype == "#define":
keep_param = False
elif partype == "char":
# FIXME: char/string parameter types should in principle be supported
print("Error: parameter "+paramtuple.module+"::"+paramtuple.parname+
" has unsupported type: \""+ paramtuple.type + "\"")
sys.exit(1)
else:
print("Error: parameter "+paramtuple.module+"::"+paramtuple.parname+
" has unsupported type: \""+ paramtuple.type + "\"")
sys.exit(1)
return keep_param, typestring
paramccl_str="""
# This param.ccl file was automatically generated by NRPy+.
# You are advised against modifying it directly; instead
# modify the Python code that generates it.
shares: grid
USES KEYWORD type
shares: WaveToyNRPy
USES REAL wavespeed
restricted:
CCTK_KEYWORD initial_data "Type of initial data"
{"""
for ID in ID_options:
paramccl_str +='''
"'''+ID+'''" :: "'''+ID+'"'
paramccl_str +='''
} "'''+ID+'''"
'''
paramccl_str +="""
restricted:
"""
for i in range(len(par.glb_Cparams_list)):
# keep_param is a boolean indicating whether we should accept or reject
# the parameter. singleparstring will contain the string indicating
# the variable type.
keep_param, singleparstring = keep_param__return_type(par.glb_Cparams_list[i])
if keep_param:
parname = par.glb_Cparams_list[i].parname
partype = par.glb_Cparams_list[i].type
singleparstring += parname + " \""+ parname +" (see NRPy+ for parameter definition)\"\n"
singleparstring += "{\n"
if partype != "bool":
singleparstring += " *:* :: \"All values accepted. NRPy+ does not restrict the allowed ranges of parameters yet.\"\n"
singleparstring += "} "+str(par.glb_Cparams_list[i].defaultval)+"\n\n"
paramccl_str += singleparstring
with open(os.path.join(outrootdir,"param.ccl"), "w") as file:
file.write(paramccl_str)
# -
# 3. `schedule.ccl`: allocates storage for gridfunctions, defines how the thorn's functions should be scheduled in a broader simulation, and specifies the regions of memory written to or read from gridfunctions. More information on this file's syntax can be found in the [official Einstein Toolkit documentation](https://einsteintoolkit.org/usersguide/UsersGuide.html#x1-187000D2.4).
#
# We specify here the standardized ETK "scheduling bins" in which we want each of our thorn's functions to run.
with open(os.path.join(outrootdir,"schedule.ccl"), "w") as file:
file.write("""
# This schedule.ccl file was automatically generated by NRPy+.
# You are advised against modifying it directly; instead
# modify the Python code that generates it.
if (CCTK_EQUALS (initial_data, "PlaneWave"))
{
schedule IDScalarWaveNRPy_param_check at CCTK_PARAMCHECK
{
LANG: C
OPTIONS: global
} "Check sanity of parameters"
}
schedule IDScalarWaveNRPy_InitialData at CCTK_INITIAL as WaveToy_InitialData
{
STORAGE: WaveToyNRPy::scalar_fields[3]
LANG: C
} "Initial data for 3D wave equation"
""")
# <a id='einstein_list'></a>
#
# ## Step 2.c: Add the C code to the Einstein Toolkit compilation list \[Back to [top](#toc)\]
# $$\label{einstein_list}$$
#
# We will also need `make.code.defn`, which indicates the list of files that need to be compiled. This thorn only has the one C file to compile.
make_code_defn_list = []
def append_to_make_code_defn_list(filename):
if filename not in make_code_defn_list:
make_code_defn_list.append(filename)
return os.path.join(outdir,filename)
with open(append_to_make_code_defn_list("InitialData.c"),"w") as file:
file.write("""
#include <math.h>
#include <stdio.h>
#include <string.h>
#include "cctk.h"
#include "cctk_Parameters.h"
#include "cctk_Arguments.h"
void IDScalarWaveNRPy_param_check(CCTK_ARGUMENTS) {
DECLARE_CCTK_ARGUMENTS;
DECLARE_CCTK_PARAMETERS;
if (kk0 == 0 && kk1 == 0 && kk2 == 0) {
CCTK_WARN(0,"kk0==kk1==kk2==0: Zero wave vector cannot be normalized. Set one of the kk's to be != 0.");
}
}
void IDScalarWaveNRPy_InitialData(CCTK_ARGUMENTS)
{
DECLARE_CCTK_ARGUMENTS
DECLARE_CCTK_PARAMETERS
const CCTK_REAL *xGF = x;
const CCTK_REAL *yGF = y;
const CCTK_REAL *zGF = z;
if (CCTK_EQUALS (initial_data, "PlaneWave")) {
#include "ScalarWave_PlaneWaveID.h"
} else if (CCTK_EQUALS (initial_data, "SphericalGaussian")) {
#include "ScalarWave_SphericalGaussianID.h"
}
}
""")
with open(os.path.join(outdir,"make.code.defn"), "w") as file:
file.write("""
# Main make.code.defn file for thorn WaveToyNRPy
# Source files in this directory
SRCS =""")
filestring = ""
for i in range(len(make_code_defn_list)):
filestring += " "+make_code_defn_list[i]
if i != len(make_code_defn_list)-1:
filestring += " \\\n"
else:
filestring += "\n"
file.write(filestring)
# <a id='latex_pdf_output'></a>
#
# # Step 3: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
# $$\label{latex_pdf_output}$$
#
# The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
# [Tutorial-ETK_thorn-IDScalarWaveNRPy.pdf](Tutorial-ETK_thorn-IDScalarWaveNRPy.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
cmd.output_Jupyter_notebook_to_LaTeXed_PDF("Tutorial-ETK_thorn-IDScalarWaveNRPy.ipynb")
|
Tutorial-ETK_thorn-IDScalarWaveNRPy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.metrics import r2_score
wine_quality = pd.read_csv("winequality/winequality-red.csv", sep=';')
wine_quality.rename (columns=lambda x: x.replace(" ", "_"), inplace=True)
eda_columns = ['volatile_acidity', 'chlorides', 'sulphates', 'alcohol', 'quality']
sns.set(style='whitegrid', context = 'notebook')
sns.pairplot (wine_quality[eda_columns], size = 2.5, x_vars = eda_columns, y_vars = eda_columns)
plt.show()
# # Correlation coefficients
corr_mat = np.corrcoef (wine_quality[eda_columns].values.T)
sns.set(font_scale=1)
full_mat = sns.heatmap(corr_mat, cbar=True, annot=True, square=True, fmt='.2f', annot_kws={'size': 15}, yticklabels=eda_columns, xticklabels=eda_columns)
plt.show()
# +
colnms = ['fixed_acidity', 'volatile_acidity', 'citric_acid', 'residual_sugar',
'chlorides', 'free_sulfur_dioxide', 'total_sulfur_dioxide', 'density',
'pH', 'sulphates', 'alcohol']
pdx = wine_quality[colnms]
pdy = wine_quality["quality"]
# -
x_train, x_test, y_train, y_test = train_test_split(pdx, pdy, train_size = 0.7, random_state = 42)
x_train_new = sm.add_constant (x_train)
x_test_new = sm.add_constant (x_test)
full_mod = sm.OLS (y_train, x_train_new)
full_res = full_mod.fit ()
print ("\n \n", full_res.summary ())
print ("\nVariance Inflation Factor")
cnames = x_train.columns
for i in np.arange (0, len (cnames)):
xvars = list (cnames)
yvar = xvars.pop (i)
mod = sm.OLS (x_train[yvar], sm.add_constant (x_train_new[xvars]))
res = mod.fit ()
vif = 1 / (1 - res.rsquared)
print (yvar, round (vif, 3))
|
books/stats/chapter2/OLS_Regression_Results.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ReactiveX in Python - baseline
# A baseline experiment with no `async` tomfoolery.
# * https://github.com/ReactiveX/RxPY
# * https://rxpy.readthedocs.io/en/latest/get_started.html
# # *Status :-)*
# # Try out with widgets
import ipywidgets as widgets
from IPython.display import display
# ## Make a widget observable
def make_push_widget(w):
def push_widget(observer, scheduler):
# make the callback to attach to the widget
def on_value_change(change):
new_value = change['new']
#print(f"ovc new_value is {new_value}")
observer.on_next(change['new'])
if new_value == 100:
observer.on_completed()
w.unobserve(on_value_change, names='value')
# attach callback to widget
w.observe(on_value_change, names='value')
# return the observation function
return push_widget
# ## Place some widgets
# +
from math import pi
v_w = widgets.FloatSlider(
value=0.0,
min=-1.0,
max=1.0,
step=0.01,
description='Sin:',
disabled=False,
continuous_update=False,
orientation='vertical',
readout=True,
readout_format='.2f',
)
h_w = widgets.FloatSlider(
value=0.0,
min=-1.0,
max=1.0,
step=0.01,
description='Cos:',
disabled=False,
continuous_update=False,
orientation='horizontal',
readout=True,
readout_format='.2f',
)
t_w = widgets.IntSlider(
description='t',
)
shutdown_b_w = widgets.Button(description="Shutdown worker")
clear_b_w = widgets.Button(description="clear")
out_w = widgets.Output(layout={'border': '1px solid black'})
display(v_w, h_w, t_w, shutdown_b_w, clear_b_w, out_w)
# -
# ## Interaction functions
# +
from math import sin, cos, pi
import rx
def slider_bender(s, v):
s.value = v
def circulate(t):
slider_bender(v_w, sin(t))
slider_bender(h_w, cos(t))
def shutdown_child(w):
with out_w:
print(f"would send shutdown from shutdown_child")
def clear_out(w):
out_w.clear_output()
# -
# ### Plug in button callbacks
shutdown_b_w.on_click(shutdown_child)
clear_b_w.on_click(clear_out)
# ## Build ReactiveX pipeline
# +
from rx import operators as op
from math import pi
t_src = rx.create(make_push_widget(t_w))
t_src.pipe(
op.map(lambda i: i/100),
op.map(lambda t: 2*pi * 2*t)
).subscribe(
on_next = circulate,
on_error = lambda e: print("Error Occurred: {0}".format(e)),
on_completed = lambda: print("Done!"),
)
# -
# ### Test
# Go up to Widgets and manipulate the **t** slider. When you're done, make the pipeline shut down by sliding it all the way to 100.
# ## UI while working
# Can these controls and responses be used while doing other work, perhaps work that is controlled by the widgets?
# Go rerun the pipeline above, verify it works by manipulating the `t` slider, and leave it working. Run the cell below, and again manipulate the slider.
# +
import asyncio
async def sleep_print():
for i in range(30):
print(f"radius is {v_w.value**2 + h_w.value**2}, run {i}")
await asyncio.sleep(1)
asyncio.create_task(sleep_print())
# -
# # Conclusions
# * The path from widget -> rx pipeline -> widget works, as long as another code block is not running.
# * When the running code block returns, the path works again
|
nbs/ReactiveX/rx-widgets-baseline.ipynb
|