code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Training Neural Networks:
# ### Classification of MNIST dataset of Handwritten Digits
# +
# Importing libraries and dataset
import torch
from torch import nn
import torch.nn.functional as F
from torchvision import datasets, transforms
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
# Download and load the training data
trainset = datasets.MNIST('~/.pytorch/MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# +
# Preparing Optimizers
from torch import optim
# Optimizers require the parameters to optimize and a learning rate
optimizer = optim.SGD(model.parameters(), lr=0.01)
# +
# Build a feed-forward network
model = nn.Sequential(nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1))
# Defining Losses and Optimizer
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003)
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
# Flatten MNIST images into a 784 long vector
images = images.view(images.shape[0], -1)
# Training pass
optimizer.zero_grad() ###Important
output = model(images)
loss = criterion(output, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
print(f"Training loss: {running_loss/len(trainloader)}")
# -
# With the network trained, we can check out it's predictions.
# +
# %matplotlib inline
import helper
images, labels = next(iter(trainloader))
img = images[0].view(1, 784)
# Turn off gradients to speed up this part
with torch.no_grad():
logps = model(img)
# Output of the network are log-probabilities, need to take exponential for probabilities
ps = torch.exp(logps)
helper.view_classify(img.view(1, 28, 28), ps)
# -
# Now the network can accurately predict the digits in our images.
|
PyTorch/3. Training Neural Networks (MNIST Handwritten Digit Classification).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
import seaborn as sns
import pingouin as pg
# %matplotlib inline
# -
# # Import the data
path_cohort_1 = '/home/ds/Ntrk2_KOs/2018_12/EPM/tracking_results_EPM.xlsx'
df_1 = pd.read_excel(path_cohort_1)
path_cohort_2 = '/home/ds/Ntrk2_KOs/2019_07/EPM/tracking_results_epm.xlsx'
df_2 = pd.read_excel(path_cohort_2)
path_cohort_3 = '/home/ds/Ntrk2_KOs/2019_12/EPM/EMP_results_new.xlsx'
df_3 = pd.read_excel(path_cohort_3)
# # Preprocess the data:
# ### Adjust column names for cohort 1 to match those of cohort 2 & 3:
# +
l_rename_columns = ['Datei', 'Nr.', 'Analyseintervall', 'von', 'bis', 'Tier Nr.', 'Gruppe',
'time_open_arms', 'visits_open_arms', 'distance_open_arms',
'Zeit %Total(o) (Z)', 'Zeit %Global(o) (Z)', 'Besuche %Total(o) (Z)',
'time_closed_arms', 'visits_closed_arms', 'distance_closed_arms',
'Zeit %Total(g) (Z)', 'Zeit %Global(g) (Z)', 'Besuche %Total(g) (Z)',
'Totalzeit', 'Totalstrecke', 'Globalzeit',
'Globalstrecke', 'Latenz(o) (Z)', 'Latenz(g) (Z)', 'Latenz(o+g) (Z)',
'Bewegungsschwelle', 'Minimale Aufenthaltsdauer']
df_1.columns = l_rename_columns
df_1['Totalbesuche'] = df_1['visits_open_arms'] + df_1['visits_closed_arms']
# -
l_columns_for_total = ['time_open_arms', 'visits_open_arms', 'distance_open_arms', 'time_closed_arms', 'visits_closed_arms', 'distance_closed_arms', 'Totalzeit', 'Totalbesuche', 'Totalstrecke']
# +
# For df_2 and df_3, the data from the individual arms has to be aggregated first:
for df in [df_2, df_3]:
#for df in [df_2]:
# Aggregate data from both open arms:
df['time_open_arms'] = df['Zeit I01 Open-up'] + df['Zeit I03 Open-down']
df['visits_open_arms'] = df['Besuche I01 Open-up'] + df['Besuche I03 Open-down']
df['distance_open_arms'] = df['Strecke I01 Open-up'] + df['Strecke I03 Open-down']
# Aggregate data from both closed arms:
df['time_closed_arms'] = df['Zeit I02 Closed-right'] + df['Zeit I04 Closed-left']
df['visits_closed_arms'] = df['Besuche I02 Closed-right'] + df['Besuche I04 Closed-left']
df['distance_closed_arms'] = df['Strecke I02 Closed-right'] + df['Strecke I04 Closed-left']
# Now we can work with all three DataFrames in the same way
l_raw_dfs = [df_1, df_2, df_3]
#_raw_dfs = [df_1, df_2]
l_preprocessed_dfs = []
for cohort in range(len(l_raw_dfs)):
# Select DataFrame and assign cohort ID:
df = l_raw_dfs[cohort]
# Calculate the total session information
for mouse in df['Tier Nr.'].unique():
group = df.loc[df['Tier Nr.'] == mouse, 'Gruppe'].values[0]
row = df.shape[0]
df.loc[row] = np.NaN
df.loc[row, ['Analyseintervall', 'Tier Nr.', 'Gruppe']] = ['total', mouse, group]
for column in l_columns_for_total:
df.loc[row, column] = df.loc[(df['Tier Nr.'] == mouse) & (df['Analyseintervall'] != 'total'), column].sum()
# Calculate the percentages of time, visits and distance in the open arms:
df['%time_open_arms'] = df['time_open_arms'] / df['Totalzeit'] * 100
df['%visits_open_arms'] = df['visits_open_arms'] / df['Totalbesuche'] * 100
df['%distance_open_arms'] = df['distance_open_arms'] / df['Totalstrecke'] * 100
# Add information about the cohort:
df.insert(7, 'Kohorte', cohort)
# Append preprocessed DataFrame to list to create Master DataFrame:
l_preprocessed_dfs.append(df)
df = pd.concat(l_preprocessed_dfs)
df = df.reset_index(drop=True)
df.head()
# -
df.to_csv('EPM_all_cohorts.csv')
# # __Calculate stats:__
# +
d_stats = {}
# List of measures (=column names) for which stats will be calculated:
l_measures = ['Totalstrecke', '%time_open_arms', '%visits_open_arms', '%distance_open_arms']
for measure in l_measures:
#Setup new dictionary in d_stats:
d_stats[measure] = {}
# Get data:
data_wt = list(df.loc[(df['Gruppe'] == 'wt') & (df['Analyseintervall'] == 'total'), measure].values)
data_tg = list(df.loc[(df['Gruppe'] == 'wt') & (df['Analyseintervall'] == 'total'), measure].values)
# Store data for annotations in plots:
d_stats[measure]['data_wt'] = data_wt
d_stats[measure]['data_tg'] = data_tg
# Test for normal distribution (Shapiro):
d_stats[measure]['normality_wt'] = (pg.normality(data_wt).loc[0, 'normal'], pg.normality(data_wt).loc[0, 'pval'].round(3))
d_stats[measure]['normality_tg'] = (pg.normality(data_tg).loc[0, 'normal'], pg.normality(data_tg).loc[0, 'pval'].round(3))
# Test for homoscesdasticity (Levenes):
d_stats[measure]['equal_var'] = (pg.homoscedasticity([data_wt, data_tg]).loc['levene', 'equal_var'], pg.homoscedasticity([data_wt, data_tg]).loc['levene', 'pval'].round(3))
# Perform either parametric or non-parametric pairwise test:
if (d_stats[measure]['normality_wt'][0] == True) & (d_stats[measure]['normality_tg'][0] == True) & (d_stats[measure]['equal_var'][0] == True):
d_stats[measure]['pairwise_test'] = ('ttest', pg.ttest(x=data_wt, y=data_tg).loc['T-test', 'p-val'].round(4) <= 0.05, pg.ttest(x=data_wt, y=data_tg).loc['T-test', 'p-val'].round(4))
else:
d_stats[measure]['pairwise_test'] = ('MWU', pg.mwu(x=data_wt, y=data_tg).loc['MWU', 'p-val'].round(4) <= 0.05, pg.mwu(x=data_wt, y=data_tg).loc['MWU', 'p-val'].round(4))
# -
# # __Plot results:__
# ### Setup figure design and annotate_stats function:
# +
SMALL_SIZE = 16
MEDIUM_SIZE = 17
BIGGER_SIZE = 19
LINE_WIDTH = 2
SIZE = 9
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=MEDIUM_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('axes', linewidth=LINE_WIDTH) # linewidth of x and y axis
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('xtick.major', size=10) # linewidth of x ticks
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick.major', size=10) # linewidth of y ticks
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
def annotate_stats(key, axis, subplot):
data_wt = d_stats[key]['data_wt']
data_tg = d_stats[key]['data_tg']
max_total = max([max(data_wt), max(data_tg)])
x1, x2 = 0, 1
y, h, col = max_total + max_total * 0.05, max_total * 0.05, 'k'
stars = '$\it{n.s.}$'
if d_stats[key]['pairwise_test'][2] < 0.001:
subplot = axis.plot([x1, x2], [y+h, y+h], lw=1.5, c=col)
stars = '***'
elif d_stats[key]['pairwise_test'][2] < 0.01:
subplot = axis.plot([x1, x2], [y+h, y+h], lw=1.5, c=col)
stars = '**'
elif d_stats[key]['pairwise_test'][2] < 0.05:
subplot = axis.plot([x1, x2], [y+h, y+h], lw=1.5, c=col)
stars = '*'
subplot = axis.text((x1+x2)*.5, max_total, stars, ha='center', va='bottom', color=col)
labels = ['WT', '$\it{Ntrk2}$$^{+/-}$']
axis.axes.set_xticklabels(labels)
axis.spines['right'].set_visible(False)
axis.spines['top'].set_visible(False)
axis.axes.set_ylabel('latency [s]')
# -
# ## Total distance travelled:
# +
data_col = 'Totalstrecke'
fig = plt.figure(figsize=(20, 7), facecolor='w')
gs = fig.add_gridspec(1,2)
# Plot data for individual intervalls:
ax1 = fig.add_subplot(gs[0,0])
sns.lineplot(data=df.loc[df['Analyseintervall'] != 'total'], x='Analyseintervall', y=data_col, hue="Gruppe", palette=['gray', 'black'], ax=ax1, linewidth=2)
# Adjust axes, labels, and title:
plt.title('total distance travelled - per minute', pad = 20)
plt.ylim(0)
plt.xlim(1,10)
plt.ylabel('total distance travelled [cm]')
plt.xlabel('minute')
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# Adjust legend:
handles, labels = ax1.get_legend_handles_labels()
for ha in handles:
ha = ha.set_linewidth(3)
labels = ['WT', '$\it{Ntrk2}$$^{+/-}$']
ax1.legend(handles, labels, ncol=1, frameon=False, loc='center right', bbox_to_anchor=(1.3, 0.5))
# Plot data for total session and annotate states:
ax2 = fig.add_subplot(gs[0,1])
plt_total = sns.stripplot(data=df.loc[df['Analyseintervall'] == 'total'], x='Gruppe', y=data_col, hue='Kohorte', palette='colorblind', size=SIZE, ax=ax2)
annotate_stats(data_col, ax2, plt_total)
# Adjust axes, labels, and title:
plt.title('total distance travelled - total session', pad = 20)
plt.ylabel('total distance travelled [cm]')
plt.ylim(0)
plt.xlabel('')
# Adjust legend:
plt.legend(title='')
current_handles, current_labels = plt.gca().get_legend_handles_labels()
current_labels = ['cohort 1', 'cohort 2', 'cohort 3']
ax2.legend(current_handles, current_labels, ncol=1, loc='center right', frameon=False, bbox_to_anchor=(1.25, 0.5))
# Save and display figure:
plt.tight_layout()
plt.savefig('EMP_total_distance.png', dpi=300)
plt.show()
# -
# ## Time in open arms:
# +
data_col = '%time_open_arms'
fig = plt.figure(figsize=(20, 7), facecolor='w')
gs = fig.add_gridspec(1,2)
# Plot data for individual intervalls:
ax1 = fig.add_subplot(gs[0,0])
sns.lineplot(data=df.loc[df['Analyseintervall'] != 'total'], x='Analyseintervall', y=data_col, hue="Gruppe", palette=['gray', 'black'], ax=ax1, linewidth=2)
# Adjust axes, labels, and title:
plt.title('time spent in open arms - per minute', pad = 20)
plt.ylim(0)
plt.xlim(1,10)
plt.ylabel('time spent in open arms [%]')
plt.xlabel('minute')
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# Adjust legend:
handles, labels = ax1.get_legend_handles_labels()
for ha in handles:
ha = ha.set_linewidth(3)
labels = ['WT', '$\it{Ntrk2}$$^{+/-}$']
ax1.legend(handles, labels, ncol=1, frameon=False, loc='center right', bbox_to_anchor=(1.3, 0.5))
# Plot data for total session and annotate states:
ax2 = fig.add_subplot(gs[0,1])
plt_total = sns.stripplot(data=df.loc[df['Analyseintervall'] == 'total'], x='Gruppe', y=data_col, hue='Kohorte', palette='colorblind', size=SIZE, ax=ax2)
annotate_stats(data_col, ax2, plt_total)
# Adjust axes, labels, and title:
plt.title('time spent in open arms - total session', pad = 20)
plt.ylabel('time spent in open arms [%]')
plt.ylim(0)
plt.xlabel('')
# Adjust legend:
plt.legend(title='')
current_handles, current_labels = plt.gca().get_legend_handles_labels()
current_labels = ['cohort 1', 'cohort 2', 'cohort 3']
ax2.legend(current_handles, current_labels, ncol=1, loc='center right', frameon=False, bbox_to_anchor=(1.25, 0.5))
# Save and display figure:
plt.tight_layout()
plt.savefig('EPM_time_open_arms.png', dpi=300)
plt.show()
# -
# ## Visits to open arms:
# +
data_col = '%visits_open_arms'
fig = plt.figure(figsize=(20, 7), facecolor='w')
gs = fig.add_gridspec(1,2)
# Plot data for individual intervalls:
ax1 = fig.add_subplot(gs[0,0])
sns.lineplot(data=df.loc[df['Analyseintervall'] != 'total'], x='Analyseintervall', y=data_col, hue="Gruppe", palette=['gray', 'black'], ax=ax1, linewidth=2)
# Adjust axes, labels, and title:
plt.title('visits to open arms - per minute', pad = 20)
plt.ylim(0)
plt.xlim(1,10)
plt.ylabel('visits to open arms [%]')
plt.xlabel('minute')
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# Adjust legend:
handles, labels = ax1.get_legend_handles_labels()
for ha in handles:
ha = ha.set_linewidth(3)
labels = ['WT', '$\it{Ntrk2}$$^{+/-}$']
ax1.legend(handles, labels, ncol=1, frameon=False, loc='center right', bbox_to_anchor=(1.3, 0.5))
# Plot data for total session and annotate states:
ax2 = fig.add_subplot(gs[0,1])
plt_total = sns.stripplot(data=df.loc[df['Analyseintervall'] == 'total'], x='Gruppe', y=data_col, hue='Kohorte', palette='colorblind', size=SIZE, ax=ax2)
annotate_stats(data_col, ax2, plt_total)
# Adjust axes, labels, and title:
plt.title('visits to open arms - total session', pad = 20)
plt.ylabel('visits to open arms [%]')
plt.ylim(0)
plt.xlabel('')
# Adjust legend:
plt.legend(title='')
current_handles, current_labels = plt.gca().get_legend_handles_labels()
current_labels = ['cohort 1', 'cohort 2', 'cohort 3']
ax2.legend(current_handles, current_labels, ncol=1, loc='center right', frameon=False, bbox_to_anchor=(1.25, 0.5))
# Save and display figure:
plt.tight_layout()
plt.savefig('EPM_visits_open_arms.png', dpi=300)
plt.show()
# -
# ## Distance in open arms:
# +
data_col = '%distance_open_arms'
fig = plt.figure(figsize=(20, 7), facecolor='w')
gs = fig.add_gridspec(1,2)
# Plot data for individual intervalls:
ax1 = fig.add_subplot(gs[0,0])
sns.lineplot(data=df.loc[df['Analyseintervall'] != 'total'], x='Analyseintervall', y=data_col, hue="Gruppe", palette=['gray', 'black'], ax=ax1, linewidth=2)
# Adjust axes, labels, and title:
plt.title('distance travelled in open arms - per minute', pad = 20)
plt.ylim(0)
plt.xlim(1,10)
plt.ylabel('distance travelled in open arms [%]')
plt.xlabel('minute')
ax1.spines['right'].set_visible(False)
ax1.spines['top'].set_visible(False)
# Adjust legend:
handles, labels = ax1.get_legend_handles_labels()
for ha in handles:
ha = ha.set_linewidth(3)
labels = ['WT', '$\it{Ntrk2}$$^{+/-}$']
ax1.legend(handles, labels, ncol=1, frameon=False, loc='center right', bbox_to_anchor=(1.3, 0.5))
# Plot data for total session and annotate states:
ax2 = fig.add_subplot(gs[0,1])
plt_total = sns.stripplot(data=df.loc[df['Analyseintervall'] == 'total'], x='Gruppe', y=data_col, hue='Kohorte', palette='colorblind', size=SIZE, ax=ax2)
annotate_stats(data_col, ax2, plt_total)
# Adjust axes, labels, and title:
plt.title('distance travelled in open arms - total session', pad = 20)
plt.ylabel('distance travelled in open arms [%]')
plt.ylim(0)
plt.xlabel('')
# Adjust legend:
plt.legend(title='')
current_handles, current_labels = plt.gca().get_legend_handles_labels()
current_labels = ['cohort 1', 'cohort 2', 'cohort 3']
ax2.legend(current_handles, current_labels, ncol=1, loc='center right', frameon=False, bbox_to_anchor=(1.25, 0.5))
# Save and display figure:
plt.tight_layout()
plt.savefig('EPM_distance_open_arms.png', dpi=300)
plt.show()
# -
|
anxiety/mice/Analyze_EPM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
from skimage.color.adapt_rgb import adapt_rgb, each_channel, hsv_value
from skimage import filters
from skimage import data
from skimage.exposure import rescale_intensity
import matplotlib.pyplot as plt
@adapt_rgb(each_channel)
def scharr_each(image):
return filters.scharr(image)
@adapt_rgb(hsv_value)
def scharr_hsv(image):
return filters.scharr(image)
image = data.coffee()
out1 = rescale_intensity(1 - scharr_each(image))
out2 = rescale_intensity(1 - scharr_hsv(image))
# -
plt.imshow(image)
plt.show()
plt.imshow(out1)
plt.show()
plt.imshow(out2)
plt.show()
|
Chapter 12/Section18_03_Filters.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# incomplete. was just using this to understand how ppo works
# https://github.com/nikhilbarhate99/PPO-PyTorch/blob/master/PPO.py
# +
import torch
import torch.nn as nn
from torch.distributions import Categorical
import gym
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# + jupyter={"source_hidden": true}
class Memory:
def __init__(self):
self.actions = []
self.states = []
self.logprobs = []
self.rewards = []
self.is_terminals = []
def clear_memory(self):
del self.actions[:]
del self.states[:]
del self.logprobs[:]
del self.rewards[:]
del self.is_terminals[:]
# -
class ActorCritic(nn.Module):
def __init__(self, state_dim, action_dim, n_latent_var):
super(ActorCritic, self).__init__()
self.affine = nn.Linear(state_dim, n_latent_var)
# actor
self.action_layer = nn.Sequential(
nn.Linear(state_dim, n_latent_var),
nn.Tanh(),
nn.Linear(n_latent_var, n_latent_var),
nn.Tanh(),
nn.Linear(n_latent_var, action_dim),
nn.Softmax(dim=-1)
)
# critic
self.value_layer = nn.Sequential(
nn.Linear(state_dim, n_latent_var),
nn.Tanh(),
nn.Linear(n_latent_var, n_latent_var),
nn.Tanh(),
nn.Linear(n_latent_var, 1)
)
def forward(self):
raise NotImplementedError
def act(self, state, memory):
state = torch.from_numpy(state).float().to(device)
action_probs = self.action_layer(state)
dist = Categorical(action_probs)
action = dist.sample()
memory.states.append(state)
memory.actions.append(action)
memory.logprobs.append(dist.log_prob(action))
return action.item()
def evaluate(self, state, action):
action_probs = self.action_layer(state)
dist = Categorical(action_probs)
action_logprobs = dist.log_prob(action)
dist_entropy = dist.entropy()
state_value = self.value_layer(state)
return action_logprobs, torch.squeeze(state_value), dist_entropy
# +
rewards = []
discounted_reward = 0
for reward, is_terminal in zip(reversed(memory.rewards), reversed(memory.is_terminals)):
if is_terminal:
discounted_reward = 0
discounted_reward = reward + (gamma * discounted_reward)
rewards.insert(0, discounted_reward)
# Normalizing the rewards:
rewards = torch.tensor(rewards).to(device)
rewards = (rewards - rewards.mean()) / (rewards.std() + 1e-5)
print(rewards)
# -
# convert list to tensor
old_states = torch.stack(memory.states).to(device).detach()
old_actions = torch.stack(memory.actions).to(device).detach()
old_logprobs = torch.stack(memory.logprobs).to(device).detach()
# +
# evaluate
action_probs = ppo.policy.action_layer(old_states)
dist = Categorical(action_probs)
action_logprobs = dist.log_prob(old_actions)
dist_entropy = dist.entropy()
# state_value = self.value_layer(state)
# return action_logprobs, torch.squeeze(state_value), dist_entropy
# -
old_logprobs
action_logprobs
action_probs
ppo.action_layer([ 0.0022, 1.4151, 0.2234, 0.1852, -0.0025, -0.0506, 0.0000, 0.0000])
action_logprobs
action_probs
dist_entropy
class PPO:
def __init__(self, state_dim, action_dim, n_latent_var, lr, betas, gamma, K_epochs, eps_clip):
self.lr = lr
self.betas = betas
self.gamma = gamma
self.eps_clip = eps_clip
self.K_epochs = K_epochs
self.policy = ActorCritic(state_dim, action_dim, n_latent_var).to(device)
self.optimizer = torch.optim.Adam(self.policy.parameters(), lr=lr, betas=betas)
self.policy_old = ActorCritic(state_dim, action_dim, n_latent_var).to(device)
self.policy_old.load_state_dict(self.policy.state_dict())
self.MseLoss = nn.MSELoss()
def update(self, memory):
# Monte Carlo estimate of state rewards:
rewards = []
discounted_reward = 0
for reward, is_terminal in zip(reversed(memory.rewards), reversed(memory.is_terminals)):
if is_terminal:
discounted_reward = 0
discounted_reward = reward + (self.gamma * discounted_reward)
rewards.insert(0, discounted_reward)
# Normalizing the rewards:
rewards = torch.tensor(rewards).to(device)
rewards = (rewards - rewards.mean()) / (rewards.std() + 1e-5)
# convert list to tensor
old_states = torch.stack(memory.states).to(device).detach()
old_actions = torch.stack(memory.actions).to(device).detach()
old_logprobs = torch.stack(memory.logprobs).to(device).detach()
# Optimize policy for K epochs:
for _ in range(self.K_epochs):
# Evaluating old actions and values :
logprobs, state_values, dist_entropy = self.policy.evaluate(old_states, old_actions)
# Finding the ratio (pi_theta / pi_theta__old):
ratios = torch.exp(logprobs - old_logprobs.detach())
# Finding Surrogate Loss:
advantages = rewards - state_values.detach()
surr1 = ratios * advantages
surr2 = torch.clamp(ratios, 1-self.eps_clip, 1+self.eps_clip) * advantages
loss = -torch.min(surr1, surr2) + 0.5*self.MseLoss(state_values, rewards) - 0.01*dist_entropy
# take gradient step
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
# Copy new weights into old policy:
self.policy_old.load_state_dict(self.policy.state_dict())
# +
############## Hyperparameters ##############
env_name = "LunarLander-v2"
# creating environment
env = gym.make(env_name)
state_dim = env.observation_space.shape[0]
action_dim = 4
render = False
solved_reward = 230 # stop training if avg_reward > solved_reward
log_interval = 20 # print avg reward in the interval
max_episodes = 50000 # max training episodes
max_timesteps = 300 # max timesteps in one episode
n_latent_var = 64 # number of variables in hidden layer
update_timestep = 2000 # update policy every n timesteps
lr = 0.002
betas = (0.9, 0.999)
gamma = 0.99 # discount factor
K_epochs = 4 # update policy for K epochs
eps_clip = 0.2 # clip parameter for PPO
random_seed = None
if random_seed:
torch.manual_seed(random_seed)
env.seed(random_seed)
# +
memory = Memory()
ppo = PPO(state_dim, action_dim, n_latent_var, lr, betas, gamma, K_epochs, eps_clip)
print(lr,betas)
# logging variables
running_reward = 0
avg_length = 0
timestep = 0
# training loop
for i_episode in range(1, max_episodes+1):
state = env.reset()
for t in range(5):
timestep += 1
# Running policy_old:
action = ppo.policy_old.act(state, memory)
state, reward, done, _ = env.step(action)
# Saving reward and is_terminal:
memory.rewards.append(reward)
memory.is_terminals.append(done)
# update if its time
if timestep % 5 == 0:
break
# ppo.update(memory)
# memory.clear_memory()
# timestep = 0
running_reward += reward
if render:
env.render()
if done:
break
break # just one episode
avg_length += t
# # stop training if avg_reward > solved_reward
# if running_reward > (log_interval*solved_reward):
# print("########## Solved! ##########")
# torch.save(ppo.policy.state_dict(), './PPO_{}.pth'.format(env_name))
# break
# # logging
# if i_episode % log_interval == 0:
# avg_length = int(avg_length/log_interval)
# running_reward = int((running_reward/log_interval))
# print('Episode {} \t avg length: {} \t reward: {}'.format(i_episode, avg_length, running_reward))
# running_reward = 0
# avg_length = 0
# -
|
LunarLander/OneActorPPO.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from arena_util import load_json
from arena_util import write_json
from arena_util import remove_seen
from arena_util import most_popular
import numpy as np
# -
train = load_json("arena_data/orig/val.json")
len(train)
song_meta = load_json("res/song_meta.json")
song_infos = {}
for t in train:
song_infos[t['id']]=[song_meta[a] for a in t['songs']]
song_vec = np.zeros(30)
def one_hot_encode(song):
song_vec = np.zeros(30)
for genre in song['song_gn_gnr_basket']:
try:
song_vec[int(int(genre[2:])/100)-1] = 1
except:
pass
#print("error in : ",genre)
return song_vec
def normalize(v):
#norm = np.linalg.norm(v)
norm = np.sum(v)
if norm == 0:
return v
return v / norm
def songs2vec(songs):
plylst_vec_list = np.zeros(30)
for i in range(len(songs)):
plylst_vec_list += one_hot_encode(songs[i])
if np.linalg.norm(plylst_vec_list):
return plylst_vec_list/np.linalg.norm(plylst_vec_list)
return plylst_vec_list
plylst_list = {}
for plylst, songs in song_infos.items():
plylst_list[plylst] = songs2vec(songs)
plylst_list
def vec_diff(p, q):
return np.linalg.norm(p-q)
def get_most_similar(song):
songs = [song]
song_vec = songs2vec(songs)
closest_plylst = plylst[0]
for plylst in plylst
vec_diff(p1,p2)
load_json('arena_data/questions/val.json')[:10]
|
practice_sheet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ##### Python Encapsulation-Erişim Engelleme
class Personel:
def __init__(self,isim,soyisim,yas,maas,uzmanlık):
self.isim=isim
self.soyisim=soyisim
self.yas=yas
self.__maas=maas
self.uzmanlık=uzmanlık
def info(self):
print("{}{}{} yasında ve maası {} olan bir {}personelimizdir.".format(self.isim,self.soyisim,self.yas,self.__maas,self.uzmanlık))
def getMaas(self):
return self.__maas
def setMaas(self,yeni_maas):
self.__maas=yeni_maas
personel=Personel("nilay","cezik",23,10000,"<NAME>")
personel.getMaas()
personel.setMaas(5000)
personel.getMaas()
# ##### Python Inheritance - Kalıtım
class Ofis:
def __init__(self,isim,soyisim,yas):
self.isim=isim
self.soyisim=soyisim
self.yas=yas
# +
class Personel(Ofis):
def __init__(self,isim,soyisim,yas):
super().__init__(isim,soyisim,yas)
def info(self):
print("{}{}{} yasında olan personelimizdir.".format(self.isim,self.soyisim,self.yas))
# -
personel=Personel("nilay","cezik",23)
# ##### Ptyhon Abstract Class- Soyut Sınıflar
from abc import ABC,abstractmethod
class Animal:
@abstractmethod
def walk(self):
print("Hayvan yürüyor")
@abstractmethod
def run(self):
print("Hayvan koşuyor")
class Leo(Animal):
def walk(self):
print("Aslan yürüyor")
@abstractmethod
def run(self):
print("Aslan koşuyor")
leo=Animal()
leo.walk()
leo_obj=Leo()
leo_obj.run()
# ##### Modül- Paket ve Kütüphaneler
# ###### Math Modülü
import math
math.factorial(6)
math.sqrt(5)
import math as matematik
matematik.pi
from math import factorial
factorial(15)
from math import *
sqrt(6)
# ###### Datetime Modülü
import datetime
now=datetime.datetime.now()
now.strftime("%d/%m/%y %H:%M:%S")
from datetime import date
today=date.today()
today.day
today.month
today.year
new=date(2022,6,23)
new
# ###### Time Modülü
from datetime import time
time=time(10,23,45,245)
time.hour
time.minute
time.second
time.microsecond
date1=date(2020,5,22)
date2=date(2021,8,16)
date1-date2
import time
time.localtime()
while True:
zaman =time.strftime("%H:%M:%S")
print(zaman)
time.sleep(1)
# ###### Hatalar ve İstisnalar
# ###### Try-Catch
def topla(x,y):
print(x+y)
if 5>1
print("5 büyük 1")
x=5
y="10"
x+y
x=int(input("bir sayı giriniz:"))
y=int(input("ikinci sayıyı giriniz:"))
x/y
try:
x=int(input("bir sayı giriniz:"))
y=int(input("ikinci sayıyı giriniz:"))
x/y
except:
print("Sıfıra bölünme hatası")
try:
x=int(input("bir sayı giriniz:"))
y=int(input("ikinci sayıyı giriniz:"))
x/y
except ValueError:
print("Lütfen bir sayı giriniz")
except TypeError:
print("Veri tiplerinde bir hata var")
except ZeroDivisionError:
print("Sıfırdan farklı bir değer giriniz")
# ###### Finally-Raise
# +
try:
x=int(input("bir sayı giriniz:"))
y=int(input("ikinci sayıyı giriniz:"))
x/y
except:
print("hata oluştu")
finally:
print("ne olursa olsun çalışacak")
# -
class SıfırHatası(Exception):
pass
# +
x=int(input("bir sayı giriniz:"))
if x==0:
raise SıfırHatası("Lütfen 0 dan farklı bir değer giriniz")
else:
print(x)
# -
# ##### Python'da Dosya İşlemleri
dosya= open("dosya.txt",mode="w",encoding="utf-8")
dosya.write("Hi")
dosya.close()
dosya= open("dosya.txt",mode="a",encoding="utf-8")
dosya.write(" Hello World")
# ###### Dosya Okuma
dosya= open("dosya.txt",mode="r",encoding="utf-8")
dosya.read()
dosya= open("dosya.txt",mode="r",encoding="utf-8")
for i in dosya:
print(i)
liste = dosya.readlines()
liste
liste[0]
# ###### With Open Yapısı
with open("cv.txt","w",encoding="utf-8") as cv:
cv.write("Hi.I am Nilay")
cv.write("I am 23 years old")
with open("cv.txt","r",encoding="utf-8") as cv:
cv.seek(5)
print(cv.read(5))
print(cv.tell())
# ##### Iterator
x="Nilay"
for i in x:
print(i)
y=[1,2,4,6,7,9]
for i in y:
print(i)
iterasyon=iter(x)
next(iterasyon)
next(iterasyon)
next(iterasyon)
next(iterasyon)
next(iterasyon)
iterasyon=iter(x)
while True:
try:
eleman=next(iterasyon)
print(eleman)
except:
break
# +
class Sayılar:
def __iter__(self):
self.sayı=0
return self
def __next__(self):
x=self.sayı
self.sayı+=10
return x
iterasyon = iter(Sayılar())
print(next(iterasyon))
print(next(iterasyon))
print(next(iterasyon))
print(next(iterasyon))
print(next(iterasyon))
print(next(iterasyon))
# -
# ##### Generator
def cift(sayi):
cift_sayilar=[]
for i in range (sayi):
cift_sayilar.append(i*2)
return cift_sayilar
cift(20)
def cift(sayi):
for i in range (sayi):
yield i*2
cift(20)
for i in cift(1000):
print(i)
|
BasicPythonExample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # 1. Rysowanie Dłonie
#
# Rozpoznawanie dłonie polega na wyznaczeniu pozycji elementów charakterystycznych dłoni. W sumie można wyznaczych ich 21. Są to między innymi stawy, nadgarstek lub końcówki palców. Współrzędne są obliczne względem położenia nagarstka.
#
# <img src=https://i.imgur.com/qpRACer.png />
#
# Rozpoczynamy od zaimportowania odpowiednich bibliotek.
#
# OpenCV pozowli na przeprowadzenie wstępnych przekształceń obrazu, w taki sposób, aby biblioteka MediaPipe mogła poprawnie rozpoznać dłoń oraz jej elementy charaktterystyczne.
import mediapipe as mp
import cv2
import numpy as np
# Wybieramy dwa obiekty klasy mp.solutions:
#
# 1. mp_drawing - pozowli na naniesienie punktów na elementy charakterystyczne dłoni oraz linii ich łączących.
# 2. mp_hands - zostanie wykorzystany do rozpoznania dłoni z wybraną dokładnością.
mp_drawing = mp.solutions.drawing_utils
mp_hands = mp.solutions.hands
# Wstępne ropoznanie dłoni i nanisieni grafiki na obraz pobrany z kamery.
# +
cap = cv2.VideoCapture(0)
with mp_hands.Hands(min_detection_confidence=0.8, min_tracking_confidence=0.5) as hands:
while cap.isOpened():
ret, frame = cap.read()
#BGR to RGB
image = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
#Flip horizontal
image = cv2.flip(image, 1)
#Set flag
image.flags.writeable = False
#Detections
results = hands.process(image)
#Set flag back to True
image.flags.writeable = True
#RGB to BGR
image = cv2.cvtColor(image, cv2.COLOR_RGB2BGR)
#print(results)
#Rendering results
if results.multi_hand_landmarks:
for num, hand in enumerate(results.multi_hand_landmarks):
mp_drawing.draw_landmarks(image, hand, mp_hands.HAND_CONNECTIONS,
mp_drawing.DrawingSpec(color=(0,255,0), thickness=2, circle_radius=4),
mp_drawing.DrawingSpec(color=(0,0,255), thickness=2, circle_radius=4))
#image = cv2.flip(image, 0)
cv2.imshow("Hand Tracking", image)
if cv2.waitKey(10) & 0xFF == ord('q'):
break
print(image.shape)
cap.release()
cv2.destroyAllWindows()
# -
# Wyniki zapisujemy w liście "results", która posiada informacje o wszystkich wykrytyach dłoniach.
results.multi_hand_landmarks[0].landmark
# # 2. Zapis pozycji elementów charakterystycznych do pliku CSV
import csv
import os
import numpy as np
# Sprawdzamy sumaryczną liczbę wszysktich elementów charakterystycznych
num_coords = len(results.multi_hand_landmarks[0].landmark)
print(num_coords)
# Tworzymy oznaczenia kolumn (klasy, współrzędne)
landmarks = ['class']
for val in range(0, num_coords):
landmarks += ['x{}'.format(val), 'y{}'.format(val), 'z{}'.format(val)]
landmarks
# Tworzymy plik CSV i zapisujemy do niego oznaczenia kolumn.
with open('coords.csv', mode='w', newline='') as f:
csv_writer = csv.writer(f, delimiter=',', quotechar='"', quoting=csv.QUOTE_MINIMAL)
csv_writer.writerow(landmarks)
# Tworzymy zmienną class_name, która będzie przechowywała informację o aktualnie przechwytywanym geście. W momencie rozpoczęcie tej części programu, będziemy zapisywać wszystkie współrzędne elementów charakterystycznych dla wybranego gestu.
class_name = "Open"
# +
cap = cv2.VideoCapture(0)
detections = 0
with mp_hands.Hands(min_detection_confidence=0.8, min_tracking_confidence=0.5) as hands:
while cap.isOpened():
ret, frame = cap.read()
#BGR to RGB
image = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
#Flip horizontal
image = cv2.flip(image, 1)
#Set flag
image.flags.writeable = False
#Detections
results = hands.process(image)
#Set flag back to True
image.flags.writeable = True
#RGB to BGR
image = cv2.cvtColor(image, cv2.COLOR_RGB2BGR)
#print(results)
#Rendering results
if results.multi_hand_landmarks:
for num, hand in enumerate(results.multi_hand_landmarks):
mp_drawing.draw_landmarks(image, hand, mp_hands.HAND_CONNECTIONS,
mp_drawing.DrawingSpec(color=(0,255,0), thickness=2, circle_radius=4),
mp_drawing.DrawingSpec(color=(0,0,255), thickness=2, circle_radius=4))
try:
hand_landmarks = results.multi_hand_landmarks[0].landmark
hand_landmarks_row = list(np.array([[landmark.x, landmark.y, landmark.z] for landmark in hand_landmarks]).flatten())
hand_landmarks_row.insert(0, class_name)
with open('coords.csv', mode='a', newline='') as f:
csv_writer = csv.writer(f, delimiter=',', quotechar='"', quoting=csv.QUOTE_MINIMAL)
csv_writer.writerow(hand_landmarks_row)
detections += 1
except:
pass
if detections == 1500:
break
#image = cv2.flip(image, 0)
cv2.imshow("Hand Tracking", image)
if cv2.waitKey(10) & 0xFF == ord('q'):
break
print(image.shape)
cap.release()
cv2.destroyAllWindows()
# -
len(hand_landmarks_row)
# # 3. Trening modeli z wykorzystaniem Scikit Learn
import pandas as pd
from sklearn.model_selection import train_test_split
# Odczytyjemy wszystkie dane z pliku CSV
df = pd.read_csv('coords.csv')
df.head()
df.tail()
df[df['class']=='Fist']
x = df.drop('class', axis=1)
y = df['class']
y
x
# Wszystkie pobrane dane dzielimy na dwie części, pierwsza posłuży do trenowania, druga do testwowania.
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=3451)
y_train.values
# # 4. Trenowanie Klasyfikujących Modeli Uczenia Maszynowego
# +
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression, RidgeClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
# -
# Tworzymy słownik przechowywujący 4 metody uczenie maszynowego wraz z metodą normalizacji.
pipelines = {
'lr':make_pipeline(StandardScaler(), LogisticRegression()),
'rd':make_pipeline(StandardScaler(), RidgeClassifier()),
'rf':make_pipeline(StandardScaler(), RandomForestClassifier()),
'gb':make_pipeline(StandardScaler(), GradientBoostingClassifier()),
}
# + active=""
# y_train
# -
# Trenujemy 4 różne modele jednocześnie
# +
fit_models = {}
for algo, pipeline in pipelines.items():
model = pipeline.fit(x_train, y_train)
fit_models[algo] = model
# -
fit_models['rf'].predict(x_test)
# # 5. Ewaluacja Modelu
from sklearn.metrics import accuracy_score
import pickle
# Porównujemy dokładność każdego modelu wykorzystując funkcję accuracy_score
for algo, model in fit_models.items():
yhat = model.predict(x_test)
print(algo, accuracy_score(y_test, yhat))
fit_models['rf'].predict(x_test)
y_test
# Najdokładniejszy model zapisujemy w postaci binarnej wykorzystując pickle.
with open('gesture_recognition.pkl', 'wb') as f:
pickle.dump(fit_models['rf'], f)
# # 5. Detekcje
# Powtórnie ładujemy model.
with open('gesture_recognition.pkl', 'rb') as f:
model = pickle.load(f)
model
model.predict(x_test)
# Testujemy działanie modelu na podstawie obrazu z kamery.
# +
cap = cv2.VideoCapture(0)
detections = 0
with mp_hands.Hands(min_detection_confidence=0.8, min_tracking_confidence=0.5) as hands:
while cap.isOpened():
ret, frame = cap.read()
#BGR to RGB
image = cv2.cvtColor(frame, cv2.COLOR_BGR2RGB)
#Flip horizontal
image = cv2.flip(image, 1)
#Set flag
image.flags.writeable = False
#Detections
results = hands.process(image)
#Set flag back to True
image.flags.writeable = True
#RGB to BGR
image = cv2.cvtColor(image, cv2.COLOR_RGB2BGR)
#print(results)
#Rendering results
if results.multi_hand_landmarks:
for num, hand in enumerate(results.multi_hand_landmarks):
mp_drawing.draw_landmarks(image, hand, mp_hands.HAND_CONNECTIONS,
mp_drawing.DrawingSpec(color=(0,255,0), thickness=2, circle_radius=4),
mp_drawing.DrawingSpec(color=(0,0,255), thickness=2, circle_radius=4))
try:
hand_landmarks = results.multi_hand_landmarks[0].landmark
hand_landmarks_row = list(np.array([[landmark.x, landmark.y, landmark.z] for landmark in hand_landmarks]).flatten())
#hand_landmarks_row.insert(0, class_name)
#Make Detections
x = pd.DataFrame([hand_landmarks_row])
#print(x)
gesture_class = model.predict(x.values)
#gesture_prob = model.predict_proba(x)[0]
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
print(gesture_class)
cv2.putText(image, gesture_class, (10,20), cv2.FONT_HERSHEY_SIMPLEX, 1, (255,255,255), 2, cv2.LINE_AA)
except:
pass
if detections == 500:
break
#image = cv2.flip(image, 0)
cv2.imshow("Hand Tracking", image)
if cv2.waitKey(10) & 0xFF == ord('q'):
break
print(image.shape)
cap.release()
cv2.destroyAllWindows()
|
.ipynb_checkpoints/Gesture Recognition-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Sequence to Sequence Classification by RNN
#
# - Creating the **data pipeline** with `tf.data`
# - Preprocessing word sequences (variable input sequence length) using `padding technique` by `user function (pad_seq)`
# - Using `tf.nn.embedding_lookup` for getting vector of tokens (eg. word, character)
# - Training **many to many classification** with `tf.contrib.seq2seq.sequence_loss`
# - Masking unvalid token with `tf.sequence_mask`
# - Creating the model as **Class**
# +
import os
import sys
import time
import string
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
import tensorflow as tf
slim = tf.contrib.slim
rnn = tf.contrib.rnn
sess_config = tf.ConfigProto(gpu_options=tf.GPUOptions(allow_growth=True))
# -
# ## Prepare example data
sentences = [['I', 'feel', 'hungry'],
['You', 'are', 'a', 'genius'],
['tensorflow', 'is', 'very', 'difficult'],
['tensorflow', 'is', 'a', 'framework', 'for', 'deep', 'learning'],
['tensorflow', 'is', 'very', 'fast', 'changing']]
pos = [['pronoun', 'verb', 'adjective'],
['pronoun', 'verb', 'preposition', 'noun'],
['noun', 'verb', 'adverb', 'adjective'],
['noun', 'verb', 'determiner', 'noun', 'preposition', 'adjective', 'noun'],
['noun', 'verb', 'adverb', 'adjective', 'verb']]
# +
# word dictionary
bag_of_words = []
for sentence in sentences:
bag_of_words += sentence
bag_of_words = list(set(bag_of_words))
bag_of_words.sort()
bag_of_words = ['<pad>'] + bag_of_words
word2idx = {word : idx for idx, word in enumerate(bag_of_words)} # word to index
idx2word = [word for word in bag_of_words] # index to word
# -
#print("word2idx: {}".format(word2idx))
word2idx
#print("idx2word: {}".format(idx2word))
idx2word
# +
# pos dictionary
bag_of_pos = []
for item in pos:
bag_of_pos += item
bag_of_pos = list(set(bag_of_pos))
bag_of_pos.sort()
bag_of_pos = ['<pad>'] + bag_of_pos
print("bag_of_pos: {}".format(bag_of_pos))
pos2idx = {pos : idx for idx, pos in enumerate(bag_of_pos)} # pos to index
idx2pos = [pos for pos in bag_of_pos] # index to pos
# -
#print("pos2idx: {}".format(pos2idx))
pos2idx
#print("idx2pos: {}".format(idx2pos))
idx2pos
# ### Create pad_seq function
def pad_seq(sequences, max_length, dic):
"""Padding sequences
Padding a special charcter '<pad>' from the end of sentence to max_length
Args:
sequences (list of characters): input data
max_length (int): max length for padding
dic (dictionary): char to index
Returns:
seq_indices (2-rank np.array):
seq_length (1-rank np.array): sequence lengthes of all data
"""
seq_length, seq_indices = [], []
for sequence in sequences:
seq_length.append(len(sequence))
seq_idx = [dic.get(char) for char in sequence]
seq_idx += (max_length - len(seq_idx)) * [dic.get('<pad>')] # 0 is idx of meaningless token "<pad>"
seq_indices.append(seq_idx)
return np.array(seq_indices), np.array(seq_length)
# ### Pre-process data
max_length = 10
X_indices, X_length = pad_seq(sequences=sentences, max_length=max_length, dic=word2idx)
print("X_indices")
print(X_indices)
print("X_length")
print(X_length)
y_string = np.array([item + ['<pad>'] * (max_length - len(item)) for item in pos])
print(y_string)
y = np.array([list(map(lambda el : pos2idx.get(el), item)) for item in y_string])
print(y)
# ### Define SimPosRNN
class PosRNN:
def __init__(self, seq_indices, seq_length, labels, num_classes, hidden_dim, max_length, word2idx):
# Data pipeline
with tf.variable_scope('input_layer'):
self._seq_indices = seq_indices
self._seq_length = seq_length
self._labels = labels
one_hot = tf.eye(len(word2idx), dtype = tf.float32)
self._one_hot = tf.get_variable(name='one_hot_embedding',
initializer=one_hot,
trainable=False) # embedding vector training 안할 것이기 때문
self._seq_embeddings = tf.nn.embedding_lookup(params=self._one_hot,
ids=self._seq_indices)
# LSTM cell (many to many)
with tf.variable_scope('lstm_cell'):
cell = rnn.BasicLSTMCell(num_units=hidden_dim, state_is_tuple=True)
score_cell = rnn.OutputProjectionWrapper(cell=cell,
output_size=num_classes)
self._outputs, _ = tf.nn.dynamic_rnn(cell=score_cell, inputs=self._seq_embeddings,
sequence_length=self._seq_length,
dtype=tf.float32)
with tf.variable_scope('seq2seq_loss'):
masks = tf.sequence_mask(lengths=self._seq_length, maxlen=max_length, dtype=tf.float32)
self.seq2seq_loss = tf.contrib.seq2seq.sequence_loss(logits=self._outputs,
targets=self._labels,
weights=masks)
with tf.variable_scope('prediction'):
self._prediction = tf.argmax(input=self._outputs,
axis=2, output_type=tf.int32)
def predict(self, sess, seq_indices, seq_length):
feed_dict = {self._seq_indices : seq_indices, self._seq_length : seq_length}
return sess.run(self._prediction, feed_dict=feed_dict)
# ### Create a model of SimPosRNN
# hyper-parameters
num_classes = len(idx2pos)
learning_rate = .003
batch_size = 2
max_epochs = 100
# ### Set up dataset with `tf.data`
#
# #### create input pipeline with `tf.data.Dataset`
## create data pipeline with tf.data
train_dataset = tf.data.Dataset.from_tensor_slices((X_indices, X_length, y))
train_dataset = train_dataset.shuffle(buffer_size = 100)
train_dataset = train_dataset.batch(batch_size = batch_size)
print(train_dataset)
# #### Define Iterator
train_iterator = train_dataset.make_initializable_iterator()
seq_indices, seq_length, labels = train_iterator.get_next()
pos_rnn = PosRNN(seq_indices=seq_indices, seq_length=seq_length,
labels=labels, num_classes=num_classes,
hidden_dim=16, max_length=max_length,
word2idx=word2idx)
# ### Creat training op and train model
## create training op
optimizer = tf.train.AdamOptimizer(learning_rate)
train_op = optimizer.minimize(pos_rnn.seq2seq_loss)
# ### `tf.Session()` and train
# +
sess = tf.Session()
sess.run(tf.global_variables_initializer())
loss_history = []
step = 0
for epochs in range(max_epochs):
start_time = time.time()
sess.run(train_iterator.initializer)
avg_loss = []
while True:
try:
_, loss_ = sess.run([train_op, pos_rnn.seq2seq_loss])
avg_loss.append(loss_)
step += 1
except tf.errors.OutOfRangeError:
#print("End of dataset") # ==> "End of dataset"
break
avg_loss_ = np.mean(avg_loss)
loss_history.append(avg_loss_)
duration = time.time() - start_time
examples_per_sec = batch_size / float(duration)
print("epochs: {}, step: {}, loss: {:g}, ({:.2f} examples/sec; {:.3f} sec/batch)".format(epochs+1, step, avg_loss_, examples_per_sec, duration))
# -
plt.plot(loss_history, label='train')
y_pred = pos_rnn.predict(sess=sess, seq_indices=X_indices, seq_length=X_length)
print(y_pred)
# +
result_str = []
for example in y_pred:
result_str.append([idx2pos[idx] for idx in example])
for examples in zip(y_string, result_str):
print(" Label: ", ' '.join(examples[0]))
print("Prediction: ", ' '.join(examples[1]))
|
tf.version.1/04.rnn/04.03.seq2seq.classification.LSTM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Author: <NAME>
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manual_seed(1)
# +
lstm = nn.LSTM(3, 3) # Input dim is 3, output dim is 3
inputs = [torch.randn(1, 3) for _ in range(5)] # make a sequence of length 5
print ('inputs: ', inputs)
# initialize the hidden state.
hidden = (torch.randn(1, 1, 3),
torch.randn(1, 1, 3))
for i in inputs:
# Step through the sequence one element at a time.
# after each step, hidden contains the hidden state.
out, hidden = lstm(i.view(1, 1, -1), hidden)
print ("hidden: ", hidden)
# alternatively, we can do the entire sequence all at once.
# the first value returned by LSTM is all of the hidden states throughout
# the sequence. the second is just the most recent hidden state
# (compare the last slice of "out" with "hidden" below, they are the same)
# The reason for this is that:
# "out" will give you access to all hidden states in the sequence
# "hidden" will allow you to continue the sequence and backpropagate,
# by passing it as an argument to the lstm at a later time
# Add the extra 2nd dimension
inputs = torch.cat(inputs).view(len(inputs), 1, -1)
hidden = (torch.randn(1, 1, 3), torch.randn(1, 1, 3)) # clean out hidden state
out, hidden = lstm(inputs, hidden)
print(out)
print(hidden)
# -
|
predict_nn/lstm_pytorch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial
# Jelle, updated May 2019
#
# This notebook shows how to do basic analysis with straxen, much like `hax.minitrees`.
# For reference, here are some jargon terms which we will introduce below:
#
# * **Context**: Holds configuration on how to process
# * **Dataframe** or **array**: table of related information produced by a plugin.
# * **Plugin**: an algorithm that produces a dataframe
# * **Data type**: specification of which columns are in a dataframe.
# * **Data kind**: e.g. 'events' or 'peaks'. Dataframes of the same kind have the same number of rows and can be merged.
#
import numpy as np
# This just ensures some comments in dataframes below display nicely
import pandas as pd
pd.options.display.max_colwidth = 100
# ## Setting up
# First we load a strax **context**, much like `hax.init()`. A strax context contains all information on *how* to process: where to read what files from, what plugins provide what data, etc.
#
# You can make a context yourselves using `strax.Context`, but straxen provides standardized contexts as well. Most future analyses will use such standardized contexts defined by analysis coordinators or straxen maintainers.
#
# Unlike `hax.init`, you can have multiple active contexts, e.g. to load analysis and MC data, or compare data processed with different settings (we will see examples of this below).
import straxen
st = straxen.contexts.demo()
# ## Finding your data
# Usually you'd be running on a XENON analysis facility with access to XENON data. This demo should run everywhere, so we'll have to download some data first:
straxen.download_test_data()
# Suposse we want to make a cS1/cS2 plot. We have to figure out which type of **dataframes** to load. A specific type of dataframe is also called a **data type**. (in hax these were called minitrees)
#
# We can find this out automatically if we know (part of) the name of a field to load:
st.search_field('*s1')
# It seems we're after one of the data types called `event_info` or `corrected_areas`. In the current context, these are provided by **plugins** called EventInfo and CorrectedAreas, respectively (but this doesn't concern us yet).
#
# Let's see what else is in these data types:
st.data_info('corrected_areas')
st.data_info('event_info')
# As you can see, `event_info` has a lot more information; let's load that one. You can see from the documentation (TODO link) that `event_info`'s job is to merge the info from `corrected_areas` and other things.
#
# ## Loading data
# Next, you'll want to select a run. The `select_runs` function will return a dataframe with all available runs; there is a separate tutorial on more advanced use of this. In this demo context, we only have high-level data for the run `180215_1029` available (and low-level data for another):
st.select_runs()
# So lets' take that 180215_1029.
#
# To actually load data, you use `get_df` to get a pandas DataFrame, or `get_array` to get a numpy (structured) array. Let's go with pandas for now:
run_id = '180215_1029'
df = st.get_df(run_id, 'event_info')
# The first time you run this, it will take a moment: it has to actually process the data somewhat. We didn't ship highest-level demo data with straxen: that would mean we'd have to constantly update the test data when the algorithms change.
#
# Just like hax.minitrees.load, we got a dataframe back. You can specify a list of runid's instead of one run, and get the concatenated result back.
#
# Though it's not related to strax, let's make a quick plot of the events we just loaded:
# +
import matplotlib.pyplot as plt
# %matplotlib inline
def event_plot(df):
plt.scatter(df.cs1, df.cs2,
c=df.s1_area_fraction_top,
vmin=0, vmax=0.3,
s=10,
cmap=plt.cm.jet,
marker='.', edgecolors='none')
plt.colorbar(label="S1 area fraction top", extend='max')
plt.xlabel('cS1 (PE)')
plt.ylabel('cS2 (PE)')
plt.xscale('symlog')
plt.yscale('log')
plt.ylim(1e2, 1e7)
event_plot(df)
# -
# Can you guess what kind of data this is?
# ## Waveform analysis
# The *peaks* data type contains the sum waveform information:
st.data_info('peaks')
# Notice the compound data types of the `data`, `width` and `saturated_channel` fields. Pandas does not support such types (well, it sort of does, but the resulting dataframes are quite inefficient), so we have to load this as a numpy array:
peaks = st.get_array(run_id, 'peaks')
type(peaks), peaks.dtype.names
# Now we can plot peak waveforms:
# +
def plot_peak(p, t0=None, **kwargs):
n = p['length']
if t0 is None:
t0 = p['time']
plt.plot((p['time'] - t0) + np.arange(n) * p['dt'],
p['data'][:n] / p['dt'],
linestyle='steps-mid',
**kwargs)
plt.xlabel("Time (ns)")
plt.ylabel("Sum waveform (PE / ns)")
plot_peak(peaks[55241])
# +
def plot_peaks(main_i, n_before=0, n_after=0, label_threshold=0):
for i in main_i + np.arange(-n_before, n_after + 1):
p = peaks[i]
label = None
if p['area'] > label_threshold:
label = '%.1f PE, %d ns dt' % (p['area'], p['dt'], )
plot_peak(p,
t0=peaks[main_i]['time'],
label=label)
plt.ylim(0, None)
plt.legend(loc='best')
plt.yscale('symlog')
plot_peaks(55240, n_after=0, n_before=2)
# -
# The abrupt termination of the S2 above is due to strax's data reduction.
# ## Configuration changes
# As you can see in the above plot, we have many events high up in the TPC at low S1. Perhaps you want to get rid of them by increasing the 'S1 coincidence requirement', i.e. the number of PMTs that must see something before a peak is labeled as S1. Then, of course, you want to load the event-level data again to see if it worked.
# First, we need to see which configuration option we have to change. Strax plugins declare what configuration they take and what other plugins they depend on, so this is not very difficult. We just ask which options with `s1` in their name influence `event_basics`:
st.show_config('event_basics', 's1*')
# Looks like we're after the `s1_min_n_channels option`. Note this is not part of the `event_basics` data type, but of a data type called `peak_classification`. As you can see from the table, this option is not set in the current context, so the default value (3) is used.
#
# To try out a different option, just pass it to get_df:
df_2 = st.get_df(run_id, 'event_info',
config=dict(s1_min_n_channels=50))
event_plot(df_2)
# Notice all the small S1 events are indeed gone now.
#
# Behind the scenes, this figured out which dataframes had to be remade: as it happens this time just `event_basics` and `peak_basics`. You will now have a new `event_basics_<somehash>` folder in `./custom_data` which contains the results, as well as a new `peak_basics_<somehash> folder`.
# ### More on configuration changes
# Changing configuration can be done in two other ways. We can change it permanently in the current context:
# ```python
# st.set_config(dict(s1_min_channels=50))
# ```
# Or we could make a new context, with this option set:
# ```python
# st_2 = st.new_context(config=dict(s1_min_channels=50))
# ```
# (feeding it to get_df just does the latter behind the scenes).
# Strax protects you from typos in the configuration. Suppose we typed `s1_min_n_channelz` instead:
df_2 = st.get_df(run_id, 'event_info',
config=dict(s1_min_n_channelz=10))
event_plot(df_2)
# The result of get_df is just the same as if the option wasn't set (just like in pax/hax), but you also get a warning about an unknown configuration option.
#
# By the way, you can use
# ```python
# import warnings
# warnings.filterwarnings("error")
# ```
# to ensure any warning raises an exception instead.
# ## Customization: new plugins
# To add or change processing algorithms, or to define new variables to use in cuts, you have to write new strax plugins. These are somewhat similar to hax's treemakers.
#
# Suppose you have a brilliant new idea for peak classification:
# +
import strax
import numpy as np
class AdvancedExpertClassification(strax.Plugin):
"""Everything is an S1!"""
# Name of the data type this plugin provides
provides = 'peak_classification'
# Data types this plugin requires. Note we don't specify
# what plugins should produce them: maybe the default PeakBasics
# has been replaced by another AdvancedExpertBlabla plugin?
depends_on = ('peak_basics',)
# Numpy datatype of the output
dtype = straxen.plugins.plugins.PeakClassification.dtype
# Version of the plugin. Increment this if you change the algorithm.
__version__ = '0.0.1'
def compute(self, peaks):
# Your code here.
# This function will be called several times with
# 'peaks' a numpy array of the datatype 'peaks'.
# Each time you'll see a small part of the run.
# You have to return a numpy array of the dtype you declared above
# or, which is often easier, a dictionary we can transform into it
# (dict keys -> field names, values -> field values)
return dict(type=np.ones(len(peaks)))
# -
# Notice the plugin provides 'peak_classification' and produces the same data type as PeakClassification plugin, which in this case is just:
AdvancedExpertClassification.dtype
# To use it in place of PeakClassification, we only have to register it. Again, we can do so permanently using
# ```python
# st.register(AdvancedExpertClassification)
# ```
# or temporarily, by feeding the registration as an extra argument to `get_df`:
df = st.get_df(run_id, 'event_info',
register=AdvancedExpertClassification)
df['s2_area'].max()
# As you can see, all events are now S1-only events, as expected. Maybe this is not the best alternative classification :-)
#
# This plugin was the most basic possible plugin. You'll also want to learn about `LoopPlugin`s and `OverlapWindowPlugin`s, but that's beyond the scope of this tutorial.
|
notebooks/tutorials/strax_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.7 64-bit (''tf2'': conda)'
# language: python
# name: python_defaultSpec_1598282886802
# ---
# +
# RefLink: https://www.tensorflow.org/tutorials/distribute/keras
import os
# Import TensorFlow and TensorFlow Datasets
import tensorflow_datasets as tfds
import tensorflow as tf
from tensorflow import keras
tfds.disable_progress_bar()
# + tags=[]
print(f"TensorFlow version: {tf.__version__}.") # Keras backend
print(f"Keras version: {keras.__version__}.")
print(f"tensorflow_datasets version: {tfds.__version__}.")
print(tf.test.is_built_with_cuda())
# + tags=[]
datasets, info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
# -
mnist_train
# + tags=[]
strategy = tf.distribute.MirroredStrategy()
# + tags=[]
print('Number of devices: {}'.format(strategy.num_replicas_in_sync))
# -
# ## Setup input pipeline
# +
# You can also do info.splits.total_num_examples to get the total
# number of examples in the dataset.
num_train_examples = info.splits['train'].num_examples
num_test_examples = info.splits['test'].num_examples
BUFFER_SIZE = 10000
BATCH_SIZE_PER_REPLICA = 64
BATCH_SIZE = BATCH_SIZE_PER_REPLICA * strategy.num_replicas_in_sync
# -
len(tf.config.list_physical_devices('XLA_GPU'))
# Pixel values, which are 0-255, have to be normalized to the 0-1 range. Define this scale in a function.
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
# Apply this function to the training and test data, shuffle the training data, and batch it for training. Notice we are also keeping an in-memory cache of the training data to improve performance.
train_dataset = mnist_train.map(scale).cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
eval_dataset = mnist_test.map(scale).batch(BATCH_SIZE)
train_dataset
# ## Create the model
# + tags=[]
with strategy.scope():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10)
])
model.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
# -
# ## Define the callbacks
# +
# Define the checkpoint directory to store the checkpoints
checkpoint_dir = './training_checkpoints'
# Name of the checkpoint files
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
def decay(epoch):
if epoch < 3:
return 1e-3
elif epoch >= 3 and epoch < 7:
return 1e-4
else:
return 1e-5
# Callback for printing the LR at the end of each epoch.
class PrintLR(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs=None):
print('\nLearning rate for epoch {} is {}'.format(epoch + 1,
model.optimizer.lr.numpy()))
log_dir = os.path.join(".", "logs")
callbacks = [
# tf.keras.callbacks.TensorBoard(log_dir=log_dir),
tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_prefix,
save_weights_only=True),
tf.keras.callbacks.LearningRateScheduler(decay),
PrintLR()
]
# -
# ## Train and evaluate
# + tags=[]
model.fit(train_dataset, epochs=12, callbacks=callbacks)
# -
|
keras_basics/tf.keras_distributed.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Cube conversion
#
# This notebooks creates an optimized version of each `SEG-Y` cube.
# The exact format (`HDF5`, `BLOSC` or their quantized versions) depends on `FORMAT` and `QUANTIZE` parameters.
#
# Pseudocode of this notebook looks like:
# ```python
# for each cube:
# mkdir
# infer geometry
# if SHOW, log to std.out
#
# convert segy to a desired format
# ```
# * The parameter `paths` controls which cubes are converted
# * `RECREATE` determines whether already converted volumes are re-converted
# * `FORMAT` and `QUANTIZE` determine the exact format to convert to
# * `SHOW` allows to control whether results are shown in the notebook itself
# * `DRY` can be used to check which operations will happen, without actually executing them
# +
import os
import sys
import warnings
from tqdm.auto import tqdm
from glob import glob
import matplotlib.pyplot as plt
sys.path.append('..')
from seismiqb import SeismicGeometry, plot_image
from seismiqb.batchflow import Notifier
# +
paths = sorted(glob('/data/seismic_data/seismic_interpretation/*_*/*.s*y'))
[print(path) for path in paths]
RECREATE = True
FORMAT = 'blosc'
QUANTIZE = True
SHOW = True
DRY_RUN = True
# -
# %%time
for path_cube in Notifier('n')(paths):
if not os.path.exists(path_cube):
continue
path_converted = '.'.join((os.path.splitext(path_cube)[0],
('q' if QUANTIZE else '') + FORMAT))
if os.path.exists(path_converted) and not RECREATE:
print(f'{path_converted} already exists, skipping')
continue
if DRY_RUN:
print(f'Will convert ::: {path_cube}\nto ::: {path_converted}\n')
continue
if SHOW:
print('▆'*60); print('▆'*60);
print('Working with', path_cube)
geometry = SeismicGeometry(
path_cube,
headers=SeismicGeometry.HEADERS_POST_FULL,
index_headers = SeismicGeometry.INDEX_POST,
collect_stats=True, spatial=True, recollect=True
)
qmap = geometry.quality_map
if SHOW:
geometry.print()
geometry.print_textual()
geometry.show()
geometry.show_quality_map()
plt.show()
geometry_converted = geometry.convert(format=FORMAT, quantize=QUANTIZE)
if SHOW:
geometry_converted.print()
print('\n'*3)
|
datasets/01_Convert_cubes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
from scipy import sparse
from scipy.sparse import csc_matrix,find,coo_matrix
import torch
from tqdm import tqdm
from multiprocessing import Pool, cpu_count
import os
import time
# +
### Variables ###
# the path of raw rule files generated by AMIE 3
data_path_list = [
'./rules_file/rules_0.txt',
'./rules_file/rules_1.txt',
'./rules_file/rules_2.txt',
'./rules_file/rules_3.txt',
'./rules_file/rules_4.txt'
]
# path
train_hrt_data_path = './ogb/wikikg90m_kddcup2021/processed/train_hrt.npy'
relation_matrix_path = './rel_ht_spmat/'
# the attribute of rule list
V_Rule = 0
V_Head_Coverage = 1
V_Std_Confidence =2
V_PCA_Confidence = 3
V_Positive_Examples = 4
V_Body_size = 5
V_PCA_Body_size = 6
V_Functional_variable = 7
# other variables
INV_NUM = 10000
# +
### Functions about rules ###
# get rules from the raw files
def get_rules_from_file(rule_file_path):
fp = open(rule_file_path)
rule_num = -1
rules_lists = []
for line in fp.readlines():
if rule_num == -1:
items = line.strip().split('\t')
else:
rule_list = line.strip().split('\t')
rule_list[1] = float(rule_list[1]) # Head Coverage
rule_list[2] = float(rule_list[2]) # Std Confidence
rule_list[3] = float(rule_list[3]) # PCA Confidence
rule_list[4] = int(rule_list[4]) # Positive Examples
rule_list[5] = int(rule_list[5]) # Body size
rule_list[6] = int(rule_list[6]) # PCA Body size
rules_lists.append(rule_list)
rule_num += 1
for i in range(rule_num):
rules_lists[i][0] = parse_rules(rules_lists[i][0])
return rules_lists
# get the number of positive and negative examples
def get_rule_PCA_examples(rules_lists):
rules_dict = {}
for i in range(len(rules_lists)):
pos_example = rules_lists[i][V_Positive_Examples]
neg_example = round( (pos_example / rules_lists[i][V_PCA_Confidence]) - pos_example )
rule = rules_lists[i][V_Rule]
if rule not in rules_dict.keys():
rules_dict[rule] = {}
rules_dict[rule]['NEG'] = neg_example
rules_dict[rule]['POS'] = pos_example
else:
rules_dict[rule]['NEG'] += neg_example
rules_dict[rule]['POS'] += pos_example
return rules_dict
# convert dict to list
# the element of rules_dict is in the form: { RULE: {NEG,NEG} }
# the element of rules_lists is in the form: [RULE, POS, NEG, PAC_CONFIDENCE]
def get_rule_list_from_dict(rules_dict):
rules_lists = []
for rule in rules_dict.keys():
pos_example = rules_dict[rule]['POS']
neg_example = rules_dict[rule]['NEG']
pca_confidence = pos_example / (pos_example + neg_example)
rules_lists.append([rule, pos_example, neg_example, pca_confidence])
return rules_lists
# parse the raw rule files
def parse_rules(rule_str):
rule_str_list = rule_str.split()
equal_index = rule_str_list.index('=>')
if equal_index // 3 == 1:
body_s1 = rule_str_list[0]
body_s2 = rule_str_list[2]
body_rel = int(rule_str_list[1])
head_s1 = rule_str_list[4]
head_s2 = rule_str_list[6]
head_rel = int(rule_str_list[5])
if head_s1 == body_s1 and head_s2 == body_s2:
return (body_rel, head_rel)
elif head_s1 == body_s2 and head_s2 == body_s1:
return (body_rel + INV_NUM, head_rel)
else:
return None
elif equal_index // 3 == 2:
body1_s1 = rule_str_list[0]
body1_s2 = rule_str_list[2]
body1_rel = int(rule_str_list[1])
body2_s1 = rule_str_list[3]
body2_s2 = rule_str_list[5]
body2_rel = int(rule_str_list[4])
head_s1 = rule_str_list[7]
head_s2 = rule_str_list[9]
head_rel = int(rule_str_list[8])
if body1_s2 == body2_s1:
if body1_s1 == head_s1 and body2_s2 == head_s2: # (a r_1 b) (b r_2 c) => (a r_3 c)
return (body1_rel, body2_rel, head_rel) # (a r_1 b) (b r_2 c) => (a r_3 c)
elif body1_s1 == head_s2 and body2_s2 == head_s1: # (c r_1 b) (b r_2 a) => (a r_3 c)
return (body2_rel + INV_NUM, body1_rel+ INV_NUM, head_rel)
else:
return None
elif body1_s1 == body2_s1:
if body1_s2 == head_s1 and body2_s2 == head_s2: # (a r_1 b) (a r_2 c) => (b r_3 c)
return (body1_rel + INV_NUM, body2_rel, head_rel)
elif body1_s2 == head_s2 and body2_s2 == head_s1: # (a r_1 b) (a r_2 c) => (c r_3 b)
return (body2_rel + INV_NUM, body1_rel, head_rel)
else:
return None
elif body1_s1 == body2_s2:
if body1_s2 == head_s1 and body2_s1 == head_s2: # (a r_1 b) (c r_2 a) => (b r_3 c)
return (body1_rel + INV_NUM, body2_rel + INV_NUM, head_rel)
elif body1_s2 == head_s2 and body2_s1 == head_s1: # (a r_1 c) (b r_2 a) => (b r_3 c)
return (body2_rel, body1_rel, head_rel)
else:
return None
elif body1_s2 == body2_s2:
if body1_s1 == head_s1 and body2_s1 == head_s2: # (b r_1 a) (c r_2 a) => (b r_3 c)
return (body1_rel, body2_rel + INV_NUM, head_rel)
elif body1_s1 == head_s2 and body2_s1 == head_s1: # (b r_1 a) (c r_2 a) => (c r_3 b)
return (body2_rel, body1_rel + INV_NUM, head_rel)
else:
return None
else:
return None
# load the relation matrix by id
def load_spmat_by_id(rel):
return sparse.load_npz(relation_matrix_path + 'rel_ht_spmat_'+str(rel%INV_NUM)+'.npz')
# make predictions by using rules,input format: (r_1, r_2, r_head) or (r_1, r_head)
def get_new_triples_by_rule_scipy(rule):
if len(rule) == 2:
r1 = rule[0]
rh = rule[1]
sp_r1 = load_spmat_by_id(r1)
sp_rh = load_spmat_by_id(rh)
# for the inverse relations
if r1 >= INV_NUM:
sp_r1 = sp_r1.T
sp_rule_head = sp_r1
sp_new_head = sp_rule_head - coo_matrix.multiply(sp_rule_head, sp_rh)
sp_new_head = sp_new_head.tocoo()
new_triples = []
for i in range(len(sp_new_head.row)):
new_triples.append((sp_new_head.row[i], rh, sp_new_head.col[i]) )
return new_triples
elif len(rule) == 3:
r1 = rule[0]
r2 = rule[1]
rh = rule[2]
sp_r1 = load_spmat_by_id(r1)
sp_r2 = load_spmat_by_id(r2)
sp_rh = load_spmat_by_id(rh)
# for the inverse relations
if r1 >= INV_NUM:
sp_r1 = sp_r1.T
if r2 >= INV_NUM:
sp_r2 = sp_r2.T
sp_rule_head = sp_r1.dot(sp_r2)
sp_new_head = sp_rule_head - coo_matrix.multiply(sp_rule_head, sp_rh)
sp_new_head = sp_new_head.tocoo()
new_triples = []
for i in range(len(sp_new_head.row)):
new_triples.append((sp_new_head.row[i], rh, sp_new_head.col[i]))
return new_triples
else:
return []
# +
### Functions about triples ###
# get the set of (h, r) from triples
def get_triples_hr_set(triples):
hr_set = set()
for triple in triples:
hr_set.add((triple[0], triple[1]))
return hr_set
# get the set of relations from triples
def get_triples_rel_set(triples):
rel_set = set()
for triple in triples:
rel_set.add(triple[1])
return rel_set
# get rule list concerning relations in rel_set
def rule_filter_rel(rules_lists, rel_set):
rules_filter = []
for i in range(len(rules_lists)):
if rules_lists[i][0][-1] in rel_set:
rules_filter.append(rules_lists[i])
return rules_filter
# filter rules by their PCA_Confidence and Positive_Examples
def rule_filter_PCA_POS(rules_lists, pca_conf=0, pos_num=0):
rules_filter = []
for i in range(len(rules_lists)):
if rules_lists[i][-1] >= pca_conf and rules_lists[i][1] >= pos_num:
rules_filter.append(rules_lists[i])
return rules_filter
# filter rules by their PCA_Confidence
def rule_filter_PCA_CONF(rules_lists, pca_conf_min=0, pca_conf_max=1.01):
rules_filter = []
for i in range(len(rules_lists)):
if rules_lists[i][-1] >= pca_conf_min and rules_lists[i][-1] < pca_conf_max:
rules_filter.append(rules_lists[i])
return rules_filter
# get the dict of r to h
def get_hr_set_dict(hr_set, rel_set):
hr_set_dict = {}
for rel in rel_set:
hr_set_dict[rel] = []
for hr in hr_set:
hr_set_dict[hr[1]].append(hr[0])
return hr_set_dict
# filter the triples concerning relations in rel_set
def filter_triples_by_relset(triples, rel_set):
filterd_triples = []
for triple in tqdm(triples):
if triple[1] in rel_set:
filterd_triples.append(triple)
return filterd_triples
# count the frequency of relations in the triples
def count_reltri_num(triples):
rel_tri_num_dict = {}
for triple in tqdm(triples):
if triple[1] in rel_tri_num_dict.keys():
rel_tri_num_dict[triple[1]] += 1
else:
rel_tri_num_dict[triple[1]] = 1
return rel_tri_num_dict
# filter triples by relations
def filter_triples_by_relset_del(triples, rel_set):
filterd_triples = []
for triple in tqdm(triples):
if triple[1] not in rel_set:
filterd_triples.append(triple)
return filterd_triples
# +
# get the relation matrix #
train_hrt = np.load(train_hrt_data_path)
num_shape = 87143637 # num_entities
def list_sparse_mat(r_list):
sp_mat = sparse.coo_matrix((np.ones(len(r_list[0])),(r_list[0],r_list[1])),shape=(num_shape, num_shape))
return sp_mat
num_relations = 1315
# get the head and tail entities of relations
rel_ht_lists = []
for rel in range(num_relations):
rel_ht_lists.append([[], []])
for i in tqdm(range(len(train_hrt))):
h = train_hrt[i][0]
r = train_hrt[i][1]
t = train_hrt[i][2]
rel_ht_lists[r][0].append(h)
rel_ht_lists[r][1].append(t)
for rel in tqdm(range(num_relations)):
sp_mat_rel = list_sparse_mat(rel_ht_lists[rel])
sparse.save_npz(relation_matrix_path + 'rel_ht_spmat_'+str(rel)+'.npz', sp_mat_rel)
# +
# get all the rules from raw rule files, and merge them
rules_lists_all = []
for data_path in data_path_list:
rules_lists_all += get_rules_from_file(data_path)
rules_dict_all = get_rule_PCA_examples(rules_lists_all)
rules_lists_all_merge = get_rule_list_from_dict(rules_dict_all)
# -
len(rules_lists_all_merge)
# +
# delete 'None' value in the rule list
# rules such as(x, x, x)(a, r, b) => (a, r, b) can get 'None' after parsing
del_index = []
len_tmp = len(rules_lists_all_merge)
for i in range(len_tmp):
if rules_lists_all_merge[i][0] == None:
del_index.append(i)
for i in range(len(del_index)):
rules_lists_all_merge.pop(del_index[i]-i)
rules_lists_all_merge = sorted(rules_lists_all_merge, key=lambda rule_list: rule_list[-1], reverse=True)
# -
len(rules_lists_all_merge)
# +
# get some dicts
num_entities = 87143637
test_hr = np.load('./ogb/wikikg90m_kddcup2021/processed/test_hr.npy').tolist()
val_hr = np.load('./ogb/wikikg90m_kddcup2021/processed/val_hr.npy').tolist()
test_val_hr = test_hr + val_hr
test_val_hr_dict = {}
for itm in test_val_hr:
if itm[1] not in test_val_hr_dict.keys():
test_val_hr_dict[itm[1]] = set()
test_val_hr_dict[itm[1]].add(itm[0])
else:
test_val_hr_dict[itm[1]].add(itm[0])
# get the set of entities
test_val_ent_set = set()
for itm in test_val_hr:
test_val_ent_set.add(itm[0])
# get the dict of entities
ent_inValTest_dict = {}
for ent in tqdm(range(num_entities)):
ent_inValTest_dict[ent] = 0
for ent in tqdm(test_val_ent_set):
ent_inValTest_dict[ent] = 1
# +
# get the rules with PCA Confidence > 0.95, the process to get the rules with PCA Confidence > 0.99 are similar.
filterd_rules = rule_filter_PCA_CONF(rules_lists_all_merge, 0.95)
filterd_rules_relDict = {}
for rule_itm in filterd_rules:
rule_head = rule_itm[0][-1]
if rule_itm[0][-1] in filterd_rules_relDict.keys():
filterd_rules_relDict[rule_head].append(rule_itm[0])
else:
filterd_rules_relDict[rule_head] = [rule_itm[0]]
len_rel = []
for key in filterd_rules_relDict.keys():
len_rel.append(len(filterd_rules_relDict[key]))
# -
len(filterd_rules)
# +
# get the predictions
pca095_path_1 = './pool_files_pca095/'
pca095_path_2 = './pool_files_pca095_filter/'
def rule_task(rel_head, rule_set):
new_triples = []
for rule in rule_set:
new_triples += get_new_triples_by_rule_scipy(rule)
new_triples = list(set(new_triples))
np.save(pca095_path_1+'pca095_rel_'+str(rel_head)+'_ruleNewTriples.npy', new_triples)
print(str(rel_head)+' DONE!')
def multi_process_task(max_pool_num):
process_pool = Pool(max_pool_num)
for key in filterd_rules_relDict.keys():
process_pool.apply_async(rule_task, args=(key,filterd_rules_relDict[key]))
print('Wait the subprocesses ......')
process_pool.close()
process_pool.join()
print('All subprocesses done!')
# -
multi_process_task(10)
# +
# keep predictions about valid and test data
def rule_task_inVALTEST_by_ent(rel_head):
print(str(rel_head)+' START!')
new_triples = []
valTest_new_triples = []
if os.path.exists(pca095_path_2+'pca095_rel_'+str(rel_head)+'_valTestENT_NewTriples.npy'):
print(str(rel_head)+' ALREADY DONE!')
else:
if os.path.exists(pca095_path_1+'pca095_rel_'+str(rel_head)+'_ruleNewTriples.npy'):
new_triples += np.load(pca095_path_1+'pca095_rel_'+str(rel_head)+'_ruleNewTriples.npy').astype(np.int32).tolist()
if new_triples != []:
valTest_new_triples = [ triple for triple in new_triples if ent_inValTest_dict[triple[2]] == 1 or ent_inValTest_dict[triple[0]] == 1 ]
np.save(pca095_path_2 + '/pca095_rel_'+str(rel_head)+'_valTestENT_NewTriples.npy', np.array(valTest_new_triples).astype(np.int32))
print(str(rel_head)+' DONE!')
else:
print(str(rel_head)+' NONE DONE!')
def multi_process_task_inVALTEST_ENT(max_pool_num):
process_pool = Pool(max_pool_num)
for rel in filterd_rules_relDict.keys():
process_pool.apply_async(rule_task_inVALTEST_by_ent, args=(rel,))
print('Wait the subprocesses ......')
process_pool.close()
process_pool.join()
print('All subprocesses done!')
# -
multi_process_task_inVALTEST_ENT(10)
# +
# save the predictions
all_new_triples = []
for rel_head in tqdm(filterd_rules_relDict.keys()):
if os.path.exists(pca095_path_2+'pca095_rel_'+str(rel_head)+'_valTestENT_NewTriples.npy'):
all_new_triples += np.load(pca095_path_2+'pca095_rel_'+str(rel_head)+'_valTestENT_NewTriples.npy').tolist()
train_hrt = np.load(train_hrt_data_path)
np.save('./enhanced_triples/train_hrt_pca095_ENT.npy',
np.vstack((train_hrt, np.array(all_new_triples).astype(np.int32))))
# -
|
inference/Rule-based_Data_Augmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# <div style='font-size:2.3em;font-weight:bold'><center>Memory Module: Hippocampus Neural Network Simulation</center></div><br>
# <div style='font-size:1.5em;'>This is an open source project. Contributers welcome, contact <a target="_blank" href="http://nmsutton.heroku.com">Nate</a> if interested.</div>
# <br>
# <div style='font-size:2em;text-decoration:underline;font-weight:bold'>Research Proposal:</div>
# <br>
# <div style='font-size:1.5em;'>
# <br><b>Introduction (Prior Work):</b>
# <br>Based on the article "Hippocampal network dynamics constrain the time lag between
# pyramidal cells across modified environments" by <NAME> Buzsáki: <a target="_blank" href="http://www.ncbi.nlm.nih.gov/pubmed/19074018">Article</a>.
# <br>Electrophysiology data availible openly <a target="_blank" href='http://crcns.org/data-sets/hc/hc-3'>here</a>.
# <br>
# <br><b>Methods:</b>
# <br>Currently: C++ and <a href="http://www.socsci.uci.edu/~jkrichma/CARLsim/">CARLSim</a>
# <br><br>Previously: Python and <a href="http://www.nest-simulator.org/">NEST</a>
# <ul><li><font color=red>Details:</font> To utilize newer GPU computing advances <a href="http://www.socsci.uci.edu/~jkrichma/CARLsim/">CARLSim</a> was chosen to be used. Articles such as <a href="http://www.ics.uci.edu/~jmoorkan/pub/gpusnn-ijcnn.pdf">"Efficient Simulation of Large-Scale Spiking Neural Networks Using CUDA Graphics Processors"</a> motivated the adoption of <a href="http://www.socsci.uci.edu/~jkrichma/CARLsim/">CARLSim</a> into the project.
# <br><br>Previously I used <a href="http://www.nest-simulator.org/">NEST</a> after also trying <a href="https://www.neuron.yale.edu/neuron/">NEURON</a> in part due to performance gains found from <a href="journal.frontiersin.org/article/10.3389/fninf.2014.00076/">"Limits to high-speed simulations of spiking neural networks using general-purpose computers"</a>.
# </li></ul>
# <br>Izhikevich neurons
# <ul><li><font color=red>Update:</font> Now using parameters for the neurons from <a href="f1000research.com/articles/3-104/v1">"Simple, biologically-constrained CA1 pyramidal cell models using an intact, whole hippocampus context"</a>
# </li></ul>
# <br>Spiking Neural Network
# <br>Reinforcement Learning
# <ul><li>Specifically the neural activity occuring during behavior tasks recorded with the rats will be modeled with reinforcement learning.
# </li></ul>
# <br>STDP
# <br>Oscillation Codes
# <br>
# <br><b>Results (Goal):</b>
# <br>This inital work aims to capture some meaningful elements of neural activity in the hippocampus, not to represent itself as a complete hippocampus simulation. An objective is from model neurons of the relevant type to train the network to have similar behavior experimentally reported.
# <br><ul><li>Input:
# <br>Simulated sensory input representing position of mice
# </li><br>
# <br><li>Output:
# <br>Have network trained to create results reported in article. See key points below for some examples of areas to further research that the trained model will work on representing.
# </li></ul>
# <br><b>Discussion:</b>
# <br>This work is intended to be created in a way that can be extended into bigger and more complex simulations. More experimental data can be used and the simulation can be modified to match it. The code can integrate into other researcher's systems.
# <br>
# <br><b>Future Work:</b>
# <br>GPU computing using CUDA
# <br>Larger neural net based on smaller one here
# <br>Modularize the simulation to be included in larger systems
# </div>
# <div style='font-size:1.5em;'>
# <div style='font-size:2em;text-decoration:underline;font-weight:bold'><hr></div>
# <br>Some key areas to work on:
# <br><ul><li>"Within a single theta cycle, the relative timing of neuronal spikes reflects the upcoming
# sequence of locations in the path of the rat, with larger time lags representing larger distances"
# </li><br><li> "As further
# support, context (i.e. track length) also affected the degree of spatial and temporal overlap of
# place fields, resulting in increased co-firing among cells during each theta cycle and increased
# overall firing in the pyramidal population on the short track, relative to the long. Interestingly,
# this change in activity resulted in decreased power and coherence in the theta-band of local
# fields measured from CA1 and CA3 regions."
# </li><br><li> "Although in this equidistant dataset the sequence compression
# correlations between time lag and distance were mostly unaffected (R = 0.76 long; R = 0.63
# short), the correlation between the time lags across tracks was noticeably weakened (R = 0.39;
# Figure 4c),"
# </li><br><li> "A robust finding in our study is that time lags between pairs are preserved despite changes to
# the tuning curves of individual neurons." and "...an important aspect of the present findings is that changes to the firing rate did not affect the timing across neuron pairs."
# </li><br><li> "How can firing rate vary without affecting timing?
# We conjecture that interneurons play a critical role: interneurons can provide a “window of
# opportunity” during which a postsynaptic neuron may spike." and "A
# network variant of the single cell model proposed by Mehta et. al (2002), illustrates our
# hypothesis (Figure 7): through recurrent and feedforward connections, changes in the drive
# from the leading assembly may modify the timing of interneurons inhibiting the trailing
# assembly, which in turn establish the time lag."
# </li></ul>
# </div>
|
.ipynb_checkpoints/memory_module_outline-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (tensorflow_cpu)
# language: python
# name: tensorflow_cpu
# ---
# +
import tensorflow as tf
from tensorflow.keras import backend as K
import matplotlib as mpl
import pickle
import matplotlib.pyplot as plt
import matplotlib
import numpy as np
import os
# Init NuScenes. Requires the dataset to be stored on disk.
from nuscenes.nuscenes import NuScenes
from nuscenes.map_expansion.map_api import NuScenesMap
matplotlib.rcParams['figure.figsize'] = (24, 18)
matplotlib.rcParams['figure.facecolor'] = 'white'
matplotlib.rcParams.update({'font.size': 20})
TRAIN_SIZE = 9800
TRAIN_TIME = 6
BATCH_SIZE = 32
BUFFER_SIZE = 500
# +
total_ped_matrix = np.load("details/total_ped_matrix.npy")
with open("details/ped_dataset.pkl", "rb") as f:
ped_dataset = pickle.load(f)
with open('details/scene_info.pkl', 'rb') as handle:
scene_info = pickle.load(handle)
# -
nusc = NuScenes(version='v1.0-trainval', \
dataroot='../../../../data/', \
verbose=False)
# +
so_map = NuScenesMap(dataroot='../../../../data/', \
map_name='singapore-onenorth')
bs_map = NuScenesMap(dataroot='../../../../data/', \
map_name='boston-seaport')
sh_map = NuScenesMap(dataroot='../../../../data/', \
map_name='singapore-hollandvillage')
sq_map = NuScenesMap(dataroot='../../../../data/', \
map_name='singapore-queenstown')
# dict mapping map name to map file
map_files = {'singapore-onenorth': so_map,
'boston-seaport': bs_map,
'singapore-hollandvillage': sh_map,
'singapore-queenstown': sq_map}
# -
# defining the custom rmse loss function
def rmse_loss(gt_path, pred_path):
'''
calculates custom rmse loss between every time point
'''
gt_path = tf.reshape(gt_path, [-1, 10, 2])
pred_path = tf.reshape(pred_path, [-1, 10, 2])
return K.mean(K.sqrt(K.sum(K.square(gt_path-pred_path), axis=1)))
# +
# loading the model
fc_model = tf.keras.models.load_model("checkpoints/mlp_best.hdf5", compile=False)
fc_model.compile(optimizer=tf.keras.optimizers.RMSprop(clipvalue=1.0),
loss=rmse_loss,
metrics=["accuracy"])
# +
# undo normalization for plotting
def move_from_origin(l, origin):
x0, y0 = origin
return [[x + x0, y + y0] for x, y in l]
def rotate_from_y(l, angle):
theta = -angle
return [(x*np.cos(theta) - y*np.sin(theta),
x*np.sin(theta) + y*np.cos(theta)) for x, y in l]
# loss calculation for test prediction
def rmse_error(l1, l2):
loss = []
if len(np.array(l1).shape) < 2:
return ((l1[0] - l2[0])**2 + (l1[1] - l2[1])**2)**0.5, None, None
for p1, p2 in zip(l1, l2):
loss.append(((p1[0] - p2[0])**2 + (p1[1] - p2[1])**2)**0.5)
loss = np.array(loss)
return np.mean(loss), loss.min(), loss.max()
# +
rmse_values = []
fde_valus = []
min_deviations = []
max_deviations = []
for test_idx in range(9800, len(ped_dataset)):
test_data = np.reshape(total_ped_matrix[test_idx,:6,:]
, (1, 42))
predictions = fc_model.predict(test_data).reshape(-1, 2)
predictions = move_from_origin(rotate_from_y(predictions, ped_dataset[test_idx]["angle"]),
ped_dataset[test_idx]["origin"])
# n_scene = ped_dataset[test_idx]["scene_no"]
# ego_poses = map_files[scene_info[str(n_scene)]["map_name"]].render_pedposes_on_fancy_map(
# nusc, scene_tokens=[nusc.scene[n_scene]['token']],
# ped_path = np.array(ped_dataset[test_idx]["translation"])[:,:2],
# verbose = False,
# render_egoposes=True, render_egoposes_range=False,
# render_legend=False)
# plt.scatter(*zip(*np.array(ped_dataset[test_idx]["translation"])[:6,:2]), c='k', s=5, zorder=2)
# plt.scatter(*zip(*np.array(ped_dataset[test_idx]["translation"])[6:,:2]), c='b', s=5, zorder=3)
# plt.scatter(*zip(*predictions), c='r', s=5, zorder=4)
# plt.show()
loss, min_dev, max_dev = rmse_error(predictions, np.array(ped_dataset[test_idx]["translation"])[6:,:2])
final_loss, _, _ = rmse_error(predictions[-1],
np.array(ped_dataset[test_idx]["translation"])[-1,:2])
min_deviations.append(min_dev)
max_deviations.append(max_dev)
rmse_values.append(loss)
fde_valus.append(final_loss)
print(f"RMSE Loss in m is {np.mean(np.array(rmse_values))}")
print(f"Loss of final position in m is {np.mean(np.array(fde_valus))}")
# +
plt.hist(rmse_values)
plt.title("RMSE errors")
plt.show()
plt.hist(fde_valus)
plt.title("FDE errors")
plt.show()
plt.hist(min_deviations)
plt.title("Minimum deviation errors")
plt.show()
plt.hist(max_deviations)
plt.title("Maximum deviation errors")
plt.show()
# -
|
python-sdk/nuscenes/map_expansion/evaluation/evaluation_mlp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # Counteracting Overfitting
#
# Overfitting is the primary cause of model innacuracy. When a model is overfitted, it performs well when predicting the class of images on which it has been trained; but does not generalize well to new images.
#
# ## Techniques for Avoiding Overfitting
#
# There are a number of ways to address overfitting during the training process. In this notebook, we'll look at two of the most common approaches.
#
# ### Dropping Feature Maps
#
# The first approach is somewhat counter-intuitive, but very effective. During the training process, the convolution and pooling layers in the feature extraction section of the model generate lots of feature maps from the training images. Randomly dropping some of these feature maps helps vary the features that are extracted in each batch, ensuring the model doesn't become overly-reliant on any one dominant feature in the training data.
#
# ### Data Augmentation
#
# In an ideal world, you'd have a huge volume of training data that is representative of all future data that you will submit to the model for inference. In reality, you must often traing a model with a limited set of training data, which can exacerbate the overfitting problem. One way to mitigate this is to perform data augmentation by making random transformations of the training images; for example by flipping, rotating, or cropping them. Because you randomly apply these data augmentation transformations during training, the same image might be presented differently from batch to batch, creating more variation in the training data and helping the model to learn features based the same objects at different orientations or scales.
# ## Adding Drop Layers and Data Augementation to a CNN
#
# Let's take a look at using these techniques when training a PyTorch model. First, we'll import the latest version of PyTorch and prepare to load our training data.
#
# > *Note: The following `pip install` commands install the CPU-based version of PyTorch on Linux, which is appropriate for the Azure Notebooks environment. For instructions on how to install the PyTorch and TorchVision packages on your own system, see https://pytorch.org/get-started/locally/*
# +
# Install PyTorch
# !pip install https://download.pytorch.org/whl/cpu/torch-1.0.1.post2-cp36-cp36m-linux_x86_64.whl
# !pip install torchvision
# Import PyTorch libraries
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
print("Libraries imported - ready to use PyTorch", torch.__version__)
# -
# ### Augment the Data
# Now we're ready to define our data loaders. At this point we can add transformations to randomly modify the images as they are added to a training batch. In this case, we'll flip images horizontally at random.
# +
# Function to ingest data using training and test loaders
def load_dataset(data_path):
# Load all of the images
transformation = transforms.Compose([
# Randomly augment the image data
transforms.RandomHorizontalFlip(0.5),
# transform to tensors
transforms.ToTensor(),
# Normalize the pixel values (in R, G, and B channels)
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
# Load all of the images, transforming them
full_dataset = torchvision.datasets.ImageFolder(
root=data_path,
transform=transformation
)
# Split into training (70% and testing (30%) datasets)
train_size = int(0.7 * len(full_dataset))
test_size = len(full_dataset) - train_size
train_dataset, test_dataset = torch.utils.data.random_split(full_dataset, [train_size, test_size])
# define a loader for the training data we can iterate through in 50-image batches
train_loader = torch.utils.data.DataLoader(
train_dataset,
batch_size=50,
num_workers=0,
shuffle=False
)
# define a loader for the testing data we can iterate through in 50-image batches
test_loader = torch.utils.data.DataLoader(
test_dataset,
batch_size=50,
num_workers=0,
shuffle=False
)
return train_loader, test_loader
import os
# The images are in a folder named 'shapes/training'
training_folder_name = '../data/shapes/training'
# The folder contains a subfolder for each class of shape
classes = sorted(os.listdir(training_folder_name))
print(classes)
# Get the iterative dataloaders for test and training data
train_loader, test_loader = load_dataset(training_folder_name)
batch_size = train_loader.batch_size
print("Data loaders ready to read", training_folder_name)
# -
# ### Add Drop Layers to the CNN
# Now we're ready to define our model, which will include some drop layers to randomly drop some of the extracted features.
# +
# Create a neural net class
class Net(nn.Module):
# Constructor
def __init__(self, num_classes=3):
super(Net, self).__init__()
# Our images are RGB, so input channels = 3. We'll apply 12 filters in the first convolutional layer
self.conv1 = nn.Conv2d(in_channels=3, out_channels=12, kernel_size=3, stride=1, padding=1)
# A second convolutional layer takes 12 input channels, and generates 24 outputs
self.conv2 = nn.Conv2d(in_channels=12, out_channels=24, kernel_size=3, stride=1, padding=1)
# We'll apply max pooling with a kernel size of 2
self.pool = nn.MaxPool2d(kernel_size=2)
# A drop layer deletes 30% of the features to help prevent overfitting
self.drop = nn.Dropout2d(p=0.3)
# Our 128x128 image tensors will be pooled twice with a kernel size of 2. 128/2/2 is 32.
# So our feature tensors are now 32 x 32, and we've generated 24 of them
# We need to flatten these and feed them to a fully-connected layer
# to map them to the probability for each class
self.fc = nn.Linear(in_features=32 * 32 * 24, out_features=num_classes)
def forward(self, x):
# Use a relu activation function after layer 1 (convolution 1 and pool)
x = F.relu(self.pool(self.conv1(x)))
# Use a relu activation function after layer 2
x = F.relu(self.pool(self.conv2(x)))
# Select some features to drop to prevent overfitting (only drop during training)
x = F.dropout(self.drop(x), training=self.training)
# Flatten
x = x.view(-1, 32 * 32 * 24)
# Feed to fully-connected layer to predict class
x = self.fc(x)
# Return class probabilities via a log_softmax function
return torch.log_softmax(x, dim=1)
device = "cpu"
if (torch.cuda.is_available()):
# if GPU available, use cuda (on a cpu, training will take a considerable length of time!)
device = "cuda"
# Create an instance of the model class and allocate it to the device
model = Net(num_classes=len(classes)).to(device)
print(model)
# -
# ### Train the Model
#
# With the layers of the CNN defined, we're ready to train the model using our randomly augmented image data. Since we're dropping some features, it may require more epochs to get the loss to drop so that the model is reasonably accurate - but the data augmentation and dropped features should help ensure that as we train for more epochs, the validation loss drops along with the training loss; meaning that the model will generalize well.
# +
def train(model, device, train_loader, optimizer, epoch):
# Set the model to training mode
model.train()
train_loss = 0
print("Epoch:", epoch)
# Process the images in batches
for batch_idx, (data, target) in enumerate(train_loader):
# Use the CPU or GPU as appropriate
data, target = data.to(device), target.to(device)
# Reset the optimizer
optimizer.zero_grad()
# Push the data forward through the model layers
output = model(data)
# Get the loss
loss = loss_criteria(output, target)
# Keep a running total
train_loss += loss.item()
# Backpropagate
loss.backward()
optimizer.step()
# Print metrics so we see some progress
print('\tTraining batch {} Loss: {:.6f}'.format(batch_idx + 1, loss.item()))
# return average loss for the epoch
avg_loss = train_loss / (batch_idx+1)
print('Training set: Average loss: {:.6f}'.format(avg_loss))
return avg_loss
def test(model, device, test_loader):
# Switch the model to evaluation mode (so we don't backpropagate or drop)
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
batch_count = 0
for data, target in test_loader:
batch_count += 1
data, target = data.to(device), target.to(device)
# Get the predicted classes for this batch
output = model(data)
# Calculate the loss for this batch
test_loss += loss_criteria(output, target).item()
# Calculate the accuracy for this batch
_, predicted = torch.max(output.data, 1)
correct += torch.sum(target==predicted).item()
# Calculate the average loss and total accuracy for this epoch
avg_loss = test_loss/batch_count
print('Validation set: Average loss: {:.6f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
avg_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
# return average loss for the epoch
return avg_loss
# Use an "Adam" optimizer to adjust weights
optimizer = optim.Adam(model.parameters(), lr=0.01)
# Specify the loss criteria
loss_criteria = nn.CrossEntropyLoss()
# Track metrics in these arrays
epoch_nums = []
training_loss = []
validation_loss = []
# Train over 10 epochs
epochs = 10
print('Training on', device)
for epoch in range(1, epochs + 1):
train_loss = train(model, device, train_loader, optimizer, epoch)
test_loss = test(model, device, test_loader)
epoch_nums.append(epoch)
training_loss.append(train_loss)
validation_loss.append(test_loss)
# -
# ### View the Loss History
# We tracked average training and validation loss for each epoch. We can plot these to verify that loss reduced as the model was trained, and to detect *over-fitting* (which is indicated by a continued drop in training loss after validation loss has levelled out or started to increase.
# +
# %matplotlib inline
from matplotlib import pyplot as plt
plt.plot(epoch_nums, training_loss)
plt.plot(epoch_nums, validation_loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['training', 'validation'], loc='upper right')
plt.show()
# -
# ### Save the Model
# Now that we have trained the model, we can save its weights. Then later, we can reload those weights into an instance of the same network and use it to predict classes from new images.
# +
# Save the model weights
model_file = 'shape-classifier.pt'
torch.save(model.state_dict(), model_file)
print("Model saved.")
# Delete the existing model variable
del model
# -
# ## Use the Model with New Data
# Now that we've trained and evaluated our model, we can use it to predict classes for new images.
#
# ### Create Functions to Prepare Data and Get Class Predictions
# Let's create a couple of functions to:
#
# - Resize new images to match the size on which the model was trained.
# - Submit the new images to the model and retrieve the predicted classes.
# +
# Helper function to resize image
def resize_image(src_img, size=(128,128), bg_color="white"):
from PIL import Image
# rescale the image so the longest edge is the right size
src_img.thumbnail(size, Image.ANTIALIAS)
# Create a new image of the right shape
new_image = Image.new("RGB", size, bg_color)
# Paste the rescaled image onto the new background
new_image.paste(src_img, (int((size[0] - src_img.size[0]) / 2), int((size[1] - src_img.size[1]) / 2)))
# return the resized image
return new_image
# Function to predict the class of an image
def predict_image(classifier, image_array):
# Set the classifer model to evaluation mode
classifier.eval()
# These are the classes our model can predict
class_names = ['circle', 'square', 'triangle']
# Apply the same transformations as we did for the training images
transformation = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])
])
# Preprocess the imagees
image_tensor = torch.stack([transformation(image).float() for image in image_array])
# Turn the input into a Variable
input_features = image_tensor
# Predict the class of each input image
predictions = classifier(input_features)
predicted_classes = []
# Convert the predictions to a numpy array
for prediction in predictions.data.numpy():
# The prediction for each image is the probability for each class, e.g. [0.8, 0.1, 0.2]
# So get the index of the highest probability
class_idx = np.argmax(prediction)
# And append the corresponding class name to the results
predicted_classes.append(class_names[class_idx])
return np.array(predicted_classes)
print("Functions created - ready to use model for inference.")
# -
# ### Predict Image Classes
# Now we're ready to use the model for predicting (often referred to as *inferencing*) the classes of some new images.
# +
import os
from random import randint
import numpy as np
from PIL import Image
from matplotlib import pyplot as plt
# %matplotlib inline
# load the saved model weights
model = Net()
model.load_state_dict(torch.load(model_file))
#get the list of test image files
test_folder = '../data/shapes/test'
test_image_files = os.listdir(test_folder)
# Empty array on which to store the images
image_arrays = []
size = (128,128)
background_color="white"
fig = plt.figure(figsize=(12, 8))
# Get the images and show the predicted classes
for file_idx in range(len(test_image_files)):
img = Image.open(os.path.join(test_folder, test_image_files[file_idx]))
# resize the image so it matches the training set - it must be the same size as the images on which the model was trained
resized_img = np.array(resize_image(img, size, background_color))
# Add the image to the array of images
image_arrays.append(resized_img)
# Get predictions from the array of image arrays
# Note that the model expects an array of 1 or more images - just like the batches on which it was trained
predictions = predict_image(model, np.array(image_arrays))
# plot easch image with its corresponding prediction
for idx in range(len(predictions)):
a=fig.add_subplot(1,len(predictions),idx+1)
imgplot = plt.imshow(image_arrays[idx])
a.set_title(predictions[idx])
|
Mod03/Exercise 01 - Counteracting Overfitting (PyTorch).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="VbkyG_K1LSnC"
# Copyright 2018 Google Inc.
#
# Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
#
# + [markdown] colab_type="text" id="EHcImnV1yZ5z"
# **This tutorial is for educational purposes purposes only and is not intended for use in clinical diagnosis or clinical decision-making or for any other clinical use.**
# + [markdown] colab_type="text" id="Q8ZHSBelKd8V"
# # Training/Inference on Breast Density Classification Model on AutoML Vision
#
# + [markdown] colab_type="text" id="XCClehsPK2Jq"
# The goal of this tutorial is to train, deploy and run inference on a breast density classification model. Breast density is thought to be a factor for an increase in the risk for breast cancer. This will emphasize using the [Cloud Healthcare API](https://cloud.google.com/healthcare/) in order to store, retreive and transcode medical images (in DICOM format) in a managed and scalable way. This tutorial will focus on using [Cloud AutoML Vision](https://cloud.google.com/vision/automl/docs/beginners-guide) to scalably train and serve the model.
#
# **Note: This is the AutoML version of the Cloud ML Engine Codelab found [here](./breast_density_cloud_ml.ipynb).**
# + [markdown] colab_type="text" id="u1OUa9pCPtqu"
# ## Requirements
# - A Google Cloud project.
# - Project has [Cloud Healthcare API](https://cloud.google.com/healthcare/docs/quickstart) enabled.
# - Project has [Cloud AutoML API ](https://cloud.google.com/vision/automl/docs/quickstart) enabled.
# - Project has [Cloud Build API](https://cloud.google.com/cloud-build/docs/quickstart-docker) enabled.
# - Project has [Kubernetes engine API](https://console.developers.google.com/apis/api/container.googleapis.com/overview?project=) enabled.
# - Project has [Cloud Resource Manager API](https://console.cloud.google.com/cloud-resource-manager) enabled.
# + [markdown] colab_type="text" id="qL-vcMmZRITm"
# ## Input Dataset
#
# The dataset that will be used for training is the [TCIA CBIS-DDSM](https://wiki.cancerimagingarchive.net/display/Public/CBIS-DDSM) dataset. This dataset contains ~2500 mammography images in DICOM format. Each image is given a [BI-RADS breast density ](https://breast-cancer.ca/densitbi-rads/) score from 1 to 4. In this tutorial, we will build a binary classifier that distinguishes between breast density "2" (*scattered density*) and "3" (*heterogeneously dense*). These are the two most common and variably assigned scores. In the literature, this is said to be [particularly difficult for radiologists to consistently distinguish](https://aapm.onlinelibrary.wiley.com/doi/pdf/10.1002/mp.12683).
# + colab={} colab_type="code" id="NSr5StGBZkYd"
project_id = "MY_PROJECT" # @param
location = "us-central1"
dataset_id = "MY_DATASET" # @param
dicom_store_id = "MY_DICOM_STORE" # @param
# Input data used by AutoML must be in a bucket with the following format.
automl_bucket_name = "gs://" + project_id + "-vcm"
# + colab={} colab_type="code" id="UW3Y6Pd6d1Ey" magic_args="-s {project_id} {location} {automl_bucket_name}" language="bash"
# # Create bucket.
# gsutil -q mb -c regional -l $2 $3
#
# # Allow Cloud Healthcare API to write to bucket.
# PROJECT_NUMBER=`gcloud projects describe $1 | grep projectNumber | sed 's/[^0-9]//g'`
# SERVICE_ACCOUNT="<EMAIL>"
# COMPUTE_ENGINE_SERVICE_ACCOUNT="${PROJECT_NUMBER}-<EMAIL>"
#
# gsutil -q iam ch serviceAccount:${SERVICE_ACCOUNT}:objectAdmin $3
# gsutil -q iam ch serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT}:objectAdmin $3
# gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${SERVICE_ACCOUNT} --role=roles/pubsub.publisher
# gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/pubsub.admin
# # Allow compute service account to create datasets and dicomStores.
# gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/healthcare.dicomStoreAdmin
# gcloud projects add-iam-policy-binding $1 --member=serviceAccount:${COMPUTE_ENGINE_SERVICE_ACCOUNT} --role roles/healthcare.datasetAdmin
# + colab={} colab_type="code" id="vgBA16ptbacM"
import json
import os
import google.auth
from google.auth.transport.requests import AuthorizedSession
credentials, project = google.auth.default()
authed_session = AuthorizedSession(credentials)
# Path to Cloud Healthcare API.
HEALTHCARE_API_URL = 'https://healthcare.googleapis.com/v1beta1'
# Create Cloud Healthcare API dataset.
path = os.path.join(HEALTHCARE_API_URL, 'projects', project_id, 'locations', location, 'datasets?dataset_id=' + dataset_id)
headers = {'Content-Type': 'application/json'}
resp = authed_session.post(path, headers=headers)
assert resp.status_code == 200, 'error creating Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Create Cloud Healthcare API DICOM store.
path = os.path.join(HEALTHCARE_API_URL, 'projects', project_id, 'locations', location, 'datasets', dataset_id, 'dicomStores?dicom_store_id=' + dicom_store_id)
resp = authed_session.post(path, headers=headers)
assert resp.status_code == 200, 'error creating DICOM store, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# + [markdown] colab_type="text" id="HKsCfbXorosM"
# Next, we are going to transfer the DICOM instances to the Cloud Healthcare API.
#
# Note: We are transfering >100GB of data so this will take some time to complete
# + colab={} colab_type="code" id="shhPzNFArpHH"
# Store DICOM instances in Cloud Healthcare API.
path = "https://healthcare.googleapis.com/v1beta1/projects/{}/locations/{}/datasets/{}/dicomStores/{}:import".format(
project_id, location, dataset_id, dicom_store_id)
headers = {'Content-Type': 'application/json'}
body = {
'gcsSource': {
'uri': 'gs://gcs-public-data--healthcare-tcia-cbis-ddsm/dicom/**'
}
}
resp = authed_session.post(path, headers=headers, json=body)
assert resp.status_code == 200, 'error creating Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
response = json.loads(resp.text)
operation_name = response['name']
# + colab={} colab_type="code" id="biHU0WoLjgYs"
import time
def wait_for_operation_completion(path, timeout, sleep_time=30):
success = False
while time.time() < timeout:
print('Waiting for operation completion...')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error polling for Operation results, code: {0}, response: {1}'.format(resp.status_code, resp.text)
response = json.loads(resp.text)
if 'done' in response:
if response['done'] == True and 'error' not in response:
success = True;
break
time.sleep(sleep_time)
print('Full response:\n{0}'.format(resp.text))
assert success, "operation did not complete successfully in time limit"
print('Success!')
return response
# + colab={} colab_type="code" id="B7pNV8uYyYmy"
path = os.path.join(HEALTHCARE_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
_ = wait_for_operation_completion(path, timeout)
# + [markdown] colab_type="text" id="mjFm5w356Z6t"
# ### Explore the Cloud Healthcare DICOM dataset (optional)
#
# This is an optional section to explore the Cloud Healthcare DICOM dataset. In the following code, we simply just list the studies that we have loaded into the Cloud Healthcare API. You can modify the *num_of_studies_to_print* parameter to print as many studies as desired.
# + colab={} colab_type="code" id="RUjYgoym7MZN"
num_of_studies_to_print = 2 # @param
path = os.path.join(HEALTHCARE_API_URL, 'projects', project_id, 'locations', location, 'datasets', dataset_id, 'dicomStores', dicom_store_id, 'dicomWeb', 'studies')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error querying Dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
response = json.loads(resp.text)
print(json.dumps(response[:num_of_studies_to_print], indent=2))
# + [markdown] colab_type="text" id="qpkeGeAsb-ec"
# ## Convert DICOM to JPEG
#
# The ML model that we will build requires that the dataset be in JPEG. We will leverage the Cloud Healthcare API to transcode DICOM to JPEG.
#
# First we will create a [Google Cloud Storage](https://cloud.google.com/storage/) bucket to hold the output JPEG files. Next, we will use the ExportDicomData API to transform the DICOMs to JPEGs.
# + colab={} colab_type="code" id="sXB41cvKeLZj"
# Folder to store input images for AutoML Vision.
jpeg_folder = automl_bucket_name + "/images/"
# + [markdown] colab_type="text" id="aIfKnxqHjE9A"
# Next we will convert the DICOMs to JPEGs using the [ExportDicomData](https://cloud.google.com/sdk/gcloud/reference/beta/healthcare/dicom-stores/export/gcs).
# + colab={} colab_type="code" id="2Ic_OPeVjM5i" magic_args="-s {jpeg_folder} {project_id} {location} {dataset_id} {dicom_store_id}" language="bash"
# gcloud beta healthcare --project $2 dicom-stores export gcs $5 --location=$3 --dataset=$4 --mime-type="image/jpeg; transfer-syntax=1.2.840.10008.172.16.31.10" --gcs-uri-prefix=$1
# + [markdown] colab_type="text" id="pVhp8IdVkVH3"
# Meanwhile, you should be able to observe the JPEG images being added to your Google Cloud Storage bucket.
# + [markdown] colab_type="text" id="liblamUVyWZw"
# Next, we will join the training data stored in Google Cloud Storage with the labels in the TCIA website. The output of this step is a [CSV file that is input to AutoML](https://cloud.google.com/vision/automl/docs/prepare). This CSV contains a list of pairs of (IMAGE_PATH, LABEL).
# + colab={} colab_type="code" id="DgDI4Esw8bXT"
# tensorflow==1.15.0 to have same versions in all environments - dataflow, automl, ai-platform
# !pip install tensorflow==1.15.0 --ignore-installed
# CSV to hold (IMAGE_PATH, LABEL) list.
input_data_csv = automl_bucket_name + "/input.csv"
import csv
import os
import re
from tensorflow.python.lib.io import file_io
import scripts.tcia_utils as tcia_utils
# Get map of study_uid -> file paths.
path_list = file_io.get_matching_files(os.path.join(jpeg_folder, '*/*/*'))
study_uid_to_file_paths = {}
pattern = r'^{0}(?P<study_uid>[^/]+)/(?P<series_uid>[^/]+)/(?P<instance_uid>.*)'.format(jpeg_folder)
for path in path_list:
match = re.search(pattern, path)
study_uid_to_file_paths[match.group('study_uid')] = path
# Get map of study_uid -> labels.
study_uid_to_labels = tcia_utils.GetStudyUIDToLabelMap()
# Join the two maps, output results to CSV in Google Cloud Storage.
with file_io.FileIO(input_data_csv, 'w') as f:
writer = csv.writer(f, delimiter=',')
for study_uid, label in study_uid_to_labels.items():
if study_uid in study_uid_to_file_paths:
writer.writerow([study_uid_to_file_paths[study_uid], label])
# + [markdown] colab_type="text" id="JDxxEp3XnFp1"
# ## Training
#
# ***This section will focus on using AutoML through its API. AutoML can also be used through the user interface found [here](https://console.cloud.google.com/vision/). The below steps in this section can all be done through the web UI .***
#
# We will use [AutoML Vision ](https://cloud.google.com/automl/) to train the classification model. AutoML provides a fully managed solution for training the model. All we will do is input the list of input images and labels. The trained model in AutoML will be able to classify the mammography images as either "2" (scattered density) or "3" (heterogeneously dense).
#
# As a first step, we will create a AutoML dataset.
#
# + colab={} colab_type="code" id="If7y8FkwZ1V-"
automl_dataset_display_name = "MY_AUTOML_DATASET" # @param
# + colab={} colab_type="code" id="VPPZsQScaZm7"
import json
import os
# Path to AutoML API.
AUTOML_API_URL = 'https://automl.googleapis.com/v1beta1'
# Path to request creation of AutoML dataset.
path = os.path.join(AUTOML_API_URL, 'projects', project_id, 'locations', location, 'datasets')
# Headers (request in JSON format).
headers = {'Content-Type': 'application/json'}
# Body (encoded in JSON format).
config = {'display_name': automl_dataset_display_name, 'image_classification_dataset_metadata': {'classification_type': 'MULTICLASS'}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'creating AutoML dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Record the AutoML dataset name.
response = json.loads(resp.text)
automl_dataset_name = response['name']
# + [markdown] colab_type="text" id="I-pK9_jQewO9"
# Next, we will import the CSV that contains the list of (IMAGE_PATH, LABEL) list into AutoML. **Please ignore errors regarding an existing ground truth.**
# + colab={} colab_type="code" id="gD3GsUBee78l"
# Path to request import into AutoML dataset.
path = os.path.join(AUTOML_API_URL, automl_dataset_name + ':importData')
# Body (encoded in JSON format).
config = {'input_config': {'gcs_source': {'input_uris': [input_data_csv]}}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'error importing AutoML dataset, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# Record operation_name so we can poll for it later.
response = json.loads(resp.text)
operation_name = response['name']
# + [markdown] colab_type="text" id="AtkvgdlhjFS2"
# The output of the previous step is an [operation](https://cloud.google.com/vision/automl/docs/models#get-operation) that will need to poll the status for. We will poll until the operation's "done" field is set to true. This will take a few minutes to complete so we will wait until completion.
# + colab={} colab_type="code" id="MSXpdV20yYnZ"
path = os.path.join(AUTOML_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
_ = wait_for_operation_completion(path, timeout)
# + [markdown] colab_type="text" id="tUrg3P6EkqNS"
# Next, we will train the model to perform classification. We will set the training budget to be a maximum of 1hr (but this can be modified below). The cost of using AutoML can be found [here](https://cloud.google.com/vision/automl/pricing). Typically, the longer the model is trained for, the more accurate it will be.
# + colab={} colab_type="code" id="kUJnoVd8k_hy"
# Name of the model.
model_display_name = "MY_MODEL_NAME" # @param
# Training budget (1 hr).
training_budget = 1 # @param
# + colab={} colab_type="code" id="voU4GkP6lWKE"
# Path to request import into AutoML dataset.
path = os.path.join(AUTOML_API_URL, 'projects', project_id, 'locations', location, 'models')
# Headers (request in JSON format).
headers = {'Content-Type': 'application/json'}
# Body (encoded in JSON format).
automl_dataset_id = automl_dataset_name.split('/')[-1]
config = {'display_name': model_display_name, 'dataset_id': automl_dataset_id, 'image_classification_model_metadata': {'train_budget': training_budget}}
resp = authed_session.post(path, headers=headers, json=config)
assert resp.status_code == 200, 'error creating AutoML model, code: {0}, response: {1}'.format(resp.status_code, contenresp.text)
print('Full response:\n{0}'.format(resp.text))
# Record operation_name so we can poll for it later.
response = json.loads(resp.text)
operation_name = response['name']
# + [markdown] colab_type="text" id="EADtTufcnPFf"
# The output of the previous step is also an [operation](https://cloud.google.com/vision/automl/docs/models#get-operation) that will need to poll the status of. We will poll until the operation's "done" field is set to true. This will take a few minutes to complete.
# + colab={} colab_type="code" id="vsl3iHa2niLo"
path = os.path.join(AUTOML_API_URL, operation_name)
timeout = time.time() + 40*60 # Wait up to 40 minutes.
sleep_time = 5*60 # Update each 5 minutes.
response = wait_for_operation_completion(path, timeout, sleep_time)
full_model_name = response['response']['name']
# + colab={} colab_type="code" id="mI3oD2AeyYnq"
# google.cloud.automl to make api calls to Cloud AutoML
# !pip install google-cloud-automl
from google.cloud import automl_v1
client = automl_v1.AutoMlClient()
response = client.deploy_model(full_model_name)
print(u'Model deployment finished. {}'.format(response.result()))
# + [markdown] colab_type="text" id="ZdkETXQqqggh"
# Next, we will check out the accuracy metrics for the trained model. The following command will return the [AUC (ROC)](https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc), [precision](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall) and [recall](https://developers.google.com/machine-learning/crash-course/classification/precision-and-recall) for the model, for various ML classification thresholds.
# + colab={} colab_type="code" id="efrr6X7zrvW2"
# Path to request to get model accuracy metrics.
path = os.path.join(AUTOML_API_URL, full_model_name, 'modelEvaluations')
resp = authed_session.get(path)
assert resp.status_code == 200, 'error getting AutoML model evaluations, code: {0}, response: {1}'.format(resp.status_code, resp.text)
print('Full response:\n{0}'.format(resp.text))
# + [markdown] colab_type="text" id="BYbmGGoooIws"
# ## Inference
#
# To allow medical imaging ML models to be easily integrated into clinical workflows, an *inference module* can be used. A standalone modality, a PACS system or a DICOM router can push DICOM instances into Cloud Healthcare [DICOM stores](https://cloud.google.com/healthcare/docs/introduction), allowing ML models to be triggered for inference. This inference results can then be structured into various DICOM formats (e.g. DICOM [structured reports](http://dicom.nema.org/MEDICAL/Dicom/2014b/output/chtml/part20/sect_A.3.html)) and stored in the Cloud Healthcare API, which can then be retrieved by the customer.
#
# The inference module is built as a [Docker](https://www.docker.com/) container and deployed using [Kubernetes](https://kubernetes.io/), allowing you to easily scale your deployment. The dataflow for inference can look as follows (see corresponding diagram below):
#
# 1. Client application uses [STOW-RS](ftp://dicom.nema.org/medical/Dicom/2013/output/chtml/part18/sect_6.6.html) to push a new DICOM instance to the Cloud Healthcare DICOMWeb API.
#
# 2. The insertion of the DICOM instance triggers a [Cloud Pubsub](https://cloud.google.com/pubsub/) message to be published. The *inference module* will pull incoming Pubsub messages and will recieve a message for the previously inserted DICOM instance.
#
# 3. The *inference module* will retrieve the instance in JPEG format from the Cloud Healthcare API using [WADO-RS](ftp://dicom.nema.org/medical/Dicom/2013/output/chtml/part18/sect_6.5.html).
#
# 4. The *inference module* will send the JPEG bytes to the model hosted on AutoML.
#
# 5. AutoML will return the prediction back to the *inference module*.
#
# 6. The *inference module* will package the prediction into a DICOM instance. This can potentially be a DICOM structured report, [presentation state](ftp://dicom.nema.org/MEDICAL/dicom/2014b/output/chtml/part03/sect_A.33.html), or even burnt text on the image. In this codelab, we will focus on just DICOM structured reports. The structured report is then stored back in the Cloud Healthcare API using STOW-RS.
#
# 7. The client application can query for (or retrieve) the structured report by using [QIDO-RS](http://dicom.nema.org/dicom/2013/output/chtml/part18/sect_6.7.html) or WADO-RS. Pubsub can also be used by the client application to poll for the newly created DICOM structured report instance.
#
# 
#
#
# To begin, we will create a new DICOM store that will store our inference source (DICOM mammography instance) and results (DICOM structured report). In order to enable Pubsub notifications to be triggered on inserted instances, we will give the DICOM store a Pubsub channel to publish on.
# + colab={} colab_type="code" id="r7VrAx6B0TQK"
# Pubsub config.
pubsub_topic_id = "MY_PUBSUB_TOPIC_ID" # @param
pubsub_subscription_id = "MY_PUBSUB_SUBSRIPTION_ID" # @param
# DICOM Store for store DICOM used for inference.
inference_dicom_store_id = "MY_INFERENCE_DICOM_STORE" # @param
pubsub_subscription_name = "projects/" + project_id + "/subscriptions/" + pubsub_subscription_id
inference_dicom_store_name = "projects/" + project_id + "/locations/" + location + "/datasets/" + dataset_id + "/dicomStores/" + inference_dicom_store_id
# + colab={} colab_type="code" id="v10GgraT7XbO" magic_args="-s {pubsub_topic_id} {pubsub_subscription_id} {project_id} {location} {dataset_id} {inference_dicom_store_id}" language="bash"
#
# # Create Pubsub channel.
# gcloud beta pubsub topics create $1
# gcloud beta pubsub subscriptions create $2 --topic $1
#
# # Create a Cloud Healthcare DICOM store that published on given Pubsub topic.
# TOKEN=`gcloud beta auth application-default print-access-token`
# NOTIFICATION_CONFIG="{notification_config: {pubsub_topic: \"projects/$3/topics/$1\"}}"
# curl -s -X POST -H "Content-Type: application/json" -d "${NOTIFICATION_CONFIG}" https://healthcare.googleapis.com/v1beta1/projects/$3/locations/$4/datasets/$5/dicomStores?access_token=${TOKEN}\&dicom_store_id=$6
#
# # Enable Cloud Healthcare API to publish on given Pubsub topic.
# PROJECT_NUMBER=`gcloud projects describe $3 | grep projectNumber | sed 's/[^0-9]//g'`
# SERVICE_ACCOUNT="<EMAIL>"
# gcloud beta pubsub topics add-iam-policy-binding $1 --member="serviceAccount:${SERVICE_ACCOUNT}" --role="roles/pubsub.publisher"
# + [markdown] colab_type="text" id="VRs-EWOf_VIU"
# Next, we will building the *inference module* using [Cloud Build API](https://cloud.google.com/cloud-build/docs/api/reference/rest/). This will create a Docker container that will be stored in [Google Container Registry](https://cloud.google.com/container-registry/). The inference module code is found in *[inference.py](./scripts/inference/inference.py)*. The build script used to build the Docker container for this module is *[cloudbuild.yaml](./scripts/inference/cloudbuild.yaml)*. Progress of build may be found on [cloud build dashboard](https://console.cloud.google.com/cloud-build/builds?project=).
# + colab={} colab_type="code" id="nolumVGiL47X" magic_args="-s {project_id}" language="bash"
# PROJECT_ID=$1
#
# gcloud builds submit --config scripts/inference/cloudbuild.yaml --timeout 1h scripts/inference
# + [markdown] colab_type="text" id="YtufvIOrdnP7"
# Next, we will deploy the *inference module* to Kubernetes.
# + [markdown] colab_type="text" id="oIWLkRKleFJS"
# Then we create a Kubernetes Cluster and a Deployment for the *inference module*.
# + colab={} colab_type="code" id="uJHRFPvjeDnZ" magic_args="-s {project_id} {location} {pubsub_subscription_name} {full_model_name} {inference_dicom_store_name}" language="bash"
# gcloud container clusters create inference-module --region=$2 --scopes https://www.googleapis.com/auth/cloud-platform --num-nodes=1
#
# PROJECT_ID=$1
# SUBSCRIPTION_PATH=$3
# MODEL_PATH=$4
# INFERENCE_DICOM_STORE_NAME=$5
#
# cat <<EOF | kubectl create -f -
# apiVersion: extensions/v1beta1
# kind: Deployment
# metadata:
# name: inference-module
# namespace: default
# spec:
# replicas: 1
# template:
# metadata:
# labels:
# app: inference-module
# spec:
# containers:
# - name: inference-module
# image: gcr.io/${PROJECT_ID}/inference-module:latest
# command:
# - "/opt/inference_module/bin/inference_module"
# - "--subscription_path=${SUBSCRIPTION_PATH}"
# - "--model_path=${MODEL_PATH}"
# - "--dicom_store_path=${INFERENCE_DICOM_STORE_NAME}"
# - "--prediction_service=AutoML"
# EOF
# + [markdown] colab_type="text" id="dgUu3dJN8spl"
# Next, we will store a mammography DICOM instance from the TCIA dataset to the DICOM store. This is the image that we will request inference for. Pushing this instance to the DICOM store will result in a Pubsub message, which will trigger the *inference module*.
# + colab={} colab_type="code" id="9CG0225T8rw2"
# DICOM Study/Series UID of input mammography image that we'll push for inference.
input_mammo_study_uid = "1.3.6.1.4.1.9590.100.1.2.85935434310203356712688695661986996009"
input_mammo_series_uid = "1.3.6.1.4.1.9590.100.1.2.374115997511889073021386151921807063992"
input_mammo_instance_uid = "1.3.6.1.4.1.9590.100.1.2.289923739312470966435676008311959891294"
# + colab={} colab_type="code" id="SRtBZf5N-ou8"
from google.cloud import storage
client = storage.Client()
bucket = client.bucket('gcs-public-data--healthcare-tcia-cbis-ddsm', user_project=project_id)
blob = bucket.blob("dicom/{}/{}/{}.dcm".format(input_mammo_study_uid,input_mammo_series_uid,input_mammo_instance_uid))
blob.download_to_filename("example.dcm")
with open("example.dcm", 'rb') as dcm:
dcm_content = dcm.read()
path = os.path.join(HEALTHCARE_API_URL, inference_dicom_store_name, 'dicomWeb', 'studies')
headers = {'Content-Type': 'application/dicom'}
authed_session.post(path, headers=headers, data=dcm_content)
# + [markdown] colab_type="text" id="SrPN8rW1wxcg"
# You should be able to observe the *inference module*'s logs by running the following command. In the logs, you should observe that the inference module successfully recieved the the Pubsub message and ran inference on the DICOM instance. The logs should also include the inference results. It can take a few minutes for the Kubernetes deployment to start up, so you many need to run this a few times. The logs should also include the inference results. It can take a few minutes for the Kubernetes deployment to start up, so you many need to run this a few times.
# + colab={} colab_type="code" id="muiDpFTuxMOk"
# !kubectl logs -l app=inference-module
# + [markdown] colab_type="text" id="l9ibc2yayM_j"
# You can also query the Cloud Healthcare DICOMWeb API (using QIDO-RS) to see that the DICOM structured report has been inserted for the study. The structured report contents can be found under tag **"0040A730"**.
#
# You can optionally also use WADO-RS to recieve the instance (e.g. for viewing).
# + colab={} colab_type="code" id="grWtbIQCyL0r" magic_args="-s {project_id} {location} {dataset_id} {inference_dicom_store_id} {input_mammo_study_uid}" language="bash"
#
# TOKEN=`gcloud beta auth application-default print-access-token`
#
# # QIDO-RS should return two results in JSON response. One for the original DICOM
# # instance, and one for the Strucured Report containing the inference results.
# curl -s https://healthcare.googleapis.com/v1beta1/projects/$1/locations/$2/datasets/$3/dicomStores/$4/dicomWeb/studies/$5/instances?includefield=all\&access_token=${TOKEN} | python -m json.tool
|
imaging/ml/ml_codelab/breast_density_auto_ml.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Unit Commitment with Energy Storage
#
# This is an extended version of the sandbox unit comitment problem used in the previous two notebooks.
#
# The model consists aus three heat generators that have to cover a heat demand. The generators are:
# * a gasfired heat only boiler
# * a back pressure steam turbine
# * a thermal heat storage
#
# A forecast for the heat load that needs to be covered is available and the models purpose is to find the
# optimal schedule to cover this load giving another forecast for the electricity prices.
#
# ## Configuration and Scenarios
#
# The configuration to this code is saved as an Excel Workbook. The workbook serves as input and contains both
# the constant plant characteristics and the forecasts. It can therefore be used to try out different scenarios.
#
# ## Code Explanation
#
# In contrast to the previous three notebooks, this one uses functions that are defined first and then called in different cells later on. This is a more typical approach when developing these kind of models: Implement the next small step as a function, when it works create another cell and use the function.
# +
#%% Imports
# pandas for tables and timeseries,
# Numpy for Numeric calculations,
# Matplotlib for plotting,
# pulp for linear program definition
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pulp import LpProblem, LpMinimize, LpVariable, LpInteger, LpStatus, value,LpAffineExpression
# little helper to interact with excel parameter file
from tools import update_excel, read_config
# This command makes the plots in this workbook interactive
# %matplotlib inline
# +
# Test read configuration file
filename='4_optimization_model_with_storage_input.xlsx'
params, ts = read_config(filename)
# Display input data
print(params)
ts.head()
# -
# Build and solve the optimization problem
def build_problem(params, ts):
#%% Einlesen und Verarbeiten der Parameter aus der Excel Datei
tsindex=ts.index
ts = ts.reset_index()
# Scale timeseries
ts['Heatload']=ts['Heatload']*params['Qlmax']
ts['EEX']=ts['EEX'] / ts['EEX'].mean() * params['k_sp']
#%% Definition des Problems als Lineare Minimierungsproblem
prob = LpProblem("Advanced Unit Commitment Problem",LpMinimize)
nts=ts.shape[0]
# Inititalize variables with boundaries and store them in a list (one per timestep)
# These variables are normalized to nominal capacity so range [0,1]
q1 = [LpVariable(f"q1{t}", 0, 1) for t in range(nts)]
q2 = [LpVariable(f"q2{t}", 0, 1/params['SKZ2']) for t in range(nts)]
p2 = [LpVariable(f"p2{t}", 0, 1) for t in range(nts)]
q3 = [LpVariable(f"q3{t}", -1, 1) for t in range(nts)]
# This is the one binary variable for the turbine operating state
z2 = [LpVariable(f"z2{t}", 0, 1, LpInteger) for t in range(nts)]
# Storage capacity is stored in hours of full heat load coverage
e3 = [LpVariable(f"e3{t}", 0, params['e3max']) for t in range(nts)]
objective={}
# Production cost of unit 1 (heat only boiler)
objective.update({q1[t]:params['Q1max']*params['k_1'] for t in range(nts)})
# Production cost of unit 2 (increase cost)
objective.update({p2[t]:params['P2max']*(params['k_21']-ts.loc[t, 'EEX']) for t in range(nts)})
# Production cost of unit 2 (constant operating cost)
objective.update({z2[t]:params['P2max']*params['k_20'] for t in range(nts)})
# Add objectives to problem
prob += LpAffineExpression(objective), "Objective function, Linear Production Cost"
# These are the conditions per timestep
for t in range(nts):
# Load constraint
prob += q1[t]*params['Q1max'] \
+ p2[t]*params['P2max']/params['SKZ2'] \
+ q3[t]*params['Qlmax'] == ts.loc[t, 'Heatload'], f"Load constraint t={t}"
# Heat storage level
prob += e3[t] == params['estart'] + sum(q3[i] for i in range(0,t+1)), f"Heat storage contraint t={t}"
# Steam turbine characteristic
prob += p2[t] == q2[t] * params['SKZ2']
# Minimum Power
prob += p2[t]*params['P2max'] >= z2[t]*params['P2min']
# Maximum Power
prob += p2[t] <= z2[t]
# Storage level at last step
prob += e3[-1] == params['estart']
return prob
# test build_problem
prob = build_problem(params, ts.copy())
print(f"Problem has {len(prob.constraints)} constraints and {len(prob.variables())} variables")
print(f"or {len(prob.variables())/len(ts):.0f} variables and {len(prob.constraints)/len(ts):.0f} constraints per timestep with a total number of {len(ts)} timesteps")
def solve(prob, ts):
# Löse das Problem
prob.solve()
print("Status:", LpStatus[prob.status])
# Each of the variables is printed with it's resolved optimum value
raw_result={}
for v in prob.variables():
raw_result[v.name]=v.varValue
# The optimised objective function value is printed to the screen
print(f"Total cost of production is {value(prob.objective):.0f} EUR.")
#%% Construct result frame
# Gets the variable values back as timeseries in correct order of timesteps given the variable name (key)
get_series = lambda key: pd.Series({int(k.replace(key,'')):raw_result[k] for k in raw_result.keys() if k.startswith(key)}, name=key)
# selection of variables to be exported to excel file
result_vars=['q1', 'q2', 'q3', 'p2', 'e3', 'z2']
# save as dataframe
df = pd.concat([get_series(k) for k in result_vars], axis=1, keys=result_vars).sort_index()
df.index = ts.index
return (LpStatus[prob.status],value(prob.objective), df)
# test solve()
result = solve(prob, ts)
def process_results(filename, result, params, ts):
update_excel(result[2], filename, 'schedule')
# show thermal production schedule in first plot
result[2][['q1','q2','q3','e3']].plot(title='Thermal production schedule')
plt.subplots()
# in the second I want EEX prive and electric prodution
ax21=ts['EEX'].plot(color='red')
ax22 = ax21.twinx()
result[2]['p2'].plot(ax=ax22)
ax22.figure.legend(loc='center left')
ax22.set_title('Electric production schedule (blue) and EEX price (red)')
# test process_results
process_results(filename, result, params, ts)
def build_and_run(filename):
params, ts = read_config(filename)
problem = build_problem(params, ts.copy())
result = solve(problem, ts)
process_results(filename, result, params, ts)
#%% Call of the defined functions
build_and_run('4_optimization_model_with_storage_input.xlsx')
|
4_optimization_model_with_storage.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Explaining Answer Set Solving
#
# This is a (relatively) short guide that shows how the different features/elements of Answer Set Programming work. We will use [clingo](https://potassco.org/clingo/) in Python for this, and throughout this document we will use the syntax that clingo uses for answer set programming.
import clingo
# (If you want to learn in more detail about any of the features of answer set programming with clingo that are explained in this guide, please have a look at the official [Potassco guide](https://github.com/potassco/guide/releases/).)
# ## Printing answer sets
#
# We start by defining a short function that uses the clingo python package to give us the answer sets of a given answer set program (and display the atoms in the answer set sorted alphabetically).
def print_answer_sets(program):
# Load the answer set program, and call the grounder
control = clingo.Control()
control.add("base", [], program)
control.ground([("base", [])])
# Define a function that will be called when an answer set is found
# This function sorts the answer set alphabetically, and prints it
def on_model(model):
sorted_model = [str(atom) for atom in model.symbols(shown=True)]
sorted_model.sort()
print("Answer set: {{{}}}".format(", ".join(sorted_model)))
# Ask clingo to find all models (using an upper bound of 0 gives all models)
control.configuration.solve.models = 0
# Call the clingo solver, passing on the function on_model for when an answer set is found
answer = control.solve(on_model=on_model)
# Print a message when no answer set was found
if answer.satisfiable == False:
print("No answer sets")
# We can use the function `print_answer_sets()` as follows to print all answer sets of a given answer set program `program`. (We will get to what answer set programs are.)
print_answer_sets("""
a :- not b.
b :- not a.
""")
# ## Answer set semantics
#
# Answer set programming is based on the *answer set semantics* for logic programs. This is easiest explained if we start looking at propositional logic programs. Such a program consists of several rules of the following form:
#
# ```
# a :- b_1, ..., b_n, not c_1, ..., not c_m.
# ```
#
# where each of $a$, $b_i$ and $c_i$ are propositional atoms (that start with a lowercase letter). In such a rule, `a` is called the *head* and `b_1, ..., not c_m` is called the *body*. The order of elements within the body of the rule does not matter. This rule is roughly interpreted as: "$a$ is true if $b_1$, ..., $b_n$ are true, and $c_1$, ..., $c_m$ are not true."
#
# You are also free to choose $n=0$, $m=0$, or both. In case both $n=0$ and $m=0$, the rule is simply written as `a.` (and the rule is interpreted as "$a$ is true"). So the following are valid rules in a logic program:
#
# ```
# a.
# a :- b_1, ..., b_n.
# a :- not c_1, ..., not c_m.
# ```
#
# An *interpretation* for a logic program is typically taken to be a set $I$ of propositional atoms. All atoms in the set $I$ are true in this interpretation, and all atoms that are not in $I$ are false in the interpretation.
#
# ### Models for positive programs
#
# Answer sets are a particular type of models for logic programs. To explain the particular property that answer sets should have, we first have a look at models for positive programs.
#
# A *positive program* is a logic program that does not contain negations (`not`). In other words, it is a set of rules that are all either of the form `a.` (interpreted as: "$a$ is true") or of the form `a :- b_1, ..., b_n.` (interpreted as "if $b_1$, ..., $b_n$ are true, then $a$ should also be true"). So, a positive program can be seen as a set of facts (`a.`) and logical implications ($(b_1 \wedge \dotsm \wedge b_n) \rightarrow a)$, written as `a :- b_1, ..., b_n`).
#
# A *model* for a positive program is an interpretation $I$ that makes all the logical statements encoded by the rules in the program true. However, some of these models make more sense than others. For example, for the program `a. b :- a.`, the interpretation $I = \{a,b\}$ is a model, but so is $I = \{a,b,c\}$. The first of these two looks reasonable, but the second not so much. For example, to make the rules in the program true, we need to include $a$ and $b$ in the interpretation, but what justification do we have for putting $c$ in?
#
# For positive programs, we are interested in *minimal models*: models $M$ such that no (strict) subset $M' \subseteq M$ also makes the program true. For a positive program $P$, we define the *answer sets* of $P$ to be the set of all minimal models of $P$. It turns out that if a positive program $P$ has a model, then there is always a single unique minimal model of $P$.
#
# So let's try this out:
print_answer_sets("""
a :- b_1, b_2, b_3.
b_1.
b_2 :- c.
b_3 :- c.
c.
d :- e.
e :- d.
""")
# Taking the unique minimal model of a positive program nicely matches with our intuition of what we want from models. We include all atoms that are declared to be true in the program (in our example: $a$ and $c$). Then we add other atoms that we must include to make all if-then rules true (for example, adding $b_2$ because we already included $c$ and because `b_2 :- c` is in the program), until we are done.
#
# In our example, we don't include $d$ and $e$, because there is no reason to add them to the model. (We could have added both to the model, and still satisfy all if-then rules.)
#
# ### Programs with negation
#
# For logic programs where some rules contain a negation (`not`), things don't turn out to be as easy as simply iterating all if-then rules until we reach a fixpoint. For example, look at the following program:
#
# ```
# a.
# c :- a, not b.
# d :- c.
# b :- d.
# ```
#
# If we would use the strategy of applying if-then rules as long as we can, we would first add $a$, then $c$ (due to the rule `c :- a, not b.`), then $d$ (`d :- c.`), and $b$ (`b :- d.`). But then by adding $b$, we made the application of the rule `c :- a, not b.` invalid (because it only works to justify adding $c$ if $b$ is not true).
#
# Nevertheless, we want to select from all the models of a program with negation those models that we are interested in (the answer sets). The idea is to guess an interpretation $I$, use this interpretation to make a version $P^I$ of the program $P$ without negation ($P^I$ is called the *reduct* of $P$ w.r.t. $I$), and then check that $I$ is the unique minimal model of $P^I$—if this is the case, then $I$ is an *answer set* of $P$.
#
# Let's see how this works with a simple example. Take the following program $P$ (lines starting with `%` are comments):
# ```
# % the program P
# c.
# d :- c, not b.
# b :- not d.
# ```
# Take also the interpretation $I_1 = \{c,d\}$. The new program $P^{I_1}$ we get from $P$ by:
# 1. Removing all rules containing some `not a` in the body such that $a \in I_1$. So in our example, we remove `b :- not d.`, because $d \in I_1$.
# 1. Removing all remaining statements `not a` from the rest of the program. For all of these statements it holds that $a \not\in I_1$, otherwise we would have removed the entire rule containing the `not a` in step (1). So in our example, we change `d :- c, not b.` into `d :- c.`.
#
# So in our example, the program $P^{I_1}$ becomes:
# ```
# % the reduct P^{I_1}
# c.
# d :- c.
# ```
#
# Now, we have that $I_1 = \{c,d\}$ is the unique minimal model of $P^{I_1}$, so $I_1$ is an answer set of $P$.
#
# Let's check with clingo what the answer sets of our example program $P$ are:
print_answer_sets("""
c.
d :- c, not b.
b :- not d.
""")
# Indeed, $\{c,d\}$ is one of the answer sets. Let us also verify why, for example, $I_2 = \{b,c,d\}$ is not an answer set. If we apply the same rules (1) and (2) to $P$ based on $I_2$, we get the program $P^{I_2}$:
# ```
# % the reduct P^{I_2}
# c.
# ```
# (We remove both of the rules `d :- c, not b.` and `b :- not d.` because both $b \in I_2$ and $d \in I_2$.)
#
# And since $I_2 = \{b,c,d\}$ is not the unique minimal model of $P^{I_2}$ (which is $\{c\}$), $I_2$ is not an answer set of $P$.
#
# ### Answer set semantics for programs with negation
#
# So, to summarize, the answer sets of a propositional logic program $P$, are all interpretations $I$ for which it holds that $I$ is the unique minimal model of $P^I$, where $P^I$ is obtained from $P$ by:
# 1. Removing all rules containing some `not a` in the body such that $a \in I$.
# 1. Removing all remaining statements `not a` from the rest of the program.
#
#
# ### Example 0: no answer sets
#
# It turns out that when we allow negation in the logic programs, it is not guaranteed that an answer set exists. Take the following example program $P$:
print_answer_sets("""
a :- not a.
""")
# With only one atom, there are only two relevant interpretations: $I_1 = \emptyset$ and $I_2 = \{a\}$. Both are not answer sets of this program $P$. We get the following two reducts $P^{I_1}$ and $P^{I_2}$:
# ```
# % the reduct P^{I_1}
# a.
#
# % the reduct P^{I_2} (empty)
# ```
# Since $I_1$ is not the minimal model of $P^{I_1}$, and $I_2$ is not the minimal model of $P^{I_2}$, neither is an answer set of $P$.
#
# ## Some (more) examples
#
# Now that we know what the definition is of answer sets for propositional logic programs, let's look at a few examples to get a bit more feeling for it.
#
# ### Example 1: binary choice
#
# Take this example:
print_answer_sets("""
a :- not b.
b :- not a.
""")
# The rules `a :- not b.` and `b :- not a.` allow us to make a binary choice between $a$ and $b$. If we take $a \in I$, these two rules are replaced by `a.` in $P^I$, and similarly, if we take $b \in I$, the two rules are replaced by `b.` in $P^I$. In other words, we can pick either $a$ or $b$, and $P^I$ will contain a fact justifying our choice.
#
# If we take $I = \{a,b\}$, then $P^I$ becomes the empty program (containing no rules), and $\{a,b\}$ is not the unique minimal model of the empty program (the empty set is), so $\{a,b\}$ is not an answer set of our program.
#
# ### Example 2: more binary choice
#
# Now take this example:
print_answer_sets("""
a :- not b.
b :- not a.
c :- not d.
d :- not c.
""")
# In this case, we took two sets of rules encoding the choice between $a$ and $b$, on the one hand, and $c$ and $d$, on the other hand. The resulting program has four answer sets, corresponding to the four combinations of choices.
#
# ### Example 3: overlapping choice
print_answer_sets("""
a :- not b.
b :- not a.
a :- not c.
c :- not a.
""")
# In this example, we again have two sets of rules that each encode a binary choice. One of these is between $a$ and $b$, and the other between $a$ and $c$. This yields two possible combinations of choices ($a,b$, and $a,c$). The answer sets of this program correspond exactly to these two combinations.
#
# ### Example 4: constraints
#
# Suppose now that we want to encode the choices $a/b$ and $c/d$, but that we want to rule out one of the combinations of choices. To do this, we can use a *constraint*, which is a rule with an empty head. For example, the rule `:- a, c.` is a constraint that can be interpreted as "$a$ and $c$ may not both be true". Another way to look at this rule is as the logical implication $(a \wedge c) \rightarrow \bot$, where $\bot$ denotes falsity.
#
# Let's see how we can use this constraint in an example:
print_answer_sets("""
a :- not b.
b :- not a.
c :- not d.
d :- not c.
:- a, c.
""")
# ### Example 5: another constraint
#
# We can also use negations in constraints. For example, the constraint `:- not a, not c.` can be interpreted as "$a$ and $c$ may not both be false."
print_answer_sets("""
a :- not b.
b :- not a.
c :- not d.
d :- not c.
:- not a, not c.
""")
# ## Variables
#
# So far, we looked at propositional atoms only. However, in many cases it would be very convenient to use (first-order) variables to range over a certain domain, rather than spelling out everything in the language of propositional logic. Fortunately, this is functionality that we can use.
#
# For example, we can use predicates with constants wherever we used propositional atoms so far. These constants can be numbers, constants (starting with a lowercase letter, e.g., `charlie`), or compound terms built up using function symbols (e.g., `bestfriend(charlie)`).
#
# Note that here the line between predicates (and propositional atoms) and function symbols is blurred a bit: we may use `bestfriend(charlie)` (a) as a unary predicate `bestfriend` applied to the constant `charlie`, or (b) as function symbol `bestfriend` applied to the constant `charlie`.
#
# Note also that terms that are syntactically different from each other are always interpreted as semantically different as well: `bestfriend(charlie)` and `bobbie` are always different (even though one can think of an interpretation where the function symbol `bestfriend` applied to `charlie` is the same as `bobbie`).
#
# Let's phrase one of our previous examples using predicats:
print_answer_sets("""
choose(a) :- not choose(b).
choose(b) :- not choose(a).
""")
# To really use the power of this first-order notation, we can use variables. Variables start with an uppercase letter. Let's start with an example:
print_answer_sets("""
choice(1).
choice(2).
choose(X,a) :- not choose(X,b), choice(X).
choose(X,b) :- not choose(X,a), choice(X).
""")
# How does this example work, exactly? Variables are universally quantified, so the rule `a(X) :- b(X).` expresses that for each $c$ for which $b(c)$ holds, also $a(c)$ must hold. What clingo does is spelling out all the different relevant instantiations of rules with variables. This is called *grounding*. (Programs without variables are called *ground programs*.) So under the hood, clingo first changed our previous example into the following:
print_answer_sets("""
choice(1).
choice(2).
choose(1,a) :- not choose(1,b), choice(1).
choose(1,b) :- not choose(1,a), choice(1).
choose(2,a) :- not choose(2,b), choice(2).
choose(2,b) :- not choose(2,a), choice(2).
""")
# ### Safe rules
#
# In order to make sure that the grounding process works, you can only use rules that are *safe*. What this means is that every variable that appears in the rule must appear in some positive (that is, non-negated) element of the body. So for example, the following rules are *unsafe* (because the variable `Y` does not appear positively in the body):
#
# ```
# a(Y) :- not b(Y).
# a(X,Y) :- c(X).
# ```
#
# If you ask clingo to find answer sets for a program that contains unsafe rules, it will throw an error message.
#
# ## Abbreviations and other additional features
#
# We have seen all the basic features of answer set programming. However, clingo and the language of answer set programming make our life easier by providing some further features. Let's look at some of them by means of some further examples.
#
# ### Example 6: enumerating numbers
#
# Suppose that we want to declare `choice(i)` for all integers between 1 and 10. Rather than spelling out ten facts, we can simply write `choice(1..10).` So we can write our previous choice example as follows:
print_answer_sets("""
choice(1..2).
choose(X,a) :- not choose(X,b), choice(X).
choose(X,b) :- not choose(X,a), choice(X).
""")
# ### Example 7: showing only some predicates in the answer sets
#
# In our choice example, we might be interested in only part of the answer set. Namely, in the binary predicate `choose`. We know that every answer set will contain `choice(1)`, etc. We can declare a statement that says we want to show the binary predicate `choose`: `#show choose/2.`. If you issue one or more show statements, then all predicates for which no show statement is issued are automatically hidden from answer sets:
print_answer_sets("""
choice(1..2).
choose(X,a) :- not choose(X,b), choice(X).
choose(X,b) :- not choose(X,a), choice(X).
#show choose/2.
""")
# ### Example 8: declaring constants
#
# Suppose that we want to use a number that we will use more often in a program, and that we want to be able to change it easily in a single place. Then we can declare this number as a constant, as follows:
print_answer_sets("""
#const k=2.
choice(1..k).
choose(X,a) :- not choose(X,b), choice(X).
choose(X,b) :- not choose(X,a), choice(X).
#show choose/2.
""")
print_answer_sets("""
#const k=3.
choice(1..k).
choose(X,a) :- not choose(X,b), choice(X).
choose(X,b) :- not choose(X,a), choice(X).
#show choose/2.
""")
# ### Example 9: abbreviating facts
#
# Instead of using `choice(1..3).`, we could also use the statement `choice(1;2;3).`:
print_answer_sets("""
choice(1;2;3).
""")
# ### Example 10: choice rules
#
# Suppose that we want a program that encodes a choice between all subsets of a given set. For example, let $A = \{a_1,a_2\}$ and suppose that we want to write a program whose answer sets (restricted to some predicate `choose/1`) correspond exactly to the four subsets of $A$. We can do this as follows, using the technique that we saw in the examples about binary choice:
print_answer_sets("""
element(a;b).
choose(X) :- not unchoose(X), element(X).
unchoose(X) :- not choose(X), element(X).
#show choose/1.
""")
# However, we can also encode this, more conveniently, using so-called choice rules. For example, the rule `{ choose(a;b) }.` represents exactly what the above example did:
print_answer_sets("""
{ choose(a;b) }.
""")
# Or, equivalently, written as:
print_answer_sets("""
{ choose(a); choose(b) }.
""")
# You can use these choice rules in the head of a rule, also with a non-empty body of the rule (e.g., `{ choose(a;b) } :- make_choice.`).
#
# ### Example 11: cardinality rules
#
# A construct that is similar to choice rules is that of cardinality rules. These are rules that encode a choice between subsets of a given set that satisfies some cardinality conditions. For example, we can modify the example above so that only subsets of size at least 1 and at most 2 are given:
print_answer_sets("""
1 { choose(a); choose(b) } 2.
""")
# We can also use these cardinality expressions in the body of a rule:
print_answer_sets("""
{ choose(a); choose(b) }.
exactly_one :- 1 { choose(a;b) } 1.
""")
# ### Example 12: conditional literals
#
# Another convenient feature is the use of conditional literals. This we can use to express a set of statements for which another property is true. This works as in the following example, where we declare several items using `item/1`, and then encode a choice of exactly two of these items using a cardinality rule where we express the set using conditional literals:
print_answer_sets("""
item(a;b;c).
2 { choose(X) : item(X) } 2.
#show choose/1.
""")
# ### Example 13: arithmetic
#
# You can use integers as constants. Moreover, you can use arithmetic operations (e.g., comparing integers, addition, multiplication, etc).
print_answer_sets("""
number(1..10).
four(4).
at_most_five(N) :- number(N), four(F), N <= F+1.
#show at_most_five/1.
""")
# However, these arithmetic operations can only be applied to variables whose value can be determined by means of other predicates. Therefore, if arithmetic operations involve variables that do not appear in a positively occurring atom in the body of the rule, clingo will throw an error message. (Such rules are not *safe*, as we explained before.)
#
# In the following example, the rule for `double(X,Y)` contains arithmetic operations on `X` and `Y`, and these variables do not occur in a positive atom in the body, and so the rule is not safe and clingo will throw an error message.
try:
print_answer_sets("""
number(1..10).
double(X,Y) :- not letter(X), not letter(Y), Y = 2*X.
#show double/2.
""")
except RuntimeError as e:
print("RuntimeError: \"{}\"".format(str(e)))
# We can make the rule for `double(X,Y)` safe as follows, for example.
print_answer_sets("""
number(1..10).
double(X,Y) :- number(X), number(Y), Y = 2*X.
#show double/2.
""")
# ### Example 14: aggregates
#
# Another useful feature that clingo offers is the use of *aggregates*: `#sum`, `#count`, `#max`, `#min`, `#even`, and `#odd`. These aggregates operate on a (multi)set of atoms.
#
# They can be used as follows, for example:
print_answer_sets("""
item(1..4).
cost(1,2).
cost(2,2).
cost(3,3).
cost(4,0).
2 { choose(I) : item(I) } 2.
total(D) :- D = #sum { C,item(I) : item(I), choose(I), cost(I,C) }.
#show total/1.
#show choose/1.
""")
# In the above example, we use `C,item(I)` in the `#sum` aggregate to make sure that whenever there are more items with the same cost, all of their costs are counted towards the total. If we were to replace `C,item(I)` by `C`, several items with the same cost `C` would (all together) only contribute `C` to the sum.
#
# Here is another example, now using the `#count` aggregate.
print_answer_sets("""
item(1..4).
total(D) :- D = #count { item(I) : item(I) }.
""")
# Finally, an example using `#max`:
print_answer_sets("""
item(1..4).
2 { choose(I) : item(I) } 2.
highest(D) :- D = #max { I : item(I), choose(I) }.
#show highest/1.
#show choose/1.
""")
# ## Optimization
#
# We can also use optimization statements, to select from all answer sets of a given answer set program those answer sets that minimize or maximize a particular property. To illustrate this, we will define a short function that will give us all optimized answer sets for a given answer set program.
def print_optimal_answer_sets(program):
# Load the answer set program, and call the grounder
control = clingo.Control()
control.add("base", [], program)
control.ground([("base", [])])
# Define a function that will be called when an answer set is found
# This function sorts the answer set alphabetically, and prints it
def on_model(model):
if model.optimality_proven == True:
sorted_model = [str(atom) for atom in model.symbols(shown=True)]
sorted_model.sort()
print("Optimal answer set: {{{}}}".format(", ".join(sorted_model)))
# Ask clingo to find all optimal models (using an upper bound of 0 gives all models)
control.configuration.solve.opt_mode = "optN"
control.configuration.solve.models = 0
# Call the clingo solver, passing on the function on_model for when an answer set is found
answer = control.solve(on_model=on_model)
# Print a message when no answer set was found
if answer.satisfiable == False:
print("No answer sets")
# With this function in place, we will illustrate how optimization statements work.
#
# Consider the following example, where we have facts declaring four items and a score for each of these items. We also have a cardinality rule that states that we should select between 2 and 3 of these items. This gives us 10 answer sets in total:
print_answer_sets("""
item(1..4).
score(1,5).
score(2,4).
score(3,4).
score(4,2).
2 { select(I) : item(I) } 3.
#show select/1.
""")
# Now let's add an optimization statement, that states that we should maximize the total score for the items that we select. This shows that only 2 of the 10 answer sets maximize this total score.
print_optimal_answer_sets("""
item(1..4).
score(1,5).
score(2,4).
score(3,4).
score(4,2).
2 { select(I) : item(I) } 3.
#maximize { S,I : select(I), score(I,S) }.
#show select/1.
""")
# How this works is as follows. The statement `{ S,I : select(I), score(I,S) }` refers to the set of all pairs `S,I` for which `select(I), score(I,S)` holds in the answer set. Then the `#maximize` statements indicates that only those answer sets should be taken for which the sum of all `S` in such pairs `S,I` is maximal. You may also use `#maximize` statements with tuples of different arity (e.g., triples, or 1-tuples). In this case, however, we need to include `I` in the tuples, because otherwise the score for item 2 and item 3 would only be counted once in the total score.
#
# This works similarly using `#minimize` instead of `#maximize`.
print_optimal_answer_sets("""
item(1..4).
score(1,5).
score(2,4).
score(3,4).
score(4,2).
2 { select(I) : item(I) } 3.
#minimize { S,I : select(I), score(I,S) }.
#show select/1.
""")
# To see why we need the tuple `S,I` in this `#minimize` statement, consider the following example, where we replace `S,I` by just `S` in the `#minimize` statement:
print_optimal_answer_sets("""
item(1..4).
score(1,5).
score(2,4).
score(3,4).
score(4,2).
2 { select(I) : item(I) } 3.
#minimize { S : select(I), score(I,S) }.
#show select/1.
""")
# Now selecting items 2 and 3 yields the mimimal total score, because both add score 4 to the set `{ S : select(I), score(I,S) }`, and now the score 4 gets only counted once, which is not what we had in mind.
# ## Disjunction
#
# There is an extension of answer set programming that allows us to use disjunction in the head of rules, and clingo supports this. The following example illustrates how we can do this (with the operator `;` in the head of a rule):
print_answer_sets("""
a.
b ; c :- a.
""")
# To make sure that we have a good foundation for this, we make sure that our definition of *answer sets* also works for programs with rules that have disjunction in the head.
#
# The idea is the same. We guess an interpretation $I$, use this interpretation to make a version $P^I$ of the program $P$ without negation (the *reduct* of $P$ w.r.t. $I$), and then check that $I$ is a minimal model of $P^I$—if this is the case, then $I$ is an *answer set* of $P$.
#
# The reduct $P^{I}$ we get from $P$ by:
# 1. Removing all rules containing some `not a` in the body such that $a \in I$.
# 1. Removing all remaining statements `not a` from the rest of the program.
# So this is also exactly the same as for the case without disjunction in the head of rules.
#
# The only thing that we need to update is what it means for $I$ to be a (minimal) model of $P^I$. We consider rules `a ; b :- c_1, ..., c_n` as the logical implication $(c_1 \wedge \dotsm \wedge c_n) \rightarrow (a \vee b)$. That is, we interpret disjunction in the head as logical disjunction in the consequent of the implication. Using this, we can use a similar definition of what an answer set is: an interpretation $I$ that is a minimal (w.r.t. set inclusion) model of the reduct $P^I$ of the program $P$ w.r.t. $I$.
#
# To take an example, consider the program that we used as example above:
# ```
# % the program P
# a.
# b ; c :- a.
# ```
# Consider the interpretation $I_1 = \{a,b\}$. The reduct $P^{I_1}$ is:
# ```
# % the reduct P^{I_1}
# a.
# b ; c :- a.
# ```
# And $I_1$ is in fact a minimal model of $P^{I_1}$. If we remove $a$ from $I_1$, we get the interpretation $\{b\}$, which does not satisfy `a.`. This is also the case if we remove $a$ and $b$ from $I_1$. If we instead only remove $b$ from $I_1$, we get the interpretation $\{a\}$, which does not satisfy `b ; c :- a.`. Thus, $I_1$ is a minimal model of $P^{I_1}$.
#
# ### Using default negation to represent disjunctive choices
#
# As we have seen above, we can add disjunction to the head of rules. However, in many cases this is not needed to express disjunctive choices. For example, as we have already seen earlier, we can encode a choice between two atoms (say, `a` and `b`) using several rules as follows:
print_answer_sets("""
a :- not b.
b :- not a.
""")
|
basics/guide-to-asp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Import all the necessary libraries
import numpy as np
import pandas as pd
from datetime import datetime as dt
import itertools
# %matplotlib inline
# +
# Read data from the CSV into a dataframe
loc = "./Datasets/PremierLeagueEng"
#raw_data_1 = pd.read_csv(loc + '2000-01.csv')
#raw_data_2 = pd.read_csv(loc + '2001-02.csv')
#raw_data_3 = pd.read_csv(loc + '2002-03.csv')
#raw_data_4 = pd.read_csv(loc + '2003-04.csv')
#raw_data_5 = pd.read_csv(loc + '2004-05.csv')
#raw_data_6 = pd.read_csv(loc + '2005-06.csv')
#raw_data_7 = pd.read_csv(loc + '2006-07.csv')
#raw_data_8 = pd.read_csv(loc + '2007-08.csv')
#raw_data_9 = pd.read_csv(loc + '2008-09.csv')
#raw_data_10 = pd.read_csv(loc + '2009-10.csv')
#raw_data_11 = pd.read_csv(loc + '2010-11.csv')
#raw_data_12 = pd.read_csv(loc + '2011-12.csv')
#raw_data_13 = pd.read_csv(loc + '2012-13.csv')
raw_data_14 = pd.read_csv(loc + 'D1_Buli_1314.csv')
raw_data_15 = pd.read_csv(loc + 'D1_Buli_1415.csv')
raw_data_16 = pd.read_csv(loc + 'D1_Buli_1516.csv')
raw_data_17 = pd.read_csv(loc + 'D1_Buli_1617.csv')
raw_data_18 = pd.read_csv(loc + 'D1_Buli_1718.csv')
# -
raw_data_18
# +
# Parse data as time
def parse_date(date):
if date == '':
return None
else:
return dt.strptime(date, '%d/%m/%Y').date()
def parse_date_other(date):
if date == '':
return None
else:
return dt.strptime(date, '%d/%m/%Y').date()
#raw_data_17.Date = raw_data_17.Date.apply(parse_date)
#raw_data_18.Date = raw_data_18.Date.apply(parse_date)
#Gets all the statistics related to draw betting strategy
columns_req = ['Date', 'HomeTeam', 'AwayTeam', 'FTR', 'B365D',
'BWD', 'IWD', 'LBD', 'PSD', 'VCD', 'WHD', 'PSCD']
odds_statistics_14 = raw_data_14[columns_req]
odds_statistics_15 = raw_data_15[columns_req]
odds_statistics_16 = raw_data_16[columns_req]
odds_statistics_17 = raw_data_17[columns_req]
odds_statistics_18 = raw_data_18[columns_req]
# -
odds_statistics_14
# +
draws_14 = odds_statistics_14.loc[odds_statistics_14['FTR'] == 'D']
draws_15 = odds_statistics_15.loc[odds_statistics_15['FTR'] == 'D']
draws_16 = odds_statistics_16.loc[odds_statistics_16['FTR'] == 'D']
draws_17 = odds_statistics_17.loc[odds_statistics_17['FTR'] == 'D']
draws_18 = odds_statistics_18.loc[odds_statistics_18['FTR'] == 'D']
blacklist = ['<NAME>']
draws_14_wo_bayern = draws_14.loc[~draws_14['HomeTeam'].isin(blacklist)]
draws_15_wo_bayern = draws_15.loc[~draws_15['HomeTeam'].isin(blacklist)]
draws_16_wo_bayern = draws_16.loc[~draws_16['HomeTeam'].isin(blacklist)]
draws_17_wo_bayern = draws_17.loc[~draws_17['HomeTeam'].isin(blacklist)]
draws_18_wo_bayern = draws_18.loc[~draws_18['HomeTeam'].isin(blacklist)]
print(len(draws_14))
print(len(draws_14_wo_bayern))
print(len(draws_15))
print(len(draws_15_wo_bayern))
print(len(draws_16))
print(len(draws_16_wo_bayern))
print(len(draws_17))
print(len(draws_17_wo_bayern))
print(len(draws_18))
print(len(draws_18_wo_bayern))
# +
# average odd b365
b365D_odd_14 = draws_14['B365D'].sum()
b365D_odd_15 = draws_15['B365D'].sum()
b365D_odd_16 = draws_16['B365D'].sum()
b365D_odd_17 = draws_17['B365D'].sum()
b365D_odd_18 = draws_18['B365D'].sum()
b365D_odd_14_wo = draws_14_wo_bayern['B365D'].sum()
b365D_odd_15_wo = draws_15_wo_bayern['B365D'].sum()
b365D_odd_16_wo = draws_16_wo_bayern['B365D'].sum()
b365D_odd_17_wo = draws_17_wo_bayern['B365D'].sum()
b365D_odd_18_wo = draws_18_wo_bayern['B365D'].sum()
print("ROI over the last 5 years:")
rlt = ((b365D_odd_18-34*9) + (b365D_odd_17-34*9) + (b365D_odd_16-34*9) +
(b365D_odd_15-34*9) + (b365D_odd_14-34*9))
print("result : " + str(rlt) + " - ")
rltwo = ((b365D_odd_18_wo-34*9) + (b365D_odd_17_wo-34*9) +
(b365D_odd_16_wo-34*9) + (b365D_odd_15_wo-34*9) +
(b365D_odd_14_wo-34*9))
print("result_wo : " + str(rltwo) + " - ")
print("\n#####################################\n")
print("2018")
print("-----")
print("odds B365:")
print("all: " + str(b365D_odd_18))
print("wo : " + str(b365D_odd_18_wo))
print("n of Draws:")
print("all: " + str(len(draws_18)))
print("wo : " + str(len(draws_18_wo_bayern)))
print("result:")
print("all: " + str(b365D_odd_18-34*9))
print("wo : " + str(b365D_odd_18_wo-34*8))
print("p of draws: " + str(len(draws_18)/((34*9)/100)))
print("p of draws wo: " + str(len(draws_18_wo_bayern)/((34*8)/100)))
print("\n#####################################\n")
print("2017")
print("-----")
print("odds B365:")
print("all: " + str(b365D_odd_17))
print("wo : " + str(b365D_odd_17_wo))
print("n of Draws:")
print("all: " + str(len(draws_17)))
print("wo : " + str(len(draws_17_wo_bayern)))
print("result:")
print("all: " + str(b365D_odd_17-34*9))
print("wo : " + str(b365D_odd_17_wo-34*8))
print("p of draws: " + str(len(draws_17)/((34*9)/100)))
print("p of draws wo: " + str(len(draws_17_wo_bayern)/((34*8)/100)))
print("\n#####################################\n")
print("2016")
print("-----")
print("odds B365:")
print("all: " + str(b365D_odd_16))
print("wo : " + str(b365D_odd_16_wo))
print("n of Draws:")
print("all: " + str(len(draws_16)))
print("wo : " + str(len(draws_16_wo_bayern)))
print("result:")
print("all: " + str(b365D_odd_16-34*9))
print("wo : " + str(b365D_odd_16_wo-34*8))
print("p of draws: " + str(len(draws_16)/((34*9)/100)))
print("p of draws wo: " + str(len(draws_16_wo_bayern)/((34*8)/100)))
print("\n#####################################\n")
print("2015")
print("-----")
print("odds B365:")
print("all: " + str(b365D_odd_15))
print("wo : " + str(b365D_odd_15_wo))
print("n of Draws:")
print("all: " + str(len(draws_15)))
print("wo : " + str(len(draws_15_wo_bayern)))
print("result:")
print("all: " + str(b365D_odd_15-34*9))
print("wo : " + str(b365D_odd_15_wo-34*8))
print("p of draws: " + str(len(draws_15)/((34*9)/100)))
print("p of draws wo: " + str(len(draws_15_wo_bayern)/((34*8)/100)))
print("\n#####################################\n")
print("2014")
print("-----")
print("odds B365:")
print("all: " + str(b365D_odd_14))
print("wo : " + str(b365D_odd_14_wo))
print("n of Draws:")
print("all: " + str(len(draws_14)))
print("wo : " + str(len(draws_14_wo_bayern)))
print("result:")
print("all: " + str(b365D_odd_14-34*9))
print("wo : " + str(b365D_odd_14_wo-34*8))
print("p of draws: " + str(len(draws_14)/((34*9)/100)))
print("p of draws wo: " + str(len(draws_14_wo_bayern)/((34*8)/100)))
# -
|
.ipynb_checkpoints/historical_view_prem_l-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#triangle of pattern
n=int(input())
i=1
while i<=n:
spaces=1
while spaces<=n-i:
print(' ',end='')
spaces+=1
j=1
p=i
while j<=i:
print(p,end='')
p+=1
j+=1
p=i-1
j = 0
while p>=1:
r=(2*i)-j-2
print(r,end='')
p-=1
j += 1
print()
i+=1
n=int(input())
i=1
while(i<=n):
j=n
while(j>=i):
print(" ",end="")
j=j-1
k=1
while(k<=2*i-1):
print("*",end="")
k=k+1
print(" ")
i=i+1
|
pattern.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
with open("poem.txt","r") as f:
for line in f:
print(line)
word_count = {}
with open("poem.txt","r") as f:
for line in f:
tokens = line.split(' ')
for token in tokens:
token=token.replace('\n','')
if token in word_count:
word_count[token]+=1
else:
word_count[token]=1
word_count
|
Data Structures/data_structures/4_HashTable_2_Collisions/Solution/exercise_poem_find_word_occurances.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: iambjudas
# language: python
# name: iambjudas
# ---
# # Genome scale model reconstruction of the smut fungus *Ustilago maydis*: Reproduction of simulations with CobraPy Notebook
# ## Introduction
#
# This notebook is an extension to the article by Liebal et al., (2022) and reproduces the comparison of experimental growth rates with predictions by the genome scale metabolic model (GSMM) of *Ustilago maydis*. Finaly, the Memote quality check is performed.
#
# ## Requirements
# Make sure that the required files are present in the notebook directory.
#
# Files:
# * ../model/iCL1079.xml: SBML file, Genome scale metabolic model of *U. maydis*
#
# Dependencies:
# * CPython 3.7.6
# * IPython 7.12.0
# * ipywidgets 7.5.1
# * matplotlib 3.1.3
# * numpy 1.18.1
# * pandas 1.0.1
# * cobra 0.17.1
# * memote 0.10.2
#
# ## Set-up compute environment
#
# In the following cell the python environment is set up. If CobraPy and Memote are not already downloaded, use the following command to download the packages them from the cell:
# # !{sys.executable} -m pip install cobra
# +
import sys
import os
import pandas as pd
import csv
import itertools
import operator
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from Bio import SeqIO
# loading cobrapy, a library dedicated to the analysis of genome scale metabolic models
from cobra.io import read_sbml_model, write_sbml_model
from cobra import Reaction, Metabolite
from escher import Builder
# loading Memote, quality assessment of GSMM
# from memote import test_model, snapshot_report
# from FastaTools import *
from iambcodes.cobra import *
from iambcodes.fasta import *
print('System initiated.')
# -
# ## Model loading
ModelFile = os.path.join('..','model', 'iUma22.xml')
model=read_sbml_model(ModelFile)
model
# model.metabolites
# ## Support functions
# +
def TestSubstrate(model, EX_Sub, Rate=10):
'''
Function for testing substrate consumption with exchange reaction.
'''
with model:
medium = model.medium
medium[EX_Sub] = Rate
medium['EX_co2_e'] = 0
medium['EX_glc__D_e'] = 0
model.medium = medium
return round(model.slim_optimize(),2)
def MetNewFromExist(MetIn):
Metout = Metabolite('{}_e'.format(MetIn.id[:-2]),
formula = MetIn.formula,
name = MetIn.name,
compartment = 'e')
return Metout
def CreateTransReact(MetIn):
reaction = Reaction('Trans_{}'.format(MetIn.id),
name = 'Transport c<->e {}'.format(MetIn.name),
lower_bound = -1000,
upper_bound = 1000)
MetOut = MetNewFromExist(MetIn)
reaction.add_metabolites({MetIn:-1.0, MetOut:1.0})
return reaction
def CSVexport(myDict, FName='BiologGrowthTest'):
fields = ['id','name','id_e','id_c','growth','CL_Growth']
with open(FName, 'w') as f:
w = csv.DictWriter(f, fields)
w.writeheader()
for k in myDict:
w.writerow({field: myDict[k].get(field) or k for field in fields})
# -
# ## Data loading
#
# Now, the external data is integrated. The excel-sheet is parsed and the GSMM file is converted to a model variable.
myxls = os.path.join('..','data','MSc-Lieven_Christian','sorted_growth_study.xlsx')
x1 = pd.ExcelFile(myxls)
df1 = x1.parse('Sheet1')
df1.head(3)
# Loading the pan genome
myECFile = os.path.join('..','data','Sequencing','EC_Annotation.txt')
EC_dict_ori = extractEC(myECFile)
len(EC_dict_ori)
# extracting all substrates from biolog list with BiGG metabolite identifiers
# for source in df1['BiGG_ID'].astype(str) if source != 'nan']
Substrate_dict = dict()
# Substrate_e = dict()
# Substrate_c = dict()
# Substrate_no = list()
for indx, Sub in enumerate(df1['BiGG_ID'].astype(str)):
Sub_e = '{}_e'.format(Sub)
Sub_c = '{}_c'.format(Sub)
Sub_eIdx = np.where([Sub_e==met.id for met in model.metabolites])[0]
Sub_cIdx = np.where([Sub_c==met.id for met in model.metabolites])[0]
CLGrowth = str(round(df1['In_Silico_Growth_Rate'][indx],2))
if Sub_cIdx.size>0 and Sub_eIdx.size>0:
Substrate_dict[Sub] = {'name': model.metabolites[Sub_cIdx[0]].name, 'id_c': model.metabolites[Sub_cIdx[0]].id, 'id_e': model.metabolites[Sub_eIdx[0]].id, 'CL_Growth': CLGrowth}
if Sub_cIdx.size>0 and Sub_eIdx.size<1:
Substrate_dict[Sub] = {'name': model.metabolites[Sub_cIdx[0]].name, 'id_c': model.metabolites[Sub_cIdx[0]].id, 'id_e': None, 'CL_Growth': CLGrowth}
if Sub_cIdx.size<1 and Sub_eIdx.size>0:
Substrate_dict[Sub] = {'name': model.metabolites[Sub_eIdx[0]].name, 'id_c': None, 'id_e': model.metabolites[Sub_eIdx[0]].id, 'CL_Growth': CLGrowth}
if Sub_cIdx.size<1 and Sub_eIdx.size<1:
Substrate_dict[Sub] = {'name': None, 'id_c': None, 'id_e': None}
# +
# change for loop to new substrate_dict with if loops to check which metabolic compartments exist
for Substrate in Substrate_dict.keys():
if Substrate_dict[Substrate]['id_e'] is not None:
EX_Sub = 'EX_{}'.format(Substrate_dict[Substrate]['id_e'])
try:
model.reactions.get_by_id(EX_Sub)
except KeyError:
with model:
model.add_boundary(model.metabolites.get_by_id(Substrate_dict[Substrate]['id_e']), type='exchange')
myGrowth = TestSubstrate(model, EX_Sub)
Substrate_dict[Substrate].update({'growth': str(myGrowth)})
# print('New exchange reaction for {} with growth: {}'.format(Substrate, myGrowth))
else:
myGrowth = TestSubstrate(model, EX_Sub)
Substrate_dict[Substrate].update({'growth': str(myGrowth)})
# print('{} with growth: {}'.format(Substrate, myGrowth))
elif Substrate_dict[Substrate]['id_c'] is not None:
myMet = model.metabolites.get_by_id(Substrate_dict[Substrate]['id_c'])
myTransport = CreateTransReact(myMet)
EX_Sub = 'EX_{}_e'.format(Substrate)
with model:
model.add_reactions([myTransport])
model.add_boundary(model.metabolites.get_by_id('{}_e'.format(Substrate)), type='exchange')
myGrowth = TestSubstrate(model, EX_Sub)
Substrate_dict[Substrate].update({'growth': str(myGrowth)})
# print('New transport+exchange reaction for {} with growth: {}'.format(Substrate, myGrowth))
# else:
# print('{} not in model.'.format(Substrate))
CSVexport(Substrate_dict)
print('Biolog-Model growth comparison exported.')
# -
# Export of gene list with locus tags
Genes_File = os.path.join('..','data','Uma_Genes.csv')
Genes = pd.DataFrame([[x.id,i.id] for x in model.genes for i in x.reactions], nrows=400, columns=['locus-tag', 'name'])
# Genes.to_csv(Genes_File, index=False)
# model.genes.get_by_id('UMAG_00518')
# model.reactions.get_by_id('ANTPPT')
# EC_dict[model.genes.get_by_id('UMAG_00518').name]
EC_dict = EC_dict_ori.copy()
Gene_common = [True if ModGene.name in EC_dict.keys() else False for ModGene in model.genes]
iUmaANDpan = [myGene.name for myGene in model.genes[Gene_common]]
iUmaNOTpan = [myGene.name for myGene in model.genes[list(map(operator.not_, Gene_common))]]
[EC_dict.pop(myGene.name, None) for myGene in model.genes]
panNOTiUma = list(EC_dict.keys())
f1 = os.path.join('..','data','Sequencing', 'Analysis', 'iUmaANDpan.txt')
f2 = os.path.join('..','data','Sequencing', 'Analysis','iUmaNOTpan.txt')
f3 = os.path.join('..','data','Sequencing', 'Analysis','panNOTiUma.txt')
with open(f1, "w") as f:
f.write("\n".join(iUmaANDpan))
with open(f2, "w") as f:
f.write("\n".join(iUmaNOTpan))
with open(f3, "w") as f:
f.write("\n".join(panNOTiUma))
print('iUma in Pan:', sum(Gene_common))
print('iUma only:', len(model.genes)-sum(Gene_common))
print('Pan only:', len(panNOTiUma))
# model.genes.get_by_id('UMAG_00037')
# model.reactions.get_by_id('1.6.5.4-RXN')
# ## Unique usti 521 genes
# +
# loading xls with all data
myseqsXls = os.path.join('..','data','Sequencing','Pan_Uma.xlsx')
MutualFig = os.path.join('..','data','Sequencing', 'Analysis','Hist_ECGeneOverlap512.svg')
myseqs = pd.read_excel(myseqsXls, skiprows=1, index_col=None, nrows=6779, false_values=' - , -') # There are only 6779 positions with U. maydis 521 genes
myseqs.replace(' - , -', False, regex=True, inplace=True)
mylist = list(myseqs['Usti_521'])
# Finding positions in the xls that are also annotated with an ec number
IndxKeep = [mylist.index(elem) for elem in mylist for gene in EC_dict_ori if gene in elem]
IndxRmve = np.ones(len(mylist), dtype=bool)
IndxRmve[IndxKeep] = False
myseqs.drop(np.arange(len(mylist))[IndxRmve], inplace=True)
# finding the distribution of genes in other strains
GeneShare = list()
for idx, row in myseqs.iterrows():
GeneShare.append(sum(1 for entry in row if isinstance(entry, str)))
# histogram with broken y-axis:
# https://stackoverflow.com/questions/60062664/y-xis-break-on-matplotlib-histogram
bin_edges = np.linspace(.5, 5.5, 6) # make the bins
bin_centres = np.linspace(1, 5, 5) # for plotting only
my_hist = np.histogram(GeneShare, bins = bin_edges)[0]
f, (ax, ax2) = plt.subplots(2,1,sharex = True) # make the axes
ax.bar(bin_centres, my_hist) # plot on top axes
ax2.bar(bin_centres, my_hist) # plot on bottom axes
ax.set_ylim([1300,1500]) # numbers here are specific to this example
ax2.set_ylim([0, 20]) # numbers here are specific to this example
ax.spines['bottom'].set_visible(False)
ax2.spines['top'].set_visible(False)
ax.xaxis.tick_bottom()
ax.tick_params(labeltop=False)
ax2.xaxis.tick_bottom()
ax2.set_xticklabels(['','512 only','+1','+2','+3','all strains'])
plt.xlabel('E.C. annotated genes among strains')
plt.savefig(MutualFig)
plt.show()
# +
# extracting the 512 unique E.C. genes and export to fasta file for KAAS analysis
ECUniqFile = os.path.join('..','data','Sequencing', 'Analysis','ECUnique512.fasta')
ECUniq = [elem.split(',')[0] for elem in myseqs.iloc[np.arange(len(GeneShare))[np.array(GeneShare)==1]]['Usti_521'].values]
myFasta = 'pangenome_AA_Uma.faa'
myDir = os.path.join('..','data','Sequencing')
myFile = os.path.join(myDir,myFasta)
records = list()
with open(myFile) as infile:
for record in SeqIO.parse(infile, 'fasta'):
if record.id in ECUniq:
records.append(record)
with open(os.path.join(ECUniqFile), 'w') as outfile:
SeqIO.write(records, outfile, "fasta")
# -
# ### export of panNOTiUma list as fasta for KAAS analysis
# +
myFasta = 'pangenome_AA_Uma.faa'
myDir = os.path.join('..','data','Sequencing')
myFile = os.path.join(myDir,myFasta)
records = list()
with open(myFile) as infile:
for record in SeqIO.parse(infile, 'fasta'):
if record.id in panNOTiUsti:
records.append(record)
with open(os.path.join(myDir,'panNOTiUsti.fasta'), 'w') as outfile:
SeqIO.write(records, outfile, "fasta")
# -
# ### Testing KEGG Biopython functions
# +
from Bio.KEGG import REST
result = REST.kegg_get('ko:k03800').read()
BRidx = result.find('BR:ko')
GOidx = result.find('map')
BRid = result[BRidx+5:BRidx+10]
GOid = result[GOidx+3:GOidx+8]
print(BRid, GOid)
print(result)
# finding multiple 'map' id in string of result
# https://stackoverflow.com/questions/47486563/how-can-i-get-index-of-two-of-more-duplicate-characters-in-a-string
# -
KAAStxt = 'KaasMap_panNOTiUsti.txt'
KAASpath = os.path.join('..','data','Sequencing','Analysis', KAAStxt)
myKAAS = pd.read_csv(KAASpath, delimiter='\t', names=['UMAG-ID','KO-ID'])
myKAAS
MAP_dict = dict()
for ko in myKAAS['KO-ID']:
if str(ko) != 'nan':
result = REST.kegg_get('ko:{}'.format(ko)).read()
MAPidx = result.find('map')
MAPid = result[MAPidx+3:MAPidx+8]
if MAPid in MAP_dict:
MAP_dict[MAPid]+=1
else:
MAP_dict[MAPid] = 1
MAP_dict
# ## Function definitions
#
# We are testing three different growth conditions with substrates methanol, glycerol, and glucose. For each of the substrates, the corresponding exchange rate has to be activated, the approriate biomass composition formula has to be selected and exchange reactions for non-used substrates need to be closed.
# ## Simulation
#
# Here, we start the simulation loop. For all substrates we use the substrate uptake rate and use the functions defined previously to update the model. The final growth rate is stored, and is then used in a plot versus the experimentally observed growth.
# +
# checking TCA consistency with objective to ATP hydrolysis/maintenance
with model as ATPM:
ATPM.objective = 'ATPS'
solution = ATPM.optimize()
print(solution.fluxes['BIOMASS_REACTION'])
print(model.summary())
# visualization
builder = Builder()
# load U. maydis ESCHER map with Pentose phosphate pathway, Glycolysis
Escher_Central = os.path.join('Maps','iUma22_MetMap_TCA.json')
Escher_Glycine = os.path.join('Maps','iUma22_MetMap_glycine.json')
builder = Builder(
map_json=Escher_Central,
model = model, # 'iCL1079.json',
)
# Run FBA with the model and add the flux data to the map
solution = builder.model.optimize()
builder.reaction_data = solution.fluxes
builder.save_html('example_map.html')
# -
# ### Dependencies and versions
# The code below was used to identify the versions of dependent packages.
# %load_ext watermark
# %watermark -v -m -p ipywidgets,matplotlib,numpy,pandas,cobra,memote,watermark
|
code/iUma22_FASTA+KAAS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3-azureml
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# ### Install required libraries
#
# Run the following cells to install required libraries. Please ignore any compatibility related errors. Please run the cells below only once.
# After your install these libraries it is recommended that you **restart** the notebook kernel from the **Kernel** menu above. After restarting the kernel, start from the `Train a deep learning model` section.
# !pip install tensorflow==2.2.0
# !pip install onnxmltools==1.7.0
# !pip install keras2onnx==1.7.0
# !pip install onnxruntime==1.4.0
# !pip install tf2onnx==1.6.3
# # Train a deep learning model
# In this notebook you will train a deep learning model to classify the descriptions of car components as compliant or non-compliant.
#
# Each document in the supplied training data set is a short text description of the component as documented by an authorized technician.
# The contents include:
# - Manufacture year of the component (e.g. 1985, 2010)
# - Condition of the component (poor, fair, good, new)
# - Materials used in the component (plastic, carbon fiber, steel, iron)
#
# The compliance regulations dictate:
# *Any component manufactured before 1995 or in fair or poor condition or made with plastic or iron is out of compliance.*
#
# For example:
# * Manufactured in 1985 made of steel in fair condition -> **Non-compliant**
# * Good condition carbon fiber component manufactured in 2010 -> **Compliant**
# * Steel component manufactured in 1995 in fair condition -> **Non-Compliant**
#
# The labels present in this data are 0 for compliant, 1 for non-compliant.
#
# The challenge with classifying text data is that deep learning models only undertand vectors (e.g., arrays of numbers) and not text. To encode the car component descriptions as vectors, we use an algorithm from Stanford called [GloVe (Global Vectors for Word Representation)](https://nlp.stanford.edu/projects/glove/). GloVe provides us pre-trained vectors that we can use to convert a string of text into a vector.
# ### Setup
#
# Execute the following cell by selecting the `>|Run` button in the command bar above.
# +
experiment_name = 'deep-learning'
project_folder = './dl'
deployment_folder = './deploy'
datasets_folder = './datasets'
onnx_export_folder = 'onnx'
# this is the URL to the CSV file containing the car component descriptions
cardata_url = ('https://quickstartsws9073123377.blob.core.windows.net/'
'azureml-blobstore-0d1c4218-a5f9-418b-bf55-902b65277b85/'
'quickstarts/connected-car-data/connected-car_components.csv')
cardata_ds_name = 'connected_car_components'
cardata_ds_description = 'Connected car components data'
# this is the name of the AML Compute cluster
cluster_name = "amlcluster"
embedding_dim = 100
training_samples = 90000
validation_samples = 5000
max_words = 10000
# -
# # Create the Azure Machine Learning resources
# The Azure Machine Learning SDK provides a comprehensive set of a capabilities that you can use directly within a notebook including:
# - Creating a **Workspace** that acts as the root object to organize all artifacts and resources used by Azure Machine Learning.
# - Creating **Experiments** in your Workspace that capture versions of the trained model along with any desired model performance telemetry. Each time you train a model and evaluate its results, you can capture that run (model and telemetry) within an Experiment.
# - Creating **Compute** resources that can be used to scale out model training, so that while your notebook may be running in a lightweight container in a notebook environment, your model training can actually occur on a powerful cluster that can provide large amounts of memory, CPU or GPU.
# - Using **Automated Machine Learning (AutoML)** to automatically train multiple versions of a model using a mix of different ways to prepare the data and different algorithms and hyperparameters (algorithm settings) in search of the model that performs best according to a performance metric that you specify.
# - Packaging a Docker **Image** that contains everything your trained model needs for scoring (prediction) in order to run as a web service.
# - Deploying your Image to either Azure Kubernetes or Azure Container Instances, effectively hosting the **Web Service**.
#
# In the Azure Machine Learning compute instance you created, all of the libraries needed for Azure Machine Learning are pre-installed. To use them, you just need to import them. Run the following cell to do so:
# +
import logging
import os
import json
from matplotlib import pyplot as plt
from matplotlib.pyplot import imshow
import numpy as np
import pandas as pd
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.core.model import Model
from azureml.core.dataset import Dataset
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
from azureml.widgets import RunDetails
from azureml.train.dnn import TensorFlow
import tensorflow
from tensorflow import keras
from tensorflow.keras.models import load_model
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
import onnxruntime
print("keras version: {} tensorflow version: {}".format(keras.__version__, tensorflow.__version__))
print("Azure ML SDK version:", azureml.core.VERSION)
# -
# ## Create and connect to an Azure Machine Learning Workspace
# Run the following cell to create a new Azure Machine Learning **Workspace** and save the configuration to disk (next to the Jupyter notebook).
#
# **Important Note**: You will be prompted to login in the text that is output below the cell. Be sure to navigate to the URL displayed and enter the code that is provided. Once you have entered the code, return to this notebook and wait for the output to read `Workspace configuration succeeded`.
ws = Workspace.from_config()
print(ws)
print('Workspace configuration succeeded')
# ### Create AML Compute Cluster
# Now you are ready to create the CPU compute cluster. Run the following cell to create a new compute cluster (or retrieve the existing cluster if it already exists). The code below will create a *CPU based* cluster where each node in the cluster is of the size `Standard_D2_V2`, and the cluster is restricted to use 1 node. This will take couple of minutes to create.
# +
### Create AML CPU based Compute Cluster
try:
compute_target = ComputeTarget(workspace=ws, name=cluster_name)
print('Found existing compute target.')
except ComputeTargetException:
print('Creating a new compute target...')
compute_config = AmlCompute.provisioning_configuration(vm_size='Standard_D2_V2',
min_nodes=1, max_nodes=1)
# create the cluster
compute_target = ComputeTarget.create(ws, cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
# Use the 'status' property to get a detailed status for the current AmlCompute.
print(compute_target.status.serialize())
# -
# ### Create and register input Datasets for training
# +
# this is the URL to the CSV file containing the GloVe vectors
glove_url = ('https://quickstartsws9073123377.blob.core.windows.net/'
'azureml-blobstore-0d1c4218-a5f9-418b-bf55-902b65277b85/'
'quickstarts/connected-car-data/glove.6B.100d.txt')
glove_ds_name = 'glove_6B_100d'
glove_ds_description ='GloVe embeddings 6B 100d'
# this is the URL to the CSV file containing the care component descriptions
cardata_url = ('https://quickstartsws9073123377.blob.core.windows.net/'
'azureml-blobstore-0d1c4218-a5f9-418b-bf55-902b65277b85/'
'quickstarts/connected-car-data/connected-car_components.csv')
cardata_ds_name = 'connected_car_components'
cardata_ds_description = 'Connected car components data'
try:
glove_ds = Dataset.get_by_name(workspace=ws, name=glove_ds_name)
print('GloVe embeddings dataset already registered.')
except:
print('Registering GloVe embeddings dataset...')
glove_ds = Dataset.File.from_files(glove_url)
glove_ds.register(workspace=ws, name=glove_ds_name, description=glove_ds_description)
print('GloVe embeddings dataset successfully registered.')
try:
cardata_ds = Dataset.get_by_name(workspace=ws, name=cardata_ds_name)
print('Connected car components dataset already registered.')
except:
print('Registering connected car components dataset...')
cardata_ds = Dataset.Tabular.from_delimited_files(path=cardata_url)
cardata_ds.register(workspace=ws, name=cardata_ds_name, description=cardata_ds_description)
print('Connected car components dataset successfully registered.')
# -
# ### Create the ScriptRunConfig with custom TensforFlow 2.0 Enviroment
from azureml.core import Environment
from azureml.core.environment import CondaDependencies
tensorflow_env = Environment.get(workspace=ws, name='AzureML-TensorFlow-2.2-CPU').clone('Custom-TensforFlow-Env')
cd = tensorflow_env.python.conda_dependencies
cd.add_pip_package('pandas==1.1.2')
cd.add_pip_package('onnxmltools==1.7.0')
cd.add_pip_package('keras2onnx==1.7.0')
cd.add_pip_package('onnxruntime==1.4.0')
cd.add_pip_package('tf2onnx==1.6.3')
tensorflow_env.register(workspace=ws)
# +
from azureml.core import ScriptRunConfig
src = ScriptRunConfig(source_directory=project_folder,
script='train.py',
arguments=['--glove_ds', glove_ds.as_named_input('glove').as_mount(),
'--cardata_ds_name', cardata_ds_name],
compute_target=compute_target,
environment=tensorflow_env)
# -
# ## Remotely train a deep learning model using the Azure ML Compute
# In the following cells, you will *not* train the model against the data you just downloaded using the resources provided by your notebook selected compute instances. Instead, you will deploy an Azure ML Compute cluster that will download the data and use a trainings script to train the model. In other words, all of the training will be performed remotely with respect to this notebook.
#
#
# create project folder
if not os.path.exists(project_folder):
os.makedirs(project_folder)
# ### Create the training script
# +
# %%writefile $project_folder/train.py
import os
import argparse
import numpy as np
import pandas as pd
import tensorflow
from tensorflow import keras
from tensorflow.keras import models
from tensorflow.keras import layers
from tensorflow.keras import optimizers
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Embedding, Flatten, Dense
from azureml.core import Run
from azureml.core.dataset import Dataset
import sys
print('Python version:', sys.version)
print("keras version: {} tensorflow version: {}".format(keras.__version__, tensorflow.__version__))
parser = argparse.ArgumentParser("train")
parser.add_argument("--glove_ds", type=str, help="glove dataset input mount path", dest="glove_ds", required=True)
parser.add_argument("--cardata_ds_name", type=str, help="dataset name", dest="cardata_ds_name", required=True)
args = parser.parse_args()
print("Argument 1: %s" % args.glove_ds)
print("Argument 2: %s" % args.cardata_ds_name)
glove_file_path = args.glove_ds
cardata_ds_name = args.cardata_ds_name
embedding_dim = 100
training_samples = 90000
validation_samples = 5000
max_words = 10000
run = Run.get_context()
ws = run.experiment.workspace
print("Loading car components data...")
cardata_ds = Dataset.get_by_name(workspace=ws, name=cardata_ds_name)
car_components_df = cardata_ds.to_pandas_dataframe()
components = car_components_df["text"].tolist()
labels = car_components_df["label"].tolist()
print("Loading car components data completed.")
# use the Tokenizer from Keras to "learn" a vocabulary from the entire car components text
print("Tokenizing data...")
tokenizer = Tokenizer(num_words=max_words)
tokenizer.fit_on_texts(components)
sequences = tokenizer.texts_to_sequences(components)
word_index = tokenizer.word_index
print('Found %s unique tokens.' % len(word_index))
data = pad_sequences(sequences, maxlen=embedding_dim)
labels = np.asarray(labels)
print('Shape of data tensor:', data.shape)
print('Shape of label tensor:', labels.shape)
indices = np.arange(data.shape[0])
np.random.seed(100)
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
x_train = data[:training_samples]
y_train = labels[:training_samples]
x_val = data[training_samples: training_samples + validation_samples]
y_val = labels[training_samples: training_samples + validation_samples]
x_test = data[training_samples + validation_samples:]
y_test = labels[training_samples + validation_samples:]
print("Tokenizing data complete.")
# apply the vectors provided by GloVe to create a word embedding matrix
print("Applying GloVe vectors...")
embeddings_index = {}
f = open(glove_file_path)
for line in f:
values = line.split()
word = values[0]
coefs = np.asarray(values[1:], dtype='float32')
embeddings_index[word] = coefs
f.close()
print('Found %s word vectors.' % len(embeddings_index))
embedding_matrix = np.zeros((max_words, embedding_dim))
for word, i in word_index.items():
if i < max_words:
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
embedding_matrix[i] = embedding_vector
print("Applying GloVe vectors compelted.")
# use Keras to define the structure of the deep neural network
print("Creating model structure...")
model = Sequential()
model.add(Embedding(max_words, embedding_dim, input_length=embedding_dim))
model.add(Flatten())
model.add(Dense(64, activation='relu'))
model.add(Dense(32, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.summary()
# fix the weights for the first layer to those provided by the embedding matrix
model.layers[0].set_weights([embedding_matrix])
model.layers[0].trainable = False
print("Creating model structure completed.")
opt = optimizers.RMSprop(lr=0.1)
print("Training model...")
model.compile(optimizer=opt,
loss='binary_crossentropy',
metrics=['acc'])
history = model.fit(x_train, y_train,
epochs=3,
batch_size=32,
validation_data=(x_val, y_val))
print("Training model completed.")
print("Saving model files...")
# create a ./outputs/model folder in the compute target
# files saved in the "./outputs" folder are automatically uploaded into run history
path = os.path.join('./outputs', 'model')
os.makedirs(path, exist_ok=True)
# save model h5
model.save(os.path.join(path, 'model.h5'))
print("model saved in ./outputs/model folder")
print("Saving model files completed.")
import onnxmltools
import os
# Convert the Keras model to ONNX
onnx_model_name = 'model.onnx'
converted_model = onnxmltools.convert_keras(model, onnx_model_name, target_opset=7)
# Save the model locally...
onnxmltools.utils.save_model(converted_model, os.path.join(path, 'model.onnx'))
print('Model exported in ONNX format...')
# -
# ## Submit the training run
# The code pattern to submit a training run to Azure Machine Learning compute targets is always:
#
# - Create an experiment to run.
# - Submit the experiment.
# - Wait for the run to complete.
# ### Create the experiment
experiment = Experiment(ws, experiment_name)
# ### Submit the experiment
run = experiment.submit(config=src)
# Wait for the run to complete by executing the following cell. Note that this process will perform the following:
# - Build and deploy the container to Azure Machine Learning compute (~8 minutes)
# - Execute the training script (~2 minutes)
#
# If you change only the training script and re-submit, it will run faster the second time because the necessary container is already prepared so the time requried is just that for executing the training script.
#
# *Run the cell below and wait till the **Run Status** is **Completed** before proceeding ahead*
RunDetails(run).show()
# ## Download the model files from the run
# In the training script, the Keras model is saved into two files, model.json and model.h5, in the outputs/models folder on the CPU cluster AmlCompute node. Azure ML automatically uploaded anything written in the ./outputs folder into run history file store. Subsequently, we can use the run object to download the model files. They are under the the outputs/model folder in the run history file store, and are downloaded into a local folder named model.
# +
# create a model folder in the current directory
os.makedirs('model', exist_ok=True)
for f in run.get_file_names():
if f.startswith('outputs/model'):
output_file_path = os.path.join('./model', f.split('/')[-1])
print('Downloading from {} to {} ...'.format(f, output_file_path))
run.download_file(name=f, output_file_path=output_file_path)
print('Download completed.')
# -
# ## Restore the model from model.h5 file
model = load_model('./model/model.h5')
print("Model loaded from disk.")
print(model.summary())
# ## Evaluate the model on test data
# You can also evaluate how accurately the model performs against data it has not seen. Run the following cell to load the test data that was not used in either training or evaluating the model.
# Run the following cell to see the accuracy on the test set (it is the second number in the array displayed, on a scale from 0 to 1).
# +
embedding_dim = 100
training_samples = 90000
validation_samples = 5000
max_words = 10000
cardata_ds_name = 'connected_car_components'
cardata_ds = Dataset.get_by_name(workspace=ws, name=cardata_ds_name)
car_components_df = cardata_ds.to_pandas_dataframe()
components = car_components_df["text"].tolist()
labels = car_components_df["label"].tolist()
# use the Tokenizer from Keras to "learn" a vocabulary from the entire car components text
print("Tokenizing data...")
tokenizer = Tokenizer(num_words=max_words)
tokenizer.fit_on_texts(components)
sequences = tokenizer.texts_to_sequences(components)
word_index = tokenizer.word_index
print('Found %s unique tokens.' % len(word_index))
data = pad_sequences(sequences, maxlen=embedding_dim)
labels = np.asarray(labels)
print('Shape of data tensor:', data.shape)
print('Shape of label tensor:', labels.shape)
indices = np.arange(data.shape[0])
np.random.seed(100)
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
x_train = data[:training_samples]
y_train = labels[:training_samples]
x_val = data[training_samples: training_samples + validation_samples]
y_val = labels[training_samples: training_samples + validation_samples]
x_test = data[training_samples + validation_samples:]
y_test = labels[training_samples + validation_samples:]
print("Tokenizing data complete.")
# -
print('Model evaluation will print the following metrics: ', model.metrics_names)
evaluation_metrics = model.evaluate(x_test, y_test)
print(evaluation_metrics)
# Log the evaluation metrics to the experiment **Run**
run.log(model.metrics_names[0], evaluation_metrics[0], 'Model test data loss')
run.log(model.metrics_names[1], evaluation_metrics[1], 'Model test data accuracy')
# **Save the run information to json file**
# +
run_info = {}
run_info["id"] = run.id
print("Saving run_info.json...")
os.makedirs('./outputs', exist_ok=True)
run_info_filepath = os.path.join('./outputs', 'run_info.json')
with open(run_info_filepath, "w") as f:
json.dump(run_info, f)
# -
# ## Converting a Keras model to ONNX
#
# In the steps that follow, you will convert Keras model you just trained to the ONNX format. This will enable you to use this model for classification in a very broad range of environments, outside of Azure Databricks including:
#
# Web services
# iOS and Android mobile apps
# Windows apps
# IoT devices
# Convert the model to ONNX by running the following cell.
# +
import onnxmltools
import os
# Convert the Keras model to ONNX
onnx_model_name = 'component_compliance.onnx'
converted_model = onnxmltools.convert_keras(model, onnx_model_name, target_opset=7)
# Save the model locally...
onnx_model_path = os.path.join(deployment_folder, onnx_export_folder)
os.makedirs(onnx_model_path, exist_ok=True)
onnxmltools.utils.save_model(converted_model, os.path.join(onnx_model_path,onnx_model_name))
print('Model exported in ONNX format...')
# -
# The above cell created a new file called component_compliance.onnx that contains the ONNX version of the model.
#
# Now try using this ONNX model to classify a component description by running the following cell. Remeber the prediction will be a value close to 0 (non-compliant) or to 1 (compliant).
#
# ## Compare ONNX Inference Performace with Keras
#
# Create an onnxruntime InferenceSession and observe the expected input shape for inference. Classify a sample data from test set using both ONNX and Keras. Remeber the prediction will be a value close to 0 (non-compliant) or to 1 (compliant).
#
# Next, we will evaluate the performance of ONNX and Keras by running the same sample 10,000 times. You will observe that ONNX is approximately 10 times faster than Keras in making inferences.
import onnxruntime
# Load the ONNX model and observe the expected input shape
onnx_session = onnxruntime.InferenceSession(
os.path.join(os.path.join(deployment_folder, onnx_export_folder), onnx_model_name))
input_name = onnx_session.get_inputs()[0].name
output_name = onnx_session.get_outputs()[0].name
print('Expected input shape: ', onnx_session.get_inputs()[0].shape)
# +
# Load the car components labeled data
print("Loading car components data...")
cardata_ds = Dataset.get_by_name(workspace=ws, name=cardata_ds_name)
car_components_df = cardata_ds.to_pandas_dataframe()
components = car_components_df["text"].tolist()
labels = car_components_df["label"].tolist()
print("Loading car components data completed.")
tokenizer = Tokenizer(num_words=max_words)
tokenizer.fit_on_texts(components)
sequences = tokenizer.texts_to_sequences(components)
word_index = tokenizer.word_index
print('Found %s unique tokens.' % len(word_index))
data = pad_sequences(sequences, maxlen=embedding_dim)
labels = np.asarray(labels)
print('Shape of data tensor:', data.shape)
print('Shape of label tensor:', labels.shape)
indices = np.arange(data.shape[0])
np.random.seed(100)
np.random.shuffle(indices)
data = data[indices]
labels = labels[indices]
x_test = data[training_samples + validation_samples:]
y_test = labels[training_samples + validation_samples:]
# +
# Grab one sample from the test data set
x_test_float = np.reshape(x_test[1502].astype(np.float32), (1,100))
print('Input shape: ', x_test_float.shape)
print('ONNX prediction: ', onnx_session.run([output_name], {input_name: x_test_float}))
# Use Keras to make predictions on the same sample
print('Keras prediction: ', model.predict(x_test_float))
# Next we will compare the performance of ONNX vs Keras
import timeit
n = 1000
# -
start_time = timeit.default_timer()
for i in range(n):
model.predict(x_test_float)
keras_elapsed = timeit.default_timer() - start_time
print('Keras performance: ', keras_elapsed)
start_time = timeit.default_timer()
for i in range(n):
onnx_session.run([output_name], {input_name : x_test_float})
onnx_elapsed = timeit.default_timer() - start_time
print('ONNX performance: ', onnx_elapsed)
print('ONNX is about {} times faster than Keras'.format(round(keras_elapsed/onnx_elapsed)))
|
Hands-on lab/notebooks/Deep Learning with Text.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="kWXTCuo1sV1I" colab_type="code" colab={}
import pandas as pd
from gensim.utils import simple_preprocess
from gensim.models import Word2Vec
from gensim.models.phrases import Phrases, Phraser
from ast import literal_eval
# + id="6TBetlmexdFw" colab_type="code" outputId="a154c295-f00b-4141-a00e-26dcb4515034" colab={"base_uri": "https://localhost:8080/", "height": 34}
# cd 'drive/My Drive/Colab Notebooks/dw_challenges/dw_four/data'
# + id="H-QzfXRyxig5" colab_type="code" outputId="c910561c-5027-4156-8f1a-49695f855370" colab={"base_uri": "https://localhost:8080/", "height": 34}
df = pd.read_csv('job_ofer.csv')
df.shape
# + id="6Gx6pAAVxrCA" colab_type="code" outputId="d0161941-c264-4087-8acd-9c53d21ad77e" colab={"base_uri": "https://localhost:8080/", "height": 459}
df.head()
# + [markdown] id="ASFsySs-x96P" colab_type="text"
# #Word2Vec
# + id="S-bJvktVx_tG" colab_type="code" colab={}
#we train our model now
corpus = df['title'].map( simple_preprocess)
# + id="mtZklecgybmQ" colab_type="code" outputId="28c0967f-2f28-40c6-d4ca-bbfd517b0aa8" colab={"base_uri": "https://localhost:8080/", "height": 221}
#we chceck how it looks like
corpus
# + id="ddKP3DCtykAP" colab_type="code" colab={}
#now we transfer the 'corpus' to our model
model = Word2Vec(corpus, size=100, window=2, min_count=1)
# + id="Dc0eEeuUy3W3" colab_type="code" outputId="4732f2b3-2abd-41c0-9a3e-8b95207dd3cf" colab={"base_uri": "https://localhost:8080/", "height": 241}
model.wv.most_similar('machine')
# + [markdown] id="YHmwPbj2z9dd" colab_type="text"
# #Some example
# + id="UF4Pg-TAz_Oh" colab_type="code" outputId="484f5a68-e7dc-4f5c-8171-1a2c2b8bf5c4" colab={"base_uri": "https://localhost:8080/", "height": 34}
corpus = [
['machine', 'learning', 'c'],
['machine', 'learning', 'x'],
['y', 'machine', 'learning', 'w'],
['q', 'machine', 'learning', 'u', 'k'],
]
bigram = Phraser( Phrases(corpus, min_count=1, threshold=1))
bigram[ ['k', 'machine', 'learning', 'c']]
# + [markdown] id="5r6CVhxx0U_g" colab_type="text"
# #Title + phrases
# + id="gPZnPj5W0XPt" colab_type="code" colab={}
title_corpus = df['title'].map(simple_preprocess)
title_bigram = Phraser( Phrases(title_corpus, min_count=1, threshold=1))
# + id="bXd5u4ua0lJG" colab_type="code" outputId="bd023514-4e64-45d2-9f51-be53598067cd" colab={"base_uri": "https://localhost:8080/", "height": 34}
title_bigram[ simple_preprocess('Deep Learning Applaied Resarcher - Chicago')]
# + id="uSDZFiRy0wYG" colab_type="code" colab={}
#we chceck the whole list now i.e. the whole phrase
title_corpus_phrase = [title_bigram[sent] for sent in title_corpus]
model = Word2Vec(title_corpus_phrase, size=100, window=2, min_count=1)
# + id="gi0iEMJ71Gag" colab_type="code" outputId="5852664f-9193-4c31-862f-a4faefe63350" colab={"base_uri": "https://localhost:8080/", "height": 241}
model.wv.most_similar('machine') #we check it
# + id="BBs2N9HE1QL1" colab_type="code" colab={}
#above model is insufficient so we define below function
def prepare_corpus(corpus, bigram):
for sent in corpus:
yield bigram[sent] + sent
# + id="ebZwZTTc1g2Q" colab_type="code" outputId="f93b5948-3b7d-40ce-92b5-313b24431aea" colab={"base_uri": "https://localhost:8080/", "height": 34}
simple_preprocess('Deep Learning Applaied Resarcher - Chicago')
# + id="4I8rZass1j6-" colab_type="code" outputId="aa2c2865-013b-45c9-e702-3524ced23c97" colab={"base_uri": "https://localhost:8080/", "height": 34}
title_bigram[ ['deep', 'learning', 'appleid', 'resarcher', 'chicago']]
# + id="6LnLpHvg1q5G" colab_type="code" colab={}
#we glue the both list together, i.e. bigram and preprocess
ext_corp = list(prepare_corpus(title_corpus, title_bigram))
title_model = Word2Vec( ext_corp, size=100, window=2, min_count=1 )
# + id="fSgYCPLb2nX1" colab_type="code" outputId="b7eca51e-8c43-40f6-9901-86a6ae469ad6" colab={"base_uri": "https://localhost:8080/", "height": 241}
#now it works as it should
title_model.wv.most_similar('machine_learning')
# + [markdown] id="UTP5MsfG3XV9" colab_type="text"
# #Description
# + id="P2FozeoR3ZXG" colab_type="code" outputId="f1918f96-9a56-4d10-aa4d-5503642439e5" colab={"base_uri": "https://localhost:8080/", "height": 1000}
simple_preprocess(df.sample()['description'].values[0])
# + id="tBZxPS4B6Jd2" colab_type="code" colab={}
#we do the same as above for bigram
descr_corpus = df['description'].map(simple_preprocess)
descr_bigram = Phraser(Phrases(descr_corpus, min_count=1, threshold=1))
# + id="3OYmi3xu6US8" colab_type="code" colab={}
ext_descr_corp = list(prepare_corpus(descr_corpus, descr_bigram))
descr_model = Word2Vec(ext_corp, size=100, window=2, min_count=1)
# + id="XzVuQXlN6b-a" colab_type="code" outputId="d64529ce-4cdf-46a4-a000-30d386d49007" colab={"base_uri": "https://localhost:8080/", "height": 241}
descr_model.wv.most_similar('nlp')
# + id="DB0QRiX067gJ" colab_type="code" outputId="cd21f347-bac5-46c8-bad5-e8b288b8d731" colab={"base_uri": "https://localhost:8080/", "height": 241}
descr_model.wv.most_similar('pytorch')
# + id="i1od8M4982th" colab_type="code" outputId="8097cb14-4baa-4b0a-932f-14895f60c826" colab={"base_uri": "https://localhost:8080/", "height": 71}
df.sample()['description'].map(literal_eval).values
# + id="WlkNxGvx8sb1" colab_type="code" outputId="59687ec5-4718-41c3-dbef-4bac6526a9fc" colab={"base_uri": "https://localhost:8080/", "height": 71}
for line in df.sample()['description'].map(literal_eval).values[0]:
print(line)
print("")
|
day4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # I2Cの認識確認
# I2Cの認識状況を確認する
# !i2cdetect -r -y 1
# # カメラの認識確認
# カメラの認識を確認する
# !dmesg | grep imx219
# # カメラ関連のデーモンの再起動
#
# カメラ関連デーモンの再起動
# !echo jetbot | sudo -S systemctl restart nvargus-daemon
# # カメラ関連のデーモンのログ確認
# カメラ関連のデーモンのログを確認する。ログの確認が終わったら、プロセスが戻ってこないので、■でユーザにより停止させる
# !journalctl -u nvargus-daemon.service -f
# # 電力モードの変更(5Wモード)
#
# CPUが2つ起動
# !echo jetbot | sudo -S nvpmodel -m 1
# # 電力モードの変更(10Wモード)
# CPUが4つ起動
# !echo jetbot | sudo -S nvpmodel -m 0
# # 電力モードの確認
# 電力モードの確認
# !nvpmodel -q --verbose
# # メモリ使用量の確認
#
# freeコマンドでメモリ使用量を確認
# !free -h
# # クロックの高速化
# クロックを高速化します。
# !echo jetbot | sudo -S jetson_clocks
# # クロックの状態の確認
#
# クロックの状態を表示します。
# !echo jetbot | sudo -S sudo jetson_clocks --show
# # Wifiへの接続
# !echo jetbot | sudo -S nmcli device wifi connect 'アクセスポイント名' password '<PASSWORD>' ifname wlan0
|
notebooks/utils/jetutil.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit
# language: python
# name: python3
# ---
inp =[1,1,5,1]
xnor, xor = 0, 0
for i in inp:
xnor = ~(xnor ^i)
xor ^= i
xor, xnor
|
leetcode/137_single_number_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
from shared_notebook_utils import *
from statsmodels.sandbox.stats.runs import mcnemar
# Add the datasets you want to analyze in 'dataset_dirnames'
# Change the directory names listed here by the ones set in your data folder.
# In this repository we include an example 'toy_dataset' that can be used to test the notebook.
dataset_dirnames = ['freesound_loops_db_4000', 'apple_loops_db', 'mixcraft_loops_db', 'looperman']
datasets = load_datasets(dirnames=dataset_dirnames, clean=True) # Load and clean datasets
# Add the datasets you want to analyze in 'methods_to_compare'
methods_to_compare = ['Percival14_essentia', 'Percival14Mod', 'Percival14']
# %matplotlib inline
# This notebook contains expriments that complement those found in the article: <NAME>., & <NAME>. (2016). Tempo Estimation for Music Loops and a Simple Confidence Measure. In Proceedings of the Int. Conf. on Music Information Retrieval (ISMIR).
# License: CC-BY-4.0
# -
# In this notebook we compare implementation variations of Percival14's method:
#
# - **Percival14**: python implementation provided by original authors.
# - **Percival14Mod**: original python implementation with small modifications (see below).
# - **Percival14_essentia**: essentia implementation of the algorithm.
#
# We observed a certain misbehaving for Percival14 results for sounds shorter than 6 seconds. In our original evaluation we zero-padded all sounds shorter than 6 seconds to be at least 6 seconds long (to prevent software crashes). This had however an unexpected positive impact on estimation accuracy as (in authors' original python implementation of the method) the evaluation of pulse trains (see algorithm) worked best if filtered flux signal contains information at the end of the window (which is what was achieved by zero-padding). We revised the python implementation and updated the code (that's what Percival14Mod method represents) to not favour information at the end of the window and to better closely follow the method as described in the paper (probably at the expense of some speed optimisations). Our Essentia implementation of the method [see *PercivalBpmEstimator* algorithm in Essentia docs] also implements the modifications from Percival14Mod.
#
# In this notebook we see how the different implementations provide quite similar results.
# ## General accuracy
# +
# Prepare figure
n_datasets = len(datasets)
if not n_datasets:
raise Exception("No datasets were specified or could be loaded!")
nrows = int(math.ceil(float(n_datasets)/2))
ncols = 1 if n_datasets < 2 else 2
fig1, axs = plt.subplots(nrows, ncols, figsize=(17, 5))
# Run analysis and plot results
all_datasets_method_results = dict()
for count, dataset in enumerate(datasets):
print title("\nGeneral tempo estimation results (%s)" % dataset.short_name, c='*')
methods_to_compare = methods_to_compare
table_header = ['Method', 'Accuracy 1e', 'Accuracy 1', 'Accuracy 2', 'N']
table_rows = list()
for method in methods_to_compare:
if method not in all_datasets_method_results:
all_datasets_method_results[method] = dict()
try:
table_row = [method]
for accuracy_func in accuracy1e, accuracy1, accuracy2:
method_results = accuracy_func(dataset.data, method,skip_zeroed_values=True)
table_row.append(100 * basic_statistics(method_results)['avg'])
if accuracy_func.__name__ not in all_datasets_method_results[method]:
all_datasets_method_results[method][accuracy_func.__name__] = list()
all_datasets_method_results[method][accuracy_func.__name__] += method_results
table_row.append(len(method_results))
table_rows.append(table_row)
except IndexError:
print "Warning: Skipping method %s (analsyis not found in dataset)" % method
continue
print ""
print_table(table_header, table_rows, sort_column=3, highlight_max=True)
if n_datasets == 1:
ax = axs
elif n_datasets == 2:
ax = axs[count]
else:
ax_col=count/2
ax_row=count%2
ax = axs[ax_col,ax_row]
N = len(methods_to_compare)
ind = np.arange(N)
accuracy_1e_means = [row[1] for row in table_rows]
accuracy_1_means = [row[2] for row in table_rows]
accuracy_2_means = [row[3] for row in table_rows]
width = 0.25
rects1 = ax.bar(ind, accuracy_1e_means, width, color=COLORS[0])
rects2 = ax.bar(ind + width, accuracy_1_means, width, color=COLORS[1])
rects3 = ax.bar(ind + 2*width, accuracy_2_means, width, color=COLORS[2])
ax.set_title(dataset.short_name)
ax.set_xticks(ind + 1.4 * width)
ax.set_xticklabels([method for method in methods_to_compare], rotation=0)
ax.legend((rects1[0], rects2[0], rects3[0]), ('Accuracy 1e', 'Accuracy 1', 'Accuracy 2'))
ax.set_ylabel('Accuracy (%)')
ax.set_ylim((0, 100))
ax.xaxis.grid(False)
plt.show()
figure_caption = """
**Figure 1**: Overall tempo estimation accuracies.
"""
IPython.display.display(IPython.display.Markdown(figure_caption))
# Show results for all datasets combined
print title("General tempo estimation results (ALL DATASETS)")
table_header = ['Method', 'Accuracy 1e', 'Accuracy 1', 'Accuracy 2', 'Mean accuracy']
table_rows = list()
for method, results in all_datasets_method_results.items():
table_row = [method]
for accuracy_measure, data in results.items():
table_row.append(100 * basic_statistics(data)['avg'])
table_rows.append(table_row + [np.mean(table_row[1:])])
print_table(table_header, table_rows, sort_column=4, highlight_max=True)
# -
# ## Accuracy vs sound duration
for dataset in datasets:
fig, ax1 = plt.subplots(1, 1, figsize=(14, 6))
ax2 = ax1.twinx()
for count, method in enumerate(methods_to_compare):
accuracies_1e = list()
accuracies_1 = list()
accuracies_2 = list()
counts = list()
steps = np.linspace(1, 40, 40)
for duration_max in steps:
try:
filtered_data = dataset.filter_data([('analysis.durations.duration__<=', duration_max)]).data
accuracies_1e.append(100 * basic_statistics(accuracy1e(filtered_data, method))['avg'])
accuracies_1.append(100 * basic_statistics(accuracy1(filtered_data, method))['avg'])
accuracies_2.append(100 * basic_statistics(accuracy2(filtered_data, method))['avg'])
counts.append(len(filtered_data))
except IndexError:
accuracies_1e.append(0)
accuracies_1.append(0)
accuracies_2.append(0)
counts.append(0)
ax1.plot(steps, accuracies_1e, color=COLORS[count], ls="--")
ax1.plot(steps, accuracies_2, color=COLORS[count], ls="--")
ax1.fill_between(steps, accuracies_1e, accuracies_2, color=COLORS[count], alpha=0.2)
ax2.plot(steps, counts, color=COLORS[count], label=method)
print title('Duration vs tempo estimation accuracy (%s)' % dataset.short_name)
ax1.set_ylabel('Accuracy (%)')
ax1.set_xlabel('Duration (s)')
ax2.set_ylabel('Number of instances')
ax2.legend(loc=3)
ax1.set_ylim((0, 100))
ax1.set_yticks([float(ax1.get_ylim()[1])*(float(i)/5) for i in range(0,6)])
ax2.set_ylim(0.0, ax2.get_ylim()[1])
ax2.set_yticks([float(ax2.get_ylim()[1])*(float(i)/5) for i in range(0,6)])
plt.show()
figure_caption = """**Figure 2 - %s **: Accuracy vs duration for %s dataset. Lower bounds of the
filled areas correspond to Accuracy 1e, while upper bounds correspond to Accuracy 2. Solid lines represent
the number of instances remaining in the dataset.
""" % (dataset.short_name, dataset.short_name)
IPython.display.display(IPython.display.Markdown(figure_caption))
# ## Accuracy vs confidence measure
# +
# Confidence measure function
# NOTE: to speed up this process here we have already precomputed the effective start and end positions
# acocrding to the envelope
def compute_confidence_measure(estimated_bpm,
duration_samples,
start_effective_duration,
end_effective_duration,
sample_rate=44100, beat_range=range(1, 128), k=0.5):
if estimated_bpm == 0:
# This condition is to skip computing other steps if estimated bpm is 0, we already know that the
# output will be 0
return 0
durations_to_check = [
duration_samples,
duration_samples - start_effective_duration,
end_effective_duration,
end_effective_duration - start_effective_duration
]
beat_duration = (60.0 * sample_rate)/estimated_bpm
L = [beat_duration * n for n in beat_range]
thr_lambda = k * beat_duration
confidences = list()
for duration in durations_to_check:
delta_l = min([abs(l - duration) for l in L])
if delta_l > thr_lambda:
confidences.append(0.0)
else:
confidences.append(1.0 - float(delta_l) / thr_lambda)
return max(confidences)
# Iterate over all instances in all datasets and for all methods
print 'Computing confidence measure values for all sounds in all datasets and for all methods...',
n_annotated = 0
for dataset in datasets:
for key, item in dataset.data.items():
for method in methods_to_compare:
try:
item['analysis'][method]['confidence_ffont'] = compute_confidence_measure(
int(round(item['analysis'][method]['bpm'])),
item['analysis']['durations']['length_samples'],
item['analysis']['durations']['start_effective_duration'],
item['analysis']['durations']['end_effective_duration']
)
n_annotated += 1
except KeyError:
continue
print 'done! \n%i annotations done' % n_annotated
if n_annotated == 0:
print 'It looks like no instances have been annotated. Make sure that the dataset has been properly analysed.'
# +
# Now do all the plotting
for dataset in datasets:
fig, ax1 = plt.subplots(1, 1, figsize=(14, 6))
ax2 = ax1.twinx()
for count, method in enumerate(methods_to_compare):
accuracies_1e = list()
accuracies_1 = list()
accuracies_2 = list()
counts = list()
steps = np.linspace(0, 1, 60)
for conf_min in steps:
try:
filtered_data = dataset.filter_data([('analysis.%s.%s__>=' % (method, 'confidence_ffont'), conf_min)]).data
accuracies_1e.append(100 * basic_statistics(accuracy1e(filtered_data, method))['avg'])
accuracies_1.append(100 * basic_statistics(accuracy1(filtered_data, method))['avg'])
accuracies_2.append(100 * basic_statistics(accuracy2(filtered_data, method))['avg'])
counts.append(len(filtered_data))
except IndexError:
raise Exception("Unable to compute basic statistics. Make sure that there is data available...")
ax1.plot(steps, accuracies_1e, color=COLORS[count], ls="--")
ax1.plot(steps, accuracies_2, color=COLORS[count], ls="--")
ax1.fill_between(steps, accuracies_1e, accuracies_2, color=COLORS[count], alpha=0.2)
ax2.plot(steps, counts, color=COLORS[count], label=method)
print title('Confidence vs tempo estimation accuracy (%s)' % dataset.short_name)
ax1.set_ylabel('Accuracy (%)')
ax1.set_xlabel('$\gamma$')
ax2.set_ylabel('Number of instances')
ax2.legend(loc=3)
ax1.set_ylim((0, 100))
ax1.set_yticks([float(ax1.get_ylim()[1])*(float(i)/5) for i in range(0,6)])
ax2.set_ylim(0.0, ax2.get_ylim()[1])
ax2.set_yticks([float(ax2.get_ylim()[1])*(float(i)/5) for i in range(0,6)])
ax1.vlines(0.95, 0, 100, color='#999999') # 95% confidence threshold
plt.show()
figure_caption = """**Figure 3 - %s **: Accuracy vs confidence measure for %s dataset. Lower bounds of the
filled areas correspond to Accuracy 1e, while upper bounds correspond to Accuracy 2. Solid lines represent
the number of instances remaining in the dataset.
""" % (dataset.short_name, dataset.short_name)
IPython.display.display(IPython.display.Markdown(figure_caption))
# -
# ### Accuracy results for confidence > 95%, 100%
# +
# Accuracy for for confidence threshold > 95%
conf_threshold = 0.95
table_header = ['Method'] + [dataset.short_name for dataset in datasets]
table_rows = list()
for method in methods_to_compare:
table_row = list()
table_row.append(method)
for dataset in datasets:
try:
filtered_data = dataset.filter_data([('analysis.%s.%s__>=' % (method, 'confidence_ffont'), conf_threshold)]).data
min_acc = 100 * basic_statistics(accuracy1e(filtered_data, method))['avg']
max_acc = 100 * basic_statistics(accuracy2(filtered_data, method))['avg']
except IndexError:
print 'Unable to compute results for method %s and dataset %s' % (method, dataset.short_name)
table_row.append('-')
continue
table_row.append('A=%.2f - %.2f%%, N=%.0f%%' % (min_acc, max_acc, 100 * float(len(filtered_data))/len(dataset.data)))
table_rows.append(table_row)
print title('\nConfidence threshold %.2f' % conf_threshold)
print_table(table_header, table_rows)
# Accuracy for for confidence threshold = 100%
conf_threshold = 1.00
table_header = ['Method'] + [dataset.short_name for dataset in datasets]
table_rows = list()
for method in methods_to_compare:
table_row = list()
table_row.append(method)
for dataset in datasets:
try:
filtered_data = dataset.filter_data([('analysis.%s.%s__>=' % (method, 'confidence_ffont'), conf_threshold)]).data
min_acc = 100 * basic_statistics(accuracy1e(filtered_data, method))['avg']
max_acc = 100 * basic_statistics(accuracy2(filtered_data, method))['avg']
except IndexError:
print 'Unable to compute results for method %s and dataset %s' % (method, dataset.short_name)
table_row.append('-')
continue
table_row.append('A=%.2f - %.2f%%, N=%.0f%%' % (min_acc, max_acc, 100 * float(len(filtered_data))/len(dataset.data)))
table_rows.append(table_row)
print title('\nConfidence threshold %.2f' % conf_threshold)
print_table(table_header, table_rows)
# -
|
data_analysis/audiocommons_ffont/tempo_estimation/paper_notebooks/Compare Percival14 variations.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cpp
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: C++17
// language: C++17
// name: xcpp17
// ---
// # Приклад поліморфізму у *С++*
// Створимо базовий клас `Figure`, який має два віртуальних метода: `area()` та `perimeter()`
class Figure {
public:
virtual double area() {return 0.0;}
virtual double perimeter() {return 0.0;}
};
// Наслідуємо від нього клас `Rectangle`, що зберігає координати вершин прямокутника, та його довжину та ширину, та перегрузимо методи базового класу.
// Тепер метод `area()` повертає площу прямокутника за формулою: $S = a * b$
// Метод `perimeter()` відтепер повертає периметер за формулою: $P = 2(a+b)$
class Rectangle : public Figure {
public:
double ax, ay, bx, by, cx, cy, dx, dy, horizontal, vertical;
Rectangle (double ax, double ay, double cx, double cy) {
this->ax = ax;
this->ay = ay;
this->bx = ax;
this->by = cy;
this->cx = cx;
this->cy = cy;
this->dx = cx;
this->dy = ay;
this->horizontal = cx - ax;
this->vertical = cy - ay;
}
double area() {
return this->horizontal * this->vertical;
}
double perimeter() {
return 2.0 * (this->vertical + this->horizontal);
}
};
// Також наслідуємо від нього клас `Circle`, що зберігає радіус кола, та перегрузимо методи базового класу.
// Тепер метод `area()` повертає площу кола за формулою: $S = \pi r^2$
// Метод `perimeter()` відтепер повертає довжину окружності за формулою: $P = 2\pi r$
// Таким чином і проявляється поліморфізм. Одні й ті самі методи виконують різні дії, що залежать від класу, для його ці методи виконуються.
// +
#include <math.h>
class Circle : public Figure {
public:
double radius;
Circle (double radius) { this->radius = radius;}
double area() {
return M_PI * pow(this->radius, 2.0);
}
double perimeter() {
return 2.00 * M_PI * this->radius;
}
};
// -
// Маємо прямокутник наступного формату:
// 
// Ініціюємо його, обчислемо площу та периметр, виведемо ці данні.
double ax = 0.0, ay = 0.0, cx = 40.0, cy = 15.0;
Rectangle rectangle(ax, ay, cx, cy);
// **Площа:**
rectangle.area()
// **Периметр:**
rectangle.perimeter()
// Також ініціюємо коло з радіусом 18.
// Викорастаємо методи обчислення площі та периметру. Через поліморфізм обчислення пройдуть іншим чином від прямокутника.
double radius = 18.00;
Circle circle(radius);
// **Площа:**
circle.area()
// **Периметр:**
circle.perimeter()
|
Notebooks/2econd/C_PlusPlus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# from torchvision.transforms import ToTensor, Resize, Compose, CenterCrop, Normalize
# transform = Compose([
# Resize(256, interpolation=2),
# CenterCrop(224),
# ToTensor(),
# Normalize(mean=[0.485, 0.456, 0.406],
# std=[0.229, 0.224, 0.225])
# ])
# dm = ImageFolderDataModule(data_dir, 128, transform)
# dm.setup()
# logger = pl.loggers.TensorBoardLogger('tb_logs', name=modelname+'_fractalDB_imagenet_nm')
# weight_path = 'FractalDB-1000_resnet50_epoch90.pth'
# trainer = pl.Trainer(gpus=1, max_epochs=max_epochs, checkpoint_callback=False, logger=logger)
# model = CNNModule(modelname, freeze_extractor=False, num_classes=len(dm.trainset.classes), weight_path=weight_path)
# trainer.fit(model, dm);
# -
# !pip show torchvision
import torchvision
# !which python
|
nbs/_02_FractalDB_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
#
# <a href="https://hub.callysto.ca/jupyter/hub/user-redirect/git-pull?repo=https%3A%2F%2Fgithub.com%2Fcallysto%2Fshorts&branch=master&subPath=Sounds.ipynb&depth=1" target="_parent"><img src="https://raw.githubusercontent.com/callysto/curriculum-notebooks/master/open-in-callysto-button.svg?sanitize=true" width="123" height="24" alt="Open in Callysto"/></a>
# # Including music and sounds
#
# Music and sounds on a computer are stored as data files, usually with the file types .wav or .mp3. You can upload such a file onto your Jupyter hub account, and then access it with HTML code or a call to Python tools.
#
# We give four examples to show the basics of how this works.
#
# ## Example 1 - A local .wav file using html
#
# We have uploaded a short music file onto this repo, called KolnShort.wav (a clip from <NAME>'s Koln concert).
#
# A few lines of html code will create a tool on the screen, click to play.
# + language="html"
# <audio controls>
# <source src="KolnShort.wav" type="audio/wav">
# Your browser does not support the audio element.
# </audio>
# -
# ## Example 2 - A remote .wav file using html
#
# You can also access a .wav stored online, and play it. Here we grab a short clip from an online resource at Stanford.
#
# A few lines of html code will create a tool on the screen, click to play.
# + language="html"
# <audio controls>
# <source src="https://ccrma.stanford.edu/workshops/mir2014/audio/T37-vibraphone-8k.wav" type="audio/wav">
# Your browser does not support the audio element.
# </audio>
# -
# ## Example 3 - Python code to play a .wav sound
#
# We can import a tool and play the sound within Python code, avoiding the HTML magic above. It works about the same.
# +
from IPython.display import Audio ## only import once per notebook
Audio(data='KolnShort.wav')
# -
# ## Example 4 - Python code to play a remote .wav sound
#
# We can also use Python code to play a clip of sound from an online resource. It works about the same as the last example.
Audio(data='https://ccrma.stanford.edu/workshops/mir2014/audio/T37-vibraphone-8k.wav')
# If you want to dive deeper into music and sound using Python on the computer, a good resource is here: https://musicinformationretrieval.com/ipython_audio.html
# [](https://github.com/callysto/curriculum-notebooks/blob/master/LICENSE.md)
|
_sources/shorts/Sounds.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dense 3D Face Correspondence
import os
os.environ["MKL_NUM_THREADS"] = "1"
os.environ["NUMEXPR_NUM_THREADS"] = "1"
os.environ["OMP_NUM_THREADS"] = "1"
# +
import pdb
import numpy as np
import re
import time
import threading
import warnings
import cv2
import ipyvolume as ipv
import scipy
from math import cos, sin
from scipy import meshgrid, interpolate
import pdb
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.spatial import ConvexHull, Delaunay
import numpy as np
from scipy.interpolate import griddata
from collections import defaultdict
# THRESHOLDS
rho = 0.5
eigen_ratio_threshold = 5000
Kq = 10
# -
# ## Read each face data
def read_wrl(file_path):
holder = []
with open(file_path, "r") as vrml:
for line in vrml:
a = line.strip().strip(",").split()
if len(a) == 3:
try:
holder.append(list(map(float, a)))
except:
pass
x,y,z = zip(*holder)
x = np.array(x)
y = np.array(y)
z = np.array(z)
return np.array(holder)
# +
file_paths = {
"path1": "F0001/F0001_AN01WH_F3D.wrl",
"path2": "F0001/F0001_AN02WH_F3D.wrl",
"path3": "F0001/F0001_AN03WH_F3D.wrl",
"path4": "F0001/F0001_AN04WH_F3D.wrl",
"path5": "F0001/F0001_DI01WH_F3D.wrl",
"path6": "F0001/F0001_DI02WH_F3D.wrl",
"path7": "F0001/F0001_DI03WH_F3D.wrl",
"path8": "F0001/F0001_DI04WH_F3D.wrl",
"path9": "F0001/F0001_FE01WH_F3D.wrl",
"path10": "F0001/F0001_FE02WH_F3D.wrl",
"path11": "F0001/F0001_FE03WH_F3D.wrl",
"path12": "F0001/F0001_FE04WH_F3D.wrl",
}
face_points = {} # key = face+index, value = extracted face data
for i in range(1, len(file_paths)+1):
face_points["face" + str(i)] = read_wrl(file_paths["path" + str(i)])
# -
# ## Normalizing faces and Interpolation
# +
def normalize_face(points):
maxind = np.argmax(points[:,2])
nosex = points[maxind,0]
nosey = points[maxind,1]
nosez = points[maxind,2]
points = points - np.array([nosex, nosey, nosez])
# points = points / np.max(points)
return points
def points2grid(points):
x1, y1, z1 = map(np.array, zip(*points))
grid_x, grid_y = np.mgrid[np.amin(x1):np.amax(x1):0.5, np.amin(y1):np.amax(y1):0.5]
grid_z = griddata((x1, y1), z1, (grid_x, grid_y), method='linear')
return [grid_x, grid_y, grid_z]
# -
# normalizing the faces and interpolating them across a grid
grid_data = {}
for i in range(1, len(file_paths)+1):
# normalization
face_points["face" + str(i)] = normalize_face(face_points["face" + str(i)])
# grid interpolation of the face data
grid_data["face" + str(i)] = points2grid(face_points["face" + str(i)])
# hull plot
first_face_id = 3 # face id (number) to plot
second_face_id = 7
points = face_points["face" + str(first_face_id)]
points2 = face_points["face" + str(second_face_id)]
ipv.quickscatter(points[:, 0], points[:, 1], points[:, 2], size=1, marker="sphere")
ipv.scatter(points2[:, 0], points2[:, 1], points2[:, 2], size=1, marker="sphere", color="blue")
ipv.show()
# ## Plot the interpolated faces
# +
face_id = 8
ipv.clear()
grid_x, grid_y, grid_z = grid_data["face" + str(face_id)]
ipv.plot_mesh(grid_x, grid_y, grid_z, wireframe=False)
ipv.show()
# -
# ## Sparse Correspondence Initialization
# ## Seed points sampling using mean 2D convex hull
# +
def hull72(points, nosex, nosey, nosez):
newhull = [[nosex, nosey, nosez]]
for theta in range(0, 360, 5):
fx = 200 * cos(theta * np.pi / 180)
fy = 200 * sin(theta * np.pi / 180)
nearest_point = min(zip(points[:, 0], points[:, 1], points[:, 2]), key=lambda p:(p[0] - fx)**2 + (p[1] - fy)**2)
newhull.append(nearest_point)
return newhull
def get_hull(points):
maxind = np.argmax(points[:,2])
# coordinates of nose, nosex = x coordinate of nose, similarly for nosey and nosez
nosex = points[maxind,0]
nosey = points[maxind,1]
nosez = points[maxind,2]
hull = np.array(hull72(points, nosex,nosey,nosez))
return hull
hull = np.zeros([73, 3])
for i in range(1, len(file_paths)+1):
hull += get_hull(face_points["face" + str(i)])
hull = hull / len(file_paths)
# -
# ### Plot of extracted seed points
first_face_index = 7
second_face_index = 4
points1 = face_points["face" + str(first_face_index)]
points2 = face_points["face" + str(second_face_index)]
plt.figure(figsize=(8,8))
plt.scatter(points1[:,0], points1[:,1], color="red")
plt.scatter(points2[:,0], points2[:,1], color="orange")
plt.scatter(hull[:,0], hull[:,1])
maxind = np.argmax(points1[:,2])
nosex = points1[maxind,0]
nosey = points1[maxind,1]
nosez = points1[maxind,2]
plt.plot(nosex,nosey,"b")
plt.show()
# ## Delaunay Triangulation
def triangulation(hull):
points2D = np.vstack([hull[:,0],hull[:,1]]).T
tri_hull = Delaunay(points2D)
return tri_hull
tri_hull = triangulation(hull)
# +
#tri_hull = triangulation(hull)
ipv.figure()
mesh = ipv.plot_trisurf(hull[:,0], hull[:,1], hull[:,2], triangles=tri_hull.simplices, color='blue')
ipv.scatter(hull[:,0], hull[:,1], hull[:,2], marker='sphere', color='red')
ipv.show()
# -
# ## Geodesic Patch Extraction
# +
def get_all_patches_from_face(points, hull, triangles):
from itertools import combinations
patch_width = 5 * rho
def distance(x,y,z,x1,y1,z1,x2,y2,z2):
a = (y2-y1)/(x2-x1)
b = -1
c = y2-x2*(y2-y1)/(x2-x1)
return abs(a*x+b*y+c)/(a**2+b**2)**0.5
patches = []
for t1,t2 in combinations(triangles,r=2): #pairwise triangles
if len(set(t1)&set(t2))==2: #triangles with a common edge
patch = []
a_ind, b_ind = list(set(t1)&set(t2))
x1, y1, z1 = hull[a_ind,:]
x2, y2, z2 = hull[b_ind,:]
for x,y,z in points: #loop over all points to find patch points
if (x-x1/2-x2/2)**2+(y-y1/2-y2/2)**2<(x1/2-x2/2)**2+(y1/2-y2/2)**2 and distance(x,y,z,x1,y1,z1,x2,y2,z2)<patch_width:
patch.append([x,y,z])
if len(patch)==0:
#print("ALERT: NO PATCH FOR AN EDGE!!!!")
pass
patches.append(np.array(patch))
return patches
# -
def get_patches(hull, triangles):
#pdb.set_trace()
patches = defaultdict(list) # key = edges, values = a list of extracted patches from all faces along that edge
for face_index in range(1, len(file_paths)+1):
all_patches = get_all_patches_from_face(face_points["face"+str(face_index)], hull, triangles)
#print(len(all_patches))
# the patches are organised in following way because the original get_patches function was modified after the whole serial code was written
try:
for edge_index in range(len(all_patches)):
patches["edge" + str(edge_index)].append(all_patches[edge_index])
except:
pdb.set_trace()
return patches
#hull= correspondence_set
patches = get_patches(hull, tri_hull.simplices)
# randomly selecting a edge, and plotting all patches along that edge across all the faces
ipv.clear()
edge_index = np.random.choice(range(len(patches)))
edge = patches["edge" + str(edge_index)]
for i in range(len(edge)):
patch = edge[i]
ipv.scatter(patch[:,0], patch[:,1], patch[:,2], size=1, marker="sphere", color=["red", "blue", "yellow", "green"][i%4])
ipv.show()
# ## Keypoint Extraction
# takes in a point and the patch it belongs to and decides whether it is a keypoint (ratio of largest two eigenvalues on the covariance matrix of its local surface) or not
def is_keypoint(point, points):
threshold = 7 * rho
nhood = points[(np.sum(np.square(points-point),axis=1)) < threshold**2]
try:
nhood = (nhood - np.min(nhood, axis=0)) / (np.max(nhood, axis=0) - np.min(nhood, axis=0))
covmat = np.cov(nhood)
eigvals = np.sort(np.abs(np.linalg.eigvalsh(covmat)))
ratio = eigvals[-1]/(eigvals[-2]+0.0001)
return ratio>30 #eigen_ratio_threshold #/ 5
except Exception as e:
return False
# +
def get_keypoints(patches):
keypoints = {} # key = edge, value = a list of keypoints extracted from the patches along that edge across all faces
for edge_index in range(1, len(patches)+1):
edge_patches = patches["edge" + str(edge_index)]
edge_keypoints = []
for patch in edge_patches:
#print(patch.shape)
if patch.shape[0]:
patch_keypoints = patch[np.apply_along_axis(is_keypoint, 1, patch, patch)] # keypoints in `patch`
else:
patch_keypoints = []
edge_keypoints.append(patch_keypoints)
keypoints["edge" + str(edge_index)] = edge_keypoints
return keypoints
keypoints = get_keypoints(patches)
# -
# plot keypoints of a face, given the face index
face_index = 1
face_keypoints = []
for edge_index in range(1, len(keypoints)+1):
try:
face_keypoints.extend(keypoints["edge" + str(edge_index)][face_index-1])
except: # not every edge has a patch and hence keypoints, indexing an empty array will give error
pass
face_keypoints = np.array(face_keypoints)
print(face_keypoints.shape)
#print(face_keypoints)
points = face_points["face" + str(face_index)]
ipv.clear()
ipv.scatter(points[:,0], points[:,1], points[:,2], size=1, marker="sphere", color="blue")
ipv.scatter(face_keypoints[:, 0], face_keypoints[:,1], face_keypoints[:,2], size=1, marker="sphere", color="red")
ipv.show()
# ## Feature Extraction
# +
def get_normal(x, y, grid_x, grid_y, grid_z):
'''
3
1 2
4
x, y are coordinates of the point for which the normal has to be calculated
'''
i = (x - grid_x[0, 0]) / (grid_x[1, 0] - grid_x[0, 0])
j = (y - grid_y[0, 0]) / (grid_y[0, 1] - grid_y[0, 0])
i,j = int(round(i)), int(round(j))
if (not 0 <= i < grid_x.shape[0]-1) or (not 0 <= j < grid_y.shape[1]-1):
warnings.warn("out of bounds error")
#pdb.set_trace()
return "None"
point1 = (grid_x[i-1, j], grid_y[i-1, j], grid_z[i-1, j])
point2 = (grid_x[i+1, j], grid_y[i+1, j], grid_z[i+1, j])
point3 = (grid_x[i, j-1], grid_y[i, j-1], grid_z[i, j-1])
point4 = (grid_x[i, j+1], grid_y[i, j+1], grid_z[i, j+1])
a1, a2, a3 = [point2[x] - point1[x] for x in range(3)]
b1, b2, b3 = [point3[x] - point4[x] for x in range(3)]
normal = np.array([a3*b2, a1*b3, -a1*b2])
return normal/np.linalg.norm(normal)
# +
# test the get_normal function and plot
'''If this snippet throws an error, rerun it'''
def normal_plot():
face_id = 8
grid_x, grid_y, grid_z = grid_data["face" + str(face_id)]
i = np.random.choice(len(grid_x))
j = np.random.choice(len(grid_y))
x, y = grid_x[i, 0], grid_y[0, j]
print(i, j, x, y)
uvn = get_normal(x, y, grid_x, grid_y, grid_z)
ipv.clear()
ipv.plot_mesh(grid_x, grid_y, grid_z, wireframe=False)
ipv.quiver(np.array([x, ]), np.array([y,]), np.array([grid_z[i, j]]), np.array([uvn[0]]), np.array([uvn[1]]), np.array([uvn[2]]), color="blue", size=10)
ipv.show()
try:
normal_plot()
except:
normal_plot()
# -
def get_keypoint_features(keypoints, face_index):
feature_list = [] # a list to store extracted features of each keypoint
final_keypoints = [] # remove unwanted keypoints, like the ones on edges etc
for point in keypoints:
point_features = []
x, y, z = point
points = face_points["face" + str(face_index)]
grid_x, grid_y, grid_z = grid_data["face" + str(face_index)]
threshold = 5 * rho
nhood = points[(np.sum(np.square(points-point), axis=1)) < threshold**2]
xy_hu_moments = cv2.HuMoments(cv2.moments(nhood[:, :2])).flatten()
yz_hu_moments = cv2.HuMoments(cv2.moments(nhood[:, 1:])).flatten()
xz_hu_moments = cv2.HuMoments(cv2.moments(nhood[:, ::2])).flatten()
hu_moments = np.concatenate([xy_hu_moments, yz_hu_moments, xz_hu_moments])
#print(hu_moments)
#i = (x - grid_x[0, 0]) / (grid_x[1, 0] - grid_x[0, 0])
#j = (y - grid_y[0, 0]) / (grid_y[0, 1] - grid_y[0, 0])
#i, j = int(round(i)), int(round(j))
#start_i, start_j = i - int(5 * rho / (grid_x[1, 0] - grid_x[0, 0])), j - int(5 * rho / (grid_y[0, 1] - grid_y[0, 0]))
#end_i, end_j = i + int(5 * rho / (grid_x[1, 0] - grid_x[0, 0])), j + int(5 * rho / (grid_y[0, 1] - grid_y[0, 0]))
#nhood = points[start_i: end_i, start_j: end_j]
#nhood_x = grid_x[start_i:end_i, start_j:end_j]
#nhood_y = grid_y[start_i:end_i, start_j:end_j]
#nhood_z = grid_z[start_i:end_i, start_j:end_j]
normal = get_normal(x, y, grid_x, grid_y, grid_z)
if normal == "None": # array comparision raises ambiguity error, so None passed as string
continue
final_keypoints.append(point)
point_features.extend(np.array([x, y, z])) # spatial location
point_features.extend(normal)
point_features.extend(hu_moments)
point_features = np.array(point_features)
feature_list.append(point_features)
final_keypoints = np.array(final_keypoints)
return final_keypoints, feature_list
# +
def get_features(keypoints):
features = {} # key = edge + edge_index, value = list of features for each keypoint across all the faces
for edge_index in range(1, len(keypoints)+1):
edgewise_keypoint_features = [] # store features of keypoints for a given edge_index across all faces
for face_index in range(1, len(file_paths)+1):
try:
edge_keypoints = keypoints["edge" + str(edge_index)][face_index-1]
final_keypoints, keypoint_features = get_keypoint_features(edge_keypoints, face_index)
keypoints["edge" + str(edge_index)][face_index-1] = final_keypoints # update the keypoint, remove unwanted keypoints like those on the edge etc
except: # for no keypoints, no features
keypoint_features = []
edgewise_keypoint_features.append(keypoint_features)
features["edge" + str(edge_index)] = edgewise_keypoint_features
return features
features = get_features(keypoints)
# -
# ## Keypoint matching
# +
def get_keypoint_under_2rho(keypoints, point):
"""return the index of the keypoint in `keypoints` which is closest to `point` if that distance is less than 2 * rho, else return None"""
try:
distance = np.sqrt(np.sum(np.square(keypoints-point), axis=1))
if (distance < 4*rho).any():
min_dist_index = np.argmin(distance)
return min_dist_index
except Exception as e: # keypoints is [], gotta return None
pass
return None
def get_matching_keypoints(edge_keypoints, edge_features, edge_index):
# check if a bunch of keypoints across the patches (across all faces) are withing 2*rho
# first get all the keypoints in a list
matching_keypoints_list = []
for face_index1 in range(len(edge_keypoints)): # take a patch along the edge among the faces
for point_index, point in enumerate(edge_keypoints[face_index1]): # take a keypoint in that patch, we have to find corresponding keypoints in each other patche along this edge
matched_keypoint_indices = [] # to store indices of matched keypoints across the patches
for face_index2 in range(len(edge_keypoints)): # find if matching keypoints exist across the patches along that edge across all faces
if face_index2 == face_index1:
matched_keypoint_indices.append(point_index)
continue
matched_keypoint = get_keypoint_under_2rho(edge_keypoints[face_index2], point)
if matched_keypoint:
#if edge_index == 36: pdb.set_trace()I#
matched_keypoint_indices.append(matched_keypoint)
else: # no keypoint was matched in the above patch (face_index2), gotta start search on other keypoint from face_index1
break
if len(matched_keypoint_indices) == len(edge_keypoints): # there's a corresponding keypoint for each patch across all faces
matching_keypoints_list.append(matched_keypoint_indices)
if len(matching_keypoints_list) == 0:
return []
# now we have those keypoints which are in vicinity of 2*rho, let's compute euclidean distance of their feature vectors
final_matched_keypoints = []
for matched_keypoints in matching_keypoints_list: # select first list of matching keypoints
# get the indices, get their corresponding features, compute euclidean distance
try:
features = np.array([edge_features[face_index][idx] for face_index, idx in zip(range(len(edge_features)), matched_keypoints)])
euc_dist_under_kq = lambda feature, features: np.sqrt(np.sum(np.square(features - feature), axis=1)) < Kq
if np.apply_along_axis(euc_dist_under_kq, 1, features, features).all() == True:
# we have got a set of matching keypoints, get their mean coordinates
matched_coords = [edge_keypoints[face_index][idx] for face_index, idx in zip(range(len(edge_features)), matched_keypoints)]
final_matched_keypoints.append(np.mean(matched_coords, axis=0))
except:
pdb.set_trace()
return final_matched_keypoints
# +
# those keypoints which are in vicinity of 2*rho are considered for matching
# matching is done using constrained nearest neighbour
# choose an edge, select a keypoint, find out keypoints on corresponding patches on other faces within a vicinity of 2*rho,
# get euclidean distance in features among all possible pair wise combinations, if the distances come out to be less than Kp are added to the global set of correspondences
def keypoint_matching_process(keypoints, features):
final_mean_keypoints = []
for edge_index in range(1, len(keypoints)):
edge_keypoints = keypoints["edge" + str(edge_index)]
edge_features = features["edge" + str(edge_index)]
matched_keypoints = get_matching_keypoints(edge_keypoints, edge_features, edge_index)
if len(matched_keypoints) == 0:
continue
#print(matched_keypoints)
final_mean_keypoints.extend(matched_keypoints)
#final_mean_keypoints = list(set(final_mean_keypoints))
final_mean_keypoints = np.array(final_mean_keypoints)
final_mean_keypoints = np.unique(final_mean_keypoints, axis=0)
return final_mean_keypoints
final_mean_keypoints = keypoint_matching_process(keypoints, features)
#print("Iteration completed")
#print(len(final_mean_keypoints), "new keypoints found")
print(final_mean_keypoints)
# -
updated_hull = np.concatenate((hull, final_mean_keypoints), axis=0)
# +
first_face_index = 7
second_face_index = 4
points1 = face_points["face" + str(first_face_index)]
points2 = face_points["face" + str(second_face_index)]
plt.figure(figsize=(8,8))
plt.scatter(points1[:,0], points1[:,1], color="red")
plt.scatter(points2[:,0], points2[:,1], color="orange")
#plt.scatter(updated_hull[:,0], updated_hull[:,1])
plt.scatter(hull[:,0], hull[:,1])
plt.scatter(final_mean_keypoints[:, 0], final_mean_keypoints[:, 1], color="yellow")
maxind = np.argmax(points1[:,2])
nosex = points1[maxind,0]
nosey = points1[maxind,1]
nosez = points1[maxind,2]
plt.plot(nosex,nosey,"b")
plt.show()
# -
ipv.clear()
ipv.scatter(points[:,0], points[:,1], points[:,2], size=1, marker="sphere", color="blue")
ipv.scatter(final_mean_keypoints[:, 0], final_mean_keypoints[:,1], final_mean_keypoints[:,2], size=2, marker="sphere", color="red")
ipv.show()
updated_tri_hull = triangulation(updated_hull)
ipv.figure()
mesh = ipv.plot_trisurf(updated_hull[:,0], updated_hull[:,1], updated_hull[:,2], triangles=updated_tri_hull.simplices, color='blue')
ipv.scatter(updated_hull[:,0], updated_hull[:,1], updated_hull[:,2], marker='sphere', color='red')
ipv.show()
updated_patches = get_patches(updated_hull, updated_tri_hull.simplices)
num_iterations = 10
correspondence_set = hull
# +
# Start correspondence densification loop
num_iterations = 10
correspondence_set = hull
for iteration in range(num_iterations):
print("\n\nStarting iteration: ", iteration)
t1 = time.time()
print("Starting Delaunay triangulation............", end="", flush=True)
tri_hull = triangulation(correspondence_set)
print("Done | time taken: %0.4f seconds" % (time.time() - t1))
t2 = time.time()
print("Starting geodesic patch extraction............", end="", flush=True)
patches = get_patches(correspondence_set, tri_hull.simplices)
print("Done | time taken: %0.4f seconds" % (time.time() - t2))
t3 = time.time()
print("Starting keypoint extraction............", end="", flush=True)
keypoints = get_keypoints(patches)
print("Done | time taken: %0.4f seconds" % (time.time() - t3))
t4 = time.time()
print("Starting feature extraction............", end="", flush=True)
features = get_features(keypoints)
print("Done | time taken: %0.4f seconds" % (time.time() - t4))
t5 = time.time()
print("Starting keypoint matching............", end="", flush=True)
final_mean_keypoints = keypoint_matching_process(keypoints, features)
print("Done | time taken: %0.4f seconds" % (time.time() - t5))
print("Total new correspondences found: ", len(final_mean_keypoints))
print("Updating correspondence set...")
correspondence_set = np.concatenate((correspondence_set, final_mean_keypoints), axis=0)
correspondence_set = np.unique(correspondence_set, axis=0)
print("Iteration completed in %0.4f seconds" % (time.time() - t1))
# -
len(correspondence_set)
#correspondence_set
# +
tri_hull = triangulation(correspondence_set)
print("done")
print("starting geodesic patch extraction............", end="", flush=True)
patches = get_patches(correspondence_set, tri_hull.simplices)
# -
patches.keys()
ipv.clear()
face_index = 3
points = face_points["face" + str(face_index)]
ipv.scatter(points[:,0], points[:,1], points[:,2], size=1, marker="sphere", color="blue")
for key in patches.keys():
patch = patches[key][face_index-1]
if len(patch):
ipv.scatter(patch[:, 0], patch[:,1], patch[:,2], size=2, marker="sphere", color="red")
ipv.show()
updated_hull = correspondence_set
updated_tri_hull = triangulation(updated_hull)
ipv.figure()
mesh = ipv.plot_trisurf(updated_hull[:,0], updated_hull[:,1], updated_hull[:,2], triangles=updated_tri_hull.simplices, color='blue')
ipv.scatter(updated_hull[:,0], updated_hull[:,1], updated_hull[:,2], marker='sphere', color='red')
ipv.show()
|
serial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # byte handling examples
#
# * bytes()
# * bytearray()
'''
empty_bytes =bytes(4)
#print(type(empty_bytes))
#print(empty_bytes)
mutable_bytes = bytearray(empty_bytes)
#print(mutable_bytes)
mutable_bytes[0] = 255
mutable_bytes.append(255)
print(mutable_bytes)
immutable_bytes = bytes(mutable_bytes)
print(immutable_bytes)
'''
empty_bytes = bytes(4)
mutable_bytes = bytearray(empty_bytes)
mutable_bytes[0] = 1
mutable_bytes[1] = 2
mutable_bytes[2] = 3
mutable_bytes[3] = 4
pad_bytes = bytes(mutable_bytes)
bins = bytes(0)
print(bins)
print(empty_bytes + pad_bytes)
'''
print(type(empty_bytes))
print(empty_bytes[0:2])
print(empty_bytes[:2])
print(empty_bytes[2:])
print(empty_bytes + pad_bytes)
'''
# # Simple web api - I
# +
from flask import Flask, url_for
app = Flask(__name__)
@app.route('/')
def api_root():
return 'Welcome'
@app.route('/articles')
def api_articles():
return 'List of ' + url_for('api_articles')
@app.route('/articles/<articleid>')
def api_article(articleid):
return 'you are reading ' + articleid
if __name__ == '__main__':
app.run()
# -
# # Simple Web Api II
# +
from flask import json, Flask, request
app = Flask(__name__)
@app.route('/messages', methods = ['POST'])
def api_message():
if request.headers['Content-Type'] == 'text/plain':
return "Text Message: " + request.data
elif request.headers['Content-Type'] == 'application/json':
return "JSON Message: " + json.dumps(request.json)
elif request.headers['Content-Type'] == 'application/octet-stream':
f = open('./binary', 'wb')
f.write(request.data)
f.close()
return "Binary message written!"
else:
return "JSON Message: " + json.dumps(request.json)
if __name__ == '__main__':
app.run()
# -
# # More detailed Web Api
# +
from flask import Flask, jsonify, abort, make_response
from flask_restful import Resource, Api
from flask_restful import reqparse
app = Flask(__name__)
tasks = [
{
'id': 1,
'title': u'Buy groceries',
'description': u'Milk, Cheese, Pizza, Fruit, Tylenol',
'done': False
},
{
'id': 2,
'title': u'Learn Python',
'description': u'Need to find a good Python tutorial on the web',
'done': False
}
]
@app.route('/todo/api/v1.0/tasks', methods=['GET'])
def get_tasks():
return jsonify({'tasks': tasks})
@app.route('/todo/api/v1.0/tasks/<int:task_id>', methods=['GET'])
def get_task(task_id):
task = [task for task in tasks if task['id'] == task_id]
if len(task) == 0:
abort(404)
return jsonify({'task': task[0]})
@app.errorhandler(404)
def not_found(error):
return make_response(jsonify({'error': 'Not found'}), 404)
if __name__ == '__main__':
app.run(host='0.0.0.0', port=80, debug=True)
# -
# # TCP Server Example
# +
# TCP server example
import socket
server_socket = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
server_socket.bind(("", 5000))
server_socket.listen(5)
print ("TCPServer Waiting for client on port 5000")
while 1:
client_socket, address = server_socket.accept()
print ("I got a connection from ", address)
while 1:
data = input('SEND( TYPE q or Q to Quit):')
if(data == 'Q' or data == 'q'):
client_socket.send (data.encode())
client_socket.close()
break
else:
client_socket.send(data.encode())
data = client_socket.recv(512).decode()
if(data == 'q' or data == 'Q'):
client_socket.close()
break;
else:
print ("RECEIVED:" , data)
break;
server_socket.close()
print("SOCKET closed... END")
# -
# # Message Class
class message():
def parse(self, bins):
json = {}
_bytes = bytearray(bins)
'''
message_type :
1. W : PC 에서 ETN DEVICE로 Data를 보내는 의미로 'W'=0x57을 보낸다.
2. R : PC 에서 ETN DEVICE로 STATUS 정보를 보내라는 의미로 'R'=0x52을 보낸다.
3. A : ETN DEVICE에서 PC로 REQ에 대한 ACK를 보낸다는 의미로 'A'=0x41을 보낸다.
'''
if _bytes[0] == 0x57:
json["message_type"] = "W"
elif _bytes[0] == 0x52:
json["message_type"] = "R"
elif _bytes[0] == 0x41:
json["message_type"] = "A"
else:
json["message_type"] = "Unknown"
'''
sound_group :
1. 현재 설정된 Group 정보가 들어 있다
1) 0x00 : WS(5 Warning Sounds) *ETNB Product (built-in buzzer)
2) 0x01 : WP(Special 5 Warning Sounds)
3) 0x02 : WM(5 sounds of melody)
4) 0x03 : WA(5 sounds of alarm)
5) 0x04 : WB(Play buzzer sound)
'''
if _bytes[1] == 0x00:
json['sound_group'] = 'WS'
elif _bytes[1] == 0x01:
json['sound_group'] = 'WP'
elif _bytes[1] == 0x02:
json['sound_group'] = 'WM'
elif _bytes[1] == 0x03:
json['sound_group'] = 'WA'
elif _bytes[1] == 0x04:
json['sound_group'] = 'WB'
else:
json['sound_group'] = 'Unknown'
'''
[lamp common setting]
1) 0x00: LAMP OFF
2) 0x01: LAMP BLINK(ON / OFF)
3) 0x02: LAMP ON
4) Else: N / A
'''
'''
red_lamp
'''
if _bytes[2] == 0x00:
json["red_lamp"] = "blink"
elif _bytes[2] == 0x01:
json["red_lamp"] = "on"
elif _bytes[2] == 0x02:
json["red_lamp"] = "blink"
else:
json["red_lamp"] = "Unknown"
'''
yellow_lamp
'''
if _bytes[3] == 0x00:
json["yellow_lamp"] = "blink"
elif _bytes[3] == 0x01:
json["yellow_lamp"] = "on"
elif _bytes[3] == 0x02:
json["yellow_lamp"] = "blink"
else:
json["yellow_lamp"] = "Unknown"
'''
green_lamp
'''
if _bytes[4] == 0x00:
json["green_lamp"] = "blink"
elif _bytes[4] == 0x01:
json["green_lamp"] = "on"
elif _bytes[4] == 0x02:
json["green_lamp"] = "blink"
else:
json["green_lamp"] = "Unknown"
'''
blue_lamp
'''
if _bytes[5] == 0x00:
json["blue_lamp"] = "blink"
elif _bytes[5] == 0x01:
json["blue_lamp"] = "on"
elif _bytes[5] == 0x02:
json["blue_lamp"] = "blink"
else:
json["blue_lamp"] = "Unknown"
'''
white_lamp
'''
if _bytes[6] == 0x00:
json["white_lamp"] = "blink"
elif _bytes[6] == 0x01:
json["white_lamp"] = "on"
elif _bytes[6] == 0x02:
json["white_lamp"] = "blink"
else:
json["white_lamp"] = "Unknown"
json["sound_channel"] = int(_bytes[7])
return json
def generate(self, json):
_bytes = bytearray(bytes(10))
'''
message_type :
1. W : PC 에서 ETN DEVICE로 Data를 보내는 의미로 'W'=0x57을 보낸다.
2. R : PC 에서 ETN DEVICE로 STATUS 정보를 보내라는 의미로 'R'=0x52을 보낸다.
3. A : ETN DEVICE에서 PC로 REQ에 대한 ACK를 보낸다는 의미로 'A'=0x41을 보낸다.
'''
if json['message_type'] == 'W':
_bytes[0] = 0x57
elif json['message_type'] == 'R':
_bytes[0] = 0x52
elif json['message_type'] == 'A':
_bytes[0] = 0x41
else:
print('error')
'''
sound_group :
1. 현재 설정된 Group 정보가 들어 있다
1) 0x00 : WS(5 Warning Sounds) *ETNB Product (built-in buzzer)
2) 0x01 : WP(Special 5 Warning Sounds)
3) 0x02 : WM(5 sounds of melody)
4) 0x03 : WA(5 sounds of alarm)
5) 0x04 : WB(Play buzzer sound)
'''
if json['sound_group'] == 'WS':
_bytes[1] = 0x00
elif json['sound_group'] == 'WP':
_bytes[1] = 0x01
elif json['sound_group'] == 'WM':
_bytes[1] = 0x02
elif json['sound_group'] == 'WA':
_bytes[1] = 0x03
elif json['sound_group'] == 'WB':
_bytes[1] = 0x04
'''
[lamp common setting]
1) 0x00: LAMP OFF
2) 0x01: LAMP BLINK(ON / OFF)
3) 0x02: LAMP ON
4) Else: N / A
'''
'''
red_lamp
'''
if json["red_lamp"] == "on":
_bytes[2] = 0x01
elif json["red_lamp"] == "blink":
_bytes[2] = 0x02
else :
_bytes[2] = 0x00
'''
yellow_lamp
'''
if json["yellow_lamp"] == "on":
_bytes[3] = 0x01
elif json["yellow_lamp"] == "blink":
_bytes[3] = 0x02
else :
_bytes[3] = 0x00
'''
green_lamp
'''
if json["green_lamp"] == "on":
_bytes[4] = 0x01
elif json["green_lamp"] == "blink":
_bytes[4] = 0x02
else:
_bytes[4] = 0x00
'''
blue_lamp
'''
if json["blue_lamp"] == "on":
_bytes[5] = 0x01
elif json["blue_lamp"] == "blink":
_bytes[5] = 0x02
else:
_bytes[5] = 0x00
'''
white_lamp
'''
if json["white_lamp"] == 'on':
_bytes[6] = 0x01
elif json["white_lamp"] == "blink":
_bytes[6] = 0x02
else:
_bytes[6] = 0x00
_bytes[7] = json["sound_channel"]
return bytes(_bytes)
# # Socket Client Example
# +
import socket
import message
json_list = []
json = {
"message_type": "W",
"sound_group": "WP",
"red_lamp": 'blink',
"yellow_lamp": 'blink',
"green_lamp": 'on',
"blue_lamp": 'blink',
"white_lamp": 'on',
"sound_channel": 1
}
json_list.append(json)
json = {
'message_type': 'W',
'sound_group': 'WA',
'red_lamp': 'blink',
'yellow_lamp': 'blink',
'green_lamp': 'on',
'blue_lamp': 'blink',
'white_lamp': 'on',
'sound_channel': 1
}
json_list.append(json)
#message.generate(json)
msg = message.message()
bin_msg = msg.generate(json)
ip = "127.0.0.1"
port = 20000
with socket.socket(socket.AF_INET, socket.SOCK_STREAM) as s:
s.connect((ip, port))
s.send(bin_msg)
if json["message_type"] == "R" :
bins = bytes(0)
while 1:
bins += s.recv(512)
if len(bins) > 9:
json = msg.parse(bins[:10])
print(json)
break
s.close()
# -
# # Socker Server Example
# +
import socket
import message
msg = message.message()
host = '127.0.0.1'
port = 20000
with socket.socket(socket.AF_INET, socket.SOCK_STREAM) as s:
s.bind((host, port))
s.listen(5)
while 1:
client, address = s.accept()
bins = bytes(0)
while 1:
bins += client.recv(512)
if len(bins) > 9:
json = msg.parse(bins[:10])
print(json)
if json["message_type"] == "R":
json["message_type"] = "A"
client.send(msg.generate(json))
break
|
flask-web-api.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Working with imbalanced data
# In machine learning it is quite usual to have to deal with imbalanced dataset. This is particularly true in online learning for tasks such as fraud detection and spam classification. In these two cases, which are binary classification problems, there are usually many more 0s than 1s, which generally hinders the performance of the classifiers we thrown at them.
#
# As an example we'll use the credit card dataset available in `river`. We'll first use a `collections.Counter` to count the number of 0s and 1s in order to get an idea of the class balance.
# +
import collections
from river import datasets
X_y = datasets.CreditCard()
counts = collections.Counter(y for _, y in X_y)
for c, count in counts.items():
print(f'{c}: {count} ({count / sum(counts.values()):.5%})')
# -
# ## Baseline
# The dataset is quite unbalanced. For each 1 there are about 578 0s. Let's now train a logistic regression with default parameters and see how well it does. We'll measure the ROC AUC score.
# +
from river import linear_model
from river import metrics
from river import evaluate
from river import preprocessing
X_y = datasets.CreditCard()
model = (
preprocessing.StandardScaler() |
linear_model.LogisticRegression()
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# ## Importance weighting
# The performance is already quite acceptable, but as we will now see we can do even better. The first thing we can do is to add weight to the 1s by using the `weight_pos` argument of the `Log` loss function.
# +
from river import optim
model = (
preprocessing.StandardScaler() |
linear_model.LogisticRegression(
loss=optim.losses.Log(weight_pos=5)
)
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# ## Focal loss
#
# The deep learning for object detection community has produced a special loss function for imbalaced learning called [focal loss](https://arxiv.org/pdf/1708.02002.pdf). We are doing binary classification, so we can plug the binary version of focal loss into our logistic regression and see how well it fairs.
# +
model = (
preprocessing.StandardScaler() |
linear_model.LogisticRegression(loss=optim.losses.BinaryFocalLoss(2, 1))
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# ## Under-sampling the majority class
# Adding importance weights only works with gradient-based models (which includes neural networks). A more generic, and potentially more effective approach, is to use undersamplig and oversampling. As an example, we'll under-sample the stream so that our logistic regression encounter 20% of 1s and 80% of 0s. Under-sampling has the additional benefit of requiring less training steps, and thus reduces the total training time.
# +
from river import imblearn
model = (
preprocessing.StandardScaler() |
imblearn.RandomUnderSampler(
classifier=linear_model.LogisticRegression(),
desired_dist={0: .8, 1: .2},
seed=42
)
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# The `RandomUnderSampler` class is a wrapper for classifiers. This is represented by a rectangle around the logistic regression bubble when we visualize the model.
model
# ## Over-sampling the minority class
# We can also attain the same class distribution by over-sampling the minority class. This will come at cost of having to train with more samples.
# +
model = (
preprocessing.StandardScaler() |
imblearn.RandomOverSampler(
classifier=linear_model.LogisticRegression(),
desired_dist={0: .8, 1: .2},
seed=42
)
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# ## Sampling with a desired sample size
#
# The downside of both `RandomUnderSampler` and `RandomOverSampler` is that you don't have any control on the amount of data the classifier trains on. The number of samples is adjusted so that the target distribution can be attained, either by under-sampling or over-sampling. However, you can do both at the same time and choose how much data the classifier will see. To do so, we can use the `RandomSampler` class. In addition to the desired class distribution, we can specify how much data to train on. The samples will both be under-sampled and over-sampled in order to fit your constraints. This is powerful because it allows you to control both the class distribution and the size of the training data (and thus the training time). In the following example we'll set it so that the model will train with 1 percent of the data.
# +
model = (
preprocessing.StandardScaler() |
imblearn.RandomSampler(
classifier=linear_model.LogisticRegression(),
desired_dist={0: .8, 1: .2},
sampling_rate=.01,
seed=42
)
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
# -
# ## Hybrid approach
#
# As you might have guessed by now, nothing is stopping you from mixing imbalanced learning methods together. As an example, let's combine `sampling.RandomUnderSampler` and the `weight_pos` parameter from the `optim.losses.Log` loss function.
# +
model = (
preprocessing.StandardScaler() |
imblearn.RandomUnderSampler(
classifier=linear_model.LogisticRegression(
loss=optim.losses.Log(weight_pos=5)
),
desired_dist={0: .8, 1: .2},
seed=42
)
)
metric = metrics.ROCAUC()
evaluate.progressive_val_score(X_y, model, metric)
|
docs/examples/imbalanced-learning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Copyright 2020 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License"); <br>
# you may not use this file except in compliance with the License.<br>
# You may obtain a copy of the License at<br>
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.<br>
#
# See the License for the specific language governing permissions and
# limitations under the License.
import numpy as np
import json
import matplotlib.pyplot as plt
from tqdm import tqdm
import random
import subprocess
import time
import os
with open("packages_npm.txt") as file:
packages = file.read().strip().split('\n')
# +
def get_seconds(time):
min_ind = time.find('m')
mins = int(time[:min_ind])
second = float(time[min_ind + 1:-1])
return mins * 60 + second
def log(file, msg):
f = open(file, 'a+')
f.write(msg + '\n')
f.close()
# +
rates_gzip = []
rates_brotli = []
times_gzip = []
times_brotli = []
speed_gzip = []
speed_brotli = []
init_sizes = []
all_urls = []
for i in range(len(packages)):
with open("package.txt", "w") as file:
file.write(packages[i])
#delete the current node_modules directories containing previous package
result = subprocess.run(["rm", "-rf", "node_modules"])
#install the package and save the names of js scripts
result = subprocess.run(["bash", "npm_install_packages.sh"])
result = subprocess.run(["bash", "find_urls_save.sh"])
with open("urls_for_package.txt") as file:
urls = file.read().strip().split('\n')
all_urls.append(urls)
#concatenate all scripts of that package together to simulate web bundle
script_concatenated = ""
for url in all_urls[i]:
if url == "":
continue
if not os.path.exists(url):
print(i)
print("DOESN'T EXIST: ", url)
continue
with open(url) as file:
script_concatenated += file.read()
rates_gzip_compressed = []
rates_brotli_compressed = []
times_gzip_compressed = []
times_brotli_compressed = []
speed_gzip_compressed = []
speed_brotli_compressed = []
with open("example2.txt", "w") as file:
file.write(script_concatenated)
size_non_compressed = os.stat("example2.txt").st_size
init_sizes.append(size_non_compressed)
# do the gzip compression with different levels
for level in range(4, 10):
result = subprocess.run(["bash", "gzip_compress.sh", str(level), "time2.txt",
"example_gzip2.txt.gz", "example2.txt"])
with open("time2.txt") as file:
user_sys = file.read().strip().split('\n')[1:]
time = get_seconds(user_sys[0].split('\t')[1]) + get_seconds(user_sys[1].split('\t')[1])
size_gzip_compressed = os.stat("example_gzip2.txt.gz").st_size
rates_gzip_compressed.append(size_non_compressed / size_gzip_compressed)
times_gzip_compressed.append(time)
speed_gzip_compressed.append(size_non_compressed / time)
# do the brotli compression with different levels
for level in range(4, 12):
result = subprocess.run(["bash", "brotli_compress.sh", str(level), "time2.txt",
"example_brotli2.txt.br", "example2.txt"])
with open("time2.txt") as file:
user_sys = file.read().strip().split('\n')[1:]
time = get_seconds(user_sys[0].split('\t')[1]) + get_seconds(user_sys[1].split('\t')[1])
size_br_compressed = os.stat("example_brotli2.txt.br").st_size
rates_brotli_compressed.append(size_non_compressed / size_br_compressed)
times_brotli_compressed.append(time)
speed_brotli_compressed.append(size_non_compressed / time)
rates_gzip.append(rates_gzip_compressed)
rates_brotli.append(rates_brotli_compressed)
times_gzip.append(times_gzip_compressed)
times_brotli.append(times_brotli_compressed)
speed_gzip.append(speed_gzip_compressed)
speed_brotli.append(speed_brotli_compressed)
if i != 0 and i % 100 == 0:
log("logs3.txt", "rates_gzip: " + str(np.mean(rates_gzip, axis=0)))
log("logs3.txt", "rates_brotli: " + str(np.mean(rates_brotli, axis=0)))
log("logs3.txt", "times_gzip: " + str(np.mean(times_gzip, axis=0)))
log("logs3.txt", "times_brotli: " + str(np.mean(times_brotli, axis=0)))
log("logs3.txt", "speed_gzip: " + str(np.mean(speed_gzip, axis=0)))
log("logs3.txt", "speed_brotli: " + str(np.mean(speed_brotli, axis=0)))
# +
import pandas as pd
frame = pd.DataFrame()
frame["name"] = ["gzip 4", "gzip 5", "gzip 6", "gzip 7", "gzip 8", "gzip 9",
"brotli 4", "brotli 5", "brotli 6", "brotli 7", "brotli 8", "brotli 9", "brotli 10", "brotli 11"]
frame["rates"] = np.hstack((np.mean(rates_gzip, axis=0), np.mean(rates_brotli, axis=0)))
frame["savings"] = 1 - 1 / np.hstack((np.mean(rates_gzip, axis=0), np.mean(rates_brotli, axis=0)))
frame["speed(MB/s)"] = np.hstack((np.mean(speed_gzip, axis=0), np.mean(speed_brotli, axis=0))) / 1000000
frame
# -
print("non compressed size range {}MB-{}MB".format(np.min(init_sizes) / 1000000, np.max(init_sizes)/ 1000000))
|
compression_experiments/npm_packages_compression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (compiler_gym)
# language: python
# name: myenv
# ---
# + [markdown] cellView="form" colab={"base_uri": "https://localhost:8080/"} id="a0kDBAHvP7jw" outputId="f0375e07-7a6a-4a30-b7da-19f3bc02b421"
# License
#
# ```
# Copyright (c) Facebook, Inc. and its affiliates.
#
# This source code is licensed under the MIT license found in the
# LICENSE file in the root directory of this source tree.
# ```
# + [markdown] id="AidRbcu8Pwxh"
# # CompilerGym Getting Started
#
# CompilerGym is a toolkit for applying reinforcement learning to compiler optimization tasks. This document provides a short walkthrough of the key concepts, using the codesize reduction task of a production-grade compiler as an example. It will take about 20 minutes to work through. Lets get started!
# + [markdown] id="SlTQST1TT2uf"
# ## Key Concepts
#
# CompilerGym exposes compiler optimization problems as environments for reinforcement learning. It uses the [OpenAI Gym](https://gym.openai.com/) interface to expose the “agent-environment loop” of reinforcement learning:
#
# 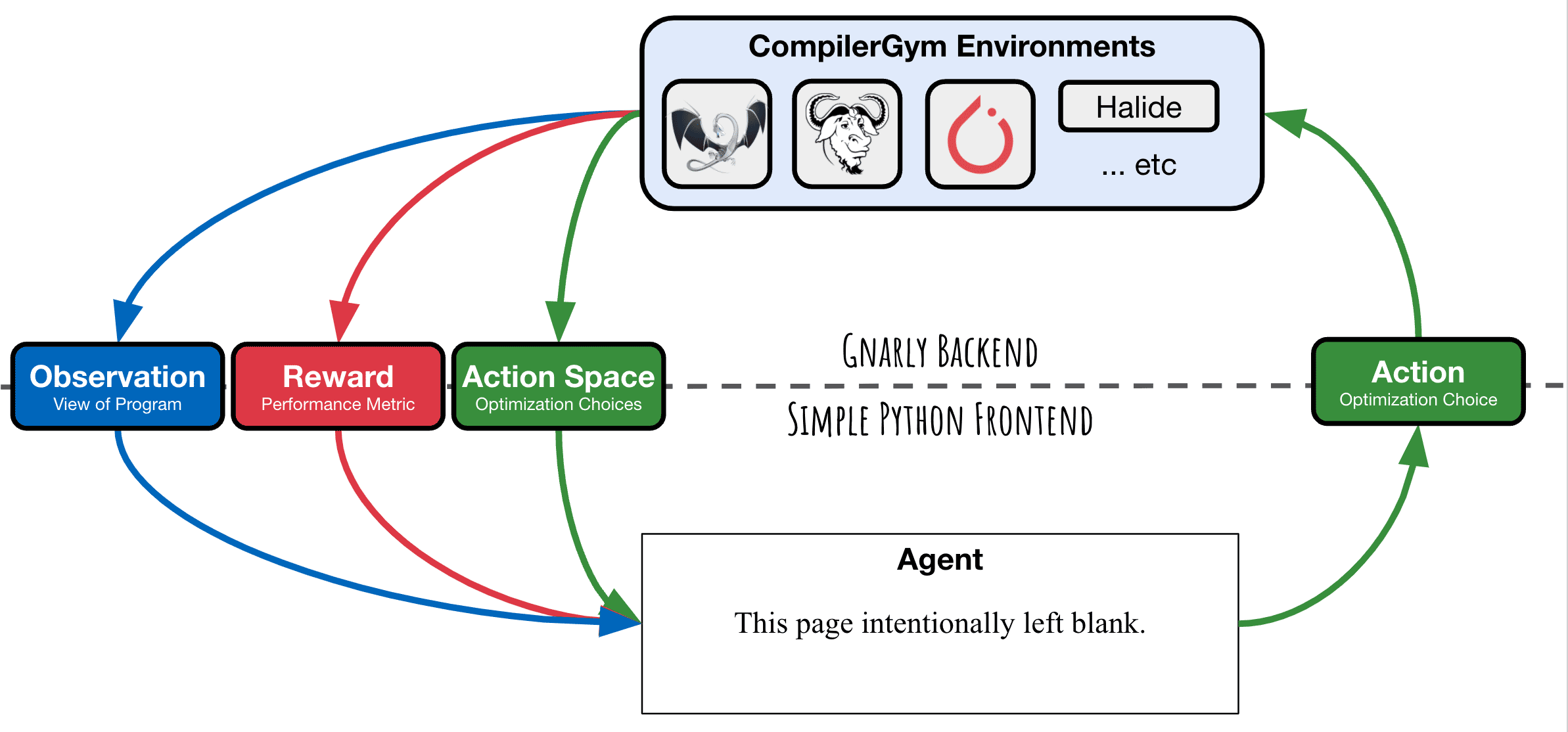
#
# The ingredients for reinforcement learning that CompilerGym provides are:
#
# * **Environment**: a compiler optimization task. For example, *optimizing a C++ graph-traversal program for codesize using LLVM*. The environment encapsulates an instance of a compiler and a particular program that is being compiled. As an agent interacts with the environment, the state of the program, and the compiler, can change.
# * **Action Space**: the actions that may be taken at the current environment state. For example, this could be a set of optimization transformations that the compiler can apply to the program.
# * **Observation**: a view of the current environment state. For example, this could be the Intermediate Representation (IR) of the program that is being compiled. The types of observations that are available depend on the compiler.
# * **Reward**: a metric indicating the quality of the previous action. For example, for a codesize optimization task this could be the change to the number of instructions of the previous action.
#
# A single instance of this “agent-environment loop” represents the compilation of a particular program. The goal is to develop an agent that maximises the cumulative reward from these environments so as to produce the best programs.
# + [markdown] id="MBiwH2xDUiy-"
# ## Installation
#
# Install the latest CompilerGym release using:
# + id="CUKVhcr2P0Ui"
# !pip install compiler_gym
# + [markdown] id="CaRZ_tt-Uqrx"
# See [Building from Source](https://github.com/facebookresearch/CompilerGym#building-from-source) for alternative installation methods.
# + [markdown] id="J6hV1NlKQdN2"
# ## Using CompilerGym
#
# To start with we import the gym module and the CompilerGym environments:
# + id="Qw0VakHSQe5J"
import gym
import compiler_gym
compiler_gym.__version__
# + [markdown] id="bXAmlDsUQ-B9"
# Importing `compiler_gym` automatically registers the compiler environments.
#
# We can see what environments are available using:
# + id="hINZesIARAXT"
compiler_gym.COMPILER_GYM_ENVS
# + [markdown] id="zKnNlIpXRAzF"
# ## Selecting an environment
#
# CompilerGym environments are named using one of the following formats:
#
# * `<compiler>-<observation>-<reward>-<version>`
# * `<compiler>-<reward>-<version>`
# * `<compiler>-<version>`
#
# Where `<compiler>` identifiers the compiler optimization task, `<observation>` is the default type of observations that are provided, and `<reward>` is the reward signal.
#
# **Note** A key concept is that CompilerGym environments enables **lazy evaluation** of observations and reward signals. This makes the environment much more computationally efficient for scenarios in which you do not need to compute a reward or observation for every step. If an environment omits a `<observation>` or `<reward>` tag, this means that no observation or reward is provided by default. See [compiler_gym.views](https://facebookresearch.github.io/CompilerGym/compiler_gym/views.html) for further details.
#
# For this tutorial, we will use the following environment:
# * **Compiler**: [LLVM](https://facebookresearch.github.io/CompilerGym/llvm/index.html)
# * **Observation Type**: [Autophase](https://facebookresearch.github.io/CompilerGym/llvm/index.html#autophase)
# * **Reward Signal**: [IR Instruction count relative to -Oz](https://facebookresearch.github.io/CompilerGym/llvm/index.html#codesize)
#
# Create an instance of this environment using:
# + id="peG5Jp_bRtTu"
env = gym.make("llvm-autophase-ic-v0")
# + [markdown] id="TXG_UcVeRufO"
# ## Installing benchmarks
#
# A compiler requires a program as input. For the purposes of CompilerGym we call these input programs *benchmarks*, and collections of benchmarks are assembled into *datasets*. You may provide your own programs to use as benchmarks, or download one of our pre-assembled datasets.
#
# The benchmarks that are available to an environment can be queried using `env.benchmarks`:
# + id="Nm2tocpER1HY"
env.benchmarks
# + [markdown] id="Cpd8uLSqR2AC"
# As you can see, there are no benchmarks installed by default. We have provided a collection of pre-assembled [LLVM benchmark datasets](https://facebookresearch.github.io/CompilerGym/llvm/index.html#datasets) that can be installed using `env.require_dataset()`. For this tutorial we will use the [NAS Parallel Benchmarks](https://www.nas.nasa.gov/publications/npb.html) dataset:
# + id="vURwmL1aSI54"
env.require_dataset("npb-v0")
# + [markdown] id="6MLbwsV_SL2W"
# Now, `env.benchmarks` lists the 123 benchmarks that comprise the dataset we just installed:
# + id="KeDzercdSOMJ"
env.benchmarks
# + [markdown] id="xwc2xlJTSPSd"
# ## The compiler environment
#
# If you have experience using [OpenAI Gym](https://gym.openai.com/), the CompilerGym environments will be familiar. If not, you can call `help()` on any function, object or method to query the documentation:
# + id="INSRF2LmSVV5"
help(env.reset)
# + [markdown] id="ci0Pc-81SWMh"
# The action space is described by `env.action_space`. The [LLVM Action Space](https://facebookresearch.github.io/CompilerGym/llvm/index.html#action-space) is discrete:
# -
env.action_space.dtype
env.action_space.n
# The observation space is described by `env.observation_space`. The [Autophase](https://facebookresearch.github.io/CompilerGym/llvm/index.html#autophase) observation space is a 56-dimension vector of integers:
env.observation_space.space.shape
env.observation_space.space.dtype
# The upper and lower bounds of the reward signal are described by `env.reward_range`:
env.reward_range
# As with other Gym environments, `reset()` must be called before a CompilerGym environment may be used:
env.reset()
# + [markdown] id="4AbDyVS2SZJ5"
# ## Interacting with the environment
#
# Once an environment has been initialized, you interact with it in the same way that you would with any other [OpenAI Gym](https://gym.openai.com/) environment. `env.render()` prints the Intermediate Representation (IR) of the program in the current state:
# + id="Ks6hQobrSi8x"
env.render()
# + [markdown] id="lFyM5PAMSgP3"
# `env.step()` runs an action:
# + id="WiS3lXSeSlQW"
observation, reward, done, info = env.step(0)
# + [markdown] id="fe4LYhV7SnWp"
# This returns four values: a new observation, a reward, a boolean value indicating whether the episode has ended, and a dictionary of additional information:
# + id="Yy1FrFQxSrf0"
observation
# + id="Z90NAUVPSsNv"
reward
# + id="9EnM69y0SsxW"
done
# + id="QI2uTajIStC9"
info
# + [markdown] id="8ZMmVE0hStV0"
# For this environment, reward represents the reduction in code size of the
# previous action, scaled to the total codesize reduction achieved with LLVM's `-Oz` optimizations enabled. A cumulative reward greater than one means that the sequence of optimizations performed yields better results than LLVM's default optimizations. Let's run 100 random actions and see how close we can get:
# + id="7p_UzcyZTRL0"
env.reset(benchmark="benchmark://npb-v0/50")
episode_reward = 0
for i in range(1, 101):
observation, reward, done, info = env.step(env.action_space.sample())
if done:
break
episode_reward += reward
print(f"Step {i}, quality={episode_reward:.2%}")
# + [markdown] id="U7CQAkTSTasn"
# Not bad, but clearly there is room for improvement! Because at each step we are taking random actions, your results will differ with every run. Try running it again. Was the result better or worse? Of course, there may be better ways of selecting actions than choosing randomly, but for the purpose of this tutorial we will leave that as an exercise for the reader :)
#
# Before we finish, lets use `env.commandline()` to produce an LLVM `opt` command line invocation that is equivalent to the sequence of actions we just run:
# + id="E2whGdgKTiSQ"
env.commandline()
# + [markdown] id="UaeTCnbZTmUe"
# We can also save the program for future reference:
# + id="_dtaMwEKTehC"
env.write_bitcode("/tmp/program.bc")
# !ls /tmp/program.bc
# + [markdown] id="uIC-ZxIeTqFH"
# Once we are finished, we must close the environment to end the compiler instance:
# + id="Atloj7dZTrVj"
env.close()
|
examples/getting-started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={"duration": 0.018154, "end_time": "2020-12-14T18:39:05.698495", "exception": false, "start_time": "2020-12-14T18:39:05.680341", "status": "completed"} tags=[]
# **This notebook is an exercise in the [Feature Engineering](https://www.kaggle.com/learn/feature-engineering) course. You can reference the tutorial at [this link](https://www.kaggle.com/matleonard/feature-generation).**
#
# ---
#
# + [markdown] papermill={"duration": 0.016788, "end_time": "2020-12-14T18:39:05.732700", "exception": false, "start_time": "2020-12-14T18:39:05.715912", "status": "completed"} tags=[]
# # Introduction
#
# In this set of exercises, you'll create new features from the existing data. Again you'll compare the score lift for each new feature compared to a baseline model. First off, run the cells below to set up a baseline dataset and model.
# + papermill={"duration": 59.581452, "end_time": "2020-12-14T18:40:05.331478", "exception": false, "start_time": "2020-12-14T18:39:05.750026", "status": "completed"} tags=[]
import numpy as np
import pandas as pd
from sklearn import preprocessing, metrics
import lightgbm as lgb
# Set up code checking
from learntools.core import binder
binder.bind(globals())
from learntools.feature_engineering.ex3 import *
# Create features from timestamps
click_data = pd.read_csv('../input/feature-engineering-data/train_sample.csv',
parse_dates=['click_time'])
click_times = click_data['click_time']
clicks = click_data.assign(day=click_times.dt.day.astype('uint8'),
hour=click_times.dt.hour.astype('uint8'),
minute=click_times.dt.minute.astype('uint8'),
second=click_times.dt.second.astype('uint8'))
# Label encoding for categorical features
cat_features = ['ip', 'app', 'device', 'os', 'channel']
for feature in cat_features:
label_encoder = preprocessing.LabelEncoder()
clicks[feature] = label_encoder.fit_transform(clicks[feature])
def get_data_splits(dataframe, valid_fraction=0.1):
dataframe = dataframe.sort_values('click_time')
valid_rows = int(len(dataframe) * valid_fraction)
train = dataframe[:-valid_rows * 2]
# valid size == test size, last two sections of the data
valid = dataframe[-valid_rows * 2:-valid_rows]
test = dataframe[-valid_rows:]
return train, valid, test
def train_model(train, valid, test=None, feature_cols=None):
if feature_cols is None:
feature_cols = train.columns.drop(['click_time', 'attributed_time',
'is_attributed'])
dtrain = lgb.Dataset(train[feature_cols], label=train['is_attributed'])
dvalid = lgb.Dataset(valid[feature_cols], label=valid['is_attributed'])
param = {'num_leaves': 64, 'objective': 'binary',
'metric': 'auc', 'seed': 7}
num_round = 1000
print("Training model. Hold on a minute to see the validation score")
bst = lgb.train(param, dtrain, num_round, valid_sets=[dvalid],
early_stopping_rounds=20, verbose_eval=False)
valid_pred = bst.predict(valid[feature_cols])
valid_score = metrics.roc_auc_score(valid['is_attributed'], valid_pred)
print(f"Validation AUC score: {valid_score}")
if test is not None:
test_pred = bst.predict(test[feature_cols])
test_score = metrics.roc_auc_score(test['is_attributed'], test_pred)
return bst, valid_score, test_score
else:
return bst, valid_score
print("Baseline model score")
train, valid, test = get_data_splits(clicks)
_ = train_model(train, valid)
# + [markdown] papermill={"duration": 0.019316, "end_time": "2020-12-14T18:40:05.375067", "exception": false, "start_time": "2020-12-14T18:40:05.355751", "status": "completed"} tags=[]
# ### 1) Add interaction features
#
# Here you'll add interaction features for each pair of categorical features (ip, app, device, os, channel). The easiest way to iterate through the pairs of features is with `itertools.combinations`. For each new column, join the values as strings with an underscore, so 13 and 47 would become `"13_47"`. As you add the new columns to the dataset, be sure to label encode the values.
# + papermill={"duration": 0.561427, "end_time": "2020-12-14T18:40:05.955742", "exception": false, "start_time": "2020-12-14T18:40:05.394315", "status": "completed"} tags=[]
import itertools
cat_features = ['ip', 'app', 'device', 'os', 'channel']
interactions = pd.DataFrame(index=clicks.index)
# Iterate through each pair of features, combine them into interaction features
for feature in cat_features:
label_encoder = preprocessing.LabelEncoder()
clicks[feature] = label_encoder.fit_transform(clicks[feature])
label_enc = LabelEncoder()
# Check your answer
q_1.check()
# + papermill={"duration": 0.02746, "end_time": "2020-12-14T18:40:06.003349", "exception": false, "start_time": "2020-12-14T18:40:05.975889", "status": "completed"} tags=[]
# Uncomment if you need some guidance
#q_1.hint()
#q_1.solution()
# + papermill={"duration": 56.681864, "end_time": "2020-12-14T18:41:02.707168", "exception": false, "start_time": "2020-12-14T18:40:06.025304", "status": "completed"} tags=[]
clicks = clicks.join(interactions)
print("Score with interactions")
train, valid, test = get_data_splits(clicks)
_ = train_model(train, valid)
# + [markdown] papermill={"duration": 0.026053, "end_time": "2020-12-14T18:41:02.760501", "exception": false, "start_time": "2020-12-14T18:41:02.734448", "status": "completed"} tags=[]
# # Generating numerical features
#
# Adding interactions is a quick way to create more categorical features from the data. It's also effective to create new numerical features, you'll typically get a lot of improvement in the model. This takes a bit of brainstorming and experimentation to find features that work well.
#
# For these exercises I'm going to have you implement functions that operate on Pandas Series. It can take multiple minutes to run these functions on the entire data set so instead I'll provide feedback by running your function on a smaller dataset.
# + [markdown] papermill={"duration": 0.021115, "end_time": "2020-12-14T18:41:02.803114", "exception": false, "start_time": "2020-12-14T18:41:02.781999", "status": "completed"} tags=[]
# ### 2) Number of events in the past six hours
#
# The first feature you'll be creating is the number of events from the same IP in the last six hours. It's likely that someone who is visiting often will download the app.
#
# Implement a function `count_past_events` that takes a Series of click times (timestamps) and returns another Series with the number of events in the last six hours. **Tip:** The `rolling` method is useful for this.
# + papermill={"duration": 0.065451, "end_time": "2020-12-14T18:41:02.890140", "exception": false, "start_time": "2020-12-14T18:41:02.824689", "status": "completed"} tags=[]
def count_past_events(series):
count_past_events
return
# Check your answer
q_2.check()
# + papermill={"duration": 0.031619, "end_time": "2020-12-14T18:41:02.944323", "exception": false, "start_time": "2020-12-14T18:41:02.912704", "status": "completed"} tags=[]
# Uncomment if you need some guidance
#q_2.hint()
#q_2.solution()
# + [markdown] papermill={"duration": 0.022206, "end_time": "2020-12-14T18:41:02.990307", "exception": false, "start_time": "2020-12-14T18:41:02.968101", "status": "completed"} tags=[]
# Because this can take a while to calculate on the full data, we'll load pre-calculated versions in the cell below to test model performance.
# + papermill={"duration": 56.490923, "end_time": "2020-12-14T18:41:59.503321", "exception": false, "start_time": "2020-12-14T18:41:03.012398", "status": "completed"} tags=[]
# Loading in from saved Parquet file
past_events = pd.read_parquet('../input/feature-engineering-data/past_6hr_events.pqt')
clicks['ip_past_6hr_counts'] = past_events
train, valid, test = get_data_splits(clicks)
_ = train_model(train, valid)
# + [markdown] papermill={"duration": 0.023724, "end_time": "2020-12-14T18:41:59.562428", "exception": false, "start_time": "2020-12-14T18:41:59.538704", "status": "completed"} tags=[]
# ### 3) Features from future information
#
# In the last exercise you created a feature that looked at past events. You could also make features that use information from events in the future. Should you use future events or not?
#
# Run the following line after you've decided your answer.
# + papermill={"duration": 0.035856, "end_time": "2020-12-14T18:41:59.621105", "exception": false, "start_time": "2020-12-14T18:41:59.585249", "status": "completed"} tags=[]
# Check your answer (Run this code cell to receive credit!)
q_3.solution()
# + [markdown] papermill={"duration": 0.024983, "end_time": "2020-12-14T18:41:59.670989", "exception": false, "start_time": "2020-12-14T18:41:59.646006", "status": "completed"} tags=[]
# ### 4) Time since last event
#
# Implement a function `time_diff` that calculates the time since the last event in seconds from a Series of timestamps. This will be ran like so:
#
# ```python
# timedeltas = clicks.groupby('ip')['click_time'].transform(time_diff)
# ```
# + papermill={"duration": 0.035193, "end_time": "2020-12-14T18:41:59.730791", "exception": false, "start_time": "2020-12-14T18:41:59.695598", "status": "completed"} tags=[]
def time_diff(series):
"""Returns a series with the time since the last timestamp in seconds."""
return series.diff().dt.total_seconds()
# Check your answer
q_4.check()
# + papermill={"duration": 0.03165, "end_time": "2020-12-14T18:41:59.787785", "exception": false, "start_time": "2020-12-14T18:41:59.756135", "status": "completed"} tags=[]
# Uncomment if you need some guidance
#q_4.hint()
#q_4.solution()
# + [markdown] papermill={"duration": 0.027922, "end_time": "2020-12-14T18:41:59.841907", "exception": false, "start_time": "2020-12-14T18:41:59.813985", "status": "completed"} tags=[]
# We'll again load pre-computed versions of the data, which match what your function would return
# + papermill={"duration": 56.745327, "end_time": "2020-12-14T18:42:56.614135", "exception": false, "start_time": "2020-12-14T18:41:59.868808", "status": "completed"} tags=[]
# Loading in from saved Parquet file
past_events = pd.read_parquet('../input/feature-engineering-data/time_deltas.pqt')
clicks['past_events_6hr'] = past_events
train, valid, test = get_data_splits(clicks.join(past_events))
_ = train_model(train, valid)
# + [markdown] papermill={"duration": 0.03156, "end_time": "2020-12-14T18:42:56.682788", "exception": false, "start_time": "2020-12-14T18:42:56.651228", "status": "completed"} tags=[]
# ### 5) Number of previous app downloads
#
# It's likely that if a visitor downloaded an app previously, it'll affect the likelihood they'll download one again. Implement a function `previous_attributions` that returns a Series with the number of times an app has been downloaded (`'is_attributed' == 1`) before the current event.
# + papermill={"duration": 0.11464, "end_time": "2020-12-14T18:42:56.824434", "exception": false, "start_time": "2020-12-14T18:42:56.709794", "status": "completed"} tags=[]
def previous_attributions(series):
"""Returns a series with the number of times an app has been downloaded."""
return series.expanding(min_periods=2).sum() - series
# Check your answer
q_5.check()
# + papermill={"duration": 0.035979, "end_time": "2020-12-14T18:42:56.888156", "exception": false, "start_time": "2020-12-14T18:42:56.852177", "status": "completed"} tags=[]
# Uncomment if you need some guidance
#q_5.hint()
#q_5.solution()
# + [markdown] papermill={"duration": 0.028717, "end_time": "2020-12-14T18:42:56.944270", "exception": false, "start_time": "2020-12-14T18:42:56.915553", "status": "completed"} tags=[]
# Again loading pre-computed data.
# + papermill={"duration": 50.275938, "end_time": "2020-12-14T18:43:47.251967", "exception": false, "start_time": "2020-12-14T18:42:56.976029", "status": "completed"} tags=[]
# Loading in from saved Parquet file
past_events = pd.read_parquet('../input/feature-engineering-data/downloads.pqt')
clicks['ip_past_6hr_counts'] = past_events
train, valid, test = get_data_splits(clicks)
_ = train_model(train, valid)
# + [markdown] papermill={"duration": 0.03146, "end_time": "2020-12-14T18:43:47.322220", "exception": false, "start_time": "2020-12-14T18:43:47.290760", "status": "completed"} tags=[]
# ### 6) Tree-based vs Neural Network Models
#
# So far we've been using LightGBM, a tree-based model. Would these features we've generated work well for neural networks as well as tree-based models?
#
# Run the following line after you've decided your answer.
# + papermill={"duration": 0.040144, "end_time": "2020-12-14T18:43:47.390820", "exception": false, "start_time": "2020-12-14T18:43:47.350676", "status": "completed"} tags=[]
# Check your answer (Run this code cell to receive credit!)
q_6.solution()
# + [markdown] papermill={"duration": 0.029313, "end_time": "2020-12-14T18:43:47.451351", "exception": false, "start_time": "2020-12-14T18:43:47.422038", "status": "completed"} tags=[]
# Now that you've generated a bunch of different features, you'll typically want to remove some of them to reduce the size of the model and potentially improve the performance. Next, I'll show you how to do feature selection using a few different methods such as L1 regression and Boruta.
# + [markdown] papermill={"duration": 0.029167, "end_time": "2020-12-14T18:43:47.510253", "exception": false, "start_time": "2020-12-14T18:43:47.481086", "status": "completed"} tags=[]
# # Keep Going
#
# You know how to generate a lot of features. In practice, you'll frequently want to pare them down for modeling. Learn to do that in the **[Feature Selection lesson](https://www.kaggle.com/matleonard/feature-selection)**.
# + [markdown] papermill={"duration": 0.029226, "end_time": "2020-12-14T18:43:47.569116", "exception": false, "start_time": "2020-12-14T18:43:47.539890", "status": "completed"} tags=[]
# ---
#
#
#
#
# *Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161443) to chat with other Learners.*
|
feature engg/exercise-feature-generation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Fk1jFUCTqfSq"
# ## টোকেনাইজেশন, অক্ষরগুলোকে সংখ্যায় আনছি ইউনিকোডে
# + [markdown] id="xILcGW6Tqdii"
#
# + colab={"base_uri": "https://localhost:8080/"} id="GutWj_UHqbJi" outputId="d17148b9-f773-4289-cc2b-1ff478e7da7f"
c= '\u0980'
ord('আ') #use Order Function()
# + colab={"base_uri": "https://localhost:8080/"} id="ayF8icZerHYR" outputId="5bba10e5-d133-4a84-c792-ca9540d5b42f"
print(c)
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="w1-S8ATdrgKI" outputId="81a61ef9-fdc6-4c4c-94f5-0f17c7c096f1"
chr(2495) #chr() method returns a character (a string) from an integer (represents unicode code point of the character)
# + colab={"base_uri": "https://localhost:8080/"} id="6Dx65XlNr7tP" outputId="f45937c3-9b64-412a-e51a-fea0afdca134"
print(ord('ক'))
print(ord('ল'))
print(ord('স'))
print(ord(' '))
# + [markdown] id="zG0JzJG2tALq"
#
# + [markdown] id="GQxqJf9rtCjY"
# ধরুন আমরা একটা শব্দ বলছি কলস, এর মধ্যে তিনটা অক্ষর আছে, যাকে আলাদা করে ইউনিকোড পয়েন্ট কোড হচ্ছে নিচের লাইনে।
# + colab={"base_uri": "https://localhost:8080/"} id="takUDFjdtEeE" outputId="3cd83937-5cd4-4c18-b1c4-b315f4049990"
import numpy as np
np.array([ord(char) for char in u"কলস"])
# + colab={"base_uri": "https://localhost:8080/"} id="jcz5gs1NtbT0" outputId="6958c8fe-fdfc-47fb-8ed9-2e2aeb6610e5"
np.array([ord(char) for char in "কলস"])
# + colab={"base_uri": "https://localhost:8080/"} id="A5JRHIKStnF3" outputId="8a5a795d-8e31-4406-89d9-fb40d3b228ff"
import tensorflow as tf
tf.strings.unicode_decode("সকল", input_encoding='UTF-8')
# + colab={"base_uri": "https://localhost:8080/"} id="shTmJe8eymhs" outputId="eb662d6a-e97c-4ef9-a43b-cafc5efdb099"
tf.strings.unicode_decode('আমি ভালবাসি বই পড়তে', 'UTF-8')
# + colab={"base_uri": "https://localhost:8080/"} id="vGcGBEwK04l9" outputId="426fc2eb-a3a2-4050-ceaf-bbf5cbf636d9"
from tensorflow.keras.preprocessing.text import Tokenizer
sentences = [
'আমি ভালবাসি বই পড়তে।'
]
tokenizer = Tokenizer(num_words= 10, filters='!।')
print(tokenizer)
# + id="ZkiHUfrl2X2_"
# tokenizer.fit_on_sequences(sentences)
# word_index = tokenizer.word_index
# print(word_index)
# + colab={"base_uri": "https://localhost:8080/"} id="J6xoNYLN3Rr_" outputId="20db649a-be7c-42bd-96d5-df33d3331c7f"
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
print(word_index)
# + colab={"base_uri": "https://localhost:8080/"} id="qaOF8TBv3jO2" outputId="d64df87e-d429-47a8-ceaf-47190d065792"
tokenizer.num_words
# + id="jUXen-NC31lu"
sentences = [
'আমি ভালবাসি বই পড়তে।',
'আমি ভালবাসি বই লিখতে!'
]
# + colab={"base_uri": "https://localhost:8080/"} id="gIsXxKrq38Mu" outputId="117c6d0a-c5a0-4b05-8349-90ab984a7ba5"
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
print(word_index)
# + colab={"base_uri": "https://localhost:8080/"} id="if5Mwjcx4gC1" outputId="f2e1a0c4-9fe2-43b8-9d06-c66bb83c566d"
tokenizer.word_counts
# + [markdown] id="5D0yQAX_8lG7"
# ## tokenizer এর ভেতরের কনফিগারেশন
#
# + id="QQcZOTbp4yud" colab={"base_uri": "https://localhost:8080/"} outputId="dcf54704-3722-4b94-f858-b52f44ef45cc"
tokenizer.get_config()
# + [markdown] id="jPaAZtBn8hzM"
#
|
NLP_tokenization_unicodeBaki.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Load libraries
# !pip install -q -r requirements.txt
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import sys
import os
import numpy as np
import pandas as pd
from PIL import Image
import torch
import torch.nn as nn
import torch.utils.data as D
from torch.optim.lr_scheduler import ExponentialLR
import torch.nn.functional as F
from torch.autograd import Variable
from torchvision import transforms
from ignite.engine import Events
from scripts.ignite import create_supervised_evaluator, create_supervised_trainer
from ignite.metrics import Loss, Accuracy
from ignite.contrib.handlers.tqdm_logger import ProgressBar
from ignite.handlers import EarlyStopping, ModelCheckpoint
from ignite.contrib.handlers import LinearCyclicalScheduler, CosineAnnealingScheduler
from tqdm import tqdm_notebook
from sklearn.model_selection import train_test_split
from efficientnet_pytorch import EfficientNet
from scripts.evaluate import eval_model
import warnings
warnings.filterwarnings('ignore')
# -
# ## Define dataset and model
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
img_dir = '../input/rxrxairgb512'
path_data = '../input/rxrxaicsv'
device = 'cuda'
batch_size = 8
torch.manual_seed(0)
model_name = 'efficientnet-b3'
# -
jitter = (0.6, 1.4)
class ImagesDS(D.Dataset):
# taken textbook from https://arxiv.org/pdf/1812.01187.pdf
transform_train = transforms.Compose([
transforms.RandomResizedCrop(448),
transforms.ColorJitter(brightness=jitter, contrast=jitter, saturation=jitter, hue=.1),
transforms.RandomHorizontalFlip(p=0.5),
# PCA Noise should go here,
transforms.ToTensor(),
transforms.Normalize(mean=(123.68, 116.779, 103.939), std=(58.393, 57.12, 57.375))
])
transform_validation = transforms.Compose([
transforms.CenterCrop(448),
transforms.ToTensor(),
transforms.Normalize(mean=(123.68, 116.779, 103.939), std=(58.393, 57.12, 57.375))
])
def __init__(self, df, img_dir=img_dir, mode='train', validation=False, site=1):
self.records = df.to_records(index=False)
self.site = site
self.mode = mode
self.img_dir = img_dir
self.len = df.shape[0]
self.validation = validation
@staticmethod
def _load_img_as_tensor(file_name, validation):
with Image.open(file_name) as img:
if not validation:
return ImagesDS.transform_train(img)
else:
return ImagesDS.transform_validation(img)
def _get_img_path(self, index, site=1):
experiment, well, plate = self.records[index].experiment, self.records[index].well, self.records[index].plate
return f'{self.img_dir}/{self.mode}/{experiment}_{plate}_{well}_s{site}.jpeg'
def __getitem__(self, index):
img1, img2 = [self._load_img_as_tensor(self._get_img_path(index, site), self.validation) for site in [1,2]]
if self.mode == 'train':
return img1, img2, int(self.records[index].sirna)
else:
return img1, img2, self.records[index].id_code
def __len__(self):
return self.len
# dataframes for training, cross-validation, and testing
df_test = pd.read_csv(path_data+'/test.csv')
ds_test = ImagesDS(df_test, mode='test', validation=True)
tloader = D.DataLoader(ds_test, batch_size=1, shuffle=False, num_workers=4)
# +
class EfficientNetTwoInputs(nn.Module):
def __init__(self):
super(EfficientNetTwoInputs, self).__init__()
self.classes = 1108
model = model = EfficientNet.from_pretrained(model_name, num_classes=1108)
num_ftrs = model._fc.in_features
model._fc = nn.Identity()
self.resnet = model
self.fc = nn.Linear(num_ftrs * 2, self.classes)
def forward(self, x1, x2):
x1_out = self.resnet(x1)
x2_out = self.resnet(x2)
N, _, _, _ = x1.size()
x1_out = x1_out.view(N, -1)
x2_out = x2_out.view(N, -1)
out = torch.cat((x1_out, x2_out), 1)
out = self.fc(out)
return out
model = EfficientNetTwoInputs()
model.load_state_dict(torch.load('models/Model_efficientnet-b3_93.pth'))
model.cuda()
# -
with torch.no_grad():
preds = []
for x1, x2, _ in tqdm_notebook(tloader):
x1 = x1.to(device)
x2 = x2.to(device)
output = model(x1,x2)
idx = output.cpu().numpy()
preds.append(idx[0])
# #### Evaluate
plate_groups = np.zeros((1108,4), int)
for sirna in range(1108):
grp = df.loc[df.sirna==sirna,:].plate.value_counts().index.values
assert len(grp) == 3
plate_groups[sirna,0:3] = grp
plate_groups[sirna,3] = 10 - grp.sum()
# +
all_test_exp = df_test.experiment.unique()
sub = pd.read_csv("./submission (13).csv")
group_plate_probs = np.zeros((len(all_test_exp),4))
for idx in range(len(all_test_exp)):
preds = sub.loc[df_test.experiment == all_test_exp[idx],'sirna'].values
pp_mult = np.zeros((len(preds),1108))
pp_mult[range(len(preds)),preds] = 1
sub_test = df_test.loc[df_test.experiment == all_test_exp[idx],:]
assert len(pp_mult) == len(sub_test)
for j in range(4):
mask = np.repeat(plate_groups[np.newaxis, :, j], len(pp_mult), axis=0) == \
np.repeat(sub_test.plate.values[:, np.newaxis], 1108, axis=1)
group_plate_probs[idx,j] = np.array(pp_mult)[mask].sum()/len(pp_mult)
# -
pd.DataFrame(group_plate_probs, index = all_test_exp)
exp_to_group = group_plate_probs.argmax(1)
with torch.no_grad():
preds = []
for x1, x2, _ in tqdm_notebook(tloader):
x1 = x1.to(device)
x2 = x2.to(device)
output = model(x1,x2)
idx = output.cpu().numpy()
preds.append(idx[0])
pre_preds = np.stack(preds).squeeze()
def select_plate_group(pp_mult, idx):
sub_test = df_test.loc[df_test.experiment == all_test_exp[idx],:]
assert len(pp_mult) == len(sub_test)
mask = np.repeat(plate_groups[np.newaxis, :, exp_to_group[idx]], len(pp_mult), axis=0) != \
np.repeat(sub_test.plate.values[:, np.newaxis], 1108, axis=1)
pp_mult[mask] = 0
return pp_mult
for idx in range(len(all_test_exp)):
indices = (df_test.experiment == all_test_exp[idx])
final_preds = pre_preds[indices,:].copy()
final_preds = select_plate_group(final_preds, idx)
sub.loc[indices,'sirna'] = final_preds.argmax(1)
(sub.sirna == pd.read_csv("./submission (13).csv").sirna).mean()
sub.to_csv('./submission_w_leak.csv', index=False, columns=['id_code','sirna'])
|
my_notebooks/plates_leak.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# name: python2
# ---
# + [markdown] id="copyright-notice" colab_type="text"
# #### Copyright 2017 Google LLC.
# + cellView="both" colab={"autoexec": {"wait_interval": 0, "startup": false}} id="copyright-notice2" colab_type="code"
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="4f3CKqFUqL2-" colab_type="text" slideshow={"slide_type": "slide"}
# # Premiers pas avec TensorFlow
# + [markdown] id="Bd2Zkk1LE2Zr" colab_type="text"
# **Objectifs d'apprentissage :**
# * Concepts fondamentaux de TensorFlow
# * Utiliser la classe `LinearRegressor` de TensorFlow pour prédire le prix médian des logements, au niveau des îlots urbains, sur la base d'une seule caractéristique d'entrée
# * Évaluer la justesse des prédictions d'un modèle en utilisant la racine carrée de l'erreur quadratique moyenne (Root Mean Squared Error, RMSE)
# * Améliorer la justesse d'un modèle en modifiant ses hyperparamètres
# + [markdown] id="MxiIKhP4E2Zr" colab_type="text"
# Les données sont basées sur le recensement de 1990 de l'État de Californie.
# + [markdown] id="6TjLjL9IU80G" colab_type="text"
# ## Configuration
# Dans cette première cellule, vous allez charger les bibliothèques nécessaires.
# + id="rVFf5asKE2Zt" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
from __future__ import print_function
import math
from IPython import display
from matplotlib import cm
from matplotlib import gridspec
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from sklearn import metrics
import tensorflow as tf
from tensorflow.python.data import Dataset
tf.logging.set_verbosity(tf.logging.ERROR)
pd.options.display.max_rows = 10
pd.options.display.float_format = '{:.1f}'.format
# + [markdown] id="ipRyUHjhU80Q" colab_type="text"
# Vous allez ensuite charger votre ensemble de données.
# + id="9ivCDWnwE2Zx" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
california_housing_dataframe = pd.read_csv("https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv", sep=",")
# + [markdown] id="vVk_qlG6U80j" colab_type="text"
# Vous allez mélanger les données de manière aléatoire, pour être sûr d'éviter les effets de classement pathologique pouvant nuire aux performances de la descente de gradient stochastique. Vous allez, en outre, mettre à l'échelle la valeur `median_house_value` pour qu'elle soit exprimée en milliers, de sorte que son apprentissage soit un peu plus facile avec des taux dans l'intervalle utilisé généralement.
# + id="r0eVyguIU80m" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
california_housing_dataframe = california_housing_dataframe.reindex(
np.random.permutation(california_housing_dataframe.index))
california_housing_dataframe["median_house_value"] /= 1000.0
california_housing_dataframe
# + [markdown] id="HzzlSs3PtTmt" colab_type="text" slideshow={"slide_type": "-"}
# ## Analyse des données
#
# Il est conseillé de se familiariser avec les données avant de les exploiter.
#
# Nous allons imprimer un bref résumé de quelques statistiques utiles sur chaque colonne : nombre d'exemples, moyenne, écart type, maximum, minimum et divers quantiles.
# + id="gzb10yoVrydW" colab_type="code" slideshow={"slide_type": "slide"} colab={"autoexec": {"startup": false, "wait_interval": 0}, "test": {"output": "ignore", "timeout": 600}} cellView="both"
california_housing_dataframe.describe()
# + [markdown] id="Lr6wYl2bt2Ep" colab_type="text" slideshow={"slide_type": "-"}
# ## Construction du premier modèle
#
# Dans cet exercice, vous allez essayer de prédire la valeur médiane d'un logement (`median_house_value`) qui deviendra l'étiquette (que l'on désigne parfois également sous le nom de cible). Vous utiliserez le nombre de pièces (`total_rooms`) comme caractéristique d'entrée.
#
# **REMARQUE :** Les données se situent au niveau de l'îlot urbain. Cette caractéristique représente donc le nombre total de pièces dans cet îlot.
#
# Pour entraîner le modèle, vous allez utiliser l'interface [LinearRegressor](https://www.tensorflow.org/api_docs/python/tf/estimator/LinearRegressor) fournie par l'API [Estimator](https://www.tensorflow.org/get_started/estimator) de TensorFlow. Cette API s'occupe d'une bonne partie des mécanismes sous-jacents du modèle de bas niveau, et propose des méthodes pratiques pour effectuer les tâches d'apprentissage du modèle, d'évaluation et d'inférence.
# + [markdown] id="0cpcsieFhsNI" colab_type="text"
# ### Étape 1 : Définir les caractéristiques et configurer les colonnes de caractéristiques
# + [markdown] id="EL8-9d4ZJNR7" colab_type="text"
# Pour qu'il soit possible d'importer les données d'apprentissage dans TensorFlow, vous devez spécifier le type de données qui se trouve dans chaque caractéristique. Vous utiliserez principalement deux types de données pour cet exercice et les suivants :
#
# * **Données catégorielles** : il s'agit de données textuelles. L'ensemble de données immobilières utilisé dans cet exercice ne contient aucune caractéristique catégorielle. Ce type de données pourrait être le style de logement, le contenu d'une annonce immobilière…
#
# * **Données numériques** : données représentant un nombre (entier ou à virgule flottante) et que vous souhaitez traiter comme tel. Comme nous le verrons par la suite, vous pouvez, dans certains cas, traiter des données numériques (un code postal, par exemple), comme si elles étaient de type catégoriel.
#
# Dans TensorFlow, le type de données d'une caractéristique est indiqué à l'aide d'une construction appelée **colonne de caractéristiques**. Les colonnes de ce type ne stockent qu'une description des données de la caractéristique ; elles ne contiennent pas les données proprement dites.
#
# Dans un premier temps, vous allez simplement utiliser une caractéristique d'entrée numérique, `total_rooms`. Le code suivant extrait les données `total_rooms` de l'ensemble `california_housing_dataframe` et définit la colonne de caractéristiques à l'aide de `numeric_column`, qui précise que ses données sont numériques :
# + id="rhEbFCZ86cDZ" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
# Define the input feature: total_rooms.
my_feature = california_housing_dataframe[["total_rooms"]]
# Configure a numeric feature column for total_rooms.
feature_columns = [tf.feature_column.numeric_column("total_rooms")]
# + [markdown] id="K_3S8teX7Rd2" colab_type="text"
# **REMARQUE :** Les données `total_rooms` se présentent sous la forme d'un tableau à une seule dimension (une liste du nombre total de pièces pour chaque îlot urbain). Il s'agit de la forme par défaut pour `numeric_column`. Par conséquent, elle ne doit pas être transmise en tant qu'argument.
# + [markdown] id="UMl3qrU5MGV6" colab_type="text"
# ### Étape 2 : Définir la cible
# + [markdown] id="cw4nrfcB7kyk" colab_type="text"
# Vous allez ensuite définir la cible, à savoir la valeur médiane d'un logement (`median_house_value`). Ici encore, vous pouvez extraire cette donnée de l'ensemble `california_housing_dataframe` :
# + id="l1NvvNkH8Kbt" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
# Define the label.
targets = california_housing_dataframe["median_house_value"]
# + [markdown] id="4M-rTFHL2UkA" colab_type="text"
# ### Étape 3 : Configurer la classe LinearRegressor
# + [markdown] id="fUfGQUNp7jdL" colab_type="text"
# Vous allez ensuite configurer un modèle de régression linéaire à l'aide de LinearRegressor. Vous allez entraîner ce modèle à l'aide de `GradientDescentOptimizer`, qui met en œuvre une descente de gradient stochastique par mini-lots. L'argument `learning_rate` détermine la taille du pas de gradient.
#
# **REMARQUE :** Par mesure de précaution, un [bornement de la norme du gradient] (https://developers.google.com/machine-learning/glossary/#gradient_clipping) est également appliqué à l'optimiseur via `clip_gradients_by_norm`. Le bornement de la norme du gradient permet de s'assurer que la magnitude des gradients reste dans des limites acceptables au cours de l'apprentissage, sans quoi la descente de gradient risque d'échouer.
# + id="ubhtW-NGU802" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
# Use gradient descent as the optimizer for training the model.
my_optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.0000001)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
# Configure the linear regression model with our feature columns and optimizer.
# Set a learning rate of 0.0000001 for Gradient Descent.
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# + [markdown] id="-0IztwdK2f3F" colab_type="text"
# ### Étape 4 : Définir la fonction d'entrée
# + [markdown] id="S5M5j6xSCHxx" colab_type="text"
# Pour importer les données immobilières de l'État de Californie dans `LinearRegressor`, une fonction d'entrée doit être définie. Cette fonction indique non seulement à TensorFlow comment effectuer le prétraitement des données, mais aussi comment les mettre en lots, les lire en mode aléatoire et les répéter pendant l'entraînement du modèle.
#
# Vous allez, tout d'abord, convertir les données de la caractéristique *pandas* en un dictionnaire de tableaux NumPy. Vous pourrez ensuite utiliser l'[API Dataset] (https://www.tensorflow.org/programmers_guide/datasets) de TensorFlow pour construire un objet d'ensemble de données à partir de ces données, puis scinder ces dernières dans des lots de `batch_size`, de sorte qu'elles soient répétées pour le nombre indiqué d'itérations (num_epochs).
#
# **REMARQUE :** Lorsque la valeur par défaut de `num_epochs=None` est transmise à `repeat()`, les données d'entrée sont répétées indéfiniment.
#
# Ensuite, si `shuffle` est défini sur `True`, les données seront lues de manière aléatoire, de façon à être transmises aléatoirement au modèle au cours de l'apprentissage. L'argument `buffer_size` indique la taille de l'ensemble de données à partir duquel `shuffle` sera échantillonné de manière aléatoire.
#
# Pour terminer, la fonction d'entrée construit un itérateur pour l'ensemble de données et renvoie le lot de données suivant à LinearRegressor.
# + id="RKZ9zNcHJtwc" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
def my_input_fn(features, targets, batch_size=1, shuffle=True, num_epochs=None):
"""Trains a linear regression model of one feature.
Args:
features: pandas DataFrame of features
targets: pandas DataFrame of targets
batch_size: Size of batches to be passed to the model
shuffle: True or False. Whether to shuffle the data.
num_epochs: Number of epochs for which data should be repeated. None = repeat indefinitely
Returns:
Tuple of (features, labels) for next data batch
"""
# Convert pandas data into a dict of np arrays.
features = {key:np.array(value) for key,value in dict(features).items()}
# Construct a dataset, and configure batching/repeating.
ds = Dataset.from_tensor_slices((features,targets)) # warning: 2GB limit
ds = ds.batch(batch_size).repeat(num_epochs)
# Shuffle the data, if specified.
if shuffle:
ds = ds.shuffle(buffer_size=10000)
# Return the next batch of data.
features, labels = ds.make_one_shot_iterator().get_next()
return features, labels
# + [markdown] id="wwa6UeA1V5F_" colab_type="text"
# **REMARQUE :** Vous continuerez à utiliser cette fonction d'entrée dans les prochains exercices. Pour en savoir plus sur les fonctions d'entrée et l'API `Dataset`, consultez le [Guide du programmeur de TensorFlow] (en anglais) (https://www.tensorflow.org/programmers_guide/datasets).
# + [markdown] id="4YS50CQb2ooO" colab_type="text"
# ### Étape 5 : Entraîner le modèle
# + [markdown] id="yP92XkzhU803" colab_type="text"
# Vous pouvez maintenant appeler `train()` sur `linear_regressor` pour entraîner le modèle. Vous allez encapsuler `my_input_fn` dans un `lambda`
# afin de pouvoir transmettre `my_feature` et `target` comme arguments (pour en savoir plus, reportez-vous à ce [didacticiel sur la fonction d'entrée TensorFlow](https://www.tensorflow.org/get_started/input_fn#passing_input_fn_data_to_your_model)). Pour commencer, vous allez effectuer
# l'apprentissage pour 100 pas.
# + id="5M-Kt6w8U803" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
_ = linear_regressor.train(
input_fn = lambda:my_input_fn(my_feature, targets),
steps=100
)
# + [markdown] id="7Nwxqxlx2sOv" colab_type="text"
# ### Étape 6 : Évaluer le modèle
# + [markdown] id="KoDaF2dlJQG5" colab_type="text"
# Vous allez faire des prédictions sur les données d'apprentissage afin de déterminer dans quelle mesure elles sont adaptées à votre modèle au cours de l'apprentissage.
#
# **REMARQUE :** L'erreur d'apprentissage mesure à quel point votre modèle est adapté aux données d'apprentissage. En revanche, elle ne mesure **_pas_** la qualité de **_généralisation du modèle aux nouvelles données_**. Au cours des prochains exercices, vous examinerez comment scinder les données afin d'évaluer la capacité de généralisation de votre modèle.
#
# + id="pDIxp6vcU809" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
# Create an input function for predictions.
# Note: Since we're making just one prediction for each example, we don't
# need to repeat or shuffle the data here.
prediction_input_fn =lambda: my_input_fn(my_feature, targets, num_epochs=1, shuffle=False)
# Call predict() on the linear_regressor to make predictions.
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
# Format predictions as a NumPy array, so we can calculate error metrics.
predictions = np.array([item['predictions'][0] for item in predictions])
# Print Mean Squared Error and Root Mean Squared Error.
mean_squared_error = metrics.mean_squared_error(predictions, targets)
root_mean_squared_error = math.sqrt(mean_squared_error)
print("Mean Squared Error (on training data): %0.3f" % mean_squared_error)
print("Root Mean Squared Error (on training data): %0.3f" % root_mean_squared_error)
# + [markdown] id="AKWstXXPzOVz" colab_type="text" slideshow={"slide_type": "slide"}
# S'agit-il d'un bon modèle ? Comment évaluer l'importance de l'erreur ?
#
# Une erreur quadratique moyenne (MSE) pouvant être difficile à interpréter, on tient plutôt compte de la racine carrée de l'erreur quadratique
# moyenne (RMSE). Une propriété intéressante de RMSE est la possibilité de l'interpréter sur la même échelle que les cibles d'origine.
#
# Comparons la RMSE à la différence des valeurs minimale et maximale de nos cibles :
# + id="7UwqGbbxP53O" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
min_house_value = california_housing_dataframe["median_house_value"].min()
max_house_value = california_housing_dataframe["median_house_value"].max()
min_max_difference = max_house_value - min_house_value
print("Min. Median House Value: %0.3f" % min_house_value)
print("Max. Median House Value: %0.3f" % max_house_value)
print("Difference between Min. and Max.: %0.3f" % min_max_difference)
print("Root Mean Squared Error: %0.3f" % root_mean_squared_error)
# + [markdown] id="JigJr0C7Pzit" colab_type="text"
# L'erreur couvre pratiquement la moitié de l'intervalle des valeurs cibles. Peut-on faire mieux ?
#
# C'est la question qui agace tous les développeurs de modèle. Élaborons quelques stratégies de base pour réduire l'erreur de modèle.
#
# Pour commencer, vous pouvez examiner dans quelle mesure les prédictions répondent aux cibles qui ont été définies, en termes de statistiques récapitulatives globales.
# + id="941nclxbzqGH" colab_type="code" slideshow={"slide_type": "-"} colab={"autoexec": {"startup": false, "wait_interval": 0}, "test": {"output": "ignore", "timeout": 600}} cellView="both"
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
calibration_data.describe()
# + [markdown] id="E2-bf8Hq36y8" colab_type="text" slideshow={"slide_type": "-"}
# Ces informations peuvent s'avérer bien utiles. Comment peut-on comparer la valeur moyenne à la valeur RMSE du modèle ? Qu'en est-il des divers quantiles ?
#
# Vous pouvez également visualiser les données et la ligne qui a été apprise. Pour rappel, la régression linéaire sur une seule caractéristique peut être représentée par une droite transformant l'entrée *x* en la sortie *y*.
#
# Vous allez d'abord obtenir un échantillon aléatoire uniforme des données, de manière à créer un diagramme de dispersion lisible.
# + id="SGRIi3mAU81H" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
sample = california_housing_dataframe.sample(n=300)
# + [markdown] id="N-JwuJBKU81J" colab_type="text"
# Vous allez ensuite représenter, sous forme graphique, la ligne qui a été apprise, en partant de la pondération de caractéristique et du biais du modèle, superposée au diagramme de dispersion. La ligne sera affichée en rouge.
# + id="7G12E76-339G" colab_type="code" slideshow={"slide_type": "-"} colab={"autoexec": {"startup": false, "wait_interval": 0}, "test": {"output": "ignore", "timeout": 600}} cellView="both"
# Get the min and max total_rooms values.
x_0 = sample["total_rooms"].min()
x_1 = sample["total_rooms"].max()
# Retrieve the final weight and bias generated during training.
weight = linear_regressor.get_variable_value('linear/linear_model/total_rooms/weights')[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
# Get the predicted median_house_values for the min and max total_rooms values.
y_0 = weight * x_0 + bias
y_1 = weight * x_1 + bias
# Plot our regression line from (x_0, y_0) to (x_1, y_1).
plt.plot([x_0, x_1], [y_0, y_1], c='r')
# Label the graph axes.
plt.ylabel("median_house_value")
plt.xlabel("total_rooms")
# Plot a scatter plot from our data sample.
plt.scatter(sample["total_rooms"], sample["median_house_value"])
# Display graph.
plt.show()
# + [markdown] id="t0lRt4USU81L" colab_type="text"
# Cette ligne initiale semble très éloignée. Voyez s'il est possible de revenir aux statistiques récapitulatives et d'examiner les mêmes informations qui y sont encodées.
#
# Ces évaluations d'intégrité laissent supposer qu'il doit être possible de trouver une bien meilleure ligne
# + [markdown] id="AZWF67uv0HTG" colab_type="text" slideshow={"slide_type": "slide"}
# ## Modifier les hyperparamètres du modèle
# Dans le cadre de cet exercice, tout le code ci-dessus a été placé dans une seule fonction pour plus de facilité. Vous pouvez appeler cette fonction avec différents paramètres pour visualiser les effets.
#
# Dans cette fonction, vous travaillerez dans 10 périodes réparties uniformément, afin de pouvoir observer l'amélioration du modèle à chaque période.
#
# Pour chaque période, vous allez calculer et représenter graphiquement la perte d'apprentissage. Cela peut vous aider à déterminer si un modèle a convergé ou si des itérations supplémentaires sont nécessaires.
#
# Vous allez également représenter graphiquement les valeurs de biais et de pondération de caractéristique apprises par le modèle au fil du temps. Il s'agit d'une autre méthode pour visualiser la convergence des éléments.
# + id="wgSMeD5UU81N" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
def train_model(learning_rate, steps, batch_size, input_feature="total_rooms"):
"""Trains a linear regression model of one feature.
Args:
learning_rate: A `float`, the learning rate.
steps: A non-zero `int`, the total number of training steps. A training step
consists of a forward and backward pass using a single batch.
batch_size: A non-zero `int`, the batch size.
input_feature: A `string` specifying a column from `california_housing_dataframe`
to use as input feature.
"""
periods = 10
steps_per_period = steps / periods
my_feature = input_feature
my_feature_data = california_housing_dataframe[[my_feature]]
my_label = "median_house_value"
targets = california_housing_dataframe[my_label]
# Create feature columns.
feature_columns = [tf.feature_column.numeric_column(my_feature)]
# Create input functions.
training_input_fn = lambda:my_input_fn(my_feature_data, targets, batch_size=batch_size)
prediction_input_fn = lambda: my_input_fn(my_feature_data, targets, num_epochs=1, shuffle=False)
# Create a linear regressor object.
my_optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
my_optimizer = tf.contrib.estimator.clip_gradients_by_norm(my_optimizer, 5.0)
linear_regressor = tf.estimator.LinearRegressor(
feature_columns=feature_columns,
optimizer=my_optimizer
)
# Set up to plot the state of our model's line each period.
plt.figure(figsize=(15, 6))
plt.subplot(1, 2, 1)
plt.title("Learned Line by Period")
plt.ylabel(my_label)
plt.xlabel(my_feature)
sample = california_housing_dataframe.sample(n=300)
plt.scatter(sample[my_feature], sample[my_label])
colors = [cm.coolwarm(x) for x in np.linspace(-1, 1, periods)]
# Train the model, but do so inside a loop so that we can periodically assess
# loss metrics.
print("Training model...")
print("RMSE (on training data):")
root_mean_squared_errors = []
for period in range (0, periods):
# Train the model, starting from the prior state.
linear_regressor.train(
input_fn=training_input_fn,
steps=steps_per_period
)
# Take a break and compute predictions.
predictions = linear_regressor.predict(input_fn=prediction_input_fn)
predictions = np.array([item['predictions'][0] for item in predictions])
# Compute loss.
root_mean_squared_error = math.sqrt(
metrics.mean_squared_error(predictions, targets))
# Occasionally print the current loss.
print(" period %02d : %0.2f" % (period, root_mean_squared_error))
# Add the loss metrics from this period to our list.
root_mean_squared_errors.append(root_mean_squared_error)
# Finally, track the weights and biases over time.
# Apply some math to ensure that the data and line are plotted neatly.
y_extents = np.array([0, sample[my_label].max()])
weight = linear_regressor.get_variable_value('linear/linear_model/%s/weights' % input_feature)[0]
bias = linear_regressor.get_variable_value('linear/linear_model/bias_weights')
x_extents = (y_extents - bias) / weight
x_extents = np.maximum(np.minimum(x_extents,
sample[my_feature].max()),
sample[my_feature].min())
y_extents = weight * x_extents + bias
plt.plot(x_extents, y_extents, color=colors[period])
print("Model training finished.")
# Output a graph of loss metrics over periods.
plt.subplot(1, 2, 2)
plt.ylabel('RMSE')
plt.xlabel('Periods')
plt.title("Root Mean Squared Error vs. Periods")
plt.tight_layout()
plt.plot(root_mean_squared_errors)
# Output a table with calibration data.
calibration_data = pd.DataFrame()
calibration_data["predictions"] = pd.Series(predictions)
calibration_data["targets"] = pd.Series(targets)
display.display(calibration_data.describe())
print("Final RMSE (on training data): %0.2f" % root_mean_squared_error)
# + [markdown] id="kg8A4ArBU81Q" colab_type="text"
# ## Tâche 1 : Obtenir une valeur RMSE inférieure ou égale à 180
#
# Modifiez les hyperparamètres du modèle pour améliorer le coût et obtenir une meilleure correspondance avec la distribution cible.
# Si, après environ cinq minutes, vous ne parvenez toujours pas à obtenir une valeur RMSE de 180, vérifiez la solution pour afficher une combinaison applicable.
# + id="UzoZUSdLIolF" colab_type="code" slideshow={"slide_type": "slide"} colab={"autoexec": {"startup": false, "wait_interval": 0}, "test": {"output": "ignore", "timeout": 600}} cellView="both"
train_model(
learning_rate=0.00001,
steps=100,
batch_size=1
)
# + [markdown] id="ajVM7rkoYXeL" colab_type="text"
# ### Solution
#
# Cliquez ci-dessous pour afficher une solution.
# + id="T3zmldDwYy5c" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
train_model(
learning_rate=0.00002,
steps=500,
batch_size=5
)
# + [markdown] id="M8H0_D4vYa49" colab_type="text"
# Il ne s'agit là que d'une configuration parmi d'autres ; d'autres combinaisons de paramètres peuvent également donner de bons résultats. Notez que le but de cet exercice n'est pas de trouver le paramètre *optimal*, mais bien de vous aider à percevoir en quoi le réglage de la configuration du modèle affecte la qualité de prédiction.
# + [markdown] id="QU5sLyYTqzqL" colab_type="text" slideshow={"slide_type": "slide"}
# ### Existe-t-il une méthode heuristique standard en matière de réglage de modèle ?
#
# Il s'agit là d'une question courante. En bref, on peut dire que les effets des différents hyperparamètres dépendent des données. Il n'existe donc pas de règles absolues. Vous devez effectuer des tests sur les données !
#
# Cela étant dit, voici quelques règles empiriques qui peuvent s'avérer utiles :
#
# * L'erreur d'apprentissage doit diminuer régulièrement, selon une pente abrupte dans un premier temps, pour finalement se stabiliser à mesure que l'apprentissage converge.
# * Si l'apprentissage n'a pas convergé, essayez de l'exécuter plus longtemps.
# * Si l'erreur d'apprentissage diminue trop lentement, augmenter le taux d'apprentissage permettra peut-être d'accélérer la diminution.
# * Cependant, il arrive parfois que l'inverse se produise si le taux d'apprentissage est trop élevé.
# * Si l'erreur d'apprentissage varie sensiblement, essayez de diminuer le taux d'apprentissage.
# * Une bonne méthode consiste généralement à diminuer le taux d'apprentissage tout en augmentant le nombre de pas ou la taille du lot.
# * Des lots de très petite taille peuvent également entraîner une instabilité. Commencez par des valeurs telles que 100 ou 1 000, et continuez à réduire la taille jusqu'à ce que vous constatiez une dégradation.
#
# Pour rappel, vous ne devez pas suivre à la lettre ces règles empiriques, car les effets dépendent des données. Vous devez toujours essayer une méthode et vérifier ensuite le résultat.
# + [markdown] id="GpV-uF_cBCBU" colab_type="text" slideshow={"slide_type": "slide"}
# ## Tâche 2 : Essayer une autre caractéristique
#
# Voyons s'il est possible d'obtenir un meilleur résultat en remplaçant la caractéristique `total_rooms` par `population`.
#
# Ne consacrez pas plus de cinq minutes à cette tâche.
# + id="YMyOxzb0ZlAH" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
# YOUR CODE HERE
# + [markdown] id="ci1ISxxrZ7v0" colab_type="text"
# ### Solution
#
# Cliquez ci-dessous pour afficher une solution.
# + id="SjdQQCduZ7BV" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0}}
train_model(
learning_rate=0.00002,
steps=1000,
batch_size=5,
input_feature="population"
)
|
ml/cc/exercises/fr/first_steps_with_tensor_flow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.6.12 64-bit (''bigdata'': conda)'
# metadata:
# interpreter:
# hash: 393438f6c0bca4a2b0b9b28a96f5952f2521bd7399947aa24a0a5b669f83e1d6
# name: python3
# ---
import os
import sys
import datetime
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pyspark.sql import functions as F
from sklearn.neighbors import DistanceMetric
head, tail = os.path.split(os.getcwd())
data_dir = os.path.join(head, 'data')
data_raw_dir = os.path.join(data_dir, 'raw')
data_raw_dir
# +
# os.listdir(data_raw_dir)
# +
# df_remor = pd.read_csv(os.path.join(data_raw_dir, 'remorquages.csv'), header=0)
# df_remor.head()
# +
# df_avg_drop_dist = df_remor[['LONGITUDE_ORIGINE', 'LATITUDE_ORIGINE', 'LONGITUDE_DESTINATION', 'LATITUDE_DESTINATION']]
# df_avg_drop_dist
# R = 6373.0
# lat1 = np.radians(df_avg_drop_dist['LATITUDE_ORIGINE'])
# lon1 = np.radians(df_avg_drop_dist['LONGITUDE_ORIGINE'])
# lat2 = np.radians(df_avg_drop_dist['LATITUDE_DESTINATION'])
# lon2 = np.radians(df_avg_drop_dist['LONGITUDE_DESTINATION'])
# dlon = lon2 - lon1
# dlat = lat2 - lat1
# # print(dlon, dlat)
# a = np.sin(dlat / 2)**2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon / 2)**2
# # print(type(a))
# c = 2 * np.arctan2(np.sqrt(a), np.sqrt(1 - a))
# # print(c)
# distance = R * c
# # print(type(distance))
# df_avg_drop_dist.loc[:, 'avg_dist'] = distance
# -
# # PYSPARK
from pyspark.rdd import RDD
from pyspark.sql import DataFrame
from pyspark.sql import SparkSession
from pyspark.sql.functions import desc
from pyspark.sql import functions as F
def init_spark():
spark = SparkSession \
.builder \
.appName("Python Spark SQL basic example") \
.config("spark.some.config.option", "some-value") \
.getOrCreate()
return spark
spark = init_spark()
data = spark.read.csv(os.path.join(data_raw_dir, 'remorquages.csv'), header=True)
data.head(2)
# +
# data = data.withColumn('LONGITUDE_ORIGINE', F.expr('radians(LONGITUDE_ORIGINE)'))\
# .withColumn('LATITUDE_ORIGINE', F.expr('radians(LATITUDE_ORIGINE)'))\
# .withColumn('LONGITUDE_DESTINATION', F.expr('radians(LONGITUDE_DESTINATION)'))\
# .withColumn('LATITUDE_DESTINATION', F.expr('radians(LATITUDE_DESTINATION)'))
# data.head(5)
# +
# # data = data.select('*', (data.LONGITUDE_DESTINATION - data.LONGITUDE_ORIGINE).alias('Diff_longitude'))
# data = data.withColumn('Diff_long', F.expr('(LONGITUDE_DESTINATION-LONGITUDE_ORIGINE)/2'))\
# .withColumn('Diff_lat', F.expr('(LATITUDE_DESTINATION-LATITUDE_ORIGINE)/2'))
# data.head(2)
# +
# data = data.withColumn('LATITUDE_DESTINATION', F.expr('cos(LATITUDE_DESTINATION)'))\
# .withColumn('LATITUDE_ORIGINE', F.expr('cos(LATITUDE_ORIGINE)'))
# data.head(2)
# +
# data = data.withColumn('Diff_long', F.expr('sin(Diff_long)'))\
# .withColumn('Diff_lat', F.expr('sin(Diff_lat)'))
# data.head(2)
# +
# # a = np.sin(dlat / 2)**2 + np.cos(lat1) * np.cos(lat2) * np.sin(dlon / 2)**2
# data = data.withColumn('A', F.expr('Diff_lat*Diff_lat + LATITUDE_DESTINATION * LATITUDE_ORIGINE * Diff_long * Diff_long'))
# data.head(2)
# +
# # c = 2 * np.arctan2(np.sqrt(a), np.sqrt(1 - a))
# data = data.withColumn('One_minus_A', F.expr('1-A'))
# data = data.withColumn('C', F.expr('2 * atan2( sqrt(A), sqrt(One_minus_A))'))
# data = data.withColumn('Distance(Km)', F.expr('6373.0*C'))
# data.head(2)
# -
data = data.\
withColumn('LONGITUDE_ORIGINE_rad', F.expr('radians(LONGITUDE_ORIGINE)')).\
withColumn('LATITUDE_ORIGINE_rad', F.expr('radians(LATITUDE_ORIGINE)')).\
withColumn('LONGITUDE_DESTINATION_rad', F.expr('radians(LONGITUDE_DESTINATION)')).\
withColumn('LATITUDE_DESTINATION_rad', F.expr('radians(LATITUDE_DESTINATION)')).\
withColumn('Diff_long', F.expr('(LONGITUDE_DESTINATION_rad-LONGITUDE_ORIGINE_rad)/2')).\
withColumn('Diff_lat', F.expr('(LONGITUDE_DESTINATION_rad-LONGITUDE_ORIGINE_rad)/2')).\
withColumn('LATITUDE_DESTINATION_cos', F.expr('cos(LATITUDE_DESTINATION_rad)')).\
withColumn('LATITUDE_ORIGINE_cos', F.expr('cos(LATITUDE_ORIGINE_rad)')).\
withColumn('Diff_long', F.expr('sin(Diff_long)')).\
withColumn('Diff_lat', F.expr('sin(Diff_lat)')).\
withColumn('A', F.expr('Diff_lat*Diff_lat + LATITUDE_DESTINATION_cos * LATITUDE_ORIGINE_cos * Diff_long * Diff_long')).\
withColumn('One_minus_A', F.expr('1-A')).\
withColumn('C', F.expr('2 * atan2( sqrt(A), sqrt(One_minus_A))')).\
withColumn('Distance_km', F.expr('6373.0*C'))
data.head(2)
df_final = data.select('DATE_ORIGINE', 'LONGITUDE_ORIGINE', 'LATITUDE_ORIGINE', 'Distance_km', 'MOTIF_REMORQUAGE')
print(df_final.count())
df_final = df_final.na.drop()
print(df_final.count())
print(df_final.filter(df_final.DATE_ORIGINE.isNotNull()).count())
# df_final.na.drop(subset=["DATE_ORIGINE"])
# print(df_final.filter(df_final.DATE_ORIGINE.isNotNull()).count())
print(df_final.filter(df_final.LONGITUDE_ORIGINE.isNotNull()).count())
# df_final.na.drop(subset=["LONGITUDE_ORIGINE"])
# print(df_final.filter(df_final.LONGITUDE_ORIGINE.isNotNull()).count())
print(df_final.filter(df_final.LATITUDE_ORIGINE.isNotNull()).count())
# df_final.na.drop(subset=["LATITUDE_ORIGINE"])
# print(df_final.filter(df_final.LATITUDE_ORIGINE.isNotNull()).count())
print(df_final.filter(df_final.Distance_km.isNotNull()).count())
# df_final.na.drop(subset=["Distance_km"])
# print(df_final.filter(df_final.Distance_km.isNotNull()).count())
print(df_final.filter(df_final.MOTIF_REMORQUAGE.isNotNull()).count())
# df_final.na.drop(subset=["MOTIF_REMORQUAGE"])
# print(df_final.filter(df_final.MOTIF_REMORQUAGE.isNotNull()).count())
|
notebooks/0.5-GS-distance_using_pyspark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Outlier Detection using EasyMiner API
#
# This example demonstrates the possibility of outlier detection using complex REST API of data mining system EasyMiner.
# <br /><br />
# To use this example, you must have a working instance of EasyMiner. For testing purposes, you can use our demo server.
#
# ## Dataset IRIS
#
# This example code is based on daset IRIS from the [UCI Repository](https://archive.ics.uci.edu/ml/datasets/iris). The file used in this exmample is located in the folder with this notebook: [iris-preprocessed.csv](./iris-preprocessed.csv)
# <br /><br />
# The dataset contains columns *sepallength*, *petalwidth*, *sepalwidth*, *petallength* and *class*. For rule miming also as for classification model building, the column *class* should be used in consequent part of rules, other columns should be used in antecedent.
# ## 1. Setup variables, import dependencies
#
# To run this example, you have to configure the following variables.
# +
# Import requested libraries
import requests
import json
import time
import urllib
# Setup details about the used file
CSV_FILE = 'iris-preprocessed.csv'
CSV_SEPARATOR = ','
CSV_ENCODING = 'utf8'
# -
# To use the integrated data mining API provided by EasyMiner, you must have an user account on a running instance of EasyMiner. Please input the URL of the API in the variable *API_URL*
# Configure access variables
API_URL = 'https://br-dev.lmcloud.vse.cz/easyminercenter/api'
# To work with EasyMiner you must register an user account.
# It can be realized using the GUI also as using the API.
# <br />
# If you already have an account, please input your API KEY in the following variable *API_KEY*:
API_KEY = ''
# In case you do not have an user account yet,
# you can register a new one using the following code:
if API_KEY == "":
user_name = 'testuser' + str(time.time())
user_email = user_name + "@domain.tld"
user_password = <PASSWORD>
# JSON configuration of the API request
json_data = json.dumps({"name": user_name, "email": user_email, "password": <PASSWORD>_password})
# Send request for miner creation
r = requests.post(API_URL + "/users?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"}, data = json_data.encode())
# Get the API key of the newly registered user account
API_KEY = r.json()["apiKey"]
# Please check the configuration using the simple API call:
# +
# Check the functionality of the user account
r = requests.get(API_URL + "/auth?apiKey=" + API_KEY, headers={"Accept": "application/json"})
# Parse the response as JSON
auth_user = r.json()
# If everything works correctly, you should get the details of your account:
auth_user
# -
# ## 2. Upload CSV file to EasyMiner server (create datasource)
# +
# HTTP request for uploading of the CSV file
r = requests.post(API_URL + '/datasources?separator=' + urllib.parse.quote(CSV_SEPARATOR) + '&encoding=' + CSV_ENCODING + '&type=limited&apiKey=' + API_KEY, files = {("file", open(CSV_FILE, 'rb'))}, headers = {"Accept": "application/json"})
# Get datasource ID (identificates the dataset on EasyMiner server) from the server response
datasource_id = r.json()["id"]
# -
# For debug purposes, print datasource_id - if the datasource was created successfully, the datasource_id should be greater than 0)
#
datasource_id
# ## 3. Create miner
# +
# Define name for the miner {optional value for your better orientation in list of miners]
miner_name = '<NAME>'
# JSON configuration of the API request (will be sent as body of the HTTP request)
json_data = json.dumps({"name": miner_name, "type": "cloud", "datasourceId": datasource_id})
# Send request for miner creation
r = requests.post(API_URL + "/miners?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"}, data = json_data.encode())
# Get ID of the created miner (identificates the miner on EasyMiner server)
miner_id = r.json()["id"]
# -
# For debug purposes, print datasource_id - if the datasource was created successfully, the datasource_id should be greater than )
#
miner_id
# ## 4. Preprocess data
# It is not possible to use the uploaded data fields from the uploaded datasource directly for definition of the data mining task. You have to generate attribute from each attribute you want to use.
# <br /><br />
# The simplest preprocessing method is to use the values of the data field "as they are" using the preprocessing method "each value - one bin".
# <br /><br />
# The uploaded data fields are identified using their names. Remember, the names has not be exactly the same as in the uploaded file (in case of duplicities etc.). You should get the list of data fields (columns) in the datasource:
# +
# Request from the EasyMiner list of columns (data fields) available in the existing datasource
r = requests.get(API_URL + '/datasources/' + str(datasource_id) + '?apiKey=' + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"})
# The response contains properties of the datasource also as the list of columns. Get only the columns...
datasource_columns = r.json()['column']
# -
# Check the list of columns:
datasource_columns
# ### Construction of preprocessing requests - simple usage of the original data values
#
# In case you want to preprocess all the columns from the data field using the method "each value - one bin", you can simple use the following code:
# +
# Define variable for collecting of list of prepared attributes
attributes_columns_map = {}
# Process all the columns...
for col in datasource_columns:
# You can work with the column name or the column ID. Both these values are parsed from the previous JSON response.
column_name = col['name']
# You have to select
attribute_name = column_name
# Construct the definition of preprocessing request;
# for identification of the column from datasource, you can use its ID (set it to property "column"), or its name (set it to property "columnName")..
json_data = json.dumps({"miner": miner_id, "name": attribute_name, "columnName": column_name, "specialPreprocessing": "eachOne"})
# Send the request and wait for the response;
# dependently on the size of the used datasource, it can take a bit longer time...
r = requests.post(API_URL + "/attributes?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"}, data = json_data.encode())
if r.status_code != 201:
break # error occurred - the preprocessing of the selected attribute failed
attributes_columns_map[column_name] = r.json()['name']
# -
# The list of prepared attributes is:
attributes_columns_map
# ### 4.b Other preprocessing methods
#
# New version of the data mining system EasyMiner supports also all
# standard preprocessing methods for preparation of attributes from data fields (datasource columns):
# - *equidistant intervals* - group numerical values to intervals with given length or to defined count of intervals
# - *equifrequent intervals* - group numerical values to given count of intervals with almost the same frequencies of values in the datasource
# - *equisized intervals* - group numerical values to intervals with requested minimal value of support
# ## 5. Define outlier detection mining task
#
# For outlier detection, the system uses all attributes prepared in the previous step (**4.**).
# In task definition request, you have to specify the minimal value of support and the name of the task.
# +
# Define minimal value of support
min_support = 0.01
# Construct the JSON request for task definition
json_data = json.dumps({"miner": miner_id, "minSupport": min_support})
# Send the request to server
r = requests.post(API_URL + "/outliers-tasks?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"}, data=json_data.encode())
# Get the ID of created task
outlier_task_id = r.json()["id"]
# -
# The ID of created task is:
outlier_task_id
# ## 6. Execute the outlier detection task
# +
# Send the request
r = requests.get(API_URL + "/outliers-tasks/" + str(outlier_task_id) + "/start?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"})
# Wait for result (dependently on the task definition and the size of analyzed data, it can take even a long tame)
while True:
time.sleep(1)
# check state
r = requests.get(API_URL + "/outliers-tasks/" + str(outlier_task_id) + "/state?apiKey=" + API_KEY, headers = {'Content-Type': 'application/json', "Accept": "application/json"})
task_state = r.json()["state"]
print("task_state:" + task_state)
if task_state == "solved":
break
if task_state == "failed":
print("task failed executing")
break
# -
# ## 7. Read the results
#
# The results of an outlier detection task are rows from the preprocessed dataset with its outlier score.
# +
# Define, which rows are you interested in
offset = 0
limit = 10
# Send the request to server
r = requests.get(API_URL + '/outliers-tasks/' + str(outlier_task_id) + '/outliers?apiKey=' + API_KEY + '&offset=' + str(offset) + '&limit=' + str(limit), headers = {"Accept": "application/json"})
# Get the results in JSON
outliers = r.json()['outlier']
# and then work with the results...
outliers
|
EasyMinerCenter API examples/Outlier detection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Introduction
# In the previous post, we read about the concepts of __Graph__ and __Session__ which describes the way the data flows in TensorFlow. In this tutorial, we'll take a look at some of the __Tensor Types__ used in TensorFlow and specially the ones commonly used in creating neural network models, namely ___Constant___, ___Variable___, and ___Placeholder___.
#
# This will also enable us to shed light on some of the points and questions left unanswered in the previous post.
#
# Remember that we need to import the TensorFlow library at the very beginning of our code using:
import tensorflow as tf
#
#
#
# ## 1. Constant
#
# As the name speaks for itself, __Constants__ are used as constant value tensors. They create a node that takes a constant value. You can simply create a constant tensor using __tf.constant__. It accepts the following arguments:
#
tf.constant(value, dtype=None, shape=None, name='Const', verify_shape=False)
# Now let's look at a very simple example.
#
# ### Example 1:
# Let's create two constants and add them together. Constant tensors can be defined simply by defining a value:
# create graph
a = tf.constant(2)
b = tf.constant(3)
c = a + b
# launch the graph in a session
with tf.Session() as sess:
print(sess.run(c))
# Perfect! Now Let's look at the created graph and generated data types:
# <img src="files/files/2_1.png" width="1000" height="2000" >
# ___Fig1. ___ __Left:__ generated graph visualized in Tensorboard, __Right:__ generated variables (screenshot captured from PyCharm debugger when running in debug mode)
#
# As it's depicted in the figure, we created 3 tensors with __"Python-names"__ _a_, _b_, and _c_. However, we didn't define any __"TensorFlow-name"__ for them. Therefore, TensorFlow assigns some default names to them which are depicted in the graph: __const__ and __const_1__ for the input constants and __add__ for the output of the addition operation. We can easily modify it and define our own names, like:
# create graph
a = tf.constant(2, name='A')
b = tf.constant(3, name='B')
c = tf.add(a, b, name='Sum')
# launch the graph in a session
with tf.Session() as sess:
print(sess.run(c))
# This time the graph and created tensors are as follows:
# <img src="files/files/2_2.png" width="1000" height="2000" >
# ___Fig2. ___ generated graph (Left) and variables (Right) with the modified names
#
#
# We can also define constants of different types (integer, float, etc.) and shapes (vectors, matrices, etc.).
#
#
# ### Example 2:
s = tf.constant(2.3, name='scalar', dtype=tf.float32)
m = tf.constant([[1, 2], [3, 4]], name='matrix')
# launch the graph in a session
with tf.Session() as sess:
print(sess.run(s))
print(sess.run(m))
# ## 2. VARIABLE
# Variables are stateful nodes which output their current value; meaning that they can retain their value over multiple executions of a graph. They have a number of useful features such as:
#
# - They can be __saved__ to your disk during and after training. This allows people from different companies and groups to save, restore and send over their model parameters to other people.
# - By default, gradient updates (used in all neural networks) will apply to all variables in your graph. In fact, variables are the things that you want to tune in order to minimize the loss.
#
# These features make variables suitable to be used as the network parameters (i.e. weights and biases).
#
# You might ask what are the differences between variables and constants? Well there are two major differences:
#
# 1. Constants are (guess what), constants. Their value doesn't change. You'd usually need your network parameters to be updated and that's where the __variable__ comes into play.
#
# 2. Constants are stored in the graph definition which makes them memory-expensive. In other words, constants with millions of entries makes the graph loading much slower.
#
#
# Again, it's important to remember that creating a variables is an operation (look at the Fig. 2 of the first tutorial for a quick recap). When we evaluate these operations in the session, we'll get the output value of the operations.
#
# ### 2.1. Create Variables
# To create a variable, you can use __tf.Variable__ as:
#
# Create a variable.
w = tf.Variable(<initial-value>, name=<optional-name>)
# Some examples of creating scalar and matrix variables are as follows:
s = tf.Variable(2, name="scalar")
m = tf.Variable([[1, 2], [3, 4]], name="matrix")
W = tf.Variable(tf.zeros([784,10]))
# Variable __W__ defined above will create a matrix with 784 rows and 10 columns which will be initialized by zeros. This can be used as a weight matrix of a feed-forward neural network (or even in a linear regression model) from a layer with 784 neuron to a layer with 10 neuron. We'll see more of this later in this turorial.
#
# __*Note:__ we use tf.Variable() with uppercase "V", and tf.constant with lowercase "c". You don't necessarily need to know the reason, but it's simply because tf.constant is an op, while tf.Variable is a class with multiple ops.
#
# __* IMPORTANT Note:__ Calling tf.Variable to create a variable is the old way of creating a variable. TensorFlow recommends to use the wraper __tf.get_variable__ which accepts the name, shape, etc as its arguments as follows:
#
tf.get_variable(name,
shape=None,
dtype=None,
initializer=None,
regularizer=None,
trainable=True,
collections=None,
caching_device=None,
partitioner=None,
validate_shape=True,
use_resource=None,
custom_getter=None,
constraint=None)
# Some examples are as follows:
s = tf.get_variable("scalar", initializer=tf.constant(2))
m = tf.get_variable("matrix", initializer=tf.constant([[0, 1], [2, 3]]))
W = tf.get_variable("weight_matrix", shape=(784, 10), initializer=tf.zeros_initializer())
# ### 2.2. Initialize Variables
# Variables need to be initialized befor being used. To do so, we have to invoke a __variable initializer operation__ and run the operation on the session. This is the easiest way to initialize variables which initializes all variables at once.
#
# The following toy example shows how we can add an op to initialize the variables.
#
# ### Example 3:
# create two variables and add them together. Then print out their value and the summation result.
# +
a = tf.get_variable(name="var_1", initializer=tf.constant(2))
b = tf.get_variable(name="var_2", initializer=tf.constant(3))
c = tf.add(a, b, name="Add1")
# launch the graph in a session
with tf.Session() as sess:
# now let's evaluate their value
print(sess.run(a))
print(sess.run(b))
print(sess.run(c))
# -
# __FailedPreconditionError: Attempting to use uninitialized value__
# As you can see, we ran into __FailedPreconditionError: Attempting to use uninitialized value__. This is because we tried to evaluate the variables before initializing them. Let's correct the code by first initializing all variables and then evaluating them.
# +
# create graph
a = tf.get_variable(name="A", initializer=tf.constant(2))
b = tf.get_variable(name="B", initializer=tf.constant(3))
c = tf.add(a, b, name="Add")
# add an Op to initialize global variables
init_op = tf.global_variables_initializer()
# launch the graph in a session
with tf.Session() as sess:
# run the variable initializer operation
sess.run(init_op)
# now let's evaluate their value
print(sess.run(a))
print(sess.run(b))
print(sess.run(c))
# -
# Let's take a quick look at the graph and generated variables:
# <img src="files/files/2_3.png" width="1000" height="2000" >
# ___Fig3. ___ generated graph (Left) and variables (Right)
#
# As you can see, two blue boxes are the generated variables (compare them with constant nodes in Fig. 2) which are added together using "Add" operation.
#
#
# __*Note:__ Variables are usually used for weights and biases in neural networks.
#
# - __weights__ are usually initialized from a normal distribution using `tf.truncated_normal_initializer()`.
#
# - __biases__ are usually initialized from zeros using `tf.zeros_initializer()`.
#
# Let's look at a very simple example of creating weight and bias variables with proper initialization:
#
# ### Example 4:
# Create the weight and bias matrices for a fully-connected layer with 2 neuron to another layer with 3 neuron.
# In this scenario, the weight and bias variables must be of size $[2, 3]$ and 3 respectively.
# +
# create graph
weights = tf.get_variable(name="W", shape=[2,3], initializer=tf.truncated_normal_initializer(stddev=0.01))
biases = tf.get_variable(name="b", shape=[3], initializer=tf.zeros_initializer())
# add an Op to initialize global variables
init_op = tf.global_variables_initializer()
# launch the graph in a session
with tf.Session() as sess:
# run the variable initializer
sess.run(init_op)
# now we can run our operations
W, b = sess.run([weights, biases])
print('weights = {}'.format(W))
print('biases = {}'.format(b))
# -
# ## 3. Placeholder:
# Placeholders are nodes whose value is fed in at execution time. If you have inputs to your network that depend on some external data and you don't want your graph to depend on any real value, placeholders are the datatype you need. In fact, you can build the graph without needing the data. Therefore, they don't need any initial value; only a datatype (such as float32) and a tensor shape so the graph still knows what to compute even though it doesn't have any stored values yet.
#
# Some examples of creating placeholders are as follows:
a = tf.placeholder(tf.float32, shape=[5])
b = tf.placeholder(dtype=tf.float32, shape=None, name=None)
X = tf.placeholder(tf.float32, shape=[None, 784], name='input')
Y = tf.placeholder(tf.float32, shape=[None, 10], name='label')
# Let's run a simple example.
#
# ### Example 5:
# Create a constant vector and a placeholder and add them together.
# +
a = tf.constant([5, 5, 5], tf.float32, name='A')
b = tf.placeholder(tf.float32, shape=[3], name='B')
c = tf.add(a, b, name="Add")
with tf.Session() as sess:
print(sess.run(c))
# -
# __InvalidArgumentError: You must feed a value for placeholder tensor 'B' with dtype float and shape $[3]$ error__
# As you can see, running this code will run into an error. As you might have guessed, it is simply because the placeholder is empty and there is no way to add an empty tensor to a constant tensor. To solve this, we need to feed the input value to tensor "a". It can be done by creating a dictionary ("d" in the following code) whose key(s) are the placeholders and their values are the desired value to be passed to the placeholder(s), and feeding it to an argument called "feed_dict". In our example, say we want to pass $[1, 2, 3]$ to the placeholder; the code needs to be modified as:
#
# +
a = tf.constant([5, 5, 5], tf.float32, name='A')
b = tf.placeholder(tf.float32, shape=[3], name='B')
c = tf.add(a, b, name="Add")
with tf.Session() as sess:
# create a dictionary:
d = {b: [1, 2, 3]}
# feed it to the placeholder
print(sess.run(c, feed_dict=d))
# -
# The generated graph and variables are as follows:
# <img src="files/files/2_4.png" width="700" height="1400" >
# ___Fig4. ___ generated graph (Left) and variables (Right)
#
#
# So far so good?
#
#
# ## Creating a Toy Neural Network
# Now, we have all the required materials to start building a toy feed-forward neural network with one hidden layer with 200 hidden units (neurons). The computational graph in Tensorflow will look like this:
#
# <img src="files/files/2_5.png" width="300" height="600" >
# ___Fig5. ___ Schematic of the graph for one layer of the neural network
#
# How many operations (or nodes) you see in this graph? Six, right? The three circles (X, W, b) and three rectangles. We'll go through them one by one and will discuss what is the best way to implement it.
#
# Let's start with the input, X. This can be an input of any type, such as images, signals, etc. The general approach is to feed all inputs to the network and train the trainable parameters (here, W and b) by backpropagating the error signal. Ideally, you need to feed all inputs together, compute the error, and update the parameters. This process is called "Gradient Descent".
#
# *Side Note: In real-world problems, we have thousands and millions of inputs which makes gradient descent computationally expensive. That's why we split the input set into several shorter pieces (called mini-batch) of size B (called mini-batch size) inputs, and feed them one by one. This is called "Stochastic Gradient Descent". The process of feeding each mini-batch of size B to the network, back-propagating errors, and updating the parameters (weights and biases) is called an iteration.
#
# We generally use Placeholders for inputs so that we can build the graph without depending on any real value. The only point is that you need to choose the proper size for the input. Here, we have a feed-forward neural network, and let's assume inputs of size 784 (similar to 28x28 images of MNIST data). The input placeholder can be written as:
# create the input placeholder
X = tf.placeholder(tf.float32, shape=[None, 784], name="X")
# You might wonder what is shape=$[None, 784]$?!
#
# Well, that's the tricky part! Read the above side note one more time. We need to feed B images of size 784 to the network in each training iteration. So the placeholder needs to be of shape=$[B, 784]$. Defining the placeholder shape as $[None, 784]$ means that you can feed any number of images of size 784 (not B images necessarily). This is especially helpful in the evaluation time where you need to feed all validation or test images to the network and compute the performance on all of them.
#
# Enough with the placeholder. Let's continue with the network parameters, W, and b. As explained in the Variable section above, they have to be defined as variables. Since in Tensorflow, gradient updates will be applied to the graph variables, by default. As mentioned, variables need to be initialized.
#
# *Note: Generally, weights (W) are initialized randomly, in it's the simplest form from a normal distribution, say normal distribution with zero mean and standard deviation of 0.01. Biases (b) can be initialized as small constant values, such as 0.
#
# Since the input dimension is 784 and we have 200 hidden units, the weight matrix will be of size $[784, 200]$. We also need 200 biases, one for each hidden unit. The code will be like:
# +
# create weight matrix initialized randomely from N(0, 0.01)
weight_initer = tf.truncated_normal_initializer(mean=0.0, stddev=0.01)
W = tf.get_variable(name="Weight", dtype=tf.float32, shape=[784, 200], initializer=weight_initer)
# create bias vector of size 200, all initialized as zero
bias_initer =tf.constant(0., shape=[200], dtype=tf.float32)
b = tf.get_variable(name="Bias", dtype=tf.float32, initializer=bias_initer)
# -
# Now let's move on to the rectangle operations. We must multiply input X$_{[None, 784]}$ and weight matrix W$_{[784, 200]}$ which gives a tensor of size $[None, 200]$, then add the bias vector b$_{[200]}$ and eventually pass the final tensor from a ReLU non-linearity:
# create MatMul node
x_w = tf.matmul(X, W, name="MatMul")
# create Add node
x_w_b = tf.add(x_w, b, name="Add")
# create ReLU node
h = tf.nn.relu(x_w_b, name="ReLU")
# Okay, we are all set. The created graph looks like this:
# <img src="files/files/2_6.png" width="400" height="800" >
# ___Fig6. ___ Data flow graph of the neural network created in Tensorflow
#
# But how can you visualize this graph? How did you create this figure?! That's the magic of __Tensorboard__. It's thoroughly explained in our next article.
#
# Before closing it, let's run a session on this graph (using 100 images generated by random pixel values) and get the output of hidden units (h). The whole code will be like this:
#
# +
# import the tensorflow library
import tensorflow as tf
import numpy as np
# create the input placeholder
X = tf.placeholder(tf.float32, shape=[None, 784], name="X")
weight_initer = tf.truncated_normal_initializer(mean=0.0, stddev=0.01)
# create network parameters
W = tf.get_variable(name="Weight", dtype=tf.float32, shape=[784, 200], initializer=weight_initer)
bias_initer =tf.constant(0., shape=[200], dtype=tf.float32)
b = tf.get_variable(name="Bias", dtype=tf.float32, initializer=bias_initer)
# create MatMul node
x_w = tf.matmul(X, W, name="MatMul")
# create Add node
x_w_b = tf.add(x_w, b, name="Add")
# create ReLU node
h = tf.nn.relu(x_w_b, name="ReLU")
# Add an Op to initialize variables
init_op = tf.global_variables_initializer()
# launch the graph in a session
with tf.Session() as sess:
# initialize variables
sess.run(init_op)
# create the dictionary:
d = {X: np.random.rand(100, 784)}
# feed it to placeholder a via the dict
print(sess.run(h, feed_dict=d))
# -
# Running this code will print out h$_{[100, 200]}$ which are the outputs of 200 hidden units in response to 100 images; i.e. 200 features extracted from 100 images.
#
# We'll continue constructing the loss function and creating the optimizer operations in the next articles. However, we need to learn Tensorboard first to use its amazing features in our neural network code.
#
# Thanks for reading! If you have any question or doubt, feel free to leave a comment below. You can also send us feedback through contact us page.
|
1_Basics/2_Tensor_Types.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tf-explain
# language: python
# name: tf-explain
# ---
# ## Tf-Explain technique of explaining neural networks
# From https://github.com/sicara/tf-explain
#
# Before you start remember to create virtual environment. Type in your shell:
#
# ```virtualenv venv -p python3.6```
#
# Create new kernel using your virtualenv (https://anbasile.github.io/posts/2017-06-25-jupyter-venv/) and turn it on in the notebook **(Top bar > Kernel > Change kernel > ...).**
# #### Install all dependencies
pip install tf-explain
pip install tensorflow==2.1.0
pip install pillow
pip install opencv-python
# #### Import all libraries and classes
# +
import os
os.environ['KERAS_BACKEND'] = 'tensorflow'
import sys
from glob import glob
from PIL import Image
sys.modules['Image'] = Image
import tensorflow as tf
import numpy as np
import keras
import cv2 as cv
from tf_explain.core import *
# -
# Be sure that your keras backend is switch to 'tensorflow' and your image data format is 'channels_last'
tf.keras.backend.set_image_data_format('channels_last')
# #### Loading pretrained model
model_vgg16 = tf.keras.applications.vgg16.VGG16(weights='imagenet', include_top=True)
model_inception = tf.keras.applications.inception_v3.InceptionV3(include_top=True, weights='imagenet')
# #### Create list of image paths and class indexes of images from ImageNet
# You have to organise your images like: *./images/xyz/* where xyz is class index from ImageNet (e.g. ./images/96/)
classes_list = glob('./images/*')
# +
data_list = []
for class_path in classes_list:
class_index = class_path.split('/')[-1]
path_for_glob = class_path + '/*.jpg'
images_paths = glob(path_for_glob)
for image in images_paths:
print(image)
data_list.append((image,int(class_index)))
# -
# #### Create diffrent types of explainers
# Start explainer
explainer_grad_cam = GradCAM()
explainer_vanilla = VanillaGradients()
explainer_smooth = SmoothGrad()
explainer_occlusion = OcclusionSensitivity()
explainer_int_grad = IntegratedGradients()
# #### Load images from path and start explaining with all five techniques and save the result images
# Make sure, you've chosen right model (inception or vgg16)
# +
for data_item in data_list:
image_path = data_item[0]
# print(image_path)
image_name = image_path.split('/')[-1][:-4]
# print(image_name)
img = tf.keras.preprocessing.image.load_img(image_path, target_size=(299, 299))
img = tf.keras.preprocessing.image.img_to_array(img)
data = ([img], None)
grid_cam = explainer_grad_cam.explain(data, model_inception, class_index=data_item[1], colormap=cv.COLORMAP_JET)
explainer_grad_cam.save(grid_cam, "./images/" + str(data_item[1])+ "/results/", image_name + "-grad_cam.png")
# grid_occlusion = explainer_occlusion.explain(data, model_inception, class_index=data_item[1], colormap=cv.COLORMAP_JET)
# explainer_occlusion.save(grid_occlusion, "./images/" + str(data_item[1])+ "/", image_name + "-occlusion_sensitivity.png")
print("-----------------DONE-------------------")
# grid_vanilla = explainer_vanilla.explain(data_np_array, model, scorpion_class_index)
# explainer_vanilla.save(grid_vanilla, ".", "vanilla_gradients.png")
# grid_smooth = explainer_smooth.explain(data, model, scorpion_class_index, 20, 1.0)
# explainer_smooth.save(grid_smooth, ".", "smoothgrad.png")
# grid_grad = explainer_int_grad.explain(data, model, scorpion_class_index, n_steps=15)
# explainer_int_grad.save(grid_grad, ".", "integrated_gradients.png")
# -
|
notebooks/tf-explain/tf-explain.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Building graph using Nobel_prize JSON data
# +
import json
import pandas as pd
file1 = '../data/Nobel_prize.json'
file2 = '../data/Nobel_laureate.json'
file3 = '../data/Nobel_country.json' # this file has simple json structure
# -
with open(file1) as json_file:
json_data1 = json.load(json_file)
# json_data
# +
# from pandas.io.json import json_normalize
# # this is not practical for the this json data
# df = json_normalize(json_data1, 'prizes')
# df.head()
# -
json_data1['prizes'][0]['laureates']
with open(file2) as json_file:
json_data2 = json.load(json_file)
json_data2['laureates'][100]
# +
# with open(file3) as json_file:
# json_data3 = json.load(json_file)
# json_data3['countries']
# -
import networkx as nx
from pprint import pprint
from graphene import graphgen
import graphene
print(graphene.__version__)
nodes_mapper = {
"nodes": [
{
"type": "Affiliations",
"path": "/prizes/affiliations",
"key" : [
{"name": "name", "raw": "/prizes/affiliations/name"}
],
"attributes": [
{"name": "name", "raw": "/prizes/affiliations/name"},
{"name": "city", "raw": "/prizes/affiliations/city"},
{"name": "country", "raw": "/prizes/affiliations/country"},
]
},
{
"type": "Prize",
"path": "/prizes",
"key" : [
{"name": "category", "raw": "/prizes/category"}
],
"attributes": [
{"name": "category", "raw": "/prizes/category"},
]
}
]
}
edges_mapper = {
"edges": [
{
"type": "Awarded",
"from": {
"type": "Affiliations",
"path": "/prizes/affiliations",
"key" : [
{"name": "name", "raw": "/prizes/affiliations/name"}
]
},
"to" : {
"type": "Prize",
"path": "/prizes",
"key" : [
{"name": "category", "raw": "/prizes/category"}
]
},
"attributes": [
{"name": "year", "raw": "/prizes/year"},
]
}
]
}
# +
g = nx.MultiDiGraph()
g = graphgen.create_graph(g, graph_mapper = nodes_mapper,
data_provider = json_data2['laureates'], add_type_to_key=True)
g = graphgen.create_graph(g, graph_mapper = edges_mapper,
data_provider = json_data2['laureates'], add_type_to_key=True)
# -
type(g)
nx.number_of_nodes(g)
nx.number_of_edges(g)
pprint(json_data2['laureates'][216])
print(g.node[('Affiliations', 'University of Cambridge',)])
print(g.node[('Prize','chemistry',)])
print(g.node[('Prize', 'physics')])
pprint(g.get_edge_data(('Affiliations', 'University of Cambridge'), ('Prize', 'chemistry')))
pprint(g.get_edge_data(('Prize', 'chemistry'), ('Affiliations', 'University of Cambridge')))
pprint(g.get_edge_data(('Affiliations', 'Munich University'), ('Prize', 'physics')))
|
examples/networkx/Nobel_prize_graph_model_one.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # process multipage pdf of bank transactions
#
# provides function process_file
#
# fn gives list of lists (which can be fed into dataframe)
#
# which are result of processing pdf file with table spanning several pages
#
# extracts only transactions data (and begin/end konto balance)
import camelot
import pandas
def remove_whitespace(x):
"""remove all whitespaces from a given string"""
if x is not None:
x = x.split()
x = ''.join(x)
return x
def extract_transactions(tables_transactions):
"""
list of processed pdf pages -> dataframe with table that contains them all
get the list of all monthly transactions, clean the data
"""
transactions_list = []
for table in tables_transactions:
trans = table.df.values.tolist()
for row in trans:
transactions_list.append(row)
transactions = pandas.DataFrame(transactions_list)
transactions = transactions.applymap(remove_whitespace)
transactions.columns = ['info', 'date', 'out', 'in']
transactions = transactions[transactions.date != 'Valuta']
transactions = transactions[transactions.date != 'zu']
transactions = transactions.fillna(value="")
transactions.index = range(len(transactions.index))
return transactions
def merge_transactions(transactions, begin_month_data, end_month_data):
"""
dataframe of transactions -> list transactions (each is a list)
merges 3 rows of one transaction into one, discard the rest
"""
list_merged_transactions = []
list_merged_transactions.append(begin_month_data)
use_this_row = 0 # we'll use 3 consecutive rows, and merge them
for index, row in transactions.iterrows():
if (row['date'] != ''):
use_this_row = 1
current_info = row['info']
current_date = row['date']
current_in = row['in']
current_out = row['out']
elif use_this_row > 0:
use_this_row += 1
if use_this_row <= 3: # unused row after row with date
current_info += ". . . ." + row['info']
if use_this_row == 3:
list_merged_transactions.append([current_info, current_date, current_out, current_in])
use_this_row = 0
list_merged_transactions.append(end_month_data)
return list_merged_transactions
# figuring out column dimensions in the console
# ```
# camelot -p 4 stream -plot text test.pdf &
# camelot -p 4 stream -plot textedge test.pdf &
# camelot -p 4 stream -plot grid test.pdf &
# ```
#
# check in the tool where are the limits
#
# final command
#
# ```
# camelot --format html --output test.html --pages 4 stream -R 0,600,600,0 -C 290,330,460 test.pdf
# ```
def process_file(input_file):
""" for a given path to a pdf file, extract the transactional data as a list of transactions (list)"""
# table_areas = top_left x, y, bottom_right x, y // 0,0 is bottom left
# read all pages in bottom 600x600 square
tables_transactions = camelot.read_pdf(input_file, flavor='stream', pages='1-end',
table_regions=['0,600,600,0'], columns=['290,330,460'])
tables_for_balance = camelot.read_pdf(input_file, pages='1-end')
trans_begin = tables_for_balance[0].df # take 3 lines
begin_month_balance = ''.join(trans_begin.iat[1,0].split())
begin_month_data = ["BEGIN " + begin_month_balance[21:28] + " = " + begin_month_balance[28:], "", "", ""]
trans_end = tables_for_balance[-1].df # take 3 lines
end_month_balance = ''.join(trans_end.iat[-2,0].split())
end_month_data = ["END " + end_month_balance[21:28] + " = " + end_month_balance[28:], "", "", ""]
return merge_transactions(extract_transactions(tables_transactions), begin_month_data, end_month_data)
|
analyse_bank_statements/process_single_month_bank_transactions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import seaborn as sns
import numpy as np
import altair as alt
import matplotlib.pyplot as plt
import os
import sys
from ocp_table_tpot.globals import Globals as gd
from tpot import TPOTRegressor
sys.path.insert(0,'..')
from sklearn.pipeline import make_pipeline, make_union
from sklearn.preprocessing import RobustScaler,MinMaxScaler,PolynomialFeatures,QuantileTransformer,Normalizer
from sklearn.decomposition import PCA
from sklearn.base import BaseEstimator, TransformerMixin, RegressorMixin, clone
from sklearn.model_selection import KFold, cross_val_score, train_test_split
from sklearn.metrics import mean_squared_error,make_scorer
from copy import copy
from tpot.builtins import StackingEstimator
from src.models.model import mase,TimeSeriesSplitImproved
from sklearn.linear_model import ElasticNet, Lasso, BayesianRidge, LassoLarsIC,RANSACRegressor,Ridge
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor
from sklearn.kernel_ridge import KernelRidge
from sklearn.neighbors import KNeighborsRegressor
from skgarden.quantile import RandomForestQuantileRegressor
from lightgbm import LGBMRegressor
import xgboost as xgb
import lightgbm as lgb
import umap
df_tsfresh = pd.read_pickle(f'../data/processed/train_test_tsfresh_6.pkl').reset_index(level = 0)
data_dict = pd.read_pickle(f'../data/processed/data_dict_all.pkl')
# +
year = 2019
tgt = 'rougher.output.recovery'
X = data_dict[year]['X_train_lagdiff']
print(X.shape)
y = data_dict[year]['y_train']
X_test = data_dict[year]['X_test_lagdiff']
mask = data_dict[year]['mask']
exclude_pts = data_dict[year]['excl'].set_index('date').tz_localize('UTC')
#mask_na_two_row=y[y[tgt].isna()].index.union(y[y[tgt].isna()].index + pd.Timedelta('1 hour')).union(y[y[tgt].isna()].index + pd.Timedelta('2 hour'))
inds = mask.index.difference(exclude_pts.index)
X=X.loc[inds,:]
y=y.loc[inds,:]
mask=mask[inds]
print(X.shape)
print(X_test.shape)
# -
print(f'1) X shape: {X.shape},y: {y.shape}')
X = X[mask]
y = y[mask][tgt]
print(f'2) Train shape: {X.shape}')
X_filt = X.filter(regex ="rougher|hour|dayw",axis = 1)
X = X_filt
train_df = pd.concat([X,y],axis= 1)
train_df.head()
# +
#Fit Isolation RF
from sklearn.ensemble import IsolationForest
irf = IsolationForest(verbose =1,contamination='auto',behaviour='new')
irf.fit(train_df[X.columns])
irf_preds = irf.predict(train_df[X.columns])
(irf_preds > 0).sum()
# -
# ## Create a function to fit a base model on `K-1` folds, predict on `1` fold
# This function takes one model and fit it to the train and test data
# It returns the model MASE, CV prediction, and test prediction
def base_fit(model, folds, features, target, trainData, testData):
# Initialize empty lists and matrix to store data
model_mase = []
model_val_predictions = np.empty((trainData.shape[0], 1))
k=0
# Loop through the index in KFolds
model_test_predictions=np.zeros((testData.shape[0],))
model_val_true=np.zeros((trainData.shape[0],1))
for train_index, val_index in folds.split(trainData):
k=k+1
# Split the train data into train and validation data
train, validation = trainData.iloc[train_index], trainData.iloc[val_index]
# Get the features and target
train_features, train_target = train[features], train[target]
validation_features, validation_target = validation[features], validation[target]
# Fit the base model to the train data and make prediciton for validation data
if (model.__class__ == xgb.sklearn.XGBRegressor) | (model.__class__ == lgb.sklearn.LGBMRegressor):
print('Fitting a boost model with limited tree rounds')
evalset = [(validation_features,np.ravel(validation_target))]
model.fit(train_features, np.ravel(train_target),eval_set =evalset,early_stopping_rounds = 20,verbose = False)
else:
model.fit(train_features, train_target.values)
if (model.__class__ == xgb.sklearn.XGBRegressor):
print(model.best_ntree_limit)
print('Using xgboost with limited tree rounds')
validation_predictions = model.predict(validation_features,ntree_limit = model.best_ntree_limit)
elif (model.__class__ == lgb.sklearn.LGBMRegressor):
print(model.best_iteration_)
print('Using lgbmboost with limited tree rounds')
validation_predictions = model.predict(validation_features,num_iteration = model.best_iteration_)
else:
print('Using generic predict')
validation_predictions = model.predict(validation_features)
# Calculate and store the MASE for validation data
print(mase(validation_predictions,validation_target))
#model_mase.append(mase(validation_predictions,validation_target))
# Save the validation prediction for level 1 model training
model_val_predictions[val_index, 0] = validation_predictions.reshape(validation.shape[0])
model_val_true[val_index,0] = validation_target.values
model_test_predictions += model.predict(testData[features])
model_test_predictions = model_test_predictions/k
# Fit the base model to the whole training data
#model.fit(trainData[features], np.ravel(trainData[target]))
# Get base model prediction for the test data
#model_test_predictions = model.predict(testData[features])
# Calculate and store the MASE for validation data
#model_val_predictions = model_val_predictions
model_mase.append(mase(model_val_predictions,model_val_true))
return(model_mase, model_val_predictions, model_test_predictions)
# ## Create a function to fit a dictionary of models, and get their OOF predictions from the training data
# Function that takes a dictionary of models and fits it to the data using baseFit
# The results of the models are then aggregated and returned for level 1 model training
def stacks(level0_models, folds, features, target, trainData, testData):
num_models = len(level0_models.keys()) #Number of models
# Initialize empty lists and matrix
level0_trainFeatures = np.empty((trainData.shape[0], num_models))
level0_testFeatures = np.empty((testData.shape[0], num_models))
# Loop through the models
for i, key in enumerate(level0_models.keys()):
print('Fitting %s -----------------------' % (key))
model_mase, val_predictions, test_predictions = base_fit(level0_models[key], folds, features, target, trainData, testData)
# Print the average MASE for the model
print('%s average MASE: %s' % (key, np.mean(model_mase)))
print('\n')
# Aggregate the base model validation and test data predictions
level0_trainFeatures[:, i] = val_predictions.reshape(trainData.shape[0])
level0_testFeatures[:, i] = test_predictions.reshape(testData.shape[0])
return(level0_trainFeatures, level0_testFeatures)
# ## Create a function that trains a dictionary of stackers
# +
# Function that takes a dictionary of classifiers and train them on base model predictions
def stackerTraining(stacker, folds, level0_trainFeatures, level0_testFeatures, trainData,target = None):
for k in stacker.keys():
print('Training stacker %s' % (k))
stacker_model = stacker[k]
stacker_mase = []
y_pred = np.zeros_like(trainData[target].values)
y_true = np.zeros_like(trainData[target].values)
for t, v in folds.split(X, y):
train, validation = level0_trainFeatures[t,:], level0_trainFeatures[v,:]
# Get the features and target
train_features, train_target = train, trainData.iloc[t][target]
validation_features, validation_target = validation, trainData.iloc[v][target]
if (stacker_model.__class__ == xgb.sklearn.XGBRegressor) | (stacker_model.__class__ == lgb.sklearn.LGBMRegressor):
print('Fitting a boost model with limited tree rounds')
evalset = [(validation_features,np.ravel(validation_target))]
stacker_model.fit(train_features, np.ravel(train_target),eval_set =evalset,early_stopping_rounds = 20,verbose = False)
print(stacker_model.best_iteration_)
else:
stacker_model.fit(level0_trainFeatures[t,:], train_target)
y_pred[v] = stacker_model.predict(level0_trainFeatures[v])
y_true[v] = trainData.iloc[v][target].values
stacker_mase =mase(y_pred,y_true)
average_mase = mase(level0_trainFeatures.mean(axis=1),y_true)
print('%s Stacker MASE: %s' % (k, stacker_mase))
print('%s Averaging MASE: %s' % (k, average_mase))
# -
# Get the K fold indexes
n_folds = 5
kf = KFold(n_splits=n_folds, shuffle=False, random_state=156)
# ## Set up the dictionaries of level 0 and level 1 models
# +
# A dictionary of base models
scaler = make_pipeline(QuantileTransformer(output_distribution='normal'),PCA(whiten=True))
level0_models = {}
# level0_models['Lasso'] = make_pipeline(scaler, Lasso(alpha =0.005, random_state=1,max_iter = 2000))
# level0_models['ElasticNet'] = make_pipeline(scaler,ElasticNet(alpha = 0.001))
# level0_models['XGB_rougher_base_a'] = xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 7, 'gamma': '44.954', 'colsample_bytree': '0.395', 'subsample': '0.993', 'min_child_weight': '133.132'},
# silent=1,
# random_state =48, nthread = -1)
# level0_models['XGB_rougher_base_b'] =xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 7, 'gamma': '44.954', 'colsample_bytree': '0.395', 'subsample': '0.993', 'min_child_weight': '133.132'},
# silent=1,
# random_state =38, nthread = -1)
# # level0_models['XGB_rougher_base_c'] = xgb.XGBRegressor(learning_rate=0.05,
# # n_estimators=400,**{'max_depth': 4, 'gamma': '5.102', 'colsample_bytree': '0.344', 'subsample': '0.884', 'min_child_weight': '9.622'},
# # silent=1,
# # random_state =82, nthread = -1)
# # level0_models['XGB_rougher_base_d'] = xgb.XGBRegressor(learning_rate=0.05,
# # n_estimators=400,**{'max_depth': 5, 'gamma': '3.906', 'colsample_bytree': '0.401', 'subsample': '0.760', 'min_child_weight': '9.563'},
# # silent=1,
# # random_state =11, nthread = -1)
level0_models['LGBM_rougher_base_a'] = lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=500,random_state=91,
**{'max_depth': 5, 'num_leaves': 40, 'feature_fraction': '0.453', 'bagging_fraction': '0.276'})
level0_models['LGBM_rougher_base_b'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=500,random_state=92,
**{'max_depth': 4, 'num_leaves': 180, 'feature_fraction': '0.322', 'bagging_fraction': '0.150'})
level0_models['LGBM_rougher_base_c'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=500,random_state=93,
** {'max_depth': 5, 'num_leaves': 80, 'feature_fraction': '0.440', 'bagging_fraction': '0.666'})
level0_models['LGBM_rougher_base_d'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=500,random_state=94,
**{'max_depth': 6, 'num_leaves': 25, 'feature_fraction': '0.555', 'bagging_fraction': '0.257'})
level0_models['LGBM_rougher_base_e']= lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=500,random_state=7,
**{'max_depth': 4, 'num_leaves': 30, 'feature_fraction': '0.658', 'bagging_fraction': '0.863'})
# -
# Train all the base models in the dictionary
level0_trainFeatures_rougher, level0_testFeatures_rougher = stacks(level0_models, kf, X.columns, tgt, train_df, X_test)
# +
# A dictionary of level 1 model to train on base model predictions
stacker = {
'Enet': ElasticNet(alpha = 0.001),
# 'BR':BayesianRidge(n_iter = int(3e3)),
# 'Ridge1':Ridge(),
'Ridge50':Ridge(alpha=60),
'Ridge1e2':Ridge(alpha=1e2),
'Ridge5e2':Ridge(alpha=5e2),
'Ridge1e3':Ridge(alpha=1e3),
'Ridge5e3':Ridge(alpha=5e3),
'Lasso': Lasso(alpha =0.005, random_state=1,max_iter = 2000),
'positive_Lasso': Lasso(alpha=0.0001,precompute=True,max_iter=1000, positive=True, random_state=9999, selection='random'),
'LGBM': lgb.LGBMRegressor(objective='mae',
learning_rate=0.07, n_estimators=500,random_state=38,
**{'max_depth': 4, 'num_leaves': 32, 'feature_fraction': '0.8', 'bagging_fraction': '0.8'})}
stackerTraining(stacker, kf, level0_trainFeatures_rougher, level0_testFeatures_rougher, train_df,target = tgt)
level1_model = stacker['Enet'].fit(level0_trainFeatures_rougher,train_df[tgt])
level1_test_pred_rougher = level1_model.predict(level0_testFeatures_rougher)
rougher_meta_train = level0_trainFeatures_rougher
rougher_meta_test = level0_testFeatures_rougher
level1_test_pred_rougher.shape
# -
# # Let's try to figure out the stacking Level 2
# +
def solve_pg(A, b, momentum=0.9, maxiter=1000):
from cvxpy import Variable,Parameter,Minimize,square,norm,Problem
M, N = A.shape
x = np.zeros(N)
AtA = A.T.dot(A)
Atb = A.T.dot(b)
stop_count = 0
# projection helper
x_ = Variable(N)
v_ = Parameter(N)
objective_ = Minimize(0.5 * norm(x_ - v_, 1))
constraints_ = [sum(x_) == 1]
problem_ = Problem(objective_, constraints_)
def gradient(x):
return AtA.dot(x) - Atb
def obj(x):
return 0.5 * np.linalg.norm(A.dot(x) - b,ord=1)
it = 0
while True:
grad = gradient(x)
# line search
alpha = 1
beta = 0.5
sigma=1e-2
old_obj = obj(x)
while True:
new_x = x - alpha * grad
new_obj = obj(new_x)
if old_obj - new_obj >= sigma * grad.dot(x - new_x):
break
else:
alpha *= beta
x_old = x[:]
x = x - alpha*grad
# projection
v_.value = x
problem_.solve()
x = np.array(x_.value.flat)
y = x + momentum * (x - x_old)
if np.abs(old_obj - obj(x)) < 1e-2:
stop_count += 1
else:
stop_count = 0
if stop_count == 3:
print('early-stopping @ it: ', it)
return x
it += 1
if it == maxiter:
return x
x = solve_pg(level0_trainFeatures_rougher, train_df[tgt].values)
print('sum x: ', np.sum(x))
print(mase(level0_trainFeatures_rougher.dot(x),train_df[tgt].values))
# -
# # Repeat the procedure with Final
# +
year = 2019
tgt = 'final.output.recovery'
X = data_dict[year]['X_train_lagdiff']
y = data_dict[year]['y_train']
X_test = data_dict[year]['X_test_lagdiff']
mask = data_dict[year]['mask']
exclude_pts = data_dict[year]['excl'].set_index('date').tz_localize('UTC')
#mask_na_two_row=y[y[tgt].isna()].index.union(y[y[tgt].isna()].index + pd.Timedelta('1 hour')).union(y[y[tgt].isna()].index + pd.Timedelta('2 hour'))
inds = mask.index.difference(exclude_pts.index)
print(X.shape)
X=X.loc[inds,:]
y=y.loc[inds,:]
mask=mask[inds]
print(X.shape)
print(f'1) X shape: {X.shape},y: {y.shape}')
X = X[mask]
y = y[mask][tgt]
train_df = pd.concat([X,y],axis= 1)
print(f'1) X shape: {X.shape},y: {y.shape}')
print(X_test.shape)
train_df.head()
# -
# ## Create dicts of stackers and base models
# +
# A dictionary of base models
scaler = make_pipeline(QuantileTransformer(output_distribution='normal'),PCA(whiten=True))
level0_models = {}
# level0_models['Lasso'] = make_pipeline(scaler, Lasso(alpha =0.005, random_state=1,max_iter = 2000))
# level0_models['ElasticNet'] = make_pipeline(scaler,ElasticNet(alpha = 0.001))
def fair_obj(preds, dtrain):
"""y = c * abs(x) - c**2 * np.log(abs(x)/c + 1)"""
x = preds - dtrain.get_labels()
c = 1
den = abs(x) + c
grad = c*x / den
hess = c*c / den ** 2
return grad, hess
# level0_models['XGB_final_base_a'] = xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 3, 'gamma': '17.158', 'colsample_bytree': '0.442', 'subsample': '0.644', 'min_child_weight': '9.733'},
# silent=1,
# random_state =48, nthread = -1)
# level0_models['XGB_final_base_b'] =xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 4, 'gamma': '18.571', 'colsample_bytree': '0.745', 'subsample': '0.681', 'min_child_weight': '9.024'},
# silent=1,
# random_state =38, nthread = -1)
# level0_models['XGB_final_base_c'] = xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 2, 'gamma': '16.491', 'colsample_bytree': '0.522', 'subsample': '0.844', 'min_child_weight': '5.096'},
# silent=1,
# random_state =82, nthread = -1)
# level0_models['XGB_final_base_d'] = xgb.XGBRegressor(learning_rate=0.05,
# n_estimators=400,**{'max_depth': 3, 'gamma': '16.766', 'colsample_bytree': '0.540', 'subsample': '0.774', 'min_child_weight': '12.674'},
# silent=1,
# random_state =11, nthread = -1)
level0_models['LGBM_final_base_a'] = lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=400,random_state=96,
**{'max_depth': 8, 'num_leaves': 150, 'feature_fraction': '0.645', 'bagging_fraction': '0.425'})
level0_models['LGBM_final_base_b'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=400,random_state=973,
**{'max_depth': 6, 'num_leaves': 15, 'feature_fraction': '0.826', 'bagging_fraction': '0.919'})
level0_models['LGBM_final_base_c'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=400,random_state=937,
**{'max_depth': 4, 'num_leaves': 195, 'feature_fraction': '0.586', 'bagging_fraction': '0.110'})
level0_models['LGBM_final_base_d'] =lgb.LGBMRegressor(objective='mae',
learning_rate=0.05, n_estimators=400,random_state=49,
**{'max_depth': 4, 'num_leaves': 210, 'feature_fraction': '0.635', 'bagging_fraction': '0.326'})
# level0_models['LGBM_final_base_e'] = lgb.LGBMRegressor(objective=obj,
# learning_rate=0.07, n_estimators=500,random_state=7,
# **{'max_depth': 4, 'num_leaves': 63, 'feature_fraction': '0.89', 'bagging_fraction': '0.757'})
# level0_models['LGBM_final_base_f'] = lgb.LGBMRegressor(objective=obj,
# learning_rate=0.07, n_estimators=500,random_state=8,
# **{'max_depth': 4, 'num_leaves': 63, 'feature_fraction': '0.879', 'bagging_fraction': '0.727'})
# level0_models['LGBM_final_base_g'] = lgb.LGBMRegressor(objective=obj,
# learning_rate=0.07, n_estimators=500,random_state=9,
# **{'max_depth': 5, 'num_leaves': 65, 'feature_fraction': '0.879', 'bagging_fraction': '0.727'})
# level0_models['LGBM_final_base_h'] = lgb.LGBMRegressor(objective=obj,
# learning_rate=0.07, n_estimators=500,random_state=10,
# **{'max_depth': 4, 'num_leaves': 60, 'feature_fraction': '0.797', 'bagging_fraction': '0.982'})
# level0_models['LGBM_final_base_i'] = lgb.LGBMRegressor(objective=obj,
# learning_rate=0.07, n_estimators=500,random_state=12,
# **{'max_depth': 5, 'num_leaves': 60, 'feature_fraction': '0.8', 'bagging_fraction': '0.92'})
# #level0_models['KNN_final_a'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 254, 'weights': 'distance', 'leaf_size': 16}))
#level0_models['KNN_final_b'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 50, 'weights': 'distance', 'leaf_size': 18}))
#level0_models['KNN_final_c'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 15, 'weights': 'distance', 'leaf_size': 30.0}))
# level0_models['KNN_final_d'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 5, 'weights': 'uniform', 'leaf_size': 24.0}))
#level0_models['KNN_rougher_b_bray'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 50, 'weights': 'distance','metric':'braycurtis', 'leaf_size': 18}))
#level0_models['KNN_rougher_c_bray'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 15, 'weights': 'distance', 'leaf_size': 30.0,'metric':'braycurtis'}))
# level0_models['KNN_rougher_d_bray'] = make_pipeline(scaler,KNeighborsRegressor(n_jobs = -1,**{'n_neighbors': 5, 'weights': 'uniform', 'leaf_size': 24.0,'metric':'braycurtis'}))
# -
# Train all the base models in the dictionary
level0_trainFeatures_final, level0_testFeatures_final = stacks(level0_models, kf, X.columns, tgt, train_df, X_test)
# +
# A dictionary of level 1 model to train on base model predictions
stacker = {
'Enet': ElasticNet(alpha = 0.001),
#'RF':RandomForestRegressor(max_depth = 3,n_estimators=200),
'BR':BayesianRidge(n_iter = int(3e3)),
'Ridge1':Ridge(),
'Ridge1e2':Ridge(alpha=1e2),
'Ridge5e2':Ridge(alpha=5e2),
'Ridge1e3':Ridge(alpha=1e3),
'Ridge5e3':Ridge(alpha=5e3),
'Lasso': Lasso(alpha =0.005, random_state=1,max_iter = 2000),
'LGBM': lgb.LGBMRegressor(objective='mae',
learning_rate=0.07, n_estimators=500,random_state=40,
**{'max_depth': 3, 'num_leaves':8, 'feature_fraction': '0.9', 'bagging_fraction': '0.7'})}
stackerTraining(stacker, kf, level0_trainFeatures_final, level0_testFeatures_final, train_df,target = tgt)
level1_model = stacker['LGBM'].fit(level0_trainFeatures_final,train_df[tgt])
level1_test_pred_final = level1_model.predict(level0_testFeatures_final)
level1_test_pred_final.shape
# -
x
# ## Make a submission:
preds = pd.DataFrame(data = {'date':X_test.index,'rougher.output.recovery':level1_test_pred_rougher, 'final.output.recovery':level0_testFeatures_final.mean(axis=1)})
stacked_preds_sub = preds
stacked_preds_sub['date'] = stacked_preds_sub['date'].dt.strftime('%Y-%m-%dT%H:%M:%SZ')
stacked_preds_sub.set_index('date',inplace=True)
#stacked_preds_sub.drop_duplicates(inplace=True)
stacked_preds_sub.to_csv('../results/stacked_sub_lgb_lasso_base_alldata_tsclean_fixed_lgbm_lagdiff.csv')
stacked_preds_sub.plot(style=['o','o'],figsize = (20,10),alpha=0.9)
# +
preds_av = pd.DataFrame(data = {'date':X_test.index,'rougher.output.recovery':level0_testFeatures_rougher.mean(axis=1), 'final.output.recovery':level0_testFeatures_final.mean(axis=1)})
preds_av['date'] = preds_av['date'].dt.strftime('%Y-%m-%dT%H:%M:%SZ')
preds_av.set_index('date',inplace=True)
preds_av.plot(figsize = (20,10),style=['o','o'],alpha=0.9)
#preds_av.to_csv('../results/stacked_sub_lgb_lasso_base_alldata_tsclean_r-filt-f-meta.fixed_best_mod_averaged_lagdiff.csv')
# +
r = np.power(level0_testFeatures_rougher.prod(axis=1),1/level0_testFeatures_rougher.shape[1])
f = np.power(level0_testFeatures_final.prod(axis=1),1/level0_testFeatures_final.shape[1])
preds_av = pd.DataFrame(data = {'date':X_test.index,'rougher.output.recovery':r, 'final.output.recovery':f})
preds_av['date'] = preds_av['date'].dt.strftime('%Y-%m-%dT%H:%M:%SZ')
preds_av.set_index('date',inplace=True)
preds_av.plot(figsize = (20,10),style=['o','o'],alpha=0.9)
# -
|
notebooks/stack_models_lagdiffs-old.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Specifying a Model
#
# One of the core features of **respy** include the flexible modeling capabilities. The guide on *example models* showcases a collection of economic models that have already been implemented. They can be accessed freely.
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">To how-to guide</span>
#
# Find out more about example models in <a
# href="how_to_example_models.html">How to load example models</a>.
# </div>
# -
# However, **respy** can also be used to implement models from scratch. This guide illustrates how to translate an economic model and underlying mathematical relations to the core objects in **respy**: `params` and `options`. As a guiding example we will follow the seminal work of Keane and Wolpin (1994) and replicate their dynamic discrete choice model of schooling and occupational choice. Insights carry over to the conceptually close model used by Keane and Wolpin (1997).
#
# ---
#
# **Note:** Only models of the Eckstein-Keane-Wolpin (EKW) class are implementable in **respy**. You can find further information about this modeling framework in the explanations section of this documentation.
#
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">Explanations</span>
#
# Find out more about EKW models in the <a
# href="../explanations/index.html">Explanations</a>.
# </div>
# -
# ---
# ## Components to modeling
#
# See the article in the explanations section linked below to find information on the exact model specification of Keane and Wolpin (1994).
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">Explanations</span>
#
# Find the details about this model specification in <a
# href="../explanations/implementation_kw94.html">Model in Keane and Wolpin (1994)</a>.
# </div>
# -
# How can we map the equations from the model into **respy** to construct a discrete choice dynamic programming model that allows us to estimate the structural parameters?
#
# A model in **respy** is defined by two components:
#
# 1. The `params` DataFrame, where model parameters reside. It should be specified as a [pandas.DataFrame](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html).
#
# 2. The `options` which specify the settings for the model solution and further restrictions on the model structure. `options` are defined in a Python `dictionary`. Examples of components that enter the options include the number of periods, type of numerical integration, unfeasible states, etc.
#
# In the next steps, we will examine these two components in detail to illustrate how they mirror the model outlined above. Since the model of Keane and Wolpin (1994) is already implemented, we can simply load it into memory.
import respy as rp
params, options, data = rp.get_example_model("kw_94_one")
# ---
#
# Note that when you specify these objects yourself, doing so in separate files might facilitate your workflow. For example, `params` could be loaded from a .csv-file and `options` from a .yaml-file.
#
# ---
# ## Specifying the `params`
#
# We first inspect the `params` DataFrame. It contains all the parameters that enter the structural model. Usually, these parameters will be estimable, but this is not mandatory. For instance, a specified shock distribution may guide the model but be exogenously set. The `params` DataFrame may also contain auxiliary parameters that aid simulation but are not directly related to the model. **respy** allows copious freedom in designing reward functions and naming parameters. However, certain rules need to be accounted for to allow **respy** to process a model correctly. Below, we discuss each parameter group of our exemplary `params` DataFrame to outline how parameters can be specified.
params
# ### Index stucture
#
# The `params` DataFrame needs to abide to a specific index structure:
#
# - **Index**: The DataFrame has a MultiIndex with two levels. The levels have to be named `category` and `name`. Categories need to be unique. Names may be repeated but never within the same category. This ensures that each parameter is uniquely identfied in the `params` DataFrame.
# - **Columns**:The parameter value needs to be saved in a column called `value`. The `params` DataFrame may contain other columns like the comment column above. They do not influence the model. This can also be useful for parameter estimation where information like bounds may need to be specified as additional columns.
#
# ### Discounting
#
# In `respy` the discount factor has a pre-defined and unmutable name: `delta`.
params.loc["delta"]
# **respy** also supports hyperbolic discounting. You can implement it in your model by adding a `category` and `name` called `beta` to your parameter vector.
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">How-to Guide</span>
#
# Find out how to implement hyperbolic discounting in <a
# href="how_to_hyperbolic_discounting.html">Impatient Robinson</a>.
# </div>
# -
# ### Choice Rewards
#
# The structural model consists of two building blocks: states and choices. Choices in general can have two types of rewards:
#
# - **pecuniary rewards**, e.g. wages, with corresponding `category`: `wage_{choice}`.
# - **non-pecuniary rewards**, e.g. intrinsic value of education, with corresponding `category`: `nonpec_{choice}`.
#
# Choices can be named freely but it is important to use the appropriate prefixes so **respy** can process the model accordingly. In our example above, choices have either exclusively pecuniary rewards (occupation *A* and *B*) or non-pecuniary rewards (*education* and *home*) but **respy** also allows for combinations of both types to define reward functions. Each parameter in `params` then corresponds to a parameter in the reward functions.
#
# #### Example: Returns to Occupation A
#
# Take for example the reward function for choosing to work in occupation *A*:
#
# $$
# R_1(t) = w_{1t} = r_{1} exp\{\alpha_{10} + \alpha_{11}s_{t} + \alpha_{12}x_{1t} - \alpha_{13}x^2_{1t} + \alpha_{14}x_{2t} - \alpha_{15}x^2_{2t} + \epsilon_{1t}\} \nonumber\\
# $$
#
# We can directly map the `params` DataFrame to the equation. All parameters are saved under the `category` of `wage_a`. The pecuniary reward associated with working in occupation A, `wage_a` is determined by state-specific returns. The index `name` collects all covariates where `value` captures the associated return. The state-variables and returns are mapped to the entries in `category` `wage_a` according to the following table:
# | Covariate | `name` | Return | `value` |
# |---------------|----------------|----------------|-----------|
# | $1$ | `constant` | $\alpha_{10}$ | $9.2100$ |
# | $s_{t}$ | `exp_edu` | $\alpha_{11}$ | $0.0380$ |
# | $x_{1t}$ | `exp_a` | $\alpha_{12}$ | $0.0330$ |
# | $x_{1t}^2$ | `exp_a_square` | $\alpha_{13}$ | $-0.0005$ |
# | $x_{2t}$ | `exp_b` | $\alpha_{14}$ | $0.0000$ |
# | $x_{2t}^2$ | `exp_b_square` | $\alpha_{15}$ | $0.0000$ |
# We can imagine the equation to be written as
#
# $$
# w_{1t} = 1 \cdot exp\{9.2100 \cdot 1 + 0.0380 \cdot h_{t} + 0.0330 \cdot k_{1t} -0.0005 \cdot k_{1t}^2 + 0.0000 \cdot k_{2t} + 0.0000 \cdot k_{2t}^2\ + \epsilon_{1t}\}.
# $$
#
#
#
# The choice-specific shock that is also part of this equation will be discussed in more detail below.
# ---
#
# **Note:** The prefix `exp_` is a special `name` in **respy** and must be complemented by the name of a choice. Parameters with this prefix indicate the return to experience in a certain choice alternative. Conversely, the names `constant` and `exp_{choice}_square` do not have this pre-specified structure. Instead, they require further user input in the `options` dictionary to be properly specified.
#
# Experience accumulation is a central component of EKW models and thus an important feature of **respy**. You will notice that `exp_home` does not appear in our `params` DataFrame. This is a direct result from our model equations: Individuals do not accumulate any experience while being at home. Omitted experience parameters indicate that experience accumulation for this alternative is not a model component. Notably, alternatives with a wage component automatically account for experience accumulation.
#
# ---
# ### Shocks
#
# For each choice reward, idiosyncratic and serially uncorrelated shocks alter the respective return. Those alternative-specific shocks are specified jointly in `category` `shocks_sdcorr`.
params.loc["shocks_sdcorr"]
# Shocks are **assumed to follow a multivariate normal distribution** with zero mean and covariance matrix $\Sigma$. The **dimensionality** of the symmetric covariance matrix equals the number of modeled choices. The specification of $\Sigma$ remains in the discretion of the user. Because the symmetry of covariance matrices, it is sufficient to specify the lower triangular matrix. However, it is mandatory to follow the order which is prescribed by **respy**.
#
# - First, the **diagonal elements (standard deviations)** are specified via `sd_{choice}` according to the following order:
#
# 1. Working alternatives (alphabetically sorted).
# 2. Non-working alternatives with experience accumulation (alphabetically sorted).
# 3. Remaining alternatives (alphabetically sorted.)
#
# - Second, the **off-diagonal elements (correlations)** are specified ordered **by rows** in the matrix.
#
# ---
# In all of the example models, the covariance matrices are specified in form of a correlation matrix following Keane and Wolpin (1994, 1997, 2000) to allow direct comparison between the parameters presented in the papers and their **respy** implementation.
#
# ---
#
#
# Aside from specifying shocks according to standard deviations and correlations, you can also specify the variance-covariance matrix. The parameters are ordered by appearance in the lower triangular. Variances have the name `var_{choice}` and covariances `cov_{choice_2}_{choice_1}` and so forth. Lastly, another option is the Cholesky factor of the variance-covariance matrix ordered by appearance in the lower triangular. The labels are either `chol_{choice}` or `chol_{choice_2}_{choice_1}` and so forth. In contrast to the other two options, Cholesky shocks are not ordered according to diagonal and off-diagonal elements. Instead they need to be ordered according to appearance by rows in the lower triangular of the shock matrix.
#
#
# ---
#
# The specification of shocks may appear a bit confusing due to the ordering requirements. Notably, **respy** will raise an error the shock parameters are not passed in correct order. The error message will help you specify the parameters in the correct order.
#
# ---
#
#
# ### Additional Parameters
#
# Aside from discounting and reward-specific parameters (pecuniary rewards, non-pecuniary rewards, and shocks) there are some additional parameters that you might want to add to specify your model. Below you find a small overview of the type of parameters you may add.
# #### Initial Conditions
#
# In many instances, you may need to add initial conditions to your model. This can include lagged choices, experience levels, and observable characteristics. Their `value` in the `params` reflect the share of individuals that exhibits a specific characteristic. Importantly, initial conditions are usually non-estimable parameters. Our example model requires two such parameter specifications.
#
# The parameter `lagged_choice_1_edu` ensures that the model logs *education* as the previous choice in period $t=-1$ for all individuals in the sample. Our model requires this specification because we include a cost of returning to school in the reward function for education, if the previous choice was another alternative. In order to compute the rewards for period $0$, **respy** thus needs to know the choice of the previous period, even if it is not directly part of the model's decision horizon.
params.loc["lagged_choice_1_edu"]
# The parameter `initial_exp_edu_10` assigns 10 periods of experience in education (i.e. 10 periods of completed schooling) to all individuals in period $0$. Adding an initial condition like this may be useful if we think about the correspondence between the model and potential empirical data. Since we are assessing occupational choices, we will be analyzing individuals of working age who will have accumulated schooling before they enter the labor market.
params.loc["initial_exp_edu_10"]
# Both of these parameters only exhibit one value that occurs for all individuals in this example. However, initial conditions are much more versatile and can be defined quite flexibility. Refer to the guide linked below for more information.
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">How-to Guide</span>
#
# Find out how to implement initial conditions in <a
# href="how_to_initial_conditions.html">Initial Conditions</a>.
# </div>
# -
# #### Maximum Experience
#
# Much like adding initial experience, we may want to limit the maximum amount of experience. In our example, individuals can complete a maximum of 20 periods of schooling. The implementation is straightforward. We define a `category` called `maximum_exp` and add a parameter `name` that corresponds to the name of a choice (e.g. `edu`). The `value` column holds the maximum level of experience.
params.loc["maximum_exp"]
# #### Unobserved Heterogeneity
#
# A component not implemented in this example is unobserved heterogeneity between individuals. **respy** allows to add such components using finite mixture approaches. Check out the guide below and example models based on Keane and Wolpin (1997) to learn more about adding unobserved heterogeneity to your model.
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">How-to Guide</span>
#
# Find out how to add unobserved heterogeneity in <a
# href="how_to_finite_mixture.html">Unobserved Heterogeneity and Finite Mixture Models</a>.
# </div>
# -
# #### Measurement Error
#
# You may also implement measurement error in wages. To do so you have to define a `category` called `meas_error` and add the parameter names `sd_{choice}` for all choices with a wage. The parameter `value` should be the standard deviations of measurement error. Check out the model parametrization of `kw_97_extended` for an example.
#
# ---
#
# Note that this parameter `category` only requires standard deviations for choices with a wage. They can be provided for *all* or *none* choices with wages, measurement errors for non-wage choices are neglected, and no correlation between measurement errors can be defined.
#
# ---
# ## Defining the `options`
#
# The `options` dictionary is the second necessary component for defining models in **respy**. As we have learned above, structural parameters are defined in a pandas.DataFrame. The `options` dictionary holds additional settings and information about the model. Thus, the `params` DataFrame and `options` dictionary should be viewed as complementary objects. Some types of parameters require additional options in order for **respy** to process them. Below we will inspect our example model's `options`.
options
# ### `n_periods`
#
# The option `n_periods` determines the number of periods that individuals take into account when evaluating their actions. That is, they decide for the action that maximizes their expected utility in an evaluation over `n_periods`. Possible values are one and higher integers. This option is mandatory as no default is supplied. In most models, the model's complexity or the number of states in the state space is exponentially increasing in the number of periods.
#
# Do not confuse this option with the number of periods for which you want to simulate the actions of individuals. This number can be lower because although actions of individuals are simulated for, say, 10 periods, their actions can still aim to maximize utility for 50 periods.
options["n_periods"]
# ### `simulation_agents`
#
# This option specifies the number of individuals which are simulated. This option is ignored if you pass data to the simulation function.
options["simulation_agents"]
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">To how-to guide</span>
# Find out more about <a href="how_to_simulation.html">Simulation</a>.
# </div>
# -
# ### `covariates`
#
# In the subsection on the [parameterization of the choice rewards](#Choice-Rewards), we discussed the special role of `exp_{choice}` in defining parameters for the pecuniary reward of occupation A. However, the parameter vector includes further covariates like a constant and squared experience terms.
#
# These covariates need further specification so **respy** knows how to process them. Covariates with no pre-defined naming convention are specified in the model `options` as a nested dictionary called `covariates`. In the `covariates` dictionary, keys correspond to the parameter `name` in `params` and dictionary values hold the definition of this parameter.
#
# For example, all parameters named `constant` return a value of 1 for every individual. The parameters `exp_a_square` and `exp_b_square` signal the return to square experience in both occupations.
#
# The other two covariates enter the reward function for *education*. `at_least_twelve_exp_edu` is a boolean that evaluates true when an individual has accumulated 12 periods of schooling or more, and triggers a cost component in the reward function. Lastly, the covariate `not_edu_last_period` is a boolean indicator for not having chosen *education* in the last period. As discussed in the section on [initial conditions](#Initial-Conditions), this requires the inclusion of a lagged choice in the `params` DataFrame.
options["covariates"]
# ---
#
# How should covariate definitions in the `options` look like to be processed? Here are some pointers:
#
# - The statements are evaluated using [pandas.eval](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.eval.html). This means you can use all arithmetic operations that this method supports.
# - The following pre-defined terms are recognized to construct covariates: `period`, `exp_{choice}`, `lagged_choice_{number of periods}`.
# - You can also define new covariates as a function of already existing covariates.
#
# ---
# ### Seeds (optional)
#
# To be able to replicate a model, the `options` for solution, simulation, and estimation allows for three seeds. The distinction enables us to vary randomness in only one component, independent from the others. The dictionary keys are
#
# - `solution_seed` for the computation of the decision rules.
# - `simulation_seed` for the simulation.
# - `estimation_seed` for the computation of the log likelihood.
{k: v for k, v in options.items() if "seed" in k}
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">To reference guide</span>
# Find out more about this topic in
# <a href="../reference_guides/randomness_and_reproducibility.html">Randomness and Reproducibility</a>.
# </div>
# -
# ### `monte_carlo_sequence` and draws (optional)
#
# `monte_carlo_sequence` and draws refer more generally to approximations of integrals with Monte Carlo simulations inside **respy**. There exist two applications for Monte Carlo simulation.
#
# 1. In the solution of a model, the value of expected value functions has to be simulated.
# 2. While computing the log likelihood, (log) choice probabilities are simulated.
#
# The number of draws controls how many points are used to evaluate an integral. The default is 500 for the solution and 200 for the estimation of choice probabilities.
{k: v for k, v in options.items() if "draws" in k}
# The option `monte_carlo_sequence` controls how points are drawn.
#
# - `"random"`: Points are drawn randomly (crude Monte Carlo).
# - `"sobol"`or `"halton"`: Points are drawn from low-discrepancy sequences (superiority in coverage). This means a given approximation error can be achieved with less points.
#
# + active=""
# <div class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">To how-to guide</span>
# Find out more about
# <a href="how_to_numerical_integration.html">Numerical Integration Methods</a>.
# </div>
# -
# ### `interpolation_points`
#
# The number of interpolation points specifies the number states or their corresponding expected value functions which are used to fit an interpolation model. The model is used to predict the expected value functions for all remaining states. The interpolation method available in **respy** is designed by Keane and Wolpin (1994). Their paper offers a detailed explanation of the method.
#
# If `interpolation_points` is set to -1, the full solution is computed.
options["interpolation_points"]
# ### `negative_choice_set`
#
# You can limit the set of available choices at different points in time using the option `negative_choice_set`. To implement a negative choice set, define a nested dictionary where keys correspond to choice alternatives and values hold a list of conditions that will eliminate the corresponding choice for periods whenever it evaluates to `True`.
#
# For example, consider a scenario where individuals can only work in occupation A after the fifth period ($t=4$) (i.e. the occupation may have an age requirement). In this case, we need to implement a negative choice set for the first five periods as follows.
options["negative_choice_set"] = {"a" : ["period < 5"]}
# ### `core_state_space_filters` (optional)
#
# Core state space filters partly complement the `negative_choice_set` option. First of all, what is the core state space? The core state space is the part of the state space spanned by the combinations of experiences and previous choices. Not all combinations are feasible, but it is not always possible to catch all invalid combinations.
#
# States with impossible combinations have no effect on the correctness of the model, but pose an additional computational burden which should be eliminated. Similar to `negative_choice_set` the `core_state_space_filters` are a list of conditions and whenever one of them is true, the state is eliminated from the state space.
#
# This option is a rather advanced feature of **respy** as it requires a sound understanding of the state space and at least partial knowledge on how it processed internally. In most cases, you would not necessarily need to add them, but they can be useful to:
#
# - Improve the computational performance of your model.
# - Implement restrictions on the choice set that cannot be implemented using the `params` or `negative_choice_set` option .
options["core_state_space_filters"]
# ---
#
# **Order is important**
#
# `negative_choice_set`'s are applied **after** initial conditions are implemented.
#
# `core_state_space_filters` are applied **before** initial conditions are implemented. Pay attention to this when you have, for example, implemented initial experience for a choice. When adding a filter based on the experience for this choice, you will have to refer to within-model experience and discard knowledge of potential previous experience.
#
#
# ---
# ### `estimation_tau`
#
# *This option is only relevant for maximum likelihood estimation.*
#
# The choice probabilities in the likelihood function are simulated, as there exists no closed-form solution for them. They are computed with the [softmax function](https://en.wikipedia.org/wiki/Softmax_function) and require the specfication of a so-called temperature parameter tau. This parameter can be specified in the **respy** options.
options["estimation_tau"]
#
# + active=""
# <div to class="d-flex flex-row gs-torefguide">
# <span class="badge badge-info">How-to Guide</span>
#
# To learn more about the temerature parameter see <a
# href="how_to_likelihood.html">Maximum Likelihood Criterion</a>.
# </div>
# -
#
#
# ## References
#
# - <NAME>., & <NAME>. (1994). The Solution and Estimation of Discrete Choice Dynamic Programming Models by Simulation and Interpolation: Monte Carlo Evidence. *The Review of Etheconomics and Statistics*, 648-672.
#
# - <NAME>., & <NAME>. (1997). The Career Decisions of Young Men. *Journal of Political Economy*, 105(3), 473-522.
|
docs/how_to_guides/how_to_specify_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
# +
import numpy as np
x = tf.constant(2.0)
del_y = []
with tf.GradientTape(persistent=True) as tape:
tape.watch(x)
y = [x, 2 * x]
for i in range(len(y)):
del_y.append(tape.gradient(y[i], x))
del tape
print(del_y)
# -
y
grad
tf.__version__
# +
x = tf.ones((2, 2))
with tf.GradientTape() as t:
t.watch(x)
y = tf.reduce_sum(x)
z = tf.multiply(y, y)
# Use the tape to compute the derivative of z with respect to the
# intermediate value y.
dz_dy = t.gradient(z, y)
# -
dz_dy
|
test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''base'': conda)'
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/Vamsi995/Paraphrase-Generator/blob/master/Paraphrase.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="8f6uVYL1XLJI"
# # **Inferential Transformer: Semantic Alignment Generation from Pre-trained Generative Model**
# + [markdown] colab_type="text" id="w2gJ5EV12trx"
# # **What models can be used**
#
# + [markdown] colab_type="text" id="V__cOHPS2t4J"
# # **Building the BART model for fine tuning**
# + [markdown] colab_type="text" id="asAs1kgl8NPr"
# ## **Install Requirements**
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="kZiXQgIsTOUS" outputId="ea2b7656-cc82-4c8a-8749-49cda86f97ea"
# !pip install pytorch-lightning
# !pip install transformers
# !pip install rouge-scorer
# -
# ## **Set Up Environemnt and Seed**
# + colab={"base_uri": "https://localhost:8080/", "height": 53} colab_type="code" id="f7izi0clHdsf" outputId="832db418-9aba-4f28-d6ef-c37ab85135d0"
import argparse
import os
import random
import pandas as pd
import numpy as np
import torch
import pytorch_lightning as pl
from torch.utils.data import Dataset, DataLoader
from transformers import AdamW, get_linear_schedule_with_warmup
from transformers import BartForConditionalGeneration, BartTokenizer
# + colab={} colab_type="code" id="Sbe6w5MaUMlA"
def set_seed(seed):
random.seed(seed)
np.random.seed(seed)
torch.manual_seed(seed)
if torch.cuda.is_available():
torch.cuda.manual_seed_all(seed)
set_seed(42)
# -
# ## **Prepare Few-shot Dataset**
train_alignment_pairs = []
val_alignment_pairs = [
{
"premise": "A man , a woman , and two dogs are walking on the beach .",
"source": "Some people and two animals",
"target": "A man , a woman , and two dogs",
},
{
"premise": "A man with a helmet is riding a bike down the road",
"source": "along a roadway",
"target": "down the road",
},
{
"premise": "A student broke a screen today in class",
"source": "a screen was broken",
"target": "student broke a screen",
},
]
# +
import pandas as pd
df = pd.read_csv("sick_alignment.csv")
df.head()
# +
counter = 0
for row in df.itertuples(index=False):
premise = row.premise
sources = row.chunks2.replace("[","").replace("]","").split(", ")
targets = row.chunks1.replace("[","").replace("]","").split(", ")
relations = row.labels.replace("[","").replace("]","").split(", ")
for i in range(len(sources)):
if relations[i] == "entailAlign":
example = {
"premise": premise,
"source": sources[i],
"target": targets[i]
}
if example["source"] == example["target"]:
continue
if counter < 240:
train_alignment_pairs.append(example)
else:
val_alignment_pairs.append(example)
counter += 1
print(len(train_alignment_pairs))
print(len(val_alignment_pairs))
# +
import copy
class AlignmentGenerationDataset(Dataset):
def __init__(self, tokenizer, examples, max_len_inp=96,max_len_out=96):
self.alignment_pairs = examples
self.max_len_input = max_len_inp
self.max_len_output = max_len_out
self.tokenizer = tokenizer
self.inputs = []
self.targets = []
self.skippedcount =0
self._build()
def __len__(self):
return len(self.inputs)
def __getitem__(self, index):
source_ids = self.inputs[index]["input_ids"].squeeze()
target_ids = self.targets[index]["input_ids"].squeeze()
src_mask = self.inputs[index]["attention_mask"].squeeze()
target_mask = self.targets[index]["attention_mask"].squeeze()
labels = copy.deepcopy(target_ids)
labels [labels==0] = -100
return {"source_ids": source_ids, "source_mask": src_mask, "target_ids": target_ids, "target_mask": target_mask,"labels":labels}
def _build(self):
for inputs in self.alignment_pairs:
premise = inputs["premise"]
source = inputs['source']
input_sent = f"Premise: {premise} <extra_id_0> Source Phrase: {source} <extra_id_1> In Premise , Source Phrase aligns to: "
ouput_sent = inputs['target']
# tokenize inputs
tokenized_inputs = self.tokenizer.batch_encode_plus(
[input_sent], max_length=self.max_len_input, pad_to_max_length=True, return_tensors="pt"
)
# tokenize targets
tokenized_targets = self.tokenizer.batch_encode_plus(
[ouput_sent], max_length=self.max_len_output, pad_to_max_length=True,return_tensors="pt"
)
self.inputs.append(tokenized_inputs)
self.targets.append(tokenized_targets)
# -
# ## **Create Fine-tuner and Model**
# +
from pytorch_lightning.loggers import TensorBoardLogger
from rouge_score import rouge_scorer
from tqdm import tqdm
class MetricsCallback(pl.Callback):
def __init__(self):
super().__init__()
self.metrics = []
def on_validation_end(self, trainer, pl_module):
self.metrics.append(trainer.callback_metrics)
class BartFineTuner(pl.LightningModule):
def __init__(self, args, train_ds, val_ds):
super(BartFineTuner, self).__init__()
self.save_hyperparameters(args)
self.args = args
self.model = BartForConditionalGeneration.from_pretrained(
args.model_name_or_path)
self.tokenizer = BartTokenizer.from_pretrained(
args.model_name_or_path)
self.scorer = rouge_scorer.RougeScorer(
['rouge1', 'rouge2', 'rougeL'], use_stemmer=True)
self.build_dataset(train_ds, val_ds)
def build_dataset(self, train_ds, val_ds):
self.train_dataset = AlignmentGenerationDataset(self.tokenizer, train_ds)
self.validation_dataset = AlignmentGenerationDataset(self.tokenizer, val_ds)
def forward(self, input_ids,
attention_mask=None,
decoder_input_ids=None,
decoder_attention_mask=None,
lm_labels=None):
outputs = self.model(
input_ids=input_ids,
decoder_input_ids=decoder_input_ids,
attention_mask=attention_mask,
decoder_attention_mask=decoder_attention_mask,
labels=lm_labels,
)
return outputs
def training_step(self, batch, batch_idx):
outputs = self.forward(
input_ids=batch["source_ids"],
attention_mask=batch["source_mask"],
decoder_input_ids = batch["target_ids"],
decoder_attention_mask=batch['target_mask'],
lm_labels=batch['labels']
)
loss = outputs[0]
self.log('train_loss',loss)
return loss
def validation_step(self, batch, batch_idx):
outputs = self.forward(
input_ids=batch["source_ids"],
attention_mask=batch["source_mask"],
decoder_input_ids = batch["target_ids"],
decoder_attention_mask=batch['target_mask'],
lm_labels=batch['labels']
)
loss = outputs[0]
self.log("val_loss",loss)
return loss
def save_core_model(self):
store_path = os.path.join(
self.args.output_dir,
self.args.name)
self.model.save_pretrained(store_path)
self.tokenizer.save_pretrained(store_path)
def configure_optimizers(self):
optimizer = AdamW(self.parameters(), lr=self.hparams.lr, eps=1e-8)
scheduler = get_linear_schedule_with_warmup(
optimizer, num_warmup_steps=self.hparams.warmup_steps,
num_training_steps=self.hparams.max_epochs * len(self.train_dataset))
return {'optimizer': optimizer, 'lr_scheduler': scheduler}
def generate_alignment(self, test_data):
results = []
self.model.eval()
for _, test_example in tqdm(enumerate(test_data)):
premise = test_example['premise']
source = test_example['source']
target = test_example["target"]
test_sent = f"Premise: {premise} <extra_id_0> Source Phrase: {source} <extra_id_1> In Premise , Source Phrase aligns to: </s>"
test_tokenized = self.tokenizer.encode_plus(test_sent, return_tensors="pt")
test_input_ids = test_tokenized["input_ids"]
test_attention_mask = test_tokenized["attention_mask"]
beam_outputs = model.model.generate(
input_ids=test_input_ids,
attention_mask=test_attention_mask,
max_length=64,
early_stopping=True,
num_beams=10,
num_return_sequences=5,
no_repeat_ngram_size=2
)
for beam_output in beam_outputs:
prediction = self.tokenizer.decode(
beam_output,
skip_special_tokens=True,
clean_up_tokenization_spaces=True)
scores = self.scorer.score(target, prediction)
result = {
"premise": premise,
"source": source,
"prediction": prediction,
"target": target,
"scores": scores
}
results.append(result)
return results
def train_dataloader(self):
return DataLoader(
self.train_dataset,
batch_size=self.hparams.train_batch_size,
num_workers=0)
def val_dataloader(self):
return DataLoader(
self.validation_dataset,
batch_size=self.hparams.eval_batch_size,
num_workers=0)
# -
# # **Fine-tune Your Own Inferential T5**
# ## **Initialize Hyperparameters and Training Arguments**
# +
import argparse
trial_number = 1
args_dict = dict(
name="inferential-bart-base",
data_dir="",
output_dir="./runs",
model_name_or_path='facebook/bart-base',
max_seq_length=512,
lr=3e-4,
weight_decay=0.0,
warmup_steps=0,
train_batch_size=1,
eval_batch_size=2,
max_epochs=5,
gradient_accumulation_steps=16,
n_gpu=1,
fp_16=False,
opt_level='O1',
max_grad_norm=1.0,
seed=42,
)
args = argparse.Namespace(**args_dict)
checkpoint_callback = pl.callbacks.ModelCheckpoint(
dirpath=os.path.join(args.output_dir, args.name),
filename="checkpoint",
monitor="val_loss",
mode="min",
save_top_k=5
)
metrics_callback = MetricsCallback()
train_params = dict(
#accumulate_grad_batches=args.gradient_accumulation_steps,
gpus=args.n_gpu,
max_epochs=args.max_epochs,
progress_bar_refresh_rate=10,
#precision= 16 if args.fp_16 else 32,
#amp_level=args.opt_level,
#gradient_clip_val=args.max_grad_norm,
checkpoint_callback=True,
callbacks=[metrics_callback, checkpoint_callback],
logger=TensorBoardLogger(
os.path.join(args.output_dir, 'logs'),
name=args.name,
version=f'trial_{trial_number}')
)
# -
# ## **Run Training and Validation Loop**
# +
import warnings
warnings.filterwarnings('ignore')
model = BartFineTuner(args, train_alignment_pairs, val_alignment_pairs)
trainer = pl.Trainer(**train_params)
print (" Training model")
trainer.fit(model)
#trainer.test(model)
print ("Saving model ... ")
model.save_core_model()
print("Model Saved")
# -
# ## **Test On Validation Set**
# +
from utils.py_io import write_json
results = model.generate_alignment(val_alignment_pairs)
write_json(results, "./results_bart.json")
# +
premise = val_alignment_pairs[0]['premise']
source = val_alignment_pairs[0]['source']
target = val_alignment_pairs[0]["target"]
test_sent = f"Premise: {premise} <extra_id_0> Source Phrase: {source} <extra_id_1> In Premise , Source Phrase aligns to: </s>"
test_tokenized = model.tokenizer.encode_plus(test_sent, return_tensors="pt")
test_input_ids = test_tokenized["input_ids"]
test_attention_mask = test_tokenized["attention_mask"]
model.model.eval()
beam_outputs = model.model.generate(
input_ids=test_input_ids,
attention_mask=test_attention_mask,
max_length=64,
early_stopping=True,
num_beams=10,
num_return_sequences=5,
no_repeat_ngram_size=2
)
print(source)
print(target)
for beam_output in beam_outputs:
sent = model.tokenizer.decode(beam_output, skip_special_tokens=True,clean_up_tokenization_spaces=True)
print (sent)
# -
|
inferential_BART.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from combined_player import player_minutes_value
from html_scraper import db
from mongo_to_db import create_master_df
import pprint
import json
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pd.set_option('display.max_columns', 50)
# # Dataframe of Players
games = db.games.find()
players = db.players.find()
final_df = player_minutes_value(games, players)
final_df.head()
# # Shot Data Dataframe
games = db.games.find()
shots_df = create_master_df(games)
shots_df.head()
# # Model Training
from model_prep import create_training_df, create_test_df, create_xG_df, create_summed_xG_df, create_test_min_df, merged_dataframes
train_data, train_y, indices, hold_test = create_training_df(shots_df)
test_data, test_y, indices1, holdout, test = create_test_df(shots_df, hold_test)
print(len(holdout))
#holdout is game_id where as the other two are shot events
print(len(train_data))
len(test_data)
# holdout is 54 games to train on again
#
# training data is 1240 shots - rougly 60 games...
#
# test data is 677 shots - roughly 34 games...
1240 / 20
# # Running XGBoost, RF, Gradient Boosting, Ensemble
from sklearn.metrics import log_loss
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier
from xgboost import XGBClassifier
columns_to_predict_on = ['shot_distance', 'shot_angle', 'assisted_shot', 'is_penalty_attempt']
# +
xgboost_model = XGBClassifier(learning_rate = 0.01, max_depth = 3, n_estimators = 300, random_state=8)
gradient_boost_model = GradientBoostingClassifier(learning_rate=0.01, max_depth=4, max_features='log2', min_samples_leaf=4, n_estimators=280, subsample=0.25, random_state=8)
random_forest_model = RandomForestClassifier(n_estimators=300, max_depth=3, verbose=1, random_state=8)
xgboost_model.fit(train_data[columns_to_predict_on], train_y)
gradient_boost_model.fit(train_data[columns_to_predict_on], train_y)
random_forest_model.fit(train_data[columns_to_predict_on], train_y)
p_random_forest = random_forest_model.predict_proba(test_data[columns_to_predict_on])
p_gradient_boost = gradient_boost_model.predict_proba(test_data[columns_to_predict_on])
p_xgboost = xgboost_model.predict_proba(test_data[columns_to_predict_on])
#need to concat these two arrays somehow...
ensemble_p_0 = (p_random_forest[:,0] + p_gradient_boost[:,0] + p_xgboost[:,0])/3
ensemble_p_1 = (p_random_forest[:,1] + p_gradient_boost[:,1] + p_xgboost[:,1])/3
# ensemble_p = np.concatenate(ensemble_p_0, ensemble_p_1, axis=0)
random_forest_ll = log_loss(test_y, p_random_forest)
gradient_boost_ll = log_loss(test_y, p_gradient_boost)
xgboost_ll = log_loss(test_y, p_xgboost)
# ensemble_ll = log_loss(test_y, ensemble_p)
print("Ensemble Log Loss " + str(ensemble_ll))
print("Gradient Boost Log Loss " + str(gradient_boost_ll))
print("Random Forest Log Loss " + str(random_forest_ll))
print("XGBoost Log Loss " + str(xgboost_ll))
# -
# # predicting on holdoutset with turned parameters
from model_prep import use_holdout_df
test_data, test_y, indiecs1 = use_holdout_df(shots_df, holdout)
# +
p_random_forest = random_forest_model.predict_proba(test_data[columns_to_predict_on])
p_gradient_boost = gradient_boost_model.predict_proba(test_data[columns_to_predict_on])
p_xgboost = xgboost_model.predict_proba(test_data[columns_to_predict_on])
random_forest_ll = log_loss(test_y, p_random_forest)
gradient_boost_ll = log_loss(test_y, p_gradient_boost)
xgboost_ll = log_loss(test_y, p_xgboost)
print("Gradient Boost Log Loss " + str(gradient_boost_ll))
print("Random Forest Log Loss " + str(random_forest_ll))
print("XGBoost Log Loss " + str(xgboost_ll))
# -
# # pickle models
import pickle
# +
rf_pkl_filename = 'rfc.pkl'
rf_pkl = open(rf_pkl_filename, 'wb')
pickle.dump(random_forest_model, rf_pkl)
rf_pkl.close()
gb_pkl_filename = 'gb.pkl'
gb_pkl = open(gb_pkl_filename, 'wb')
pickle.dump(gradient_boost_model, gb_pkl)
gb_pkl.close()
xgb_pkl_filename = 'xgb.pkl'
xgb_pkl = open(xgb_pkl_filename, 'wb')
pickle.dump(xgboost_model, xgb_pkl)
xgb_pkl.close()
# -
# # xG and minutes for various models
# +
rf_xg = create_xG_df(test_data, test_y, p_random_forest)
rf_contributions = create_summed_xG_df(rf_xg)
gb_xg = create_xG_df(test_data, test_y, p_gradient_boost)
gb_contributions = create_summed_xG_df(gb_xg)
xgb_xg = create_xG_df(test_data, test_y, p_xgboost)
xgb_contributions = create_summed_xG_df(xgb_xg)
# ensem_xg = create_xG_df(test_data, test_y, ensemble_p)
# ensem_contributions = create_summed_xG_df(ensem_xg)
# -
rf_contributions.head(20)
gb_contributions.head(20)
xgb_contributions.head(20)
# # looking at probability by area
from create_shot_coordinates import shot_probability_player, coord_table
six, eighteen, eighteen_plus, left_box, right_box = shot_probability_player()
# ### average probability of shot in the six yard box
# +
p_random_forest6 = random_forest_model.predict_proba(six)
p_gradient_boost6 = gradient_boost_model.predict_proba(six)
p_xgboost6 = xgboost_model.predict_proba(six)
p_6_rf = p_random_forest6.sum(axis=0)[1] / len(p_random_forest6)
p_6_gb = p_gradient_boost6.sum(axis=0)[1] / len(p_gradient_boost6)
p_6_xgb = p_xgboost6.sum(axis=0)[1] / len(p_xgboost6)
print(p_6_rf)
print(p_6_gb)
print(p_6_xgb)
# -
six_yard_shot = coord_table(-10, 10, 2, 2, 6, 2)
fig, ax = plt.subplots()
ax.scatter(six_yard_shot['shot_coord_x1'], six_yard_shot['shot_coord_y1'])
# ax.scatter(shot_distance_df['pass_coord_x1'], shot_distance_df['pass_coord_y1'], color='red')
# ax.scatter(transposed_df['pass_coord_x2'], transposed_df['pass_coord_y2'], color='yellow')
ax.set_title('xG of shots six yard box (rf:0.33, gb: 0.43, xgb: 0.39)')
ax.set_xlim([88.88, 0])
ax.set_ylim([-30.76, 30.76])
ax.axvline(6)
ax.axvline(18)
ax.axhline(10, xmax=6)
ax.axhline(-10, xmax=6)
ax.axhline(22, xmax=18)
ax.axhline(-22, xmax=18)
ax.set_facecolor('xkcd:lightgreen')
# ### average probability of shot in the eighteen yard box
# +
p_random_forest18 = random_forest_model.predict_proba(eighteen)
p_gradient_boost18 = gradient_boost_model.predict_proba(eighteen)
p_xgboost18 = xgboost_model.predict_proba(eighteen)
p_18_rf = p_random_forest18.sum(axis=0)[1] / len(p_random_forest18)
p_18_gb = p_gradient_boost18.sum(axis=0)[1] / len(p_gradient_boost18)
p_18_xgb = p_xgboost18.sum(axis=0)[1] / len(p_xgboost18)
print(p_18_rf)
print(p_18_gb)
print(p_18_xgb)
# -
eighteen_yard_shot = coord_table(-10, 10, 2, 8, 18, 2)
fig, ax = plt.subplots()
ax.scatter(eighteen_yard_shot['shot_coord_x1'], eighteen_yard_shot['shot_coord_y1'], color='red')
# ax.scatter(shot_distance_df['pass_coord_x1'], shot_distance_df['pass_coord_y1'], color='red')
# ax.scatter(transposed_df['pass_coord_x2'], transposed_df['pass_coord_y2'], color='yellow')
ax.set_title('xG of shots in 18-yard box (rf:0.12, gb: 0.13, xgb: 0.14)')
ax.set_xlim([88.88, 0])
ax.set_ylim([-30.76, 30.76])
ax.axvline(6)
ax.axvline(18)
ax.axhline(10, xmax=6)
ax.axhline(-10, xmax=6)
ax.axhline(22, xmax=18)
ax.axhline(-22, xmax=18)
ax.set_facecolor('xkcd:lightgreen')
# ### average probability of shot beyond eighteen yard box
# +
p_random_forest18p = random_forest_model.predict_proba(eighteen_plus)
p_gradient_boost18p = gradient_boost_model.predict_proba(eighteen_plus)
p_xgboost18p = xgboost_model.predict_proba(eighteen_plus)
p_18p_rf = p_random_forest18p.sum(axis=0)[1] / len(p_random_forest18p)
p_18p_gb = p_gradient_boost18p.sum(axis=0)[1] / len(p_gradient_boost18p)
p_18p_xgb = p_xgboost18p.sum(axis=0)[1] / len(p_xgboost18p)
print(p_18p_rf)
print(p_18p_gb)
print(p_18p_xgb)
# -
beyond_eighteen_yard_shot = coord_table(-22, 22, 2, 20, 30, 2)
fig, ax = plt.subplots()
ax.scatter(beyond_eighteen_yard_shot['shot_coord_x1'], beyond_eighteen_yard_shot['shot_coord_y1'], color='yellow')
# ax.scatter(shot_distance_df['pass_coord_x1'], shot_distance_df['pass_coord_y1'], color='red')
# ax.scatter(transposed_df['pass_coord_x2'], transposed_df['pass_coord_y2'], color='yellow')
ax.set_title('xG of shots beyond 18-yard box (rf:0.06, gb: 0.05, xgb: 0.04)')
ax.set_xlim([88.88, 0])
ax.set_ylim([-30.76, 30.76])
ax.axvline(6)
ax.axvline(18)
ax.axhline(10, xmax=6)
ax.axhline(-10, xmax=6)
ax.axhline(22, xmax=18)
ax.axhline(-22, xmax=18)
ax.set_facecolor('xkcd:lightgreen')
# ### average probability of shot left of six
# +
p_random_forest6l = random_forest_model.predict_proba(left_box)
p_gradient_boost6l = gradient_boost_model.predict_proba(left_box)
p_xgboost6l = xgboost_model.predict_proba(left_box)
p_6l_rf = p_random_forest6l.sum(axis=0)[1] / len(p_random_forest6l)
p_6l_gb = p_gradient_boost6l.sum(axis=0)[1] / len(p_gradient_boost6l)
p_6l_xgb = p_xgboost6l.sum(axis=0)[1] / len(p_xgboost6l)
print(p_6l_rf)
print(p_6l_gb)
print(p_6l_xgb)
# -
left_six_yard_shot = coord_table(12, 22, 2, 3, 18, 3)
fig, ax = plt.subplots()
ax.scatter(left_six_yard_shot['shot_coord_x1'], left_six_yard_shot['shot_coord_y1'], color='green')
ax.set_title('xG of shots beyond left of six yard box (rf:0.07, gb: 0.07, xgb: 0.06)')
ax.set_xlim([88.88, 0])
ax.set_ylim([-30.76, 30.76])
ax.axvline(6)
ax.axvline(18)
ax.axhline(10, xmax=6)
ax.axhline(-10, xmax=6)
ax.axhline(22, xmax=18)
ax.axhline(-22, xmax=18)
ax.set_facecolor('xkcd:lightgreen')
# ### average probability of shot right of six
# +
p_random_forest6r = random_forest_model.predict_proba(right_box)
p_gradient_boost6r = gradient_boost_model.predict_proba(right_box)
p_xgboost6r = xgboost_model.predict_proba(right_box)
p_6r_rf = p_random_forest6r.sum(axis=0)[1] / len(p_random_forest6r)
p_6r_gb = p_gradient_boost6r.sum(axis=0)[1] / len(p_gradient_boost6r)
p_6r_xgb = p_xgboost6r.sum(axis=0)[1] / len(p_xgboost6r)
print(p_6r_rf)
print(p_6r_gb)
print(p_6r_xgb)
# -
right_six_yard_shot = coord_table(-12, -22, -2, 3, 18, 3)
fig, ax = plt.subplots()
ax.scatter(right_six_yard_shot['shot_coord_x1'], right_six_yard_shot['shot_coord_y1'], color='purple')
ax.set_title('xG of shots beyond left of six yard box (rf:0.08, gb: 0.08, xgb: 0.07)')
ax.set_xlim([88.88, 0])
ax.set_ylim([-30.76, 30.76])
ax.axvline(6)
ax.axvline(18)
ax.axhline(10, xmax=6)
ax.axhline(-10, xmax=6)
ax.axhline(22, xmax=18)
ax.axhline(-22, xmax=18)
ax.set_facecolor('xkcd:lightgreen')
# +
# fig, ax = plt.subplots()
# ax.scatter(six_yard_shot['shot_coord_x1'], six_yard_shot['shot_coord_y1'])
# ax.scatter(eighteen_yard_shot['shot_coord_x1'], eighteen_yard_shot['shot_coord_y1'], color='red')
# ax.scatter(beyond_eighteen_yard_shot['shot_coord_x1'], beyond_eighteen_yard_shot['shot_coord_y1'], color='yellow')
# ax.scatter(left_six_yard_shot['shot_coord_x1'], left_six_yard_shot['shot_coord_y1'], color='green')
# ax.scatter(right_six_yard_shot['shot_coord_x1'], right_six_yard_shot['shot_coord_y1'], color='purple')
# # ax.scatter(shot_distance_df['pass_coord_x1'], shot_distance_df['pass_coord_y1'], color='red')
# # ax.scatter(transposed_df['pass_coord_x2'], transposed_df['pass_coord_y2'], color='yellow')
# ax.set_title('xG of Shots in Box for Tomás Pochettino x: blue:0.79, red: 0.80, yellow: 0.79, green: 0.80, purple: 0.80')
# ax.set_xlim([88.88, 0])
# ax.set_ylim([-30.76, 30.76])
# ax.axvline(6)
# ax.axvline(18)
# ax.axhline(10, xmax=6)
# ax.axhline(-10, xmax=6)
# ax.axhline(22, xmax=18)
# ax.axhline(-22, xmax=18)
# ax.set_facecolor('xkcd:lightgreen')
# -
# # Parameter tuning
from model_prep import stage_score_plot
train_data, train_y, indices, hold_test = create_training_df(shots_df)
test_data, test_y, indices1, holdout, test = create_test_df(shots_df, hold_test)
columns_to_predict_on = ['shot_distance', 'shot_angle', 'assisted_shot', 'is_penalty_attempt']
# +
gbm1 = GradientBoostingClassifier(learning_rate=0.01, max_depth=1, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm2 = GradientBoostingClassifier(learning_rate=0.01, max_depth=2, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm3 = GradientBoostingClassifier(learning_rate=0.01, max_depth=3, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm4 = GradientBoostingClassifier(learning_rate=0.01, max_depth=4, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm5 = GradientBoostingClassifier(learning_rate=0.01, max_depth=5, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm6 = GradientBoostingClassifier(learning_rate=0.01, max_depth=6, max_features='log2', min_samples_leaf=4, n_estimators=300, subsample=0.25, random_state=8)
gbm1.fit(train_data[columns_to_predict_on], train_y)
gbm2.fit(train_data[columns_to_predict_on], train_y)
gbm3.fit(train_data[columns_to_predict_on], train_y)
gbm4.fit(train_data[columns_to_predict_on], train_y)
gbm5.fit(train_data[columns_to_predict_on], train_y)
gbm6.fit(train_data[columns_to_predict_on], train_y)
pgb1 = gbm1.predict_proba(test_data[columns_to_predict_on])
pgb2 = gbm2.predict_proba(test_data[columns_to_predict_on])
pgb3 = gbm3.predict_proba(test_data[columns_to_predict_on])
pgb4 = gbm4.predict_proba(test_data[columns_to_predict_on])
pgb5 = gbm5.predict_proba(test_data[columns_to_predict_on])
pgb6 = gbm6.predict_proba(test_data[columns_to_predict_on])
gb1_ll = log_loss(test_y, pgb1)
gb2_ll = log_loss(test_y, pgb2)
gb3_ll = log_loss(test_y, pgb3)
gb4_ll = log_loss(test_y, pgb4)
gb5_ll = log_loss(test_y, pgb5)
gb6_ll = log_loss(test_y, pgb6)
print("GB depth 1 log loss " + str(gb1_ll))
print("GB depth 2 log loss " + str(gb2_ll))
print("GB depth 3 log loss " + str(gb3_ll))
print("GB depth 4 log loss " + str(gb4_ll))
print("GB depth 5 log loss " + str(gb5_ll))
print("GB depth 6 log loss " + str(gb6_ll))
# -
# ### best gb is depth of 3, 188 trees
stage_score_plot(gbm1, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
stage_score_plot(gbm2, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
stage_score_plot(gbm3, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
stage_score_plot(gbm4, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
stage_score_plot(gbm5, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
stage_score_plot(gbm6, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
# ### tuning xgboost
train_data, train_y, indices, hold_test = create_training_df(shots_df)
test_data, test_y, indices1, holdout, test = create_test_df(shots_df, hold_test)
columns_to_predict_on = ['shot_distance', 'shot_angle', 'assisted_shot', 'is_penalty_attempt']
# +
xgb1 = XGBClassifier(learning_rate=0.01, n_estimators=200, random_state=8)
xgb2 = XGBClassifier(learning_rate=0.01, n_estimators=300, random_state=8)
xgb3 = XGBClassifier(learning_rate=0.01, n_estimators=400, random_state=8)
xgb4 = XGBClassifier(learning_rate=0.01, n_estimators=500, random_state=8)
xgb5 = XGBClassifier(learning_rate=0.01, n_estimators=600, random_state=8)
xgb1.fit(train_data[columns_to_predict_on], train_y)
xgb2.fit(train_data[columns_to_predict_on], train_y)
xgb3.fit(train_data[columns_to_predict_on], train_y)
xgb4.fit(train_data[columns_to_predict_on], train_y)
xgb5.fit(train_data[columns_to_predict_on], train_y)
xgb_p1 = xgb1.predict_proba(test_data[columns_to_predict_on])
xgb_p2 = xgb2.predict_proba(test_data[columns_to_predict_on])
xgb_p3 = xgb3.predict_proba(test_data[columns_to_predict_on])
xgb_p4 = xgb4.predict_proba(test_data[columns_to_predict_on])
xgb_p5 = xgb5.predict_proba(test_data[columns_to_predict_on])
xgb1_ll = log_loss(test_y, xgb_p1)
xgb2_ll = log_loss(test_y, xgb_p2)
xgb3_ll = log_loss(test_y, xgb_p3)
xgb4_ll = log_loss(test_y, xgb_p4)
xgb5_ll = log_loss(test_y, xgb_p5)
print("GB depth 1 log loss " + str(xgb1_ll))
print("GB depth 2 log loss " + str(xgb2_ll))
print("GB depth 3 log loss " + str(xgb3_ll))
print("GB depth 4 log loss " + str(xgb4_ll))
print("GB depth 5 log loss " + str(xgb5_ll))
# -
stage_score_plot(xgb1, train_data[columns_to_predict_on], train_y, test_data[columns_to_predict_on], test_y)
|
archives/_model_comparisons.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Volume and Surface are of a cone
# +
import math
pi = math.pi
# Function to calculate Volume of Cone
def volume(r, h):
return (1 / 3) * pi * r * r * h
# Function To Calculate Surface Area of Cone
def surfacearea(r, s):
return pi * r * s + pi * r * r
# Driver Code
radius = float(5)
height = float(12)
slat_height = float(13)
print( "Volume Of Cone : ", volume(radius, height) )
print( "Surface Area Of Cone : ", surfacearea(radius, slat_height) )
# -
|
Day 6 Assignment 2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas
import requests
# %matplotlib inline
from matplotlib.pyplot import figure
from seaborn import lineplot, barplot, color_palette, set_palette
# +
from bs4 import BeautifulSoup
def extract_table_rows(url):
from bs4 import BeautifulSoup
html = BeautifulSoup(requests.get(url).text, 'lxml')
return html.find_all('tr')
url = 'https://h1bdata.info/index.php?em=&job=&city=DALLAS&year=All+Years'
rows = extract_table_rows(url)
print(f"The table for Dallas (`dal.htm`) has {len(rows)} rows, including the header.")
print(f"The returned object, `rows`, has type `{type(rows)}`.")
# +
def inspect_html_table_row(rows, frontmatter=None):
if frontmatter is not None:
print(frontmatter)
cols = rows
for col_num, col in enumerate(cols):
print("[{}] '{}'".format(col_num, col.text))
print(" - Type: {}".format(type(col)))
print(" - Raw HTML: '{}'".format(str(col)))
header = rows[0]
print("=== HEADER ===\n")
inspect_html_table_row(header)
# -
first_data_row = rows[1]
inspect_html_table_row(first_data_row, frontmatter="=== FIRST DATA ROW (`rows[1]`) ===\n")
last_data_row = rows[-1]
inspect_html_table_row(last_data_row, frontmatter="=== LAST DATA ROW (`rows[-1]`) ===\n")
# +
def raw_rows_to_pandas(rows):
from pandas import DataFrame
df_rows = []
for row in rows:
cols = list(row)
if cols[6].text == 'CERTIFIED':
df_rows.append([cols[0].text # EMPLOYER
, cols[1].text # JOB TITLE
, cols[3].text # LOCATION
, int(cols[2].text.replace(',', '')) # BASE SALARY
, int(cols[4].text[-4:]) # START YEAR
])
return DataFrame(df_rows,
columns=['EMPLOYER', 'JOB TITLE', 'LOCATION', 'BASE SALARY', 'YEAR'])
dal = raw_rows_to_pandas(rows[1:])
print("Found", len(dal), "rows")
dal.sample(5)
# -
dal = dal[dal['JOB TITLE'].str.contains('.*DATA.*')]
dal_job_titles = dal['JOB TITLE'].unique()
print(f"There are {len(dal_job_titles)} unique job titles in the Dallas dataset.")
print(f"They are:\n{dal_job_titles[:20]}...")
def subset_series_str(s, pattern):
from pandas import Series
if not isinstance(s, Series):
s = Series(s)
return s[s.str.contains(pattern)]
jobs_with_data_followed_by_scientist = subset_series_str(dal_job_titles, r'.*DATA.*SCIENTIST.*')
jobs_with_data_followed_by_scientist
# +
def filter_jobs(df, target_jobs):
from pandas import DataFrame
assert isinstance(df, DataFrame)
assert df.columns.contains('JOB TITLE')
assert all([isinstance(j, str) for j in target_jobs])
keep_job = df['JOB TITLE'].str.contains('|'.join(target_jobs))
return df[keep_job]
target_job_list = ['DATA ANALYST', 'DATABASE ADMINISTRATOR', 'DATA SCIENTIST', 'DATA ENGINEER']
dal_target_jobs = filter_jobs(dal, target_job_list)
print(dal_target_jobs['JOB TITLE'].unique())
# -
def normalize_series(s, target):
from pandas import Series
assert isinstance(s, Series), f"Object `s` has type `{type(s)}`, not `Series`."
assert isinstance(target, str), f"`target` is a `{type(target)}`, not a string."
return s.str.replace('.*' + target + '.*', target)
# +
TARGET_JOBS = ['DATA SCIENTIST', 'DATA ANALYST', 'DATA ENGINEER', 'DATABASE ADMINISTRATOR']
def reduce_jobs(df, target_jobs=TARGET_JOBS):
df_reduced = df.copy()
for title in target_jobs:
df_reduced['JOB TITLE'] = normalize_series(df_reduced['JOB TITLE'], title)
return df_reduced
dal_reduced = reduce_jobs(dal)
dal_reduced.sample(20)
# -
dal_reduced_job_counts = dal_reduced['JOB TITLE'].value_counts()
dal_reduced_job_counts.head(10)
# +
# Base salaries change over time
dal_reduced2 = dal_reduced.loc[dal_reduced['JOB TITLE'].isin(TARGET_JOBS)]
fig = figure(figsize=(12, 6))
lineplot(x='YEAR', y='BASE SALARY', hue='JOB TITLE', data=dal_reduced2)
set_palette(color_palette('colorblind'))
# +
def get_median_salaries_by_title(df):
from pandas import DataFrame
assert isinstance(df, DataFrame)
df_return = df[['JOB TITLE', 'BASE SALARY']].groupby('JOB TITLE').median().reset_index()
df_return['BASE SALARY'] = df_return['BASE SALARY'].astype(int)
return df_return
get_median_salaries_by_title(dal_reduced2)
# +
CITY_NAMES = {'nyc': 'NEW YORK',
'sfo': 'SAN FRANCISCO',
'hou': 'HOUSTON',
'aus': 'AUSTIN',
'dal': 'DALLAS'}
df_list = []
for city_code, city_name in CITY_NAMES.items():
url = f'https://h1bdata.info/index.php?em=&job=&city={city_name}&year=All+Years'
df_city = filter_jobs(reduce_jobs(raw_rows_to_pandas(extract_table_rows(url)[1:])), TARGET_JOBS)
df_city['LOCATION'] = city_name
df_list.append(df_city)
df_all = pandas.concat(df_list)
df_summary = df_all[['JOB TITLE', 'LOCATION', 'BASE SALARY']] \
.groupby(['JOB TITLE', 'LOCATION']) \
.median() \
.reset_index()
df_summary['BASE SALARY'] = df_summary['BASE SALARY'].astype(int)
display(df_summary)
# -
# Median base salaries compared across 5 cities
figure(figsize=(12, 6))
g = barplot(x='JOB TITLE', y='BASE SALARY', hue='LOCATION', data=df_summary)
set_palette(color_palette('colorblind'))
|
H1B Data Job in Dallas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: feml
# language: python
# name: feml
# ---
# ## Predicting Survival on the Titanic
#
# ### History
# Perhaps one of the most infamous shipwrecks in history, the Titanic sank after colliding with an iceberg, killing 1502 out of 2224 people on board. Interestingly, by analysing the probability of survival based on few attributes like gender, age, and social status, we can make very accurate predictions on which passengers would survive. Some groups of people were more likely to survive than others, such as women, children, and the upper-class. Therefore, we can learn about the society priorities and privileges at the time.
#
# ### Assignment:
#
# Build a Machine Learning Pipeline, to engineer the features in the data set and predict who is more likely to Survive the catastrophe.
#
# Follow the Jupyter notebook below, and complete the missing bits of code, to achieve each one of the pipeline steps.
# +
import re
# to handle datasets
import pandas as pd
import numpy as np
# for visualization
import matplotlib.pyplot as plt
# to divide train and test set
from sklearn.model_selection import train_test_split
# feature scaling
from sklearn.preprocessing import StandardScaler
# to build the models
from sklearn.linear_model import LogisticRegression
# to evaluate the models
from sklearn.metrics import accuracy_score, roc_auc_score
# to persist the model and the scaler
import joblib
# to visualise al the columns in the dataframe
pd.pandas.set_option('display.max_columns', None)
# -
# ## Prepare the data set
# +
# load the data - it is available open source and online
data = pd.read_csv('https://www.openml.org/data/get_csv/16826755/phpMYEkMl')
# display data
data.head()
# +
# replace interrogation marks by NaN values
data = data.replace('?', np.nan)
# +
# retain only the first cabin if more than
# 1 are available per passenger
def get_first_cabin(row):
try:
return row.split()[0]
except:
return np.nan
data['cabin'] = data['cabin'].apply(get_first_cabin)
# +
# extracts the title (Mr, Ms, etc) from the name variable
def get_title(passenger):
line = passenger
if re.search('Mrs', line):
return 'Mrs'
elif re.search('Mr', line):
return 'Mr'
elif re.search('Miss', line):
return 'Miss'
elif re.search('Master', line):
return 'Master'
else:
return 'Other'
data['title'] = data['name'].apply(get_title)
# +
# cast numerical variables as floats
data['fare'] = data['fare'].astype('float')
data['age'] = data['age'].astype('float')
# +
# drop unnecessary variables
data.drop(labels=['name','ticket', 'boat', 'body','home.dest'], axis=1, inplace=True)
# display data
data.head()
# +
# save the data set
data.to_csv('titanic.csv', index=False)
# -
# ## Data Exploration
#
# ### Find numerical and categorical variables
target = 'survived'
# +
vars_num = [c for c in data.columns if data[c].dtypes!='O' and c!=target]
vars_cat = [c for c in data.columns if data[c].dtypes=='O']
print('Number of numerical variables: {}'.format(len(vars_num)))
print('Number of categorical variables: {}'.format(len(vars_cat)))
# -
# ### Find missing values in variables
# +
# first in numerical variables
data[vars_num].isnull().mean()
# +
# now in categorical variables
data[vars_cat].isnull().mean()
# -
# ### Determine cardinality of categorical variables
data[vars_cat].nunique()
# ### Determine the distribution of numerical variables
data[vars_num].hist(bins=30, figsize=(10,10))
plt.show()
# ## Separate data into train and test
# +
X_train, X_test, y_train, y_test = train_test_split(
data.drop('survived', axis=1), # predictors
data['survived'], # target
test_size=0.2, # percentage of obs in test set
random_state=0) # seed to ensure reproducibility
X_train.shape, X_test.shape
# -
# ## Feature Engineering
#
# ### Extract only the letter (and drop the number) from the variable Cabin
# +
X_train['cabin'] = X_train['cabin'].str[0] # captures the first letter
X_test['cabin'] = X_test['cabin'].str[0] # captures the first letter
X_train['cabin'].unique()
# -
# ### Fill in Missing data in numerical variables:
#
# - Add a binary missing indicator
# - Fill NA in original variable with the median
# +
for var in ['age', 'fare']:
# add missing indicator
X_train[var+'_NA'] = np.where(X_train[var].isnull(), 1, 0)
X_test[var+'_NA'] = np.where(X_test[var].isnull(), 1, 0)
# replace NaN by median
median_val = X_train[var].median()
X_train[var].fillna(median_val, inplace=True)
X_test[var].fillna(median_val, inplace=True)
X_train[['age', 'fare']].isnull().sum()
# -
# ### Replace Missing data in categorical variables with the string **Missing**
X_train[vars_cat] = X_train[vars_cat].fillna('Missing')
X_test[vars_cat] = X_test[vars_cat].fillna('Missing')
X_train.isnull().sum()
X_test.isnull().sum()
# ### Remove rare labels in categorical variables
#
# - remove labels present in less than 5 % of the passengers
# +
def find_frequent_labels(df, var, rare_perc):
# function finds the labels that are shared by more than
# a certain % of the passengers in the dataset
df = df.copy()
tmp = df.groupby(var)[var].count() / len(df)
return tmp[tmp > rare_perc].index
for var in vars_cat:
# find the frequent categories
frequent_ls = find_frequent_labels(X_train, var, 0.05)
# replace rare categories by the string "Rare"
X_train[var] = np.where(X_train[var].isin(
frequent_ls), X_train[var], 'Rare')
X_test[var] = np.where(X_test[var].isin(
frequent_ls), X_test[var], 'Rare')
# -
X_train[vars_cat].nunique()
X_test[vars_cat].nunique()
# ### Perform one hot encoding of categorical variables into k-1 binary variables
#
# - k-1, means that if the variable contains 9 different categories, we create 8 different binary variables
# - Remember to drop the original categorical variable (the one with the strings) after the encoding
# +
for var in vars_cat:
# to create the binary variables, we use get_dummies from pandas
X_train = pd.concat([X_train,
pd.get_dummies(X_train[var], prefix=var, drop_first=True)
], axis=1)
X_test = pd.concat([X_test,
pd.get_dummies(X_test[var], prefix=var, drop_first=True)
], axis=1)
X_train.drop(labels=vars_cat, axis=1, inplace=True)
X_test.drop(labels=vars_cat, axis=1, inplace=True)
X_train.shape, X_test.shape
# +
# Note that we have one less column in the test set
# this is because we had 1 less category in embarked.
# we need to add that category manually to the test set
X_train.head()
# -
X_test.head()
# +
# we add 0 as values for all the observations, as Rare
# was not present in the test set
X_test['embarked_Rare'] = 0
# +
# Note that now embarked_Rare will be at the end of the test set
# so in order to pass the variables in the same order, we will
# create a variables variable:
variables = [c for c in X_train.columns]
variables
# -
# ### Scale the variables
#
# - Use the standard scaler from Scikit-learn
# +
# create scaler
scaler = StandardScaler()
# fit the scaler to the train set
scaler.fit(X_train[variables])
# transform the train and test set
X_train = scaler.transform(X_train[variables])
X_test = scaler.transform(X_test[variables])
# -
# ## Train the Logistic Regression model
#
# - Set the regularization parameter to 0.0005
# - Set the seed to 0
# +
# set up the model
# remember to set the random_state / seed
model = LogisticRegression(C=0.0005, random_state=0)
# train the model
model.fit(X_train, y_train)
# -
# ## Make predictions and evaluate model performance
#
# Determine:
# - roc-auc
# - accuracy
#
# **Important, remember that to determine the accuracy, you need the outcome 0, 1, referring to survived or not. But to determine the roc-auc you need the probability of survival.**
# +
# make predictions for test set
class_ = model.predict(X_train)
pred = model.predict_proba(X_train)[:,1]
# determine mse and rmse
print('train roc-auc: {}'.format(roc_auc_score(y_train, pred)))
print('train accuracy: {}'.format(accuracy_score(y_train, class_)))
print()
# make predictions for test set
class_ = model.predict(X_test)
pred = model.predict_proba(X_test)[:,1]
# determine mse and rmse
print('test roc-auc: {}'.format(roc_auc_score(y_test, pred)))
print('test accuracy: {}'.format(accuracy_score(y_test, class_)))
print()
# -
# That's it! Well done
#
# **Keep this code safe, as we will use this notebook later on, to build production code, in our next assignement!!**
|
section-04-research-and-development/titanic-assignment/02-predicting-survival-titanic-solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Step 0: load necessary libraries
import xarray as xr
import datetime
import pandas as pd
import numpy as np
import xesmf as xe
import time
import gc
import matplotlib.pyplot as plt
# +
def regrid_data_2006(var, start_year, end_year, interval, height=True):
t0 = time.time()
print("******Start to process "+var+"******")
ds = []
# load the data
start_time = time.time()
for s_year in np.arange(start_year,end_year,interval):
#print(s_year)
e_year = s_year+interval-1
s_s_year = str(s_year)
s_e_year = str(e_year)
print(CMIP_dir+mod+"/"+var+"_day_"+mod+rcp+s_s_year+"0101-"+s_e_year+"1231.nc")
temp_ds = xr.open_dataset(CMIP_dir+mod+"/"+var+"_day_"+mod+rcp+s_s_year+"0101-"+s_e_year+"1231.nc")[var]
ds.append(temp_ds)
del temp_ds
gc.collect()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to load the data")
# merge the time series
print("*********Start to merge*********")
start_time = time.time()
ds_merge_ts = xr.merge(ds).sel(time=slice("2006-01-01", "2015-12-31"))
del ds
gc.collect()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to merge the time series")
# build the regridder
print("*********Start to build the regridder*********")
start_time = time.time()
regridder = xe.Regridder(ds_merge_ts, ds_out, 'patch', periodic=True, reuse_weights=True)
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to build the regridder")
# regrid the layer
print("*********Start to regrid the layer*********")
start_time = time.time()
ds_merge_ts_reg = regridder(ds_merge_ts[var])
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to regrid the layer")
# mask the layer
print("*********Start to mask the layer*********")
start_time = time.time()
ds_merge_ts_reg_mask = ds_merge_ts_reg.where(mask)
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to mask the layer")
# plot the layer
print("*********Start to plot the layer*********")
start_time = time.time()
fig, ((ax1, ax2, ax3)) = plt.subplots(nrows=1, ncols=3,figsize=(18,3))
ds_merge_ts[var].loc["2015-12-31"].plot(ax=ax1,
vmax=ds_merge_ts[var].loc["2015-12-31"].max(),
vmin=ds_merge_ts[var].loc["2015-12-31"].min())
ds_merge_ts_reg.loc["2015-12-31"].plot(ax=ax2,
vmax=ds_merge_ts[var].loc["2015-12-31"].max(),
vmin=ds_merge_ts[var].loc["2015-12-31"].min())
ds_merge_ts_reg_mask.loc["2015-12-31"].plot(ax=ax3,
vmax=ds_merge_ts[var].loc["2015-12-31"].max(),
vmin=ds_merge_ts[var].loc["2015-12-31"].min())
plt.show()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to plot the layer")
elapsed_time = time.time() - t0
print("It takes elapsed_time", elapsed_time, "to deal with "+var+" in total")
print("******End "+var+"******")
print("\n")
if (height):
return ds_merge_ts_reg_mask.rename(var).drop("height")
else:
return ds_merge_ts_reg_mask.rename(var)
def regrid_data_2061(var, start_year, end_year, interval, height=True):
t0 = time.time()
print("******Start to process "+var+"******")
ds = []
# load the data
start_time = time.time()
for s_year in np.arange(start_year,end_year,interval):
#print(s_year)
e_year = s_year+interval-1
s_s_year = str(s_year)
s_e_year = str(e_year)
print(CMIP_dir+mod+"/"+var+"_day_"+mod+rcp+s_s_year+"0101-"+s_e_year+"1231.nc")
temp_ds = xr.open_dataset(CMIP_dir+mod+"/"+var+"_day_"+mod+rcp+s_s_year+"0101-"+s_e_year+"1231.nc")[var]
ds.append(temp_ds)
del temp_ds
gc.collect()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to load the data")
# merge the time series
print("*********Start to merge*********")
start_time = time.time()
ds_merge_ts = xr.merge(ds).sel(time=slice("2061-01-01", "2070-12-31"))
del ds
gc.collect()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to merge the time series")
# build the regridder
print("*********Start to build the regridder*********")
start_time = time.time()
regridder = xe.Regridder(ds_merge_ts, ds_out, 'patch', periodic=True, reuse_weights=True)
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to build the regridder")
# regrid the layer
print("*********Start to regrid the layer*********")
start_time = time.time()
ds_merge_ts_reg = regridder(ds_merge_ts[var])
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to regrid the layer")
# mask the layer
print("*********Start to mask the layer*********")
start_time = time.time()
ds_merge_ts_reg_mask = ds_merge_ts_reg.where(mask)
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to mask the layer")
# plot the layer
print("*********Start to plot the layer*********")
start_time = time.time()
fig, ((ax1, ax2, ax3)) = plt.subplots(nrows=1, ncols=3,figsize=(18,3))
ds_merge_ts[var].loc["2070-12-31"].plot(ax=ax1,
vmax=ds_merge_ts[var].loc["2070-12-31"].max(),
vmin=ds_merge_ts[var].loc["2070-12-31"].min())
ds_merge_ts_reg.loc["2070-12-31"].plot(ax=ax2,
vmax=ds_merge_ts[var].loc["2070-12-31"].max(),
vmin=ds_merge_ts[var].loc["2070-12-31"].min())
ds_merge_ts_reg_mask.loc["2070-12-31"].plot(ax=ax3,
vmax=ds_merge_ts[var].loc["2070-12-31"].max(),
vmin=ds_merge_ts[var].loc["2070-12-31"].min())
plt.show()
elapsed_time = time.time() - start_time
print("It takes elapsed_time", elapsed_time, "to plot the layer")
elapsed_time = time.time() - t0
print("It takes elapsed_time", elapsed_time, "to deal with "+var+" in total")
print("******End "+var+"******")
print("\n")
if (height):
return ds_merge_ts_reg_mask.rename(var).drop("height")
else:
return ds_merge_ts_reg_mask.rename(var)
#########################################################################################################
def get_ds_2006(start_year, end_year, interval):
# define the variable list *****
var_ls_height = ["tasmax"]
# get a list of variable DataArray
temp_var = []
for var in var_ls_height:
temp_var.append(regrid_data_2006(var, start_year, end_year, interval, height=True))
ds_merge = xr.merge(temp_var)
return ds_merge
def get_ds_2061(start_year, end_year, interval):
# define the variable list *****
var_ls_height = ["tasmax"]
# get a list of variable DataArray
temp_var = []
for var in var_ls_height:
temp_var.append(regrid_data_2061(var, start_year, end_year, interval, height=True))
ds_merge = xr.merge(temp_var)
return ds_merge
def get_urban_df(ds):
start_time = time.time()
df_all = ds.to_dataframe()
df = df_all[~np.isnan(df_all["tasmax"])]
print("It takes elapsed_time", time.time()-start_time, "to convert to dataframe and get urban grid")
return df
# -
# # Step 1: define the grid and mask
# +
# define the model
mod = "MIROC-ESM"
rcp = "_rcp85_r1i1p1_"
# define the grid mask
CESM = xr.open_dataset("/glade/collections/cdg/data/cesmLE/CESM-CAM5-BGC-LE/lnd/proc/tseries/daily/TREFMXAV_U/b.e11.BRCP85C5CNBDRD.f09_g16.002.clm2.h1.TREFMXAV_U.20060101-20801231.nc")
grid = CESM["TREFMXAV_U"].loc["2006-01-02"]
mask = CESM["TREFMXAV_U"].loc["2006-01-02"].notnull().squeeze()
ds_out = xr.Dataset({'lat':(['lat'], grid["lat"].values),
'lon':(['lon'], grid["lon"].values)})
# define the load directory *****
CMIP_dir = "/glade/scratch/zhonghua/CMIP5_tasmax_nc/"
# define the save directory *****
CMIP_save_dir = "/glade/scratch/zhonghua/CMIP5_tasmax_csv/"
# -
# # Step 2: 2006-2015
ds = get_ds_2006(2006, 2101, 95)
df = get_urban_df(ds)
start_time=time.time()
df.to_csv(CMIP_save_dir+mod+"/2006.csv")
print(time.time()-start_time)
# # Step 3: 2061-2070
del ds, df
gc.collect()
ds = get_ds_2061(2006, 2101, 95)
df = get_urban_df(ds)
start_time=time.time()
df.to_csv(CMIP_save_dir+mod+"/2061.csv")
print(time.time()-start_time)
|
1_data_prep/CMIP_gridcell_temp_prep/CPU_MIROC-ESM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/priyanshgupta1998/Programming-/blob/master/python/mergeSort_of_linked_list.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="SFcrla8ofLXY" colab_type="code" colab={}
# + id="A3houMbnfLrr" colab_type="code" colab={}
# + id="nk9QwGGAfL-C" colab_type="code" colab={}
# + [markdown] id="yI1tMR0pfQd6" colab_type="text"
# #Merge Sort for Linked Lists
# + id="c-4ERggCfL7E" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 238} outputId="701570c3-982b-44f2-a48b-4af24a022ef6"
# Python3 program to merge sort of linked list
# create Node using class Node.
import random
class Node:
def __init__(self, data):
self.data = data
self.next = None
class LinkedList:
#-----------------------------------------------#
def __init__(self):
self.head = None
#-----------------------------------------------#
# push new value to linked list using append method
def append(self, new_value):
# Allocate new node
new_node = Node(new_value)
# if head is None, initialize it to new node
if self.head is None:
self.head = new_node
return
curr_node = self.head
while curr_node.next is not None:
curr_node = curr_node.next
# Append the new node at the end of the linked list
curr_node.next = new_node
#-----------------------------------------------#
def sortedMerge(self, a, b):
get = random.randint(1,10)
result = None
# Base cases
if a == None:
return b
if b == None:
return a
# pick either a or b and recur..
if a.data <= b.data:
result = a
result.next = self.sortedMerge(a.next, b)
else:
result = b
result.next = self.sortedMerge(a, b.next)
print(result.data,"with get value : " , get)
return result
#-----------------------------------------------#
# Utility function to get the middle of the linked list
def getMiddle(self, head):
if (head == None):
return head
slow = head
fast = head
while (fast.next != None and
fast.next.next != None):
slow = slow.next
fast = fast.next.next
return slow
#-----------------------------------------------#
def mergeSort(self, h):
# Base case if head is None
if h == None or h.next == None:
return h
# get the middle of the list
middle = self.getMiddle(h)
nexttomiddle = middle.next
# set the next of middle node to None
middle.next = None
# Apply mergeSort on left list
left = self.mergeSort(h)
# Apply mergeSort on right list
right = self.mergeSort(nexttomiddle)
# Merge the left and right lists
sortedlist = self.sortedMerge(left, right)
return sortedlist
# Utility function to print the linked list
def printList(head):
if head is None:
print(' ')
return
curr_node = head
while curr_node:
print(curr_node.data, end = " ")
curr_node = curr_node.next
print(' ')
li = LinkedList()
# Let us create a unsorted linked list to test the functions created. The list shall be a: 2->3->20->5->10->15
li.append(15)
li.append(10)
li.append(5)
li.append(20)
li.append(3)
li.append(2)
print ("before sorting the Linked List is:")
printList(li.head)
# Apply merge Sort
li.head = li.mergeSort(li.head)
print ("after Sorting the Linked List is:")
printList(li.head)
# + id="HAqa_d6pfL5X" colab_type="code" colab={}
# + id="fe_RKTWxoSkR" colab_type="code" colab={}
# + id="5-XekQRuoSeK" colab_type="code" colab={}
# + id="YYJD_rhZoScl" colab_type="code" colab={}
# + id="zLsd54GVoTdE" colab_type="code" colab={}
# + id="4_oppWmaoTYh" colab_type="code" colab={}
# + id="KD8jXx8_oTW7" colab_type="code" colab={}
# + id="5tUAELSBoTVU" colab_type="code" colab={}
# + id="w6ZZmYAKoTTj" colab_type="code" colab={}
# + id="bKtLP6Q3oTQ3" colab_type="code" colab={}
# + id="fPmM1LfUoTNI" colab_type="code" colab={}
# + id="45VlQkXzoR94" colab_type="code" colab={}
# + id="jsMf3fh6fL3v" colab_type="code" colab={}
# + id="rhX4FxbofL2i" colab_type="code" colab={}
# + id="OiB4PceJfL1U" colab_type="code" colab={}
# + id="I_wAJQt6fLz_" colab_type="code" colab={}
# + id="_UlWio5FfLyE" colab_type="code" colab={}
# + id="4phjDpdMfLvn" colab_type="code" colab={}
# + id="-y1nzOrNfLpB" colab_type="code" colab={}
# + id="JI7XKMjKfLlj" colab_type="code" colab={}
# + id="MjwGRXSAfLkK" colab_type="code" colab={}
# + id="h8BHeDJWfLim" colab_type="code" colab={}
# + id="2z0iSLSyfLhO" colab_type="code" colab={}
# + id="lDtUqj2zfLf3" colab_type="code" colab={}
# + id="EEbiMkuEfLeW" colab_type="code" colab={}
# + id="ZtnbWAJ0fLbm" colab_type="code" colab={}
|
python/mergeSort_of_linked_list.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:fairness3]
# language: python
# name: conda-env-fairness3-py
# ---
# # Introducing The IgnoringBiasEstimator
# Recently, a friend of mine, 26 years old, told me about her experience interviewing for a resident position (_"arts in opleiding tot specialist (aios)"_ in Dutch). Everything went well and she got the position. But she did tell me one specificic part of the conversation that baffled me: when planning her educational program for the next ten years, the dean just planned her maternity leave with it - not that she's pregnant, but he already planned it because he figured she would. I probably shouldn't have been surprised. Many female friends have shared similar experiences since.
#
# Now this blog is about AI, but AI is about the real world. In the real world, biases often lead to uneven outcomes. In the story above, my friend did get the position, but in many instances, groups may be disadvantaged. When these decision processes would be automated through AI, the model might learn the biases with it: perphaps that it should hire females at a smaller rate. This has in fact happened on many occasions [in the real world](https://towardsdatascience.com/real-life-examples-of-discriminating-artificial-intelligence-cae395a90070), and was a driver for one of the biggest scandals in the Netherlands in recent years: the ["Toeslagenaffaire"](https://www.rtlnieuws.nl/nieuws/nederland/artikel/5037966/belastingdienst-toeslagenaffaire-ministerie-van-financien).
#
# While there is a lot of attention for bias mitigation in AI, I feel it is still lacking: it requires more work, gives worse outcomes and less flexibility. To me, this is unacceptable. I work for the organisation I do, because I feel it helps society. Therefore, I developed an easy wrapper around `sklearn`-models that mitigates biases. I call it the `IgnoringBiasEstimator`. It has the following advantages:
# * It is **extremely easy to implement**, as it is just a wrapper around sklearn models that are ubiquitous in data science. I will investigate this in this Part 1 of the series.
# * It is **very flexible**: unlike many bias mitigation algorithms, it works with both regression and classification and for both continuous and binary/categorical data. I will look into this further in further installments of the series.
# * Most importantly, it **removes disparate treatment very well**, also when the bias is non-linear and/or correlated, which I will also investigate further in next installments.
# * As a bonus, it **gives insight in the current biases** in the data set, which may be used to decrease the bias in the real world as well.
#
# The IgnoringBiasEstimator consciously learns the bias in the data during training time, so it can adequately ignore it at prediction time.
#
# ## Outline
# ### The blog series
# The introduction and comparison of the IgnoringEstimator is split into three parts
# 1. [Introducing the IgnoringEstimator](https://github.com/SjoerdCor/fairness/blob/main/blog/1.IntroducingTheIgnoringEstimator.ipynb) introduces measures of fairness and shows how naive approaches do not solve them, and on the other hand shows how easily the IgnoringEstimator is implemented and solves them well
# 1. [Dealing with more complex biases](https://github.com/SjoerdCor/fairness/blob/main/blog/2.DealingWithMoreComplexBiases.ipynb) first shows how common complex biases are: non-linear, correlated with other attributes and for continuous features, and shows how easy it is to mitigate the disparate treatment with the `IgnoringBiasEstimator`. I also show how little attention there seems to be for this problem in existing approaches.
# 1. [Ignoring bias for cassification poblems](https://github.com/SjoerdCor/fairness/blob/main/blog/3.IgnoringBiasForClassificationProblems.ipynb) finally shows how to use the Ignoring Estimator for the classic classification problems - since these are more prolific, we can also compare against a wide variety of existing approaches and see the `IgnoringBiasEstimator` does equally well or better both in terms of bias mitigation and accuracy.
#
# ### This installment introduces the problem, measures of fairness and compares naive approaches with the IgnoringEstimator
#
# * First, I will show the problem by generating a biased data set and showing how it leads to biased models
# * For this, I will also define the notions of disparate impact and disparate treatment
# * Secondly, I will show passive bias mitigation strategies of ignoring the sensitive attributes does not solve the problem if these attributes are correlated with other, non-sensitive attributes (as is often the case)
# * Lastly, I will quickly show how to run the the IgnoringBiasEstimator and how well it does both in terms of fairness and accuracy. A deeper investigation will follow in parts 2 and 3.
#
# ## Generating biased data: salaries for employees
#
# To investigate fairness, imagine there is a company with 2500 employees that is concerned with salary differences, and they set out to give everyone a fair salary, but with the same mean salary. I generate a toy dataset consisting of three employee characteristics: Gender (0 or 1), Education (between 4 and 20) and Experience, a continuous variable between 0 and 40. It also has a SalaryTrue column, which is the monthly salary of each employee. The SalarySkill column contains what should be paid to each employee, if the salary were based purely on the skill. It is based on Education (150 per level) and experience (30 per level), with a standard deviation of 150 per employee for other characteristics. Unfortunately, in the true world, one does not observe this - one only observes the paid salary.
#
# Now imagine this company has a gender bias, where the people with gender 1 are structurally paid less 200 every month. This is what is observed in the SalaryTrue column.
#
# <img src="./figures/DGP_Salary_Uncorrelated.PNG" title="The data generating process for salary for an imaginary company with biases in employee salaries"/>
# +
import copy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import sklearn.model_selection
import sklearn.metrics
from sklearn.inspection import plot_partial_dependence
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from fairness import fairestimator
from fairness.blog import utils
np.random.seed(42)
# +
coefficients = pd.DataFrame({'True world': {'Education': 150, 'Experience': 30, 'Gender': -200, 'Intercept': 100},
'Skills-based': {'Education': 150, 'Experience': 30, 'Gender': 0, 'Intercept': 0}}
)
coefficients.plot(kind='barh', title='In the True world, Gender influences salary,\nbut it does not in the Skills-based coefficients')
plt.xlabel('Coefficient')
plt.show()
# -
# *Note that the intercept is 100 larger in the True world so that the same mean salary is paid for the entire company.*
# +
def generate_employees_uncorrelated(size=2500):
X = (pd.DataFrame({'Gender': np.random.randint(2, size=size),
'Education': 4 + 16 * np.random.rand(size),
'Experience': 40*np.random.rand(size)
}
)
)
return X
def add_salaries(df):
weights = {'Gender': 0,
'Education': 150,
'Experience': 30,
}
gender_bias = -100 # -100 for Gender 1 and +100 for Gender 0, because Gender is standardized first
error = np.random.normal(0, 150, size=len(df))
df = df.assign(SalarySkill = lambda df: df.mul(weights).sum('columns').add(error),
SalaryTrue = lambda df: df['SalarySkill'].add(utils.generate_bias(df['Gender'], effect_size=gender_bias)))
return df
# +
df = generate_employees_uncorrelated().pipe(add_salaries)
def display_df(df, n=10):
display(df.sample(n, random_state=42)
.style.format({'Education': "{:.2f}", 'Experience': '{:.2f}', 'Gender': "{:d}",
'SalarySkill': "€{:.2f}", 'SalaryTrue': '€{:.2f}'})
)
display_df(df)
# -
# Above, a small subset of the employee data is shown.
# ## Training a model on biased data gives biased outcomes
# Now the company sets out to predict salaries for all employees - first making a nice train and test split, and then fitting and validating a model. It does so very naively, with no bias mitigation in place.
(X_train, X_test, y_train, y_test,
y_skill_train, y_skill_test) = sklearn.model_selection.train_test_split(df.filter(['Education', 'Experience', 'Gender', ]),
df['SalaryTrue'],
df['SalarySkill'])
# +
lr = LinearRegression()
lr.fit(X_train, y_train)
print(f'The mean absolute error of the fitted model is {sklearn.metrics.mean_absolute_error(lr.predict(X_test), y_test): .2f} ')
# -
# ## Fairness is a matter of definition: disparate impact vs. disparate treatment
# That looks very good, for such a simple model. But we're also interested in fairness. In fact, it is not so easy to define fairness. While I will not dive too deep in all definitions (for more, see e.g. [here](https://towardsdatascience.com/a-tutorial-on-fairness-in-machine-learning-3ff8ba1040cb)), we do need two different notions of fairness:
# * **Disparate treatment** is when a decision process, such as an algorithm, directly or indirectly makes different decisions based on sensitive attributes, such as gender or age.
# * **Disparate impact** is when a decision process, such as an algorithm, leads to different outcomes for some sensitive attributes.
#
# There may be a disparate impact without disparate treatment if the sensitive attribute correlates with other, important features - we will see this in a bit.
# ### No mitigation just propagates biases
# Disparate impact is easiest to show. I plot both the mean predicted salary with error for both groups:
y_pred = utils.predict_series(lr, X_test)
y_pred_per_gender = y_pred.groupby(X_test['Gender']).agg(['mean', 'sem'])
ax = y_pred_per_gender.plot(y='mean', xerr='sem', kind='barh', title='Disparate impact\nGender 1 structurally gets paid less than group 0')
ax.set_xlabel('Salary')
plt.show()
# In this case, there is definitely a disparate impact. That in itself, may already be enough to find the algorithm is unfair, but others may argue that experience and level of education are valuable to the company and that in fact should pay more. Therefore, let's quickly look into disparate treatment as well.
#
# The model has a coefficient of -200 for gender 1 (closely mimicking the real, biased world), so there is a disparate treatment.
coefficients['No bias mitigation'] = utils.coefs_to_series(lr, X_train.columns.tolist())
coefficients.plot(kind='barh', title='Disparate Treatment\nThe model learned to pay employees of gender 1\n200 less than employees of gender 0 ')
plt.show()
# The Disparate impact and Disparate treatment are also shown in the plot below. I calculate them as follows:
# **Calculating Disparate Impact**
# 1. Disparate impact is the difference in average salary between the genders
#
# **Calculating Disparate Treatment**
# 1. Calculate the difference between the skill-based salary and the predicted salary for each employee; which is the bias per employee
# 1. Calculate the mean bias per gender.
# 1. Disparate treatment is the difference between the two means calculated in the previous step.
# Note that I can only do step 1, because I generated the data, and therefore have access to the salary based purely on skills.
#
# Again, we see the model suffers from both disparate impact and disparate treatment.
# +
predictions = {'No bias mitigation': y_pred}
utils.plot_fairness_metrics(predictions, y_skill_test, X_test['Gender'])
plt.show()
# -
# ## A generally inadequate bias mitigation approach: Unawareness
# One way of dealing with this is 'Unawareness': drop the protected attributes and fit the model without it, so it does not account for the protected attribute.
X_train_unaware = X_train.drop(columns=['Gender'])
X_test_unaware = X_test.drop(columns=['Gender'])
lr_unaware = LinearRegression()
lr_unaware.fit(X_train_unaware, y_train)
print(f'The mean absolute error of the fitted model is {sklearn.metrics.mean_absolute_error(lr_unaware.predict(X_test_unaware), y_test): .2f} ')
# At the cost of a bit of accuracy, the company now has a model that does not take Gender into account. Let's see what this does with out fairness measures.
y_pred_unaware = utils.predict_series(lr_unaware, X_test_unaware)
# +
predictions['Unaware'] = y_pred_unaware
utils.plot_fairness_metrics(predictions, y_skill_test, X_test['Gender'])
plt.show()
# -
# So for this case, we now have a fair model on both metrics. Is this then the way to deal with sensitive attributes: just drop them from the data set? No. This toy dataset is unrealistic because there are no correlations
#
# Unawareness is insufficient because in the real world the protected attribute often correlates with other, non-protected and perhaps even relevant attributes.
sns.heatmap(X_train.corr(), cmap='RdBu_r', vmin=-0.8, vmax=0.8, annot=True, fmt='.0%')
plt.suptitle('Correlation Matrix\nThis toy dataset is unrealistic because there are no correlations between the features')
plt.show()
# ## Unawareness only solves the problem for trivial toy datasets
# In this part I will show that neither approach works if the protected attribute is in fact correlated with other attributes. This is almost always the case in real life, and often in very complicated ways.
#
# For our example, let's investigate a simple case where due to societal expectations and developments a gender that is disadvantaged is also biased against in getting education and experience, as shown in the following process:
#
# <img src="./figures/DGP_Salary_Correlated.PNG" title="The data generating process for salary for an imaginary company with biases in employee salaries, where experience and education correlate with gender"/>
def generate_employees_correlated(size=2500):
'''
Generating employees, where attributes are correlated with gender
Gender 1 generally has lower education and experience
'''
X = (pd.DataFrame({'Gender': np.random.randint(2, size=size),})
.assign(Education = lambda df: 4 + 16 * np.random.rand(size) * np.where(df['Gender'] == 0, 1, np.random.rand(size)) ,
Experience = lambda df: (40*np.random.rand(size) + np.random.normal(df['Gender'].mul(-1).add(1).mul(10), 5)).clip(0, 40),
)
)
return X
df_corr = generate_employees_correlated().pipe(add_salaries)
display_df(df_corr)
# The table has the same columns, only the values are correlated now.
X_corr_train, X_corr_test, y_corr_train, y_corr_test, y_corr_skill_train, y_corr_skill_test = sklearn.model_selection.train_test_split(
df_corr.filter(['Education', 'Experience', 'Gender', ]),
df_corr['SalaryTrue'],
df_corr['SalarySkill'])
X_corr_train_unaware = X_corr_train.drop(columns=['Gender']) # So we can train an unaware regressor
X_corr_test_unaware = X_corr_test.drop(columns=['Gender'])
sns.heatmap(X_corr_train.corr(), cmap='RdBu_r', vmin=-0.8, vmax=0.8, annot=True, fmt='.0%')
plt.suptitle('Correlation Matrix\nIn this generated data set, gender is correlated with other, informative features')
plt.show()
# ### Training the same models on the new data set gives biased models
# Again, we train the same two models as before: one where we do not apply any bias mitigation, and one _unaware_ model. While the the bias is not as bad in the unaware model as in the model that explicitly allows for the dependency, it is still clearly there, with people of Gender 1 getting ~50 less per month based on their gender.
lr = LinearRegression()
lr.fit(X_corr_train, y_corr_train)
y_corr_pred = utils.predict_series(lr, X_corr_test)
lr_unaware = LinearRegression()
lr_unaware.fit(X_corr_train_unaware, y_corr_train)
y_corr_pred_unaware = utils.predict_series(lr_unaware, X_corr_test_unaware)
# + tags=[]
predictions = {'No bias mitigation': y_corr_pred,
'Unaware': y_corr_pred_unaware,
}
utils.plot_fairness_metrics(predictions, y_corr_skill_test, X_corr_test['Gender'])
plt.show()
# -
# How is this possible if the model is unaware of Gender? Unawareness compensates the lack of direct information through correlated variables
#
# The model _overestimates_ the importance of Experience and Education and through this keeps the biases partially intact. To keep the same mean salary, it also has a negative intercept: everyone is paid less, and then people with higher experience and education (mostly of Gender 1) are compensated.
# +
coefficients['No bias mitigation'] = utils.coefs_to_series(lr, X_corr_train.columns.tolist())
coefficients['Unawareness'] = utils.coefs_to_series(lr_unaware, X_corr_train_unaware.columns.tolist())
coefficients.plot(kind='barh')
plt.show()
# -
# ## Removing the disparate treatment with the IgnoringBiasEstimator
#
# So we conclude that something must be done to reach a fair algorithm. Therefore, I built the `IgnoringBiasEstimator` which learns the biases in the data and ignores them at prediction.
#
# There are generally 3 moments to work towards fairness, which I will quickly describe. For more information, see e.g. [here](https://towardsdatascience.com/a-tutorial-on-fairness-in-machine-learning-3ff8ba1040cb)
# * During **preprocessing** by transforming the dataset in such a way that downstream estimators learn in a fair way. Note that dropping protected attributes was in this category (in a very naive way), but much more sophisticated approaches exist. A great advantage is that you no longer need the protected attributes after this is done, but it generally does not reach the performance (both in terms of fairness and accuracy) of the other approaches.
# * During **inprocessing** by modifying the estimator (be it a classifier or a regressor) and the loss function (or constraints for this). This is generally harder from a technical perspective, but may reach very good results for a given definition of fairness.
# * During **postprocessing**, which is the most flexible, but as a drawback does require access to protected attributes at test time.
#
# ### The workings of the IgnoringBiasEstimator
# What I will is use inprocessing modification of the algorithm, by combining the two unsuccesfull approaches applied above:
# * The first model had access to the protected attribute - and we clearly saw how biased it learned to be during training
# * The second model did not have access - and this was better during prediction, but had an unfortunate effect during training where it learned biases through other variables.
#
# I will combine this by learning the biases during fitting and then *ignoring them at prediction time*. The fact that the model has access to the sensitive attributes during training prevents the model from learning the biases through other variables (which is what happened in the unaware model). Then, when predicting new instances, the protected attribute is hidden (in our example: the Gender) and filled with a neutral value for all instances (by default, this is the mean, but a custom value can be chosen). This allows us to discard the biases to work towards fairer salaries.
#
#
# The implementation is available on [my Github](https://github.com/SjoerdCor/fairness/blob/main/fairestimator.py).
# ### Applying the IgnoringBiasEstimator: simple and effective
#
#
# When applying the IgnoringBiasEstimator, you'll see two twings:
# 1. The IgnoringBiasEstimator is very easy to apply: it's just a wrapper around the fundamental estimator we're using (in our case, a simple LinearRegression) and the user has to indicate which column contains the sensitive attribute. Note that because of this, it is also very flexible: it can be used everything that's in `scikit-learn`: from a simple LinearRegression to more complex models such as Gradient Boosting. You also specify the index of the column which should be ignored at prediction time.
# 1. It's effective: the disparate treatment is fully gone.
ib = fairestimator.IgnoringBiasRegressor(LinearRegression(), ignored_cols=[-1]) # Ignore the Gender at prediction time, which is encoded in the last column
ib.fit(X_corr_train, y_corr_train)
y_corr_pred_ib = utils.predict_series(ib, X_corr_test)
predictions['IgnoringBias'] = y_corr_pred_ib
utils.plot_fairness_metrics(predictions, y_corr_skill_test, X_corr_test['Gender'])
plt.show()
#
#
# ### Additional advantage: the method can give insight into the biases at play here
# A bonus of this approach is that the model learned all the biases, and by observing what the model learned, a user might be able to influence the real world. For this, I like the [partial dependence plot](https://scikit-learn.org/stable/modules/generated/sklearn.inspection.plot_partial_dependence.html). It shows the expected output for a given input. In the plot below, it can be seen that the salary increases with increasing Education and Experience, but is lower for Gender 1 than for Gender 0 (during training - not during prediction, since it is hidden during prediction). While in this case, this was already clear from the plots before, the partial dependence plot can be very useful for more complex, non-parametric models (unlike the simple Linear Regression I performed) and/or non-linear biases. I will investigate that in Part 2 of this series about fairness.
#
# We might use this to influence the real world; understanding where it comes from and perhaps training the people responsible for it to prevent it from happening.
pdd = plot_partial_dependence(ib.estimator, X_corr_train, X_corr_train.columns)
pdd.axes_[0][2].set_title('Real-world bias\nthat was learned')
plt.show()
# ## Two closing remarks on fairness
# Before concluding this blog, I would like to share two general remarks on fairness in AI:
#
# * There is a trade-off between disparate impact and disparate treatment
# * Fairness does not hurt the true accuracy
#
# ### There is a trade-off between disparate impact and disparate treatment
# For some people or use cases, removing disparate treatment might be the definition of fair. For others, it might not be: there is still a disparate impact where employees of Gender 1 get a lower salary of ~900 a month, due to their lower experience and education on average, which may in turn be driven by societal biases. What you should note though, is that is a choice, and you cannot have it both ways. Below, I train a model that has a Disparate Impact of 0. This on the other hand leads to a disparate treatment towards employees of gender 0: for equal experience and education, they would now receive a lower salary. There is no fundamental good or bad - this is a matter of vision.
# +
lr_di = copy.deepcopy(lr)
lr_di.coef_[2] = 900
y_corr_pred_di = utils.predict_series(lr_di, X_corr_test)
predictions['No Disparate Impact'] = y_corr_pred_di
utils.plot_fairness_metrics(predictions, y_corr_skill_test, X_corr_test['Gender'])
plt.show()
# -
del predictions['No Disparate Impact']
# ### Fairness does not hurt the true accuracy
# A lot of places state that there is a trade-off beteween fairness and accuracy. I disagree. The trade-off is only there because we do not observe what we would like to observe. Improving fairness you might decrease the _observed_ accuracy (which would still be worth it), but we do not _want_ to match the observed salaries in the first place - the whole point was to remove the biases that we see in the real world. In fact, the plots below show that the predictions of match the skills-based salaries _better_ when improving fairness. The only thing is that in a real world application we would not have access to those. But it is still very important to keep in mind that accuracy only decreases because we observe bad targets.
measurable_accuracy = {name: sklearn.metrics.mean_absolute_error(y_pred, y_corr_test)
for name, y_pred in predictions.items()}
ax = plt.barh(range(len(measurable_accuracy)), measurable_accuracy.values(), color=['lightgrey', 'lightgrey', 'darkblue', 'lightgrey'])
plt.bar_label(ax, fmt='%d', padding=3)
plt.yticks(range(len(measurable_accuracy)), measurable_accuracy.keys())
plt.suptitle('More fairness leads to larger observed errors')
plt.ylabel("Bias mitigation strategy")
plt.xlabel('Observed mean absolute error\n(lower is better)')
plt.show()
true_accuracy = {name: sklearn.metrics.mean_absolute_error(y_pred, y_corr_skill_test)
for name, y_pred in predictions.items()}
ax = plt.barh(range(len(true_accuracy)), true_accuracy.values(), color=['lightgrey', 'lightgrey', 'darkblue', 'lightgrey'])
plt.bar_label(ax, fmt='%d', padding=3)
plt.yticks(range(len(true_accuracy)), true_accuracy.keys())
plt.ylabel("Bias mitigation strategy")
plt.xlabel('Skills-based mean absolute error\n(lower is better)')
plt.suptitle('More fairness leads to smaller true errors')
plt.show()
# ## Conclusion and outlook
# In this blog series, I quickly introduced the problem of bias in AI models, due to biased datasets and inadequate bias mitigation. Passive bias mitigation through either ignoring bias exists and leaving the sensitive attributes in the dataset, or dropping the sensitive attribute and then ignoring the problem propage biases into biased models. Furthermore, I quickly introduced two notions of fairness: disparate treatment (or different _decisions_ for sensitive groups) versus disparate impact (or different _outcomes_ for senstive groups).
#
#
# As a solution, I propsed the IgnoringBiasEstimator and saw the following things:
# * It was in fact very easy to use,
# * It worked very well to remove the disparate treatment
# * It gives insight into the biases at play.
#
# In the following installment of this series, I will show how flexible it is with continuous sensitive attributes and non-linear biases and classification targets and compare it to other bias mitigation strategies. I hope this will contribute to more fairness in decision processes.
|
blog/1.IntroducingTheIgnoringEstimator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lista Prodotti DOP - Italia
#
# La lista dei prodotti di qualità viene prodotta e aggiornata dal Ministero delle Politiche Agricole.
# https://www.politicheagricole.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/2090
import pdftables_api
import requests
import pandas as pd
import numpy as np
from openpyxl import load_workbook
import os.path
# +
config = {}
config_path = os.path.join(os.path.abspath('..'))
config_name = r'config.py'
config_file = os.path.join(config_path,config_name)
exec(open(config_file).read(),config)
# Key and Secret
pdf_key=config['TOKEN_PDF'] #https://pdftables.com/pdf-to-excel-api
# -
#Leggo il PDF dei prodotti DOP e IGP e lo trasformo in .xlsx
# https://www.politicheagricole.it/flex/cm/pages/ServeBLOB.php/L/IT/IDPagina/2090
if not os.path.isfile("Prodotti_DOP_IGP_KO.xlsx"):
PDFfilename = "https://www.politicheagricole.it/flex/cm/pages/ServeAttachment.php/L/IT/D/2%252Fb%252F0%252FD.3da391285cd6983b8cec/P/BLOB%3AID%3D2090/E/pdf"
r = requests.get(PDFfilename)
with open('Prodotti_DOP_IGP.pdf', 'wb') as f:
f.write(r.content)
c = pdftables_api.Client(pdf_key)
c.xlsx('Prodotti_DOP_IGP.pdf', 'Prodotti_DOP_IGP_KO')
# +
#Trasformo xlsx in pandas Dataframe ed effettuo DataQuality
df = pd.DataFrame()
for i in range(11):
df1 = pd.read_excel('Prodotti_DOP_IGP_KO.xlsx', sheetname=i, header=None)
df = df.append(df1)
cols = [7,9]
df.drop(df.columns[cols],axis=1,inplace=True)
header = df.iloc[[1]].values[0]
df.columns = header
df.reset_index(drop=True, inplace = True)
to_drop = df[df.isnull()['Denominazione']==True].index.values
to_drop = np.append(to_drop,1)
df = df.drop(df.index[[to_drop]]) # rimuovo le righe vuote
df.reset_index(drop=True, inplace = True)
# -
df.head(2)
df.count()['N'] # Totale Numero Prodotti DOP, IGP e STG
df_agg = df.groupby('Cat.').count()
df_agg['N'] # Suddivisione dei prodotti
df[df['Cat.']=='D.O.P.'].head(2)
df[df['Cat.']=='I.G.P.'].head(2)
df[df['Cat.']=='S.T.G.'].head(2)
df.to_excel('Prodotti_DOP_IGP.xlsx')
# +
#os.remove("Prodotti_DOP_IGP_KO.xlsx")
#os.remove("Prodotti_DOP_IGP.pdf")
|
Lista_Prodotti_DOP_IT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import psycopg2
import config as creds
import sqlalchemy
from sqlalchemy import create_engine
import numpy as np
from numpy.random import randn
import pandas as pd
from scipy import stats
from datetime import datetime
# + active=""
# GAS for years 2018-2019, INDIVIDUAL BUILDING TYPES
# Foreign keys: One Hot encode categorical features YEARBUILT and WARD, exclude DCREALPROPERTYID
# Numeric features: sqft, awnd, cldd, htdd, snow
# Target feature: kbtu
# VotingRegressor - "Services"
# -
# CONNECT TO DATABASE:
# +
user=creds.PGUSER
password=<PASSWORD>
host=creds.PGHOST
port=5432
database=creds.PGDATABASE
engine_str=f"postgresql+psycopg2://{user}:{password}@{host}:{port}/{database}"
engine = create_engine(engine_str)
conn = engine.raw_connection()
print('Connected')
cur = conn.cursor()
print('Cursor created')
# -
# EXTRACT DATASET:
# +
query='''
SELECT b.kbtu
,b.REPORTEDBUILDINGGROSSFLOORAREA
,b.dcrealpropertyid
,b.ward
,b.yearbuilt
,b.primarypropertytype_selfselect
,b.elegas
,n.awnd
,n.cldd
,n.htdd
,n.snow
,n.tavg
,n.wdf2
,n.wdf5
,n.wsf2
,n.wsf5
,n.date
FROM buildings_data b
LEFT OUTER join noaa_data n
ON b.REPORTINGYEAR = n.WEATHERYEAR
WHERE b.MONTH = n.MONTH
AND b.ELEGAS = 'N'
AND b.PRIMARYPROPERTYTYPE_SELFSELECT = '16'
AND b.REPORTINGYEAR BETWEEN 2018 AND 2019
AND b.YEARBUILT > 0
AND b.REPORTEDBUILDINGGROSSFLOORAREA > 50000;
'''
data=pd.read_sql(query,conn)
data.head()
# -
data.isnull().values.any()
# FORMAT COLUMNS:
# +
#CONVERT 'Date' COLUMN TO datetime format
#data["reportingyear"] = data["reportingyear"].astype(str)
#data['month']=data['month'].apply(lambda x: '{0:0>2}'.format(x))
#data['date_time'] = data[['reportingyear', 'month']].agg('-'.join, axis=1)
#data['date_time'] = (data.date_time + "-01")
#data['date_time'] = datetime.strptime('date_time', "%Y-%m-%d")
data['datetime']=pd.to_datetime(data['date'])
# -
data['primarypropertytype_selfselect'].dtype
data['primarypropertytype_selfselect']=data['primarypropertytype_selfselect'].astype('int32')
data.set_index('datetime', inplace=True)
data.head()
data.shape
data.columns
data.dtypes
import matplotlib.pyplot as plt
import seaborn as sns
plt.figure(figsize=(25,15))
ftr = list(["kbtu", "reportedbuildinggrossfloorarea", "ward", "yearbuilt", "awnd", "cldd", "htdd", "snow"])
corrMatrix = data[ftr].corr()
sns.heatmap(corrMatrix, annot=True, fmt='.1f', linewidths=.5)
# DEFINE FEATURES:
# +
TARGET = "kbtu"
COLS = ['reportedbuildinggrossfloorarea', 'ward', 'yearbuilt', 'awnd', 'cldd', 'htdd', 'snow', 'datetime']
def make_sklearn_data(df=data, target=TARGET, cols=COLS):
df = df.reset_index()
X, y = df[cols], df[target]
return X, y
# -
features = ['reportedbuildinggrossfloorarea', 'ward', 'yearbuilt', 'awnd', 'cldd', 'htdd', 'snow']
X, y = make_sklearn_data(cols=features)
# +
#Rank2D
from yellowbrick.features import Rank2D
# Instantiate the visualizer with the Pearson ranking algorithm
visualizer = Rank2D(algorithm='pearson', features=features, size=(1080, 720))
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
# +
# Instantiate the visualizer with the Covariance algorithm
visualizer = Rank2D(algorithm='covariance', features=features, size=(1080, 720))
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
# +
#Feature Importances
import yellowbrick as yb
from sklearn.ensemble import RandomForestRegressor
from yellowbrick.features import RadViz
from yellowbrick.features import FeatureImportances
model = RandomForestRegressor(n_estimators=10)
viz = FeatureImportances(model, labels=features, size=(1080, 720))
viz.fit(X, y)
viz.show()
# +
#Feature Importances
import yellowbrick as yb
from sklearn.linear_model import Lasso
from yellowbrick.features import RadViz
from yellowbrick.features import FeatureImportances
model = Lasso()
viz = FeatureImportances(model, labels=features, size=(1080, 720))
viz.fit(X, y)
viz.show()
# +
#CYCLIC ENCODER: to capture temporal cycles (yearly).
from sklearn.base import BaseEstimator, TransformerMixin
class CyclicEncoder(BaseEstimator, TransformerMixin):
def __init__(self, date_extract="month"):
if date_extract not in {"minute", "hour", "week", "month", "year"}:
raise ValueError(f"specify correct date component to extract, not {date_extract}")
self.date_extract = date_extract
def get_date_component(self, x):
if self.date_extract == "month":
return x.dt.month
elif self.date_extract == "year":
return x.dt.year
else:
raise NotImplementedError(f"{self.date_extract} date component not implemented yet")
def fit(self, X, y=None):
self.cycle_max_ = self.get_date_component(X).max()
return self
def transform(self, X, y=None):
cols = []
names = []
x = self.get_date_component(X)
xn = 2 * np.pi * x / self.cycle_max_
cols.append(np.cos(xn))
names.append(f"{X.name}_cos")
cols.append(np.sin(xn))
names.append(f"{X.name}_sin")
return pd.DataFrame(np.asarray(cols).T, columns=names)
ce = CyclicEncoder().fit_transform(data.reset_index()["datetime"])
ce.plot(x="datetime_cos", y="datetime_sin", kind="scatter")
# +
#FEATURE EXTRACTION
from sklearn.base import clone
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import FeatureUnion, Pipeline
from sklearn.preprocessing import OneHotEncoder
extraction = Pipeline([
('column_selection', ColumnTransformer([
('time_components', FeatureUnion([
('month', CyclicEncoder(date_extract='month')),
('year', CyclicEncoder(date_extract='year')),
]), 'datetime'),
('ward_one_hot', OneHotEncoder(handle_unknown='ignore'), ['ward']),
('yearbuilt_one_hot', OneHotEncoder(handle_unknown='ignore'), ['yearbuilt']),
], remainder="passthrough")),
])
def make_energy_pipeline(model, append_transformers=None, fe=extraction):
pipe = clone(fe)
if append_transformers:
for step in append_transformers:
pipe.steps.append(step)
pipe.steps.append(["model", clone(model)])
return pipe
# +
#Test the Feature Extraction Pipeline
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split as tts
X_train, X_test, y_train, y_test = tts(*make_sklearn_data(), test_size=0.2)
model = make_energy_pipeline(LinearRegression())
model.fit(X_train, y_train)
model.score(X_test, y_test)
# +
#TIME SERIES CROSS VALIDATION
from functools import partial
from sklearn.metrics import make_scorer
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
rmse = partial(mean_squared_error, squared=False)
def time_series_evaluate(model, X, y):
"""
Performs time series cross validation on the model, returning the
cross validated r2, mse, and mae of the regressor, along with the
final fitted model, fitted on all of the data.
"""
cv = TimeSeriesSplit(12)
scores = {}
scores["r2"] = cross_val_score(model, X, y, cv=cv, scoring=make_scorer(r2_score))
scores["mse"] = cross_val_score(model, X, y, cv=cv, scoring=make_scorer(mean_squared_error))
# scores["rmse"] = cross_val_score(model, X, y, cv=cv, scoring=make_scorer(rmse))
scores["mae"] = cross_val_score(model, X, y, cv=cv, scoring=make_scorer(mean_absolute_error))
model.fit(X, y)
return model, scores
# -
# LINEAR MODEL
X, y = make_sklearn_data()
lm = make_energy_pipeline(LinearRegression())
time_series_evaluate(lm, X, y)
# +
#Second order polynomial regression
from sklearn.linear_model import SGDRegressor
from sklearn.preprocessing import PolynomialFeatures
qm = make_energy_pipeline(SGDRegressor(), [('quad', PolynomialFeatures(2))])
time_series_evaluate(qm, X, y)
# +
from sklearn.ensemble import RandomForestRegressor
rfm = make_energy_pipeline(RandomForestRegressor(n_estimators=10, max_depth=3))
time_series_evaluate(rfm, X, y)
# +
import time
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import VotingRegressor
start = time.time()
r1 = LinearRegression()
r2 = RandomForestRegressor(n_estimators=10, random_state=1)
X, y = make_sklearn_data()
er = make_energy_pipeline(VotingRegressor([('lr', r1), ('rf', r2)]))
print(time_series_evaluate(er, X, y))
print("Time = {:0.3f} seconds".format(time.time()-start))
# -
conn.close()
print('Closed')
|
machine_learning/Roman_SERVICES_GAS_wardyearbuilt_kbtu.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="y3dwviL1Cpv1"
# # Data Loading
# + id="2Vmx8HBb0sdz"
import matplotlib.pyplot as plt
import numpy as np
import gdown
import zipfile
from tqdm import tqdm
# + colab={"base_uri": "https://localhost:8080/", "height": 108} id="Ul9gq2ja1Xw0" outputId="eb2014e3-76bd-4510-9ec1-afb281dff645"
gdown.download('https://drive.google.com/uc?export=download&id=1naL2i9KKcx7hd7oCEQIVStQjSH6j9gDW', 'dataset.zip', quiet=False)
# + colab={"base_uri": "https://localhost:8080/"} id="DvQQ5jh62DOs" outputId="abd3d44f-9c63-4a7e-e9da-e07d9fcd0768"
with zipfile.ZipFile('dataset.zip', mode='r') as zip_file:
for zf in tqdm(zip_file.infolist(), desc="Extracting"):
try:
zip_file.extract(zf)
except Exception as e:
print(e)
zip_file.close()
# + [markdown] id="YRqa3-2eCtXM"
# # Preprocessing Data
# + colab={"base_uri": "https://localhost:8080/"} id="WcdiML7X3SeQ" outputId="e97679df-8f2c-4d3a-b068-ab456ad464c8"
from google.colab import drive
drive.mount('/content/drive')
# + id="SDTxbcxp9cN_"
import os
import shutil
import tensorflow as tf
from tensorflow.keras.preprocessing.image import ImageDataGenerator
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="s0ffUlry9FHu" outputId="74049567-5541-41bb-d1e4-990f7263caf0"
shutil.move('/content/content/content/dataset', '/content/')
# + id="Hg5pLgQv9x_Z"
shutil.rmtree('/content/content')
# + [markdown] id="OFZXJh4HDZCJ"
# ## Split Data
# + id="RF-Uvt4fDaXk"
def split_data(data, train_size=0.8, random_seed=42):
"""Fungsi ini untuk memisahkan data menjadi train set dan validation_set
dengan urutan hasil return : data_train, data_validasi"""
np.random.seed(int(random_seed))
test_size=1-train_size
panjang_train = int(train_size*len(data))
panjang_val = int(test_size*len(data))
selisih =len(data) - (panjang_train + panjang_val)
# print(len(data), " - ( ",panjang_train, " + ", panjang_val," ) = ",selisih)
if selisih > 0:
panjang_train +=selisih
data_train = []
#memilih data train dari data
while len(data_train) != panjang_train:
bantu = np.random.randint(0, (len(data)-1))
if data[bantu] not in data_train:
data_train.append(data[bantu])
del data[bantu]
#Sisanya Dicopy kedalam Train
data_validasi = data.copy()
del data
print("\nPanjang train : ",panjang_train)
print("Panjang validasi : ",panjang_val,"\n")
return data_train, data_validasi
# + id="5EM3xWjiDbbG"
#Selanjutnya pindahkan ke folder terpisah
#Membuat fungsi untuk membuat folder penyimpanan dan memindahkan data yang telah dipisahkan kedalam folder tersebut
def move(data_train, data_val, data_path, train_path, val_path):
"""Fungsi ini untuk membuat folder penyimpanan dan
memasukan data yang telah dipisahkan dengan folder tersebut"""
#Memeriksa apakan folder sudah ada, jika belum maka tambahkan folder
if not (os.path.exists(train_path) and os.path.exists(val_path)):
os.makedirs(train_path)
os.makedirs(val_path)
else:
print('Folder Sudah ada')
#memindahkan ke folder terpisah
for i in range(len(data_train)):
shutil.move(os.path.join(data_path, data_train[i]), os.path.join(train_path, data_train[i]))
#memindahkan ke folder terpisah
for i in range(len(data_val)):
shutil.move(os.path.join(data_path, data_val[i]), os.path.join(val_path, data_val[i]))
# + id="7xpm_ryLDeSu"
def split_and_move_data(path='', random_seed=42, train_size=0.8):
path_dict = {}
for i in os.listdir(path):
path_dict[i] = os.listdir(os.path.join(path, i))
print(i, "=> sebanyak ", len(os.listdir(os.path.join(path, i))))
dict_train_test = {}
for cls in path_dict.keys():
dict_train_test[cls] = split_data(path_dict[cls],random_seed=random_seed,train_size=train_size)
for cls in path_dict.keys():
move(
data_train = dict_train_test[cls][0],
data_val = dict_train_test[cls][1],
data_path = os.path.join(path, cls),
train_path = os.path.join(os.path.join(path,'train'),cls),
val_path = os.path.join(os.path.join(path,'test'),cls)
)
shutil.rmtree(os.path.join(path, cls))
len_train = 0
len_test = 0
train = os.path.join(path,'train')
test = os.path.join(path,'test')
for cls in os.listdir(train):
len_train += len(os.listdir((os.path.join(train,cls))))
len_test += len(os.listdir((os.path.join(test,cls))))
print('train : {} data'.format(len_train))
print('test : {} data'.format(len_test))
# + colab={"base_uri": "https://localhost:8080/"} id="P22zNaqhDipm" outputId="900547b6-9d46-4279-f03f-7f227158f38a"
split_and_move_data('/content/dataset', train_size=0.85)
# + [markdown] id="UC6Jms_HEZR4"
# # Data Generator
# + id="DL9QbPI8EcEH"
train_dir = 'dataset/train'
test_dir = 'dataset/test'
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=45,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
brightness_range=[0.6, 1.5],
horizontal_flip=True,
fill_mode='nearest')
test_datagen = ImageDataGenerator(
rescale=1./255
)
# + colab={"base_uri": "https://localhost:8080/"} id="HTBHpQ3zFS6u" outputId="b55aadcc-7a4b-4021-dda8-f581c3d1293d"
train_generator = train_datagen.flow_from_directory(
directory=train_dir,
target_size=(224, 224),
batch_size=128,
class_mode='categorical',
shuffle=True
)
test_generator = test_datagen.flow_from_directory(
directory=test_dir,
target_size=(224, 224),
batch_size=434,
class_mode='categorical'
)
# + id="Bi8mlE-YqClR"
from tensorflow.keras.models import load_model
from tensorflow.keras import Input, Model, Sequential
from tensorflow.keras.regularizers import l2, l1_l2
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.layers import Dense, Dropout, LeakyReLU, BatchNormalization
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
# + colab={"base_uri": "https://localhost:8080/"} id="dk6eFSLS6fgI" outputId="36651aca-6bb8-4e39-ae35-5c852b2dc83d"
model = load_model('/content/drive/MyDrive/Orbit_final_project/bestModel9/checkpoint_34')
model.summary()
# + id="QnCy-jnQ7yCB"
model.layers[0].trainable = False
model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=1e-4),
loss='categorical_crossentropy',
metrics=['accuracy'])
# + id="kyQrHBgo83cK"
def checkpoint(filepath, monitor='val_loss'):
return ModelCheckpoint(filepath=filepath, monitor=monitor, verbose=1, save_best_only=False, save_freq='epoch')
# + colab={"base_uri": "https://localhost:8080/"} id="0xpfrtKP-siw" outputId="dc9e5729-24ea-4391-e360-6b9f621383c2"
model_checkpoint = checkpoint('/content/drive/MyDrive/Orbit_final_project/bestModel8/checkpoint_{epoch:02d}', monitor='val_accuracy',)
learningrate_decay = ReduceLROnPlateau(monitor='val_accuracy', factor=0.5,
patience=10, verbose=1, min_lr=1e-20)
earlystopping = EarlyStopping(monitor='val_accuracy', patience=20, verbose=1)
train_steps_per_epoch = train_generator.n // train_generator.batch_size
val_steps = test_generator.n // test_generator.batch_size
print(train_steps_per_epoch, val_steps)
# + [markdown] id="4LtHRr73Iopc"
# # Transfer Learning
# + colab={"base_uri": "https://localhost:8080/"} id="NzLxnKOt_Yvw" outputId="23b6c4e8-056e-4283-910e-327c2f7affd0"
history = model.fit(train_generator, validation_data=test_generator, epochs=100,
verbose=1, callbacks=[model_checkpoint, learningrate_decay, earlystopping],
steps_per_epoch=train_steps_per_epoch, validation_steps=val_steps)
# + id="__rth6noJmNZ" colab={"base_uri": "https://localhost:8080/", "height": 530} outputId="9268182d-2f69-42b1-f2b6-1d1deeabb920"
plt.figure(figsize=(20,9))
plt.subplot(121)
plt.title('grafik loss')
plt.plot(history.history['loss'], label='training')
plt.plot(history.history['val_loss'], label='validation')
plt.legend()
plt.subplot(122)
plt.title('grafik accuracy')
plt.plot(history.history['accuracy'], label='training')
plt.plot(history.history['val_accuracy'], label='validation')
plt.legend()
plt.show()
|
Machine-learning-model/BestModel8.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # TD8
// ## Tours de Hanoï
// Exemple : http://championmath.free.fr/tourhanoi.htm
void deplacements(int n, String src, String tmp, String dest) {
if (n > 0) {
deplacements(n - 1, src, dest, tmp);
System.out.println("Déplace 1 élément de " + src + " vers " + dest);
deplacements(n - 1, tmp, src, dest);
}
}
deplacements(1, "T1", "T2", "T3");
/* Doit afficher :
Déplace 1 élément de T1 vers T3 */
deplacements(2, "T1", "T2", "T3");
/* Doit afficher :
Déplace 1 élément de T1 vers T2
Déplace 1 élément de T1 vers T3
Déplace 1 élément de T2 vers T3 */
deplacements(3, "T1", "T2", "T3");
/* Doit afficher :
Déplace 1 élément de T1 vers T3
Déplace 1 élément de T1 vers T2
Déplace 1 élément de T3 vers T2
Déplace 1 élément de T1 vers T3
Déplace 1 élément de T2 vers T1
Déplace 1 élément de T2 vers T3
Déplace 1 élément de T1 vers T3 */
deplacements(4, "T1", "T2", "T3");
// ## Fibonnaci
// ### Récursive
int fibonnaci_recursive(int n) {
if (n==0) { return 0; }
else if (n==1) { return 1; }
else { return fibonnaci_recursive(n-1) + fibonnaci_recursive(n-2); }
}
for (int i = 0; i < 10; i++) {
System.out.println("i: " + i + " | f(i): " + fibonnaci_recursive(i));
}
// ### Dynamique
// +
int MAX = 100;
private int[] memory = new int[MAX];
memory[0] = 0;
memory[1] = 1;
int fibonnaci_dynamic(int n) {
if (n >= 2 && memory[n] == 0) {
memory[n] = fibonnaci_dynamic(n-1) + fibonnaci_dynamic(n-2);
}
return memory[n];
}
// -
for (int i = 0; i < 10; i++) {
System.out.println("i: " + i + " | f(i): " + fibonnaci_dynamic(i));
}
// ### Itérative
int fibonnaci_iterative(int n) {
if (n == 0) { return 0; }
int fn_minus_1 = 0;
int fn = 1;
for (int i = 1; i < n; i++) {
int fn_plus_1 = fn + fn_minus_1;
fn_minus_1 = fn;
fn = fn_plus_1;
}
return fn;
}
for (int i = 0; i < 10; i++) {
System.out.println("i: " + i + " | f(i): " + fibonnaci_iterative(i));
}
|
notebooks/TD8-solution.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .scala
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Scala
// language: scala
// name: scala
// ---
// + [markdown] slideshow={"slide_type": "slide"}
// <div style="text-align:center">
// <h1>Scala - Structuring Programs</h1>
// <h3><NAME> <br/> Departement of Mathematics and Computer Science</h3>
// </div>
// + [markdown] slideshow={"slide_type": "slide"}
// # Outline
//
// - Repetition: The basic building blocks
// - Scala - the simple parts
// - Objects
// - Groups
// - Collections
// - For-loops
// - Algebraic data types
// - Case study: Scalismo's IO Methods and ```Try```
// + [markdown] slideshow={"slide_type": "slide"}
// # Expression, types and values
//
// 
// + [markdown] slideshow={"slide_type": "slide"}
// # Blocks
//
// * Sequence of expression
// * Itself an expression
// * Last line determines value
// * Can be named
//
// ```scala
// val result = {
// val x = 1 + 1
// x + 1
// }
// ```
// + [markdown] slideshow={"slide_type": "slide"}
// # Functions
//
// * Expressions that take parameter
//
// 
// + [markdown] slideshow={"slide_type": "slide"}
// # Functions
//
// * Functions are blocks are expressions and hence can be named
//
// ```scala
// val f = (x : Int) => {
// val y = 1
// x + y
// }
// ```
// + [markdown] slideshow={"slide_type": "slide"}
// # Object-oriented programming
//
// Scala has
// * classes
// * objects
// * traits (interfaces)
// + [markdown] slideshow={"slide_type": "slide"}
// # Object-oriented programming
//
// ```scala
//
// trait Printable {
// def printToString(s : String) : String
// }
//
// class MyNumber(number : Double) extends Printable {
// override def printToString(s + number) : String = {
// s + number.toString
// }
// }
//
// ```
// + [markdown] slideshow={"slide_type": "slide"}
// # Case-classes and objects
//
// #### Case class
//
// * Class with proper equality to organize data
//
// ```scala
// case class Point(x : Double, y : Double)
// ```
//
// #### Object
//
// * One instance only
//
// ```scala
// object Universe {
// val mass = 4.5e51 //kg
// }
//
// ```
//
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Pattern matching
//
// * Generalizes switch/case statement from java
//
// ```scala
// expression match {
// case pattern1 => expression1
// case pattern2 => expression2
// // ...
// }
// ```
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Parametric types
//
// > Types in Scala can be parametric
//
// ```scala
// case class Pair[A, B](first : A, second : B)
// ```
//
// Usage:
// ```scala
// val pair1 = Pair(3, 5.0)
// val pair2 : Pair[String, Int] = Pair("abc", 5)
// ```
//
//
// * Types are inferred automatically when possible
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Scala - the simple parts
//
// Slides are loosely based on
// * [Scala - the simple parts](https://www.slideshare.net/Odersky/scala-the-simple-parts) by <NAME>
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Simple vs Easy
//
//
// + [markdown] slideshow={"slide_type": "fragment"}
// > Simple is often erroneously mistaken for easy.
// >
// > * "Easy" means "to be at hand", "to be approachable".
// > * "Simple" is the opposite of "complex" which means "being intertwined", "being tied together".
// >
// > <NAME> (from the talk [Simple Made Easy](https://www.infoq.com/presentations/Simple-Made-Easy)
//
// + [markdown] slideshow={"slide_type": "slide"}
// # (almost) Everything is an expression
//
// * Everything can be composed
// +
val a = 5
val s = "abc"
println(if (a == 3) "abc" else "cde")
val c: Int = s match {
case "abc" =>
try {
new java.io.FileInputStream(new java.io.File("I do not Exist"))
7
} catch {
case (e : java.io.FileNotFoundException) => 0
}
case _ => 2
}
// + [markdown] slideshow={"slide_type": "slide"}
// # Everything is an object
//
// * We always interact with any value by
// * Calling methods
// * Accessing fields
//
// Example:
// ```scala
// 1 + 3
// ```
//
// * 1 is object
// * ```+``` is method
// * 3 is Argument
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Mini exercises
//
//
// Create a class Complex for representing complex numbers
//
// ```scala
// case class Complex(re : Double, imag : Double)
// ```
//
// * Implement a method called ```+``` to add two complex numbers
// * Try out the method:
// * Do you need the ```.``` to call it?
// * Do you need the paranthesis?
//
// * Implement a method called ```#*--!```
//
//
// +
// type your solution here
// + [markdown] slideshow={"slide_type": "slide"}
// # Groups
//
// * Everything can be grouped and nested
// * Static uniform scoping rules
// * Allows naming of thing
// * Allows keeping local things in local context
//
// +
def foo() : Unit = {
import collection.immutable.List
case class KeyValue(key : String, value : Int)
val list = List(KeyValue("A", 3), KeyValue("B", 2))
def keyIsA(kv : KeyValue) : Boolean = { kv.key == "A" }
list.count(keyIsA)
}
// + [markdown] slideshow={"slide_type": "slide"}
// # Collections
//
// * Collections aggregate data
// * Transformed to manipulate data
// * updates not possible with default collections
// * Uniform interface - Learn once, use everywhere
//
//
// > Essence of functional programming
// + [markdown] slideshow={"slide_type": "slide"}
// # Collections - Basic operations
// + slideshow={"slide_type": "fragment"}
val people = Seq("<NAME>", "<NAME>", "<NAME>")
// + slideshow={"slide_type": "fragment"}
people.map(name => name.toUpperCase)
// + slideshow={"slide_type": "fragment"}
people.filter(name => name.startsWith("b"))
// + slideshow={"slide_type": "fragment"}
people.flatMap(name => name.split(" "))
// + [markdown] slideshow={"slide_type": "slide"}
// # Mini exercise
//
// * Create a sequence of values from 1 to 10
// * Double each value in the sequence
// * Filter out the values that can be divided by 7
// * Create a sequence of values like this:
// ```1, 2, 3, 2, 3, 4, 3, 4, 5, ...```
// * Create the cartesian product of the numbers 1 to 10 using only map and flatmap
//
// + [markdown] slideshow={"slide_type": "slide"}
// # For - loops
//
// > Scala has also for loops
// + slideshow={"slide_type": "fragment"}
for (i <- 0 until 10) {
print(i + " ")
}
// + slideshow={"slide_type": "fragment"}
val evenNumbers = for (i <- 0 until 10) yield {
i * 2
}
// + [markdown] slideshow={"slide_type": "slide"}
// # Not your father's for loops
//
// > For loops are only syntactic sugar
//
// The two expressions are the same:
// ```scala
// (0 until 10).map(i => i * 2)
// ```
// ```scala
// for (i <- 0 until 10) yield {
// i * 2
// }
// ```
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Not your father's for loops
//
// > For loops are only syntactic sugar
//
// The two expressions are the same:
// ```scala
// (0 until 10).filter(i => i % 2 == 0)
// ```
// ```scala
// for (i <- 0 until 10 if i % 2 == 0) yield {
// i
// }
// ```
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Not your father's for loops
//
// > For loops are only syntactic sugar
//
// The two expressions are the same:
// ```scala
// (0 until 10).flatMap(i =>(i until i + 2))
// ```
// ```scala
// for (i <- (0 until 10;
// iSeq <- i until i + 2) yield iSeq
// ```
//
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Not your father's for loops
//
// > For loops are only syntactic sugar
//
// Makes complicated expressions look simple
// ```scala
// for (i <- 0 until 10;
// j <- 0 until 10;
// if (i + j) == 7) yield (i , j)
// ```
//
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Algebraic data types
//
//
// > Sum types
// * A is either B or C
//
// ```scala
// trait A
// case class B() extends A
// case class C() extends A
// ```
//
// + [markdown] slideshow={"slide_type": "slide"}
// # Algebraic data types
//
// > Product types
// * A and B
//
// ```scala
// case class C(a : A, b : B)
// ```
// + [markdown] slideshow={"slide_type": "slide"}
// # Algebraic data types: Example
// +
trait Expression
case class Number(n : Int) extends Expression
case class Plus(a : Expression, b : Expression) extends Expression
case class Minus(a : Expression, b : Expression) extends Expression
val expression = Plus(Number(5), Minus(Number(3), Number(1)))
// + [markdown] slideshow={"slide_type": "slide"}
// # Taking things apart
//
// > Sum types are desctructed by *pattern matching*
// + slideshow={"slide_type": "fragment"}
def evaluate(expr : Expression) : Int = {
expr match {
case Number(n) => n
case Plus(a, b) => evaluate(a) + evaluate(b)
case Minus(a, b) => evaluate(a) - evaluate(b)
}
}
// + [markdown] slideshow={"slide_type": "slide"}
// # Time to get started
//
// 
|
notebooks/Scala-structuring.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:root] *
# language: python
# name: conda-root-py
# ---
# ## Performance Python
# Import relevant libraries
# +
# numpy is the 'Numerical Python' package
import numpy as np
# Numpy's methods for pseudorandom number generation
import numpy.random as rnd
# For plotting
import matplotlib.pyplot as plt
# scipy is the 'Scientific Python' package
# We'll use the stats package to get some p.d.f.s.
from scipy import stats
# %config InlineBackend.figure_format = 'retina'
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Sampling a Laplace distribution with MCMC
#
# $$ X \sim \mathsf{Laplace}(\mu, \lambda) \quad \Rightarrow \quad f_X(x) = \frac{1}{2\lambda} \exp \,\Bigl\{ \frac{| x - \mu | }{\lambda} \Bigr\} \,. $$
# + cell_style="split" slideshow={"slide_type": "-"}
xs = np.linspace(-5,5, 500)
plt.plot(xs, stats.laplace.pdf(xs), 'r');
# -
def sample(R):
rng = rnd.default_rng(1)
π = stats.laplace.pdf
X = np.empty(R)
X[0] = 0
for n in range(1, R):
Y = X[n-1] + rng.normal()
α = π(Y) / π(X[n-1])
if rng.uniform() < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
# ### Measure the problem
# Before timing any code, put turn off battery saver modes.
# %time X = sample(10**2)
26.5 / 1000 * 100
# %time X = sample(10**4)
1.68 * 100 / 60
# %timeit X = sample(1)
# %load_ext line_profiler
# %lprun -f sample sample(10**4)
# %lprun -f stats.laplace.pdf sample(10**4)
# %load_ext heat
# +
# %%heat
import numpy as np
import numpy.random as rnd
from scipy import stats
rng = rnd.default_rng(1)
R = 10**4
pi = stats.laplace.pdf
X = np.empty(R)
X[0] = 0
for n in range(1, R):
Y = X[n-1] + rng.normal()
alpha = pi(Y) / pi(X[n-1])
if rng.uniform() < alpha:
X[n] = Y
else:
X[n] = X[n-1]
# -
# %load_ext snakeviz
# %snakeviz X = sample(10**4)
# ### Check improvements one-by-one
# #### Replace built-in Laplace p.d.f. with a version we have made.
# + cell_style="split" slideshow={"slide_type": "-"}
xs = np.linspace(-5, 5, 11)
old = stats.laplace.pdf(xs)
new = np.exp(-np.abs(xs))/2
old - new
# -
xs = np.linspace(-5, 5, 10**5)
# %timeit stats.laplace.pdf(xs)
# %timeit np.exp(-np.abs(xs)) # Don't need normalising constant
5.58 / 1.2
xs = np.linspace(-5, 5, 10**5)
# %timeit [stats.laplace.pdf(x) for x in xs]
# %timeit [np.exp(-np.abs(x)) for x in xs]
7.37 / 0.233
samplePrev = sample
def sample(R):
rng = rnd.default_rng(1)
π = lambda x: np.exp(-np.abs(x))
X = np.empty(R)
X[0] = 0
for n in range(1, R):
Y = X[n-1] + rng.normal()
α = π(Y) / π(X[n-1])
if rng.uniform() < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
print(samplePrev(5))
print(sample(5))
# %time X = samplePrev(10**5)
# %time X = sample(10**5)
16.3 / 0.987
# %lprun -f sample sample(10**5)
# #### Let's try vectorising the random number generation
samplePrev = sample
def sample(R):
rng = rnd.default_rng(1)
π = lambda x: np.exp(-np.abs(x))
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
uniforms = rng.uniform(size=R-1)
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
α = π(Y) / π(X[n-1])
if uniforms[n-1] < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
print(samplePrev(5))
print(sample(5))
# %time X = samplePrev(10**6)
# %time X = sample(10**6)
9.98 / 6.14
# %lprun -f sample sample(10**6)
# #### Let's try getting rid of the exponential in the p.d.f.
samplePrev = sample
def sample(R):
rng = rnd.default_rng(1)
logπ = lambda x: -np.abs(x)
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
exponentials = np.log(rng.uniform(size=R-1)) # Seems faster than rng.exponential
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
logα = logπ(Y) - logπ(X[n-1])
if exponentials[n-1] < logα:
X[n] = Y
else:
X[n] = X[n-1]
return X
print(samplePrev(5))
print(sample(5))
# %time X = samplePrev(10**6)
# %time X = sample(10**6)
6.06 / 3.5
# ### Sample from a truncated Laplace distribution
def sample(R):
rng = rnd.default_rng(1)
π = lambda x: (x > -1) * (x < 1) * np.exp(-np.abs(x))
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
uniforms = rng.uniform(size=R-1)
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
α = π(Y) / π(X[n-1])
if uniforms[n-1] < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
# +
# %time X = sample(10**5)
plt.plot(X)
plt.show()
plt.hist(X, 40);
# -
np.mean(np.diff(X) == 0)
samplePrev = sample
def sample(R):
rng = rnd.default_rng(1)
πUn = lambda x: np.exp(-np.abs(x))
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
uniforms = rng.uniform(size=R-1)
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
# Check the constraint first
if Y <= -1 or Y >= 1:
X[n] = X[n-1]
continue
# Then, if a valid proposal,
# calculate the acceptance prob.
α = πUn(Y) / πUn(X[n-1])
if uniforms[n-1] < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
print(samplePrev(5))
print(sample(5))
# %time X = samplePrev(10**6)
# %time X = sample(10**6)
14.6 / 4.11
# ### Try compiling the algorithm with numba
from numba import njit
samplePrev = sample
@njit
def sample(R):
rng = rnd.default_rng(1)
πUn = lambda x: np.exp(-np.abs(x))
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
uniforms = rng.uniform(size=R-1)
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
# Check the constraint first
if Y <= -1 or Y >= 1:
X[n] = X[n-1]
continue
# Then, if a valid proposal,
# calculate the acceptance prob.
α = πUn(Y) / πUn(X[n-1])
if uniforms[n-1] < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
sample(5)
# +
def sample(R):
rng = rnd.default_rng(1)
X = np.empty(R)
X[0] = 0
jumps = rng.normal(size=R-1)
uniforms = rng.uniform(size=R-1)
sample_jit(X, jumps, uniforms)
return X
@njit
def sample_jit(X, jumps, uniforms):
R = len(X)
πUn = lambda x: np.exp(-np.abs(x))
for n in range(1, R):
Y = X[n-1] + jumps[n-1]
# Check the constraint first
if Y <= -1 or Y >= 1:
X[n] = X[n-1]
continue
# Then, if a valid proposal,
# calculate the acceptance prob.
α = πUn(Y) / πUn(X[n-1])
if uniforms[n-1] < α:
X[n] = Y
else:
X[n] = X[n-1]
# -
# %time X = sample(10**6)
# %time X = sample(10**6)
print(samplePrev(5))
print(sample(5))
# %time X = samplePrev(10**6)
# %time X = sample(10**6)
4.67 / 0.0419
from numba import int64, float64
samplePrev = sample
@njit(float64[:](int64))
def sample(R):
rnd.seed(123)
X = np.empty(R)
X[0] = 0
for n in range(1, R):
Y = X[n-1] + rnd.normal(0, 1)
α = (Y > -1) * (Y < 1) * np.exp(-np.abs(Y)+np.abs(X[n-1]))
if rnd.uniform(0, 1) < α:
X[n] = Y
else:
X[n] = X[n-1]
return X
# %time X = sample(10**7)
# %time X = sample(10**7)
# %timeit X = samplePrev(10**7)
# %timeit X = sample(10**7)
# +
plt.plot(X[:10**6])
plt.show()
plt.hist(X[:10**6], 40);
# -
# Can get a little faster by noticing that each `π` function call is called (at least) twice with the same arguments. If the result is stored/cached, then we get faster but uglier code, so I'll stop here.
# Similarly, one can try to [simulate using a truncated proposal](https://darrenjw.wordpress.com/2012/06/04/metropolis-hastings-mcmc-when-the-proposal-and-target-have-differing-support/) so that invalid points are never proposed.
# ### Keep in mind
#
# Improvements to the algorithm and your choice of hyperparameters are often a better starting point than going down a rabbit-hole of performance optimisations!
#
# Updating Python and its packages may give you a free small speed boost (or maybe it will slow things down). With this numpy update, I tested CMC before and after and the time went from 5m 4s down to 3m 54s.
from IPython.display import Image
Image("numpy_update.png")
|
codedemos/CodeL3_Performance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # zip function
#
# zip() makes an iterator that aggregates elements from each of the iterables.
# - iterators: https://www.w3schools.com/python/python_iterators.asp
# - also : https://wiki.python.org/moin/Iterator
#
# Returns an iterator of tuples, where the i-th tuple contains the i-th element from each of the argument sequences or iterables. The iterator stops when the shortest input iterable is exhausted. With a single iterable argument, it returns an iterator of 1-tuples. With no arguments, it returns an empty iterator.
#
# zip() is equivalent to:
#
# def zip(*iterables):
# # zip('ABCD', 'xy') --> Ax By
# sentinel = object()
# iterators = [iter(it) for it in iterables]
# while iterators:
# result = []
# for it in iterators:
# elem = next(it, sentinel)
# if elem is sentinel:
# return
# result.append(elem)
# yield tuple(result)
#
#
# zip() should only be used with unequal length inputs when you don’t care about trailing, unmatched values from the longer iterables.
#
# Let's see it in action in some examples:
#
# ## Examples
# +
x = [1,2,3]
y = [4,5,6]
# Zip the lists together
list(zip(x,y))
# -
# Note how tuples are returned. What if one iterable is longer than the other?
# +
x = [1,2,3]
y = [4,5,6,7,8]
# Zip the lists together
list(zip(x,y))
# -
# Note how the zip is defined by the shortest iterable length. Its generally advised not to zip unequal length iterables unless your very sure you only need partial tuple pairings.
#
# What happens if we try to zip together dictionaries?
# +
d1 = {'a':1,'b':2}
d2 = {'c':4,'d':5}
list(zip(d1,d2))
# -
# This makes sense because simply iterating through the dictionaries will result in just the keys. We would have to call methods to mix keys and values:
list(zip(d2,d1.values()))
# Great! Finally lets use zip() to switch the keys and values of the two dictionaries:
def switcharoo(d1,d2):
dout = {}
for d1key,d2val in zip(d1,d2.values()):
dout[d1key] = d2val
return dout
switcharoo(d1,d2)
|
1.Chapter-Python/2-Python_Basis/courses/45-Zip.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
from selenium import webdriver
import time
import csv
csvFile = "results.csv" #where to store results
## Ticker symbols to pull data for ##
tickers = [
"CAB",
"DKS"
]
## Statistics to pull from Yahoo Finance "Key Statistcs" Page
keyStatistics = [
"Market Cap (intraday)",
"Forward P/E",
"Revenue",
"EBITDA",
"Total Cash",
"Total Debt",
"Forward Annual Dividend Yield",
"Payout Ratio",
"52-Week Change",
"Short % of Float",
]
def findTDValue(tds,tdRelatedText):
# The pattern of the td we want
pattern = './/span[text()="' + tdRelatedText + '"]'
try:
want = filter(lambda x: len(x.find_elements_by_xpath(pattern)) > 0, tds)
# return the text of sibling td
return [str(want[0].find_element_by_xpath('.//following-sibling::td').text)]
except:
return ["N/A"]
# Because the data is read by javascript, so I used selenium
if __name__ == '__main__':
browser = webdriver.Chrome()
resultTable = [["Ticker"] + keyStatistics] #append ticker as first column of results
for ticker in tickers: #iterate through tickers
print "Scraping ticker " + ticker
print "=" * 50
page = 'http://finance.yahoo.com/q/ks?s='+ticker+'+Key+Statistics' #pull page data
browser.get(page)
# Sleep 2s to make sure the web browser render the whole page
time.sleep(2)
all_tds = browser.find_elements_by_xpath('//td')
resultRow = [ticker] #start new result row with first item as the ticker symbol
for keyStatistic in keyStatistics: #iterate through remaining statistic items, and append to row
print "Looking for keyStatistic " + keyStatistic
print "*" * 25
resultRow += findTDValue(all_tds, keyStatistic)
resultTable += [resultRow] #write entire row as new record in table
with open(csvFile, "w") as output:
writer = csv.writer(output, lineterminator='\n')
writer.writerows(resultTable)
# -
|
ScrapYahooKeyStat.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="bnzPmx8P52UF"
# # Amostragem
# + [markdown] id="DTxzWPl_Vel4"
# ## Carregamento da base de dados
# + id="rLSrGHxI52uB"
import pandas as pd
import random
import numpy as np
# + id="MQX_JYAH6T58"
dataset = pd.read_csv('census.csv')
# + id="GKW5CXUU6amv" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234690710, "user_tz": 180, "elapsed": 725, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="47a22ce6-8727-4101-c9fe-4d57cc7f5c8f"
dataset.shape
# + id="d9HaTD8Y6gGK" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599068580282, "user_tz": 180, "elapsed": 1041, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="4a069883-b8ac-4dd0-e93b-d61cd841a40f"
dataset.head()
# + id="3X7iatIf61Xf" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599068665062, "user_tz": 180, "elapsed": 1093, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="d06b50af-cea9-440d-c502-69b99451ca43"
dataset.tail()
# + [markdown] id="RrDiirdZ9_m5"
# ## Amostragem aleatória simples
# + id="30PSAsow6_HS"
df_amostra_aleatoria_simples = dataset.sample(n = 100, random_state = 1)
# + id="Ja1ErgYX7OaP" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234700034, "user_tz": 180, "elapsed": 694, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="e0a9af56-5703-46ef-852f-cabaa65e466e"
df_amostra_aleatoria_simples.shape
# + id="1ZJG2Qc87UJw" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599234702511, "user_tz": 180, "elapsed": 762, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="facf0870-2e74-4c95-b59c-669709875af3"
df_amostra_aleatoria_simples.head()
# + id="lk7eAB_R8IiT"
def amostragem_aleatoria_simples(dataset, amostras):
return dataset.sample(n = amostras, random_state=1)
# + id="08X9Bov_8TBP" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234706841, "user_tz": 180, "elapsed": 859, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="e8f50eb7-e13f-44c4-9a1d-a735b7ad1bb2"
df_amostra_aleatoria_simples = amostragem_aleatoria_simples(dataset, 100)
df_amostra_aleatoria_simples.shape
# + id="5L3-p9_q8bXS" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599234708275, "user_tz": 180, "elapsed": 814, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="d190700c-a14a-48ea-ca12-839440bbd674"
df_amostra_aleatoria_simples.head()
# + [markdown] id="LuNZ29C3A8nc"
# ## Amostragem sistemática
# + id="R1eCebNe-uBK" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234716051, "user_tz": 180, "elapsed": 813, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="52adb43b-d8b5-46e9-ef7d-99f5c074e637"
dataset.shape
# + id="FWPHL6nq-y69" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234718105, "user_tz": 180, "elapsed": 775, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="d309f06e-6a15-4f5e-e46e-44736dd0f9c9"
len(dataset) // 100
# + id="hX1U_jiW_MAY" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234719379, "user_tz": 180, "elapsed": 633, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="ee151249-57b1-4132-87a9-3d704e6f2fdb"
random.seed(1)
random.randint(0, 325)
# + id="n6orOz0N_l2J" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599069929408, "user_tz": 180, "elapsed": 888, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="af2d07c8-dba6-4926-aa58-ea3f7bfd4a56"
68 + 325
# + id="dtHieJi5_tiX" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599069944867, "user_tz": 180, "elapsed": 1064, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="db5f1504-e15e-4c6c-dc3d-732acc206c51"
393 + 325
# + id="1L5t6aCh_z9v" colab={"base_uri": "https://localhost:8080/", "height": 248} executionInfo={"status": "ok", "timestamp": 1599070017367, "user_tz": 180, "elapsed": 1318, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="103f6355-fe51-423e-b6f2-7fe51e73a909"
np.arange(68, len(dataset), step = 325)
# + id="pJe3yAXhAGti"
def amostragem_sistematica(dataset, amostras):
intervalo = len(dataset) // amostras
random.seed(1)
inicio = random.randint(0, intervalo)
indices = np.arange(inicio, len(dataset), step = intervalo)
amostra_sistematica = dataset.iloc[indices]
return amostra_sistematica
# + id="F4m8_IGIAtVu" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234726094, "user_tz": 180, "elapsed": 1034, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="6386931c-545d-4aaf-d1d8-75908030f1f1"
df_amostra_sistematica = amostragem_sistematica(dataset, 100)
df_amostra_sistematica.shape
# + id="JvVQYpU-A23b" colab={"base_uri": "https://localhost:8080/", "height": 368} executionInfo={"status": "ok", "timestamp": 1599234726958, "user_tz": 180, "elapsed": 419, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="51fa5d64-0df3-4dd9-c4a8-e60d345e7b09"
df_amostra_sistematica.head()
# + [markdown] id="gc3aea8QHqz9"
# ## Amostragem por grupos
# + id="h5gX9qckCfNM" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599070686656, "user_tz": 180, "elapsed": 1087, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="a90338fa-e794-465f-fe46-f4c32ec2a23a"
len(dataset) / 10
# + id="ChAf82zGCpuq"
grupos = []
id_grupo = 0
contagem = 0
for _ in dataset.iterrows():
grupos.append(id_grupo)
contagem += 1
if contagem > 3256:
contagem = 0
id_grupo += 1
# + id="3xdjYE8tDSaX" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599070889209, "user_tz": 180, "elapsed": 1474, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="009198cc-ec33-4e0e-82f5-61a88a0443c4"
print(grupos)
# + id="bj5vkGXaDYaO" colab={"base_uri": "https://localhost:8080/", "height": 72} executionInfo={"status": "ok", "timestamp": 1599070950240, "user_tz": 180, "elapsed": 1334, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="a625e9ff-fadc-48ae-fce9-f8a7939c8a40"
np.unique(grupos, return_counts=True)
# + id="SYduRE7ZD0Z3" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599071038715, "user_tz": 180, "elapsed": 1120, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="3734fe1f-896d-47da-8fb6-befe1e0f6ce2"
np.shape(grupos), dataset.shape
# + id="etnxze3hEEVr"
dataset['grupo'] = grupos
# + id="22_i_6S1D_bp" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599071118996, "user_tz": 180, "elapsed": 1075, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="98a591ec-86cd-48b9-ff22-37ff19672727"
dataset.head()
# + id="L5fwzhRMEQdJ" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599071133128, "user_tz": 180, "elapsed": 1148, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="5605cb11-3fe9-4427-dffa-a60d2d055df9"
dataset.tail()
# + id="Q5b-qPrHEVLC" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599071173268, "user_tz": 180, "elapsed": 1012, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="4c2c5816-7f7e-40ba-d4ed-c43fed2358f3"
random.randint(0, 9)
# + id="zGC9nZIaEdG5" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599071220946, "user_tz": 180, "elapsed": 942, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="5484cffc-5af8-4b95-8843-328f2e12f719"
df_agrupamento = dataset[dataset['grupo'] == 7]
df_agrupamento.shape
# + id="OnBJQcVdEpz1" colab={"base_uri": "https://localhost:8080/", "height": 72} executionInfo={"status": "ok", "timestamp": 1599071250528, "user_tz": 180, "elapsed": 1098, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="4f7b4d23-5845-4554-ef15-a0d4c3f667d8"
df_agrupamento['grupo'].value_counts()
# + id="d8PhN_47Eyp3"
def amostragem_agrupamento(dataset, numero_grupos):
intervalo = len(dataset) / numero_grupos
grupos = []
id_grupo = 0
contagem = 0
for _ in dataset.iterrows():
grupos.append(id_grupo)
contagem += 1
if contagem > intervalo:
contagem = 0
id_grupo += 1
dataset['grupo'] = grupos
random.seed(1)
grupo_selecionado = random.randint(0, numero_grupos)
return dataset[dataset['grupo'] == grupo_selecionado]
# + id="A2Qk3HP5F-W-" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599071594955, "user_tz": 180, "elapsed": 2079, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="368b02e1-6306-4ee4-e205-f9243eba31b7"
len(dataset) / 325
# + id="24TKEMjiGFFL" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599071612364, "user_tz": 180, "elapsed": 1125, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="90f2600e-71f2-43ba-b930-86f0dbfc7c50"
325 * 100
# + id="tELlhSEZFP9u" colab={"base_uri": "https://localhost:8080/", "height": 72} executionInfo={"status": "ok", "timestamp": 1599234751306, "user_tz": 180, "elapsed": 2955, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="89b75d85-7465-4d02-b92f-d15195981cda"
df_amostra_agrupamento = amostragem_agrupamento(dataset, 325)
df_amostra_agrupamento.shape, df_amostra_agrupamento['grupo'].value_counts()
# + id="24EIgr3cGVwe" colab={"base_uri": "https://localhost:8080/", "height": 386} executionInfo={"status": "ok", "timestamp": 1599234752520, "user_tz": 180, "elapsed": 606, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="a115cef4-ad01-4ce7-f28c-6d8a6f1003ac"
df_amostra_agrupamento.head()
# + [markdown] id="PNtASp3qI4mL"
# ## Amostra estratificada
# + id="FbVBHWkJIZqq"
from sklearn.model_selection import StratifiedShuffleSplit
# + id="SOTB_dzMIxFO" colab={"base_uri": "https://localhost:8080/", "height": 90} executionInfo={"status": "ok", "timestamp": 1599234767474, "user_tz": 180, "elapsed": 974, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="3a52159c-1cd7-4e74-b432-71d983acd710"
dataset['income'].value_counts()
# + id="831nuOvXI69-" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599072401052, "user_tz": 180, "elapsed": 1237, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="927f4473-a676-415b-abe1-c8a31511ed32"
7841 / len(dataset), 24720 / len(dataset)
# + id="D6IGsbaFJMTB" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599072429930, "user_tz": 180, "elapsed": 1250, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="f2e82f82-a4a9-4195-ca28-c2a399431627"
0.2408095574460244 + 0.7591904425539756
# + id="DVhs0ihfKirI" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599072794169, "user_tz": 180, "elapsed": 900, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="40229684-8be0-44eb-a677-c8cca73f3eea"
100 / len(dataset)
# + id="JXVu9lPWJdSI"
split = StratifiedShuffleSplit(test_size=0.0030711587481956942)
for x, y in split.split(dataset, dataset['income']):
df_x = dataset.iloc[x]
df_y = dataset.iloc[y]
# + id="0vWiOkaSKEDF" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599072813933, "user_tz": 180, "elapsed": 1066, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="4dbac9b6-2214-46bb-e80e-7867367c7114"
df_x.shape, df_y.shape
# + id="ycbOGCYcKOeN" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599072836261, "user_tz": 180, "elapsed": 965, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="0a0532ca-e241-4f9e-8128-2809b721768e"
df_y.head()
# + id="XMGjRyrEK1Dc" colab={"base_uri": "https://localhost:8080/", "height": 90} executionInfo={"status": "ok", "timestamp": 1599072864898, "user_tz": 180, "elapsed": 1110, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="1203b5e9-90ac-4583-97a9-630d321eb8b8"
df_y['income'].value_counts()
# + id="W5jDYrBt7itv"
def amostragem_estratificada(dataset, percentual):
split = StratifiedShuffleSplit(test_size=percentual, random_state=1)
for _, y in split.split(dataset, dataset['income']):
df_y = dataset.iloc[y]
return df_y
# + id="YrWqVax077Ca" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236782724, "user_tz": 180, "elapsed": 607, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="d504313f-1685-4cd5-b51f-b212482e46cb"
df_amostra_estratificada = amostragem_estratificada(dataset, 0.0030711587481956942)
df_amostra_estratificada.shape
# + [markdown] id="_b3662yh0h5M"
# ## Amostragem de reservatório
# + id="9TTcCTUZ0jty"
stream = []
for i in range(len(dataset)):
stream.append(i)
# + id="0ALiX_1B1Oe1" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599234964993, "user_tz": 180, "elapsed": 1003, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="37c82d79-0a39-4c22-aab3-cc00c28adf75"
print(stream)
# + id="0djdo1vP1b5x"
def amostragem_reservatorio(dataset, amostras):
stream = []
for i in range(len(dataset)):
stream.append(i)
i = 0
tamanho = len(dataset)
reservatorio = [0] * amostras
for i in range(amostras):
reservatorio[i] = stream[i]
while i < tamanho:
j = random.randrange(i + 1)
if j < amostras:
reservatorio[j] = stream[i]
i += 1
return dataset.iloc[reservatorio]
# + id="stjfeIID2ea7" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599235316333, "user_tz": 180, "elapsed": 821, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="ce92f70d-2698-45ba-aff4-0701c52477da"
df_amostragem_reservatorio = amostragem_reservatorio(dataset, 100)
df_amostragem_reservatorio.shape
# + id="Opskb8zu2n1p" colab={"base_uri": "https://localhost:8080/", "height": 351} executionInfo={"status": "ok", "timestamp": 1599235335174, "user_tz": 180, "elapsed": 704, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="dca741e7-ae2c-4db3-c2b6-3e2eee43f17f"
df_amostragem_reservatorio.head()
# + [markdown] id="5CKJPA5L7S9q"
# ## Comparativo dos resultados
# + id="NTIZlSOQ7Usc" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236811998, "user_tz": 180, "elapsed": 788, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="0e507b6c-c933-459f-987b-fcbbd15696b1"
dataset['age'].mean()
# + id="ygori0T_8VD1" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236842031, "user_tz": 180, "elapsed": 636, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="a7341788-44c3-451e-9272-437e4809fb2b"
df_amostra_aleatoria_simples['age'].mean()
# + id="3UF_48Rb8cRZ" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236862380, "user_tz": 180, "elapsed": 1392, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="e7fb23c3-419a-4837-b027-75a580b865dd"
df_amostra_sistematica['age'].mean()
# + id="qA6-4Ltt8i6G" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236919722, "user_tz": 180, "elapsed": 757, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="a847ef6d-2b92-429d-b289-c47e4af5e7da"
df_amostra_agrupamento['age'].mean()
# + id="-2p78djJ8vM6" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236943324, "user_tz": 180, "elapsed": 1297, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gj-HFBSchv13C5VeiDZcZd2tVCvD_pOSKexaPmQ=s64", "userId": "10042675233362078631"}} outputId="8041e35c-a299-4a11-8a3c-2951eb7fed43"
df_amostra_estratificada['age'].mean()
# + id="7i0sdi5W80xC" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1599236963549, "user_tz": 180, "elapsed": 652, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/<KEY>", "userId": "10042675233362078631"}} outputId="8dcc9b7c-24a1-48d1-8c20-97f8dde77a1f"
df_amostragem_reservatorio['age'].mean()
|
populacaoeamostra/probability_sampling/Tipos de Amostragens e Comparativo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: aiEnv
# language: python
# name: aienv
# ---
import os
import pandas as pd
from tqdm import tqdm
# !ls 'BanglaLekha-Isolated'
labels = os.listdir(os.path.abspath('BanglaLekha-Isolated/Images/'))
train = []
val = []
# +
for label in tqdm(labels):
images = [os.path.abspath(os.path.join(dirpath, f))
for dirpath, dirnames, filenames in os.walk('BanglaLekha-Isolated/Images/' + label)
for f in filenames]
for i, img in enumerate(images):
if i % 20 == 0:
val.append([os.path.abspath(img), int(label)-1])
else:
train.append([os.path.abspath(img), int(label)-1])
len(train), len(val)
# +
train_df = pd.DataFrame(train)
val_df = pd.DataFrame(val)
train_df.to_csv('train_manifest.csv', header=None, index=None)
val_df.to_csv('val_manifest.csv', header=None, index=None)
# -
len(labels)
train_df.groupby([1]).size()
os.path.basename(val_df[0][0])
|
manifest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Toy Examples of complex graph measures
# This script includes the creation of the following figures:
# * Node degree - toy example
# * Graph partitioning - toy example
# * Hierarchy index - toy example
# * Rich club coefficient - toy example
# +
# IMPORTS
import os
import cv2
import json
import numpy as np
import re
import matplotlib.pyplot as plt
import pandas as pd
import networkx as nx
import glob
import scipy.cluster.vq as clusters
import scipy.sparse as sparse
import warnings
import random_graph
warnings.simplefilter(action='ignore', category=FutureWarning)
from scipy.special import binom as nchoosek
from pandas.plotting import autocorrelation_plot as AC_plot
from statsmodels.graphics import tsaplots
from statsmodels.tsa.stattools import acf
from skimage.filters import gaussian
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import LinearSegmentedColormap
from mpl_toolkits.axes_grid1 import make_axes_locatable, axes_size
from skimage.transform.pyramids import pyramid_expand as expand
from skimage.transform.pyramids import pyramid_reduce as reduce
from matplotlib import gridspec
from matplotlib.colors import ListedColormap
from itertools import combinations
import pickle
from matplotlib.axes._axes import _log as matplotlib_axes_logger
matplotlib_axes_logger.setLevel('ERROR')
# Git Paths
DATA_PATH = '/Users/lessmann/Desktop/PaperFigures/'
# load the city map image
white_bg_img = cv2.imread("./ressources/map_white.png")
# Visuals - global variables
fontsize = 20
fontweight = 'bold'
labelfontsize = 30
figurelabels = ['A','B','C','D']
# COLOR
# color defs
green = [0.40,0.80,0.42]
blue = [0.27,0.38,0.99]
yellow = [0.96,0.73,0.23]
darkblue = [0.18, 0.19, 0.69]
lightyellow = [0.9763, 0.9831, 0.0538]
grey = [0.75,0.75,0.75]
white = [1,1,1]
black = [0,0,0]
# implement parula color map scheme from matlab
cm_data = [[0.2081, 0.1663, 0.5292], [0.2116238095, 0.1897809524, 0.5776761905],
[0.212252381, 0.2137714286, 0.6269714286], [0.2081, 0.2386, 0.6770857143],
[0.1959047619, 0.2644571429, 0.7279], [0.1707285714, 0.2919380952,
0.779247619], [0.1252714286, 0.3242428571, 0.8302714286],
[0.0591333333, 0.3598333333, 0.8683333333], [0.0116952381, 0.3875095238,
0.8819571429], [0.0059571429, 0.4086142857, 0.8828428571],
[0.0165142857, 0.4266, 0.8786333333], [0.032852381, 0.4430428571,
0.8719571429], [0.0498142857, 0.4585714286, 0.8640571429],
[0.0629333333, 0.4736904762, 0.8554380952], [0.0722666667, 0.4886666667,
0.8467], [0.0779428571, 0.5039857143, 0.8383714286],
[0.079347619, 0.5200238095, 0.8311809524], [0.0749428571, 0.5375428571,
0.8262714286], [0.0640571429, 0.5569857143, 0.8239571429],
[0.0487714286, 0.5772238095, 0.8228285714], [0.0343428571, 0.5965809524,
0.819852381], [0.0265, 0.6137, 0.8135], [0.0238904762, 0.6286619048,
0.8037619048], [0.0230904762, 0.6417857143, 0.7912666667],
[0.0227714286, 0.6534857143, 0.7767571429], [0.0266619048, 0.6641952381,
0.7607190476], [0.0383714286, 0.6742714286, 0.743552381],
[0.0589714286, 0.6837571429, 0.7253857143],
[0.0843, 0.6928333333, 0.7061666667], [0.1132952381, 0.7015, 0.6858571429],
[0.1452714286, 0.7097571429, 0.6646285714], [0.1801333333, 0.7176571429,
0.6424333333], [0.2178285714, 0.7250428571, 0.6192619048],
[0.2586428571, 0.7317142857, 0.5954285714], [0.3021714286, 0.7376047619,
0.5711857143], [0.3481666667, 0.7424333333, 0.5472666667],
[0.3952571429, 0.7459, 0.5244428571], [0.4420095238, 0.7480809524,
0.5033142857], [0.4871238095, 0.7490619048, 0.4839761905],
[0.5300285714, 0.7491142857, 0.4661142857], [0.5708571429, 0.7485190476,
0.4493904762], [0.609852381, 0.7473142857, 0.4336857143],
[0.6473, 0.7456, 0.4188], [0.6834190476, 0.7434761905, 0.4044333333],
[0.7184095238, 0.7411333333, 0.3904761905],
[0.7524857143, 0.7384, 0.3768142857], [0.7858428571, 0.7355666667,
0.3632714286], [0.8185047619, 0.7327333333, 0.3497904762],
[0.8506571429, 0.7299, 0.3360285714], [0.8824333333, 0.7274333333, 0.3217],
[0.9139333333, 0.7257857143, 0.3062761905], [0.9449571429, 0.7261142857,
0.2886428571], [0.9738952381, 0.7313952381, 0.266647619],
[0.9937714286, 0.7454571429, 0.240347619], [0.9990428571, 0.7653142857,
0.2164142857], [0.9955333333, 0.7860571429, 0.196652381],
[0.988, 0.8066, 0.1793666667], [0.9788571429, 0.8271428571, 0.1633142857],
[0.9697, 0.8481380952, 0.147452381], [0.9625857143, 0.8705142857, 0.1309],
[0.9588714286, 0.8949, 0.1132428571], [0.9598238095, 0.9218333333,
0.0948380952], [0.9661, 0.9514428571, 0.0755333333],
[0.9763, 0.9831, 0.0538]]
parula_map = LinearSegmentedColormap.from_list('parula', cm_data)
plt.rcParams.update({'font.family':'Arial'})
# -
# # Node Degree Toy
# +
# example degree list to create graph
degree_list = [1,1,2,2,2,3,3,3,3,3,3,4,4,4,4,5,5,5,6,6,7,8]
edges = random_graph.sample_simple_graph(degree_list)
# create graph
G_nd = nx.Graph()
G_nd = nx.from_edgelist(edges)
# get degree dictionary and degree list of the graph (degree list is obsolete, just for consistency)
degree_dict = dict(G_nd.degree)
degree_list = list(degree_dict.values())
# FIGURE
figgy = plt.figure(figsize=(18,8))
gs = gridspec.GridSpec(ncols=2, nrows=1,
width_ratios=[1, 1],
wspace=0.1)
# plot degree distribution on the left axis
ax1 = figgy.add_subplot(gs[0])
plt.hist(degree_list, len(np.unique(degree_list)), color=blue, ec='k')
plt.xlabel('Node Degree', fontsize=20, weight='bold')
plt.ylabel('Frequency', fontsize=20, weight='bold')
ax1.tick_params(axis = 'both', which = 'major', labelsize = fontsize)
ax1.tick_params(axis = 'both', which = 'minor', labelsize = fontsize)
# plot color-coded graph on the right axis
ax2 = figgy.add_subplot(gs[0:, -1])
nx.draw_networkx(G_nd, node_color=degree_list, node_size=500, font_size=15, with_labels=False)
vmin = np.min(degree_list)
vmax = np.max(degree_list)
sm = plt.cm.ScalarMappable(cmap=parula_map, norm=plt.Normalize(vmin=vmin, vmax=vmax))
sm.set_array([])
cbar = plt.colorbar(sm)
cbar.ax.tick_params(labelsize=20)
cbar.set_label('Node Degree', size=20, weight='bold')
# SAVING
plt.savefig(DATA_PATH + "Toy_NodeDegree.png",
dpi=200,
format="PNG",
facecolor='white',
transparent=False,
bbox_inches = "tight")
# -
# ## Basic statistics
# +
mean = np.mean(degree_list)
std = np.std(degree_list)
print('Mean Degree:'
+ str(round(mean,2))
+ ', STD: '
+ str(round(std,2))
+ ', one sigma at: ' + str(round(mean+std,2))
+ ', two sigma at: ' + str(round(mean+2*std,2))
)
# -
# # Partitioning Toy
# +
# Example adjacency matrix to create the graph
adj_matrix_cluster = np.array([[0, 1, 1, 1, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 1, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 1, 1, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0, 0, 0, 0, 0],
[0, 1, 1, 1, 0, 0, 1, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 1, 0, 0, 1, 1, 1],
[0, 0, 0, 0, 0, 1, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 1, 1, 1, 0, 1],
[0, 0, 0, 0, 0, 1, 1, 0, 1, 0]])
# create graph
G_cluster = nx.from_numpy_matrix(adj_matrix_cluster)
# get the laplacian matrix
laplacian_matrix = nx.laplacian_matrix(G_cluster)
laplacian_matrix = sparse.csr_matrix.toarray(laplacian_matrix)
# Get the eigenvalues and vectors
Eigenvalue, Eigenvector = np.linalg.eig(laplacian_matrix)
# sort Eigenvalues in ascending order and use index to sort eigenvectors
index_array = np.argsort(Eigenvalue)
# get second smallest Eigenvalue and corresponding eigenvector
Eigenvalue_2 = Eigenvalue[index_array[1]]
Eigenvector_2 = Eigenvector[:,index_array[1]]
# sort the eigenvector and sorting index
vec_arg = np.argsort(Eigenvector_2)
vec_sort = np.sort(Eigenvector_2)
# split the eigenvector into positive and negative component (based on its entries)
eig_pos = vec_sort[vec_sort>=0]
eig_neg = vec_sort[vec_sort<0]
# for the correct colored plotting of the sparsity pattern matrix
colors = []
for i in Eigenvector_2:
if i >= 0:
colors.append(blue)
else:
colors.append(green)
# get a sorted adjacency matrix according to the sorting index of the 2nd smallest eigenvector
adj = sparse.csr_matrix.toarray(nx.adjacency_matrix(G_cluster, nodelist=vec_arg))
# create a copy of the adjacency matrix for color-coded plotting
adj_colors = np.empty((adj.shape[0], adj.shape[1], 3))
# iterate through the matrix
for row in range(adj.shape[0]):
for col in range(adj.shape[1]):
# if the entry is 0, assign white to the entry
if adj[row,col] == 0:
adj_colors[row,col,:] = white
# if the entry is 1 assign blue, green, or black according to the cluster
# Since this is a constructed example, the cluster size of 5 nodes each is known and used here
elif adj[row,col] == 1:
# if the edge connects nodes from the first cluster (known), assign blue
if row <= 4 and col <=4:
adj_colors[row,col,:] = blue
# if the edge connects nodes from the second cluster (known), assign green
elif row > 4 and col > 4:
adj_colors[row,col,:] = green
# if the edge connects nodes from the two clusters (known), assign black
elif ((row > 4) and not (col > 4)) or (not (row > 4) and (col > 4)):
adj_colors[row,col,:] = black
# PLOTTING
figgy = plt.figure(figsize=(15,10))
# create grid for different subplots
gs = gridspec.GridSpec(ncols=2, nrows=2,
width_ratios=[1, 2.5],
height_ratios=[1, 1],
wspace=0.2,
hspace=0.5)
# plot the color-coded sparsity pattern matrix on the top left axis
ax1 = figgy.add_subplot(gs[0])
node_colors = ListedColormap([white, grey])
plt.imshow(adj_colors)
plt.plot([9.5,-0.5],[4.5,4.5], color=yellow, linewidth=5)
plt.plot([4.5,4.5],[-0.5,9.5], color=yellow, linewidth=5)
# settings
plt.xlabel('Matrix Entry', fontsize=fontsize, weight='bold')
plt.ylabel('Matrix Entry', fontsize=fontsize, weight='bold')
plt.xticks([0,2,4,6,8])
plt.yticks([0,2,4,6,8])
ax1.tick_params(axis = 'both', which = 'major', labelsize = fontsize)
ax1.tick_params(axis = 'both', which = 'minor', labelsize = fontsize)
# plot the color-coded second smallest eigenvector on the bottom left axis
ax2 = figgy.add_subplot(gs[0:, -1])
nx.draw_networkx(G_cluster, node_color=colors, node_size=1000, font_size=20, with_labels = False)
# plot the color-coded graph on the right axis
ax3 = figgy.add_subplot(gs[2])
plt.plot(range(len(eig_neg)), eig_neg, linewidth=6, color=blue)
plt.plot(range(len(eig_pos),len(vec_sort)), eig_pos, linewidth=6, color=green)
neg_max = max(eig_neg)
pos_min = min(eig_pos)
# plot a line between them
plt.plot([4,4.5],[neg_max,0], color=blue, linewidth=6)
plt.plot([4.5,5],[0,pos_min], color=green, linewidth=6)
# settings
plt.xlabel('Eigenvector Entries', fontsize=fontsize, weight='bold')
plt.ylabel('Eigenvector Value', fontsize=fontsize, weight='bold')
ax3.tick_params(axis = 'both', which = 'major', labelsize = fontsize)
ax3.tick_params(axis = 'both', which = 'minor', labelsize = fontsize)
# SAVING
plt.savefig(DATA_PATH + "Toy_Partitioning.png",
dpi=200,
format="PNG",
facecolor='white',
transparent=False,
bbox_inches = "tight")
# -
# # Hierarchy Toy
# +
# Example adjacency matrix to create the graph
adj_matrix_hier = np.array([[0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0],
[1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0 ,1 ,1 ,1, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0 ,1 ,1 ,1, 0, 1, 0, 0, 0]])
# create the graph
G_hier = nx.from_numpy_matrix(adj_matrix_hier)
# get the degree dictionary, list and median degree (as a later threshold)
degree_dict = dict(G_hier.degree)
degree_list = list(degree_dict.values())
median_degree = np.median(degree_list)
# get a list of unique degree values
UniqueDegree = np.unique(degree_list)
UniqueDegreeMed = UniqueDegree[UniqueDegree >= median_degree]
# get the frequency of each degree value (also for the data above the median)
DegreeFrequency = dict()
for degree in UniqueDegree:
DegreeFrequency[degree] = np.sum(degree_list==degree)
# above the median
DegreeFrequencyMed = np.array(list(DegreeFrequency.values()))[UniqueDegree >= median_degree]
# do a linear fit of the log data of Unique Degree over Frequency
linear_model=np.polyfit(np.log(UniqueDegreeMed),np.log(DegreeFrequencyMed),1)
linear_model_fn=np.poly1d(linear_model)
# get the hierarchy index (the negative slope of the linear fit)
hierarchy_index = -linear_model[0]
# print the value
print('Hierarchy Index:' + str(hierarchy_index))
# PLOTTING
figgy = plt.figure(figsize=(15,15))
gs = gridspec.GridSpec(ncols=2, nrows=2,
width_ratios=[1, 1],
height_ratios=[1, 1.3],
wspace=0.3)
# plot the node degree distribution the top left axis
figgy.add_subplot(gs[0])
plt.hist(degree_list, bins=9, color=blue, ec='k')
plt.xlabel('Node Degree', fontsize=20, weight='bold')
plt.ylabel('Frequency', fontsize=20, weight='bold')
plt.rc('xtick', labelsize = fontsize)
plt.rc('ytick', labelsize = fontsize)
# plot the example graph on the top right axis
figgy.add_subplot(gs[1])
nx.draw_networkx(G_hier, node_color=blue, node_size=800, font_size=15, with_labels=False)
# plot the scatter plot of Degree value against frequency with the linear fit on the bottom axis
figgy.add_subplot(gs[1, 0:2])
plt.scatter(np.log(UniqueDegree),np.log(list(DegreeFrequency.values())), 200, color=blue)
x_s=np.arange(np.log(median_degree) ,max(np.log(UniqueDegree)+0.5))
plt.plot(x_s, linear_model_fn(x_s),color=green, linewidth=8)
# settings
plt.xlabel('Degree (log)', fontsize=fontsize, weight='bold')
plt.ylabel('Frequency (log)', fontsize=fontsize, weight='bold')
plt.rc('xtick', labelsize=fontsize)
plt.rc('ytick', labelsize=fontsize)
plt.yticks([0,0.5,1,1.5])
# SAVING
plt.savefig(DATA_PATH + "Toy_Hierarchy.png",
dpi=200,
format="PNG",
facecolor='white',
transparent=False,
bbox_inches = "tight")
# -
# ## Basic statistics
# +
mean = np.mean(degree_list)
std = np.std(degree_list)
print('Mean Degree:'
+ str(round(mean,2))
+ ', STD: '
+ str(round(std,2))
+ ', one sigma at: ' + str(round(mean+std,2))
+ ', two sigma at: ' + str(round(mean+2*std,2))
)
# -
# # <NAME>
# +
# Example adjacency matrix to create the graph
adj_matrix_rich = np.array([[0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1],
[1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]])
# create the graph
G_rich = nx.from_numpy_matrix(adj_matrix_rich)
# get the degree dictionary and list
degree_dict = dict(G_rich.degree)
degree_list = list(degree_dict.values())
# calculate the rich club coefficient
RC = nx.rich_club_coefficient(G_rich, normalized=False, seed=1)
# create a random graph for the rich club weighting with the same degree distribution
edges = random_graph.sample_simple_graph(degree_list)
randomG = nx.Graph()
randomG = nx.from_edgelist(edges)
# calculate the ric club for the random graph
RC_random = nx.rich_club_coefficient(randomG, normalized=False, seed=2)
RichClub = np.array(list(RC.values()))/np.array(list(RC_random.values()))
# Save the rich club array
np.savetxt(DATA_PATH+"RichClub.csv",
RichClub,
delimiter =", ",
fmt ='% s')
# +
# PLOTTING
# node sizes for plotting
node_size = [1000, 1000,1000,1000,1000,500,500,500,500,500,500,500,500,500,500]
figgy = plt.figure(figsize=(20,12))
gs = gridspec.GridSpec(ncols=2, nrows=2,
width_ratios=[1, 2],
height_ratios=[1, 1],
wspace=0.1,
hspace=0.3)
# plot the node degree distribution the top left axis
ax1 = figgy.add_subplot(gs[0])
plt.hist(degree_list, color=blue, ec='k', bins=9)
plt.xlabel('Node Degree', fontsize=20, weight='bold')
plt.ylabel('Frequency', fontsize=20, weight='bold')
ax1.tick_params(axis = 'both', which = 'major', labelsize = fontsize)
ax1.tick_params(axis = 'both', which = 'minor', labelsize = fontsize)
# plot the color- and size-coded graph on the right axis
ax2 = figgy.add_subplot(gs[0:, -1])
nx.draw_networkx(G_rich, node_color=degree_list, node_size=node_size, font_size=15, with_labels=False)
vmin = np.min(degree_list)
vmax = np.max(degree_list)
sm = plt.cm.ScalarMappable(cmap=parula_map, norm=plt.Normalize(vmin=vmin, vmax=vmax))
sm.set_array([])
cbar = plt.colorbar(sm)
cbar.ax.tick_params(labelsize=20)
cbar.set_label('Node Degree', size=20, weight='bold')
# plot the rich club array on the bottom left axis
ax3 = figgy.add_subplot(gs[2])
plt.plot(RichClub, color=green, linewidth=5)
plt.xlabel('Node Degree', fontsize=20, weight='bold')
plt.ylabel('Rich Club (Real/Random)', fontsize=20, weight='bold')
ax3.tick_params(axis = 'both', which = 'major', labelsize = fontsize)
ax3.tick_params(axis = 'both', which = 'minor', labelsize = fontsize)
# SAVING
plt.savefig(DATA_PATH + "Toy_RichClub.png",
dpi=200,
format="PNG",
facecolor='white',
transparent=False,
bbox_inches = "tight")
|
analysis/ToyExamplesGraphMeasures.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.2 64-bit (''dev'': conda)'
# language: python
# name: python38264bitdevconda06c7c692422b4cb59f191a8cff7c413e
# ---
# # Automating DFT Exercises
#
# ## Exercise 01: QChem Input/Outputs
#
#
# Another important DFT code for MP is QChem. VASP uses a plane-wave basis, which makes it very efficient for periodic crystalline systems, but not very efficient for molecules. There are a number of DFT codes that use Gaussian functions to build the basis, such as Gaussian and QChem. Let's begin this example by loading the molecular structure of Ethylene Carbonate
#
# Let's start by loading a `Molecule` object from pymatgen and importing the `ethylene_carbonate.xyz` as a `Molecule` object
# +
from pymatgen import Molecule
mol = Molecule.from_file("ethylene_carbonate.xyz")
print(mol)
# -
# This is an XYZ file, which is a standard format for molecular structures. Several other formats are supported using the openbabel package that can be optionally installed.
#
#
# For the purpose of this example, we've provided a completed QChem calculation under `QChem_ethylene_carboante`. Let's use pymatgen to read the inputs in this directory.
#
# Use `tab` and `shift`+`tab` to explore the `pymatgen.io.qchem.inputs` module and find something that well let you read a QChem Input.
# +
from pymatgen.io.qchem.inputs import ____
qcinp = ____.from_file("./QChem_etlyene_carbonate/mol.qin.gz")
print(qcinp.molecule)
# -
# For QChem, the input structure is much simpler as it is all contained in one file, this mol.qin file. The output comes directly from QChem as mostly a single file caled the QCOutput file. We have a corresponding object in pymatgen to read this file.
#
# Let's do the same as above for outputs. Explore the `pymatgen.io.qchem.outputs` module and find something to read a QChem Output
# +
from pymatgen.io.qchem.outputs import ____
qcoutput = ____(filename="./QChem_etlyene_carbonate/mol.qout.gz")
# -
# The data for this is all contained a single `data` attribute which is a dictionary with parsed information. Find the key that will get you the optimized output molecule geometry from the calculation.
qcoutput.data.keys()
qcoutput.data[____]
# Note that the optimized geoemtry has new coordinates that should be the minimum energy configuration for ethylene carbonate.
# ## Exercise 2: QChem Input Sets
#
# We also have InputSets for QChem, which act very similarly to VASP. Because the input for QChem is much simpler, these sets just represent a single input file. Let's load the molecule again just incase.
# +
from pymatgen import Molecule
mol = Molecule.from_file("ethylene_carbonate.xyz")
print(mol)
# -
# Explore the `pymatgen.io.qchem.sets` module and find an Input set to "Opt" or optimize the given molecule
from pymatgen.io.qchem.sets import ____
# Now load up an input set and print what the QChem Input should look like
opt_set = ____(molecule=mol)
print(opt_set)
# Now let's do the same to calculate the frequencies of a given Molecule
from pymatgen.io.qchem.sets import ____
freq_set = ____(mol)
print(freq_set)
# Now inspect the parameters of the frequency calculation input set using either `help` or `shift`+2x`tab`
help(freq_set.__init__)
# The QChem InputSets just like the VASP InputSets are designed to be flexible for various DFT parameters such as the level of theory and the solvation environment.
#
# Now try changing the DFT Rung
freq_set = ____(mol,dft_rung=1)
print(freq_set)
|
workshop/lessons/05_automated_dft/Exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Evaluating surface wave breaking parameterizations in WaveWatchIII
#
# This notebook compares several well-known surface wave breaking parameterizations used in the NEMO model to the Salish Sea configuration of the WaveWatchIII model.
#
# ***
# +
import numpy as np
import xarray as xr
from matplotlib import pyplot as plt, colors
from scipy.optimize import curve_fit
from datetime import datetime, timedelta
from salishsea_tools import nc_tools
from tqdm.notebook import tqdm
# %matplotlib inline
# -
plt.rcParams['font.size'] = 12
# ***
#
# ### Theory
#
# The effect of surface wave breaking on TKE ($\overline{e}$) is parameterized in terms of the surface wind forcing in NEMO in the following two ways:
#
# 1. The surface TKE boundary condition $\overline{e}_0$ ([Madec et al. 2017](https://zenodo.org/record/3248739), Eq. 10.10)
#
# $$\overline{e}_0 = \frac{1}{2}\left(15.8\alpha_{CB}\right)^{2/3}\frac{\tau}{\rho_0}$$
#
# 2. The surface dissipation length scale boundary condition $l_0$ (Charnock's relation, [Madec et al. 2017](https://zenodo.org/record/3248739), Eq. 10.11)
#
# $$l_0 = \kappa z_0 = \kappa\beta\frac{\tau}{g\rho_0}$$
#
# where $z_0$ is the surface roughness length, $\kappa$ is the von Kármán constant, $\tau$ is the surface wind stress, $\rho_0$ is the background seawater density, $g$ is the gravitational acceleration, and $\alpha_{CB}$ and $\beta$ are tuneable parameters. Literature values for $\alpha_{CB}$ and $\beta$ have been reported in a handful of studies (e.g., $\alpha_{CB} = 100$ [Craig and Banner 1994](https://journals.ametsoc.org/view/journals/phoc/24/12/1520-0485_1994_024_2546_mwetit_2_0_co_2.xml), $\beta = 2\times10^5$ [Stacey 1999](https://journals.ametsoc.org/view/journals/phoc/29/6/1520-0485_1999_029_1363_sotwfn_2.0.co_2.xml)).
#
# In practice, these parameters vary widely according to sea state and fetch, and thus need to be determined specifically for the Salish Sea. One approach is to link these parameters to wind forcing using the concept of "wave age" $c_p/u_*$ ([Mellor and Blumberg 2004](https://journals.ametsoc.org/view/journals/phoc/34/3/2517.1.xml)), where $c_p$ is the surface wave phase speed and $u_*=\sqrt{\tau/\rho_{air}}$ is the air side friction velocity. The reasoning behind this concept is that $c_p$ increases relative to $u_*$ as waves develop over time. Mellor and Blumberg (2004) summarize the proposed parameter definitions across several studies as the following:
#
# $$\alpha_{CB} = 15\frac{c_p}{u_*}\exp\left\{-\left(0.04\frac{c_p}{u_*}\right)^4\right\} \hspace{0.5cm} \text{(cited from Terray et al. 1996, 1997 JPO)}$$
#
# $$\beta \approx 665\left(\frac{c_p}{u_*}\right)^{1.5} \hspace{0.5cm} \text{(cited from Donelan 1990, Smith et al. 1992, Janssen 2001)}$$
#
# Craig and Banner (1994) have suggested that $l_0$ is more important in determining surface mixing than $\overline{e}_0$, and the NEMO authors agree (Madec et al. 2017). We therefore focus our initial tuning efforts on constraining the Charnock parameter $\beta$. [Rascle et al. (2008)](https://www.sciencedirect.com/science/article/abs/pii/S1463500308001017) propose an empirical fit for wave age in terms of $u_*$
#
# $$\frac{c_p}{u_*} = A_{max}\tanh \frac{2u_{*ref}}{u_*}$$
#
# where $A_{max}$ and $u_{*ref}$ are tuneable fit parameters. The Charnock relation is then modified in terms of the significant wave height $H_s$
#
# $$z_0 = r_HH_s = \frac{\beta}{1}\frac{\tau}{g\rho_0}$$
#
# where $r_{H}$ is the ratio of significant wave height $H_s$ to surface roughness length $z_0$ and can vary between approximately 0.5 and 2 as summarized by Rascle et al. (2008).
#
# ***
#
# ### Analysis
#
# The modified Charnock relation in terms of $H_s$ given by Rascle et al. (2008) provides a framework for tuning the surface dissipation length scale parameterization for SalishSeaCast using the WaveWatch3 hindcast. Specifically, we seek to optimize the values of $A_{max}$, $u_{*ref}$ and $r_{H}$.
def calc_Cd(u2):
"""Calculate the surface drag coefficient according to
Hellerman and Rosenstein (1983) JPO, neglecting T effects
"""
return 0.934e-3 + 0.788e-4 * np.sqrt(u2) - 0.616e-6 * u2
# Load hourly WW3 results for 2020 and spatial average over SoG water points
# +
# Specify start date and SoG water points
startdate = datetime(2020, 1, 1)
slc = {'latitude': slice(160, 450), 'longitude': slice(120, 470)}
with xr.open_dataset(nc_tools.get_WW3_path(startdate)) as ds:
mask = ds.MAPSTA.isel(slc).values.ravel().astype(bool)
# Loop through each day of hourly results files and extract variables
Hs, cp, u2 = [], [], []
for day in tqdm(range(360)):
fn = nc_tools.get_WW3_path(startdate + timedelta(days=day))
with xr.open_dataset(fn).isel(slc) as ds:
hs, lm, t02, u, v = [ds[var].values.reshape(48, -1)[:, mask].mean(axis=1) for var in ('hs', 'lm', 't02', 'uwnd', 'vwnd')]
Hs.append(hs)
cp.append(lm/t02)
u2.append(u**2 + v**2)
# Concatenate arrays
Hs = np.hstack(Hs)
cp = np.hstack(cp)
u2 = np.hstack(u2)
# -
# Calculate diagnostics
rho_ratio, g = 28, 9.81
ustar = np.sqrt(calc_Cd(u2) * u2)
ustar_plot = np.linspace(0.001, 1, 100)
index = ustar > 0
Hs, cp, ustar = Hs[index], cp[index], ustar[index]
# +
def calc_waveage(ustar, A_max, ustar_ref):
return A_max * np.tanh(2 * ustar_ref / ustar)
def calc_Hs(ustar, A_max, ustar_ref):
return 665 * calc_waveage(ustar, A_max, ustar_ref)**(1.5) * (ustar / rho_ratio)**2 / g
p0 = [30, 0.3]
functions = {'waveage': calc_waveage, 'Hs': calc_Hs}
# -
fig, axs = plt.subplots(2, 1, figsize=(10, 15))
xlim, xlabel = [0, 0.8], 'Airside friction velocity $u_*$ [m/s]'
for ax, func, yplot, ymax, ylabel in zip(axs, ['waveage', 'Hs'], [cp/ustar, Hs], [100, 2], ['Wave age $c_p/u_*$', 'Significant wave height $H_s$ [m]']):
ylim = [0, ymax]
_, _, _, c = ax.hist2d(ustar, yplot, bins=100, range=[xlim, ylim], norm=colors.LogNorm(vmin=1, vmax=100))
yfit = functions[func](ustar_plot, *p0)
label = f'$A_{{max}}=${p0[0]:.1f}, $u*_{{ref}}=${p0[1]:.3f} (default)'
ax.plot(ustar_plot, yfit, 'r-', lw=3, label=label)
popt, pcov = curve_fit(calc_Hs, ustar, Hs, p0=p0)
yfit = functions[func](ustar_plot, *popt)
label = f'$A_{{max}}=${popt[0]:.1f}, $u*_{{ref}}=${popt[1]:.3f}'
ax.plot(ustar_plot, yfit, 'r--', lw=3, label=label)
ax.set_xlim(xlim)
ax.set_ylim(ylim)
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
axs[0].legend()
|
notebooks/wavemixing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="lJz6FDU1lRzc"
"""
You can run either this notebook locally (if you have all the dependencies and a GPU) or on Google Colab.
Instructions for setting up Colab are as follows:
1. Open a new Python 3 notebook.
2. Import this notebook from GitHub (File -> Upload Notebook -> "GITHUB" tab -> copy/paste GitHub URL)
3. Connect to an instance with a GPU (Runtime -> Change runtime type -> select "GPU" for hardware accelerator)
4. Run this cell to set up dependencies.
5. Restart the runtime (Runtime -> Restart Runtime) for any upgraded packages to take effect
"""
# If you're using Google Colab and not running locally, run this cell.
## Install dependencies
# !pip install wget
# !apt-get install sox libsndfile1 ffmpeg
# !pip install unidecode
# !pip install matplotlib>=3.3.2
## Install NeMo
BRANCH = 'main'
# !python -m pip install git+https://github.com/NVIDIA/NeMo.git@$BRANCH#egg=nemo_toolkit[all]
## Grab the config we'll use in this example
# !mkdir configs
# !wget -P configs/ https://raw.githubusercontent.com/NVIDIA/NeMo/$BRANCH/examples/asr/conf/config.yaml
"""
Remember to restart the runtime for the kernel to pick up any upgraded packages (e.g. matplotlib)!
Alternatively, you can uncomment the exit() below to crash and restart the kernel, in the case
that you want to use the "Run All Cells" (or similar) option.
"""
# exit()
# -
# # Streaming ASR
# In this tutorial, we will look at one way to use one of NeMo's pretrained Conformer-CTC models for streaming inference. We will first look at some use cases where we may need streaming inference and then we will work towards developing a method for transcribing a long audio file using streaming.
# + [markdown] id="v1Jk9etFlRzf"
# # Why Stream?
# Streaming inference may be needed in one of the following scenarios:
# * Real-time or close to real-time inference for live transcriptions
# * Offline transcriptions of very long audio
#
# In this tutorial, we will mainly focus on streaming for handling long form audio and close to real-time inference with CTC based models. For training ASR models we usually use short segments of audio (<20s) that may be smaller chunks of a long audio that is aligned with the transcriptions and segmented into smaller chunks (see [tools/](https://github.com/NVIDIA/NeMo/tree/main/tools) for some great tools to do this). For running inference on long audio files we are restricted by the available GPU memory that dictates the maximum length of audio that can be transcribed in one inference call. We will take a look at one of the ways to overcome this restriction using NeMo's Conformer-CTC ASR model.
# -
# # Conformer-CTC
# Conformer-CTC models distributed with NeMo use a combination of self-attention and convolution modules to achieve the best of the two approaches, the self-attention layers can learn the global interaction while the convolutions efficiently capture the local correlations. Use of self-attention layers comes with a cost of increased memory usage at a quadratic rate with the sequence length. That means that transcribing long audio files with Conformer-CTC models needs streaming inference to break up the audio into smaller chunks. We will develop one method to do such inference through the course of this tutorial.
# # Data
# To demonstrate transcribing a long audio file we will use utterances from the dev-clean set of the [mini Librispeech corpus](https://www.openslr.org/31/).
# If something goes wrong during data processing, un-comment the following line to delete the cached dataset
# # !rm -rf datasets/mini-dev-clean
# !mkdir -p datasets/mini-dev-clean
# !python ../../scripts/dataset_processing/get_librispeech_data.py \
# --data_root "datasets/mini-dev-clean/" \
# --data_sets dev_clean_2
manifest = "datasets/mini-dev-clean/dev_clean_2.json"
# Let's create a long audio that is about 15 minutes long by concatenating audio from dev-clean and also create the corresponding concatenated transcript.
import json
def concat_audio(manifest_file, final_len=3600):
concat_len = 0
final_transcript = ""
with open("concat_file.txt", "w") as cat_f:
while concat_len < final_len:
with open(manifest_file, "r") as mfst_f:
for l in mfst_f:
row = json.loads(l.strip())
if concat_len >= final_len:
break
cat_f.write(f"file {row['audio_filepath']}\n")
final_transcript += (" " + row['text'])
concat_len += float(row['duration'])
return concat_len, final_transcript
# +
new_duration, ref_transcript = concat_audio(manifest, 15*60)
concat_audio_path = "datasets/mini-dev-clean/concatenated_audio.wav"
# !ffmpeg -t {new_duration} -safe 0 -f concat -i concat_file.txt -c copy -t {new_duration} {concat_audio_path} -y
print("Finished concatenating audio file!")
# -
# # Streaming with CTC based models
# Now let's try to transcribe the long audio file created above using a conformer-large model.
import torch
import nemo.collections.asr as nemo_asr
import contextlib
import gc
device = 'cuda' if torch.cuda.is_available() else 'cpu'
device
# We are mainly concerned about decoding on the GPU in this tutorial. CPU decoding may be able to handle longer files but would also not be as fast as GPU decoding. Let's check if we can run transcribe() on the long audio file that we created above.
# Clear up memory
torch.cuda.empty_cache()
gc.collect()
model = nemo_asr.models.EncDecCTCModelBPE.from_pretrained("stt_en_conformer_ctc_large", map_location=device)
device = 'cuda' if torch.cuda.is_available() else 'cpu'
# device = 'cpu' # You can transcribe even longer samples on the CPU, though it will take much longer !
model = model.to(device)
# Helper for torch amp autocast
if torch.cuda.is_available():
autocast = torch.cuda.amp.autocast
else:
@contextlib.contextmanager
def autocast():
print("AMP was not available, using FP32!")
yield
# The call to transcribe() below should fail with a "CUDA out of memory" error when run on a GPU with 32 GB memory.
with autocast():
transcript = model.transcribe([concat_audio_path], batch_size=1)[0]
# Clear up memory
torch.cuda.empty_cache()
gc.collect()
# # Buffer mechanism for streaming long audio files
# One way to transcribe long audio with a Conformer-CTC model would be to split the audio into consecutive smaller chunks and running inference on each chunk. Care should be taken to have enough context for audio at either edges for accurate transcription. Let's introduce some terminology here to help us navigate the rest of this tutorial.
#
# * Buffer size is the length of audio on which inference is run
# * Chunk size is the length of new audio that is added to the buffer.
#
# An audio buffer is made up of a chunk of audio with some padded audio from previous chunk. In order to make the best predictions with enough context for the beginning and end portions of the buffer, we only collect tokens for the middle portion of the buffer of length equal to the size of each chunk.
#
# Let's suppose tha the maximum length of audio that can be transcribed with conformer-large model is 20s, then we can use 20s as the buffer size and use 15s (for example) as the chunk size, so one hour of audio is broken into 240 chunks of 15s each. Let's take a look at a few audio buffers that may be created for this audio.
# A simple iterator class to return successive chunks of samples
class AudioChunkIterator():
def __init__(self, samples, frame_len, sample_rate):
self._samples = samples
self._chunk_len = chunk_len_in_secs*sample_rate
self._start = 0
self.output=True
def __iter__(self):
return self
def __next__(self):
if not self.output:
raise StopIteration
last = int(self._start + self._chunk_len)
if last <= len(self._samples):
chunk = self._samples[self._start: last]
self._start = last
else:
chunk = np.zeros([int(self._chunk_len)], dtype='float32')
samp_len = len(self._samples) - self._start
chunk[0:samp_len] = self._samples[self._start:len(self._samples)]
self.output = False
return chunk
# a helper function for extracting samples as a numpy array from the audio file
import soundfile as sf
def get_samples(audio_file, target_sr=16000):
with sf.SoundFile(audio_file, 'r') as f:
dtype = 'int16'
sample_rate = f.samplerate
samples = f.read(dtype=dtype)
if sample_rate != target_sr:
samples = librosa.core.resample(samples, sample_rate, target_sr)
samples=samples.astype('float32')/32768
samples = samples.transpose()
return samples
# Let's take a look at each chunk of speech that is used for decoding.
import matplotlib.pyplot as plt
samples = get_samples(concat_audio_path)
sample_rate = model.preprocessor._cfg['sample_rate']
chunk_len_in_secs = 1
chunk_reader = AudioChunkIterator(samples, chunk_len_in_secs, sample_rate)
count = 0
for chunk in chunk_reader:
count +=1
plt.plot(chunk)
plt.show()
if count >= 5:
break
# Now, let's plot the actual buffers at each stage after a new chunk is added to the buffer. Audio buffer can be thought of as a fixed size queue with each incoming chunk added at the end of the buffer and the oldest samples removed from the beginning.
# +
import numpy as np
context_len_in_secs = 1
buffer_len_in_secs = chunk_len_in_secs + 2* context_len_in_secs
buffer_len = sample_rate*buffer_len_in_secs
sampbuffer = np.zeros([buffer_len], dtype=np.float32)
chunk_reader = AudioChunkIterator(samples, chunk_len_in_secs, sample_rate)
chunk_len = sample_rate*chunk_len_in_secs
count = 0
for chunk in chunk_reader:
count +=1
sampbuffer[:-chunk_len] = sampbuffer[chunk_len:]
sampbuffer[-chunk_len:] = chunk
plt.plot(sampbuffer)
plt.show()
if count >= 5:
break
# -
# Now that we have a method to split the long audio into smaller chunks, we can now work on transcribing the individual buffers and merging the outputs to get the trancription of the whole audio.
# First, we implement some helper functions to help load the buffers into the datalayer.
# +
from nemo.core.classes import IterableDataset
def speech_collate_fn(batch):
"""collate batch of audio sig, audio len
Args:
batch (FloatTensor, LongTensor): A tuple of tuples of signal, signal lengths.
This collate func assumes the signals are 1d torch tensors (i.e. mono audio).
"""
_, audio_lengths = zip(*batch)
max_audio_len = 0
has_audio = audio_lengths[0] is not None
if has_audio:
max_audio_len = max(audio_lengths).item()
audio_signal= []
for sig, sig_len in batch:
if has_audio:
sig_len = sig_len.item()
if sig_len < max_audio_len:
pad = (0, max_audio_len - sig_len)
sig = torch.nn.functional.pad(sig, pad)
audio_signal.append(sig)
if has_audio:
audio_signal = torch.stack(audio_signal)
audio_lengths = torch.stack(audio_lengths)
else:
audio_signal, audio_lengths = None, None
return audio_signal, audio_lengths
# simple data layer to pass audio signal
class AudioBuffersDataLayer(IterableDataset):
def __init__(self):
super().__init__()
def __iter__(self):
return self
def __next__(self):
if self._buf_count == len(self.signal) :
raise StopIteration
self._buf_count +=1
return torch.as_tensor(self.signal[self._buf_count-1], dtype=torch.float32), \
torch.as_tensor(self.signal_shape[0], dtype=torch.int64)
def set_signal(self, signals):
self.signal = signals
self.signal_shape = self.signal[0].shape
self._buf_count = 0
def __len__(self):
return 1
# -
# Next we implement a class that implements transcribing audio buffers and merging the tokens corresponding to a chunk of audio within each buffer.
#
# For each buffer, we pick tokens corresponding to one chunk length of audio. The chunk within each buffer is chosen such that there is equal left and right context available to the audio within the chunk.
#
# For example, if the chunk size is 1s and buffer size is 3s, we collect tokents corresponding to audio starting from 1s to 2s within each buffer. Conformer-CTC models have a model stride of 4, i.e., a token is produced for every 4 feature vectors in the time domain. MelSpectrogram features are generated once every 10 ms, so a token is produced for every 40 ms of audio.
#
# **Note:** The inherent assumption here is that the output tokens from the model are well aligned with corresponding audio segments. This may not always be true for models trained with CTC loss, so this method of streaming inference may not always work with CTC based models.
from torch.utils.data import DataLoader
import math
class ChunkBufferDecoder:
def __init__(self,asr_model, stride, chunk_len_in_secs=1, buffer_len_in_secs=3):
self.asr_model = asr_model
self.asr_model.eval()
self.data_layer = AudioBuffersDataLayer()
self.data_loader = DataLoader(self.data_layer, batch_size=1, collate_fn=speech_collate_fn)
self.buffers = []
self.all_preds = []
self.chunk_len = chunk_len_in_secs
self.buffer_len = buffer_len_in_secs
assert(chunk_len_in_secs<=buffer_len_in_secs)
feature_stride = asr_model._cfg.preprocessor['window_stride']
self.model_stride_in_secs = feature_stride * stride
self.n_tokens_per_chunk = math.ceil(self.chunk_len / self.model_stride_in_secs)
self.blank_id = len(asr_model.decoder.vocabulary)
self.plot=False
@torch.no_grad()
def transcribe_buffers(self, buffers, merge=True, plot=False):
self.plot = plot
self.buffers = buffers
self.data_layer.set_signal(buffers[:])
self._get_batch_preds()
return self.decode_final(merge)
def _get_batch_preds(self):
device = self.asr_model.device
for batch in iter(self.data_loader):
audio_signal, audio_signal_len = batch
audio_signal, audio_signal_len = audio_signal.to(device), audio_signal_len.to(device)
log_probs, encoded_len, predictions = self.asr_model(input_signal=audio_signal, input_signal_length=audio_signal_len)
preds = torch.unbind(predictions)
for pred in preds:
self.all_preds.append(pred.cpu().numpy())
def decode_final(self, merge=True, extra=0):
self.unmerged = []
self.toks_unmerged = []
# index for the first token corresponding to a chunk of audio would be len(decoded) - 1 - delay
delay = math.ceil((self.chunk_len + (self.buffer_len - self.chunk_len) / 2) / self.model_stride_in_secs)
decoded_frames = []
all_toks = []
for pred in self.all_preds:
ids, toks = self._greedy_decoder(pred, self.asr_model.tokenizer)
decoded_frames.append(ids)
all_toks.append(toks)
for decoded in decoded_frames:
self.unmerged += decoded[len(decoded) - 1 - delay:len(decoded) - 1 - delay + self.n_tokens_per_chunk]
if self.plot:
for i, tok in enumerate(all_toks):
plt.plot(self.buffers[i])
plt.show()
print("\nGreedy labels collected from this buffer")
print(tok[len(tok) - 1 - delay:len(tok) - 1 - delay + self.n_tokens_per_chunk])
self.toks_unmerged += tok[len(tok) - 1 - delay:len(tok) - 1 - delay + self.n_tokens_per_chunk]
print("\nTokens collected from succesive buffers before CTC merge")
print(self.toks_unmerged)
if not merge:
return self.unmerged
return self.greedy_merge(self.unmerged)
def _greedy_decoder(self, preds, tokenizer):
s = []
ids = []
for i in range(preds.shape[0]):
if preds[i] == self.blank_id:
s.append("_")
else:
pred = preds[i]
s.append(tokenizer.ids_to_tokens([pred.item()])[0])
ids.append(preds[i])
return ids, s
def greedy_merge(self, preds):
decoded_prediction = []
previous = self.blank_id
for p in preds:
if (p != previous or previous == self.blank_id) and p != self.blank_id:
decoded_prediction.append(p.item())
previous = p
hypothesis = self.asr_model.tokenizer.ids_to_text(decoded_prediction)
return hypothesis
# To see how this chunk based decoder comes together, let's call the decoder with a few buffers we create from our long audio file.
# Some interesting experiments to try would be to see how changing sizes of the chunk and the context affects transcription accuracy.
# +
chunk_len_in_secs = 4
context_len_in_secs = 2
buffer_len_in_secs = chunk_len_in_secs + 2* context_len_in_secs
n_buffers = 5
buffer_len = sample_rate*buffer_len_in_secs
sampbuffer = np.zeros([buffer_len], dtype=np.float32)
chunk_reader = AudioChunkIterator(samples, chunk_len_in_secs, sample_rate)
chunk_len = sample_rate*chunk_len_in_secs
count = 0
buffer_list = []
for chunk in chunk_reader:
count +=1
sampbuffer[:-chunk_len] = sampbuffer[chunk_len:]
sampbuffer[-chunk_len:] = chunk
buffer_list.append(np.array(sampbuffer))
if count >= n_buffers:
break
# -
stride = 4 # 8 for Citrinet
asr_decoder = ChunkBufferDecoder(model, stride=stride, chunk_len_in_secs=chunk_len_in_secs, buffer_len_in_secs=buffer_len_in_secs )
transcription = asr_decoder.transcribe_buffers(buffer_list, plot=True)
# Final transcription after CTC merge
print(transcription)
# Time to evaluate our streaming inference on the whole long file that we created.
# +
# WER calculation
from nemo.collections.asr.metrics.wer import word_error_rate
# Collect all buffers from the audio file
sampbuffer = np.zeros([buffer_len], dtype=np.float32)
chunk_reader = AudioChunkIterator(samples, chunk_len_in_secs, sample_rate)
buffer_list = []
for chunk in chunk_reader:
sampbuffer[:-chunk_len] = sampbuffer[chunk_len:]
sampbuffer[-chunk_len:] = chunk
buffer_list.append(np.array(sampbuffer))
asr_decoder = ChunkBufferDecoder(model, stride=stride, chunk_len_in_secs=chunk_len_in_secs, buffer_len_in_secs=buffer_len_in_secs )
transcription = asr_decoder.transcribe_buffers(buffer_list, plot=False)
wer = word_error_rate(hypotheses=[transcription], references=[ref_transcript])
print(f"WER: {round(wer*100,2)}%")
|
tutorials/asr/Streaming_ASR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Assignment:
#
# Beat the performance of my Lasso regression by **using different feature engineering steps ONLY!!**.
#
# The performance of my current model, as shown in this notebook is:
# - test rmse: 44798.497576784845
# - test r2: 0.7079639526659389
#
# To beat my model you will need a test r2 bigger than 0.71 and a rmse smaller than 44798.
#
#
# ### Conditions:
#
# - You MUST NOT change the hyperparameters of the Lasso.
# - You MUST use the same seeds in Lasso and train_test_split as I show in this notebook (random_state)
# - You MUST use all the features of the dataset (except Id) - you MUST NOT select features
#
#
# ### If you beat my model:
#
# Make a pull request with your notebook to this github repo:
# https://github.com/solegalli/udemy-feml-challenge
#
# Remember that you need to fork this repo first, upload your winning notebook to your repo, and then make a PR (pull request) to my repo. I will then revise and accept the PR, which will appear in my repo and be available to all the students in the course. This way, other students can learn from your creativity when transforming the variables in your dataset.
# ## House Prices dataset
# +
from math import sqrt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# for the model
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Lasso
from sklearn.pipeline import Pipeline
from sklearn.metrics import mean_squared_error, r2_score
# for feature engineering
from sklearn.preprocessing import StandardScaler
from feature_engine import missing_data_imputers as mdi
from feature_engine import discretisers as dsc
from feature_engine import categorical_encoders as ce
from feature_engine import variable_transformers as vt
# -
# ### Load Datasets
# +
# load dataset
data = pd.read_csv('../houseprice.csv')
# +
# make lists of variable types
categorical = [var for var in data.columns if data[var].dtype == 'O']
year_vars = [var for var in data.columns if 'Yr' in var or 'Year' in var]
discrete = [
var for var in data.columns if data[var].dtype != 'O'
and len(data[var].unique()) < 20 and var not in year_vars
]
numerical = [
var for var in data.columns if data[var].dtype != 'O'
if var not in discrete and var not in ['Id', 'SalePrice']
and var not in year_vars
]
print('There are {} continuous variables'.format(len(numerical)))
print('There are {} discrete variables'.format(len(discrete)))
print('There are {} temporal variables'.format(len(year_vars)))
print('There are {} categorical variables'.format(len(categorical)))
# -
# ### Separate train and test set
# +
# IMPORTANT: keep the random_state to zero for reproducibility
# Let's separate into train and test set
X_train, X_test, y_train, y_test = train_test_split(data.drop(
['Id', 'SalePrice'], axis=1),
data['SalePrice'],
test_size=0.1,
random_state=0)
# +
# calculate elapsed time
def elapsed_years(df, var):
# capture difference between year variable and
# year the house was sold
df[var] = df['YrSold'] - df[var]
return df
for var in ['YearBuilt', 'YearRemodAdd', 'GarageYrBlt']:
X_train = elapsed_years(X_train, var)
X_test = elapsed_years(X_test, var)
# -
# drop YrSold
X_train.drop('YrSold', axis=1, inplace=True)
X_test.drop('YrSold', axis=1, inplace=True)
# capture the column names for use later in the notebook
final_columns = X_train.columns
# ## Feature Engineering Pipeline
# +
# I will treat discrete variables as if they were categorical
# to treat discrete as categorical using Feature-engine
# we need to re-cast them as object
X_train[discrete] = X_train[discrete].astype('O')
X_test[discrete] = X_test[discrete].astype('O')
# -
house_pipe = Pipeline([
# missing data imputation - section 4
('missing_ind',
mdi.AddMissingIndicator(
variables=['LotFrontage', 'MasVnrArea', 'GarageYrBlt'])),
('imputer_num',
mdi.MeanMedianImputer(imputation_method='median', variables=['LotFrontage'])),
('imputer_num2',
mdi.RandomSampleImputer(random_state = 29, variables=['MasVnrArea', 'GarageYrBlt'])),
('imputer_cat',
mdi.CategoricalVariableImputer(variables=categorical)),
# categorical encoding - section 6
('rare_label_enc1',
ce.RareLabelCategoricalEncoder(tol=0.15, n_categories=6, variables=categorical+discrete)),
('categorical_enc',
ce.OrdinalCategoricalEncoder(encoding_method='ordered', variables=categorical+discrete)),
# feature Scaling - section 10
('scaler',
StandardScaler(with_mean=True, with_std=True)),
# regression
('lasso', Lasso(random_state=0))
])
# +
# let's fit the pipeline
house_pipe.fit(X_train, y_train)
# let's get the predictions
X_train_preds = house_pipe.predict(X_train)
X_test_preds = house_pipe.predict(X_test)
# +
# check model performance:
print('train mse: {}'.format(mean_squared_error(y_train, X_train_preds)))
print('train rmse: {}'.format(sqrt(mean_squared_error(y_train, X_train_preds))))
print('train r2: {}'.format(r2_score(y_train, X_train_preds)))
print()
print('test mse: {}'.format(mean_squared_error(y_test, X_test_preds)))
print('test rmse: {}'.format(sqrt(mean_squared_error(y_test, X_test_preds))))
print('test r2: {}'.format(r2_score(y_test, X_test_preds)))
# +
# plot predictions vs real value
plt.scatter(y_test,X_test_preds)
plt.xlabel('True Price')
plt.ylabel('Predicted Price')
# +
# let's explore the importance of the features
# the importance is given by the absolute value of the coefficient
# assigned by the Lasso
importance = pd.Series(np.abs(house_pipe.named_steps['lasso'].coef_))
importance.index = list(final_columns)+['LotFrontage_na', 'MasVnrArea_na', 'GarageYrBlt_na']
importance.sort_values(inplace=True, ascending=False)
importance.plot.bar(figsize=(18,6))
|
StudentsSolutions_old/13-Assignment-NievesMerino.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="_DWiFEBR_rf-"
# ## CSP 502 - Assignment 2 & 3 [FACE RECOGNITION USING SIFT ALGORITHM]
# + [markdown] id="gXLOW_aM_Wom"
# # Team Name: Bit Coders
# + [markdown] id="dHOoSvyD_bd8"
# ## Name: <NAME> - AU 2044011
# + [markdown] id="pKI1zYjA_eb5"
# ## Name: <NAME> - AU 1841051
# + [markdown] id="AvQMTmTjgSCM"
# # Mount your drive if you want to use our face database.
#
# Ask <EMAIL> OR <EMAIL> for access to our face database.
# + colab={"base_uri": "https://localhost:8080/"} id="njZqHzB6iRhk" outputId="bb8adeff-d8ff-4d7c-ad7c-1f3fd2c3a45a"
from google.colab import drive
drive.mount('/gdrive')
# + [markdown] id="60f7H9hcNKe6"
# # Imports and helper functions
# + [markdown] id="ITZUwJMEE9vn"
# ## Libraries
# + id="Xyi9aHVDvGOS" colab={"base_uri": "https://localhost:8080/"} outputId="97e097f1-c1c5-4d23-e304-884287ddf9d3"
# !pip install opencv-contrib-python==3.4.2.16
from IPython.display import display, Javascript, Image
from google.colab.output import eval_js
from base64 import b64decode, b64encode
from pathlib import Path
import cv2
import numpy as np
import PIL
import io
import html
import time
import pandas as pd
import cv2 as cv
import matplotlib.pyplot as plt
import os
from skimage import io
from IPython.display import clear_output
from google.colab.patches import cv2_imshow
import cv2
# + [markdown] id="ubtLtOpwE_Y-"
# ## SIFT algorithm
# + id="Qry-dY-vEN87"
# SIFT implementation
# MIN_MATCH_COUNT = 10
def sift_match(test, image, plot=False, MIN_MATCH_COUNT=10):
isMatch = False
# Initiate SIFT detector
sift = cv2.xfeatures2d.SIFT_create()
# img1 = cv.imread(test,cv.IMREAD_GRAYSCALE)# queryImage
img1 = test
img2 = cv.imread(image,cv.IMREAD_GRAYSCALE) # trainImage
# find the keypoints and descriptors with SIFT
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks = 50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1,des2,k=2)
# store all the good matches as per Lowe's ratio test.
good = []
for m,n in matches:
if m.distance < 0.7*n.distance:
good.append(m)
if len(good)>MIN_MATCH_COUNT:
src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1,1,2)
dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1,1,2)
M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC,5.0)
matchesMask = mask.ravel().tolist()
h,w = img1.shape
pts = np.float32([ [0,0],[0,h-1],[w-1,h-1],[w-1,0] ]).reshape(-1,1,2)
dst = cv2.perspectiveTransform(pts,M)
img2 = cv2.polylines(img2,[np.int32(dst)],True,255,3, cv2.LINE_AA)
# print("MATCH FOUND")
isMatch = True
else:
# print("Not enough matches are found - %d/%d" % (len(good),MIN_MATCH_COUNT))
isMatch = False
if plot:
matchesMask = None
draw_params = dict(matchColor = (0,255,0), # draw matches in green color
singlePointColor = None,
matchesMask = matchesMask, # draw only inliers
flags = 2)
img3 = cv2.drawMatches(img1,kp1,img2,kp2,good,None,**draw_params)
plt.imshow(img3, 'gray'),plt.show()
return (isMatch, len(good))
# + [markdown] id="qHx9V64CIijQ"
# ## SURF algorithm
# + id="-ubUw2AXYlAs"
# SURF implementation
# MIN_MATCH_COUNT = 10
def surf_match(test, image, plot=False, MIN_MATCH_COUNT=10):
isMatch = False
# Initiate SIFT detector
surf = cv2.xfeatures2d.SURF_create(400)
# img1 = cv.imread(test,cv.IMREAD_GRAYSCALE)# queryImage
img1 = test
img2 = cv.imread(image,cv.IMREAD_GRAYSCALE) # trainImage
# find the keypoints and descriptors with SIFT
kp1, des1 = surf.detectAndCompute(img1,None)
kp2, des2 = surf.detectAndCompute(img2,None)
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks = 50)
flann = cv2.FlannBasedMatcher(index_params, search_params)
matches = flann.knnMatch(des1,des2,k=2)
# store all the good matches as per Lowe's ratio test.
good = []
for m,n in matches:
if m.distance < 0.7*n.distance:
good.append(m)
if len(good)>MIN_MATCH_COUNT:
src_pts = np.float32([ kp1[m.queryIdx].pt for m in good ]).reshape(-1,1,2)
dst_pts = np.float32([ kp2[m.trainIdx].pt for m in good ]).reshape(-1,1,2)
M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC,5.0)
matchesMask = mask.ravel().tolist()
h,w = img1.shape
pts = np.float32([ [0,0],[0,h-1],[w-1,h-1],[w-1,0] ]).reshape(-1,1,2)
dst = cv2.perspectiveTransform(pts,M)
img2 = cv2.polylines(img2,[np.int32(dst)],True,255,3, cv2.LINE_AA)
# print("MATCH FOUND")
isMatch = True
else:
# print("Not enough matches are found - %d/%d" % (len(good),MIN_MATCH_COUNT))
isMatch = False
if plot:
matchesMask = None
draw_params = dict(matchColor = (0,255,0), # draw matches in green color
singlePointColor = None,
matchesMask = matchesMask, # draw only inliers
flags = 2)
img3 = cv2.drawMatches(img1,kp1,img2,kp2,good,None,**draw_params)
plt.imshow(img3, 'gray'),plt.show()
return (isMatch, len(good))
# + [markdown] id="sI184cZsFDrz"
# ## Image helper functions
# + id="o7x4vBOW_Bxe"
def take_photo(filename='photo.jpg', quality=0.8):
js = Javascript('''
async function takePhoto(quality) {
const div = document.createElement('div');
const capture = document.createElement('button');
capture.textContent = 'Capture';
div.appendChild(capture);
const video = document.createElement('video');
video.style.display = 'block';
const stream = await navigator.mediaDevices.getUserMedia({video: true});
document.body.appendChild(div);
div.appendChild(video);
video.srcObject = stream;
await video.play();
// Resize the output to fit the video element.
google.colab.output.setIframeHeight(document.documentElement.scrollHeight, true);
// Wait for Capture to be clicked.
await new Promise((resolve) => capture.onclick = resolve);
const canvas = document.createElement('canvas');
canvas.width = video.videoWidth;
canvas.height = video.videoHeight;
canvas.getContext('2d').drawImage(video, 0, 0);
stream.getVideoTracks()[0].stop();
div.remove();
return canvas.toDataURL('image/jpeg', quality);
}
''')
display(js)
data = eval_js('takePhoto({})'.format(quality))
binary = b64decode(data.split(',')[1])
with open(filename, 'wb') as f:
f.write(binary)
return filename
# + [markdown] id="Z6cGBpLtFhVj"
# ## Video helper functions
# + id="U74F7ehhAUyT"
# function to convert the JavaScript object into an OpenCV image
def js_to_image(js_reply):
"""
Params:
js_reply: JavaScript object containing image from webcam
Returns:
img: OpenCV BGR image
"""
# decode base64 image
image_bytes = b64decode(js_reply.split(',')[1])
# convert bytes to numpy array
jpg_as_np = np.frombuffer(image_bytes, dtype=np.uint8)
# decode numpy array into OpenCV BGR image
img = cv2.imdecode(jpg_as_np, flags=1)
img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
return img
# function to convert OpenCV Rectangle bounding box image into base64 byte string to be overlayed on video stream
def bbox_to_bytes(bbox_array):
"""
Params:
bbox_array: Numpy array (pixels) containing rectangle to overlay on video stream.
Returns:
bytes: Base64 image byte string
"""
# convert array into PIL image
bbox_PIL = PIL.Image.fromarray(bbox_array, 'RGBA')
iobuf = io.BytesIO()
# format bbox into png for return
bbox_PIL.save(iobuf, format='png')
# format return string
bbox_bytes = 'data:image/png;base64,{}'.format((str(b64encode(iobuf.getvalue()), 'utf-8')))
return bbox_bytes
# + id="FOQcw4lI-BaN"
# JavaScript to properly create our live video stream using our webcam as input
def video_stream():
js = Javascript('''
var video;
var div = null;
var stream;
var captureCanvas;
var imgElement;
var labelElement;
var pendingResolve = null;
var shutdown = false;
function removeDom() {
stream.getVideoTracks()[0].stop();
video.remove();
div.remove();
video = null;
div = null;
stream = null;
imgElement = null;
captureCanvas = null;
labelElement = null;
}
function onAnimationFrame() {
if (!shutdown) {
window.requestAnimationFrame(onAnimationFrame);
}
if (pendingResolve) {
var result = "";
if (!shutdown) {
captureCanvas.getContext('2d').drawImage(video, 0, 0, 640, 480);
result = captureCanvas.toDataURL('image/jpeg', 0.8)
}
var lp = pendingResolve;
pendingResolve = null;
lp(result);
}
}
async function createDom() {
if (div !== null) {
return stream;
}
div = document.createElement('div');
div.style.border = '2px solid black';
div.style.padding = '3px';
div.style.width = '100%';
div.style.maxWidth = '600px';
document.body.appendChild(div);
const modelOut = document.createElement('div');
modelOut.innerHTML = "<span>Status:</span>";
labelElement = document.createElement('span');
labelElement.innerText = 'No data';
labelElement.style.fontWeight = 'bold';
modelOut.appendChild(labelElement);
div.appendChild(modelOut);
video = document.createElement('video');
video.style.display = 'block';
video.width = div.clientWidth - 6;
video.setAttribute('playsinline', '');
video.onclick = () => { shutdown = true; };
stream = await navigator.mediaDevices.getUserMedia(
{video: { facingMode: "environment"}});
div.appendChild(video);
imgElement = document.createElement('img');
imgElement.style.position = 'absolute';
imgElement.style.zIndex = 1;
imgElement.onclick = () => { shutdown = true; };
div.appendChild(imgElement);
const instruction = document.createElement('div');
instruction.innerHTML =
'<span style="color: red; font-weight: bold;">' +
'When finished, click here or on the video to stop this demo</span>';
div.appendChild(instruction);
instruction.onclick = () => { shutdown = true; };
video.srcObject = stream;
await video.play();
captureCanvas = document.createElement('canvas');
captureCanvas.width = 640; //video.videoWidth;
captureCanvas.height = 480; //video.videoHeight;
window.requestAnimationFrame(onAnimationFrame);
return stream;
}
async function stream_frame(label, imgData) {
if (shutdown) {
removeDom();
shutdown = false;
return '';
}
var preCreate = Date.now();
stream = await createDom();
var preShow = Date.now();
if (label != "") {
labelElement.innerHTML = label;
}
if (imgData != "") {
var videoRect = video.getClientRects()[0];
imgElement.style.top = videoRect.top + "px";
imgElement.style.left = videoRect.left + "px";
imgElement.style.width = videoRect.width + "px";
imgElement.style.height = videoRect.height + "px";
imgElement.src = imgData;
}
var preCapture = Date.now();
var result = await new Promise(function(resolve, reject) {
pendingResolve = resolve;
});
shutdown = false;
return {'create': preShow - preCreate,
'show': preCapture - preShow,
'capture': Date.now() - preCapture,
'img': result};
}
''')
display(js)
def video_frame(label, bbox):
data = eval_js('stream_frame("{}", "{}")'.format(label, bbox))
return data
# + [markdown] id="ubZBdbm8Azq6"
# # Choose your face data directory path
# + [markdown] id="JS3-qNVXmbqA"
# Our directory will be loaded at '/gdrive/MyDrive/BitCoders/Assignment2/'.
# Feel free to load a blank directory and create your own database.
# + id="BFRBWvcBA4Hv"
main_dir = '/gdrive/MyDrive/BitCoders/Assignment2/'
# + [markdown] id="ihqdgHwVQ4N2"
# ## Load the database
# + id="t7uBqBVmSabL"
image_database = {}
pathlist = Path(str(main_dir)).rglob('*.jpg')
for path in pathlist:
path_in_str = str(path)
image_database[path_in_str] = path_in_str.split('/')[-2]
# + [markdown] id="MK4Ku-hhNMck"
# # Add yourself to the face database
# + id="v7XWivaI_rAA" cellView="form"
#@title Your Information:
#@markdown This info will help us to analyse your face and identify you in future.
# Name = 'Insert Name here (eg. Supan / Bhumiti)'
Name = 'supan' #@param {type: "string"}
#@markdown More number of images = better face recognition !!
#@markdown So, please consider clicking atleast around 20 images.
Number_of_images = 25 #@param {type: "slider", min: 1, max: 40}
#@markdown ---
class NameError(Exception):
pass
if Name == 'Insert Name here (eg. Supan / Bhumiti)':
raise NameError("Enter name please!")
elif len(Name)<2:
raise NameError("Enter name atleast bigger than 2 characters!")
elif os.path.exists(main_dir):
raise NameError("Person already exists. Try a different Name")
else:
print("Hi, ", Name)
print("Let's begin taking your photos")
os.chdir(main_dir)
main = os.path.join(main_dir, '{}'.format(Name))
try:
os.mkdir('{}'.format(Name))
except:
raise NameError("Couldn't create your folder somehow. Try again!")
main = os.path.join(main_dir, '{}'.format(Name))
os.chdir(main)
for i in range(1, Number_of_images+1):
print("Click image number {}".format(i))
try:
filename = take_photo('{}.jpg'.format(i))
print('Saved image number {}'.format(i))
clear_output()
except Exception as err:
print(str(err))
print("Thank you!")
print("Your face is now registered with us!")
# + [markdown] id="zlW531UBSDrL"
# # Face Detection
# + [markdown] id="OqOp733-Q9sU"
# ## Face Recognition
# + [markdown] id="5qzOoZ_goj5E"
# Run the below cell to recognise your face against our face database!
# + id="zSoYUIJz-r7y"
# start streaming video from webcam
video_stream()
# label for video
label_html = 'Detecting...'
# initialze bounding box to empty
bbox = ''
count = 0
detected = False
while not detected:
js_reply = video_frame(label_html, bbox)
if not js_reply:
break
img = js_to_image(js_reply["img"])
# gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# gray = cv.imread(test,cv.IMREAD_GRAYSCALE)
best_match = ''
highest = 0
for key, value in image_database.items():
try:
match, num_matches = sift_match(img, key)
if match:
# label_html = 'Hello, {}'.format(value)
if num_matches > highest:
highest = num_matches
best_match = value
except:
pass
if len(best_match)>0:
label_html = 'Hello, {}'.format(best_match)
detected = True
else:
label_html = 'You seem to be new here...'
clear_output()
print(label_html)
final_frame = cv2.cvtColor(img, cv2.COLOR_GRAY2RGB)
plt.imshow(final_frame)
plt.title(label_html)
plt.axis('off')
plt.show()
# + [markdown] id="xzxNryw9kQ6V"
# # Measuring Accuracy on current database
# + [markdown] id="pKOVb_ZJZQVO"
# ## SIFT
# + colab={"base_uri": "https://localhost:8080/", "height": 198} id="XaMZuIrykVCA" outputId="54809fad-f5df-4b68-c1eb-dacfff5ad85f"
image_sources = list(image_database.keys())
labels = list(image_database.values())
data = pd.DataFrame()
data['Image_Sources'] = image_sources
data['Labels'] = labels
data.head()
# + id="kD89xMhhrnwW"
from sklearn.model_selection import train_test_split
X = data['Image_Sources']
y = data['Labels']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.5, random_state = 0, stratify=y)
# + id="NmmDk-NusDc0"
y_cap = []
for test_image_path in X_test:
test_image = cv.imread(test_image_path,cv.IMREAD_GRAYSCALE)
best_match = ''
highest_matches = 0
for train_image, label in zip(X_train, y_train):
try:
match, num_matches = sift_match(test_image, train_image)
if match and num_matches > highest_matches:
highest_matches = num_matches
best_match = label
except:
pass
# print('Error')
if len(best_match)<1:
y_cap.append('Unknown')
else:
y_cap.append(best_match)
# + id="oczK35jO5Vyv"
classes = list(set(y_test))
classes.append('Unknown')
# + [markdown] id="Yt_xdOa6-xaz"
# ### Overall Accuracy : 95.71%
# + colab={"base_uri": "https://localhost:8080/"} id="EhxY1jf67_VN" outputId="c8c6bf70-42eb-4701-979f-3dd3f4402f30"
from sklearn.metrics import accuracy_score
print("Accuracy is:", np.round(accuracy_score(y_test, y_cap)*100,3),"%")
# + [markdown] id="li6a8pj1-zl9"
# ### Overall weighted F1 score: 97.48%
# + colab={"base_uri": "https://localhost:8080/"} id="HwmZgvt_7_X3" outputId="4160090d-043b-483a-ed9f-fe92996398fa"
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_cap, average='weighted')
print("F1 Score is:",np.round(f1*100, 3), "%")
# + [markdown] id="K5HLd_nT-8Gc"
# ### Confusion Matrix
# + id="6A301ECLqpMs"
from sklearn.metrics import confusion_matrix
cf_matrix = confusion_matrix(y_test, y_cap, labels=classes)
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="4MEvJuFt3kIB" outputId="e8550acc-9be1-4803-eab8-47e95c0cd1d5"
import seaborn as sns
ax= plt.subplot()
sns.heatmap(cf_matrix, annot=True, ax = ax);
# sns.heatmap(cf_matrix, annot=True)
ax.set_xlabel('Predicted labels');
ax.set_ylabel('True labels');
ax.set_title('Confusion Matrix');
ax.xaxis.set_ticklabels(classes);
ax.yaxis.set_ticklabels(classes);
plt.show()
# + [markdown] id="Xx8E3dQ6HmIe"
# ## SVM
# + [markdown] id="KNU30bwMH04x"
# ### Splitting our database for SVM training
# + colab={"base_uri": "https://localhost:8080/"} id="-HQqp7rDtXFh" outputId="ca557113-15a6-4d7c-95e5-5b7e1457fba5"
image_paths = []
image_classes = []
class_id = 0
main_dir = '/gdrive/MyDrive/BitCoders/Assignment2SVM'
train_path = os.path.join(main_dir, 'Train')
people = os.listdir(train_path)
def imageList(path):
return [os.path.join(path, file) for file in os.listdir(path)]
for training_name in people:
dir = os.path.join(train_path, training_name)
class_path = imageList(dir)
image_paths += class_path
image_classes += [class_id]*len(class_path)
class_id += 1
des_list = []
for image_path in image_paths:
kpt, desc = sift(image_path)
des_list.append((image_path, desc))
descriptors = des_list[0][1]
for image_path, descriptor in des_list[1:]:
descriptors = np.vstack((descriptors, descriptor))
descriptors_float = descriptors.astype(float)
from scipy.cluster.vq import kmeans, vq
k=200
voc, variance = kmeans(descriptors_float, k, 1)
image_features = np.zeros((len(image_paths), k), "float32")
for i in range(len(image_paths)):
words, distance = vq(des_list[i][1], voc)
for word in words:
image_features[i][word] += 1
#TF-IDF
occurences = np.sum((image_features>0)*1, axis=0)
idf = np.array(np.log((1.0*len(image_paths)+1) / (1.0*occurences+1)), "float32")
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler().fit(image_features)
image_features = scaler.transform(image_features)
from sklearn.svm import LinearSVC
clf = LinearSVC(max_iter=10000)
clf.fit(image_features, np.array(image_classes))
from sklearn.externals import joblib
joblib.dump((clf, people, scaler, k, voc), '/gdrive/MyDrive/BitCoders/trainedSVM.pkl', compress=3)
# + [markdown] id="G856Z82vH76w"
# ### Fitting SVM Classifier and plotting Confusion Matrix
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="2LRAiqb1TA0m" outputId="b4c2d9b2-5101-44a1-ae18-aa1f15ec100d"
from sklearn.multiclass import OneVsOneClassifier, OneVsRestClassifier
from sklearn.svm import SVC
model = SVC()
ovo = OneVsOneClassifier(model)
ovo.fit(image_features, np.array(image_classes))
y_train = [people[i] for i in image_classes]
yhat = [people[i] for i in ovo.predict(image_features)]
accuracy = accuracy_score(y_train, yhat)
print ("accuracy = ", accuracy)
cm1 = confusion_matrix(y_train, yhat)
plt.matshow(cm1)
plt.title('Confusion matrix')
plt.colorbar()
plt.show()
# + id="ztQCJ7SaQOyK"
y_train = [people[i] for i in image_classes]
y_train_pred = [people[i] for i in clf.predict(image_features)]
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="UL5-iFnMLAC1" outputId="eaf9b09b-8f18-4d96-8d1f-4fc1cb7be0c3"
from sklearn.metrics import confusion_matrix, accuracy_score
clf1, class_names1, stdScalar1, k1, voc1 = joblib.load('/gdrive/MyDrive/BitCoders/trainedSVM.pkl')
test_path = os.path.join(main_dir, 'Test')
test_classes = os.listdir(test_path)
test_image_paths = []
test_image_classes = []
test_class_id = 0
for test_class in test_classes:
dir = os.path.join(test_path, test_class)
class_path = imageList(dir)
test_image_paths+=class_path
test_image_classes+=[test_class_id]*len(class_path)
test_class_id+=1
test_des_list = []
for image_path in test_image_paths:
kpt, desc = sift(image_path)
test_des_list.append((image_path, desc))
test_descriptors = test_des_list[0][1]
for image_path, descriptor in test_des_list[0:]:
test_descriptors = np.vstack((test_descriptors, descriptor))
test_features = np.zeros((len(test_image_paths), k1), "float32")
for i in range(len(test_image_paths)):
words, distance = vq(test_des_list[i][1],voc1)
for w in words:
test_features[i][w] += 1
nbr_occurences = np.sum( (test_features > 0) * 1, axis = 0)
idf = np.array(np.log((1.0*len(test_image_paths)+1) / (1.0*nbr_occurences + 1)), 'float32')
test_features = stdScalar1.transform(test_features)
y_test = [class_names1[i] for i in test_image_classes]
y_test_pred = [class_names1[i] for i in clf1.predict(test_features)]
accuracy = accuracy_score(y_test, y_test_pred)
print ("accuracy = ", accuracy)
cm = confusion_matrix(y_test, y_test_pred)
plt.matshow(cm)
plt.title('Confusion matrix')
plt.colorbar()
plt.show()
# + id="f-<KEY>"
from sklearn.preprocessing import label_binarize
y = label_binarize(y, classes=people)
n_classes = y.shape[1]
# + id="bQJ1Qz6MWzMf"
y_test_bin = label_binarize(y_test, classes=people)
# + id="K-zxA40rVfjx"
from sklearn import svm
random_state = np.random.RandomState(0)
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
random_state=random_state))
y_score = classifier.fit(image_features, y_train).decision_function(test_features)
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test_bin[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# + [markdown] id="wfiU1GLvIFdx"
# ### ROC Curve
# + colab={"base_uri": "https://localhost:8080/", "height": 677} id="41zvagluVfc_" outputId="a149959f-cfa0-4a1d-d3c6-f5f75d099e7d"
from scipy import interp
from itertools import cycle
fpr["micro"], tpr["micro"], _ = roc_curve(y_test_bin.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))
# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
mean_tpr += interp(all_fpr, fpr[i], tpr[i])
# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])
# Plot all ROC curves
plt.figure(figsize=(10,10))
plt.plot(fpr["micro"], tpr["micro"],
label='micro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["micro"]),
color='deeppink', linestyle=':', linewidth=4)
plt.plot(fpr["macro"], tpr["macro"],
label='macro-average ROC curve (area = {0:0.2f})'
''.format(roc_auc["macro"]),
color='navy', linestyle=':', linewidth=4)
colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
plt.plot(fpr[i], tpr[i], color=color, lw=lw,
label='ROC curve of class {0} (area = {1:0.2f})'
''.format(i, roc_auc[i]))
plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend(loc="lower right")
plt.show()
# + [markdown] id="S8lj6Ca5ZTyP"
# ## SURF
# + colab={"base_uri": "https://localhost:8080/", "height": 198} id="Cr9ONgNFZaDK" outputId="0d7aff34-9a66-4a67-a874-13b03e393cac"
image_sources = list(image_database.keys())
labels = list(image_database.values())
data = pd.DataFrame()
data['Image_Sources'] = image_sources
data['Labels'] = labels
data.head()
# + id="_AOlXYnHZaDN"
from sklearn.model_selection import train_test_split
X = data['Image_Sources']
y = data['Labels']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.5, random_state = 0, stratify=y)
# + id="AkQZJ3xkZaDN"
y_cap = []
for test_image_path in X_test:
test_image = cv.imread(test_image_path,cv.IMREAD_GRAYSCALE)
best_match = ''
highest_matches = 0
for train_image, label in zip(X_train, y_train):
try:
match, num_matches = surf_match(test_image, train_image)
if match and num_matches > highest_matches:
highest_matches = num_matches
best_match = label
except:
pass
# print('Error')
if len(best_match)<1:
y_cap.append('Unknown')
else:
y_cap.append(best_match)
# + id="q6uASEn9ZaDO"
classes = list(set(y_test))
classes.append('Unknown')
# + [markdown] id="eijGPFWzZaDP"
# ### Overall Accuracy : 98.57%
# + colab={"base_uri": "https://localhost:8080/"} id="lHrbyVtbZaDP" outputId="c34be713-969f-456b-d8ab-824fc615f831"
from sklearn.metrics import accuracy_score
print("Accuracy is:", np.round(accuracy_score(y_test, y_cap)*100,3),"%")
# + [markdown] id="MHDHi9-xZaDQ"
# ### Overall weighted F1 score: 99.5%
# + colab={"base_uri": "https://localhost:8080/"} id="ElIJ77sPZaDQ" outputId="b8424a40-bf7a-423b-f5c3-7df7f75e531f"
from sklearn.metrics import f1_score
f1 = f1_score(y_test, y_cap, average='weighted')
print("F1 Score is:",np.round(f1*100, 3), "%")
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="I_Zm-eHgfTL6" outputId="4d3b5292-03cd-45a0-a7f8-68fd11b99193"
from sklearn.metrics import confusion_matrix
cf_matrix = confusion_matrix(y_test, y_cap, labels=classes)
import seaborn as sns
ax= plt.subplot()
sns.heatmap(cf_matrix, annot=True, ax = ax);
# sns.heatmap(cf_matrix, annot=True)
ax.set_xlabel('Predicted labels');
ax.set_ylabel('True labels');
ax.set_title('Confusion Matrix');
ax.xaxis.set_ticklabels(classes);
ax.yaxis.set_ticklabels(classes);
plt.show()
# + [markdown] id="Wi2XkZpvZaDR"
# ### Confusion Matrix
# + id="TADP0GkUZaDR"
from sklearn.metrics import confusion_matrix
cf_matrix = confusion_matrix(y_test, y_cap, labels=classes)
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="pcCTstL1ZaDS" outputId="6c8640a7-9418-445e-c117-ae88dccdddb1"
import seaborn as sns
ax= plt.subplot()
sns.heatmap(cf_matrix, annot=True, ax = ax);
# sns.heatmap(cf_matrix, annot=True)
ax.set_xlabel('Predicted labels');
ax.set_ylabel('True labels');
ax.set_title('Confusion Matrix');
ax.xaxis.set_ticklabels(classes);
ax.yaxis.set_ticklabels(classes);
plt.show()
# + [markdown] id="vP9Beqr3BqAK"
# # Sample Outputs of our SIFT algorithm
# + colab={"base_uri": "https://localhost:8080/", "height": 177} id="NfzFWropB-sv" outputId="dc16b5cf-c06f-4fc2-ffbd-cdcf6330a6c3"
test_image = cv.imread(X_test[131],cv.IMREAD_GRAYSCALE)
match, num_matches = sift_match(test_image, X_train[120], plot=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 177} id="dm_2WLEIDRrA" outputId="bc518e18-efde-4ffc-f594-5241ed9d462c"
test_image = cv.imread(X_test[20],cv.IMREAD_GRAYSCALE)
match, num_matches = sift_match(test_image, X_train[33], plot=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 177} id="hcgGhs0bClR6" outputId="3c86a5fb-dc1b-453a-fff0-0578095b01f4"
test_image = cv.imread(X_test[0],cv.IMREAD_GRAYSCALE)
match, num_matches = sift_match(test_image, X_train[18], plot=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 177} id="F2fjmXO0C129" outputId="a486f6a2-371e-485f-dce8-ded06f937cbc"
test_image = cv.imread(X_test[16],cv.IMREAD_GRAYSCALE)
match, num_matches = sift_match(test_image, X_train[18], plot=True)
# + [markdown] id="nWZ2rjMjPBCk"
# # Testing other team's data (BuggerDebugger Group)
# + id="8AOQWsTrPvLx"
other_team_dir = '/gdrive/MyDrive/BitCoders/Assignment2_other_team_data'
# + colab={"base_uri": "https://localhost:8080/", "height": 198} id="hTcEmO2WQMrY" outputId="8c669c0a-6018-4f4e-8a35-6eb259d647ee"
image_database_1 = {}
pathlist_1 = Path(str(other_team_dir)).rglob('*.jpg')
for path in pathlist_1:
path_in_str = str(path)
image_database_1[path_in_str] = path_in_str.split('/')[-2]
image_sources_1 = list(image_database_1.keys())
labels_1 = list(image_database_1.values())
data_1 = pd.DataFrame()
data_1['Image_Sources'] = image_sources_1
data_1['Labels'] = labels_1
data_1.head()
# + id="9RNieXwWP6NY"
from sklearn.model_selection import train_test_split
X_1 = data_1['Image_Sources']
y_1 = data_1['Labels']
X_train_1, X_test_1, y_train_1, y_test_1 = train_test_split(X_1, y_1, test_size = 0.5, random_state = 0, stratify=y_1)
# + colab={"base_uri": "https://localhost:8080/", "height": 236} id="dihZDZgXSHsb" outputId="96e47306-3a82-4e3e-eea3-7b55511f431a"
# a1 = cv.imread(X_train_1[0], cv.IMREAD_GRAYSCALE)
# cv2_imshow(a1)
a2 = cv.imread(X_test_1[45], cv.IMREAD_GRAYSCALE)
# cv2_imshow(a2)
sift_match(a2, X_train_1[50], plot=True)
# + id="SPfrtT7rTTSX"
test_image = cv.imread(X_test_1[131],cv.IMREAD_GRAYSCALE)
match, num_matches = sift_match(test_image, X_train[120], plot=True)
# + id="QDeBl9ILQj50"
y_cap_1 = []
for test_image_path in X_test_1:
test_image = cv.imread(test_image_path,cv.IMREAD_GRAYSCALE)
best_match = ''
highest_matches = 0
for train_image, label in zip(X_train_1, y_train_1):
try:
match, num_matches = sift_match(test_image, train_image, MIN_MATCH_COUNT=1)
if match and num_matches > highest_matches:
highest_matches = num_matches
best_match = label
except:
pass
# print('Error')
if len(best_match)<1:
y_cap_1.append('Unknown')
else:
y_cap_1.append(best_match)
# + id="w23SfK-fRgDZ"
classes_1 = list(set(y_test_1))
classes_1.append('Unknown')
# + colab={"base_uri": "https://localhost:8080/"} id="pRasht6hRfvb" outputId="81615c9c-0247-4e25-db08-7cf3a06d379d"
from sklearn.metrics import accuracy_score
print("Accuracy is:", np.round(accuracy_score(y_test_1, y_cap_1)*100,3),"%")
# + colab={"base_uri": "https://localhost:8080/"} id="ZDjaAH6jR0ib" outputId="a39636a1-924a-4b0c-d921-d4fb8eb2dc8e"
from sklearn.metrics import f1_score
f1_1 = f1_score(y_test_1, y_cap_1, average='weighted')
print("F1 Score is:",np.round(f1_1*100, 3), "%")
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="RL0hbFSwXn5-" outputId="1156f96c-4a81-4c03-b39d-2ae6f3a7e025"
from sklearn.metrics import confusion_matrix
import seaborn as sns
cf_matrix_1 = confusion_matrix(y_test_1, y_cap_1, labels=classes_1)
ax1= plt.subplot()
sns.heatmap(cf_matrix_1, annot=True, ax = ax1);
# sns.heatmap(cf_matrix, annot=True)
ax1.set_xlabel('Predicted labels');
ax1.set_ylabel('True labels');
ax1.set_title('Confusion Matrix');
ax1.xaxis.set_ticklabels(classes_1);
ax1.yaxis.set_ticklabels(classes_1);
plt.show()
# + [markdown] id="JMHWaaqP9enk"
# # Testing other team's data (YK Group)
# + id="Ltne6exBCFxq"
other_team_train = '/gdrive/MyDrive/BitCoders/CVAss22/Train'
other_team_test = '/gdrive/MyDrive/BitCoders/CVAss22/Test'
image_database_1 = {}
pathlist_1 = Path(str(other_team_train)).rglob('*.pgm')
for path in pathlist_1:
path_in_str = str(path)
image_database_1[path_in_str] = path_in_str.split('/')[-1].split('_')[0][-2:]
test_image_database_1 = {}
pathlist_2 = Path(str(other_team_test)).rglob('*.pgm')
for path in pathlist_2:
path_in_str = str(path)
test_image_database_1[path_in_str] = path_in_str.split('/')[-1].split('_')[0][-2:]
X_train_1 = list(image_database_1.keys())
y_train_1 = list(image_database_1.values())
X_test_1 = list(test_image_database_1.keys())
y_test_1 = list(test_image_database_1.values())
# + id="5Q1SMfpDD-bD"
y_cap_1 = []
for test_image_path in X_test_1:
test_image = cv.imread(test_image_path,cv.IMREAD_GRAYSCALE)
best_match = ''
highest_matches = 0
for train_image, label in zip(X_train_1, y_train_1):
try:
match, num_matches = sift_match(test_image, train_image, MIN_MATCH_COUNT=1)
if match and num_matches > highest_matches:
highest_matches = num_matches
best_match = label
except:
pass
# print('Error')
if len(best_match)<1:
y_cap_1.append('Unknown')
else:
y_cap_1.append(best_match)
# + id="TuDGkgxTD-X-"
classes_1 = list(set(y_test_1))
classes_1.append('Unknown')
# + colab={"base_uri": "https://localhost:8080/"} id="CDaxf9KED-Tg" outputId="3ac800d4-b09e-44b4-c987-7b5731227abd"
from sklearn.metrics import accuracy_score
print("Accuracy is:", np.round(accuracy_score(y_test_1, y_cap_1)*100,3),"%")
# + colab={"base_uri": "https://localhost:8080/"} id="cAvQKOt1D-Qb" outputId="9e88313f-c0c7-4f81-aca6-2919a38e46ee"
from sklearn.metrics import f1_score
f1_1 = f1_score(y_test_1, y_cap_1, average='weighted')
print("F1 Score is:",np.round(f1_1*100, 3), "%")
# + colab={"base_uri": "https://localhost:8080/", "height": 295} id="8v77Yfi8ESyf" outputId="ec97595c-e229-4fc2-e7e3-5e609f04efb2"
from sklearn.metrics import confusion_matrix
import seaborn as sns
cf_matrix_1 = confusion_matrix(y_test_1, y_cap_1, labels=classes_1)
ax1= plt.subplot()
sns.heatmap(cf_matrix_1, annot=True, ax = ax1);
# sns.heatmap(cf_matrix, annot=True)
ax1.set_xlabel('Predicted labels');
ax1.set_ylabel('True labels');
ax1.set_title('Confusion Matrix');
ax1.xaxis.set_ticklabels(classes_1);
ax1.yaxis.set_ticklabels(classes_1);
plt.show()
# + id="EXHpYB-2EWVQ"
# + colab={"base_uri": "https://localhost:8080/", "height": 273} id="XnGjlk7U92b9" outputId="d916d1fe-d26e-45e7-dbc2-b4668418d9f5"
test_image = cv2.imread(image_database_2[26],cv.IMREAD_GRAYSCALE)
# cv2_imshow(test_image)
sift_match(test_image,image_database_2[9], plot=True, MIN_MATCH_COUNT=3)
# + [markdown] id="wpBxrIHQ_JxA"
# # And we're DONE !
|
Assignment 2 & 3/Bhumiti - Assignment 2 & 3/Face_Recognition_Challenge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
# <script>
# window.dataLayer = window.dataLayer || [];
# function gtag(){dataLayer.push(arguments);}
# gtag('js', new Date());
#
# gtag('config', 'UA-59152712-8');
# </script>
#
# # Tutorial-IllinoisGRMHD: harm_utoprim_2d.c
#
# ## Authors: <NAME> & <NAME>
#
# <font color='red'>**This module is currently under development**</font>
#
# ## In this tutorial module we explain the conservative-to-primitive algorithm used by `HARM`. This module will likely be absorbed by another one once we finish documenting the code.
#
# ### Required and recommended citations:
#
# * **(Required)** <NAME>., <NAME>., <NAME>., <NAME>., and <NAME>. IllinoisGRMHD: an open-source, user-friendly GRMHD code for dynamical spacetimes. Class. Quantum Grav. 32 (2015) 175009. ([arxiv:1501.07276](http://arxiv.org/abs/1501.07276)).
# * **(Required)** <NAME>., <NAME>., <NAME>., <NAME>. Primitive Variable Solvers for Conservative General Relativistic Magnetohydrodynamics. Astrophysical Journal, 641, 626 (2006) ([astro-ph/0512420](https://arxiv.org/abs/astro-ph/0512420)).
# * **(Recommended)** <NAME>., <NAME>., <NAME>. An efficient shock-capturing central-type scheme for multidimensional relativistic flows - II. Magnetohydrodynamics. A&A 400 (2) 397-413 (2003). DOI: 10.1051/0004-6361:20021641 ([astro-ph/0210618](https://arxiv.org/abs/astro-ph/0210618)).
# <a id='toc'></a>
#
# # Table of Contents
# $$\label{toc}$$
#
# This module is organized as follows
#
# 0. [Step 0](#src_dir): **Source directory creation**
# 1. [Step 1](#introduction): **Introduction**
# 1. [Step 2](#harm_utoprim_2d__c__eos_indep): **EOS independent routines**
# 1. [Step 2.a](#utoprim_2d): *The `Utoprim_2d()` function*
# 1. [Step 2.a.i](#utoprim_2d__bi_and_alpha): Setting $B^{i}_{\rm HARM}$ and $\alpha$
# 1. [Step 2.a.ii](#utoprim_2d__converting): Preparing the variables to be used by the `Utoprim_new_body()` function
# 1. [Step 2.b](#utoprim_new_body): *The `Utoprim_new_body()` function*
# 1. [Step 2.b.i](#utoprim_new_body__basic_quantities): Computing basic quantities
# 1. [Step 2.b.ii](#utoprim_new_body__wlast): Determining $W$ from the previous iteration, $W_{\rm last}$
# 1. [Step 2.b.iii](#utoprim_new_body__vsqlast_and_recompute_w_and_vsq): Compute $v^{2}_{\rm last}$, then update $v^{2}$ and $W$
# 1. [Step 2.b.iv](#utoprim_new_body__compute_prims): Computing the primitive variables
# 1. [Step 2.c](#vsq_calc): *The `vsq_calc()` function*
# 1. [Step 2.d](#x1_of_x0): *The `x1_of_x0()` function*
# 1. [Step 2.e](#validate_x): *The `validate_x()` function*
# 1. [Step 2.f](#general_newton_raphson): *The `general_newton_raphson()` function*
# 1. [Step 2.g](#func_vsq): *The `func_vsq()` function*
# 1. [Step 3](#harm_utoprim_2d__c__eos_dep): **EOS dependent routines**
# 1. [Step 3.a](#pressure_w_vsq): *The `pressure_W_vsq()` function*
# 1. [Step 3.b](#dpdw_calc_vsq): *The `dpdW_calc_vsq()` function*
# 1. [Step 3.c](#dpdvsq_calc): *The `dpdvsq_calc()` function*
# 1. [Step 3.c.i](#dpdvsq_calc__basic_quantities): Setting basic quantities and computing $P_{\rm cold}$ and $\epsilon_{\rm cold}$
# 1. [Step 3.c.ii](#dpdvsq_calc__dpcolddvsq): Computing $\frac{\partial P_{\rm cold}}{\partial\left(v^{2}\right)}$
# 1. [Step 3.c.iii](#dpdvsq_calc__depscolddvsq): Computing $\frac{\partial \epsilon_{\rm cold}}{\partial\left(v^{2}\right)}$
# 1. [Step 3.c.iv](#dpdvsq_calc__dpdvsq): Computing $\frac{\partial p_{\rm hybrid}}{\partial\left(v^{2}\right)}$
# 1. [Step 4](#code_validation): **Code validation**
# 1. [Step 5](#latex_pdf_output): **Output this notebook to $\LaTeX$-formatted PDF file**
# <a id='src_dir'></a>
#
# # Step 0: Source directory creation \[Back to [top](#toc)\]
# $$\label{src_dir}$$
#
# We will now use the [cmdline_helper.py NRPy+ module](Tutorial-Tutorial-cmdline_helper.ipynb) to create the source directory within the `IllinoisGRMHD` NRPy+ directory, if it does not exist yet.
# +
# Step 0: Creation of the IllinoisGRMHD source directory
# Step 0a: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os,sys
nrpy_dir_path = os.path.join("..","..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
# Step 0b: Load up cmdline_helper and create the directory
import cmdline_helper as cmd
IGM_src_dir_path = os.path.join("..","src")
cmd.mkdir(IGM_src_dir_path)
# Step 0c: Create the output file path
outfile_path__harm_utoprim_2d__c = os.path.join(IGM_src_dir_path,"harm_utoprim_2d.c")
# -
# <a id='introduction'></a>
#
# # Step 1: Introduction \[Back to [top](#toc)\]
# $$\label{introduction}$$
#
# Comment on license: `HARM` uses GPL, while `IllinoisGRMHD` uses BSD.
# <a id='harm_utoprim_2d__c__eos_indep'></a>
#
# # Step 2: EOS independent routines \[Back to [top](#toc)\]
# $$\label{harm_utoprim_2d__c__eos_indep}$$
#
# Let us now start documenting the `harm_utoprim_2d.c`, which is a part of the `Harm` code. Our main reference throughout this discussion will be the required citation [Noble *et al.* (2006)](https://arxiv.org/abs/astro-ph/0512420).
#
# We will start with the code's required preamble.
# +
# %%writefile $outfile_path__harm_utoprim_2d__c
#ifndef __HARM_UTOPRIM_2D__C__
#define __HARM_UTOPRIM_2D__C__
/***********************************************************************************
Copyright 2006 <NAME>, <NAME>, <NAME>,
<NAME>, and <NAME>
HARM version 1.0 (released May 1, 2006)
This file is part of HARM. HARM is a program that solves hyperbolic
partial differential equations in conservative form using high-resolution
shock-capturing techniques. This version of HARM has been configured to
solve the relativistic magnetohydrodynamic equations of motion on a
stationary black hole spacetime in Kerr-Schild coordinates to evolve
an accretion disk model.
You are morally obligated to cite the following two papers in his/her
scientific literature that results from use of any part of HARM:
[1] <NAME>., <NAME>., \& Toth, G.\ 2003,
Astrophysical Journal, 589, 444.
[2] <NAME>., <NAME>., <NAME>., \& <NAME>, L. \ 2006,
Astrophysical Journal, 641, 626.
Further, we strongly encourage you to obtain the latest version of
HARM directly from our distribution website:
http://rainman.astro.uiuc.edu/codelib/
HARM is free software; you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 2 of the License, or
(at your option) any later version.
HARM is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with HARM; if not, write to the Free Software
Foundation, Inc., 51 Franklin St, Fifth Floor, Boston, MA 02110-1301 USA
***********************************************************************************/
/*************************************************************************************/
/*************************************************************************************/
/*************************************************************************************
utoprim_2d.c:
---------------
Uses the 2D method:
-- solves for two independent variables (W,v^2) via a 2D
Newton-Raphson method
-- can be used (in principle) with a general equation of state.
-- Currently returns with an error state (>0) if a negative rest-mass
density or internal energy density is calculated. You may want
to change this aspect of the code so that it still calculates the
velocity and so that you can floor the densities. If you want to
change this aspect of the code please comment out the "return(retval)"
statement after "retval = 5;" statement in Utoprim_new_body();
******************************************************************************/
static const int NEWT_DIM=2;
// Declarations:
static CCTK_REAL vsq_calc(CCTK_REAL W,CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D);
static int Utoprim_new_body(eos_struct eos, CCTK_REAL U[], CCTK_REAL gcov[NDIM][NDIM], CCTK_REAL gcon[NDIM][NDIM], CCTK_REAL gdet, CCTK_REAL prim[],long &n_iter);
static int general_newton_raphson( eos_struct eos, CCTK_REAL x[], int n, long &n_iter, void (*funcd) (eos_struct, CCTK_REAL [], CCTK_REAL [], CCTK_REAL [], CCTK_REAL [][NEWT_DIM], CCTK_REAL *, CCTK_REAL *, int,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &),CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D);
static void func_vsq( eos_struct eos, CCTK_REAL [], CCTK_REAL [], CCTK_REAL [], CCTK_REAL [][NEWT_DIM], CCTK_REAL *f, CCTK_REAL *df, int n,CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D);
static CCTK_REAL x1_of_x0(CCTK_REAL x0, CCTK_REAL &Bsq, CCTK_REAL &QdotBsq, CCTK_REAL &Qtsq, CCTK_REAL &Qdotn, CCTK_REAL &D ) ;
static CCTK_REAL pressure_W_vsq(eos_struct eos, CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D) ;
static CCTK_REAL dpdW_calc_vsq(CCTK_REAL W, CCTK_REAL vsq);
static CCTK_REAL dpdvsq_calc(eos_struct eos, CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D);
/**********************************************************************/
/******************************************************************
Utoprim_2d():
-- Driver for new prim. var. solver. The driver just translates
between the two sets of definitions for U and P. The user may
wish to alter the translation as they see fit. Note that Greek
indices run 0,1,2,3 and Latin indices run 1,2,3 (spatial only).
/ rho u^t \
U = | T^t_t + rho u^t | sqrt(-det(g_{\mu\nu}))
| T^t_i |
\ B^i /
/ rho \
P = | uu |
| \tilde{u}^i |
\ B^i /
Arguments:
U[NPR] = conserved variables (current values on input/output);
gcov[NDIM][NDIM] = covariant form of the metric ;
gcon[NDIM][NDIM] = contravariant form of the metric ;
gdet = sqrt( - determinant of the metric) ;
prim[NPR] = primitive variables (guess on input, calculated values on
output if there are no problems);
-- NOTE: for those using this routine for special relativistic MHD and are
unfamiliar with metrics, merely set
gcov = gcon = diag(-1,1,1,1) and gdet = 1. ;
******************************************************************/
# -
# <a id='utoprim_2d'></a>
#
# ## Step 2.a: The `Utoprim_2d()` function \[Back to [top](#toc)\]
# $$\label{utoprim_2d}$$
#
# The `Utoprim_2d()` function is the driver function of the `HARM` conservative-to-primitive algorithm. We remind you from the definitions of primitive and conservative variables used in the code:
#
# $$
# \begin{align}
# \boldsymbol{P}_{\rm HARM} &= \left\{\rho_{b},u,\tilde{u}^{i},B^{i}_{\rm HARM}\right\}\ ,\\
# \boldsymbol{C}_{\rm HARM} &= \left\{\sqrt{-g}\rho_{b}u^{0},\sqrt{-g}\left(T^{0}_{\ 0}+\rho_{b}u^{0}\right),\sqrt{-g}T^{0}_{\ i},\sqrt{-g}B^{i}_{\rm HARM}\right\}\ .
# \end{align}
# $$
#
# <a id='utoprim_2d__bi_and_alpha'></a>
#
# ### Step 2.a.i: Setting $B^{i}_{\rm HARM}$ and $\alpha$ \[Back to [top](#toc)\]
# $$\label{utoprim_2d__bi_and_alpha}$$
#
# Let
#
# $$
# \tilde{B}^{i}_{\rm HARM} \equiv \sqrt{-g}B^{i}_{\rm HARM}\ .
# $$
#
# The code starts by relating
#
# $$
# \boxed{B^{i}_{\rm HARM} = \frac{\tilde{B}^{i}_{\rm HARM}}{\sqrt{-g}}}\ ,
# $$
#
# and setting
#
# $$
# \boxed{\alpha = \frac{1}{\sqrt{-g^{00}}}} \ .
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
int Utoprim_2d(eos_struct eos, CCTK_REAL U[NPR], CCTK_REAL gcov[NDIM][NDIM], CCTK_REAL gcon[NDIM][NDIM],
CCTK_REAL gdet, CCTK_REAL prim[NPR], long &n_iter)
{
CCTK_REAL U_tmp[NPR], prim_tmp[NPR];
int i, ret;
CCTK_REAL alpha;
if( U[0] <= 0. ) {
return(-100);
}
/* First update the primitive B-fields */
for(i = BCON1; i <= BCON3; i++) prim[i] = U[i] / gdet ;
/* Set the geometry variables: */
alpha = 1.0/sqrt(-gcon[0][0]);
# -
# <a id='utoprim_2d__converting'></a>
#
# ### Step 2.a.ii: Preparing the variables to be used by the `Utoprim_new_body()` function \[Back to [top](#toc)\]
# $$\label{utoprim_2d__converting}$$
#
# The conservative-to-primitive algorithm uses the `Utoprim_new_body()` function. However, this function assumes a *different* set of primitive/conservative variables. Thus, we must perform the proper conversion. First, let us ease on the notation a bit by defining:
#
# $$
# \boldsymbol{C} \equiv \left\{\rho_{\star},u_{\star},\tilde{S}_{i},\tilde{B}^{i}_{\rm HARM}\right\} \equiv \left\{\sqrt{-g}\rho_{b}u^{0},\sqrt{-g}\left(T^{0}_{\ 0}+\rho_{b}u^{0}\right),\sqrt{-g}T^{0}_{\ i},\sqrt{-g}B^{i}_{\rm HARM}\right\}\ .
# $$
#
#
#
# Below we list the main differences in the conservative variables:
#
# | `Utoprim_2d()` | `Utoprim_new_body()` |
# |------------------------------------------|---------------------------------------------------------------------------|
# | $\color{blue}{\textbf{Conservatives}}$ | $\color{red}{\textbf{Conservatives}}$ |
# | $\color{blue}{\rho_{\star}}$ | $\color{red}{\frac{\alpha}{\sqrt{-g}}\rho_{\star}}$ |
# | $\color{blue}{u_{\star}}$ | $\color{red}{\frac{\alpha}{\sqrt{-g}}\left(u_{\star}-\rho_{\star}\right)}$|
# | $\color{blue}{\tilde{S}_{i}}$ | $\color{red}{\frac{\alpha}{\sqrt{-g}}\tilde{S}_{i}}$ |
# | $\color{blue}{\tilde{B}^{i}_{\rm HARM}}$ | $\color{red}{\frac{\alpha}{\sqrt{-g}}\tilde{B}^{i}_{\rm HARM}}$ |
#
# These are necessary conversions because while `Utoprim_2d()` assumes the set of conservatives above, `Utoprim_new_body()` assumes
#
# $$
# \left\{\gamma\rho_{b},\alpha T^{0}_{\ \ 0}, \alpha T^{0}_{\ \ i}, \alpha B^{i}_{\rm HARM}\right\}\ .
# $$
#
# Let us first pause to understand the table above. From definition (15) in [Noble *et al.* (2006)](https://arxiv.org/abs/astro-ph/0512420) and the discussion just below it, we know that $\gamma = \alpha u^{0}$. Thus
#
# $$
# \rho_{\star} = \sqrt{-g}\rho_{b}u^{0} = \sqrt{-g}\left(\frac{\gamma}{\alpha}\rho_{b}\right)\implies\boxed{\gamma \rho_{b} = \frac{\alpha}{\sqrt{-g}}\rho_{\star}}\ .
# $$
#
# Then we have
#
# $$
# u_{\star} = \sqrt{-g}\left(T^{0}_{\ \ 0} + \rho_{b}u^{0}\right)= \sqrt{-g}\left(T^{0}_{\ \ 0} + \frac{\rho_{\star}}{\sqrt{-g}}\right) = \sqrt{-g}T^{0}_{\ \ 0} + \rho_{\star} \implies \boxed{\alpha T^{0}_{\ \ 0} = \frac{\alpha}{\sqrt{-g}}\left(u_{\star}-\rho_{\star}\right)}\ .
# $$
#
# The other two relations are more straightforward. We have
#
# $$
# \tilde{S}_{i} = \sqrt{-g}T^{0}_{\ \ i} \implies \boxed{\alpha T^{0}_{\ \ i} = \frac{\alpha}{\sqrt{-g}}\tilde{S}_{i}}\ ,
# $$
#
# and
#
# $$
# \tilde{B}^{i}_{\rm HARM} = \sqrt{-g}B^{i}_{\rm HARM}\implies \boxed{\alpha B^{i}_{\rm HARM} = \frac{\alpha}{\sqrt{-g}}\tilde{B}^{i}_{\rm HARM}}\ .
# $$
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* Transform the CONSERVED variables into the new system */
U_tmp[RHO] = alpha * U[RHO] / gdet;
U_tmp[UU] = alpha * (U[UU] - U[RHO]) / gdet ;
for( i = UTCON1; i <= UTCON3; i++ ) {
U_tmp[i] = alpha * U[i] / gdet ;
}
for( i = BCON1; i <= BCON3; i++ ) {
U_tmp[i] = alpha * U[i] / gdet ;
}
# Below we list the necessary transformations on the primitive variables:
#
# | `Utoprim_2d()` | `Utoprim_new_body()` |
# |-------------------------------------|----------------------------------------|
# | $\color{blue}{\textbf{Primitives}}$ | $\color{red}{\textbf{Primitives}}$ |
# | $\color{blue}{\rho_{b}}$ | $\color{red}{\rho_{b}}$ |
# | $\color{blue}{u}$ | $\color{red}{u}$ |
# | $\color{blue}{\tilde{u}^{i}}$ | $\color{red}{\tilde{u}^{i}}$ |
# | $\color{blue}{B^{i}_{\rm HARM}}$ | $\color{red}{\alpha B^{i}_{\rm HARM}}$ |
#
# After this slight modification we call the `Utoprim_new_body()` function. If it returns without errors, than the variables ${\rm prim\_tmp}$ will now contain the values of the primitives. We then update the ${\rm prim}$ variables with these newly computed values.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* Transform the PRIMITIVE variables into the new system */
for( i = 0; i < BCON1; i++ ) {
prim_tmp[i] = prim[i];
}
for( i = BCON1; i <= BCON3; i++ ) {
prim_tmp[i] = alpha*prim[i];
}
ret = Utoprim_new_body(eos, U_tmp, gcov, gcon, gdet, prim_tmp,n_iter);
/* Transform new primitive variables back if there was no problem : */
if( ret == 0 || ret == 5 || ret==101 ) {
for( i = 0; i < BCON1; i++ ) {
prim[i] = prim_tmp[i];
}
}
return( ret ) ;
}
# -
# <a id='utoprim_new_body'></a>
#
# ## Step 2.b: The `Utoprim_new_body()` function \[Back to [top](#toc)\]
# $$\label{utoprim_new_body}$$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/**********************************************************************************
Utoprim_new_body():
-- Attempt an inversion from U to prim using the initial guess prim.
-- This is the main routine that calculates auxiliary quantities for the
Newton-Raphson routine.
-- assumes that
/ rho gamma \
U = | alpha T^t_\mu |
\ alpha B^i /
/ rho \
prim = | uu |
| \tilde{u}^i |
\ alpha B^i /
return: (i*100 + j) where
i = 0 -> Newton-Raphson solver either was not called (yet or not used)
or returned successfully;
1 -> Newton-Raphson solver did not converge to a solution with the
given tolerances;
2 -> Newton-Raphson procedure encountered a numerical divergence
(occurrence of "nan" or "+/-inf" ;
j = 0 -> success
1 -> failure: some sort of failure in Newton-Raphson;
2 -> failure: utsq<0 w/ initial p[] guess;
3 -> failure: W<0 or W>W_TOO_BIG
4 -> failure: v^2 > 1
5 -> failure: rho,uu <= 0 ;
**********************************************************************************/
static int Utoprim_new_body(eos_struct eos, CCTK_REAL U[NPR], CCTK_REAL gcov[NDIM][NDIM],
CCTK_REAL gcon[NDIM][NDIM], CCTK_REAL gdet, CCTK_REAL prim[NPR], long &n_iter)
{
CCTK_REAL x_2d[NEWT_DIM];
CCTK_REAL QdotB,Bcon[NDIM],Bcov[NDIM],Qcov[NDIM],Qcon[NDIM],ncov[NDIM],ncon[NDIM],Qsq,Qtcon[NDIM];
CCTK_REAL rho0,u,p,w,gammasq,gamma,gtmp,W_last,W,utsq,vsq;
int i,j, n, retval, i_increase;
n = NEWT_DIM ;
// Assume ok initially:
retval = 0;
# -
# <a id='utoprim_new_body__basic_quantities'></a>
#
# ## Step 2.b.i: Computing basic quantities \[Back to [top](#toc)\]
# $$\label{utoprim_new_body__basic_quantities}$$
#
# We start by computing basic quantities from the input variables. Notice that this conservative-to-primitive algorithm does not need to update the magnetic field, thus
#
# $$
# \boxed{B_{\rm prim}^{i} = B_{\rm conserv}^{i}}\ .
# $$
#
# Since they are both equal, we will not distinguish between prim and conserv in what follows. We also set $B^{0} = 0$. Then we define
#
# $$
# \boxed{Q_{\mu} \equiv \alpha T^{0}_{\ \ \mu}}\ .
# $$
#
# From these, the following quantities are then computed:
#
# $$
# \boxed{
# \begin{align}
# B_{i} &= g_{i\mu}B^{\mu}\\
# Q^{\mu} &= g^{\mu\nu}Q_{\nu}\\
# B^{2} &= B_{i}B^{i}\\
# Q\cdot B &= Q_{\mu}B^{\mu}\\
# \left(Q\cdot B\right)^{2} &= \left(Q\cdot B\right)\left(Q\cdot B\right)\\
# n_{\mu} &= \left(-\alpha,0,0,0\right)\\
# n^{\mu} &= g^{\mu\nu}n_{\nu}\\
# \left(Q\cdot n\right) &= Q^{\mu}n_{\mu}\\
# Q^{2} &= Q_{\mu}Q^{\mu}\\
# \tilde{Q}^{2} &= Q^{2} + \left(Q\cdot n\right)\left(Q\cdot n\right)\\
# D &\equiv \gamma \rho_{b}
# \end{align}
# }\ .
# $$
# %%writefile -a $outfile_path__harm_utoprim_2d__c
for(i = BCON1; i <= BCON3; i++) prim[i] = U[i] ;
// Calculate various scalars (Q.B, Q^2, etc) from the conserved variables:
Bcon[0] = 0. ;
for(i=1;i<4;i++) Bcon[i] = U[BCON1+i-1] ;
lower_g(Bcon,gcov,Bcov) ;
for(i=0;i<4;i++) Qcov[i] = U[QCOV0+i] ;
raise_g(Qcov,gcon,Qcon) ;
CCTK_REAL Bsq = 0. ;
for(i=1;i<4;i++) Bsq += Bcon[i]*Bcov[i] ;
QdotB = 0. ;
for(i=0;i<4;i++) QdotB += Qcov[i]*Bcon[i] ;
CCTK_REAL QdotBsq = QdotB*QdotB ;
ncov_calc(gcon,ncov) ;
// FIXME: The exact form of n^{\mu} can be found
// in eq. (2.116) and implementing it
// directly is a lot more efficient than
// performing n^{\mu} = g^{\mu\nu}n_{nu}
raise_g(ncov,gcon,ncon);
CCTK_REAL Qdotn = Qcon[0]*ncov[0] ;
Qsq = 0. ;
for(i=0;i<4;i++) Qsq += Qcov[i]*Qcon[i] ;
CCTK_REAL Qtsq = Qsq + Qdotn*Qdotn ;
CCTK_REAL D = U[RHO] ;
# <a id='utoprim_new_body__wlast'></a>
#
# ## Step 2.b.ii: Determining $W$ from the previous iteration, $W_{\rm last}$ \[Back to [top](#toc)\]
# $$\label{utoprim_new_body__wlast}$$
#
# The quantity $W$ is defined as
#
# $$
# W \equiv w\gamma^{2}\ ,
# $$
#
# where
#
# $$
# \begin{align}
# w &= \rho_{b} + u + p\ ,\\
# \gamma^{2} &= 1 + g_{ij}\tilde{u}^{i}\tilde{u}^{j}\ .
# \end{align}
# $$
#
# Thus the quantities $g_{ij}\tilde{u}^{i}\tilde{u}^{j}$ and then $\gamma^{2}$ and $\gamma$. Thus, by computing $\rho_{b}$ and $p$ from the input variables, i.e. $D$, one can determine $w$ and then compute the value of $W$ from the input values (previous iteration), which we denote by $W_{\rm last}$.
#
# **Dependecy note:** Note that this function depends on the `pressure_rho0_u()` function, which is *not* EOS independent.
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* calculate W from last timestep and use for guess */
utsq = 0. ;
for(i=1;i<4;i++)
for(j=1;j<4;j++) utsq += gcov[i][j]*prim[UTCON1+i-1]*prim[UTCON1+j-1] ;
if( (utsq < 0.) && (fabs(utsq) < 1.0e-13) ) {
utsq = fabs(utsq);
}
if(utsq < 0. || utsq > UTSQ_TOO_BIG) {
retval = 2;
return(retval) ;
}
gammasq = 1. + utsq ;
gamma = sqrt(gammasq);
// Always calculate rho from D and gamma so that using D in EOS remains consistent
// i.e. you don't get positive values for dP/d(vsq) .
rho0 = D / gamma ;
u = prim[UU] ;
p = pressure_rho0_u(eos, rho0,u) ;
w = rho0 + u + p ;
W_last = w*gammasq ;
// Make sure that W is large enough so that v^2 < 1 :
i_increase = 0;
while( (( W_last*W_last*W_last * ( W_last + 2.*Bsq )
- QdotBsq*(2.*W_last + Bsq) ) <= W_last*W_last*(Qtsq-Bsq*Bsq))
&& (i_increase < 10) ) {
W_last *= 10.;
i_increase++;
}
# <a id='utoprim_new_body__vsqlast_and_recompute_w_and_vsq'></a>
#
# ## Step 2.b.iii: Compute $v^{2}_{\rm last}$, then update $v^{2}$ and $W$ \[Back to [top](#toc)\]
# $$\label{utoprim_new_body__vsqlast_and_recompute_w_and_vsq}$$
#
# Then we use equation (28) in [Noble *et al.* (2006)](https://arxiv.org/abs/astro-ph/0512420) to determine $v^{2}$:
#
# $$
# \boxed{v^{2} = \frac{\tilde{Q}^{2}W^{2} + \left(Q\cdot B\right)^{2}\left(B^{2}+2W\right)}{\left(B^{2}+W\right)^{2}W^{2}}}\ .
# $$
#
# This is done by calling the `x1_of_x0()` function, where $x_{0} = W$ and $x_{1} = v^{2}$, which itself calls the `vsq_calc()` function which implements the boxed equation above.
#
# After we have $\left\{W_{\rm last},v^{2}_{\rm last}\right\}$ we use them as the initial guess for the `general_newton_raphson()`, which returns the updated values $\left\{W,v^{2}\right\}$.
#
# All functions mentioned above are documented in this tutorial notebook, so look at the [Table of Contents](#toc) for more information.
# %%writefile -a $outfile_path__harm_utoprim_2d__c
// Calculate W and vsq:
x_2d[0] = fabs( W_last );
x_2d[1] = x1_of_x0( W_last , Bsq,QdotBsq,Qtsq,Qdotn,D) ;
retval = general_newton_raphson( eos, x_2d, n, n_iter, func_vsq, Bsq,QdotBsq,Qtsq,Qdotn,D) ;
W = x_2d[0];
vsq = x_2d[1];
/* Problem with solver, so return denoting error before doing anything further */
if( (retval != 0) || (W == FAIL_VAL) ) {
retval = retval*100+1;
return(retval);
}
else{
if(W <= 0. || W > W_TOO_BIG) {
retval = 3;
return(retval) ;
}
}
// Calculate v^2:
if( vsq >= 1. ) {
vsq = 1.-2.e-16;
//retval = 4;
//return(retval) ;
}
# <a id='utoprim_new_body__compute_prims'></a>
#
# ## Step 2.b.iv: Computing the primitive variables \[Back to [top](#toc)\]
# $$\label{utoprim_new_body__compute_prims}$$
#
# Now that we have $\left\{W,v^{2}\right\}$, we recompute the primitive variables. We start with
#
# $$
# \left\{
# \begin{align}
# \tilde{g} &\equiv \sqrt{1-v^{2}}\\
# \gamma &= \frac{1}{\tilde{g}}
# \end{align}
# \right.
# \implies
# \boxed{\rho_{b} = D\tilde{g}}\ .
# $$
#
# Then, we determine the pressure $p$ using the `pressure_rho0_w()` function and
#
# $$
# w = W\left(1-v^{2}\right)
# \implies
# \boxed{u = w - \left(\rho_{b} + p\right)}\ .
# $$
#
# **Dependecy note:** Note that this function depends on the `pressure_rho0_w()` function, which is *not* EOS independent.
#
# Finally, we can obtain $\tilde{u}^{i}$ using eq. 31 in [Noble *et al.* (2006)](https://arxiv.org/abs/astro-ph/0512420)
#
# $$
# \boxed{
# \tilde{u}^{i} = \frac{\gamma}{\left(W+B^{2}\right)}\left[\tilde{Q}^{i} + \frac{\left(Q\cdot B\right)}{W}B^{i}\right]
# }\ ,
# $$
#
# where
#
# $$
# \tilde{Q}^{i} = Q^{i} + \left(Q\cdot n\right)n^{i}\ .
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
// Recover the primitive variables from the scalars and conserved variables:
gtmp = sqrt(1. - vsq);
gamma = 1./gtmp ;
rho0 = D * gtmp;
w = W * (1. - vsq) ;
p = pressure_rho0_w(eos, rho0,w) ;
u = w - (rho0 + p) ; // u = rho0 eps, w = rho0 h
if( (rho0 <= 0.) || (u <= 0.) ) {
// User may want to handle this case differently, e.g. do NOT return upon
// a negative rho/u, calculate v^i so that rho/u can be floored by other routine:
retval = 5;
//return(retval) ;
}
/*
if(retval==5 && fabs(u)<1e-16) {
u = fabs(u);
CCTK_VInfo(CCTK_THORNSTRING,"%e\t%e\t%e",1.0-w/(rho0 + p),rho0,p);
retval=0;
}
*/
prim[RHO] = rho0 ;
prim[UU] = u ;
for(i=1;i<4;i++) Qtcon[i] = Qcon[i] + ncon[i] * Qdotn;
for(i=1;i<4;i++) prim[UTCON1+i-1] = gamma/(W+Bsq) * ( Qtcon[i] + QdotB*Bcon[i]/W ) ;
/* set field components */
for(i = BCON1; i <= BCON3; i++) prim[i] = U[i] ;
/* done! */
return(retval) ;
}
# -
# <a id='vsq_calc'></a>
#
# ## Step 2.c: The `vsq_calc()` function \[Back to [top](#toc)\]
# $$\label{vsq_calc}$$
#
# This function implements eq. (28) in [Noble *et al.* (2006)](https://arxiv.org/abs/astro-ph/0512420) to determine $v^{2}$:
#
# $$
# \boxed{v^{2} = \frac{\tilde{Q}^{2}W^{2} + \left(Q\cdot B\right)^{2}\left(B^{2}+2W\right)}{\left(B^{2}+W\right)^{2}W^{2}}}\ .
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/****************************************************************************
vsq_calc():
-- evaluate v^2 (spatial, normalized velocity) from
W = \gamma^2 w
****************************************************************************/
static CCTK_REAL vsq_calc(CCTK_REAL W,CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D)
{
CCTK_REAL Wsq,Xsq;
Wsq = W*W ;
Xsq = (Bsq + W) * (Bsq + W);
return( ( Wsq * Qtsq + QdotBsq * (Bsq + 2.*W)) / (Wsq*Xsq) );
}
# -
# <a id='x1_of_x0'></a>
#
# ## Step 2.d: The `x1_of_x0()` function \[Back to [top](#toc)\]
# $$\label{x1_of_x0}$$
#
# This function computes $v^{2}$, as described [above](#vsq_calc), then performs physical checks on $v^{2}$ (i.e. whether or not it is superluminal). This function assumes $W$ is physical.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/********************************************************************
x1_of_x0():
-- calculates v^2 from W with some physical bounds checking;
-- asumes x0 is already physical
-- makes v^2 physical if not;
*********************************************************************/
static CCTK_REAL x1_of_x0(CCTK_REAL x0, CCTK_REAL &Bsq, CCTK_REAL &QdotBsq, CCTK_REAL &Qtsq, CCTK_REAL &Qdotn, CCTK_REAL &D )
{
CCTK_REAL vsq;
CCTK_REAL dv = 1.e-15;
vsq = fabs(vsq_calc(x0,Bsq,QdotBsq,Qtsq,Qdotn,D)) ; // guaranteed to be positive
return( ( vsq > 1. ) ? (1.0 - dv) : vsq );
}
# -
# <a id='validate_x'></a>
#
# ## Step 2.e: The `validate_x()` function \[Back to [top](#toc)\]
# $$\label{validate_x}$$
#
# This function performs physical tests on $\left\{W,v^{2}\right\}$ based on their definitions.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/********************************************************************
validate_x():
-- makes sure that x[0,1] have physical values, based upon
their definitions:
*********************************************************************/
static void validate_x(CCTK_REAL x[2], CCTK_REAL x0[2] )
{
CCTK_REAL dv = 1.e-15;
/* Always take the absolute value of x[0] and check to see if it's too big: */
x[0] = fabs(x[0]);
x[0] = (x[0] > W_TOO_BIG) ? x0[0] : x[0];
x[1] = (x[1] < 0.) ? 0. : x[1]; /* if it's too small */
x[1] = (x[1] > 1.) ? (1. - dv) : x[1]; /* if it's too big */
return;
}
# -
# <a id='general_newton_raphson'></a>
#
# ## Step 2.f: The `general_newton_raphson()` function \[Back to [top](#toc)\]
# $$\label{general_newton_raphson}$$
#
# This function implements a [multidimensional Newton-Raphson method](https://en.wikipedia.org/wiki/Newton%27s_method#k_variables,_k_functions). We will not make the effort of explaining the algorithm exhaustively since it is pretty standard, so we will settle for a summary of the method.
#
# Given a system of $N$ non-linear of equations and $N$ variables, $\left\{\vec{F}\!\left(\vec{x}\right),\vec{x}\right\}$, the Newton-Raphson method attempts to determine the root vector, $\vec{x}_{\star}$, iteratively through
#
# $$
# \begin{align}
# \vec{x}_{n+1} = \vec{x}_{n} - J^{-1}_{F}\!\left(\vec{x}_{n}\right)\vec{F}\!\left(\vec{x}\right)\ ,
# \end{align}
# $$
#
# where $J^{-1}_{F}$ is the Jacobian matrix
#
# $$
# \left(J_{F}\right)^{i}_{\ \ j} = \frac{\partial F^{i}}{\partial x^{j}}\ .
# $$
#
# The index $n$ above is an *iteration* index and $\vec{x}_{n+1}$ represents an improved approximation to $\vec{x}_{\star}$ when compared to $\vec{x}_{n}$.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/************************************************************
general_newton_raphson():
-- performs Newton-Rapshon method on an arbitrary system.
-- inspired in part by Num. Rec.'s routine newt();
*****************************************************************/
static int general_newton_raphson( eos_struct eos, CCTK_REAL x[], int n, long &n_iter,
void (*funcd) (eos_struct, CCTK_REAL [], CCTK_REAL [], CCTK_REAL [],
CCTK_REAL [][NEWT_DIM], CCTK_REAL *,
CCTK_REAL *, int,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &,CCTK_REAL &),CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D)
{
CCTK_REAL f, df, dx[NEWT_DIM], x_old[NEWT_DIM];
CCTK_REAL resid[NEWT_DIM], jac[NEWT_DIM][NEWT_DIM];
CCTK_REAL errx, x_orig[NEWT_DIM];
int id, i_extra, doing_extra;
int keep_iterating;
// Initialize various parameters and variables:
errx = 1. ;
df = f = 1.;
i_extra = doing_extra = 0;
for( id = 0; id < n ; id++) x_old[id] = x_orig[id] = x[id] ;
n_iter = 0;
/* Start the Newton-Raphson iterations : */
keep_iterating = 1;
while( keep_iterating ) {
(*funcd) (eos, x, dx, resid, jac, &f, &df, n, Bsq,QdotBsq,Qtsq,Qdotn,D); /* returns with new dx, f, df */
/* Save old values before calculating the new: */
errx = 0.;
for( id = 0; id < n ; id++) {
x_old[id] = x[id] ;
}
/* Make the newton step: */
for( id = 0; id < n ; id++) {
x[id] += dx[id] ;
}
/****************************************/
/* Calculate the convergence criterion */
/****************************************/
errx = (x[0]==0.) ? fabs(dx[0]) : fabs(dx[0]/x[0]);
/****************************************/
/* Make sure that the new x[] is physical : */
/****************************************/
validate_x( x, x_old ) ;
/*****************************************************************************/
/* If we've reached the tolerance level, then just do a few extra iterations */
/* before stopping */
/*****************************************************************************/
if( (fabs(errx) <= NEWT_TOL) && (doing_extra == 0) && (EXTRA_NEWT_ITER > 0) ) {
doing_extra = 1;
}
if( doing_extra == 1 ) i_extra++ ;
if( ((fabs(errx) <= NEWT_TOL)&&(doing_extra == 0))
|| (i_extra > EXTRA_NEWT_ITER) || (n_iter >= (MAX_NEWT_ITER-1)) ) {
keep_iterating = 0;
}
n_iter++;
} // END of while(keep_iterating)
/* Check for bad untrapped divergences : */
if( (finite(f)==0) || (finite(df)==0) ) {
return(2);
}
if( fabs(errx) > MIN_NEWT_TOL){
//CCTK_VInfo(CCTK_THORNSTRING,"%d %e %e %e %e",n_iter,f,df,errx,MIN_NEWT_TOL);
return(1);
}
if( (fabs(errx) <= MIN_NEWT_TOL) && (fabs(errx) > NEWT_TOL) ){
return(0);
}
if( fabs(errx) <= NEWT_TOL ){
return(0);
}
return(0);
}
# -
# <a id='func_vsq'></a>
#
# ## Step 2.g: The `func_vsq()` function \[Back to [top](#toc)\]
# $$\label{func_vsq}$$
#
# This function is used by the `general_newton_raphson()` function to compute the residuals and stepping. We will again not describe it in great detail since the method itself is relatively straightforward.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/*********************************************************************************
func_vsq():
-- calculates the residuals, and Newton step for general_newton_raphson();
-- for this method, x=W,vsq here;
Arguments:
x = current value of independent var's (on input & output);
dx = Newton-Raphson step (on output);
resid = residuals based on x (on output);
jac = Jacobian matrix based on x (on output);
f = resid.resid/2 (on output)
df = -2*f; (on output)
n = dimension of x[];
*********************************************************************************/
static void func_vsq(eos_struct eos, CCTK_REAL x[], CCTK_REAL dx[], CCTK_REAL resid[],
CCTK_REAL jac[][NEWT_DIM], CCTK_REAL *f, CCTK_REAL *df, int n,
CCTK_REAL &Bsq,CCTK_REAL &QdotBsq,CCTK_REAL &Qtsq,CCTK_REAL &Qdotn,CCTK_REAL &D)
{
CCTK_REAL W, vsq, Wsq, p_tmp, dPdvsq, dPdW;
CCTK_REAL t11;
CCTK_REAL t16;
CCTK_REAL t18;
CCTK_REAL t2;
CCTK_REAL t21;
CCTK_REAL t23;
CCTK_REAL t24;
CCTK_REAL t25;
CCTK_REAL t3;
CCTK_REAL t35;
CCTK_REAL t36;
CCTK_REAL t4;
CCTK_REAL t40;
CCTK_REAL t9;
// vv TESTING vv
// CCTK_REAL D,gtmp,gamma,rho0,w,p,u;
// ^^ TESTING ^^
W = x[0];
vsq = x[1];
Wsq = W*W;
// vv TESTING vv
/*
D = U[RHO] ;
gtmp = sqrt(1. - vsq);
gamma = 1./gtmp ;
rho0 = D * gtmp;
w = W * (1. - vsq) ;
p = pressure_rho0_w(eos, rho0,w) ;
u = w - (rho0 + p) ;
if(u<=0 && 1==1) {
vsq = 0.9999999 * (1.0-(rho0+p)/W);
w = W * (1. - vsq) ;
p = pressure_rho0_w(eos, rho0,w) ;
u = w - (rho0 + p) ;
//CCTK_VInfo(CCTK_THORNSTRING,"%e check",u);
}
*/
// ^^ TESTING ^^
p_tmp = pressure_W_vsq( eos, W, vsq , D);
dPdW = dpdW_calc_vsq( W, vsq );
dPdvsq = dpdvsq_calc( eos, W, vsq, D );
// These expressions were calculated using Mathematica, but made into efficient
// code using Maple. Since we know the analytic form of the equations, we can
// explicitly calculate the Newton-Raphson step:
t2 = -0.5*Bsq+dPdvsq;
t3 = Bsq+W;
t4 = t3*t3;
t9 = 1/Wsq;
t11 = Qtsq-vsq*t4+QdotBsq*(Bsq+2.0*W)*t9;
t16 = QdotBsq*t9;
t18 = -Qdotn-0.5*Bsq*(1.0+vsq)+0.5*t16-W+p_tmp;
t21 = 1/t3;
t23 = 1/W;
t24 = t16*t23;
t25 = -1.0+dPdW-t24;
t35 = t25*t3+(Bsq-2.0*dPdvsq)*(QdotBsq+vsq*Wsq*W)*t9*t23;
t36 = 1/t35;
dx[0] = -(t2*t11+t4*t18)*t21*t36;
t40 = (vsq+t24)*t3;
dx[1] = -(-t25*t11-2.0*t40*t18)*t21*t36;
//detJ = t3*t35; // <- set but not used...
jac[0][0] = -2.0*t40;
jac[0][1] = -t4;
jac[1][0] = t25;
jac[1][1] = t2;
resid[0] = t11;
resid[1] = t18;
*df = -resid[0]*resid[0] - resid[1]*resid[1];
*f = -0.5 * ( *df );
}
# -
# <a id='harm_utoprim_2d__c__eos_dep'></a>
#
# # Step 3: EOS dependent routines \[Back to [top](#toc)\]
# $$\label{harm_utoprim_2d__c__eos_dep}$$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************
**********************************************************************
The following routines specify the equation of state. All routines
above here should be indpendent of EOS. If the user wishes
to use another equation of state, the below functions must be replaced
by equivalent routines based upon the new EOS.
**********************************************************************
**********************************************************************/
# -
# <a id='pressure_w_vsq'></a>
#
# ## Step 3.a: The `pressure_W_vsq()` function \[Back to [top](#toc)\]
# $$\label{pressure_w_vsq}$$
#
# This function computes $p\left(W,v^{2}\right)$. For a $\Gamma$-law equation of state,
#
# $$
# p_{\Gamma} = \left(\Gamma-1\right)u\ ,
# $$
#
# and with the definitions
#
# $$
# \begin{align}
# \gamma^{2} &= \frac{1}{1-v^{2}}\ ,\\
# W &= \gamma^{2}w\ ,\\
# D &= \gamma\rho_{b}\ ,\\
# w &= \rho_{b} + u + p\ ,
# \end{align}
# $$
#
# we have
#
# $$
# \begin{align}
# p_{\Gamma} &= \left(\Gamma-1\right)u\\
# &= \left(\Gamma-1\right)\left(w - \rho_{b} - p_{\Gamma}\right)\\
# &= \left(\Gamma-1\right)\left(\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\right) - \left(\Gamma-1\right)p_{\Gamma}\\
# \implies
# &\boxed{
# p_{\Gamma} = \frac{\left(\Gamma-1\right)}{\Gamma}\left(\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\right)
# }\ .
# \end{align}
# $$
#
# Thus, the pre-PPEOS Patch version of this function was
#
# ```c
# /**********************************************************************/
# /**********************************************************************
# pressure_W_vsq():
#
# -- Gamma-law equation of state;
# -- pressure as a function of W, vsq, and D:
# **********************************************************************/
# static CCTK_REAL pressure_W_vsq(CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D)
# {
#
# CCTK_REAL gtmp;
# gtmp = 1. - vsq;
#
# return( (GAMMA - 1.) * ( W * gtmp - D * sqrt(gtmp) ) / GAMMA );
#
# }
# ```
#
# We are now, however, interested in the hybrid EOS of the form
#
# $$
# p_{\rm hybrid} = P_{\rm cold} + P_{\rm th}\ ,
# $$
#
# where $P_{\rm cold}$ is given by a single or piecewise polytrope EOS,
#
# $$
# P_{\rm cold} = K_{i}\rho_{b}^{\Gamma_{i}}\ ,
# $$
#
# $P_{\rm th}$ accounts for thermal effects and is given by
#
# $$
# P_{\rm th} = \left(\Gamma_{\rm th} - 1\right)\epsilon_{\rm th}\ ,
# $$
#
# and
#
# $$
# \begin{align}
# \epsilon \equiv \frac{u}{\rho_{b}} &= \epsilon_{\rm th}+\epsilon_{\rm cold}\ ,\\
# \epsilon_{\rm cold} &= \int d\rho \frac{P_{\rm cold}(\rho)}{\rho^{2}}\ .
# \end{align}
# $$
#
# We then have
#
# $$
# \begin{align}
# p_{\rm hybrid} &= P_{\rm cold} + P_{\rm th}\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\rho_{b}\epsilon_{\rm th}\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\rho_{b}\left(\epsilon - \epsilon_{\rm cold}\right)\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\left(u - \frac{D}{\gamma}\epsilon_{\rm cold}\right)\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\left(w - \rho_{b} - p_{\rm hybrid} - \frac{D}{\gamma}\epsilon_{\rm cold}\right)\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\left(\frac{W}{\gamma^{2}} - \frac{D}{\gamma} - \frac{D}{\gamma}\epsilon_{\rm cold}\right)-\left(\Gamma_{\rm th}-1\right)p_{\rm hybrid}\\
# &= P_{\rm cold} + \left(\Gamma_{\rm th}-1\right)\left[\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\left(1+\epsilon_{\rm cold}\right)\right]-\left(\Gamma_{\rm th}-1\right)p_{\rm hybrid}\\
# \implies
# &\boxed{ p_{\rm hybrid} = \frac{P_{\rm cold}}{\Gamma_{\rm th}} + \frac{\left(\Gamma_{\rm th}-1\right)}{\Gamma_{\rm th}}\left[\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\left(1+\epsilon_{\rm cold}\right)\right] }
# \end{align}
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/**********************************************************************
pressure_W_vsq():
-- Hybrid single and piecewise polytropic equation of state;
-- pressure as a function of P_cold, eps_cold, W, vsq, and D:
**********************************************************************/
static CCTK_REAL pressure_W_vsq(eos_struct eos, CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D)
{
#ifndef ENABLE_STANDALONE_IGM_C2P_SOLVER
DECLARE_CCTK_PARAMETERS;
#endif
// Compute gamma^{-2} = 1 - v^{2} and gamma^{-1}
CCTK_REAL inv_gammasq = 1.0 - vsq;
CCTK_REAL inv_gamma = sqrt(inv_gammasq);
// Compute rho_b = D / gamma
CCTK_REAL rho_b = D*inv_gamma;
// Compute P_cold and eps_cold
CCTK_REAL P_cold, eps_cold;
compute_P_cold__eps_cold(eos,rho_b, P_cold,eps_cold);
// Compute p = P_{cold} + P_{th}
return( ( P_cold + (Gamma_th - 1.0)*( W*inv_gammasq - D*inv_gamma*( 1.0 + eps_cold ) ) )/Gamma_th );
}
# -
# <a id='dpdw_calc_vsq'></a>
#
# ## Step 3.b: The `dpdW_calc_vsq()` function \[Back to [top](#toc)\]
# $$\label{dpdw_calc_vsq}$$
#
# This function computes $\frac{\partial p\left(W,v^{2}\right)}{\partial W}$. For a $\Gamma$-law equation of state, remember that
#
# $$
# p_{\Gamma} = \frac{\left(\Gamma-1\right)}{\Gamma}\left(\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\right)\ ,
# $$
#
# which then implies
#
# $$
# \boxed{\frac{\partial p_{\Gamma}}{\partial W} = \frac{\Gamma-1}{\Gamma \gamma^{2}} = \frac{\left(\Gamma-1\right)\left(1-v^{2}\right)}{\Gamma}}\ .
# $$
#
# Thus, the pre-PPEOS Patch version of this function was
#
# ```c
# /**********************************************************************/
# /**********************************************************************
# dpdW_calc_vsq():
#
# -- partial derivative of pressure with respect to W;
# **********************************************************************/
# static CCTK_REAL dpdW_calc_vsq(CCTK_REAL W, CCTK_REAL vsq)
# {
#
# return( (GAMMA - 1.) * (1. - vsq) / GAMMA ) ;
#
# }
# ```
#
# For the case of a hybrid, single or piecewise polytropic EOS, we have
#
# $$
# p_{\rm hybrid} = \frac{P_{\rm cold}}{\Gamma_{\rm th}} + \frac{\left(\Gamma_{\rm th}-1\right)}{\Gamma_{\rm th}}\left[\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\left(1+\epsilon_{\rm cold}\right)\right]\ .
# $$
#
# It is important to notice that the cold components of $p_{\rm hybrid}$ are *not* functions of $W$, but instead functions of $D$: $P_{\rm cold} = P_{\rm cold}(\rho_{b}) = P_{\rm cold}(D)$ and $\epsilon_{\rm cold} = \epsilon_{\rm cold}(\rho_{b}) = \epsilon_{\rm cold}(D)$. Thus
#
# $$
# \boxed{\frac{\partial p_{\rm hybrid}}{\partial W} = \frac{\Gamma_{\rm th}-1}{\Gamma_{\rm th} \gamma^{2}} = \frac{\left(\Gamma_{\rm th}-1\right)\left(1-v^{2}\right)}{\Gamma_{\rm th}}}\ .
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/**********************************************************************
dpdW_calc_vsq():
-- partial derivative of pressure with respect to W;
**********************************************************************/
static CCTK_REAL dpdW_calc_vsq(CCTK_REAL W, CCTK_REAL vsq)
{
#ifndef ENABLE_STANDALONE_IGM_C2P_SOLVER
DECLARE_CCTK_PARAMETERS;
#endif
return( (Gamma_th - 1.0) * (1.0 - vsq) / Gamma_th ) ;
}
# -
# <a id='dpdvsq_calc'></a>
#
# ## Step 3.c: The `dpdvsq_calc()` function \[Back to [top](#toc)\]
# $$\label{dpdvsq_calc}$$
#
# This function computes $\frac{\partial p\left(W,v^{2}\right)}{\partial W}$. For a $\Gamma$-law equation of state, remember that
#
# $$
# p_{\Gamma} = \frac{\left(\Gamma-1\right)}{\Gamma}\left(\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\right) = \frac{\left(\Gamma-1\right)}{\Gamma}\left[W\left(1-v^{2}\right) - D\sqrt{1-v^{2}}\right]\ ,
# $$
#
# which then implies
#
# $$
# \boxed{\frac{\partial p_{\Gamma}}{\partial\left(v^{2}\right)} = \frac{\Gamma-1}{\Gamma}\left(\frac{D}{2\sqrt{1-v^{2}}}-W\right)} \ .
# $$
#
# Thus, the pre-PPEOS Patch version of this function was
#
# ```c
# /**********************************************************************/
# /**********************************************************************
# dpdvsq_calc():
#
# -- partial derivative of pressure with respect to vsq
# **********************************************************************/
# static CCTK_REAL dpdvsq_calc(CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D)
# {
# return( (GAMMA - 1.) * ( 0.5 * D / sqrt(1.-vsq) - W ) / GAMMA ) ;
# }
# ```
#
# <a id='dpdvsq_calc__basic_quantities'></a>
#
# ### Step 3.c.i: Setting basic quantities and computing $P_{\rm cold}$ and $\epsilon_{\rm cold}$ \[Back to [top](#toc)\]
# $$\label{dpdvsq_calc__basic_quantities}$$
#
# For the case of a hybrid, single or piecewise polytropic EOS, we have
#
# $$
# p_{\rm hybrid} = \frac{P_{\rm cold}}{\Gamma_{\rm th}} + \frac{\left(\Gamma_{\rm th}-1\right)}{\Gamma_{\rm th}}\left[\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\left(1+\epsilon_{\rm cold}\right)\right]\ .
# $$
#
# Let us thus begin by setting the necessary parameters from the hybrid EOS.
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/**********************************************************************/
/**********************************************************************
dpdvsq_calc():
-- partial derivative of pressure with respect to vsq
**********************************************************************/
static CCTK_REAL dpdvsq_calc(eos_struct eos, CCTK_REAL W, CCTK_REAL vsq, CCTK_REAL &D)
{
// This sets Gamma_th
#ifndef ENABLE_STANDALONE_IGM_C2P_SOLVER
DECLARE_CCTK_PARAMETERS;
#endif
// Set gamma and rho
CCTK_REAL gamma = 1.0/sqrt(1.0 - vsq);
CCTK_REAL rho_b = D/gamma;
// Compute P_cold and eps_cold
CCTK_REAL P_cold, eps_cold;
compute_P_cold__eps_cold(eos,rho_b, P_cold,eps_cold);
// Set basic polytropic quantities
int polytropic_index = find_polytropic_K_and_Gamma_index(eos,rho_b);
CCTK_REAL Gamma_ppoly_tab = eos.Gamma_ppoly_tab[polytropic_index];
# -
# <a id='dpdvsq_calc__dpcolddvsq'></a>
#
# ### Step 3.c.ii: Computing $\frac{\partial P_{\rm cold}}{\partial\left(v^{2}\right)}$ \[Back to [top](#toc)\]
# $$\label{dpdvsq_calc__dpcolddvsq}$$
#
# Next, remember that $P_{\rm cold} = P_{\rm cold}(\rho_{b}) = P_{\rm cold}(D,v^{2})$ and also $\epsilon_{\rm cold} = \epsilon_{\rm cold}(D,v^{2})$. Therefore, we must start by finding the derivatives of $P_{\rm cold}$ and $\epsilon_{\rm cold}$ with respect to $v^{2}$.
#
# Let us first notice that
#
# $$
# \frac{\partial\gamma}{\partial\left(v^{2}\right)} = \frac{\partial}{\partial\left(v^{2}\right)}\left[\frac{1}{\sqrt{1-v^{2}}}\right] = \frac{1}{2}\left(1-v^{2}\right)^{-3/2} = \frac{\gamma^{3}}{2}\ .
# $$
#
# Thus, for a general power
#
# $$
# \frac{\partial\gamma^{a}}{\partial\left(v^{2}\right)} = a\gamma^{a-1}\frac{\partial\gamma}{\partial\left(v^{2}\right)} = a\gamma^{a-1}\left(\frac{\gamma^{3}}{2}\right) = \frac{a}{2}\gamma^{a+2}
# $$
#
# Thus we have
#
# $$
# \begin{align}
# \frac{\partial P_{\rm cold}}{\partial \left(v^{2}\right)}
# &= \frac{\partial}{\partial\left(v^{2}\right)}\left(K_{\rm poly}\rho_{b}^{\Gamma_{\rm poly}}\right)\\
# &= \frac{\partial}{\partial\left(v^{2}\right)}\left[K_{\rm poly}\left(\frac{D}{\gamma}\right)^{\Gamma_{\rm poly}}\right]\\
# &= K_{\rm poly}D^{\Gamma_{\rm poly}}\frac{\partial}{\partial\left(v^{2}\right)}\left[\gamma^{-\Gamma_{\rm poly}/2}\right]\\
# &=K_{\rm poly}D^{\Gamma_{\rm poly}}\left[\frac{-\Gamma_{\rm poly}/2}{2}\gamma^{-\Gamma_{\rm poly}/2 + 2}\right]\\
# &=K_{\rm poly}\left(\frac{D}{\gamma}\right)^{\Gamma_{\rm poly}}\gamma^{-\frac{\Gamma_{\rm poly}}{2} + 2 + \Gamma_{\rm poly}}\\
# \implies &\boxed{ \frac{\partial P_{\rm cold}}{\partial \left(v^{2}\right)} = \gamma^{2+\frac{\Gamma_{\rm poly}}{2}}P_{\rm cold}}\ .
# \end{align}
# $$
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* Now we implement the derivative of P_cold with respect
* to v^{2}, given by
* ----------------------------------------------------
* | dP_cold/dvsq = gamma^{2 + Gamma_{poly}/2} P_{cold} |
* ----------------------------------------------------
*/
CCTK_REAL dPcold_dvsq = P_cold * pow(gamma,2.0 + 0.5*Gamma_ppoly_tab);
# <a id='dpdvsq_calc__depscolddvsq'></a>
#
# ### Step 3.c.iii: Computing $\frac{\partial \epsilon_{\rm cold}}{\partial\left(v^{2}\right)}$ \[Back to [top](#toc)\]
# $$\label{dpdvsq_calc__depscolddvsq}$$
#
# Now, obtaining $\epsilon_{\rm cold}$ from $P_{\rm cold}$ requires an integration and, therefore, generates an integration constant. Since we are interested in a *derivative* of $\epsilon_{\rm cold}$, however, we will simply drop the constant altogether. Remember that:
#
# $$
# \epsilon_{\rm cold} = K_{\rm poly}\int d\rho_{b} \rho_{b}^{\Gamma_{\rm poly}-2} = \frac{K_{\rm poly}\rho_{b}^{\Gamma_{\rm poly}-1}}{\Gamma_{\rm poly}-1} = \frac{P_{\rm cold}}{\rho_{b}\left(\Gamma_{\rm poly}-1\right)} = \frac{\gamma P_{\rm cold}}{D\left(\Gamma_{\rm poly}-1\right)}\ .
# $$
#
# Thus
#
# $$
# \begin{align}
# \frac{\partial \epsilon_{\rm cold}}{\partial \left(v^{2}\right)}
# &= \frac{1}{D\left(\Gamma_{\rm poly}-1\right)}\left[\gamma\frac{\partial P_{\rm cold}}{\partial \left(v^{2}\right)} + P_{\rm cold}\frac{\partial\gamma}{\partial \left(v^{2}\right)}\right]\\
# &=\frac{1}{D\left(\Gamma_{\rm poly}-1\right)}\left[\gamma\frac{\partial P_{\rm cold}}{\partial \left(v^{2}\right)} + P_{\rm cold}\left(\frac{\gamma^{3}}{2}\right)\right]\\
# \implies &\boxed{
# \frac{\partial \epsilon_{\rm cold}}{\partial \left(v^{2}\right)} = \frac{\gamma}{D\left(\Gamma_{\rm poly}-1\right)}\left[\frac{\partial P_{\rm cold}}{\partial \left(v^{2}\right)} + \frac{\gamma^{2} P_{\rm cold}}{2}\right]\ .
# }
# \end{align}
# $$
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* Now we implement the derivative of eps_cold with respect
* to v^{2}, given by
* -----------------------------------------------------------------------------------
* | deps_cold/dvsq = gamma/(D*(Gamma_ppoly_tab-1)) * (dP_cold/dvsq + gamma^{2} P_cold / 2) |
* -----------------------------------------------------------------------------------
*/
CCTK_REAL depscold_dvsq = ( gamma/(D*(Gamma_ppoly_tab-1.0)) ) * ( dPcold_dvsq + 0.5*gamma*gamma*P_cold );
# <a id='dpdvsq_calc__dpdvsq'></a>
#
# ### Step 3.c.iv: Computing $\frac{\partial p_{\rm hybrid}}{\partial\left(v^{2}\right)}$ \[Back to [top](#toc)\]
# $$\label{dpdvsq_calc__dpdvsq}$$
#
# Finally, remembering that
#
# $$
# \begin{align}
# p_{\rm hybrid} &= \frac{P_{\rm cold}}{\Gamma_{\rm th}} + \frac{\left(\Gamma_{\rm th}-1\right)}{\Gamma_{\rm th}}\left[\frac{W}{\gamma^{2}} - \frac{D}{\gamma}\left(1+\epsilon_{\rm cold}\right)\right]\ ,\\
# \frac{\partial\gamma^{a}}{\partial\left(v^{2}\right)} &= \frac{a}{2}\gamma^{a+2}\ ,
# \end{align}
# $$
#
# we have
#
# $$
# \boxed{
# \frac{\partial p_{\rm hybrid}}{\partial\left(v^{2}\right)}
# = \frac{1}{\Gamma_{\rm th}}\left\{\frac{\partial P_{\rm cold}}{\partial\left(v^{2}\right)} + \left(\Gamma_{\rm th}-1\right)\left[-W + \frac{D\gamma}{2}\left(1+\epsilon_{\rm cold}\right) - \frac{D}{\gamma}\frac{\partial \epsilon_{\rm cold}}{\partial\left(v^{2}\right)}\right]\right\}\ .
# }
# $$
# +
# %%writefile -a $outfile_path__harm_utoprim_2d__c
/* Now we implement the derivative of p_hybrid with respect
* to v^{2}, given by
* -----------------------------------------------------------------------------
* | dp/dvsq = Gamma_th^{-1}( dP_cold/dvsq |
* | + (Gamma_{th}-1)*(-W |
* | + D gamma (1 + eps_cold)/2 |
* | - (D/gamma) * deps_cold/dvsq) ) |
* -----------------------------------------------------------------------------
*/
return( ( dPcold_dvsq + (Gamma_th-1.0)*( -W + D*gamma*(1+eps_cold)/2.0 - D*depscold_dvsq/gamma ) )/Gamma_th );
}
/******************************************************************************
END OF UTOPRIM_2D.C
******************************************************************************/
#endif
# -
# <a id='code_validation'></a>
#
# # Step 4: Code validation \[Back to [top](#toc)\]
# $$\label{code_validation}$$
#
# First we download the original `IllinoisGRMHD` source code and then compare it to the source code generated by this tutorial notebook.
# +
# Verify if the code generated by this tutorial module
# matches the original IllinoisGRMHD source code
# First download the original IllinoisGRMHD source code
import urllib
from os import path
original_IGM_file_url = "https://bitbucket.org/zach_etienne/wvuthorns/raw/5611b2f0b17135538c9d9d17c7da062abe0401b6/IllinoisGRMHD/src/harm_utoprim_2d.c"
original_IGM_file_name = "harm_utoprim_2d-original.c"
original_IGM_file_path = os.path.join(IGM_src_dir_path,original_IGM_file_name)
# Then download the original IllinoisGRMHD source code
# We try it here in a couple of ways in an attempt to keep
# the code more portable
try:
original_IGM_file_code = urllib.request.urlopen(original_IGM_file_url).read().decode("utf-8")
# Write down the file the original IllinoisGRMHD source code
with open(original_IGM_file_path,"w") as file:
file.write(original_IGM_file_code)
except:
try:
original_IGM_file_code = urllib.urlopen(original_IGM_file_url).read().decode("utf-8")
# Write down the file the original IllinoisGRMHD source code
with open(original_IGM_file_path,"w") as file:
file.write(original_IGM_file_code)
except:
# If all else fails, hope wget does the job
# !wget -O $original_IGM_file_path $original_IGM_file_url
# Perform validation
# Validation__harm_utoprim_2d__c = !diff $original_IGM_file_path $outfile_path__harm_utoprim_2d__c
if Validation__harm_utoprim_2d__c == []:
# If the validation passes, we do not need to store the original IGM source code file
# !rm $original_IGM_file_path
print("Validation test for harm_utoprim_2d.c: PASSED!")
else:
# If the validation fails, we keep the original IGM source code file
print("Validation test for harm_utoprim_2d.c: FAILED!")
# We also print out the difference between the code generated
# in this tutorial module and the original IGM source code
print("Diff:")
for diff_line in Validation__harm_utoprim_2d__c:
print(diff_line)
# -
# <a id='latex_pdf_output'></a>
#
# # Step 5: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
# $$\label{latex_pdf_output}$$
#
# The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
# [Tutorial-IllinoisGRMHD__harm_utoprim_2d.pdf](Tutorial-IllinoisGRMHD__harm_utoprim_2d.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means).
latex_nrpy_style_path = os.path.join(nrpy_dir_path,"latex_nrpy_style.tplx")
# #!jupyter nbconvert --to latex --template $latex_nrpy_style_path --log-level='WARN' Tutorial-IllinoisGRMHD__harm_utoprim_2d.ipynb
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__harm_utoprim_2d.tex
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__harm_utoprim_2d.tex
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__harm_utoprim_2d.tex
# !rm -f Tut*.out Tut*.aux Tut*.log
|
IllinoisGRMHD/doc/Tutorial-IllinoisGRMHD__harm_utoprim_2d.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <!--<badge>--><a href="https://colab.research.google.com/github/huggingface/workshops/blob/main/mlops-world/dynamic-quantization.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a><!--</badge>-->
# # Dynamic Quantization with Hugging Face Optimum
# In this session, you will learn how to apply _dynamic quantization_ to a 🤗 Transformers model. You will quantize a [DistilBERT model](https://huggingface.co/optimum/distilbert-base-uncased-finetuned-banking77) that's been fine-tuned on the [Banking77 dataset](https://huggingface.co/datasets/banking77) for intent classification.
#
# Along the way, you'll learn how to use two open-source libraries:
#
# * [🤗 Optimum](https://github.com/huggingface/optimum): an extension of 🤗 Transformers, which provides a set of performance optimization tools enabling maximum efficiency to train and run models on targeted hardware.
# * [🤗 Evaluate](https://github.com/huggingface/evaluate): a library that makes evaluating and comparing models and reporting their performance easier and more standardized.
#
#
# By the end of this session, you see how quantization with 🤗 Optimum can significantly decrease model latency while keeping almost 100% of the full-precision model.
#
#
# > This tutorial was created and run on a c6i.xlarge AWS EC2 Instance.
# ## Learning objectives
#
# By the end of this session, you will know how to:
#
# * Setup a development environment
# * Convert a 🤗 Transformers model to ONNX for inference
# * Apply dynamic quantization using `ORTQuantizer` from 🤗 Optimum
# * Test inference with the quantized model
# * Evaluate the model performance with 🤗 Evaluate
# * Compare the latency of the quantized model against the original one
# * Push the quantized model to the Hub
# * Load and run inference with a quantized model from the Hub
#
#
# Let's get started! 🚀
# + [markdown] tags=[]
# ## 1. Setup development environment
# -
# Our first step is to install 🤗 Optimum, along with 🤗 Evaluate and some other libraries. Running the following cell will install all the required packages for us including 🤗 Transformer, PyTorch, and ONNX Runtime utilities:
# Remove the mkl-include and mkl dependencies if running on Colab
# %pip install "optimum[onnxruntime]==1.2.2" "evaluate[evaluator]" sklearn mkl-include mkl
# > If you want to run inference on a GPU, you can install 🤗 Optimum with `pip install optimum[onnxruntime-gpu]`.
# While we're at it, let's turn off some of the warnings from the 🤗 Datasets library and the tokenizer:
# +
import datasets
datasets.logging.set_verbosity_error()
# %env TOKENIZERS_PARALLELISM=false
# -
# ## 2. Convert a 🤗 Transformers model to ONNX for inference
# Before we can optimize and quantize our model, we first need to export it to the ONNX format. To do this we will use the `ORTModelForSequenceClassification` class and call the `from_pretrained()` method. This method will download the PyTorch weights from the Hub and export them via the `from_transformers` argument. The model we are using is `optimum/distilbert-base-uncased-finetuned-banking77`, which is a fine-tuned DistilBERT model on the Banking77 dataset achieving an accuracy score of 92.5% and as the feature (task) text-classification:
# +
from pathlib import Path
from optimum.onnxruntime import ORTModelForSequenceClassification
from transformers import AutoTokenizer
model_id = "optimum/distilbert-base-uncased-finetuned-banking77"
dataset_id = "banking77"
onnx_path = Path("onnx")
# load vanilla transformers and convert to onnx
model = ORTModelForSequenceClassification.from_pretrained(
model_id, from_transformers=True
)
tokenizer = AutoTokenizer.from_pretrained(model_id)
# -
# One neat thing about 🤗 Optimum, is that allows you to run ONNX models with the `pipeline()` function from 🤗 Transformers. This means that you get all the pre- and post-processing features for free, without needing to re-implement them for each model! Here's how you can run inference with our vanilla ONNX model:
# +
from transformers import pipeline
vanilla_clf = pipeline("text-classification", model=model, tokenizer=tokenizer)
vanilla_clf("Could you assist me in finding my lost card?")
# -
# This looks good, so let's save the model and tokenizer to disk for later usage:
# save onnx checkpoint and tokenizer
model.save_pretrained(onnx_path)
tokenizer.save_pretrained(onnx_path)
# If we inspect the `onnx` directory where we've saved the model and tokenizer:
# !ls {onnx_path}
# we can see that there's a `model.onnx` file that corresponds to our exported model. Let's now go ahead and optimize this!
# ## 3. Apply dynamic quantization using `ORTQuantizer` from 🤗 Optimum
# To apply quantization in 🤗 Optimum, we do this by:
#
# * Creating an optimizer based on our ONNX model
# * Defining the type of optimizations via a configuration class
# * Exporting the optimized model as a new ONNX file
#
# The following code snippet does these steps for us:
# +
from optimum.onnxruntime import ORTQuantizer
from optimum.onnxruntime.configuration import AutoQuantizationConfig
# create ORTQuantizer and define quantization configuration
dynamic_quantizer = ORTQuantizer.from_pretrained(model_id, feature=model.pipeline_task)
dqconfig = AutoQuantizationConfig.avx512_vnni(is_static=False, per_channel=False)
# apply the quantization configuration to the model
model_quantized_path = dynamic_quantizer.export(
onnx_model_path=onnx_path / "model.onnx",
onnx_quantized_model_output_path=onnx_path / "model-quantized.onnx",
quantization_config=dqconfig,
)
# -
# Here we can see that we've specifed in the configuration the type of execution engine to use with the Intel AVX512-VNNI CPU. If we now take a look at our `onnx` directory:
# !ls {onnx_path}
# we can see we have a new ONNX file called `model-quantized-dynamic.onnx`. Let's do a quick size comparison of the two models:
# +
import os
# get model file size
size = os.path.getsize(onnx_path / "model.onnx") / (1024 * 1024)
quantized_model = os.path.getsize(onnx_path / "model-quantized.onnx") / (1024 * 1024)
print(f"Model file size: {size:.2f} MB")
print(f"Quantized Model file size: {quantized_model:.2f} MB")
# -
# Nice, dynamic quantization has reduced the model size by around a factor of 2! This should allow us to speed up the inference time by a similar factor, so let's now see how we can test the latency of our models.
# ## 4. Test inference with the quantized model
# As we saw earlier, Optimum has built-in support for transformers pipelines. This allows us to leverage the same API that we know from using PyTorch and TensorFlow models. Therefore we can load our quantized model with `ORTModelForSequenceClassification` class and the transformers `pipeline()` function:
# +
model = ORTModelForSequenceClassification.from_pretrained(
onnx_path, file_name="model-quantized.onnx"
)
tokenizer = AutoTokenizer.from_pretrained(onnx_path)
quantized_clf = pipeline("text-classification", model=model, tokenizer=tokenizer)
quantized_clf("Could you assist me in finding my lost card?")
# -
# ## 5. Evaluate the model performance with 🤗 Evaluate
# It is always a good idea to evaluate the performance of your quantized model on a dedicated test set to ensure the optimizations haven't impacted the model too strongly. To evaluate our model, we'll use the handy `evaluator()` function from 🤗 Evaluate. This function is similar to the `pipeline()` function from 🤗 Transformers, in the sense that it handles the evaluation loop for you automatically!
#
# Here's how you can load an evaluator for text classification and feed in the quantized pipeline:
# +
from datasets import load_dataset
from evaluate import evaluator
eval_pipe = evaluator("text-classification")
eval_dataset = load_dataset("banking77", split="test")
label_mapping = model.config.label2id
results = eval_pipe.compute(
model_or_pipeline=quantized_clf,
data=eval_dataset,
metric="accuracy",
input_column="text",
label_column="label",
label_mapping=label_mapping,
strategy="simple",
)
print(results)
# -
# Not bad! The resulting accuracy isn't too far from the original model - let's see how much exactly:
print(f"Vanilla model: 92.5%")
print(f"Quantized model: {results['accuracy']*100:.2f}%")
print(
f"The quantized model achieves {round(results['accuracy']/0.925,4)*100:.2f}% accuracy of the fp32 model"
)
# ## 6. Compare the latency of the quantized model against the original one
# Okay, now let's test the performance (latency) of our quantized model. We are going to use a payload with a sequence length of 128 for the benchmark. To keep it simple, we are going to use a Python loop and calculate the avgerage and p95 latencies for our vanilla model and for the quantized model:
# +
from time import perf_counter
import numpy as np
payload = (
"Hello my name is Philipp. I am getting in touch with you because i didn't get a response from you. What do I need to do to get my new card which I have requested 2 weeks ago? Please help me and answer this email in the next 7 days. Best regards and have a nice weekend "
* 2
)
print(f'Payload sequence length: {len(tokenizer(payload)["input_ids"])}')
def measure_latency(pipe):
latencies = []
# warm up
for _ in range(10):
_ = pipe(payload)
# Timed run
for _ in range(300):
start_time = perf_counter()
_ = pipe(payload)
latency = perf_counter() - start_time
latencies.append(latency)
# Compute run statistics
time_avg_ms = 1000 * np.mean(latencies)
time_std_ms = 1000 * np.std(latencies)
time_p95_ms = 1000 * np.percentile(latencies, 95)
return (
f"P95 latency (ms) - {time_p95_ms}; Average latency (ms) - {time_avg_ms:.2f} +\- {time_std_ms:.2f};",
time_p95_ms,
)
vanilla_model = measure_latency(vanilla_clf)
quantized_model = measure_latency(quantized_clf)
print(f"Vanilla model: {vanilla_model[0]}")
print(f"Quantized model: {quantized_model[0]}")
print(
f"Improvement through quantization: {round(vanilla_model[1]/quantized_model[1],2)}x"
)
# -
# Nice, our model is model is almost two times faster, despite losing little to no accuracy!
# 
# ## 6. Push the quantized model to the Hub
# The Optimum model classes like `ORTModelForSequenceClassification` are integrated with the Hugging Face Model Hub, which means you can not only load model from the Hub, but also push your models to the Hub with the `push_to_hub()` method. That way we can now save our qunatized model on the Hub to be for example used inside our inference API.
#
# We have to make sure that we are also saving the tokenizer as well as the `config.json` to have a good inference experience.
#
# If you haven't logged into the Hub yet you can use the `notebook_login` function to do so:
# +
from huggingface_hub import notebook_login
notebook_login()
# -
# It's then a simple mater of saving our files to a local directory and running the `push_to_hub()` method:
# +
tmp_store_directory = "onnx_hub_repo"
repository_id = "quantized-distilbert-banking77"
model_file_name = "model-quantized.onnx"
model.latest_model_name = model_file_name # workaround for PR #214
model.save_pretrained(tmp_store_directory)
dynamic_quantizer.tokenizer.save_pretrained(tmp_store_directory)
model.push_to_hub(tmp_store_directory, repository_id=repository_id, use_auth_token=True)
# -
# ## 7. Load and run inference from the Hub
# Now that our model is on the Hub, we can use it from anywhere! Here's a demo to show how we can load the model and tokenizer, before passing them to the `pipeline()` function:
# +
model = ORTModelForSequenceClassification.from_pretrained(
"lewtun/quantized-distilbert-banking77"
)
tokenizer = AutoTokenizer.from_pretrained("lewtun/quantized-distilbert-banking77")
remote_clf = pipeline("text-classification", model=model, tokenizer=tokenizer)
remote_clf("Could you assist me in finding my lost card?")
# -
|
mlops-world/dynamic-quantization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ---
#
# _You are currently looking at **version 1.0** of this notebook. To download notebooks and datafiles, as well as get help on Jupyter notebooks in the Coursera platform, visit the [Jupyter Notebook FAQ](https://www.coursera.org/learn/python-text-mining/resources/d9pwm) course resource._
#
# ---
# *Note: Some of the cells in this notebook are computationally expensive. To reduce runtime, this notebook is using a subset of the data.*
# # Case Study: Sentiment Analysis
# ### Data Prep
# +
import pandas as pd
import numpy as np
# Read in the data
df = pd.read_csv('Amazon_Unlocked_Mobile.csv')
# Sample the data to speed up computation
# Comment out this line to match with lecture
df = df.sample(frac=0.1, random_state=10)
df.head()
# +
# Drop missing values
df.dropna(inplace=True)
# Remove any 'neutral' ratings equal to 3
df = df[df['Rating'] != 3]
# Encode 4s and 5s as 1 (rated positively)
# Encode 1s and 2s as 0 (rated poorly)
df['Positively Rated'] = np.where(df['Rating'] > 3, 1, 0)
df.head(10)
# -
# Most ratings are positive
df['Positively Rated'].mean()
# +
from sklearn.model_selection import train_test_split
# Split data into training and test sets
X_train, X_test, y_train, y_test = train_test_split(df['Reviews'],
df['Positively Rated'],
random_state=0)
# -
print('X_train first entry:\n\n', X_train.iloc[0])
print('\n\nX_train shape: ', X_train.shape)
# # CountVectorizer
# +
from sklearn.feature_extraction.text import CountVectorizer
# Fit the CountVectorizer to the training data
vect = CountVectorizer().fit(X_train)
# -
vect.get_feature_names()[::2000]
len(vect.get_feature_names())
# +
# transform the documents in the training data to a document-term matrix
X_train_vectorized = vect.transform(X_train)
X_train_vectorized
# +
from sklearn.linear_model import LogisticRegression
# Train the model
model = LogisticRegression()
model.fit(X_train_vectorized, y_train)
# +
from sklearn.metrics import roc_auc_score
# Predict the transformed test documents
predictions = model.predict(vect.transform(X_test))
print('AUC: ', roc_auc_score(y_test, predictions))
# +
# get the feature names as numpy array
feature_names = np.array(vect.get_feature_names())
# Sort the coefficients from the model
sorted_coef_index = model.coef_[0].argsort()
# Find the 10 smallest and 10 largest coefficients
# The 10 largest coefficients are being indexed using [:-11:-1]
# so the list returned is in order of largest to smallest
print('Smallest Coefs:\n{}\n'.format(feature_names[sorted_coef_index[:10]]))
print('Largest Coefs: \n{}'.format(feature_names[sorted_coef_index[:-11:-1]]))
# -
# # Tfidf
# +
from sklearn.feature_extraction.text import TfidfVectorizer
# Fit the TfidfVectorizer to the training data specifiying a minimum document frequency of 5
vect = TfidfVectorizer(min_df=5).fit(X_train)
len(vect.get_feature_names())
# +
X_train_vectorized = vect.transform(X_train)
model = LogisticRegression()
model.fit(X_train_vectorized, y_train)
predictions = model.predict(vect.transform(X_test))
print('AUC: ', roc_auc_score(y_test, predictions))
# +
feature_names = np.array(vect.get_feature_names())
sorted_tfidf_index = X_train_vectorized.max(0).toarray()[0].argsort()
print('Smallest tfidf:\n{}\n'.format(feature_names[sorted_tfidf_index[:10]]))
print('Largest tfidf: \n{}'.format(feature_names[sorted_tfidf_index[:-11:-1]]))
# +
sorted_coef_index = model.coef_[0].argsort()
print('Smallest Coefs:\n{}\n'.format(feature_names[sorted_coef_index[:10]]))
print('Largest Coefs: \n{}'.format(feature_names[sorted_coef_index[:-11:-1]]))
# -
# These reviews are treated the same by our current model
print(model.predict(vect.transform(['not an issue, phone is working',
'an issue, phone is not working'])))
# # n-grams
# +
# Fit the CountVectorizer to the training data specifiying a minimum
# document frequency of 5 and extracting 1-grams and 2-grams
vect = CountVectorizer(min_df=5, ngram_range=(1,2)).fit(X_train)
X_train_vectorized = vect.transform(X_train)
len(vect.get_feature_names())
# +
model = LogisticRegression()
model.fit(X_train_vectorized, y_train)
predictions = model.predict(vect.transform(X_test))
print('AUC: ', roc_auc_score(y_test, predictions))
# +
feature_names = np.array(vect.get_feature_names())
sorted_coef_index = model.coef_[0].argsort()
print('Smallest Coefs:\n{}\n'.format(feature_names[sorted_coef_index[:10]]))
print('Largest Coefs: \n{}'.format(feature_names[sorted_coef_index[:-11:-1]]))
# -
# These reviews are now correctly identified
print(model.predict(vect.transform(['not an issue, phone is working',
'an issue, phone is not working'])))
|
lab/week3/Module+2+(Python+3).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Changelog
#
# ### Version 18
#
# * Use additional dataset from https://www.kaggle.com/shymammoth/shopee-reviews
# * No longer modify y_train
#
# ### Version 14
#
# * Replace Bag of Words (BoW) with TF-IDF
#
# ### Version 13
#
# * Use NaiveBayes
# * Use Bigram
# * Change all y_train rating 4->5
#
# ### Version 12
#
# * Replace TF-IDF with Bag of Words (BoW)
#
# ### Version 11
#
# * Change replace char & delete remove char
# * Set `min_df=20` for TF-IDF
# * Use SVM (with GridSearchCV)
# * Enable replace/remove char
#
# ### Version 6
#
# * Add Confusion Matrix
# * Set `min_df=5` for TF-IDF
# * Import library used to set SEED
# * Lemmatization for EN & Stemming for ID
# * Disable replace/remove char
# * Revert RandomForestClassifier parameter
#
# ### Version 5
#
# * Change RandomForestClassifier parameter
# * Set SEED
#
# ### Version 4
#
# * Use RandomForestClassifier
# * `min_df=20` for TF-IDF
# * Change generic model function position
#
# ### Version 3
#
# * Fix submission.csv column name
#
# ### Version 2
#
# * Use MultinomialNB
#
# ### Version 1
#
# * Initialize code
# # Library
# !pip install pyenchant pysastrawi
# !wget http://archive.ubuntu.com/ubuntu/pool/main/libr/libreoffice-dictionaries/hunspell-id_6.4.3-1_all.deb
# !dpkg -i hunspell-id_6.4.3-1_all.deb
# !apt update && apt install -y enchant libenchant1c2a hunspell hunspell-en-us libhunspell-1.6-0
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import re
import os
import gc
import random
import numpy as np
import pandas as pd
import sklearn
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
import nltk
import enchant
# -
# !pip freeze > requirements.txt
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
print('Numpy version:', np.__version__)
print('Pandas version:', pd.__version__)
print('Scikit-Learn version:', sklearn.__version__)
print('Matplotlib version:', matplotlib.__version__)
print('Seaborn version:', sns.__version__)
print('NLTK version:', nltk.__version__)
# +
SEED = 42
os.environ['PYTHONHASHSEED']=str(SEED)
random.seed(SEED)
np.random.seed(SEED)
# -
nltk.download('wordnet')
# # Dataset
# !ls -lha /kaggle/input
# !ls -lha /kaggle/input/student-shopee-code-league-sentiment-analysis
df_train = pd.read_csv('/kaggle/input/student-shopee-code-league-sentiment-analysis/train.csv')
df_train.sample(10)
# +
df_train2 = pd.read_csv('/kaggle/input/shopee-reviews/shopee_reviews.csv')
def to_int(r):
try:
return np.int32(r)
except:
return np.nan
df_train2['label'] = df_train2['label'].apply(to_int)
df_train2 = df_train2.dropna()
df_train2['label'] = df_train2['label'].astype(np.int32)
df_train2
# -
df_test = pd.read_csv('/kaggle/input/student-shopee-code-league-sentiment-analysis/test.csv')
df_test.sample(10)
# +
X_train = pd.concat([df_train['review'], df_train2['text']], axis=0)
X_train = X_train.reset_index(drop=True)
y_train = pd.concat([df_train['rating'], df_train2['label']], axis=0)
y_train = y_train.reset_index(drop=True)
X_test = df_test['review']
# -
# # Class weight
# +
rating_count = y_train.value_counts().sort_index().to_list()
total_rating = sum(rating_count)
lowest_rating_count = min(rating_count)
rating_weight = [lowest_rating_count/rc for rc in rating_count]
print(rating_count)
print(total_rating)
print(rating_weight)
# -
class_weight = np.empty((total_rating,))
for i in range(total_rating):
class_weight[i] = rating_weight[y_train[i] - 1]
# # Preprocess
# +
from nltk.stem import WordNetLemmatizer
from Sastrawi.Stemmer.StemmerFactory import StemmerFactory
lemmatizer = WordNetLemmatizer() # for en
factory = StemmerFactory() # for id
stemmer = factory.create_stemmer() # for id
tweet_tokenizer = nltk.tokenize.TweetTokenizer(preserve_case=False, strip_handles=True, reduce_len=True)
eng_dict = enchant.Dict('en')
ind_dict = enchant.Dict('id_ID')
def remove_char(text):
text = re.sub(r'[^a-z ]', ' ', text)
return text
def stem_lemma(tokens):
new_token = []
for token in tokens:
if eng_dict.check(token):
new_token.append(lemmatizer.lemmatize(token))
elif ind_dict.check(token):
new_token.append(stemmer.stem(token))
else:
new_token.append(token)
return new_token
def upper_or_lower(tokens):
new_token = []
for token in tokens:
total_lower = len(re.findall(r'[a-z]',token))
total_upper = len(re.findall(r'[A-Z]',token))
if total_lower == 0 or total_upper == 0:
new_token.append(token)
elif total_lower > total_upper:
new_token.append(token.lower())
else:
new_token.append(token.upper())
return new_token
def preprocess(X):
X = X.apply(tweet_tokenizer.tokenize)
X = X.apply(lambda token: [t for t in token if t != ''])
X = X.apply(upper_or_lower)
X = X.apply(stem_lemma)
# X = X.apply(lambda token: ' '.join(token)) # need to join token because sklearn tf-idf only accept string, not list of string
# X = X.apply(remove_char)
return X
# -
X_train = preprocess(X_train)
X_test = preprocess(X_test)
X_train.sample(10)
# # Word representation
# +
from sklearn.feature_extraction.text import TfidfVectorizer
bow_vectorizer = TfidfVectorizer(lowercase=False, ngram_range=(1,2), analyzer=lambda t:t, min_df=5, sublinear_tf=True)
X_train = bow_vectorizer.fit_transform(X_train)
X_test = bow_vectorizer.transform(X_test)
# -
print(X_train.shape)
print(X_test.shape)
# # Model functions
# +
from sklearn.metrics import classification_report, f1_score, confusion_matrix
def predict(model, X):
y = model.predict(X)
return y
def metrics(y_true, y_pred):
print('F1 Score :', f1_score(y_true, y_pred, average='macro'))
print(classification_report(y_true, y_pred))
cm = confusion_matrix(y_true, y_pred)
cm = pd.DataFrame(cm, [1,2,3,4,5], [1,2,3,4,5])
sns.heatmap(cm, annot=True, cmap="YlGnBu", fmt="d")
plt.show()
# -
# # MultinomialNB
from sklearn.naive_bayes import MultinomialNB
clf = MultinomialNB()
clf.fit(X_train, y_train, class_weight)
y_train_pred = predict(clf, X_train)
metrics(y_train, y_train_pred)
# +
y_test_pred = predict(clf, X_test)
df_submission = pd.concat([df_test['review_id'], pd.Series(y_test_pred, name='rating')], axis=1)
df_submission.to_csv('submission_MultinomialNB.csv', index=False)
df_submission
# -
# # ComplementNB
from sklearn.naive_bayes import ComplementNB
clf = ComplementNB()
clf.fit(X_train, y_train, class_weight)
y_train_pred = predict(clf, X_train)
metrics(y_train, y_train_pred)
# +
y_test_pred = predict(clf, X_test)
df_submission = pd.concat([df_test['review_id'], pd.Series(y_test_pred, name='rating')], axis=1)
df_submission.to_csv('submission_ComplementNB.csv', index=False)
df_submission
# -
# # RandomForestClassifier
# +
# from sklearn.ensemble import RandomForestClassifier
# clf = RandomForestClassifier(random_state=SEED)
# clf.fit(X_train, y_train)
# +
# y_train_pred = predict(clf, X_train)
# metrics(y_train, y_train_pred)
# +
# y_test_pred = predict(clf, X_test)
# df_submission = pd.concat([df_test['review_id'], pd.Series(y_test_pred, name='rating')], axis=1)
# df_submission.to_csv('submission.csv', index=False)
# df_submission
# -
# # SVM
# +
# from sklearn.svm import SVC
# clf = SVC(kernel='rbf', C=1, cache_size=10240)
# clf.fit(X_train, y_train)
# +
# y_train_pred = predict(clf, X_train)
# metrics(y_train, y_train_pred)
# +
# y_test_pred = predict(clf, X_test)
# df_submission = pd.concat([df_test['review_id'], pd.Series(y_test_pred, name='rating')], axis=1)
# df_submission.to_csv('submission.csv', index=False)
# df_submission
|
02c_sklearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: PySpark3
# name: pyspark3kernel
# ---
# # Read and write from Spark to SQL
# A typical big data scenario is large scale ETL in Spark and writing the processed data to SQLServer. The following samples shows
# - reading a HDFS file,
# - some basic processing on it and
# - then processed data to SQL Server table.
#
# Need a database precreated in SQL for this sample. Here we are using database name "MyTestDatabase" that can be created using SQL statements below.
#
# ``` sql
# Create DATABASE MyTestDatabase
# GO
# ```
#
# +
#Read a file and then write it to the SQL table
datafile = "/spark_data/AdultCensusIncome.csv"
df = spark.read.format('csv').options(header='true', inferSchema='true', ignoreLeadingWhiteSpace='true', ignoreTrailingWhiteSpace='true').load(datafile)
df.show(5)
# +
#Process this data. Very simple data cleanup steps. Replacing "-" with "_" in column names
columns_new = [col.replace("-", "_") for col in df.columns]
df = df.toDF(*columns_new)
df.show(5)
# +
#Write from Spark to SQL table using JDBC
print("Use build in JDBC connector to write to SQLServer master instance in Big data ")
servername = "jdbc:sqlserver://mssql-master-pool-0.service-master-pool"
dbname = "MyTestDatabase"
url = servername + ";" + "databaseName=" + dbname + ";"
c = "dbo.AdultCensus"
user = "sa"
password = "****"
print("url is ", url)
try:
df.write \
.format("jdbc") \
.mode("overwrite") \
.option("url", url) \
.option("dbtable", dbtable) \
.option("user", user) \
.option("password", password)\
.save()
except ValueError as error :
print("JDBC Write failed", error)
print("JDBC Write done ")
# +
#Read to Spark from SQL table using JDBC
print("read data from SQL server table ")
jdbcDF = spark.read \
.format("jdbc") \
.option("url", url
) \
.option("dbtable", dbtable) \
.option("user", user) \
.option("password", password) \
.load()
jdbcDF.show(5)
|
samples/features/sql-big-data-cluster/spark/spark_to_sql/spark_to_sql_jdbc.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # USING PYTHON FOR ACCESSING DATABASE VIA SQL QUERIES
# Install ipython-sql
# ! pip install ipython-sql
# Load sql
# + jupyter={"outputs_hidden": false}
# %load_ext sql
# + jupyter={"outputs_hidden": false}
# %sql sqlite://
# -
# ### SQL Syntax
# Create Table
# + jupyter={"outputs_hidden": false} language="sql"
# CREATE TABLE writer (first_name, last_name, year_of_death);
# INSERT INTO writer VALUES ('William', 'Shakespeare', 1616);
# INSERT INTO writer VALUES ('Bertold', 'Brecht', 1956);
# INSERT INTO writer VALUES ('William', 'Brecht', 2020);
# INSERT INTO writer VALUES ('Bertold', 'Shakespeare', 2010);
# + jupyter={"outputs_hidden": false}
# %sql select * from writer
# + jupyter={"outputs_hidden": false} magic_args="writers << select first_name, year_of_death" language="sql"
# from writer
# -
writers
var = 'last_name'
# %sql select * from writer where {var} = 'Brecht'
# + magic_args="select * from writer " language="sql"
# where {var} = 'Brecht'
# -
|
Data Science and Machine Learning/Machine-Learning-In-Python-THOROUGH/PYTHON_SQL/01_Python_SQL_writers.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from collections import defaultdict
import matplotlib.pyplot as plt
import numpy as np
from config import multi_run_results_file_path, MAX_CASE
# -
def plot_results(filename):
list_case = []
list_tau_fixed = []
list_tau_adaptive = []
list_loss = []
list_acc = []
keys = []
keys_adaptive = []
with open(filename) as f:
for line in f:
l = line.replace('\n', '').split(',')
type = l[0]
simulation = l[1]
case = l[2]
tau_fixed = l[3]
loss = l[4]
accuracy = l[5]
tau_adaptive = l[6]
if (simulation != 'Simulation') and (type != 'centralized'):
list_case.append(int(case))
list_tau_fixed.append(int(tau_fixed))
list_loss.append(float(loss))
list_acc.append(float(accuracy))
keys.append((int(case), int(tau_fixed)))
if tau_fixed == '-1':
list_tau_adaptive.append(float(tau_adaptive))
keys_adaptive.append((int(case), int(tau_fixed)))
if type == 'centralized':
list_case.append(case)
list_tau_fixed.append((tau_fixed))
list_loss.append(float(loss))
list_acc.append(float(accuracy))
keys.append((case, tau_fixed))
list_tau_fixed = list(set(list_tau_fixed))
try:
i = list_tau_fixed.index('nan')
del list_tau_fixed[i]
except: # Exception if no centralized result exists
pass
list_tau_fixed = sorted([i for i in list_tau_fixed])
def avg_over_simulations(keys, values, list_ref):
i = iter(keys)
j = iter(values)
k = list(zip(i, j))
intermediate = defaultdict(list)
d = []
for key, value in k:
intermediate[key].append(value)
for key, value in intermediate.items():
d.append((key, sum(value) / len(value)))
d = dict(d)
# Centralized
centralized = d.get(('None', 'nan'), None)
ncase = list(range(0, MAX_CASE))
case = []
for i in range(0, len(ncase)):
case.append([])
for i in range(0, len(ncase)):
for j in range(0, len(list_ref)):
a = d.get((ncase[i], list_ref[j]), '')
case[i].append(a)
return [centralized, case]
loss_centralized, avg_list_loss = avg_over_simulations(keys, list_loss, list_tau_fixed)
accuracy_centralized, avg_list_acc = avg_over_simulations(keys, list_acc, list_tau_fixed)
_, tauAvg = avg_over_simulations(keys_adaptive, list_tau_adaptive, list_tau_fixed)
N_CASES = 4
color_cases = ['blue', 'green', 'red', 'yellow']
fixed_local_it_indexes = [i for i, x in enumerate(list_tau_fixed) if x > 0]
adapt_local_it_indexes = [i for i, x in enumerate(list_tau_fixed) if x == -1]
adapt_thres_local_it_indexes = [i for i, x in enumerate(list_tau_fixed) if x == -2]
xaxis = [list_tau_fixed[i] for i in fixed_local_it_indexes]
single_point = np.ones(len(xaxis))
if len(adapt_thres_local_it_indexes) == 0:
tauAvgIndex = 0
else:
tauAvgIndex = 1 # because -2 is less than -1
plt.figure(1)
for c in range(0, N_CASES):
plt.semilogx(xaxis, [avg_list_loss[c][i] for i in fixed_local_it_indexes], label='Case' + str(c),
color=color_cases[c])
plt.plot(tauAvg[c][tauAvgIndex], ([avg_list_loss[c][i] for i in adapt_local_it_indexes] * single_point)[0],
marker='o', markersize=8, color=color_cases[c])
if loss_centralized is not None:
plt.semilogx(xaxis, loss_centralized * single_point, '--', label='Centralized case', color='black')
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=2, ncol=2, mode="expand", borderaxespad=0.)
plt.xlabel('Value of \\tau')
plt.ylabel('Loss function Value (on Training Data)')
plt.figure(2)
for c in range(0, N_CASES):
plt.semilogx(xaxis, [avg_list_acc[c][i] for i in fixed_local_it_indexes], label='Case' + str(c),
color=color_cases[c])
plt.plot(tauAvg[c][tauAvgIndex], ([avg_list_acc[c][i] for i in adapt_local_it_indexes] * single_point)[0],
marker='o', markersize=8, color=color_cases[c])
if accuracy_centralized is not None:
plt.semilogx(xaxis, accuracy_centralized * single_point, '--', label='Centralized case', color='black')
plt.legend(bbox_to_anchor=(0., 1.02, 1., .102), loc=2, ncol=2, mode="expand", borderaxespad=0.)
plt.xlabel('Value of \\tau')
plt.ylabel('Classification Accuracy (on Testing Data)')
plt.show()
plot_results(multi_run_results_file_path)
plot_results(multi_run_results_file_path)
plot_results(multi_run_results_file_path)
|
notebooks/plots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ___
# # Simulación de escenarios de desescalada con el modelo SIR-D
# ___
#
#
# En este notebook se realiza una simulación de desescalada por edades utilizando el modelo SIR-D para epidemias.
# ## Importo librerías:
from funcs import *
# Semilla aleatoria
np.random.seed(2019)
# Pandas
pd.set_option("display.max_colwidth", 1000)
# Matplotlib
plt.style.use("seaborn-ticks")
plt.rcParams["xtick.direction"] = "in"
plt.rcParams["ytick.direction"] = "in"
plt.rcParams["font.size"] = 11.0
plt.rcParams["figure.figsize"] = (12, 6)
# # Concepto teórico: Modelo SIR-D
# Debido a que estamos midiendo el número de casos fatales y de casos recuperados por separado, podemos utilizar dos variables ("Recuperados" y "Muertes") en lugar de "Recuperados + Muertes" en el modelo matemático.
# ### ¿Qué es el modelo SIR-D?
# * S: Susceptible
# * I: Infectado
# * R: Recuperado
# * D: Muertes
#
# Modelo:
# \begin{align*}
# \mathrm{S} \overset{\beta I}{\longrightarrow}\ & \mathrm{I} \overset{\gamma}{\longrightarrow} \mathrm{R} \\
# & \mathrm{I} \overset{\alpha}{\longrightarrow} \mathrm{D} \\
# \end{align*}
#
# $\alpha$: Tasa de mortalidad [1/min]
# $\beta$: Tasa de contacto efectiva [1/min]
# $\gamma$: Tasa de recuperación [1/min]
#
# Ecuación diferencial ordinaria:
# \begin{align*}
# & \frac{\mathrm{d}S}{\mathrm{d}T}= - N^{-1}\beta S I \\
# & \frac{\mathrm{d}I}{\mathrm{d}T}= N^{-1}\beta S I - (\gamma + \alpha) I \\
# & \frac{\mathrm{d}R}{\mathrm{d}T}= \gamma I \\
# & \frac{\mathrm{d}D}{\mathrm{d}T}= \alpha I \\
# \end{align*}
#
# Donde $N=S+I+R+D$ es la población total, $T$ es el tiempo transcurrido desde la fecha de inicio.
# ### Modelo SIR-D no dimensional
# Set $(S, I, R, D) = N \times (x, y, z, w)$ and $(T, \alpha, \beta, \gamma) = (\tau t, \tau^{-1} \kappa, \tau^{-1} \rho, \tau^{-1} \sigma)$.
#
# Esto resulta en que las ecuaciones diferenciales son:
# \begin{align*}
# & \frac{\mathrm{d}x}{\mathrm{d}t}= - \rho x y \\
# & \frac{\mathrm{d}y}{\mathrm{d}t}= \rho x y - (\sigma + \kappa) y \\
# & \frac{\mathrm{d}z}{\mathrm{d}t}= \sigma y \\
# & \frac{\mathrm{d}w}{\mathrm{d}t}= \kappa y \\
# \end{align*}
#
# Donde $N$ es la población total y $\tau$ es un coeficiente ([min], es un entero para simplificar).
#
# El rango de variables y parámetros:
# \begin{align*}
# & 0 \leq (x, y, z, w, \kappa, \rho, \sigma) \leq 1 \\
# \end{align*}
# \begin{align*}
# & 1\leq \tau \leq 1440 \\
# \end{align*}
#
# El número de reproducción puede definirse como
# \begin{align*}
# R_0 = \rho (\sigma + \kappa)^{-1} = \beta (\gamma + \alpha)^{-1}
# \end{align*}
#
# Valores medios estimados de $R_0$:
# $R_0$ ("R nada") significa "el número medio de infecciones secundarias causadas por un huésped infectado".
# 2.06: Zika en América del Sur, 2015-2016
# 1,51: Ebola en Guinea, 2014
# 1,33: <NAME> en Sudáfrica, 2009
# 3.5 : El SRAS en 2002-2003
# 1,68: <NAME> en EE.UU., 1957
# 3.8 : Ola de otoño de la gripe española de 1918 en Génova
# 1.5 : Ola de primavera de 1918 de la gripe española en Génova
# Primero de todo descargo la pirámide poblacional de España, para saber cuantas personas hay de cada edad en el país. El virus ataca más en edades avanzadas. Los datos de la pirámide poblacional se han obtenido de https://www.populationpyramid.net/es/espa%C3%B1a/2019/.
# Por otro lado, también se ha hecho uso de la tasa de mortalidad por edades obtenido de https://coronavirus-resumen.herokuapp.com/.
#
# <img src='tasa_mortalidad.png'></img>
edades = pd.read_csv('./data/piramide_2019.csv')
poblacion_total = edades['Hombres'].sum() + edades['Mujeres'].sum()
edades[:3]
print(u'La población total en España es de {} personas'.format(poblacion_total))
# ___
# # 1.- Desescalada con apertura total:
# ___
# Por ejemplo, establece $R_0 = 2.5, \kappa=0.005, \rho=0.2$ y los valores iniciales $(x_{(0)}, y_{(0)}, z_{(0)}, w_{(0)}) = (0.999, 0.001, 0, 0)$.
#(numero reproductivo, tasa mortalidad * tau, tasa efectiva contagio * tau)
r0, kappa, rho = (2.5, 0.005, 0.2)
sigma = rho / r0 - kappa
# (susceptibles, infectados, recuperados, fallecidos)
initials = (0.999, 0.001, 0, 0)
display(Markdown(rf"$\kappa = {kappa},\ \rho = {rho},\ \sigma = {sigma}$."))
# Suponemos que el día inicial es el 5 de Mayo de 2020. $\tau=1440$ minutos y abrimos al total de la población $N=46.736.782$.
tau = 1440
dia_inicial = datetime.datetime(2020, 5, 5)
poblacion = poblacion_total
# %%time
df = simulation(SIRD, initials, step_n=200, kappa=kappa, rho=rho, sigma=sigma)
df.tail()
ori_df = pd.DataFrame(
{
"Date": (df["t"] * tau).apply(lambda x: timedelta(minutes=x)) + dia_inicial,
"Group": "Stopping",
"País": "España",
"Province": "-",
"Susceptible": 0,
"Confirmed": 0,
"Infected": (df["y"] * poblacion).astype(np.int64)
}
)
ori_df["Recovered"] = (df["z"] * poblacion).astype(np.int64)
ori_df["Deaths"] = (df["w"] * poblacion).astype(np.int64)
ori_df["Confirmed"] = ori_df[["Infected", "Recovered", "Deaths"]].sum(axis=1)
ori_df["Susceptible"] = poblacion - ori_df["Confirmed"]
ori_df.tail()
line_plot(
ori_df.set_index("Date")[["Susceptible", "Infected", "Recovered", "Deaths"]],
"Modelo SIR-D desconfinando a todos",
h=poblacion,
y_integer=True
)
print(u'El número total de fallecimientos es de: {}'.format(ori_df['Deaths'].max()))
print(u'Fallece un {} % de la población'.format(np.round((ori_df['Deaths'].max()/poblacion)*100,2)))
# # 2.- Desescalada por edades
# ___
# ## 2.1.- Apertura a < 50 años:
# ___
poblacion_menor_50 = edades.loc[edades['Tasa mortalidad']<=0.5][['Hombres', 'Mujeres']].sum().sum()
poblacion_menor_50
# Establecemos $R_0 = 2.5, \kappa=0.0004, \rho=0.2$ y los valores iniciales $(x_{(0)}, y_{(0)}, z_{(0)}, w_{(0)}) = (0.999, 0.001, 0, 0)$.
#(numero reproductivo, tasa mortalidad * tau, tasa efectiva contagio * tau)
r0, kappa, rho = (2.5, 0.0004, 0.2)
sigma = rho / r0 - kappa
# (susceptibles, infectados, recuperados, fallecidos)
initials = (0.999, 0.001, 0, 0)
display(Markdown(rf"$\kappa = {kappa},\ \rho = {rho},\ \sigma = {sigma}$."))
# Suponemos que el día inicial es el 5 de Mayo de 2020. $\tau=1440$ minutos y abrimos a la población de menos de 50 años.
tau = 1440
dia_inicial = datetime.datetime(2020, 5, 5)
poblacion = poblacion_menor_50
# %%time
df = simulation(SIRD, initials, step_n=90, kappa=kappa, rho=rho, sigma=sigma)
df.tail()
ori_df = pd.DataFrame(
{
"Date": (df["t"] * tau).apply(lambda x: timedelta(minutes=x)) + dia_inicial,
"Group": "Stopping",
"País": "España",
"Province": "-",
"Susceptible": 0,
"Confirmed": 0,
"Infected": (df["y"] * poblacion).astype(np.int64)
}
)
ori_df["Recovered"] = (df["z"] * poblacion).astype(np.int64)
ori_df["Deaths"] = (df["w"] * poblacion).astype(np.int64)
ori_df["Confirmed"] = ori_df[["Infected", "Recovered", "Deaths"]].sum(axis=1)
ori_df["Susceptible"] = poblacion - ori_df["Confirmed"]
ori_df.tail()
line_plot(
ori_df.set_index("Date")[["Susceptible", "Infected", "Recovered", "Deaths"]],
"Modelo SIR-D desconfinando por edades -- fase 2, apertura < 50 años",
h=poblacion,
y_integer=True
)
print(u'El número total de fallecimientos es de: {}'.format(ori_df['Deaths'].max()))
print(u'Fallece un {} % de la población'.format(np.round((ori_df['Deaths'].max()/poblacion)*100,2)))
# ## 2.2.- Apertura a >= 50 y <70 años:
# ___
poblacion_mayor_50_menor_70 = edades.loc[(edades['Tasa mortalidad']>1) &
(edades['Tasa mortalidad']<4)][['Hombres', 'Mujeres']].sum().sum()
poblacion_mayor_50_menor_70
condicion_inicial = ori_df.loc[ori_df['Date']==ori_df['Date'].max()]
condicion_inicial
susceptibles = poblacion_mayor_50_menor_70 + condicion_inicial['Susceptible'].values[0]
infectados = condicion_inicial['Infected'].values[0]
recuperados = condicion_inicial['Recovered'].values[0]
fallecidos = condicion_inicial['Deaths'].values[0]
ini_sus = susceptibles/(susceptibles+infectados+recuperados+fallecidos)
ini_inf = infectados/(susceptibles+infectados+recuperados+fallecidos)
ini_recup = recuperados/(susceptibles+infectados+recuperados+fallecidos)
ini_fall = fallecidos/(susceptibles+infectados+recuperados+fallecidos)
ini_sus, ini_inf, ini_recup, ini_fall
# Ahora aumentamos la tasa de mortalidad esperada, ya que el nuevo grupo es más mayor: $R_0 = 2.5, \kappa=0.003, \rho=0.2$.
#(numero reproductivo, tasa mortalidad * tau, tasa efectiva contagio * tau)
r0, kappa, rho = (2.5, 0.003, 0.2)
sigma = rho / r0 - kappa
# (susceptibles, infectados, recuperados, fallecidos)
initials = (ini_sus, ini_inf, ini_recup, ini_fall)
display(Markdown(rf"$\kappa = {kappa},\ \rho = {rho},\ \sigma = {sigma}$."))
# Suponemos que el día inicial es el 3 de Agosto de 2020. $\tau=1440$ minutos y abrimos también a la población de entre 50 y 70 años.
tau = 1440
dia_inicial = datetime.datetime(2020, 8, 3)
poblacion = susceptibles + infectados + recuperados + fallecidos
# %%time
df = simulation(SIRD, initials, step_n=90, kappa=kappa, rho=rho, sigma=sigma)
df.tail()
ori_df = pd.DataFrame(
{
"Date": (df["t"] * tau).apply(lambda x: timedelta(minutes=x)) + dia_inicial,
"Group": "Stopping",
"País": "España",
"Province": "-",
"Susceptible": 0,
"Confirmed": 0,
"Infected": (df["y"] * poblacion).astype(np.int64)
}
)
ori_df["Recovered"] = (df["z"] * poblacion).astype(np.int64)
ori_df["Deaths"] = (df["w"] * poblacion).astype(np.int64)
ori_df["Confirmed"] = ori_df[["Infected", "Recovered", "Deaths"]].sum(axis=1)
ori_df["Susceptible"] = poblacion - ori_df["Confirmed"]
ori_df.tail()
line_plot(
ori_df.set_index("Date")[["Susceptible", "Infected", "Recovered", "Deaths"]],
"Modelo SIR-D desconfinando por edades -- fase 2, apertura < 70 años",
h=poblacion,
y_integer=True
)
print(u'El número total de fallecimientos es de: {}'.format(ori_df['Deaths'].max()))
print(u'Fallece un {} % de la población'.format(np.round((ori_df['Deaths'].max()/poblacion)*100,2)))
# ## 2.3.- Apertura a >= 70:
# ___
poblacion_mayor_70 = edades.loc[(edades['Tasa mortalidad']>4)][['Hombres', 'Mujeres']].sum().sum()
poblacion_mayor_70
condicion_inicial = ori_df.loc[ori_df['Date']==ori_df['Date'].max()]
condicion_inicial
susceptibles = poblacion_mayor_70 + condicion_inicial['Susceptible'].values[0]
infectados = condicion_inicial['Infected'].values[0]
recuperados = condicion_inicial['Recovered'].values[0]
fallecidos = condicion_inicial['Deaths'].values[0]
ini_sus = susceptibles/(susceptibles+infectados+recuperados+fallecidos)
ini_inf = infectados/(susceptibles+infectados+recuperados+fallecidos)
ini_recup = recuperados/(susceptibles+infectados+recuperados+fallecidos)
ini_fall = fallecidos/(susceptibles+infectados+recuperados+fallecidos)
ini_sus, ini_inf, ini_recup, ini_fall
# Volvemos a subir la tasa de mortalidad $R_0 = 2.5, \kappa=0.005, \rho=0.2$.
r0, kappa, rho = (2.5, 0.005, 0.2) #(numero reproductivo, tasa mortalidad * tau, tasa efectiva contagio * tau)
sigma = rho / r0 - kappa
initials = (ini_sus, ini_inf, ini_recup, ini_fall) # (susceptibles, infectados, recuperados, fallecidos)
display(Markdown(rf"$\kappa = {kappa},\ \rho = {rho},\ \sigma = {sigma}$."))
# Suponemos que el día inicial es el 1 de Noviembre de 2020. $\tau=1440$ minutos y abrimos al total de la población.
tau = 1440
dia_inicial = datetime.datetime(2020, 11, 1)
poblacion = susceptibles + infectados + recuperados + fallecidos
# %%time
df = simulation(SIRD, initials, step_n=20, kappa=kappa, rho=rho, sigma=sigma)
df.tail()
ori_df = pd.DataFrame(
{
"Date": (df["t"] * tau).apply(lambda x: timedelta(minutes=x)) + dia_inicial,
"Group": "Stopping",
"País": "España",
"Province": "-",
"Susceptible": 0,
"Confirmed": 0,
"Infected": (df["y"] * poblacion).astype(np.int64)
}
)
ori_df["Recovered"] = (df["z"] * poblacion).astype(np.int64)
ori_df["Deaths"] = (df["w"] * poblacion).astype(np.int64)
ori_df["Confirmed"] = ori_df[["Infected", "Recovered", "Deaths"]].sum(axis=1)
ori_df["Susceptible"] = poblacion - ori_df["Confirmed"]
ori_df.tail()
line_plot(
ori_df.set_index("Date")[["Susceptible", "Infected", "Recovered", "Deaths"]],
"Modelo SIR-D desconfinando por edades -- fase 3, apertura total",
h=poblacion,
y_integer=True
)
print(u'El número total de fallecimientos es de: {}'.format(ori_df['Deaths'].max()))
print(u'Fallece un {} % de la población'.format(np.round((ori_df['Deaths'].max()/poblacion)*100,2)))
|
Escenarios_Covid19_Espania.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="CGq7iPsZyiOD" colab_type="code" colab={}
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import cross_val_score
# + id="IAZrSiqkzcvr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="cbf4e46d-e172-4138-df5e-cbeb4401483a" executionInfo={"status": "ok", "timestamp": 1581602526465, "user_tz": -60, "elapsed": 465, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
# cd "/content/drive/My Drive/Colab Notebooks/dw_matrix"
# + id="O0cfgKh3z_lC" colab_type="code" colab={}
df = pd.read_csv('data/men_shoes.csv', low_memory=False)
# + id="EuHQurF50GkQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b2cd5315-0c23-4263-de3e-9d97f6c3ddb1" executionInfo={"status": "ok", "timestamp": 1581602541359, "user_tz": -60, "elapsed": 548, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.shape
# + id="LcgW5wOn0bA2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="55d4c8a5-ce4d-4f41-850c-3a36f2052027" executionInfo={"status": "ok", "timestamp": 1581602542716, "user_tz": -60, "elapsed": 546, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.columns
# + id="SJt9JK7_0p4_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="ce650494-779d-435f-af24-e98bed64ac2d" executionInfo={"status": "ok", "timestamp": 1581602543327, "user_tz": -60, "elapsed": 758, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
mean_price = np.mean( df['prices_amountmin'])
mean_price
# + id="sC4-ORft04k5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="579356a9-6147-4df1-9ef1-a1ab29181199" executionInfo={"status": "ok", "timestamp": 1581603139523, "user_tz": -60, "elapsed": 628, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
y_true = df['prices_amountmin']
y_pred = [mean_price] * y_true.shape[0]
mean_absolute_error(y_true, y_pred)
# + id="tv8MWPUt1msL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="0d7650ec-e4b8-46c0-8869-43e8b66e74bd" executionInfo={"status": "ok", "timestamp": 1581603200182, "user_tz": -60, "elapsed": 1008, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df['prices_amountmin'].hist(bins=100)
# + id="qmbPp8_O5ZhP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="8b9557df-9326-4b5b-b4ae-ba53904a5f4b" executionInfo={"status": "ok", "timestamp": 1581603323134, "user_tz": -60, "elapsed": 825, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
np.log1p(df['prices_amountmin']).hist(bins=100)
# + id="qZzblCm05jyt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="8edc53d9-facd-44cf-ea63-2c4586bd2d31" executionInfo={"status": "ok", "timestamp": 1581603421550, "user_tz": -60, "elapsed": 538, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
y_true = df['prices_amountmin']
y_pred = [np.median(y_true)] * y_true.shape[0]
mean_absolute_error(y_true, y_pred)
# + id="QcqRmIvz6PrY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="3cccba13-cb63-4455-ced2-76d12f8ecce1" executionInfo={"status": "ok", "timestamp": 1581604050163, "user_tz": -60, "elapsed": 532, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
y_true = df['prices_amountmin']
price_log_mean = np.expm1(np.mean(np.log1p(y_true)))
y_pred = [price_log_mean] * y_true.shape[0]
mean_absolute_error(y_true, y_pred)
# + id="cGotTniT8m9L" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="19f3922a-b69b-4694-c1fb-faec371d9147" executionInfo={"status": "ok", "timestamp": 1581604084379, "user_tz": -60, "elapsed": 476, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.columns
# + id="SUP8KTvo8vl6" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="bb3e1b14-aad8-48ba-b481-78bef646d9b7" executionInfo={"status": "ok", "timestamp": 1581604128034, "user_tz": -60, "elapsed": 606, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.brand.value_counts()
# + id="yfcms5gR831Y" colab_type="code" colab={}
df['brand_cat'] = df['brand'].factorize()[0]
# + id="KPzYjcij9Lcq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="92fcf6f6-7238-43f6-b283-4afa8c38b07c" executionInfo={"status": "ok", "timestamp": 1581604463859, "user_tz": -60, "elapsed": 609, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
feats=['brand_cat']
X =df[feats].values
y = df['prices_amountmin'].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error')
np.mean(scores), np.std(scores)
# + id="87w9DBTB99B3" colab_type="code" colab={}
def run_model(feats):
X =df[feats].values
y = df['prices_amountmin'].values
model = DecisionTreeRegressor(max_depth=5)
scores = cross_val_score(model, X, y, scoring='neg_mean_absolute_error')
return np.mean(scores), np.std(scores)
# + id="_qR9jEvI-9sf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e8fb6a7a-b308-49ec-c6bb-dc566a69fd32" executionInfo={"status": "ok", "timestamp": 1581604692281, "user_tz": -60, "elapsed": 621, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
run_model(['brand_cat'])
# + id="7HP__AnB_DjL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="3aabb1d4-cca3-4e63-f919-274e556a1e56" executionInfo={"status": "ok", "timestamp": 1581604768082, "user_tz": -60, "elapsed": 740, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.manufacturer.value_counts()
# + id="mFMWXHnI_Var" colab_type="code" colab={}
df['manufacturer_cat'] = df['manufacturer'].factorize()[0]
# + id="auGAbtdd_oIM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="aedb714d-eae3-4855-8f0b-0fb40a3bd960" executionInfo={"status": "ok", "timestamp": 1581605235091, "user_tz": -60, "elapsed": 488, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
run_model(['brand_cat', 'manufacturer_cat'])
# + id="6-K8ByV1A3Gd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 185} outputId="d05504c8-48a6-41a9-d181-bd4bc8c82bd8" executionInfo={"status": "ok", "timestamp": 1581605476554, "user_tz": -60, "elapsed": 654, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df.sample()
# + id="tRKM3E0PBQTY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="4aac8c82-051d-4806-f2eb-227327ed7aaa" executionInfo={"status": "ok", "timestamp": 1581605317500, "user_tz": -60, "elapsed": 683, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
df['colors'].value_counts()
# + id="CSf73NsLBXFP" colab_type="code" colab={}
df['colors_cat'] = df['colors'].factorize()[0]
# + id="uxn7cMQcBmiT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="1cee4142-f328-4b3e-9202-653a8048d16f" executionInfo={"status": "ok", "timestamp": 1581605366027, "user_tz": -60, "elapsed": 486, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
run_model(['brand_cat', 'manufacturer_cat', 'colors_cat'])
# + id="SZUiEYR2Bqa-" colab_type="code" colab={}
df['prices_currency_cat'] = df['prices_currency'].factorize()[0]
# + id="fnaLdiWKB5Tm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="4e82e89f-f598-4376-cb93-09a5f0af789c" executionInfo={"status": "ok", "timestamp": 1581605458650, "user_tz": -60, "elapsed": 654, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "13342956792212140438"}}
run_model(['brand_cat', 'manufacturer_cat', 'prices_currency_cat'])
# + id="mz6K0AN_CA_n" colab_type="code" colab={}
|
matrix_one/day4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # System building
# ## Import modules
# +
import warnings
warnings.simplefilter(action='ignore',category=FutureWarning)
import model_openface as mo ## helper module for model build
import helper_module as hm ## helper module with custom functions
import cv2 ## openCV
import os
import numpy as np
import matplotlib.pyplot as plt
import pickle
# %matplotlib inline
original_path = os.getcwd()
# -
# ## Build a predefined model/weights for face embedding ([OpenFace](https://github.com/iwantooxxoox/Keras-OpenFace))
# This may take some time..
model = mo.model_openface()
mo.load_weight_openface(model)
# ## Hyperparams
# If the euclidian distance between faces is <= `face_recog_thresh`, recognize them as the same face. If not, as n/a.
face_recog_thresh = 0.75
# ## Testing on images: what is going to be embedded?
# To build a reliable face database, it is important to consider:
# * input image needs to contain only a single frontal-looking face
# * use `flag='db'` in `detect_face()` --> process images in the gray scale to increase the face detection accuracy
#
#
# **Only the face** is cropped to be embedded.
testing_img_sean = cv2.imread('sean.jpg')
testing_img_sean = cv2.resize(testing_img_sean,(550,750),interpolation=cv2.INTER_AREA)
hm.detect_face(testing_img_sean,flag='db',plot=True)
# ## Database embedding
# * If you are using the prepared Insight embeddings, simply load the provided **'insight_embedding.pkl'**.
# * If you want to create your own embedding database, CREATE a folder named 'image_database' and place your database images there.
# +
####################################################
##### ONLY RUN THIS CELL TO CREATE YOUR OWN DB #####
####################################################
saving_file_name = 'insight_embedding'
database_embeddings = hm.database_face_embedding(model)
registered_name = list(database_embeddings.keys())
print('Current database contains {} images: \n{}'.format(len(database_embeddings),[key.upper() for key in registered_name]))
## save embeddings
pickle.dump(database_embeddings,open(saving_file_name+'.pkl','wb'))
# -
## load embeddings
database_embeddings = pickle.load(open(saving_file_name+'.pkl','rb'))
# ## Model validation
# For validation, used the identical picture stored in the database --> 0 distance from *SEAN* **(model confirmed!)**
#
# About the wrongly-detected blue bounding boxes:
# * This problem is partially because `recog_face` uses `detect_face(flag='new')` --> RGB images are fed.
# * This issue was mainly caused by the performance of OpenCV's `face_cascade.detectMultiScale()`. A better face detection algorithm will solve this problem.
# * `helper_module.py` can be customized not to display these wrongly detected bounding boxes.
hm.recog_face(testing_img_sean,database_embeddings,model,face_recog_thresh=face_recog_thresh,verbose=True)
# ## Face recognition testing on new images!
# Place your own testing images in the 'test' folder!
testing_file_name = 'sean.jpeg'
test_img = hm.load_test_img(testing_file_name)
hm.recog_face(test_img,database_embeddings,model,face_recog_thresh=face_recog_thresh,verbose=True)
|
OpenFace_Workshop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 64-bit
# name: python3
# ---
# ------ Chapter 12 of MLAPP: Generalized Linear Models ------
#
# @author <NAME> / <NAME>
#
# @date 5 nov 2021
# In this demo I will try to re-obtain some distributions by modifying the parameters in the general formula for the Exponential Family Models.
#
# List : Bernoulli, Binomial, Poisson, Exponential, Normal
#
# In every block of code, I re-define the formula of the functions, but the rest of the codes are just duplicated each time. I have to do in this way because what changes in the general exponential family formula is not the value of some parameters, but the form of the functions in the formula. I didn't find another efficient way to modify the form of the functions.
#
# [Reference](https://en.wikipedia.org/wiki/Exponential_family)
# Bernoulli
# +
import numpy as np
import matplotlib.pyplot as plt
# Definition of the formula
x = np.arange(0,1.1,0.05)
h = 1
T = x
def eta(theta):
return np.log(theta/(1-theta))
def A(eta):
return np.log(1+np.exp(eta))
# plot the pdf generated 2 ways
fig, ax = plt.subplots(1, 2)
for p in np.arange(0.2,0.8,0.2):
# FEF
pdf = h * np.exp(np.dot(eta(p),x)-A(eta(p)))
ax[0].plot(x,pdf,'-o')
## original form
pdf2 = p**x*(1-p)**(1-x)
ax[1].plot(x,pdf2,'-o')
plt.show()
# -
# Binomial with time of trials (n) = 50
# +
import numpy as np
import matplotlib.pyplot as plt
import math as m
# Definition of the formula
x_set = np.arange(0,51,1)
n = 40
def h(n,x):
return m.comb(n,x)
def T(x):
return x
def eta(theta):
return np.log(theta/(1-theta))
def A(eta):
return n*np.log(1+np.exp(eta))
pdf = np.zeros(51)
pdf2 = np.zeros(51)
# plot the pdf generated 2 ways
fig, ax = plt.subplots(2, 1)
for p in np.arange(0.1,0.5,0.1):
for x in x_set:
# FEF
pdf[x] = np.dot(h(n,x), np.exp( np.dot(eta(p),x) - A(eta(p)) ) )
## original form
pdf2[x] = m.comb(n,x)*(p**x)*(1-p)**(n-x)
ax[0].plot(x_set,pdf,'o-')
ax[1].plot(x_set,pdf2,'o-')
plt.show()
# -
# Poisson
#
# Notes: The result generated with 2 methods are slightly different. When calculated with the standard formula (second figure), the data is rounded to 0 from the 18th point.
# +
import numpy as np
import matplotlib.pyplot as plt
import math as m
# Definition of the formula
x_set_len = 25
x_set = np.arange(0,x_set_len,1)
# to keep the convention, we replace the \lambda in the formula by p
n = 40
def h(x):
return 1/(m.factorial(x))
def T(x):
return x
def eta(theta):
return np.log(theta)
def A(eta):
return np.exp(eta)
pdf = np.zeros(x_set_len)
pdf2 = np.zeros(x_set_len)
# plot the pdf generated 2 ways
fig, ax = plt.subplots(2, 1)
for p in np.arange(1,16,4):
for x in x_set:
# FEF
pdf[x] = np.dot(h(x), np.exp( np.dot(eta(p),x) - A(eta(p)) ) )
## original form
pdf2[x] = (p**x*np.exp(-p))/(m.factorial(x))
ax[0].plot(x_set,pdf,'o-')
ax[1].plot(x_set,pdf2,'o-')
plt.show()
# -
# Exponential
# +
import numpy as np
import matplotlib.pyplot as plt
import math as m
# Definition of the formula
x_set_len = 5
x_set = np.arange(0,x_set_len,1)
# to keep the convention, we replace the \lambda in the formula by p
n = 40
def h(x):
return 1
def T(x):
return x
def eta(theta):
return -p
def A(eta):
return -np.log(-eta)
pdf = np.zeros(x_set_len)
pdf2 = np.zeros(x_set_len)
# plot the pdf generated 2 ways
fig, ax = plt.subplots(2, 1)
for p in np.arange(0,2,0.5):
for x in x_set:
# FEF
pdf[x] = np.dot(h(x), np.exp( np.dot(eta(p),x) - A(eta(p)) ) )
## original form
pdf2[x] = p * np.exp(-p*x)
ax[0].plot(x_set,pdf,'-o')
ax[1].plot(x_set,pdf2,'-o')
plt.show()
# -
# Normal
#
# For this part I reuse the code of my 1st version of demo. The principal is the same even though the code might seem a big different.
#
# I will rewrite the code in a similar structure in the file GLM_general.ipynb. I did so because the 1st example given in GLM_general.ipynb is the linear regression model. If everything goes write, we should get a pdf of Normal Distribution at the end of that part, because that's part of the hypothesis adopted by the linear regression model.
# +
import numpy as np
import matplotlib.pyplot as plt
def univariate_normal(x, mean, variance):
"""pdf of the univariate normal distribution."""
return ((1. / np.sqrt(2 * np.pi * variance)) *
np.exp(-(x - mean)**2 / (2 * variance)))
# Plot different Univariate Normals
x = np.linspace(-3, 5, num=150)
fig, axs = plt.subplots(1, 2)
# FFE
sigma = 1
mu = 0
Z = np.sqrt(2*np.pi)*np.exp((mu**2)/(2*sigma**2))
N = (1/Z) * np.exp( mu/(sigma**2)*x+ (-1/(2*sigma**2))*x**2)
axs[0].plot(x,N)
sigma = np.sqrt(3)
mu = 2
Z = np.sqrt(2*np.pi)*sigma*np.exp((mu**2)/(2*sigma**2))
N = (1/Z) * np.exp( mu/(sigma**2)*x+ (-1/(2*sigma**2))*x**2)
axs[0].plot(x,N)
sigma = np.sqrt(0.2)
mu = 0
Z = np.sqrt(2*np.pi)*sigma*np.exp((mu**2)/(2*sigma**2))
N = (1/Z) * np.exp( mu/(sigma**2)*x+ (-1/(2*sigma**2))*x**2)
axs[0].plot(x,N)
# original form
axs[1].plot(
x, univariate_normal(x, mean=0, variance=1),
label="$N(0, 1)$",)
axs[1].plot(
x, univariate_normal(x, mean=2, variance=3),
label="$n(2, 3)$")
axs[1].plot(
x, univariate_normal(x, mean=0, variance=0.2),
label="$n(0, 0.2)$")
fig.subplots_adjust(bottom=0.15)
plt.show()
|
ExpFam_general.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + raw_mimetype="text/html" active=""
# <style>
# pre {
# white-space: pre-wrap !important;
# }
# .table-striped > tbody > tr:nth-of-type(odd) {
# background-color: #f9f9f9;
# }
# .table-striped > tbody > tr:nth-of-type(even) {
# background-color: white;
# }
# .table-striped td, .table-striped th, .table-striped tr {
# border: 1px solid black;
# border-collapse: collapse;
# margin: 1em 2em;
# }
# .rendered_html td, .rendered_html th {
# text-align: left;
# vertical-align: middle;
# padding: 4px;
# }
# </style>
#
# -
# <div class="alert alert-info">
#
# **Note:** vaex.ml is under heavy development, consider this document as a sneak preview.
#
# </div>
# # Vaex-ml - Machine Learning
# The `vaex.ml` package brings some machine learning algorithms to vaex. Install it by running `pip install vaex-ml`.
#
# Vaex.ml stays close to the authoritative ML package: scikit-learn. We will first show two examples, KMeans and PCA, to see how they compare and differ, and what the gain is in performance.
import vaex.ml.cluster
import vaex.ml.datasets
import numpy as np
# %matplotlib inline
# We use the well known [iris flower dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set), a classical for machine learning.
df = vaex.ml.datasets.load_iris()
df.scatter(df.petal_width, df.petal_length, c_expr=df.class_)
df
# ## KMeans
# We use two features to do a KMeans, and roughly put the two features on the same scale by a simple division. We then construct a KMeans object, quite similar to what you would do in [sklearn](http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html), and fit it.
features = ['petal_width/2', 'petal_length/5']
init = [[0, 1/5], [1.2/2, 4/5], [2.5/2, 6/5]] #
kmeans = vaex.ml.cluster.KMeans(features=features, init=init, verbose=True)
kmeans.fit(df)
# We now transform the original DataFrame, similar to sklearn. However, we now end up with a new DataFrame, which contains an extra column (prediction_kmeans).
df_predict = kmeans.transform(df)
df_predict
# Although this column is special, it is actually a virtual column, it does not use up any memory and will be computed on the fly when needed, saving us precious ram. Note that the other columns reference the original data as well, so this new DataFrame (ds_predict) almost takes up no memory at all, which is ideal for very large datasets, and quite different from what sklearn will do.
df_predict.virtual_columns['prediction_kmeans']
# By making a simple scatter plot we can see the KMeans does a pretty good job.
# +
import matplotlib.pylab as plt
fig, ax = plt.subplots(1, 2, figsize=(12,5))
plt.sca(ax[0])
plt.title('original classes')
df.scatter(df.petal_width, df.petal_length, c_expr=df.class_)
plt.sca(ax[1])
plt.title('predicted classes')
df_predict.scatter(df_predict.petal_width, df_predict.petal_length, c_expr=df_predict.prediction_kmeans)
# -
# ## KMeans benchmark
# To demonstrate the performance and scaling of vaex, we continue with a special version of the iris dataset that has $\sim10^7$ rows, by repeating the rows many times.
df = vaex.ml.datasets.load_iris_1e7()
# We now use random initial conditions, and execute 10 runs in parallel (n_init), for a maximum of 5 iterations and benchmark it.
features = ['petal_width/2', 'petal_length/5']
kmeans = vaex.ml.cluster.KMeans(features=features, n_clusters=3, init='random', random_state=1,
max_iter=5, verbose=True, n_init=10)
# %%timeit -n1 -r1 -o
kmeans.fit(df)
time_vaex = _
# We now do the same using sklearn.
from sklearn.cluster import KMeans
kmeans_sk = kmeans = KMeans(n_clusters=3, init='random', max_iter=5, verbose=True, algorithm='full', n_jobs=-1,
precompute_distances=False, n_init=10)
# Doing an unfortunate memory copy
X = np.array(df[features])
# %%timeit -n1 -r1 -o
kmeans_sk.fit(X)
time_sklearn = _
# We see that vaex is quite fast:
print('vaex is approx', time_sklearn.best / time_vaex.best, 'times faster for KMeans')
# But also, sklean will need to copy the data, while vaex will be very careful not to do unnecessary copies, and minimal amounts of passes of the data (Out-of-core). Therefore vaex will happily scale to massive datasets, while with sklearn you will be limited to the size of the RAM.
# ## PCA Benchmark
# We now continue with benchmarking a PCA on 4 features:
features = [k.expression for k in [df.col.petal_width, df.col.petal_length, df.col.sepal_width, df.col.sepal_length]]
pca = df.ml.pca(features=features)
# %%timeit -n1 -r3 -o
pca = df.ml.pca(features=features)
time_vaex = _
# Since sklearn takes too much memory with this dataset, we only use 10% for sklearn, and correct later.
# on my laptop this takes too much memory with sklearn, use only a subset
factor = 0.1
df.set_active_fraction(factor)
len(df)
from sklearn.decomposition import PCA
pca_sk = PCA(n_components=2, random_state=33, svd_solver='full', whiten=False)
X = np.array(df.trim()[features])
# %%timeit -n1 -r3 -o
pca_sk.fit(X)
time_sklearn = _
print('vaex is approx', time_sklearn.best / time_vaex.best / factor, 'times faster for a PCA')
# Again we see that vaex not only will outperform sklearn, but more importantly it will scale to much larger datasets.
#
# ## A billion row PCA
# We now run a PCA on **a billion rows**.
df_big = vaex.ml.datasets.load_iris_1e9()
# %%timeit -n1 -r2 -o
pca = df_big.ml.pca(features=features)
# Note the although this dataset is $10\times$ larger, it takes more than $10\times$ to execute. This is because this dataset did not fit into memory this time, and is limited to the harddrive speed. But note that it *possible* to actually run it, instead of giving a MemoryError!
# ## XGBoost
# This example shows integration with xgboost, this is work in progress.
import vaex.ml.xgboost
df = vaex.ml.datasets.load_iris()
features = [k.expression for k in [df.col.petal_width, df.col.petal_length, df.col.sepal_width, df.col.sepal_length]]
df_train, df_test = df.ml.train_test_split()
param = {
'max_depth': 3, # the maximum depth of each tree
'eta': 0.3, # the training step for each iteration
'silent': 1, # logging mode - quiet
'objective': 'multi:softmax', # error evaluation for multiclass training
'num_class': 3} # the number of classes that exist in this datset
xgmodel = vaex.ml.xgboost.XGBModel(features=features, num_round=10, param=param)
xgmodel.fit(df_train, df_train.class_, copy=True)
df_predict = xgmodel.transform(df_test)
df_predict
# +
import matplotlib.pylab as plt
fig, ax = plt.subplots(1, 2, figsize=(12,5))
plt.sca(ax[0])
plt.title('original classes')
df_predict.scatter(df_predict.petal_width, df_predict.petal_length, c_expr=df_predict.class_)
plt.sca(ax[1])
plt.title('predicted classes')
df_predict.scatter(df_predict.petal_width, df_predict.petal_length, c_expr=df_predict.xgboost_prediction)
# -
# ## One hot encoding
# Shortly showing one hot encoding
encoder = df.ml_one_hot_encoder([df.col.class_])
df_encoded = encoder.transform(df)
df_encoded
|
docs/source/ml.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from basicMod import showDfInfo
import pandas as pd
import pandasgui as pdg
dfTrain = pd.read_csv('./titanic_DataSet/train.csv')
showDfInfo(dfTrain)
dfTrain['Fare'] = dfTrain['Fare'].astype(float)
dfTrain['Survived'] = dfTrain['Survived'].astype(int)
dfTest = pd.read_csv('./titanic_DataSet/test.csv')
showDfInfo(dfTest)
# ## <font color='blue'>01.Explore Data for Training set</font>
pdg.show(dfTrain)
# ----
# ## <font color='blue'>Compare with Train and Test</font>
# # ========== Test Zone ==========
|
2021-02-07_Class Examples/20210206_PandasGUI Examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction to MicroQiskit
#
# *This workshop covers topics from the [Introduction to Python and Qiskit]() section of the textbook [Learn Quantum Computation using Qiskit](https://community.qiskit.org).*
#
# Qiskit is the largest, most feature rich and most well developed framework for quantum computing. This is obviously a good thing in general, but it can be overwhelming for those getting started.
#
# For that reason, we have created MicroQiskit: the smallest, least feature rich and least developed framework for quantum computing! It has everything you need to get to know single and two qubit circuits, and do so with the same syntax as Qiskit. By mastering MicroQiskit, you'll be well on your way to mastering Qiskit.
#
# MicroQiskit has also been designed to be able to work on microcontroller devices. This includes the PewPew, as well as many other devices used for education and hobbies. It is compatible with MicroPython and CircuitPython, both of which are minimal implementations of Python designed to run on microcontrollers. Many Python packages have minimal versions made to be compatible with these implementations. MicroQiskit is similarly the MicroPython-compatible version of Qiskit.
#
# ## Basics of MicroQiskit (and Qiskit)
#
# ### Quantum Circuits
#
# The heart of quantum computing is the circuit. In Qiskit and MicroQiskit, our circuit is represented by a Python object, known as the `QuantumCircuit` object. The following line creates such an object, and names it `qc`.
#
# ```python
# qc = QuantumCircuit(n,n)
# ```
#
# Here the first `n` is the number of qubits, and the second `n` is the number of output bits. In Qiskit, these can be different numbers in general. However, they are often simply chosen to be equal. MicroQiskit restricts us to this standard case. MicroQiskit also retricts to `n` being either 1 or 2, as it cannot similate larger numbers of qubits. Many interesting things can be done with just two qubits, so this will not hamper us. However, Qiskit supports any number of qubits.
#
# ### Quantum gates
#
# The gates that can be added to a quantum circuit are
#
# ```python
# qc.x(j)
# qc.rx(theta,j)
# qc.h(j)
# qc.cx(j,k)
# ```
#
# Here `j` is the number representing the qubit: `0` for a single qubit circuit, or `0` and `1` for a two qubit circuit.
#
# Other gates are also available in Qiskit. However, since everything can be built out of the basic operations we have here, nothing is lost in MicroQiskit by restricting to them.
#
# ### Measurements
#
# Measurement is the process of extracting an output from a qubit. These outputs take the form of normal bits. Measurement can be performed using the command
#
# ```python
# qc.measure(j,j)
# ```
#
# This measures qubit `j` and places the result in output bit `j`. In Qiskit, these two arguments do not neccessarily need to be equal: the labelling of a qubit and the bit used for its output can be different. However, they are often chosen to be the same. MicroQiskit only supports this standard case, so the two arguments must be equal.
#
# Measurements in Qiskit can be placed at any point in the circuit. The simulators of Qiskit will quite happily run such quantum programs. However, when running on current prototype quantum hardware, the only supported case is to have all measurements made at the very end. This is also only case supported by MicroQiskit, so no gates for a given qubit should be placed after its measurement.
#
# ### Simulating a Circuit
#
# In standard Qiskit, circuits can be run on real quantum devices as well as various simulators. The procedure for running circuits and extracting results in Qiskit reflects the need to handle all these various use cases.
#
# In MicroQiskit, there is only one way to run a circuit: to simulate it on the MicroQiskit simulator. The process is implemented by a single function, called `simulate()`. This has an argument `shots`, which determines how many times you wish to repeatedly run the circuit to extract statistics. It also has an argument `get` which determines the form in which the results are given.
#
# For example, to get a list of `shots=5` output bit strings, use
#
# ```python
# m = simulate(qc,shots=5,get='memory')
# ```
#
# The result will look something like `m = ['11','00','01','01','00']`.
#
# To get a dictionary detailing how many of `shots=1024` samples result in each output, use
#
# ```python
# c = simulate(qc,shots=1024,get='counts')
# ```
#
# The result will look something like `c = {'00':240,'01':275,'10':212,'11':299}`.
#
# To get a state vector describing the state at output, no measurement gates or output bits are required. You are therefore able to initialize the circuit with
#
# ```python
# qc = QuantumCircuit(n)
# ```
#
# The state vector is extracted with
#
# ```python
# state = simulate(qc,shots=1024,get='statevector')
# ```
#
# The Qiskit equivalents of the execute commands listed above are
#
# ```python
# m = execute(qc,shots=5).result().get_memory()
# c = execute(qc,shots=1024).result().get_counts()
# state = execute(qc,shots=1024).result().get_statevector()
# ```
#
# Note also that the format for complex numbers in the statevector is different in MicroQiskit. A complex number of the form $a + i b$ is represented by the list `[a,b]` in MicroQiskit, rather than `a + bj` as in Qiskit. A statevector composed only of real numbers can be initialized with a list of real numbers as normal.
#
# ## Using MicroQiskit
#
# We will now use our quantum tools on the PewPew. To do this, take the file named 'MicroQiskit.py', included in this folder, and place it on your PewPew. You will then be able to run the program below. If you are using an emulator, make sure that 'MicroQiskit.py' is in the same folder as the 'Pew.py' file.
#
# The following program shows a simple example of using MicroQiskit. It is largely the same as the program in the last section. The main difference is that it no longer checks for user input inside the loop, but instead executes a two qubit quantum program designed to randomly generate random outputs (details regarding how this works will follow in later workshops).
#
# ```python
# qc = QuantumCircuit(2,2) # create an empty circuit with two qubits and two output bits
# # put a hadamard on both qubits
# qc.h(0)
# qc.h(1)
# # put a measurement on both qubit, whose results go to the corresponding output bit
# qc.measure(0,0)
# qc.measure(1,1)
# ```
#
# The results are extracted using `shots=1` and `get='memory'`.
#
# ```python
# m = simulate(qc,shots=1,get='memory')
# ```
#
# The result contained in `m` is a list containing a single result. This will one of the four possible two-bit outputs: `'00'`, `'01'`, `'10'` and `'11'`. This is accessed by looking at the first (and only) element of the list `m` using `m[0]`.
#
# These four outputs can be interpreted as the binary representations of the numbers 0, 1 , 2 and 3. Since these are exactly the allowed values for the brightness on a PewPew, let's convert them to an integer using `int(m[0],2)` and use them as the brightness of pixel (1,2). This replaces the user input from the previous program.
# %matplotlib notebook
# +
import pew # setting up tools for the pewpew
from microqiskit import QuantumCircuit, simulate # setting up tools for quantum
pew.init() # initialize the game engine...
screen = pew.Pix() # ...and the screen
qc = QuantumCircuit(2,2) # create an empty circuit with two qubits and two output bits
# put a hadamard on both qubits
qc.h(0)
qc.h(1)
# put a measurement on both qubit, whose results go to the corresponding output bit
qc.measure(0,0)
qc.measure(1,1)
# loop over the square centered on (1,2) and make all dim
(X,Y) = (1,2)
for dX in [+1,0,-1]:
for dY in [+1,0,-1]:
screen.pixel(X+dX,Y+dY,2)
screen.pixel(X,Y,0) # turn off pixel at (1,2)
while True: # loop which checks for user input and responds
# execute the circuit and get a single sample of memory
m = simulate(qc,shots=1,get='memory')
# the resulting bit string m[0] is converted to the corresponding number and used as brightness
screen.pixel(X,Y,int(m[0],2))
pew.show(screen) # update screen to display the above changes
pew.tick(1/6) # pause for a sixth of a second
# -
# Another way to display the outputs `'00'`, `'01'`, `'10'` and `'11'` is to use two squares: one for each bit value. We can turn the pixel at (1,2) on and off to show whether the left bit is `1` or `0`, and do the same for the right bit and pixel (6,2). The left bit value is accessed using `m[0][0]`, and the right bit value using `m[0][1]`.
# +
import pew # setting up tools for the pewpew
from microqiskit import QuantumCircuit, simulate # setting up tools for quantum
pew.init() # initialize the game engine...
screen = pew.Pix() # ...and the screen
qc = QuantumCircuit(2,2) # create an empty circuit with two qubits and two output bits
# put a hadamard on both qubits
qc.h(0)
qc.h(1)
# put a measurement on both qubit, whose results go to the corresponding output bit
qc.measure(0,0)
qc.measure(1,1)
# loop over the squares centered on (1,2) and (6,2) and make all dim
for (X,Y) in [(1,2),(6,2)]:
for dX in [+1,0,-1]:
for dY in [+1,0,-1]:
screen.pixel(X+dX,Y+dY,2)
for (X,Y) in [(1,2),(6,2)]:
screen.pixel(X,Y,0) # turn off the center pixels of the squares
while True: # loop which checks for user input and responds
# execute the circuit and get a single sample of memory
m = simulate(qc,shots=1,get='memory')
# turn the pixel (1,2) on or off depending on whether the first bit value is 1 or 0
if m[0][0]=='1':
screen.pixel(1,2,3)
else:
screen.pixel(1,2,0)
# do the same for pixel (6,2)
if m[0][1]=='1':
screen.pixel(6,2,3)
else:
screen.pixel(6,2,0)
pew.show(screen) # update screen to display the above changes
pew.tick(1/6) # pause for a sixth of a second
# -
# These programs were a simple 'Hello World', just to show that MicroQiskit is working. Now let's do something with it.
# **[Click here for the next notebook](Atoms-Computation.ipynb)**
|
Introduction-MicroQiskit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Problem Set 1: Descriptive Analytics
#
# * Authors: `<NAME>, <NAME>`
# * Emails: `<EMAIL>, <EMAIL>`
# # Problem Description
#
# * A telecom company is interested in segmenting loyal customers in order to optimize customer retention effort.
# * Our goal is to describe the data in preparation for this task.
# * It is our assumption to claim that the following are important factors in deciding whether a customer is valuable:
# * His/her tenure (the longer, the better)
# * His/her monthly charges (the higher, the better)
# * Note: the type of services that customers subscribe to is less important since they are reflected in monthly charges.
# # Section I: Importing Data & Data Cleaning
# ### Import data
# Import packages
# %matplotlib inline
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statistics as sts
from scipy.stats import ttest_ind
from scipy.stats import f_oneway
# +
# Import .csv file as a dataframe
data = pd.read_csv('Telco-Customer-Churn.csv')
# Count number of observations and features
obs, nvar = data.shape
print('Number of observations (all): {x:}'.format(x=obs))
print('Number of variables: {x:}'.format(x=nvar))
# View table
data.head()
# -
# ### Check missing data
# Are they empty cells?
for i in range(len(data.columns)):
counter = 0
for j in range(len(data)):
if data[data.columns[i]][j]==' ':
counter += 1
print('Empty cells in {f:}: {n:}'.format(f=data.columns[i], n=counter))
# ### Check and fix some variable types
# +
# `TotalCharges` should be a numeric feature
print('BEFORE Variable type of `TotalCharges`: {t:}'.format(t=type(data['TotalCharges'][0])))
# Convert to float
data['TotalCharges'] = pd.to_numeric(data['TotalCharges'], errors='coerce')
print('AFTER Variable type of `TotalCharges`: {t:}'.format(t=type(data['TotalCharges'][0])))
# -
# ### Impute mean values for empty cells (for now)
data['TotalCharges'].loc[data['TotalCharges'].isnull()] = np.mean(data)['TotalCharges']
# ### Count different types of variables
# +
# Describe variable types
n_nom = 0 # number of nominal variables
n_num = 0 # number of numeric variables
n_ord = 0 # number of ordinal variables
for i,j in enumerate(data.columns):
if type(data[j][0]) == str:
n_nom += 1
elif len(set(data[j])) <= 2:
n_nom += 1
else:
if j=='SeniorCitizen':
print(set(data[j]))
n_num += 1
print('Number of nominal variables: {n:}'.format(n=n_nom))
print('Number of ordinal variables: {n:}'.format(n=n_ord))
print('Number of numeric (continuous) variables: {n:}'.format(n=n_num))
# -
# ### Work only with loyal customers from now on (exclude churns)
data = data[data.Churn == 'No']
print('Number of observations (no churns): {x:}'.format(x=len(data[data.Churn=='No'])))
# # Section II: Descriptive Statistics
# ### Statistics about continuous variables
# +
# Print basic statistics
print('Average monthly charges: {x:.2f}'.format(x=np.mean(data.MonthlyCharges)))
print('Min, Max: {x:}'.format(x=[np.min(data.MonthlyCharges), np.max(data.MonthlyCharges)]))
print('Median: {x:.2f}'.format(x=sts.median(data.MonthlyCharges)))
print('Mode: {x:.2f}'.format(x=sts.mode(data.MonthlyCharges)))
print('SD: {x:.2f}\n'.format(x=np.std(data.MonthlyCharges)))
print('Average total charges: {x:.2f}'.format(x=np.mean(data.TotalCharges)))
print('Min, Max: {x:}'.format(x=[np.min(data.TotalCharges), np.max(data.TotalCharges)]))
print('Median: {x:.2f}'.format(x=sts.median(data.TotalCharges)))
print('Mode: {x:.2f}'.format(x=sts.mode(data.TotalCharges)))
print('SD: {x:.2f}\n'.format(x=np.std(data.TotalCharges)))
print('Average tenure: {x:.2f}'.format(x=np.mean(data.tenure)))
print('Min, Max: {x:}'.format(x=[np.min(data.tenure), np.max(data.tenure)]))
print('Median: {x:.2f}'.format(x=sts.median(data.tenure)))
print('Mode: {x:.2f}'.format(x=sts.mode(data.tenure)))
print('SD: {x:.2f}'.format(x=np.std(data.tenure)))
plt.boxplot([data.MonthlyCharges, data.tenure])
plt.title('Boxplots of Monthly Charges and Tenure')
plt.xticks([1,2], ['Monthly Charges','Tenure'])
plt.grid()
plt.show()
# Histograms
fig, ax = plt.subplots(1,2)
ax[0].hist(data.MonthlyCharges)
ax[0].set_title('Distribution of Monthly Charges')
ax[0].set_ylabel('Number of customers')
ax[0].set_xlabel('Monthly Charges')
ax[1].hist(data.tenure)
ax[1].set_title('Distribution of Tenure')
ax[1].set_ylabel('Number of customers')
ax[1].set_xlabel('Tenure')
plt.subplots_adjust(left=None, bottom=None, right=1.5, top=None)
plt.show()
sns.pairplot(data[['tenure','MonthlyCharges','TotalCharges']])
# -
# ### Customer demographics summary
# Summarize demographic attributes
pd.pivot_table(data,index=['gender','SeniorCitizen','Partner','Dependents'],values='Contract',aggfunc=len,margins=True)
# * With the pivot table, we are able to trace total number of customers in any specific demographic group
# ### Count Plots
# +
# Count plots of different attributes
fig, ax = plt.subplots(2,2)
fig.set_figheight(12)
fig.set_figwidth(12)
plt.subplots_adjust(left=None, bottom=None, right=None, top=None, wspace=0.3, hspace=0.3)
sns.countplot(data.gender, ax=ax[0,0]).set_title('Female vs. Male Counts')
sns.countplot(data.SeniorCitizen, ax=ax[0,1]).set_title('Non-Senior (0) vs. Senior (1) Counts')
sns.countplot(data.Partner, ax=ax[1,0]).set_title('Partner vs. Non-Partner Counts')
sns.countplot(data.Dependents, ax=ax[1,1]).set_title('Dependents vs. No Dependents Counts')
# -
# * Male vs. female and Parter vs. Non-partner ratios seem roughly even.
# * However, we can suspect that there is significant difference in the number of customers in: Senior vs. Non-senior and Dependents vs. No dependents groups
# # Section III: T-tests on Means
def ttest(vector1, vector2):
"""
Takes in two numeric vectors and compares their means via t-test.
Parameters
----------
vector1, vector2: numeric vectors (possibly with different lengths)
Returns
-------
t: t-statistic
p: two tailed p-value
se: standard error
"""
t, pval = ttest_ind(vector1, vector2)
se = np.sqrt(np.var(vector1)/len(vector1) + np.var(vector2)/len(vector2))
return t, pval, se
# ### All groups with binary values
# +
# Lists to collect p-values, t-statistics, and standard errors
p_month = []
t_month = []
se_month = []
p_tenure = []
t_tenure = []
se_tenure = []
# Define groups to test
groups = ['gender','SeniorCitizen','Partner','Dependents','PaperlessBilling']
for i,j in enumerate(groups):
print(pd.pivot_table(data,index=j,values=['MonthlyCharges','tenure'],aggfunc='mean'))
print('------------------------------------------------\n')
labels = list(set(data[j]))
vector1 = data.MonthlyCharges[data[j]==labels[0]]
vector2 = data.MonthlyCharges[data[j]==labels[1]]
# T-test
t, pval, se = ttest(vector1, vector2)
# Update lists
t_month.append(t)
p_month.append(pval)
se_month.append(se)
# Same thing for tenure
vector1 = data.tenure[data[j]==labels[0]]
vector2 = data.tenure[data[j]==labels[1]]
t, pval, se = ttest(vector1, vector2)
t_tenure.append(t)
p_tenure.append(pval)
se_tenure.append(se)
# -
# ### Contract Type (3 values)
pd.pivot_table(data,index='Contract',values=['MonthlyCharges','tenure'],aggfunc='mean')
# +
F_month = []
P_an_month=[]
F_tenure=[]
P_an_tenure=[]
vector1=data.MonthlyCharges[data['Contract']=='Month-to-month']
vector2=data.MonthlyCharges[data['Contract']=='One year']
vector3=data.MonthlyCharges[data['Contract']=='Two year']
f,p=f_oneway(vector1,vector2,vector3)
F_month.append(f)
P_an_month.append(p)
vector1=data.tenure[data['Contract']=='Month-to-month']
vector2=data.tenure[data['Contract']=='One year']
vector3=data.tenure[data['Contract']=='Two year']
f,p=f_oneway(vector1,vector2,vector3)
F_tenure.append(f)
P_an_tenure.append(p)
# -
# ### Payment method (4 values)
pd.pivot_table(data,index='PaymentMethod',values=['MonthlyCharges','tenure'],aggfunc='mean')
# +
vector1=data.MonthlyCharges[data['PaymentMethod']=='Bank transfer (automatic)']
vector2=data.MonthlyCharges[data['PaymentMethod']=='Credit card (automatic)']
vector3=data.MonthlyCharges[data['PaymentMethod']=='Electronic check']
vector4=data.MonthlyCharges[data['PaymentMethod']=='Mailed check']
f_oneway(vector1,vector2,vector3)
f,p=f_oneway(vector1,vector2,vector3)
F_month.append(f)
P_an_month.append(p)
vector1=data.tenure[data['PaymentMethod']=='Bank transfer (automatic)']
vector2=data.tenure[data['PaymentMethod']=='Credit card (automatic)']
vector3=data.tenure[data['PaymentMethod']=='Electronic check']
vector4=data.tenure[data['PaymentMethod']=='Mailed check']
f,p=f_oneway(vector1,vector2,vector3)
F_tenure.append(f)
P_an_tenure.append(p)
# -
# ### Visualize p-values and t-statistics
# +
x = list(range(len(p_month)))
critical_value = np.ones(len(x)) * 0.05
fig, axes = plt.subplots(1,2)
fig.set_figwidth(12)
axes[0].scatter(x, p_month)
axes[0].plot(x, critical_value,'--r')
axes[0].set_xticks([0,1,2,3,4])
axes[0].set_xticklabels(groups, rotation=30)
axes[0].set_ylabel('P-value')
axes[0].set_title('MonthlyCharges: T-test on the difference of means')
axes[1].scatter(x, p_tenure)
axes[1].plot(x, critical_value,'--r')
axes[1].set_xticks([0,1,2,3,4])
axes[1].set_xticklabels(groups, rotation=30)
axes[1].set_ylabel('P-value')
axes[1].set_title('Tenure: T-test on the difference of means')
axes[0].grid()
axes[1].grid()
plt.show()
# -
# * With the exception of `gender`, all other groups report having statistically different means in `MonthlyCharges` AND `tenure` at the 5% significance level.
# +
x = list(range(len(p_month)))
critical_value = np.ones(len(x)) * 0.05
fig, axes = plt.subplots(1,2)
fig.set_figwidth(12)
t_month = np.array(t_month)
se_month = np.array(se_month)
t_tenure = np.array(t_tenure)
se_tenure = np.array(se_tenure)
axes[0].scatter(x, t_month)
axes[0].errorbar(x, t_month, fmt='m',linestyle='None', yerr=1.96*se_month)
axes[0].set_xticks([0,1,2,3,4])
axes[0].set_xticklabels(groups, rotation=30)
axes[0].set_ylabel('t-statistic')
axes[0].set_title('MonthlyCharges: T-test on the difference of means')
axes[1].scatter(x, t_tenure)
axes[1].errorbar(x, t_tenure, fmt='m',linestyle='None', yerr=1.96*se_tenure)
axes[1].set_xticks([0,1,2,3,4])
axes[1].set_xticklabels(groups, rotation=30)
axes[1].set_ylabel('t-statistic')
axes[1].set_title('Tenure: T-test on the difference of means')
axes[0].grid()
axes[1].grid()
plt.show()
# -
# * Same interpretation as the p-value graphs: only the confidence interval of the t-statistic for `gender` includes 0, which makes it the only group where the means are not statistically different.
# +
# Histograms of Monthly Charges
fig, axes = plt.subplots(1,4)
axes[0].hist(data.MonthlyCharges[data.gender=='Male'], alpha=0.5)
axes[0].hist(data.MonthlyCharges[data.gender=='Female'], alpha=0.5)
axes[0].legend(['Male','Female'])
axes[0].set_xlabel('Monthly Charges')
axes[0].set_ylabel('Number of Customers')
axes[1].hist(data.MonthlyCharges[data.SeniorCitizen==0], alpha=0.5)
axes[1].hist(data.MonthlyCharges[data.SeniorCitizen==1], alpha=0.5)
axes[1].legend(['Non-Senior','Senior'])
axes[1].set_xlabel('Monthly Charges')
axes[2].hist(data.MonthlyCharges[data.Partner=='No'], alpha=0.5)
axes[2].hist(data.MonthlyCharges[data.Partner=='Yes'], alpha=0.5)
axes[2].legend(['Non-Partner','Partner'])
axes[2].set_xlabel('Monthly Charges')
axes[3].hist(data.MonthlyCharges[data.Dependents=='No'], alpha=0.5)
axes[3].hist(data.MonthlyCharges[data.Dependents=='Yes'], alpha=0.5)
axes[3].legend(['No Dependents','Has Dependents'])
axes[3].set_xlabel('Monthly Charges')
plt.subplots_adjust(left=None, bottom=None, right=2.3, top=None)
plt.show()
# Histogram of tenure
fig, axes = plt.subplots(1,4)
axes[0].hist(data.tenure[data.gender=='Male'], alpha=0.5)
axes[0].hist(data.tenure[data.gender=='Female'], alpha=0.5)
axes[0].legend(['Male','Female'])
axes[0].set_xlabel('Tenure')
axes[0].set_ylabel('Number of Customers')
axes[1].hist(data.tenure[data.SeniorCitizen==0], alpha=0.5)
axes[1].hist(data.tenure[data.SeniorCitizen==1], alpha=0.5)
axes[1].legend(['Non-Senior','Senior'])
axes[1].set_xlabel('Tenure')
axes[2].hist(data.tenure[data.Partner=='No'], alpha=0.5)
axes[2].hist(data.tenure[data.Partner=='Yes'], alpha=0.5)
axes[2].legend(['Non-Partner','Partner'])
axes[2].set_xlabel('Tenure')
axes[3].hist(data.tenure[data.Dependents=='No'], alpha=0.5)
axes[3].hist(data.tenure[data.Dependents=='Yes'], alpha=0.5)
axes[3].legend(['No Dependents','Has Dependents'])
axes[3].set_xlabel('Tenure')
plt.subplots_adjust(left=None, bottom=None, right=2.3, top=None)
plt.show()
# -
# ### Visualize Annova F-values and p-values
print(F_month,F_tenure)
print(P_an_month,P_an_tenure)
# +
x = list(range(len(F_month)))
print(x)
#critical_value = np.ones(len(x)) * 0.05 #Change to give crit value for F-val
fig,axes = plt.subplots(2,2)
fig.set_figwidth(12)
F_month = np.array(F_month)
P_an_month = np.array(P_an_month)
F_tenure = np.array(F_tenure)
P_an_tenure = np.array(P_an_tenure)
axes[0,0].scatter(x,F_month)
#axes[0].errorbar(x, t_month, fmt='m',linestyle='None', yerr=1.96*se_month)
axes[0,0].set_xticks([0,1])
axes[0,0].set_xticklabels(['Contract Length','Payment Method'], rotation=0)
axes[0,0].set_ylabel('F-value')
axes[0,0].set_title('MonthlyCharges: ANOVA test: F-values')
axes[0,1].scatter(x, F_tenure)
#axes[1].errorbar(x, t_tenure, fmt='m',linestyle='None', yerr=1.96*se_tenure)
axes[0,1].set_xticks([0,1])
axes[0,1].set_xticklabels(['Contract Length','Payment Method'], rotation=0)
axes[0,1].set_ylabel('F-Value')
axes[0,1].set_title('Tenure: ANOVA test: F-values')
axes[1,0].scatter(x, P_an_month)
#axes[1].errorbar(x, t_tenure, fmt='m',linestyle='None', yerr=1.96*se_tenure)
axes[1,0].set_xticks([0,1])
axes[1,0].set_xticklabels(['Contract Length','Payment Method'], rotation=0)
axes[1,0].set_ylabel('P-Value')
axes[1,0].set_title('Tenure: ANOVA test: P-values')
axes[1,1].scatter(x, P_an_tenure)
#axes[1].errorbar(x, t_tenure, fmt='m',linestyle='None', yerr=1.96*se_tenure)
axes[1,1].set_xticks([0,1])
axes[1,1].set_xticklabels(['Contract Length','Payment Method'], rotation=0)
axes[1,1].set_ylabel('P-Value')
axes[1,1].set_title('Tenure: ANOVA test: P-values')
axes[0,0].grid()
axes[0,1].grid()
axes[1,0].grid()
axes[1,1].grid()
plt.show()
# -
# * Likely the above means that all hypotheses that the factors are insignificant are rejected.
|
ProblemSet1/.ipynb_checkpoints/MGT-415 PS1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cv2
import imageio
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from skimage.transform import resize
from IPython.display import HTML
from tqdm import tqdm
from matplotlib import pyplot as plt
import warnings
warnings.filterwarnings("ignore")
# +
source_image = imageio.imread('/home/wintersoldier/Downloads/forDeepFake.jpg')
driving_video = imageio.mimread('/home/wintersoldier/Downloads/my_video3.mp4',memtest=False)
# source_image2 = imageio.imread('/home/wintersoldier/Downloads/chris.jpg')
source_image = resize(source_image, (256, 256))[..., :3]
# source_image2 = resize(source_image2, (256, 256))[..., :3]
source_image = resize(source_image, (256, 256))[..., :3]
driving_video = [resize(frame, (256, 256))[..., :3] for frame in driving_video]
# +
#Resize image and video to 256x256
def display(source, driving, generated=None):
fig = plt.figure(figsize=(8 + 4 * (generated is not None), 6))
ims = []
for i in range(len(driving)):
cols = [source]
cols.append(driving[i])
if generated is not None:
cols.append(generated[i])
im = plt.imshow(np.concatenate(cols, axis=1), animated=True)
plt.axis('off')
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=50, repeat_delay=1000)
plt.close()
return ani
# HTML(display(source_image, driving_video).to_html5_video())
# -
from demo import load_checkpoints
generator, kp_detector = load_checkpoints(config_path='config/vox-256.yaml',
checkpoint_path='/media/wintersoldier/Gaming_Disk/Downloads/vox-cpk.pth.tar')
# +
from demo import make_animation
from skimage import img_as_ubyte
predictions = make_animation(source_image, driving_video, generator, kp_detector, relative=True)
#save resulting video
# imageio.mimsave('../generated.mp4', [img_as_ubyte(frame) for frame in predictions])
#video can be downloaded from /content folder
# +
from demo import make_animation
# from skimage import img_as_ubyte
cap = cv2.VideoCapture(0)
driving_video=[]
while True:
if cv2.waitKey(1) & 0xFF == ord('q'):
break
ret, frame = cap.read()
frame = cv2.resize(cv2.cvtColor(frame,cv2.COLOR_BGR2RGB),(256,256))
cv2.imshow('the',frame)
print(len(driving_video))
driving_video.append(frame)
if(len(driving_video)==256):
predictions = make_animation(source_image, driving_video, generator, kp_detector, relative=True)
try:
predictions = np.reshape(predictions,(10,256,256,3))
cv2.imshow('this',predictions[8])
except:
pass
driving_video=[]
cap.release()
cv2.destroyAllWindows()
# -
cap.release()
HTML(display(source_image, driving_video, predictions).to_html5_video())
# +
# main_prediction=np.reshape(main_prediction,(100,256,256,3))
# +
# HTML(display(source_image, driving_video, main_prediction).to_html5_video())
# -
np.shape(temp_driving_video)
temp_driving_video = driving_video[121:122]
# +
from demo import make_animation
from skimage import img_as_ubyte
k=100
for i in range(k, k+1):
temp_driving_video = driving_video[i:i+15]
predictions = make_animation(source_image, temp_driving_video, generator, kp_detector, relative=True)
HTML(display(source_image, temp_driving_video, predictions).to_html5_video())
#save resulting video
# imageio.mimsave('../generated.mp4', [img_as_ubyte(frame) for frame in predictions])
#video can be downloaded from /content folder
# +
cap = cv2.VideoCapture(0)
recorded=[]
while True:
ret, frame = cap.read()
frame = cv2.resize(cv2.cvtColor(frame,cv2.COLOR_BGR2RGB),(256,256))
cv2.imshow('the',frame)
print(len(driving_video))
recorded.append(frame)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
# -
import cv2
plt.imshow(predictions[1])
HTML(display(source_image, driving_video, predictions).to_html5_video())
np.shape(predictions)
for frame in predictions:
frame = np.array(frame,'uint8')
cv2.imshow('',frame)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cv2.destroyAllWindows()
for frame in predictions:
frame = np.array(frame,'uint8')
print(np.shape(frame))
np.shape(predictions)
cv2.destroyAllWindows()
predictions[0][0]
def display(source, driving, generated=None):
fig = plt.figure(figsize=(8 + 4 * (generated is not None), 6))
ims = []
for i in range(len(driving)):
cols = [source]
cols=[[]]
cols.append(driving[i])
if generated is not None:
cols.append(generated[i])
im = plt.imshow(np.concatenate(cols, axis=1), animated=True)
plt.axis('off')
ims.append([im])
ani = animation.ArtistAnimation(fig, ims, interval=50, repeat_delay=1000)
plt.close()
return ani
arr = [img_as_ubyte(frame) for frame in predictions]
# + active=""
#
# -
import time
for frame in arr:
cv2.imshow('',frame)
time.sleep(1)
cv2.destroyAllWindows()
imageio.mimsave('/home/wintersoldier/Desktop/generated.mp4', [img_as_ubyte(frame) for frame in predictions])
imageio.imsave('/home/wintersoldier/Desktop/generated.png', img_as_ubyte(predictions[4]))
arr=[]
cap = cv2.VideoCapture(0)
while True:
ret, frame = cap.read()
cv2.imshow('', frame)
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
# +
import urllib
import cv2
import numpy as np
import time
arr=[]
# Replace the URL with your own IPwebcam shot.jpg IP:port
url='http://192.168.1.103:8080/shot.jpg'
while True:
# Use urllib to get the image from the IP camera
imgResp = urllib.request.urlopen(url)
# Numpy to convert into a array
imgNp = np.array(bytearray(imgResp.read()),dtype=np.uint8)
# Finally decode the array to OpenCV usable format ;)
img = cv2.imdecode(imgNp,-1)
img = cv2.resize(img, (256,256))
# put the image on screen
cv2.imshow('IPWebcam',img)
arr.append(img)
predictions = make_animation(source_image, arr, generator, kp_detector, relative=True)
imageio.imsave('/home/wintersoldier/Desktop/cache.png', img_as_ubyte(predictions[0]))
readImg= plt.imread('/home/wintersoldier/Desktop/cache.png')
cv2.imshow('',readImg)
arr = []
#To give the processor some less stress
#time.sleep(0.1)
# Quit if q is pressed
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cv2.destroyAllWindows()
# -
|
Realtime FaceCloning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### HTML 데이터 파싱을 이용한 크롤링
# - 네이버 실시간 검색어 순위
# - HTML 포멧의 문자열을 가져오는 URL 찾음
# - 요청 -> 응답(HTML 포멧(문자열)의 데이터를 저장)
# - 데이터 파싱
# - bs4 패키지의 BeautifulSoup 클래스를 이용해서 dom(Document) 객체를 생성
# - dom 객체에서 우리가 원하는 데이터를 css-selector를 이용해서 수집
# - 데이터 프레임으로 만들기
import requests
import pandas as pd
from bs4 import BeautifulSoup
# #### 1. requests 이용하여 HTML 코드 문자열 데이터 가져오기
url = "https://www.naver.com/"
response = requests.get(url)
response
# #### 2. BeautifulSoup을 이용하여 css-selector를 사용할 수 있는 객체로 파싱
# html로 파싱
dom = BeautifulSoup(response.content, "html.parser")
# #### 3. css-selector를 이용하여 원하는 데이터 수집
# - select : 여러개의 엘리먼트 객체들을 리스트로 가져옴
# - type : list
# - select_one : 하나의 엘리먼트 객체를 가져옴
# - type : bs4.element.Tag
# Chrome에 있는 copy selector 사용해도 된다.
elements = dom.select(".ah_roll_area > .ah_l > .ah_item")
type(elements[0]), elements[0]
elements[0].select_one(".ah_k").text
# #### 4. 수집한 데이터를 데이터 프레임으로 만들기
# +
datas = []
for element in elements:
# rank = element.select_one(".ah_r").text
# keyword = element.select_one(".ah_k").text
datas.append({
"rank": element.select_one(".ah_r").text,
"keyword": element.select_one(".ah_k").text,
})
naver_keywords = pd.DataFrame(datas)
naver_keywords.tail(3)
# -
# #### 5. 함수로 만들기
def naver_keywords():
response = requests.get("https://www.naver.com/")
dom = BeautifulSoup(response.content, "html.parser")
elements = dom.select(".ah_roll_area > .ah_l > .ah_item")
datas = []
for element in elements:
datas.append({
"rank": element.select_one(".ah_r").text,
"keyword": element.select_one(".ah_k").text,
})
return pd.DataFrame(datas)
df = naver_keywords()
df.tail(2)
# - 다음 실시간 검색어 순위 데이터 수집
response = requests.get("https://daum.net/")
dom = BeautifulSoup(response.content, "html.parser")
elements = dom.select(".realtime_part > .list_hotissue.issue_row > li")
len(elements)
rank = elements[0].select_one(".ir_wa").text
keyword = elements[0].select_one(".link_issue").text
print(rank, keyword)
# +
datas = []
for element in elements:
datas.append({
"rank": element.select_one(".ir_wa").text,
"keyword": element.select_one(".link_issue").text
})
daum_keywords = pd.DataFrame(datas)
daum_keywords.tail(2)
# -
naver_df = naver_keywords()
daum_df = pd.DataFrame(datas)
set(naver_df["keyword"]) & set(daum_df["keyword"])
|
Crawling/07_requests_html.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# # Introduction
#
# This tutorial will explain the concept of document-oriented databases using MongoDB in Python. Because document-oriented databases do not express relations among data, they are less structured. However, operations in document-oriented databases are much faster than analogous operations in a relational database such as MySQL. For this reason, document-oriented databases such as MongoDB scale better than their SQL counterparts, and they are useful for big data.
#
# This tutorial will focus on using a MongoDB database as opposed to the implementation of a MongoDB database. Therefore, topics such as file storage, replication, load balancing, and sharding will not be covered in this tutorial. See the References section at the end for further reading.
# ## Tutorial Content
#
# In this tutorial, we will cover the basics of MongoDB, including CRUD (create, read, update, delete) operations, the aggregation pipeline, map_reduce, indexing, and text search.
#
# ### Table of Contents
#
# * [Installing the Libraries](#Installing-the-Libraries)
# * [Document-Oriented vs. Relational DB's](#Document-Oriented-vs.-Relational-DB's)
# * [An Introduction to MongoDB](#An-Introduction-to-MongoDB)
# * [Operations in MongoDB](#Operations-in-MongoDB)
# * [The Aggregation Pipeline](#The-Aggregation-Pipeline)
# * [Map_Reduce](#Map_Reduce)
# * [Indexing and Text Search](#Indexing-and-Text-Search)
# * [Summary](#Summary)
# * [References](#References)
# ## Installing the Libraries
#
# You'll need to install MongoDB and the Python library pymongo.
#
# If you have brew, you can brew MongoDB in the following way.
#
# ```
# $ brew update
# $ brew install mongodb
# ```
#
# If you want to install MongoDB with TLS/SSL, you can run
#
# ```
# $ brew install mongodb --with-openssl
# ```
#
# If not, you can install MongoDB [here](https://www.mongodb.com/download-center "MongoDB Download").
#
# Now you should install pymongo, the Python library for MongoDB.
#
# ```
# $ pip install --upgrade pymongo
# ```
# # Document-Oriented vs. Relational DB's
#
# We will begin by comparing and contrasting document-oriented databases and relational databases. We begin with an example. Suppose you are taking 2 classes. For both of these classes, you have an associated list of test scores, which you have stored as `classes.csv`. We can view this data as a relational database in the following way.
import sqlite3
from MongoTutorialLibrary import load_sql, pretty_print, pretty_print_remove_id
conn = sqlite3.connect(":memory:")
load_sql(conn, "classes.csv")
# This is very straightforward. We have a list of classes and corresponding test scores. However, this is more complicated when we have unequal number of tests. For example, say you scored a 95% on your fourth test in 15-213. If you tried to add this to the table, you'd have to add a fourth column for 15-213, and the table would be uneven. (Note that we could represent classes as grades in seperate tables, with one table for classes and another table for the relations between classes and grades. We represent data in the following manner for the sake of example.)
#
# Here we introduce the *document-oriented database*. Suppose I have the same data for these classes stored in some `classes.json`.
import json
classes_file = open('classes.json', 'r')
classes = json.load(classes_file)
print pretty_print(classes)
classes_file.close()
# A document-oriented database allows us to represent a group of *documents* collectively known as a *collection*. In our example, each class is a *document*, and the collection of classes is a *collection*.
#
# Noteably, each document does not have to have the same information, and we are able to add our fourth exam score to our 15-213 document with no problem! But how do we add the data to our document? To do this, we will introduce MongoDB.
# # An Introduction to MongoDB
#
# In this section we will learn a popular implementation of a document-oriented database, MongoDB.
#
# Let's first set up our database from our `classes.json`.
#
# Note that this will require a MongoDB instance running on your local machine. To accomplish this, simply run
#
# ```
# $ mongod
# ```
#
# Note that you may have to pass additional flags or arguments. Run
#
# ```
# $ mongod --help
# ```
#
# for more information.
#
# Notably, you should set up MongoDB to to store information in a directory `data/` and with some subdirectory `db/` (so `<absolute_path>/data/db/`) and record logs in a file within a directory `log/`. You can achieve these with the flags `--dbpath` and `--dbpath`, respectively, as shown below.
#
# ```
# $ mongod --dbpath <path>data/db/ --logpath <path>log/mongo.log
# ```
# +
import bson, pymongo
from pymongo import MongoClient
conn = MongoClient()
# create db if it doesn't already exist
db = conn.test_database
# create collection grades
grades = db.grades
# make sure grades is empty, so we can run this function multiple times
grades.delete_many({})
# add entries, initialize list of id's of objects
id_objects = grades.insert_many(classes)
ids = id_objects.inserted_ids
# analogous to "SELECT * FROM classes;"
grades_list = grades.find()
# print all grades
for grade in grades_list:
print grade
# -
# And we have successfully created a collection with our grades. But you want to put your great test score in the collection! Let's take a look at how to modify a document.
#
# If we know the ID of the document, this process is quite simple. We can find a *single* document with `<collection>.find_one()` and update a collection with `<collection>.update_one()`.
# +
# this is the id we want
courseId = ids[1]
print courseId
# print newline and the document
print
print grades.find_one({"_id": courseId})
# update the document
grades.update_one({'_id': courseId}, {"$set": {'scores.midterm_4': 95}}, upsert=True)
# print newline and the updated document
print
print grades.find_one({"_id": courseId})
# -
# Let's make a few notes. Firstly, we use the keyword `$set` to set the key `'scores.midterm_4'` to value `95`. Also, we need to pass the parameter upsert=True to indicate that we wish to add this field if it doesn't exist already.
#
# Now you have received a great homework grade for 15-388: 100%! You are anxious to add this score, but unfortunately, we have lost our list of id's!
id_objects = None
ids = []
# We will have to find the document using only the information that the `course` is `15-388`. Fortunately, we have an alternate way to select documents!
# +
# print the document
print grades.find_one({"course": '15-388'})
# update the document
grades.update_one({"course": '15-388'}, {"$set": {'scores.homework_1': 100}}, upsert=True)
# print newline and the updated document
print
print grades.find_one({"course": '15-388'})
# -
# You notice there's an error! In your database, your midterm 2 score in 15-388 is a 70%, but you actually got a 90%. You're going to need to change that! To change a value, we use the same syntax as adding a value. The only difference is we don't need `upsert=True`, and so we will eliminate this parameter (`upsert=False` by default).
# +
# update the document
grades.update_one({"course": '15-388'}, {"$set": {'scores.midterm_2': 90}})
# print the updated document
print grades.find_one({"course": '15-388'})
# -
# Finally, we will show you how to remove a document.
#
# You don't like 15-150, and so you are electing to drop the course. You want to remove it from your schedule.
#
# To remove a document, we use the `.delete_one()` function to remove one document or `.delete_many()` to remove several documents. Since we only want to remove one document, we will simply use `.delete_one()`.
# +
# remove the document
grades.delete_one({"course": '15-150'})
# print the updated document
for course in grades.find():
print course
# -
# And we've removed the course!
# # Operations in MongoDB
#
# It's midsemester and you want to calculate your midsemester grade! To do this, you'll need to understand a little about operations in MongoDB.
#
# Let's start by averaging midterm scores for each class. Of course, we can select each class as a python object and iterate through them.
avgs = {}
for class_ in grades.find():
total = 0
count = 0
for _, score in class_['scores'].iteritems():
total += score
count += 1
avgs[class_['course']] = float(total) / count
print avgs
# But we have to write our own code, and this is inefficient. As a better solution, we introduce the Aggregation Pipeline.
# # The Aggregation Pipeline
#
# Here we introducte the topic of the *aggregation*. To simplify this transition, we will define a new database with the same information stored differently. This database will allow for a more intuitive explanation of the concept of the *aggregation pipeline*.
# +
# create collection grades
grades_by_test = db.grades_by_test
# make sure grades is empty, so we can run this function multiple times
grades_by_test.delete_many({})
# add entries, initialize list of id's of objects
classes_by_test_file = open('classes-by-test.json', 'r')
id_objects = grades_by_test.insert_many(json.load(classes_by_test_file))
ids = id_objects.inserted_ids
classes_by_test_file.close()
# analogous to "SELECT * FROM classes;"
grades_by_test_list = grades_by_test.find()
# print all grades
for grade in grades_by_test_list:
print grade
# -
# We will use the aggregation framework. Aggregation is useful when we want to perform very general tasks on a set of data. For example, we can easily take the average of all a student's scores.
#
# The aggregation pipeline is a set of *stages*. We begin with our set of documents, and then each *stage* modifies the documents and passes resulting documents to the next stage. In our example we only have one stage, a `$group`. We group documents by `course` and compute the average of each document's `score` field. Note that this example is intentionally simple, and we go over a more in-depth example with multiple stages in the next section.
#
# Note that a full list of stages can be found [here](https://docs.mongodb.com/manual/reference/operator/aggregation-pipeline/ "MongoDB Aggregate Stages")
# +
pipeline = [{
'$group': {
"_id": "$course",
"avg_score": {
"$avg":"$score"
}
}
}]
print pretty_print(list(grades_by_test.aggregate(pipeline)))
# -
# Let's walk through a more difficult example. We begin by constructing a new database that is more easy to analyze. We have three students each taking several classes.
# +
# create collection grades
students = db.students
# make sure grades is empty, so we can run this function multiple times
students.delete_many({})
# add entries, initialize list of id's of objects
students_file = open('students.json', 'r')
id_objects = students.insert_many(json.load(students_file))
ids = id_objects.inserted_ids
students_file.close()
# analogous to "SELECT * FROM classes;"
students_list = students.find()
# print all grades
for student in students_list:
print student
# -
# We want to calculate each student's grade in each class. We begin with an `$unwind` stage. Unwind creates a document for each element of a list within a document. Using unwind, we pass the path to the `courses` list and create a new document for each course an individual is in. Further information on `$unwind` is available [here](https://docs.mongodb.com/manual/reference/operator/aggregation/unwind/).
#
# Note that we are completing each stage of the aggregation pipeline separately to demonstrate the effect of each stage individually.
# +
pipeline = [{
'$unwind': {
"path": "$courses"
}
}]
# special print function removes id
print pretty_print_remove_id(students, pipeline)
# -
# We then use a `$project` stage, which is able to pass along a subset of data or perform computations on data. We construct a dictionary of what we want and do not want to include. We can create a new field with key, value `<new_field_name>: <formula`>, or we can select certain information to include with `<existing_field_name>: True` (or, equivalently, `<existing_field_name>: 1`). We can also choose to remove the id element with `_id: False`. Note that this is the only element we can remove.
# +
pipeline = [{
'$unwind': {
"path": "$courses"
}}, {
'$project': {
'homework_avg': {'$avg': '$courses.homeworks'},
'midterm_avg': {'$avg': '$courses.midterms'},
'course': '$courses.course',
'name': True,
'_id': False
}
}]
print pretty_print(list(students.aggregate(pipeline)))
# -
# We then group the documents back together. `$group` takes a field `_id` which is what you want the elements to be grouped by. In this case, we group by `$name`. We then construct some formula to combine all documents with this `_id`. In this case, we simply want to copy all fields. We use the `$push` operation, which creates a list and pushes all values (given by `$push: <value>`) onto the list.
# +
pipeline = [{
'$unwind': {
"path": "$courses"
}}, {
'$project': {
'homework_avg': {'$avg': '$courses.homeworks'},
'midterm_avg': {'$avg': '$courses.midterms'},
'course': '$courses.course',
'name': True,
'_id': False
}}, {
'$group': {
'_id': '$name',
'courses': {
'$push': {'course': '$course', 'homework_avg': '$homework_avg', 'midterm_avg': '$midterm_avg'}
}
}
}]
print pretty_print(list(students.aggregate(pipeline)))
# -
# We were able to compute each students' homework average and midterm average with just the aggregation pipeline. However, more complex operations often require the more versatile `map_reduce` function.
# # Map_Reduce
#
# In this section we will discuss `map_reduce` in MongoDB. This is a method to aggregate large amounts of data into some convenient representation. Note that map and reduce must be JavaScript functions, and so this section will require some knowledge of JavaScript. [Here](https://developer.mozilla.org/en-US/docs/Web/JavaScript "JavaScript Documentation") is a link to JavaScript Docs, which includes a good tutorial that can be found [here](https://developer.mozilla.org/en-US/docs/Web/JavaScript/Guide "JavaScript Guide"). I also personally endorse [Codecademy's JavaScript tutorial](https://www.codecademy.com/learn/javascript "Codecademy JavaScript") as a brief introduction to the language.
#
# We first discuss the **map** step of this process. In general, *mapping* is a concept in functional programming where we map every element of some list L to some element in a new list L'. In MongoDB, this is achieved by *emitting* key-value pairs for each element in the list L. Note that each element of list L can emit an arbitrary number of key, value pairs (including 0). After emitting, each key `k` has a corresponding list `L` of values `[l1, ..., ln]` such that for each `li` (`k`, `li`) was emitted by map.
#
# We construct a function `mapper` that will be given each document as input. We can reference the document with the keyword `this`.
#
# After mapping, we **reduce** our key-value pairs. We use a function that processes the accumulated list `L` and returns some value `v` that will be associated with each key.
#
# Let's begin writing our aggregation as a `map_reduce`! We first want to select which key-value pair to emit. `course`, `score` makes sense because a list of scores associated with each course could simply be averaged after the map step. We can then reduce by simply computing the average for each list `L`. Don't worry too much about the JavaScript syntax.
# +
from bson.code import Code
# emits course, score
mapper = Code("""
function() {
emit(this.course, this.score);
}
""")
# computes average of each list of test scores
reducer = Code("""
function(key, values) {
var total = 0;
var length = values.length;
for (var i = 0; i < length; i++) { //compute average
total += values[i];
}
return total / length;
}
""")
# mapreduce to find averages
averages = grades_by_test.map_reduce(mapper, reducer, "averages")
for average in averages.find():
print average
# -
# And we have a list of averages, like before. What's more interesting though is that `map_reduce` can be used on our original dataset! Let's try this.
# +
# emits course, score
mapper = Code("""
function() {
for (var key in this.scores) { //iterate through dictionary and emit course, score
emit(this.course, this.scores[key]);
}
}
""")
# mapreduce to find averages
averages_2 = grades.map_reduce(mapper, reducer, "averages_2")
for average in averages_2.find():
print average
# -
# Notice that our map function on this dataset yielded the same result as last time, so we can use the same reduce function.
# # Indexing and Text Search
#
# Now you want to lookup Bob's schedule and grades. But you forgot his last name! You'll need some kind of search feature.
#
# To enable search, we first must *index* our data. We assign each document a unique index, defined by one or more fields of each document. In this case, we choose to index on `name`. Note that we must specify the type on which we index (in this case `text`).
#
# More information such as weighting text fields is available [here](https://docs.mongodb.com/v3.2/core/index-text/ "MongoDB Text Indexes").
# +
result = students.create_index([('name', 'text')])
for student in students.find():
print student
# -
# Using our find method, we can now search the data using the following syntax.
search_result = students.find({"$text": {"$search": 'Bob'}})
for student in search_result:
print student
# # Summary
#
# In this tutorial we have discussed CRUD (create, read, update, delete) operations, the aggregation pipeline, map_reduce, indexing, and text search. However, there is still much to learn about MongoDB. See the references section below for additional information.
# # References
#
# Document-Oriented Databases:
# 1. [Wikipedia Document-Oriented Database](https://en.wikipedia.org/wiki/Document-oriented_database "Wikipedia Document-Oriented Database")
# 2. [Document-Oriented Databases and MongoDB](https://www.mongodb.com/document-databases "Document-Oriented Databases and MongoDB")
#
# MongoDB:
# 1. [MongoDB Manual](https://docs.mongodb.com/manual/ "MongoDB Manual")
# 2. [Aggregation Pipeline](https://docs.mongodb.com/manual/core/aggregation-pipeline/ "Aggregation Pipeline")
# 3. [Map-Reduce](https://docs.mongodb.com/manual/core/map-reduce/ "Map-Reduce")
# 4. [Sharding](https://docs.mongodb.com/manual/sharding/ "Sharding")
#
# PyMongo:
# 1. [Pymongo Documentation](https://api.mongodb.com/python/current/ "Pymongo Documentation")
# 2. [Getting Started MongoDB - Python](https://docs.mongodb.com/getting-started/python/ "Getting Started MongoDB - Python")
#
# JavaScript:
# 1. [JavaScript Documentation](https://developer.mozilla.org/en-US/docs/Web/JavaScript "JavaScript Documentation")
# 2. [JavaScript Guide](https://developer.mozilla.org/en-US/docs/Web/JavaScript/Guide "JavaScript Guide")
# 3. [Codecademy JavaScript](https://www.codecademy.com/learn/javascript "Codecademy JavaScript")
|
2016/tutorial_final/9/Document-Oriented Database and MongoDB Tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import pymssql
import mysql.connector
pd.set_option('display.width', 75)
pd.set_option('display.max_columns', 5)
pd.options.display.float_format = '{:,.2f}'.format
sqlselect = "Select studentid, school, sex, age, famsize,\
medu As mothereducation, fedu As fathereducation,\
traveltime, studytime, failures, famrel, freetime,\
goout, g1 As gradeperiod1, g2 As gradeperiod2,\
g3 As gradeperiod3 From studentmath"
server = "pdcc.c9sqqzd5fulv.us-west-2.rds.amazonaws.com"
user = "pdccuser"
password = "<PASSWORD>"
database = "pdcctest"
conn = pymssql.connect(server=server,
user=user, password=password, database=database)
studentmath = pd.read_sql(sqlselect,conn)
conn.close()
host = "pdccmysql.c9sqqzd5fulv.us-west-2.rds.amazonaws.com"
user = "pdccuser"
password = "<PASSWORD>"
database = "pdccschema"
connmysql = mysql.connector.connect(host=host,
database=database,user=user,password=password)
studentmath = pd.read_sql(sqlselect,connmysql)
connmysql.close()
studentmath.dtypes
studentmath.head()
newcolorder = ['studentid', 'gradeperiod1', 'gradeperiod2',
'gradeperiod3', 'school', 'sex', 'age', 'famsize',
'mothereducation', 'fathereducation', 'traveltime',
'studytime', 'freetime', 'failures', 'famrel',
'goout']
studentmath = studentmath[newcolorder]
studentmath.studentid.count()
studentmath.studentid.nunique()
studentmath.set_index('studentid', inplace=True)
studentmath.count()
# +
setvalues={"famrel":{1:"1:very bad",2:"2:bad",3:"3:neutral",
4:"4:good",5:"5:excellent"},
"freetime":{1:"1:very low",2:"2:low",3:"3:neutral",
4:"4:high",5:"5:very high"},
"goout":{1:"1:very low",2:"2:low",3:"3:neutral",
4:"4:high",5:"5:very high"},
"mothereducation":{0:np.nan,1:"1:k-4",2:"2:5-9",
3:"3:secondary ed",4:"4:higher ed"},
"fathereducation":{0:np.nan,1:"1:k-4",2:"2:5-9",
3:"3:secondary ed",4:"4:higher ed"}}
studentmath.replace(setvalues, inplace=True)
setvalueskeys = [k for k in setvalues]
studentmath[setvalueskeys].memory_usage(index=False)
for col in studentmath[setvalueskeys].columns:
studentmath[col] = studentmath[col].astype('category')
studentmath[setvalueskeys].memory_usage(index=False)
studentmath['famrel'].value_counts(sort=False, normalize=True)
# -
studentmath[['freetime', 'goout']].apply(pd.Series.value_counts, sort=False, normalize=True)
studentmath[['mothereducation', 'fathereducation']].apply(pd.Series.value_counts, sort=False, normalize=True)
|
Python-Data-Cleaning-Cookbook-master/1_ImportingTabularData/importing_sql.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.4.2
# language: julia
# name: julia-1.4
# ---
#
# <a id='ree'></a>
# <div id="qe-notebook-header" style="text-align:right;">
# <a href="https://quantecon.org/" title="quantecon.org">
# <img style="width:250px;display:inline;" src="https://assets.quantecon.org/img/qe-menubar-logo.svg" alt="QuantEcon">
# </a>
# </div>
# # Rational Expectations Equilibrium
# ## Contents
#
# - [Rational Expectations Equilibrium](#Rational-Expectations-Equilibrium)
# - [Overview](#Overview)
# - [Defining Rational Expectations Equilibrium](#Defining-Rational-Expectations-Equilibrium)
# - [Computation of an Equilibrium](#Computation-of-an-Equilibrium)
# - [Exercises](#Exercises)
# - [Solutions](#Solutions)
# > “If you’re so smart, why aren’t you rich?”
# ## Overview
#
# This lecture introduces the concept of *rational expectations equilibrium*.
#
# To illustrate it, we describe a linear quadratic version of a famous and important model
# due to Lucas and Prescott [[LP71]](../zreferences.html#lucasprescott1971).
#
# This 1971 paper is one of a small number of research articles that kicked off the *rational expectations revolution*.
#
# We follow Lucas and Prescott by employing a setting that is readily “Bellmanized” (i.e., capable of being formulated in terms of dynamic programming problems).
#
# Because we use linear quadratic setups for demand and costs, we can adapt the LQ programming techniques described in [this lecture](../dynamic_programming/lqcontrol.html).
#
# We will learn about how a representative agent’s problem differs from a planner’s, and how a planning problem can be used to compute rational expectations quantities.
#
# We will also learn about how a rational expectations equilibrium can be characterized as a [fixed point](https://en.wikipedia.org/wiki/Fixed_point_%28mathematics%29) of a mapping from a *perceived law of motion* to an *actual law of motion*.
#
# Equality between a perceived and an actual law of motion for endogenous market-wide objects captures in a nutshell what the rational expectations equilibrium concept is all about.
#
# Finally, we will learn about the important “Big $ K $, little $ k $” trick, a modeling device widely used in macroeconomics.
#
# Except that for us
#
# - Instead of “Big $ K $” it will be “Big $ Y $”
# - Instead of “little $ k $” it will be “little $ y $”
# ### The Big $ Y $, little $ y $ trick
#
# This widely used method applies in contexts in which a “representative firm” or agent is a “price taker” operating within a competitive equilibrium.
#
# We want to impose that
#
# - The representative firm or individual takes *aggregate* $ Y $ as given when it chooses individual $ y $, but $ \ldots $.
# - At the end of the day, $ Y = y $, so that the representative firm is indeed representative.
#
#
# The Big $ Y $, little $ y $ trick accomplishes these two goals by
#
# - Taking $ Y $ as beyond control when posing the choice problem of who chooses $ y $; but $ \ldots $.
# - Imposing $ Y = y $ *after* having solved the individual’s optimization problem.
#
#
# Please watch for how this strategy is applied as the lecture unfolds.
#
# We begin by applying the Big $ Y $, little $ y $ trick in a very simple static context.
# #### A simple static example of the Big $ Y $, little $ y $ trick
#
# Consider a static model in which a collection of $ n $ firms produce a homogeneous good that is sold in a competitive market.
#
# Each of these $ n $ firms sells output $ y $.
#
# The price $ p $ of the good lies on an inverse demand curve
#
#
# <a id='equation-ree-comp3d-static'></a>
# $$
# p = a_0 - a_1 Y \tag{1}
# $$
#
# where
#
# - $ a_i > 0 $ for $ i = 0, 1 $
# - $ Y = n y $ is the market-wide level of output
#
#
# Each firm has total cost function
#
# $$
# c(y) = c_1 y + 0.5 c_2 y^2,
# \qquad c_i > 0 \text{ for } i = 1,2
# $$
#
# The profits of a representative firm are $ p y - c(y) $.
#
# Using [(1)](#equation-ree-comp3d-static), we can express the problem of the representative firm as
#
#
# <a id='equation-max-problem-static'></a>
# $$
# \max_{y} \Bigl[ (a_0 - a_1 Y) y - c_1 y - 0.5 c_2 y^2 \Bigr] \tag{2}
# $$
#
# In posing problem [(2)](#equation-max-problem-static), we want the firm to be a *price taker*.
#
# We do that by regarding $ p $ and therefore $ Y $ as exogenous to the firm.
#
# The essence of the Big $ Y $, little $ y $ trick is *not* to set $ Y = n y $ *before* taking the first-order condition with respect
# to $ y $ in problem [(2)](#equation-max-problem-static).
#
# This assures that the firm is a price taker.
#
# The first order condition for problem [(2)](#equation-max-problem-static) is
#
#
# <a id='equation-bigysimplefonc'></a>
# $$
# a_0 - a_1 Y - c_1 - c_2 y = 0 \tag{3}
# $$
#
# At this point, *but not before*, we substitute $ Y = ny $ into [(3)](#equation-bigysimplefonc)
# to obtain the following linear equation
#
#
# <a id='equation-staticy'></a>
# $$
# a_0 - c_1 - (a_1 + n^{-1} c_2) Y = 0 \tag{4}
# $$
#
# to be solved for the competitive equilibrium market wide output $ Y $.
#
# After solving for $ Y $, we can compute the competitive equilibrium price $ p $ from the inverse demand curve [(1)](#equation-ree-comp3d-static).
# ### Further Reading
#
# References for this lecture include
#
# - [[LP71]](../zreferences.html#lucasprescott1971)
# - [[Sar87]](../zreferences.html#sargent1987), chapter XIV
# - [[LS18]](../zreferences.html#ljungqvist2012), chapter 7
# ### Setup
# + hide-output=true
using InstantiateFromURL
# optionally add arguments to force installation: instantiate = true, precompile = true
github_project("QuantEcon/quantecon-notebooks-julia", version = "0.8.0")
# + hide-output=false
using LinearAlgebra, Statistics
# -
# ## Defining Rational Expectations Equilibrium
#
#
# <a id='index-1'></a>
# Our first illustration of a rational expectations equilibrium involves a market with $ n $ firms, each of which seeks to maximize the discounted present value of profits in the face of adjustment costs.
#
# The adjustment costs induce the firms to make gradual adjustments, which in turn requires consideration of future prices.
#
# Individual firms understand that, via the inverse demand curve, the price is determined by the amounts supplied by other firms.
#
# Hence each firm wants to forecast future total industry supplies.
#
# In our context, a forecast is generated by a belief about the law of motion for the aggregate state.
#
# Rational expectations equilibrium prevails when this belief coincides with the actual
# law of motion generated by production choices induced by this belief.
#
# We formulate a rational expectations equilibrium in terms of a fixed point of an operator that maps beliefs into optimal beliefs.
#
#
# <a id='ree-ce'></a>
# ### Competitive Equilibrium with Adjustment Costs
#
#
# <a id='index-2'></a>
# To illustrate, consider a collection of $ n $ firms producing a homogeneous good that is sold in a competitive market.
#
# Each of these $ n $ firms sells output $ y_t $.
#
# The price $ p_t $ of the good lies on the inverse demand curve
#
#
# <a id='equation-ree-comp3d'></a>
# $$
# p_t = a_0 - a_1 Y_t \tag{5}
# $$
#
# where
#
# - $ a_i > 0 $ for $ i = 0, 1 $
# - $ Y_t = n y_t $ is the market-wide level of output
#
#
#
# <a id='ree-fp'></a>
# #### The Firm’s Problem
#
# Each firm is a price taker.
#
# While it faces no uncertainty, it does face adjustment costs
#
# In particular, it chooses a production plan to maximize
#
#
# <a id='equation-ree-obj'></a>
# $$
# \sum_{t=0}^\infty \beta^t r_t \tag{6}
# $$
#
# where
#
#
# <a id='equation-ree-comp2'></a>
# $$
# r_t := p_t y_t - \frac{ \gamma (y_{t+1} - y_t )^2 }{2},
# \qquad y_0 \text{ given} \tag{7}
# $$
#
# Regarding the parameters,
#
# - $ \beta \in (0,1) $ is a discount factor
# - $ \gamma > 0 $ measures the cost of adjusting the rate of output
#
#
# Regarding timing, the firm observes $ p_t $ and $ y_t $ when it chooses $ y_{t+1} $ at at time $ t $.
#
# To state the firm’s optimization problem completely requires that we specify dynamics for all state variables.
#
# This includes ones that the firm cares about but does not control like $ p_t $.
#
# We turn to this problem now.
# #### Prices and Aggregate Output
#
# In view of [(5)](#equation-ree-comp3d), the firm’s incentive to forecast the market price translates into an incentive to forecast aggregate output $ Y_t $.
#
# Aggregate output depends on the choices of other firms.
#
# We assume that $ n $ is such a large number that the output of any single firm has a negligible effect on aggregate output.
#
# That justifies firms in regarding their forecasts of aggregate output as being unaffected by their own output decisions.
# #### The Firm’s Beliefs
#
# We suppose the firm believes that market-wide output $ Y_t $ follows the law of motion
#
#
# <a id='equation-ree-hlom'></a>
# $$
# Y_{t+1} = H(Y_t) \tag{8}
# $$
#
# where $ Y_0 $ is a known initial condition.
#
# The *belief function* $ H $ is an equilibrium object, and hence remains to be determined.
# #### Optimal Behavior Given Beliefs
#
# For now let’s fix a particular belief $ H $ in [(8)](#equation-ree-hlom) and investigate the firm’s response to it.
#
# Let $ v $ be the optimal value function for the firm’s problem given $ H $.
#
# The value function satisfies the Bellman equation
#
#
# <a id='equation-comp4'></a>
# $$
# v(y,Y) = \max_{y'} \left\{ a_0 y - a_1 y Y - \frac{ \gamma (y' - y)^2}{2} + \beta v(y', H(Y))\right\} \tag{9}
# $$
#
# Let’s denote the firm’s optimal policy function by $ h $, so that
#
#
# <a id='equation-comp9'></a>
# $$
# y_{t+1} = h(y_t, Y_t) \tag{10}
# $$
#
# where
#
#
# <a id='equation-ree-opbe'></a>
# $$
# h(y, Y) := \mathop{\mathrm{arg\,max}}_{y'}
# \left\{ a_0 y - a_1 y Y - \frac{ \gamma (y' - y)^2}{2} + \beta v(y', H(Y))\right\} \tag{11}
# $$
#
# Evidently $ v $ and $ h $ both depend on $ H $.
# #### First-Order Characterization of $ h $
#
# In what follows it will be helpful to have a second characterization of $ h $, based on first order conditions.
#
# The first-order necessary condition for choosing $ y' $ is
#
#
# <a id='equation-comp5'></a>
# $$
# -\gamma (y' - y) + \beta v_y(y',H(Y)) =0 \tag{12}
# $$
#
# An important useful envelope result of Benveniste-Scheinkman [[BS79]](../zreferences.html#benvenistescheinkman1979) implies that to
# differentiate $ v $ with respect to $ y $ we can naively differentiate
# the right side of [(9)](#equation-comp4), giving
#
# $$
# v_y(y,Y) = a_0 - a_1 Y + \gamma (y' - y)
# $$
#
# Substituting this equation into [(12)](#equation-comp5) gives the *Euler equation*
#
#
# <a id='equation-ree-comp7'></a>
# $$
# -\gamma (y_{t+1} - y_t) + \beta [a_0 - a_1 Y_{t+1} + \gamma (y_{t+2} - y_{t+1} )] =0 \tag{13}
# $$
#
# The firm optimally sets an output path that satisfies [(13)](#equation-ree-comp7), taking [(8)](#equation-ree-hlom) as given, and subject to
#
# - the initial conditions for $ (y_0, Y_0) $
# - the terminal condition $ \lim_{t \rightarrow \infty } \beta^t y_t v_y(y_{t}, Y_t) = 0 $
#
#
# This last condition is called the *transversality condition*, and acts as a first-order necessary condition “at infinity”.
#
# The firm’s decision rule solves the difference equation [(13)](#equation-ree-comp7) subject to the given initial condition $ y_0 $ and the transversality condition.
#
# Note that solving the Bellman equation [(9)](#equation-comp4) for $ v $ and then $ h $ in [(11)](#equation-ree-opbe) yields
# a decision rule that automatically imposes both the Euler equation [(13)](#equation-ree-comp7) and the transversality condition.
# #### The Actual Law of Motion for $ \{Y_t\} $
#
# As we’ve seen, a given belief translates into a particular decision rule $ h $.
#
# Recalling that $ Y_t = ny_t $, the *actual law of motion* for market-wide output is then
#
#
# <a id='equation-ree-comp9a'></a>
# $$
# Y_{t+1} = n h(Y_t/n, Y_t) \tag{14}
# $$
#
# Thus, when firms believe that the law of motion for market-wide output is [(8)](#equation-ree-hlom), their optimizing behavior makes the actual law of motion be [(14)](#equation-ree-comp9a).
#
#
# <a id='ree-def'></a>
# ### Definition of Rational Expectations Equilibrium
#
# A *rational expectations equilibrium* or *recursive competitive equilibrium* of the model with adjustment costs is a decision rule $ h $ and an aggregate law of motion $ H $ such that
#
# 1. Given belief $ H $, the map $ h $ is the firm’s optimal policy function.
# 1. The law of motion $ H $ satisfies $ H(Y)= nh(Y/n,Y) $ for all.
# $ Y $
#
#
# Thus, a rational expectations equilibrium equates the perceived and actual laws of motion [(8)](#equation-ree-hlom) and [(14)](#equation-ree-comp9a).
# #### Fixed point characterization
#
# As we’ve seen, the firm’s optimum problem induces a mapping $ \Phi $ from a perceived law of motion $ H $ for market-wide output to an actual law of motion $ \Phi(H) $.
#
# The mapping $ \Phi $ is the composition of two operations, taking a perceived law of motion into a decision rule via [(9)](#equation-comp4)–[(11)](#equation-ree-opbe), and a decision rule into an actual law via [(14)](#equation-ree-comp9a).
#
# The $ H $ component of a rational expectations equilibrium is a fixed point of $ \Phi $.
# ## Computation of an Equilibrium
#
#
# <a id='index-3'></a>
# Now let’s consider the problem of computing the rational expectations
# equilibrium.
# ### Misbehavior of $ \Phi $
#
# Readers accustomed to dynamic programming arguments might try to address this problem by choosing some guess $ H_0 $ for the aggregate law of motion and then iterating with $ \Phi $.
#
# Unfortunately, the mapping $ \Phi $ is not a contraction.
#
# In particular, there is no guarantee that direct iterations on $ \Phi $ converge <sup><a href=#fn-im id=fn-im-link>[1]</a></sup>.
#
# Fortunately, there is another method that works here.
#
# The method exploits a general connection between equilibrium and Pareto optimality expressed in
# the fundamental theorems of welfare economics (see, e.g, [[MCWG95]](../zreferences.html#mcwg1995)).
#
# Lucas and Prescott [[LP71]](../zreferences.html#lucasprescott1971) used this method to construct a rational expectations equilibrium.
#
# The details follow.
#
#
# <a id='ree-pp'></a>
# ### A Planning Problem Approach
#
#
# <a id='index-4'></a>
# Our plan of attack is to match the Euler equations of the market problem with those for a single-agent choice problem.
#
# As we’ll see, this planning problem can be solved by LQ control ([linear regulator](../dynamic_programming/lqcontrol.html)).
#
# The optimal quantities from the planning problem are rational expectations equilibrium quantities.
#
# The rational expectations equilibrium price can be obtained as a shadow price in the planning problem.
#
# For convenience, in this section we set $ n=1 $.
#
# We first compute a sum of consumer and producer surplus at time $ t $
#
#
# <a id='equation-comp10'></a>
# $$
# s(Y_t, Y_{t+1})
# := \int_0^{Y_t} (a_0 - a_1 x) \, dx - \frac{ \gamma (Y_{t+1} - Y_t)^2}{2} \tag{15}
# $$
#
# The first term is the area under the demand curve, while the second measures the social costs of changing output.
#
# The *planning problem* is to choose a production plan $ \{Y_t\} $ to maximize
#
# $$
# \sum_{t=0}^\infty \beta^t s(Y_t, Y_{t+1})
# $$
#
# subject to an initial condition for $ Y_0 $.
# ### Solution of the Planning Problem
#
# Evaluating the integral in [(15)](#equation-comp10) yields the quadratic form $ a_0
# Y_t - a_1 Y_t^2 / 2 $.
#
# As a result, the Bellman equation for the planning problem is
#
#
# <a id='equation-comp12'></a>
# $$
# V(Y) = \max_{Y'}
# \left\{a_0 Y - {a_1 \over 2} Y^2 - \frac{ \gamma (Y' - Y)^2}{2} + \beta V(Y') \right\} \tag{16}
# $$
#
# The associated first order condition is
#
#
# <a id='equation-comp14'></a>
# $$
# -\gamma (Y' - Y) + \beta V'(Y') = 0 \tag{17}
# $$
#
# Applying the same Benveniste-Scheinkman formula gives
#
# $$
# V'(Y) = a_0 - a_1 Y + \gamma (Y' - Y)
# $$
#
# Substituting this into equation [(17)](#equation-comp14) and rearranging leads to the Euler
# equation
#
#
# <a id='equation-comp16'></a>
# $$
# \beta a_0 + \gamma Y_t - [\beta a_1 + \gamma (1+ \beta)]Y_{t+1} + \gamma \beta Y_{t+2} =0 \tag{18}
# $$
# ### The Key Insight
#
# Return to equation [(13)](#equation-ree-comp7) and set $ y_t = Y_t $ for all $ t $.
#
# (Recall that for this section we’ve set $ n=1 $ to simplify the
# calculations)
#
# A small amount of algebra will convince you that when $ y_t=Y_t $, equations [(18)](#equation-comp16) and [(13)](#equation-ree-comp7) are identical.
#
# Thus, the Euler equation for the planning problem matches the second-order difference equation
# that we derived by
#
# 1. finding the Euler equation of the representative firm and
# 1. substituting into it the expression $ Y_t = n y_t $ that “makes the representative firm be representative”
#
#
# If it is appropriate to apply the same terminal conditions for these two difference equations, which it is, then we have verified that a solution of the planning problem is also a rational expectations equilibrium quantity sequence
#
# It follows that for this example we can compute equilibrium quantities by forming the optimal linear regulator problem corresponding to the Bellman equation [(16)](#equation-comp12).
#
# The optimal policy function for the planning problem is the aggregate law of motion
# $ H $ that the representative firm faces within a rational expectations equilibrium.
# #### Structure of the Law of Motion
#
# As you are asked to show in the exercises, the fact that the planner’s
# problem is an LQ problem implies an optimal policy — and hence aggregate law
# of motion — taking the form
#
#
# <a id='equation-ree-hlom2'></a>
# $$
# Y_{t+1}
# = \kappa_0 + \kappa_1 Y_t \tag{19}
# $$
#
# for some parameter pair $ \kappa_0, \kappa_1 $.
#
# Now that we know the aggregate law of motion is linear, we can see from the
# firm’s Bellman equation [(9)](#equation-comp4) that the firm’s problem can also be framed as
# an LQ problem.
#
# As you’re asked to show in the exercises, the LQ formulation of the firm’s
# problem implies a law of motion that looks as follows
#
#
# <a id='equation-ree-ex5'></a>
# $$
# y_{t+1} = h_0 + h_1 y_t + h_2 Y_t \tag{20}
# $$
#
# Hence a rational expectations equilibrium will be defined by the parameters
# $ (\kappa_0, \kappa_1, h_0, h_1, h_2) $ in [(19)](#equation-ree-hlom2)–[(20)](#equation-ree-ex5).
# ## Exercises
#
#
# <a id='ree-ex1'></a>
# ### Exercise 1
#
# Consider the firm problem [described above](#ree-fp).
#
# Let the firm’s belief function $ H $ be as given in [(19)](#equation-ree-hlom2).
#
# Formulate the firm’s problem as a discounted optimal linear regulator problem, being careful to describe all of the objects needed.
#
# Use the type `LQ` from the [QuantEcon.jl](http://quantecon.org/quantecon-jl) package to solve the firm’s problem for the following parameter values:
#
# $$
# a_0= 100, a_1= 0.05, \beta = 0.95, \gamma=10, \kappa_0 = 95.5, \kappa_1 = 0.95
# $$
#
# Express the solution of the firm’s problem in the form [(20)](#equation-ree-ex5) and give the values for each $ h_j $.
#
# If there were $ n $ identical competitive firms all behaving according to [(20)](#equation-ree-ex5), what would [(20)](#equation-ree-ex5) imply for the *actual* law of motion [(8)](#equation-ree-hlom) for market supply.
#
#
# <a id='ree-ex2'></a>
# ### Exercise 2
#
# Consider the following $ \kappa_0, \kappa_1 $ pairs as candidates for the
# aggregate law of motion component of a rational expectations equilibrium (see
# [(19)](#equation-ree-hlom2)).
#
# Extending the program that you wrote for exercise 1, determine which if any
# satisfy [the definition](#ree-def) of a rational expectations equilibrium
#
# - (94.0886298678, 0.923409232937)
# - (93.2119845412, 0.984323478873)
# - (95.0818452486, 0.952459076301)
#
#
# Describe an iterative algorithm that uses the program that you wrote for exercise 1 to compute a rational expectations equilibrium.
#
# (You are not being asked actually to use the algorithm you are suggesting)
#
#
# <a id='ree-ex3'></a>
# ### Exercise 3
#
# Recall the planner’s problem [described above](#ree-pp)
#
# 1. Formulate the planner’s problem as an LQ problem.
# 1. Solve it using the same parameter values in exercise 1
#
# - $ a_0= 100, a_1= 0.05, \beta = 0.95, \gamma=10 $
#
# 1. Represent the solution in the form $ Y_{t+1} = \kappa_0 + \kappa_1 Y_t $.
# 1. Compare your answer with the results from exercise 2.
#
#
#
# <a id='ree-ex4'></a>
# ### Exercise 4
#
# A monopolist faces the industry demand curve [(5)](#equation-ree-comp3d) and chooses $ \{Y_t\} $ to maximize $ \sum_{t=0}^{\infty} \beta^t r_t $ where
#
# $$
# r_t = p_t Y_t - \frac{\gamma (Y_{t+1} - Y_t)^2 }{2}
# $$
#
# Formulate this problem as an LQ problem.
#
# Compute the optimal policy using the same parameters as the previous exercise.
#
# In particular, solve for the parameters in
#
# $$
# Y_{t+1} = m_0 + m_1 Y_t
# $$
#
# Compare your results with the previous exercise. Comment.
# ## Solutions
# ### Exercise 1
# + hide-output=false
using QuantEcon, Printf, LinearAlgebra
# -
# To map a problem into a [discounted optimal linear control
# problem](http://quant-econ.net/jl/lqcontrol.html), we need to define
#
# - state vector $ x_t $ and control vector $ u_t $
# - matrices $ A, B, Q, R $ that define preferences and the law of
# motion for the state
#
#
# For the state and control vectors we choose
#
# $$
# x_t = \begin{bmatrix} y_t \\ Y_t \\ 1 \end{bmatrix},
# \qquad
# u_t = y_{t+1} - y_{t}
# $$
#
# For $ , B, Q, R $ we set
#
# $$
# A =
# \begin{bmatrix}
# 1 & 0 & 0 \\
# 0 & \kappa_1 & \kappa_0 \\
# 0 & 0 & 1
# \end{bmatrix},
# \quad
# B = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} ,
# \quad
# R =
# \begin{bmatrix}
# 0 & a_1/2 & -a_0/2 \\
# a_1/2 & 0 & 0 \\
# -a_0/2 & 0 & 0
# \end{bmatrix},
# \quad
# Q = \gamma / 2
# $$
#
# By multiplying out you can confirm that
#
# - $ x_t' R x_t + u_t' Q u_t = - r_t $
# - $ x_{t+1} = A x_t + B u_t $
#
#
# We’ll use the module `lqcontrol.jl` to solve the firm’s problem at the
# stated parameter values.
#
# This will return an LQ policy $ F $ with the interpretation
# $ u_t = - F x_t $, or
#
# $$
# y_{t+1} - y_t = - F_0 y_t - F_1 Y_t - F_2
# $$
#
# Matching parameters with $ y_{t+1} = h_0 + h_1 y_t + h_2 Y_t $ leads
# to
#
# $$
# h_0 = -F_2, \quad h_1 = 1 - F_0, \quad h_2 = -F_1
# $$
#
# Here’s our solution
# + hide-output=false
# model parameters
a0 = 100
a1 = 0.05
β = 0.95
γ = 10.0
# beliefs
κ0 = 95.5
κ1 = 0.95
# formulate the LQ problem
A = [1 0 0
0 κ1 κ0
0 0 1]
B = [1.0, 0.0, 0.0]
R = [ 0 a1/2 -a0/2
a1/2 0 0
-a0/2 0 0]
Q = 0.5 * γ
# solve for the optimal policy
lq = QuantEcon.LQ(Q, R, A, B; bet = β)
P, F, d = stationary_values(lq)
hh = h0, h1, h2 = -F[3], 1 - F[1], -F[2]
@printf("F = [%.3f, %.3f, %.3f]\n", F[1], F[2], F[3])
@printf("(h0, h1, h2) = [%.3f, %.3f, %.3f]\n", h0, h1, h2)
# -
# The implication is that
#
# $$
# y_{t+1} = 96.949 + y_t - 0.046 \, Y_t
# $$
#
# For the case $ n > 1 $, recall that $ Y_t = n y_t $, which,
# combined with the previous equation, yields
#
# $$
# Y_{t+1}
# = n \left( 96.949 + y_t - 0.046 \, Y_t \right)
# = n 96.949 + (1 - n 0.046) Y_t
# $$
# ### Exercise 2
#
# To determine whether a $ \kappa_0, \kappa_1 $ pair forms the
# aggregate law of motion component of a rational expectations
# equilibrium, we can proceed as follows:
#
# - Determine the corresponding firm law of motion
# $ y_{t+1} = h_0 + h_1 y_t + h_2 Y_t $.
# - Test whether the associated aggregate law
# :$ Y_{t+1} = n h(Y_t/n, Y_t) $ evaluates to
# $ Y_{t+1} = \kappa_0 + \kappa_1 Y_t $.
#
#
# In the second step we can use $ Y_t = n y_t = y_t $, so that
# $ Y_{t+1} = n h(Y_t/n, Y_t) $ becomes
#
# $$
# Y_{t+1} = h(Y_t, Y_t) = h_0 + (h_1 + h_2) Y_t
# $$
#
# Hence to test the second step we can test $ \kappa_0 = h_0 $ and
# $ \kappa_1 = h_1 + h_2 $.
#
# The following code implements this test
# + hide-output=false
candidates = ([94.0886298678, 0.923409232937],
[93.2119845412, 0.984323478873],
[95.0818452486, 0.952459076301])
for (k0, k1) in candidates
A = [1 0 0
0 k1 k0
0 0 1]
lq = QuantEcon.LQ(Q, R, A, B; bet=β)
P, F, d = stationary_values(lq)
hh = h0, h1, h2 = -F[3], 1 - F[1], -F[2]
if isapprox(k0, h0; atol = 1e-4) && isapprox(k1, h1 + h2; atol = 1e-4)
@printf("Equilibrium pair = (%.6f, %.6f)\n", k0, k1)
@printf("(h0, h1, h2) = [%.6f, %.6f, %.6f]\n", h0, h1, h2)
end
end
# -
# The output tells us that the answer is pair (iii), which implies
# $ (h_0, h_1, h_2) = (95.0819, 1.0000, -.0475) $.
#
# (Notice we use `isapprox` to test equality of floating point numbers,
# since exact equality is too strict)
#
# Regarding the iterative algorithm, one could loop from a given
# $ (\kappa_0, \kappa_1) $ pair to the associated firm law and then to
# a new $ (\kappa_0, \kappa_1) $ pair.
#
# This amounts to implementing the operator $ \Phi $ described in the
# lecture.
#
# (There is in general no guarantee that this iterative process will
# converge to a rational expectations equilibrium)
# ### Exercise 3
#
# We are asked to write the planner problem as an LQ problem.
#
# For the state and control vectors we choose
#
# $$
# x_t = \begin{bmatrix} Y_t \\ 1 \end{bmatrix},
# \quad
# u_t = Y_{t+1} - Y_{t}
# $$
#
# For the LQ matrices we set
#
# $$
# A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},
# \quad
# B = \begin{bmatrix} 1 \\ 0 \end{bmatrix},
# \quad
# R = \begin{bmatrix} a_1/2 & -a_0/2 \\ -a_0/2 & 0 \end{bmatrix},
# \quad
# Q = \gamma / 2
# $$
#
# By multiplying out you can confirm that
#
# - $ x_t' R x_t + u_t' Q u_t = - s(Y_t, Y_{t+1}) $
# - $ x_{t+1} = A x_t + B u_t $
#
#
# By obtaining the optimal policy and using $ u_t = - F x_t $ or
#
# $$
# Y_{t+1} - Y_t = -F_0 Y_t - F_1
# $$
#
# we can obtain the implied aggregate law of motion via
# $ \kappa_0 = -F_1 $ and $ \kappa_1 = 1-F_0 $
# + hide-output=false
# formulate the planner's LQ problem
A = I + zeros(2, 2)
B = [1.0, 0.0]
R = [ a1 / 2.0 -a0 / 2.0
-a0 / 2.0 0.0]
Q = γ / 2.0
# solve for the optimal policy
lq = QuantEcon.LQ(Q, R, A, B; bet=β)
P, F, d = stationary_values(lq)
# print the results
κ0, κ1 = -F[2], 1 - F[1]
println("κ0=$κ0\tκ1=$κ1")
# -
# The output yields the same $ (\kappa_0, \kappa_1) $ pair obtained as
# an equilibrium from the previous exercise.
# ### Exercise 4
#
# The monopolist’s LQ problem is almost identical to the planner’s problem
# from the previous exercise, except that
#
# $$
# R = \begin{bmatrix}
# a_1 & -a_0/2 \\
# -a_0/2 & 0
# \end{bmatrix}
# $$
#
# The problem can be solved as follows
# + hide-output=false
# formulate the monopolist's LQ problem
A = I + zeros(2, 2)
B = [1.0, 0.0]
R = [ a1 -a0 / 2.0
-a0 / 2.0 0.0]
Q = γ / 2.0
# solve for the optimal policy
lq = QuantEcon.LQ(Q, R, A, B; bet=β)
P, F, d = stationary_values(lq)
# print the results
m0, m1 = -F[2], 1 - F[1]
println("m0=$m0\tm1=$m1")
# -
# We see that the law of motion for the monopolist is approximately
# $ Y_{t+1} = 73.4729 + 0.9265 Y_t $.
#
# In the rational expectations case the law of motion was approximately
# $ Y_{t+1} = 95.0819 + 0.9525 Y_t $.
#
# One way to compare these two laws of motion is by their fixed points,
# which give long run equilibrium output in each case.
#
# For laws of the form $ Y_{t+1} = c_0 + c_1 Y_t $, the fixed point is
# $ c_0 / (1 - c_1) $.
#
# If you crunch the numbers, you will see that the monopolist adopts a
# lower long run quantity than obtained by the competitive market,
# implying a higher market price.
#
# This is analogous to the elementary static-case results
# **Footnotes**
#
# <p><a id=fn-im href=#fn-im-link><strong>[1]</strong></a> A literature that studies whether models populated with agents
# who learn can converge to rational expectations equilibria features
# iterations on a modification of the mapping $ \Phi $ that can be
# approximated as $ \gamma \Phi + (1-\gamma)I $. Here $ I $ is the
# identity operator and $ \gamma \in (0,1) $ is a *relaxation parameter*.
# See [[MS89]](../zreferences.html#marcetsargent1989) and [[EH01]](../zreferences.html#evanshonkapohja2001) for statements
# and applications of this approach to establish conditions under which
# collections of adaptive agents who use least squares learning converge to a
# rational expectations equilibrium.
|
multi_agent_models/rational_expectations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/sokrypton/ColabFold/blob/main/batch/AlphaFold2_batch.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="G4yBrceuFbf3"
# #ColabFold: AlphaFold2 w/ MMseqs2 BATCH
#
# <img src="https://raw.githubusercontent.com/sokrypton/ColabFold/main/.github/ColabFold_Marv_Logo_Small.png" height="256" align="right" style="height:256px">
#
# Easy to use AlphaFold2 [(Jumper et al. 2021)](https://www.nature.com/articles/s41586-021-03819-2) protein structure prediction using multiple sequence alignments generated through an MMseqs2 API. For details, refer to our manuscript:
#
# [<NAME>, <NAME>, <NAME>. ColabFold - Making protein folding accessible to all.
# *bioRxiv*, 2021](https://www.biorxiv.org/content/10.1101/2021.08.15.456425v1)
#
# - This notebook provides basic functionality, for more advanced options (such as modeling heterocomplexes, increasing recycles, sampling, etc.) see our [advanced notebook](https://colab.research.google.com/github/sokrypton/ColabFold/blob/main/beta/AlphaFold2_advanced.ipynb).
# - This notebook replaces the homology detection of AlphaFold2 with MMseqs2. For a comparision against the [Deepmind Colab](https://colab.research.google.com/github/deepmind/alphafold/blob/main/notebooks/AlphaFold.ipynb) and the full [AlphaFold2](https://github.com/deepmind/alphafold) system read our [preprint](https://www.biorxiv.org/content/10.1101/2021.08.15.456425v1).
#
#
#
# **Usage**
#
# `input_dir` directory with only fasta files or MSAs stored in Google Drive. MSAs need to be A3M formatted and have an `.a3m` extention. For MSAs MMseqs2 will not be called.
#
# `result_dir` results will be written to the result directory in Google Drive
#
#
# <strong>For more details, see <a href="#Instructions">bottom</a> of the notebook and checkout the [ColabFold GitHub](https://github.com/sokrypton/ColabFold). </strong>
# + id="AwvIWN3HDyUJ" cellView="form"
#@title Mount google drive
from google.colab import drive
drive.mount('/content/drive')
# + id="kOblAo-xetgx" cellView="form"
#@title Input protein sequence, then hit `Runtime` -> `Run all`
input_dir = '/content/drive/MyDrive/input_fasta' #@param {type:"string"}
result_dir = '/content/drive/MyDrive/result' #@param {type:"string"}
# number of models to use
#@markdown ---
#@markdown ### Advanced settings
msa_mode = "MMseqs2 (UniRef+Environmental)" #@param ["MMseqs2 (UniRef+Environmental)", "MMseqs2 (UniRef only)","single_sequence","custom"]
num_models = 5 #@param [1,2,3,4,5] {type:"raw"}
stop_at_score = 100 #@param {type:"string"}
use_msa = True if msa_mode.startswith("MMseqs2") else False
use_custom_msa = False
use_amber = False #@param {type:"boolean"}
use_templates = False #@param {type:"boolean"}
do_not_overwrite_results = True #@param {type:"boolean"}
homooligomer = 1
with open(f"run.log", "w") as text_file:
text_file.write("num_models=%s\n" % num_models)
text_file.write("use_amber=%s\n" % use_amber)
text_file.write("use_msa=%s\n" % use_msa)
text_file.write("msa_mode=%s\n" % msa_mode)
text_file.write("use_templates=%s\n" % use_templates)
# + id="iccGdbe_Pmt9" cellView="form"
#@title Install dependencies
# %%bash -s $use_amber $use_msa $use_templates
set -e
USE_AMBER=$1
USE_MSA=$2
USE_TEMPLATES=$3
# Trick for dev stage because otherwise pip won't install newer git versions
pip install -q 'git+https://github.com/sokrypton/ColabFold.git#egg=ColabFold[alphafold]'
# Download params (~1min)
python -m colabfold.download
# setup conda
if [ ${USE_AMBER} == "True" ] || [ ${USE_TEMPLATES} == "True" ]; then
if [ ! -f CONDA_READY ]; then
wget -qnc https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh
bash Miniconda3-latest-Linux-x86_64.sh -bfp /usr/local 2>&1 1>/dev/null
rm Miniconda3-latest-Linux-x86_64.sh
touch CONDA_READY
fi
fi
# setup template search
if [ ${USE_TEMPLATES} == "True" ] && [ ! -f HH_READY ]; then
conda install -y -q -c conda-forge -c bioconda kalign3=3.2.2 hhsuite=3.3.0 python=3.7 2>&1 1>/dev/null
touch HH_READY
fi
# setup openmm for amber refinement
if [ ${USE_AMBER} == "True" ] && [ ! -f AMBER_READY ]; then
conda install -y -q -c conda-forge openmm=7.5.1 python=3.7 pdbfixer 2>&1 1>/dev/null
wget -qnc https://raw.githubusercontent.com/deepmind/alphafold/main/docker/openmm.patch
(cd /usr/local/lib/python3.7/site-packages; patch -s -p0 < /content/openmm.patch)
wget -qnc https://git.scicore.unibas.ch/schwede/openstructure/-/raw/7102c63615b64735c4941278d92b554ec94415f8/modules/mol/alg/src/stereo_chemical_props.txt
touch AMBER_READY
fi
# + id="hUYApPElB30u" cellView="form"
#@title Run Prediction
import sys
from colabfold.batch import get_queries, run
from colabfold.download import default_data_dir
from colabfold.utils import setup_logging
from pathlib import Path
# For some reason we need that to get pdbfixer to import
if use_amber and '/usr/local/lib/python3.7/site-packages/' not in sys.path:
sys.path.insert(0, '/usr/local/lib/python3.7/site-packages/')
setup_logging(Path(result_dir).joinpath("log.txt"))
queries, is_complex = get_queries(input_dir)
run(
queries=queries,
result_dir=result_dir,
use_templates=use_templates,
use_amber=use_amber,
msa_mode=msa_mode,
num_models=num_models,
model_order=[3, 4, 5, 1, 2],
is_complex=is_complex,
data_dir=default_data_dir,
keep_existing_results=do_not_overwrite_results,
rank_mode="auto",
pair_mode="unpaired+paired",
stop_at_score=stop_at_score,
)
# + [markdown] id="UGUBLzB3C6WN"
# # Instructions <a name="Instructions"></a>
# **Quick start**
# 1. Upload your single fasta files to a folder in your Google Drive
# 2. Define path to the fold containing the fasta files (`input_dir`) define an outdir (`output_dir`)
# 3. Press "Runtime" -> "Run all".
#
# **Result zip file contents**
#
# At the end of the job a all results `jobname.result.zip` will be uploaded to your (`output_dir`) Google Drive. Each zip contains one protein.
#
# 1. PDB formatted structures sorted by avg. pIDDT. (unrelaxed and relaxed if `use_amber` is enabled).
# 2. Plots of the model quality.
# 3. Plots of the MSA coverage.
# 4. Parameter log file.
# 5. A3M formatted input MSA.
# 6. BibTeX file with citations for all used tools and databases.
#
#
# **Troubleshooting**
# * Check that the runtime type is set to GPU at "Runtime" -> "Change runtime type".
# * Try to restart the session "Runtime" -> "Factory reset runtime".
# * Check your input sequence.
#
# **Known issues**
# * Google Colab assigns different types of GPUs with varying amount of memory. Some might not have enough memory to predict the structure for a long sequence.
# * Google Colab assigns different types of GPUs with varying amount of memory. Some might not have enough memory to predict the structure for a long sequence.
# * Your browser can block the pop-up for downloading the result file. You can choose the `save_to_google_drive` option to upload to Google Drive instead or manually download the result file: Click on the little folder icon to the left, navigate to file: `jobname.result.zip`, right-click and select \"Download\" (see [screenshot](https://pbs.twimg.com/media/E6wRW2lWUAEOuoe?format=jpg&name=small)).
#
# **Limitations**
# * Computing resources: Our MMseqs2 API can handle ~20-50k requests per day.
# * MSAs: MMseqs2 is very precise and sensitive but might find less hits compared to HHblits/HMMer searched against BFD or Mgnify.
# * We recommend to additionally use the full [AlphaFold2 pipeline](https://github.com/deepmind/alphafold).
#
# **Description of the plots**
# * **Number of sequences per position** - We want to see at least 30 sequences per position, for best performance, ideally 100 sequences.
# * **Predicted lDDT per position** - model confidence (out of 100) at each position. The higher the better.
# * **Predicted Alignment Error** - For homooligomers, this could be a useful metric to assess how confident the model is about the interface. The lower the better.
#
# **Bugs**
# - If you encounter any bugs, please report the issue to https://github.com/sokrypton/ColabFold/issues
#
#
# **Acknowledgments**
# - We thank the AlphaFold team for developing an excellent model and open sourcing the software.
#
# - [Söding Lab](https://www.mpibpc.mpg.de/soeding) for providing the computational resources for the MMseqs2 server
#
# - Do-Yoon Kim for creating the ColabFold logo.
#
# - A colab by <NAME> ([@sokrypton](https://twitter.com/sokrypton)), <NAME> ([@milot_mirdita](https://twitter.com/milot_mirdita)) and <NAME> ([@thesteinegger](https://twitter.com/thesteinegger)).
#
|
batch/AlphaFold2_batch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.7 64-bit (''midnight'': conda)'
# language: python
# name: python3
# ---
# [](https://colab.research.google.com/github/nahuelalmeira/midnight/blob/main/notebooks/notebook.ipynb)
# !pip install --quiet git+https://github.com/nahuelalmeira/midnight
# +
# Graphics
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from IPython.display import display
sns.set()
sns.set_context("talk")
matplotlib.rcParams["figure.figsize"] = (12, 8)
# -
from midnight.player import Player
from midnight.game import Game
from midnight.strategy import (
ConservativeStrategy,
MiddleStrategy,
AlwaysConservativeStrategy,
AlwaysMiddleStrategy,
)
sample_conservative = pd.Series(ConservativeStrategy.sample(100000))
sample_middle = pd.Series(MiddleStrategy.sample(100000))
samples = {"Conservative": sample_conservative, "Middle": sample_middle}
fig, ax = plt.subplots()
ax.set_xlabel("Score")
ax.set_ylabel("Probability")
ax.hist(samples.values(), bins=range(0, 25), density=True, label=list(samples.keys()))
plt.legend()
plt.show()
fig, ax = plt.subplots()
for name, sample in samples.items():
(
sample.value_counts(normalize=True)
.sort_index(ascending=False)
.drop(0)
.cumsum()
.plot(marker="o", xlabel="Score", ylabel="Tie or win probability", label=name, ax=ax)
)
ax.legend()
plt.show()
# +
n_rounds = 10000
n_players = 2
initial_stake = 1000
print("-----------------")
print("Game settings")
print(f"Number of players: {n_players}")
print(f"Number of rounds: {n_rounds}")
print(f"Initial stake: {initial_stake}")
print("-----------------")
print()
Player.reset_counter()
game = Game(n_rounds=n_rounds)
player1 = Player(
strategy=AlwaysConservativeStrategy(), initial_stake=initial_stake
)
game.add_player(player1)
player2 = Player(
strategy=AlwaysMiddleStrategy(), initial_stake=initial_stake
)
game.add_player(player2)
# Play game
game.play()
print("-----------------")
print("Game stats")
stats = game.get_game_stats()
display(stats.head(10))
print("-----------------")
print()
print(f"Final relative stakes: {game.relative_stakes}")
print()
print("-----------------")
print("Scores")
scores = game.get_all_scores()
display(scores.head())
print("-----------------")
print()
print("-----------------")
print("Qualification rate per player:")
display((scores > 0).mean())
print("-----------------")
print()
print("-----------------")
print("Win rate per player:")
display(stats["WINNER"].value_counts(normalize=True))
print("-----------------")
print()
# -
|
notebooks/notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: venv
# language: python
# name: venv
# ---
import json
import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
import joblib
df = pd.read_csv('https://raw.githubusercontent.com/pplonski/datasets-for-start/master/adult/data.csv', skipinitialspace=True)
x_cols = [c for c in df.columns if c!= 'income']
X=df[x_cols]
y=df['income']
df.head()
#split datasets to train and test
X_train, X_test, y_train, y_test = train_test_split(X,y, test_size=0.3, random_state=1234)
#fill empty values
train_mode = dict(X_train.mode().iloc[0])
X_train = X_train.fillna(train_mode)
print(train_mode)
#encode string to numerical
encoders={}
for column in ['workclass','education','marital-status','occupation','relationship','race','sex','native-country']:
categorical_convert = LabelEncoder()
X_train[column] = categorical_convert.fit_transform(X_train[column])
encoders[column]=categorical_convert
#training random forest algorithm
rf = RandomForestClassifier(n_estimators=100)
rf = rf.fit(X_train,y_train)
#train extra trees algorithm
et = ExtraTreesClassifier(n_estimators = 100)
et = et.fit(X_train,y_train)
#save preprocessing objects and ml algorithms
joblib.dump(train_mode,"./train_mode-joblib",compress=True)
joblib.dump(encoders,"./encoders.joblib",compress=True)
joblib.dump(rf,"./random_forest.joblib",compress=True)
joblib.dump(et,"extra_trees.joblib",compress=True)
|
research/train_income_classifier.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cpp
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: C++14
// language: C++14
// name: xeus-cling-cpp14
// ---
// # Array-based List
// https://opendsa-server.cs.vt.edu/ODSA/Books/CS2/html/ListADT.html
//
// ## Table of Contents
// - **[List Definition](#intro)** <br>
// - **[Defining List ADT](#adt)** <br>
// - **[Using List ADT](#app)**<br>
// <a id="intro"></a>
// ## List
// - C++ STL provides several data structures/containers; often we need to design our own
// - we'll build **list** Abstract Data Type (ADT) in this chapter
// - **list**: finite, sequence of data items/elements
// - some terminologies and definitions:
// - a list is said to be **empty** when it contains no elements
// - number of elements currently stored is called the **length**
// - the beginning of the list is called **head**
// - the end of the list is called **tail**
// <a id="adt"></a>
// ## Defining List ADT
// - how do we store elements? C-Array is one of the easier options!
// - what basic operations do we want our list to support?
// - some intuition and experience in using STL container says, we want our list to be able to:
// 1. add more elements
// 2. delete elements
// 3. clear elements
// 4. access elements
// 5. know the length and many more...
// - operations similar to STL Vector
// - Tricky Operations:
// - insert element in the middle
// - remove element from the middle
// +
#pragma once
#include <iostream>
#include <cassert>
#include <stdexcept>
using namespace std;
// + code_folding=[65, 72, 81, 87, 93, 99, 105, 119, 125, 140, 151, 158, 176, 189, 195, 204, 223]
/*
Class interface and definition for dynamic array-based ListType template.
Class template definition can't be in separate file because
the compiler needs to know all the implementation details of the class
so it can instantiate different versions of the code, depending on the
actual types provided for each template parameters.
Remember that a template doesn't represent code directly, but a
template for several versions of that code.
*/
template <class T>
class ListType
{
private:
T *list;
int length;
int maxSize;
public:
ListType(size_t max = 10000); // constructor
ListType(const ListType<T> &other); // copy constructor
~ListType(); // destructor
// **** LIST META-DATA AND CAPACITY INFO ****
// return true if list is empty
bool isEmpty() const;
// return true if list is full
bool isFull() const;
// get the length/size of the list
int listSize() const;
// get the max list size
int listMaxSize() const;
// **** ELEMENT ACCESS ****
// retrieve the element at given index
T at(size_t index) const;
// access the last/back element
T back();
// access the first element
T front();
// overload operator[] as member function
T operator[](int index) const;
// **** MODIFIERS ***
// insert at the end of the list
void pushBack(const T &item);
// delete the last element
void popBack();
// insert given item at the given index
void insertAt(size_t index, const T &item);
// deletes all the elements in the list and resets the list
void clear();
// replace element at index with new item
void replaceAt(size_t index, const T &item);
// remove the element at given index
void removeAt(size_t index);
// do a linear search on given searchItem and return index if found -1 otherwise
int search(const T &searchItem);
// find the item in the container and remove it
void remove(const T &item);
};
template <class T>
ListType<T>::ListType(size_t max) {
this->maxSize = max;
this->length = 0;
this->list = new T[maxSize]; // dynamic array!
}
template <class T>
ListType<T>::ListType(const ListType<T> &other) {
this->length = other.length;
this->maxSize = other.maxSize;
this->list = new T[maxSize];
for (int i = 0; i<other.length; i++)
this->list[i] = other.list[i];
}
template <class T>
ListType<T>::~ListType() {
delete[] list;
}
// return true if list is empty
template <class T>
bool ListType<T>::isEmpty() const {
return (length == 0);
}
// return true if list is full
template <class T>
bool ListType<T>::isFull() const {
return (length == maxSize);
}
// return size/length of the list
template <class T>
int ListType<T>::listSize() const {
return this->length;
}
// return the max size of list
template <class T>
int ListType<T>::listMaxSize() const {
return this->maxSize;
}
// retrieve the element at given index
template <class T>
T ListType<T>::at(size_t index) const {
if (index < 0 || index >= length)
throw out_of_range("Index out of range.");
return list[index];
}
template<class T>
T ListType<T>::back() {
// doesn't check if the list is empty!
return list[length-1];
}
template<class T>
T ListType<T>::front() {
// doesn't check if the list is empty!
return list[0];
}
//return the reference to the value at given index
template <class T>
T ListType<T>::operator[](int index) const {
if (index < 0 || index >= length)
throw out_of_range("Index out of range.");
return list[index];
}
// insert at the end of the list
template <class T>
void ListType<T>::pushBack(const T &item) {
if (isFull())
throw overflow_error("List is full.");
else {
list[length] = item;
length++;
}
}
// delete the last element
template <class T>
void ListType<T>::popBack() {
removeAt(length-1);
}
// insert item at the index
// Exception: out_of_range thrown when list it full or index is out of bounds
template <class T>
void ListType<T>::insertAt(size_t index, const T &item) {
if (index < 0 || index >= length)
throw out_of_range("Index out of range.");
else if (isFull()) {
throw overflow_error("List is full.");
}
else {
// move the elements down from the index
// starting from the end
for (int i = length; i > index; i--)
list[i] = list[i - 1];
list[index] = item; // insert the item at the specified index
length++; // increment the length
}
}
// remove the element at given index
template <class T>
void ListType<T>::removeAt(size_t index) {
if (index < 0 || index >= length)
throw out_of_range("Index out of range.");
else {
// move elements up one position one at a time
for (int i = index; i < length - 1; i++)
list[i] = list[i + 1];
length--; // decrease list length by 1
}
}
// deletes all the elements in the list and resets the list
template <class T>
void ListType<T>::clear() {
length = 0;
}
// replace element at index with new item
template <class T>
void ListType<T>::replaceAt(size_t index, const T &item) {
if (index < 0 || index >= length)
throw out_of_range("Index out of range.");
else
list[index] = item;
}
// do a linear search on given searchItem and return index if found, -1 otherwise
template <class T>
int ListType<T>::search(const T &searchItem) {
int index = 0;
bool found = false;
while (index < length && !found)
{
if (list[index] == searchItem)
found = true;
else
index++;
}
if (found)
return index;
else
return -1;
}
// find the item in the container and remove it
template <class T>
void ListType<T>::remove(const T &item)
{
int index = -1;
if (isEmpty())
throw underflow_error("List is empty.");
else
{
index = seqSearch(item);
if (index != -1)
removeAt(index);
}
}
// + code_folding=[3]
// print all the elements in the list
// overload operator<<
template<class T>
ostream& operator<<(ostream& out, const ListType<T>& alist){
out << "max size = " << alist.listMaxSize() << endl;
out << "length = " << alist.listSize() << endl;
out << "list contents: " << endl;
for (int i = 0; i<alist.listSize(); i++)
out << alist[i] << " ";
out << endl;
return out;
}
// -
// <a id="app"></a>
// ## Using ListType ADT
// Test ListType
ListType<int> ilist(100);
ilist.pushBack(10);
cout << ilist;
ilist.insertAt(0, 20);
cout << ilist;
ilist.clear();
cout << ilist;
ilist.replaceAt(0, 200);
cout << ilist;
int i;
i = ilist.search(10);
if (i < 0)
cout << "element not found...";
else
cout << "element found at index: " << i << endl;
// ### Exercise
// - In an array-based list, the successive elements in the list:
// 1. Need not occupy contiguous space in memory
// - Must occupy contiguous space in memory
// - None of these
// - Must not occupy contigious space in memory
|
ArrayList.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/AnthonyGachuru/DS-Unit-1-Sprint-2-Data-Wrangling-and-Storytelling/blob/master/AnthonyG_LS_DS_123_Make_Explanatory_Visualizations.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="-8-trVo__vRE"
# _Lambda School Data Science_
#
# # Make Explanatory Visualizations
#
# ### Objectives
#
# - identify misleading visualizations and how to fix them
# - use Seaborn to visualize distributions and relationships with continuous and discrete variables
# - add emphasis and annotations to transform visualizations from exploratory to explanatory
# - remove clutter from visualizations
#
# ### Links
#
# - [How to Spot Visualization Lies](https://flowingdata.com/2017/02/09/how-to-spot-visualization-lies/)
# - [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
# - [Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
# - [Searborn example gallery](http://seaborn.pydata.org/examples/index.html) & [tutorial](http://seaborn.pydata.org/tutorial.html)
# - [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
# - [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
# - [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
# + [markdown] id="s-24T844-8qv" colab_type="text"
# # Avoid Misleading Visualizations
#
# Did you find/discuss any interesting misleading visualizations in your Walkie Talkie?
# + [markdown] id="Qzxt9ntsNjs0" colab_type="text"
# ## What makes a visualization misleading?
#
# [5 Ways Writers Use Misleading Graphs To Manipulate You](https://venngage.com/blog/misleading-graphs/)
# + [markdown] id="q7_DUiENNvxk" colab_type="text"
# ## Two y-axes
#
# <img src="https://kieranhealy.org/files/misc/two-y-by-four-sm.jpg" width="800">
#
# Other Examples:
# - [Spurious Correlations](https://tylervigen.com/spurious-correlations)
# - <https://blog.datawrapper.de/dualaxis/>
# - <https://kieranhealy.org/blog/archives/2016/01/16/two-y-axes/>
# - <http://www.storytellingwithdata.com/blog/2016/2/1/be-gone-dual-y-axis>
# + [markdown] id="oIijNBDMNv2k" colab_type="text"
# ## Y-axis doesn't start at zero.
#
# <img src="https://i.pinimg.com/originals/22/53/a9/2253a944f54bb61f1983bc076ff33cdd.jpg" width="600">
# + [markdown] id="ISB2p8vZNv6r" colab_type="text"
# ## Pie Charts are bad
#
# <img src="https://i1.wp.com/flowingdata.com/wp-content/uploads/2009/11/Fox-News-pie-chart.png?fit=620%2C465&ssl=1" width="600">
# + [markdown] id="67CsAzu1NwBJ" colab_type="text"
# ## Pie charts that omit data are extra bad
#
# - A guy makes a misleading chart that goes viral
#
# What does this chart imply at first glance? You don't want your user to have to do a lot of work in order to be able to interpret you graph correctly. You want that first-glance conclusions to be the correct ones.
#
# <img src="https://pbs.twimg.com/media/DiaiTLHWsAYAEEX?format=jpg&name=medium" width='600'>
#
# <https://twitter.com/michaelbatnick/status/1019680856837849090?lang=en>
#
# - It gets picked up by overworked journalists (assuming incompetency before malice)
#
# <https://www.marketwatch.com/story/this-1-chart-puts-mega-techs-trillions-of-market-value-into-eye-popping-perspective-2018-07-18>
#
# - Even after the chart's implications have been refuted, it's hard a bad (although compelling) visualization from being passed around.
#
# <https://www.linkedin.com/pulse/good-bad-pie-charts-karthik-shashidhar/>
#
# **["yea I understand a pie chart was probably not the best choice to present this data."](https://twitter.com/michaelbatnick/status/1037036440494985216)**
# + [markdown] id="FYXmlToEOOTC" colab_type="text"
# ## Pie Charts that compare unrelated things are next-level extra bad
#
# <img src="http://www.painting-with-numbers.com/download/document/186/170403+Legalizing+Marijuana+Graph.jpg" width="600">
#
# + [markdown] id="IwtMQpY_QFUw" colab_type="text"
# ## Be careful about how you use volume to represent quantities:
#
# radius vs diameter vs volume
#
# <img src="https://static1.squarespace.com/static/5bfc8dbab40b9d7dd9054f41/t/5c32d86e0ebbe80a25873249/1546836082961/5474039-25383714-thumbnail.jpg?format=1500w" width="600">
# + [markdown] id="tTuAWjSBRsc7" colab_type="text"
# ## Don't cherrypick timelines or specific subsets of your data:
#
# <img src="https://wattsupwiththat.com/wp-content/uploads/2019/02/Figure-1-1.png" width="600">
#
# Look how specifically the writer has selected what years to show in the legend on the right side.
#
# <https://wattsupwiththat.com/2019/02/24/strong-arctic-sea-ice-growth-this-year/>
#
# Try the tool that was used to make the graphic for yourself
#
# <http://nsidc.org/arcticseaicenews/charctic-interactive-sea-ice-graph/>
#
# + [markdown] id="Xs13S7p4Srme" colab_type="text"
# ## Use Relative units rather than Absolute Units
#
# <img src="https://imgs.xkcd.com/comics/heatmap_2x.png" width="600">
# + [markdown] id="CIMt5OiuTlrr" colab_type="text"
# ## Avoid 3D graphs unless having the extra dimension is effective
#
# Usually you can Split 3D graphs into multiple 2D graphs
#
# 3D graphs that are interactive can be very cool. (See Plotly and Bokeh)
#
# <img src="https://thumbor.forbes.com/thumbor/1280x868/https%3A%2F%2Fblogs-images.forbes.com%2Fthumbnails%2Fblog_1855%2Fpt_1855_811_o.jpg%3Ft%3D1339592470" width="600">
# + [markdown] id="GATMu9IqUlIj" colab_type="text"
# ## Don't go against typical conventions
#
# <img src="http://www.callingbullshit.org/twittercards/tools_misleading_axes.png" width="600">
# + [markdown] id="g6bKgZ0m_ynS" colab_type="text"
# # Tips for choosing an appropriate visualization:
# + [markdown] id="WtBsVnO4VHiJ" colab_type="text"
# ## Use Appropriate "Visual Vocabulary"
#
# [Visual Vocabulary - Vega Edition](http://ft.com/vocabulary)
# + [markdown] id="H_QM9FHqVT7T" colab_type="text"
# ## What are the properties of your data?
# - Is your primary variable of interest continuous or discrete?
# - Is in wide or long (tidy) format?
# - Does your visualization involve multiple variables?
# - How many dimensions do you need to include on your plot?
#
# Can you express the main idea of your visualization in a single sentence?
#
# How hard does your visualization make the user work in order to draw the intended conclusion?
# + [markdown] id="5EqXxnJeB89_" colab_type="text"
# ## Which Visualization tool is most appropriate?
#
# [Choosing a Python Visualization Tool flowchart](http://pbpython.com/python-vis-flowchart.html)
# + [markdown] id="4mDuzLeNn23m" colab_type="text"
# ## Anatomy of a Matplotlib Plot
# + id="h-aIS1Vdn2RR" colab_type="code" outputId="9da54117-8b82-4a79-b099-e86120ef1a9a" colab={"base_uri": "https://localhost:8080/", "height": 555}
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import AutoMinorLocator, MultipleLocator, FuncFormatter
np.random.seed(19680801)
X = np.linspace(0.5, 3.5, 100)
Y1 = 3+np.cos(X)
Y2 = 1+np.cos(1+X/0.75)/2
Y3 = np.random.uniform(Y1, Y2, len(X))
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(1, 1, 1, aspect=1)
def minor_tick(x, pos):
if not x % 1.0:
return ""
return "%.2f" % x
ax.xaxis.set_major_locator(MultipleLocator(1.000))
ax.xaxis.set_minor_locator(AutoMinorLocator(4))
ax.yaxis.set_major_locator(MultipleLocator(1.000))
ax.yaxis.set_minor_locator(AutoMinorLocator(4))
ax.xaxis.set_minor_formatter(FuncFormatter(minor_tick))
ax.set_xlim(0, 4)
ax.set_ylim(0, 4)
ax.tick_params(which='major', width=1.0)
ax.tick_params(which='major', length=10)
ax.tick_params(which='minor', width=1.0, labelsize=10)
ax.tick_params(which='minor', length=5, labelsize=10, labelcolor='0.25')
ax.grid(linestyle="--", linewidth=0.5, color='.25', zorder=-10)
ax.plot(X, Y1, c=(0.25, 0.25, 1.00), lw=2, label="Blue signal", zorder=10)
ax.plot(X, Y2, c=(1.00, 0.25, 0.25), lw=2, label="Red signal")
ax.plot(X, Y3, linewidth=0,
marker='o', markerfacecolor='w', markeredgecolor='k')
ax.set_title("Anatomy of a figure", fontsize=20, verticalalignment='bottom')
ax.set_xlabel("X axis label")
ax.set_ylabel("Y axis label")
ax.legend()
def circle(x, y, radius=0.15):
from matplotlib.patches import Circle
from matplotlib.patheffects import withStroke
circle = Circle((x, y), radius, clip_on=False, zorder=10, linewidth=1,
edgecolor='black', facecolor=(0, 0, 0, .0125),
path_effects=[withStroke(linewidth=5, foreground='w')])
ax.add_artist(circle)
def text(x, y, text):
ax.text(x, y, text, backgroundcolor="white",
ha='center', va='top', weight='bold', color='blue')
# Minor tick
circle(0.50, -0.10)
text(0.50, -0.32, "Minor tick label")
# Major tick
circle(-0.03, 4.00)
text(0.03, 3.80, "Major tick")
# Minor tick
circle(0.00, 3.50)
text(0.00, 3.30, "Minor tick")
# Major tick label
circle(-0.15, 3.00)
text(-0.15, 2.80, "Major tick label")
# X Label
circle(1.80, -0.27)
text(1.80, -0.45, "X axis label")
# Y Label
circle(-0.27, 1.80)
text(-0.27, 1.6, "Y axis label")
# Title
circle(1.60, 4.13)
text(1.60, 3.93, "Title")
# Blue plot
circle(1.75, 2.80)
text(1.75, 2.60, "Line\n(line plot)")
# Red plot
circle(1.20, 0.60)
text(1.20, 0.40, "Line\n(line plot)")
# Scatter plot
circle(3.20, 1.75)
text(3.20, 1.55, "Markers\n(scatter plot)")
# Grid
circle(3.00, 3.00)
text(3.00, 2.80, "Grid")
# Legend
circle(3.70, 3.80)
text(3.70, 3.60, "Legend")
# Axes
circle(0.5, 0.5)
text(0.5, 0.3, "Axes")
# Figure
circle(-0.3, 0.65)
text(-0.3, 0.45, "Figure")
color = 'blue'
ax.annotate('Spines', xy=(4.0, 0.35), xytext=(3.3, 0.5),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.annotate('', xy=(3.15, 0.0), xytext=(3.45, 0.45),
weight='bold', color=color,
arrowprops=dict(arrowstyle='->',
connectionstyle="arc3",
color=color))
ax.text(4.0, -0.4, "Made with http://matplotlib.org",
fontsize=10, ha="right", color='.5')
plt.show()
# + [markdown] id="5_na7Oy3NGKA" colab_type="text"
# # Making Explanatory Visualizations with Seaborn
# + [markdown] id="ORUwQD6F-VYg" colab_type="text"
# Today we will reproduce this [example by FiveThirtyEight:](https://fivethirtyeight.com/features/al-gores-new-movie-exposes-the-big-flaw-in-online-movie-ratings/)
#
#
# + colab_type="code" id="ya_w5WORGs-n" outputId="9fffcac4-02bf-43e2-a015-50442f40485c" colab={"base_uri": "https://localhost:8080/", "height": 355}
from IPython.display import display, Image
url = 'https://fivethirtyeight.com/wp-content/uploads/2017/09/mehtahickey-inconvenient-0830-1.png'
example = Image(url=url, width=400)
display(example)
# + [markdown] colab_type="text" id="HP4DALiRG3sC"
# Using this data: https://github.com/fivethirtyeight/data/tree/master/inconvenient-sequel
# + [markdown] colab_type="text" id="HioPkYtUG03B"
# Links
# - [Strong Titles Are The Biggest Bang for Your Buck](http://stephanieevergreen.com/strong-titles/)
# - [Remove to improve (the data-ink ratio)](https://www.darkhorseanalytics.com/blog/data-looks-better-naked)
# - [How to Generate FiveThirtyEight Graphs in Python](https://www.dataquest.io/blog/making-538-plots/)
# + [markdown] colab_type="text" id="0w_iMnQ6-VoQ"
# ## Make prototypes
#
# This helps us understand the problem
# + colab_type="code" id="5uz0eEaEN-GO" outputId="8dadcdb6-8c7f-4716-fdff-6fe2b38b195f" colab={"base_uri": "https://localhost:8080/", "height": 285}
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.style.use('fivethirtyeight')
fake = pd.Series([38, 3, 2, 1, 2, 4, 6, 5, 5, 33],
index=range(1,11))
fake.plot.bar(color='C1', width=0.9);
# + colab_type="code" id="KZ0VLOV8OyRr" outputId="f3ea484a-be58-4b95-9bd3-69b3d1629cba" colab={"base_uri": "https://localhost:8080/", "height": 289}
fake2 = pd.Series(
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2,
3, 3, 3,
4, 4,
5, 5, 5,
6, 6, 6, 6,
7, 7, 7, 7, 7,
8, 8, 8, 8,
9, 9, 9, 9,
10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10])
fake2.value_counts().sort_index().plot.bar(color='C1', width=0.9);
# + [markdown] colab_type="text" id="mZb3UZWO-q05"
# ## Annotate with text
# + colab_type="code" id="f6U1vswr_uWp" outputId="f6606c96-86dd-4858-b359-30893afba9ad" colab={"base_uri": "https://localhost:8080/", "height": 307}
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
fig = plt.figure()
fig.patch.set_facecolor('blue')
#Make figure color 0% opaque (transparent)
#fig.patch.set_alpha(0)
#fig.patch.set(facecolor = 'white')
ax = fake.plot.bar(color = 'C1', width = 0.9)
ax.set(facecolor = 'red')
#Makes axes facecolor to 0% opaque (transparent)
#ax.patch.set_alpha(.1)
plt.xlabel('Rating')
plt.ylabel('Perent of total votes')
plt.show()
# + id="4Av7qk0dTMhM" colab_type="code" outputId="f9bf5207-ae8a-44ad-b756-fd08719d781a" colab={"base_uri": "https://localhost:8080/", "height": 355}
display(example)
# + id="PuthbdkkTdIP" colab_type="code" outputId="8428b141-03be-4518-d80d-265869bb345b" colab={"base_uri": "https://localhost:8080/", "height": 335}
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
fig = plt.figure()
#fig.patch.set_facecolor('blue')
#Make figure color 0% opaque (transparent)
#fig.patch.set_alpha(0)
fig.patch.set(facecolor = 'white')
ax = fake.plot.bar(color = '#ED713A', width = 0.9)
ax.set(facecolor = 'white')
#Makes axes facecolor to 0% opaque (transparent)
#ax.patch.set_alpha(.1)
ax.text(x = -2, y = 43, s = 'IMDB Ratings for the film as of Aug. 29', fontsize = 12)
#Fix tick labels to be upright
#ax.set_xticklabels(labels = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], rotation = 0) or
ax.set_xticklabels(range(1, 11, 1), rotation = 0)
ax.set_yticks(range(0, 50, 10))
plt.xlabel('Rating', fontsize = 10, fontweight = 'bold')
plt.ylabel('Perent of total votes', fontsize = '10', fontweight = 'bold')
plt.title("'An Inconvenient sequel: Truth to power' is divisive", fontsize = '12', fontweight = 'bold', x = -0.1, y = 1.1, loc = 'left')
plt.show()
# + id="fbV9nVTUtocC" colab_type="code" outputId="15b615d3-50fb-490e-8f08-0dd785718c20" colab={"base_uri": "https://localhost:8080/", "height": 35}
print(range(1, 11))
# + id="TmDLgDUqtrjO" colab_type="code" outputId="bffb88ee-3613-4d73-b637-760f0476be69" colab={"base_uri": "https://localhost:8080/", "height": 35}
#Cast the range to a list
print(list(range(1, 11)))
# + id="OBk9W8gKuDLQ" colab_type="code" outputId="ab017863-9acc-47aa-be3b-b67ad20875c5" colab={"base_uri": "https://localhost:8080/", "height": 35}
print(list(range(10, 50, 10)))
# + [markdown] colab_type="text" id="x8jRZkpB_MJ6"
# ## Reproduce with real data
# + colab_type="code" id="3SOHJckDUPI8" outputId="0d8387c4-aa71-4ca4-c526-1e8f5c462143" colab={"base_uri": "https://localhost:8080/", "height": 1000}
df = pd.read_csv('https://raw.githubusercontent.com/fivethirtyeight/data/master/inconvenient-sequel/ratings.csv')
print(df.shape)
df.head(20)
# + id="ToV9-nXMAaVz" colab_type="code" outputId="21c218bd-0aca-411b-c8af-f081ad15b539" colab={"base_uri": "https://localhost:8080/", "height": 1000}
df.tail(20)
# + id="Di_MgIKb-Al7" colab_type="code" outputId="c2e65889-c6d5-465a-8b60-f31631bc4b18" colab={"base_uri": "https://localhost:8080/", "height": 127}
df.columns
# + id="bvp6CurlAlC7" colab_type="code" outputId="d7de48c2-4b2c-44a6-9c06-5190a437b006" colab={"base_uri": "https://localhost:8080/", "height": 531}
df.dtypes
# + id="879_ANiNAtpq" colab_type="code" outputId="7542dc6a-d522-4b44-f6d1-4ac7fa883e9f" colab={"base_uri": "https://localhost:8080/", "height": 146}
df['timestamp'] = pd.to_datetime(df['timestamp'])
df['timestamp'].describe()
# + colab_type="code" id="cDltXxhC_yG-" outputId="877e4f11-2fa4-4cb4-c536-38ed6273dd83" colab={"base_uri": "https://localhost:8080/", "height": 1000}
#Fix this
df.set_index('timestamp', inplace = True)
df['2017-08-29']
# + id="ak6fHwgi_g1y" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="2973f795-7b20-43cb-e4e1-ae8bdfc4ec2d"
lastday = df['2017-08-29']
lastday_filtered = lastday[lastday['category'] == 'IMDb users']
lastday_filtered.tail(30)
# + id="ySD5GjYWAaHH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="656016ed-574a-4ea4-bd77-fe35143bb15b"
df['category'].value_counts
# + id="e8K2YaBNAcvL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 314} outputId="e07cfe97-d6cd-439f-d074-741c7ac23a9c"
lastday_filtered.respondents.plot()
# + id="bHpk3f3FBGMH" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 865} outputId="cb853fe6-781b-4178-d086-e60599d27a3f"
final = lastday_filtered.tail(1)
final.T
# + id="mMPiaBWXKv2l" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 363} outputId="52ecd551-1514-4345-e2c5-8f70c6183d32"
pct_columns = ['1_pct', '2_pct', '3_pct', '4_pct', '5_pct',
'6_pct', '7_pct', '8_pct', '9_pct', '10_pct']
final[pct_columns].T
# + id="auAqDRoHLVVa" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 363} outputId="48c14a53-da1b-4d29-f36f-4c91be6feb7c"
plot_data = final[pct_columns].T
plot_data.index = range(1, 11)
plot_data
# + id="vKY1jqhkLjU_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 353} outputId="8a0f4ef6-1568-46d7-ebb4-bf97b08b1ae3"
plt.style.use('fivethirtyeight')
fig = plt.figure()
#fig.patch.set_facecolor('blue')
#Make figure color 0% opaque (transparent)
#fig.patch.set_alpha(0)
fig.patch.set(facecolor = 'white')
ax = plot_data.plot.bar(color = '#ED713A', width = 0.9)
ax.set(facecolor = 'white')
#Makes axes facecolor to 0% opaque (transparent)
#ax.patch.set_alpha(.1)
ax.text(x = -2, y = 43, s = 'IMDB Ratings for the film as of Aug. 29', fontsize = 12)
#Fix tick labels to be upright
ax.set_xticklabels(labels = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], rotation = 0) #or
ax.set_xticklabels(range(1, 11, 1), rotation = 0)
ax.set_yticks(range(0, 50, 10))
#Remove legend
ax.get_legend().remove()
plt.xlabel('Rating', fontsize = 10, fontweight = 'bold')
plt.ylabel('Perent of total votes', fontsize = '10', fontweight = 'bold')
plt.title("'An Inconvenient sequel: Truth to power' is divisive", fontsize = '12', fontweight = 'bold', x = -0.1, y = 1.1, loc = 'left')
plt.show()
|
AnthonyG_LS_DS_123_Make_Explanatory_Visualizations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Many questions at once
# From Python
from moodlexport import Question, Category
# +
category = Category("My little catgory from python")
question = Question("essay")
question.text("What is the derivative of $f(x) = e^x + 0.5 \Vert x \Vert^2$?")
question.grade(1.5)
question.addto(category)
question = Question("multichoice")
question.text("Is every symmetric matrix invertible?")
question.grade(2.0)
question.answer("Yes", False)
question.answer("No", True)
question.addto(category)
category.save()
# -
from moodlexport import latextomoodle
latextomoodle('mycategory.tex')
|
examples/many_questions_at_once.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Recommending Movies to a User
# > We will explore content-based and colaborative filtering recommendation systems.
#
# - toc: true
# - branch: master
# - badges: true
# - comments: true
# - categories: [recommender sytems]
# Recommendation systems are a collection of algorithms used to recommend items to users based on information taken from the user. These systems have become ubiquitous, and can commonly be seen in online stores, movie databases, and job finders. In this blog post, we will explore **content-based** and **colaborative filtering** recommendation systems.
#
# The dataset we'll be working on has been acquired from [GroupLens](https://grouplens.org/datasets/movielens/). It consists of 27 million ratings and 1.1 million tag applications applied to 58,000 movies by 280,000 users.
# import libraries
import pandas as pd
from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# +
# store the movie information into a pandas dataframe
movies_df = pd.read_csv('movies1.csv')
# store the ratings information into a pandas dataframe
ratings_df = pd.read_csv('ratings.csv')
# -
movies_df.head()
# Each movie has a unique ID, a title with its release year along with it (which may contain unicode characters) and several different genres in the same field.
# dimensions of the dataframes
print(movies_df.shape)
print(ratings_df.shape)
# ---
# ### Preprocessing the data
# Let's remove the year from the 'title' column and store it in a new 'year' column.
# +
# use regular expressions to find a year stored between parantheses
# we specify the parantheses so we don't conflict with movies that have years in their titles
movies_df['year'] = movies_df.title.str.extract('(\(\d\d\d\d\))', expand=False)
# remove the parentheses
movies_df['year'] = movies_df.year.str.extract('(\d\d\d\d)', expand=False)
# remove the years from the 'title' column
movies_df['title'] = movies_df.title.str.replace('(\(\d\d\d\d\))', '')
# apply the strip finction to get rid of any ending whitespace characters that may have appeared
movies_df['title'] = movies_df['title'].apply(lambda x: x.strip())
movies_df.head()
# -
# Let's also split the values in the 'genres' column into a 'list of genres' to simplify future use. Apply Python's split string function on the genres column.
# every genre is separated by a |. So call the split function on |.
movies_df['genres'] = movies_df.genres.str.split('|')
movies_df.head()
# Since keeping genres in a list format isn't optimal for the content-based recommendation system technique, we will use the One Hot Encoding technique to convert the list of genres to a vector where each column corresponds to one possible value of the feature. This encoding is needed for feeding categorical data.
# In this case, we store every differrent genre in columns that contain either 1 or 0. 1 shows that a movie has that genre and 0 shows that it doesn't. Let's also store this dataframe in another variable since genres won't be important for our first recommendation system.
# +
# # copy the movie dataframe into a new one
moviesWithGenres_df = movies_df.copy()
# for every row in the dataframe, iterate through the list of genres and place a 1 in the corresponding column
for index, row in movies_df.iterrows():
for genre in row['genres']:
moviesWithGenres_df.at[index, genre] = 1
# fill in the NaN values with 0 to show that a movie doesn't have that column's genre
moviesWithGenres_df = moviesWithGenres_df.fillna(0)
moviesWithGenres_df.head()
# -
# Now, let's focus on the ratings dataframe.
ratings_df.head()
# Every row in the ratings dataframe has a userId associated with at least one movie, a rating and a timestamp showing when they reviewed it. We won't be needing the timestamp column, so let's drop it.
ratings_df = ratings_df.drop('timestamp',1)
ratings_df.head()
# --
# ## Content-based recommendation system
# This technique attempts to figure out what a user's favorite aspects of an item are, and then recommends items that present those aspects. In our case, we're going to try to figure out the input's favorite genres from the movies and ratings given.
#
# Advantages of content-based filtering:
# - it learns the user's preferences.
# - it's highly personalized for the user.
#
# Disadvantages of content-based filtering:
# - it doesn't take into account what others think of the item, so low quality item recommendations might happen.
# - Extracting data is not always intuitive.
# - Determining what characteristics of the item the user dislikes or likes is not always obvious.
#
# Create an input to recommend movies to.
userInput = [
{'title':'Mission: Impossible - Fallout', 'rating':5},
{'title':'Top Gun', 'rating':4.5},
{'title':'<NAME>', 'rating':3},
{'title':'Vanilla Sky', 'rating':2.5},
{'title':'Minority Report', 'rating':4},
]
inputMovies = pd.DataFrame(userInput)
inputMovies
# Add movieId to input user.
# Extract the input movie's ID from the movies dataframe and add it to the input.
# +
# filter the movies by title
inputId = movies_df[movies_df['title'].isin(inputMovies['title'].tolist())]
# merge it to get the movieId
inputMovies = pd.merge(inputId, inputMovies)
# drop information we won't use from the input dataframe
inputMovies = inputMovies.drop('genres', 1).drop('year', 1)
# final input dataframe
inputMovies
# -
# We will learn the input's preferences. So let's get the subset of movies that the input has watched from the dataframe containing genres defined with binary values.
# filter out the movies from the input
userMovies = moviesWithGenres_df[moviesWithGenres_df['movieId'].isin(inputMovies['movieId'].tolist())]
userMovies
# We only need the actual genre table. Reset the index and drop the unnecessary columns.
# +
# reset the index
userMovies = userMovies.reset_index(drop=True)
# drop unnecessary columns
userGenreTable = userMovies.drop('movieId', 1).drop('title', 1).drop('genres', 1).drop('year', 1)
userGenreTable
# -
# Now we learn the input preferences.
# We turn each genre into weights using the input's reviews and multiplying them into the input's genre table, and then summing up the resulting table by column.
inputMovies['rating']
# +
# dot product to get weights
userProfile = userGenreTable.transpose().dot(inputMovies['rating'])
# the user profile
userProfile
# -
# Now we have the weights for each of the user's preferences. This is the **User Profile**. Using this, we can recommend movies that satisfy the user's preferences.
# Let's start by extracting the genre table from the original dataframe.
# +
# get the genre of every movie in our original dataframe
genreTable = moviesWithGenres_df.set_index(moviesWithGenres_df['movieId'])
# drop unnecessary columns
genreTable = genreTable.drop('movieId', 1).drop('title', 1).drop('genres', 1).drop('year', 1)
genreTable.head()
# -
genreTable.shape
# With the input's profile and the complete list of movies and their genres in hand, we're going to take the weighted average of every movie based on the input profile and recommend the top twenty movies that most satisfy it.
# multiply the genre by the weights and then take the weighted average
recommendationTable_df = ((genreTable*userProfile).sum(axis=1)) / (userProfile.sum())
recommendationTable_df.head()
# Here is the recommendation table.
movies_df.loc[movies_df['movieId'].isin(recommendationTable_df.head(20).keys())]
# These are the top 20 movies to recommend to the user based on a content-based recommendation system.
# ---
# ## Collaborative Filtering
# This technique uses other users to recommend items to the input user. It attempts to find users that have similar preferences and opinions as the input and then recommends items that they have liked to the input. there are several methods of finding similar users, and the one we will be using here is going to be based on the Pearson Correlation Function.
#
# The process for creating a user-based recommendation system is as follows:
# - Select a user with the movies the user has watched.
# - Based on his ratings of movies, find the top X neighbours.
# - Get the watched movie record of the user for each neighbour.
# - Calculate a similarity score using some formula.
# - Recommend the items with the highest score.
#
# Advantages of collaborative filtering:
# - It takes other user's ratings into consideration
# - It doesn't need to study or extract information from the recommended item
# - It adapts to the user's interestes which might change over time
#
# Disadvantages of collaborative filtering:
# - The approximation function can be slow.
# - There might be a low amount of users to approximate
# - There might be privacy issues when trying to learn the user's experiences.
#
# Let's create an input user to recommend movies to.
userInput = [
{'title':'Mission: Impossible - Fallout', 'rating':5},
{'title':'Top Gun', 'rating':4.5},
{'title':'<NAME>', 'rating':3},
{'title':'Vanilla Sky', 'rating':2.5},
{'title':'Minority Report', 'rating':4},
]
inputMovies = pd.DataFrame(userInput)
inputMovies
# +
# filter the movies by title
inputId = movies_df[movies_df['title'].isin(inputMovies['title'].tolist())]
# merge it to get the movieId
inputMovies = pd.merge(inputId, inputMovies)
# drop information we won't use from the input dataframe
inputMovies = inputMovies.drop('genres', 1).drop('year', 1)
# final input dataframe
inputMovies
# -
# #### The users who have seen the same movies
# Now, with the movie IDs in our input, we can get the subset of users that have watched and reviewd the movies in our input.
# filter out users that have watched movies that the input has watched and storing it
userSubset = ratings_df[ratings_df['movieId'].isin(inputMovies['movieId'].tolist())]
userSubset.head()
# Group the rows by userId.
# groupby creates several sub dataframes where they all have the same value in the column specified as the parameter
userSubsetGroup = userSubset.groupby(['userId'])
# Let's look at one of these users - userId = 4
userSubsetGroup.get_group(4)
# Let's sort these groups so the users that share the most movies in common with the input have higher priority. This provides a richer recommendation since we won't go through every single user.
userSubsetGroup = sorted(userSubsetGroup, key=lambda x: len(x[1]), reverse=True)
# Now let's look at the first user.
userSubsetGroup[0:3]
# Next, we are going to compare users to our specified user and find the one that is most similar.
# We're going to find out how similar each user is to the input through the Pearson Correlation Coefficient. It is used to measure the strength of a linear association between two variables.
#
# We will select a subset of users to iterate through. The limit is imposed because we don't want to waste too much time going through every single user.
userSubsetGroup = userSubsetGroup[0:100]
# Calculate the Pearson Correlation between the input user and the subset group, and store it in a dictionary, where the key is the userId and the value is the coefficient.
# +
pearsonCorrelationDict = {}
#For every user group in our subset
for name, group in userSubsetGroup:
#Let's start by sorting the input and current user group so the values aren't mixed up later on
group = group.sort_values(by='movieId')
inputMovies = inputMovies.sort_values(by='movieId')
#Get the N for the formula
nRatings = len(group)
#Get the review scores for the movies that they both have in common
temp_df = inputMovies[inputMovies['movieId'].isin(group['movieId'].tolist())]
#And then store them in a temporary buffer variable in a list format to facilitate future calculations
tempRatingList = temp_df['rating'].tolist()
#Let's also put the current user group reviews in a list format
tempGroupList = group['rating'].tolist()
#Now let's calculate the pearson correlation between two users, so called, x and y
Sxx = sum([i**2 for i in tempRatingList]) - pow(sum(tempRatingList),2)/float(nRatings)
Syy = sum([i**2 for i in tempGroupList]) - pow(sum(tempGroupList),2)/float(nRatings)
Sxy = sum( i*j for i, j in zip(tempRatingList, tempGroupList)) - sum(tempRatingList)*sum(tempGroupList)/float(nRatings)
#If the denominator is different than zero, then divide, else, 0 correlation.
if Sxx != 0 and Syy != 0:
pearsonCorrelationDict[name] = Sxy/sqrt(Sxx*Syy)
else:
pearsonCorrelationDict[name] = 0
# -
pearsonCorrelationDict.items()
pearsonDF = pd.DataFrame.from_dict(pearsonCorrelationDict, orient='index')
pearsonDF.columns = ['similarityIndex']
pearsonDF['userId'] = pearsonDF.index
pearsonDF.index = range(len(pearsonDF))
pearsonDF.head()
# #### The top x similar users to the input user
# Let's get the top 50 users that are most similar to the input.
topUsers = pearsonDF.sort_values(by='similarityIndex', ascending=False)[0:50]
topUsers.head()
# Now let's start recommending movies to the input user.
#
# #### Rating of selected users to all movies
#
# We're going to do this by taking the weighted average of the ratings of the movies using the Pearson Correlation as the weight. But to do this, we first need to get the movies watched by the users in our pearsonDF from the ratings dataframe, and then store their correlation in a new column called 'similarityIndex'.
# merge two tables
topUsersRating=topUsers.merge(ratings_df, left_on='userId', right_on='userId', how='inner')
topUsersRating.head()
# Now we multiply the movie rating by its weight (the similarity index), then sum up the new ratings and divide it by the sum of the weights.
# We can easily do this by simply multiplying two columns, then grouping up the dataframe by movieId and then dividing two columns.
# It shows the idea of all similar users to candidate movies for the input user.
# multiply the similarity by the user's ratings
topUsersRating['weightedRating'] = topUsersRating['similarityIndex']*topUsersRating['rating']
topUsersRating.head()
# apply a sum to the topUsers after grouping it by userId
tempTopUsersRating = topUsersRating.groupby('movieId').sum()[['similarityIndex','weightedRating']]
tempTopUsersRating.columns = ['sum_similarityIndex','sum_weightedRating']
tempTopUsersRating.head()
# +
# create an empty dataframe
recommendation_df = pd.DataFrame()
# take the weighted average
recommendation_df['weighted average recommendation score'] = tempTopUsersRating['sum_weightedRating']/tempTopUsersRating['sum_similarityIndex']
recommendation_df['movieId'] = tempTopUsersRating.index
recommendation_df.head()
# -
# Let's sort this and see the top 20 movies that the algorithm recommended.
recommendation_df = recommendation_df.sort_values(by='weighted average recommendation score', ascending=False)
recommendation_df.head()
movies_df.loc[movies_df['movieId'].isin(recommendation_df.head(20)['movieId'].tolist())]
# These are the top 20 movies to recommend to the user based on a collaborative filtering recommendation system.
#
#
# ---
|
_notebooks/2020-03-15-recommending-movies.ipynb
|