code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# %load_ext autoreload
# %autoreload 2
import cPickle as pickle
import os; import sys; sys.path.append('..')
import gp
import gp.nets as nets
from nolearn.lasagne.visualize import plot_loss
from nolearn.lasagne.visualize import plot_conv_weights
from nolearn.lasagne.visualize import plot_conv_activity
from nolearn.lasagne.visualize import plot_occlusion
from matplotlib.pyplot import imshow
import matplotlib.pyplot as plt
# %matplotlib inline
# -
PATCH_PATH = ('cylinder2_rgba_small')
X_train, y_train, X_test, y_test = gp.Patch.load_rgba(PATCH_PATH)
gp.Util.view_rgba(X_train[100], y_train[100])
cnn = nets.RGBANet()
cnn = cnn.fit(X_train, y_train)
cnn = cnn.fit(X_train, y_train)
test_accuracy = cnn.score(X_test, y_test)
test_accuracy
plot_loss(cnn)
plot_conv_weights(cnn.layers_['conv2'])
# store CNN
sys.setrecursionlimit(1000000000)
with open(os.path.expanduser('~/Projects/gp/nets/RGBA.p'), 'wb') as f:
pickle.dump(cnn, f, -1)
with open(os.path.expanduser('~/Projects/gp/nets/RGBA.p'), 'rb') as f:
net = pickle.load(f)
from sklearn.metrics import classification_report, accuracy_score, roc_curve, auc, precision_recall_fscore_support, f1_score, precision_recall_curve, average_precision_score, zero_one_loss
test_prediction = net.predict(X_test)
test_prediction_prob = net.predict_proba(X_test)
print
print 'Precision/Recall:'
print classification_report(y_test, test_prediction)
|
ipy_train/train_RGBA.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 1.1 - Python 101
#
# Python is an easy to learn, powerful programming language with efficient high-level data structures and object-oriented programming. Python’s elegant syntax and dynamic typing, together with its interpreted nature, make it an ideal language for scripting and rapid application development in many areas on most platforms.
# ### Jupyter Notebook
# What you are reading now is an example of a Jupyter Notebook. The basic concept is that of a "notebook" containing text and programming code. You can easily edit the notebook using your web browser, run the programs in the ipython server in the background and see the output of the programs within the notebook. This is a powerful paradigm that is well suited to machine learning research, particularly when collaborating with other people.
# For Reference:
# - https://ipython.org/notebook.html
# - https://jupyter.org/
# Python also works as your basic calculator directly through the interpreter
5**7/5*4+3-6**5 # ** is exponentation
# Declare a few variables. Set <code style="background-color:#dddddd">newnum</code> as integer, <code style="background-color:#dddddd">newstring</code> as string, and <code style="background-color:#dddddd">mylist</code> as a list of integers (using list comprehension).
# +
#Your code here
# SHIFT + ENTER to execute a cell
# -
# <h2>Exercise 1</h2><br>
# Iterate through the values in the list and run those numbers through a function that produces their squares.
# +
#Your code here
# -
# ## Exercise 2
# Find the sum of the largest 10 numbers. You may find Sorted and Sum functions useful
L =[20, 22, 18, 100, 40, 71, 34, 76, 94, 7, 6, 82, 3, 86, 46, 5, 36, 70, 54, 56, 57, 21, 99, 87, 40, 15, 100,
87, 97, 45, 87, 11, 37, 100, 46, 21, 44, 60, 32, 88, 46, 38, 31, 65, 78, 47, 20, 30, 3, 65, 14, 3, 3, 100,
3, 97, 42, 44, 46, 94, 64, 29, 79, 70, 27, 83, 85, 47, 98, 27, 48, 58, 51, 7, 96, 31, 79, 87, 80, 8, 96, 88,
4, 79, 52, 15, 57, 83, 21, 59, 25, 28, 74, 75, 70, 79, 73, 11, 7, 42]
ans = None# your code here
# ## Exercise 3
# Convert given integer input of seconds into hours, minutes, and seconds.
# +
#Your code here
# -
# ## Exercise 4
# Write a function to generate a fibonacci series upto n terms.
# +
#Your code here
# -
# ## Exercise 5
# Calculate the sum of all prime numbers between 3000 and 42000
# +
#Your code here
# -
# ## Exercise 6
# Use the split and join functions to produce the required string.
dum_str = "A few gems, diamonds, rubies, and I'm rich."
string_to_be_produced = "A few gems, rubies, diamonds, and I'm rich."
# ## Exercise 7
# Deal four sets of cards using the given dictionary.
# The solution looks something like this
#
# ><code style="background-color:#eeeeee;border-radius:5px;padding:5px">Deal 1: Ace of Spades, Queen of Hearts, 2 of Clubs and 7 of Clubs<br> Deal 2: 4 of Hearts, 5 of Clubs, Jack of Spades and Queen of Clubs<br> Deal 3: 7 of Clubs, 8 of Diamonds, 8 of Spades and 10 of Diamonds</code>
#
# The deals must be random. You will find the documentation of the [Random Module](https://docs.python.org/2/library/random.html) helpful
ranks = ["Ace"] + [str(x) for x in range(2,11)] + ["Jack","Queen","King"]
cards = {
"Spades":ranks,
"Diamonds":ranks,
"Clubs":ranks,
"Hearts":ranks
}
# ans str(cards[list(cards.keys())[1]][1])+" of "+str(list(cards.keys())[1])
# ## Exercise 8
# Create a Function to transpose a matrix.
def transpose(A):
#Your code here
pass
A = [
[1,2,1],
[4,2,7],
[6,4,5],
[7,8,9]
]
transpose(A)
|
Session1/Assignments/Assignment 1.1 - Python 101.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This notebook is designed to allow you to tweak how you might like your walkers initialized. Edit the cells as you see fit and then proceed to evaluate each cell and save the final `pos0.npy` file.
import numpy as np
# Generally, you want at least a few walkers for each dimension you may be exploring. For the **truncated** model, there are 13 parameters.
nparam = 13
nwalkers = 4 * nparam
print(nwalkers)
# If you are fixing distance, then you should change the previous line to
#
# nparam = 12
#
# and then comment out the `dpc` row below. Below, we create an array of starting walker positions, similar to how `emcee` is initialized. You should tweak the `low` and `high` ranges to correspond to a small guess around your starting position.
p0 = np.array([np.random.uniform(1.03, 1.05, nwalkers), # mass [M_sun]
np.random.uniform(30., 50.0, nwalkers), #r_c [AU]
np.random.uniform(110., 115, nwalkers), #T_10 [K]
np.random.uniform(0.70, 0.71, nwalkers), # q
np.random.uniform(0.0, 1.5, nwalkers), # gamma_e
np.random.uniform(-3.4, -3.5, nwalkers), #log10 Sigma_c [log10 g/cm^2]
np.random.uniform(0.17, 0.18, nwalkers), #xi [km/s]
np.random.uniform(144.0, 145.0, nwalkers), #dpc [pc]
np.random.uniform(159.0, 160.0, nwalkers), #inc [degrees]
np.random.uniform(40.0, 41.0, nwalkers), #PA [degrees]
np.random.uniform(-0.1, 0.1, nwalkers), #vz [km/s]
np.random.uniform(-0.1, 0.1, nwalkers), #mu_a [arcsec]
np.random.uniform(-0.1, 0.1, nwalkers)]) #mu_d [arcsec]
# Just to check we have the right shape
p0.shape
# Save the new position file to disk
np.save("pos0.npy", p0)
# Just to check that we have written the file, you can read it back in and check that it has the proper shape.
np.load("pos0.npy").shape
|
assets/InitializeWalkers.truncated.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 基本程序设计
# - 一切代码输入,请使用英文输入法
print('123')
# ## 编写一个简单的程序
# - 圆公式面积: area = radius \* radius \* 3.1415
# ### 在Python里面不需要定义数据的类型
# ## 控制台的读取与输入
# - input 输入进去的是字符串
# - eval
bianchang = int(input('请输入正方形边长'))
area = bianchang * bianchang
print(area)
import os
input_=input('good')
os.system('say'+ input_)
# - 在jupyter用shift + tab 键可以跳出解释文档
# ## 变量命名的规范
# - 由字母、数字、下划线构成
# - 不能以数字开头 \*
# - 标识符不能是关键词(实际上是可以强制改变的,但是对于代码规范而言是极其不适合)
# - 可以是任意长度
# - 驼峰式命名
# ## 变量、赋值语句和赋值表达式
# - 变量: 通俗理解为可以变化的量
# - x = 2 \* x + 1 在数学中是一个方程,而在语言中它是一个表达式
# - test = test + 1 \* 变量在赋值之前必须有值
# ## 同时赋值
# var1, var2,var3... = exp1,exp2,exp3...
# ## 定义常量
# - 常量:表示一种定值标识符,适合于多次使用的场景。比如PI
# - 注意:在其他低级语言中如果定义了常量,那么,该常量是不可以被改变的,但是在Python中一切皆对象,常量也是可以被改变的
# ## 数值数据类型和运算符
# - 在Python中有两种数值类型(int 和 float)适用于加减乘除、模、幂次
# <img src = "../Photo/01.jpg"></img>
# ## 运算符 /、//、**
# ## 运算符 %
# ## EP:
# - 25/4 多少,如果要将其转变为整数该怎么改写
# - 输入一个数字判断是奇数还是偶数
# - 进阶: 输入一个秒数,写一个程序将其转换成分和秒:例如500秒等于8分20秒
# - 进阶: 如果今天是星期六,那么10天以后是星期几? 提示:每个星期的第0天是星期天
int(25/4)
num = eval(input('数字'))
if num % 2 == 0:
print('oushu')
else:
print('jishu')
shu = int(input('输入秒数'))
fen = shu // 60
miao = shu % 60
print(fen,'分' ,miao,'秒')
shu = eval(input('输入一个数'))
if shu % 2 == 0 ;
print(ou)
week = eval(input('..'))
se = (week + 10 ) % 7
print('今天是星期'+str(week),'10天之后是星期'+str(se))
# ## 科学计数法
# - 1.234e+2
# - 1.234e-2
# ## 计算表达式和运算优先级
# <img src = "../Photo/02.png"></img>
# <img src = "../Photo/03.png"></img>
x = 10
y = 6
a = 0
b = 1
c = 1
yi = (3+4*x)/5
er = 10*(y-5)*(a+b+c)/x
san = 9*((4/x)+(9+x)/y)
sum= yi-er+san
print(yi)
print(er)
print(san)
print(sum)
# ## 增强型赋值运算
# <img src = "../Photo/04.png"></img>
# ## 类型转换
# - float -> int
# - 四舍五入 round
# ## EP:
# - 如果一个年营业税为0.06%,那么对于197.55e+2的年收入,需要交税为多少?(结果保留2为小数)
# - 必须使用科学计数法
round((0.06e-2)*(197.55e+2),2)
# # Project
# - 用Python写一个贷款计算器程序:输入的是月供(monthlyPayment) 输出的是总还款数(totalpayment)
# 
# # Homework
# - 1
# <img src="../Photo/06.png"></img>
celsius = eval(input('摄氏温度'))
fahrenheit = (9 / 5) * celsius + 32
print('华氏温度为:'+str(fahrenheit))
pr
# - 2
# <img src="../Photo/07.png"></img>
r = eval(input('半径'))
h = eval(input('高'))
PI = 3.14
area = r * r * PI
volume = area * h
print('该圆的底面积为:',+area)
print('该圆的体积为:',+volume)
# - 3
# <img src="../Photo/08.png"></img>
feet = eval(input('输入英尺'))
meters = 0.305 * feet
print(str(feet)+'英尺等于'+str(meters)+'米')
# - 4
# <img src="../Photo/10.png"></img>
water = eval(input('水量'))
initial = eval(input('初始温度'))
final = eval(input('最终温度'))
Q = water * (final - initial) * 4184
print('需要的能量为'+str(Q)+'焦耳')
# - 5
# <img src="../Photo/11.png"></img>
balance,rate = eval(input('差额,年利率'))
interest = balance * (rate / 1200)
print('利息为'+str(interest))
# - 6
# <img src="../Photo/12.png"></img>
v0,v1,t = eval(input('初速度,末速度,所用时间'))
a = (v1 - v0) / t
print('平均加速度为:'+str(a))
# - 7 进阶
# <img src="../Photo/13.png"></img>
# +
x = eval(input('存入金额 '))
mon = 0.00417
s = 0
for y in range (6):
s = x * (1 + mon)
# s = s
x = s + 100
print(s,x)
# -
# - 8 进阶
# <img src="../Photo/14.png"></img>
import random
x = random.randint(0,1000)
a = x % 10
b = (x // 10) % 10
c = x // 100
s = a + b + c
print('随即获取:',x)
print('位数之和为',s)
|
910.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2
import numpy as np
from matplotlib import pyplot as plt
import os
import xlsxwriter
import pandas as pd # Excel
import struct # Binary writing
import scipy.io as sio # Read .mat files
import h5py
from grading import *
# -
# Convert .mat arrays to binary files
path = r'V:\Tuomas\PTASurfaceImages'
savepath = r'V:\Tuomas\PTASurfaceImages_binary'
filelist = os.listdir(path)
for k in range(len(filelist)):
#Load file
file = os.path.join(path,filelist[k])
try:
file = sio.loadmat(file)
Mz = file['Mz']
sz = file['sz']
except NotImplementedError:
file = h5py.File(file)
Mz = file['Mz'][()]
sz = file['sz'][()]
# Save file
dtype = 'double'
Mz = np.float64(Mz)
sz = np.float64(sz)
name = filelist[k]
print(filelist[k])
writebinaryimage(savepath + '\\' + name[:-4] + '_mean.dat', Mz, dtype)
writebinaryimage(savepath + '\\' + name[:-4] + '_std.dat', sz, dtype)
# Convert .mat arrays to .png files
path = r'V:\Tuomas\PTASurfaceImages'
savepath = r'V:\Tuomas\PTASurfaceImages_png'
filelist = os.listdir(path)
for k in range(len(filelist)):
#Load file
file = os.path.join(path,filelist[k])
try:
file = sio.loadmat(file)
Mz = file['Mz']
sz = file['sz']
except NotImplementedError:
file = h5py.File(file)
Mz = file['Mz'][()]
sz = file['sz'][()]
# Save file
dtype = 'double'
mx = np.amax(np.float64(Mz))
mn = np.amin(np.float64(Mz))
Mbmp = (np.float64(Mz) - mn) * (255 / (mx - mn))
sx = np.amax(np.float64(sz))
sn = np.amin(np.float64(sz))
sbmp = (np.float64(sz) - sn) * (255 / (sx - sn))
name = filelist[k]
print(filelist[k])
#print(savepath + '\\' + name[:-4] +'_mean.png')
cv2.imwrite(savepath + '\\' + name[:-4] +'_mean.png', Mbmp)
cv2.imwrite(savepath + '\\' + name[:-4] +'_std.png', sbmp)
|
training/notebooks/Conversions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# <a href="https://colab.research.google.com/github/DingLi23/s2search/blob/pipelining/pipelining/exp-csse/exp-csse_csse_1w_ale_plotting.ipynb" target="_blank"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# ### Experiment Description
#
#
#
# > This notebook is for experiment \<exp-csse\> and data sample \<csse\>.
# ### Initialization
# +
# %load_ext autoreload
# %autoreload 2
import numpy as np, sys, os
in_colab = 'google.colab' in sys.modules
# fetching code and data(if you are using colab
if in_colab:
# !rm -rf s2search
# !git clone --branch pipelining https://github.com/youyinnn/s2search.git
sys.path.insert(1, './s2search')
# %cd s2search/pipelining/exp-csse/
pic_dir = os.path.join('.', 'plot')
if not os.path.exists(pic_dir):
os.mkdir(pic_dir)
# -
# ### Loading data
# +
sys.path.insert(1, '../../')
import numpy as np, sys, os, pandas as pd
from getting_data import read_conf
from s2search_score_pdp import pdp_based_importance
sample_name = 'csse'
f_list = [
'title', 'abstract', 'venue', 'authors',
'year',
'n_citations'
]
ale_xy = {}
ale_metric = pd.DataFrame(columns=['feature_name', 'ale_range', 'ale_importance', 'absolute mean'])
for f in f_list:
file = os.path.join('.', 'scores', f'{sample_name}_1w_ale_{f}.npz')
if os.path.exists(file):
nparr = np.load(file)
quantile = nparr['quantile']
ale_result = nparr['ale_result']
values_for_rug = nparr.get('values_for_rug')
ale_xy[f] = {
'x': quantile,
'y': ale_result,
'rug': values_for_rug,
'weird': ale_result[len(ale_result) - 1] > 20
}
if f != 'year' and f != 'n_citations':
ale_xy[f]['x'] = list(range(len(quantile)))
ale_xy[f]['numerical'] = False
else:
ale_xy[f]['xticks'] = quantile
ale_xy[f]['numerical'] = True
ale_metric.loc[len(ale_metric.index)] = [f, np.max(ale_result) - np.min(ale_result), pdp_based_importance(ale_result, f), np.mean(np.abs(ale_result))]
# print(len(ale_result))
print(ale_metric.sort_values(by=['ale_importance'], ascending=False))
print()
# -
# ### ALE Plots
# +
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.ticker import MaxNLocator
categorical_plot_conf = [
{
'xlabel': 'Title',
'ylabel': 'ALE',
'ale_xy': ale_xy['title']
},
{
'xlabel': 'Abstract',
'ale_xy': ale_xy['abstract']
},
{
'xlabel': 'Authors',
'ale_xy': ale_xy['authors'],
# 'zoom': {
# 'inset_axes': [0.3, 0.3, 0.47, 0.47],
# 'x_limit': [89, 93],
# 'y_limit': [-1, 14],
# }
},
{
'xlabel': 'Venue',
'ale_xy': ale_xy['venue'],
# 'zoom': {
# 'inset_axes': [0.3, 0.3, 0.47, 0.47],
# 'x_limit': [89, 93],
# 'y_limit': [-1, 13],
# }
},
]
numerical_plot_conf = [
{
'xlabel': 'Year',
'ylabel': 'ALE',
'ale_xy': ale_xy['year'],
# 'zoom': {
# 'inset_axes': [0.15, 0.4, 0.4, 0.4],
# 'x_limit': [2019, 2023],
# 'y_limit': [1.9, 2.1],
# },
},
{
'xlabel': 'Citations',
'ale_xy': ale_xy['n_citations'],
# 'zoom': {
# 'inset_axes': [0.4, 0.65, 0.47, 0.3],
# 'x_limit': [-1000.0, 12000],
# 'y_limit': [-0.1, 1.2],
# },
},
]
def pdp_plot(confs, title):
fig, axes_list = plt.subplots(nrows=1, ncols=len(confs), figsize=(20, 5), dpi=100)
subplot_idx = 0
plt.suptitle(title, fontsize=20, fontweight='bold')
# plt.autoscale(False)
for conf in confs:
axes = axes if len(confs) == 1 else axes_list[subplot_idx]
sns.rugplot(conf['ale_xy']['rug'], ax=axes, height=0.02)
axes.axhline(y=0, color='k', linestyle='-', lw=0.8)
axes.plot(conf['ale_xy']['x'], conf['ale_xy']['y'])
axes.grid(alpha = 0.4)
# axes.set_ylim([-2, 20])
axes.xaxis.set_major_locator(MaxNLocator(integer=True))
axes.yaxis.set_major_locator(MaxNLocator(integer=True))
if ('ylabel' in conf):
axes.set_ylabel(conf.get('ylabel'), fontsize=20, labelpad=10)
# if ('xticks' not in conf['ale_xy'].keys()):
# xAxis.set_ticklabels([])
axes.set_xlabel(conf['xlabel'], fontsize=16, labelpad=10)
if not (conf['ale_xy']['weird']):
if (conf['ale_xy']['numerical']):
axes.set_ylim([-1.5, 1.5])
pass
else:
axes.set_ylim([-8, 15])
pass
if 'zoom' in conf:
axins = axes.inset_axes(conf['zoom']['inset_axes'])
axins.xaxis.set_major_locator(MaxNLocator(integer=True))
axins.yaxis.set_major_locator(MaxNLocator(integer=True))
axins.plot(conf['ale_xy']['x'], conf['ale_xy']['y'])
axins.set_xlim(conf['zoom']['x_limit'])
axins.set_ylim(conf['zoom']['y_limit'])
axins.grid(alpha=0.3)
rectpatch, connects = axes.indicate_inset_zoom(axins)
connects[0].set_visible(False)
connects[1].set_visible(False)
connects[2].set_visible(True)
connects[3].set_visible(True)
subplot_idx += 1
pdp_plot(categorical_plot_conf, f"ALE for {len(categorical_plot_conf)} categorical features")
# plt.savefig(os.path.join('.', 'plot', f'{sample_name}-1wale-categorical.png'), facecolor='white', transparent=False, bbox_inches='tight')
pdp_plot(numerical_plot_conf, f"ALE for {len(numerical_plot_conf)} numerical features")
# plt.savefig(os.path.join('.', 'plot', f'{sample_name}-1wale-numerical.png'), facecolor='white', transparent=False, bbox_inches='tight')
|
pipelining/exp-csse/exp-csse_csse_1w_ale_plotting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Corpus and BGRF Composition
#
# We describe and analyse the status quo of the corpus with respect to criteria like author gender, year of first publication, narrative form etc. Then we compare it to the "baseline" of the Bibliographie du genre romanesque français, 1751-1800 (BGRF).
#
# **Table of Contents**
# * [Prerequisites](#Prerequisites)
# * [Corpus Metadata](#Corpus-Metadata)
# - [Author Gender](#Author-Gender)
# - [Text Length](#Text-Length)
# - [Publication Date](#Year-of-first-publication)
# - [Narrative Form](#Narrative-Form)
# * [BGRF Metadata from Wikibase](#BGRF-Metadata-from-Wikibase)
# - [Configuration](#Configuration)
# - [Data Loading](#Data-Loading)
# - [Author Gender](#Author-Gender-(BGRF))
# - [Text Length](#Text-Length-(BGRF))
# - [Publication Date](#Publication-Date-(BGRF))
# - [Narrative Form](#Narrative-Form-(BGRF))
# * [Comparison](#Comparison)
# - [Publication Date](#Publication-Date-(Corpus-vs-BGRF))
#
# ## Prerequisites
# +
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
sns.set()
# Install with e.g. `pip install sparqlwrapper`
from SPARQLWrapper import SPARQLWrapper, JSON
# Make plots appear directly in the notebook.
# %matplotlib inline
from pprint import pprint
# -
# The later parts also require access to a Wikibase instance, which is only accessible in/over the university network.
# ## Corpus Metadata
# Adjust the URL to the .tsv file as needed.
DATA_URL = 'https://raw.githubusercontent.com/MiMoText/roman18/master/XML-TEI/xml-tei_metadata.tsv'
corpus = pd.read_csv(DATA_URL, sep='\t')
print('Available column names:', corpus.columns.values)
# ### Author Gender
#
# Data is in the column 'au-gender'. Possible values are 'F', 'M' and 'U'.
gender = corpus['au-gender'].astype('category')
print('Set of all occuring values:', set(gender.values))
ratio_female = (gender == 'F').sum() / gender.count()
ratio_male = (gender == 'M').sum() / gender.count()
ratio_other = 1 - ratio_female - ratio_male
print(
f'% of female authors: \t{ratio_female:.3f}\n'
f'% of male authors: \t{ratio_male:.3f}\n'
f'% of unknown/other: \t{ratio_other:.3f}'
)
sns.countplot(x=gender)
plt.xlabel('Author gender')
plt.ylabel('Count in corpus')
# ### Text Length
# Data is in the column 'size', possible values are 'short', 'medium', 'long'.
size = corpus['size']
ratio_size_short = (size == 'short').sum() / size.count()
ratio_size_med = (size == 'medium').sum() / size.count()
ratio_size_long = (size == 'long').sum() / size.count()
print(
f'% of short texts: \t{ratio_size_short:.3f}\n'
f'% of medium texts: \t{ratio_size_med:.3f}\n'
f'% of long texts: \t{ratio_size_long:.3f}'
)
sns.countplot(x=size)
plt.xlabel('Text length')
plt.ylabel('Count in corpus')
# ### Year of first publication
# Data is in the column 'firsted-yr'. However, possible values can be single years `(yyyy)`, year spans `(yyyy-yyyy)`, the floating point number value `NaN`, or even a string like `'unknown'`. Therefore, we need to clean up a bit before we can use it. In case of year ranges, we simply use the first year.
# + raw_mimetype="text/x-python"
pubyear = pd.to_datetime(corpus['firsted-yr'], format='%Y')
time_range = pubyear.max().year - pubyear.min().year
plot = sns.displot(x=pubyear, bins=time_range, height=5, aspect=16/8)
plot.set_xticklabels(rotation=90)
pubyear.head()
# -
pd.to_datetime(corpus['firsted-yr'])
# ### Narrative form
# Data is in the column 'form'. Possible values include `'mixed'`, `'autodiegetic'`, `'heterodiegetic'`, `'homodiegetic'`, `'epistolary'`, `'dialogue novel'` and also `NaN`.
form = corpus['form'].astype('category')
print('Set of all values: ', set(form.values))
print('\n'.join([
f'% of {kind}: \t{((form==kind).sum()/form.count()):.3f}'
for kind in [
'mixed', 'autodiegetic', 'heterodiegetic', 'homodiegetic',
'epistolary', 'dialogue novel'
]
]))
plot = sns.countplot(x=form)
_ = plt.xticks(rotation=30, horizontalalignment='right')
# ## BGRF Metadata from Wikibase
# Data is pulled from Wikibase. For the moment, our instance on port 53100 is used. This may change in the future, which then will not only affect the URL but also the IDs of the items and predicates. Adjust these accordingly in the [Configuration Section](#Configuration).
# ### Configuration
# Adjust these values whenever another Wikibase instance is to be used.
WB_URL = 'http://zora.uni-trier.de:11100'
ITEM_IDS = {
'publication_date': 'P7',
'publication_date_str': 'P42', # hard to use, since not normalized
'sex_or_gender': 'P28',
'narrative_form': 'P54', # the wikibase label is "narrative perspective"
'narrative_form_str': 'P46', # the wikibase label is "narrative perspective_string"
'page_count': 'P34', # the wikibase label is "number of pages"
'page_count_str': 'P44', # the wikibase label is "number of pages_string"
'distribution_format_str': 'P45',
'distribution_format': 'P37',
}
# ### Data Loading
# We use the SPARQL endpoint to query the bibliography metadata. Each metadatum gets its own query for simplicity's sake.
# +
bgrf = pd.DataFrame()
wb_endpoint = f'{WB_URL}/proxy/wdqs/bigdata/namespace/wdq/sparql'
def get_data(endpoint, query):
'''Given an endpoint URL and a SPARQL query, return
the data as JSON.
'''
user_agent = 'jupyter notebook'
sparql = SPARQLWrapper(endpoint, agent=user_agent)
sparql.setQuery(query)
sparql.setReturnFormat(JSON)
return sparql.query().convert()["results"]["bindings"]
# -
# This wrapper function conveniently provides the data as python dictionaries.
# For example, to get all the data values for the property `narrative_form_str`,
# we can use the following:
ex_query = 'SELECT DISTINCT ?form WHERE { ?item wdt:P46 ?form. }'
results = get_data(wb_endpoint, ex_query)
print('Number of distinct values:', len(results))
print('Each entry has the following form (NPI):', results[0])
# The key `'form'` corresponds to us choosing `?form` as the output variable in our SPARQL query.
# ### Author Gender (BGRF)
# Author gender
# NOTE: currently no data in Wikibase at :44100.
query = ''.join([
'SELECT ?item ?gender ',
'WHERE { ?item wdt:',
ITEM_IDS['sex_or_gender'],
' ?gender. }'
])
gender = get_data(wb_endpoint, query)
# ### Text Length (BGRF)
#
# For the bibliography we do not have e.g. the word count. We do however have both a page count (as custom string, in 'page_count_str'/P45) and information about the page format (in 'distribution_format_str'/P46). We can use this to estimate a text length.
#
# Interestingly though, historically formats vary substantially (see [Wikipedia](https://fr.wikipedia.org/wiki/Reliure#Formats_des_feuilles_et_des_reliures) and [other source](http://home.page.ch/pub/reliurebcapt@vtx.ch/format.htm)).
# Formats are, in order, 'in-plano', 'in-folio', 'in-4', 'in-8', 'in-12', 'in-16', 'in-18'.
# Taken from https://fr.wikipedia.org/wiki/Reliure#Formats_des_feuilles_et_des_reliures and
# http://home.page.ch/pub/reliurebcapt@vtx.ch/format.htm
# Note, that both tables are NOT in complete agreement with each other.
formats = {
'colombier': [(90, 63), (63,45), (45,31.5), (30,21), (21, 14), (22.5,15.7), (21,15)],
'jesus': [(70,54), (54,35), (35,27), (27,18), (23, 9), (17.5,13.7), (18.3, 11.6)],
'raisin': [(65,50), (49,32), (32,24), (24,16), (21, 8), (16.2,12.5), (16.6, 10.8)],
}
areas = {
key: [w*h for (w, h) in value]
for key, value in formats.items()
}
# Ratio of one format and the next smaller one, for each convention.
ratios = {
key: [f'{a/b:.2f}' for a, b in zip(values[1:], values[:-1])]
for key, values in areas.items()
}
from pprint import pprint
pprint(list(ratios.values()))
# As we can see, the ratio from one format to another is, if not identical, still pretty consistent for each column (as it should be, considering how they are derived). If we assume that the entries in the bibliography are at least internally consistent, we can use _any_ of the conventions and multiply by the number of pages to get a "combined page area" for each text. This can of course not simply be mapped to the actual text length. But as a heuristic, maybe we can assume that the combined area is roughly proportional to the text length. If this is the case, we can use this value to categorize texts into 'short', 'medium' and 'long' (although these labels are independent of, and can differ from, the ones used for the corpus, which directly use word count).
# First, let's query both `page_count_string` and `distribution_format_string`.
# Page count
query = ''.join([
'SELECT ?item ?page_count ?page_format ',
'WHERE { ?item wdt:',
ITEM_IDS['page_count_str'],
' ?page_count;',
' wdt:',
ITEM_IDS['distribution_format_str'],
' ?page_format.',
' }'
])
print(query)
results = get_data(wb_endpoint, query)
pprint(results[0])
# Unsurprisingly, both `page_count_string` and `distribution_format_string` need some cleaning up and normalization. To keep this notebook tidy and allow for both easier re-use and easier testing, the corresponding parsing functions have been outsourced into their own `utils.py` module in the same folder as this notebook.
# +
# Have a look at ./utils.py if you are interested in the implementation details.
from utils import parse_distribution_format
from utils import parse_page_count
# Note: parse_page_count() ignores page numbers given in roman numerals by default.
# To include them in the sum, call parse_page_count() with `count_preface=True`.
# For more info about these functions use help():
#help(parse_page_count)
#help(parse_distribution_count)
# Adjust as needed:
INCLUDE_PREFACE = False
bgrf['page_count'] = pd.Series(
data=[sum(parse_page_count(entry['page_count']['value'], count_preface=INCLUDE_PREFACE))
for entry in results],
index=[entry['item']['value'] for entry in results],
dtype='Int64'
)
bgrf['dist_format'] = pd.Series(
data=[parse_distribution_format(entry['page_format']['value'])
for entry in results],
index=[entry['item']['value'] for entry in results],
)
print('"page_count" column:\n', bgrf['page_count'].head(2))
print('"dist_format" column:\n', bgrf['dist_format'].head(2))
sns.countplot(x=bgrf['dist_format'], order=['in-1', 'in-2', 'in-4', 'in-8', 'in-12', 'in-16', 'in-18', 'in-24', 'in-32'])
plt.show()
sns.displot(x=bgrf['page_count'])
plt.show()
# -
# In order to estimate the cummulative page area of each text, we need to choose any of the conventions listed at the start of this section.
# **However, for some of the formats like 'in-24' we do not have any estimate!** The following code simply uses NaN in these cases, but this is obviously not a real solution.
page_areas = {
format: area
for format, area
in zip(['in-1', 'in-2', 'in-4', 'in-8', 'in-12', 'in-16', 'in-18'], areas['jesus'])
}
pprint(page_areas)
bgrf['page_area'] = bgrf['dist_format'].apply(lambda f: page_areas.get(f, np.nan))
# +
# Calculate an estimated 'cummulative page area' for each work.
bgrf['cumm_area'] = bgrf['page_area'] * bgrf['page_count']
sns.displot(x=bgrf['cumm_area'])
plt.show()
bgrf['estimated_length'] = pd.cut(bgrf['cumm_area'], bins=3, labels=['short', 'medium', 'long'])
sns.countplot(x=bgrf['estimated_length'])
plt.show()
# There is only one work described as 'long' by this procedure:
only_long = bgrf['estimated_length'][bgrf['estimated_length'] == 'long']
print('The only work categorized as "long" is actually a collection of novels:\n', only_long)
# -
# The only work which is categorized as long by this procedure is actually a collection of novels. This probably means that our binning is rather meaningless. Domain-specific knowledge would be necessary to choose adequate limits for the three bins.
# ### Publication Date (BGRF)
# +
# Publication date
import datetime as dt
query = ''.join([
'SELECT ?item ?pubdate ',
'WHERE { ?item wdt:',
ITEM_IDS['publication_date'],
' ?pubdate. }'
])
pubdate = get_data(wb_endpoint, query)
bgrf['pubyear'] = pd.Series(
data=[dt.date.fromisoformat(entry['pubdate']['value'].split('T')[0]) for entry in pubdate],
index=[entry['item']['value'] for entry in pubdate],
dtype='datetime64[ns]'
)
print('The new data Series looks like this:\n', bgrf['pubyear'].head(3))
year_range = bgrf['pubyear'].max().year - bgrf['pubyear'].min().year
plot = sns.displot(x=bgrf['pubyear'], bins=time_range, height=5, aspect=16/8)
plot.set_xticklabels(rotation=90)
# -
# ### Narrative Form (BGRF)
# +
# Narrative form
query = ''.join([
'SELECT ?item ?form ?label ',
'WHERE { ?item wdt:',
ITEM_IDS['narrative_form'],
' ?form.',
' ?form rdfs:label ?label .',
' FILTER(LANG(?label) = "en") }'
])
form = get_data(wb_endpoint, query)
form = pd.Series(
data=[entry['label']['value'] for entry in form],
index=[entry['item']['value'] for entry in form],
dtype='category'
)
#print('\n'.join([i for i in set(bgrf['form'].values) ]))
bgrf['form'] = form
plot = sns.countplot(x=bgrf['form'])
_ = plt.xticks(rotation=30, horizontalalignment='right')
# -
# ## Comparison
# ### Publication Date (Corpus vs BGRF)
# +
# Publication year of corpus texts:
year_corpus = pd.to_datetime(corpus['firsted-yr'], format='%Y')
# Publication year of BGRF items:
year_bgrf = bgrf['pubyear']
# Create a date index which includes the whole data range
# so that we can fill in missing data points.
idx = pd.date_range(start='1730', end='1800', freq='YS', closed=None)
# In previous visualizations we have used absolute value counts.
# For comparison we obviously need to use relative frequencies instead.
df = pd.DataFrame(index=idx)
df['freq_corpus'] = year_corpus.value_counts(normalize=True)
df['freq_bgrf'] = year_bgrf.value_counts(normalize=True)
df['year'] = df.index.year
print('The data in "wide form"\n', df.head(4), '\n')
# For the visualization we need the data in "long form", i.e. all the
# relative frequencies are in one single column, with another column
# specifying whether it stems from the corpus or the bibliography.
long = pd.melt(
df, id_vars=['year'], value_vars=['freq_corpus', 'freq_bgrf'],
var_name='origin', value_name='rel_freq')
print('The data in "long form"\n', long.head(4))
# -
sns.catplot(x='year', y='rel_freq', hue='origin', kind='bar', data=long, height=5, aspect=3, legend_out=False)
plt.xlabel('Publication Year')
plt.ylabel('Share of all texts in collection')
_ = plt.xticks(rotation=90)
# The outlier with publication year 1731 makes the above chart a bit harder to read than necessary. So let's create the same graph with data starting at 1751.
sns.catplot(x='year', y='rel_freq', hue='origin', kind='bar', data=long[long['year'] > 1750], height=5, aspect=3,
legend_out=False)
plt.xlabel('Publication Year')
plt.ylabel('Share of all texts\nin resp. collection')
_ = plt.xticks(rotation=90)
|
balance_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_braket
# language: python
# name: conda_braket
# ---
# # Testing the tensor network simulator with 2-local Hayden-Preskill circuits
#
# **Abstract:** We study a class of random quantum circuits known as Hayden-Preskill circuits using the tensor network simulator backend in Amazon Braket. The goal is to understand the degree to which the tensor network simulator is capable of detecting a hidden local structure in a quantum circuit, while simultaneously building experience with the Amazon Braket service and SDK. We find that the TN1 tensor network simulator can efficiently simulate local random quantum circuits, even when the local structure is obfuscated by permuting the qubit indices. Conversely, when running genuinely non-local versions of the quantum circuits, the simulator's performance is significantly degraded.
#
# This notebook is aimed at users who are familiar with Amazon Braket and have a working knowledge of quantum computing and quantum circuits.
# <div class="alert alert-block alert-warning">
# <b>NOTE:</b> Remember to update your S3 bucket.
# </div>
# +
from braket.circuits import Circuit
from braket.aws import AwsDevice
from braket.devices import LocalSimulator
import numpy as np
import random
import matplotlib.pyplot as plt
import time
import os
# Please enter the S3 bucket you created during onboarding
# (or any other S3 bucket starting with 'amazon-braket-' in your account) in the code below
my_bucket = f"amazon-braket-Your-Bucket-Name" # the name of the bucket
my_prefix = "Your-Folder-Name" # the name of the folder in the bucket
s3_folder = (my_bucket, my_prefix)
# -
# #### Setup the tensor network simulator:
# In this notebook we will use the TN1 simulator on Amazon Braket [[1]](#References):
device = AwsDevice("arn:aws:braket:::device/quantum-simulator/amazon/tn1")
# ## Local Hayden-Preskill Circuits
# Hayden-Preskill circuits are a class of unstructured, random quantum circuits. To produce a Hayden-Preskill circuit, one chooses a gate at random from some universal gate set at each time step and applies this gate to random target qubits. For example, one can choose to either apply a random single qubit rotation to a random qubit, or a CZ gate to a random pair of qubits at each time step. As a concrete example, consider the following pseudocode:
# ```
# Choose either {single qubit, two qubit} gate w/ prob. {1/2, 1/2}
#
# If single qubit:
# Choose either {Rx, Ry, Rz, H} randomly w/ prob. {1/4, 1/4, 1/4, 1/4}
# Apply the chosen gate to a randomly chosen qubit
# If the gate is Rx, Ry, or Rz, rotate by a randomly chosen angle
#
# If two qubit gate:
# Choose (qubit 1, qubit 2) to be two randomly chosen qubits out of the set of N qubits
# Apply CZ(qubit 1, qubit 2) # This means the couplings are long range, all-to-all
# ```
#
# Using the strategy above, one can quickly generate random circuits with all-to-all, long-range couplings. These circuits generate unitaries that rapidly converge to Haar random unitaries, and they are difficult to simulate.
#
# A much simpler class of random circuits, which we call **local Hayden-Preskill circuits**, can be generated using the same strategy as above, but in which the two qubit CZ gates are applied to nearest neighbour qubits instead of random pairs:
# ```
# Choose a random qubit j from [0, N-2]
# Apply CZ(qubit j, qubit j+1)
# ```
# #### In this notebook, we will focus on both local and non-local Hayden-Preskill circuits, defined using the helper functions below.
# +
def CZtuple_generator(qubits):
"""Yields a CZ between a random qubit and its next nearest neighbor.
For simplicity, we choose a random qubit from the first N-1 qubits for
the control and we set the target to be qubit i+1, where i is the control."""
a = np.random.choice(range(len(qubits)-1), 1, replace=True)[0]
yield Circuit().cz(qubits[a],qubits[a+1])
def local_Hayden_Preskill_generator(qubits,numgates):
"""Yields the circuit elements for a scrambling unitary.
Generates a circuit with numgates gates by laying down a
random gate at each time step. Gates are chosen from single
qubit unitary rotations by a random angle, Hadamard, or a
controlled-Z between a qubit and its nearest neighbor (i.e.,
incremented by 1)."""
for i in range(numgates):
yield np.random.choice([
Circuit().rx(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().ry(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().rz(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().h(np.random.choice(qubits,1,replace=True)),
CZtuple_generator(qubits), # For all-to-all: Circuit().cz(*np.random.choice(qubits,2,replace=False)),
],1,replace=True,p=[1/8,1/8,1/8,1/8,1/2])
def non_local_Hayden_Preskill_generator(qubits,numgates):
"""Yields the circuit elements for a scrambling unitary.
Generates a circuit with numgates gates by laying down a
random gate at each time step. Gates are chosen from single
qubit unitary rotations by a random angle, Hadamard, or a
controlled-Z between a qubit and its nearest neighbor (i.e.,
incremented by 1)."""
for i in range(numgates):
yield np.random.choice([
Circuit().rx(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().ry(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().rz(np.random.choice(qubits,1,replace=True),np.random.ranf()),
Circuit().h(np.random.choice(qubits,1,replace=True)),
Circuit().cz(*np.random.choice(qubits,2,replace=False)),
],1,replace=True,p=[1/8,1/8,1/8,1/8,1/2])
# -
# We use the helper functions above to generate local Hayden-Preskill (random) quantum circuits. For example:
# Generate an example of a local Hayden Preskill circuit
test_circuit = Circuit()
test_circuit.add(local_Hayden_Preskill_generator(range(5),20))
print(test_circuit)
# Generate an example of a non-local Hayden Preskill circuit
test_circuit = Circuit()
test_circuit.add(non_local_Hayden_Preskill_generator(range(5),20))
print(test_circuit)
# ## Simulating _local_ random circuits using the TN1 tensor network simulator
# ### Testing and timing
# Let's start with a reasonably sized circuit
num_qubits = 20 # Number of qubits
num_layers = 10 # Number of layers. A layer consists of num_qubits gates.
numgates = num_qubits * num_layers # Total number of gates.
print(f"{num_qubits} qubits, {num_layers} layers = {numgates} total gates")
circ = Circuit()
circ.add(local_Hayden_Preskill_generator(range(num_qubits), numgates)); # Create the circuit with numgates gates.
# Time this circuit using TN1. It should take about a minute or so.
# +
# %%time
# define task
print(f"Running: {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
task = device.run(circ, s3_folder, shots=1000, poll_timeout_seconds = 1000)
# get id and status of submitted task
task_id = task.id
status = task.state()
print('ID of task:', task_id)
print('Status of task:', status)
# wait for job to complete
terminal_states = ['COMPLETED', 'FAILED', 'CANCELLED']
while status not in terminal_states:
time.sleep(20) # Update this for shorter circuits.
status = task.state()
print('Status:', status)
# get results of task
result = task.result()
# get measurement shots
counts = result.measurement_counts
plt.bar(counts.keys(), counts.values());
# -
# ### The importance of locality in circuits
# The goal of this section is to understand the importance of a local structure in quantum circuits being simulated in the tensor network simulator. We will first generate and benchmark a local Hayden-Preskill circuit, and then we will re-run the exact same circuit with the qubits randomly permuted. By permuting the qubits, we produce a circuit that appears to be have non-local, long-range coupling, but for which we know that there exists an underlying local structure.
#
# An example of a circuit and its permuted version is shown below. A local Hayden-Preskill circuit is generated, and then a version of the same circuit is created in which the qubits are randomly permuted, according to the permutation [0,1,2,3,4,5]$\mapsto$[5,2,4,1,0,3].
from IPython.display import Image
Image(filename='permuted_circuit.png', width=400)
# With these two circuits (that seem to have vastly different locality, but which are "secretly" the same), we can explore the tensor network simulator's ability to discern structure in a given circuit.
# First generate a modest sized local Hayden-Preskill circuit. Then make a copy of that circuit by permuting the qubit indices randomly. We'll compare the runtime to sample from the outputs of these two circuits.
# +
num_qubits = 50 # Number of qubits
num_layers = 10 # Number of layers. A layer consists of num_qubits gates.
numgates = num_qubits * num_layers # Total number of gates.
qubits=range(num_qubits) # Generate the (1D) qubits
print(f"{num_qubits} qubits, {num_layers} layers = {numgates} total gates")
# Generate the circuit with numgates gates acting on qubits.
circ = Circuit()
circ.add(local_Hayden_Preskill_generator(qubits,numgates));
# Choose a random permutation of the qubits
permuted_qubits=np.random.permutation(qubits)
# Copy the circuit circ acting on the permuted qubits
perm = Circuit().add_circuit(circ, target_mapping=dict(zip(qubits, permuted_qubits)))
##Uncomment for testing:
# print(permuted_qubits)
# print(circ)
# print(perm)
# -
# Time both circuits using the tensor network simulator for a **single shot**.
# +
# %%time
# define task
task = device.run(circ, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
counts = result.measurement_counts
print(f"The sample was: {next(iter(counts))}.")
# +
# %%time
# define task
task = device.run(perm, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the non-local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
counts = result.measurement_counts
print(f"The sample was: {next(iter(counts))}.")
# -
# If you repeat these experiments, you'll find that the two runtimes are (typically) very similar! Even though the permuted circuit seems to be highly non-local at first glance, the simulator discovers the underlying local structure, and the total runtime is comparable to the manifestly local circuit. This similarity is due to the rehearsal phase of the tensor network simulation [[1]](#References). A sophisticated algorithm works behind the scenes to find an efficient path for contracting the tensor network. Thus, when the tensor network has an underlying structure, the tensor network simulator can often tease it out.
# ## Simulating _non-local_ random circuits using the TN1 tensor network simulator
# Let us now compare the efficiency of simulating local and genuinely non-local random quantum circuits. When using the non-local Hayden Preskill circuits above, the circuits we generate have no underlying structure, making them especially difficult for the tensor network simulator.
# We will generate one local random circuit and one non-local quantum circuit of the same size, and we will compare their runtimes. In this section, the we will not be comparing identical quantum circuits as we were above, so our results can be understood by repeating these experiments several times and noting that our claims are true on average.
# +
num_qubits = 50 # Number of qubits
num_layers = 8 # Number of layers. A layer consists of num_qubits gates.
numgates = num_qubits * num_layers # Total number of gates.
qubits=range(num_qubits) # Generate the (1D) qubits
print(f"{num_qubits} qubits, {num_layers} layers = {numgates} total gates")
# Generate the local circuit with numgates gates acting on qubits.
localcirc = Circuit()
localcirc.add(local_Hayden_Preskill_generator(qubits,numgates));
# Generate the non-local circuit with numgates gates acting on qubits.
nonlocalcirc = Circuit()
nonlocalcirc.add(non_local_Hayden_Preskill_generator(qubits,numgates));
##Uncomment for testing:
# print(permuted_qubits)
# print(circ)
# print(perm)
# -
# Run the local circuit:
# +
# %%time
# define task
task = device.run(localcirc, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
counts = result.measurement_counts
print(f"The sample was: {next(iter(counts))}.")
# -
# Run the non-local circuit:
# +
# %%time
# define task
task = device.run(nonlocalcirc, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the non-local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
counts = result.measurement_counts
print(f"The sample was: {next(iter(counts))}.")
# -
# When running this notebook several times, we find that the non-local circuit generally takes 2-3 times longer to run than the local circuit. However, on occasion the non-local circuit fails to run, for a reason we will explore below.
# ## Non-local circuits quickly become too difficult for tensor network methods
# In this section, we will compare larger circuits with and without locality. We will see that the local circuits execute very efficiently on the tensor network simulator, whereas the non-local circuits actually fail in the rehearsal phase.
#
# We start by generating these larger circuits:
# +
num_qubits = 50 # Number of qubits
num_layers = 20 # Number of layers. A layer consists of num_qubits gates.
numgates = num_qubits * num_layers # Total number of gates.
qubits=range(num_qubits) # Generate the (1D) qubits
print(f"{num_qubits} qubits, {num_layers} layers = {numgates} total gates")
# Generate the circuit with numgates gates acting on qubits.
localcirc = Circuit()
localcirc.add(local_Hayden_Preskill_generator(qubits,numgates));
# Generate the circuit with numgates gates acting on qubits.
nonlocalcirc = Circuit()
nonlocalcirc.add(non_local_Hayden_Preskill_generator(qubits,numgates));
##Uncomment for testing:
# print(permuted_qubits)
# print(circ)
# print(perm)
# -
# The local Hayden Preskill circuit executes in a reasonable amount of time, generally about a minute or so:
# +
# %%time
# define task
task = device.run(localcirc, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
counts = result.measurement_counts
print(f"The sample was: {next(iter(counts))}.")
# -
# Conversely, the non-local Hayden Preskill circuit actually fails to execute:
#
# <div class="alert alert-block alert-info">
# <b>Note:</b> The following cell can take several minutes to run on TN1. It is only present to illustrate a task that will result in a FAILED state.
# </div>
# +
# %%time
# define task
task = device.run(nonlocalcirc, s3_folder, shots=1, poll_timeout_seconds = 1000)
# get results of task
result = task.result()
# get measurement shots
print(f"Running the non-local circuit with {num_qubits} qubits, {num_layers} layers = {numgates} total gates")
# counts = result.measurement_counts
# print(f"The sample was: {next(iter(counts))}.")
# -
# To see why this circuit `FAILED` to run, we can check the `failureReason` in the task's `_metadata`:
print(task._metadata['failureReason'])
# Evidently, without any structure to exploit, this tensor network would take too long to simulate, and the simulator returns with a `FAILED` state.
# ## Conclusions
# We saw that structured quantum circuits can be simulated much more efficiently than unstructured random quantum circuits. That said, structure in a quantum circuit may not be immediately evident, as the tensor network simulator was able to discover the hidden structure in our permuted quantum circuits, leading to efficiency on-par with their unpermuted, local counterparts. Note, however, that discovering this underlying structure is analogous to the graph isomorphism problem, and finding an efficient contraction path for a tensor network is a hard problem.
# ## Appendix
# Check SDK version
# alternative: braket.__version__
# !pip show amazon-braket-sdk | grep Version
# ## References
# [1] [Amazon Braket Documentation: Tensor Network Simulator](https://docs.aws.amazon.com/braket/latest/developerguide/braket-devices.html#braket-simulator-tn1)
|
examples/braket_features/TN1_demo_local_vs_non-local_random_circuits.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.3
# language: julia
# name: julia-0.6
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Solving Partial Differential Equations in Julia
#
# ## JuliaCon 2018
#
# ## <NAME>
#
# ## University of Maryland, Baltimore
# ## University of California, Irvine
# + [markdown] slideshow={"slide_type": "slide"}
# ## The goal of this workshop is to show how very disparate parts of the package ecosystem can be joined together to solve PDEs
#
# How are finite elements, multigrid methods, ODE solvers, etc. all the same topic?
#
# Teach a man to fish: we won't be going over pre-built domain specific PDE solvers, instead we will be going over the tools which are used to build PDE solvers.
#
# #### While the basics of numerically solving PDEs is usually taught in mathematics courses, the way it is described is not suitable for high performance scientific computing. Instead, we will describe the field in a very practical "I want to compute things fast and accurately" style.
# + [markdown] slideshow={"slide_type": "slide"}
# ## What is a PDE?
#
# A partial differential equation (PDE) is a differential equation which has partial derivatives. Let's unpack that.
#
# A differential equation describes a value (function) by how it changes. `u' = f(u,p,t)` gives you a solution `u(t)` by you inputing / describing its derivative. Scientific equations are encoded in differential equations since experiments uncovers laws about what happens when entities change.
#
# A partial differential equation describes a value by how it changes in multiple directions: how it changes in the `x` vs `y` physical directions, and how it changes in time.
#
# Thus spatial properties, like the heat in a 3D room at a given time, `u(x,y,z,t)` are described by physical equations which are PDEs. Values like how a drug is distributed throughout the liver, or how stress propogates through an airplane hull, are examples of phonomena described by PDEs.
#
# You are interested in PDEs.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 1: Representations of PDEs as other mathematical problems
#
# This will either be an overview where I will reframe the most common method of solution, or your first walkthrough of a PDE solver!
# + [markdown] slideshow={"slide_type": "slide"}
# ## The best way to solve a PDE is...
# + [markdown] slideshow={"slide_type": "slide"}
# ## By converting it into another problem!
#
# Generally, PDEs are converted into:
#
# - Linear systems: `Ax = b` find `x`.
# - Nonlinear systems: `G(x) = 0` find `x`.
# - ODEs: `u' = f(u,p,t)`, find `u`.
#
# There are others:
#
# - SDEs: `du = f(u,p,t)dt + g(u,p,t)dW`, find `mean(u)`.
#
# ... Yes experts, there are more but we will stick to the usual stuff.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Learning by example: the Poisson Equation
#
# Let's introduce some shorthand: $u_x = \frac{\partial u}{\partial x}$. The Poisson Equation is the PDE:
#
# $$ \Delta u(x) = b(x) $$
#
# for $ x \in [0,1]$. In one dimension:
#
# $$u_{xx} = b$$
#
# $b(x)$ is some known constant function (known as "the data"). Given the data (the second derivative), find $u$.
#
# ### How do we solve this PDE?
# + [markdown] slideshow={"slide_type": "slide"}
# ## First Choice: Computational Representation of a Function
#
# First we have to choose how to computationally represent our continuous function $u(x)$ by finitely many numbers. Let's start with the most basic way (and we'll revisit the others later!). Let $\Delta x$ be some constant discretization size and let $x_i = i\Delta x$. Then we represent our function $u(x) \approx {u_i} = {u(x_i)}$, i.e. we represent a continuous function by values on a grid (and we can assume some interpolation, like linear interpolation)
# + slideshow={"slide_type": "slide"}
Δx = 0.1
x = 0:Δx:1
u(x) = sin(2π*x)
using Plots
plot(u,0,1,lw=3)
scatter!(x,u.(x))
plot!(x,u.(x),lw=3)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Second Choice: Discretization of Derivatives
#
# Forward difference: $ u_x \approx \delta^+ u = \frac{u_{i+1} - u_{i}}{\Delta x} $
#
# Backward difference: $ u_x \approx \delta^- u = \frac{u_{i} - u_{i-1}}{\Delta x} $
#
# $$ u_{xx} = \frac{\partial u_x}{\partial x} $$
#
# Central difference for 2nd derivative: $ u_{xx} \approx \delta u_{x} = \frac{\delta^+ u_x - \delta^- u_x}{\Delta x}$
#
# This gives the well-known central difference formula:
#
# $$ u_{xx} \approx \frac{u_{i+1} - 2u_i + u_{i-1}}{\Delta x^2} $$
# + [markdown] slideshow={"slide_type": "slide"}
# ## Quick Recap
#
# We just made **two choices**:
#
# - Represent our function by an evenly spaced grid of points
# - Represent the derivative by the central difference formula
#
# Given these two choices, how can we re-write our PDE?
# + [markdown] slideshow={"slide_type": "slide"}
# ## The Representation of Our PDE
#
# Remember we want to solve $ \Delta u = b $ on $ x \in [0,1] $
#
# - $u(x)$ is now a vector of points $u_i = u(x_i)$
# - $b(x)$ is now a vector of points $b_i = b(x_i)$
# - The second derivative is now the function $\frac{\partial^2 u}{\partial x}(x_i) = \frac{u_{i+1} - 2u_i + u_{i-1}}{\Delta x^2}$
#
# Thus we have a system of $i$ equations:
#
# $$ \frac{u_{i+1} - 2u_i + u_{i-1}}{\Delta x^2} = b_i $$
# + [markdown] slideshow={"slide_type": "slide"}
# ## But Wait...
#
# What happens at $i=0$?
#
# $$ \frac{u_1 - 2u_0 + u_{i-1}}{\Delta x^2} = b_0 $$
#
# Translating back to $u_i = u(x_i) = u(i\Delta x)$:
#
# $$ u(\Delta x) - 2u(0) + u(-\Delta x)$$
#
# The last point is out of the domain! In order to solve this problem we have to impose **boundary conditions**. For example, let's add the following condition to our problem: $u(0) = u(1) = 0$. Then the $0$th point is determined: $u_0 = 0$, and the 1st point is:
#
# $$ b_1 = \frac{u_2 - 2u_1 + u_0}{\Delta x^2} = \frac{u_2 - 2u_1}{\Delta x^2} $$
#
# so we can solve it!
# + [markdown] slideshow={"slide_type": "slide"}
# ## The Linear Representation of Our Derivative
#
# Notice that if $$ U=\left[\begin{array}{c}
# u_{1}\\
# u_{2}\\
# \vdots\\
# u_{N-1}\\
# u_{N}
# \end{array}\right], $$ then
#
# $$ AU=\frac{1}{\Delta x^{2}}\left[\begin{array}{ccccc}
# -2 & 1\\
# 1 & -2 & 1\\
# & \ddots & \ddots & \ddots\\
# & & 1 & -2 & 1\\
# & & & 1 & -2
# \end{array}\right]\left[\begin{array}{c}
# u_{1}\\
# u_{2}\\
# \vdots\\
# u_{N-1}\\
# u_{N}
# \end{array}\right]=\frac{1}{\Delta x^{2}}\left[\begin{array}{c}
# u_{2}-2u_{1}\\
# u_{3}-2u_{2}+u_{1}\\
# \vdots\\
# u_{N}-2u_{N-1}+u_{N-2}\\
# -2u_{N}+u_{N-1}
# \end{array}\right]=\left[\begin{array}{c}
# b_{1}\\
# b_{2}\\
# \vdots\\
# b_{N-1}\\
# b_{N}
# \end{array}\right]=B $$
# + [markdown] slideshow={"slide_type": "slide"}
# ## This is a linear equation!
#
# We know $A$, $B$ is given to us, find $U$.
#
# Let's walk through a concrete version with some Julia code now. Let's solve:
#
# $$ u_{xx} = sin(2\pi x) $$
# + slideshow={"slide_type": "slide"}
Δx = 0.1
x = Δx:Δx:1-Δx # Solve only for the interior: the endpoints are known to be zero!
N = length(x)
B = sin.(2π*x)
A = zeros(N,N)
for i in 1:N, j in 1:N
abs(i-j)<=1 && (A[i,j]+=1)
i==j && (A[i,j]-=3)
end
A = A/(Δx^2)
# + slideshow={"slide_type": "slide"}
# Now we want to solve AU=B, so we use backslash:
U = A\B
plot([0;x;1],[0;U;0],label="U")
# + [markdown] slideshow={"slide_type": "slide"}
# ## Did we do that correctly?
#
# This equation is simple enough we can check via the analytical solution.
#
# $$ u_{xx} = sin(2\pi x) $$
#
# Integrate it twice:
#
# $$ u(x) = -\frac{sin(2\pi x)}{4\pi^2} $$
# + slideshow={"slide_type": "slide"}
# Now we want to solve AU=B, so we use backslash:
plot([0;x;1],[0;U;0],label="U")
plot!([0;x;1],-sin.(2π*[0;x;1])/4(π^2),label="Analytical Solution")
# + [markdown] slideshow={"slide_type": "slide"}
# ## Recap
#
# We solved the PDE $$\Delta u = b $$ by transforming our functions into vectors of numbers $U$ and $B$, transforming second derivative into a linear operator (a matrix) $A$, and solving $AU = B$ using backslash.
#
# Does this method generally apply?
#
# Pretty much.
#
# #### Because derivatives are linear, when you discretize a function, the derivative operators become linear operators = matrices
# + [markdown] slideshow={"slide_type": "slide"}
# ## Semilinear Poisson Equation
#
# $$ \Delta u = f(u) $$
#
# Now the right hand side is dependent on $u$! Let's choose the same discretization and the same representation of the derivatives. Then once again $ \Delta u = AU$ for the same matrix $A$. Now we get the equation:
#
# $$ AU = f(U) $$
#
# Find the vector of $U$ which satisfy this nonlinear system! If we redefine:
#
# $$ G(U) = f(U) - AU $$
#
# then we are looking for the vector $U$ which causes $G(U) = 0$.
#
# #### tl;dr: Semilinear equations convert into nonlinear rootfinding problems
# + [markdown] slideshow={"slide_type": "slide"}
# ## Semilinear Heat Equation
#
# $$ u_t = u_{xx} + f(u,t) $$
#
# Discretize the function the same way as before. This once again makes $u_{xx} = AU$. Thus letting $U_t$ be the time derivative of each point in the vector, we get:
#
# $$ U_t = AU + f(U,t) $$
#
# but since there's now only one coordinate, let the derivative be by time. Then we can write this as:
#
# $$ U' = AU + f(U,t) $$
#
# This is an ODE!
#
# #### tl;dr: Time-dependent PDEs (can) convert into ODE problems!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Loose End: Higher Dimensions Do The Same Thing
#
# Now let's look at $$ \Delta u = u_{xx} + u_{yy} = b(x,y) $$ on $x \in [0,1], y \in [0,1]$.
#
# In this case, you can let $u_{i,j} = u(x_i,y_i)$ where $x_i = i\Delta x$ and $y_i = i\Delta y$. You can list out all of the $u_{i,j}$ into a vector $U$ by lexicographic ordering:
#
# $$ U=\left[\begin{array}{c}
# u_{1,1}\\
# u_{2,1}\\
# \vdots\\
# u_{N-1,}\\
# u_{N,1}\\
# u_{1,2}\\
# \vdots\\
# u_{N,M}
# \end{array}\right] $$
#
# $$ \Delta u = u_{xx} + u_{yy} \approx \frac{u_{i+1,j} - 2u_{i,j} + u_{i-1,j}}{\Delta x^2} + \frac{u_{i,j+1} -2 u_{i,j} + u_{i,j-1}}{\Delta y^2} = AU$$
#
# for some A. Now solve $AU=B$
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 1 Summary
#
# To solve a PDE,
#
# - You choose a way to represent functions.
# - You choose a way to represent your derivative (and on the function representation, your derivative representation is a matrix!)
#
# Then when you write out your PDE, you get one of the following problems:
#
# - Linear systems: `Ax = b` find `x`.
# - Nonlinear systems: `G(x) = 0` find `x`.
# - ODEs: `u' = f(u,p,t)`, find `u`.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 2: The Many Ways to Discretize
#
# There are thus 4 types of packages in the PDE solver pipeline:
#
# - Packages with ways to represent functions as vectors of numbers and their derivatives as matrices
# - Packages which solve linear systems
# - Packages which solve nonlinear rootfinding problems
# - Packages which solve ODEs
#
# In this part we will look at the many ways you can discretize a PDE.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 2.1: Packages to Represent Functions and Derivatives
#
# There are four main ways to represet functions and derivatives as vectors:
#
# - Finite difference method (FDM): functions are represented on a grid. Packages: DiffEqOperators.jl (still developing)
# - Finite volume method (FVM): functions are represented by a discretization of its integral. Currently no strong generic package support.
# - Finite element method (FEM): functions are represented by a local basis. FEniCS.jl, JuliaFEM and JuAFEM.jl
# - Spectral methods: functions are represented by a global basis. FFTW.jl and ApproxFun.jl
# + [markdown] slideshow={"slide_type": "slide"}
# ## Finite Difference method: DiffEqOperators.jl
#
# DiffEqOperators.jl is part of the JuliaDiffEq ecosystem. It automatically develops lazy operators for finite difference discretizations (functions represented on a grid). For example, to represent $u_{xx}$, we'd do:
# + slideshow={"slide_type": "fragment"}
using DiffEqOperators
# Second order approximation to the second derivative
order = 2
deriv = 2
Δx = 0.1
N = 9
A = DerivativeOperator{Float64}(order,deriv,Δx,N,:Dirichlet0,:Dirichlet0)
# + [markdown] slideshow={"slide_type": "fragment"}
# This `A` is lazy: it acts `A*u` like it was a matrix but without ever building the matrix by overloading `*` and directly computing the coefficients. This makes it efficient, using $\mathcal{O}(1)$ memory while not having the overhead of sparse matrices!
# + [markdown] slideshow={"slide_type": "slide"}
# This package also makes it easy to generate the matrices without much work. For example, let's get a 2nd order discretization of $u_{xxxx}$:
# + slideshow={"slide_type": "fragment"}
full(DerivativeOperator{Float64}(4,2,Δx,N,:Dirichlet0,:Dirichlet0))
# + [markdown] slideshow={"slide_type": "fragment"}
# #### This package is still in heavy development: improved boundary condition handling and irregular grid support is coming
# + [markdown] slideshow={"slide_type": "slide"}
# ## Brief brief brief overview of finite element methods
#
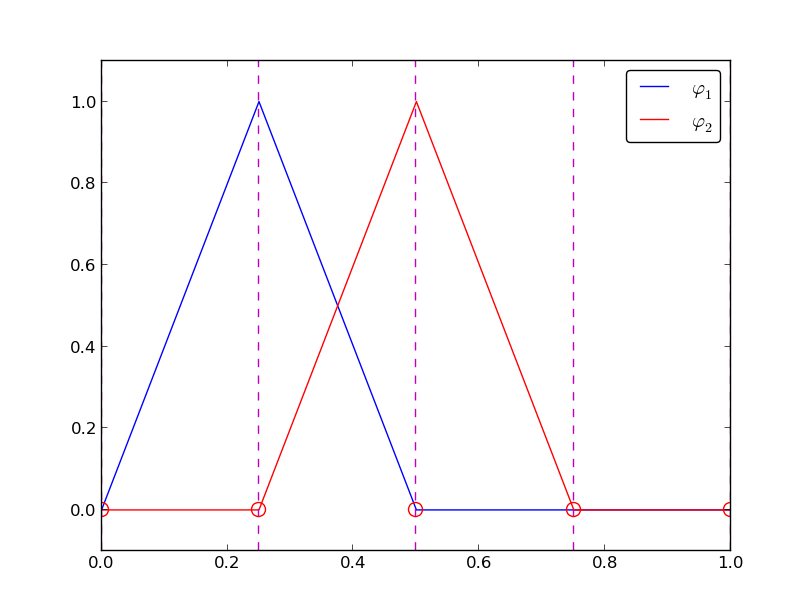
# Represent your function $u(x) = \sum_i c_i \varphi_i(x) $ with some chosen basis $\varphi_i(x)$.
#
# "Matrix Assembly" = calculate the matrix representations of the derivatives in this function representation. The core of an FEM package is its matrix assembly tools.
#
# #### Finite difference method is good if your domain is a square / hypercube. Finite element methods can solve PDEs on more complicated domains
# + [markdown] slideshow={"slide_type": "slide"}
# ## 1D Basis Example
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
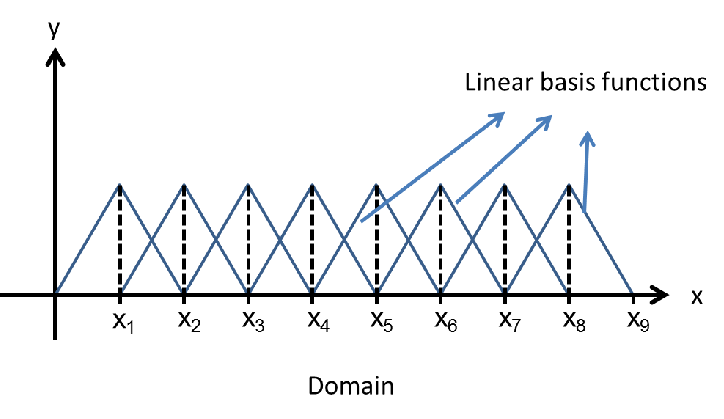
# 
# + [markdown] slideshow={"slide_type": "slide"}
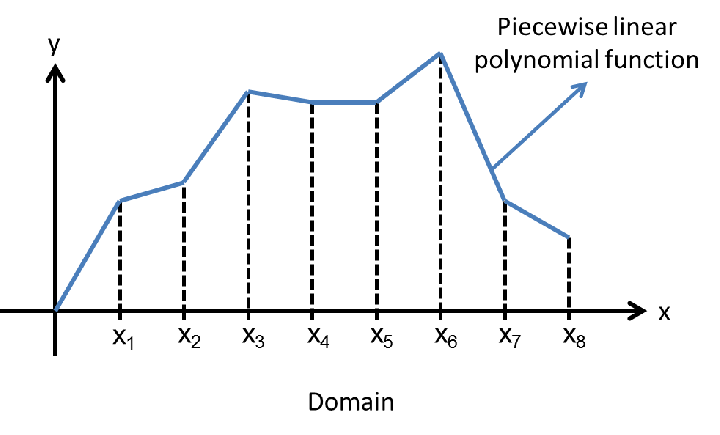
# 
# + [markdown] slideshow={"slide_type": "slide"}
# ## 2D Basis Elements
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
# ## FEM Easily Handle Difficult Domains
#
# 
# + [markdown] slideshow={"slide_type": "slide"}
# 
# + [markdown] slideshow={"slide_type": "slide"}
# ## FEM Package 1: FEniCS.jl
#
# FEniCS is a well-known finite element package for Python (fellow NumFOCUS project!). It lets you describe the kind of PDE you want to solve and what elements (basis functions) you want to discretize with in a DSL, and it handles the rest.
#
# FEniCS.jl is a wrapper over FEniCS which is maintained by the JuliaDiffEq organization.
#
# - Pro: very full featured (since it's wrapping an existing package). Linear solvers are built in.
# - Con: not Julia-based, so it's missing a lot of the fancy Julia features (generic programming, arbitrary number types, etc.)
# + slideshow={"slide_type": "slide"}
using FEniCS
mesh = UnitSquareMesh(8,8)
V = FunctionSpace(mesh,"P",1)
u_D = Expression("1+x[0]*x[0]+2*x[1]*x[1]", degree=2)
u = TrialFunction(V)
bc1 = DirichletBC(V,u_D, "on_boundary")
v = TestFunction(V)
f = Constant(-6.0)
a = dot(grad(u),grad(v))*dx
L = f*v*dx
U = FEniCS.Function(V)
lvsolve(a,L,U,bc1) #linear variational solver
# + [markdown] slideshow={"slide_type": "slide"}
# ## FEM Package 2: JuliaFEM
#
# JuliaFEM is an organization with a suite of packages for performing finite element discretizations. It focuses on FEM discretizations of physical PDEs and integrates with Julia's linear solver, nonlinear rootfinding, and DifferentialEquations.jl libraries to ease the full PDE solving process.
# + [markdown] slideshow={"slide_type": "slide"}
# ## FEM Package 3: JuAFEM.jl
#
# JuAFEM.jl is a FEM toolbox. It gives you functionality that makes it easier to write matrix assembly routines.
# + slideshow={"slide_type": "slide"}
function doassemble(cellvalues::CellScalarValues{dim}, K::SparseMatrixCSC, dh::DofHandler) where {dim}
n_basefuncs = getnbasefunctions(cellvalues)
Ke = zeros(n_basefuncs, n_basefuncs)
fe = zeros(n_basefuncs)
f = zeros(ndofs(dh))
assembler = start_assemble(K, f)
@inbounds for cell in CellIterator(dh)
fill!(Ke, 0)
fill!(fe, 0)
reinit!(cellvalues, cell)
for q_point in 1:getnquadpoints(cellvalues)
dΩ = getdetJdV(cellvalues, q_point)
for i in 1:n_basefuncs
v = shape_value(cellvalues, q_point, i)
∇v = shape_gradient(cellvalues, q_point, i)
fe[i] += v * dΩ
for j in 1:n_basefuncs
∇u = shape_gradient(cellvalues, q_point, j)
Ke[i, j] += (∇v ⋅ ∇u) * dΩ
end
end
end
assemble!(assembler, celldofs(cell), fe, Ke)
end
return K, f
end
K, f = doassemble(cellvalues, K, dh);
apply!(K, f, ch)
u = K \ f;
# + [markdown] slideshow={"slide_type": "slide"}
# ## Spectral Methods
#
# Like finite element methods, spectral methods represent a function in a basis: $u(x) = \sum_i c_i \varphi_i(x) $ with some chosen basis $\varphi_i(x)$.
#
# "Spectral" usually refers to global basis functions. For example, the Fourier basis of sines and cosines.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Spectral Packages 1: FFTW.jl
#
# Okay, this is not necessarily a spectral discretization package. However, it is a package to change from a pointwise representation of a function to a Fourier representation via a Fast Fourier Transform (FFT). Thus if you want to find the coefficients $c_ki$ for
#
# $$ u(x) = \sum_k c_k sin(kx) $$
#
# you'd use:
# + slideshow={"slide_type": "slide"}
using FFTW
x = linspace(0,2π,100)
u(x) = sin(x)
freqs = fft(u.(x))[1:length(x)÷2 + 1]
c = 2*abs.(freqs/length(x))'
# + [markdown] slideshow={"slide_type": "fragment"}
# This corresponds to basically saying that $sin(x)$ is represented in the Fourier basis as:
#
# $$ sin(x) \approx 5\times 10^{-18} sin(0x) + 0.9948sin(x) + 0.014sin(2x) + 0.0076sin(3x) + \ldots $$
#
# It almost got it, and you can see the slight discretization error. This goes away as you add more points. But now you can represent any periodic function!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Spectral Packages 2: ApproxFun.jl
#
# ApproxFun.jl is a package for easily approximating functions and their derivatives in a given basis, making it an ideal package for building spectral discretizations of PDEs. It utilizes lazy representations of infinite matrices to be efficient and save memory. It uses a type system to make the same code easy to translate between different basis choices.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Representing a Function and its Derivative in the Fourier Basis
#
# Let's represent
#
# $$ r(x) = cos(cos(x-0.1)), $$
#
# in the Fourier basis, and build a matrix representation of the second derivative in this basis:
# + slideshow={"slide_type": "slide"}
S = Fourier()
n = 100
T = ApproxFun.plan_transform(S, n)
Ti = ApproxFun.plan_itransform(S, n)
x = points(S, n)
r = (T*cos.(cos.(x-0.1)))'
# + slideshow={"slide_type": "slide"}
D2 = Derivative(S,2)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Now let's change to the Chebyshev basis:
#
# This basis is $$ \sum_k c_k T_k(x) $$ for $T_k$ the Chebyschev polynomials $(1, x, 2x^2-1, 4x^3 - 3x, \ldots)$
# + slideshow={"slide_type": "slide"}
S = Chebyshev()
n = 100
T = ApproxFun.plan_transform(S, n)
Ti = ApproxFun.plan_itransform(S, n)
x = points(S, n)
r = (T*cos.(cos.(x-0.1)))'
# + slideshow={"slide_type": "slide"}
D2 = Derivative(S,2)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 2 Summary
#
# Using these packages, you can easily translate your PDE functions to coefficient vectors and your derivatives to matrices:
#
# - Use spectral methods or finite difference methods for cases with "simple enough" boundary conditions and on simple (square) domains
# - Use finite element packages to discretize complex spatial domains
#
# There are a lot more factors. Sometimes given discretizations are better/worse on given PDEs. There are mathematicians who spend their entire life researching the differences between discretization methods!
# + [markdown] slideshow={"slide_type": "slide"}
# ## But now...
#
# Our PDE functions are now vectors of coefficients. Our PDE derivatives are now matrices. We are left with one of the following to solve:
#
# - Linear systems: `Ax = b` find `x`.
# - Nonlinear systems: `G(x) = 0` find `x`.
# - ODEs: `u' = f(u,p,t)`, find `u`.
#
# Each of these problems is a specific area of research in and of itself!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3: Equation Solving
#
# In order to do equation solving correctly, we must make note of one important fact:
#
# #### The matrices which come out of a derivative discretization are often very sparse!
#
# - The finite difference matrix `[1 -2 1]` only has 3 non-zero values per row no matter what `N` is! This type of matrix is called tridiagonal.
# - For matrices which have more general semi-diagonal structures which are only non-zero near the center, they are called banded matrices.
# - Derivatives in Fourier space are diagonal!
# - Generic sparse matrices arise from FEM discretizations (since the derivatives only depend on nearby basis elements which are very few!).
#
# Thus solving PDEs is more specifically **equation solving with large numbers of equations and high sparsity with structure**
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.1: Solving Large Sparse Linear Systems
#
# When solving $AU=B$ where $A$ arises from the derivative term in the PDE discretization, the structure of $A$ determines what type of method and what pacakage to use.
#
# - If `A` is tridiagonal, then Julia's `\` will use a specialized fast method.
# - If `A` is small enough, then `\` is a multithreaded LU or QR factorization which is fine.
# - If `A` is a banded matrix (many spectral discertizations and finite difference methods), then uses `BandedMatrix(A)\B` from BandedMatrices.jl utilizes a fast LU/QR for this matrix type.
# - If `A` is a block banded matrix (blocking arises from lexicographical ordering when 2+ dimensional), then `BlockBandedMatrix(A)\B` from BlockBandedMatrices.jl utilizes a fast LU/QR for this matrix type.
# - If `A` is a small enough sparse matrix, then Julia's Base `\` will use SuperLUMT, a multithreaded sparse LU which will be fast if it has enough memory (hence small enough).
# - If `A` is a large sparse matrix (or matrix-free), then iterative methods are required. For this, there is IterativeSolvers.jl and JuliaSmoothOptimizers/Krylov.jl
# + [markdown] slideshow={"slide_type": "slide"}
# ## Iterative Solvers
#
# Iterative solvers repeatedly calculate `A*U_k` in order to find a sequence such that $U_k \rightarrow U $ where $AU=B$.
#
# #### Because iterative solvers only use multiplication, "matrix-free" operators, i.e. Julia types which just define `*`, can be used in these methods!
#
# IterativeSolvers.jl has many methods which are specialized for different forms of sparsity structures. For example, `cg` is a fast method for symmetric positive definite matrices. The fallback method for a general `A` is `gmres`. Let's give it a try on some random `AU=B` problem.
# + slideshow={"slide_type": "slide"}
n = 10
A = rand(n, n)
B = rand(n)
# Let's use the gmres method from IterativeSolvers.jl
using IterativeSolvers
# Same thing as A\B
U = gmres(A, B, tol = 1e-8) # Get at least within 1e-8 of the solution!
norm(A*U - B)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Using a Matrix-Free Type
#
# Let's create a type that is the second order central difference derivative `[1 -2 1]` and solve the Poisson equation $\Delta u = b$ with our matrix-free operator by using `gmres` instead of `\`. We could just use DiffEqOperators.jl's lazy matrix here, but let's build the full example from scratch:
# + slideshow={"slide_type": "slide"}
struct SizedStrangMatrix
size::Tuple{Int,Int}
end
Base.eltype(A::SizedStrangMatrix) = Float64
Base.size(A::SizedStrangMatrix) = A.size
Base.size(A::SizedStrangMatrix,i::Int) = A.size[i]
A = SizedStrangMatrix((length(B),length(B)))
function Base.A_mul_B!(C,A::SizedStrangMatrix,B)
for i in 2:length(B)-1
C[i] = B[i-1] - 2B[i] + B[i+1]
end
C[1] = -2B[1] + B[2]
C[end] = B[end-1] - 2B[end]
C
end
Base.:*(A::SizedStrangMatrix,B::AbstractVector) = (C = similar(B); A_mul_B!(C,A,B))
using IterativeSolvers
U = gmres(A,B,tol=1e-14)
norm(A*U - B)
# + [markdown] slideshow={"slide_type": "slide"}
# ### LinearMaps.jl is a nice package for helping build matrix-free discretizations!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Preconditioning
#
# To solve the linear system $AU=B$ faster, you can use a preconditioners to partial solve the linear problem and thereby present a simpler problem to the iterative method. This is a deep deep area of research and the best preconditioner for your problem is highly dependent on your PDE, so I'm just going to point to some of the best packages in the area:
#
# - ILU.jl : Incomplete LU decompositions
# - IncompleteSelectedInversion.jl : incomplete LDLt decompositions
# - AlgebraicMultigrid.jl : An algebraic multigrid method
#
# You take one of these, plop it in as an additional argument to `gmres` and then it can go faster!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Linear Solver Parallelism Libraries
#
# Because of the ubiquity of solving large sparse linear systems in PDEs, there exists libraries which are dedicated to parallelizing the large scale sparse linear algebra. Julia packages for this are:
#
# - PETSc.jl
# - Trilinos.jl
# - Elemental.jl
#
# These packages allow you to distibute a linear solve computation amongst a whole cluster mixed with GPUs! But fundamentally the techniques are the same.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.1 Recap
#
# Linear solving requires specializing on the matrix type:
#
# - If small enough or the structure is known, special methods should be used
# - If large enough or no sparsity structure to explot, Krylov methods like `gmres` need to be used.
# - If iterative (Krylov) methods are used, then a good preconditioner can heavily speed up the solving.
# - `\`, Julia's LinearAlgebra special matrix types, BandedMatrices.jl, BlockBandedMatrices.jl, and IterativeSolvers.jl are your friends!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.2 Nonlinear Solvers
#
# Recall that if your data is a nonlinear function of your unknown then your PDE discretization doesn't produce a linear system but instead a nonlinear system $G(x) = 0$. There are a few packages for this case:
#
# - NLSolve.jl
# - Sundials.jl (KINSOL)
# - MINPACK.jl
#
# These have not been benchmarked against each other ( https://github.com/JuliaNLSolvers/NLsolve.jl/issues/159 go do it!) but have different characteristics.
#
# **But due to features, KINSOL.jl is the recommended one for now for PDEs, with NLsolve features coming soon**
# + [markdown] slideshow={"slide_type": "slide"}
# ## Quick Note: Don't use optimization routines to solve rootfinding problems
#
# $G(x) = 0$ is theoretically the same as finding the minimum of $\Vert G(x) \Vert$ (which should be zero!). However, this is bad:
#
# - Optimization methods are generally rootfinding methods on the derivative, since an optima is found when the derivative is zero!
# - Optimization methods generally use higher order derivatives. For example, Newton's method for optimization uses the second derivative (the Hessian), instead of the first derivative (the Jacobian), so it's more error prone and more expensive.
#
# Just don't do it.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Newton's Method
#
# $$z_{n+1} = z_n - J^{-1}(z_n)*G(z_n) $$
#
# where $J(z_n)$ is the Jacobian of $G(z_n)$. To solve this without needed inverses, you can rewrite this with $dz = z_{n+1} - z_n$ and see that
#
# $$G(z_n)dz = G(z_n)$$
#
# Thus every step of Newton's method is actually a linear solving problem, where the matrix is the Jacobian of $G$. Since $G$ is from our discretized PDE and all of the nonlinear behavior is local, the Jacobian of $G$ has the same structure and sparsity pattern as the $A$ from before! This means that:
#
# #### Newton's method is essentially nonlinear solving via repeat linear solving. Almost all of the time is spent linear solving
#
# All of the same tricks from before apply: we want to specialize on banded matrices, we want to use Krylov methods, and preconditioners, etc.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.2 Recap
#
# To solve nonlinear systems $G(x) = 0$, you either do:
#
# - Some simple iteration scheme (Picard iteration, Powell iterations, Anderson acceleration). These have a smaller area of convergence and converge slower, but do not require solving linear systems.
# - Some form of Newton's method. This requires solving linear systems.
#
# Usually a Newton method is required. In this case, **almost all of the cost comes from solving the linear systems**. Right now, KINSOL in Sundials.jl is the best tool because of the flexibility it gives in the linear solver choices, though NLsolve.jl will be adding similar features shortly (PRs are in progress).
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.3 ODE Solvers
#
# Recall that if you leave a derivative un-discretized you get an ODE system. Example:
#
# $$ u_t = u_xx + f(u,t) => u' = Au + f(u,t) $$
#
# You could discretize this time derivative the same way as you did space, getting a two-dimensional system and solving a big linear/nonlinear equation. But there can be advantages to leaving it as an ODE:
#
# - The full linear/nonlinear system is much larger. If you have $N$ points in space and $M$ time points, then you have $u$ as a size $NM$ vector! This grows fast!
# * This can take a prohibative amount of memory
# * The cost of the nonlinear solving can grow quadratically or cubically, so it would grow like $\mathcal{O}((NM)^k)$
# - Newton's method requires a good starting point. For a huge system in time and space, initial values for $u(x_i,t_j)$ can be hard to come by, and Newton's method can diverge.
#
# Keeping one part undiscretized and solving the ODE can alieviate these problems.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Features of a PDE-derived ODE
#
# A PDE-derived ODE tends to have the following features:
#
# - Stiffness. This is due to the CFL condition which doesn't requires $\frac{\Delta t}{\Delta x^k} < 1 $ for stability
# - Large sparse Jacobian. This is because of the matrices from the derivative terms!
#
# What ODE methods are applicable to this case?
#
# #### DifferentialEquations.jl has a wealth of unique options specifically for reducing the cost of integration on these types of problems
# + [markdown] slideshow={"slide_type": "slide"}
# ## Quick Note: Order of Integrator
#
# FAQ: I did a second order discretization in space, does it make sense to use a higher than second order integrator in time?
#
# Answer: Yes! The order of the integrator isn't just for reducing error. Higher order integrators can be more efficient! You can always incrase the error by taking larger time steps (increasing the tolernace) and thereby use less steps with a more efficient method.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Implicit and Rosenbrock ODE Integrators
#
# These methods step by **repeatedly solving nonlinear systems**. Remember that solving nonlinear systems boils down to repeatedly solving linear systems. Thus for the ODE $u'=f(u,p,t)$ with Jacobian $J$, an implicit ODE solver spends most of its time solving:
#
# $$ (I - \gamma J)x = b $$
#
# Since this $J$ has the same characteristics as before, solving this efficiently requires specializing the linear solver to the sparsity pattern (bandedness, etc.) or using a good preconditioner in an iterative solver.
#
# Good choices in DifferentialEquations.jl:
#
# - `CVODE_BDF`
# - `KenCarp4`
# - `Rodas5`
# + [markdown] slideshow={"slide_type": "slide"}
# ## Example: Spectral time stepping for Heat Equation in Fourier Space
# + slideshow={"slide_type": "slide"}
using ApproxFun, Sundials, Plots; gr()
S = Fourier(); n = 100; x = points(S, n)
T = ApproxFun.plan_transform(S, n); Ti = ApproxFun.plan_itransform(S, n)
u₀ = T*cos.(cos.(x-0.1)) # Convert the initial condition to Fourier space
D2 = Derivative(S,2); L = D2[1:n,1:n]
function heat(du,u,L,t)
A_mul_B!(du, L, u) # The equation is trivial in Fourier space
end
prob = ODEProblem(heat, u₀, (0.0,10.0),L)
# Specialize the linear solver on the diagonalness of the Jacobian
u = solve(prob, CVODE_BDF(linear_solver=:Diagonal); reltol=1e-8,abstol=1e-8);
# + slideshow={"slide_type": "slide"}
plot(x,Ti*u(0.0)) # The solution is in Fourier space, so use inverse to transform back
plot!(x,Ti*u(0.5)); plot!(x,Ti*u(2.0)); plot!(x,Ti*u(10.0))
# + [markdown] slideshow={"slide_type": "slide"}
# ## Pseudospectral Solving the Reaction-Diffusion Equation
#
# Take the PDE
#
# $$ u_t = u_{xx} + f(u,t)$$
#
# For some nonlinear $u$. In the Fourier basis, $u_{xx} = Au$ for a diagonal matrix $u$, so this is a nice way to solve the Heat Equation as above (by solving in Fourier space, and converting the solution back). We can solve a nonlinear equation by, whenever we need to apply the nonlinear $f$, transform $u$ back to the origional coordinates and applying $f$ on $u$ before transforming back. This pseudospectral discretization is seen as:
#
# $$ \mathcal{F}u' = A\mathcal{F}u + \mathcal{F}(f(\mathcal{F}^{-1}\mathcal{F}u,t)) $$
#
# gives an ODE for how $\mathcal{F}u$ evolves, and from that we can recover the true solution via the inverse Fourier transform $\mathcal{F}^{-1}(\mathcal{F}u)$
# + [markdown] slideshow={"slide_type": "slide"}
# ## Implicit-Explicit (IMEX) Integrators
#
# But wait, we shouldn't solve this as one whole ODE. If we split the ODE into two parts:
#
# $$ u' = f(u,p,t) = f_1(u,p,t) + f_2(u,p,t) $$
#
# then we notice that the first part is the linear part and has the stiff term, while the second part is nonlinear and (can be) non-stiff. **If we only are implicit on the first part, we can use a linear solver instead of a nonlinear solver to significantly reduce the amount of work!** Integrators which allow you to split and do two separate methods at the same time are called IMEX integrators.
#
# In DifferentialEquations.jl, IMEX integrators to be aware of are:
#
# - `CNAB2`
# - `SBDF2`
# - `KenCarp3`
# - `KenCarp4`
# + slideshow={"slide_type": "slide"}
# By making it Diagonal, DiffEq internally specializes the linear solver
using DiffEqOperators; A = DiffEqArrayOperator(Diagonal(L))
function f(dû,û,tmp,t)
A_mul_B!(tmp,Ti,û) # Transform u back to point-space
@. tmp = 0.75sqrt(tmp) - tmp # apply nonlinear function 0.75sqrt(u)-u in point-space
A_mul_B!(dû,T,tmp) # Transform back to Fourier space
end
# Define u' = Au + f
prob = SplitODEProblem(A, f, u₀, (0.0,10.0),similar(u₀))
u = solve(prob, KenCarp4())
plot(x,Ti*u(0.0)); plot!(x,Ti*u(0.5)); plot!(x,Ti*u(1.0)); plot!(x,Ti*u(2.0))
# + [markdown] slideshow={"slide_type": "slide"}
# ## Exponential Integrators
#
# A more recent set of integrators are the exponential integrators. These methods do not require solving a linear system, thus avoiding the most costly calculation of the implicit methods. However, they must perform a Krylov version of matrix exponential times vector multiplications, $w = exp(\gamma A)v$. Recent literature has been showing large performance gains of exponential integrators over traditional implicit methods. DifferentialEquations.jl is the first open source library in a high performance language to include exponential integrators, and a brand new (adaptive) Krylov-based approach for large sparse systems was just released as part of GSoC 2018. These methods will be continued to be improved but are ready for widespread use and benchmarking is to come.
# + slideshow={"slide_type": "slide"}
u = solve(prob, ETDRK4(), dt=0.1)
plot(x,Ti*u(0.0))
plot!(x,Ti*u(0.5))
plot!(x,Ti*u(1.0))
plot!(x,Ti*u(2.0))
# + [markdown] slideshow={"slide_type": "slide"}
# ## Note
#
# Additional methods in DifferentialEquations.jl should be explored. The Runge-Kutta Chebyshev methods are stabilized explicit methods which can solve stiff equations without linear solving. Options allow for swapping out the internal Newton method to Picard and Anderson iteration to not require linear solving. Passing a `linsolve` allows you to take control over the linear solver technique: make it an AMG-preconditioned GMRES. Please see the documentation for a full feature list.
#
# ## SSP Methods
#
# Strong-Stability Presurving Runge-Kutta methods are "more stable" explicit methods for PDEs. Some PDEs, like hyperbolic PDEs, are not amenable to implicit solvers and thus require explicit solvers. SSPRK methods can increase the allowable stepsize to increase the efficiency!
# + [markdown] slideshow={"slide_type": "slide"}
# ## Part 3.3 Recap
#
# PDEs can also be solved by leaving an axis undiscretized and using an ODE solver. This can increase efficiency, stability, and reduce memory consumption. Classes of methods to utilize are:
#
# - Implicit and Rosenbrock(-W) Methods
# - IMEX Methods
# - Exponential Integrators
# - Runge-Kutta Chebyshev Methods
# - SSPRK Methods
# + [markdown] slideshow={"slide_type": "slide"}
# ## Why Julia?
#
# - IterativeSolvers.jl is compatible with matrix-free types via `*` overloads able to be used in the nonlinear and ODE solvers
# - BandedMatrices.jl and BlockBandedMatrices.jl are packages for specialization of linear solvers on common PDE matrix types
# - KINSOL from Sundials.jl, and soon NLsolve.jl, are:
# * A globalized Newton method with the ability to chose preconditioned-Krylov linear solvers
# * Able to utilize Anderson acceleration to avoid linear solving
# - DifferentialEquations.jl is:
# * One of 3 open-source ODE suites with IMEX integrators (Sundials ARKODE and PETSc).
# * One of 3 open-source ODE suites (EXPINT and ExpoKit in MATLAB) with exponential integrators, and the only one with the newest class of EPIRK methods.
# * One of two suites with Runge-Kutta Chebyshev methods (Hairer's Suite). It is the only one with high order adaptive SSPRK methods.
# - Julia is a language which allows for zero-cost abstractions, letting one compile code specific to the application and compose packages without extra overhead
#
# The native Julia methods of DifferentialEquations.jl also let you swap in all of the Julia tools for linear solvers and allows type-genericity (which allows the use of GPUs for example), allowing you to utilize the full arsenal of tools with these unique implementations.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Conclusion: Solving PDEs Takes Layers of Tools
#
# You need discretization tooling, linear solvers, nonlinear solvers, and finally ODE solvers to build an efficient PDE solver.
#
# We showed how you can use simple loops to write simple PDE solvers, but the efficient methods require using packages in order to get the latest and most efficient methods.
#
# Many of the latest and most efficient methods only have implementations in Julia, and the JuliaDiffEq organization is committed to continuing the development of such toolling.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Near Future
#
# In the near future we with to provide a set of problem types and algorithms for common PDEs. Example: Reaction-Diffusion Equation
#
# $$ u_t = u_{xx} + f(u,t) $$
# + slideshow={"slide_type": "fragment"}
# Define the PDE problem to solve
prob = ReactionDiffusionProblem(domain,discretization,f)
# Solve it with a pseudospectral IMEX method
solve(prob,Pseudospectral(KenCarp4())
# Or an EPIRK method
solve(prob,FiniteDifference(EXPRB53s3()))
# + [markdown] slideshow={"slide_type": "fragment"}
# #### We are now very close.
# + [markdown] slideshow={"slide_type": "slide"}
# # Acknowledgments
#
# I am deeply indebted to every JuliaDiffEq contributor. I would like to especially those who have specifically been involved in developing and funding the large range of tools which have been demonstrated in this talk:
#
# - <NAME> (@YingboMa)
# - <NAME> (@shivin9)
# - <NAME> (@sipah00)
# - <NAME> (@MSeeker1340)
# - <NAME> (@ysimillides)
# - <NAME> (@dlfivefifty)
# - <NAME> (@pkofod)
# - <NAME> (@haampie)
# - @dextorious
# - <NAME> (@barche)
# - <NAME> (@devmotion)
# - <NAME> (@ranocha)
# - <NAME> (@alyst)
# - <NAME> (@sglyon)
# - <NAME> (@jiahao)
# - <NAME> (@ViralBShah)
# - <NAME> (@vjd)
# - <NAME> (@jlperla)
# - <NAME> (@KristofferC)
# - An<NAME> (@antoine-levitt)
# - <NAME> (@ahojukka5)
|
PDEWorkshop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import pandas as pd
# # 1 - Create A Series Object from A Python List
# +
ice_cream = ["Chocolate", "Vanilla", "Strawberry", "Rum Raisin"]
pd.Series(ice_cream)
# +
loterry = [3, 9, 11, 14, 23, 45]
pd.Series(loterry)
# +
registations = [True, False, False, False, True]
pd.Series(registations)
# -
# # 2 - Create A Series Object from a Dictionary
# +
webster = {"Aardvark" : "An animal",
"Banana" : " A Delicious fruit",
"Cyan" : "A color"}
web = pd.Series(webster)
# -
# # Exercise 1
# +
###############################################################
# DO NOT DELETE THIS CODE. IT IS NEEDED FOR THE TESTS TO RUN. #
from unittest.mock import MagicMock #
import pandas as pd #
pd.Series = MagicMock() #
###############################################################
# Assume the pandas library has already been imported and assigned
# the alias "pd".
# Create a list with 4 countries - United States, France, Germany, Italy
# Create a new Series by passing in the list of countries
# Assign the Series to a "countries" variable
countries_list = ["Unites States", "France", Germany]
countries = pd.Series(countries_list)
# Create a list with 3 colors - red, green, blue
# Create a new Series by passing in the list of colors
# Assign the Series to a "colors" variable
colors_list = ["red", "green", "blue"]
colors = pd.Series(colors_list)
# Given the "recipe" dictionary below,
# create a new Series by passing in the dictionary as the data source
# Assign the resulting Series to a "series_dict" variable
recipe = {
"Flour": True,
"Sugar": True,
"Salt": False
}
series_dict = pd.Series(recipe)
# -
# # Intro a Attributes
about_me = ["Smart", "Handsome", "Charming", "Brilliant", "Humble"]
s = pd.Series(about_me)
s
s.values
s.index
s.dtype
# # Intro a Methods
prices = [2.99, 4.45, 1.36]
s = pd.Series(prices)
s
s.sum()
# É preciso colocar () ao final de <strong>Methods</strong> porque ele está construindo, fazendo algum tipo de operação, tipo de calculo por exemplo, ele faz algo, ao contrário de <strong>Attributes</strong> que apenas trazem o valor
s.product()
s.mean()
# # Parameters and Arguments
# +
# Difficulty - Easy, Medium, Hard
## Difficulty na programação seria o paramether e a escolha seria os argument
# Volume - 1 through 10
# Subtitles - True / False
# +
fruits = ["Apple", "Orange", "Plum", "Grape", "Blueberry"]
weekdays = ["Monday", "Tuesday", "Wednesday", "Thursday", "Friday"]
pd.Series(fruits, weekdays) # se segurar shift e apertar tab mostrara a doc do parameter
pd.Series(data = fruits, index = weekdays)
pd.Series(fruits, index=weekdays)
# -
# # Import Series with the read_csv Method
pokemon = pd.read_csv("pokemon.csv", usecols=["Pokemon"], squeeze=True)
pokemon
# Data frames são usados para amarzenar mais de uma coluna, e Series apenas uma
# + active=""
# google = pd.read_csv("google_stock_price.csv", squeeze=True)
# google
# -
# # Exercise 2
# +
###############################################################
# DO NOT DELETE THIS CODE. IT IS NEEDED FOR THE TESTS TO RUN. #
from unittest.mock import MagicMock #
import pandas as pd #
pd.read_csv = MagicMock(spec = pd.read_csv) #
###############################################################
# Assume the pandas library has already been imported and assigned the alias "pd".
# Let's say we have a foods.csv CSV file with 3 columns: Item Number, Menu Item, Price
# The raw CSV data looks like this:
#
# Item Number,Menu Item,Price
# 1,Big Mac,4.99
# 2,McNuggets,7.99
# 3,Quarter Pounder,3.99
#
# Import the CSV file into a Pandas Series object
# The Series should have the standard Pandas numeric index
# The Series values should be the string values from the "Menu Item" column
# Assign the Series object to a "foods" variable
foods = pd.read_csv("foods.csv", usecols=["Menu Item"], squeeze=True)
# -
# # The .head() and .tail() Methods
pokemon = pd.read_csv("pokemon.csv", usecols=["Pokemon"], squeeze=True)
google = pd.read_csv("google_stock_price.csv", squeeze=True)
pokemon.head(1)
google.tail(1)
|
pandas/notebooks/Series.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Heave Compensation Example Script
# This script demonstrates the use of boolean operators to plot heave corrected data. It also provides an example of using the ProcessedData.view() method to plot a subset of the data.
# ## Setup
# +
# -*- coding: utf-8 -*-
# %matplotlib nbagg
# %matplotlib
from matplotlib.pyplot import figure, show, subplots_adjust
from echolab2.instruments import EK60
from echolab2.plotting.matplotlib import echogram
# -
# ## Read in the data
# +
# Specify some raw files that have heave data and transducer depth in the raw
# data.
rawfiles = ['./data/EK60/DY1706_EK60-D20170625-T061707.raw',
'./data/EK60/DY1706_EK60-D20170625-T062521.raw']
# Create an instance of the EK60 instrument and read the data.
ek60 = EK60.EK60()
ek60.read_raw(rawfiles)
# -
# ## Parse the data
# +
# Get the 38 kHz raw data.
raw_data_38 = ek60.get_raw_data(channel_number=2)
# Get a ProcessedData object containing the heave corrected Sv on a depth grid.
heave_corrected_Sv = raw_data_38.get_Sv(heave_correct=True)
print(heave_corrected_Sv)
# Extract a portion of the data to plot "zoomed in". We can use the view method
# to return a ProcessedData object with data attributes that are views into
# our heave_corrected_Sv data attributes.
#
# The view method takes 2 arguments, which are themselves tuples that define the
# start, stop, stride of the ping axes and sample axes, to view the first 100
# pings and first 100 samples of the data.
subset_Sv = heave_corrected_Sv.view((0, 100, 1), (0, 100, 1))
print(subset_Sv)
# -
# ## Plot the data
# +
# Create a matplotlib figure to plot our echograms on.
fig = figure()
# Get some properties for the sub plot layout.
subplots_adjust(left=0.1, bottom=0.09, right=0.98, top=.93, wspace=None,
hspace=0.5)
# Create an axis.
ax_1 = fig.add_subplot(2, 1, 1)
# Create an echogram which will display on our heave corrected data.
echogram_1 = echogram.Echogram(ax_1, heave_corrected_Sv, threshold=[-70, -34])
ax_1.set_title("heave compensated Sv on depth grid")
# Create another axis.
ax_2 = fig.add_subplot(2, 1, 2)
# Create an echogram which will display the Sv data on a range grid.
echogram_2 = echogram.Echogram(ax_2, subset_Sv, threshold=[-70, -34])
ax_2.set_title("zoomed view of heave compensated Sv on depth grid")
# Display our figure.
show()
# -
|
examples/not_updated/heave_compensation_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1><center> Análise de pellets plásticos como ferramenta para o estudo de permanência de microplásticos em praias arenosas. </center></h1>
#
# <NAME>
# # 03. Recortando Área de Interesse (Pellet)
#
# - Recortar área de interesse
# - Ver se o programa funciona para maior parte das imagens
# +
import skimage
import matplotlib.pyplot as plt
import numpy as np
from glob import glob
from pathlib import Path
#--- Importando as imagens que serão analisadas ---#
from skimage import io
#existem x pastas nomeadas "dados_partex" pois meu computador não tinha ram pra tudo rsrs
#lista_fotos = sorted(glob("dados_partei/*.jpg"))
#lista_fotos = sorted(glob("dados_parteii/*.jpg"))
lista_fotos = sorted(glob("dados_parteiii/*.jpg"))
images = {}
for name in lista_fotos:
images.update(
{
Path(name).stem: io.imread(name)
}
)
# +
from skimage import segmentation
from skimage import filters, morphology
from skimage.color import rgb2gray
from skimage.measure import label, regionprops
def remove_background(foto):
img = rgb2gray(foto)
mask = img > filters.threshold_otsu(img)
clean_border = segmentation.clear_border(mask).astype(np.int64)
img_edges = segmentation.mark_boundaries(img, clean_border)
label_img = label(clean_border)
regions = regionprops(label_img)
area = 0
for region in regions:
if region.area > area:
area = region.area
pellet = region
maskr = morphology.remove_small_objects(mask, pellet.area)
masked = foto.copy()
masked[~maskr] = 255
return masked, maskr
# +
#--- Recortando a área de interesse (pellet) ---#
images_nobg = {}
for foto, data in images.items():
masked = remove_background(data)
images_nobg.update({foto: masked})
# -
def plot_recorte(foto):
plt.figure(figsize=(4, 4))
plt.imshow(images_nobg[foto][0])
plt.title(foto)
for foto, (masked, maskr) in images_nobg.items():
plot_recorte(foto)
# +
#Quantas fotos do banco foram recortadas
imgs_rec = len(sorted(glob("dados_parteiii/*.jpg"))) + len(sorted(glob("dados_parteii/*.jpg"))) + len(sorted(glob("dados_partei/*.jpg")))
imgs_tot = 236 #total de imagens no banco
porc_imgs = imgs_rec*100/imgs_tot
print(round(porc_imgs,2),"% das fotos foram recortadas")
# -
# ## Observações
#
# - 148 das 236 fotos o recorte funcionou
# - A maioria das que não foram recortadas são "translúcidas" ou "beeeem amarelas"
# - Algumas das que não foram cortadas são de pellets coloridos (indiferente pra pesquisa)
|
notebooks/rotina_03_recortepellet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:jcopml]
# language: python
# name: conda-env-jcopml-py
# ---
# +
import numpy as np
import pandas as pd
from luwiji.pandas import illustration
# -
# ## Import Data
df = pd.read_csv('data/cereal_imp.csv', index_col='name')
df.head()
df.rating > 70
df[df.rating > 70]
~ (df.shelf == 1)
df[(df.rating > 50) & (df.fat == 0)]
df[(df.rating > 70) | (df.vitamins == 'FDA_100')]
df[df.mfr.isin(['K', 'N']) | (df.rating > 70)]
df_my_preferences = df[((df.rating) > 60) & (df.mfr.isin(['K', 'N']))].copy()
df_my_preferences
df_my_preferences.sort_values("rating", ascending=False, inplace=True)
df_my_preferences
# ## Group by (optional)
df.groupby("shelf").mean()
df.groupby(['mfr', 'shelf']).mean()
df.groupby(['mfr', 'shelf']).size()
df.pivot_table(index='mfr', columns='vitamins', values='rating', aggfunc='mean')
# ## New column and drop column
df.shape
df["kolom_baru"] = np.random.rand(len(df))
df.head()
df.drop(columns='kolom_baru', inplace=True)
df.head()
# ## Map, Apply, and Transform
df['shelf_name'] = df.shelf.map({1: 'atas', 2: 'tengah', 3: 'atas'})
df.head()
# +
def convert_g_to_mg(x):
return 1000 * x
def convert_to_lower(x):
return x.lower()
# -
df['fat_mg'] = df.fat.apply(convert_g_to_mg)
df['mfr_lower'] = df.mfr.apply(convert_to_lower)
df.head()
f = lambda x: x * 1000
df['protein_mg'] = df.protein.apply(lambda x: x * 1000)
df.head()
df['scaled_rating'] = df.rating.transform(lambda x: (x - x.min()) / (x.max() - x.min()))
df.head()
df.drop(columns=['shelf_name', 'fat_mg', 'mfr_lower', 'protein_mg', 'scaled_rating'], inplace=True)
df.head()
# # One-Hot Encoding / Dummy Variable
df = pd.get_dummies(df, columns=['vitamins'], prefix_sep='__')
df.head()
# ## Binning
df.sodium.hist(bins=10)
df['sodium_bin'] = pd.cut(df.sodium, bins=3, labels=['low', 'medium', 'high'])
df.head()
df['sodium_bin'] = pd.cut(df.sodium, bins=[0,100,200,df.sodium.max()], labels=['0-100', '101-200', '>200'])
df.head()
df.rating.hist(bins=50)
df['Grade'] = pd.cut(df.rating, bins=[0, 40, 70, df.rating.max()], labels=['C', 'B', 'A'])
df.head()
|
02 - Pandas Introduction/Part 2 - Conditional and more pandas.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.7.1
# language: julia
# name: julia-1.7
# ---
# # Programming a Deep Neural Network with Flux
#
# ## MNIST Data Set
#
# The MNIST data set consists of 70,000 images of hand written digits, 60,000 of which are typically used as labeled training examples and the other 10,000 used for testing your learning model on. The following picture represent a sample of some of the images.
#
# <img src="MnistExamples.png" alt="Drawing" style="width: 500px;"/>
#
# We can load this dataset with the ```MLDatasets.jl``` package. Load this data by running the following code.
#
#
# ---
# +
using MLDatasets, Flux
using Plots, Images
using Statistics
# load full training set
train_x, train_y = MNIST.traindata(Float32)
# load full test set
test_x, test_y = MNIST.testdata(Float32)
# -
# ---
#
# Each image is comprised of a $28\times 28$ grey scaled grid of pixel values. These values are floating point numbers in the interval $(0,1)$, where darker pixels will have values closer to $1$ and lighter pixels will have values closer to $0$. The following image represents one such example.
#
# <img src="MNIST-Matrix.png" alt="Drawing" style="width: 600px;"/>
#
# We can view the image of one of these matrices by running the following code.
#
# ---
#
# Images.colorview
colorview(Gray, train_x[:, :, 1]')
# ---
#
# Tensors are simply multi-dimensional matrices. The data structures ```train_x``` and ```test_x``` are stored as 3 dimensional tensors.
#
# <img src="order-3-tensor.png" alt="Drawing" style="width: 300px;"/>
#
# This can be varified by viewing the size of these variables.
#
#
# ---
# +
# Show the dimensions of the training data
@show size(train_x)
@show size(train_y)
println()
# Show the dimensions of the testing data
@show size(test_x)
@show size(test_y)
println()
# -
# ---
#
# ## Image Flattening
#
# Simple **dense neural networks** take as input feature vectors which are column vectors. In order to feed our images into such a network we must **flatten** the matrix into a column vector.
#
# <img src="flatten.png" alt="Drawing" style="width: 500px;"/>
#
# We can do this for each image matrix we are considering by calling the ```Flux.flatten()```. Note, that $784 = 28 \times 28$. By running the following code we reshape our images and store them in new variables.
#
# ## One-Hot Encoding
#
# <img src="onehot.jpeg" alt="Drawing" style="width: 500px;"/>
#
# ## Row Features and Column Instances
# Unlike most Python machine learning API's, Flux.jl and other Julia machine learning API's, we will store our training and testing data with feature measurements in the rows of our arrays and columns being instances. In the case of our 3-dimensional tensor, the 3rd dimension represents the number of instances of our data, i.e., the number of digits .
#
# ---
# +
# Reshape Data in order to flatten each image into a linear array
xtrain = Flux.flatten(train_x)
xtest = Flux.flatten(test_x)
# One-hot-encode the labels
ytrain, ytest = Flux.onehotbatch(train_y, 0:9), Flux.onehotbatch(test_y, 0:9)
# Print the dimensions of training feature matrices and training label matrices
println("xtrain dimensions = $(size(xtrain))")
println("ytrain dimensions = $(size(ytrain))")
# +
# Get the dimensions of train_x
(m, n, z) = size(train_x)
# Chain together functions!
model = Flux.Chain(
Dense(m*n, 60, Flux.σ),
Dense(60, 60, Flux.σ),
Dense(60, 60, Flux.σ),
Dense(60, 10, Flux.σ),
)
# Define mean squared error loss function
loss(x, y) = Flux.Losses.mse(model(x), y)
# Define the accuracy
accuracy(x, y) = Statistics.mean(Flux.onecold(model(x)) .== Flux.onecold(y))
# ADAM would be the perferred optimizer for serious deep learning
#opt = Flux.ADAM()
# Define gradient descent optimizer
# Flux.Descent
opt = Descent(0.23)
# Format your data
data = [(xtrain, ytrain)]
# Collect weights and bias for your model
parameters = Flux.params(model)
println("Old Loss = $(loss(xtrain, ytrain))")
println("Old Accuracy = $(accuracy(xtrain, ytrain)) \n")
# Train the model over one epoch
Flux.train!(loss, parameters, data, opt)
println("New Loss = $(loss(xtrain, ytrain))")
println("New Accuracy = $(accuracy(xtrain, ytrain))")
# +
#using Flux: @epochs
println("Old Loss = $(loss(xtrain, ytrain))")
println("Old Accuracy = $(accuracy(xtrain, ytrain)) \n")
(m, n) = size(xtrain)
# Train the model over 100_000 epochs
for epoch in 1:100_000
# Randomly select a entry of training data
i = rand(1:n)
data = [(xtrain[:, i], ytrain[:, i])]
# Implement Stochastic Gradient Descent
Flux.train!(loss, parameters, data, opt)
# Print loss function values
if epoch % 10_000 == 0
println("Epoch: $(epoch)")
@show loss(xtrain, ytrain)
@show accuracy(xtrain, ytrain)
println()
end
end
# +
i = rand(1:1_000)
predict(i) = argmax(model(xtest[:, i])) - 1
digit = predict(i)
println("Predict digit: $(digit)")
println(argmax(ytest[:, i]) - 1)
colorview(Gray, test_x[:,:,i]')
# +
i = rand(1:1_000)
predict(i) = argmax(model(xtest[:, i])) - 1
digit = predict(i)
println("Predict digit: $(digit)")
println(argmax(ytest[:, i]) - 1)
colorview(Gray, test_x[:,:,i]')
# +
using TensorBoardLogger, Logging
# Create tensorboard logger
# TensorBoardLogger.TBLogger
logger = TBLogger("content/log", tb_overwrite)
# Log some images as samples (not needed)
with_logger(logger) do
images = TBImage(train_x[:, :, 1:10], WHN)
@info "mnist/samples" pics = images log_step_increment=0
end
# Function to get dictionary of model parameters
function fill_param_dict!(dict, m, prefix)
if m isa Chain
for (i, layer) in enumerate(m.layers)
fill_param_dict!(dict, layer, prefix*"layer_"*string(i)*"/"*string(layer)*"/")
end
else
for fieldname in fieldnames(typeof(m))
val = getfield(m, fieldname)
if val isa AbstractArray
val = vec(val)
end
dict[prefix*string(fieldname)] = val
end
end
end
# Callback to log information after every epoch
function TBCallback()
param_dict = Dict{String, Any}()
fill_param_dict!(param_dict, model, "")
with_logger(logger) do
@info "model" params=param_dict log_step_increment=0
@info "train" loss=loss(xtrain, ytrain) acc=accuracy(xtrain, ytrain) log_step_increment=0
@info "test" loss=loss(xtest, ytest) acc=accuracy(xtest, ytest)
end
end
# +
# Get the dimensions of train_x
(m, n, z) = size(train_x)
# Chain together functions!
model = Flux.Chain(
Dense(m*n, 60, Flux.σ),
Dense(60, 60, Flux.σ),
Dense(60, 60, Flux.σ),
Dense(60, 10, Flux.σ),
)
# Define mean squared error loss function
loss(x, y) = Flux.Losses.mse(model(x), y)
# Define the accuracy
accuracy(x, y) = Statistics.mean(Flux.onecold(model(x) |> cpu) .== Flux.onecold(y |> cpu))
# ADAM would be the perferred optimizer for serious deep learning
opt = Flux.ADAM()
# Format your data
data = [(xtrain, ytrain)]
# Collect weights and bias for your model
parameters = Flux.params(model)
println("Old Loss = $(loss(xtrain, ytrain))")
# Train the model over 100 epochs
for epoch in 1:100
Flux.train!(loss, parameters, data, opt, cb = Flux.throttle(TBCallback, 5))
end
println("New Loss = $(loss(xtrain, ytrain))")
# -
|
Episode_9_and_10_Flux_/mnist_flux.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PEEWEE ORM
#
# Here I will demonstrate how to use PEEWEE ORM to get the world bank data into a database.
# +
from peewee import *
from playhouse.postgres_ext import PostgresqlDatabase
import pandas as pd
from tqdm import tqdm
from os.path import join
from time import sleep
from IPython import display
import matplotlib.pyplot as pl
import seaborn as sns
# %matplotlib inline
# +
db = PostgresqlDatabase('ads')
class BaseModel(Model):
class Meta:
database = db
class Country(BaseModel):
id = PrimaryKeyField()
name = CharField()
class LifeExpectancy(BaseModel):
id = PrimaryKeyField()
country = ForeignKeyField(
Country,
index=True,
null=False,
related_name='life_expectancy',
on_delete='cascade'
)
year = IntegerField(null=False)
value = FloatField(null=True)
class Population(BaseModel):
id = PrimaryKeyField()
country = ForeignKeyField(
Country,
index=True,
null=False,
related_name='population',
on_delete='cascade'
)
year = IntegerField(null=False)
value = FloatField(null=True)
class GDP(BaseModel):
id = PrimaryKeyField()
country = ForeignKeyField(
Country,
index=True,
null=False,
related_name='gdp',
on_delete='cascade'
)
year = IntegerField(null=False)
value = FloatField(null=True)
models = [
Country,
LifeExpectancy,
Population,
GDP,
]
# -
# +
def rearrange_dataframe(df, indicator_name):
country = 'Country Name'
years = [c for c in df.columns if c[0] == '1' or c[0] == '2']
df = pd.melt(df[[country] + years], id_vars=country, var_name='year')
df.rename(columns={'value': indicator_name}, inplace=True)
return df
db.drop_tables(models, safe=True, cascade=True)
db.create_tables(models, safe=True)
sources = [
('API_SP.DYN.LE00.IN_DS2_en_csv_v2_713010', 'Life expectency at birth', LifeExpectancy),
('API_SP.POP.TOTL_DS2_en_csv_v2_713131', 'Total population', Population ),
('API_NY.GDP.PCAP.CD_DS2_en_csv_v2_713080', 'GDP per capita', GDP ),
]
for source, key, model in sources:
df = rearrange_dataframe(pd.read_csv(join(source, '{}.csv'.format(source)), skiprows=4), key)
print(df.head())
for ri, row in tqdm(df.iterrows()):
country, inserted = Country.get_or_create(name=row['Country Name'])
model.create(
country=country,
year=int(row['year']),
value=row[key]
)
# For faster insersion, the insert_many method may be used.
# -
#GDP.select().count()
print(GDP.select())
#type(lq[0])
#lq[0].value
#lq[0]
# +
q = GDP.select().limit(10)
print(q)
lq = list(q)
print(lq)
print(lq[0])
print(lq[0].country.name)
# +
c1 = Country.select().where(Country.id == 110).get()
c1.name
# -
list(Population.select().dicts())
db.rollback()
list(Country.select(
Country.name,
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
).where(
Country.id == 110
).join(
GDP,
on=Country.id == GDP.country_id
).join(
Population,
on=(Country.id == Population.country_id) & (GDP.year == Population.year)
).dicts())
list(Country.select(
Country.name,
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
).where(
Country.id == 110
).join(
GDP,
on=Country.id == GDP.country_id
).join(
Population,
on=(Country.id == Population.country_id) & (GDP.year == Population.year)
).limit(10).dicts())
df = pd.DataFrame(list(Country.select(
Country.name,
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
LifeExpectancy.value.alias('le'),
).where(
Country.id == 110
).join(
GDP,
on=Country.id == GDP.country_id
).join(
Population,
on=(Country.id == Population.country_id) & (GDP.year == Population.year)
).join(
LifeExpectancy,
on=(Country.id == LifeExpectancy.country_id) & (GDP.year == LifeExpectancy.year)
).dicts()))
df.set_index('year', inplace=True)
del df['name']
df.plot(subplots=True, figsize=(10,10));
c = Country.select(
Country.name,
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
LifeExpectancy.value.alias('le'),
).where(
Country.id == 59
).join(
GDP,
on=Country.id == GDP.country_id
).join(
Population,
on=(Country.id == Population.country_id) & (GDP.year == Population.year)
).join(
LifeExpectancy,
on=(Country.id == LifeExpectancy.country_id) & (GDP.year == LifeExpectancy.year)
)
cur = db.cursor()
print(cur.mogrify(*c.sql()))
# +
df = pd.DataFrame(list(GDP.select(
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
LifeExpectancy.value.alias('le'),
).join(
Population,
on=(GDP.year == Population.year) & (GDP.country_id == Population.country_id)
).join(
LifeExpectancy,
on=(GDP.year == LifeExpectancy.year) & (GDP.country_id == LifeExpectancy.country_id)
).join(
Country,
on=GDP.country_id == Country.id
).where(
Country.name == 'United Kingdom'
).dicts()))
df.set_index('year', inplace=True)
df.head()
# -
df.plot(subplots=True, figsize=(10, 10));
# +
df = pd.DataFrame(list(GDP.select(
Country.name.alias('country'),
GDP.year,
GDP.value.alias('gdp'),
Population.value.alias('pop'),
LifeExpectancy.value.alias('le'),
).join(
Population,
on=(GDP.year == Population.year) & (GDP.country_id == Population.country_id)
).join(
LifeExpectancy,
on=(GDP.year == LifeExpectancy.year) & (GDP.country_id == LifeExpectancy.country_id)
).join(
Country,
on=GDP.country_id == Country.id
).dicts()))
df.head()
# +
countries = {
'United States',
'China',
'India'
}
keys = ('pop', 'le', 'gdp')
fig, axes = pl.subplots(3, 1, figsize=(10, 10))
for country, group in df.groupby('country'):
if country in countries:
for ax, key in zip(axes, keys):
ax.plot(group.year, group[key], label=country)
for ax, key in zip(axes, keys):
pl.sca(ax)
pl.title(key)
pl.legend()
# -
df.describe()
# +
x = 'gdp'# per capita'
y = 'le'
s = 'pop'
do_legend = True
def pw_scatter(df, year):
current_palette = sns.color_palette()
alpha = 0.25
for i, c in enumerate(countries):
country = Country.select().where(Country.name == c).get()
gdp = GDP.select().where(GDP.country_id == country, GDP.year == year).get()
pop = Population.select().where(Population.country_id == country, Population.year == year).get()
le = LifeExpectancy.select().where(LifeExpectancy.country_id == country, LifeExpectancy.year == year).get()
ax.plot(gdp.value, le.value, marker='o', linestyle='', color=current_palette[i], ms=pop.value / 1e7, label=c, alpha=alpha)
ax.set_xlabel(x)
ax.set_ylabel(y)
ax.set_xlim([0, 75000])
ax.set_ylim([df[y].min()*0.9, df[y].max()*1.1])
ax.set_title(year)
# Animated version
fig, ax = pl.subplots(figsize=[15 ,10])
#countries = ['United Kingdom', 'France', 'Germany']
for year in range(1960, 2017):
pw_scatter(df, year)
if do_legend:
lgnd = ax.legend()
for i in range(len(countries)):
lgnd.legendHandles[i]._legmarker.set_markersize(20)
lgnd.legendHandles[i]._legmarker.set_alpha(1.0)
do_legend = False
display.clear_output(wait=True)
display.display(pl.gcf())
sleep(0.02)
# -
|
03_data_transformation_and_integration/03-peewee-orm-worldbank-demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Matplotlib
# ## Basics
#
# <NAME> (<EMAIL>)
#
# The latest version of this notebook is available at [https://github.com/escape2020/school2021](https://github.com/escape2020/school2021)
# +
# %matplotlib inline
import matplotlib as ml
import numpy as np
import sys
plt = ml.pyplot
ml.rcParams['figure.figsize'] = (10.0, 5.0)
print(f"Python version: {sys.version}\n"
f"NumPy version: {np.__version__}\n"
f"Matplotlib version: {ml.__version__}\n")
rng = np.random.default_rng(42) # initialise our random number generator
# -
n = 100
xs = np.linspace(0, 2*np.pi, n)
ys = np.sinc(xs)
plt.plot(xs, ys)
plot = plt.plot(xs, ys)
plot
# not that good to overuse plot, because when we use title and so on we are fucking up hidden things of the library
# ## Figure
# it is much better to create your own object, that is a plt.figure()
fig = plt.figure()
ax = fig.add_axes([0, 0, 1, 1])
# the figure is like defining a canvas, now with add_axes we are setting the grid of the canvas
fig
ax.scatter(xs, ys, label="sensor Q")
# the grid can be completed with a scatterplot, a continuous function, ...
fig
sub_ax = fig.add_axes([0.5, 0.5, 0.4, 0.4])
# We can also insert another grid environment inside our main axes. The syntax is add_axes(lower x position, lower y position, )
fig
sub_ax.plot(xs, np.sin(xs), color="salmon", label="sensor P")
sub_ax.plot(xs, np.sin(xs)*0.9, color="steelblue", linestyle="-.", label="lower/upper")
fig
ax.set_xlabel("time [s]")
ax.set_ylabel("voltage [mV]")
fig
sub_ax.set_xlabel("time [s]")
sub_ax.set_ylabel(r"current [$\mu$A]")
fig
ax.legend()
sub_ax.legend()
# Both our plots can have legends, titles and so on
fig
ax.axhline(0.15, linestyle=":", color="#aabbcc")
fig
toi = 2.13 # time [s]
opts = dict(linestyle="-", color="deepskyblue", linewidth=2)
ax.axvline(toi, **opts)
sub_ax.axvline(toi, **opts)
fig
ax.grid(color="#dddddd")
sub_ax.grid(color="slategrey")
fig
for axis in [ax.xaxis, ax.yaxis]:
axis.label.set_fontsize(20)
# we make a for loop to change the font size of both our labels of our plots
fig
sub_ax.set_position([0.45, 0.4, 0.52, 0.5])
# we may want to shift the smaller subplot with respect to the larger, make it bigger
fig
fig
import scipy.signal
# we may want to underline the peaks of our plot with other markers
peak_idx = scipy.signal.find_peaks_cwt(ys, np.arange(1, 5))
peak_idx
ax.scatter(xs[peak_idx], ys[peak_idx], c="red", marker="X", s=100)
fig
# we also may want to save the plots in another type of file, for example a pdf or a png
fig.savefig("the_plot.pdf", bbox_inches="tight") # the filename extension defines the media type
fig.savefig("the_plot.png", bbox_inches="tight")
# ## Working with subplots
#
# The `plt.subplots()` utility wrapper makes it convenient to create common layouts of
# subplots, including the enclosing figure object, in a single call.
fig, ax = plt.subplots() # a one-shot to create a figure with an axes
fig, axes = plt.subplots(nrows=2, ncols=3)
# this creates in one shot a lot of plots with pre determined distances. We divided the figure in different parts
# As we see, the situation now is that we have an array of objects (an array of subplots)
axes
axes[0]
axes[1]
axes[0, 2].scatter(xs, np.cos(xs))
# we can therefore fill with a scatterplot just one object
fig
list
axes.flat[4].scatter(xs, ys)
fig
# +
colors = plt.cm.viridis(np.linspace(0, 1, len(axes.flat)))
for func, ax, color in zip([np.cos, np.sin, np.sinc, np.tan, np.tanh, np.exp], axes.flat, colors):
ax.plot(xs, func(xs), color=color)
# -
# we can make use of colormaps to get functions in different colors. The firs line of code defines an interval (0,1) divided into steps that colro the plot
fig
plt.cm.viridis(np.linspace(0, 1, len(axes.flat)))
plt.cm.viridis(0.5)
fig, ax = plt.subplots()
n = 100
xs = rng.random(n)
ys = rng.random(n)
ms = rng.random(n)
ax.scatter(rng.random(n), rng.random(n), c=ms, cmap="plasma")
# +
fig, ax = plt.subplots()
n = 100
xs = np.linspace(-7, 7, n)
N = 40
colors = iter(plt.cm.viridis(np.linspace(0, 1, N)))
for k in range(-N//2, N//2):
color = "salmon" if k == 8 else next(colors)
ax.plot(xs, k / (xs**2 + 4), c=color)
ax.grid()
# -
# ## Histograms
data1 = rng.normal(23, 5, 1000)
data2 = rng.normal(42, 5, 10000)
fig, ax = plt.subplots()
ax.hist(data1, bins=100)
ax.hist(data2, bins=100)
fig
# +
N = 100000
data1 = rng.normal(23, 5, N)
data2 = rng.normal(42, 5, N)
fig, ax = plt.subplots()
ax.hist2d(data1, data2, bins=100);
# -
|
matplotlib/Matplotlib Introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import cv2
import numpy as np
import matplotlib.pyplot as plt
# # First, set the path to the image to use and the number of colours
imagePath = "testImage.png"
completedPatternPath = "testImagePattern.txt"
noOfColours = 3
# # Apply K means clustering to split the image into the correct number of colours
image = cv2.imread(imagePath)
# https://www.thepythoncode.com/article/kmeans-for-image-segmentation-opencv-python
imageRGB = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
pixelValues = np.float32(imageRGB.reshape((-1, 3)))
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 100, 0.2)
_, labels, (centers) = cv2.kmeans(pixelValues, noOfColours, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS)
centers = np.uint8(centers)
labels = labels.flatten()
segmentedImage = centers[labels]
segmentedImage = segmentedImage.reshape(image.shape)
plt.imshow(segmentedImage)
plt.show()
# should show up as the input image with the given number of colours
# # Assign names to the colours
squareSize = 1
testImage = np.zeros((squareSize * noOfColours, squareSize, 3), dtype=np.uint8)
for i in range(noOfColours):
testImage[i:i+squareSize, :] = centers[i]
plt.imshow(testImage)
plt.title(str(noOfColours) + " extracted colours")
plt.show()
# Enter colour names in order of where they appear in the plot above (top colour first, second colour second etc)
colourNames = ['B', 'Y', 'W']
assert len(colourNames) == noOfColours, "Set the names of colours as they should appear on the pattern. Number of names given does not match how many colours where extracted."
# convert image to an array of the same shape, but with the element being the colour name
height = image.shape[0]
width = image.shape[1]
colourNameImage = np.zeros((height, width), dtype=object)
for j in range(height):
for i in range(width):
# find corresponding colour
colourIndex = 0
foundColour = False
for k in range(noOfColours):
if (segmentedImage[j, i] == centers[k]).all():
colourIndex = k
foundColour = True
break
if foundColour:
colourNameImage[j, i] = colourNames[colourIndex]
else:
assert False, "Something went wrong at " + str(i) + "," + str(j)
# +
finishedPattern = False
pattern = ""
file = open(completedPatternPath, 'w')
# start at the bottom right
x = width - 1
y = height - 1
xstep = 1
ystep = -1
row = 0
startType = "INC"
while not finishedPattern:
finishedDiagonal = False
line = []
while not finishedDiagonal:
colour = colourNameImage[y, x]
line.append(colour)
if x == 0 and y == 0:
finishedDiagonal = True
finishedPattern = True
x += xstep
y += ystep
if x >= width and y < 0:
# top right corner
finishedDiagonal = True
x -= 2 * xstep
y -= ystep
nextStartType = "DEC"
elif x >= width and y >= 0:
# bottom right area, off the right
finishedDiagonal = True
x -= xstep
nextStartType = "INC"
elif x >= 0 and y >= height:
# bottom right, off the bottom
finishedDiagonal = True
y -= ystep
nextStartType = "INC"
elif x < 0:
# left
finishedDiagonal = True
x -= xstep
y -= 2 * ystep
nextStartType = "DEC"
elif y < 0:
# top
finishedDiagonal = True
x -= 2 * xstep
y -= ystep
nextStartType = "DEC"
# have finished diagonal at this point
xstep *= -1
ystep *= -1
row += 1
currentColour = line[0]
currentColourCount = 0
formattedLine = str(row) + ": " + startType + str(currentColour)
for i in range(1, len(line)):
if line[i] == currentColour:
currentColourCount += 1
else:
if currentColourCount > 0:
formattedLine += " " + str(currentColourCount) + str(currentColour) + ","
currentColour = line[i]
currentColourCount = 1
if currentColourCount > 0:
formattedLine += " " + str(currentColourCount) + str(currentColour)
pattern += formattedLine + " (total row count=" + str(len(line)) + ")" + "\n"
startType = nextStartType
print(pattern)
file.write(pattern)
file.close()
# -
|
c2cGen.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# -
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
return data[:, :-1], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4)
class LRClassifier(object):
def __init__(self, max_iter=200, learning_rate=0.01):
self.max_iter = max_iter
self.learning_rate = learning_rate
def sigmoid(self, x):
return 1 / (1 + exp(-x))
def data_matrix(self, X):
data_mat = list()
for d in X:
data_mat.append([1.0, *d])
return data_mat
def fit(self, X, y):
data_mat = self.data_matrix(X)
self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
for iter_ in range(self.max_iter):
for i in range(len(X)):
result = self.sigmoid(np.dot(data_mat[i], self.weights))
error = y[i] - result
self.weights += self.learning_rate * error * np.transpose([data_mat[i]])
print('LogisticRegression Model(learning_rate={},max_iter={})'.format(self.learning_rate, self.max_iter))
def score(self, X_test, y_test):
right = 0
X_test = self.data_matrix(X_test)
for x, y in zip(X_test, y_test):
result = np.dot(x, self.weights)
if (result > 0 and y == 1) or (result < 0 and y == 0):
right += 1
return right / len(X_test)
lr_clf = LRClassifier()
lr_clf.fit(X_train, y_train)
lr_clf.score(X_test, y_test)
# +
x_ponits = np.arange(4, 8)
y_ = -(lr_clf.weights[1]*x_ponits + lr_clf.weights[0])/lr_clf.weights[2]
plt.plot(x_ponits, y_)
#lr_clf.show_graph()
plt.scatter(X[:50,0],X[:50,1], label='0')
plt.scatter(X[50:,0],X[50:,1], label='1')
plt.legend()
# -
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
print(clf.coef_, clf.intercept_)
# +
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_ponits + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_ponits, y_)
plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0')
plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
# +
import math
from copy import deepcopy
class MaxEntropy:
def __init__(self, EPS=0.005):
self._samples = []
self._Y = set() # 标签集合,相当去去重后的y
self._numXY = {} # key为(x,y),value为出现次数
self._N = 0 # 样本数
self._Ep_ = [] # 样本分布的特征期望值
self._xyID = {} # key记录(x,y),value记录id号
self._n = 0 # 特征键值(x,y)的个数
self._C = 0 # 最大特征数
self._IDxy = {} # key为(x,y),value为对应的id号
self._w = []
self._EPS = EPS # 收敛条件
self._lastw = [] # 上一次w参数值
def loadData(self, dataset):
self._samples = deepcopy(dataset)
for items in self._samples:
y = items[0]
X = items[1:]
self._Y.add(y) # 集合中y若已存在则会自动忽略
for x in X:
if (x, y) in self._numXY:
self._numXY[(x, y)] += 1
else:
self._numXY[(x, y)] = 1
self._N = len(self._samples)
self._n = len(self._numXY)
self._C = max([len(sample)-1 for sample in self._samples])
self._w = [0]*self._n
self._lastw = self._w[:]
self._Ep_ = [0] * self._n
for i, xy in enumerate(self._numXY): # 计算特征函数fi关于经验分布的期望
self._Ep_[i] = self._numXY[xy]/self._N
self._xyID[xy] = i
self._IDxy[i] = xy
def _Zx(self, X): # 计算每个Z(x)值
zx = 0
for y in self._Y:
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
zx += math.exp(ss)
return zx
def _model_pyx(self, y, X): # 计算每个P(y|x)
zx = self._Zx(X)
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
pyx = math.exp(ss)/zx
return pyx
def _model_ep(self, index): # 计算特征函数fi关于模型的期望
x, y = self._IDxy[index]
ep = 0
for sample in self._samples:
if x not in sample:
continue
pyx = self._model_pyx(y, sample)
ep += pyx/self._N
return ep
def _convergence(self): # 判断是否全部收敛
for last, now in zip(self._lastw, self._w):
if abs(last - now) >= self._EPS:
return False
return True
def predict(self, X): # 计算预测概率
Z = self._Zx(X)
result = {}
for y in self._Y:
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
pyx = math.exp(ss)/Z
result[y] = pyx
return result
def train(self, maxiter=1000): # 训练数据
for loop in range(maxiter): # 最大训练次数
print("iter:%d" % loop)
self._lastw = self._w[:]
for i in range(self._n):
ep = self._model_ep(i) # 计算第i个特征的模型期望
self._w[i] += math.log(self._Ep_[i]/ep)/self._C # 更新参数
print("w:", self._w)
if self._convergence(): # 判断是否收敛
break
dataset = [['no', 'sunny', 'hot', 'high', 'FALSE'],
['no', 'sunny', 'hot', 'high', 'TRUE'],
['yes', 'overcast', 'hot', 'high', 'FALSE'],
['yes', 'rainy', 'mild', 'high', 'FALSE'],
['yes', 'rainy', 'cool', 'normal', 'FALSE'],
['no', 'rainy', 'cool', 'normal', 'TRUE'],
['yes', 'overcast', 'cool', 'normal', 'TRUE'],
['no', 'sunny', 'mild', 'high', 'FALSE'],
['yes', 'sunny', 'cool', 'normal', 'FALSE'],
['yes', 'rainy', 'mild', 'normal', 'FALSE'],
['yes', 'sunny', 'mild', 'normal', 'TRUE'],
['yes', 'overcast', 'mild', 'high', 'TRUE'],
['yes', 'overcast', 'hot', 'normal', 'FALSE'],
['no', 'rainy', 'mild', 'high', 'TRUE']]
maxent = MaxEntropy()
x = ['overcast', 'mild', 'high', 'FALSE']
maxent.loadData(dataset)
maxent.train()
print('predict:', maxent.predict(x))
# -
|
chapter06/LR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#from sklearn.linear_model import Perceptron
from sklearn.neural_network import MLPClassifier
from sklearn.metrics import accuracy_score
#from matplotlib.colors import ListedColormap
#import matplotlib.pyplot as plt
#from matplotlib import rcParams
# +
iris = datasets.load_iris()
X = iris.data
y = iris.target
# -
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
# +
sc = StandardScaler()
# fit the scaler to the training feature set ONLY
sc.fit(X_train)
# scale (transform) the training and the testing sets
# using the scaler that was fitted to training data
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
# -
np.unique(y,return_counts= True)
X_train_std.shape
X_test_std.shape
# +
# create the perceptron instance
#model = Perceptron(max_iter=40,tol=None,eta0=0.1,random_state=0)
model = MLPClassifier(solver='lbfgs',alpha=1e-5,hidden_layer_sizes=(5,2),random_state=0)
# fit
model.fit(X_train_std,y_train)
# make predictions
y_pred = model.predict(X_test_std)
acc = accuracy_score(y_test,y_pred)
print(acc)
# -
model.coefs_
# weights
# from input to hidden layer 1
model.coefs_[0].shape
# from hidden layer 1 to hidden layer 2
model.coefs_[1].shape
# from hidden layer 2 to output
model.coefs_[2].shape
|
perceptron_multi_layer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Identity Normalization in Residual Networks
#
# This notebook contains the compact (residual) neural network, datasets and empirical results for the aforementioned paper.
# ### Dataset(s)
#
# The first dataset used for empirical benchmarking is the Fruits-360 dataset, which was formerly a Kaggle competition. It consists of images of fruit labeled by fruit type and the variety.
#
# 1. There are a total of 47 types of fruit (e.g., Apple, Orange, Pear, etc) and 81 varieties.
# 2. On average, there are 656 images per variety.
# 3. Each image is 128x128 RGB.
#
#
# !gsutil cp gs://cloud-samples-data/air/fruits360/fruits360-combined.zip .
# !ls
# !unzip -qn fruits360-combined.zip
# ## Setup
#
# Install:
# 1. Tensorflow (1.13) machine learning framework
# 2. Tensorflow integration of Keras API for building and training models.
# 3. Numpy for general image/matrix manipulation.
# 4. OpenCV for reading and preprocessing of images.
# 5. Scikit-Learn for splitting datasets
# +
import tensorflow as tf
from tensorflow.keras.applications.resnet50 import ResNet50
from tensorflow.keras.preprocessing import image
from tensorflow.keras.applications.resnet50 import preprocess_input, decode_predictions
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.layers import GlobalAveragePooling2D, Dense
from tensorflow.keras import Sequential, Model, Input, optimizers
from tensorflow.keras.layers import Conv2D, Flatten, MaxPooling2D, Dense, Dropout, BatchNormalization, ReLU
from tensorflow.keras.models import load_model
from tensorflow.keras.utils import to_categorical
import tensorflow.keras.layers as layers
from sklearn.model_selection import train_test_split
import numpy as np
import cv2
import os
# -
# ## Steps
#
# *Benchmark Fruits-360*
# 1. Create the Coarse Dataset for Training, Evaluation and Test
# 2. Define training routines
# 3. Run Benchmarks
#
# *Benchmark Intel Image Classification*
# 1. Create the Dataset for Training, Evaluation and Test
# 2. Run Benchmarks
#
# *Benchmark Columbia University COIL-100*
# 11. Create the Dataset for Training, Evaluation and Test
# 12. Run Benchmarks
#
# # Coarse Fruits-360 Dataset
#
# ## (Step 1) Make Coarse Category Dataset
#
#
# ### Define Function to Make Coarse Train/Test Dataset from Fruits-360 dataset
#
# This makes the by Fruit Type dataset.
def Fruits(root):
n_label = 0
images = []
labels = []
classes = {}
os.chdir(root)
classes_ = os.scandir('./')
for class_ in classes_:
print(class_.name)
os.chdir(class_.name)
classes[class_.name] = n_label
# Finer Level Subdirectories per Coarse Level
subclasses = os.scandir('./')
for subclass in subclasses:
os.chdir(subclass.name)
files = os.listdir('./')
for file in files:
image = cv2.imread(file)
images.append(image)
labels.append(n_label)
os.chdir('../')
os.chdir('../')
n_label += 1
os.chdir('../')
images = np.asarray(images)
# standardization of the pixel data
mean = np.mean(images)
std = np.std(images)
images = ((images - mean) / std).astype(np.float32)
# convert to one-hot encoded labels
labels = to_categorical(labels, n_label)
print("Images", images.shape, "Labels", labels.shape, "Classes", classes, "Mean", mean, "Stddev", std)
# Split the processed image dataset into training and test data
x_train, x_test, y_train, y_test = train_test_split(images, labels, test_size=0.20, shuffle=True)
return x_train, x_test, y_train, y_test, classes, mean, std
# ### Generate the preprocessed Coarse Dataset
# !free -m
x_train, x_test, y_train, y_test, fruits_classes, mean, std = Fruits('Training')
# !free -m
# ### Split Coarse Training Dataset (by Fruit) further into Train and Validation
#
# Next split out 10% of train to use for validation during training.
#
# - Train: 80%
# - Train: 90%
# - Validation: 10%
# - Test : 20%
# +
# Split out 10% of Train to use for Validation
pivot = int(len(x_train) * 0.9)
x_val = x_train[pivot:]
y_val = y_train[pivot:]
x_train = x_train[:pivot]
y_train = y_train[:pivot]
print("train", x_train.shape, y_train.shape)
print("val ", x_val.shape, y_val.shape)
print("test ", x_test.shape, y_test.shape)
# !free -m
# -
# ## (Step 2) Define Training Routines
#
# Define the routines we will use for training.
#
# ### Make Feeder
#
# Prepare the Feeder mechanism for training the neural networkm using ImageDataGenerator.
#
# Add image augmentation for:
#
# 1. Horizontal Flip
# 2. Verticial Flip
# 3. Random Rotation +/- 30 degrees
def Feeder():
datagen = ImageDataGenerator(horizontal_flip=True, vertical_flip=True, rotation_range=30,
width_shift_range=0.15, height_shift_range=0.15, shear_range=0.2)
return datagen
# ### Make Trainer
#
# Prepare a training session:
#
# 1. Epochs defaults to 10
# 2. Batch size defaults to 32
# 3. Train with validation data
# 4. Final evaluation with test data (holdout set).
def Train(model, datagen, x_train, y_train, x_test, y_test, epochs=10, batch_size=32):
model.fit_generator(datagen.flow(x_train, y_train, batch_size=batch_size, shuffle=True),
steps_per_epoch=len(x_train) / batch_size, epochs=epochs, verbose=1, validation_data=(x_test, y_test))
scores = model.evaluate(x_train, y_train, verbose=1)
print("Train", scores)
# ## (Step 3) Build Base Model
#
# See paper for detailed description
# +
from keras import Input, Model
import keras.layers as layers
import keras.optimizers as optimizers
def ConvNetA(input_shape, nclasses):
''' Compact Neural Network with Batch Normalization (Model 2)'''
def stem(inputs):
''' The stem convolutional group '''
# Two 3x3 convolutional layers, representational equivalent to single 5x5,
# which reduces computational complexity (trainable weights) by 75%
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(inputs)
x = layers.BatchNormalization()(x)
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(x)
x = layers.BatchNormalization()(x)
# Reduce the feature map sizes by 75%
x = layers.MaxPooling2D(2, strides=2)(x)
return x
def conv_groups(x):
''' Residual Groups (ResNet34 style) '''
# transition convolution for identity link, delay downsampling
shortcut = layers.Conv2D(128, (1,1), strides=1, padding='same')(x)
x = layers.BatchNormalization()(x)
# residual block - double filters (Replace two 3,3 with 3,3 and 1,1)
x = layers.Conv2D(128, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.BatchNormalization()(x)
x = layers.Conv2D(128, (3,1), strides=1, padding='same', activation='relu')(x)
x = layers.BatchNormalization()(x)
# identity link
x = layers.add([shortcut, x])
x = layers.Dropout(0.50)(x)
# transition convolution for identity link
shortcut = layers.Conv2D(256, (1,1), strides=1, padding='same')(x)
# residual block - double filters
x = layers.Conv2D(256, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.BatchNormalization()(x)
x = layers.Conv2D(256, (3,1), strides=1, padding='same', activation='relu')(x)
x = layers.BatchNormalization()(x)
# identity link
x = layers.add([shortcut, x])
# pooling for final downsampling in convolutional layers
x = layers.MaxPooling2D(2, strides=2, name='encoder')(x)
return x
def bottleneck(x):
''' The bottleneck layer '''
# Use fast form of pooling: single value per feature map,
# which reduces the size substantially more than a Flatten().
x = layers.GlobalAveragePooling2D(name='bottleneck')(x)
return x
def classifier(x, nclasses):
''' The classifier layer '''
x = layers.Dense(nclasses, activation='softmax')(x)
return x
inputs = Input(input_shape)
x = stem(inputs)
x = conv_groups(x)
x = bottleneck(x)
outputs = classifier(x, nclasses)
return Model(inputs, outputs)
def ConvNetB(input_shape, nclasses):
''' Compact Neural Network with Identity Normalization (Model 3)'''
def stem(inputs):
''' The stem convolutional group '''
# Two 3x3 convolutional layers, representational equivalent to single 5x5,
# which reduces computational complexity (trainable weights) by 75%
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(inputs)
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(x)
# Reduce the feature map sizes by 75%
x = layers.MaxPooling2D(2, strides=2)(x)
return x
def conv_groups(x):
''' Residual Groups (ResNet34 style) '''
# transition convolution for identity link, delay downsampling
shortcut = layers.Conv2D(128, (1,1), strides=1, padding='same')(x)
# residual block - double filters (Replace two 3,3 with 3,3 and 1,1)
x = layers.Conv2D(128, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(128, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
x = layers.Dropout(0.50)(x)
# transition convolution for identity link
shortcut = layers.Conv2D(256, (1,1), strides=1, padding='same')(x)
# residual block - double filters
x = layers.Conv2D(256, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(256, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
x = layers.BatchNormalization()(x)
# pooling for final downsampling in convolutional layers
x = layers.MaxPooling2D(2, strides=2, name='encoder')(x)
return x
def bottleneck(x):
''' The bottleneck layer '''
# Use fast form of pooling: single value per feature map,
# which reduces the size substantially more than a Flatten().
x = layers.GlobalAveragePooling2D(name='bottleneck')(x)
return x
def classifier(x, nclasses):
''' The classifier layer '''
x = layers.Dense(nclasses, activation='softmax')(x)
return x
inputs = Input(input_shape)
x = stem(inputs)
x = conv_groups(x)
x = bottleneck(x)
outputs = classifier(x, nclasses)
return Model(inputs, outputs)
def ConvNetC(input_shape, nclasses):
''' Compact Neural Network without Normalization (Model 1)'''
def stem(inputs):
''' The stem convolutional group '''
# Two 3x3 convolutional layers, representational equivalent to single 5x5,
# which reduces computational complexity (trainable weights) by 75%
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(inputs)
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(x)
# Reduce the feature map sizes by 75%
x = layers.MaxPooling2D(2, strides=2)(x)
return x
def conv_groups(x):
''' Residual Groups (ResNet34 style) '''
# transition convolution for identity link, delay downsampling
shortcut = layers.Conv2D(128, (1,1), strides=1, padding='same')(x)
# residual block - double filters (Replace two 3,3 with 3,3 and 1,1)
x = layers.Conv2D(128, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(128, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
x = layers.Dropout(0.50)(x)
# transition convolution for identity link
shortcut = layers.Conv2D(256, (1,1), strides=1, padding='same')(x)
# residual block - double filters
x = layers.Conv2D(256, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(256, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
# pooling for final downsampling in convolutional layers
x = layers.MaxPooling2D(2, strides=2, name='encoder')(x)
return x
def bottleneck(x):
''' The bottleneck layer '''
# Use fast form of pooling: single value per feature map,
# which reduces the size substantially more than a Flatten().
x = layers.GlobalAveragePooling2D(name='bottleneck')(x)
return x
def classifier(x, nclasses):
''' The classifier layer '''
x = layers.Dense(nclasses, activation='softmax')(x)
return x
inputs = Input(input_shape)
x = stem(inputs)
x = conv_groups(x)
x = bottleneck(x)
outputs = classifier(x, nclasses)
return Model(inputs, outputs)
# Remove this (obsolete)
def ConvNetD(input_shape, nclasses):
def stem(inputs):
''' The stem convolutional group '''
# Two 3x3 convolutional layers, representational equivalent to single 5x5,
# which reduces computational complexity (trainable weights) by 75%
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(inputs)
x = layers.Conv2D(64, 3, strides=2, padding='same', activation='relu')(x)
# Reduce the feature map sizes by 75%
x = layers.MaxPooling2D(2, strides=2)(x)
return x
def conv_groups(x):
''' Residual Groups (ResNet34 style) '''
# transition convolution for identity link, delay downsampling
shortcut = layers.Conv2D(128, (1,1), strides=1, padding='same')(x)
# residual block - double filters (Replace two 3,3 with 3,3 and 1,1)
x = layers.Conv2D(128, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(128, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
x = layers.BatchNormalization()(x)
x = layers.Dropout(0.50)(x)
# transition convolution for identity link
shortcut = layers.Conv2D(256, (1,1), strides=1, padding='same')(x)
# residual block - double filters
x = layers.Conv2D(256, (3,3), strides=1, padding='same', activation='relu')(x)
x = layers.Conv2D(256, (1,1), strides=1, padding='same', activation='relu')(x)
# identity link
x = layers.add([shortcut, x])
x = layers.BatchNormalization()(x)
# pooling for final downsampling in convolutional layers
x = layers.MaxPooling2D(2, strides=2, name='encoder')(x)
return x
def bottleneck(x):
''' The bottleneck layer '''
# Use fast form of pooling: single value per feature map,
# which reduces the size substantially more than a Flatten().
x = layers.GlobalAveragePooling2D(name='bottleneck')(x)
return x
def classifier(x, nclasses):
''' The classifier layer '''
x = layers.Dense(nclasses, activation='softmax')(x)
return x
inputs = Input(input_shape)
x = stem(inputs)
x = conv_groups(x)
x = bottleneck(x)
outputs = classifier(x, nclasses)
return Model(inputs, outputs)
# -
# ## Benchmark Fruits-360 with Models 2 and 3
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Benchmark Fruits-360 with Model 1
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Benchmark Fruits-360 with modified Model 3
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetD((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# !ls ../
# ## Dataset for Intel Image Classification
# +
import cv2
import numpy as np
from keras.utils import to_categorical
import random
root_train = "../intel-image-classification/seg_train"
root_test = "../intel-image-classification/seg_test"
def loadImages(root):
data = []
labels = []
classes = {}
nclass = 0
subdirs = os.scandir(root)
for subdir in subdirs:
classes[subdir.name] = nclass
images = []
files = os.scandir(subdir.path)
for file in files:
image = cv2.imread(file.path)
image = cv2.resize(image, (150, 150))
images.append(image)
data.append(np.asarray(images))
labels.append(np.asarray([nclass for _ in range(len(images))]))
nclass += 1
data = np.concatenate(np.asarray(data))
mean = np.mean(data)
std = np.std(data)
data = (( data - mean ) / std).astype(np.float32)
labels = to_categorical(np.concatenate(labels))
return data, labels, classes
data, labels, classes = loadImages(root_train)
n = data.shape[0]
random.seed(101)
random.shuffle(data)
random.seed(101)
random.shuffle(labels)
pivot = int(n * .9)
x_train = data[0:pivot]
y_train = labels[0:pivot]
x_val = data[pivot:]
y_val = labels[pivot:]
print(x_train.shape, y_train.shape)
print(x_val.shape, y_val.shape)
data = None
labels = None
x_test, y_test, _= loadImages(root_test)
# -
# ## Benchmarks for Intel Image Classification for Models 1, 2 and 3
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Benchmarks for Fruits-360 for He-normal for Models 1, 2 and 3
# He-Normal
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, 20)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Benchmarks for Fruits-360 and batch=128 for Models 1, 2 and 3
# batch 128 / fruits-360
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((100, 100, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Benchmarks for Intel Image Classification and batch=128 for Models 1, 2
# batch 128 / intel
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((150, 150, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=128)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Dataset for Columbia University COIL-100
# +
import cv2
import numpy as np
from keras.utils import to_categorical
import random
from sklearn.model_selection import train_test_split
root = '/usr/local/google/home/aferlitsch/Desktop/Datasets/coil-100'
def loadImages(root):
nfiles=0
images = []
labels = []
classes = {}
nclass = 0
files = os.scandir(root)
for file in files:
pair = file.name.split('_')
label = pair[0][3:]
image = cv2.imread(file.path)
if image is None:
continue
image = cv2.resize(image, (128, 128))
images.append(image)
labels.append(int(label))
nfiles += 1
return nfiles, np.asarray(images).astype(np.float32), np.asarray(labels)
nfiles, images, labels = loadImages(root)
print(nfiles)
labels = to_categorical(labels)
mean = np.mean(images)
std = np.mean(images)
images = (images - mean) / std
x_train, x_test, y_train, y_test = train_test_split(images, labels, test_size=0.20, random_state=42)
pivot = int(len(x_train) * 0.9)
x_val = x_train[pivot:]
y_val = y_train[pivot:]
x_train = x_train[:pivot]
y_train = y_train[:pivot]
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)
print(x_val.shape, y_val.shape)
# -
# ## Benchmarks for COIL-100 for Models 1, 2 and 3
# COIL-100
import keras.optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((128, 128, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((128, 128, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((128, 128, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
# ## Dataset for CIFAR-10
#
# +
from keras.datasets import cifar10
from keras.utils import to_categorical
import numpy as np
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
mean = np.mean(x_train)
std = np.std(x_train)
x_train = ((x_train - mean) / std).astype(np.float32)
x_test = ((x_test - mean) / std).astype(np.float32)
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
pivot = int(len(x_train) * 0.9)
x_val = x_train[pivot:]
y_val = y_train[pivot:]
x_train = x_train[:pivot]
y_train = y_train[:pivot]
# -
# ## Benchmarks for CIFAR-10 for Models 1, 2 and 3
# CIFAR-10
import keras.optimizers as optimizers
for lr in [0.1, 0.01, 0.001, 0.0001]:
optimizer = optimizers.Adam(lr=lr)
for i in range(3):
print("RESNET WITHOUT BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetC((32, 32, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH LAYER BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetA((32, 32, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
for i in range(3):
print("RESNET WITH IDENTITY BATCHNORM, lr =", lr, "ITER = ", i)
model = ConvNetB((32, 32, 3), y_train.shape[1])
model.compile(loss='categorical_crossentropy', optimizer=optimizer, metrics=['accuracy'])
datagen = Feeder()
Train(model, datagen, x_train, y_train, x_val, y_val, epochs=20, batch_size=32)
scores = model.evaluate(x_test, y_test, verbose=1)
print("Test", scores)
|
papers/Identity Normalization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from database.market import Market
# +
##pulled from https://finance.yahoo.com/quote/BTC-USD/history/
# -
btc = pd.read_csv("BTC-USD.csv")
market = Market()
market.connect()
market.store_data("btc",btc)
market.close()
|
boiler/bitcoin_extraction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Video Processing
#
# This notebook loads the saved model and processes detection on a video.
# +
import keras
import keras.preprocessing.image
from keras_retinanet.models.resnet import custom_objects
from keras_retinanet.preprocessing.csv_generator import CSVGenerator
import imageio
imageio.plugins.ffmpeg.download()
from moviepy.editor import VideoFileClip
import PIL.Image
import time
import numpy as np
import cv2
# -
# `VideoFileClip` needs an instance to hold the test generator. This `VideoProcessor` instance retains the generator instance and also provides a processing function.
class VideoProcessor():
def __init__(self, threshold):
self.model = keras.models.load_model('./snapshots/resnet50_csv_18.h5', custom_objects=custom_objects)
# create image data generator object for the preprocessing functionality
generator = keras.preprocessing.image.ImageDataGenerator()
self.csv_generator = CSVGenerator(
'./data/test.csv',
'./data/classes.csv',
generator,
batch_size=1,
)
self.threshold = threshold
def process_image(self, image):
# copy to draw on
draw = image.copy()
# preprocess image for network
image = self.csv_generator.preprocess_image(image)
image, scale = self.csv_generator.resize_image(image)
# process image
start = time.time()
_, _, detections = self.model.predict_on_batch(np.expand_dims(image, axis=0))
# compute predicted labels and scores
predicted_labels = np.argmax(detections[0, :, 4:], axis=1)
scores = detections[0, np.arange(detections.shape[1]), 4 + predicted_labels]
# correct for image scale
detections[0, :, :4] /= scale
# visualize detections
for idx, (label, score) in enumerate(zip(predicted_labels, scores)):
if score < self.threshold:
continue
b = detections[0, idx, :4].astype(int)
cv2.rectangle(draw, (b[0], b[1]), (b[2], b[3]), (0, 0, 255), 3)
caption = "{} {:.3f}".format(self.csv_generator.label_to_name(label), score)
cv2.putText(draw, caption, (b[0], b[1] - 10), cv2.FONT_HERSHEY_PLAIN, 1.5, (0, 0, 0), 3)
cv2.putText(draw, caption, (b[0], b[1] - 10), cv2.FONT_HERSHEY_PLAIN, 1.5, (255, 255, 255), 2)
return draw
def process_video(processor, input_path, output_path):
clip = VideoFileClip (input_path)
result = clip.fl_image(processor.process_image)
# %time result.write_videofile (output_path, audio=False)
ironman_processor = VideoProcessor(threshold=0.09)
process_video(ironman_processor, './videos/ironman.mp4', './videos/ironman_result.mp4')
selfie_processor = VideoProcessor(threshold=0.25)
process_video(selfie_processor, './videos/selfie.mp4', './videos/selfie_result.mp4')
|
video.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
arr = np.array([(1,2,5,4),(5,6,5,8)])
print(arr)
arr.ndim
arr.itemsize
arr
type(arr)
d = [23,43]
type(d)
arr.dtype
arr.shape
arr.transpose()
arr.reshape(4,2)
np.linspace(1,4,25)
arr.max()
arr.min()
arr.mean()
arr.sum()
np.sqrt(arr)
np.linspace(4, 2, 52)
np.std(arr)
(1,2,3)+(4,5,6)
[4,5,6]+[5,6,2]
arr+arr
arr
arr(arr)
print(arr, arr)
arr.vstack(arr)
np.vstack((arr, arr))
np.hstack((arr, arr))
[[23,24],[34,45]] + [[46,68],[67,86]]
np.exp((arr), 3)
np.log(arr)
|
MCA/Machine Learning/numpy array functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: venv36
# language: python
# name: venv36
# ---
# # ART decision tree classifier attack
# This notebook shows how to compute adversarail examples on decision trees (as described in by Papernot et al. in https://arxiv.org/abs/1605.07277). Due to the structure of the decision tree, an adversarial example can be computed without any explicit gradients, only by traversing the learned tree structure.
#
# Consider the following simple decision tree for four dimensional data, where we go to the left if a condition is true:
#
# F1<3
#
# F2<5 F2>2
#
# F4>3 C1 F3<1 C3*
#
# C1 C2 C3 C1
#
# Given sample [4,4,1,1], the tree outputs C3 (as indicated by the star). To misclassify the sample, we walk one node up and explore the subtree on the left. We find the leaf outputting C1 and change the two features, obtaining [4,1.9,0.9,1]. In this implementation, we change only the features with the wrong values, and specify the offset in advance.
# ## Applying the attack
# +
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_digits
from matplotlib import pyplot as plt
import numpy as np
from art.attacks import DecisionTreeAttack
from art.classifiers import SklearnClassifier
# +
digits = load_digits()
X = digits.data
y = digits.target
clf = DecisionTreeClassifier()
clf.fit(X,y)
clf_art = SklearnClassifier(clf)
print(clf.predict(X[:14]))
plt.imshow(X[0].reshape(8,8))
plt.colorbar()
# -
# We now craft adversarial examples and plot their classification. The differnce is really small, and often only one or two features are changed.
attack = DecisionTreeAttack(clf_art)
adv = attack.generate(X[:14])
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
# plt.imshow((X[0]-adv[0]).reshape(8,8)) ##use this to plot the difference
# The change is possibly larger if we specify which class the sample should be classified as. To do this, we just specify a label for each attack point.
adv = attack.generate(X[:14],np.array([6,6,7,7,8,8,9,9,1,1,2,2,3,3]))
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
# Finally, the attack has an offset parameter which specifies how close the new value of the feature is compared to the learned threshold of the tree. The default value is very small (0.001), however the value can be set larger when desired. Setting it to a very large value might however yield adversarial examples outside the range or normal features!
attack = DecisionTreeAttack(clf_art,offset=20.0)
adv = attack.generate(X[:14])
print(clf.predict(adv))
plt.imshow(adv[0].reshape(8,8))
plt.colorbar()
|
notebooks/attack_decision_tree.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:PyData] *
# language: python
# name: conda-env-PyData-py
# ---
# %matplotlib inline
from matplotlib import style
style.use('fivethirtyeight')
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import datetime as dt
import sqlalchemy
from pprint import pprint
from sqlalchemy.ext.automap import automap_base
from sqlalchemy.orm import Session
from sqlalchemy import create_engine, func, distinct, inspect
engine = create_engine("sqlite:///Resources/hawaii.sqlite")
Base = automap_base()
Base.prepare(engine, reflect=True)
from sqlalchemy import inspect
inspector = inspect(engine)
inspector.get_table_names()
Measurement = Base.classes.measurement
Station = Base.classes.station
session = Session(engine)
# +
Measurement_Columns=inspector.get_columns('measurement')
for columns in Measurement_Columns:
print(columns['name'])
# +
Station_Columns=inspector.get_columns('station')
for columns in Station_Columns:
print(columns['name'])
# +
last=session.query(Measurement).order_by(Measurement.date.desc()).limit(1).all()
last_date= " "
for info in last:
last_date=info
print(last_date.date)
# -
first_day=dt.date(2017,8,23)-dt.timedelta(days=365)
results=session.query(Measurement.date, Measurement.prcp).filter(Measurement.date>= first_day).all()
percip_df=pd.DataFrame(results, columns=['date', 'percipitation'])
percip_df.set_index(['date'], inplace=True)
final_df= percip_df.sort_values('date')
final_df.head()
final_df.plot(rot=45)
plt.xlabel('Date')
plt.ylabel('Inches')
plt.legend()
plt.show()
final_df.describe()
# +
station_count=session.query(func.count(Station.id)).all()
print(f'There is a total of {station_count[0][0]} stations')
# -
active_stations = (
session.query(Measurement.station, Station.name, func.count(Measurement.id))
.filter(Measurement.station == Station.station)
.group_by(Measurement.station)
.order_by(func.count(Measurement.id).desc())
.all()
)
print("Most active stations are:")
pprint(active_stations)
# +
station_record = (
session.query(
func.min(Measurement.tobs),
func.max(Measurement.tobs),
func.avg(Measurement.tobs),
)
.filter(Measurement.station == active_stations[0][0])
.all()
)
print(
f"Most active station is {active_stations[0][0]} - {active_stations[0][1]}. Following are its records:"
)
print(f"Highest Temperature: {station_record[0][1]}F")
print(f"Lowest Temperature: {station_record[0][0]}F")
print(f"Average Temperature: {station_record[0][2]}F")
# +
temp_results = (
session.query(Measurement.date, Measurement.tobs)
.filter(Measurement.date > first_day)
.filter(Measurement.station == active_stations[0][0])
.order_by(Measurement.date)
.all()
)
temp_df = pd.DataFrame(temp_results)
temp_df = temp_df.set_index("date").sort_index(ascending=True)
temp_df.plot(kind="hist", bins=12, alpha=0.85, figsize=(9, 8))
plt.xlabel("Temperature")
plt.ylabel("Frequency")
plt.show()
# +
def calc_temps(start_date, end_date):
"""TMIN, TAVG, and TMAX for a list of dates.
Args:
start_date (string): A date string in the format %Y-%m-%d
end_date (string): A date string in the format %Y-%m-%d
Returns:
TMIN, TAVE, and TMAX
"""
return session.query(func.min(Measurement.tobs), func.avg(Measurement.tobs), func.max(Measurement.tobs)).\
filter(Measurement.date >= start_date).filter(Measurement.date <= end_date).all()
print(calc_temps('2012-02-28', '2012-03-05'))
# +
trip_dates = "2017-12-05 to 2017-12-13"
prev_year = "2016-12-05 - \n 2016-12-13"
prev_year_start = dt.date(2017, 12, 5) - dt.timedelta(days=365)
prev_year_end = dt.date(2017, 12, 13) - dt.timedelta(days=365)
temps = calc_temps(prev_year_start, prev_year_end)
temp_min, temp_avg, temp_max = temps[0]
print(f" Min Temp : {temp_min}F")
print(f" Avg Temp : {temp_avg}F")
print(f" Max Temp : {temp_max}F")
# +
error = temp_max - temp_min
xpos = 1
plt.figure(figsize=(4, 8))
plt.bar(xpos, temp_avg, yerr=error, alpha=0.75,)
plt.title(f"Trip Avg Temp")
plt.ylabel("Temp (F)")
plt.xticks([])
plt.yticks(np.arange(0, 120, 20))
plt.tight_layout()
plt.xlim(0.45, 1.55)
plt.ylim(0, 105)
plt.show()
# +
trip_start = "2016-12-05"
trip_end = "2016-12-13"
rain_station = (
session.query(
Station.station,
Station.name,
Station.latitude,
Station.longitude,
Station.elevation,
func.avg(Measurement.prcp),
)
.filter(
Measurement.station == Station.station,
Measurement.date.between(trip_start, trip_end),
)
.group_by(Station.station)
.order_by(func.avg(Measurement.prcp).desc())
.all()
)
rain_df = pd.DataFrame(np.array(rain_station))
rain_df = rain_df.rename(
columns={
0: "Station",
1: "Location",
2: "Latitude",
3: "Longitude",
4: "Elevation",
5: "Total Precipitation",
}
)
rain_df
# +
def daily_normals(date):
"""Daily Normals.
Args:
date (str): A date string in the format '%m-%d'
Returns:
A list of tuples containing the daily normals, tmin, tavg, and tmax
"""
sel = [
func.min(Measurement.tobs),
func.avg(Measurement.tobs),
func.max(Measurement.tobs),
]
return (
session.query(*sel)
.filter(func.strftime("%m-%d", Measurement.date) == date)
.all()
)
daily_normals("01-01")
# +
trip_startdate = dt.date(2018, 1, 1)
trip_enddate = dt.date(2018, 1, 7)
date_range = pd.date_range(trip_startdate, trip_enddate)
date_list = [d.strftime("%m-%d") for d in date_range]
daily_normal = [daily_normals(d)[0] for d in date_list]
pprint(daily_normal)
# -
normal_df = pd.DataFrame(
daily_normal, columns=["tmin", "tavg", "tmax"], index=date_range
)
normal_df.index.name = "Date"
normal_df
normal_df.plot(kind="area", stacked=False, x_compat=True, alpha=0.333, figsize=(7, 6))
plt.xlabel("Date")
plt.ylabel("Temperature")
plt.show()
|
climate_starter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
print(ord('h'))
print(chr(ord('h')))
# +
# hash?
# -
a = []
a.insert(0,3)
a.insert(0,4)
if 5 not in a:
a.insert(0,5)
a
a.remove(7)
a
# # solution
# +
# python3
class Query:
def __init__(self, query):
self.type = query[0]
if self.type == 'check':
self.ind = int(query[1])
else:
self.s = query[1] #s is string
class QueryProcessor:
_multiplier = 263
_prime = 1000000007
def __init__(self, bucket_count):
self.bucket_count = bucket_count
# store all strings in one list
self.elems = [[] for i in range(bucket_count)]
def _hash_func(self, s):
ans = 0
for c in reversed(s):
ans = (ans * self._multiplier + ord(c)) % self._prime
return ans % self.bucket_count
def write_search_result(self, was_found):
print('yes' if was_found else 'no')
def write_chain(self, chain): #prints a list as a string.
print(' '.join(chain))
def read_query(self):
return Query(input().split())
def process_query(self, query):
if query.type == "check":
self.write_chain(self.elems[query.ind])
# use reverse order, because we append strings to the end
# self.write_chain(cur for cur in reversed(self.elems)
# if self._hash_func(cur) == query.ind)
else:
temp_hash = self._hash_func(query.s)
if query.type == 'add' and (query.s not in self.elems[temp_hash]):
self.elems[temp_hash].insert(0,query.s)
elif query.type == 'find':
if query.s in self.elems[temp_hash]:
print('yes')
else:
print('no')
elif query.type == 'del':
# if query.s in self.elems[temp_hash]:
try:
self.elems[temp_hash].remove(query.s)
except ValueError:
pass
# try:
# ind = self.elems.index(query.s)
# except ValueError:
# ind = -1
# if query.type == 'find':
# self.write_search_result(ind != -1)
# elif query.type == 'add':
# if ind == -1:
# self.elems.append(query.s)
# else:
# if ind != -1:
# self.elems.pop(ind)
def process_queries(self):
n = int(input())
for i in range(n):
self.process_query(self.read_query())
if __name__ == '__main__':
bucket_count = int(input())
proc = QueryProcessor(bucket_count)
proc.process_queries()
# -
# # starter solution from coursera
# +
# python3
class Query:
def __init__(self, query):
self.type = query[0]
if self.type == 'check':
self.ind = int(query[1])
else:
self.s = query[1]
class QueryProcessor:
_multiplier = 263
_prime = 1000000007
def __init__(self, bucket_count):
self.bucket_count = bucket_count
# store all strings in one list
self.elems = []
def _hash_func(self, s):
ans = 0
for c in reversed(s):
ans = (ans * self._multiplier + ord(c)) % self._prime
return ans % self.bucket_count
def write_search_result(self, was_found):
print('yes' if was_found else 'no')
def write_chain(self, chain):
print(' '.join(chain))
def read_query(self):
return Query(input().split())
def process_query(self, query):
if query.type == "check":
# use reverse order, because we append strings to the end
self.write_chain(cur for cur in reversed(self.elems)
if self._hash_func(cur) == query.ind)
else:
try:
ind = self.elems.index(query.s)
except ValueError:
ind = -1
if query.type == 'find':
self.write_search_result(ind != -1)
elif query.type == 'add':
if ind == -1:
self.elems.append(query.s)
else:
if ind != -1:
self.elems.pop(ind)
def process_queries(self):
n = int(input())
for i in range(n):
self.process_query(self.read_query())
if __name__ == '__main__':
bucket_count = int(input())
proc = QueryProcessor(bucket_count)
proc.process_queries()
|
week4/hash_chains/hashing with chains.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Hats
# Train hats, both class consistent and class discriminatory
# +
import dense_correspondence_manipulation.utils.utils as utils
utils.add_dense_correspondence_to_python_path()
from dense_correspondence.training.training import *
import sys
import logging
# utils.set_default_cuda_visible_devices()
utils.set_cuda_visible_devices([1]) # use this to manually set CUDA_VISIBLE_DEVICES
from dense_correspondence.training.training import DenseCorrespondenceTraining
from dense_correspondence.dataset.spartan_dataset_masked import SpartanDataset
logging.basicConfig(level=logging.INFO)
# +
config_filename = os.path.join(utils.getDenseCorrespondenceSourceDir(), 'config', 'dense_correspondence',
'dataset', 'composite', 'hat_train_6.yaml')
config = utils.getDictFromYamlFilename(config_filename)
train_config_file = os.path.join(utils.getDenseCorrespondenceSourceDir(), 'config', 'dense_correspondence',
'training', 'training.yaml')
train_config = utils.getDictFromYamlFilename(train_config_file)
dataset = SpartanDataset(config=config)
logging_dir = "code/data_volume/pdc/trained_models/caterpillar_new"
num_iterations = 3500
num_image_pairs = 100
TRAIN = True
EVALUATE = True
# -
# ## Class Consistent
# +
descriptor_dim = [3,6,9]
M_background_list = [0.5, 2.0]
for M_background in M_background_list:
for d in descriptor_dim:
print "\n"
print "d:", d
print "M_background:", M_background
print "training descriptor of dimension %d" %(d)
train_config = utils.getDictFromYamlFilename(train_config_file)
train = DenseCorrespondenceTraining(dataset=dataset, config=train_config)
name = "hats_consistent_M_background_%.3f_%s" %(M_background, d)
train._config["training"]["logging_dir"] = logging_dir
train._config["training"]["logging_dir_name"] = name
train._config["dense_correspondence_network"]["descriptor_dimension"] = d
train._config["loss_function"]["M_background"] = M_background
if TRAIN:
train.run()
print "finished training descriptor of dimension %d" %(d)
model_folder = os.path.join(logging_dir, name)
model_folder = utils.convert_to_absolute_path(model_folder)
if EVALUATE:
DCE = DenseCorrespondenceEvaluation
DCE.run_evaluation_on_network(model_folder, num_image_pairs=num_image_pairs, cross_scene=False)
# -
# ## Instance Specific
# +
descriptor_dim = [3,6,9]
M_background_list = [0.5, 2.0]
for M_background in M_background_list:
for d in descriptor_dim:
print "\n"
print "d:", d
print "M_background:", M_background
print "training descriptor of dimension %d" %(d)
train_config = utils.getDictFromYamlFilename(train_config_file)
train = DenseCorrespondenceTraining(dataset=dataset, config=train_config)
name = "hats_specific_M_background_%.3f_%s" %(M_background, d)
train._config["training"]["logging_dir"] = logging_dir
train._config["training"]["logging_dir_name"] = name
train._config["dense_correspondence_network"]["descriptor_dimension"] = d
train._config["loss_function"]["M_background"] = M_background
# DIFFERENT_OBJECT
train._config["training"]["data_type_probabilities"]["DIFFERENT_OBJECT"] = 0.25
train._config["training"]["data_type_probabilities"]["SINGLE_OBJECT_WITHIN_SCENE"] = 0.75
if TRAIN:
train.run()
print "finished training descriptor of dimension %d" %(d)
model_folder = os.path.join(logging_dir, name)
model_folder = utils.convert_to_absolute_path(model_folder)
if EVALUATE:
DCE = DenseCorrespondenceEvaluation
DCE.run_evaluation_on_network(model_folder, num_image_pairs=num_image_pairs, cross_scene=False)
|
dense_correspondence/experiments/hats/training_hats.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Classification MNSIT Datasets
# - 로컬 컴퓨터를 이용할 때는 에폭을 낮게 지정(단지 실행이 되는지만 확인)
# - Kaggle이나 gcp를 이용할 때는 GPU를 사용하여 실제 훈련 실시
# ## 라이브러리 import
import torch
import torchvision
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import numpy as np
# %matplotlib inline
# ## Datasets 다운로드 및 불러오기
# +
# Dataset & DataLoader
transform = transforms.Compose(
[
transforms.ToTensor(),
transforms.Normalize([0], [1])
])
trainset = torchvision.datasets.MNIST(root = './data', train = True,
download = True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size = 128,
shuffle = True, num_workers=1)
testset = torchvision.datasets.MNIST(root = './data', train = False,
download = True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size = 128,
shuffle = True, num_workers=1)
classes = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'}
print(trainset)
print('*'*100)
print(testset)
# -
# ## Datasets 확인하기
# +
# Visualization Datasets
def show(img):
print(img.size())
grid = torchvision.utils.make_grid(img, padding = 0) # make_grid 함수는 3채널로 만든다(모두 같은 format으로)
print(grid.size())
tranimg = grid.permute(1,2,0)
print(tranimg.size())
plt.imshow(tranimg, aspect = 'auto')
images, labels = iter(trainloader).next()
show(images)
# -
# # Model 구축하기
# +
# Make Model
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, 7, padding = 3)
self.conv2 = nn.Conv2d(10, 50, 7, padding = 3)
self.conv3 = nn.Conv2d(50, 120, 7, padding = 3)
self.conv4 = nn.Conv2d(120, 100, 5)
self.conv5 = nn.Conv2d(100, 20, 5)
self.conv6 = nn.Conv2d(20, 10, 5)
self.conv7 = nn.Conv2d(10, 10, 3)
self.pool = nn.MaxPool2d(2,2)
self.fc1 = nn.Linear(10 * 8 * 8, 120)
self.fc2 = nn.Linear(120, 360)
self.fc3 = nn.Linear(360, 50)
self.fc4 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(self.conv1(x)) # 28 28
x = F.relu(self.conv2(x)) # 28 28
x = F.relu(self.conv3(x)) # 28 28
x = F.relu(self.conv4(x)) # 24 24
x = F.relu(self.conv5(x)) # 20 20
x = self.pool(F.relu(self.conv6(x))) # 8 8
x = x.view(-1, 10 * 8 * 8)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
# -
# ## GPU 사용 여부 판단하기
# GPU 사용여부 판단
if torch.cuda.is_available():
device = torch.device('cuda')
print('We can use GPU')
else:
device = torch.device('cpu')
print('We can use CPU')
# ## Model 및 Optimizer 생성
# - Model Parameters 확인
# +
import torch.optim as optim
model = Net().to(device)
loss_func = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr = 0.1)
print(loss_func, optimizer)
# -
for p in model.parameters():
print(p.size())
# ## 모델 작동상태 확인하기
model.eval()
with torch.no_grad():
images, labels = next(iter(trainloader))
images, labels = images.to(device), labels.to(device)
print(images.size())
example = model(images)
print('Test : ', example)
# ## 학습하기
# +
# Train
import time
EPOCH = 1
for e in range(1, EPOCH+1):
model.train()
start_time = time.time()
running_loss = 0
for i, data in enumerate(trainloader):
images, labels = data
images, labels = images.to(device), labels.to(device)
optimizer.zero_grad()
outputs = model(images)
loss = loss_func(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss
now = time.time()
print('\r[%d/%d]-----[%d/%d] LOSS : %.3f------ Time : %d'
%(e, EPOCH, i, 60000/128, running_loss, now - start_time), end = '')
print('\n')
# -
# ## Model 저장하기
torch.save(model, 'data/mnist_classifier.pth')
test_model = torch.load('data/mnist_classifier.pth')
test_model
# # 예측이 작동하는지 확인하기
with torch.no_grad():
classes = ('0', '1', '2', '3', '4', '5', '6', '7', '8', '9')
testloader = torch.utils.data.DataLoader(testset, batch_size = 8,
shuffle = True, num_workers=1)
test_data = iter(testloader)
test_images, test_labels = test_data.next()
show(test_images)
test_images, test_labels = test_images.cuda(), test_labels.cuda()
test_outputs = test_model(test_images)
_, predicted = torch.max(test_outputs, 1)
print('GroundTruth : ', ' '.join(classes[test_labels[j]] for j in range(8)))
print('Predicted : ', ' '.join(classes[predicted[i]] for i in range(8)))
# ## Model 성능 시험하기
# +
correct = 0
total = 0
model.eval()
with torch.no_grad():
for data in testloader:
val_images, val_labels = data
val_images, val_labels = val_images.to(device), val_labels.to(device)
val_outputs = model(val_images)
#_, val_predicted = torch.max(val_outputs.data, 1) # 이것 보다는
pred = val_outputs.argmax(dim=1, keepdim=True)
#correct += (val_predicted == val_labels).sum().item() # 이것 보다는
correct += pred
print('Accuracy of the network on the 10000 test images : %.3f %%' %(100 * correct / total))
# -
isinstance(Net(), nn.Conv2d)
type(nn.Conv2d)
type(nn.Conv2d(1, 10, 7)) == nn.Conv2d
type(model.conv1) == nn.Conv2d
self.conv1 = nn.Conv2d(1, 10, 7, padding = 3)
a = 10
if a == (9 or 10):
print('g')
# +
def weight_init(m):
if ((type(m) == nn.Conv2d) or (type(m) == nn.Linear)):
print('0')
torch.nn.init.xavier_uniform_(m.weight)
m.bias.data.fill_(0)
model.apply(weight_init)
# -
nn.init.xavier_normal(torch.zeros(3,5))
|
1. Beginner/Pytorch5_1_CNN_Classifier_MNSIT.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Ruby 2.3.1
# language: ruby
# name: ruby
# ---
require 'daru'
df = Daru::DataFrame.new({b: [11,12,13,14,15], a: [1,2,3,4,5],
c: [11,22,33,44,55]},
order: [:a, :b, :c],
index: [:one, :two, :three, :four, :five])
df.to_html
a = Daru::Vector.new([1,2,3,4,5])
a.to_html
a.to_html_thead
a.to_html_tbody
# +
tuples = [
[:a, :one, :foo],
[:a, :two, :bar],
[:b, :one, :bar],
[:b, :two, :baz]
]
multi_index = Daru::MultiIndex.from_tuples(tuples)
# -
vec_mi = Daru::Vector.new [1,2,3,4], name: :mi, index: multi_index
vec_mi.to_html
vec_mi.to_html_tbody
vec_mi.to_html_thead
|
spec/dummy_iruby/Some daru examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# In this notebook, I will use the best of both the worlds:
#
# - Use `tsfresh` to extract features
# - Use `Dask` for parallelization and handling larger than memory dataset
# - Dask will distribute the jobs across multiple cores (single machine or distributed cluster)
# - Dask DataFrame utlizes out of core computing
#
# This notebook is divided into two sections
# - Dask Basics
# - Automated FE using `tsfresh` & `Dask`
# +
import glob
import os
import sys
import pandas as pd
import numpy as np
import dask
from dask.distributed import Client, LocalCluster
import dask.dataframe as dd
# +
def get_segment_id_from_path(df, path):
"""
Returns the segment_id from the path of the file
"""
df.segment_id = df.segment_id.str.replace(path, "", regex=False)
df.segment_id = df.segment_id.str.replace(".csv", "", regex=False)
df.segment_id = df.segment_id.astype(np.int64)
return df
def append_time_column(df):
df["time"] = range(0, len(df))
return df
# Path for raw data
DATA_DIR = "/datadrive/arnab/vssexclude/kaggle/volcano/data/train"
# Path to save generated features
FEATURE_PATH = "/datadrive/arnab/vssexclude/kaggle/volcano/data/features"
# Define the datatypes for different sensor data
data_types = {"sensor_1" : np.float32,
"sensor_2" : np.float32,
"sensor_3" : np.float32,
"sensor_4" : np.float32,
"sensor_5" : np.float32,
"sensor_6" : np.float32,
"sensor_7" : np.float32,
"sensor_8" : np.float32,
"sensor_9" : np.float32,
"sensor_10" : np.float32}
# -
# # Dask Basics
# ### Dask Architechture
#
# Technically, Dask is a centrally managed distributed service with distributed storage and execution with the workers and peer to peer communication.
# <img src="../images/dask_architechture_diagram.png" width="600" height="200" style="border-style: solid;">
# #### What is a Client?
#
# The Client connects users to a Dask cluster. After a Dask cluster is setup, we initialize a Client by pointing it to the address of a Scheduler:
#
# ```python
# from distributed import Client
# client = Client("1.2.3.4:8786")
# ```
#
#
# Here we are creating a Local Cluster and then connecting the Dask Client to the Local Cluster.
#
# By specifying `n_worker=10`, we have asked to dask to start `10` independent python processes. Based on the nature of the cluster, they may run in the same machine or different machines.
# +
cluster = LocalCluster(n_workers=8,
threads_per_worker=1,
scheduler_port=8786,
memory_limit='2GB')
client = Client(cluster)
client
# -
# ### Read Data
# !ls -lrt {DATA_DIR}/1408*.csv | wc -l
# %%time
ddf = dd.read_csv(
urlpath=f"{DATA_DIR}/1408*.csv",
blocksize=None,
dtype=data_types,
include_path_column='segment_id')
# #### What just happened:
# - Dask just checked the input path and found that there are multiple CSV files matching the path description
# - It has not really loaded the content of the individual CSV files yet.
# - Nothing happens in the Dask UI, because these operations are just setting up a task graph which will be executed later
# - Dask is lazy by default. It will load all the CSV files into the memory **in parallel** only when we ask for any result
# - We can ask for result by invoking `compute()` method
#
# Note:
# - None value for `blocksize` creates single partition for each CSV file
ddf
# ### What is Dask DataFrame?
#
# - Dask DataFrame API extends Pandas to work on **larger than memory** datasets on laptops or distributed datasets across the clusters
# - It reuses lot of Pandas' code and extends the scale.
#
# ### How Dask DataFrame is constructed?
# <img src="../images/pandas_vs_dask_DF.png" width="400" height="200" style="border-style: solid;">
# #### Observations
# - This Dask DataFrame is composed of 4 Pandas DataFrame
# - It has the column names and data types
# - It has 4 tasks, i.e. 4 small Python functions which must be run to execute this entire Dask DataFrame.
ddf.visualize()
# #### Let's compute the maximum value of the `sensor_1` feature
ddf.sensor_1.max()
ddf.sensor_1.max().visualize()
ddf.sensor_1.max().compute()
type(ddf.sensor_1.max().compute())
# #### What just happened?
# - Dask checked the input path. Identified the matching files
# - A bunch of jobs were created. Here, one job per chunk/partition.
# - Each CSV file is read from the memory and loaded into a Pandas Dataframe
# - For each Pandas DataFrame, maximum value of `sensor_1` feature is computed
# - Results from multiple Pandas DataFrame are combined to get the final result, i.e., the maximum value of `sensor_1` across all the CSVs
# - Look at the Dask Dashboard before and after the compute()
#
#
# - Note: **The result of `compute()` must fit in-memory.**
#
# ## How to parallelize a custom function working on individual partitions?
#
# #### Problem Statement
#
# - I have a function which works well on one Pandas DataFrame. How can I parallelize it over multiple Pandas DataFrame?
#
# `map_partitions()` is the answer. It applies the function in an **embarrassingly parallel** way to multiple Pandas DataFrame
# #### Calculate the percentage of missing values across sensors for all the segments
def get_missing_sensors(df):
"""
Returns a DataFrame consisting percentage of missing data per sensor
"""
df_missing_percentage = df.isna().mean().to_frame().transpose()
df_missing_percentage = df_missing_percentage.astype(np.float16)
return df_missing_percentage
df_train_seg_missing = ddf.map_partitions(get_missing_sensors).compute()
ddf.map_partitions(get_missing_sensors).visualize()
client.close()
cluster.close()
# # Automated FE using `tsfresh` & `Dask`
# Here, input data starts from the hard drive & output (extracted features) will end on the hard drive.
#
# In between, Dask will read input data chunk by chunk, extract features and write to hard drive.
# ### Steps
#
# - Create a Dask Cluster and connect a Client to it.
# - Read data using Dask DataFrame from hard drive.
# - Extract features using `tsfresh.feature_extraction.extract_features`. Dask parallelizes execution of this function using `map_partitions`.
# - Write the extracted features to hard drive segment by segment.
# ### 1. Create a Dask Cluster and connect a Client to it
# +
cluster = LocalCluster(n_workers=8,
threads_per_worker=1,
scheduler_port=8786,
memory_limit='3GB')
client = Client(cluster)
client
# -
# ### 2. Read Data using Dask DataFrame
# +
ddf = dd.read_csv(
urlpath=f"{DATA_DIR}/1*.csv",
blocksize=None,
usecols=["sensor_1", "sensor_4"],
dtype=data_types,
include_path_column='segment_id')
# Use the first 1000 observations
ddf = ddf.loc[0:999, :]
# Insert a new column with segment_id along with the values from 10 sensors
ddf = ddf.map_partitions(get_segment_id_from_path, f"{DATA_DIR}/")
# Add a column named time with ascending values staring from 0 representing time
ddf = ddf.map_partitions(append_time_column)
ddf = ddf.fillna(0)
# -
ddf
# ### 3. Generate Features for individual partitions in parallel using Dask
#
# Here I am going to parallize the function `tsfresh.feature_extraction.extract_features()` using
# +
from tsfresh.feature_extraction import extract_features
from tsfresh.feature_extraction.settings import MinimalFCParameters
def custom_extract_features(df, column_id, column_sort, default_fc_parameters):
"""
Generate features using `extract_features` of `tsfresh` and then rename and
reset axis.
Setting `n_jobs` to 0 disable multiprocessing functionality
"""
feature_df = extract_features(df,
column_id=column_id,
column_sort=column_sort,
n_jobs=0,
default_fc_parameters=default_fc_parameters,
disable_progressbar=True)
feature_df = feature_df.rename_axis("segment_id").reset_index(drop=False)
feature_df.segment_id = feature_df.segment_id.astype('category')
return feature_df
# +
my_fc = {
'maximum': None,
'minimum': None
}
ddf_features = ddf.map_partitions(custom_extract_features,
column_id='segment_id',
column_sort='time',
default_fc_parameters=my_fc)
# -
ddf_features
# ### 4. Write extracted features back to hard drive
ddf_features.to_parquet(
path=f"{FEATURE_PATH}",
write_index=False,
partition_on="segment_id",
engine="pyarrow",
append=False)
# ### 5. Read generated features for verification
# Read using Pandas
# +
SEGMENT_ID = "1999605295"
df = pd.read_parquet(f"{FEATURE_PATH}/segment_id={SEGMENT_ID}")
df.head()
# -
# Read using Dask
ddf_features_from_disk = dd.read_parquet(path=f"{FEATURE_PATH}/*/*.parquet")
ddf_features_from_disk
ddf_features_from_disk.partitions[3].compute()
client.close()
cluster.close()
|
notebooks/3_fe_on_large_data_dask.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 2021년 5월 22일 토요일
# ### BaekJoon - 통계학 (Python)
# ### 문제 : https://www.acmicpc.net/problem/2108
# ### 블로그 : https://somjang.tistory.com/entry/BaekJoon-2108%EB%B2%88-%ED%86%B5%EA%B3%84%ED%95%99-Python
# ### Solution (PyPy3)
# +
from collections import Counter
numbers = []
for _ in range(int(input())):
num = int(input())
numbers.append(num)
numbers.sort()
cnt = Counter(numbers).most_common(2)
print(round(sum(numbers) / len(numbers)))
print(numbers[len(numbers) // 2])
if len(numbers) > 1:
if cnt[0][1] == cnt[1][1]:
print(cnt[1][0])
else:
print(cnt[0][0])
else:
print(cnt[0][0])
print(max(numbers) - min(numbers))
# -
# ### Solution (Python3)
# +
from collections import Counter
import sys
numbers = []
for _ in range(int(sys.stdin.readline())):
num = int(sys.stdin.readline())
numbers.append(num)
numbers.sort()
cnt = Counter(numbers).most_common(2)
print(round(sum(numbers) / len(numbers)))
print(numbers[len(numbers) // 2])
if len(numbers) > 1:
if cnt[0][1] == cnt[1][1]:
print(cnt[1][0])
else:
print(cnt[0][0])
else:
print(cnt[0][0])
print(max(numbers) - min(numbers))
|
DAY 301 ~ 400/DAY373_[BaekJoon] 통계학 (Python).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Assignment 1 | Data Types
#
# Add code cells as needed for your answers.
# ### Exercise 1: Manipulating Lists
# Create a list containing the numbers 10, 20, and 30. Store your list as a variable named `a`. Then create a second list containing the numbers 30, 60, and 90. Call this this `b`.
a = [10,20,30]
b = [30,60,90]
# In the cells below, write Python expressions to create the following four outputs by combining `a` and `b` in creative ways:
#
# 1. [[10, 20, 30], [30, 60, 90]]
#
# 2. [10, 20, 30, 30, 60, 90]
#
# 3. [10, 20, 60, 90]
#
# 4. [20, 40, 60]
print ([a , b])
print (a + b)
print (a[:2] + b[1:3])
print ([a[1] , (a[0] + a[2]) , b[1]])
# ### Exercise 2. Working with Lists
#
# Create a list that contains the sums of each of the lists in G.
#
# `G = [[13, 9, 8], [14, 6, 12], [10, 13, 11], [7, 18, 9]]`
#
# Your output should look like:
#
# - `[30, 32, 34, 34]`
#
# Hint: try computing the sum for just one list first.
import math
G = [[13, 9, 8], [14, 6, 12], [10, 13, 11], [7, 18, 9]]
g1 = sum(G[0])
g2 = sum(G[1])
g3 = sum(G[2])
g4 = sum(G[3])
print ([g1,g2,g3,g4])
# ### Exercise 3: String Manipulation
#
# Turn the string below into 'all good countrymen' using the minimum amount of code, using only the methods we've covered so far. A couple of lines of code should do the trick. Note: this requires string and list methods.
s = 'Now is the time for all good men to come to the aid of their country!'
ag = s[20:28]
ag
men = s[29:32]
men
cnty = s[60:68]
cnty
phrase = ag + cnty + men
phrase
# ### Exercise 4: String Manipulation and Type Conversion
#
# Define a variable `a = "Sarah earns $96500 in a year"`. Then maniuplate the value of `a` in order to print the following string: `Sarah earns $8041.67 monthly`
#
# Start by doing it in several steps and then combine them one step at a time until you can do it in one line.
a = "Sarah earns $96500 in a year"
aint = int(a[13:18])
rounded = aint - 88458.33
num = (round (rounded,2))
num
a.find("i")
a.find("y")
a = a.strip("96500 in a year")
m = " monthly"
newa = []
newa.append(a)
newa = newa + [num] + [m]
newa_str = ''.join(map(str, newa))
newa_str
# ### Exercise 5: Create and Query a Dictionary on State Demographics
#
# Create two dictionaries, one for California and one for New York state, based on the data in the following table:
#
# | States | Pop Density | Prop White | Prop Afr Amer | Prop Asian | Prop Other | Owners | Renters |
# | --- | ---: | ---: | ---: | ---: | ---: | ---: | ---: |
# | CA | 239.1 | 0.57 | 0.06 | 0.13 | 0.22 | 7035371 | 5542127 |
# | NY | 411.2 | 0.65 | 0.15 | 0.07 | 0.22 | 3897837 | 3419918 |
#
# Each dictionary should have the following keys and value types: `name: (string)` , `population density: (float)`, `race (dict)`, `tenure: (dict)`.
#
# 1. Create one dictionary called CA and one called NY that contain dictionaries containing name, pop_density, race as a dictionary, and tenure for California and New York. Now combine these into a dictionary called "states", making it a dictionary of dictionaries, or a nested dictionary.
#
# 1. Check if Texas is in our state dictionary (we know it isn't but show us).
#
# 1. Print the White population in New York as a percentage
#
# 1. Assume there was a typo in the data, and update the White population fraction of NY to 0.64. Verify that it was updated by printing the percentage again.
#
# 1. Print the percentage of households that are renters in California, with two decimal places
# +
CA = {}
r_dict_CA = {'White': 0.57, 'Afr Amer': 0.06, 'Asian': 0.13, 'Other': 0.22}
t_dict_CA = {'Owners': 7035371, 'Renters':5542127}
CA = {'name': 'CA', 'population density': 239.1, 'race': r_dict_CA, 'tenure': t_dict_CA}
NY = {}
r_dict_NY = {'White': 0.65, 'Afr Amer': 0.15, 'Asian': 0.07, 'Other': 0.22}
t_dict_NY = {'Owners': 3897837, 'Renters':3419918}
NY = {'name': 'NY', 'population density': 411.2, 'race': r_dict_NY, 'tenure': t_dict_NY}
states = {}
states = {'California':CA, 'New York': NY}
states
# -
states['Texas']
print("{:.0%}".format(NY['race']['White']))
states['New York']['race']['White'] = 0.64
print("{:.0%}".format(NY['race']['White']))
# +
rent_CA = states['California']['tenure']['Renters']
own_CA = states['California']['tenure']['Owners']
tenure_tot = rent_CA + own_CA
perc_rent = rent_CA/tenure_tot
perc_rent
print ("{:.2%}".format(perc_rent))
# -
# ### Exercise 6: Working with Numpy Arrays
#
# 1. Create and print a 4 x 4 array named `a` with value 3 everywhere.
#
# 1. Create and print a 4 x 4 array named `b` with elements drawn from a uniform random distribution
#
# 1. Create and print array `c` by dividing a by b
#
# 1. Compute and print the min, mean, max, median, and 90th percentile values of `c`
#
# 1. Compute and print the sum of the second column in `c`
import numpy as np
list= [3,3,3,3]
a=np.array([list, list, list, list])
a
list_r1=np.random.uniform(low=0.0, high=100, size=4)
list_r2=np.random.uniform(low=0.0, high=100, size=4)
list_r3=np.random.uniform(low=0.0, high=100, size=4)
list_r4=np.random.uniform(low=0.0, high=100, size=4)
b=np.array([list_r1, list_r2, list_r3, list_r4])
b
c = a / b
c
np.min(c)
np.max(c)
np.mean(c)
np.median(c)
np.percentile(c,90)
col2_sum = c[:,1].sum(axis=0)
print (col2_sum)
|
assignments/assignment_1/assignment_1_Harasym_Gregory.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="MF7BncmmLBeO"
import os
import numpy as np
import matplotlib.pyplot as plt
import torch
from sklearn.datasets import load_digits
from sklearn import datasets
from torch.utils.data import Dataset, DataLoader
import torch.nn as nn
import torch.nn.functional as F
# -
# **DISCLAIMER**
#
# The presented code is not optimized, it serves an educational purpose. It is written for CPU, it uses only fully-connected networks and an extremely simplistic dataset. However, it contains all components that can help to understand how a hierarchical Variational Auto-Encoder (VAE) works, and it should be rather easy to extend it to more sophisticated models. This code could be run almost on any laptop/PC, and it takes a couple of minutes top to get the result.
# + [markdown] id="RKsmjLumL5A2"
# ## Dataset: Digits
# -
# In this example, we go wild and use a dataset that is simpler than MNIST! We use a scipy dataset called Digits. It consists of ~1500 images of size 8x8, and each pixel can take values in $\{0, 1, \ldots, 16\}$.
#
# The goal of using this dataset is that everyone can run it on a laptop, without any gpu etc.
# + id="hSWUnXAYLLif"
class Digits(Dataset):
"""Scikit-Learn Digits dataset."""
def __init__(self, mode='train', transforms=None):
digits = load_digits()
if mode == 'train':
self.data = digits.data[:1000].astype(np.float32)
elif mode == 'val':
self.data = digits.data[1000:1350].astype(np.float32)
else:
self.data = digits.data[1350:].astype(np.float32)
self.transforms = transforms
def __len__(self):
return len(self.data)
def __getitem__(self, idx):
sample = self.data[idx]
if self.transforms:
sample = self.transforms(sample)
return sample
# + [markdown] id="xQyrkrqAL7p8"
# ## Auxiliary functions and classes
# -
# <NAME>., & <NAME>. (2016). Gaussian error linear units (gelus). arXiv preprint arXiv:1606.08415.
class GELU(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return x * torch.sigmoid(1.702 * x)
# + [markdown] id="tw00sH-6L9yg"
# ### Distributions
# + id="AJh8NiXxLNf9"
PI = torch.from_numpy(np.asarray(np.pi))
EPS = 1.e-7
def log_categorical(x, p, num_classes=256, reduction=None, dim=None):
x_one_hot = F.one_hot(x.long(), num_classes=num_classes)
log_p = x_one_hot * torch.log(torch.clamp(p, EPS, 1. - EPS))
if reduction == 'avg':
return torch.mean(log_p, dim)
elif reduction == 'sum':
return torch.sum(log_p, dim)
else:
return log_p
def log_bernoulli(x, p, reduction=None, dim=None):
pp = torch.clamp(p, EPS, 1. - EPS)
log_p = x * torch.log(pp) + (1. - x) * torch.log(1. - pp)
if reduction == 'avg':
return torch.mean(log_p, dim)
elif reduction == 'sum':
return torch.sum(log_p, dim)
else:
return log_p
def log_normal_diag(x, mu, log_var, reduction=None, dim=None):
log_p = -0.5 * torch.log(2. * PI) - 0.5 * log_var - 0.5 * torch.exp(-log_var) * (x - mu)**2.
if reduction == 'avg':
return torch.mean(log_p, dim)
elif reduction == 'sum':
return torch.sum(log_p, dim)
else:
return log_p
def log_standard_normal(x, reduction=None, dim=None):
log_p = -0.5 * torch.log(2. * PI) - 0.5 * x**2.
if reduction == 'avg':
return torch.mean(log_p, dim)
elif reduction == 'sum':
return torch.sum(log_p, dim)
else:
return log_p
# Chakraborty & Chakravarty, "A new discrete probability distribution with integer support on (−∞, ∞)",
# Communications in Statistics - Theory and Methods, 45:2, 492-505, DOI: 10.1080/03610926.2013.830743
def log_min_exp(a, b, epsilon=1e-8):
"""
Source: https://github.com/jornpeters/integer_discrete_flows
Computes the log of exp(a) - exp(b) in a (more) numerically stable fashion.
Using:
log(exp(a) - exp(b))
c + log(exp(a-c) - exp(b-c))
a + log(1 - exp(b-a))
And note that we assume b < a always.
"""
y = a + torch.log(1 - torch.exp(b - a) + epsilon)
return y
def log_integer_probability(x, mean, logscale):
scale = torch.exp(logscale)
logp = log_min_exp(
F.logsigmoid((x + 0.5 - mean) / scale),
F.logsigmoid((x - 0.5 - mean) / scale))
return logp
def log_integer_probability_standard(x):
logp = log_min_exp(
F.logsigmoid(x + 0.5),
F.logsigmoid(x - 0.5))
return logp
# + [markdown] id="qSP2qiMqMICK"
# ## Hierarchical Variational Auto-Encoder
# -
# **NOTE** Please note that we use a single class unlike in previous implementations of VAEs. We do it for clarity.
# + id="GRYA6JA4LWEC"
class HierarchicalVAE(nn.Module):
def __init__(self, nn_r_1, nn_r_2, nn_delta_1, nn_delta_2, nn_z_1, nn_x, num_vals=256, D=64, L=16, likelihood_type='categorical'):
super(HierarchicalVAE, self).__init__()
print('Hierachical VAE by JT.')
# bottom-up path
self.nn_r_1 = nn_r_1
self.nn_r_2 = nn_r_2
self.nn_delta_1 = nn_delta_1
self.nn_delta_2 = nn_delta_2
# top-down path
self.nn_z_1 = nn_z_1
self.nn_x = nn_x
# other params
self.D = D
self.L = L
self.num_vals = num_vals
self.likelihood_type = likelihood_type
def reparameterization(self, mu, log_var):
std = torch.exp(0.5*log_var)
eps = torch.randn_like(std)
return mu + std * eps
def forward(self, x, reduction='avg'):
#=====
# bottom-up
# step 1
r_1 = self.nn_r_1(x)
r_2 = self.nn_r_2(r_1)
#step 2
delta_1 = self.nn_delta_1(r_1)
delta_mu_1, delta_log_var_1 = torch.chunk(delta_1, 2, dim=1)
delta_log_var_1 = F.hardtanh(delta_log_var_1, -7., 2.)
# step 3
delta_2 = self.nn_delta_2(r_2)
delta_mu_2, delta_log_var_2 = torch.chunk(delta_2, 2, dim=1)
delta_log_var_2 = F.hardtanh(delta_log_var_2, -7., 2.)
# top-down
# step 4
z_2 = self.reparameterization(delta_mu_2, delta_log_var_2)
# step 5
h_1 = self.nn_z_1(z_2)
mu_1, log_var_1 = torch.chunk(h_1, 2, dim=1)
# step 6
z_1 = self.reparameterization(mu_1 + delta_mu_1, log_var_1 + delta_log_var_1)
# step 7
h_d = self.nn_x(z_1)
if self.likelihood_type == 'categorical':
b = h_d.shape[0]
d = h_d.shape[1]//self.num_vals
h_d = h_d.view(b, d, self.num_vals)
mu_d = torch.softmax(h_d, 2)
elif self.likelihood_type == 'bernoulli':
mu_d = torch.sigmoid(h_d)
#=====ELBO
# RE
if self.likelihood_type == 'categorical':
RE = log_categorical(x, mu_d, num_classes=self.num_vals, reduction='sum', dim=-1).sum(-1)
elif self.likelihood_type == 'bernoulli':
RE = log_bernoulli(x, mu_d, reduction='sum', dim=-1)
# KL
KL_z_2 = 0.5 * (delta_mu_2**2 + torch.exp(delta_log_var_2) - delta_log_var_2 - 1).sum(-1)
KL_z_1 = 0.5 * (delta_mu_1**2 / torch.exp(log_var_1) + torch.exp(delta_log_var_1) -\
delta_log_var_1 - 1).sum(-1)
KL = KL_z_1 + KL_z_2
error = 0
if np.isnan(RE.detach().numpy()).any():
print('RE {}'.format(RE))
print('KL {}'.format(KL))
error = 1
if np.isnan(KL.detach().numpy()).any():
print('RE {}'.format(RE))
print('KL {}'.format(KL))
error = 1
if error == 1:
raise ValueError()
# Final ELBO
if reduction == 'sum':
loss = -(RE - KL).sum()
else:
loss = -(RE - KL).mean()
return loss
def sample(self, batch_size=64):
# step 1
z_2 = torch.randn(batch_size, self.L)
# step 2
h_1 = self.nn_z_1(z_2)
mu_1, log_var_1 = torch.chunk(h_1, 2, dim=1)
# step 3
z_1 = self.reparameterization(mu_1, log_var_1)
# step 4
h_d = self.nn_x(z_1)
if self.likelihood_type == 'categorical':
b = batch_size
d = h_d.shape[1]//self.num_vals
h_d = h_d.view(b, d, self.num_vals)
mu_d = torch.softmax(h_d, 2)
# step 5
p = mu_d.view(-1, self.num_vals)
x_new = torch.multinomial(p, num_samples=1).view(b, d)
elif self.likelihood_type == 'bernoulli':
mu_d = torch.sigmoid(h_d)
# step 5
x_new = torch.bernoulli(mu_d)
return x_new
# + [markdown] id="vUoPkTmrMVnx"
# ## Evaluation and Training functions
# + [markdown] id="JvwmRoi7MVto"
# **Evaluation step, sampling and curve plotting**
# + id="JHx4RIqDLZe9"
def evaluation(test_loader, name=None, model_best=None, epoch=None):
# EVALUATION
if model_best is None:
# load best performing model
model_best = torch.load(name + '.model')
model_best.eval()
loss = 0.
N = 0.
for indx_batch, test_batch in enumerate(test_loader):
loss_t = model_best.forward(test_batch, reduction='sum')
loss = loss + loss_t.item()
N = N + test_batch.shape[0]
loss = loss / N
if epoch is None:
print(f'FINAL LOSS: nll={loss}')
else:
print(f'Epoch: {epoch}, val nll={loss}')
return loss
def samples_real(name, test_loader):
# REAL-------
num_x = 4
num_y = 4
x = next(iter(test_loader)).detach().numpy()
fig, ax = plt.subplots(num_x, num_y)
for i, ax in enumerate(ax.flatten()):
plottable_image = np.reshape(x[i], (8, 8))
ax.imshow(plottable_image, cmap='gray')
ax.axis('off')
plt.savefig(name+'_real_images.pdf', bbox_inches='tight')
plt.close()
def samples_generated(name, data_loader, extra_name=''):
x = next(iter(data_loader)).detach().numpy()
# GENERATIONS-------
model_best = torch.load(name + '.model')
model_best.eval()
num_x = 4
num_y = 4
x = model_best.sample(batch_size=num_x * num_y)
x = x.detach().numpy()
fig, ax = plt.subplots(num_x, num_y)
for i, ax in enumerate(ax.flatten()):
plottable_image = np.reshape(x[i], (8, 8))
ax.imshow(plottable_image, cmap='gray')
ax.axis('off')
plt.savefig(name + '_generated_images' + extra_name + '.pdf', bbox_inches='tight')
plt.close()
def plot_curve(name, nll_val):
plt.plot(np.arange(len(nll_val)), nll_val, linewidth='3')
plt.xlabel('epochs')
plt.ylabel('nll')
plt.savefig(name + '_nll_val_curve.pdf', bbox_inches='tight')
plt.close()
# + [markdown] id="umU3VYKzMbDt"
# **Training step**
# + id="NxkUZ1xVLbm_"
def training(name, max_patience, num_epochs, model, optimizer, training_loader, val_loader):
nll_val = []
best_nll = 1000.
patience = 0
# Main loop
for e in range(num_epochs):
# TRAINING
model.train()
for indx_batch, batch in enumerate(training_loader):
loss = model.forward(batch)
optimizer.zero_grad()
loss.backward(retain_graph=True)
optimizer.step()
# Validation
loss_val = evaluation(val_loader, model_best=model, epoch=e)
nll_val.append(loss_val) # save for plotting
if e == 0:
print('saved!')
torch.save(model, name + '.model')
best_nll = loss_val
else:
if loss_val < best_nll:
print('saved!')
torch.save(model, name + '.model')
best_nll = loss_val
patience = 0
samples_generated(name, val_loader, extra_name="_epoch_" + str(e))
else:
patience = patience + 1
if patience > max_patience:
break
nll_val = np.asarray(nll_val)
return nll_val
# + [markdown] id="0BXJ9dN0MinB"
# ## Experiments
# + [markdown] id="KsF7f-Q-MkWu"
# **Initialize datasets**
# -
transforms = None
# + id="fqZKMNM0LdQ1"
train_data = Digits(mode='train', transforms=transforms)
val_data = Digits(mode='val', transforms=transforms)
test_data = Digits(mode='test', transforms=transforms)
training_loader = DataLoader(train_data, batch_size=64, shuffle=True)
val_loader = DataLoader(val_data, batch_size=64, shuffle=False)
test_loader = DataLoader(test_data, batch_size=64, shuffle=False)
# + [markdown] id="6lEKUznpMns7"
# **Hyperparameters**
# + id="ANQo7LrGLjIN"
D = 64 # input dimension
L = 8 # number of latents
M = 256 # the number of neurons in scale (s) and translation (t) nets
lr = 1e-3 # learning rate
num_epochs = 1000 # max. number of epochs
max_patience = 20 # an early stopping is used, if training doesn't improve for longer than 20 epochs, it is stopped
# + [markdown] id="-7APXeunMrDh"
# **Creating a folder for results**
# + id="bjSUn1eWLkWm"
name = 'vae_hierarchical' + '_' + str(L)
result_dir ='results/' + name + '/'
if not(os.path.exists(result_dir)):
os.mkdir(result_dir)
# + [markdown] id="Hpwm6LWUMulQ"
# **Initializing the model: (i) determining the conditional likelihood distribution, (ii) defininig encoder and decoder nets, and a prior**
# + colab={"base_uri": "https://localhost:8080/"} id="FrnNsCqQLmK3" outputId="5f0cf2b1-0a96-4f5c-da9e-f78f909a5259"
likelihood_type = 'categorical'
if likelihood_type == 'categorical':
num_vals = 17
elif likelihood_type == 'bernoulli':
num_vals = 1
nn_r_1 = nn.Sequential(nn.Linear(D, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, M), nn.GELU()
)
nn_r_2 = nn.Sequential(nn.Linear(M, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, M), nn.LeakyReLU()
)
nn_delta_1 = nn.Sequential(nn.Linear(M, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, 2 * (L * 2)),
)
nn_delta_2 = nn.Sequential(nn.Linear(M, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, 2 * L),
)
nn_z_1 = nn.Sequential(nn.Linear(L, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, 2 * (L * 2))
)
nn_x = nn.Sequential(nn.Linear(L * 2, M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M,M), GELU(),
nn.BatchNorm1d(M),
nn.Linear(M, D * num_vals)
)
# Eventually, we initialize the full model
model = HierarchicalVAE(nn_r_1, nn_r_2, nn_delta_1, nn_delta_2, nn_z_1, nn_x, num_vals=num_vals, D=D, L=L, likelihood_type=likelihood_type)
# + [markdown] id="3SzTemY3NSxO"
# **Optimizer - here we use Adamax**
# + id="R9TZtLVtLoWc"
# OPTIMIZER
optimizer = torch.optim.Adamax([p for p in model.parameters() if p.requires_grad == True], lr=lr)
# + [markdown] id="dNf__W_ONVHA"
# **Training loop**
# + colab={"base_uri": "https://localhost:8080/"} id="KhqHgluGLqIC" outputId="c52fa1e4-3376-4bff-9f87-6f03613c4e42"
# Training procedure
nll_val = training(name=result_dir + name, max_patience=max_patience, num_epochs=num_epochs, model=model, optimizer=optimizer,
training_loader=training_loader, val_loader=val_loader)
# + [markdown] id="-3XTxgEcNXfp"
# **The final evaluation**
# + colab={"base_uri": "https://localhost:8080/"} id="okK1mV_-LrRU" outputId="4664693f-742d-4453-94cf-d051d2efa9be"
test_loss = evaluation(name=result_dir + name, test_loader=test_loader)
f = open(result_dir + name + '_test_loss.txt', "w")
f.write(str(test_loss))
f.close()
samples_real(result_dir + name, test_loader)
plot_curve(result_dir + name, nll_val)
samples_generated(result_dir + name, test_loader, extra_name='FINAL')
|
vaes/vae_hierarchical_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TensorFlow MNIST Tutorial
import tensorflow as tf
import numpy as np
import datetime
import matplotlib.pyplot as plt
# %matplotlib inline
# Lets load MNIST data and check random image
mnist = input_data.read_data_sets('../../datasets/MNIST', one_hot=True)
batch = mnist.train.next_batch(1)
sample_image = batch[0].reshape([28, 28])
print('Label %s' % np.argmax(batch[1]))
plt.imshow(sample_image, cmap='Greys')
# ## Helper functions
#
# Helper functions for building CNN
# +
def weight_variable(shape):
initial = tf.truncated_normal(shape, stddev=0.1)
return tf.Variable(initial)
def bias_variable(shape):
initial = tf.constant(0.1, shape=shape)
return tf.Variable(initial)
def conv2d(x, W):
return tf.nn.conv2d(x, W, strides=[1, 1, 1, 1], padding='SAME')
def max_pool_2x2(x):
return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')
# -
# ## Build regression model
#
# Lets start we simple regression model
# +
# Place holders for data
x_input = tf.placeholder(tf.float32, shape=[None, 784])
y_input = tf.placeholder(tf.float32, shape=[None, 10])
# First convolution layer
x_image = tf.reshape(x_input, [-1, 28, 28, 1])
W_conv1 = weight_variable([5, 5, 1, 32])
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
# Second convolution layer
W_conv2 = weight_variable([5, 5, 32, 64])
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)
# First dense layer
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
W_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# Dropout
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)
# Output layer
W_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])
y_conv = tf.matmul(h_fc1_drop, W_fc2) + b_fc2
# -
# ## Train
# +
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=y_input, logits=y_conv))
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
correct_prediction = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_input, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(20000):
batch = mnist.train.next_batch(50)
if i % 1000 == 0:
train_accuracy = accuracy.eval(
feed_dict={x_input: batch[0], y_input: batch[1], keep_prob: 1.0})
print('step %d, training accuracy %g' % (i, train_accuracy))
train_step.run(feed_dict={x_input: batch[0], y_input: batch[1], keep_prob: 0.5})
print('test accuracy %g' % accuracy.eval(feed_dict={
x_input: mnist.test.images, y_input: mnist.test.labels, keep_prob: 1.0}))
|
notebook/Tutorials/tf-mnist.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import matplotlib.pyplot as plt
import csv
file = open('./train.csv', encoding='utf-8')
reader = csv.reader(file)
next(reader)
X = np.ndarray((0, 2))
y = np.ndarray((0,))
y_mapping = {'Bob': 0, 'Kate': 1, 'Mark': 2, 'Sue': 3}
i = 0
for row in reader:
i += 1
X = np.vstack((X, np.array(row[0:2])))
y = np.append(y, y_mapping[row[2]])
X = X.astype(np.float)
y = y.astype(np.float)
file.close()
plt.scatter(X[y == 0, 0], X[y == 0, 1], label='Bob', c='red', linewidths=0)
plt.scatter(
X[y == 1, 0], X[y == 1, 1], label='Kate', c='lightgreen', linewidths=0)
plt.scatter(
X[y == 2, 0], X[y == 2, 1], label='Mark', c='lightblue', linewidths=0)
plt.scatter(X[y == 3, 0], X[y == 3, 1], label='Sue', c='purple', linewidths=0)
plt.show()
# +
from IPython.display import Image
from IPython.display import display
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score
from sklearn.model_selection import GridSearchCV
pipe1 = Pipeline([['sc', StandardScaler()], ['clf', LogisticRegression(C=10, random_state=0)]])
pipe2 = Pipeline([['clf', DecisionTreeClassifier(max_depth=3, random_state=0)]])
pipe3 = Pipeline([['sc', StandardScaler()], ['clf', KNeighborsClassifier(n_neighbors=5)]])
# +
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=3)
clf_labels = ['LogisticRegression', 'DecisionTree', 'KNN']
print('[Individual]')
for pipe, label in zip([pipe1, pipe2, pipe3], clf_labels):
scores = cross_val_score(estimator=pipe, X=X_train, y=y_train, cv=10, scoring='accuracy')
print('%s: %.3f (+/- %.3f)' % (label, scores.mean(), scores.std()))
# +
from sklearn.ensemble import VotingClassifier
import itertools
print('[Voting]')
best_vt, best_w, best_score = None, (), -1
for a, b, c in list(itertools.permutations(range(0,3))): # try some weight combination
clf = VotingClassifier(estimators=[('lr', pipe1), ('dt', pipe2), ('knn', pipe3)],
voting='soft', weights=[a,b,c])
scores = cross_val_score(estimator=clf, X=X_train, y=y_train, cv=10, scoring='accuracy')
print('%s: %.3f (+/- %.3f)' % ((a,b,c), scores.mean(), scores.std()))
if best_score < scores.mean():
best_vt, best_w, best_score = clf, (a, b, c), scores.mean()
print('\nBest %s: %.3f' % (best_w, best_score))
# +
from sklearn.ensemble import BaggingClassifier
tree = DecisionTreeClassifier(criterion='entropy', max_depth=None, random_state=0)
bag = BaggingClassifier(base_estimator=tree, n_estimators=500,
max_samples=0.7, bootstrap=True,
max_features=1.0, bootstrap_features=False,
n_jobs=1, random_state=1)
# +
from sklearn.metrics import accuracy_score
# single DecisionTree
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('[DecisionTree] accuracy-train = %.3f, accuracy-test = %.3f' % (tree_train, tree_test))
# Bagging
bag = bag.fit(X_train, y_train)
y_train_pred = bag.predict(X_train)
y_test_pred = bag.predict(X_test)
bag_train = accuracy_score(y_train, y_train_pred)
bag_test = accuracy_score(y_test, y_test_pred)
print('[Bagging] auc-train = %.3f, auc-test = %.3f' % (bag_train, bag_test))
# +
from sklearn.ensemble import AdaBoostClassifier
tree = DecisionTreeClassifier(criterion='entropy', max_depth=1)
# single decision tree
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('[DecisionTree] accuracy-train = %.3f, accuracy-test = %.3f' %
(tree_train, tree_test))
# adaboost
ada = AdaBoostClassifier(base_estimator=tree, n_estimators=500)
ada = ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train, y_train_pred)
ada_test = accuracy_score(y_test, y_test_pred)
print('[AdaBoost] accuracy-train = %.3f, accuracy-test = %.3f' %
(ada_train, ada_test))
# +
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
print("Decision Tree nested CV grid search")
outer_cv = KFold(n_splits=5, shuffle=True, random_state=1)
inner_cv = KFold(n_splits=10, shuffle=True, random_state=1)
outer_scores = []
tree = DecisionTreeClassifier(criterion='entropy')
# outer folds
for i, (train_idx, test_idx) in enumerate(outer_cv.split(X, y)):
print('[Outer fold %d/5]' % (i + 1))
X_train, X_test = X[train_idx], X[test_idx]
y_train, y_test = y[train_idx], y[test_idx]
# hyperparameter tuning by grid search CV
param_grid = {'max_depth':[1,3,5,7,9]}
gs = GridSearchCV(estimator=tree, param_grid=param_grid,
scoring='accuracy', cv=inner_cv)
gs.fit(X_train, y_train)
best_clf = gs.best_estimator_
best_clf.fit(X_train, y_train)
outer_scores.append(best_clf.score(X_test, y_test))
print('Test accuracy: %.2f (n_neighbors=%d selected by inner 10-fold CV)' %
(outer_scores[i], gs.best_params_['max_depth']))
print('\nTest accuracy: %.2f (5x10 nested CV)' % np.mean(outer_scores))
# +
tree = DecisionTreeClassifier(criterion='entropy', max_depth=7)
# single decision tree
tree = tree.fit(X_train, y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train, y_train_pred)
tree_test = accuracy_score(y_test, y_test_pred)
print('[DecisionTree] accuracy-train = %.3f, accuracy-test = %.3f' %
(tree_train, tree_test))
# adaboost
ada = AdaBoostClassifier(base_estimator=tree, n_estimators=500)
ada = ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train, y_train_pred)
ada_test = accuracy_score(y_test, y_test_pred)
print('[AdaBoost] accuracy-train = %.3f, accuracy-test = %.3f' %
(ada_train, ada_test))
# +
outer_cv = KFold(n_splits=5, shuffle=True, random_state=1)
inner_cv = KFold(n_splits=10, shuffle=True, random_state=1)
print("KNN nested CV grid search")
outer_scores = []
# outer folds
for i, (train_idx, test_idx) in enumerate(outer_cv.split(X, y)):
print('[Outer fold %d/5]' % (i + 1))
X_train, X_test = X[train_idx], X[test_idx]
y_train, y_test = y[train_idx], y[test_idx]
pipe = Pipeline([['sc', StandardScaler()], ['clf', KNeighborsClassifier()]])
# hyperparameter tuning by grid search CV
param_grid = {'clf__n_neighbors':[1, 2, 3]}
gs = GridSearchCV(estimator=pipe, param_grid=param_grid,
scoring='accuracy', cv=inner_cv)
gs.fit(X_train, y_train)
best_clf = gs.best_estimator_
best_clf.fit(X_train, y_train)
outer_scores.append(best_clf.score(X_test, y_test))
print('Test accuracy: %.2f (n_neighbors=%d selected by inner 10-fold CV)' %
(outer_scores[i], gs.best_params_['clf__n_neighbors']))
print('\nTest accuracy: %.2f (5x10 nested CV)' % np.mean(outer_scores))
# +
from sklearn.svm import SVC
print("SVC nested CV grid search")
outer_cv = KFold(n_splits=5, shuffle=True, random_state=1)
inner_cv = KFold(n_splits=10, shuffle=True, random_state=1)
param_C = [0.1, 1.0, 10.0, 100.0, 1000.0, 10000.0]
param_gamma = [0.00001, 0.0001, 0.001, 0.01, 0.1, 1.0]
for i, (train_idx, test_idx) in enumerate(outer_cv.split(X, y)):
print('[Outer fold %d/5]' % (i + 1))
X_train, X_test = X[train_idx], X[test_idx]
y_train, y_test = y[train_idx], y[test_idx]
pipe = Pipeline([('scl', StandardScaler()),
('clf', SVC(random_state=0))])
# hyperparameter tuning by grid search CV
param_grid = [{'clf__C': param_C,
'clf__gamma': param_gamma,
'clf__kernel': ['rbf']}]
gs = GridSearchCV(
estimator=pipe, param_grid=param_grid, scoring='accuracy', cv=inner_cv)
gs.fit(X_train, y_train)
best_clf = gs.best_estimator_
best_clf.fit(X_train, y_train)
outer_scores.append(best_clf.score(X_test, y_test))
print('Test accuracy: %.2f (C=%d gamma=%6f selected by inner 10-fold CV)' %
(outer_scores[i], gs.best_params_['clf__C'],gs.best_params_['clf__gamma']))
print('\nTest accuracy: %.2f (5x10 nested CV)' % np.mean(outer_scores))
# +
pipe_svc_b = Pipeline([['sc', StandardScaler()],
['bag', BaggingClassifier(base_estimator=SVC(random_state=0,kernel='rbf',C=10000,gamma=0.1),
max_samples=0.7,n_estimators=500,random_state=0)]])
pipe_svc_b.fit(X_train,y_train)
y_train_pred = pipe_svc_b.predict(X_train)
y_pred = pipe_svc_b.predict(X_test)
svc_train = accuracy_score(y_train, y_train_pred)
svc_val = accuracy_score(y_test,y_pred)
print('[bagging with SVM] accuracy-train = %.3f, accuracy-test = %.3f' % (svc_train, svc_val))
# +
ada_tree = AdaBoostClassifier(base_estimator=DecisionTreeClassifier(criterion='entropy', max_depth=7), n_estimators=500)
pipe_knn = Pipeline([['sc', StandardScaler()], ['knn', KNeighborsClassifier(n_neighbors=3)]])
pipe_svc_b = Pipeline([['sc', StandardScaler()],
['bag', BaggingClassifier(base_estimator=SVC(random_state=0,kernel='rbf',C=10000,gamma=0.1),
max_samples=0.7,n_estimators=100,random_state=0)]])
clf_labels = ['Adaboost(decision tree base)', 'KNN', 'SVC w/ bagging']
print('[Individual]')
for pipe, label in zip([ada_tree, pipe_knn, pipe_svc_b], clf_labels):
scores = cross_val_score(estimator=pipe, X=X_train, y=y_train, cv=10, scoring='accuracy')
print('%s: %.3f (+/- %.3f)' % (label, scores.mean(), scores.std()))
# -
print('[Voting]')
best_vt, best_w, best_score = None, (), -1
for a, b, c in list(itertools.permutations(range(0, 3))): # try some weight combination
clf = VotingClassifier(
estimators=[('adaboost', ada_tree), ('knn', pipe_knn), ('svm', pipe_svc_b)],voting='soft',weights=[a, b, c])
scores = cross_val_score(estimator=clf, X=X, y=y, cv=10)
print('%s: %.3f (+/- %.3f)' % ((a, b, c), scores.mean(), scores.std()))
if best_score < scores.mean():
best_vt, best_w, best_score = clf, (a, b, c), scores.mean()
[Voting]
(0, 1, 2): 0.870 (+/- 0.033)
(0, 2, 1): 0.866 (+/- 0.041)
(1, 0, 2): 0.878 (+/- 0.034)
(1, 2, 0): 0.844 (+/- 0.037)
(2, 0, 1): 0.837 (+/- 0.040)
(2, 1, 0): 0.832 (+/- 0.039)
|
week_8/Lab08.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
a = [[1,5,6], [3,5,1], [9,4,0]]
arr = np.array(a)
arr
def triclusterToChromosome(self, tricluster, problem):
chromosome = problem.generateEmptyIndividual()
lL = self.data.shape[0]
lC = self.data.shape[1]
# lT = self.data.shape[2]
lIR= self.data.shape[0]
for row in tricluster.rows:
chromosome.features[row] = 1
for col in tricluster.cols:
chromosome.features[lL + col] = 1
# for time in tricluster.times:
# chromosome.features[lL+lC+time] = 1
for invRow in tricluster.inverted_rows:
chromosome.features[lL+lC+invRow] = 1
return(chromosome)
|
examples/Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
"""
Create a list called numbers containing 1 through 15, then perforin the following tasks:
a) Use the built-in function filter with a lambda to select only numbers’ even elements. Create a new list containing rhe result.
b) Use the built-in function map with a lambda to square the values of numbers’ elements. Create a new list containing the result.
c) Filter numbers’ even elements, then map them to their squares. Create a new list containing the result.
"""
# + tags=[]
numbers = list(range(1,16))
print(list(filter(lambda i: i%2==0, numbers)))
print(list(map(lambda i: i**2, numbers)))
print(list(map(lambda i: i**2,filter(lambda i: i%2==0, numbers))))
|
filtering, mapping, lambda.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=[]
# <title><h1><b>Web Scraping e Análise Exploratória</b></h1></title>
# -
# Neste projeto vou realizar:
# 1. Extração de dados de uma página web;
# 2. Análise exploratória dos dados.
# Os dados serão extraídos do portal de vagas Indeed: https://br.indeed.com/
# Na Etapa 1, utilizarei a biblioteca Selenium, seu WebDriver Chromium e, a biblioteca Beautiful Soup.
#
# Selenium - é um conjunto de ferramentas para automação de navegadores web, utilizado principalmente para testes automatizados de software. Aqui, utilizarei para automatizar alguns cliques na página com o intuito de acessar os dados.
#
# Beautiful Soup - é uma biblioteca para extração de dados de documentos HTML e XML.
# Na Etapa 2, realizo análise exploratória dos dados obtidos, que neste momento serão recuperados de um arquivo csv. Nesta análise, além do sumário estatístico e das visualizações de dados, utilizo também o pacote NLTK para quebrar as sentenças de texto em palavras, para então fazer o processamento e análise de textos.
#
# NLTK - Natural Language Toolkit é uma plataforma de ferramentas para trabalhar com dados de linguagem natural e processamento de texto.
# ## Setup
# ### Importação dos Pacotes
from bs4 import BeautifulSoup
from selenium import webdriver
import pandas
from matplotlib import pyplot
import nltk
from nltk import word_tokenize
from nltk.corpus import stopwords
from collections import Counter
# ### Outras Configurações
# +
# Download do Chromium Driver
# https://sites.google.com/a/chromium.org/chromedriver/home
# Salve o Chromium na mesma pasta do projeto
# -
# ## Etapa 1 - Web Scraping
# ### Acessar a página e obter o documento HTML
URL = "https://br.indeed.com/jobs?q=ciencia+de+dados&l=brasil"
# Instanciar uma sessão do Chrome WebDriver
driver = webdriver.Chrome("./chromedriver")
# Navegar para Url
driver.get(URL)
driver.implicitly_wait(15)
# Aceitar os cookies da página
aceitar_cookies = driver.find_element_by_id("onetrust-accept-btn-handler")
aceitar_cookies.click()
# Obtendo o documento
jobsearch = driver.find_elements_by_class_name("result")
# ### Realizando a extração do dados
# +
jobs = pandas.DataFrame(columns = ['title', 'company', 'salary', 'location', 'remote', 'jobdesc'])
for jobcard in jobsearch:
html_doc = jobcard.get_attribute('innerHTML')
soup = BeautifulSoup(html_doc, 'html.parser')
try: title = soup.find("h2", class_="title").a.text.replace('\n', '')
except: title = ' '
try: company = soup.find(class_="company").string.replace('\n', ' ').strip()
except: company = 'não informada'
try: salary = soup.find(class_="salaryText").string.replace('\n', ' ').strip()
except: salary = ' '
try: location = soup.find(class_="location").string
except: location = ' '
try: remote = soup.find(class_="remote").string
except: remote = ' '
# Clica no card para acessar o sumário do job
jobcard.find_element_by_class_name('summary').click()
jobdesc = driver.find_element_by_id('vjs-desc').text.replace('\n', ' ').strip()
jobs = jobs.append(
{
'title': title,
'company': company,
'salary': salary,
'location': location,
'remote': remote,
'jobdesc': jobdesc
},
ignore_index = True)
# -
# Uma pré visualização
jobs.head()
# Vamos salvar os dados obtidos em um arquivo CSV
jobs.to_csv("./jobs.csv", encoding="utf-8", index=False)
# ## Etapa 2 - Análise Exploratória
# A partir deste ponto vou recuperar os dados do arquivo csv que criei, e não mais acessar a página para buscar estes dados.
# Importar os dados do arquivo CSV
mass = pandas.read_csv("./jobs.csv", encoding="utf-8").fillna('')
# Uma pré visualização
mass.head()
# Aqui, faço a contagem de quais empresas possuem mais vagas
company_jobs = mass.groupby('company').count()['title'].sort_values(ascending=False)
company_jobs
company_jobs.plot(kind='bar', figsize=(12,4), rot=60, color="blue")
pyplot.show()
# Aqui, faço a contagem de quais localidades possuem mais vagas
location_jobs = mass.groupby('location').count()['title'].sort_values(ascending=False)
location_jobs
location_jobs.plot(kind='bar', figsize=(12,4), rot=60, color="green")
pyplot.show()
# Agora vou analisar os dados de texto, aplicando um processamento de linguagem natural
# Função de limpeza dos dados
def limpa_dados(desc):
desc = word_tokenize(desc)
desc = [word.lower() for word in desc if word.isalpha() and len(word) > 2]
desc = [word for word in desc if word not in stop_words_pt]
desc = [word for word in desc if word not in stop_words_en]
return desc
# Vamos definir a lista de stopwords em português
stop_words_pt = stopwords.words('portuguese')
# Vamos definir a lista de stopwords em inglês
stop_words_en = stopwords.words('english')
# Aplicamos a função de limpeza a coluna de descrição da vaga
desc_jobs = mass["jobdesc"].apply(limpa_dados)
# Visualiza os dados
desc_jobs.head()
# Vamos sumarizar as descrições das vagas
desc_itens = desc_jobs.apply(Counter).sum().items()
# Ordenamos o resultado
desc_itens = sorted(desc_itens, key = lambda kv: kv[1], reverse = True)
# Criamos uma série
desc_itens_serie = pandas.Series({k: v for k, v in desc_itens})
# Visualizamos os dados, com a contagem de palavras mais frequentes nas descrições das vagas
desc_itens_serie.head(15)
# Vamos criar uma lista de skills e pesquisar como eles aparecem nas descrições das vagas
# Usamoas as palavras em minúsculo pois ao limpar os dados convertemos tudo para minúsculo
skills = ["python", "statistics", "analytics", "business", "projects", "develop"]
# Filtramos a série com os skills
filtro_skills = desc_itens_serie.filter(items = skills)
# Criamos o plot
filtro_skills.plot(kind = 'bar', figsize = (18,6), color = "brown", rot = 30)
|
WebScraping/proj_20210616_Scraping_and_Analyses/.ipynb_checkpoints/scraping_analyse-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="4hHdaXD02QFo"
x=20
# + colab={"base_uri": "https://localhost:8080/"} id="fjUmUwc32WhI" outputId="c373bac8-6de0-4c94-e091-9e41a86ba0f7"
if x>10 :
print("x>10")
# + id="hZJOI0FI2riw"
x=20
# + colab={"base_uri": "https://localhost:8080/"} id="_Gk_LxHH3HVH" outputId="7a916f9f-e734-48b3-ad45-b32e65cdb4c8"
if x>10 :
print("x is greater than 10")
if x<10 :
print ("x is less than 10 ")
if x==10 :
print("x is equal to 10 ")
# + colab={"base_uri": "https://localhost:8080/"} id="t_Rio6_U3lZn" outputId="cb428fac-eb54-4950-ef19-6cc901a178c4"
x=int(input(" enter your marks "))
if x<100 :
print("failed")
if x==100 :
print("just pass")
if x>100 :
print("passed")
# + colab={"base_uri": "https://localhost:8080/"} id="hIzmep7a-rjZ" outputId="ee1c75d4-b377-4184-ce2a-84c8719241cd"
inc.ome= int(input("enter your taxable income in india"))
if income<=250000 :
print("tax not needed")
if income>=250000 :
print(income*10/100)
# + id="zGDkaPj0FZ71"
|
PythonBasics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# [Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# # Nonlinear Filtering
#format the book
# %matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
# ## Introduction
#
# The Kalman filter that we have developed uses linear equations, and so the filter can only handle linear problems. But the world is nonlinear, and so the classic filter that we have been studying to this point can have very limited utility.
#
# There can be nonlinearity in the process model. Suppose we want to track an object falling through the atmosphere. The acceleration of the object depends on the drag it encounters. Drag depends on air density, and the air density decreases with altitude. In one dimension this can be modelled with the nonlinear differential equation
#
# $$\ddot x = \frac{0.0034ge^{-x/22000}\dot x^2}{2\beta} - g$$
#
# A second source of nonlinearity comes from the measurements. For example, radars measure the slant range to an object, and we are typically interested in the aircraft's position over the ground. We invoke Pythagoras and get the nonlinear equation:
#
# $$x=\sqrt{\mathtt{slant}^2 - \mathtt{altitude}^2}$$
#
# These facts were not lost on the early adopters of the Kalman filter. Soon after Dr. Kalman published his paper people began working on how to extend the Kalman filter for nonlinear problems.
#
# It is almost true to state that the only equation anyone knows how to solve is $\mathbf{Ax}=\mathbf{b}$. We only really know how to do linear algebra. I can give you any linear set of equations and you can either solve it or prove that it has no solution.
#
# Anyone with formal education in math or physics has spent years learning various analytic ways to solve integrals, differential equations and so on. Yet even trivial physical systems produce equations that cannot be solved analytically. I can take an equation that you are able to integrate, insert a $\log$ term, and render it insolvable. This leads to jokes about physicists stating "assume a spherical cow on a frictionless surface in a vacuum...". Without making extreme simplifications most physical problems do not have analytic solutions.
#
# How do we do things like model airflow over an aircraft in a computer, or predict weather, or track missiles with a Kalman filter? We retreat to what we know: $\mathbf{Ax}=\mathbf{b}$. We find some way to linearize the problem, turning it into a set of linear equations, and then use linear algebra software packages to compute an approximate solution.
#
# Linearizing a nonlinear problem gives us inexact answers, and in a recursive algorithm like a Kalman filter or weather tracking system these small errors can sometimes reinforce each other at each step, quickly causing the algorithm to spit out nonsense.
#
# What we are about to embark upon is a difficult problem. There is not one obvious, correct, mathematically optimal solution anymore. We will be using approximations, we will be introducing errors into our computations, and we will forever be battling filters that *diverge*, that is, filters whose numerical errors overwhelm the solution.
#
# In the remainder of this short chapter I will illustrate the specific problems the nonlinear Kalman filter faces. You can only design a filter after understanding the particular problems the nonlinearity in your problem causes. Subsequent chapters will then teach you how to design and implement different kinds of nonlinear filters.
# ## The Problem with Nonlinearity
#
# The mathematics of the Kalman filter is beautiful in part due to the Gaussian equation being so special. It is nonlinear, but when we add and multiply them we get another Gaussian as a result. That is very rare. $\sin{x}*\sin{y}$ does not yield a $\sin$ as an output.
#
# What I mean by linearity may be obvious, but there are some subtleties. The mathematical requirements are twofold:
#
# * additivity: $f(x+y) = f(x) + f(y)$
# * homogeneity: $f(ax) = af(x)$
#
#
# This leads us to say that a linear system is defined as a system whose output is linearly proportional to the sum of all its inputs. A consequence of this is that to be linear if the input is zero than the output must also be zero. Consider an audio amp - if I sing into a microphone, and you start talking, the output should be the sum of our voices (input) scaled by the amplifier gain. But if the amplifier outputs a nonzero signal such as a hum for a zero input the additive relationship no longer holds. This is because linearity requires that $amp(voice) = amp(voice + 0)$. This clearly should give the same output, but if amp(0) is nonzero, then
#
# $$
# \begin{aligned}
# amp(voice) &= amp(voice + 0) \\
# &= amp(voice) + amp(0) \\
# &= amp(voice) + non\_zero\_value
# \end{aligned}
# $$
#
# which is clearly nonsense. Hence, an apparently linear equation such as
#
# $$L(f(t)) = f(t) + 1$$
#
# is not linear because $L(0) = 1$. Be careful!
# ## An Intuitive Look at the Problem
#
# I particularly like the following way of looking at the problem, which I am borrowing from <NAME>'s *Optimal State Estimation* [[1]](#[1]). Consider a tracking problem where we get the range and bearing to a target, and we want to track its position. The reported distance is 50 km, and the reported angle is 90$^\circ$. Assume that the errors in both range and angle are distributed in a Gaussian manner. Given an infinite number of measurements what is the expected value of the position?
#
# I have been recommending using intuition to gain insight, so let's see how it fares for this problem. We might reason that since the mean of the range will be 50 km, and the mean of the angle will be 90$^\circ$, that the answer will be x=0 km, y=50 km.
#
# Let's plot that and find out. Here are 3000 points plotted with a normal distribution of the distance of 0.4 km, and the angle having a normal distribution of 0.35 radians. We compute the average of the all of the positions, and display it as a star. Our intuition is displayed with a large circle.
# +
import numpy as np
from numpy.random import randn
import matplotlib.pyplot as plt
N = 5000
a = np.pi/2. + (randn(N) * 0.35)
r = 50.0 + (randn(N) * 0.4)
xs = r * np.cos(a)
ys = r * np.sin(a)
plt.scatter(xs, ys, label='Sensor', color='k',
alpha=0.4, marker='.', s=1)
xmean, ymean = sum(xs) / N, sum(ys) / N
plt.scatter(0, 50, c='k', marker='o', s=200, label='Intuition')
plt.scatter(xmean, ymean, c='r', marker='*', s=200, label='Mean')
plt.axis('equal')
plt.legend();
# -
# We can see that out intuition failed us because the nonlinearity of the problem forced all of the errors to be biased in one direction. This bias, over many iterations, can cause the Kalman filter to diverge. Even if it doesn't diverge the solution will not be optimal. Linear approximations applied to nonlinear problems yields inaccurate results.
# ## The Effect of Nonlinear Functions on Gaussians
#
# Gaussians are not closed under an arbitrary nonlinear function. Recall the equations of the Kalman filter - at each evolution we pass the Gaussian representing the state through the process function to get the Gaussian at time $k$. Our process function was always linear, so the output was always another Gaussian. Let's look at that on a graph. I will take an arbitrary Gaussian and pass it through the function $f(x) = 2x + 1$ and plot the result. We know how to do this analytically, but let's use sampling. I will generate 500,000 points with a normal distribution, pass them through $f(x)$, and plot the results. I do it this way because the next example will be nonlinear, and we will have no way to compute this analytically.
# +
from numpy.random import normal
data = normal(loc=0., scale=1., size=500000)
plt.hist(2*data + 1, 1000);
# -
# This is an unsurprising result. The result of passing the Gaussian through $f(x)=2x+1$ is another Gaussian centered around 1. Let's look at the input, nonlinear function, and output at once.
# +
from kf_book.book_plots import set_figsize, figsize
from kf_book.nonlinear_plots import plot_nonlinear_func
def g1(x):
return 2*x+1
plot_nonlinear_func(data, g1)
# -
# > I explain how to plot Gaussians, and much more, in the Notebook *Computing_and_Plotting_PDFs* in the
# Supporting_Notebooks folder. You can also read it online [here](https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb)[1]
#
# The plot labeled 'Input' is the histogram of the original data. This is passed through the function $f(x)=2x+1$ which is displayed in the chart on the bottom left. The red lines shows how one value, $x=0$ is passed through the function. Each value from input is passed through in the same way to the output function on the right. For the output I computed the mean by taking the average of all the points, and drew the results with the dotted blue line. A solid blue line shows the actual mean for the point $x=0$. The output looks like a Gaussian, and is in fact a Gaussian. We can see that the variance in the output is larger than the variance in the input, and the mean has been shifted from 0 to 1, which is what we would expect given the transfer function $f(x)=2x+1$ The $2x$ affects the variance, and the $+1$ shifts the mean The computed mean, represented by the dotted blue line, is nearly equal to the actual mean. If we used more points in our computation we could get arbitrarily close to the actual value.
#
# Now let's look at a nonlinear function and see how it affects the probability distribution.
# +
def g2(x):
return (np.cos(3*(x/2 + 0.7))) * np.sin(0.3*x) - 1.6*x
plot_nonlinear_func(data, g2)
# -
# This result may be somewhat surprising to you. The function looks "fairly" linear, but the probability distribution of the output is completely different from a Gaussian. Recall the equations for multiplying two univariate Gaussians:
#
# $$\begin{aligned}
# \mu &=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2} \\
# \sigma &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}}
# \end{aligned}$$
#
# These equations do not hold for non-Gaussians, and certainly do not hold for the probability distribution shown in the 'Output' chart above.
#
# Here's another way to look at the same data as scatter plots.
N = 30000
plt.subplot(121)
plt.scatter(data[:N], range(N), alpha=.1, s=1.5)
plt.title('Input')
plt.subplot(122)
plt.title('Output')
plt.scatter(g2(data[:N]), range(N), alpha=.1, s=1.5);
# The original data is clearly Gaussian, but the data passed through `g2(x)` is no longer normally distributed. There is a thick band near -3, and the points are unequally distributed on either side of the band. If you compare this to the pdf labelled 'output' in the previous chart you should be able to see how the pdf shape matches the distribution of `g(data)`.
#
# Think of what this implies for the Kalman filter algorithm of the previous chapter. All of the equations assume that a Gaussian passed through the process function results in another Gaussian. If this is not true then all of the assumptions and guarantees of the Kalman filter do not hold. Let's look at what happens when we pass the output back through the function again, simulating the next step time step of the Kalman filter.
y = g2(data)
plot_nonlinear_func(y, g2)
# As you can see the probability function is further distorted from the original Gaussian. However, the graph is still somewhat symmetric around x=0, let's see what the mean is.
print('input mean, variance: %.4f, %.4f' %
(np.mean(data), np.var(data)))
print('output mean, variance: %.4f, %.4f' %
(np.mean(y), np.var(y)))
# Let's compare that to the linear function that passes through (-2,3) and (2,-3), which is very close to the nonlinear function we have plotted. Using the equation of a line we have
#
# $$m=\frac{-3-3}{2-(-2)}=-1.5$$
# +
def g3(x):
return -1.5 * x
plot_nonlinear_func(data, g3)
out = g3(data)
print('output mean, variance: %.4f, %.4f' %
(np.mean(out), np.var(out)))
# -
# Although the shapes of the output are very different, the mean and variance of each are almost the same. This may lead us to reasoning that perhaps we can ignore this problem if the nonlinear equation is 'close to' linear. To test that, we can iterate several times and then compare the results.
# +
out = g3(data)
out2 = g2(data)
for i in range(10):
out = g3(out)
out2 = g2(out2)
print('linear output mean, variance: %.4f, %.4f' %
(np.average(out), np.std(out)**2))
print('nonlinear output mean, variance: %.4f, %.4f' %
(np.average(out2), np.std(out2)**2))
# -
# Unfortunately the nonlinear version is not stable. It drifted significantly from the mean of 0, and the variance is half an order of magnitude larger.
#
# I minimized the issue by using a function that is quite close to a straight line. What happens if the function is $y(x)=-x^2$?
# +
def g3(x):
return -x*x
data = normal(loc=1, scale=1, size=500000)
plot_nonlinear_func(data, g3)
# -
# Despite the curve being smooth and reasonably straight at $x=1$ the probability distribution of the output doesn't look anything like a Gaussian and the computed mean of the output is quite different than the value computed directly. This is not an unusual function - a ballistic object moves in a parabola, and this is the sort of nonlinearity your filter will need to handle. If you recall we've tried to track a ball and failed miserably. This graph should give you insight into why the filter performed so poorly.
# ## A 2D Example
# It is hard to look at probability distributions and reason about what will happen in a filter. So let's think about tracking an aircraft with radar. The estimate may have a covariance that looks like this:
# +
import kf_book.nonlinear_internal as nonlinear_internal
nonlinear_internal.plot1()
# -
# What happens when we try to linearize this problem? The radar gives us a range to the aircraft. Suppose the radar is directly under the aircraft (x=10) and the next measurement states that the aircraft is 3 miles away (y=3). The positions that could match that measurement form a circle with radius 3 miles, like so.
nonlinear_internal.plot2()
# We can see by inspection that the probable position of the aircraft is somewhere near x=11.4, y=2.7 because that is where the covariance ellipse and range measurement overlap. But the range measurement is nonlinear so we have to linearize it. We haven't covered this material yet, but the Extended Kalman filter will linearize at the last position of the aircraft - (10,2). At x=10 the range measurement has y=3, and so we linearize at that point.
nonlinear_internal.plot3()
# Now we have a linear representation of the problem (literally a straight line) which we can solve. Unfortunately you can see that the intersection of the line and the covariance ellipse is a long way from the actual aircraft position.
nonlinear_internal.plot4()
# That sort of error often leads to disastrous results. The error in this estimate is large. But in the next innovation of the filter that very bad estimate will be used to linearize the next radar measurement, so the next estimate is likely to be markedly worse than this one. After only a few iterations the Kalman filter will diverge, and start producing results that have no correspondence to reality.
#
# This covariance ellipse spans miles. I exaggerated the size to illustrate the difficulties of highly nonlinear systems. In real radar tracking problems the nonlinearity is usually not that bad, but the errors will still accumulate. Other systems you might work with could have this amount of nonlinearity - this was not an exaggeration only to make a point. You will always be battling divergence when working with nonlinear systems.
# ## The Algorithms
# You may be impatient to solve a specific problem, and wondering which filter to use. I will quickly survey the options. The subsequent chapters are somewhat independent of each other, and you can fruitfully skip around, though I recommend reading linearly if you truly want to master all of the material.
#
# The workhorses of nonlinear filters are the *linearized Kalman filter* and *extended Kalman filter* (EKF). These two techniques were invented shortly after Kalman published his paper and they have been the main techniques used since then. The flight software in airplanes, the GPS in your car or phone almost certainly use one of these techniques.
#
# However, these techniques are extremely demanding. The EKF linearizes the differential equations at one point, which requires you to find a solution to a matrix of partial derivatives (a Jacobian). This can be difficult or impossible to do analytically. If impossible, you have to use numerical techniques to find the Jacobian, but this is expensive computationally and introduces more error into the system. Finally, if the problem is quite nonlinear the linearization leads to a lot of error being introduced in each step, and the filters frequently diverge. You can not throw some equations into some arbitrary solver and expect to to get good results. It's a difficult field for professionals. I note that most Kalman filtering textbooks merely gloss over the EKF despite it being the most frequently used technique in real world applications.
#
# Recently the field has been changing in exciting ways. First, computing power has grown to the point that we can use techniques that were once beyond the ability of a supercomputer. These use *Monte Carlo* techniques - the computer generates thousands to tens of thousands of random points and tests all of them against the measurements. It then probabilistically kills or duplicates points based on how well they match the measurements. A point far away from the measurement is unlikely to be retained, whereas a point very close is quite likely to be retained. After a few iterations there is a clump of particles closely tracking your object, and a sparse cloud of points where there is no object.
#
# This has two benefits. First, the algorithm is robust even for extremely nonlinear problems. Second, the algorithm can track arbitrarily many objects at once - some particles will match the behavior of one object, and other particles will match other objects. So this technique is often used to track automobile traffic, people in crowds, and so on.
#
# The costs should be clear. It is computationally expensive to test tens of thousands of points for every step in the filter. But modern CPUs are very fast, and this is a good problem for GPUs because the part of the algorithm is parallelizable. Another cost is that the answer is not mathematical. With a Kalman filter my covariance matrix gives me important information about the amount of error in the estimate. The particle filter does not give me a rigorous way to compute this. Finally, the output of the filter is a cloud of points; I then have to figure out how to interpret it. Usually you will be doing something like taking the mean and standard deviations of the points, but this is a difficult problem. There are still many points that do not 'belong' to a tracked object, so you first have to run some sort of clustering algorithm to first find the points that seem to be tracking an object, and then you need another algorithm to produce a state estimate from those points. None of this is intractable, but it is all quite computationally expensive.
#
#
# Finally, we have a new algorithm called the *unscented Kalman filter* (UKF). It does not require you to find analytic solutions to nonlinear equations, and yet almost always performs better than the EKF. It does well with nonlinear problems - problems where the EKF has significant difficulties. Designing the filter is extremely easy. Some will say the jury is still out on the UKF, but to my mind the UKF is superior in almost every way to the EKF. I suggest that the UKF should be the starting point for any implementation, especially if you are not a Kalman filter professional with a graduate degree in control theory. The main downside is that the UKF can be a few times slower than the EKF, but this really depends on whether the EKF solves the Jacobian analytically or numerically. If numerically the UKF is almost certainly faster. It has not been proven (and probably it cannot be proven) that the UKF always yields more accurate results than the EKF. In practice it almost always does, often significantly so. It is very easy to understand and implement, and I strongly suggest this filter as your starting point.
# ## Summary
# The world is nonlinear, but we only really know how to solve linear problems. This introduces significant difficulties for Kalman filters. We've looked at how nonlinearity affects filtering in 3 different but equivalent ways, and I've given you a brief summary of the major appoaches: the linearized Kalman filter, the extended Kalman filter, the Unscented Kalman filter, and the particle filter.
#
# Until recently the linearized Kalman filter and EKF have been the standard way to solve these problems. They are very difficult to understand and use, and they are also potentially very unstable.
#
# Recent developments have offered what are to my mind superior approaches. The UKF dispenses with the need to find solutions to partial differential equations, yet it is also usually more accurate than the EKF. It is easy to use and understand. I can get a basic UKF going in a few minutes by using FilterPy. The particle filter dispenses with mathematical modeling completely in favor of a Monte Carlo technique of generating a random cloud of thousands of points. It runs slowly, but it can solve otherwise intractable problems with relative ease.
#
# I get more email about the EKF than anything else; I suspect that this is because most treatments in books, papers, and on the internet use the EKF. If your interest is in mastering the field of course you will want to learn about the EKF. But if you are just trying to get good results I point you to the UKF and particle filter first. They are much easier to implement, understand, and use, and they are typically far more stable than the EKF.
#
# Some will quibble with that advice. A lot of recent publications are devoted to a comparison of the EKF, UKF, and perhaps a few other choices for a given problem. Do you not need to perform a similar comparison for your problem? If you are sending a rocket to Mars then of course you do. You will be balancing issues such as accuracy, round off errors, divergence, mathematical proof of correctness, and the computational effort required. I can't imagine not knowing the EKF intimately.
#
# On the other hand the UKF works spectacularly! I use it at work for real world applications. I mostly haven't even tried to implement an EKF for these applications because I can verify that the UKF is working fine. Is it possible that I might eke out another 0.2% of performance from the EKF in certain situations? Sure! Do I care? No! I completely understand the UKF implementation, it is easy to test and verify, I can pass the code to others and be confident that they can understand and modify it, and I am not a masochist that wants to battle difficult equations when I already have a working solution. If the UKF or particle filters start to perform poorly for some problem then I will turn to other techniques, but not before then. And realistically, the UKF usually provides substantially better performance than the EKF over a wide range of problems and conditions. If "really good" is good enough I'm going to spend my time working on other problems.
#
# I'm belaboring this point because in most textbooks the EKF is given center stage, and the UKF is either not mentioned at all or just given a 2 page gloss that leaves you completely unprepared to use the filter. The UKF is still relatively new, and it takes time to write new editions of books. At the time many books were written the UKF was either not discovered yet, or it was just an unproven but promising curiosity. But as I am writing this now, the UKF has had enormous success, and it needs to be in your toolkit. That is what I will spend most of my effort trying to teach you.
# ## References
#
# <A name="[1]">[1]</A> https://github.com/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/Supporting_Notebooks/Computing_and_plotting_PDFs.ipynb
|
09-Nonlinear-Filtering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# `파이토치(PyTorch) 기본 익히기 <intro.html>`_ ||
# `빠른 시작 <quickstart_tutorial.html>`_ ||
# `텐서(Tensor) <tensorqs_tutorial.html>`_ ||
# `Dataset과 Dataloader <data_tutorial.html>`_ ||
# `변형(Transform) <transforms_tutorial.html>`_ ||
# `신경망 모델 구성하기 <buildmodel_tutorial.html>`_ ||
# `Autograd <autogradqs_tutorial.html>`_ ||
# **최적화(Optimization)** ||
# `모델 저장하고 불러오기 <saveloadrun_tutorial.html>`_
#
# 모델 매개변수 최적화하기
# ==========================================================================
#
# 이제 모델과 데이터가 준비되었으니, 데이터에 매개변수를 최적화하여 모델을 학습하고, 검증하고, 테스트할 차례입니다.
# 모델을 학습하는 과정은 반복적인 과정을 거칩니다; (*에폭(epoch)*\ 이라고 부르는) 각 반복 단계에서 모델은 출력을 추측하고,
# 추측과 정답 사이의 오류(\ *손실(loss)*\ )를 계산하고, (`이전 장 <autograd_tutorial.html>`_\ 에서 본 것처럼)
# 매개변수에 대한 오류의 도함수(derivative)를 수집한 뒤, 경사하강법을 사용하여 이 파라매터들을 **최적화(optimize)**\ 합니다.
# 이 과정에 대한 자세한 설명은 `3Blue1Brown의 역전파 <https://www.youtube.com/watch?v=tIeHLnjs5U8>`__ 영상을 참고하세요.
#
# 기본(Pre-requisite) 코드
# ------------------------------------------------------------------------------------------
# 이전 장인 `Dataset과 DataLoader <data_tutorial.html>`_\ 와 `신경망 모델 구성하기 <buildmodel_tutorial.html>`_\ 에서
# 코드를 기져왔습니다.
#
# +
import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor, Lambda
training_data = datasets.FashionMNIST(
root="data",
train=True,
download=True,
transform=ToTensor()
)
test_data = datasets.FashionMNIST(
root="data",
train=False,
download=True,
transform=ToTensor()
)
train_dataloader = DataLoader(training_data, batch_size=64)
test_dataloader = DataLoader(test_data, batch_size=64)
class NeuralNetwork(nn.Module):
def __init__(self):
super(NeuralNetwork, self).__init__()
self.flatten = nn.Flatten()
self.linear_relu_stack = nn.Sequential(
nn.Linear(28*28, 512),
nn.ReLU(),
nn.Linear(512, 512),
nn.ReLU(),
nn.Linear(512, 10),
)
def forward(self, x):
x = self.flatten(x)
logits = self.linear_relu_stack(x)
return logits
model = NeuralNetwork()
# -
# 하이퍼파라매터(Hyperparameter)
# ------------------------------------------------------------------------------------------
#
# 하이퍼파라매터(Hyperparameter)는 모델 최적화 과정을 제어할 수 있는 조절 가능한 매개변수입니다.
# 서로 다른 하이퍼파라매터 값은 모델 학습과 수렴율(convergence rate)에 영향을 미칠 수 있습니다.
# (하이퍼파라매터 튜닝(tuning)에 대해 `더 알아보기 <https://tutorials.pytorch.kr/beginner/hyperparameter_tuning_tutorial.html>`__)
#
# 학습 시에는 다음과 같은 하이퍼파라매터를 정의합니다:
# - **에폭(epoch) 수** - 데이터셋을 반복하는 횟수
# - **배치 크기(batch size)** - 매개변수가 갱신되기 전 신경망을 통해 전파된 데이터 샘플의 수
# - **학습률(learning rate)** - 각 배치/에폭에서 모델의 매개변수를 조절하는 비율. 값이 작을수록 학습 속도가 느려지고, 값이 크면 학습 중 예측할 수 없는 동작이 발생할 수 있습니다.
#
#
#
learning_rate = 1e-3
batch_size = 64
epochs = 5
# 최적화 단계(Optimization Loop)
# ------------------------------------------------------------------------------------------
#
# 하이퍼파라매터를 설정한 뒤에는 최적화 단계를 통해 모델을 학습하고 최적화할 수 있습니다.
# 최적화 단계의 각 반복(iteration)을 **에폭**\ 이라고 부릅니다.
#
# 하나의 에폭은 다음 두 부분으로 구성됩니다:
# - **학습 단계(train loop)** - 학습용 데이터셋을 반복(iterate)하고 최적의 매개변수로 수렴합니다.
# - **검증/테스트 단계(validation/test loop)** - 모델 성능이 개선되고 있는지를 확인하기 위해 테스트 데이터셋을 반복(iterate)합니다.
#
# 학습 단계(training loop)에서 일어나는 몇 가지 개념들을 간략히 살펴보겠습니다. 최적화 단계(optimization loop)를 보려면
# `full-impl-label` 부분으로 건너뛰시면 됩니다.
#
# 손실 함수(loss function)
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#
# 학습용 데이터를 제공하면, 학습되지 않은 신경망은 정답을 제공하지 않을 확률이 높습니다. **손실 함수(loss function)**\ 는
# 획득한 결과와 실제 값 사이의 틀린 정도(degree of dissimilarity)를 측정하며, 학습 중에 이 값을 최소화하려고 합니다.
# 주어진 데이터 샘플을 입력으로 계산한 예측과 정답(label)을 비교하여 손실(loss)을 계산합니다.
#
# 일반적인 손실함수에는 회귀 문제(regression task)에 사용하는 `nn.MSELoss <https://pytorch.org/docs/stable/generated/torch.nn.MSELoss.html#torch.nn.MSELoss>`_\ (평균 제곱 오차(MSE; Mean Square Error))나
# 분류(classification)에 사용하는 `nn.NLLLoss <https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss>`_ (음의 로그 우도(Negative Log Likelihood)),
# 그리고 ``nn.LogSoftmax``\ 와 ``nn.NLLLoss``\ 를 합친 `nn.CrossEntropyLoss <https://pytorch.org/docs/stable/generated/torch.nn.CrossEntropyLoss.html#torch.nn.CrossEntropyLoss>`_
# 등이 있습니다.
#
# 모델의 출력 로짓(logit)을 ``nn.CrossEntropyLoss``\ 에 전달하여 로짓(logit)을 정규화하고 예측 오류를 계산합니다.
#
#
# 손실 함수를 초기화합니다.
loss_fn = nn.CrossEntropyLoss()
# 옵티마이저(Optimizer)
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#
# 최적화는 각 학습 단계에서 모델의 오류를 줄이기 위해 모델 매개변수를 조정하는 과정입니다. **최적화 알고리즘**\ 은 이 과정이 수행되는 방식(여기에서는 확률적 경사하강법(SGD; Stochastic Gradient Descent))을 정의합니다.
# 모든 최적화 절차(logic)는 ``optimizer`` 객체에 캡슐화(encapsulate)됩니다. 여기서는 SGD 옵티마이저를 사용하고 있으며, PyTorch에는 ADAM이나 RMSProp과 같은 다른 종류의 모델과 데이터에서 더 잘 동작하는
# `다양한 옵티마이저 <https://pytorch.org/docs/stable/optim.html>`_\ 가 있습니다.
#
# 학습하려는 모델의 매개변수와 학습률(learning rate) 하이퍼파라매터를 등록하여 옵티마이저를 초기화합니다.
#
#
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
# 학습 단계(loop)에서 최적화는 세단계로 이뤄집니다:
# * ``optimizer.zero_grad()``\ 를 호출하여 모델 매개변수의 변화도를 재설정합니다. 기본적으로 변화도는 더해지기(add up) 때문에 중복 계산을 막기 위해 반복할 때마다 명시적으로 0으로 설정합니다.
# * ``loss.backwards()``\ 를 호출하여 예측 손실(prediction loss)을 역전파합니다. PyTorch는 각 매개변수에 대한 손실의 변화도를 저장합니다.
# * 변화도를 계산한 뒤에는 ``optimizer.step()``\ 을 호출하여 역전파 단계에서 수집된 변화도로 매개변수를 조정합니다.
#
#
#
# 전체 구현
# ------------------------------------------------------------------------------------------
#
# 최적화 코드를 반복하여 수행하는 ``train_loop``\ 와 테스트 데이터로 모델의 성능을 측정하는 ``test_loop``\ 를 정의하였습니다.
#
#
# +
def train_loop(dataloader, model, loss_fn, optimizer):
size = len(dataloader.dataset)
for batch, (X, y) in enumerate(dataloader):
# 예측(prediction)과 손실(loss) 계산
pred = model(X)
loss = loss_fn(pred, y)
# 역전파
optimizer.zero_grad()
loss.backward()
optimizer.step()
if batch % 100 == 0:
loss, current = loss.item(), batch * len(X)
print(f"loss: {loss:>7f} [{current:>5d}/{size:>5d}]")
def test_loop(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
test_loss, correct = 0, 0
with torch.no_grad():
for X, y in dataloader:
pred = model(X)
test_loss += loss_fn(pred, y).item()
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches
correct /= size
print(f"Test Error: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
# -
# 손실 함수와 옵티마이저를 초기화하고 ``train_loop``\ 와 ``test_loop``\ 에 전달합니다.
# 모델의 성능 향상을 알아보기 위해 자유롭게 에폭(epoch) 수를 증가시켜 볼 수 있습니다.
#
#
# +
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
epochs = 10
for t in range(epochs):
print(f"Epoch {t+1}\n-------------------------------")
train_loop(train_dataloader, model, loss_fn, optimizer)
test_loop(test_dataloader, model, loss_fn)
print("Done!")
# -
# 더 읽어보기
# ------------------------------------------------------------------------------------------
# - `Loss Functions <https://pytorch.org/docs/stable/nn.html#loss-functions>`_
# - `torch.optim <https://pytorch.org/docs/stable/optim.html>`_
# - `Warmstart Training a Model <https://tutorials.pytorch.kr/recipes/recipes/warmstarting_model_using_parameters_from_a_different_model.html>`_
#
#
#
|
docs/_downloads/a085acf892f1c661e019dd5c0fc402fd/optimization_tutorial.ipynb
|
% -*- coding: utf-8 -*-
% ---
% jupyter:
% jupytext:
% text_representation:
% extension: .m
% format_name: light
% format_version: '1.5'
% jupytext_version: 1.14.4
% kernelspec:
% display_name: Octave
% language: octave
% name: octave
% ---
% # Chapitre 0.1 - Prise en main
%
% Vous vous trouvez actuellement sur la première page d'un ensemble de notebook dédié au rattrapage du cours sur le langage Matlab. Cet ensemble peut être vu comme un "cahier de vacances" et ne fera l'objet d'aucun cours officiels. Ainsi, nous profitons de cet espace pour vous expliquer comment vous allez procéder. Chaque notion importante sera représentée par un notebook. L'objectif est de suivre pas à pas chacun des notebook pour vous mettre à niveau.
%
% ## Comment ça marche ?
%
%
% Les notebooks sont une suite de cellules. Vous avez plusieurs types de cellules :
%
% - Les cellules "codes" : permettent de saisir du code et de l'interpréter (le langage change en fonction du noyau actif);
% - Les cellules "markdown" : permettent de saisir du texte;
%
% Les cellules "markdown" n'ont pas d'intérêt pour vous, celles que nous vous demanderons de remplir seront principalement des cellules "codes". Pour exécuter le code présent dans la fenêtre de commande, il vous suffit de cliquer sur l'onglet "Run" situer dans la barre des tâches juste au-dessus.
%
% 
%
% Vous pouvez également utiliser le raccourci "Shift+Entree". Essayez d'exécuter le code présent dans la fenêtre suivante :
2+2
% Comme vous pouvez le constater, vous avez un retour console qui dit : "ans = 4". Ainsi, vous comprenez que la réponse à votre question est 4. Vous pouvez par ailleurs effectuer des opérations plus compliquées, lancez les lignes de commandes suivantes :
x = 0:2*pi/100:2*pi;
plot(x,sin(x))
xlabel('X axis name')
ylabel('Y axis name')
legend('sinus x')
% **NB :** Lorsque vous voyez d'écrit **In [ \* ]** sur la partie gauche d'une cellule de code, c'est que le notebook est en train d'exécuter du code. Il est possible que votre code fasse une boucle infini lors des exercices, et donc que le notebook soit bloqué. Pour stopper l'exécution d'une cellule "code", il faut que vous alliez dans l'onglet *"Kernel -> Restart"*. Si jamais cela ne fonctionne pas, vous pouvez faire un *"Kernel -> Restart & Clear Output"*, les résultats précédents seront alors effacés.
%
% Bien entendu, il vous est possible de modifier n'importe quelles cellules du document (à l'exception de celles non protégées par nos soins). En cas de problème, il vous suffit juste de recharger la page ou de relançer le lien binder. Vous repartirez alors de 0, ce qui pose évidemment le problème de la sauvegarde de votre progression que nous verrons dans le prochain Notebook.
% ## Différence Octave Matlab ?
%
% Pour être exact, le langage de programmation que vous utilisez n'est pas Matlab, il s'agit du logiciel Octave son équivalent OpenSource de Matlab, vous pouvez bien entendu l'installer sur votre machine en suivant le lien en [1].
% Il faut savoir que la différence entre Matlab et Octave est très mince, surtout pour la base du langage. Les différences interviendront notamment lorsque vous aurez à prendre en main le System Development Kit de Matlab (l'interface graphique Matlab). Pour cela, nous proposons dans les cours en complément un rapide tour sur l'interface graphique Matlab.
% En espérant que ce format puisse vous convenir et que vous puissiez progresser tranquillement ! N'hésitez pas à faire remonter les éventuels problèmes, les questions ou des oublis en envoyant un mail à l'adresse suivante : <<EMAIL>>. Pour participer à la création, consultez le chapitre 0.3.
|
Chapitre 0 - Guide d'utilisation/Chapitre 0.1 - Prise en main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img style="float: left;;" src='../Imagenes/iteso.jpg' width="50" height="100"/></a>
#
# # <center> <font color= #000047> Módulo II: Aprendizaje No supervizado: Kmeans
#
# ## Introducción
#
# K-Means es un algoritmo no supervisado de Clustering. Se utiliza cuando tenemos un montón de datos sin etiquetar. El objetivo de este algoritmo es el de encontrar “K” grupos (clusters) entre los datos crudos.
# **¿Cómo funciona?**
# El algoritmo trabaja iterativamente para asignar a cada “muestra” uno de los “K” grupos basado en sus características. Son agrupados en base a la similitud de sus features (las columnas). Como resultado de ejecutar el algoritmo tendremos:
#
#
# > Los `“centroids”` de cada grupo que serán unas “coordenadas” de cada uno de los K conjuntos qu>e se utilizarán para poder etiquetar nuevas muestras.
#
# > `Etiquetas` para el conjunto de datos de entrenamiento. Cada etiqueta perteneciente a uno de los K grupos formados.
#
# Los grupos se van definiendo de manera “orgánica”, es decir que se va ajustando su posición en cada iteración del proceso, hasta que converge el algoritmo. Una vez hallados los centroids deberemos analizarlos para ver cuales son sus características únicas, frente a la de los otros grupos. Estos grupos son las etiquetas que genera el algoritmo.
# ## Casos de Uso de K-Means
# Algunos casos de uso son:
#
# > **Segmentación por Comportamiento:** relacionar el carrito de compras de un usuario, sus tiempos de acción e información del perfil.
#
# > **Categorización de Inventario:** agrupar productos por actividad en sus ventas
# Detectar anomalías o actividades sospechosas: según el comportamiento en una web reconocer un troll -o un bot- de un usuario normal
#
# ## Algoritmo K-means
# El algoritmo utiliza una proceso **iterativo** en el que se van ajustando los grupos para producir el resultado final. Para ejecutar el algoritmo deberemos pasar como entrada el `conjunto de datos` y un valor de `K`. El conjunto de datos serán las características o features para cada punto. Las posiciones iniciales de los K centroids serán asignadas de manera aleatoria de cualquier punto del conjunto de datos de entrada. Luego se itera en dos pasos:
#
# > 1.- **Paso de asignación** $argmin_{c_i \in C} dist(c_i, x)^2$
#
# > 2.- **Paso de actualización del Centroide** En este paso los centroides de cada grupo son recalculados. Esto se hace tomando una media de todos los puntos asignados en el paso anterior. $c_i = \frac{1}{|s_i|}\sum_{x_i \in s_i} x_i$
#
# El algoritmo itera entre estos pasos hasta cumplir un criterio de detención:
# * si no hay cambios en los puntos asignados a los grupos,
# * o si la suma de las distancias se minimiza,
# * o se alcanza un número máximo de iteraciones.
#
# El algoritmo converge a un resultado que puede ser el óptimo local, por lo que será conveniente volver a ejecutar más de una vez con puntos iniciales aleatorios para confirmar si hay una salida mejor.
#
#
# ## Criterios de Elección de Grupos
#
# > Criterio del codo
#
# > Criterio del gradiente
# ## Ejemplo 1
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
#%% Generar datos aleatorios
#%% Aplicar el algoritmo Kmeans
#%% Criterio de selección
#%% Definiendo el número de grupos optimos
#%% Aplicar el algoritmo Kmeans con 2 grupos
# ## Ejemplo 2
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd
# +
#%% Leer los datos
#%% drop de columnas time y class
#%% Estandarizar los datos
# -
#%% Aplicar el algoritmo de clustering
# Aplicar el criterio de selección del codo
# plot de las inercias
#%% Ejecutar el algoritmo con k = 11
#%% Obtener los centroides
# +
# Eligiendo 3 variables para plotear
# Creating figure
# Creating plot
# -
# ## Ejemplo 2
#
# Tiene un centro comercial de supermercado y, a través de las tarjetas de membresía, tiene algunos datos básicos sobre sus clientes, como ID de cliente, edad, sexo, ingresos anuales y puntaje de gastos.
#
# Usted es el propietario del centro comercial y desea comprender a sus clientes. Desea saber quienes clientes pueden ser clientes objetivos para que el equipo de marketing planifique una campaña.
#
# **¿Quiénes son sus clientes objetivo con los que puede iniciar la estrategia de marketing?**
#
# Para responder la pregunta anterior necesitamos realizar lo siguiente:
#
# >1.- data quality report dqr
#
# >2.- Limpieza de datos
#
# >3.- Analisis exploratorio de datos EDA
#
# >4.- Aplicar el criterio de selección de grupos -> el número opt de grupos
#
# >5.- Aplican kmeans con el num opt de grupos
#
# >6.- Conclusiones o comentarios acerca de los resultados
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from CDIN import CDIN as cd
#%% Leer los datos
#%% 1.- data quality report dqr
# +
#%% 2.- Limpieza de datos
# -
#%% 3.- EDA
## 1er insight
# +
## 2do insight (rango de edades)
# -
#%% 4.- Aplicar el criterio de selección de grupos
# +
# Visualizando el criterio del codo, se observa que con 5 grupos
# se puede obtener una buena clasificación
# -
#%% 5.- Aplican kmeans con el num opt de grupos
#%% 6.- Conclusiones o comentarios acerca de los resultados
# Visualizar todos los clusters
# ## Actividad 3
#
# Agrupar usuarios Twitter de acuerdo a su personalidad con K-means.
#
# >1.- data quality report dqr
#
# >2.- Limpieza de datos
#
# >3.- Analisis exploratorio de datos EDA (obtener al menos 3 insights)
#
# >4.- Aplicar el criterio de selección de grupos -> el número opt de grupos
#
# >5.- Aplican kmeans con el num opt de grupos
#
# >6.- Graficar, concluir y comentar acerca de los resultados.
#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sb
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin_min
from mpl_toolkits.mplot3d import Axes3D
#Leer datos
## tabla de información estadística que nos provee Pandas dataframe:
# dqr del dataframe
# El archivo contiene diferenciadas 9 categorías -actividades laborales- que son:
#
# 1-> Actor/actriz
#
# 2->Cantante
#
# 3->Modelo
#
# 4->Tv, series
#
# 5->Radio
#
# 6->Tecnología
#
# 7->Deportes
#
# 8->Politica
#
# 9->Escritor
#
## Histogramas
# Las variables que nos pueden servir para la agrupación pueden ser `["op","ex","ag"]`
# +
# Crear la figura
# Plotear
# -
# ## Elección de los grupos óptimos
#
# Vamos a hallar el valor de K mediante el criterio del codo
#
# +
# Criterio del codo
# plot de las inercias
# -
# Realmente la curva es bastante “suave”. Considero a 5 como un buen número para K. Según vuestro criterio podría ser otro.
#Aplicar kmeans con el num opt de grupos
# ### Clasificar nuevas muestras
#
# podemos agrupar y etiquetar nuevos usuarios twitter con sus características y clasificarlos.
# +
## Obtener el grupo de una nueva muestra
# -
# # Ejemplo 4
# +
## Importatr digitos
# +
# Cluster por Kmeans
# -
|
Modulo2/Code/2.3.-Aprendizaje No supervizado Kmeans.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Treasury Bond Fund Simulator
#
# This is based off of [longinvest's post on bogleheads][1]. He implemented it all in a spreadsheet (which is linked in the thread).
#
# The goal is to calculate returns of a simulated bond fund given a bunch of interest rates. By having returns (instead of rates) we can perform backtesting with historical data.
#
# Keep in mind that this a simulation so it has some simplifying things that will make it slightly different from the real world. This is not a comprehensive list:
#
# * It assumes no transaction costs. This is mostly truish for Treasuries, though.
# * It assumes an extremely liquid marketplace where there is no margin when selling. This is mostly truish for Treasuries, as well.
# * Because bonds are only rolled once a year, [the duration of the fund shifts a bit][2].
# * Real funds [shift their durations all the time][3], even if only by small amounts. Our simulated shifts and their actual shifts are unlikely to line up exactly.
# * All interest is reinvested rather than being paid out. This actually works in our favor, since total returns are what we care about for backtesting anyway.
#
# First we need to import some libraries....
#
# [1]: https://www.bogleheads.org/forum/viewtopic.php?f=10&t=179425
# [2]: https://www.bogleheads.org/forum/viewtopic.php?f=10&t=179425&start=100#p2998433
# [3]: https://www.bogleheads.org/forum/viewtopic.php?f=10&t=179425&start=100#p2998031
# + deletable=true editable=true
import numpy
from collections import deque
import pandas
import math
# + [markdown] deletable=true editable=true
# # Simulating the Bond Fund
# Simulating the bond fund is conceptually straightforward.
#
# You have a ladder of bonds, one for each year. Something like this:
#
# deque([Maturity: 1 | Yield: 5.00% | Face Value: $50.00,
# Maturity: 2 | Yield: 5.00% | Face Value: $52.50,
# Maturity: 3 | Yield: 5.00% | Face Value: $55.12,
# Maturity: 4 | Yield: 5.00% | Face Value: $57.88,
# Maturity: 5 | Yield: 5.00% | Face Value: $60.78,
# Maturity: 6 | Yield: 5.00% | Face Value: $63.81,
# Maturity: 7 | Yield: 5.00% | Face Value: $67.00,
# Maturity: 8 | Yield: 5.00% | Face Value: $70.36,
# Maturity: 9 | Yield: 5.00% | Face Value: $73.87])
#
# Every year three things will happen:
#
# 1. All of the bonds will pay out their cash coupon. This is based on their yield and their face value.
# 1. When a bond gets "too young" (I'll come back to this) we sell it. The exact price will also be explained later. Every year you will sell one bond of the youngest maturity.
# 1. Now you've got a pile of cash and one fewer bond. Use the cash to buy a new bond of the longest maturity.
#
# ## Youngest maturity & oldest maturity
#
# When you create the bond fund, you can select the youngest maturity and the oldest maturity. Say that you want fund where the oldest bond has a 10-year maturity and the youngest bond has a 2-year maturity. As a shorthand, we'll call that a 10-2 fund. Every year a 2-year bond becomes a 1-year bond and will be sold and replaced with a brand new 10-year bond.
# + deletable=true editable=true
def iterate_fund(ladder, yield_curve, max_maturity):
reduce_maturity(ladder)
payments = get_payments(ladder)
sold_bond = ladder.popleft()
payments += sold_bond.value(yield_curve)
new_bond = Bond(payments, yield_curve[max_maturity-1], max_maturity)
ladder.append(new_bond)
# This happens *after* we sell the shortest bond and buy a new long one
# (at least, that's what longinvest does...)
nav = get_nav(ladder, yield_curve)
return (ladder, payments, nav)
def get_nav(ladder, rates):
return sum((b.value(rates) for b in ladder))
def get_payments(ladder):
return sum((b.gen_payment() for b in ladder))
def reduce_maturity(ladder):
for b in ladder:
b.maturity -= 1
return ladder
# + [markdown] deletable=true editable=true
# # Bond Mechanics
#
# A bond is just three things: a yield, a face value, and a maturity. If you called up your broker you would say, "I want to buy $100 of the 10-year Treasury that is yielding 3.2%." The maturity is 10-years; the face value is $100; and the yield is 3.2%.
#
# There are only two things you can do with a bond.
#
# ### Receive your payment
# Every year the bond will generate a payment -- a "coupon" in bond-speak. This is simply the **yield × face value**. Going back to the previous example, with a face value of $100 and a yield of 3.2%, every year you would get a payment of $3.20. (Not very impressive, admittedly.)
#
# ### Check the current value of the bond
# Bonds are designed to be held until their maturity. At that point you'll receive a payment for the face value. In our example, that would mean after holding the bond for 10 years you would get your full $100 back.
#
# But what if you wanted to sell the bond **before** maturity? That's (usually) possible but the exact price will depend on current rates. Say we want to sell our bond after 9 years. In essence, we have a 1-year bond that yields 3.2%. What if the current going yield for 1-year bonds was 2.5%? Then our bond will be worth a little more. If the current going yield for 1-year bonds is 4.2% then our bond will be worth a little less.
#
# Here's how it actually gets calculated:
#
# * take the current maturity remaining on the bond
# * take the current yield on bonds of that maturity
# * take the bond face value
#
# Then mix all of them into present value calculation: **pv(current yield, current maturity, face value)**. (The pv function is found in every spreadsheet and many calculators.)
#
# If the current yields are 2.5% and you have a face value of $100 then the present value is $97.56. This calculates the "exact" value of the bond. In the real world, someone would probably offer you slightly less, maybe $97.25, because they are offering you liquidity and taking some risk. For Treasuries that is a very small number, so ignoring it is probably good enough.
#
# ### From rates to returns
# At the end of the day, checking the current value of the bonds we hold is what we're trying to achieve. By adding up the value of all the bonds we hold we can figure out the Net Asset Value (NAV) of our fund. And then we compare that NAV over time. This is what we wanted: to be able to calculate the returns of a (simulated) bond fund.
# + deletable=true editable=true
class Bond:
def __init__(self, face_value, yield_pct, maturity):
self.face_value = face_value
self.yield_pct = yield_pct
self.maturity = maturity
def __repr__(self):
return ('Maturity: %d | Yield: %.2f%% | Face Value: $%.2f' % (self.maturity, self.yield_pct * 100, self.face_value))
def gen_payment(self):
return self.face_value * self.yield_pct
def value(self, rates):
value = numpy.pv(rates[self.maturity - 1], self.maturity, self.gen_payment(), self.face_value)
return -value
# + [markdown] deletable=true editable=true
# # Bootstrapping the Ladder
#
# Our bond ladder is straightforward enough. Sell the youngest bond and buy another one of the old bonds, using whatever cash we currently have available.
#
# But how do you get the ladder **started**? Where do those first bonds come from?
#
# Here's where things get a little bit unavoidably hacky. In the real world, you could slowly build up a ladder over time. For instance, buy 1/10th of the ladder every year for a decade. That takes, well, a decade. Which means there's an entire decade in our simulation with no results. We can shortcut that at the cost of a slight loss of accuracy for those first few years.
#
# If we're building a 10-2 ladder then we have 9 bonds (we don't have a bond with 1-year maturity, hence only 9 bonds). We bootstrap the ladder by buying all 9 instantly. That means they will all have the same yield -- whatever the current yield is.
# + deletable=true editable=true
def bootstrap(yield_curve, max_bonds, min_maturity):
bond_yield = yield_curve[max_bonds - 1]
ladder = deque()
starting_face_value = 50 # chosen arbitrarily (to match longinvest)
for i, j in zip(range(max_bonds), range(min_maturity, max_bonds+1)):
face_value = pow(1 + bond_yield, i) * starting_face_value
b = Bond(face_value, bond_yield, j)
ladder.append(b)
return ladder
bootstrap([.0532]*10, 10, 2)
# + [markdown] deletable=true editable=true
# Why do we have a different face value for each one? Why not just $50 for each? That's how we ensure that each rung of the ladder has equivalent value. If they each had a face value of $50 then the longer-term bonds would actually be worth less than the younger-term bonds. [For more explanation, refer to this post by longinvest][1].
#
# [1]: https://www.bogleheads.org/forum/viewtopic.php?p=3142416#p3142416
# + [markdown] deletable=true editable=true
# # Rates
#
# Now that we understand how the ladder works and how to bootstrap it, we need a source of rates in order to drive the engine.
#
# We have a number of sources of rate data.
#
# * Shiller provides 10 year yields on Treasuries, going back to 1871
# * Shiller provides 1 year interest rates, going back to 1871
# * [FRED provides 1-, 2-, 3-, 5-, 7-, 20-, and 30-year rates][1]. The data begins in the 1954-1977 range. When available, we prefer the FRED data over Shiller data.
# * NBER provides [historical data (1942-1962)][2] for 20-year rates
# * NBER provides [yields on long-term bonds (1919-1944)][3]
#
# So we will start by importing those. (I've spliced them all into a single CSV file to make importing things simpler; [you can get the CSV from github][4])
#
# [1]: https://fred.stlouisfed.org/categories/115
# [2]: https://fred.stlouisfed.org/series/M13058USM156NNBR
# [3]: https://fred.stlouisfed.org/series/M1333AUSM156NNBR
# [4]: https://github.com/hoostus/prime-harvesting/blob/master/bond_rates.csv
# + deletable=true editable=true
HISTORICAL_RATES = pandas.read_csv('bond_rates.csv', index_col=0)
HISTORICAL_RATES.head()
# + [markdown] deletable=true editable=true
# ## Rate interpolation
#
# For a given year, we will have **some** rate data. At the very least we will have the 1-year and 10-year rates; the data on those go back the further thanks to Shiller.
#
# However, we may *also* have other rate data from FRED.
#
# But we need to have rate data for every year on the yield curve. That is: 1-, 2-, 3-, 4-, 5-, 6-, 7-, 9-, and 10-year rates. When we don't have the data available we will perform linear interpolation from data we *do* have to fill in the gaps.
#
# So if we only have the 1- and 10-year data then we need to do a linear interpolation for the other 8 years. If we have 1-, 3-, and 10-year data then we do linear interpolation between the 1- and 3-year data to fill in the 2-year data. And we'll do linear interpolation between the 3- and 10-year data for the rest.
#
# ### Missing data & flat yield curve
#
# We can only do linear interpolation if we have two sets of data. We *always* have data for 1-year and 10-year rates, so we can fill in that part of the yield curve. But before the FRED data series of the mid-20th century we don't have any rates beyond 10 years. How do we fill that part of the rate yield curve when we don't have anything to interpolate?
#
# We don't interpolate: we just create a flat yield curve. That is, the 11-year rate is the same as the 10-year rate. And the 20-year rate is *also* the same as the 10-year rate. And the 30-year rate is **also** the same as the 10-year rate.
#
# This is obviously far from idea. So you should take with a large grain of salt any results before 1954. longinvest has [some comments on the longer terms starting approximately here][2].
#
# ### Potential problems with linear interpolation
#
# This linear interpolation is not perfect: it assumes that the yield curve is linear and that may not be the case. In particular, [look at this post from Fryxell][1] where he notes that before the 1920s the yield curve may have looked very different from what it did today.
#
# Still, trying to handle that is beyond the scope of this simulation. The more historical data (like those extra FRED data points) that we have, the less of this linear interpolation we need to do. That makes our post-1954 numbers better than the earlier numbers.
#
# [1]: https://www.bogleheads.org/forum/viewtopic.php?f=10&t=179425&start=100#p2973643
# [2]: https://www.bogleheads.org/forum/viewtopic.php?f=10&t=179425&start=100#p3013350
# + deletable=true editable=true
def splice_data(raw_rates, series):
# Start by loading the data we get from Shiller.
# This will always exist.
series.iloc[0] = raw_rates['1 year']
series.iloc[9] = raw_rates['10 year']
# Try to load any FRED rates.
series.iloc[1] = raw_rates['GS2']
series.iloc[2] = raw_rates['GS3']
series.iloc[4] = raw_rates['GS5']
series.iloc[6] = raw_rates['GS7']
series.iloc[19] = raw_rates['GS20']
series.iloc[29] = raw_rates['GS30']
def safe_add(series_index, rate_index):
# Don't overwrite any data we already have.
if math.isnan(series.iloc[series_index]):
series.iloc[series_index] = raw_rates[rate_index]
# These are in order of preference. This is try to use M13058 before
# trying to use M1333.
safe_add(19, 'M13058')
safe_add(19, 'M1333')
# See the note below under "Going Beyond 30 Years" about how longinvest got these numbers
safe_add(19, 'longinvest 20')
safe_add(29, 'longinvest 30')
def build_yield_curve(raw_rates, yield_curve_size=30):
s = pandas.Series(math.nan, index=numpy.arange(yield_curve_size))
# We use NaN to indicate "the data needs to be interpolated"
# We have a few different data series that we splice together.
splice_data(raw_rates, s)
def left_number(series, index):
""" Find the index of first number to the left """
if not math.isnan(series.iloc[index]):
return index
else:
return left_number(series, index-1)
def right_number(series, index):
""" Find the index of the first number to the right """
if not math.isnan(series.iloc[index]):
return index
else:
return right_number(series, index+1)
# now fill in the gaps with linear interpolation.
for i in range(yield_curve_size):
if math.isnan(s.iloc[i]):
# First, try to find any existing data on the left and right.
# We might not find any, for instance when we look beyond 10-years
# before we have FRED data.
try:
left = left_number(s, i)
except IndexError:
left = None
try:
right = right_number(s, i)
except IndexError:
right = None
if (left is None) and (right is None):
raise IndexError("Couldn't find any rate data to fill out the yield curve.")
if left is None:
# If we can't find any data to the left then we can't do any linear interpolation
# So just fill from the right
s.iloc[i] = s.iloc[right]
elif right is None:
# If we can't find any data to the right then fill from the left
# Both of these will result in a flat yield curve, which isn't ideal
s.iloc[i] = s.iloc[left]
else:
# We can actually do linear interpolation
steps = right - left
rate = s.iloc[left] + ((s.iloc[right] - s.iloc[left]) * (i - left) / steps)
s.iloc[i] = rate
return s.tolist()
# + deletable=true editable=true
['%.2f' % (s*100) for s in build_yield_curve(HISTORICAL_RATES.iloc[0])]
# + [markdown] deletable=true editable=true
# # Putting it all together
#
# Now we have all the building blocks. We have a source of rates. We have a way to bootstrap our ladder. We have a way to see how the NAV changes over time.
#
# We only have one decision left to make -- what are the youngest & oldest maturities that we care about? Do we want a 10-2 fund? Or 10-4 fund? Or a 3-2 fund? Or how about a 7-4 fund?
#
# The maximum you can chose is 30 and the minimum is 1.
#
# Do you want a 10-2 fund, or 10-4 fund, or something else? That's actually done by the way you create the bootstrap ladder. This is how you build a 10-4 ladder.
# + deletable=true editable=true
bootstrap(build_yield_curve(HISTORICAL_RATES.iloc[0]), 10, 4)
# + deletable=true editable=true
def loop(ladder, rates, max_maturity, start_year, end_year):
df = pandas.DataFrame(columns=['NAV', 'Payments', 'Change'], index=numpy.arange(start_year, end_year + 1))
for (year, current_rates) in rates:
(ladder, payments, nav) = iterate_fund(ladder, build_yield_curve(current_rates), max_maturity)
df.loc[year] = {'NAV' : nav, 'Payments' : payments}
calculate_returns(df)
return df
def calculate_returns(df):
# Longinvest calculates the return based on comparison's to
# next year's NAV. So I'll do the same. Even though that seems
# weird to me. Maybe it's because the rates are based on January?
# Hmmm...that sounds plausible.
max_row = df.shape[0]
for i in range(max_row - 1):
next_nav = df.iloc[i+1]['NAV']
nav = df.iloc[i]['NAV']
change = (next_nav - nav) / nav
df.iloc[i]['Change'] = change
return df
def simulate(max_maturity, min_maturity, rates):
""" This is just something to save on typing...and make clearer what the bounds on the fund are """
ladder = bootstrap(build_yield_curve(rates.iloc[0]), max_maturity, min_maturity)
start_year = int(rates.iloc[0].name)
end_year = int(rates.iloc[-1].name)
return loop(ladder, rates.iterrows(), max_maturity, start_year, end_year)
# + [markdown] deletable=true editable=true
# # Simulate All The Things
#
# Now we can simulate a 10-2 fund.
# + deletable=true editable=true
simulate(10, 2, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# Or a 10-4 fund.
# + deletable=true editable=true
simulate(10, 4, HISTORICAL_RATES).head()
# + deletable=true editable=true
simulate(4, 2, HISTORICAL_RATES).head()
# + deletable=true editable=true
simulate(3, 2, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # Holding to maturity
#
# Our previous examples all sell prior to bond maturity.
#
# If you want to hold until maturity, then specify a minimum duration of 1.
# + deletable=true editable=true
simulate(10, 1, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # Only holding a single maturity
#
# If you only want to fund to hold a single maturity, specify the same number twice. This constructs fund that only holds bonds of 2-year maturity. That is, every year it sells them and buys new 2-year bonds.
# + deletable=true editable=true
simulate(2, 2, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # The "naive" approach
#
# Other bond return simulations don't hold a ladder, they just sell the bond after a single year. That is, buy a 10-year bond, sell it after 1-year and buy another 10-year bond. That's the same as holding a single maturity (above) but with a 10-year maturity.
# + deletable=true editable=true
simulate(10, 10, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # Going beyond 30 years
#
# Keeping in mind the caveats above about results before we have FRED data from the mid-1950s...we can also build longer term bond funds.
#
# ### Warning: Extra interpolation
#
# There are a few gaps in the FRED data. In the FRED 20-year series, there is no data for 1987-1993. (They weren't issued in those years, IIRC.)
#
# In the FRED 30-year series, there is no data for 2003-2006.
#
# longinvest does a linear interpolation **across years** to fill in the missing data. **I currently do not do this, so my results differ from those in the spreadsheet.**
#
# The way it works is:
#
# There is no 20-year data for 1987. But there *is* 30-year data. longinvest looks back at 1986 and sees that the spread between 20-year and 30-year in 1986 was -0.19%. Then he looks forward to 1994 and sees that the spread then was -0.10%. Then he assumes the spread changed linearly over the missing years 1987-1993. That is:
# * 1987: -0.178%
# * 1988: -0.167%
# * 1989: -0.156%
# * 1990: -0.145%
# * 1991: -0.133%
# * 1992: -0.122%
# * 1993: -0.111%
#
# Then he applies that calculated spread to the known 30-year rates.
#
# When the 30-year rates are missing, a similar calculation is done based on the years 2002 & 2007 and the known 20-year rates.
#
# This is captured in the CSV as two new data series "longinvest 20" and "longinvest 30".
# + deletable=true editable=true
simulate(30, 11, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # Crazy Funds
#
# You can select any set of maturities you want, since the computer does all the heavy lifting. Want to simulate a fund that is **28-14** or **17-9**? That's easy.
# + deletable=true editable=true
simulate(28, 14, HISTORICAL_RATES).head()
# + deletable=true editable=true
simulate(17, 9, HISTORICAL_RATES).head()
# + [markdown] deletable=true editable=true
# # Saving to CSV
# To do anything useful, you probably want to save the results to a CSV file. Here's a commented-out example of how to do that.
# + deletable=true editable=true
#simulate(10, 5, HISTORICAL_RATES).to_csv('10-5.csv')
# + deletable=true editable=true
import numpy
from collections import deque
import pandas
import math
import pandas_datareader.data as web
import datetime
import requests
import requests_cache
import xlrd
import tempfile
def get_morningstar(secid):
url = 'http://mschart.morningstar.com/chartweb/defaultChart?type=getcc&secids=%s&dataid=8225&startdate=1900-01-01&enddate=2016-11-18¤cy=&format=1' % secid
expire_after = datetime.timedelta(days=3)
session = requests_cache.CachedSession(cache_name='data-cache', backend='sqlite', expire_after=expire_after)
# TODO: why doesn't this work!?!
#r = session.get(url)
r = requests.get(url)
j = r.json()
# The Morningstar data is pretty deeply nested....
m = j['data']['r'][0]
assert m['i'] == secid
actual_data = m['t'][0]['d']
# convert from strings to real data types
as_dict = dict([(datetime.datetime.strptime(n['i'], '%Y-%m-%d'), float(n['v'])) for n in m['t'][0]['d']])
# Strip out data?
# Do we only want start of month, end of month, start of year, end of year, etc?
s = pandas.Series(as_dict, name=secid)
return s
barclays_index = get_morningstar('XIUSA000MJ')
# Use only final value for each calendar year
def annual(series):
return series.groupby(by=lambda x: x.year).last()
# Use only final value for each calendar month
def monthly(series):
return series.groupby(by=lambda x: datetime.date(x.year, x.month, 1)).last()
def calculate_change_prev(df, column):
max_row = df.shape[0]
series = pandas.Series()
for i in range(max_row - 1):
val = df.iloc[i][column]
prev_val = df.iloc[i-1][column]
change = (val - prev_val) / prev_val
series.loc[df.iloc[i].name] = change
return series
def calculate_change_next(df, column):
max_row = df.shape[0]
series = pandas.Series()
for i in range(max_row - 1):
val = df.iloc[i][column]
next_val = df.iloc[i+1][column]
change = (next_val - val) / val
series.loc[df.iloc[i].name] = change
return series
barclays_index = annual(barclays_index)
# + deletable=true editable=true
sim_10_4 = simulate(10, 4, HISTORICAL_RATES)
sim_10_10 = simulate(10, 10, HISTORICAL_RATES)
# + deletable=true editable=true
joined = pandas.concat([sim_10_4, barclays_index], axis=1, join='outer')
s_ind = calculate_change_prev(joined, 'XIUSA000MJ')
s_nav = calculate_change_next(joined, 'NAV')
joined = joined.assign(Change=s_nav, index_change=s_ind)
joined.to_csv('check.csv')
print(joined[["Change", "index_change"]].corr())
# + deletable=true editable=true
joined = pandas.concat([sim_10_10, barclays_index], axis=1, join='outer')
s_ind = calculate_change_prev(joined, 'XIUSA000MJ')
s_nav = calculate_change_next(joined, 'NAV')
joined = joined.assign(Change=s_nav, index_change=s_ind)
print(joined[["Change", "index_change"]].corr())
# + deletable=true editable=true
|
Bond Fund Simulator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Compute transforms from aspect solution DY/DZ to CHIPX/CHIPY
#
# A key part of the process to apply dynamic ACA offsets to each observation is
# computing the required DY/DZ aspect solution value to move the aimpoint to the
# specified CHIPX/CHIPY coordinate. This notebook computes these transforms
# for each ACIS and HRC chip.
#
# The final results are used in the `chandra_aca.drift` module.
#
# This notebook was originally based on the `absolute_pointing_uncertainty` notebook
# in this repository.
# +
from __future__ import print_function, division
import argparse
import re
import time
from itertools import izip, cycle
import functools
from pprint import pprint
import numpy as np
import Ska.DBI
from astropy.table import Table, vstack
from astropy.time import Time
import mica.archive.obspar
from mica.archive import asp_l1
import Ska.Shell
from Ska.quatutil import yagzag2radec
from Quaternion import Quat
from Ska.quatutil import radec2yagzag
from sherpa import ui
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# Sherpa is too chatty so just turn off all logging (attempts to do this more selectively
# did not work on first try)
import logging
logging.disable(50)
# Nominal SIM focus and TSC positions. This is run once with cell below and values
# are filled in to avoid repeating this exercise. Originally use:
# sim_x_nom = {}
# sim_z_nom = {}
sim_x_nom = {
'ACIS-I': -0.78090834371672724,
'ACIS-S': -0.68282252473119054,
'HRC-I': -1.0388663562382989,
'HRC-S': -1.526339935833849}
sim_z_nom = {
'ACIS-I': -233.58743446082869,
'ACIS-S': -190.1400660498719,
'HRC-I': 126.98297998998621,
'HRC-S': 250.46603308020099}
if not sim_x_nom or not sim_z_nom:
from Ska.DBI import DBI
db = DBI(server='sybase', dbi='sybase', user='aca_read')
dat = db.fetchall('select detector, sim_x, sim_z from obspar where obsid>12000 and obsid<18000')
for det in ('ACIS-S', 'ACIS-I', 'HRC-S', 'HRC-I'):
ok = dat['detector'] == det
sim_x_nom[det] = np.median(dat['sim_x'][ok])
sim_z_nom[det] = np.median(dat['sim_z'][ok])
db.conn.close()
from pprint import pprint
pprint(sim_x_nom)
pprint(sim_z_nom)
# +
aimpoint_data_cache = {}
acis_pixscale = 0.492 # arcsec / pixel
def get_aimpoint_data(det):
"""
Read aimpoint data provided by <NAME> and define additional columns
that make it easier to compare with fid light drift data.
"""
if det not in aimpoint_data_cache:
filename = 'optics_aimpoint/{}_ap_pos.rdb'.format(re.sub(r'-', '', det).lower())
dat = Table.read(filename, format='ascii.rdb')
y_off = dat['y_det_offset'] * 60 / acis_pixscale # pix / arcmin
z_off = dat['z_det_offset'] * 60 / acis_pixscale # pix / arcmin
aimpoint_data_cache[det] = dat
return aimpoint_data_cache[det]
# -
def get_zero_offset_aimpoint_data(det, min_year=2010):
"""
Return aimpoint data for observations with zero target offset.
This simplifies the correlation of aspect solution and dmcoords
results with the published POG plots (chapter 4) of aimpoint drift.
"""
dat = get_aimpoint_data(det)
ok = (dat['y_det_offset'] == 0) & (dat['z_det_offset'] == 0) & (dat['year'] > min_year)
return dat[ok]
# +
dats = get_zero_offset_aimpoint_data('ACIS-S', 2010)
dati = get_zero_offset_aimpoint_data('ACIS-I', 2010)
hrcs = get_zero_offset_aimpoint_data('HRC-S', 2010)
hrci = get_zero_offset_aimpoint_data('HRC-I', 2010)
observations = vstack([dats, dati, hrcs, hrci])
# +
# Use the obspar for each obsid to fill in some additional
# columns. Yag and Zag represent the local frame position
# (arcsec) of the target in the nominal frame.
noms = ('ra_nom', 'dec_nom', 'roll_nom')
for nom in noms:
observations[nom] = 0.0
observations['yag'] = 0.0
observations['zag'] = 0.0
observations['ra_pnt'] = 0.0
observations['dec_pnt'] = 0.0
observations['detector'] = 'ACIS-S'
for obs in observations:
obspar = mica.archive.obspar.get_obspar(obs['obsid'])
for nom in noms:
obs[nom] = obspar[nom]
obs['ra_targ'] = obspar['ra_targ']
obs['dec_targ'] = obspar['dec_targ']
obs['ra_pnt'] = obspar['ra_pnt']
obs['dec_pnt'] = obspar['dec_pnt']
obs['detector'] = obspar['detector']
q_nom = Quat([obs[nom] for nom in noms])
obs['yag'], obs['zag'] = radec2yagzag(obspar['ra_targ'], obspar['dec_targ'], q_nom)
observations['yag'] *= 3600
observations['zag'] *= 3600
# -
ok = observations['detector'] == 'HRC-I'
observations[ok][:5]
# ### Use dmcoords to relate detector, dy, dz to chipx, chipy
#
# This will be an approximation that applies over small displacements (of order 100 pixels).
ciaoenv = Ska.Shell.getenv('source /soft/ciao/bin/ciao.sh')
dmcoords_cmd = ['dmcoords', 'none',
'asolfile=none',
'detector="{detector}"',
'fpsys="{fpsys}"',
'opt=cel',
'ra={ra}',
'dec={dec}',
'celfmt=deg',
'ra_nom=0',
'dec_nom=0',
'roll_nom=0',
'ra_asp=")ra_nom"',
'dec_asp=")dec_nom"',
'roll_asp=")roll_nom"',
'sim="{simx} 0 {simz}"',
'displace="0 {dy} {dz} 0 0 0"',
'verbose=0']
dmcoords_cmd = ' '.join(dmcoords_cmd)
ciaorun = functools.partial(Ska.Shell.bash, env=ciaoenv)
# ### Derive the typical offset between _TARG and _NOM values in observation data
#
# There is normally around an 17 arcsec offset between the target and nominal coordinates in the obspar or event file header values. It's basically the difference between two rotation matrices in our system:
#
# - `ACA_MISALIGN`: MNC (HRMA optical axis) to ACA frame misalignment.
# - `ODB_SI_ALIGN`: Misalignment used to transform from science target coordinates to ACA (PCAD) pointing direction that gets used on-board.
#
# My recollection is that the fact that these are not the same is a relic of a decision during OAC, but I'm not entirely certain of that.
def get_obspars(start='2010:001', stop='2016:001'):
from Ska.DBI import DBI
from cxotime import CxoTime
tstart = CxoTime(start).secs
tstop = CxoTime(stop).secs
db = DBI(server='sybase', dbi='sybase', user='aca_read')
obspars = db.fetchall('select obsid, ra_nom, dec_nom, roll_nom, ra_targ, dec_targ, detector, '
'date_obs, y_det_offset, z_det_offset, sched_exp_time from obspar'
' where tstart>{} and tstop<{} and obsid<40000 and sched_exp_time>8000'.format(tstart, tstop))
db.conn.close()
return obspars
# #### Use ODB_SI_ALIGN (OFSL) and CXC CALALIGN to infer required target RA, DEC
calalign = Table.read('/soft/ciao/CALDB/data/chandra/pcad/align/pcadD2012-09-13alignN0009.fits',
hdu='CALALIGN')
ODB_SI_ALIGN = np.array([[1.0, 3.3742E-4, 2.7344E-4],
[-3.3742E-4, 1.0, 0.0],
[-2.7344E-4, 0.0, 1.0]])
calalign
# These are the values of ra_targ, dec_targ which will result in the target being at
# the zero-offset aimpoint for ra_pnt = ra_nom = dec_pnt = dec_nom = roll = 0
detectors = ('ACIS-S', 'ACIS-I', 'HRC-S', 'HRC-I')
ra_dec_0 = {}
for cal in calalign:
rot = cal['ACA_MISALIGN'].dot(ODB_SI_ALIGN)
qrot = Quat(rot)
ra = -np.degrees(qrot.q[2] * 2)
dec = np.degrees(qrot.q[1] * 2)
det = cal['INSTR_ID'].strip()
ra_dec_0[det] = (ra, dec)
print(det, ra * 3600, dec * 3600)
# ### Now let's confirm this with data using obspars
obspars = Table(get_obspars('2006:001'))
obspars['yag'] = np.zeros(len(obspars))
obspars['zag'] = np.zeros(len(obspars))
for i, op in enumerate(obspars):
q = Quat([op['ra_nom'], op['dec_nom'], op['roll_nom']])
obspars['yag'][i], obspars['zag'][i] = radec2yagzag(op['ra_targ'], op['dec_targ'], q)
obspars['yag'] = obspars['yag'] * 3600 - obspars['y_det_offset'] * 60
obspars['zag'] = obspars['zag'] * 3600 - obspars['z_det_offset'] * 60
obspars[:5]
# +
plt.figure(figsize=(10, 10))
from itertools import count
for color, det, i in zip('gbrc', detectors, count()):
ok = obspars['detector'] == det
op = obspars[ok]
if len(op) > 5:
plt.subplot(2, 2, i + 1)
plt.plot(op['yag'], op['zag'], '.', color=color, alpha=0.4)
plt.title(det)
print(det, np.median(op['yag']), np.median(op['zag']))
plt.xlim(-25, -5)
plt.ylim(-10, 15)
for color, det, i in zip('gbrc', detectors, count()):
plt.subplot(2, 2, i + 1)
x, y = (val * 3600 for val in ra_dec_0[det])
plt.plot(x, y, 'o', color='k', markersize=10)
plt.plot(x, y, 'o', color=color, markersize=7)
plt.grid()
# -
obspars[:2]
def dmcoords_chipx_chipy(det, dy, dz, verbose=False):
"""
Get the dmcoords-computed chipx and chipy for given detector and
aspect solution DY and DZ values. NOTE: the ``dy`` and ``dz`` inputs
to dmcoords are flipped in sign from the ASOL values. Generally the
ASOL DY/DZ are positive and dmcoord input values are negative. This
sign flip is handled *here*, so input to this is ASOL DY/DZ.
:param det: detector (ACIS-S, ACIS-I, HRC-S, HRC-I)
:param dy: aspect solution DY value (mm)
:param dz: aspect solution DZ value (mm)
"""
# See the absolute_pointing_uncertainty notebook in this repo for the
# detailed derivation of this -15.5, 6.0 arcsec offset factor. See the
# cell below for the summary version.
ra0, dec0 = ra_dec_0[det]
ciaorun('punlearn dmcoords')
fpsys_map = {'HRC-I': 'HI1',
'HRC-S': 'HS2',
'ACIS-I': 'ACIS',
'ACIS-S': 'ACIS'}
cmd = dmcoords_cmd.format(ra=ra0, dec=dec0,
detector=(det if det.startswith('HRC') else 'ACIS'),
fpsys=fpsys_map[det],
simx=sim_x_nom[det], simz=sim_z_nom[det],
dy=-dy, dz=-dz)
ciaorun(cmd)
if verbose:
print(cmd)
return [float(x) for x in ciaorun('pget dmcoords chipx chipy chip_id')]
def get_dy_dz(obsid):
"""
Get statistical summary data for aspect solution DY/DZ for ``obsid``.
:param obsid: ObsID
:returns: min_dy, median_dy, max_dy, min_dz, median_dz, max_dz (mm)
"""
asolfiles = asp_l1.get_files(obsid=obsid, content=['ASPSOL'])
asol = Table.read(asolfiles[0])
min_dy, median_dy, max_dy = (np.min(asol['dy']),
np.median(asol['dy']),
np.max(asol['dy']))
min_dz, median_dz, max_dz = (np.min(asol['dz']),
np.median(asol['dz']),
np.max(asol['dz']))
return min_dy, median_dy, max_dy, min_dz, median_dz, max_dz
# ### Do some exploration / validation of methods
# What are CHIPX/Y for HRC-I at DY/Z = 0, 0
dmcoords_chipx_chipy('HRC-I', 0, 0)
# #### Compare P. Zhao values to expected from dmcoords_chipx_chipy for ACIS-S and ACIS-I obsids
#
# This is not incredibly independent since Zhao values also use dmcoords, but in a slightly different way.
dati['obsid', 'ap_chipx', 'ap_chipy'][:1]
min_dy, median_dy, max_dy, min_dz, median_dz, max_dz = get_dy_dz(11613)
dmcoords_chipx_chipy(det='ACIS-I', dy=median_dy, dz=median_dz)
dats['obsid', 'ap_chipx', 'ap_chipy'][:1]
min_dy, median_dy, max_dy, min_dz, median_dz, max_dz = get_dy_dz(12351)
dmcoords_chipx_chipy(det='ACIS-S', dy=median_dy, dz=median_dz)
hrcs['obsid', 'ap_chipx', 'ap_chipy'][:1]
min_dy, median_dy, max_dy, min_dz, median_dz, max_dz = get_dy_dz(10665)
dmcoords_chipx_chipy(det='HRC-S', dy=median_dy, dz=median_dz, verbose=True)
hrci['obsid', 'ap_chipx', 'ap_chipy'][:1]
min_dy, median_dy, max_dy, min_dz, median_dz, max_dz = get_dy_dz(10980)
dmcoords_chipx_chipy(det='HRC-I', dy=median_dy, dz=median_dz, verbose=True)
# ### DY and DZ correspond to adding values to Y_A and Z_A
#
# <img src="http://cxc.harvard.edu/proposer/POG/html/images/simc.png">
# ### Find DY/DZ values corresponding to each ACIS-I and HRC-S chip
# The third number of the output is the chip_id
dmcoords_chipx_chipy(det='ACIS-I', dy=-10.0, dz=-10.0)
dmcoords_chipx_chipy(det='ACIS-I', dy=10.0, dz=10.0)
dmcoords_chipx_chipy(det='ACIS-I', dy=10.0, dz=-10.0)
dmcoords_chipx_chipy(det='ACIS-I', dy=-10.0, dz=10.0)
dmcoords_chipx_chipy(det='HRC-S', dy=100, dz=0)
dmcoords_chipx_chipy(det='HRC-S', dy=-100, dz=0)
# ### Use Sherpa and dmcoords to empirically determine the transformation DY/Z to CHIPX/Y for each chip
def dyz_to_chipxy(pars, x):
"""
Define a function to transform from DY/Z to CHIPX/Y
CHIPX, CHIPY = c0 + cyz * [DY, DZ] (dot product)
"""
c0x, c0y, cyx, czx, cyy, czy = pars
c0 = np.array([[c0x],
[c0y]])
cyz = np.array([[cyx, czx],
[cyy, czy]])
x = np.array(x).reshape(-1, 2).transpose()
y = c0 + cyz.dot(x)
return y.transpose().flatten()
pars = [971.91, 963.07, 0.0, +41.74, -41.74, 0.0]
x = [-1, -1, 0, -1, -1, -2.0]
# x = [-1, -1]
dyz_to_chipxy(pars, x)
def fit_xform(det, chip_id, dy0, dz0):
"""
Fit the transform model to 3 points forming an "L" on the chip around
the ``dy0`` and ``dz0`` DY/Z values.
:param det: detector (can be lower case)
:param chip_id: numerical chip ID using dmcoord convention (ACIS=0 to 9, HRC=0 to 3)
:param dy0: asol DY center value (mm)
:param dz0: asol DZ center value (mm)
:returns: sherpa fit_results() object
"""
det = det.upper()
x = []
y = []
for ddy, ddz in ((0, 0), (1, 0), (0, 1)):
dy = dy0 + ddy
dz = dz0 + ddz
cx, cy, cid = dmcoords_chipx_chipy(det, dy, dz)
if cid != chip_id:
raise ValueError('Chip mismatch {} != {}'.format(cid, chip_id))
x.extend([dy, dz])
y.extend([cx, cy])
ui.load_arrays(1, np.array(x), np.array(y))
ui.load_user_model(dyz_to_chipxy, 'xform_mdl')
ui.add_user_pars('xform_mdl', ['c0x', 'c0y', 'cyx', 'czx', 'cyy', 'czy'])
ui.set_model(xform_mdl)
ui.fit()
return ui.get_fit_results()
fr = fit_xform('ACIS-I', 3, 0.0, 0.0)
fr.parvals
fr = fit_xform(det='HRC-I', chip_id=0, dy0=0.0, dz0=0.0)
fr.parvals
# ### Do the fitting for each chip on ACIS and HRC
det_ids = (('acis-i', 3, 0, 0),
('acis-i', 0, 10, -10),
('acis-i', 1, -10, -10),
('acis-i', 2, 10, 10),
('acis-s', 7, 0, 0),
('acis-s', 6, 25, 0),
('acis-s', 5, 50, 0),
('acis-s', 4, 75, 0),
('acis-s', 8, -25, 0),
('acis-s', 9, -50, 0),
('hrc-i', 0, 0, 0),
('hrc-s', 1, -100, 0),
('hrc-s', 2, 0, 0),
('hrc-s', 3, 100, 0),
)
xforms = {}
for det, chip_id, dy0, dz0 in det_ids:
key = det.upper(), chip_id
if key in xforms:
continue
print(key)
fr = fit_xform(det, chip_id, dy0, dz0)
xforms[key] = fr.parvals
# ### Compare model prediction to actual
print(dyz_to_chipxy(xforms['ACIS-I', 1], [-10, -10]))
print(dmcoords_chipx_chipy(det='ACIS-I', dy=-10.0, dz=-10.0))
print(dyz_to_chipxy(xforms['ACIS-S', 7], [0, 0]))
print(dmcoords_chipx_chipy(det='ACIS-S', dy=0.0, dz=0.0))
print(dyz_to_chipxy(xforms['HRC-I', 0], [0, 0]))
print(dmcoords_chipx_chipy(det='HRC-I', dy=0.0, dz=0.0))
print(dyz_to_chipxy(xforms['HRC-S', 2], [0, 0]))
print(dmcoords_chipx_chipy(det='HRC-S', dy=0.0, dz=0.0))
# ### Make a nicer format to copy into chandra_aca.drift module
xforms_out = {}
for key, val in xforms.items():
vals = [round(x, 3) for x in val]
xforms_out[key] = {'c0': [vals[0], vals[1]],
'cyz': [[vals[2], vals[3]],
[vals[4], vals[5]]]}
from pprint import pprint
pprint(xforms_out)
|
asol_to_chip_transforms.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] Collapsed="false" _cell_guid="d3b04218-0413-4e6c-8751-5d8a404d73a9" _uuid="0bca9739b82d5d51e1229243e03ea1b6db35c17e"
# ## Introduction
#
# This kernel shows how to use NBSVM (Naive Bayes - Support Vector Machine) to create a strong baseline for the [Toxic Comment Classification Challenge](https://www.kaggle.com/c/jigsaw-toxic-comment-classification-challenge) competition. NBSVM was introduced by <NAME> and <NAME> in the paper [Baselines and Bigrams: Simple, Good Sentiment and Topic Classification](https://nlp.stanford.edu/pubs/sidaw12_simple_sentiment.pdf). In this kernel, we use sklearn's logistic regression, rather than SVM, although in practice the two are nearly identical (sklearn uses the liblinear library behind the scenes).
#
# If you're not familiar with naive bayes and bag of words matrices, I've made a preview available of one of fast.ai's upcoming *Practical Machine Learning* course videos, which introduces this topic. Here is a link to the section of the video which discusses this: [Naive Bayes video](https://youtu.be/37sFIak42Sc?t=3745).
# + Collapsed="false" _cell_guid="ef06cd19-66b6-46bc-bf45-184e12d3f7d4" _uuid="cca038ca9424a3f66e10262fc9129de807b5f855"
import pandas as pd, numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
# + Collapsed="false" _cell_guid="a494f561-0c2f-4a38-8973-6b60c22da357" _uuid="f70ebe669fcf6b434c595cf6fb7a76120bf7809c"
train = pd.read_csv('train.csv')
# test = pd.read_csv('test.csv')
# subm = pd.read_csv('sample_submission.csv')
# + [markdown] Collapsed="false" _cell_guid="3996a226-e1ca-4aa8-b39f-6524d4dadb07" _uuid="2c18461316f17d1d323b1959c8eb4e5448e8a44e"
# ## Looking at the data
#
# The training data contains a row per comment, with an id, the text of the comment, and 6 different labels that we'll try to predict.
# + [markdown] Collapsed="false" _cell_guid="b3b071fb-7a2c-4195-9817-b01983d11c0e" _uuid="004d2e823056e98afc5adaac433b7afbfe93b82d"
# Here's a couple of examples of comments, one toxic, and one with no labels.
# + [markdown] Collapsed="false" _cell_guid="b8515824-b2dd-4c95-bbf9-dc74c80355db" _uuid="0151ab55887071aed82d297acb2c6545ed964c2b"
# We'll create a list of all the labels to predict, and we'll also create a 'none' label so we can see how many comments have no labels. We can then summarize the dataset.
# + Collapsed="false" _cell_guid="c66f79d1-1d9f-4d94-82c1-8026af198f2a" _uuid="4ba6ef86c82f073bf411785d971a694348c3efa9"
label_cols = ['toxic', 'severe_toxic', 'obscene', 'threat', 'insult', 'identity_hate']
train['none'] = 1-train[label_cols].max(axis=1)
train.describe()
# + [markdown] Collapsed="false" _cell_guid="1b221e62-e23f-422a-939d-6747edf2d613" _uuid="bfdcf59624717b37ca4ffc0c99d2c28a2d419b06"
# There are a few empty comments that we need to get rid of, otherwise sklearn will complain.
# + Collapsed="false" _cell_guid="fdba531c-7ef2-4967-88e2-fc2b04f6f2ef" _uuid="1e1229f403225f1889c7a7b4fc9be90fda818af5"
COMMENT = 'comment_text'
train[COMMENT].fillna("unknown", inplace=True)
test[COMMENT].fillna("unknown", inplace=True)
# + [markdown] Collapsed="false" _cell_guid="480780f1-00c0-4f9a-81e5-fc1932516a80" _uuid="f2e77e8e6df5e29b620c7a2a0add1438c35af932"
# ## Building the model
#
# We'll start by creating a *bag of words* representation, as a *term document matrix*. We'll use ngrams, as suggested in the NBSVM paper.
# + Collapsed="false" _cell_guid="b7f11db7-5c12-4eb8-9f2d-0323d629fed9" _uuid="b043a3fb66c443fab0129e863c134ec813dadb87"
import re, string
re_tok = re.compile(f'([{string.punctuation}“”¨«»®´·º½¾¿¡§£₤‘’])')
def tokenize(s): return re_tok.sub(r' \1 ', s).split()
# + [markdown] Collapsed="false" _cell_guid="bfdebf11-133c-4b12-8664-8bf64757d6cc" _uuid="941759df15c71d42853515e4d1006f4ab000ce75"
# It turns out that using TF-IDF gives even better priors than the binarized features used in the paper. I don't think this has been mentioned in any paper before, but it improves leaderboard score from 0.59 to 0.55.
# + Collapsed="false" _cell_guid="31ad6c98-d054-426c-b3bd-b3b18f52eb6f" _uuid="75f3f27d56fb2d7d539e65c292d9e77c92ceead3"
n = train.shape[0]
vec = TfidfVectorizer(ngram_range=(1,2), tokenizer=tokenize,
min_df=3, max_df=0.9, strip_accents='unicode', use_idf=1,
smooth_idf=1, sublinear_tf=1 )
trn_term_doc = vec.fit_transform(train[COMMENT])
test_term_doc = vec.transform(test[COMMENT])
# + [markdown] Collapsed="false" _cell_guid="4cf3ec26-8237-452b-90c9-831cb0297955" _uuid="6d215bc460e64d88b08f501d5c5a67c290e40635"
# This creates a *sparse matrix* with only a small number of non-zero elements (*stored elements* in the representation below).
# + Collapsed="false" _cell_guid="4c7bdbcc-4451-4477-944c-772e99bac777" _uuid="8816cc35f66b9fed9c12978fbdef5bb68fae10f4"
trn_term_doc, test_term_doc
# + [markdown] Collapsed="false" _cell_guid="59131479-a861-4f46-add9-b2af09a51976" _uuid="5fc487461f4c6fdaea25f2cd471fc801856c6689"
# Here's the basic naive bayes feature equation:
# + Collapsed="false" _cell_guid="45fc6070-ba13-455b-9274-5c2611e2809c" _uuid="8b277f01cecd575ed4fcae2e630c0dd8ce979793"
def pr(y_i, y):
p = x[y==y_i].sum(0)
return (p+1) / ((y==y_i).sum()+1)
# + Collapsed="false" _cell_guid="2299d24b-5515-4d37-92d9-e7f6b16a290a" _uuid="926eaa2e40e588f4ef2b86e0a28f8e575c9ed5f4"
x = trn_term_doc
test_x = test_term_doc
# + [markdown] Collapsed="false" _cell_guid="c0b494ac-0dfc-4faa-a909-0a6d7696d1fc" _uuid="dc5cafeab86d17ac4f036d58658437636a885a87"
# Fit a model for one dependent at a time:
# + Collapsed="false" _cell_guid="b756c889-a383-4952-9ee9-eca79fd3454f" _uuid="8652ab2f5f84e77fa395252be9b60be1e44fd583"
def get_mdl(y):
y = y.values
r = np.log(pr(1,y) / pr(0,y))
m = LogisticRegression(C=4, dual=False)
x_nb = x.multiply(r)
return m.fit(x_nb, y), r
# + Collapsed="false" _cell_guid="33fd5f8c-adfc-45a1-9fde-1769a0993e76" _uuid="0fa103b5406aabdc36ea9ef21612d343e4982fc4"
preds = np.zeros((len(test), len(label_cols)))
for i, j in enumerate(label_cols):
print('fit', j)
m,r = get_mdl(train[j])
preds[:,i] = m.predict_proba(test_x.multiply(r))[:,1]
# + [markdown] Collapsed="false" _cell_guid="1a99c4d9-916f-4189-9a25-fedcb7700336" _uuid="5525045116474e6d12b6edc890250d30c0790f06"
# And finally, create the submission file.
# + Collapsed="false" _cell_guid="bc6a4575-fbbb-47ea-81ac-91fa702dc194" _uuid="5dd033a93e6cf32cdbdaa0a8b05cd8d27de2b21d"
submid = pd.DataFrame({'id': subm["id"]})
submission = pd.concat([submid, pd.DataFrame(preds, columns = label_cols)], axis=1)
submission.to_csv('submission.csv', index=False)
# + Collapsed="false" _cell_guid="1c345d02-b768-491c-8c03-8c3459a552a8" _uuid="adbbfb0156952a6a43833e337b8a418ccac257aa" jupyter={"outputs_hidden": true}
|
Machine Learning/Natural Language Processing/nb-svm-strong-linear-baseline.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Working With STAC
#
# Need to run at scale? checkout https://github.com/developmentseed/titiler/blob/master/Notebooks/WorkingWithSTAC.ipynb
#
# ###### Requirements
#
# `pip install tdqm stac-tiler rio-color`
# +
import os
import json
import base64
import requests
import datetime
import itertools
import urllib.parse
from io import BytesIO
from functools import partial
from concurrent import futures
from rasterio.plot import reshape_as_image
from rasterio.features import bounds as featureBounds
from stac_tiler import STACReader
from rio_color.operations import parse_operations
from rio_color.utils import scale_dtype, to_math_type
from tqdm.notebook import tqdm
# %pylab inline
# STAC API hosted by element84
stac_endpoint = "https://earth-search.aws.element84.com/v0/search"
# -
# #### Define Area of Interest (AOI)
# +
# use geojson.io
geojson = {
"type": "FeatureCollection",
"features": [
{
"type": "Feature",
"properties": {},
"geometry": {
"type": "Polygon",
"coordinates": [
[
[
30.810813903808594,
29.454247067148533
],
[
30.88600158691406,
29.454247067148533
],
[
30.88600158691406,
29.51879923863822
],
[
30.810813903808594,
29.51879923863822
],
[
30.810813903808594,
29.454247067148533
]
]
]
}
}
]
}
bounds = featureBounds(geojson)
# -
# ## STAC Search
#
# Use STAC API to search for data over our AOI
#
# Doc: https://github.com/radiantearth/stac-api-spec
# +
# Date filter
date_min="2019-01-01"
date_max="2019-12-11"
start = datetime.datetime.strptime(date_min, "%Y-%m-%d").strftime("%Y-%m-%dT00:00:00Z")
end = datetime.datetime.strptime(date_max, "%Y-%m-%d").strftime("%Y-%m-%dT23:59:59Z")
query = {
"collections": ["sentinel-s2-l2a-cogs"], # Make sure to query only sentinel-2 COGs collection
"datetime": f"{start}/{end}",
"query": {
"eo:cloud_cover": {
"lt": 5
} # Use low cloud cover
},
"intersects": geojson["features"][0]["geometry"],
"limit": 1000,
"fields": {
'include': ['id', 'properties.datetime', 'properties.eo:cloud_cover'], # Make returned response ligth
'exclude': ['assets', 'links']
}
}
headers = {
"Content-Type": "application/json",
"Accept-Encoding": "gzip",
"Accept": "application/geo+json",
}
data = requests.post(stac_endpoint, headers=headers, json=query).json()
print(data["context"])
print()
print("Example:")
print(json.dumps(data["features"][0], indent=4))
sceneid = [f["id"] for f in data["features"]]
cloudcover = [f["properties"]["eo:cloud_cover"] for f in data["features"]]
dates = [f["properties"]["datetime"][0:10] for f in data["features"]]
# -
# #### Plot Cloud cover / dates
# +
fig = plt.figure(dpi=100)
fig.autofmt_xdate()
ax = fig.add_subplot(1, 1, 1)
ax.plot(dates, cloudcover, label="Cloud Cover", color="tab:red", linewidth=0.4, linestyle="-.")
ax.legend()
# -
# ### Read DATA
#
# ```
# # TILE
# with STACReader("stac.json") as stac:
# tile, mask = stac.tile(1, 2, 3, tilesize=256, assets=["red", "green"])
#
# # With expression
# with STACReader("stac.json") as stac:
# tile, mask = cog.tile(1, 2, 3, tilesize=256, expression="red/green")
#
# # PART
# with STACReader("stac.json") as stac:
# data, mask = stac.part((10, 10, 20, 20), assets=["red", "green"])
#
# # Limit output size (default is set to 1024)
# with STACReader("stac.json") as stac:
# data, mask = stac.part((10, 10, 20, 20), max_size=2000, assets=["red", "green"])
#
# # Read high resolution
# with STACReader("stac.json") as stac:
# data, mask = stac.part((10, 10, 20, 20), max_size=None, assets=["red", "green"])
#
# # With expression
# with STACReader("stac.json") as stac:
# data, mask = stac.part((10, 10, 20, 20), expression="red/green")
#
# # POINT
# with STACReader("stac.json") as stac:
# pts = stac.point(-100, 25, assets=["red", "green"])
#
# # With expression
# with STACReader("stac.json") as stac:
# pts = stac.point(-100, 25, expression="red/green")
#
# ```
#
url_template = "https://earth-search.aws.element84.com/v0/collections/sentinel-s2-l2a-cogs/items/{id}"
# ### Visualize One Item
# +
item = url_template.format(id=sceneid[0])
with STACReader(item) as stac:
data, _ = stac.preview(assets=["B04", "B03", "B02"], max_size=256)
imshow(reshape_as_image(data))
# -
# ### Make the data look nice
# +
color_formula = "Gamma RGB 3.5 Saturation 1.7 Sigmoidal RGB 15 0.35"
data[data < 0] = 0
for ops in parse_operations(color_formula):
data = scale_dtype(ops(to_math_type(data)), numpy.uint8)
data = data.astype(numpy.uint8)
imshow(reshape_as_image(data))
# -
# ### NDVI
# +
with STACReader(item) as stac:
data, _ = stac.preview(expression="(B08-B04)/(B08+B04)", max_size=256)
imshow(data[0])
# -
# ### Part reading
# +
with STACReader(item) as stac:
data, _ = stac.part(bounds, assets=["B04", "B03", "B02"], max_size=256)
data[data < 0] = 0
for ops in parse_operations(color_formula):
data = scale_dtype(ops(to_math_type(data)), numpy.uint8)
data = data.astype(numpy.uint8)
imshow(reshape_as_image(data))
# +
with STACReader(item) as stac:
data, _ = stac.part(bounds, expression="(B08-B04)/(B08+B04)", max_size=256)
imshow(data[0])
# -
# ### GET Point values
def _worker(sceneid):
item = url_template.format(id=sceneid)
lon, lat = 30.87, 29.48
with STACReader(item) as stac:
return stac.point(lon, lat, expression="(B08-B04)/(B08+B04)")
with futures.ThreadPoolExecutor(max_workers=10) as executor:
future_work = [
executor.submit(_worker, scene) for scene in sceneid
]
for f in tqdm(futures.as_completed(future_work), total=len(future_work)):
pass
# +
fig, ax1 = plt.subplots(dpi=150)
fig.autofmt_xdate()
ax1.plot(dates, [f.result()[0][0] for f in future_work], label="NDVI")
ax1.set_xlabel("Dates")
ax1.set_ylabel("Normalized Difference Vegetation Index")
ax1.legend()
# -
|
Notebooks/WorkingWithSTAC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # "[NDIR] (ENG) Hard-negative Mining for Mir-Flickr 1M Dataset"
# > NDIR tech review
#
# - toc: false
# - badges: false
# - comments: false
# - categories: [near-duplicate image detection, tech-review]
# - hide_{github,colab,binder,deepnote}_badge: true
# + [markdown] jp-MarkdownHeadingCollapsed=true tags=[]
# # 1. Overview
# __Hard-negative mining__ is one of __sampling method__ that is usually used in object detection task. The hard-negative sample means __difficult__ negative data like not high distance value but it is negative samples. Therefore, the hard-negative mining pick first hard-negative samples.<br><br>
#
# In near-duplicate image retrieval task, it means that the method firstly choose the hard-negative pair. As a representative example, following paper used this method.
#
# > 2019, Expert Systems and Applications, <NAME>, "Benchmarking Unsupervised Near-Duplicate Image Detection"
#
# In above paper, they have to use Mir-Flickr 1M dataset which contain one million images. Generally, when we solve the ndir task by agglomeraive hierachical clustering algorithm, we have to use very big memory space, and also it takes at least $O(n^3)$ time complexity. Although we use parallel computing, that cannot be implemented. First of all, we can substitute clustering to binary classification task to solve clustering problem. If there are $n$ numbers of data, it can be $n \choose 2$ numbers of pair which can be classified to ND or NND. If that is ND, it can be 1, or not 0. Following paper used this method.
#
# > 2020, Mathematics, <NAME>, "Near-Duplicate Image Detection System Using Coarse-to-Fine Matching Scheme Based on Global and Local CNN Features"
#
# In above method, we need to consider transivity property for each pairs. If there ise cluster which is classified ND, every elements satisfy transivity property in cluster. However, in binary classification problem,
#
# $$
# \text{If} \,\ _{I_i} \text{ND}_{I_j} \,\ \text{and} \,\ _{I_j} \text{ND}_{I_k}, \,\ \text{then} \,\
# $$
# $(I_i, I_k)$ is not ND pair generally. In contrast, it is more general case, therefore we can consider it can be used.<br><br>
#
#
# What is left is the time complexity. The number of MFND dataset is 10e6 and the number of pairs is 4.999995e11. From now on, we will consider hard-negative mining algorithm to approximate score.
# + [markdown] tags=[]
# # 2. Hard-negative mining for MFND dataset
#
# - Extract randomly selected query images and a compact set of NND from a large image collection that does not contain any near-duplicate match for each query image and element of collection.
# - EX) Extract $K = 4400$ numbers of randomly selected query images and $M = 80000$ numbers of element to create a compact set from $1,000,000$ numbers of dataset.
# - For each query image, we can compute distance with all of data in collection, and it will be $K \times M$ matrix.
# - For each row, extract NND pair which have minimum distance in that row. ($hn_1$)
# - EX) $|hn_1| = 4400$
# - For each sorted row, extract K-nearest neighbors from query image. ($hn_2$)
# - EX) $|hn_2| = 4400 \times 5$
#
# > $hn_2$ is more "difficult" sample than $hn_1$.
# -
# # Commnets
# - It seems like a good way to deal with really large datasets like MFND in parallel and in parallel.
# - This is a method of selecting a negative sample, and it should not be confused with selecting a sample that is well representative of the distribution.
# - It is a simple and good method, but it seems to be a bad method under the assumption that the concept of ND can be extended to IND and NIND. Expansion of this concept may define a new concept that can quantitatively evaluate the degree from Duplicate to NND.
|
_notebooks/tech-review/(eng)hard-negative-mining-for-mir-flickr-1m-dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import Preprocess as util
import pandas as pd
import seaborn as sns
inputs,labels = util.load_data()
df = pd.DataFrame(inputs, columns = ['Reviews','Size','Installs','Type','Price','Content Rating','Genres'])
# # Distribution of Review Feature
sns.distplot(df["Reviews"])
# # Distribution of Size Feature
sns.distplot(df["Size"])
# # Distribution of Installs Feature
sns.distplot(df["Installs"])
# # Distribution of Type Feature
sns.distplot(df["Type"])
|
Data Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 ('base')
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from requests import get
from bs4 import BeautifulSoup
directions = {
"N": 0,
"NNE": 23,
"NE": 45,
"NEE": 68,
"E":90,
"SEE": 113,
"SE": 135,
"SSE": 158,
"S": 180,
"SSW": 203,
"SW": 225,
"SWW": 248,
"W": 270,
"NWW": 293,
"NW": 315,
"NNW": 338
}
url = "https://www.ndbc.noaa.gov/station_page.php?station=51201"
res = get(url)
soup = BeautifulSoup(res.content)
float(soup.find('div', id='data').find_all('tr')[1].find_all('td')[2].text.strip().split()[0])
avg_period_9_h = float(soup.find('table', class_='dataTable').find_all('tr')[19].find_all('td')[8].text)
avg_period_9_h
avg_period_6_h = float(soup.find('table', class_='dataTable').find_all('tr')[13].find_all('td')[8].text)
avg_period_6_h
# +
dominant_wave_direction = int(soup.find("div", id="data").find_all("tr")[4].find_all("td")[2].text.strip().split()[2])
dominant_wave_direction
# -
dominant_wave_direction_6_h = directions[soup.find('table', class_='dataTable').find_all('tr')[13].find_all('td')[9].text]
dominant_wave_direction_6_h
avg_period_1_h = float(soup.find('table', class_='dataTable').find_all('tr')[3].find_all('td')[8].text)
avg_period_1_h
dominant_period_1_5_h = float(soup.find('table', class_='dataTable').find_all('tr')[4].find_all('td')[7].text)
dominant_period_1_5_h
dominant_period_6_h = float(soup.find('table', class_='dataTable').find_all('tr')[13].find_all('td')[7].text)
dominant_period_6_h
wave_height_3_h = float(soup.find('table', class_='dataTable').find_all('tr')[7].find_all('td')[6].text)
wave_height_3_h
url = "https://www.ndbc.noaa.gov/station_page.php?station=oouh1"
res = get(url)
soup2 = BeautifulSoup(res.content)
wind_direction = int(soup2.find("div", id="data").find_all("tr")[1].find_all('td')[2].text.split()[2])
wind_direction
wind_speed = float(soup2.find("div", id="data").find_all("tr")[2].find_all('td')[2].text.split()[0])
wind_speed
|
scratch/noaa_scrape.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # <center> PORTFOLIO BLOG </center>
# INFO 7390
#
#
# <NAME>
#
#
# NUID: 001886775
#
# ## What is Alzheimer's Disease?
# Alzheimer's disease is the most common cause of dementia — a group of brain disorders that cause the loss of intellectual and social skills. In Alzheimer's disease, the brain cells degenerate and die, causing a steady decline in memory and mental function.
from IPython.display import Image
from IPython.core.display import HTML
Image(url= "https://www.nia.nih.gov/sites/default/files/inline-images/brain_slices_alzheimers_0.jpg")
# ## What are we trying to do?
# In this blog, we are trying to explain how we can build Machine Learning classification models to detect the presence of Alzheimer's Disease using existing medical data.
#
# Before we proceed let's define some essential concepts which are to be known.
#
# ### Supervised Learning:
# Supervised learning is where you have input variables (x) and an output variable (Y) and you use an algorithm to learn the mapping function from the input to the output.
#
# Y = f(X)
#
# The goal is to approximate the mapping function so well that when you have new input data (x) that you can predict the output variables (Y) for that data.
#
# It is called supervised learning because the process of an algorithm learning from the training dataset can be thought of as a teacher supervising the learning process.
#
# ### Classification:
# A classification model attempts to draw some conclusion from observed values. Given one or more inputs a classification model will try to predict the value of one or more outcomes. Outcomes are labels that can be applied to a dataset. For example, when filtering emails “spam” or “not spam”.
#
# There are various classification models in Machine Learning such as Random Forests Classifier and Naive Baye's Classifier.
#
# ### Neural Networks:
# Artificial neural networks (ANNs) or connectionist systems are computing systems vaguely inspired by the biological neural networks that constitute animal brains.
#
# Such systems "learn" (i.e. progressively improve performance on) tasks by considering examples, generally without task-specific programming.
#
# A deep neural network (DNN) is an artificial neural network (ANN) with multiple hidden layers between the input and output layers.
#
# ## Let's get started!
#
# We still start off by obtaining the dataset which we are going to use.
#
# The dataset has been obtained from https://www.oasis-brains.org/.
#
# - This set consists of a longitudinal collection of 150 subjects aged 60 to 96. Each subject was scanned on two or more visits, separated by at least one year for a total of 373 imaging sessions.
# - For each subject, 3 or 4 individual T1-weighted MRI scans obtained in single scan sessions are included. The subjects are all right-handed and include both men and women.
# - 72 of the subjects were characterized as nondemented throughout the study. 64 of the included subjects were characterized as demented at the time of their initial visits and remained so for subsequent scans, including 51 individuals with mild to moderate Alzheimer’s disease.
# - Another 14 subjects were characterized as nondemented at the time of their initial visit and were subsequently characterized as demented at a later visit.
#
# ### The first step is to import all the required packages
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import tree
from sklearn import datasets, linear_model, metrics
from sklearn.metrics import confusion_matrix,accuracy_score
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.decomposition import PCA
from sklearn.cross_validation import KFold
from sklearn.preprocessing import normalize, StandardScaler
from scipy.stats import multivariate_normal
from collections import Counter
from sklearn.preprocessing import LabelEncoder
from sklearn.preprocessing import OneHotEncoder, LabelBinarizer
from keras.wrappers.scikit_learn import KerasClassifier
from keras.models import Sequential
from keras.layers import Dense, Activation
# ### Next we clean the dataset of null values and unwanted columns
df=pd.read_csv('oasis_longitudinal.csv')
df2=df
df.isnull().sum()
df = df.fillna(method='ffill')
df.isnull().sum()
df = df.drop('Hand',1)
# Now our data is ready for preprocessing and analysis!
#
# It is important to remove irrelevant columns from our dataset because they could affect the performance of our model.
# ### Preprocessing
# We map categorical values to integer values and we standardize our data using StandardScaler() because some classification models perform better with standardized data.
# +
X = df.drop('Group', axis=1)
X = X.drop(['Subject ID','MRI ID','M/F','SES','Visit'], axis=1)
y = df['Group']
size_mapping={'Demented':1,'Nondemented':2,'Converted':3,'M':4,'F':5}
df2['Group'] = df2['Group'].map(size_mapping)
from sklearn.preprocessing import normalize, StandardScaler
sc_x = StandardScaler()
X2 = sc_x.fit_transform(X)
size_mapping={'Demented':1,'Nondemented':2,'Converted':3,'M':4,'F':5}
df2['Group'] = df2['Group'].map(size_mapping)
# -
# ### Split data into a Training Set and a Test Set
#
# The training set contains a known output and the model learns on this data in order to be generalized to other data later on.
#
# We have the test dataset (or subset) in order to test our model’s prediction on this subset.
#
#
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
X_train2, X_test2, y_train2, y_test2 = train_test_split(X2, y, random_state=1)
# -
# ### Selecting best features for classification
# All kinds of tree methods calculate their splits by mathematically determining which split will most effectively help distinguish the classes.
#
# This is how the Random Forest method ranks it's features based on their importances depending on which feature allows the best split.
# +
from sklearn.ensemble import RandomForestClassifier
random_forest = RandomForestClassifier(n_estimators=40, max_depth=5, random_state=1,max_features=5)
random_forest.fit(X_train, y_train)
importances=100*random_forest.feature_importances_
sorted_feature_importance = sorted(zip(importances, list(X_train)), reverse=True)
features_pd = pd.DataFrame(sorted_feature_importance)
print(features_pd)
sns.barplot(x=0, y=1, data=features_pd,palette='Reds');
plt.show()
# -
# Clinical Dementia Rating (CDR) seems to be the most important feature.
#
#
# The Clinical Dementia Rating or CDR is a numeric scale used to quantify the severity of symptoms of dementia.
#
# CDR:
# - 0 No dementia
# - 0.5 Slightly Dementia
# - 1 Demented
# - 2 Severely Demented
#
#
# We may eliminate the 3 lowest features to improve the accuracy of our model.
#
# ## Classification of data
# Now as we have cleaned, pre-processed, split and selected features for our dataset, we may finally apply the classification models and view the results produced.
#
# ### **We start off with the Support Vector Classifier.**
#
# A Support Vector Machine (SVM) is a discriminative classifier formally defined by a separating hyperplane. In other words, given labeled training data (supervised learning), the algorithm outputs an optimal hyperplane which categorizes new examples.
#
# First we create the model with desired parameters.
Image(url= "http://38.media.tumblr.com/0e459c9df3dc85c301ae41db5e058cb8/tumblr_inline_n9xq5hiRsC1rmpjcz.jpg")
from sklearn.svm import SVC
supvc = SVC(kernel='linear',C=2)
# We attempt to fit our training data into the model we just created
supvc.fit(X_train2,y_train2)
# Now that the model has sucessfully fit the data, we may predict new values using the test data.
#
# Then using the accuray_score module from Sci-Kit learn's metrics set, we may view how well the model performed
y_predict = supvc.predict(X_test2)
svcscore=accuracy_score(y_test2,y_predict)*100
print('Accuracy of Support vector classifier is ')
print(100*accuracy_score(y_test2,y_predict))
# Let us construct the confusion matrix to view the exact number of accurate predictions
# +
from sklearn.metrics import confusion_matrix
pd.DataFrame(
confusion_matrix(y_test, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True Alzheimers','True converted']
)
# -
# Observations:
# - Extremely low accuracy of 56% when using the RBF kernel.
# - High computation time on poly kernel & 90% accuracy.
# - Highest accuracy obtained on the linear kernel with 92.55%.
# - Accuracy slightly increases when penalty parameter C is set to 2.
#
#
#
# We have sucessfully classified patients into "Demented" or "Nondemented" with Support Vector Classifier with an accuracy of 92.55%!
#
# ##### Similarly, this process can be repeated with several other classification models provided by Sci-Kit Learn to perform classification.
#
# You can choose from the following classification models and discover the most accurate one for this cause.
# http://scikit-learn.org/stable/auto_examples/classification/plot_classifier_comparison.html
# ### **Using Random Forests Classifier**
#
# A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and use averaging to improve the predictive accuracy and control over-fitting.
Image(url= "http://www.globalsoftwaresupport.com/wp-content/uploads/2018/02/ggff5544hh.png")
# +
from sklearn.metrics import accuracy_score
y_predict = random_forest.predict(X_test)
rfscore = 100*accuracy_score(y_test, y_predict)
print('Accuracy of Random Forests Classifier Accuracy is ')
print(100*accuracy_score(y_test,y_predict))
from sklearn.metrics import confusion_matrix
pd.DataFrame(
confusion_matrix(y_test, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True Alzheimers','True converted']
)
# -
# Observations:
# - The highest accuracy was attained when max_features was set to 5.
# - When 5 features are considered for the best split, we obtain the greatest accuracy in this model (92.55%)
# - Standardization does not make a difference to the accuracy.
#
#
# ### **Using K Nearest Neighbors**
#
# K nearest neighbors is a simple algorithm that stores all available cases and classifies new cases based on a similarity measure (e.g., distance functions).
# +
Image(url= "http://adataanalyst.com/wp-content/uploads/2016/07/kNN-1.png")
# -
from sklearn.neighbors import KNeighborsClassifier
nneighbor = KNeighborsClassifier(n_neighbors=8,metric='euclidean')
nneighbor.fit(X_train2, y_train2)
y_predict = nneighbor.predict(X_test2)
knscore = 100*accuracy_score(y_test2, y_predict)
print('Accuracy of K Nearest Neighbors Classifier is ')
print(100*accuracy_score(y_test2,y_predict))
pd.DataFrame(
confusion_matrix(y_test2, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True Alzheimers','True converted']
)
# Observations:
# - Accuracy plateaus after using 8 neighbors.
# - Accuracy remains the same with all distance measures ( minkowski, manhattan, euclidean ).
#
#
# ### **Using Decision Tree Classifier**
#
# Decision tree learning uses a decision tree (as a predictive model) to go from observations about an item (represented in the branches) to conclusions about the item's target value (represented in the leaves).
# +
Image(url= "http://dataaspirant.com/wp-content/uploads/2017/01/B03905_05_01-compressor.png")
# -
from sklearn.tree import DecisionTreeClassifier
dectree = DecisionTreeClassifier(max_features=5)
dectree.fit(X_train, y_train)
y_predict = dectree.predict(X_test)
decscore=100*accuracy_score(y_test, y_predict)
print('Accuracy of Decision Tree Classifier is ')
print(100*accuracy_score(y_test,y_predict))
pd.DataFrame(
confusion_matrix(y_test, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True Alzheimers','True converted']
)
# Observations:
# - Max_features is selected as 5, this means that when 5 features are selected for the best split, accuracy is the highest.
#
# ### **Using Naive Baye's Classifier**
#
# Naive Bayes is a kind of classifier which uses the Bayes Theorem. It predicts membership probabilities for each class such as the probability that given record or data point belongs to a particular class. The class with the highest probability is considered as the most likely class.
Image(url= "http://www.saedsayad.com/images/Bayes_rule.png")
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train,y_train)
y_predict = gnb.predict(X_test)
nbscore = 100*accuracy_score(y_test, y_predict)
print('Accuracy of Naive Bayes Classifier is ')
print(100*accuracy_score(y_test,y_predict))
pd.DataFrame(
confusion_matrix(y_test, y_predict),
columns=['Predicted Healthy', 'Predicted alzheimers','Predicted Converted'],
index=['True Healthy', 'True alzheimers','True converted']
)
# Observations:
# - Parameters have not been tuned because the only parameter available for tuning is priors (Prior probabilities of the class).
# - It is best to leave priors at 'None' because the priors will be adjusted automatically based on the data.
#
# ### **Using Ada Boost Classifier**
#
# Ada-boost classifier combines weak classifier algorithm to form strong classifier. A single algorithm may classify the objects poorly. But if we combine multiple classifiers with selection of training set at every iteration and assigning right amount of weight in final voting, we can have good accuracy score for overall classifier.
#
#
# +
Image(url= "https://www.researchgate.net/profile/Brendan_Marsh3/publication/306054843/figure/fig3/AS:393884896120846@1470920885933/Training-of-an-AdaBoost-classifier-The-first-classifier-trains-on-unweighted-data-then.png")
# -
from sklearn.ensemble import AdaBoostClassifier
abc = AdaBoostClassifier(algorithm='SAMME')
abc.fit(X_train2,y_train2)
y_predict = abc.predict(X_test2)
abcscore=accuracy_score(y_test2,y_predict)*100
print('Accuracy of ADA Boost classifier is ')
print(100*accuracy_score(y_test2,y_predict))
pd.DataFrame(
confusion_matrix(y_test2, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True alzheimers','True converted']
)
# Observations:
# - Yields higher accuracy when the algorithm used is SAMME and not the default SAMME.R.
# - SAMME is a boosting algorithm which works better for multiclass classification, SAMME.R works is conventionally used for binary classification problems.
# - Accuracy greatly increases after using standardised data(From 50% to 90%).
# ### Using a Multilayered Perceptron Classifier
#
# Multilayer perceptron classifier is a classifier based on the feedforward artificial neural network. MLPC consists of multiple layers of nodes. Each layer is fully connected to the next layer in the network. Nodes in the input layer represent the input data. All other nodes map inputs to outputs by a linear combination of the inputs with the node’s weights w and bias b and applying an activation function.
#
# We are using 3 hidden layers of nodes.
#
# The solver is used for weight optimization.
# +
Image(url= "https://www.researchgate.net/profile/Mouhammd_Alkasassbeh/publication/309592737/figure/fig2/AS:423712664100865@1478032379613/MultiLayer-Perceptron-MLP-sturcture-334-MultiLayer-Perceptron-Classifier-MultiLayer.jpg")
# +
from sklearn.neural_network import MLPClassifier
mlp = MLPClassifier(max_iter=500,solver='lbfgs',hidden_layer_sizes=(10,30,20),activation='tanh')
mlp.fit(X_train2,y_train2)
y_predict = mlp.predict(X_test2)
mlpscore = 100*accuracy_score(y_test2,y_predict)
print(mlpscore)
from sklearn.metrics import classification_report,confusion_matrix
pd.DataFrame(
confusion_matrix(y_test2, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True alzheimers','True converted']
)
# -
# Observations:
# - Performance greatly increased from 50% to 81.23% after using scaled data.
# - Accuracy remains unaffected on changing activation functions.
# - According to scikit learn documentation, the solver 'lbfgs' is more appropriate for smaller datasets compared to other solvers such as 'adam'.
# ### Using a Feed Forward Deep Learning Neural Network
#
# [This Code was Adapted From: https://machinelearningmastery.com/multi-class-classification-tutorial-keras-deep-learning-library/ Author: <NAME>]
#
# The feedforward neural network was the first and simplest type of artificial neural network devised. In this network, the information moves in only one direction, forward, from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network.
# +
Image(url= "https://cs.stanford.edu/people/eroberts/courses/soco/projects/neural-networks/Architecture/images/feedforward.jpg")
# -
# - Multi-class labels need to be converted to binary labels(belong or does not belong to the class). LabelBinarizer makes this process easy with the transform method. At prediction time, one assigns the class for which the corresponding model gave the greatest confidence.
# +
lb = LabelBinarizer()
y_train3 =lb.fit_transform(y_train2)
# -
# - The Keras library provides a convenient wrapper for deep learning models to be used as classification or regression estimators in scikit-learn.
# - The KerasClassifier class in Keras take an argument build_fn which is the name of the function to call to get your model. You must define a function that defines your model, compiles it and returns it.
# +
def baseline_model():
classifier = Sequential()
# Adding the input layer and the first hidden layer
classifier.add(Dense(activation = 'relu', input_dim = 8, units = 8, kernel_initializer = 'uniform'))
# Adding the second hidden layer
classifier.add(Dense( activation = 'relu', units = 15, kernel_initializer = 'uniform'))
# Adding the third hidden layer
# Adding the output layer
classifier.add(Dense(activation = 'sigmoid', units = 3, kernel_initializer = 'uniform' ))
# Compiling the ANN
classifier.compile(optimizer = 'adamax', loss = 'categorical_crossentropy', metrics = ['accuracy'])
# Fitting the ANN to the Training set
return classifier
# -
# - In the example below, it is called "baseline_model". We pass this function name to the KerasClassifier.
#
estimator = KerasClassifier(build_fn=baseline_model, epochs=150, batch_size=5, verbose=0)
# - The model is automatically bundled up and passed on to the fit() function which is called internally by the KerasClassifier class.
estimator.fit(X_train2, y_train2)
y_predict = estimator.predict(X_test2)
ffdnscore = 100*accuracy_score(y_test2,y_predict)
ffdnscore
pd.DataFrame(
confusion_matrix(y_test2, y_predict),
columns=['Predicted Healthy', 'Predicted Alzheimers','Predicted Converted'],
index=['True Healthy', 'True alzheimers','True converted']
)
# Observations:
# - Using the Adamax optimizer we obtain the highest accuracy.
# - We start with the input layer, followed by two hidden layers with relu activation functions.
# - The output layer is added and the model is compiled.
# ## Comparing our classification models
# We have run all five classifiers and obtained the accuracies for each, we will attempt to visaulize the acccuracies to determine the best possible classifier for predicting Alzheimer's disease.
# +
scorearray = [svcscore,nbscore,decscore,knscore,rfscore,abcscore,mlpscore,ffdnscore]
score_arr = [{'Classifier':'SVC','Accuracy':svcscore},
{'Classifier':'NB','Accuracy':nbscore},
{'Classifier':'DEC','Accuracy':decscore},
{'Classifier':'KNN','Accuracy':knscore},
{'Classifier':'RF','Accuracy':rfscore}
,{'Classifier':'ABC','Accuracy':abcscore},
{'Classifier':'MLP','Accuracy':mlpscore},
{'Classifier':'FFDN','Accuracy':ffdnscore}]
score_df = pd.DataFrame(score_arr)
score_df = score_df.sort_values('Accuracy')
print(score_df)
sns.barplot(x="Classifier", y="Accuracy", data=score_df,palette='Reds');
plt.show()
# -
# ### Observations
# - We can hence clearly observe that the best classifier is the Support Vector Classifier & Random Forest Classifier with 92.55% accuracy.
#
# - The deep learning Multilayer Perceptron with 3 layers yields 87% accuracy, this could possibly be due to the small size of the dataset resulting in overfitting of the model.
#
# - The Deep Learning Network Using Keras Classifier performs better than a tri-layered MLP but the conventional classifiers outperform this network.
#
# - The other classifiers' performances were average with the Decision Tree Classifier being the worst performer with 77.12% accuracy.
#
# - Since Neural Networks are stochastic in nature, they produce random results every time.
#
# - Conventional Machine Learning classifiers perform better than Neural Network models. This could possibly be due to the small size of the dataset which in turn leads to the model overfitting the data. Regularization and data augmentation can be used to solve this problem.
# ### Thank you!
# I hope this tutorial was helpful, if you have any questions please e-mail me at <EMAIL>
|
NEU_ADS_Student_Project_Portfolio_Examples/Detection of Brain Illnesses using Machine Learning/Project/PortfolioBlog.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from keras.layers import Convolution2D
from keras.layers import MaxPooling2D
from keras.layers import Flatten
from keras.layers import Dense
from keras.models import Sequential
model = Sequential()
#inputlayer : apply filters
model.add(Convolution2D(filters=32,
kernel_size=(3,3),
activation='relu',
input_shape=(64, 64, 3)
))
# pooling layer where we are doing maxpooling
model.add(MaxPooling2D(pool_size=(2, 2)))
#modification for increasing accuracy
model.add(Convolution2D(filters=32,
kernel_size=(3,3),
activation='relu',
))
#modification for increasing accuracy
model.add(MaxPooling2D(pool_size=(2, 2)))
#layer inwhich we areconverting 2d/3d image to 1d image i.e flattening
model.add(Flatten())
# layer: appling relu to give positive output
# from here our hidden layerrs starts
model.add(Dense(units=128, activation='relu'))
#output layer : to provide binary output using sigmoid function
model.add(Dense(units=6, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
from keras_preprocessing.image import ImageDataGenerator
#image augmentation
#url : https://keras.io/api/preprocessing/image/
train_datagen = ImageDataGenerator(
rescale=1./255,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
test_datagen = ImageDataGenerator(rescale=1./255)
training_set = train_datagen.flow_from_directory(
'seg_train/',
target_size=(64,64),
batch_size=32,
class_mode='categorical')
test_set = test_datagen.flow_from_directory(
'seg_test/',
target_size=(64,64),
batch_size=32,
class_mode='categorical')
training_set.class_indices # to see classes of our dataset
# +
#model.fit(
# training_set,
# steps_per_epoch=2300,
# epochs=3,
# validation_data=test_set,
# validation_steps=12000)
# -
# +
#model.save("cnn-placeimage_model.h5") #save model
# -
from keras.models import load_model
model=load_model("cnn-intel-image-model.h5") #load model <- this has run on 3 epochs with ~85% accuracy
from keras.preprocessing import image
test_image = image.load_img("seg_pred/14.jpg",target_size=(64,64))
#test_image = image.load_img("C:/Users/ASUS/Desktop/cat.jpg",target_size=(64,64))
test_image #since this format is PIL or pillow so it can be printed
test_image = image.img_to_array(test_image) #convert PIL image to numpy array
import numpy as np
test_image = np.expand_dims(test_image,axis=0)
#since keras uses tensor flow and for tensorflow it needs 4d image so we converted 3d image to 4d image using above
result = model.predict(test_image)
result
if result[0][0]==1:
print("Buildings")
elif result[0][1]==1:
print("Forest")
elif result[0][2]==1:
print("Glacier")
elif result[0][3]==1:
print("Mountain")
elif result[0][4]==1:
print("Sea")
else:
print("Street")
|
Intel-Placeimage-Classification using cnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import time
import pickle
import numpy as np
from sklearn import metrics
from sklearn.linear_model import LogisticRegression
t = time.time()
# -
# ## Creating the LR pickle for tfidf vectors
def read_pickle(filename: str):
'''Read pickle to get the info'''
list_pickle = pickle.load(open(filename,"rb"))
return list_pickle
# We assume that we have train_tf_idf.pickle and test_tf_idf in folder
train_tf_idf = read_pickle('train_tf_idf.pickle')
test_tf_idf = read_pickle('test_tf_idf.pickle')
def get_X_vectors(batch):
'''Input : batch
Output : Array of vectors'''
X = []
for i in range(len(batch)):
X.append(np.concatenate((batch[i][2], batch[i][3])))
return np.array(X)
def get_y_vector(batch):
'''Input : batch
Output : array of integers (0 or 1)'''
list_bool = [list(elem[4]) for elem in batch]
preprocessed_list_bool = []
for boolean in list_bool:
if boolean == [False]:
preprocessed_list_bool.append(0)
else:
preprocessed_list_bool.append(1)
return np.array(preprocessed_list_bool)
# +
X_train = get_X_vectors(train_tf_idf)
y_train = get_y_vector(train_tf_idf)
X_test = get_X_vectors(test_tf_idf)
y_test = get_y_vector(test_tf_idf)
# -
logreg = LogisticRegression(penalty='l1', C=1.0, solver='liblinear')
logreg.fit(X_train, y_train)
outfile = open('LR_model_fit.pickle', 'wb')
pickle.dump(logreg, outfile)
outfile.close()
# ## Defining a function that takes vectors in entry and return LR probabilities
def get_batch_LR_proba(query_vecs, doc_vecs, logreg):
'''Input :
query_vecs, doc_vecs : tfidf vectors of query and doc (2D array)
logreg : fitted logistic regression
Output : array of probabilites returned by LR'''
if len(query_vecs)!=len(doc_vecs):
raise ValueError('Arrays are not of the same size')
X = []
for i in range(len(query_vecs)):
X.append(np.concatenate((query_vecs[i], doc_vecs[i])))
y_scores = logreg.predict_proba(X)
LR_results = [y_scores[i,0] for i in range(len(y_scores))]
return np.array(LR_results)
# Testing the function
query_vecs_list = [train_tf_idf[i][2] for i in range(10)]
query_vecs = np.array(query_vecs_list)
doc_vecs_list = [train_tf_idf[i][3] for i in range(10)]
doc_vecs = np.array(doc_vecs_list)
get_batch_LR_proba(query_vecs, doc_vecs, logreg)
print(f"Execution time : {time.strftime('%H:%M:%S', time.gmtime(time.time()-t))}")
|
misc/saving_LR_results.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # matplotlib
#
# Matplotlib is the core plotting package in scientific python. There are others to explore as well (which we can chat about on slack).
# <div class="alert alert-block alert-warning">
#
# There are different interfaces for interacting with matplotlib, an interactive, function-driven (state machine) command-set and an object-oriented version. We'll focus on the OO interface.
#
# </div>
# We want matplotlib to work inline in the notebook.
import numpy as np
import matplotlib.pyplot as plt
# ## Matplotlib concepts
#
# Matplotlib was designed with the following goals (from mpl docs):
#
# * Plots should look great -- publication quality (e.g. antialiased)
# * Postscript output for inclusion with TeX documents
# * Embeddable in a graphical user interface for application development
# * Code should be easy to understand it and extend
# * Making plots should be easy
#
# Matplotlib is mostly for 2-d data, but there are some basic 3-d (surface) interfaces.
#
# Volumetric data requires a different approach
# ### Gallery
#
# Matplotlib has a great gallery on their webpage -- find something there close to what you are trying to do and use it as a starting point:
#
# https://matplotlib.org/stable/gallery/index.html
#
# ### Importing
#
# There are several different interfaces for matplotlib (see https://matplotlib.org/3.1.1/faq/index.html)
#
# Basic ideas:
#
# * `matplotlib` is the entire package
# * `matplotlib.pyplot` is a module within matplotlib that provides easy access to the core plotting routines
# * `pylab` combines pyplot and numpy into a single namespace to give a MatLab like interface. You should avoid this—it might be removed in the future.
#
# There are a number of modules that extend its behavior, e.g. `basemap` for plotting on a sphere, `mplot3d` for 3-d surfaces
#
# ### Anatomy of a figure
#
# Figures are the highest level obect and can inlcude multiple axes
# 
#
# (figure from: http://matplotlib.org/faq/usage_faq.html#parts-of-a-figure )
#
# ### State-machine vs. OO interface
#
# The state-machine interface is similar to matlab -- high level functions are provided to work on the current axes in the current figure
#
# The objected oriented interface is more pythonic -- you create figure and axes objects and interact with them. It is the preferred way to use matplotlib.
#
# Note: when looking for help online, you often see these two approaches mixed.
#
# See this: https://matplotlib.org/3.2.2/tutorials/introductory/lifecycle.html
# ### Backends
#
# Interactive backends: pygtk, wxpython, tkinter, ...
#
# Hardcopy backends: PNG, PDF, PS, SVG, ...
#
#
# # Basic plotting
# ## State-machine interface
# plot() is the most basic command. Here we also see that we can use LaTeX notation for the axes
# +
x = np.linspace(0,2.0*np.pi, num=50)
y = np.cos(x)
plt.plot(x,y)
plt.xlabel(r"$x$")
plt.ylabel(r"$\cos(x)$", fontsize="x-large")
plt.xlim(0, 2.0*np.pi)
# -
# Note that when we use the `plot()` command like this, matplotlib automatically creates a figure and an axis for us and it draws the plot on this for us. This is the _state machine_ interface.
# ## OO Interface
# +
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.set_xlabel(r"$x$")
ax.set_ylabel(r"$\cos(x)$")
ax.set_xlim(0, 2*np.pi)
# -
# <div class="alert alert-block alert-info"><h3><span class="fa fa-flash"></span> Quick Exercise:</h3>
#
#
# We can plot 2 lines on a plot simply by calling plot twice. Make a plot with both `sin(x)` and `cos(x)` drawn
#
# </div>
# we can use symbols instead of lines pretty easily too—and label them
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, np.sin(x), "o", label="sine")
ax.plot(x, np.cos(x), "x", label="cosine")
ax.set_xlim(0.0, 2.0*np.pi)
ax.legend()
# Here we specified the format using a "format string" (see https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.plot.html)
#
# This has the form `'[marker][line][color]'`
# most functions take a number of optional named arguments too
ax.clear()
ax.plot(x, np.sin(x), linestyle="--", linewidth=3.0)
ax.plot(x, np.cos(x), linestyle="-")
fig
# There are predefined styles that can be used too. Generally you need to start from the figure creation for these to take effect
print(plt.style.available)
# +
plt.style.use("seaborn-darkgrid")
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x, np.sin(x), linestyle="--", linewidth=3.0)
ax.plot(x, np.cos(x), linestyle="-")
ax.set_xlim(0.0, 2.0*np.pi)
# -
plt.style.use("default")
# # Multiple axes
# there are a wide range of methods for putting multiple axes on a grid. We'll look at the simplest method.
#
# The `add_subplot()` method we've been using can take 3 numbers: the number of rows, number of columns, and current index
# +
fig = plt.figure()
ax1 = fig.add_subplot(211)
x = np.linspace(0,5,100)
ax1.plot(x, x**3 - 4*x)
ax1.set_xlabel("x")
ax1.set_ylabel(r"$x^3 - 4x$", fontsize="large")
ax2 = fig.add_subplot(212)
ax2.plot(x, np.exp(-x**2))
ax2.set_xlabel("x")
ax2.set_ylabel("Gaussian")
# log scale
ax2.set_yscale("log")
# set the figure size
fig.set_size_inches(6, 8)
# tight_layout() makes sure things don't overlap
fig.tight_layout()
# -
# # Visualizing 2-d array data
# 2-d datasets consist of (x, y) pairs and a value associated with that point. Here we create a 2-d Gaussian, using the `meshgrid()` function to define a rectangular set of points.
# +
def g(x, y):
return np.exp(-((x-0.5)**2)/0.1**2 - ((y-0.5)**2)/0.2**2)
N = 100
x = np.linspace(0.0, 1.0, N)
y = x.copy()
xv, yv = np.meshgrid(x, y)
# -
# A "heatmap" style plot assigns colors to the data values. A lot of work has gone into the latest matplotlib to define a colormap that works good for colorblindness and black-white printing.
fig = plt.figure()
ax = fig.add_subplot(111)
im = ax.imshow(g(xv, yv), origin="lower")
plt.colorbar(im, ax=ax)
# Sometimes we want to show just contour lines—like on a topographic map. The `contour()` function does this for us.
fig = plt.figure()
ax = fig.add_subplot(111)
contours = ax.contour(g(xv, yv))
ax.axis("equal") # this adjusts the size of image to make x and y lengths equal
# <div class="alert alert-block alert-info"><h3><span class="fa fa-flash"></span> Quick Exercise:</h3>
#
# Contour plots can label the contours, using the `ax.clabel()` function.
# Try adding labels to this contour plot.
# </div>
# # Error bars
# For experiments, we often have errors associated with the $y$ values. Here we create some data and add some noise to it, then plot it with errors.
# +
def y_experiment(a1, a2, sigma, x):
""" return the experimental data in a linear + random fashion a1
is the intercept, a2 is the slope, and sigma is the error """
N = len(x)
# randn gives samples from the "standard normal" distribution
r = np.random.randn(N)
y = a1 + a2*x + sigma*r
return y
N = 40
x = np.linspace(0.0, 100.0, N)
sigma = 25.0*np.ones(N)
y = y_experiment(10.0, 3.0, sigma, x)
# -
fig = plt.figure()
ax = fig.add_subplot(111)
ax.errorbar(x, y, yerr=sigma, fmt="o")
# <div class="alert alert-block alert-info"><h3><span class="fa fa-flash"></span> Quick Exercise:</h3>
#
# Make an error plot with error bars in both x and y
# </div>
# # Annotations
# adding text to the plot is easy
xx = np.linspace(0, 2.0*np.pi, 1000)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xx, np.sin(xx))
ax.text(np.pi/2, np.sin(np.pi/2), r"maximum")
# we can also turn off the top and right "splines"
ax.spines['right'].set_visible(False)
ax.spines['top'].set_visible(False)
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
fig
# Annotations with an arrow are also possible
# +
#example from http://matplotlib.org/examples/pylab_examples/annotation_demo.html
fig = plt.figure()
ax = fig.add_subplot(111, projection='polar')
r = np.arange(0, 1, 0.001)
theta = 2*2*np.pi*r
line, = ax.plot(theta, r, color='#ee8d18', lw=3)
ind = 800
thisr, thistheta = r[ind], theta[ind]
ax.plot([thistheta], [thisr], 'o')
ax.annotate('a polar annotation',
xy=(thistheta, thisr), # theta, radius
xytext=(0.05, 0.05), # fraction, fraction
textcoords='figure fraction',
arrowprops=dict(facecolor='black', shrink=0.05),
horizontalalignment='left',
verticalalignment='bottom')
# -
# # Surface plots
# matplotlib can't deal with true 3-d data (i.e., x,y,z + a value), but it can plot 2-d surfaces and lines in 3-d.
# +
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.gca(projection="3d")
# parametric curves
N = 100
theta = np.linspace(-4*np.pi, 4*np.pi, N)
z = np.linspace(-2, 2, N)
r = z**2 + 1
x = r*np.sin(theta)
y = r*np.cos(theta)
ax.plot(x,y,z)
# +
fig = plt.figure()
ax = fig.gca(projection="3d")
X = np.arange(-5,5, 0.25)
Y = np.arange(-5,5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap="coolwarm")
# and the view (note: most interactive backends will allow you to rotate this freely)
ax.azim = 45
ax.elev = 40
# -
# # Plotting on a sphere
# the map funcationality expects stuff in longitude and latitude, so if you want to plot x,y,z on the surface of a sphere using the idea of spherical coordinates, remember that the spherical angle from z (theta) is co-latitude
#
# note: you need the python-basemap package installed for this to work
#
# This also illustrates getting access to a matplotlib toolkit
# +
def to_lonlat(x,y,z):
SMALL = 1.e-100
rho = np.sqrt((x + SMALL)**2 + (y + SMALL)**2)
R = np.sqrt(rho**2 + (z + SMALL)**2)
theta = np.degrees(np.arctan2(rho, z + SMALL))
phi = np.degrees(np.arctan2(y + SMALL, x + SMALL))
# latitude is 90 - the spherical theta
return (phi, 90-theta)
from mpl_toolkits.basemap import Basemap
# other projections are allowed, e.g. "ortho", moll"
map = Basemap(projection='moll', lat_0 = 45, lon_0 = 45,
resolution = 'l', area_thresh = 1000.)
map.drawmapboundary()
map.drawmeridians(np.arange(0, 360, 15), color="0.5", latmax=90)
map.drawparallels(np.arange(-90, 90, 15), color="0.5", latmax=90) #, labels=[1,0,0,1])
# unit vectors (+x, +y, +z)
points = [(1,0,0), (0,1,0), (0,0,1)]
labels = ["+x", "+y", "+z"]
for i in range(len(points)):
p = points[i]
print(p)
lon, lat = to_lonlat(p[0], p[1], p[2])
xp, yp = map(lon, lat)
s = plt.text(xp, yp, labels[i], color="b", zorder=10)
# draw a great circle arc between two points
lats = [0, 0]
lons = [0, 90]
map.drawgreatcircle(lons[0], lats[0], lons[1], lats[1], linewidth=2, color="r")
# -
# also, if you really are interested in earth...
# +
map = Basemap(projection='ortho', lat_0 = 45, lon_0 = 45,
resolution = 'l', area_thresh = 1000.)
map.drawcoastlines()
map.drawmapboundary()
# -
# # Histograms
# here we generate a bunch of gaussian-normalized random numbers and make a histogram. The probability distribution should match
# $$y(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-x^2/(2\sigma^2)}$$
# +
N = 10000
r = np.random.randn(N)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.hist(r, density=True, bins=20)
x = np.linspace(-5,5,200)
sigma = 1.0
ax.plot(x, np.exp(-x**2/(2*sigma**2))/(sigma*np.sqrt(2.0*np.pi)),
c="r", lw=2)
ax.set_xlabel("x")
# -
# # Plotting data from a file
# numpy.loadtxt() provides an easy way to read columns of data from an ASCII file
data = np.loadtxt("test1.exact.128.out")
print(data.shape)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(data[:,1], data[:,2]/np.max(data[:,2]), label=r"$\rho$")
ax.plot(data[:,1], data[:,3]/np.max(data[:,3]), label=r"$u$")
ax.plot(data[:,1], data[:,4]/np.max(data[:,4]), label=r"$p$")
ax.plot(data[:,1], data[:,5]/np.max(data[:,5]), label=r"$T$")
ax.set_ylim(0,1.1)
ax.legend(frameon=False, fontsize=12)
# # Final fun
# if you want to make things look hand-drawn in the style of xkcd, rerun these examples after doing
# plt.xkcd()
plt.xkcd()
|
content/04-python-matplotlib/matplotlib-basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="Fi4s3f_Pcfi8"
# # Fast RCNN for object detection
# Este notebook apresenta:
# - como usar o [SDK](https://platiagro.github.io/sdk/) para carregar datasets, salvar modelos e outros artefatos.
# - como declarar parâmetros e usá-los para criar componentes reutilizáveis.
#
#
# **Este Notebook seguirá os seguintes tutoriais:**
# - Faster RCNN Train <br>
# https://www.kaggle.com/pestipeti/pytorch-starter-fasterrcnn-train <br>
# - Faster RCNN Inference <br>
# https://www.kaggle.com/pestipeti/pytorch-starter-fasterrcnn-inference <br>
# - Faster RCNN Metric + scrpit details <br>
# https://www.kaggle.com/pestipeti/competition-metric-details-script <br>
# - TORCHVISION OBJECT DETECTION FINETUNING TUTORIAL <br>
# https://pytorch.org/tutorials/intermediate/torchvision_tutorial.html <br>
# - TRANSFER LEARNING FOR COMPUTER VISION TUTORIAL <br>
# https://pytorch.org/tutorials/beginner/transfer_learning_tutorial.html#transfer-learning-for-computer-vision-tutorial
# + [markdown] id="VS0WZkTKcfi9"
# ## Declare parâmetros e hiperparâmetros para o modelo
# Os componentes podem declarar (e usar) estes parâmetros como padrão:
# - dataset
# - target
#
# Use estes parâmetros para carregar/salvar conjutos de dados, modelos, métricas e figuras com a ajuda do [SDK da PlatIAgro](https://platiagro.github.io/sdk/). <br>
# É possível também declarar parâmetros personalizados para serem definidos ao executar um experimento.
#
# Selecione os hiperparâmetros e seus respectivos valores para serem usados ao treinar o modelo:
# - language
#
# Estes parâmetros são alguns dos oferecidos pela classe do modelo, você também pode utilizar outros existentes. <br>
# Dê uma olhada nos [parâmetros do modelo](https://scikit-learn.org/stable/modules/generated/sklearn.impute.SimpleImputer.html#sklearn-impute-simpleimputer) para mais informações.
# + id="3F2NzQcfcfi_" tags=["parameters"]
# parâmetros
dataset = "" #@param {type:"string"}
target = "sentiment" #@param {type:"string", label:"Atributo alvo", description:"Seu modelo será treinado para prever os valores do alvo."}
#Hyperparâametros
train_batch_size = 2 #@param {type:"integer"}
valid_batch_size = 4 #@param {type:"integer"}
test_batch_size = 2 #@param {type:"integer"}
max_epochs = 2 #@param {type:"integer"}
accumulate_grad_batches = 8 #@param {type:"integer"}
learning_rate = 0.005 #@param {type:"number"}
momentum = 0.9 #@param {type:"number"}
weight_decay = 0.0005 #@param {type:"number"}
num_classes = 2 #@param {type:"integer"}
detection_threshold = 0.5 #@param {type:"number"}
seed =7 #@param {type:"integer"}
# selected features to perform the model
filter_type = "incluir" #@param ["incluir","remover"] {type:"string",label:"Modo de seleção das features", description:"Se deseja informar quais features deseja incluir no modelo, selecione a opção [incluir]. Caso deseje informar as features que não devem ser utilizadas, selecione [remover]. "}
model_features = "review" #@param {type:"string",multiple:true,label:"Features para incluir/remover no modelo",description:"Seu modelo será feito considerando apenas as features selecionadas. Caso nada seja especificado, todas as features serão utilizadas"}
coord_format = "coco" #@param ["coco","pascal_voc"] {type:"string"}
# + [markdown] id="2xOAGNc3kKc7"
# ## Estapas Google Coolab
# + id="IOkTulvykOH8" executionInfo={"status": "ok", "timestamp": 1601552328596, "user_tz": 180, "elapsed": 44126, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="d02e1ae1-9afd-4f9d-8223-b4a15cfb0528" colab={"base_uri": "https://localhost:8080/", "height": 245}
# ! pip install torchvision --quiet
# ! pip install pytorch-lightning==0.8.4 --quiet
# ! pip install transformers --quiet
# ! pip install ftfy --quiet
# ! pip install -U git+https://github.com/albumentations-team/albumentations --quiet
# ! pip install numba --quiet
# + id="WQgpuceG9oW-" executionInfo={"status": "ok", "timestamp": 1601468937549, "user_tz": 180, "elapsed": 2509, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="914f211f-6478-46dd-ccc1-5a3c053f1543" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# ! pip freeze
# + id="REX4zqqhkQm5" executionInfo={"status": "ok", "timestamp": 1601400453573, "user_tz": 180, "elapsed": 35886, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="9d6bae81-2fb4-4d93-89ad-83e121fa28f1" colab={"base_uri": "https://localhost:8080/", "height": 82}
#Mount drive
print("\nMounting Drive...\n")
from google.colab import drive
drive.mount('/content/drive')
# + id="A-WNn7tlkWRi"
import pandas as pd
import numpy as np
import cv2
import os
import re
from PIL import Image
import albumentations as A
from albumentations.pytorch.transforms import ToTensorV2
import torch
import torchvision
from torchvision.models.detection.faster_rcnn import FastRCNNPredictor
from torchvision.models.detection import FasterRCNN
from torchvision.models.detection.rpn import AnchorGenerator
from torch.utils.data import DataLoader, Dataset
from torch.utils.data.sampler import SequentialSampler
from matplotlib import pyplot as plt
DIR_INPUT = '/content/drive/My Drive/Computer_Vision/datasets_imagem/wheat-detection'
DIR_TRAIN = f'{DIR_INPUT}/train'
DIR_TEST = f'{DIR_INPUT}/test'
# + [markdown] id="ylc859l2kLMc"
# ## Configurações Gerais
#
#
# + [markdown] id="-VWoVX87lIl2"
# Definindo GPU como padrão e verificando status de hardware
# + id="C1jVexlxkKPB" executionInfo={"status": "ok", "timestamp": 1601400459327, "user_tz": 180, "elapsed": 41610, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="518b39d0-7e58-4f89-e5ce-da4e07defbe8" colab={"base_uri": "https://localhost:8080/"}
from multiprocessing import cpu_count
import torch
dev = "cuda:0" if torch.cuda.is_available() else "cpu"
device = torch.device(dev)
if dev == "cpu":
print(f"number of CPU cores: {cpu_count()}")
else:
print(f"GPU: {torch.cuda.get_device_name(0)}, number of CPU cores: {cpu_count()}")
# + [markdown] id="54N1AM5lgcQZ"
# Impedir excesso de logs
# + id="Wp7cKKJakymt"
import logging
logging.getLogger("transformers.configuration_utils").setLevel(logging.WARNING)
logging.getLogger("transformers.modeling_utils").setLevel(logging.WARNING)
logging.getLogger("lightning").setLevel(logging.WARNING)
# + [markdown] id="NkSLj_sZk_IG"
# Fixar semente de pesos aleatporios para replicabilidade
# + id="1JqH82K-k2QI"
import random
random.seed(seed)
torch.random.manual_seed(seed)
torch.cuda.manual_seed(seed)
# + [markdown] id="Fg9s8gudcfjF"
# ## Acesso ao conjunto de dados
#
# O conjunto de dados utilizado nesta etapa será o mesmo carregado através da plataforma.<br>
# O tipo da variável retornada depende do arquivo de origem:
# - [pandas.DataFrame](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.html) para CSV e compressed CSV: .csv .csv.zip .csv.gz .csv.bz2 .csv.xz
# - [Binary IO stream](https://docs.python.org/3/library/io.html#binary-i-o) para outros tipos de arquivo: .jpg .wav .zip .h5 .parquet etc
# + id="mR0o0ezkcfjG" executionInfo={"status": "ok", "timestamp": 1601400459694, "user_tz": 180, "elapsed": 41908, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="8a78a089-d127-4f57-91b1-3c8a0caa2dc7" colab={"base_uri": "https://localhost:8080/", "height": 191}
import pandas as pd
train_df = pd.read_csv(f'{DIR_INPUT}/train.csv')
test_df = pd.read_csv(f'{DIR_INPUT}/sample_submission.csv')
train_df.head()
# + [markdown] id="GbQg7f51mRXP"
# ## Manipulando os dados
# + id="_AYwbrnKmYWt" executionInfo={"status": "ok", "timestamp": 1601400460897, "user_tz": 180, "elapsed": 43077, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="5198abf3-a590-4bd5-88c5-ed2f0765a1e1" colab={"base_uri": "https://localhost:8080/", "height": 191}
train_df['x'] = -1
train_df['y'] = -1
train_df['w'] = -1
train_df['h'] = -1
def expand_bbox(x):
r = np.array(re.findall("([0-9]+[.]?[0-9]*)", x))
if len(r) == 0:
r = [-1, -1, -1, -1]
return r
train_df[['x', 'y', 'w', 'h']] = np.stack(train_df['bbox'].apply(lambda x: expand_bbox(x)))
train_df.drop(columns=['bbox'], inplace=True)
train_df['x'] = train_df['x'].astype(np.float)
train_df['y'] = train_df['y'].astype(np.float)
train_df['w'] = train_df['w'].astype(np.float)
train_df['h'] = train_df['h'].astype(np.float)
train_df.head()
# + id="37ypOiYmmmv-" executionInfo={"status": "ok", "timestamp": 1601400460900, "user_tz": 180, "elapsed": 43024, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="a75fee55-d6d3-42bd-be8b-b50b0018ad66" colab={"base_uri": "https://localhost:8080/", "height": 33}
image_ids = train_df['image_id'].unique()
valid_ids = image_ids[-665:]
train_ids = image_ids[:-665]
valid_df = train_df[train_df['image_id'].isin(valid_ids)]
train_df = train_df[train_df['image_id'].isin(train_ids)]
valid_df.shape, train_df.shape
# + id="BAzvLYdJ75wQ" executionInfo={"status": "ok", "timestamp": 1601400460901, "user_tz": 180, "elapsed": 43001, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="58ca3c71-73b9-4109-8b89-4cdd25a3b34f" colab={"base_uri": "https://localhost:8080/", "height": 191}
test_df.head()
# + [markdown] id="Ubjtx5tVnT2Y"
# ## Criação do Dataset -> Utilizando formato Pascal Voc
#
#
#
# * pascal_voc: min/max coordinates ```[x_min, y_min, x_max, y_max] ```<br>
# * coco: width/height instead of maxes ```[x_min, y_min, width, height]```
#
#
#
# + id="yNvzUuEanWB7" executionInfo={"status": "ok", "timestamp": 1601400460902, "user_tz": 180, "elapsed": 42949, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="42e8a0a8-17f1-436c-cd7c-c3106f3c636f" colab={"base_uri": "https://localhost:8080/", "height": 33}
# %%writefile Dataset.py
from torch.utils.data import Dataset
import torch
import cv2
import numpy as np
import pandas as pd
class WheatDataset(Dataset):
def __init__(self, dataframe, image_dir, transforms=None,step = "Experiment"):
super().__init__()
self.image_ids = dataframe['image_id'].unique()
self.df = dataframe
self.image_dir = image_dir
self.transforms = transforms
self.step = step
def __getitem__(self, index: int):
image_id = self.image_ids[index]
records = self.df[self.df['image_id'] == image_id]
image = cv2.imread(f'{self.image_dir}/{image_id}.jpg', cv2.IMREAD_COLOR)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB).astype(np.float32)
image /= 255.0
if self.step == "Experiment":
# transforming [x_min, y_min, width, height] to x_min, y_min, x_max, y_max]
# it is an albumentations requirement
boxes = records[['x', 'y', 'w', 'h']].values
boxes[:, 2] = boxes[:, 0] + boxes[:, 2]
boxes[:, 3] = boxes[:, 1] + boxes[:, 3]
area = (boxes[:, 3] - boxes[:, 1]) * (boxes[:, 2] - boxes[:, 0])
area = torch.as_tensor(area, dtype=torch.float32)
# there is only one class
labels = torch.ones((records.shape[0],), dtype=torch.int64)
# suppose all instances are not crowd
iscrowd = torch.zeros((records.shape[0],), dtype=torch.int64)
target = {}
target['boxes'] = boxes
target['labels'] = labels
# target['masks'] = None
target['image_id'] = torch.tensor([index])
target['area'] = area
target['iscrowd'] = iscrowd
if self.transforms:
sample = {'image': image,'bboxes': target['boxes'],'labels': labels}
sample = self.transforms(**sample)
image = sample['image']
# Reempilia as bboxes em m tensor só como estava antes
stacked_boxes = torch.stack(tuple(map(torch.tensor, zip(*sample['bboxes'])))).permute(1, 0)
target['boxes'] = torch.as_tensor(stacked_boxes, dtype=torch.float32)
return image, image_id,target
if self.step == "Deployment":
if self.transforms:
sample = {'image': image,}
sample = self.transforms(**sample)
image = sample['image']
return image, image_id
def __len__(self) -> int:
return self.image_ids.shape[0]
# + id="W-HDG8NEuSz-"
# %run Dataset.py
# + [markdown] id="gfn7TXcAuTz-"
# Transformações com Albumentations
# + id="Y7rAc10NoTzr"
def get_debug_transform():
return A.Compose([
A.Flip(0.5),
ToTensorV2(p=1.0)
], bbox_params={'format': 'pascal_voc', 'label_fields': ['labels']})
# + id="ZYkBMi83oYv0" executionInfo={"status": "ok", "timestamp": 1601400460906, "user_tz": 180, "elapsed": 42849, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="c4191c08-1394-4acd-c0e9-35486cd60815" colab={"base_uri": "https://localhost:8080/", "height": 1000}
ds_debug = WheatDataset(train_df, DIR_TRAIN, get_debug_transform())
print("------->Testando Dataset<-------")
image, target, image_id = ds_debug[0]
print(image)
print(target)
print(image_id)
# + [markdown] id="_94SZT0No69y"
# ## Criação do Dataloader
# + [markdown] id="S6zrMk6npxag"
# Collate para colocar batch em tuplas
# + id="yEDRnLGTo-kD"
def collate_fn(batch):
return tuple(zip(*batch))
# + [markdown] id="qjb7ceIrqULV"
# Criando dataloader
# + id="byZ_sc0cp4P_"
debug_loader = DataLoader(
ds_debug,
batch_size=4,
shuffle=False,
num_workers=cpu_count(),
collate_fn=collate_fn
)
# + [markdown] id="4474yq12p4pY"
# Testando dataloader
# + id="TudvkVV_qVv0" executionInfo={"status": "ok", "timestamp": 1601400462398, "user_tz": 180, "elapsed": 44253, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="f0bccea4-9239-46d7-a400-028de8d30382" colab={"base_uri": "https://localhost:8080/", "height": 1000}
print("------->Testando Dataloader <-------")
next(iter(debug_loader))
# + [markdown] id="Z4KwkcwBqkZC"
# ## Testando um exemplar
# + [markdown] id="i8KJXqOHrFle"
# Recuperando elementos do dataset/dataloader
# + id="1cVRcRpuqxKU"
images, image_ids,targets = next(iter(debug_loader))
images = list(image.to(device) for image in images)
targets = [{k: v.to(device) for k, v in t.items()} for t in targets]
# + [markdown] id="PpQDpJN4rIcx"
# Recuperando boxes e a imagem
# + id="BADDZb6LrI0i"
boxes = targets[2]['boxes'].cpu().numpy().astype(np.int32)
sample = images[2].permute(1,2,0).cpu().numpy()
# + [markdown] id="sYLRGJMxrRue"
# Plotando Imagem
# + id="KxZg8hF-rUHQ" executionInfo={"status": "ok", "timestamp": 1601400473249, "user_tz": 180, "elapsed": 55006, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="ac04d7f1-b4ab-465a-8d57-dd4869a42989" colab={"base_uri": "https://localhost:8080/", "height": 498}
fig, ax = plt.subplots(1, 1, figsize=(16, 8))
for box in boxes:
cv2.rectangle(sample,
(box[0], box[1]),
(box[2], box[3]),
(220, 0, 0), 3)
ax.set_axis_off()
ax.imshow(sample)
# + [markdown] id="INZe4iBRcfjL"
# ## Acesso aos metadados do conjunto de dados
#
# Utiliza a função `stat_dataset` do [SDK da PlatIAgro](https://platiagro.github.io/sdk/) para carregar metadados. <br>
# Por exemplo, arquivos CSV possuem `metadata['featuretypes']` para cada coluna no conjunto de dados (ex: categorical, numerical, or datetime).
# + id="PWJfCTTacfjL"
import numpy as np
# from platiagro import stat_dataset
# metadata = stat_dataset(name=dataset)
# featuretypes = metadata["featuretypes"]
#columns = df.columns.to_numpy()
# featuretypes = np.array(featuretypes)
#target_index = np.argwhere(columns == target)
#columns = np.delete(columns, target_index)
# featuretypes = np.delete(featuretypes, target_index)
# + [markdown] id="qL-gCSEWcfjP"
# ## Remoção de linhas com valores faltantes no atributo alvo
#
# Caso haja linhas em que o atributo alvo contenha valores faltantes, é feita a remoção dos casos faltantes.
# + id="LRdnKbyKcfjQ"
# from sklearn.preprocessing import LabelEncoder
# df.dropna(subset = [target],inplace=True)
# y = df[target].to_numpy()
# label_encoder = LabelEncoder()
# y = label_encoder.fit_transform(y)
# + [markdown] id="7jmjr4rTcfjU"
# ## Filtragem das features
#
# Seleciona apenas as features que foram declaradas no parâmetro model_features. Se nenhuma feature for especificada, todo o conjunto de dados será utilizado para a modelagem.
# + id="XcZs3X2WcfjU"
# if filter_type == 'incluir':
# if len(model_features) >= 1:
# columns_index = (np.where(np.isin(columns,model_features)))[0]
# columns_index.sort()
# columns_to_filter = columns[columns_index]
# featuretypes = featuretypes[columns_index]
# else:
# columns_to_filter = columns
# else:
# if len(model_features) >= 1:
# columns_index = (np.where(np.isin(columns,model_features)))[0]
# columns_index.sort()
# columns_to_filter = np.delete(columns,columns_index)
# featuretypes = np.delete(featuretypes,columns_index)
# else:
# columns_to_filter = columns
# # keep the features selected
# df_model = df[columns_to_filter]
# X = df_model.to_numpy()
# + [markdown] id="qkG4CvuIcfjZ"
# ## Divisão do datset em subconjuntos de treino e teste
#
# Subconjunto de Treino: amostras de dados usado para treinar o modelo (``fit``). <br>
# Subconjunto de Teste: a amostra de dados usada para fornecer uma avaliação imparcial de um modelo adequado ao conjunto de dados de treinamento.
# + id="A833KX9BgcRA"
# from sklearn.model_selection import train_test_split
# from sklearn.model_selection import StratifiedShuffleSplit
# X_train, X_, y_train, y_ = train_test_split(X, y, train_size=0.8,random_state=seed,stratify = y)
# X_valid, X_test, y_valid, y_test = train_test_split(X_, y_, train_size=0.5,stratify = y_)
# + [markdown] id="HWuuyglUpO_g"
# ## Classe para tirar a média entre as losses
# + [markdown] id="eJ7s_V7FpS17"
# Diversas funções de custo são levadas em consideração. Será tirada uma média entre elas para se ter uma única função de otimização. Estas são:
#
# * loss_box_reg
# * loss_classifier
# * loss_objectness
# * loss_rpn_box_reg
#
#
# + id="Cuympe-2pR0A" executionInfo={"status": "ok", "timestamp": 1601400473257, "user_tz": 180, "elapsed": 54788, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="45e2e918-9b34-40f2-e71f-03823e99e60b" colab={"base_uri": "https://localhost:8080/", "height": 33}
# %%writefile Averager.py
class Averager:
def __init__(self):
self.current_total = 0.0
self.iterations = 0.0
def send(self, value):
self.current_total += value
self.iterations += 1
@property
def value(self):
if self.iterations == 0:
return 0
else:
return 1.0 * self.current_total / self.iterations
def reset(self):
self.current_total = 0.0
self.iterations = 0.0
# + id="dQ4Vojz9XSNs" executionInfo={"status": "ok", "timestamp": 1601400473259, "user_tz": 180, "elapsed": 54736, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="ec0e6ef9-b46f-46ab-e39b-8272709eac09" colab={"base_uri": "https://localhost:8080/", "height": 33}
# %run Averager.py
# + [markdown] id="wAjwq493gcR8"
# ## Recuperando os pesos
# + id="salI94ZvgcR8" executionInfo={"status": "ok", "timestamp": 1601400473260, "user_tz": 180, "elapsed": 54697, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="9360717b-7485-4562-963c-92c9bff6449e" colab={"base_uri": "https://localhost:8080/", "height": 35}
import os
cwd = os.getcwd()
cwd
# + id="td-3utusgcSA"
# # ! gsutil cp gs://platiagro/Glove_Bag_Of_Embeddings_For_Sentence_Classification/epoch=199.ckpt /home/jovyan/tasks/GloVe_Bag_Of_Sentence_Classification
# + [markdown] id="1UeXhI5K7GMf"
# ## Funções que calculam a métrica de precisão baseada em Intersect Over Union (IOU)
# Foi escolhido fazer por fora do modelo e enviar as funções para que seja possível utilizar a biblioteca Numba, paralelizando o processamento em CPU
# + id="EhI1jR10r2Km"
from numba import jit
@jit(nopython=True)
def calculate_iou(gt, pr, form='coco') -> float:
"""Calculates the Intersection over Union.
Args:
gt: (np.ndarray[Union[int, float]]) coordinates of the ground-truth box
pr: (np.ndarray[Union[int, float]]) coordinates of the prdected box
form: (str) gt/pred coordinates format
- pascal_voc: [xmin, ymin, xmax, ymax]
- coco: [xmin, ymin, w, h]
Returns:
(float) Intersection over union (0.0 <= iou <= 1.0)
"""
if form == 'coco':
gt = gt.copy()
pr = pr.copy()
gt[2] = gt[0] + gt[2]
gt[3] = gt[1] + gt[3]
pr[2] = pr[0] + pr[2]
pr[3] = pr[1] + pr[3]
# Calculate overlap area
dx = min(gt[2], pr[2]) - max(gt[0], pr[0]) + 1
if dx < 0:
return 0.0
dy = min(gt[3], pr[3]) - max(gt[1], pr[1]) + 1
if dy < 0:
return 0.0
overlap_area = dx * dy
# Calculate union area
union_area = (
(gt[2] - gt[0] + 1) * (gt[3] - gt[1] + 1) +
(pr[2] - pr[0] + 1) * (pr[3] - pr[1] + 1) -
overlap_area
)
return overlap_area / union_area
@jit(nopython=True)
def find_best_match(gts, pred, pred_idx, threshold = 0.5, form = 'pascal_voc', ious=None) -> int:
"""Returns the index of the 'best match' between the
ground-truth boxes and the prediction. The 'best match'
is the highest IoU. (0.0 IoUs are ignored).
Args:
gts: (List[List[Union[int, float]]]) Coordinates of the available ground-truth boxes
pred: (List[Union[int, float]]) Coordinates of the predicted box
pred_idx: (int) Index of the current predicted box
threshold: (float) Threshold
form: (str) Format of the coordinates
ious: (np.ndarray) len(gts) x len(preds) matrix for storing calculated ious.
Return:
(int) Index of the best match GT box (-1 if no match above threshold)
"""
best_match_iou = -np.inf
best_match_idx = -1
for gt_idx in range(len(gts)):
if gts[gt_idx][0] < 0:
# Already matched GT-box
continue
iou = -1 if ious is None else ious[gt_idx][pred_idx]
if iou < 0:
iou = calculate_iou(gts[gt_idx], pred, form=form)
if ious is not None:
ious[gt_idx][pred_idx] = iou
if iou < threshold:
continue
if iou > best_match_iou:
best_match_iou = iou
best_match_idx = gt_idx
return best_match_idx
@jit(nopython=True)
def calculate_precision(gts, preds, threshold = 0.5, form = 'coco', ious=None) -> float:
"""Calculates precision for GT - prediction pairs at one threshold.
Args:
gts: (List[List[Union[int, float]]]) Coordinates of the available ground-truth boxes
preds: (List[List[Union[int, float]]]) Coordinates of the predicted boxes,
sorted by confidence value (descending)
threshold: (float) Threshold
form: (str) Format of the coordinates
ious: (np.ndarray) len(gts) x len(preds) matrix for storing calculated ious.
Return:
(float) Precision
"""
n = len(preds)
tp = 0
fp = 0
# for pred_idx, pred in enumerate(preds_sorted):
for pred_idx in range(n):
best_match_gt_idx = find_best_match(gts, preds[pred_idx], pred_idx,
threshold=threshold, form=form, ious=ious)
if best_match_gt_idx >= 0:
# True positive: The predicted box matches a gt box with an IoU above the threshold.
tp += 1
# Remove the matched GT box
gts[best_match_gt_idx] = -1
else:
# No match
# False positive: indicates a predicted box had no associated gt box.
fp += 1
# False negative: indicates a gt box had no associated predicted box.
fn = (gts.sum(axis=1) > 0).sum()
return tp / (tp + fp + fn)
@jit(nopython=True)
def calculate_image_precision(gts, preds, thresholds = (0.5, ), form = 'coco') -> float:
"""Calculates image precision.
Args:
gts: (List[List[Union[int, float]]]) Coordinates of the available ground-truth boxes
preds: (List[List[Union[int, float]]]) Coordinates of the predicted boxes,
sorted by confidence value (descending)
thresholds: (float) Different thresholds
form: (str) Format of the coordinates
Return:
(float) Precision
"""
n_threshold = len(thresholds)
image_precision = 0.0
ious = np.ones((len(gts), len(preds))) * -1
# ious = None
for threshold in thresholds:
precision_at_threshold = calculate_precision(gts.copy(), preds, threshold=threshold,
form=form, ious=ious)
image_precision += precision_at_threshold / n_threshold
return image_precision
# + [markdown] id="M_O9CvCwn2Mq"
# ## Modelo Pytorch Lightning
# + id="itIgwqsWj8-3" executionInfo={"status": "ok", "timestamp": 1601400474017, "user_tz": 180, "elapsed": 55372, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="5945ea5f-e4f5-4315-8297-11f1599d4433" colab={"base_uri": "https://localhost:8080/", "height": 33}
# %%writefile Model_Lightning.py
#general
from torch.utils.data import DataLoader
from multiprocessing import cpu_count
import pytorch_lightning as pl
import torch
import functools
import traceback
import psutil
import pandas as pd
import numpy as np
import cv2
#albumentations
import albumentations as A
from albumentations.pytorch.transforms import ToTensorV2
#torchvision
import torchvision
from torchvision.models.detection.faster_rcnn import FastRCNNPredictor
from torchvision.models.detection import FasterRCNN
from torchvision.models.detection.rpn import AnchorGenerator
#numba -> CPU paralelisation
from numba import jit
class FastRCNNFinetuner(pl.LightningModule):
def __init__(self,
hyperparams,
model_parameters,
dataset_infos,
extra_infos):
super(FastRCNNFinetuner, self).__init__()
#---------- hyperparams
self.learning_rate = hyperparams['learning_rate']
self.momentum = hyperparams['momentum']
self.weight_decay = hyperparams['weight_decay']
self.detection_threshold = hyperparams['detection_threshold']
self.train_batch_size = hyperparams['train_batch_size']
self.valid_batch_size = hyperparams['valid_batch_size']
self.test_batch_size = hyperparams['test_batch_size']
#---------- model_parameters
self.num_classes = model_parameters['num_classes'] # 1 class (wheat) + background
self.coord_format = model_parameters['coord_format'] # coco ou pascal_voc
self.Averager = model_parameters['Averager']
self.loss_hist = self.Averager()
self.calculate_image_precision = model_parameters['calculate_image_precision']
self.calculate_precision = model_parameters['calculate_precision']
self.find_best_match = model_parameters['find_best_match']
self.calculate_iou = model_parameters['calculate_iou']
#---------- dataset_infos
self.all_data = dataset_infos['all_data']
self.DIR_TRAIN = dataset_infos['DIR_TRAIN']
self.DIR_TEST = dataset_infos['DIR_TEST']
self.CustomDataset = dataset_infos['CustomDataset']
#---------- extra_infos
self.overfit = extra_infos['overfit']
#---------- other_infos
self.predict_proba = torch.nn.Softmax(dim=1)
self.step = 'Experiment'
#---------- Dados para gráfico de Acurácia e Loss
self.df_performance_train_batch = pd.DataFrame(columns=['train_batch_loss'])
self.df_performance_train_epoch = pd.DataFrame(columns=['train_epoch_loss'])
self.df_performance_valid_batch = pd.DataFrame(columns=['valid_batch_loss','valid_batch_iou'])
self.df_performance_valid_epoch = pd.DataFrame(columns=['valid_epoch_loss','valid_epoch_iou'])
self.df_performance_test_batch = pd.DataFrame(columns=['test_batch_iou'])
self.df_performance_test_epoch = pd.DataFrame(columns=['test_epoch_iou'])
#---------- Carregamento datasets
if self.overfit:
self.train_dataset = self.CustomDataset(self.all_data[0], self.DIR_TRAIN, self.get_train_transform())
self.valid_dataset = self.CustomDataset(self.all_data[0], self.DIR_TRAIN, self.get_train_transform())
self.test_dataset = self.CustomDataset(self.all_data[0], self.DIR_TRAIN, self.get_train_transform())
else:
self.train_dataset = self.CustomDataset(self.all_data[0], self.DIR_TRAIN, self.get_train_transform())
self.valid_dataset = self.CustomDataset(self.all_data[1], self.DIR_TRAIN, self.get_valid_transform())
self.test_dataset = self.CustomDataset(self.all_data[2], self.DIR_TRAIN, self.get_valid_transform())
#---------- Resultados
self.df_valid = pd.DataFrame(columns=['IMAGE_ID','PREDICTION_STRING','PRECISION_IOU'])
self.df_test = pd.DataFrame(columns=['IMAGE_ID','PREDICTION_STRING','PRECISION_IOU'])
self.result_valid = []
self.result_test = []
#---------- Preditor Fast-RCNN
# load a model; pre-trained on COCO
self.model = torchvision.models.detection.fasterrcnn_resnet50_fpn(pretrained=True)
# get number of input features for the classifier
in_features = self.model.roi_heads.box_predictor.cls_score.in_features
# replace the pre-trained head with a new one
self.model.roi_heads.box_predictor = FastRCNNPredictor(in_features, self.num_classes)
def predict(self,df, image_dir):
self.step = "Deployment"
inference_dataset = self.CustomDataset(df, image_dir,self.get_test_transform(),step = self.step)
dataloader = DataLoader(inference_dataset, batch_size=self.test_batch_size,shuffle=False, num_workers=cpu_count(),collate_fn=self.my_collate)
for batch in dataloader:
self.test_step(batch, None)
return self.df_test
def forward(self, images, image_ids,targets = None,info_requested='loss'):
if info_requested == 'loss':
self.model.train()
images = list(image for image in images)
targets = [{k: v for k, v in t.items()} for t in targets]
loss_dict = self.model(images, targets)
losses = sum(loss for loss in loss_dict.values())
loss_value = losses.item()
self.loss_hist.send(loss_value)
retorno = losses
if info_requested == 'predictions':
self.model.eval()
results = []
images = list(image for image in images)
outputs = self.model(images)
for i, image in enumerate(images):
boxes = outputs[i]['boxes'].data.cpu().numpy()
scores = outputs[i]['scores'].data.cpu().numpy()
# Sort highest confidence -> lowest confidence
boxes_sorted_idx = np.argsort(scores)[::-1]
boxes = boxes[boxes_sorted_idx]
#eliminate boxes with scores under detection_threshold
# if you enter model in pascal_voc it will output in pascal_voc
boxes = boxes[scores >= self.detection_threshold].astype(np.int32)
boxes_prediction_string = boxes.copy()
scores = scores[scores >= self.detection_threshold]
image_id = image_ids[i]
#Converting from Pascal Voc to COCO-> Only for prediction String
boxes_prediction_string[:, 2] = boxes_prediction_string[:, 2] - boxes_prediction_string[:, 0]
boxes_prediction_string[:, 3] = boxes_prediction_string[:, 3] - boxes_prediction_string[:, 1]
result = {
'image_id': image_id,
'boxes':boxes,
'scores':scores,
'PredictionString': self.format_prediction_string(boxes_prediction_string, scores)
}
results.append(result)
retorno = results
return retorno
def training_step(self, batch, batch_nb):
# batch
images, image_ids,targets = batch
# loss
loss = self.forward(images, image_ids,targets,'loss')
# What to log
tensorboard_logs = {'loss': loss}
self.df_performance_train_batch = self.df_performance_train_batch.append(pd.Series([loss.item()], index=self.df_performance_train_batch.columns ), ignore_index=True)
return {'loss': loss, 'train_loss_batch': loss,'log': tensorboard_logs}
def training_epoch_end(self, outputs):
if not outputs: return {}
temp_avg_loss_batch = [x['train_loss_batch'] for x in outputs]
avg_train_loss = torch.stack(temp_avg_loss_batch).mean()
self.df_performance_train_epoch = self.df_performance_train_epoch.append(pd.Series([avg_train_loss.item()], index=self.df_performance_train_epoch.columns ), ignore_index=True)
tensorboard_logs = {'avg_train_loss': avg_train_loss}
return {'log': tensorboard_logs}
def validation_step(self, batch, batch_nb):
# batch
images, image_ids,targets = batch
# loss
loss = self.forward(images, image_ids,targets,'loss')
# Inference
outputs = self.forward(images, image_ids,targets,'predictions')
#constructing dataframe
ious = np.zeros(len(targets))
for iter in zip(enumerate(outputs),targets):
i = iter[0][0]
output = iter[0][1]
target = iter[1]
gts_boxes = target['boxes'].data.cpu().numpy().astype(np.int32)
pred_boxes = output['boxes']
image = images[i].permute(1,2,0).cpu().numpy()
image_id = output['image_id']
prediction_string = output['PredictionString']
image_precision = self.calculate_image_precision(gts_boxes, pred_boxes,(self.detection_threshold,),'pascal_voc')
ious[i] = image_precision
self.df_valid = self.df_valid.append(pd.Series([image_id,prediction_string,image_precision], index=self.df_valid.columns), ignore_index=True)
self.result_valid.append({'image_id':image_id,'image':image,'gts_boxes':gts_boxes, 'pred_boxes':pred_boxes})
#mean batch dataframe
mean_batch_ious = np.mean(ious)
self.df_performance_valid_batch = self.df_performance_valid_batch.append(pd.Series([loss.item(),mean_batch_ious], index=self.df_performance_valid_batch.columns ), ignore_index=True)
return {'valid_iou_batch': mean_batch_ious, 'valid_loss_batch': loss}
def validation_epoch_end(self, outputs):
if not outputs: return {}
temp_avg_loss_batch = [x['valid_loss_batch'] for x in outputs]
temp_avg_iou_batch = [x['valid_iou_batch'] for x in outputs]
avg_valid_loss = torch.stack(temp_avg_loss_batch).mean()
avg_valid_iou = np.mean(temp_avg_iou_batch)
self.df_performance_valid_epoch = self.df_performance_valid_epoch.append(pd.Series([avg_valid_loss.item(),avg_valid_iou], index=self.df_performance_valid_epoch.columns ), ignore_index=True)
tensorboard_logs = {'avg_valid_iou': avg_valid_iou,'avg_valid_loss': avg_valid_loss}
return {'avg_valid_iou': avg_valid_iou, 'log': tensorboard_logs}
def test_step(self, batch, batch_nb):
# batch
if self.step == "Experiment":
# batch
images, image_ids,targets = batch
# Inference
outputs = self.forward(images, image_ids,targets,'predictions')
#constructing dataframe
ious = np.zeros(len(targets))
for iter in zip(enumerate(outputs),targets):
i = iter[0][0]
output = iter[0][1]
target = iter[1]
gts_boxes = target['boxes'].data.cpu().numpy().astype(np.int32)
pred_boxes = output['boxes'].astype(np.int32)
image = images[i].permute(1,2,0).cpu().numpy()
image_id = output['image_id']
prediction_string = output['PredictionString']
image_precision = self.calculate_image_precision(gts_boxes, pred_boxes,(self.detection_threshold,),'pascal_voc')
ious[i] = image_precision
self.df_test = self.df_test.append(pd.Series([image_id,prediction_string,image_precision], index=self.df_test.columns), ignore_index=True)
self.result_test.append({'image_id':image_id,'image':image,'gts_boxes':gts_boxes, 'pred_boxes':pred_boxes})
#mean batch dataframe
mean_batch_ious = np.mean(ious)
self.df_performance_test_batch = self.df_performance_test_batch.append(pd.Series([mean_batch_ious], index=self.df_performance_test_batch.columns), ignore_index=True)
retorno = {'test_iou_batch': mean_batch_ious}
if self.step == "Deployment":
# batch
images, image_ids = batch
# Inference
outputs = self.forward(images, image_ids,'predictions')
not_apply_list = ['N/A'] * len(outputs)
#constructing dataframe
for iter in zip(enumerate(outputs),not_apply_list):
i = iter[0][0]
output = iter[0][1]
na = iter[1]
pred_boxes = output['boxes'].astype(np.int32)
image = images[i].permute(1,2,0).cpu().numpy()
image_id = output['image_id']
prediction_string = output['PredictionString']
self.df_test = self.df_test.append(pd.Series([image_id,prediction_string,na], index=self.df_test.columns), ignore_index=True)
self.result_test.append({'image_id':image_id,'image':image,'pred_boxes':pred_boxes})
retorno = None
return retorno
def test_epoch_end(self, outputs):
if not outputs: return {}
if self.step == "Experiment":
avg_test_iou = np.mean([x['test_iou_batch'] for x in outputs])
tensorboard_logs = {'avg_test_iou': avg_test_iou}
retorno = {'avg_test_iou': avg_test_iou, 'log': tensorboard_logs}
if self.step == "Deployment":
retorno = None
return retorno
def configure_optimizers(self):
params = [p for p in self.parameters() if p.requires_grad]
return torch.optim.SGD( params,
lr=self.learning_rate,
momentum=self.momentum,
weight_decay=self.weight_decay)
def my_collate(self,batch):
return tuple(zip(*batch))
def gpu_mem_restore(func):
@functools.wraps(func)
def wrapper(*args, **kwargs):
try:
return func(*args, **kwargs)
except:
type, val, tb = sys.exc_info()
traceback.clear_frames(tb)
raise type(val).with_traceback(tb) from None
return wrapper
# Albumentations
def get_train_transform(self):
return A.Compose([
A.Flip(0.5),
ToTensorV2(p=1.0)
], bbox_params={'format': 'pascal_voc', 'label_fields': ['labels']})
def get_valid_transform(self):
return A.Compose([
ToTensorV2(p=1.0)
], bbox_params={'format': 'pascal_voc', 'label_fields': ['labels']})
def get_test_transform(self):
return A.Compose([
# A.Resize(512, 512),
ToTensorV2(p=1.0)
])
def format_prediction_string(self, boxes, scores):
pred_strings = []
for j in zip(scores, boxes):
pred_strings.append("{0:.4f} {1} {2} {3} {4}".format(j[0], j[1][0], j[1][1], j[1][2], j[1][3]))
return " ".join(pred_strings)
@gpu_mem_restore
def train_dataloader(self):
return DataLoader(self.train_dataset, batch_size=self.train_batch_size, shuffle=False,num_workers=cpu_count(), collate_fn=self.my_collate)
@gpu_mem_restore
def val_dataloader(self):
return DataLoader(self.valid_dataset, batch_size=self.valid_batch_size,shuffle=False, num_workers=cpu_count(),collate_fn=self.my_collate)
@gpu_mem_restore
def test_dataloader(self):
return DataLoader(self.valid_dataset, batch_size=self.test_batch_size,shuffle=False, num_workers=cpu_count(),collate_fn=self.my_collate)
# + id="JB__zx5_gcSH"
# %run Model_Lightning.py
# + id="n7dGd1S3q6Hk" executionInfo={"status": "error", "timestamp": 1601400505666, "user_tz": 180, "elapsed": 935, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="2919c70e-646c-4f6d-ee7d-81ca8b6610e2" colab={"base_uri": "https://localhost:8080/", "height": 158}
del model
# + [markdown] id="5Upw48c-gcSK"
# Parâmetros do Modelo
# + id="7xBiXR7ggcSL"
all_data = [train_df,valid_df,test_df]
hyperparams = {'learning_rate':learning_rate,'momentum':momentum,'weight_decay':weight_decay,'detection_threshold':detection_threshold,'train_batch_size':train_batch_size,'valid_batch_size':valid_batch_size,'test_batch_size':test_batch_size}
model_parameters = {'num_classes': num_classes,'coord_format':coord_format,'Averager':Averager,'calculate_iou':calculate_iou,'find_best_match':find_best_match,'calculate_precision':calculate_precision,'calculate_image_precision':calculate_image_precision}
dataset_infos = {'all_data':all_data,'CustomDataset':WheatDataset,'DIR_TRAIN':DIR_TRAIN,'DIR_TEST':DIR_TEST}
extra_infos = {'overfit':False}
# + id="OG9D3AU5gcSP" executionInfo={"status": "error", "timestamp": 1601400502696, "user_tz": 180, "elapsed": 7051, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="9fe725e3-3226-41a7-cdbd-2d77c541234c" colab={"base_uri": "https://localhost:8080/", "height": 345}
model = FastRCNNFinetuner(hyperparams=hyperparams,
model_parameters=model_parameters,
dataset_infos=dataset_infos,
extra_infos = extra_infos)
sum([torch.tensor(x.size()).prod() for x in model.parameters() if x.requires_grad]) # trainable parameters
# + id="ugTD3owOgcSS"
trainer = pl.Trainer(gpus=0,
checkpoint_callback=False, # Disable checkpoint saving.
fast_dev_run=True)
trainer.fit(model)
# + id="JDJ2nUtkgcSV"
trainer.test(model)
# + [markdown] id="TauA-JssgcSY"
# Recuperando ou treinando o modelo
# + id="7M34zSVlQqVP" executionInfo={"status": "ok", "timestamp": 1601400540633, "user_tz": 180, "elapsed": 30939, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="f7d31f55-4ef0-49ca-9617-24319af0b871" colab={"base_uri": "https://localhost:8080/", "height": 605, "referenced_widgets": ["181762a947bd42509b8813b9cf12bc68", "c9ebf858e5034ed193fe3abaa6e64cda", "<KEY>", "<KEY>", "fb85ce40bde14ec387105560cab07b98", "6ee64816a46c4c55854feb613bad138a", "<KEY>", "<KEY>", "914f03520d5741e683b54221e78497e3", "5946ad946a564d9d8b12a3861a842d3f", "<KEY>", "c2f6a3e74d6a42d1bbfeaaba883f50ed", "<KEY>", "c0df0f08ea7244a98dfd88db00485833", "d3373ced4fc94d7199df9cdfe1ad6f76", "d144b2f2aa7a4aa6bc41df3f339d2108"]}
from pytorch_lightning.callbacks import ModelCheckpoint
import os
cwd = '/content/drive/My Drive/Computer_Vision/Object_Detection/FastRCNN/checkpoints'
checkpoint_path = cwd + '/epoch=1.ckpt'
checkpoint_dir = os.path.dirname(os.path.abspath(checkpoint_path))
print(f'Files in {checkpoint_dir}: {os.listdir(checkpoint_dir)}')
print(f'Saving checkpoints to {checkpoint_dir}')
checkpoint_callback = ModelCheckpoint(filepath=checkpoint_dir, save_top_k=-1) # Keeps all checkpoints.
resume_from_checkpoint = None
if os.path.exists(checkpoint_path):
weights_retrieved = True
print(f"Restoring checkpoint: {checkpoint_path}")
resume_from_checkpoint = checkpoint_path
else:
weights_retrieved = False
trainer = pl.Trainer(gpus=1,
max_epochs=2,
check_val_every_n_epoch=1,
profiler=True,
checkpoint_callback=checkpoint_callback,
progress_bar_refresh_rate=1,
resume_from_checkpoint=resume_from_checkpoint)
model = FastRCNNFinetuner(hyperparams=hyperparams,
model_parameters=model_parameters,
dataset_infos=dataset_infos,
extra_infos = extra_infos)
trainer.fit(model)
# + id="q39ZAPr30Mxx" executionInfo={"status": "ok", "timestamp": 1601400730190, "user_tz": 180, "elapsed": 217072, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="7d236f04-0d6d-4d83-c7f7-a39c8f1a3079" colab={"base_uri": "https://localhost:8080/", "height": 182, "referenced_widgets": ["d8b7489f84e94e93ad666be1cc77c872", "5ce09163bbd048519eae714cc2a9213b", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "80e7c900ea66409d8edda3bca264dc93", "a9f3fb0dfad645a8b44d20755601835b"]}
trainer.test(model)
# + [markdown] id="Kp0Cp-9DgcSi"
# Visualizando resultados
# + id="Zu1OeX8f_HKi" executionInfo={"status": "ok", "timestamp": 1601400730194, "user_tz": 180, "elapsed": 183644, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="16fc8a59-f0a6-4932-ac9a-07770363d7f8" colab={"base_uri": "https://localhost:8080/", "height": 277}
model.df_valid
# + id="k371h_Xm0NYv" executionInfo={"status": "ok", "timestamp": 1601400731114, "user_tz": 180, "elapsed": 182486, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="e518d8f3-96f7-4b50-ee3b-bb041f2493ef" colab={"base_uri": "https://localhost:8080/", "height": 391}
model.df_test
# + [markdown] id="AZrnbPzjxvRa"
# ## Salva métricas
#
# Utiliza a função `save_metrics` do [SDK da PlatIAgro](https://platiagro.github.io/sdk/) para salvar métricas. Por exemplo: `accuracy`, `precision`, `r2_score`, `custom_score` etc.<br>
# + id="I5Cl7HVdzAEZ" outputId="f6b87420-cdf1-4b07-9beb-681b3074fc03"
from platiagro import save_metrics
save_metrics(confusion_matrix=confusion_matrix,commom_metrics=commom_metrics)
# + [markdown] id="Gr2CzFwgy67g"
# ## Salva figuras
#
# Utiliza a função `save_figures` do [SDK da PlatIAgro](https://platiagro.github.io/sdk/) para salvar figuras do [matplotlib](https://matplotlib.org/3.2.1/gallery/index.html). <br>
#
# A avaliação do desempenho do modelo pode ser feita por meio da análise da [Curva ROC (ROC)](https://pt.wikipedia.org/wiki/Caracter%C3%ADstica_de_Opera%C3%A7%C3%A3o_do_Receptor). Esse gráfico permite avaliar a performance de um classificador binário para diferentes pontos de cortes. A métrica [AUC (Area under curve)](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve) também é calculada e indicada na legenda do gráfico.<br>
# Se a variável resposta tiver mais de duas categorias, o cálculo da curva ROC e AUC é feito utilizando o algoritmo [one-vs-rest](https://scikit-learn.org/stable/modules/model_evaluation.html#roc-metrics), ou seja, calcula-se a curva ROC e AUC de cada classe em relação ao restante.
# + id="-EQgFvXAy7uC" executionInfo={"status": "ok", "timestamp": 1601401319582, "user_tz": 180, "elapsed": 15626, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="7584c303-1979-4303-f0a2-385fc1ebeca8" colab={"base_uri": "https://localhost:8080/", "height": 1000, "output_embedded_package_id": "1LsluGOvzHz0LBhqR6KsvgGanohHvqfGO"}
from matplotlib.pyplot import cm
#from platiagro import save_figure
#from platiagro import list_figures
from sklearn.metrics import roc_curve, auc
from sklearn import preprocessing
import matplotlib.pyplot as plt
import numpy as np
def overlaping_multiple_plots(rows,columns,results):
fig=plt.figure(figsize=(15, 15))
ax = []
for i in range(1, columns*rows +1):
result = results[i]
sample = result['image']
sample = cv2.cvtColor(sample, cv2.COLOR_BGR2RGB)
for pred_box in result['pred_boxes']:
cv2.rectangle(
sample,
(pred_box[0], pred_box[1]),
(pred_box[2],pred_box[3]),
(220, 0, 0), 2
)
for gt_box in result['gts_boxes']:
cv2.rectangle(
sample,
(gt_box[0], gt_box[1]),
(gt_box[2], gt_box[3]),
(0, 0, 220), 2
)
ax.append( fig.add_subplot(rows, columns, i) )
ax[-1].set_title(result['image_id'])
fig.suptitle("RED: Predicted | BLUE - Ground-truth")
plt.imshow(sample)
plt.show()
plt.close()
def inference_multiple_plots(rows,columns,results):
fig=plt.figure(figsize=(15, 15))
ax = []
for i in range(1, columns*rows +1):
result = results[i]
sample = result['image']
sample = cv2.cvtColor(sample, cv2.COLOR_BGR2RGB)
for pred_box in result['pred_boxes']:
cv2.rectangle(
sample,
(pred_box[0], pred_box[1]),
(pred_box[2],pred_box[3]),
(220, 0, 0), 2
)
ax.append( fig.add_subplot(rows, columns, i) )
ax[-1].set_title(result['image_id'])
fig.suptitle("RED: Predicted")
plt.imshow(sample)
plt.show()
plt.close()
def performance_loss_visualization(loss_list,epoch_or_batch="Epoch",step = "Train"):
x = range(len(loss_list))
# Loss plot
plt.xlabel(epoch_or_batch)
plt.ylabel("Loss")
plt.plot(x, loss_list, '-')
plt.title(step + ' Loss Performance')
plt.suptitle(epoch_or_batch + ' - ' + step)
plt.show()
def performance_loss_iou_visualization(loss_list, iou_list,epoch_or_batch="Epoch",step = "Valid"):
x = range(len(loss_list))
# Loss plot
plt.subplot(1, 2, 1)
plt.xlabel(epoch_or_batch)
plt.ylabel("Loss")
plt.plot(x, loss_list, '-')
plt.title(step + ' Loss Performance')
# Precision plot
plt.subplot(1, 2, 2)
plt.xlabel(epoch_or_batch)
plt.ylabel("IOU")
plt.plot(x, iou_list, '-')
plt.title(step + ' IOU Performance')
#show
plt.subplots_adjust(wspace=0.4)
plt.suptitle(epoch_or_batch + ' - ' + step)
plt.show()
def performance_iou_visualization(iou_list,epoch_or_batch="Epoch",step = "Train"):
x = range(len(iou_list))
# Loss plot
plt.xlabel(epoch_or_batch)
plt.ylabel("IOU")
plt.plot(x, iou_list, '-')
plt.title(step + ' IOU Performance')
plt.suptitle(epoch_or_batch + ' - ' + step)
plt.show()
overlaping_multiple_plots(2,2,model.result_valid)
inference_multiple_plots(2,2,model.result_test)
if not weights_retrieved:
performance_loss_visualization(model.df_performance_train_batch['train_batch_loss'].to_numpy(), epoch_or_batch="Batch",step = "Train")
performance_loss_visualization(model.df_performance_train_epoch['train_epoch_loss'].to_numpy(), epoch_or_batch="Epoch",step = "Train")
performance_loss_iou_visualization(model.df_performance_valid_batch['valid_batch_loss'].to_numpy(), model.df_performance_valid_batch['valid_batch_iou'].to_numpy(),epoch_or_batch="Batch",step = "Valid")
performance_loss_iou_visualization(model.df_performance_valid_epoch['valid_epoch_loss'].to_numpy(), model.df_performance_valid_epoch['valid_epoch_iou'].to_numpy(),epoch_or_batch="Epoch",step = "Valid")
performance_iou_visualization(model.df_performance_test_batch['test_batch_iou'].to_numpy(), epoch_or_batch="Batch",step = "Test")
performance_iou_visualization(model.df_performance_test_epoch['test_epoch_iou'].to_numpy(), epoch_or_batch="Epoch",step = "Test")
# + [markdown] id="msQktuMzcfkR"
# ## Salva modelo e outros artefatos
#
# Utiliza a função `save_model` do [SDK da PlatIAgro](https://platiagro.github.io/sdk/) para salvar modelos e outros artefatos.<br>
# Essa função torna estes artefatos disponíveis para o notebook de implantação.
# + [markdown] id="CNlNmytZgcTG"
# Modelo Pytorch Lightining
# + id="6UolfjpfgcTH" executionInfo={"status": "error", "timestamp": 1601400935395, "user_tz": 180, "elapsed": 2089, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="dc0a45d8-10eb-4315-bff0-0f5b6e44e66e" colab={"base_uri": "https://localhost:8080/", "height": 312}
file_name = 'pytorch_model.pt'
torch.save(model.state_dict(), f'/tmp/data/{file_name}')
# + [markdown] id="M0Gfr-OugcTL"
# Artefatos
# + id="DF_B2lfQcfkS" executionInfo={"status": "error", "timestamp": 1601400935400, "user_tz": 180, "elapsed": 1283, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjD_7RtHYeeADzApH8kYC-0xfA7jniYSXIeyBR4=s64", "userId": "01542215021181445417"}} outputId="84f0be0e-c0c7-45d4-f60b-78de349fd783" colab={"base_uri": "https://localhost:8080/", "height": 260}
import pickle
dataset_infos = {'all_data':all_data}
deployment_infos = {'columns':columns,'X_test':X_test}
artifacts = {'hyperparams':hyperparams,'model_parameters':model_parameters,'dataset_infos':dataset_infos,'extra_infos':extra_infos,'deployment_infos':deployment_infos}
file_name = 'artifacts.p'
pickle.dump(artifacts, open(f'/tmp/data/{file_name}', "wb" ))
|
samples/vc-fast-rcnn-object-detection/Experiment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Function Practice Exercises
#
# Problems are arranged in increasing difficulty:
# * Warmup - these can be solved using basic comparisons and methods
# * Level 1 - these may involve if/then conditional statements and simple methods
# * Level 2 - these may require iterating over sequences, usually with some kind of loop
# * Challenging - these will take some creativity to solve
# ## WARMUP SECTION:
# #### LESSER OF TWO EVENS: Write a function that returns the lesser of two given numbers *if* both numbers are even, but returns the greater if one or both numbers are odd
# lesser_of_two_evens(2,4) --> 2
# lesser_of_two_evens(2,5) --> 5
def lesser_of_two_evens(a,b):
if (a % 2 == 0 and b % 2 == 0):
result = (b if a > b else a)
else:
result = (a if a > b else b)
return result
# Check
lesser_of_two_evens(2,4)
# Check
lesser_of_two_evens(2,5)
# #### ANIMAL CRACKERS: Write a function takes a two-word string and returns True if both words begin with same letter
# animal_crackers('Levelheaded Llama') --> True
# animal_crackers('Crazy Kangaroo') --> False
# +
def animal_crackers(text):
words = text.split()
if len(words) != 2:
return -1
return words[0][0] == words[1][0]
# -
# Check
animal_crackers('Levelheaded Llama')
# Check
animal_crackers('<NAME>')
# #### MAKES TWENTY: Given two integers, return True if the sum of the integers is 20 *or* if one of the integers is 20. If not, return False
#
# makes_twenty(20,10) --> True
# makes_twenty(12,8) --> True
# makes_twenty(2,3) --> False
def makes_twenty(n1,n2):
return (n1 + n2 == 20) or (n1 == 20) or (n2 == 20)
# Check
makes_twenty(20,10)
# Check
makes_twenty(2,3)
# # LEVEL 1 PROBLEMS
# #### OLD MACDONALD: Write a function that capitalizes the first and fourth letters of a name
#
# old_macdonald('macdonald') --> MacDonald
#
# Note: `'macdonald'.capitalize()` returns `'Macdonald'`
def old_macdonald(name):
if len(name) < 4:
return -1
name = name.capitalize()
return name[0:3] + name[3].upper() + name[4:]
# Check
old_macdonald('macdonald')
# #### MASTER YODA: Given a sentence, return a sentence with the words reversed
#
# master_yoda('I am home') --> 'home am I'
# master_yoda('We are ready') --> 'ready are We'
#
# Note: The .join() method may be useful here. The .join() method allows you to join together strings in a list with some connector string. For example, some uses of the .join() method:
#
# >>> "--".join(['a','b','c'])
# >>> 'a--b--c'
#
# This means if you had a list of words you wanted to turn back into a sentence, you could just join them with a single space string:
#
# >>> " ".join(['Hello','world'])
# >>> "Hello world"
def master_yoda(text):
text = text[::-1]
words_reversed = text.split()
lst = list(map(lambda word:word[::-1],words_reversed))
reversed_words = " ".join(lst)
return reversed_words
# Check
master_yoda('I am home')
# Check
master_yoda('We are ready')
# #### ALMOST THERE: Given an integer n, return True if n is within 10 of either 100 or 200
#
# almost_there(90) --> True
# almost_there(104) --> True
# almost_there(150) --> False
# almost_there(209) --> True
#
# NOTE: `abs(num)` returns the absolute value of a number
def almost_there(n):
return abs(n - 100) <= 10 or abs(n-200) <= 10
# Check
almost_there(104)
# Check
almost_there(150)
# Check
almost_there(209)
# # LEVEL 2 PROBLEMS
# #### FIND 33:
#
# Given a list of ints, return True if the array contains a 3 next to a 3 somewhere.
#
# has_33([1, 3, 3]) → True
# has_33([1, 3, 1, 3]) → False
# has_33([3, 1, 3]) → False
def has_33(nums):
lst = "".join([str(n) for n in nums])
return '33' in lst
# Check
has_33([1, 3, 3])
# Check
has_33([1, 3, 1, 3])
# Check
has_33([3, 1, 3])
# #### PAPER DOLL: Given a string, return a string where for every character in the original there are three characters
# paper_doll('Hello') --> 'HHHeeellllllooo'
# paper_doll('Mississippi') --> 'MMMiiissssssiiippppppiii'
def paper_doll(text):
text = "".join(list(map(lambda word:word*3,text)))
return text
# Check
paper_doll('Hello')
# Check
paper_doll('Mississippi')
# #### BLACKJACK: Given three integers between 1 and 11, if their sum is less than or equal to 21, return their sum. If their sum exceeds 21 *and* there's an eleven, reduce the total sum by 10. Finally, if the sum (even after adjustment) exceeds 21, return 'BUST'
# blackjack(5,6,7) --> 18
# blackjack(9,9,9) --> 'BUST'
# blackjack(9,9,11) --> 19
def blackjack(a,b,c):
if not all(1 <= num <= 11 for num in [a,b,c]):
return 'Wrong Input'
sum = a + b + c
if sum > 21 and 11 in (a,b,c):
sum -= 10
if sum > 21:
sum = 'BUST'
return sum
# Check
blackjack(5,6,7)
# Check
blackjack(9,9,9)
# Check
blackjack(9,9,11)
# #### SUMMER OF '69: Return the sum of the numbers in the array, except ignore sections of numbers starting with a 6 and extending to the next 9 (every 6 will be followed by at least one 9). Return 0 for no numbers.
#
# summer_69([1, 3, 5]) --> 9
# summer_69([4, 5, 6, 7, 8, 9]) --> 9
# summer_69([2, 1, 6, 9, 11]) --> 14
def summer_69(arr):
sum = 0
lst = []
for n in arr:
if n == 6:
lst.append('a')
elif n == 9 and lst != []:
lst.pop()
elif lst == []:
sum += n
return sum
# Check
summer_69([1, 3, 5])
# Check
summer_69([4, 5, 6, 7, 8, 9,6,5,4,3,6,5,4,3,9,7,9,1])
# Check
summer_69([2, 1, 6, 9, 11])
# # CHALLENGING PROBLEMS
# #### SPY GAME: Write a function that takes in a list of integers and returns True if it contains 007 in order
#
# spy_game([1,2,4,0,0,7,5]) --> True
# spy_game([1,0,2,4,0,5,7]) --> True
# spy_game([1,7,2,0,4,5,0]) --> False
#
def spy_game(nums):
str1 = ""
for i in nums:
if i == 0 or i == 7:
str1 += str(i)
return '007' in str1
# Check
spy_game([1,2,4,0,0,7,5])
# Check
spy_game([1,0,2,4,0,5,7])
# Check
spy_game([1,7,2,0,4,5,0])
# #### COUNT PRIMES: Write a function that returns the *number* of prime numbers that exist up to and including a given number
# count_primes(100) --> 25
#
# By convention, 0 and 1 are not prime.
# +
def count_primes(num):
count = 0
for i in range(num+1):
if is_prime(i):
count += 1
return count
def is_prime(val):
prime = True
if(val >= 2):
for i in range(2,val):
if(val % i == 0):
prime = False
break
else:
prime = False
return prime
# -
# Check
count_primes(100)
# ### Just for fun:
# #### PRINT BIG: Write a function that takes in a single letter, and returns a 5x5 representation of that letter
# print_big('a')
#
# out: *
# * *
# *****
# * *
# * *
# HINT: Consider making a dictionary of possible patterns, and mapping the alphabet to specific 5-line combinations of patterns. <br>For purposes of this exercise, it's ok if your dictionary stops at "E".
def print_big(letter):
letter = letter.lower();
dict = {
'a': ' * \n * * \n*****\n* *\n* *',
'b': '**** \n* *\n*****\n* *\n**** ',
'c': ' ****\n* \n* \n* \n ****',
'd': '**** \n* *\n* *\n* *\n**** ',
'e': '*****\n* \n*****\n* \n*****'
}
print(dict.get(letter))
print_big('a')
# ## Great Job!
|
02-Function Practice Exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
class PastSampler:
'''
Forms training samples for predicting future values from past value
'''
def __init__(self, N, K, sliding_window = True):
'''
Predict K future sample using N previous samples
'''
self.K = K
self.N = N
self.sliding_window = sliding_window
def transform(self, A):
M = self.N + self.K #Number of samples per row (sample + target)
#indexes
if self.sliding_window:
I = np.arange(M) + np.arange(A.shape[0] - M + 1).reshape(-1, 1)
else:
if A.shape[0]%M == 0:
I = np.arange(M)+np.arange(0,A.shape[0],M).reshape(-1,1)
else:
I = np.arange(M)+np.arange(0,A.shape[0] -M,M).reshape(-1,1)
B = A[I].reshape(-1, M * A.shape[1], A.shape[2])
ci = self.N * A.shape[1] #Number of features per sample
return B[:, :ci], B[:, ci:] #Sample matrix, Target matrix
#data file path
dfp = '../data/bitcoin2015to2019.csv'
#Columns of price data to use
columns = ['Close']
# df = pd.read_csv(dfp).dropna().tail(1000000)
df = pd.read_csv(dfp)
time_stamps = df['Timestamp']
df = df.loc[:,columns]
# original_df = pd.read_csv(dfp).dropna().tail(1000000).loc[:,columns]
original_df = pd.read_csv(dfp).loc[:,columns]
# -
file_name='../data/bitcoin2015to2019_close.h5'
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
# normalization
for c in columns:
df[c] = scaler.fit_transform(df[c].values.reshape(-1,1))
# #%%Features are channels
A = np.array(df)[:,None,:]
original_A = np.array(original_df)[:,None,:]
time_stamps = np.array(time_stamps)[:,None,None]
# #%%Make samples of temporal sequences of pricing data (channel)
NPS, NFS = 256, 16 #Number of past and future samples
ps = PastSampler(NPS, NFS, sliding_window=False)
B, Y = ps.transform(A)
input_times, output_times = ps.transform(time_stamps)
original_B, original_Y = ps.transform(original_A)
import h5py
with h5py.File(file_name, 'w') as f:
f.create_dataset("inputs", data = B)
f.create_dataset('outputs', data = Y)
f.create_dataset("input_times", data = input_times)
f.create_dataset('output_times', data = output_times)
f.create_dataset("original_datas", data=np.array(original_df))
f.create_dataset('original_inputs',data=original_B)
f.create_dataset('original_outputs',data=original_Y)
# f.create_dataset('original_times', data=time_stamps)
B.shape
|
data/PastSampler.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.display import Image
# %matplotlib inline
# +
# this code cell unzips mnist
import sys
import gzip
import shutil
import os
if (sys.version_info > (3, 0)):
writemode = 'wb'
else:
writemode = 'w'
zipped_mnist = [f for f in os.listdir() if f.endswith('ubyte.gz')]
for z in zipped_mnist:
with gzip.GzipFile(z, mode='rb') as decompressed, open(z[:-3], writemode) as outfile:
outfile.write(decompressed.read())
# -
# # mnist dataset
# +
import os
import struct
import numpy as np
def load_mnist(path, kind='train'):
"""Load MNIST data from `path`"""
labels_path = os.path.join(path,
'%s-labels-idx1-ubyte' % kind)
images_path = os.path.join(path,
'%s-images-idx3-ubyte' % kind)
with open(labels_path, 'rb') as lbpath:
magic, n = struct.unpack('>II',
lbpath.read(8))
labels = np.fromfile(lbpath,
dtype=np.uint8)
with open(images_path, 'rb') as imgpath:
magic, num, rows, cols = struct.unpack(">IIII",
imgpath.read(16))
images = np.fromfile(imgpath,
dtype=np.uint8).reshape(len(labels), 784)
images = ((images / 255.) - .5) * 2
return images, labels
# -
X_train, y_train = load_mnist('', kind='train')
print('Rows: %d, columns: %d' % (X_train.shape[0], X_train.shape[1]))
X_test, y_test = load_mnist('', kind='t10k')
print('Rows: %d, columns: %d' % (X_test.shape[0], X_test.shape[1]))
# Visualize the first digit of each class:
# +
import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(10):
img = X_train[y_train == i][0].reshape(28, 28)
ax[i].imshow(img, cmap='Greys')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
# plt.savefig('images/12_5.png', dpi=300)
plt.show()
# -
# Visualize 25 different versions of "7":
# +
fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True,)
ax = ax.flatten()
for i in range(25):
img = X_train[y_train == 7][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
# +
import numpy as np
np.savez_compressed('mnist_scaled.npz',
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test)
# -
mnist = np.load('mnist_scaled.npz')
mnist.files
# +
X_train, y_train, X_test, y_test = [mnist[f] for f in ['X_train', 'y_train',
'X_test', 'y_test']]
del mnist
X_train.shape
# +
import numpy as np
import sys
class NeuralNetMLP(object):
def __init__(self, n_hidden=30,
l2=0., epochs=100, eta=0.001,
shuffle=True, minibatch_size=1, seed=None):
self.random = np.random.RandomState(seed)
self.n_hidden = n_hidden
self.l2 = l2
self.epochs = epochs
self.eta = eta
self.shuffle = shuffle
self.minibatch_size = minibatch_size
def _onehot(self, y, n_classes):
onehot = np.zeros((n_classes, y.shape[0]))
for idx, val in enumerate(y.astype(int)):
onehot[val, idx] = 1.
return onehot.T
def _sigmoid(self, z):
return 1. / (1. + np.exp(-np.clip(z, -250, 250)))
def _forward(self, X):
# step 1: net input of hidden layer
# [n_examples, n_features] dot [n_features, n_hidden]
# -> [n_examples, n_hidden]
z_h = np.dot(X, self.w_h) + self.b_h
# step 2: activation of hidden layer
a_h = self._sigmoid(z_h)
# step 3: net input of output layer
# [n_examples, n_hidden] dot [n_hidden, n_classlabels]
# -> [n_examples, n_classlabels]
z_out = np.dot(a_h, self.w_out) + self.b_out
# step 4: activation output layer
a_out = self._sigmoid(z_out)
return z_h, a_h, z_out, a_out
def _compute_cost(self, y_enc, output):
# -y log yhat - (1-y)log(1-yhat) categorical entropy
L2_term = (self.l2 *
(np.sum(self.w_h ** 2.) +
np.sum(self.w_out ** 2.)))
term1 = -y_enc * (np.log(output))
term2 = (1. - y_enc) * np.log(1. - output)
cost = np.sum(term1 - term2) + L2_term
return cost
def predict(self, X):
z_h, a_h, z_out, a_out = self._forward(X)
y_pred = np.argmax(z_out, axis=1)
return y_pred
def fit(self, X_train, y_train, X_valid, y_valid):
n_output = np.unique(y_train).shape[0] # number of class labels
n_features = X_train.shape[1]
########################
# Weight initialization
########################
# weights for input -> hidden
self.b_h = np.zeros(self.n_hidden)
self.w_h = self.random.normal(loc=0.0, scale=0.1,
size=(n_features, self.n_hidden))
# weights for hidden -> output
self.b_out = np.zeros(n_output)
self.w_out = self.random.normal(loc=0.0, scale=0.1,
size=(self.n_hidden, n_output))
epoch_strlen = len(str(self.epochs)) # for progress formatting
self.eval_ = {'cost': [], 'train_acc': [], 'valid_acc': []}
y_train_enc = self._onehot(y_train, n_output)
# iterate over training epochs
for i in range(self.epochs):
# iterate over minibatches
indices = np.arange(X_train.shape[0])
if self.shuffle:
self.random.shuffle(indices)
for start_idx in range(0, indices.shape[0] - self.minibatch_size +
1, self.minibatch_size):
batch_idx = indices[start_idx:start_idx + self.minibatch_size]
# forward propagation
z_h, a_h, z_out, a_out = self._forward(X_train[batch_idx])
# Backpropagation
# [n_examples, n_classlabels]
delta_out = a_out - y_train_enc[batch_idx]
# [n_examples, n_hidden]
sigmoid_derivative_h = a_h * (1. - a_h)
# [n_examples, n_classlabels] dot [n_classlabels, n_hidden]
# -> [n_examples, n_hidden]
delta_h = (np.dot(delta_out, self.w_out.T) *
sigmoid_derivative_h)
# [n_features, n_examples] dot [n_examples, n_hidden]
# -> [n_features, n_hidden]
grad_w_h = np.dot(X_train[batch_idx].T, delta_h)
grad_b_h = np.sum(delta_h, axis=0)
# [n_hidden, n_examples] dot [n_examples, n_classlabels]
# -> [n_hidden, n_classlabels]
grad_w_out = np.dot(a_h.T, delta_out)
grad_b_out = np.sum(delta_out, axis=0)
# Regularization and weight updates
delta_w_h = (grad_w_h + self.l2*self.w_h)
delta_b_h = grad_b_h # bias is not regularized
self.w_h -= self.eta * delta_w_h
self.b_h -= self.eta * delta_b_h
delta_w_out = (grad_w_out + self.l2*self.w_out)
delta_b_out = grad_b_out # bias is not regularized
self.w_out -= self.eta * delta_w_out
self.b_out -= self.eta * delta_b_out
#############
# Evaluation
#############
# Evaluation after each epoch during training
z_h, a_h, z_out, a_out = self._forward(X_train)
cost = self._compute_cost(y_enc=y_train_enc,
output=a_out)
y_train_pred = self.predict(X_train)
y_valid_pred = self.predict(X_valid)
train_acc = ((np.sum(y_train == y_train_pred)).astype(np.float) /
X_train.shape[0])
valid_acc = ((np.sum(y_valid == y_valid_pred)).astype(np.float) /
X_valid.shape[0])
sys.stderr.write('\r%0*d/%d | Cost: %.2f '
'| Train/Valid Acc.: %.2f%%/%.2f%% ' %
(epoch_strlen, i+1, self.epochs, cost,
train_acc*100, valid_acc*100))
sys.stderr.flush()
self.eval_['cost'].append(cost)
self.eval_['train_acc'].append(train_acc)
self.eval_['valid_acc'].append(valid_acc)
return self
# -
n_epochs = 200
# +
nn = NeuralNetMLP(n_hidden=100,
l2=0.01,
epochs=n_epochs,
eta=0.0005,
minibatch_size=100,
shuffle=True,
seed=1)
nn.fit(X_train=X_train[:55000],
y_train=y_train[:55000],
X_valid=X_train[55000:],
y_valid=y_train[55000:])
# -
import matplotlib.pyplot as plt
plt.plot(range(nn.epochs), nn.eval_['cost'])
plt.ylabel('Cost')
plt.xlabel('Epochs')
plt.show()
plt.plot(range(nn.epochs), nn.eval_['train_acc'],
label='Training')
plt.plot(range(nn.epochs), nn.eval_['valid_acc'],
label='Validation', linestyle='--')
plt.ylabel('Accuracy')
plt.xlabel('Epochs')
plt.legend(loc='lower right')
plt.savefig('images/12_08.png', dpi=300)
plt.show()
# +
y_test_pred = nn.predict(X_test)
acc = (np.sum(y_test == y_test_pred)
.astype(np.float) / X_test.shape[0])
print('Test accuracy: %.2f%%' % (acc * 100))
# +
miscl_img = X_test[y_test != y_test_pred][:25]
correct_lab = y_test[y_test != y_test_pred][:25]
miscl_lab = y_test_pred[y_test != y_test_pred][:25]
fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(25):
img = miscl_img[i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_title('%d) t: %d p: %d' % (i+1, correct_lab[i], miscl_lab[i]))
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()
|
ann.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Plot classification probability
#
#
# Plot the classification probability for different classifiers. We use a 3 class
# dataset, and we classify it with a Support Vector classifier, L1 and L2
# penalized logistic regression with either a One-Vs-Rest or multinomial setting,
# and Gaussian process classification.
#
# Linear SVC is not a probabilistic classifier by default but it has a built-in
# calibration option enabled in this example (`probability=True`).
#
# The logistic regression with One-Vs-Rest is not a multiclass classifier out of
# the box. As a result it has more trouble in separating class 2 and 3 than the
# other estimators.
#
#
# +
print(__doc__)
# Author: <NAME> <<EMAIL>>
# License: BSD 3 clause
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import accuracy_score
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.gaussian_process import GaussianProcessClassifier
from sklearn.gaussian_process.kernels import RBF
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:, 0:2] # we only take the first two features for visualization
y = iris.target
n_features = X.shape[1]
C = 10
kernel = 1.0 * RBF([1.0, 1.0]) # for GPC
# Create different classifiers.
classifiers = {
'L1 logistic': LogisticRegression(C=C, penalty='l1',
solver='saga',
multi_class='multinomial',
max_iter=10000),
'L2 logistic (Multinomial)': LogisticRegression(C=C, penalty='l2',
solver='saga',
multi_class='multinomial',
max_iter=10000),
'L2 logistic (OvR)': LogisticRegression(C=C, penalty='l2',
solver='saga',
multi_class='ovr',
max_iter=10000),
'Linear SVC': SVC(kernel='linear', C=C, probability=True,
random_state=0),
'GPC': GaussianProcessClassifier(kernel)
}
n_classifiers = len(classifiers)
plt.figure(figsize=(3 * 2, n_classifiers * 2))
plt.subplots_adjust(bottom=.2, top=.95)
xx = np.linspace(3, 9, 100)
yy = np.linspace(1, 5, 100).T
xx, yy = np.meshgrid(xx, yy)
Xfull = np.c_[xx.ravel(), yy.ravel()]
for index, (name, classifier) in enumerate(classifiers.items()):
classifier.fit(X, y)
y_pred = classifier.predict(X)
accuracy = accuracy_score(y, y_pred)
print("Accuracy (train) for %s: %0.1f%% " % (name, accuracy * 100))
# View probabilities:
probas = classifier.predict_proba(Xfull)
n_classes = np.unique(y_pred).size
for k in range(n_classes):
plt.subplot(n_classifiers, n_classes, index * n_classes + k + 1)
plt.title("Class %d" % k)
if k == 0:
plt.ylabel(name)
imshow_handle = plt.imshow(probas[:, k].reshape((100, 100)),
extent=(3, 9, 1, 5), origin='lower')
plt.xticks(())
plt.yticks(())
idx = (y_pred == k)
if idx.any():
plt.scatter(X[idx, 0], X[idx, 1], marker='o', c='w', edgecolor='k')
ax = plt.axes([0.15, 0.04, 0.7, 0.05])
plt.title("Probability")
plt.colorbar(imshow_handle, cax=ax, orientation='horizontal')
plt.show()
|
01 Machine Learning/scikit_examples_jupyter/classification/plot_classification_probability.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="2xg1OCvqO6YI"
# Welcome to the module on Advanced Regression. In this module, we will learn how to deal with variables which do not exhibit a linear relationship with the target variable. Furthermore, we will learn how to avoid the perils of overfitting and make a generalisable model.
# + [markdown] id="cWQy3TsbPV2W"
# Lets start off with a quick recap of simple linear regression. In the first example. we will try to model sales of an online retailer with the help of the marketing spend. Lets see how we go about it
# + id="VdA4-7WU1iil"
# importing the requisite libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
import warnings
warnings.filterwarnings('ignore')
# + [markdown] id="RLXIuxCrmee3"
# ### 1.1 Simple Linear Regression
# + [markdown] id="Itaw8n9i26ay"
# #### We will build a model using TV spend on advertisements to predict sales
# + id="S1xgV8ct3Sev"
# Reading the dataset
df = pd.read_csv('https://cdn.upgrad.com/UpGrad/temp/098bb2e9-83fb-48df-9dd1-fac56fbb25ca/advertising.csv')
# + colab={"base_uri": "https://localhost:8080/"} id="QvemyN_NTXpQ" outputId="04ef5b38-e858-4dea-fda3-d35c19463cc0"
df.info()
# -
data = df[["TV", "Sales"]]
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="lqEh0unm4Mtu" outputId="746407f3-cbf8-4141-997c-af3036395799"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'TV' , y = 'Sales')
# + [markdown] id="1q4YGqIH4Mt0"
# As you can infer from the above plot, the relationship between the two variables seems to be linear.
# + id="YvfGT9qB4Mt0"
# Splitting the dataset into X and y
X = np.array(data['TV']).reshape(-1,1) # predictor variable
y = np.array(data['Sales']).reshape(-1,1) # response variable
# + colab={"base_uri": "https://localhost:8080/"} id="zRL8EyJy4Mt3" outputId="2471e95c-f8c3-4ff1-d365-c8996e4390a4"
# Building the regression model
reg = LinearRegression()
reg.fit(X,y)
# + id="pK0ZEIO74Mt6"
# Predictions on the basis of the model
y_pred = reg.predict(X)
# y_pred
# + colab={"base_uri": "https://localhost:8080/"} id="sYPVxiBK4Mt9" outputId="3d093d26-37fb-4f70-f6c1-c63c370a41b4"
# Find the value of r squared
r2_score(y , y_pred)
# The advertising spends on TV explain about 81.21% of the variation in the Sales
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="3Udh-iIC4MuB" outputId="9ae3777e-632d-4174-db19-67a7935e2584"
# Visualizing the model fit
plt.scatter( X , y , color = 'blue')
plt.plot(X , y_pred , color = 'red' , linewidth = 3)
plt.xlabel("TV (Million $)")
plt.ylabel("Sales (Million $)")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="58u4eynH4MuH" outputId="ed3d3a2b-6af3-4ac1-e664-bd658c4e10ff"
# Model Coefficients: beta0 and beta1
print(reg.intercept_)
print(reg.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="TAQv59Wa4MuJ" outputId="c88c26a9-b0f5-474c-d152-a9dcb220a0a7"
# Metrics to assess model performance
rss = np.sum(np.square(y - y_pred)) # sum of the squared difference between the actual and the predicted values
print(rss)
mse = mean_squared_error(y, y_pred) # MSE is RSS divided by the number of observations
print(mse)
rmse = mse**0.5 # RMSE is square root of MSE
print(rmse)
# -
# #### Checking for assumptions
# + id="eXCl-vtJ4MuM"
# Residual analysis
y_res = y - y_pred # Residuals
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="nOQV3CfY4MuT" outputId="c71c4da5-f1f1-4741-f2a7-b472fc579fbf"
# Residual v/s predictions plot
data['res'] = y_res
plt.scatter( y_pred , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("TV Spend (Million $)")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="9nsuKqbL4MuX" outputId="8b60c7d1-9bd7-4c4a-a6ff-f95a49c0137d"
# Distribution of errors
p = sns.distplot(y_res,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residuals")
plt.show()
# -
# + [markdown] id="4INVAOzkKBgn"
# ### Normal Equations
#
# #### Regression Equation
# $\hat{y_i} = b_{0} + b_{1}{x_i}$<br>
# where slope of trend line is calculated as:<br>
# $b_{1}=\frac{\sum (x_i-\bar{x})*(y_i-\bar{y})}{\sum (x_i-\bar{x})^{2}}$<br>
# and the intercept is computed as:<br>
# $b_{0}=\bar{y}-b_{1}\bar{x}$
# + id="HvPFFcOdtALQ"
# Computing X and Y
X = data['TV'].values # advertising spend on TV
Y = data['Sales'].values # Sales
# + id="6-v1ghJMJWRe"
# Mean X and Y
mean_x = np.mean(X)
mean_y = np.mean(Y)
# Total number of values
n = len(X)
# + colab={"base_uri": "https://localhost:8080/"} id="iM-mh5gyJX9h" outputId="06981a81-9aeb-4e6f-cbba-b9e4d288af5e"
# Using the formula to calculate 'b0' and 'b1'
numer = 0
denom = 0
for i in range(n): # for each observation in the data
numer += (X[i] - mean_x) * (Y[i] - mean_y) # compute the expression and sum over all observations using for loop
denom += (X[i] - mean_x) ** 2
b1 = numer / denom
b0 = mean_y - (b1 * mean_x)
# Printing coefficients
print("Coefficients")
print(b0, b1)
# + [markdown] id="O-cQ6OnvKM44"
# ### Linear Regression Model Estimates using Matrix Multiplications
#
# $\widehat{\beta}=(X^{T}.X)^{-1}.X^{T}.Y$
# + id="pCotKXTvKM5L"
# We use NumPy’s vstack to create a 2-d numpy array from two 1d-arrays and create X_mat.
X_mat=np.vstack((np.ones(len(X)), X)).T
# -
X_mat
Y
# $\widehat{\beta}=(X^{T}.X)^{-1}.X^{T}.Y$
# + id="QvYamwvoKM5e"
# We can implement this using NumPy’s linalg module’s matrix inverse function and matrix multiplication function.
beta_hat = np.linalg.inv(X_mat.T.dot(X_mat)).dot(X_mat.T).dot(Y)
# + colab={"base_uri": "https://localhost:8080/"} id="vKAfauQbKM5l" outputId="f6b2fbb8-062f-46d0-af94-1b7c0fb8a6db"
beta_hat
# -
# + [markdown] id="Ts_s172rmjBA"
# ### 1.2 Multiple Linear Regression
#
# + [markdown] id="ud3Gp7DPrNOf"
# #### We predict the sales based on the expenditure on TV, Radio and Newspaper advertisements
# + id="HRkxl_hTubB3"
# Reading the dataset
df = pd.read_csv('https://cdn.upgrad.com/UpGrad/temp/098bb2e9-83fb-48df-9dd1-fac56fbb25ca/advertising.csv')
# -
df.info()
# + colab={"base_uri": "https://localhost:8080/"} id="_WgdTDpzubCA" outputId="b17246cc-d23e-42fe-ac81-9754404e6695"
# Inspecting the dataset
print(df.head())
# + id="4uITUQ79ubCE"
data = df
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="LsovL1I7ubCH" outputId="de9e243d-3ce3-4601-ec8d-65e92dbf0512"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'TV' , y = 'Sales') # advertising spend on TV vs Sales
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="8hmtqnhXu3h2" outputId="d1a3682e-2dcf-4c7c-a3b0-be731ce12426"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'Radio' , y = 'Sales') # Advertising spend on radio versus Sales
# + colab={"base_uri": "https://localhost:8080/", "height": 296} id="gJPGW-yju87i" outputId="31309c1f-4cf0-467a-883a-1fd2900b6415"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'Newspaper' , y = 'Sales') # Advertising spend on Newspaper versus Sales
# +
# Linear Regression model
# + id="b1JLDnk-ubCL"
# Splitting the dataset into X and y
X = data[['TV' , 'Newspaper', 'Radio']]
y = np.array(data['Sales']).reshape(-1,1)
# + colab={"base_uri": "https://localhost:8080/"} id="lPQgkRnRubCO" outputId="653ecfdc-b224-4f73-dc66-9e89b8e8fda2"
# Building the regression model
reg = LinearRegression()
reg.fit(X,y)
# + id="cgSU1I9rubCQ"
# Predictions on the basis of the model
y_pred = reg.predict(X)
# y_pred
# + colab={"base_uri": "https://localhost:8080/"} id="QAlm0hxPubCU" outputId="ec0fdeb4-87ff-40b1-d8a9-5771dafc40ae"
# Find the value of r squared
r2_score(y , y_pred) # The three predictors considered explain about 90.25% of the variation in the data
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="kTiEkPPSubCZ" outputId="c2e46c8d-9fc1-4b7e-af94-4afe1511f3dc"
# Visual comparison between predicted and actual values
plt.scatter( X['Radio'] , y , color = 'blue') # actual values
plt.scatter( X['Radio'] , y_pred , color = 'red' ) # predicted values
plt.xlabel("Radio (Million $)")
plt.ylabel("Sales (Million $)")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="zEr6b9EowVmd" outputId="24b004eb-acf3-47f1-8060-4c8bed04fe77"
plt.scatter( X['TV'] , y , color = 'blue') # actual values
plt.scatter( X['TV'] , y_pred , color = 'red' ) # predicted values
plt.xlabel("TV (Million $)")
plt.ylabel("Sales (Million $)")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="WCDIpH-qwhSO" outputId="cc035249-27b3-446e-dd1f-71796855cf8c"
plt.scatter( X['Newspaper'] , y , color = 'blue') # actual values
plt.scatter( X['Newspaper'] , y_pred , color = 'red' ) # predicted values
plt.xlabel("TV (Million $)")
plt.ylabel("Newspaper (Million $)")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="A92ve7F3ubCe" outputId="5874627c-ddd4-4301-d547-6eb32fbbc1ab"
# Calculate beta coefficients.
print(reg.intercept_)
print(reg.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="5LZbp19uubCh" outputId="2272fd45-7fbf-43fe-c874-80719e57d768"
# Metrics to give an overall sense of error in the model
rss = np.sum(np.square(y - y_pred))
print(rss)
mse = mean_squared_error(y, y_pred)
print(mse)
rmse = mse**0.5
print(rmse)
# + id="4irnIzqNubCk"
# Residual analysis
y_res = y - y_pred
#y_res
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="-izhZAUyE2Cw" outputId="56e58622-902f-4393-e30e-3ae3f54da81a"
data['res'] = y_res
plt.scatter( y_pred , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Predictions")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="EtNaSD1subCt" outputId="1fa0b6c9-276f-4635-9b3d-1a2bbbb73820"
# Distribution of errors
p = sns.distplot(y_res,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residuals")
plt.show()
# -
# + [markdown] id="RG2gLSFMxXD-"
# ### Linear Regression Model Estimates using Matrix Multiplications
# + id="8V4fmWu-ym8n"
# We use NumPy’s vstack to create a 2-d numpy array from two 1d-arrays and create X_mat.
X_mat=np.vstack((np.ones(len(X)), X.T)).T
# + id="mvuRvl2I4s8M"
#X_mat
# -
# #### $\widehat{\beta}=(X^{T}.X)^{-1}.X^{T}.Y$
# + id="OdIDxc4_xxdx"
# We can implement this using NumPy’s linalg module’s matrix inverse function and matrix multiplication function.
beta_hat = np.linalg.inv(X_mat.T.dot(X_mat)).dot(X_mat.T).dot(y)
# + colab={"base_uri": "https://localhost:8080/"} id="DK-v2WKpysgO" outputId="78ff4820-5b24-4988-e524-37f661586916"
beta_hat
# + id="Ca_mcHPWSuqt"
beta_hat_list = [beta_hat[i][0] for i in range(len(beta_hat))]
coefficients = ['b0', 'b1(TV)', 'b2(Radio)', 'b3(Newspaper)']
betas = dict(zip(coefficients, beta_hat_list))
# + colab={"base_uri": "https://localhost:8080/"} id="ToRCGj3sSuqu" outputId="ad18e603-cb65-4f28-964d-ca7b0468f545"
betas
# -
# + [markdown] id="AB-7WEzzmvET"
# ### Modeling non-linear relationships using data transformation
# + [markdown] id="8k50BFpznpkw"
# Here, we need to make a model which predicts how much distance is covered by a truck in a given time unit after a break is applied.
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="OCXjKgllP0Lk" outputId="66a7078b-57d3-4f38-9d16-b975e5cfb2ae"
dist = pd.read_csv(r"AR - Examples - 1.5.csv")
dist.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="OVCCqjyvQRRt" outputId="e838537d-6b15-42e0-d83d-f8c94be5caad"
# Plotting a scatter plot
sns.scatterplot( data = dist , x ='time' , y='distance')
plt.show()
# + id="J7ixDMYcQ0ZI"
# Splitting the dataset into X and y
X = np.array(dist['time']).reshape(-1,1)
y = np.array(dist['distance']).reshape(-1,1)
# + id="4qSfoX2TQbDE"
# Building the regression model
model = LinearRegression()
# + colab={"base_uri": "https://localhost:8080/"} id="7zQZyMkYQxZd" outputId="b051d971-1002-4ef8-8951-cc39d717d955"
model.fit(X, y)
# + id="QYPbYCKfRVck"
# Predictions on the basis of the model
y_pred2 = model.predict(X)
# y_pred2
# + colab={"base_uri": "https://localhost:8080/"} id="YOHRRYgYRnZh" outputId="72bfe849-d798-4d72-bad6-205b17e7be9e"
# Find the value of r squared
r2_score(y, y_pred2)
# -
plt.scatter( X , y , color = 'blue')
plt.plot(X , y_pred2 , color = 'red' , linewidth = 3)
plt.xlabel("time")
plt.ylabel("distance")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="Ed_rLssSU_AN" outputId="b78421f2-6606-4ef5-e28c-ab2e6cebf5a4"
# Calculate beta0 and beta1.
print(model.intercept_)
print(model.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="SdZ4Pg2qU_A0" outputId="4836caae-db67-47aa-c5f5-5603cee9ad5e"
# Metrics to give an overall sense of error in the model
rss = np.sum(np.square(y - y_pred2))
print(rss)
mse = mean_squared_error(y, y_pred2)
print(mse)
rmse = mse**0.5
print(rmse)
# + id="yjkyLZthRyrz"
#residual
residual = y - y_pred2
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="yq1zygHBR7uT" outputId="f27ea7ca-d988-4917-e850-e0e51b6f435c"
# Scatter plot of the predicted values on the x-axis and the residuals on the y-axis
plt.scatter( y_pred2 , residual)
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Predicted Distance (metres)")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="kWRnv8RmU_A7" outputId="a8e7d2a1-031d-4560-8b24-a1b69508ae15"
# Distribution of errors
p = sns.distplot(residual,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residual")
plt.show()
# + id="iZydkRm_GZTg"
# As we can see that the residuals do not fulfill the conditions for linear regression, Lets see if we can make some changes so that the residuals are normally distributed.
dist['time (seconds)(log)'] = np.log(dist['time'])
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="L5pRvbyzP56h" outputId="7af6a666-ce87-4403-a297-107aa6206297"
# Plotting a scatter plot
sns.scatterplot( data = dist , x ='time (seconds)(log)' , y='distance')
plt.show()
# + id="eGaZ6aH2GeR5"
# Splitting the dataset into X and y
X = np.array(dist['time (seconds)(log)']).reshape(-1,1)
y = np.array(dist['distance']).reshape(-1,1)
# + colab={"base_uri": "https://localhost:8080/"} id="F4CkavBbGeli" outputId="2286623e-5e91-4910-cdfc-d13621fb7e0e"
# Building the regression model
model = LinearRegression()
model.fit(X, y)
# + id="w0tcA9ZYGe7l"
# Predictions on the basis of the model
y_pred2 = model.predict(X)
# y_pred2
# + colab={"base_uri": "https://localhost:8080/"} id="mi0YdcvhGfKv" outputId="1d537eb9-ad82-4787-be89-3ded842b5d02"
# Find the value of r squared
r2_score(y, y_pred2)
# -
plt.scatter( X , y , color = 'blue')
plt.plot(X , y_pred2 , color = 'red' , linewidth = 3)
plt.xlabel("time (seconds)(log)")
plt.ylabel("distance")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="F5_SnhXPGgGR" outputId="e513dd1f-37c2-435a-b121-da2d5d5ce2d3"
# Calculate beta0 and beta1.
print(model.intercept_)
print(model.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="Awrqfc0TGt9H" outputId="b86551f6-c6b9-445d-b72a-0697c29f75b6"
# Metrics to give an overall sense of error in the model
rss = np.sum(np.square(y - y_pred2))
print(rss)
mse = mean_squared_error(y, y_pred2)
print(mse)
rmse = mse**0.5
print(rmse)
# + id="o-eMLCGCGfi_"
#residual
residual = y - y_pred2
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="YxL2MJuLGf1r" outputId="15fe8454-1ac3-4986-a710-6d88ed64e623"
plt.scatter( y_pred2 , residual)
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Predicted Distance (metres)")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="Mo-yITcvGt2s" outputId="97073303-7ea3-48dd-be9d-7c7153778d21"
# Distribution of errors
p = sns.distplot(residual,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residual")
plt.show()
# + [markdown] id="UyR0EdRHm3lb"
# ### Modeling non-linear relationship using Polynomial Regression
# + colab={"base_uri": "https://localhost:8080/", "height": 197} id="8KNPRGw2VYJ6" outputId="25a3699b-9d5e-4f02-eb02-ad9bf00e61e2"
# Model to predict marks given the number of courses taken and the time the student gives to study
# on a daily basis.
data = pd.read_csv("AR - Examples - 1.6.csv")
data.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="nQQC0bwpYH0n" outputId="25a683cc-3f4b-4c05-d1cf-d0af104ee455"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'number_courses' , y = 'Marks')
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="H-YVPqtbYH0r" outputId="18162b51-9138-471d-b0cc-e64289337b7d"
# Plotting a scatter plot
sns.scatterplot( data = data , x = 'time_study' , y = 'Marks')
# + id="wyzsOLxvYH0y"
# Splitting the dataset into X and y
X = data[['number_courses' , 'time_study']]
y = np.array(data['Marks']).reshape(-1,1)
# + colab={"base_uri": "https://localhost:8080/"} id="aGX4nAAPYH00" outputId="c71b4f7f-1814-49e8-db12-933b3d99ceee"
# Building the regression model
reg = LinearRegression()
reg.fit(X,y)
# + id="IqDN8e84YH02"
# Predictions on the basis of the model
y_pred = reg.predict(X)
#y_pred
# + colab={"base_uri": "https://localhost:8080/"} id="pegMvW_DYH04" outputId="025439ea-a0db-43cd-9704-87ae35b5064c"
# Find the value of r squared
r2_score(y , y_pred)
# + colab={"base_uri": "https://localhost:8080/"} id="ekn8Kn8ZYH1D" outputId="ebabda98-0c29-4619-df98-f847ded60701"
# Calculate beta0 and beta1.
print(reg.intercept_)
print(reg.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="cdlVIYH1YH1F" outputId="9788d1f4-ebcf-4be1-cd10-10b5ff1ac144"
# Metrics to give an overall sense of error in the model
rss = np.sum(np.square(y - y_pred))
print(rss)
mse = mean_squared_error(y, y_pred)
print(mse)
rmse = mse**0.5
print(rmse)
# + id="J9PaDywRYH1H"
# Residual analysis
y_res = y - y_pred
#y_res
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="TLShNOYsM737" outputId="2fa5e851-d1ae-4d5b-8a42-f7ce20396de0"
data['res'] = y_res
plt.scatter( y_pred , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Predictions")
plt.ylabel("Residual")
plt.show()
# -
# Checking which variable is non-linearly related to the response value
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="EAT8NM-KYH1K" outputId="27374649-55a5-48a2-903f-a22b55d4ed9a"
data['res'] = y_res
plt.scatter( data['number_courses'] , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Number courses")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="5Y2GAw74Z2yf" outputId="237cf08b-abff-4f4c-bc15-a5f72048478e"
plt.scatter( data['time_study'] , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Time study")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="SR569GE7YH1M" outputId="710718a1-3c36-4b01-fa73-9678758bc784"
# Distribution of errors
p = sns.distplot(y_res,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residuals")
plt.show()
# -
# + [markdown] id="2sJeRTkqvtW5"
# ### Fitting Polynomial Regression Model
# + id="1Y7IkfB4aGhC"
# Transforming the time_study variable
data['time_study_squared'] = data['time_study']*data['time_study']
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="dYSB-UWCQ2Jq" outputId="7b3a9777-4c89-4244-81bc-5483e3d5a001"
plt.scatter( data['time_study_squared'] , data['Marks'])
plt.xlabel("Time study squared")
plt.ylabel("Marks")
plt.show()
# + id="Asbt6moioop2"
# Splitting the dataset into X and y
X = data[['number_courses' , 'time_study', 'time_study_squared']]
y = np.array(data['Marks']).reshape(-1,1)
# + colab={"base_uri": "https://localhost:8080/"} id="aRbQ3STYoop6" outputId="19a14aa4-1866-40cb-9fa1-799bcc35dc40"
# Building the regression model
reg = LinearRegression()
reg.fit(X,y)
# + id="iwlR0PG6oop9"
# Predictions on the basis of the model
y_pred = reg.predict(X)
# y_pred
# + colab={"base_uri": "https://localhost:8080/"} id="bUGyZkBSooqA" outputId="5e5eec22-86c8-400d-e804-6cb54fcce2fa"
# Find the value of r squared
r2_score(y , y_pred)
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="HgAjmrchooqC" outputId="50ee458f-827c-4112-c36b-6d67525f7351"
plt.scatter( X['number_courses'] , y , color = 'red')
plt.scatter( X['number_courses'] , y_pred , color = 'blue' )
plt.xlabel("Number Courses")
plt.ylabel("Marks")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="yFdPbj-EooqE" outputId="c3cefee6-e229-480d-f0f6-7e3f035ddb99"
plt.scatter( X['time_study_squared'] , y , color = 'red')
plt.scatter( X['time_study_squared'] , y_pred , color = 'blue' )
plt.xlabel("Time Study Squared")
plt.ylabel("Marks")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="nr6m2q7PooqG" outputId="3c650133-d5b3-4537-d724-fffc008de93d"
# Calculate beta0 and beta1.
print(reg.intercept_)
print(reg.coef_)
# + colab={"base_uri": "https://localhost:8080/"} id="AgaZ_6gbooqI" outputId="bf68d9f5-53b0-4405-e5f0-160965c41e3c"
#Residual Sum of Squares = Mean_Squared_Error * Total number of datapoints
rss = np.sum(np.square(y - y_pred))
print(rss)
mse = mean_squared_error(y, y_pred)
print(mse)
rmse = mse**0.5
print(rmse)
# + id="jHrr08xdooqK"
# Residual analysis
y_res = y - y_pred
#y_res
# -
data['res'] = y_res
plt.scatter( y_pred , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Predictions")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="YH1-x6xlooqN" outputId="30f892d7-d5e8-4372-9be3-732af82daf69"
data['res'] = y_res
plt.scatter( data['number_courses'] , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Number courses")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 278} id="XcE_5tXRooqP" outputId="019f5996-4ef9-4ceb-dabe-3ea615623a61"
plt.scatter( data['time_study_squared'] , data['res'])
plt.axhline(y=0, color='r', linestyle=':')
plt.xlabel("Time study Squared")
plt.ylabel("Residual")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 294} id="806WZJMvooqT" outputId="9a324797-ebc9-422e-cf8e-be8fc1b832cf"
# Distribution of errors
p = sns.distplot(y_res,kde=True)
p = plt.title('Normality of error terms/residuals')
plt.xlabel("Residuals")
plt.show()
# + id="arw-Zo8mSRV7"
|
8. Machine Learning-2/1. Advanced Regression/.ipynb_checkpoints/Linear+Regression-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "-"}
# # Semi Project team 4 데이터 탐색 및 전처리 프로젝트 (EDA)
# + [markdown] slideshow={"slide_type": "-"}
# # 1. 개요
#
# - 월별 전국 아파트 분양가격 데이터를 전처리하고, 어떻게 아파트에 투자해야 좋을지 가설을 세우고 분석한 결과
#
#
# # 2. 분석과제
#
# ### 아파트 가격정보를 보고 어떻게 아파트를 투자해야 좋을지 분석해보세요.
# - 데이터셋 - https://www.data.go.kr/dataset/3035522/fileData.do
# - 분양가격이 실제 아파트 가격 상승과 깊은 관계가 있다는 가정하에 분석해보세요.
# - 위의 tips와 같이 3가지 이상의 가설을 세워 분석해보세요.
# - 가설, 분석과정, 결과 확인에 대한 설명 주석을 달아주세요.
#
#
# # 3. 분석방법
#
# - 팀원이 각각 가설을 제안하고, 가설 별로 하나씩 담당해 분석하여 결과를 취합
#
#
# # 4. 가설
#
# 1) 새학기, 인사이동 등 국내인구이동이 많이 일어나는 겨울, 봄 계절의 분양가격이 여름, 가을 분양가격보다 비쌀 것이다.
#
# 2) 2016년 9-10월, 2017년 11월~18년 2월에 경북지역의 아파트 분양가격이 하락했을 것이다.
#
# 3) 해가 갈수록 서울, 수도권 지역 분양가격 상승률이 타 지역에 비해 높을 것이다.
#
# 4) 전용면적이 넓어질수록 분양가격이 하락할 것이다.
#
# # 5. 가설 별 분석결과
# -
# ## 가설 1) 분석
# ## 가설설정
#
#
#
# 1. 가설 :
# - 새학기, 인사이동 등 국내인구이동이 많이 일어나는 겨울,봄 계절의 분양가격이 여름,가을 분양가격보다 비쌀것이다.
#
#
#
# 2. 가설근거
#
#
# 1) 인구이동
#
# ㅇ 관련근거
# - 통계청 발간 2018년 7월 국내인구이동 보도자료
#
# ㅇ 최근 3년간 인구이동 추이
# - 인구이동량 : 겨울, 봄 > 여름,가을
#
# 2) 계절정의
#
# ㅇ 관련근거
# - 한국학중앙연구원육성법 시행령
# - 한국민족문화대백과사전 자연지리/개념용어 '계절'
#
# ㅇ 계절정의
# - 봄 : 3 ~ 5월
# - 여름 : 6 ~ 8월
# - 가을 : 9월 ~ 11월
# - 겨울 : 12월 ~ 2월
# ## 분석방법
#
# #### 1. '규모구분' 칼럼 내 '전체' 데이터 중에서 월별 평균 분양가격 추이 분석
#
# ##### 2. '규모구분' 칼럼 내 '전체' 데이터 중에서 '서울', '경기', '인천', '부산', '세종', '대전'을 제외한 지역의 월별 평균 분양가격 추이 분석
#
# ##### 3. '규모구분' 칼럼 내 전용면적 별로 월별 평균 분양가격 추이 분석
#
# ##### 4. '규모구분' 칼럼 내 전용면적 별로 '서울', '경기', '인천', '부산', '세종', '대전'을 제외한 지역의 평균 분양가격 추이 분석
#
# ## 분석중점
#
# - 월별 평균 분양가격 추이 확인으로 가설검증
# ## 분석결과
#
# - 가설과 무관하게 시간의 흐름에 따라 분양가격은 상승곡선을 그리는 추이
# ## 분석과정
# ### 분석방법 1. '규모구분' 칼럼 내 '전체' 데이터 중에서 월별 평균 분양가격 분석
# +
## < 분석과정 요약 >
## 1. 데이터 프레임 내 평균 계산 등 연산을 위한 noise 데이터 제거 및 데이터 형태 int화 : step 1. ~ step 6.
## 2. 'year'과 'month'를 기준으로 'price' 추이변화 확인을 위한 'price' 평균계산 및 그룹바이 : step 7. ~ step 10.
## 3. "increase rate from a month ago(전월대비 분양가 상승률)" 생성 및 확인 : step 11. ~ step 12.
## step 1. 원본데이터 로드
## step 2. 컬럼이름 및 데이터 변수이름 변경
## step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
## step 4. 'nan' 값 제거
## step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
## step 6. 'price' 칼럼형식 int형으로 변경
## step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
## step 8. 'size' 칼럼삭제
## step 9. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
## step 10. 연산결과 두자리수에서 반올림
## step 11. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
## step 12. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
## < 세부 분석과정 >
# step 1. 원본데이터 로드
import pandas as pd
total_df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
# step 2. 컬럼이름 및 데이터 변수이름 변경
total_df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
total_df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
# step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
total_df["price(㎡)"].replace(' ', np.nan, inplace = True )
# step 4. 'nan' 값 제거
total_df.dropna(inplace = True)
# step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
total_df["price(㎡)"] = total_df["price(㎡)"].apply(lambda x: x.replace(',',''))
# step 6. 'price' 칼럼형식 int형으로 변경
total_df["price(㎡)"] = total_df["price(㎡)"].astype(int)
# step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
partial_df = total_df[total_df["size"] == 'avg'].reset_index(drop=True)
partial_df
# step 8. 'size' 칼럼삭제
partial_df.drop("size", axis=1, inplace=True)
partial_df
# step 9. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
step1_df = partial_df.groupby([partial_df["year"],partial_df["month"]]).mean()["price(㎡)"].reset_index()
# step 10. 연산결과 두자리수에서 반올림
step1_df = round(step1_df,2)
# step 11. "increase rate from a month ago" 생성
price_list = [step1_df.loc[0]["price(㎡)"]]
def increase_rate(price):
price_list_pop = price_list.pop()
increase_rate = round((price / price_list_pop * 100),2)
price_list.append(price)
return increase_rate
step1_df["increase rate from a month ago"] = step1_df["price(㎡)"].apply(increase_rate)
del price_list
# step 12. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
step1_df["increase rate from a month ago"] = step1_df["increase rate from a month ago"].astype('str')
step1_df["increase rate from a month ago"] = step1_df["increase rate from a month ago"].apply(lambda data : data + " %")
step1_df
# -
import matplotlib.font_manager as fm
font_location = "C:\Windows\Fonts\H2GTRM.TTF"
font_name = fm.FontProperties(fname=font_location).get_name()
print(font_name)
mpl.rc('font', family=font_name)
mpl.rcParams["font.family"]
# ### 분석방법 2.'규모구분' 칼럼 내 '전체' 데이터 중에서 '서울', '경기', '인천', '부산', '세종', '대전'을 제외한 지역의 월별 평균 분양가격 추이 분석
# +
## < 분석과정 요약 >
## 1. 데이터 프레임 내 평균 계산 등 연산을 위한 noise 데이터 제거 및 데이터 형태 int화 : step 1. ~ step 6.
## 2. 'year'과 'month'를 기준으로 'price' 추이변화 확인을 위한 'price' 평균계산 및 그룹바이 : step 7. ~ step 11.
## 3. "increase rate from a month ago(전월대비 분양가 상승률)" 생성 및 확인 : step 12. ~ step 13.
## step 1. 원본데이터 로드
## step 2. 컬럼이름 및 데이터 변수이름 변경
## step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
## step 4. 'nan' 값 제거
## step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
## step 6. 'price' 칼럼형식 int형으로 변경
## step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
## step 8. 'city' 컬럼에서 '서울', '경기', '인천', '부산', '세종', '대전' 데이터 제거
## step 9. 'size' 컬럼 제거
## step 10. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
## step 11. 연산결과 두자리수에서 반올림
## step 12. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
## step 13. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
## < 세부 분석과정 >
# step 1. 원본데이터 로드
import pandas as pd
total_df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
# step 2. 컬럼이름 및 데이터 변수이름 변경
total_df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
total_df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
# step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
total_df["price(㎡)"].replace(' ', np.nan, inplace = True )
# step 4. 'nan' 값 제거
total_df.dropna(inplace = True)
# step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
total_df["price(㎡)"] = total_df["price(㎡)"].apply(lambda x: x.replace(',',''))
# step 6. 'price' 칼럼형식 int형으로 변경
total_df["price(㎡)"] = total_df["price(㎡)"].astype(int)
# step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
partial = total_df[total_df["size"] == 'avg'].reset_index(drop =True)
# step 8. 'city' 컬럼에서 '서울', '경기', '인천', '부산', '세종', '대전' 데이터 제거
partial6 = partial[~partial["city"].isin(["서울","경기","인천",'부산','세종','대전'])]
# step 9. 'size' 컬럼 제거
partial6.drop("size",axis=1,inplace = True)
## step 10. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
result = partial6.groupby([partial6["year"],partial6["month"]]).mean()["price(㎡)"].reset_index()
## step 11. 연산결과 두자리수에서 반올림
result = round(result,2)
## step 12. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
price_list = [result.loc[0]["price(㎡)"]]
def increase_rate(price):
price_list_pop = price_list.pop()
increase_rate = round((price / price_list_pop * 100),2)
price_list.append(price)
return increase_rate
result["increase rate from a month ago"] = result["price(㎡)"].apply(increase_rate)
del price_list
## step 13. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
result["increase rate from a month ago"] = result["increase rate from a month ago"].astype('str')
result["increase rate from a month ago"] = result["increase rate from a month ago"].apply(lambda data : data + " %")
result
# -
# ### 분석방법 3. '규모구분' 칼럼 내 전용면적 별로 월별 평균 분양가격 추이 분석
# +
## < 분석과정 요약 >
## 1. 데이터 프레임 내 평균 계산 등 연산을 위한 noise 데이터 제거 및 데이터 형태 int화 : step 1. ~ step 6.
## 2. 'year'과 'month'를 기준으로 'price' 추이변화 확인을 위한 'price' 평균계산 및 그룹바이 : step 7. ~ step 10.
## 3. "increase rate from a month ago(전월대비 분양가 상승률)" 생성 및 확인 : step 11. ~ step 13.
## step 1. 원본데이터 로드
## step 2. 컬럼이름 및 데이터 변수이름 변경
## step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
## step 4. 'nan' 값 제거
## step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
## step 6. 'price' 칼럼형식 int형으로 변경
## step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
## step 8. 'size' 컬럼에서 'size' 별로 확인 할 수 있도록 코드작성. 아래와 같이 주석처리하여 선택가능
## step 9. 'size' 컬럼 제거
## step 10. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
## step 11. 연산결과 두자리수에서 반올림
## step 12. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
## step 13. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
## < 세부 분석과정 >
# step 1. 원본데이터 로드
import pandas as pd
total_df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
# step 2. 컬럼이름 및 데이터 변수이름 변경
total_df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
total_df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
# step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
total_df["price(㎡)"].replace(' ', np.nan, inplace = True )
# step 4. 'nan' 값 제거
total_df.dropna(inplace = True)
# step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
total_df["price(㎡)"] = total_df["price(㎡)"].apply(lambda x: x.replace(',',''))
# step 6. 'price' 칼럼형식 int형으로 변경
total_df["price(㎡)"] = total_df["price(㎡)"].astype(int)
# step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
partial = total_df[total_df['size'] != 'avg'].reset_index(drop =True)
# step 8. 'size' 컬럼에서 'size' 별로 확인 할 수 있도록 코드작성. 아래와 같이 주석처리하여 선택가능
partial1 = partial[partial['size'] == '~ 60㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '60㎡ ~ 85㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '85㎡ ~ 102㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '102㎡ ~'].reset_index(drop=True)
# step 9. 'size' 컬럼 제거
partial1.drop("size",axis=1,inplace = True)
# step 10. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
result = partial1.groupby([partial1["year"],partial1["month"]]).mean()["price(㎡)"].reset_index()
# step 11. 연산결과 두자리수에서 반올림
result = round(result,2)
# step 12. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
price_list = [result.loc[0]["price(㎡)"]]
def increase_rate(price):
price_list_pop = price_list.pop()
increase_rate = round((price / price_list_pop * 100),2)
price_list.append(price)
return increase_rate
result["increase rate from a month ago"] = result["price(㎡)"].apply(increase_rate)
del price_list
# step 13. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
result["increase rate from a month ago"] = result["increase rate from a month ago"].astype('str')
result["increase rate from a month ago"] = result["increase rate from a month ago"].apply(lambda data : data + " %")
result
# -
# ### 분석방법 4. '규모구분' 칼럼 내 전용면적 별로 '서울', '경기', '인천', '부산', '세종', '대전'을 제외한 지역의 평균 분양가격 추이 분석
# +
## < 분석과정 요약 >
## 1. 데이터 프레임 내 평균 계산 등 연산을 위한 noise 데이터 제거 및 데이터 형태 int화 : step 1. ~ step 6.
## 2. 'year'과 'month'를 기준으로 'price' 추이변화 확인을 위한 'price' 평균계산 및 그룹바이 : step 7. ~ step 10.
## 3. "increase rate from a month ago(전월대비 분양가 상승률)" 생성 및 확인 : step 11. ~ step 13.
## step 1. 원본데이터 로드
## step 2. 컬럼이름 및 데이터 변수이름 변경
## step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
## step 4. 'nan' 값 제거
## step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
## step 6. 'price' 칼럼형식 int형으로 변경
## step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
## step 8. 'size' 컬럼에서 'size' 별로 확인 할 수 있도록 코드작성. 아래와 같이 주석처리하여 선택가능
## step 9. 'city' 컬럼에서 '서울', '경기', '인천', '부산', '세종', '대전' 데이터 제거
## step 10. 'size' 컬럼 제거
## step 11. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
## step 12. 연산결과 두자리수에서 반올림
## step 13. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
## step 14. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
## < 세부 분석과정 >
# step 1. 원본데이터 로드
import pandas as pd
total_df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
# step 2. 컬럼이름 및 데이터 변수이름 변경
total_df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
total_df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
# step 3. 'price' 컬럼에서 공백을 'nan' 값으로 변경
total_df["price(㎡)"].replace(' ', np.nan, inplace = True )
# step 4. 'nan' 값 제거
total_df.dropna(inplace = True)
# step 5. 'price' 칼럼 내 데이터 중 ','을 포함한 데이터에서 ','제거
total_df["price(㎡)"] = total_df["price(㎡)"].apply(lambda x: x.replace(',',''))
# step 6. 'price' 칼럼형식 int형으로 변경
total_df["price(㎡)"] = total_df["price(㎡)"].astype(int)
# step 7. 'size' 칼럼에서 'avg' 데이터만 전시 , index 재설정
partial = total_df[total_df['size'] != 'avg'].reset_index(drop =True)
# step 8. 'size' 컬럼에서 'size' 별로 확인 할 수 있도록 코드작성. 아래와 같이 주석처리하여 선택가능
partial = partial[partial['size'] == '~ 60㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '60㎡ ~ 85㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '85㎡ ~ 102㎡'].reset_index(drop=True)
# partial = partial[partial['size'] == '102㎡ ~'].reset_index(drop=True)
# step 9. 'city' 컬럼에서 '서울', '경기', '인천', '부산', '세종', '대전' 데이터 제거
partial6 = partial[~partial["city"].isin(["서울","경기","인천",'부산','세종','대전'])]
# step 10. 'size' 컬럼 제거
partial6.drop("size",axis=1,inplace = True)
# step 11. 'year'과 'month' 칼럼을 기준으로 price 칼럼 평균을 출력해주는 groupby 실행, 추가로 index 재설정
result = partial6.groupby([partial6["year"],partial6["month"]]).mean()["price(㎡)"].reset_index()
# step 12. 연산결과 두자리수에서 반올림
result = round(result,2)
# step 13. "increase rate from a month ago(전월대비 분양가 상승률)" 생성
price_list = [result.loc[0]["price(㎡)"]]
def increase_rate(price):
price_list_pop = price_list.pop()
increase_rate = round((price / price_list_pop * 100),2)
price_list.append(price)
return increase_rate
result["increase rate from a month ago"] = result["price(㎡)"].apply(increase_rate)
del price_list
# step 14. "increase rate from a month ago" 칼럼 데이터 뒤에 '%' 추가
result["increase rate from a month ago"] = result["increase rate from a month ago"].astype('str')
result["increase rate from a month ago"] = result["increase rate from a month ago"].apply(lambda data : data + " %")
result
# -
# ## 결론
#
# 월별로 분양가 차이나 특이점이 없었고 수도권 비수도권 구분 없이 분양가는 지속적으로 상승하는 추세로 본 가설과 무방한 결과 도출
# ## 가설 2) 분석
# ## 가설설정
#
# 1. 가설 :
#
# - **2016년 9-10월, 2017년 11월~18년 2월에 경북지역의 아파트 분양가격이 하락했을 것이다.**
#
#
# 2. 가설근거
#
# ㅇ 지진피해 발생
# - 행정안전부 2016 재해연보(145-147), 2017 재해연보(106-110)
#
# ㅇ 현상인식
# - '16년 9월 경상북도 경주, 17년 11월 경상북도 포항을 중심으로 리히터 규모 5이상의 지진으로 인명 및 재산피해 발생
# ## 분석방법
#
#
# 1. 지역 칼럼에서 '경북'에 해당하는 데이터만 추출 후, 규모구분 칼럼 내 '전체' 데이터의 월별 분양가격 상승률 계산 및 비교분석
#
#
# 2. 경북 지역 각 전용면적마다의 월별 분양가격 상승률 계산 및 비교분석
#
#
# 3. 전국 모든 시,도의 규모구분 '전체' 데이터 추출 후 월별 분양가격 상승률 계산, 예측한 시기의 경북지역 상승률과 타 지역들의 상승률 비교
#
#
#
# ## 분석중점
#
#
# - 경북 지역에서의 아파트 분양가격 상승률 추이를 월별로 비교하여 다른 시기에 비해 예측한 시기 분양가격이 하락하는지 확인
#
#
# - 예측한 시기의 전국 모든 시, 도의 아파트 분양가격 상승률 추이를 비교하여 경북지역의 분양가격이 타지역에 비해 하락했는지 확인
#
# ## 분석결과
#
# - 가설과 정반대로, 지진이 발생한 시기에 경북 지역의 아파트 분양가격은 오히려 상승하는 경향을 보임
# ## 분석과정
# #### 데이터 전처리
df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
df.head()
# +
# 분양가격 column에서 공백, 즉 가격데이터가 없는 값들을 nan으로 바꿔주고, nan값인 행들을 제거합니다.
df["price(㎡)"].replace(' ', np.nan, inplace = True)
df.dropna(inplace = True)
# 가격 내 쉼표를 제거합니다.
df["price(㎡)"] = df["price(㎡)"].apply(lambda x: x.replace(',',''))
# str이었던 가격을 int로 바꿔줍니다.
df['price(㎡)'] = df['price(㎡)'].astype('int')
# index를 reset해줍니다.
df.reset_index(drop = True, inplace = True)
df.tail()
# -
# +
# rise = [np.nan]
# def rising_price(price):
# for index in range(len(price)-1):
# a = round(list(price)[index+1] / list(price)[index] * 100, 2)
# rise.append(a)
# return rise
# list(df_kb_all['price(㎡)'])[0] / list(df_kb_all['price(㎡)'])[1] * 100
# 처음에 이렇게 함수를 선언해서 상승률을 계산했는데 pandas 내부 기능으로 lambda를 사용해 apply하는 방법으로 수정,개선하였습니다.
# -
# #### 분석 1. 경북지역 아파트 '전체' 월별 분양가격 상승률 계산 및 비교분석
# +
# 경북지역 중 size가 전체인 것들끼리 분양가격을 비교하기 위해 새 dataframe을 만듭니다.
df_kb_all = df[df['city'] == '경북']
df_kb_all = df_kb_all[df_kb_all['size'] == 'avg']
df_kb_all.reset_index(drop=True, inplace=True)
# 아래 lambda 함수에서 상승률을 계산하기 위해 index값을 밸류값으로 하는 column을 생성합니다.
df_kb_all['index'] =list(range(len(df_kb_all)))
# lambda함수로 상승률을 계산해 apply함수를 이용하여 'rate_of_rise'라는 새로운 칼럼에 넣어줍니다.
df_kb_all['rate_of_rise'] = df_kb_all['index'].apply(lambda x : np.nan if x == 0 \
else round(df_kb_all['price(㎡)'][x] / df_kb_all['price(㎡)'][x-1] * 100, 2))
# 오로지 상승률 계산을 위해 만들었던 index칼럼을 드랍합니다.
df_kb_all.drop(columns = 'index', inplace = True)
# pivot으로 연도별, 월별로 보기 좋게 정리합니다.
df_kb_all = df_kb_all.pivot("month", "year", "rate_of_rise")
df_kb_all
# -
#예측한 시기의 분양가격 상승률
df_kb_all[2016][9], df_kb_all[2016][10], df_kb_all[2017][11], df_kb_all[2017][12], df_kb_all[2018][1], df_kb_all[2018][2]
# - 분석 1의 결과
# >예측했던 것과는 정반대로,
# 2016년 9월에서 10월, 2017년 11월에서 2018년 2월까지 분양가격이 오히려 상승했거나 변동이 없었음을 확인할 수 있습니다.
# #### 분석 2. 경북 지역 각 전용면적마다의 월별 분양가격 상승률 계산 및 비교분석
# ##### 1) 전용면적 60㎡ 이하
# +
df_kb_60_lower = df[df['city'] == '경북']
df_kb_60_lower = df_kb_60_lower[df_kb_60_lower['size'] == '~ 60㎡']
df_kb_60_lower.reset_index(drop=True, inplace=True)
df_kb_60_lower['index'] =list(range(len(df_kb_60_lower)))
df_kb_60_lower['rate_of_rise'] = df_kb_60_lower['index'].apply(lambda x : np.nan if x == 0 \
else round(df_kb_60_lower['price(㎡)'][x] / df_kb_60_lower['price(㎡)'][x-1] * 100, 2))
df_kb_60_lower.tail()
df_kb_60_lower.drop(columns = 'index', inplace = True)
df_kb_60_lower = df_kb_60_lower.pivot("month", "year", "rate_of_rise")
df_kb_60_lower
# -
# ##### 2) 전용면적 60㎡ 초과 85㎡ 이하
# +
df_kb_60_to_85 = df[df['city'] == '경북']
df_kb_60_to_85 = df_kb_60_to_85[df_kb_60_to_85['size'] == '60㎡ ~ 85㎡']
df_kb_60_to_85.reset_index(drop=True, inplace=True)
df_kb_60_to_85['index'] =list(range(len(df_kb_60_to_85)))
df_kb_60_to_85['rate_of_rise'] = df_kb_60_to_85['index'].apply(lambda x : np.nan if x == 0 \
else round(df_kb_60_to_85['price(㎡)'][x] / df_kb_60_to_85['price(㎡)'][x-1] * 100, 2))
df_kb_60_to_85.tail()
df_kb_60_to_85.drop(columns = 'index', inplace = True)
df_kb_60_to_85 = df_kb_60_to_85.pivot("month", "year", "rate_of_rise")
df_kb_60_to_85
# -
# ##### 3) 전용면적 85㎡ 초과 102㎡ 이하
# +
df_kb_85_to_102 = df[df['city'] == '경북']
df_kb_85_to_102 = df_kb_85_to_102[df_kb_85_to_102['size'] == '85㎡ ~ 102㎡']
df_kb_85_to_102.reset_index(drop=True, inplace=True)
df_kb_85_to_102['index'] =list(range(len(df_kb_85_to_102)))
df_kb_85_to_102['rate_of_rise'] = df_kb_85_to_102['index'].apply(lambda x : np.nan if x == 0 \
else round(df_kb_85_to_102['price(㎡)'][x] / df_kb_85_to_102['price(㎡)'][x-1] * 100, 2))
df_kb_85_to_102.tail()
df_kb_85_to_102.drop(columns = 'index', inplace = True)
df_kb_85_to_102 = df_kb_85_to_102.pivot("month", "year", "rate_of_rise")
df_kb_85_to_102
# -
# ##### 4) 전용면적 102㎡ 초과
# +
df_kb_102_up = df[df['city'] == '경북']
df_kb_102_up = df_kb_102_up[df_kb_102_up['size'] == '102㎡ ~']
df_kb_102_up.reset_index(drop=True, inplace=True)
df_kb_102_up['index'] =list(range(len(df_kb_102_up)))
df_kb_102_up['rate_of_rise'] = df_kb_102_up['index'].apply(lambda x : np.nan if x == 0 \
else round(df_kb_102_up['price(㎡)'][x] / df_kb_102_up['price(㎡)'][x-1] * 100, 2))
df_kb_102_up.tail()
df_kb_102_up.drop(columns = 'index', inplace = True)
df_kb_102_up = df_kb_102_up.pivot("month", "year", "rate_of_rise")
df_kb_102_up
# +
#예측한 시기의 단위면적별 분양가격 상승률
#60㎡ 이하
df_kb_60_lower[2016][9], df_kb_60_lower[2016][10], df_kb_60_lower[2017][11], df_kb_60_lower[2017][12], df_kb_60_lower[2018][1], df_kb_60_lower[2018][2]
# -
#60㎡ 초과 85㎡ 이하
df_kb_60_to_85[2016][9], df_kb_60_to_85[2016][10], df_kb_60_to_85[2017][11], df_kb_60_to_85[2017][12], df_kb_60_to_85[2018][1], df_kb_60_to_85[2018][2]
#85㎡ 초과 102㎡ 이하
df_kb_85_to_102[2016][9], df_kb_85_to_102[2016][10]
#102㎡ 초과
df_kb_102_up[2016][9], df_kb_102_up[2016][10], df_kb_102_up[2017][11], df_kb_102_up[2017][12], df_kb_102_up[2018][1], df_kb_102_up[2018][2]
# - 분석 2의 결과
# > 예측한 기간동안 모든 면적에서 대체적으로 분양가격이 상승하는 경향이 보이고, 그 상승률의 크기는 면적이 커질수록 작아진다.
# #### 분석 3. 예측 시기 전국 모든 시,도의 아파트 '전체' 월별 분양가격 상승률과 경북지역 상승률 비교
#전국의 아파트 분양가격을 '전체'로만 비교하기 위한 데이터프레임을 생성합니다.
df= df[df['size'] == 'avg']
df.reset_index(inplace = True)
df.head()
# 가격, 지역, 월별로 피봇테이블을 생성합니다.
df_pt = df.pivot_table('price(㎡)',['city'], ['year','month'])
#df_pt.columns = df_pt.columns.droplevel()
df_pt.head()#.reset_index().head()
len(df_pt)
# +
#위 테이블의 밸류값을 월별 분양가격 상승률로 바꿔주기 위해 우선 지역별로, 즉 row 마다 상승률을 계산해 rising이라는 리스트에 넣어줍니다.
rising=[]
for index in range(17): #전체 행 개수
rising.append(np.nan)
for index2 in range(33): #전체 열 개수
a = round(df_pt.values[index][index2+1] / df_pt.values[index][index2] * 100, 2)
rising.append(a)
# +
#위에서 뽑은 상승률 리스트를 행렬로 만들고 테이블 모양과 동일하게 reshape해줍니다.
na = np.array(rising).reshape(17,34)
na
# +
#reshape한 상승률 행렬로 원래 테이블의 밸류값을 교체하여 상승률 테이블을 만듭니다.
df_pt.loc[:,:] = na
df_pt.head()
# +
#지진발생시기의 분양가격 상승률만을 비교하고자 하기 때문에 그 시기에 해당하는 column만 뽑습니다.
df_compare = df_pt[2017][[11,12]].combine_first(df_pt[2018][[1,2]])
cols = df_compare.columns.tolist()
cols = cols[2:]+cols[:2]
cols
# df_compare_2017 = df_compare[cols]
# df_compare_2017
# -
df_compare_2016 = df_pt[2016][[9,10]]
df_compare_2016
# - 분석 3의 결과
# > 지진피해의 영향권 밖에 있는 경북 이외 지역들에서의 분양가격은 해당 시기에 각 지역들에 존재하는 다양한 외부 요인에 의해 상승 혹은 하락한다. 따라서 지진이 발생하지 않은 지역에 비해 지진이 발생한 지역의 아파트 분양가격 상승률이 더 높다는 결론은 내리기 힘들다.
# ## 결론
#
# 지진이 발생한 시기에 피해지역의 아파트 분양가격은 대체적으로 전월대비 상승하는 형태를 보인다.
#
# 해당 시기 전용면적별 상승률을 비교해보면, 전용면적이 작을수록 상승률이 높게 나타난다.
#
# 그러나 지진 발생 시기에 피해지역 이외의 분양가격 상승률과 피해지역의 분양가격 상승률을 비교하기는 어렵다.
#
# 사실 분양가격 변동에는 각 지역별로 아파트의 단지조건, 학군, 주변 환경 등 다양한 요인이 원인으로 작용하기 때문에,
#
# 단순히 '지진발생'이라는 요인만을 기준으로 상승률을 분석해 어떤 결론을 내리고 그 결론을 일반화하기에는 무리가 있다고 판단된다.
# ## 가설 3) 분석
# ## 가설설정
#
# 1. 가설 :
# - 해가 갈수록 서울, 수도권 지역 분양가격 상승률이 타 지역에 비해 높을 것이다.
# ## 분석방법
#
# ##### 1. 수도권 지역 월별 평균 분양 가격 분석
#
# ##### 2. 수도권 외 지역 월별 평균 분양 가격 분석
#
# ##### 3. 수도권 지역과 수도권 외 지역 월별 평균 분양 가격 비교 분석
#
# ##### 4. 수도권 지역 연간 평균 분양 가격 분석
#
# ##### 5. 수도권 외 지역 연간 평균 분양 가격 분석
#
# ##### 6. 수도권 지역과 수도권 외 지역 연간 평균 분양 가격 비교 분석
#
# ## 분석중점
#
# - 수도권과 수도권 외 지역의 평균 분양가격 추이 확인으로 의미있는 분석결과 도출
# ## 분석결과
#
# - 아파트 분양가는 수도권 지역이 수도권 외 지역 보다 1.5배 정도 높음
#
# - 아파트 분양가 상승률은 수도권 외 지역이 수도권 지역보다 다소 높음
# ## 분석과정
# ### 데이터 전처리
# +
import warnings
warnings.simplefilter('ignore')
import numpy as np
import pandas as bpd
# 데이터 로드
df_price = pd.read_csv("apt_2018_7.csv", encoding="euc-kr")
# 칼럼명 변경
df_price.rename(columns={"지역명":"city", "규모구분":"size", "연도":"year", "월":"mon", "분양가격(㎡)":"price(㎡)"}, inplace=True)
# 데이터가 존재하지 않는(NaN) 칼럼이 하나라도 포함되거나 price(㎡) 칼럼 내 데이터가 공백으로만 구성된 행 제외
df_price = df_price[(df_price.notnull().all(axis=1)) & (df_price["price(㎡)"].str.strip() != "")]
# 인덱스 리셋
df_price.reset_index(drop=True, inplace=True)
# price(㎡) 칼럼 내 쉼표를 제거
df_price["price(㎡)"] = df_price["price(㎡)"].str.replace(",", "")
# price(㎡) 칼럼의 타입을 정수형으로 변경
df_price["price(㎡)"] = df_price["price(㎡)"].astype("int")
# size 컬럼의 데이터를 인식하기 쉽게 변경
df_price["size"].replace({"전용면적 60㎡이하":"~60㎡", "전용면적 60㎡초과 85㎡이하":"60㎡~85㎡",\
"전용면적 85㎡초과 102㎡이하":"85㎡~102㎡", "전용면적 102㎡초과":"102㎡~", "전체":"All"}, inplace=True)
df_price.tail()
# -
# ##### 수도권
# 우리나라의 중심지인 서울 특별시와 그 주변에 있는 경기도와 인천 광역시를 말한다.
# 지역 조회
df_price["city"].unique()
# ### 분석방법 1. 수도권 지역 월별 평균 분양 가격
# +
# 수도권 지역 데이터만 추출
df_price_metro = df_price[df_price["city"].isin(["서울","인천","경기"])]
# size는 All(전체)를 대상으로 함
df_price_metro_all = df_price_metro[df_price_metro["size"]=="All"]
# 년도, 월에 따라 그룹핑 후 분양가의 평균을 구함
df_price_metro_all_mean = df_price_metro_all.groupby(["year", "mon"]).mean()["price(㎡)"].reset_index()
# 전월 대비 분양 가격 상승률 칼럼 추가
df_price_metro_all_mean["rate"] = [100. if i == 0 else \
round(df_price_metro_all_mean["price(㎡)"][i] / df_price_metro_all_mean["price(㎡)"][i-1] * 100, 2) \
for i in range(len(df_price_metro_all_mean))]
# 수도권 표식 칼럼 추가(0:수도권 외 지역, 1:수도권 지역)
df_price_metro_all_mean["metropolis"] = 1
df_price_metro_all_mean
# -
# ### 분석방법 2. 수도권 외 지역 월별 평균 분양 가격
# +
# 수도권 외 지역 데이터만 추출
df_price_outer = df_price[~df_price["city"].isin(["서울","인천","경기"])]
# size는 All(전체)를 대상으로 함
df_price_outer_all = df_price_outer[df_price_outer["size"]=="All"]
# 년도, 월에 따라 그룹핑 후 분양가의 평균을 구함
df_price_outer_all_mean = df_price_outer_all.groupby(["year", "mon"]).mean()["price(㎡)"].reset_index()
# 전월 대비 분양 가격 상승률 칼럼 추가
df_price_outer_all_mean["rate"] = [100. if i == 0 else \
round(df_price_outer_all_mean["price(㎡)"][i] / df_price_outer_all_mean["price(㎡)"][i-1] * 100, 2) \
for i in range(len(df_price_outer_all_mean))]
# 수도권 표식 칼럼 추가(0:수도권 외 지역, 1:수도권 지역)
df_price_outer_all_mean["metropolis"] = 0
df_price_outer_all_mean
# -
# ### 분석방법 3. 수도권 지역과 수도권 외 지역 월별 평균 분양 가격 비교
# +
# 수도권 지역과 수도권 외 지역의 월별 평균 분양가 데이터 프레임을 세로로 합침
df_price_all_mean = df_price_metro_all_mean.append(df_price_outer_all_mean, ignore_index=True)
# 피벗 테이블로 표시
df_price_all_mean.pivot_table("rate", ["year", "mon"], ["metropolis"])
# -
# ### 분석방법 4. 수도권 지역 연간 평균 분양 가격
# +
# 수도권 지역 데이터만 추출
df_price_metro = df_price[df_price["city"].isin(["서울","인천","경기"])]
# size는 All(전체)를 대상으로 함
df_price_metro_all = df_price_metro[df_price_metro["size"]=="All"]
# 년도에 따라 그룹핑 후 분양가의 평균을 구함
df_price_metro_all_mean = df_price_metro_all.groupby("year").mean()["price(㎡)"].reset_index()
# 전년 대비 분양 가격 상승률 칼럼 추가
df_price_metro_all_mean["rate"] = [100. if i == 0 else \
round(df_price_metro_all_mean["price(㎡)"][i] / df_price_metro_all_mean["price(㎡)"][i-1] * 100, 2) \
for i in range(len(df_price_metro_all_mean))]
# 수도권 표식 칼럼 추가(0:수도권 외 지역, 1:수도권 지역)
df_price_metro_all_mean["metropolis"] = 1
df_price_metro_all_mean
# -
# ### 분석방법 5. 수도권 외 지역 연간 평균 분양 가격
# +
# 수도권 외 지역 데이터만 추출
df_price_outer = df_price[~df_price["city"].isin(["서울","인천","경기"])]
# size는 All(전체)를 대상으로 함
df_price_outer_all = df_price_outer[df_price_outer["size"]=="All"]
# 년도에 따라 그룹핑 후 분양가의 평균을 구함
df_price_outer_all_mean = df_price_outer_all.groupby("year").mean()["price(㎡)"].reset_index()
# 전년 대비 분양 가격 상승률 칼럼 추가
df_price_outer_all_mean["rate"] = [100. if i == 0 else \
round(df_price_outer_all_mean["price(㎡)"][i] / df_price_outer_all_mean["price(㎡)"][i-1] * 100, 2) \
for i in range(len(df_price_outer_all_mean))]
# 수도권 표식 칼럼 추가(0:수도권 외 지역, 1:수도권 지역)
df_price_outer_all_mean["metropolis"] = 0
df_price_outer_all_mean
# -
# ### 분석방법 6. 수도권 지역과 수도권 외 지역 연간 평균 분양 가격 비교
# +
# 수도권 지역과 수도권 외 지역의 연간 평균 분양가 데이터 프레임을 세로로 합침
df_price_all_mean = df_price_metro_all_mean.append(df_price_outer_all_mean, ignore_index=True)
# 피벗 테이블로 표시
df_price_all_mean.pivot("year", "metropolis", "rate")
# -
# ## 결론
#
# - 아파트 분양가는 수도권 지역이 수도권 외 지역 보다 1.5배 정도 높음
#
# - 아파트 분양가 상승률은 수도권 외 지역이 수도권 지역보다 다소 높음
#
# - 연간 데이터 샘플이 다르기 때문에 다른 방법을 통해 형평성을 고려해야 함
#
# ## 가설 4) 분석
# ## 가설설정
#
#
#
# 1. 가설 :
# - 전용면적이 넓어질수록 분양가격이 하락할 것이다.
#
#
#
# 2. 가설근거
#
#
# 1) 규모가 커지면 면적당 분양가격이 상승할 것이라고 판단
# 2) 물건을 팔 때 여러개를 한 번에 팔면 할인을 해줄 수 있듯이 넓은 면적일수록 단위 전용면적 당 분양가격이 하락할 것이라고 예상
# 3) 전용면적이 높을수록 관리비 부담이 커지기 때문에 단위 전용면적 당 분양가가 하락 할 것으로 예상
#
# ## 분석방법
#
# ##### 1. 각 규모구분과 다음 구간 규모구분과의 분양가격 차이를 구한다.
#
# ##### 2. 각 규모구분 분양가격 차이를 기준 규모로 나누어 상승률을 구한다.
#
# ##### 3. 전체 지역별로 각 규모구분 분양가격 상승률을 구해서 한 표에 합친다.
#
# ##### 4. 상승률이 양수(%)이면 다음 구간이 전 구간 보다 상승한 것이고 음수(%)이면 하락한 것이다.
#
#
# ## 분석중점
#
# - 상승률에 양수(%)가 많은지 음수(%)가 많은지 확인한다. 일반적으로 한쪽이 많은지 본다.
# ## 분석결과
#
# - 가설과 무관하게 일정한 흐름이 없이 전용면적이 하락하거나 상승했을 때 일정하게 분양가격이 증감하지 않는다.
# # 분석과정
#
# ### 분석방법 - 각 구간별 상승률을 구한다.
df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
df.head()
# +
df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"price(㎡)"}, inplace = True)
df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
df["price(㎡)"] = df["price(㎡)"].ffill().apply(lambda x: x.replace(',','')) # nan인 값들을 다음 데이터 값으로 채워줌, 데이터 내 쉼표 제거
df["price(㎡)"].replace(' ', np.nan, inplace = True) # 공백, 즉 가격데이터가 없는 값들을 nan으로 바꿔줌
df.dropna(inplace = True) # 가격이 nan인 행을 모두 드랍
df['price(㎡)'] = df['price(㎡)'].astype('int') # str이었던 가격을 int로 바꿔줌
# -
# ## 분석 방법 (함수로 실행한다.)
#
# ##### 1. 각 규모구분과 다음 구간 규모구분과의 분양가격 차이를 구한다.
#
# ##### 2. 각 규모구분 분양가격 차이를 기준 규모로 나누어 상승률을 구한다.
#
# ##### 3. 전체 지역별로 각 규모구분 분양가격 상승률을 구해서 한 표에 합친다.
# 각 지역별 규모구분과 다음 규모구분의 상승률 차이를 계산하는 함수
def func_rate(dft, city_ls):
new_df = pd.DataFrame() # return할 dataframe을 생성한다.
for c in city_ls: # 각 지역별로 돌린다.
for n in range(3): # 구간이 5개인데 전체구간은 해당되지 않으므로 제외하고 4구간에서 구간 간격은 3이므로
if n == 0:
s = "~ 60㎡" # 기준 전용면적
ne = "60㎡ ~ 85㎡" # 비교할 대상 전용면적
elif n == 1:
s = "60㎡ ~ 85㎡"
ne = "85㎡ ~ 102㎡"
else:
s = "85㎡ ~ 102㎡"
ne = "102㎡ ~"
df_rise = dft[dft['city'] == c] # 해당 지역의 데이터를 넣는다.
df_rise = df_rise[df_rise['size'] == s] # 기준 구간의 데이터를 넣는다.
df_rise.reset_index(drop=True, inplace=True)
df_rise_next = dft[dft['city'] == c] # 비교할 지역의 데이터를 넣는다.
df_rise_next = df_rise_next[df_rise_next['size'] == ne] # 다음 구간의 데이터를 추춣한다.
df_rise_next.reset_index(drop=True, inplace=True)
df_rise['next'] = df_rise_next['price(㎡)'] # 다음 구간의 데이터를 넣는다.
df_rise.reset_index(drop=True, inplace=True)
df_rise['sub'] = df_rise['next'] - df_rise['price(㎡)'] # 다음 구간 데이터와의 차를 구한다.
df_rise.reset_index(drop=True, inplace=True)
# 나누기를 할 때 분모가 0이나 공백이면 안 된다. 구간 간격 분양가격 차이를 기준 분양가격으로 나누어 상승률을 계산한다.
df_rise['rate'] = round(df_rise['sub'] / df_rise['price(㎡)'] * 100, 2) if df_rise['price(㎡)'] is not np.nan and df_rise['price(㎡)'] is not 0 else np.nan
df_rise['size'] = s + " / " + ne # 어느 기준 구간과 다음 구간의 상승률인지 표시한다.
# 합계를 구하기 위해 개수를 구한다.
df_tmp = df_rise[["city", "size", "rate"]]
df_avg = df_tmp.groupby(["city", "size"]).size().reset_index(name="counts")
# 평균를 구하기 위해 합계를 구한다.
df_avg['sum'] = df_tmp['rate'].agg('sum')
# 평균을 구한다.
df_avg['avg'] = round(df_avg['sum'] / df_avg['counts'], 2)
if float(df_avg['avg']) > 0.00:
df_avg['updown'] = "증가"
else:
df_avg['updown'] = "감소"
# dataframe 하단에 계속 추가한다.
new_df = pd.concat([new_df, df_avg]).reset_index(drop=True)
# 불필요한 컬럼을 삭제한다.
new_df.drop(columns = 'counts', inplace = True)
new_df.drop(columns = 'sum', inplace = True)
new_df.reset_index(drop=True)
# 컬럼 순서가 바뀔 수 있기 때문에 다시 지정한다.
cols = ['city', 'size', 'avg', 'updown']
new_df = new_df[cols]
return new_df
# +
# 각 지역별 규모구분과 다음 규모구분의 상승률 차이를 계산한다.
re_df = func_rate(df, ['강원', '경기', '경남', '경북', '광주', '대구', '대전', '부산', '서울', '세종', '울산', '인천', '전남', '전북', '제주', '충남', '충북'])
re_df
# city - 지역, size - 기준 구간 / 다음 구간, avg - 구간 상승률, updown - 다음 구간에서 증가했는가 감소했는가
# -
# ## 결론
#
# 가설과 무관하게 일정한 흐름이 없이 전용면적이 하락하거나 상승했을 때 일정하게 분양가격이 증감하지 않는다. 상승률에 양수(%)와 음수(%)가 일정한 패턴으로 있지 않고 불규칙적으로 있어서 전용면적이 늘어날수록 분양가격이 상승하거나 하락한다고 말 할 수 없다.
# ## 다른 방법으로 전처리
#
# #### pivot을 사용하지 않고 간단하게 원하는 표와 그래프를 만들어 보여줄 수 있도록 하였습니다.
df = pd.read_csv("apt_2018_7.csv", encoding='euc-kr')
df.head()
# +
df.rename(columns = {"지역명":"city","규모구분":"size","연도":"year","월":"month","분양가격(㎡)":"rate(㎡)"}, inplace = True)
df.replace(('전용면적 102㎡초과','전용면적 85㎡초과 102㎡이하','전용면적 60㎡초과 85㎡이하','전용면적 60㎡이하','전체'),\
('102㎡ ~','85㎡ ~ 102㎡', '60㎡ ~ 85㎡','~ 60㎡','avg'), inplace = True)
df["rate(㎡)"] = df["rate(㎡)"].ffill().apply(lambda x: x.replace(',','')) # nan인 값들을 다음 데이터 값으로 채워줌, 데이터 내 쉼표 제거
#df["rate(㎡)"].replace(' ', np.nan, inplace = True) # 공백, 즉 가격데이터가 없는 값들을 nan으로 바꿔줌
df["rate(㎡)"].replace(' ', 0, inplace = True)
# 공백, 즉 가격데이터가 없는 값들을 0으로 바꿔줌.
# 일단 공백 행이 있어야 하는데 int로 형변환을 위해 0으로 바꿔줌. 나중에 다시 공백으로 바꿔야 한다.
#df.dropna(inplace = True) # 가격이 nan인 행을 모두 드랍 # 우선 행의 개수를 맞춰야 하기 때문에 나중에 필요하면 실행한다.
df['rate(㎡)'] = df['rate(㎡)'].astype('int') # str이었던 가격을 int로 바꿔줌
# +
import matplotlib as mpl # 그래프를 그리는 모듈
import matplotlib.pyplot as plt # 그래프를 그리는 모듈
from matplotlib import rc, font_manager # 한글 깨짐 방지하기 위해 필요
# 마지막 실행 결과만 출력되지 않고 중간 실행 결과도 모두 출력하기
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
# 표가 중간에 짤리지 않고 모두 나오도록. 스크롤 생김
pd.set_option('display.large_repr', 'truncate')
pd.set_option('display.max_columns', 0)
pd.set_option('max_colwidth', 800)
# -
# ## 세로로 나열된 표를 보기 쉽도록 구성
# +
df_ym = df[["year", "month"]] # 표의 가로 축(columns)에 년도와 월이 나오도록 년도, 월 데이터를 추출한다.
df_ym = df_ym.drop_duplicates() # 중복제거
df_year = list(df_ym["year"]) # year의 data를 뽑는다.
df_month = list(df_ym["month"]) # month의 data를 뽑니다.
# https://datascienceschool.net/view-notebook/a49bde24674a46699639c1fa9bb7e213/
df_cs = df[["city", "size"]] # 표의 세로 축(index)에 지역과 규모구분이 나오도록 지역, 규모구분 데이트를 추출한다.
df_cs = df_cs.drop_duplicates() # 중복제거
df_city = list(df_cs["city"]) # city의 data를 뽑는다.
df_size = list(df_cs["size"]) # size의 data를 뽑는다.
# 위에서 뽑은 데이터로 표의 인덱스, 컬럼을 구성한다.
df_all = pd.DataFrame(index = [df_city, df_size], columns = [df_year, df_month])
df_all.columns.names = ["year", "month"] # columns에 이름을 붙인다.
df_all.index.names = ["city", "size"] # index에 이름을 붙인다.
n = int(len(df.index) / len(df_all.index)) # 반복해야 하는 열의 수를 구한다.
# 데이터를 첫번째 열 부터 마지막 열 까지 열 단위로 넣는다.
for i in range(n):
df_all[df_all.columns[i]] = list(df["rate(㎡)"][len(df_all.index)*i:len(df_all.index)*(i+1)])
# 분양가격 column에서 공백, 즉 가격데이터가 없는 값들을 공백으로 바꿔준다.
df_all.replace(0, "", inplace = True)
#df_all.dropna(inplace = True) # 공백이 포함된 행이 없어지므로 실행하지 않음
# 새로 구성한 표를 보여준다.
df_all
# -
# pivot을 이용하면 바로 가능함을 알게 되었음.
df_pt = df.pivot_table('rate(㎡)',['city','size'],['year','month'])
df_pt
# +
# 참고 - stack(): 열 인덱스 -> 행 인덱스로 변환, unstack(): 행 인덱스 -> 열 인덱스로 변환
# df_tmp.stack("year") # 열 인덱스를 행 인덱스로 변환 가능
# df_tmp.stack("month") # 열 인덱스를 행 인덱스로 변환 가능
# df_tmp.unstack("year") # error. 이미 행 인덱스
# df_tmp.unstack("month") # error. 이미 행 인덱스
# df_tmp.stack("city") # error. 이미 열 인덱스
# df_tmp.stack("size") # error. 이미 열 인덱스
# df_tmp.unstack("city") # 행 인덱스를 열 인덱스로 변환 가능
# df_tmp.unstack("size") # 행 인덱스를 열 인덱스로 변환 가능
# -
# ## 원하는 구간을 바로 표로 보여줄 수 있는 함수
def func_df_view(df, s_city="서울", s_size="avg", e_city="제주", e_size="102㎡ ~", s_year=2015, s_month=10, e_year=2018, e_month=7, x=1, y=1):
df_idx = list(df.index)
df_clm = list(df.columns)
df_idx_s = df_idx.index((s_city, s_size))
df_idx_e = df_idx.index((e_city, e_size))
df_clm_s = df_clm.index((s_year, s_month))
df_clm_e = df_clm.index((e_year, e_month))
return df[df_idx_s:df_idx_e+1:x][df.columns[df_clm_s:df_clm_e+1:y]]
func_df_view(df_all)
# 전체 지역의 전체(avg) 규모구분의 2017년 데이터를 보고 싶다.
df_all_avg_2017 = func_df_view(df_all, s_city="서울", s_size="avg", e_city="제주", e_size="avg", s_year=2017, s_month=1, e_year=2017, e_month=12, x=5, y=1)
df_all_avg_2017
# 서울의 각 규모구분별 2017년 데이터를 보고 싶다.
df_seoul_2017 = func_df_view(df_all, s_city="서울", s_size="avg", e_city="서울", e_size="102㎡ ~", s_year=2017, s_month=1, e_year=2017, e_month=12, x=1, y=1)
df_seoul_2017
# ## pivot을 이용해서 보여주는 방법과 비교
# +
# 서울의 전체 규모구분의 2017년 데이터를 pivot을 이용해서 보여줌
df_so_2017 = df[df['city'] == '서울']
df_so_2017 = df_so_2017[df_so_2017['year'] == 2017]
df_so_2017.reset_index(drop=True, inplace=True)
df_so_2017.pivot_table('rate(㎡)',['city','size'],['year','month'])
# pivot을 이용하면 자동적으로 재정렬을 하는데 문자열의 경우도 자동적으로 정렬하기 때문에 순서가 오히려 이상하게 될 수 있다.
# 지역의 경우 가나다 순으로 강원부터 보여주고 규모구분의 경우 순서가 이상하게 되었다.
# +
# 표의 모양은 같으나 index, columns을 출력하면 다르다는 것을 알 수 있음.
# 표를 그려서 한 방법의 index, columns
df_seoul_2017.index
df_seoul_2017.columns
# 초기 데이터에서 rate(㎡)의 값을 제외한 값들이 인덱스, 컬럼으로 되었음.
# +
# pivot으로 한 방법의 index, columns
df_so_2017.index
df_so_2017.columns
# 구조가 초기 데이터와 같음. stop은 값의 개수
# -
# ## 간단하게 그래프로 그리기
# +
# 그래프 설정
SMALL_SIZE = 12
MEDIUM_SIZE = 14
BIGGER_SIZE = 16
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=SMALL_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
# 한글 설정
#font_name = font_manager.FontProperties(fname="c:/Windows/Fonts/malgun.ttf").get_name()
#rc('font', family=font_name)
# -
def func_draw_df(df):
gf_x = list(df.columns.levels[1]) # 그래프의 가로줄에 넣을 컬럼을 넣는다.
#print(gf_x)
# 행의 개수에 따라서 넣는 변수 개수가 다르기 때문에 각 개수 영역별로 함수를 호출한다.
if len(df) == 1:
gf = plt.plot(gf_x, df[0:1:].values[0], marker="o")
elif len(df) == 2:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], marker="o")
elif len(df) == 3:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], marker="o")
elif len(df) == 4:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0], marker="o")
elif len(df) == 5:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], marker="o")
elif len(df) == 6:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], marker="o")
elif len(df) == 7:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], marker="o")
elif len(df) == 8:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0], marker="o")
elif len(df) == 9:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], marker="o")
elif len(df) == 10:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], marker="o")
elif len(df) == 11:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0], marker="o")
elif len(df) == 12:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], marker="o")
elif len(df) == 13:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], gf_x, df[12:13:].values[0], marker="o")
elif len(df) == 14:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], gf_x, df[12:13:].values[0], gf_x, df[13:14:].values[0], marker="o")
elif len(df) == 15:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], gf_x, df[12:13:].values[0], gf_x, df[13:14:].values[0],\
gf_x, df[14:15:].values[0], marker="o")
elif len(df) == 16:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], gf_x, df[12:13:].values[0], gf_x, df[13:14:].values[0],\
gf_x, df[14:15:].values[0], gf_x, df[15:16:].values[0], marker="o")
else:
gf = plt.plot(gf_x, df[0:1:].values[0], gf_x, df[1:2:].values[0], gf_x, df[2:3:].values[0], gf_x, df[3:4:].values[0],\
gf_x, df[4:5:].values[0], gf_x, df[5:6:].values[0], gf_x, df[6:7:].values[0], gf_x, df[7:8:].values[0],\
gf_x, df[8:9:].values[0], gf_x, df[9:10:].values[0], gf_x, df[10:11:].values[0],\
gf_x, df[11:12:].values[0], gf_x, df[12:13:].values[0], gf_x, df[13:14:].values[0],\
gf_x, df[14:15:].values[0], gf_x, df[15:16:].values[0], gf_x, df[16:17:].values[0], marker="o")
return gf
df_all_avg_2017 # 2017년 전체 구간에 대한 분양가격을 표로 보여준다.
# 2017년 전체 구간에 대한 분양가격을 간단하게 그래프로 보여준다.
gf_all_avg_2017 = func_draw_df(df_all_avg_2017)
|
Apartment_price_data_analysis/semi_project_team4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import xarray as xr
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
from pathlib import Path
import sklearn
import numpy as np
import torch
import torchvision
from torch import nn, optim
from torchvision import transforms, datasets
import matplotlib.colors as colors
import pandas as pd
import openpyxl
import cartopy
import cartopy.crs as ccrs
from cartopy.mpl.gridliner import LONGITUDE_FORMATTER, LATITUDE_FORMATTER
import shapely
from shapely.geometry import Point, Polygon
xr.__version__
# -
pwd
# +
#Uploading Satellite data
file = Path('../../DATA/UK_SMARTBUOY/SatS2/','satDowsS2.csv')
satDows = pd.read_csv(file)
file = Path('../../DATA/UK_SMARTBUOY/SatS2/','satLivBayS2.csv')
satLivS2 = pd.read_csv(file)
file = Path('../../DATA/UK_SMARTBUOY/SatS2/','satThamesS2.csv')
satThamesS2 = pd.read_csv(file)
file = Path('../../DATA/UK_SMARTBUOY/SatS2/','satWGabS2.csv')
satWGabS2 = pd.read_csv(file)
# +
# # Uploading initu of WestGab then making into a complete one together.
# file3 = Path('../../DATA/UK_SMARTBUOY/','In-situ/WESTGAB_20160510.csv') # first = path to notebook, 2nd = to file
# insituWGab16 = pd.read_csv(file3)
# file3 = Path('../../DATA/UK_SMARTBUOY/','In-situ/WESTGAB2_20201023.csv') # first = path to notebook, 2nd = to file
# insituWGab20 = pd.read_csv(file3)
# #converting the datetime from type object to datetime
# insituWGab20['DateTime'] = pd.to_datetime(insituWGab20['DateTime'])
# # then converting the date string into same as other insitu
# insituWGab20['DateTime'] = insituWGab20['DateTime'].dt.strftime('%Y-%m-%d %H:%M:%S')
# #both Wgab in-situ
# insituWGab = pd.concat([insituWGab16,insituWGab20])
# insituWGab
# insituWGab.to_csv(r'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/insituWGAb.csv')
# +
file2 = Path('../../DATA/UK_SMARTBUOY/','In-situ/DOWSING_20190514.csv') # first = path to notebook, 2nd = to file
insituDows = pd.read_csv(file2)
file3 = Path('../../DATA/UK_SMARTBUOY/','In-situ/TH1_20200702.csv') # first = path to notebook, 2nd = to file
insituThames = pd.read_csv(file3)
file3 = Path('../../DATA/UK_SMARTBUOY/','In-situ/LIVBAY_20200930.csv') # first = path to notebook, 2nd = to file
insituLiv = pd.read_csv(file3)
file3 = Path('../../DATA/UK_SMARTBUOY/','In-situ/insituWGAb.csv') # first = path to notebook, 2nd = to file
insituWGab = pd.read_csv(file3)
# -
# ## Getting readable Datetime format
# +
import ee
import numpy as np
import pandas as pd
import os
## Trigger the authentication flow.
ee.Authenticate()
## Initialise the library.
ee.Initialize()
# -
# # Adding Lat/Lon to Satellite data
# +
def addinglat_lon2sat(lat,lon,satDows): # takes lat,lon and the satellite dataframe as input
#lat = 53.53133
#lon = 1.053167
lat = [lat]*499
lon = [lon]*499
lat = pd.Series(lat) #making series for datafram
lat = lat.rename("LATITUDE") #naming series
lon = pd.Series(lon)
lon = lon.rename("LONGITUDE")
satDows.insert(1,"LATITUDE",lat,True) #(adds cluster at column 1)
satDows.insert(1,"LONGITUDE",lon,True) #(adds cluster at column 1)
return satDows #returns an sat df with lat/lon added in
# -
# Adding all locations to satellite data
satLivS2 = addinglat_lon2sat(53.531833,-3.367833,satLivS2)
satThamesS2 = addinglat_lon2sat(51.52650,1.029700,satThamesS2)
satWGabS2 = addinglat_lon2sat(51.954583,2.109600,satWGabS2)
satDows = addinglat_lon2sat(53.531333,1.053167,satDows)
# +
print(satLivS2.iloc[0,28] # checking date is in right column)
#satDows.iloc[0,5] # testing for the converting datetime!
date = ee.Date(int(satDows.iloc[168,28])).format().getInfo()
# making timestamp into readable date (int->format-> get info)
date
# -
# # Converting all datetime of dataframe:
def convertDTindexintodatetime(satDows):
datetime = []
for i in range(0,satDows.shape[0]):
a = satDows.iloc[i,28]
date_i = ee.Date(int(a)).format().getInfo() # making timestamp into readable date (int->format-> get info)
datetime.append(date_i)
datetime = pd.Series(datetime)
datetime = datetime.rename("TIMEDATE")
satDows.insert(1,"TIMEDATE",datetime,True) #(adds new date/time at column 3)
satDows.loc[100,'TIMEDATE'] #testing at random time
return satDows
# +
satLivS2 = convertDTindexintodatetime(satLivS2)
satDows = convertDTindexintodatetime(satDows)
satWGabS2= convertDTindexintodatetime(satWGabS2)
satThamesS2 = convertDTindexintodatetime(satThamesS2)
satLivS2
# +
### Getting the temp/salinity in-situ in separate columns.
def seperating_tempsal(insituDows):
lat = []
lon =[]
DT = []
temp = []
sal = []
for i in range(0,(insituDows.shape[0])):
if insituDows.loc[i, 'parameter'] == 'TEMP' :
temp.append(insituDows.loc[i, 'value'])
lat.append(insituDows.loc[i,'latitude'])
lon.append(insituDows.loc[i,'longitude'])
DT.append(insituDows.loc[i,'DateTime'])
sal.append(0)
if insituDows.loc[i, 'parameter'] == 'SAL':
sal.append(insituDows.loc[i, 'value'])
lat.append(insituDows.loc[i,'latitude'])
lon.append(insituDows.loc[i,'longitude'])
DT.append(insituDows.loc[i,'DateTime'])
temp.append(0)
#Converting all lists to Dataframes
temp_df = pd.DataFrame(temp ,columns=['Temperature'])
sal_df = pd.DataFrame(sal ,columns=['Salinity'])
lat_df = pd.DataFrame(lat ,columns=['Latitude'])
lon_df = pd.DataFrame(lon ,columns=['Longitude'])
dateandtime_df = pd.DataFrame(DT ,columns=['DateandTime'])
InsituDows2 = pd.concat([lat_df,lon_df,dateandtime_df,temp_df,sal_df], axis=1)
return InsituDows2
# -
def mergingzerorowstempsal(InsituDows2):
# Merging the zero rows of temp and salinity
lat = []
lon =[]
DT = []
temp = []
sal = []
for i in range(0,InsituDows2.shape[0]-1):
if InsituDows2.iloc[i,2] == InsituDows2.iloc[i+1,2] and (InsituDows2.iloc[i,3] == 0 or InsituDows2.iloc[i+1,3] == 0):
temp.append(max((InsituDows2.loc[i, 'Temperature'],InsituDows2.loc[i+1, 'Temperature'])))
lat.append(InsituDows2.loc[i,'Latitude'])
lon.append(InsituDows2.loc[i,'Longitude'])
DT.append(InsituDows2.loc[i,'DateandTime'])
sal.append(max((InsituDows2.loc[i, 'Salinity'],InsituDows2.loc[i+1, 'Salinity'])))
i= i +1;
else:
lat.append(InsituDows2.loc[i,'Latitude'])
lon.append(InsituDows2.loc[i,'Longitude'])
DT.append(InsituDows2.loc[i,'DateandTime'])
sal.append(InsituDows2.loc[i, 'Salinity'])
temp.append(InsituDows2.loc[i,'Temperature'])
#Converting all lists to Dataframes
temp_df = pd.DataFrame(temp ,columns=['Temperature'])
sal_df = pd.DataFrame(sal ,columns=['Salinity'])
lat_df = pd.DataFrame(lat ,columns=['Latitude'])
lon_df = pd.DataFrame(lon ,columns=['Longitude'])
dateandtime_df = pd.DataFrame(DT ,columns=['DateandTime'])
InsituDows2 = pd.concat([lat_df,lon_df,dateandtime_df,temp_df,sal_df], axis=1)
InsituDows2
#downsampling to remove the repeated values/ zeros
InsituDows2 = InsituDows2.iloc[::3, :]
InsituDows2 = InsituDows2.reset_index(drop=True)
return InsituDows2
# +
# insituDows = seperating_tempsal(insituDows)
# insituLiv = seperating_tempsal(insituLiv)
# insituThames = seperating_tempsal(insituThames)
# insituWGab = seperating_tempsal(insituWGab)
#merging the rows of redundant data
insituDows = mergingzerorowstempsal(insituDows)
insituLiv = mergingzerorowstempsal(insituLiv)
insituThames = mergingzerorowstempsal(insituThames)
insituWGab = mergingzerorowstempsal(insituWGab)
insituWGab
# -
# ## Plotting In-situ Temp vs Time
# +
InsituDows2
ax = plt.axes()
fig = plt.figure(figsize=(15, 8))
DateTime = MatchedInsitu['DateandTime']
Temp = MatchedInsitu['Temperature']
ax.scatter(DateTime, Temp, s=0.1)
# -
# # Matching Data:
# +
def matchingdata(satDows,InsituDows2): # taking as inputs Sat/Insitu
#taking closest time_diff in-situ matches for each reflectance point so just have one match
import datetime
margin = datetime.timedelta(hours=1) #datetime allowed hour difference
begin_time = datetime.datetime.now()
#Make empty lists which will apped match values to:
temp = []
sal = []
DT =[]
lat = []
lon = []
SatMatched = satDows.columns.values # Rrs column titles
for i in range(0,satDows.shape[0]): #iterate throough rows of Satellite
time_diff_list = []
n_matched = []
#print(i)
if InsituDows2.equals(insituWGab): #thames data had milisecond sin middle
for n in range(163933,InsituDows2.shape[0]-1): # rows of in-situ non-zero start (longer timeseries)
# this is where matching...
#insiturow = TempSal.iloc[n,:]
#print(n)
#converting string to datetime
day = (satDows.iloc[i,1])
datesat = datetime.datetime.strptime(day, '%Y-%m-%dT%H:%M:%S')
day2 = (InsituDows2.iloc[n,2])
dateinsitu = datetime.datetime.strptime(day2,'%Y-%m-%d %H:%M:%S')
#Difference intime between in-situ and Reflectance values
time_diff = abs(dateinsitu - datesat)
#If matching location and time save temp, sal etc and RRS values
if time_diff <= margin :#/
# code that inputs those matched values into dateframe df
n_matched.append(n)
time_diff_list.append(time_diff) #appending matched values to the list
else:
for n in range(0,InsituDows2.shape[0]-1): # rows of in-situ non-zero start (longer timeseries)
# this is where matching...
#insiturow = TempSal.iloc[n,:]
#print(n)
#converting string to datetime
day = (satDows.iloc[i,1])
datesat = datetime.datetime.strptime(day, '%Y-%m-%dT%H:%M:%S')
day2 = (InsituDows2.iloc[n,2])
dateinsitu = datetime.datetime.strptime(day2,'%Y-%m-%d %H:%M:%S')
#Difference intime between in-situ and Reflectance values
time_diff = abs(dateinsitu - datesat)
#If matching location and time save temp, sal etc and RRS values
if time_diff <= margin :#/
# code that inputs those matched values into dateframe df
n_matched.append(n)
time_diff_list.append(time_diff) #appending matched values to the list
time_diff_array = np.array(time_diff_list)
n_matched_array = np.array(n_matched) #making arrays of time_diff next to the row number
stacked = np.vstack((n_matched_array,time_diff_array))
transposed = np.transpose(stacked)
sortedArr = transposed[transposed[:,1].argsort()] #sorting the array based on time
#taking only the smallest 1 time differences.
top10rows = sortedArr[0:1,:]
for m in top10rows[:,0]:
temp.append(InsituDows2.iloc[m,3])
sal.append(InsituDows2.iloc[m,4])
DT.append(InsituDows2.iloc[m,2])
lon.append(InsituDows2.iloc[m,1])
lat.append(InsituDows2.iloc[m,0])
matchsat = satDows.iloc[i,:].to_numpy()
SatMatched = np.vstack((SatMatched,matchsat))
#print('Length of Temp list =', len(temp))
if i == 0:
# print(datetime.datetime.now() - begin_time)
print((datetime.datetime.now() - begin_time)*len(satDows)) #Estimating length of running code
### Satellite only run this once!!
#Converting SatMatched array to DF, putting first row as column header then resseting index.
SatMatched = pd.DataFrame(SatMatched)
SatMatched.columns = SatMatched.iloc[0]
SatMatched = SatMatched.drop(SatMatched.index[0])
SatMatched = SatMatched.reset_index(drop=True)
# INSITU: Converting all lists to Dataframes
temp_df = pd.DataFrame(temp ,columns=['Temperature'])
sal_df = pd.DataFrame(sal ,columns=['Salinity'])
lat_df = pd.DataFrame(lat ,columns=['Latitude'])
lon_df = pd.DataFrame(lon ,columns=['Longitude'])
dateandtime_df = pd.DataFrame(DT ,columns=['DateandTime'])
MatchedInsitu = pd.concat([lat_df,lon_df,dateandtime_df,temp_df,sal_df], axis=1)
MatchedInsituDows = MatchedInsitu
#Moving the Lat/lon and Time columns to begining of Satellite dataframe
first_column = SatMatched.pop('LATITUDE')
SatMatched.insert(0,'LATITUDE',first_column,allow_duplicates = False)
first_column = SatMatched.pop('LONGITUDE')
SatMatched.insert(0,'LONGITUDE',first_column,allow_duplicates = False)
first_column = SatMatched.pop('TIMEDATE')
SatMatched.insert(0,'TIMEDATE',first_column,allow_duplicates = False)
SatMatchedSal = pd.concat([sal_df,SatMatched], axis=1)
SatMatchedTemp = pd.concat([temp_df,SatMatched], axis=1)
#moving the sal/temp column from first to 3rd
first_column = SatMatchedSal.pop('Salinity')
SatMatchedSal.insert(3,'SALINITY',first_column,allow_duplicates = False)
first_column = SatMatchedTemp.pop('Temperature')
SatMatchedTemp.insert(3,'TEMPERATURE',first_column,allow_duplicates = False)
return SatMatchedTemp,SatMatchedSal
# -
#dropping unnamed:0 column
# check the column index
SatMatchedTemp.columns[4]
# +
def TempSalDATAclean(SatMatchedTemp,SatMatchedSal):
#dropping unnamed:0 column
# check the column index
SatMatchedTemp.drop(SatMatchedTemp.columns[4], axis = 1, inplace = True)
SatMatchedSal.drop(SatMatchedSal.columns[4], axis = 1, inplace = True)
# #Downsampling to every other row (removing repeated values)
# SatMatchedSal = SatMatchedSal.iloc[::2, :]
# SatMatchedSal = SatMatchedSal.reset_index(drop=True)
# #Downsampling to every other row (removing repeated values)
# SatMatchedTemp = SatMatchedTemp.iloc[::2, :]
# SatMatchedTemp = SatMatchedTemp.reset_index(drop=True)
#Dropping columns with Nans (for modelling)
SatMatchedTemp= SatMatchedTemp.dropna(axis=1)
SatMatchedSal= SatMatchedSal.dropna(axis=1)
# Now Making salinity/ temp values Nan from zero
# take out as series then replace and add back in.
first_column = SatMatchedSal.pop('SALINITY')
first_column = first_column.replace([0], np.nan)
SatMatchedSal.insert(0,'SALINITY',first_column,allow_duplicates = False)
first_column = SatMatchedTemp.pop('TEMPERATURE')
first_column = first_column.replace([0], np.nan)
SatMatchedTemp.insert(0,'TEMPERATURE',first_column,allow_duplicates = False)
# Removing the rows with Temp/Sal Nan
SatMatchedTemp = SatMatchedTemp.dropna(axis=0)
SatMatchedSal = SatMatchedSal.dropna(axis=0)
return SatMatchedTemp,SatMatchedSal
# +
import datetime
day2 = (insituWGab.iloc[(163933),2])
day2
#dateinsitu =
#datetime.datetime.strptime(day2,'%Y-%m-%d %H:%M:%S')
# +
#getting matched temp/sal from Sat/insitu for different ones.
# Can use function but insitu have miliseconds in middle of data
#S2TempThames, S2SalThames = matchingdata(satThamesS2, insituThames)
#S2TempLiv, S2SalLiv = matchingdata(satLivS2, insituLiv)
#S2TempWGab, S2SalWGab = matchingdata(satWGabS2, insituWGab)
#S2TempDows, S2SalDows = matchingdata(satDows, insituDows)
#doing cleaning of them all
#S2TempDows, S2SalDows = TempSalDATAclean(S2TempDows, S2SalDows) # thames and dows need downsmapled
#S2TempThames, S2SalThames = TempSalDATAclean(S2TempThames, S2SalThames)
#S2TempLiv, S2SalLiv = TempSalDATAclean(S2TempLiv, S2SalLiv)
#S2TempWGab, S2SalWGab = TempSalDATAclean(S2TempWGab, S2SalWGab)
# +
# insituThames.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/In-situ/insituThames.csv')
# insituWGab.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/In-situ/insituWGab.csv')
# insituLiv.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/In-situ/insituLiv.csv')
# insituDows.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/In-situ/insituDows.csv')
# Make sure keep the location data!
# +
#Saving the outputs as csv (!!)
S2TempUk = pd.concat([S2TempDows, S2TempThames, S2TempLiv, S2TempWGab])
S2SalUk = pd.concat([S2SalDows, S2SalThames, S2SalLiv, S2SalWGab])
#again dropping the Nan columns
S2SalUk = S2SalUk.dropna(axis=1)
S2TempUk = S2TempUk.dropna(axis=1)
S2TempUk = S2TempUk.reset_index(drop=True)
S2SalUk = S2SalUk.reset_index(drop=True)
S2TempUk.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/SatS2/Matched/S2TempUk.csv')
S2SalUk.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/SatS2/Matched/S2SalUk.csv')
# -
# trying to save all neatly as a list
# #satlistS2 = [S2TempDows, S2SalDows, S2TempThames, S2SalThames, S2TempLiv, S2SalLiv, S2TempWGab, S2SalWGab ]
# satlistS2 = [satDows,satLivS2,satWGabS2]
# #satDows.name
# for n in satlistS2:
# i =0
# m = satlistS2[i].astype(str)
# n.to_csv(f'C:/Users/s2113022/Documents/PhD/DATA/UK_SMARTBUOY/SatS2/Matched/{m}.csv')
# i = i+1
|
Matching Satellite UK Smart Buoy (Dowsing) (4).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial 01: Running Sumo Simulations
#
# This tutorial walks through the process of running non-RL traffic simulations in Flow. Simulations of this form act as non-autonomous baselines and depict the behavior of human dynamics on a network. Similar simulations may also be used to evaluate the performance of hand-designed controllers on a network. This tutorial focuses primarily on the former use case, while an example of the latter may be found in `exercise07_controllers.ipynb`.
#
# In this exercise, we simulate a initially perturbed single lane ring road. We witness in simulation that as time advances the initially perturbations do not dissipate, but instead propagates and expands until vehicles are forced to periodically stop and accelerate. For more information on this behavior, we refer the reader to the following article [1].
#
# ## 1. Components of a Simulation
# All simulations, both in the presence and absence of RL, require two components: a *scenario*, and an *environment*. Scenarios describe the features of the transportation network used in simulation. This includes the positions and properties of nodes and edges constituting the lanes and junctions, as well as properties of the vehicles, traffic lights, inflows, etc. in the network. Environments, on the other hand, initialize, reset, and advance simulations, and act the primary interface between the reinforcement learning algorithm and the scenario. Moreover, custom environments may be used to modify the dynamical features of an scenario.
#
# ## 2. Setting up a Scenario
# Flow contains a plethora of pre-designed scenarios used to replicate highways, intersections, and merges in both closed and open settings. All these scenarios are located in flow/scenarios. In order to recreate a ring road network, we begin by importing the scenario `LoopScenario`.
from flow.scenarios.loop import LoopScenario
# This scenario, as well as all other scenarios in Flow, is parametrized by the following arguments:
# * name
# * vehicles
# * net_params
# * initial_config
# * traffic_lights
#
# These parameters allow a single scenario to be recycled for a multitude of different network settings. For example, `LoopScenario` may be used to create ring roads of variable length with a variable number of lanes and vehicles.
#
# ### 2.1 Name
# The `name` argument is a string variable depicting the name of the scenario. This has no effect on the type of network created.
name = "ring_example"
# ### 2.2 Vehicles
# The `Vehicles` class stores state information on all vehicles in the network. This class is used to identify the dynamical behavior of a vehicle and whether it is controlled by a reinforcement learning agent. Morover, information pertaining to the observations and reward function can be collected from various get methods within this class.
#
# The initial configuration of this class describes the number of vehicles in the network at the start of every simulation, as well as the properties of these vehicles. We begin by creating an empty `Vehicles` object.
# +
from flow.core.vehicles import Vehicles
vehicles = Vehicles()
# -
# Once this object is created, vehicles may be introduced using the `add` method. This method specifies the types and quantities of vehicles at the start of a simulation rollout. For a description of the various arguements associated with the `add` method, we refer the reader to the following documentation (reference readthedocs).
#
# When adding vehicles, their dynamical behaviors may be specified either by the simulator (default), or by user-generated models. For longitudinal (acceleration) dynamics, several prominent car-following models are implemented in Flow. For this example, the acceleration behavior of all vehicles will be defined by the Intelligent Driver Model (IDM) [2].
from flow.controllers.car_following_models import IDMController
# Another controller we define is for the vehicle's routing behavior. For closed network where the route for any vehicle is repeated, the `ContinuousRouter` controller is used to perpetually reroute all vehicles to the initial set route.
from flow.controllers.routing_controllers import ContinuousRouter
# Finally, we add 22 vehicles of type "human" with the above acceleration and routing behavior into the `Vehicles` class.
vehicles.add("human",
acceleration_controller=(IDMController, {}),
routing_controller=(ContinuousRouter, {}),
num_vehicles=22)
# ### 2.3 NetParams
#
# `NetParams` are network-specific parameters used to define the shape and properties of a network. Unlike most other parameters, `NetParams` may vary drastically depending on the specific network configuration, and accordingly most of its parameters are stored in `additional_params`. In order to determine which `additional_params` variables may be needed for a specific scenario, we refer to the `ADDITIONAL_NET_PARAMS` variable located in the scenario file.
# +
from flow.scenarios.loop import ADDITIONAL_NET_PARAMS
print(ADDITIONAL_NET_PARAMS)
# -
# Importing the `ADDITIONAL_NET_PARAMS` dict from the ring road scenario, we see that the required parameters are:
#
# * **length**: length of the ring road
# * **lanes**: number of lanes
# * **speed**: speed limit for all edges
# * **resolution**: resolution of the curves on the ring. Setting this value to 1 converts the ring to a diamond.
#
#
# At times, other inputs (for example `no_internal_links`) may be needed from `NetParams` to recreate proper network features/behavior. These requirements can be founded in the scenario's documentation. For the ring road, no attributes are needed aside from the `additional_params` terms. Furthermore, for this exercise, we use the scenario's default parameters when creating the `NetParams` object.
# +
from flow.core.params import NetParams
net_params = NetParams(additional_params=ADDITIONAL_NET_PARAMS)
# -
# ### 2.4 InitialConfig
#
# `InitialConfig` specifies parameters that affect the positioning of vehicle in the network at the start of a simulation. These parameters can be used to limit the edges and number of lanes vehicles originally occupy, and provide a means of adding randomness to the starting positions of vehicles. In order to introduce a small initial disturbance to the system of vehicles in the network, we set the `perturbation` term in `InitialConfig` to 1m.
# +
from flow.core.params import InitialConfig
initial_config = InitialConfig(spacing="uniform", perturbation=1)
# -
# ### 2.5 TrafficLights
#
# `TrafficLights` are used to desribe the positions and types of traffic lights in the network. These inputs are outside the scope of this tutorial, and instead are covered in `exercise06_traffic_lights.ipynb`. For our example, we create an empty `TrafficLights` object, thereby ensuring that none are placed on any nodes.
# +
from flow.core.traffic_lights import TrafficLights
traffic_lights = TrafficLights()
# -
# ## 3. Setting up an Environment
#
# Several envionrments in Flow exist to train autonomous agents of different forms (e.g. autonomous vehicles, traffic lights) to perform a variety of different tasks. These environments are often scenario or task specific; however, some can be deployed on an ambiguous set of scenarios as well. One such environment, `AccelEnv`, may be used to train a variable number of vehicles in a fully observable network with a *static* number of vehicles.
from flow.envs.loop.loop_accel import AccelEnv
# Although we will not be training any autonomous agents in this exercise, the use of an environment allows us to view the cumulative reward simulation rollouts receive in the absence of autonomy.
#
# Envrionments in Flow are parametrized by three components:
# * `EnvParams`
# * `SumoParams`
# * `Scenario`
#
# ### 3.1 SumoParams
# `SumoParams` specifies simulation-specific variables. These variables include the length a simulation step (in seconds) and whether to render the GUI when running the experiment. For this example, we consider a simulation step length of 0.1s and activate the GUI.
# +
from flow.core.params import SumoParams
sumo_params = SumoParams(sim_step=0.1, render=True)
# -
# ### 3.2 EnvParams
#
# `EnvParams` specify environment and experiment-specific parameters that either affect the training process or the dynamics of various components within the scenario. Much like `NetParams`, the attributes associated with this parameter are mostly environment specific, and can be found in the environment's `ADDITIONAL_ENV_PARAMS` dictionary.
# +
from flow.envs.loop.loop_accel import ADDITIONAL_ENV_PARAMS
print(ADDITIONAL_ENV_PARAMS)
# -
# Importing the `ADDITIONAL_ENV_PARAMS` variable, we see that it consists of only one entry, "target_velocity", which is used when computing the reward function associated with the environment. We use this default value when generating the `EnvParams` object.
# +
from flow.core.params import EnvParams
env_params = EnvParams(additional_params=ADDITIONAL_ENV_PARAMS)
# -
# ## 4. Setting up and Running the Experiment
# Once the inputs to the scenario and environment classes are ready, we are ready to set up a `SumoExperiment` object.
from flow.core.experiment import SumoExperiment
# These objects may be used to simulate rollouts in the absence of reinforcement learning agents, as well as acquire behaviors and rewards that may be used as a baseline with which to compare the performance of the learning agent. In this case, we choose to run our experiment for one rollout consisting of 3000 steps (300 s).
#
# **Note**: When executing the below code, remeber to click on the <img style="display:inline;" src="img/play_button.png"> Play button after the GUI is rendered.
# +
# create the scenario object
scenario = LoopScenario(name="ring_example",
vehicles=vehicles,
net_params=net_params,
initial_config=initial_config,
traffic_lights=traffic_lights)
# create the environment object
env = AccelEnv(env_params, sumo_params, scenario)
# create the experiment object
exp = SumoExperiment(env, scenario)
# run the experiment for a set number of rollouts / time steps
exp.run(1, 3000)
# -
# As we can see from the above simulation, the initial perturbations in the network instabilities propogate and intensify, eventually leading to the formation of stop-and-go waves after approximately 180s.
# ## 5. Modifying the Simulation
# This tutorial has walked you through running a single lane ring road experiment in Flow. As we have mentioned before, these simulations are highly parametrizable. This allows us to try different representations of the task. For example, what happens if no initial perturbations are introduced to the system of homogenous human-driven vehicles?
#
# ```
# initial_config = InitialConfig()
# ```
#
# In addition, how does the task change in the presence of multiple lanes where vehicles can overtake one another?
#
# ```
# net_params = NetParams(
# additional_params={
# 'length': 230,
# 'lanes': 2,
# 'speed_limit': 30,
# 'resolution': 40
# }
# )
# ```
#
# Feel free to experiment with all these problems and more!
#
# ## Bibliography
# [1] Sugiyama, Yuki, et al. "Traffic jams without bottlenecks—experimental evidence for the physical mechanism of the formation of a jam." New journal of physics 10.3 (2008): 033001.
#
# [2] Treiber, Martin, <NAME>, and <NAME>. "Congested traffic states in empirical observations and microscopic simulations." Physical review E 62.2 (2000): 1805.
|
tutorials/tutorial01_sumo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="n0y62ggtoZmE"
# # Practice Exercise 1: Exploring Correlation with Python
#
# To start things off, we would need to download the libraries for NumPy, Plotlib, Pandas, Seaborn, and SciPy. These will be required to solve the following exercise.
#
# Write your code here:
# + id="p7UkiZGypUJZ" active=""
# dir()
# + [markdown] id="rjrkZgKSpV5x"
# Next up, we want to read the General Esports dataset along with loading it as we will use it for this exercise
#
# Write your code here:
# + id="_Dd4S7Jfqqey"
# + [markdown] id="__9En-RdqrCf"
# Print the description for the General Esports dataset
#
# Write your code here:
# + id="qrEu8g0WrN-R"
# + [markdown] id="QstdmNCqrOuf"
# Print a correlation for the General Esports dataset
#
# Write your code here:
# + id="UW6jfqg4rgAZ"
# + [markdown] id="pF-dm8xhrnaq"
# # Practice Exercise 2: Calculating Pearson Correlation Coefficient in Python with Numpy
#
# First, let's import the numpy module, alongside the pyplot module from Matplotlib. We'll be using Matplotlib to visualize the correlation later on.
#
# Write your code here:
# + id="E3fyXDMusJsS"
# + [markdown] id="Nh1xP0oksLiT"
# We'll use the same values from the manual example from before. Let's store that into x_simple and compute the correlation matrix.
#
# Write your code here:
# + id="3Z7Vmcj6sYSH"
# + [markdown] id="xRaDJeZwsYgq"
# The following is the output correlation matrix. Note the ones on the diagonals, indicating that the correlation coefficient of a variable with itself is one:
#
# [Output]
# + [markdown] id="lnU36k4es4uU"
# # Practice Exercise 3: Linear Regression with scikit-learn
#
# The first step for this exercise is to import the package numpy and the class LinearRegression from sklearn.linear_model. They will have all the functionalities you need to implement linear regression.
#
# Write your code here:
# + id="ejE4P_fkuVNy"
# + [markdown] id="Mm2mn65UuVVQ"
# The second step is defining data to work with. The inputs (regressors, 𝑥) and output (predictor, 𝑦) should be arrays (the instances of the class numpy.ndarray) or similar objects. This is the simplest way of providing data for regression.
#
# Write your code here:
# + id="0iZrKj1suwkm"
# + [markdown] id="io_afxokuw11"
# The next step is to create a linear regression model and fit it using the existing data.
#
# Let’s create an instance of the class LinearRegression, which will represent the regression model. This statement creates the variable model as the instance of LinearRegression.
#
# Write your code here:
# + id="YKe6XvjwwKl8"
# + [markdown] id="qaZk5iIdwKvq"
# It’s time to start using the model. First, you need to call .fit() on model.
#
# Write your code here:
# + id="smnXeLErwZsG"
# + [markdown] id="-ndvQFoCwZ-d"
# With .fit(), you calculate the optimal values of the weights 𝑏₀ and 𝑏₁, using the existing input and output (x and y) as the arguments. In other words, .fit() fits the model. It returns self, which is the variable model itself. Replace the last two statements with another (and shorter) one.
#
# Write your code here:
# + id="IZbWncvjwnub"
# + [markdown] id="Y-kaJv5OwoWI"
# For our next step, we want to get the results of the regression. Once you have your model fitted, you can get the results to check whether the model works satisfactorily and interpret it. Write a solution to obtain the coefficient of determination with .score() called on model.
#
# Write your code here:
# + id="xNjjIjV_xPF2"
# + [markdown] id="aH2v7H-IxPP_"
# Write the attributes for the model: the intercept and coefficient.
#
# Write your code here:
# + id="K48nCWx1xkbw"
# + [markdown] id="hFBgVnvixkkJ"
# Our final step is to predict the response with either existing or new data.
#
# Use .predict() to obtain thee predicted response
#
# Write your code here:
# + id="zqp4TIKZyNgc"
# + [markdown] id="kIFsJ-vfyNnG"
# Use a fitted model to calculate the outputs based on new inputs for the prediction
#
# Write your code here:
# + id="rPTA6CojylpN"
# + [markdown] id="ZFjRkXnfymP0"
# # Practice Exercise 4: Multiple Linear Reregression with scikit-learn
#
# The first and second steps will be completed in one piece of code. First, you import numpy and sklearn.linear_model.LinearRegression and provide known inputs and output
#
# Write your code here:
# + id="zuchYt9gzK_b"
# + [markdown] id="Hd1ybok3zLGv"
# The next step is to create the regression model as an instance of LinearRegression and fit it with .fit()
#
# Write your code here:
# + id="sODUi_dMzRaP"
# + [markdown] id="ocnfO8JDzRls"
# The next step is to get the results. You can obtain the properties of the model the same way as in the case of simple linear regression.
#
# Write your code here:
# + id="OK1WlZADzaWf"
# + [markdown] id="vFreYbJ5zakh"
# The final step is to predict the response, which works in a similar fashion as with in simple linear regression.
#
# Write your code here:
# + id="zV27taTfz8gF"
# + [markdown] id="zN53823qz8nq"
# You can predict the output values by multiplying each column of the input with the appropriate weight, summing the results and adding the intercept to the sum. Apply the model to new data.
#
# Write your code here:
# + id="2cFRUmn20MnG"
# + [markdown] id="1zF46b5M0jPe"
# # Practice Exercise 5: Decision Tree Clarification with Python
#
# Let's start off by loading the required libraries (Pandas, DecisionTreeClassifier, train_test_split, metrics)
#
# Write your code here:
# + id="Z15g9QL91CcJ"
# + [markdown] id="fRtnRNPS1Cvy"
# load the required General Esports dataset using pandas' read CSV function.
#
# Write your code here:
# + id="OyEsM9kL1P6u"
# + [markdown] id="Roa3wUq_1QEy"
# Next, divide given columns into two types of variables dependent(or target variable) and independent variable(or feature variables)
#
# Write your code here:
# + id="KYbxdy4A1XkU"
# + [markdown] id="cF3UqbYx1Xuy"
# To understand model performance, dividing the dataset into a training set and a test set is a good strategy.
#
# Let's split the dataset by using function train_test_split(). You need to pass 3 parameters features, target, and test_set size.
#
# Write your code here:
# + id="GqyBMzox1emr"
# + [markdown] id="pH0UP9gD1e29"
# Let's create a Decision Tree Model using Scikit-learn.
#
# Write your code here:
# + id="uIP7LuLB1jsI"
# + [markdown] id="Gce4Y9KE13SX"
# Write a piece of code to visualize the Decision Tree you just created.
#
# Write your code here:
# + id="a1_UpgN819Lj"
|
code/4 Data Analytics/Practice Exercises 4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 재귀에서 반복문으로
# +
import numpy as np
class Variable:
def __init__(self, data):
self.data = data
self.grad = None
self.creator = None
def set_creator(self, func):
self.creator = func
def backward(self):
funcs = [self.creator]
while funcs:
f = funcs.pop() # 1. Get a function
x, y = f.input, f.output # 2. Get the function's input/output
x.grad = f.backward(y.grad) # 3. Call the function's backward
if x.creator is not None:
funcs.append(x.creator)
class Function:
def __call__(self, input):
x = input.data
y = self.forward(x)
output = Variable(y)
output.set_creator(self)
self.input = input
self.output = output
return output
def forward(self, x):
raise NotImplementedError()
def backward(self, gy):
raise NotImplementedError()
class Square(Function):
def forward(self, x):
y = x ** 2
return y
def backward(self, gy):
x = self.input.data
gx = 2 * x * gy
return gx
class Exp(Function):
def forward(self, x):
y = np.exp(x)
return y
def backward(self, gy):
x = self.input.data
gx = np.exp(x) * gy
return gx
A = Square()
B = Exp()
C = Square()
x = Variable(np.array(0.5))
a = A(x)
b = B(a)
y = C(b)
# backward
y.grad = np.array(1.0)
y.backward()
print(x.grad)
# -
|
Deep Learning/backpropagation/step08.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# .. _asmens_userguide:
#
# Asmens koda Strings
# ============
# + active=""
# Introduction
# ------------
#
# The function :func:`clean_lt_asmens() <dataprep.clean.clean_lt_asmens.clean_lt_asmens>` cleans a column containing Lithuanian personal number (Asmens koda) strings, and standardizes them in a given format. The function :func:`validate_lt_asmens() <dataprep.clean.clean_lt_asmens.validate_lt_asmens>` validates either a single Asmens koda strings, a column of Asmens koda strings or a DataFrame of Asmens koda strings, returning `True` if the value is valid, and `False` otherwise.
# -
# Asmens koda strings can be converted to the following formats via the `output_format` parameter:
#
# * `compact`: only number strings without any seperators or whitespace, like "33309240064"
# * `standard`: Asmens koda strings with proper whitespace in the proper places. Note that in the case of Asmens koda, the compact format is the same as the standard one.
# * `birthdate`: split the date parts from the number and return the birth date, like "1933-09-24".
#
# Invalid parsing is handled with the `errors` parameter:
#
# * `coerce` (default): invalid parsing will be set to NaN
# * `ignore`: invalid parsing will return the input
# * `raise`: invalid parsing will raise an exception
#
# The following sections demonstrate the functionality of `clean_lt_asmens()` and `validate_lt_asmens()`.
# ### An example dataset containing Asmens koda strings
import pandas as pd
import numpy as np
df = pd.DataFrame(
{
"asmens": [
'33309240064',
'33309240164',
'7542011030',
'7552A10004',
'8019010008',
"hello",
np.nan,
"NULL",
],
"address": [
"123 Pine Ave.",
"main st",
"1234 west main heights 57033",
"apt 1 789 s maple rd manhattan",
"robie house, 789 north main street",
"1111 S Figueroa St, Los Angeles, CA 90015",
"(staples center) 1111 S Figueroa St, Los Angeles",
"hello",
]
}
)
df
# ## 1. Default `clean_lt_asmens`
#
# By default, `clean_lt_asmens` will clean asmens strings and output them in the standard format with proper separators.
from dataprep.clean import clean_lt_asmens
clean_lt_asmens(df, column = "asmens")
# ## 2. Output formats
# This section demonstrates the output parameter.
# ### `standard` (default)
clean_lt_asmens(df, column = "asmens", output_format="standard")
# ### `compact`
clean_lt_asmens(df, column = "asmens", output_format="compact")
# ### `birthdate`
clean_lt_asmens(df, column = "asmens", output_format="birthdate")
# ## 3. `inplace` parameter
#
# This deletes the given column from the returned DataFrame.
# A new column containing cleaned Asmens koda strings is added with a title in the format `"{original title}_clean"`.
clean_lt_asmens(df, column="asmens", inplace=True)
# ## 4. `errors` parameter
# ### `coerce` (default)
clean_lt_asmens(df, "asmens", errors="coerce")
# ### `ignore`
clean_lt_asmens(df, "asmens", errors="ignore")
# ## 4. `validate_lt_asmens()`
# `validate_lt_asmens()` returns `True` when the input is a valid Asmens koda. Otherwise it returns `False`.
#
# The input of `validate_lt_asmens()` can be a string, a Pandas DataSeries, a Dask DataSeries, a Pandas DataFrame and a dask DataFrame.
#
# When the input is a string, a Pandas DataSeries or a Dask DataSeries, user doesn't need to specify a column name to be validated.
#
# When the input is a Pandas DataFrame or a dask DataFrame, user can both specify or not specify a column name to be validated. If user specify the column name, `validate_lt_asmens()` only returns the validation result for the specified column. If user doesn't specify the column name, `validate_lt_asmens()` returns the validation result for the whole DataFrame.
from dataprep.clean import validate_lt_asmens
print(validate_lt_asmens('33309240064'))
print(validate_lt_asmens('33309240164'))
print(validate_lt_asmens('7542011030'))
print(validate_lt_asmens('7552A10004'))
print(validate_lt_asmens('8019010008'))
print(validate_lt_asmens("hello"))
print(validate_lt_asmens(np.nan))
print(validate_lt_asmens("NULL"))
# ### Series
validate_lt_asmens(df["asmens"])
# ### DataFrame + Specify Column
validate_lt_asmens(df, column="asmens")
# ### Only DataFrame
validate_lt_asmens(df)
|
docs/source/user_guide/clean/clean_lt_asmens.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # <NAME>., et al. "Symmetric Rydberg controlled-Z gates with adiabatic pulses." Physical Review A 101.6 (2020): 062309.
#
# In this simulation, we shape $\Omega1$ and let $\Omega2$, $\Delta1$ and $\Delta2$ be constants.
# %cd /home/thc/Ubuntu_data/IAMS-Rydberg-atom-quantum-computing
# +
from IPython.display import clear_output
from qutip import *
import math
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display, clear_output
from rdquantum.pulse_shape import Saffman_shape
from rdquantum.fidelity import fidelity
from rdquantum.optimizer.de import de
# + [markdown] tags=[]
# # Physical system
# +
### Hamiltonian ###
def Hamiltonian(shape_omega1, value_omega2, value_delta1, value_delta2):
rho = [] # 0, 1, p, r, d
for i in range(5):
rho.append(ket2dm(basis(5,i)))
I = qeye(5)
H_omega1 = np.zeros((5,5))
H_omega1[2][1] = 2*np.pi / 2
H_omega1[1][2] = 2*np.pi / 2
H_omega1 = Qobj(H_omega1)
# Let Omega2, Delta1 and Delta2 be constants.
H_omega2 = np.zeros((5,5))
H_omega2[3][2] = 2*np.pi / 2 * value_omega2[0]
H_omega2[2][3] = 2*np.pi / 2 * value_omega2[0]
H_omega2 = Qobj(H_omega2)
H_delta1 = np.zeros((5,5))
H_delta1[2][2] = 2*np.pi * value_delta1[0]
H_delta1 = Qobj(H_delta1)
value_delta = value_delta1[0] + value_delta2[0]
H_delta = np.zeros((5,5))
H_delta[3][3] = 2*np.pi * value_delta
H_delta = Qobj(H_delta)
B = 2*np.pi * 500 # (MHz) Strength of Rydberg states interaction
Brr = np.zeros((5,5))
Brr[3][3] = np.sqrt(B)
Brr = tensor(Qobj(Brr), Qobj(Brr))
H = [[tensor(H_omega1, I) + tensor(I, H_omega1), shape_omega1],
[tensor(H_omega2, I) + tensor(I, H_omega2), '1'],
[tensor(H_delta1, I) + tensor(I, H_delta1), '1'],
[tensor(H_delta, I) + tensor(I, H_delta), '1'],
[Brr, '1']]
return H
### Pulse shape omega1(t), omega2(t) and delta1(t) ###
def PulseShape(times, Pulses, T_gate, n_seg):
def shape_omega1(t, arg):
return Saffman_shape(t, Pulses['Omega1'],T_gate, n_seg)
value_omega2 = Pulses['Omega2']
value_delta1 = Pulses['Delta1']
value_delta2 = Pulses['Delta2']
return shape_omega1, value_omega2, value_delta1, value_delta2
### Decay term, c_ops ###
def Decay(gammap=1/0.155, gammar=1/540):
# gammap: (1/mu s) population decay rate of the Rydberg state
# gammar: (1/mu s) population decay rate of the P state
c_ops = []
I = qeye(5)
L0p = np.zeros((5,5))
L0p[0][2] = np.sqrt(1/16 * gammap)
c_ops.append(tensor(Qobj(L0p), I))
c_ops.append(tensor(I, Qobj(L0p)))
L0r = np.zeros((5,5))
L0r[0][3] = np.sqrt(1/32 * gammar)
c_ops.append(tensor(Qobj(L0r), I))
c_ops.append(tensor(I, Qobj(L0r)))
L1p = np.zeros((5,5))
L1p[1][2] = np.sqrt(1/16 * gammap)
c_ops.append(tensor(Qobj(L1p), I))
c_ops.append(tensor(I, Qobj(L1p)))
L1r = np.zeros((5,5))
L1r[1][3] = np.sqrt(1/32 * gammar)
c_ops.append(tensor(Qobj(L1r), I))
c_ops.append(tensor(I, Qobj(L1r)))
Ldp = np.zeros((5,5))
Ldp[4][2] = np.sqrt(7/8 * gammap)
c_ops.append(tensor(Qobj(Ldp), I))
c_ops.append(tensor(I, Qobj(Ldp)))
Ldr = np.zeros((5,5))
Ldr[4][3] = np.sqrt(7/16 * gammar)
c_ops.append(tensor(Qobj(Ldr), I))
c_ops.append(tensor(I, Qobj(Ldr)))
Lpr = np.zeros((5,5))
Lpr[2][3] = np.sqrt(1/2 * gammar)
c_ops.append(tensor(Qobj(Lpr), I))
c_ops.append(tensor(I, Qobj(Lpr)))
return c_ops
### Create two qubits state as density matrix, dm(control_qubit, target_qubit) ###
# def dm(control_qubit, target_qubit):
# return ket2dm( tensor(basis(5, control_qubit), basis(5, target_qubit)) )
# -
# # Gate Operation
# Gate operation
def GateOp(Pulses, rho_init, targets):
times = np.linspace(0.0, 1, 100)
T_gate = 1 # (mu s) Total gate time
n_seg = 2*len(Omega1) # Number of segments
shape_omega1, value_omega2, value_delta1, value_delta2 = PulseShape(times, Pulses, T_gate, n_seg)
H = Hamiltonian(shape_omega1, value_omega2, value_delta1, value_delta2)
c_ops = Decay(1/0.155, 1/540)
results = mesolve(H, rho_init, times, c_ops, targets, options=Options(nsteps=10000))
return results
# + [markdown] tags=[]
# # Outpout
# +
Omega1 = [1.38, 10.30, 25.54, 42.85, 82.50, 93.35]
Omega2 = [175]
Delta1 = [300]
Delta2 = [300]
Pulses = {'Omega1': Omega1, 'Omega2': Omega2, 'Delta1': Delta1, 'Delta2': Delta2}
PulsesRange = {'Omega1': [0, 100], 'Omega2': [0, 200], 'Delta1': [300, 450], 'Delta2': [-450, -300]}
Had = np.zeros((5,5))
Had[0][0] = 1
Had[0][1] = 1
Had[1][0] = 1
Had[1][1] = -1
I = qeye(5)
Had = Qobj(Had/np.sqrt(2))
ket00 = tensor(basis(5,0), basis(5,0))
ket01 = tensor(basis(5,0), basis(5,1))
ket10 = tensor(basis(5,1), basis(5,0))
ket11 = tensor(basis(5,1), basis(5,1))
# Target Bell state, rho_bell = 1/sqrt(2) * (|01> + |10>)
rho0101 = tensor(I, Had) * ket2dm(ket01) * tensor(I, Had)
rho1010 = tensor(I, Had) * ket2dm(ket10) * tensor(I, Had)
rho0110 = tensor(I, Had) * (ket10 * ket01.dag()) * tensor(I, Had)
rho_bell = [rho0101, rho1010, rho0110]
# Initial state, rhoi = |01><01|
rhoi = tensor(Had, Had) * ket2dm(ket01) * tensor(Had, Had)
bell_fidelity = fidelity(GateOp)
print(bell_fidelity.get_fidelity(Pulses, rhoi, rho_bell))
# -
# # Differentail Evolution
# + tags=[]
K = len(Pulses)
# diffevo = de(bell_fidelity, K, 0, 500)
diffevo = de(bell_fidelity, rhoi, rho_bell)
diffevo.createPopulations(Pulses, PulsesRange)
diffevo.start(itr=2, batch=10)
# + tags=[]
fig, ax1 = plt.subplots(figsize=(12,8))
ax1.plot(diffevo.data_fidelity, label="Fi")
ax1.set_xlabel("test time", fontsize=20)
ax1.set_ylabel("Fidelity", fontsize=20)
fig.legend(bbox_to_anchor=(.84, .68), fontsize=16)
# -
testnpy = np.load("out.npz")
print(diffevo.op_pulse)
# Pulse shape
T_gate = 1 # (mu s) Total gate time
n = 12 # Number of segments
dt = T_gate/n # (mu s) Duration of each segment
def Pshape(t, pulse_coe):
ith = int( (t - dt/2) // dt )
ti = dt/2 + dt*ith
ti1 = ti + dt
if t < dt/2 or t > (T_gate - dt/2):
fi = pulse_coe[0]
fi1 = pulse_coe[0]
ft = (fi + fi1)/2
else:
if ith < 5:
ith1 = ith + 1
fi = pulse_coe[ith]
fi1 = pulse_coe[ith1]
ft = ( (fi + fi1)/2 + ( (fi1-fi)/2 ) * math.erf( (5/dt) * ( t - (ti + ti1)/2 ) ) )
elif ith == 5:
ith1 = ith
fi = pulse_coe[ith]
fi1 = pulse_coe[ith1]
ft = ( (fi + fi1)/2 + ( (fi1-fi)/2 ) * math.erf( (5/dt) * ( t - (ti + ti1)/2 ) ) )
elif ith > 5:
ith1 = ith + 1
fi = pulse_coe[n-ith-1]
fi1 = pulse_coe[n-ith1-1]
ft = ( (fi + fi1)/2 + ( (fi1-fi)/2 ) * math.erf( (5/dt) * ( t - (ti + ti1)/2 ) ) )
return ft
# +
Omega1 = diffevo.op_pulse['Omega1']
Omega2 = diffevo.op_pulse['Omega2'][0]
Delta1 = diffevo.op_pulse['Delta1'][0]
times = np.linspace(0.0, 1, 100)
pulse_Omega1 = []
for t in times:
pulse_Omega1.append( Pshape(t, Omega1))
# pulse_Omega2.append( Pshape(t, Omega2))
# delta1.append( Pshape(t, Delta1))
fig, ax1 = plt.subplots(figsize=(12,8))
ax1.plot(times, pulse_Omega1, label=r'$\Omega_1$')
ax1.hlines(y=Omega2, xmin=0, xmax=1, label=r'$\Omega_2$', color='r')
ax2 = ax1.twinx()
ax2.hlines(y=Delta1, xmin=0, xmax=1, label=r'$\Delta_1$', color='g')
ax2.hlines(y=Delta2, xmin=0, xmax=1, label=r'$\Delta_2$', color='y')
ax1.set_xlabel('Time' r'$(\mu s)$', fontsize=20)
ax1.set_ylabel(r'$\Omega / 2 \pi$' '(MHz)', fontsize=20)
ax2.set_ylabel(r'$\Delta_1 / 2 \pi$' '(MHz)', fontsize=20)
plt.title("Fidelity = %.4f" %diffevo.op_fidelity, fontsize=24)
fig.legend(bbox_to_anchor=(.84, .68), fontsize=16)
# -
|
results/run_Saffman_shape-o1tgate_fixo2d1d2/examples/Saffman_shape-o1_fix-o2d1d2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Assignment 3
# Loading the libraries
import pandas as pd
import numpy as np
from surprise import KNNWithMeans,Dataset, accuracy,Reader
from surprise.model_selection import train_test_split
import warnings
warnings.filterwarnings("ignore")
# reading all the files
ratings = pd.read_csv("ratings.csv")
movies = pd.read_csv("movies.csv")
links = pd.read_csv("links.csv")
tags = pd.read_csv("tags.csv")
ratings.head()
ratings.shape
movies.head()
movies.shape
links.head()
links.shape
tags.head()
tags.shape
# ## 1. Create recommender system using ratings.csv file
#reader class to mention the rating scale
reader = Reader(rating_scale=(1,5))
data = Dataset.load_from_df(ratings[["userId","movieId","rating"]],reader)
#divide dataset in trainset and test set
[trainset,testset] = train_test_split(data,test_size=.15,shuffle=True)
recom = KNNWithMeans(k=40, sim_options={"Name":"Cosine","user_based":True})
recom.fit(data.build_full_trainset())
test_pred = recom.test(testset)
RMSE = accuracy.rmse(test_pred)
print("RMSE =",RMSE)
# ## 2. Display predicted rating for a particular userID and MovieID combinations (both taken as keyboard input)
userID = int(input("USER ID = "))
movieID = int(input("MOVIE ID = "))
print("The rating value for USER ID:",userID,"and","MOVIE ID:",movieID,"=",round((recom.predict(userID,movieID)[3]),2))
# ## 3. Recommend a user to watch top 10 movies, which has not watched yet (as per his rating predictions).Take userID as a keyboard input. Fix the threshold rating as 2.5
# +
# creating empty dictionary -> userID as key and movieID as value
movie_list = {}
userID = int(input("USER ID = "))
for movieID in movies["movieId"]:
if recom.predict(userID,movieID)[3] > 2.5:
movie_list[movieID] = recom.predict(userID,movieID)[3]
# finding 10 highest values in a Dictionary
from collections import Counter
k = Counter(movie_list)
high = k.most_common(10)
print("Top 10 movies for user",userID,"are listed below")
for i in range(10):
print(i+1,"\t",list(movies[movies["movieId"]==high[i][0]]["title"])[0])
# -
# ## 4. Display the MovieID, IMDB ID, Average User Rating (excluding predictions), genres and tag of all the movies found in Step 3 as a data frame
df = pd.merge(movies[["movieId","genres"]],tags[["movieId","tag"]],how="left",on="movieId")
df1 = pd.merge(df,links[["movieId","imdbId"]],how="left",on="movieId")
df1.head()
ls = []
for i in range(10):
ls.append(high[i][0])
df_final = df1[df1["movieId"].isin(ls)]
df_final
# finding average user rating
avg_usr_rating = {}
for i in df_final["movieId"]:
avg_usr_rating[i] = round((ratings[ratings["movieId"]==i]['rating'].mean()),2)
avg_usr_rating
# +
id_rating = [(x,y) for x,y in avg_usr_rating.items() if x in ls]
avg_rating = []
for i in range(10):
avg_rating.append(id_rating[i][1])
df_final["avg_usr_rating"] = avg_rating
# printing MovieID, IMDB ID,Average User Rating,genres and tag for all the movies in step 3
df_final
# -
|
IMDB_Recommendation_System.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Customer Segmentation
#
# We will be using E-commerce dataset of user purchases and try develop a model that allow us to do two things:
#
# 1. Classifying customers into segments.
# 2. Anticipate the purchases that will be made by a new customer, during the following year and
# this, from its first purchase by assigning them appropriate cluster/segment
#
from __future__ import division
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import datetime, nltk, warnings
import matplotlib.cm as cm
import itertools
from pathlib import Path
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples, silhouette_score
from sklearn import preprocessing, model_selection, metrics, feature_selection
from sklearn.model_selection import GridSearchCV, learning_curve
from sklearn.svm import SVC
from sklearn.metrics import confusion_matrix
from sklearn import neighbors, linear_model, svm, tree, ensemble
from wordcloud import WordCloud, STOPWORDS
from sklearn.ensemble import AdaBoostClassifier
from sklearn.decomposition import PCA
from IPython.display import display, HTML
#import plotly.plotly as py
#import plotly.graph_objs as go
#from plotly.offline import init_notebook_mode,iplot
#init_notebook_mode(connected=True)
#warnings.filterwarnings("ignore")
#plt.rcParams["patch.force_edgecolor"] = True
#plt.style.use('fivethirtyeight')
#mpl.rc('patch', edgecolor = 'dimgray', linewidth=1)
# %matplotlib inline
# # ** Data Preparation **
#Reading train and test data
train = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
train.info()
#Let us have a look at the structure of data in each file
print("Train data structure -> ","Rows: ",train.shape[0],'\t',"Cols: ",train.shape[1])
print("Test data structure ->", "Rows: ",test.shape[0],'\t',"Cols: ",test.shape[1])
train.head(10).append(train.tail(10))
train.isnull().sum()
train['Gender'].unique()
train['Profession'].unique()
train['Spending_Score'].unique()
train['Var_1'].unique()
train['Segmentation'].unique()
#use of simple map function
map_Gender ={"Male" : 1 , "Female" : 2}
train['Gender'] = train['Gender'].map(map_Gender)
map_Ever_Married ={"Yes" : 0 , "No" : 1}
train['Ever_Married'] = train['Ever_Married'].map(map_Ever_Married)
map_Graduated ={"Yes" : 0 , "No" : 1}
train['Graduated'] = train['Graduated'].map(map_Graduated)
map_Spending_Score ={"Low" : 1 , "Average" : 2 , "High" : 3 }
train['Spending_Score'] = train['Spending_Score'].map(map_Spending_Score)
map_Var_1 ={"Cat_1" : 1 , "Cat_2" : 2 , "Cat_3" : 3 , "Cat_4" : 4 , "Cat_5" : 5 , "Cat_6" : 6 , "Cat_7" : 7 }
train['Var_1'] = train['Var_1'].map(map_Var_1)
map_Profession ={"Healthcare" : 1 , "Engineer" : 2 , "Lawyer" : 3 , "Entertainment" : 4 , "Artist" : 5 , "Executive" : 6 , "Doctor" : 7 , "Homemaker" : 8 , "Marketing" : 9 }
train['Profession'] = train['Profession'].map(map_Profession)
map_Segmentation ={"A" : 1 , "B" : 2 , "C" : 3 , "D" : 4}
train['Segmentation'] = train['Segmentation'].map(map_Segmentation)
train.head(10).append(train.tail(10))
display(train.describe())
train.isnull().sum()
train.loc[(train['Family_Size'].isnull() == True), 'Family_Size'] = train['Family_Size'].mean()
train.loc[(train['Work_Experience'].isnull() == True), 'Work_Experience'] = train['Work_Experience'].mean()
train.loc[(train['Ever_Married'].isnull() == True), 'Ever_Married'] = train['Ever_Married'].mean()
train.loc[(train['Var_1'].isnull() == True), 'Var_1'] = train['Var_1'].mean()
train.loc[(train['Graduated'].isnull() == True), 'Graduated'] = train['Graduated'].mean()
train.loc[(train['Profession'].isnull() == True), 'Profession'] = train['Profession'].mean()
train.drop('ID', axis = 1 , inplace = True)
# +
plt.figure(figsize=(10,50))
for i in range(len(train.columns)):
plt.subplot(10, 1, i+1)
sns.distplot(train[train.columns[i]], kde_kws={"color": "b", "lw": 3, "label": "KDE"}, hist_kws={"color": "g"})
plt.title(train.columns[i])
plt.tight_layout()
# -
# Check product correlation
plt.subplots(figsize=(15,5))
sns.heatmap(train.corr(),cmap='coolwarm',annot=True)
print('Duplicate data entries: {}'.format(train.duplicated().sum()))
train.drop_duplicates(inplace = True)
# +
#x = train.values #returns a numpy array
#min_max_scaler = preprocessing.MinMaxScaler()
#x_scaled = min_max_scaler.fit_transform(x)
#train = pd.DataFrame(x_scaled)
# -
# # APPLY K MEAN
# Let's scale the data first
scaler = StandardScaler()
train_scaled = scaler.fit_transform(train)
train_scaled.shape
train_scaled
kmeans.fit(train_scaled[:,:7])
# +
score_1 = []
range_values = range(1,20)
for i in range_values:
kmeans = KMeans(n_clusters =i)
kmeans.fit(train_scaled)
score_1.append(kmeans.inertia_)
plt.plot(score_1, 'bx-')
# +
#above is optimal
# -
kmeans = KMeans(4)
kmeans.fit(train_scaled)
labels = kmeans.labels_
kmeans.cluster_centers_.shape
cluster_centers = pd.DataFrame(data = kmeans.cluster_centers_, columns = [train.columns])
cluster_centers
# In order to understand what these numbers mean, let's perform inverse transformation
cluster_centers = scaler.inverse_transform(cluster_centers)
cluster_centers = pd.DataFrame(data = cluster_centers, columns = [train.columns])
cluster_centers
y_kmeans = kmeans.fit_predict(train_scaled)
y_kmeans
# concatenate the clusters labels to our original dataframe
train_cluster = pd.concat([train, pd.DataFrame({'cluster':labels})], axis = 1)
train_cluster.head()
# Plot the histogram of various clusters
for i in train.columns:
plt.figure(figsize = (35, 5))
for j in range(4):
plt.subplot(1,4,j+1)
cluster = train_cluster[train_cluster['cluster'] == j]
cluster[i].hist(bins = 20)
plt.title('{} \nCluster {} '.format(i,j))
plt.show()
|
Cust_segmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial 6: Important Methods in Pandas
import pandas as pd
import numpy as np
s=pd.Series([1,2,3,4],
index=["a","b","c","d"])
s
s["a"]
s2=s.reindex(["b","d","a","c","e"])
s2
s3=pd.Series(["blue","yellow","purple"],
index=[0,2,4])
s3
s3.reindex(range(6),method="ffill")
df=pd.DataFrame(np.arange(9).reshape(3,3),
index=["a","c","d"],
columns=["Tim","Tom","Kate"])
df
df2=df.reindex(["d","c","b","a"])
df2
names=["Kate","Tim","Tom"]
df.reindex(columns=names)
df.loc[["c","d","a"]]
s=pd.Series(np.arange(5.),
index=["a","b","c","d","e"])
s
new_s=s.drop("b")
new_s
s.drop(["c","d"])
data=pd.DataFrame(np.arange(16).reshape(4,4),
index=["Kate","Tim",
"Tom","Alex"],
columns=list("ABCD"))
data
data.drop(["Kate","Tim"])
data.drop("A",axis=1)
data.drop("Kate",axis=0)
data
data.mean(axis="index")
data.mean(axis="columns")
# Don't forget to follow us on our youtube channel http://youtube.com/tirendazakademi and our medium page http://tirendazacademy.medium.com.
|
jupyter/pandas-tut/06-Important Methods.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_tensorflow_p36
# language: python
# name: conda_tensorflow_p36
# ---
# # Amazon SageMaker Experiment Trials for Distirbuted Training of Mask-RCNN
#
# This notebook is a step-by-step tutorial on Amazon SageMaker Experiment Trials for distributed tranining of [Mask R-CNN](https://arxiv.org/abs/1703.06870) implemented in [TensorFlow](https://www.tensorflow.org/) framework.
#
# Concretely, we will describe the steps for SagerMaker Experiment Trials for training [TensorPack Faster-RCNN/Mask-RCNN](https://github.com/tensorpack/tensorpack/tree/master/examples/FasterRCNN) and [AWS Samples Mask R-CNN](https://github.com/aws-samples/mask-rcnn-tensorflow) in [Amazon SageMaker](https://aws.amazon.com/sagemaker/) using [Amazon S3](https://aws.amazon.com/s3/) as data source.
#
# The outline of steps is as follows:
#
# 1. Stage COCO 2017 dataset in [Amazon S3](https://aws.amazon.com/s3/)
# 2. Build SageMaker training image and push it to [Amazon ECR](https://aws.amazon.com/ecr/)
# 3. Configure data input channels
# 4. Configure hyper-prarameters
# 5. Define training metrics
# 6. Define training job
# 7. Define SageMaker Experiment Trials to start the training jobs
#
# Before we get started, let us initialize two python variables ```aws_region``` and ```s3_bucket``` that we will use throughout the notebook:
aws_region = # aws-region-code e.g. us-east-1
s3_bucket = # your-s3-bucket-name
# ## Stage COCO 2017 dataset in Amazon S3
#
# We use [COCO 2017 dataset](http://cocodataset.org/#home) for training. We download COCO 2017 training and validation dataset to this notebook instance, extract the files from the dataset archives, and upload the extracted files to your Amazon [S3 bucket](https://docs.aws.amazon.com/en_pv/AmazonS3/latest/gsg/CreatingABucket.html) with the prefix ```mask-rcnn/sagemaker/input/train```. The ```prepare-s3-bucket.sh``` script executes this step.
#
# !cat ./prepare-s3-bucket.sh
# Using your *Amazon S3 bucket* as argument, run the cell below. If you have already uploaded COCO 2017 dataset to your Amazon S3 bucket *in this AWS region*, you may skip this step. The expected time to execute this step is 20 minutes.
# %%time
# !./prepare-s3-bucket.sh {s3_bucket}
# ## Build and push SageMaker training images
#
# For this step, the [IAM Role](https://docs.aws.amazon.com/IAM/latest/UserGuide/id_roles.html) attached to this notebook instance needs full access to Amazon ECR service. If you created this notebook instance using the ```./stack-sm.sh``` script in this repository, the IAM Role attached to this notebook instance is already setup with full access to ECR service.
#
# Below, we have a choice of two different implementations:
#
# 1. [TensorPack Faster-RCNN/Mask-RCNN](https://github.com/tensorpack/tensorpack/tree/master/examples/FasterRCNN) implementation supports a maximum per-GPU batch size of 1, and does not support mixed precision. It can be used with mainstream TensorFlow releases.
#
# 2. [AWS Samples Mask R-CNN](https://github.com/aws-samples/mask-rcnn-tensorflow) is an optimized implementation that supports a maximum batch size of 4 and supports mixed precision. This implementation uses custom TensorFlow ops. The required custom TensorFlow ops are available in [AWS Deep Learning Container](https://github.com/aws/deep-learning-containers/blob/master/available_images.md) images in ```tensorflow-training``` repository with image tag ```1.15.2-gpu-py36-cu100-ubuntu18.04```, or later.
#
# It is recommended that you build and push both SageMaker training images and use either image for training later.
#
# ### TensorPack Faster-RCNN/Mask-RCNN
#
# Use ```./container/build_tools/build_and_push.sh``` script to build and push the TensorPack Faster-RCNN/Mask-RCNN training image to Amazon ECR.
# !cat ./container/build_tools/build_and_push.sh
# Using your *AWS region* as argument, run the cell below.
# %%time
# ! ./container/build_tools/build_and_push.sh {aws_region}
# Set ```tensorpack_image``` below to Amazon ECR URI of the image you pushed above.
tensorpack_image = # mask-rcnn-tensorpack-sagemaker ECR URI
# ### AWS Samples Mask R-CNN
# Use ```./container-optimized/build_tools/build_and_push.sh``` script to build and push the AWS Samples Mask R-CNN training image to Amazon ECR.
# !cat ./container-optimized/build_tools/build_and_push.sh
# Using your *AWS region* as argument, run the cell below.
# %%time
# ! ./container-optimized/build_tools/build_and_push.sh {aws_region}
# Set ```aws_samples_image``` below to Amazon ECR URI of the image you pushed above.
aws_samples_image = # mask-rcnn-tensorflow-sagemaker ECR URI
# ## SageMaker Initialization
# First we upgrade SageMaker to 2.3.0 API. If your notebook is already using latest Sagemaker 2.x API, you may skip the next cell.
#
# ! pip install --upgrade pip
# ! pip install sagemaker==2.3.0
# We have staged the data and we have built and pushed the training docker image to Amazon ECR. Now we are ready to start using Amazon SageMaker.
# +
# %%time
import os
import time
import boto3
import sagemaker
from sagemaker import get_execution_role
from sagemaker.estimator import Estimator
role = get_execution_role() # provide a pre-existing role ARN as an alternative to creating a new role
print(f'SageMaker Execution Role:{role}')
client = boto3.client('sts')
account = client.get_caller_identity()['Account']
print(f'AWS account:{account}')
session = boto3.session.Session()
region = session.region_name
print(f'AWS region:{region}')
# -
# Next, we set ```training_image``` to the Amazon ECR image URI you saved in a previous step.
training_image = # set to tensorpack_image or aws_samples_image
print(f'Training image: {training_image}')
# ## Define SageMaker Data Channels
#
# Next, we define the *train* data channel using EFS file-system. To do so, we need to specify the EFS file-system id, which is shown in the output of the command below.
# !df -kh | grep 'fs-' | sed 's/\(fs-[0-9a-z]*\).*/\1/'
# Set the EFS ```file_system_id``` below to the ouput of the command shown above. In the cell below, we define the `train` data input channel.
# +
from sagemaker.inputs import FileSystemInput
# Specify EFS ile system id.
file_system_id = # 'fs-xxxxxxxx'
print(f"EFS file-system-id: {file_system_id}")
# Specify directory path for input data on the file system.
# You need to provide normalized and absolute path below.
file_system_directory_path = '/mask-rcnn/sagemaker/input/train'
print(f'EFS file-system data input path: {file_system_directory_path}')
# Specify the access mode of the mount of the directory associated with the file system.
# Directory must be mounted 'ro'(read-only).
file_system_access_mode = 'ro'
# Specify your file system type
file_system_type = 'EFS'
train = FileSystemInput(file_system_id=file_system_id,
file_system_type=file_system_type,
directory_path=file_system_directory_path,
file_system_access_mode=file_system_access_mode)
# -
# Next, we define the model output location in S3 bucket.
prefix = "mask-rcnn/sagemaker" #prefix in your bucket
s3_output_location = f's3://{s3_bucket}/{prefix}/output'
print(f'S3 model output location: {s3_output_location}')
# ## Configure Hyper-parameters
# Next, we define the hyper-parameters.
#
# Note, some hyper-parameters are different between the two implementations. The batch size per GPU in TensorPack Faster-RCNN/Mask-RCNN is fixed at 1, but is configurable in AWS Samples Mask-RCNN. The learning rate schedule is specified in units of steps in TensorPack Faster-RCNN/Mask-RCNN, but in epochs in AWS Samples Mask-RCNN.
#
# The detault learning rate schedule values shown below correspond to training for a total of 24 epochs, at 120,000 images per epoch.
#
# <table align='left'>
# <caption>TensorPack Faster-RCNN/Mask-RCNN Hyper-parameters</caption>
# <tr>
# <th style="text-align:center">Hyper-parameter</th>
# <th style="text-align:center">Description</th>
# <th style="text-align:center">Default</th>
# </tr>
# <tr>
# <td style="text-align:center">mode_fpn</td>
# <td style="text-align:left">Flag to indicate use of Feature Pyramid Network (FPN) in the Mask R-CNN model backbone</td>
# <td style="text-align:center">"True"</td>
# </tr>
# <tr>
# <td style="text-align:center">mode_mask</td>
# <td style="text-align:left">A value of "False" means Faster-RCNN model, "True" means Mask R-CNN moodel</td>
# <td style="text-align:center">"True"</td>
# </tr>
# <tr>
# <td style="text-align:center">eval_period</td>
# <td style="text-align:left">Number of epochs period for evaluation during training</td>
# <td style="text-align:center">1</td>
# </tr>
# <tr>
# <td style="text-align:center">lr_schedule</td>
# <td style="text-align:left">Learning rate schedule in training steps</td>
# <td style="text-align:center">'[240000, 320000, 360000]'</td>
# </tr>
# <tr>
# <td style="text-align:center">batch_norm</td>
# <td style="text-align:left">Batch normalization option ('FreezeBN', 'SyncBN', 'GN', 'None') </td>
# <td style="text-align:center">'FreezeBN'</td>
# </tr>
# <tr>
# <td style="text-align:center">images_per_epoch</td>
# <td style="text-align:left">Images per epoch </td>
# <td style="text-align:center">120000</td>
# </tr>
# <tr>
# <td style="text-align:center">data_train</td>
# <td style="text-align:left">Training data under data directory</td>
# <td style="text-align:center">'coco_train2017'</td>
# </tr>
# <tr>
# <td style="text-align:center">data_val</td>
# <td style="text-align:left">Validation data under data directory</td>
# <td style="text-align:center">'coco_val2017'</td>
# </tr>
# <tr>
# <td style="text-align:center">resnet_arch</td>
# <td style="text-align:left">Must be 'resnet50' or 'resnet101'</td>
# <td style="text-align:center">'resnet50'</td>
# </tr>
# <tr>
# <td style="text-align:center">backbone_weights</td>
# <td style="text-align:left">ResNet backbone weights</td>
# <td style="text-align:center">'ImageNet-R50-AlignPadding.npz'</td>
# </tr>
# <tr>
# <td style="text-align:center">load_model</td>
# <td style="text-align:left">Pre-trained model to load</td>
# <td style="text-align:center"></td>
# </tr>
# <tr>
# <td style="text-align:center">config:</td>
# <td style="text-align:left">Any hyperparamter prefixed with <b>config:</b> is set as a model config parameter</td>
# <td style="text-align:center"></td>
# </tr>
# </table>
#
#
# <table align='left'>
# <caption>AWS Samples Mask-RCNN Hyper-parameters</caption>
# <tr>
# <th style="text-align:center">Hyper-parameter</th>
# <th style="text-align:center">Description</th>
# <th style="text-align:center">Default</th>
# </tr>
# <tr>
# <td style="text-align:center">mode_fpn</td>
# <td style="text-align:left">Flag to indicate use of Feature Pyramid Network (FPN) in the Mask R-CNN model backbone</td>
# <td style="text-align:center">"True"</td>
# </tr>
# <tr>
# <td style="text-align:center">mode_mask</td>
# <td style="text-align:left">A value of "False" means Faster-RCNN model, "True" means Mask R-CNN moodel</td>
# <td style="text-align:center">"True"</td>
# </tr>
# <tr>
# <td style="text-align:center">eval_period</td>
# <td style="text-align:left">Number of epochs period for evaluation during training</td>
# <td style="text-align:center">1</td>
# </tr>
# <tr>
# <td style="text-align:center">lr_epoch_schedule</td>
# <td style="text-align:left">Learning rate schedule in epochs</td>
# <td style="text-align:center">'[(16, 0.1), (20, 0.01), (24, None)]'</td>
# </tr>
# <tr>
# <td style="text-align:center">batch_size_per_gpu</td>
# <td style="text-align:left">Batch size per gpu ( Minimum 1, Maximum 4)</td>
# <td style="text-align:center">4</td>
# </tr>
# <tr>
# <td style="text-align:center">batch_norm</td>
# <td style="text-align:left">Batch normalization option ('FreezeBN', 'SyncBN', 'GN', 'None') </td>
# <td style="text-align:center">'FreezeBN'</td>
# </tr>
# <tr>
# <td style="text-align:center">images_per_epoch</td>
# <td style="text-align:left">Images per epoch </td>
# <td style="text-align:center">120000</td>
# </tr>
# <tr>
# <td style="text-align:center">data_train</td>
# <td style="text-align:left">Training data under data directory</td>
# <td style="text-align:center">'train2017'</td>
# </tr>
# <tr>
# <td style="text-align:center">data_val</td>
# <td style="text-align:left">Validation data under data directory</td>
# <td style="text-align:center">'val2017'</td>
# </tr>
# <tr>
# <td style="text-align:center">resnet_arch</td>
# <td style="text-align:left">Must be 'resnet50' or 'resnet101'</td>
# <td style="text-align:center">'resnet50'</td>
# </tr>
# <tr>
# <td style="text-align:center">backbone_weights</td>
# <td style="text-align:left">ResNet backbone weights</td>
# <td style="text-align:center">'ImageNet-R50-AlignPadding.npz'</td>
# </tr>
# <tr>
# <td style="text-align:center">load_model</td>
# <td style="text-align:left">Pre-trained model to load</td>
# <td style="text-align:center"></td>
# </tr>
# <tr>
# <td style="text-align:center">config:</td>
# <td style="text-align:left">Any hyperparamter prefixed with <b>config:</b> is set as a model config parameter</td>
# <td style="text-align:center"></td>
# </tr>
# </table>
hyperparameters = {
"mode_fpn": "True",
"mode_mask": "True",
"eval_period": 1,
"batch_norm": "FreezeBN"
}
# ## Define Training Metrics
# Next, we define the regular expressions that SageMaker uses to extract algorithm metrics from training logs and send them to [AWS CloudWatch metrics](https://docs.aws.amazon.com/en_pv/AmazonCloudWatch/latest/monitoring/working_with_metrics.html). These algorithm metrics are visualized in SageMaker console.
metric_definitions=[
{
"Name": "fastrcnn_losses/box_loss",
"Regex": ".*fastrcnn_losses/box_loss:\\s*(\\S+).*"
},
{
"Name": "fastrcnn_losses/label_loss",
"Regex": ".*fastrcnn_losses/label_loss:\\s*(\\S+).*"
},
{
"Name": "fastrcnn_losses/label_metrics/accuracy",
"Regex": ".*fastrcnn_losses/label_metrics/accuracy:\\s*(\\S+).*"
},
{
"Name": "fastrcnn_losses/label_metrics/false_negative",
"Regex": ".*fastrcnn_losses/label_metrics/false_negative:\\s*(\\S+).*"
},
{
"Name": "fastrcnn_losses/label_metrics/fg_accuracy",
"Regex": ".*fastrcnn_losses/label_metrics/fg_accuracy:\\s*(\\S+).*"
},
{
"Name": "fastrcnn_losses/num_fg_label",
"Regex": ".*fastrcnn_losses/num_fg_label:\\s*(\\S+).*"
},
{
"Name": "maskrcnn_loss/accuracy",
"Regex": ".*maskrcnn_loss/accuracy:\\s*(\\S+).*"
},
{
"Name": "maskrcnn_loss/fg_pixel_ratio",
"Regex": ".*maskrcnn_loss/fg_pixel_ratio:\\s*(\\S+).*"
},
{
"Name": "maskrcnn_loss/maskrcnn_loss",
"Regex": ".*maskrcnn_loss/maskrcnn_loss:\\s*(\\S+).*"
},
{
"Name": "maskrcnn_loss/pos_accuracy",
"Regex": ".*maskrcnn_loss/pos_accuracy:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/IoU=0.5",
"Regex": ".*mAP\\(bbox\\)/IoU=0\\.5:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/IoU=0.5:0.95",
"Regex": ".*mAP\\(bbox\\)/IoU=0\\.5:0\\.95:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/IoU=0.75",
"Regex": ".*mAP\\(bbox\\)/IoU=0\\.75:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/large",
"Regex": ".*mAP\\(bbox\\)/large:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/medium",
"Regex": ".*mAP\\(bbox\\)/medium:\\s*(\\S+).*"
},
{
"Name": "mAP(bbox)/small",
"Regex": ".*mAP\\(bbox\\)/small:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/IoU=0.5",
"Regex": ".*mAP\\(segm\\)/IoU=0\\.5:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/IoU=0.5:0.95",
"Regex": ".*mAP\\(segm\\)/IoU=0\\.5:0\\.95:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/IoU=0.75",
"Regex": ".*mAP\\(segm\\)/IoU=0\\.75:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/large",
"Regex": ".*mAP\\(segm\\)/large:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/medium",
"Regex": ".*mAP\\(segm\\)/medium:\\s*(\\S+).*"
},
{
"Name": "mAP(segm)/small",
"Regex": ".*mAP\\(segm\\)/small:\\s*(\\S+).*"
}
]
# ## Define SageMaker Experiment
#
# To define SageMaker Experiment, we first install `sagemaker-experiments` package.
# ! pip install sagemaker-experiments==0.1.20
# Next, we import the SageMaker Experiment modules.
from smexperiments.experiment import Experiment
from smexperiments.trial import Trial
from smexperiments.trial_component import TrialComponent
from smexperiments.tracker import Tracker
import time
# Next, we define a `Tracker` for tracking input data used in the SageMaker Trials in this Experiment. Specify the S3 URL of your dataset in the `value` below and change the name of the dataset if you are using a different dataset.
sm = session.client('sagemaker')
with Tracker.create(display_name="Preprocessing", sagemaker_boto_client=sm) as tracker:
# we can log the s3 uri to the dataset used for training
tracker.log_input(name="coco-2017-dataset",
media_type="s3/uri",
value= f's3://{s3_bucket}/{prefix}/input/train' # specify S3 URL to your dataset
)
# Next, we create a SageMaker Experiment.
mrcnn_experiment = Experiment.create(
experiment_name=f"mask-rcnn-experiment-{int(time.time())}",
description="Mask R-CNN experiment",
sagemaker_boto_client=sm)
print(mrcnn_experiment)
# We run the training job in your private VPC, so we need to set the ```subnets``` and ```security_group_ids``` prior to running the cell below. You may specify multiple subnet ids in the ```subnets``` list. The subnets included in the ```sunbets``` list must be part of the output of ```./stack-sm.sh``` CloudFormation stack script used to create this notebook instance. Specify only one security group id in ```security_group_ids``` list. The security group id must be part of the output of ```./stack-sm.sh``` script.
security_group_ids = # ['sg-xxxxxxxx']
subnets = # ['subnet-xxxxxxx', 'subnet-xxxxxxx', 'subnet-xxxxxxx']
sagemaker_session = sagemaker.session.Session(boto_session=session)
# Next, we use SageMaker [Estimator](https://sagemaker.readthedocs.io/en/stable/estimators.html) API to define a SageMaker Training Job for each SageMaker Trial we need to run within the SageMaker Experiment.
#
# We recommned using 8 GPUs, so we set ```train_instance_count=1``` and ```train_instance_type='ml.p3.16xlarge'```, because there are 8 Tesla V100 GPUs per ```ml.p3.16xlarge``` instance. We recommend using 100 GB [Amazon EBS](https://aws.amazon.com/ebs/) storage volume with each training instance, so we set ```train_volume_size = 100```. We want to replicate training data to each training instance, so we set ```input_mode= 'File'```.
#
# Next, we will iterate through the Trial parameters and start two trials, one for ResNet architecture `resnet50`, and a second Trial for `resnet101`.
# +
trial_params = [ ('resnet50', 'ImageNet-R50-AlignPadding.npz'),
('resnet101', 'ImageNet-R101-AlignPadding.npz')]
for resnet_arch, backbone_weights in trial_params:
hyperparameters['resnet_arch'] = resnet_arch
hyperparameters['backbone_weights'] = backbone_weights
trial_name = f"mask-rcnn-{resnet_arch}-{int(time.time())}"
mrcnn_trial = Trial.create(
trial_name=trial_name,
experiment_name=mrcnn_experiment.experiment_name,
sagemaker_boto_client=sm,
)
# associate the proprocessing trial component with the current trial
mrcnn_trial.add_trial_component(tracker.trial_component)
print(mrcnn_trial)
mask_rcnn_estimator = Estimator(image_uri=training_image,
role=role,
instance_count=4,
instance_type='ml.p3.16xlarge',
volume_size = 100,
max_run = 400000,
input_mode= 'File',
output_path=s3_output_location,
sagemaker_session=sagemaker_session,
hyperparameters = hyperparameters,
metric_definitions = metric_definitions,
subnets=subnets,
security_group_ids=security_group_ids)
# Specify directory path for log output on the EFS file system.
# You need to provide normalized and absolute path below.
# For example, '/mask-rcnn/sagemaker/output/log'
# Log output directory must not exist
file_system_directory_path = f'/mask-rcnn/sagemaker/output/{mrcnn_trial.trial_name}'
print(f"EFS log directory:{file_system_directory_path}")
# Create the log output directory.
# EFS file-system is mounted on '$HOME/efs' mount point for this notebook.
home_dir=os.environ['HOME']
local_efs_path = os.path.join(home_dir,'efs', file_system_directory_path[1:])
print(f"Creating log directory on EFS: {local_efs_path}")
assert not os.path.isdir(local_efs_path)
# ! sudo mkdir -p -m a=rw {local_efs_path}
assert os.path.isdir(local_efs_path)
# Specify the access mode of the mount of the directory associated with the file system.
# Directory must be mounted 'rw'(read-write).
file_system_access_mode = 'rw'
log = FileSystemInput(file_system_id=file_system_id,
file_system_type=file_system_type,
directory_path=file_system_directory_path,
file_system_access_mode=file_system_access_mode)
data_channels = {'train': train, 'log': log}
mask_rcnn_estimator.fit(inputs=data_channels,
job_name=mrcnn_trial.trial_name,
logs=True,
experiment_config={"TrialName": mrcnn_trial.trial_name,
"TrialComponentDisplayName": "Training"},
wait=False)
# sleep in between starting two trials
time.sleep(2)
# -
search_expression = {
"Filters":[
{
"Name": "DisplayName",
"Operator": "Equals",
"Value": "Training",
},
{
"Name": "metrics.maskrcnn_loss/accuracy.max",
"Operator": "LessThan",
"Value": "1",
}
],
}
# +
from sagemaker.analytics import ExperimentAnalytics
trial_component_analytics = ExperimentAnalytics(
sagemaker_session=sagemaker_session,
experiment_name=mrcnn_experiment.experiment_name,
search_expression=search_expression,
sort_by="metrics.maskrcnn_loss/accuracy.max",
sort_order="Descending",
parameter_names=['resnet_arch']
)
# -
analytic_table = trial_component_analytics.dataframe()
for col in analytic_table.columns:
print(col)
bbox_map=analytic_table[['resnet_arch',
'mAP(bbox)/small - Max',
'mAP(bbox)/medium - Max',
'mAP(bbox)/large - Max']]
bbox_map
segm_map=analytic_table[['resnet_arch',
'mAP(segm)/small - Max',
'mAP(segm)/medium - Max',
'mAP(segm)/large - Max']]
segm_map
|
advanced_functionality/distributed_tensorflow_mask_rcnn/mask-rcnn-experiment-trials.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.1 64-bit
# language: python
# name: python38164bitdbd76ed984a5488496eb976b9e8b3b8e
# ---
# +
# dataset: tf_idf_part (333, 688)
# algorithms need to test: BaggingClassifier, RandomForestClassifier, AdaBoostClassifier, GradientBoostingClassifier
# generator : input_shape:688(features dims)+20(noise dims) hidden layer nodes:256 output layer nodes:128
# subsititude detector: 128 - 256 - 1
# +
from tensorflow.keras.layers import Input
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import Activation
from tensorflow.keras.layers import Maximum, Concatenate
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from VOTEClassifier import VOTEClassifier
import config
from pathlib import Path
# -
|
Classifier/.ipynb_checkpoints/GAN_Ensemble_Classifier-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.3 64-bit (''base'': conda)'
# metadata:
# interpreter:
# hash: 61a9efb557ee20b19fda2d58cb63f9a3bf86c2530fcd43d63aa6e0adea42a5e4
# name: 'Python 3.8.3 64-bit (''base'': conda)'
# ---
import pandas as pd
import numpy as np
import datetime
# %matplotlib inline
print(f"This notebook last ran at {datetime.datetime.now()}")
# ## A df
df = pd.DataFrame({"time":np.arange(0, 10, 0.1)})
df["amplitude"] = np.sin(df.time)
df.head(5)
ax = df.plot()
|
tests/fixtures/with_mknotebooks/docs/demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# [View in Colaboratory](https://colab.research.google.com/github/marksandler2/models/blob/master/research/slim/nets/mobilenet/mobilenet_example.ipynb)
# + [markdown] colab_type="toc" id="aUVxY7xOGD1G"
# >[Prerequisites (downloading tensorflow_models and checkpoints)](#scrollTo=T_cETKXHDTXu)
#
# >[Checkpoint based inference](#scrollTo=fxMe7_pkk_Vo)
#
# >[Frozen inference](#scrollTo=PlwvpK3ElBk6)
#
#
# + [markdown] colab_type="text" id="T_cETKXHDTXu"
# # Prerequisites (downloading tensorflow_models and checkpoints)
# + colab={} colab_type="code" id="zo5GyseklSVH"
# !git clone https://github.com/tensorflow/models
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="obaW6O8bz3mA" outputId="5b096d87-68dc-4475-bf49-0d4e80c4f42e"
from __future__ import print_function
from IPython import display
base_name = 'mobilenet_v2_1.0_224' #@param
url = 'https://storage.googleapis.com/mobilenet_v2/checkpoints/' + base_name + '.tgz'
print('Downloading from ', url)
# !wget {url}
print('Unpacking')
# !tar -xvf {base_name}.tgz
checkpoint = base_name + '.ckpt'
display.clear_output()
print('Successfully downloaded checkpoint from ', url,
'. It is available as', checkpoint)
# + colab={"base_uri": "https://localhost:8080/", "height": 215} colab_type="code" id="qZDfLegf3hpw" outputId="ea332b4f-8073-4913-97bd-733be77544b7"
# !wget https://upload.wikimedia.org/wikipedia/commons/f/fe/Giant_Panda_in_Beijing_Zoo_1.JPG -O panda.jpg
# + colab={"base_uri": "https://localhost:8080/", "height": 17} colab_type="code" id="g0H2RDadndug" outputId="f239ad90-64ec-49e4-b5da-fa018c7eca24"
# setup path
import sys
sys.path.append('/content/models/research/slim')
# + [markdown] colab_type="text" id="fxMe7_pkk_Vo"
# # Checkpoint based inference
# + colab={"base_uri": "https://localhost:8080/", "height": 17} colab_type="code" id="GrQemT66CxXt" outputId="d533c94d-26f2-45ff-d889-02785cfceeaf"
import tensorflow as tf
from nets.mobilenet import mobilenet_v2
tf.reset_default_graph()
# For simplicity we just decode jpeg inside tensorflow.
# But one can provide any input obviously.
file_input = tf.placeholder(tf.string, ())
image = tf.image.decode_jpeg(tf.read_file(file_input))
images = tf.expand_dims(image, 0)
images = tf.cast(images, tf.float32) / 128. - 1
images.set_shape((None, None, None, 3))
images = tf.image.resize_images(images, (224, 224))
# Note: arg_scope is optional for inference.
with tf.contrib.slim.arg_scope(mobilenet_v2.training_scope(is_training=False)):
logits, endpoints = mobilenet_v2.mobilenet(images)
# Restore using exponential moving average since it produces (1.5-2%) higher
# accuracy
ema = tf.train.ExponentialMovingAverage(0.999)
vars = ema.variables_to_restore()
saver = tf.train.Saver(vars)
# + colab={"base_uri": "https://localhost:8080/", "height": 666} colab_type="code" id="TJbLYo_FCxXy" outputId="60f490cb-baca-4146-d110-fd9f0e208b48"
from IPython import display
import pylab
from datasets import imagenet
import PIL
display.display(display.Image('panda.jpg'))
with tf.Session() as sess:
saver.restore(sess, checkpoint)
x = endpoints['Predictions'].eval(feed_dict={file_input: 'panda.jpg'})
label_map = imagenet.create_readable_names_for_imagenet_labels()
print("Top 1 prediction: ", x.argmax(),label_map[x.argmax()], x.max())
# + [markdown] colab_type="text" id="PlwvpK3ElBk6"
# # Frozen inference
# + colab={"base_uri": "https://localhost:8080/", "height": 17} colab_type="code" id="o0BIbQUUlVrf" outputId="029626e1-6b6d-4768-db76-e4a22c7cbd48"
import numpy as np
img = np.array(PIL.Image.open('panda.jpg').resize((224, 224))).astype(np.float) / 128 - 1
gd = tf.GraphDef.FromString(open(base_name + '_frozen.pb', 'rb').read())
inp, predictions = tf.import_graph_def(gd, return_elements = ['input:0', 'MobilenetV2/Predictions/Reshape_1:0'])
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="qSU2h5NRlN7V" outputId="1fbdbade-b0e8-422d-a2b2-9a6b6192ee6a"
with tf.Session(graph=inp.graph):
x = predictions.eval(feed_dict={inp: img.reshape(1, 224,224, 3)})
label_map = imagenet.create_readable_names_for_imagenet_labels()
print("Top 1 Prediction: ", x.argmax(),label_map[x.argmax()], x.max())
# + colab={} colab_type="code" id="CU8dJF8kCo6X"
|
models/mobilenet/mobilenet_example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### EJEMPLO DE CORRIDA DEL ALGORITMO: PARTICLE SWARM
# +
import sys
sys.path.append('../')
from src.models import particle_swarm as ps
# +
# Definición del grafo cerrado
df_Dummy = [[0, 1, 1],
[0, 2, 3],
[0, 3, 4],
[0, 4, 5],
[1, 2, 1],
[1, 3, 4],
[1, 4, 8],
[2, 3, 5],
[2, 4, 1],
[3, 4, 2],
]
# Definición de hiperparámetros
dict_Hiper = {'Iteraciones': 10,
'Particulas': 10,
'Alfa': .9,
'Beta': 1
}
# +
# Se instancia el objeto
PS = ps.ParticleSwarm(df_Dummy, dict_Hiper)
# Ejecución de particle swarm
PS.Ejecutar()
# Resultados del algoritmo:
print('Tiempo de ejecución: ', PS.nbr_TiempoEjec)
print('Mejor distancia encontrada: ', PS.nbr_MejorCosto)
print('MejorCamino: ', PS.lst_MejorCamino)
|
notebooks/borradores/Ejemplo_ParticleSwarm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project 2: Investigate the dataset TMDb movie data
#
# ## Table of Contents
# <ul>
# <li><a href="#intro">Introduction</a></li>
# <li><a href="#wrangling">Data Wrangling</a></li>
# <li><a href="#eda">Exploratory Data Analysis</a></li>
# <li><a href="#conclusions">Conclusions</a></li>
# </ul>
# <a id='intro'></a>
# ## Introduction
# To create this analysis I choose the dataset called 'TMDb movie data'. This data set contains information about 10,000 movies collected from The Movie Database (TMDb), including user ratings and revenue.
# The questions that I will answer on this report are the next ones:
#
# - Which genres are most popular from year to year?
# - What kinds of properties are associated with movies that have high revenues?
# <a id='wrangling'></a>
# ## Data Wrangling
#
# ### General Properties
# First of all I will load the libraries that I will use in this analysis.
# Import the libraries
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
% matplotlib inline
# Next I will load the dataset from the CSV file called 'tmdb-movies.csv'.
# +
# Read the data
df = pd.read_csv('tmdb-movies.csv')
#Show the first 5 rows
df.head()
# -
#Shape of the dataset
df.shape
# As we can see from the previous preview, this dataset contains in total 21 columns and 10866 rows.
#
# Now I will check the number of NA and datatype of each feature.
#Check the number of NA and data type of each feature
df.info()
# In this case we can see that some columns like 'homepage' and 'cast' they have missing values. So this means that I will have to impute this missing values or drop this rows.
# ### Data Cleaning
#
# First of all I will remove the columns that they are not useful for the analysis.
#Get the list of the names of the columns
df.columns
# If I check the preview that I did before I can see that there are some columns that they are not usefull for this analysis, like for example 'id', 'idmb_id' and 'homepage'. So I will drop this columns before doing the analysis.
# +
#Drop the useless columns
df.drop(['id','imdb_id','homepage','overview'], axis = 1, inplace = True)
#Check again the name of the columns
df.head(2)
# -
# Now we also can see the column 'keywords', in the first preview this column was hiden because the number of columns was too big.
#
# Another thing we can see from this dataset is that there are some columns that they contain multiple values splited by a vertical bar '|'. This means that later I will have to split this columns into multiple rows to do the analysis.
#
# Once I have removed the columns I will not use let's check again the number of NA for each column.
#Check the number of NA and datatype of each column
df.info()
# As I can see there are 3 columns that they have more than 1000 missing values, this are 'tagline', 'keywords' and 'production_companies'. Even that this columns can be really interestin to do some analysis, in this analysis they will not be needed to answer the questions that I want to answer. So insted of losing data from other columns, I will remove this 3 columns.
# +
#Drop the 3 columns with more NA
df.drop(['tagline', 'keywords', 'production_companies'], axis = 1, inplace = True)
#Check the header again
df.head(1)
# -
# Finally I will remove the rows that they have NA so I will make sure that all the rows contains values for each column.
#Check the number of columns before drop all NA
df.shape
# +
#Drop all the rows with NA
df.dropna(inplace = True)
#Check again the number of columns after the drop
df.shape
# -
# As we can see after the cleaning we have lost 134 rows and 7 columns.
#
# Finally I will check if there are some duplicated rows, so then I will remove this that are duplicated.
#Check if there are duplicated rows
sum(df.duplicated())
# As we can see there is 1 duplicated row so I will remove this one before doing the EDA.
#Drop duplicated rows
df.drop_duplicates(inplace = True)
# Before going to the EDA let's do a final check for all the columns.
#Check the number of NA and datatype of each column
df.info()
# <a id='eda'></a>
# ## Exploratory Data Analysis
#
# ### Which genres are most popular from year to year?
# To answer this question I will use the column 'popularity', 'release_year' and 'genres'. The tricky thing in this case is that the genres column contains multiple values splited by a vertical bar. This means I will have to split this column into multiples rows.
# +
#Select the columns I will use
popular_year = df[['popularity','release_year','genres']]
#Show the head of the table
popular_year.head(3)
# -
# Before continuo I also would like to explore the variable 'release_year' to know how many years and films there are per year.
# +
#Count the number of films for each year
count_year = popular_year[['popularity', 'release_year']].groupby(['release_year'], as_index = False).count()
#Rename column 'popularity' to 'n'
count_year.rename(columns={'popularity': 'n'}, inplace = True)
#Show the header
count_year.head()
# -
# Once I have a table with the number of fils for each year I will do a plot visualitzation to see better how many films there are for each year.
#Create plot with the number of fils for each year
plt.plot(count_year.release_year, count_year.n)
plt.xlabel("Year")
plt.ylabel("Number of films")
plt.title("Number of films for each year")
plt.show()
# As I can see from the previous plot, the number of films has increased exponentially during the last years.
#
# Another nice thing to see it would be to see the film with the maximum popularity each year, just to see if there is some years that the popularity went really bad or even if there is a trend in the fils in where every x years there is a film with a really high popularity. To do this I will do it kind of similar than before.
# +
#Select for each year the maximum popularity
max_popularity_year = df[['popularity', 'release_year']].groupby(['release_year'], as_index = False).max()
#Show the head
max_popularity_year.head()
# -
#Show the tail
max_popularity_year.tail()
# Now let's plot this data in a lineplot to see better what is the max popularity for each year.
#Create plot with the max popularity for each year
plt.plot(max_popularity_year.release_year, max_popularity_year.popularity)
plt.xlabel("Year")
plt.ylabel("Popularity")
plt.title("Max popularity for each year")
plt.show()
# As I can see from the previous plot, the popularity of the movies has increased really a lot specially the last 2 years in where the max popularity it is above 24, meanwhile the popularity in the previous years was lower than 15.
#
# So I know the popularity and the amount of films per year let's go to answer the main question. To do that, first I need to split the column 'genres' into multiple rows (one row for each genre in each row).
#
# To do that I used the recommendation of this [link](https://stackoverflow.com/questions/39504079/take-column-of-string-data-in-pandas-dataframe-and-split-into-separate-columns).
# +
#Split the column 'genres' into multiple columns
popular_year_split = popular_year.set_index(['popularity','release_year']).genres.str.split('|', expand=True).reset_index()
#Show the header
popular_year_split.head()
# -
# As I can see there is maximum 5 different type of genres for each film. Now I will melt all the dataframe and create a row for each genre and film. I know melt because I know quite well R and I use it with the library reshape2 to melt a dplyr dataframe.
# +
#Melt the dataframe
popular_year_split_melt = pd.melt(popular_year_split, id_vars = ['popularity','release_year'])
#Show the header
popular_year_split_melt.head()
# -
# Now I will drop the column 'variable' because it's not useful for our analysis.
# +
#Drop column 'variable'
popular_year_split_melt.drop(['variable'], axis = 1, inplace = True)
#Show the header
popular_year_split_melt.head()
# -
# Finally I will aggregate per year and genre by summing the popularity and finally I will take the max of each year.
# +
#Agregate by year and genre and sum the popularity
genre_year = popular_year_split_melt.groupby(['release_year','value']).sum().reset_index()
#Show head
genre_year.head()
# -
# Now that I have the table with the total sum of popularity for each year and genre I will choose the genre with the highest popularity for each year. To do that, I found some help in this [link](https://stackoverflow.com/questions/41815079/pandas-merge-join-two-data-frames-on-multiple-columns).
# +
#Select the highest popularity of each year
list_highest_popularity_year = genre_year.groupby(['release_year']).agg({'popularity' : 'max'}).reset_index()
#Join the list of the highest popularity of each year with the list of 'genre_year' to get the name of the genre of each year
list_highest_popularity_year = pd.merge(genre_year, list_highest_popularity_year, how = 'inner',
left_on = ['release_year','popularity'], right_on = ['release_year','popularity'])
#Show the head
list_highest_popularity_year.head()
# -
# Finally I got the table in where I can see for each year which genre was more popular for that year.
#
# Now I will pivot this table and create a column for each different genre and then plot in a bar plot for each year. To this I found some help in this [link](https://stackoverflow.com/questions/48958035/pandas-convert-some-rows-to-columns-in-python) in where it is explained how to do a pivot and also in this [link](https://pandas.pydata.org/pandas-docs/version/0.15.0/visualization.html) in where I can do a stacked bar plot.
#Stacket bar plot in where I can see the genre most popular for each year and the popularity of each genre for each year
list_highest_popularity_year.rename(columns = {'value': 'genre'})\
.pivot(index='release_year', columns='genre', values='popularity').reset_index()\
.plot(kind='bar',x='release_year', stacked=True, figsize=(10,5));
plt.xlabel("Year");
plt.ylabel("Popularity");
plt.title("Genre most popular for each year and the total sum of popularity");
plt.show();
# In the previous plot we can see clearly that the genre that is more popular almost all the years is the 'Drama'.
#
# If we want to see this more clear, I will aggragate the data and count the total for each genre.
list_highest_popularity_year[['value','popularity']].groupby(['value']).count().reset_index()\
.plot(kind='bar',x='value',y='popularity');
plt.xlabel("Genre");
plt.ylabel("Nº years");
plt.title("Nº of years that each genre is the most popular from 1960 until 2015");
plt.show();
# As I can see, the winner is the genre 'Drama' with 39 times and the next one is 'Comedy' with 9.
# ### What kinds of properties are associated with movies that have high revenues?
#
# To asnwer this question it gets more tricky so first let's see the columns and see which of them can be interesting to answer this question.
#Show the header
df.head(3)
# The first thing to take into account is that to answer this questions we can do it using numerical variables and categorical variables. For example, can be that some actors or directors they maybe have a high probavility to have a high revenue. Also can affect the genres and other factors.
#
# As we can see, there are two columns with the budget and the revenue. This is because during the last years the inflation makes the things more expensive so the columns that they end with `_adj` means that they are adjusted with the inflation. So to check the revenue I will use the adjusted columns.
#
# In this case, I will focus only with the numerical columns. This are the 'popularity', 'runtime', 'vote_count', 'release_year', 'budget_adj' and 'revenue_adj'.
# +
#Filter the original dataset with only the numerical columns
numeric_df = df[['popularity','runtime','vote_count','release_year','budget_adj','revenue_adj']].copy()
#Show the header
numeric_df.head()
# -
#Show the information of this dataset
numeric_df.info()
# As I can see the values in 'budget_adj' and 'revenue_adj' are really big so I will divide by 1 million and convert it to int.
# +
#Change the datatype of the column 'budget_adj' from float to int
numeric_df['budget_adj'] = (numeric_df['budget_adj'] / 1000000).astype(int)
#Change the datatype of the column 'revenue_adj' from float to int
numeric_df['revenue_adj'] = (numeric_df['revenue_adj'] / 1000000).astype(int)
numeric_df.info()
# -
# Now let's check again the data.
#Show the header
numeric_df.head()
# The first thing I will do is create a histogram for each column to see the distribution of each feature.
#Create a histogram for each feature
numeric_df.hist(figsize=(12,8), bins = 50);
# As I can see, in this case there is a lot of 0 in this data or at least low values. Using this data it will be dificult to see if there is a correlation between this features. So before looking for correlations, let's clean more this data.
#
# The first thing I will look is to check the number of films that they have 0 as a revenue.
#Number of rows with the value of revenue 0
numeric_df.query('revenue_adj == 0.0').shape[0]
# As excepected, the number of rows in where the revenue is 0 is really big! So almost half of the films they don't have revenue, this in reality is really unlikely. So probably is missing this data and it was just imputed with a 0.
#
# Then I will remove this lines before checking the features that they are more correlated with the revenue. And also I will remove the lines with budget 0 because it also doesn't make sense to make a film without budget.
# +
#Drop the lines with revenue 0
numeric_df.drop(numeric_df.query('revenue_adj == 0.0').index, axis = 0, inplace = True)
#Drop the lines with budget 0
numeric_df.drop(numeric_df.query('budget_adj == 0.0').index, axis = 0, inplace = True)
#Show size
numeric_df.shape
# -
# At the end I only have 3546 rows. Now let's plot again the histogram.
#Create a histogram for each feature
numeric_df.hist(figsize=(12,8), bins = 50);
# Now I will do a scatter plot for each of them.
#
# To do that I will use the library seaborn in where I will be available to create a scatter plot for all the different features and also a bar plot. To do that I found the documentation in this [link](https://seaborn.pydata.org/generated/seaborn.pairplot.html).
sns.set(style="ticks", color_codes=True);
sns.pairplot(numeric_df);
# As I can see from the previous plot, the feature `revenue_adj` doesn't have any column with a right strong correlation. Maybe the one is more correlated could be with the `vote_count`.
#
# To see better this scatterplot I will plot it individually using the library matplotlib.
#Create a scatter plot
plt.scatter(x = numeric_df.revenue_adj, y = numeric_df.vote_count);
plt.xlabel("Revenue adjusted");
plt.ylabel("Vote count");
plt.title("Scatter plot of the revenue and the vote count");
plt.show();
# Another whey to see if there are correlations is using a correlation matrix. To do that I will use the function `corr()`. To do this I found the code in this [link](https://stackoverflow.com/questions/29432629/plot-correlation-matrix-using-pandas).
#Correlation matrix of the dataframe 'numeric_df'
numeric_df.corr().style.background_gradient(cmap='coolwarm')
# <a id='conclusions'></a>
# ## Conclusions
#
# As a conclusion of the first question I can say that the genre most popular during the last years is the `Drama` followed by the `Comedy`. But the winner is clear with a big difference compared to the other gendres.
#
# For the second question, as I said before this question can be really general and big to answer because the revenue can depend in a lot of things and even I could use more external data to unser this questions but just to not make really big this project I choose only to use the numeric variables. With this variables I coudln't see a big correlations with the revenue. The highest one was 0.64 with the `vote_count` column follower by the `budget_adj` with 0.55. This doesn't mean that this are really key to determine the revenue of the film but it make sense because a film with a high budget and a lot of votes is high probability that it will have a big revenue.
#
#
# ## Submitting your Project
from subprocess import call
call(['python', '-m', 'nbconvert', 'Investigate_a_Dataset.ipynb'])
|
Investigate_a_Dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/maruvadaItis/Movie-Recommender-System/blob/master/image_classify.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="N6gYMne3WPcw" colab_type="code" outputId="c4b8a231-3f1b-4e3d-e60c-8d0215be19f1" colab={"base_uri": "https://localhost:8080/", "height": 522}
# !pip install tensorflow-gpu==2.0.0-rc0
# + id="IZYFXhFcgDFZ" colab_type="code" outputId="9cc5e66b-cbf1-4908-82d5-95e09ee458cb" colab={"base_uri": "https://localhost:8080/", "height": 33}
import tensorflow as tf
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Flatten, Dense, Dropout, BatchNormalization, Conv2D, MaxPool2D
from tensorflow.keras.optimizers import Adam
from tensorflow.keras.preprocessing import image
print(tf.__version__)
# + id="ikM_aifdgDC9" colab_type="code" colab={}
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from tqdm import tqdm
# + id="V46PtXI4gDBo" colab_type="code" outputId="82c752b1-e1e2-4f60-a37a-aca8800f8371" colab={"base_uri": "https://localhost:8080/", "height": 150}
# !git clone https://github.com/laxmimerit/Movies-Poster_Dataset.git
# + id="IBHmD4s8gC-B" colab_type="code" outputId="631f0e42-1922-48c9-aa31-2526919e7f1c" colab={"base_uri": "https://localhost:8080/", "height": 33}
data = pd.read_csv('/content/Movies-Poster_Dataset/train.csv')
data.shape
# + id="-d4bQbr7XC_y" colab_type="code" outputId="3ad11441-2374-43ac-fedb-7ad53442ef70" colab={"base_uri": "https://localhost:8080/", "height": 333}
data.head()
# + id="P5C9vMAZXC8c" colab_type="code" outputId="e42dc6e6-93ef-42a5-e789-29d8f77911c3" colab={"base_uri": "https://localhost:8080/", "height": 33}
img_width = 350
img_height = 350
X = []
for i in tqdm(range(data.shape[0])):
path = '/content/Movies-Poster_Dataset/Images/' + data['Id'][i] + '.jpg'
img = image.load_img(path, target_size=(img_width, img_height, 3))
img = image.img_to_array(img)
img = img/255.0
X.append(img)
X = np.array(X)
# + id="V1m2Y69fXC6Q" colab_type="code" outputId="eca03256-71f7-45fb-cc62-c6819806af18" colab={"base_uri": "https://localhost:8080/", "height": 33}
X.shape
# + id="eZztCZUwXC3s" colab_type="code" outputId="838c7f68-6df5-45e4-c850-533bb2d92b1d" colab={"base_uri": "https://localhost:8080/", "height": 286}
plt.imshow(X[1])
# + id="MNIJPLa3XC1O" colab_type="code" outputId="18858d5c-cdff-4355-f481-09a7c29e82da" colab={"base_uri": "https://localhost:8080/", "height": 33}
data['Genre'][1]
# + id="AD0H1LdeXCyr" colab_type="code" outputId="846d19f9-1872-4d5e-bc0a-b16fedb99aad" colab={"base_uri": "https://localhost:8080/", "height": 33}
y = data.drop(['Id', 'Genre'], axis = 1)
y = y.to_numpy()
y.shape
# + id="G_PCSAL7XCv5" colab_type="code" outputId="93ef78d1-ef1b-4592-8322-996823369e9c" colab={"base_uri": "https://localhost:8080/", "height": 33}
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state = 0, test_size = 0.15)
X_train[0].shape
# + id="WRZoCM9xXCs-" colab_type="code" colab={}
model = Sequential()
model.add(Conv2D(16, (3,3), activation='relu', input_shape = X_train[0].shape))
model.add(BatchNormalization())
model.add(MaxPool2D(2,2))
model.add(Dropout(0.3))
model.add(Conv2D(32, (3,3), activation='relu'))
model.add(BatchNormalization())
model.add(MaxPool2D(2,2))
model.add(Dropout(0.3))
model.add(Conv2D(64, (3,3), activation='relu'))
model.add(BatchNormalization())
model.add(MaxPool2D(2,2))
model.add(Dropout(0.4))
model.add(Conv2D(128, (3,3), activation='relu'))
model.add(BatchNormalization())
model.add(MaxPool2D(2,2))
model.add(Dropout(0.5))
model.add(Flatten())
model.add(Dense(128, activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.5))
model.add(Dense(128, activation='relu'))
model.add(BatchNormalization())
model.add(Dropout(0.5))
model.add(Dense(25, activation='sigmoid'))
# + id="mxjUV-HMXCqh" colab_type="code" outputId="2b703bbd-2f99-4368-aaf5-b2f2af798846" colab={"base_uri": "https://localhost:8080/", "height": 953}
model.summary()
# + id="zWvu9GZRXCn8" colab_type="code" outputId="11e08cff-e4db-472c-ec13-478aa98b7d38" colab={"base_uri": "https://localhost:8080/", "height": 321}
model.compile(optimizer='adam', loss = 'binary_crossentropy', metrics=['accuracy'])
history = model.fit(X_train, y_train, epochs=8, validation_data=(X_test, y_test))
# + id="dcjDmXJkbtZv" colab_type="code" colab={}
def plot_learningCurve(history, epoch):
# Plot training & validation accuracy values
epoch_range = range(1, epoch+1)
plt.plot(epoch_range, history.history['accuracy'])
plt.plot(epoch_range, history.history['val_accuracy'])
plt.title('Model accuracy')
plt.ylabel('Accuracy')
plt.xlabel('Epoch')
plt.legend(['Train', 'Val'], loc='upper left')
plt.show()
# Plot training & validation loss values
plt.plot(epoch_range, history.history['loss'])
plt.plot(epoch_range, history.history['val_loss'])
plt.title('Model loss')
plt.ylabel('Loss')
plt.xlabel('Epoch')
plt.legend(['Train', 'Val'], loc='upper left')
plt.show()
# + id="iv7Pr-ZibtWk" colab_type="code" outputId="30f6b663-0965-499c-a418-3b8b7be95526" colab={"base_uri": "https://localhost:8080/", "height": 573}
plot_learningCurve(history, 8)
# + id="az3kKI40btUS" colab_type="code" outputId="f4717642-6b56-4dff-9158-e7ee5eb2259e" colab={"base_uri": "https://localhost:8080/", "height": 420}
img = image.load_img('/content/housefull4.jpg', target_size=(img_width, img_height, 3))
plt.imshow(img)
img = image.img_to_array(img)
img = img/255.0
img = img.reshape(1, img_width, img_height, 3)
classes = data.columns[2:]
print(classes)
y_prob = model.predict(img)
top4 = np.argsort(y_prob[0])[:-5:-1]
for i in range(4):
print(classes[top4[i]])
# + id="kqxbSLV4btRu" colab_type="code" outputId="1b266810-97d1-47b5-8998-4b2450f0c322" colab={"base_uri": "https://localhost:8080/", "height": 134}
y_prob[0]
# + id="_RU-i8ZnbtPL" colab_type="code" colab={}
# + id="QMUSUvo8btMl" colab_type="code" colab={}
|
image_classify.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TASKS
# This notebook is for solutions to the various task assignments part of the Fundamentals of Data Analysis Module at GMIT.
#
# **The author is me, <NAME> - <EMAIL>**
# ## Task 1 Brief - Write a Python function called Counts
# This function takes a list as input and returns a dictionary of unique items in the list as keys and the number of times each item appears as values. So, with an input of ['A','A','B','C','A'], should return the output {'A': 3,'B': 1,'C': 1}.
#
# Your code should not depend on any module from the standard library or otherwise. You should research the task first and include a description with references of your algorithm in the notebook.
# ## Research and thoughts on the problem
# At face value to count the number of occurences of each value in a list will first need to loop through every item in list. As it loops through item by item check has this item already been seen, if so increment some counter by 1, if not set a count of 1 for the current item.
# In python terms:
# - Need a list as an input
# - A dict to store the items of the list (key)
# - A count of the number of occurences of that specific item (value)
# - And finally the input list will be iterated through using a for loop.
#
# The list and for loop are pretty self-explanatory but how to add items to a dictionary and check if one has already been added is the interesting part.
#creating a dict object and assigning a value to a key
#dictionaries operate as a key-pair or key-value, where when you supply a key to a dict object it
# returns the corresponding value
test_dict = {}
print(type(test_dict))
test_dict['a'] = 1
print(f"Printing the entire dict - {test_dict}")
print(f"Printing the dict's key-value - {test_dict['a']}")
# To check whether key exists already or not, dict.get() seems like a good approach.
# [dict.get() documentation](https://docs.python.org/3/library/stdtypes.html?highlight=#dict.get)
# The first argument passed to dict.get() represents the key we are trying to get, the second optional argument is what to return if the key cannot be found, if supplying no value here *None* is returned
#
# The next cell is testing this idea out in a for loop and then turning that bit of logic into a function.
#
# +
#first I need a list to test with
test_list = ['A', 'B', 'X', 'Y', 'X', 'A', 'A']
#next I will need a dictionary for storing the key-value pairs
test_dict = {}
#simple for loop to iterate through the list
for i in test_list:
print(i, end=' ')
#second arg for .get is 0, .get returns this value should the key not exist
test_dict[i] = test_dict.get(i,0) + 1
'''
Older solution, can be done in single line instead taking advantage of get return value if nothing found
if test_dict.get(i, False) == False:
test_dict[i] = 1 #add key and set value to one
else:
test_dict[i] += 1 #increment key value
'''
print() #introduce a new line between previous print and next print
print(test_dict)
# -
# ## Taking tested solution and enclosing with function
# +
def counts(input_list):
#initialise blank dict
output_dict = {}
#loop through provided list
for item in input_list:
#taking advantage of dict.get return, if item not found in dict return 0 then add 1
output_dict[item] = output_dict.get(item, 0) + 1
return output_dict #return the dictionary
# -
print(f"Provided list - {test_list}")
returned_dict = counts(test_list) #store the result from function call in variable my_dict, then print it
print(f"Count of items in list - {returned_dict}")
# +
from IPython.display import clear_output #Clearing the notebook cell https://stackoverflow.com/questions/24816237/ipython-notebook-clear-cell-output-in-code
'''
Here for a bit of fun I wanted to refamiliarise myself with taking a user input from
one of the previous modules.
'''
user_list = []
user_in = str(input("Enter some values and stop with blank input:"))
while user_in != '':
clear_output() #after every input clear the output cell
user_list.append(user_in) #after every input append it to list of user inputs
user_in = str(input("Enter again if you would like, stop with a blank input: "))
print("You have entered the following: ", user_list)
counts(user_list)
# -
# ## Alternate way of getting same count
# Instead of using dict.get to verify whether key already exists or not, it's simpler to just use list.count() to return a count of the specified item within the list. - [see list.count() in python3 datastructures documentation](https://docs.python.org/3/tutorial/datastructures.html)
#
# Interestingly the count function likewise works for tuples.
#initially did this without a set, but can make it more efficient if using a set to first convert the list to just it's unique items
#in practice this will probably not generally be an issue, but in cases of massive lists, would probably be a very efficient approach
unique_items_set = set(test_list)
print(unique_items_set)
my_dict = {}
for i in unique_items_set:
my_dict[i] = test_list.count(i)
print(my_dict)
def list_count_to_dict(input_list):
#convert list into set to get unique values of the list
input_set = set(input_list)
#initialise blank dictionary
output_dict = {}
#iterate through each item in set (e.g. each unique value from input_list)
for item in input_set:
output_dict[item] = input_list.count(item) #output_dict keys are equal to the count of that item from the list
return output_dict
#Returns the counted dict object
print(f"Provided list - {test_list}")
returned_dict = list_count_to_dict(test_list)
print(f"Count of items in list - {returned_dict}")
# +
'''To test the functions against one another, thought it would be neat to make a large list of random strings'''
import numpy as np #importing numpy for it's random package
import string #importing string to return a string containing letters of the alphabet upper and lowercase
alphabet_list = list(string.ascii_letters) #https://stackoverflow.com/questions/2823316/generate-a-random-letter-in-python
random_array = np.random.choice(alphabet_list, size=10000)
#annoyingly but maybe obviously, list_count_to_dict function can't handle numpy arrays as it relies on list.count
#https://numpy.org/doc/stable/reference/generated/numpy.ndarray.tolist.html
big_test_list = random_array.tolist()
# -
# %%timeit
counts(big_test_list)
# %%timeit
list_count_to_dict(big_test_list)
# # Summary and Conclusion of Task 1
# I found 2 different ways of getting the number of times an item appears in a list.
# The first was the more obvious solution to me, knowing that as we iterate through a list we can simply add to the dictionary and increment as we go but also accounting for when the item does not already exist in the dictionary.
#
# - First was simply to iterate through the list, checking whether the item was already present in the dictionary object, if it was not present add the item to the dictionary and set its value to 1, if it is present increment its value by 1
# - Alternative solution is to create a set out of the given list to get all of the unique values, then iterating through the set add each item to the dictionary object and set its value equal to the count of that item from the list. This solution has a quirk by changing the order the list items appear in, so if the order of items appearing in the list were to matter this would not work as a solution.
#
# In practice I would gravitate more towards the second function which uses a Set to get just the unique items in the list and then iterating through the Set assign each item as a key in the dictionary and put its value as the count of that item from the list - the advantage of this approach is you are not looping through for every item in a list, instead you loop through each unique item in the list by taking advantage of how Sets work and inbuilt list functions.
# However despite my preference, as we can see with the above %%timeit magic commands, the list_to_dict function (which relies on inbuilt dict functions) runs far quicker than it's list_count_to_dict function counterpart (which makes use of sets and list inbuilt functions).
# ***
#
# # Task 2 Brief - Write a Python function called dicerolls
# The task this time is to create a function that simulates rolling dice, it should take two parameters, the number of dice and the number of times to roll them. The function will simulate random rolls of the dice and keep track of the total number of occurences of the sum of the dice rolls.
#
# After the function has finished it returns a dictionary object holding the number of occurrences the different dice face totals occurred.
#
# `{2:19,3:50,4:82,5:112,6:135,7:174,8:133,9:114,10:75,11:70,12:36}`
# +
#With this function I want to show what kind of size of dictionary will eventually be returned by the dicerolls function
#the more dice you add, the more face totals there will be
def exploring_dicerolls(n_dice, n_rolls):
print(f"Number of dice selected {n_dice} to roll {n_rolls} times")
print(f"Minimum face total = {n_dice}")
print(f"Maximum face total = {n_dice*6}")
#try different numbers of dice to show min and max face totals
exploring_dicerolls(2,1000)
exploring_dicerolls(4,10)
# -
# ## Research and attempts
# ***
# Exploring the task in earnest now, I can see that we will need to use a library to produce random numbers, unfortunately given the task brief I can only make use of the Standard Python Library, which in this case rules out numpy.random.
#
# Handily though the Standard Python Library does have a package that should do exactly what is needed for the dice rolls https://docs.python.org/3/library/random.html
#
# Specifically the module random.randint is relevant here as I only want to return an integer value and want to specify 2 numbers as the limits.
#
# Initially I thought of a shortcut, where instead of doing individual dice rolls I could instead just get a random number between the min and max of the face totals of the dice rolled, however in practice I saw the issue with this pretty quickly and have imported matplotlib below to illustrate.
# +
import random
import matplotlib.pyplot as plt
n_dice = 2
n_rolls = 100000
my_list = []
for i in range(n_rolls):
my_list.append(random.randint(n_dice, n_dice*6))
plt.hist(my_list);
# -
# The above histogram plot was very surprising, I expected to see a uniform (practically flat) distribution but instead see a peak around 12.
#
# After a bit of playing around with the histogram plot I realised it was down to the number of bins used, as you can see above the last bar around 12 is about twice the height of all the other bars so the bar at 12 is actually covering 11 and 12, see corrected histogram plot below.
# want the number of bins to be 1 greater than the max minus the min
# as we want our bins to be inclusive of every point on the range.
num_bins = ((n_dice*6) - n_dice) + 1
plt.hist(my_list, bins=num_bins);
# The issue with the above is that it is not representative of what we would expect to see when rolling dice, when rolling dice (and as illustrated with example Ian provided in the Assignment) we should see a normal distribution, where values to the min and max of the range appear less frequently than those in the middle.
#
# If we rolled two dice a number of times, values like 2 and 12 occur less frequently than more central values like and the reason for this is very simple. You can only get 2 and 12 by rolling 1, 1 and 6, 6 respectively, but for other values like say 5, can instead be made up by a number of potential dice rolls (5 could be rolled with a combination of a 1 and 4, 2 and 3 and those combinations in reverse too as the order they occured could change).
#
# So for 2 and 12 there is only 1 scenario where we can get either face total, but for 5 we have 4 possible scenarios, therefore 5 is more likely to be seen more frequently.
#
# What this means for the function is we need to do independent dice rolls, e.g. a random number between 1 and 6 2 times as opposed to a random number between 2 and 12.
#keeping same structure as before
n_dice = 2
n_rolls = 100000
my_list = []
#but changing how the for loop works
for i in range(n_rolls):
face_total = 0
for j in range(n_dice):
face_total += random.randint(1,6)
my_list.append(face_total)
plt.hist(my_list, bins=num_bins);
# The above histogram plot looks much more like what I initially expected to see for the dice rolls.
my_dict = list_count_to_dict(my_list) #using the previous function from Task 1 to count the list
print(my_dict)
# ***
# ## Function - diceRolls
# ***
# From the last few cells I think I now have a pretty good way of getting the face totals and their count into a dictionary, so now to convert that into a function that takes inputs
def diceRolls(n_dice, n_rolls):
face_total_list = []
#loop by number of rolls
for i in range(n_rolls):
face_total = 0 #set face_total to 0 on every new roll
for j in range(n_dice): #for every dice to be rolled n_dice
face_total += random.randint(1,6) #pick a random number from 1 to 6 and add it to face_total
face_total_list.append(face_total) #after finishing loop to tally face_total, continue roll loop
#finally return a dictionary object in the format {face total : number of occurence} using solution from first task
return counts(face_total_list)
print(diceRolls(1,1000))
print(diceRolls(100,1))
print(diceRolls(10, 10000))
# ## Task 2 Summary and Conclusion
#
# For generating the above dice rolls the only packages imported were python's inbuilt random package for generating random numbers and matplotlib for showing the distribution of dice rolls.
#
# To simulate the dice rolls I created a function that takes two input arguments, n_dice for the number of dice to use and n_rolls for the number of rolls, esentially the amount of dice to throw per roll and the number of rolls total.
#
# Within the function it loops through the number of rolls and per roll it has an inner loop for each of the dice thrown, the for loops simulate the dice rolls to be performed (using random.randint(1,6)) and the outcome of each set of dice rolls is kept track of in face_total_list variable.
#
# As the face_total_list variable contains a list of the sum of all dice rolls, we can pass it as an argument to the list_to_dict function from Task 1, which will return a dictionary object counting the amount of times each sum of dice roll - which the above function diceRolls returns.
# ***
# # Task 3
# ## Distribution of coin flips
#
# The third task is to simulate coin flips, specifically it is to simulate the number of heads occurring after 100 coin flips and then simulate that 1000 times, visualising the resulting list/array of 1000 numbers (this assumes that the coin is fair, so either heads or tails is equally likely).
#
# First I will set up a random number generator to provide random values.
import numpy as np
rng = np.random.default_rng() #using a default_rng object instead of numpy.random functions directly https://numpy.org/doc/stable/reference/random/generator.html
print("quick test of random number generator -", rng.integers(10))
# ## Brief bit of theory around Binomial Distributions
#
# [Wikipedia Entry on Binomial Distribution](https://en.wikipedia.org/wiki/Binomial_distribution)
#
# [Statistics How To Link](https://www.statisticshowto.com/probability-and-statistics/binomial-theorem/binomial-distribution-formula/)
#
# A binomial distribution in simple terms is a distribution that shows the amount of times some event occurs when there are two possible outcomes and given it has a fixed probability of occurring and all occurrences are independent (an example of this for coin flip being yes/no for heads over 100 coin flips).
#
# I've skipped ahead a bit and produced a binomial distribution which can be seen in the below image, here the y axis shows the probability for each of the bins, the bins are along the x-axis and this represents the number of heads from coin flips (the bin size in this case is in steps of 5 starting from 20 ending at 80), and in this case the probability of getting between 50 and 55 is around 0.35.
#
# 
#
#
# ## Binomial Distribution function in numpy package
#
# From the numpy.random documentation the binomial distribution function takes 3 arguments, n for number of trials, p for probability and size for the size of the array to return.
#
# https://numpy.org/doc/stable/reference/random/generated/numpy.random.Generator.binomial.html#numpy.random.Generator.binomial
#
# From the task definition from Ian, we know that our size (n) is 100 as we want to flip a coin 100 times and observe the result, secondly we know that our probability (p) is 0.5 as there's a 50% chance for either heads or tails and lastly or size is 1000 as we are simulating this 1000 times overall.
#
# In the case of this example whether we are counting the occurrences of heads or tails with the distribution is subjective (as either event is just as likely), in fact with the binomial function we are not explicitly asking it to tell us the number of occurences of heads, instead what we are asking of the function is to show us the number of occurrences for an event with a 50% chance of happening, happens over 100 tries and then repeating that 1000 times.
#
# This then gives us our distribution showing the total number of 'wins' or 'heads' that occurred for each set of 100 tries over the 1000 repeats.
coinflip_binomial = rng.binomial(n=100,p=0.5,size=1000)
print("What the output of the binomial function returns for distribution of 100 coinflips simulated 1000 times\n", coinflip_binomial)
print("Minimum number of heads for 100 coinflips -", min(coinflip_binomial))
print("Minimum number of heads for 100 coinflips -", max(coinflip_binomial))
print("Mean number of heads for 100 coinflips -", np.mean(coinflip_binomial))
print("Standard Deviation of heads per 100 coinflips -", np.std(coinflip_binomial))
# ## Visualising the binomial distribution for coin flips
# From looking at seaborn documentation it appears that distplot is most appropriate way to visualise the binomial distribution as it combines both a histogram and [kernel density estimation](https://en.wikipedia.org/wiki/Kernel_density_estimation) into a single plot.
# https://seaborn.pydata.org/generated/seaborn.distplot.html
import seaborn as sns
sns.distplot(coinflip_binomial, color='orange').set_title('binomial distribution for 1000 games of 100 coinflips')
plt.xlabel('Heads');
# We can see from the above distplot that the values do indeed center around 50 with values out towards 40 and 60 being less probable and beyond that very unlikely.
# If a larger dataset were to be generated where size argument was 10,000 instead of 1,000, then you would get a smoother distribution.
#
# ### Saving Binomial Distribution as image
'''
This cell is what I did to get an image to use in the markdown text above, this proved an interesting enough exercise
so I decided to leave it in it's own standalone cell.
On the face of it, it was simple to do but as soon as I went about describing it I realised I needed to determine what the
'''
bin_steps=np.linspace(start=20,stop=80,num=13) #steps to use for bins I want steps of 5 between (and inclusive of) 20 to 80
plt.tick_params(which='minor', length=5, color='black')
plt.tick_params(which='minor', length=4, color='r')
plt.hist(coinflip_binomial, weights=np.ones(len(coinflip_binomial))/len(coinflip_binomial), color='orange', bins=bin_steps) #in order to get y axis as percentage not sum of total occurences I have, this argument for weights
plt.title('Fair Coin Flip Simulation')
plt.ylabel('Probability')
plt.xlabel('Flips')
plt.xticks(bin_steps); #this one was surprisingly tricky as mostly guides show examples using subplot not plot, only myself to blame for sticking with plot - https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.tick_params.html
#plt.savefig('images/binomial_example.png') #Uncomment this to save your own version
coinflip_binomial = rng.binomial(n=100,p=0.5,size=10000)
sns.distplot(coinflip_binomial, color='orange').set_title('binomial distribution for 1000 games of 100 coinflips')
plt.xlabel('Heads');
# ***
# ### Tangent to the original task
# In the next cell I thought it would be interesting to show the binomial distribution of an unfair coin flip, where instead of it being p=0.5 for heads (or tails) I would instead specify p=0.75 to represent a coin that was weighted so as to return heads 75% of the time.
#
# By shifting the value for p, so to does the center of the distribution which makes sense, if we are doing 100 coin flips with 75% probability of getting heads then after 1000 repetitions of this we should see that on average we are mostly getting 75 heads.
# Similarly if we set p=1 we would get 100 heads for every single repetition as there's 100% chance of getting heads
#little tweak to the binomial distribution showing an uneven weighting for the coin
unfair_coinflip_binomial = rng.binomial(n=100,p=0.75,size=1000)
#print("What the output of the binomial function returns for distribution of 100 coinflips simulated 1000 times\n", unfair_coinflip_binomial)
print("Minimum number of heads for 100 coinflips -", min(unfair_coinflip_binomial))
print("Minimum number of heads for 100 coinflips -", max(unfair_coinflip_binomial))
sns.distplot(unfair_coinflip_binomial, color='orange').set_title('binomial distribution for 1000 games of 100 coinflips')
plt.xlabel('Heads');
#little tweak to the binomial distribution showing an uneven weighting for the coin
reallyunfair_coinflip_binomial = rng.binomial(n=100,p=0.99,size=1000)
print("Minimum number of heads for 100 coinflips -", min(reallyunfair_coinflip_binomial))
print("Minimum number of heads for 100 coinflips -", max(reallyunfair_coinflip_binomial))
sns.distplot(reallyunfair_coinflip_binomial, color='orange').set_title('binomial distribution for 1000 games of 100 coinflips')
plt.xlabel('Heads');
# Interestingly when we give a really close to 1 value for p we get what multiple peaks for our Kernel Density Estimate, what I think is happening here is due to the proximity to 100 which is the max possible wins it removes what would be the right side of the distribution which would even it out.
# ***
# ### Recreating the Binomial Distribution without using binomial function
# Based on the following line of the task brief I am attempting to recreate the binomial distribution using other numpy.random functions
#
# - <i>"Write some python code that simulates flipping a coin 100 times. Then run this code 1,000 times, keeping track of the number of heads in each of the 1,000 simulations."</i>
#
# To do so I use numpy.random.choice to recreate the 100 coin flips and will then loop through that 1000 times to simulate 1000 games of 100 coin flips while keeping track of the total heads for each game.
# https://numpy.org/doc/stable/reference/random/generated/numpy.random.Generator.choice.html
#
# Alternately I could use np.random.integers to represent 1/0 for head/tails but I like the idea that with choice we can explicitly state the probability for each option.
#
# I could also use a list of ['Heads','Tails'] similarly but that would then make summing the total heads more involved.
coinface_list = [1,0] #here 1 is representing heads and 0 represents tails
coinflip_choice = rng.choice(a=coinface_list,p=[0.5,0.5]) #p=[0.5,0.5] as need to supply the probabilities for both 1 and 0 for argument a
print(coinflip_choice)
# Summing an array - https://numpy.org/doc/stable/reference/generated/numpy.sum.html
coinflip_choice = rng.choice(a=coinface_list,p=[0.5,0.5], size=100) #size=100 as want to get an array returned representing 100 coinflips
heads = sum(coinflip_choice) #as we have 1's representing heads and 0's representing tails can get the total heads by simply summing the array
print(heads)
heads_list = [] #declare empty list to be appended to
for i in range(1000):
coinflip_choice = rng.choice(a=coinface_list,p=[0.5,0.5], size=100) #per loop get 100 results
heads = sum(coinflip_choice) #get sum of current total heads
heads_list.append(heads) #append to heads list
sns.distplot(heads_list, color='orange')
plt.title('Number of heads over 100 coinflips, repeated 1000 times')
plt.xlabel('Heads');
# ## Task 3 Summary and Conclusion
#
# With this task I took two different approaches to generate a distribution for coinflips, first I generated the 1000 repeats of 100 coinflips using the numpy binomial function and second using numpy's choice function within a for loop.
#
# While the binomial distribution option is by far the more simple and direct version it was interesting exploring how to reproduce it without using the binomial function explicitly.
#
# I took a tangent to the task to see what unfair coin flips would look like where the probabilities aren't equal.
#
# Finally I also used the seaborn libraries distplot function to visualise both a histogram and a kernel density estimate line to show the distribution.
# ***
# # Task 4
# ## Simpson's Paradox
#
# The objective for this task is to demonstrate the Simpson's Paradox.
#
# The Simpson's Paradox is a phenomenon in probability and statistics where a general trend that can be seen across various groups when viewed independently is reversed when they are grouped together, Simpson's Paradox highlights how misleading statistics can be when presented without being properly considered what's being shown.
#
# A simple example of this would be to imagine some figures are being published based on crime rates across different demographics, when viewed independently by their demographic group the trend may show a decline in crime rate, however if someone naievly (or as is often the case - if the outlet reporting this has an agenda and does so maliciously) groups all this data together it would show a trend upwards, suggesting crime rates are increasing.
#x1 goes from 0 to 10 in 10 steps
x1 = np.linspace(1,10, 10)
y1 = 4*x1+20
#x2 goes from 5 to 15 in 10 steps
x2 = np.linspace(5,15,10)
y2 = 1*x2
#in an effort to create a single combined dataset in order to show the line of fit for x1 and x2 and y1 and y2
x1x2 = np.concatenate((x1,x2), axis=None) #x1x2 gives array of x2 concatenated on top of x1
y1y2 = np.concatenate((y1,y2), axis=None)
plt.scatter(x1,y1, color='r')
plt.scatter(x2,y2, color='g')
m,c = np.polyfit(x1x2,y1y2,1) #as shown by Ian in video on 'Fitting Lines'
plt.plot(np.unique(x1x2), m*np.unique(x1x2)+c);
# With the simple example above we have an illustration of the simpsons paradox, whereby two datasets each show a clear upward linear trend. However when line of fit is acquired for both datasets together it shows a downward linear trend
#
# ### Adding some randomness to the data
# +
#introducing some randomness to the line's so they are no longer perfectly linear
rng = np.random.default_rng() #first declare a random num generator
x3 = np.linspace(1,10,100)
y3 = 5*x3+40+rng.normal(0.0,3,len(x3))
m3,c3 = np.polyfit(x3,y3,1)
x4 = np.linspace(10, 20, 100)
y4 = 5*x4-50+rng.normal(0.0,5,len(x4))
m4,c4 = np.polyfit(x4,y4, 1)
#in an effort to create a single combined dataset in order to show the line of fit for x1 and x2 and y1 and y2
x3x4 = np.concatenate((x3,x4), axis=None)
y3y4 = np.concatenate((y3,y4), axis=None)
comb_m, comb_c = np.polyfit(x3x4,y3y4,1)
# -
plt.figure(figsize=(10,6))
plt.plot(np.unique(x3), m3*np.unique(x3)+c3, 'orange', linewidth=2) #want the line underneath the transparent dot's
plt.scatter(x3,y3, marker='o', alpha=0.75, label='x3 and y3') #set the scatter dots to be slightly transparent
plt.scatter(x4,y4, label='x4 and y4')
plt.plot(np.unique(x4), m4*np.unique(x4)+c4, 'green', linewidth=2) #want the line underneath the transparent dot's
plt.plot(np.unique(x3x4), comb_m*np.unique(x3x4)+comb_c, color='black', label='Simpsons Paradox Line')
plt.legend()
plt.title('x3 and x4 vs. y3 and y4')
# By doing the previous example I can now see a general feel for how to generate complimentary datasets that will show the Simpson's Paradox, and that is when you have a fairly consistent slope (m) by increasing the intercept (b) fairly significantly it leads to a downwards trend when grouping the two together.
#
# ## Demonstrating Simpson's Paradox with 4 datasets on single trend
# +
x1 = np.linspace(1,10,100)
y1 = -5*x1+50+rng.normal(0.0,3,len(x1))
m1,c1 = np.polyfit(x1,y1,1)
x2 = np.linspace(1, 20, 100)
y2 = -5*x2+100+rng.normal(0.0,5,len(x2))
m2,c2 = np.polyfit(x2,y2, 1)
x3 = np.linspace(5,30,100)
y3 = -5*x3+200+rng.normal(0.0,3,len(x3))
m3,c3 = np.polyfit(x3,y3,1)
x4 = np.linspace(20, 40, 100)
y4 = -5*x4+300+rng.normal(0.0,5,len(x4))
m4,c4 = np.polyfit(x4,y4, 1)
#in an effort to create a single combined dataset in order to show the line of fit for x1 and x2 and y1 and y2
x_all = np.concatenate((x1,x2,x3,x4), axis=None)
y_all = np.concatenate((y1,y2,y3,y4), axis=None)
m_all,c_all = np.polyfit(x_all,y_all, 1)
#comb_a, comb_b = np.polyfit(x3x4,y3y4,1)
plt.figure(figsize=(10,6))
plt.plot(np.unique(x1), m1*np.unique(x1)+c1, 'orange', linewidth=2) #want the line underneath the transparent dot's
plt.scatter(x1,y1, marker='o', alpha=0.75, label='x1 and y1') #set the scatter dots to be slightly transparent
plt.scatter(x2,y2, label='x2 and y2')
plt.plot(np.unique(x2), m2*np.unique(x2)+c2, 'green', linewidth=2) #want the line underneath the transparent dot's
#plt.plot(np.unique(x3x4), comb_a*np.unique(x3x4)+comb_b, color='black', label='Simpsons Paradox Line')
plt.plot(np.unique(x3), m3*np.unique(x3)+c3, 'purple', linewidth=2) #want the line underneath the transparent dot's
plt.scatter(x3,y3, marker='o', alpha=0.75, label='x3 and y3') #set the scatter dots to be slightly transparent
plt.scatter(x4,y4, label='x4 and y4')
plt.plot(np.unique(x4), m4*np.unique(x4)+c4, 'green', linewidth=2) #want the line underneath the transparent dot's
plt.plot(np.unique(x_all), m_all*np.unique(x_all)+c_all, color='black', label='Simpsons Paradox Line')
plt.legend()
plt.title('x1,x2,x3,x4 vs. y1,y2,y3,y4');
# -
# ## Task 4 Summary and Conclusion
#
# With this task I have tried to demonstrate the Simpson's paradox where established trends in groups of data are shown to be reversed when viewing groups together.
#
# To do so I generated groupings of data (x1,y1 and x2,y2 etc.)
# to show linear relationships among their groups and used numpy.polyfit to generate a line of fit for each group.
# Then to combine the different groups together I simply concatenated them one on top of another and again used numpy.polyfit on the concatenated dataset.
#
# The datasets were plotted using matplotlib.pyplot library and functions in particular were scatter for showing the individual data points and plot for showing the lines of fit.
|
Tasks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Imports
import pandas as pd
import seaborn as sns
import numpy as np
import os
import matplotlib.pyplot as plt
import pandas_profiling
# # 1. Load Data
df = pd.read_csv("/Users/stevenzonneveld/Desktop/data301/project-group35-project/data/raw/MileStone1.csv")
df
# # 2. Clean Data
# Checking for NaN Values
nan_in_df = df.isnull().values.any()
nan_in_df
# +
# No NaN Values
# -
# Dropping columns
df_cleaned = df.drop(columns = ['Unnamed: 0', 'price', 'title_status', 'color', 'state'], axis = 0).sort_values(by = ['brand'])
df_cleaned
# +
# Droping rows
df_cleaned.drop( df_cleaned [ df_cleaned ['brand'] == 'peterbilt'].index, inplace=True)
df_cleaned.drop( df_cleaned [ df_cleaned ['mileage'] == 0.0 ].index, inplace=True)
df_cleaned
# Don't want undriven cars / missing values.
# Peterbilts are semi trucks, we are looking at cars.
# +
# Research Questions: What car brand is the longest lasting on average, based on the model year of the car and the milage
# -
# # 3. Process Data / 4. Wrangle Data --> Dropping Unnecessary Columns, per each graph.
# +
# Longest lasting by Mileage
# Data Wrangling - Dropping Columns
df_mileage = df_cleaned.drop(columns = ['year'], axis = 0)
# Data Wrangling - Renamming Columns
df_mileage = df_mileage.rename(columns = {"brand": "Manufacturer", "mileage": "Mileage"})
df_mileage
# -
# # 3. Process Data / 4. Wrangle Data --> Dropping Unnecessary Columns, per each graph.
#
# +
# Longest Lasting by Year
df_year = df_cleaned
# Data Wrangling - Dropping Columns
df_year = df_year.drop(columns = ['mileage'])
# Data Wrangling - Renamming Columns
df_year = df_year.rename(columns = {"brand": "Manufacturer", "year": "Model Year"})
df_year
# -
# ### Beginning of Method Chaining
# #### Method Chaining by Year
def load_and_process_df_Method_Chain_by_Year(path_to_csv_file):
df_Method_Chain_by_Year1 = (
pd.read_csv("/Users/stevenzonneveld/Desktop/data301/project-group35-project/data/raw/MileStone1.csv")
.drop(columns = ['Unnamed: 0', 'price', 'title_status', 'color', 'state', 'mileage'], axis = 0)
.sort_values(by = ['brand'])
#.drop( df_cleaned [ df_cleaned ['brand'] == 'peterbilt'].index, inplace=True) #could not figure out how to use .drop in method chaining.
.rename(columns = {"brand": "Manufacturer", "year": "Model Year"})
)
df_Method_Chain_by_Year2 = df_Method_Chain_by_Year1.drop( df_Method_Chain_by_Year1 [ df_Method_Chain_by_Year1 ['Manufacturer'] == 'peterbilt'].index)
return df_Method_Chain_by_Year2
# +
# practice code (Method chain minus the function)
df_Method_Chain_by_Year1 = (
pd.read_csv("/Users/stevenzonneveld/Desktop/data301/project-group35-project/data/raw/MileStone1.csv")
.drop(columns = ['Unnamed: 0', 'price', 'title_status', 'color', 'state', 'mileage'], axis = 0)
.sort_values(by = ['brand'])
#.drop( df_cleaned [ df_cleaned ['brand'] == 'peterbilt'].index, inplace=True) #could not figure out how to use .drop in method chaining.
.rename(columns = {"brand": "Manufacturer", "year": "Model Year"})
)
df_Method_Chain_by_Year2 = df_Method_Chain_by_Year1.drop( df_Method_Chain_by_Year1 [ df_Method_Chain_by_Year1 ['Manufacturer'] == 'peterbilt'].index)
df_Method_Chain_by_Year2
# -
# #### Method Chaining by Mileage
def load_and_process_df_Method_Chain_by_Mileage(path_to_csv_file):
df_Method_Chain_by_Mileage1 = (
pd.read_csv("/Users/stevenzonneveld/Desktop/data301/project-group35-project/data/raw/MileStone1.csv")
.drop(columns = ['Unnamed: 0', 'price', 'title_status', 'color', 'state', 'year'], axis = 0)
.sort_values(by = ['brand'])
#.drop( df_cleaned [ df_cleaned ['brand'] == 'peterbilt'].index, inplace=True) #could not figure out how to use .drop in method chaining.
#.drop( df_cleaned [ df_cleaned ['mileage'] == 0.0 ].index, inplace=True) #could not figure out how to use .drop in method chaining.
.rename(columns = {"brand": "Manufacturer", "mileage": "Mileage"})
)
df_Method_Chain_by_Mileage2 = df_Method_Chain_by_Mileage1.drop( df_Method_Chain_by_Mileage1 [ df_Method_Chain_by_Mileage1 ['Manufacturer'] == 'peterbilt'].index)
df_Method_Chain_by_Mileage3 = df_Method_Chain_by_Mileage2.drop( df_Method_Chain_by_Mileage2 [ df_Method_Chain_by_Mileage2 ['Mileage'] == 0.0 ].index)
return df_Method_Chain_by_Mileage3
# +
# practice code (Method chain minus the function)
df_Method_Chain_by_Mileage1 = (
pd.read_csv("/Users/stevenzonneveld/Desktop/data301/project-group35-project/data/raw/MileStone1.csv")
.drop(columns = ['Unnamed: 0', 'price', 'title_status', 'color', 'state', 'year'], axis = 0)
.sort_values(by = ['brand'])
#.drop( df_cleaned [ df_cleaned ['brand'] == 'peterbilt'].index, inplace=True) #could not figure out how to use .drop in method chaining.
#.drop( df_cleaned [ df_cleaned ['mileage'] == 0.0 ].index, inplace=True) #could not figure out how to use .drop in method chaining.
.rename(columns = {"brand": "Manufacturer", "mileage": "Mileage"})
)
df_Method_Chain_by_Mileage2 = df_Method_Chain_by_Mileage1.drop( df_Method_Chain_by_Mileage1 [ df_Method_Chain_by_Mileage1 ['Manufacturer'] == 'peterbilt'].index)
df_Method_Chain_by_Mileage3 = df_Method_Chain_by_Mileage2.drop( df_Method_Chain_by_Mileage2 [ df_Method_Chain_by_Mileage2 ['Mileage'] == 0.0 ].index)
df_Method_Chain_by_Mileage3
# -
|
analysis/Steven1/Milestone2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="copyright"
# Copyright 2021 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="title:generic"
# # Vertex AI Pipelines: Metrics visualization and run comparison using the KFP SDK
#
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/official/pipelines/metrics_viz_run_compare_kfp.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
# </a>
# </td>
# <td>
# <a href="https://github.com/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/official/pipelines/metrics_viz_run_compare_kfp.ipynb">
# <img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
# View on GitHub
# </a>
# </td>
# <td>
# <a href="https://console.cloud.google.com/vertex-ai/notebooks/deploy-notebook?download_url=https://github.com/GoogleCloudPlatform/vertex-ai-samples/blob/master/notebooks/official/pipelines/metrics_viz_run_compare_kfp.ipynb">
# Open in Vertex AI Workbench
# </a>
# </td>
# </table>
# <br/><br/><br/>
# + [markdown] id="overview:pipelines,metrics"
# ## Overview
#
# This notebook shows how to use [the Kubeflow Pipelines (KFP) SDK](https://www.kubeflow.org/docs/components/pipelines/) to build [Vertex AI Pipelines](https://cloud.google.com/vertex-ai/docs/pipelines) that generate model metrics and metrics visualizations, and comparing pipeline runs.
# + [markdown] id="dataset:wine,lcn,sklearn"
# ### Dataset
#
# The dataset used for this tutorial is the [Wine dataset](https://archive.ics.uci.edu/ml/datasets/wine) from [Scikit-learn builtin datasets](https://scikit-learn.org/stable/datasets.html).
#
# The dataset predicts the origin of a wine.
# + [markdown] id="dataset:iris,lcn,sklearn"
# ### Dataset
#
# The dataset used for this tutorial is the [Iris dataset](https://scikit-learn.org/stable/auto_examples/datasets/plot_iris_dataset.html) from [Scikit-learn builtin datasets](https://scikit-learn.org/stable/datasets.html).
#
# The dataset predicts the type of Iris flower species from a class of three species: setosa, virginica, or versicolor.
# + [markdown] id="objective:pipelines,metrics"
# ### Objective
#
# The steps performed include:
#
# - Generate ROC curve and confusion matrix visualizations for classification results
# - Write metrics
# - Compare metrics across pipeline runs
# + [markdown] id="costs"
# ### Costs
#
# This tutorial uses billable components of Google Cloud:
#
# * Vertex AI
# * Cloud Storage
#
# Learn about [Vertex AI
# pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
# pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
# Calculator](https://cloud.google.com/products/calculator/)
# to generate a cost estimate based on your projected usage.
# + [markdown] id="setup_local"
# ### Set up your local development environment
#
# If you are using Colab or Google Cloud Notebook, your environment already meets all the requirements to run this notebook. You can skip this step.
#
# Otherwise, make sure your environment meets this notebook's requirements. You need the following:
#
# - The Cloud Storage SDK
# - Git
# - Python 3
# - virtualenv
# - Jupyter notebook running in a virtual environment with Python 3
#
# The Cloud Storage guide to [Setting up a Python development environment](https://cloud.google.com/python/setup) and the [Jupyter installation guide](https://jupyter.org/install) provide detailed instructions for meeting these requirements. The following steps provide a condensed set of instructions:
#
# 1. [Install and initialize the SDK](https://cloud.google.com/sdk/docs/).
#
# 2. [Install Python 3](https://cloud.google.com/python/setup#installing_python).
#
# 3. [Install virtualenv](Ihttps://cloud.google.com/python/setup#installing_and_using_virtualenv) and create a virtual environment that uses Python 3.
#
# 4. Activate that environment and run `pip3 install Jupyter` in a terminal shell to install Jupyter.
#
# 5. Run `jupyter notebook` on the command line in a terminal shell to launch Jupyter.
#
# 6. Open this notebook in the Jupyter Notebook Dashboard.
#
# + [markdown] id="install_aip:mbsdk"
# ## Installation
#
# Install the latest version of Vertex AI SDK for Python.
# + id="install_aip:mbsdk"
import os
# Google Cloud Notebook
if os.path.exists("/opt/deeplearning/metadata/env_version"):
USER_FLAG = "--user"
else:
USER_FLAG = ""
# ! pip3 install --upgrade google-cloud-aiplatform $USER_FLAG
# + [markdown] id="install_storage"
# Install the latest GA version of *google-cloud-storage* library as well.
# + id="install_storage"
# ! pip3 install -U google-cloud-storage $USER_FLAG
# + [markdown] id="install_kfp"
# Install the latest GA version of *KFP SDK* library as well.
# + id="install_kfp"
# ! pip3 install $USER kfp --upgrade
# + id="install_matplotlib"
if os.environ["IS_TESTING"]:
# ! pip3 install --upgrade matplotlib $USER_FLAG
# + [markdown] id="restart"
# ### Restart the kernel
#
# Once you've installed the additional packages, you need to restart the notebook kernel so it can find the packages.
# + id="restart"
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
# + [markdown] id="check_versions"
# Check the versions of the packages you installed. The KFP SDK version should be >=1.6.
# + id="check_versions:kfp"
# ! python3 -c "import kfp; print('KFP SDK version: {}'.format(kfp.__version__))"
# + [markdown] id="before_you_begin:nogpu"
# ## Before you begin
#
# ### GPU runtime
#
# This tutorial does not require a GPU runtime.
#
# ### Set up your Google Cloud project
#
# **The following steps are required, regardless of your notebook environment.**
#
# 1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
#
# 2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
#
# 3. [Enable the Vertex AI APIs, Compute Engine APIs, and Cloud Storage.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component,storage-component.googleapis.com)
#
# 4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Google Cloud Notebook.
#
# 5. Enter your project ID in the cell below. Then run the cell to make sure the
# Cloud SDK uses the right project for all the commands in this notebook.
#
# **Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$`.
# + id="set_project_id"
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
# + id="autoset_project_id"
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
shell_output = ! gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
# + id="set_gcloud_project_id"
# ! gcloud config set project $PROJECT_ID
# + [markdown] id="region"
# #### Region
#
# You can also change the `REGION` variable, which is used for operations
# throughout the rest of this notebook. Below are regions supported for Vertex AI. We recommend that you choose the region closest to you.
#
# - Americas: `us-central1`
# - Europe: `europe-west4`
# - Asia Pacific: `asia-east1`
#
# You may not use a multi-regional bucket for training with Vertex AI. Not all regions provide support for all Vertex AI services.
#
# Learn more about [Vertex AI regions](https://cloud.google.com/vertex-ai/docs/general/locations)
# + id="region"
REGION = "us-central1" # @param {type: "string"}
# + [markdown] id="timestamp"
# #### Timestamp
#
# If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append the timestamp onto the name of resources you create in this tutorial.
# + id="timestamp"
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
# + [markdown] id="gcp_authenticate"
# ### Authenticate your Google Cloud account
#
# **If you are using Google Cloud Notebook**, your environment is already authenticated. Skip this step.
#
# **If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
#
# **Otherwise**, follow these steps:
#
# In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
#
# **Click Create service account**.
#
# In the **Service account name** field, enter a name, and click **Create**.
#
# In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex" into the filter box, and select **Vertex Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
#
# Click Create. A JSON file that contains your key downloads to your local environment.
#
# Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
# + id="gcp_authenticate"
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
import os
import sys
# If on Google Cloud Notebook, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
# %env GOOGLE_APPLICATION_CREDENTIALS ''
# + [markdown] id="bucket:mbsdk"
# ### Create a Cloud Storage bucket
#
# **The following steps are required, regardless of your notebook environment.**
#
# When you initialize the Vertex AI SDK for Python, you specify a Cloud Storage staging bucket. The staging bucket is where all the data associated with your dataset and model resources are retained across sessions.
#
# Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
# + id="bucket"
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
# + id="autoset_bucket"
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
# + [markdown] id="create_bucket"
# **Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
# + id="create_bucket"
# ! gsutil mb -l $REGION $BUCKET_NAME
# + [markdown] id="validate_bucket"
# Finally, validate access to your Cloud Storage bucket by examining its contents:
# + id="validate_bucket"
# ! gsutil ls -al $BUCKET_NAME
# + [markdown] id="set_service_account"
# #### Service Account
#
# **If you don't know your service account**, try to get your service account using `gcloud` command by executing the second cell below.
# + id="set_service_account"
SERVICE_ACCOUNT = "[your-service-account]" # @param {type:"string"}
# + id="autoset_service_account"
if (
SERVICE_ACCOUNT == ""
or SERVICE_ACCOUNT is None
or SERVICE_ACCOUNT == "[your-service-account]"
):
# Get your GCP project id from gcloud
# shell_output = !gcloud auth list 2>/dev/null
SERVICE_ACCOUNT = shell_output[2].strip()
print("Service Account:", SERVICE_ACCOUNT)
# + [markdown] id="set_service_account:pipelines"
# #### Set service account access for Vertex AI Pipelines
#
# Run the following commands to grant your service account access to read and write pipeline artifacts in the bucket that you created in the previous step -- you only need to run these once per service account.
# + id="set_service_account:pipelines"
# ! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectCreator $BUCKET_NAME
# ! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectViewer $BUCKET_NAME
# + [markdown] id="setup_vars"
# ### Set up variables
#
# Next, set up some variables used throughout the tutorial.
# ### Import libraries and define constants
# + id="import_aip:mbsdk"
import google.cloud.aiplatform as aip
# + [markdown] id="pipeline_constants"
# #### Vertex AI Pipelines constants
#
# Setup up the following constants for Vertex AI Pipelines:
# + id="pipeline_constants"
PIPELINE_ROOT = "{}/pipeline_root/iris".format(BUCKET_NAME)
# + [markdown] id="additional_imports"
# Additional imports.
# + id="import_pipelines"
from kfp.v2 import dsl
from kfp.v2.dsl import ClassificationMetrics, Metrics, Output, component
# + [markdown] id="init_aip:mbsdk"
# ## Initialize Vertex AI SDK for Python
#
# Initialize the Vertex AI SDK for Python for your project and corresponding bucket.
# + id="init_aip:mbsdk"
aip.init(project=PROJECT_ID, staging_bucket=BUCKET_NAME)
# + [markdown] id="define_component:wine_classification"
# ### Define pipeline components using scikit-learn
#
# In this section, you define some Python function-based components that use scikit-learn to train some classifiers and produce evaluations that can be visualized.
#
# Note the use of the `@component()` decorator in the definitions below. You can optionally set a list of packages for the component to install; the base image to use (the default is a Python 3.7 image); and the name of a component YAML file to generate, so that the component definition can be shared and reused.
#
# #### Define wine_classification component
#
# The first component shows how to visualize an *ROC curve*.
# Note that the function definition includes an output called `wmetrics`, of type `Output[ClassificationMetrics]`. You can visualize the metrics in the Pipelines user interface in the Cloud Console.
#
# To do this, this example uses the artifact's `log_roc_curve()` method. This method takes as input arrays with the false positive rates, true positive rates, and thresholds, as [generated by the `sklearn.metrics.roc_curve` function](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.roc_curve.html).
#
# When you evaluate the cell below, a task factory function called `wine_classification` is created, that is used to construct the pipeline definition. In addition, a component YAML file is created, which can be shared and loaded via file or URL to create the same task factory function.
# + id="define_component:wine_classification"
@component(
packages_to_install=["sklearn"],
base_image="python:3.9",
output_component_file="wine_classification_component.yaml",
)
def wine_classification(wmetrics: Output[ClassificationMetrics]):
from sklearn.datasets import load_wine
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_curve
from sklearn.model_selection import cross_val_predict, train_test_split
X, y = load_wine(return_X_y=True)
# Binary classification problem for label 1.
y = y == 1
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
rfc = RandomForestClassifier(n_estimators=10, random_state=42)
rfc.fit(X_train, y_train)
y_scores = cross_val_predict(rfc, X_train, y_train, cv=3, method="predict_proba")
fpr, tpr, thresholds = roc_curve(
y_true=y_train, y_score=y_scores[:, 1], pos_label=True
)
wmetrics.log_roc_curve(fpr, tpr, thresholds)
# + [markdown] id="define_component:iris_sgdclassifier"
# #### Define iris_sgdclassifier component
#
# The second component shows how to visualize a *confusion matrix*, in this case for a model trained using `SGDClassifier`.
#
# As with the previous component, you create a `metricsc` output artifact of type `Output[ClassificationMetrics]`. Then, use the artifact's `log_confusion_matrix` method to visualize the confusion matrix results, as generated by the [sklearn.metrics.confusion_matrix](https://scikit-learn.org/stable/modules/generated/sklearn.metrics.confusion_matrix.html) function.
# + id="define_component:iris_sgdclassifier"
@component(packages_to_install=["sklearn"], base_image="python:3.9")
def iris_sgdclassifier(
test_samples_fraction: float,
metricsc: Output[ClassificationMetrics],
):
from sklearn import datasets, model_selection
from sklearn.linear_model import SGDClassifier
from sklearn.metrics import confusion_matrix
iris_dataset = datasets.load_iris()
train_x, test_x, train_y, test_y = model_selection.train_test_split(
iris_dataset["data"],
iris_dataset["target"],
test_size=test_samples_fraction,
)
classifier = SGDClassifier()
classifier.fit(train_x, train_y)
predictions = model_selection.cross_val_predict(classifier, train_x, train_y, cv=3)
metricsc.log_confusion_matrix(
["Setosa", "Versicolour", "Virginica"],
confusion_matrix(
train_y, predictions
).tolist(), # .tolist() to convert np array to list.
)
# + [markdown] id="define_component:iris_logregression"
# #### Define iris_logregression component
#
# The third component also uses the "iris" dataset, but trains a `LogisticRegression` model. It logs model `accuracy` in the `metrics` output artifact.
# + id="define_component:iris_logregression"
@component(
packages_to_install=["sklearn"],
base_image="python:3.9",
)
def iris_logregression(
input_seed: int,
split_count: int,
metrics: Output[Metrics],
):
from sklearn import datasets, model_selection
from sklearn.linear_model import LogisticRegression
# Load digits dataset
iris = datasets.load_iris()
# # Create feature matrix
X = iris.data
# Create target vector
y = iris.target
# test size
test_size = 0.20
# cross-validation settings
kfold = model_selection.KFold(
n_splits=split_count, random_state=input_seed, shuffle=True
)
# Model instance
model = LogisticRegression()
scoring = "accuracy"
results = model_selection.cross_val_score(model, X, y, cv=kfold, scoring=scoring)
print(f"results: {results}")
# split data
X_train, X_test, y_train, y_test = model_selection.train_test_split(
X, y, test_size=test_size, random_state=input_seed
)
# fit model
model.fit(X_train, y_train)
# accuracy on test set
result = model.score(X_test, y_test)
print(f"result: {result}")
metrics.log_metric("accuracy", (result * 100.0))
# + [markdown] id="define_pipeline:metrics"
# ### Define the pipeline
#
# Next, define a simple pipeline that uses the components that were created in the previous section.
# + id="define_pipeline:metrics"
PIPELINE_NAME = "metrics-pipeline-v2"
@dsl.pipeline(
# Default pipeline root. You can override it when submitting the pipeline.
pipeline_root=PIPELINE_ROOT,
# A name for the pipeline.
name="metrics-pipeline-v2",
)
def pipeline(seed: int, splits: int):
wine_classification_op = wine_classification() # noqa: F841
iris_logregression_op = iris_logregression( # noqa: F841
input_seed=seed, split_count=splits
)
iris_sgdclassifier_op = iris_sgdclassifier(test_samples_fraction=0.3) # noqa: F841
# + [markdown] id="compile_pipeline"
# ## Compile the pipeline
#
# Next, compile the pipeline.
# + id="compile_pipeline"
from kfp.v2 import compiler # noqa: F811
compiler.Compiler().compile(
pipeline_func=pipeline,
package_path="tabular classification_pipeline.json".replace(" ", "_"),
)
# + [markdown] id="run_pipeline:metrics"
# ## Run the pipeline
#
# Next, run the pipeline.
# + id="run_pipeline:metrics"
DISPLAY_NAME = "iris_" + TIMESTAMP
job = aip.PipelineJob(
display_name=DISPLAY_NAME,
template_path="tabular classification_pipeline.json".replace(" ", "_"),
job_id=f"tabular classification-v2{TIMESTAMP}-1".replace(" ", ""),
pipeline_root=PIPELINE_ROOT,
parameter_values={"seed": 7, "splits": 10},
)
job.run()
# + [markdown] id="view_pipeline_run:metrics"
# Click on the generated link to see your run in the Cloud Console.
#
# <!-- It should look something like this as it is running:
#
# <a href="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" target="_blank"><img src="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" width="40%"/></a> -->
#
# In the UI, many of the pipeline DAG nodes will expand or collapse when you click on them.
# + [markdown] id="compare_pipeline_runs:ui"
# ## Comparing pipeline runs in the UI
#
# Next, generate another pipeline run that uses a different `seed` and `split` for the `iris_logregression` step.
#
# Submit the new pipeline run:
# + id="compare_pipeline_runs:ui"
job = aip.PipelineJob(
display_name="iris_" + TIMESTAMP,
template_path="tabular classification_pipeline.json".replace(" ", "_"),
job_id=f"tabular classification-pipeline-v2{TIMESTAMP}-2".replace(" ", ""),
pipeline_root=PIPELINE_ROOT,
parameter_values={"seed": 5, "splits": 7},
)
job.run()
# + [markdown] id="compare_pipeline_runs:ui"
# When both pipeline runs have finished, compare their results by navigating to the pipeline runs list in the Cloud Console, selecting both of them, and clicking **COMPARE** at the top of the Console panel.
# + [markdown] id="compare_pipeline_runs"
# ## Compare the parameters and metrics of the pipelines run from their tracked metadata
#
# Next, you use the Vertex AI SDK for Python to compare the parameters and metrics of the pipeline runs. Wait until the pipeline runs have finished to run the next cell.
# + id="compare_pipeline_runs"
pipeline_df = aip.get_pipeline_df(pipeline=PIPELINE_NAME)
print(pipeline_df.head(2))
# + [markdown] id="plot_coord_runs"
# ### Plot parallel coordinates of parameters and metrics
#
# With the metric and parameters in a dataframe, you can perform further analysis to extract useful information. The following example compares data from each run using a parallel coordinate plot.
# + id="plot_coord_runs"
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
plt.rcParams["figure.figsize"] = [15, 5]
pipeline_df["param.input:seed"] = pipeline_df["param.input:seed"].astype(np.float16)
pipeline_df["param.input:splits"] = pipeline_df["param.input:splits"].astype(np.float16)
ax = pd.plotting.parallel_coordinates(
pipeline_df.reset_index(level=0),
"run_name",
cols=["param.input:seed", "param.input:splits", "metric.accuracy"],
)
ax.set_yscale("symlog")
ax.legend(bbox_to_anchor=(1.0, 0.5))
# + [markdown] id="plot_roc_runs"
# ### Plot ROC curve and calculate AUC number
#
# In addition to basic metrics, you can extract complex metrics and perform further analysis using the `get_pipeline_df` method.
# + id="plot_roc_runs"
try:
df = pd.DataFrame(pipeline_df["metric.confidenceMetrics"][0])
auc = np.trapz(df["recall"], df["falsePositiveRate"])
plt.plot(df["falsePositiveRate"], df["recall"], label="auc=" + str(auc))
plt.legend(loc=4)
plt.show()
except Exception as e:
print(e)
# + [markdown] id="cleanup:pipelines"
# # Cleaning up
#
# To clean up all Google Cloud resources used in this project, you can [delete the Google Cloud
# project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
#
# Otherwise, you can delete the individual resources you created in this tutorial -- *Note:* this is auto-generated and not all resources may be applicable for this tutorial:
#
# - Dataset
# - Pipeline
# - Model
# - Endpoint
# - Batch Job
# - Custom Job
# - Hyperparameter Tuning Job
# - Cloud Storage Bucket
# + id="cleanup:pipelines"
delete_dataset = True
delete_pipeline = True
delete_model = True
delete_endpoint = True
delete_batchjob = True
delete_customjob = True
delete_hptjob = True
delete_bucket = True
try:
if delete_model and "DISPLAY_NAME" in globals():
models = aip.Model.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
model = models[0]
aip.Model.delete(model)
print("Deleted model:", model)
except Exception as e:
print(e)
try:
if delete_endpoint and "DISPLAY_NAME" in globals():
endpoints = aip.Endpoint.list(
filter=f"display_name={DISPLAY_NAME}_endpoint", order_by="create_time"
)
endpoint = endpoints[0]
endpoint.undeploy_all()
aip.Endpoint.delete(endpoint.resource_name)
print("Deleted endpoint:", endpoint)
except Exception as e:
print(e)
if delete_dataset and "DISPLAY_NAME" in globals():
if "tabular" == "tabular":
try:
datasets = aip.TabularDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TabularDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "tabular" == "image":
try:
datasets = aip.ImageDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.ImageDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "tabular" == "text":
try:
datasets = aip.TextDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TextDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "tabular" == "video":
try:
datasets = aip.VideoDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.VideoDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
try:
if delete_pipeline and "DISPLAY_NAME" in globals():
pipelines = aip.PipelineJob.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
pipeline = pipelines[0]
aip.PipelineJob.delete(pipeline.resource_name)
print("Deleted pipeline:", pipeline)
except Exception as e:
print(e)
if delete_bucket and "BUCKET_NAME" in globals():
# ! gsutil rm -r $BUCKET_NAME
|
gc-ai-notebook-tutorials/tutorials/vertex_samples/pipelines/metrics_viz_run_compare_kfp.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Complex NetCDF to Zarr Recipe: TerraClimate
#
# ## About the Dataset
#
# From http://www.climatologylab.org/terraclimate.html:
#
# > TerraClimate is a dataset of monthly climate and climatic water balance for global terrestrial surfaces from 1958-2019. These data provide important inputs for ecological and hydrological studies at global scales that require high spatial resolution and time-varying data. All data have monthly temporal resolution and a ~4-km (1/24th degree) spatial resolution. The data cover the period from 1958-2019. We plan to update these data periodically (annually).
#
# ## What makes it tricky
#
# This is an advanced example that illustrates the following concepts
# - _MultiVariable recipe_: There is one file per year for a dozen different variables.
# - _Complex Preprocessing_: We want to apply different preprocessing depending on the variable. This example shows how.
# - _Inconsistent size of data in input files_: This means we have to scan each input file and cache its metadata before we can start writing the target.
#
# This recipe requires a new storage target, a `metadata_cache`. In this example, this is just another directory. You could hypothetically use a database or other key/value store for this.
from pangeo_forge.recipe import NetCDFtoZarrMultiVarSequentialRecipe
from pangeo_forge.patterns import VariableSequencePattern
import xarray as xr
# ## Define Filename Pattern
#
# To keep this example smaller, we just use two years instead of the whole record.
# +
target_chunks = {"lat": 1024, "lon": 1024, "time": 12}
# only do two years to keep the example small; it's still big!
years = list(range(1958, 1960))
variables = [
"aet",
"def",
"pet",
"ppt",
"q",
"soil",
"srad",
"swe",
"tmax",
"tmin",
"vap",
"ws",
"vpd",
"PDSI",
]
pattern = VariableSequencePattern(
fmt_string="https://climate.northwestknowledge.net/TERRACLIMATE-DATA/TerraClimate_{variable}_{year}.nc",
keys={'variable': variables, 'year': years}
)
pattern
# -
# ## Define Preprocessing Functions
#
# These functions apply masks for each variable to remove invalid data.
# +
rename_vars = {'PDSI': 'pdsi'}
mask_opts = {
"PDSI": ("lt", 10),
"aet": ("lt", 32767),
"def": ("lt", 32767),
"pet": ("lt", 32767),
"ppt": ("lt", 32767),
"ppt_station_influence": None,
"q": ("lt", 2147483647),
"soil": ("lt", 32767),
"srad": ("lt", 32767),
"swe": ("lt", 10000),
"tmax": ("lt", 200),
"tmax_station_influence": None,
"tmin": ("lt", 200),
"tmin_station_influence": None,
"vap": ("lt", 300),
"vap_station_influence": None,
"vpd": ("lt", 300),
"ws": ("lt", 200),
}
def apply_mask(key, da):
"""helper function to mask DataArrays based on a threshold value"""
if mask_opts.get(key, None):
op, val = mask_opts[key]
if op == "lt":
da = da.where(da < val)
elif op == "neq":
da = da.where(da != val)
return da
def preproc(ds):
"""custom preprocessing function for terraclimate data"""
rename = {}
station_influence = ds.get("station_influence", None)
if station_influence is not None:
ds = ds.drop_vars("station_influence")
var = list(ds.data_vars)[0]
if var in rename_vars:
rename[var] = rename_vars[var]
if "day" in ds.coords:
rename["day"] = "time"
if station_influence is not None:
ds[f"{var}_station_influence"] = station_influence
with xr.set_options(keep_attrs=True):
ds[var] = apply_mask(var, ds[var])
if rename:
ds = ds.rename(rename)
return ds
# -
# ## Define Recipe
#
# We are now ready to define the recipe.
# We also specify the desired chunks of the target dataset.
#
# A key property of this recipe is `nitems_per_input=None`, which triggers caching of input metadata.
# +
chunks = {"lat": 1024, "lon": 1024, "time": 12}
recipe = NetCDFtoZarrMultiVarSequentialRecipe(
input_pattern=pattern,
sequence_dim="time", # TODO: raise error if this is not specified
target_chunks=target_chunks,
nitems_per_input=None, # don't know how many timesteps in each file
process_chunk=preproc
)
recipe
# -
# ## Define Storage Targets
#
# Since our recipe needs to cache input metadata, we need to suply a `metadata_cache` target.
# +
import tempfile
from fsspec.implementations.local import LocalFileSystem
from pangeo_forge.storage import FSSpecTarget, CacheFSSpecTarget
fs_local = LocalFileSystem()
target_dir = tempfile.TemporaryDirectory()
target = FSSpecTarget(fs_local, target_dir.name)
cache_dir = tempfile.TemporaryDirectory()
cache_target = CacheFSSpecTarget(fs_local, cache_dir.name)
meta_dir = tempfile.TemporaryDirectory()
meta_store = FSSpecTarget(fs_local, meta_dir.name)
recipe.target = target
recipe.input_cache = cache_target
recipe.metadata_cache = meta_store
recipe
# -
# ## Execute with Prefect
#
# This produces A LOT of output because we turn on logging.
# +
# logging will display some interesting information about our recipe during execution
import logging
import sys
logging.basicConfig(
format='%(asctime)s [%(levelname)s] %(name)s - %(message)s',
level=logging.INFO,
datefmt='%Y-%m-%d %H:%M:%S',
stream=sys.stdout,
)
logger = logging.getLogger("pangeo_forge.recipe")
logger.setLevel(logging.INFO)
# -
from pangeo_forge.executors import PrefectPipelineExecutor
pipelines = recipe.to_pipelines()
executor = PrefectPipelineExecutor()
plan = executor.pipelines_to_plan(pipelines)
executor.execute_plan(plan)
# ## Check and Plot Target
ds_target = xr.open_zarr(target.get_mapper(), consolidated=True)
ds_target
# As an example calculation, we compute and plot the seasonal climatology of soil moisture.
with xr.set_options(keep_attrs=True):
soil_clim = ds_target.soil.groupby('time.season').mean('time').coarsen(lon=12, lat=12).mean()
soil_clim
soil_clim.plot(col='season', col_wrap=2, robust=True, figsize=(18, 8))
|
docs/tutorials/terraclimate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: tensorflow2env
# language: python
# name: tensorflow2env
# ---
# We begin similar to the tutorial:
import numpy as np
import matplotlib.pyplot as pp
data=np.loadtxt("../Datasets/weight-height.csv",skiprows=1,usecols=(1,2),delimiter=",")
data[:,0]*=2.54 #Here, we use the *= shorthand, which is the same as data[:,0]=data[:,0]*2.54
data[:,1]*=0.45359237
# The first exercise was to only plot the first N points. This is easy with Python's flexible tensor indexing, no for loops needed.
N=20
pp.scatter(data[:N,0],data[:N,1],marker=".")
pp.title("Relation of height and weight")
pp.xlabel("Height (centimeters)")
pp.ylabel("Weight (kilograms)")
# The second exercise was to visualize how the mean of height changes when you compute it from different amounts of data. The key lesson here is that mean computed from noisy data is also noisy, i.e., mean of random variables is also random variable.
# Above, we've already used the ":" symbol to denote "all indices". It can also be used for defining arbitrary ranges. Note the following:
# * The indexing is zero-based, i.e., index 1 is the second element and index 0 is the first.
# * A range a:b includes a but not b. Instead, the last index in the range is b-1.
#
# Thus, this is how you print three elements starting from the second one:
# +
#we will use up to this many data points
maxData=1000
#allocate a Numpy array for the results
means=np.zeros(maxData)
#loop over the ranges
for i in range(maxData):
means[i]=np.mean(data[:i+1,0])
pp.plot(means)
pp.title("Mean of height with different amounts of data")
pp.xlabel("Number of data points")
pp.ylabel("Mean")
|
Code/Jupyter/DataAndTensors_solutions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Functions
# We have used functions is past lessions. Functions have a name and parameters. Some of them return a result, others don't. We typically call them using `result = name(parameters)`.
#
# See also
# * [Python functions](https://www.tutorialspoint.com/python/python_functions.htm)
# * [List of built-in functions](https://docs.python.org/3/library/functions.html)
#
# Let's take a look at some functions, for example `print(text)` and `pow(x, y)`. The print function takes a parameter (or multiple parameters) and returns nothing:
result = print('Hello world')
result
# The [pow](https://docs.python.org/3/library/functions.html#pow) function has two parameters and returns a result:
result = pow(2, 3)
result
# ## Custom functions
# You can DEFine your own functions using the `def` statement. After the def statement, you should specify your functions' name and in brackets its parameters. Afterwards follows a colon `:` and all following lines of code which are indented are part of this function. A final `return` statement sends the result back to from where the function was called.
def sum_numbers(a, b):
result = a + b
return result
# You can then call your function as often as you like
sum_numbers(3, 4)
sum_numbers(5, 6)
# Sometimes, you want to save the result of your function in a variable.
c = sum_numbers(4, 5)
print(c)
# ## Simplify code using functions
# Assume you have a complicated algorithm which can tell you if a number if odd or even. Let's put this algorithm in a function and call it later on. For our algorithm, we will use the [modulo operator %](https://en.wikipedia.org/wiki/Modulo_operation).
def print_odd_or_even(number):
if number % 2 == 0:
print(number, "is even")
else:
print(number, "is odd")
print_odd_or_even(3)
print_odd_or_even(4)
print_odd_or_even(10)
# Thus, instead of writing the same `if-else` block again and again, we can just call our custom `print_odd_or_even` function.
# ## Documenting functions
# You can document what a function does in its so called doc string. The doc string follows right after the functions header and looks like this:
def square(number):
'''
Squares a number by multiplying it with itself and returns its result.
'''
return number * number
# You can then later read the documentation of the function like this:
print(square.__doc__)
# Also try this if you want to have the docstring shown side-by-side in your notebook:
# +
# square?
# -
# By the way, you can do this with any function:
import math
print(math.sqrt.__doc__)
print(math.exp.__doc__)
# ## Exercise
# Write a function that takes two parameters: `number_of_points_in_exam` and `number_of_total_points_in_exam` and returns a grade from 1 to 5. Students with > 95% of the points get grade 1, above 80% they get grade 2, above 60% grade 3 and above 50% grade 4. Students with less than 50% get grade 5 and have to repeat the exam. Then, call the function for three students who had 15, 25 and 29 points in an exam with 30 total points.
|
docs/02_python_basics/09_custom_functions.ipynb
|
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# export
import time,os,shutil
from sys import stdout
from warnings import warn
from fastprogress.core import *
# +
#default_exp fastprogress
# -
# ## Base class
#export
class ProgressBar():
update_every,first_its = 0.2,5
def __init__(self, gen, total=None, display=True, leave=True, parent=None, master=None, comment=''):
self.gen,self.parent,self.master,self.comment = gen,parent,master,comment
self.total = len(gen) if total is None else total
self.last_v = 0
if parent is None: self.leave,self.display = leave,display
else:
self.leave,self.display=False,False
parent.add_child(self)
self.last_v = None
def on_iter_begin(self):
if self.master is not None: self.master.on_iter_begin()
def on_interrupt(self):
if self.master is not None: self.master.on_interrupt()
def on_iter_end(self):
if self.master is not None: self.master.on_iter_end()
def on_update(self, val, text): pass
def __iter__(self):
if self.total != 0: self.update(0)
try:
for i,o in enumerate(self.gen):
if i >= self.total: break
yield o
self.update(i+1)
except Exception as e:
self.on_interrupt()
raise e
def update(self, val):
if self.last_v is None:
self.on_iter_begin()
self.last_v = 0
if val == 0:
self.start_t = self.last_t = time.time()
self.pred_t,self.last_v,self.wait_for = 0,0,1
self.update_bar(0)
elif val <= self.first_its or val >= self.last_v + self.wait_for or val >= self.total:
cur_t = time.time()
avg_t = (cur_t - self.start_t) / val
self.wait_for = max(int(self.update_every / (avg_t+1e-8)),1)
self.pred_t = avg_t * self.total
self.last_v,self.last_t = val,cur_t
self.update_bar(val)
if val >= self.total:
self.on_iter_end()
self.last_v = None
def update_bar(self, val):
elapsed_t = self.last_t - self.start_t
remaining_t = format_time(self.pred_t - elapsed_t)
elapsed_t = format_time(elapsed_t)
end = '' if len(self.comment) == 0 else f' {self.comment}'
if self.total == 0:
warn("Your generator is empty.")
self.on_update(0, '100% [0/0]')
else: self.on_update(val, f'{100 * val/self.total:.2f}% [{val}/{self.total} {elapsed_t}<{remaining_t}{end}]')
class VerboseProgressBar(ProgressBar):
def on_iter_begin(self): super().on_iter_begin(); print("on_iter_begin")
def on_interrupt(self): print("on_interrupt")
def on_iter_end(self): print("on_iter_end"); super().on_iter_end()
def on_update(self, val, text): print(f"on_update {val}")
from contextlib import redirect_stdout
import io
# +
tst_pb = VerboseProgressBar(range(6))
s = io.StringIO()
with redirect_stdout(s):
for i in tst_pb: time.sleep(0.1)
assert s.getvalue() == '\n'.join(['on_iter_begin'] + [f'on_update {i}' for i in range(7)] + ['on_iter_end']) + '\n'
# +
tst_pb = VerboseProgressBar(range(6))
s = io.StringIO()
with redirect_stdout(s):
for i in range(7):
tst_pb.update(i)
time.sleep(0.1)
assert s.getvalue() == '\n'.join(['on_iter_begin'] + [f'on_update {i}' for i in range(7)] + ['on_iter_end']) + '\n'
# -
#export
class MasterBar(ProgressBar):
def __init__(self, gen, cls, total=None):
self.main_bar = cls(gen, total=total, display=False, master=self)
def on_iter_begin(self): pass
def on_interrupt(self): pass
def on_iter_end(self): pass
def add_child(self, child): pass
def write(self, line): pass
def update_graph(self, graphs, x_bounds, y_bounds): pass
def __iter__(self):
for o in self.main_bar:
yield o
def update(self, val): self.main_bar.update(val)
class VerboseMasterBar(MasterBar):
def __init__(self, gen, total=None): super().__init__(gen, VerboseProgressBar, total=total)
def on_iter_begin(self): print("master_on_iter_begin")
def on_interrupt(self): print("master_on_interrupt")
def on_iter_end(self): print("master_on_iter_end")
#def on_update(self, val, text): print(f"master_on_update {val}")
tst_mb = VerboseMasterBar(range(6))
for i in tst_mb: time.sleep(0.1)
#hide
#Test an empty progress bar doesn't crash
for i in ProgressBar([]): pass
# ## Notebook progress bars
#export
if IN_NOTEBOOK:
try:
from IPython.display import clear_output, display, HTML
import matplotlib.pyplot as plt
except:
warn("Couldn't import ipywidgets properly, progress bar will use console behavior")
IN_NOTEBOOK = False
#export
class NBProgressBar(ProgressBar):
def on_iter_begin(self):
super().on_iter_begin()
self.progress = html_progress_bar(0, self.total, "")
if self.display: self.out = display(HTML(self.progress), display_id=True)
self.is_active=True
def on_interrupt(self):
self.on_update(0, 'Interrupted', interrupted=True)
super().on_interrupt()
self.on_iter_end()
def on_iter_end(self):
if not self.leave and self.display: self.out.update(HTML(''))
self.is_active=False
super().on_iter_end()
def on_update(self, val, text, interrupted=False):
self.progress = html_progress_bar(val, self.total, text, interrupted)
if self.display: self.out.update(HTML(self.progress))
elif self.parent is not None: self.parent.show()
tst = NBProgressBar(range(100))
for i in tst: time.sleep(0.05)
tst = NBProgressBar(range(100))
for i in range(50):
time.sleep(0.05)
tst.update(i)
tst.on_interrupt()
#hide
for i in NBProgressBar([]): pass
#export
class NBMasterBar(MasterBar):
names = ['train', 'valid']
def __init__(self, gen, total=None, hide_graph=False, order=None, clean_on_interrupt=False, total_time=False):
super().__init__(gen, NBProgressBar, total)
if order is None: order = ['pb1', 'text', 'pb2']
self.hide_graph,self.order = hide_graph,order
self.report,self.clean_on_interrupt,self.total_time = [],clean_on_interrupt,total_time
self.inner_dict = {'pb1':self.main_bar, 'text':""}
self.text,self.lines = "",[]
def on_iter_begin(self):
self.html_code = '\n'.join([html_progress_bar(0, self.main_bar.total, ""), ""])
self.out = display(HTML(self.html_code), display_id=True)
def on_interrupt(self):
if self.clean_on_interrupt: self.out.update(HTML(''))
def on_iter_end(self):
if hasattr(self, 'imgs_fig'):
plt.close()
self.imgs_out.update(self.imgs_fig)
if hasattr(self, 'graph_fig'):
plt.close()
self.graph_out.update(self.graph_fig)
if self.text.endswith('<p>'): self.text = self.text[:-3]
if self.total_time:
total_time = format_time(time.time() - self.main_bar.start_t)
self.text = f'Total time: {total_time} <p>' + self.text
self.out.update(HTML(self.text))
def add_child(self, child):
self.child = child
self.inner_dict['pb2'] = self.child
#self.show()
def show(self):
self.inner_dict['text'] = self.text
to_show = [name for name in self.order if name in self.inner_dict.keys()]
self.html_code = '\n'.join([getattr(self.inner_dict[n], 'progress', self.inner_dict[n]) for n in to_show])
self.out.update(HTML(self.html_code))
def write(self, line, table=False):
if not table: self.text += line + "<p>"
else:
self.lines.append(line)
self.text = text2html_table(self.lines)
def show_imgs(self, imgs, titles=None, cols=4, imgsize=4, figsize=None):
if self.hide_graph: return
rows = len(imgs)//cols if len(imgs)%cols == 0 else len(imgs)//cols + 1
plt.close()
if figsize is None: figsize = (imgsize*cols, imgsize*rows)
self.imgs_fig, imgs_axs = plt.subplots(rows, cols, figsize=figsize)
if titles is None: titles = [None] * len(imgs)
for img, ax, title in zip(imgs, imgs_axs.flatten(), titles): img.show(ax=ax, title=title)
for ax in imgs_axs.flatten()[len(imgs):]: ax.axis('off')
if not hasattr(self, 'imgs_out'): self.imgs_out = display(self.imgs_fig, display_id=True)
else: self.imgs_out.update(self.imgs_fig)
def update_graph(self, graphs, x_bounds=None, y_bounds=None, figsize=(6,4)):
if self.hide_graph: return
if not hasattr(self, 'graph_fig'):
self.graph_fig, self.graph_ax = plt.subplots(1, figsize=figsize)
self.graph_out = display(self.graph_ax.figure, display_id=True)
self.graph_ax.clear()
if len(self.names) < len(graphs): self.names += [''] * (len(graphs) - len(self.names))
for g,n in zip(graphs,self.names): self.graph_ax.plot(*g, label=n)
self.graph_ax.legend(loc='upper right')
if x_bounds is not None: self.graph_ax.set_xlim(*x_bounds)
if y_bounds is not None: self.graph_ax.set_ylim(*y_bounds)
self.graph_out.update(self.graph_ax.figure)
mb = NBMasterBar(range(5))
for i in mb:
for j in NBProgressBar(range(10), parent=mb, comment=f'first bar stat'):
time.sleep(0.01)
#mb.child.comment = f'second bar stat'
mb.write(f'Finished loop {i}.')
mb = NBMasterBar(range(5))
mb.update(0)
for i in range(5):
for j in NBProgressBar(range(10), parent=mb):
time.sleep(0.01)
#mb.child.comment = f'second bar stat'
mb.main_bar.comment = f'first bar stat'
mb.write(f'Finished loop {i}.')
mb.update(i+1)
# ## Console progress bars
#export
NO_BAR = False
WRITER_FN = print
FLUSH = True
SAVE_PATH = None
SAVE_APPEND = False
MAX_COLS = 160
#export
def printing():
return False if NO_BAR else (stdout.isatty() or IN_NOTEBOOK)
#export
class ConsoleProgressBar(ProgressBar):
fill:str='█'
end:str='\r'
def __init__(self, gen, total=None, display=True, leave=True, parent=None, master=None, txt_len=60):
self.cols,_ = shutil.get_terminal_size((100, 40))
if self.cols > MAX_COLS: self.cols=MAX_COLS
self.length = self.cols-txt_len
self.max_len,self.prefix = 0,''
#In case the filling char returns an encoding error
try: print(self.fill, end='\r', flush=FLUSH)
except: self.fill = 'X'
super().__init__(gen, total, display, leave, parent, master)
def on_interrupt(self):
super().on_interrupt()
self.on_iter_end()
def on_iter_end(self):
if not self.leave and printing():
print(f'\r{self.prefix}' + ' ' * (self.max_len - len(f'\r{self.prefix}')), end='\r', flush=FLUSH)
super().on_iter_end()
def on_update(self, val, text):
if self.display:
if self.length > self.cols-len(text)-len(self.prefix)-4:
self.length = self.cols-len(text)-len(self.prefix)-4
filled_len = int(self.length * val // self.total) if self.total else 0
bar = self.fill * filled_len + '-' * (self.length - filled_len)
to_write = f'\r{self.prefix} |{bar}| {text}'
if val >= self.total: end = '\r'
else: end = self.end
if len(to_write) > self.max_len: self.max_len=len(to_write)
if printing(): WRITER_FN(to_write, end=end, flush=FLUSH)
tst = ConsoleProgressBar(range(100))
for i in tst: time.sleep(0.05)
tst = ConsoleProgressBar(range(100))
for i in range(50):
time.sleep(0.05)
tst.update(i)
tst.on_interrupt()
#export
def print_and_maybe_save(line):
WRITER_FN(line)
if SAVE_PATH is not None:
attr = "a" if os.path.exists(SAVE_PATH) else "w"
with open(SAVE_PATH, attr) as f: f.write(line + '\n')
#export
class ConsoleMasterBar(MasterBar):
def __init__(self, gen, total=None, hide_graph=False, order=None, clean_on_interrupt=False, total_time=False):
super().__init__(gen, ConsoleProgressBar, total)
self.total_time = total_time
def add_child(self, child):
self.child = child
self.child.prefix = f'Epoch {self.main_bar.last_v+1}/{self.main_bar.total} :'
self.child.display = True
def on_iter_begin(self):
super().on_iter_begin()
if SAVE_PATH is not None and os.path.exists(SAVE_PATH) and not SAVE_APPEND:
with open(SAVE_PATH, 'w') as f: f.write('')
def write(self, line, table=False):
if table:
text = ''
if not hasattr(self, 'names'):
self.names = [name + ' ' * (8-len(name)) if len(name) < 8 else name for name in line]
text = ' '.join(self.names)
else:
for (t,name) in zip(line,self.names): text += t + ' ' * (2 + len(name)-len(t))
print_and_maybe_save(text)
else: print_and_maybe_save(line)
if self.total_time:
total_time = format_time(time() - self.start_t)
print_and_maybe_save(f'Total time: {total_time}')
def show_imgs(*args): pass
def update_graph(*args): pass
mb = ConsoleMasterBar(range(5))
for i in mb:
for j in ConsoleProgressBar(range(10), parent=mb):
time.sleep(0.01)
#mb.child.comment = f'second bar stat'
mb.main_bar.comment = f'first bar stat'
mb.write(f'Finished loop {i}.')
mb = ConsoleMasterBar(range(5))
mb.update(0)
for i in range(5):
for j in ConsoleProgressBar(range(10), parent=mb):
time.sleep(0.01)
#mb.child.comment = f'second bar stat'
mb.main_bar.comment = f'first bar stat'
mb.write(f'Finished loop {i}.')
mb.update(i+1)
#export
if IN_NOTEBOOK: master_bar, progress_bar = NBMasterBar, NBProgressBar
else: master_bar, progress_bar = ConsoleMasterBar, ConsoleProgressBar
#export
_all_ = ['master_bar', 'progress_bar']
#export
def force_console_behavior():
"Return the console progress bars"
return ConsoleMasterBar, ConsoleProgressBar
#export
def workaround_empty_console_output():
"Change console output behaviour to correctly show progress in consoles not recognizing \r at the end of line"
ConsoleProgressBar.end = ''
# ## Export -
from nbdev.export import notebook2script
notebook2script()
|
nbs/01_fastprogress.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from keras.datasets import mnist
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# +
from keras.datasets import mnist
from scipy.misc import imsave
import numpy as np
import math
(X_train, y_train), (X_test, y_test) = mnist.load_data()
#generate a separate image for training and test sets
for (dataset, name) in [(X_train, "mnist_train"), (X_test, "mnist_test")]:
#We will make a square grid which can contain s*s images
s = math.ceil(math.sqrt(dataset.shape[0]))
#Our image will be of size w*h. In the case of MNIST w=h
w = s*dataset.shape[1]
h = s*dataset.shape[2]
#Create empty tensor
allimgs = np.empty([w, h])
#Fill the newly created tensor
for index in range(dataset.shape[0]):
iOffset = (index%s)*dataset.shape[1] #remainder of the Euclidian division
jOffset = (index//s)*dataset.shape[2] #quotient of the Euclidian division
for i in range(dataset.shape[1]):
for j in range(dataset.shape[2]):
allimgs[iOffset+i,jOffset+j] = dataset[index, i, j] #Copy the pixel value
#Generate the image
imsave(name+".png", allimgs)
# +
import numpy as np
np.random.seed(1337) # for reproducibility
import os
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.optimizers import RMSprop
from keras.utils import np_utils
batch_size = 128 #Number of images used in each optimization step
nb_classes = 10 #One class per digit
nb_epoch = 20 #Number of times the whole data is used to learn
(X_train, y_train), (X_test, y_test) = mnist.load_data()
#Flatten the data, MLP doesn't use the 2D structure of the data. 784 = 28*28
X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)
#Make the value floats in [0;1] instead of int in [0;255]
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
#Display the shapes to check if everything's ok
print(X_train.shape[0], 'train samples')
print(X_test.shape[0], 'test samples')
# convert class vectors to binary class matrices (ie one-hot vectors)
Y_train = np_utils.to_categorical(y_train, nb_classes)
Y_test = np_utils.to_categorical(y_test, nb_classes)
#Define the model achitecture
model = Sequential()
model.add(Dense(512, input_shape=(784,)))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))
model.add(Dense(10)) #Last layer with one output per class
model.add(Activation('softmax')) #We want a score simlar to a probability for each class
#Use rmsprop to do the gradient descent see http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
#and http://cs231n.github.io/neural-networks-3/#ada
rms = RMSprop()
#The function to optimize is the cross entropy between the true label and the output (softmax) of the model
model.compile(loss='categorical_crossentropy', optimizer=rms, metrics=["accuracy"])
#Make the model learn
model.fit(X_train, Y_train,
batch_size=batch_size, nb_epoch=nb_epoch,
verbose=2,
validation_data=(X_test, Y_test))
#Evaluate how the model does on the test set
score = model.evaluate(X_test, Y_test, verbose=0)
print('Test score:', score[0])
print('Test accuracy:', score[1])
# -
|
python/deep_learning/Keras/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import numpy as np
import os
import glob as gb
import cv2 as cv
import matplotlib.pyplot as plt
import pandas as pd
# # Data preparation
df=pd.read_csv('./train.csv')
df.head()
df.info()
from sklearn.model_selection import train_test_split
train_set, validation_set = train_test_split(df, test_size=0.2, random_state=42)
print(train_set.shape, validation_set.shape)
import shutil
from shutil import copyfile
source= "./Images"
TRAIN_DIR="./temp/train"
# +
for index, data in train_set.iterrows():
labels=df.columns[np.argmax(data[1:])]
filepath=os.path.join(source, "Train_"+str(index)+'.jpg')
destination=os.path.join(TRAIN_DIR, labels, "Train_"+str(index)+".jpg")
copyfile(filepath, destination)
for subdir in os.listdir(TRAIN_DIR):
print(subdir, len(os.listdir(os.path.join(TRAIN_DIR, subdir))))
# -
|
Crop ditection/ crop detection.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Q#
# language: qsharp
# name: iqsharp
# ---
# # Quantum error correction - bit-flip code quantum kata
#
# The **"Quantum error correction - bit-flip code"** quantum kata is a series of exercises designed to get you familiar with quantum error correction (QEC) and programming in Q#. It introduces you to the simplest of QEC codes - the three-qubit bit-flip code, which encodes each logical qubit in three physical qubits and protects against single bit-flip error (equivalent to applying an X gate). In practice quantum systems can have other types of errors, which will be considered in the following katas on quantum error correction.
#
# Each task is wrapped in one operation preceded by the description of the task.
# Your goal is to fill in the blank (marked with // ... comment)
# with some Q# code that solves the task. To verify your answer, run the cell using Ctrl/⌘+Enter.
#
# The tasks are given in approximate order of increasing difficulty.
# To begin, first prepare this notebook for execution (if you skip this step, you'll get "Syntax does not match any known patterns" error when you try to execute Q# code in the next cells; if you skip the second step, you'll get "Invalid test name" error):
%package Microsoft.Quantum.Katas::0.10.1910.3107
# > The package versions in the output of the cell above should always match. If you are running the Notebooks locally and the versions do not match, please install the IQ# version that matches the version of the `Microsoft.Quantum.Katas` package.
# > <details>
# > <summary><u>How to install the right IQ# version</u></summary>
# > For example, if the version of `Microsoft.Quantum.Katas` package above is 0.6.1905.301, the installation steps are as follows:
# >
# > 1. Stop the kernel.
# > 2. Uninstall the existing version of IQ#:
# > dotnet tool uninstall microsoft.quantum.iqsharp -g
# > 3. Install the matching version:
# > dotnet tool install microsoft.quantum.iqsharp -g --version 0.6.1905.301
# > 4. Reinstall the kernel:
# > dotnet iqsharp install
# > 5. Restart the Notebook.
# > </details>
#
%workspace reload
# ### Task 1. Parity Measurements
#
# **Input:** three qubits (stored as an array of length 3) in an unknown basis state or in a superposition of basis states of the same parity.
#
# **Output:** the parity of this state encoded as a value of `Result` type: `Zero` for parity 0 and `One` for parity 1. The parity of basis state $| x_{0} x_{1} x_{2}\rangle$ is defined as $(x_{0} \otimes x_{1} \otimes x_{2})$. After applying the operation the state of the qubits should not change. You can use exactly one measurement.
#
# **Example:** $|000 \rangle$, $|101\rangle$ and $|011\rangle$ all have parity 0, while $|010\rangle$ and $|111\rangle$ have parity 1.
# +
%kata T01_MeasureParity_Test
operation MeasureParity (register : Qubit[]) : Result {
// ...
return Zero;
}
# -
# ### Task 2. Encoding Codewords
#
# **Input**: three qubits in the state $| \psi \rangle \otimes |00\rangle$, where $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ is the state of the first qubit, i.e., `register[0]`.
#
# **Goal**: create a state $|\bar{\psi}\rangle := \alpha |000\rangle + \beta |111\rangle$ on these qubits.
# +
%kata T02_Encode_Test
operation Encode (register : Qubit[]) : Unit {
// ...
}
# -
# ### Task 3. Error Detection I
#
# **Inputs:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in the state $X\mathbb{11} |\bar{\psi}\rangle = \alpha |100\rangle + \beta |011\rangle$.
#
# > Note that the second state is the first state with X applied to the first qubit, which corresponds to an X error happening on the first qubit.
#
# **Output:** `Zero` if the input is $|\bar{\psi}\rangle$ (state without the error), `One` if the input is $X\mathbb{11} |\bar{\psi}\rangle$ (state with the error). After applying the operation the state of the qubits should not change.
# +
%kata T03_DetectErrorOnLeftQubit_Test
operation DetectErrorOnLeftQubit (register : Qubit[]) : Result {
// ...
return ...;
}
# -
# ### Task 4. Error Correction I
#
# **Input:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in the state $X\mathbb{11} |\bar{\psi}\rangle = \alpha |100\rangle + \beta |011\rangle$.
#
# **Goal:** make sure that the qubits are returned to the state $|\bar{\psi}\rangle$ (i.e., determine whether an X error has occurred, and if so, fix it).
#
# <br/>
# <details>
# <summary>Need a hint? Click here </summary>
# You can use task 3 to figure out which state you are given.
# </details>
# +
%kata T04_CorrectErrorOnLeftQubit_Test
operation CorrectErrorOnLeftQubit (register : Qubit[]) : Unit {
// ...
}
# -
# ### Task 5. Error Detection II
#
# **Input:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in one of the states $X\mathbb{11} |\bar{\psi}\rangle$, $\mathbb{1}X\mathbb{1} |\bar{\psi}\rangle$ or $\mathbb{11}X |\bar{\psi}\rangle$ (i.e., state $|\bar{\psi}\rangle$ with an X error applied to one of the qubits).
#
# **Goal:** determine whether an X error has occurred, and if so, on which qubit.
#
# | Error | Output |
# |---------------------------|--------|
# | None | 0 |
# | $X\mathbb{11}$ | 1 |
# | $\mathbb{1}X\mathbb{1}$ | 2 |
# | $\mathbb{11}X$ | 3 |
#
# After applying the operation the state of the qubits should not change.
# +
%kata T05_DetectErrorOnAnyQubit_Test
operation DetectErrorOnAnyQubit (register : Qubit[]) : Int {
// ...
return -1;
}
# -
# ### Task 6. Error Correction II
#
# **Input:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in one of the states $X\mathbb{11} |\bar{\psi}\rangle$, $\mathbb{1}X\mathbb{1} |\bar{\psi}\rangle$ or $\mathbb{11}X |\bar{\psi}\rangle$ (i.e., the qubits start in state $|\bar{\psi}\rangle$ with an X error possibly applied to one of the qubits).
#
# **Goal:** make sure that the qubits are returned to the state $|\bar{\psi}\rangle$ (i.e., determine whether an X error has occurred on any qubit, and if so, fix it).
# +
%kata T06_CorrectErrorOnAnyQubit_Test
operation CorrectErrorOnAnyQubit (register : Qubit[]) : Unit {
// ...
}
# -
# > All the tasks in this kata have been dealing with X errors on single qubit. The bit-flip code doesn't allow one to detect or correct a Z error or multiple X errors. Indeed,
# * A Z error on a logical state $|\psi\rangle = \alpha |0\rangle + \beta |1\rangle$ encoded using the bit-flip code would convert the encoded state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ into $\alpha |000\rangle - \beta |111\rangle$, which is a correct code word for logical state $\alpha |0\rangle - \beta |1\rangle$.
# * Two X errors (say, on qubits 1 and 2) would convert $|\bar{\psi}\rangle$ to $\alpha |110\rangle + \beta |001\rangle$, which is a code word for logical state $\beta |0\rangle + \alpha |1\rangle$ with one X error on qubit 3.
# ### Task 7. Logical X Gate
#
# **Input:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in one of the states $X\mathbb{11} |\bar{\psi}\rangle$, $\mathbb{1}X\mathbb{1} |\bar{\psi}\rangle$ or $\mathbb{11}X |\bar{\psi}\rangle$ (i.e., state $|\bar{\psi}\rangle$ with an X error applied to one of the qubits).
#
# **Goal:** apply a logical X operator, i.e., convert the qubits to the state $\bar{X} |\bar{\psi}\rangle = \beta |000\rangle + \alpha |111\rangle$ or one of the states that can be represented as $\bar{X} |\bar{\psi}\rangle$ with an X error applied to one of the qubits (for example, $\beta |010\rangle + \alpha |101\rangle$). If the state has an error, you can fix it, but this is not necessary.
# +
%kata T07_LogicalX_Test
operation LogicalX (register : Qubit[]) : Unit {
// ...
}
# -
# ### Task 8. Logical Z Gate
#
# **Input:** three qubits that are either in the state $|\bar{\psi}\rangle = \alpha |000\rangle + \beta |111\rangle$ or in one of the states $X\mathbb{11} |\bar{\psi}\rangle$, $\mathbb{1}X\mathbb{1} |\bar{\psi}\rangle$ or $\mathbb{11}X |\bar{\psi}\rangle$ (i.e., state $|\bar{\psi}\rangle$ with an X error applied to one of the qubits).
#
# **Goal:** apply a logical Z operator, i.e., convert the qubits to the state $\bar{Z} \bar{\psi}\rangle = \alpha |000\rangle - \beta |111\rangle$ or one of the states that can be represented as $\bar{Z} |\bar{\psi}\rangle$ with an X error applied to one of the qubits (for example, $\alpha |010\rangle - \beta |101\rangle$ ). If the state has an error, you can fix it, but this is not necessary.
# +
%kata T08_LogicalZ_Test
operation LogicalZ (register : Qubit[]) : Unit {
// ...
}
|
QEC_BitFlipCode/QEC_BitFlipCode.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="NXW9aGLroXsV"
# <img src="https://miro.medium.com/max/2652/1*eTkBMyqdg9JodNcG_O4-Kw.jpeg" width="100%">
#
# [Image Source](https://medium.com/stanford-ai-for-healthcare/its-a-no-brainer-deep-learning-for-brain-mr-images-f60116397472)
#
# # Brain Tumor Auto-Segmentation for Magnetic Resonance Imaging (MRI)
# Welcome to the final part of the "Artificial Intelligence for Medicine" course 1!
#
# You will learn how to build a neural network to automatically segment tumor regions in brain, using [MRI (Magnetic Resonance Imaging](https://en.wikipedia.org/wiki/Magnetic_resonance_imaging)) scans.
#
# The MRI scan is one of the most common image modalities that we encounter in the radiology field.
# Other data modalities include:
# - [Computer Tomography (CT)](https://en.wikipedia.org/wiki/CT_scan),
# - [Ultrasound](https://en.wikipedia.org/wiki/Ultrasound)
# - [X-Rays](https://en.wikipedia.org/wiki/X-ray).
#
# In this assignment we will be focusing on MRIs but many of our learnings applies to other mentioned modalities as well. We'll walk you through some of the steps of training a deep learning model for segmentation.
#
# **You will learn:**
#
# - What is in an MR image
# - Standard data preparation techniques for MRI datasets
# - Metrics and loss functions for segmentation
# - Visualizing and evaluating segmentation models
# -
# ## Outline
# Use these links to jump to particular sections of this assignment!
#
# - [1. Dataset](#1)
# - [1.1 What is an MRI?](#1-1)
# - [1.2 MRI Data Processing](#1-2)
# - [1.3 Exploring the Dataset](#1-3)
# - [1.4 Data Preprocessing](#1-4)
# - [1.4.1 Sub-volume Sampling](#1-4-1)
# - [1.4.2 Standardization](#1-4-2)
# - [2. Model: 3D U-Net](#2)
# - [3. Metrics](#3)
# - [3.1 Dice Coefficient](#3-1)
# - [3.2 Soft Dice Loss](#3-2)
# - [4. Training](#4)
# - [5. Evaluation](#5)
# - [5.1 Overall Performance](#5-1)
# - [5.2 Patch-level Predictions](#5-2)
# - [5.3 Running on Entire Scans](#5-3)
# + [markdown] colab_type="text" id="pTHrazBFcAtl"
# ## Packages
#
# In this assignment, we'll make use of the following packages:
#
# - `keras` is a framework for building deep learning models.
# - `keras.backend` allows us to perform math operations on tensors.
# - `nibabel` will let us extract the images and labels from the files in our dataset.
# - `numpy` is a library for mathematical and scientific operations.
# - `pandas` is what we'll use to manipulate our data.
#
# ## Import Packages
#
# Run the next cell to import all the necessary packages, dependencies and custom util functions.
# + colab={"base_uri": "https://localhost:8080/", "height": 148} colab_type="code" id="sJz-IbUycEhT" outputId="49ae7bfe-c506-4b1a-c6ea-7a831bedfc09"
import keras
import json
import numpy as np
import pandas as pd
import nibabel as nib
import matplotlib.pyplot as plt
from tensorflow.keras import backend as K
import util
# + [markdown] colab_type="text" id="B563bDC1hUvr"
# <a name="1"></a>
# # 1 Dataset
# <a name="1-1"></a>
# ## 1.1 What is an MRI?
#
# Magnetic resonance imaging (MRI) is an advanced imaging technique that is used to observe a variety of diseases and parts of the body.
#
# As we will see later, neural networks can analyze these images individually (as a radiologist would) or combine them into a single 3D volume to make predictions.
#
# At a high level, MRI works by measuring the radio waves emitting by atoms subjected to a magnetic field.
#
# <img src="https://miro.medium.com/max/1740/1*yC1Bt3IOzNv8Pp7t1v7F1Q.png">
#
# In this assignment, we'll build a multi-class segmentation model. We'll identify 3 different abnormalities in each image: edemas, non-enhancing tumors, and enhancing tumors.
#
# <a name="1-2"></a>
# -
# ## 1.2 MRI Data Processing
#
# We often encounter MR images in the [DICOM format](https://en.wikipedia.org/wiki/DICOM).
# - The DICOM format is the output format for most commercial MRI scanners. This type of data can be processed using the [pydicom](https://pydicom.github.io/pydicom/stable/getting_started.html) Python library.
#
# In this assignment, we will be using the data from the [Decathlon 10 Challenge](https://decathlon-10.grand-challenge.org). This data has been mostly pre-processed for the competition participants, however in real practice, MRI data needs to be significantly pre-preprocessed before we can use it to train our models.
# + [markdown] colab_type="text" id="aTg4vp-Eo86-"
# <a name="1-3"></a>
# ## 1.3 Exploring the Dataset
#
# Our dataset is stored in the [NifTI-1 format](https://nifti.nimh.nih.gov/nifti-1/) and we will be using the [NiBabel library](https://github.com/nipy/nibabel) to interact with the files. Each training sample is composed of two separate files:
#
# The first file is an image file containing a 4D array of MR image in the shape of (240, 240, 155, 4).
# - The first 3 dimensions are the X, Y, and Z values for each point in the 3D volume, which is commonly called a voxel.
# - The 4th dimension is the values for 4 different sequences
# - 0: FLAIR: "Fluid Attenuated Inversion Recovery" (FLAIR)
# - 1: T1w: "T1-weighted"
# - 2: t1gd: "T1-weighted with gadolinium contrast enhancement" (T1-Gd)
# - 3: T2w: "T2-weighted"
#
# The second file in each training example is a label file containing a 3D array with the shape of (240, 240, 155).
# - The integer values in this array indicate the "label" for each voxel in the corresponding image files:
# - 0: background
# - 1: edema
# - 2: non-enhancing tumor
# - 3: enhancing tumor
#
# We have access to a total of 484 training images which we will be splitting into a training (80%) and validation (20%) dataset.
#
# Let's begin by looking at one single case and visualizing the data! You have access to 10 different cases via this notebook and we strongly encourage you to explore the data further on your own.
# + [markdown] colab_type="text" id="Gqgu96ccW0cJ"
# We'll use the [NiBabel library](https://nipy.org/nibabel/nibabel_images.html) to load the image and label for a case. The function is shown below to give you a sense of how it works.
# + colab={} colab_type="code" id="AoW-WFWNW0cN"
# set home directory and data directory
HOME_DIR = "./BraTS-Data/"
DATA_DIR = HOME_DIR
def load_case(image_nifty_file, label_nifty_file):
# load the image and label file, get the image content and return a numpy array for each
image = np.array(nib.load(image_nifty_file).get_fdata())
label = np.array(nib.load(label_nifty_file).get_fdata())
return image, label
# + [markdown] colab_type="text" id="CzRraO9TW0cT"
# We'll now visualize an example. For this, we use a pre-defined function we have written in the `util.py` file that uses `matplotlib` to generate a summary of the image.
#
# The colors correspond to each class.
# - Red is edema
# - Green is a non-enhancing tumor
# - Blue is an enhancing tumor.
#
# Do feel free to look at this function at your own time to understand how this is achieved.
# + colab={"base_uri": "https://localhost:8080/", "height": 457} colab_type="code" id="ihLR2ZD-W0cU" outputId="dcf534ac-8c15-46d5-9851-a0fe35e05411"
image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
image = util.get_labeled_image(image, label)
util.plot_image_grid(image)
# + [markdown] colab_type="text" id="14GxIOrQW0ce"
# We've also written a utility function which generates a GIF that shows what it looks like to iterate over each axis.
# + colab={"base_uri": "https://localhost:8080/", "height": 257} colab_type="code" id="TJubVx44W0cf" outputId="a5ac10ef-be99-491f-cc04-1ace92434e25"
image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
util.visualize_data_gif(util.get_labeled_image(image, label))
# -
# **Reminder:** You can explore more images in the `imagesTr` directory by changing the image name file.
# + [markdown] colab_type="text" id="dulCuzOnW0ch"
# <a name="1-4"></a>
# ## 1.4 Data Preprocessing using patches
#
# While our dataset is provided to us post-registration and in the NIfTI format, we still have to do some minor pre-processing before feeding the data to our model.
#
# ##### Generate sub-volumes
#
# We are going to first generate "patches" of our data which you can think of as sub-volumes of the whole MR images.
# - The reason that we are generating patches is because a network that can process the entire volume at once will simply not fit inside our current environment's memory/GPU.
# - Therefore we will be using this common technique to generate spatially consistent sub-volumes of our data, which can be fed into our network.
# - Specifically, we will be generating randomly sampled sub-volumes of shape \[160, 160, 16\] from our images.
# - Furthermore, given that a large portion of the MRI volumes are just brain tissue or black background without any tumors, we want to make sure that we pick patches that at least include some amount of tumor data.
# - Therefore, we are only going to pick patches that have at most 95% non-tumor regions (so at least 5% tumor).
# - We do this by filtering the volumes based on the values present in the background labels.
#
# ##### Standardization (mean 0, stdev 1)
#
# Lastly, given that the values in MR images cover a very wide range, we will standardize the values to have a mean of zero and standard deviation of 1.
# - This is a common technique in deep image processing since standardization makes it much easier for the network to learn.
#
# Let's walk through these steps in the following exercises.
# + [markdown] colab_type="text" id="H8GLemPeW0cj"
# <a name="1-4-1"></a>
# ### 1.4.1 Sub-volume Sampling
# Fill in the function below takes in:
# - a 4D image (shape: \[240, 240, 155, 4\])
# - its 3D label (shape: \[240, 240, 155\]) arrays,
#
# The function returns:
# - A randomly generated sub-volume of size \[160, 160, 16\]
# - Its corresponding label in a 1-hot format which has the shape \[3, 160, 160, 160\]
#
# Additionally:
# 1. Make sure that at most 95% of the returned patch is non-tumor regions.
# 2. Given that our network expects the channels for our images to appear as the first dimension (instead of the last one in our current setting) reorder the dimensions of the image to have the channels appear as the first dimension.
# 3. Reorder the dimensions of the label array to have the first dimension as the classes (instead of the last one in our current setting)
# 4. Reduce the labels array dimension to only include the non-background classes (total of 3 instead of 4)
# -
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>Check the lecture notebook for a similar example in 1 dimension</li>
# <li>To check the ratio of background to the whole sub-volume, the numerator is the number of background labels in the sub-volume. The last dimension of the label array at index 0 contains the labels to identify whether the voxel is a background (value of 1) or not a a background (value of 0).
# </li>
# <li>For the denominator of the background ratio, this is the volume of the output (see <code>output_x</code>, <code>output_y</code>, <code>output_z</code> in the function parameters).</li>
# <li><a href="https://www.tensorflow.org/api_docs/python/tf/keras/utils/to_categorical">keras.utils.to_categorical(y, num_classes=)</a></li>
# <li><a href="https://docs.scipy.org/doc/numpy/reference/generated/numpy.moveaxis.html" > np.moveaxis </a> can help you re-arrange the dimensions of the arrays </li>
# <li> <a href="https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.random.randint.html">np.random.randint</a> for random sampling</li>
# <li> When taking a subset of the label <code>'y'</code> that excludes the background class, remember which dimension contains the <code>'num_classes'</code> channel after re-ordering the axes. </li>
# </ul>
# </p>
# + colab={} colab_type="code" id="AXKV1epOSuUl"
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def get_sub_volume(image, label,
orig_x = 240, orig_y = 240, orig_z = 155,
output_x = 160, output_y = 160, output_z = 16,
num_classes = 4, max_tries = 1000,
background_threshold=0.95):
"""
Extract random sub-volume from original images.
Args:
image (np.array): original image,
of shape (orig_x, orig_y, orig_z, num_channels)
label (np.array): original label.
labels coded using discrete values rather than
a separate dimension,
so this is of shape (orig_x, orig_y, orig_z)
orig_x (int): x_dim of input image
orig_y (int): y_dim of input image
orig_z (int): z_dim of input image
output_x (int): desired x_dim of output
output_y (int): desired y_dim of output
output_z (int): desired z_dim of output
num_classes (int): number of class labels
max_tries (int): maximum trials to do when sampling
background_threshold (float): limit on the fraction
of the sample which can be the background
returns:
X (np.array): sample of original image of dimension
(num_channels, output_x, output_y, output_z)
y (np.array): labels which correspond to X, of dimension
(num_classes, output_x, output_y, output_z)
"""
# Initialize features and labels with `None`
X = None
y = None
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
tries = 0
while tries < max_tries:
# randomly sample sub-volume by sampling the corner voxel
# hint: make sure to leave enough room for the output dimensions!
start_x = np.random.randint(0, orig_x - output_x+1)
start_y = np.random.randint(0, orig_y - output_y+1)
start_z = np.random.randint(0, orig_z - output_z+1)
# extract relevant area of label
y = label[start_x: start_x + output_x,
start_y: start_y + output_y,
start_z: start_z + output_z]
# One-hot encode the categories.
# This adds a 4th dimension, 'num_classes'
# (output_x, output_y, output_z, num_classes)
y = keras.utils.to_categorical(y, num_classes=num_classes)
# compute the background ratio
bgrd_ratio = np.sum(y[:, :, :, 0])/(output_x * output_y * output_z)
# increment tries counter
tries += 1
# if background ratio is below the desired threshold,
# use that sub-volume.
# otherwise continue the loop and try another random sub-volume
if bgrd_ratio < background_threshold:
# make copy of the sub-volume
X = np.copy(image[start_x: start_x + output_x,
start_y: start_y + output_y,
start_z: start_z + output_z, :])
# change dimension of X
# from (x_dim, y_dim, z_dim, num_channels)
# to (num_channels, x_dim, y_dim, z_dim)
X = np.moveaxis(X, 3, 0)
# change dimension of y
# from (x_dim, y_dim, z_dim, num_classes)
# to (num_classes, x_dim, y_dim, z_dim)
y = np.moveaxis(y, 3, 0)
### END CODE HERE ###
# take a subset of y that excludes the background class
# in the 'num_classes' dimension
y = y[1:, :, :, :]
return X, y
# if we've tried max_tries number of samples
# Give up in order to avoid looping forever.
print(f"Tried {tries} times to find a sub-volume. Giving up...")
# -
# ### Test Case:
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="FfL0EzHrYs4A" outputId="30916a33-23dc-4800-9847-549cf4102efa"
np.random.seed(3)
image = np.zeros((4, 4, 3, 1))
label = np.zeros((4, 4, 3))
for i in range(4):
for j in range(4):
for k in range(3):
image[i, j, k, 0] = i*j*k
label[i, j, k] = k
print("image:")
for k in range(3):
print(f"z = {k}")
print(image[:, :, k, 0])
print("\n")
print("label:")
for k in range(3):
print(f"z = {k}")
print(label[:, :, k])
# -
# #### Test: Extracting (2, 2, 2) sub-volume
# +
sample_image, sample_label = get_sub_volume(image,
label,
orig_x=4,
orig_y=4,
orig_z=3,
output_x=2,
output_y=2,
output_z=2,
num_classes = 3)
print("Sampled Image:")
for k in range(2):
print("z = " + str(k))
print(sample_image[0, :, :, k])
# -
# #### Expected output:
#
# ```Python
# Sampled Image:
# z = 0
# [[0. 2.]
# [0. 3.]]
# z = 1
# [[0. 4.]
# [0. 6.]]
# ```
print("Sampled Label:")
for c in range(2):
print("class = " + str(c))
for k in range(2):
print("z = " + str(k))
print(sample_label[c, :, :, k])
# #### Expected output:
#
# ```Python
# Sampled Label:
# class = 0
# z = 0
# [[1. 1.]
# [1. 1.]]
# z = 1
# [[0. 0.]
# [0. 0.]]
# class = 1
# z = 0
# [[0. 0.]
# [0. 0.]]
# z = 1
# [[1. 1.]
# [1. 1.]]
# ```
# + [markdown] colab_type="text" id="uXWxfMmXW0ct"
# You can run the following cell to look at a candidate patch and ensure that the function works correctly. We'll look at the enhancing tumor part of the label.
# + colab={"base_uri": "https://localhost:8080/", "height": 306} colab_type="code" id="otA9p2lRW0cu" outputId="e0888053-f1ca-4afd-e946-2416446d423e"
image, label = load_case(DATA_DIR + "imagesTr/BRATS_001.nii.gz", DATA_DIR + "labelsTr/BRATS_001.nii.gz")
X, y = get_sub_volume(image, label)
# enhancing tumor is channel 2 in the class label
# you can change indexer for y to look at different classes
util.visualize_patch(X[0, :, :, :], y[2])
# + [markdown] colab_type="text" id="QEjatQCQW0cy"
# <a name="1-4-2"></a>
# ### 1.4.2 Standardization
#
# Next, fill in the following function that given a patch (sub-volume), standardizes the values across each channel and each Z plane to have a mean of zero and standard deviation of 1.
# -
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li> Check that the standard deviation is not zero before dividing by it.
# </ul>
# </p>
# + colab={} colab_type="code" id="kNht6sVLW0c0"
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def standardize(image):
"""
Standardize mean and standard deviation
of each channel and z_dimension.
Args:
image (np.array): input image,
shape (num_channels, dim_x, dim_y, dim_z)
Returns:
standardized_image (np.array): standardized version of input image
"""
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# initialize to array of zeros, with same shape as the image
standardized_image = np.zeros(image.shape)
# iterate over channels
for c in range(image.shape[0]):
# iterate over the `z` dimension
for z in range(image.shape[3]):
# get a slice of the image
# at channel c and z-th dimension `z`
image_slice = image[c,:,:,z]
# subtract the mean
centered = image_slice - np.mean(image_slice)
# divide by the standard deviation
if np.std(centered) != 0:
centered_scaled = centered / np.std(centered)
# update the slice of standardized image
# with the scaled centered and scaled image
standardized_image[c, :, :, z] = centered_scaled
### END CODE HERE ###
return standardized_image
# + [markdown] colab_type="text" id="_b3XeEYtW0c4"
# And to sanity check, let's look at the output of our function:
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="xt1DAVhRW0c5" outputId="e5dee9cc-5183-4ede-88b1-5cb0ccb7a26b"
X_norm = standardize(X)
print("standard deviation for a slice should be 1.0")
print(f"stddv for X_norm[0, :, :, 0]: {X_norm[0,:,:,0].std():.2f}")
# + [markdown] colab_type="text" id="D_Q1xXkXkr3D"
# Let's visualize our patch again just to make sure (it won't look different since the `imshow` function we use to visualize automatically normalizes the pixels when displaying in black and white).
# + colab={"base_uri": "https://localhost:8080/", "height": 306} colab_type="code" id="XcMiq-3FOYHe" outputId="b910aa87-4499-473d-9779-42b30a7a40bc"
util.visualize_patch(X_norm[0, :, :, :], y[2])
# + [markdown] colab_type="text" id="PnYAP0SQK7NL"
# <a name="2"></a>
# # 2 Model: 3D U-Net
# Now let's build our model. In this assignment we will be building a [3D U-net](https://arxiv.org/abs/1606.06650).
# - This architecture will take advantage of the volumetric shape of MR images and is one of the best performing models for this task.
# - Feel free to familiarize yourself with the architecture by reading [this paper](https://arxiv.org/abs/1606.06650).
#
# <img src="https://lmb.informatik.uni-freiburg.de/people/ronneber/u-net/u-net-architecture.png" width="50%">
# + [markdown] colab_type="text" id="P0tVtbIshBXq"
# <a name="3"></a>
# # 3 Metrics
# + [markdown] colab_type="text" id="XOWndz7GecSh"
# <a name="3-1"></a>
# ## 3.1 Dice Similarity Coefficient
#
# Aside from the architecture, one of the most important elements of any deep learning method is the choice of our loss function.
#
# A natural choice that you may be familiar with is the cross-entropy loss function.
# - However, this loss function is not ideal for segmentation tasks due to heavy class imbalance (there are typically not many positive regions).
#
# A much more common loss for segmentation tasks is the Dice similarity coefficient, which is a measure of how well two contours overlap.
# - The Dice index ranges from 0 (complete mismatch)
# - To 1 (perfect match).
#
# In general, for two sets $A$ and $B$, the Dice similarity coefficient is defined as:
# $$\text{DSC}(A, B) = \frac{2 \times |A \cap B|}{|A| + |B|}.$$
#
# Here we can interpret $A$ and $B$ as sets of voxels, $A$ being the predicted tumor region and $B$ being the ground truth.
#
# Our model will map each voxel to 0 or 1
# - 0 means it is a background voxel
# - 1 means it is part of the segmented region.
#
# In the dice coefficient, the variables in the formula are:
# - $x$ : the input image
# - $f(x)$ : the model output (prediction)
# - $y$ : the label (actual ground truth)
#
# The dice coefficient "DSC" is:
#
# $$\text{DSC}(f, x, y) = \frac{2 \times \sum_{i, j} f(x)_{ij} \times y_{ij} + \epsilon}{\sum_{i,j} f(x)_{ij} + \sum_{i, j} y_{ij} + \epsilon}$$
#
# - $\epsilon$ is a small number that is added to avoid division by zero
#
# <img src="https://www.researchgate.net/publication/328671987/figure/fig4/AS:688210103529478@1541093483784/Calculation-of-the-Dice-similarity-coefficient-The-deformed-contour-of-the-liver-from.ppm" width="30%">
#
# [Image Source](https://www.researchgate.net/figure/Calculation-of-the-Dice-similarity-coefficient-The-deformed-contour-of-the-liver-from_fig4_328671987)
#
# Implement the dice coefficient for a single output class below.
#
# - Please use the [Keras.sum(x,axis=)](https://www.tensorflow.org/api_docs/python/tf/keras/backend/sum) function to compute the numerator and denominator of the dice coefficient.
# + colab={} colab_type="code" id="DRZUNCaM_9x7"
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def single_class_dice_coefficient(y_true, y_pred, axis=(0, 1, 2),
epsilon=0.00001):
"""
Compute dice coefficient for single class.
Args:
y_true (Tensorflow tensor): tensor of ground truth values for single class.
shape: (x_dim, y_dim, z_dim)
y_pred (Tensorflow tensor): tensor of predictions for single class.
shape: (x_dim, y_dim, z_dim)
axis (tuple): spatial axes to sum over when computing numerator and
denominator of dice coefficient.
Hint: pass this as the 'axis' argument to the K.sum function.
epsilon (float): small constant added to numerator and denominator to
avoid divide by 0 errors.
Returns:
dice_coefficient (float): computed value of dice coefficient.
"""
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
dice_numerator = 2. * K.sum(y_true * y_pred, axis=axis) + epsilon
dice_denominator = K.sum(y_true, axis=axis) + K.sum(y_pred, axis=axis) + epsilon
dice_coefficient = (dice_numerator) / (dice_denominator)
### END CODE HERE ###
return dice_coefficient
# + colab={"base_uri": "https://localhost:8080/", "height": 323} colab_type="code" id="XOugSRoF_8jN" outputId="a0a1b9ff-aa7b-46eb-96a3-7ee443ea9831"
# TEST CASES
sess = K.get_session()
#sess = tf.compat.v1.Session()
with sess.as_default() as sess:
pred = np.expand_dims(np.eye(2), -1)
label = np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), -1)
print("Test Case #1")
print("pred:")
print(pred[:, :, 0])
print("label:")
print(label[:, :, 0])
# choosing a large epsilon to help check for implementation errors
dc = single_class_dice_coefficient(pred, label,epsilon=1)
print(f"dice coefficient: {dc.eval():.4f}")
print("\n")
print("Test Case #2")
pred = np.expand_dims(np.eye(2), -1)
label = np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), -1)
print("pred:")
print(pred[:, :, 0])
print("label:")
print(label[:, :, 0])
# choosing a large epsilon to help check for implementation errors
dc = single_class_dice_coefficient(pred, label,epsilon=1)
print(f"dice_coefficient: {dc.eval():.4f}")
# -
# ##### Expected output
#
# If you get a different result, please check that you implemented the equation completely.
# ```Python
# Test Case #1
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 0.]]
# dice coefficient: 0.6000
#
#
# Test Case #2
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 1.]]
# dice_coefficient: 0.8333
# ```
# + [markdown] colab_type="text" id="1s3uVww0C01C"
# ### Dice Coefficient for Multiple classes
# Now that we have the single class case, we can think about how to approach the multi class context.
# - Remember that for this task, we want segmentations for each of the 3 classes of abnormality (edema, enhancing tumor, non-enhancing tumor).
# - This will give us 3 different dice coefficients (one for each abnormality class).
# - To combine these, we can just take the average. We can write that the overall dice coefficient is:
#
# $$DC(f, x, y) = \frac{1}{3} \left ( DC_{1}(f, x, y) + DC_{2}(f, x, y) + DC_{3}(f, x, y) \right )$$
#
# - $DC_{1}$, $DC_{2}$ and $DC_{3}$ are edema, enhancing tumor, and non-enhancing tumor dice coefficients.
#
# For any number of classes, the equation becomes:
# $$DC(f, x, y) = \frac{1}{N} \sum_{c=1}^{C} \left ( DC_{c}(f, x, y) \right )$$
#
# In this case, with three categories, $C = 3$
#
# Implement the mean dice coefficient below. This should not be very different from your singe-class implementation.
#
#
# Please use the [K.mean](https://keras.io/backend/#mean) function to take the average of the three classes.
# - Apply the mean to the ratio that you calculate in the last line of code that you'll implement.
# + colab={} colab_type="code" id="r0G9ND3_W0dC"
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def dice_coefficient(y_true, y_pred, axis=(1, 2, 3),
epsilon=0.00001):
"""
Compute mean dice coefficient over all abnormality classes.
Args:
y_true (Tensorflow tensor): tensor of ground truth values for all classes.
shape: (num_classes, x_dim, y_dim, z_dim)
y_pred (Tensorflow tensor): tensor of predictions for all classes.
shape: (num_classes, x_dim, y_dim, z_dim)
axis (tuple): spatial axes to sum over when computing numerator and
denominator of dice coefficient.
Hint: pass this as the 'axis' argument to the K.sum
and K.mean functions.
epsilon (float): small constant add to numerator and denominator to
avoid divide by 0 errors.
Returns:
dice_coefficient (float): computed value of dice coefficient.
"""
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
dice_numerator = 2. * K.sum(y_true * y_pred, axis=axis) + epsilon
dice_denominator = K.sum(y_true, axis=axis) + K.sum(y_pred, axis=axis) + epsilon
dice_coefficient = K.mean((dice_numerator)/(dice_denominator))
### END CODE HERE ###
return dice_coefficient
# + colab={"base_uri": "https://localhost:8080/", "height": 629} colab_type="code" id="bQi8Trze4jGR" outputId="d07e46f0-bc8e-4379-dc4d-46576a2911b5"
# TEST CASES
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #1")
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = dice_coefficient(pred, label,epsilon=1)
print(f"dice coefficient: {dc.eval():.4f}")
print("\n")
print("Test Case #2")
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), 0), -1)
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = dice_coefficient(pred, label,epsilon=1)
print(f"dice coefficient: {dc.eval():.4f}")
print("\n")
print("Test Case #3")
pred = np.zeros((2, 2, 2, 1))
pred[0, :, :, :] = np.expand_dims(np.eye(2), -1)
pred[1, :, :, :] = np.expand_dims(np.eye(2), -1)
label = np.zeros((2, 2, 2, 1))
label[0, :, :, :] = np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), -1)
label[1, :, :, :] = np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), -1)
print("pred:")
print("class = 0")
print(pred[0, :, :, 0])
print("class = 1")
print(pred[1, :, :, 0])
print("label:")
print("class = 0")
print(label[0, :, :, 0])
print("class = 1")
print(label[1, :, :, 0])
dc = dice_coefficient(pred, label,epsilon=1)
print(f"dice coefficient: {dc.eval():.4f}")
# -
# #### Expected output:
#
# ```Python
# Test Case #1
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 0.]]
# dice coefficient: 0.6000
#
#
# Test Case #2
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 1.]]
# dice coefficient: 0.8333
#
#
# Test Case #3
# pred:
# class = 0
# [[1. 0.]
# [0. 1.]]
# class = 1
# [[1. 0.]
# [0. 1.]]
# label:
# class = 0
# [[1. 1.]
# [0. 0.]]
# class = 1
# [[1. 1.]
# [0. 1.]]
# dice coefficient: 0.7167
# ```
# + [markdown] colab_type="text" id="4UFpujr1Mo8m"
# <a name="3-2"></a>
# ## 3.2 Soft Dice Loss
#
# While the Dice Coefficient makes intuitive sense, it is not the best for training.
# - This is because it takes in discrete values (zeros and ones).
# - The model outputs *probabilities* that each pixel is, say, a tumor or not, and we want to be able to backpropagate through those outputs.
#
# Therefore, we need an analogue of the Dice loss which takes real valued input. This is where the **Soft Dice loss** comes in. The formula is:
#
# $$\mathcal{L}_{Dice}(p, q) = 1 - \frac{2\times\sum_{i, j} p_{ij}q_{ij} + \epsilon}{\left(\sum_{i, j} p_{ij}^2 \right) + \left(\sum_{i, j} q_{ij}^2 \right) + \epsilon}$$
#
# - $p$ is our predictions
# - $q$ is the ground truth
# - In practice each $q_i$ will either be 0 or 1.
# - $\epsilon$ is a small number that is added to avoid division by zero
#
# The soft Dice loss ranges between
# - 0: perfectly matching the ground truth distribution $q$
# - 1: complete mismatch with the ground truth.
#
# You can also check that if $p_i$ and $q_i$ are each 0 or 1, then the soft Dice loss is just one minus the dice coefficient.
#
#
# ### Multi-Class Soft Dice Loss
#
# We've explained the single class case for simplicity, but the multi-class generalization is exactly the same as that of the dice coefficient.
# - Since you've already implemented the multi-class dice coefficient, we'll have you jump directly to the multi-class soft dice loss.
#
# For any number of categories of diseases, the expression becomes:
#
# $$\mathcal{L}_{Dice}(p, q) = 1 - \frac{1}{N} \sum_{c=1}^{C} \frac{2\times\sum_{i, j} p_{cij}q_{cij} + \epsilon}{\left(\sum_{i, j} p_{cij}^2 \right) + \left(\sum_{i, j} q_{cij}^2 \right) + \epsilon}$$
#
# Please implement the soft dice loss below!
#
# As before, you will use K.mean()
# - Apply the average the mean to ratio that you'll calculate in the last line of code that you'll implement.
# + colab={} colab_type="code" id="aMR9KO7mHVl5"
# UNQ_C5 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def soft_dice_loss(y_true, y_pred, axis=(1, 2, 3),
epsilon=0.00001):
"""
Compute mean soft dice loss over all abnormality classes.
Args:
y_true (Tensorflow tensor): tensor of ground truth values for all classes.
shape: (num_classes, x_dim, y_dim, z_dim)
y_pred (Tensorflow tensor): tensor of soft predictions for all classes.
shape: (num_classes, x_dim, y_dim, z_dim)
axis (tuple): spatial axes to sum over when computing numerator and
denominator in formula for dice loss.
Hint: pass this as the 'axis' argument to the K.sum
and K.mean functions.
epsilon (float): small constant added to numerator and denominator to
avoid divide by 0 errors.
Returns:
dice_loss (float): computed value of dice loss.
"""
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
dice_numerator = 2. * K.sum(y_true * y_pred, axis=axis) + epsilon
dice_denominator = K.sum(y_true**2, axis=axis) + K.sum(y_pred**2, axis=axis) + epsilon
dice_loss = 1 - K.mean((dice_numerator)/(dice_denominator))
### END CODE HERE ###
return dice_loss
# -
# #### Test Case 1
# + colab={"base_uri": "https://localhost:8080/", "height": 969} colab_type="code" id="FuUigtIO9QVh" outputId="d534083d-9b40-40e5-8e9b-f1bcd3a609c2"
# TEST CASES
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #1")
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss:{dc.eval():.4f}")
# -
# #### Expected output:
#
# ```Python
# Test Case #1
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 0.]]
# soft dice loss:0.4000
# ```
# #### Test Case 2
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #2")
pred = np.expand_dims(np.expand_dims(0.5*np.eye(2), 0), -1)
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss: {dc.eval():.4f}")
# #### Expected output:
#
# ```Python
# Test Case #2
# pred:
# [[0.5 0. ]
# [0. 0.5]]
# label:
# [[1. 1.]
# [0. 0.]]
# soft dice loss: 0.4286
# ```
# #### Test Case 3
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #3")
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), 0), -1)
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss: {dc.eval():.4f}")
# #### Expected output:
#
# ```Python
# Test Case #3
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 1.]]
# soft dice loss: 0.1667
# ```
# #### Test Case 4
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #4")
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
pred[0, 0, 1, 0] = 0.8
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), 0), -1)
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss: {dc.eval():.4f}")
# #### Expected output:
#
# ```Python
# Test Case #4
# pred:
# [[1. 0.8]
# [0. 1. ]]
# label:
# [[1. 1.]
# [0. 1.]]
# soft dice loss: 0.0060
# ```
# #### Test Case 5
sess = K.get_session()
with sess.as_default() as sess:
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #5")
pred = np.zeros((2, 2, 2, 1))
pred[0, :, :, :] = np.expand_dims(0.5*np.eye(2), -1)
pred[1, :, :, :] = np.expand_dims(np.eye(2), -1)
pred[1, 0, 1, 0] = 0.8
label = np.zeros((2, 2, 2, 1))
label[0, :, :, :] = np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), -1)
label[1, :, :, :] = np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), -1)
print("pred:")
print("class = 0")
print(pred[0, :, :, 0])
print("class = 1")
print(pred[1, :, :, 0])
print("label:")
print("class = 0")
print(label[0, :, :, 0])
print("class = 1")
print(label[1, :, :, 0])
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss: {dc.eval():.4f}")
# #### Expected output:
#
# ```Python
# Test Case #5
# pred:
# class = 0
# [[0.5 0. ]
# [0. 0.5]]
# class = 1
# [[1. 0.8]
# [0. 1. ]]
# label:
# class = 0
# [[1. 1.]
# [0. 0.]]
# class = 1
# [[1. 1.]
# [0. 1.]]
# soft dice loss: 0.2173
# ```
# #### Test Case 6
# +
# Test case 6
pred = np.array([
[
[
[1.0, 1.0], [0.0, 0.0]
],
[
[1.0, 0.0], [0.0, 1.0]
]
],
[
[
[1.0, 1.0], [0.0, 0.0]
],
[
[1.0, 0.0], [0.0, 1.0]
]
],
])
label = np.array([
[
[
[1.0, 0.0], [1.0, 0.0]
],
[
[1.0, 0.0], [0.0, 0.0]
]
],
[
[
[0.0, 0.0], [0.0, 0.0]
],
[
[1.0, 0.0], [0.0, 0.0]
]
]
])
sess = K.get_session()
print("Test case #6")
with sess.as_default() as sess:
dc = soft_dice_loss(pred, label, epsilon=1)
print(f"soft dice loss",dc.eval())
# -
# #### Expected Output
# ```Python
# Test case #6
# soft dice loss: 0.4375
# ```
#
# Note, if you don't have a scalar, and have an array with more than one value, please check your implementation!
# + [markdown] colab_type="text" id="6HXdsoV9OVEV"
# <a name="4"></a>
# # 4 Create and Train the model
#
# Once you've finished implementing the soft dice loss, we can create the model!
#
# We'll use the `unet_model_3d` function in `utils` which we implemented for you.
# - This creates the model architecture and compiles the model with the specified loss functions and metrics.
# - Check out function `util.unet_model_3d(loss_function)` in the `util.py` file.
# -
model = util.unet_model_3d(loss_function=soft_dice_loss, metrics=[dice_coefficient])
# + [markdown] colab_type="text" id="lQ-JvVotW0dS"
# <a name="4-1"></a>
# ## 4.1 Training on a Large Dataset
#
# In order to facilitate the training on the large dataset:
# - We have pre-processed the entire dataset into patches and stored the patches in the [`h5py`](http://docs.h5py.org/en/stable/) format.
# - We also wrote a custom Keras [`Sequence`](https://www.tensorflow.org/api_docs/python/tf/keras/utils/Sequence) class which can be used as a `Generator` for the keras model to train on large datasets.
# - Feel free to look at the `VolumeDataGenerator` class in `util.py` to learn about how such a generator can be coded.
#
# Note: [Here](https://www.geeksforgeeks.org/keras-fit-and-keras-fit_generator/) you can check the difference between `fit` and `fit_generator` functions.
#
# To get a flavor of the training on the larger dataset, you can run the following cell to train the model on a small subset of the dataset (85 patches). You should see the loss going down and the dice coefficient going up.
#
# Running `model.fit()` on the Coursera workspace may cause the kernel to die.
# - Soon, we will load a pre-trained version of this model, so that you don't need to train the model on this workspace.
# + [markdown] colab={} colab_type="code" id="bcBeF80jf54b"
# ```Python
# # Run this on your local machine only
# # May cause the kernel to die if running in the Coursera platform
#
# base_dir = HOME_DIR + "processed/"
#
# with open(base_dir + "config.json") as json_file:
# config = json.load(json_file)
#
# # Get generators for training and validation sets
# train_generator = util.VolumeDataGenerator(config["train"], base_dir + "train/", batch_size=3, dim=(160, 160, 16), verbose=0)
# valid_generator = util.VolumeDataGenerator(config["valid"], base_dir + "valid/", batch_size=3, dim=(160, 160, 16), verbose=0)
#
# steps_per_epoch = 20
# n_epochs=10
# validation_steps = 20
#
# model.fit_generator(generator=train_generator,
# steps_per_epoch=steps_per_epoch,
# epochs=n_epochs,
# use_multiprocessing=True,
# validation_data=valid_generator,
# validation_steps=validation_steps)
#
# # run this cell if you to save the weights of your trained model in cell section 4.1
# #model.save_weights(base_dir + 'my_model_pretrained.hdf5')
# ```
# + [markdown] colab_type="text" id="-Oq1qG5UW0dY"
# <a name="4-2"></a>
# ## 4.2 Loading a Pre-Trained Model
# As in assignment 1, instead of having the model train for longer, we'll give you access to a pretrained version. We'll use this to extract predictions and measure performance.
# -
# run this cell if you didn't run the training cell in section 4.1
base_dir = HOME_DIR + "processed/"
with open(base_dir + "config.json") as json_file:
config = json.load(json_file)
# Get generators for training and validation sets
train_generator = util.VolumeDataGenerator(config["train"], base_dir + "train/", batch_size=3, dim=(160, 160, 16), verbose=0)
valid_generator = util.VolumeDataGenerator(config["valid"], base_dir + "valid/", batch_size=3, dim=(160, 160, 16), verbose=0)
# + colab={} colab_type="code" id="iYJ3cdSGeR5l"
model.load_weights(HOME_DIR + "model_pretrained.hdf5")
# -
model.summary()
# + [markdown] colab_type="text" id="22JSeC5yOnty"
# <a name="5"></a>
# # 5 Evaluation
#
# Now that we have a trained model, we'll learn to extract its predictions and evaluate its performance on scans from our validation set.
# + [markdown] colab_type="text" id="DjK9oMJ3iEeW"
# <a name="5-1"></a>
# ## 5.1 Overall Performance
# + [markdown] colab_type="text" id="akLh2sTIhkTj"
# First let's measure the overall performance on the validation set.
# - We can do this by calling the keras [evaluate_generator](https://keras.io/models/model/#evaluate_generator) function and passing in the validation generator, created in section 4.1.
#
# #### Using the validation set for testing
# - Note: since we didn't do cross validation tuning on the final model, it's okay to use the validation set.
# - For real life implementations, however, you would want to do cross validation as usual to choose hyperparamters and then use a hold out test set to assess performance
#
# Python Code for measuring the overall performance on the validation set:
#
# ```python
# val_loss, val_dice = model.evaluate_generator(valid_generator)
#
# print(f"validation soft dice loss: {val_loss:.4f}")
# print(f"validation dice coefficient: {val_dice:.4f}")
# ```
#
# #### Expected output:
#
# ```Python
# validation soft dice loss: 0.4742
# validation dice coefficient: 0.5152
# ```
#
# **NOTE:** Do not run the code shown above on the Coursera platform as it will exceed the platform's memory limitations. However, you can run the code shown above locally on your machine or in Colab to practice measuring the overall performance on the validation set.
#
#
# Like we mentioned above, due to memory limitiations on the Coursera platform we won't be runing the above code, however, you should take note of the **expected output** below it. We should note that due to the randomness in choosing sub-volumes, the values for soft dice loss and dice coefficient will be different each time that you run it.
# + [markdown] colab_type="text" id="JGZ-GLXPiCXH"
# <a name="5-2"></a>
# ## 5.2 Patch-level predictions
#
# When applying the model, we'll want to look at segmentations for individual scans (entire scans, not just the sub-volumes)
# - This will be a bit complicated because of our sub-volume approach.
# - First let's keep things simple and extract model predictions for sub-volumes.
# - We can use the sub-volume which we extracted at the beginning of the assignment.
# + colab={"base_uri": "https://localhost:8080/", "height": 306} colab_type="code" id="D3Zx9gSiAhEC" outputId="4fb5d166-2dbe-4cfc-84ce-8ebab9867729"
util.visualize_patch(X_norm[0, :, :, :], y[2])
# + [markdown] colab_type="text" id="BRJF6bR9i4n7"
# #### Add a 'batch' dimension
# We can extract predictions by calling `model.predict` on the patch.
# - We'll add an `images_per_batch` dimension, since the `predict` method is written to take in batches.
# - The dimensions of the input should be `(images_per_batch, num_channels, x_dim, y_dim, z_dim)`.
# - Use [numpy.expand_dims](https://docs.scipy.org/doc/numpy/reference/generated/numpy.expand_dims.html) to add a new dimension as the zero-th dimension by setting axis=0
# + colab={} colab_type="code" id="_GKVqDNbjUIF"
X_norm_with_batch_dimension = np.expand_dims(X_norm, axis=0)
patch_pred = model.predict(X_norm_with_batch_dimension)
# + [markdown] colab_type="text" id="c11FN5SJjXxT"
# #### Convert prediction from probability into a category
# Currently, each element of `patch_pred` is a number between 0.0 and 1.0.
# - Each number is the model's confidence that a voxel is part of a given class.
# - You will convert these to discrete 0 and 1 integers by using a threshold.
# - We'll use a threshold of 0.5.
# - In real applications, you would tune this to achieve your required level of sensitivity or specificity.
# + colab={} colab_type="code" id="VCsVNiKJBvcC"
# set threshold.
threshold = 0.5
# use threshold to get hard predictions
patch_pred[patch_pred > threshold] = 1.0
patch_pred[patch_pred <= threshold] = 0.0
# + [markdown] colab_type="text" id="AenKy0OGjs-C"
# Now let's visualize the original patch and ground truth alongside our thresholded predictions.
# + colab={"base_uri": "https://localhost:8080/", "height": 663} colab_type="code" id="vf6N-lzLjov4" outputId="071f06c1-a440-4267-99bf-cf261c82efff"
print("Patch and ground truth")
util.visualize_patch(X_norm[0, :, :, :], y[2])
plt.show()
print("Patch and prediction")
util.visualize_patch(X_norm[0, :, :, :], patch_pred[0, 2, :, :, :])
plt.show()
# + [markdown] colab_type="text" id="_JAEdpA3llCJ"
# #### Sensitivity and Specificity
#
# The model is covering some of the relevant areas, but it's definitely not perfect.
# - To quantify its performance, we can use per-pixel sensitivity and specificity.
#
# Recall that in terms of the true positives, true negatives, false positives, and false negatives,
#
# $$\text{sensitivity} = \frac{\text{true positives}}{\text{true positives} + \text{false negatives}}$$
#
# $$\text{specificity} = \frac{\text{true negatives}}{\text{true negatives} + \text{false positives}}$$
#
# Below let's write a function to compute the sensitivity and specificity per output class.
# -
#
# <details>
# <summary>
# <font size="3" color="darkgreen"><b>Hints</b></font>
# </summary>
# <p>
# <ul>
# <li>Recall that a true positive occurs when the class prediction is equal to 1, and the class label is also equal to 1</li>
# <li>Use <a href="https://docs.scipy.org/doc/numpy/reference/generated/numpy.sum.html" > numpy.sum() </a> </li>
#
# </ul>
# </p>
# + colab={} colab_type="code" id="B2ajAYw0bQ50"
# UNQ_C6 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
def compute_class_sens_spec(pred, label, class_num):
"""
Compute sensitivity and specificity for a particular example
for a given class.
Args:
pred (np.array): binary arrary of predictions, shape is
(num classes, height, width, depth).
label (np.array): binary array of labels, shape is
(num classes, height, width, depth).
class_num (int): number between 0 - (num_classes -1) which says
which prediction class to compute statistics
for.
Returns:
sensitivity (float): precision for given class_num.
specificity (float): recall for given class_num
"""
# extract sub-array for specified class
class_pred = pred[class_num]
class_label = label[class_num]
### START CODE HERE (REPLACE INSTANCES OF 'None' with your code) ###
# compute true positives, false positives,
# true negatives, false negatives
tp = np.sum((class_pred == 1) & (class_label == 1))
tn = np.sum((class_pred == 0) & (class_label == 1))
fp = np.sum((class_pred == 1) & (class_label == 0))
fn = np.sum((class_pred == 0) & (class_label == 0))
# compute sensitivity and specificity
sensitivity = tp / (tp + fn)
specificity = tn / (tn + fp)
### END CODE HERE ###
return sensitivity, specificity
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" id="mcTtD1JdYnGj" outputId="b3d1b2f4-224e-4855-cd48-d53dc7a9fb04"
# TEST CASES
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 0.0]]), 0), -1)
print("Test Case #1")
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
sensitivity, specificity = compute_class_sens_spec(pred, label, 0)
print(f"sensitivity: {sensitivity:.4f}")
print(f"specificity: {specificity:.4f}")
# -
# #### Expected output:
#
# ```Python
# Test Case #1
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 0.]]
# sensitivity: 0.5000
# specificity: 0.5000
# ```
# +
print("Test Case #2")
pred = np.expand_dims(np.expand_dims(np.eye(2), 0), -1)
label = np.expand_dims(np.expand_dims(np.array([[1.0, 1.0], [0.0, 1.0]]), 0), -1)
print("pred:")
print(pred[0, :, :, 0])
print("label:")
print(label[0, :, :, 0])
sensitivity, specificity = compute_class_sens_spec(pred, label, 0)
print(f"sensitivity: {sensitivity:.4f}")
print(f"specificity: {specificity:.4f}")
# -
# #### Expected output:
#
# ```Python
# Test Case #2
# pred:
# [[1. 0.]
# [0. 1.]]
# label:
# [[1. 1.]
# [0. 1.]]
# sensitivity: 0.6667
# specificity: 1.0000
# ```
# +
# Note: we must explicity import 'display' in order for the autograder to compile the submitted code
# Even though we could use this function without importing it, keep this import in order to allow the grader to work
from IPython.display import display
print("Test Case #3")
df = pd.DataFrame({'y_test': [1,1,0,0,0,0,0,0,0,1,1,1,1,1],
'preds_test': [1,1,0,0,0,1,1,1,1,0,0,0,0,0],
'category': ['TP','TP','TN','TN','TN','FP','FP','FP','FP','FN','FN','FN','FN','FN']
})
display(df)
pred = np.array( [df['preds_test']])
label = np.array( [df['y_test']])
sensitivity, specificity = compute_class_sens_spec(pred, label, 0)
print(f"sensitivity: {sensitivity:.4f}")
print(f"specificity: {specificity:.4f}")
# -
# #### Expected Output
#
# ```Python
# Test case #3
# ...
# sensitivity: 0.2857
# specificity: 0.4286
# ```
# + [markdown] colab_type="text" id="sjDw9Fg9c21a"
# #### Sensitivity and Specificity for the patch prediction
#
# Next let's compute the sensitivity and specificity on that patch for expanding tumors.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="Kp4SJDWmc0L5" outputId="f8735867-131d-4d25-d84d-e008e9a68d5f"
sensitivity, specificity = compute_class_sens_spec(patch_pred[0], y, 2)
print(f"Sensitivity: {sensitivity:.4f}")
print(f"Specificity: {specificity:.4f}")
# -
# #### Expected output:
#
# ```Python
# Sensitivity: 0.7891
# Specificity: 0.9960
# ```
# + [markdown] colab_type="text" id="MdSeKsZEntHG"
# We can also display the sensitivity and specificity for each class.
# + colab={} colab_type="code" id="0LuVZHUKnp4t"
def get_sens_spec_df(pred, label):
patch_metrics = pd.DataFrame(
columns = ['Edema',
'Non-Enhancing Tumor',
'Enhancing Tumor'],
index = ['Sensitivity',
'Specificity'])
for i, class_name in enumerate(patch_metrics.columns):
sens, spec = compute_class_sens_spec(pred, label, i)
patch_metrics.loc['Sensitivity', class_name] = round(sens,4)
patch_metrics.loc['Specificity', class_name] = round(spec,4)
return patch_metrics
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="lBPqWFmspQHj" outputId="7efafc97-ed71-4e28-ae74-4be3d5533322"
df = get_sens_spec_df(patch_pred[0], y)
print(df)
# -
# #### Expected output
# ```Python
# Edema Non-Enhancing Tumor Enhancing Tumor
# Sensitivity 0.9085 0.9505 0.7891
# Specificity 0.9848 0.9961 0.996
# ```
# + [markdown] colab_type="text" id="PoRrKnBmW0dk"
# <a name="5-3"></a>
# ## 5.3 Running on entire scans
# As of now, our model just runs on patches, but what we really want to see is our model's result on a whole MRI scan.
#
# - To do this, generate patches for the scan.
# - Then we run the model on the patches.
# - Then combine the results together to get a fully labeled MR image.
#
# The output of our model will be a 4D array with 3 probability values for each voxel in our data.
# - We then can use a threshold (which you can find by a calibration process) to decide whether or not to report a label for each voxel.
#
# We have written a function that stitches the patches together: `predict_and_viz(image, label, model, threshold)`
# - Inputs: an image, label and model.
# - Ouputs: the model prediction over the whole image, and a visual of the ground truth and prediction.
#
# Run the following cell to see this function in action!
#
# #### Note: the prediction takes some time!
# - The first prediction will take about 7 to 8 minutes to run.
# - You can skip running this first prediction to save time.
# + colab={"base_uri": "https://localhost:8080/", "height": 415} colab_type="code" id="-DUANuJD2_sm" outputId="d008adb5-f69c-4b98-e886-e70e8d759ed7"
# uncomment this code to run it
# image, label = load_case(DATA_DIR + "imagesTr/BRATS_001.nii.gz", DATA_DIR + "labelsTr/BRATS_001.nii.gz")
# pred = util.predict_and_viz(image, label, model, .5, loc=(130, 130, 77))
# + [markdown] colab_type="text" id="-mI85bMEW0ds"
# Here's a second prediction.
# - Takes about 7 to 8 minutes to run
#
# Please run this second prediction so that we can check the predictions.
# + colab={"base_uri": "https://localhost:8080/", "height": 415} colab_type="code" id="18m8pkA9W0dt" outputId="673151b3-2120-4609-f0d6-154b47e8516a"
image, label = load_case(DATA_DIR + "imagesTr/BRATS_003.nii.gz", DATA_DIR + "labelsTr/BRATS_003.nii.gz")
pred = util.predict_and_viz(image, label, model, .5, loc=(130, 130, 77))
# + [markdown] colab_type="text" id="PaiZrDrG7cHt"
# #### Check how well the predictions do
#
# We can see some of the discrepancies between the model and the ground truth visually.
# - We can also use the functions we wrote previously to compute sensitivity and specificity for each class over the whole scan.
# - First we need to format the label and prediction to match our functions expect.
# + colab={} colab_type="code" id="H7pB-ZgPsl2N"
whole_scan_label = keras.utils.to_categorical(label, num_classes = 4)
whole_scan_pred = pred
# move axis to match shape expected in functions
whole_scan_label = np.moveaxis(whole_scan_label, 3 ,0)[1:4]
whole_scan_pred = np.moveaxis(whole_scan_pred, 3, 0)[1:4]
# + [markdown] colab_type="text" id="Iic-P_jl7viR"
# Now we can compute sensitivity and specificity for each class just like before.
# + colab={"base_uri": "https://localhost:8080/", "height": 68} colab_type="code" id="tpljPNBJ6k0k" outputId="adb78f68-6de9-4c8e-9ffb-163458a68b2f"
whole_scan_df = get_sens_spec_df(whole_scan_pred, whole_scan_label)
print(whole_scan_df)
# + [markdown] colab_type="text" id="lglxceyGW0d0"
# # That's all for now!
# Congratulations on finishing this challenging assignment! You now know all the basics for building a neural auto-segmentation model for MRI images. We hope that you end up using these skills on interesting and challenging problems that you face in the real world.
#
#
#
#
|
AI for Medical Diagnosis/utf-8''C1M3_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Single network model theory
#
# ## Foundation
# To understand network models, it is crucial to understand the concept of a network as a random quantity, taking a probability distribution. We have a realization $A$, and we think that this realization is random in some way. Stated another way, we think that there exists a network-valued random variable $\mathbf A$ that governs the realizations we get to see. Since $\mathbf A$ is a random variable, we can describe it using a probability distribution. The distribution of the random network $\mathbf A$ is the function $\mathbb P$ which assigns probabilities to every possible configuration that $\mathbf A$ could take. Notationally, we write that $\mathbf A \sim \mathbb P$, which is read in words as "the random network $\mathbf A$ is distributed according to $\mathbb P$."
#
# In the preceding description, we made a fairly substantial claim: $\mathbb P$ assigns probabilities to every possible configuration that realizations of $\mathbf A$, denoted by $A$, could take. How many possibilities are there for a network with $n$ nodes? Let's limit ourselves to simple networks: that is, $A$ takes values that are unweighted ($A$ is *binary*), undirected ($A$ is *symmetric*), and loopless ($A$ is *hollow*). In words, $\mathcal A_n$ is the set of all possible adjacency matrices $A$ that correspond to simple networks with $n$ nodes. Stated another way: every $A$ that is found in $\mathcal A$ is a *binary* $n \times n$ matrix ($A \in \{0, 1\}^{n \times n}$), $A$ is symmetric ($A = A^\top$), and $A$ is *hollow* ($diag(A) = 0$, or $A_{ii} = 0$ for all $i = 1,...,n$). We describe $\mathcal A_n$ as:
#
# \begin{align*}
# \mathcal A_n = \left\{A : A \textrm{ is an $n \times n$ matrix with $0$s and $1$s}, A\textrm{ is symmetric}, A\textrm{ is hollow}\right\}
# \end{align*}
#
# To summarize the statement that $\mathbb P$ assigns probabilities to every possible configuration that realizations of $\mathbf A$ can take, we write that $\mathbb P : \mathcal A_n \rightarrow [0, 1]$. This means that for any $A \in \mathcal A_n$ which is a possible realization of a random network $\mathbf A$, that $\mathbb P(\mathbf A = A)$ is a probability (it takes a value between $0$ and $1$). If it is completely unambiguous what the random variable $\mathbf A$ refers to, we might abbreviate $\mathbb P(\mathbf A = A)$ with $\mathbb P(A)$. This statement can alternatively be read that the probability that the random variable $\mathbf A$ takes the value $A$ is $\mathbb P(A)$. Finally, let's address that question we had in the previous paragraph. How many possible adjacency matrices are in $\mathcal A_n$?
#
# Let's imagine what just one $A \in \mathcal A_n$ can look like. Note that each matrix $A$ has $n \times n = n^2$ possible entries, in total, since $A$ is an $n \times n$ matrix. There are $n$ possible self-loops for a network, but since $\mathbf A$ is simple, it is loopless. This means that we can subtract $n$ possible edges from $n^2$, leaving us with $n^2 - n = n(n-1)$ possible edges that might not be unconnected. If we think in terms of a realization $A$, this means that we are ignoring the diagonal entries $a_{ii}$, for all $i \in [n]$. Remember that a simple network is also undirected. In terms of the realization $A$, this means that for every pair $i$ and $j$, that $a_{ij} = a_{ji}$. If we were to learn about an entry in the upper triangle of $A$ where $a_{ij}$ is such that $j > i$, note that we have also learned what $a_{ji}$ is, too. This symmetry of $A$ means that of the $n(n-1)$ entries that are not on the diagonal of $A$, we would, in fact, "double count" the possible number of unique values that $A$ could have. This means that $A$ has a total of $\frac{1}{2}n(n - 1)$ possible entries which are *free*, which is equal to the expression $\binom{n}{2}$. Finally, note that for each entry of $A$, that the adjacency can take one of two possible values: $0$ or $1$. To write this down formally, for every possible edge which is randomly determined, we have *two* possible values that edge could take. Let's think about building some intuition here:
# 1. If $A$ is $2 \times 2$, there are $\binom{2}{2} = 1$ unique entry of $A$, which takes one of $2$ values. There are $2$ possible ways that $A$ could look:
# \begin{align*}
# \begin{bmatrix}
# 0 & 1 \\
# 1 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 0 \\
# 0 & 0
# \end{bmatrix}
# \end{align*}
# 2. If $A$ is $3 \times 3$, there are $\binom{3}{2} = \frac{3 \times 2}{2} = 3$ unique entries of $A$, each of which takes one of $2$ values. There are $8$ possible ways that $A$ could look:
# \begin{align*}
# &\begin{bmatrix}
# 0 & 1 & 1 \\
# 1 & 0 & 1 \\
# 1 & 1 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 1 & 0 \\
# 1 & 0 & 1 \\
# 0 & 1 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 0 & 1 \\
# 0 & 0 & 1 \\
# 1 & 1 & 0
# \end{bmatrix}
# \textrm{ or }\\
# &\begin{bmatrix}
# 0 & 1 & 1 \\
# 1 & 0 & 0 \\
# 1 & 0 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 0 & 1 \\
# 0 & 0 & 0 \\
# 1 & 0 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 0 & 0 \\
# 0 & 0 & 1 \\
# 0 & 1 & 0
# \end{bmatrix}\textrm{ or }\\
# &\begin{bmatrix}
# 0 & 1 & 0 \\
# 1 & 0 & 0 \\
# 0 & 0 & 0
# \end{bmatrix}\textrm{ or }
# \begin{bmatrix}
# 0 & 0 & 0 \\
# 0 & 0 & 0 \\
# 0 & 0 & 0
# \end{bmatrix}
# \end{align*}
#
# How do we generalize this to an arbitrary choice of $n$? The answer is to use *combinatorics*. Basically, the approach is to look at each entry of $A$ which can take different values, and multiply the total number of possibilities by $2$ for every element which can take different values. Stated another way, if there are $2$ choices for each one of $x$ possible items, we have $2^x$ possible ways in which we could select those $x$ items. But we already know how many different elements there are in $A$, so we are ready to come up with an expression for the number. In total, there are $2^{\binom n 2}$ unique adjacency matrices in $\mathcal A_n$. Stated another way, the *cardinality* of $\mathcal A_n$, described by the expression $|\mathcal A_n|$, is $2^{\binom n 2}$. The **cardinality** here just means the number of elements that the set $\mathcal A_n$ contains. When $n$ is just $15$, note that $\left|\mathcal A_{15}\right| = 2^{\binom{15}{2}} = 2^{105}$, which when expressed as a power of $10$, is more than $10^{30}$ possible networks that can be realized with just $15$ nodes! As $n$ increases, how many unique possible networks are there? In the below figure, look at the value of $|\mathcal A_n| = 2^{\binom n 2}$ as a function of $n$. As we can see, as $n$ gets big, $|\mathcal A_n|$ grows really really fast!
# + tags=["hide-input"]
import seaborn as sns
import numpy as np
from math import comb
n = np.arange(2, 51)
logAn = np.array([comb(ni, 2) for ni in n])*np.log10(2)
ax = sns.lineplot(x=n, y=logAn)
ax.set_title("")
ax.set_xlabel("Number of Nodes")
ax.set_ylabel("Number of Possible Graphs $|A_n|$ (log scale)")
ax.set_yticks([50, 100, 150, 200, 250, 300, 350])
ax.set_yticklabels(["$10^{{{pow:d}}}$".format(pow=d) for d in [50, 100, 150, 200, 250, 300, 350]])
ax;
# -
# So, now we know that we have probability distributions on networks, and a set $\mathcal A_n$ which defines all of the adjacency matrices that every probability distribution must assign a probability to. Now, just what is a network model? A **network model** is a set $\mathcal P$ of probability distributions on $\mathcal A_n$. Stated another way, we can describe $\mathcal P$ to be:
# \begin{align*}
# \mathcal P &\subseteq \{\mathbb P: \mathbb P\textrm{ is a probability distribution on }\mathcal A_n\}
# \end{align*}
#
# In general, we will simplify $\mathcal P$ through something called *parametrization*. We define $\Theta$ to be the set of all possible parameters of the random network model, and $\theta \in \Theta$ is a particular parameter choice that governs the parameters of a specific network-valued random variaable $\mathbf A$. In this case, we will write $\mathcal P$ as the set:
# \begin{align*}
# \mathcal P(\Theta) &= \left\{\mathbb P_\theta : \theta \in \Theta\right\}
# \end{align*}
# If $\mathbf A$ is a random network that follows a network model, we will write that $\mathbf A \sim \mathbb P_\theta$, for some choice $\theta$. We will often use the shorthand $\mathbf A \sim \mathbb P$.
#
# If you are used to traditional univariate or multivariate statistical modelling, an extremely natural choice for when you have a discrete sample space (like $\mathcal A_n$, which is discrete because we can count it) would be to use a categorical model. In the categorical model, we would have a single parameter for all possible configurations of an $n$-node network; that is, $|\theta| = \left|\mathcal A_n\right| = 2^{\binom n 2}$. What is wrong with this model? The limitations are two-fold:
# 1. As we explained previously, when $n$ is just $15$, we would need over $10^{30}$ bits of storage just to define $\theta$. This amounts to more than $10^{8}$ zetabytes, which exceeds the storage capacity of *the entire world*.
# 2. With a single network observed (or really, any number of networks we could collect in the real world) we would never be able to get a reasonable estimate of $2^{\binom n 2}$ parameters for any reasonably non-trivial number of nodes $n$. For the case of one observed network $A$, an estimate of $\theta$ (referred to as $\hat\theta$) would simply be for $\hat\theta$ to have a $1$ in the entry corresponding to our observed network, and a $0$ everywhere else. Inferentially, this would imply that the network-valued random variable $\mathbf A$ which governs realizations $A$ is deterministic, even if this is not the case. Even if we collected potentially *many* observed networks, we would still (with very high probability) just get $\hat \theta$ as a series of point masses on the observed networks we see, and $0$s everywhere else. This would mean our parameter estimates $\hat\theta$ would not generalize to new observations at *all*, with high probability.
#
# So, what are some more reasonable descriptions of $\mathcal P$? We explore some choices below. Particularly, we will be most interested in the *independent-edge* networks. These are the families of networks in which the generative procedure which governs the random networks assume that the edges of the network are generated *independently*. **Statistical Independence** is a property which greatly simplifies many of the modelling assumptions which are crucial for proper estimation and rigorous statistical inference, which we will learn more about in the later chapters.
#
# ### Equivalence Classes
#
# In all of the below models, we will explore the concept of the **probability equivalence class**, or an *equivalence class*, for short. The probability is a function which in general, describes how effective a particular observation can be described by a random variable $\mathbf A$ with parameters $\theta$, written $\mathbf A \sim F(\theta)$. The probability will be used to describe the probability $\mathbb P_\theta(\mathbf A)$ of observing the realization $A$ if the underlying random variable $\mathbf A$ has parameters $\theta$. Why does this matter when it comes to equivalence classes? An equivalence class is a subset of the sample space $E \subseteq \mathcal A_n$, which has the following properties. Holding the parameters $\theta$ fixed:
#
# 1. If $A$ and $A'$ are members of the same equivalence class $E$ (written $A, A' \in E$), then $\mathbb P_\theta(A) = \mathbb P_\theta(A')$.
# 2. If $A$ and $A''$ are members of different equivalence classes; that is, $A \in E$ and $A'' \in E'$ where $E, E'$ are equivalence classes, then $\mathbb P_\theta(A) \neq \mathbb P_\theta(A'')$.
# 3. Using points 1 and 2, we can establish that if $E$ and $E'$ are two different equivalence classes, then $E \cap E' = \varnothing$. That is, the equivalence classes are **mutually disjoint**.
# 4. We can use the preceding properties to deduce that given the sample space $\mathcal A_n$ and a probability function $\mathbb P_\theta$, we can define a partition of the sample space into equivalence classes $E_i$, where $i \in \mathcal I$ is an arbitrary indexing set. A **partition** of $\mathcal A_n$ is a sequence of sets which are mutually disjoint, and whose union is the whole space. That is, $\bigcup_{i \in \mathcal I} E_i = \mathcal A_n$.
#
# We will see more below about how the equivalence classes come into play with network models, and in a later section, we will see their relevance to the estimation of the parameters $\theta$.
#
# (representations:whyuse:networkmodels:iern)=
# ### Independent-Edge Random Networks
#
# The below models are all special families of something called **independent-edge random networks**. An independent-edge random network is a network-valued random variable, in which the collection of edges are all independent. In words, this means that for every adjacency $\mathbf a_{ij}$ of the network-valued random variable $\mathbf A$, that $\mathbf a_{ij}$ is independent of $\mathbf a_{i'j'}$, any time that $(i,j) \neq (i',j')$. When the networks are simple, the easiest thing to do is to assume that each edge $(i,j)$ is connected with some probability (which might be different for each edge) $p_{ij}$. We use the $ij$ subscript to denote that this probability is not necessarily the same for each edge. This simple model can be described as $\mathbf a_{ij}$ has the distribution $Bern(p_{ij})$, for every $j > i$, and is independent of every other edge in $\mathbf A$. We only look at the entries $j > i$, since our networks are simple. This means that knowing a realization of $\mathbf a_{ij}$ also gives us the realizaaion of $\mathbf a_{ji}$ (and thus $\mathbf a_{ji}$ is a *deterministic* function of $\mathbf a_{ij}$). Further, we know that the random network is loopless, which means that every $\mathbf a_{ii} = 0$. We will call the matrix $P = (p_{ij})$ the **probability matrix** of the network-valued random variable $\mathbf A$. In general, we will see a common theme for the probabilities of a realization $A$ of a network-valued random variable $\mathbf A$, which is that it will greatly simplify our computation. Remember that if $\mathbf x$ and $\mathbf y$ are binary variables which are independent, that $\mathbb P(\mathbf x = x, \mathbf y = y) = \mathbb P(\mathbf x = x) \mathbb P(\mathbf y = y)$. Using this fact:
#
# \begin{align*}
# \mathbb P(\mathbf A = A) &= \mathbb P(\mathbf a_{11} = a_{11}, \mathbf a_{12} = a_{12}, ..., \mathbf a_{nn} = a_{nn}) \\
# &= \mathbb P(\mathbf a_{ij} = a_{ij} \text{ for all }j > i) \\
# &= \prod_{j > i}\mathbb P(\mathbf a_{ij} = a_{ij}), \;\;\;\;\textrm{Independence Assumption}
# \end{align*}
# Next, we will use the fact that if a random variable $\mathbf a_{ij}$ has the Bernoulli distribution with probability $p_{ij}$, that $\mathbb P(\mathbf a_{ij} = a_{ij}) = p_{ij}^{a_{ij}}(1 - p_{ij})^{1 - p_{ij}}$:
# \begin{align*}
# \mathbb P_\theta(A) &= \prod_{j > i}p_{ij}^{a_{ij}}(1 - p_{ij})^{1 - p_{ij}}
# \end{align*}
#
# Now that we've specified a probability and a very generalizable model, we've learned the full story behind network models and are ready to skip to estimating parameters, right? *Wrong!* Unfortunately, if we tried too estimate anything about each $p_{ij}$ individually, we would obtain that $p_{ij} = a_{ij}$ if we only have one realization $A$. Even if we had many realizations of $\mathbf A$, this still would not be very interesting, since we have a *lot* of $p_{ij}$s to estimate, and we've ignored any sort of structural model that might give us deeper insight into $\mathbf A$. In the below sections, we will learn successively less restrictive (and hence, *more expressive*) assumptions about $p_{ij}$s, which will allow us to convey fairly complex random networks, but *still* enable us with plenty of intteresting things to learn about later on.
# ## Erdös-Rényi (ER) Random Networks
#
# The Erdös Rényi model formalizes this relatively simple situation with a single parameter and an $iid$ assumption:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $p$ | $[0, 1]$ | Probability that an edge exists between a pair of nodes, which is identical for all pairs of nodes |
#
# From here on out, when we talk about an Erdös Rényi random variable, we will simply call it an ER network. In an ER network, each pair of nodes is connected with probability $p$, and therefore not connected with probability $1-p$. Statistically, we say that for each edge $\mathbf{a}_{ij}$ for every pair of nodes where $j > i$ (in terms of the adjacency matrix, this means all of the edges in the *upper right* triangle), that $\mathbf{a}_{ij}$ is sampled independently and identically from a *Bernoulli* distribution with probability $p$. The word "independent" means that edges in the network occurring or not occurring do not affect one another. For instance, this means that if we knew a student named Alice was friends with Bob, and Alice was also friends with Chadwick, that we do not learn any information about whether Bob is friends with Chadwick. The word "identical" means that every edge in the network has the same probability $p$ of being connected. If Alice and Bob are friends with probability $p$, then Alice and Chadwick are friends with probability $p$, too. We assume here that the networks are undirected, which means that if an edge $\mathbf a_{ij}$ exists from node $i$ to $j$, then the edge $\mathbf a_{ji}$ also exists from node $j$ to node $i$. We also assume that the networks are loopless, which means that no edges $\mathbf a_{ii}$ can go from node $i$ to itself. If $\mathbf A$ is the adjacency matrix for an ER network with probability $p$, we write that $\mathbf A \sim ER_n(p)$.
#
# Next, let's formalize an example of one of the limitations of an ER random network. Remember that we said that ER random networks are often too simple. Well, one way in which they are simple is called **degree homogeneity**, which is a property in which *all* of the nodes in an ER network have the *exact* same expected node degree! What this means is that if we were to take an ER random network $\mathbf A$, we would expect that *all* of the nodes in the network had the same degree. Let's see how this works:
#
# ```{admonition} Working Out the Expected Degree in an Erdös-Rényi Network
# Suppose that $\mathbf A$ is a simple network which is random. The network has $n$ nodes $\mathcal V = (v_i)_{i = 1}^n$. Recall that the in a simple network, the node degree is $deg(v_i) = \sum_{j = 1}^n \mathbf a_{ij}$. What is the expected degree of a node $v_i$ of a random network $\mathbf A$ which is Erdös-Rényi?
#
# To describe this, we will compute the expectated value of the degree $deg(v_i)$, written $\mathbb E\left[deg(v_i)\right]$. Let's see what happens:
# \begin{align*}
# \mathbb E\left[deg(v_i)\right] &= \mathbb E\left[\sum_{j = 1}^n \mathbf a_{ij}\right] \\
# &= \sum_{j = 1}^n \mathbb E[\mathbf a_{ij}]
# \end{align*}
# We use the *linearity of expectation* in the line above, which means that the expectation of a sum with a finite number of terms being summed over ($n$, in this case) is the sum of the expectations. Finally, by definition, all of the edges $A_{ij}$ have the same distribution: $Bern(p)$. The expected value of a random quantity which takes a Bernoulli distribution is just the probability $p$. This means every term $\mathbb E[\mathbf a_{ij}] = p$. Therefore:
# \begin{align*}
# \mathbb E\left[deg(v_i)\right] &= \sum_{j = 1}^n p = n\cdot p
# \end{align*}
# Since all of the $n$ terms being summed have the same expected value. This holds for *every* node $v_i$, which means that the expected degree of all nodes is an undirected ER network is the same number, $n \cdot p$.
# ```
#
# ### Probability
#
# What is the probability for realizations of Erdös-Rényi networks? Remember that for Independent-edge graphs, that the probability can be written:
#
# \begin{align*}
# \mathbb P_{\theta}(A) &= \prod_{j > i} \mathbb P_\theta(\mathbf{a}_{ij} = a_{ij})
# \end{align*}
#
# Next, we recall that by assumption of the ER model, that the probability matrix $P = (p)$, or that $p_{ij} = p$ for all $i,j$. Therefore:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \prod_{j > i} p^{a_{ij}}(1 - p)^{1 - a_{ij}} \\
# &= p^{\sum_{j > i} a_{ij}} \cdot (1 - p)^{\binom{n}{2} - \sum_{j > i}a_{ij}} \\
# &= p^{m} \cdot (1 - p)^{\binom{n}{2} - m}
# \end{align*}
#
# This means that the probability $\mathbb P_\theta(A)$ is a function *only* of the number of edges $m = \sum_{j > i}a_{ij}$ in the network represented by adjacency matrix $A$. The equivalence class on the Erdös-Rényi networks are the sets:
#
# \begin{align*}
# E_{i} &= \left\{A \in \mathcal A_n : m = i\right\}
# \end{align*}
#
# where $i$ index from $0$ (the minimum number of edges possible) all the way up to $n^2$ (the maximum number of edges possible). All of the relationships for equivalence classes discussed above apply to the sets $E_i$.
# ## Network Models for networks which aren't simple
#
# To make the discussions a little more easy to handle, in the above descriptions and all our successive descriptions, we will describe network models for **simple networks**. To recap, networks which are simple are binary networks which are both loopless and undirected. Stated another way, simple networks are networks whose adjacency matrices are only $0$s and $1$s, they are hollow (the diagonal is entirely *0*), and symmetric (the lower and right triangles of the adjacency matrix are the *same*). What happens our networks don't quite look this way?
#
# For now, we'll keep the assumption that the networks are binary, but we will discuss non-binary network models in a later chapter. We have three possibilities we can consider, and we will show how the "relaxations" of the assumptions change a description of a network model. A *relaxation*, in statistician speak, means that we are taking the assumptions that we had (in this case, that the networks are *simple*), and progressively making the assumptions weaker (more *relaxed*) so that they apply to other networks, too. We split these out so we can be as clear as possible about how the generative model changes with each relaxation step.
#
# We will compare each relaxation to the statement about the generative model for the ER generative model. To recap, for a simple network, we wrote:
#
# "Statistically, we say that for each edge $\mathbf{a}_{ij}$ for every pair of nodes where $j > i$ (in terms of the adjacency matrix, this means all of the nodes in the *upper right* triangle), that $\mathbf{a}_{ij}$ is sampled independently and identically from a *Bernoulli* distribution with probability $p$.... We assume here that the networks are undirected, which means that if an edge $\mathbf a_{ij}$ exists from node $i$ to $j$, then the edge $\mathbf a_{ji}$ also exists from node $j$ to node $i$. We also assume that the networks are loopless, which means that no edges $\mathbf a_{ii}$ can go from node $i$ to itself."
#
# Any additional parts that are added are expressed in **<font color='green'>green</font>** font. Omitted parts are struck through with <font color='red'><strike>red</strike></font> font.
#
# Note that these generalizations apply to *any* of the successive networks which we describe in the Network Models section, and not just the ER model!
#
# ### Binary network model which has loops, but is undirected
#
# Here, all we want to do is relax the assumption that the network is loopless. We simply ignore the statement that edges $\mathbf a_{ii}$ cannot exist, and allow that the $\mathbf a_{ij}$ which follow a Bernoulli distribution (with some probability which depends on the network model choice) *now* applies to $j \geq i$, and not just $j > i$. We keep that an edge $\mathbf a_{ij}$ existing implies that $\mathbf a_{ji}$ also exists, which maintains the symmetry of $\mathbf A$ (and consequently, the undirectedness of the network).
#
# Our description of the ER network changes to:
#
# Statistically, we say that for each edge $\mathbf{a}_{ij}$ for every pair of nodes where $\mathbf{\color{green}{j \geq i}}$ (in terms of the adjacency matrix, this means all of the nodes in the *upper right* triangle **<font color='green'>and the diagonal</font>**), that $\mathbf{a}_{ij}$ is sampled independently and identically from a *Bernoulli* distribution with probability $p$.... We assume here that the networks are undirected, which means that if an edge $\mathbf a_{ij}$ exists from node $i$ to $j$, then the edge $\mathbf a_{ji}$ also exists from node $j$ to node $i$. <font color='red'><strike>We also assume that the networks are loopless, which means that no edges $\mathbf a_{ii}$ can go from node $i$ to itself.</strike></font>
#
# ### Binary network model which is loopless, but directed
#
# Like above, we simply ignore the statement that $\mathbf a_{ji} = \mathbf a_{ij}$, which removes the symmetry of $\mathbf A$ (and consequently, removes the undirectedness of the network). We allow that the $\mathbf a_{ij}$ which follows a Bernoulli distribution now apply to $j \neq i$, and not just $j > i$. We keep that $\mathbf a_{ii} = 0$, which maintains the hollowness of $\mathbf A$ (and consequently, the undirectedness of the network).
#
# Our description of the ER network changes to:
#
# Statistically, we say that for each edge $\mathbf{a}_{ij}$ for every pair of nodes where $\mathbf{\color{green}{j \neq i}}$ (in terms of the adjacency matrix, this means all of the nodes <strike><font color='red'>in the *upper right* triangle</font></strike>**<font color='green'>which are not along the diagonal</font>**), that $\mathbf{a}_{ij}$ is sampled independently and identically from a *Bernoulli* distribution with probability $p$.... <font color='red'><strike>We assume here that the networks are undirected, which means that if an edge $\mathbf a_{ij}$ exists from node $i$ to $j$, then the edge $\mathbf a_{ji}$ also exists from node $j$ to node $i$.</strike></font> We also assume that the networks are loopless, which means that no edges $\mathbf a_{ii}$ can go from node $i$ to itself.
#
# ### Binary network model which is has loops and is directed
#
# Finally, for a network which has loops and is directed, we combine the above two approaches. We ignore the statements that $\mathbf a_{ji} = \mathbf a_{ij}$, and the statement that $\mathbf a_{ii} = 0$.
#
# Our descriptiomn of the ER network changes to:
#
#
# Statistically, we say that for each edge $\mathbf{a}_{ij}$ <font color='red'><strike>where $j > i$ (in terms of the adjacency matrix, this means all of the nodes in the *upper right* triangle)</strike></font>, that $\mathbf{a}_{ij}$ is sampled independently and identically from a *Bernoulli* distribution with probability $p$, <font color='green'>for all possible combinations of nodes $j$ and $i$</font>. <font color='red'><strike>We assume here that the networks are undirected, which means that if an edge $\mathbf a_{ij}$ exists from node $i$ to $j$, then the edge $\mathbf a_{ji}$ also exists from node $j$ to node $i$. We also assume that the networks are loopless, which means that no edges $\mathbf a_{ii}$ can go from node $i$ to itself.</strike></font>
# ## *A Priori* Stochastic Block Model
#
# The *a priori* SBM is an SBM in which we know ahead of time (*a priori*) which nodes are in which communities. Here, we will use the variable $K$ to denote the maximum number of different communities. The ordering of the communities does not matter; the community we call $1$ versus $2$ versus $K$ is largely a symbolic distinction (the only thing that matters is that they are *different*). The *a priori* SBM has the following parameter:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $B$ | [0,1]$^{K \times K}$ | The block matrix, which assigns edge probabilities for pairs of communities |
#
# To describe the *A Priori* SBM, we will designate the community each node is a part of using a vector, which has a single community assignment for each node in the network. We will call this **node assignment vector** $\vec{\tau}$, and it is a $n$-length vector (one element for each node) with elements which can take values from $1$ to $K$. In symbols, we would say that $\vec\tau \in \{1, ..., K\}^n$. What this means is that for a given element of $\vec \tau$, $\tau_i$, that $\tau_i$ is the community assignment (either $1$, $2$, so on and so forth up to $K$) for the $i^{th}$ node. If there we hahd an example where there were $2$ communities ($K = 2$) for instance, and the first two nodes are in community $1$ and the second two in community $2$, then $\vec\tau$ would be a vector which looks like:
# \begin{align*}
# \vec\tau &= \begin{bmatrix}1 & 1 & 2 & 2\end{bmatrix}^\top
# \end{align*}
#
# Next, let's discuss the matrix $B$, which is known as the **block matrix** of the SBM. We write down that $B \in [0, 1]^{K \times K}$, which means that the block matrix is a matrix with $K$ rows and $K$ columns. If we have a pair of nodes and know which of the $K$ communities each node is from, the block matrix tells us the probability that those two nodes are connected. If our networks are simple, the matrix $B$ is also symmetric, which means that if $b_{kk'} = p$ where $p$ is a probability, that $b_{k'k} = p$, too. The requirement of $B$ to be symmetric exists *only* if we are dealing with undirected networks.
#
# Finally, let's think about how to write down the generative model for the *a priori* SBM. Intuitionally what we want to reflect is, if we know that node $i$ is in community $k'$ and node $j$ is in community $k$, that the $(k', k)$ entry of the block matrix is the probability that $i$ and $j$ are connected. We say that given $\tau_i = k'$ and $\tau_j = k$, $\mathbf a_{ij}$ is sampled independently from a $Bern(b_{k' k})$ distribution for all $j > i$. Note that the adjacencies $\mathbf a_{ij}$ are not *necessarily* identically distributed, because the probability depends on the community of edge $(i,j)$. If $\mathbf A$ is an *a priori* SBM network with parameter $B$, and $\vec{\tau}$ is a realization of the node-assignment vector, we write that $\mathbf A \sim SBM_{n,\vec \tau}(B)$.
#
# ### Probability
#
# What does the probability for the *a priori* SBM look like? In our previous description, we admittedly simplified things to an extent to keep the wording down. In truth, we model the *a priori* SBM using a *latent variable* model, which means that the node assignment vector, $\vec{\pmb \tau}$, is treated as *random*. For the case of the *a priori* SBM, it just so happens that we *know* the specific value that this latent variable $\vec{\pmb \tau}$ takes, $\vec \tau$, ahead of time.
#
# Fortunately, since $\vec \tau$ is a *parameter* of the *a priori* SBM, the probability is a bit simpler than for the *a posteriori* SBM. This is because the *a posteriori* SBM requires an integration over potential realizations of $\vec{\pmb \tau}$, whereas the *a priori* SBM does not, since we already know that $\vec{\pmb \tau}$ was realized as $\vec\tau$.
#
# Putting these steps together gives us that:
# \begin{align*}
# \mathbb P_\theta(A) &= \mathbb P_{\theta}(\mathbf A = A | \vec{\pmb \tau} = \vec\tau) \\
# &= \prod_{j > i} \mathbb P_\theta(\mathbf a_{ij} = a_{ij} | \vec{\pmb \tau} = \vec\tau),\;\;\;\;\textrm{Independence Assumption}
# \end{align*}
#
# Next, for the *a priori* SBM, we know that each edge $\mathbf a_{ij}$ only *actually* depends on the community assignments of nodes $i$ and $j$, so we know that $\mathbb P_{\theta}(\mathbf a_{ij} = a_{ij} | \vec{\pmb \tau} = \vec\tau) = \mathbb P(\mathbf a_{ij} = a_{ij} | \tau_i = k', \tau_j = k)$, where $k$ and $k'$ are any of the $K$ possible communities. This is because the community assignments of nodes that are not nodes $i$ and $j$ do not matter for edge $ij$, due to the independence assumption.
#
# Next, let's think about the probability matrix $P = (p_{ij})$ for the *a priori* SBM. We know that, given that $\tau_i = k'$ and $\tau_j = k$, each adjacency $\mathbf a_{ij}$ is sampled independently and identically from a $Bern(b_{k',k})$ distribution. This means that $p_{ij} = b_{k',k}$. Completing our analysis from above:
# \begin{align*}
# \mathbb P_\theta(A) &= \prod_{j > i} b_{k'k}^{a_{ij}}(1 - b_{k'k})^{1 - a_{ij}} \\
# &= \prod_{k,k' \in [K]}b_{k'k}^{m_{k'k}}(1 - b_{k'k})^{n_{k'k} - m_{k'k}}
# \end{align*}
#
# Where $n_{k' k}$ denotes the total number of edges possible between nodes assigned to community $k'$ and nodes assigned to community $k$. That is, $n_{k' k} = \sum_{j > i} \mathbb 1_{\tau_i = k'}\mathbb 1_{\tau_j = k}$. Further, we will use $m_{k' k}$ to denote the total number of edges observed between these two communities. That is, $m_{k' k} = \sum_{j > i}\mathbb 1_{\tau_i = k'}\mathbb 1_{\tau_j = k}a_{ij}$. Note that for a single $(k',k)$ community pair, that the probability is analogous to the probability of a realization of an ER random variable.
#
# <!--- We can formalize this a bit more explicitly. If we let $A^{\ell k}$ be defined as the subgraph *induced* by the edges incident nodes in community $\ell$ and those in community $k$, then we can say that $A^{\ell k}$ is a directed ER random network, --->
#
# Like the ER model, there are again equivalence classes of the sample space $\mathcal A_n$ in terms of their probability. For a two-community setting, with $\vec \tau$ and $B$ given, the equivalence classes are the sets:
# \begin{align*}
# E_{a,b,c}(\vec \tau, B) &= \left\{A \in \mathcal A_n : m_{11} = a, m_{21}=m_{12} = b, m_{22} = c\right\}
# \end{align*}
#
# The number of equivalence classes possible scales with the number of communities, and the manner in which nodes are assigned to communities (particularly, the number of nodes in each community).
#
#
# ## *A Posteriori* Stochastic Block Model
#
# In the *a posteriori* Stochastic Block Model (SBM), we consider that node assignment to one of $K$ communities is a random variable, that we *don't* know already like te *a priori* SBM. We're going to see a funky word come up, that you're probably not familiar with, the **$K$ probability simplex**. What the heck is a probability simplex?
#
# The intuition for a simplex is probably something you're very familiar with, but just haven't seen a word describe. Let's say I have a vector, $\vec\pi = (\pi_k)_{k \in [K]}$, which has a total of $K$ elements. $\vec\pi$ will be a vector, which indicates the *probability* that a given node is assigned to each of our $K$ communities, so we need to impose some additional constraints. Symbolically, we would say that, for all $i$, and for all $k$:
# \begin{align*}
# \pi_k = \mathbb P(\pmb\tau_i = k)
# \end{align*}
# The $\vec \pi$ we're going to use has a very special property: all of its elements are non-negative: for all $\pi_k$, $\pi_k \geq 0$. This makes sense since $\pi_k$ is being used to represent the probability of a node $i$ being in group $k$, so it certainly can't be negative. Further, there's another thing that we want our $\vec\pi$ to have: in order for each element $\pi_k$ to indicate the probability of something to be assigned to $k$, we need all of the $\pi_k$s to sum up to one. This is because of something called the Law of Total Probability. If we have $K$ total values that $\pmb \tau_i$ could take, then it is the case that:
# \begin{align*}
# \sum_{k=1}^K \mathbb P(\pmb \tau_i = k) = \sum_{k = 1}^K \pi_k = 1
# \end{align*}
# So, back to our question: how does a probability simplex fit in? Well, the $K$ probability simplex describes all of the possible values that our vector $\vec\pi$ could take! In symbols, the $K$ probability simplex is:
# \begin{align*}
# \left\{\vec\pi : \text{for all $k$ }\pi_k \geq 0, \sum_{k = 1}^K \pi_k = 1 \right\}
# \end{align*}
# So the $K$ probability simplex is just the space for all possible vectors which could indicate assignment probabilities to one of $K$ communities.
#
# What does the probability simplex look like? Below, we take a look at the $2$-probability simplex (2-d $\vec\pi$s) and the $3$-probability simplex (3-dimensional $\vec\pi$s):
# + tags=["hide-input"]
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
import matplotlib.pyplot as plt
fig=plt.figure(figsize=plt.figaspect(.5))
fig.suptitle("Probability Simplexes")
ax=fig.add_subplot(1,2,1)
x=[1,0]
y=[0,1]
ax.plot(x,y)
ax.set_xticks([0,.5,1])
ax.set_yticks([0,.5,1])
ax.set_xlabel("$\pi_1$")
ax.set_ylabel("$\pi_2$")
ax.set_title("2-probability simplex")
ax=fig.add_subplot(1,2,2,projection='3d')
x = [1,0,0]
y = [0,1,0]
z = [0,0,1]
verts = [list(zip(x,y,z))]
ax.add_collection3d(Poly3DCollection(verts, alpha=.6))
ax.view_init(elev=20,azim=10)
ax.set_xticks([0,.5,1])
ax.set_yticks([0,.5,1])
ax.set_zticks([0,.5,1])
ax.set_xlabel("$\pi_1$")
ax.set_ylabel("$\pi_2$")
h=ax.set_zlabel("$\pi_3$", rotation=0)
ax.set_title("3-probability simplex")
plt.show()
# -
# The values of $\vec\pi = (\pi)$ that are in the $K$-probability simplex are indicated by the shaded region of each figure. This comprises the $(\pi_1, \pi_2)$ pairs that fall along a diagonal line from $(0,1)$ to $(1,0)$ for the $2$-simplex, and the $(\pi_1, \pi_2, \pi_3)$ tuples that fall on the surface of the triangular shape above with nodes at $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$.
# This model has the following parameters:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $\vec \pi$ | the $K$ probability simplex | The probability of a node being assigned to community $K$ |
# | $B$ | [0,1]$^{K \times K}$ | The block matrix, which assigns edge probabilities for pairs of communities |
#
# The *a posteriori* SBM is a bit more complicated than the *a priori* SBM. We will think about the *a posteriori* SBM as a variation of the *a priori* SBM, where instead of the node-assignment vector being treated as a known fixed value (the community assignments), we will treat it as *unknown*. $\vec{\pmb \tau}$ is called a *latent variable*, which means that it is a quantity that is never actually observed, but which will be useful for describing our model. In this case, $\vec{\pmb \tau}$ takes values in the space $\{1,...,K\}^n$. This means that for a given realization of $\vec{\pmb \tau}$, denoted by $\vec \tau$, that for each of the $n$ nodes in the network, we suppose that an integer value between $1$ and $K$ indicates which community a node is from. Statistically, we write that the node assignment for node $i$, denoted by $\pmb \tau_i$, is sampled independently and identically from $Categorical(\vec \pi)$. Stated another way, the vector $\vec\pi$ indicates the probability $\pi_k$ of assignment to each community $k$ in the network.
#
# The matrix $B$ behaves exactly the same as it did with the *a posteriori* SBM. Finally, let's think about how to write down the generative model in the *a posteriori* SBM. The model for the *a posteriori* SBM is, in fact, nearly the same as for the *a priori* SBM: we still say that given $\tau_i = k'$ and $\tau_j = k$, that $\mathbf a_{ij}$ are independent $Bern(b_{k'k})$. Here, however, we also describe that $\pmb \tau_i$ are sampled independent and identically from $Categorical(\vec\pi)$, as we learned above. If $\mathbf A$ is the adjacency matrix for an *a posteriori* SBM network with parameters $\vec \pi$ and $B$, we write that $\mathbf A \sim SBM_n(\vec \pi, B)$.
#
# ### Probability
#
# What does the probability for the *a posteriori* SBM look like? In this case, $\theta = (\vec \pi, B)$ are the parameters for the model, so the probability for a realization $A$ of $\mathbf A$ is:
# \begin{align*}
# \mathbb P_\theta(A) &= \mathbb P_\theta(\mathbf A = A)
# \end{align*}
# Next, we use the fact that the probability that $\mathbf A = A$ is, in fact, the *integration* (over realizations of $\vec{\pmb \tau}$) of the joint $(\mathbf A, \vec{\pmb \tau})$. In this case, we will let $\mathcal T = \{1,...,K\}^n$ be the space of all possible realizations that $\vec{\pmb \tau}$ could take:
# \begin{align}
# \mathbb P_\theta(A)&= \sum_{\vec \tau \in \mathcal T} \mathbb P_\theta(\mathbf A = A, \vec{\pmb \tau} = \vec \tau)
# \end{align}
# Next, remember that by definition of a conditional probability for a random variable $\mathbf x$ taking value $x$ conditioned on random variable $\mathbf y$ taking the value $y$, that $\mathbb P(\mathbf x = x | \mathbf y = y) = \frac{\mathbb P(\mathbf x = x, \mathbf y = y)}{\mathbb P(\mathbf y = y)}$. Note that by multiplying through by $\mathbf P(\mathbf y = y)$, we can see that $\mathbb P(\mathbf x = x, \mathbf y = y) = \mathbb P(\mathbf x = x| \mathbf y = y)\mathbb P(\mathbf y = y)$. Using this logic for $\mathbf A$ and $\vec{\pmb \tau}$:
# \begin{align*}
# \mathbb P_\theta(A) &=\sum_{\vec \tau \in \mathcal T} \mathbb P_\theta(\mathbf A = A| \vec{\pmb \tau} = \vec \tau)\mathbb P(\vec{\pmb \tau} = \vec \tau)
# \end{align*}
# Intuitively, for each term in the sum, we are treating $\vec{\pmb \tau}$ as taking a fixed value, $\vec\tau$, to evaluate this probability statement.
#
# We will start by describing $\mathbb P(\vec{\pmb \tau} = \vec\tau)$. Remember that for $\vec{\pmb \tau}$, that each entry $\pmb \tau_i$ is sampled *independently and identically* from $Categorical(\vec \pi)$.The probability mass for a $Categorical(\vec \pi)$-valued random variable is $\mathbb P(\pmb \tau_i = \tau_i; \vec \pi) = \pi_{\tau_i}$. Finally, note that if we are taking the products of $n$ $\pi_{\tau_i}$ terms, that many of these values will end up being the same. Consider, for instance, if the vector $\tau = [1,2,1,2,1]$. We end up with three terms of $\pi_1$, and two terms of $\pi_2$, and it does not matter which order we multiply them in. Rather, all we need to keep track of are the counts of each $\pi$ term. Written another way, we can use the indicator that $\tau_i = k$, given by $\mathbb 1_{\tau_i = k}$, and a running counter over all of the community probability assignments $\pi_k$ to make this expression a little more sensible. We will use the symbol $n_k = \sum_{i = 1}^n \mathbb 1_{\tau_i = k}$ to denote this value, which is the number of nodes in community $k$:
# \begin{align*}
# \mathbb P_\theta(\vec{\pmb \tau} = \vec \tau) &= \prod_{i = 1}^n \mathbb P_\theta(\pmb \tau_i = \tau_i),\;\;\;\;\textrm{Independence Assumption} \\
# &= \prod_{i = 1}^n \pi_{\tau_i} ,\;\;\;\;\textrm{p.m.f. of a Categorical R.V.}\\
# &= \prod_{k = 1}^K \pi_{k}^{n_k},\;\;\;\;\textrm{Reorganizing what we are taking products of}
# \end{align*}
# Next, let's think about the conditional probability term, $\mathbb P_\theta(\mathbf A = A \big | \vec{\pmb \tau} = \vec \tau)$. Remember that the entries are all independent conditional on $\vec{\pmb \tau}$ taking the value $\vec\tau$. It turns out this is exactly the same result that we obtained for the *a priori* SBM:
# \begin{align*}
# \mathbb P_\theta(\mathbf A = A \big | \vec{\pmb \tau} = \vec \tau)
# &= \prod_{k',k} b_{\ell k}^{m_{k' k}}(1 - b_{k' k})^{n_{k' k} - m_{k' k}}
# \end{align*}
#
# Combining these into the integrand gives:
# \begin{align*}
# \mathbb P_\theta(A) &= \sum_{\vec \tau \in \mathcal T} \mathbb P_\theta(\mathbf A = A \big | \vec{\pmb \tau} = \vec \tau) \mathbb P_\theta(\vec{\pmb \tau} = \vec \tau) \\
# &= \sum_{\vec \tau \in \mathcal T} \prod_{k = 1}^K \left[\pi_k^{n_k}\cdot \prod_{k'=1}^K b_{k' k}^{m_{k' k}}(1 - b_{k' k})^{n_{k' k} - m_{k' k}}\right]
# \end{align*}
#
# Evaluating this sum explicitly proves to be relatively tedious and is a bit outside of the scope of this book, so we will omit it here.
#
# ## Degree-Corrected Stochastic Block Model (DCSBM)
#
# Let's think back to our school example for the Stochastic Block Model. Remember, we had 100 students, each of whom could go to one of two possible schools: school one or school two. Our network had 100 nodes, representing each of the students. We said that the school for which each student attended was represented by their node assignment $\tau_i$ to one of two possible communities. The matrix $B$ was the block probaability matrix, where $b_{11}$ was the probability that students in school one were friends, $b_{22}$ was the probability that students in school two were friends, and $b_{12} = b_{21}$ was the probability that students were friends if they did not go to the same school. In this case, we said that $\mathbf A$ was an $SBM_n(\tau, B)$ random network.
#
# When would this setup not make sense? Let's say that Alice and Bob both go to the same school, but Alice is more popular than Bob. In general since Alice is more popular than Bob, we might want to say that for any clasasmate, Alice gets an additional "popularity benefit" to her probability of being friends with the other classmate, and Bob gets an "unpopularity penalty." The problem here is that within a single community of an SBM, the SBM assumes that the **node degree** (the number of nodes each nodes is connected to) is the *same* for all nodes within a single community. This means that we would be unable to reflect this benefit/penalty system to Alice and Bob, since each student will have the same number of friends, on average. This problem is referred to as **community degree homogeneity** in a Stochastic Block Model Network. Community degree homogeneity just means that the node degree is *homogeneous*, or the same, for all nodes within a community.
#
#
# ```{admonition} Degree Homogeneity in a Stochastic Block Model Network
# Suppose that $\mathbf A \sim SBM_{n, \vec\tau}(B)$, where $\mathbf A$ has $K=2$ communities. What is the node degree of each node in $\mathbf A$?
#
# For an arbitrary node $v_i$ which is in community $k$ (either one or two), we will compute the expectated value of the degree $deg(v_i)$, written $\mathbb E\left[deg(v_i); \tau_i = k\right]$. We will let $n_k$ represent the number of nodes whose node assignments $\tau_i$ are to community $k$. Let's see what happens:
# \begin{align*}
# \mathbb E\left[deg(v_i); \tau_i = k\right] &= \mathbb E\left[\sum_{j = 1}^n \mathbf a_{ij}\right] \\
# &= \sum_{j = 1}^n \mathbb E[\mathbf a_{ij}]
# \end{align*}
# We use the *linearity of expectation* again to get from the top line to the second line. Next, instead of summing over all the nodes, we'll break the sum up into the nodes which are in the same community as node $i$, and the ones in the *other* community $k'$. We use the notation $k'$ to emphasize that $k$ and $k'$ are different values:
#
# \begin{align*}
# \mathbb E\left[deg(v_i); \tau_i = k\right] &= \sum_{j : i \neq j, \tau_j = k} \mathbb E\left[\mathbf a_{ij}\right] + \sum_{j : \tau_j =k'} \mathbb E[\mathbf a_{ij}]
# \end{align*}
# In the first sum, we have $n_k-1$ total edges (the number of nodes that aren't node $i$, but are in the same community), and in the second sum, we have $n_{k'}$ total edges (the number of nodes that are in the other community). Finally, we will use that the probability of an edge in the same community is $b_{kk}$, but the probability of an edge between the communities is $b_{k' k}$. Finally, we will use that the expected value of an adjacency $\mathbf a_{ij}$ which is Bernoulli distributed is its probability:
# \begin{align*}
# \mathbb E\left[deg(v_i); \tau_i = k\right] &= \sum_{j : i \neq j, \tau_j = k} b_{kk} + \sum_{j : \tau_j = \ell} b_{kk'},\;\;\;\;\mathbf a_{ij}\textrm{ are Bernoulli distributed} \\
# &= (n_k - 1)b_{kk} + n_{k'} b_{kk'}
# \end{align*}
# This holds for any node $i$ which is in community $k$. Therefore, the expected node degree is the same, or **homogeneous**, within a community of an SBM.
# ```
#
# To address this limitation, we turn to the Degree-Corrected Stochastic Block Model, or DCSBM. As with the Stochastic Block Model, there is both a *a priori* and *a posteriori* DCSBM.
# ### *A Priori* DCSBM
#
# Like the *a priori* SBM, the *a priori* DCSBM is where we know which nodes are in which communities ahead of time. Here, we will use the variable $K$ to denote the number of different communiies. The *a priori* DCSBM has the following two parameters:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $B$ | [0,1]$^{K \times K}$ | The block matrix, which assigns edge probabilities for pairs of communities |
# | $\vec\theta$ | $\mathbb R^n_+$ | The degree correction vector, which adjusts the degree for pairs of nodes |
#
# The latent community assignment vector $\vec{\pmb \tau}$ with a known *a priori* realization $\vec{\tau}$ and the block matrix $B$ are exactly the same for the *a priori* DCSBM as they were for the *a priori* SBM.
#
# The vector $\vec\theta$ is the degree correction vector. Each entry $\theta_i$ is a positive scalar. $\theta_i$ defines how much more (or less) edges associated with node $i$ are connected due to their association with node $i$.
#
# Finally, let's think about how to write down the generative model for the *a priori* DCSBM. We say that $\tau_i = k'$ and $\tau_j = k$, $\mathbf a_{ij}$ is sampled independently from a $Bern(\theta_i \theta_j b_{k'k})$ distribution for all $j > i$. As we can see, $\theta_i$ in a sense is "correcting" the probabilities of each adjacency to node $i$ to be higher, or lower, depending on the value of $\theta_i$ that that which is given by the block probabilities $b_{\ell k}$. If $\mathbf A$ is an *a priori* DCSBM network with parameters and $B$, we write that $\mathbf A \sim DCSBM_{n,\vec\tau}(\vec \theta, B)$.
# #### Probability
#
# The derivation for the probability is the same as for the *a priori* SBM, with the change that $p_{ij} = \theta_i \theta_j b_{k'k}$ instead of just $b_{k'k}$. This gives that the probability turns out to be:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \prod_{j > i} \left(\theta_i \theta_j b_{k'k}\right)^{a_{ij}}\left(1 - \theta_i \theta_j b_{k'k}\right)^{1 - a_{ij}}
# \end{align*}
# The expression doesn't simplify much more due to the fact that the probabilities are dependent on the particular $i$ and $j$, so we can't just reduce the statement in terms of $n_{k'k}$ and $m_{k'k}$ like for the SBM.
# ### *A Posteriori* DCSBM
# The *a posteriori* DCSBM is to the *a posteriori* SBM what the *a priori* DCSBM was to the *a priori* SBM. The changes are very minimal, so we will omit explicitly writing it all down here so we can get this section wrapped up, with the idea that the preceding section on the *a priori* DCSBM should tell you what needs to change. We will leave it as an exercise to the reader to write down a model and probability statement for realizations of the DCSBM.
#
# ## Random Dot Product Graph (RDPG)
#
# ### *A Priori* RDPG
#
# The *a priori* Random Dot Product Graph is an RDPG in which we know *a priori* the latent position matrix $X$. The *a priori* RDPG has the following parameter:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $X$ | $ \mathbb R^{n \times d}$ | The matrix of latent positions for each node $n$. |
#
# $X$ is called the **latent position matrix** of the RDPG. We write that $X \in \mathbb R^{n \times d}$, which means that it is a matrix with real values, $n$ rows, and $d$ columns. We will use the notation $\vec x_i$ to refer to the $i^{th}$ row of $X$. $\vec x_i$ is referred to as the **latent position** of a node $i$. This looks something like this:
# \begin{align*}
# X = \begin{bmatrix}
# \vec x_{1}^\top \\
# \vdots \\
# \vec x_n^\top
# \end{bmatrix}
# \end{align*}
# Noting that $X$ has $d$ columns, this implies that $\vec x_i \in \mathbb R^d$, or that each node's latent position is a real-valued $d$-dimensional vector.
#
# What is the generative model for the *a priori* RDPG? As we discussed above, given $X$, for all $j > i$, $\mathbf a_{ij} \sim Bern(\vec x_i^\top \vec x_j)$ independently. If $i < j$, $\mathbf a_{ji} = \mathbf a_{ij}$ (the network is *undirected*), and $\mathbf a_{ii} = 0$ (the network is *loopless*). If $\mathbf A$ is an *a priori* RDPG with parameter $X$, we write that $\mathbf A \sim RDPG_n(X)$.
#
#
# <!-- TODO: return to add equivalence classes -->
# #### Probability
#
# Given $X$, the probability for an RDPG is relatively straightforward, as an RDPG is another Independent-Edge Random Graph. The independence assumption vastly simplifies our resulting expression. We will also use many of the results we've identified above, such as the p.m.f. of a Bernoulli random variable. Finally, we'll note that the probability matrix $P = (\vec x_i^\top \vec x_j)$, so $p_{ij} = \vec x_i^\top \vec x_j$:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \mathbb P_\theta(A) \\
# &= \prod_{j > i}\mathbb P(\mathbf a_{ij} = a_{ij}),\;\;\;\; \textrm{Independence Assumption} \\
# &= \prod_{j > i}(\vec x_i^\top \vec x_j)^{a_{ij}}(1 - \vec x_i^\top \vec x_j)^{1 - a_{ij}},\;\;\;\; a_{ij} \sim Bern(\vec x_i^\top \vec x_j)
# \end{align*}
#
# Unfortunately, the probability equivalence classes are a bit harder to understand intuitionally here compared to the ER and SBM examples so we won't write them down here, but they still exist!
# ### *A Posteriori* RDPG
#
# Like for the *a posteriori* SBM, the *a posteriori* RDPG introduces another strange set: the **intersection of the unit ball and the non-negative orthant**. Huh? This sounds like a real mouthful, but it turns out to be rather straightforward. You are probably already very familiar with a particular orthant: in two-dimensions, an orthant is called a quadrant. Basically, an orthant just extends the concept of a quadrant to spaces which might have more than $2$ dimensions. The non-negative orthant happens to be the orthant where all of the entries are non-negative. We call the **$K$-dimensional non-negative orthant** the set of points in $K$-dimensional real space, where:
# \begin{align*}
# \left\{\vec x \in \mathbb R^K : x_k \geq 0\text{ for all $k$}\right\}
# \end{align*}
# In two dimensions, this is the traditional upper-right portion of the standard coordinate axis. To give you a picture, the $2$-dimensional non-negative orthant is the blue region of the following figure:
# + tags=["hide-input"]
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axisartist import SubplotZero
import matplotlib.patches as patch
class myAxes():
def __init__(self, xlim=(-5,5), ylim=(-5,5), figsize=(6,6)):
self.xlim = xlim
self.ylim = ylim
self.figsize = figsize
self.__scale_arrows()
def __drawArrow(self, x, y, dx, dy, width, length):
plt.arrow(
x, y, dx, dy,
color = 'k',
clip_on = False,
head_width = self.head_width,
head_length = self.head_length
)
def __scale_arrows(self):
""" Make the arrows look good regardless of the axis limits """
xrange = self.xlim[1] - self.xlim[0]
yrange = self.ylim[1] - self.ylim[0]
self.head_width = min(xrange/30, 0.25)
self.head_length = min(yrange/30, 0.3)
def __drawAxis(self):
"""
Draws the 2D cartesian axis
"""
# A subplot with two additional axis, "xzero" and "yzero"
# corresponding to the cartesian axis
ax = SubplotZero(self.fig, 1, 1, 1)
self.fig.add_subplot(ax)
# make xzero axis (horizontal axis line through y=0) visible.
for axis in ["xzero","yzero"]:
ax.axis[axis].set_visible(True)
# make the other axis (left, bottom, top, right) invisible
for n in ["left", "right", "bottom", "top"]:
ax.axis[n].set_visible(False)
# Plot limits
plt.xlim(self.xlim)
plt.ylim(self.ylim)
ax.set_yticks([-1, 1, ])
ax.set_xticks([-2, -1, 0, 1, 2])
# Draw the arrows
self.__drawArrow(self.xlim[1], 0, 0.01, 0, 0.3, 0.2) # x-axis arrow
self.__drawArrow(0, self.ylim[1], 0, 0.01, 0.2, 0.3) # y-axis arrow
self.ax=ax
def draw(self):
# First draw the axis
self.fig = plt.figure(figsize=self.figsize)
self.__drawAxis()
axes = myAxes(xlim=(-2.5,2.5), ylim=(-2,2), figsize=(9,7))
axes.draw()
rectangle =patch.Rectangle((0,0), 3, 3, fc='blue',ec="blue", alpha=.2)
axes.ax.add_patch(rectangle)
plt.show()
# -
# Now, what is the unit ball? You are probably familiar with the idea of the unit ball, even if you haven't heard it called that specifically. Remember that the Euclidean norm for a point $\vec x$ which has coordinates $x_i$ for $i=1,...,K$ is given by the expression:
# \begin{align*}
# \left|\left|\vec x\right|\right|_2 = \sqrt{\sum_{i = 1}^K x_i^2}
# \end{align*}
# The Euclidean unit ball is just the set of points whose Euclidean norm is at most $1$. To be more specific, the **closed unit ball** with the Euclidean norm is the set of points:
# \begin{align*}
# \left\{\vec x \in \mathbb R^K :\left|\left|\vec x\right|\right|_2 \leq 1\right\}
# \end{align*}
#
# We draw the $2$-dimensional unit ball with the Euclidean norm below, where the points that make up the unit ball are shown in red:
# + tags=["hide-input"]
axes = myAxes(xlim=(-2.5,2.5), ylim=(-2,2), figsize=(9,7))
axes.draw()
circle =patch.Circle((0,0), 1, fc='red',ec="red", alpha=.3)
axes.ax.add_patch(circle)
plt.show()
# -
# Now what is their intersection? Remember that the intersection of two sets $A$ and $B$ is the set:
# \begin{align*}
# A \cap B &= \{x : x \in A, x \in B\}
# \end{align*}
# That is, each element must be in *both* sets to be in the intersection. The interesction of the unit ball and the non-negative orthant will be the set:
#
# \begin{align*}
# \mathcal X_K = \left\{\vec x \in \mathbb R^K :\left|\left|\vec x\right|\right|_2 \leq 1, x_k \geq 0 \textrm{ for all $k$}\right\}
# \end{align*}
#
# visually, this will be the set of points in the *overlap* of the unit ball and the non-negative orthant, which we show below in purple:
# + tags=["hide-input"]
axes = myAxes(xlim=(-2.5,2.5), ylim=(-2,2), figsize=(9,7))
axes.draw()
circle =patch.Circle((0,0), 1, fc='red',ec="red", alpha=.3)
axes.ax.add_patch(circle)
rectangle =patch.Rectangle((0,0), 3, 3, fc='blue',ec="blue", alpha=.2)
axes.ax.add_patch(rectangle)
plt.show()
# + [markdown] tags=["hide-input"]
# This space has an *incredibly* important corollary. It turns out that if $\vec x$ and $\vec y$ are both elements of $\mathcal X_K$, that $\left\langle \vec x, \vec y \right \rangle = \vec x^\top \vec y$, the **inner product**, is at most $1$, and at least $0$. Without getting too technical, this is because of something called the Cauchy-Schwartz inequality and the properties of $\mathcal X_K$. If you remember from linear algebra, the Cauchy-Schwartz inequality states that $\left\langle \vec x, \vec y \right \rangle$ can be at most the product of $\left|\left|\vec x\right|\right|_2$ and $\left|\left|\vec y\right|\right|_2$. Since $\vec x$ and $\vec y$ have norms both less than or equal to $1$ (since they are on the *unit ball*), their inner-product is at most $1$. Further, since $\vec x$ and $\vec y$ are in the non-negative orthant, their inner product can never be negative. This is because both $\vec x$ and $\vec y$ have entries which are not negative, and therefore their element-wise products can never be negative.
#
# -
# The *a posteriori* RDPG is to the *a priori* RDPG what the *a posteriori* SBM was to the *a priori* SBM. We instead suppose that we do *not* know the latent position matrix $X$, but instead know how we can characterize the individual latent positions. We have the following parameter:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | F | inner-product distributions | A distribution which governs each latent position. |
#
# The parameter $F$ is what is known as an **inner-product distribution**. In the simplest case, we will assume that $F$ is a distribution on a subset of the possible real vectors that have $d$-dimensions with an important caveat: for any two vectors within this subset, their inner product *must* be a probability. We will refer to the subset of the possible real vectors as $\mathcal X_K$, which we learned about above. This means that for any $\vec x_i, \vec x_j$ that are in $\mathcal X_K$, it is always the case that $\vec x_i^\top \vec x_j$ is between $0$ and $1$. This is essential because like previously, we will describe the distribution of each edge in the adjacency matrix using $\vec x_i^\top \vec x_j$ to represent a probability. Next, we will treat the latent position matrix as a matrix-valued random variable which is *latent* (remember, *latent* means that we don't get to see it in our real data). Like before, we will call $\vec{\mathbf x}_i$ the random latent positions for the nodes of our network. In this case, each $\vec {\mathbf x}_i$ is sampled independently and identically from the inner-product distribution $F$ described above. The latent-position matrix is the matrix-valued random variable $\mathbf X$ whose entries are the latent vectors $\vec {\mathbf x}_i$, for each of the $n$ nodes.
#
# The model for edges of the *a posteriori* RDPG can be described by conditioning on this unobserved latent-position matrix. We write down that, conditioned on $\vec {\mathbf x}_i = \vec x$ and $\vec {\mathbf x}_j = \vec y$, that if $j > i$, then $\mathbf a_{ij}$ is sampled independently from a $Bern(\vec x^\top \vec y)$ distribution. As before, if $i < j$, $\mathbf a_{ji} = \mathbf a_{ij}$ (the network is *undirected*), and $\mathbf a_{ii} = 0$ (the network is *loopless*). If $\mathbf A$ is the adjacency matrix for an *a posteriori* RDPG with parameter $F$, we write that $\mathbf A \sim RDPG_n(F)$.
#
# #### Probability
#
# The probability for the *a posteriori* RDPG is fairly complicated. This is because, like the *a posteriori* SBM, we do not actually get to see the latent position matrix $\mathbf X$, so we need to use *integration* to obtain an expression for the probability. Here, we are concerned with realizations of $\mathbf X$. Remember that $\mathbf X$ is just a matrix whose rows are $\vec {\mathbf x}_i$, each of which individually have have the distribution $F$; e.g., $\vec{\mathbf x}_i \sim F$ independently. For simplicity, we will assume that $F$ is a disrete distribution on $\mathcal X_K$. This makes the logic of what is going on below much simpler since the notation gets less complicated, but does not detract from the generalizability of the result (the only difference is that sums would be replaced by multivariate integrals, and probability mass functions replaced by probability density functions).
#
# We will let $p$ denote the probability mass function (p.m.f.) of this discrete distribution function $F$. The strategy will be to use the independence assumption, followed by integration over the relevant rows of $\mathbf X$:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \mathbb P_\theta(\mathbf A = A) \\
# &= \prod_{j > i} \mathbb P(\mathbf a_{ij} = a_{ij}), \;\;\;\;\textrm{Independence Assumption} \\
# \mathbb P(\mathbf a_{ij} = a_{ij})&= \sum_{\vec x \in \mathcal X_K}\sum_{\vec y \in \mathcal X_K}\mathbb P(\mathbf a_{ij} = a_{ij}, \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y),\;\;\;\;\textrm{integration over }\vec {\mathbf x}_i \textrm{ and }\vec {\mathbf x}_j
# \end{align*}
# Next, we will simplify this expression a little bit more, using the definition of a conditional probability like we did before for the SBM:
#
# \begin{align*}
# \\
# \mathbb P(\mathbf a_{ij} = a_{ij}, \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) &= \mathbb P(\mathbf a_{ij} = a_{ij}| \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) \mathbb P(\vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y)
# \end{align*}
#
# Further, remember that if $\mathbf a$ and $\mathbf b$ are independent, then $\mathbb P(\mathbf a = a, \mathbf b = b) = \mathbb P(\mathbf a = a)\mathbb P(\mathbf b = b)$. Using that $\vec x_i$ and $\vec x_j$ are independent, by definition:
#
# \begin{align*}
# \mathbb P(\vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) &= \mathbb P(\vec{\mathbf x}_i = \vec x) \mathbb P(\vec{\mathbf x}_j = \vec y)
# \end{align*}
#
# Which means that:
#
# \begin{align*}
# \mathbb P(\mathbf a_{ij} = a_{ij}, \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) &= \mathbb P(\mathbf a_{ij} = a_{ij} | \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y)\mathbb P(\vec{\mathbf x}_i = \vec x) \mathbb P(\vec{\mathbf x}_j = \vec y)
# \end{align*}
# Finally, we that conditional on $\vec{\mathbf x}_i = \vec x_i$ and $\vec{\mathbf x}_j = \vec x_j$, $\mathbf a_{ij}$ is $Bern(\vec x_i^\top \vec x_j)$. This means that in terms of our probability matrix, each entry $p_{ij} = \vec x_i^\top \vec x_j$. Therefore:
#
# \begin{align*}
# \mathbb P(\mathbf a_{ij} = a_{ij}| \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) &= (\vec x^\top \vec y)^{a_{ij}}(1 - \vec x^\top\vec y)^{1 - a_{ij}}
# \end{align*}
# This implies that:
# \begin{align*}
# \mathbb P(\mathbf a_{ij} = a_{ij}, \vec{\mathbf x}_i = \vec x, \vec{\mathbf x}_j = \vec y) &= (\vec x^\top \vec y)^{a_{ij}}(1 - \vec x^\top\vec y)^{1 - a_{ij}}\mathbb P(\vec{\mathbf x}_i = \vec x) \mathbb P(\vec{\mathbf x}_j = \vec y)
# \end{align*}
#
#
# So our complete expression for the probability is:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \prod_{j > i}\sum_{\vec x \in \mathcal X_K}\sum_{\vec y \in \mathcal X_K} (\vec x^\top \vec y)^{a_{ij}}(1 - \vec x^\top\vec y)^{1 - a_{ij}}\mathbb P(\vec{\mathbf x}_i = \vec x) \mathbb P(\vec{\mathbf x}_j = \vec y)
# \end{align*}
# + [markdown] tags=[]
# ## Generalized Random Dot Product Graph (GRDPG)
#
# The Generalized Random Dot Product Graph, or GRDPG, is the most general random network model we will consider in this book. Note that for the RDPG, the probability matrix $P$ had entries $p_{ij} = \vec x_i^\top \vec x_j$. What about $p_{ji}$? Well, $p_{ji} = \vec x_j^\top \vec x_i$, which is exactly the same as $p_{ij}$! This means that even if we were to consider a directed RDPG, the probabilities that can be captured are *always* going to be symmetric. The generalized random dot product graph, or GRDPG, relaxes this assumption. This is achieved by using *two* latent positin matrices, $X$ and $Y$, and letting $P = X Y^\top$. Now, the entries $p_{ij} = \vec x_i^\top \vec y_j$, but $p_{ji} = \vec x_j^\top \vec y_i$, which might be different.
#
# ### *A Priori* GRDPG
#
# The *a priori* GRDPG is a GRDPG in which we know *a priori* the latent position matrices $X$ and $Y$. The *a priori* GRDPG has the following parameters:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $X$ | $ \mathbb R^{n \times d}$ | The matrix of left latent positions for each node $n$. |
# | $Y$ | $ \mathbb R^{n \times d}$ | The matrix of right latent positions for each node $n$. |
#
# $X$ and $Y$ behave nearly the same as the latent position matrix $X$ for the *a priori* RDPG, with the exception that they will be called the **left latent position matrix** and the **right latent position matrix** respectively. Further, the vectors $\vec x_i$ will be the left latent positions, and $\vec y_i$ will be the right latent positions, for a given node $i$, for each node $i=1,...,n$.
#
# What is the generative model for the *a priori* GRDPG? As we discussed above, given $X$ and $Y$, for all $j \neq i$, $\mathbf a_{ij} \sim Bern(\vec x_i^\top \vec y_j)$ independently. If we consider only loopless networks, $\mathbf a_{ij} = 0$. If $\mathbf A$ is an *a priori* GRDPG with left and right latent position matrices $X$ and $Y$, we write that $\mathbf A \sim GRDPG_n(X, Y)$.
#
# ### *A Posteriori* GRDPG
#
# The *A Posteriori* GRDPG is very similar to the *a posteriori* RDPG. We have two parameters:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | F | inner-product distributions | A distribution which governs the left latent positions. |
# | G | inner-product distributions | A distribution which governs the right latent positions. |
#
# Here, we treat the left and right latent position matrices as latent variable matrices, like we did for *a posteriori* RDPG. That is, the left latent positions are sampled independently and identically from $F$, and the right latent positions $\vec y_i$ are sampled independently and identically from $G$.
#
# The model for edges of the *a posteriori* RDPG can be described by conditioning on the unobserved left and right latent-position matrices. We write down that, conditioned on $\vec {\mathbf x}_i = \vec x$ and $\vec {\mathbf y}_j = \vec y$, that if $j \neq i$, then $\mathbf a_{ij}$ is sampled independently from a $Bern(\vec x^\top \vec y)$ distribution. As before, assuming the network is loopless, $\mathbf a_{ii} = 0$. If $\mathbf A$ is the adjacency matrix for an *a posteriori* RDPG with parameter $F$, we write that $\mathbf A \sim GRDPG_n(F, G)$.
#
# -
# ## Inhomogeneous Erdös-Rényi (IER)
#
# In the preceding models, we typically made assumptions about how we could characterize the edge-existence probabilities using fewer than $\binom n 2$ different probabilities (one for each edge). The reason for this is that in general, $n$ is usually relatively large, so attempting to actually learn $\binom n 2$ different probabilities is not, in general, going to be very feasible (it is *never* feasible when we have a single network, since a single network only one observation for each independent edge). Further, it is relatively difficult to ask questions for which assuming edges share *nothing* in common (even if they don't share the same probabilities, there may be properties underlying the probabilities, such as the *latent positions* that we saw above with the RDPG, that we might still want to characterize) is actually favorable.
#
# Nonetheless, the most general model for an independent-edge random network is known as the Inhomogeneous Erdös-Rényi (IER) Random Network. An IER Random Network is characterized by the following parameters:
#
# | Parameter | Space | Description |
# | --- | --- | --- |
# | $P$ | [0,1]$^{n \times n}$ | The edge probability matrix. |
#
# The probability matrix $P$ is an $n \times n$ matrix, where each entry $p_{ij}$ is a probability (a value between $0$ and $1$). Further, if we restrict ourselves to the case of simple networks like we have done so far, $P$ will also be symmetric ($p_{ij} = p_{ji}$ for all $i$ and $j$). The generative model is similar to the preceding models we have seen: given the $(i, j)$ entry of $P$, denoted $p_{ij}$, the edges $\mathbf a_{ij}$ are independent $Bern(p_{ij})$, for any $j > i$. Further, $\mathbf a_{ii} = 0$ for all $i$ (the network is *loopless*), and $\mathbf a_{ji} = \mathbf a_{ij}$ (the network is *undirected*). If $\mathbf A$ is the adjacency maatrix for an IER network with probability matarix $P$, we write that $\mathbf A \sim IER_n(P)$.
#
# It is worth noting that *all* of the preceding models we have discussed so far are special cases of the IER model. This means that, for instance, if we were to consider only the probability matrices where all of the entries are the same, we could represent the ER models. Similarly, if we were to only to consider the probability matrices $P$ where $P = XX^\top$, we could represent any RDPG.
#
# The IER Random Network can be thought of as the limit of Stochastic Block Models, as the number of communities equals the number of nodes in the network. Stated another way, an SBM Random Network where each node is in its own community is equivalent to an IER Random Network. Under this formulation, note that the block matarix for such an SBM, $B$, would have $n \times n$ unique entries. Taking $P$ to be this block matrix shows that the IER is a limiting case of SBMs.
#
# ### Probability
#
# The probability for a network which is IER is very straightforward. We use the independence assumption, and the p.m.f. of a Bernoulli-distributed random-variable $\mathbf a_{ij}$:
#
# \begin{align*}
# \mathbb P_\theta(A) &= \mathbb P(\mathbf A = A) \\
# &= \prod_{j > i}p_{ij}^{a_{ij}}(1 - p_{ij})^{1 - a_{ij}}
# \end{align*}
|
network_machine_learning_in_python/representations/ch5/single-network-models_theory.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Connecting to Presto
#
# Presto ships with a CLI. Run `docker exec -it classroom-presto_presto_1 bin/presto-cli` do access it from the Presto container. the Presto CLI supports autocompletion, history, progress bars and other useful features. For quickly testing queries the CLI is very helpful.
#
# In a environment like a Jupyter notebook, we can use a Presto Python client. The Presto client library implements the Python DBAPI2.0 interface that is used by common database client libraries for querying MySQL, PostgreSQL and SQLite.
#
# DBAPI2.0 defines a API with a `Connection`. Queries then happen with a `cursor`. Presto supports transaction. The level of isolation depends on the connectors involved in a query.
#
# The three mandatory arguments to create a connection are *host*, *port*, and *user*.
# Other arguments such as *source* allow to identify the origin of the query. A common use case is to use it to tell which service, tool, or code sent the query.
#
# Let's create a connection:
# +
import prestodb.dbapi as presto
conn = presto.Connection(host="presto", port=8080, user="demo")
cur = conn.cursor()
cur
# -
# ## Configuration
#
# Presto's general configuration is documented in the [deployment](https://prestodb.github.io/docs/current/installation/deployment.html) page. There are 4 types of configuration files:
# - Node Properties: to configure the coordinator (main server) and worker nodes.
# - JVM Config: command line options for the Java Virtual Machine that runs Presto.
# - Config Properties: configuration for the Presto server
# - Catalog Properties: configuration for Connectors (data sources)
#
# In the repository, the configuration is in `etc/`. The main file to configure Presto is `config.properties`:
#
# ```
# coordinator=true
# node-scheduler.include-coordinator=true
# http-server.http.port=8080
# discovery-server.enabled=true
# discovery.uri=http://localhost:8080
# ```
#
# The discovery is what allows worker nodes to find the coordinator and register themselves. Then they will participate in the execution of queries.
# ## Catalogs
#
# A catalog is mapped to a connector. The name of configuration file for a catalgo defines the catalog's name. Here `etc/catalog/mysql.properties` configures the `mysql` catalog. We could name it `events` or `users`:
#
# ```
# connector.name=mysql
# connection-url=jdbc:mysql://mysql:3306
# connection-user=USER
# connection-password=PASSWORD
# ```
#
# We did the same with `etc/catalog/mongodb.properties`:
#
# ```
# connector.name=mongodb
# mongodb.seeds=mongodb
# ```
#
# Adding a catalog is a simple as adding a file with the catalog properties and named after the catalog's name.
#
#
# Below we list the available catalogs on the Presto cluster we are running:
cur.execute("SHOW catalogs")
cur.fetchall()
# ## How Does Presto Execute a Query?
#
# If you are curious about what Presto translate a SQL query to and what it will run, you can you `EXPLAIN`:
# +
conn = presto.Connection(host="presto", port=8080, user="demo", catalog="tcph", schema="sf10")
cur = conn.cursor()
cur.execute("explain (type distributed, format graphviz) select * from tcph.sf100.lineitem l join orders o on l.orderkey = o.orderkey")
plan = cur.fetchall()
import graphviz
graphviz.Source(plan[0][0])
# -
# Here we asked Presto to return the query plan in graphviz format.
#
# Each box is a *stage* and the boundaries delimit when Presto has to exchange data between nodes.
# ## Create a Table in MySQL
#
# Let's use the MySQL client to create the table. Then we will switch to Presto to manipulate the data:
# +
import mysql.connector
mysql = mysql.connector.connect(
host='mysql',
user='root',
password='<PASSWORD>'
)
cur = mysql.cursor()
cur.execute("CREATE DATABASE IF NOT EXISTS presto")
cur.fetchall()
cur.execute("""
CREATE TABLE IF NOT EXISTS presto.events (event LONGTEXT)
CHARSET utf8mb4 ENGINE=InnoDB
""")
cur.fetchall()
cur.execute("DESC presto.events")
for row in cur.fetchall():
print("{table}: [{props}]".format(
table=row[0],
props=', '.join(str(i) for i in row[1:])))
# -
# ## Load Data in MySQL
#
# Let's now load data from [GH Archive](http://www.gharchive.org/) into MySQL and MongoDB.
# Each file from GH Archive contains lines of JSON structs that represent events from the public GitHub timeline, for example repository creation or code push.
#
# Now that the table is create in MySQL, we can insert rows with Presto by using the existing `conn` object created above. You can open http://localhost:8080 to see the execution Presto queries.
# +
import gzip
import io
import json
import re
import requests
# Load events happening between 4-5pm.
# Feel free to load more hours or more days.
# We limit the dataset to one hour here to not overload
# the machine that will run the queries as this tutorial
# is expected to run on a laptop.
# It is going to take some time. For the demo, i pre-loaded
# the data with the mysql client to avoid the overhead of creating
# Python objects.
zdata = requests.get("https://data.gharchive.org/2015-04-28-16.json.gz")
data = gzip.decompress(zdata.content)
rows = []
# load ``ROW_COUNT`` rows. Feel free to set a greater value if it
# works well in your environment. Using a small value on purpose
# to avoid loading data for a long time.
ROW_COUNT = 50
cur = conn.cursor()
for n, line in enumerate(io.BytesIO(data)):
row = line.strip().decode('utf8')
sql = "INSERT INTO mysql.presto.events (event) VALUES ('{}')".format(row.replace("'", "''"))
cur.execute(sql)
cur.fetchall()
if n == ROW_COUNT - 1:
break
# -
cur = conn.cursor()
cur.execute("SELECT json_extract(json_parse(event), '$.type') FROM mysql.presto.events TABLESAMPLE BERNOULLI (1) LIMIT 1")
cur.fetchall()
# +
cur = conn.cursor()
cur.execute("""
SELECT ev_type, repo_name, count(*) FROM (
SELECT
TRY(json_extract_scalar(ev, '$.repo.name')) as repo_name,
TRY(json_extract_scalar(ev, '$.type')) as ev_type FROM (
SELECT try(json_parse(event)) as ev FROM mysql.presto.events))
WHERE repo_name is not null and ev_type = 'PushEvent'
GROUP BY ev_type, repo_name
ORDER BY 3 DESC
LIMIT 10
""")
rows = cur.fetchall()
import pandas as pd
from IPython.display import display
print(rows)
df = pd.DataFrame(sorted(rows, key=lambda x: x[2], reverse=True))
display(df)
# -
cur = conn.cursor()
cur.execute("CREATE TABLE mongodb.events.all AS SELECT * FROM mysql.presto.events")
cur.fetchall()
|
jupyter/f8_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: apache-sedona
# language: python
# name: apache-sedona
# ---
import findspark
findspark.init()
from IPython.display import display, HTML
from pyspark.sql import SparkSession
from pyspark import StorageLevel
import pandas as pd
from pyspark.sql.types import StructType, StructField,StringType, LongType, IntegerType, DoubleType, ArrayType
from pyspark.sql.functions import regexp_replace
from sedona.register import SedonaRegistrator
from sedona.utils import SedonaKryoRegistrator, KryoSerializer
from pyspark.sql.functions import col, split, expr
from pyspark.sql.functions import udf, lit
from sedona.utils import SedonaKryoRegistrator, KryoSerializer
from pyspark.sql.functions import col, split, expr
from pyspark.sql.functions import udf, lit
# # Create Spark Session for application
# +
spark = SparkSession.\
builder.\
master("local[*]").\
appName("Demo-app").\
config("spark.serializer", KryoSerializer.getName).\
config("spark.kryo.registrator", SedonaKryoRegistrator.getName) .\
config("spark.executor.cores", 3) .\
config("spark.driver.memory", "4G") .\
config("spark.kryoserializer.buffer.max.value", "4096") .\
config("spark.sql.crossJoin.enabled", "true") .\
getOrCreate()
SedonaRegistrator.registerAll(spark)
sc = spark.sparkContext
# -
# # Geotiff Loader
#
# 1. Loader takes as input a path to directory which contains geotiff files or a parth to particular geotiff file
# 2. Loader will read geotiff image in a struct named image which contains multiple fields as shown in the schema below which can be extracted using spark SQL
# Path to directory of geotiff images
DATA_DIR = "./data/raster/"
df = spark.read.format("geotiff").option("dropInvalid",True).load(DATA_DIR)
df.printSchema()
df = df.selectExpr("image.origin as origin","ST_GeomFromWkt(image.wkt) as Geom", "image.height as height", "image.width as width", "image.data as data", "image.nBands as bands")
df.show(5)
# # Extract a particular band from geotiff dataframe using RS_GetBand()
#
# +
''' RS_GetBand() will fetch a particular band from given data array which is the concatination of all the bands'''
df = df.selectExpr("Geom","RS_GetBand(data, 1,bands) as Band1","RS_GetBand(data, 2,bands) as Band2","RS_GetBand(data, 3,bands) as Band3", "RS_GetBand(data, 4,bands) as Band4")
df.createOrReplaceTempView("allbands")
df.show(5)
# -
# # Map Algebra operations on band values
# +
''' RS_NormalizedDifference can be used to calculate NDVI for a particular geotiff image since it uses same computational formula as ndvi'''
NomalizedDifference = df.selectExpr("RS_NormalizedDifference(Band1, Band2) as normDiff")
NomalizedDifference.show(5)
# -
''' RS_Mean() can used to calculate mean of piel values in a particular spatial band '''
meanDF = df.selectExpr("RS_Mean(Band1) as mean")
meanDF.show(5)
""" RS_Mode() is used to calculate mode in an array of pixels and returns a array of double with size 1 in case of unique mode"""
modeDF = df.selectExpr("RS_Mode(Band1) as mode")
modeDF.show(5)
''' RS_GreaterThan() is used to mask all the values with 1 which are greater than a particular threshold'''
greaterthanDF = spark.sql("Select RS_GreaterThan(Band1,1000.0) as greaterthan from allbands")
greaterthanDF.show()
# +
''' RS_GreaterThanEqual() is used to mask all the values with 1 which are greater than a particular threshold'''
greaterthanEqualDF = spark.sql("Select RS_GreaterThanEqual(Band1,360.0) as greaterthanEqual from allbands")
greaterthanEqualDF.show()
# -
''' RS_LessThan() is used to mask all the values with 1 which are less than a particular threshold'''
lessthanDF = spark.sql("Select RS_LessThan(Band1,1000.0) as lessthan from allbands")
lessthanDF.show()
''' RS_LessThanEqual() is used to mask all the values with 1 which are less than equal to a particular threshold'''
lessthanEqualDF = spark.sql("Select RS_LessThanEqual(Band1,2890.0) as lessthanequal from allbands")
lessthanEqualDF.show()
''' RS_AddBands() can add two spatial bands together'''
sumDF = df.selectExpr("RS_AddBands(Band1, Band2) as sumOfBand")
sumDF.show(5)
''' RS_SubtractBands() can subtract two spatial bands together'''
subtractDF = df.selectExpr("RS_SubtractBands(Band1, Band2) as diffOfBand")
subtractDF.show(5)
''' RS_MultiplyBands() can multiple two bands together'''
multiplyDF = df.selectExpr("RS_MultiplyBands(Band1, Band2) as productOfBand")
multiplyDF.show(5)
''' RS_DivideBands() can divide two bands together'''
divideDF = df.selectExpr("RS_DivideBands(Band1, Band2) as divisionOfBand")
divideDF.show(5)
''' RS_MultiplyFactor() will multiply a factor to a spatial band'''
mulfacDF = df.selectExpr("RS_MultiplyFactor(Band2, 2) as target")
mulfacDF.show(5)
''' RS_BitwiseAND() will return AND between two values of Bands'''
bitwiseAND = df.selectExpr("RS_BitwiseAND(Band1, Band2) as AND")
bitwiseAND.show(5)
''' RS_BitwiseOR() will return OR between two values of Bands'''
bitwiseOR = df.selectExpr("RS_BitwiseOR(Band1, Band2) as OR")
bitwiseOR.show(5)
''' RS_Count() will calculate the total number of occurence of a target value'''
countDF = df.selectExpr("RS_Count(RS_GreaterThan(Band1,1000.0), 1.0) as count")
countDF.show(5)
''' RS_Modulo() will calculate the modulus of band value with respect to a given number'''
moduloDF = df.selectExpr("RS_Modulo(Band1, 21.0) as modulo ")
moduloDF.show(5)
''' RS_SquareRoot() will calculate calculate square root of all the band values upto two decimal places'''
rootDF = df.selectExpr("RS_SquareRoot(Band1) as root")
rootDF.show(5)
''' RS_LogicalDifference() will return value from band1 if value at that particular location is not equal tp band1 else it will return 0'''
logDiff = df.selectExpr("RS_LogicalDifference(Band1, Band2) as loggDifference")
logDiff.show(5)
''' RS_LogicalOver() will iterate over two bands and return value of first band if it is not equal to 0 else it will return value from later band'''
logOver = df.selectExpr("RS_LogicalOver(Band3, Band2) as logicalOver")
logOver.show(5)
# # Visualising Geotiff Images
#
# 1. Normalize the bands in range [0-255] if values are greater than 255
# 2. Process image using RS_Base64() which converts in into a base64 string
# 3. Embedd results of RS_Base64() in RS_HTML() to embedd into IPython notebook
# 4. Process results of RS_HTML() as below:
# +
''' Plotting images as a dataframe using geotiff Dataframe.'''
df = spark.read.format("geotiff").option("dropInvalid",True).load(DATA_DIR)
df = df.selectExpr("image.origin as origin","ST_GeomFromWkt(image.wkt) as Geom", "image.height as height", "image.width as width", "image.data as data", "image.nBands as bands")
df = df.selectExpr("RS_GetBand(data,1,bands) as targetband", "height", "width", "bands", "Geom")
df_base64 = df.selectExpr("Geom", "RS_Base64(height,width,RS_Normalize(targetBand), RS_Array(height*width,0), RS_Array(height*width, 0)) as red","RS_Base64(height,width,RS_Array(height*width, 0), RS_Normalize(targetBand), RS_Array(height*width, 0)) as green", "RS_Base64(height,width,RS_Array(height*width, 0), RS_Array(height*width, 0), RS_Normalize(targetBand)) as blue","RS_Base64(height,width,RS_Normalize(targetBand), RS_Normalize(targetBand),RS_Normalize(targetBand)) as RGB" )
df_HTML = df_base64.selectExpr("Geom","RS_HTML(red) as RedBand","RS_HTML(blue) as BlueBand","RS_HTML(green) as GreenBand", "RS_HTML(RGB) as CombinedBand")
df_HTML.show(5)
# -
display(HTML(df_HTML.limit(2).toPandas().to_html(escape=False)))
# # User can also create some UDF manually to manipulate Geotiff dataframes
# +
''' Sample UDF calculates sum of all the values in a band which are greater than 1000.0 '''
def SumOfValues(band):
total = 0.0
for num in band:
if num>1000.0:
total+=1
return total
calculateSum = udf(SumOfValues, DoubleType())
spark.udf.register("RS_Sum", calculateSum)
sumDF = df.selectExpr("RS_Sum(targetband) as sum")
sumDF.show()
# +
''' Sample UDF to visualize a particular region of a GeoTiff image'''
def generatemask(band, width,height):
for (i,val) in enumerate(band):
if (i%width>=12 and i%width<26) and (i%height>=12 and i%height<26):
band[i] = 255.0
else:
band[i] = 0.0
return band
maskValues = udf(generatemask, ArrayType(DoubleType()))
spark.udf.register("RS_MaskValues", maskValues)
df_base64 = df.selectExpr("Geom", "RS_Base64(height,width,RS_Normalize(targetband), RS_Array(height*width,0), RS_Array(height*width, 0), RS_MaskValues(targetband,width,height)) as region" )
df_HTML = df_base64.selectExpr("Geom","RS_HTML(region) as selectedregion")
display(HTML(df_HTML.limit(2).toPandas().to_html(escape=False)))
|
binder/ApacheSedonaRaster_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
"""
Get data of google search results of books and authors to create book/author poularity.
functions used:
book_google(book,author,date) from fictiondb.py
book_google2(book,author,date) from fictiondb.py (improve search results)
Output: book_history_2 (search results that make more sense)
"""
# +
from bs4 import BeautifulSoup
import requests
import time, os
from selenium import webdriver
from selenium.webdriver.common.keys import Keys
from selenium.webdriver.support.ui import WebDriverWait
from selenium.webdriver.common.by import By
from selenium.webdriver.support import expected_conditions as EC
from selenium.webdriver.common.action_chains import ActionChains
import pandas as pd
import numpy as np
import pickle
import sys
sys.path.append('/Users/katiehuang/Documents/metis/projects/onl_ds5_project_2/py')
from loadpage import *
import importlib
from fictiondb import *
# -
chromedriver = "/Applications/chromedriver" # path to the chromedriver executable
os.environ["webdriver.chrome.driver"] = chromedriver
# %run -i '../py/fictiondb.py'
driver.get("https://www.google.com")
# Load combined_df to get author,book,release_date of movie
combined_df = pd.read_pickle('../dump/combined_data')
essential_df = combined_df[['movie_title','author']].copy()
essential_df['date'] = combined_df.release_date.dt.strftime('%Y-%m-%d')
essential_df = essential_df.drop_duplicates(subset=['movie_title','date']).copy()
essential_df.info()
# Create list to for searching
title_list = list(essential_df.movie_title)
author_list = list(essential_df.author)
date_list = list(essential_df.date)
lng = len(title_list)
# %run -i '../py/fictiondb.py'
book_history = []
for i in range(lng):
book = title_list[i]
author = author_list[i]
date = date_list[i]
print(i,book) #keep track the scraping progress
info = book_google(book,author,date)
book_history.append(info)
len(book_history)
import pickle
# Save the list to pickle
with open('../dump/book_history_list','wb') as f:
pickle.dump(book_history,f)
book_history_df = pd.DataFrame(book_history)
# Save the data to pickle file
book_history_df.to_pickle('../dump/book_history_data')
book_history_df.head()
# Test load the pickled df
book_history_df = pd.read_pickle('../dump/book_history_data')
# Check book_popularity and author_popularity
book_popularity_df = book_history_df[['title','book_popularity','author_popularity']].dropna()
book_popularity_df[book_popularity_df.book_popularity == 0]
# ### Improve book popularity
# (Include genre in general search: added book_google2() in fictiondb.py)
import pandas as pd
# Since 'budget' is the bottle neck in dropna process, use that to narrow down the search list
all_df = pd.read_pickle('../dump/all_data').dropna(subset=['budget'])
all_df['date'] = all_df.release_date.dt.strftime('%Y-%m-%d')
all_df.info()
# Create list to search
title_list = list(all_df.movie_title)
author_list = list(all_df.author)
date_list = list(all_df.date)
genre_list = list(all_df.genre)
lng = len(title_list)
# %run -i '../py/fictiondb.py'
book_history_2 = []
for i in range(lng):
book = title_list[i]
author = author_list[i]
date = date_list[i]
genre = genre_list[i]
print(i,book)
info = book_google2(book,author,date,genre)
book_history_2.append(info)
book_history_2
book_history_2_df = pd.DataFrame(book_history_2)
book_history_2_df.to_pickle('../data/book_history_2_data')
|
notebooks/07_scrape_google.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Overview
#
# This a notebook that inspects the results of a WarpX simulation.
#
# # Instruction
#
# Enter the path of the data you wish to visualize below. Then execute the cells one by one, by selecting them with your mouse and typing `Shift + Enter`
# Import statements
import yt ; yt.funcs.mylog.setLevel(50)
import numpy as np
import scipy.constants as scc
import matplotlib.pyplot as plt
# %matplotlib notebook
# ## Read data in the simulation frame
# +
ds = yt.load( './diags/plotfiles/plt00200' ) # Create a dataset object
sl = yt.SlicePlot(ds, 2, 'Ex', aspect=.2) # Create a sliceplot object
sl.set_xlabel(r'$x (\mu m)$') # Set labels x
sl.set_ylabel(r'$z (\mu m)$') # Set labels y
sl.annotate_particles(width=(10.e-6, 'm'), p_size=2, ptype='ions', col='black') # Plot particles species=ions
sl.annotate_particles(width=(10.e-6, 'm'), p_size=2, ptype='electrons', col='black')
sl.annotate_particles(width=(10.e-6, 'm'), p_size=2, ptype='beam', col='black')
sl.annotate_grids() # Show grids
sl.show() # Show the plot
#############################
### OTHER USEFUL COMMANDS ###
#############################
# # List all fields in the datasert
# ds.field_list
# # Get All Data from the dataset
# # Then get some data. ".v" converts arrays from units-aware yt arrays to numpy arrays.
# ad = ds.all_data()
# Bx = ad['boxlib', 'Bx'].v
# # Get All Data from the dataset, on a given level and given dimension.
# # Then get some data. ".v" converts arrays from units-aware yt arrays to numpy arrays.
# # This is similar to the 2 lines above, except that F has the proper shape.
# all_data_level_0 = ds.covering_grid(level=0,left_edge=ds.domain_left_edge, dims=ds.domain_dimensions)
# Bx = all_data_level_0['boxlib', 'Bx'].v.squeeze()
# # particle
# # CAREFUL! For the moment, 2d WarpX simulations use (x, z) spatial coordinate
# # but they are stored as (particle_position_x, particle_position_y) in Yt
# x = ad['beam', 'particle_position_x'].v
# z = ad['beam', 'particle_position_y'].v
# # For 2d simulations, WarpX and Yt use (ux, uz)
# # ux/c should be the nirmalized momentum
# ux = ad['beam', 'particle_momentum_x'].v
# uy = ad['beam', 'particle_momentum_y'].v
# uz = ad['beam', 'particle_momentum_z']
# w = ad['beam', 'particle_weight'].v
# # Set figure size
# sl.figure_size = (9, 7)
# # Save image
# sl.save('./toto.pdf')
# # This returns the domain boundaries
# sl.bounds
# -
# ## Read data back-transformed to the lab frame when the simulation runs in the boosted frame (example: 2D run)
# read_raw_data.py is located in warpx/Tools.
import os, glob
import read_raw_data
# For the moment, the back-transformed diagnostics must be read with
# custom functions like this one.
# It should be OpenPMD-compliant hdf5 files soon, making this part outdated.
def get_particle_field(snapshot, species, field):
fn = snapshot + '/' + species
files = glob.glob(os.path.join(fn, field + '_*'))
files.sort()
all_data = np.array([])
for f in files:
data = np.fromfile(f)
all_data = np.concatenate((all_data, data))
return all_data
# +
species = 'beam'
iteration = 3
field = 'Ex'
snapshot = './lab_frame_data/' + 'snapshot' + str(iteration).zfill(5)
header = './lab_frame_data/Header'
allrd, info = read_raw_data.read_lab_snapshot(snapshot, header) # Read field data
F = allrd[field]
print( "Available info: ", *list(info.keys()) )
print("Available fields: ", info['field_names'])
nx = info['nx']
nz = info['nz']
x = info['x']
z = info['z']
xbo = get_particle_field(snapshot, species, 'x') # Read particle data
ybo = get_particle_field(snapshot, species, 'y')
zbo = get_particle_field(snapshot, species, 'z')
uzbo = get_particle_field(snapshot, species, 'uz')
plt.figure(figsize=(6, 3))
extent = np.array([info['zmin'], info['zmax'], info['xmin'], info['xmax']])
plt.imshow(F, aspect='auto', extent=extent, cmap='seismic')
plt.colorbar()
plt.plot(zbo, xbo, 'g.', markersize=1.)
# -
# ## Read back-transformed data with hdf5 format (example: 3D run)
import h5py
import matplotlib.pyplot as plt
f = h5py.File('HDF5_lab_frame_data/snapshot00003', 'r')
print( list(f.keys())
# plt.figure()
# plt.imshow(f['Ey'][:,,:])
|
Tools/Visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/mengwailoh/geovelo/blob/master/PyTorch_Tutorial_OReilly.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="5fP31OuG98Xj"
# # Introduction to PyTorch - Neural Nets and Beyond
#
# ## <NAME> - Head of Data Science at Podium Education
#
#
# <!---->
#
# <!------>
#
# <!------>
#
# <!---->
#
# 
#
# 
# + [markdown] id="C8MMEUpx98Xk"
# ---
# # Using PyTorch on Google Server
#
# Google has made a version of Jupyter Notebook available online for **free** that allow us to use GPUs for faster training time! I do not recommend you use the local installation unless you don't have access to the internet.
#
# Go to https://colab.research.google.com and sign in with your Google account. If you do not have a Google account you can create one. From there you can create a new notebook.
# + [markdown] id="FmihBmzK-r04"
# # PyTorch on Google
#
# Google Colab has already pre-installed PyTorch (and many other libraries) so no need to re-install on our virtual machines.
#
# + id="wM7YJvTf98Xl"
# usual suspects
import os
import time
import shutil
import requests
import zipfile
from PIL import Image
from io import BytesIO
import numpy as np
import pandas as pd
from cycler import cycler
# the good stuff
import torch
import torch.nn as nn
from torch.autograd import Variable
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import torchvision
from torchvision import datasets, models, transforms
from torchsummary import summary
# standard sklearn import
from sklearn.metrics import accuracy_score
# minor changes to plotting functions
import matplotlib.pyplot as plt
cmap=plt.cm.tab10
c = cycler('color', cmap(np.linspace(0,1,10)))
plt.rcParams["axes.prop_cycle"] = c
# see if GPU is available
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# %matplotlib inline
# + id="Dm78sdz_v0Qa" outputId="8f213421-eb56-44b5-dca1-24247661c54c" colab={"base_uri": "https://localhost:8080/"}
# Output should be: device(type='cuda', index=0)
# If not, restart runtime with GPU enabled.
device
# + id="2XgbYeYa98Xn"
# Download all necessary files for the live tutorial
data_url = 'https://www.dropbox.com/s/k8ywqfx2hvrh9ny/pytorch_data.zip?dl=1'
if not os.path.exists('data'):
# Download the data zip file.
response = requests.get(data_url, stream=True)
zip_path = 'pytorch_data.zip'
with open(zip_path, 'wb') as f:
shutil.copyfileobj(response.raw, f)
# Unzip the file.
with zipfile.ZipFile(zip_path, 'r') as z:
z.extractall()
# Clean up.
os.remove(zip_path)
# + [markdown] id="d9lpGce498Xp"
# # PyTorch
#
# What is PyTorch?
#
# * It is a replacement for NumPy to use GPUs
# * A deep learning platform built for flexibility and speed
#
#
# ## Tensor Overview
# What are tensors?
#
# Tensors are similar to NumPy's `ndarrays`
#
# We normally think of tensors as a generalization of matrices. In fact, matrices are 2-D tensors!
#
# 
#
# Here is a great visualization of tensors from 1-D to 5-D
#
# 
#
# As mentioned before, since tensors are generalizations of matrices, we should be able to create them in similar ways. We can also expect *most* operations to stay the same. In particular, addition of tensors is the same as for matrices. Multiplication is a bit different, but we won't have to concern ourselves with that in this lecture.
# + [markdown] id="SCw6QKH298Xq"
# ### Tensor Types
#
# Torch defines eight CPU tensor types and eight GPU tensor types:
#
# | Data type | dtype | CPU Tensor | GPU Tensor |
# |--------------------------|-----------------------------------|----------------------|---------------------------|
# | 32-bit floating point | `torch.float32` or `torch.float` | `torch.FloatTensor` | `torch.cuda.FloatTensor` |
# | 64-bit floating point | `torch.float64` or `torch.double` | `torch.DoubleTensor` | `torch.cuda.DoubleTensor` |
# | 16-bit floating point | `torch.float16` or `torch.half` | `torch.HalfTensor` | `torch.cuda.HalfTensor` |
# | 8-bit integer (unsigned) | `torch.uint8` | `torch.ByteTensor` | `torch.cuda.ByteTensor` |
# | 8-bit integer (signed) | `torch.int8` | `torch.CharTensor` | `torch.cuda.CharTensor` |
# | 16-bit integer (signed) | `torch.int16` or `torch.short` | `torch.ShortTensor` | `torch.cuda.ShortTensor` |
# | 32-bit integer (signed) | `torch.int32` or `torch.int` | `torch.IntTensor` | `torch.cuda.IntTensor` |
# | 64-bit integer (signed) | `torch.int64` or `torch.long` | `torch.LongTensor` | `torch.cuda.LongTensor` |
#
# **Note**: Tensor types need to match when doing calculations with them.
# + [markdown] id="9b_Zh-XD98Xq"
# ### Numpy ndarrays vs PyTorch Tensors
#
# Let's look at the differences between these two common methods of handling arrays.
# + id="cDuKQwQo98Xr"
# In numpy, we create tensors (arrays) in the following way
x1 = np.random.rand(5,3)
print(f"x1 =\n {x1}\n")
# Similar to numpy we can create random tensors
t1 = torch.rand(5,3, dtype=torch.float64)
print(f"t1 =\n {t1}")
# + id="qYXbEFaJ98Xt"
# check the type
print(f"t1 is a {type(t1)}")
print(f"x1 is a {type(x1)}")
# + id="Ckve1bS898Xu"
print(f"t1 is dtype {t1.dtype}")
print(f"x1 is dtype {x1.dtype}")
# + id="iC9nKptd98Xw"
# create a 3-D tensor in torch and numpy
t2 = torch.rand(2, 3, 5)
print(f"t2 =\n {t2}\n")
x2 = np.random.rand(2, 3, 5)
print(f"x2 =\n {x2}")
# + id="TLLno7I498Xy"
long_tensor = torch.zeros(5,3, dtype=torch.long)
long_tensor
# + id="WjJxk3x898X1"
float_tensor = torch.zeros(5,3, dtype=torch.float64)
float_tensor
# + id="O1zfR0H198X4"
long_tensor + float_tensor
# + id="GJXNRaUC98X7"
# we can also create explicit tensors
x = torch.tensor([2., 3])
x, x.type()
# + id="2x8zEP4S98X9"
# this method creates a new tensor "y" that has the same properties (e.g. dtype) as the original tensor "x"
y = x.new_ones(5,3)
print(f'{y.type()}\n {y}')
# + id="1ldBCZ-Q98X_"
# there's a size method as well
y.size()
# + id="TVYmRi0m98YB"
# We can add tensors as well in the usual way you expect
x = torch.rand(5,3)
x + y
# + id="z56pRLLn98YD"
# We can also add like this
torch.add(x, y)
# + id="S0PQJ4bI98YE"
# OR like this!
# The `*_` method works just like `inplace=True` in pandas
y.add_(x)
# + id="38U4RzTj98YG"
# see!
y
# + id="4KD9jmwr98YI"
# Indexing/Slicing works just like in numpy
y[2, :]
# + id="Hfs11ngt98YX"
# We can reshape tensors as well though it's called "view" in pytorch
# support for 'reshape' has been added
x = torch.randn(4,4)
y = x.view(16)
z = x.view(-1, 8)
w = x.reshape(2, -1)
print(x.size(), y.size(), z.size(), w.size())
# + [markdown] id="XatTg6M498Ya"
# More on torch operations can be found here: https://pytorch.org/docs/stable/torch.html
# + id="oUce2CSj98Yb"
# Converting to/from PyTorch & NumPy is easy
a = torch.ones(5)
a
# + id="H10V5GL098Ye"
# convert to numpy
b = a.numpy()
b
# + id="uxEOtLfN98Yg"
# what do we expect this result to be?
a.add_(1)
print(a)
print(b)
# + id="CqnuTdCJ98Yi"
# Convert from numpy to torch
c = np.random.randn(4,5)
print(c)
d = torch.from_numpy(c)
print(d)
# + [markdown] id="UvnyYAJ698Yk"
# ## Autograd - AKA why PyTorch is awesome
#
# Central to all Neural Networks in PyTorch is the `autograd` package.
#
# The `autograd` package provides automatic differentiation for all operations on Tensors. It is a define-by-run framework,
# which means that your backprop is defined by how your code is run, and that every single iteration can be different.
#
# Let's look at a basic example of this before turning to Neural Networks.
# + id="AqIAiQl798Yk" outputId="41dc14a9-fd2c-4962-8de1-c01355a31981" colab={"base_uri": "https://localhost:8080/", "height": 198}
# Create a tensor and set requires_grad=True to track computation with it
x = torch.ones(2,2, requires_grad=True)
print(x)
# + id="5hCV7jWG98Ym"
# Do some operation on said tensor
y = 3*x + 7
print(y)
# + id="OpzudC3v98Yn"
# Because y was created as a result of an operation, it now has a grad_fn method
y.grad_fn
# + id="xl0fduSM98Yo"
# We can do more stuff to y (and thus x) and calculate its derivatives
z = 2*y**2
w = z.mean()
print(z, w)
# + [markdown] id="3Fz1lXOm4LwQ"
# Let's do that derivative by hand and see that we get the same result.
#
# $\frac{\partial w}{\partial x} = \frac{\partial w}{\partial z} \frac{\partial z}{\partial y} \frac{\partial y}{\partial x}$
#
# Which gives us
#
# $w(x) = \frac{1}{4} z(x)^2 = \frac{1}{2} (3x+7)^2$
#
# $w'(x) = (3x+7)*3|_{x=1} = 30$
# + id="U-9pbJF698Yp" outputId="8bb86a16-45a2-42aa-b102-f6c99994a3c3" colab={"base_uri": "https://localhost:8080/", "height": 181}
# Backpropagation in one line!
w.backward()
# + id="GrscC7cq98Yr"
# et voila!
x.grad
# + [markdown] id="cZBQt0mX98Yt"
# ## Linear Regression Example
# + id="KeTo0Pb_98Yu"
n=1000
# + id="hJ4LRmVQ98Yv"
x = torch.ones(n,2)
x[:,0].uniform_(-1.,1)
x[:5]
# + id="Yrp1OMEe98Yx"
a = torch.tensor([3.,2]); a
# + id="P2k3oBNf98Yy"
y = x@a + torch.randn(n)/3
# + id="lPFm3Yy798Y0"
plt.scatter(x[:,0], y);
# + id="YGjHe8Hz98Y2"
def mse(y, y_pred):
return ((y - y_pred)**2).mean()
# + id="BKgWWEro98Y3"
a_guess = torch.tensor([-1.,1])
# + id="IlVJnrog98Y5"
y_hat = x@a_guess # @ is matrix multiplication
mse(y_hat, y)
# + id="sv6Qha9A98Y7"
plt.scatter(x[:,0],y)
plt.scatter(x[:,0],y_hat);
# + id="K4ahptpE98Y8"
a_guess = nn.Parameter(a_guess)
a_guess
# + id="75TK6zOR98Y9"
def update():
'''
function to update tensor using SGD
'''
y_hat = x@a_guess
loss = mse(y, y_hat)
if t % 10 == 0: print(loss)
loss.backward()
with torch.no_grad():
a_guess.sub_(lr * a_guess.grad)
a_guess.grad.zero_()
# + id="Ce9_sd1v98Y-"
lr = 1e-1
for t in range(100):
update()
# + id="DeUXfjdV98ZB"
plt.scatter(x[:,0], y)
plt.scatter(x[:,0], x@a_guess.detach()); # detach() removes gradient from `a` so it can be plotted. otherwise matplotlib gives error
# + [markdown] id="FSjr7WCF98ZG"
# ### Normal Equations
# Although we solved for the line of best fit using stochastic gradient descent,
# we could have also used the [Normal Equations](https://en.wikipedia.org/wiki/Linear_least_squares#Derivation_of_the_normal_equations) given by
#
# $$ \theta = (X^T X)^{-1} X^T \vec y$$
#
# where $\theta$ is the vector we called `a` in the linear regression code above
# + id="G9Qwa5o498ZG"
# Exercise:
# Use pytorch to solve for theta using the normal equations
# plot your result when you are finished
# HINT:
# matrix inverse in pytorch: x.inverse()
# matrix transpose in pytorch: torch.t(x)
# Code goes here
# + [markdown] id="XhcElduD98ZH"
# ---
# # Neural Nets
# + [markdown] id="IUSiq8Hs98ZI"
# Neural networks (NNs) are special forms of nonlinear regressions where the decision system for which the NN is built mimics the way
# the brain is supposed to work (whether it works like a NN is up for grabs, of course).
#
# Like many of the algorithms we have seen in classical machine learning, it is a supervised learning technique that can perform complex tasks.
# + [markdown] id="nQ814fgi98ZI"
# ## Perceptrons
# + [markdown] id="5YQwp2rp98ZJ"
# The basic building block of a neural network is a perceptron. A perceptron is like a neuron in a human brain. It takes inputs
# (e.g. sensory in a real brain) and then produces an output signal. An entire network of perceptrons is called a neural net.
#
# 
# + [markdown] id="00sR2ipX98ZJ"
# In general, a perceptron could have more or fewer inputs.
# + [markdown] id="XldQsuBe98ZK"
# Instead of assigning equal weight to each of the inputs, we can assign real numbers $w_1, w_2, \ldots$ expressing the importance of the respective inputs to the output. The nueron's output, 0 or 1, is determined whether the weighted sum $\sum_j w_j x_j$ is less than or greater than some *threshold value*.
#
# Perceptrons may emit continuous signals or binary $(0,1)$ signals. In the case of a credit card application, the final perceptron is a binary one (approved or denied). Such perceptrons are implemented by means of squashing functions. For example, a really simple squashing function is one that issues a 1 if the function value is positive and a $-1$ if it is negative.
# + [markdown] id="tb28h7Ll98ZK"
# To put this in more mathematical terms, let $z = \sum_{j=0}^n w_j x_j$ .
# Then the *activation function* $\phi(z)$ is defined as
#
# $$
# \phi(z) =
# \begin{cases}
# -1 & \text{if } z < \theta\\
# 1 & \text{if } z \geq \theta
# \end{cases}
# $$
# + [markdown] id="if9rqZt-98ZL"
# 
# + [markdown] id="b5JMM3rJ98ZL"
# The whole point of the perceptron is to mimic how a single nueron in the brain works: it either *fires* or it doesn't. Thus, the
# perceptron rule is fairly simple and can be summarized by the following steps.
#
# * Initialize the weights to zero or small random numbers
# * For each training sample $\textbf{x}_n$ perform the following steps:
# * Compute the output value $y$
# * Calculate error in $y$ vs $\hat y$
# * Update the weights
#
# Here, the output value is the class label predicted by the activation function that we defined earlier, and the
# simultaneous update of weight $w_j$ in the weight vector $\textbf{w}$ can be more formally written as
#
# $$\bar w_j = w_j + \Delta w_j$$
#
# + [markdown] id="sLSxoMS198ZM"
# ## Fitting a model
#
# Let's go back to our linear perceptron. It has the following parameters:
#
# * $x_i$: inputs
# * $y$ : output
# * $w_i$: learned weights
#
# What we would like to do is adjust the $w_i$'s until our model has the best fit.
#
# First, initialize the $w_i$'s in some meaningful way (usually they're drawn from a randon uniform distribution).
#
# Then, we put it into the usual **algorithm workflow:**
#
# * calculate prediction $\hat y$
# * calculate Loss function $L(y, \hat y)$
# * update weights using backpropagation
#
# ### Loss function and backpropagation
#
# To figure out how well our prediction was during each epoch, we'll use a basic loss function, mean squared error (MSE):
#
# $L(y,\hat{y}) = ||~ y-\hat{y} ~||^2$,
#
# ultimately trying to find $L_{\rm min}$, defined by the point in parameter space where $\nabla_{w_i} L = 0$.
#
# Per-iteration update:
#
# $ w_i \to w_i - \eta \nabla_{w_i} L $,
#
# where $\eta$ is known as the learning rate; too small and takes very long to converge, too big and you oscillate about the minimum.
#
# + [markdown] id="kd5YUrwu98ZM"
# ## A basic example
#
# We'll build a Rube Goldberg adding machine that will illustrate how neural nets work.
# + id="7YHrn_ov98ZM"
model = nn.Sequential(
nn.Linear(2, 1, bias=False))
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.MSELoss()
print(model)
# + id="LJrYvWGK98ZO"
total_loss = []
num_samples = 10_000
for num in range(1, num_samples+1):
# Progress bar indicator
if num % (num_samples//5) == 0:
print('{0}: %: {1:.3f}'.format(num,num/num_samples * 100))
# data prep
x = 4*torch.rand(2) #generate two random numbers uniformly on (0,4)
data, target = Variable(x), Variable(x[0] + x[1])
# Feed forward through NN
output = model(data)
loss = criterion(output, target)
total_loss.append(loss)
# Backpropagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# + id="xOtHnPe598ZP"
fig,ax=plt.subplots(figsize=(11,8))
ax.plot(total_loss,marker='.',ls='',markersize=1.)
ax.set_ylim(0,);ax.set_xlim(0,);ax.grid(alpha=0.2);
ax.set_xlabel('training examples');ax.set_ylabel('mean squared loss');
# + id="ZPNZtx5598ZQ"
x,y=np.linspace(-5,8,100),[]
for xx in x:
yy=model(torch.tensor([xx,2], dtype=torch.float32)).data.cpu().numpy()[0]
y.append(yy)
y=np.array(y)
fig,ax=plt.subplots(figsize=(11,8))
ax.plot([-5,8],[-3,10],lw=2.0,label='actual',alpha=0.7)
ax.fill_betweenx([-3,10],0,4,alpha=0.2)
ax.scatter(x,y,marker='.',s=3.,label='prediction',color='r')
ax.text(0.2,0,'Where we have \ntraining data')
ax.legend()
ax.set_ylim(-3,10);ax.set_xlim(-5,8);
ax.grid(alpha=0.2);
# + [markdown] id="xgmsSRw198ZR"
# ## Feedforward Neural Network
#
# 
#
# For our case of learning linear relationships, the modification to the linear regression architecture is depicted below:
#
#
# 
#
# where
#
# $$\varphi(z) = \frac{1}{1+e^{-z}}$$
#
# is the so-called sigmoid function; this is typically the activation function that is first introduced, I think because of historical reasons. In modern practice, it finds most of its use in transforming single outputs from a NN into a probability. It's worth noting that if your NN will output multiple probabilities, for example, if your NN will categorize between black cats, red cats, white cats, etc., a multi-dimensional generalization of the sigmoid, called the softmax function, is typically used.
#
# The motivation behind adding an activation function is the hope that the NN model may capture non-linear relationships that exist in the data. Below are some commonly used activation functions.
#
# 
#
# In practice, a lot of architectures use the rectified linear unit (ReLU), along with it's close cousin, the so-called leaky-ReLU. In introducing this idea though, we'll focus on the sigmoid which maps real numbers from $(-\infty,\infty) \to [0,1]$.
#
# Of course our data is linear in the case of a straight line (!) but let's see what happens if we try to force a non-linear activation layer to capture a linear relationship..
# + [markdown] id="tcvWinIf98ZR"
# ## Non-linear model for a linear relationship
#
# ### Deep Feedforward Network with sigmoid activation
# + id="r4Qatq-r98ZS"
model = nn.Sequential(
nn.Linear(2, 20),
nn.Sigmoid(),
nn.Linear(20, 20),
nn.Sigmoid(),
nn.Linear(20, 20),
nn.Sigmoid(),
nn.Linear(20, 1))
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.MSELoss()
print(model)
# + id="LJV3Gs4Z98ZT"
total_loss = []
num_samples = 10_000
for num in range(1, num_samples+1):
# Progress bar indicator
if num % (num_samples//5) == 0:
print('{0}: %: {1:.3f}'.format(num,num/num_samples * 100))
# data prep
x = 4*torch.rand(2) #generate two random numbers uniformly on (0,4)
data, target = Variable(x), Variable(x[0] + x[1])
# Feed forward through NN
output = model(data)
loss = criterion(output, target)
total_loss.append(loss)
# Backpropagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# + id="sg8t7Nju98ZU"
fig,ax=plt.subplots(figsize=(11,8))
ax.plot(total_loss,marker='.',ls='',markersize=.8)
ax.set_ylim(0,);ax.set_xlim(0,);ax.grid(alpha=0.2);
ax.set_xlabel('training examples');ax.set_ylabel('mean squared loss');
x,y=np.linspace(-5,8,100),[]
for xx in x:
yy=model(torch.tensor([xx,2],dtype=torch.float32)).data.cpu().numpy()[0]
y.append(yy)
y=np.array(y)
fig,ax=plt.subplots(figsize=(11,8))
ax.plot([-5,8],[-3,10],lw=2.0,label='actual',alpha=0.7)
ax.fill_betweenx([-3,10],0,4,alpha=0.2)
ax.scatter(x,y,marker='.',s=3.,label='prediction',color='r')
ax.text(0.2,0,'Where we have \ntraining data')
ax.legend()
ax.set_ylim(-3,10);ax.set_xlim(-5,8);
ax.grid(alpha=0.2);
ax.set_title('Sigmoid activation function');
# + [markdown] id="8MF1JD0898ZV"
# ## ReLU activation function
# + id="OkrdWaTZ98ZX"
model = nn.Sequential(
nn.Linear(2, 20),
nn.ReLU(),
nn.Linear(20, 20),
nn.ReLU(),
nn.Linear(20, 20),
nn.ReLU(),
nn.Linear(20, 1))
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.MSELoss()
print(model)
# + id="81jF1PRV98ZY"
total_loss = []
num_samples = 10_000
for num in range(1, num_samples+1):
# Progress bar indicator
if num % (num_samples//5) == 0:
print('{0}: %: {1:.3f}'.format(num,num/num_samples * 100))
# data prep
x = 4*torch.rand(2) #generate two random numbers uniformly on (0,4)
data, target = Variable(x), Variable(x[0] + x[1])
# Feed forward through NN
output = model(data)
loss = criterion(output, target)
total_loss.append(loss)
# Backpropagation
optimizer.zero_grad()
loss.backward()
optimizer.step()
# + id="_8lVbhVS98ZZ"
fig,ax=plt.subplots(figsize=(11,8))
ax.plot(total_loss,marker='.',ls='',markersize=.8)
ax.set_ylim(0,);ax.set_xlim(0,);ax.grid(alpha=0.2);
ax.set_xlabel('training examples');ax.set_ylabel('mean squared loss');
x,y=np.linspace(-5,8,100),[]
for xx in x:
yy=model(torch.tensor([xx,2],dtype=torch.float32)).data.cpu().numpy()[0]
y.append(yy)
y=np.array(y)
fig,ax=plt.subplots(figsize=(11,8))
ax.plot([-5,8],[-3,10],lw=2.0,label='actual',alpha=0.7)
ax.fill_betweenx([-3,10],0,4,alpha=0.2)
ax.scatter(x,y,marker='.',s=3.,label='prediction',color='r')
ax.text(0.2,0,'Where we have \ntraining data')
ax.legend()
ax.set_ylim(-3,10);ax.set_xlim(-5,8);
ax.grid(alpha=0.2);
ax.set_title('ReLu activation function');
# + [markdown] id="ge84bd3z98Za"
# ## Teaching a machine to draw circles
#
# Here the NN learns attempts to learn the 2d rotation matrix, parameterized by the generator of rotations in two dimensions:
#
# $R={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}$
# + id="D-LHtrI998Zb"
# First some helper functions for plotting and model training
def train_models(models, optimizers, num_samples=1000, circle_interval=1.0, save_models=False, cuda=torch.cuda.is_available(), recurrent=False):
total_loss = []
for num in range(1, num_samples+1):
# progress indicator
if num % (num_samples//20) ==0:
print('{0}: %: {1:.3f}'.format(num, num/num_samples * 100))
# data calc
# take a random point on the circle of radius 1
x, theta = torch.ones(2), circle_interval*2*np.pi*torch.rand(1)
R = torch.zeros(2,2)
R[0,:] = torch.Tensor([np.cos(theta[0]),-np.sin(theta[0])])
R[1,:] = torch.Tensor([np.sin(theta[0]), np.cos(theta[0])])
data, target = Variable(theta), Variable(torch.mv(R,x))
# Check if GPU can be used
if cuda:
data, target = data.cuda(), target.cuda()
# learning phases
for idx, model in enumerate(models):
loss_iter = []
# forward
if recurrent:
output = model(data,None)
else:
output = model(data)
loss = criterion(output, target)
loss_iter.append(loss.data.item())
# backward
optimizers[idx].zero_grad()
loss.backward()
optimizers[idx].step()
total_loss.append(np.mean(loss_iter))
# save model state
if save_models:
for l,model in enumerate(models):
torch.save(model.state_dict(), 'rotations_{}.pth'.format(l))
return total_loss,theta
def plot_circles(models, offset=0, CI=False):
fig, axes = plt.subplots(figsize=(5*3,3.9),ncols=3)
x = torch.ones(2)
for k,ax in enumerate(axes):
ax.scatter(x[0],x[1], facecolors='none', edgecolors='r')
ax.scatter(x[0],x[1], facecolors='none', edgecolors='b')
x_real, y_real = [],[]
x_mean, y_mean = [],[]
x_std, y_std = [],[]
for theta in np.linspace((k+offset) *2*np.pi,(k+1+offset) *2*np.pi,300):
x_model,y_model = [],[]
# synthetic (real) data
data = Variable(torch.Tensor([theta]))#.cuda()
R = torch.zeros(2,2)
R[0,:] = torch.Tensor([np.cos(theta),-np.sin(theta)])
R[1,:] = torch.Tensor([np.sin(theta), np.cos(theta)])
real = torch.mv(R,x)
x_real.append(real[0].numpy())
y_real.append(real[1].numpy())
# predict w/ all models
for model in models:
if torch.cuda.is_available():
model.cpu()
outputs=model(data).data
xx_model, yy_model = outputs[0],outputs[1]
x_model.append(xx_model.numpy())
y_model.append(yy_model.numpy())
else:
outputs=model(data).data
xx_model, yy_model = outputs[0],outputs[1]
x_model.append(xx_model.numpy())
y_model.append(yy_model.numpy())
# summarize all model predictions
x_mean.append(np.mean(x_model))
y_mean.append(np.mean(y_model))
x_std.append(np.std(x_model))
y_std.append(np.std(y_model))
# plotting data
ax.scatter(x_real,y_real, facecolors='none', edgecolors='r',label='real data',s=2.)
ax.scatter(x_mean,y_mean, facecolors='none', edgecolors='k',label='model data', alpha=0.9,s=2.)
if CI:
ax.fill_betweenx(y_mean,x_mean-3*np.array(x_std),x_mean+3*np.array(x_std), alpha=0.1,color='b')
ax.fill_between(x_mean,y_mean-3*np.array(y_std),y_mean+3*np.array(y_std), alpha=0.1,color='b')
ax.legend()
ax.set_ylim(-2,2);ax.set_xlim(-2,2);ax.grid(alpha=0.3)
ax.set_title(r'${}\pi \leq \theta \leq {}\pi$'.format(2*(k+offset),2*(k+1+offset)),y=1.01);
return x_mean, y_mean, np.array(x_std), np.array(y_std)
def weight_init(m): # so-called xavier normalization https://arxiv.org/abs/1211.5063
if isinstance(m, nn.Linear):
size = m.weight.size()
fan_out = size[0]
fan_in = size[1]
variance = np.sqrt(2.0/(fan_in + fan_out))
m.weight.data.normal_(0.0, variance)
# + id="aLPdSOBI98Zd"
num_nodes=10
# Usually we define neural nets as a class in pytorch
class Rotations(nn.Module):
def __init__(self):
super(Rotations, self).__init__()
self.layer1 = nn.Sequential(
nn.Linear(1,num_nodes),
nn.Sigmoid(),
nn.Linear(num_nodes,2))
def forward(self, x):
out=self.layer1(x)
return out
model = Rotations().to(device)
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.MSELoss()
print(model)
total_loss, theta = train_models([model], [optimizer], num_samples=100000, circle_interval=2.0)
fig,ax = plt.subplots(figsize=(11,8))
ax.plot(total_loss,marker='.',ls='',markersize=.8)
ax.set_ylim(0,);ax.set_xlim(0,);ax.grid(alpha=0.2);
ax.set_xlabel('training examples');ax.set_ylabel('mean squared loss');
output=plot_circles([model],offset=0,CI=False)
# + [markdown] id="vXBgBf1O98Zg"
# ### Will a deeper network perform better?
# + id="Gk0GC2Ry98Zg"
# Add more layers to the model and see if performance on the test set increases
num_nodes=10
class Rotations(nn.Module):
def __init__(self):
super(Rotations, self).__init__()
self.layer1 = nn.Sequential(
nn.Linear(1,num_nodes),
nn.Sigmoid(),
nn.Linear(num_nodes,num_nodes),
nn.Sigmoid(),
nn.Linear(num_nodes,num_nodes),
nn.Sigmoid(),
nn.Linear(num_nodes,2))
def forward(self, x):
out=self.layer1(x)
return out
model=Rotations().to(device)
optimizer=torch.optim.Adam(model.parameters())
criterion=nn.MSELoss()
print(model)
total_loss,theta=train_models([model],[optimizer],num_samples=100000,circle_interval=2.0)
fig,ax=plt.subplots(figsize=(7,5))
ax.plot(total_loss,marker='.',ls='',markersize=.8)
ax.set_ylim(0,);ax.set_xlim(0,);ax.grid(alpha=0.2);
ax.set_xlabel('training examples');ax.set_ylabel('mean squared loss');
output=plot_circles([model],offset=0,CI=False)
# + [markdown] id="qajejnfa98Zh"
# ## Parallel approach
# + [markdown] id="AABjjzF098Zh"
# One simple approach to apply the method described by <NAME>, is to take multiple of the same models and train them independently. This allows each model to take independent paths through parameter space, usually finding their way near some optimal minima. In practice, this allows you to hedge the risk of getting stuck in some local minima and missing out on the global one, if it exists.
#
# A visual way of understanding the situation of training a machine learning model, in general, is by considering a 3D surface plot where the x and y dimensions are two parameters you may modify, with the loss on the z axis, or height, which your aim is to minimize.
#
# 
#
# The surface that the data carves out in this space is predicated by the data; the aim of the model design is then to build a model flexible and robust enough to find the global minima, but not overly complex enough to overfit and get stuck at a local minima. Also, if your model is too simple, it can skip right over all the minima altogether, and not learn the nuance of the process described by the data. Having too high/low of a learning rate can also make the training process difficult.
# + [markdown] id="gsWWfgQY98Zi"
# ---
# # Image Recognition and Transfer Learning
#
# 
# + [markdown] id="J8r6k9iz98Zi"
# # Transfer Learning
#
# Transfer learning is one of the most useful discoveries to come out of the computer vision community. Stated simply, transfer learning allows one model that was trained on different types of images, e.g. dogs vs cats, to be used for a different set of images, e.g. planes vs trains, while reducing the training time dramatically. When Google released ImageNet, they stated it took them over 14 **days** to train the model on some of the most powerful GPUs available at the time. Now, with transfer learning, we will train an, albeit smaller, model in less than 5 minutes.
#
# + [markdown] id="EF9D_vi898Zi"
# The philosophy behind transfer learning is simple. We keep the "base" layers of a model frozen since the weights have already been tuned to identify patterns such as lines, circles, and other shapes, and insert layers at the end that will be tuned for the specific task at hand.
#
# 
#
# 
#
#
# For our task, let's take a look at the King and Queen of the Miami food scene:
#
# **The Cuban Sandwich**
#
# 
#
# **The Stuffed Arepa**
#
# 
# + id="HHazrBAH98Zj"
normalize = transforms.Normalize(mean=[0.485, 0.456, 0.406],
std=[0.229, 0.224, 0.225])
data_transforms = {
'train':
transforms.Compose([
transforms.Resize((224,224)),
transforms.RandomAffine(0, shear=10, scale=(0.8,1.2)),
transforms.RandomHorizontalFlip(),
transforms.ToTensor()]),
'validation':
transforms.Compose([
transforms.Resize((224,224)),
transforms.ToTensor()])}
image_datasets = {
'train':
datasets.ImageFolder('data/cva_data/train', data_transforms['train']),
'validation':
datasets.ImageFolder('data/cva_data/validation', data_transforms['validation'])}
dataloaders = {
'train':
torch.utils.data.DataLoader(
image_datasets['train'],
batch_size=32,
shuffle=True,
num_workers=4),
'validation':
torch.utils.data.DataLoader(
image_datasets['validation'],
batch_size=32,
shuffle=False,
num_workers=4)}
# + id="aYDftGNq98Zk"
model = models.resnet50(pretrained=True).to(device)
# freeze the weights
for param in model.parameters():
param.requires_grad = False
# modify the final layer of resnet50 (called 'fc')
# originally model.fc = nn.Linear(2048, 1000) for the 1000 image classes
# we modify it to our specific needs
model.fc = nn.Sequential(
nn.Linear(2048, 128),
# inplace=True is a shortcut to not modify the forward method
nn.ReLU(inplace=True),
nn.Linear(128, 2)).to(device)
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.fc.parameters())
# + id="3IikbBD698Zl"
# Get estimate of model size: number of parameters, storage, etc.
# input size is based off of the dimensions of a single example in our dataset.
summary(model, input_size=(3, 224, 224))
# + id="Uvz_TM4_98Zm"
def train_model(model, criterion, optimizer, num_epochs=3):
for epoch in range(num_epochs):
print(f'Epoch {epoch + 1}/{num_epochs}')
print('-' * 10)
for phase in ['train', 'validation']:
if phase == 'train':
model.train()
else:
model.eval()
running_loss = 0.0
running_corrects = 0
for inputs, labels in dataloaders[phase]:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss = criterion(outputs, labels)
if phase == 'train':
optimizer.zero_grad()
loss.backward()
optimizer.step()
_, preds = torch.max(outputs, 1)
running_loss += loss.item() * inputs.size(0)
running_corrects += torch.sum(preds == labels.data)
epoch_loss = running_loss / len(image_datasets[phase])
epoch_acc = running_corrects.double() / len(image_datasets[phase])
print(f'{phase} loss: {epoch_loss}, acc: {epoch_acc}')
return model
model_trained = train_model(model, criterion, optimizer, num_epochs=3)
# + [markdown] id="HG3txGvM98Zn"
# ### Saving Models
# + id="ZStqUrY998Zo"
torch.save(model_trained.state_dict(),'models/cva_weights_new.pt')
# + [markdown] id="dbmTmF8m98Zq"
# ### Loading Models
# + id="2xhvK0Zj98Zq"
model = models.resnet50(pretrained=False).to(device)
model.fc = nn.Sequential(
nn.Linear(2048, 128),
nn.ReLU(inplace=True),
nn.Linear(128, 2)).to(device)
model.load_state_dict(torch.load('models/cva_weights.h5'))
model.eval() # stop training model
# + [markdown] id="J-W0-scw98Zr"
# ### Make predictions on test images
# + id="Yg5NP4fr98Zr"
validation_img_paths = ["data/cva_data/validation/arepas/00000165.jpg",
"data/cva_data/validation/cubanos/00000037.jpg",
"data/cva_data/validation/cubanos/00000061.jpg",
"data/cva_data/validation/arepas/00000003.jpeg"]
img_list = [Image.open(img_path) for img_path in validation_img_paths]
# + id="mGkOZaCd98Zs"
validation_batch = torch.stack([data_transforms['validation'](img).to(device)
for img in img_list])
pred_logits_tensor = model(validation_batch)
pred_probs = F.softmax(pred_logits_tensor, dim=1).cpu().data.numpy()
# + id="nyEbGi4N98Zt"
fig, axs = plt.subplots(1, len(img_list), figsize=(20, 5))
for i, img in enumerate(img_list):
ax = axs[i]
ax.axis('off')
ax.set_title("{:.0f}% Arepa, {:.0f}% Cubano".format(100*pred_probs[i,0],
100*pred_probs[i,1]))
ax.imshow(img)
# + [markdown] id="F3f9DSrp98Zt"
# # CNN from Scratch
# + [markdown] id="IFfDZV5a98Zu"
# ### `Datasets` and `Dataloaders`
#
# In PyTorch, you'll usually create or import a `Dataset` subclass to represent your data. Once you've done that, you can use it to instantiate a `Dataloader` object which allows you to easily iterate over your training set in `BATCH_SIZE` chunks.
# + id="rDY2WCgj98Zu"
image_size = 28
num_classes = 10
num_channels = 1
batch_size = 64
id_to_label = {
0 :'T-shirt/top',
1 :'Trouser',
2 :'Pullover',
3 :'Dress',
4 :'Coat',
5 :'Sandal',
6 :'Shirt',
7 :'Sneaker',
8 :'Bag',
9 :'Ankle boot'}
class FashionDataset(Dataset):
def __init__(self, path,
image_size, num_channels, image_transform=None):
self.num_channels = num_channels
self.image_size = image_size
self.image_transform = image_transform
data_df = pd.read_csv(path)
self.X = data_df.values[:, 1:]
self.X = self.X.reshape(-1, image_size, image_size, num_channels)
self.X = self.X.astype('float32')
self.y = data_df.values[:, 0]
def __getitem__(self, index):
batch_X, batch_y = self.X[index], self.y[index]
if self.image_transform is not None:
batch_X = self.image_transform(batch_X)
return batch_X, batch_y
def __len__(self):
return len(self.X)
# This simple transform coverts the image from an numpy array
# to a PyTorch tensor and remaps its values from 0-255 to 0-1.
# Many other types of transformations are available, and they
# can easily be composed into a pipeline. For more info see:
# https://pytorch.org/docs/stable/torchvision/transforms.html
image_transform = transforms.Compose([transforms.ToTensor()])
train_dataset = FashionDataset(
'fashionmnist/fashion-mnist_train.csv',
image_size,
num_channels,
image_transform)
train_dataloader = DataLoader(
dataset=train_dataset,
batch_size=batch_size,
shuffle=True)
val_dataset = FashionDataset(
'fashionmnist/fashion-mnist_test.csv',
image_size,
num_channels,
image_transform)
val_dataloader = DataLoader(
dataset=train_dataset,
batch_size=batch_size)
# + [markdown] id="87tWdYgJ98Zv"
# ### Show some examples from the training set
# + id="G3_1m7hh98Zw"
def plot_images(data, labels, image_size):
fig, axes = plt.subplots(
1, data.shape[0], figsize=(16, 4),
subplot_kw={'xticks':[], 'yticks':[]},
gridspec_kw=dict(hspace=0.1, wspace=0.1))
for i, ax in enumerate(axes.flat):
ax.imshow(data[i].reshape(image_size, image_size), cmap='binary')
ax.set_xlabel(labels[i])
images = train_dataset.X[:10]
class_ids = train_dataset.y[:10]
class_labels = [id_to_label[class_id] for class_id in class_ids]
plot_images(images, class_labels, image_size)
# + [markdown] id="wiTMWwoN98Zy"
# ## Modeling
# + [markdown] id="lHn8Z9og98Zy"
# This baseline network uses a single convolution with only 4 filters. Because of the simplicity of our dataset, it still manages to achieve nearly 90% accuracy after only 5 epochs.
#
# Experiment and see if you can increase the accuracy on the validation set to above 95%.
#
# Things you might try:
#
# * Increasing the number of filters per convolution.
# * Adding more convolutions.
# * Adding a `BatchNorm2d` layer after `Conv2d`.
# * Increasing the number of epochs.
# * Changing the kernel size.
# * Using different types of pooling or using stride > 1 in convolutional layers instead of pooling.
#
# You might also find the [PyTorch API reference](https://pytorch.org/docs/stable/nn.html) useful.
# + [markdown] id="mrKe0kZU98Zy"
# ### Determining Output Size after Convolution and MaxPool
#
# When dealing with any neural net model, we have to ensure that each one of our layers is receiving the correct input size from its previous layers. This is easier said than done as, in Computer Vision, we have to convert from 2D layers such as convolutions, batch normalizations, and max pooling layers to communicate properly with a linear layer that follows. To do this, we have to ensure that our calculations for the **input** to each layer is correct when we instantiate our model.
#
# Linear layers are simple, the output size is stated when we instantiate. The difficulty lies in Conv2D layers since PyTorch calculates the output size using a formula and we need to determine what that size is by hand if we need it to pass it as input for other layers.
#
# To determine the output size after 2D layers we usually have to do it separately for our height and width, but since we are dealing with square images they will give us the same result. Furthermore, we'll remove any values that are set to zero in our model to reduce the complexity of the equation. For more information on output size for different functions, refer to the PyTorch API.
#
# #### Conv2D
#
# $$H_{out} = \frac{H_{in} - kernel + 2 * padding}{stride} + 1$$
#
#
# #### MaxPool2D
# $$H_{out} = \frac{H_{in} - kernel + 2*padding}{stride} + 1$$
#
#
#
# Let's use the numbers from our `FashionModel` (see below) to determine what the outputs are after our first combo of `Conv2d` and `MaxPool2d`
#
# Since our images are square, (28x28) we only need to do this calcluation once.
#
# **Size of image:** 28
#
# **Output size after Conv2d:**
# $$H_{out} = \frac{28 - 3 + 2*1}{1} + 1 = 28$$
#
# **Output size after MaxPool2d:**
# $$H_{out} = \frac{28 - 2 + 2*0}{2} + 1 = 14$$
#
#
# If passing to a linear layer we need to multiply `output_channels` from our `Conv2d` times the `output_size_height` and `output_size_width` (in our case they are the same) to properly rescale our tensor.
#
# **Output channels (after Conv2d):** 16
#
# **MaxPool Output Size:** 14 (same for both height and width)
#
# Thus, our linear layer needs and input of size `14 * 14 * 16`
#
# For more info see [here.](https://www.quora.com/How-can-I-calculate-the-size-of-output-of-convolutional-layer)
# + id="ksWzfB3m98Zy"
class FashionModel(nn.Module):
def __init__(self, num_channels, num_classes):
super().__init__()
self.conv_1 = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=3, stride=1, padding=1),
nn.BatchNorm2d(16),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2, padding=0))
# Add more conv2d layers
# recall that the input channel size for the new layer is 16!
# Make the outputs 32 and 64 to create 3 total convolution layers
# ------------- CODE GOES HERE ------------- #
# to determine the correct inputs for the last linear layer you'll need the formulas:
# output_size of conv2d = (input_width - kernel_size + 2*padding)/stride + 1
# output_size of maxpool = (output_size of conv2d - kernel_size + 2*padding)/stride + 1
# See cell above for more detail
# If adding an extra conv layers, the input into nn.Linear needs to change!
self.linear = nn.Linear(14 * 14 * 16, num_classes)
def forward(self, x):
x = self.conv_1(x)
# Uncomment as more convolution layers are added
# x = self.conv_2(x)
# x = self.conv_3(x)
x = x.reshape(x.size(0), -1)
x = self.linear(x)
return x
# Instantiate the model.
model = FashionModel(num_channels, num_classes)
# Send the model's tensors to the GPU (if available).
model = model.to(device)
# + [markdown] id="xMphQPq_98Zz"
# ## Training
# + id="v63uptok98Z0"
num_epochs = 10
log_freq = 100
checkpoint_path = 'checkpoint.pickle'
optimizer = torch.optim.Adam(model.parameters())
criterion = nn.CrossEntropyLoss()
for epoch in range(1, num_epochs + 1):
model.train() # Switch to training mode.
print(f'Starting epoch {epoch}.')
epoch_start_time = time.time()
running_loss = 0.0
running_accuracy = 0.0
for batch_id, (batch_X, batch_y) in enumerate(train_dataloader):
batch_X = batch_X.to(device)
batch_y = batch_y.to(device)
output = model(batch_X)
loss = criterion(output, batch_y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# Periodically print the loss and prediction accuracy.
running_loss += loss.item()
y_pred = output.argmax(dim=-1)
running_accuracy += accuracy_score(batch_y.cpu(), y_pred.cpu())
if batch_id % log_freq == log_freq - 1:
average_loss = running_loss / log_freq
average_accuracy = running_accuracy / log_freq
print(f'Mini-batch: {batch_id + 1}/{len(train_dataloader)} '
f'Loss: {average_loss:.5f} Accuracy: {average_accuracy:.5f}')
running_loss = 0.0
running_accuracy = 0.0
# Log elapsed_time for the epoch.
elapsed_time = time.time() - epoch_start_time
print(f'\nEpoch {epoch} completed in {elapsed_time // 60:.0f} minutes '
f'{elapsed_time % 60:.0f} seconds.')
# Calculate and log loss on validation set.
with torch.no_grad():
model.eval()
running_loss = 0.0
running_accuracy = 0.0
for batch_id, (batch_X, batch_y) in enumerate(val_dataloader):
batch_X = batch_X.to(device)
batch_y = batch_y.to(device)
output = model(batch_X)
loss = criterion(output, batch_y)
running_loss += loss.item()
y_pred = output.argmax(dim=-1)
running_accuracy += accuracy_score(batch_y.cpu(), y_pred.cpu())
average_loss = running_loss / len(val_dataloader)
average_accuracy = running_accuracy / len(val_dataloader)
print(f'Val Loss: {average_loss:.5f} Val Accuracy: {average_accuracy:.5f}\n')
# + [markdown] id="eAuXhyQb98Z6"
# # Semi-Supervised Learning - Style Transfer
#
# Style transfer, to me, is one of the coolest "discoveries" in the computer vision and deep learning community from the past few years. In essence, it allows us to take the "content" from an image (shapes, objects, arrangements) and reproduce a new target that is in the "style" (style, colors, textures) of another.
#
# We'll be taking inspiration from the paper, [Image Style Transfer Using Convolutional Neural Networks, by Gatys](https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Gatys_Image_Style_Transfer_CVPR_2016_paper.pdf), and implementing the model in PyTorch.
#
# In the paper, style transfer uses the features found in the 19-layer VGG Network, which are comprised of a series of convolutional and pooling layers, and a few fully-connected layers. (Recall that this is similar to many of the computer vision models discussed earlier)
#
# In the image below, the convolutional layers are named by stack and their order in the stack.
#
# For example, `Conv_1_1` is the first convolutional layer that an image is passed through in the *first* stack. `Conv_2_1` is the first convolutional layer in the *second* stack. The deepest convolutional layer in the network is `Conv_5_4`.
#
# <img src='https://github.com/robert-alvarez/pytorch_tutorial/blob/master/data/img/vgg19_convlayers.png?raw=1' width=80% />
#
# Style transfer relies on separating the content and style of an image. To do so, we aim to create a new **target** image which should contain our desired content and style components.
#
# **Note:**
# * objects and their arrangement are similar to that of the **content image**
# * style, colors, and textures are similar to that of the **style image**
#
# <img src='https://github.com/robert-alvarez/pytorch_tutorial/blob/master/data/img/style-transfer-example.jpg?raw=1' width=80% />
# + [markdown] id="kH93VNUL98Z6"
# ## Load VGG19
#
# VGG19 is split into two portions:
# * `vgg19.features` - contains all the convolutional and pooling layers
# * `vgg19.classifier` - contains the three fully connected layers layers at the end
#
# We only need the `features` portion, which we're going to load in and "freeze" the weights of. This is similar to what we did for our transfer learning section.
# + id="hQXtdum498Z7"
# get the "features" portion of VGG19
vgg = models.vgg19(pretrained=True).features
# freeze all VGG parameters since we're only optimizing the target image
for param in vgg.parameters():
param.requires_grad_(False)
# + id="3KCR6u8L98Z9"
# move the model to GPU (if available)
vgg.to(device)
# + [markdown] id="rVGVbkt_98Z-"
# ### Load in Content and Style Images
#
# Load in any images you want! The code below is a helper function for loading in any type and size of image. The `load_image` function also converts images to normalized Tensors.
# + id="emPYYCP398Z_"
def load_image(img_path, max_size=400, shape=None):
''' Load in and transform an image, making sure the image
is <= 400 pixels in the x-y dims.'''
if "http" in img_path:
response = requests.get(img_path)
image = Image.open(BytesIO(response.content)).convert('RGB')
else:
image = Image.open(img_path).convert('RGB')
# large images will slow down processing
if max(image.size) > max_size:
size = max_size
else:
size = max(image.size)
if shape is not None:
size = shape
in_transform = transforms.Compose([
transforms.Resize(size),
transforms.ToTensor(),
transforms.Normalize((0.485, 0.456, 0.406),
(0.229, 0.224, 0.225))])
# discard the transparent, alpha channel (that's the :3) and add the batch dimension
image = in_transform(image)[:3,:,:].unsqueeze(0)
return image
# + id="4z1U5NhX98Z_"
# load in content and style image
content = load_image('data/img/Nala.jpg').to(device)
# Resize style to match content, makes code easier
style = load_image('data/img/style_images/dayofthedead.jpg', shape=content.shape[-2:]).to(device)
# + id="QIzfP7-M98aA"
# helper function for un-normalizing an image
# and converting it from a Tensor image to a NumPy image for display
def im_convert(tensor):
""" Display a tensor as an image. """
image = tensor.to("cpu").clone().detach()
image = image.numpy().squeeze()
image = image.transpose(1,2,0)
image = image * np.array((0.229, 0.224, 0.225)) + np.array((0.485, 0.456, 0.406))
image = image.clip(0, 1)
return image
# + id="8YQn4XdO98aB"
# display the images
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 10))
# content and style ims side-by-side
ax1.imshow(im_convert(content))
ax2.imshow(im_convert(style))
# + [markdown] id="M_SLPHnw98aC"
# ## VGG19 Layers
#
# To get the content and style representations of an image, we have to pass an image forward throug the VGG19 network until we get to the desired layer(s) and then get the output from that layer.
# + id="qjOozSKG98aC"
# print out VGG19 model so you can see the names of all the layers
print(vgg)
# + [markdown] id="EOKXQcXC98aE"
# ## Content and Style Features
#
# Below, complete the mapping of layer names to the names found in the paper for the _content representation_ and the _style representation_.
# + id="-P8dLNmi98aE"
def get_features(image, model, layers=None):
""" Run an image forward through a model and get the features for
a set of layers. Default layers are for VGGNet matching Gatys et al (2016)
"""
## Here we gather the layers need to preserve style and content of an image
if layers is None:
layers = {'1': 'relu1_1',
'6': 'relu2_1',
'11': 'relu3_1',
'20': 'relu4_1',
'13': 'relu3_2', ## content representation
'29': 'relu5_1'}
features = {}
x = image
# model._modules is a dictionary holding each module in the model
for name, layer in model._modules.items():
x = layer(x)
if name in layers:
features[layers[name]] = x
return features
# + [markdown] id="U_9ncp6S98aH"
# ## Gram Matrix
#
# The output of every convolutional layer is a Tensor with dimensions associated with the `batch_size`, a depth, `d` and some height and width (`h`, `w`). The Gram matrix of a convolutional layer can be calculated as follows:
# * Get the depth, height, and width of a tensor using `batch_size, d, h, w = tensor.size`
# * Reshape that tensor so that the spatial dimensions are flattened
# * Calculate the gram matrix by multiplying the reshaped tensor by it's transpose
# + id="3l1_Lb-X98aH"
def gram_matrix(tensor):
""" Calculate the Gram Matrix of a given tensor
Gram Matrix: https://en.wikipedia.org/wiki/Gramian_matrix
"""
# get the batch_size, depth, height, and width of the Tensor
_, d, h, w = tensor.size()
# reshape so we're multiplying the features for each channel
tensor = tensor.view(d, h * w)
# calculate the gram matrix
gram = tensor @ tensor.t()
return gram
# + [markdown] id="tJIQ9riA98aK"
# ## We're Almost there!
#
# Here's what our helper functions do:
#
# * Extract the features for our content and style images from VGG19
# * Compute the Gram Matrix for a given convolutional layer
#
#
# What we need:
# * Put it all together!
# + id="1b8fo8gg98aK"
# get content and style features only once before training
content_features = get_features(content, vgg)
style_features = get_features(style, vgg)
# calculate the gram matrices for each layer of our style representation
style_grams = {layer: gram_matrix(style_features[layer]) for layer in style_features}
# create a third "target" image and prep it for change
# it is a good idea to start off with the target as a copy of our *content* image
# then iteratively change its style
target = content.clone().requires_grad_(True).to(device)
# + [markdown] id="kzb2iaqA98aL"
# ## Loss and Weights
#
# #### Individual Layer Style Weights
#
# In the script below, we have the option to weight the style representation at each relevant layer. This will allow us to fine tune what effect size we want for each layer - earlier layers have larger style artifacts and later layers place emphasis on smaller features. Remember, each layer is a different size and by combining them we can create multi-scale style representations.
#
# The paper suggests using a range between 0-1 to weight the layers.
#
# #### Content and Style Weight
#
# The paper defines a **style ratio** of $\alpha/\beta$, where $\alpha$ is the `content_weight` and $\beta$ is the `style_weight`. This ratio will affect how _stylized_ the final image is. It's recommended that to leave the content_weight = 1 and set the style_weight to achieve the ratio needed for a desired effect style. Note that this is not exact science, there will be lots of tuning of the ratio and the weights of the layers to get a result we're pleased with.
#
# Remember - the reason this is called "Semi-Supervised" is because there is no right answer. We decide when to stop the training based on intermediate results we plot and stop when we are happy with what we see.
# + id="-GXW_90X98aL"
# weights for each style layer
# weighting earlier layers more will result in *larger* style artifacts
# notice we are excluding `conv4_2` our content representation
style_weights = {'relu1_1': 1.,
'relu2_1': 0.75,
'relu3_1': 0.4,
'relu4_1': 0.3,
'relu5_1': 0.2}
content_weight = 1 # alpha
style_weight = 1e8 # beta
# + [markdown] id="U-Aa1VAY98aM"
# ## Update the Target & Calculate Losses
#
# Like in every training loop we've seen before, we need to decide on how many passes we want to do on our model (via gradient descent). The difference here is that we will be changing our **target** image and nothing about the VGG19 model or our original content and style images. Since this is semi-supervised, the number of steps to choose is up to you. Keep in mind that after ~50,000 steps you probably won't see any noticeable differences in the images and by using ~2,000 steps you can see early on whether the style ratio ($\alpha/\beta$) is giving the desired effect.
#
# Experiment with different weights or images to see some really cool effects!
#
# #### Content Loss
#
# The content loss will be the mean squared difference between the target and content features at layer `conv4_2`. This can be calculated as follows: (see paper)
# ```
# content_loss = torch.mean(torch.abs(target_features['conv4_2'] - content_features['conv4_2']))
# ```
#
# #### Style Loss
#
# The style loss is calculated in a similar way, but we have to iterate through the layers specified by name in our dictionary `style_weights`.
#
# > Calculate the gram matrix for the target image, `target_gram` and style image `style_gram` at each of these layers and compare those gram matrices, calculating the `layer_style_loss`.
#
# #### Total Loss
#
# Finally, the total loss is calculated by adding up the individual style and content losses and weighting them with the specified alpha and beta values chosen.
#
# Intermittently, we'll print out an intermediate image and its loss - don't be alarmed if the loss is very large! It takes some time for an image's style to change and you should focus on the appearance of your target image rather than any loss value, but we should still be seeing the loss go down over time.
# + id="tydP-K9c98aM"
# for displaying the target image, intermittently
show_every = 400
# iteration hyperparameters
optimizer = torch.optim.Adam([target], lr=0.003)
steps = 2000 # decide how many iterations to update your image
for step in range(1, steps+1):
# get the features from your target image
target_features = get_features(target, vgg)
# the content loss
content_loss = torch.mean(torch.abs(target_features['relu3_2'] - content_features['relu3_2']))
# the style loss
# initialize the style loss to 0
style_loss = 0
# then add to it for each layer's gram matrix loss
for layer in style_weights:
# get the "target" style representation for the layer
target_feature = target_features[layer]
target_gram = gram_matrix(target_feature)
_, d, h, w = target_feature.shape
# get the "style" style representation
style_gram = style_grams[layer]
# the style loss for one layer, weighted appropriately
layer_style_loss = style_weights[layer] * torch.mean((target_gram - style_gram)**2)
# add to the style loss
style_loss += layer_style_loss / (d * h * w)
# calculate the *total* loss
total_loss = content_weight * content_loss + style_weight * style_loss
# update your target image
optimizer.zero_grad()
total_loss.backward()
optimizer.step()
# display intermediate images and print the loss
if step % show_every == 0:
print('Total loss: ', total_loss.item())
plt.imshow(im_convert(target))
plt.show()
# + [markdown] id="US9otQ0e98aN"
# ## Display the Target Image
# + id="dVB8O5_998aO"
# display content and target image
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 10))
ax1.imshow(im_convert(content))
ax2.imshow(im_convert(target))
# + id="r9IvOCk598aP"
# display style and target image
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(20, 10))
ax1.imshow(im_convert(style))
ax2.imshow(im_convert(target))
# + id="Vo6F3GOJrISA"
plt.imshow(im_convert(target))
# + id="XdzRCNyauoww"
fig, ax = plt.subplots(1,1,figsize=(20,20))
ax.imshow(im_convert(target))
ax.spines['top'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['bottom'].set_visible(False)
ax.spines['right'].set_visible(False)
ax.set_xticks([])
ax.set_yticks([])
plt.savefig("nala_mod.png",bbox_inches="tight",pad_inches=0.02,dpi=300)
plt.show()
# + id="a_ZqoJnWyDEz"
# display fully stylized image vs style
file_path = '/content/data/img/nala_mod.png'
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(20, 10))
ax1.imshow(im_convert(content))
ax2.imshow(im_convert(style))
ax3.imshow(Image.open(file_path))
# + [markdown] id="_UZVR5_V98aR"
# ---
# # RNN Character Level Generation
#
# Text generation is a fun way to familiarize yourself with Recurrent Neural Nets.
#
# In this notebook, we will deal with **character-level** text generation and why they can be just as useful as word-level text generation.
#
# For this example, we'll be using text files to generate code similar to our input. In other words, if we put in Trump tweets, our generator should output words that sound like Trump.
#
# ### Our current understanding of RNNs
# 
#
#
# ### Reminder
#
# 
#
# #### "RNNs have a hidden state that feeds back into the cell at the next time step"
# + [markdown] id="2_GV03CE98aR"
# ## What is actually going on?
#
# ### Example with sequence length 5
# + [markdown] id="2W1SYysW98aR"
# 
# + [markdown] id="-s_MsXJM98aR"
# ### What about the backwards pass?
# + [markdown] id="V3fvQzdk98aS"
# 
# + [markdown] id="_AXEdHUq98aS"
# ## Preprocessing
# + id="9licgHnh98aS"
# install unidecode
# !pip install unidecode
# + id="EwM19pvC98aU"
# Read in text and change unicode characters to ASCII
import unidecode
import string
import random
import re
all_characters = string.printable
n_characters = len(all_characters)
# + id="5nkrsGUh98aV"
# read in file to train RNN
file = unidecode.unidecode(open('data/shakespeare.txt').read())
file_len = len(file)
print(f'file_len = {file_len}')
# + [markdown] id="ReHlckvd98aW"
# To give our model inputs from this large string of text, we'll split it up into chunks
# + id="lKIIRWCE98aW"
chunk_len = 400
def random_chunk():
start_index = random.randint(0, file_len - chunk_len)
end_index = start_index + chunk_len + 1
return file[start_index:end_index]
print(random_chunk())
# + [markdown] id="pi0rBFSe98aW"
# ## Build Model
#
# This model will take as input the character for step $t$ and is expected to output the next character for step $t+1$. There are three layers - one linear layer that encodes the input character into an internal state, one GRU layer (which may itself have multiple layers) that operates on that internal state and a hidden state, and a decoder layer that outputs the probability distribution.
# + id="GDk8bHgi98aX"
class RNN(nn.Module):
def __init__(self, input_size, hidden_size, output_size, n_layers=1):
super(RNN, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.output_size = output_size
self.n_layers = n_layers
self.encoder = nn.Embedding(input_size, hidden_size)
self.gru = nn.GRU(hidden_size, hidden_size, n_layers)
self.decoder = nn.Linear(hidden_size, output_size)
def forward(self, input, hidden):
output = self.encoder(input.view(1, -1))
output, hidden = self.gru(output.view(1, 1, -1), hidden)
output = self.decoder(output.view(1, -1))
return output, hidden
def init_hidden(self):
return Variable(torch.randn(self.n_layers, 1, self.hidden_size))
# + [markdown] id="fXw2G1Fu98aZ"
# ## Inputs and Targets
#
# Now that we've defined our model, we need to give it both input data, via our chunks, and our target data. Each character is one-hot encoded to the vocab size
# + id="JYBv5jbj98aZ"
def char2tensor(string):
tensor = torch.zeros(len(string)).long()
for char in range(len(string)):
if string[char] in all_characters:
tensor[char] = all_characters.index(string[char])
else:
tensor[char] = 94 #predict space if character unknown
return Variable(tensor)
# Let's see it in action.
print(char2tensor('Podium0123abczABC'))
# + [markdown] id="KQeU8ig398aa"
# Now that we can generate chunks of data, we can build our inputs and targets.
#
# Our inputs will be all of the chunk except for the last letter.
#
# Our target will be all of the chunk except for the first letter.
# + id="-3WJANx798aa"
def random_training_set():
chunk = random_chunk()
inp = char2tensor(chunk[:-1])
target = char2tensor(chunk[1:])
return inp, target
# + [markdown] id="cgVLzwWA98aa"
# ## Evaluating the Model
#
# To evaluate the network we will feed one character at a time, use the outputs of the network as a probability distribution for the next character, and repeat. To start generation we pass a priming string to start building up the hidden state, from which we then generate one character at a time.
# + id="rbdP6olM98ab"
def evaluate(model, prime_str='A', predict_len=100, temperature=0.8):
hidden = model.init_hidden()
prime_input = char2tensor(prime_str)
predicted = prime_str
# use priming string to build up hidden state
for p in range(len(prime_str) - 1):
_, hidden = model(prime_input[p], hidden)
inp = prime_input[-1]
for p in range(predict_len):
output, hidden = model(inp, hidden)
# Sample from the network as a multinomial distribution
output_dist = output.data.view(-1).div(temperature).exp()
top_i = torch.multinomial(output_dist, 1)[0]
# Add predicted character to string and use as next input
predicted_char = all_characters[top_i]
predicted += predicted_char
inp = char2tensor(predicted_char)
return predicted
# + [markdown] id="BCXSgyAq98ac"
# ## Training
# + id="RFvGhOSG98ac"
# helper function
import time, math
def time_since(since):
s = time.time() - since
m = math.floor(s/60)
s -= m*60
return '%dm %ds' % (m, s)
# + id="S4VVSZk598ac"
# The actual training part
def train(inp, target):
hidden = model.init_hidden()
model.zero_grad()
loss = 0
for char in range(chunk_len):
output, hidden = model(inp[char], hidden)
loss += criterion(output, target[char].unsqueeze(0))
loss.backward()
model_optimizer.step()
return loss.data.item() / chunk_len
# + id="MZGTd4Ta98ad"
# parameters
n_epochs = 1000
print_every = 100
plot_every = 10
hidden_size = 256
n_layers = 2
learning_rate = 0.001
# model declaration
model = RNN(n_characters, hidden_size, n_characters, n_layers)
model_optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()
start = time.time()
all_losses = []
loss_avg = 0
for epoch in range(1, n_epochs + 1):
loss = train(*random_training_set())
loss_avg += loss
if epoch % print_every == 0:
print('[%s (%d %d%%) %.4f]' % (time_since(start), epoch, epoch / n_epochs * 100, loss))
print(evaluate(model, 'A ', 100), '\n')
if epoch % plot_every == 0:
all_losses.append(loss_avg / plot_every)
loss_avg = 0
# + id="eH0W9ZUD98ae"
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
# %matplotlib inline
plt.figure()
plt.plot(all_losses)
# + [markdown] id="RUFswDvk98af"
# ### Load pre-trained models
# + id="hmgQhWKUVJ8o"
# model declaration
hidden_size = 256
billy = RNN(n_characters, hidden_size, n_characters, n_layers=2)
billy.load_state_dict(torch.load('data/models/shakespeare_weights.h5'))
cells = RNN(n_characters, hidden_size, n_characters, n_layers=2)
cells.load_state_dict(torch.load('data/models/cell_weights.h5'))
# + id="jGtRIvOi98ah"
# Evaluate <NAME>
print(evaluate(billy, 'To be or not to be: ', predict_len=200, temperature=0.7))
# + id="ZKYO0B8A98ai"
# Evaluate NLP model of math biology latex file
print(evaluate(cells, 'The equation ', predict_len=200, temperature=0.4))
# + [markdown] id="nzJ43EHb98aj"
# # Resources
#
# [tensor images](https://hackernoon.com/learning-ai-if-you-suck-at-math-p4-tensors-illustrated-with-cats-27f0002c9b32)
#
# [alien vs predator](https://deepsense.ai/keras-vs-pytorch-avp-transfer-learning/)
#
# [unreasonable reffectiveness of neural nets](http://karpathy.github.io/2015/05/21/rnn-effectiveness/)
#
# [pytorch.org](https://pytorch.org/tutorials/beginner/deep_learning_60min_blitz.html)
#
# [<NAME>](https://richardagalvez.github.io/)
#
# [Visualizing and Understanding Convolutional Networks](https://arxiv.org/pdf/1311.2901.pdf)
#
# [Image Style Transfer](https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/Gatys_Image_Style_Transfer_CVPR_2016_paper.pdf)
#
# [Transfer Learning Image](https://www.researchgate.net/figure/Illustration-of-transfer-learning-concept-where-the-rst-layers-in-network-A-and-network-B_fig2_316748306)
#
# [Udacity](https://github.com/udacity/deep-learning-v2-pytorch)
#
|
PyTorch_Tutorial_OReilly.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## This code is used to simulate some experiment using a wrapper module
#
# ### The steps of simulations are following:
# - Create folder "data/op/"
# - Import "sd/" modules
# - Initialize radar, datetime of the run (typically run for a day for a radar)
# - Initialize clustering category, type, and associated parameters
# - Strat simulation
# +
import datetime as dt
import argparse
from dateutil import parser as dparser
from optimize import Model, _del_
def to_argparse(_dict_):
""" Take parameters as dictionary and convert to argparse """
parser = argparse.ArgumentParser()
parser.add_argument("-c", "--category", default=_dict_["category"], help="Algorithm category")
parser.add_argument("-m", "--model", default=_dict_["model"], help="Algorithm name")
parser.add_argument("-nc", "--n_clusters", type=int, default=_dict_["n_clusters"], help="Number of clusters (default 8)")
parser.add_argument("-r", "--rad", default="sas", help="SuperDARN radar code (default sas)")
parser.add_argument("-s", "--start", default=_dict_["start"], help="Start date (default 2018-04-05)",
type=dparser.isoparse)
parser.add_argument("-e", "--end", default=_dict_["end"], help="End date (default 2018-04-05T01)",
type=dparser.isoparse)
parser.add_argument("-cl", "--clear", default=_dict_["clear"], help="Clear pervious stored files (default False)")
parser.add_argument("-sk", "--skills", default=_dict_["skills"], help="Run skill estimate (default False)")
parser.add_argument("-pl", "--plot", default=_dict_["plot"], help="Plot estimations (default True)")
parser.add_argument("-v", "--verbose", default=_dict_["verbose"], help="Increase output verbosity (default False)")
parser.add_argument("-sv", "--save", default=_dict_["save"], help="Increase output verbosity (default True)")
args = parser.parse_args()
if args.verbose:
print("\n Parameter list for simulation ")
for k in vars(args).keys():
print(" ", k, "->", vars(args)[k])
return args
def run_model(args):
""" Run the model with all keywords"""
Model(args.rad, args.start, args.end, args)
_del_()
return
# Setup default dictionary
_dic_ = {
"category": "density",
"model": "dbscan",
"n_clusters": "4",
"rad": "sas",
"start": dt.datetime(2018, 4, 5),
"end": dt.datetime(2018, 4, 6),
"clear": True,
"skills": True,
"plot": True,
"verbose": True,
"save": True,
}
# +
# Change parameters defined in dictionary (_dic_)
# Run the model with defined parameters
run_model(to_argparse(_dic_))
# -
import sys
sys.path.append("algorithm/")
from partitional import KMedoids
|
sd/SimulationExperimentCode.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.feature_selection import SelectFromModel
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier
#import data
data = pd.read_csv('airline_tweets.csv')
print(data)
#show one column
print(data['text'])
#show two columns
print(data[['text','airline_sentiment']])
#show one record
print(data.loc[0,:])
#show some more records
print(data.loc[0:5,:])
#show one column of one record
print(data.loc[0,'text'])
#select columns
data = data[['tweet_id','text','airline_sentiment','airline']]
print(data)
# +
#convert sentiment into numbers
def sentiment2int(sentiment):
if sentiment == 'positive':
return 1
elif sentiment == 'neutral':
return 0
elif sentiment == 'negative':
return -1
else:
return np.NaN
data['rating'] = data['airline_sentiment'].apply(sentiment2int)
print(data)
# -
#alternatively, use encoder
encoder = LabelEncoder()
encoder.fit(data['airline_sentiment'])
data['encoded'] = encoder.transform(data['airline_sentiment'])
print(data)
#average sentiment of airlines
filter = data['airline'] == 'Virgin America'
virgin = data[filter]
print(virgin['rating'].mean())
# +
#tfidf
vectorizer = TfidfVectorizer(min_df=3, stop_words='english',ngram_range=(1, 2))
vectorizer.fit(data['text'])
X = vectorizer.transform(data['text'])
#get labels
y = np.array(data['rating'])
print(X)
print(X.shape)
print(y)
print(y.shape)
# -
#test train split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, stratify=y, random_state=1234)
print(X_train.shape)
print(X_test.shape)
#naive bayes
nb = MultinomialNB()
nb.fit(X_train,y_train)
print(nb.score(X_test,y_test))
nb_preds = nb.predict(X_test)
print(nb_preds)
#logistic regression
lr = LogisticRegression(penalty='l1',C=1)
lr.fit(X_train,y_train)
print(lr.score(X_test,y_test))
lr_preds = lr.predict(X_test)
print(lr_preds)
#random forest
rf = RandomForestClassifier(n_estimators=100)
rf.fit(X_train,y_train)
print(rf.score(X_test,y_test))
rf_preds = rf.predict(X_test)
print(rf_preds)
|
Misc/Python4ML/sklearn_tweets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Clean Evaluation
#
# dataset
# - cifar10
# - svhn
#
# model_name
# - resnet18
# - [soft-pruning]
# - resnet18_sfP
# - resnet18_sfP-mixup
# - resnet18_sfP-cutout
# - [post-training pruning]
# - resnet18_PX_0.Y
# - X = 2, 3, 4
# - Y = 3, 6, 9
# +
import numpy as np
import pandas as pd
import os
import torch
import json
from utils_model import *
dir_results = './results/'
# -
model_names = ['resnet18', 'resnet18_sfP', 'resnet18_sfP-mixup', 'resnet18_sfP-cutout']
for layer in [2, 3, 4]:
for prune_pct in ['0.3', '0.6', '0.9']:
model_names.append('resnet18_P%i-%s' % (layer, prune_pct))
model_names
# + active=""
# all_results = []
#
# for dataset in ['cifar10', 'svhn']:
#
# for model_name in model_names:
#
# model = get_model(model_name, dataset)
# testloader = get_testdata(dataset)
#
# top, top_probs, top1acc, top5acc, outputs, labels = evaluate(model, testloader)
#
# print('Top 1 accuracy', sum(top1acc) / len(labels))
# print('Top 5 accuracy', sum(top5acc) / len(labels))
#
# dict_entry = {}
# dict_entry['model_name'] = model_name
# dict_entry['dataset'] = dataset
# dict_entry['top1acc'] = sum(top1acc) / len(labels)
# dict_entry['top5acc'] = sum(top5acc) / len(labels)
#
# for i in range(10):
# dict_entry['label_dist%i' % i] = sum(outputs == i) / len(labels)
#
# all_results.append(dict_entry)
# pd.DataFrame(all_results).to_csv(dir_results + 'eval_clean.csv')
# -
df = pd.read_csv(dir_results + 'eval_clean.csv', index_col = 0)
df[df['dataset'] == 'cifar10']
df[df['dataset'] == 'svhn']
|
11-02 eval_clean.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python
# name: conda-env-python-py
# ---
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <a href="https://www.bigdatauniversity.com"><img src="https://ibm.box.com/shared/static/cw2c7r3o20w9zn8gkecaeyjhgw3xdgbj.png" width="400" align="center"></a>
#
# <h1 align="center"><font size="5">COLLABORATIVE FILTERING</font></h1>
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Recommendation systems are a collection of algorithms used to recommend items to users based on information taken from the user. These systems have become ubiquitous can be commonly seen in online stores, movies databases and job finders. In this notebook, we will explore recommendation systems based on Collaborative Filtering and implement simple version of one using Python and the Pandas library.
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <h1>Table of contents</h1>
#
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <ol>
# <li><a href="#ref1">Acquiring the Data</a></li>
# <li><a href="#ref2">Preprocessing</a></li>
# <li><a href="#ref3">Collaborative Filtering</a></li>
# </ol>
# </div>
# <br>
# <hr>
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
#
#
# <a id="ref1"></a>
# # Acquiring the Data
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# To acquire and extract the data, simply run the following Bash scripts:
# Dataset acquired from [GroupLens](http://grouplens.org/datasets/movielens/). Lets download the dataset. To download the data, we will use **`!wget`** to download it from IBM Object Storage.
# __Did you know?__ When it comes to Machine Learning, you will likely be working with large datasets. As a business, where can you host your data? IBM is offering a unique opportunity for businesses, with 10 Tb of IBM Cloud Object Storage: [Sign up now for free](http://cocl.us/ML0101EN-IBM-Offer-CC)
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
# !wget -O moviedataset.zip https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/ML0101ENv3/labs/moviedataset.zip
print('unziping ...')
# !unzip -o -j moviedataset.zip
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now you're ready to start working with the data!
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <hr>
#
# <a id="ref2"></a>
# # Preprocessing
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# First, let's get all of the imports out of the way:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Dataframe manipulation library
import pandas as pd
#Math functions, we'll only need the sqrt function so let's import only that
from math import sqrt
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now let's read each file into their Dataframes:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Storing the movie information into a pandas dataframe
movies_df = pd.read_csv('movies.csv')
#Storing the user information into a pandas dataframe
ratings_df = pd.read_csv('ratings.csv')
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Let's also take a peek at how each of them are organized:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Head is a function that gets the first N rows of a dataframe. N's default is 5.
movies_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# So each movie has a unique ID, a title with its release year along with it (Which may contain unicode characters) and several different genres in the same field. Let's remove the year from the title column and place it into its own one by using the handy [extract](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.str.extract.html#pandas.Series.str.extract) function that Pandas has.
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Let's remove the year from the __title__ column by using pandas' replace function and store in a new __year__ column.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Using regular expressions to find a year stored between parentheses
#We specify the parantheses so we don't conflict with movies that have years in their titles
movies_df['year'] = movies_df.title.str.extract('(\(\d\d\d\d\))',expand=False)
#Removing the parentheses
movies_df['year'] = movies_df.year.str.extract('(\d\d\d\d)',expand=False)
#Removing the years from the 'title' column
movies_df['title'] = movies_df.title.str.replace('(\(\d\d\d\d\))', '')
#Applying the strip function to get rid of any ending whitespace characters that may have appeared
movies_df['title'] = movies_df['title'].apply(lambda x: x.strip())
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Let's look at the result!
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
movies_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# With that, let's also drop the genres column since we won't need it for this particular recommendation system.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Dropping the genres column
movies_df = movies_df.drop('genres', 1)
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Here's the final movies dataframe:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
movies_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <br>
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Next, let's look at the ratings dataframe.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
ratings_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Every row in the ratings dataframe has a user id associated with at least one movie, a rating and a timestamp showing when they reviewed it. We won't be needing the timestamp column, so let's drop it to save on memory.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Drop removes a specified row or column from a dataframe
ratings_df = ratings_df.drop('timestamp', 1)
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Here's how the final ratings Dataframe looks like:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
ratings_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <hr>
#
# <a id="ref3"></a>
# # Collaborative Filtering
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now, time to start our work on recommendation systems.
#
# The first technique we're going to take a look at is called __Collaborative Filtering__, which is also known as __User-User Filtering__. As hinted by its alternate name, this technique uses other users to recommend items to the input user. It attempts to find users that have similar preferences and opinions as the input and then recommends items that they have liked to the input. There are several methods of finding similar users (Even some making use of Machine Learning), and the one we will be using here is going to be based on the __Pearson Correlation Function__.
#
# <img src="https://ibm.box.com/shared/static/1ql8cbwhtkmbr6nge5e706ikzm5mua5w.png" width=800px>
#
#
# The process for creating a User Based recommendation system is as follows:
# - Select a user with the movies the user has watched
# - Based on his rating to movies, find the top X neighbours
# - Get the watched movie record of the user for each neighbour.
# - Calculate a similarity score using some formula
# - Recommend the items with the highest score
#
#
# Let's begin by creating an input user to recommend movies to:
#
# Notice: To add more movies, simply increase the amount of elements in the userInput. Feel free to add more in! Just be sure to write it in with capital letters and if a movie starts with a "The", like "The Matrix" then write it in like this: 'Matrix, The' .
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
userInput = [
{'title':'Breakfast Club, The', 'rating':5},
{'title':'Toy Story', 'rating':3.5},
{'title':'Jumanji', 'rating':2},
{'title':"Pulp Fiction", 'rating':5},
{'title':'Akira', 'rating':4.5}
]
inputMovies = pd.DataFrame(userInput)
inputMovies
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# #### Add movieId to input user
# With the input complete, let's extract the input movies's ID's from the movies dataframe and add them into it.
#
# We can achieve this by first filtering out the rows that contain the input movies' title and then merging this subset with the input dataframe. We also drop unnecessary columns for the input to save memory space.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Filtering out the movies by title
inputId = movies_df[movies_df['title'].isin(inputMovies['title'].tolist())]
#Then merging it so we can get the movieId. It's implicitly merging it by title.
inputMovies = pd.merge(inputId, inputMovies)
#Dropping information we won't use from the input dataframe
inputMovies = inputMovies.drop('year', 1)
#Final input dataframe
#If a movie you added in above isn't here, then it might not be in the original
#dataframe or it might spelled differently, please check capitalisation.
inputMovies
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# #### The users who has seen the same movies
# Now with the movie ID's in our input, we can now get the subset of users that have watched and reviewed the movies in our input.
#
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Filtering out users that have watched movies that the input has watched and storing it
userSubset = ratings_df[ratings_df['movieId'].isin(inputMovies['movieId'].tolist())]
userSubset.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# We now group up the rows by user ID.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Groupby creates several sub dataframes where they all have the same value in the column specified as the parameter
userSubsetGroup = userSubset.groupby(['userId'])
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# lets look at one of the users, e.g. the one with userID=1130
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
userSubsetGroup.get_group(1130)
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Let's also sort these groups so the users that share the most movies in common with the input have higher priority. This provides a richer recommendation since we won't go through every single user.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Sorting it so users with movie most in common with the input will have priority
userSubsetGroup = sorted(userSubsetGroup, key=lambda x: len(x[1]), reverse=True)
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now lets look at the first user
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
userSubsetGroup[0:3]
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# #### Similarity of users to input user
# Next, we are going to compare all users (not really all !!!) to our specified user and find the one that is most similar.
# we're going to find out how similar each user is to the input through the __Pearson Correlation Coefficient__. It is used to measure the strength of a linear association between two variables. The formula for finding this coefficient between sets X and Y with N values can be seen in the image below.
#
# Why Pearson Correlation?
#
# Pearson correlation is invariant to scaling, i.e. multiplying all elements by a nonzero constant or adding any constant to all elements. For example, if you have two vectors X and Y,then, pearson(X, Y) == pearson(X, 2 * Y + 3). This is a pretty important property in recommendation systems because for example two users might rate two series of items totally different in terms of absolute rates, but they would be similar users (i.e. with similar ideas) with similar rates in various scales .
#
# 
#
# The values given by the formula vary from r = -1 to r = 1, where 1 forms a direct correlation between the two entities (it means a perfect positive correlation) and -1 forms a perfect negative correlation.
#
# In our case, a 1 means that the two users have similar tastes while a -1 means the opposite.
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# We will select a subset of users to iterate through. This limit is imposed because we don't want to waste too much time going through every single user.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
userSubsetGroup = userSubsetGroup[0:100]
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now, we calculate the Pearson Correlation between input user and subset group, and store it in a dictionary, where the key is the user Id and the value is the coefficient
#
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Store the Pearson Correlation in a dictionary, where the key is the user Id and the value is the coefficient
pearsonCorrelationDict = {}
#For every user group in our subset
for name, group in userSubsetGroup:
#Let's start by sorting the input and current user group so the values aren't mixed up later on
group = group.sort_values(by='movieId')
inputMovies = inputMovies.sort_values(by='movieId')
#Get the N for the formula
nRatings = len(group)
#Get the review scores for the movies that they both have in common
temp_df = inputMovies[inputMovies['movieId'].isin(group['movieId'].tolist())]
#And then store them in a temporary buffer variable in a list format to facilitate future calculations
tempRatingList = temp_df['rating'].tolist()
#Let's also put the current user group reviews in a list format
tempGroupList = group['rating'].tolist()
#Now let's calculate the pearson correlation between two users, so called, x and y
Sxx = sum([i**2 for i in tempRatingList]) - pow(sum(tempRatingList),2)/float(nRatings)
Syy = sum([i**2 for i in tempGroupList]) - pow(sum(tempGroupList),2)/float(nRatings)
Sxy = sum( i*j for i, j in zip(tempRatingList, tempGroupList)) - sum(tempRatingList)*sum(tempGroupList)/float(nRatings)
#If the denominator is different than zero, then divide, else, 0 correlation.
if Sxx != 0 and Syy != 0:
pearsonCorrelationDict[name] = Sxy/sqrt(Sxx*Syy)
else:
pearsonCorrelationDict[name] = 0
# -
pearsonCorrelationDict.items()
pearsonDF = pd.DataFrame.from_dict(pearsonCorrelationDict, orient='index')
pearsonDF.columns = ['similarityIndex']
pearsonDF['userId'] = pearsonDF.index
pearsonDF.index = range(len(pearsonDF))
pearsonDF.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# #### The top x similar users to input user
# Now let's get the top 50 users that are most similar to the input.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
topUsers=pearsonDF.sort_values(by='similarityIndex', ascending=False)[0:50]
topUsers.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now, let's start recommending movies to the input user.
#
# #### Rating of selected users to all movies
# We're going to do this by taking the weighted average of the ratings of the movies using the Pearson Correlation as the weight. But to do this, we first need to get the movies watched by the users in our __pearsonDF__ from the ratings dataframe and then store their correlation in a new column called _similarityIndex". This is achieved below by merging of these two tables.
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
topUsersRating=topUsers.merge(ratings_df, left_on='userId', right_on='userId', how='inner')
topUsersRating.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now all we need to do is simply multiply the movie rating by its weight (The similarity index), then sum up the new ratings and divide it by the sum of the weights.
#
# We can easily do this by simply multiplying two columns, then grouping up the dataframe by movieId and then dividing two columns:
#
# It shows the idea of all similar users to candidate movies for the input user:
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Multiplies the similarity by the user's ratings
topUsersRating['weightedRating'] = topUsersRating['similarityIndex']*topUsersRating['rating']
topUsersRating.head()
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Applies a sum to the topUsers after grouping it up by userId
tempTopUsersRating = topUsersRating.groupby('movieId').sum()[['similarityIndex','weightedRating']]
tempTopUsersRating.columns = ['sum_similarityIndex','sum_weightedRating']
tempTopUsersRating.head()
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
#Creates an empty dataframe
recommendation_df = pd.DataFrame()
#Now we take the weighted average
recommendation_df['weighted average recommendation score'] = tempTopUsersRating['sum_weightedRating']/tempTopUsersRating['sum_similarityIndex']
recommendation_df['movieId'] = tempTopUsersRating.index
recommendation_df.head()
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# Now let's sort it and see the top 20 movies that the algorithm recommended!
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
recommendation_df = recommendation_df.sort_values(by='weighted average recommendation score', ascending=False)
recommendation_df.head(20)
# + button=false deletable=true jupyter={"outputs_hidden": false} new_sheet=false run_control={"read_only": false}
movies_df.loc[movies_df['movieId'].isin(recommendation_df.head(20)['movieId'].tolist())]
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# ### Advantages and Disadvantages of Collaborative Filtering
#
# ##### Advantages
# * Takes other user's ratings into consideration
# * Doesn't need to study or extract information from the recommended item
# * Adapts to the user's interests which might change over time
#
# ##### Disadvantages
# * Approximation function can be slow
# * There might be a low of amount of users to approximate
# * Privacy issues when trying to learn the user's preferences
# + [markdown] button=false deletable=true new_sheet=false run_control={"read_only": false}
# <h2>Want to learn more?</h2>
#
# IBM SPSS Modeler is a comprehensive analytics platform that has many machine learning algorithms. It has been designed to bring predictive intelligence to decisions made by individuals, by groups, by systems – by your enterprise as a whole. A free trial is available through this course, available here: <a href="http://cocl.us/ML0101EN-SPSSModeler">SPSS Modeler</a>
#
# Also, you can use Watson Studio to run these notebooks faster with bigger datasets. Watson Studio is IBM's leading cloud solution for data scientists, built by data scientists. With Jupyter notebooks, RStudio, Apache Spark and popular libraries pre-packaged in the cloud, Watson Studio enables data scientists to collaborate on their projects without having to install anything. Join the fast-growing community of Watson Studio users today with a free account at <a href="https://cocl.us/ML0101EN_DSX">Watson Studio</a>
#
# <h3>Thanks for completing this lesson!</h3>
#
# <h4>Author: <a href="https://ca.linkedin.com/in/saeedaghabozorgi"><NAME></a></h4>
# <p><a href="https://ca.linkedin.com/in/saeedaghabozorgi"><NAME></a>, PhD is a Data Scientist in IBM with a track record of developing enterprise level applications that substantially increases clients’ ability to turn data into actionable knowledge. He is a researcher in data mining field and expert in developing advanced analytic methods like machine learning and statistical modelling on large datasets.</p>
#
# <hr>
#
# <p>Copyright © 2018 <a href="https://cocl.us/DX0108EN_CC">Cognitive Class</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.</p>
|
ML0101EN-RecSys-Collaborative-Filtering-movies-py-v1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
print('Hello World!')
a = 34
b = 1126
print('a + b =', a + b)
fname = '高尾'
name = '基史'
print('私の名前は,{} {}です.'.format(fname, name))
import matplotlib.pyplot as plt
import numpy as np
import math
x = np.linspace(0, 10, 100)
print(x)
y = np.sin(x)
print(y)
plt.figure(figsize = (6,3))
plt.rcParams['font.family'] = 'Arial'
plt.plot(x,y, color = 'red')
plt.xlim([0,10])
# ## forループ
a = 10
for i in range(5):
a = a + i
print(a)
for i in range(5):
# 0, 1, 2, 3, 4
print(i)
nums = [0,1,2,3,4]
names = ['Mike', 'Ken', 'キティ']
for s in names:
print('私の名前は,{}です.'.format(s))
# if 文
for i in range(1, 10):
print(i)
if i == 1:
print('偶数')
elif i % 2 == 0:
print('偶数')
else:
print('奇数')
|
hre/test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import pandas as pd
import numpy as np
# # Creating a data frame
#
#
# +
#when writing a data frame from scratch pandas will take data in the form of a dictionary
data ={'ones':np.ones(10),
'zeros':np.zeros(10)
}
#making a data frame from scratch
#start with any data or colum names that you want to input
data_frame = pd.DataFrame(data,columns=['ones','zeros'])
print (data_frame)
# +
#to add additional colums afterwards define them as follows:
#simply define your new colum anme and assign data to it
data_frame['new_colum']=np.ones(10)+1
print (data_frame)
# +
#creating a pd.DataFrame from lists
#your lists of data
fruit= ('Apple','Banana','Pineapple')
shape=('round','long','spikey')
#define keys
list_keys=('Fruit','Shape')
#create master list of data
list_data=[fruit,shape]
#zip data with coresponding keys
zipped_data = list(zip(list_keys,list_data))
#make into a dictionary
df_input_data = dict(zipped_data)
#read in as data frame
df_fruit = pd.DataFrame(df_input_data)
print(df_fruit)
# +
#adding a new colum with nans
df_fruit['number']=[1,5,np.nan]
#print(df_fruit)
#adding a new row of 'oranges'
fruit2={'Fruit':['orange','Kiwi','Grapes'],
'Shape':['round',np.nan,'roundish'],
'number':[1,np.nan,100.5]}
df_fruit2=pd.DataFrame(fruit2,columns=(['Fruit','Shape','number']))
print df_fruit2
df_fruit.append(df_fruit2, ignore_index=True)
#when appending one df into another there is some truble with how to access the merged frame
# in this case the command df_fruit.ix[3] will not work!!
# -
# # Reading and writing files
#
# If you have an exsisting file or want to write our table into a file you can easily do this with pandas
#
# # pandas file types
#
# pandas reads a wide variety of file types (csv,txt and alsp pickled files).
# It is even possible to execute sql queries! (not showing that today)
#
# It does NOT read fits files!
#
# To read / write data define what type you want (i.e pd.read_XYZ)
# +
#reading in the data file
filename='cereal.csv'
df=pd.read_csv(filename)
#other read functions include
#pd.read_table
#pd.read_text
# + active=""
# Other options for the various read methods include what deliminators to use.
# These can be defined with 'sep =' when reading in the file.
# ','-comma
# ' '- whitespace
# '\t'-tap
# For excell files/workbooks you can define the sheet_name that you want to read in
# If you dont want the total file you can define the number of rows to read in
# Also define whether or not you are reading in the header (header=)or rename the colums
# Excluding the header means you colums will not be named!!
#
#
# -
# # retriving data frame information
#
# a full list / cheat sheet regarding pandas is availible with this material!
# +
#basic info
#comment and uncomment to have a look at the various methods
#df.info() # basic information regarding your colums and number of objects in each column (will flag nans)
#df.count() # number coun in each colum with theyr respective keys
#df.shape # shape of your data frame (as usual)
#df.columns # names of your columns
#df.index # unique index list
#df.keys() #list of your keys to access column data
#df.describe() # returns basic info for each column (count,unique etc.)
#df.idxmin() #minimum or maximim index value (doens't work with example data set)
# -
# # Selecting
# +
#selecting rows
#by label i.e the index number (unique identifier assosiated with a dataentry)
print(df.ix[1])
#by position
print (df.iloc[1])
#slicing
print (df[76:])
#selecting colums
#by keys
print (df['name'])
# or select in both rows and colums
print (df.ix[1,'name'])
# +
# for a brief look at some of your data call head or tail (also works well if previously you sorted your data frame!)
#will return you the top 5 elements in your data frame
print (df['cups'].head())
#will return the last 5 elements in your data frame
print (df['cups'].tail())
# an example of sorting and using the tail method
print df.sort(columns=['cups','sugars']).head()
# if you want to access sorted data say the fourth entry in you r sorted table use iloc not ix!!!
print df.sort(columns=['cups','sugars']).iloc[[3]]
# -
# # Applying functions
# +
# one way to write a function to count he lenght of the name of each cereal
def count_string(data):
lenght =[]
for i in data:
lenght.append(len(i))
return lenght
name_lenght=count_string(df['name'])
#alternative much shorter version !!
f = lambda x: len(x)
df['name'].apply(f)
#if you wanted to apply his not only to the name version but you wanted to know the length of any object in your data frame :
df.applymap(f)
# -
# # removing nans and replacing values
# +
#at this stage you can try using any of the other kaggle datasets in the folder to have a play around
#just make sure you adjust all the column names accordingly!
filename='cereal2.csv'
df=pd.read_csv(filename, nrows=50, usecols=[0,9,15])
#if you skip rows and do not define a set of colum names it will assign the values it finds in the first row...
#other method for this specific example is to use df.keys()[x] to determine the relevant names
df_extra_rows=pd.read_csv(filename,skiprows=51,usecols=[0,9,15], names=['name','sugars','rating'])
#check that we didn't download a row twice
print(df.ix[49],df_extra_rows.ix[0]) #using an index of -1 won't work
df_columns=pd.read_csv(filename,usecols=[1,11])
# +
# find out where there are nan's
# returns you how many null objects
df.info()
# THIS WILL NOT WORK!! as np.nan==np.nan will return False!!!
df['sugars']==np.nan
#However this will!! to filter out nans use the np.isnan function
df['sugars'].apply(np.isnan)
#this way you can find the idex of each nan value
np.where(df['sugars'].apply(np.isnan))
#if you know the location of the nan use df.loc[x]
df['sugars'].ix[np.where(df['sugars'].apply(np.isnan))]=(1,1,1,1,1)
#alternatively use the pd.fillna function
#just select what filler you want for you nan's
df.fillna(('nothing to see here'))
# -
# # merging data frames
#
# a number of data frames have been created for you above. Using the merge and concat function in pandas try stitching them back together.
# (start with
# +
# use the merge function on the various data frames above
help(pd.merge)
#df_merged=
# +
# use the merge function on the various data frames above
help(pd.concat)
#df_concat=
# +
# making a new colum using the apply function
df['name_length']=df['name'].apply(f)
df.keys()
#overwriting colums
df['name_length']=df['name_length']+1
# -
# # saving files
# +
#similar to reading in files you can write into all file formats using the pd.to_xyz command
#pandas can even write to latex files !!!!!!!
help(pd.DataFrame.to_csv)
df.to_csv('merged_csv', sep='\t')
# -
|
tutorials/pandas_intro/Pandas intro.ipynb
|