code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Dependencies
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _kg_hide-input=true _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import json, warnings, shutil
from scripts_step_lr_schedulers import *
from tweet_utility_scripts import *
from tweet_utility_preprocess_roberta_scripts import *
from transformers import TFRobertaModel, RobertaConfig
from tokenizers import ByteLevelBPETokenizer
from tensorflow.keras.models import Model
from tensorflow.keras import optimizers, metrics, losses, layers
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint, LearningRateScheduler
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
# -
# # Load data
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _kg_hide-input=true _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
database_base_path = '/kaggle/input/tweet-dataset-7fold-roberta-64-clean/'
k_fold = pd.read_csv(database_base_path + '5-fold.csv')
display(k_fold.head())
# Unzip files
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_1.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_2.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_3.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_4.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_5.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_6.tar.gz
# !tar -xf /kaggle/input/tweet-dataset-7fold-roberta-64-clean/fold_7.tar.gz
# -
# # Model parameters
# +
vocab_path = database_base_path + 'vocab.json'
merges_path = database_base_path + 'merges.txt'
base_path = '/kaggle/input/qa-transformers/roberta/'
config = {
"MAX_LEN": 64,
"BATCH_SIZE": 32,
"EPOCHS": 2,
"LEARNING_RATE": 1e-4,
"ES_PATIENCE": 2,
"N_FOLDS": 7,
"question_size": 4,
"base_model_path": base_path + 'roberta-base-tf_model.h5',
"config_path": base_path + 'roberta-base-config.json'
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
# -
# # Tokenizer
# + _kg_hide-output=true
tokenizer = ByteLevelBPETokenizer(vocab_file=vocab_path, merges_file=merges_path,
lowercase=True, add_prefix_space=True)
tokenizer.save('./')
# + _kg_hide-input=true
# pre-process
k_fold['jaccard'] = k_fold.apply(lambda x: jaccard(x['text'], x['selected_text']), axis=1)
k_fold['text_tokenCnt'] = k_fold['text'].apply(lambda x : len(tokenizer.encode(x).ids))
k_fold['selected_text_tokenCnt'] = k_fold['selected_text'].apply(lambda x : len(tokenizer.encode(x).ids))
# -
# ## Learning rate schedule
# + _kg_hide-input=true
lr_min = 1e-6
lr_start = 0
lr_max = config['LEARNING_RATE']
train_size = len(k_fold[k_fold['fold_1'] == 'train'])
step_size = train_size // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
rng = [i for i in range(0, total_steps, config['BATCH_SIZE'])]
y = [one_cycle_schedule(tf.cast(x, tf.float32), total_steps=total_steps,
lr_start=lr_min, lr_max=lr_max) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
# -
# # Model
# +
module_config = RobertaConfig.from_pretrained(config['config_path'], output_hidden_states=False)
def model_fn(MAX_LEN):
input_ids = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='input_ids')
attention_mask = layers.Input(shape=(MAX_LEN,), dtype=tf.int32, name='attention_mask')
base_model = TFRobertaModel.from_pretrained(config['base_model_path'], config=module_config, name="base_model")
last_hidden_state, _ = base_model({'input_ids': input_ids, 'attention_mask': attention_mask})
logits = layers.Dense(2, name="qa_outputs", use_bias=False)(last_hidden_state)
start_logits, end_logits = tf.split(logits, 2, axis=-1)
start_logits = tf.squeeze(start_logits, axis=-1, name='y_start')
end_logits = tf.squeeze(end_logits, axis=-1, name='y_end')
model = Model(inputs=[input_ids, attention_mask], outputs=[start_logits, end_logits])
return model
# -
# # Train
# + _kg_hide-input=true
def get_training_dataset(x_train, y_train, batch_size, buffer_size, seed=0):
dataset = tf.data.Dataset.from_tensor_slices(({'input_ids': x_train[0], 'attention_mask': x_train[1]},
(y_train[0], y_train[1])))
dataset = dataset.repeat()
dataset = dataset.shuffle(2048, seed=seed)
dataset = dataset.batch(batch_size, drop_remainder=True)
dataset = dataset.prefetch(buffer_size)
return dataset
def get_validation_dataset(x_valid, y_valid, batch_size, buffer_size, repeated=False, seed=0):
dataset = tf.data.Dataset.from_tensor_slices(({'input_ids': x_valid[0], 'attention_mask': x_valid[1]},
(y_valid[0], y_valid[1])))
if repeated:
dataset = dataset.repeat()
dataset = dataset.shuffle(2048, seed=seed)
dataset = dataset.batch(batch_size, drop_remainder=True)
dataset = dataset.cache()
dataset = dataset.prefetch(buffer_size)
return dataset
# + _kg_hide-input=true _kg_hide-output=true
AUTO = tf.data.experimental.AUTOTUNE
history_list = []
for n_fold in range(config['N_FOLDS']):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
# Load data
base_data_path = 'fold_%d/' % (n_fold)
x_train = np.load(base_data_path + 'x_train.npy')
y_train = np.load(base_data_path + 'y_train.npy')
x_valid = np.load(base_data_path + 'x_valid.npy')
y_valid = np.load(base_data_path + 'y_valid.npy')
step_size = x_train.shape[1] // config['BATCH_SIZE']
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
model = model_fn(config['MAX_LEN'])
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
lr = lambda: one_cycle_schedule(tf.cast(optimizer.iterations, tf.float32),
total_steps=total_steps, lr_start=lr_min,
lr_max=lr_max)
optimizer = optimizers.Adam(learning_rate=lr)
model.compile(optimizer, loss=[losses.CategoricalCrossentropy(label_smoothing=0.2, from_logits=True),
losses.CategoricalCrossentropy(label_smoothing=0.2, from_logits=True)])
history = model.fit(get_training_dataset(x_train, y_train, config['BATCH_SIZE'], AUTO, seed=SEED),
validation_data=(get_validation_dataset(x_valid, y_valid, config['BATCH_SIZE'], AUTO, repeated=False, seed=SEED)),
epochs=config['EPOCHS'],
steps_per_epoch=step_size,
callbacks=[checkpoint, es],
verbose=2).history
history_list.append(history)
# Make predictions
predict_eval_df(k_fold, model, x_train, x_valid, get_test_dataset, decode, n_fold, tokenizer, config, config['question_size'])
### Delete data dir
shutil.rmtree(base_data_path)
# -
# # Model loss graph
# + _kg_hide-input=true
for n_fold in range(config['N_FOLDS']):
print('Fold: %d' % (n_fold+1))
plot_metrics(history_list[n_fold])
# -
# # Model evaluation
# + _kg_hide-input=true
display(evaluate_model_kfold(k_fold, config['N_FOLDS']).style.applymap(color_map))
# -
# # Visualize predictions
# + _kg_hide-input=true
k_fold['jaccard_mean'] = 0
for n in range(config['N_FOLDS']):
k_fold['jaccard_mean'] += k_fold[f'jaccard_fold_{n+1}'] / config['N_FOLDS']
display(k_fold[['text', 'selected_text', 'sentiment', 'text_tokenCnt',
'selected_text_tokenCnt', 'jaccard', 'jaccard_mean'] + [c for c in k_fold.columns if (c.startswith('prediction_fold'))]].head(15))
|
Model backlog/Train/281-tweet-train-7fold-roberta-onecycle.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## Strings
# ### Criando uma String
# Para criar uma string em Python você pode usar aspas simples ou duplas. Por exemplo:
# Uma única palavra
'Oi'
# Uma frase
'Criando uma string em Python'
# Podemos usar aspas duplas
"Podemos usar aspas duplas ou simples para strings em Python"
# Você pode combinar aspas duplas e simples
"Testando strings em 'Python'"
# ### Imprimindo uma String
print ('Testando Strings em Python')
print ('Testando \nStrings \nem \nPython')
print ('\n')
# ### Indexando Strings
# Atribuindo uma string
s = 'Data Science Academy'
print(s)
# Primeiro elemento da string.
s[0]
s[1]
s[2]
# Podemos usar um : para executar um slicing que faz a leitura de tudo até um ponto designado. Por exemplo:
# Retorna todos os elementos da string, começando pela posição (lembre-se que Python começa a indexação pela posição 0),
# até o fim da string.
s[1:]
# A string original permanece inalterada
s
# Retorna tudo até a posição 3
s[:3]
s[:]
# Nós também podemos usar a indexação negativa e ler de trás para frente.
s[-1]
# Retornar tudo, exceto a última letra
s[:-1]
# Nós também podemos usar a notação de índice e fatiar a string em pedaços específicos (o padrão é 1). Por exemplo, podemos usar dois pontos duas vezes em uma linha e, em seguida, um número que especifica a frequência para retornar elementos. Por exemplo:
s[::1]
s[::2]
s[::-1]
# ### Propriedades de Strings
s
# Alterando um caracter
s[0] = 'x'
# Concatenando strings
s + ' é a melhor maneira de estar preparado para o mercado de trabalho em Ciência de Dados!'
s = s + ' é a melhor maneira de estar preparado para o mercado de trabalho em Ciência de Dados!'
print(s)
# Podemos usar o símbolo de multiplicação para criar repetição!
letra = 'w'
letra * 3
# ### Funções Built-in de Strings
s
# Upper Case
s.upper()
# Lower case
s.lower()
# Dividir uma string por espaços em branco (padrão)
s.split()
# Dividir uma string por um elemento específico
s.split('y')
# ### Funções String
s = 'seja bem vindo ao universo de python'
s.capitalize()
s.count('a')
s.find('p')
s.center(20, 'z')
s.isalnum()
s.isalpha()
s.islower()
s.isspace()
s.endswith('o')
s.partition('!')
# ### Comparando Strings
print("Python" == "R")
print("Python" == "Python")
# # Fim
|
001-Curso-De-Python/001-DSA/001-Variaveis-Tipos-Estrutura-De-Dados/005-Strings.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
import os
import os.path as path
from sklearn.model_selection import train_test_split
base_path = 'data'
original_data = path.join(base_path, 'AM_test_original.npz')
data = np.load(original_data)
x_data = data['trainimg']
y_data = data['trainlabel']
img_shape = (341, 341, 3)
x_2d_data = x_data.reshape((len(x_data), *img_shape))
y_label = np.argmax(y_data, axis=1)
y_text = ['bed', 'bird', 'cat', 'dog', 'house', 'tree']
y_table = {i:text for i, text in enumerate(y_text)}
y_table_array = np.array([(i, text) for i, text in enumerate(y_text)])
# +
x_train_temp, x_test, y_train_temp, y_test = train_test_split(
x_2d_data, y_label, test_size=0.2, random_state=42, stratify=y_label)
x_train, x_val, y_train, y_val = train_test_split(
x_train_temp, y_train_temp, test_size=0.25, random_state=42, stratify=y_train_temp)
x_train.shape, y_train.shape, x_val.shape, y_val.shape, x_test.shape, y_test.shape
# -
np.savez_compressed(path.join(base_path, 'imagenet_6_class_train_data.npz'),
x_data=x_train, y_data=y_train, y_table_array=y_table_array)
np.savez_compressed(path.join(base_path, 'imagenet_6_class_val_data.npz'),
x_data=x_val, y_data=y_val, y_table_array=y_table_array)
np.savez_compressed(path.join(base_path, 'imagenet_6_class_test_data.npz'),
x_data=x_test, y_data=y_test, y_table_array=y_table_array)
x_data = data['valimg']
y_data = data['vallabel']
img_shape = (341, 341, 3)
x_2d_data = x_data.reshape((len(x_data), *img_shape))
np.savez_compressed(path.join(base_path, 'imagenet_6_class_vis_data.npz'),
x_data=x_2d_data, y_data=y_data, y_table_array=y_table_array)
|
make_imagenet_6_class_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/aparna2903/letsupgreade-Python-Batch-7/blob/master/Assignment1_and_Assignment2_Day6_Batch7.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="16a1D5XMaOPQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 221} outputId="87be08f0-596b-4bdf-af84-1887ee76db22"
#Question 1 : for this challenge, create a bank account class that has two attributes:
#owner_name
#balance
#and two methods
#deposit
#withdraw
#As an added requirement, withdrawals may not exceed the available balance
#Instantiate your class, make several deposites and withdrawals and test to make sure the account can't be overdrawn.
#Solution :
class Bank_Account:
def __init__(self, Owner_name):
self.balance = 0
self.Owner_name = Owner_name
print(f"Hello!!! {self.Owner_name} Welcome to the Deposit & Withdrawal Machine")
def deposit(self):
amount=float(input("Enter amount to be Deposited: "))
self.balance += amount
print("\n Amount Deposited:", amount)
def withdraw(self):
amount = float(input("Enter amount to be Withdrawn: "))
if self.balance>=amount:
self.balance-=amount
print("\n You Withdrew:", amount)
else:
print("\n Insufficient balance ")
def display(self):
print("\n Net Available Balance=",self.balance)
# creating an object of class
s = Bank_Account(input('Enter Your name'))
# Calling functions with that class object
s.deposit()
s.withdraw()
s.display()
#Question 2 : for this challenge, create a cone class that has two attributes:
#R=radius,
#h=height
#and two method
#volume = pi * r*r*(h/3)
#surface area : base : pi*r*r, side : pi*r*(r**2+h**2)/2
#Make only one class with functions as in where required import maths
#solution :
# Importing Math library for value Of PI
import math
pi = math.pi
class Cone:
def __init__(self, r, h):
self.r = r
self.h = h
# Function to calculate Volume of Cone
def volume(self):
return (1 / 3) * pi * self.r**2 * self.h
# Function To Calculate Surface Area of Cone
def surfacearea(self):
base = (pi * self.r **2)
side = (pi * self.r * math.sqrt((self.r**2) + (self.h**2)))
return (pi * self.r **2) + (pi * self.r * math.sqrt((self.r**2) + (self.h**2)))
calc_volume = Cone(5,12)
print(f"Volume Of Cone : {calc_volume.volume()}")
calc_surface = Cone(5,12)
print(f"Surface Area Of Cone : {calc_surface.surfacearea()}")
|
Assignment1_and_Assignment2_Day6_Batch7.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/ahmadhajmosa/3d-force-graph/blob/master/Session_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="rmSUExzC-ZBV" colab_type="text"
#
# + [markdown] id="wgWZldyi-Zef" colab_type="text"
# # Lab on Machine Learning and Applications in Intelligent Vehicles
# ## Session 1: Introduction
#
# + [markdown] id="j1T4XAd1_fJk" colab_type="text"
# ### Course Plan:
#
# This lab is a continuation to the Machine learning lecture, the objective of this course is to learn how to model and implement neural networks using deep learning python frameworks:
# 1. Tensorflow
# 2. Keras
# 3. Pytorch
#
# Useing these frameworks, we will go through the following topics and use cases:
#
# #### Session 1: 05.06 - 09:00 - 11:00 :
#
# >#### Presentation: 05.06 - 09:00 - 10:30:
# >1. Introduction to deep learning frameworks
# 2. Deep learning in Numpy
#
# >#### Break: 05.06 - 10:30 - 10:45
# >#### Assignment: 05.06 - 10:45 - 11:45 :
# >* Implementation of backprop using numpy
#
# >1. Tensorflow backround
# 2. Implementation of feedforward neural networks using Tensorflow
#
# >#### Break: 05.06 - 10:00 - 10:15
# >#### Assignment: 05.06 - 10:15 - 10:45 :
#
# >* play around with tensorflow and build your first neural network
#
#
#
# #### Session 2: 05.06 - 11:00 - 12:00 :
#
# >#### Presentation: 05.06 - 11:00 - 12:00:
#
#
# >3. Implementation of CNN useing Tensorflow
# 4. Tensorboard
#
# >#### Break: 05.06 - 12:00 - 13:00
# >#### Assignment: 05.06 - 13:00 - 13:30 :
#
#
# #### Session 3: 05.06 - 13:30 - 15:00 :
#
# >#### Presentation: 05.06 - 13:00 - 14:00:
#
# >5. Introduction to Keras
# 6. CNN using Keras
# >#### Break: 05.06 - 14:00 - 14:15
# >#### Assignment: 05.06 - 14:15 - 14:45 :
#
# #### Session 4: 05.06 - 15:00 - 16:30 :
#
# >#### Presentation: 05.06 - 15:00 - 15:45:
#
# >7. LSTM using Keras
#
# >#### Break: 05.06 - 15:45 - 16:00
# >#### Assignment: 05.06 - 16:00 - 16:30 :
#
#
# 8. VGG, Inceptaion, ResNet models using Keras
#
# 9. Autoencoders using Keras
#
# 10. Sequence to Sequence Models using Keras
#
# 11. Attention Mechanism using Keras
# 12. GANS
# 13. Introduction to Pytorch
# 14. Machine translation using Pytorch
# 15. Introduction to Allennlp
# 16. Deep Reinforcment Learning using Keras
# 17. Use case: building self driving car using Unity and tensorflow
#
#
#
#
#
#
#
#
#
# + [markdown] id="a75NLOuwKXSs" colab_type="text"
# #Session 1: 05.06 - 09:00 - 11:00 :
#
# + [markdown] id="ciUtGM-W_ehP" colab_type="text"
#
#
# ## Deep learning frameworks:
#
# In the past decade, many deep learning frameworks have been developed to ease and scale the research and development of AI. Many big technology providers including Google, IBM, Microsoft and Facebook have entered the race to provide the best and most popluar frameworks. To enter such a race, mainly four features are considered in the provided framework:
#
# 1. Uses a popular language for data scientists (Python, Scale, C++ or R)
# 2. Flexible in creating and adjusting deep learning architectures -> Functional programming
# 3. Easy for computing gradients
# 4. Interface with GPUs for parallel processing
#
#
# In the following we see the most popular provided deep learning frameworks with their providers
# https://towardsdatascience.com/deep-learning-framework-power-scores-2018-23607ddf297a
#
# 
#
# ## Tensorflow
# TensorFlow is the undisputed heavyweight champion. It has the most GitHub activity, Google searches, Medium articles, books on Amazon and ArXiv articles. It also has the most developers using it and is listed in the most online job descriptions. TensorFlow is backed by Google.
#
# ## Keras
# Keras has an “API designed for human beings, not machines.” It is the second most popular framework in nearly all evaluation areas. Keras sits on top of TensorFlow, Theano, or CNTK. Start with Keras if you are new to deep learning.
#
# ## Pytorch
#
# PyTorch is the third most popular overall framework and the second most popular stand-alone framework. It is younger than TensorFlow and has grown rapidly in popularity. It allows customization that TensorFlow does not. It has the backing of Facebook.
#
# ## Theano
#
# Theano was developed at the University of Montreal in 2007 and is the oldest significant Python deep learning framework. It has lost much of its popularity and its leader stated that major releases were no longer on the roadmap. However, updates continue to be made. Theano still the fifth highest scoring framework.
#
# # Comparision:
#
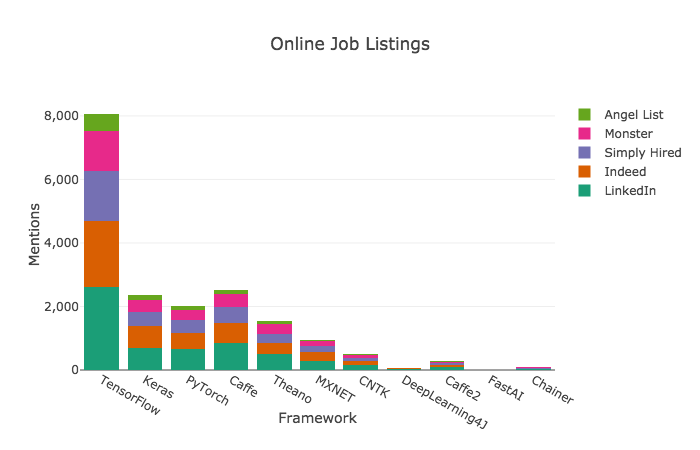
# ## Criteria 1: Online Job Listings
#
# TensorFlow is the clear winner when it comes to frameworks mentioned in job listings. Learn it if you want a job doing deep learning.
#
# >> 
#
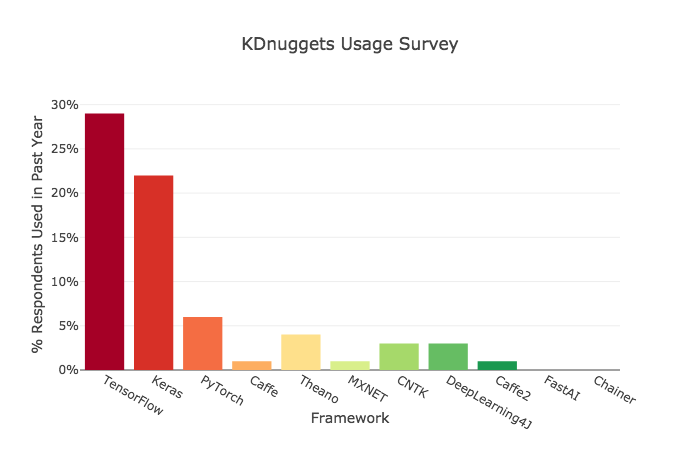
# ## Criteria 2: Usage
#
#
# Keras showed a surprising amount of use — nearly as much as TensorFlow. It’s interesting that US employers are overwhelmingly looking for TensorFlow skills, when — at least internationally — Keras is used almost as frequently.
#
# >> 
#
#
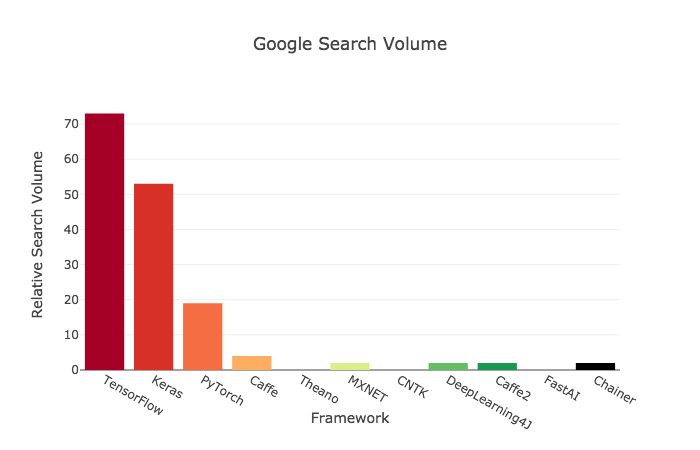
# ## Criteria 4: Google Search Activity
#
# >> 
#
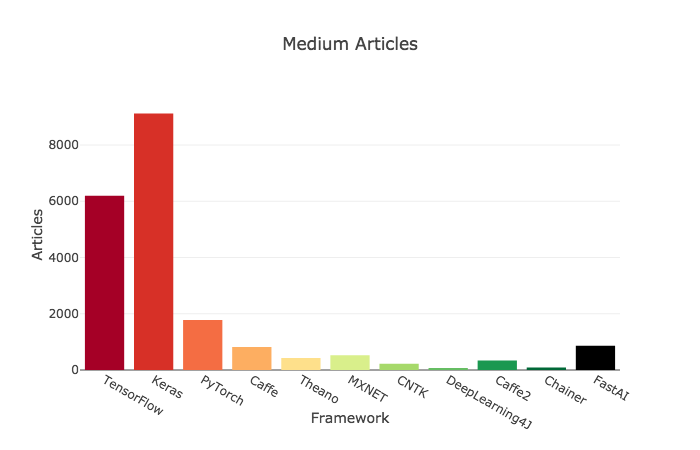
# ## Criteria 5: Medium Articles
#
# >> 
#
#
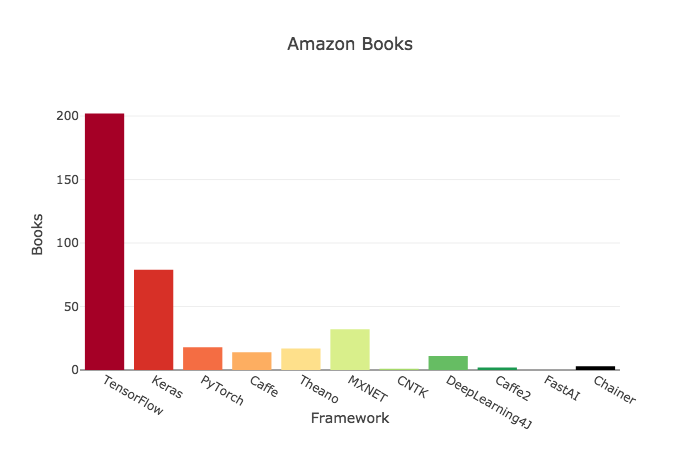
# ## Criteria 6: Amazon Books
#
# >> 
#
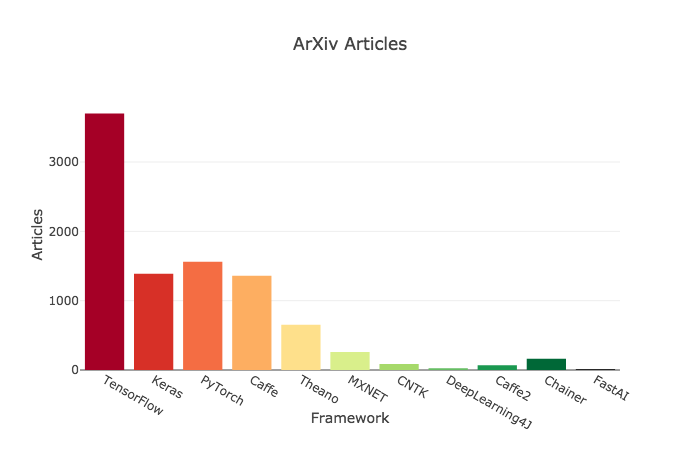
# ## Criteria 7 : ArXiv Articles
#
# >> 
#
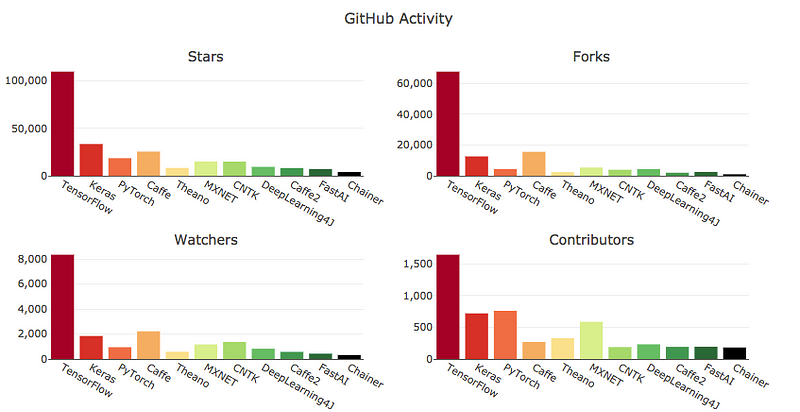
# ## Criteria 8: GitHub Activity
#
# >> 
#
# --------------------------------
#
#
#
#
#
#
#
#
#
#
# + [markdown] id="9v3V8ztAKDCg" colab_type="text"
#
#
# ```
# # This is formatted as code
# ```
#
#
# Before we jump into Tensorflow, we will implemented our first neural network model using Python Numpy package. NumPy is the fundamental package for scientific computing with Python, such as:
#
# 1. Linear Algebra
# 2. Statistics
# 3. Calculus
#
# ## A brief intro to Numpy operations:
#
# 1. Creating a Vector:
# Here we use Numpy to create a 1-D Array which we then call a vector.
#
#
#
#
# + id="GTf7M4r7Lgj9" colab_type="code" colab={}
#Load Library
import numpy as np
#Create a vector as a Row
vector_row = np.array([1,2,3])
#Create vector as a Column
vector_column = np.array([[1],[2],[3]])
# + [markdown] id="JYFjSo0OLqA3" colab_type="text"
# 2. Creating a Matrix
# We Create a 2-D Array in Numpy and call it a Matrix. It contains 2 rows and 3 columns.
# + id="fJlDBq5rLmA-" colab_type="code" colab={}
#Load Library
import numpy as np
#Create a Matrix
matrix = np.array([[1,2,3],[4,5,6]])
print(matrix)
# + [markdown] id="wv99hZqULygH" colab_type="text"
# 3. Selecting Elements
#
# + id="ZLQlxFzkPrKM" colab_type="code" colab={}
#Load Library
import numpy as np
#Create a vector as a Row
vector_row = np.array([ 1,2,3,4,5,6 ])
#Create a Matrix
matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(matrix)
#Select 3rd element of Vector
print(vector_row[2])
#Select 2nd row 2nd column
print(matrix[1,1])
#Select all elements of a vector
print(vector_row[:])
#Select everything up to and including the 3rd element
print(vector_row[:3])
#Select the everything after the 3rd element
print(vector_row[3:])
#Select the last element
print(vector_row[-1])
#Select the first 2 rows and all the columns of the matrix
print(matrix[:2,:])
#Select all rows and the 2nd column of the matrix
print(matrix[:,1:2])
# + [markdown] id="QO3vTGEKQhm7" colab_type="text"
# 4. Describing a Matrix
# + id="q8bDjBhhQpg5" colab_type="code" colab={}
import numpy as np
#Create a Matrix
matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])
#View the Number of Rows and Columns
print(matrix.shape)
#View the number of elements (rows*columns)
print(matrix.size)
#View the number of Dimensions(2 in this case)
print(matrix.ndim)
# + [markdown] id="eKISvY8kQtA0" colab_type="text"
# 5. Finding the max and min values
# + id="abPJd0JrQ4mM" colab_type="code" colab={}
#Load Library
import numpy as np
#Create a Matrix
matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(matrix)
#Return the max element
print(np.max(matrix))
#Return the min element
print(np.min(matrix))
#To find the max element in each column
print(np.max(matrix,axis=0))
#To find the max element in each row
print(np.max(matrix,axis=1))
# + [markdown] id="3Qm64s_eR0zQ" colab_type="text"
# 6. Reshaping Arrays
#
# + id="Pwepq7h_SBBD" colab_type="code" colab={}
#Load Library
import numpy as np
#Create a Matrix
matrix = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(matrix)
#Reshape
print(matrix.reshape(9,1))
#Here -1 says as many columns as needed and 1 row
print(matrix.reshape(1,-1))
#If we provide only 1 value Reshape would return a 1-d array of that length
print(matrix.reshape(9))
#We can also use the Flatten method to convert a matrix to 1-d array
print(matrix.flatten())
# + [markdown] id="cJU3xABuVem_" colab_type="text"
# 7. Calculating Dot Products
# + id="cPKg382VVivy" colab_type="code" colab={}
#Load Library
import numpy as np
#Create vector-1
vector_1 = np.array([ 1,2,3 ])
#Create vector-2
vector_2 = np.array([ 4,5,6 ])
#Calculate Dot Product
print(np.dot(vector_1,vector_2))
#Alternatively you can use @ to calculate dot products
print(vector_1 @ vector_2)
# + [markdown] id="cB-jK7jEXY7F" colab_type="text"
# ##Linear regression in Numpy:
#
# ---
#
#
#
# Write the numpy code for the following model:
#
# $Y=WX+B$
#
# where $X$ is 3x10 matrix: 10 samples and 3 features
#
# $Y$ is 4x10 matrix: 10 samples and 4 outputs
#
# $W$ is the weights matrix with the shape 4x3: connecting 3 inputs to 4 outputs
#
# $b$ is a vector with a size 4 ( one bias per output)
#
# + id="_EtM5LVtWCpm" colab_type="code" colab={}
#Load Library
import numpy as np
# Generate a random X (we do not have a real data)
X = np.random.rand(3,10)
display(X.shape)
# Generate a random weights vector
W = np.random.rand(4,3)
# Generate a random bias
b = np.random.rand(4,1)
# Calculate Y
Y= np.dot(W,X) + b
display(Y.shape)
# + [markdown] id="hMIoucH9hFfr" colab_type="text"
# ## One neuron model in numpy:
#
# A single neuron has multiple inputs and one output, in addition to the linear regression model, we need to add non linearity through an activation function:
#
# $Y= f(WX+B)$
#
# where $X$ is n x m matrix: m samples and n features/inputs
#
# $f(g)= \frac{1}{1+\exp(-g)}$ is a sigmoid acitavation function
#
# $Y$ is nh1 x m matrix: m samples and ny outputs
#
# $W$ is the weights matrix with the shape nh1 x n: connecting 3 inputs to 4 outputs
#
# $b$ is a vector with a size nh1 ( one bias per output)
#
#
#
#
# + id="Qry1JDGEiLmx" colab_type="code" colab={}
# load Library
import numpy as np
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
# Generate a random X (we do not have a real data)
X = np.random.rand(3,10)
# Generate a random weights vector
W = np.random.rand(1,3)
# Generate a random bias
b = np.random.rand()
# Calculate Y
Y= f(np.dot(W,X) + b)
display(Y)
# + [markdown] id="aSnbti9ooIIs" colab_type="text"
# ## One hidden layer model in numpy:
#
# The difference from the one neuron model is simple: we need only to change the number of output "ny"
# + id="ZAY3o6zBnpA0" colab_type="code" colab={}
# load Library
import numpy as np
#Suppose we have the following NN architecture
m = 10 # Number of samples
ni= 3 # Number of input neurons
h = 1 # Number of hidden layers
nh1 = 4 # Number of neurons in the hidden layer 1
no =1 # Number of neurons in the output layer
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
# Generate a random X (we do not have a real data)
X = np.random.rand(ni,m)
# Generate a random weights vector for the first hidden layer
W1 = np.random.rand(nh1,ni)
# Generate a random bias for the first hidden layer
b1 = np.random.rand(nh1,1)
# Generate a random weights vector for the output layer
W2 = np.random.rand(no,nh1)
# Generate a random bias for the output layer
b2 = np.random.rand(no,1)
# Calculate output of the first hidden layer
Yh1= f(np.dot(W1,X) + b1)
# Calculate output of the output layer
Y= f(np.dot(W2,Yh1) + b2)
display(Yh1.shape)
display(Y.shape)
# + [markdown] id="11fqb_bQvIEi" colab_type="text"
# ## Gradient descent in Numpy:
# Let us now start training a neural network
# We start by implementing a simple gradient descent for linear regression
# + id="mzBJxwb7FFZ2" colab_type="code" colab={}
# + id="QaQyLoxk2FyG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 70} outputId="d50165d2-7fa1-48af-8d81-7e1da9c47783"
import numpy as np
converged = False
iter = 0
m = 10 # Number of samples
ni= 1 # Number of input neurons
h = 1 # Number of hidden layers
no =1 # Number of neurons in the output layer
# Generate a random X (we do not have a real data)
X = np.random.rand(m)
display(X)
# learning rate
alpha =0.01
# early stop criteria
ep=0.001
# maximum number of training iterations
max_iter=100
# Generate a random weights vector for the output layer
W1 = np.random.rand()
# Generate a random bias for the output layer
b1 = np.random.rand()
# Generate a random ground truth
Y_gr = np.random.rand(m)
J = sum([(b1 + W1*X[i] - Y_gr[i])**2 for i in range(m)])
while not converged:
# for each training sample, compute the gradient (d/d_theta j(theta))
grad0 = 1.0/m * sum([(b1 + W1*X[i] - Y_gr[i]) for i in range(m)])
grad1 = 1.0/m * sum([(b1 + W1*X[i] - Y_gr[i])*X[i] for i in range(m)])
# update the theta_temp
temp0 = W1 - alpha * grad0
temp1 = b1 - alpha * grad1
# update theta
W1 = temp0
b1 = temp1
# sum squared error
e = sum([(b1 + W1*X[i] - Y_gr[i])**2 for i in range(m)])
if abs(J-e) <= ep:
print('Converged, iterations: ', iter, '!!!')
converged = True
J = e # update error
iter += 1 # update iter
if iter == max_iter:
print('Max interactions exceeded!')
converged = True
# + [markdown] id="jRqCCVlmFIZl" colab_type="text"
# ##Assignment 1
# ### Backpropagation in Numpy:
#
# + id="7sW8ZoEVMb9I" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 7181} outputId="1186687f-26f8-43a5-a229-d84a4eb74d51"
num_inputs = 4
hidden_layer_1_outputs = 4
hidden_layer_2_outputs = 3
num_samples = 10
f = lambda x: 1.0/(1.0 + np.exp(-x)) # activation function (use sigmoid)
X = np.random.rand(num_samples,num_inputs-1) # 10x4
X = np.hstack((np.ones((X.shape[0], 1)), X))
display(X.shape)
# Generate a random weights vector for the first hidden layer
W_h1 = np.random.rand(num_inputs,hidden_layer_1_outputs) # 4x4
# Generate a random weights vector for the second hidden layer
W_h2 = np.random.rand(hidden_layer_1_outputs+1,hidden_layer_2_outputs)
# Calculate output of hidden layer 1
h1= f(np.dot(X,W_h1))
display(h1.shape)
# Calculate output of hidden layer 2
#h2= f(np.dot(h1,W_h2))
#display(h2.shape)
# learning rate
alpha =0.01
# early stop criteria
ep=0.001
# maximum number of training iterations
max_iter=100
# Generate a random ground truth
Y_gr = np.random.rand(hidden_layer_2_outputs,num_samples)
#J = sum([(h2 - Y_gr[:,i])**2 for i in range(num_samples)]) #cost function sum of squared error
print(J)
#while not converged:
for i in range(100):
#print('Interations:' , iter)
# forward prop
# Calculate output of hidden layer 1
h1= f(np.dot(X,W_h1))
# append a column with ones representing bias inputs
h1 = np.hstack((np.ones((h1.shape[0], 1)), h1))
# Calculate output of hidden layer 2
h2= f(np.dot(h1,W_h2))
#error/error
J = np.sum(np.square(h2- Y_gr.T))
# gradient of the output layer
grad_h2 = h2*J
# error
#display('h1', (h1[:, 1:] * (1 - h1[:, 1:])).shape)
#display('dot ', np.dot(grad_h2, W_h2.T[:, 1:]).shape)
hidden_error = (h1[:, 1:] * (1 - h1[:, 1:])) * np.dot(grad_h2, W_h2.T[:, 1:])
#print(h1.shape)
#print(hidden_error.shape)
grad_h1= h1[:, :, np.newaxis]*hidden_error[:, np.newaxis, :]
# average gradient
total_hidden_gradient_h2 = np.average(grad_h2, axis=0)
total_output_gradient_h1 = np.average(grad_h1, axis=0)
#print(grad_h1.shape)
#print(W_h1.shape)
# update weights
W_h2 += - alpha * total_hidden_gradient_h2
W_h1 += - alpha * total_output_gradient_h1[1:,:]
print('iter',i)
print('cost',J)
|
Session_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Online Retails Purchase
# ### Introduction:
#
#
#
# ### Step 1. Import the necessary libraries
# ### Step 2. Import the dataset from this [address](https://raw.githubusercontent.com/guipsamora/pandas_exercises/master/07_Visualization/Online_Retail/Online_Retail.csv).
# ### Step 3. Assign it to a variable called online_rt
# Note: if you receive a utf-8 decode error, set `encoding = 'latin1'` in `pd.read_csv()`.
# ### Step 4. Create a histogram with the 10 countries that have the most 'Quantity' ordered except UK
# ### Step 5. Exclude negative Quantity entries
# ### Step 6. Create a scatterplot with the Quantity per UnitPrice by CustomerID for the top 3 Countries (except UK)
# ### Step 7. Investigate why the previous results look so uninformative.
#
# This section might seem a bit tedious to go through. But I've thought of it as some kind of a simulation of problems one might encounter when dealing with data and other people. Besides there is a prize at the end (i.e. Section 8).
#
# (But feel free to jump right ahead into Section 8 if you want; it doesn't require that you finish this section.)
#
# #### Step 7.1 Look at the first line of code in Step 6. And try to figure out if it leads to any kind of problem.
# ##### Step 7.1.1 Display the first few rows of that DataFrame.
# ##### Step 7.1.2 Think about what that piece of code does and display the dtype of `UnitPrice`
# ##### Step 7.1.3 Pull data from `online_rt`for `CustomerID`s 12346.0 and 12347.0.
# #### Step 7.2 Reinterpreting the initial problem.
#
# To reiterate the question that we were dealing with:
# "Create a scatterplot with the Quantity per UnitPrice by CustomerID for the top 3 Countries"
#
# The question is open to a set of different interpretations.
# We need to disambiguate.
#
# We could do a single plot by looking at all the data from the top 3 countries.
# Or we could do one plot per country. To keep things consistent with the rest of the exercise,
# let's stick to the latter oprion. So that's settled.
#
# But "top 3 countries" with respect to what? Two answers suggest themselves:
# Total sales volume (i.e. total quantity sold) or total sales (i.e. revenue).
# This exercise goes for sales volume, so let's stick to that.
#
# ##### Step 7.2.1 Find out the top 3 countries in terms of sales volume.
# ##### Step 7.2.2
#
# Now that we have the top 3 countries, we can focus on the rest of the problem:
# "Quantity per UnitPrice by CustomerID".
# We need to unpack that.
#
# "by CustomerID" part is easy. That means we're going to be plotting one dot per CustomerID's on our plot. In other words, we're going to be grouping by CustomerID.
#
# "Quantity per UnitPrice" is trickier. Here's what we know:
# *One axis will represent a Quantity assigned to a given customer. This is easy; we can just plot the total Quantity for each customer.
# *The other axis will represent a UnitPrice assigned to a given customer. Remember a single customer can have any number of orders with different prices, so summing up prices isn't quite helpful. Besides it's not quite clear what we mean when we say "unit price per customer"; it sounds like price of the customer! A reasonable alternative is that we assign each customer the average amount each has paid per item. So let's settle that question in that manner.
#
# #### Step 7.3 Modify, select and plot data
# ##### Step 7.3.1 Add a column to online_rt called `Revenue` calculate the revenue (Quantity * UnitPrice) from each sale.
# We will use this later to figure out an average price per customer.
# ##### Step 7.3.2 Group by `CustomerID` and `Country` and find out the average price (`AvgPrice`) each customer spends per unit.
# ##### Step 7.3.3 Plot
# #### Step 7.4 What to do now?
# We aren't much better-off than what we started with. The data are still extremely scattered around and don't seem quite informative.
#
# But we shouldn't despair!
# There are two things to realize:
# 1) The data seem to be skewed towaards the axes (e.g. we don't have any values where Quantity = 50000 and AvgPrice = 5). So that might suggest a trend.
# 2) We have more data! We've only been looking at the data from 3 different countries and they are plotted on different graphs.
#
# So: we should plot the data regardless of `Country` and hopefully see a less scattered graph.
#
# ##### Step 7.4.1 Plot the data for each `CustomerID` on a single graph
# ##### Step 7.4.2 Zoom in so we can see that curve more clearly
# ### 8. Plot a line chart showing revenue (y) per UnitPrice (x).
#
# Did Step 7 give us any insights about the data? Sure! As average price increases, the quantity ordered decreses. But that's hardly surprising. It would be surprising if that wasn't the case!
#
# Nevertheless the rate of drop in quantity is so drastic, it makes me wonder how our revenue changes with respect to item price. It would not be that surprising if it didn't change that much. But it would be interesting to know whether most of our revenue comes from expensive or inexpensive items, and how that relation looks like.
#
# That is what we are going to do now.
#
# #### 8.1 Group `UnitPrice` by intervals of 1 for prices [0,50), and sum `Quantity` and `Revenue`.
# #### 8.3 Plot.
# #### 8.4 Make it look nicer.
# x-axis needs values.
# y-axis isn't that easy to read; show in terms of millions.
# ### BONUS: Create your own question and answer it.
|
07_Visualization/Online_Retail/Exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Tyred/TimeSeries_OCC-PUL/blob/main/Notebooks/OC_SVM.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Emi8F7ZFdSrK"
# ## Imports
# + id="nnoW8j3yNpuZ"
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import OneClassSVM
from sklearn.metrics import precision_score, accuracy_score, recall_score, f1_score
import tensorflow as tf
from tensorflow import keras
from sklearn.decomposition import PCA
from sklearn.manifold import MDS
# + [markdown] id="6y-sBkgCb8GM"
# ## Reading the dataset from Google Drive
#
# + id="hn5JbVRONu1T" colab={"base_uri": "https://localhost:8080/"} outputId="fa9ddcce-1268-42b6-e4d7-2138b5957b8d"
path = 'drive/My Drive/UFSCar/FAPESP/IC/Data/UCRArchive_2018'
dataset = input('Dataset: ')
tr_data = np.genfromtxt(path + "/" + dataset + "/" + dataset + "_TRAIN.tsv", delimiter="\t",)
te_data = np.genfromtxt(path + "/" + dataset + "/" + dataset + "_TEST.tsv", delimiter="\t",)
labels = te_data[:, 0]
print("Labels:", np.unique(labels))
# + [markdown] id="R0l2RpHUcHaB"
# ## Splitting in Train-Test data
# + id="xLaE6_vANwQL" colab={"base_uri": "https://localhost:8080/"} outputId="95f1f3a8-219b-401c-cdfa-09a245794887"
class_label = int(input('Positive class label: '))
train_data = tr_data[tr_data[:, 0] == class_label, 1:] # train
test_data = te_data[:, 1:] # test
print("Train data shape:", train_data.shape)
print("Test data shape:", test_data.shape)
# + [markdown] id="UcC1Ru1McR5b"
# ## Labeling for OCC Task
# <li> Label 1 for positive class </li>
# <li> Label -1 for other class(es) </li>
# + id="wEFEYrdWOHl_" colab={"base_uri": "https://localhost:8080/"} outputId="8d26296a-004c-40fe-d7a8-df263ceefa78"
occ_labels = [1 if x == class_label else -1 for x in labels]
print("Positive samples:", occ_labels.count(1))
print("Negative samples:", occ_labels.count(-1))
# + [markdown] id="G-Pi8UleecbW"
# # MDS Plot
# + colab={"base_uri": "https://localhost:8080/"} id="gVJivoUqHHer" outputId="e8121822-002d-4877-a080-01dbc5ea994e"
embedding = MDS(n_components=2, random_state=42)
mds_data = embedding.fit_transform(train_data)
mds_test = embedding.fit_transform(test_data)
print(mds_data.shape)
print(mds_test.shape)
# + [markdown] id="HuY7WPf3egU0"
# ## Train
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="3f3Wx0XRGqM3" outputId="c1ad80a0-0f6a-4fb4-860e-ab830db3d731"
x = [row[0] for row in mds_data]
y = [row[1] for row in mds_data]
plt.plot(x, y, 'x',label='train data')
plt.title('MDS Training Data')
plt.legend()
plt.show()
# + [markdown] id="ddWCsjXBeih3"
# ## Test
# + id="TzXgqXdHP639"
negative_mds_test = np.array([x for x in mds_test[np.where(labels!=class_label)]])
positive_mds_test = np.array([x for x in mds_test[np.where(labels==class_label)]])
# + colab={"base_uri": "https://localhost:8080/", "height": 281} id="K52-1KVCNPtR" outputId="38a375b6-4e74-4195-8710-438ef485a2a3"
x_positive = [row[0] for row in positive_mds_test]
y_positive = [row[1] for row in positive_mds_test]
x_negative = [row[0] for row in negative_mds_test]
y_negative = [row[1] for row in negative_mds_test]
plt.plot(x_positive, y_positive, 'x', label='positive class', c = 'blue')
plt.plot(x_negative, y_negative, 'o', label='negative class', c = 'red')
plt.title('MDS Test Data')
plt.legend()
plt.show()
# + [markdown] id="vF69fFp98esV"
# # Feature extraction
#
# + [markdown] id="0to8-3vv8gn-"
# ## PCA
# + id="scNbHiyg_0qM" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="1c92bf05-bb29-4b8c-a90d-33c4bede521a"
"""pca = PCA(svd_solver='full')
train_data = pca.fit_transform(train_data)
test_data = pca.transform(test_data)
print(train_data.shape)"""
# + [markdown] id="BWmsaj478iVD"
# ## Convolutional Autoencoder
#
# + id="hQ68Z_Yn8nXy"
# Convolutional Autoencoder with MaxPooling:
class ConvAutoencoder(tf.keras.Model):
def __init__(self, serie_length):
super(ConvAutoencoder, self).__init__()
self.conv_1 = keras.layers.Conv1D(serie_length[0]//16, 3, activation='swish', padding='same', input_shape=(serie_length))
self.max_1 = keras.layers.MaxPooling1D(2, padding='same')
self.conv_2 = keras.layers.Conv1D(serie_length[0]//8, 3, activation='swish', padding='same')
self.max_2 = keras.layers.MaxPooling1D(2, padding='same')
self.conv_3 = keras.layers.Conv1D(1, 3, activation='swish', padding='same')
# encoded representation
self.encoded = keras.layers.MaxPooling1D(2, padding='same')
# decoder layers
self.conv_4 = keras.layers.Conv1D(1, 3, activation='swish', padding='same')
self.up_1 = keras.layers.UpSampling1D(2)
self.conv_5 = keras.layers.Conv1D(serie_length[0]//8, 3, activation='swish', padding='same')
self.up_2 = keras.layers.UpSampling1D(2)
self.conv_6 = keras.layers.Conv1D(serie_length[0], 3, activation='swish', padding='same')
self.up_3 = keras.layers.UpSampling1D(2)
# decoded output
self.decoded = keras.layers.Conv1D(1, 3, activation='linear', padding='same')
def encode(self, inputs):
if self.padding != 0:
inputs = keras.layers.ZeroPadding1D(padding=(8 + 8-self.padding, 0))(inputs)
x = self.conv_1(inputs)
x = self.max_1(x)
x = self.conv_2(x)
x = self.max_2(x)
x = self.conv_3(x)
return self.encoded(x)
def call(self, inputs):
self.padding = inputs.shape[1] % 8
x = self.encode(inputs)
x = self.conv_4(x)
x = self.up_1(x)
x = self.conv_5(x)
x = self.up_2(x)
x = self.conv_6(x)
x = self.up_3(x)
if self.padding != 0:
x = keras.layers.Cropping1D(cropping=(8 + 8-self.padding, 0))(x)
return self.decoded(x)
def model(self):
x = keras.layers.Input(shape=(serie_length, 1))
return tf.keras.Model(inputs=[x], outputs=self.call(x))
# + [markdown] id="YFq9IKqQ-S9T"
# ### Initializing and training the Conv Autoencoder
# + colab={"base_uri": "https://localhost:8080/"} id="SgM_5LPm-ceG" outputId="15c9c6a5-d9ab-4b29-effe-21c39bfc3ca5"
serie_length = train_data.shape[1]
model = ConvAutoencoder((serie_length, 1))
model.compile(optimizer='adam', loss='mse')
# Train
batch_size = 16
epochs = 50
train_data = train_data[..., np.newaxis]
test_data = test_data[..., np.newaxis]
model.fit(train_data, train_data, epochs=epochs, batch_size=batch_size)
# + colab={"base_uri": "https://localhost:8080/"} id="Z8MD8TRkZJW7" outputId="d32e1f0b-11b5-467e-f2b2-431fe245a419"
model.model().summary()
# + [markdown] id="Tuia1i6pc63Q"
# # Results
# + [markdown] id="fkrvRx9oeC6V"
# ## Data extracted by the ConvAutoencoder
# + [markdown] id="q9gnUq6pfdZj"
# ### OC-SVM Fitting
# + id="F7U2LY8YPbLW"
train_data_encoded = np.array(model.encode(train_data))
train_data_encoded = np.squeeze(train_data_encoded)
clf_cae = OneClassSVM(gamma='scale', nu=0.2, kernel='rbf').fit(train_data_encoded)
# + [markdown] id="4EXqf35HfoZu"
# ### Scores
# + id="wXfI9NmGQKAw" colab={"base_uri": "https://localhost:8080/"} outputId="94e11d22-7039-4259-dc99-e1dc329bfef2"
test_data_encoded = np.array(model.encode(test_data))
test_data_encoded = np.squeeze(test_data_encoded)
result_labels = clf_cae.predict(test_data_encoded)
acc = accuracy_score(occ_labels, result_labels)
precision = precision_score(occ_labels, result_labels)
recall = recall_score(occ_labels, result_labels)
f1 = f1_score(occ_labels, result_labels)
print("Accuracy: %.2f" % (acc*100) + "%")
print("Precision: %.2f" % (precision*100) + "%")
print("Recall: %.2f" % (recall*100) + "%")
print("F1-Score: %.2f" % (f1*100) + "%")
# + [markdown] id="JOpjLAoMdc8W"
# ## Raw Data
# + [markdown] id="8bhO6UkmchYB"
# ### OC-SVM Fitting
# + id="Yml7N8ElfiVF"
train_data_raw = np.squeeze(train_data)
clf = OneClassSVM(gamma='scale', nu=0.2, kernel='rbf').fit(train_data_raw)
# + [markdown] id="1jMGult_fkL6"
# ### Scores
# + colab={"base_uri": "https://localhost:8080/"} id="Hr8onWKieQ6U" outputId="1eadf556-23c6-4c7d-f271-a53e3bf1c061"
test_data_raw = np.squeeze(test_data)
result_labels = clf.predict(test_data_raw)
acc = accuracy_score(occ_labels, result_labels)
precision = precision_score(occ_labels, result_labels)
recall = recall_score(occ_labels, result_labels)
f1 = f1_score(occ_labels, result_labels)
print("Accuracy: %.2f" % (acc*100) + "%")
print("Precision: %.2f" % (precision*100) + "%")
print("Recall: %.2f" % (recall*100) + "%")
print("F1-Score: %.2f" % (f1*100) + "%")
|
Notebooks/algorithms/OC_SVM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import scipy
from scipy import stats, signal
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (15,10)
# ## **HW 4**
# #### **Problem 0**
# Making 'fake' data
# +
#Generating a time scale
t = np.linspace(0,np.pi*100,np.int(1e5))
#Creating an offset sin wave
N = 10+np.sin(t)
#Creating a background distribution that depends on N
bkgd = stats.norm.rvs(size = np.int(1e5))*np.sqrt(N)+N
# -
# #### **Problem 1**
# ##### **A)** Make a scatter plot of the first 1000 data points
plt.plot(t[0:1001],bkgd[0:1001],'o')
plt.xlabel('Time')
plt.title('First 1000 Data Points')
plt.show()
# ##### **B)** Generalize your code so you can make a plot of any X contiguous points and produce an example plot of a set of data somethere in the middle of your array
def slice_plt(x,y,start,length):
plt.plot(t[start-1:start+length+1],bkgd[start-1:start+length+1],'o')
plt.title('Slice Plot from ' + str(np.round(x[start-1],4)) + ' to ' + str(np.round(x[start+length+1],4)))
plt.show()
slice_plt(t,bkgd,500,2000)
# ##### **C)** Sometimes you want to sample the data, such as plotting every 100th point. Make a plot of the full data range, but only every 100th point.
index = np.arange(0,np.int(1e5),100)
plt.plot(t[index],bkgd[index],'o')
plt.title('Entire Range Sampling every 100th Point')
plt.show()
# #### **Problem 2**
# ##### **A)** Make a 2d histogram plot
plt.hist2d(t,bkgd,bins = [100,50], density = True)
plt.colorbar()
plt.show()
# ##### **B)** Clearly explain what is being plotted in your plot
#
# The plot above shows the probability density of getting a certain range of values in a certain range of time. The closer to yellow a region is the more likely that measurement is to occur. The higher probability regions are mostly localized about the center of the plot at 10. They follow a roughly wavelike path about this center.
#
# #### **Problem 3**
# ##### **A)** Make a scatter plot of all your data, but now folded.
t2 = t%(2*np.pi)
plt.plot(t2,bkgd,'o',alpha=0.4)
plt.show()
# ##### **B)** Make a 2D histogram plot of your folded data
blocks = plt.hist2d(t,bkgd,bins = [100,50], density = True)
plt.colorbar()
plt.show()
# ##### **C)** Calculate the average as a function of the folded variable. You can then overplot this on the 2d histogram to show the average as a function of folded time.
mean = np.zeros(100)
for i in range(0,100):
mean[i] = sum(blocks[2][1:]*blocks[0][i,:]/sum(blocks[0][i,:]))
plt.hist2d(t,bkgd,bins = [100,50], density = True)
plt.plot(blocks[1][1:],mean, linewidth = 2, color = 'black')
plt.colorbar()
plt.show()
|
Homework/.ipynb_checkpoints/HW4-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] _uuid="93d7b4b8f5f6e5289cfc0312d650744e64905bc7"
#
# + [markdown] _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
# # The purpose of this notebook
#
# **UPDATE 1:** *In version 5 of this notebook, I demonstrated that the model is capable of reaching the LB score of 0.896. Now, I would like to see if the augmentation idea from [this kernel](https://www.kaggle.com/jiweiliu/lgb-2-leaves-augment) would help us to reach an even better score.*
#
# **UPDATE 2:** *Version 10 of this notebook shows that the augmentation idea does not work very well for the logistic regression -- the CV score clearly went down to 0.892. Good to know -- no more digging in this direction.*
#
# I have run across [this nice script](https://www.kaggle.com/ymatioun/santander-linear-model-with-additional-features) by Youri Matiounine in which a number of new features are added and linear regression is performed on the resulting data set. I was surprised by the high performance of this simple model: the LB score is about 0.894 which is close to what you can get using the heavy artillery like LighGBM. At the same time, I felt like there is a room for improvement -- after all, this is a classification rather than a regression problem, so I was wondering what will happen if we perform a logistic regression on Matiounine's data set. This notebook is my humble attempt to answer this question.
#
# Matiounine's features can be used in other models as well. To avoid the necessety of re-computing them every time when we switch from one model to another, I show how to store the processed data in [feather files](https://pypi.org/project/feather-format/), so that next time they can be loaded very fast into memory. This is much faster and safer than using CSV format.
#
# # Computing the new features
#
# Importing libraries.
# + _uuid="319c9748ad2d9b82cc875000f58afa2129aeb9c3"
import os
import gc
import sys
import time
import shutil
import feather
import numpy as np
import pandas as pd
from scipy.stats import norm, rankdata
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import StratifiedKFold
from sklearn.metrics import roc_curve, auc, roc_auc_score
# + [markdown] _uuid="31a0c430046df842333652c410b3181d800f0551"
# Now, let's read the CSV files containing the training and testing data and measure how long it takes.
#
# Train:
# + _uuid="0d080b4a0bf27808a316196c71948a96280ef177"
path_train = '../input/train.feather'
path_test = '../input/test.feather'
print("Reading train data...")
start = time.time()
train = pd.read_csv('../input/train.csv')
end = time.time()
print("It takes {0:.2f} seconds to read 'train.csv'.".format(end - start))
# + [markdown] _uuid="1e6904f34859901e764adde45ed0bb3bc13e4f58"
# Test:
# + _uuid="0fca1a0b7f595147cc5c3641b1a45c9d7f8e2340"
start = time.time()
print("Reading test data...")
test = pd.read_csv('../input/test.csv')
end = time.time()
print("It takes {0:.2f} seconds to read 'test.csv'.".format(end - start))
# + [markdown] _uuid="9c74d587203855a0a8eb7da6b2f6abb3090bb60d"
# Saving the 'target' and 'ID_code' data.
# + _uuid="74a87959eb66d371c314180f4877d1afdde136b7"
target = train.pop('target')
train_ids = train.pop('ID_code')
test_ids = test.pop('ID_code')
# + [markdown] _uuid="8c2c537288b4915a1f860065a2046e47cae19459"
# Saving the number of rows in 'train' for future use.
# + _uuid="b1026519541d70d9206f9941fc29d19005fa1dcd"
len_train = len(train)
# + [markdown] _uuid="af2947142503c41f3c26e9c805e14e033fceb955"
# Merging test and train.
# + _uuid="fc7bb057b85c4a8b12b102e7432e261ff6a92954"
merged = pd.concat([train, test])
# + [markdown] _uuid="5b29b8bd47b43d76ee650e12e063c34c3c1ad189"
# Removing data we no longer need.
# + _uuid="bca8a00d9d62f3a4479c524b66d6e906ac155b7e"
del test, train
gc.collect()
# + [markdown] _uuid="ef8301089d9bfd8880ad0165e3d1c248a5fb1fde"
# Saving the list of original features in a new list `original_features`.
# + _uuid="134f8d281a4fafdbbbd51fb3429015d271d895ac"
original_features = merged.columns
# + [markdown] _uuid="8787d83673d27fe9529524257c660933af610ab2"
# Adding more features.
# + _uuid="06df646dee338e944955dd6059df57cd6c73afa0"
for col in merged.columns:
# Normalize the data, so that it can be used in norm.cdf(),
# as though it is a standard normal variable
merged[col] = ((merged[col] - merged[col].mean())
/ merged[col].std()).astype('float32')
# Square
merged[col+'^2'] = merged[col] * merged[col]
# Cube
merged[col+'^3'] = merged[col] * merged[col] * merged[col]
# 4th power
merged[col+'^4'] = merged[col] * merged[col] * merged[col] * merged[col]
# Cumulative percentile (not normalized)
merged[col+'_cp'] = rankdata(merged[col]).astype('float32')
# Cumulative normal percentile
merged[col+'_cnp'] = norm.cdf(merged[col]).astype('float32')
# + [markdown] _uuid="d5fd487e4440606deb9e936346e982513f0718c9"
# Getting the list of names of the added features.
# + _uuid="456a64b4d2c1ada1b6db546a1d004537df4bd238"
new_features = set(merged.columns) - set(original_features)
# + [markdown] _uuid="8188eb856e421905972cc6f34ab4b43e87dd41f8"
# Normalize the data. Again.
# + _uuid="7180731459fe9ce60f95b94b77f3d7f9a565823d"
for col in new_features:
merged[col] = ((merged[col] - merged[col].mean())
/ merged[col].std()).astype('float32')
# + [markdown] _uuid="3f1039a0b002c1db092a9b3d590759531facc3e6"
# Saving the data to feather files.
# + _uuid="9f04f23ad704daa0207a03c9c6e5d680ac0caed8"
path_target = 'target.feather'
path_train_ids = 'train_ids_extra_features.feather'
path_test_ids = 'test_ids_extra_features.feather'
path_train = 'train_extra_features.feather'
path_test = 'test_extra_features.feather'
print("Writing target to a feather files...")
pd.DataFrame({'target' : target.values}).to_feather(path_target)
print("Writing train_ids to a feather files...")
pd.DataFrame({'ID_code' : train_ids.values}).to_feather(path_train_ids)
print("Writing test_ids to a feather files...")
pd.DataFrame({'ID_code' : test_ids.values}).to_feather(path_test_ids)
print("Writing train to a feather files...")
feather.write_dataframe(merged.iloc[:len_train], path_train)
print("Writing test to a feather files...")
feather.write_dataframe(merged.iloc[len_train:], path_test)
# + [markdown] _uuid="640948a1a36e2d3d73f18ceb9cfb816be6d11d7b"
# Removing data we no longer need.
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
del target, train_ids, test_ids, merged
gc.collect()
# + [markdown] _uuid="837f988316528d5c3d4530043448fe5849be3fa5"
# # Loading the data from feather files
#
# Now let's load of these data back into memory. This will help us to illustrate the advantage of using the feather file format.
# + _uuid="60b26db1cf85167b14f9223af995a8656bdaa316"
path_target = 'target.feather'
path_train_ids = 'train_ids_extra_features.feather'
path_test_ids = 'test_ids_extra_features.feather'
path_train = 'train_extra_features.feather'
path_test = 'test_extra_features.feather'
print("Reading target")
start = time.time()
y = feather.read_dataframe(path_target).values.ravel()
end = time.time()
print("{0:5f} sec".format(end - start))
# + _uuid="2f60516cb907e9e62f97eb99ebb00db079edc6e3"
print("Reading train_ids")
start = time.time()
train_ids = feather.read_dataframe(path_train_ids).values.ravel()
end = time.time()
print("{0:5f} sec".format(end - start))
# + _uuid="4c8ad8191f0a4cd976645e7d7b59f7c16c48311f"
print("Reading test_ids")
start = time.time()
test_ids = feather.read_dataframe(path_test_ids).values.ravel()
end = time.time()
print("{0:5f} sec".format(end - start))
# + _uuid="afe5ba0c48d46a05e09c2de00b094a5a479fded6"
print("Reading training data")
start = time.time()
train = feather.read_dataframe(path_train)
end = time.time()
print("{0:5f} sec".format(end - start))
# + _uuid="4764997b330eb79e2962c6ea207b2bf43d75b7a0"
print("Reading testing data")
start = time.time()
test = feather.read_dataframe(path_test)
end = time.time()
print("{0:5f} sec".format(end - start))
# + [markdown] _uuid="d3d1c00f01bdcc40525a6d59cf3bc463bdbcef11"
# Hopefully now you can see the great advantage of using the feather files: it is blazing fast. Just compare the timings shown above with those measured for the original CSV files: the processed data sets (stored in the feather file format) that we have just loaded are much bigger in size that the original ones (stored in the CSV files) but we can load them in almost no time!
#
# # Logistic regession with the added features.
#
# Now let's finally do some modeling! More specifically, we will build a straighforward logistic regression model to see whether or not we can improve on linear regression result (LB 0.894).
#
# Setting things up for the modeling phase.
# + _uuid="72ddd6eee811099caba7f2cc610e7f099d8fa84f"
NFOLDS = 5
RANDOM_STATE = 871972
feature_list = train.columns
test = test[feature_list]
X = train.values.astype('float32')
X_test = test.values.astype('float32')
folds = StratifiedKFold(n_splits=NFOLDS, shuffle=True,
random_state=RANDOM_STATE)
oof_preds = np.zeros((len(train), 1))
test_preds = np.zeros((len(test), 1))
roc_cv =[]
del train, test
gc.collect()
# + [markdown] _uuid="6e5750e889c0aab08e0230a00641bb589a723d04"
# Defining a function for the augmentation proceduer (for deltails, see [this kernel](https://www.kaggle.com/jiweiliu/lgb-2-leaves-augment)):
# + _uuid="8bdee398862caef3ddcfeaabadfc025e2fea280a"
def augment(x,y,t=2):
if t==0:
return x, y
xs,xn = [],[]
for i in range(t):
mask = y>0
x1 = x[mask].copy()
ids = np.arange(x1.shape[0])
for c in range(x1.shape[1]):
np.random.shuffle(ids)
x1[:,c] = x1[ids][:,c]
xs.append(x1)
del x1
gc.collect()
for i in range(t//2):
mask = y==0
x1 = x[mask].copy()
ids = np.arange(x1.shape[0])
for c in range(x1.shape[1]):
np.random.shuffle(ids)
x1[:,c] = x1[ids][:,c]
xn.append(x1)
del x1
gc.collect()
print("The sizes of x, xn, and xs are {}, {}, {}, respectively.".format(sys.getsizeof(x),
sys.getsizeof(xn),
sys.getsizeof(xs)
)
)
xs = np.vstack(xs)
xn = np.vstack(xn)
print("The sizes of x, xn, and xs are {}, {}, {}, respectively.".format(sys.getsizeof(x)/1024**3,
sys.getsizeof(xn),
sys.getsizeof(xs)
)
)
ys = np.ones(xs.shape[0])
yn = np.zeros(xn.shape[0])
y = np.concatenate([y,ys,yn])
print("The sizes of y, yn, and ys are {}, {}, {}, respectively.".format(sys.getsizeof(y),
sys.getsizeof(yn),
sys.getsizeof(ys)
)
)
gc.collect()
return np.vstack([x,xs, xn]), y
# + [markdown] _uuid="0f8952de31eb35a24d805e2f05234419a787c2b5"
# Modeling.
# + _uuid="bac555a0224df2ec57edea0d9efc2bea6087a1b9"
for fold_, (trn_, val_) in enumerate(folds.split(y, y)):
print("Current Fold: {}".format(fold_))
trn_x, trn_y = X[trn_, :], y[trn_]
val_x, val_y = X[val_, :], y[val_]
NAUGMENTATIONS=1#5
NSHUFFLES=0#2 # turning off the augmentation by shuffling since it did not help
val_pred, test_fold_pred = 0, 0
for i in range(NAUGMENTATIONS):
print("\nFold {}, Augmentation {}".format(fold_, i+1))
trn_aug_x, trn_aug_y = augment(trn_x, trn_y, NSHUFFLES)
trn_aug_x = pd.DataFrame(trn_aug_x)
trn_aug_x = trn_aug_x.add_prefix('var_')
clf = Pipeline([
#('scaler', StandardScaler()),
#('qt', QuantileTransformer(output_distribution='normal')),
('lr_clf', LogisticRegression(solver='lbfgs', max_iter=1500, C=10))
])
clf.fit(trn_aug_x, trn_aug_y)
print("Making predictions for the validation data")
val_pred += clf.predict_proba(val_x)[:,1]
print("Making predictions for the test data")
test_fold_pred += clf.predict_proba(X_test)[:,1]
val_pred /= NAUGMENTATIONS
test_fold_pred /= NAUGMENTATIONS
roc_cv.append(roc_auc_score(val_y, val_pred))
print("AUC = {}".format(roc_auc_score(val_y, val_pred)))
oof_preds[val_, :] = val_pred.reshape((-1, 1))
test_preds += test_fold_pred.reshape((-1, 1))
# + [markdown] _uuid="bdaeb55ef0787d12809ef93cb039f20a9ea48420"
# Predicting.
# + _uuid="4f9c059d80cd7f3a88ec54c6981d5bf61175372c"
test_preds /= NFOLDS
# + [markdown] _uuid="01b3796195161127820576b0bf6874a0c2730b3b"
# Evaluating the cross-validation AUC score (we compute both the average AUC for all folds and the AUC for combined folds).
# + _uuid="2a717d9ff79b7d7debb7cfc12a01437925fa659d"
roc_score_1 = round(roc_auc_score(y, oof_preds.ravel()), 5)
roc_score = round(sum(roc_cv)/len(roc_cv), 5)
st_dev = round(np.array(roc_cv).std(), 5)
print("Average of the folds' AUCs = {}".format(roc_score))
print("Combined folds' AUC = {}".format(roc_score_1))
print("The standard deviation = {}".format(st_dev))
# + [markdown] _uuid="6f8f29301f1a46851bbd8d73b53b42e3cf1b78b2"
# Creating the submission file.
# + _uuid="cf48c73f9a06e7396c8a34dff4e80ba1b21fc59b"
print("Saving submission file")
sample = pd.read_csv('../input/sample_submission.csv')
sample.target = test_preds.astype(float)
sample.ID_code = test_ids
sample.to_csv('submission.csv', index=False)
# + [markdown] _uuid="6ae9818982ca118b293d82ef58e8bdc5e11370e1"
# The LB score is now 0.896 versus 0.894 for linear regression. The mprovement of 0.001 is obviously very small. It looks like for this data linear and logistic regression work equally well! Moving forward, I think it would be interesting to see how the feature engineering presented here would affect other classification models (e.g. Gaussian Naive Bayes, LDA, LightGBM, XGBoost, CatBoost).
# + _uuid="e3b88b41d876338362d22fbeb552bf3ec6db964b"
|
12 customer prediction/logistic-regression-with-new-features-feather.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.8 64-bit (''base'': conda)'
# name: python3
# ---
# ## Gateways reached by a Sensor
from datetime import datetime, timedelta
import subprocess
import pandas as pd
from dateutil.parser import parse
from dateutil import tz
from label_map import dev_id_lbls, gtw_lbls
# +
DEVICES = [
'3148 E 19th, Anc',
'3414 E 16th, Anc',
'3424 E 18th, Anc',
'122 N Bliss',
'122 N Bliss Unit',
'1826 Columbine, Anc',
'Phil ELT-2 3692',
'Phil LT22222 436E',
'Phil CO2 26D8',
]
# Days of Data to Show
DAYS = 4
GATEWAY_FILE = '~/gateways.tsv'
# -
# Make DateTime objects for time period analyze
tz_ak = tz.gettz('US/Alaska')
start_ts = (datetime.now(tz_ak) - timedelta(days=DAYS)).replace(
tzinfo=None, minute=0, second=0, microsecond=0)
end_ts = datetime.now(tz_ak).replace(
tzinfo=None, minute=0, second=0, microsecond=0)
start_ts, end_ts
# +
# Pick a device to use for testing the script
device = DEVICES[3]
df = pd.read_csv(GATEWAY_FILE,
sep='\t',
parse_dates=['ts', 'ts_hour'],
index_col='ts',
low_memory=False)
df = df.loc[str(start_ts):]
df['dev_id'] = df.dev_id.map(dev_id_lbls)
df.query('dev_id == @device', inplace=True)
def gtw_map(gtw_eui):
return gtw_lbls.get(gtw_eui, gtw_eui)
df['gateway'] = df.gateway.map(gtw_map)
df.head()
# -
# Determine the "Any" gateway counts by dropping duplicate readings
df_any = df[['ts_hour', 'counter']].drop_duplicates(subset=['counter'])
df_any_count = df_any.groupby('ts_hour').count()
df_any_count.columns = ['Any' ]
df_any_count
# Determine counts for individual gateways
df_cts = pd.pivot_table(df, index='ts_hour', columns='gateway', values='counter', aggfunc='count')
df_cts
# +
# Combine the two DataFrames, horizontally (combine columns)
df_final = pd.concat([df_any_count, df_cts], axis=1)
# Make a new index that fills in any missing hours
new_ix = pd.date_range(start_ts, end_ts, freq='1H')
df_final = df_final.reindex(new_ix)
# Replace NaN values with zero and then convert values to integers
df_final.fillna(0, inplace=True)
df_final = df_final.astype('int32')
df_final = df_final[:-1] # drop last hour because likely incomplete
# Convert index into a string so we can change drop the seconds from display
df_final.index = df_final.index.strftime("%Y-%m-%d %H:%M")
df_final
# +
def color_cells(val):
color_scale = {
0: '#FF3131',
1: '#FFFF00',
2: '#FFD822',
}
color = color_scale.get(val, '#EEEEEE')
return 'background: %s' % color
s = df_final.style
s.applymap(color_cells)
s.set_properties(**{'width': '70px', 'text-align': 'center'})
styles = [
dict(selector="td", props=[('padding', "0px")]),
]
s.set_table_styles(styles)
s
|
sensor-gateway.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="mHDxn9VHjxKn"
# ##### Copyright 2019 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="3x19oys5j89H"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="hFDUpbtvv_3u"
# # Save and serialize models with Keras
# + [markdown] colab_type="text" id="V94_3U2k9rWV"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/guide/keras/save_and_serialize"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/keras/save_and_serialize.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/keras/save_and_serialize.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/keras/save_and_serialize.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="ZwiVWAQc9tk7"
# The first part of this guide covers saving and serialization for Keras models built using the Functional and Sequential APIs. Saving and serialization is exactly same for both of these model APIs.
#
# The second part of this guide covers "[saving and loading subclassed models](save_and_serialize.ipynb#saving-subclassed-models)". The subclassing API differs from the Keras sequential and functional API.
# + [markdown] colab_type="text" id="uqSgPMHguAAs"
# ## Setup
# + colab={} colab_type="code" id="bx5w4U5muDAo"
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
tf.keras.backend.clear_session() # For easy reset of notebook state.
# + [markdown] colab_type="text" id="wwCxkE6RyyPy"
# ## Part I: Saving Sequential models or Functional models
#
# Let's consider the following model:
# + colab={} colab_type="code" id="ILmySACTvSA9"
from tensorflow import keras
from tensorflow.keras import layers
inputs = keras.Input(shape=(784,), name='digits')
x = layers.Dense(64, activation='relu', name='dense_1')(inputs)
x = layers.Dense(64, activation='relu', name='dense_2')(x)
outputs = layers.Dense(10, name='predictions')(x)
model = keras.Model(inputs=inputs, outputs=outputs, name='3_layer_mlp')
model.summary()
# + [markdown] colab_type="text" id="xPRqbd0yw8hY"
# Optionally, let's train this model, just so it has weight values to save, as well as an optimizer state.
# Of course, you can save models you've never trained, too, but obviously that's less interesting.
# + colab={} colab_type="code" id="gCygTeGQw74g"
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
model.compile(loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=keras.optimizers.RMSprop())
history = model.fit(x_train, y_train,
batch_size=64,
epochs=1)
# Reset metrics before saving so that loaded model has same state,
# since metric states are not preserved by Model.save_weights
model.reset_metrics()
# + colab={} colab_type="code" id="htnmbhz-iOwh"
# Save predictions for future checks
predictions = model.predict(x_test)
# + [markdown] colab_type="text" id="opP1KROHwWwd"
#
# ### Whole-model saving
#
# You can save a model built with the Functional API into a single file. You can later recreate the same model from this file, even if you no longer have access to the code that created the model.
#
# This file includes:
#
# - The model's architecture
# - The model's weight values (which were learned during training)
# - The model's training config (what you passed to `compile`), if any
# - The optimizer and its state, if any (this enables you to restart training where you left)
# + colab={} colab_type="code" id="HqHvq6Igw3wx"
# Save the model
model.save('path_to_my_model.h5')
# Recreate the exact same model purely from the file
new_model = keras.models.load_model('path_to_my_model.h5')
# + colab={} colab_type="code" id="mmIcF6UOItJE"
import numpy as np
# Check that the state is preserved
new_predictions = new_model.predict(x_test)
np.testing.assert_allclose(predictions, new_predictions, rtol=1e-6, atol=1e-6)
# Note that the optimizer state is preserved as well:
# you can resume training where you left off.
# + [markdown] colab_type="text" id="-WEPW3n8ICyz"
# ### Export to SavedModel
#
# You can also export a whole model to the TensorFlow `SavedModel` format. `SavedModel` is a standalone serialization format for TensorFlow objects, supported by TensorFlow serving as well as TensorFlow implementations other than Python.
# + colab={} colab_type="code" id="cKASRTKCU5nv"
# Export the model to a SavedModel
model.save('path_to_saved_model', save_format='tf')
# Recreate the exact same model
new_model = keras.models.load_model('path_to_saved_model')
# Check that the state is preserved
new_predictions = new_model.predict(x_test)
np.testing.assert_allclose(predictions, new_predictions, rtol=1e-6, atol=1e-6)
# Note that the optimizer state is preserved as well:
# you can resume training where you left off.
# + [markdown] colab_type="text" id="4AWgwkKWIhfj"
# The `SavedModel` files that were created contain:
#
# - A TensorFlow checkpoint containing the model weights.
# - A `SavedModel` proto containing the underlying TensorFlow graph.
# + [markdown] colab_type="text" id="GkY8XP_XxgMI"
# ### Architecture-only saving
#
# Sometimes, you are only interested in the architecture of the model, and you don't need to save the weight values or the optimizer. In this case, you can retrieve the "config" of the model via the `get_config()` method. The config is a Python dict that enables you to recreate the same model -- initialized from scratch, without any of the information learned previously during training.
# + colab={} colab_type="code" id="yQGGvo2Fw4o-"
config = model.get_config()
reinitialized_model = keras.Model.from_config(config)
# Note that the model state is not preserved! We only saved the architecture.
new_predictions = reinitialized_model.predict(x_test)
assert abs(np.sum(predictions - new_predictions)) > 0.
# + [markdown] colab_type="text" id="WsNBBvDgxsTS"
# You can alternatively use `to_json()` from `from_json()`, which uses a JSON string to store the config instead of a Python dict. This is useful to save the config to disk.
# + colab={} colab_type="code" id="5a0z7_6XxqWV"
json_config = model.to_json()
reinitialized_model = keras.models.model_from_json(json_config)
# + [markdown] colab_type="text" id="SGC7R6IIxy0o"
# ### Weights-only saving
#
# Sometimes, you are only interested in the state of the model -- its weights values -- and not in the architecture. In this case, you can retrieve the weights values as a list of Numpy arrays via `get_weights()`, and set the state of the model via `set_weights`:
# + colab={} colab_type="code" id="B8tHwEvkxw5E"
weights = model.get_weights() # Retrieves the state of the model.
model.set_weights(weights) # Sets the state of the model.
# + [markdown] colab_type="text" id="Ydwtw-u2x7xC"
# You can combine `get_config()`/`from_config()` and `get_weights()`/`set_weights()` to recreate your model in the same state. However, unlike `model.save()`, this will not include the training config and the optimizer. You would have to call `compile()` again before using the model for training.
# + colab={} colab_type="code" id="LWVtuxtrx5lb"
config = model.get_config()
weights = model.get_weights()
new_model = keras.Model.from_config(config)
new_model.set_weights(weights)
# Check that the state is preserved
new_predictions = new_model.predict(x_test)
np.testing.assert_allclose(predictions, new_predictions, rtol=1e-6, atol=1e-6)
# Note that the optimizer was not preserved,
# so the model should be compiled anew before training
# (and the optimizer will start from a blank state).
# + [markdown] colab_type="text" id="prk0GzwCyIYy"
# The save-to-disk alternative to `get_weights()` and `set_weights(weights)`
# is `save_weights(fpath)` and `load_weights(fpath)`.
#
# Here's an example that saves to disk:
# + colab={} colab_type="code" id="2irLnOUbyHlI"
# Save JSON config to disk
json_config = model.to_json()
with open('model_config.json', 'w') as json_file:
json_file.write(json_config)
# Save weights to disk
model.save_weights('path_to_my_weights.h5')
# Reload the model from the 2 files we saved
with open('model_config.json') as json_file:
json_config = json_file.read()
new_model = keras.models.model_from_json(json_config)
new_model.load_weights('path_to_my_weights.h5')
# Check that the state is preserved
new_predictions = new_model.predict(x_test)
np.testing.assert_allclose(predictions, new_predictions, rtol=1e-6, atol=1e-6)
# Note that the optimizer was not preserved.
# + [markdown] colab_type="text" id="KBxcFAPHyYi5"
# But remember that the simplest, recommended way is just this:
# + colab={} colab_type="code" id="DE4b3ndNyQh3"
model.save('path_to_my_model.h5')
del model
model = keras.models.load_model('path_to_my_model.h5')
# + [markdown] colab_type="text" id="yKikmbdC3O_i"
# ### Weights-only saving using TensorFlow checkpoints
#
# Note that `save_weights` can create files either in the Keras HDF5 format,
# or in the [TensorFlow Checkpoint format](https://www.tensorflow.org/api_docs/python/tf/train/Checkpoint). The format is inferred from the file extension you provide: if it is ".h5" or ".keras", the framework uses the Keras HDF5 format. Anything else defaults to Checkpoint.
# + colab={} colab_type="code" id="0pYKb6LV3h2l"
model.save_weights('path_to_my_tf_checkpoint')
# + [markdown] colab_type="text" id="ZFwKv6JC3kyu"
# For total explicitness, the format can be explicitly passed via the `save_format` argument, which can take the value "tf" or "h5":
# + colab={} colab_type="code" id="oN9vOaWU34lA"
model.save_weights('path_to_my_tf_checkpoint', save_format='tf')
# + [markdown] colab_type="text" id="xXgtNRCSyuIW"
# ## Part II: Saving and Loading of Subclassed Models
# + [markdown] colab_type="text" id="mJqOn0snzCRy"
# Sequential models and Functional models are datastructures that represent a DAG of layers. As such,
# they can be safely serialized and deserialized.
#
# A subclassed model differs in that it's not a datastructure, it's a piece of code. The architecture of the model
# is defined via the body of the `call` method. This means that the architecture of the model cannot be safely serialized. To load a model, you'll need to have access to the code that created it (the code of the model subclass). Alternatively, you could be serializing this code as bytecode (e.g. via pickling), but that's unsafe and generally not portable.
#
# For more information about these differences, see the article ["What are Symbolic and Imperative APIs in TensorFlow 2.0?"](https://medium.com/tensorflow/what-are-symbolic-and-imperative-apis-in-tensorflow-2-0-dfccecb01021).
# + [markdown] colab_type="text" id="Pkwyu5dVz12P"
# Let's consider the following subclassed model, which follows the same structure as the model from the first section:
# + colab={} colab_type="code" id="4Onp-8rGyeQG"
class ThreeLayerMLP(keras.Model):
def __init__(self, name=None):
super(ThreeLayerMLP, self).__init__(name=name)
self.dense_1 = layers.Dense(64, activation='relu', name='dense_1')
self.dense_2 = layers.Dense(64, activation='relu', name='dense_2')
self.pred_layer = layers.Dense(10, name='predictions')
def call(self, inputs):
x = self.dense_1(inputs)
x = self.dense_2(x)
return self.pred_layer(x)
def get_model():
return ThreeLayerMLP(name='3_layer_mlp')
model = get_model()
# + [markdown] colab_type="text" id="wwT_YoKA0yQW"
# First of all, *a subclassed model that has never been used cannot be saved*.
#
# That's because a subclassed model needs to be called on some data in order to create its weights.
#
# Until the model has been called, it does not know the shape and dtype of the input data it should be
# expecting, and thus cannot create its weight variables. You may remember that in the Functional model from the first section, the shape and dtype of the inputs was specified in advance (via `keras.Input(...)`) -- that's why Functional models have a state as soon as they're instantiated.
#
# Let's train the model, so as to give it a state:
# + colab={} colab_type="code" id="xqP4kIFN0fTZ"
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
model.compile(loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=keras.optimizers.RMSprop())
history = model.fit(x_train, y_train,
batch_size=64,
epochs=1)
# Reset metrics before saving so that loaded model has same state,
# since metric states are not preserved by Model.save_weights
model.reset_metrics()
# + [markdown] colab_type="text" id="rvGCpyX72HOC"
# There are three different approaches to save and restore a subclassed model. The following sections provides more details on those three approaches.
#
# ### Approach 1:
# The recommended way to save a subclassed model is to use `save_weights` to create a TensorFlow SavedModel checkpoint, which will contain the value of all variables associated with the model:
# - The layers' weights
# - The optimizer's state
# - Any variables associated with stateful model metrics (if any)
#
#
# + colab={} colab_type="code" id="gMg87Tz01cxQ"
model.save_weights('path_to_my_weights', save_format='tf')
# + colab={} colab_type="code" id="KOKNBojtsl0F"
# Save predictions for future checks
predictions = model.predict(x_test)
# Also save the loss on the first batch
# to later assert that the optimizer state was preserved
first_batch_loss = model.train_on_batch(x_train[:64], y_train[:64])
# + [markdown] colab_type="text" id="h2PM_PL1SzPo"
# To restore your model, you will need access to the code that created the model object.
#
# Note that in order to restore the optimizer state and the state of any stateful metric, you should
# compile the model (with the exact same arguments as before) and call it on some data before calling `load_weights`:
# + colab={} colab_type="code" id="OOSGiSkHTERy"
# Recreate the model
new_model = get_model()
new_model.compile(loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
optimizer=keras.optimizers.RMSprop())
# This initializes the variables used by the optimizers,
# as well as any stateful metric variables
new_model.train_on_batch(x_train[:1], y_train[:1])
# Load the state of the old model
new_model.load_weights('path_to_my_weights')
# Check that the model state has been preserved
new_predictions = new_model.predict(x_test)
np.testing.assert_allclose(predictions, new_predictions, rtol=1e-6, atol=1e-6)
# The optimizer state is preserved as well,
# so you can resume training where you left off
new_first_batch_loss=new_model.train_on_batch(x_train[:64], y_train[:64])
assert first_batch_loss == new_first_batch_loss
# + [markdown] colab_type="text" id="nQkIRxdNusS9"
# ### Approach 2:
# Second approach is by using `model.save` to save whole model and by using `load_model` to restore previously stored subclassed model. The following code snippets describe how to implement them.
# + colab={} colab_type="code" id="52c8x8Tcuqb4"
# Save the model
model.save('path_to_my_model',save_format='tf')
# Recreate the exact same model purely from the file
new_model = keras.models.load_model('path_to_my_model')
# + [markdown] colab_type="text" id="ZRQ-3rOfzutA"
# ### Approach 3:
# Third approach is by using `tf.saved_model.save`. This is equivalent to the `tf` format in `model.save`. You can once again call `load_model` to restore the previously saved subclassed model. The following code snippets describe how to implement them.
# + colab={} colab_type="code" id="GTX03SNh0Lvm"
# Save the model
tf.saved_model.save(model,'my_saved_model')
# Restoring the model
restored_saved_model = keras.models.load_model('my_saved_model')
|
site/en/guide/keras/save_and_serialize.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h2>Understanding the working of perceptron</h2><br>
# <p>
# Perceptron is an algorithm for learning a binary classifier: a function that maps its input x (a real-valued vector) to an output value f(x) (a single binary value):
# </p>
# <img src="perceptron1.png">
# <p>
# h(X) represents the hyper plane that would be able to split the data into positives and negatives. Perceptron trains a random h(X) and improves the h(X) so that the misclassification error is minimized.<br>
# This is done so using the 2 update equations :
# </p>
# <img src="perceptron2.png">
# <h2>Creating a sample program to understand the working of perceptron</h2>
# +
"""Importing the required modules"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.colors
from mpl_toolkits.mplot3d import Axes3D
# +
"""creating a feature X1"""
X1 = np.array([1,4,1,4])
X1
# +
"""creating a feature X2"""
X2 = np.array([1,1,3,3])
X2
# +
"""combine X1 and X2"""
X = np.vstack((X1,X2))
X
# -
y = np.array([1, -1, 1, -1])
y
# +
"""a function to create the graph for each iteration """
def show_graph(beta, beta0, X, y, x = None):
"""creating sample values for understanding the new hyperplane"""
sampleX2 = np.array([0, 1, 2, 3, 4, 5])
"""checking if the denominatoe is 0"""
if(beta[0] != 0):
sampleX1 = -(( beta0) + np.multiply(beta[1] , sampleX2))/ (beta[0])
else:
sampleX1 = np.zeros(len(sampleX2))
"""plotting the chart"""
colors=["red", "limegreen"]
cmap = matplotlib.colors.ListedColormap(colors)
plt.scatter(X[0], X[1], c = y, cmap = cmap, marker = 'o', s = 200)
"""checking and marking the misclassified point"""
if x is not None:
plt.annotate('wrongly classified', xy = (x[0],x[1]), xytext=(x[0],x[1]))
plt.xlabel('X1')
plt.ylabel('X2')
plt.plot(sampleX1,sampleX2)
plt.show()
"""perceptron learning algorithm"""
def learn_perceptron(beta, beta0, X, y, alpha, epoch):
"""iterate for a fixed number of epoch"""
for i in range(epoch):
"""set initial set of errors as zero"""
errors = 0
print('########Epoch {}###########'.format(i))
"""iterate over the X and y data"""
for x,yi in zip(X.T, y):
"""if the hyper plane wrongly classifies add error and compute new beta values"""
if(yi * (beta0 + np.dot(beta, x)) <= 0):
errors = errors + 1
beta = beta + alpha * yi * x
beta0 = beta0 + alpha * yi
show_graph(beta, beta0, X, y, x)
"""print each iteration values for better understanding"""
print ('x = ',x)
print ('beta ={} , beta0 = {}\n'.format(beta, beta0))
print ('error = ', errors)
"""if the error is zero for a complete iteration throught the values then converged"""
if( errors == 0):
print ('###########\nx',x)
print ('beta ={} , beta0 = {}\n'.format(beta, beta0))
print ('error = ', errors)
print('converged')
"""show the learned hyperplane"""
show_graph(beta, beta0, X, y)
break
# -
# <h2>Perceptron learning on linearly seperable data</h2>
# +
"""calling the function with the values for X and y"""
learn_perceptron(np.array([1, -1]), -1, X, y, 1, 20)
# -
# <h2>Perceptron learning on linearly unseperable data</h2>
X_new = np.array([[2, 2, -1, -1],[2, -1, -1, 2]], np.int32)
X_new
y_new = np.array([1, -1, 1, -1])
y_new
learn_perceptron(np.array([1, -1]), -1, X_new, y_new, 1, 2)
# <h4>No matter how many iteration the perceptron tries to learn the data is not linearly seperable in 2 Dimension<h4>
# <h2> The Kernal Trick to seperate linearly inseperable data</h2>
# <p> It's better not to explain about the kernel trick and let the image explain it for you</p>
# <p> image url :http://www.eric-kim.net/eric-kim-net/posts/1/kernel_trick.html</p>
# <img src="perceptron3.png" >
# <p> we use a trick and convert the data into a larger dimension and now try to split it using a hyperplane as can be seen from the image. The circle points were not linearly seperable so we converted the data into 3D and here the points are linearly seperable.</p>
y_new = np.array([1, -1, 1, -1])
y_new
X_new1 = np.array([[2, 2, -1, -1],[2, -1, -1, 2],[1, 4, 2, 6]], np.int32)
X_new1
fig = plt.figure(figsize = (15,10))
ax = fig.add_subplot(111, projection='3d')
colors=["red", "limegreen"]
cmap = matplotlib.colors.ListedColormap(colors)
ax.scatter(X_new1[0], X_new1[1], X_new1[2], c=y_new, cmap =cmap, s=100)
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
# <h4>Now the same 4 points from the previous unseperable data can be seperated using a plane in 3D if a suitable kernal is used. In machine learning, the (Gaussian) radial basis function kernel, or RBF kernel, is a popular kernel function used in various kernelized learning algorithms. In particular, it is commonly used in support vector machine classification.</h4>
|
Perceptron/Perceptron.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: py3sglyon
# language: python
# name: py3sglyon
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Web Scraping
# + [markdown] slideshow={"slide_type": "fragment"}
# More and more data is becoming available via APIs and other computer-friendly protocols.
# + [markdown] slideshow={"slide_type": "fragment"}
# However, not all of us can be so lucky to work on projects that are fed by APIs.
# + [markdown] slideshow={"slide_type": "fragment"}
# Today we learn a skill to combat this issue: web-scraping
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Overview
#
# Web-scraping can be as complex as the web itself, but we will cover the foundations and learn the core tools to use
# + [markdown] slideshow={"slide_type": "fragment"}
# Our outline is:
#
# - [HTML basics](02_html.ipynb)
# - Intro to scrapy
# - Example: Scrapy spiders crawling IMDb
# -
|
Year19-20/2020-02-07_web_scraping/01_intro.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (n36)
# language: python
# name: n36
# ---
# # Preprocess
# +
import shutil
import os
import glob
import random
import json
rnd_seed = 1234
random.seed(rnd_seed)
import spacy
# -
def clean_dir(dirname):
try:
shutil.rmtree(dirname)
except FileNotFoundError:
pass
os.mkdir(dirname)
allowed = set('ADJ NOUN VERB'.split())
nlp = spacy.load('en_core_web_sm', disable=['parser', 'ner'])
nlp.max_length = 10000000
def plain_text(infile, outdir, max_pairs=None):
clean_dir(outdir)
with open(infile) as inf:
for line_idx, line in enumerate(inf):
if max_pairs and line_idx >= max_pairs:
break
pair = json.loads(line)
pair_id = pair['id']
for idx, text in enumerate(pair['pair']):
text_idx = pair_id + '_' + str(idx)
tokens = nlp(text)
if not tokens:
continue
new_fn = f'{outdir}/{text_idx}.txt'
with open(new_fn, 'w') as f:
for t in tokens:
if t.pos_ in allowed and t.is_alpha and not t.is_stop:
w = t.text.lower()
if len(w) > 1:
f.write(w + ' ')
plain_text(infile='datasets/pan20-authorship-verification-training-small/pairs.jsonl',
outdir='plain_text_train_small',
max_pairs=None)
|
clef20/authorship-verification/tm_preprocessing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (reco_gpu)
# language: python
# name: reco_gpu
# ---
# <i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
#
# <i>Licensed under the MIT License.</i>
# # Neural Collaborative Filtering on MovieLens dataset.
#
# Neural Collaborative Filtering (NCF) is a well known recommendation algorithm that generalizes the matrix factorization problem with multi-layer perceptron.
#
# This notebook provides an example of how to utilize and evaluate NCF implementation in the `recommenders`. We use a smaller dataset in this example to run NCF efficiently with GPU acceleration on a [Data Science Virtual Machine](https://azure.microsoft.com/en-gb/services/virtual-machines/data-science-virtual-machines/).
# %load_ext autoreload
# %autoreload 2
# +
import sys
import pandas as pd
import tensorflow as tf
tf.get_logger().setLevel('ERROR') # only show error messages
from recommenders.utils.timer import Timer
from recommenders.models.ncf.ncf_singlenode import NCF
from recommenders.models.ncf.dataset import Dataset as NCFDataset
from recommenders.datasets import movielens
from recommenders.utils.notebook_utils import is_jupyter
from recommenders.datasets.python_splitters import python_chrono_split
from recommenders.evaluation.python_evaluation import (rmse, mae, rsquared, exp_var, map_at_k, ndcg_at_k, precision_at_k,
recall_at_k, get_top_k_items)
print("System version: {}".format(sys.version))
print("Pandas version: {}".format(pd.__version__))
print("Tensorflow version: {}".format(tf.__version__))
# -
# Set the default parameters.
# + tags=["parameters"]
# top k items to recommend
TOP_K = 10
# Select MovieLens data size: 100k, 1m, 10m, or 20m
MOVIELENS_DATA_SIZE = '100k'
# Model parameters
EPOCHS = 50
BATCH_SIZE = 256
SEED = 42
# -
# ### 1. Download the MovieLens dataset
df = movielens.load_pandas_df(
size=MOVIELENS_DATA_SIZE,
header=["userID", "itemID", "rating", "timestamp"]
)
# ### 2. Split the data using the Spark chronological splitter provided in utilities
train, test = python_chrono_split(df, 0.75)
# Generate an NCF dataset object from the data subsets.
data = NCFDataset(train=train, test=test, seed=SEED)
# ### 3. Train the NCF model on the training data, and get the top-k recommendations for our testing data
#
# NCF accepts implicit feedback and generates prospensity of items to be recommended to users in the scale of 0 to 1. A recommended item list can then be generated based on the scores. Note that this quickstart notebook is using a smaller number of epochs to reduce time for training. As a consequence, the model performance will be slighlty deteriorated.
model = NCF (
n_users=data.n_users,
n_items=data.n_items,
model_type="NeuMF",
n_factors=4,
layer_sizes=[16,8,4],
n_epochs=EPOCHS,
batch_size=BATCH_SIZE,
learning_rate=1e-3,
verbose=10,
seed=SEED
)
# +
with Timer() as train_time:
model.fit(data)
print("Took {} seconds for training.".format(train_time))
# -
# In the movie recommendation use case scenario, seen movies are not recommended to the users.
# +
with Timer() as test_time:
users, items, preds = [], [], []
item = list(train.itemID.unique())
for user in train.userID.unique():
user = [user] * len(item)
users.extend(user)
items.extend(item)
preds.extend(list(model.predict(user, item, is_list=True)))
all_predictions = pd.DataFrame(data={"userID": users, "itemID":items, "prediction":preds})
merged = pd.merge(train, all_predictions, on=["userID", "itemID"], how="outer")
all_predictions = merged[merged.rating.isnull()].drop('rating', axis=1)
print("Took {} seconds for prediction.".format(test_time))
# -
# ### 4. Evaluate how well NCF performs
# The ranking metrics are used for evaluation.
# +
eval_map = map_at_k(test, all_predictions, col_prediction='prediction', k=TOP_K)
eval_ndcg = ndcg_at_k(test, all_predictions, col_prediction='prediction', k=TOP_K)
eval_precision = precision_at_k(test, all_predictions, col_prediction='prediction', k=TOP_K)
eval_recall = recall_at_k(test, all_predictions, col_prediction='prediction', k=TOP_K)
print("MAP:\t%f" % eval_map,
"NDCG:\t%f" % eval_ndcg,
"Precision@K:\t%f" % eval_precision,
"Recall@K:\t%f" % eval_recall, sep='\n')
# -
if is_jupyter():
# Record results with papermill for tests
import papermill as pm
import scrapbook as sb
sb.glue("map", eval_map)
sb.glue("ndcg", eval_ndcg)
sb.glue("precision", eval_precision)
sb.glue("recall", eval_recall)
sb.glue("train_time", train_time.interval)
sb.glue("test_time", test_time.interval)
|
examples/00_quick_start/ncf_movielens.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Approximating square root
#
# There are a lot of useful functions that have no closed form solution, meaning we can't just do a computation and return the value. Instead, we need to use an iterative method to approximate the function value. We can use this to approximate sine (with Taylor series expansion), approximate square root (as we'll do in this lecture), or optimize a cost or error function (gradient descent in next lecture).
#
# As with the previous uniform random variable lecture, we must translate a recurrence relation to Python. Instead of returning a single value in the recurrence series, we will look for **convergence of the series**. In other words, if we run the series out far enough, $x_{i+1}$ will be close to $x_i$ leaving $x_i$ as a very accurate approximation of square root. This will teach us the basics of iterative computing and prepare us for the more complicated function optimization material.
#
# ## Babylonian method
#
# To approximate square root, the idea is to pick an initial estimate, $x_0$, and then iterate with better and better estimates, $x_i$, using the ([Babylonian method](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots#Babylonian_method)) recurrence relation:
#
# $x_{i+1} = \frac{1}{2}(x_i + \frac{n}{x_i})$
#
# There’s a great deal on the web you can read to learn more about why this process works but it relies on the average (midpoint) of $x_i$ and $n/x_i$ getting us closer to the square root of n. The cool thing is that the iteration converges quickly.
#
# Our goal is to write a function that takes a single number and returns it square root. What do we know about this function before even beginning to code? Well, we have a clear description of the problem per our function workplan, and we also have the function signature we want:
#
# ```python
# def sqrt(n):
# ```
#
# Because we are implementing a recurrence relation, we know that we will have a loop that computes $x_{i+1}$ from $x_{i}$.
# ### Convergence
#
# The terminating condition of the loop is when we have reached convergence or close to it. Convergence just means that $x_{i+1}$ is pretty close to $x_i$. Because we can never compare to real numbers for equality, we have to check for the difference being smaller than some precision like 0.00000001.
# ### Iterative method outline
#
# Just as we have an outline for an analytics program, iterative methods all share the same basic outline. (I'm assuming here that $x_{i+1}$ depends only on a single previous value and that $i$ implicitly increments as the loop goes around.)
#
# *set $x_0$ to initial value*<br>
# *repeat:*<br>
# $x_{i+1} =$ function-giving-next-value$(x_i)$<br>
# *until $abs(x_{i+1} - x_i) \lt precision$<br>
# return $x_{i+1}$*<br>
#
# Because Python does not have a repeat-until loop, we fake it with an infinite loop containing a conditional that breaks us out upon convergence:
#
# *set $x_0$ to initial value*<br>
# *while True:*<br>
# $x_{i+1} =$ function-giving-next-value$(x_i)$<br>
# *if $abs(x_{i+1} - x_i) \lt precision$<br>
# return $x_{i+1}$*<br>
#
# That is a fairly straightforward implementation of the recurrence relation, but you will notice that we don't actually need to keep all previous $x_i$ around except for the new value and the previous value. Here is a Python implementation that tracks only two values and follows the infinite loop pattern:
def sqrt(n):
"compute square root of n"
PRECISION = 0.00000001 # stop iterating when we converge with this delta
x_0 = 1.0 # pick any old initial value
x_prev = x_0
while True: # Python doesn't have repeat-until loop so fake it
x_new = 0.5 * (x_prev + n/x_prev)
if abs(x_new - x_prev) < PRECISION:
return x_new
x_prev = x_new # x_i+1 becomes x_i (previous value)
# To test our square root approximation, we can compare it to `math.sqrt()` and use numpy's `isclose` to do the comparison.
# +
import math
import numpy as np
def check(n):
assert np.isclose(sqrt(n), math.sqrt(n))
def test_sqrt():
check(125348)
check(89.2342)
check(100)
check(1)
check(0)
test_sqrt()
# -
# As you can see we can define a function within a function. It's not special in any way except that code outside of `test_sqrt()` cannot see function `check()`. On the other hand, `check()` **can** see the symbols outside of `test_sqrt()`, such as our `sqrt()`.
# ### Exercise
#
# Type in (don't cut/paste) the `sqrt(n)` function and test with, for example, `sqrt(125348.0)`. Make sure you get the right answer (354.045195) and then add print statements so that you can see the sequence of $x_{i}$ values. I get:
#
# ```
# 1.0
# 62674.5
# 31338.249992
# 15671.1249162
# 7839.56178812
# 3927.77547356
# 1979.84435152
# 1021.5781996
# 572.139273508
# 395.612894667
# 356.228988269
# 354.051888518
# 354.045194918
# 354.045194855
# ```
#
# Notice how quickly it converges!
# +
def sqrt_with_trace(n):
"compute square root of n"
PRECISION = 0.00000001 # stop iterating when we converge with this delta
x_0 = 1.0 # pick any old initial value
x_prev = x_0
while True: # Python doesn't have repeat-until loop so fake it
print x_prev
x_new = 0.5 * (x_prev + n/x_prev)
if abs(x_new - x_prev) < PRECISION:
return x_new
x_prev = x_new
sqrt_with_trace(125348.000000)
# -
# Now that we know how to implement a recurrence relation that converges, let's take a look at function optimization. At first glance, it seems completely different, but uses the same extraction of an iterative method.
|
notes/sqrt.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// ***Good, you have jupyter notebooks installed and running!!***
//
// Let's start by talking a little about the FRC robot environment and about WPIlib. You will generally be grogramming on your own laptop or a teal laptop (one of the driver stations). From your laptop you download code to the robot to run the robot, and you upload code to github so it can be easily shared between team members and so we have a history of all the changes made to code, and the version of the code that we ran at each of the competitions
//
// We program the robot in Java as that is one of the languages supported by
// [WPIlib](https://docs.wpilib.org/en/stable/).
// **What is Java, and how does it compare to other languages?**
// Java is a relatively old language (see the [Wikipedia](https://en.wikipedia.org/wiki/Java_(programming_language)) artcle) originally released in the mid 1990's in my experience with languages I would characterize these aspects
// of Java:
// * **declarative vs implerative** - Java is an imperative language. I read an article recently that
// characterized declarative languages as ones where you declare the intent and it just happens vs.
// imperative languages where you explicitly describe what must be done to achieve the intent. The
// example they used was how you would describe meeting somewhere, i.e. "Let's meet at Kickstand in
// Hood River for coffee and 9:30AM" is declarative. It describes intent without going into any details
// of how you get to kickstand at 9:30AM - you figure that out.
//
// In an imperative language concepts are low-level and the description would start with where you are
// and explicitly describe when you should leave which streets you take, where you turn, landmarks,
// etc., to descibe the exact path you would take to get to Kickstand. Oddly, in the imperative approach
// the address might never be revealed since the imperitives get you there.
//
// The difference between these two is that in the imperitive case you are relying on the programmer to
// make the best decision about how to get from where someone is to kickstand. In the declarative case you
// describe what you want to happen, and leave the details to be taken care of by the programming language - or,
// in this case, a person who is using google maps who might want to run a couple errands along the way.
//
// In Java you will find that there are a lot of libraries that have declarative capabilities for certain
// tasks. WPIlib is an example of that, which lets you declare what you want parts of the robot to do
// (i.e. set the speed of a motor) rather than describing the intricate details of interacting with
// controllers and encoders encoders, applying PID loops to control speed or distance, etc.
//
// * **structured vs unstructured** - Java is a very structured language. While I have found different
// interpretations of *structured*, the most useful describe structured as encouraging building
// and packaging *reusable* blocks of code. Others reference address the rigidity of syntax structure.
// Java has both.
//
// * **object-oriented** - Java is object-oriented. What this means is a bit more abstract to describe - but,
// say, for example, I want to work with a motor controller. In a non-object oriented language I would have
// methods like
//
// * **strongly typed vs. inferred types** - Java is strongly typed
// * **compiled vs. interpreted** - Java is compiled
// * **platform (hardware and operating system) independence** - Java compiles to bytecode - which is
// intended to be platform independent. You should be able to run it on any computer.
|
jupyter/01 - Getting Started.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Assignment
#
# 1. Create a video and attach border of diffrent colour.
# 2. Save the video
|
essential/a11.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: SageMath 9.5
# language: sage
# name: sagemath-9.5
# ---
# # Протоколы аутентификации с нулевым разглашением
IS_DEBUG = 1
def trace(*args, **kwargs):
"""
Отладочная трассировка
"""
global IS_DEBUG
if IS_DEBUG:
print('[TRACE]', end=' ')
print(*args, **kwargs)
# ---
# +
# Генерация простых чисел
from Crypto.Util import number
# КГПСЧ
from Crypto.Random import random
# Понадобится в протоколе Шнорра
from Crypto.PublicKey import RSA
from Crypto.Signature import pss
from Crypto.Hash import SHA256
# Немного математики
import gmpy2
# Для генерации идентификаторов клиентов
import uuid
# -
# ---
# +
def randint(a, b) -> gmpy2.mpz:
"""
Генерация случайного числа в отрезке [a, b] с помощью КГПСЧ с поддержкой gmpy2
"""
native_a = int(a)
native_b = int(b)
return gmpy2.mpz(random.randint(native_a, native_b))
def getrandbits(n) -> gmpy2.mpz:
"""
Генерация случайного числа длиной n бит с помощью КГПСЧ с поддержкой gmpy2
"""
native_n = int(n)
return gmpy2.mpz(random.getrandbits(native_n))
# -
# ----
# ## Протокол Фиата-Шамира
# 
class FiatShamirCA(object):
PRIME_BITS = 1024
def __init__(self):
"""
Инициализация доверенного центра.
Генерируются два простых числа и их произведение.
"""
self._db = {}
self._p = number.getPrime(FiatShamirCA.PRIME_BITS)
self._q = number.getPrime(FiatShamirCA.PRIME_BITS)
self._modulus = gmpy2.mul(self._p, self._q)
trace('[FiatShamirCA]', f'Modulus = {self._modulus}')
def register_client(self, client_id: uuid.UUID, client_public_key: gmpy2.mpz) -> None:
"""
Регистрация клиента. На вход принимает идентификатор клиента и его открытый ключ.
Ничего не возвращает.
Выбрасывает исключение, если клиент уже существует.
"""
trace('[FiatShamirCA]', f'''Attempting to register client {client_id}
with public key {client_public_key}''')
if client_id in self._db:
trace('[FiatShamirCA]', 'User already exists')
raise ValueError(f'Client {client_id} is already registered')
#
# Теперь сохраняю открытый ключ
#
self._db[client_id] = client_public_key
trace('[FiatShamirCA]', 'Client registered successfully')
def get_public_key(self, client_id: uuid.UUID) -> gmpy2.mpz:
"""
Получение открытого ключа клиента. Получает на вход идентификатор клиента.
Возвращает открытый ключ.
Выбрасывает исключение, если пользователь отсутствует.
"""
return self._db[client_id]
@property
def modulus(self) -> gmpy2.mpz:
"""
Возвращает модуль.
"""
return self._modulus
class FiatShamirClient(object):
def __init__(self, modulus: gmpy2.mpz, *,
fake_data: tuple[uuid.UUID, gmpy2.mpz] = None):
"""
Инициализация клиента с выработкой ключевой пары и идентификатора.
Последний параметр требуются для демонстрации неудачной аутентификации.
"""
self._id = uuid.uuid4() if fake_data is None else fake_data[0]
self._r = None
self._private_key = FiatShamirClient._generate_coprime(modulus)
self._public_key = gmpy2.powmod(self._private_key, 2, modulus) if fake_data is None else fake_data[1]
trace('[FiatShamirClient]', f'Client {self._id}')
trace('[FiatShamirClient]', f'Public key = {self._public_key}')
@property
def public_key(self) -> gmpy2.mpz:
"""
Получение открытого ключа.
"""
return self._public_key
@property
def identifier(self) -> uuid.UUID:
"""
Получение идентификатора.
"""
return self._id
def get_x(self, modulus: gmpy2.mpz) -> gmpy2.mpz:
"""
Получение случайного значения, вычисляемого по формуле:
x = r ** 2 mod n,
где n - модуль, r - случайное целое число из отрезка [1, n - 1].
Значение r сохраняется.
"""
self._r = randint(1, modulus - 1)
return gmpy2.powmod(self._r, 2, modulus)
def get_y(self, e: gmpy2.mpz, modulus: gmpy2.mpz) -> gmpy2.mpz:
"""
Получение числа, вычисляемого по формуле:
y = r * s ** e mod n,
где n - модуль, s - закрытый ключ пользователя, r - сгенерированное
функцией get_x внутреннее значение, e - целое число из отрезка [0, 1],
пришедшее от проверяющего.
"""
product = gmpy2.mul(self._r, gmpy2.powmod(self._private_key, e, modulus))
return gmpy2.t_mod(product, modulus)
@staticmethod
def _generate_coprime(modulus: gmpy2.mpz) -> gmpy2.mpz:
"""
Генерация случайного числа из отрезка [1, n - 1], взаимно
простого с n, где n - модуль.
"""
#
# Генерирую число до тех пор, пока оно не станет взаимно простым с модулем
#
result = randint(1, modulus - 1)
while gmpy2.gcd(result, modulus) != 1:
result = randint(1, modulus - 1)
return result
class FiatShamirVerifier(object):
def __init__(self, iterations: int):
"""
Инициализация проверяющего. Задает коичество итераций проверки.
"""
self._iterations = iterations
def authenticate(self, client: FiatShamirClient, ca: FiatShamirCA) -> bool:
"""
Аутентификация клиента. На вход принимает дескрипторы клиента и СА.
Возвращает True в случае успешной аутентификации.
"""
trace('[FiatShamirVerifier]', f'Attempt to authenticate client {client.identifier}')
trace('[FiatShamirVerifier]', f'Number of iterations = {self._iterations}')
is_successful = True
for i in range(self._iterations):
x = client.get_x(ca.modulus)
trace('[FiatShamirVerifier]', f'[Iteration {i + 1}] {x = }')
e = randint(0, 1)
trace('[FiatShamirVerifier]', f'[Iteration {i + 1}] {e = }')
y = client.get_y(e, ca.modulus)
trace('[FiatShamirVerifier]', f'[Iteration {i + 1}] {y = }')
pk = ca.get_public_key(client.identifier)
product = gmpy2.mul(x, gmpy2.powmod(pk, e, ca.modulus))
successful_iteration = gmpy2.powmod(y, 2, ca.modulus) == gmpy2.t_mod(product, ca.modulus)
is_successful &= successful_iteration
trace('[FiatShamirVerifier]', f'[Iteration {i + 1}] success: {successful_iteration}')
if not successful_iteration:
break
print(f'Authentication successful: {is_successful}')
return is_successful
# ----
# Создаю доверенный центр
ca = FiatShamirCA()
# Создаю двух пользователей:
# - Алису - валидного пользователя
# - Еву - пользователя, представляющегося Алисой. но не знающего закрытого ключа Алисы
alice = FiatShamirClient(ca.modulus)
eve = FiatShamirClient(ca.modulus,
fake_data=(alice.identifier, alice.public_key))
# Регистрирую валидного пользователя
ca.register_client(alice.identifier, alice.public_key)
# +
# Для простоты будет 3 итерации
ITERATIONS = 3
# Создаю проверяющую сторону
verifier = FiatShamirVerifier(ITERATIONS)
# -
# Произвожу аутентификацию валидного пользователя
verifier.authenticate(alice, ca)
# Произвожу аутентификацию невалидного пользователя
verifier.authenticate(eve, ca)
# ---
# ## Протокол Шнорра
# 
class SchnorrCA(object):
RSA_KEY_LENGTH = 4096
def __init__(self):
"""
Инициализация доверенного центра
Генерация простых чисел p, q и элемента g, а также ключевой пары СА
"""
self._db = {}
#
# Генерация параметров протокола
#
self._p, self._q, self._g = SchnorrCA._generate_parameters()
#
# Ключевая пара RSA для СА
#
self._private_key = RSA.generate(SchnorrCA.RSA_KEY_LENGTH)
self._public_key = self._private_key.publickey()
trace('[SchnorrCA]', f'RSA public key = {(self._public_key.e, self._public_key.n)}')
def register_client(self,
client_id: uuid.UUID,
client_public_key: gmpy2.mpz) -> tuple[uuid.UUID, gmpy2.mpz, bytes]:
"""
Регистрация клиента. Принимает на вход идентификатор клиента и его открытый ключ.
Возвращает подписанный сервером сертификат.
Выбрасывает исключение, если клиент уже зарегистрирован.
"""
if client_id in self._db:
trace('[SchnorrCA]', 'User already exists')
raise ValueError(f'Client {client_id} is already registered')
#
# Создаю сертификат
#
h = SHA256.new(str(client_id).encode() + number.long_to_bytes(int(client_public_key)))
signature = pss.new(self._private_key).sign(h)
certificate = (client_id, client_public_key, signature)
trace('[SchnorrCA]', f'Certificate = {certificate}')
#
# Сохраняю его и возвращаю
#
self._db[client_id] = certificate
return certificate
def verify_certificate(self, certificate: tuple[uuid.UUID, gmpy2.mpz, bytes]) -> bool:
"""
Проверка сертификата.
Возвращает признак валидности сертификата.
"""
client_id, client_public_key, signature = certificate
if client_id not in self._db:
trace('[SchnorrCA]', f"Client {client_id} doesn't exist")
raise ValueError("Client doesn't exist")
h = SHA256.new(str(client_id).encode() + number.long_to_bytes(int(client_public_key)))
verifier = pss.new(self.public_key)
try:
verifier.verify(h, signature)
return True
except:
return False
@property
def public_key(self):
"""
Получение открытого ключа СА.
"""
return self._public_key
@property
def parameters(self) -> tuple[gmpy2.mpz, gmpy2.mpz, gmpy2.mpz]:
"""
Параметры протокола (p, q, g)
"""
return self._p, self._q, self._g
@staticmethod
def _generate_parameters() -> tuple[gmpy2.mpz, gmpy2.mpz, gmpy2.mpz]:
"""
Генерация параметров протокола (p, q, g).
"""
Q_LENGTH = 160
P_LENGTH = 1024
q = gmpy2.mpz(number.getPrime(Q_LENGTH))
p = gmpy2.mul(getrandbits(P_LENGTH - Q_LENGTH), q) + 1
while not gmpy2.is_prime(p):
p = gmpy2.mul(getrandbits(P_LENGTH - Q_LENGTH), q) + 1
#
# Сгенерирую число, взаимно простое с p
#
tmp = getrandbits(P_LENGTH)
while gmpy2.gcd(tmp, p) != 1:
tmp = getrandbits(P_LENGTH)
#
# По малой теореме Ферма такой g будет иметь порядок q
#
g = gmpy2.powmod(tmp, (p - 1) // q, p)
trace('[SchnorrCA]', f'{p = }, {q = }, {g = }')
return p, q, g
class SchnorrClient(object):
def __init__(self, parameters: tuple[gmpy2.mpz, gmpy2.mpz, gmpy2.mpz], *,
fake_data: tuple[uuid.UUID, gmpy2.mpz, tuple] = None):
"""
Инициализация клиента. Генерирует идентификатор клиента,
ключевую пару.
Последний параметр необходим для демонстрации неуспешной аутентификации.
"""
self._p, self._q, self._g = parameters
self._id = uuid.uuid4() if fake_data is None else fake_data[0]
self._cert = None if fake_data is None else fake_data[2]
self._r = None
self._private_key = randint(1, self._q - 1)
self._public_key = gmpy2.powmod(
self._g, -self._private_key, self._p) if fake_data is None else fake_data[1]
trace('[SchnorrClient]', f'Client {self._id}')
trace('[SchnorrClient]', f'Public key = {self._public_key}')
def register(self, ca: SchnorrCA) -> None:
"""
Регистрация клиента на СА. Принимает дескриптор СА.
"""
self._cert = ca.register_client(self.identifier, self.public_key)
def get_x(self) -> gmpy2.mpz:
"""
Получение числа х, получаемого по формуле:
x = g ** r mod p
где r - случайное целое число из отрезка [1, q - 1].
Сохраняет значение r.
"""
self._r = randint(1, self._q - 1)
return gmpy2.powmod(self._g, self._r, self._p)
def get_y(self, e, security_parameter) -> gmpy2.mpz:
"""
Получение числа х, получаемого по формуле:
x = a * e + r mod q
где r - сохраненное в get_x служебное значение, e - число,
полученное от проверяющего, a - закрытый ключ клиента.
"""
if e > 2 ** security_parameter or e < 1:
trace('[SchnorrClient]', f'Invalid {e = }')
raise ValueError('Invalid e')
pre_result = gmpy2.mul(self._private_key, e) + self._r
return gmpy2.t_mod(pre_result, self._q)
@property
def certificate(self):
"""
Получение сертификата клиента.
"""
return self._cert
@property
def public_key(self) -> gmpy2.mpz:
"""
Получение открытого ключа клиента.
"""
return self._public_key
@property
def identifier(self) -> uuid.UUID:
"""
Получение идентификатора клиента.
"""
return self._id
class SchnorrVerifier(object):
def __init__(self, parameters, security_parameter):
"""
Инициализация проверяющего. Фактически только закрепляет параметры протокола.
"""
self._p, self._q, self._g = parameters
self._security_parameter = security_parameter
assert security_parameter > 0 and 2 ** security_parameter < self._q
self._e_values = set()
def authenticate(self, client: SchnorrClient, ca: SchnorrCA) -> bool:
"""
Аутентификация клиента. На вход принимает дескрипторы клиента и СА.
Возвращает True в случае успешной аутентификации.
"""
#
# Получаю с клиента x и его сертификат
#
x, cert = client.get_x(), client.certificate
trace('[SchnorrVerifier]', f'{x = }')
#
# Если сертификат битый или невалидный, то это плохо
#
if not ca.verify_certificate(cert):
trace('[SchnorrVerifier]', f'Invalid certificate {cert}')
return False
#
# Генерирую число е и отдаю его клиенту
#
e = randint(1, 2 ** self._security_parameter)
while e in self._e_values:
e = randint(1, 2 ** self._security_parameter)
self._e_values.add(e)
trace('[SchnorrVerifier]', f'{e = }')
y = client.get_y(e, self._security_parameter)
trace('[SchnorrVerifier]', f'{y = }')
#
# Вычисляю значение, которое необходимо сравнить с полученным от клиента х
# И сразу же сравниваю их
#
product = gmpy2.mul(gmpy2.powmod(self._g, y, self._p),
gmpy2.powmod(client.public_key, e, self._p))
z = gmpy2.t_mod(product, self._p)
trace('[SchnorrVerifier]', f'{z = }')
is_successful = x == z
print(f'Authentication successful: {is_successful}')
return is_successful
# ----
# Создаю доверенный центр
ca = SchnorrCA()
# Создам Алису - валидного пользователя
alice = SchnorrClient(ca.parameters)
# Регистрирую валидного пользователя
alice.register(ca)
# +
# Параметр безопасности положим равным 10 для демонстрации
security_parameter = 10
# Создаю проверяющую сторону
verifier = SchnorrVerifier(ca.parameters, security_parameter)
# -
# Произвожу аутентификацию валидного пользователя
verifier.authenticate(alice, ca)
# Создаю Еву - клиента, который пытается представиться Алисой
eve = SchnorrClient(ca.parameters,
fake_data=(alice.identifier, alice.public_key, alice.certificate))
# Произвожу аутентификацию невалидного пользователя
verifier.authenticate(eve, ca)
|
Lab 2/Lab 2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Wijuva/Programacion_Basica_Plazi/blob/master/TallerPython.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="GPMWnJo7wpiT"
# # Introduccion a Colab de Google
# ---
# + [markdown] id="cQNx7sNuwyBI"
# Colaboraty es una plataforma online de google gratuita para la ejecucion de Jupyter Notebooks https://jupyter.org/
# Tiene una integracion con drive
# + [markdown] id="g2UePZCIZhUh"
# Para montar una unidad de drive diferente a la sesion actual iniciada
# + colab={"base_uri": "https://localhost:8080/"} id="5_LYrfzPbW-U" outputId="d23cbcce-5b9b-4a85-b930-b4c00466c03a"
from google.colab import drive
drive.mount('/gdrive')
# %cd /gdrive/My\ Drive/Taller
# + colab={"base_uri": "https://localhost:8080/"} id="kfKr7gZCaWcM" outputId="7688ad88-8cd1-460a-c524-3e0c62c93002"
# %cd
# %cd ..
drive.flush_and_unmount()
# + [markdown] id="J4RRPnwhZnuB"
# Si se monta la misma unidad, cambiar a una carpeta especifica indicando la ruta
# + colab={"base_uri": "https://localhost:8080/"} id="cqonOhSNcP81" outputId="9b0205ab-a6d4-43f2-eee7-bc888cd606ff"
from google.colab import drive
drive.mount('/content/drive')
# %cd content/drive/MyDrive/Taller
# + [markdown] id="--06O21cZ0PZ"
# Obtener la ubicacion actual dentro de las carpetas del computador
# + colab={"base_uri": "https://localhost:8080/"} id="onqcKXJAi31j" outputId="2273a62a-30fe-4377-d321-539dfcdaba99"
# !pwd
# + [markdown] id="zO2cTWReZ9wc"
# Obtener los documentos dentro de la carpeta
# + colab={"base_uri": "https://localhost:8080/"} id="7J7F2Bv8cxBX" outputId="9f903d24-67aa-4fc1-b13e-90e917ee03b7"
# !ls
# + [markdown] id="k0iAsxAxe28A"
# Mostrar la imagen test.png
#
# Otros comandos de la consola https://www.hostinger.co/tutoriales/linux-comandos
# + colab={"base_uri": "https://localhost:8080/", "height": 435} id="ndKjOEKoenen" outputId="5e4fa9a5-2cec-4f5a-bb16-cdfc1828243f"
from IPython.display import Image
Image('test.png')
# + [markdown] id="zghYWigwssvt"
# # Operaciones Basicas
#
# ---
#
#
# + [markdown] id="KEpBPsYLsKzL"
# ### Suma
# + colab={"base_uri": "https://localhost:8080/"} id="kjaxA6KWr5-W" outputId="a7a65e3c-4a21-449b-d94a-8f688e773da2"
O_sum = 3 + 11
O_sum += 5
O_sum
# + [markdown] id="vQmLaItLsRkn"
# ### Multiplicacion
# + colab={"base_uri": "https://localhost:8080/"} id="nNX_LKZqsR1g" outputId="8c07ed92-e9a2-43ee-ad8d-0a4d8daedd71"
O_mult = 3 * 10
O_mult *= 3
O_mult
# + [markdown] id="6b23uzuJsTQS"
# ### Division
# + colab={"base_uri": "https://localhost:8080/"} id="2vxzlXHusTYg" outputId="a33f10b0-a53e-4f6b-9e11-b1849f98cd25"
O_div = 7 / 10
O_div
# + [markdown] id="x1j27NJBsSK3"
# ### Exponencial
# + colab={"base_uri": "https://localhost:8080/"} id="GHxRLMPssSUs" outputId="977c815b-d305-462d-b6cd-e6d1692fd227"
O_exp = 2 ** 6
O_exp
# + [markdown] id="-vlBLk3qsTjN"
# ### Modulo
# + colab={"base_uri": "https://localhost:8080/"} id="uEpf7f3-sTq6" outputId="cce0b048-563b-4660-aa94-2ade81d93627"
O_mod = 20 % 3
O_mod
# + [markdown] id="juFhRQh2qXPF"
# ### Cociente
# + colab={"base_uri": "https://localhost:8080/"} id="3EVwC1SoqMMd" outputId="9e216ab6-3121-48c4-f509-ae132ebf1206"
O_coci = 20 // 3
O_coci
# + [markdown] id="0mqceXvYxXnm"
# ### Operaciones de comparacion
# + colab={"base_uri": "https://localhost:8080/"} id="6zFyT6oKxaad" outputId="b7fbdd13-2c2f-45d0-ba1f-75b8b1d40e1b"
mi_boolean = 2 == 3
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="KkeMZ4w9xfJ2" outputId="fad14d91-f342-491d-cc76-976cd9b0729b"
mi_boolean = 'hola' != "hola"
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="O4cn2bi1yB7j" outputId="67bb8735-2b67-4435-fd76-5a4b234aaea5"
mi_boolean = 34 < 10
mi_boolean
# + id="KmOqilzHy9mr" colab={"base_uri": "https://localhost:8080/"} outputId="d91d5f2f-9a82-4e17-d61b-9b08b8a92e61"
mi_boolean = 35 >= 35
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="xeZqvfLJCIwV" outputId="ec1d7b63-4f3a-45cd-888c-0cfbef1d8767"
mi_boolean = 35 == 35 and 2 > 10
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="2y2kA8cyCPOm" outputId="3da67c4d-26aa-4494-b158-d6f16125f7b5"
mi_boolean = 14 <= 15 or 16 > 20
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="E8wOAV_dCW7q" outputId="9d64caef-71ba-4c79-b2c9-3d9bb1d00f6b"
mi_boolean = not 'hola' != "hola"
mi_boolean
# + [markdown] id="MJOnD8aepBEs"
# # Variables String (alfanumerico)
# ---
# + [markdown] id="cqRgwPhQpJbw"
# ### String
# + [markdown] id="ophnuP0jpbU3"
# Se puede usar tanto comillas dobles " " como comillas simples ' ' y sera interpretado como tipo string
# + colab={"base_uri": "https://localhost:8080/"} id="_Vy23nABpIwX" outputId="aad5460a-7925-4a85-c74d-95576255732c"
mensaje = 'Hola mundo'
print(type(mensaje))
mensaje = "Hola mundo"
print(type(mensaje))
# + [markdown] id="Zoj0kNAkrgyJ"
# ### Concatenar string
# + colab={"base_uri": "https://localhost:8080/"} id="CtRpMXgHpWzb" outputId="61719b4d-74f8-42b8-d5dc-9a75c496c86c"
mensaje += '\nBienvenidos'
print(mensaje)
# + [markdown] id="NBGIAhBmq8oI"
# ### Replicar String
# + colab={"base_uri": "https://localhost:8080/"} id="FPs4MfbLsOMd" outputId="005d1f95-9e96-469b-b22c-3d5f6fec6bd3"
mensaje = mensaje + '\n'*3 + 'Hello world '*2
print(mensaje)
# + [markdown] id="FOqThhNytFsr"
# ### Obtener una entrada del usuario
# + colab={"base_uri": "https://localhost:8080/"} id="NzUBRSuYswgG" outputId="659dc7d8-308f-43c3-9c93-321f2b831520"
x = input()
print(x)
type(x)
# + [markdown] id="OtoyZSXh_CPS"
# ### String format
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="Cs8gcwgi_EDU" outputId="e5c36604-b97f-4fec-8b20-c04f54c19f44"
mensaje = 'El nombre de la ciudad es {} del pais {}'.format('Bogota', 'Colombia')
mensaje
# + [markdown] id="WyDWnDtBGokl"
# # Tipos de conjuntos
# ---
# + [markdown] id="fuJgZ7x5fI28"
# ### Tuple
# + [markdown] id="vtNgFtbffkxX"
# Tuple vacia
# + id="Cqgg48_ffLW7"
mi_tuple = ()
mi_tuple
# + [markdown] id="cIVH2ylzfnNc"
# Se pueden guardar multiple tipos de archivos en una tupla
# + id="J1NMGpDGfSiP"
mi_tuple = (1, 2, 'hola')
mi_tuple
# + [markdown] id="EOIvhI0HfsmE"
# Se usa los [ ] para llamar a los elementos de una tupla, iniciando desde el elemento 0 en *adelante*
# + id="ABZ6x0tOfYaV"
numero1 = mi_tuple[0]
numero1
# + [markdown] id="0gcxJAytgGuD"
# Llamar multiples elementos
# + id="8jxbpn6ggF6Y"
print(mi_tuple[0:3:2])
# + [markdown] id="uHXlEeNFG86e"
# ### List
# + [markdown] id="lD1I0l94HPEF"
# Lista vacia
# + id="3SwmJzp5G_JY"
mi_lista = []
mi_lista
# + [markdown] id="DbpzfBxRH1WY"
# Agregar elementos a una lista
# + id="7vqWTrMHH3-9"
mi_lista.append('Hola')
mi_lista.append('Mundo')
mi_lista
# + [markdown] id="LgS7mR4MHZgO"
# Lista con 3 elementos tipo string
# + id="2NYZEdDXHfgp"
mi_lista = ['Andres', 'Andrea', 'Karen']
print(mi_lista)
print(len(mi_lista)) # len(list) devuelve el tamaño de una lista
mi_lista[0]
# + [markdown] id="wxeNDVAXIXFW"
# Lista con elemntos tipo float y string
# + id="YWAngqdBIa-c"
mi_lista = [4.5, 'hola']
print(type(mi_lista[0]))
print(type(mi_lista[1]))
mi_lista
# + [markdown] id="AOhjEB8OfLsQ"
# ### Diccionarios
# + colab={"base_uri": "https://localhost:8080/"} id="4FnjPo6b75ow" outputId="16c44fc7-3529-4cbc-e9a3-53808d8bd516"
diccionario = {
"Andres": [24, 173],
"Andrea": [25, 175],
1: 123
}
diccionario['Andres']
# + colab={"base_uri": "https://localhost:8080/"} id="IzJrbyEgz1Kp" outputId="ff4ce859-9bc4-44b8-ecf6-8f1970deffcd"
lista = diccionario.get("Andrea")
print(lista, type(lista))
# + colab={"base_uri": "https://localhost:8080/"} id="Oj4l8x1vz-79" outputId="c0d5cc93-9715-499e-a264-844ca81d584f"
diccionario[1]
# + colab={"base_uri": "https://localhost:8080/"} id="al54hj7I00kS" outputId="5b488ee2-f8a6-4800-9188-ae9d2cd8f29b"
diccionario.pop(1)
# + colab={"base_uri": "https://localhost:8080/"} id="c22vEuJS1mrp" outputId="818474a5-383a-4593-e2ac-47e5676ab5f9"
diccionario['Alex'] = [21, 124]
diccionario
# + id="85Aixabp1fRq"
diccionario.clear()
# + colab={"base_uri": "https://localhost:8080/"} id="v9JdJtKV1kpV" outputId="475f035a-03ad-462a-eb5e-b990f984bc40"
diccionario
# + [markdown] id="vYlDXCJ5st66"
# # Estructuras de Control
# ---
# + [markdown] id="7xU3J9c2vWMK"
# ### Clase booleana
# + id="o7n2DcwLtggy" colab={"base_uri": "https://localhost:8080/"} outputId="6ac400a7-2d5a-4322-b0f1-899183d95b7d"
mi_boolean = True
mi_boolean
# + id="1R8Uy942wc4p" colab={"base_uri": "https://localhost:8080/"} outputId="8396acd3-3a3e-452b-fa3a-843afa02a681"
mi_boolean = not(mi_boolean)
mi_boolean
# + colab={"base_uri": "https://localhost:8080/"} id="Nc2m5OQu23Ss" outputId="267746cd-554d-4b7f-d44f-0000eac1e9de"
booleano = "Andres" in diccionario
booleano
# + [markdown] id="Eb2rtit22t2m"
# ### Declaracion If, Else y Elif
# + id="421AI3Kq22XB" colab={"base_uri": "https://localhost:8080/"} outputId="454379f9-a328-4cbf-e6e9-33d631bbf89a"
a = 3
if a < 10:
print('Menor que 10')
# + id="mi4uX8sd9u62" colab={"base_uri": "https://localhost:8080/"} outputId="9641d74d-16c3-4ec2-a4ce-13403a695c19"
if a > 10:
print('Mayor que 10')
else:
print('Menor que 10')
# + id="cLtgTCpw-GxS" colab={"base_uri": "https://localhost:8080/"} outputId="aa8aad2f-86a4-446b-af9d-c3c6edf02218"
a = float(input())
if a == 10:
print('Igual que 10')
elif a > 10:
print('Mayor que 10')
else:
print('Menor que 10')
# + [markdown] id="BfD-RJK729sL"
# ### For
# + [markdown] id="xs0nHlfLKQlT"
# Se usa in para iteral en cada uno de los elementos de una lista
# + colab={"base_uri": "https://localhost:8080/"} id="lfKlE-wR4fW4" outputId="46401ede-4985-46d5-f92b-39b5c7dc5409"
lista = [0, 1, 2, 3, 4, 5]
for i in lista:
print(i)
# + colab={"base_uri": "https://localhost:8080/"} id="kDhHVAdT63IK" outputId="b4aeb0ff-ea44-4313-9bb8-af1a45839083"
lista = ['Andres', 'Andrea', 'Felipe']
for i in lista:
print(i)
# + [markdown] id="3uAuNsTRDvit"
# Uso de range
# + colab={"base_uri": "https://localhost:8080/"} id="VNJktad8Du8p" outputId="e5f5e755-25b8-4085-9b5a-d9894706d364"
for i in range(0, 6, 1):
print(i)
# + colab={"base_uri": "https://localhost:8080/"} id="y_3n2FCJFzXN" outputId="1bd7609b-0dbf-4b40-d39e-1eef3a2c1eb3"
lista1 = [1 ,2, 3, 4, 5]
lista2 = ['a', 'b', 'c', 'd', 'e']
lista3 = [1.73, 1.86, 1.84, 1.62, 1.70]
for i, j, k in zip(lista1, lista2, lista3):
print(i, j, k)
# + [markdown] id="Y9JSan6yKBe_"
# For else, sirve para realizar acciones en caso de no ejecutarse un "break"
# + colab={"base_uri": "https://localhost:8080/"} id="Q5RVVQimJPDY" outputId="e940046d-6388-4e05-dcc5-faf22d9e0c5e"
lista1 = [1 ,2, 3, 4, 5]
lista2 = ['a', 'b', 'c', 'd', 'e']
lista3 = [1.73, 1.86, 1.84, 1.62, 1.70]
numero = 3
for i, j, k in zip(lista1, lista2, lista3):
print(i, j, k)
if numero <= 1:
break
numero -= 1
else:
print('Todos los elementos fueron impresos')
# + [markdown] id="Ytgs_rJ6JLKT"
# ### While
# + id="njE8EmoyMFbP" colab={"base_uri": "https://localhost:8080/"} outputId="18567c70-ce39-42ce-a65f-9a300b97b734"
print('hola')
# + colab={"base_uri": "https://localhost:8080/"} id="gtS4TAeLOMs5" outputId="9d1ffeef-9f76-42fa-b4b5-38f539267915"
print('funciona?')
# + [markdown] id="_87Pd4xVTs6F"
# # Debugging en Jupyter Notebook
#
# + [markdown] id="pHbJcZhPT1s7"
# ### Debug despues de un error
# + id="kZheR25zT5pM"
a = 14
b = 5
b -= (a + 1)/3
Division = a / b
Division
# + id="UkDcSJfMUVXv"
# %debug
# + [markdown] id="jTGDLA5PUoL2"
# ### Debugging y breakpoints
# + [markdown] id="Ki-sFSj7U7R2"
# Para ejecutar el codigo paso a paso creamos una funcion Code_debug y usamos la libreria de debug de Ipython
# + id="mtBRAlPZU49d"
def Code_debug():
from IPython.core.debugger import set_trace
set_trace() # Se crea un breakpoint
a = 14
b = 5
b -= (a + 1)/3
Division = a / b
Code_debug()
# + [markdown] id="z4XM27rwXTap"
# ### Debugging a funciones
# + id="CK0AgbbnXZkT"
from IPython.core.debugger import set_trace
def Funcion1(a=1):
set_trace()
b = a ** 10
c = a / b
return c
Funcion1()
# + [markdown] id="hcVn-3wRRB99"
# # Bibliotecas Numpy y Sympy
# + [markdown] id="iU4zYzQwRKBD"
# ### Funciones
# + id="z1nfZ5mWRBLd"
import numpy as np
def f(x):
return np.sqrt(x + 2)
x = np.array([-2, -1, 0, 2, 4, 6]) # Creando el vector de valores de x
y = f(x)
list(zip(x, y))
# + [markdown] id="2HyPmL2rQ6xb"
# ### Derivadas
# + id="MehTzZ1TJWR-"
from sympy import Derivative, diff, simplify, Symbol
x = Symbol('x') # Creando el simbolo x.
fx = (2*x + 1)*(x**3 + 2)
dx = Derivative(fx, x).doit()
dx
# + id="cssJCFdiJX2X"
# simplificando los resultados
simplify(dx)
# + id="akHkxrMJJYKe"
# Derivada de segundo orden con el 3er argumento.
Derivative(fx, x, 2).doit()
# + id="BbWnLQHZJYhM"
# Calculando derivada de (3x +1) / (2x)
fx = (3*x + 1) / (2*x)
dx = Derivative(fx, x).doit()
simplify(dx)
# + id="zMBlmQwLJY1U"
# la función diff nos da directamente el resultado
simplify(diff(fx, x))
# + id="5Nrgi-JOJaTJ"
# con el metodo subs sustituimos el valor de x
# para obtener el resultado numérico. Ej x = 1.
diff(fx, x).subs(x, 1)
# + [markdown] id="ePWitZ1_R634"
# ### Integrales
# + id="Y2bKtcufSB4N"
from sympy import Integral, integrate
fx = x**3 - 6*x
dx = Integral(fx, x).doit()
dx
# + id="tbw7RujLSMPS"
# la función integrate nos da el mismo resultado
integrate(fx, x)
# + id="Rk7R6LUxSPA3"
# Calculando integral definida para [0, 3]
Integral(fx, (x, 0, 3)).doit()
|
TallerPython.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # MLE for GPP and ER models in Nakano et al., 2022
#
# (c) 2021 <NAME>
#
# - Estimate model parameters by MLE with AIC
# - Variance is assumed unknown
# - Observation $ y_i \sim N(x_i, \sigma^2) $
# - Model $ x_i = f_i(\theta) = f_{Ti}(E) \cdot f_{PARi}(a, b, c) $
# +
# !python --version
import numpy as np
import scipy
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
print('numpy', np.__version__)
print('scipy', scipy.__version__)
print('pandas', pd.__version__)
print('matplotlib', matplotlib.__version__)
# -
# # Observation
#
# - Daily GPP, ER, mean water temperature, and total PAR in data.csv
#
# ```csv
# Date, GPP, ER, meanWT, totalPAR
# 2016/2/19, 1.76, -3.16, 4.27, 30.6
# :
# ```
# +
f = 'data.csv'
df = pd.read_csv(f, parse_dates=[0], index_col=0).sort_values('GPP')
df.ER *= -1
Nfree = df.shape[0]
print('Degree of freedom observation is', Nfree)
sigma_obs = df.GPP.std(ddof=1)
print(r'Initial observation error standard deviation set by GPP data:', sigma_obs)
# -
# # Model
#
# $ R = f(T,I|R_{20}, E,a,b,c) = R_{20} \cdot \exp \left( \frac{E(T-T_{20})}{kTT_{20}} \right) \cdot (a I^2 + b I + c) $
# - GPP: c=0
# - ER: c=1
# +
from scipy import optimize
class Model():
"""
Base model
"""
def __init__(self, data, T, I):
self.data = data
self.T = T
self.I = I
self.fi = None
def ftemp(self, E):
k = 8.62e-5
T = self.T + 273.
T20 = 20. + 273.
return np.exp(E * (T - T20) / (k * T * T20))
def fi1(self, b, c):
return b * self.I + c
def fi2(self, a, b, c):
return a * self.I ** 2 + b * self.I + c
def estimate(self, xcoef):
E, *param = xcoef
return self.ftemp(E) * self.fi(*param)
class F1(Model):
"""
Linear function with R20
"""
def __init__(self, *args, c=0):
Model.__init__(self, *args)
self.fi = self.fi1
self.pname = 'R20 E b'.split()
self.c = c
def estimate(self, xcoef):
R20, E, b = xcoef
return R20 * self.ftemp(E) * self.fi(b, self.c)
class F2(Model):
"""
Quadratic function with R20
"""
def __init__(self, *args, c=0):
Model.__init__(self, *args)
self.fi = self.fi2
self.pname = 'R20 E a b'.split()
self.c = c
def estimate(self, xcoef):
R20, E, a, b = xcoef
return R20 * self.ftemp(E) * self.fi(a, b, self.c)
# set model
GPP1 = F1(df['GPP'], df['meanWT'], df['totalPAR'], c=0)
GPP2 = F2(df['GPP'], df['meanWT'], df['totalPAR'], c=0)
ER2 = F2(df['ER'], df['meanWT'], df['totalPAR'], c=1)
# test (first guess)
x0 = [1., 0.4, 0.7]
est = GPP1.estimate(x0)
ax = df.assign(GPPest=est).plot.scatter(x='GPP', y='GPPest')
x0 = [1., 0.4, -0.002, 0.7]
GPPest0 = GPP2.estimate(x0)
ERest0 = ER2.estimate(x0)
df.assign(GPPest=GPPest0).plot.scatter(x='GPP', y='GPPest', ax=ax, c='C1')
ax.legend(['Linear model', 'Quadratic model'])
ax.plot([0,30],[0,30], lw=0.5, c='k')
ax.set_title('First guess')
# -
# # MLE (Maximum Likelihood Estimation)
#
# - Log likelihood: $ \log L(\theta, \sigma^2) = −\frac{n}{2} \log(2 \pi) −\frac{n}{2} \log(\sigma^2) − \frac{1}{2 \sigma^2} \sum^n_{i=1} (f_i(\theta) − y_i)^2 $
#
# - Standard Error (SE) calculated by Fisher information
#
# - Model selection: $ \mathrm {AIC} =-2\log L+2k $
# +
class MLE():
"""
Maximum Likelihood Estimation
"""
def __init__(self, model, x0, sigma):
"""
model: model class (object)
x0: initial parameter values (array-like)
sigma: initial sigma value (scaler)
"""
self.model = model
self.x0 = np.append(np.array(x0), sigma) # estimate parameters
def logL(self, x):
xv = x * self.x0
*xv, sigma = xv
Hx = self.model.estimate(xv)
y = self.model.data
d = y - Hx
n = d.shape[0]
return -0.5*n * np.log(2*np.pi*sigma*sigma) -0.5/sigma/sigma * np.sum(d*d)
def deviance(self, x):
return -2 * self.logL(x)
def optimize(self, disp=False):
x0 = np.ones_like(self.x0)
res = optimize.minimize(self.deviance, x0, method='BFGS', options={'disp':disp, 'maxiter':10000})
res.x_scaled = res.x * self.x0
res.se_scaled = np.sqrt(np.diag(res.hess_inv)) * np.abs(self.x0)
return res
def AIC(self, x):
D = self.deviance(x)
return D + 2*len(x)
def main(model, x0, sigma, plot=False, fout=None):
"""
Main function
Return: dict
"""
mle = MLE(model, x0=x0, sigma=sigma)
# optimize
res = mle.optimize(disp=False)
*x_opt, sigma_opt = res.x_scaled
#print(res.x_scaled, res.message)
print(res.message)
# output
x = res.x_scaled
se = res.se_scaled
out = {'k':len(res.x)}
for i, pname in enumerate(model.pname):
out[pname] = x[i]
out[pname+'_se'] = se[i]
out['sigma'] = x[-1]
out['sigma_se'] = se[-1]
out.update({
'logL':mle.logL(res.x),
'deviance':mle.deviance(res.x),
'AIC':mle.AIC(res.x)
})
return out, x, se, res.message
def run_iter(model, x0, seed=0):
np.random.seed(seed)
out, xopt, se, m = main(model, x0=x0, sigma=sigma_obs)
for i in range(1,10):
if m == 'Optimization terminated successfully.' and i>1:
return out
x, xse = xopt[:-1]*(1/i), se[:-1]*(1/i)
s, sse = xopt[-1]*(1/i), se[-1]*(1/i)
out, xopt, se, m = main(model, x0=np.random.normal(x, xse), sigma=np.random.normal(s, sse))
# test
x0 = [10., 0.1, -0.001, 10.]
GPPopt = run_iter(GPP2, x0, seed=0)
# -
# # Estimate GPP
# +
GPPopt = run_iter(GPP2, x0, seed=0)
est = GPP2.estimate([GPPopt[vname] for vname in 'R20 E a b'.split()])
ax = df.assign(GPPest=GPPest0).plot.scatter(x='GPP', y='GPPest', c='lightgrey')
ax = df.assign(GPPest=est).plot.scatter(x='GPP', y='GPPest', c='k', ax=ax)
ax.legend(['First guess', 'MLE'])
ax.plot([0,30],[0,30], lw=0.5, c='k')
# -
# # Estimate ER
# +
ERopt = run_iter(ER2, x0, seed=0)
est = ER2.estimate([ERopt[vname] for vname in 'R20 E a b'.split()])
ax = df.assign(ERest=ERest0).plot.scatter(x='ER', y='ERest', c='lightgrey')
ax = df.assign(ERest=est).plot.scatter(x='ER', y='ERest', c='k', ax=ax)
ax.legend(['First guess', 'MLE'])
ax.plot([0,30],[0,30], lw=0.5, c='k')
# -
# # Export CSV file
# +
f = 'MLE.csv'
raw = pd.DataFrame([GPPopt, ERopt], index='GPP ER'.split())
raw = raw[GPPopt.keys()]
raw.to_csv(f'raw_{f}')
with open(f, 'w', encoding='utf-8') as f:
f.write(' , k, b0, E, a, b, sigma, logL, Deviance, AIC\n')
for i, row in raw.iterrows():
f.write('{}, {:.0f}, {:.2f}±{:.2f}, {:.3f}±{:.3f}, {:.4f}±{:.4f}, {:.3f}±{:.3f}, {:.2f}±{:.2f}, {:.1f}, {:.1f}, {:.1f}\n'.format(i, *row))
|
MLE.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: "Python 3.7 (Intel\xAE oneAPI)"
# language: python
# name: c009-intel_distribution_of_python_3_oneapi-beta05-python
# ---
# # Introduction to JupyterLab and Notebooks
# If you are familiar with Jupyter skip below and head to the first exercise.
#
# <video controls src="src/Introduction_to_Jupyter.mp4" width="720"/>
# __JupyterLab__ is a sequence of boxes referred to as "cells". Each cell will contain text, like this one, or C++ or Python code that may be executed as part of this tutorial. As you proceed, please note the following:
#
# * The active cell is indicated by the blue bar on the left. Click on a cell to select it.
#
# * Use the __"run"__ ▶ button at the top or __Shift+Enter__ to execute a selected cell, starting with this one.
# * Note: If you mistakenly press just Enter, you will enter the editing mode for the cell. To exit editing mode and continue, press Shift+Enter.
#
#
# * Unless stated otherwise, the cells containing code within this tutorial MUST be executed in sequence.
#
# * You may save the tutorial at any time, which will save the output, but not the state. Saved Jupyter Notebooks will save sequence numbers which may make a cell appear to have been executed when it has not been executed for the new session. Because state is not saved, re-opening or __restarting a Jupyter Notebook__ will required re-executing all the executable steps, starting in order from the beginning.
#
# * If for any reason you need to restart the tutorial from the beginning, you may reset the state of the Jupyter Notebook and clear all output. Use the menu at the top to select __Kernel -> "Restart Kernel and Clear All Outputs"__
#
# * Cells containing Markdown can be executed and will render. However, there is no indication of execution, and it is not necessary to explicitly execute Markdown cells.
#
# * Cells containing executable code will have "a [ ]:" to the left of the cell:
# * __[ ]__ blank indicates that the cell has not yet been executed.
# * __[\*]__ indicates that the cell is currently executing.
# * Once a cell is done executing, a number will appear in the small brackets with each cell execution to indicate where in the sequence the cell has been executed. Any output (e.g. print()'s) from the code will appear below the cell.
# ### Code editing, Compiling and Running in Jupyter Notebooks
# This code shows a simple C++ Hello world. Inspect code, there are no modifications necessary:
# 1. Inspect the code cell below and click run ▶ to save the code to file
# 2. Next run ▶ the cell in the __Build and Run__ section below the code to compile and execute the code.
#
# +
# %%writefile src/hello.cpp
#include <iostream>
#define RESET "\033[0m"
#define RED "\033[31m" /* Red */
#define BLUE "\033[34m" /* Blue */
int main(){
std::cout << RED << "Hello World" << RESET << std::endl;
}
# -
# ### Build and Run
# Select the cell below and click run ▶ to compile and execute the code above:
# ! chmod 755 q; chmod 755 run_hello.sh;if [ -x "$(command -v qsub)" ]; then ./q run_hello.sh; else run_hello.sh; fi
# <html><body><span style="color:green"><h1>Get started on Module 1</h1></span></body></html>
#
# [Click Here](../01_oneAPI_Intro/oneAPI_Intro.ipynb)
# ### Refresh Your Jupyter Notebooks
# If it's been awhile since you started exploring the notebooks, you will likely need to update them for compatibility with Intel® DevCloud for oneAPI and the Intel® oneAPI DPC++ Compiler to keep up with the latest updates.
#
# Run the cell below to get latest and replace with latest version of oneAPI Essentials Modules:
# !/data/oneapi_workshop/get_jupyter_notebooks.sh
|
DirectProgramming/DPC++/Jupyter/oneapi-essentials-training/00_Introduction_to_Jupyter/Introduction_to_Jupyter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ! ls /Users/guillermogonzalez/ga/evan_github/input/
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# ### Train Data EDA
df_train = pd.read_csv('../input/train.csv')
columns = df_train.columns
for col in columns:
print(col)
print(df_train[col].value_counts().sort_values(ascending=False))
df_train['Date'].nunique()
df_train.nunique()
train = df_train.drop(labels=['Address','Block','Street',
'AddressNumberAndStreet',
'AddressAccuracy'],axis=1)
train['Date'] = pd.to_datetime(train['Date']) # convert dtype to date
train.info()
plt.hist(x=train['WnvPresent'])
plt.show()
plt.hist(x=train['NumMosquitos'])
plt.show()
train['Species'].sort_values()
plt.hist(x=train['Species'].sort_values(),orientation='vertical')
plt.xticks(x=train['Species'], rotation='vertical')
plt.title('Species Histogram')
plt.xlabel('Species',size='large')
plt.ylabel('Counts',size='large')
plt.show()
# ### Test Data EDA
df_test = pd.read_csv('../input/test.csv')
# +
columns_test = df_test.columns
for col in columns_test:
print(col)
print(df_test[col].value_counts())
# -
df_test[ df_test['Trap']=='T094B' ]
df_test['Trap'].nunique()
df_test['Date'].nunique()
df_test['Id'].nunique()
test = df_test.drop(labels=['Address','Block','Street',
'AddressNumberAndStreet',
'AddressAccuracy'],axis=1)
test['Date'] = pd.to_datetime(test['Date']) # convert date dtype to date
test.info()
plt.hist(x=test['Species'].sort_values(),orientation='vertical')
plt.xticks(x=test['Species'], rotation='vertical')
plt.title('Species Histogram')
plt.xlabel('Species',size='large')
plt.ylabel('Counts',size='large')
plt.show()
# ### Weather data EDA
df_weather = pd.read_csv('../input/weather.csv')
df_weather.nunique()
columns_w = df_weather.columns
for col in columns_w:
print(col)
print(df_weather[col].value_counts())
df_weather.columns
# +
code_list = list(set([i[j] for i in [title.split() for title in bt.pd.get_dummies(pro_w.df.CodeSum).columns.tolist()] for j in range(len(i))]))
for code in code_list:
pro_w.df[code] = [1 if code in pro_w.df.CodeSum[i] else 0 for i in range(pro_w.df.CodeSum.shape[0])]
# -
weather = df_weather.drop(['CodeSum','Depth','Water1','SnowFall',
],axis=1)
weather['Date'] = pd.to_datetime(weather['Date']) # convert date dtype to date
weather[['Tavg','WetBulb','Heat','Cool']] = weather[['Tavg','WetBulb','Heat','Cool']].copy().astype(dtype='int') # M to 0
weather[['Sunrise','Sunset']] = weather[['Sunrise','Sunset']].copy().astype(dtype='int') # converting - to 0
weather['PrecipTotal'] = weather['PrecipTotal'].copy().astype(dtype='float') # T and M to 0
weather.head()
weather.info()
# Farenheit to Celcius for RH calculation
weather[['Tavg(C)','DewPoint(C)']]=weather[['Tavg','DewPoint']].apply(lambda x: (x-32)*(5/9)).round(1)
#Calculation Relative Humidity
weather['RH'] = (100*(1.8096 + np.exp(17.2694*weather['DewPoint(C)']/(237.3 + weather['DewPoint(C)'])))/
(1.8096 + np.exp((17.2694*weather['Tavg(C)']/(237.3 + weather['Tavg(C)']))))).round(1)
weather.shape
weather.groupby('Date')[['Tmax','Tmin','Tavg','DewPoint','WetBulb','Heat','Cool']].mean().shape
# ### Spray Data EDA
df_spray = pd.read_csv('/Users/guillermogonzalez/ga/evan_github/input/spray.csv')
df_spray.nunique()
columns_spray = df_spray.columns
for col in columns_spray:
print(col)
print(df_spray[col].value_counts())
df_spray.isnull().sum()
spray = df_spray.copy()
spray['Time']
# ### Sample Submission data EDA
df_sample = pd.read_csv('/Users/guillermogonzalez/ga/evan_github/input/sampleSubmission.csv')
df_sample.nunique()
# ### Date Ranges
print(' Min Max')
print('train = ',df_train['Date'].min(),' ', df_train['Date'].max())
print('test = ',df_test['Date'].min(),' ', df_test['Date'].max())
print('weather =',df_weather['Date'].min(),' ', df_weather['Date'].max())
print('spray = ',df_spray['Date'].min(),' ', df_spray['Date'].max())
|
working/.ipynb_checkpoints/WestNile-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="wcq6dWzy1ZR0"
# # Payment Date Prediction
# + [markdown] id="2778654e"
#
# ### Importing related Libraries
# + id="304c9e38"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# + [markdown] id="8724f5ee"
# ### Store the dataset into the Dataframe
#
# + id="415db50a"
data = pd.read_csv('dataset.csv')
# + [markdown] id="42e37f05"
# ### Check the shape of the dataframe
#
# + id="27cc0907"
data.shape
# + [markdown] id="b68c955d"
# ### Check the Detail information of the dataframe
# + id="e092ec9e"
data.info()
# + [markdown] id="112f2d0e"
# ### Display All the column names
# + id="1416e2fd"
print(data.columns)
# + [markdown] id="d465ed7a"
# ### Describe the entire dataset
# + id="25f65e1b"
data.describe()
# + [markdown] id="0f2c8d02"
# # Data Cleaning
#
# - Show top 5 records from the dataset
# + id="8f876212"
data.head()
# + [markdown] id="92b044e4"
# ### Display the Null values percentage against every columns (compare to the total number of records)
#
# - Output expected : area_business - 100% null, clear_data = 20% null, invoice_id = 0.12% null
# + id="24c7b13d"
# creating a list of features with missing values
features_with_nill = [x for x in data.columns if data[x].isnull().sum() > 0]
# printing out that list
for i in features_with_nill:
print(i,'= ', np.round(data[i].isnull().mean()*100, 4), '% null')
# + [markdown] id="2c46a98b"
# ### Display Invoice_id and Doc_Id
#
# - Note - Many of the would have same invoice_id and doc_id
#
# + id="038f24bb"
data[['invoice_id', 'doc_id']]
# -
data.loc[data['invoice_id'] != data['doc_id']]
# There are only 6 values that are not same, because they have null values in invoice id
# + [markdown] id="18cfe10a"
# #### Write a code to check - 'baseline_create_date',"document_create_date",'document_create_date.1' - these columns are almost same.
#
# - Please note, if they are same, we need to drop them later
#
#
# -
data[['baseline_create_date','document_create_date','document_create_date.1']].head()
# From the above table we can see that they are quite similar
# Now we are trying to prove the same
data['baseline_create_date'].astype(int)
# + id="cf5b40ff"
# comparing baseline_create_date and document_create_date
result = data['baseline_create_date'].ge(data['document_create_date']) | np.isclose(data['baseline_create_date'], data['document_create_date'])
# -
result.value_counts()
# From above, we can see that both columns are very much similar
# +
# comparing baseline_create_date and document_create_date.1
result1 = data['baseline_create_date'].ge(data['document_create_date.1']) | np.isclose(data['baseline_create_date'], data['document_create_date.1'])
# -
result1.value_counts()
# document_create_date.1 is almost equal to baseline_create_date
# From the above data, we can conclude that the three columns are very much similar to each other and can be dropped later
# + [markdown] id="33110576"
# #### Please check, Column 'posting_id' is constant columns or not
#
# + id="ecce2664"
print(data.posting_id.nunique())
# + [markdown] id="e5fb8daf"
# #### Please check 'isOpen' is a constant column and relevant column for this project or not
# + id="8db9956b"
print(data.isOpen.nunique())
# -
print(data.isOpen.value_counts())
# isOpen is only contains 2 values. Hence, it is not relavant for this project
# + [markdown] id="45a11a62"
# ### Write the code to drop all the following columns from the dataframe
#
# - 'area_business'
# - "posting_id"
# - "invoice_id"
# - "document_create_date"
# - "isOpen"
# - 'document type'
# - 'document_create_date.1
# + id="270d85d1"
data = data.drop(columns=['area_business', 'posting_id', 'invoice_id', 'document_create_date', 'isOpen', 'document type', 'document_create_date.1'])
# + [markdown] id="K5LHAM2XVGnk"
# ### Please check from the dataframe whether all the columns are removed or not
# + id="ef3f7d2b"
print(data.columns)
# -
data.shape
# + [markdown] id="6bc052c7"
# ### Show all the Duplicate rows from the dataframe
# + id="1ae3c7e4"
data.loc[data.duplicated() == True]
# + [markdown] id="464fab09"
# ### Display the Number of Duplicate Rows
# -
data.duplicated().sum()
# + [markdown] id="827a6718"
# ### Drop all the Duplicate Rows
# + id="5d10151c"
data.drop_duplicates(inplace=True)
# + [markdown] id="7e5d1f9b"
# #### Now check for all duplicate rows now
#
# - Note - It must be 0 by now
# + id="9accc9fc"
data.duplicated().sum()
# -
# There are 0 True values
# + [markdown] id="d0704898"
# ### Check for the number of Rows and Columns in your dataset
# + id="582748a8"
data.shape
# + [markdown] id="4o9c5UodWRtl"
# ### Find out the total count of null values in each columns
# + id="b0612cb5"
data.isnull().sum()
# + [markdown] id="7abdb98b"
# # Data type Conversion
# + [markdown] id="LPfSUSp-WpPj"
# ### Please check the data type of each column of the dataframe
# + id="689c8592"
data.dtypes
# + [markdown] id="0nsem0_3XzOt"
# ### Check the datatype format of below columns
#
# - clear_date
# - posting_date
# - due_in_date
# - baseline_create_date
# + id="-yyODyW3X6pL"
print(data['clear_date'].dtype)
print(data['posting_date'].dtype)
print(data['due_in_date'].dtype)
print(data['baseline_create_date'].dtype)
# + [markdown] id="11cf9478"
# ### converting date columns into date time formats
#
# - clear_date
# - posting_date
# - due_in_date
# - baseline_create_date
#
#
# - **Note - You have to convert all these above columns into "%Y%m%d" format**
# -
import datetime as dt
data['clear_date'] = pd.to_datetime(data['clear_date'])
data['posting_date'] = pd.to_datetime(data['posting_date'])
# + id="9a8c6c71"
data['due_in_date'] = data['due_in_date'].astype(str) # converting into string type
data['due_in_date'] = data['due_in_date'].str.slice(0,9) # slicing the number part
data['due_in_date'] = pd.to_datetime(data['due_in_date']) # converting into datetime dtype
# -
data['baseline_create_date'] = data['baseline_create_date'].astype(str) # converting into string type
data['baseline_create_date'] = data['baseline_create_date'].str.slice(0,9) # slicing the number part
data['baseline_create_date'] = pd.to_datetime(data['baseline_create_date']) # converting into datetime dtype
data.head()
# + [markdown] id="7adq0wSIYSCS"
# ### Please check the datatype of all the columns after conversion of the above 4 columns
# + id="fd028c61"
data.dtypes
# -
# Checking for null values in datetime columns
data['clear_date'].isnull().value_counts()
print(data['posting_date'].isnull().value_counts())
print(data['due_in_date'].isnull().value_counts())
print(data['baseline_create_date'].isnull().value_counts())
# + [markdown] id="8c9882fa"
# #### the invoice_currency column contains two different categories, USD and CAD
#
# - Please do a count of each currency
# + id="72085397"
data.invoice_currency.value_counts()
# + [markdown] id="6cbe26ee"
# #### display the "total_open_amount" column value
# -
data['total_open_amount']
# + id="6c49f2ab"
data.total_open_amount.sum()
# + [markdown] id="df899966"
# ### Convert all CAD into USD currency of "total_open_amount" column
#
# - 1 CAD = 0.7 USD
# - Create a new column i.e "converted_usd" and store USD and convered CAD to USD
# -
data.reset_index(inplace=True, drop=True)
data.invoice_currency.value_counts()
# + id="8eb2f1c5"
for i in range(len(data)):
if(data.at[i,'invoice_currency'] == 'USD'):
data.at[i,'converted_usd'] = data.at[i,'total_open_amount']
else:
data.at[i,'converted_usd'] = data.at[i,'total_open_amount']*0.7
# -
data.head()
# + [markdown] id="f9f6ef1d"
# ### Display the new "converted_usd" column values
# + id="1fc1a178"
data['converted_usd']
# + [markdown] id="6XLXX17kayuy"
# ### Display year wise total number of record
#
# - Note - use "buisness_year" column for this
# + id="00c9f6ee"
data['buisness_year'].value_counts()
# + [markdown] id="05c35904"
# ### Write the code to delete the following columns
#
# - 'invoice_currency'
# - 'total_open_amount',
# + id="4ac28aa5"
data = data.drop(columns=['invoice_currency','total_open_amount'])
# + [markdown] id="bDBJ_Kvwc086"
# ### Write a code to check the number of columns in dataframe
# + id="ea360a8c"
len(data.columns)
# + [markdown] id="b8f63655"
# # Splitting the Dataset
# + [markdown] id="a00f749d"
# ### Look for all columns containing null value
#
# - Note - Output expected is only one column
# + id="148c801e"
data.isnull().any()
# + [markdown] id="a094a290"
# #### Find out the number of null values from the column that you got from the above code
# + id="30bfb113"
data['clear_date'].isnull().sum()
# + [markdown] id="7f6d939b"
# ### On basis of the above column we are spliting data into dataset
#
# - First dataframe (refer that as maindata) only containing the rows, that have NO NULL data in that column ( This is going to be our train dataset )
# - Second dataframe (refer that as nulldata) that contains the columns, that have Null data in that column ( This is going to be our test dataset )
# +
main_dataset=data[data['clear_date'].isnull()==False]
nulldata=data[data['clear_date'].isnull()==True]
# + [markdown] id="3P8riRBHd_r6"
# ### Check the number of Rows and Columns for both the dataframes
# + id="0693a464"
main_dataset.shape
# + id="7f86bc74"
nulldata.shape
# + [markdown] id="0747165d"
# ### Display the 5 records from maindata and nulldata dataframes
# + id="dec2ec36"
main_dataset.head()
# + id="eee2d68a"
nulldata.head()
# + [markdown] id="24aa6746"
# ## Considering the **maindata**
# + [markdown] id="f92c4aa7"
# #### Generate a new column "Delay" from the existing columns
#
# - Note - You are expected to create a new column 'Delay' from two existing columns, "clear_date" and "due_in_date"
# - Formula - Delay = clear_date - due_in_date
# + id="8eeceb9c"
delay = main_dataset.clear_date - main_dataset.due_in_date
# -
main_dataset['delay'] = delay
main_dataset.head()
# + [markdown] id="f482144e"
# ### Generate a new column "avgdelay" from the existing columns
#
# - Note - You are expected to make a new column "avgdelay" by grouping "name_customer" column with reapect to mean of the "Delay" column.
# - This new column "avg_delay" is meant to store "customer_name" wise delay
# - groupby('name_customer')['Delay'].mean(numeric_only=False)
# - Display the new "avg_delay" column
# + id="d18d2f8d"
avg_delay = main_dataset.groupby('name_customer')['delay'].mean(numeric_only=False)
# -
avg_delay
# + [markdown] id="64b995e8"
# You need to add the "avg_delay" column with the maindata, mapped with "name_customer" column
#
# - Note - You need to use map function to map the avgdelay with respect to "name_customer" column
# + id="e1e1f3d9"
main_dataset['avg_delay'] = main_dataset['name_customer'].map(avg_delay)
# -
main_dataset.head()
# + [markdown] id="1d332525"
# ### Observe that the "avg_delay" column is in days format. You need to change the format into seconds
#
# - Days_format : 17 days 00:00:00
# - Format in seconds : 1641600.0
# -
main_dataset['avg_delay'] = main_dataset['avg_delay'] / np.timedelta64(1, 's')
# + [markdown] id="OvgtHSsx_O-n"
# ### Display the maindata dataframe
# + id="97ca9c45"
main_dataset.head()
# + [markdown] id="ae24c7bb"
# ### Since you have created the "avg_delay" column from "Delay" and "clear_date" column, there is no need of these two columns anymore
#
# - You are expected to drop "Delay" and "clear_date" columns from maindata dataframe
# + id="78a61ab9"
main_dataset = main_dataset.drop(columns=['delay', 'clear_date'])
# -
main_dataset.head()
main_dataset.shape
# + [markdown] id="ae724bfc"
# # Splitting of Train and the Test Data
# + [markdown] id="cb6f0264"
# ### You need to split the "maindata" columns into X and y dataframe
#
# - Note - y should have the target column i.e. "avg_delay" and the other column should be in X
#
# - X is going to hold the source fields and y will be going to hold the target fields
# + id="75ab29ab"
y = main_dataset['avg_delay']
# + id="6412c62b"
X = main_dataset.drop(columns=['avg_delay'])
# -
X.shape
X.head()
y.shape
y.head()
# + [markdown] id="1c2942bf"
# #### You are expected to split both the dataframes into train and test format in 60:40 ratio
#
# - Note - The expected output should be in "X_train", "X_loc_test", "y_train", "y_loc_test" format
# + id="d92160a5"
from sklearn.model_selection import train_test_split
# -
X_train, X_loc_test, y_train, y_loc_test = train_test_split(X, y, test_size=0.4)
# + [markdown] id="p4OME62pDufR"
# ### Please check for the number of rows and columns of all the new dataframes (all 4)
# + id="48328d0a"
print('X_train ->', X_train.shape)
print('X_loc_test ->', X_loc_test.shape)
print('y_train ->', y_train.shape)
print('y_loc_test ->', y_loc_test.shape)
# + [markdown] id="4a68ed71"
# ### Now you are expected to split the "X_loc_test" and "y_loc_test" dataset into "Test" and "Validation" (as the names given below) dataframe with 50:50 format
#
# - Note - The expected output should be in "X_val", "X_test", "y_val", "y_test" format
# + id="b56c62f2"
X_val, X_test, y_val, y_test = train_test_split(X_loc_test, y_loc_test, test_size=0.5)
# + [markdown] id="bJTSAskvERH1"
# ### Please check for the number of rows and columns of all the 4 dataframes
# + id="845d7564"
print('X_val ->', X_val.shape)
print('X_test ->', X_test.shape)
print('y_val ->', y_val.shape)
print('y_test ->', y_test.shape)
# + [markdown] id="110fa872"
# # Exploratory Data Analysis (EDA)
# + [markdown] id="ffc8fe0f"
# ### Distribution Plot of the target variable (use the dataframe which contains the target field)
#
# - Note - You are expected to make a distribution plot for the target variable
# + id="ba2bf8ed"
sns.displot(y, bins=35)
# + [markdown] id="d0e323a3"
# ### You are expected to group the X_train dataset on 'name_customer' column with 'doc_id' in the x_train set
#
# ### Need to store the outcome into a new dataframe
#
# - Note code given for groupby statement- X_train.groupby(by=['name_customer'], as_index=False)['doc_id'].count()
# + id="f7acf0ee"
new_data = X_train.groupby(by=['name_customer'], as_index=False)['doc_id'].count()
# + [markdown] id="cA43bFffFt6i"
# ### You can make another distribution plot of the "doc_id" column from x_train
# + id="9576bf33"
sns.displot(X_train['doc_id'], bins=20)
# + [markdown] id="fba2c44f"
# #### Create a Distribution plot only for business_year and a seperate distribution plot of "business_year" column along with the doc_id" column
#
# + id="4fecec77"
sns.displot(X_train['buisness_year'], bins=20)
# + id="qr1jGhfOKjnw"
sns.displot(X_train['buisness_year'], bins=20)
sns.displot(X_train['doc_id'], bins=20)
# + [markdown] id="968fbcc9"
# # Feature Engineering
# + [markdown] id="jbh6CyGqH3XE"
# ### Display and describe the X_train dataframe
# + id="e6bcf307"
X_train.head()
# + id="08ccc819"
X_train.describe()
# + [markdown] id="abd7ac8b"
# #### The "business_code" column inside X_train, is a categorical column, so you need to perform Labelencoder on that particular column
#
# - Note - call the Label Encoder from sklearn library and use the fit() function on "business_code" column
# - Note - Please fill in the blanks (two) to complete this code
# + id="7c223545"
from sklearn.preprocessing import LabelEncoder
business_coder = LabelEncoder()
business_coder.fit(X_train['business_code'])
# + [markdown] id="f86f7d9c"
# #### You are expected to store the value into a new column i.e. "business_code_enc"
#
# - Note - For Training set you are expected to use fit_trainsform()
# - Note - For Test set you are expected to use the trainsform()
# - Note - For Validation set you are expected to use the trainsform()
#
#
# - Partial code is provided, please fill in the blanks
# + id="4269c307"
X_train['business_code_enc'] = business_coder.fit_transform(X_train['business_code'])
# + id="70a53712"
X_val['business_code_enc'] = business_coder.transform(X_val['business_code'])
X_test['business_code_enc'] = business_coder.transform(X_test['business_code'])
# + [markdown] id="gdNYxTkqNfmz"
# ### Display "business_code" and "business_code_enc" together from X_train dataframe
# + id="1196a002"
X_train[['business_code','business_code_enc']]
# + [markdown] id="11477224"
# #### Create a function called "custom" for dropping the columns 'business_code' from train, test and validation dataframe
#
# - Note - Fill in the blank to complete the code
# + id="1052868a"
def custom(col ,traindf = X_train,valdf = X_val,testdf = X_test):
traindf.drop(col, axis =1,inplace=True)
valdf.drop(col,axis=1 , inplace=True)
testdf.drop(col,axis=1 , inplace=True)
return traindf,valdf ,testdf
# + [markdown] id="rI--ZuMbNLne"
# ### Call the function by passing the column name which needed to be dropped from train, test and validation dataframes. Return updated dataframes to be stored in X_train ,X_val, X_test
#
# - Note = Fill in the blank to complete the code
# + id="1a0f955c"
X_train , X_val , X_test = custom(['business_code'])
# + [markdown] id="28b5b27e"
# ### Manually replacing str values with numbers, Here we are trying manually replace the customer numbers with some specific values like, 'CCCA' as 1, 'CCU' as 2 and so on. Also we are converting the datatype "cust_number" field to int type.
#
# - We are doing it for all the three dataframes as shown below. This is fully completed code. No need to modify anything here
#
#
# + id="85dd129e"
X_train['cust_number'] = X_train['cust_number'].str.replace('CCCA',"1").str.replace('CCU',"2").str.replace('CC',"3").astype(int)
X_test['cust_number'] = X_test['cust_number'].str.replace('CCCA',"1").str.replace('CCU',"2").str.replace('CC',"3").astype(int)
X_val['cust_number'] = X_val['cust_number'].str.replace('CCCA',"1").str.replace('CCU',"2").str.replace('CC',"3").astype(int)
# + [markdown] id="U8vA-zmdPnJ8"
# #### It differs from LabelEncoder by handling new classes and providing a value for it [Unknown]. Unknown will be added in fit and transform will take care of new item. It gives unknown class id.
#
# #### This will fit the encoder for all the unique values and introduce unknown value
#
# - Note - Keep this code as it is, we will be using this later on.
# + id="151f48ba"
#For encoding unseen labels
class EncoderExt(object):
def __init__(self):
self.label_encoder = LabelEncoder()
def fit(self, data_list):
self.label_encoder = self.label_encoder.fit(list(data_list) + ['Unknown'])
self.classes_ = self.label_encoder.classes_
return self
def transform(self, data_list):
new_data_list = list(data_list)
for unique_item in np.unique(data_list):
if unique_item not in self.label_encoder.classes_:
new_data_list = ['Unknown' if x==unique_item else x for x in new_data_list]
return self.label_encoder.transform(new_data_list)
# + [markdown] id="254c64e6"
# ### Use the user define Label Encoder function called "EncoderExt" for the "name_customer" column
#
# - Note - Keep the code as it is, no need to change
# + id="62b17eff"
label_encoder = EncoderExt()
label_encoder.fit(X_train['name_customer'])
X_train['name_customer_enc']=label_encoder.transform(X_train['name_customer'])
X_val['name_customer_enc']=label_encoder.transform(X_val['name_customer'])
X_test['name_customer_enc']=label_encoder.transform(X_test['name_customer'])
# + [markdown] id="mK7LMoy2QZhy"
# ### As we have created the a new column "name_customer_enc", so now drop "name_customer" column from all three dataframes
#
# - Note - Keep the code as it is, no need to change
# + id="ef85f1c0"
X_train ,X_val, X_test = custom(['name_customer'])
# + [markdown] id="3aa09d22"
# ### Using Label Encoder for the "cust_payment_terms" column
#
# - Note - Keep the code as it is, no need to change
# + id="6f9ab642"
label_encoder1 = EncoderExt()
label_encoder1.fit(X_train['cust_payment_terms'])
X_train['cust_payment_terms_enc']=label_encoder1.transform(X_train['cust_payment_terms'])
X_val['cust_payment_terms_enc']=label_encoder1.transform(X_val['cust_payment_terms'])
X_test['cust_payment_terms_enc']=label_encoder1.transform(X_test['cust_payment_terms'])
# + id="55f9a7c2"
X_train ,X_val, X_test = custom(['cust_payment_terms'])
# + [markdown] id="0788f42b"
# ## Check the datatype of all the columns of Train, Test and Validation dataframes realted to X
#
# - Note - You are expected yo use dtype
# + id="bc79a316"
X_train.dtypes
# + id="b33242d8"
X_test.dtypes
# + id="6bd4da71"
X_val.dtypes
# + [markdown] id="LVfvuPiWPeMB"
# ### From the above output you can notice their are multiple date columns with datetime format
#
# ### In order to pass it into our model, we need to convert it into float format
# + [markdown] id="9d344db9"
# ### You need to extract day, month and year from the "posting_date" column
#
# 1. Extract days from "posting_date" column and store it into a new column "day_of_postingdate" for train, test and validation dataset
# 2. Extract months from "posting_date" column and store it into a new column "month_of_postingdate" for train, test and validation dataset
# 3. Extract year from "posting_date" column and store it into a new column "year_of_postingdate" for train, test and validation dataset
#
#
#
# - Note - You are supposed yo use
#
# * dt.day
# * dt.month
# * dt.year
#
#
#
#
#
# + id="6e3cdfd6"
X_train['day_of_postingdate'] = X_train['posting_date'].dt.day
X_train['month_of_postingdate'] = X_train['posting_date'].dt.month
X_train['year_of_postingdate'] = X_train['posting_date'].dt.year
X_val['day_of_postingdate'] = X_val['posting_date'].dt.day
X_val['month_of_postingdate'] = X_val['posting_date'].dt.month
X_val['year_of_postingdate'] = X_val['posting_date'].dt.year
X_test['day_of_postingdate'] = X_test['posting_date'].dt.day
X_test['month_of_postingdate'] = X_test['posting_date'].dt.month
X_test['year_of_postingdate'] = X_test['posting_date'].dt.year
# + [markdown] id="GyI-F853Rxa7"
# ### pass the "posting_date" column into the Custom function for train, test and validation dataset
# + id="FQHtQkrnRx_V"
X_train ,X_val, X_test = custom(['posting_date'])
# + [markdown] id="GMnCaEcKReSw"
# ### You need to extract day, month and year from the "baseline_create_date" column
#
# 1. Extract days from "baseline_create_date" column and store it into a new column "day_of_createdate" for train, test and validation dataset
# 2. Extract months from "baseline_create_date" column and store it into a new column "month_of_createdate" for train, test and validation dataset
# 3. Extract year from "baseline_create_date" column and store it into a new column "year_of_createdate" for train, test and validation dataset
#
#
#
# - Note - You are supposed yo use
#
# * dt.day
# * dt.month
# * dt.year
#
#
# - Note - Do as it is been shown in the previous two code boxes
# + [markdown] id="ee4d83d0"
# ### Extracting Day, Month, Year for 'baseline_create_date' column
# + id="32b240e1"
X_train['day_of_createdate'] = X_train['baseline_create_date'].dt.day
X_train['month_of_createdate'] = X_train['baseline_create_date'].dt.month
X_train['year_of_createdate'] = X_train['baseline_create_date'].dt.year
X_val['day_of_createdate'] = X_val['baseline_create_date'].dt.day
X_val['month_of_createdate'] = X_val['baseline_create_date'].dt.month
X_val['year_of_createdate'] = X_val['baseline_create_date'].dt.year
X_test['day_of_createdate'] = X_test['baseline_create_date'].dt.day
X_test['month_of_createdate'] = X_test['baseline_create_date'].dt.month
X_test['year_of_createdate'] = X_test['baseline_create_date'].dt.year
# + [markdown] id="cFgwkS5rSDDs"
# ### pass the "baseline_create_date" column into the Custom function for train, test and validation dataset
# + id="RGYa2BEQSDg3"
X_train , X_val , X_test = custom(['baseline_create_date'])
# + [markdown] id="77c7a0df"
# ### You need to extract day, month and year from the "due_in_date" column
#
# 1. Extract days from "due_in_date" column and store it into a new column "day_of_due" for train, test and validation dataset
# 2. Extract months from "due_in_date" column and store it into a new column "month_of_due" for train, test and validation dataset
# 3. Extract year from "due_in_date" column and store it into a new column "year_of_due" for train, test and validation dataset
#
#
#
# - Note - You are supposed yo use
#
# * dt.day
# * dt.month
# * dt.year
#
# - Note - Do as it is been shown in the previous code
# + id="5c745547"
X_train['day_of_due'] = X_train['due_in_date'].dt.day
X_train['month_of_due'] = X_train['due_in_date'].dt.month
X_train['year_of_due'] = X_train['due_in_date'].dt.year
X_val['day_of_due'] = X_val['due_in_date'].dt.day
X_val['month_of_due'] = X_val['due_in_date'].dt.month
X_val['year_of_due'] = X_val['due_in_date'].dt.year
X_test['day_of_due'] = X_test['due_in_date'].dt.day
X_test['month_of_due'] = X_test['due_in_date'].dt.month
X_test['year_of_due'] = X_test['due_in_date'].dt.year
# + [markdown] id="FYLLzulGSvRd"
# pass the "due_in_date" column into the Custom function for train, test and validation dataset
# + id="1-s6QuY9Svrh"
X_train , X_val , X_test = custom(['due_in_date'])
# + [markdown] id="1ae5d052"
# ### Check for the datatypes for train, test and validation set again
#
# - Note - all the data type should be in either int64 or float64 format
#
# + id="aee9d828"
X_train.dtypes
# -
X_val.dtypes
X_test.dtypes
# + [markdown] id="65810f55"
# # Feature Selection
# + [markdown] id="4bb1ad9f"
# ### Filter Method
#
# - Calling the VarianceThreshold Function
# - Note - Keep the code as it is, no need to change
# + id="e882509f"
from sklearn.feature_selection import VarianceThreshold
constant_filter = VarianceThreshold(threshold=0)
constant_filter.fit(X_train)
len(X_train.columns[constant_filter.get_support()])
# + [markdown] id="V9531H3jR-W2"
# - Note - Keep the code as it is, no need to change
#
# + id="c77c12e1"
constant_columns = [column for column in X_train.columns
if column not in X_train.columns[constant_filter.get_support()]]
print(len(constant_columns))
# + [markdown] id="6d9b8610"
# - transpose the feature matrice
# - print the number of duplicated features
# - select the duplicated features columns names
#
# - Note - Keep the code as it is, no need to change
#
# + id="0fb7db95"
x_train_T = X_train.T
print(x_train_T.duplicated().sum())
duplicated_columns = x_train_T[x_train_T.duplicated()].index.values
# + [markdown] id="510fa831"
# ### Filtering depending upon correlation matrix value
# - We have created a function called handling correlation which is going to return fields based on the correlation matrix value with a threshold of 0.8
#
# - Note - Keep the code as it is, no need to change
# + id="67731abc"
def handling_correlation(X_train,threshold=0.8):
corr_features = set()
corr_matrix = X_train.corr()
for i in range(len(corr_matrix .columns)):
for j in range(i):
if abs(corr_matrix.iloc[i, j]) >threshold:
colname = corr_matrix.columns[i]
corr_features.add(colname)
return list(corr_features)
# + [markdown] id="JaE_6qVgSXl3"
# - Note : Here we are trying to find out the relevant fields, from X_train
# - Please fill in the blanks to call handling_correlation() function with a threshold value of 0.85
# + id="dd91d1a2"
train=X_train.copy()
handling_correlation(train.copy(),threshold=0.85)
# + [markdown] id="154da511"
# ### Heatmap for X_train
#
# - Note - Keep the code as it is, no need to change
# + id="2e8f2fe4"
colormap = plt.cm.RdBu
plt.figure(figsize=(14,12))
plt.title('Pearson Correlation of Features', y=1.05, size=20)
sns.heatmap(X_train.merge(y_train , on = X_train.index ).corr(),linewidths=0.1,vmax=1.0,
square=True, cmap='gist_rainbow_r', linecolor='white', annot=True)
# + [markdown] id="e3b0d745"
# #### Calling variance threshold for threshold value = 0.8
#
# - Note - Fill in the blanks to call the appropriate method
# + id="a9b2080f"
from sklearn.feature_selection import VarianceThreshold
sel = VarianceThreshold(0.8)
sel.fit(X_train)
# + id="6cb8c3dc"
sel.variances_
# + [markdown] id="62633a84"
# ### Features columns are
# - 'year_of_createdate'
# - 'year_of_due'
# - 'day_of_createdate'
# - 'year_of_postingdate'
# - 'month_of_due'
# - 'month_of_createdate'
# + [markdown] id="651f1ad0"
# # Modelling
#
# #### Now you need to compare with different machine learning models, and needs to find out the best predicted model
#
# - Linear Regression
# - Decision Tree Regression
# - Random Forest Regression
# - Support Vector Regression
# - Extreme Gradient Boost Regression
# + [markdown] id="PicEhSuUUOkt"
# ### You need to make different blank list for different evaluation matrix
#
# - MSE
# - R2
# - Algorithm
# + id="701e12b0"
MSE_Score = []
R2_Score = []
Algorithm = []
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# + [markdown] id="29310119"
# ### You need to start with the baseline model Linear Regression
#
# - Step 1 : Call the Linear Regression from sklearn library
# - Step 2 : make an object of Linear Regression
# - Step 3 : fit the X_train and y_train dataframe into the object
# - Step 4 : Predict the output by passing the X_test Dataset into predict function
#
#
#
#
# - Note - Append the Algorithm name into the algorithm list for tracking purpose
# + id="6bdea395"
from sklearn.linear_model import LinearRegression
Algorithm.append('LinearRegression')
regressor = LinearRegression()
regressor.fit(X_train, y_train)
predicted= regressor.predict(X_test)
# + [markdown] id="G02cpnBhXJ14"
# ### Check for the
#
# - Mean Square Error
# - R Square Error
#
# for y_test and predicted dataset and store those data inside respective list for comparison
# + id="0f69ca19"
MSE_Score.append(mean_squared_error(y_test, predicted))
R2_Score.append(r2_score(y_test, predicted))
# + [markdown] id="CsmScbHjYMv1"
# ### Check the same for the Validation set also
# + colab={"base_uri": "https://localhost:8080/"} id="fe653295" outputId="0c7429ca-50d0-42a2-96a1-effaa92f549e"
predict_test= regressor.predict(X_val)
mean_squared_error(y_val, predict_test, squared=False)
# + [markdown] id="LokxV2LGYUVh"
# ### Display The Comparison Lists
# + colab={"base_uri": "https://localhost:8080/"} id="9c405bd3" outputId="9d78f4a9-33fc-48d1-edc8-c997eca38de0"
for i in Algorithm, MSE_Score, R2_Score:
print(i,end=',')
# + [markdown] id="b0e65c86"
# ### You need to start with the baseline model Support Vector Regression
#
# - Step 1 : Call the Support Vector Regressor from sklearn library
# - Step 2 : make an object of SVR
# - Step 3 : fit the X_train and y_train dataframe into the object
# - Step 4 : Predict the output by passing the X_test Dataset into predict function
#
#
#
#
# - Note - Append the Algorithm name into the algorithm list for tracking purpose
# + id="ccb5de08"
from sklearn.svm import SVR
svr = SVR()
svr.fit(X_train, y_train)
# -
svr_predicted= svr.predict(X_test)
Algorithm.append('Suppor Vector Regressor')
# + [markdown] id="zz9kcrViYt7e"
# ### Check for the
#
# - Mean Square Error
# - R Square Error
#
# for "y_test" and "predicted" dataset and store those data inside respective list for comparison
# + id="5bb9db76"
MSE_Score.append(mean_squared_error(y_test, svr_predicted))
R2_Score.append(r2_score(y_test, svr_predicted))
# + [markdown] id="0YAxd8N9Y0hJ"
# ### Check the same for the Validation set also
# + id="d6ee71b1"
predict_test= svr.predict(X_val)
mean_squared_error(y_val, predict_test, squared=False)
# + [markdown] id="eGcqS5EcY4BI"
# ### Display The Comparison Lists
# + id="aa72c1ec"
for i in Algorithm, MSE_Score, R2_Score:
print(i,end=',')
# + [markdown] id="dad18bb3"
# ### Your next model would be Decision Tree Regression
#
# - Step 1 : Call the Decision Tree Regressor from sklearn library
# - Step 2 : make an object of Decision Tree
# - Step 3 : fit the X_train and y_train dataframe into the object
# - Step 4 : Predict the output by passing the X_test Dataset into predict function
#
#
#
#
# - Note - Append the Algorithm name into the algorithm list for tracking purpose
# + id="1b6a51eb"
from sklearn.tree import DecisionTreeRegressor
Algorithm.append('Decision Tree')
decision_tree = DecisionTreeRegressor()
decision_tree.fit(X_train, y_train)
dt_predicted= decision_tree.predict(X_test)
# + [markdown] id="AOzfgfeOZo3F"
# ### Check for the
#
# - Mean Square Error
# - R Square Error
#
# for y_test and predicted dataset and store those data inside respective list for comparison
# + id="776e6983"
MSE_Score.append(mean_squared_error(y_test, dt_predicted))
R2_Score.append(r2_score(y_test, dt_predicted))
# + [markdown] id="eI6d49DQZrhW"
# ### Check the same for the Validation set also
# + id="155fb55c"
predict_test= decision_tree.predict(X_val)
mean_squared_error(y_val, predict_test, squared=False)
# + [markdown] id="sbGXvBLQZw5E"
# ### Display The Comparison Lists
# + id="1d74d515"
for i in Algorithm, MSE_Score, R2_Score:
print(i,end=',')
# + [markdown] id="4ae9979b"
# ### Your next model would be Random Forest Regression
#
# - Step 1 : Call the Random Forest Regressor from sklearn library
# - Step 2 : make an object of Random Forest
# - Step 3 : fit the X_train and y_train dataframe into the object
# - Step 4 : Predict the output by passing the X_test Dataset into predict function
#
#
#
#
# - Note - Append the Algorithm name into the algorithm list for tracking purpose
# + id="a69e476a"
from sklearn.ensemble import RandomForestRegressor
Algorithm.append('Random Forest Regressor')
rf = RandomForestRegressor()
rf.fit(X_train, y_train)
rf_predicted= rf.predict(X_test)
# + [markdown] id="XNcEJF-6anof"
# ### Check for the
#
# - Mean Square Error
# - R Square Error
#
# for y_test and predicted dataset and store those data inside respective list for comparison
# + id="826f63f4"
MSE_Score.append(mean_squared_error(y_test, rf_predicted))
R2_Score.append(r2_score(y_test, rf_predicted))
# + [markdown] id="yMbyr9V4ati1"
# ### Check the same for the Validation set also
# + id="55b9fb54"
predict_test= rf.predict(X_val)
mean_squared_error(y_val, predict_test, squared=False)
# + [markdown] id="tiBawcCsaw_Z"
# ### Display The Comparison Lists
#
# + id="8277c13e"
for i in Algorithm, MSE_Score, R2_Score:
print(i,end=',')
# + [markdown] id="e6b21881"
# ### The last but not the least model would be XGBoost or Extreme Gradient Boost Regression
#
# - Step 1 : Call the XGBoost Regressor from xgb library
# - Step 2 : make an object of Xgboost
# - Step 3 : fit the X_train and y_train dataframe into the object
# - Step 4 : Predict the output by passing the X_test Dataset into predict function
#
#
#
#
# - Note - Append the Algorithm name into the algorithm list for tracking purpose### Extreme Gradient Boost Regression
# - Note - No need to change the code
# + id="705a38ec"
import xgboost as xgb
Algorithm.append('XGB Regressor')
regressor = xgb.XGBRegressor()
regressor.fit(X_train, y_train)
predicted = regressor.predict(X_test)
# + [markdown] id="ierNZkb9bQDD"
# ### Check for the
#
# - Mean Square Error
# - R Square Error
#
# for y_test and predicted dataset and store those data inside respective list for comparison
# + id="507a9d2f"
MSE_Score.append(mean_squared_error(y_test, predicted))
R2_Score.append(r2_score(y_test, predicted))
# + [markdown] id="84UZ2ojsbWaH"
# ### Check the same for the Validation set also
# + id="e78ac250"
predict_test= regressor.predict(X_val)
mean_squared_error(y_val, predict_test, squared=False)
# + [markdown] id="9FJFyaVbbbAH"
# ### Display The Comparison Lists
#
# + id="f765ba35"
for i in Algorithm, MSE_Score, R2_Score:
print(i,end=',')
# + [markdown] id="a71bc90f"
# ## You need to make the comparison list into a comparison dataframe
# + id="ff5159a7"
comparison_list = pd.DataFrame(list(zip(Algorithm, MSE_Score, R2_Score)), columns=['Algorithm', 'MSE_Score', 'R2_Score'])
# -
comparison_list
# + [markdown] id="62e61c60"
# ## Now from the Comparison table, you need to choose the best fit model
#
# - Step 1 - Fit X_train and y_train inside the model
# - Step 2 - Predict the X_test dataset
# - Step 3 - Predict the X_val dataset
#
#
# - Note - No need to change the code
# + id="3e07c258"
regressorfinal = xgb.XGBRegressor()
regressorfinal.fit(X_train, y_train)
predictedfinal = regressorfinal.predict(X_test)
predict_testfinal = regressorfinal.predict(X_val)
# + [markdown] id="8e4df6c4"
# ### Calculate the Mean Square Error for test dataset
#
# - Note - No need to change the code
# + id="5fb466d0"
mean_squared_error(y_test,predictedfinal,squared=False)
# + [markdown] id="ce27f87f"
# ### Calculate the mean Square Error for validation dataset
# + id="b47978ea"
predict_testfinal= regressorfinal.predict(X_val)
mean_squared_error(y_val, predict_testfinal, squared=False)
# + [markdown] id="30014dbd"
# ### Calculate the R2 score for test
# + id="8a162737"
r2_score(y_test, predictedfinal)
# + [markdown] id="1c9853b0"
# ### Calculate the R2 score for Validation
# + id="1a6dc77c"
r2_score(y_val, predict_testfinal)
# + [markdown] id="499522d9"
# ### Calculate the Accuracy for train Dataset
# -
from sklearn.metrics import accuracy_score
# + id="7a4f1ce8"
regressorfinal.score(X_train, y_train)
# + [markdown] id="12a1c921"
# ### Calculate the accuracy for validation
# + id="d2579b4f"
regressorfinal.score(X_val, y_val)
# + [markdown] id="79b82e84"
# ### Calculate the accuracy for test
# + id="f09e6431"
regressorfinal.score(X_test, y_test)
# + [markdown] id="9488a5d9"
# ## Specify the reason behind choosing your machine learning model
#
# - Note : Provide your answer as a text here
# -
# As the MSE Score is the lowest and R2 score is the highest among all the other algorithms, I have chosen XGB Regressor for my ML Model
# + [markdown] id="387a6519"
# ## Now you need to pass the Nulldata dataframe into this machine learning model
#
# #### In order to pass this Nulldata dataframe into the ML model, we need to perform the following
#
# - Step 1 : Label Encoding
# - Step 2 : Day, Month and Year extraction
# - Step 3 : Change all the column data type into int64 or float64
# - Step 4 : Need to drop the useless columns
# + [markdown] id="I7JuxAkdiAdI"
# ### Display the Nulldata
# + id="6d6a51d2"
nulldata
# + [markdown] id="Vamx5xqtiHCH"
# ### Check for the number of rows and columns in the nulldata
# + id="59de1092"
nulldata.shape
# + [markdown] id="BxzHNbBjpqXL"
# ### Check the Description and Information of the nulldata
# + id="a6294d29"
nulldata.info()
# -
nulldata.describe()
# + [markdown] id="fe860d94"
# ### Storing the Nulldata into a different dataset
# # for BACKUP
# + id="16352034"
temp_null = nulldata.copy()
# + [markdown] id="00f35b8c"
# ### Call the Label Encoder for Nulldata
#
# - Note - you are expected to fit "business_code" as it is a categorical variable
# - Note - No need to change the code
# + id="baf04b17"
from sklearn.preprocessing import LabelEncoder
business_codern = LabelEncoder()
business_codern.fit(nulldata['business_code'])
nulldata['business_code_enc'] = business_codern.transform(nulldata['business_code'])
# + [markdown] id="ZCPBK9karIR-"
# ### Now you need to manually replacing str values with numbers
# - Note - No need to change the code
# + id="c64924be"
nulldata['cust_number'] = nulldata['cust_number'].str.replace('CCCA',"1").str.replace('CCU',"2").str.replace('CC',"3").astype(int)
# + [markdown] id="9a55f5f6"
# ## You need to extract day, month and year from the "clear_date", "posting_date", "due_in_date", "baseline_create_date" columns
#
#
# ##### 1. Extract day from "clear_date" column and store it into 'day_of_cleardate'
# ##### 2. Extract month from "clear_date" column and store it into 'month_of_cleardate'
# ##### 3. Extract year from "clear_date" column and store it into 'year_of_cleardate'
#
#
#
# ##### 4. Extract day from "posting_date" column and store it into 'day_of_postingdate'
# ##### 5. Extract month from "posting_date" column and store it into 'month_of_postingdate'
# ##### 6. Extract year from "posting_date" column and store it into 'year_of_postingdate'
#
#
#
#
# ##### 7. Extract day from "due_in_date" column and store it into 'day_of_due'
# ##### 8. Extract month from "due_in_date" column and store it into 'month_of_due'
# ##### 9. Extract year from "due_in_date" column and store it into 'year_of_due'
#
#
#
#
# ##### 10. Extract day from "baseline_create_date" column and store it into 'day_of_createdate'
# ##### 11. Extract month from "baseline_create_date" column and store it into 'month_of_createdate'
# ##### 12. Extract year from "baseline_create_date" column and store it into 'year_of_createdate'
#
#
#
#
# - Note - You are supposed To use -
#
# * dt.day
# * dt.month
# * dt.year
# + id="4166fbe4"
nulldata['day_of_cleardate'] = nulldata['clear_date'].dt.day
nulldata['month_of_cleardate'] = nulldata['clear_date'].dt.month
nulldata['year_of_cleardate'] = nulldata['clear_date'].dt.year
nulldata['day_of_postingdate'] = nulldata['posting_date'].dt.day
nulldata['month_of_postingdate'] = nulldata['posting_date'].dt.month
nulldata['year_of_postingdate'] = nulldata['posting_date'].dt.year
nulldata['day_of_due'] = nulldata['due_in_date'].dt.day
nulldata['month_of_due'] = nulldata['due_in_date'].dt.month
nulldata['year_of_due'] = nulldata['due_in_date'].dt.year
nulldata['day_of_createdate'] = nulldata['baseline_create_date'].dt.day
nulldata['month_of_createdate'] = nulldata['baseline_create_date'].dt.month
nulldata['year_of_createdate'] = nulldata['baseline_create_date'].dt.year
# + [markdown] id="QeHWJYrAvOC6"
# ### Use Label Encoder1 of all the following columns -
# - 'cust_payment_terms' and store into 'cust_payment_terms_enc'
# - 'business_code' and store into 'business_code_enc'
# - 'name_customer' and store into 'name_customer_enc'
#
# Note - No need to change the code
# + id="bac330e2"
nulldata['cust_payment_terms_enc']=label_encoder1.transform(nulldata['cust_payment_terms'])
nulldata['business_code_enc']=label_encoder1.transform(nulldata['business_code'])
nulldata['name_customer_enc']=label_encoder.transform(nulldata['name_customer'])
# + [markdown] id="zD9I-XqQwC28"
# ### Check for the datatypes of all the columns of Nulldata
# -
nulldata.dtypes
# + [markdown] id="17cd5452"
# ### Now you need to drop all the unnecessary columns -
#
# - 'business_code'
# - "baseline_create_date"
# - "due_in_date"
# - "posting_date"
# - "name_customer"
# - "clear_date"
# - "cust_payment_terms"
# - 'day_of_cleardate'
# - "month_of_cleardate"
# - "year_of_cleardate"
# + id="d7c82076"
nulldata.drop(columns=['business_code','baseline_create_date',
'due_in_date','posting_date','name_customer',
'clear_date','cust_payment_terms',
'day_of_cleardate','month_of_cleardate',
'year_of_cleardate'])
# + [markdown] id="Q_NCr9IPweVq"
# ### Check the information of the "nulldata" dataframe
# + id="4e7ffee0"
nulldata.info()
# + [markdown] id="-XvjhWqmwi-C"
# ### Compare "nulldata" with the "X_test" dataframe
#
# - use info() method
# + id="02f4b62d"
X_test.info()
# + [markdown] id="Us3ey-9zwqjq"
# ### You must have noticed that there is a mismatch in the column sequence while compairing the dataframes
#
# - Note - In order to fed into the machine learning model, you need to edit the sequence of "nulldata", similar to the "X_test" dataframe
# + [markdown] id="vduVNt1kxPW-"
# - Display all the columns of the X_test dataframe
# - Display all the columns of the Nulldata dataframe
# - Store the Nulldata with new sequence into a new dataframe
#
#
# - Note - The code is given below, no need to change
# + id="6729353e"
X_test.columns
# + id="47bd9c5e"
nulldata.columns
# + id="aa5a2103"
final_df=nulldata[['cust_number', 'buisness_year', 'doc_id', 'converted_usd',
'business_code_enc', 'name_customer_enc', 'cust_payment_terms_enc',
'day_of_postingdate', 'month_of_postingdate', 'year_of_postingdate',
'day_of_createdate', 'month_of_createdate', 'year_of_createdate',
'day_of_due', 'month_of_due', 'year_of_due']]
# + [markdown] id="1dc8b021"
# ### Display the Final Dataset
# + id="2f39785a"
final_df.head()
# + [markdown] id="27b88c5a"
# ### Now you can pass this dataset into you final model and store it into "final_result"
# + id="9e0b6388"
final_result = regressorfinal.predict(final_df)
# + [markdown] id="9653d3c6"
# ### you need to make the final_result as dataframe, with a column name "avg_delay"
#
# - Note - No need to change the code
# + id="25ef814d"
final_result = pd.Series(final_result,name='avg_delay')
# -
final_result = final_result.to_frame()
# + [markdown] id="C86staIhyf2C"
# ### Display the "avg_delay" column
# + id="4fd46406"
final_result['avg_delay']
# + [markdown] id="44f71a7e"
# ### Now you need to merge this final_result dataframe with the BACKUP of "nulldata" Dataframe which we have created in earlier steps
# + id="e8f0969d"
temp_null.reset_index(drop=True,inplace=True)
Final = temp_null.merge(final_result , on = nulldata.index )
# + [markdown] id="G-hLtxXgy4GZ"
# ### Display the "Final" dataframe
# + id="71fb4dc0"
Final
# + [markdown] id="4sc27Uz-y-0O"
# ### Check for the Number of Rows and Columns in your "Final" dataframe
# + id="5iUXOIhzy_HR"
Final.shape
# + [markdown] id="48886d2c"
# ### Now, you need to do convert the below fields back into date and time format
#
# - Convert "due_in_date" into datetime format
# - Convert "avg_delay" into datetime format
# - Create a new column "clear_date" and store the sum of "due_in_date" and "avg_delay"
# - display the new "clear_date" column
# - Note - Code is given below, no need to change
# + id="243abc2d"
Final['clear_date'] = pd.to_datetime(Final['due_in_date']) + pd.to_timedelta(Final['avg_delay'], unit='s')
# + [markdown] id="9QcX_fAjIkYR"
# ### Display the "clear_date" column
# + id="740e1486"
Final['clear_date']
# + [markdown] id="MSkNLq6-z7rZ"
# ### Convert the average delay into number of days format
#
# - Note - Formula = avg_delay//(24 * 3600)
# - Note - full code is given for this, no need to change
# + id="ce6b618a"
Final['avg_delay'] = Final.apply(lambda row: row.avg_delay//(24 * 3600), axis = 1)
# + [markdown] id="wbBBZPjP0W7o"
# ### Display the "avg_delay" column
# + id="a494982f"
Final['avg_delay']
# + [markdown] id="815d8811"
# ### Now you need to convert average delay column into bucket
#
# - Need to perform binning
# - create a list of bins i.e. bins= [0,15,30,45,60,100]
# - create a list of labels i.e. labels = ['0-15','16-30','31-45','46-60','Greatar than 60']
# - perform binning by using cut() function from "Final" dataframe
#
#
# - Please fill up the first two rows of the code
# + id="c797e4b5"
bins= [0,15,30,45,60,100]
labels =['0-15','16-30','31-45','46-60','61-100']
Final['Aging Bucket'] = pd.cut(Final['avg_delay'], bins=bins, labels=labels, right=False)
# + [markdown] id="1c35725f"
# ### Now you need to drop "key_0" and "avg_delay" columns from the "Final" Dataframe
# + id="b31bc6a3"
Final.drop(columns=['key_0','avg_delay'], inplace=True, axis=1)
# + [markdown] id="Ui-tyIvU0-5u"
# ### Display the count of each categoty of new "Aging Bucket" column
# + id="a6e16218"
Final['Aging Bucket'].value_counts()
# + [markdown] id="kgYegy551GKJ"
# ### Display your final dataset with aging buckets
# + id="c4bc87ec"
Final
# + [markdown] id="Ji7AoDCB1L_x"
# ### Store this dataframe into the .csv format
# + id="727d0b8d"
Final.to_csv('HRC82285W_ADITYA_MISHRA.csv')
# + [markdown] id="FK0fabl61SkC"
# # END OF THE PROJECT
|
src/HRC82285W_ADITYA_MISHRA_prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Galaxy simulations
#
# Now we'll use some initial conditions from the ```Gadget-2``` particle simulation code to do our own simulations of galaxies! We'll start with some low resolution data.
#
# There are only 2 types of particles - particle #1 is a star particle and particle #2 is a dark matter particle.
# +
# usual things:
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# We'll read data in using np.genfromtxt. This is the "opposite" function of the np.savetxt we used before to save text files.
#
# Note we can use it to even read from the web! Or you can download these galaxy snapshots from the Day 5 webpage as well.
# this is a 100 particle (in stars and DM) initial conditions
# each row is a particle
# Ptype is the particle type (dark matter or stars)
# and then x,y,z give coordinates of each particle
# vx,vy,vz give each velocity component
names = ('Ptype', 'x', 'y', 'z', 'vx', 'vy', 'vz')
formats= ('f8', 'f8', 'f8','f8', 'f8','f8', 'f8')
galaxy_data = np.genfromtxt("https://jnaiman.github.io/csci-p-14110/lesson04/galaxySnaps/snap_001_fac1n3.txt",
delimiter=",",
dtype={'names':names,
'formats':formats})
# Now let's take a quick peak at what the array looks like:
galaxy_data
# We'll convert this data into a form that our hermite solver knows how to use with the `convert_galaxy_data.py` library. Make sure this is in the same folder as this ipynb notebook!
# +
# convert galaxy data
from convert_galaxy_data import convert_galaxy_data
masses, pos, vel = convert_galaxy_data(galaxy_data)
# -
# What do they look like? Here are the masses (in grams):
masses
# We'll use a slightly different version of the `do_hermite` function: the `do_hermite_galaxies` that is tailored to doing galaxy simulations:
# +
# import the galaxy library
from hermite_library import do_hermite_galaxies
# note: this will likely take a good long while to run
# note that tfinal has changed - this is because our scales are very different!
# time is in seconds and is 10^7 years
r_h, v_h, t_h, e_h = do_hermite_galaxies(masses, pos, vel, tfinal=3.15e7*1e7, Nsteps = 100)
# -
# Finally, plot!
# +
# let's plot in multi-d
fig, ax = plt.subplots(1, 4, figsize = (10*2, 10))
fig.suptitle('Coordinates Plot')
# for plots 0->2
ax[0].set_xlabel('x in kpc')
ax[0].set_ylabel('y in kpc')
ax[1].set_xlabel('x in kpc')
ax[1].set_ylabel('z in kpc')
ax[2].set_xlabel('y in kpc')
ax[2].set_ylabel('z in kpc')
# plot Euler's solution, particle 1, x-y
for i in range(len(masses)):
ax[0].plot(r_h[i,0,:], r_h[i,1,:], lw=3)
for i in range(len(masses)):
ax[1].plot(r_h[i,0,:], r_h[i,2,:], lw=3)
for i in range(len(masses)):
ax[2].plot(r_h[i,1,:], r_h[i,2,:], lw=3)
ax[3].set_xlabel('Time in years')
ax[3].set_ylabel('Energy')
# re-norm energy
ax[3].plot(t_h, e_h)
plt.show()
# -
# ### Exercise
# Calculate the merger of these two objects and plot the particle trajectories. To do this, you'll need many more timesteps and a larger tfinal.
#
# Note that you might want to color each type of particle a different way instead of having matplotlib choose colors for you - how do you think you can go about doing that?
#
# Bonus: try higher resolutions - how much longer does it take? How to quantify this? (hint: google "time library python")
#
# Bonus bonus: how would you go about making an animation of this?
|
lesson05/Optional_galaxySimulations_3d_lesson05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
train_data = pd.read_csv("data/train_data.csv", index_col="id")
print(train_data.shape)
train_data.head()
np.sum(train_data['y'] == 1) / train_data['y'].count(), np.sum(train_data['y'] == 0) / train_data['y'].count()
train_data.info()
# ## 両チームの最大レベルは?
pd.concat([train_data['A1-level'], train_data['A2-level'], train_data['A3-level'], train_data['A4-level'], train_data['B1-level'], train_data['B2-level'], train_data['B3-level'], train_data['B4-level']]).max()
train_data['A1-level']
train_data.sort_values('A1-level', ascending=False)['A1-level'][:10]
from sklearn.preprocessing import MultiLabelBinarizer
mlb = MultiLabelBinarizer()
mlb.fit([set(train_data['A1-weapon'].unique())])
MultiLabelBinarizer(classes=None, sparse_output=False)
# +
def trans_weapon(df, columns=['A1-weapon', 'A2-weapon', 'A3-weapon', 'A4-weapon']):
weapon = df.fillna('none')
weapon_binarized = mlb.transform(weapon[columns].values)
return pd.DataFrame(weapon_binarized, columns=mlb.classes_)
def make_input_output(df, with_y=False):
a_weapon = trans_weapon(df, ['A1-weapon', 'A2-weapon', 'A3-weapon', 'A4-weapon'])
b_weapon = trans_weapon(df, ['B1-weapon', 'B2-weapon', 'B3-weapon', 'B4-weapon'])
X = pd.concat([a_weapon, b_weapon], axis=1)
if with_y:
y = df['y']
return X, y, a_weapon, b_weapon
return X, a_weapon, b_weapon
# -
X, y, a_weapon, b_weapon = make_input_output(train_data, with_y=True)
X
X.info()
a_weapon
b_weapon
X.shape
X['splatroller']
X['splatroller']
# +
#scikit-learnライブラリをimport
import sklearn
from sklearn.ensemble import RandomForestClassifier
#線形回帰モデルのインスタンス化
model = RandomForestClassifier()
#予測モデルの作成
model.fit(X, y)
# -
list(reversed(sorted(list(zip(model.feature_importances_, X.columns)))))[:10]
# accuracyの出力
from sklearn.metrics import accuracy_score
y_true = y
y_pred = model.predict(X)
print(accuracy_score(y_true, y_pred))
path_test = "data/test_data.csv"
test_data = pd.read_csv(path_test, index_col='id')
test_data.head()
test_X, _, _ = make_input_output(test_data)
#テスト結果の出力
test_predicted = model.predict(test_X)
submit_df = pd.DataFrame({'y': test_predicted})
submit_df.index.name = 'id'
submit_df.to_csv('tuto_submission.csv')
train_data['game-ver'].unique()
train_data['lobby-mode'].unique()
train_data['lobby'].unique()
train_data['mode'].unique()
train_data['stage'].unique()
pd.concat([train_data['A1-level'], train_data['A2-level'], train_data['A3-level'], train_data['A4-level'], train_data['B1-level'], train_data['B2-level'], train_data['B3-level'], train_data['B4-level']]).max()
|
tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="RjCjlskvBfgX"
# The dataset includes several data wranglings. The most important issue is that the columns Xi which indicate the day should be rows instead of columns. Also the measurements should be columns instead of rows.
#
# Also we can observe that there are some null values and some inconsistencies with some of the rows.
# + id="WQ4fgl6vE_vB" executionInfo={"status": "ok", "timestamp": 1618252733701, "user_tz": -270, "elapsed": 1310, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
import pandas as pd
# + id="7-rp8vkPFhWg" executionInfo={"status": "ok", "timestamp": 1618252734383, "user_tz": -270, "elapsed": 1835, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df = pd.read_csv('weather.csv', index_col=0)
# + colab={"base_uri": "https://localhost:8080/", "height": 224} id="6DEsH_Ncj3XB" executionInfo={"status": "ok", "timestamp": 1618252742283, "user_tz": -270, "elapsed": 724, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="59be92c8-8e63-40bf-b877-298c97bbd574"
df.head()
# + [markdown] id="vIqT6dqgjtWk"
# Column X is just an index, so let's drop it!
# + id="rrUbQ6F2FpSa" executionInfo={"status": "ok", "timestamp": 1618252746601, "user_tz": -270, "elapsed": 687, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df.drop(['X'], axis=1, inplace=True)
# + id="s1ToLEnGcv6w" executionInfo={"status": "ok", "timestamp": 1618260475708, "user_tz": -270, "elapsed": 1112, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2 = df.pivot(index=['year', 'month'], columns='measure').stack(0).reset_index()
df2.rename(columns={'level_2': "day"}, inplace=True)
df2.columns.name = None
# + colab={"base_uri": "https://localhost:8080/", "height": 456} id="tjszjLL2q_Au" executionInfo={"status": "ok", "timestamp": 1618257657890, "user_tz": -270, "elapsed": 865, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="d26d3873-0d93-40d2-e5ab-71798838d22a"
df2
# + colab={"base_uri": "https://localhost:8080/", "height": 309} id="3DTyi5TRuy6B" executionInfo={"status": "ok", "timestamp": 1618260477966, "user_tz": -270, "elapsed": 774, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="3afc1149-cdcf-4e08-d0ca-2509aba174f7"
dates = pd.to_datetime(df2.apply(lambda x: f"{x[0]}-{x[1]}-{x[2][1:]}", axis=1))
df2.insert(0, 'Date', dates)
df2.drop(columns=['year', 'month', 'day'], inplace=True)
df2.head()
# + [markdown] id="2uoUbp700JLM"
# We can see in the above cell that some values in the `PrecipitationIn` column are set to *T* which probably mean NaN. We can subsitute them with 0 for that column:
# + id="1PYvimAL08i9" executionInfo={"status": "ok", "timestamp": 1618260480243, "user_tz": -270, "elapsed": 601, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2['PrecipitationIn'].replace(['T','0'], inplace=True)
# + [markdown] id="MQ2xQG3l2-dr"
# Let's go for columns with empty values:
# + colab={"base_uri": "https://localhost:8080/"} id="axe8uHGZ3UOq" executionInfo={"status": "ok", "timestamp": 1618260919711, "user_tz": -270, "elapsed": 727, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="de836693-3328-447b-c10a-816aa7e3caf0"
df2.isna().any()
# + [markdown] id="1-EswYj239EZ"
# Let's fill in the empty values:
# + colab={"base_uri": "https://localhost:8080/"} id="gT1E4R0M4qgw" executionInfo={"status": "ok", "timestamp": 1618261261442, "user_tz": -270, "elapsed": 1740, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="8daf37a3-8c92-45a8-84f2-2e62f5e7bb8a"
df2['Max.Gust.SpeedMPH'].unique()
# + id="dsjuH_EG4Ate" executionInfo={"status": "ok", "timestamp": 1618261312750, "user_tz": -270, "elapsed": 763, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2.fillna({'Events': 'Sunny', 'Max.Gust.SpeedMPH': '0'}, inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 193} id="x3CQv3XH6Hzs" executionInfo={"status": "ok", "timestamp": 1618261719054, "user_tz": -270, "elapsed": 903, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="9a68f0b4-8178-4bdb-95b5-5c530e215769"
df2.drop(columns=['Date', 'Events']).describe()
# + id="7vE3Uh9B7Ga0" executionInfo={"status": "ok", "timestamp": 1618261939183, "user_tz": -270, "elapsed": 751, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
numerical_cols = df2.columns.difference(['Date', 'Events'])
# + id="x43wB9mF48Pf" executionInfo={"status": "ok", "timestamp": 1618261980608, "user_tz": -270, "elapsed": 762, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2[numerical_cols] = df2[numerical_cols].apply(pd.to_numeric, errors='ignore')
# + colab={"base_uri": "https://localhost:8080/", "height": 317} id="cdPg238o7kJn" executionInfo={"status": "ok", "timestamp": 1618262028533, "user_tz": -270, "elapsed": 752, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="6c54d0b9-b69f-4658-baa3-0faa6259c319"
df2.describe()
# + [markdown] id="OmwJHLLj7yYm"
# As we can see in the cell above, `Mean.VisibilityMiles` has some rows with value -1 which is not a valid mean value. So let's change that:
# + id="f8m0lSTQ7pE8" executionInfo={"status": "ok", "timestamp": 1618262185065, "user_tz": -270, "elapsed": 715, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2.loc[df2['Mean.VisibilityMiles'] < 0, 'Mean.VisibilityMiles'] = 0
# + [markdown] id="VWaU3MbX8V5w"
# We can also observe that in some rows `Max.Humidity` is above 100% so let's fix that too:
# + id="yY6wpaJq8RaH" executionInfo={"status": "ok", "timestamp": 1618262259869, "user_tz": -270, "elapsed": 738, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}}
df2.loc[df2['Max.Humidity'] > 100, 'Max.Humidity'] = 100
# + [markdown] id="YZWtMSNp9Joh"
# Let's check the statistics again:
# + colab={"base_uri": "https://localhost:8080/", "height": 317} id="3MKm76Ed8nVN" executionInfo={"status": "ok", "timestamp": 1618262492147, "user_tz": -270, "elapsed": 742, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14Gi1OueG9sGfZPOEpshnIKiyStiVabJwtjvgrIbsrw=s64", "userId": "16815373180648766477"}} outputId="cf6e1af1-fc5e-4bf3-d252-f43d71d51f02"
df2.describe()
|
Homeworks/03. Get the most relevant song using LSH and GloVe/02. Intro to data cleaning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## import local
from __future__ import print_function
# __file__ = !cd .. ;pwd
__file__ = __file__[0]
__file__
import sys
from random import random
sys.path.append(__file__)
sys.path
# + active=""
# ## paso's Train, Valid, Test DataSet Creation and Cross-Validation
# -
# view the source code for the x,y,z,a and e class. You are free to use and modify this code.
# As we saw in [lesson-1](), we need to startup **paso** services.
# +
import numpy as np
import pandas as pd
import warnings
warnings.filterwarnings("ignore")
import matplotlib as mpl
from matplotlib import pyplot as plt
from matplotlib import cm
# %reload_ext autoreload
# %autoreload 2
# %matplotlib inline
import matplotlib
import seaborn as sns
from paso.base import Paso,Log,PasoError
from loguru import logger
session = Paso(parameters_filepath='../parameters/lesson.4.yaml').startup()
# -
# Next, we load the ``boston``data set into the ``City``dataframe. We will munge City up to show what the **paso** cleaners can do.
# +
from sklearn.datasets import load_boston
boston = load_boston()
City = pd.DataFrame(boston.data, columns = boston.feature_names )
City['MEDV'] = boston.target
logger.info(boston.DESCR)
City.head()
# -
# ## paso Class for Determining a Feature's SHAP Value
# When evaluating different settings (“hyperparameters”) for estimators, such as the C setting that must be manually set for an SVM, there is still a risk of overfitting on the test set because the parameters can be tweaked until the estimator performs optimally. This way, knowledge about the test set can “leak” into the model and evaluation metrics no longer report on generalization performance. To solve this problem, yet another part of the dataset can be held out as a so-called “validation set”: training proceeds on the training set, after which evaluation is done on the validation set, and when the experiment seems to be successful, final evaluation can be done on the test set.
# However, by partitioning the available data into three sets, we drastically reduce the number of samples which can be used for learning the model, and the results can depend on a particular random choice for the pair of (train, validation) sets.
# A solution to this problem is a procedure called cross-validation (CV for short). A test set should still be held out for final evaluation, but the validation set is no longer needed when doing CV. In the basic approach, called k-fold CV, the training set is split into k smaller sets (other approaches are described below, but generally follow the same principles). The following procedure is followed for each of the k “folds”:
# A model is trained using
# k
# −
# 1
# of the folds as training data;
# the resulting model is validated on the remaining part of the data (i.e., it is used as a test set to compute a performance measure such as accuracy).
# The performance measure reported by k-fold cross-validation is then the average of the values computed in the loop. This approach can be computationally expensive, but does not waste too much data (as is the case when fixing an arbitrary validation set), which is a major advantage in problems such as inverse inference where the number of samples is very small.
#
#
#
#
#
#
# ## Summary
#
# Other lessons on **paso** are:
# 1. [**paso**'s Offering of Logging and Parameter Services for your Python Project](https://github.com/bcottman/paso/blob/master/lessons/lesson_1.ipynb)
# In the future, we will cover **paso** in more depth with the following lesons:
# - Overview of **paso** scalers and handling data outliers.
# - Overview of **paso** encoders.
# - Overview of **paso** machine learning and deep learning models.
# - Using **paso** on GPUs.
# - and yet more…
#
# If you have a service or feature or see a bug, then leave the **paso** project a [note](https://github.com/bcottman/paso/issues).
#
#
#
#
#
#
|
lessons/lesson-5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Color Fundamentals
#
# This notebook describes a few fundamental aspects of how we perceive colors, and then proceeds to quantify a couple different colormaps in that context.
#
# We will start by describing the color matching function, then the response function of the three cones in a human eye. Links to data are included. Following this, we'll demonstrate how colormaps fit into the spectrum, and how to use the package [palettable](https://jiffyclub.github.io/palettable/).
# + deletable=true editable=true
# %matplotlib inline
# + deletable=true editable=true
import matplotlib.pyplot as plt
import csv
import numpy as np
plt.rcParams["figure.figsize"] = (12, 10)
plt.style.use("seaborn")
# -
# ## Colors and Eyes
#
# We'll load up the Stiles & Burch 1955 2-degree color matching functions, via http://www.cvrl.org/database/text/cmfs/sbrgb2.htm .
#
# This will give us the chromatic responses for an observer.
# + deletable=true editable=true
with open("sbrgb2.csv") as f:
data = [[] for _ in 'Wrgb']
reader = csv.reader(f)
for row in csv.reader(f):
for l, v in zip(data, row):
l.append(float(v))
wavelength = np.array(data[0])
data = np.array([data[1], data[2], data[3]])
# -
# We'll plot them now, so that we can see the wavelength and response.
# + deletable=true editable=true
plt.plot(wavelength, data[0], '-r')
plt.plot(wavelength, data[1], '-g')
plt.plot(wavelength, data[2], '-b')
plt.xlabel("Wavelength [nm]", fontsize=18)
plt.ylabel("Color Matching Function", fontsize=18)
# + [markdown] deletable=true editable=true
# Now, let's convert these to the sensitivity of LMS.
# + deletable=true editable=true
# Now we convert these to LMS; Stockman, MacLeod & Johnson 1993
coeffs = np.array([
[0.214808, 0.751035, 0.045156],
[0.022882, 0.940534, 0.076827],
[0.000000, 0.016500, 0.999989]
])
L, M, S = (data[0] * coeffs[i,0]
+ data[1] * coeffs[i,1]
+ data[2] * coeffs[i,2] for i in range(3))
# -
# We'll plot these now.
# + deletable=true editable=true
plt.plot(wavelength, L, '-r')
plt.plot(wavelength, M, '-g')
plt.plot(wavelength, S, '-b')
plt.xlabel("Wavelength [nm]", fontsize=18)
plt.ylabel("Responsivity", fontsize=18)
# + [markdown] deletable=true editable=true
# Now we'll convert wavelength to RGB; this code was heavily borrowed from http://www.noah.org/wiki/Wavelength_to_RGB_in_Python
#
# Note that this isn't necessarily the *best* way to generate RGB curves; in fact, it does not cover the full spectrum of colors expressible in RGB. We'll demonstrate that below.
# + deletable=true editable=true
wavelength = np.mgrid[wavelength[0]:wavelength[-1]:1024j]
gamma = 0.8
i1 = (wavelength >= 380) & (wavelength < 440)
i2 = (wavelength >= 440) & (wavelength < 490)
i3 = (wavelength >= 490) & (wavelength < 510)
i4 = (wavelength >= 510) & (wavelength < 580)
i5 = (wavelength >= 580) & (wavelength < 645)
i6 = (wavelength >= 645) & (wavelength < 750)
R, G, B = (np.zeros_like(wavelength) for _ in 'RGB')
a1 = attenuation = 0.3 + 0.7 * (wavelength[i1] - 380) / (440 - 380)
R[i1] = ((-(wavelength[i1] - 440) / (440 - 380)) * a1) ** gamma
G[i1] = 0.0
B[i1] = (1.0 * a1) ** gamma
R[i2] = 0.0
G[i2] = ((wavelength[i2] - 440) / (490 - 440)) ** gamma
B[i2] = 1.0
R[i3] = 0.0
G[i3] = 1.0
B[i3] = (-(wavelength[i3] - 510) / (510 - 490)) ** gamma
R[i4] = ((wavelength[i4] - 510) / (580 - 510)) ** gamma
G[i4] = 1.0
B[i4] = 0.0
R[i5] = 1.0
G[i5] = (-(wavelength[i5] - 645) / (645 - 580)) ** gamma
B[i5] = 0.0
a2 = 0.3 + 0.7 * (750 - wavelength[i6]) / (750 - 645)
R[i6] = (1.0 * a2) ** gamma
G[i6] = 0.0
B[i6] = 0.0
# + deletable=true editable=true
plt.plot(wavelength, R, '-r')
plt.plot(wavelength, G, '-g')
plt.plot(wavelength, B, '-b')
# -
# Above, you can see the RGB values as a line plot. Below, we'll plot the RGB as a color, across these wavelengths.
# + deletable=true editable=true
im = np.ones((wavelength.size, wavelength.size, 4))
im[:,:,0] *= R
im[:,:,1] *= G
im[:,:,2] *= B
im *= 255
im = im.astype("uint8")
plt.imshow(im, extent = [0.0, 1.0, 0.0, 1.0], aspect = 1.0/5)
# -
# What do some of our colormaps look like? We'll check out viridis, which is a pretty awesome colormap.
# + deletable=true editable=true
import matplotlib.cm as cm
# + deletable=true editable=true
viridis = cm.viridis(np.mgrid[0.0:1.0:256j])[:,:3]
im = np.ones((viridis.shape[0], viridis.shape[0], 4))
im[...,:3] *= viridis[None,:,:]
im *= 255
im = im.astype("uint8")
plt.imshow(im, extent = [0.0, 1.0, 0.0, 1.0], aspect = 1.0/5)
# -
# ## Colormaps
#
# Now that is a nice looking colormap! So what happens if we try to restrict this to the RGB values we've identified in our image above, when we generated the rainbow? We'll try to find the "nearest" RGB values by looking at the L2 norm of the distance.
# + deletable=true editable=true
# Now we need to get our reversal to wavelength from an RGB value.
# We don't have that many wavelengths, so let's just do an L2 norm for each.
rgb = np.array([R,G,B]).T
def get_rgb(cmap_name):
colors = cm.cmap_d[cmap_name](np.mgrid[0.0:1.0:256j])[:,:3]
closest = np.sqrt(np.abs((rgb[:,None,:] - colors)**2.0).sum(axis=2)).argmin(axis=0)
return closest
rgbi = get_rgb("viridis")
# + deletable=true editable=true
im = np.ones((rgbi.size, rgbi.size, 4))
im[:,:,0] *= R[rgbi]
im[:,:,1] *= G[rgbi]
im[:,:,2] *= B[rgbi]
im *= 255
im = im.astype("uint8")
plt.imshow(im, extent = [0.0, 1.0, 0.0, 1.0])
# -
# Yuck! Not quite as nice. The way we've generated the spectra here, where we varied a reasonably simple function along one dimension, doesn't allow for the expressiveness that we need for really nice looking colors.
# We'll take a look at a couple colormaps now, to see what they look like in both color and RGB space. The plots you'll see will have the colormap at the bottom, and in the top panel they'll show the R, G, B lines from 0 to 1, to show the relative composition.
# + deletable=true editable=true
def plot_rgb(cmap_name):
N = 256
colors = cm.cmap_d[cmap_name](np.mgrid[0.0:1.0:N * 1j])[:,:3]
plt.clf()
fig = plt.figure()
ax = fig.add_axes([0.0, 0.15, 1.0, 0.8])
plt.plot(np.mgrid[0.0:1.0:N*1j], colors[:,0], '-r')
plt.plot(np.mgrid[0.0:1.0:N*1j], colors[:,1], '-g')
plt.plot(np.mgrid[0.0:1.0:N*1j], colors[:,2], '-b')
plt.xlim(0.0, 1.0)
plt.ylim(0.0, 1.01)
ax.xaxis.set_ticklabels([])
ax.yaxis.set_ticklabels([])
ax = fig.add_axes([0.0, 0.0, 1.0, 0.2])
im = np.ones((1, N, 3), dtype="uint8")
im *= (colors*255).astype("uint8")[None, :, :]
ax.imshow(im, interpolation='nearest', extent = [0.0, 1.0, 0.0, 1.0], aspect = 20.0/N)
plt.xlim(0.0, 1.0)
ax.xaxis.set_ticklabels([])
ax.xaxis.set_visible(False)
ax.yaxis.set_ticklabels([])
ax.yaxis.set_visible(False)
# -
# viridis is the new default colormap in matplotlib. For a great description of how this was developed and why, see <NAME>'s [talk from SciPy 2015](https://www.youtube.com/watch?v=xAoljeRJ3lU).
# + deletable=true editable=true
plot_rgb('viridis')
# -
# Let's also take a look at 'jet'. For a long time, jet was the default colormap; part of this stems from the similairites between the API for matplotlib and matlab, long ago. We'll explore some of the odd quirks in jet in another notebook.
# + deletable=true editable=true
plot_rgb("jet")
# -
# This is the gray colormap, which just grows linearly from 0..1 simultaneously in all three channels.
# + deletable=true editable=true
plot_rgb("gray")
# -
# This is a colormap called "GIST Stern." According to https://gist.github.com/endolith/2719900 , this came from the Yorick package, and before that, IDL. I used to use this one a lot in astronomy. I'm not a huge fan anymore.
# + deletable=true editable=true
plot_rgb("gist_stern")
# -
# Don't use this colormap. I mean, there might be reasons one could hazard to use it but ... I don't know of any good ones.
# + deletable=true editable=true
plot_rgb("flag")
# -
# Magma is another good, new colormap from matplotlib designed for accessibility and perceptual uniformity.
# + deletable=true editable=true
plot_rgb("magma")
# -
# ## Palettes
#
# We're going to experiment with color palettes, as well. This will use the [palettable](https://jiffyclub.github.io/palettable/) library from <NAME>.
#
# We're going to talk about basically three different ways of thinking of palettes: qualitative (categorical), diverging, and sequential.
#
# In general, qualitative are for situations where you wish to express different categories, diverging when you wish to express deviation from a baseline value, and sequential when the baseline is moved away from only in one direction.
# + deletable=true editable=true
import palettable
# -
# First, the qualitative colormaps. Note how they don't work that well as continuous images!
# + deletable=true editable=true
from palettable.colorbrewer.qualitative import Set1_9
Set1_9.show_discrete_image(size=(12,2))
Set1_9.show_continuous_image(size=(12,2))
# -
# Let's write some simple functions so that we can play with the colormaps via widgets. We'll write one for each type of colormap.
# + deletable=true editable=true
def get_cb_diverging(name = "Spectral", number = 9):
number = min(number, max(int(_) for _ in palettable.colorbrewer.COLOR_MAPS["Diverging"][name]))
m = palettable.colorbrewer.get_map(name, map_type="diverging", number=number)
m.show_discrete_image(size=(12,2))
m.show_continuous_image(size=(12,2))
# + deletable=true editable=true
def get_cb_qualitative(name = "Set1", number = 9):
number = min(number, max(int(_) for _ in palettable.colorbrewer.COLOR_MAPS["Qualitative"][name]))
m = palettable.colorbrewer.get_map(name, map_type="qualitative", number=number)
m.show_discrete_image(size=(12,2))
m.show_continuous_image(size=(12,2))
# + deletable=true editable=true
def get_cb_sequential(name = "Blues", number = 9):
number = min(number, max(int(_) for _ in palettable.colorbrewer.COLOR_MAPS["Sequential"][name]))
m = palettable.colorbrewer.get_map(name, map_type="sequential", number=number)
m.show_discrete_image(size=(12,2))
m.show_continuous_image(size=(12,2))
# -
# As you look at these next few cells, note how things change with each colormap as well as with each count and type of colormap.
# + deletable=true editable=true
import ipywidgets
# + deletable=true editable=true
ipywidgets.interact(get_cb_diverging, name = list(palettable.colorbrewer.COLOR_MAPS["Diverging"].keys()), number = (1, 12))
# + deletable=true editable=true
ipywidgets.interact(get_cb_qualitative, name = list(palettable.colorbrewer.COLOR_MAPS["Qualitative"].keys()), number = (1, 12))
# + deletable=true editable=true
ipywidgets.interact(get_cb_sequential, name = list(palettable.colorbrewer.COLOR_MAPS["Sequential"].keys()), number = (1, 12))
# -
# Finally, cubehelix is a nice colormap for when you need to print out and get the same perceptual look as when its viewed in color.
# + deletable=true editable=true
palettable.cubehelix.classic_16.show_continuous_image(size=(10,2))
# + deletable=true editable=true
|
week06/examples_color01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import networkx as nx
class RandomGraph(object):
def __init__(self, node_num, p, seed, k=4, m=5, graph_mode="ER"):
self.node_num = node_num
self.p = p
self.k = k
self.m = m
self.seed = seed
self.graph_mode = graph_mode
self.graph = self.make_graph()
def make_graph(self):
# reference
# https://networkx.github.io/documentation/networkx-1.9/reference/generators.html
if self.graph_mode is "ER":
graph = nx.random_graphs.erdos_renyi_graph(self.node_num, self.p, self.seed)
elif self.graph_mode is "WS":
graph = nx.random_graphs.watts_strogatz_graph(self.node_num, self.k, self.p, self.seed)
elif self.graph_mode is "BA":
graph = nx.random_graphs.barabasi_albert_graph(self.node_num, self.m, self.seed)
return graph
def get_graph_info(self):
in_edges = {}
in_edges[0] = []
nodes = [0]
end = []
for node in self.graph.nodes():
neighbors = list(self.graph.neighbors(node))
# print(node, neighbors)
edges = []
check = []
for neighbor in neighbors:
if node > neighbor:
edges.append(neighbor + 1)
check.append(neighbor)
if not edges:
edges.append(0)
in_edges[node + 1] = edges
if check == neighbors:
end.append(node + 1)
nodes.append(node + 1)
in_edges[self.node_num + 1] = end
nodes.append(self.node_num + 1)
# print(nodes, in_edges)
return nodes, in_edges
# +
import torch
import torch.nn as nn
import torch.nn.functional as F
from graph import RandomGraph
# reference, Thank you.
# https://github.com/tstandley/Xception-PyTorch/blob/master/xception.py
class SeparableConv2d(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size=1, stride=1, padding=0, dilation=1, bias=False):
super(SeparableConv2d, self).__init__()
self.conv = nn.Conv2d(in_channels, in_channels, kernel_size, stride, padding, dilation, groups=in_channels, bias=bias)
self.pointwise = nn.Conv2d(in_channels, out_channels, 1, 1, 0, 1, 1, bias=bias)
def forward(self, x):
x = self.conv(x)
x = self.pointwise(x)
return x
# ReLU-convolution-BN triplet
class Unit(nn.Module):
def __init__(self, in_channels, out_channels, stride=1):
super(Unit, self).__init__()
self.unit = nn.Sequential(
nn.ReLU(),
SeparableConv2d(in_channels, out_channels, stride=stride),
nn.BatchNorm2d(out_channels)
)
def forward(self, x):
return self.unit(x)
class Node(nn.Module):
def __init__(self, in_degree, in_channels, out_channels, stride=1):
super(Node, self).__init__()
self.in_degree = in_degree
if len(self.in_degree) > 1:
self.weights = nn.Parameter(torch.ones(len(self.in_degree)), requires_grad=True)
self.unit = Unit(in_channels, out_channels, stride=stride)
def forward(self, *input):
if len(self.in_degree) > 1:
x = (input[0] * self.weights[0])
for index in range(1, len(input)):
x += (input[index][0] * self.weights[index])
x = torch.sigmoid(x)
out = self.unit(x)
else:
out = self.unit(input[0])
return out
class RandWire(nn.Module):
def __init__(self, node_num, p, seed, in_channels, out_channels):
super(RandWire, self).__init__()
self.node_num = node_num
self.p = p
self.seed = seed
self.in_channels = in_channels
self.out_channels = out_channels
# get graph nodes and in edges
graph = RandomGraph(self.node_num, self.p, self.seed)
self.nodes, self.in_edges = graph.get_graph_info()
# define input Node
self.module_list = nn.ModuleList([Node(self.in_edges[0], self.in_channels, self.out_channels, stride=2)])
# define the rest Node
self.module_list.extend([Node(self.in_edges[node], self.out_channels, self.out_channels) for node in self.nodes if node > 0])
self.memory = {}
def forward(self, x):
# start vertex
out = self.module_list[0].forward(x)
self.memory[0] = out
# the rest vertex
for node in range(1, len(self.nodes) - 1):
if len(self.in_edges[node]) > 1:
out = self.module_list[node].forward(*[self.memory[in_vertex] for in_vertex in self.in_edges[node]])
else:
out = self.module_list[node].forward(self.memory[self.in_edges[node][0]])
self.memory[node] = out
out = self.module_list[self.node_num + 1].forward(*[self.memory[in_vertex] for in_vertex in self.in_edges[self.node_num + 1]])
return out
# -
class Model(nn.Module):
def __init__(self, node_num, p, seed, in_channels, out_channels):
super(Model, self).__init__()
self.node_num = node_num
self.p = p
self.seed = seed
self.in_channels = in_channels
self.out_channels = out_channels
self.conv1 = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=self.out_channels // 2, kernel_size=3, stride=2, padding=1),
nn.BatchNorm2d(self.out_channels // 2),
nn.ReLU()
)
self.conv2 = nn.Sequential(
nn.Conv2d(in_channels=self.in_channels // 2, out_channels=self.out_channels, kernel_size=3, stride=2, padding=1),
nn.BatchNorm2d(self.out_channels),
nn.ReLU()
)
self.rand_wire1 = nn.Sequential(
RandWire(self.node_num, self.p, self.seed, self.in_channels, self.out_channels * 2)
)
self.rand_wire2 = nn.Sequential(
RandWire(self.node_num, self.p, self.seed, self.in_channels * 2, self.out_channels * 2)
)
self.conv_output = nn.Sequential(
nn.Conv2d(self.in_channels * 2, 1280, kernel_size=1, stride=2),
nn.BatchNorm2d(1280)
)
self.output = nn.Linear(1280, 10)
def forward(self, x):
x = self.conv1(x)
x = self.conv2(x)
x = self.rand_wire1(x)
x = self.rand_wire2(x)
x = self.conv_output(x)
# global average pooling
x = F.avg_pool2d(x, kernel_size=x.size()[2:])
x = torch.squeeze(x)
x = F.softmax(self.output(x), dim=-1)
return x
# +
import argparse
from torchviz import make_dot
from torch.autograd import Variable
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
model = Model(7, 0.4, 12, 2, 2)
x = torch.randn(2, 3, 32, 32)
y = model(x)
g = make_dot(y.mean(), params=dict(model.named_parameters()))
g.format='svg'
g.filename = 'image'
g.render(view=False)
# -
g
# !cairosvg image.svg -o image.png
|
visualize_graph/graphviz_module/RandWiredNetworkGraphVizualize_graphviz.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py35]
# language: python
# name: conda-env-py35-py
# ---
# ### Palindromes
#
# Some fun with palindromes.
#
#
# See [The LeetCode example problem](https://leetcode.com/problems/palindrome-number/description/)
# +
debugging = False
debugging = True
logging = True
def dprint(f, *args):
if debugging:
print((' DBG:' + f).format(*args))
def log(f, *args):
if logging:
print((f).format(*args))
def logError(f, *args):
if logging:
print(('*** ERROR:' + f).format(*args))
def className(instance):
return type(instance).__name__
# -
class Solution1(object):
""" Front to back, digit by digit compare using magnitudes to get leftmost digits """
def isPalindrome(self, x):
"""
:type x: int
:rtype: bool
"""
if x < 0:
return False # negative numbers are not palindromes
if x < 10:
return True # A single digit is a palindrome
n = x
digits = 1
mag = 1
# Count the number of digits in x.
while n > 9:
digits += 1
mag *= 10
n = n // 10
while digits > 0:
firstdigit = x // mag
lastdigit = x % 10
if firstdigit != lastdigit:
return False
x = x - firstdigit * mag
x = x // 10
mag //= 100
digits -= 2
return True
class Solution2(object):
""" Recursive string converted test for Palindrome """
def isPalindrome(self, x):
"""
:type x: int
:rtype: bool
"""
if isinstance(x, int):
return self.isPalindrome(str(x))
return len(x) < 2 or (x[0] == x[-1] and len(x) == 2) or ((x[0] == x[-1]) and self.isPalindrome(x[1:-1]))
class Solution3(object):
""" fastest numeric modulo reverse of only first half of number """
def isPalindrome(self, x):
"""
:type x: int
:rtype: bool
"""
if x < 0 or ( x % 10 == 0 and x != 0):
return False
if x < 10:
return True
revx = 0
n = x
while (n > revx):
digit = n % 10
revx *= 10
revx += digit
n //= 10
return n == revx or n == revx//10
tdata = [0, 1, 22, 10001, 123454321, 12344321]
fdata = [-1, 41, 123421]
testClasses = [Solution1, Solution2, Solution3]
testcycles = 10000 # Do enough to make the elapsed times meaningful.
# +
import time
from datetime import timedelta
for tclass in testClasses:
instance = tclass()
start_time = time.time()
for v in range(testcycles):
true_tests = [instance.isPalindrome(x) for x in tdata]
false_tests = [not instance.isPalindrome(x) for x in fdata]
elapsed_time = time.time() - start_time
success = all(true_tests) and all(false_tests)
if success:
log("- Class {0} works great! (ELAPSED time={1} )", className(instance), timedelta(seconds=elapsed_time))
else:
logError("Test Failure in {0}", className(instance))
log("- Passing True cases: {0}", true_tests)
for passed, val in zip(true_tests, tdata):
if not passed:
log("--- {0} is a palindrome, but was NOT recognized as one.", val)
log("- Passing False cases: {0}", false_tests)
for failed, val in zip(false_tests, fdata):
if not failed:
log("--- {0} is a NOT palindrome, but was recognized as one.", val)
# +
def isPalindrome(s, i, n):
""" true if s[i:i+n] is a Palindrome """
if n<=1:
return True
#log(" left={0} right={1}", s[i], s[i+n-1])
even = n % 2 == 0
m = n // 2
left = s[i:i+m]
right = s[i+m:i+n] if even else s[i+m+1:i+n]
#log("isPalindrome(s[]={0}, left={1} right={2} i={3}, m={4} n={5}", s[i:i+n], left, right, i, m, n)
return left == right[::-1]
def longestPalindrome(s):
"""
:type s: str
:rtype: str
"""
n = len(s)
while n > 1:
#for i in range(len(s)-n, -1, -1):
for i in range(0, len(s)-n+1):
if isPalindrome(s, i, n):
return s[i:i+n]
n -= 1
return s[0]
# -
isPalindrome("abbaxyabbazz", 2, 4)
#"abcd"[::-1]
longestPalindrome("thius baabad is a test")
zz="mwwfjysbkebpdjyabcfkgprtxpwvhglddhmvaprcvrnuxifcrjpdgnktvmggmguiiquibmtviwjsqwtchkqgxqwljouunurcdtoeygdqmijdympcamawnlzsxucbpqtuwkjfqnzvvvigifyvymfhtppqamlgjozvebygkxawcbwtouaankxsjrteeijpuzbsfsjwxejtfrancoekxgfyangvzjkdskhssdjvkvdskjtiybqgsmpxmghvvicmjxqtxdowkjhmlnfcpbtwvtmjhnzntxyfxyinmqzivxkwigkondghzmbioelmepgfttczskvqfejfiibxjcuyevvpawybcvvxtxycrfbcnpvkzryrqujqaqhoagdmofgdcbhvlwgwmsmhomknbanvntspvvhvccedzzngdywuccxrnzbtchisdwsrfdqpcwknwqvalczznilujdrlevncdsyuhnpmheukottewtkuzhookcsvctsqwwdvfjxifpfsqxpmpwospndozcdbfhselfdltmpujlnhfzjcgnbgprvopxklmlgrlbldzpnkhvhkybpgtzipzotrgzkdrqntnuaqyaplcybqyvidwcfcuxinchretgvfaepmgilbrtxgqoddzyjmmupkjqcypdpfhpkhitfegickfszermqhkwmffdizeoprmnlzbjcwfnqyvmhtdekmfhqwaftlyydirjnojbrieutjhymfpflsfemkqsoewbojwluqdckmzixwxufrdpqnwvwpbavosnvjqxqbosctttxvsbmqpnolfmapywtpfaotzmyjwnd"
longestPalindrome(zz)
# +
longestPalindrome("a"*1000)
# -
# ### Python O(n^2) method with some optimization, 88ms.
#
# Basic thought is simple. when you increase s by 1 character, you could only increase maxPalindromeLen by 1 or 2, and that new maxPalindrome includes this new character. Proof: if on adding 1 character, maxPalindromeLen increased by 3 or more, say the new maxPalindromeLen is Q, and the old maxPalindromeLen is P, and Q>=P+3. Then it would mean, even without this new character, there would be a palindromic substring ending in the last character, whose length is at least Q-2. Since Q-2 would be >P, this contradicts the condition that P is the maxPalindromeLen without the additional character.
#
# So, it becomes simple, you only need to scan from beginning to the end, adding one character at a time, keeping track of maxPalindromeLen, and for each added character, you check if the substrings ending with this new character, with length P+1 or P+2, are palindromes, and update accordingly.
#
# Now, this is O(n^2) as taking substrings and checking palindromicity seem O(n) time. We can speed up it by realizing that strings are immutable, and there are memory slicing tricks will help to speed these operations up. comparing string equality with "==" is O(1), and using slicing to substring and reverse is ̶a̶l̶s̶o̶ ̶O̶(̶1̶)̶ ̶(̶n̶o̶t̶ ̶t̶o̶t̶a̶l̶l̶y̶ ̶s̶u̶r̶e̶ ̶a̶b̶o̶u̶t̶ ̶t̶h̶e̶ ̶s̶l̶i̶c̶i̶n̶g̶ ̶t̶h̶o̶u̶g̶h̶.̶ ̶ ̶I̶ ̶t̶h̶i̶n̶k̶ ̶i̶t̶ ̶i̶s̶ ̶O̶(̶1̶)̶,̶ ̶b̶u̶t̶ ̶c̶o̶u̶l̶d̶ ̶n̶o̶t̶ ̶f̶i̶n̶d̶ ̶a̶n̶y̶ ̶s̶o̶l̶i̶d̶ ̶l̶i̶t̶e̶r̶a̶t̶u̶r̶e̶ ̶a̶b̶o̶u̶t̶ ̶i̶t̶.̶ O(n) (thanks to ChuntaoLu). But as slicing is optimized by the interpreter's C code, it should run pretty fast. I'm pretty new to Python. Would appreciate you would give more insights or further optimization.
#
# Thus, here is the O(n) method:
def longestPalindrome(s):
if len(s)==0:
return 0
maxLen=1
start=0
for i in range(len(s)):
if i-maxLen >=1 and s[i-maxLen-1:i+1]==s[i-maxLen-1:i+1][::-1]:
start=i-maxLen-1
maxLen+=2
continue
if i-maxLen >=0 and s[i-maxLen:i+1]==s[i-maxLen:i+1][::-1]:
start=i-maxLen
maxLen+=1
return s[start:start+maxLen]
zz="aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaabcaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa"
len(zz)
len(longestPalindrome(zz))
longestPalindrome("zzabbaxyxbbxz")
# +
def isPalindrome(s, i, n):
""" true if s[i:i+n] is a Palindrome """
if n<=1:
return True
if i<0 or i+n > len(s):
return False
#log(" left={0} right={1}", s[i], s[i+n-1])
even = n % 2 == 0
m = n // 2
left = s[i:i+m]
right = s[i+m:i+n] if even else s[i+m+1:i+n]
log("isPalindrome(s[]={0}, left={1} right={2} i={3}, m={4} n={5}", s[i:i+n], left, right, i, m, n)
isone = left == right[::-1]
if isone: log('"{0}" is a palindrome', s[i:i+n])
return isone
def longestPalindrome(s):
"""
:type s: str
:rtype: str
"""
maxlen = 1
p = 0 # location of the longest palindrome (the first character is always valid
for i in range(len(s)):
qp = i - maxlen
# Check for longer palindrome
if isPalindrome(s, qp-1, maxlen+2):
p = qp-1
maxlen += 2
continue
if isPalindrome(s, qp, maxlen+1):
p = qp
maxlen += 1
return s[p:p+maxlen]
# -
longestPalindrome("aaaabaaa")
|
Palindromes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:rec_to_binaries] *
# language: python
# name: conda-env-rec_to_binaries-py
# ---
# %reload_ext autoreload
# %autoreload 2
# ## File structure before running extraction
#
# Note: the data (`20190902_lotus_06_r3.rec`, `20190902_lotus_06_r3.1.h264`) has to be in the date folder (`20190902`). It cannot be contained within a subfolder.
# !tree ../test_data
# ### Extraction
#
# 1. Add spike gadgets to path
# +
import logging
import os
from rec_to_binaries import extract_trodes_rec_file
SPIKE_GADGETS_PATH = os.path.join(os.path.expanduser('~'), 'SpikeGadgets')
os.environ['PATH'] += os.pathsep + SPIKE_GADGETS_PATH
print(os.environ['PATH'])
# -
# 2. Extract animal `lotus` from `test_data` directory
# +
logging.basicConfig(level='INFO', format='%(asctime)s %(message)s',
datefmt='%d-%b-%y %H:%M:%S')
data_dir = os.path.join(os.pardir, 'test_data')
animal = 'lotus'
extract_trodes_rec_file(data_dir, animal, parallel_instances=4, overwrite=True)
# -
# ### File structure after extraction
#
# Notice that there is now a preprocessing directory
# !tree ../test_data
|
notebooks/Extract_Rec_to_Binaries.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.6 64-bit
# name: python3
# ---
# # Demo outlier detection with Proximity-Based (kNN)
#
# <NAME> - 20424037
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors
# +
# Import dataset
X = np.genfromtxt('./datasets/wine-data.csv', delimiter=',') # The wine dataset of scikit-learn
data = X
feature_space = pd.DataFrame(data)
# Visual dataset
plt.scatter(X[:, 0], X[:, 1], color='black', marker='o')
plt.xlabel('Concentration of flavanoids', fontsize=16)
plt.ylabel('Color intensity', fontsize=16)
plt.title("Outlier detection on wine dataset", fontsize=20)
plt.show()
feature_space
# -
k = 3
# Train kNN
nbrs = NearestNeighbors(n_neighbors = k).fit(data)
distances, indexes = nbrs.kneighbors(data)
distances = distances[:,1:k]
r = 0.5
# If any object has distances > r is a outlier, because in such a case, there are fewer than k objects that are in the r-neighborhood.
outliers = data[np.unique(np.where(distances > r)[0])]
plt.xlabel('Concentration of flavanoids', fontsize=16)
plt.ylabel('Color intensity', fontsize=16)
plt.title("Outlier detection on wine dataset", fontsize=20)
plt.scatter(X[:, 0], X[:, 1], color='black', marker='o')
plt.scatter(outliers[:, 0], outliers[:, 1], color = "r")
plt.show()
|
src/knn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
my_list = [1,2,3,4,5,6]
my_list
my_list
a = np.array(my_list)
print(a)
my_list%2
#it throws an error. we cannot iterate
#through the list to find out which are the off numbers present inside a list
a%2
#numpy is fastest package for mathematical operations- optimised memory allocation
# +
#2D array
# +
#multi dimensional arrays
my_matrix = [[1,2,3],[4,'hello',6],[7,8,9]]
# -
my_matrix
a = np.array(my_matrix)
print(a)
print(type(a))
#numpy.array is a function that returns a numpy.ndarray. There is no object type numpy.array.
#converting array to list
a.tolist()
# +
#working with dimensions
#1-D array
a = np.array([2,3,4,5])
print(a)
print(a.ndim) #gives the number of dimension whether a 1D array or 2D array
print(a.size) #gives the number of elements
# +
#working with dimensions
#2-D array
a = np.array([[2,3],[4,5]])
print(a)
print(a.ndim)#gives the number of dimension whether a 1D array or 2D array
print(a.shape) #gives the shape of the array
print(a.size) #gives the number of elements
# +
#working with dimensions
#3-D array
a = np.array([[[2,3],[4,5]]])
print(a)
print(a.ndim) #gives the number of dimension whether a 1D array or 2D array
print(a.size) #gives the number of elements
print(a.shape)
# -
# ## Built-in Methods
#
# There are lots of built-in ways to generate Arrays
# ### arange
#
# Return evenly spaced values within a given interval.
np.arange(0,10,2)
np.linspace(0,10,5000)
np.arange(0,13,4)
# ### zeros and ones
#
# Generate arrays of zeros or ones
np.zeros(3)
np.ones(5)*5
np.zeros((5,5))
#passing as a tuple
np.zeros([5,5])
#passing as a lost
np.eye(3)
np.ones(3)
np.ones((3,3))
np.ones(4)*5
np.full([2,4],-45)
#3D matrix of zeros
np.zeros([2,3,4])
# ### linspace
# Return evenly spaced numbers over a specified interval.
np.linspace(0,1,10)
np.linspace(0,10,5)
# ## eye
#
# Creates an identity matrix
np.eye(4)
np.identity(4)
# ## Random
#
# Numpy also has lots of ways to create random number arrays:
#
# ### rand
# Create an array of the given shape and populate it with
# random samples from a uniform distribution
# over ``[0, 1)``.
np.random.rand(5)
#values between 0 and 1
np.random.rand(5,5)
# ### randn
#
# Return a sample (or samples) from the "standard normal" distribution. Unlike rand which is uniform:
np.random.randn(2)
np.random.randint(1,10,size=(4,5,3))
np.randint(1,10,3)
np.random.randn(5,5)
# ### randint
# Return random integers from `low` (inclusive) to `high` (exclusive).
np.random.randint(1,100)
arr1 = np.random.randint(1,100,50)
arr1
a = np.array(np.random.randint(2,10,(3,3)))
print(a)
a = np.array(np.random.randint(2,10,(3,3,3)))
print(a)
# ## Array Attributes and Methods
#
# Let's discuss some useful attributes and methods or an array:
arr1 = np.random.randint(0,50,10)
arr1
arr = np.arange(25)
arr
import numpy as np
a = np.arange(0,25)
a
# ## Reshape
# Returns an array containing the same data with a new shape.
a.reshape(5,5)
a=np.random.randint(0,1000,50)
a
# ### max,min,argmax,argmin
#
# These are useful methods for finding max or min values. Or to find their index locations using argmin or argmax
arr1
a.max()
a.argmax()
a.min()
a.argmin()
# ## Shape
#
# Shape is an attribute that arrays have (not a method):
# Vector
arr.shape
# Notice the two sets of brackets
arr.reshape(25,)
arr1.reshape(5,10)
arr.reshape(25,1).shape
# ### dtype
#
# You can also grab the data type of the object in the array:
arr.dtype
|
01-NumPy Arrays.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from deep_rl import *
import matplotlib.pyplot as plt
import torch
# %load_ext autoreload
# %reload_ext autoreload
# %autoreload 2
# +
def dsr_feature(**kwargs):
generate_tag(kwargs)
kwargs.setdefault('log_level', 0)
config = Config()
config.merge(kwargs)
config.task_fn = lambda: Task(config.game)
config.eval_env = config.task_fn()
config.c = 0.1
config.optimizer_fn = lambda params: torch.optim.RMSprop(params, 0.001)
config.network_fn = lambda: SRNet(config.action_dim, FCBody(config.state_dim))
# config.network_fn = lambda: DuelingNet(config.action_dim, FCBody(config.state_dim))
# config.replay_fn = lambda: Replay(memory_size=int(1e4), batch_size=10)
config.replay_fn = lambda: AsyncReplay(memory_size=int(1e4), batch_size=10)
config.random_action_prob = LinearSchedule(1.0, 0.1, 1e4)
config.discount = 0.99
config.target_network_update_freq = 200
config.exploration_steps = 1000
# config.double_q = True
config.double_q = False
config.sgd_update_frequency = 4
config.gradient_clip = 5
config.eval_interval = int(5e3)
config.max_steps = 1e5
config.async_actor = False
run_steps(DSRAgent(config))
# DQN
def dqn_feature(**kwargs):
generate_tag(kwargs)
kwargs.setdefault('log_level', 0)
config = Config()
config.merge(kwargs)
config.task_fn = lambda: Task(config.game)
config.eval_env = config.task_fn()
config.optimizer_fn = lambda params: torch.optim.RMSprop(params, 0.001)
config.network_fn = lambda: VanillaNet(config.action_dim, FCBody(config.state_dim))
# config.network_fn = lambda: DuelingNet(config.action_dim, FCBody(config.state_dim))
# config.replay_fn = lambda: Replay(memory_size=int(1e4), batch_size=10)
config.replay_fn = lambda: AsyncReplay(memory_size=int(1e4), batch_size=10)
config.random_action_prob = LinearSchedule(1.0, 0.1, 1e4)
config.discount = 0.99
config.target_network_update_freq = 200
config.exploration_steps = 1000
# config.double_q = True
config.double_q = False
config.sgd_update_frequency = 4
config.gradient_clip = 5
config.eval_interval = int(5e3)
config.max_steps = 1e5
config.async_actor = False
run_steps(DQNAgent(config))
# -
mkdir('log')
mkdir('tf_log')
set_one_thread()
random_seed()
select_device(-1)
game = 'FourRooms'
dsr_feature(game=game)
game = 'FourRooms'
dqn_feature(game=game)
import re
# %ls log/
def log2list(filename):
returns_train = []
returns_test = []
with open(filename, 'rb') as f:
while True:
line = f.readline()
split = re.split('\s', str(line))
if not line:
break
if('episodic_return_train' in split):
returns_train.append(float(split[-1][:-3]))
if('episodic_return_test' in split):
returns_test.append(float(split[-1][:-10]))
return returns_train, returns_test
dsr_file = 'log/FourRooms--run-0-200302-131223.txt'
# dqn_file = 'log/FourRooms--run-0-200301-161113.txt'
train_dsr, test_dsr = log2list(dsr_file)
# train_dqn, test_dqn = log2list(dqn_file)
# train_max = min(len(train_dsr), len(train_dqn))
# test_max = min(len(test_dsr), len(test_dqn))
# +
import matplotlib.pyplot as plt
plt.figure(figsize=(12,6), dpi=100)
# plt.plot(train_dqn[:train_max], label='DQN')
plt.plot(train_dsr[:], label='DSR')
plt.title('Train returns on 4 rooms')
plt.xlabel('episodes'), plt.legend()
plt.show()
plt.figure(figsize=(12,6), dpi=100)
# plt.plot(test_dqn[:test_max], '.-', label='DQN')
plt.plot(test_dsr[:], '.-', label='DSR')
plt.title('Test return on 4rooms')
plt.xlabel('test iteration'), plt.legend()
plt.show()
# -
|
notebooks/dsr-with-repLearn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Estimating the carbon content of marine bacteria and archaea
#
# In order to estimate the characteristic carbon content of marine bacteria and archaea, we rely on two main methodologies - volume based estimates and amino acid based estimates.
#
# ## Volume-based estimates
# We collected measurements of the characeteristic volume of bacteria and archaea in the marine deep subsurface from 4 different studies. For 3 of those studies, we collected reported average cell volumes. Here are the average values we collected from those three studies:
import pandas as pd
import numpy as np
from scipy.stats import gmean
import sys
sys.path.insert(0, '../../../statistics_helper')
from CI_helper import *
pd.options.display.float_format = '{:,.2f}'.format
volumes = pd.read_excel('marine_deep_subsurface_prok_carbon_content_data.xlsx','Volume based')
volumes
# In addition we used data from [Braun et al.](http://dx.doi.org/10.3389/fmicb.2016.01375) which measured cell volumes for three cell morphologies (coccoid, elongated and filamentous), along with the relative fraction of each morphology in each site sampled. Here is the data extracted from Braun et al.:
braun_volumes = pd.read_excel('marine_deep_subsurface_prok_carbon_content_data.xlsx','Braun', skiprows=1)
braun_volumes
# We first calculate the characteristic volume of a single cell from the data in Braun et al. to be able to compare it with the other resources:
# +
# Group by depth
braun_depth_binned = braun_volumes.groupby(['Depth (m)'])
# Define the function which will to the weighted average of volume based on the fraction of the
# population of each cell type
def groupby_weighted_average(input):
return np.average(input['Mean volume (µm^3)'],weights=input['Fraction FM'])
# Calculate the weighted average volume for each depth sample
braun_weighted_average = braun_depth_binned.apply(groupby_weighted_average)
# Calculate the geometric mean of the volumes from different depths
braun_characteristic_volume = gmean(braun_weighted_average)
print(r'The characteristic volume of bacterial and archaeal cells in the marine deep subsurface based on Braun et al. is ≈%.2fµm^3' %braun_characteristic_volume)
volumes.append(pd.DataFrame.from_dict([{'Study': 'Braun et al.', 'Mean cell volume (µm^3)':braun_characteristic_volume}]))
# -
# In order to covert the five different estimates for the characteristic volume of bacterial and archaeal cell in the marine deep subsurface into estimates of carbon content, we use two independent models that have been used in the literature: [Fry et al.](http://dx.doi.org/10.1016/S0580-9517(08)70239-3) which estimates ≈300 fg C per $µm^3$, and [Simon & Azam](http://dx.doi.org/10.3354/meps051201), which developed an allometric model of the carbon content of cells with different volumes. The allometric model they developed is:
# $$C = 88.1 \times V^{0.59}$$
# Where C is the carbon content of a single cell [fg C cell$^{-1}$], and V is cell volume [$µm^3$]. We apply these two independent conversion equations to the volumes we gathered from the literature to produce 10 estimates for the characteristic carbon content of bacterial and archaeal cells in the marine deep subsurface.
# +
# Apply the conversion equations to the volumes reported in the literature
volumes['Fry et al.'] = volumes['Mean cell volume (µm^3)']*310
volumes['Simon and Azam'] = 88.1*volumes['Mean cell volume (µm^3)']**0.59
volumes
# -
# We calculate the geometric mean of the values from different studies using the same conversion equation to generate a characteristic carbon content for each conversion method.
# +
fry_volume_mean = gmean(volumes['Fry et al.'])
sa_volume_mean = gmean(volumes['Simon and Azam'])
print('The characteristic carbon content of a single bacterial or archaeal cell in the marine deep subsurface based on cell volume converted using the conversion equation from Fry et al. is ≈%.0f fg C cell^-1\n' %fry_volume_mean)
print('The characteristic carbon content of a single bacterial or archaeal cell in the marine deep subsurface based on cell volume converted using the conversion equation from Simon & Azam is ≈%.0f fg C cell^-1' %sa_volume_mean)
# -
# We compute the geometric mean of the characteristic values from the two volume to carbon content conversion methods and use it as our best estimate for the carbon content of bacterial and archaeal cells in the marine deep subsurface, based on volume measurements.
vol_best_carbon_content = gmean([fry_volume_mean,sa_volume_mean])
print('Our best volume-based estimate for the carbon content of bacterial and archaeal cells in the marine deep subsurface is %.0f fg C cell^-1' %vol_best_carbon_content)
# ## Amino acid-based estimate
# We rely on the study by Braun et al., which measured carobon content of bacterial and archaeal cells in the marine deep subsurface based on amino acid carbon mass, and assuming ≈55% of the carbon mass of single cells is stored in amino acids. Here are the values reported by Braun et al.:
aa_based = pd.read_excel('marine_deep_subsurface_prok_carbon_content_data.xlsx', 'Amino acid based', skiprows=1)
aa_based
# We use the geometric mean of the values reported by Braun et al. as our best estimate for the amino acid-based estimate of the carbon content of bacterial and archaeal cells in the marine deep subsurface.
# +
aa_best_carbon_content = gmean(aa_based['Carbon content (fg C cell-1)'])
print('Our best amino acid-based estimate for the carbon content of bacterial and archaeal cells in the marine deep subsurface is %.0f fg C cell^-1' %aa_best_carbon_content)
# -
# As our best estimate for the carbon content of bacterial and archaeal cells in the marine deep subsurface, we use the geometric mean of the volume-based and amino acid-based estimates.
best_estimate = gmean([vol_best_carbon_content,aa_best_carbon_content])
print('Our best estimate for the carbon content of bacterial and archaeal cells in the marine deep subsurface is %.0f fg C cell^-1' %best_estimate)
# # Uncertainty analysis
# To calculate the uncertainty associated with the estimate for the total number of of bacteria and archaea in the marine deep subsurface, we first collect all available uncertainties and then take the largest value as our best projection for the uncertainty.
#
# ## Volume-based
#
# ### intra-study uncertainty
# For the volume based approaches, we had data on intra-study uncertainty only for the Braun et al. study. We calculate the intra study uncertainty of the volumes reported in Braun et al. by calculating the 95% confidence interval of the values reported in Braun et al.
vol_braun_intra_CI = geo_CI_calc(braun_weighted_average)
print('The intra-study uncertainty for Braun et al. is ≈%.1f-fold' %vol_braun_intra_CI)
# ### Interstudy uncertainty
# As a measure of the interstudy uncertainty, we compare the 95% confidence interval for the geometric mean of the carbon content from different studies, using the same conversion method.
# We also use the 95% confidence interval for the geometric mean of the carbon content estimates from the two different conversion methods (Fry et al. and Simon & Azam) as a measure of interstudy uncertainty.
# +
carbon_content_fry_CI = geo_CI_calc(volumes['Fry et al.'])
carbon_content_sa_CI = geo_CI_calc(volumes['Simon and Azam'])
print('The interstudy uncertainty of the geometric mean of carbon content using the conversion method of Fry et al. is ≈%.1f-fold' %carbon_content_fry_CI)
print('The interstudy uncertainty of the geometric mean of carbon content using the conversion method of Simon & Azam is ≈%.1f-fold' %carbon_content_sa_CI)
carbon_content_vol_CI = geo_CI_calc([fry_volume_mean,sa_volume_mean])
print('The interstudy uncertainty of the geometric mean of carbon content between conversion methods is ≈%.1f-fold' %carbon_content_vol_CI)
# -
# ## Amino acid-based
#
# ### Intra-study uncertainty
# We calculate the 95% confidence interval of the geometric mean of values for the carbon content from Braun et al. as a measure of the intra-study uncertainty.
aa_intra_CI = geo_CI_calc(aa_based['Carbon content (fg C cell-1)'])
print('The intra-study uncertainty of amino acid-based carbon content estimates from Braun et al. is ≈%.1f-fold' %aa_intra_CI)
# ## Inter-method uncertainty
# As another measure of uncertainty we calculate the 95% confidence interval of the geometric mean of the estimates for carbon content calculated using either the volume-based method or the amino acid-based method.
inter_method_CI = geo_CI_calc([vol_best_carbon_content,aa_best_carbon_content])
print('The intra-method uncertainty for the caron content of bacretial and archaeal cells in the marine deep subsurface is ≈%.1f-fold' %inter_method_CI)
# We use the highest uncertainty among this collection, which is ≈2.2-fold, as our best projection of the uncertainty associated with our estimate of the carbon content of bacterial and archaeal cells in the marine deep subsurface.
#
# Our final parameters are:
# +
# Take the maximal uncetainty as our best projection of uncertainty
mul_CI = np.max([inter_method_CI,aa_intra_CI,carbon_content_vol_CI,carbon_content_fry_CI,carbon_content_sa_CI,vol_braun_intra_CI])
print('Carbon content of bacterial and archaeal cells in the marine deep subsurface: %.0f fg C' % best_estimate)
print('Uncertainty associated with the carbon content of bacterial and archaeal cells in the marine deep subsurface: %.1f-fold' % mul_CI)
old_results = pd.read_excel('../marine_deep_subsurface_prok_biomass_estimate.xlsx')
result = old_results.copy()
result.loc[1] = pd.Series({
'Parameter': 'Carbon content of bacterial and archaeal cells in the marine deep subsurface',
'Value': int(best_estimate),
'Units': 'fg C cell^-1',
'Uncertainty': "{0:.1f}".format(mul_CI)
})
result.to_excel('../marine_deep_subsurface_prok_biomass_estimate.xlsx',index=False)
|
bacteria_archaea/marine_deep_subsurface/carbon_content/marine_deep_subsurface_prok_carbon_content.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="3rZiB3wop9pt" colab_type="text"
# #Principal Componenent Analysis (PCA)
# + id="sNNVHMngp5p_" colab_type="code" outputId="7a9087f4-8d3b-41d3-fdbb-acf6ddbdb1b9" executionInfo={"status": "ok", "timestamp": 1574824414656, "user_tz": 240, "elapsed": 2376, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}} colab={"base_uri": "https://localhost:8080/", "height": 202}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# Download and load iris dataset
url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal length','sepal width','petal length','petal width','target']
df = pd.read_csv(url, names=names)
df.head()
# + id="rVORIEc1qI0J" colab_type="code" outputId="ea38e7ed-c19f-46a8-98f8-8ca5dd6cd263" executionInfo={"status": "ok", "timestamp": 1574824457847, "user_tz": 240, "elapsed": 918, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}} colab={"base_uri": "https://localhost:8080/", "height": 52}
# Standardize data to 0 mean and 1 variance
features = names[:-1]
x = df.loc[:, features].values
y = df.loc[:,['target']].values
x = StandardScaler().fit_transform(x)
print(x[0])
print(x[1])
# + id="xL5mutyCq4ae" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 202} outputId="74027780-0a2f-4f1b-9026-6575a3bb098a" executionInfo={"status": "ok", "timestamp": 1574824583237, "user_tz": 240, "elapsed": 501, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}}
# Perform PCA using two componenents (k=2)
pca = PCA(n_components=2)
principalComponents = pca.fit_transform(x)
principalDf = pd.DataFrame(data = principalComponents, columns = ['PC1', 'PC2'])
principalDf.head()
# + id="4pPyzXTOuH7f" colab_type="code" outputId="d0aa1925-eb14-43e8-f813-0f80659ed2db" executionInfo={"status": "ok", "timestamp": 1574824597141, "user_tz": 240, "elapsed": 504, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}} colab={"base_uri": "https://localhost:8080/", "height": 69}
# Let's look at our components
print(pca.components_)
# Let's print the explained variance by each componenent using np.around to round to two decimal places
print(np.around(pca.explained_variance_ratio_*100, 2))
# + id="rYTjIcFcwEZD" colab_type="code" outputId="f68dba25-04fd-4c34-84c4-48e1b2500237" executionInfo={"status": "ok", "timestamp": 1574824648022, "user_tz": 240, "elapsed": 1317, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}} colab={"base_uri": "https://localhost:8080/", "height": 330}
#cumulative sum of variance explained with [n] features
var = np.cumsum(np.round(pca.explained_variance_ratio_, decimals=3)*100)
print(var)
plt.ylabel('% Variance Explained')
plt.xlabel('# of Features')
plt.title('PCA Analysis')
plt.ylim(30,100.5)
plt.style.context('seaborn-whitegrid')
plt.plot(var)
# + id="CoMzAdvWt3Ky" colab_type="code" colab={}
# Merge or concatenate our PCA dataset with our target column
finalDf = pd.concat([principalDf, df[['target']]], axis = 1)
# + id="Cm-nlBAuq6mO" colab_type="code" outputId="abac5c47-7997-4276-b1a8-00fb90d42209" executionInfo={"status": "ok", "timestamp": 1574824706559, "user_tz": 240, "elapsed": 1333, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mCGo6aIm0tOcd5EhqWlYb0rime9sBvHS9YMpx0D2w=s64", "userId": "08597265227091462140"}} colab={"base_uri": "https://localhost:8080/", "height": 523}
# Plot
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(1,1,1)
explained = np.around(pca.explained_variance_ratio_*100, 2)
ax.set_xlabel('PC1 ({}%)'.format(explained[0]), fontsize = 15)
ax.set_ylabel('PC2 ({}%)'.format(explained[1]), fontsize = 15)
ax.set_title('Two-Component PCA', fontsize = 20)
targets = ['Iris-setosa', 'Iris-versicolor', 'Iris-virginica']
colors = ['r', 'g', 'b']
for target, color in zip(targets,colors):
indicesToKeep = finalDf['target'] == target
ax.scatter(finalDf.loc[indicesToKeep, 'PC1']
, finalDf.loc[indicesToKeep, 'PC2']
, c = color
, s = 50)
ax.legend(targets)
ax.grid()
# + id="EQxXVFSOuWsi" colab_type="code" colab={}
|
notebooks/22.3 Principal Component Analysis + Visualizations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Laboratorio 2
import numpy as np
from scipy import linalg
# ## Ejercicio 1
#
# Dados dos NumPy array, `x` e `y` unidimensionales, construye su matriz de Cauchy `C`tal que
#
# (1 punto)
#
# $$
# c_{ij} = \frac{1}{x_i - y_j}
# $$
def cauchy_matrix(x, y):
m = x.shape[0]
n = y.shape[0]
C = np.empty(shape=(m, n))
for i in range(m):
for j in range(n):
C[i,j] = 1/(x[i] - y[j])
return C
x = np.arange(10, 101, 10)
y = np.arange(5)
cauchy_matrix(x, y)
# ## Ejercicio 2
#
# (1 punto)
#
# Implementa la multiplicación matricial a través de dos ciclos `for`. Verifica que tu implementación está correcta y luego compara los tiempos de tu implementación versus la de NumPy.
def my_mul(A, B):
m, n = A.shape
p, q = B.shape
if n != p:
raise ValueError("Las dimensiones de las matrices no calzan!")
C = np.empty(shape=(m,q))
for i in range(m):
for j in range(q):
C[i, j] = np.sum(A[i]*B[:,j])
return C
A = np.arange(15).reshape(-1, 5)
B = np.arange(20).reshape(5, -1)
my_mul(A, B)
# Validation
np.allclose(my_mul(A, B), A @ B)
# %%timeit
my_mul(A, B)
# %%timeit
A @ B
# ## Ejercicio 3
#
# (1 punto)
#
# Crea una función que imprima todos los bloques contiguos de tamaño $3 \times 3$ para una matriz de $5 \times 5$.
# Hint: Deben ser 9 bloques!
def three_times_three_blocks(A):
m, n = A.shape
counter = 1
for i in range(3):
for j in range(3):
block = A[i:i+3,j:j+3:]
print(f"Block {counter}:")
print(block)
print("\n")
counter += 1
A = np.arange(1, 26).reshape(5, 5)
A
three_times_three_blocks(A)
# ## Ejercicio 4
#
# (1 punto)
#
# Has tu propio implementación de la matriz de Hilbert de orden $n$ y luego compara los tiempos de ejecución versus la función [`scipy.linalg.hilbert`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.hilbert.html#scipy.linalg.hilbert). Finalmente, verifica que la inversa de tu implementación (utilizando `linalg.inv`) es idéntica a la obtenida con la función [`scipy.linalg.invhilbert`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.invhilbert.html#scipy.linalg.invhilbert).
def my_hilbert(n):
H = np.empty((n, n))
for i in range(n):
for j in range(n):
H[i,j] = 1/(i + j + 1)
return H
n = 5
np.allclose(my_hilbert(n), linalg.hilbert(n))
# %timeit my_hilbert(n)
# %timeit linalg.hilbert(n)
# +
# Verificacion inversas
np.allclose(linalg.inv(my_hilbert(n)),linalg.invhilbert(n))
# -
# Vuelve a probar pero con $n=10$. ¿Cambia algo? ¿Por qué podría ser?
n = 10
np.allclose(my_hilbert(n), linalg.hilbert(n))
# %timeit my_hilbert(n)
# %timeit linalg.hilbert(n)
# __Respuesta:__ Sí, para $n = 5$ es más rápido `my_hilbert`, mientras que para $n = 10$ es más rápido `scipy.linalg.hilbert`. Esto se debe probablemente a que el algoritmo de `scipy.linalg.hilbert` este pensado para trabajar con muchos datos, por tanto es eficiente para $n$ suficientemente grande, lo que lo puede hacer ineficientes para $n$ pequeños.
|
labs/lab02.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# [Table of contents](../toc.ipynb)
#
# # Workflows and beyond
#
# This final theory notebook will be a short summary of different workflows and software development processes. The goal is to get a high level overview of the methods.
#
# Add to this, two methods for collaborative software development are outlined.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Keywords
#
# You probably heard about keywords and concepts like
#
# * Inner Source,
# * Open Source,
# * Waterfall,
# * Agile?
#
# The first two keywords are about collaboration models and the latter about project management (or its absence).
#
# Let us take a short look at Open and Inner Source first.
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Collaboration
#
# ### Open Source
#
# <a href="https://de.wikipedia.org/wiki/Open_Source"><img src="https://upload.wikimedia.org/wikipedia/commons/thumb/4/42/Opensource.svg/170px-Opensource.svg.png" alt="Open Source" width="100" align="right"></a>
#
# Nowadays, there is no need to tell much about [open source](https://en.wikipedia.org/wiki/Open_source) because it is virtually everywhere and very successful. Especially if you are using Python, you build entirely on open source software.
#
# The main strengths of open source are:
# * reuse of software,
# * often better quality than proprietary software,
# * you can propose extensions,
# * more trustworthy because you can read the code,
# * close to customer, you can change the part of software you want,
# * ...
#
# This was just a short list of arguments.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Inner Source
#
# <a href="http://innersourcecommons.org/"><img src="http://innersourcecommons.org/assets/img/isc-border.png" alt="Inner Source" width="100" align="right"></a>
#
# [Inner Source](https://en.wikipedia.org/wiki/Inner_source) is a rather recent initiative to apply open source principles inside companies. Larger companies face basically the same challenges that lead to open source culture. These challenges are:
#
# * Software development is highly distributed in space (countries, departments) and time (time locations).
# * Redundant software development is waste of money, reuse of existing software makes more sense.
# * It is hard to shape high quality software culture without sharing code.
# * Organizational boundaries slow down development and do not contribute to quality.
# + [markdown] slideshow={"slide_type": "subslide"}
# <a href="http://innersourcecommons.org/assets/img/AdoptingInnerSource.jpg"><img src="http://innersourcecommons.org/assets/img/AdoptingInnerSource.jpg" alt="Inner Source Book" width="100" align="right"></a>
#
# Add to these challenges, inner source benefits are:
# * Flexible utilization of developers (you do not need to change the department to fix a bug in a project).
# * Higher motivated developers.
#
# A great source of company experience with inner source is [[Cooper2018]](../references.bib).
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Silo thinking
#
# <img width="150" alt="silo" src="../_static/silo.jpg" align="right">
#
# Last but not least, probably the majority of software within companies is still written in silos. The common problems with silo thinking in general are:
#
# * It is hard to find someone who is in charge.
# * Much redundant is work is done.
# * The quality is usually poorer than in shared projects because no one else can see the mess behind.
# * Individual software parts within a company are not compatible because there is not need to work together.
# * Specification, negotiation, internal contracting wastes many resources.
# * Blaming more common than solving problems.
# * ...
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Development paradigms
#
# ### Waterfall model
#
# The [waterfall model](https://en.wikipedia.org/wiki/Waterfall_model) is the oldest project management principle and is seen as "not so hot today".
#
# The waterfall model is a sequential development where **product requirements** are converted into a
# **software design**, the **implementation** is made within this design, the software is **verified**, and **maintained**.
#
# Main criticism is with respect to sequential development. **Usually, neither costumers nor product managers know all requirements at beginning** and in practice the **requirements change over time**. With waterfall, you need to wait until end of verification to change the requirements and start from scratch, which is very time consuming.
# + [markdown] slideshow={"slide_type": "subslide"}
# <a title="CC BY 3.0 by Geek and Poke" href="http://geek-and-poke.com/geekandpoke/2012/10/1/doad.html"><img width="350" alt="almost done" src="http://s3.media.squarespace.com/production/2129687/19317774/.a/6a00d8341d3df553ef017ee3e6a10f970d-800wi" align="right"></a>
#
# ### Agile
#
# Compared with waterfall, the term [Agile](https://en.wikipedia.org/wiki/Agile_software_development) is very hot and a lot of consulting agencies make money out of this fact.
#
# Agile originates from the [agile manifesto](https://agilemanifesto.org/) which makes the following suggestions:
#
# * **Individuals and Interactions** over processes and tools
# * **Working Software** over comprehensive documentation
# * **Customer Collaboration** over contract negotiation
# * **Responding to Change** over following a plan
# + [markdown] slideshow={"slide_type": "subslide"}
# <a title="CC BY 3.0 by Geek and Poke" href="http://geek-and-poke.com/geekandpoke/2016/4/26/finally-agile"><img width="350" alt="finally agile" src="https://images.squarespace-cdn.com/content/v1/518f5d62e4b075248d6a3f90/1461706611560-F89DIXX8PVBXMHFH2AIE/ke17ZwdGBToddI8pDm48kKPkarJTiB48oWPGUQ76BaN7gQa3H78H3Y0txjaiv_0faShnVfr-ySw9qgw5FxrvM0_-U88Vz3_ValeR7UJawSO8tYm6j2RpB0d1Gi3SQHdgOqpeNLcJ80NK65_fV7S1UR5Xs9DxgCAdpDMB2e4IT-ha50phGt447LzNOTZrI4UdM14nZUo0tVr0uKhdsAoztA/image-asset.jpeg?format=1000w" align="right"></a>
#
# Therefore from its roots, **agile is quite the opposite to what large organizations are used to work with**.
#
# This is why a lot of consulting agencies bend agile into a form which is convenient for large companies so that they can say they are working agile but stick to their old culture.
#
# Agile is often used in combination or as substitute for terms like **Scrum** and **Kanban**, which complicates things further. Instead of a lengthly explanation what Agile is, I prefer to provide a very short explanation and a warning and links to expert resources.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Agile in a nutshell
#
# <img width="500" alt="agile" src="agile.png" align="center">
#
# * Agile is iterative development.
# * Working software is delivered frequently (weeks no months).
# * Simplicity is what counts! MVP minimum viable product (bare minimum for the client).
# * Regular meetings: daily standup (what did I, what I am working on, problems), sprint planning (slice features into stories, estimate effort in story points), sprint review (team presents what is delivered), retrospectives (what went wrong or well, continuous improvement).
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Sad story: some experts recommend to abandon Agile
#
# Experts who developed the agile manifesto actually recommend developers to [abandon agile](https://ronjeffries.com/articles/018-01ff/abandon-1/) because the process people flood all agile conferences with a very process driven view on agile.
#
# As result, many agile implementations in large companies are process driven and already the first principle "**Individuals and Interactions** over processes and tools" is not realized. This process driven implementations are known as [dark scrum](https://ronjeffries.com/articles/016-09ff/defense/).
#
# More serious warnings are stated in these conference video casts:
#
# * [The death of Agile - <NAME>](https://www.youtube.com/watch?v=vSnCeJEka_s)
# * [GOTO 2015 • Agile is Dead • Pragmatic Dave Thomas](https://www.youtube.com/watch?v=a-BOSpxYJ9M)
# * [Agile in 2018](https://www.youtube.com/watch?v=G_y2pNj0zZg)
# + [markdown] slideshow={"slide_type": "subslide"}
# #### Books on Agile development
#
# <a href="https://www.oreilly.com/library/view/clean-agile-back/9780135782002/"><img src="https://www.oreilly.com/library/cover/9780135782002/250w/" alt="Clean Agile" width="100" align="right"></a>
#
#
# As there are so many authors and consulting agencies make money out of the agile hype, it is not so easy to find the original concept behind agile. Here are two trustworthy sources from my point of view.
#
# * [Agile Software Guide blog on martinfowler.com](https://martinfowler.com/agile.html)
# * [[Martin2019]](../references.bib)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Congrats
#
# <img src="../_static/flower.jpg" alt="Flower" width="350" align="right">
#
# These were the basics in software development I wanted to share. The topic is much larger, but with the given outline you will be able to understand and implement more advanced concepts.
#
# The final part of this course is a collection of mini projects.
|
03_software-development/05_workflows.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={} tags=[]
# <img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
#
# + [markdown] papermill={} tags=[]
# # Plotly - Create Bubble chart
# <a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Plotly/Create%20Bubble%20chart.ipynb" target="_parent"><img src="https://img.shields.io/badge/-Open%20in%20Naas-success?labelColor=000000&logo=data:image/svg+xml;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiPz4KPHN2ZyB3aWR0aD0iMTAyNHB4IiBoZWlnaHQ9IjEwMjRweCIgdmlld0JveD0iMCAwIDEwMjQgMTAyNCIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayIgdmVyc2lvbj0iMS4xIj4KIDwhLS0gR2VuZXJhdGVkIGJ5IFBpeGVsbWF0b3IgUHJvIDIuMC41IC0tPgogPGRlZnM+CiAgPHR<KEY>
# + [markdown] papermill={} tags=[]
# **Tags:** #plotly #chart #bubblechart #dataviz
# + [markdown] papermill={} tags=[]
# Learn more on the Plotly doc : https://plotly.com/python/bubble-charts/
# + [markdown] papermill={} tags=[]
# ## Input
# + [markdown] papermill={} tags=[]
# ### Import library
# + papermill={} tags=[]
import plotly.express as px
# + [markdown] papermill={} tags=[]
# ## Model
# + [markdown] papermill={} tags=[]
# ### Bubble chart
# + papermill={} tags=[]
df = px.data.gapminder()
fig = px.scatter(df.query("year==2007"), x="gdpPercap", y="lifeExp",
size="pop", color="continent",
hover_name="country", log_x=True, size_max=60)
# + [markdown] papermill={} tags=[]
# ## Output
# + [markdown] papermill={} tags=[]
# ### Display result
# + papermill={} tags=[]
fig.show()
|
Plotly/Create Bubble chart.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Multi-Band Auto-Encoder
# ### This Network should learn to compress the information from multiple 2400 channel spectrograms of different window lengths into a low dimensional latent space.
#
# ### - This latent space can then be used to train a `Text -> Feature -> Vocoder` setup in place of typical Mel-Spectrograms.
#
# ### - The latent space should contain multiple windows worth of information, and potentially encode the types of noise occuring in the frame.
#
# ---
#
# - ### Updated to add iso226 volume scaling for features. (noticed far too much model focus on 11Khz+ channels)
#
# ---
# # -1 - Install ISO226
try:
import iso226
except:
# !git clone https://github.com/jacobbaylesssmc/iso226
# !cd iso226; python3 -m pip install ./
# # 0 - Import Dependancies/Modules
#
# +
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import os
os.environ["LRU_CACHE_CAPACITY"] = "3"
import random
from CookieTTS.utils.dataset.utils import load_wav_to_torch, load_filepaths_and_text
# -
# ---
#
# # 1 - Load Dataset
# +
import os
import random
from glob import glob
from CookieTTS.utils.dataset.utils import load_wav_to_torch
from CookieTTS.utils.audio.stft import STFT
from CookieTTS.utils.audio.audio_processing import window_sumsquare, dynamic_range_compression, dynamic_range_decompression
class AudioDataset(torch.utils.data.Dataset):
def __init__(self, model_config, gpu_dataloading, directory, wildcard_filter = "*.wav"):
self.gpu_dataloading = gpu_dataloading
print("Finding Audio Files...")
self.audio_files = glob( os.path.join(directory, "**", wildcard_filter), recursive=True)
print("Done")
random.seed(1234)
random.shuffle(self.audio_files)
self.len = len(self.audio_files)
self.max_len_s = model_config['max_len_s']
self.win_lens = model_config['window_lengths']
self.hop_len = model_config['hop_length']
self.fil_len = model_config['filter_length']
self.stfts = []
for win_len in self.win_lens:
stft = STFT(filter_length=self.fil_len,
hop_length=self.hop_len,
win_length=win_len,)
stft = stft.cuda() if self.gpu_dataloading else stft
self.stfts.append(stft)
self.directory = directory
self.wildcard_filter = wildcard_filter
def get_mel(self, audio):
"""Take audio and convert to multi-res spectrogram"""
melspec = []
for stft in self.stfts:
spect = stft.transform(audio.unsqueeze(0), return_phase=False)[0].squeeze(0)# -> [n_mel, dec_T]
#print(spect.shape)
melspec.append(spect)
return torch.cat(melspec, dim=0)# [[n_mel, dec_T], ...] -> [n_stft*n_mel, dec_T]
def __getitem__(self, index):
audio_path = self.audio_files[index]
audio, sampling_rate, max_mag = load_wav_to_torch(audio_path) # load mono audio from file
audio = audio / max_mag # normalize to range [-1, 1]
#noisy_audio = audio.clone()
#noisy_audio += torch.randn(*audio.shape) * random.uniform(self.min_noise_str, self.max_noise_str)
#noisy_audio = noisy_audio.clamp(min=-0.999, max=0.999)
#noisy_spect = dynamic_range_compression(self.get_mel(noisy_audio))
if audio.shape[0] > int(self.max_len_s*sampling_rate):
max_start = audio.shape[0] - int(self.max_len_s*sampling_rate)
start = (torch.rand(1)*max_start).int()
audio = audio[start:start+int(self.max_len_s*sampling_rate)]
audio = audio.cuda() if self.gpu_dataloading else audio
spect = self.get_mel(audio)
spect = dynamic_range_compression(spect)
spect_length = spect.shape[1]
return (spect, spect_length)
def __len__(self):
return self.len
# -
class MelCollate():
def __init__(self):
pass
def __call__(self, batch):
B = len(batch)
lengths = [x[0].shape[1] for x in batch]
n_mel = batch[0][0].shape[0]
max_length = max(*lengths)
b_spect = [x[0] for x in batch]
b_spect = torch.cat(b_spect, dim=1).unsqueeze(0)# [1, n_stft*n_mel, sum(dec_T)]
#for i in range(B):
# spect = batch[i][0]
# b_spect[i, :, :spect.shape[1]] = spect
spect_lengths = torch.tensor([sum(lengths),])
model_inputs = (b_spect, spect_lengths)
return model_inputs
# ---
#
# # 2 - Init Model
# +
class TemporalBlock(nn.Module):
def __init__(self, input_dim, output_dim, n_layers, n_dim, kernel_w, bias=True, act_func=nn.LeakyReLU(negative_slope=0.1, inplace=True), dropout=0.0, res=False):
super(TemporalBlock, self).__init__()
self.layers = nn.ModuleList()
for i in range(n_layers):
in_dim = input_dim if i == 0 else n_dim
out_dim = output_dim if i+1 == n_layers else n_dim
pad = (kernel_w - 1)//2
conv = nn.Conv1d(in_dim, out_dim, kernel_w, padding=pad, bias=bias)
self.layers.append(conv)
self.act_func = act_func
self.dropout = dropout
self.res = res
if self.res:
assert input_dim == output_dim, 'residual connection requires input_dim and output_dim to match.'
def forward(self, x): # [B, in_dim, T]
skip = x
for i, layer in enumerate(self.layers):
is_last_layer = bool( i+1 == len(self.layers) )
x = layer(x)
if not is_last_layer:
x = self.act_func(x)
if self.dropout > 0.0 and self.training:
x = F.dropout(x, p=self.dropout, training=self.training, inplace=True)
if self.res:
x += skip
return x # [B, out_dim, T]
class Coder(nn.Module):
def __init__(self, model_config, input_dim=None, output_dim=None, output_batchnorm=False):
super(Coder, self).__init__()
self.input_dim = ((model_config['filter_length']//2) + 1) * len(model_config['window_lengths']) if input_dim is None else input_dim
self.output_dim = model_config['latent_dim'] if output_dim is None else output_dim
self.device = "cuda"
self.temporalblocks = nn.ModuleList()
for i in range(model_config['n_blocks']):
b_first_block = bool(i == 0)
b_last_block = bool(i+1 == model_config['n_blocks'])
in_dim = self.input_dim if b_first_block else model_config['n_dim']
out_dim = self.output_dim if b_last_block else model_config['n_dim']
res = True if (model_config['residual_connections'] and in_dim == out_dim) else False
n_layers = model_config['bottleneck_n_layers'] if b_first_block or b_last_block else model_config['n_layers']
temp_block = TemporalBlock(in_dim, out_dim, n_layers, model_config['n_dim'],
model_config['kernel_width'], bias = model_config['bias'],
dropout = model_config['dropout'], res=res)
self.temporalblocks.append(temp_block)
if output_batchnorm:
self.bn_out = nn.BatchNorm1d(self.output_dim, momentum=0.05, affine=False)
def forward(self, spect):
assert spect.shape[1] == self.input_dim, f'input Tensor is wrong shape ({spect.shape}). Expected {self.input_dim} channels.'
spect = spect.to(self.device)
for block in self.temporalblocks:
spect = block(spect)
spect = spect.clone()
if hasattr(self, 'bn_out'):
spect = self.bn_out(spect)
return spect
class AutoEncoder(nn.Module):
def __init__(self, model_config):
super(AutoEncoder, self).__init__()
self.in_out_dim = ((model_config['filter_length']//2) + 1) * len(model_config['window_lengths'])
self.latent_dim = model_config['latent_dim']
self.encoder = Coder(model_config, self.in_out_dim, self.latent_dim, output_batchnorm=True)
self.decoder = Coder(model_config, self.latent_dim, self.in_out_dim)
def get_specs(self, audio):
spects = []
for stft in self.stfts:
spect = stft.transform(audio.unsqueeze(0), return_phase=False)[0].squeeze(0)# -> [n_mel, dec_T]
spects.append(spect)
spect = torch.cat(spects, dim=0)# [[n_mel, dec_T], ...] -> [n_stft*n_mel, T//hop_len]
spect = dynamic_range_compression(spect)# change to clamped log-scale magnitudes
return spect.unsqueeze(0)# -> [1, n_stft*n_mel, T//hop_len]
def encode_audiopath(self, audio_path):
audio, sampling_rate, max_mag = load_wav_to_torch(audio_path) # load mono audio from file
audio /= max_mag # normalize to range [-1, 1]
return self.encode_audio(audio)
def encode_audio(self, audio):
"""Encoder [T] Tensor into Z learned latent representation."""
spect = self.get_specs(audio.cuda())# -> [B, n_stfts*n_fft, T]
z = self.encoder(spect)# -> [B, z_dim, T]
return z
def forward(self, inputs):
spect, spect_lengths = inputs
z = self.encoder(spect)
rec_spect = self.decoder(z)
return rec_spect.clone()
# +
import torch
import numpy as np
import iso226
import math
from CookieTTS.utils.model.utils import get_mask_from_lengths
# https://www.desmos.com/calculator/4nac7kvt7p
# Squash smaller values together so that mse loss is lower on quieter parts of the spectrogram.
def vol_rescale_loss(mel, power=0.5, min=-11.55):
mel = mel + (power/(-min*2))*(mel**2)
return mel
class LossFunction(nn.Module):
def __init__(self, model_config):
super(LossFunction, self).__init__()
iso226_spl_from_freq = iso226.iso226_spl_itpl(L_N=60, hfe=True)# get InterpolatedUnivariateSpline for Perc Sound Pressure Level at Difference Frequencies with 60DB ref.
self.freq_weights = torch.tensor([(2**(60./10))/(2**(iso226_spl_from_freq(freq)/10)) for freq in np.linspace(0, model_config['sampling_rate']//2, (model_config['filter_length']//2)+1)])
self.freq_weights = self.freq_weights.cuda().repeat(len(model_config['window_lengths']))[None, :, None]# [B, n_mel, T]
self.loud_loss_priority_str = model_config['loud_loss_priority']
def forward(self, y, x):
gt_spect, lengths = x
gt_spect = gt_spect.cuda()
pred_spect = y
mask = get_mask_from_lengths(lengths.cuda())
mask = mask.expand(gt_spect.size(1), mask.size(0), mask.size(1))
mask = mask.permute(1, 0, 2)
#gt_spect.detach()[~mask] = 0.0
#pred_spect.detach()[~mask] = 0.0
if self.loud_loss_priority_str > 0:
pred_spect = vol_rescale_loss(pred_spect, power=self.loud_loss_priority_str)
gt_spect = vol_rescale_loss(gt_spect, power=self.loud_loss_priority_str)
MAE = F.mse_loss(pred_spect, gt_spect, reduction='none')
MAE = MAE * self.freq_weights# [B, n_mel, T] * [1, n_mel, 1]
MAE = torch.masked_select(MAE, mask)# [B, n_mel, T] -> [n_mel*sum(n_frames)]
return MAE.mean()
# -
# # 2.9 - Plot Data
# +
import matplotlib
# %matplotlib inline
import matplotlib.pylab as plt
import IPython.display as ipd
def plot_data(data, title=None, figsize=(20, 7.5), range_=[-11.6, 2.0]):
"""
data: list([height, width], [height, width], ...)
"""
#for i in range(len(data)):
# data[i][0,0] = range_[0]
# data[i][0,1] = range_[1]
fig, axes = plt.subplots(1, len(data), figsize=figsize)
for i in range(len(data)):
if title:
axes[i].set_title(title[i])
axes[i].imshow(data[i], aspect='auto', origin='bottom',
interpolation='none')
plt.show()
# %matplotlib inline
# -
# ---
#
# # 3 - Train and Eval
# Config
# ---
# ```
# ----- Previous Models -----
# AEF1 - 160 Channels with 12*5 Coder Layers, Learned Mean/STD
# AEF4 - 160 Channels with 3*1 Coder Layers, Learned Mean/STD
# AEF5 - 512 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF6 - 256 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF7 - 128 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF8 - 192 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# ```
# ---
# +
model_config = {
"model_name": "AEF8",
"audio_directory": "/media/cookie/Samsung 860 QVO/ClipperDatasetV2",#r"H:\ClipperDatasetV2\SlicedDialogue",
"wildcard_filter": "*.wav",
"batch_size": 8,
'max_len_s': 6.0,
"learning_rate": 5e-5,
"latent_dim": 192,
"loud_loss_priority": 0.1,# squash smaller values so model will prioritise louder parts of the spectrogram. # 0.0 = Off, 1.0 = Nearly parts have 0.0 loss.
"sampling_rate": 48000,
"window_lengths": [600, 1200, 2400],
"hop_length": 600,
"filter_length": 2400,
"n_blocks": 1,#3,
"n_layers": 3,
"bottleneck_n_layers": 1,
"n_dim": 256,
"kernel_width": 1,
"residual_connections": True,
"bias": True,
"dropout": 0.00,
}
gpu_dataloading = True
# -
# ---
#
# The rest
# +
from torch.utils.data import DataLoader
n_epochs = 200
dataset = AudioDataset(model_config, gpu_dataloading, model_config['audio_directory'], model_config['wildcard_filter'])
# +
# Initialize Training
collate_fn = MelCollate()
train_loader = DataLoader(dataset, num_workers=0 if gpu_dataloading else 12, shuffle=True,
batch_size=model_config['batch_size'],
pin_memory=False, drop_last=True,
collate_fn=collate_fn)
criterion = LossFunction(model_config)
# +
# Initialize/Reset Model
model = AutoEncoder(model_config).cuda()
optimizer = torch.optim.Adam(model.parameters(), lr=model_config['learning_rate'])
iteration = 0
avg_improvement = 0.0
avg_training_loss = 2.0
# +
#checkpoint_path = "MelAutoEncoder_50000_AEF7.pt"
#checkpoint_dict = torch.load(checkpoint_path, map_location='cpu')
#model.load_state_dict(checkpoint_dict['model'])
#optimizer.load_state_dict(checkpoint_dict['optimizer'])
#iteration = checkpoint_dict['iteration']
#model_config = checkpoint_dict['model_config']
# +
model.train()
for epoch in range(n_epochs):
print(f"Epoch: {epoch}")
for i, batch in enumerate(train_loader):
learning_rate = 2e-4
if iteration > 50000:
learning_rate = 1e-4
if iteration > 75000:
learning_rate = 0.5e-4
if iteration > 100000:
learning_rate = 0.25e-4
if iteration > 110000:
learning_rate = 0.125e-4
if iteration > 120000:
learning_rate = 0.0625e-4
learning_rate *= 0.74
for param_group in optimizer.param_groups:
param_group['lr'] = learning_rate
model.zero_grad()
outputs = model(batch)
loss = criterion(outputs, batch)
reduced_loss = loss.item()
loss.backward()
optimizer.step()
avg_training_loss = avg_training_loss*0.99 + reduced_loss*(1-0.99)
if iteration%100 == 0:
print(f"\n[Iter {iteration:<6}] [Training Loss {reduced_loss:5.3f} Avg {avg_training_loss:5.3f}]", end='')
else:
print(".", end='')
if True and iteration%10000 == 0:
plot_data([x[0][:,:400].float().cpu().detach().numpy() for x in batch[0:1]]+\
[outputs[0][:,:400].float().cpu().detach().numpy()],
figsize=(24, 48))
if iteration%25000==0:
filepath = "/media/cookie/Samsung PM961/TwiBot/CookiePPPTTS/CookieTTS/scripts/MelAutoEncoder"+f"_{iteration}_{model_config['model_name']}.pt"
saving_dict = {
'model': model.state_dict(),
'iteration': iteration,
'optimizer': optimizer.state_dict(),
'learning_rate': learning_rate,
'model_config': model_config}
torch.save(saving_dict, filepath)
iteration+=1
# +
# save model
#filepath = r"G:\TwiBot\CookiePPPTTS\CookieTTS\scripts\MelAutoEncoder"+f"_{iteration}.pt"
filepath = "/media/cookie/Samsung PM961/TwiBot/CookiePPPTTS/CookieTTS/scripts/MelAutoEncoder"+f"_{iteration}_{model_config['model_name']}.pt"
print(f"Saving checkpoint to '{filepath}'")
saving_dict = {
'model': model.state_dict(),
'iteration': iteration,
'optimizer': optimizer.state_dict(),
'learning_rate': learning_rate,
'model_config': model_config,
}
torch.save(saving_dict, filepath)
print("Done")
# -
# ---
#
# # 4 - Convert Dataset to new Latent features.
#
# #### `.wav` -> `.npy`
# ```
# AEF1 - 160 Channels with 12*5 Coder Layers, Learned Mean/STD
# AEF4 - 160 Channels with 3*1 Coder Layers, Learned Mean/STD
# AEF5 - 512 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF6 - 256 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF7 - 128 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
# AEF8 - 192 Channels with 3*3 Coder Layers, Zero Mean Unit Variance
#
# (edited)
# ```
# +
checkpoint_path = "MelAutoEncoder_150000_AEF6.pt"
checkpoint_dict = torch.load(checkpoint_path, map_location='cpu')
iteration = checkpoint_dict['iteration']
model_config = checkpoint_dict['model_config']
# load model
model = AutoEncoder(model_config).cuda()
model.load_state_dict(checkpoint_dict['model'])
_ = model.eval()
# +
hop_len = 600
# update as needed!
model.stfts = []
for win_len in model_config['window_lengths']:
stft = STFT(filter_length=model_config['filter_length'],
hop_length=hop_len, win_length=win_len,).cuda()
model.stfts.append(stft)
# +
from glob import glob
directory = "/media/cookie/Samsung 860 QVO/ClipperDatasetV2"
with torch.no_grad():
audiopaths = glob( os.path.join(directory, "**", "*.wav"), recursive=True)
len_audiopaths = len(audiopaths)
for i, audiopath in enumerate(audiopaths):
latent_z = model.encode_audiopath(audiopath).squeeze(0)
print(f'{i:6}/{len_audiopaths:<6} {latent_z.shape}', end='\r')
new_save_path = audiopath.replace('.wav','.npy')
#print(torch.from_numpy(np.load(new_save_path)).shape)
np.save(new_save_path, latent_z.data.squeeze().float().cpu().numpy())
print("\nDone!")
# -
|
CookieTTS/scripts/MultiResMel-AutoEncoder.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#当采用交叉熵,在train函数中:
#_,prediction = torch.max(F.softmax(prediction.data), 1),_代表的是概率值
#_,prediction = torch.max(prediction.data, 1),_代表的不是是概率值
#注意outputs = model(inputs)的outputs为Variable,而用于torch.max中的应为Tensor
#_, preds = torch.max(F.softmax(outputs.data), 1)
#局部微调:
#model = torchvision.models.resnet18(pretrained=True)
#for param in model.parameters():
#param.requires_grad = False
#model.fc = nn.Linear(512, 100)
#a = torch.from_numpy(a)
# +
# Author: 孙立波 created on 2018-04-01
# +
##############################环境设置#######################
import torch
import pretrainedmodels
from torch.autograd import Variable ## torch中自动计算梯度模块
import torch.nn as nn # 神经网络模块
import torch.utils.data as data
import torch.nn.functional as F #神经网络模块中的常用功能
import torch.multiprocessing as mp
from torch import optim
from torch.optim import *
from torch.optim import lr_scheduler
from torch.optim.lr_scheduler import *
from torch.utils.data import DataLoader,Dataset
import torchvision
import torchvision.transforms as transforms
import torchvision.datasets as datasets
from torchvision.utils import make_grid
from torchvision import datasets, models
from torchvision.models import *
from __future__ import print_function, division
import matplotlib.pyplot as plt
import numpy as np
import random
import cv2
import time
import os
import copy
from tqdm import tqdm
import pandas as pd
from skimage import io, transform
from PIL import Image
# %matplotlib inline
plt.ion() # interactive mode
# %config InlineBackend.figure_format = 'retina'
#显示中文字体设置
plt.rcParams["font.sans-serif"] = ["Droid Sans Fallback"]
plt.rcParams['axes.unicode_minus'] = False #为了正常显示是"-"减号
# +
############################## 准备 #######################
MODELS=[ 'inceptionresnetv2', 'inceptionv4']
OPTIMIZERS = {"SGD":SGD,"ASGD":ASGD,"Adam":Adam,"Adagrad":Adagrad}
# classes = [ 'collar_design_labels','neckline_design_labels','skirt_length_labels',
# 'sleeve_length_labels', 'neck_design_labels', 'lapel_design_labels',
# 'pant_length_labels','coat_length_labels']
#classes = ['collar_design_labels', 'neckline_design_labels', 'neck_design_labels']
classes = ['neck_design_labels']
label_count = {'coat_length_labels':8,
'collar_design_labels':5,
'lapel_design_labels':5,
'neck_design_labels':5,
'neckline_design_labels':10,
'pant_length_labels':6,
'skirt_length_labels':6,
'sleeve_length_labels':9}
attrs_cls_label_map = {
'skirt_length_labels':['群不可见Invisible', '短群Short', '及膝群Knee', '旗袍裙群Midi', '及脚群Ankle', '接地群Floor'],
'coat_length_labels': ['衣不可见Invisible','高腰衣HighWaistLength','常规衣RegularLength','长衣LongLength','加长衣MicroLength',
'及膝衣Knee Length','旗袍衣MidiLength','及地衣Ankle&FloorLength'],
'collar_design_labels': ['衣领不可见Invisible','衬衫领ShirtCollar','彼得潘女士小圆领PeterPan','清道夫领PuritanCollar','螺纹领RibCollar'],
'lapel_design_labels':['翻领不可见Invisible','缺口领Notched','无领Collarless','披肩围巾式领ShawlCollar','大号披肩围巾式领PlusSizeShawl'],
'neck_design_labels':['脖颈不可见Invisible','长高领TurtleNeck', '荷叶半高领RuffleSemi-HighCollar','低圆领LowTurtleNeck','翻领Draped Collar'],
'neckline_design_labels':['颈领线不可见Invisible','无肩带领StraplessNeck','深V领DeepVNeckline', '直领StraightNeck', 'V领VNeckline',
'方领SquareNeckline', '出肩领OffShoulder', '圆领RoundNeckline', '桃形领SweatHeartNeck', '单肩领OneShoulderNeckline'],
'pant_length_labels':[ '裤不可见Invisible', '短裤ShortPant', '中裤Mid Length', '7分裤3/4Length', '9分裤CroppedPant', '长裤FullLength'],
'sleeve_length_labels':['袖不可见Invisible', '无袖Sleeveless', '杯袖CupSleeves', '短袖ShortSleeves', '肘中袖ElbowSleeves',
'7分袖Sleeves', '及腕9分袖WristLength', '长袖LongSleeves', '超长袖ExtraLongSleeves']}
# +
############################## 参数设置 #######################
#参数设置
#设置可见的GPU数,注意不是并行训练的设置
#os.environ["CUDA_DEVICE_ORDER"]="PCI_BUS_ID"
#os.environ["CUDA_VISIBLE_DEVICES"]="0,1"
os.environ["CUDA_VISIBLE_DEVICES"] = "1"
#若gpu可用则返回True
use_gpu = torch.cuda.is_available()
#sgd = SGD(lr=0.01, decay=0.01/45, momentum=0.9, nesterov=True)
#adam = optimizers.Adam(lr=1e-4)
#optimizer=sgd(lr=0.001, momentum=0.9, nesterov=True))
#adam = Adam(lr=0.0001)
#保存文件后缀,即月份和日为版本尾号
#version = ""
version = 'ouside-inceptionresnet-fainet1'
image_width =299
epochs_num = 30
scheduler_step_size = 4#设置含参变量的学习率变化,为多少个epoch做一次步进的衰减
learning_rate = 0.01
split_ratio = 0.2
batch_size = 64
stepepochs_gamma = 0.2
# +
########################### 定义数据集类和预处理类及操作和数据集实例化测试 #######################
######################################################################################
#Data augmentation and normalization for training,Just normalization for validation
#Transforms on PIL Image
#过时class torchvision.transforms.Scale(size, interpolation=2) #按照规定的尺寸重新调节PIL.Image
#class torchvision.transforms.Resize(size, interpolation=2)
#class torchvision.transforms.CenterCrop(size) #将给定的PIL.Image进行中心切割,得到给定的size,size可以是tuple,(target_height, target_width)。size也可以是一个Integer,在这种情况下,切出来的图片的形状是正方形
#class torchvision.transforms.RandomCrop(size, padding=0) #切割中心点的位置随机选取。size可以是tuple也可以是Integer。
#class torchvision.transforms.RandomHorizontalFlip(p=0.5) #随机水平翻转给定的PIL.Image,概率为0.5。即:一半的概率翻转,一半的概率不翻转。
#过时class torchvision.transforms.RandomSizedCrop(size, interpolation=2) #先将给定的PIL.Image随机切,然后再resize成给定的size大小。
#class torchvision.transforms.RandomResizedCrop(size, scale=(0.08, 1.0), ratio=(0.75, 1.3333333333333333), interpolation=2)
#class torchvision.transforms.FiveCrop(size) #可能不匹配batchsize,见官网。Crop the given PIL Image into four corners and the central crop
#class torchvision.transforms.TenCrop(size, vertical_flip=False)
#class torchvision.transforms.ColorJitter(brightness=0, contrast=0, saturation=0, hue=0) #Randomly change the brightness, contrast and saturation of an image.
#class torchvision.transforms.RandomRotation(degrees, resample=False, expand=False, center=None)
#class torchvision.transforms.RandomAffine(degrees, translate=None, scale=None, shear=None, resample=False, fillcolor=0)
#Transforms on torch.*Tensor
#class torchvision.transforms.Normalize(mean, std) #给定均值:(R,G,B) 方差:(R,G,B),将会把Tensor的每个通道矩阵值规范化到正态分布上。即:Normalized_image=(image-mean)/std。
#Conversion Transforms
#class torchvision.transforms.ToTensor #Convert a PIL Image or numpy.ndarray to tensor.如把一个取值范围是[0,255]的PIL.Image或者shape为(H,W,C)的numpy.ndarray,转换成形状为[C,H,W],取值范围是[0.0,1.0]的torch.FloadTensor
#class torchvision.transforms.ToPILImage(mode=None)
#class torchvision.transforms.Lambda(lambd) #使用转换器
#Lambda(lambda crops: torch.stack([ToTensor()(crop) for crop in crops]))
#应加入的数据增强:对fai一定不要用transforms.RandomCrop(size, padding=0)
#transforms.Resize(image_width, interpolation=2) #一般放缩到224*224,并保持边长比不变
#transforms.RandomHorizontalFlip(p=0.65) #这个很有用!!!
#transforms.ColorJitter(brightness=0.3, contrast=0.2, saturation=0.2, hue=0.2) #是随机的,赋值为增益因子
#transforms.RandomRotation(20, resample=False, expand=False, center=None)
#可能轻微的影响transforms.RandomResizedCrop(image_width, scale=(0.95, 1.0), ratio=(0.75, 1.3333333333333333), interpolation=2)
#可能会有用,可用于测试阶段transforms.CenterCrop((224,180)),如:transforms.CenterCrop(256,224)#注意不是随机裁剪,即高不变,裁剪的宽变化
################################################################################
#注:定义的dataset经自定义的transform或库自带的基于PIL的数据变换返回的图像和label都应是Tensor形式,而用库自带的变换,需用PIL读取图像!
#定义数据预处理
#######################transforms.RandomRotation(10)#改变10度
###############################transforms.ColorJitter(0.05, 0.05, 0.05, 0.05)#微小抖动
fai_data_transforms = {
'train': transforms.Compose([
transforms.Resize(image_width, interpolation=2),
transforms.RandomHorizontalFlip(),
#transforms.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1),
#transforms.RandomRotation(10, resample=False, expand=False, center=None),
#transforms.RandomResizedCrop(image_width, scale=(0.95, 1.0), ratio=(0.75, 1.3333333333333333), interpolation=2),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])
]),
'val': transforms.Compose([
#transforms.Resize(256),
#transforms.CenterCrop(256,224),
transforms.Resize(image_width, interpolation=2),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])
]),
'test': transforms.Compose([
#transforms.Resize(256),
#transforms.CenterCrop(256,224),
transforms.Resize(image_width, interpolation=2),
transforms.ToTensor(),
transforms.Normalize([0.5, 0.5, 0.5], [0.5, 0.5, 0.5])
])
}
#定义数据集
#当变换中含有 transforms.ToTensor(),处理后为RGB CHW 0-1.0数据,当含有transforms.Normalize()会返回一个分布在(x-mean)/std,这时值的范围就不是0-1.0了
def pil_loader(path):
with open(path, 'rb') as f:
with Image.open(f) as img:
return img.convert('RGB').resize((image_width,image_width),Image.ANTIALIAS)
def accimage_loader(path):
import accimage
try:
return accimage.Image(path)
except IOError:
# Potentially a decoding problem, fall back to PIL.Image
return pil_loader(path)
def default_loader(path):
from torchvision import get_image_backend
if get_image_backend() == 'accimage':
return accimage_loader(path)
else:
return pil_loader(path)
#定义数据集
class FaiTrainDataset(Dataset):
"""FaiTrainDataset dataset."""
def __init__(self, train_csv_path_and_file, train_val_images_root_dir, train =True, split_ratio=0.2,transform=None,target_transform=None,loader=default_loader):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.df = pd.read_csv(train_csv_path_and_file)
#self.df_load = df.sample(frac=1).reset_index(drop=True)
self.df_load = self.df.copy()
#df.iloc[np.random.permutation(len(df))]
self.split_ratio = split_ratio
self.cut_idx = int(len(self.df_load)-round(len(self.df_load)*self.split_ratio))#int(round(0.1 * self.df_load.shape[0]))
self.df_train= self.df_load.iloc[:self.cut_idx]
self.df_val = self.df_load.iloc[self.cut_idx:]
self.df_train_load = self.df_train.copy()
self.df_val_load = self.df_val.copy()
self.df_train_load.columns = ['image_id', 'class', 'label']
self.df_val_load.columns = ['image_id', 'class', 'label']
self.df_train_load.reset_index(inplace= True,drop=True)
self.df_val_load.reset_index(inplace= True,drop=True)
self.train_images = self.df_train_load['image_id'].tolist()
self.train_labels = self.df_train_load['label'].tolist()
self.val_images = self.df_val_load['image_id'].tolist()
self.val_labels = self.df_val_load['label'].tolist()
n1=len(self.df_train_load)
n2=len(self.df_val_load)
#不用转化为one-hot,根据所用的交叉熵形式
#self.train_y = np.zeros((n1, label_count[self.df_train_load['class'][0]]), dtype=np.uint8)
#self.val_y = np.zeros((n2, label_count[self.df_val_load['class'][0]]), dtype=np.uint8)
self.train_y = np.zeros(n1, dtype=np.uint8)
self.val_y = np.zeros(n2, dtype=np.uint8)
for i in range(n1):
tmp_label1=self.train_labels[i]
self.train_y[i]=tmp_label1.find('y')
for j in range(n2):
tmp_label2=self.val_labels[j]
self.val_y[j]=tmp_label2.find('y')
self.train_data = list(zip(self.train_images,self.train_y))
self.val_data = list(zip(self.val_images,self.val_y))
#print("训练集:batch化需要的元组样例是{0}:".format(self.train_data[0]))
#print("验证集:batch化需要的元组样例是{0}:".format(self.val_data[0]))
self.train_val_images_root_dir = train_val_images_root_dir
self.transform = transform
self.target_transform = target_transform
self.loader = loader
self.train = train
def __len__(self):
if self.train == True:
return len(self.df_train_load)
else:
return len(self.df_val_load)
def __getitem__(self, index): #最终返回的是Tensor
if self.train == True:
train_image_path, train_label = self.train_data[index]
train_img_name = os.path.join(self.train_val_images_root_dir,train_image_path)
#image = io.imread(img_name) #用的skimage.io,读入为uint8,RGB,HWc图像
train_img = self.loader(train_img_name)
if self.transform is not None:
train_img = self.transform(train_img) #处理后为RGB CHW ,个位整数的数据
if self.target_transform is not None:
train_label = self.target_transform(train_label)
return train_img,train_label
else:
val_image_path, val_label = self.val_data[index]
val_img_name = os.path.join(self.train_val_images_root_dir,val_image_path)
#image = io.imread(img_name) #用的skimage.io,读入为uint8,RGB,HWc图像
val_img = self.loader(val_img_name)
if self.transform is not None:
val_img = self.transform(val_img) ##处理后为RGB CHW ,个位整数的数据
if self.target_transform is not None:
val_label = self.target_transform(val_label)
return val_img,val_label #返回值是Tensor
#定义测试数据集
class FaiTestDataset(Dataset):
"""FaiTestDataset dataset."""
def __init__(self, test_csv_path_and_file, test_images_root_dir, attr, transform=None,target_transform=None,loader=default_loader):
"""
Args:
csv_file (string): Path to the csv file with annotations.
root_dir (string): Directory with all the images.
transform (callable, optional): Optional transform to be applied
on a sample.
"""
self.df_test = pd.read_csv(test_csv_path_and_file)
#定义各列名称
self.df_test.columns = ['image_id', 'class', 'x']
del self.df_test['x']
self.attr = attr
self.df_test_load = self.df_test[(self.df_test['class'] == self.attr)].copy()
self.df_test_load.reset_index(inplace= True,drop= True)
self.test_images = self.df_test_load['image_id'].tolist()
#n=len(self.df_test_load)
#self.test_y = np.zeros((n, label_count[self.attr]), dtype=np.uint8)
#self.test_data = list(zip(self.test_images,self.test_y))
self.test_data = self.test_images
#print("测试集(不含label):batch化需要的元组样例是{0}:".format(self.test_data[0]))
self.transform = transform
self.target_transform = target_transform
self.loader = loader
self.test_images_root_dir = test_images_root_dir
def __len__(self):
return len(self.df_test_load)
def __getitem__(self, index):
test_path = self.test_data[index]
test_img_name = os.path.join(self.test_images_root_dir,test_path)
#test_image = io.imread(test_img_name) 只能用PIL读图像,因为系统要求
test_img = self.loader(test_img_name)
if self.transform is not None:
test_img = self.transform(test_img) #处理后为RGB CHW ,个位整数的数据
return test_img #返回值为Tensor
################################################## 对定义的数据集做测试 以classes[0]属性为例 ####################
#定义的dataset经自定义的transform或库自带的基于PIL的数据变换返回的图像和label都应是Tensor形式,而用库自带的变换,需用PIL读取图像!
#测试训练,验证和测试数据上的数据增强
fai_train_dataset = FaiTrainDataset(train_csv_path_and_file='../train/Annotations/{0}.csv'.format(classes[0]),
train_val_images_root_dir='../train/',
train =True, split_ratio=split_ratio,
transform = fai_data_transforms['train'])
fai_val_dataset = FaiTrainDataset(train_csv_path_and_file='../train/Annotations/{0}.csv'.format(classes[0]),
train_val_images_root_dir='../train/',
train =False, split_ratio=split_ratio,
transform = fai_data_transforms['val'])
image_datasets = {'train': fai_train_dataset, 'val':fai_val_dataset}
#关于训练验证集
dataloaders = {'train': torch.utils.data.DataLoader(image_datasets['train'], batch_size=4,shuffle=True, num_workers=4),
'val': torch.utils.data.DataLoader(image_datasets['val'], batch_size=4,shuffle=False, num_workers=4),
}
dataset_lengths = {x: len(image_datasets[x]) for x in ['train', 'val']}
#关于测试集
fai_test_dataset = FaiTestDataset(test_csv_path_and_file='../test/Tests/question.csv',
test_images_root_dir='../test/',
attr =classes[0],
transform = fai_data_transforms['test'])
test_dataloader = torch.utils.data.DataLoader(fai_test_dataset, batch_size=4,shuffle=False, num_workers=4)
test_dataset_length = len(fai_test_dataset)
print()
# print("dataloaders['train']的一个batch输出为:")
# print(next(iter(dataloaders['train'])))
# print("dataloaders['val']的一个batch输出为:")
# print(next(iter(dataloaders['val'])))
# print("test_dataloader的一个batch输出为:")
# print(next(iter(test_dataloader)))
print()
print("train,val,test的一个batch输出shape分别为:")
train_sample1,train_sample2= next(iter(dataloaders['train']))
print("train#",'1个batch图像数据:',train_sample1.size(),'1个batch的labels:',train_sample2.size())
val_sample1,val_sample2= next(iter(dataloaders['val']))
print("val#",'1个batch图像数据:',val_sample1.size(),'1个batch的labels:',val_sample2.size())
test_sample1= next(iter(test_dataloader))
print("test#",'1个batch图像数据:',test_sample1.size())
print()
#测试定义的数据,一个batch的数据可视化
def fai_augment_visualize(inp, title=None):
"""Imshow for Tensor."""
inp = inp.numpy().transpose((1, 2, 0)) #若用cv显示则是:inp = inp.numpy().transpose((1, 2, 0))*255
mean = np.array([0.5, 0.5, 0.5])
std = np.array([0.5, 0.5, 0.5])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
plt.imshow(inp)
if title is not None:
plt.title(title)
#plt.pause(0.001) # pause a bit so that plots are updated
# opencv
#img2 = data[i][0].numpy()*255
#img2 = img2.astype('uint8')
#img2 = np.transpose(img2, (1,2,0))
#img2=img2[:,:,::-1]#RGB->BGR
#cv2.imshow('img2', img2)
#cv2.waitKey()
print("Attr:{0}.Train样本数:{1} ,Val样本数:{2},Test样本数:{3}".format(classes[0],len(fai_train_dataset),len(fai_val_dataset),len(fai_test_dataset)))
#torch.utils.data.DataLoader是一个提供功能的迭代器。其中一个蛮有趣的参数是collate_fn。
#可用collate_fn来指定如何读取一批的样本。然而,默认的collate在大部分的情况下都表现得很好。
# Get a batch of training data
inputs1, classes1 = next(iter(dataloaders['train']))
inputs2, classes2 = next(iter(dataloaders['val']))
inputs3 = next(iter(test_dataloader))
# Make a grid from batch and visualize输出
plt.figure(0)
out1 = torchvision.utils.make_grid(inputs1) #为CHW,RGB 0.0-1.0图像,用plt显示需转化为HWC形式
fai_augment_visualize(out1, title='train-augment-{0}'.format(classes[0]))
plt.figure(1)
out2 = torchvision.utils.make_grid(inputs2)
fai_augment_visualize(out2, title='val-augment-{0}'.format(classes[0]))
plt.figure(3)
out3 = torchvision.utils.make_grid(inputs3)
fai_augment_visualize(out3, title='test-augment-{0}'.format(classes[0]))
# +
########################### 定义训练和测试及其他可视化函数 #######################
#定义训练模型的具体步骤及参数设置
def fai_train_model(model, criterion, optimizer, scheduler, batch_size,split_ratio,num_epochs,attr,model_key,version):
since = time.time()
best_model_wts = copy.deepcopy(model.state_dict())
best_acc = 0.0
#测试训练,验证和测试数据上的数据增强
training_fai_train_dataset = FaiTrainDataset(train_csv_path_and_file='../train/Annotations/{0}.csv'.format(attr),
train_val_images_root_dir='../train/',
train =True, split_ratio=split_ratio,
transform= fai_data_transforms['train'])
training_fai_val_dataset = FaiTrainDataset(train_csv_path_and_file='../train/Annotations/{0}.csv'.format(attr),
train_val_images_root_dir='../train/',
train =False, split_ratio=split_ratio,
transform= fai_data_transforms['val'])
training_image_datasets = {'train': training_fai_train_dataset, 'val':training_fai_val_dataset}
#关于训练验证集的封装
training_dataloaders = {'train': torch.utils.data.DataLoader(image_datasets['train'], batch_size=4,shuffle=True, num_workers=4),
'val': torch.utils.data.DataLoader(image_datasets['val'], batch_size=4,shuffle=False, num_workers=4),
}
training_dataset_lengths = {x: len(training_image_datasets[x]) for x in ['train', 'val']}
print("摘要:Attr:{0}.Train样本数:{1} ,Val样本数:{2}".format(attr,training_dataset_lengths['train'],training_dataset_lengths['val']))
for epoch in range(num_epochs):
print('Epoch {}/{}'.format(epoch, num_epochs - 1))
print('-' * 10)
# Each epoch has a training and validation phase
for phase in ['train', 'val']:
#每batch一次train,就val一次
if phase == 'train':
#与Optimizer类似的是,其主要功能体现在step()方法中,用于更新optimizer对象每个param_group字典的lr键的值。
#scheduler = torch.optim.ReduceLROnPlateau(optimizer, 'min'),这应用在函数体外
scheduler.step() #
model.train(True) # Set model to training mode
else:
model.train(False) # Set model to evaluate mode
running_loss = 0.0
running_corrects = 0
# Iterate over data.
for data in training_dataloaders[phase]:
# get the inputs(每次一个batch)
inputs, labels = data
# wrap them in Variable
if use_gpu:
inputs = Variable(inputs.cuda())
labels = Variable(labels.long().cuda())
else:
inputs, labels = Variable(inputs,volatile=True), Variable(labels,volatile=True)
# zero the parameter gradients
optimizer.zero_grad()
# forward
outputs = model(inputs)
#_, preds = torch.max(F.softmax(utputs.data), 1)
_, preds = torch.max(outputs.data, 1) #第一个是最大值的张量(注意此处不是概率值),第二个是索引值
loss = criterion(outputs, labels)
# backward + optimize only if in training phase
if phase == 'train':
loss.backward()
optimizer.step()
# statistics
# 即用的总loss而不是平均loss
running_loss += loss.data[0] * inputs.size(0) #inputs.size(0):每个batchsize的大小
running_corrects += torch.sum(preds == labels.data) #可知标签不用转化为one-hot
epoch_loss = running_loss / training_dataset_lengths[phase]
epoch_acc = running_corrects / training_dataset_lengths[phase]
#if phase == 'val':
#scheduler.step(epoch_acc)
print('{} Loss: {:.4f} Acc: {:.4f}'.format(phase, epoch_loss, epoch_acc))
# deep copy the model
if phase == 'val' and epoch_acc > best_acc:
best_acc = epoch_acc
best_model_wts = copy.deepcopy(model.state_dict())
print()
time_elapsed = time.time() - since
print('Training complete in {:.0f}m {:.0f}s'.format(time_elapsed // 60, time_elapsed % 60))
print('Best val Acc: {:4f}'.format(best_acc))
# load best model weights
model.load_state_dict(best_model_wts)
#保存最好的模型
print("开始保存模型")
prefix_cls = attr.split('_')[0]
PATH = '../models/{0}/pytorch_{0}_{1}_{2}'.format(prefix_cls, model_key, version)
torch.save(model.state_dict(), PATH)
#model = 你定义的模型class封装
#model.load_state_dict(torch.load(PATH))
print("保存最好的模型完成")
return model
######这是将训练好的模型用于测试集上,输出对应属性的也测结果到csv文件
#CPU版本的函数
def fai_predict(predictor,attr,model_key,version):
fai_test_dataset = FaiTestDataset(test_csv_path_and_file='../test/Tests/question.csv',
test_images_root_dir='../test/',
attr =attr,
transform= fai_data_transforms['test'])
test_dataloader = torch.utils.data.DataLoader(fai_test_dataset, batch_size=64,shuffle=False, num_workers=4)
model = predictor.cpu()
model.train(False)
model.eval() #model.train(False) # Set model to evaluate mode
#len(test_dataloader)返回的是len(相应dataset)/batch_size
#for i_batch in tqdm(range(len(test_dataloader))):
#在测试集上预测并保存结果
df_test_load = fai_test_dataset.df_test_load
print("测试属性:Attr:{0}".format(attr))
print('测试数据集的样本数为:{0},迭代器需要的迭代次数是:{1}次batchsize的迭代'.format(len(fai_test_dataset),len(test_dataloader)))
result = []
prefix_cls = attr.split('_')[0]
for i,batch_x in enumerate(test_dataloader):
batch_x = Variable(batch_x, volatile=True)
out = model(batch_x)
out = F.softmax(out,dim=1) #把输出的正负数转到0-1之间
test_np=out.data.numpy()
#tmp_list = test_np.tolist()
for jj in test_np:
tmp_result = ''
for tmp_ret in jj:
tmp_result += '{:.5f};'.format(tmp_ret)
#不要最后一个分号
result.append(tmp_result[:-1])
#预测结果导入内存表格的result列
df_test_load['result'] = result
df_test_load.to_csv('../result/pytorch/pytorch_{0}_{1}_{2}.csv'.format(prefix_cls, model_key, version), header=None, index=False)
print('#######完成{0}:{1}下的测试集上的csv文件输出'.format(model_key,attr))
######这是可视化预测输出函数,用于测试集上的预测可视化,测试一个batch的输出(设置batchsize大小的是n_pictures)
#predictor:模型分类器#attr:要测试的属性#n_pictures:要测试的图片数,最好别大于8,因为输出为1*n的形式
#CPU+cuda版本的函数
def fai_predict_test_data_visualize(predictor, attr, n_pictures=8,use_gpu= False):
fai_test_dataset = FaiTestDataset(test_csv_path_and_file='../test/Tests/question.csv',
test_images_root_dir='../test/',
attr =attr,
transform= fai_data_transforms['test'])
test_dataloader = torch.utils.data.DataLoader(fai_test_dataset, batch_size=n_pictures,shuffle=False, num_workers=4)
test_dataset_length = len(fai_test_dataset) #注:len(test_dataloader)返回的是len(相应dataset)/batch_size
if use_gpu:
model = predictor.cuda()
model.train(False)
model.eval()
else:
model = predictor.cpu()
model.train(False)
model.eval()
# get some random training images
dataiter = iter(test_dataloader)
batch_x= dataiter.next()
if use_gpu:
batch_xx = Variable(batch_x.cuda(), volatile=True)
else:
batch_xx = Variable(batch_x,volatile=True)
outputs = model(batch_xx)
_, predicted = torch.max(outputs.data, 1) #此时predicted为Tensor类型的索引列表
if use_gpu:
aa = predicted.cpu().numpy()
else:
aa = predicted.numpy()
fig,axes = plt.subplots(ncols=n_pictures,figsize=(4*n_pictures,4))
print('{0}张图片预测得到的索引:'.format(n_pictures))
print(aa)
for i in range(n_pictures):
"""Imshow for Tensor."""
inp = batch_x[i].numpy().transpose((1, 2, 0)) #若用cv显示则是:inp = inp.numpy().transpose((1, 2, 0))*255
mean = np.array([0.5, 0.5, 0.5])
std = np.array([0.5, 0.5, 0.5])
inp = std * inp + mean
inp = np.clip(inp, 0, 1)
k = aa[i]
axes[i].set_title("pred-vis-{0},\nPred:{1}".format(attr,attrs_cls_label_map[attr][k]),color='r')
axes[i].imshow(inp)
print('完成测试集上的一个batchsize测试!')
#plt.savefig('../images/{0}/pytorch_{0}_{1}_{2}.png'.format(prefix_cls, KEY, version),bbox_inches='tight')
# +
################################### 迁移学习添加新层 ############################
class FAINET(nn.Module): #model为需要finetune的base model,对于resnet最后两层分别为pooling和fc,此模型只去除最后一层,然后做一定的修改
def __init__(self, model,fai_classes_num, fai_num_ftrs=1024,hidden_feature_size = 512): #,classes_num为分类数,hidden_feature_size是三层全连接间的隐藏层神经元个数,属于倒数第二层数
super(FAINET, self).__init__()
#self.fai_base_features = nn.Sequential(*list(model.children())[:-2])
#self.fai_base_features = nn.Sequential(*list(model.children())[:-1])#即去除最后一层全连接层(一般是由卷积得来的2048维),*是解包操作
#若不让输出保证与原模型一样可用:
#self.fai_num_ftrs = fai_num_ftrs #特征图数 #
self.hidden_feature_size = hidden_feature_size
self.fai_num_ftrs = model.last_linear.in_features #原模型的fc-Module输入维度,in_features为Linear类的输入参数
model.last_linear = nn.Linear(self.fai_num_ftrs, self.hidden_feature_size)
self.fai_base_features =model
#下面是新增的操作
# self.fai_conv =nn.Sequential(
# nn.Conv2d(self.fai_num_ftrs, 32, kernel_size=4, stride=1, padding=2), # in:如(bs,self.fai_num_ftrs,60,160)
# nn.BatchNorm2d(32),
# nn.LeakyReLU(0.2, inplace=True),
# nn.MaxPool2d(kernel_size=2), # out:(bs,32,30,80)
# nn.Conv2d(32, 64, kernel_size=4, stride=1, padding=2),
# nn.BatchNorm2d(64),
# nn.LeakyReLU(0.2, inplace=True),
# nn.MaxPool2d(kernel_size=2), # out:(bs,64,15,40)
# nn.Conv2d(64, 64, kernel_size=3 ,stride=1, padding=1),
# nn.BatchNorm2d(64),
# nn.LeakyReLU(0.2, inplace=True),
# nn.MaxPool2d(kernel_size=2) # out:(bs,64,7,20)
# )
self.fai_end_classifier = nn.Sequential(
nn.Dropout(0.5),
nn.Linear(hidden_feature_size, fai_classes_num),
# nn.BatchNorm1d(hidden_feature_size),
# nn.ELU(inplace=True),
# nn.Dropout(0.5),
# nn.Linear(hidden_feature_size, fai_classes_num)
#在次加入softmax则部署模型时输出的是概率值,不过也可以不加,在预测的时候加入也可以做转化,影响不大
)
def forward(self, x):
x = self.fai_base_features(x)
#加入自定义的卷积层
#x = self.fai_conv(x)
#加入全局池化
#x = F.average_pool2d(x, kernel_size=input.size()[2:]) #加全局均值采样得到的是batch-size*特征图的个数
#其实若加入了全局卷积池化就不用展平操作了
x = x.view(x.size(0), -1) #相当于numpy的reshape和keras的Flatten层,将二维压成一维
x = self.fai_end_classifier(x)
return x
#x = Dropout(0.5)(x)
#x = Flatten(name='flatten')(x)
#x = Dense(1024, activation='relu', name='fc1')(x)
# n_class为对应属性的分类个数
#x = Dense(512, activation='relu', kernel_initializer=initializers.he_uniform(seed=None),name='fc2')(x)
#x = Dropout(0.5)(x)
#x = Dense(n_class, activation='softmax', name='softmax')(x)
# +
################################### 实例化训练和测试 ############################
#加载预训练模型并重写全连接层。
#state_dict = torch.utils.model_zoo.load_url('https://s3.amazonaws.com/pytorch/models/resnet18-5c106cde.pth')
#the_model = TheModelClass(*args, **kwargs)
#the_model.load_state_dict(torch.load(PATH))
#下面是冻结卷积层的方法
# fai_model = torchvision.models.resnet18(pretrained=True)
# for param in fai_model.parameters():
# param.requires_grad = False
# Parameters of newly constructed modules have requires_grad=True by default
#model.fc = nn.Linear(512, 100)
# Optimize only the classifier
#optimizer = optim.SGD(model.fc.parameters(), lr=1e-2, momentum=0.9)
for KEY in MODELS:
print('######################在{0}下训练8个分类器####################'.format(KEY))
print()
for KEY2,OPTIMIZER in OPTIMIZERS.items():
print('######################在{0}:{1}下训练8个分类器####################'.format(KEY,KEY2))
print()
for cur_class in classes:
print('#######{0}:{1}:{2}####################'.format(KEY,KEY2, cur_class))
#预结构
base_model = pretrainedmodels.__dict__[KEY](num_classes=1000, pretrained='imagenet')
fai_model = FAINET(base_model,fai_classes_num = label_count[cur_class])
#打印含参数各层的名字
#params = fai_model.state_dict()
#for k,v in params.items():
# print(k)#打印网络中的变量名
#print(fai_model)#可查最后一层Module类对象的名和输入参数,输出参数名,如(fc): Linear(in_features=512, out_features=5, bias=True)
if use_gpu:
#If you need to move a model to GPU via .cuda(), please do so before constructing optimizers for it.
fai_model = fai_model.cuda()
#多GPU训练用:
#fai_model = torch.nn.DataParallel(module=fai_model.cuda(), device_ids=[0, 3],output_device=0).cuda()#前向在 device_ids,梯度汇总和更新在output_device上
#设置采用多分类的交叉熵loss
criterion = nn.CrossEntropyLoss()
# 设置优化器,fai_model.parameters()表示优化全部参数@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@@这里可设置两部优化法
#torch.optim.Adadelta(params, lr=1.0, rho=0.9, eps=1e-06, weight_decay=0)
#torch.optim.Adagrad(params, lr=0.01, lr_decay=0, weight_decay=0)
#torch.optim.Adam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
#torch.optim.SparseAdam(params, lr=0.001, betas=(0.9, 0.999), eps=1e-08)
#class torch.optim.Adamax(params, lr=0.002, betas=(0.9, 0.999), eps=1e-08, weight_decay=0)
#class torch.optim.RMSprop(params, lr=0.01, alpha=0.99, eps=1e-08, weight_decay=0, momentum=0, centered=False)
#torch.optim.Rprop(params, lr=0.01, etas=(0.5, 1.2), step_sizes=(1e-06, 50))
#torch.optim.SGD(params, lr=<object object>, momentum=0, dampening=0, weight_decay=0, nesterov=False)
optimizer = OPTIMIZER(fai_model.parameters(), lr=learning_rate)
#optimizer = optim.Adam(ai_model.parameters(), lr = learning_rate)#olearning_rate=0.0001,optimizer = optim.Adam([var1, var2], lr = 0.0001)
# Decay LR by a factor of 0.1 every 7 epochs
#与Optimizer类似的是,其主要功能体现在step()方法中,用于更新optimizer对象每个param_group字典的lr键的值。
#scheduler = torch.optim.ReduceLROnPlateau(optimizer, 'min') scheduler.step(val_loss)
fai_lr_scheduler = lr_scheduler.StepLR(optimizer, step_size=scheduler_step_size, gamma=0.1)
#fai_lr_scheduler = ReduceLROnPlateau(optimizer, 'max',patience=10,factor = 0.1,verbose = False)
#训练和评估
model = fai_train_model(fai_model, criterion, optimizer, fai_lr_scheduler, batch_size=batch_size,split_ratio=split_ratio,num_epochs=epochs_num,attr=cur_class,model_key=KEY,version=version)
#在测试集上运用训练好的模型,输出csv文件
print('#######{0}:{1}训练完毕,开始在测试集上测试'.format(KEY,cur_class ))
#在cpu上测试
model = model.cpu()
fai_predict(predictor = model,attr=cur_class,model_key=KEY,version=version)
#fai_predict_test_data_visualize(predictor= model, attr=cur_class, n_pictures=8,use_gpu= False)
# +
##############################模型实例部署并进行可视化测试#############################################
#自定义载入相应模型来自finetune或者是model来自你定义的模型class封装,并进行可视化测试
#下面是finetune示例
#KEY = finetune改进的模型类型,在此为对应的字符串
#预结构
#fai_model = models.MODELS[KEY](pretrained=True)
#改进的自定义添加
#num_ftrs = fai_model.fc.in_features
#fai_model.fc = nn.Linear(num_ftrs, label_count[cur_class])
#prefix_cls = classes[0].split('_')[0]
#PATH = '../models/{0}/pytorch_{0}_{1}_{2}'.format(prefix_cls, model_key=KEY, version=version)
#torch.save(model.state_dict(), PATH)
#装入训练好的模型的权重
#model.load_state_dict(torch.load(PATH))
#fai_predict_test_data_visualize(predictor = fai_model, classes[0], n_pictures = batch_size,use_gpu= False):
|
src/jupyter_notebooks/jupyter-fai-b/pytorch_instance _outside_inceptionresnet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="1czVdIlqnImH"
# # Deep Convolutional GAN (DCGAN)
# + [markdown] colab_type="text" id="1KD3ZgLs80vY"
# ### Goal
# In this notebook, you're going to create another GAN using the MNIST dataset. You will implement a Deep Convolutional GAN (DCGAN), a very successful and influential GAN model developed in 2015.
#
# *Note: [here](https://arxiv.org/pdf/1511.06434v1.pdf) is the paper if you are interested! It might look dense now, but soon you'll be able to understand many parts of it :)*
#
# ### Learning Objectives
# 1. Get hands-on experience making a widely used GAN: Deep Convolutional GAN (DCGAN).
# 2. Train a powerful generative model.
#
#
# 
#
# Figure: Architectural drawing of a generator from DCGAN from [Radford et al (2016)](https://arxiv.org/pdf/1511.06434v1.pdf).
# + [markdown] colab_type="text" id="wU8DDM6l9rZb"
# ## Getting Started
#
# #### DCGAN
# Here are the main features of DCGAN (don't worry about memorizing these, you will be guided through the implementation!):
#
# <!-- ```
# Architecture guidelines for stable Deep Convolutional GANs
# • Replace any pooling layers with strided convolutions (discriminator) and fractional-strided
# convolutions (generator).
# • Use BatchNorm in both the generator and the discriminator.
# • Remove fully connected hidden layers for deeper architectures.
# • Use ReLU activation in generator for all layers except for the output, which uses Tanh.
# • Use LeakyReLU activation in the discriminator for all layers.
# ``` -->
#
#
# * Use convolutions without any pooling layers
# * Use batchnorm in both the generator and the discriminator
# * Don't use fully connected hidden layers
# * Use ReLU activation in the generator for all layers except for the output, which uses a Tanh activation.
# * Use LeakyReLU activation in the discriminator for all layers except for the output, which does not use an activation
#
# You will begin by importing some useful packages and data that will help you create your GAN. You are also provided a visualizer function to help see the images your GAN will create.
# + colab={} colab_type="code" id="JfkorNJrnmNO"
import torch
from torch import nn
from tqdm.auto import tqdm
from torchvision import transforms
from torchvision.datasets import MNIST
from torchvision.utils import make_grid
from torch.utils.data import DataLoader
import matplotlib.pyplot as plt
torch.manual_seed(0) # Set for testing purposes, please do not change!
def show_tensor_images(image_tensor, num_images=25, size=(1, 28, 28)):
'''
Function for visualizing images: Given a tensor of images, number of images, and
size per image, plots and prints the images in an uniform grid.
'''
image_tensor = (image_tensor + 1) / 2
image_unflat = image_tensor.detach().cpu()
image_grid = make_grid(image_unflat[:num_images], nrow=5)
plt.imshow(image_grid.permute(1, 2, 0).squeeze())
plt.show()
# + [markdown] colab_type="text" id="P1A1M6kpnfxw"
# ## Generator
# The first component you will make is the generator. You may notice that instead of passing in the image dimension, you will pass the number of image channels to the generator. This is because with DCGAN, you use convolutions which don’t depend on the number of pixels on an image. However, the number of channels is important to determine the size of the filters.
#
# You will build a generator using 4 layers (3 hidden layers + 1 output layer). As before, you will need to write a function to create a single block for the generator's neural network.
# <!-- From the paper, we know to "[u]se batchnorm in both the generator and the discriminator" and "[u]se ReLU activation in generator for all layers except for the output, which uses Tanh." -->
# Since in DCGAN the activation function will be different for the output layer, you will need to check what layer is being created. You are supplied with some tests following the code cell so you can see if you're on the right track!
#
# At the end of the generator class, you are given a forward pass function that takes in a noise vector and generates an image of the output dimension using your neural network. You are also given a function to create a noise vector. These functions are the same as the ones from the last assignment.
#
# <details>
# <summary>
# <font size="3" color="green">
# <b>Optional hint for <code><font size="4">make_gen_block</font></code></b>
# </font>
# </summary>
#
# 1. You'll find [nn.ConvTranspose2d](https://pytorch.org/docs/master/generated/torch.nn.ConvTranspose2d.html) and [nn.BatchNorm2d](https://pytorch.org/docs/master/generated/torch.nn.BatchNorm2d.html) useful!
# </details>
# + colab={} colab_type="code" id="EvO7h0LYnEJZ"
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: Generator
class Generator(nn.Module):
'''
Generator Class
Values:
z_dim: the dimension of the noise vector, a scalar
im_chan: the number of channels in the images, fitted for the dataset used, a scalar
(MNIST is black-and-white, so 1 channel is your default)
hidden_dim: the inner dimension, a scalar
'''
def __init__(self, z_dim=10, im_chan=1, hidden_dim=64):
super(Generator, self).__init__()
self.z_dim = z_dim
# Build the neural network
self.gen = nn.Sequential(
self.make_gen_block(z_dim, hidden_dim * 4),
self.make_gen_block(hidden_dim * 4, hidden_dim * 2, kernel_size=4, stride=1),
self.make_gen_block(hidden_dim * 2, hidden_dim),
self.make_gen_block(hidden_dim, im_chan, kernel_size=4, final_layer=True),
)
def make_gen_block(self, input_channels, output_channels, kernel_size=3, stride=2, final_layer=False):
'''
Function to return a sequence of operations corresponding to a generator block of DCGAN,
corresponding to a transposed convolution, a batchnorm (except for in the last layer), and an activation.
Parameters:
input_channels: how many channels the input feature representation has
output_channels: how many channels the output feature representation should have
kernel_size: the size of each convolutional filter, equivalent to (kernel_size, kernel_size)
stride: the stride of the convolution
final_layer: a boolean, true if it is the final layer and false otherwise
(affects activation and batchnorm)
'''
# Steps:
# 1) Do a transposed convolution using the given parameters.
# 2) Do a batchnorm, except for the last layer.
# 3) Follow each batchnorm with a ReLU activation.
# 4) If its the final layer, use a Tanh activation after the deconvolution.
# Build the neural block
if not final_layer:
return nn.Sequential(
#### START CODE HERE ####
nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
nn.BatchNorm2d(output_channels),
nn.ReLU(inplace=True)
#### END CODE HERE ####
)
else: # Final Layer
return nn.Sequential(
#### START CODE HERE ####
nn.ConvTranspose2d(input_channels, output_channels, kernel_size, stride),
nn.Tanh()
#### END CODE HERE ####
)
def unsqueeze_noise(self, noise):
'''
Function for completing a forward pass of the generator: Given a noise tensor,
returns a copy of that noise with width and height = 1 and channels = z_dim.
Parameters:
noise: a noise tensor with dimensions (n_samples, z_dim)
'''
return noise.view(len(noise), self.z_dim, 1, 1)
def forward(self, noise):
'''
Function for completing a forward pass of the generator: Given a noise tensor,
returns generated images.
Parameters:
noise: a noise tensor with dimensions (n_samples, z_dim)
'''
x = self.unsqueeze_noise(noise)
return self.gen(x)
def get_noise(n_samples, z_dim, device='cpu'):
'''
Function for creating noise vectors: Given the dimensions (n_samples, z_dim)
creates a tensor of that shape filled with random numbers from the normal distribution.
Parameters:
n_samples: the number of samples to generate, a scalar
z_dim: the dimension of the noise vector, a scalar
device: the device type
'''
return torch.randn(n_samples, z_dim, device=device)
# +
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
'''
Test your make_gen_block() function
'''
gen = Generator()
num_test = 100
# Test the hidden block
test_hidden_noise = get_noise(num_test, gen.z_dim)
test_hidden_block = gen.make_gen_block(10, 20, kernel_size=4, stride=1)
test_uns_noise = gen.unsqueeze_noise(test_hidden_noise)
hidden_output = test_hidden_block(test_uns_noise)
# Check that it works with other strides
test_hidden_block_stride = gen.make_gen_block(20, 20, kernel_size=4, stride=2)
test_final_noise = get_noise(num_test, gen.z_dim) * 20
test_final_block = gen.make_gen_block(10, 20, final_layer=True)
test_final_uns_noise = gen.unsqueeze_noise(test_final_noise)
final_output = test_final_block(test_final_uns_noise)
# Test the whole thing:
test_gen_noise = get_noise(num_test, gen.z_dim)
test_uns_gen_noise = gen.unsqueeze_noise(test_gen_noise)
gen_output = gen(test_uns_gen_noise)
# + [markdown] colab_type="text" id="vBnOVbTpzW2M"
# Here's the test for your generator block:
# + colab={} colab_type="code" id="osbCUvkWk_LI"
# UNIT TESTS
assert tuple(hidden_output.shape) == (num_test, 20, 4, 4)
assert hidden_output.max() > 1
assert hidden_output.min() == 0
assert hidden_output.std() > 0.2
assert hidden_output.std() < 1
assert hidden_output.std() > 0.5
assert tuple(test_hidden_block_stride(hidden_output).shape) == (num_test, 20, 10, 10)
assert final_output.max().item() == 1
assert final_output.min().item() == -1
assert tuple(gen_output.shape) == (num_test, 1, 28, 28)
assert gen_output.std() > 0.5
assert gen_output.std() < 0.8
print("Success!")
# + [markdown] colab_type="text" id="r9fScH98nkYH"
# ## Discriminator
# The second component you need to create is the discriminator.
#
# You will use 3 layers in your discriminator's neural network. Like with the generator, you will need create the function to create a single neural network block for the discriminator.
# <!-- From the paper, we know that we need to "[u]se LeakyReLU activation in the discriminator for all layers." And for the LeakyReLUs, "the slope of the leak was set to 0.2" in DCGAN. -->
# There are also tests at the end for you to use.
# <details>
# <summary>
# <font size="3" color="green">
# <b>Optional hint for <code><font size="4">make_disc_block</font></code></b>
# </font>
# </summary>
#
# 1. You'll find [nn.Conv2d](https://pytorch.org/docs/master/generated/torch.nn.Conv2d.html), [nn.BatchNorm2d](https://pytorch.org/docs/master/generated/torch.nn.BatchNorm2d.html), and [nn.LeakyReLU](https://pytorch.org/docs/master/generated/torch.nn.LeakyReLU.html) useful!
# </details>
# + colab={} colab_type="code" id="aA4AxGnmpuPq"
# UNQ_C3 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: Discriminator
class Discriminator(nn.Module):
'''
Discriminator Class
Values:
im_chan: the number of channels in the images, fitted for the dataset used, a scalar
(MNIST is black-and-white, so 1 channel is your default)
hidden_dim: the inner dimension, a scalar
'''
def __init__(self, im_chan=1, hidden_dim=16):
super(Discriminator, self).__init__()
self.disc = nn.Sequential(
self.make_disc_block(im_chan, hidden_dim),
self.make_disc_block(hidden_dim, hidden_dim * 2),
self.make_disc_block(hidden_dim * 2, 1, final_layer=True),
)
def make_disc_block(self, input_channels, output_channels, kernel_size=4, stride=2, final_layer=False):
'''
Function to return a sequence of operations corresponding to a discriminator block of DCGAN,
corresponding to a convolution, a batchnorm (except for in the last layer), and an activation.
Parameters:
input_channels: how many channels the input feature representation has
output_channels: how many channels the output feature representation should have
kernel_size: the size of each convolutional filter, equivalent to (kernel_size, kernel_size)
stride: the stride of the convolution
final_layer: a boolean, true if it is the final layer and false otherwise
(affects activation and batchnorm)
'''
# Steps:
# 1) Add a convolutional layer using the given parameters.
# 2) Do a batchnorm, except for the last layer.
# 3) Follow each batchnorm with a LeakyReLU activation with slope 0.2.
# Build the neural block
if not final_layer:
return nn.Sequential(
#### START CODE HERE #### #
nn.Conv2d(input_channels, output_channels, kernel_size, stride),
nn.BatchNorm2d(output_channels),
nn.LeakyReLU(negative_slope=0.2, inplace=True)
#### END CODE HERE ####
)
else: # Final Layer
return nn.Sequential(
#### START CODE HERE #### #
nn.Conv2d(input_channels, output_channels, kernel_size, stride),
#### END CODE HERE ####
)
def forward(self, image):
'''
Function for completing a forward pass of the discriminator: Given an image tensor,
returns a 1-dimension tensor representing fake/real.
Parameters:
image: a flattened image tensor with dimension (im_dim)
'''
disc_pred = self.disc(image)
return disc_pred.view(len(disc_pred), -1)
# +
# UNQ_C4 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
'''
Test your make_disc_block() function
'''
num_test = 100
gen = Generator()
disc = Discriminator()
test_images = gen(get_noise(num_test, gen.z_dim))
# Test the hidden block
test_hidden_block = disc.make_disc_block(1, 5, kernel_size=6, stride=3)
hidden_output = test_hidden_block(test_images)
# Test the final block
test_final_block = disc.make_disc_block(1, 10, kernel_size=2, stride=5, final_layer=True)
final_output = test_final_block(test_images)
# Test the whole thing:
disc_output = disc(test_images)
# + [markdown] colab_type="text" id="tsOvZwjIzQ0F"
# Here's a test for your discriminator block:
# + colab={} colab_type="code" id="GemvBkChn0_k"
# Test the hidden block
assert tuple(hidden_output.shape) == (num_test, 5, 8, 8)
# Because of the LeakyReLU slope
assert -hidden_output.min() / hidden_output.max() > 0.15
assert -hidden_output.min() / hidden_output.max() < 0.25
assert hidden_output.std() > 0.5
assert hidden_output.std() < 1
# Test the final block
assert tuple(final_output.shape) == (num_test, 10, 6, 6)
assert final_output.max() > 1.0
assert final_output.min() < -1.0
assert final_output.std() > 0.3
assert final_output.std() < 0.6
# Test the whole thing:
assert tuple(disc_output.shape) == (num_test, 1)
assert disc_output.std() > 0.25
assert disc_output.std() < 0.5
print("Success!")
# + [markdown] colab_type="text" id="qRk_8azSq3tF"
# ## Training
# Now you can put it all together!
# Remember that these are your parameters:
# * criterion: the loss function
# * n_epochs: the number of times you iterate through the entire dataset when training
# * z_dim: the dimension of the noise vector
# * display_step: how often to display/visualize the images
# * batch_size: the number of images per forward/backward pass
# * lr: the learning rate
# * beta_1, beta_2: the momentum term
# * device: the device type
#
# <!-- In addition, be warned that **this runs very slowly on the default CPU**. One way to run this more quickly is to download the .ipynb and upload it to Google Drive, then open it with Google Colab, click on `Runtime -> Change runtime type` and set hardware accelerator to GPU and replace
# `device = "cpu"`
# with
# `device = "cuda"`. The code should then run without any more changes, over 1,000 times faster. -->
#
# + colab={} colab_type="code" id="IFLQ039u-qdu"
criterion = nn.BCEWithLogitsLoss()
z_dim = 64
display_step = 500
batch_size = 128
# A learning rate of 0.0002 works well on DCGAN
lr = 0.0002
# These parameters control the optimizer's momentum, which you can read more about here:
# https://distill.pub/2017/momentum/ but you don’t need to worry about it for this course!
beta_1 = 0.5
beta_2 = 0.999
device = 'cuda'
# You can tranform the image values to be between -1 and 1 (the range of the tanh activation)
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)),
])
dataloader = DataLoader(
MNIST('.', download=False, transform=transform),
batch_size=batch_size,
shuffle=True)
# + [markdown] colab_type="text" id="24Var22i_Ccs"
# Then, you can initialize your generator, discriminator, and optimizers.
# + colab={} colab_type="code" id="sDFRZ8tg_Y57"
gen = Generator(z_dim).to(device)
gen_opt = torch.optim.Adam(gen.parameters(), lr=lr, betas=(beta_1, beta_2))
disc = Discriminator().to(device)
disc_opt = torch.optim.Adam(disc.parameters(), lr=lr, betas=(beta_1, beta_2))
# You initialize the weights to the normal distribution
# with mean 0 and standard deviation 0.02
def weights_init(m):
if isinstance(m, nn.Conv2d) or isinstance(m, nn.ConvTranspose2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
if isinstance(m, nn.BatchNorm2d):
torch.nn.init.normal_(m.weight, 0.0, 0.02)
torch.nn.init.constant_(m.bias, 0)
gen = gen.apply(weights_init)
disc = disc.apply(weights_init)
# + [markdown] colab_type="text" id="7iCTg3w4_Zw6"
# Finally, you can train your GAN!
# For each epoch, you will process the entire dataset in batches. For every batch, you will update the discriminator and generator. Then, you can see DCGAN's results!
# + [markdown] colab_type="text" id="-5dhXMXLvt7l"
# Here's roughly the progression you should be expecting. On GPU this takes about 30 seconds per thousand steps. On CPU, this can take about 8 hours per thousand steps. You might notice that in the image of Step 5000, the generator is disproprotionately producing things that look like ones. If the discriminator didn't learn to detect this imbalance quickly enough, then the generator could just produce more ones. As a result, it may have ended up tricking the discriminator so well that there would be no more improvement, known as mode collapse:
# 
#
# + colab={} colab_type="code" id="UXptQZcwrBrq"
n_epochs = 50
cur_step = 0
mean_generator_loss = 0
mean_discriminator_loss = 0
for epoch in range(n_epochs):
# Dataloader returns the batches
for real, _ in tqdm(dataloader):
cur_batch_size = len(real)
real = real.to(device)
## Update discriminator ##
disc_opt.zero_grad()
fake_noise = get_noise(cur_batch_size, z_dim, device=device)
fake = gen(fake_noise)
disc_fake_pred = disc(fake.detach())
disc_fake_loss = criterion(disc_fake_pred, torch.zeros_like(disc_fake_pred))
disc_real_pred = disc(real)
disc_real_loss = criterion(disc_real_pred, torch.ones_like(disc_real_pred))
disc_loss = (disc_fake_loss + disc_real_loss) / 2
# Keep track of the average discriminator loss
mean_discriminator_loss += disc_loss.item() / display_step
# Update gradients
disc_loss.backward(retain_graph=True)
# Update optimizer
disc_opt.step()
## Update generator ##
gen_opt.zero_grad()
fake_noise_2 = get_noise(cur_batch_size, z_dim, device=device)
fake_2 = gen(fake_noise_2)
disc_fake_pred = disc(fake_2)
gen_loss = criterion(disc_fake_pred, torch.ones_like(disc_fake_pred))
gen_loss.backward()
gen_opt.step()
# Keep track of the average generator loss
mean_generator_loss += gen_loss.item() / display_step
## Visualization code ##
if cur_step % display_step == 0 and cur_step > 0:
print(f"Step {cur_step}: Generator loss: {mean_generator_loss}, discriminator loss: {mean_discriminator_loss}")
show_tensor_images(fake)
show_tensor_images(real)
mean_generator_loss = 0
mean_discriminator_loss = 0
cur_step += 1
# -
|
Build Basic Generative Adversarial Networks (GANs)/week2/C1_W2_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="http://landlab.github.io"><img style="float: left" src="../../../landlab_header.png"></a>
# # Using the ChiFinder Component
#
# The `ChiFinder` component creates a map of the $\chi$ drainage network index from a digital elevation model. The $\chi$ index, described by Perron and Royden (2013), is a function of drainage area, $A$, and elevation, $\eta$:
#
# $$\chi = \int\limits_{x_b}^{x} \left(\frac{A_0}{A(x)}\right)^\theta dx$$
#
# where $x_b$ is the location of the outlet of a watershed of interest, $x$ is a position on a channel somewhere upstream, $A_0$ is a drainage area scale, and $\theta$ is the concavity index parameter, often taken to be $\approx$0.5.
#
# This tutorial shows briefly how to use the `ChiFinder` on natural or synthetic data.
# ## Imports and inline docs
#
# First, import what we'll need:
import copy
import numpy as np
import matplotlib as mpl
from landlab import RasterModelGrid, imshow_grid
from landlab.io import read_esri_ascii
from landlab.components import FlowAccumulator, ChiFinder
# The docstring describes the component and provides some simple examples:
print(ChiFinder.__doc__)
# ## Example
#
# In this example, we read in a small digital elevation model (DEM) from NASADEM for an area on the Colorado high plains (USA) that includes a portion of an escarpment along the west side of a drainage known as West Bijou Creek (see Rengers & Tucker, 2014).
#
# The DEM file is in ESRI Ascii format, but is in a geographic projection, with horizontal units of decimal degrees. To calculate slope gradients properly, we'll first read the DEM into a Landlab grid object that has this geographic projec. Then we'll create a second grid with 30 m cell spacing (approximately equal to the NASADEM's resolution), and copy the elevation field from the geographic DEM. This isn't a proper projection of course, but it will do for purposes of this example.
# read the DEM
(grid_geog, elev) = read_esri_ascii('west_bijou_escarpment_snippet.asc')
grid = RasterModelGrid((grid_geog.number_of_node_rows,
grid_geog.number_of_node_columns), xy_spacing=30.0)
grid.add_field('topographic__elevation', elev, at='node')
cmap = copy.copy(mpl.cm.get_cmap("pink"))
imshow_grid(grid, elev, cmap=cmap, colorbar_label='Elevation (m)')
# The `ChiFinder` needs to have drainage areas pre-calculated. We'll do that with the `FlowAccumulator` component. We'll have the component do D8 flow routing (each DEM cell drains to whichever of its 8 neighbors lies in the steepest downslope direction), and fill pits (depressions in the DEM that would otherwise block the flow) using the `LakeMapperBarnes` component. The latter two arguments below tell the lake mapper to update the flow directions and drainage areas after filling the pits.
fa = FlowAccumulator(grid,
flow_director='FlowDirectorD8', # use D8 routing
depression_finder='LakeMapperBarnes', # pit filler
method='D8', # pit filler use D8 too
redirect_flow_steepest_descent=True, # re-calculate flow dirs
reaccumulate_flow=True, # re-calculate drainagea area
)
fa.run_one_step() # run the flow accumulator
cmap = copy.copy(mpl.cm.get_cmap("Blues"))
imshow_grid(grid,
np.log10(grid.at_node['drainage_area'] + 1.0), # sq root helps show drainage
cmap=cmap,
colorbar_label='Log10(drainage area (m2))'
)
# Now run the `ChiFinder` and display the map of $\chi$ values:
cf = ChiFinder(grid,
reference_concavity=0.5,
min_drainage_area=1.0,
clobber=True,
)
cf.calculate_chi()
cmap = copy.copy(mpl.cm.get_cmap("viridis"))
imshow_grid(grid,
grid.at_node['channel__chi_index'],
cmap=cmap,
colorbar_label='Chi index',
)
# ## References
#
# <NAME>., <NAME>. (2012). An integral approach to bedrock river
# profile analysis Earth Surface Processes and Landforms 38(6), 570-576. https://dx.doi.org/10.1002/esp.3302
#
# <NAME>., & <NAME>. (2014). Analysis and modeling of gully headcut dynamics, North American high plains. Journal of Geophysical Research: Earth Surface, 119(5), 983-1003. https://doi.org/10.1002/2013JF002962
# For more Landlab tutorials, click here: https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html
|
notebooks/tutorials/terrain_analysis/chi_finder/chi_finder.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 with local CP4S env
# language: python
# name: python3_local_cp4s
# ---
# ## Load CP4S Data
# !pip install matplotlib
# !pip install sklearn
# !pip install git+https://github.com/IBM/ibm-cp4s-client.git
from cp4s.client import CP4S
from os import environ as env
ac = CP4S(url=env['CP4S_API_ENDPOINT'],
username=env['CP4S_APIKEY_USERNAME'],
password=env['<PASSWORD>'])
mdf = ac.search_df(
query="[ipv4-addr:value = '127.0.0.1']",
configs="all")
# ## Interactive analysis
# +
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.dates as md
from matplotlib import pyplot as plt
from sklearn import preprocessing
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from datetime import datetime
from sklearn.ensemble import IsolationForest
# method to extract child count
def getChildCount(row):
value=0
for x in new_df.index:
if row['process_pid']==new_df['process_parent_pid'][x]:
value=value+1
return value
# +
# drop and rename
File1=mdf.drop(columns=['domain_name','process_binary_name','process_creator_user_ref','process_opened_connection_binary_hashes_md5','process_opened_connection_binary_name','process_opened_connection_command_line','process_opened_connection_created','process_opened_connection_creator_user_ref', 'process_opened_connection_name','process_opened_connection_opened_connection_','process_opened_connection_parent_name','process_opened_connection_parent_pid', 'process_opened_connection_pid','process_opened_connection_src_addr','process_parent_binary_hashes_md5', 'process_parent_binary_name'])
new_df=File1.rename(columns={'process_creator_user_user_id':'proc_username','process_opened_connection_count':'proc_netconn_count','process_parent_name':'parent_name','user_account_user_id':'proc_hostname','process_binary_hashes_md5':'proc_md5','process_command_line':'proc_cmdline'})
# add child count and duration
new_df['proc_child_count'] = new_df.apply(getChildCount, axis=1)
new_df['duration']=(pd.to_datetime(new_df['last_observed']))-(pd.to_datetime(new_df['first_observed']))
# drop more
new_df=new_df.drop(columns=['created_by_ref','first_observed','id','last_observed','network_traffic_src_addr','process_created','tod','cmd_len', 'network_traffic_dst_addr' ,'process_parent_pid', 'process_pid' ,'proc_hostname','process_opened_connection_dst_addr'])
# +
# create dictionary to store count of unique txts in each column
def CreateCountDict():
FinalDict={}
cols=['proc_username','proc_cmdline','proc_md5','parent_name','proc_child_count','proc_netconn_count','process_name']
for x in cols:
dict1=(pd.DataFrame(new_df[x].value_counts())).to_dict()
FinalDict.update(dict1)
return FinalDict
# get the desired representation of data
def CountNormRepresntation(ProcessData):
ProcessDataC=ProcessData.copy(deep=False)
totalLength=len(ProcessDataC.index)
cols=['proc_username','proc_cmdline','proc_md5','parent_name','proc_child_count','proc_netconn_count','process_name']
for x in cols:
y=ProcessDataC[x].unique()
for i in y:
ProcessDataC[x]=ProcessDataC[x].replace(i,FinalDict_x[x][i])
return ProcessDataC
# +
# replace unknown by label Unk
new_df=new_df.fillna("UnK")
# create dictionary and final data form
FinalDict_x=CreateCountDict()
ProcessDataC=CountNormRepresntation(new_df)
# normalize the data
cols_to_norm = ['proc_username','proc_cmdline','proc_md5','parent_name','process_name','proc_netconn_count','proc_child_count']
ProcessDataC[cols_to_norm] = ProcessDataC[cols_to_norm].apply(lambda x: (x - x.mean()) / (x.std()))
# remove the cols are not adding any info as same value
ProcessDataC=ProcessDataC.drop(columns=['proc_netconn_count','proc_child_count','duration'])
# +
# pca for visualisation
pca = PCA(n_components=2)
datanew = pca.fit_transform(ProcessDataC)
# standardize these 2 new features
min_max_scaler = preprocessing.StandardScaler()
np_scaled = min_max_scaler.fit_transform(datanew)
datanew = pd.DataFrame(np_scaled)
# elbow method to decide on number of clusters
from sklearn.cluster import KMeans
n_cluster = range(1, 11)
kmeans = [KMeans(n_clusters=i).fit(datanew) for i in n_cluster]
scores = [kmeans[i].score(datanew) for i in range(len(kmeans))]
fig, ax = plt.subplots()
ax.plot(n_cluster, scores)
plt.show()
ProcessDataC['cluster'] = kmeans[1].predict(datanew)
print(ProcessDataC['cluster'].value_counts())
ProcessDataC['principal_feature1'] = datanew[0]
ProcessDataC['principal_feature2'] = datanew[1]
# plot the clusters
fig, ax = plt.subplots()
colors = {0:'red', 1:'blue'}
ax.scatter(ProcessDataC['principal_feature1'],ProcessDataC['principal_feature2'],c=ProcessDataC["cluster"].apply(lambda x: colors[x]))
plt.show()
# -
x=new_df.loc[ProcessDataC["cluster"] == 0,:]
x['proc_cmdline'].unique()
#in cluster 0
x
#in cluster 1
x=new_df.loc[ProcessDataC["cluster"] == 1,:]
x
# ## Open a CP4S Case
|
cp4s-notebooks/udi-examples/udi_clustering_processes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#importing libraries
import math
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
import ipywidgets as widgets
plt.style.use('fivethirtyeight')
# %matplotlib inline
# +
#data file
file = "./close_price (1) (2).csv"
# +
#importing file to create data frame
data = pd.read_csv(file)
# +
#first 5 rows of the dataset
data.head()
# +
#last 5 rows of the dataset
data.tail()
# +
#list of ll the columns
data.columns
# +
#dropdown to select the stock
title = widgets.Dropdown(
options=list(data.columns[1:]),
description='Stock :',
)
#Text
winSize = widgets.IntText(value=30,
description='Window :',
)
# +
#global variables
pnl_dict = {}
tradeCount_dict = {}
SMA = pd.DataFrame()
call_df = pd.DataFrame()
# +
#buysell indicators
def buysell(df,stock,title):
'''
INPUT:
df - DataFrame having stock name, closing price, SMA values
stock - stocks column
title - SMA values column
OUTPUT:
buy - List with buy calls
sell - List with sell calls
'''
flag = -1
buy = []
sell = []
for i in range(len(df)):
if df[stock][i] > df[title][i]:
if flag != 1:
buy.append(df[stock][i])
sell.append(np.nan)
flag = 1
else: #to hold
buy.append(np.nan)
sell.append(np.nan)
elif df[stock][i] < df[title][i]:
if flag != 0:
buy.append(np.nan)
sell.append(df[stock][i])
flag = 0
else: #to wait
buy.append(np.nan)
sell.append(np.nan)
else: #crossing point
buy.append(np.nan)
sell.append(np.nan)
return buy, sell
# -
def indicators_visualise(df,stock,title):
'''
INPUT:
df - DataFrame having stock name, closing price, SMA values
stock - stocks column
title - SMA values column
OUTPUT:
A plot with technical indicators
'''
plt.figure(figsize=(15.5,6.5))
plt.plot(df[stock],label = stock,alpha = 0.3)
plt.plot(df[title],label = 'With SMA',alpha = 0.3)
plt.scatter(df.index, df['Buy'], label = 'Buy', marker = '^', c = 'green')
plt.scatter(df.index, df['Sell'], label = 'Sell', marker = 'v', c = 'red')
plt.title('Buy and Sell indicators for '+ stock + ' stock')
plt.legend(loc = 'upper left')
plt.xlabel('1/1/2008 - 11/30/2018')
plt.ylabel('Daily Close Price (INR)')
plt.show()
def pnl_calculate(df,stock):
'''
INPUT:
df - DataFrame having stock name, closing price, SMA values
stock - stocks column
OUTPUT:
PnL - P&L
'''
PnL = np.nansum(df['Sell']) - np.nansum(df['Buy'])
#total number of trades
trades_count = len(df['Sell'])-df['Sell'].isnull().sum() + len(df['Buy'])-df['Buy'].isnull().sum()
pnl_dict[stock] = PnL
tradeCount_dict[stock] = trades_count
return PnL
def sma_calculate(df,name,title,win):
'''
INPUT:
df - DataFrame having stock name, closing price
stock - stocks column
title - SMA values column name (that needs to be created)
win - SMA window size
OUTPUT:
df1 - DataFrame having stock name, closing price, SMA values
'''
df1 = pd.DataFrame()
df1[name] = df[name]
df1[title] = df1[name].rolling(window = win).mean()
return df1
def PnL_chart(pnl_dict):
'''
INPUT:
pnl_dict - Dictionary populated in the pnl_calculate function with stock wise P&L value
OUTPUT:
P&L bar plot
'''
PnL_df = pd.Series(pnl_dict).to_frame('PnL')
PnL_df['Stock'] = PnL_df.index
col = []
for val in PnL_df['PnL']:
if val < 0:
col.append('red')
elif val >= 0:
col.append('green')
PnL_df.plot.bar(x='Stock', y='PnL', rot=90,figsize=(15,8),fontsize=13,color = col,legend=False)
plt.title("P/L corresponding to each stock")
plt.xlabel("Stock")
plt.ylabel("P/L in INR")
def return_profit(call_df,pnl_dict):
'''
INPUT:
call_df - DataFrame having all the buy & sell calls
pnl_dict - Dictionary populated in the pnl_calculate function with stock wise P&L value
OUTPUT:
mrpt - Mean Return per Trade
profit_factor - Profit Factor
'''
returns = (np.nansum(call_df['Sell'])-np.nansum(call_df['Buy']))/(np.nansum(call_df['Buy']))
calls = len(call_df['Sell'])-call_df['Sell'].isnull().sum() + len(call_df['Buy'])-call_df['Buy'].isnull().sum()
mrpt = returns/calls
total_profit = sum([val for val in pnl_dict.values() if val>=0])
total_loss = sum([val for val in pnl_dict.values() if val<0])
if abs(total_loss)!=0:
profit_factor = total_profit/abs(total_loss)
else:
profit_factor = float('inf')
return mrpt, profit_factor
# +
#Main Function
def mainFunc(name, win):
stock_title = name + ' Closing Price'
SMA = sma_calculate(data,name,stock_title,win)
smatitle = 'SMA with Window Size: ' + str(win)
plt.figure(figsize=(15.5,6.5))
plt.plot(data[name],label = name)
plt.plot(SMA[stock_title],label = smatitle,alpha = 0.7)
plt.title(stock_title)
plt.legend(loc = 'upper left')
plt.xlabel('1/1/2008 - 11/30/2018')
plt.ylabel('Daily Close Price (INR)')
plt.show()
buy,sell = buysell(SMA,name,stock_title)
SMA['Buy'] = buy
SMA['Sell'] = sell
indicators_visualise(SMA,name,stock_title)
call_df['Buy'] = buy
call_df['Sell'] = sell
#total p&l
for i in data.columns[1:]:
temp_title = i + ' Closing Price'
temp_SMA = sma_calculate(data,i,temp_title,win)
buy,sell = buysell(temp_SMA,i,temp_title)
temp_SMA['Buy'] = buy
temp_SMA['Sell'] = sell
temp_PnL = pnl_calculate(temp_SMA,i)
mrpt, profit_factor = return_profit(call_df,pnl_dict)
print("Total no. of trades of {}: {}".format(name,(len(SMA['Sell'])-SMA['Sell'].isnull().sum() + len(SMA['Buy'])-SMA['Buy'].isnull().sum())))
print("="*113)
print("Total no. of trades : {}".format(sum(tradeCount_dict.values())))
print("="*113)
print("P/L for {} stock : {:.2f}".format(name, pnl_calculate(SMA,name)))
print("="*113)
print("Mean Return per Trade for {} stock : {}".format(name, mrpt))
print("="*113)
print("Profit Factor : {:.2f}".format(profit_factor))
print("="*113)
print("Total P/L : {:.2f}".format(sum(pnl_dict.values())))
print("="*113)
PnL_chart(pnl_dict)
# +
# Triggering the widgets
widgets.interact(mainFunc,name = title, win = winSize);
|
Technical Indicators.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Model Specification for 1st-Level fMRI Analysis
#
# Nipype provides also an interfaces to create a first level Model for an fMRI analysis. Such a model is needed to specify the study-specific information, such as **condition**, their **onsets**, and **durations**. For more information, make sure to check out [nipype.algorithms.modelgen](http://nipype.readthedocs.io/en/latest/interfaces/generated/nipype.algorithms.modelgen.html).
# ## General purpose model specification
#
# The `SpecifyModel` provides a generic mechanism for model specification. A mandatory input called `subject_info` provides paradigm specification for each run corresponding to a subject. This has to be in the form of a `Bunch` or a list of `Bunch` objects (one for each run). Each `Bunch` object contains the following attributes.
# ### Required for most designs
#
# - **`conditions`** : list of names
#
#
# - **`onsets`** : lists of onsets corresponding to each condition
#
#
# - **`durations`** : lists of durations corresponding to each condition. Should be left to a single 0 if all events are being modeled as impulses.
# ### Optional
#
# - **`regressor_names`**: list of names corresponding to each column. Should be None if automatically assigned.
#
#
# - **`regressors`**: list of lists. values for each regressor - must correspond to the number of volumes in the functional run
#
#
# - **`amplitudes`**: lists of amplitudes for each event. This will be ignored by SPM's Level1Design.
#
#
# The following two (`tmod`, `pmod`) will be ignored by any `Level1Design` class other than `SPM`:
#
# - **`tmod`**: lists of conditions that should be temporally modulated. Should default to None if not being used.
#
# - **`pmod`**: list of Bunch corresponding to conditions
# - `name`: name of parametric modulator
# - `param`: values of the modulator
# - `poly`: degree of modulation
# Together with this information, one needs to specify:
#
# - whether the durations and event onsets are specified in terms of scan volumes or secs.
#
# - the high-pass filter cutoff,
#
# - the repetition time per scan
#
# - functional data files corresponding to each run.
#
# Optionally you can specify realignment parameters, outlier indices. Outlier files should contain a list of numbers, one per row indicating which scans should not be included in the analysis. The numbers are 0-based
# ## Example
#
# An example Bunch definition:
# +
from nipype.interfaces.base import Bunch
condnames = ['Tapping', 'Speaking', 'Yawning']
event_onsets = [[0, 10, 50],
[20, 60, 80],
[30, 40, 70]]
durations = [[0],[0],[0]]
subject_info = Bunch(conditions=condnames,
onsets = event_onsets,
durations = durations)
# -
subject_info
# ## Input via textfile
#
# Alternatively, you can provide condition, onset, duration and amplitude
# information through event files. The event files have to be in 1, 2 or 3
# column format with the columns corresponding to Onsets, Durations and
# Amplitudes and they have to have the name event_name.run<anything else>
# e.g.: `Words.run001.txt`.
#
# The event_name part will be used to create the condition names. `Words.run001.txt` may look like:
#
# # Word Onsets Durations
# 0 10
# 20 10
# ...
#
# or with amplitudes:
#
# # Word Onsets Durations Amplitudes
# 0 10 1
# 20 10 1
# ...
# ## Example based on dataset
#
# Now let's look at a TSV file from our tutorial dataset.
# !cat /data/ds000114/task-fingerfootlips_events.tsv
# We can also use [pandas](http://pandas.pydata.org/) to create a data frame from our dataset.
import pandas as pd
trialinfo = pd.read_table('/data/ds000114/task-fingerfootlips_events.tsv')
trialinfo.head()
# Before we can use the onsets, we first need to split them into the three conditions:
for group in trialinfo.groupby('trial_type'):
print(group)
# The last thing we now need to to is to put this into a ``Bunch`` object and we're done:
# +
from nipype.interfaces.base import Bunch
conditions = []
onsets = []
durations = []
for group in trialinfo.groupby('trial_type'):
conditions.append(group[0])
onsets.append(group[1].onset.tolist())
durations.append(group[1].duration.tolist())
subject_info = Bunch(conditions=conditions,
onsets=onsets,
durations=durations)
subject_info.items()
# -
# # Sparse model specification
#
# In addition to standard models, `SpecifySparseModel` allows model generation for sparse and sparse-clustered acquisition experiments. Details of the model generation and utility are provided in [Ghosh et al. (2009) OHBM 2009](https://www.researchgate.net/publication/242810827_Incorporating_hemodynamic_response_functions_to_improve_analysis_models_for_sparse-acquisition_experiments)
|
notebooks/basic_model_specification_fmri.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Learning Objectives
#
# - How we can dump large dataset on S3 and read it by using Boto
#
# - Learn this by uploading churn dataset on S3, train a Keras DL model by `Churn_Modelling.csv`
# ### Why use Cloud to Store Data?
#
# - changes to the dataset are more consistently shared around the company
# - and it's more effiecient resource allocation, data stored in one place rather than everyone has their own copy on their machine
#
#
#
# S3 + Boto:
# - pip install awscli (!pip install awscli on Google Colab)
# - $ aws configure (!aws configure on Google Colab)
# - AWS Access Key ID [None]: ...
# - AWS Secret Access Key [None]: ...
# - Default region name [None]: ...
# - Default output format [None]: ...
# +
# from this blog: https://dluo.me/s3databoto3
# use this when installing packages like Boto3: --use-feature=2020-resolver
# using the AWS API
import boto3
client = boto3.client('s3') #low-level functional API
BUCKET_NAME = '' # this is SENSITIVE!
resource = boto3.resource('s3') #high-level object-oriented API
my_bucket = resource.Bucket(BUCKET_NAME) #subsitute this for your s3 bucket name.
# making a Pandas DF
import pandas as pd
# Bucket refer to the name of the bucket
# key refers to the file path, once in the bucket
obj = client.get_object(Bucket=BUCKET_NAME, Key='')
df = pd.read_csv(obj['Body'])
# use environment variables, even if the repo is PRIVATE!
# -
df
# +
import pandas as pd
import boto3
# bucket = "makeschooldata"
# file_name = "data/Churn_Modelling.csv"
s3 = boto3.client('s3')
# 's3' is a key word. create connection to S3 using default config and all buckets within S3
obj = s3.get_object(Bucket=bucket, Key=file_name)
# get object and file (key) from bucket
df = pd.read_csv(obj['Body']) # 'Body' is a key word
print(df.head())
# -
# # Churn Prediction
#
# - Lets first read: https://medium.com/@pushkarmandot/build-your-first-deep-learning-neural-network-model-using-keras-in-python-a90b5864116d
# +
import pandas as pd
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import keras
from keras.models import Sequential
from keras.layers import Dense
from sklearn.metrics import confusion_matrix
print(df.head())
# get features and output of dataset
X = df.iloc[:, 3:13].values
y = df.iloc[:, 13].values
print(X)
print(X.shape)
print(y)
label_encoder_X_1 = LabelEncoder()
X[:, 1] = label_encoder_X_1.fit_transform(X[:, 1])
label_encoder_X_2 = LabelEncoder()
X[:, 2] = label_encoder_X_2.fit_transform(X[:, 2])
print(X)
print(X.shape)
one_hot_encoder = OneHotEncoder(categorical_features=[1])
X = one_hot_encoder.fit_transform(X).toarray()
X = X[:, 1:]
# print('M:')
# print(X[:, :10])
# print(X[:, 10])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# Feature Scaling
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
print(X_train.shape)
# MLP network
classifier = Sequential()
# Adding the input layer and the first hidden layer
classifier.add(Dense(output_dim=6, init='uniform', activation='relu', input_dim=11))
# Adding the second hidden layer
classifier.add(Dense(output_dim=6, init='uniform', activation='relu'))
# Adding the output layer
classifier.add(Dense(output_dim=1, init='uniform', activation='sigmoid'))
# Compiling Neural Network
classifier.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
# Fitting our model
classifier.fit(X_train, y_train, batch_size=10, nb_epoch=50, verbose=1)
# Predicting the Test set results
y_predict = classifier.predict(X_test)
print(y_predict)
y_predict = (y_predict > 0.5)
cm = confusion_matrix(y_test, y_predict)
print(cm)
# -
# ## SQL
#
# Review the basics of SQL vs NonSQL (BEW 1.1):
#
# SQL (less priority)
#
# - not a db
# - Structured Query Language
# - lets you write db queries in a structured way
# - lots of keywords
# - tables = samples of one Resource
# - usually used with relational db
# - lots of tables for the resources
# - assume that they are related to each other in some way
# - three ways in way this exisits is in BEW 1.1!
# - kinds of relationships are 1:1, 1:+1, +1:1, or +1:+1
# - Many to Many - it's a table in between two tables, which both have a one-to-many relationship to each other!
# - Schema = fields of a resource, for one table in the db
# - fields = columns
# - rows = records, or samples
# - all records in the table must have a value for all the fields
# - "adhering to the schema"
#
#
# NonSQL:
#
# -
# +
import sqlite3 as lite # sqlite3 lets you run SQL in your Python code, doesn't need to be installed with pip
con = lite.connect('population.db') # population db is referred to using P, and table is with lower p
with con:
cur = con.cursor()
# set the schema
"""cur.execute("CREATE TABLE Population(id INTEGER PRIMARY KEY, country TEXT, population INT)")
# adding records
cur.execute("INSERT INTO Population VALUES(NULL,'Germany',81197537)")
cur.execute("INSERT INTO Population VALUES(NULL,'France', 66415161)")
cur.execute("INSERT INTO Population VALUES(NULL,'Spain', 46439864)")
cur.execute("INSERT INTO Population VALUES(NULL,'Italy', 60795612)")
cur.execute("INSERT INTO Population VALUES(NULL,'Spain', 46439864)")
"""
# -
import pandas as pd
# connect to db
con = lite.connect('population.db')
# write query
search = "SELECT country FROM Population where population > 50000000;"
# get the records
print(pd.read_sql_query(search, con))
# +
import pandas as pd
import sqlite3
# listing the countries in the db, using SQL queries
conn = sqlite3.connect('population.db')
# countries must have population above a certain population size
query = "SELECT country FROM Population WHERE population > 50000000;"
# if you did SELECT * - that means all FIELDS of the records that are queried in the db
'''From here, it's all up to your Pandas skills'''
# making a df from the query, (1 column)
df = pd.read_sql_query(query, conn)
for country in df['country']:
print(country)
# +
# connect to the db
con = lite.connect('population.db')
# make the query
query = "SELECT country FROM Population WHERE country LIKE 'S%'" # % is like a regex?
# get the records
countries_start_with_s = pd.read_sql_query(query, con)
# output the result
for country in countries_start_with_s['country']:
print(country)
# osther SQL exercises:
# 1. how to get duplicate values, or count them?
# Cool thing? A lot of Pandas commands completely condense SQL query equivalents!
# -
# ## On NonSQL or "MongoDB world"
#
# NonSQL - what is it?
#
# MongoDB - most popular nonsql db
#
# NonSQL don't have tables, but collections
#
# Collections are made of documents
#
# - like rows in SQL - except they don't need to have all the same schema!
# - much more flexible!
#
# - no relations in NonSQL though, much less relied upon
# - instead, all info put in one place
# - more popular at ealrier stage in the website for a business
# - therefore, queries are less used
#
#
# SQL vs. NonSQL - which is better?
# Neither! Both have their own strengths and weaknesses, are good for certain use cases
#
# Scalability:
#
# 1. Horizontal Scaling - NonSQL is easier to do this, because no relationships, no hindrances
#
# - we add more power, by adding more servers
# - have to distribute db against the servers
# - often NOT supported in SQL
#
# 2. Vertical Scaling
#
# - adding more power to a single server
#
#
# SQL
# - multiple read/write operations can be problematic, if you're doing very complicated queries
#
#
# NonSQL
# - if data related, nonSQl is redundant
# - data is typically merged and nested in a few collections
#
# - data is structured like JSON
# - table in SQL = collection in NoSQL
# - record in SQL = document in NoSQL
# - field in SQL = kinda like key value pair of a doc in NoSQL
#
# The hard truth
# - you can pretty much build any application you want, with either kind of db
# - SQL vs NonSQL really only presents problems at SCALE
# ## Setup the MongoDB and insert and have query in Python
#
# Read: https://marcobonzanini.com/2015/09/07/getting-started-with-mongodb-and-python/
# +
from pymongo import MongoClient
from datetime import datetime
# set up connection
client = MongoClient()
# get db, and the collection
db = client['tutorial']
coll = db['articles']
# add a new doc to the db
doc = {
"title": "An article about MongoDB and Python",
"author": "Marco",
"publication_date": datetime.utcnow(),
# more fields
}
doc_id = coll.insert_one(doc).inserted_id
# +
from pymongo import MongoClient
# reading from the db
client = MongoClient()
db = client['tutorial']
coll = db['articles']
for doc in coll.find():
print(doc)
# -
# ### Syntaxes:
#
# sudo mkdir -p /data/db
#
# whoami
#
# sudo chown miladtoutounchian /data/db
#
# ./bin/mongod
#
# ## Download MongoDB Compass
# # GitHub RESTful API example
# +
import requests # package for calling public APIs, along with urllib.requests
url = 'https://api.github.com/search/repositories?q=tensorflow&type=python'
tf_repos = requests.get(url)
repos = tf_repos.json()
# print the top 10
for item in repos['items'][:10]:
print(item['full_name'])
# -
# ## Review
#
# 1. Why We Use Cloud Storage
# 2. Using SQL and NoSQL
# 3. Using Public APIs using Requests package
|
Lessons/S3_Boto.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
import random
# Reading of file
def ReadFile(file):
f=open(file,"r")
lines=f.read().splitlines()
f.close()
items=[]
for i in range(len(lines)):
line=lines[i].split(',')
feature=[]
for j in line:
feature.append(float(j))
items.append(feature)
return items
def Figure(items):
plt.figure(figsize=(20,10))
for item in items:
plt.scatter(item[0],item[1],c='b',s=70)
plt.title('Before applying K Means')
plt.show()
def FinalFigure(items,clusters):
plt.figure(figsize=(20,10))
for i in range(len(items)):
colors=['k','b','y','g','r']
plt.scatter(items[i][0],items[i][1],c=colors[clusters[i]-1],s=70)
plt.title('After applying K Means')
plt.show()
def SpearmanCorrelation(obj1,obj2):
l1=list(obj1)
l1.sort()
l2=list(obj2)
l2.sort()
Rankobj1={}
Rankobj2={}
for i in range(1,len(l1)+1):
Rankobj1[l1[i-1]]=i
Rankobj2[l2[i-1]]=i
d=[]
for j in range(len(obj1)):
d.append(abs(Rankobj1[obj1[j]]-Rankobj2[obj2[j]]))
dsq=[]
for j in range(len(obj1)):
dsq.append(math.pow(d[j],2))
sum=0
for j in range(len(obj1)):
sum+=dsq[j]
n=len(obj1)
return (1-6*sum/(n*(n*n-1)))
def Correlation(items,means):
k=len(means)
correlations=[]
for i in range(k):
correlation=[]
for item in items:
cor=SpearmanCorrelation(item,means[i])
correlation.append(cor)
correlations.append(correlation)
return correlations
def InitializeMeans(items, k):
no_f = len(items[0]);
means =[]
while(len(means)!=k):
mean=list(random.choice(items))
if mean not in means:
means.append(mean)
return means
def CalculateMean(items,clusters,i,j):
sum=0.0
count=0
z=len(items)
for k in range(z):
if(clusters[k]==j+1):
sum+=items[k][i]
count+=1
if(count!=0):
return(sum/float(count))
else:
return -1
def UpdateMean(items,clusters,means):
a=len(means)
b=len(means[0])
for j in range(a):
for i in range(b):
num=CalculateMean(items,clusters,i,j)
if(num!=-1):
means[j][i]=num
return means
def ClusterAssigning(clusters,Correlations):
for j in range(len(clusters)):
max=-2
for i in range(len(Correlations)):
if max<Correlations[i][j]:
max=Correlations[i][j]
clusters[j]=i+1
return clusters
def KMeans(file,no_clus,num_of_iterations):
items=ReadFile(file)
Figure(items)
clusters=[0 for i in range(len(items))]
means=InitializeMeans(items,no_clus)
while(num_of_iterations):
Correlations=Correlation(items,means)
clusters=ClusterAssigning(clusters,Correlations)
#print("---------------Means---------------------------")
#print(means)
means=UpdateMean(items,clusters,means)
#print("---------------Clusters---------------------------")
#print(clusters)
#print()
num_of_iterations-=1
FinalFigure(items,clusters)
print('Points\t\tCluster')
print('----------------------')
for i in range(len(items)):
print(items[i],'\t',clusters[i])
# Parameters : ( File_Name, No_of_Clusters, No_of_Iterations )
KMeans('sample.txt',3,50)
|
K_Means/K_Means_Using_SpearmanCorrelationCoefficent.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
df = pd.read_csv("decision_tree_regression.csv",sep = ";", header = None)
df
x = df.iloc[:,0].values.reshape(-1,1)
y = df.iloc[:,1].values.reshape(-1,1)
x,y
#decision tree regression
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor() # random sate = 0
tree_reg.fit(x,y)
tree_reg.predict([[5.4]])
y_head = tree_reg.predict(x)
y_head
plt.scatter(x,y,color="red")
plt.plot(x,y_head,color = "green")
plt.xlabel("seat level")
plt.ylabel("price")
plt.show()
x_ = np.arange(min(x),max(x), 0.01).reshape(-1,1)
#tree_reg.predict([[1.47]])
y_head = tree_reg.predict(x_)
y_head
plt.scatter(x,y,color="red")
plt.plot(x_,y_head,color = "green")
plt.xlabel("seat level")
plt.ylabel("price")
plt.show()
|
decision_tree_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Chapter 1 - The Machine Learning Landscape
# This chapter primarily introduces a lot of the fundamental concepts and jargon that everyone practicing ML should know.
# + [markdown] pycharm={"name": "#%% md\n"}
# ## 1.1 What is Machine Learning
#
# - Machine Learning is the science (and art) of programming computers so they can *learn from data*
# - The set of data that a machine learning system uses to learn from is called the *training set*
# + [markdown] pycharm={"name": "#%% md\n"}
# ## 1.2 Why Use Machine Learning
#
# - It is great for problems for which existing solutions require a lot of fine-tuning or long lists of rules
# - Often, a ML algorithm can simplify code and perform better than the traditional approach
# - ML techniques can possibly find a solution for complex problems for which using a traditional approach doesn't yield
# a good solution
# - ML systems can easily adapt to new data from fluctuating environments
# - Getting insights about complex problems and large amounts of data
# - Applying ML techniques to dig into large amounts of data can help discover patterns that were not immediately apparent
# is called *data mining*
# + [markdown] pycharm={"name": "#%% md\n"}
# ## 1.3 Examples of Applications
# - *Image Classification* is the analysis of images in an attempt to automatically identify them as particular objects/shapes/etc.
# - Typically performed using convolutional neural networks (CNN)
# - *Semantic Segmentation* is the analysis of an image where each pixel is classified
# - Typically performed using convolutional neural networks
# - Used to determine the exact location and shape of tumors
# - *Text Classification*
# - Automatically flagging offensive comments on discussion forums
# - Is a part of Natural Language Processing (NLP)
# - *Text Summarization*
# - Automatically summarizing long documents
# - Also NLP
# - *Chatbot*
# - Involves NLP components including understanding and question-answering modules
# - *Regression*
# - Forecasting company revenue next year based on performance metrics
# - Can be performed using Linear Regression, Polynomial Regression, Support Vector Machine (SVM), Random Forest,
# Neural Network
# - *Speech Recognition*
# - Audio samples are processed for speech recognition
# - Typically uses Recurrent Neural Networks (RNNs), CNN, or transformers
# - *Anomaly Detection*
# - Detecting fraud
# - *Clustering*
# - Segmenting clients based on their purchases so that you can design a different marketing strategy for each segment
# - *Dimensionality Reduction*
# - *Recommender Systems*
# - Usually done with the use of Neural Networks
# - *AI Bots for Games*
# - Usually done through reinforcement learning (RL)
# + [markdown] pycharm={"name": "#%% md\n"}
# ## 1.4 Types of Machine Learning Systems
#
# - Machine Learning systems can be broadly classified into these broad categories:
# - Whether or not they are training with human supervision (supervised, unsupervised, semisupervised, and reinforcement learning)
# - Whether or not they can learn incrementally on the fly
# - Whether they work by simply comparing new data points to known data points or instead by detecting patterns in the training data
# and building a predictive models (instance-based versus model-based learning)
#
# ### 1.4.1 Supervised/Unsupervised Learning
#
# - There are 4 major categories (how they learn):
# - Supervised learning
# - Unsupervised learning
# - Semisupervised learning
# - Reinforcement learning
#
# #### 1.4.1.1 Supervised Learning
#
# - In *supervised learning*, the training set you feed to the algorithm includes the desired solutions called *labels*
# - A typical supervised learning task is *classification*
# - Another typical task is to predict *target* numeric values given a set of *features* called *predictors* called *regression*
# - An *attribute* is a data type
# - A *feature* generally means an attribute with its value
#
# #### 1.4.1.2 Unsupervised Learning
#
# - In *unsupervised learning* the training data in unlabeled
# - The system will try to learn without any intervention
# - Some important unsupervised learning tasks include:
# - Dimensionality reduction
# - Anomaly detection
# - Novelty detection
# - Association rule learning
#
# #### 1.4.1.3 Semisupervised Learning
#
# - This type of learning system deals with data where the data is only partially labelled
# - Most semisupervised learning algorithms are combinations of unsupervised and supervised algorithms
#
# #### 1.4.1.4 Reinforcement Learning
#
# - This system involves an *agent* that can observe the "environment", select and perform actions, and get *rewards* in return
# - These rewards can be positive or negative (penalties)
# - The system then learns by itself what the best strategy is, called a *policy*, where it maximizes the reward over time
#
# ### 1.4.2 Batch and Online Learning
#
# #### 1.4.2.1 Batch Learning
#
# - In *batch learning*, the system is incapable of learning incrementally meaning it must be trained using all the available data
# - The system is training, and then it is launched into production and runs without learning anymore; it just applies what
# it has learned called *offline learning*
# - If you want a batch learning system to know about new data, yuo need to train a new version of the system from scratch
# on the full dataset and replace the old one with the new one
#
# #### 1.4.2.2 Online Learning
#
# - In *online learning*, you train the system incrementally by feeding it data instances sequentially, either individually
# or in small groups called *mini-batches*
# - *Online learning* is great for system that need to adapt to change rapidly
# - *Online learning* can also be used to training systems on huge datasets that cannot fit in one machine's main memory
# (called *out-of-core* learning)
# - An important parameter of online learning systems is how fast they should adapt to changing data: this is called the
# *learning rate*
# - High learning rates mean the system will rapidly adapt to new data but will also quickly forget what it has learned
# - Low learning rates mean the system will remember longer but also adapt to new data more slowly
#
# ### 1.4.3 Instance-Based Versus Model-Based Learning
#
# - One more way to categorize ML systems is by how they *generalize*
# - How well does the system adapt to new (unseen) data?
# - Two main approaches to generalization:
# - Instance-based learning
# - Model-based learning
#
# #### 1.4.3.1 Instance-Based Learning
#
# - Instance-based learning is basically "learning by heart" or using existing examples, and flagging new examples when they
# are identical to previous examples
# - The other method to instance-based learning is using a *measure of similarity* where new examples are compared to previous
# examples, and if they meet some threshold, are identified as such
#
# #### 1.4.3.2 Model-Based Learning
#
# - Model-based learning is the method of generalizing from a set of examples by building a model from those examples, and then
# using the model to make *predictions*
# - In order to do model-based learning, you need to specify a performance measure
# - This is often done through defining a *utility function* (or *fitness function*) that measures how good the model is
# - This can also be defined as a *cost function* (or how bad a model is)
# - For Linear Regression, the cost function typically revolves around a measure of distance between the predictions and
# the actual values, and the model works to minimize this distance
#
#
# + [markdown] pycharm={"name": "#%% md"}
# ## 1.5 Main Challenges of Machine Learning
#
# - The two things that can go wrong are "bad algorithm" and "bad data"
#
# ### 1.5.1 Insufficient Quantity of Training Data
#
# - In general, given enough data, simple ML models can perform just as well (or better) as more complex models
# - There is an inherent trade-off that must be considered when thinking about spending time and money on algorithm development
# and corpus development (training data)
#
# ### 1.5.2 Nonrepresentative Training Data
#
# - In order to generalize well, it is crucial that your training data be representative of the new cases you want to generalize to
# - It is crucial to use a training set that is representative of the cases you want to generalize to
# - If the sample is too small, you will have *sampling noise* (nonrepresentative data as a result of chance)
# - Another source of error is from *sampling bias*, when the sampling method is flawed
#
# ### 1.5.3 Poor-Quality Data
#
# - If the training data is full of errors, outliers, and noise, it will be harder for the algorithm to detect patterns, and thus
# your system is highly likely to perform poorly
# - Severe outliers can be be discarded or dealt with manually
# - Whenever a feature is missing a lot of information, action must be taken whether it is to:
# - Ignore the feature
# - Fill in the missing values
# - Ignore the instances of missing values
# - Train two models with and without the feature
#
# ### 1.5.4 Irrelevant Features
#
# - One of the most important parts of a successful ML project is *feature engineering*, or coming up with a good set of features
# to train on. This process involves the following steps:
# - *Feature selection*: selecting the most useful features to train on among existing features
# - *Feature extraction*: combining existing features to produce a more useful one
# - Creating new features by gathering new data
#
# ### 1.5.5 Overfitting the Training Data
#
# - Overfitting is when the model performs well on the training data, but does not generalize well to new data
# - Complex models such as deep neural networks are able to detect subtle patterns in data and because of this, if a dataset
# is noisy or too small, the model will likely feel like the noise is useful information
# - Overfitting can be solved by:
# - Simplifying the model
# - Selecting a model with fewer parameters
# - Reducing the number of attributes in the training data
# - Constraining the model
# - Gathering more training data
# - Reduce the noise in the training data
# - Fix errors
# - Remove outliers
# - Constraining a model to make it simpler and reduce the risk of overfitting is called *regularization*
# - The ultimate objective is to find the right balance between fitting the training data and keeping the model simple so that
# it can generalize well
# - Regularization is typically controlled through *hyperparameters*
# - *Hyperparameters* are parameters of a learning algorithm and not the model itself
#
# ### 1.5.6 Underfitting the Training Data
#
# - This occurs when the model is too simple to learn the underlying structure of the data
# - The main options for solving this problem are:
# - Selecting a more powerful model, with more parameters
# - Feed better features to the learning algorithm (feature engineering)
# - Reduce the constraints on the model (reduce the regularization parameters)
#
# ### 1.5.7 Stepping Back
#
# - ML is about making machines get better at some task by learning from data instead of having to explicitly code rules
# - There are many different types of ML systems: supervised or not, batch or online, instance-based or model-based
# - In an ML project, you gather data in a training set, feed the training set to a learning algorithm:
# - If the algorithm is model-based, it tunes some parameters to fit the model to the training data
# - If the algorithm is instance-based, it just learns the examples by heart and generalizes to new instances by using
# a similarity metric
# - The system will not perform well if your training set:
# - Is too small
# - Not representative
# - Is noisy
# - Is polluted with irrelevant features
# + [markdown] pycharm={"name": "#%% md\n"}
# ## 1.6 Testing and Validating
#
# - The only way to know how well a model will generalize to new cases is to actually try it out on new cases
# - This is accomplished by splitting your data into two sets:
# - The *training set*
# - The *test set*
# - It is very common to use 80% of the data for training and 20% on testing
# - The error rate on new cases is called the *generalization error* and this estimate can be determined by the performance
# of the model on the *test set*
# - If the training error is low, but the generalization error is high, it means that your model is overfitting the training
# data
#
# ### 1.6.1 Hyperparameter Tuning and Model Selection
#
# - Evaluating a model is done on the *test set*
# - A common solution to solving generalization error on a *test set* is to use a *holdout validation* set or *validation set*
# - You can use this set to evaluate several models and select the best one
# - This is also the time to experiment with different hyperparameters
# - The pitfalls of using a single validation set are solved through repeated *cross-validation*
# - This uses many small *validation sets*
# - Each model is evaluated once per validation set after it is training on the rest of the data
# - The error measure on all those models will give a better measure of the performance
#
# ### 1.6.2 Data Mismatch
#
# - This is when the data is not perfectly representative of the data that will be used in production
|
notes/chapter_01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from tensorflow.keras.applications.inception_v3 import preprocess_input
from tensorflow.keras.preprocessing.image import img_to_array
from tensorflow.keras.models import load_model
import numpy as np
import cv2
import os
# +
import tensorflow as tf
from tensorflow.python.framework.convert_to_constants import convert_variables_to_constants_v2
"""loaded = tf.saved_model.load('modelpb')
infer = loaded.signatures['serving_default']
f = tf.function(infer).get_concrete_function(input_1=tf.TensorSpec(shape=[None, 150, 150, 3], dtype=tf.float32))
f2 = convert_variables_to_constants_v2(f)
graph_def = f2.graph.as_graph_def()
# Export frozen graph
with tf.io.gfile.GFile('frozen_graph.pb', 'wb') as f:
f.write(graph_def.SerializeToString())"""
# +
prototxtPath = os.path.sep.join(["/home/soundarzozm/Desktop/mask_detector", "deploy.prototxt"])
weightsPath = os.path.sep.join(["/home/soundarzozm/Desktop/mask_detector", "res10_300x300_ssd_iter_140000.caffemodel"])
net = cv2.dnn.readNet(prototxtPath, weightsPath)
model = load_model("model.h5")
# +
image = cv2.imread("try1.jpg")
orig = image.copy()
(h, w) = image.shape[:2]
blob = cv2.dnn.blobFromImage(image, 1.0, (256, 256), (104.0, 177.0, 123.0))
net.setInput(blob)
detections = net.forward()
# -
detections
# +
for i in range(0, detections.shape[2]):
confidence = detections[0, 0, i, 2]
if confidence > 0.3:
box = detections[0, 0, i, 3:7] * np.array([w, h, w, h])
(startX, startY, endX, endY) = box.astype("int")
(startX, startY) = (max(0, startX), max(0, startY))
(endX, endY) = (min(w - 1, endX), min(h - 1, endY))
face = image[startY:endY, startX:endX]
face = cv2.cvtColor(face, cv2.COLOR_BGR2RGB)
face = cv2.resize(face, (256, 256))
face = img_to_array(face)
face = preprocess_input(face)
face = np.expand_dims(face, axis=0)
mask = model.predict(face)[0][0]
no_mask = 1 - mask
label = "Mask" if mask < no_mask else "No Mask"
color = (0, 255, 0) if label == "Mask" else (0, 0, 255)
label = "{}: {:.2f}%".format(label, max(mask, no_mask) * 100)
cv2.putText(image, label, (startX, startY - 10), cv2.FONT_HERSHEY_SIMPLEX, 0.45, color, 2)
cv2.rectangle(image, (startX, startY), (endX, endY), color, 2)
cv2.imshow("Output", image)
cv2.imwrite("try1mod.jpg", image)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
photo_implementation_notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] heading_collapsed=true
# # Data Wrangling with Pandas
#
# **Author**: <NAME> - Missouri University of Science and Technology
#
# This notebook provides an overview of data manipulation using Pandas, a Python package that provides similar functionality to spreadsheet programs like Excel or Google Sheets.
#
# You can read more details about Pandas __[here](https://pandas.pydata.org/pandas-docs/stable/getting_started/index.html)__
#
# In this notebook we will briefly demonstrate the following capabilities of pandas:
# - Reading data from comma and space-delimited files into pandas dataframes
# - Manipulating data in a dataframe
# - Writing dataframes to files
#
# <div class="alert alert-info">
# <b>Terminology:</b>
#
# - *dataframe*: The equivalent of a spreadsheet in Python.
#
# - *Series*: A single column of a Pandas dataframe; equivalent to a column in a spreadsheet
#
# - *tropospheric zenith delay*: The precise atmospheric delay satellite signals experience when propagating through the troposphere.
# </div>
#
# Estimated time to run notebook: 15 minutes
# + [markdown] heading_collapsed=true hidden=true
# ## Table of Contents:
# <a id='example_TOC'></a>
# + [markdown] hidden=true
# [**Overview of the pandas package**](#overview)
# [1. Reading data from files](#reading-data)
# [2. Manipulating data in dataframes](#manip-data)
# [3. Writing data to files](#write-data)
# + [markdown] heading_collapsed=true hidden=true
# ## Prep: Initial setup of the notebook
# + [markdown] hidden=true
# Below we set up the directory structure for this notebook exercise. In addition, we load the required modules into our python environment using the **`import`** command.
#
# <div class="alert alert-info">
# You can customize the location of your home and working directory when running this notebook by modifying the cell below.
# </div>
#
# + hidden=true
import numpy as np
import os
import matplotlib.pyplot as plt
import pandas as pd
## Defining the home and data directories
tutorial_home_dir = os.path.abspath(os.getcwd())
work_dir = os.path.abspath(os.getcwd())
print("Tutorial directory: ", tutorial_home_dir)
print("Work directory: ", work_dir)
# -
# ## Overview of the Pandas Package
# <a id='overview'></a>
# ### Reading data from files
# <a id='reading-data'></a>
# Let's start by loading a simple .csv dataset into a pandas dataframe
df = pd.read_csv('data/sample_data.csv')
df.head()
# +
# It's also possible to read space-delimited and excel files using pandas
# df = pd.read_csv('space_delimited_file.txt', delim_whitespace=True)
# df = pd.read_excel('excel_file.xlsx') # You may need to install xlrd or openpyxl to read excel files
# -
# ### Manipulating data in pandas
# <a id='manip-data'></a>
# Pandas uses an "index" to keep track of rows. By default it uses integers
print(df.index)
# You can change the index to a column in the dataframe, for example a datetime
df = df.set_index('Datetime')
df.head()
# You can reset the index as well
df = df.reset_index()
df.head()
# By default Pandas reads datetimes from files as strings.
# we can convert them to actual Python datetimes
df['Datetime'] = pd.to_datetime(df['Datetime'])
df = df.set_index('Datetime')
df.head()
# We can get a subset of the data using the column name
df_jme2 = df[df['ID'] == 'JME2']
df_jme2.head()
# It's possible to plot data directly using Pandas
df_jme2['ZTD'].plot()
# We can perform operations on columns:
'Station_' + df['ID']
# Or mathematical operations:
noisy = np.nanmean(df['ZTD']) + np.nanstd(df['ZTD'])*np.random.randn(len(df))
print(noisy)
# We can assign the output of an operation to a new column
df['ZTD_noisy'] = noisy
# And we can take operations of several columns
df['ZTD_diff'] = df['ZTD'] - df['ZTD_noisy']
# +
# We can define functions and then call them as operators on a dataframe column or index
def dt2fracYear(date):
import datetime as dt
import time
def sinceEpoch(date): # returns seconds since epoch
return time.mktime(date.timetuple())
s = sinceEpoch
# check that the object is a datetime
try:
year = date.year
except AttributeError:
date = numpyDT64ToDatetime(date)
year = date.year
startOfThisYear = dt.datetime(year=year, month=1, day=1)
startOfNextYear = dt.datetime(year=year+1, month=1, day=1)
yearElapsed = s(date) - s(startOfThisYear)
yearDuration = s(startOfNextYear) - s(startOfThisYear)
fraction = yearElapsed/yearDuration
date_frac = date.year + fraction
return date_frac
def numpyDT64ToDatetime(dt64):
'''
Convert a numpy datetime64 object to a python datetime object
'''
import datetime
import numpy as np
unix_epoch = np.datetime64(0, 's')
one_second = np.timedelta64(1, 's')
seconds_since_epoch = (dt64 - unix_epoch) / one_second
dt = datetime.datetime.utcfromtimestamp(seconds_since_epoch)
return dt
# -
# We can assign the index to be a column, operate on it, and then drop the added column
df['dt'] = df.index
df['fracYear'] = df['dt'].apply(lambda x: dt2fracYear(x))
df.drop('dt', axis=1)
# We can look at summary statistics
df.describe()
# We can group variables as needed
station_stats = df.value_counts('ID')
station_stats.head()
# We can create different plots, depending on the type of variable we are interested in
df['ZTD'].plot.hist(bins=100)
plt.xlabel('ZTD (m)')
# See the API documentation for keyword arguments, etc.
df.plot.scatter(x='ZTD', y='ZTD_noisy', s=1, c='k')
# ### Writing dataframes to a file
# <a id='write-data'></a>
# Pandas can write to various file formats, including xcel, JSON, HTML, HDF5, STATA, SQL, and pickle formats.
#
# Using the __[Scipy.io](https://docs.scipy.org/doc/scipy/reference/io.html)__ module, you can also export data from Python to a .mat file that can be read in Matlab.
#
# You can the Pandas I/O documentation __[here](https://pandas.pydata.org/pandas-docs/stable/user_guide/io.html)__.
# We can export a dataframe to a .csv file
df_jme2.to_csv(os.path.join(work_dir, 'Station_JME2_ZTD.csv'), index = False)
# export to a .mat file by first converting the dataframe to a dictionary
import scipy.io as sio
sio.savemat('Station_JME2_ZTD.mat', {'data': df_jme2.to_dict()})
|
notebooks/Pandas_tutorial/Pandas_tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Source
# ***
# ### Yahoo Finance
# The majority of the information pulled into the system and processed comes from *Yahoo Finance* one of the top sources for free stock market data. Yahoo Finance used to be considered the golder standard for stock data until they shut down thier API in 2017. However by using the **yfinance** python library we can connect to the new API provided by Yahoo Finance.
#
# Library Source : https://github.com/ranaroussi/yfinance
#
# #### What data do we need to start?
# **Tickers** : A list of ticker values is the only thing needed to initialize the program. These can be found from any stock source site and are representative of which companies stock you are looking at. For example: Tesla is (TSLA). Ford Motors is (F).
#
# ***
# ### What data do we pull?
# ***
# #### Time Frame
# We only pull seven years of historical data for each stock
#
#
# #### Meta Data
# *Short Name* : The actual name of the company
# <br>
# *Sector* : This is the economic area the company covers
# <br>
# *Full Time Employees* : This value denotes the number of employees in the company
# <br>
# *Exchange* : Which stock exchange the company is on
#
# #### Daily Data
# *Date* : This is the date that the record is tied to
# <br>
# *Open* : The value of the stock when the markets opened
# <br>
# *High* : The highest value the stock reached during that trading day
# <br>
# *Low* : The lowest value the stock reached during the trading day
# <br>
# *Close* : The value of the stock when the markets closed at the end of the trading day
# <br>
# *Volume* : The amount of stock that was traded in that day
# <br>
# *Dividends* : The amount of money paid to each stock holder as a dividended during that trading day
# <br>
# *Stock Split* : This value shows if the stock split during the trading day and how it split during the day of trading
#
# ### Location in Code
# The data here is pulled in with the *Initalize Database* code, saved to *Master DB* sqlite database and is queried with the *SQL Queries* section of the code
|
notebooks/Documentation_Data_Source.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# + [markdown] slideshow={"slide_type": "-"}
# ## Finite-Window data
# * Filament: Axoneme-488
# * Dynein: 1067-SNAP-Cy3 diluted by 1000
# * Condition: 2 mM ATP in DAB (50 mM K-Ac, 10 mM Mg-Ac2)
# * Number of frame: 500
# * Total time = 27.3 s
#
# Created on Wed May 15 07:49:41 2019 @author: <NAME>
# + slideshow={"slide_type": "slide"}
# Import library
from __future__ import division, print_function, absolute_import
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt
# %matplotlib inline
from matplotlib import cm
import sys
sys.path.append("../finite_window/finite_window")
import config
#from my_funcs import generate_trace, find_dwell
data_dir = config.data_dir
data_files = config.data_files
print(data_dir)
print(data_files)
# + [markdown] slideshow={"slide_type": "slide"}
# ## Read a movie file (*.tif)
# + slideshow={"slide_type": "slide"}
# Open a time lapse movie
filename = data_dir / 'data1' / 'data1.tif'
movie = Image.open(filename)
n_frame = movie.n_frames
n_row = movie.size[1]
n_col = movie.size[0]
print('File name = ', filename)
print('[frame, row, col] = [%d, %d, %d] \n' %(n_frame, n_row, n_col))
# Pixel intensity is saved in I[frame, row, col]
I_frame = np.zeros((n_frame, n_row, n_col), dtype=int)
for i in range(n_frame):
movie.seek(i) # Move to i-th frame
I_frame[i,] = np.array(movie, dtype=int)
# -
# ## Create a maximum projection image
# +
# Maximum projection
I_max = np.max(I_frame, axis=0)
fig, ax = plt.subplots(figsize=(10, 10))
ax.imshow(I_max, cmap=cm.gray)
ax.set_title('Maximum intensity')
# -
# ## Find local maximum intensity peaks
# +
# Find peaks from local maximum
from skimage.feature import peak_local_max
spot_size = 3
min_distance = 5
peaks = peak_local_max(I_max, min_distance)
n_peak = len(peaks[:, 1])
row = peaks[::-1,0]
col = peaks[::-1,1]
print('Found', n_peak, 'spots. ')
fig, ax = plt.subplots(figsize=(10, 10))
ax.imshow(I_max, cmap=cm.gray)
for i in range(n_peak):
ax.plot(col[i], row[i], 'ro', ms=3, alpha=0.5)
ax.set_title('Peaks = %d, Spot size = %d, Min_distance = %d' % (n_peak, spot_size, min_distance))
# -
# ## Get the intensity traces at each spot
# +
I_peak = ['None']*n_peak
s = int(spot_size/2)
for i in range(n_peak):
I_peak[i] = np.mean(np.mean(I_frame[:,row[i]-s:row[i]+s,col[i]-s:col[i]+s], axis=2), axis=1) # Mean intensity around the peak
fig, (ax1, ax2) = plt.subplots(1,2,figsize=(15,5))
ax1.hist([I_peak[i].max() for i in range(n_peak)], 100, color='k', histtype='step', lw=1)
ax1.set_xlabel('Intensity')
ax1.set_ylabel('Occurrence')
ax1.set_title('Maximum intensity at each spot')
ax2.hist([I_peak[i].min() for i in range(n_peak)], 100, color='k', histtype='step', lw=1)
ax1.set_xlabel('Intensity')
ax1.set_ylabel('Occurrence')
ax2.set_title('Minimum intensity at each spot')
# -
# ## Normalize intensity traces at each spot
# +
def lowpass(I, n):
m = int(n/2)
x = np.convolve(I, np.ones((n,))/n, mode='valid')
x0 = np.array(x[:m])
x1 = np.array(x[-m:])
return np.concatenate((x0, x, x1))
def normalize(I):
# Lowpass filter
I_lp = lowpass(I, 3)
# Normalize by min and max
I_lp = I_lp - np.min(I_lp)
I_lp = I_lp/np.max(I_lp)
# Renormalize by median of upper and lower parts
I_up = np.median(I[I_lp > 0.5])
I_low = np.median(I[I_lp < 0.5])
I_norm = (I - I_low)/(I_up - I_low)
return I_norm
I_peak = [normalize(I_peak[i]) for i in range(n_peak)]
# -
# ## Check the noise level at each spot
# +
def reject_outliers(data, m = 3.):
d = np.abs(data - np.median(data))
mdev = np.median(d)
s = d/mdev if mdev else 0.
return data[s<m]
def find_noise(I):
noise = I - lowpass(I, 3)
noise = reject_outliers(noise)
return np.std(noise)
noise = np.array([find_noise(I_peak[i]) for i in range(n_peak)])
fig, ax = plt.subplots(figsize=(10, 5))
ax.hist(noise[noise<1], 100, color='k', histtype='step', lw=1)
ax.set_xlabel('Noise')
ax.set_ylabel('Occurrence')
# -
# # Discard spots with high noise level
# +
noise_cutoff = 0.2
I_mol = [I_peak[i] for i in range(n_peak) if noise[i] < noise_cutoff]
n_mol = len(I_mol)
print('Found %d molecules. Discarded %d spots.' %(n_mol, (n_peak-n_mol)))
# -
# ## Show traces as an example
n_fig = 4
fig, ax = plt.subplots(1, n_fig, figsize=(4*n_fig, 5))
for i in range(n_fig):
ax[i].plot(I_mol[i], 'k', lw=1)
ax[i].axhline(y=1, ls='--', lw=1, c='k')
ax[i].axhline(y=0.5, ls='--', lw=1, c='k')
ax[i].axhline(y=0, ls='--', lw=1, c='k')
ax[i].set_xlabel('Frame')
ax[i].set_ylabel('Normalized intensity')
fig.tight_layout()
# ## Lowpass filter (smothen) the signal
# +
I_lp = [lowpass(I_mol[i], 3) for i in range(n_mol)]
fig, ax = plt.subplots(1, n_fig, figsize=(4*n_fig, 5))
for i in range(n_fig):
ax[i].plot(I_lp[i], 'b', lw=1)
ax[i].axhline(y=1, ls='--', lw=1, c='k')
ax[i].axhline(y=0.5, ls='--', lw=1, c='k')
ax[i].axhline(y=0, ls='--', lw=1, c='k')
ax[i].set_xlabel('Frame')
ax[i].set_ylabel('Smoothened intensity')
fig.tight_layout()
# -
# ## Find the traces using piecewise constant (PWC) algorithm
# ### Ref: Generalized Methods and Solvers for Noise Removal from Piecewise Constant Signals (2010)
# +
# Use Jump Penalty algorithm among PWC since it is less sensitive to noise.
from pwc_jumppenalty import pwc_jumppenalty
from pwc_cluster import pwc_cluster
I_fit = ['None']*n_mol
for i in range(n_mol):
I_fit[i] = pwc_jumppenalty(I_lp[i], square=True, gamma=1.0, display=False, maxiter=10, full=False)
# I_fit[i] = pwc_cluster(I_mol[i], K=2, soft=False, beta=0.1, biased=True, display=False, stoptol=1e-5, maxiter=20) # Likelihood mean-shift
# Plot the fitting result
f, ax = plt.subplots(1, n_fig, figsize=(4*n_fig, 5))
for i in range(n_fig):
ax[i].plot(I_lp[i], 'b', lw=1)
ax[i].plot(I_fit[i], 'r', lw=3)
ax[i].axhline(y=1, ls='--', lw=1, c='k')
ax[i].axhline(y=0.5, ls='--', lw=1, c='k')
ax[i].axhline(y=0, ls='--', lw=1, c='k')
ax[i].set_xlabel('Frame')
ax[i].set_ylabel('Smoothened intensity')
ax[i].set_title('PWC fitting result')
f.tight_layout()
# -
# ## Define state [unbound, bound] = [0, 1] in each trace based on the PWC fitting result
# +
# If I_fit > 0.5, then it is bound state. Otherwise, it is unbound state.
state = [I_fit[i] > 0.5 for i in range(n_mol)]
# Plot the fitting result
f, ax = plt.subplots(1, n_fig, figsize=(4*n_fig, 5))
for i in range(n_fig):
ax[i].plot(I_mol[i], 'k', lw=1)
ax[i].plot(state[i], 'r', lw=3)
ax[i].axhline(y=1, ls='--', lw=1, c='k')
ax[i].axhline(y=0.5, ls='--', lw=1, c='k')
ax[i].axhline(y=0, ls='--', lw=1, c='k')
ax[i].set_xlabel('Frame')
ax[i].set_ylabel('Intensity')
ax[i].set_title('Bound/Unbound states')
f.tight_layout()
# -
# ## Now, we find the dwell time from each trace
# +
# Variable to save bound and unbound dwell
dwell = [] # Dwell time
for i in range(n_mol):
t_b = [] # Frame number at binding
t_u = [] # Frame number at unbinding
s = state[i] # State of ith molecule
for j in range(len(s)-1):
# Frame at binding
if (s[j] == False) & (s[j+1] == True):
t_b.append(j)
# Frame at unibnding
if (s[j] == True) & (s[j+1] == False):
t_u.append(j)
# Stop if there's no complete binding/unbinding
if len(t_b)*len(t_u) == 0:
continue
# Remove pre-existing binding
if t_u[0] < t_b[0]:
del t_u[0]
# Stop if there's no complete binding/unbinding
if len(t_b)*len(t_u) == 0:
continue
# Remove unfinished binding
if t_u[-1] < t_b[-1]:
del t_b[-1]
# Stop if there's no complete binding/unbinding
if len(t_b)*len(t_u) == 0:
continue
# Dwell time of each molecule
t_bu = [t_u[k] - t_b[k] for k in range(len(t_b))]
# Dwell time of overall molecules
dwell.extend(t_bu)
print('%d events are found.' %(len(dwell)))
# -
# ## Histogram and mean dwell time
# +
mean_dwell = np.mean(dwell)
bins = np.linspace(0, max(dwell), 20)
norm = len(dwell)*(bins[1]-bins[0])
t = np.linspace(min(dwell), max(dwell), 100)
exp_mean = np.exp(-t/mean_dwell)/mean_dwell
exp_mean = exp_mean*norm
fig, (ax1, ax2) = plt.subplots(1,2,figsize=(15,5))
ax1.hist(dwell, bins, color='k', histtype='step', lw=1)
ax1.plot(t, exp_mean, 'r')
ax1.set_xlabel('Frame')
ax1.set_ylabel('Occurrence')
ax1.set_title('Dwell time distribution (N = %d)' %(len(dwell)))
ax2.hist(dwell, bins, color='k', histtype='step', lw=1)
ax2.plot(t, exp_mean, 'r')
ax2.set_yscale('log')
ax2.set_xlabel('Frame')
ax2.set_ylabel('Occurrence')
ax2.set_title('Mean dwell time = %.1f [frame]' %(mean_dwell))
# -
# # Finally, we got the mean dwell time of the entire molecules.
# ## Add drift correction
# ## Jupyter Github
# ## else?
import numpy
|
notebooks/02_exp_1067_ATP.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Tutorial 3: An Introduction To MoleculeNet
#
# One of the most powerful features of DeepChem is that it comes "batteries included" with datasets to use. The DeepChem developer community maintains the MoleculeNet [1] suite of datasets which maintains a large collection of different scientific datasets for use in machine learning applications. The original MoleculeNet suite had 17 datasets mostly focused on molecular properties. Over the last several years, MoleculeNet has evolved into a broader collection of scientific datasets to facilitate the broad use and development of scientific machine learning tools.
#
# These datasets are integrated with the rest of the DeepChem suite so you can conveniently access these these through functions in the `dc.molnet` submodule. You've already seen a few examples of these loaders already as you've worked through the tutorial series. The full documentation for the MoleculeNet suite is available in our docs [2].
#
# [1] <NAME>, et al. "MoleculeNet: a benchmark for molecular machine learning." Chemical science 9.2 (2018): 513-530.
#
# [2] https://deepchem.readthedocs.io/en/latest/moleculenet.html
#
# ## Colab
#
# This tutorial and the rest in this sequence can be done in Google colab. If you'd like to open this notebook in colab, you can use the following link.
#
# [](https://colab.research.google.com/github/deepchem/deepchem/blob/master/examples/tutorials/02_Working_With_Datasets.ipynb)
#
#
# ## Setup
#
# To run DeepChem within Colab, you'll need to run the following installation commands. This will take about 5 minutes to run to completion and install your environment. You can of course run this tutorial locally if you prefer. In that case, don't run these cells since they will download and install Anaconda on your local machine.
# !curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
import conda_installer
conda_installer.install()
# !/root/miniconda/bin/conda info -e
# !pip install --pre deepchem
# We can now import the `deepchem` package to play with.
import deepchem as dc
dc.__version__
# # MoleculeNet Overview
#
# In the last two tutorials we loaded the Delaney dataset of molecular solubilities. Let's load it one more time.
tasks, datasets, transformers = dc.molnet.load_delaney(featurizer='GraphConv', split='random')
# Notice that the loader function we invoke `dc.molnet.load_delaney` lives in the `dc.molnet` submodule of MoleculeNet loaders. Let's take a look at the full collection of loaders available for us
[method for method in dir(dc.molnet) if "load_" in method ]
# The set of MoleculeNet loaders is actively maintained by the DeepChem community and we work on adding new datasets to the collection. Let's see how many datasets there are in MoleculeNet today
len([method for method in dir(dc.molnet) if "load_" in method ])
# # MoleculeNet Dataset Categories
#
# There's a lot of different datasets in MoleculeNet. Let's do a quick overview of the different types of datasets available. We'll break datasets into different categories and list loaders which belong to those categories. More details on each of these datasets can be found at https://deepchem.readthedocs.io/en/latest/moleculenet.html. The original MoleculeNet paper [1] provides details about a subset of these papers. We've marked these datasets as "V1" below. All remaining dataset are "V2" and not documented in the older paper.
#
# ## Quantum Mechanical Datasets
#
# MoleculeNet's quantum mechanical datasets contain various quantum mechanical property prediction tasks. The current set of quantum mechanical datasets includes QM7, QM7b, QM8, QM9. The associated loaders are
#
# - [`dc.molnet.load_qm7`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_qm7): V1
# - [`dc.molnet.load_qm7b_from_mat`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_qm7): V1
# - [`dc.molnet.load_qm8`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_qm8): V1
# - [`dc.molnet.load_qm9`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_qm9): V1
#
# ## Physical Chemistry Datasets
#
# The physical chemistry dataset collection contain a variety of tasks for predicting various physical properties of molecules.
#
# - [`dc.molnet.load_delaney`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_delaney): V1. This dataset is also referred to as ESOL in the original paper.
# - [`dc.molnet.load_sampl`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_sampl): V1. This dataset is also referred to as FreeSolv in the original paper.
# - [`dc.molnet.load_lipo`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_lipo): V1. This dataset is also referred to as Lipophilicity in the original paper.
# - [`dc.molnet.load_thermosol`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_thermosol): V2.
# - [`dc.molnet.load_hppb`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_hppb): V2.
# - [`dc.molnet.load_hopv`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_hopv): V2. This dataset is drawn from a recent publication [3]
#
# ## Chemical Reaction Datasets
#
# These datasets hold chemical reaction datasets for use in computational retrosynthesis / forward synthesis.
#
# - [`dc.molnet.load_uspto`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_uspto)
#
# ## Biochemical/Biophysical Datasets
#
# These datasets are drawn from various biochemical/biophysical datasets that measure things like the binding affinity of compounds to proteins.
#
# - [`dc.molnet.load_pcba`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_pcba): V1
# - [`dc.molnet.load_nci`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_nci): V2.
# - [`dc.molnet.load_muv`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_muv): V1
# - [`dc.molnet.load_hiv`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_hiv): V1
# - [`dc.molnet.load_ppb`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#ppb-datasets): V2.
# - [`dc.molnet.load_bace_classification`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bace_classification): V1. This loader loads the classification task for the BACE dataset from the original MoleculeNet paper.
# - [`dc.molnet.load_bace_regression`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bace_regression): V1. This loader loads the regression task for the BACE dataset from the original MoleculeNet paper.
# - [`dc.molnet.load_kaggle`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_kaggle): V2. This dataset is from Merck's drug discovery kaggle contest and is described in [4].
# - [`dc.molnet.load_factors`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_factors): V2. This dataset is from [4].
# - [`dc.molnet.load_uv`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_uv): V2. This dataset is from [4].
# - [`dc.molnet.load_kinase`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_kinase): V2. This datset is from [4].
#
# ## Molecular Catalog Datasets
#
# These datasets provide molecular datasets which have no associated properties beyond the raw SMILES formula or structure. These types of datasets are useful for generative modeling tasks.
#
# - [`dc.molnet.load_zinc15`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_zinc15): V2
# - [`dc.molnet.load_chembl`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_chembl): V2
# - [`dc.molnet.load_chembl25`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#chembl25-datasets): V2
#
# ## Physiology Datasets
#
# These datasets measure physiological properties of how molecules interact with human patients.
#
# - [`dc.molnet.load_bbbp`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bbbp): V1
# - [`dc.molnet.load_tox21`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_tox21): V1
# - [`dc.molnet.load_toxcast`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_toxcast): V1
# - [`dc.molnet.load_sider`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_sider): V1
# - [`dc.molnet.load_clintox`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_clintox): V1
# - [`dc.molnet.load_clearance`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_clearance): V2.
#
# ## Structural Biology Datasets
#
# These datasets contain 3D structures of macromolecules along with associated properties.
#
# - [`dc.molnet.load_pdbbind`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_pdbbind): V1
#
#
# ## Microscopy Datasets
#
# These datasets contain microscopy image datasets, typically of cell lines. These datasets were not in the original MoleculeNet paper.
#
# - [`dc.molnet.load_bbbc001`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bbbc001): V2
# - [`dc.molnet.load_bbbc002`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bbbc002): V2
# - [`dc.molnet.load_cell_counting`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#cell-counting-datasets): V2
#
# ## Materials Properties Datasets
#
# These datasets compute properties of various materials.
#
# - [`dc.molnet.load_bandgap`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_bandgap): V2
# - [`dc.molnet.load_perovskite`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_perovskite): V2
# - [`dc.molnet.load_mp_formation_energy`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_mp_formation_energy): V2
# - [`dc.molnet.load_mp_metallicity`](https://deepchem.readthedocs.io/en/latest/moleculenet.html#deepchem.molnet.load_mp_metallicity): V2
#
#
# [3] <NAME>., et al. "The Harvard organic photovoltaic dataset." Scientific data 3.1 (2016): 1-7.
#
# [4] <NAME>, et al. "Is multitask deep learning practical for pharma?." Journal of chemical information and modeling 57.8 (2017): 2068-2076.
# # MoleculeNet Loaders Explained
# All MoleculeNet loader functions take the form `dc.molnet.load_X`. Loader functions return a tuple of arguments `(tasks, datasets, transformers)`. Let's walk through each of these return values and explain what we get:
#
# 1. `tasks`: This is a list of task-names. Many datasets in MoleculeNet are "multitask". That is, a given datapoint has multiple labels associated with it. These correspond to different measurements or values associated with this datapoint.
# 2. `datasets`: This field is a tuple of three `dc.data.Dataset` objects `(train, valid, test)`. These correspond to the training, validation, and test set for this MoleculeNet dataset.
# 3. `transformers`: This field is a list of `dc.trans.Transformer` objects which were applied to this dataset during processing.
#
# This is abstract so let's take a look at each of these fields for the `dc.molnet.load_delaney` function we invoked above. Let's start with `tasks`.
tasks
# We have one task in this dataset which corresponds to the measured log solubility in mol/L. Let's now take a look at `datasets`:
datasets
# As we mentioned previously, we see that `datasets` is a tuple of 3 datasets. Let's split them out.
train, valid, test = datasets
train
valid
test
# Let's peek into one of the datapoints in the `train` dataset.
train.X[0]
# Note that this is a `dc.feat.mol_graphs.ConvMol` object produced by `dc.feat.ConvMolFeaturizer`. We'll say more about how to control choice of featurization shortly. Finally let's take a look at the `transformers` field:
transformers
# So we see that one transformer was applied, the `dc.trans.NormalizationTransformer`.
#
# After reading through this description so far, you may be wondering what choices are made under the hood. As we've briefly mentioned previously, datasets can be processed with different choices of "featurizers". Can we control the choice of featurization here? In addition, how was the source dataset split into train/valid/test as three different datasets?
#
# At present, MoleculeNet has some limited support for allowing users to control the choice of featurizer and dataset. You can use the 'featurizer' and 'split' keyword arguments and pass in different strings. Common possible choices for 'featurizer' are 'ECFP', 'GraphConv', 'Weave' and 'smiles2img' corresponding to the `dc.feat.CircularFingerprint`, `dc.feat.ConvMolFeaturizer`, `dc.feat.WeaveFeaturizer` and `dc.feat.SmilesToImage` featurizers. Common possible choices for 'split' are `None`, 'index', 'random', 'scaffold' and 'stratified' corresponding to no split, `dc.splits.IndexSplitter`, `dc.splits.RandomSplitter`, `dc.splits.SingletaskStratifiedSplitter`. We haven't talked much about splitters yet, but intuitively they're way to partition a dataset based on different criteria. We'll say more in a future tutorial.
#
# This keyword API is a little awkward. It doesn't provide for a convenient way for you to use a custom featurizer/splitter or to specify the transformations you want to apply to the dataset. We're working on ways to refactor this API to make it more friendly. In the meanwhile, let's try out some different keyword arguments to see how they behave in practice.
tasks, datasets, transformers = dc.molnet.load_delaney(featurizer="ECFP", split="scaffold")
(train, valid, test) = datasets
train
train.X[0]
# Note that unlike the earlier invocation we have numpy arrays produced by `dc.feat.CircularFingerprint` instead of `ConvMol` objects produced by `dc.feat.ConvMolFeaturizer`.
#
# Give it a try for yourself. Try invoking MoleculeNet to load some other datasets and experiment with dfiferent featurizer/split options and see what happens!
# # Congratulations! Time to join the Community!
#
# Congratulations on completing this tutorial notebook! If you enjoyed working through the tutorial, and want to continue working with DeepChem, we encourage you to finish the rest of the tutorials in this series. You can also help the DeepChem community in the following ways:
#
# ## Star DeepChem on [GitHub](https://github.com/deepchem/deepchem)
# This helps build awareness of the DeepChem project and the tools for open source drug discovery that we're trying to build.
#
# ## Join the DeepChem Gitter
# The DeepChem [Gitter](https://gitter.im/deepchem/Lobby) hosts a number of scientists, developers, and enthusiasts interested in deep learning for the life sciences. Join the conversation!
|
examples/tutorials/03_An_Introduction_To_MoleculeNet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Robustness curves for binary toy classification problem
# +
import os
os.chdir("../")
import sys
import json
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set(context='paper')
from utils import NumpyEncoder
# -
# ## Plot settings:
# +
SMALL_SIZE = 14
MEDIUM_SIZE = 18
BIGGER_SIZE = 26
plt.rc('font', size=SMALL_SIZE) # controls default text sizes
plt.rc('axes', titlesize=MEDIUM_SIZE) # fontsize of the axes title
plt.rc('axes', labelsize=MEDIUM_SIZE) # fontsize of the x and y labels
plt.rc('xtick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('ytick', labelsize=SMALL_SIZE) # fontsize of the tick labels
plt.rc('legend', fontsize=SMALL_SIZE) # legend fontsize
plt.rc('figure', titlesize=BIGGER_SIZE) # fontsize of the figure title
plt.rc('text', usetex=True)
# dictionary that maps color string to 'good looking' seaborn colors that are easily distinguishable
colors = {
"orange": sns.xkcd_rgb["yellowish orange"],
"red": sns.xkcd_rgb["pale red"],
"green": sns.xkcd_rgb["medium green"],
"blue": sns.xkcd_rgb["denim blue"],
"yellow": sns.xkcd_rgb["amber"],
"purple": sns.xkcd_rgb["dusty purple"],
"cyan": sns.xkcd_rgb["cyan"]
}
# -
# ## Calculate data:
#
# Runtime: < 10 minutes
# +
data_path = 'res/toy_data.npz'
if os.path.exists(data_path):
np_data = np.load(data_path)
points = np_data['points']
labels = np_data['labels']
dists_l1 = np_data['dists_l1']
dists_linf = np_data['dists_linf']
dists_l2 = np_data['dists_l2']
X = np_data['X']
Y = np_data['Y']
probs = np_data['probs']
else:
if not os.path.exists("res"):
os.makedirs("res")
X = np.linspace(-2 * np.pi, 2 * np.pi, 1000)
Y = np.sin(X)
boundary = np.vstack((X, Y))
n = 1000000
r_points = np.random.rand(n, 2)
r_points[:, 0] *= 4 * np.pi
r_points[:, 0] -= 2 * np.pi
r_points[:, 1] *= 4.5
r_points[:, 1] -= 2.25
def min_dist(point, boundary, p):
difs = point.reshape(2, 1) - boundary
distances = np.linalg.norm(difs, axis=0, ord=p)
return np.min(distances)
dists_l2 = np.zeros(n)
for i, p in enumerate(r_points):
dists_l2[i] = min_dist(p, boundary, 2)
chosen = np.all([dists_l2 < 1.001, dists_l2 > 0.999], axis=0)
points = r_points[chosen, :]
dists_l2 = dists_l2[chosen]
labels = np.array([y < np.sin(x) for (x, y) in points])
n_points = np.count_nonzero(chosen)
dists_l1 = np.zeros(n_points)
dists_linf = np.zeros(n_points)
for i, p in enumerate(points):
dists_l1[i] = min_dist(p, boundary, 1)
dists_linf[i] = min_dist(p, boundary, np.inf)
add = [0, 1.1 * np.max(dists_l1)]
dists_l1 = np.append(dists_l1, add)
dists_l2 = np.append(dists_l2, add)
dists_linf = np.append(dists_linf, add)
dists_l1 = np.sort(dists_l1)
dists_linf = np.sort(dists_linf)
dists_l2 = np.sort(dists_l2)
probs = np.linspace(0, 1, n_points + 2)
np.savez(data_path,
points=points,
labels=labels,
dists_l1=dists_l1,
dists_linf=dists_linf,
dists_l2=dists_l2,
probs=probs,
X=X,
Y=Y)
# -
# ## Plot:
# +
save_name = 'fig_rc_synthetic_data'
n_rows = 1
n_cols = 2
fig, axx = plt.subplots(n_rows,
n_cols,
figsize=(12,5))
ax = axx[0]
ax.plot(X, Y, c='black', label="decision boundary")
ax.scatter(points[labels, 0],
points[labels, 1],
c=colors["blue"],
alpha=0.11,
s=5,
label="point with class 0")
ax.scatter(points[np.logical_not(labels), 0],
points[np.logical_not(labels), 1],
c=colors["red"],
alpha=0.11,
s=5,
label="point with class 0")
ax.set_title("data and classifier")
ax.set_xlabel("feature 1")
ax.set_ylabel("feature 2")
ax.legend()
ax = axx
alpha = 1.0
ax[1].plot(dists_linf,
probs,
c=colors["blue"],
alpha=alpha,
label="$\ell_{\infty}$ robustness curve")
ax[1].plot(dists_l2,
probs,
c=colors["red"],
alpha=alpha,
label="$\ell_{2}$ robustness curve")
ax[1].plot(dists_l1,
probs,
c=colors["green"],
alpha=alpha,
label="$\ell_{1}$ robustness curve")
ax[1].set_xlabel("perturbation size $\epsilon$")
ax[1].set_ylabel("test set loss")
ax[1].set_title("robustness curves")
ax[1].legend()
fig.tight_layout()
fig.savefig('res/{}.pdf'.format(save_name))
|
experiments/rob_curves_for_toy_classification_problem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Ebnable HTML/CSS
from IPython.core.display import HTML
HTML("<link href='https://fonts.googleapis.com/css?family=Passion+One' rel='stylesheet' type='text/css'><style>div.attn { font-family: 'Helvetica Neue'; font-size: 30px; line-height: 40px; color: #FFFFFF; text-align: center; margin: 30px 0; border-width: 10px 0; border-style: solid; border-color: #5AAAAA; padding: 30px 0; background-color: #DDDDFF; }hr { border: 0; background-color: #ffffff; border-top: 1px solid black; }hr.major { border-top: 10px solid #5AAA5A; }hr.minor { border: none; background-color: #ffffff; border-top: 5px dotted #CC3333; }div.bubble { width: 65%; padding: 20px; background: #DDDDDD; border-radius: 15px; margin: 0 auto; font-style: italic; color: #f00; }em { color: #AAA; }div.c1{visibility:hidden;margin:0;height:0;}div.note{color:red;}</style>")
# ___
# Enter Team Member Names here (*double click to edit*):
#
# - Name 1:<NAME>
# - Name 2:<NAME>
# - Name 3:<NAME>
# - Name 4:<NAME>
# ___
# # In Class Assignment Four
# In the following assignment you will be asked to fill in python code and derivations for a number of different problems. Please read all instructions carefully and turn in the rendered notebook (or HTML of the rendered notebook) before the end of class (or right after class). The initial portion of this notebook is given before class and the remainder is given during class. Please answer the initial questions before class, to the best of your ability. Once class has started you may rework your answers as a team for the initial part of the assignment.
#
# <a id="top"></a>
# ## Contents
# * <a href="#LoadingKDD">Loading KDDCup Data</a>
# * <a href="#kdd_eval">KDDCup Evaluation and Cross Validation</a>
# * <a href="#data_snooping">More Cross Validation</a>
# * <a href="#stats">Statistical Comparison</a>
#
# **Before coming to class**, please make sure you have the latest version of `scikit-learn`. This notebook was created for version 0.18 and higher.
#
# ________________________________________________________________________________________________________
#
# <a id="LoadingKDD"></a>
# <a href="#top">Back to Top</a>
# ## Loading KDDCup Data
#
# Please run the following code to read in the "KDD Cup" dataset from sklearn's data loading module. It consists of examples of different simulated attacks for the 1998 DARPA Intrusion Detection System (IDS).
#
# This will load the data into the variable `ds`. `ds` is a `bunch` object with fields like `ds.data` and `ds.target`. The field `ds.data` is a numpy matrix of the continuous features in the dataset. **The object is not a pandas dataframe. It is a numpy matrix.** Each row is a set of observed instances, each column is a different feature. It also has a field called `ds.target` that is an integer value we are trying to predict (i.e., a specific integer represents a specific person). Each entry in `ds.target` is a label for each row of the `ds.data` matrix.
# +
# fetch the dataset
from sklearn.datasets import fetch_kddcup99
from sklearn import __version__ as sklearn_version
print('Sklearn Version:',sklearn_version)
ds = fetch_kddcup99(subset='http')
# +
import numpy as np
# get some of the specifics of the dataset
X = ds.data
y = ds.target != b'normal.'
n_samples, n_features = X.shape
n_classes = len(np.unique(y))
print("n_samples: {}".format(n_samples))
print("n_features: {}".format(n_features))
print("n_classes: {}".format(n_classes))
# +
unique, counts = np.unique(y, return_counts=True)
np.asarray((unique, counts)).T
# -
# ___
# **Question 1:** How many instances are in the binary classification problem loaded above? How many instances are in each class? **Plot a pie chart or bar chart of the number of instances in each of the classes.**
# +
from matplotlib import pyplot as plt
# %matplotlib inline
plt.style.use('ggplot')
plt.pie(bi, labels=np.unique(y), startangle=90, autopct='%.1f%%')
plt.show()
#=== Fill in code below========
print('Number of instances in each class:',np.asarray((unique, counts)).T)
# -
# <a id="kdd_eval"></a>
# <a href="#top">Back to Top</a>
# ## KDDCup Evaluation and Cross Validation
# +
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold, ShuffleSplit
from sklearn.model_selection import StratifiedKFold, StratifiedShuffleSplit
from sklearn.metrics import make_scorer, accuracy_score
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn.linear_model import LogisticRegression
# select model
clf = LogisticRegression()
#select cross validation
cv = KFold(n_splits=10)
# select evaluation criteria
my_scorer = make_scorer(accuracy_score)
# run model training and cross validation
per_fold_eval_criteria = cross_val_score(estimator=clf,
X=X,
y=y,
cv=cv,
scoring=my_scorer
)
plt.bar(range(len(per_fold_eval_criteria)),per_fold_eval_criteria)
plt.ylim([min(per_fold_eval_criteria)-0.01,max(per_fold_eval_criteria)])
# -
# ____
# **Question 2** Is the code above a proper separation of training and testing sets for the given dataset (i.e., using KFold)? Why or why not?
#
#
# *Enter your answer here (double click)*
#
# *Yes or No and why*
#
# No
#
# there is two reasons :
# 1- because the data is split into 10 fold without making sure that each fold has the same percantage of the two classes like the orignal one
#
# 2-the classfier should be trained on any 9 fold andtestedon the remaining one fold
#
#
#
#
# ___
# **Question 3:** Is the evaluation metric chosen in the above code appropriate for the dataset (i.e., using accuracy)? Why or Why not?
# *Enter your answer here (double click)*
#
# *Yes or No and why*
#
# No
#
# because the prediction might have a high accuracy with a high variance , so we need to look at the accuracy variance and the biase
#
# ___
# **Exercise 1:** If the code above is not a proper separation of the train or does not use the proper evaluation criteria, fix the code in the block below to use appropriate train/test separation and appropriate evaluation criterion (criteria). **Mark changes in the code with comments.**
# +
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import KFold, ShuffleSplit
from sklearn.model_selection import StratifiedKFold, StratifiedShuffleSplit
from sklearn.metrics import make_scorer, accuracy_score
from sklearn.metrics import precision_score, recall_score, f1_score
from sklearn.linear_model import LogisticRegression
# these imports above might help you
#=====Write your code below here=================
# select model
clf = LogisticRegression()
#select cross validation
#cv = KFold(n_splits=10)
rs=StratifiedShuffleSplit(n_splits=10, random_state=1)
# select evaluation criteria
my_scorer = make_scorer(accuracy_score)
# run model training and cross validation
per_fold_eval_criteria = cross_val_score(estimator=clf,
X=X,
y=y,
cv=rs,
scoring=my_scorer
)
plt.bar(range(len(per_fold_eval_criteria)),per_fold_eval_criteria)
plt.ylim([min(per_fold_eval_criteria)-0.01,max(per_fold_eval_criteria)])
# -
# ____
# **Question 4**: Does the learning algorithm perform well based on the evaluation criteria? Why or why not?
#
# *Enter you answer here (double click to edit)*
#
#
# yes it dose, becasue we presrved the percentage of samples for each class in each folds
#
# <a id="data_snooping"></a>
# <a href="#top">Back to Top</a>
#
# ## More Cross Validation
#
# **Exercise 2:** Does the code below contain any errors in the implementation of the cross validation? If so, fix the code below so that there are no longer any errors in the cross validation.
# there is two erorrs in the code :
# 1- the best practice is to first scale data then do dimensionalty reduction and after that start our learning algrothem
# 2-use StratifiedShuffleSplit to presrved the percentage of samples for each class
# +
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
#======If there are errors, fix them below======
n_components = 1
pca = PCA(n_components=n_components)
Xpca = pca.fit_transform(X)
clf = Pipeline([('scl',StandardScaler()),
('clf',LogisticRegression())])
per_fold_eval_criteria = cross_val_score(estimator=clf,
X=Xpca,
y=y,
cv=cv,
scoring=my_scorer
)
plt.bar(range(len(per_fold_eval_criteria)),per_fold_eval_criteria)
plt.ylim([min(per_fold_eval_criteria)-0.01,max(per_fold_eval_criteria)])
# =====fixed code======
# write the fixed code (if needed) below
clf = Pipeline([('scl',StandardScaler()),
('pca',PCA(n_components=n_components)),
('clf',LogisticRegression())])
per_fold_eval_criteria = cross_val_score(estimator=clf,
X=X,
y=y,
cv=rs,
scoring=my_scorer
)
plt.bar(range(len(per_fold_eval_criteria)),per_fold_eval_criteria)
plt.ylim([min(per_fold_eval_criteria)-0.01,max(per_fold_eval_criteria)])
# -
# ___
#
# # Circumstances Change
# For this question, the circumstances for the DARPA KDD99 cup are changed in the following way:
# - When the model for detecting attacks is deployed, we now think that it will often need to be retrained because new attacks will emerge.
# - DARPA anticipates that there will be a handful of different style attacks on their systems that have never been seen before. To detect these new attacks, they are employing programmers and analysts to find them manually every day.
# - DARPA believes the perpetrators of these new attacks are more sophisticated, so finding the new attacks will take priority over detecting the older, known attacks.
# - DARPA wants to use your learning algorithm for detecting only these new attacks. However, they tell you that the amount of training data for the new attacks will be extremely small. That is, the analysts can only identify a handful of new style attacks each day (so you will only have about 3-5 examples of the attacks for training).
# - **DARPA asks you: Do you think its a good idea to employ retraining your model each day to find these new attacks?** They need an answer in the next 20 minutes.
#
# **Question 5**: How would you change the method of cross validation to answer this question from DARPA? That is, how can you change your cross validation method to better mirror how your system will be used and deployed by DARPA when there are only 3-5 attack examples avaliable for training? *Note: you do not have access to these new training examples. You need to change you cross validation method with the existing data to answer this question.*
# *Enter your answer here (double click)*
#
# *We could... and why*
# ___
#plotting function for use in next question
# takes input 'test_scores', axis labels, and an x-axis label
def plot_filled(test_scores,train_x_axis, xlabel=''):
test_mean = np.percentile(test_scores,50, axis=1)
test_max = np.percentile(test_scores,95, axis=1)
test_min = np.percentile(test_scores,5, axis=1)
plt.plot(train_x_axis, test_mean,
color='blue', linestyle='--',
marker='s', markersize=5,
label='validation set')
plt.fill_between(train_x_axis,
test_min,
test_max,
alpha=0.15, color='blue')
plt.grid(True)
plt.xlabel(xlabel)
plt.ylabel('Evaluation Criterion')
plt.legend(loc='lower right')
plt.tight_layout()
# ___
# DARPA is also concerned about how much training data they will need from the analysts in order to have a high performing model. They would like to use the current dataset to help answer that question. The code below is written for you to help answer DARPA's question about how many examples will be needed for training. Examine the code and the output that is already run for you, then answer the following question:
#
# **Question 6**: Based on the analysis graphed below, how many positive examples are required to have a good tradeoff between bias and variance for the given evaluation criteria? Why? *Note: the x-axis really is a percentage, so the value 0.1 is actually 0.1%.*
# +
clf = LogisticRegression()
test_scores = []
train_sizes=np.linspace(5e-4,5e-3,10)
for size in train_sizes:
cv = StratifiedShuffleSplit(n_splits=100,
train_size = size,
test_size = 1-size,
)
test_scores.append(cross_val_score(estimator=clf,X=X,y=y,cv=cv,scoring=my_scorer))
plot_filled(np.array(test_scores), train_sizes*100, 'Percentage training data (%)')
# -
# ___
# *Enter you answer here (double click)*
#
# It seems that .3% (177 samples) is the best point, because the accuracy is the maxmum at this point and the variance in the lowest
#
# however as showen above after .2% the variance did not change at all, so if we are intrested in minmizing the data size , we can say that .2% is a good size in terms of accuracy since we only got a .002 % increase when going from .2% data size to .3% data size
#
#
#
# ___
# ___
# <a id="stats"></a>
# <a href="#top">Back to Top</a>
#
# # Statistical Comparison
# Now lets create a few different models and see if any of them have statistically better performances.
#
# We are creating three different classifiers below to compare to one another. For creating different training and testing splits, we are using stratified shuffle splits on the datasets.
#
#
# +
clf1 = LogisticRegression(C=100)
clf2 = LogisticRegression(C=1)
clf3 = LogisticRegression(C=0.1)
train_size = 0.003 # small training size
cv = StratifiedShuffleSplit(n_splits=10,train_size=train_size,test_size=1-train_size)
evals1 = cross_val_score(estimator=clf1,X=X,y=y,scoring=my_scorer,cv=cv)
evals2 = cross_val_score(estimator=clf2,X=X,y=y,scoring=my_scorer,cv=cv)
evals3 = cross_val_score(estimator=clf3,X=X,y=y,scoring=my_scorer,cv=cv)
# -
# **Question 7**: Given the code above, what statistical test is more appropriate for selecting confidence intervals, and **why**? Your options are:
# - **A**: approximating the evaluation criterion as a binomial distribution and bounding by the variance (the first option we used in the flipped lecture video)
# - **B**: approximating the bounds using the folds of the cross validation to get mean and variance (the second option we used in the flipped lecture video)
# - **C**: Either are acceptable statistical tests for obtaining confidence intervals
#
# The reason that I think (B) is correct is because the three classifiers are not independent but they all are correlated into each other, since they all using the same data this means that if classifier 1 did slightly better then classifier 2 would do slightly better and same goes to classfier 3
# ___
# **Final Exercise:** With 95% confidence, perform the statistical test that you selected above. Is any model or set of models statistically the best performer(s)? Or can we not say if the models are different with greater than 95% confidence?
#
# If you chose option A, use a multiplier of Z=1.96. The number of instances used in testing can be calculated from the variable `train_size`.
#
# If you chose option B, use a multiplier of t=2.26 and k=10.
# +
#===================================================
# Enter your code below
clf1 = LogisticRegression(C=100, solver='lbfgs')
clf2 = LogisticRegression(C=1, solver='lbfgs')
clf3 = LogisticRegression(C=0.1, solver='lbfgs')
train_size = 0.003 # small training size
cv = StratifiedShuffleSplit(n_splits=10,train_size=train_size,test_size=1-train_size)
evals1 = cross_val_score(estimator=clf1,X=X,y=y,scoring=my_scorer,cv=cv)
evals2 = cross_val_score(estimator=clf2,X=X,y=y,scoring=my_scorer,cv=cv)
evals3 = cross_val_score(estimator=clf3,X=X,y=y,scoring=my_scorer,cv=cv)
test_scores1 = []
test_scores1.append(evals1)
test_scores2 = []
test_scores2.append(evals2)
test_scores3 = []
test_scores3.append(evals3)
e1=1-np.array(test_scores1)
e2=1-np.array(test_scores2)
e3=1-np.array(test_scores3)
var1=np.mean(e1e2)
t=2.26/np.sqrt(10)
# comparing E1 with E2----------------------
e1e2=e1[0]-e2[0]
e1e2_m=np.mean(e1e2)
std12=np.std(e1e2)
conf12=t*std12
print(e1e2_m,conf12)
print('since the mean of the diffrance is positive and no zero crossing this means that classfier 2 is better than classfier 1')
print('')
# comparing E2 with E3-------------------------
e2e3=e2[0]-e3[0]
e2e3_m=np.mean(e2e3)
std23=np.std(e1e2)
conf23=t*std23
print(e2e3_m,conf23)
print('since the mean of the diffrance is negative and no zero crossing this means that classfier 2 is better than classfier 3 ')
print(' ')
print('Model 2 has statistically the best XXX with 95% confidence')
#===================================================
# -
# ________________________________________________________________________________________________________
#
# That's all! Please **save (make sure you saved!!!) and upload your rendered notebook** and please include **team member names** in the notebook submission.
|
ICA/ICA4_MachineLearning (1) (1).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Project 1 - Penguin Dataset
#
# ### About the dataset:
# Please refer to the official [Github](https://github.com/allisonhorst/palmerpenguins/blob/master/README.md) page for details and license information. The details below have also been
# taken from there.
# Artwork: [@allison_horst](https://www.kaggle.com/allison)
#
# ### Summary:
#
# The data folder contains a csv file: penguins_size.csv
# - penguins_size.csv: Simplified data from original penguin data sets.
#
# Contains variables:
# - species: penguin species (Chinstrap, Adélie, or Gentoo)
# - culmen_length_mm: culmen length (mm)
# - culmen_depth_mm: culmen depth (mm)
# - flipper_length_mm: flipper length (mm)
# - body_mass_g: body mass (g)
# - island: island name (Dream, Torgersen, or Biscoe) in the Palmer Archipelago (Antarctica)
# - sex: penguin sex
#
# ### TASK:
#
# To predict the class of Penguin Species
# +
import joblib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from time import time
from sklearn.model_selection import train_test_split
from sklearn.model_selection import learning_curve
from sklearn.datasets import load_digits
from sklearn.model_selection import ShuffleSplit
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score, precision_score, recall_score
import warnings
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings('ignore', category=DeprecationWarning)
##warnings.filterwarnings('ignore', category=UndefinedMetricWarning)
##warnings.filterwarnings('ignore', category=ConvergenceWarning)
# %matplotlib inline
penguins = pd.read_csv('penguins_size.csv')
penguins.head()
# -
penguins.info()
# ## Task 1: To perform a detailed EDA
# 1. Fill in the missing values
# 2. Drop irrelevant/repetetive variables (sex)
# 3. Convert **species** and **island** into numeric variables.
# Fill missing values for **culmen_length_mm, culmen_depth_mm, flipper_length_mm & body_mass_g**
penguins.isnull().sum()
# +
# Fill in the missing values for the following 4 attributes :
penguins['culmen_length_mm'].fillna(penguins['culmen_length_mm'].mean(), inplace=True)
penguins['culmen_depth_mm'].fillna(penguins['culmen_depth_mm'].mean(), inplace=True)
penguins['flipper_length_mm'].fillna(penguins['flipper_length_mm'].mean(), inplace=True)
penguins['body_mass_g'].fillna(penguins['body_mass_g'].mean(), inplace=True)
# -
# Drop unnnecessary variables
penguins.drop(['sex'], axis=1, inplace=True)
# Convert **species** and **island** to numeric variables
# +
species_num = {'Chinstrap' : 0, 'Adelie' : 1, 'Gentoo' : 2}
penguins['species'] = penguins['species'].map(species_num)
island_num = {'Dream' : 0, 'Torgersen' : 1, 'Biscoe' : 2}
penguins['island'] = penguins['island'].map(island_num)
# -
penguins.head()
# +
## Plotting the features
for i, col in enumerate(['island', 'culmen_length_mm', 'culmen_depth_mm', 'flipper_length_mm', 'body_mass_g']):
plt.figure(i)
sns.catplot(x='species', y=col, data=penguins, kind='point', aspect=2,)
# -
# ## Task 2: Split the data into two different ratios (training - validation - test) :-
#
# ### 1. 60-20-20 (Ratio 1)
#
penguins.head(10)
# +
features = penguins.drop('species', axis=1)
labels = penguins['species']
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.4, random_state=42)
X_test, X_val, y_test, y_val = train_test_split(X_test, y_test, test_size=0.5, random_state=42)
# -
for dataset in [y_train, y_val, y_test]:
print(round(len(dataset) / len(labels), 2))
# Write out data
# +
X_train.to_csv('train_features1.csv', index=False)
X_val.to_csv('val_features1.csv', index=False)
X_test.to_csv('test_features1.csv', index=False)
y_train.to_csv('train_labels1.csv', index=False)
y_val.to_csv('val_labels1.csv', index=False)
y_test.to_csv('test_labels1.csv', index=False)
# -
# ### 2. 80-10-10 (Ratio 2)
# +
features = penguins.drop('species', axis=1)
labels = penguins['species']
X_train, X_test, y_train, y_test = train_test_split(features, labels, test_size=0.2, random_state=42)
X_test, X_val, y_test, y_val = train_test_split(X_test, y_test, test_size=0.5, random_state=42)
# -
for dataset in [y_train, y_val, y_test]:
print(round(len(dataset) / len(labels), 2))
# +
X_train.to_csv('train_features2.csv', index=False)
X_val.to_csv('val_features2.csv', index=False)
X_test.to_csv('test_features2.csv', index=False)
y_train.to_csv('train_labels2.csv', index=False)
y_val.to_csv('val_labels2.csv', index=False)
y_test.to_csv('test_labels2.csv', index=False)
# -
# #### Function for plotting Learning Curves
def plot_learning_curve(
estimator,
title,
X,
y,
axes=None,
ylim=None,
cv=None,
n_jobs=None,
train_sizes=np.linspace(0.1, 1.0, 5),
):
if axes is None:
_, axes = plt.subplots(1, 3, figsize=(20, 5))
axes[0].set_title(title)
if ylim is not None:
axes[0].set_ylim(*ylim)
axes[0].set_xlabel("Training examples")
axes[0].set_ylabel("Score")
train_sizes, train_scores, test_scores, fit_times, _ = learning_curve(
estimator,
X,
y,
cv=cv,
n_jobs=n_jobs,
train_sizes=train_sizes,
return_times=True,
)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
fit_times_mean = np.mean(fit_times, axis=1)
fit_times_std = np.std(fit_times, axis=1)
# Plot learning curve
axes[0].grid()
axes[0].fill_between(
train_sizes,
train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std,
alpha=0.1,
color="r",
)
axes[0].fill_between(
train_sizes,
test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std,
alpha=0.1,
color="g",
)
axes[0].plot(
train_sizes, train_scores_mean, "o-", color="r", label="Training score"
)
axes[0].plot(
train_sizes, test_scores_mean, "o-", color="g", label="Cross-validation score"
)
axes[0].legend(loc="best")
# Plot n_samples vs fit_times
axes[1].grid()
axes[1].plot(train_sizes, fit_times_mean, "o-")
axes[1].fill_between(
train_sizes,
fit_times_mean - fit_times_std,
fit_times_mean + fit_times_std,
alpha=0.1,
)
axes[1].set_xlabel("Training examples")
axes[1].set_ylabel("fit_times")
axes[1].set_title("Scalability of the model")
# Plot fit_time vs score
fit_time_argsort = fit_times_mean.argsort()
fit_time_sorted = fit_times_mean[fit_time_argsort]
test_scores_mean_sorted = test_scores_mean[fit_time_argsort]
test_scores_std_sorted = test_scores_std[fit_time_argsort]
axes[2].grid()
axes[2].plot(fit_time_sorted, test_scores_mean_sorted, "o-")
axes[2].fill_between(
fit_time_sorted,
test_scores_mean_sorted - test_scores_std_sorted,
test_scores_mean_sorted + test_scores_std_sorted,
alpha=0.1,
)
axes[2].set_xlabel("fit_times")
axes[2].set_ylabel("Score")
axes[2].set_title("Performance of the model")
return plt
# ## Task 3: Experiment with two different ratios using the following algorithms :-
#
# ### 1. Random Forest Classifier
#
# #### For Ratio 1
rf_features1 = pd.read_csv('train_features1.csv')
rf_labels1 = pd.read_csv('train_labels1.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
rf1 = RandomForestClassifier()
parameters = {
'n_estimators': [5, 50, 250],
'max_depth': [2, 4, 8, 16, None]
}
cv = GridSearchCV(rf1, parameters, cv=5)
cv.fit(rf_features1, rf_labels1.values.ravel())
print_results(cv)
# -
cv.best_estimator_
# Write out the model
joblib.dump(cv.best_estimator_, 'RF_model1.pkl')
# **_Reading out the data for split ratio 1_**
# +
tr_features1 = pd.read_csv('train_features1.csv')
tr_labels1 = pd.read_csv('train_labels1.csv')
val_features1 = pd.read_csv('val_features1.csv')
val_labels1 = pd.read_csv('val_labels1.csv')
te_features1 = pd.read_csv('test_features1.csv')
te_labels1 = pd.read_csv('test_labels1.csv')
# -
# **_Fit the best models on the Training set_**
# +
rfA = RandomForestClassifier(n_estimators=50, max_depth=16)
rfA.fit(tr_features1, tr_labels1.values.ravel())
rfB = RandomForestClassifier(n_estimators=50, max_depth=8)
rfB.fit(tr_features1, tr_labels1.values.ravel())
rfC = RandomForestClassifier(n_estimators=250, max_depth=None)
rfC.fit(tr_features1, tr_labels1.values.ravel())
# -
# **_Evaluate the models on the Validation Set_**
for mdl in [rfA, rfB, rfC]:
y_pred = mdl.predict(val_features1)
accuracy = round(accuracy_score(val_labels1, y_pred), 3)
precision = round(precision_score(val_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels1, y_pred, average="macro"), 3)
print('MAX DEPTH: {} / # OF EST: {} -- A: {} / P: {} / R: {}'.format(mdl.max_depth,
mdl.n_estimators,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = rfA.predict(te_features1)
accuracy = round(accuracy_score(te_labels1, y_pred), 3)
precision = round(precision_score(te_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels1, y_pred, average="macro"), 3)
print('MAX DEPTH: {} / # OF EST: {} -- A: {} / P: {} / R: {}'.format(rfA.max_depth,
rfA.n_estimators,
accuracy,
precision,
recall))
# #### For ratio 2
rf_features2 = pd.read_csv('train_features2.csv')
rf_labels2 = pd.read_csv('train_labels2.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
rf2 = RandomForestClassifier()
parameters = {
'n_estimators': [5, 50, 250],
'max_depth': [2, 4, 8, 16, 32, None]
}
cv = GridSearchCV(rf2, parameters, cv=5)
cv.fit(rf_features2, rf_labels2.values.ravel())
print_results(cv)
# -
cv.best_estimator_
# Write out the model
joblib.dump(cv.best_estimator_, 'RF_model2.pkl')
# **_Read out data for split ratio 2_**
# +
tr_features2 = pd.read_csv('train_features2.csv')
tr_labels2 = pd.read_csv('train_labels2.csv')
val_features2 = pd.read_csv('val_features2.csv')
val_labels2 = pd.read_csv('val_labels2.csv')
te_features2 = pd.read_csv('test_features2.csv')
te_labels2 = pd.read_csv('test_labels2.csv')
# -
# **_Fit the best models on the Training set_**
# +
rfA = RandomForestClassifier(n_estimators=5, max_depth=None)
rfA.fit(tr_features2, tr_labels2.values.ravel())
rfB = RandomForestClassifier(n_estimators=50, max_depth=8)
rfB.fit(tr_features2, tr_labels2.values.ravel())
rfC = RandomForestClassifier(n_estimators=250, max_depth=16)
rfC.fit(tr_features2, tr_labels2.values.ravel())
# -
# **_Evaluate the results on the Validation Set_**
for mdl in [rfA, rfB, rfC]:
y_pred = mdl.predict(val_features2)
accuracy = round(accuracy_score(val_labels2, y_pred), 3)
precision = round(precision_score(val_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels2, y_pred, average="macro"), 3)
print('MAX DEPTH: {} / # OF EST: {} -- A: {} / P: {} / R: {}'.format(mdl.max_depth,
mdl.n_estimators,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = rfC.predict(te_features2)
accuracy = round(accuracy_score(te_labels2, y_pred), 3)
precision = round(precision_score(te_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels2, y_pred, average="macro"), 3)
print('MAX DEPTH: {} / # OF EST: {} -- A: {} / P: {} / R: {}'.format(rfC.max_depth,
rfC.n_estimators,
accuracy,
precision,
recall))
# **_Sketching the learning curves for Random Forest_**
# +
fig, axes = plt.subplots(3, 2, figsize=(10, 15))
X, y = load_digits(return_X_y=True)
title = "Learning Curves (Ratio 1: Random Forest)"
# Cross validation with 50 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=50, test_size=0.2, random_state=0)
estimator = RandomForestClassifier()
plot_learning_curve(
estimator, title, tr_features1, tr_labels1.values.ravel(), axes=axes[:, 0], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
title = "Learning Curves (Ratio 2: Random Forest)"
# Cross validation with 50 iterations to get smoother mean test and train
# score curves, each time with 10% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=50, test_size=0.1, random_state=0)
estimator = RandomForestClassifier()
plot_learning_curve(
estimator, title, tr_features2, tr_labels2.values.ravel(), axes=axes[:, 1], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
plt.show()
# -
# ### 2. Support Vector Machines (SVM)
# #### For Ratio 1
svm_features1 = pd.read_csv('train_features1.csv')
svm_labels1 = pd.read_csv('train_labels1.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
svc = SVC()
parameters = {
'kernel': ['linear', 'rbf'],
'C': [0.1, 1, 10]
}
cv = GridSearchCV(svc, parameters, cv=5)
cv.fit(svm_features1, svm_labels1.values.ravel())
print_results(cv)
# -
cv.best_estimator_
joblib.dump(cv.best_estimator_, 'SVM_model1.pkl')
# **_Read out data for split ratio 1_**
# +
tr_features1 = pd.read_csv('train_features1.csv')
tr_labels1 = pd.read_csv('train_labels1.csv')
val_features1 = pd.read_csv('val_features1.csv')
val_labels1 = pd.read_csv('val_labels1.csv')
te_features1 = pd.read_csv('test_features1.csv')
te_labels1 = pd.read_csv('test_labels1.csv')
# -
# **_Fit the best models on the Training set_**
# +
svmA = SVC(kernel='linear', C=0.1)
svmA.fit(tr_features1, tr_labels1.values.ravel())
svmB = SVC(kernel='linear', C=10)
svmB.fit(tr_features1, tr_labels1.values.ravel())
svmC = SVC(kernel='rbf', C=1)
svmC.fit(tr_features1, tr_labels1.values.ravel())
# -
# **_Evaluate the results on the Validation Set_**
for mdl in [svmA, svmB, svmC]:
y_pred = mdl.predict(val_features1)
accuracy = round(accuracy_score(val_labels1, y_pred), 3)
precision = round(precision_score(val_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels1, y_pred, average="macro"), 3)
print('Kernel: {} / C: {} -- A: {} / P: {} / R: {}'.format(mdl.kernel,
mdl.C,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = svmB.predict(te_features1)
accuracy = round(accuracy_score(te_labels1, y_pred), 3)
precision = round(precision_score(te_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels1, y_pred, average="macro"), 3)
print('Kernel: {} / C: {} -- A: {} / P: {} / R: {}'.format(svmB.kernel,
svmB.C,
accuracy,
precision,
recall))
# #### For Ratio 2
svm_features2 = pd.read_csv('train_features2.csv')
svm_labels2 = pd.read_csv('train_labels2.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
svc2 = SVC()
parameters = {
'kernel': ['linear', 'rbf'],
'C': [0.1, 1, 10]
}
cv = GridSearchCV(svc2, parameters, cv=5)
cv.fit(svm_features2, svm_labels2.values.ravel())
print_results(cv)
# -
cv.best_estimator_
joblib.dump(cv.best_estimator_, 'SVM_model2.pkl')
# **_Read out data for split ratio 2_**
# +
tr_features2 = pd.read_csv('train_features2.csv')
tr_labels2 = pd.read_csv('train_labels2.csv')
val_features2 = pd.read_csv('val_features2.csv')
val_labels2 = pd.read_csv('val_labels2.csv')
te_features2 = pd.read_csv('test_features2.csv')
te_labels2 = pd.read_csv('test_labels2.csv')
# -
# **_Fit the best models on the Training set_**
# +
svmA = SVC(kernel='linear', C=0.1)
svmA.fit(tr_features2, tr_labels2.values.ravel())
svmB = SVC(kernel='linear', C=1)
svmB.fit(tr_features2, tr_labels2.values.ravel())
svmC = SVC(kernel='linear', C=10)
svmC.fit(tr_features2, tr_labels2.values.ravel())
# -
# **_Evaluate the results on the Validation Set_**
for mdl in [svmA, svmB, svmC]:
y_pred = mdl.predict(val_features2)
accuracy = round(accuracy_score(val_labels2, y_pred), 3)
precision = round(precision_score(val_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels2, y_pred, average="macro"), 3)
print('Kernel: {} / C: {} -- A: {} / P: {} / R: {}'.format(mdl.kernel,
mdl.C,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = svmC.predict(te_features2)
accuracy = round(accuracy_score(te_labels2, y_pred), 3)
precision = round(precision_score(te_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels2, y_pred, average="macro"), 3)
print('Kernel: {} / C: {} -- A: {} / P: {} / R: {}'.format(svmC.kernel,
svmC.C,
accuracy,
precision,
recall))
# **_Sketching the Learning Curves for Support Vector Machines_**
# +
fig, axes = plt.subplots(3, 2, figsize=(10, 15))
X, y = load_digits(return_X_y=True)
title = "Learning Curves (Ratio 1: SVM)"
# Cross validation with 50 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=50, test_size=0.2, random_state=0)
estimator = SVC()
plot_learning_curve(
estimator, title, tr_features1, tr_labels1.values.ravel(), axes=axes[:, 0], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
title = r"Learning Curves (Ratio 2: SVM)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=50, test_size=0.1, random_state=0)
estimator = SVC()
plot_learning_curve(
estimator, title, tr_features2, tr_labels2.values.ravel(), axes=axes[:, 1], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
plt.show()
# -
# ### 3. Logistic Regression
# #### For Ratio 1
lr_features1 = pd.read_csv('train_features1.csv')
lr_labels1 = pd.read_csv('train_labels1.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
lr1 = LogisticRegression()
parameters = {
'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]
}
cv = GridSearchCV(lr1, parameters, cv=5)
cv.fit(lr_features1, lr_labels1.values.ravel())
print_results(cv)
# -
cv.best_estimator_
joblib.dump(cv.best_estimator_, 'LR_model1.pkl')
# **_Read out data for split ratio 1_**
# +
tr_features1 = pd.read_csv('train_features1.csv')
tr_labels1 = pd.read_csv('train_labels1.csv')
val_features1 = pd.read_csv('val_features1.csv')
val_labels1 = pd.read_csv('val_labels1.csv')
te_features1 = pd.read_csv('test_features1.csv')
te_labels1 = pd.read_csv('test_labels1.csv')
# -
# **_Fit the best models on the Training set_**
# +
lrA = LogisticRegression(C=0.01)
lrA.fit(tr_features1, tr_labels1.values.ravel())
lrB = LogisticRegression(C=0.1)
lrB.fit(tr_features1, tr_labels1.values.ravel())
lrC = LogisticRegression(C=100)
lrC.fit(tr_features1, tr_labels1.values.ravel())
# -
# **_Evaluate the results on the Validation Set_**
for mdl in [lrA, lrB, lrC]:
y_pred = mdl.predict(val_features1)
accuracy = round(accuracy_score(val_labels1, y_pred), 3)
precision = round(precision_score(val_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels1, y_pred, average="macro"), 3)
print('C: {} -- A: {} / P: {} / R: {}'.format(mdl.C,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = lrB.predict(te_features1)
accuracy = round(accuracy_score(te_labels1, y_pred), 3)
precision = round(precision_score(te_labels1, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels1, y_pred, average="macro"), 3)
print('C: {} -- A: {} / P: {} / R: {}'.format(lrB.C,
accuracy,
precision,
recall))
# #### For Ratio 2
lr_features2 = pd.read_csv('train_features2.csv')
lr_labels2 = pd.read_csv('train_labels2.csv')
# **_Hyperparameter Tuning_**
def print_results(results):
print('BEST PARAMS: {}\n'.format(results.best_params_))
means = results.cv_results_['mean_test_score']
stds = results.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, results.cv_results_['params']):
print('{} (+/-{}) for {}'.format(round(mean, 3), round(std * 2, 3), params))
# +
lr2 = LogisticRegression()
parameters = {
'C': [0.001, 0.01, 0.1, 1, 10, 100, 1000]
}
cv = GridSearchCV(lr2, parameters, cv=5)
cv.fit(lr_features2, lr_labels2.values.ravel())
print_results(cv)
# -
cv.best_estimator_
joblib.dump(cv.best_estimator_, 'LR_model2.pkl')
# **_Read out data for Split ratio 2_**
# +
tr_features2 = pd.read_csv('train_features2.csv')
tr_labels2 = pd.read_csv('train_labels2.csv')
val_features2 = pd.read_csv('val_features2.csv')
val_labels2 = pd.read_csv('val_labels2.csv')
te_features2 = pd.read_csv('test_features2.csv')
te_labels2 = pd.read_csv('test_labels2.csv')
# -
# **_Fit the best models on the Training set_**
# +
lrA = LogisticRegression(C=0.01)
lrA.fit(tr_features2, tr_labels2.values.ravel())
lrB = LogisticRegression(C=10)
lrB.fit(tr_features2, tr_labels2.values.ravel())
lrC = LogisticRegression(C=1000)
lrC.fit(tr_features2, tr_labels2.values.ravel())
# -
# **_Evaluate the results on the Validation Set_**
for mdl in [lrA, lrB, lrC]:
y_pred = mdl.predict(val_features2)
accuracy = round(accuracy_score(val_labels2, y_pred), 3)
precision = round(precision_score(val_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(val_labels2, y_pred, average="macro"), 3)
print('C: {} -- A: {} / P: {} / R: {}'.format(mdl.C,
accuracy,
precision,
recall))
# **_Evaluating the best model on the Test set_**
y_pred = lrC.predict(te_features2)
accuracy = round(accuracy_score(te_labels2, y_pred), 3)
precision = round(precision_score(te_labels2, y_pred, average="macro"), 3)
recall = round(recall_score(te_labels2, y_pred, average="macro"), 3)
print('C: {} : -- A: {} / P: {} / R: {}'.format(lrC.C,
accuracy,
precision,
recall))
# **_Sketching the Learning Curves for Logistic Regression_**
# +
fig, axes = plt.subplots(3, 2, figsize=(10, 15))
X, y = load_digits(return_X_y=True)
title = "Learning Curves (Ratio 1: Logistic Regression)"
# Cross validation with 50 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=50, test_size=0.2, random_state=0)
estimator = LogisticRegression()
plot_learning_curve(
estimator, title, tr_features1, tr_labels1.values.ravel(), axes=axes[:, 0], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
title = r"Learning Curves (Ratio 2: Logistic Regression)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=50, test_size=0.1, random_state=0)
estimator = LogisticRegression()
plot_learning_curve(
estimator, title, tr_features2, tr_labels2.values.ravel(), axes=axes[:, 1], ylim=(0.7, 1.01), cv=cv, n_jobs=4
)
plt.show()
# -
# ## Task 4: Model Comparison
#
# #### For Ratio 1
# +
val_features = pd.read_csv('val_features1.csv')
val_labels = pd.read_csv('val_labels1.csv')
te_features = pd.read_csv('test_features1.csv')
te_labels = pd.read_csv('test_labels1.csv')
# +
models = {}
for mdl in ['RF', 'SVM', 'LR']:
models[mdl] = joblib.load('{}_model1.pkl'.format(mdl))
# -
models
# **_Evaluate the models on the Validation Set_**
def evaluate_model(name, model, features, labels):
start = time()
pred = model.predict(features)
end = time()
accuracy = round(accuracy_score(labels, pred), 3)
precision = round(precision_score(labels, pred, average="macro"), 3)
recall = round(recall_score(labels, pred, average="macro"), 3)
print('{} -- Accuracy: {} / Precision: {} / Recall: {} / Latency: {}ms'.format(name,
accuracy,
precision,
recall,
round((end - start)*1000, 1)))
for name, mdl in models.items():
evaluate_model(name, mdl, val_features, val_labels)
# Since the LR model has the least latency on this split ratio, we can say that **LR is the best model**.
# **_Evaluating the best model on the Test set_**
evaluate_model('Logistic Regression', models['LR'], te_features, te_labels)
# #### For Ratio 2
# +
val_features = pd.read_csv('val_features2.csv')
val_labels = pd.read_csv('val_labels2.csv')
te_features = pd.read_csv('test_features2.csv')
te_labels = pd.read_csv('test_labels2.csv')
# +
models = {}
for mdl in ['RF', 'SVM', 'LR']:
models[mdl] = joblib.load('{}_model2.pkl'.format(mdl))
# -
models
# **_Evaluate the models on the Validation Set_**
def evaluate_model(name, model, features, labels):
start = time()
pred = model.predict(features)
end = time()
accuracy = round(accuracy_score(labels, pred), 3)
precision = round(precision_score(labels, pred, average="macro"), 3)
recall = round(recall_score(labels, pred, average="macro"), 3)
print('{} -- Accuracy: {} / Precision: {} / Recall: {} / Latency: {}ms'.format(name,
accuracy,
precision,
recall,
round((end - start)*1000, 1)))
for name, mdl in models.items():
evaluate_model(name, mdl, val_features, val_labels)
# Since the LR model has the least latency on this split ratio, we can say that **LR is the best model**. Even though the accuracy, precision and recall values of the RF model are the highest, the LR model has got the lowest latency.
# **_Evaluating the best model on the Test set_**
evaluate_model('Logistic Regression', models['LR'], te_features, te_labels)
# ## Task 5: Determine the better Split ratio
# After evaluating the best model on the test set for both the split ratios, we can see that the best model on split ratio 1 ($60-20-20$) has lesser latency than the best model on split ratio 2 ($80-10-10$).
# Hence, the split ratio 1 is better than split ratio 2.
|
project1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import functions as fn
import pickle
# ## Load Data into Data Frame and Save it
# #### EXECUTED JUST ONCE AT THE BEGINNING
df = fn.create_dataframe()
df = df.drop_duplicates(subset='url')
# This function below saves the dataframe we have created into one csv file, so that we can just import it instead of recreating it every time.
df.to_csv(r'./data.csv', index = False)
# #### READ ONLY THE COLUMNS THAT WE NEED IN THE DATAFRAME CREATED
df = pd.read_csv("./data.csv") #to read
df
# #### Before starting we want to define some useful functions that we will use to save dictionaries into pickle files and load them back every time we might need them
# +
#Useful functions to save and load files in pickle format
def save_dict(obj, name ):
with open(f'{name}.pickle', 'wb') as f:
pickle.dump(obj, f)
def load_obj(name ):
with open(f'{name}.pickle', 'rb') as f:
return pickle.load(f)
# -
# # Q2. Search Engine
# ## 2.1. Conjunctive query
# In this firts version of the search engine we just want to evaluate conjuctive queries (AND) with respect of only the **plot** of the books
# ### Examine Null Values
df['plot'].isnull().sum()
# #### substitute nulla values in the plot with a string
df['plot'].fillna('unknown',inplace = True)
df['plot'].isnull().sum()
# The first thing to do, when building a search engine is creating a **vocabulary**. We will first look at all the unique words into the plot of each book and create a list of them, then, from this list, we will map each word to an integer, that we will call **term_id** and will be useful in the future creation of the **inverted index**.
# #### The next two cells were runned just one time at the beginning
dictionary = fn.build_dictionary(df)
save_dict(dictionary,'vocabulary') #to save
# #### Everytime that we restart the kernel we just need to load the file that we have already created, using the command below:
dictionary = load_obj('vocabulary') #to load
# Now, before calculating the inverted index we will determine, for each document, the frequency of each word in the document:
frequency_of_words = fn.frequency_of_words_per_book(df,dictionary)
# We now have all the tools needed to create our first **inverted index**: we will run the cell below just one time and store the inverted index in a pickle file so that we can recall it every time we need it.
# #### The next two cells were runned just one time at the beginning
inverted_index_1 = fn.inverted_index1(df,dictionary,frequency_of_words)
save_dict(inverted_index_1,'inverted_index_1') #to save
# #### Everytime that we restart the kernel we just need to load the file that we have already created, using the command below:
inverted_index_1 = load_obj('inverted_index_1') #to load
# Let's now give in input a query:
query = input()
# We have to pre-process the query as well if we want to recall it inside our inverted index
query = fn.query_processed(query)
query
# ### SEARCH ENGINE 1
# Now we have **everything** so we can implement our very first **search engine**
output = fn.search_engine1(query,df,inverted_index_1,dictionary)
output[['bookTitle','plot','url']].head(10)
# ## 2.2 Conjunctive query & Ranking score
# ### For the second search engine, given a query, we want to get the top-k documents related to the query. In particular:
# - Find all the documents that contains all the words in the query.
# - Sort them by their similarity with the query
# - Return in output k documents, or all the documents with non-zero similarity with the query when the results are less than k.
df = df[['bookTitle','plot','url']]
df
df.isnull().sum()
# To answer this question we first need to define the concepts of **TF-IDF score** and **cosine similarity**.
#
# **TF-IDF** stands for **Term Frequency-Inverse Document Frequency**. This tecnique is used to quantify the words inside a document by giving a weigth to each word in proportion with its importance.
#
# So, this score is given by two main components:
# - *Term Frequency*: that measures the frequency of a word in a document. It is given by: $\textrm{tf}(t,d)=\frac{\textrm{count of t in d}}{\textrm{number of words in d}}$
#
#
# - *Document Frequency*: it measures the importance of the document by counting the number of documents is which a certain word is present (at least one time):
# $\textrm{df}(t) = \textrm{occurrence of t in documents}$
#
# But we actually need the *Inverse Document Frequency*:
# it measures the informativeness of the term t in the document. IDF will be small if the occurence of the words is very big and viceversa:
# $\textrm{idf}(t) = \frac{N}{\textrm{df}}$
#
# There may be some problems with $IDF$, in particular in the cases where the corpus is really large, so in this case it may be convenient to take the log of it.
# Also, if a word that is not in the pre-determined vocabolary occurs, its df will be equal to $0$, but then we would have a division with 0 at the denominator, which, of course, is going to lead to an error. To solve this issue we are just going to add a 1 to the denominator. So, the final formula is: $\textrm{idf}(t) = \textrm{log}(\frac{N}{\textrm{df}+1})$
#
# Finally, the TD-IDF score is defined by:
#
# $\textrm{tf}-\textrm{idf}(t,d) = \textrm{tf}(t,d)*\textrm{log}(\frac{N}{\textrm{df}+1})$
#
# ## Step 1: calculate TF-IDF score
# #### The next four cells were runned just one time at the beginning
tf_score = fn.tf(df,dictionary,frequency_of_words)
idf_score = fn.idf(df,dictionary,frequency_of_words)
tf_idf_scores = fn.tf_idf_score(df,dictionary,tf_score,idf_score)
save_dict(tf_idf_scores,'tf_idf_scores') #to save
# #### Everytime that we restart the kernel we just need to load the file that we have already created, using the command below:
tf_idf_scores = load_obj('tf_idf_scores') #to load
# ## Step 2: from list of words calculate inverted index
# #### The next two cells were runned just one time at the beginning
inverted_index_2 = fn.inverted_index2(df,dictionary,tf_idf_scores,frequency_of_words)
save_dict(inverted_index_2,'inverted_index_2') #to save
# #### Everytime that we restart the kernel we just need to load the file that we have already created, using the command below:
inverted_index_2 = load_obj('inverted_index_2') #to load
# ## Step 3: calculate cosine similarity
# Let's now talk about **cosine similarity**:
# this is just a metric used to measure how similar the documents regardless their size. Geometrically speaking this consists of measuring the cosine of the angle between two vectors (where the vector corresponds to a word in the document). The formula to use is the following: $\textrm{cos}(\hat{\theta}) = \textrm{cos}(\vec{x},\vec{y}) = \frac{\vec{x}\cdot\vec{y}}{||\vec{x}||\cdot||\vec{y}||}=\frac{\sum_{i=1}^{m} x_i\cdot y_i}{||\vec{x}||\cdot||\vec{y}||}$
#
#
#
# In our specific case the final formula will be the following:
# $\textrm{score} (\vec{q},\vec{d_i}) = \frac{1}{||\vec{q}||}\cdot \frac{1}{||\vec{d_i}||} \cdot \sum_{j=1}^{m} \vec{q_j}\vec{d_j^i}$
#
#
# <p> </p>
# First, we need in input a query from the user:
query2 = input()
# Then, we want to pre-process the query so that it can be found in the inverted index
query2 = fn.query_processed(query2)
query2
# Now we can calculate the cosine similarity score:
cosine_similarity_score = fn.cosine_similarity(query2,df,tf_idf_scores)
# ### SEARCH ENGINE 2
# Finally, we can look at the output we want, sorted in decreasing order based on the book's cosine similarity score:
output2 = fn.search_engine2(df,query2,inverted_index_1,dictionary,cosine_similarity_score)
output2
# # Q3: Define a new score!
# **for this part the aim is to define a new score metrics different from other score metrics, such as cosine-similarity. This metric has to take into account other variables which are in the provided dataset as a result of the parsing. For this purpose has been defined a new metric called user_score: the user score is substantially a weighted average of 4 different scores: the cosine similarity, the rate_score,the lenght_score and the date_release score. The weight of these scores are choosen directly from users, who can give a vote from 0 to 5 which represents the importance of that feature in their search**
# **rate_score**
#
# the rate_score gives a measure which encompasses both the number of rates (e.g 549,545,666) and the rate value (e.g 4.5/5). the formula to compute it is the following:
#
# $\sum_{i=0}^{m} \frac{ratevalue_{doc_i}\log(1+ratenumber_{doc_i})}{maxratevalue_{docs}\log(1.00000001+maxratenumber_{docs})}$
#
# where
# 1. m=number of documents which contains the query
# 2. doc_i= specific document
# 3. docs= set of documents found by the query
# 4. ratevalue= integer value between [0,5]
# 5. ratenumber= number of rates for each document
# 6. maxratevalue= max rate value among the documents found
# 7. maxratenumber= max rate number among the documents found
#
# this score is included betwenn [0,1]
# it is 1 when the document found by the search engine is both the document with more ratings and with the best vote (rate value). it is 0 when the documents has no ratings or has a vote that is 0.
#
# it has been added a constant of 0.00000001 in the denominator in order to avoid a zero division error.
#
# rate score provides a measure both of the popularity of the book and of the users appreciation of the book.
# **lenght_score**
#
# $ lenghtscore= (\sum_{i=0}^{m1} 1-(k x_i)$ where k= 1/m1 and where m1 is (m-na number)) if $x_i\neq x_{i-1}$
#
# $lenghtscore_{i}= lenghtscore_{i-1}$ if $x_{i}=x_{i-1}$
#
# $lenghtscore_{i}$= 0 if $x_{i}=na$
#
# the lenght score, given a number of pages in input by the user, aims to find what are the books closer to this specific user request. This score is a positional score: the score to a book is given taking into account the ranking of books ordered in ascending order by absolute value of number of pages difference. However this metric, even if the number of pages between books differs, will give a score of 1 if the book has the minimum difference among all. the score of 0 is assigned for books which don't provide the number of pages value in the dataset.
# the score is diminished each time by a coefficient proportional to the ranking number and the inverse of the lenght of books considered.
# **date_release_score**
#
# DRS= ($\sum_{i=0}^{m1} 1-(k x_i)$ where k= 1/m1 and where m1 is (m-na number)) if $x_i\neq x_{i-1}$
#
#
# $DRS_{i}$= $DRS_{i-1}$ if $x_{i}=x_{i-1}$
#
#
# $DRS_{i}$= 0 if $x_{i}=na$
#
# the date release score has the same mechanism of the lenght score but, instead of taking into account the book pages, deals with the year of pubblication of the book. As in lenght score the user will give in input a desired year for the book searched and the score will be maximixed for the books most closer in time to user request.
# *in the following cells the user gives in input the desired number of pages and the desired year of pubblication*
desired_lenght=int(input("please insert the desired lenght for your new book giving the number of pages\n").strip())
desired_year=int(input("please insert the desired year for your new book in the format xxxx\n").strip())
# +
cosine_similarity=fn.cosine_similarity(query,output,tf_idf_scores)
rate_score=fn.rating_score(output)
book_lenght_score=fn.lenght_score(output,desired_lenght)
publish_date_score=fn.publish_score(output,desired_year)
# -
# **in this section the user has to provide his preferences about the importance of the parameters for his research**
# +
print("you are asked to tell us how much important is for you the number of pages of the book\n")
k_pages=fn.input_vote()
# +
print("you are asked to tell us how much important is for you the year of pubblication of the book\n")
k_date=fn.input_vote()
# +
print("you are asked to tell us how much important is for you the similarity of your description with the plot of the book\n")
k_cosine=fn.input_vote()
# +
print("you are asked to tell us how much is important for you the popularity and the users vote for your searched book\n")
k_rate=fn.input_vote()
# -
k_list=[k_pages,k_date,k_cosine,k_rate]
fn.similarity_score(output,cosine_similarity,rate_score,book_lenght_score,publish_date_score,k_list)
# # Q4: Make a nice visualization
# #### Import only the columns of the Dataset useful for this part
df = pd.read_csv("./data.csv", usecols= ['bookTitle','bookSeries','numberOfPages','published','url'])
# #### Remove rows of books that don't belong to a series
df = df.drop(df[df['bookSeries'].isnull()].index)
df = df.reset_index()
df
# #### Create two new columns
# These columns were created starting from the BookSeries Column and by splitting it in two:
# - the name of the serie
# - the number of the book in the serie
df = fn.split_series_and_book_series(df)
# Now we want to determine which are the first 10 series in order of appearence that we want to analyze
series_to_analyze = fn.series_to_analyze(df)
series_to_analyze
# #### Create a new dataframe in which there are only the rows corresponding to the series that we want to analyze
df1 = fn.create_new_dataframe(df,series_to_analyze)
df1.head(10)
# Here we want to convert the column *published* into a datetime object so that we can later compare the years of publishment of the different books in the serie
df1['published'] = pd.to_datetime(df1['published'])
df1.info()
# #### We have everything that we need to create the plots
# We are going to create **10 different plots**: one for each book series we want to analyze. These plots will have on:
# - the **x axis**: the years that have passed since the first publication of the first book in the serie (considering year 0 the year of publication of book1)
# - the **y axis**: the cumulative page count of the books in the series
fn.plot_series(series_to_analyze,df1)
|
HW3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import VotingClassifier
import warnings
warnings.filterwarnings('ignore')
# -
# # Bagging Classifier with Titanic Dataset
#load already pre-processed titanic trianing dataset
X = np.load("tatanic_X_train.npy")
y = np.load("tatanic_y_train.npy")
X[0]
y[:10]
# +
from sklearn.ensemble import BaggingClassifier
clf2 = DecisionTreeClassifier(random_state=1)
eclf = BaggingClassifier(clf2, oob_score=True)
# +
from sklearn.model_selection import cross_val_score
cross_val_score(eclf, X, y, cv=5).mean()
# -
params = {
"n_estimators": [10, 20, 30, 40, 50, 55, 100],
"max_samples": [0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1]
}
# +
from sklearn.model_selection import GridSearchCV
grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
grid = grid.fit(X, y)
# -
grid.best_score_
grid.best_params_
# ## Random Forest
# +
from sklearn.ensemble import RandomForestClassifier
eclf = RandomForestClassifier(n_estimators=100, max_features=int(len(X[0])/3), n_jobs=7, oob_score=True)
# -
cross_val_score(eclf, X, y, cv=5).mean()
# +
params = {
"n_estimators": [10, 20, 30, 40, 50, 55, 100],
"max_features": [1,2,3,4,5,6,7, 10, 15, 20, 25]
}
grid = GridSearchCV(estimator=eclf, param_grid=params, cv=5)
grid = grid.fit(X, y)
# -
grid.best_score_
grid.best_params_
|
ensemble/bagging_random_forest.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc="true"
# # Table of Contents
# <p><div class="lev1 toc-item"><a href="#Clip" data-toc-modified-id="Clip-1"><span class="toc-item-num">1 </span>Clip</a></div><div class="lev2 toc-item"><a href="#Exemplos" data-toc-modified-id="Exemplos-11"><span class="toc-item-num">1.1 </span>Exemplos</a></div><div class="lev2 toc-item"><a href="#Exemplo-com-ponto-flutuante" data-toc-modified-id="Exemplo-com-ponto-flutuante-12"><span class="toc-item-num">1.2 </span>Exemplo com ponto flutuante</a></div><div class="lev1 toc-item"><a href="#Documentação-Oficial-Numpy" data-toc-modified-id="Documentação-Oficial-Numpy-2"><span class="toc-item-num">2 </span>Documentação Oficial Numpy</a></div>
# -
# # Clip
#
# A função clip substitui os valores de um array que estejam abaixo de um limiar mínimo ou que estejam acima de um limiar máximo, por esses limiares mínimo e máximo, respectivamente. Esta função é especialmente útil em processamento de imagens para evitar que os índices ultrapassem os limites das imagens.
#
# ## Exemplos
# +
import numpy as np
a = np.array([11,1,2,3,4,5,12,-3,-4,7,4])
print('a = ',a)
print('np.clip(a,0,10) = ', np.clip(a,0,10))
# -
# ## Exemplo com ponto flutuante
#
# Observe que se os parâmetros do clip estiverem em ponto flutuante, o resultado também será em ponto flutuante:
a = np.arange(10).astype(np.int)
print('a=',a)
print('np.clip(a,2.5,7.5)=',np.clip(a,2.5,7.5))
# # Documentação Oficial Numpy
#
# - [clip](http://docs.scipy.org/doc/numpy/reference/generated/numpy.clip.html)
|
master/tutorial_numpy_1_10.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "subslide"}
# # 16 - Recurrent Neural Netwoks and LSTM
#
# by [<NAME>](albahnsen.com/) and [<NAME>](https://github.com/jesugome)
#
# version 1.6, June 2020
#
#
# ## Part of the class [AdvancedMethodsDataAnalysisClass](https://github.com/albahnsen/AdvancedMethodsDataAnalysisClass/tree/master/notebooks)
#
#
#
# This notebook is licensed under a [Creative Commons Attribution-ShareAlike 3.0 Unported License](http://creativecommons.org/licenses/by-sa/3.0/deed.en_US).
# -
# ## Recurrent Neuural Network (RNN)
# Being human, when we watch a movie, we don’t think from scratch every time while understanding any event. We rely on the recent experiences happening in the movie and learn from them. But, a conventional neural network is unable to learn from the previous events because the information does not pass from one step to the next. On contrary, RNN learns information from immediate previous step.
#
# For example, there is a scene in a movie where a person is in a basketball court. We will improvise the basketball activities in the future frames: an image of someone running and jumping probably be labeled as playing basketball, and an image of someone sitting and watching is probably a spectator watching the game.
#
#
# <img src="https://raw.githubusercontent.com/albahnsen/AppliedDeepLearningClass/master/notebooks/images/RNN-rolled.png" width="20%" height="20%">
#
# A typical RNN (Source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
# <img src="https://raw.githubusercontent.com/albahnsen/AppliedDeepLearningClass/master/notebooks/images/RNN-unrolled.png" >
#
# A typical RNN looks like above-where X(t) is input, h(t) is output and A is the neural network which gains information from the previous step in a loop. The output of one unit goes into the next one and the information is passed.
#
# But, sometimes we don’t need our network to learn only from immediate past information. Suppose we want to predict the blank word in the text ‘ David, a 36-year old man lives in San Francisco. He has a female friend Maria. Maria works as a cook in a famous restaurant in New York whom he met recently in a school alumni meet. Maria told him that she always had a passion for _________ . Here, we want our network to learn from dependency ‘cook’ to predict ‘cooking. There is a gap between the information what we want to predict and from where we want it to get predicted . This is called long-term dependency. We can say that anything larger than trigram as a long term dependency. Unfortunately, RNN does not work practically in this situation.
# ### Why RNN does not work practically
# During the training of RNN, as the information goes in loop again and again which results in very large updates to neural network model weights. This is due to the accumulation of error gradients during an update and hence, results in an unstable network. At an extreme, the values of weights can become so large as to overflow and result in NaN values.The explosion occurs through exponential growth by repeatedly multiplying gradients through the network layers that have values larger than 1 or vanishing occurs if the values are less than 1.
# # Long Short Term Memory Networks (LSTM)
# Long Short Term Memory networks – usually just called “LSTMs” – are a special kind of RNN, capable of learning long-term dependencies. They were introduced by [Hochreiter & Schmidhuber (1997)](http://www.bioinf.jku.at/publications/older/2604.pdf), and were refined and popularized by many people in following work.1 They work tremendously well on a large variety of problems, and are now widely used.
#
# LSTMs are explicitly designed to avoid the long-term dependency problem. Remembering information for long periods of time is practically their default behavior, not something they struggle to learn!
#
# All recurrent neural networks have the form of a chain of repeating modules of neural network. In standard RNNs, this repeating module will have a very simple structure, such as a single tanh layer.
# <img src="https://raw.githubusercontent.com/albahnsen/AppliedDeepLearningClass/master/notebooks/images/LSTM3-SimpleRNN.png" width="100%" height="100%">
#
# The repeating module in a standard RNN contains a single layer.
# (Source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
# LSTMs also have this chain like structure, but the repeating module has a different structure. Instead of having a single neural network layer, there are four, interacting in a very special way.
# <img src="https://raw.githubusercontent.com/albahnsen/AppliedDeepLearningClass/master/notebooks/images/LSTM3-chain.png" width="100%" height="100%">
#
# The repeating module in an LSTM contains four interacting layers.
# (Source: http://colah.github.io/posts/2015-08-Understanding-LSTMs/)
# ### Detailed process
# <img src="https://raw.githubusercontent.com/albahnsen/AppliedDeepLearningClass/master/notebooks/images/1_Niu_c_FhGtLuHjrStkB_4Q.png" width="60%" height="60%">
#
# The repeating module in an LSTM contains four interacting layers.
# (Source: https://towardsdatascience.com/understanding-lstm-and-its-quick-implementation-in-keras-for-sentiment-analysis-af410fd85b47)
# The symbols used here have following meaning:
#
# - $x$ : Scaling of information
#
# - $+$ : Adding information
#
# - $\sigma$ : Sigmoid layer
#
# - $tanh$: tanh layer
#
# - $h_{t-1}$ : Output of last LSTM unit
#
# - $c_{t-1}$ : Memory from last LSTM unit
#
# - $X_t$ : Current input
#
# - $c_t$ : New updated memory
#
# - $h_t$ : Current output
# Information passes through many such LSTM units.There are three main components of an LSTM unit which are labeled in the diagram:
#
# 1) LSTM has a special architecture which enables it to forget the unnecessary information .The sigmoid layer takes the input $X_t$ and $h_{t-1}$ and decides which parts from old output should be removed (by outputting a 0). In our example, when the input is ‘He has a female friend Maria’, the gender of ‘David’ can be forgotten because the subject has changed to ‘Maria’. This gate is called forget gate $f(t)$. The output of this gate is $f(t) \cdot c_{t-1}$.
#
# 2) The next step is to decide and store information from the new input $X_t$ in the cell state. A Sigmoid layer decides which of the new information should be updated or ignored. A tanh layer creates a vector of all the possible values from the new input. These two are multiplied to update the new cell sate. This new memory is then added to old memory $c_{t-1}$ to give $c_{t}$. In our example, for the new input ‘ He has a female friend Maria’, the gender of Maria will be updated. When the input is ‘Maria works as a cook in a famous restaurant in New York whom he met recently in a school alumni meet’, the words like ‘famous’, ‘school alumni meet’ can be ignored and words like ‘cook, ‘restaurant’ and ‘New York’ will be updated.
#
# 3) Finally, we need to decide what we’re going to output. A sigmoid layer decides which parts of the cell state we are going to output. Then, we put the cell state through a tanh generating all the possible values and multiply it by the output of the sigmoid gate, so that we only output the parts we decided to. In our example, we want to predict the blank word, our model knows that it is a noun related to ‘cook’ from its memory, it can easily answer it as ‘cooking’. Our model does not learn this answer from the immediate dependency, rather it learnt it from long term dependency.
#
# We just saw that there is a big difference in the architecture of a typical RNN and a LSTM. In LSTM, our model learns what information to store in long term memory and what to get rid of.
#
#
# # Example phishing URL detection
# Based on the paper:
# - <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>, “Classifying phishing urls using recurrent neural networks,” in Electronic Crime Research (eCrime), 2017 APWG Symposium on. IEEE, 2017, pp. 1–8.
# https://albahnsen.com/wp-content/uploads/2018/05/classifying-phishing-urls-using-recurrent-neural-networks_cameraready.pdf
import pandas as pd
data = pd.read_csv('https://raw.githubusercontent.com/albahnsen/PracticalMachineLearningClass/master/datasets/phishing.csv')
data.head()
data.tail()
# #### Model using RF
# +
keywords = ['https', 'login', '.php', '.html', '@', 'sign']
for keyword in keywords:
data['keyword_' + keyword] = data.url.str.contains(keyword).astype(int)
data['lenght'] = data.url.str.len() - 2
domain = data.url.str.split('/', expand=True).iloc[:, 2]
data['lenght_domain'] = domain.str.len()
data['isIP'] = (domain.str.replace('.', '') * 1).str.isnumeric().astype(int)
data['count_com'] = data.url.str.count('com')
X = data.drop(['url', 'phishing'], axis=1)
y = data.phishing
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=42)
clf = RandomForestClassifier(n_jobs=-1, n_estimators=100)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print((y_pred == y_test).mean())
# -
# ## Using LSTM
#
# In the previous experiement, we designed a set of features
# extracted from a URL and fed them into a classification model
# to predict whether a URL is a case of phishing. We now
# approach the problem in a different way. Instead of manually
# extracting the features, we directly learn a representation from
# the URL’s character sequence.
#
# Each character sequence exhibits correlations, that is,
# nearby characters in a URL are likely to be related to each
# other. These sequential patterns are important because they can
# be exploited to improve the performance of the predictors.
import keras
from keras import backend as K
from keras.models import Sequential
from keras.layers.recurrent import LSTM
from keras.layers.core import Dense, Dropout
from keras.layers.embeddings import Embedding
from keras.preprocessing import sequence
from livelossplot import PlotLossesKeras
# %matplotlib inline
# #### Create vocabulary
X = data['url'].tolist()
# For vocabulary only the intersec characters is used to avoid issues with data collection
voc = set(''.join(X))
vocabulary = {x: idx + 1 for idx, x in enumerate(set(voc))}
vocabulary
# #### Create embeeding
# Max len
max_url_len = 150
X = [x[:max_url_len] for x in X]
# Convert characters to int and pad
X = [[vocabulary[x1] for x1 in x if x1 in vocabulary.keys()] for x in X]
X[0]
X_pad = sequence.pad_sequences(X, maxlen=max_url_len)
X_pad
# #### Create the network
X_train, X_test, y_train, y_test = train_test_split(X_pad, y, test_size=0.33, random_state=42)
# +
model = Sequential()
model.add(Embedding(len(vocabulary) + 1, 128, input_length=max_url_len))
model.add(LSTM(32))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='rmsprop', metrics=['accuracy'])
model.summary()
# -
model.fit(X_train, y_train, validation_data=[X_test, y_test],
batch_size=128, epochs=10, verbose=1,
callbacks=[PlotLossesKeras()])
# +
y_pred = model.predict_classes(X_test)[:,0]
print((y_pred == y_test).mean())
|
notebooks/16-RecurrentNeuralNetworks_LSTM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Demo: MoveActivity
# The basic steps to set up an OpenCLSim simulation are:
# * Import libraries
# * Initialise simpy environment
# * Define object classes
# * Create objects
# * Create sites
# * Create vessels
# * Create activities
# * Register processes and run simpy
#
# ----
#
# This notebook shows the basic contours of a first OpenCLSim simulation. It defines a from_site and moves vessel01 from there to a to_site. No volume is shifted yet.
# #### 0. Import libraries
# +
import datetime, time
import simpy
import shapely.geometry
import pandas as pd
import openclsim.core as core
import openclsim.model as model
import openclsim.plot as plot
# -
# #### 1. Initialise simpy environment
# setup environment
simulation_start = 0
my_env = simpy.Environment(initial_time=simulation_start)
# #### 2. Define object classes
# +
# create a Site object based on desired mixin classes
Site = type(
"Site",
(
core.Identifiable,
core.Log,
core.Locatable,
core.HasContainer,
core.HasResource,
),
{},
)
# create a TransportProcessingResource object based on desired mixin classes
TransportProcessingResource = type(
"TransportProcessingResource",
(
core.Identifiable,
core.Log,
core.ContainerDependentMovable,
core.HasResource,
core.Processor,
),
{},
)
# -
# #### 3. Create objects
# ##### 3.1. Create site object(s)
# +
# prepare input data for from_site
location_from_site = shapely.geometry.Point(4.18055556, 52.18664444)
# prepare input data for from_site
location_to_site = shapely.geometry.Point(4.25222222, 52.11428333)
data_to_site = {"env": my_env,
"name": "to_site",
"geometry": location_to_site,
"capacity": 100,
"level": 100
}
# instantiate to_site
to_site = Site(**data_to_site)
# -
# ##### 3.2. Create vessel object(s)
# prepare input data for vessel_01
data_vessel01 = {"env": my_env,
"name": "vessel01",
"geometry": location_from_site,
"capacity": 5,
"compute_v": lambda x: 10
}
# instantiate vessel_01
vessel01 = TransportProcessingResource(**data_vessel01)
# ##### 3.3 Create activity/activities
# initialise registry
registry = {}
activity = model.MoveActivity(
env=my_env,
name="Move activity",
registry=registry,
mover=vessel01,
destination=to_site,
)
# #### 4. Register processes and run simpy
# initate the simpy processes defined in the 'move activity' and run simpy
model.register_processes([activity])
my_env.run()
# #### 5. Inspect results
# ##### 5.1 Inspect logs
# We can now inspect the logs. Since the model only contains a move activity not volume was shifted.
display(plot.get_log_dataframe(activity))
# Note that the log shows only uuids, and not human readable names. Add a list of activities for which you want the unique uuids to be mapped to the (not necesassily unique) human readable names. So you have to suppply the activity object twice.
display(plot.get_log_dataframe(activity, [activity]))
display(plot.get_log_dataframe(vessel01, [activity]))
# Observe that there was movement. There was no amount shifting.
|
notebooks/02_MoveActivity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="iO7crgZlJKIS"
# # Initialize
# + [markdown] id="pQzJcaz0q-JE"
# ## Import all libraries
# + colab={"base_uri": "https://localhost:8080/"} id="3qWATYI9rHX_" executionInfo={"status": "ok", "timestamp": 1637193024323, "user_tz": 420, "elapsed": 24345, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="09ea8a52-2717-4f35-bc6f-0ee36cd0d16e"
from google.colab import drive
drive.mount('/content/drive/')
# + id="fvPMUsBC73Ur" executionInfo={"status": "ok", "timestamp": 1637193025393, "user_tz": 420, "elapsed": 1079, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
import pandas as pd
import numpy as np
from scipy.sparse import csr_matrix
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from sklearn.metrics import silhouette_samples, silhouette_score
# + id="WlEjFtZM87K3" executionInfo={"status": "ok", "timestamp": 1637193029271, "user_tz": 420, "elapsed": 3375, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# import all data Movielens 100K
df_movies = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/movies.csv")
df_ratings = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/ratings.csv")
df_tags = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/tags.csv")
df_links = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/links.csv")
# df_genome_scores = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/genome-scores.csv")
# df_genome_tags = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/genome-tags.csv")
# df_links = pd.read_csv("/content/drive/MyDrive/MovieLensRecommendationEngine/data/links.csv")
# + [markdown] id="Oks40y8ErYdf"
# ## Let's look at the data
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="H6_13Ybe89-Y" executionInfo={"status": "ok", "timestamp": 1637193029273, "user_tz": 420, "elapsed": 41, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="c27dd3b7-db0c-4418-ec07-2e2c87138fbc"
print(len(df_movies))
df_movies.head(1)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="z3zvf3Dp8980" executionInfo={"status": "ok", "timestamp": 1637193029274, "user_tz": 420, "elapsed": 36, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="025d2f2a-2b40-41ba-e20f-650f69874f86"
print(len(df_ratings))
df_ratings.head(1)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="JGiCw8TGrjJ8" executionInfo={"status": "ok", "timestamp": 1637193029275, "user_tz": 420, "elapsed": 34, "user": {"displayName": "<NAME>ia", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="b5b39bb1-c5a0-4599-c141-6add12b709eb"
print(len(df_tags))
df_tags.head(1)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="Xp0qWz18895t" executionInfo={"status": "ok", "timestamp": 1637193029276, "user_tz": 420, "elapsed": 33, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="2ceaa377-979b-40d1-baf5-8ddbf2c27379"
print(len(df_links))
df_links.head(1)
# + [markdown] id="TIeiZnh_5cfS"
# # Data Cleaning
# + [markdown] id="xyU67V38r_Ge"
# ## Few movies are missing year of release, let's add that
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="aBAcmQRh6244" executionInfo={"status": "ok", "timestamp": 1637193029276, "user_tz": 420, "elapsed": 31, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="479e7d74-ebdb-4f77-f764-a19548981698"
df_movies.head(1)
# + id="YYB-J9eO9pge" executionInfo={"status": "ok", "timestamp": 1637193029277, "user_tz": 420, "elapsed": 31, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
add_year = {'Babylon 5':1994, 'Ready Player One':2018,'Hyena Road':2016,'The Adventures of Sherlock Holmes and Doctor Watson':1980,'Nocturnal Animals':2016,'Paterson':2016,'Moonlight':2016,'The OA':2016,'Maria Bamford: Old Baby':2017,'Generation Iron 2':2017,'Black Mirror':2011}
# + colab={"base_uri": "https://localhost:8080/"} id="2-_unr-l5i-Z" executionInfo={"status": "ok", "timestamp": 1637193030155, "user_tz": 420, "elapsed": 908, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="c0de3d3b-0c70-47b2-c84e-71273590d06f"
for index,movie in df_movies.iterrows():
if '(' not in movie['title']:
if movie['title'] in add_year:
moviename = movie['title']+' ('+str(add_year[movie['title']])+')'
df_movies.loc[index,'title'] = str(moviename)
else:
# remove the movie from db
print('Dropped ',movie['title'])
df_movies = df_movies.drop(index)
# + id="vgkVeN_eDRam" executionInfo={"status": "ok", "timestamp": 1637193030156, "user_tz": 420, "elapsed": 18, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# Add year column separately from the title
# If this works without error, then there aren't any movies with no release year
temp = df_movies.copy()
temp['year'] = temp['title'].apply(lambda x: str(x).split('(')[1].split(')')[0])
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="x9N2__74DSNL" executionInfo={"status": "ok", "timestamp": 1637193030157, "user_tz": 420, "elapsed": 18, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="341801b6-4ef0-4175-981e-3c7c24498cdf"
temp.head()
# + [markdown] id="7OzHNnKNBRyc"
# ## Genres - Not being used, but useful
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="-RrVtCyc893h" executionInfo={"status": "ok", "timestamp": 1637193030422, "user_tz": 420, "elapsed": 276, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="a704073e-fdd3-4fd2-af51-1059b5ebdaf1"
df_movies.head(1)
# + id="Pg7Sfosj891J" executionInfo={"status": "ok", "timestamp": 1637193030423, "user_tz": 420, "elapsed": 21, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
genre_list = ['Action','Adventure','Animation','Children\'s','Comedy','Crime','Documentary','Drama','Fantasy','Film-Noir','Horror','Musical','Mystery','Romance','Sci-Fi','Thriller','War','Western','(no genres listed)']
# + colab={"base_uri": "https://localhost:8080/"} id="EgSMXHKe89zm" executionInfo={"status": "ok", "timestamp": 1637193030424, "user_tz": 420, "elapsed": 21, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="d5ae9130-e14f-4750-bb1c-7db9dc805cdb"
for genre in genre_list:
mov = df_movies[df_movies['genres'].str.contains(genre)]
print(mov)
rate = df_ratings[df_ratings['movieId'].isin(mov['movieId'])]
print(rate)
break
# + id="NUGy-sxe89yO" executionInfo={"status": "ok", "timestamp": 1637193030425, "user_tz": 420, "elapsed": 21, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# + [markdown] id="nXlV4IhbxF5p"
# # Clustering - K-means
# + [markdown] id="PK75AylYs5_D"
# ## Let's create the dataset
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="kjRohpuFq4X0" executionInfo={"status": "ok", "timestamp": 1637193034326, "user_tz": 420, "elapsed": 165, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="b9542b8f-9eea-4583-992e-e96ac08fb688"
ratings = pd.merge(df_ratings, df_movies[['movieId', 'title']], on='movieId' )
ratings.head()
# + colab={"base_uri": "https://localhost:8080/"} id="zP5lEuGa89xF" executionInfo={"status": "ok", "timestamp": 1637193034887, "user_tz": 420, "elapsed": 394, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="27366c5a-dce2-461d-c20f-e3501ae39716"
# Pivot
user_movies = pd.pivot_table(ratings, index='userId', columns= 'title', values='rating')
print('Dimensions',user_movies.shape)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="yLxJP6HT89tC" executionInfo={"status": "ok", "timestamp": 1637193034888, "user_tz": 420, "elapsed": 7, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="04770ec0-2fe2-4e1e-8b89-5821be0f6992"
user_movies.head(2)
# + [markdown] id="XIOf6AmFt76G"
# ## The dataset is sparse
# - Very few values are there
# - Sort by most rated movies and users who have rated the most number of movies - dense region on top
# - We will use top 5000 movies for now, then increase to the total dataset
# + id="sIsN4cHN89qj" executionInfo={"status": "ok", "timestamp": 1637193037071, "user_tz": 420, "elapsed": 167, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
#let's sort this based on the most rated movies first
num_movies = 1000
user_movie_rated = user_movies.append(user_movies.count(), ignore_index=True)
# user_movies['count'] = pd.Series(user_movies.count(axis=1))
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="lFkLyD8UvcX4" executionInfo={"status": "ok", "timestamp": 1637193037292, "user_tz": 420, "elapsed": 226, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="3ca658f6-4991-4407-af6b-17a3685561a6"
user_movie_rated.tail(1)
# + id="NP0veGptwWwM" executionInfo={"status": "ok", "timestamp": 1637193037293, "user_tz": 420, "elapsed": 8, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
user_movie_ratings_sorted = user_movie_rated.sort_values(len(user_movie_rated)-1, axis=1, ascending=False)
user_movie_ratings_sorted = user_movie_ratings_sorted.drop(user_movie_ratings_sorted.tail(1).index)
# + id="n9XvedVlwnkG" executionInfo={"status": "ok", "timestamp": 1637193037294, "user_tz": 420, "elapsed": 9, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# slice the count
most_rated_movies = user_movie_ratings_sorted.iloc[:, :num_movies]
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="iwbqIZt-wv2A" executionInfo={"status": "ok", "timestamp": 1637193037517, "user_tz": 420, "elapsed": 231, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="751c403e-a3c8-4961-9741-da726ea0e449"
print(len(most_rated_movies))
most_rated_movies.tail()
# + id="llHeNShJ89og" executionInfo={"status": "ok", "timestamp": 1637193037518, "user_tz": 420, "elapsed": 23, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# all_user_movies = user_movies.sort_values('count', ascending=False)
# + id="nVVawxTU89mP" executionInfo={"status": "ok", "timestamp": 1637193037518, "user_tz": 420, "elapsed": 21, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# most_rated_user_movies = all_user_movies.iloc[:num_movies, :]
# most_rated_user_movies = most_rated_user_movies.drop(['count'], axis=1)
# + id="RHXDzOkp94ud" executionInfo={"status": "ok", "timestamp": 1637193037519, "user_tz": 420, "elapsed": 21, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# most_rated_user_movies.head(5)
# + [markdown] id="vMtiAdYUxlla"
# ## Let's create the CSR matrix
# + id="bTjc9kd-7M-8" executionInfo={"status": "ok", "timestamp": 1637193038981, "user_tz": 420, "elapsed": 490, "user": {"displayName": "<NAME>ia", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
sdf = most_rated_movies.astype(pd.SparseDtype("float", np.nan))
# + colab={"base_uri": "https://localhost:8080/"} id="6F7Fy83Y89jo" executionInfo={"status": "ok", "timestamp": 1637193038982, "user_tz": 420, "elapsed": 6, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="ea0c376f-f5c3-4b55-c45c-2aeff62d2eaa"
sdf.sparse.density
# + id="2Fsq1iQl89gz" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1637193039186, "user_tz": 420, "elapsed": 19, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="f2b6ea97-3326-452e-e643-6d2658385f3e"
sdf.sparse.to_coo()
# + id="h8AK8G-x89bF" executionInfo={"status": "ok", "timestamp": 1637193039187, "user_tz": 420, "elapsed": 16, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# Let's check it back
sparse_ratings = csr_matrix(sdf.sparse.to_coo())
# + id="kcCRapnH89QG" colab={"base_uri": "https://localhost:8080/", "height": 0} executionInfo={"status": "ok", "timestamp": 1637193039632, "user_tz": 420, "elapsed": 461, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="d0b1ec3b-e6f8-45ae-cc9d-eff1d337cdca"
check = pd.DataFrame.sparse.from_spmatrix(sparse_ratings)
check.head()
# + [markdown] id="hGF9IHT6PHcd"
# # Visualize
# + id="yypx67mVPJct"
# + [markdown] id="pXS0ltIN5_8e"
# # Optimal K - Run only once - Current K selected = 6
# - Silhoutte method
#
# + colab={"base_uri": "https://localhost:8080/"} id="Q8dUX7dQIJ4P" executionInfo={"status": "ok", "timestamp": 1637171291165, "user_tz": 420, "elapsed": 195, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="9faa907b-1f61-4d08-8bb2-5b5c1139a751"
possible_k_values = range(2, 25, 1)
k_val = [a for a in possible_k_values]
sil_avg = []
samp_sil_val = []
print(k_val)
# + colab={"base_uri": "https://localhost:8080/"} id="7EvgQFdGIM-8" executionInfo={"status": "ok", "timestamp": 1637171305630, "user_tz": 420, "elapsed": 11661, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="9844443f-9a41-454f-ee58-01454baae6a6"
for n_clusters in possible_k_values:
clusterer = KMeans(n_clusters=n_clusters,algorithm='full')
cluster_labels = clusterer.fit_predict(sparse_ratings)
silhouette_avg = silhouette_score(sparse_ratings, cluster_labels)
sil_avg.append(silhouette_avg)
sample_silhouette_values = silhouette_samples(sparse_ratings,cluster_labels)
samp_sil_val.append(sample_silhouette_values)
print('For cluster {}, the average silhouette score is {}'.format(n_clusters, silhouette_avg))
# + colab={"base_uri": "https://localhost:8080/"} id="Bdyd8fCi7lt9" executionInfo={"status": "ok", "timestamp": 1637171308536, "user_tz": 420, "elapsed": 184, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="7bbde21c-dd90-4b09-b224-d5f8b1ebc64a"
print(sil_avg)
print(k_val)
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="cMTXWdHn8MxI" executionInfo={"status": "ok", "timestamp": 1637171309716, "user_tz": 420, "elapsed": 341, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="7b8c81ca-fc5e-4c75-9f8e-5efb4896d07e"
plt.plot(k_val, sil_avg)
# So, we will select 6 clusters
# + [markdown] id="h5zToQKsyx2V"
# # Previous values - Hide
# + [markdown] id="vKCambMqM3Yd"
# - For cluster 5, the average silhouette score is -0.007949007135515532
# - For cluster 10, the average silhouette score is -0.007319061829631084
# - For cluster 15, the average silhouette score is 0.06596843169848818
# - For cluster 20, the average silhouette score is -0.0024835502092100813
# - For cluster 25, the average silhouette score is 0.00025261324755294673
# - For cluster 30, the average silhouette score is -0.12377465329012385
# - For cluster 35, the average silhouette score is 0.0014136607876502078
# - For cluster 40, the average silhouette score is -0.005981263657415396
# - For cluster 45, the average silhouette score is -0.07360037732190812
# - For cluster 50, the average silhouette score is -0.05782397788418093
# - For cluster 55, the average silhouette score is -0.01600257577134178
# - For cluster 60, the average silhouette score is -0.051782711838991934
# - For cluster 65, the average silhouette score is 0.0025508372858048687
# - For cluster 70, the average silhouette score is -0.011208975638347142
# - For cluster 75, the average silhouette score is -0.034637484845428376
# - For cluster 80, the average silhouette score is -0.005327163404530266
# - For cluster 85, the average silhouette score is -0.025301259018795097
# - For cluster 90, the average silhouette score is 0.014095549716863559
# - For cluster 95, the average silhouette score is -0.02436565607848807
# - For cluster 100, the average silhouette score is -0.02935330031976765
# - For cluster 105, the average silhouette score is -0.012487055216700507
# - For cluster 110, the average silhouette score is -0.03655599363132131
# - For cluster 115, the average silhouette score is -0.0011293262147994228
# - For cluster 120, the average silhouette score is -0.02473405994612815
# - For cluster 125, the average silhouette score is -0.0892131623590398
# - For cluster 130, the average silhouette score is -0.00044310630183416755
# - For cluster 135, the average silhouette score is 0.0001835752194179131
# - For cluster 140, the average silhouette score is -0.025734967286221346
#
#
# Let's choose K=90
# + colab={"base_uri": "https://localhost:8080/"} id="K7iRYhglMQWA" executionInfo={"status": "ok", "timestamp": 1636822190236, "user_tz": 420, "elapsed": 204843, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="80606c0a-c4aa-4fcf-d4e1-eb79f0c8c7ff"
# possible_k_values = range(100, 14, 5)
# for n_clusters in possible_k_values:
# clusterer = KMeans(n_clusters=n_clusters,algorithm='full')
# cluster_labels = clusterer.fit_predict(sparse_ratings)
# silhouette_avg = silhouette_score(sparse_ratings, cluster_labels)
# sample_silhouette_values = silhouette_samples(sparse_ratings,cluster_labels)
# print('For cluster {}, the average silhouette score is {}'.format(n_clusters, silhouette_avg))
# + colab={"base_uri": "https://localhost:8080/"} id="9D5AVZgsHjlm" outputId="d973f3ff-d8e7-4072-e076-cfedfd10db37"
possible_k_values = [10, 15, 25, 35, 65, 90, 135]
for n_clusters in possible_k_values:
clusterer = KMeans(n_clusters=n_clusters,algorithm='full')
cluster_labels = clusterer.fit_predict(sparse_ratings)
silhouette_avg = silhouette_score(sparse_ratings, cluster_labels)
sample_silhouette_values = silhouette_samples(sparse_ratings,cluster_labels)
print('For cluster {}, the average silhouette score is {}'.format(n_clusters, silhouette_avg))
# + id="5KZQfA13Hjiz"
import matplotlib.cm as cm
# + id="zbjRZ3cJHjfh"
for n_clusters in range_n_clusters:
fig=plt.figure()
# Subplot with 1 row and 2 columns
# fig,(ax1,ax2) = plt.subplot(1,2,1)
ax1 = plt.subplot(1,2,1)
fig.set_size_inches(10,5)
# 1st plot is the silhouette plot - x: score, y: no. of clusters
# x-axis range - (-1,1)
# but we saw in all values, the score is between (-0.1,1)
ax1.set_xlim([-0.1,1])
# y axis let's see the blackspace as well
ax1.set_ylim([0,len(X)+(n_clusters+1*10)])
# Initilize clusterer with random generator seed of 10 for reproducibility
clusterer = KMeans(n_clusters=n_clusters, random_state=10)
cluster_labels = clusterer.fit_predict(X)
# Score gives the average value for all the samples
# Gives a perspective into the density and separation of the formed clusters
silhouette_avg = silhouette_score(X, cluster_labels)
# Compute for each sample
sample_silhouette_values = silhouette_samples(X,cluster_labels)
print('For cluster {}, the average silhouette score is {}'.format(n_clusters, silhouette_avg))
y_lower = 10
for i in range(n_clusters):
ith_cluster_score = sample_silhouette_values[cluster_labels == i]
ith_cluster_score.sort()
size_cluster_i = ith_cluster_score.shape[0]
y_upper = y_lower + size_cluster_i
color = cm.nipy_spectral(float(i)/n_clusters)
ax1.fill_betweenx(np.arange(y_lower, y_upper),0,ith_cluster_score, facecolor=color, edgecolor=color,alpha=0.7)
ax1.text(-0.05, y_lower+0.5*size_cluster_i,str(i))
y_lower = y_upper+10
ax1.set_title('The silhouette point for various clusters')
ax1.set_xlabel('The silhouette coefficient values')
ax1.set_ylabel('Cluster label')
ax1.axvline(x=silhouette_avg,color='red',linestyle='-')
ax1.set_yticks([])
ax1.set_xticks([-0.1,0,0.2,0.4,0.6,0.8,1])
ax2 = plt.subplot(1,2,2)
colors = cm.nipy_spectral(cluster_labels.astype(float)/n_clusters)
ax2.scatter(X[:,0],X[:,1],s=30,marker='.',c=colors,lw=0,alpha=0.7, edgecolor='k')
centers = clusterer.cluster_centers_
ax2.scatter(centers[:,0],centers[:,1], marker='o',c='white',alpha=1, s=200, edgecolor='k')
ax2.set_title('The visualization of the clustered data')
ax2.set_xlabel('Feature space for the 1st feature')
ax2.set_ylabel('Feature space for the 2nd feature')
# fig.set_title('Silhouette analysis')
# + id="-ZOZTTiiHjXX"
# + id="DkxyTABJ6E-O"
# + id="8wOcTVVi6E7M"
# + id="9u7wJfZE6E5A"
# + id="lSPun4xL6E19"
# + id="LWnOA1CR6Ey8"
# + id="N_DNC4Jp6Epe"
# + [markdown] id="dsam-8H26q7V"
# # Clustering
# + id="E5_A5piM6r9W" executionInfo={"status": "ok", "timestamp": 1637193055536, "user_tz": 420, "elapsed": 638, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
predictions = KMeans(n_clusters=10, algorithm='full').fit_predict(sparse_ratings)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="thcxcHS1-KB4" executionInfo={"status": "ok", "timestamp": 1637193055769, "user_tz": 420, "elapsed": 239, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="912c9c85-549d-457f-e71d-fb662cf21e01"
most_rated_movies.head(1)
# + id="BFFZWZq468DE" executionInfo={"status": "ok", "timestamp": 1637193055771, "user_tz": 420, "elapsed": 20, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
max_users = 70
max_movies = 50
clustered = pd.concat([most_rated_movies.reset_index(), pd.DataFrame({'group':predictions})], axis=1)
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="EoRN4O-Y7mRk" executionInfo={"status": "ok", "timestamp": 1637193055772, "user_tz": 420, "elapsed": 20, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="649c128e-0c2a-44eb-c1e5-b891774863d1"
print(clustered['group'].unique())
print(clustered['group'].value_counts())
clustered.head()
# + id="qgUMf5FuAydi" executionInfo={"status": "ok", "timestamp": 1637193055773, "user_tz": 420, "elapsed": 17, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# clustered['user_id']
# + id="RUc_rj6k7xf-" executionInfo={"status": "ok", "timestamp": 1637193055774, "user_tz": 420, "elapsed": 18, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# a = clustered.reset_index()
# a.head()
# + [markdown] id="de27iAHT7RK8"
# ## Helper function to draw clusters
# + id="_sHInlEj7Htx" executionInfo={"status": "ok", "timestamp": 1637193056143, "user_tz": 420, "elapsed": 386, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
def get_most_rated_movies(user_movie_ratings, max_number_of_movies):
# 1- Count
user_movie_ratings = user_movie_ratings.append(user_movie_ratings.count(), ignore_index=True)
# 2- sort
user_movie_ratings_sorted = user_movie_ratings.sort_values(len(user_movie_ratings)-1, axis=1, ascending=False)
user_movie_ratings_sorted = user_movie_ratings_sorted.drop(user_movie_ratings_sorted.tail(1).index)
# 3- slice
most_rated_movies = user_movie_ratings_sorted.iloc[:, :max_number_of_movies]
return most_rated_movies
def get_users_who_rate_the_most(most_rated_movies, max_number_of_movies):
# Get most voting users
# 1- Count
most_rated_movies['counts'] = pd.Series(most_rated_movies.count(axis=1))
# 2- Sort
most_rated_movies_users = most_rated_movies.sort_values('counts', ascending=False)
# 3- Slice
most_rated_movies_users_selection = most_rated_movies_users.iloc[:max_number_of_movies, :]
most_rated_movies_users_selection = most_rated_movies_users_selection.drop(['counts'], axis=1)
return most_rated_movies_users_selection
def draw_movies_heatmap(most_rated_movies_users_selection, axis_labels=True):
# Reverse to match the order of the printed dataframe
#most_rated_movies_users_selection = most_rated_movies_users_selection.iloc[::-1]
fig = plt.figure(figsize=(15,4))
ax = plt.gca()
# Draw heatmap
heatmap = ax.imshow(most_rated_movies_users_selection, interpolation='nearest', vmin=0, vmax=5, aspect='auto')
if axis_labels:
ax.set_yticks(np.arange(most_rated_movies_users_selection.shape[0]) , minor=False)
ax.set_xticks(np.arange(most_rated_movies_users_selection.shape[1]) , minor=False)
ax.invert_yaxis()
ax.xaxis.tick_top()
labels = most_rated_movies_users_selection.columns.str[:40]
ax.set_xticklabels(labels, minor=False)
ax.set_yticklabels(most_rated_movies_users_selection.index, minor=False)
plt.setp(ax.get_xticklabels(), rotation=90)
else:
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
ax.grid(False)
ax.set_ylabel('User id')
# Separate heatmap from color bar
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
# Color bar
cbar = fig.colorbar(heatmap, ticks=[5, 4, 3, 2, 1, 0], cax=cax)
cbar.ax.set_yticklabels(['5 stars', '4 stars','3 stars','2 stars','1 stars','0 stars'])
plt.show()
def draw_movie_clusters(clustered, max_users, max_movies):
c=1
for cluster_id in clustered.group.unique():
# To improve visibility, we're showing at most max_users users and max_movies movies per cluster.
# You can change these values to see more users & movies per cluster
d = clustered[clustered.group == cluster_id].drop(['index', 'group'], axis=1)
n_users_in_cluster = d.shape[0]
# d = sort_by_rating_density(d, max_movies, max_users)
most_rated_movies = get_most_rated_movies(d, max_movies)
d = get_users_who_rate_the_most(most_rated_movies, max_users)
d = d.reindex(d.mean().sort_values(ascending=False).index, axis=1)
d = d.reindex(d.count(axis=1).sort_values(ascending=False).index)
d = d.iloc[:max_users, :max_movies]
n_users_in_plot = d.shape[0]
# We're only selecting to show clusters that have more than 9 users, otherwise, they're less interesting
if len(d) > 9:
print('cluster # {}'.format(cluster_id))
print('# of users in cluster: {}.'.format(n_users_in_cluster), '# of users in plot: {}'.format(n_users_in_plot))
fig = plt.figure(figsize=(15,4))
ax = plt.gca()
ax.invert_yaxis()
ax.xaxis.tick_top()
labels = d.columns.str[:40]
ax.set_yticks(np.arange(d.shape[0]) , minor=False)
ax.set_xticks(np.arange(d.shape[1]) , minor=False)
ax.set_xticklabels(labels, minor=False)
ax.get_yaxis().set_visible(False)
# Heatmap
heatmap = plt.imshow(d, vmin=0, vmax=5, aspect='auto')
ax.set_xlabel('movies')
ax.set_ylabel('User id')
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.05)
# Color bar
cbar = fig.colorbar(heatmap, ticks=[5, 4, 3, 2, 1, 0], cax=cax)
cbar.ax.set_yticklabels(['5 stars', '4 stars','3 stars','2 stars','1 stars','0 stars'])
plt.setp(ax.get_xticklabels(), rotation=90, fontsize=9)
plt.tick_params(axis='both', which='both', bottom='off', top='off', left='off', labelbottom='off', labelleft='off')
#print('cluster # {} \n(Showing at most {} users and {} movies)'.format(cluster_id, max_users, max_movies))
plt.show()
# Let's only show 5 clusters
# Remove the next three lines if you want to see all the clusters
# Contribution welcomed: Pythonic way of achieving this
# c = c+1
# if c > 6:
# break
# + id="-wKL3pwv7VVa" executionInfo={"status": "ok", "timestamp": 1637193056144, "user_tz": 420, "elapsed": 10, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# + [markdown] id="Bc6szWZd7XHa"
# # Let's visualize
# + colab={"base_uri": "https://localhost:8080/", "height": 0} id="r9LO4kkl7Xwt" executionInfo={"status": "ok", "timestamp": 1637193070465, "user_tz": 420, "elapsed": 12833, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="dbb48d99-2081-410e-fb99-fd4acf34f498"
max_users = 70
max_movies = 50
draw_movie_clusters(clustered, max_users, max_movies)
# + [markdown] id="x1se3sWJCoXB"
# # Prediction
# + colab={"base_uri": "https://localhost:8080/", "height": 304} id="uoMoVRlZJBGO" executionInfo={"status": "ok", "timestamp": 1637193093051, "user_tz": 420, "elapsed": 244, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="128134c0-5820-4efb-ead5-05488064e6ba"
clustered.head(1)
# + id="eR5h384v_Sf8" executionInfo={"status": "ok", "timestamp": 1637193093053, "user_tz": 420, "elapsed": 14, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# + colab={"base_uri": "https://localhost:8080/"} id="XTU-SW6-7hn0" executionInfo={"status": "ok", "timestamp": 1637193188473, "user_tz": 420, "elapsed": 7, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="3401d8dc-fbbd-41b9-9b26-775bd8a48c3e"
cluster_num = 3
num_users = 75
num_movies = 300
cluster = clustered[clustered.group == cluster_num].drop(['index','group'],axis=1)
# sort by rating density
most_rated_movies = get_most_rated_movies(cluster, max_movies)
cluster = get_users_who_rate_the_most(most_rated_movies, max_users)
cluster.index
# draw_movies_heatmap(cluster)
# + id="Q6Ku3YMk_fRA" executionInfo={"status": "ok", "timestamp": 1637193196307, "user_tz": 420, "elapsed": 262, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# + colab={"base_uri": "https://localhost:8080/", "height": 400} id="bPjxV4pmI59d" executionInfo={"status": "ok", "timestamp": 1637193196703, "user_tz": 420, "elapsed": 173, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="a19d1952-a94d-4acd-d4aa-c00ad3e71eb8"
cluster.fillna('').head()
# + colab={"base_uri": "https://localhost:8080/"} id="hSTxlepMJtM7" executionInfo={"status": "ok", "timestamp": 1637193200032, "user_tz": 420, "elapsed": 163, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="fa88288d-c9a0-4795-aac0-46d060769c4b"
movie_name = "Matrix, The (1999)"
cluster[movie_name].mean()
# + colab={"base_uri": "https://localhost:8080/"} id="rwmweDi7FD0r" executionInfo={"status": "ok", "timestamp": 1637193201288, "user_tz": 420, "elapsed": 5, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="9ba992fd-61dc-4020-cf41-252064233819"
movie_name = "Silence of the Lambs, The (1991)"
cluster[movie_name].mean()
# + colab={"base_uri": "https://localhost:8080/"} id="PF2jxcLQFKAf" executionInfo={"status": "ok", "timestamp": 1637193202488, "user_tz": 420, "elapsed": 169, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="18ba5408-878e-4291-970b-a623c12462b5"
movie_name = "Star Wars: Episode IV - A New Hope (1977)"
cluster[movie_name].mean()
# + id="-SBsQF20GN42" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1637193206307, "user_tz": 420, "elapsed": 172, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="aaecb7b4-54c6-4595-fb92-81519594e363"
movie_name = "Star Wars: Episode VI - Return of the Jedi (1983)"
cluster[movie_name].mean()
# + [markdown] id="AeNlavgDGPBO"
# # Recommendation
# + colab={"base_uri": "https://localhost:8080/"} id="DbrlITAeGQ2Z" executionInfo={"status": "ok", "timestamp": 1637193210461, "user_tz": 420, "elapsed": 161, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="6f714314-a769-4806-9162-d649a53bacb3"
cluster.mean().head(20)
# + colab={"base_uri": "https://localhost:8080/"} id="5_SssFIlWmqX" executionInfo={"status": "ok", "timestamp": 1637193215277, "user_tz": 420, "elapsed": 167, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="e5880b17-1d22-4354-d302-f12f46aa4bda"
user_id = 24
print('USER {} ALREADY RATED THESE MOVIES - '.format(user_id))
print()
user_2_ratings = cluster.loc[user_id, :]
user_2_ratings.dropna()
# + colab={"base_uri": "https://localhost:8080/"} id="8z5TZcOEJ_Ca" executionInfo={"status": "ok", "timestamp": 1637193220329, "user_tz": 420, "elapsed": 169, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="57031770-0778-462e-e6ed-cf9b7a17667f"
# Get all this user's ratings
user_2_ratings = cluster.loc[user_id, :]
# Which movies did they not rate? (We don't want to recommend movies they've already rated)
user_2_unrated_movies = user_2_ratings[user_2_ratings.isnull()]
# What are the ratings of these movies the user did not rate?
avg_ratings = pd.concat([user_2_unrated_movies, cluster.mean()], axis=1, join='inner').loc[:,0]
# Let's sort by rating so the highest rated movies are presented first
print('RECOMMENDATIONS FOR USER = {} - '.format(user_id))
print()
avg_ratings.sort_values(ascending=False)[:20]
# + colab={"base_uri": "https://localhost:8080/", "height": 335} id="Mwnb3tqyJdTR" executionInfo={"status": "ok", "timestamp": 1637193229767, "user_tz": 420, "elapsed": 175, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="6fb345a6-0041-443f-e53c-de154f1ae67d"
clustered.head(2)
# + id="54Fg74xQKRle" executionInfo={"status": "ok", "timestamp": 1637193231795, "user_tz": 420, "elapsed": 165, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
prediction_series = avg_ratings.sort_values(ascending=False)[:20]
# + id="BHcp_O0SLRpp" executionInfo={"status": "ok", "timestamp": 1637193233514, "user_tz": 420, "elapsed": 191, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}}
# + colab={"base_uri": "https://localhost:8080/", "height": 394} id="N5jLcxyULmSy" executionInfo={"status": "ok", "timestamp": 1637193233694, "user_tz": 420, "elapsed": 5, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="3a84fb1e-9e63-453c-9884-a81ce3aea65b"
df_prediction = df_movies[df_movies['title'].isin(list(avg_ratings.sort_values(ascending=False)[:10].index))]
df_prediciton = df_prediction.set_index('title')
df_prediciton['score'] = prediction_series
df_prediciton.sort_values(by='score',ascending=False).reset_index().set_index('movieId')
# + [markdown] id="x9tg2hV0aVMF"
# # Evaluation
# + colab={"base_uri": "https://localhost:8080/"} id="bNzLour9aWtD" executionInfo={"status": "ok", "timestamp": 1637194223693, "user_tz": 420, "elapsed": 1727, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="d80ce3e8-e0d6-461a-db94-1e41afe82831"
k = 10
rmse_list = []
mape_list = []
for i in range(0,k):
num_users = 75
num_movies = 300
cluster = clustered[clustered.group == i].drop(['index','group'],axis=1)
# sort by rating density
most_rated_movies = get_most_rated_movies(cluster, max_movies)
cluster = get_users_who_rate_the_most(most_rated_movies, max_users)
# print(cluster.index)
# print(cluster)
# print(most_rated_movies)
# print('Predicted scores -----')
# print(cluster.mean().head(20))
recommendation = cluster.mean().head(20)
# print(recommendation)
# for each user find the movies he rated
# Get all this user's ratings
for user_id in cluster.index:
# print(user_id,'Movies he rated ---- ')
user_2_ratings = cluster.loc[user_id, :]
user_2_ratings = user_2_ratings.dropna()
# print(user_2_ratings)
comb = pd.concat([recommendation, user_2_ratings], keys=['recommendation', 'rating'],axis=1)
# print(comb.columns)
comb = comb.dropna()
rmse = ((comb['recommendation'] - comb['rating']) ** 2).mean() ** .5
mape = np.mean(np.abs((comb['rating'] - comb['recommendation']) / comb['rating'])) * 100
mape_list.append(mape)
# print(rmse)
rmse_list.append(rmse)
# break
print('Avg RMSE',np.mean(rmse_list))
print('Avg MAPE',np.mean(mape_list))
# comb = comb.dropna()
# print(np.mean(np.abs((comb['rating'] - comb['recommendation']) / comb['rating'])) * 100)
# print(((comb[0] - comb[1]) ** 2).mean() ** .5)
# comb
# for index, row in df.iterrows():
# + [markdown] id="FSp8YWAyQw9r"
# # Testing Other Clustering techniques
# + [markdown] id="Qclz81HrQ3RR"
# ## Spectral Clustering - Skip
# + id="6uDclb7-Q2GT"
from scipy.stats import multivariate_normal # for generating pdf
from sklearn.cluster import SpectralClustering
# + colab={"base_uri": "https://localhost:8080/", "height": 457} id="SBtlaDfRSnHh" executionInfo={"status": "ok", "timestamp": 1636908349372, "user_tz": 420, "elapsed": 814, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="521a39c9-1d52-4314-ebf2-30231d3fb9fb"
sc = SpectralClustering(n_clusters=10).fit_predict(sparse_ratings)
max_users = 70
max_movies = 50
clusteredsc = pd.concat([most_rated_movies.reset_index(), pd.DataFrame({'group':sc})], axis=1)
clusteredsc.head(5)
# + colab={"base_uri": "https://localhost:8080/"} id="4ep3Uyt3S17H" executionInfo={"status": "ok", "timestamp": 1636908351384, "user_tz": 420, "elapsed": 7, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GhGIP-wL4j7fK3ABlEIun2k_GiNB-B1gk0UyTBw=s64", "userId": "04031563484628966258"}} outputId="14c53d88-f35f-4a91-f690-7a4641f48cb4"
print(clusteredsc['group'].unique())
print(clusteredsc['group'].value_counts())
# clusteredsc.head()
# + id="Xl6aB0BSTEnk"
|
Collaborative Filtering -- K-Means.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Imports
# +
import math
import pandas as pd
import pennylane as qml
import time
from keras.datasets import mnist
from matplotlib import pyplot as plt
from pennylane import numpy as np
from pennylane.templates import AmplitudeEmbedding, AngleEmbedding
from pennylane.templates.subroutines import ArbitraryUnitary
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# -
# # Model Params
# +
np.random.seed(131)
initial_params = np.random.random([48])
INITIALIZATION_METHOD = 'Angle'
BATCH_SIZE = 20
EPOCHS = 400
STEP_SIZE = 0.01
BETA_1 = 0.9
BETA_2 = 0.99
EPSILON = 0.00000001
TRAINING_SIZE = 0.78
VALIDATION_SIZE = 0.07
TEST_SIZE = 1-TRAINING_SIZE-VALIDATION_SIZE
initial_time = time.time()
# -
# # Import dataset
(train_X, train_y), (test_X, test_y) = mnist.load_data()
examples = np.append(train_X, test_X, axis=0)
examples = examples.reshape(70000, 28*28)
classes = np.append(train_y, test_y)
x = []
y = []
for (example, label) in zip(examples, classes):
if label in [0, 2, 4, 6, 8]:
x.append(example)
y.append(-1)
else:
x.append(example)
y.append(1)
# +
x = np.array(x)
y = np.array(y)
# Normalize pixels values
x = x / 255
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=TEST_SIZE, shuffle=True)
# -
validation_indexes = np.random.random_integers(len(X_train), size=(math.floor(len(X_train)*VALIDATION_SIZE),))
X_validation = [X_train[n] for n in validation_indexes]
y_validation = [y_train[n] for n in validation_indexes]
# +
pca = PCA(n_components=8)
pca.fit(X_train)
X_train = pca.transform(X_train)
X_validation = pca.transform(X_validation)
X_test = pca.transform(X_test)
preprocessing_time = time.time()
# -
# # Circuit creation
device = qml.device("default.qubit", wires=8)
def unitary(params, wire1, wire2):
# qml.RZ(0, wires=wire1)
qml.RY(params[0], wires=wire1)
# qml.RZ(0, wires=wire1)
# qml.RZ(0, wires=wire2)
qml.RY(params[1], wires=wire2)
# qml.RZ(0, wires=wire2)
qml.CNOT(wires=[wire2, wire1])
# qml.RZ(0, wires=wire1)
qml.RY(params[2], wires=wire2)
qml.CNOT(wires=[wire1, wire2])
qml.RY(params[3], wires=wire2)
qml.CNOT(wires=[wire2, wire1])
# qml.RZ(0, wires=wire1)
qml.RY(params[4], wires=wire1)
# qml.RZ(0, wires=wire1)
# qml.RZ(0, wires=wire2)
qml.RY(params[5], wires=wire2)
# qml.RZ(0, wires=wire2)
@qml.qnode(device)
def circuit(features, params):
# Load state
if INITIALIZATION_METHOD == 'Amplitude':
AmplitudeEmbedding(features=features, wires=range(8), normalize=True, pad_with=0.)
else:
AngleEmbedding(features=features, wires=range(8), rotation='Y')
# First layer
unitary(params[0:6], 0, 1)
unitary(params[6:12], 2, 3)
unitary(params[12:18], 4, 5)
unitary(params[18:24], 6, 7)
# Second layer
unitary(params[24:30], 1, 2)
unitary(params[36:42], 5, 6)
# Third layer
unitary(params[42:48], 2, 5)
# Measurement
return qml.expval(qml.PauliZ(5))
# ## Circuit example
features = X_train[0]
print(f"Inital parameters: {initial_params}\n")
print(f"Example features: {features}\n")
print(f"Expectation value: {circuit(features, initial_params)}\n")
print(circuit.draw())
# # Accuracy test definition
def measure_accuracy(x, y, circuit_params):
class_errors = 0
for example, example_class in zip(x, y):
predicted_value = circuit(example, circuit_params)
if (example_class > 0 and predicted_value <= 0) or (example_class <= 0 and predicted_value > 0):
class_errors += 1
return 1 - (class_errors/len(y))
# # Training
# +
params = initial_params
opt = qml.AdamOptimizer(stepsize=STEP_SIZE, beta1=BETA_1, beta2=BETA_2, eps=EPSILON)
test_accuracies = []
best_validation_accuracy = 0.0
best_params = []
for i in range(len(X_train)):
features = X_train[i]
expected_value = y_train[i]
def cost(circuit_params):
value = circuit(features, circuit_params)
return ((expected_value - value) ** 2)/len(X_train)
params = opt.step(cost, params)
if i % BATCH_SIZE == 0:
print(f"epoch {i//BATCH_SIZE}")
if i % (10*BATCH_SIZE) == 0:
current_accuracy = measure_accuracy(X_validation, y_validation, params)
test_accuracies.append(current_accuracy)
print(f"accuracy: {current_accuracy}")
if current_accuracy > best_validation_accuracy:
print("best accuracy so far!")
best_validation_accuracy = current_accuracy
best_params = params
if len(test_accuracies) == 30:
print(f"test_accuracies: {test_accuracies}")
if np.allclose(best_validation_accuracy, test_accuracies[0]):
params = best_params
break
del test_accuracies[0]
# +
print("Optimized rotation angles: {}".format(params))
training_time = time.time()
# -
# # Testing
# +
accuracy = measure_accuracy(X_test, y_test, params)
print(accuracy)
test_time = time.time()
# -
print(f"pre-processing time: {preprocessing_time-initial_time}")
print(f"training time: {training_time - preprocessing_time}")
print(f"test time: {test_time - training_time}")
print(f"total time: {test_time - initial_time}")
|
notebooks/tg/ttn/general/real/mnist_even_odd.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Twitter HOWTO
# ## Overview
#
# This document is an overview of how to use NLTK to collect and process Twitter data. It was written as an IPython notebook, and if you have IPython installed, you can download [the source of the notebook](https://raw.githubusercontent.com/nltk/nltk/develop/nltk/test/twitter.ipynb) from the NLTK GitHub repository and run the notebook in interactive mode.
#
# Most of the tasks that you might want to carry out with 'live' Twitter data require you to authenticate your request by registering for API keys. This is usually a once-only step. When you have registered your API keys, you can store them in a file on your computer, and then use them whenever you want. We explain what's involved in the section [First Steps](#first_steps).
#
# If you have already obtained Twitter API keys as part of some earlier project, [storing your keys](#store_keys) explains how to save them to a file that NLTK will be able to find. Alternatively, if you just want to play around with the Twitter data that is distributed as part of NLTK, head over to the section on using the [`twitter-samples` corpus reader](#corpus_reader).
#
# Once you have got authentication sorted out, we'll show you [how to use NLTK's `Twitter` class](#simple). This is made as simple as possible, but deliberately limits what you can do.
#
# ## <a name="first_steps">First Steps</a>
#
# As mentioned above, in order to collect data from Twitter, you first need to register a new *application* — this is Twitter's way of referring to any computer program that interacts with the Twitter API. As long as you save your registration information correctly, you should only need to do this once, since the information should work for any NLTK code that you write. You will need to have a Twitter account before you can register. Twitter also insists that [you add a mobile phone number to your Twitter profile](https://support.twitter.com/articles/110250-adding-your-mobile-number-to-your-account-via-web) before you will be allowed to register an application.
#
# These are the steps you need to carry out.
#
# ### <a name="api_keys">Getting your API keys from Twitter</a>
#
# 1. Sign in to your Twitter account at https://apps.twitter.com. You should then get sent to a screen that looks something like this:
# <img src="images/twitter_app1.tiff" width="600px">
# Clicking on the **Create New App** button should take you to the following screen:
# <img src="images/twitter_app2.tiff" width="600px">
# The information that you provide for **Name**, **Description** and **Website** can be anything you like.
#
# 2. Make sure that you select **Read and Write** access for your application (as specified on the *Permissions* tab of Twitter's Application Management screen):
# <img src="images/twitter_app3.tiff" width="600px">
#
# 3. Go to the tab labeled **Keys and Access Tokens**. It should look something like this, but with actual keys rather than a string of Xs:
# <img src="images/twitter_app4.png" width="650px">
# As you can see, this will give you four distinct keys: consumer key, consumer key secret, access token and access token secret.
#
# ### <a name="store_keys">Storing your keys</a>
#
# 1. Create a folder named `twitter-files` in your home directory. Within this folder, use a text editor to create a new file called `credentials.txt`. Make sure that this file is just a plain text file. In it, you should create which you should store in a text file with the following structure:
# ```
# app_key=YOUR CONSUMER KEY
# app_secret=YOUR CONSUMER SECRET
# oauth_token=YOUR ACCESS TOKEN
# oauth_token_secret=YOUR ACCESS TOKEN SECRET
# ```
# Type the part up to and includinge the '=' symbol exactly as shown. The values on the right-hand side of the '=' — that is, everything in caps — should be cut-and-pasted from the relevant API key information shown on the Twitter **Keys and Access Tokens**. Save the file and that's it.
#
# 2. It's going to be important for NLTK programs to know where you have stored your
# credentials. We'll assume that this folder is called `twitter-files`, but you can call it anything you like. We will also assume that this folder is where you save any files containing tweets that you collect. Once you have decided on the name and location of this
# folder, you will need to set the `TWITTER` environment variable to this value.
#
# On a Unix-like system (including MacOS), you will set the variable something like this:
# ```bash
# export TWITTER="/path/to/your/twitter-files"
# ```
# Rather than having to give this command each time you start a new session, it's advisable to add it to your shell's configuration file, e.g. to `.bashrc`.
#
# On a Windows machine, right click on “My Computer” then select `Properties > Advanced > Environment Variables > User Variables > New...`
#
# One important thing to remember is that you need to keep your `credentials.txt` file private. So do **not** share your `twitter-files` folder with anyone else, and do **not** upload it to a public repository such as GitHub.
#
# 3. Finally, read through Twitter's [Developer Rules of the Road](https://dev.twitter.com/overview/terms/policy). As far as these rules are concerned, you count as both the application developer and the user.
# ### <a name="twython">Install Twython</a>
#
# The NLTK Twitter package relies on a third party library called [Twython](https://twython.readthedocs.org/). Install Twython via [pip](https://pip.pypa.io):
# ```bash
# $ pip install twython
# ```
#
# or with [easy_install](https://pythonhosted.org/setuptools/easy_install.html):
#
# ```bash
# $ easy_install twython
# ```
# We're now ready to get started. The next section will describe how to use the `Twitter` class to talk to the Twitter API.
# *More detail*:
# Twitter offers are two main authentication options. OAuth 1 is for user-authenticated API calls, and allows sending status updates, direct messages, etc, whereas OAuth 2 is for application-authenticated calls, where read-only access is sufficient. Although OAuth 2 sounds more appropriate for the kind of tasks envisaged within NLTK, it turns out that access to Twitter's Streaming API requires OAuth 1, which is why it's necessary to obtain *Read and Write* access for your application.
# ## <a name="simple">Using the simple `Twitter` class</a>
#
# ### Dipping into the Public Stream
#
# The `Twitter` class is intended as a simple means of interacting with the Twitter data stream. Later on, we'll look at other methods which give more fine-grained control.
#
# The Twitter live public stream is a sample (approximately 1%) of all Tweets that are currently being published by users. They can be on any topic and in any language. In your request, you can give keywords which will narrow down the Tweets that get delivered to you. Our first example looks for Tweets which include either the word *love* or *hate*. We limit the call to finding 10 tweets. When you run this code, it will definitely produce different results from those shown below!
from nltk.twitter import Twitter
tw = Twitter()
tw.tweets(keywords='love, hate', limit=10) #sample from the public stream
# The next example filters the live public stream by looking for specific user accounts. In this case, we 'follow' two news organisations, namely `@CNN` and `@BBCNews`. [As advised by Twitter](https://dev.twitter.com/streaming/reference/post/statuses/filter), we use *numeric userIDs* for these accounts. If you run this code yourself, you'll see that Tweets are arriving much more slowly than in the previous example. This is because even big new organisations don't publish Tweets that often.
#
# A bit later we will show you how to use Python to convert usernames such as `@CNN` to userIDs such as `759251`, but for now you might find it simpler to use a web service like [TweeterID](http://tweeterid.com) if you want to experiment with following different accounts than the ones shown below.
tw = Twitter()
tw.tweets(follow=['759251', '612473'], limit=10) # see what CNN and BBC are talking about
# ### Saving Tweets to a File
#
# By default, the `Twitter` class will just print out Tweets to your computer terminal. Although it's fun to view the Twitter stream zipping by on your screen, you'll probably want to save some tweets in a file. We can tell the `tweets()` method to save to a file by setting the flag `to_screen` to `False`.
#
# The `Twitter` class will look at the value of your environmental variable `TWITTER` to determine which folder to use to save the tweets, and it will put them in a date-stamped file with the prefix `tweets`.
tw = Twitter()
tw.tweets(to_screen=False, limit=25)
# So far, we've been taking data from the live public stream. However, it's also possible to retrieve past tweets, for example by searching for specific keywords, and setting `stream=False`:
tw.tweets(keywords='hilary clinton', stream=False, limit=10)
# ## <a name="onwards">Onwards and Upwards</a>
#
# In this section, we'll look at how to get more fine-grained control over processing Tweets. To start off, we will import a bunch of stuff from the `twitter` package.
from nltk.twitter import Query, Streamer, Twitter, TweetViewer, TweetWriter, credsfromfile
# In the following example, you'll see the line
# ``` python
# oauth = credsfromfile()
# ```
# This gets hold of your stored API key information. The function `credsfromfile()` by default looks for a file called `credentials.txt` in the directory set by the environment variable `TWITTER`, reads the contents and returns the result as a dictionary. We then pass this dictionary as an argument when initializing our client code. We'll be using two classes to wrap the clients: `Streamer` and `Query`; the first of these calls [the Streaming API](https://dev.twitter.com/streaming/overview) and the second calls Twitter's [Search API](https://dev.twitter.com/rest/public) (also called the REST API).
# *More detail*: For more detail, see this blog post on [The difference between the Twitter Firehose API, the Twitter Search API, and the Twitter Streaming API](http://www.brightplanet.com/2013/06/twitter-firehose-vs-twitter-api-whats-the-difference-and-why-should-you-care/)
#
# After initializing a client, we call the `register()` method to specify whether we want to view the data on a terminal or write it to a file. Finally, we call a method which determines the API endpoint to address; in this case, we use `sample()` to get a random sample from the the Streaming API.
oauth = credsfromfile()
client = Streamer(**oauth)
client.register(TweetViewer(limit=10))
client.sample()
# The next example is similar, except that we call the `filter()` method with the `track` parameter followed by a string literal. The string is interpreted as a list of search terms where [comma indicates a logical OR](https://dev.twitter.com/streaming/overview/request-parameters#track). The terms are treated as case-insensitive.
client = Streamer(**oauth)
client.register(TweetViewer(limit=10))
client.filter(track='refugee, germany')
# Whereas the Streaming API lets us access near real-time Twitter data, the Search API lets us query for past Tweets. In the following example, the value `tweets` returned by `search_tweets()` is a generator; the expression `next(tweets)` gives us the first Tweet from the generator.
#
# Although Twitter delivers Tweets as [JSON](http://www.json.org) objects, the Python client encodes them as dictionaries, and the example pretty-prints a portion of the dictionary corresponding the Tweet in question.
client = Query(**oauth)
tweets = client.search_tweets(keywords='nltk', limit=10)
tweet = next(tweets)
from pprint import pprint
pprint(tweet, depth=1)
# Twitter's own documentation [provides a useful overview of all the fields in the JSON object](https://dev.twitter.com/overview/api/tweets) and it may be helpful to look at this [visual map of a Tweet object](http://www.scribd.com/doc/30146338/map-of-a-tweet).
#
# Since each Tweet is converted into a Python dictionary, it's straightforward to just show a selected field, such as the value of the `'text'` key.
for tweet in tweets:
print(tweet['text'])
client = Query(**oauth)
client.register(TweetWriter())
client.user_tweets('timoreilly', 10)
# Given a list of user IDs, the following example shows how to retrieve the screen name and other information about the users.
userids = ['759251', '612473', '15108702', '6017542', '2673523800']
client = Query(**oauth)
user_info = client.user_info_from_id(userids)
for info in user_info:
name = info['screen_name']
followers = info['followers_count']
following = info['friends_count']
print("{}, followers: {}, following: {}".format(name, followers, following))
# A list of user IDs can also be used as input to the Streaming API client.
client = Streamer(**oauth)
client.register(TweetViewer(limit=10))
client.statuses.filter(follow=userids)
# To store data that Twitter sents by the Streaming API, we register a `TweetWriter` instance.
client = Streamer(**oauth)
client.register(TweetWriter(limit=10))
client.statuses.sample()
# Here's the full signature of the `Tweetwriter`'s `__init__()` method:
# ```python
# def __init__(self, limit=2000, upper_date_limit=None, lower_date_limit=None,
# fprefix='tweets', subdir='twitter-files', repeat=False,
# gzip_compress=False):
# ```
# If the `repeat` parameter is set to `True`, then the writer will write up to the value of `limit` in file `file1`, then open a new file `file2` and write to it until the limit is reached, and so on indefinitely. The parameter `gzip_compress` can be used to compress the files once they have been written.
# ## <a name="corpus_reader">Using a Tweet Corpus</a>
#
# NLTK's Twitter corpus currently contains a sample of 20k Tweets (named '`twitter_samples`')
# retrieved from the Twitter Streaming API, together with another 10k which are divided according to sentiment into negative and positive.
from nltk.corpus import twitter_samples
twitter_samples.fileids()
# We follow standard practice in storing full Tweets as line-separated
# JSON. These data structures can be accessed via `tweets.docs()`. However, in general it
# is more practical to focus just on the text field of the Tweets, which
# are accessed via the `strings()` method.
strings = twitter_samples.strings('tweets.20150430-223406.json')
for string in strings[:15]:
print(string)
# The default tokenizer for Tweets (`casual.py`) is specialised for 'casual' text, and
# the `tokenized()` method returns a list of lists of tokens.
tokenized = twitter_samples.tokenized('tweets.20150430-223406.json')
for toks in tokenized[:5]:
print(toks)
# ### Extracting Parts of a Tweet
#
# If we want to carry out other kinds of analysis on Tweets, we have to work directly with the file rather than via the corpus reader. For demonstration purposes, we will use the same file as the one in the preceding section, namely `tweets.20150430-223406.json`. The `abspath()` method of the corpus gives us the full pathname of the relevant file. If your NLTK data is installed in the default location on a Unix-like system, this pathname will be `'/usr/share/nltk_data/corpora/twitter_samples/tweets.20150430-223406.json'`.
from nltk.corpus import twitter_samples
input_file = twitter_samples.abspath("tweets.20150430-223406.json")
# The function `json2csv()` takes as input a file-like object consisting of Tweets as line-delimited JSON objects and returns a file in CSV format. The third parameter of the function lists the fields that we want to extract from the JSON. One of the simplest examples is to extract just the text of the Tweets (though of course it would have been even simpler to use the `strings()` method of the corpus reader).
from nltk.twitter.common import json2csv
with open(input_file) as fp:
json2csv(fp, 'tweets_text.csv', ['text'])
# We've passed the filename `'tweets_text.csv'` as the second argument of `json2csv()`. Unless you provide a complete pathname, the file will be created in the directory where you are currently executing Python.
#
# If you open the file `'tweets_text.csv'`, the first 5 lines should look as follows:
#
# ```
# RT @KirkKus: Indirect cost of the UK being in the EU is estimated to be costing Britain £170 billion per year! #BetterOffOut #UKIP
# VIDEO: Sturgeon on post-election deals http://t.co/BTJwrpbmOY
# RT @LabourEoin: The economy was growing 3 times faster on the day David Cameron became Prime Minister than it is today.. #BBCqt http://t.co…
# RT @GregLauder: the UKIP east lothian candidate looks about 16 and still has an msn addy http://t.co/7eIU0c5Fm1
# RT @thesundaypeople: UKIP's housing spokesman rakes in £800k in housing benefit from migrants. http://t.co/GVwb9Rcb4w http://t.co/c1AZxcLh…
# ```
# However, in some applications you may want to work with Tweet metadata, e.g., the creation date and the user. As mentioned earlier, all the fields of a Tweet object are described in [the official Twitter API](https://dev.twitter.com/overview/api/tweets).
#
# The third argument of `json2csv()` can specified so that the function selects relevant parts of the metadata. For example, the following will generate a CSV file including most of the metadata together with the id of the user who has published it.
with open(input_file) as fp:
json2csv(fp, 'tweets.20150430-223406.tweet.csv',
['created_at', 'favorite_count', 'id', 'in_reply_to_status_id',
'in_reply_to_user_id', 'retweet_count', 'retweeted',
'text', 'truncated', 'user.id'])
for line in open('tweets.20150430-223406.tweet.csv').readlines()[:5]:
print(line)
# The first nine elements of the list are attributes of the Tweet, while the last one, `user.id`, takes the user object associated with the Tweet, and retrieves the attributes in the list (in this case only the id). The object for the Twitter user is described in the [Twitter API for users](https://dev.twitter.com/overview/api/users).
# The rest of the metadata of the Tweet are the so-called [entities](https://dev.twitter.com/overview/api/entities) and [places](https://dev.twitter.com/overview/api/places). The following examples show how to get each of those entities. They all include the id of the Tweet as the first argument, and some of them include also the text for clarity.
# +
from nltk.twitter.common import json2csv_entities
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.hashtags.csv',
['id', 'text'], 'hashtags', ['text'])
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.user_mentions.csv',
['id', 'text'], 'user_mentions', ['id', 'screen_name'])
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.media.csv',
['id'], 'media', ['media_url', 'url'])
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.urls.csv',
['id'], 'urls', ['url', 'expanded_url'])
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.place.csv',
['id', 'text'], 'place', ['name', 'country'])
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.place_bounding_box.csv',
['id', 'name'], 'place.bounding_box', ['coordinates'])
# -
# Additionally, when a Tweet is actually a retweet, the original tweet can be also fetched from the same file, as follows:
with open(input_file) as fp:
json2csv_entities(fp, 'tweets.20150430-223406.original_tweets.csv',
['id'], 'retweeted_status', ['created_at', 'favorite_count',
'id', 'in_reply_to_status_id', 'in_reply_to_user_id', 'retweet_count',
'text', 'truncated', 'user.id'])
# Here the first id corresponds to the retweeted Tweet, and the second id to the original Tweet.
#
# ### Using Dataframes
#
# Sometimes it's convenient to manipulate CSV files as tabular data, and this is made easy with the [Pandas](http://pandas.pydata.org/) data analysis library. `pandas` is not currently one of the dependencies of NLTK, and you will probably have to install it specially.
#
# Here is an example of how to read a CSV file into a `pandas` dataframe. We use the `head()` method of a dataframe to just show the first 5 rows.
import pandas as pd
tweets = pd.read_csv('tweets.20150430-223406.tweet.csv', index_col=2, header=0, encoding="utf8")
tweets.head(5)
# Using the dataframe it is easy, for example, to first select Tweets with a specific user ID and then retrieve their `'text'` value.
tweets.loc[tweets['user.id'] == 557422508]['text']
# ## Expanding a list of Tweet IDs
#
# Because the Twitter Terms of Service place severe restrictions on the distribution of Tweets by third parties, a workaround is to instead distribute just the Tweet IDs, which are not subject to the same restrictions. The method `expand_tweetids()` sends a request to the Twitter API to return the full Tweet (in Twitter's terminology, a *hydrated* Tweet) that corresponds to a given Tweet ID.
#
# Since Tweets can be deleted by users, it's possible that certain IDs will only retrieve a null value. For this reason, it's safest to use a `try`/`except` block when retrieving values from the fetched Tweet.
# +
from io import StringIO
ids_f =\
StringIO("""\
588665495492124672
588665495487909888
588665495508766721
588665495513006080
588665495517200384
588665495487811584
588665495525588992
588665495487844352
88665495492014081
588665495512948737""")
oauth = credsfromfile()
client = Query(**oauth)
hydrated = client.expand_tweetids(ids_f)
for tweet in hydrated:
id_str = tweet['id_str']
print('id: {}'.format(id_str))
text = tweet['text']
if text.startswith('@null'):
text = "[Tweet not available]"
print(text + '\n')
# -
# Although we provided the list of IDs as a string in the above example, the standard use case is to pass a file-like object as the argument to `expand_tweetids()`.
|
nltkma/test/twitter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: jup_oct_kernel
# language: python
# name: jup_oct_kernel
# ---
# # Deutsch-Jozsa Algorithm
#
# ## Problem statement:
#
# Given: a function $f$ acting on bit strings $f:\{0,1\}^n \rightarrow \{0,1\}^n$ and a promise that $f(x)=f(x \oplus s)$ for all $x$ (addition mod 2). The goal is to use Simon's algorithm to find the unknown string $s$.
#
#
#
|
04-Deutsch-Jozsa_Algorithm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R [conda env:Georg_animal_feces-phyloseq]
# language: R
# name: conda-env-Georg_animal_feces-phyloseq-r
# ---
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Goal" data-toc-modified-id="Goal-1"><span class="toc-item-num">1 </span>Goal</a></span></li><li><span><a href="#Var" data-toc-modified-id="Var-2"><span class="toc-item-num">2 </span>Var</a></span></li><li><span><a href="#Init" data-toc-modified-id="Init-3"><span class="toc-item-num">3 </span>Init</a></span></li><li><span><a href="#Load" data-toc-modified-id="Load-4"><span class="toc-item-num">4 </span>Load</a></span></li><li><span><a href="#Compare-pass/fail" data-toc-modified-id="Compare-pass/fail-5"><span class="toc-item-num">5 </span>Compare pass/fail</a></span><ul class="toc-item"><li><span><a href="#check/format" data-toc-modified-id="check/format-5.1"><span class="toc-item-num">5.1 </span>check/format</a></span></li><li><span><a href="#Summary" data-toc-modified-id="Summary-5.2"><span class="toc-item-num">5.2 </span>Summary</a></span><ul class="toc-item"><li><span><a href="#Success-rate" data-toc-modified-id="Success-rate-5.2.1"><span class="toc-item-num">5.2.1 </span>Success rate</a></span><ul class="toc-item"><li><span><a href="#Writing-table-of-samples" data-toc-modified-id="Writing-table-of-samples-5.2.1.1"><span class="toc-item-num">5.2.1.1 </span>Writing table of samples</a></span></li></ul></li><li><span><a href="#No.-of-samples" data-toc-modified-id="No.-of-samples-5.2.2"><span class="toc-item-num">5.2.2 </span>No. of samples</a></span></li><li><span><a href="#Passed-per-species" data-toc-modified-id="Passed-per-species-5.2.3"><span class="toc-item-num">5.2.3 </span>Passed per species</a></span></li><li><span><a href="#Mapping-onto-host-tree" data-toc-modified-id="Mapping-onto-host-tree-5.2.4"><span class="toc-item-num">5.2.4 </span>Mapping onto host tree</a></span><ul class="toc-item"><li><span><a href="#Host-metadata" data-toc-modified-id="Host-metadata-5.2.4.1"><span class="toc-item-num">5.2.4.1 </span>Host metadata</a></span></li></ul></li></ul></li></ul></li><li><span><a href="#sessionInfo" data-toc-modified-id="sessionInfo-6"><span class="toc-item-num">6 </span>sessionInfo</a></span></li></ul></div>
# -
# # Goal
#
# * Summary of NGS pass/fail samples
# * how many succeeded of the total?
#
# # Var
# +
work_dir = '/ebio/abt3_projects/Georg_animal_feces/data/16S_arch/NGS/'
# all samples
metadata_file = '/ebio/abt3_projects/Georg_animal_feces/data/mapping/unified_metadata_complete_200429.tsv'
# host tree for all species
host_tree_file = '/ebio/abt3_projects/Georg_animal_feces/data/animal/phylogeny/TT/unified_metadata_complete_20190416_rn.nwk'
## all samples & taxa
physeq_all_file = file.path('/ebio/abt3_projects/Georg_animal_feces/data/16S_arch/MiSeq-Runs-116-122-126-189-190/LLA/merged/phyloseq/physeq_all.RDS')
## 16S-arch phyloseq object (one sample per individual)
physeq_arch_IndD_file = '/ebio/abt3_projects/Georg_animal_feces/data/16S_arch/MiSeq-Runs-116-122-126-189-190/LLA/merged/phyloseq/physeq_arch_IndD.RDS'
# params
threads = 8
# -
# # Init
library(dplyr)
library(tidyr)
library(ggplot2)
library(ape)
library(phyloseq)
library(LeyLabRMisc)
df.dims()
# # Load
# all sample metadata
metadata = read.delim(metadata_file, sep='\t')
metadata
# host tree
host_tree = read.tree(host_tree_file)
host_tree
# all samples
physeq_all = readRDS(physeq_all_file)
## filtering
x = physeq_all %>% sample_names
x = x[grepl('Neg_control', x)]
physeq_all_neg = subset_samples(physeq_all, SampleID %in% x) %>%
filter_taxa(function(x) max(x) > 0, TRUE)
## summary
physeq_all_neg
# all passed samples
physeq_arch_IndD = readRDS(physeq_arch_IndD_file)
physeq_arch_IndD
# +
# formatting
otu = physeq_arch_IndD %>%
phyloseq2df(otu_table, long=TRUE) %>%
group_by(Sample) %>%
mutate(Total_count = sum(Count)) %>%
ungroup() %>%
filter(Count > 0)
tax = physeq_arch_IndD %>%
phyloseq2df(tax_table) %>%
filter(Class == 'Bathyarchaeia')
otu = otu %>%
inner_join(tax, c('OTU'))
otu %>% .$Sample %>% table
# -
# summary
physeq_arch_IndD %>%
phyloseq2df(tax_table) %>%
distinct(Phylum, Class) %>%
arrange(Phylum, Class)
# +
# MiSeq runs 116-122-126
samps = c('1_Eurasian_Beaver', '2_Raccoon_Dog', '5_European_Hare', '21_Yellow_necked_Field_Mouse',
'43_European_Badger', '66_Mouflon', '73_One_humped_Camel', '77_Onager', '78_Indian_Gazelle',
'81_Wolf', '87_Garden_Dormouse', '88_European_Rabbit', '101_Horse', '102_Kulan', '111_West_European_Hedgehog',
'122_Wild_Boar', '137_Gaur', '140_Sambar', '144_Cattle', '152_Tree_Shrew', '198_Human',
'206_Red_Sheep', '237_Red_shanked_Douc_Langur', '272_Black_Grouse', '275_Barnacle_Goose',
'279_Western_Grey_Kangaroo', '285_Short_beaked_Echidna', '287_Common_Brushtail', '289_Eastern_Grey_Kangaroo',
'311_Domestic_Cat', '320_Red_Deer', '376_Kulan', '395_Przewalski_horse', '407_African_Bush_Elephant',
'417_Giraffe', '419_African_Buffalo', '422_Common_Hippopotamus', '424_Quagga', '95_Meadow_Viper',
'123_Alpine_Chamois', '128_Alpine_Marmot', '129_Alpine_Ibex', '131_Rock_Ptarmigan', '155_Long_tailed_Field_Mouse',
'169_Great_Cormorant', '268_Rook', '351_Grass_Snake', '389_Indian_Rhinoceros', '7_European_Otter',
'9_Indian_Gazelle', '11_Onager', '13_Wolf', '15_Tawny_Owl', '16_Fat_Dormouse', '22_European_Rabbit',
'23_Garden_Dormouse', '31_Chicken', '32_Greylag_Goose', '33_Wild_Turkey', '34_Mallard_Duck',
'40_Bactrian_Camel', '41_Pika', '42_Goitered_Gazelle', '60_European_Chub', '85_Domestic_Dog',
'93_Red_Sheep', '94_Mangalica', '96_European_Hare', '116_Common_Kestrel', '121_Raccoon_Dog',
'135_Horse', '138_Gaur', '139_Sambar', '141_Red_cheeked_Gibbon', '150_Cattle', '154_Tree_Shrew',
'157_Grey_Heron', '158_White_tailed_Eagle', '164_Greylag_Goose', '170_Tawny_Owl', '172_European_Greenfinch',
'174_Great_Tit', '195_Domestic_Cat', '196_Domestic_Cat', '197_Human', '199_Human', '200_Human',
'203_Red_Deer', '205_Red_Sheep', '207_Red_Sheep', '208_Red_Sheep', '209_Red_Sheep', '210_Red_Sheep',
'211_Red_Sheep', '212_Goose', '213_Goose', '214_Goose', '215_Goose', '218_Goose', '219_Goose',
'221_Alpine_Ibex', '223_Human', '224_Domestic_Cat', '225_Domestic_Cat', '226_Domestic_Cat',
'228_Domestic_Cat', '230_Carrion_Crow', '234_Beech_Marten', '238_Hanuman_Langur',
'240_Southern_White_cheeked_Gibbon', '252_Eurasian_Lynx', '259_Mute_Swan', '263_White_Stork',
'265_Western_Marsh_Harrier', '270_Common_Pheasant', '271_Common_Pheasant', '276_Barnacle_Goose',
'280_Western_Grey_Kangaroo', '283_Koala', '284_Koala', '286_Short_beaked_Echidna', '290_Eastern_Grey_Kangaroo',
'301_European_Hare', '302_European_Hare', '303_European_Hare', '304_European_Hare', '305_European_Hare',
'306_European_Hare', '307_European_Hare', '308_European_Hare', '309_Domestic_Cat', '310_Domestic_Cat',
'312_Domestic_Cat', '313_Red_Deer', '314_Red_Deer', '315_Red_Deer', '316_Red_Deer', '317_Red_Deer',
'318_Red_Deer', '319_Red_Deer', '322_Red_Deer', '324_Red_Deer', '330_Ide', '332_Harbor_Porpoise',
'333_Gray_Seal', '336_Sei_Whale', '338_White_beaked_Dolphin', '339_White_beaked_Dolphin',
'340_Western_Lowland_Gorilla', '341_Western_Lowland_Gorilla', '344_Indian_Rhinoceros', '347_Brown_Bear',
'348_European_Rabbit', '352_Kinkajou', '353_Raccoon', '355_Hoffmanns_Two_toed_Sloth', '356_Northern_Tamandua',
'360_White_tailed_Deer', '362_Gray_Four_eyed_Opossum', '363_Desmarests_Spiny_Pocket_Mouse',
'368_European_Ground_Squirrel', '369_Koala', '370_African_Bush_Elephant', '371_Linnaeus_Two_toed_Sloth',
'372_Emu', '378_Fat_Sand_Rat', '379_Koala', '390_European_Ground_Squirrel', '391_European_Ground_Squirrel',
'393_European_Rabbit', '394_Przewalski_horse', '396_Morelets_crocodile', '397_Penguin', '404_Brown_Greater_Galago',
'408_African_Bush_Elephant', '409_Impala', '410_Impala', '411_Leopard', '412_Lion', '414_Vervet_Monkey',
'415_White_Rhinoceros', '416_White_Rhinoceros', '418_Giraffe', '420_Cattle', '421_Common_Hippopotamus',
'423_Quagga', '426_Ural_Owl', '427_Great_Spotted_Woodpecker', '428_African_Bush_Elephant', '429_Giraffe',
'430_Giraffe', '432_Vervet_Monkey', '433_Raccoon', '434_Blue_Wildebeest', '435_Bactrian_Camel',
'F14_Common_Bream', 'F35_Red_Deer', 'F36_Red_Deer', 'F44_Fallow_Deer', 'F45_Red_Deer', 'F46_Red_Deer',
'F47_Red_Deer', 'F48_Red_Deer', 'Pos_control_7', 'Neg_control_7', 'F53_Mouflon', 'F66_Wild_Boar',
'F68_Red_Deer', 'F69_Red_Deer', 'F70_Red_Deer', 'F80_Red_Deer', 'F90_Domestic_Dog', '108_Striped_Desert_Hamster',
'109_Red_Fox', '117_Long_eared_Owl', '119_Ural_Owl', '192_Common_Frog', '194_Agile_Frog', '125_Common_Carp',
'126_White_Stork', '130_Alpine_Ibex', '146_Cattle', '153_Bank_Vole', '179_Roach', '233_Aesculapian_Snake',
'236_Pygmy_Slow_Loris', '241_Italian_wall_lizard', '242_Dalmatian_Tortoise', '243_Noctule',
'247_Common_Hamster', '260_Blackbird', '264_Eurasian_Magpie', '266_Western_Marsh_Harrier',
'288_Common_Brushtail', '292_Central_Bearded_Dragon', '297_Horsfields_Bronze_Cuckoo',
'326_Silver_Bream', '327_Silver_Bream', '328_Prussian_Carp', '349_Smooth_Newt', '350_Smooth_Newt',
'380_Wild_Boar', '381_Wild_Boar', '382_Arctic_Wolf', '383_Arctic_Wolf', 'Pos_control_9',
'384_Eurasian_Lynx', '386_Scalloped_Hammerhead', '400_House_Mouse', 'Neg_control_9', '43_European_Badger',
'66_Mouflon', '73_One_humped_Camel', '77_Onager', '88_European_Rabbit', '101_Horse', '102_Kulan',
'111_West_European_Hedgehog', '122_Wild_Boar', '137_Gaur', '140_Sambar', '144_Cattle', '206_Red_Sheep',
'237_Red_shanked_Douc_Langur', '279_Western_Grey_Kangaroo', '285_Short_beaked_Echidna', '287_Common_Brushtail',
'289_Eastern_Grey_Kangaroo', '320_Red_Deer', '376_Kulan', '395_Przewalski_horse', '407_African_Bush_Elephant',
'417_Giraffe', '419_African_Buffalo', '422_Common_Hippopotamus', '424_Quagga', '95_Meadow_Viper',
'123_Alpine_Chamois', '128_Alpine_Marmot', '129_Alpine_Ibex', '131_Rock_Ptarmigan', '268_Rook',
'351_Grass_Snake', '389_Indian_Rhinoceros', '7_European_Otter', '11_Onager', '13_Wolf', '23_Garden_Dormouse',
'31_Chicken', '32_Greylag_Goose', '34_Mallard_Duck', '40_Bactrian_Camel', '42_Goitered_Gazelle',
'60_European_Chub', '94_Mangalica', '96_European_Hare', '116_Common_Kestrel', '121_Raccoon_Dog',
'135_Horse', '138_Gaur', '139_Sambar', '150_Cattle', '154_Tree_Shrew', '172_European_Greenfinch',
'174_Great_Tit', '203_Red_Deer', '205_Red_Sheep', '207_Red_Sheep', '208_Red_Sheep', '209_Red_Sheep',
'210_Red_Sheep', '211_Red_Sheep', '212_Goose', '213_Goose', '214_Goose', '215_Goose', '218_Goose',
'219_Goose', '221_Alpine_Ibex', '238_Hanuman_Langur', '240_Southern_White_cheeked_Gibbon',
'270_Common_Pheasant', '271_Common_Pheasant', '280_Western_Grey_Kangaroo', '283_Koala',
'286_Short_beaked_Echidna', '290_Eastern_Grey_Kangaroo', '313_Red_Deer', '314_Red_Deer',
'315_Red_Deer', '316_Red_Deer', '317_Red_Deer', '318_Red_Deer', '319_Red_Deer', '322_Red_Deer',
'324_Red_Deer', '330_Ide', '333_Gray_Seal', '336_Sei_Whale', '339_White_beaked_Dolphin',
'340_Western_Lowland_Gorilla', '341_Western_Lowland_Gorilla', '344_Indian_Rhinoceros',
'352_Kinkajou', '356_Northern_Tamandua', '360_White_tailed_Deer', '368_European_Ground_Squirrel',
'369_Koala', '370_African_Bush_Elephant', '371_Linnaeus_Two_toed_Sloth', '372_Emu', '378_Fat_Sand_Rat',
'390_European_Ground_Squirrel', '396_Morelets_crocodile', '408_African_Bush_Elephant', '409_Impala',
'410_Impala', '411_Leopard', '415_White_Rhinoceros', '416_White_Rhinoceros', '418_Giraffe', '420_Cattle',
'421_Common_Hippopotamus', '423_Quagga', '428_African_Bush_Elephant', '429_Giraffe', '430_Giraffe',
'432_Vervet_Monkey', '434_Blue_Wildebeest', '435_Bactrian_Camel', 'F14_Common_Bream', 'F35_Red_Deer',
'F36_Red_Deer', 'F44_Fallow_Deer', 'F45_Red_Deer', 'F46_Red_Deer', 'F47_Red_Deer', 'F48_Red_Deer',
'F53_Mouflon', 'F66_Wild_Boar', 'F68_Red_Deer', 'F69_Red_Deer', 'F70_Red_Deer', 'F80_Red_Deer',
'F90_Domestic_Dog', '117_Long_eared_Owl', '130_Alpine_Ibex', '146_Cattle', '179_Roach',
'233_Aesculapian_Snake', '236_Pygmy_Slow_Loris', '242_Dalmatian_Tortoise', '247_Common_Hamster',
'266_Western_Marsh_Harrier', '288_Common_Brushtail', '327_Silver_Bream', '328_Prussian_Carp',
'349_Smooth_Newt', '350_Smooth_Newt', '380_Wild_Boar', '381_Wild_Boar', '382_Arctic_Wolf')
samps = unique(samps)
samps = samps[!grepl('_control_', samps)]
samps %>% length
# -
# function to read in PCR results
read_file = function(F, D){
x = read.delim(file.path(D, F), sep='\t')
x$labware_name = gsub('.+(plate[0-9]).+', '\\1', F)
x$labware_type = '96 Well Eppendorf TwinTec PCR'
return(x)
}
# PCR results
rfu_files = c(
'sd_2019-11-05_11-00-40_Connect1_1.PCR_Georg_16S_Archaea_plate1_2.part_End_Point_Results.txt',
'sd_2019-11-05_11-03-35_Connect2_1.PCR_Georg_16S_Archaea_plate2_2.part_End_Point_Results.txt',
'sd_2019-11-05_11-06-07_Connect3_1.PCR_Georg_16S_Archaea_plate3_2.part_End_Point_Results.txt'
)
D = file.path(work_dir, '191000_SilkeD-prep', 'PCR-step1_plate2')
rfu_sd = rfu_files %>%
as.list %>%
lapply(read_file, D=D) %>%
do.call(rbind, .) %>%
filter(!grepl('control', Sample))
rfu_sd
# plate maps
F = file.path(work_dir, '191000_SilkeD-prep', 'PCR_step1_plate1', 'TECAN_NGS_amplicon_PCR1_map.txt')
plate_map = read.delim(F, sep='\t') %>%
filter(!grepl('control', SampleID)) %>%
mutate(SampleID = SampleID %>% as.character)
plate_map
# summary
all_samps = c(as.character(rfu_sd$Sample), samps, plate_map$SampleID)
all_samps = all_samps[!grepl('control', all_samps)]
all_samps = gsub('^([^X])', 'X\\1', all_samps)
all_samps = gsub('^(^XF)', 'F', all_samps)
all_samps = all_samps %>% unique %>% sort
all_samps %>% length %>% print
all_samps %>% print
# # Compare pass/fail
physeq_arch_IndD %>%
phyloseq2df(otu_table, long = TRUE) %>%
group_by(Sample) %>%
summarize(Count = sum(Count), .groups='drop') %>%
.$Count %>% summary_x
# ## check/format
# checking overlap
overlap(physeq_arch_IndD %>% sample_names, all_samps)
overlap(metadata$SampleID, all_samps)
overlap(metadata$SampleID, all_samps, to_return='diff_y')
metadata = metadata %>%
filter(SampleID %in% all_samps) %>%
mutate(NGS_pass = SampleID %in% (physeq_arch_IndD %>% sample_names))
metadata
# summary
metadata$NGS_pass %>% summary
# filter by class
metadata = metadata %>%
filter(class != 'Chondrichthyes')
metadata$NGS_pass %>% summary
# ## Summary
# ### Success rate
df.dims(20)
metadata %>%
group_by(class) %>%
summarize(n_samples = n(), .groups='drop')
df.dims()
# overall success rate
sr_class = metadata %>%
group_by(class) %>%
mutate(n_samples = n()) %>%
group_by(class, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Class') %>%
rename('feature' = class)
sr_class
# overall success rate
sr_st = metadata %>%
group_by(sample_type) %>%
mutate(n_samples = n()) %>%
group_by(sample_type, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Sample type') %>%
rename('feature' = sample_type)
sr_st
# overall success rate
sr_diet = metadata %>%
group_by(diet) %>%
mutate(n_samples = n()) %>%
group_by(diet, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Diet') %>%
rename('feature' = diet)
sr_diet
# overall success rate
sr_digsys = metadata %>%
mutate(digestive_system = gsub('fermentation activity ', '', digestive_system)) %>%
group_by(digestive_system) %>%
mutate(n_samples = n()) %>%
group_by(digestive_system, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Digestive system') %>%
rename('feature' = digestive_system)
sr_digsys
# overall success rate
sr_hab = metadata %>%
group_by(habitat) %>%
mutate(n_samples = n()) %>%
group_by(habitat, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Habitat') %>%
rename('feature' = habitat)
sr_hab
# overall success rate
sr_cw = metadata %>%
group_by(captive_wild) %>%
mutate(n_samples = n()) %>%
group_by(captive_wild, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Wild/captive') %>%
rename('feature' = captive_wild)
sr_cw
sr = list(sr_class, sr_st, sr_diet, sr_digsys, sr_cw) %>%
do.call(rbind, .)
df.dims(20)
sr
df.dims()
# +
p = sr %>%
ggplot(aes(feature, rate, fill=n_samples)) +
geom_bar(stat='identity') +
scale_fill_gradient('No. of\nsamples', low='blue', high='orange') +
labs(x='Category', y='Success rate (%)') +
facet_wrap(~ category, scales='free_x') +
theme_bw() +
theme(
axis.text.x = element_text(angle=55, hjust=1)
)
p.dims(7,5.5)
plot(p)
# +
p = sr %>%
filter(category %in% c('Class', 'Diet', 'Sample type', 'Wild/captive')) %>%
ggplot(aes(feature, rate, fill=n_samples)) +
geom_bar(stat='identity') +
scale_fill_gradient('No. of\nsamples', low='blue', high='orange') +
labs(x='Category', y='Success rate (%)') +
facet_wrap(~ category, scales='free_x') +
theme_bw() +
theme(
axis.text.x = element_text(angle=55, hjust=1)
)
p.dims(6,5.5)
plot(p)
# -
# overall success rate
sr_order = metadata %>%
filter(class == 'Mammalia') %>%
group_by(order) %>%
mutate(n_samples = n()) %>%
group_by(order, NGS_pass) %>%
summarize(rate = n() / first(n_samples) * 100,
n_samples = first(n_samples),
.groups='drop') %>%
filter(NGS_pass == TRUE) %>%
mutate(category = 'Order') %>%
rename('feature' = order)
sr_order
# +
p = sr_order %>%
mutate(feature = feature %>% reorder(-rate)) %>%
ggplot(aes(feature, rate, fill=n_samples)) +
geom_bar(stat='identity') +
scale_fill_gradient('No. of\nsamples', low='blue', high='orange') +
labs(x='Host order', y='Success rate (%)') +
theme_bw() +
theme(
axis.text.x = element_text(angle=55, hjust=1)
)
p.dims(5,3)
plot(p)
# -
# #### Writing table of samples
out_file = file.path(work_dir, 'NGS_pass-fail_metadata.tsv')
metadata %>%
dplyr::select(SampleID, class, order, family, genus, scientific_name,
diet, sample_type, NGS_pass) %>%
mutate(NGS_pass = ifelse(NGS_pass == TRUE, 'pass', 'fail')) %>%
arrange(class, order, family, genus, scientific_name) %>%
write_table(out_file)
# ### No. of samples
# +
# number of sample samples
p = metadata %>%
group_by(class, NGS_pass) %>%
summarize(N = n(), .groups='drop') %>%
ggplot(aes(class, N, fill=NGS_pass)) +
geom_bar(stat='identity') +
scale_fill_discrete('In final\nGS dataset?') +
labs(x='Host class', y='No. of samples') +
theme_bw() +
theme(
axis.text.x = element_text(angle=45, hjust=1)
)
p.dims(4, 3)
p
# +
# number of sample samples
p = metadata %>%
group_by(sample_type, NGS_pass) %>%
summarize(N = n(), .groups='drop') %>%
ggplot(aes(sample_type, N, fill=NGS_pass)) +
geom_bar(stat='identity') +
scale_fill_discrete('In final\nGS dataset?') +
labs(x='Sample type', y='No. of samples') +
theme_bw() +
theme(
axis.text.x = element_text(angle=45, hjust=1)
)
p.dims(4, 3)
p
# -
# ### Passed per species
# +
# samples per individual
x = metadata %>%
filter(!is.na(scientific_name)) %>%
group_by(scientific_name) %>%
summarize(n_samples = n(), .groups='drop')
# species with >1 sample
x %>% filter(n_samples > 1) %>% nrow
# all species
x %>% nrow
# -
# samples per individual
metadata %>%
filter(!is.na(scientific_name)) %>%
group_by(scientific_name) %>%
summarize(n_samples = n(), .groups='drop') %>%
.$n_samples %>% summary_x
# % of individuals passed per species
meta_s = metadata %>%
filter(!is.na(scientific_name)) %>%
group_by(class, scientific_name, NGS_pass) %>%
summarize(N = n(), .groups='drop') %>%
spread(NGS_pass, N, fill=0) %>%
mutate(perc_pass = `TRUE` / (`TRUE` + `FALSE`) * 100)
meta_s$perc_pass %>% summary_x
meta_s
# +
# plotting
p = meta_s %>%
group_by(class) %>%
mutate(n_species = n()) %>%
ungroup() %>%
ggplot(aes(class, perc_pass, fill=n_species)) +
geom_boxplot() +
scale_fill_gradient('No. of\nspecies', low='blue', high='orange') +
labs(x='Host class', y='Per-species\nsuccess rate') +
theme_bw() +
theme(
axis.text.x = element_text(angle=45, hjust=1)
)
p.dims(4.5, 3)
p
# -
# % of individuals passed per species (just those with >1 sample)
meta_s = metadata %>%
filter(!is.na(scientific_name)) %>%
group_by(scientific_name) %>%
mutate(n_samples = n()) %>%
ungroup() %>%
filter(n_samples > 1) %>%
group_by(class, scientific_name, NGS_pass) %>%
summarize(N = n(), .groups='drop') %>%
spread(NGS_pass, N, fill=0) %>%
mutate(perc_pass = `TRUE` / (`TRUE` + `FALSE`) * 100)
meta_s$perc_pass %>% summary_x
meta_s
# ### Mapping onto host tree
overlap(meta_s$scientific_name, host_tree$tip.label)
overlap(meta_s$scientific_name, host_tree$tip.label, to_return='diff_x')
# filtering the tree
to_rm = setdiff(host_tree$tip.label, meta_s$scientific_name)
host_tree_f = ape::drop.tip(host_tree, to_rm)
host_tree_f
# +
# creating itol mapping
df = meta_s %>%
dplyr::select(scientific_name, `FALSE`, `TRUE`) %>%
rename('passed' = `TRUE`,
'failed' = `FALSE`) %>%
as.data.frame
rownames(df) = df$scientific_name
df$scientific_name = NULL
F = file.path(work_dir, 'NGS_pass-fail_itol-bar.txt')
itol_multibar(df, 'NGS_pass_fail', F)
# -
# writing out tree
F = file.path(work_dir, 'NGS_pass-fail_SpecD.nwk')
write.tree(host_tree_f, F)
cat('File written:', F, '\n')
# #### Host metadata
#
# # sessionInfo
sessionInfo()
|
00_misc/01_NGS_pass-fail.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# # Transformations, Eigenvectors, and Eigenvalues
#
# Matrices and vectors are used together to manipulate spatial dimensions. This has a lot of applications, including the mathematical generation of 3D computer graphics, geometric modeling, and the training and optimization of machine learning algorithms. We're not going to cover the subject exhaustively here; but we'll focus on a few key concepts that are useful to know when you plan to work with machine learning.
#
# ## Linear Transformations
# You can manipulate a vector by multiplying it with a matrix. The matrix acts a function that operates on an input vector to produce a vector output. Specifically, matrix multiplications of vectors are *linear transformations* that transform the input vector into the output vector.
#
# For example, consider this matrix ***A*** and vector ***v***:
#
# $$ A = \begin{bmatrix}2 & 3\\5 & 2\end{bmatrix} \;\;\;\; \vec{v} = \begin{bmatrix}1\\2\end{bmatrix}$$
#
# We can define a transformation ***T*** like this:
#
# $$ T(\vec{v}) = A\vec{v} $$
#
# To perform this transformation, we simply calculate the dot product by applying the *RC* rule; multiplying each row of the matrix by the single column of the vector:
#
# $$\begin{bmatrix}2 & 3\\5 & 2\end{bmatrix} \cdot \begin{bmatrix}1\\2\end{bmatrix} = \begin{bmatrix}8\\9\end{bmatrix}$$
#
# Here's the calculation in Python:
# +
import numpy as np
v = np.array([1,2])
A = np.array([[2,3],
[5,2]])
t = A@v
print (t)
# -
# In this case, both the input vector and the output vector have 2 components - in other words, the transformation takes a 2-dimensional vector and produces a new 2-dimensional vector; which we can indicate like this:
#
# $$ T: \rm I\!R^{2} \to \rm I\!R^{2} $$
#
# Note that the output vector may have a different number of dimensions from the input vector; so the matrix function might transform the vector from one space to another - or in notation, ${\rm I\!R}$<sup>n</sup> -> ${\rm I\!R}$<sup>m</sup>.
#
# For example, let's redefine matrix ***A***, while retaining our original definition of vector ***v***:
#
# $$ A = \begin{bmatrix}2 & 3\\5 & 2\\1 & 1\end{bmatrix} \;\;\;\; \vec{v} = \begin{bmatrix}1\\2\end{bmatrix}$$
#
# Now if we once again define ***T*** like this:
#
# $$ T(\vec{v}) = A\vec{v} $$
#
# We apply the transformation like this:
#
# $$\begin{bmatrix}2 & 3\\5 & 2\\1 & 1\end{bmatrix} \cdot \begin{bmatrix}1\\2\end{bmatrix} = \begin{bmatrix}8\\9\\3\end{bmatrix}$$
#
# So now, our transformation transforms the vector from 2-dimensional space to 3-dimensional space:
#
# $$ T: \rm I\!R^{2} \to \rm I\!R^{3} $$
#
# Here it is in Python:
# +
import numpy as np
v = np.array([1,2])
A = np.array([[2,3],
[5,2],
[1,1]])
t = A@v
print (t)
# +
import numpy as np
v = np.array([1,2])
A = np.array([[1,2],
[2,1]])
t = A@v
print (t)
# -
# ## Transformations of Magnitude and Amplitude
#
# When you multiply a vector by a matrix, you transform it in at least one of the following two ways:
# * Scale the length (*magnitude*) of the matrix to make it longer or shorter
# * Change the direction (*amplitude*) of the matrix
#
# For example consider the following matrix and vector:
#
# $$ A = \begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \;\;\;\; \vec{v} = \begin{bmatrix}1\\0\end{bmatrix}$$
#
# As before, we transform the vector ***v*** by multiplying it with the matrix ***A***:
#
# \begin{equation}\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}\end{equation}
#
# In this case, the resulting vector has changed in length (*magnitude*), but has not changed its direction (*amplitude*).
#
# Let's visualize that in Python:
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
v = np.array([1,0])
A = np.array([[2,0],
[0,2]])
t = A@v
print (t)
# Plot v and t
vecs = np.array([t,v])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
# -
# The original vector ***v*** is shown in orange, and the transformed vector ***t*** is shown in blue - note that ***t*** has the same direction (*amplitude*) as ***v*** but a greater length (*magnitude*).
#
# Now let's use a different matrix to transform the vector ***v***:
# \begin{equation}\begin{bmatrix}0 & -1\\1 & 0\end{bmatrix} \cdot \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}0\\1\end{bmatrix}\end{equation}
#
# This time, the resulting vector has been changed to a different amplitude, but has the same magnitude.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
v = np.array([1,0])
A = np.array([[0,-1],
[1,0]])
t = A@v
print (t)
# Plot v and t
vecs = np.array([v,t])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'blue'], scale=10)
plt.show()
# -
# Now let's see change the matrix one more time:
# \begin{equation}\begin{bmatrix}2 & 1\\1 & 2\end{bmatrix} \cdot \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\1\end{bmatrix}\end{equation}
#
# Now our resulting vector has been transformed to a new amplitude *and* magnitude - the transformation has affected both direction and scale.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
v = np.array([1,0])
A = np.array([[2,1],
[1,2]])
t = A@v
print (t)
# Plot v and t
vecs = np.array([v,t])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'blue'], scale=10)
plt.show()
# -
# ### Afine Transformations
# An Afine transformation multiplies a vector by a matrix and adds an offset vector, sometimes referred to as *bias*; like this:
#
# $$T(\vec{v}) = A\vec{v} + \vec{b}$$
#
# For example:
#
# \begin{equation}\begin{bmatrix}5 & 2\\3 & 1\end{bmatrix} \cdot \begin{bmatrix}1\\1\end{bmatrix} + \begin{bmatrix}-2\\-6\end{bmatrix} = \begin{bmatrix}5\\-2\end{bmatrix}\end{equation}
#
# This kind of transformation is actually the basis of linear regression, which is a core foundation for machine learning. The matrix defines the *features*, the first vector is the *coefficients*, and the bias vector is the *intercept*.
#
# here's an example of an Afine transformation in Python:
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
v = np.array([1,1])
A = np.array([[5,2],
[3,1]])
b = np.array([-2,-6])
t = A@v + b
print (t)
# Plot v and t
vecs = np.array([v,t])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'blue'], scale=15)
plt.show()
# -
# ## Eigenvectors and Eigenvalues
# So we can see that when you transform a vector using a matrix, we change its direction, length, or both. When the transformation only affects scale (in other words, the output vector has a different magnitude but the same amplitude as the input vector), the matrix multiplication for the transformation is the equivalent operation as some scalar multiplication of the vector.
#
# For example, earlier we examined the following transformation that dot-mulitplies a vector by a matrix:
#
# $$\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}$$
#
# You can achieve the same result by mulitplying the vector by the scalar value ***2***:
#
# $$2 \times \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}$$
#
# The following python performs both of these calculation and shows the results, which are identical.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
v = np.array([1,0])
A = np.array([[2,0],
[0,2]])
t1 = A@v
print (t1)
t2 = 2*v
print (t2)
fig = plt.figure()
a=fig.add_subplot(1,1,1)
# Plot v and t1
vecs = np.array([t1,v])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
a=fig.add_subplot(1,2,1)
# Plot v and t2
vecs = np.array([t2,v])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
# -
# In cases like these, where a matrix transformation is the equivelent of a scalar-vector multiplication, the scalar-vector pairs that correspond to the matrix are known respectively as eigenvalues and eigenvectors. We generally indicate eigenvalues using the Greek letter lambda (λ), and the formula that defines eigenvalues and eigenvectors with respect to a transformation is:
#
# $$ T(\vec{v}) = \lambda\vec{v}$$
#
# Where the vector ***v*** is an eigenvector and the value ***λ*** is an eigenvalue for transformation ***T***.
#
# When the transformation ***T*** is represented as a matrix multiplication, as in this case where the transformation is represented by matrix ***A***:
#
# $$ T(\vec{v}) = A\vec{v} = \lambda\vec{v}$$
#
# Then ***v*** is an eigenvector and ***λ*** is an eigenvalue of ***A***.
#
# A matrix can have multiple eigenvector-eigenvalue pairs, and you can calculate them manually. However, it's generally easier to use a tool or programming language. For example, in Python you can use the ***linalg.eig*** function, which returns an array of eigenvalues and a matrix of the corresponding eigenvectors for the specified matrix.
#
# Here's an example that returns the eigenvalue and eigenvector pairs for the following matrix:
#
# $$A=\begin{bmatrix}2 & 0\\0 & 3\end{bmatrix}$$
import numpy as np
A = np.array([[2,0],
[0,3]])
eVals, eVecs = np.linalg.eig(A)
print(eVals)
print(eVecs)
# So there are two eigenvalue-eigenvector pairs for this matrix, as shown here:
#
# $$ \lambda_{1} = 2, \vec{v_{1}} = \begin{bmatrix}1 \\ 0\end{bmatrix} \;\;\;\;\;\; \lambda_{2} = 3, \vec{v_{2}} = \begin{bmatrix}0 \\ 1\end{bmatrix} $$
#
# Let's verify that multiplying each eigenvalue-eigenvector pair corresponds to the dot-product of the eigenvector and the matrix. Here's the first pair:
#
# $$ 2 \times \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}2 \\ 0\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 0\\0 & 3\end{bmatrix} \cdot \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}2 \\ 0\end{bmatrix} $$
#
# So far so good. Now let's check the second pair:
#
# $$ 3 \times \begin{bmatrix}0 \\ 1\end{bmatrix} = \begin{bmatrix}0 \\ 3\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 0\\0 & 3\end{bmatrix} \cdot \begin{bmatrix}0 \\ 1\end{bmatrix} = \begin{bmatrix}0 \\ 3\end{bmatrix} $$
#
# So our eigenvalue-eigenvector scalar multiplications do indeed correspond to our matrix-eigenvector dot-product transformations.
#
# Here's the equivalent code in Python, using the ***eVals*** and ***eVecs*** variables you generated in the previous code cell:
# +
vec1 = eVecs[:,0]
lam1 = eVals[0]
print('Matrix A:')
print(A)
print('-------')
print('lam1: ' + str(lam1))
print ('v1: ' + str(vec1))
print ('Av1: ' + str(A@vec1))
print ('lam1 x v1: ' + str(lam1*vec1))
print('-------')
vec2 = eVecs[:,1]
lam2 = eVals[1]
print('lam2: ' + str(lam2))
print ('v2: ' + str(vec2))
print ('Av2: ' + str(A@vec2))
print ('lam2 x v2: ' + str(lam2*vec2))
# -
# You can use the following code to visualize these transformations:
# +
t1 = lam1*vec1
print (t1)
t2 = lam2*vec2
print (t2)
fig = plt.figure()
a=fig.add_subplot(1,1,1)
# Plot v and t1
vecs = np.array([t1,vec1])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
a=fig.add_subplot(1,2,1)
# Plot v and t2
vecs = np.array([t2,vec2])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
# -
# Similarly, earlier we examined the following matrix transformation:
#
# $$\begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}$$
#
# And we saw that you can achieve the same result by mulitplying the vector by the scalar value ***2***:
#
# $$2 \times \begin{bmatrix}1\\0\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}$$
#
# This works because the scalar value 2 and the vector (1,0) are an eigenvalue-eigenvector pair for this matrix.
#
# Let's use Python to determine the eigenvalue-eigenvector pairs for this matrix:
import numpy as np
A = np.array([[2,0],
[0,2]])
eVals, eVecs = np.linalg.eig(A)
print(eVals)
print(eVecs)
# So once again, there are two eigenvalue-eigenvector pairs for this matrix, as shown here:
#
# $$ \lambda_{1} = 2, \vec{v_{1}} = \begin{bmatrix}1 \\ 0\end{bmatrix} \;\;\;\;\;\; \lambda_{2} = 2, \vec{v_{2}} = \begin{bmatrix}0 \\ 1\end{bmatrix} $$
#
# Let's verify that multiplying each eigenvalue-eigenvector pair corresponds to the dot-product of the eigenvector and the matrix. Here's the first pair:
#
# $$ 2 \times \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}2 \\ 0\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}1 \\ 0\end{bmatrix} = \begin{bmatrix}2 \\ 0\end{bmatrix} $$
#
# Well, we already knew that. Now let's check the second pair:
#
# $$ 2 \times \begin{bmatrix}0 \\ 1\end{bmatrix} = \begin{bmatrix}0 \\ 2\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 0\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}0 \\ 1\end{bmatrix} = \begin{bmatrix}0 \\ 2\end{bmatrix} $$
#
# Now let's use Pythonto verify and plot these transformations:
# +
vec1 = eVecs[:,0]
lam1 = eVals[0]
print('Matrix A:')
print(A)
print('-------')
print('lam1: ' + str(lam1))
print ('v1: ' + str(vec1))
print ('Av1: ' + str(A@vec1))
print ('lam1 x v1: ' + str(lam1*vec1))
print('-------')
vec2 = eVecs[:,1]
lam2 = eVals[1]
print('lam2: ' + str(lam2))
print ('v2: ' + str(vec2))
print ('Av2: ' + str(A@vec2))
print ('lam2 x v2: ' + str(lam2*vec2))
# Plot the resulting vectors
t1 = lam1*vec1
t2 = lam2*vec2
fig = plt.figure()
a=fig.add_subplot(1,1,1)
# Plot v and t1
vecs = np.array([t1,vec1])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
a=fig.add_subplot(1,2,1)
# Plot v and t2
vecs = np.array([t2,vec2])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
# -
# Let's take a look at one more, slightly more complex example. Here's our matrix:
#
# $$\begin{bmatrix}2 & 1\\1 & 2\end{bmatrix}$$
#
# Let's get the eigenvalue and eigenvector pairs:
# +
import numpy as np
A = np.array([[2,1],
[1,2]])
eVals, eVecs = np.linalg.eig(A)
print(eVals)
print(eVecs)
# -
# This time the eigenvalue-eigenvector pairs are:
#
# $$ \lambda_{1} = 3, \vec{v_{1}} = \begin{bmatrix}0.70710678 \\ 0.70710678\end{bmatrix} \;\;\;\;\;\; \lambda_{2} = 1, \vec{v_{2}} = \begin{bmatrix}-0.70710678 \\ 0.70710678\end{bmatrix} $$
#
# So let's check the first pair:
#
# $$ 3 \times \begin{bmatrix}0.70710678 \\ 0.70710678\end{bmatrix} = \begin{bmatrix}2.12132034 \\ 2.12132034\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 1\\0 & 2\end{bmatrix} \cdot \begin{bmatrix}0.70710678 \\ 0.70710678\end{bmatrix} = \begin{bmatrix}2.12132034 \\ 2.12132034\end{bmatrix} $$
#
# Now let's check the second pair:
#
# $$ 1 \times \begin{bmatrix}-0.70710678 \\ 0.70710678\end{bmatrix} = \begin{bmatrix}-0.70710678\\0.70710678\end{bmatrix} \;\;\;and\;\;\; \begin{bmatrix}2 & 1\\1 & 2\end{bmatrix} \cdot \begin{bmatrix}-0.70710678 \\ 0.70710678\end{bmatrix} = \begin{bmatrix}-0.70710678\\0.70710678\end{bmatrix} $$
#
# With more complex examples like this, it's generally easier to do it with Python:
# +
vec1 = eVecs[:,0]
lam1 = eVals[0]
print('Matrix A:')
print(A)
print('-------')
print('lam1: ' + str(lam1))
print ('v1: ' + str(vec1))
print ('Av1: ' + str(A@vec1))
print ('lam1 x v1: ' + str(lam1*vec1))
print('-------')
vec2 = eVecs[:,1]
lam2 = eVals[1]
print('lam2: ' + str(lam2))
print ('v2: ' + str(vec2))
print ('Av2: ' + str(A@vec2))
print ('lam2 x v2: ' + str(lam2*vec2))
# Plot the results
t1 = lam1*vec1
t2 = lam2*vec2
fig = plt.figure()
a=fig.add_subplot(1,1,1)
# Plot v and t1
vecs = np.array([t1,vec1])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
a=fig.add_subplot(1,2,1)
# Plot v and t2
vecs = np.array([t2,vec2])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['blue', 'orange'], scale=10)
plt.show()
# -
# ## Eigendecomposition
# So we've learned a little about eigenvalues and eigenvectors; but you may be wondering what use they are. Well, one use for them is to help decompose transformation matrices.
#
# Recall that previously we found that a matrix transformation of a vector changes its magnitude, amplitude, or both. Without getting too technical about it, we need to remember that vectors can exist in any spatial orientation, or *basis*; and the same transformation can be applied in different *bases*.
#
# We can decompose a matrix using the following formula:
#
# $$A = Q \Lambda Q^{-1}$$
#
# Where ***A*** is a trasformation that can be applied to a vector in its current base, ***Q*** is a matrix of eigenvectors that defines a change of basis, and ***Λ*** is a matrix with eigenvalues on the diagonal that defines the same linear transformation as ***A*** in the base defined by ***Q***.
#
# Let's look at these in some more detail. Consider this matrix:
#
# $$A=\begin{bmatrix}3 & 2\\1 & 0\end{bmatrix}$$
#
# ***Q*** is a matrix in which each column is an eigenvector of ***A***; which as we've seen previously, we can calculate using Python:
# +
import numpy as np
A = np.array([[3,2],
[1,0]])
l, Q = np.linalg.eig(A)
print(Q)
# -
# So for matrix ***A***, ***Q*** is the following matrix:
#
# $$Q=\begin{bmatrix}0.96276969 & -0.48963374\\0.27032301 & 0.87192821\end{bmatrix}$$
#
# ***Λ*** is a matrix that contains the eigenvalues for ***A*** on the diagonal, with zeros in all other elements; so for a 2x2 matrix, Λ will look like this:
#
# $$\Lambda=\begin{bmatrix}\lambda_{1} & 0\\0 & \lambda_{2}\end{bmatrix}$$
#
# In our Python code, we've already used the ***linalg.eig*** function to return the array of eigenvalues for ***A*** into the variable ***l***, so now we just need to format that as a matrix:
L = np.diag(l)
print (L)
# So ***Λ*** is the following matrix:
#
# $$\Lambda=\begin{bmatrix}3.56155281 & 0\\0 & -0.56155281\end{bmatrix}$$
#
# Now we just need to find ***Q<sup>-1</sup>***, which is the inverse of ***Q***:
Qinv = np.linalg.inv(Q)
print(Qinv)
# The inverse of ***Q*** then, is:
#
# $$Q^{-1}=\begin{bmatrix}0.89720673 & 0.50382896\\-0.27816009 & 0.99068183\end{bmatrix}$$
#
# So what does that mean? Well, it means that we can decompose the transformation of *any* vector multiplied by matrix ***A*** into the separate operations ***QΛQ<sup>-1</sup>***:
#
# $$A\vec{v} = Q \Lambda Q^{-1}\vec{v}$$
#
# To prove this, let's take vector ***v***:
#
# $$\vec{v} = \begin{bmatrix}1\\3\end{bmatrix} $$
#
# Our matrix transformation using ***A*** is:
#
# $$\begin{bmatrix}3 & 2\\1 & 0\end{bmatrix} \cdot \begin{bmatrix}1\\3\end{bmatrix} $$
#
# So let's show the results of that using Python:
# +
v = np.array([1,3])
t = A@v
print(t)
# Plot v and t
vecs = np.array([v,t])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'b'], scale=20)
plt.show()
# -
# And now, let's do the same thing using the ***QΛQ<sup>-1</sup>*** sequence of operations:
# +
import math
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
t = (Q@(L@(Qinv)))@v
# Plot v and t
vecs = np.array([v,t])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'b'], scale=20)
plt.show()
# -
# So ***A*** and ***QΛQ<sup>-1</sup>*** are equivalent.
#
# If we view the intermediary stages of the decomposed transformation, you can see the transformation using ***A*** in the original base for ***v*** (orange to blue) and the transformation using ***Λ*** in the change of basis decribed by ***Q*** (red to magenta):
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
t1 = Qinv@v
t2 = L@t1
t3 = Q@t2
# Plot the transformations
vecs = np.array([v,t1, t2, t3])
origin = [0], [0]
plt.axis('equal')
plt.grid()
plt.ticklabel_format(style='sci', axis='both', scilimits=(0,0))
plt.quiver(*origin, vecs[:,0], vecs[:,1], color=['orange', 'red', 'magenta', 'blue'], scale=20)
plt.show()
# -
# So from this visualization, it should be apparent that the transformation ***Av*** can be performed by changing the basis for ***v*** using ***Q*** (from orange to red in the above plot) applying the equivalent linear transformation in that base using ***Λ*** (red to magenta), and switching back to the original base using ***Q<sup>-1</sup>*** (magenta to blue).
# ## Rank of a Matrix
#
# The **rank** of a square matrix is the number of non-zero eigenvalues of the matrix. A **full rank** matrix has the same number of non-zero eigenvalues as the dimension of the matrix. A **rank-deficient** matrix has fewer non-zero eigenvalues as dimensions. The inverse of a rank deficient matrix is singular and so does not exist (this is why in a previous notebook we noted that some matrices have no inverse).
#
# Consider the following matrix ***A***:
#
# $$A=\begin{bmatrix}1 & 2\\4 & 3\end{bmatrix}$$
#
# Let's find its eigenvalues (***Λ***):
import numpy as np
A = np.array([[1,2],
[4,3]])
l, Q = np.linalg.eig(A)
L = np.diag(l)
print(L)
# $$\Lambda=\begin{bmatrix}-1 & 0\\0 & 5\end{bmatrix}$$
#
# This matrix has full rank. The dimensions of the matrix is 2. There are two non-zero eigenvalues.
#
# Now consider this matrix:
#
# $$B=\begin{bmatrix}3 & -3 & 6\\2 & -2 & 4\\1 & -1 & 2\end{bmatrix}$$
#
# Note that the second and third columns are just scalar multiples of the first column.
#
# Let's examine it's eigenvalues:
B = np.array([[3,-3,6],
[2,-2,4],
[1,-1,2]])
lb, Qb = np.linalg.eig(B)
Lb = np.diag(lb)
print(Lb)
# $$\Lambda=\begin{bmatrix}3 & 0& 0\\0 & -6\times10^{-17} & 0\\0 & 0 & 3.6\times10^{-16}\end{bmatrix}$$
#
# Note that matrix has only 1 non-zero eigenvalue. The other two eigenvalues are so extremely small as to be effectively zero. This is an example of a rank-deficient matrix; and as such, it has no inverse.
# ## Inverse of a Square Full Rank Matrix
# You can calculate the inverse of a square full rank matrix by using the following formula:
#
# $$A^{-1} = Q \Lambda^{-1} Q^{-1}$$
#
# Let's apply this to matrix ***A***:
#
# $$A=\begin{bmatrix}1 & 2\\4 & 3\end{bmatrix}$$
#
# Let's find the matrices for ***Q***, ***Λ<sup>-1</sup>***, and ***Q<sup>-1</sup>***:
# +
import numpy as np
A = np.array([[1,2],
[4,3]])
l, Q = np.linalg.eig(A)
L = np.diag(l)
print(Q)
Linv = np.linalg.inv(L)
Qinv = np.linalg.inv(Q)
print(Linv)
print(Qinv)
# -
# So:
#
# $$A^{-1}=\begin{bmatrix}-0.70710678 & -0.4472136\\0.70710678 & -0.89442719\end{bmatrix}\cdot\begin{bmatrix}-1 & -0\\0 & 0.2\end{bmatrix}\cdot\begin{bmatrix}-0.94280904 & 0.47140452\\-0.74535599 & -0.74535599\end{bmatrix}$$
#
# Let's calculate that in Python:
Ainv = (Q@(Linv@(Qinv)))
print(Ainv)
# That gives us the result:
#
# $$A^{-1}=\begin{bmatrix}-0.6 & 0.4\\0.8 & -0.2\end{bmatrix}$$
#
# We can apply the ***np.linalg.inv*** function directly to ***A*** to verify this:
print(np.linalg.inv(A))
|
MathsToML/Module03-Vectors and Matrices/03-05-Transformations Eigenvectors and Eigenvalues.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.3 64-bit (''base'': conda)'
# metadata:
# interpreter:
# hash: bdff06bd94e17c36ce62dbd42a532c4255a44c9d38880a633082aa091992cee7
# name: 'Python 3.8.3 64-bit (''base'': conda)'
# ---
# # Author : <NAME>
#
# ## Task 2 : Prediction using Unsupervised Machine Learning
# ## GRIP @ The Sparks Foundation
#
# In this K-means clustering task I tried to predict the optimum number of clusters and represent it visually from the given ‘Iris’ dataset.
#
#
# ## Technical Stack : Scikit Learn, Numpy Array, Scipy, Pandas, Matplotlib
from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
from sklearn.cluster import KMeans
import matplotlib.patches as mpatches
import sklearn.metrics as sm
from mpl_toolkits.mplot3d import Axes3D
from scipy.cluster.hierarchy import linkage,dendrogram
from sklearn.cluster import DBSCAN
from sklearn.decomposition import PCA
# ## Step 1 - Loading the dataset
iris = datasets.load_iris()
print(iris.data)
print(iris.target_names)
print(iris.target)
x = iris.data
y = iris.target
# ## Step 2 - Visualizing the input data and its Hierarchy
# +
#Plotting
fig = plt.figure(1, figsize=(7,5))
ax = Axes3D(fig, rect=[0, 0, 0.95, 1], elev=48, azim=134)
ax.scatter(x[:, 3], x[:, 0], x[:, 2], edgecolor="k", s=50)
ax.set_xlabel("Petal width")
ax.set_ylabel("Sepal length")
ax.set_zlabel("Petal length")
plt.title("Iris Clustering K Means=3", fontsize=14)
plt.show()
#Hierachy Clustering
hier=linkage(x,"ward")
max_d=7.08
plt.figure(figsize=(15,8))
plt.title('Iris Hierarchical Clustering Dendrogram')
plt.xlabel('Species')
plt.ylabel('distance')
dendrogram(
hier,
truncate_mode='lastp',
p=50,
leaf_rotation=90.,
leaf_font_size=8.,
)
plt.axhline(y=max_d, c='k')
plt.show()
# -
# ## Step 3 - Data Preprocessing
x = pd.DataFrame(iris.data, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width'])
y = pd.DataFrame(iris.target, columns=['Target'])
x.head()
y.head()
# ## Step 4 - Model Training
iris_k_mean_model = KMeans(n_clusters=3)
iris_k_mean_model.fit(x)
print(iris_k_mean_model.labels_)
print(iris_k_mean_model.cluster_centers_)
# ## Step 5 - Visualizing the Model Cluster
# +
plt.figure(figsize=(14,6))
colors = np.array(['red', 'green', 'blue'])
predictedY = np.choose(iris_k_mean_model.labels_, [1, 0, 2]).astype(np.int64)
plt.subplot(1, 2, 1)
plt.scatter(x['Petal Length'], x['Petal Width'], c=colors[y['Target']])
plt.title('Before classification')
plt.legend(handles=[red_patch, green_patch, blue_patch])
plt.subplot(1, 2, 2)
plt.scatter(x['Petal Length'], x['Petal Width'], c=colors[predictedY])
plt.title("Model's classification")
plt.legend(handles=[red_patch, green_patch, blue_patch])
# -
# ## Step 6 - Calculating the Accuracy and Confusion Matrix
sm.accuracy_score(predictedY, y['Target'])
sm.confusion_matrix(predictedY, y['Target'])
# In a confusion matrix, the predicted class labels (0, 1, 2) are written along the top (column names). The true class labels (Iris-setosa, etc.) are written along the right side. Each cell in the matrix is a count of how many instances of a true class where classified as each of the predicted classes.
#
#
# ## Conclusion
# ### I was able to successfully carry-out prediction using Unsupervised Machine Learning task and was able to evaluate the model's clustering accuracy score.
# # Thank You
|
Task-2_Clustering.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import cv2 as cv
from matplotlib import pyplot as plt
img = cv.imread('messi5.jpg')
mask = np.zeros(img.shape[:2],np.uint8)
bgdModel = np.zeros((1,65),np.float64)
fgdModel = np.zeros((1,65),np.float64)
rect = (50,50,450,290)
cv.grabCut(img,mask,rect,bgdModel,fgdModel,5,cv.GC_INIT_WITH_RECT)
mask2 = np.where((mask==2)|(mask==0),0,1).astype('uint8')
img = img*mask2[:,:,np.newaxis]
plt.imshow(img),plt.colorbar(),plt.show()
# +
import os
import sys
import random
import math
import re
import time
import numpy as np
import tensorflow as tf
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.patches as patches
# Root directory of the project
ROOT_DIR = os.path.abspath("../../")
# Import Mask RCNN
sys.path.append(ROOT_DIR) # To find local version of the library
from mrcnn import utils
from mrcnn import visualize
from mrcnn.visualize import display_images
import mrcnn.model as modellib
from mrcnn.model import log
from samples.aerial_building import aerial
# %matplotlib inline
# Directory to save logs and trained model
MODEL_DIR = os.path.join(ROOT_DIR, "logs")
# Path to Ballon trained weights
# You can download this file from the Releases page
# https://github.com/matterport/Mask_RCNN/releases
BALLON_WEIGHTS_PATH = "/mask_rcnn_coco_1.h5" # TODO: update this path
# -
config = aerial.AerialConfig()
AERIAL_DIR = os.path.join(ROOT_DIR, "datasets/aerial")
# +
# Override the training configurations with a few
# changes for inferencing.
class InferenceConfig(config.__class__):
# Run detection on one image at a time
GPU_COUNT = 1
IMAGES_PER_GPU = 1
config = InferenceConfig()
config.display()
# +
# Device to load the neural network on.
# Useful if you're training a model on the same
# machine, in which case use CPU and leave the
# GPU for training.
DEVICE = "/gpu:0" # /cpu:0 or /gpu:0
# Inspect the model in training or inference modes
# values: 'inference' or 'training'
# TODO: code for 'training' test mode not ready yet
TEST_MODE = "inference"
# -
def get_ax(rows=1, cols=1, size=16):
"""Return a Matplotlib Axes array to be used in
all visualizations in the notebook. Provide a
central point to control graph sizes.
Adjust the size attribute to control how big to render images
"""
_, ax = plt.subplots(rows, cols, figsize=(size*cols, size*rows))
return ax
# +
dataset = aerial.AerialDataset()
dataset.load_aerial(AERIAL_DIR, "train")
dataset.prepare()
print("Images: {}\nClasses: {}".format(len(dataset.image_ids), dataset.class_names))
# -
# Create model in inference mode
with tf.device(DEVICE):
model = modellib.MaskRCNN(mode="training", model_dir=MODEL_DIR,
config=config)
# +
# Set path to balloon weights file
# Download file from the Releases page and set its path
# https://github.com/matterport/Mask_RCNN/releases
#weights_path = "/path/to/mask_rcnn_balloon.h5"
#weights_path = "/mask_rcnn_balloon.h5"
# Or, load the last model you trained
#weights_path = model.find_last()
weights_path = "D:/Hamzah/JobPrep/GPU_Projects/MapDataset/MatterPortGit/Mask_RCNN/mask_rcnn_coco_1.h5"
# Load weights
print("Loading weights ", weights_path)
model.load_weights(weights_path, by_name=True, exclude =[ "mrcnn_class_logits", "mrcnn_bbox_fc", "mrcnn_bbox", "mrcnn_mask"])
#exclude=
#image_ids = next(os.walk(dataset_dir))[1]
#Have sloved:use”image_ids = os.listdir(dataset_dir)
# ”replace” image_ids = next(os.walk(dataset_dir))[1]”
# +
#image_id = random.choice(dataset.image_ids)
image_id = 24
image, image_meta, gt_class_id, gt_bbox, gt_mask = modellib.load_image_gt(dataset, config, image_id, use_mini_mask=False)
info = dataset.image_info[image_id]
print("image ID: {}.{} ({}) {}".format(info["source"], info["id"], image_id,
dataset.image_reference(image_id)))
# Run object detection
results = model.detect([image], verbose=1)
# Display results
ax = get_ax(1)
r = results[0]
visualize.display_instances(image, r['rois'], r['masks'], r['class_ids'],
dataset.class_names, r['scores'], ax=ax,
title="Predictions")
log("gt_class_id", gt_class_id)
log("gt_bbox", gt_bbox)
log("gt_mask", gt_mask)
# +
# fresh start
# Training dataset
dataset_train = aerial.AerialDataset()
dataset_train.load_aerial(AERIAL_DIR, "train")
dataset_train.prepare()
dataset_val = aerial.AerialDataset()
dataset_val.load_aerial(AERIAL_DIR, "val")
dataset_val.prepare()
model.train(dataset_train, dataset_val,
learning_rate=config.LEARNING_RATE,
epochs=1,
layers='all')
# -
####
'''
next steps for
create dataset - buildings, pools etc.,u7
x,y,z formt mei images
middle east
mapbox
tiles to geojson
'''
|
building_extraction_mrcnn/samples/Demo_aerial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Analyzing out-of-this world data
# Using data collected from the Open Exoplanet Catalogue database: https://github.com/OpenExoplanetCatalogue/open_exoplanet_catalogue/
#
# ## Data License
# Copyright (C) 2012 <NAME>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy of this database and associated scripts (the "Database"), to deal in the Database without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Database, and to permit persons to whom the Database is furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Database. A reference to the Database shall be included in all scientific publications that make use of the Database.
#
# THE DATABASE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE DATABASE OR THE USE OR OTHER DEALINGS IN THE DATABASE.
#
# ## Setup
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
# -
# ## EDA
planets = pd.read_csv('data/planets.csv')
planets.head()
# ### Looking for correlated features
# It's important to perform an in-depth exploration of the data before modeling. This includes consulting domain experts, looking for correlations between variables, examining distributions, etc. The visualizations covered in chapters 5 and 6 will prove indispensible for this process. One such visualization is the heatmap which we can use to look for correlated features:
fig = plt.figure(figsize=(7, 7))
sns.heatmap(
planets.drop(columns='discoveryyear').corr(),
center=0, vmin=-1, vmax=1, square=True, annot=True,
cbar_kws={'shrink': 0.8}
)
# ### Looking at Orbit shape
# | Eccentricity | Orbit Shape |
# | :---: | :---: |
# | 0 | Circular |
# | (0, 1) | Elliptical |
# | 1 | Parabolic |
# | > 1 | Hyperbolic |
planets.eccentricity.min(), planets.eccentricity.max()
# All of the planets in the data have circular or elliptical orbits. Let's see the distribution:
planets.eccentricity.hist()
plt.xlabel('eccentricity')
plt.ylabel('frequency')
plt.title('Orbit Eccentricities')
# ### Understanding the semi-major axis
# An ellipse, being an elongated circle, has 2 axes: **major** and **minor** for the longest and smallest ones, respectively. The *semi*-major axis is half the major axis. When compared to a circle, the axes are like the diameter crossing the entire shape and the semis are akin to the radius being half the diameter.
from visual_aids import misc_viz
misc_viz.elliptical_orbit()
# ### Checking data values
# With just the variables of interest, we have a lot of missing data:
planets[['period', 'eccentricity', 'semimajoraxis', 'mass']].info()
# If we drop it, we are left with about 30% of it:
planets[['period', 'eccentricity', 'semimajoraxis', 'mass']].dropna().shape
# We use `describe()` to get a summary of the variables of interest:
planets[['period', 'eccentricity', 'semimajoraxis', 'mass']].describe()
# ### Visualizing Year and Orbit Length
# We have information on the planet list each planet belongs to. We may be wondering: are these planets are controversial because they are so far away?
sns.scatterplot(
x=planets.semimajoraxis, y=planets.period,
hue=planets.list, alpha=0.5
)
plt.title('period vs. semimajoraxis')
plt.legend(title='')
# Since semi-major axis is highly correlated with period, let's see how the planets compare and label those in our solar system:
fig, ax = plt.subplots(1, 1, figsize=(10, 10))
in_solar_system = (planets.list == 'Solar System').rename('in solar system?')
sns.scatterplot(
x=planets.semimajoraxis,
y=planets.period,
hue=in_solar_system,
ax=ax
)
ax.set_yscale('log')
solar_system = planets[planets.list == 'Solar System']
for planet in solar_system.name:
data = solar_system.query(f'name == "{planet}"')
ax.annotate(
planet,
(data.semimajoraxis, data.period),
(7 + data.semimajoraxis, data.period),
arrowprops=dict(arrowstyle='->')
)
ax.set_title('log(orbital period) vs. semi-major axis')
# ## Finding Similar Planets with k-Means Clustering
# Since we want to perform clustering to learn more about the data, we will build our pipeline standardizing the data before running k-means and fit it on the all the data:
# +
from sklearn.cluster import KMeans
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
kmeans_pipeline = Pipeline([
('scale', StandardScaler()),
('kmeans', KMeans(8, random_state=0))
])
# -
# Grab the data and fit the model:
kmeans_data = planets[['semimajoraxis', 'period']].dropna()
kmeans_pipeline.fit(kmeans_data)
# We can recreate our plot from before and this time, color by the cluster k-means put each planet in:
fig, ax = plt.subplots(1, 1, figsize=(7, 7))
sns.scatterplot(
x=kmeans_data.semimajoraxis,
y=kmeans_data.period,
hue=kmeans_pipeline.predict(kmeans_data),
ax=ax, palette='Accent'
)
ax.set_yscale('log')
solar_system = planets[planets.list == 'Solar System']
for planet in solar_system.name:
data = solar_system.query(f'name == "{planet}"')
ax.annotate(
planet,
(data.semimajoraxis, data.period),
(7 + data.semimajoraxis, data.period),
arrowprops=dict(arrowstyle='->')
)
ax.get_legend().remove()
ax.set_title('KMeans Clusters')
# The elbow point method can be used to pick a good value for `k`. This value will be were we begin to see diminishing returns in the reduction of the value of the objective function:
# +
from ml_utils.elbow_point import elbow_point
ax = elbow_point(
kmeans_data,
Pipeline([
('scale', StandardScaler()),
('kmeans', KMeans(random_state=0))
])
)
ax.annotate(
'possible appropriate values for k', xy=(2, 900), xytext=(2.5, 1500),
arrowprops=dict(arrowstyle='->')
)
ax.annotate(
'', xy=(3, 480), xytext=(4.4, 1450), arrowprops=dict(arrowstyle='->')
)
# -
# k-means with the "optimal" k of 2
# +
kmeans_pipeline_2 = Pipeline([
('scale', StandardScaler()),
('kmeans', KMeans(2, random_state=0))
]).fit(kmeans_data)
fig, ax = plt.subplots(1, 1, figsize=(7, 7))
sns.scatterplot(
x=kmeans_data.semimajoraxis,
y=kmeans_data.period,
hue=kmeans_pipeline_2.predict(kmeans_data),
ax=ax
)
ax.set_yscale('log')
solar_system = planets[planets.list == 'Solar System']
for planet in solar_system.name:
data = solar_system.query(f'name == "{planet}"')
ax.annotate(
planet,
(data.semimajoraxis, data.period),
(7 + data.semimajoraxis, data.period),
arrowprops=dict(arrowstyle='->')
)
ax.get_legend().remove()
ax.set_title('KMeans Clusters')
# -
# ### Visualizing the cluster space
# Since we standardized the data, looking at the centers tells us the second cluster contains "outliers" for period and semi-major axis:
kmeans_pipeline_2.named_steps['kmeans'].cluster_centers_
# We can also visualize the clusters:
# +
# set up layout
fig = plt.figure(figsize=(8, 6))
outside = fig.add_axes([0.1, 0.1, 0.9, 0.9])
inside = fig.add_axes([0.6, 0.2, 0.35, 0.35])
# scaled data and cluster distance data
scaled = kmeans_pipeline_2.named_steps['scale']\
.fit_transform(kmeans_data)
cluster_distances = kmeans_pipeline_2\
.fit_transform(kmeans_data)
for ax, data, title, axes_labels in zip(
[outside, inside], [scaled, cluster_distances],
['Visualizing Clusters', 'Cluster Distance Space'],
['standardized', 'distance to centroid']
):
sns.scatterplot(
x=data[:,0], y=data[:,1], ax=ax, alpha=0.75, s=100,
hue=kmeans_pipeline_2.named_steps['kmeans'].labels_
)
ax.get_legend().remove()
ax.set_title(title)
ax.set_xlabel(f'semimajoraxis ({axes_labels})')
ax.set_ylabel(f'period ({axes_labels})')
ax.set_ylim(-1, None)
# add the centroids to the outside plot
cluster_centers = kmeans_pipeline_2.named_steps['kmeans'].cluster_centers_
for color, centroid in zip(['blue', 'orange'], cluster_centers):
outside.plot(*centroid, color=color, marker='x')
outside.annotate(
f'{color} center', xy=centroid, xytext=centroid + [0, 5],
arrowprops=dict(arrowstyle='->')
)
# -
# #### Notes on the `scikit-learn` API
#
# |Method|Action|Used when...|
# |---|---|---|
# |`fit()`|Train the model or preprocessor|Modeling, preprocessing|
# |`transform()`|Transform the data into the new space|Clustering, preprocessing|
# |`fit_transform()`|Run `fit()`, followed by `transform()`|Clustering, preprocessing|
# |`score()`|Evaluate the model using the default scoring method|Modeling|
# |`predict()`|Use model to predict output values for given inputs|Modeling|
# |`fit_predict()`|Run `fit()`, followed by `predict()`|Modeling|
# |`predict_proba()`|Like `predict()`, but returns the probability of belonging to each class|Classification|
#
#
# #### Evaluation of model
# There are many metrics to choose from, but since we don't know the true labels of our data, we can only use unsupervised ones. We will use a few different metrics to get a more well-rounded view of our performance:
#
# ##### Silhouette Score
# - true labels not known
# - higher = better defined (more separated) clusters
# - -1 is worst, 1 is best, near 0 indicates overlapping clusters
from sklearn.metrics import silhouette_score
silhouette_score(kmeans_data, kmeans_pipeline.predict(kmeans_data))
# ##### Davies-Bouldin Score
# - true labels not known
# - ratio of within-cluster distances to between-cluster distances
# - zero is the best partition
from sklearn.metrics import davies_bouldin_score
davies_bouldin_score(kmeans_data, kmeans_pipeline.predict(kmeans_data))
# ##### Calinski and Harabasz Score
# - true labels not known
# - higher = better defined (more separated) clusters
from sklearn.metrics import calinski_harabasz_score
calinski_harabasz_score(kmeans_data, kmeans_pipeline.predict(kmeans_data))
# ## Predicting Length of Year in Earth Days (Period)
# 1. separate x and y data, dropping nulls
# 2. create the training and testing sets
# 3. train a linear regression model (no preprocessing since we want to interpret the coefficients)
# 4. isolate the coefficients from the model
# 5. evaluate the model
#
# Step 1:
data = planets[
['semimajoraxis', 'period', 'mass', 'eccentricity']
].dropna()
X = data[['semimajoraxis', 'mass', 'eccentricity']]
y = data.period
# Step 2:
# +
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.25, random_state=0
)
# -
# ### Linear Regression
# Step 3:
from sklearn.linear_model import LinearRegression
lm = LinearRegression().fit(X_train, y_train)
# ### Get equation
# Step 4:
# get intercept
lm.intercept_
# get coefficients
[(col, coef) for col, coef in zip(X_train.columns, lm.coef_)]
# ### Evaluation of model
# Step 5
#
# In order to evaluate our model's predictions against the actual values, we need to make predictions for the test set:
preds = lm.predict(X_test)
# We can then plot the predictions and actual values:
fig, axes = plt.subplots(1, 1, figsize=(5, 3))
axes.plot(X_test.semimajoraxis, y_test, 'ob', label='actuals', alpha=0.5)
axes.plot(X_test.semimajoraxis, preds, 'or', label='predictions', alpha=0.5)
axes.set(xlabel='semimajoraxis', ylabel='period')
axes.legend()
axes.set_title('Linear Regression Results')
# The correlation between the predictions and the actual values tells us they trend together, but we need to look at other metrics to quantify the errors our model makes:
np.corrcoef(y_test, preds)[0][1]
# #### Residuals
# Our residuals have no pattern (left subplot); however, the distribution has some negative skew, and the residuals aren't quite centered around zero (right subplot):
# +
from ml_utils.regression import plot_residuals
plot_residuals(y_test, preds)
# -
# #### R<sup>2</sup>
# By default, the `score()` method of the `LinearRegression` object will give us the $R^2$:
lm.score(X_test, y_test)
# If not, we can use the `r2_score()` function from `sklearn.metrics`:
from sklearn.metrics import r2_score
r2_score(y_test, preds)
# #### Adjusted R<sup>2</sup>
# $R^2$ increases when we add regressors whether or not they actually improve the model. Adjusted $R^2$ penalizes additional regressors to address this:
from ml_utils.regression import adjusted_r2
adjusted_r2(lm, X_test, y_test)
# #### Problems with R<sup>2</sup>
# $R^2$ doesn't tell us about the prediction errors or if we specified the model correctly. Consider Anscombe's quartet from chapter 1:
#
# ##### Anscombe's Quartet
# All four data sets have the same summary statistics (mean, standard deviation, correlation coefficient), despite having different data:
anscombe = sns.load_dataset('anscombe').groupby('dataset')
anscombe.describe()
# When fitted with a regression line, they all have the same $R^2$ despite some of them not indicating a linear relationship between x and y:
from visual_aids import stats_viz
stats_viz.anscombes_quartet(r_squared=True)
# #### Explained Variance
# The percentage of the variance in the data is explained by our model:
from sklearn.metrics import explained_variance_score
explained_variance_score(y_test, preds)
# #### Mean Absolute Error (MAE)
# This gives us an idea of how far off our predictions are on average (in Earth days):
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, preds)
# #### Root Mean Squared Error (RMSE)
# We can use this to punish large errors more:
from sklearn.metrics import mean_squared_error
np.sqrt(mean_squared_error(y_test, preds))
# #### Median Absolute Error
# We can also look at the median absolute error to ignore any outliers in prediction errors and get a better picture of our error:
from sklearn.metrics import median_absolute_error
median_absolute_error(y_test, preds)
# <hr>
# <div style="overflow: hidden; margin-bottom: 10px;">
# <div style="float: left;">
# <a href="../../ch_08/anomaly_detection.ipynb">
# <button>← Chapter 8</button>
# </a>
# <a href="./planet_data_collection.ipynb">
# <button>Planet Data Collection</button>
# </a>
# <a href="./preprocessing.ipynb">
# <button>Preprocessing</button>
# </a>
# <a href="./red_wine.ipynb">
# <button>Red Wine</button>
# </a>
# <a href="./wine.ipynb">
# <button>Red + White Wine</button>
# </a>
# </div>
# <div style="float: right;">
# <a href="../../solutions/ch_09/exercise_1.ipynb">
# <button>Solutions</button>
# </a>
# <a href="../ch_10/red_wine.ipynb">
# <button>Chapter 10 →</button>
# </a>
# </div>
# </div>
# <hr>
|
ch_09/planets_ml.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# `` Creating a dataframe containing postal code, borough and neighborhoods present in canada``
# !pip install bs4
# +
import pandas as pd # for data manipulation
# import numpy as np
import requests # to fetch data from given url
from bs4 import BeautifulSoup # for webscrapping
# +
url = 'https://en.wikipedia.org/wiki/List_of_postal_codes_of_Canada:_M'
html_data = requests.get(url).text
# -
soup = BeautifulSoup(html_data, features='html5lib')
# +
table_contents=[]
table=soup.find('table')
for row in table.findAll('td'):
cell = {}
if row.span.text=='Not assigned':
pass
else:
cell['PostalCode'] = row.p.text[:3]
cell['Borough'] = (row.span.text).split('(')[0]
cell['Neighborhood'] = (((((row.span.text).split('(')[1]).strip(')')).replace(' /',',')).replace(')',' ')).strip(' ')
table_contents.append(cell)
# print(table_contents)
df=pd.DataFrame(table_contents)
df['Borough']=df['Borough'].replace({'Downtown TorontoStn A PO Boxes25 The Esplanade':'Downtown Toronto Stn A',
'East TorontoBusiness reply mail Processing Centre969 Eastern':'East Toronto Business',
'EtobicokeNorthwest':'Etobicoke Northwest','East YorkEast Toronto':'East York/East Toronto',
'MississaugaCanada Post Gateway Processing Centre':'Mississauga'})
# -
df.head()
df.shape
|
Part_01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/dansarmiento/ColaboratoryRunningAnalysis/blob/main/PlotlyCandlestick.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="8ZyPcGAIPcF0" outputId="e1ab96ac-b925-4be0-8273-0bda9a7bca07"
# !pip install yfinance
# + id="GISYZiQhPlD9"
import yfinance as yf
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="jMhffxnoPu1p" outputId="78ede627-b66d-49cd-eca6-ba2fd9719e9d"
mdrx = yf.Ticker('MDRX')
hist = mdrx.history(periods='max', auto_adjust=True)
hist.describe()
# + colab={"base_uri": "https://localhost:8080/"} id="dtF7LCLUQtKZ" outputId="d2652856-053c-4a56-c716-35e1b24195ac"
df = yf.download("MDRX", start="2019-1-1",end="2022-3-30")
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="OfieC0fXShrm" outputId="03971052-7b8e-47bf-cb3a-27cf6f19ca8d"
import plotly.graph_objects as go
import pandas as pd
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="bhto4Dn6TOfQ" outputId="81ca0320-67cf-4d04-a0a4-41ba6f6c3734"
df.index
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="6o0lpXsfTTem" outputId="f5195bb5-f53d-42b7-dc0e-fe6bf630e8dc"
df.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 542} id="KbGnbQiUTVyE" outputId="5640939b-a69f-4751-9fae-0379216e06b8"
# Create an interactive candlestick chart
figure = go.Figure(
data = [go.Candlestick(
x = df.index,
low = df.Low, high = df.High, close = df.Close, open = df.Open,
increasing_line_color = 'green', decreasing_line_color = 'red'
)
]
)
figure.show()
# + id="hvm61MmuUtjJ"
|
PlotlyCandlestick.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from tensorflow.keras.layers import Input, Lambda, Dense, Flatten,Dropout
from tensorflow.keras.models import Model
from tensorflow.keras.applications import EfficientNetB0
from tensorflow.keras.applications.vgg16 import preprocess_input
from tensorflow.keras.preprocessing import image
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import Adam
import numpy as np
from glob import glob
# +
IMAGE_SIZE = [224, 224]
train_path = 'train'
valid_path = 'test'
# +
# add preprocessing layer to the front of VGG
pretrained_model = EfficientNetB0(input_shape=IMAGE_SIZE + [3], weights='imagenet', include_top=False)
# don't train existing weights
for layer in pretrained_model.layers:
layer.trainable = False
pretrained_model.layers[-1].trainable = True
pretrained_model.layers[-2].trainable = True
pretrained_model.layers[-3].trainable = True
# +
# our layers - you can add more if you want
x = Flatten()(pretrained_model.output)
x2 = Dense(256, activation='relu')(x)
x3 = Dropout(0.2)(x2)
prediction = Dense(5, activation='softmax')(x3)
# create a model object
model = Model(inputs=pretrained_model.input, outputs=prediction)
# view the structure of the model
model.summary()
optimizer = Adam(lr = 0.0003)
# tell the model what cost and optimization method to use
model.compile(
loss='categorical_crossentropy',
optimizer=optimizer,
metrics=['accuracy'])
# +
train_datagen = ImageDataGenerator(
shear_range = 0.1,
zoom_range = 0.1,
horizontal_flip = True)
test_datagen = ImageDataGenerator()
training_set = train_datagen.flow_from_directory(train_path,
target_size = (IMAGE_SIZE),
batch_size = 32,
shuffle = True,
class_mode = 'categorical')
test_set = test_datagen.flow_from_directory(valid_path,
target_size = (IMAGE_SIZE),
batch_size = 32,
shuffle = True,
class_mode = 'categorical')
# -
r = model.fit_generator(
training_set,
validation_data=test_set,
epochs=5,
steps_per_epoch=len(training_set),
validation_steps=len(test_set)
)
# serialize model to JSON
model_json = model.to_json()
with open("model.json", "w") as json_file:
json_file.write(model_json)
# serialize weights to HDF5
model.save_weights("model.h5")
print("Saved model to disk")
|
emotion_detection _classification/training.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Display a Web Scene Tutorial
#
# This is the completed solution for the [Diplay a web scene](https://developers.arcgis.com/labs/develop/python/display-a-web-scene) ArcGIS tutorial.
#
# [ArcGIS tutorials](https://developers.arcgis.com/labs/) are short guides demonstrating the three phases of building geospatial apps: Data, Design, Develop.
# +
from arcgis.gis import GIS
gis = GIS()
# -
webscene_search = gis.content.search(query="LA Trails *", item_type="Web Scene")
webscene_search
webscene_item = webscene_search[2]
webscene_item
# ## To display a web scene in your notebook, query the `WebScene` object.
from arcgis.mapping import WebScene
la_trails = WebScene(webscene_item)
la_trails
# ## Challenge
op_layers = la_trails['operationalLayers']
print("The web scene has {} layers".format(len(op_layers)))
for lyr in op_layers:
print("{}\n\t{}".format(lyr['title'], lyr['url']))
|
labs/display_web_scene.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Homework 1: Numerical Integration (20 points)
#
# Group Members: <NAME> (el442, <EMAIL>), <NAME> (kd400, <EMAIL>), <NAME> (qo452, <EMAIL>)
#
# Due on Friday, 01.05.2020.
#Load standard libraries
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# ## Introduction
#
# In this exercise we will numerically evaluate the integral
#
# $$ y_n = y_n(a) = \int_0^1 \left( \frac{x^n}{x+a} \right) dx = \frac{1}{n} - a y_{n-1} .$$
# ### a) Plot the integrand for $a = 5$ and $n = 1, 5, 10, 20, 30, 50$ in the domain $0 \leq x \leq 1$.
# +
#Variables
a = 5
n = np.array([1, 5, 10, 20, 30, 50])
x = np.linspace(0,1,100)
#Define function
def integrand(x,n):
return x**n/(x+a)
#Create a plot for each value in array n from blue to brown
for nval in n:
plt.plot(x, integrand(x, nval))
# -
# ### b) Write a computer program that reads the value of $a$, the starting values $n_0$ and $y_0$, and the final value $n_1$, and performs the iteration from $n_0$ to $n_1$ (either backward or forward, depending on whether $n_1 < n_0$ or $n_0 < n_1$).
# +
#Read the value of a, n_0, y_0 and n_1
a = 5
n0 = 0
n1 = 30
y0 = np.log((1+a)/a)
#Function that returns y_n dependent on y_{n-1}
def yn_forward(a,n,y):
return 1/n - a * y
#Function that returns y_{n-1} dependent on y_n
def yn_backward(a,n,y):
return 1/(n*a) - y/a
#Final function that performs the iterations from n_0 to n_1
y = y0
def yn(a,n0,n1,y):
if n0 < n1: #perform the forward iteration
for i in range(n0,n1):
y = yn_forward(a,i+1,y)
return y
if n0 == n1: #no iteration, return y_0
return y
if n0 > n1: #perform the backward iteration
for i in range(n1,n0):
y = yn_backward(a,n0-(i-n1),y)
return y
print(yn(a,n0,n1,y0))
# -
# ### c) Experiment how this series behaves for iterations from $n_0 = 0$ to $n_1 = 30$ for $y_0 =\ln[(1 + a)/a]$ with $a = 5$. Also try starting with $n_0 = 50$ and iterate back to $n_1 = 30$ for any starting value $y_0$.
# +
#Read the value of a, n_0, y_0 and n_1
a = 5
n0 = 0
n1 = 30
y0 = np.log((1+a)/a)
print(yn(a,n0,n1,y0))
# -
# ### Summary of the results:
#
# - The series diverges for the forward iteration when $a > 1$.
# - It yields unreasonable results, since $y_n$ should never get negative!
# +
#Try backward iteration
a = 5
n0 = 50
n1 = 30
for y in np.linspace(0,5,11):
print(yn(a,n0,n1,y))
# -
# ### Summary of the results:
#
# - The series converges for the backward iteration, no matter what $a$ is.
# - The backward iteration is very stable, independent of the start value $y_0$!
|
Exercise1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# <table>
# <tr align=left><td><img align=left src="./images/CC-BY.png">
# <td>Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) <NAME></td>
# </table>
# # Discussion 1: Introduction to Python
#
# So you want to code in Python? We will do some basic manipulations and demonstrate some of the basics of the notebook interface that we will be using extensively throughout the course.
#
# Topics:
# - Math
# - Variables
# - Lists
# - Control flow
# - Coding style
# - Other data structures
# - IPython/Jupyter notebooks
#
# Other intros:
# - [Basic Python](https://docs.python.org/2/tutorial/introduction.html)
# - [Software Carpentry - Programming in Python](http://swcarpentry.github.io/python-novice-inflammation/)
#
# ## Python Math
#
# Lets start with some basic functions:
2 + 2
32 - (4 + 2)**2
1 / 2
# Why do we get the answer above rather than what we would expect?
#
# The answer has to do with the type of number being used. Python is a "dynamically" typed language and automatically determines what kind of number to allocate for us. Above, because we did not include a decimal, Python automatically treated the expression as integers (`int` type) and according to integer arithmetic, `1 / 2 = 0`. Now if we include a decimal we get:
1.0 / 2
# Note that Python will make the output a `float` in this case. What happens for the following though?
4.0 + 4**(3/2)
4.0 + 4.0**(3.0 / 2.0)
# Good practice to just add a decimal after any number you really want to treat as a `float`.
#
# Additional types of numbers include `complex`, `Decimal` and `Fraction`.
3+5j
# Note that to use "named" functions such as `sqrt` or `sin` we need to `import` a module so that we have access to those functions. When you `import` a module (or package) in Python we are asking Python to go look for the code that is named and make them active in our workspace (also called a namespace in more general parlance). Here is an example where we use Python's builtin `math` module:
import math
math.sqrt(4)
math.sin(math.pi / 2.0)
math.exp(-math.pi / 4.0)
# Note that in order to access these functions we need to prepend the `math.` to the functions and the constant $\pi$. We can forgo this and import all of what `math` holds if we do the following:
from math import *
sin(pi / 2.0)
# Note that many of these functions always return a `float` number regardless of their input.
# ## Variables
#
# Assign variables like you would in any other language:
num_students = 80
room_capacity = 85
(room_capacity - num_students) / room_capacity * 100.0
# Note that we do not get what we expect from this expression as we expected from above. What would we have to change to get this to work?
#
# We could go back to change our initializations but we could also use the function `float` to force these values to be of `float` type:
float(room_capacity - num_students) / float(room_capacity) * 100.0
# Note here we have left the defined variables as integers as it makes sense that they remain that way (fractional students aside).
a = 10
b = a + 2
print b
# ## Lists
#
# One of the most useful data structures in Python is the `list`.
grades = [90.0, 67.0, 85.0, 76.0, 98.0, 70.0]
# Lists are defined with square brackets and delineated by commas. Note that there is another data type called `sequences` denoted by `( )` which are immutable (cannot be changed) once created. Lets try to do some list manipulations with our list of grades above.
# Access a single value in a list
grades[3]
# Note that Python is 0 indexed, i.e. the first value in the list is accessed by `0`.
# Find the length of a list
len(grades)
# Add values to a list
grades = grades + [62.0, 82.0, 59.0]
print grades
# Slicing is another important operation
grades[2:5]
grades[0:4]
grades[:4]
grades[4:]
# Note that the range of values does not include the last indexed! This is important to remember for more than lists but we will get to that later.
grades[4:11]
# Another property of lists is that you can put different types in them at the same time. This can be important to remember if you may have both `int` and `float` types.
remember = ["2", 2, 2.0]
remember[0] / 1
remember[1] / 1
remember[2] / 1
# Finally, one of the more useful list creation functions is `range` which creates a list with the bounds requested
count = range(3,7)
print count
# ## Control Flow
#
# ### `if`
# Most basic logical control
x = 4
if x > 5:
print "x is greater than 5"
elif x < 5:
print "x is less than 5"
else:
print "x is equal to 5"
# ### `for`
#
# The `for` statements provide the most common type of loops in Python (there is also a `while` construct).
for i in range(5):
print i
for i in range(3,7):
print i
for animal in ['cat', 'dog', 'chinchilla']:
print animal
# Related to the `for` statement are the control statements `break` and `continue`. Ideally we can create a loop with logic that can avoid these but sometimes code can be more readable with judiciuos use of these statements.
for n in range(2, 10):
is_prime = True
for x in range(2, n):
if n % x == 0:
print n, 'equals', x, '*', n / x
is_prime = False
break
if is_prime:
print "%s is a prime number" % (n)
# The `pass` statement might appear fairly useless as it simply does nothing but can provide a stub to remember to come back and implement something
def my_func(x):
# Remember to implement this later!
pass
# + [markdown] slideshow={"slide_type": "slide"}
# ### Defining Functions
#
# The last statement above defines a function in Python with an argument called `x`. Functions can be defined and do lots of different things, here are a few examples.
# + slideshow={"slide_type": "subslide"}
def my_print_function(x):
print x
my_print_function(3)
# + slideshow={"slide_type": "subslide"}
def my_add_function(a, b):
return a + b
my_add_function(3.0, 5.0)
# + slideshow={"slide_type": "subslide"}
def my_crazy_function(a, b, c=1.0):
d = a + b**c
return d
my_crazy_function(2.0, 3.0), my_crazy_function(2.0, 3.0, 2.0), my_crazy_function(2.0, 3.0, c=2.0)
# + slideshow={"slide_type": "subslide"}
def my_other_function(a, b, c=1.0):
return a + b, a + b**c, a + b**(3.0 / 7.0)
my_other_function(2.0, 3.0, c=2.0)
# + [markdown] slideshow={"slide_type": "subslide"}
# Let's try writing a bit more of a complex (and useful) function. The Fibinocci sequence is formed by adding the previous two numbers of the sequence to get the next value (starting with `[0, 1]`).
# + slideshow={"slide_type": "subslide"}
def fibonacci(n):
"""Return a list of the Fibonacci sequence up to n"""
values = [0, 1]
while values[-1] <= n:
values.append(values[-1] + values[-2])
print values
return values
fibonacci(100)
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Coding Style
#
# Very important in practice to write readable and understandable code. Here are a few things to keep in mind while programming in and out of this class, we will work on this actively as the semester progresses as well. The standard for which Python program are written to is called [PEP 8](http://www.python.org/dev/peps/pep-0008) and contains the following basic guidelines:
# - Use 4-space indentation, no tabs
# - Wrap lines that exceed 80 characters
# - Use judicious use of blank lines to separate out functions, classes, and larger blocks of contained code
# - Comment! Also, put comments on their own line when possible
# - Use `docstrings` (function descriptions)
# - Use spaces around operators and after commas, `a = f(1, 2) + g(3, 4)`
# - Name your classes and functions consistently.
# - Use `CamelCase` for classes
# - Use `lower_case_with_underscores` for functions and variables
# - When in doubt be verbose with your comments and names of variables, functions, and classes
# -
# To help all of us learn from each other what coding styles are easier to read we will be doing peer-reviews of the coding portions of the assignments. After the first asssignment is turned in we will review a general template for code review which you will need to fill out for each of your peer's homework. Please be as thorough and helpful as you can!
# ## IPython/Jupyter Notebooks
#
# We will use a lot of IPython/Jupyter notebooks in this class for both class notes (what you are looking at now) and for turning in homework. The IPython notebook allows for the inline inclusion of a number of different types of input, the most critical will be
# - Code (python or otherwise) and
# - Markdown which includes
# - LaTeX,
# - HTML, and
# - JavaScript.
# IPython notebooks allow us to organize and comment on our efforts together along with writing active documents that can be modified in-situ to our work. This can lead to better practice of important ideas such as reproducibility in our work.
|
01_intro_to_python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Creating a graph of a Home Assistant sensor
# This notebook contains a simple example that creates a graph with data stored by Home Assistant in the local database. For a introduction to [matplotlib](http://matplotlib.org/) check the [matplotlib - 2D and 3D plotting in Python](http://nbviewer.jupyter.org/github/jrjohansson/scientific-python-lectures/blob/master/Lecture-4-Matplotlib.ipynb) notebook.
# ### Setup
# matplotlib for plotting the data
# %pylab inline
# +
# Instead of SQLAlchemy is the built-in Python support for SQLite used.
import sqlite3
import datetime
from matplotlib import dates
# -
conn = sqlite3.connect('/path/to/.homeassistant/home-assistant_v2.db')
# ### Query
data = conn.execute("SELECT state, last_changed FROM states WHERE entity_id = 'sensor.random' AND state != 'unknown'")
# ### Prepare data for graph
values = []
timestamps = []
for x in data:
timestamps.append(dates.date2num(datetime.datetime.strptime(x[1], '%Y-%m-%d %H:%M:%S.%f')))
values.append(float(x[0]))
# ### Plot the graph
plt.plot_date(x=timestamps, y=values, fmt="r-")
plt.ylabel('Values')
plt.xlabel('Time line')
|
other/graph-single-sensor.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Logistic Regression with a Neural Networks
#
# We will build a logistic regression classifier to recognize cats and dogs.
#
# -We do not use loops (for/while) in our code, unless extremely necessary.
#
# **We learn to:**
# - Build the general architecture of a learning algorithm, including:
# - Initializing parameters
# - Calculating the cost function and its gradient
# - Using an optimization algorithm (gradient descent)
# - Gather all three functions above into a main model function, in the right order.
# ## 1 - Packages ##
# Import all the packages that you will need.
import numpy as np
import matplotlib.pyplot as plt
import h5py
import scipy
from PIL import Image
from scipy import ndimage
from skimage.transform import resize
#from lr_utils import load_dataset
import os, shutil
# %matplotlib inline
# ## 2 - Overview of the Problem set ##
#
# **Problem Statement**: We have a dataset containing:
# - a training set of m_train(2000) images labeled as cat (y=1) or dog (y=0)
# - a test set of m_test(1000) images labeled as cat or dog
# - each image is of different shape. We reshape it to be (num_px, num_px, 3) where 3 is for the 3 channels (RGB). Thus, each image is square (height = num_px) and (width = num_px).
#
# We will build a simple image-recognition algorithm that can correctly classify pictures as cat or dog.
#
# Let's get more familiar with the dataset. Load the data by running the following code.
# +
# Loading the data (cat/dog)
base_dir_train = '/Users/nayeem/Documents/Code/DeepLearning/ConvNets/cats_dogs_small/train/'
base_dir_test = '/Users/nayeem/Documents/Code/DeepLearning/ConvNets/cats_dogs_small/test/'
train_dir = os.path.join(base_dir_train,'trg_set/')
test_dir = os.path.join(base_dir_test,'test_set/')
train_set_x_orig = list()
train_set_y = list()
for file in os.listdir(train_dir):
# print(file)
label = 1.0
if file.startswith('dog'):
label = 0.0
im = np.asarray(Image.open(train_dir+file))
# print(im.shape)
im_resized = resize(im, (200,200,3))
# print(im_resized.shape)
# plt.imshow(im_resized)
train_set_x_orig.append(im_resized)
train_set_y.append(label)
train_set_x_orig = np.asarray(train_set_x_orig)
train_set_y = np.asarray(train_set_y)
train_set_y= train_set_y.reshape(1,train_set_y.shape[0])
test_set_x_orig = list()
test_set_y = list()
for file in os.listdir(test_dir):
# print(file)
label = 1.0
if file.startswith('dog'):
label = 0.0
im = np.asarray(Image.open(test_dir+file))
# print(im.shape)
im_resized = resize(im, (200,200,3))
# print(im_resized.shape)
# plt.imshow(im_resized)
test_set_x_orig.append(im_resized)
test_set_y.append(label)
test_set_x_orig = np.asarray(test_set_x_orig)
test_set_y = np.asarray(test_set_y)
test_set_y= test_set_y.reshape(1,test_set_y.shape[0])
# -
print(train_set_x_orig.shape)
print(test_set_x_orig.shape)
print(train_set_y.shape)
print(test_set_y.shape)
# We added "_orig" at the end of image datasets (train and test) because we are going to preprocess them. After preprocessing, we will end up with train_set_x and test_set_x (the labels train_set_y and test_set_y don't need any preprocessing).
#
# Each line of your train_set_x_orig and test_set_x_orig is an array representing an image. You can visualize an example by running the following code. Feel free also to change the `index` value and re-run to see other images.
# Example of a picture
index = 25
plt.imshow(train_set_x_orig[index])
print ("y = " + str(train_set_y[:, index]))
# Many software bugs in deep learning come from having matrix/vector dimensions that don't fit. If you can keep your matrix/vector dimensions straight you will go a long way toward eliminating many bugs.
#
# **Data dimensions:**
# - m_train (number of training examples)
# - m_test (number of test examples)
# - num_px (= height = width of a training image)
# Remember that `train_set_x_orig` is a numpy-array of shape (m_train, num_px, num_px, 3). For instance, you can access `m_train` by writing `train_set_x_orig.shape[0]`.
# +
m_train = train_set_y.shape[1]
m_test = test_set_y.shape[1]
num_px = train_set_x_orig[0].shape[0]
print ("Number of training examples: m_train = " + str(m_train))
print ("Number of testing examples: m_test = " + str(m_test))
print ("Height/Width of each image: num_px = " + str(num_px))
print ("Each image is of size: (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_set_x shape: " + str(train_set_x_orig.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x shape: " + str(test_set_x_orig.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
# -
# For convenience, we reshape images of shape (num_px, num_px, 3) in a numpy-array of shape (num_px $*$ num_px $*$ 3, 1). After this, our training (and test) dataset is a numpy-array where each column represents a flattened image. There should be m_train (respectively m_test) columns.
#
#
# A trick when you want to flatten a matrix X of shape (a,b,c,d) to a matrix X_flatten of shape (b$*$c$*$d, a) is to use:
# ```python
# X_flatten = X.reshape(X.shape[0], -1).T # X.T is the transpose of X
# ```
# +
# Reshape the training and test examples
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T
print ("train_set_x_flatten shape: " + str(train_set_x_flatten.shape))
print ("train_set_y shape: " + str(train_set_y.shape))
print ("test_set_x_flatten shape: " + str(test_set_x_flatten.shape))
print ("test_set_y shape: " + str(test_set_y.shape))
print ("sanity check after reshaping: " + str(train_set_x_flatten[0:5,0]))
# -
# To represent color images, the red, green and blue channels (RGB) must be specified for each pixel, and so the pixel value is actually a vector of three numbers ranging from 0 to 255.
# One common preprocessing step in machine learning is to center and standardize your dataset, meaning that you substract the mean of the whole numpy array from each example, and then divide each example by the standard deviation of the whole numpy array. But for picture datasets, it is simpler and more convenient and works almost as well to just divide every row of the dataset by 255 (the maximum value of a pixel channel).
# Let's standardize our dataset.
train_set_x = train_set_x_flatten/255.
test_set_x = test_set_x_flatten/255.
# ## 3 - General Architecture of the learning algorithm ##
#
# It's time to design a simple algorithm to distinguish cat images from dog images.
#
# Build a Logistic Regression, using a Neural Network mindset. The following Figure explains why **Logistic Regression is actually a very simple Neural Network!**
#
# <img src="images/logregNN.jpg" >
#
# **Mathematical expression of the algorithm**:
#
# For one example $x^{(i)}$:
# $$z^{(i)} = w^T x^{(i)} + b \tag{1}$$
# $$\hat{y}^{(i)} = a^{(i)} = sigmoid(z^{(i)})\tag{2}$$
# $$ \mathcal{L}(a^{(i)}, y^{(i)}) = - y^{(i)} \log(a^{(i)}) - (1-y^{(i)} ) \log(1-a^{(i)})\tag{3}$$
#
# The cost is then computed by summing over all training examples:
# $$ J = \frac{1}{m} \sum_{i=1}^m \mathcal{L}(a^{(i)}, y^{(i)})\tag{6}$$
#
# **Key steps**:
#
# - Initialize the parameters of the model
# - Learn the parameters for the model by minimizing the cost
# - Use the learned parameters to make predictions (on the test set)
# - Analyse the results and conclude
# ## 4 - Building the parts of our algorithm ##
#
# The main steps for building a Neural Network are:
# 1. Define the model structure (such as number of input features)
# 2. Initialize the model's parameters
# 3. Loop:
# - Calculate current loss (forward propagation)
# - Calculate current gradient (backward propagation)
# - Update parameters (gradient descent)
#
# You often build 1-3 separately and integrate them into one function we call `model()`.
#
# ### 4.1 - Helper functions
#
# We need to compute $sigmoid( w^T x + b) = \frac{1}{1 + e^{-(w^T x + b)}}$ to make predictions.
def sigmoid(z):
"""
Compute the sigmoid of z
Arguments:
z -- A scalar or numpy array of any size.
Return:
s -- sigmoid(z)
"""
s = 1/(1+np.exp(-z))
return s
##test
print ("sigmoid([0, 2]) = " + str(sigmoid(np.array([0,2]))))
# ### 4.2 - Initializing parameters
def initialize_with_zeros(dim):
"""
This function creates a vector of zeros of shape (dim, 1) for w and initializes b to 0.
Argument:
dim -- size of the w vector we want (or number of parameters in this case)
Returns:
w -- initialized vector of shape (dim, 1)
b -- initialized scalar (corresponds to the bias)
"""
w = np.zeros((dim,1))
b = 0
assert(w.shape == (dim, 1))
assert(isinstance(b, float) or isinstance(b, int))
return w, b
# Test
dim = 2
w, b = initialize_with_zeros(dim)
print ("w = " + str(w))
print ("b = " + str(b))
# For image inputs, w will be of shape (num_px $\times$ num_px $\times$ 3, 1).
# ### 4.3 - Forward and Backward propagation
#
# Now that your parameters are initialized, do the "forward" and "backward" propagation steps for learning the parameters.
#
#
# Forward Propagation:
# - You get X
# - You compute $A = \sigma(w^T X + b) = (a^{(0)}, a^{(1)}, ..., a^{(m-1)}, a^{(m)})$
# - You calculate the cost function: $J = -\frac{1}{m}\sum_{i=1}^{m}y^{(i)}\log(a^{(i)})+(1-y^{(i)})\log(1-a^{(i)})$
#
# Here are the two formulas we will be using:
#
# $$ \frac{\partial J}{\partial w} = \frac{1}{m}X(A-Y)^T\tag{7}$$
# $$ \frac{\partial J}{\partial b} = \frac{1}{m} \sum_{i=1}^m (a^{(i)}-y^{(i)})\tag{8}$$
def propagate(w, b, X, Y):
"""
Implement the cost function and its gradient for the propagation explained above
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if non-cat, 1 if cat) of size (1, number of examples)
Return:
cost -- negative log-likelihood cost for logistic regression
dw -- gradient of the loss with respect to w, thus same shape as w
db -- gradient of the loss with respect to b, thus same shape as b
"""
m = X.shape[1]
# FORWARD PROPAGATION (FROM X TO COST)
A = sigmoid(np.dot(w.T,X)+b) # compute activation
cost = (-1/m)*np.sum(Y*np.log(A)+ (1-Y)*np.log(1-A)) # compute cost
# BACKWARD PROPAGATION (TO FIND GRAD)
dw = (1/m)*np.dot(X,(A-Y).T)
db = (1/m)*np.sum(A-Y)
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost)
assert(cost.shape == ())
grads = {"dw": dw,
"db": db}
return grads, cost
#Test
w, b, X, Y = np.array([[1.],[2.]]), 2., np.array([[1.,2.,-1.],[3.,4.,-3.2]]), np.array([[1,0,1]])
grads, cost = propagate(w, b, X, Y)
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
print ("cost = " + str(cost))
# ### d) Optimization
# - You have initialized your parameters.
# - You are also able to compute a cost function and its gradient.
# - Now, you want to update the parameters using gradient descent.
#
# **Goal:** The goal is to learn $w$ and $b$ by minimizing the cost function $J$. For a parameter $\theta$, the update rule is $ \theta = \theta - \alpha \text{ } d\theta$, where $\alpha$ is the learning rate.
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
"""
This function optimizes w and b by running a gradient descent algorithm
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of shape (num_px * num_px * 3, number of examples)
Y -- true "label" vector (containing 0 if dog, 1 if cat), of shape (1, number of examples)
num_iterations -- number of iterations of the optimization loop
learning_rate -- learning rate of the gradient descent update rule
print_cost -- True to print the loss every 100 steps
Returns:
params -- dictionary containing the weights w and bias b
grads -- dictionary containing the gradients of the weights and bias with respect to the cost function
costs -- list of all the costs computed during the optimization, this will be used to plot the learning curve.
Tips:
You basically need to write down two steps and iterate through them:
1) Calculate the cost and the gradient for the current parameters. Use propagate().
2) Update the parameters using gradient descent rule for w and b.
"""
costs = []
for i in range(num_iterations):
# Cost and gradient calculation
grads, cost = propagate(w, b, X, Y)
# Retrieve derivatives from grads
dw = grads["dw"]
db = grads["db"]
# update rule
w = w - learning_rate*dw
b = b - learning_rate*db
# Record the costs
if i % 100 == 0:
costs.append(cost)
# Print the cost every 100 training examples
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
# +
# Test
params, grads, costs = optimize(w, b, X, Y, num_iterations= 100, learning_rate = 0.009, print_cost = False)
print ("w = " + str(params["w"]))
print ("b = " + str(params["b"]))
print ("dw = " + str(grads["dw"]))
print ("db = " + str(grads["db"]))
# -
# The previous function will output the learned w and b. We are able to use w and b to predict the labels for a dataset X. Implement the `predict()` function. There is two steps to computing predictions:
#
# 1. Calculate $\hat{Y} = A = \sigma(w^T X + b)$
#
# 2. Convert the entries of a into 0 (if activation <= 0.5) or 1 (if activation > 0.5), stores the predictions in a vector `Y_prediction`.
def predict(w, b, X):
'''
Predict whether the label is 0 or 1 using learned logistic regression parameters (w, b)
Arguments:
w -- weights, a numpy array of size (num_px * num_px * 3, 1)
b -- bias, a scalar
X -- data of size (num_px * num_px * 3, number of examples)
Returns:
Y_prediction -- a numpy array (vector) containing all predictions (0/1) for the examples in X
'''
m = X.shape[1]
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0], 1)
# Compute vector "A" predicting the probabilities of a cat/dog being present in the picture
A = sigmoid(np.dot(w.T,X)+b)
for i in range(A.shape[1]):
# Convert probabilities A[0,i] to actual predictions p[0,i]
if A[0,i] <= 0.5:
Y_prediction[0,i] = 0
else:
Y_prediction[0,i] = 1
assert(Y_prediction.shape == (1, m))
return Y_prediction
w = np.array([[0.1124579],[0.23106775]])
b = -0.3
X = np.array([[1.,-1.1,-3.2],[1.2,2.,0.1]])
print ("predictions = " + str(predict(w, b, X)))
# ## 5 - Merge all functions into a model ##
#
# You will now see how the overall model is structured by putting together all the building blocks (functions implemented in the previous parts) together, in the right order.
#
# Implement the model function. Use the following notation:
# - Y_prediction for your predictions on the test set
# - Y_prediction_train for your predictions on the train set
# - w, costs, grads for the outputs of optimize()
def model(X_train, Y_train, X_test, Y_test, num_iterations = 2000, learning_rate = 0.05, print_cost = False):
"""
Builds the logistic regression model by calling the function you've implemented previously
Arguments:
X_train -- training set represented by a numpy array of shape (num_px * num_px * 3, m_train)
Y_train -- training labels represented by a numpy array (vector) of shape (1, m_train)
X_test -- test set represented by a numpy array of shape (num_px * num_px * 3, m_test)
Y_test -- test labels represented by a numpy array (vector) of shape (1, m_test)
num_iterations -- hyperparameter representing the number of iterations to optimize the parameters
learning_rate -- hyperparameter representing the learning rate used in the update rule of optimize()
print_cost -- Set to true to print the cost every 100 iterations
Returns:
d -- dictionary containing information about the model.
"""
# initialize parameters with zeros
w, b = initialize_with_zeros(X_train.shape[0])
# Gradient descent
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# Retrieve parameters w and b from dictionary "parameters"
w = parameters["w"]
b = parameters["b"]
# Predict test/train set examples
Y_prediction_test = predict(w,b,X_test)
Y_prediction_train = predict(w,b,X_train)
# Print train/test accuracy
print("train accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
print("test accuracy: {} %".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))
d = {"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediction_train" : Y_prediction_train,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations}
return d
# Run the following cell to train your model.
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1500, learning_rate = 0.01, print_cost = False)
# ## 6 - Analysis to pick learning rates ##
#
# #### Choice of learning rate ####
#
# **Reminder**:
# In order for Gradient Descent to work you must choose the learning rate wisely. The learning rate $\alpha$ determines how rapidly we update the parameters. If the learning rate is too large we may "overshoot" the optimal value. Similarly, if it is too small we will need too many iterations to converge to the best values. That's why it is crucial to use a well-tuned learning rate.
#
# Compare the learning curve of our model with several choices of learning rates.
# +
#learning_rates = [0.1,0.05,0.01, 0.001, 0.0001]
learning_rates = [0.5]
models = {}
for i in learning_rates:
print ("learning rate is: " + str(i))
models[str(i)] = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 1000000, learning_rate = i, print_cost = False)
print ('\n' + "-------------------------------------------------------" + '\n')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]["costs"]), label= str(models[str(i)]["learning_rate"]))
plt.ylabel('cost')
plt.xlabel('iterations')
legend = plt.legend(loc='upper center', shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
# -
|
Notebooks/LogRegressionUsingNeuralNetworks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Face Detection
# ### For pictures
# importing lib
import cv2
import matplotlib.pyplot as plt
# reading image
img = cv2.imread("image.jpg")
# ploting image by default it is bgr so it is inversing color
plt.imshow(img)
# converting bgr to rbg
img_rgb = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
# ploting rgb image
plt.imshow(img_rgb)
# loading classifier for face detection
obj = cv2.CascadeClassifier(r"C:\Users\Aditya\AppData\Local\Programs\Python\Python39\Lib\site-packages\cv2\data//haarcascade_frontalface_default.xml")
# detecting face
face = obj.detectMultiScale(img)
# fetching face co-ordinates
x,y,w,h = face[0]
# slicing face from image
face = img_rgb[y:y+h,x:x+w]
# ploting image
plt.imshow(face)
# highlighting face area by putting rectangle
cv2.rectangle(img_rgb, (x,y), (x+w,y+h), (255,0,0),3)
plt.imshow(img_rgb)
# ### For realtime Video capturing
# +
# importing lib
import cv2
# opening vdo stream
vdo = cv2.VideoCapture(0)
# initializing classifier
obj = cv2.CascadeClassifier(r"C:\Users\Aditya\AppData\Local\Programs\Python\Python39\Lib\site-packages\cv2\data//haarcascade_frontalface_default.xml")
while True:
# reading each frame of vdo as frames from vdo stream
flag,frames = vdo.read()
# detecting each frame
face = obj.detectMultiScale(frames)
# from every detectable face
for f in face:
x,y,w,h = f
# putting rectangle
cv2.rectangle(frames, (x,y), (x+w,y+h), (255,0,0),3)
#
cv2.imshow("vdo",frames)
key = cv2.waitKey(1)
if key==ord("q"):
break
|
KNN-CLASSIFICATION/FACE_DETECTION/main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: EQTransformer
# language: python
# name: eqtransformer
# ---
# +
import numpy as np
test = np.load('EQTransformer/ModelsAndSampleData/test.npy')
selectDataSize=8000
csv_file = "../../MLData/metadata_11_13_19.csv"
file_name = "../../MLData/waveforms_11_13_19.hdf5"
# -
len(test)
import pandas as pd
df = pd.read_csv(csv_file)
test[0] in list(df.trace_name)
from EQTransformer.core.trainer import trainer
trainer(input_hdf5='EQTransformer/ModelsAndSampleData/100samples.hdf5',
input_csv='EQTransformer/ModelsAndSampleData/100samples.csv',
output_name='test_trainer',
cnn_blocks=2,
lstm_blocks=1,
padding='same',
activation='relu',
drop_rate=0.2,
label_type='gaussian',
add_event_r=0.6,
add_gap_r=0.2,
shift_event_r=0.9,
add_noise_r=0.5,
mode='generator',
train_valid_test_split=[0.60, 0.20, 0.20],
batch_size=20,
epochs=10,
patience=2,
gpuid=None,
gpu_limit=None)
from EQTransformer.core.tester import tester
tester(input_hdf5='EQTransformer/ModelsAndSampleData/100samples.hdf5',
input_testset='test_trainer_outputs/test.npy',
input_model='EQTransformer/ModelsAndSampleData/EqT_model.h5',
output_name='test_tester',
detection_threshold=0.20,
P_threshold=0.1,
S_threshold=0.1,
number_of_plots=3,
estimate_uncertainty=True,
number_of_sampling=2,
input_dimention=(6000, 3),
normalization_mode='std',
mode='generator',
batch_size=10,
gpuid=None,
gpu_limit=None)
|
test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:PythonWebMongo]
# language: python
# name: conda-env-PythonWebMongo-py
# ---
from splinter import Browser
from bs4 import BeautifulSoup
import time
#https://splinter.readthedocs.io/en/latest/drivers/chrome.html
# !which chromedriver
executable_path = {'executable_path': '/usr/local/bin/chromedriver'}
browser = Browser('chrome', **executable_path, headless=False)
url = 'https://mars.nasa.gov/news/'
browser.visit(url)
# +
html = browser.html
soup = BeautifulSoup(html, 'html.parser')
news_title = soup.find(class_='content_title')
news_title_text = news_title.a.text
news_title_text
# +
news_p = soup.find(class_='article_teaser_body')
news_p_text = news_p.text
news_p_text
# -
# # MARS IMAGE
#https://splinter.readthedocs.io/en/latest/drivers/chrome.html
# !which chromedriver
executable_path = {'executable_path': '/usr/local/bin/chromedriver'}
browser = Browser('chrome', **executable_path, headless=False)
# +
img_url = 'https://www.jpl.nasa.gov/spaceimages/?search=&category=Mars'
browser.visit(img_url)
browser.click_link_by_partial_text('FULL IMAGE')
img_html = browser.html
img_soup = BeautifulSoup(img_html, 'html.parser')
# -
img_address = img_soup.find_all('a', class_='fancybox')[0].get('data-fancybox-href').strip()
print(img_address)
featured_image_url = "https://www.jpl.nasa.gov"+img_address
print(featured_image_url)
# # MARS FACTS
import pandas as pd
facts_url = 'https://space-facts.com/mars/'
table = pd.read_html(facts_url)
table
df = table
type(df)
#first table only for Mars only data
df2 = df[0]
df2.columns = ['Mars Profile', 'Values']
df2
html_table = df2.to_html()
html_table
df2.to_html('table.html')
# !open table.html
# # MARS HEMISPHERES
hemisphere_image_urls = [
{"title": "Valles Marineris Hemisphere", "img_url": "https://astropedia.astrogeology.usgs.gov/download/Mars/Viking/valles_marineris_enhanced.tif/full.jpg"},
{"title": "Cerberus Hemisphere", "img_url": "https://astropedia.astrogeology.usgs.gov/download/Mars/Viking/cerberus_enhanced.tif/full.jpg"},
{"title": "Schiaparelli Hemisphere", "img_url": "https://astropedia.astrogeology.usgs.gov/download/Mars/Viking/schiaparelli_enhanced.tif/full.jpg"},
{"title": "Syrtis Major Hemisphere", "img_url": "https://astropedia.astrogeology.usgs.gov/download/Mars/Viking/syrtis_major_enhanced.tif/full.jpg"},
]
# # MARS WEATHER
# +
# scrape twitter for latest tweet
# -
executable_path = {"executable_path": "/usr/local/bin/chromedriver"}
browser = Browser("chrome", **executable_path, headless=False)
twitter_url = "https://twitter.com/marswxreport?lang=en"
browser.visit(twitter_url)
html = browser.html
weather_soup = BeautifulSoup(html, "html.parser")
mars_weather_tweet = weather_soup.find('p', class_='TweetTextSize').text
print(mars_weather_tweet)
|
Mission_to_Mars/mission_to_mars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:py3k]
# language: python
# name: conda-env-py3k-py
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings("ignore")
import datetime as dt
import scipy.stats as sps
# %matplotlib inline
mydata = pd.read_csv("alldata_risk_table.csv")
mydata.shape
mydata['RANDOM']=np.random.ranf(len(mydata))
mydata.describe()
goods=mydata[mydata['fraud_label']==0]
goods.shape
bads=mydata[mydata['fraud_label']==1]
bads.shape
numgoods=len(goods)
numbads=len(bads)
KS = pd.DataFrame(np.zeros((mydata.shape[1],3)))
i=0
for column in mydata:
print(i,column)
KS.loc[i,0]=column
i = i+1
KS
KS.columns=['field','ks','FDR']
KS
# %%time
i=0
for column in mydata:
KS['ks'][i]=sps.ks_2samp(goods[column],bads[column])[0]
i = i+1
KS.sort_values(by='ks',ascending= False, inplace= True)
KS
# %%time
topRows=int(round(len(mydata)*0.03))
j=0
for column in mydata:
temp1=mydata.sort_values(column,ascending=False).head(topRows)
temp2=mydata.sort_values(column,ascending=True).head(topRows)
needed1=temp1.loc[:,'fraud_label']
needed2=temp2.loc[:,'fraud_label']
FDR1=sum(needed1)/numbads
FDR2=sum(needed2)/numbads
FDRate=np.maximum(FDR1,FDR2)
# print j, column, FDR1, FDR2, FDRate
KS.loc[j,"FDR"]=FDRate
j = j+1
KS.sort_values(by=['ks'],ascending=False,inplace=True)
KS
KS.sort_values(by=['FDR'],ascending=False,inplace=True)
KS
KS['rank_ks']=KS['ks'].rank(ascending=True)
KS['rank_FDR']=KS['FDR'].rank(ascending=True)
KS.head(10)
KS['average_rank']=(KS['rank_ks']+KS['rank_FDR'])/2
KS.sort_values(by=['average_rank'],ascending=False,inplace=True)
KS.head(10)
KS.tail(10)
## export to csv
KS.to_csv("KS_FDR_AllVariables.csv",index=False)
|
Fraud/3_KS_FDR_AllVariables-3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.3 64-bit
# name: python373jvsc74a57bd07945e9a82d7512fbf96246d9bbc29cd2f106c1a4a9cf54c9563dadf10f2237d4
# ---
# + [markdown] id="4w2e0D-hni2p"
# # HOME ASSIGNMENT #3: SLACK API - TO GSHEET
# + [markdown] id="yitICPVzpRI2"
# ## 0. Load Modules
# + id="G_HCucZ5rSHq"
import requests #-> Để gọi API
import re #-> Để xử lý data dạng string
from datetime import datetime as dt #-> Để xử lý data dạng datetime
import gspread #-> Để update data lên Google Spreadsheet
from gspread_dataframe import set_with_dataframe #-> Để update data lên Google Spreadsheet
import pandas as pd #-> Để update data dạng bản
import json
from oauth2client.service_account import ServiceAccountCredentials #-> Để nhập Google Spreadsheet Credentials
import os
print("done")
# + id="tFPqT2pirhy4"
with open('env_variable.json', 'r') as j:
json_data = json.load(j)
# + id="wAzmaVTLrpvH"
## Load SLACK_BEARER_TOKEN
os.environ['SLACK_BEARER_TOKEN'] = json_data['SLACK_BEARER_TOKEN']
# + id="K_TrDTx138jD"
## Gọi API từ Endpoints (Input - Token được đưa vào Headers)
## Challenge: Thử gọi API này bằng Postman
endpoint = "https://slack.com/api/users.list"
headers = {"Authorization": "Bearer {}".format(os.environ['SLACK_BEARER_TOKEN'])}
response_json = requests.post(endpoint, headers=headers).json()
user_dat = response_json['members']
# + [markdown] id="rqEti4Y50tdB"
# ### TODO #1
# Hoàn tất đoạn code sau
# + id="P0qbkdhtD9ww"
## Loop qua JSON file và extract các thông tin quan trọng (id, name, display_name, real_name_normalized, title, phone, is_bot)
## Hint: Bạn có thể dùng Postman hoặc in user_dat JSON để xem cấu trúc (schema), dùng Ctrl+F để tìm các keys (id, name, display_name, real_name_normalized, title, phone, is_bot)
user_dict = {'user_id':[], 'name':[], 'display_name':[],'real_name':[],'title':[],'phone':[],'is_bot':[]}
for i in range(len(user_dat)):
user_dict['user_id'].append(user_dat[i]['id'])
user_dict['name'].append(user_dat[i]['name'])
user_dict['display_name'].append(user_dat[i]['profile']['display_name'])
user_dict['real_name'].append(user_dat[i]['profile']['real_name_normalized'])
user_dict['title'].append(user_dat[i]['profile']['title'])
user_dict['phone'].append(user_dat[i]['profile']['phone'])
user_dict['is_bot'].append(user_dat[i]['is_bot'])
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="yGNvsCauF8_w" outputId="dfc4c6f7-845c-4202-8fc7-43aeb328554a"
user_df = pd.DataFrame(user_dict) ## Dùng pandas để convert dictionaries thành bảng
user_df.head(5) ## Chỉ in 5 dòng đầu (chủ yếu để xem cấu trúc)
# + colab={"base_uri": "https://localhost:8080/", "height": 80} id="rjFcaWdt2ABM" outputId="1a114985-7608-4421-aa51-1e406cc427eb"
user_df[user_df.display_name == 'MAD'] ## Lọc thông tin của MAD, trên DataFrame (bạn có thể Google thêm)
# -
user_df[user_df.name == 'lovelylife.158']
# + [markdown] id="1TZrcaWZyE07"
# -------------- HẾT PHẦN BẮT BUỘC ---------------------
# + [markdown] id="P3_b7zw-1A6s"
# ## Option 1: Update data => Google SpreadSheet
# + colab={"base_uri": "https://localhost:8080/"} id="4NEQFu-DNvFC" outputId="a855fe34-b409-4152-a218-67bfa240396f"
## Authorize bằng JSON
scope = ['https://spreadsheets.google.com/feeds',
'https://www.googleapis.com/auth/drive']
credentials = ServiceAccountCredentials.from_json_keyfile_name(
'assignment3-gg.json', scope)
gc = gspread.authorize(credentials)
print("DONE!")
# + id="XlZ8JNB3bZbw"
# ACCES GOOGLE SHEET
sheet_index_no = 0
spreadsheet_key = '<KEY>' # input SPREADSHEET_KEY HERE
sh = gc.open_by_key(spreadsheet_key)
worksheet = sh.get_worksheet(sheet_index_no) #-> 0 - first sheet, 1 - second sheet etc.
# APPEND DATA TO SHEET
set_with_dataframe(worksheet, user_df) #-> Upload user_df vào Sheet đầu tiên trong Spreadsheet
# DONE: Bây giờ bạn có thể mở spreadsheet và kiểm tra nội dung đã update chứ
# + [markdown] id="5I15m3ilyA3Y"
# Result: https://docs.google.com/spreadsheets/d/1pXjtLvF6yLv33htSd-B8UgoLkV99vdAZPJ1Yj3lhoIY/edit?usp=sharing
#
# + [markdown] id="9aRN9KSczkmr"
# ## Option 2: Ai đã nộp bài?
#
# + [markdown] id="Pw81ioUz2N0v"
# ### Slack API: Channel List
# + id="fcdaDaGdz60p"
## Gọi SLACK API để list tất cả các channel
endpoint = "https://slack.com/api/conversations.list"
headers = {"Authorization": "Bearer {}".format(os.environ['SLACK_BEARER_TOKEN'])}
response = requests.post(endpoint, headers=headers).json()
channel_ls = response['channels']
# + colab={"base_uri": "https://localhost:8080/"} id="47dUJAPi0Jg5" outputId="2762f1e8-ff65-4994-c3e5-1ab0f5dc9205"
channel_ls[2] ## Thử extract record đầu tiên để xem schema => name: general, id: C01B4PVGLVB
# + [markdown] id="CNFTcFC00l8g"
# ### TODO#3
# * Tìm id của channel #atom-assignment2
# -
for c in range(len(channel_ls)):
if channel_ls[c]['name']=='atom-assignment2':
print(channel_ls[c]['id'])
# + [markdown] id="EnCvdYAn2R47"
# ### Slack API: List messages trong 1 channel
# + id="1UsSESN8rtnk"
endpoint = "https://slack.com/api/conversations.history"
data = {"channel": "C021FSDN7LJ"} ## This is ID of assignment#2 channel
headers = {"Authorization": "Bearer {}".format(os.environ['SLACK_BEARER_TOKEN'])}
# + id="i8eJw3LBr4lY"
response_json = requests.post(endpoint, data=data, headers=headers).json()
msg_ls = response_json['messages']
# + colab={"base_uri": "https://localhost:8080/"} id="KkYO1KcBtZa9" outputId="7a76397b-202b-445e-aa26-f4b30cfc9a53"
msg_ls[24]
# -
"github.com" in msg_ls[24]['text']
# + id="BsW8CXAXv-tC"
not_learners_id = ['U01BE2PR6LU']
# -
sub = {'SubTime':[], 'user ID submit':[], 'User ID review':[],'latest reply':[],'link github':[]}
for i in range(len(msg_ls)):
ts = dt.fromtimestamp(float(msg_ls[i]['ts'])) # -> Convert timestamp Epoch thành dàng dễ đọc
user = msg_ls[i]['user'] # -> Lấy thông tin người post messages
if msg_ls[i]['user'] not in not_learners_id:
if "github.com" in msg_ls[i]['text']:
text = msg_ls[i]['text']
github_link = re.findall('(?:https?://)?(?:www[.])?github[.]com/[\w-]+/?', text) #-> Submission là các message có link github
if len(github_link) > 0: github = github_link[0]
if 'reply_count' in msg_ls[i].keys(): reply_count = msg_ls[i]['reply_count'] #-> Extract số review
if 'reply_users_count' in msg_ls[i].keys(): reply_users_count = msg_ls[i]['reply_users_count']
if 'reply_users' in msg_ls[i].keys(): reply_users = msg_ls[i]['reply_users']
if 'latest_reply' in msg_ls[i].keys(): latest_reply = dt.fromtimestamp(float(msg_ls[i]['latest_reply']))
print(ts, user, reply_users_count, reply_users, latest_reply, github)
sub['SubTime'].append(ts)
sub['user ID submit'].append(user)
sub['User ID review'].append(reply_users)
sub['latest reply'].append(latest_reply)
sub['link github'].append(github)
len(sub['SubTime'])
sub = pd.DataFrame(sub) ## Dùng pandas để convert dictionaries thành bảng
sub.head(5) ## Chỉ in 5 dòng đầu (chủ yếu để xem cấu trúc)
# + [markdown] id="SgSC21qO3kKA"
# ### TODO#4
# * Tạo thành 1 bảng chứa các thông tin trên và update lên Spreadsheet (Sheet: Assignment#2 Submission)
# -
ws2 = sh.add_worksheet("Assignment#2 Submit",1000,256) #create new worksheet
set_with_dataframe(ws2,sub) # APPEND DATA TO SHEET
# Result: https://docs.google.com/spreadsheets/d/1pXjtLvF6yLv33htSd-B8UgoLkV99vdAZPJ1Yj3lhoIY/edit?usp=sharing
|
assignment_3/home_assignment_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img align="center" style="max-width: 1000px" src="banner.png">
# + [markdown] id="B0cP5Z789_rr"
# <img align="right" style="max-width: 200px; height: auto" src="hsg_logo.png">
#
# ## Lab 05 - Convolutional Neural Networks (CNNs)
#
# EMBA 60 W10 / EMBA 61 W5: Coding und Künstliche Intelligenz, University of St. Gallen
# -
# The lab environment of the "AI Coding for Executives" EMBA course at the University of St. Gallen (HSG) is based on Jupyter Notebooks (https://jupyter.org), which allow to perform a variety of statistical evaluations and data analyses.
# + [markdown] id="Rno8GqfC9_rz"
# In this lab, we will learn how to enhance vanilla Artificial Neural Networks (ANNs) using `PyTorch` to classify even more complex images. Therefore, we use a special type of deep neural network referred to **Convolutional Neural Networks (CNNs)**. CNNs encompass the ability to take advantage of the hierarchical pattern in data and assemble more complex patterns using smaller and simpler patterns. Therefore, CNNs are capable to learn a set of discriminative features 'pattern' and subsequently utilize the learned pattern to classify the content of an image.
#
# We will again use the functionality of the `PyTorch` library to implement and train an CNN based neural network. The network will be trained on a set of tiny images to learn a model of the image content. Upon successful training, we will utilize the learned CNN model to classify so far unseen tiny images into distinct categories such as aeroplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks.
#
# The figure below illustrates a high-level view on the machine learning process we aim to establish in this lab.
# + [markdown] id="nswYOXvk9_r0"
# <img align="center" style="max-width: 900px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/classification.png">
# + [markdown] id="r93JK2DH9_r0"
# (Image of the CNN architecture created via http://alexlenail.me/)
#
# As always, pls. don't hesitate to ask all your questions either during the lab, post them in our CANVAS (StudyNet) forum (https://learning.unisg.ch), or send us an email (using the course email).
# + [markdown] id="eW6dySzs9_r1"
# ## 1. Lab Objectives:
# + [markdown] id="2uzc9Xr69_r1"
# After today's lab, you should be able to:
#
# > 1. Understand the basic concepts, intuitions and major building blocks of **Convolutional Neural Networks (CNNs)**.
# > 2. Know how to **implement and to train a CNN** to learn a model of tiny image data.
# > 3. Understand how to apply such a learned model to **classify images** images based on their content into distinct categories.
# > 4. Know how to **interpret and visualize** the model's classification results.
# + [markdown] id="iPRKkkig9_r2"
# ## 2. Setup of the Jupyter Notebook Environment
# + [markdown] id="7mZL4i6W9_r2"
# Similar to the previous labs, we need to import a couple of Python libraries that allow for data analysis and data visualization. We will mostly use the `PyTorch`, `Numpy`, `Sklearn`, `Matplotlib`, `Seaborn` and a few utility libraries throughout this lab:
# + id="A9cwWtab9_r2"
# import standard python libraries
import os, urllib, io
from datetime import datetime
import numpy as np
# + [markdown] id="FrB_51t89_r3"
# Import Python machine / deep learning libraries:
# + id="ZH6LhB_q9_r3"
# import the PyTorch deep learning library
import torch, torchvision
import torch.nn.functional as F
from torch import nn, optim
from torch.autograd import Variable
# + [markdown] id="sfgYux7K9_r3"
# Import the sklearn classification metrics:
# + id="cFptYrnr9_r4"
# import sklearn classification evaluation library
from sklearn import metrics
from sklearn.metrics import classification_report, confusion_matrix
# + [markdown] id="WJJ5kfaf9_r4"
# Import Python plotting libraries:
# + id="usAgsocK9_r4"
# import matplotlib, seaborn, and PIL data visualization libary
import matplotlib.pyplot as plt
import seaborn as sns
from PIL import Image
# + [markdown] id="kZft6q1B9_r5"
# Enable notebook matplotlib inline plotting:
# + id="BXnX3zt_9_r5"
# %matplotlib inline
# + [markdown] id="ZfE3I18r9_r5"
# Create notebook folder structure to store the data as well as the trained neural network models:
# + id="nMFO6m7k9_r6"
# create the data sub-directory
data_directory = './data_cifar10'
if not os.path.exists(data_directory): os.makedirs(data_directory)
# create the models sub-directory
models_directory = './models_cifar10'
if not os.path.exists(models_directory): os.makedirs(models_directory)
# + [markdown] id="wcYgp4Gl9_r6"
# Set a random `seed` value to obtain reproducable results:
# + id="vdbqEjHb9_r7"
# init deterministic seed
seed_value = 1234
np.random.seed(seed_value) # set numpy seed
torch.manual_seed(seed_value) # set pytorch seed CPU
# + [markdown] id="XH1CSkRV9_r8"
# ## 3. Dataset Download and Data Assessment
# + [markdown] id="UWDn7IQE9_r8"
# The **CIFAR-10 database** (**C**anadian **I**nstitute **F**or **A**dvanced **R**esearch) is a collection of images that are commonly used to train machine learning and computer vision algorithms. The database is widely used to conduct computer vision research using machine learning and deep learning methods:
# + [markdown] id="awuRyFMd9_r8"
# <img align="center" style="max-width: 500px; height: 500px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/cifar10.png">
#
# (Source: https://www.kaggle.com/c/cifar-10)
# + [markdown] id="pjdI5VVN9_r8"
# Further details on the dataset can be obtained via: *<NAME>., 2009. "Learning Multiple Layers of Features from Tiny Images",
# ( https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf )."*
# + [markdown] id="IaD13bmO9_r9"
# The CIFAR-10 database contains **60,000 color images** (50,000 training images and 10,000 validation images). The size of each image is 32 by 32 pixels. The collection of images encompasses 10 different classes that represent airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. Let's define the distinct classs for further analytics:
# + id="1WlB2yXu9_r-"
cifar10_classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
# + [markdown] id="kRslZNGV9_r-"
# Thereby the dataset contains 6,000 images for each of the ten classes. The CIFAR-10 is a straightforward dataset that can be used to teach a computer how to recognize objects in images.
#
# Let's download, transform and inspect the training images of the dataset. Therefore, we first will define the directory we aim to store the training data:
# + id="B2Bmhc-c9_r-"
train_path = './data/train_cifar10'
# + [markdown] id="b6AGBP_K9_r_"
# Now, let's download the training data accordingly:
# + id="G_-Zs4EU9_sA"
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform training images
cifar10_train_data = torchvision.datasets.CIFAR10(root=train_path, train=True, transform=transf, download=True)
# + [markdown] id="g79sdHOw9_sA"
# Verify the volume of training images downloaded:
# + id="uiKFBLrI9_sA"
# get the length of the training data
len(cifar10_train_data)
# + [markdown] id="CDDjW4jk9_sA"
# Furthermore, let's investigate a couple of the training images:
# + id="h8j19ga29_sA"
# set (random) image id
image_id = 1800
# retrieve image exhibiting the image id
cifar10_train_data[image_id]
# + [markdown] id="pZsiUhXb9_sB"
# Ok, that doesn't seem easily interpretable ;) Let's first seperate the image from its label information:
# + id="oe3JTrQO9_sB"
cifar10_train_image, cifar10_train_label = cifar10_train_data[image_id]
# + [markdown] id="D7vnZCRy9_sB"
# Great, now we are able to visually inspect our sample image:
# + id="yNRCdqHO9_sB"
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: "{}"'.format(str(image_id), str(cifar10_classes[cifar10_train_label])))
# un-normalize cifar 10 image sample
cifar10_train_image_plot = cifar10_train_image / 2.0 + 0.5
# plot 10 image sample
plt.imshow(trans(cifar10_train_image_plot))
# + [markdown] id="mWcoDhr_9_sC"
# Fantastic, right? Let's now decide on where we want to store the evaluation data:
# + id="hKFBcveC9_sC"
eval_path = './data/eval_cifar10'
# + [markdown] id="nB5OpV4z9_sC"
# And download the evaluation data accordingly:
# + id="L-OOVFFs9_sD"
# define pytorch transformation into tensor format
transf = torchvision.transforms.Compose([torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# download and transform validation images
cifar10_eval_data = torchvision.datasets.CIFAR10(root=eval_path, train=False, transform=transf, download=True)
# + [markdown] id="WF4VrcHG9_sD"
# Verify the volume of validation images downloaded:
# + id="vhZRDL4X9_sD"
# get the length of the training data
len(cifar10_eval_data)
# + [markdown] id="B9Xivz3j9_sD"
# ## 4. Neural Network Implementation
# + [markdown] id="5Reatmz29_sD"
# In this section we, will implement the architecture of the **neural network** we aim to utilize to learn a model that is capable of classifying the 32x32 pixel CIFAR 10 images according to the objects contained in each image. However, before we start the implementation, let's briefly revisit the process to be established. The following cartoon provides a birds-eye view:
# + [markdown] id="cLOtA61_9_sE"
# <img align="center" style="max-width: 900px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/process.png">
# + [markdown] id="F1qQOztA9_sE"
# Our CNN, which we name 'CIFAR10Net' and aim to implement consists of two **convolutional layers** and three **fully-connected layers**. In general, convolutional layers are specifically designed to learn a set of **high-level features** ("patterns") in the processed images, e.g., tiny edges and shapes. The fully-connected layers utilize the learned features to learn **non-linear feature combinations** that allow for highly accurate classification of the image content into the different image classes of the CIFAR-10 dataset, such as, birds, aeroplanes, horses.
# + [markdown] id="aLZ0MWtL9_sE"
# Let's implement the network architecture and subsequently have a more in-depth look into its architectural details:
# + id="XU-lZiqJ9_sF"
# implement the CIFAR10Net network architecture
class CIFAR10Net(nn.Module):
# define the class constructor
def __init__(self):
# call super class constructor
super(CIFAR10Net, self).__init__()
# specify convolution layer 1
self.conv1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=5, stride=1, padding=0)
# define max-pooling layer 1
self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)
# specify convolution layer 2
self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0)
# define max-pooling layer 2
self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)
# specify fc layer 1 - in 16 * 5 * 5, out 120
self.linear1 = nn.Linear(16 * 5 * 5, 120, bias=True) # the linearity W*x+b
self.relu1 = nn.ReLU(inplace=True) # the non-linearity
# specify fc layer 2 - in 120, out 84
self.linear2 = nn.Linear(120, 84, bias=True) # the linearity W*x+b
self.relu2 = nn.ReLU(inplace=True) # the non-linarity
# specify fc layer 3 - in 84, out 10
self.linear3 = nn.Linear(84, 10) # the linearity W*x+b
# add a softmax to the last layer
self.logsoftmax = nn.LogSoftmax(dim=1) # the softmax
# define network forward pass
def forward(self, images):
# high-level feature learning via convolutional layers
# define conv layer 1 forward pass
x = self.pool1(self.relu1(self.conv1(images)))
# define conv layer 2 forward pass
x = self.pool2(self.relu2(self.conv2(x)))
# feature flattening
# reshape image pixels
x = x.view(-1, 16 * 5 * 5)
# combination of feature learning via non-linear layers
# define fc layer 1 forward pass
x = self.relu1(self.linear1(x))
# define fc layer 2 forward pass
x = self.relu2(self.linear2(x))
# define layer 3 forward pass
x = self.logsoftmax(self.linear3(x))
# return forward pass result
return x
# + [markdown] id="4lJGh5Er9_sF"
# You may have noticed that we applied two more layers (compared to the MNIST example described in the last lab) before the fully-connected layers. These layers are referred to as **convolutional** layers and are usually comprised of three operations, (1) **convolution**, (2) **non-linearity**, and (3) **max-pooling**. Those operations are usually executed in sequential order during the forward pass through a convolutional layer.
# + [markdown] id="keu5KR4x9_sF"
# In the following, we will have a detailed look into the functionality and number of parameters in each layer. We will start with providing images of 3x32x32 dimensions to the network, i.e., the three channels (red, green, blue) of an image each of size 32x32 pixels.
# + [markdown] id="QYN6Dedt9_sF"
# ### 4.1. High-Level Feature Learning by Convolutional Layers
# + [markdown] id="3TqfN3Db9_sG"
# Let's first have a look into the convolutional layers of the network as illustrated in the following:
# + [markdown] id="G9oo9YFi9_sG"
# <img align="center" style="max-width: 600px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/convolutions.png">
# + [markdown] id="9Oud8yJy9_sG"
# **First Convolutional Layer**: The first convolutional layer expects three input channels and will convolve six filters each of size 3x5x5. Let's briefly revisit how we can perform a convolutional operation on a given image. For that, we need to define a kernel which is a matrix of size 5x5, for example. To perform the convolution operation, we slide the kernel along with the image horizontally and vertically and obtain the dot product of the kernel and the pixel values of the image inside the kernel ('receptive field' of the kernel).
# + [markdown] id="-UjRWKlQ9_sG"
# The following illustration shows an example of a discrete convolution:
# + [markdown] id="z4eguT5B9_sG"
# <img align="center" style="max-width: 800px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/convsample.png">
# + [markdown] id="LjqYlMyq9_sH"
# The left grid is called the input (an image or feature map). The middle grid, referred to as kernel, slides across the input feature map (or image). At each location, the product between each element of the kernel and the input element it overlaps is computed, and the results are summed up to obtain the output in the current location. In general, a discrete convolution is mathematically expressed by:
# + [markdown] id="kUA4C9GX9_sH"
# <center> $y(m, n) = x(m, n) * h(m, n) = \sum^{m}_{j=0} \sum^{n}_{i=0} x(i, j) * h(m-i, n-j)$, </center>
# + [markdown] id="1QzATC029_sH"
# where $x$ denotes the input image or feature map, $h$ the applied kernel, and, $y$ the output.
# + [markdown] id="ZogbXkwc9_sH"
# When performing the convolution operation the 'stride' defines the number of pixels to pass at a time when sliding the kernel over the input. While 'padding' adds the number of pixels to the input image (or feature map) to ensure that the output has the same shape as the input. Let's have a look at another animated example:
# + [markdown] id="JwygKDeh9_sI"
# <img align="center" style="max-width: 800px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/convsample_animated.gif">
# + [markdown] id="TRQDoCeG9_sI"
# (Source: https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53)
#
# In our implementation padding is set to 0 and stride is set to 1. As a result, the output size of the convolutional layer becomes 6x28x28, since (32 input pixel - 5 kernel pixel) + 1 stride pixel = 28. This layer exhibits ((5 kernel pixel x 5 kernel pixel x 3 input channels) + 1 stride pixel) x 6 output channels = 456 parameter.
# + [markdown] id="q0ALYEOE9_sI"
# **First Max-Pooling Layer:** The max-pooling process is a sample-based discretization operation. The objective is to down-sample an input representation (image, hidden-layer output matrix, etc.), reducing its dimensionality and allowing for assumptions to be made about features contained in the sub-regions binned.
#
# To conduct such an operation, we again need to define a kernel. Max-pooling kernels are usually a tiny matrix of, e.g, of size 2x2. To perform the max-pooling operation, we slide the kernel along the image horizontally and vertically (similarly to a convolution) and compute the maximum pixel value of the image (or feature map) inside the kernel (the receptive field of the kernel).
# + [markdown] id="Ji0FT1ra9_sI"
# The following illustration shows an example of a max-pooling operation:
# + [markdown] id="ZKQSTgI09_sI"
# <img align="center" style="max-width: 500px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/poolsample.png">
# + [markdown] id="N9T8zXVc9_sI"
# The left grid is called the input (an image or feature map). The middle grid, referred to as kernel, slides across the input feature map (or image). We use a stride of 2, meaning the step distance for stepping over our input will be 2 pixels and won't overlap regions. At each location, the max value of the region that overlaps with the elements of the kernel and the input elements it overlaps is computed, and the results are obtained in the output of the current location.
# + [markdown] id="8uy4wuah9_sI"
# In our implementation, we do max-pooling with a 2x2 kernel and stride 2 this effectively drops the original image size from 6x28x28 to 6x14x14. Let's have a look at an exemplary visualization of 64 features learnt in the first convolutional layer on the CIFAR- 10 dataset:
# -
# <img align="center" style="max-width: 700px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/cnnfeatures.png">
# (Source: <NAME>, <NAME>, <NAME>, and <NAME>, **"Mixed Pooling for Convolutional Neural Networks"**, International Conference on Rough Sets and Knowledge Technology, pp. 364-375. Springer, Cham, 2014)
# + [markdown] id="y3rD6ai29_sJ"
# **Second Convolutional Layer:** The second convolutional layer expects 6 input channels and will convolve 16 filters each of size 6x5x5x. Since padding is set to 0 and stride is set 1, the output size is 16x10x10, since (14 input pixel - 5 kernel pixel) + 1 stride pixel = 10. This layer therefore has ((5 kernel pixel x 5 kernel pixel x 6 input channels) + 1 stride pixel x 16 output channels) = 2,416 parameter.
#
# **Second Max-Pooling Layer:** The second down-sampling layer uses max-pooling with 2x2 kernel and stride set to 2. This effectively drops the size from 16x10x10 to 16x5x5.
# + [markdown] id="rUeMEeHa9_sJ"
# ### 4.2. Flattening of Learned Features
# -
# The output of the final-max pooling layer needs to be flattened so that we can connect it to a fully connected layer. This is achieved using the `torch.Tensor.view` method. Setting the parameter of the method to `-1` will automatically infer the number of rows required to handle the mini-batch size of the data.
# + [markdown] id="Bx3f3t1q9_sJ"
# ### 4.3. Learning of Feature Classification
# + [markdown] id="WEM5tSzd9_sJ"
# Let's now have a look into the non-linear layers of the network illustrated in the following:
# + [markdown] id="xXJ0uhtZ9_sJ"
# <img align="center" style="max-width: 600px" src="https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/main/lab_05/fullyconnected.png">
# + [markdown] id="v8rkmInp9_sJ"
# The first fully connected layer uses 'Rectified Linear Units' (ReLU) activation functions to learn potential nonlinear combinations of features. The layers are implemented similarly to the fifth lab. Therefore, we will only focus on the number of parameters of each fully-connected layer:
# + [markdown] id="yTtcghkz9_sK"
# **First Fully-Connected Layer:** The first fully-connected layer consists of 120 neurons, thus in total exhibits ((16 x 5 x 5) + 1) x 120 = 48,120 parameter.
#
# **Second Fully-Connected Layer:** The output of the first fully-connected layer is then transferred to second fully-connected layer. The layer consists of 84 neurons equipped with ReLu activation functions, this in total exhibits (120 + 1) x 84 = 10,164 parameter.
# + [markdown] id="3HbTqZdz9_sK"
# The output of the second fully-connected layer is then transferred to the output-layer (third fully-connected layer). The output layer is equipped with a softmax (that you learned about in the previous lab 05) and is made up of ten neurons, one for each object class contained in the CIFAR-10 dataset. This layer exhibits (84 + 1) x 10 = 850 parameter.
#
#
# As a result our CIFAR-10 convolutional neural exhibits a total of 456 + 2,416 + 48,120 + 10,164 + 850 = 62,006 parameter.
#
# (Source: https://www.stefanfiott.com/machine-learning/cifar-10-classifier-using-cnn-in-pytorch/)
# + [markdown] id="UcPpgIWI9_sK"
# Now, that we have implemented our first Convolutional Neural Network we are ready to instantiate a network model to be trained:
# + id="YGRVLvKS9_sK"
model = CIFAR10Net()
# + [markdown] id="wofRVIpA9_sL"
# Once the model is initialized we can visualize the model structure and review the implemented network architecture by execution of the following cell:
# + id="6XyE60fD9_sL"
# print the initialized architectures
print('[LOG] CIFAR10Net architecture:\n\n{}\n'.format(model))
# + [markdown] id="Wl5fE-TU9_sL"
# Looks like intended? Brilliant! Finally, let's have a look into the number of model parameters that we aim to train in the next steps of the notebook:
# + id="gkipagYv9_sL"
# init the number of model parameters
num_params = 0
# iterate over the distinct parameters
for param in model.parameters():
# collect number of parameters
num_params += param.numel()
# print the number of model paramters
print('[LOG] Number of to be trained CIFAR10Net model parameters: {}.'.format(num_params))
# + [markdown] id="MvqKcKUV9_sM"
# Ok, our "simple" CIFAR10Net model already encompasses an impressive number 62'006 model parameters to be trained.
# + [markdown] id="-_s14kxw9_sM"
# Now that we have implemented the CIFAR10Net, we are ready to train the network. However, before starting the training, we need to define an appropriate loss function. Remember, we aim to train our model to learn a set of model parameters $\theta$ that minimize the classification error of the true class $c^{i}$ of a given CIFAR-10 image $x^{i}$ and its predicted class $\hat{c}^{i} = f_\theta(x^{i})$ as faithfully as possible.
#
# In this lab we use (similarly to lab 05) the **'Negative Log-Likelihood (NLL)'** loss. During training the NLL loss will penalize models that result in a high classification error between the predicted class labels $\hat{c}^{i}$ and their respective true class label $c^{i}$. Now that we have implemented the CIFAR10Net, we are ready to train the network. Before starting the training, we need to define an appropriate loss function. Remember, we aim to train our model to learn a set of model parameters $\theta$ that minimize the classification error of the true class $c^{i}$ of a given CIFAR-10 image $x^{i}$ and its predicted class $\hat{c}^{i} = f_\theta(x^{i})$ as faithfully as possible.
# + [markdown] id="5iALpp3l9_sM"
# Let's instantiate the NLL via the execution of the following PyTorch command:
# + id="LayFcR6V9_sM"
# define the optimization criterion / loss function
nll_loss = nn.NLLLoss()
# + [markdown] id="HgICsmcF9_sN"
# Based on the loss magnitude of a certain mini-batch PyTorch automatically computes the gradients. But even better, based on the gradient, the library also helps us in the optimization and update of the network parameters $\theta$.
#
# We will use the **Stochastic Gradient Descent (SGD) optimization** and set the `learning-rate to 0.001`. Each mini-batch step the optimizer will update the model parameters $\theta$ values according to the degree of classification error (the NLL loss).
# + id="FwFN6G8m9_sN"
# define learning rate and optimization strategy
learning_rate = 0.001
optimizer = optim.SGD(params=model.parameters(), lr=learning_rate)
# + [markdown] id="Ydpb5vlt9_sN"
# Now that we have successfully implemented and defined the three CNN building blocks let's take some time to review the `CIFAR10Net` model definition as well as the `loss`. Please, read the above code and comments carefully and don't hesitate to let us know any questions you might have.
# + [markdown] id="sWU9hWb_9_sO"
# ## 5. Neural Network Model Training
# + [markdown] id="jdQLICDt9_sO"
# In this section, we will train our neural network model (as implemented in the section above) using the transformed images. More specifically, we will have a detailed look into the distinct training steps as well as how to monitor the training progress.
# + [markdown] id="EVM_dXkv9_sP"
# ### 5.1. Preparing the Network Training
# + [markdown] id="DY85Fiwh9_sP"
# So far, we have pre-processed the dataset, implemented the CNN and defined the classification error. Let's now start to train a corresponding model for **20 epochs** and a **mini-batch size of 128** CIFAR-10 images per batch. This implies that the whole dataset will be fed to the CNN 20 times in chunks of 128 images yielding to **391 mini-batches** (50.000 training images / 128 images per mini-batch) per epoch. After the processing of each mini-batch, the parameters of the network will be updated.
# + id="dZCKjFy49_sP"
# specify the training parameters
num_epochs = 20 # number of training epochs
mini_batch_size = 128 # size of the mini-batches
# + [markdown] id="L--PU3IN9_sP"
# Furthermore, lets specifiy and instantiate a corresponding PyTorch data loader that feeds the image tensors to our neural network:
# + id="GX4M4zsl9_sP"
cifar10_train_dataloader = torch.utils.data.DataLoader(cifar10_train_data, batch_size=mini_batch_size, shuffle=True)
# + [markdown] id="KTNmPRRR9_sQ"
# ### 5.2. Running the Network Training
# + [markdown] id="mAjOouhW9_sQ"
# Finally, we start training the model. The training procedure for each mini-batch is performed as follows:
#
# >1. do a forward pass through the CIFAR10Net network,
# >2. compute the negative log-likelihood classification error $\mathcal{L}^{NLL}_{\theta}(c^{i};\hat{c}^{i})$,
# >3. do a backward pass through the CIFAR10Net network, and
# >4. update the parameters of the network $f_\theta(\cdot)$.
#
# To ensure learning while training our CNN model, we will monitor whether the loss decreases with progressing training. Therefore, we obtain and evaluate the classification performance of the entire training dataset after each training epoch. Based on this evaluation, we can conclude on the training progress and whether the loss is converging (indicating that the model might not improve any further).
#
# The following elements of the network training code below should be given particular attention:
#
# >- `loss.backward()` computes the gradients based on the magnitude of the reconstruction loss,
# >- `optimizer.step()` updates the network parameters based on the gradient.
# + id="NLpad5OX9_sQ"
# init collection of training epoch losses
train_epoch_losses = []
# set the model in training mode
model.train()
# train the CIFAR10 model
for epoch in range(num_epochs):
# init collection of mini-batch losses
train_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(cifar10_train_dataloader):
# run forward pass through the network
output = model(images)
# reset graph gradients
model.zero_grad()
# determine classification loss
loss = nll_loss(output, labels)
# run backward pass
loss.backward()
# update network paramaters
optimizer.step()
# collect mini-batch reconstruction loss
train_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
train_epoch_loss = np.mean(train_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] epoch: {} train-loss: {}'.format(str(now), str(epoch), str(train_epoch_loss)))
# save model to local directory
model_name = 'cifar10_model_epoch_{}.pth'.format(str(epoch))
torch.save(model.state_dict(), os.path.join("./models", model_name))
# determine mean min-batch loss of epoch
train_epoch_losses.append(train_epoch_loss)
# + [markdown] id="Ygw3kQHe9_sQ"
# Upon successfull training let's visualize and inspect the training loss per epoch:
# + id="cYsSBemy9_sQ"
# prepare plot
fig = plt.figure()
ax = fig.add_subplot(111)
# add grid
ax.grid(linestyle='dotted')
# plot the training epochs vs. the epochs' classification error
ax.plot(np.array(range(1, len(train_epoch_losses)+1)), train_epoch_losses, label='epoch loss (blue)')
# add axis legends
ax.set_xlabel("[training epoch $e_i$]", fontsize=10)
ax.set_ylabel("[Classification Error $\mathcal{L}^{NLL}$]", fontsize=10)
# set plot legend
plt.legend(loc="upper right", numpoints=1, fancybox=True)
# add plot title
plt.title('Training Epochs $e_i$ vs. Classification Error $L^{NLL}$', fontsize=10);
# + [markdown] id="Cr_sgAbk9_sR"
# Ok, fantastic. The training error converges nicely. We could definitely train the network a couple more epochs until the error converges. But let's stay with the 20 training epochs for now and continue with evaluating our trained model.
# + [markdown] id="N8NnkvgF9_sR"
# ## 6. Neural Network Model Evaluation
# + [markdown] id="2ORj_4Gh9_sR"
# Prior to evaluating our model, let's load the best performing model. Remember, that we stored a snapshot of the model after each training epoch to our local model directory. We will now load the last snapshot saved.
# + id="siwd2xJr9_sR"
# restore pre-trained model snapshot
best_model_name = 'https://raw.githubusercontent.com/HSG-AIML-Teaching/EMBA2022-Lab/master/lab_05/models/cifar10_model_epoch_19.pth'
# read stored model from the remote location
model_bytes = urllib.request.urlopen(best_model_name)
# load model tensor from io.BytesIO object
model_buffer = io.BytesIO(model_bytes.read())
# init pre-trained model class
best_model = CIFAR10Net()
# load pre-trained models
best_model.load_state_dict(torch.load(model_buffer, map_location=torch.device('cpu')))
# + [markdown] id="-AJmXdBr9_sR"
# Let's inspect if the model was loaded successfully:
# + id="Ia3UASaI9_sR"
# set model in evaluation mode
best_model.eval()
# + [markdown] id="O68AXMgf9_sS"
# In order to evaluate our trained model, we need to feed the CIFAR10 images reserved for evaluation (the images that we didn't use as part of the training process) through the model. Therefore, let's again define a corresponding PyTorch data loader that feeds the image tensors to our neural network:
# + id="HyJfMnfL9_sS"
cifar10_eval_dataloader = torch.utils.data.DataLoader(cifar10_eval_data, batch_size=10000, shuffle=False)
# + [markdown] id="9lMsauia9_sS"
# We will now evaluate the trained model using the same mini-batch approach as we did when training the network and derive the mean negative log-likelihood loss of all mini-batches processed in an epoch:
# + id="sM691HZH9_sS"
# init collection of mini-batch losses
eval_mini_batch_losses = []
# iterate over all-mini batches
for i, (images, labels) in enumerate(cifar10_eval_dataloader):
# run forward pass through the network
output = best_model(images)
# determine classification loss
loss = nll_loss(output, labels)
# collect mini-batch reconstruction loss
eval_mini_batch_losses.append(loss.data.item())
# determine mean min-batch loss of epoch
eval_loss = np.mean(eval_mini_batch_losses)
# print epoch loss
now = datetime.utcnow().strftime("%Y%m%d-%H:%M:%S")
print('[LOG {}] eval-loss: {}'.format(str(now), str(eval_loss)))
# + [markdown] id="8rrVTPcz9_sS"
# Ok, great. The evaluation loss looks in-line with our training loss. Let's now inspect a few sample predictions to get an impression of the model quality. Therefore, we will again pick a random image of our evaluation dataset and retrieve its PyTorch tensor as well as the corresponding label:
# + id="_RWjAuPv9_sT"
# set (random) image id
image_id = 777
# retrieve image exhibiting the image id
cifar10_eval_image, cifar10_eval_label = cifar10_eval_data[image_id]
# + [markdown] id="lVxTWZQ59_sT"
# Let's now inspect the true class of the image we selected:
# + id="dIIU_7HW9_sT"
cifar10_classes[cifar10_eval_label]
# + [markdown] id="In4-hd8Z9_sT"
# Ok, the randomly selected image should contain a two (2). Let's inspect the image accordingly:
# + id="HeME1Kuf9_sT"
# define tensor to image transformation
trans = torchvision.transforms.ToPILImage()
# set image plot title
plt.title('Example: {}, Label: {}'.format(str(image_id), str(cifar10_classes[cifar10_eval_label])))
# un-normalize cifar 10 image sample
cifar10_eval_image_plot = cifar10_eval_image / 2.0 + 0.5
# plot cifar 10 image sample
plt.imshow(trans(cifar10_eval_image_plot))
# + [markdown] id="liRyC0t79_sT"
# Ok, let's compare the true label with the prediction of our model:
# + id="bLjo87kl9_sX"
cifar10_eval_image.unsqueeze(0).shape
best_model(cifar10_eval_image.unsqueeze(0))
# + [markdown] id="q_3oz6t09_sX"
# We can even determine the likelihood of the most probable class:
# + id="ggPTl-gz9_sX"
cifar10_classes[torch.argmax(best_model(Variable(cifar10_eval_image.unsqueeze(0))), dim=1).item()]
# + [markdown] id="4ERjK-u79_sY"
# Let's now obtain the predictions for all the CIFAR-10 images of the evaluation data:
# + id="PmKPLlar9_sY"
predictions = torch.argmax(best_model(iter(cifar10_eval_dataloader).next()[0]), dim=1)
# + [markdown] id="IxEmgtiD9_sY"
# Furthermore, let's obtain the overall classification accuracy:
# + id="49xGbTlV9_sY"
metrics.accuracy_score(cifar10_eval_data.targets, predictions.detach())
# + [markdown] id="7nafaYuD9_sY"
# Let's also inspect the confusion matrix of the model predictions to determine major sources of misclassification:
# + id="hgUvHNl49_sY"
# determine classification matrix of the predicted and target classes
mat = confusion_matrix(cifar10_eval_data.targets, predictions.detach())
# initialize the plot and define size
plt.figure(figsize=(8, 8))
# plot corresponding confusion matrix
sns.heatmap(mat.T, square=True, annot=True, fmt='d', cbar=False, cmap='YlOrRd_r', xticklabels=cifar10_classes, yticklabels=cifar10_classes)
plt.tick_params(axis='both', which='major', labelsize=8, labelbottom = False, bottom=False, top = False, left = False, labeltop=True)
# set plot title
plt.title('CIFAR-10 classification matrix')
# set plot axis lables
plt.xlabel('[true label]')
plt.ylabel('[predicted label]');
# + [markdown] id="dVNmm42q9_sZ"
# Ok, we can easily see that our current model confuses images of cats and dogs as well as images of trucks and cars quite often. This is again not surprising since those image categories exhibit a high semantic and therefore visual similarity.
# + [markdown] id="ST0oDfsq9_sk"
# ## 7. Lab Summary:
# + [markdown] id="Yghg1eFi9_sk"
# In this lab, a step by step introduction into **design, implementation, training and evaluation** of convolutional neural networks CNNs to classify tiny images of objects is presented. The code and exercises presented in this lab may serves as a starting point for developing more complex, deeper and more tailored CNNs.
|
lab_05/lab_05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Peak Picking, Integration, and lineshape fitting
# ## Example Notebook
#
# ### Description
# This workbook demonstrates how to extract peak heights ('abundance') from a mass spectrrum object, and also how to compute the area (integrated, using a trapezoidal function), and also how to fit the peak lineshape using a defined function (i.e. Gaussian).
#
# #### Author
# <NAME>
# <EMAIL>
#
# #### Version and Release Notes
# 2021-02-09: Initial version. Demonstrate CoreMS, lmfit, and pso curve fitting. Works with CoreMS - 23.0.1.beta
# First, import the key packages for the pipeline
from pathlib import Path
import numpy as np
import matplotlib.pyplot as plt
from corems.transient.input.brukerSolarix import ReadBrukerSolarix
from corems.encapsulation.factory.parameters import MSParameters
# %matplotlib inline
# Define the data location - here a test dataset included with the repo
#
# Also define the signal processing parameters, including:
# 1. apodisation ('windowing') function,
# 2. number of truncations (to the transient),
# 3. number of zero fills,
# 4. and the peak picking method
# +
file_location = Path("../../tests/tests_data") / "ESI_NEG_SRFA.d"
MSParameters.transient.apodization_method = "Hanning"
MSParameters.transient.number_of_truncations = 0
MSParameters.transient.number_of_zero_fills = 1
MSParameters.mass_spectrum.threshold_method = 'auto'
# -
# Read in the bruker file object, read the transient, and then get the mass spectrum object
bruker_reader = ReadBrukerSolarix(file_location)
bruker_transient = bruker_reader.get_transient()
msobj = bruker_transient.get_mass_spectrum(plot_result=False, auto_process=True)
# Plot the profile spectrum just to check it loaded OK
msobj.plot_mz_domain_profile()
# Extract a specific peak and plot it to visualise the datapoints 'describing' the peak
# +
mspeak = msobj.mspeaks[970]
mzlim = mspeak.mz_exp
ylim = mspeak.abundance
width = 0.005
msobj.plot_mz_domain_profile()
mspeak.plot()
plt.xlim(mzlim-width,mzlim+width)
plt.ylim(0-(np.sqrt(ylim)),ylim*1.05)
# -
# Lets report some key properties of the peak:
mspeak.abundance # peak height
mspeak.area #integrated area
# %%time
mzdom, fit_peak = mspeak.fit_peak()
fit_peak.values['amplitude'] #peak area from fit
# lmfit module produces nice diagnostic plots for curve fitting
fit_peak.plot()
# Figure above shows the fit is reasonably good, however there is a limited digital resolution which makes the overall lineshape appear blocky. Increased zero-filling will better describe the peak shape.
#
# Next, lets plot the profile spectrum with the initial and final fit peakshape superimposed
fig,ax=plt.subplots(figsize=(9,6))
msobj.plot_mz_domain_profile()
plt.xlim(mzlim-width,mzlim+width)
plt.ylim(0-(np.sqrt(ylim)),ylim*1.05)
ax.plot(mzdom,fit_peak.init_fit,'k--',label='initial fit')
ax.plot(mzdom,fit_peak.best_fit,'r-',label='best fit')
plt.legend()
ax.ticklabel_format(useOffset=False, style='plain')
# ##### Redo with improved zero filling
# Having seen the fit quality, we can repeat the process with 3x zero filling (not 1) and improve our peakshape
MSParameters.transient.number_of_zero_fills = 3
bruker_reader = ReadBrukerSolarix(file_location)
bruker_transient = bruker_reader.get_transient()
msobj = bruker_transient.get_mass_spectrum(plot_result=False, auto_process=True)
# Note the peak index is different - more zero filling has changed the overall number of peaks detected. Generally, more zero-filling is better.
#
# We can also explicitly call a peak function ('gaussian') and a mz_extend value - i.e. how many extra data points in the x-axis to include in the fit. This can help better describe the tails of the broad functions.
mspeak = msobj.mspeaks[953]
print(mspeak.abundance) # peak height
print(mspeak.area) #integrated area
mspeak.plot()
mzdom, fit_peak = mspeak.fit_peak(model='Voigt',mz_extend=20)
print(fit_peak.values['amplitude'])
mspeak.mz_exp
fit_peak.plot()
fig,ax=plt.subplots(figsize=(9,6))
msobj.plot_mz_domain_profile()
plt.xlim(mzlim-width,mzlim+width)
plt.ylim(0-(np.sqrt(ylim)),ylim*1.05)
ax.plot(mzdom,fit_peak.init_fit,'k--',label='initial fit')
ax.plot(mzdom,fit_peak.best_fit,'r-',label='best fit')
plt.legend()
ax.ticklabel_format(useOffset=False, style='plain')
# ## Particle Swarm Optimised Peak Fitting
# It is also possible to use pyswarm to fit an optimised peakshape.
# This package is more computationaly expensive than lmfit, but should return more accurate results
# %%time
xopt, fopt, psfit, psfit_hdp = mspeak.fit_peak_pso(mz_extend=20)
# Note that the PSO fit took ~2s, whereas the lmfit model took ~10ms.
#
# Note that the PSO model has currently fixed arguments viz maxiter and swarm size, but these could be optimised or expanded, affecting performance
fig,ax=plt.subplots(figsize=(9,6))
msobj.plot_mz_domain_profile()
plt.xlim(mzlim-width,mzlim+width)
plt.ylim(0-(np.sqrt(ylim)),ylim*1.05)
ax.plot(mzdom,fit_peak.best_fit,'r-',label='lmfit best fit')
ax.plot(mzdom,psfit,'b--',label='pso fit')
ax.plot(psfit_hdp[0],psfit_hdp[1],'b-',label='pso upsampled fit')
plt.legend()
ax.ticklabel_format(useOffset=False, style='plain')
# For sufficient digital resolution, the PSO fit offers limited advantages over the lmfit model
# Interestingly, the precise apex position appears shifted by the voigt fit in either case
# ## Resolving Power Comparison
# CoreMS calculates peak resolving power using the function:
# However, it is possible to compare the calculated resolving power with these fit lineshapes too.
print(mspeak.fwhm) # CoreMS FWHM
print(fit_peak.values['fwhm']) # Lmfit calculated value
print(xopt[1]) # PSO calculated value
# The peak widths (fwhm) above differ by reasonable amounts.
#
# Converted to resolving power numbers:
print(mspeak.mz_exp/mspeak.fwhm) # CoreMS FWHM
print(mspeak.mz_exp/fit_peak.values['fwhm']) # Lmfit calculated value
print(mspeak.mz_exp/xopt[1]) # PSO calculated value
# We can loop through all the peaks in the msobj and calculate their resolving powers.
#
# Commented out the PSO function as that is much slower
# %%time
corems_rp_measure = []
corems_rp_theor = []
lmfit_rp = []
#pso_rp = []
for mspeak in msobj.mspeaks:
corems_rp_measure.append(mspeak.resolving_power)
corems_rp_theor.append(mspeak.resolving_power_calc(12,1.1185))
mzdom, fit_peak = mspeak.fit_peak(model='Voigt',mz_extend=20)
lmfit_rp.append(mspeak.mz_exp/fit_peak.values['fwhm'])
# pso_rp.append(mspeak.resolution)
print(len(msobj.mspeaks))
# Note it took ~15s to iterate through 1093 peaks
fig,ax = plt.subplots(figsize=(10,10))
xaxis = msobj.mz_exp
ax.scatter(xaxis,corems_rp_theor,c='k',label='CoreMS Theor. RP',alpha=0.5)
ax.scatter(xaxis,corems_rp_measure,c='r',label='CoreMS Measured RP',alpha=0.5)
ax.scatter(xaxis,lmfit_rp,c='b',label='lmfit Fit RP',alpha=0.5)
#ax.plot(pso_rp,'k--',label='PSO Fit RP')
plt.legend()
plt.show()
# Note that CoreMS values follow discrete bands, whereas the lmfit values better reflect true resolving powers (which follow continuous distributions)
# CoreMS also calculates some values higher-than-possible above m/z 600, whereas lmfit better reflects the true numbers
fig,axes = plt.subplots(3,figsize=(10,12))
xaxis = msobj.mz_exp
axes[0].scatter(xaxis,corems_rp_theor,c='k',label='CoreMS Theor. RP')
axes[1].scatter(xaxis,corems_rp_measure,c='r',label='CoreMS Measured RP')
axes[2].scatter(xaxis,lmfit_rp,c='b',label='lmfit Fit RP')
#ax.plot(pso_rp,'k--',label='PSO Fit RP')
plt.show()
|
examples/notebooks/MS_Peak_Fitting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ## Dictionaries
#
# **custom key value pairs**
d = {"I":2, "am":3, "Rajat":1000}
len(d)
a = d.copy()
a
c = dict([ (10,"a"), (2,4), (15,24) ])
c
e = dict.fromkeys(["hello", "a", "b"])
e
e = dict.fromkeys(["hello", "a", "b"], 20)
e
# ## Access Data from the Dictionary
a = {1:2, 3:4, "list":[1,2,3], "dict":{1:23}}
a[1]
a["list"]
a.get(1)
a.get("list")
a["Hi"]
a.get("Hi")
a.get("Hi", "Not Found")
a.keys()
a.values()
a.items()
for i in a:
print(i)
for i in a:
print(i, a[i])
for i in a.values():
print(i)
"list" in a
"Hi" in a
# ## Add or Delete Data
a
a["t"] = (1,2,3)
a
a[1] = 10
a
b = {3:5, 'the':4, 2:100}
a.update(b)
print(a)
# +
##Remove Data
a.pop()
# -
a.pop("t")
print(a)
del a[1]
a
a.clear()
a
del a
a
# ## Print all the words having frequency K
s = "This a word string haing many many word"
k = 2
words = s.split()
print(l)
d = dict.fromkeys(words, 0)
for word in words:
d[word] += 1
d
# +
## another way for doing same
d = {}
for word in words:
if word in d:
d[word] += 1
else:
d[word] = 1
# -
d
# +
## another way
d = {}
for word in words:
d[word] = d.get(word, 0) + 1
# -
d
for word in d:
if d[word] == k:
print(word)
# +
## function
def printKfreq(string, k):
words = string.split()
d = {}
for word in words:
d[word] = d.get(word,0) + 1
for w in d:
if d[w] == k:
print(w)
# -
printKfreq(s, 2)
printKfreq(s, 1)
# ## Maximum Frequency
#
# Given a list of integers print that occurs max time
def maxOccur():
arr = list(map(int, input().split()))
d = {}
for ele in arr:
d[ele] = d.get(ele, 0) + 1
max_ = max(d.values())
for e in d:
if d[e] == max_:
return e
maxOccur()
# ## Pair Sum to Zero
arr = [-2, 2, 6, -2, 2, -6, 3]
d = {}
for e in arr:
d[e] = d.get(e,0) + 1
if -e in d:
print(e, -e)
def sumToZero(arr):
d = {}
for e in arr:
d[e] = d.get(e,0) + 1
if -e in d:
print(e, -e)
# ## Creating own Hashmap
# +
class MapNode:
def __init__(self, key, value):
self.key = key
self.value = value
self.next = None
class Map:
def __init__(self):
self.bucketSize = 10
self.buckets = [None for i in range(self.bucketSize)]
self.count = 0
def size(self):
return self.count
def getBucketIndex(self, hc):
return abs(hc) % self.bucketSize
def rehash(self):
temp = self.buckets
self.buckets = [None for i in range(2*self.bucketSize)]
self.bucketSize = 2*self.bucketSize
self.count = 0
for head in temp:
while head is not None:
self.insert(head.key, head.value)
head = head.next
def load_factor(self):
return self.count / self.bucketSize
def insert(self, key, value):
hc = hash(key)
index = self.getBucketIndex(hc)
head = self.buckets[index]
while head is not None:
if head.key == key:
head.value = value
return
head = head.next
head = self.buckets[index]
newNode = MapNode(key, value)
newNode.next = head
self.buckets[index] = newNode
self.count += 1
load_factor = self.count / self.bucketSize
if load_factor >= 0.7:
self.rehash()
def search(self, key):
hc = hash(key)
index = self.getBucketIndex(hc)
head = self.buckets[index]
while head is not None:
if head.key == key:
return head.value
head = head.next
return None
def remove(self, key):
hc = hash(key)
index = self.getBucketIndex(hc)
head = self.buckets[index]
prev = None
while head is not None:
if head.key == key:
self.count -= 1
if prev == None:
self.buckets[index] = head.next
else:
prev.next = head.next
return head.value
prev = head
head = head.next
return None
# -
m = Map()
m.insert("Rajat", 4)
print(m.size())
m.insert("Rohan", 5)
print(m.size())
m.insert("Rajat", 10)
print(m.size())
m.search("Rajat")
m.search("Hello")
m.remove("Rohan")
print(m.search("Rohan"))
m1 = Map()
for i in range(10):
m1.insert('abc' + str(i), i+1)
print(m1.load_factor(), m1.bucketSize)
# ## Extract Unique characters
#
# Send Feedback
#
# Given a string S, you need to remove all the duplicates. That means, the output string should contain each character only once. The respective order of characters should remain same, as in the input string.
#
# Input format:
#
# The first and only line of input contains a string, that denotes the value of S.
#
# Output format :
#
# The first and only line of output contains the updated string, as described in the task.
#
# Constraints :
#
# 0 <= Length of S <= 10^8
#
# Time Limit: 1 sec
#
# Sample Input 1 :
#
# ababacd
#
# Sample Output 1 :
#
# abcd
#
# Sample Input 2 :
#
# abcde
#
# Sample Output 2 :
#
# abcde
s = "ababacd"
t = ""
for i in s:
if i not in t:
t += i
print(t)
# ## Longest Consequent Subsequence from Array
arr = [9,1,8,6,3,4,2,7,10,15]
d = {}
for i in arr:
d[i] = d.get(i, 0) + 1
d
i = 9
len_temp = 1
for a in range(i+1, 20):
if a in d:
len_temp+= 1
print(True)
else:
break
for b in range(i-1, -1, -1):
if b in d:
len_temp += 1
print(True)
else:
small_temp = b+1
break
print(small_temp, len_temp)
# +
maxLen = 0
start = 0
for i in d:
if d[i] != 0:
len_temp = 1
for a in range(i+1, 100):
if a in d:
len_temp += 1
d[a] = 0
else:
break
for b in range(i-1, -1, -1):
if b in d:
len_temp += 1
d[b] = 0
else:
small_temp = b+1
break
d[i] = 0
if len_temp > maxLen:
maxLen = len_temp
start = small_temp
print(start, start+maxLen-1)
# -
arr = [9,1,8,6,3,4,2,7,10,15]
d = {}
for i in arr:
d[i] = d.get(i, 0) + 1
def longest_Cons_Subseq(arr):
d = {}
for i in arr:
d[i] = d.get(i, 0) + 1
maxLen = 0
start = -1
for i in d:
if d[i] != 0:
len_temp = 1
for a in range(i+1, 1000):
if a in d:
len_temp += 1
d[a] = 0
else:
break
for b in range(i-1, -1, -1):
if b in d:
len_temp += 1
d[b] = 0
else:
temp_start = b+1
break
d[i] = 0
if maxLen < len_temp:
maxLen = len_temp
start = temp_start
if maxLen == len_temp and temp_start == i:
start = i
return start, start+maxLen-1
arr = [9,1,8,6,3,4,2,7,10,15]
print(longest_Cons_Subseq(arr))
arr= [3,7,2,9,1,8,41]
print(longest_Cons_Subseq(arr))
d
# +
arr = [3,1,4,1,5]
k = 0
d = {}
for i in arr:
d[i] = d.get(i, 0) + 1
print(d)
# +
count = 0
for i in d:
if i+k in d:
count = count + 1
print(count)
# -
d
count = 0
if k== 0:
for i in d:
count += d[i]-1
print(count)
arr = [6,3,-1,2,-4,3,1,-2,20]
# +
# A python program to find maximum length subarray
# with 0 sum in o(n) time
# Returns the maximum length
def maxLen(arr):
# NOTE: Dictonary in python in implemented as Hash Maps
# Create an empty hash map (dictionary)
hash_map = {}
# Initialize result
max_len = 0
# Initialize sum of elements
curr_sum = 0
# Traverse through the given array
for i in range(len(arr)):
# Add the current element to the sum
curr_sum += arr[i]
if arr[i] is 0 and max_len is 0:
max_len = 1
if curr_sum is 0:
max_len = i + 1
# NOTE: 'in' operation in dictionary to search
# key takes O(1). Look if current sum is seen
# before
if curr_sum in hash_map:
max_len = max(max_len, i - hash_map[curr_sum] )
else:
# else put this sum in dictionary
hash_map[curr_sum] = i
return max_len
# test array
arr = [15, -2, 2, -8, 1, 7, 10, 13]
print "Length of the longest 0 sum subarray is % d" % maxLen(arr)
|
CN DSA/Dictionay (Hashmap).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Watch Me Code 3: Understanding Function Variable Scope
#
#
def area_incorrect():
area = length * width # these are in the global scope!!!!
return area
# +
## This is a bad idea
length = 10
width = 5
area = area_incorrect()
print ("length=",length, "width=",width, "area=",area)
# +
## Always pass in arguments from the global scope!
def area_correct(length, width):
area = length * width # these are local copies from the global scope...
length = 0
width = 0 # what happens here, stays here!
return area
# -
# in the global scope
length = 5
width = 10
area = area_correct(length,width)
print ("length=",length, "width=",width, "area=",area)
|
lessons/05-Functions/WMC3-Function-Scope.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python
# name: conda-env-python-py
# ---
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-PY0101EN-SkillsNetwork/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# # 1D Numpy in Python
#
# Estimated time needed: **30** minutes
#
# ## Objectives
#
# After completing this lab you will be able to:
#
# * Import and use the `numpy` library
# * Perform operations with `numpy`
#
# <h2>Table of Contents</h2>
# <div class="alert alert-block alert-info" style="margin-top: 20px">
# <ul>
# <li><a href="pre">Preparation</a></li>
# <li>
# <a href="numpy">What is Numpy?</a>
# <ul>
# <li><a href="type">Type</a></li>
# <li><a href="val">Assign Value</a></li>
# <li><a href="slice">Slicing</a></li>
# <li><a href="list">Assign Value with List</a></li>
# <li><a href="other">Other Attributes</a></li>
# </ul>
# </li>
# <li>
# <a href="op">Numpy Array Operations</a>
# <ul>
# <li><a href="add">Array Addition</a></li>
# <li><a href="multi">Array Multiplication</a></li>
# <li><a href="prod">Product of Two Numpy Arrays</a></li>
# <li><a href="dot">Dot Product</a></li>
# <li><a href="cons">Adding Constant to a Numpy Array</a></li>
# </ul>
# </li>
# <li><a href="math">Mathematical Functions</a></li>
# <li><a href="lin">Linspace</a></li>
# </ul>
#
# </div>
#
# <hr>
#
# <h2 id="pre">Preparation</h2>
#
# + tags=[]
# Import the libraries
import time
import sys
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# +
# Plotting functions
def Plotvec1(u, z, v):
ax = plt.axes()
ax.arrow(0, 0, *u, head_width=0.05, color='r', head_length=0.1)
plt.text(*(u + 0.1), 'u')
ax.arrow(0, 0, *v, head_width=0.05, color='b', head_length=0.1)
plt.text(*(v + 0.1), 'v')
ax.arrow(0, 0, *z, head_width=0.05, head_length=0.1)
plt.text(*(z + 0.1), 'z')
plt.ylim(-2, 2)
plt.xlim(-2, 2)
def Plotvec2(a,b):
ax = plt.axes()
ax.arrow(0, 0, *a, head_width=0.05, color ='r', head_length=0.1)
plt.text(*(a + 0.1), 'a')
ax.arrow(0, 0, *b, head_width=0.05, color ='b', head_length=0.1)
plt.text(*(b + 0.1), 'b')
plt.ylim(-2, 2)
plt.xlim(-2, 2)
# -
# Create a Python List as follows:
#
# +
# Create a python list
a = ["0", 1, "two", "3", 4]
# -
# We can access the data via an index:
#
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-PY0101EN-SkillsNetwork/labs/Module%205/images/NumOneList.png" width="660" />
#
# We can access each element using a square bracket as follows:
#
# +
# Print each element
print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])
# -
# <hr>
#
# <h2 id="numpy">What is Numpy?</h2>
#
# A numpy array is similar to a list. It's usually fixed in size and each element is of the same type. We can cast a list to a numpy array by first importing `numpy`:
#
# +
# import numpy library
import numpy as np
# -
# We then cast the list as follows:
#
# +
# Create a numpy array
a = np.array([0, 1, 2, 3, 4])
a
# -
# Each element is of the same type, in this case integers:
#
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-PY0101EN-SkillsNetwork/labs/Module%205/images/NumOneNp.png" width="500" />
#
# As with lists, we can access each element via a square bracket:
#
# +
# Print each element
print("a[0]:", a[0])
print("a[1]:", a[1])
print("a[2]:", a[2])
print("a[3]:", a[3])
print("a[4]:", a[4])
# -
# <h3 id="type">Type</h3>
#
# If we check the type of the array we get <b>numpy.ndarray</b>:
#
# +
# Check the type of the array
type(a)
# -
# As numpy arrays contain data of the same type, we can use the attribute "dtype" to obtain the data type of the array’s elements. In this case, it's a 64-bit integer:
#
# +
# Check the type of the values stored in numpy array
a.dtype
# -
# We can create a numpy array with real numbers:
#
# +
# Create a numpy array
b = np.array([3.1, 11.02, 6.2, 213.2, 5.2])
# -
# When we check the type of the array we get <b>numpy.ndarray</b>:
#
# +
# Check the type of array
type(b)
# -
# If we examine the attribute <code>dtype</code> we see float 64, as the elements are not integers:
#
# +
# Check the value type
b.dtype
# -
# <h3 id="val">Assign value</h3>
#
# We can change the value of the array. Consider the array <code>c</code>:
#
# +
# Create numpy array
c = np.array([20, 1, 2, 3, 4])
c
# -
# We can change the first element of the array to 100 as follows:
#
# +
# Assign the first element to 100
c[0] = 100
c
# -
# We can change the 5th element of the array to 0 as follows:
#
# +
# Assign the 5th element to 0
c[4] = 0
c
# -
# <h3 id="slice">Slicing</h3>
#
# Like lists, we can slice the numpy array. We can select the elements from 1 to 3 and assign it to a new numpy array <code>d</code> as follows:
#
# +
# Slicing the numpy array
d = c[1:4]
d
# -
# We can assign the corresponding indexes to new values as follows:
#
# +
# Set the fourth element and fifth element to 300 and 400
c[3:5] = 300, 400
c
# -
# <h3 id="list">Assign Value with List</h3>
#
# Similarly, we can use a list to select more than one specific index.
# The list `select` contains several values:
#
# + tags=[]
# Create the index list
select = [0, 2, 3]
# -
# We can use the list as an argument in the brackets. The output is the elements corresponding to the particular indexes:
#
# +
# Use List to select elements
d = c[select]
d
# -
# We can assign the specified elements to a new value. For example, we can assign the values to 100 000 as follows:
#
# +
# Assign the specified elements to new value
c[select] = 100000
c
# -
# <h3 id="other">Other Attributes</h3>
#
# Let's review some basic array attributes using the array <code>a</code>:
#
# +
# Create a numpy array
a = np.array([0, 1, 2, 3, 4])
a
# -
# The attribute <code>size</code> is the number of elements in the array:
#
# +
# Get the size of numpy array
a.size
# -
# The next two attributes will make more sense when we get to higher dimensions but let's review them. The attribute <code>ndim</code> represents the number of array dimensions, or the rank of the array. In this case, one:
#
# +
# Get the number of dimensions of numpy array
a.ndim
# -
# The attribute <code>shape</code> is a tuple of integers indicating the size of the array in each dimension:
#
# +
# Get the shape/size of numpy array
a.shape
# + tags=[]
# Create a numpy array
a = np.array([1, -1, 1, -1])
# +
# Get the mean of numpy array
mean = a.mean()
mean
# +
# Get the standard deviation of numpy array
standard_deviation=a.std()
standard_deviation
# +
# Create a numpy array
b = np.array([-1, 2, 3, 4, 5])
b
# +
# Get the biggest value in the numpy array
max_b = b.max()
max_b
# +
# Get the smallest value in the numpy array
min_b = b.min()
min_b
# -
# <hr>
#
# <h2 id="op">Numpy Array Operations</h2>
#
# <h3 id="add">Array Addition</h3>
#
# Consider the numpy array <code>u</code>:
#
u = np.array([1, 0])
u
# Consider the numpy array <code>v</code>:
#
v = np.array([0, 1])
v
# We can add the two arrays and assign it to z:
#
# +
# Numpy Array Addition
z = u + v
z
# -
# The operation is equivalent to vector addition:
#
# +
# Plot numpy arrays
Plotvec1(u, z, v)
# -
# <h3 id="multi">Array Multiplication</h3>
#
# Consider the vector numpy array <code>y</code>:
#
# +
# Create a numpy array
y = np.array([1, 2])
y
# -
# We can multiply every element in the array by 2:
#
# +
# Numpy Array Multiplication
z = 2 * y
z
# -
# This is equivalent to multiplying a vector by a scaler:
#
# <h3 id="prod">Product of Two Numpy Arrays</h3>
#
# Consider the following array <code>u</code>:
#
# +
# Create a numpy array
u = np.array([1, 2])
u
# -
# Consider the following array <code>v</code>:
#
# +
# Create a numpy array
v = np.array([3, 2])
v
# -
# The product of the two numpy arrays <code>u</code> and <code>v</code> is given by:
#
# +
# Calculate the production of two numpy arrays
z = u * v
z
# -
# <h3 id="dot">Dot Product</h3>
#
# The dot product of the two numpy arrays <code>u</code> and <code>v</code> is given by:
#
# +
# Calculate the dot product
np.dot(u, v)
# -
# <h3 id="cons">Adding Constant to a Numpy Array</h3>
#
# Consider the following array:
#
# +
# Create a constant to numpy array
u = np.array([1, 2, 3, -1])
u
# -
# Adding the constant 1 to each element in the array:
#
# +
# Add the constant to array
u + 1
# -
# The process is summarised in the following animation:
#
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-PY0101EN-SkillsNetwork/labs/Module%205/images/NumOneAdd.gif" width="500" />
#
# <hr>
#
# <h2 id="math">Mathematical Functions</h2>
#
# We can access the value of <code>pi</code> in numpy as follows :
#
# +
# The value of pi
np.pi
# -
# We can create the following numpy array in Radians:
#
# +
# Create the numpy array in radians
x = np.array([0, np.pi/2 , np.pi])
# -
# We can apply the function <code>sin</code> to the array <code>x</code> and assign the values to the array <code>y</code>; this applies the sine function to each element in the array:
#
# +
# Calculate the sin of each elements
y = np.sin(x)
y
# -
# <hr>
#
# <h2 id="lin">Linspace</h2>
#
# A useful function for plotting mathematical functions is <code>linspace</code>. Linspace returns evenly spaced numbers over a specified interval. We specify the starting point of the sequence and the ending point of the sequence. The parameter "num" indicates the Number of samples to generate, in this case 5:
#
# +
# Makeup a numpy array within [-2, 2] and 5 elements
np.linspace(-2, 2, num=5)
# -
# If we change the parameter <code>num</code> to 9, we get 9 evenly spaced numbers over the interval from -2 to 2:
#
# +
# Make a numpy array within [-2, 2] and 9 elements
np.linspace(-2, 2, num=9)
# -
# We can use the function <code>linspace</code> to generate 100 evenly spaced samples from the interval 0 to 2π:
#
# +
# Make a numpy array within [0, 2π] and 100 elements
x = np.linspace(0, 2*np.pi, num=100)
# -
# We can apply the sine function to each element in the array <code>x</code> and assign it to the array <code>y</code>:
#
# + tags=[]
# Calculate the sine of x list
y = np.sin(x)
# +
# Plot the result
plt.plot(x, y)
# -
# <hr>
#
# <h2 id="quiz">Quiz on 1D Numpy Array</h2>
#
# Implement the following vector subtraction in numpy: u-v
#
# +
# Write your code below and press Shift+Enter to execute
u = np.array([1, 0])
v = np.array([0, 1])
u-v
# -
# <details><summary>Click here for the solution</summary>
#
# ```python
# u - v
# ```
#
# </details>
#
# <hr>
#
# Multiply the numpy array z with -2:
#
# +
# Write your code below and press Shift+Enter to execute
z = np.array([2, 4])
-2*z
# -
# <details><summary>Click here for the solution</summary>
#
# ```python
# -2 * z
# ```
#
# </details>
#
# <hr>
#
# Consider the list <code>\[1, 2, 3, 4, 5]</code> and <code>\[1, 0, 1, 0, 1]</code>. Cast both lists to a numpy array then multiply them together:
#
# Write your code below and press Shift+Enter to execute
a=np.array([1, 2, 3, 4, 5])
b=np.array([1, 0, 1, 0, 1])
a*b
# <details><summary>Click here for the solution</summary>
#
# ```python
# a = np.array([1, 2, 3, 4, 5])
# b = np.array([1, 0, 1, 0, 1])
# a * b
# ```
#
# </details>
#
# <hr>
#
# Convert the list <code>\[-1, 1]</code> and <code>\[1, 1]</code> to numpy arrays <code>a</code> and <code>b</code>. Then, plot the arrays as vectors using the fuction <code>Plotvec2</code> and find their dot product:
#
# Write your code below and press Shift+Enter to execute
a=np.array([-1,1])
b=np.array([1,1])
Plotvec2(a,b)
print(np.dot(a,b))
# <details><summary>Click here for the solution</summary>
#
# ```python
# a = np.array([-1, 1])
# b = np.array([1, 1])
# Plotvec2(a, b)
# print("The dot product is", np.dot(a,b))
#
# ```
#
# </details>
#
# <hr>
#
# Convert the list <code>\[1, 0]</code> and <code>\[0, 1]</code> to numpy arrays <code>a</code> and <code>b</code>. Then, plot the arrays as vectors using the function <code>Plotvec2</code> and find their dot product:
#
# Write your code below and press Shift+Enter to execute
a=np.array([1,0])
b=np.array([0,1])
Plotvec2(a,b)
print(np.dot(a,b))
# <details><summary>Click here for the solution</summary>
#
# ```python
# a = np.array([1, 0])
# b = np.array([0, 1])
# Plotvec2(a, b)
# print("The dot product is", np.dot(a, b))
#
# ```
#
# </details>
#
# <hr>
#
# Convert the list <code>\[1, 1]</code> and <code>\[0, 1]</code> to numpy arrays <code>a</code> and <code>b</code>. Then plot the arrays as vectors using the fuction <code>Plotvec2</code> and find their dot product:
#
# Write your code below and press Shift+Enter to execute
a=np.array([1,1])
b=np.array([0,1])
Plotvec2(a,b)
print(np.dot(a,b))
# <details><summary>Click here for the solution</summary>
#
# ```python
# a = np.array([1, 1])
# b = np.array([0, 1])
# Plotvec2(a, b)
# print("The dot product is", np.dot(a, b))
# print("The dot product is", np.dot(a, b))
#
# ```
#
# </details>
#
# <hr>
#
# Why are the results of the dot product for <code>\[-1, 1]</code> and <code>\[1, 1]</code> and the dot product for <code>\[1, 0]</code> and <code>\[0, 1]</code> zero, but not zero for the dot product for <code>\[1, 1]</code> and <code>\[0, 1]</code>? <p><i>Hint: Study the corresponding figures, pay attention to the direction the arrows are pointing to.</i></p>
#
# Write your code below and press Shift+Enter to execute
When a and b are at 90 Degree, the dot product is
# <details><summary>Click here for the solution</summary>
#
# ```python
# The vectors used for question 4 and 5 are perpendicular. As a result, the dot product is zero.
#
# ```
#
# </details>
#
# <hr>
# <h2>The last exercise!</h2>
# <p>Congratulations, you have completed your first lesson and hands-on lab in Python. However, there is one more thing you need to do. The Data Science community encourages sharing work. The best way to share and showcase your work is to share it on GitHub. By sharing your notebook on GitHub you are not only building your reputation with fellow data scientists, but you can also show it off when applying for a job. Even though this was your first piece of work, it is never too early to start building good habits. So, please read and follow <a href="https://cognitiveclass.ai/blog/data-scientists-stand-out-by-sharing-your-notebooks/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkPY0101ENSkillsNetwork19487395-2021-01-01" target="_blank">this article</a> to learn how to share your work.
# <hr>
#
# ## Author
#
# <a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkPY0101ENSkillsNetwork19487395-2021-01-01" target="_blank"><NAME></a>
#
# ## Other contributors
#
# <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a"><NAME></a>
#
# ## Change Log
#
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# |---|---|---|---|
# | 2020-08-26 | 2.0 | Lavanya | Moved lab to course repo in GitLab |
# | | | | |
# | | | | |
#
# <hr/>
#
# ## <h3 align="center"> © IBM Corporation 2020. All rights reserved. <h3/>
#
|
PY0101EN-5-1-Numpy1D.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from google.cloud import storage
import pandas as pd
import numpy as np
from io import StringIO
def split_data(dest_bucket, dest_file, split_time, preprocess=False):
# Read in the data from the GCS bucket and format the data
data_loc = "gs://{0}/{1}".format(dest_bucket, dest_file)
data = pd.read_csv(data_loc, index_col=0)
#data.index.rename('time', inplace=True)
first_idx = data.index.values[0]
# Split the data based on the split_time param
data = data.sort_index()
train_data = data.loc[first_idx:split_time] # Note: this is 'inclusive' so the last data point in train data
test_data = data.loc[split_time:] # shows up as the first data point in the test data
# This shouldn't be a big deal for this dataset
# Preprocess the data (if applicable)
if preprocess:
scaler = MinMaxScaler()
X_train = scaler.fit_transform(train_data)
X_test = scaler.transform(test_data)
else:
X_train = train_data.to_numpy()
X_test = test_data.to_numpy()
scaled_train_data = pd.DataFrame(X_train, columns=data.columns)
scaled_test_data = pd.DataFrame(X_test, columns=data.columns)
# Save the data splits off to GCS bucket
train_f = StringIO()
test_f = StringIO()
scaled_train_data.to_csv(train_f)
scaled_test_data.to_csv(test_f)
train_f.seek(0)
test_f.seek(0)
train_dest_file = "train.csv"
test_dest_file = "test.csv"
client = storage.Client()
client.get_bucket(dest_bucket).blob(train_dest_file).upload_from_file(train_f, content_type='text/csv')
client.get_bucket(dest_bucket).blob(test_dest_file).upload_from_file(test_f, content_type='text/csv')
# Return the location of the new data splits
return (dest_bucket, train_dest_file, test_dest_file)
# +
dest_bucket = "rrusson-kubeflow-test"
dest_file = "raw_data_v2.csv"
split_time = "2004-02-15 12:52:39"
preprocess = True
split_data(dest_bucket, dest_file, split_time, preprocess=preprocess)
# -
import time
print("file_{}".format(time.perf_counter()))
|
nasa-iot-demo/explore-train-test-split.ipynb
|
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
#|hide
#|skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
# some dependencies to get the dataset
# ! pip install rarfile av
# ! pip install -Uq pyopenssl
# # Tutorial - Using fastai on sequences of Images
#
# > How to use fastai to train an image sequence to image sequence job.
#
# This tutorial uses fastai to process sequences of images. We are going to look at two tasks:
# - First we will do video classification on the [UCF101 dataset](https://www.crcv.ucf.edu/data/UCF101.php). You will learn how to convert the video to individual frames. We will also build a data processing piepline using fastai's mid level API.
# - Secondly we will build some simple models and assess our accuracy.
# - Finally we will train a SotA transformer based architecture.
# +
#|all_slow
# -
from fastai.vision.all import *
# ## UCF101 Action Recognition
#
# > UCF101 is an action recognition data set of realistic action videos, collected from YouTube, having 101 action categories. This data set is an extension of UCF50 data set which has 50 action categories.
#
# _"With 13320 videos from 101 action categories, UCF101 gives the largest diversity in terms of actions and with the presence of large variations in camera motion, object appearance and pose, object scale, viewpoint, cluttered background, illumination conditions, etc, it is the most challenging data set to date. As most of the available action recognition data sets are not realistic and are staged by actors, UCF101 aims to encourage further research into action recognition by learning and exploring new realistic action categories"_
# ### setup
# We have to download the UCF101 dataset from their website. It is a big dataset (6.5GB), if your connection is slow you may want to do this at night or in a terminal (to avoid blocking the notebook). fastai's `untar_data` is not capable of downloading this dataset, so we will use `wget` and then unrar the files using `rarfile`.
#
# `fastai`'s datasets are located inside `~/.fastai/archive`, we will download UFC101 there.
# +
#|slow
# # !wget -P ~/.fastai/archive/ --no-check-certificate https://www.crcv.ucf.edu/data/UCF101/UCF101.rar
# -
# > you can run this command on a terminal to avoid blocking the notebook
# Let's make a function to`unrar` the downloaded dataset. This function is very similar to `untar_data`, but handles `.rar` files.
# +
from rarfile import RarFile
def unrar(fname, dest):
"Extract `fname` to `dest` using `rarfile`"
dest = URLs.path(c_key='data')/fname.name.withsuffix('') if dest is None else dest
print(f'extracting to: {dest}')
if not dest.exists():
fname = str(fname)
if fname.endswith('rar'):
with RarFile(fname, 'r') as myrar:
myrar.extractall(dest.parent)
else:
raise Exception(f'Unrecognized archive: {fname}')
rename_extracted(dest)
return dest
# -
# To be consistent, we will extract UCF dataset in `~/.fasta/data`. This is where fastai stores decompressed datasets.
ucf_fname = Path.home()/'.fastai/archive/UCF101.rar'
dest = Path.home()/'.fastai/data/UCF101'
# > unraring a large file like this one is very slow.
#|slow
path = unrar(ucf_fname, dest)
# The file structure of the dataset after extraction is one folder per action:
path.ls()
# inside, you will find one video per instance, the videos are in `.avi` format. We will need to convert each video to a sequence of images to able to work with our fastai vision toolset.
# > Note: torchvision has a built-in video reader that may be capable of simplifying this task
# ```
# UCF101-frames
#
# ├── ApplyEyeMakeup
# | |── v_ApplyEyeMakeup_g01_c01.avi
# | ├── v_ApplyEyeMakeup_g01_c02.avi
# | | ...
# ├── Hammering
# | ├── v_Hammering_g01_c01.avi
# | ├── v_Hammering_g01_c02.avi
# | ├── v_Hammering_g01_c03.avi
# | | ...
# ...
# ├── YoYo
# ├── v_YoYo_g01_c01.avi
# ...
# ├── v_YoYo_g25_c03.avi
#
# ```
# we can grab all videos at one using `get_files` and passing the `'.avi` extension
video_paths = get_files(path, extensions='.avi')
video_paths[0:4]
# We can convert the videos to frames using `av`:
import av
def extract_frames(video_path):
"convert video to PIL images "
video = av.open(str(video_path))
for frame in video.decode(0):
yield frame.to_image()
frames = list(extract_frames(video_paths[0]))
frames[0:4]
# We have`PIL.Image` objects, so we can directly show them using fastai's `show_images` method
show_images(frames[0:5])
# let's grab one video path
video_path = video_paths[0]
video_path
# We want to export all videos to frames, les't built a function that is capable of exporting one video to frames, and stores the resulting frames on a folder of the same name.
#
# Let's grab de folder name:
video_path.relative_to(video_path.parent.parent).with_suffix('')
# we will also create a new directory for our `frames` version of UCF. You will need at least 7GB to do this, afterwards you can erase the original UCF101 folder containing the videos.
path_frames = path.parent/'UCF101-frames'
if not path_frames.exists(): path_frames.mkdir()
# we will make a function that takes a video path, and extracts the frames to our new `UCF-frames` dataset with the same folder structure.
def avi2frames(video_path, path_frames=path_frames, force=False):
"Extract frames from avi file to jpgs"
dest_path = path_frames/video_path.relative_to(video_path.parent.parent).with_suffix('')
if not dest_path.exists() or force:
dest_path.mkdir(parents=True, exist_ok=True)
for i, frame in enumerate(extract_frames(video_path)):
frame.save(dest_path/f'{i}.jpg')
avi2frames(video_path)
(path_frames/video_path.relative_to(video_path.parent.parent).with_suffix('')).ls()
# Now we can batch process the whole dataset using fastcore's `parallel`. This could be slow on a low CPU count machine. On a 12 core machine it takes 4 minutes.
# +
#|slow
#parallel(avi2frames, video_paths)
# -
# after this you get a folder hierarchy that looks like this
#
# ```
# UCF101-frames
#
# ├── ApplyEyeMakeup
# | |── v_ApplyEyeMakeup_g01_c01
# | │ ├── 0.jpg
# | │ ├── 100.jpg
# | │ ├── 101.jpg
# | | ...
# | ├── v_ApplyEyeMakeup_g01_c02
# | │ ├── 0.jpg
# | │ ├── 100.jpg
# | │ ├── 101.jpg
# | | ...
# ├── Hammering
# | ├── v_Hammering_g01_c01
# | │ ├── 0.jpg
# | │ ├── 1.jpg
# | │ ├── 2.jpg
# | | ...
# | ├── v_Hammering_g01_c02
# | │ ├── 0.jpg
# | │ ├── 1.jpg
# | │ ├── 2.jpg
# | | ...
# | ├── v_Hammering_g01_c03
# | │ ├── 0.jpg
# | │ ├── 1.jpg
# | │ ├── 2.jpg
# | | ...
# ...
# ├── YoYo
# ├── v_YoYo_g01_c01
# │ ├── 0.jpg
# │ ├── 1.jpg
# │ ├── 2.jpg
# | ...
# ├── v_YoYo_g25_c03
# ├── 0.jpg
# ├── 1.jpg
# ├── 2.jpg
# ...
# ├── 136.jpg
# ├── 137.jpg
#
# ```
# ## Data pipeline
# we have converted all the videos to images, we are ready to start building our fastai data pieline
data_path = Path.home()/'.fastai/data/UCF101-frames'
data_path.ls()[0:3]
# we have one folder per action category, and inside one folder per instance of the action.
def get_instances(path):
" gets all instances folders paths"
sequence_paths = []
for actions in path.ls():
sequence_paths += actions.ls()
return sequence_paths
# with this function we get individual instances of each action, **these are the image sequences that we need to clasiffy.**. We will build a pipeline that takes as input **instance path**'s.
instances_path = get_instances(data_path)
instances_path[0:3]
# we have to sort the video frames numerically. We will patch pathlib's `Path` class to return a list of files conttaines on a folde sorted numerically. It could be a good idea to modify fastcore's `ls` method with an optiional argument `sort_func`.
@patch
def ls_sorted(self:Path):
"ls but sorts files by name numerically"
return self.ls().sorted(key=lambda f: int(f.with_suffix('').name))
instances_path[0].ls_sorted()
# let's grab the first 5 frames
frames = instances_path[0].ls_sorted()[0:5]
show_images([Image.open(img) for img in frames])
# We will build a tuple that contains individual frames and that can show themself. We will use the same idea that on the `siamese_tutorial`. As a video can have many frames, and we don't want to display them all, the `show` method will only display the 1st, middle and last images.
class ImageTuple(fastuple):
"A tuple of PILImages"
def show(self, ctx=None, **kwargs):
n = len(self)
img0, img1, img2= self[0], self[n//2], self[n-1]
if not isinstance(img1, Tensor):
t0, t1,t2 = tensor(img0), tensor(img1),tensor(img2)
t0, t1,t2 = t0.permute(2,0,1), t1.permute(2,0,1),t2.permute(2,0,1)
else: t0, t1,t2 = img0, img1,img2
return show_image(torch.cat([t0,t1,t2], dim=2), ctx=ctx, **kwargs)
ImageTuple(PILImage.create(fn) for fn in frames).show();
# we will use the mid-level API to create our Dataloader from a transformed list.
class ImageTupleTfm(Transform):
"A wrapper to hold the data on path format"
def __init__(self, seq_len=20):
store_attr()
def encodes(self, path: Path):
"Get a list of images files for folder path"
frames = path.ls_sorted()
n_frames = len(frames)
s = slice(0, min(self.seq_len, n_frames))
return ImageTuple(tuple(PILImage.create(f) for f in frames[s]))
tfm = ImageTupleTfm(seq_len=5)
hammering_instance = instances_path[0]
hammering_instance
tfm(hammering_instance).show()
# with this setup, we can use the `parent_label` as our labelleing function
parent_label(hammering_instance)
splits = RandomSplitter()(instances_path)
# We will use fastai`Datasets` class, we have to pass a `list` of transforms. The first list `[ImageTupleTfm(5)]` is how we grab the `x`'s and the second list `[parent_label, Categorize]]` is how we grab the `y`'s.' So, from each instance path, we grab the first 5 images to construct an `ImageTuple` and we grad the label of the action from the parent folder using `parent_label` and the we `Categorize` the labels.
ds = Datasets(instances_path, tfms=[[ImageTupleTfm(5)], [parent_label, Categorize]], splits=splits)
len(ds)
dls = ds.dataloaders(bs=4, after_item=[Resize(128), ToTensor],
after_batch=[IntToFloatTensor, Normalize.from_stats(*imagenet_stats)])
# refactoring
def get_action_dataloaders(files, bs=8, image_size=64, seq_len=20, val_idxs=None, **kwargs):
"Create a dataloader with `val_idxs` splits"
splits = RandomSplitter()(files) if val_idxs is None else IndexSplitter(val_idxs)(files)
itfm = ImageTupleTfm(seq_len=seq_len)
ds = Datasets(files, tfms=[[itfm], [parent_label, Categorize]], splits=splits)
dls = ds.dataloaders(bs=bs, after_item=[Resize(image_size), ToTensor],
after_batch=[IntToFloatTensor, Normalize.from_stats(*imagenet_stats)], drop_last=True, **kwargs)
return dls
dls = get_action_dataloaders(instances_path, bs=32, image_size=64, seq_len=5)
dls.show_batch()
# ## A Baseline Model
# We will make a simple baseline model. It will encode each frame individually using a pretrained resnet. We make use of the `TimeDistributed` layer to apply the resnet to each frame identically. This simple model will just average the probabilities of each frame individually. A `simple_splitter` function is also provided to avoid destroying the pretrained weights of the encoder.
# +
class SimpleModel(Module):
def __init__(self, arch=resnet34, n_out=101):
self.encoder = TimeDistributed(create_body(arch, pretrained=True))
self.head = TimeDistributed(create_head(512, 101))
def forward(self, x):
x = torch.stack(x, dim=1)
return self.head(self.encoder(x)).mean(dim=1)
def simple_splitter(model): return [params(model.encoder), params(model.head)]
# -
# > Note: We don't need to put a `sigmoid` layer at the end, as the loss function will fuse the Entropy with the sigmoid to get more numerical stability. Our models will output one value per category. you can recover the predicted class using `torch.sigmoid` and `argmax`.
model = SimpleModel().cuda()
x,y = dls.one_batch()
# It is always a good idea to check what is going inside the model, and what is coming out.
print(f'{type(x) = },\n{len(x) = } ,\n{x[0].shape = }, \n{model(x).shape = }')
# We are ready to create a Learner. The loss function is not mandatory, as the `DataLoader` already has the Binary Cross Entropy because we used a `Categorify` transform on the outputs when constructing the `Datasets`.
dls.loss_func
# We will make use of the `MixedPrecision` callback to speed up our training (by calling `to_fp16` on the learner object).
# > Note: The `TimeDistributed` layer is memory hungry (it pivots the image sequence to the batch dimesion) so if you get OOM errors, try reducing the batchsize.
#
# As this is a classification problem, we will monitor classification `accuracy`. You can pass the model splitter directly when creating the learner.
learn = Learner(dls, model, metrics=[accuracy], splitter=simple_splitter).to_fp16()
learn.lr_find()
learn.fine_tune(3, 1e-3, freeze_epochs=3)
# 68% not bad for our simple baseline with only 5 frames.
learn.show_results()
# We can improve our model by passing the outputs of the image encoder to an `nn.LSTM` to get some inter-frame relation. To do this, we have to get the features of the image encoder, so we have to modify our code and make use of the `create_body` function and add a pooling layer afterwards.
arch = resnet34
encoder = nn.Sequential(create_body(arch, pretrained=True), nn.AdaptiveAvgPool2d(1), Flatten()).cuda()
# if we check what is the output of the encoder, for each image, we get a feature map of 512.
encoder(x[0]).shape
tencoder = TimeDistributed(encoder)
tencoder(torch.stack(x, dim=1)).shape
# this is perfect as input for a recurrent layer. Let's refactor and add a linear layer at the end. We will output the hidden state to a linear layer to compute the probabilities. The idea behind, is that the hidden state encodes the temporal information of the sequence.
class RNNModel(Module):
def __init__(self, arch=resnet34, n_out=101, num_rnn_layers=1):
self.encoder = TimeDistributed(nn.Sequential(create_body(arch, pretrained=True), nn.AdaptiveAvgPool2d(1), Flatten()))
self.rnn = nn.LSTM(512, 512, num_layers=num_rnn_layers, batch_first=True)
self.head = LinBnDrop(num_rnn_layers*512, n_out)
def forward(self, x):
x = torch.stack(x, dim=1)
x = self.encoder(x)
bs = x.shape[0]
_, (h, _) = self.rnn(x)
return self.head(h.view(bs,-1))
# let's make a splitter function to train the encoder and the rest separetely
def rnnmodel_splitter(model):
return [params(model.encoder), params(model.rnn)+params(model.head)]
model2 = RNNModel().cuda()
learn = Learner(dls, model2, metrics=[accuracy], splitter=rnnmodel_splitter).to_fp16()
learn.lr_find()
learn.fine_tune(5, 5e-3)
# this models is harder to train. A good idea would be to add some Dropout. Let's try increasing the sequence lenght. Another approach would be to use a better layer for this type of task, like the [ConvLSTM](https://paperswithcode.com/method/convlstm) or a Transformer for images that are capable of modelling the spatio-temporal relations in a more sophisticated way.
# Some ideas:
# - Try sampling the frames differently, (randomly spacing, more frames, etc...)
# ## A Transformer Based models
# > A quick tour on the new transformer based archs
#
# There are a bunch of transformer based image models that have appeared recently after the introduction of the [Visual Transformer (ViT). ](https://github.com/google-research/vision_transformer). We currently have many variants of this architecture with nice implementation in pytorch integrated to [timm](https://github.com/rwightman/pytorch-image-models) and [@lucidrains](https://github.com/lucidrains/vit-pytorch) maintains a repository with all the variants and elegant pytorch implementations.
#
# Recently the image models have been extended to video/image-sequences, hey use the transformer to encode space and time jointly. Here we will train the [TimeSformer](https://arxiv.org/abs/2102.05095) architecture on the action recognition task as it appears to be the easier to train from scratch. We will use [@lucidrains](https://github.com/lucidrains/TimeSformer-pytorch) implementation.
#
# Currently we don't have access to pretrained models, but loading the `ViT` weights on some blocks could be possible, but it is not done here.
#
#
# ### Install
# First things first, we will need to install the model:
#
# ```
# # !pip install -Uq timesformer-pytorch
# ```
from timesformer_pytorch import TimeSformer
# ### Train
# the `TimeSformer` implementation expects a sequence of images in the form of: `(batch_size, seq_len, c, w, h)`. We need to wrap the model to stack the image sequence before feeding the forward method
class MyTimeSformer(TimeSformer):
def forward(self, x):
x = torch.stack(x, dim=1)
return super().forward(x)
timesformer = MyTimeSformer(
dim = 128,
image_size = 128,
patch_size = 16,
num_frames = 5,
num_classes = 101,
depth = 12,
heads = 8,
dim_head = 64,
attn_dropout = 0.1,
ff_dropout = 0.1
).cuda()
learn_tf = Learner(dls, timesformer, metrics=[accuracy]).to_fp16()
learn_tf.lr_find()
learn_tf.fit_one_cycle(12, 5e-4)
learn_tf.show_results()
|
nbs/24_tutorial.image_sequence.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This repository contains an implementation of the algorithm presented in
# *Black-box density function estimation using recursive partitioning*
# [arXiv](https://arxiv.org/abs/2010.13632), referred to as DEFER (DEnsity Function Estimation using Recursive partitioning). The paper was presented at the International Conference on Machine Learning (ICML) 2021.
#
# DEFER allows efficient Bayesian inference on general problems involving up to about ten random variables or dimensions,
# without the need to specify anything else than
# - the unnormalised density function (which can be black-box),
# - domain bounds (enclosing the typical set, although allowed to be doing so with very large margins),
# - a density function evaluation budget.
#
# The code comes with a high-level interface intended for ease-of-use.
# Below we will show:
# - How the DEFER algorithm can be used to approximate arbitrary distributions (of moderate dimension),
# such as posterior distributions which are allowed to be e.g. multimodal, discontinuous, exhibit complicated correlations, and have zero density regions.
# - Some available operations the approximation provides, including:
# - fast, constant time sampling,
# - computation of normalisation constant,
# - analytical expectations of functions with respect to the approximation,
# - conditionals to be derived quickly, and
# - approximate marginalisation of a subset of variables or dimensions.
import corner
import matplotlib.pylab as plt
from defer.helpers import *
from defer.variables import Variable
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
# Configure plot defaults
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['grid.color'] = '#666666'
# %config InlineBackend.figure_format = 'png'
# ### Density function example
# The DEFER algorithm constructs a distribution approximation given a provided (arbitrary) unnormalised density function $f$ which can be point-wise evaluated.
#
# In this example we provide the algorithm with such a function, namely where the density value at a given location depends on the distance to the closest point of a shape embedded in the same space. The particular shape used is a spiral embedded in three dimensions. The distance (as a function of $x$) is used as the energy function of a Gibbs distribution.
#
# Note that the DEFER algorithm does not need to know what the function $f$ is or represents; it will simply query it with inputs and construct an approximation which allows operations that typically is not available using the original function $f$ (except for trivial $f$ and corresponding distributions).
# +
def spiral(t):
w = 6 * np.pi
v = 0.9
c = 1
return np.array([
t,
(v * t + c) * np.cos(w * t),
(v * t + c) * np.sin(w * t),
]).transpose()
# Domain bounds
curve_lower_x = -1
curve_upper_x = 1
other_dims_lower = [-2, -2]
other_dims_upper = [2, 2]
lower = [curve_lower_x] + other_dims_lower
upper = [curve_upper_x] + other_dims_upper
def find_shortest_distance(
x, curve, lower_x=curve_lower_x, upper_x=curve_upper_x):
trial_input_points = np.linspace(lower_x, upper_x, num=5000)
curve_points = curve(trial_input_points)
distances = np.linalg.norm(np.abs(curve_points - x), axis=1)
index = int(np.argmin(distances))
shortest_distance = distances[index]
return shortest_distance
# Unnormalised density function. This can be any continuous-input function returning a density value.
def f(x):
distance_to_closest_point_on_curve = find_shortest_distance(x, curve=spiral)
energy = distance_to_closest_point_on_curve
return np.exp(-30 * energy)
# + [markdown] pycharm={"name": "#%% md\n"}
# #### Variables
# Declare the random variables, corresponding to the parameters of the density function $f$.
# In this example, we only have a single parameter $x$, and thus only one random variable.
#
# The Variables object produces the density function domain (variables.domain) - or sample space. It will also keep track of mappings between variables (or slices of them using []) to the corresponding dimensions.
#
# Note that the variables do not have any state - they simply act as semantic collections of dimensions with defined boundaries. Having the variables kept together as a collection in the Variables object will be particularly useful for keeping track of what remains when deriving conditionals or marginals (more on that later).
# + pycharm={"name": "#%%\n"}
x = Variable(
lower=lower,
upper=upper,
name="x"
)
variables = Variables([x])
joint_distribution = None
x1 = None
x2 = None
x3 = None
x4 = None
x5 = None
# -
# #### Construct approximation
# Here we use a high-level wrapper around the DEFER algorithm which given the $f$-function definition and the variables (setting the domain boundaries), returns a distribution approximation.
#
# The budget of the algorithm, in terms of number of evaluations of $f$, is set using 'num_fn_calls'. Note that this number may differ slightly from the calls actually used (by a few evaluations). This is because the construction of each partition (see paper) requires more than one density evaluations, and thus the total may not add up exactly to the provided number.
#
# Note that 'is_log_fn' also needs to be specified. 'is_log_fn' should be set to True if the $f$ function returns the logarithm of the density value rather than the density value.
# +
approx_posterior = construct(
fn=joint_distribution,
variables=Variables([x1, x2, x3, x4, x5]),
is_log_fn=True,
num_fn_calls=10000,
callback=lambda i, current_approx: print(
"#Iterations: %s. #Evaluations: %s. Log Z: %.2f" %
(
i,
current_approx.num_partitions,
np.log(current_approx.z)
)),
callback_freq_fn_calls=100,
)
evidence = approx_posterior.z
differential_entropy = approx_posterior.expectation(
lambda f, x, z: -np.log(f / z))
sampler = approx_posterior.sampler()
posterior_samples = sampler(num_samples=1000000)
approx_conditional_posterior = approx_posterior.conditional({
x1: np.array([0.5, 0.5])
})
conditional_sampler = approx_conditional_posterior.sampler()
...
# -
# Analytical expectation of functions with respect to the distribution approximation.
# Due to the piece-wise constant approximation being used, this simply corresponds to a weighted summation. The 'expectation' method is for convenience for computing expectations of functions provided the function, taking the integrand ($f$) value, the corresponding parameters (concatenated to a vector), and the normalisation constant $z$, as parameters. In the below example the differential entropy is computed this way.
# + pycharm={"name": "#%%\n"}
differential_entropy = approx_joint.expectation(lambda f, x, z: -np.log(f / z))
# -
# A few, very common such expectations are provided as methods (such as mean and variance), which are internally using the 'expectation' method.
# + pycharm={"name": "#%%\n"}
mean = approx_joint.mean()
var = approx_joint.var()
# -
# The (estimated) mode is provided by the 'mode' method. This is simply the centroid of the partition of the approximation which has the highest associated $f$ value.
mode = approx_joint.mode()
# The approximation of the density function can be queried just as the original function $f$ by calling with the same parameter(s). A normalised version (the probability density) is provided using the 'prob' method.
# + pycharm={"name": "#%%\n"}
x_test = np.array([0.5, 0.5, 0.5])
f_test = approx_joint(x_test)
p_test = approx_joint.prob(x_test)
# -
# Often what one is interested in is posterior samples.
# To obtain samples from the distribution approximation, we first construct a sampler function using the 'sampler' method. Internally it performs the pre-processing required to be able to sample very quickly.
# + pycharm={"name": "#%%\n"}
sampler = approx_joint.sampler()
# -
# The sampler function allows sampling from the distribution in constant time per sample.
# Below we draw one million samples.
# Returned is a list of numpy arrays - one array of samples per variable.
# In our example, however, we only have the $x$ variable (with three dimensions).
# + pycharm={"name": "#%%\n"}
x_samples, = sampler(num_samples=1000000)
x_samples.shape
# -
# The DensityFunctionApproximation can easily be saved or loaded using the 'save' and 'load' methods. Internally the tree-structure of partitions (only) are saved/loaded, instead of the whole Python object.
# + pycharm={"name": "#%%\n"}
approx_joint.save("/tmp/approx_joint.pickle")
approx_joint.load("/tmp/approx_joint.pickle")
# -
# We will now plot the samples in a corner plot in order to visualize the distribution.
# + pycharm={"name": "#%%\n"}
def plot(density: DensityFunctionApproximation, samples=None):
if samples is None:
print("Preparing sampler..")
sampler = density.sampler()
print("Sampling..")
samples_per_variable = sampler(num_samples=10 ** 6)
samples = np.concatenate(samples_per_variable, axis=-1)
print("Plotting..")
figure = corner.corner(
samples,
range=density.variables.bounds,
labels=[
"%s: dim %s" % (var.name, index)
for var in density.variables.variable_slices
for index in var.indices
],
plot_contours=False,
no_fill_contours=True,
bins=100,
plot_datapoints=False,
)
plt.show()
plot(approx_joint, samples=x_samples)
# -
# #### Conditionals
# We can easily derive a conditional using the 'conditional' method,
# yielding a new approximation of the same type.
# In this example we condition the last dimension of the $x$ variable to 0.5.
# + pycharm={"name": "#%%\n"}
approx_conditional: DensityFunctionApproximation = approx_joint.conditional({
x[-1]: np.array([0.5])
})
# -
# Let us plot samples from the derived conditional in a corner plot to visualize it.
# + pycharm={"name": "#%%\n"}
plot(approx_conditional)
# -
# The conditional of the approximation, being of the same type, provides the same methods and properties.
# Including its normalisation constant, mode, and methods for returning density values and computing expectations.
# + pycharm={"name": "#%%\n"}
z = approx_conditional.z
approx_conditional.mode()
approx_conditional.expectation(lambda f, x, z: -np.log(f / z))
approx_conditional.mean()
approx_conditional.var()
approx_conditional.prob(np.array([0.5, 0.5]))
# -
# #### Marginalisation
# We may also marginalise variables (or dimensions of variables) using the 'construct_marginal' helper function. Internally it treats marginalisation as just another problem for the DEFER algorithm: now where each $f$ evaluation requires (approximate) integration over some variables - which using this helper function is performed using DEFER as well, i.e. in an inner-loop.
#
# Returned is a DensityFunctionApproximation similar to in the previously discussed cases.
#
# Note that in this example the provided $f$ is the constructed approximation of $f$, rather than $f$ itself. This can allow a significant speed-up if $f$ takes relatively much time to evaluate (more than several milliseconds). Alternatively $f$ can be passed in instead.
#
# In the below example the first dimension of the $x$ variable is marginalised, returning a distribution now only two dimensions rather than three.
# + pycharm={"name": "#%%\n"}
approx_marginal: DensityFunctionApproximation = construct_marginal(
fn=approx_joint,
variables=variables,
marginalize_variable_slices=[x[0]],
is_log_fn=False,
num_outer_fn_calls=5000,
num_inner_fn_calls=15,
callback=lambda i, density:
print("#Evals: %s. Log Z: %.2f" %
(density.num_partitions, np.log(density.z))),
callback_freq_fn_calls=500,
)
# + pycharm={"name": "#%%\n"}
plot(approx_marginal)
# + pycharm={"name": "#%%\n"}
approx_marginal.z
approx_marginal.mode()
approx_marginal.expectation(lambda f, x, z: -np.log(f / z))
approx_marginal.mean()
approx_marginal.var()
approx_marginal.prob(np.array([0.5, 0.5]))
# -
# #### Combining operations arbitrarily.
# As the marginal approximation provides the same operations,
# we can of course, for example, derive a conditional of the marginal similar to before - or use any of the other operations, in any order.
# + pycharm={"name": "#%%\n"}
approx_conditional_of_marginal = approx_marginal.conditional({
x[-1]: np.array([0.5])
})
# + pycharm={"name": "#%%\n"}
plot(approx_conditional_of_marginal)
# + pycharm={"name": "#%%\n"}
approx_conditional_of_marginal.z
approx_conditional_of_marginal.mode()
approx_conditional_of_marginal.expectation(lambda f, x, z: -np.log(f / z))
approx_conditional_of_marginal.mean()
approx_conditional_of_marginal.var()
approx_conditional_of_marginal.prob(np.array([0.5]))
|
notebooks/README.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from joblib import Parallel, delayed
from math import sqrt
from pathlib import Path
from lxml import etree
from tqdm import tqdm
import pickle
import dateparser
from bs4 import BeautifulSoup
import pandas as pd
import swifter
import pandas as pd
import sqlite3
from cleantext import clean
from pathlib import Path
import numpy as np
import swifter
from somajo import Tokenizer, SentenceSplitter
from tqdm import tqdm
import multiprocessing
from joblib import Parallel, delayed
num_cores = multiprocessing.cpu_count()
import numpy as np
# -
df1 = pd.read_pickle('comments.pkl')
df2 = pd.read_pickle('comments_more.pkl')
df2.columns = ['text', 'date']
df = pd.concat([df1, df2])
def parse(x):
idx = x.find('—')
return dateparser.parse(x[idx:], languages=['de'])
parsed = Parallel(n_jobs=4)(delayed(parse)(i) for i in tqdm(df['date'].values))
df['parsed'] = parsed
df.to_pickle('fin_com.pkl')
df = pd.read_pickle('fin_com.pkl')
def get_sents(texts):
tokenizer = Tokenizer(split_camel_case=True, token_classes=False, extra_info=False)
sentence_splitter = SentenceSplitter(is_tuple=False)
results = []
for text in texts:
text = clean(text, lang='de', lower=False)
tokens = tokenizer.tokenize_paragraph(text)
sentences = sentence_splitter.split(tokens)
cleaned = [clean(' '.join(s), no_urls=True, no_digits=True, no_punct=True, no_line_breaks=True, lang='de') for s in sentences]
results.append(cleaned)
return results
def chunks(l, n):
"""Yield successive n-sized chunks from l."""
for i in range(0, len(l), n):
yield l[i:i + n]
df
df['text'].values[:1]
df['text'] = df['text'].astype(str)
df['text'].values
results = Parallel(n_jobs=4)(delayed(get_sents)(row) for row in tqdm(list(chunks(df['text'].values, 1000))))
results
cleaned = pd.read_pickle('/mnt/data2/ptf/cleaned.pkl')
cleaned = cleaned[['cleaned']]
cleaned = cleaned['cleaned'].values
cnt = 0
for d in cleaned:
cnt += len([x for x in d if len(x) > 0])
len(cleaned)
cnt
with open('zo.txt', 'w') as outfile:
for d in cleaned:
outfile.write('\n'.join(d))
cleaned.cleaned.str.len().min()
cleaned.values[0]
|
notebooks/03_scrape/04_preprocess.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/cfusco77/Amazon_Vine_Analysis/blob/main/Vine_Review_Analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + colab={"base_uri": "https://localhost:8080/"} id="qtsRmh0XB0Yk" outputId="368ed239-6e68-4f8f-c7d5-a4577b242d7d"
import os
# Find the latest version of spark 3.0 from http://www.apache.org/dist/spark/ and enter as the spark version
# For example:
# spark_version = 'spark-3.0.3'
spark_version = 'spark-3.0.3'
os.environ['SPARK_VERSION']=spark_version
# Install Spark and Java
# !apt-get update
# !apt-get install openjdk-11-jdk-headless -qq > /dev/null
# !wget -q http://www.apache.org/dist/spark/$SPARK_VERSION/$SPARK_VERSION-bin-hadoop2.7.tgz
# !tar xf $SPARK_VERSION-bin-hadoop2.7.tgz
# !pip install -q findspark
# Set Environment Variables
import os
os.environ["JAVA_HOME"] = "/usr/lib/jvm/java-11-openjdk-amd64"
os.environ["SPARK_HOME"] = f"/content/{spark_version}-bin-hadoop2.7"
# Start a SparkSession
import findspark
findspark.init()
# + id="dNt0pr0aCEI7"
from pyspark.sql import SparkSession
spark = SparkSession.builder.appName("M16-Amazon-Challenge").config("spark.driver.extraClassPath","/content/postgresql-42.2.16.jar").getOrCreate()
# + [markdown] id="zPm5MTGqCGm9"
# Load Amazon Data into Spark DataFrame
# + colab={"base_uri": "https://localhost:8080/"} id="WL4b367OCHWh" outputId="8351e0cf-3912-4250-b091-a39674b2ff97"
from pyspark import SparkFiles
url = "https://s3.amazonaws.com/amazon-reviews-pds/tsv/amazon_reviews_us_Furniture_v1_00.tsv.gz"
spark.sparkContext.addFile(url)
df = spark.read.option("encoding", "UTF-8").csv(SparkFiles.get(""), sep="\t", header=True, inferSchema=True)
df.show()
# + [markdown] id="QafWyX9xCN2f"
# Create DataFrames to match tables
# + id="xiotTysACOa8"
from pyspark.sql.functions import to_date
# Read in the Review dataset as a DataFrame
# + colab={"base_uri": "https://localhost:8080/"} id="-4oTQJliCUBI" outputId="75a7f580-d6f2-4256-fd8c-c9e1230b03e8"
# Create the vine_table. DataFrame
# vine_df = df.select([])
vine_df = df.select(["review_id", "star_rating", "helpful_votes", "total_votes", "vine", "verified_purchase"])
vine_df.show()
# + colab={"base_uri": "https://localhost:8080/"} id="2_nzADVVCZJy" outputId="f212b6a5-62d0-460d-d04d-17406a490ef1"
#Filter the data and create a new Dataframe to retrieve all the rows where the totoal_botes count is equal to or greater than 20
filtered_reviews = vine_df.filter(vine_df["total_votes"]>=20)
filtered_reviews.show()
# + colab={"base_uri": "https://localhost:8080/"} id="_CIsQl2HCcNt" outputId="ecfe136f-56e5-4121-9011-61d9cb49918b"
#Filter the data and create a new Dataframe to retrieve all the rows where the number of helpful_votes divided by the total_votes is equal to or greater than 50%
helpful_reviews = filtered_reviews.filter((filtered_reviews["helpful_votes"]/filtered_reviews["total_votes"])>=.5)
helpful_reviews.show()
# + colab={"base_uri": "https://localhost:8080/"} id="UZAXx2E3Ce-k" outputId="14904cc2-663f-45b6-9bfe-0c60f476c7c8"
#Filter the DataFrame to retrieve rows where a review was written as part of the Vine program (paid)
paid_reviews = helpful_reviews.filter(helpful_reviews["vine"] =='Y')
paid_reviews.show()
# + colab={"base_uri": "https://localhost:8080/"} id="zN_zB9n2ChUT" outputId="e3b4c6f0-3d2a-428f-cd22-b30a391fc573"
#Filter the DataFrame to retrieve rows where a review was written as not part of the Vine program (unpaid)
unpaid_reviews = helpful_reviews.filter(helpful_reviews["vine"] =='N')
unpaid_reviews.show()
# + colab={"base_uri": "https://localhost:8080/"} id="pXXPzsamlZ1g" outputId="faab41a1-858c-497a-858c-954711517aa6"
#Overall Summary
helpful_reviews_count = helpful_reviews.count()
helpful_five_star = helpful_reviews.filter(helpful_reviews["star_rating"]==5).count()
helpful_five_star_percent = round(((helpful_five_star / helpful_reviews_count)*100), 2)
#Create Paid Dataframe
helpful_df = spark.createDataFrame([
("Total Reviews", str(helpful_reviews_count)),
("Total 5-Star Reviews", str(helpful_five_star)),
("Percentage of 5-Star Reviews", str(helpful_five_star_percent))
], [" Helpful Review Summary", "Count"])
helpful_df.show()
# + colab={"base_uri": "https://localhost:8080/"} id="R6lS-G_JNX1p" outputId="2eaccd3f-7e1c-4fbc-d80d-3c542ccff7ed"
#Determine the total number of reviews, the number of 5-star reviews, and the percentage of 5-star reviews for the two types of review (paid vs unpaid).
#Paid Summary
paid_reviews_count = paid_reviews.count()
paid_five_star = paid_reviews.filter(paid_reviews["star_rating"]==5).count()
paid_five_star_percent = round(((paid_five_star / paid_reviews_count)*100), 2)
#Create Paid Dataframe
paid_df = spark.createDataFrame([
("Total Reviews", str(paid_reviews_count)),
("Total 5-Star Reviews", str(paid_five_star)),
("Percentage of 5-Star Reviews", str(paid_five_star_percent))
], [" Paid Summary", "Count"])
paid_df.show()
# + colab={"base_uri": "https://localhost:8080/"} id="L4L7yFPQUrbT" outputId="246d5310-6aea-4f9b-cd04-880988bb09d8"
#UnPaid Summary
unpaid_reviews_count = unpaid_reviews.count()
unpaid_five_star = unpaid_reviews.filter(unpaid_reviews["star_rating"]==5).count()
unpaid_five_star_percent = round(((unpaid_five_star / unpaid_reviews_count)*100), 2)
#Create UnPaid Dataframe
unpaid_df = spark.createDataFrame([
("Total Reviews", str(unpaid_reviews_count)),
("Total 5-Star Reviews", str(unpaid_five_star)),
("Percentage of 5-Star Reviews", str(unpaid_five_star_percent))
], ["Unpaid Summary", "Count"])
unpaid_df.show()
|
Vine_Review_Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
# #### Quick look at the data structure
housing = pd.read_csv("housing.csv")
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
print(housing.describe())
# #### Looking for correlation
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)
housing["rooms_per_household"] = housing["total_rooms"] / housing["population"]
housing["population_per_household"] = housing["population"] / housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending=False)
# #### Prepare the data for Machine Learning algorithms
housing[housing.isnull().any(axis=1)].head(10)
# housing = housing.dropna(subset=["total_bedrooms"]) # option 1
housing = housing.drop("total_bedrooms", axis=1) # option 2
# median = housing["total_bedrooms"].median() # option 3
# housing["total_bedrooms"].fillna(median, inplace=True) # option 3
housing
# #### Handling Text and Categorical Attributes
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
# +
# 分類作法 A
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
housing_cat = housing["ocean_proximity"]
housing_cat_encoded = encoder.fit_transform(housing_cat)
housing_cat_encoded
# -
print(encoder.classes_)
# +
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder(categories='auto')
housing_cat_1hot = encoder.fit_transform(housing_cat_encoded.reshape(-1,1))
housing_cat_1hot
# -
housing_cat_1hot.toarray()
# +
# 分類作法 B
from sklearn.preprocessing import LabelBinarizer
encoder = LabelBinarizer()
encoder.fit_transform(housing_cat)
# -
# #### combine housing and categorical
pd.DataFrame(housing_cat_1hot.toarray()).iloc[:, 1:].head()
housing_final = pd.concat([housing, pd.DataFrame(housing_cat_1hot.toarray()).iloc[:, 1:]], axis=1)
housing_final.head()
# # Prepare the data for Machine Learning algorithms
X = housing_final.drop("median_house_value", axis=1).drop("ocean_proximity", axis=1)
X.head()
y = housing_final[["median_house_value"]]
y.head()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
# sc_X.fit_transform(X_train["longitude"])
X_train.head()
X_train[['longitude', 'latitude']] = sc_X.fit_transform(X_train[['longitude', 'latitude']])
X_train.head()
# +
# # Feature Scaling
# from sklearn.preprocessing import StandardScaler
# sc_X = StandardScaler()
# X_train = sc_X.fit_transform(X_train)
# X_test = sc_X.transform(X_test)
# sc_y = StandardScaler()
# y_train = sc_y.fit_transform(y_train)
# -
type(y_train)
type(X_train)
# #### null detection
# +
# 方法 A
# y_train.isnull().any(axis=1)
# X_train.isnull().any(axis=1)
# 方法 B
# np.isnan(y_train).any()
# np.isnan(X_train).any()
# -
# # Prepare the data for Machine Learning algorithms
# +
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
# +
# lin_reg.predict(X_train)
# lin_reg.predict(X_test)
# -
# #### 檢驗 train set 績效
# +
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(X_train)
lin_mse = mean_squared_error(y_train, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)
from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(y_train, housing_predictions)
print(lin_mae)
# -
# #### 檢驗 test set 績效
# +
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(X_test)
lin_mse = mean_squared_error(y_test, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)
from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(y_test, housing_predictions)
print(lin_mae)
# -
# #### 模型換決策樹
# +
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(X_train, y_train)
# housing_predictions = tree_reg.predict(housing_prepared)
# tree_mse = mean_squared_error(housing_labels, housing_predictions)
# tree_rmse = np.sqrt(tree_mse)
# tree_rmse
# -
# #### 檢驗 train set的績效
# +
from sklearn.metrics import mean_squared_error
housing_predictions = tree_reg.predict(X_train)
lin_mse = mean_squared_error(y_train, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)
from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(y_train, housing_predictions)
print(lin_mae)
# -
# #### 檢驗 test set 績效
# +
from sklearn.metrics import mean_squared_error
housing_predictions = tree_reg.predict(X_test)
lin_mse = mean_squared_error(y_test, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
print(lin_rmse)
from sklearn.metrics import mean_absolute_error
lin_mae = mean_absolute_error(y_test, housing_predictions)
print(lin_mae)
# -
# # Fine-tune your model
# +
from sklearn.model_selection import cross_val_score
tree_scores = cross_val_score(tree_reg, X_train, y_train,
scoring="neg_mean_squared_error", cv=10)
tree_rmse_scores = np.sqrt(-tree_scores)
# -
tree_rmse_scores
# +
def display_scores(scores):
print("Scores:", scores)
print("Mean:", scores.mean())
print("Standard deviation:", scores.std())
display_scores(tree_rmse_scores)
# -
lin_scores = cross_val_score(lin_reg, X_train, y_train,
scoring="neg_mean_squared_error", cv=10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
# +
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(X_train, y_train)
housing_predictions = forest_reg.predict(X_train)
forest_mse = mean_squared_error(y_train, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
# +
from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, X_train, y_train,
scoring="neg_mean_squared_error", cv=10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
# -
scores = cross_val_score(lin_reg, X_train, y_train, scoring="neg_mean_squared_error", cv=10)
pd.Series(np.sqrt(-scores)).describe()
# +
from sklearn.svm import SVR
svm_reg = SVR(kernel="linear")
svm_reg.fit(X_train, y_train)
housing_predictions = svm_reg.predict(X_train)
svm_mse = mean_squared_error(y_train, housing_predictions)
svm_rmse = np.sqrt(svm_mse)
svm_rmse
# +
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)
# -
grid_search.best_params_
grid_search.best_estimator_
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
pd.DataFrame(grid_search.cv_results_)
# +
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
param_distribs = {
'n_estimators': randint(low=1, high=200),
'max_features': randint(low=1, high=8),
}
forest_reg = RandomForestRegressor()
rnd_search = RandomizedSearchCV(forest_reg, param_distributions=param_distribs,
n_iter=10, cv=5, scoring='neg_mean_squared_error')
rnd_search.fit(X_train, y_train)
# -
cvres = rnd_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
|
02_end_to_end_machine_learning_project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import csv
fn = r"D:\Project\Uber data\uber-raw-data-apr14.csv"
data = []
with open(fn) as f:
for record in csv.DictReader(f):
data.append(record)
len(data)
data[0]
# %pylab inline
longitudes = []
for record in data:
lon = record['Lon']
longitudes.append(float(lon))
longitudes[:5]
hist(longitudes, range = (-74.05, -73.9), bins = 100)
latitudes = []
for record in data:
lat = record['Lat']
latitudes.append(float(lat))
latitudes[:10]
# +
hist(latitudes, range=(40.5, 41), bins = 100)
# -
figure(figsize=(20,20))
plot(longitudes, latitudes, '.', ms=1)
ylim(40.65, 40.8)
xlim(-74.05, -73.85)
datetimes = []
for record in data:
dt = record['Date/Time']
datetimes.append(dt)
# +
datetimes[:10]
# -
dt = '4/1/2014 0:11:00'
hours = []
for dt in datetimes:
time = dt.split(' ')[1]
hour = int(time.split(':')[0])
hours.append(hour)
hours[:10]
hist(hours, bins=24)
grid()
xlabel('hour of the day')
ylabel('frequency of drop-off')
title('histogram of drop-offs by hour')
import collections
hours_counter = collections.Counter(hours)
# +
hours_counter
# +
hours_counter.most_common(5)
# +
collections.Counter(datetimes).most_common(20)
# +
dates = []
for dt in datetimes:
date = dt.split(' ')[0]
dates.append(date)
# -
by_date = collections.Counter(dates).most_common(31)
counts = []
for r in by_date:
counts.append(r[1])
counts
# +
bar(range(1,31),counts)
# -
labels = []
for val in by_date:
date = val[0]
dom = date.split('/')[1]
labels.append(dom)
# +
bar(range(1,31),counts)
xticks(range(1,31), labels, rotation=75)
# +
Analysis of Uber's Ridership Data for NYC.
Early in 2017, the NYC Taxi and Limousine Commission (TLC) released a dataset about Uber's ridership between September 2014
and August 2015. The data contains features distinct from those in the set previously released and throughly explored by
FiveThirtyEight and the Kaggle community.
This project aims to:
visualize Uber's ridership growth in NYC during the period
characterize the demand based on identified patterns in the time series
estimate the value of the NYC market for Uber, and its revenue growth
other insights about the usage of the service
attempt to predict the demand's growth beyond 2015 [IN PROGRESS]
|
Exploring Uber data using vanilla Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="1l8bWGmIJuQa"
# ##### Copyright 2019 The TensorFlow Authors.
#
#
# + cellView="form" colab={} colab_type="code" id="CPSnXS88KFEo"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="89xNCIO5hiCj"
# # Save and load a model using a distribution strategy
# + [markdown] colab_type="text" id="9Ejs4QVxIdAm"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/tutorials/distribute/save_and_load"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/tutorials/distribute/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/tutorials/distribute/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/tutorials/distribute/save_and_load.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
#
# </table>
# + [markdown] colab_type="text" id="A0lG6qgThxAS"
# ## Overview
#
# It's common to save and load a model during training. There are two sets of APIs for saving and loading a keras model: a high-level API, and a low-level API. This tutorial demonstrates how you can use the SavedModel APIs when using `tf.distribute.Strategy`. To learn about SavedModel and serialization in general, please read the [saved model guide](../../guide/saved_model.ipynb), and the [Keras model serialization guide](../../guide/keras/saving_and_serializing.ipynb). Let's start with a simple example:
# + [markdown] colab_type="text" id="FITHltVKQ4eZ"
# Import dependencies:
# + colab={} colab_type="code" id="RWG5HchAiOrZ"
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow_datasets as tfds
import tensorflow as tf
tfds.disable_progress_bar()
# + [markdown] colab_type="text" id="qqapWj98ptNV"
# Prepare the data and model using `tf.distribute.Strategy`:
# + colab={} colab_type="code" id="yrYiAf_ziRyw"
mirrored_strategy = tf.distribute.MirroredStrategy()
def get_data():
datasets, ds_info = tfds.load(name='mnist', with_info=True, as_supervised=True)
mnist_train, mnist_test = datasets['train'], datasets['test']
BUFFER_SIZE = 10000
BATCH_SIZE_PER_REPLICA = 64
BATCH_SIZE = BATCH_SIZE_PER_REPLICA * mirrored_strategy.num_replicas_in_sync
def scale(image, label):
image = tf.cast(image, tf.float32)
image /= 255
return image, label
train_dataset = mnist_train.map(scale).cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
eval_dataset = mnist_test.map(scale).batch(BATCH_SIZE)
return train_dataset, eval_dataset
def get_model():
with mirrored_strategy.scope():
model = tf.keras.Sequential([
tf.keras.layers.Conv2D(32, 3, activation='relu', input_shape=(28, 28, 1)),
tf.keras.layers.MaxPooling2D(),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(loss='sparse_categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
return model
# + [markdown] colab_type="text" id="qmU4Y3feS9Na"
# Train the model:
# + colab={} colab_type="code" id="zmGurbJmS_vN"
model = get_model()
train_dataset, eval_dataset = get_data()
model.fit(train_dataset, epochs=2)
# + [markdown] colab_type="text" id="L01wjgvRizHS"
# ## Save and load the model
#
# Now that you have a simple model to work with, let's take a look at the saving/loading APIs.
# There are two sets of APIs available:
#
# * High level keras `model.save` and `tf.keras.models.load_model`
# * Low level `tf.saved_model.save` and `tf.saved_model.load`
#
#
# + [markdown] colab_type="text" id="FX_IF2F1tvFs"
# ### The Keras APIs
# + [markdown] colab_type="text" id="O8xfceg4Z3H_"
# Here is an example of saving and loading a model with the Keras APIs:
# + colab={} colab_type="code" id="LYOStjV5knTQ"
keras_model_path = "/tmp/keras_save"
model.save(keras_model_path) # save() should be called out of strategy scope
# + [markdown] colab_type="text" id="yvQIdQp3zNMp"
# Restore the model without `tf.distribute.Strategy`:
# + colab={} colab_type="code" id="WrXAAVtrzRgv"
restored_keras_model = tf.keras.models.load_model(keras_model_path)
restored_keras_model.fit(train_dataset, epochs=2)
# + [markdown] colab_type="text" id="gYAnskzorda-"
# After restoring the model, you can continue training on it, even without needing to call `compile()` again, since it is already compiled before saving. The model is saved in the TensorFlow's standard `SavedModel` proto format. For more information, please refer to [the guide to `saved_model` format](../../guide/saved_model.ipynb).
#
# It is important to only call the `model.save()` method out of the scope of `tf.distribute.strategy`. Calling it within the scope is not supported.
#
# Now to load the model and train it using a `tf.distribute.Strategy`:
# + colab={} colab_type="code" id="wROPrJaAqBQz"
another_strategy = tf.distribute.OneDeviceStrategy("/cpu:0")
with another_strategy.scope():
restored_keras_model_ds = tf.keras.models.load_model(keras_model_path)
restored_keras_model_ds.fit(train_dataset, epochs=2)
# + [markdown] colab_type="text" id="PdiiPmL5tQk5"
# As you can see, loading works as expected with `tf.distribute.Strategy`. The strategy used here does not have to be the same strategy used before saving.
# + [markdown] colab_type="text" id="3CrXIbmFt0f6"
# ### The `tf.saved_model` APIs
# + [markdown] colab_type="text" id="HtGzPp6et4Em"
# Now let's take a look at the lower level APIs. Saving the model is similar to the keras API:
# + colab={} colab_type="code" id="4y6T31APuCqK"
model = get_model() # get a fresh model
saved_model_path = "/tmp/tf_save"
tf.saved_model.save(model, saved_model_path)
# + [markdown] colab_type="text" id="q1QNRYcwuRll"
# Loading can be done with `tf.saved_model.load()`. However, since it is an API that is on the lower level (and hence has a wider range of use cases), it does not return a Keras model. Instead, it returns an object that contain functions that can be used to do inference. For example:
# + colab={} colab_type="code" id="aaEKqBSPwAuM"
DEFAULT_FUNCTION_KEY = "serving_default"
loaded = tf.saved_model.load(saved_model_path)
inference_func = loaded.signatures[DEFAULT_FUNCTION_KEY]
# + [markdown] colab_type="text" id="x65l7AaHUZCA"
# The loaded object may contain multiple functions, each associated with a key. The `"serving_default"` is the default key for the inference function with a saved Keras model. To do an inference with this function:
# + colab={} colab_type="code" id="5Ore5q8-UjW1"
predict_dataset = eval_dataset.map(lambda image, label: image)
for batch in predict_dataset.take(1):
print(inference_func(batch))
# + [markdown] colab_type="text" id="osB1LY8WwUJZ"
# You can also load and do inference in a distributed manner:
# + colab={} colab_type="code" id="iDYvu12zYTmT"
another_strategy = tf.distribute.MirroredStrategy()
with another_strategy.scope():
loaded = tf.saved_model.load(saved_model_path)
inference_func = loaded.signatures[DEFAULT_FUNCTION_KEY]
dist_predict_dataset = another_strategy.experimental_distribute_dataset(
predict_dataset)
# Calling the function in a distributed manner
for batch in dist_predict_dataset:
another_strategy.experimental_run_v2(inference_func,
args=(batch,))
# + [markdown] colab_type="text" id="hWGSukoyw3fF"
# Calling the restored function is just a forward pass on the saved model (predict). What if yout want to continue training the loaded function? Or embed the loaded function into a bigger model? A common practice is to wrap this loaded object to a Keras layer to achieve this. Luckily, [TF Hub](https://www.tensorflow.org/hub) has [hub.KerasLayer](https://github.com/tensorflow/hub/blob/master/tensorflow_hub/keras_layer.py) for this purpose, shown here:
# + colab={} colab_type="code" id="clfk3hQoyKu6"
import tensorflow_hub as hub
def build_model(loaded):
x = tf.keras.layers.Input(shape=(28, 28, 1), name='input_x')
# Wrap what's loaded to a KerasLayer
keras_layer = hub.KerasLayer(loaded, trainable=True)(x)
model = tf.keras.Model(x, keras_layer)
return model
another_strategy = tf.distribute.MirroredStrategy()
with another_strategy.scope():
loaded = tf.saved_model.load(saved_model_path)
model = build_model(loaded)
model.compile(loss='sparse_categorical_crossentropy',
optimizer=tf.keras.optimizers.Adam(),
metrics=['accuracy'])
model.fit(train_dataset, epochs=2)
# + [markdown] colab_type="text" id="Oe1z_OtSJlu2"
# As you can see, `hub.KerasLayer` wraps the result loaded back from `tf.saved_model.load()` into a Keras layer that can be used to build another model. This is very useful for transfer learning.
# + [markdown] colab_type="text" id="KFDOZpK5Wa3W"
# ### Which API should I use?
# + [markdown] colab_type="text" id="GC6GQ9HDLxD6"
# For saving, if you are working with a keras model, it is almost always recommended to use the Keras's `model.save()` API. If what you are saving is not a Keras model, then the lower level API is your only choice.
#
# For loading, which API you use depends on what you want to get from the loading API. If you cannot (or do not want to) get a Keras model, then use `tf.saved_model.load()`. Otherwise, use `tf.keras.models.load_model()`. Note that you can get a Keras model back only if you saved a Keras model.
#
# It is possible to mix and match the APIs. You can save a Keras model with `model.save`, and load a non-Keras model with the low-level API, `tf.saved_model.load`.
# + colab={} colab_type="code" id="Ktwg2GwnXE8v"
model = get_model()
# Saving the model using Keras's save() API
model.save(keras_model_path)
another_strategy = tf.distribute.MirroredStrategy()
# Loading the model using lower level API
with another_strategy.scope():
loaded = tf.saved_model.load(keras_model_path)
# + [markdown] colab_type="text" id="hJTWOnC9iuA3"
# ### Caveats
# + [markdown] colab_type="text" id="Tzog2ti7YYgy"
# A special case is when you have a Keras model that does not have well-defined inputs. For example, a Sequential model can be created without any input shapes (`Sequential([Dense(3), ...]`). Subclassed models also do not have well-defined inputs after initialization. In this case, you should stick with the lower level APIs on both saving and loading, otherwise you will get an error.
#
# To check if your model has well-defined inputs, just check if `model.inputs` is `None`. If it is not `None`, you are all good. Input shapes are automatically defined when the model is used in `.fit`, `.evaluate`, `.predict`, or when calling the model (`model(inputs)`).
#
# Here is an example:
# + colab={} colab_type="code" id="gurSIbDFjOBc"
class SubclassedModel(tf.keras.Model):
output_name = 'output_layer'
def __init__(self):
super(SubclassedModel, self).__init__()
self._dense_layer = tf.keras.layers.Dense(
5, dtype=tf.dtypes.float32, name=self.output_name)
def call(self, inputs):
return self._dense_layer(inputs)
my_model = SubclassedModel()
# my_model.save(keras_model_path) # ERROR!
tf.saved_model.save(my_model, saved_model_path)
|
site/en/tutorials/distribute/save_and_load.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import os.path
import requests
import json
root_path = os.path.dirname(os.getcwd())
# Import food inspection data
inspections = pd.read_csv(os.path.join(root_path, "DATA/food_inspections.csv"))
# +
# Create weather dataframe with entry for each inspection
weather = pd.DataFrame({
"inspection_id": inspections.inspection_id,
"date": inspections.inspection_date,
})
# Create list of weather data columns
features = [
"precip_intensity",
"temperature_max",
"wind_speed",
"humidity"
]
# Add empty columns
weather = pd.concat([weather, pd.DataFrame(columns=features)])
# -
# Check if weather data exists, import or start empty dataframe
if os.path.isfile(os.path.join(root_path, "DATA/weather.csv")):
print("records found")
old_weather = pd.read_csv(os.path.join(root_path, "DATA/weather.csv"))
else:
old_weather = pd.DataFrame(columns=weather.columns)
# Register for a free key at https://darksky.net/dev/register
KEY = "c30a95e4e9f7f2e90966361288918b9e"
# +
# Check if weather record can be found in old data
# If not,request record from darksky.net
# All records pertain to a single location in central Chicago
limit_reached = False
def get_weather(group):
global limit_reached
date = group.iloc[0].date
record = old_weather[old_weather.date == date]
if (not record.empty) & (not record.isnull().values.any()):
print(date, "record found")
group.loc[:, features] = record.iloc[0][features].values
elif not limit_reached:
url = "https://api.darksky.net/forecast/%s/41.836944,-87.684722,%s" % (KEY, date)
response = requests.get(url)
if response.status_code == 200:
print(date, "request successful")
data = response.json()["daily"]["data"][0]
group[features] = [
data["precipIntensity"],
data["temperatureMax"],
data["windSpeed"],
data["humidity"]
]
elif response.status_code == 403:
print("request limit reached")
limit_reached = True
else:
print(response)
return group
# -
# Time consuming
weather = weather.groupby(by="date").apply(get_weather)
# Check if process is complete
if weather.isnull().values.any():
print("Process incomplete, records missing")
else:
print("Process complete, all records obtained")
# Darksky.net limits free accounts to 1000 calls per day. If records are missing, save the result and run the notebook from the top after waiting 24 hours, upgrading your account or obtaining a new API key.
# Save result
weather.to_csv(os.path.join(root_path, "DATA/weather.csv"), index=False)
|
CODE/16_weather_download.ipynb
|