code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python2
# language: python
# name: conda_python2
# ---
# # Feature processing with Spark, training with XGBoost and deploying as Inference Pipeline
#
# Typically a Machine Learning (ML) process consists of few steps: gathering data with various ETL jobs, pre-processing the data, featurizing the dataset by incorporating standard techniques or prior knowledge, and finally training an ML model using an algorithm.
#
# In many cases, when the trained model is used for processing real time or batch prediction requests, the model receives data in a format which needs to pre-processed (e.g. featurized) before it can be passed to the algorithm. In the following notebook, we will demonstrate how you can build your ML Pipeline leveraging Spark Feature Transformers and SageMaker XGBoost algorithm & after the model is trained, deploy the Pipeline (Feature Transformer and XGBoost) as an Inference Pipeline behind a single Endpoint for real-time inference and for batch inferences using Amazon SageMaker Batch Transform.
#
# In this notebook, we use Amazon Glue to run serverless Spark. Though the notebook demonstrates the end-to-end flow on a small dataset, the setup can be seamlessly used to scale to larger datasets.
# ## Objective: predict the age of an Abalone from its physical measurement
# The dataset is available from [UCI Machine Learning](https://archive.ics.uci.edu/ml/datasets/abalone). The aim for this task is to determine age of an Abalone (a kind of shellfish) from its physical measurements. At the core, it's a regression problem. The dataset contains several features - `sex` (categorical), `length` (continuous), `diameter` (continuous), `height` (continuous), `whole_weight` (continuous), `shucked_weight` (continuous), `viscera_weight` (continuous), `shell_weight` (continuous) and `rings` (integer).Our goal is to predict the variable `rings` which is a good approximation for age (age is `rings` + 1.5).
#
# We'll use SparkML to process the dataset (apply one or many feature transformers) and upload the transformed dataset to S3 so that it can be used for training with XGBoost.
# ## Methodologies
# The Notebook consists of a few high-level steps:
#
# * Using AWS Glue for executing the SparkML feature processing job.
# * Using SageMaker XGBoost to train on the processed dataset produced by SparkML job.
# * Building an Inference Pipeline consisting of SparkML & XGBoost models for a realtime inference endpoint.
# * Building an Inference Pipeline consisting of SparkML & XGBoost models for a single Batch Transform job.
# # Using AWS Glue for executing the SparkML job
# We'll be running the SparkML job using [AWS Glue](https://aws.amazon.com/glue). AWS Glue is a serverless ETL service which can be used to execute standard Spark/PySpark jobs. Glue currently only supports `Python 2.7`, hence we'll write the script in `Python 2.7`.
# ## Permission setup for invoking AWS Glue from this Notebook
# In order to enable this Notebook to run AWS Glue jobs, we need to add one additional permission to the default execution role of this notebook. We will be using SageMaker Python SDK to retrieve the default execution role and then you have to go to [IAM Dashboard](https://console.aws.amazon.com/iam/home) to edit the Role to add AWS Glue specific permission.
# ### Finding out the current execution role of the Notebook
# We are using SageMaker Python SDK to retrieve the current role for this Notebook which needs to be enhanced.
# Import SageMaker Python SDK to get the Session and execution_role
import sagemaker
from sagemaker import get_execution_role
sess = sagemaker.Session()
role = get_execution_role()
print(role[role.rfind('/') + 1:])
# ### Adding AWS Glue as an additional trusted entity to this role
# This step is needed if you want to pass the execution role of this Notebook while calling Glue APIs as well without creating an additional **Role**. If you have not used AWS Glue before, then this step is mandatory.
#
# If you have used AWS Glue previously, then you should have an already existing role that can be used to invoke Glue APIs. In that case, you can pass that role while calling Glue (later in this notebook) and skip this next step.
# On the IAM dashboard, please click on **Roles** on the left sidenav and search for this Role. Once the Role appears, click on the Role to go to its **Summary** page. Click on the **Trust relationships** tab on the **Summary** page to add AWS Glue as an additional trusted entity.
#
# Click on **Edit trust relationship** and replace the JSON with this JSON.
# ```
# {
# "Version": "2012-10-17",
# "Statement": [
# {
# "Effect": "Allow",
# "Principal": {
# "Service": [
# "sagemaker.amazonaws.com",
# "glue.amazonaws.com"
# ]
# },
# "Action": "sts:AssumeRole"
# }
# ]
# }
# ```
# Once this is complete, click on **Update Trust Policy** and you are done.
# ## Downloading dataset and uploading to S3
# SageMaker team has downloaded the dataset from UCI and uploaded to one of the S3 buckets in our account. In this Notebook, we will download from that bucket and upload to your bucket so that AWS Glue can access the data. The default AWS Glue permissions we just added expects the data to be present in a bucket with the string `aws-glue`. Hence, after we download the dataset, we will create an S3 bucket in your account with a valid name and then upload the data to S3.
# !wget https://s3-us-west-2.amazonaws.com/sparkml-mleap/data/abalone/abalone.csv
# ### Creating an S3 bucket and uploading this dataset
# Next we will create an S3 bucket with the `aws-glue` string in the name and upload this data to the S3 bucket. In case you want to use some existing bucket to run your Spark job via AWS Glue, you can use that bucket to upload your data provided the `Role` has access permission to upload and download from that bucket.
#
# Once the bucket is created, the following cell would also update the `abalone.csv` file downloaded locally to this bucket under the `input/abalone` prefix.
# +
import boto3
import botocore
from botocore.exceptions import ClientError
boto_session = sess.boto_session
s3 = boto_session.resource('s3')
account = boto_session.client('sts').get_caller_identity()['Account']
region = boto_session.region_name
default_bucket = 'aws-glue-{}-{}'.format(account, region)
try:
if region == 'us-east-1':
s3.create_bucket(Bucket=default_bucket)
else:
s3.create_bucket(Bucket=default_bucket, CreateBucketConfiguration={'LocationConstraint': region})
except ClientError as e:
error_code = e.response['Error']['Code']
message = e.response['Error']['Message']
if error_code == 'BucketAlreadyOwnedByYou':
print ('A bucket with the same name already exists in your account - using the same bucket.')
pass
# Uploading the training data to S3
sess.upload_data(path='abalone.csv', bucket=default_bucket, key_prefix='input/abalone')
# -
# ## Writing the feature processing script using SparkML
#
# The code for feature transformation using SparkML can be found in `abalone_processing.py` file written in the same directory. You can go through the code itself to see how it is using standard SparkML constructs to define the Pipeline for featurizing the data.
#
# Once the Spark ML Pipeline `fit` and `transform` is done, we are splitting our dataset into 80-20 train & validation as part of the script and uploading to S3 so that it can be used with XGBoost for training.
# ### Serializing the trained Spark ML Model with [MLeap](https://github.com/combust/mleap)
# Apache Spark is best suited batch processing workloads. In order to use the Spark ML model we trained for low latency inference, we need to use the MLeap library to serialize it to an MLeap bundle and later use the [SageMaker SparkML Serving](https://github.com/aws/sagemaker-sparkml-serving-container) to perform realtime and batch inference.
#
# By using the `SerializeToBundle()` method from MLeap in the script, we are serializing the ML Pipeline into an MLeap bundle and uploading to S3 in `tar.gz` format as SageMaker expects.
# ## Uploading the code and other dependencies to S3 for AWS Glue
# Unlike SageMaker, in order to run your code in AWS Glue, we do not need to prepare a Docker image. We can upload the code and dependencies directly to S3 and pass those locations while invoking the Glue job.
# ### Upload the SparkML script to S3
# We will be uploading the `abalone_processing.py` script to S3 now so that Glue can use it to run the PySpark job. You can replace it with your own script if needed. If your code has multiple files, you need to zip those files and upload to S3 instead of uploading a single file like it's being done here.
script_location = sess.upload_data(path='abalone_processing.py', bucket=default_bucket, key_prefix='codes')
# ### Upload MLeap dependencies to S3
# For our job, we will also have to pass MLeap dependencies to Glue. MLeap is an additional library we are using which does not come bundled with default Spark.
#
# Similar to most of the packages in the Spark ecosystem, MLeap is also implemented as a Scala package with a front-end wrapper written in Python so that it can be used from PySpark. We need to make sure that the MLeap Python library as well as the JAR is available within the Glue job environment. In the following cell, we will download the MLeap Python dependency & JAR from a SageMaker hosted bucket and upload to the S3 bucket we created above in your account.
#
# If you are using some other Python libraries like `nltk` in your code, you need to download the wheel file from PyPI and upload to S3 in the same way. At this point, Glue only supports passing pure Python libraries in this way (e.g. you can not pass `Pandas` or `OpenCV`). However you can use `NumPy` & `SciPy` without having to pass these as packages because these are pre-installed in the Glue environment.
# !wget https://s3-us-west-2.amazonaws.com/sparkml-mleap/0.9.6/python/python.zip
# !wget https://s3-us-west-2.amazonaws.com/sparkml-mleap/0.9.6/jar/mleap_spark_assembly.jar
python_dep_location = sess.upload_data(path='python.zip', bucket=default_bucket, key_prefix='dependencies/python')
jar_dep_location = sess.upload_data(path='mleap_spark_assembly.jar', bucket=default_bucket, key_prefix='dependencies/jar')
# ## Defining output locations for the data and model
# Next we define the output location where the transformed dataset should be uploaded. We are also specifying a model location where the MLeap serialized model would be updated. This locations should be consumed as part of the Spark script using `getResolvedOptions` method of AWS Glue library (see `abalone_processing.py` for details).
#
# By designing our code in that way, we can re-use these variables as part of other SageMaker operations from this Notebook (details below).
# +
from time import gmtime, strftime
import time
timestamp_prefix = strftime("%Y-%m-%d-%H-%M-%S", gmtime())
# Input location of the data, We uploaded our train.csv file to input key previously
s3_input_bucket = default_bucket
s3_input_key_prefix = 'input/abalone'
# Output location of the data. The input data will be split, transformed, and
# uploaded to output/train and output/validation
s3_output_bucket = default_bucket
s3_output_key_prefix = timestamp_prefix + '/abalone'
# the MLeap serialized SparkML model will be uploaded to output/mleap
s3_model_bucket = default_bucket
s3_model_key_prefix = s3_output_key_prefix + '/mleap'
# -
# ### Calling Glue APIs
# Next we'll be creating Glue client via Boto so that we can invoke the `create_job` API of Glue. `create_job` API will create a job definition which can be used to execute your jobs in Glue. The job definition created here is mutable. While creating the job, we are also passing the code location as well as the dependencies location to Glue.
#
# `AllocatedCapacity` parameter controls the hardware resources that Glue will use to execute this job. It is measures in units of `DPU`. For more information on `DPU`, please see [here](https://docs.aws.amazon.com/glue/latest/dg/add-job.html).
glue_client = boto_session.client('glue')
job_name = 'sparkml-abalone-' + timestamp_prefix
response = glue_client.create_job(
Name=job_name,
Description='PySpark job to featurize the Abalone dataset',
Role=role, # you can pass your existing AWS Glue role here if you have used Glue before
ExecutionProperty={
'MaxConcurrentRuns': 1
},
Command={
'Name': 'glueetl',
'ScriptLocation': script_location
},
DefaultArguments={
'--job-language': 'python',
'--extra-jars' : jar_dep_location,
'--extra-py-files': python_dep_location
},
AllocatedCapacity=5,
Timeout=60,
)
glue_job_name = response['Name']
print(glue_job_name)
# The aforementioned job will be executed now by calling `start_job_run` API. This API creates an immutable run/execution corresponding to the job definition created above. We will require the `job_run_id` for the particular job execution to check for status. We'll pass the data and model locations as part of the job execution parameters.
job_run_id = glue_client.start_job_run(JobName=job_name,
Arguments = {
'--S3_INPUT_BUCKET': s3_input_bucket,
'--S3_INPUT_KEY_PREFIX': s3_input_key_prefix,
'--S3_OUTPUT_BUCKET': s3_output_bucket,
'--S3_OUTPUT_KEY_PREFIX': s3_output_key_prefix,
'--S3_MODEL_BUCKET': s3_model_bucket,
'--S3_MODEL_KEY_PREFIX': s3_model_key_prefix
})['JobRunId']
print(job_run_id)
# ### Checking Glue job status
# Now we will check for the job status to see if it has `succeeded`, `failed` or `stopped`. Once the job is succeeded, we have the transformed data into S3 in CSV format which we can use with XGBoost for training. If the job fails, you can go to [AWS Glue console](https://us-west-2.console.aws.amazon.com/glue/home), click on **Jobs** tab on the left, and from the page, click on this particular job and you will be able to find the CloudWatch logs (the link under **Logs**) link for these jobs which can help you to see what exactly went wrong in the job execution.
job_run_status = glue_client.get_job_run(JobName=job_name,RunId=job_run_id)['JobRun']['JobRunState']
while job_run_status not in ('FAILED', 'SUCCEEDED', 'STOPPED'):
job_run_status = glue_client.get_job_run(JobName=job_name,RunId=job_run_id)['JobRun']['JobRunState']
print (job_run_status)
time.sleep(30)
# ## Using SageMaker XGBoost to train on the processed dataset produced by SparkML job
# Now we will use SageMaker XGBoost algorithm to train on this dataset. We already know the S3 location
# where the preprocessed training data was uploaded as part of the Glue job.
# ### We need to retrieve the XGBoost algorithm image
# We will retrieve the XGBoost built-in algorithm image so that it can leveraged for the training job.
# +
from sagemaker.amazon.amazon_estimator import get_image_uri
training_image = get_image_uri(sess.boto_region_name, 'xgboost', repo_version="latest")
print (training_image)
# -
# ### Next XGBoost model parameters and dataset details will be set properly
# We have parameterized this Notebook so that the same data location which was used in the PySpark script can now be passed to XGBoost Estimator as well.
# +
s3_train_data = 's3://{}/{}/{}'.format(s3_output_bucket, s3_output_key_prefix, 'train')
s3_validation_data = 's3://{}/{}/{}'.format(s3_output_bucket, s3_output_key_prefix, 'validation')
s3_output_location = 's3://{}/{}/{}'.format(s3_output_bucket, s3_output_key_prefix, 'xgboost_model')
xgb_model = sagemaker.estimator.Estimator(training_image,
role,
train_instance_count=1,
train_instance_type='ml.m5.xlarge',
train_volume_size = 20,
train_max_run = 3600,
input_mode= 'File',
output_path=s3_output_location,
sagemaker_session=sess)
xgb_model.set_hyperparameters(objective = "reg:linear",
eta = .2,
gamma = 4,
max_depth = 5,
num_round = 10,
subsample = 0.7,
silent = 0,
min_child_weight = 6)
train_data = sagemaker.session.s3_input(s3_train_data, distribution='FullyReplicated',
content_type='text/csv', s3_data_type='S3Prefix')
validation_data = sagemaker.session.s3_input(s3_validation_data, distribution='FullyReplicated',
content_type='text/csv', s3_data_type='S3Prefix')
data_channels = {'train': train_data, 'validation': validation_data}
# -
# ### Finally XGBoost training will be performed.
xgb_model.fit(inputs=data_channels, logs=True)
# # Building an Inference Pipeline consisting of SparkML & XGBoost models for a realtime inference endpoint
# Next we will proceed with deploying the models in SageMaker to create an Inference Pipeline. You can create an Inference Pipeline with upto five containers.
#
# Deploying a model in SageMaker requires two components:
#
# * Docker image residing in ECR.
# * Model artifacts residing in S3.
#
# **SparkML**
#
# For SparkML, Docker image for MLeap based SparkML serving is provided by SageMaker team. For more information on this, please see [SageMaker SparkML Serving](https://github.com/aws/sagemaker-sparkml-serving-container). MLeap serialized SparkML model was uploaded to S3 as part of the SparkML job we executed in AWS Glue.
#
# **XGBoost**
#
# For XGBoost, we will use the same Docker image we used for training. The model artifacts for XGBoost was uploaded as part of the training job we just ran.
# ### Passing the schema of the payload via environment variable
# SparkML serving container needs to know the schema of the request that'll be passed to it while calling the `predict` method. In order to alleviate the pain of not having to pass the schema with every request, `sagemaker-sparkml-serving` allows you to pass it via an environment variable while creating the model definitions. This schema definition will be required in our next step for creating a model.
#
# We will see later that you can overwrite this schema on a per request basis by passing it as part of the individual request payload as well.
import json
schema = {
"input": [
{
"name": "sex",
"type": "string"
},
{
"name": "length",
"type": "double"
},
{
"name": "diameter",
"type": "double"
},
{
"name": "height",
"type": "double"
},
{
"name": "whole_weight",
"type": "double"
},
{
"name": "shucked_weight",
"type": "double"
},
{
"name": "viscera_weight",
"type": "double"
},
{
"name": "shell_weight",
"type": "double"
},
],
"output":
{
"name": "features",
"type": "double",
"struct": "vector"
}
}
schema_json = json.dumps(schema)
print(schema_json)
# ### Creating a `PipelineModel` which comprises of the SparkML and XGBoost model in the right order
#
# Next we'll create a SageMaker `PipelineModel` with SparkML and XGBoost.The `PipelineModel` will ensure that both the containers get deployed behind a single API endpoint in the correct order. The same model would later be used for Batch Transform as well to ensure that a single job is sufficient to do prediction against the Pipeline.
#
# Here, during the `Model` creation for SparkML, we will pass the schema definition that we built in the previous cell.
# +
from sagemaker.model import Model
from sagemaker.pipeline import PipelineModel
from sagemaker.sparkml.model import SparkMLModel
sparkml_data = 's3://{}/{}/{}'.format(s3_model_bucket, s3_model_key_prefix, 'model.tar.gz')
# passing the schema defined above by using an environment variable that sagemaker-sparkml-serving understands
sparkml_model = SparkMLModel(model_data=sparkml_data, env={'SAGEMAKER_SPARKML_SCHEMA' : schema_json})
xgb_model = Model(model_data=xgb_model.model_data, image=training_image)
model_name = 'inference-pipeline-' + timestamp_prefix
sm_model = PipelineModel(name=model_name, role=role, models=[sparkml_model, xgb_model])
# -
# ### Deploying the `PipelineModel` to an endpoint for realtime inference
# Next we will deploy the model we just created with the `deploy()` method to start an inference endpoint and we will send some requests to the endpoint to verify that it works as expected.
endpoint_name = 'inference-pipeline-ep-' + timestamp_prefix
sm_model.deploy(initial_instance_count=1, instance_type='ml.c4.xlarge', endpoint_name=endpoint_name)
# ### Invoking the newly created inference endpoint with a payload to transform the data
# Now we will invoke the endpoint with a valid payload that SageMaker SparkML Serving can recognize. There are three ways in which input payload can be passed to the request:
#
# * Pass it as a valid CSV string. In this case, the schema passed via the environment variable will be used to determine the schema. For CSV format, every column in the input has to be a basic datatype (e.g. int, double, string) and it can not be a Spark `Array` or `Vector`.
#
# * Pass it as a valid JSON string. In this case as well, the schema passed via the environment variable will be used to infer the schema. With JSON format, every column in the input can be a basic datatype or a Spark `Vector` or `Array` provided that the corresponding entry in the schema mentions the correct value.
#
# * Pass the request in JSON format along with the schema and the data. In this case, the schema passed in the payload will take precedence over the one passed via the environment variable (if any).
# #### Passing the payload in CSV format
# We will first see how the payload can be passed to the endpoint in CSV format.
from sagemaker.predictor import json_serializer, csv_serializer, json_deserializer, RealTimePredictor
from sagemaker.content_types import CONTENT_TYPE_CSV, CONTENT_TYPE_JSON
payload = "F,0.515,0.425,0.14,0.766,0.304,0.1725,0.255"
predictor = RealTimePredictor(endpoint=endpoint_name, sagemaker_session=sess, serializer=csv_serializer,
content_type=CONTENT_TYPE_CSV, accept=CONTENT_TYPE_CSV)
print(predictor.predict(payload))
# #### Passing the payload in JSON format
# We will now pass a different payload in JSON format.
# +
payload = {"data": ["F",0.515,0.425,0.14,0.766,0.304,0.1725,0.255]}
predictor = RealTimePredictor(endpoint=endpoint_name, sagemaker_session=sess, serializer=json_serializer,
content_type=CONTENT_TYPE_JSON, accept=CONTENT_TYPE_CSV)
print(predictor.predict(payload))
# -
# #### [Optional] Passing the payload with both schema and the data
# Next we will pass the input payload comprising of both the schema and the data. If you notice carefully, this schema will be slightly different than what we have passed via the environment variable. The locations of `length` and `sex` column have been swapped and so the data. The server now parses the payload with this schema and works properly.
# +
payload = {
"schema": {
"input": [
{
"name": "length",
"type": "double"
},
{
"name": "sex",
"type": "string"
},
{
"name": "diameter",
"type": "double"
},
{
"name": "height",
"type": "double"
},
{
"name": "whole_weight",
"type": "double"
},
{
"name": "shucked_weight",
"type": "double"
},
{
"name": "viscera_weight",
"type": "double"
},
{
"name": "shell_weight",
"type": "double"
},
],
"output":
{
"name": "features",
"type": "double",
"struct": "vector"
}
},
"data": [0.515,"F",0.425,0.14,0.766,0.304,0.1725,0.255]
}
predictor = RealTimePredictor(endpoint=endpoint_name, sagemaker_session=sess, serializer=json_serializer,
content_type=CONTENT_TYPE_JSON, accept=CONTENT_TYPE_CSV)
print(predictor.predict(payload))
# -
# ### [Optional] Deleting the Endpoint
# If you do not plan to use this endpoint, then it is a good practice to delete the endpoint so that you do not incur the cost of running it.
sm_client = boto_session.client('sagemaker')
sm_client.delete_endpoint(EndpointName=endpoint_name)
# # Building an Inference Pipeline consisting of SparkML & XGBoost models for a single Batch Transform job
# SageMaker Batch Transform also supports chaining multiple containers together when deploying an Inference Pipeline and performing a single batch transform jobs to transform your data for a batch use-case similar to the real-time use-case we have seen above.
# ### Preparing data for Batch Transform
# Batch Transform requires data in the same format described above, with one CSV or JSON being per line. For this Notebook, SageMaker team has created a sample input in CSV format which Batch Transform can process. The input is basically a similar CSV file to the training file with only difference is that it does not contain the label (``rings``) field.
#
# Next we will download a sample of this data from one of the SageMaker buckets (named `batch_input_abalone.csv`) and upload to your S3 bucket. We will also inspect first five rows of the data post downloading.
# !wget https://s3-us-west-2.amazonaws.com/sparkml-mleap/data/batch_input_abalone.csv
# !printf "\n\nShowing first five lines\n\n"
# !head -n 5 batch_input_abalone.csv
# !printf "\n\nAs we can see, it is identical to the training file apart from the label being absent here.\n\n"
batch_input_loc = sess.upload_data(path='batch_input_abalone.csv', bucket=default_bucket, key_prefix='batch')
# ### Invoking the Transform API to create a Batch Transform job
# Next we will create a Batch Transform job using the `Transformer` class from Python SDK to create a Batch Transform job.
input_data_path = 's3://{}/{}/{}'.format(default_bucket, 'batch', 'batch_input_abalone.csv')
output_data_path = 's3://{}/{}/{}'.format(default_bucket, 'batch_output/abalone', timestamp_prefix)
job_name = 'serial-inference-batch-' + timestamp_prefix
transformer = sagemaker.transformer.Transformer(
# This was the model created using PipelineModel and it contains feature processing and XGBoost
model_name = model_name,
instance_count = 1,
instance_type = 'ml.m5.xlarge',
strategy = 'SingleRecord',
assemble_with = 'Line',
output_path = output_data_path,
base_transform_job_name='serial-inference-batch',
sagemaker_session=sess,
accept = CONTENT_TYPE_CSV
)
transformer.transform(data = input_data_path,
job_name = job_name,
content_type = CONTENT_TYPE_CSV,
split_type = 'Line')
transformer.wait()
|
advanced_functionality/inference_pipeline_sparkml_xgboost_abalone/inference_pipeline_sparkml_xgboost_abalone.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: pymedphys-master
# language: python
# name: pymedphys-master
# ---
# +
import functools
import numpy as np
import matplotlib.pyplot as plt
import shapely.geometry
import skimage.draw
import tensorflow as tf
import pydicom
import pymedphys
import pymedphys._dicom.structure as dcm_struct
# -
dcm_path = pymedphys.data_path("example_structures.dcm")
dcm = pydicom.read_file(str(dcm_path), force=True)
dcm_struct.list_structures(dcm)
# +
i = 7
x, y, z = dcm_struct.pull_structure('ANT Box', dcm)
x = x[i]
y = y[i]
# -
plt.plot(x, y)
plt.axis('equal')
# +
dx, dy = 2, 2
Cx, Cy = -100, -300
Ox, Oy = 1, 1
# -
r = (y - Cy) / dy * Oy
c = (x - Cx) / dx * Ox
r
np.array(list(zip(r*4, c*4)))
img_size = 128
expansion = 4
expanded_mask = skimage.draw.polygon2mask((img_size * expansion, img_size * expansion), np.array(list(zip(r*expansion, c*expansion))))
plt.pcolormesh(expanded_mask)
def reduce_expanded_mask(expanded_mask, img_size, expansion):
expanded_mask = tf.dtypes.cast(expanded_mask, tf.float32)
return tf.reduce_mean(
tf.reduce_mean(
tf.reshape(expanded_mask, (img_size, expansion, img_size, expansion)),
axis=1,
),
axis=2,
)
mask = reduce_expanded_mask(expanded_mask, img_size, expansion)
plt.pcolormesh(mask)
|
prototyping/auto-segmentation/sb/00-stage-0-prototyping/01-mask-with-edge-falloff.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Train/Validation/Test Splits
#
# This notebooks is used to generate the train, validation, and test splits from the full dataset.
#
# The key here is to ensure that all intervals generated for each dataset are distinct and contain no overlap with intervals in the other datasets. This ensures we are not at risk for data leakage when training and testing our model.
# +
# %matplotlib widget
from collections import defaultdict, Counter
import datetime as dt
import glob
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import numpy as np
np.random.seed(12345)
import pandas as pd
from tqdm.notebook import tqdm
# -
df = pd.read_csv('../utils/sta_dataset_labels.txt', header=0, parse_dates=['start_time', 'stop_time'])
df.label.value_counts() / len(df)
icmes = df[df.label.eq(1)]
validation_size = 0.15
nval = round(validation_size * icmes.shape[0])
train_size = 0.70
ntrain = round(train_size * icmes.shape[0])
test_size = 0.1
ntest = round(test_size * icmes.shape[0])
sum([nval, ntrain, ntest]) == icmes.shape[0]
sum([ntrain, ntest, nval])
# +
def plot_interval_span(
ax,
df,
c='r',
hatch='*',
label='',
):
j = 0
for i, row in df.iterrows():
if j == 0:
ax.axvspan(row['start_time'], row['stop_time'], facecolor=c, alpha=0.3, label=label, hatch=hatch)
else:
ax.axvspan(row['start_time'], row['stop_time'], facecolor=c, alpha=0.3, hatch=hatch)
j+=1
return ax
def plot_train_test_val_intervals(
val_df,
test_df,
train_df,
xlim=(dt.datetime(2009,1,1), dt.datetime(2010,1, 1))
):
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 3))
plot_interval_span(ax, val_df, c='r', label='val', hatch=None)
plot_interval_span(ax, test_df, c='b', label='test', hatch=None)
plot_interval_span(ax, train_df, c='g', label='train', hatch=None)
ax.tick_params(which='both', axis='y', labelleft=False, left=False)
ax.xaxis.set_major_formatter(
mdates.ConciseDateFormatter(
locator=mdates.MonthLocator(interval=2),
formats=['%Y', '%b', '%d', '%H:%M', '%H:%M', '%S.%f'],
offset_formats=[
'%Y',
'%b',
'%b %d, %Y',
'%b %d, %Y',
'%b %d, %Y',
'%b %d, %Y'
],
zero_formats=['', '%Y', '%b', '%b-%d', '%H:%M', '%H:%M'],
show_offset=False
)
)
ax.legend(loc='upper left', bbox_to_anchor=(1.01, 0.9), edgecolor='k')
ax.set_xlim(xlim)
fig.savefig('interval_check.jpg', format='jpg', dpi=250, bbox_inches='tight')
# +
def get_pos_samples(positive_class, df, nsamples, used_intervals=None, for_train=False):
dout = defaultdict(list)
if used_intervals is not None:
intervals_to_exclude = list(
zip(used_intervals['start_time'], used_intervals['stop_time'])
)
else:
intervals_to_exclude=[]
while len(dout['fname']) < nsamples:
pos_sample = positive_class.sample(1)
if intervals_to_exclude is not None:
distinct = check_used_intervals(intervals_to_exclude, pos_sample)
else:
distinct = True
if not distinct:
positive_class = positive_class.drop(index=pos_sample.index)
continue
# Get this sample and the following one from the full df
pos_cut = df.loc[pos_sample.index[0]: pos_sample.index[0]+1]
try:
tdiff = (pos_cut['start_time'].iloc[1] - pos_cut['start_time'].iloc[0]) / np.timedelta64(1,'D')
except IndexError:
continue
# if these samples are consecutive and both contain ICMEs continue
if tdiff == 0.75 and all(pos_cut.label.eq(1)):
# consecutive interval and we are goo
for i, row in pos_cut.iterrows():
dout['fname'].append(row['fname'])
dout['label'].append(row['label'])
dout['start_time'].append(row['start_time'])
dout['stop_time'].append(row['stop_time'])
dout['index'].append(i)
# intervals_to_exclude.append((row['start_time'], row['stop_time']))
else:
# try the current sample and the previous one
pos_cut = df.loc[pos_sample.index[0] - 1 : pos_sample.index[0]]
try:
tdiff = (pos_cut['start_time'].iloc[1] - pos_cut['start_time'].iloc[0]) / np.timedelta64(1,'D')
except IndexError:
continue
# print(tdiff, pos_cut.label.eq(1).iloc[0])
if tdiff == 0.75 and all(pos_cut.label.eq(1)):
# consecutive interval and we are good
for i, row in pos_cut.iterrows():
dout['fname'].append(row['fname'])
dout['label'].append(row['label'])
dout['start_time'].append(row['start_time'])
dout['stop_time'].append(row['stop_time'])
dout['index'].append(i)
else:
# print('Resampling...')
continue
return dout
def get_neg_samples(negative_class, df, nsamples, used_intervals):
dout = defaultdict(list)
intervals_to_exclude = list(zip(used_intervals['start_time'], used_intervals['stop_time']))
while len(dout['fname']) < nsamples:
neg_sample = negative_class.sample(1)
distinct = check_used_intervals(intervals_to_exclude, neg_sample)
if distinct:
for i, row in neg_sample.iterrows():
dout['fname'].append(row['fname'])
dout['label'].append(row['label'])
dout['start_time'].append(row['start_time'])
dout['stop_time'].append(row['stop_time'])
dout['index'].append(i)
else:
continue
return dout
def check_used_intervals(intervals_to_exclude, sample):
distinct = []
for start, stop in intervals_to_exclude:
if sample['start_time'].iloc[0] == start and sample['stop_time'].iloc[0] == stop:
distinct.append(False)
elif sample['stop_time'].iloc[0] < start or sample['start_time'].iloc[0] > stop:
distinct.append(True)
else:
distinct.append(False)
return all(distinct)
def trim_df(df, indices_to_drop, N):
print(f'Found {N} samples... trimming original df')
orig_shape = df.shape
df = df.drop(index=indices_to_drop)
new_shape = df.shape
print(f"{orig_shape} --> {new_shape}")
return df
def generate_test_train_split(df, ntest=20, ntrain=20, nval=20):
positive_class = df[df.label.eq(1)]
negative_class = df[df.label.eq(0)]
train = defaultdict(list)
test = defaultdict(list)
pos_val = defaultdict(list)
neg_val = defaultdict(list)
used_intervals = defaultdict(list)
# build the validation set
print('Finding positive validation set')
pos_val = get_pos_samples(positive_class, df, nval)
used_intervals['start_time'] += pos_val['start_time']
used_intervals['stop_time'] += pos_val['stop_time']
print('Finding negative validation set')
neg_val = get_neg_samples(negative_class, df, nval, used_intervals)
used_intervals['start_time'] += neg_val['start_time']
used_intervals['stop_time'] += neg_val['stop_time']
print('Finding positive test set')
pos_test = get_pos_samples(positive_class, df, ntest, used_intervals)
used_intervals['start_time'] += pos_test['start_time']
used_intervals['stop_time'] += pos_test['stop_time']
print('Finding negative test set')
neg_test = get_neg_samples(negative_class, df, ntest, used_intervals)
used_intervals['start_time'] += neg_test['start_time']
used_intervals['stop_time'] += neg_test['stop_time']
print('Finding positive train set')
pos_train = get_pos_samples(positive_class, df, ntrain, used_intervals, for_train=True)
used_intervals['start_time'] += pos_train['start_time']
used_intervals['stop_time'] += pos_train['stop_time']
print('Finding negative train set')
neg_train = get_neg_samples(negative_class, df, ntrain, used_intervals)
used_intervals['start_time'] += neg_train['start_time']
used_intervals['stop_time'] += neg_train['stop_time']
validation_set = defaultdict(list)
testing_set = defaultdict(list)
training_set = defaultdict(list)
# Combine the positive and negative classes for each set into single
# dictionary and convert that to a dataframe
for key in pos_val.keys():
validation_set[key] += pos_val[key]
validation_set[key] += neg_val[key]
for key in pos_test.keys():
testing_set[key] += pos_test[key]
testing_set[key] += neg_test[key]
for key in pos_train.keys():
training_set[key] += pos_train[key]
training_set[key] += neg_train[key]
val_df = pd.DataFrame(validation_set, index=validation_set['index'])
test_df = pd.DataFrame(testing_set, index=testing_set['index'])
train_df = pd.DataFrame(training_set, index=training_set['index'])
return val_df, test_df, train_df
# -
val_df, test_df, train_df = generate_test_train_split(
df, nval=nval, ntrain=ntrain, ntest=ntest
)
# Check to make sure there is no overlap between the train/validation/test sets
train_f = set(train_df['fname'])
test_f = set(test_df['fname'])
val_f = set(val_df['fname'])
print(train_f.intersection(test_f))
print(train_f.intersection(val_f))
print(val_f.intersection(test_f))
fig = plot_train_test_val_intervals(val_df, test_df, train_df)
for df in [val_df, test_df, train_df]:
df['fname_img'] = df.fname.str.replace('ts_interval','img_interval').str.replace('.txt','.npy')
val_df.to_csv('../data/sta_validation_set.txt', header=True, index=False)
test_df.to_csv('../data/sta_test_set.txt', header=True, index=False)
train_df.to_csv('../data/sta_train_set.txt', header=True, index=False)
|
notebooks/train_test_validation_splits.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import sklearn
import string
import nltk
nltk.download('stopwords')
nltk.download('wordnet')
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
from nltk.stem import WordNetLemmatizer
from nltk.corpus import wordnet
import re
# !pip install wordcloud
from wordcloud import WordCloud, STOPWORDS
import time
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
from sklearn.metrics import classification_report
# -
file = r"C:\Users\<NAME>\Desktop\PROJECT\PRINT FOLDER\uci-news-aggregator.csv"
news = pd.read_csv(file)
news
news.head()
# #### Independent Features- [ID,TITLE,URL,PUBLISHER,STORY,HOSTNAME,TIMESTAMP]
# #### Dependent Feature- 'CATEGORY'
news.dtypes
news.isnull().sum()
news.info()
news["PUBLISHER"].value_counts()
news['PUBLISHER'] = news['PUBLISHER'].fillna(news['PUBLISHER'].mode()[0])
news.isnull().sum()
news.info()
news.shape
print(news.duplicated())==True
print(' News Data Size {}'.format(news.shape))
if(any(news.duplicated())==True):
print('Duplicate rows found')
print('Number of duplicate rows= ',news[news.duplicated()].shape[0])
df.drop_duplicates(inplace=True,keep='first')
df.reset_index(inplace=True,drop=True)
print('Dropping duplicates\n')
print(news.shape)
else:
print('NO Duplicate Data Found')
# #### Distribution of 'CATEGORY' (Dependent Variable)
news.head()
news["CATEGORY"].value_counts()
sns.set(font_scale=1.5)
plt.figure(figsize=(12,12))
sns.countplot(news['CATEGORY'])
def label_to_name(label):
if(label=='e'):
return 'entertainment'
elif(label=='b'):
return 'business'
elif(label=='t'):
return 'science and technology'
else:
return 'health'
news['CATEGORY'] = news['CATEGORY'].apply(label_to_name)
news["CATEGORY"].value_counts()
print('Distribution of labels in %\n')
print(news['CATEGORY'].value_counts()/news.shape[0]*100)
sns.set(font_scale=1.5)
plt.figure(figsize=(12,12))
sns.countplot(news['CATEGORY'])
# +
# Dropping features [ID,URL,PUBLISHER,STORY,HOSTNAME,TIMESTAMP]
# -
news.drop(columns=['ID','URL','PUBLISHER','STORY','HOSTNAME','TIMESTAMP'],inplace=True)
# lowercasing
news['lower'] = news['TITLE'].str.lower()
news.head()
# +
## Punctuation removing
PUNCT_TO_REMOVE = string.punctuation
def remove_punctuation(text):
"""custom function to remove the punctuation"""
return text.translate(str.maketrans('', '', PUNCT_TO_REMOVE))
news["punc_removed"] = news["lower"].apply(lambda text: remove_punctuation(text))
# -
news.head()
# +
## stopwords removing
STOPWORDS = set(stopwords.words('english'))
# -
STOPWORDS
def remove_stopwords(text):
return " ".join([word for word in str(text).split() if word not in STOPWORDS])
news["stopwords_removed"] = news["punc_removed"].apply(lambda text: remove_stopwords(text))
news.head()
# #### A Wordcloud (or Tag cloud) is a visual representation of text data. It displays a list of words, the importance of each beeing shown with font size or color. This format is useful for quickly perceiving the most prominent terms. Python is.
# ### Wordcloud Tutorial = https://www.datacamp.com/community/tutorials/wordcloud-python
comment_words = " "
comment_words
stopwords = set(STOPWORDS)
stopwords
for val in news.stopwords_removed[0:10000]:
tokens = val.split()
for words in tokens:
comment_words = comment_words + words + ' '
wordcloud = WordCloud(width = 1000, height = 900, background_color ='white',
stopwords = stopwords, min_font_size = 15).generate(comment_words)
plt.figure(figsize = (12, 12))
plt.imshow(wordcloud)
plt.axis("off")
plt.tight_layout(pad = 0)
plt.show()
# ### Dealing with catogorical data
news.head()
news.CATEGORY.value_counts()
le = LabelEncoder()
news['CATEGORY']=le.fit_transform(news['CATEGORY'])
news.head()
news.CATEGORY.value_counts()
# #### Results using CountVectorizer
vectorizer = CountVectorizer()
x = vectorizer.fit_transform(news['stopwords_removed'])
y = news['CATEGORY']
# #### splitting the data
# ?train_test_split
# #### stratify : array-like or None (default=None)
# #### If not None, data is split in a stratified fashion, using this as
# ##### the class labels.
x_train,x_test,y_train,y_test = train_test_split(x , y , test_size=0.2 , random_state=42 , stratify = news["CATEGORY"])
x_train.shape
y_train.shape
x_test.shape
y_test.shape
result = pd.DataFrame(columns=['Model_Name','Accuracy_Score','F1-score'])
result
models_name = ['Logistic Regression' , 'Multinomial NaiveBayes']
models_name
model_clf = [LogisticRegression() , MultinomialNB()]
model_clf
for index,model in enumerate(model_clf):
clf = model.fit(x_train, y_train)
predictions = model.predict(x_test)
result.loc[index] = [models_name[index],accuracy_score(y_test, predictions),f1_score(y_test , predictions ,
average = 'weighted')]
result
result
confusion_matrix(predictions , y_test)
print(classification_report(predictions , y_test))
# #### result using TF-IDF
# #### TF-IDF stands for “Term Frequency — Inverse Data Frequency”.
# #### Term Frequency (tf): gives us the frequency of the word in each document in the corpus.
# #### It is the ratio of number of times the word appears in a document compared to the total number of words in that document
tfidf = TfidfVectorizer()
x = tfidf.fit_transform(news['stopwords_removed'].values)
y = news['CATEGORY']
x_train , x_test , y_train , y_test = train_test_split(x , y , test_size=0.2 , random_state=42 , stratify=news.CATEGORY)
x_train.shape
y_train.shape
x_test.shape
y_test.shape
result = pd.DataFrame(columns=['Model_Name' , 'Accuracy_score' ,'F1-score'])
result
models_name = ['Logistic Regression' , 'Multinomial NaiveBayes']
models_name
model_clfs = [LogisticRegression() , MultinomialNB()]
model_clfs
for index,model in enumerate(model_clfs):
clfs = model.fit(x_train, y_train)
predictions = model.predict(x_test)
result.loc[index] = [models_name[index] , accuracy_score(y_test, predictions) , f1_score(y_test, predictions, average = 'weighted')]
result
result
confusion_matrix(predictions , y_test)
print(classification_report(predictions , y_test))
# #### LSTM for deep learning model
# #### The Long Short-Term Memory network, or LSTM for short, is a type of recurrent neural network that achieves state-of-the-art results on challenging prediction problems.
# +
import keras
from keras.layers import Dense, Embedding, LSTM, SpatialDropout1D
from keras.models import Sequential
from sklearn.feature_extraction.text import CountVectorizer
from keras.preprocessing.text import Tokenizer
from keras.preprocessing.sequence import pad_sequences
from sklearn.model_selection import train_test_split
from keras.utils.np_utils import to_categorical
from keras.callbacks import EarlyStopping,ModelCheckpoint
import os
# -
news_labels = to_categorical(news['CATEGORY'], num_classes=4)
news_labels
n_most_common_words = 11000
max_len = 130
tokenizer = Tokenizer(num_words=n_most_common_words, filters='!"#$%&()*+,-./:;<=>?@[\]^_`{|}~', lower=True)
tokenizer
tokenizer.fit_on_texts(news["lower"].values)
sequence = tokenizer.texts_to_sequences(news["lower"].values)
sequence
word_index = tokenizer.word_index
word_index
print('Found %s unique tokens.' % len(word_index))
# #### This function transforms a list (of length num_samples ) of sequences (lists of integers) into a 2D Numpy array of shape (num_samples, num_timesteps) .
# #### Sequences longer than num_timesteps are truncated so that they fit the desired length
# ?pad_sequences
X = pad_sequences(sequence , maxlen = max_len)
X
x_train, x_test, y_train, y_test = train_test_split(X , news_labels, test_size=0.2, random_state=42, stratify = news.CATEGORY)
X.shape
x_train.shape
x_test.shape
y_train.shape
y_test.shape
epochs = 11
emb_dim = 160
batch_size = 258
# ?Sequential
model = Sequential()
model.add(Embedding(n_most_common_words, emb_dim, input_length = X.shape[1]))
# #### An alternative way to use dropout with convolutional neural networks is to dropout entire feature maps from the convolutional layer which are then not used during pooling. This is called spatial dropout (or “SpatialDropout“). ... — Efficient Object Localization Using Convolutional Networks
model.add(SpatialDropout1D(0.2))
# ?LSTM
model.add(LSTM(100, dropout=0.15, recurrent_dropout=0.15))
model.add(Dense(4, activation='softmax'))
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])
print(model.summary())
# #### How to load a model from an HDF5 file in Keras
# #### https://intellipaat.com/community/2962/how-to-load-a-model-from-an-hdf5-file-in-keras
# #### https://stackoverflow.com/questions/35074549/how-to-load-a-model-from-an-hdf5-file-in-keras
filepath="weights.best.hdf5"
# ?ModelCheckpoint
checkpoint = ModelCheckpoint(filepath, monitor='val_acc', verbose=1, save_best_only=True, mode='max')
callback_list = [checkpoint]
history = model.fit(x_train, y_train, epochs = epochs, batch_size = batch_size, validation_data=(x_test,y_test),
callbacks = callback_list)
plt.figure(figsize=(20,12))
plt.subplot()
plt.title("Loss Curves")
plt.plot(history.history["loss"], color="g", label="Training loss",linewidth=4)
plt.plot(history.history["val_loss"], color="b", label="Validation loss",linewidth=4)
plt.legend(['Training loss : 0.0702', 'Validation Loss : 0.2181'],fontsize=18)
plt.xlabel('Epochs ',fontsize=18)
plt.ylabel('Loss',fontsize=18)
plt.tight_layout()
plt.show()
plt.figure(figsize=(20,12))
plt.plot(history.history['loss'],'g',linewidth=4)
plt.plot(history.history['val_loss'],'b',linewidth=4)
plt.legend(['Training loss : 0.0702', 'Validation Loss : 0.2181'],fontsize=18)
plt.xlabel('Epochs ',fontsize=18)
plt.ylabel('Loss',fontsize=18)
plt.title('Loss Curves',fontsize=18)
plt.show()
plt.figure(figsize=(20,12))
plt.subplot()
plt.title("Accuracy Curves")
plt.plot(history.history["acc"], color="g", label="Training Accuracy")
plt.plot(history.history["val_acc"], color="b", label="Validation Accuracy")
plt.legend(loc="best")
plt.xlabel('Epochs ',fontsize=18)
plt.ylabel('Accuracy',fontsize=18)
plt.tight_layout()
plt.show()
plt.figure(figsize=(20,12))
plt.subplot()
plt.plot(history.history['acc'],'g',linewidth=4)
plt.plot(history.history['val_acc'],'b',linewidth=4)
plt.legend(['Training Accuracy', 'Validation Accuracy'],fontsize=15)
plt.xlabel('Epochs ',fontsize=15)
plt.ylabel('Accuracy',fontsize=15)
plt.title('Accuracy Curves',fontsize=15)
plt.tight_layout()
plt.show()
print("** Results for LSTM Model **\n")
predictions = model.predict_classes(x_test)
print("Accuracy score: ", accuracy_score(y_test.argmax(1), predictions))
print("F1 score: ", f1_score(y_test.argmax(1), predictions, average = 'weighted'))
print("** Results for LSTM Model **\n")
predictions = model.predict_classes(x_test)
print("Accuracy score: ", accuracy_score(y_test.argmax(1), predictions))
print("F1 score: ", f1_score(y_test.argmax(1), predictions, average = 'weighted'))
BATCH_SIZE = 32
score, acc = model.evaluate(x_test, y_test, batch_size = BATCH_SIZE , verbose = 0)
print("Test score: %.3f, accuracy: %.3f" % (score,acc))
|
NEWS-AGGRIGATOR DATASET.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import k3d
import numpy as np
from numpy import sin,cos,pi
from ipywidgets import interact, interactive, fixed
import ipywidgets as widgets
import time
import math
plot = k3d.plot()
plot.camera_auto_fit = False
T = 1.618033988749895
r = 4.77
zmin,zmax = -r,r
xmin,xmax = -r,r
ymin,ymax = -r,r
Nx,Ny,Nz = 77,77,77
x = np.linspace(xmin,xmax,Nx)
y = np.linspace(ymin,ymax,Ny)
z = np.linspace(zmin,zmax,Nz)
x,y,z = np.meshgrid(x,y,z,indexing='ij')
p = 2 - (cos(x + T*y) + cos(x - T*y) + cos(y + T*z) + cos(y - T*z) + cos(z - T*x) + cos(z + T*x))
iso = k3d.marching_cubes(p.astype(np.float32),xmin=xmin,xmax=xmax,ymin=ymin,ymax=ymax, zmin=zmin, zmax=zmax, level=0.0)
plot += iso
plot.display()
# +
@interact(x=widgets.FloatSlider(value=0,min=-3,max=4,step=0.01))
def g(x):
iso.level=x
@interact(rad=widgets.FloatSlider(value=0,min=0,max=2*math.pi,step=0.01))
def g(rad):
plot.camera = [3*r*sin(rad),3*r*cos(rad),0,
0,0,0,
0,0,1]
# +
# camera [posx,posy,posz,targetx,targety,targetz,upx,upy,upz]
# -
plot.camera_reset()
|
examples/camera_manipulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="yq0SJEcqqlK2" executionInfo={"status": "ok", "timestamp": 1606544273611, "user_tz": 360, "elapsed": 2028, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
import pandas as pd
import sklearn.datasets as datasets
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.cluster import MeanShift
from sklearn.tree import DecisionTreeClassifier
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
import sklearn.metrics as metrics
# + [markdown] id="WMH06LDcMVaO"
# # Get Data
# ---
# + id="fZWntuXdAR5Q" executionInfo={"status": "ok", "timestamp": 1606544273625, "user_tz": 360, "elapsed": 2033, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
wines = datasets.load_wine()
# + id="KuCtcmG-AZJf" executionInfo={"status": "ok", "timestamp": 1606544273626, "user_tz": 360, "elapsed": 2030, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
x = pd.DataFrame(wines.data, columns=wines.feature_names)
y = pd.DataFrame(wines.target, columns=['Target'])
# + id="9PJlGMaXDqNU" executionInfo={"status": "ok", "timestamp": 1606544273629, "user_tz": 360, "elapsed": 2030, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
y_classes = wines.target
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="fTeEkhppDPt6" executionInfo={"status": "ok", "timestamp": 1606544286117, "user_tz": 360, "elapsed": 680, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="984d30c1-c77c-4ea5-9904-c30592b14782"
plt.scatter(x['alcohol'], x['color_intensity'], c = y_classes, s=30)
plt.xlabel('Alcohol', fontsize=10)
plt.ylabel('Color intensity', fontsize=10)
# + [markdown] id="xQYLjRq2MUic"
# # Preprocess data
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 270} id="6Dqm4gYoZJzP" executionInfo={"status": "ok", "timestamp": 1606544291363, "user_tz": 360, "elapsed": 1757, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="2605e32a-d546-40a0-a176-a46c030c57cf"
x.plot( kind = 'box', subplots = True, layout = (3,5), sharex = False, sharey = False, color='black')
plt.show()
# + id="9LsFR8Ujabwg" executionInfo={"status": "ok", "timestamp": 1606544291364, "user_tz": 360, "elapsed": 1746, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
# Data normalization
norm = MinMaxScaler().fit(x)
x_norm = norm.transform(x)
# + colab={"base_uri": "https://localhost:8080/", "height": 267} id="U-pjl5Y6axmD" executionInfo={"status": "ok", "timestamp": 1606544292401, "user_tz": 360, "elapsed": 2772, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="af582b34-3ea6-4248-f61c-3517a502e295"
pd.DataFrame(x_norm, columns=wines.feature_names).plot( kind = 'box', subplots = True, layout = (3,5), sharex = False, sharey = False, color='black')
plt.show()
# + id="WmYttFA4X4jZ" executionInfo={"status": "ok", "timestamp": 1606544292402, "user_tz": 360, "elapsed": 2764, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}}
#Data standardization
std_scaler = StandardScaler()
data_scaled = x_norm.copy()
data_scaled = pd.DataFrame(data_scaled, columns=wines.feature_names)
# + id="B4XTqAIIYPYQ" colab={"base_uri": "https://localhost:8080/", "height": 267} executionInfo={"status": "ok", "timestamp": 1606544293565, "user_tz": 360, "elapsed": 3912, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="9e9c3b1e-f522-4e1d-b256-c3ee8011b1fe"
data_scaled.plot( kind = 'box', subplots = True, layout = (3,5), sharex = False, sharey = False, color='black')
plt.show()
# + [markdown] id="VHF2azSvffcu"
# # Build model and calculate accuracy
# ---
# + id="0fysdfW4bDxI" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606544293567, "user_tz": 360, "elapsed": 2900, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="71c9cd59-8d84-4d0f-bb64-3f540ec19ca1"
model = KMeans(n_clusters=3, max_iter=1000)
model.fit(data_scaled)
# + id="23YDq-VRbLdL" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606544293568, "user_tz": 360, "elapsed": 2892, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="7bede4e0-321b-4c2e-e400-cc36779f57ab"
y_kmeans=model.predict(data_scaled)
print("Predictions: ", y_kmeans)
# + id="BDFm82K-bVtX" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606544293569, "user_tz": 360, "elapsed": 2882, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GgjfNB2uyC2lVg8674ETEVLSjngqmA_8kmonP1o7Q=s64", "userId": "15192017473037818811"}} outputId="d4475b4d-e213-4329-d462-35ba778f890f"
accuracy = metrics.adjusted_rand_score(y_classes, y_kmeans)
accuracy
|
Wines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
pd.set_option("display.max_columns", 500)
pd.set_option("display.max_rows", 500)
# ## DM_RETAIL_CLIE
# +
chunks = pd.read_csv(f"../Datasets/DM_RETAIL_CLIE.csv",
sep=",",
encoding='latin1',
decimal=",",
chunksize=1000000)
df_retail = pd.concat(chunks)
# -
df_retail.dtypes
df_retail.head(5)
df_retail.isna().mean().sort_values(ascending=False)
df_retail = df_retail.loc[:,df_retail.isna().mean() < .8]
fechas = [col for col in df_retail.columns if "F_U" in col or "F_C" in col or "FECHA" in col]
df_retail[fechas]
df_retail = df_retail.drop(fechas, axis=1)
df_retail.to_feather("../Datasets/retail.feather")
|
notebooks/1. Analysis/samples/2 - Analizando dataset nuevo DM_RETAIL_CLIE.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_python3
# language: python
# name: conda_python3
# ---
# ### Creating corpus - combine revision text data with blocks data
# +
# import necessary packages
import os
import pandas as pd
import numpy as np
import re
# set options
pd.options.display.max_colwidth = 50
pd.set_option('display.max_colwidth', -1)
pd.options.mode.chained_assignment = None # default='warn'
#2219
# -
# #### Process Blocks data
# read ipblocks
df_ipblocks = pd.read_csv("/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/ipblocks_fulldump_new.csv")
df_ipblocks = df_ipblocks.drop(df_ipblocks.columns[0],axis=1)
df_ipblocks.shape
# +
# convert object dtype to string ; keep in mind expiry with timestamp will be unusable
df_ipblocks['ipb_address'] = df_ipblocks['ipb_address'].astype('str') #ipaddress -> string
df_ipblocks['date'] = pd.to_datetime(df_ipblocks['date'], format = "%Y%m%d")
# replace NAN with empty strings
df_ipblocks.ipb_reason = df_ipblocks.ipb_reason.replace(np.nan,'', regex=True)
# -
# #### Reg Ex extraction of block keywords
# +
key1 = df_ipblocks['ipb_reason'].str.extractall(r'\[\[WP:(.*?)\]\]').unstack().apply(lambda x:','.join(x.dropna()), axis=1)
key2 = df_ipblocks['ipb_reason'].str.extractall(r'{{(.*)}}').unstack().apply(lambda x:','.join(x.dropna()), axis=1)
df_ipblocks = pd.concat([df_ipblocks,key1,key2], axis=1)
# -
df_ipblocks["key3"] = np.nan
df_ipblocks["key3"][df_ipblocks['ipb_reason'].str.contains("\[\[User:.*\]\]",regex=True)] = "Sock Puppetry"
# +
# to get word count list
#blocks = df_ipblocks[df_ipblocks['ipb_reason'].notnull()]
#import re
#def pre_process(text):
# lowercase
# text=text.lower()
# remove special characters and digits
# text=re.sub("(\\d|\\W)+"," ",text)
# return text
#blocks['ipb_reason'] = blocks['ipb_reason'].apply(lambda x:pre_process(x))
#textlist = blocks['ipb_reason']
#wordlist = [word for line in textlist for word in line.split() if word not in stoplist]
#from collections import Counter
#counts = Counter(wordlist)
#print(counts)
#with open('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/blockswordcount.csv', 'w',newline='') as csv_file:
# writer = csv.writer(csv_file)
# for key, value in counts.items():
# writer.writerow([key, value])
# -
# #### Extract keywords from ipb_reason based on list of known words
df_ipblocks.head()
# clean df
df_ipblocks = df_ipblocks.drop(columns = ['ipb_id','ipb_create_account','ipb_expiry'])
df_ipblocks.columns = ['userid','username','blockdate','reason','k1','k2','k3']
df_ipblocks.k1 = df_ipblocks.k1.replace(np.nan,'', regex=True)
df_ipblocks.k2 = df_ipblocks.k2.replace(np.nan,'', regex=True)
df_ipblocks.k3 = df_ipblocks.k3.replace(np.nan,'', regex=True)
cols = ['k1', 'k2', 'k3']
df_ipblocks['keyreason'] = df_ipblocks[cols].apply(lambda row: ','.join(row.values.astype(str)), axis=1)
df_ipblocks.keyreason = df_ipblocks.keyreason.replace(',,',',', regex=True)
df_ipblocks.keyreason = df_ipblocks.keyreason.replace(r'^,','', regex=True)
df_ipblocks = df_ipblocks.drop(columns = ['k1','k2','k3'])
df_ipblocks.head()
# +
#df_ipblocks[df_ipblocks['reason'].str.contains("\[\[User:.*\]\]",regex=True)]
# -
# #### Process XML data
# Split Contributor into UserID and Username
df_revtxt = pd.read_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/revision_text_data_final3.txt', sep = '\t')
df_revtxt.shape
# +
#df_revtxt.head(20)
#df_revtxt.NAMESPACE.value_counts()
# split CONTRIBUTOR into userid and username
namesplit = df_revtxt["CONTRIBUTOR"].str.split(",", n = 1, expand = True)
df_revtxt["USERID"] = namesplit[0]
df_revtxt["username"] = namesplit[1]
# refine columns
df_revtxt["USERID"] = df_revtxt["USERID"].str.replace("Contributor\(id=",'')
df_revtxt["USERID"] = df_revtxt["USERID"].str.strip()
df_revtxt["username"] = df_revtxt["username"].str.replace("user_text='",'')
df_revtxt["username"] = df_revtxt["username"].str[:-2]
df_revtxt["username"] = df_revtxt["username"].str.strip()
df_revtxt.head()
# -
df_data = pd.merge(df_revtxt, df_ipblocks, on=['username'], how='inner')
df_data.shape
df_data['TIMESTAMP'] = df_data['TIMESTAMP'].astype('str') #timestamp -> string
df_data['TIMESTAMP'] = df_data['TIMESTAMP'].str[0:8]
df_data['TIMESTAMP'] = pd.to_datetime(df_data['TIMESTAMP'], format = "%Y%m%d")
df_data = df_data.drop(columns = ['CONTRIBUTOR','PAGE_ID','REVISION_ID','TEXT','userid'])
# check if userid doesnt match
df_data.head()
df_data = df_data.rename(columns={'NAMESPACE':'namespace','TIMESTAMP':'revision_date','DIFF_TEXT':'text','USERID': 'userid','TITLE':'title'})
df_data = df_data[['userid','username','revision_date','namespace','title','text','blockdate','keyreason','reason']]
df_data.head()
# dump final dataframe to csv
header = ['userid','username','revision_date','namespace','title','text','blockdate','keyreason','reason']
df_data.to_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/blockcorpus3.txt', sep = '\t',encoding='utf-8',header = True,index=False)
# #### Combine files into 1 block corpus
# +
file_list = [x for x in os.listdir("/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/") if x.startswith("blockcorpus")]
df_list = []
for file in file_list:
print(file)
df_list.append(pd.read_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/' + file, sep = '\t'))
big_df = pd.concat(df_list)
# save file as .csv
header = ['userid','username','revision_date','namespace','title','text','blockdate','keyreason','reason']
big_df.to_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/blockcorpus.txt', sep = '\t',encoding='utf-8',header = True,index=False)
# -
# #### Read Corpus
df_blockcorpus = pd.read_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/blockcorpus.txt', sep = '\t')
df_blockcorpus.shape
df_blockcorpus.head()
df_blockcorpus.namespace.value_counts()
df_blockcorpus.username.nunique()
# list of blocked users
df_name = df_blockcorpus.username.unique()
df_name = pd.DataFrame(df_name)
# save file as .csv
header = ['username']
df_name.to_csv('/home/ec2-user/SageMaker/s3fs-fuse/bucket/wiki_trust/xml_dump_processed/blockuserlist.txt', sep = '\t',encoding='utf-8',header = True,index=False)
|
Misc/xml_data/xml_blockcorpus.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 04 - Multiclass logistic regression from scratch
from __future__ import print_function
import numpy as np
import mxnet as mx
from mxnet import gluon
# Setting random seed
mx.random.seed(1)
# Set context
data_ctx = mx.cpu()
model_ctx = mx.cpu()
# ## Data preprocessing
# Transforming the data from range 0-255 to 0-1
def transform(data, label):
return data.astype(np.float32) / 255, label.astype(np.float32)
# ## Loading MNIST dataset
mnist_train = gluon.data.vision.MNIST(train=True,
transform=transform)
mnist_test = gluon.data.vision.MNIST(train=False,
transform=transform)
image, label = mnist_train[0]
image.shape
label
# ## Showing data example
im = mx.nd.tile(image, (1,1,3))
print(im.shape)
import matplotlib.pyplot as plt
plt.imshow(im.asnumpy())
plt.show()
# ## Data Information / Model Parameters
num_inputs = 784
num_outputs = 10
num_examples = 60000
# ## Data Iterators
batch_size = 64
train_data = gluon.data.DataLoader(dataset=mnist_train,
batch_size=batch_size,
shuffle=True)
test_data = gluon.data.DataLoader(dataset=mnist_test,
batch_size=batch_size,
shuffle=False)
# ## Model Parameters
# +
W = mx.nd.random_normal(shape=(num_inputs, num_outputs),
ctx=model_ctx)
b = mx.nd.random_normal(shape=num_outputs,
ctx=model_ctx)
params = [W, b]
# -
# ## Gradients
for param in params:
param.attach_grad()
# ## Softmax
def softmax(y_linear):
exp = mx.nd.exp(y_linear - mx.nd.max(y_linear, axis=1).reshape((-1, 1)))
norms = mx.nd.sum(exp,
axis=1).reshape((-1, 1))
return exp / norms
# ### Example
sample_y_linear = mx.nd.random_normal(shape=(1, 3))
sample_yhat = softmax(sample_y_linear)
print(sample_y_linear)
print(sample_yhat)
print(mx.nd.sum(sample_yhat, axis=1))
# ## Define the model
def net(X):
y_linear = mx.nd.dot(X, W) + b
yhat = softmax(y_linear)
return yhat
# ## Cross-entropy loss function
def cross_entropy(yhat, y):
return - mx.nd.sum(y * mx.nd.log(yhat + 1e-6))
# ## Stochastic Gradient Descent (SGD)
def SGD(params, lr):
for param in params:
param[:] = param - lr * param.grad
# ## Accuracy calculations
def evaluate_accuracy(data_iterator, net):
# Numerator stores number of correct prediction
numerator = 0.
# Denominator stores number of all samples
denominator = 0.
for i, (data, label) in enumerate(data_iterator):
data = data.as_in_context(model_ctx).reshape((-1, 784))
label = label.as_in_context(model_ctx)
label_one_hot = mx.nd.one_hot(label, 10)
output = net(data)
predictions = mx.nd.argmax(output,
axis=1)
numerator += mx.nd.sum(predictions == label)
denominator += data.shape[0]
return (numerator / denominator).asscalar()
# ## Accuracy of randomly initialized network
evaluate_accuracy(test_data, net)
# ## Training
# +
epochs = 5
learning_rate = .005
for e in range(epochs + 1):
cumulative_loss = 0
for i, (data, label) in enumerate(train_data):
data = data.as_in_context(model_ctx).reshape((-1,784))
label = label.as_in_context(model_ctx)
label_one_hot = mx.nd.one_hot(label, 10)
with mx.autograd.record():
output = net(data)
loss = cross_entropy(output, label_one_hot)
loss.backward()
SGD(params, learning_rate)
cumulative_loss += mx.nd.sum(loss).asscalar()
test_accuracy = evaluate_accuracy(test_data, net)
train_accuracy = evaluate_accuracy(train_data, net)
print("Epoch %s. Loss: %s, Train_acc %s, Test_acc %s" % (e, cumulative_loss / num_examples, train_accuracy, test_accuracy))
# -
# ## Prediction
# Define the function to do prediction
def model_predict(net,data):
output = net(data)
return mx.nd.argmax(output, axis=1)
# let's sample 10 random data points from the test set
sample_data = gluon.data.DataLoader(mnist_test, 10, shuffle=True)
for i, (data, label) in enumerate(sample_data):
data = data.as_in_context(model_ctx)
print(data.shape)
im = mx.nd.transpose(data,(1,0,2,3))
im = mx.nd.reshape(im,(28,10*28,1))
imtiles = mx.nd.tile(im, (1,1,3))
plt.imshow(imtiles.asnumpy())
plt.show()
pred=model_predict(net,data.reshape((-1,784)))
print('model predictions are:', pred)
break
|
In Progress - Deep Learning - The Straight Dope/02 - Introduction to Supervised Learning/04 - Multiclass logistic regression from scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
matplotlib.style.use('ggplot')
# %pylab inline
# -
from sitka.general.settings import *
from sitka.io.time import *
from sitka.io.weather import *
from sitka.calculations.solar import *
from sitka.components.site import *
dir_path = os.getcwd()
weather_file = os.path.join(dir_path, 'USA_WA_Seattle-Boeing.Field.727935_TMY3.epw')
start_hour = 0
end_hour = 8760
time_steps_per_hour = 4
# +
# Simulation run parameters
settings = Settings(dir_path)
time = Time(start_hour=start_hour, end_hour=end_hour, time_steps_per_hour=time_steps_per_hour)
weather = EPW(settings, time, weather_file)
print(weather.location)
# Setup site
site = Site(weather.latitude, weather.longitude, weather.elevation)
print(site.latitude)
print(site.longitude)
# Solar angles
solar_angles = SolarAngles(time, site)
# -
# # Analysis
# ## Inputs
# Comfort criteria
min_dry_bulb_temperature = 15 # deg C
max_dry_bulb_temperature = 25 # deg C
# ## Comfort Determination
# +
# Determine whether dry-bulb temperature is within the comfort criteria
comfort = pd.DataFrame({
'dry_bulb_temperature': weather.dry_bulb_temperature,
'comfortable': np.ones(weather.dry_bulb_temperature.count())*0,
})
criteria = ((comfort['dry_bulb_temperature'] >= min_dry_bulb_temperature) & (comfort['dry_bulb_temperature'] <= max_dry_bulb_temperature))
comfort[criteria] = 1
comfort = comfort.resample('1H').min().resample('1D').sum().resample('1M').mean()
comfort.index = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun', 'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec']
ax = comfort['comfortable'].plot(legend=False, color=['blue', 'red', 'purple'], figsize=(16, 6))
ax.set_ylabel('Number of Hours', fontsize=20)
ax.set_xlabel('Month', fontsize=20)
|
Weather Analysis/Climate Type Determination.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TDEM response of a conductive permeable casing
#
# **Author:** [<NAME>](https://github.com/lheagy)
#
# This example examines follows up on the FDEM surface to borehole logging example similar to that discussed in [Augustin et al. (1989)](https://doi.org/10.1190/1.1442581) and conducts a similar experiment in the time domain. This notebook was used to produce Figures 13 and 14 in Heagy and Oldenburg (2018)
#
# If you encounter problems when running this notebook, please [open an issue](https://github.com/simpeg-research/heagy_2018_emcyl/issues).
# ## Setup and Software environment
#
# The requirements to run this example are in [requirements.txt](../requirements.txt). Uncomment the following cell if you need to install them.
# +
# # !pip install -r ../requirements.txt
# +
# core python packages
import numpy as np
import scipy.sparse as sp
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from scipy.constants import mu_0, inch, foot
import ipywidgets
import properties
import time
# SimPEG and discretize
import discretize
from discretize import utils
from SimPEG.EM import TDEM
from SimPEG import Utils, Maps, Versions
from SimPEG.Utils import Zero
from pymatsolver import Pardiso
# casing utilities
import casingSimulations as casingSim
# %matplotlib inline
# -
# ## Model Parameters
# create a simulation directory where results can be saved.
simDir = 'TDEM_Augustin'
# We will two classes of examples
# - permeable wells, one example is run for each $\mu_r$ in `casing_mur`. The conductivity of this well is `sigma_permeable_casing`
# - conductive wells ($\mu_r$=1), one example is run for each $\sigma$ value in `sigma_casing`
#
# To add model runs to the simulation, just add to the list
# +
# permeabilities to model
casing_mur = [100]
sigma_casing = [1e8]
sigma_permeable_casing = 1e6
# +
# background parameters
sigma_air = 1e-4
sigma_back = 1e-4
casing_t = 10e-3 # 10mm thick casing
casing_d = 100e-3 # 10cm diameter
casing_l = 2000
def get_model(mur, sigc):
model = casingSim.model.CasingInHalfspace(
directory = simDir,
sigma_air = sigma_air,
sigma_casing = sigc, # conductivity of the casing (S/m)
sigma_back = sigma_back, # conductivity of the background (S/m)
sigma_inside = sigma_back, # fluid inside the well has same conductivity as the background
casing_d = casing_d-casing_t, # 135mm is outer casing diameter
casing_l = casing_l,
casing_t = casing_t,
mur_casing = mur,
src_a = np.r_[0., 0., 0.],
src_b = np.r_[0., 0., 0.]
)
return model
# -
# ## store the different models
#
# +
model_names_permeable = ["casing_{}".format(mur) for mur in casing_mur]
model_names_conductive = ["casing_{:1.0e}".format(sig) for sig in sigma_casing]
# conductive, permeable models
model_dict_permeable = {
key: get_model(mur, sigma_permeable_casing) for key, mur in zip(model_names_permeable, casing_mur)
}
model_dict_conductive = {
key: get_model(1, sig) for key, sig in zip(model_names_conductive, sigma_casing)
}
model_names = model_names_conductive + model_names_permeable
model_dict = {}
model_dict.update(model_dict_permeable)
model_dict.update(model_dict_conductive)
# -
model_dict["baseline"] = model_dict[model_names[0]].copy()
model_dict["baseline"].sigma_casing = model_dict["baseline"].sigma_back
model_names = ["baseline"] + model_names
model_names
# ## Create a mesh
# +
# parameters defining the core region of the mesh
csx2 = 25. # cell size in the x-direction in the second uniform region of the mesh (where we measure data)
csz = 2.5 # cell size in the z-direction
domainx2 = 100 # go out 500m from the well
# padding parameters
npadx, npadz = 23, 30 # number of padding cells
pfx2 = 1.4 # expansion factor for the padding to infinity in the x-direction
pfz = 1.4
# set up a mesh generator which will build a mesh based on the provided parameters
# and casing geometry
def get_mesh(mod):
return casingSim.CasingMeshGenerator(
directory=simDir, # directory where we can save things
modelParameters=mod, # casing parameters
npadx=npadx, # number of padding cells in the x-direction
npadz=npadz, # number of padding cells in the z-direction
domain_x=domainx2, # extent of the second uniform region of the mesh
# hy=hy, # cell spacings in the
csx1=mod.casing_t/4., # use at least 4 cells per across the thickness of the casing
csx2=csx2, # second core cell size
csz=csz, # cell size in the z-direction
pfx2=pfx2, # padding factor to "infinity"
pfz=pfz # padding factor to "infinity" for the z-direction
)
# -
mesh_generator = get_mesh(model_dict[model_names[0]])
mesh_generator.mesh.plotGrid()
# ## Physical Properties
# Assign physical properties on the mesh
physprops = {
name: casingSim.model.PhysicalProperties(mesh_generator, mod)
for name, mod in model_dict.items()
}
# ### conductivity
# +
# Plot the models
xlim = np.r_[-1, 1] # x-limits in meters
zlim = np.r_[-1.5*casing_l, 10.] # z-limits in meters. (z-positive up)
fig, ax = plt.subplots(1, len(model_names), figsize=(6*len(model_names), 5))
if len(model_names) == 1:
ax = [ax]
for a, title in zip(ax, model_names):
pp = physprops[title]
pp.plot_sigma(
ax=a,
pcolorOpts={'norm':LogNorm()} # plot on a log-scale
)
a.set_title('{} \n\n $\sigma$ = {:1.2e}S/m'.format(title, pp.modelParameters.sigma_casing), fontsize=13)
# cylMeshGen.mesh.plotGrid(ax=a, slice='theta') # uncomment to plot the mesh on top of this
a.set_xlim(xlim)
a.set_ylim(zlim)
# -
# ### permeability
# +
# Plot the models
xlim = np.r_[-1, 1] # x-limits in meters
zlim = np.r_[-1.5*casing_l, 10.] # z-limits in meters. (z-positive up)
fig, ax = plt.subplots(1, len(model_names), figsize=(6*len(model_names), 5))
if len(model_names) == 1:
ax = [ax]
for a, title in zip(ax, model_names):
pp = physprops[title]
pp.plot_mur(
ax=a,
pcolorOpts={'norm':LogNorm()} # plot on a log-scale
)
a.set_title('{} \n\n $\mu_r$ = {:1.2e}'.format(title, pp.modelParameters.mur_casing), fontsize=13)
# cylMeshGen.mesh.plotGrid(ax=a, slice='theta') # uncomment to plot the mesh on top of this
a.set_xlim(xlim)
a.set_ylim(zlim)
# -
# ## Set up the time domain EM problem
#
# We run a time domain EM simulation with a large loop source (100m radius) and a b-field reciever down-hole at a depth of 500m.
# +
nsteps = 40
timeSteps = [
(1e-6, nsteps), (5e-6, nsteps), (1e-5, nsteps), (5e-5, nsteps), (1e-4, nsteps),
(5e-4, nsteps), (1e-3, nsteps), (5e-3, nsteps), (1e-2, nsteps+60), (5e-2, nsteps)
]
for mod in model_dict.values():
mod.timeSteps = timeSteps
# -
times = np.hstack([0, model_dict[model_names[0]].timeSteps]).cumsum()
print("latest time: {:1.1f}s".format(times.max()))
rx = TDEM.Rx.Point_b(locs=np.array([0., 0., -500.]), times=times, orientation="z")
src_list = [
TDEM.Src.CircularLoop(
[rx],
loc=np.r_[0., 0., 0.], orientation="z", radius=100,
)
]
# ## Set up the simulation
# +
wires = physprops[model_names[0]].wires # keeps track of which model parameters are sigma and which are mu
prob = TDEM.Problem3D_b(
mesh=mesh_generator.mesh, sigmaMap=wires.sigma, timeSteps=timeSteps,
Solver=Pardiso
)
# -
survey = TDEM.Survey(srcList=src_list)
prob.pair(survey)
# ## Run the simulation
#
# - for each permeability model we run the simulation for 2 conductivity models (casing = $10^6$S/m and $10^{-4}$S/m
# - each simulation takes 15s-20s on my machine: the next cell takes ~ 4min to run
# +
# %%time
fields_dict = {}
for key in model_names:
t = time.time()
pp = physprops[key]
prob.mu = pp.mu
print('--- Running {} ---'.format(key))
fields_dict[key] = prob.fields(pp.model)
print(" ... done. Elapsed time {}\n".format(time.time() - t))
# -
# ## Compute data at the receiver
# - bz data 500m below the surface, coaxial with casing
for src in src_list:
src.rxList = [rx]
# +
# %%time
data = {}
for key in model_names:
t = time.time()
pp = physprops[key]
prob.mu = pp.mu
print('--- Running {} ---'.format(key))
data[key] = survey.dpred(pp.model, f=fields_dict[key])
print(" ... done. Elapsed time {} \n".format(time.time() - t))
# -
# ## Plot Data
def plot_data(ax=None, scale='loglog', view=None, models=None):
"""
Plot the time domain EM data.
- scale can be and of ["loglog", "semilogx", "semilogy", "plot"]
- view can be ["nsf", "secondary-wholespace", "secondary-conductive"] or None (None plots the data)
- models is a list of model names to plot
"""
if ax is None:
fig, ax = plt.subplots(1, 1, dpi=400)
ax = [ax]
plot_models = model_names[1:]
if models is not None:
if isinstance(models, list):
plot_models = models
else:
if models.lower() == "permeable":
plot_models = model_names_permeable
elif models.lower() == "conductive":
plot_models = model_names_conductive
for i, key in enumerate(plot_models):
mod = model_dict[key]
label = "$\sigma = {:1.0e}$, $\mu_r$ = {}".format(mod.sigma_casing, mod.mur_casing)
# get property to plot
if view is not None:
if view.lower() in ["secondary-wholespace", "nsf"]:
plotme = data[key] - data['baseline']
if view.lower() == "nsf":
plotme = plotme / data['baseline'][0]
elif subtract.lower() == "secondary-conductive":
plotme = data[key] - data[model_names[1]]
else:
plotme = data[key]
# conductive casing
getattr(ax[0], scale)(rx.times, plotme, "-", color="C{}".format(i), label=label)
if scale.lower() not in ["semilogx", "plot"]:
getattr(ax[0], scale)(rx.times, -plotme, "--", color="C{}".format(i))
# background
if view is None:
getattr(ax[0], scale)(
rx.times, data['baseline'], "-", color='k', label="background"
)
if scale.lower() not in ["semilogx", "plot"]:
getattr(ax[0], scale)(
rx.times, -data['baseline'], "--", color='k'
)
[a.set_xlabel("time (s)") for a in ax]
[a.set_ylabel("magnetic field $b_z$ (T)") for a in ax]
[a.grid(which='both', alpha=0.4) for a in ax]
[a.legend() for a in ax]
plt.tight_layout()
return ax
# ## Figure 13: Normalized secondary field
fig, ax = plt.subplots(1, 1, dpi=300)
ax = plot_data(scale="semilogx", view="NSF", models=["casing_1e+08", "casing_100"], ax=[ax])
ax[0].set_xlim([3e-6, 2])
ax[0].set_ylim([-0.2, 1.2])
ax[0].set_ylabel("NSF")
fig.savefig("../figures/tdemNSF")
fig.savefig("../arxiv-figures/tdemNSF", dpi=200)
sim_dict = {}
for key in model_names:
sim = casingSim.run.SimulationTDEM(
directory=simDir,
meshGenerator=mesh_generator,
modelParameters=model_dict[key],
formulation=prob._fieldType[0],
)
sim._prob = prob
sim._survey = survey
sim_dict[key] = sim
# # Build a widget
# ## View the fields and fluxes
#
# This is a widget for interrogating the results.
# - `max_r`: maximum radial extent of the plot (m)
# - `min_depth`: minimum depth (m)
# - `max_depth`: maximum depth (m)
# - `clim_min`: minimum colorbar limit. If `0`, then the colorbar limits are the plotting defaults
# - `clim_max`: maximum colorbar limit. If `0`, then the colorbar limits are the plotting defaults
# - `model_key`: model which we are viewing
# - `view`: field or physical property that is plotted
# - `prim_sec`: `primary` plots the background, `secondary` subtracts the `primary` response from the current value (note that if you select `background` and `secondary` the value will be zero and an error thrown
# - `time_ind`: index of the time-step we are plotting
# - `show_mesh`: if checked, the mesh will be plotted on the right hand half of the plot
# - `use_aspect`: if checked, the aspect ratio of the axes is set to 1 (eg. no vertical or horizontal exxageration)
# - `casing_outline`: draws the outline of the casing
viewer = casingSim.FieldsViewer(
model_keys=model_names, sim_dict=sim_dict, fields_dict=fields_dict,
primary_key='baseline'
)
viewer.widget_cross_section(defaults={'view': 'b', "time_ind": 1})
# ## Figure 14
from matplotlib import rcParams
rcParams['font.size'] = 16
# +
fig, ax = plt.subplots(2, 5, figsize=(3.5*5, 5.5*2))
fig.subplots_adjust(bottom=0.8)
clim = [3e-13, 3e-8]
max_depth = 2500
top = 10
max_r = 0.14
view='b'
# primsec="secondary"
tinds = [10, 52, 128, 207, 287]
for i, tind in enumerate(tinds):
for j, m in enumerate(["casing_1e+08", "casing_100"]):
a = ax[j, i]
out = viewer.plot_cross_section(
ax=a, clim=clim, xlim=max_r * np.r_[-1., 1.],
zlim = np.r_[-max_depth, top],
view=view, model_key=m,
prim_sec="secondary",
casing_outline=True,
time_ind=tind,
show_cb=False
)
if j == 0:
a.set_title("{:1.0e} s".format(times[tind]))
a.set_xticklabels(['']*len(a.get_xticklabels()))
a.set_xlabel('')
else:
a.set_title("")
a.set_xlabel("x (m)")
if i > 0:
a.set_yticklabels(['']*len(a.get_yticklabels()))
a.set_ylabel('')
else:
a.set_ylabel('z (m)')
mod = model_dict[m]
a.text(
-0.13, -2400, "$\sigma = ${:1.0e}, $\mu_r = $ {:1.0f}".format(mod.sigma_casing, mod.mur_casing),
color="w", fontsize=18
)
plt.tight_layout()
cbar_ax = fig.add_axes([0.15, -0.02, 0.75, 0.02])
cb = fig.colorbar(out[0], cbar_ax, orientation='horizontal')
cb.set_label('Magnetic flux density (T)')
# -
fig.savefig("../figures/btdem", dpi=300, bbox_inches="tight")
fig.savefig("../arxiv-figures/btdem", dpi=150, bbox_inches="tight")
Versions()
|
notebooks/7_TDEM_Permeability.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# + [markdown] toc="true"
# # Table of Contents
# <p><div class="lev1 toc-item"><a href="#Summary" data-toc-modified-id="Summary-1"><span class="toc-item-num">1 </span>Summary</a></div><div class="lev1 toc-item"><a href="#Version-Control" data-toc-modified-id="Version-Control-2"><span class="toc-item-num">2 </span>Version Control</a></div><div class="lev1 toc-item"><a href="#Change-Log" data-toc-modified-id="Change-Log-3"><span class="toc-item-num">3 </span>Change Log</a></div><div class="lev1 toc-item"><a href="#Setup" data-toc-modified-id="Setup-4"><span class="toc-item-num">4 </span>Setup</a></div><div class="lev1 toc-item"><a href="#Convolutional-Neural-Networks" data-toc-modified-id="Convolutional-Neural-Networks-5"><span class="toc-item-num">5 </span>Convolutional Neural Networks</a></div><div class="lev2 toc-item"><a href="#CS231n-Winter-2016:-Lecture-7:-Convolutional-Neural-Networks-for-Visual-Recognition" data-toc-modified-id="CS231n-Winter-2016:-Lecture-7:-Convolutional-Neural-Networks-for-Visual-Recognition-51"><span class="toc-item-num">5.1 </span>CS231n Winter 2016: Lecture 7: Convolutional Neural Networks for Visual Recognition</a></div><div class="lev1 toc-item"><a href="#Key-Terms" data-toc-modified-id="Key-Terms-6"><span class="toc-item-num">6 </span>Key Terms</a></div><div class="lev2 toc-item"><a href="#Architecture" data-toc-modified-id="Architecture-61"><span class="toc-item-num">6.1 </span>Architecture</a></div><div class="lev2 toc-item"><a href="#Hubel-and-Wesiel" data-toc-modified-id="Hubel-and-Wesiel-62"><span class="toc-item-num">6.2 </span>Hubel and Wesiel</a></div><div class="lev2 toc-item"><a href="#Additional-Reading" data-toc-modified-id="Additional-Reading-63"><span class="toc-item-num">6.3 </span>Additional Reading</a></div><div class="lev2 toc-item"><a href="#Addional-Videos" data-toc-modified-id="Addional-Videos-64"><span class="toc-item-num">6.4 </span>Addional Videos</a></div><div class="lev3 toc-item"><a href="#CS231n-Winter-2016:-Lecture-6:-Neural-Networks-Part-3-/-Intro-to-ConvNets" data-toc-modified-id="CS231n-Winter-2016:-Lecture-6:-Neural-Networks-Part-3-/-Intro-to-ConvNets-641"><span class="toc-item-num">6.4.1 </span>CS231n Winter 2016: Lecture 6: Neural Networks Part 3 / Intro to ConvNets</a></div><div class="lev2 toc-item"><a href="#Other-resources" data-toc-modified-id="Other-resources-65"><span class="toc-item-num">6.5 </span>Other resources</a></div><div class="lev3 toc-item"><a href="#CIFAR-10-ConvNet-Demo---very-good!" data-toc-modified-id="CIFAR-10-ConvNet-Demo---very-good!-651"><span class="toc-item-num">6.5.1 </span>CIFAR-10 ConvNet Demo - very good!</a></div>
# -
# # Summary
# Notes taken to help for the second project, image recognition, for the [Deep Learning Foundations Nanodegree](https://www.udacity.com/course/deep-learning-nanodegree-foundation--nd101) course delivered by Udacity.
#
# My Github repo for this project can be found here: [adriantorrie/udacity_dlfnd_project_2](https://github.com/adriantorrie/udacity_dlfnd_project_1)
# # Version Control
# %run ../../../code/version_check.py
# # Change Log
# Date Created: 2017-03-24
#
# Date of Change Change Notes
# -------------- ----------------------------------------------------------------
# 2017-03-24 Initial draft
# # Setup
# +
# %matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from IPython.display import YouTubeVideo
plt.style.use('bmh')
matplotlib.rcParams['figure.figsize'] = (15, 4)
# -
# [[Top]](#Table-of-Contents)
# # Convolutional Neural Networks
# ## CS231n Winter 2016: Lecture 7: Convolutional Neural Networks for Visual Recognition
# * <NAME>
# * Published 27 Jan 2016
# * Reddit /r/cs231n
# * Standard YouTube Licence
#
# [Supporting notes](https://cs231n.github.io/convolutional-networks/#overview)
YouTubeVideo("LxfUGhug-iQ", height=365, width=650)
# # Key Terms
# * Filter = Kernel => The filter "slides" over the input image
# * Slide = Number of pixels the filter moves
# * Padding = The padding around the image to allow the filter output to be the same dimensions as the input
# [[Top]](#Table-of-Contents)
# ## Architecture
#
# The general architecture of a covnet is seen below. It has been influenced by the Hubel and Weseil studies (below).
#
# <img src="https://cs231n.github.io/assets/cnn/cnn.jpeg",width=450,height=200>
# ## <NAME> Wesiel
# Hubel and Wesiel did studies in 1959, 1962, 1968, using cats to determine how the visual cortex worked.
#
# * <span style="color:red">Input</span>
# * <span style="color:blue">1st filter bank with multiple activation maps</span>
# * 2nd Dotted layer</span> is another filter bank
# * <span style="color:gray">3rd filter bank with multiple activation maps</span>
#
# All layers are 3-dimensional, with the 3 filter layers above progressing from (left to right) fine detail to large object recognition, the image below shows the same feature hierarchy for object recognition, oriented from bottom to top.
# * 1st <span style="color:blue">blue</span> layer is the simple cell / <span style="background-color: #e6e6e6">low level layer</span> in the image below
# * 2nd Dotted layer is the complex cell / <span style="background-color: #e6e6e6">mid level layer</span> in the image below
# * 3rd <span style="color:gray">gray</span> layer is the hyper-complex cell / <span style="background-color: #e6e6e6">high level layer</span> in the image below
#
# <img src="http://cns-alumni.bu.edu/~slehar/webstuff/pcave/hubel.jpg" />
# Directly quoted from [here](https://cs231n.github.io/convolutional-networks/#conv)
#
# > **To summarize, the Conv Layer:**
# >
# > * Accepts a volume of size $W_1 \times H_1 \times D_1$
# > * Requires four hyperparameters:
# > * the number of filters $K$
# > * their spatial extent $F$
# > * the stride $S$
# > * the amount of zero padding $P$
# > * Produces a volume of size $W_2 \times H_2 \times D_2$ where:
# > * $W_2 = (W_1 − F + 2_P) / S + 1$
# > * $H_2 = (H_1 − F + 2_P) / S + 1$ (i.e. width and height are computed equally by symmetry)
# > * $D_2 = K$
# > * With parameter sharing, it introduces:
# > * $F \times F \times D_1$ weights per filter
# > * for a total of $F \times F \times D_1 \times K$ weights
# > * and $K$ biases
# > * In the output volume, the $d$-th depth slice (of size $W_2 \times H_2$) is the result of performing:
# > * a valid convolution of the $d$-th filter over the input volume
# > * with a stride of $S$, and then
# > * offset by $d$-th bias
# > * A common setting of the hyperparameters is:
# > * $F = 3$
# > * $S = 1$
# > * $P = 1$
# >
# > However, there are common conventions and rules of thumb that motivate these hyperparameters. See the [ConvNet architectures section](https://cs231n.github.io/convolutional-networks/#architectures) ...
# [[Top]](#Table-of-Contents)
# +
x = np.linspace(start=-10, stop=11, num=100)
y = sigmoid(x)
upper_bound = np.repeat([1.0,], len(x))
success_threshold = np.repeat([0.5,], len(x))
lower_bound = np.repeat([0.0,], len(x))
plt.plot(
# upper bound
x, upper_bound, 'w--',
# success threshold
x, success_threshold, 'w--',
# lower bound
x, lower_bound, 'w--',
# sigmoid
x, y
)
plt.grid(False)
plt.xlabel(r'$x$')
plt.ylabel(r'Probability of success')
plt.title('Sigmoid Function Example')
plt.show()
# -
# [[Top]](#Table-of-Contents)
# ## Additional Reading
#
# * [CS231n Convolutional Neural Networks for Visual Recognition](https://cs231n.github.io/)
# * [Deep Learning Book - Chapter 9: Convolutional Networks](http://www.deeplearningbook.org/contents/convnets.html)
#
# [[Top]](#Table-of-Contents)
# ## Addional Videos
#
# ### CS231n Winter 2016: Lecture 6: Neural Networks Part 3 / Intro to ConvNets
# * <NAME>
# * Published 27 Jan 2016
# * Reddit /r/cs231n
# * Standard YouTube Licence
YouTubeVideo("v=hd_KFJ5ktUc", height=365, width=650)
# [[Top]](#Table-of-Contents)
YouTubeVideo("v=u6aEYuemt0M", height=365, width=650)
# [[Top]](#Table-of-Contents)
# ## Other resources
#
# ### CIFAR-10 ConvNet Demo - very good!
# [CIFAR-10 ConvNet Demo](https://cs.stanford.edu/people/karpathy/convnetjs/demo/cifar10.html)
# [[Top]](#Table-of-Contents)
|
content/downloads/notebooks/udacity/deep_learning_foundations_nanodegree/project_2_notes_convolutional_neural_networks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Datasets for the book
#
# Here we provide links to the datasets used in the book.
#
# Important Notes:
#
# 1. Note that these datasets are provided on external servers by third parties
# 2. Due to security issues with github you will have to cut and paste FTP links (they are not provided as clickable URLs)
# # Python and the Surrounding Software Ecology
#
# ### Interfacing with R via rpy2
#
# * sequence.index
# Please FTP from this URL(cut and paste)
#
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/historical_data/former_toplevel/sequence.index
# # Next-generation Sequencing (NGS)
#
# ## Working with modern sequence formats
# * SRR003265.filt.fastq.gz
# Please FTP from this URL (cut and paste)
#
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/data/NA18489/sequence_read/SRR003265.filt.fastq.gz
#
# ## Working with BAM files
# * NA18490_20_exome.bam
# Please FTP from this URL (cut and paste)
#
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/data/NA18489/exome_alignment/NA18489.chrom20.ILLUMINA.bwa.YRI.exome.20121211.bam
#
# * NA18490_20_exome.bam.bai
# Please FTP from this URL (cut and paste)
#
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/data/NA18489/exome_alignment/NA18489.chrom20.ILLUMINA.bwa.YRI.exome.20121211.bam.bai
#
# ## Analyzing data in Variant Call Format (VCF)
#
# * tabix link:
# ftp://ftp-trace.ncbi.nih.gov/1000genomes/ftp/release/20130502/supporting/vcf_with_sample_level_annotation/ALL.chr22.phase3_shapeit2_mvncall_integrated_v5_extra_anno.20130502.genotypes.vcf.gz
# # Genomics
#
# ### Working with high-quality reference genomes
#
# * [falciparum.fasta](http://plasmodb.org/common/downloads/release-9.3/Pfalciparum3D7/fasta/data/PlasmoDB-9.3_Pfalciparum3D7_Genome.fasta)
#
# ### Dealing with low low-quality genome references
#
#
# * gambiae.fa.gz
# Please FTP from this URL (cut and paste)
# ftp://ftp.vectorbase.org/public_data/organism_data/agambiae/Genome/agambiae.CHROMOSOMES-PEST.AgamP3.fa.gz
#
# * [atroparvus.fa.gz](https://www.vectorbase.org/download/anopheles-atroparvus-ebroscaffoldsaatre1fagz)
#
#
# ### Traversing genome annotations
#
# * [gambiae.gff3.gz](http://www.vectorbase.org/download/anopheles-gambiae-pestbasefeaturesagamp42gff3gz)
#
# # PopGen
#
# ### Managing datasets with PLINK
#
# * [hapmap.map.bz2](http://hapmap.ncbi.nlm.nih.gov/downloads/genotypes/hapmap3/plink_format/draft_2/hapmap3_r2_b36_fwd.consensus.qc.poly.map.bz2)
# * [hapmap.ped.bz2](http://hapmap.ncbi.nlm.nih.gov/downloads/genotypes/hapmap3/plink_format/draft_2/hapmap3_r2_b36_fwd.consensus.qc.poly.ped.bz2)
# * [relationships.txt](http://hapmap.ncbi.nlm.nih.gov/downloads/genotypes/hapmap3/plink_format/draft_2/relationships_w_pops_121708.txt)
# # PDB
#
# ### Parsing mmCIF files with Biopython
#
# * [1TUP.cif](http://www.rcsb.org/pdb/download/downloadFile.do?fileFormat=cif&compression=NO&structureId=1TUP)
# # Python for Big genomics datasets
#
# ### Setting the stage for high-performance computing
#
# These are the exact same files as _Managing datasets with PLINK_ above
#
# ### Programing with lazyness
# * SRR003265_1.filt.fastq.gz Please ftp from this URL (cut and paste):
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/data/NA18489/sequence_read/SRR003265_1.filt.fastq.gz
#
#
# * SRR003265_2.filt.fastq.gz Please ftp from this URL (cut and paste):
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/data/NA18489/sequence_read/SRR003265_2.filt.fastq.gz
# # Python for Big genomics datasets
#
# ### Inferring shared chromosomal segments with Germline
#
# ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase1/analysis_results/shapeit2_phased_haplotypes/
#
|
Datasets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="AkjPFfsEYp4D" colab_type="code" colab={}
# + [markdown] id="ptW-CjKGY81u" colab_type="text"
# ```
# # x is examples in training set
# # y is set of attributes
# # labels is labeled data
# # Node is a class which has properties values, childs, and next
# # root is top node in the decision tree
# # Declare:
# x = # Multi dimensional arrays
# y = # Column names of x
# labels = # Classification values, for example {0, 1, 0, 1}
# # correspond that row 1 is false, row 2 is true, and so on
# root = ID3(x, y, label, root)
# # Define:
# ID3(x, y, label, node)
# initialize node as a new node instance
# if all rows in x only have single classification c, then:
# insert label c into node
# return node
# if x is empty, then:
# insert dominant label in x into node
# return node
# bestAttr is an attribute with maximum information gain in x
# insert attribute bestAttr into node
# for vi in values of bestAttr:
# // For example, Outlook has three values: Sunny, Overcast, and Rain
# insert value vi as branch of node
# create viRows with rows that only contains value vi
# if viRows is empty, then:
# this node branch ended by a leaf with value is dominant label in x
# else:
# newY = list of attributes y with bestAttr removed
# nextNode = next node connected by this branch
# nextNode = ID3(viRows, newY, label, nextNode)
# return node
#
# ```
# + id="Dp3TzgUOYsi3" colab_type="code" colab={}
import re
import math
from collections import deque
# x is examples in training set
# y is set of attributes
# label is target attributes
# Node is a class which has properties values, childs, and next
# root is top node in the decision tree
class Node(object):
def __init__(self):
self.value = None
self.next = None
self.childs = None
# Simple class of Decision Tree
# Aimed for who want to learn Decision Tree, so it is not optimized
class DecisionTree(object):
def __init__(self, sample, attributes, labels):
self.sample = sample
self.attributes = attributes
self.labels = labels
self.labelCodes = None
self.labelCodesCount = None
self.initLabelCodes()
# print(self.labelCodes)
self.root = None
self.entropy = self.getEntropy([x for x in range(len(self.labels))])
def initLabelCodes(self):
self.labelCodes = []
self.labelCodesCount = []
for l in self.labels:
if l not in self.labelCodes:
self.labelCodes.append(l)
self.labelCodesCount.append(0)
self.labelCodesCount[self.labelCodes.index(l)] += 1
def getLabelCodeId(self, sampleId):
return self.labelCodes.index(self.labels[sampleId])
def getAttributeValues(self, sampleIds, attributeId):
vals = []
for sid in sampleIds:
val = self.sample[sid][attributeId]
if val not in vals:
vals.append(val)
# print(vals)
return vals
def getEntropy(self, sampleIds):
entropy = 0
labelCount = [0] * len(self.labelCodes)
for sid in sampleIds:
labelCount[self.getLabelCodeId(sid)] += 1
# print("-ge", labelCount)
for lv in labelCount:
# print(lv)
if lv != 0:
entropy += -lv/len(sampleIds) * math.log(lv/len(sampleIds), 2)
else:
entropy += 0
return entropy
def getDominantLabel(self, sampleIds):
labelCodesCount = [0] * len(self.labelCodes)
for sid in sampleIds:
labelCodesCount[self.labelCodes.index(self.labels[sid])] += 1
return self.labelCodes[labelCodesCount.index(max(labelCodesCount))]
def getInformationGain(self, sampleIds, attributeId):
gain = self.getEntropy(sampleIds)
attributeVals = []
attributeValsCount = []
attributeValsIds = []
for sid in sampleIds:
val = self.sample[sid][attributeId]
if val not in attributeVals:
attributeVals.append(val)
attributeValsCount.append(0)
attributeValsIds.append([])
vid = attributeVals.index(val)
attributeValsCount[vid] += 1
attributeValsIds[vid].append(sid)
# print("-gig", self.attributes[attributeId])
for vc, vids in zip(attributeValsCount, attributeValsIds):
# print("-gig", vids)
gain -= vc/len(sampleIds) * self.getEntropy(vids)
return gain
def getAttributeMaxInformationGain(self, sampleIds, attributeIds):
attributesEntropy = [0] * len(attributeIds)
for i, attId in zip(range(len(attributeIds)), attributeIds):
attributesEntropy[i] = self.getInformationGain(sampleIds, attId)
maxId = attributeIds[attributesEntropy.index(max(attributesEntropy))]
return self.attributes[maxId], maxId
def isSingleLabeled(self, sampleIds):
label = self.labels[sampleIds[0]]
for sid in sampleIds:
if self.labels[sid] != label:
return False
return True
def getLabel(self, sampleId):
return self.labels[sampleId]
def id3(self):
sampleIds = [x for x in range(len(self.sample))]
attributeIds = [x for x in range(len(self.attributes))]
self.root = self.id3Recv(sampleIds, attributeIds, self.root)
def id3Recv(self, sampleIds, attributeIds, root):
root = Node() # Initialize current root
if self.isSingleLabeled(sampleIds):
root.value = self.labels[sampleIds[0]]
return root
# print(attributeIds)
if len(attributeIds) == 0:
root.value = self.getDominantLabel(sampleIds)
return root
bestAttrName, bestAttrId = self.getAttributeMaxInformationGain(
sampleIds, attributeIds)
# print(bestAttrName)
root.value = bestAttrName
root.childs = [] # Create list of children
for value in self.getAttributeValues(sampleIds, bestAttrId):
# print(value)
child = Node()
child.value = value
root.childs.append(child) # Append new child node to current
# root
childSampleIds = []
for sid in sampleIds:
if self.sample[sid][bestAttrId] == value:
childSampleIds.append(sid)
if len(childSampleIds) == 0:
child.next = self.getDominantLabel(sampleIds)
else:
# print(bestAttrName, bestAttrId)
# print(attributeIds)
if len(attributeIds) > 0 and bestAttrId in attributeIds:
toRemove = attributeIds.index(bestAttrId)
attributeIds.pop(toRemove)
child.next = self.id3Recv(
childSampleIds, attributeIds, child.next)
return root
def printTree(self):
if self.root:
roots = deque()
roots.append(self.root)
while len(roots) > 0:
root = roots.popleft()
print(root.value)
if root.childs:
for child in root.childs:
print('({})'.format(child.value))
roots.append(child.next)
elif root.next:
print(root.next)
def test():
f = open('playtennis.csv')
attributes = f.readline().split(',')
attributes = attributes[1:len(attributes)-1]
print(attributes)
sample = f.readlines()
f.close()
for i in range(len(sample)):
sample[i] = re.sub('\d+,', '', sample[i])
sample[i] = sample[i].strip().split(',')
labels = []
for s in sample:
labels.append(s.pop())
# print(sample)
# print(labels)
decisionTree = DecisionTree(sample, attributes, labels)
print("System entropy {}".format(decisionTree.entropy))
decisionTree.id3()
decisionTree.printTree()
# if __name__ == '__main__':
# test()
# + id="bZbdIJW6aKoj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 306} outputId="28ce8c10-042d-421b-a20e-418b34b4cd19"
test()
# + id="nDE8e4SXaOdR" colab_type="code" colab={}
|
final/notebooks/scratch/id3-from-scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
from scipy.io import arff
import numpy as np
import math
from sklearn.svm import SVC
from sklearn.model_selection import GridSearchCV, train_test_split, cross_val_score, cross_validate
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier
import os
import time
from tqdm.notebook import trange, tqdm
import warnings
warnings.filterwarnings('ignore')
file_pwd = os.getcwd() + "\Data"
res = os.walk(file_pwd)
file_list = [i[2] for i in res][0]
file_list
# +
#输入data,输出log2D列的数据
def preprocess(df):
head_list = df.columns.values.tolist()
#标准化
data_without_YN = df.drop("Defective",axis = 1)
data_normalize = (data_without_YN-data_without_YN.mean())/(data_without_YN.std())
data_normalize['Defective'] = df.Defective
row_yes_data = df[df.Defective == b'Y']
row_yes_data = row_yes_data.drop("Defective",axis = 1).values
row_no_data = df[df.Defective == b'N']
row_no_data = row_no_data.drop("Defective",axis = 1).values
yes_samples = data_normalize[data_normalize.Defective == b"Y"]
yes_samples = yes_samples.drop("Defective",axis = 1)
no_samples = data_normalize[data_normalize.Defective == b"N"]
no_samples = no_samples.drop("Defective",axis = 1)
k = len(no_samples)//len(yes_samples)
yes_samples_array = yes_samples.values
no_samples_array = no_samples.values
array = [[np.sqrt(np.sum(np.square(x-y))) for y in no_samples_array]for x in yes_samples_array]
array = np.array(array).argsort()[:,:k]
w = {i:0 for i in range(yes_samples.shape[1])}
for i in range(array.shape[0]):
for j in array[i]:
ds = np.abs(row_yes_data[i,:] - row_no_data[j,:])
ds = pd.Series(ds).rank(method='min')
for index in range(len(ds)):
w[index] += ds[index]
a = sorted(w.items(),key=lambda x:x[1],reverse=True)
b = [i[0] for i in a ]
c = np.array(head_list)
column = list(c[b])
df2 = df.loc[:,column].copy()
# d = df2.shape[1]
# log2d = math.ceil(math.log2(d))
# df2 = df2.iloc[:,:log2d]
return df2
# -
#返回十次十折交叉验证的平均auc
def SVM(data,label):
clf = SVC(gamma='auto')
auc_list = []
data["label"] = label
for i in tqdm(range(10)):
data = data.sample(frac=1)
scores = cross_val_score(clf,data.iloc[:,:-1],data.label,cv=10,scoring="roc_auc")
auc_list.append(scores.mean())
return np.mean(auc_list)
#贝叶斯分类
def NB(data,label):
clf = MultinomialNB()
auc_list = []
data["label"] = label
for i in tqdm(range(10)):
data = data.sample(frac=1)
scores = cross_val_score(clf,data.iloc[:,:-1],data.label,cv=10,scoring="roc_auc")
auc_list.append(scores.mean())
return np.mean(auc_list)
#决策树分类
def DT(data,label):
clf = DecisionTreeClassifier()
auc_list = []
data["label"] = label
for i in tqdm(range(10)):
data = data.sample(frac=1)
scores = cross_val_score(clf,data.iloc[:,:-1],data.label,cv=10,scoring="roc_auc")
auc_list.append(scores.mean())
return np.mean(auc_list)
real_start = time.clock()
for each in tqdm(file_list):
res_list = []
data = arff.loadarff('./data/{}'.format(each))
df = pd.DataFrame(data[0])
if df.columns[-1] == "label":
df.rename(columns={'label':'Defective'},inplace=True)
defective = df.Defective.copy()
defective[defective==b'N'] = 0
defective[defective==b'Y'] = 1
#得到排好序的数据
data = preprocess(df)
head_list = data.columns
for every_feature in tqdm(head_list):
start = time.clock()
X = data.loc[:,head_list[0]:every_feature]
label = defective.astype(int)
svm_auc = SVM(X.copy(),label)
destree_auc = DT(X.copy(),label)
nb_auc = NB(X.copy(),label)
print("*"*20)
print("数据尺寸:{}".format(X.shape))
print("文件名:{}".format("CM1"))
print("feature:{}:{}".format(head_list[0],every_feature))
print("SVM--->{}:".format(svm_auc))
print("决策树--->{}:".format(destree_auc))
print("贝叶斯--->{}".format(nb_auc))
spend = (time.clock()-start)
print("use time:{}".format(spend))
print("="*20)
make_dic = {
"size":X.shape,
"feature":every_feature,
"SVM":svm_auc,
"tree":destree_auc,
"nb":nb_auc
}
res_list.append(make_dic)
print(res_list)
info = {key:[]for key in res_list[0].keys()}
for one in res_list:
for key,value in one.items():
info[key].append(value)
info = pd.DataFrame(info)
info.to_csv("{}.csv".format(each))
print("总共耗时:",(time.clock()-real_start))
# +
# real_start = time.clock()
# res_list = []
# for each in file_list:
# data = arff.loadarff('./data/{}'.format(each))
# df = pd.DataFrame(data[0])
# if df.columns[-1] == "label":
# df.rename(columns={'label':'Defective'},inplace=True)
# defective = df.Defective.copy()
# defective[defective==b'N'] = 0
# defective[defective==b'Y'] = 1
# start = time.clock()
# #分为数据和标签
# data = preprocess(df)
# label = defective.astype(int)
# svm_auc = SVM(data,label)
# destree_auc = DT(data,label)
# nb_auc = NB(data,label)
# print("*"*20)
# print("数据尺寸:{}".format(data.shape))
# print("文件名:{}".format(each))
# print("log2D:{}".format(data.shape[1]))
# print("SVM--->{}:".format(svm_auc))
# print("决策树--->{}:".format(destree_auc))
# print("贝叶斯--->{}".format(nb_auc))
# spend = (time.clock()-start)
# print("use time:{}".format(spend))
# print("="*20)
# make_dic = {
# "size":data.shape,
# "name":each,
# "log2D":data.shape[1],
# "SVM":svm_auc,
# "tree":destree_auc,
# "nb":nb_auc
# }
# res_list.append(make_dic)
# print("总共耗时:",(time.clock()-real_start))
# print(res_list)
# +
# data = {key:[]for key in res_list[0].keys()}
# for one in res_list:
# for key,value in one.items():
# data[key].append(value)
# data.pop("size")
# data = pd.DataFrame(data,index=range(1,13))
# data.to_csv("log2D.csv")
# -
|
数据挖掘与数据仓库/实验三/.ipynb_checkpoints/实验三相关度高的特征子集-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/unicamp-dl/IA025_2022S1/blob/main/ex03/Guilherme_Pereira/Aula_3_Guilherme_Pereira.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="zK-o03OW4rWq"
# ### Escreva aqui seu nome:
# + [markdown] id="B5_ZRWRfCZtI"
# # PyTorch: Gradientes e Grafo Computacional
# + [markdown] id="mQcJKilSCZtO"
# ## Objetivos
# + [markdown] id="OFWv6Mi-CZtQ"
# Este notebook introduz
# - o conceito de autograd do PyTorch,
# - uma interpretação numérica intuitiva do gradiente, e o
# - grafo computacional, utilizado para o cálculo automático do gradiente de uma função.
# + [markdown] id="BIlQdKAuCZtR"
# Um dos principais fundamentos para que o PyTorch seja adequado para deep learning é a sua habilidade de
# calcular o gradiente automaticamente a partir da expressões definidas. Essa facilidade é implementada
# pelo tensor através do cálculo automático do gradiente pela construção dinâmica do grafo computacional.
# + [markdown] id="ZF_-dJ2nCZtT"
# ## Grafo computacional
# + [markdown] id="jboejVQMCZtU"
# ```
# y_pred = x * w
# e = y_pred - y
# e2 = e**2
# J = e2.sum()
# ```
# + [markdown] id="KeeEBKl4CZtV"
# <img src="https://raw.githubusercontent.com/robertoalotufo/files/master/figures/GrafoComputacional.png" width="600pt"/>
# + [markdown] id="8yZun7wrCZtX"
# Para conhecer com maior profundidade a diferenciação automática usando grafo computacional, veja esta nota de aula:
# https://cs231n.github.io/optimization-2/
# + id="HlT2d-4fCZtZ"
import torch
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="xX0QwUduCZtf" outputId="de0af6c3-f1e6-4a34-e1f6-6dd160beef6f"
torch.__version__
# + [markdown] id="vsqzALS4CZtl"
# ## Se um tensor possui .requires_grad=True
# + colab={"base_uri": "https://localhost:8080/"} id="foaAb94aCZtm" outputId="4232725b-79db-4d46-c68f-03b915f70ff6"
y = 2 * torch.arange(0,4).float()
y
# + colab={"base_uri": "https://localhost:8080/"} id="no6SdSyICZtr" outputId="fb804e79-0b1c-4a43-a6df-474e57595823"
x = torch.arange(0,4).float(); x
# + colab={"base_uri": "https://localhost:8080/"} id="eL_i1mwGCZtw" outputId="96ca5ceb-006b-4022-abcc-a77c7234b0c2"
w = torch.ones(1,requires_grad=True); w
# + [markdown] id="qjEl-0l7CZt0"
# ## Cálculo automático do gradiente da função perda J
# + [markdown] id="8pUh-SCnCZt1"
# Seja a expressão: $$ J = \sum ((x w) - y)^2 $$
#
# Queremos calcular a derivada de $J$ em relação a $w$.
# + [markdown] id="eMwwVtJ1CZt2"
# ### Montagem do grafo computacional
# + colab={"base_uri": "https://localhost:8080/"} id="zp2aK4YhCZt3" outputId="312d1066-f045-46f1-91b5-0933ccbd3d44"
# predict (forward)
y_pred = x * w
# cálculo da perda J: loss
e = y_pred - y
e2 = e.pow(2)
J = e2.sum()
J
# + [markdown] id="XC96wB7PCZt8"
# ## Auto grad - processa o grafo computacional backwards
# + [markdown] id="kKbf4D0CCZt-"
# O `backward()` varre o grafo computacional a partir da variável a ele associada e calcula o gradiente para todos os tensores que possuem o atributo `requires_grad` como verdadeiro.
# O `backward()` destroi o grafo após sua execução. Isso é intrínsico ao PyTorch pelo fato dele ser uma rede dinâmica.
# + colab={"base_uri": "https://localhost:8080/"} id="Z1lnkb0GCZt_" outputId="6fde2689-a80f-4b71-c521-bea2b3129802"
J.backward()
print(w.grad)
# + id="NJWgpQbICZuD"
w.grad.data.zero_();
# + colab={"base_uri": "https://localhost:8080/"} id="x2JAGn9lVtvx" outputId="0f2a24ea-6f89-45da-c50b-8928d612faf2"
w.grad
# + [markdown] id="j-HTDCpBCZuH"
# ## Interpretação do Gradiente
# + [markdown] id="aQCUPkozCZuI"
# O gradiente de uma variável final (J) com respeito à outra variável de entrada (w) pode ser interpretado como o quanto a variável final J vai aumentar se houver um pequeno aumento na variável de entrada (w).
# Por exemplo suponha que o gradiente seja 28. Isto significa se aumentarmos a variável w de 0.001, então J vai aumentar de 0.028.
# + colab={"base_uri": "https://localhost:8080/"} id="VNUws23uCZuK" outputId="c2710545-0f75-4776-bb0a-3fe0df6ee80d"
eps = 0.001
y_pred = x * (w + eps)
J_new = (y_pred - y).pow(2).sum()
J_new
# + colab={"base_uri": "https://localhost:8080/"} id="iYghg1bnCZuP" outputId="0bd02dc6-4f12-4499-9fb3-4d7f281a388c"
print(J_new - J)
# + [markdown] id="Zlm30rdnCZuT"
# ## Backpropagation
# + [markdown] id="GREsFSQWCZuU"
# Uma forma equivalente explícita de calcular o gradiente é fazendo o processamento do backpropagation no grafo computacional, de forma explícita.
# Apenas como ilustração.
# + colab={"base_uri": "https://localhost:8080/"} id="8rF7eTWUYWjs" outputId="fd5a105d-aabe-428e-bab0-5dcf83b2545d"
e.data.numpy()
# + colab={"base_uri": "https://localhost:8080/"} id="JYmJImp2CZuW" outputId="bb19a44a-12e6-44cc-8a9d-c6671934cedc"
import numpy as np
dJ = 1.
de2 = dJ * np.ones((4,))
de = de2 * 2 * e.data.numpy()
dy_pred = de
dw = (dy_pred * x.data.numpy()).sum()
print(dJ)
print(de2)
print(de)
print(dw)
# + [markdown] id="r6-bQzqsCZuZ"
# ## Visualizando o grafo computacional
# + id="pjGruWPTCZub" colab={"base_uri": "https://localhost:8080/"} outputId="0285a1cb-e1b9-41a1-b025-b094ab6db0cb"
# !pip install torchviz
# + colab={"base_uri": "https://localhost:8080/", "height": 528} id="Lbi_GDjWCZuf" outputId="729d0b93-6d2d-4261-ee12-a00f79532a3d"
import torchviz
J = ((w * x) - y).pow(2).sum()
p = {'w':w} # dicionário de parâmetros
out = torchviz.make_dot(J,params=p)
out
# + [markdown] id="bRCxXDiIzYT7"
# Iremos agora visualizar a Resnet, que é uma rede neural bastante popular em visão computacional.
# + id="dmhanmVFzhiQ" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="4d077211-ca56-4372-87f7-2d6c666d86dc"
import torch
model = torch.hub.load('pytorch/vision:v0.9.0', 'resnet18', pretrained=True)
x_temp = torch.randn(1,3,224,224) # First, create a random image.
y_temp = model(x_temp) # We need one forward pass so the graph can be build.
out = torchviz.make_dot(y_temp, params=dict(model.named_parameters())) # Create a figure from the computaional graph..
torchviz.dot.resize_graph(out, size_per_element=0.05) # Resize to fit on the screen.
out
# + [markdown] id="7mIP_gnbral2"
# # Exercício 1
#
# O que acontece com o grafo computacional após execução do `backward()`?
# + [markdown] id="Dg34dQHdk5KG"
# Resposta: o grafo é diferenciado utilizando a regra da cadeia
# + [markdown] id="0RkjpqfprZ_t"
# # Exercício 2
#
# Execute um passo de atualização do valor de w, pelo
# gradiente descendente. Utilize um fator de aprendizado (*learning rate*) de 0.01
# para atualizar o `w`. Após, recalcule a função de perda:
#
# - w = w - lr * w.grad.data
# - Verifique o quanto que a perda J diminuiu
# + id="Np7D022AO2gM" colab={"base_uri": "https://localhost:8080/"} outputId="644ee9d8-45b1-4b8e-f921-7378c1de9b7c"
lr = 0.01
y = 2 * torch.arange(0,4).float()
x = torch.arange(0,4).float()
w = torch.ones(1,requires_grad=True)
J = (w*x - y).pow(2).sum()
J.backward()
w = w - lr * w.grad.data
J_new = (w*x - y).pow(2).sum()
print(f'Loss antiga: {J}')
print(f'Loss nova: {J_new}')
# + colab={"base_uri": "https://localhost:8080/"} id="SiO_v7fDzZIm" outputId="a676d965-a073-40af-847c-a59ff85775e4"
eps = 0.001
y_pred = x * (w + eps)
J_new = (y_pred - y).pow(2).sum()
J_new
# + [markdown] id="hozksnNDXx4G"
# ## Treinando uma rede no Pytorch
#
# Para ajudar na entendimento dos exercícios abaixo, apresentamos o código em Pytorch para treinar uma rede de uma camada não-linear, com pesos `w` e `b`:
# $y' = \sigma(wx + b)$
# + [markdown] id="Fp9dSVjXy4gy"
# <img src="https://github.com/robertoalotufo/files/blob/master/figures/simple_graph.png?raw=true" width="600pt"/>
# + id="9KYYzSqoZ3iM" colab={"base_uri": "https://localhost:8080/"} outputId="ea3eeaf3-87f0-463c-bb94-e1726ca7d695"
# É importante fixar as seeds para passar nos asserts abaixo.
import random
import numpy as np
import torch
random.seed(123)
np.random.seed(123)
torch.manual_seed(123)
# + id="VhXl4fkxYv2z" colab={"base_uri": "https://localhost:8080/"} outputId="7ccb6f77-72d9-41a5-a4a1-7535cedfc345"
from typing import List
class NonLinearPytorch(torch.nn.Module):
def __init__(self):
super(NonLinearPytorch, self).__init__()
self.layer1 = torch.nn.Linear(1, 1)
# Inicializa os pesos w e b em zero.
self.layer1.load_state_dict(dict(weight=torch.zeros(1,1), bias=torch.zeros(1)))
def forward(self, x):
y_pred = torch.sigmoid(self.layer1(x))
return y_pred
learning_rate = 0.1
model = NonLinearPytorch()
loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate)
x = torch.tensor([-5], dtype=torch.float)
y_target = torch.tensor([0.76], dtype=torch.float)
num_iterations = 50
for i in range(num_iterations):
# Zere os gradientes dos passo anterior.
optimizer.zero_grad()
# Rode a um passo forward do modelo.
y_pred = model.forward(x)
# Calcule a loss
loss = loss_fn(y_pred, y_target)
# Calcule os gradientes
loss.backward()
# Atualize os pesos
optimizer.step()
print(f'iter:{i}: y_prime: {y_pred}')
# + [markdown] id="-dCpic0_XhKE"
# # Exercício 3
#
# Vamos agora escrever nosso próprio código para calcular os gradientes da rede apresentada acima.
#
# Para tanto, temos que primeiro implementar a classe Tensor, que é parecida com a classe Tensor do pytorch. Quando instanciada, o objeto resultante armazena o valor do tensor e uma referencia para o nó do grafo computacional que gerou os valores do tensor, quando houver. Com isso podemos construir percorrer o grafo computacional no sentido reverso, realizando o passo `backward` do algoritmo de backpropagation.
#
# Para simplificar a implementação, o gradiente também pode ser armazenado nesta variável. Com isso, podemos tratar os pesos da rede como Tensor's. Isso dispensa a necessidade de criarmos a classe Parameters, como é feito no pytorch.
# + id="T3vkPX65NYAS"
class Tensor():
def __init__(self, data: float, previous_node=None):
self.data = data
self.previous_node = previous_node
self.grad = 0
def backward(self, upstream_grad: float = 1.0):
self.grad = self.grad + upstream_grad
if self.previous_node:
self.previous_node.backward(self.grad)
# Implementar as funções abaixo é opcional.
def __add__(self, other: 'Tensor'):
return Tensor(self.data + other.data)
def __sub__(self, other: 'Tensor'):
return Tensor(self.data - other.data)
def __mul__(self, other: 'Tensor'):
return Tensor(self.data * other.data)
def __pow__(self, other: 'Tensor'):
return Tensor(self.data ** other.data)
# + [markdown] id="9PWNVg4wMS9t"
# A seguir, implementaremos as funções `forward` e `backward` de cada um dos nós do grafo acima, além do nó de subtração, que é usado pela função de custo.
# Vamos começar pelo nó da função sigmoid ($\sigma$), cuja derivada é:
#
# $\frac{\delta\sigma}{\delta x} = \sigma(x)(1-\sigma(x))$
# + id="Up1GixP9PFjG"
class SigmoidNode():
def forward(self, x: Tensor):
self.x = x
resultado = 1 / (1 + np.exp(-x.data))
self.z = Tensor(resultado)
return self.z
def backward(self, upstream_grad: float = 1.0):
self.z.grad = upstream_grad
derivada = self.z.data * (1 - self.z.data)
self.x.backward(derivada * upstream_grad)
# + [markdown] id="BWxNzGVZXvU7"
# Implementamos agora o `forward` e `backward` do nó da soma $z = x + y$, cujas derivadas parciais em relação a cada entrada $x$ e $y$ são:
#
# $\frac{\delta z}{\delta x} = 1$
#
# $\frac{\delta z}{\delta y} = 1$
# + id="iiGB3rhaXvxC"
class AddNode():
def forward(self, x: Tensor, y: Tensor):
self.x = x
self.y = y
self.z = x + y
self.z.previous_node = self
return self.z
def backward(self, upstream_grad: float = 1.0):
self.z.grad = upstream_grad
self.x.backward(upstream_grad)
self.y.backward(upstream_grad)
# + [markdown] id="-XbKz0z0VfdC"
# Implementamos agora o `forward` e `backward` do nó da subtração $z = x - y$, cujas derivadas parciais em relação a cada entrada $x$ e $y$ são:
#
# $\frac{\delta z}{\delta x} = 1$
#
# $\frac{\delta z}{\delta y} = -1$
# + id="ztsGOWudV3X7"
class SubNode():
def forward(self, x: Tensor, y: Tensor):
self.x = x
self.y = y
self.z = x - y
self.z.previous_node = self
return self.z
def backward(self, upstream_grad: float = 1.0):
self.z.grad = upstream_grad
self.x.backward(upstream_grad)
self.y.backward(-upstream_grad)
# + [markdown] id="HSEUWtP_qSqW"
# Implementamos agora o `forward` e `backward` do nó da multiplicação $z = xy$, cujas derivadas parciais em relação a cada entrada $x$ e $y$ são:
#
# $\frac{\delta z}{\delta x} = y$
#
# $\frac{\delta z}{\delta y} = x$
# + id="BWzSxUU-Zlel"
class MulNode():
def forward(self, x: Tensor, y: Tensor):
self.x = x
self.y = y
self.z = x * y
self.z.previous_node = self
return self.z
def backward(self, upstream_grad: float = 1.0):
self.z.grad = upstream_grad
self.x.backward(upstream_grad * self.y.data)
self.y.backward(upstream_grad * self.x.data)
# + [markdown] id="zoc-eOzznNUR"
# Implementamos agora o `forward` e `backward` do nó da exponenciação $z = x^2$, cuja derivada parcial em relação a $x$ é:
#
# $\frac{\delta z}{\delta x} = 2*x$
# + id="FG6CYy7ljRIm"
class SqrNode():
def forward(self, x: Tensor):
self.x = x
self.z = x ** Tensor(2)
self.z.previous_node = self
return self.z
def backward(self, upstream_grad: float = 1.):
self.z.grad = upstream_grad
self.x.backward(upstream_grad * 2 * self.x.data)
# + [markdown] id="61FgtL-6Z0y2"
# Agora que temos todos os nós implementados, podemos implementar as funções `forward` e `backward` de uma camada não-linear.
# + id="o1N4eVVMaCIP"
class NonLinear():
def __init__(self):
self.w = Tensor(0)
self.b = Tensor(0)
self.mul = MulNode()
self.add = AddNode()
self.sig = SigmoidNode()
def forward(self, x: Tensor):
self.x = x
m = self.mul.forward(x, self.w)
a = self.add.forward(m, self.b)
self.output = self.sig.forward(a)
self.output.previous_node = self
return self.output
def backward(self, upstream_grad: float = 1.0):
self.output.grad = upstream_grad
self.sig.backward(upstream_grad)
# + [markdown] id="IIb90Wu1aGB3"
# Para treinar esta rede, usaremos a função de custo Mean Squared Error (MSE):
#
# $L = (y_\text{pred} - y_\text{target})^2$
#
# Como por simplicidade optamos por não criar o nó de exponenciação, iremos substituir a operação de elevar ao quadrado pela multiplicacão das diferenças:
# $L = (y_\text{pred} - y_\text{target}) * (y_\text{pred} - y_\text{target})$
#
# + id="prm0OP27pynW"
def compute_loss(y_target: Tensor, y_pred: Tensor):
sub = SubNode().forward(y_pred, y_target)
exp = SqrNode().forward(sub)
return exp
# + [markdown] id="12HHy6jV6bfc"
# Também precisamos criar a classe do optimizador SGD, para atualizar os pesos da rede.
# + id="4R8_Qyfj6avq"
class SGD():
def __init__(self, parameters: List[Tensor], learning_rate: float):
self.parameters = parameters
self.lr = learning_rate
def step(self):
for param in self.parameters:
param.data = param.data - self.lr * param.grad
def zero_grad(self):
for param in self.parameters:
param.grad = 0
# + [markdown] id="plTCBJWjpwCp"
# Por fim, vamos aprender os pesos `w` e `b` para mapear um valor de entrada $x$ para um valor de saída $y_\text{target}$. Para isso, inicializamos o grafo da rede e rodamos o laço de optimização, que vai aplicar a descida do gradiente a cada iteração:
# + id="rp5ttTsGaPmA" colab={"base_uri": "https://localhost:8080/"} outputId="9162ecc1-7356-4431-e3a4-2683b31c0761"
lr = 0.1
model = NonLinear()
optimizer = SGD(parameters=[model.w, model.b], learning_rate=lr)
x = Tensor(-5)
y_target = Tensor(0.76)
num_iterations = 50
loss_history = []
for i in range(num_iterations):
# Zera os gradientes dos passo anterior.
optimizer.zero_grad()
# Roda a um passo forward do modelo.
y_pred = model.forward(x)
# Calcula o gradiente do erro, data a predição do modelo.
loss = compute_loss(y_target=y_target, y_pred=y_pred)
# Calcula agora os gradientes de w e b usando a função backward do modelo.
loss.backward()
# Atualiza os pesos w e b usando os seus respectivos gradientes.
optimizer.step()
loss_history.append(loss.data)
print(f'iter:{i}: y_prime: {y_pred.data:.5f}')
# + id="xJxSgYiwA6xf"
# Assert do histórico de losses
target_loss_history = np.array([
0.06760000000000001,
0.03108006193722489,
0.015220506198982053,
0.008060932337170576,
0.004541161563163106,
0.002676716778416733,
0.0016309590258538709,
0.0010186197676265991,
0.0006482050773556802,
0.0004184778055808091,
0.0002732213666940629,
0.0001799723631408175,
0.00011938724006066084,
7.964556795580347e-05,
5.337529235755546e-05,
3.590189694852957e-05,
2.4221066975987528e-05,
1.6380519943303855e-05,
1.1100104701260794e-05,
7.534158921382263e-06,
5.1206312225268915e-06,
3.484091178521846e-06,
2.372728572773017e-06,
1.6170734761536686e-06,
1.102751559255297e-06,
7.523936056219261e-07,
5.135628032851034e-07,
3.506642035854199e-07,
2.395039343745027e-07,
1.6361975051076568e-07,
1.1180029104756559e-07,
7.64046255502172e-08,
5.222203675240293e-08,
3.5697304881109e-08,
2.440373411811497e-08,
1.6684360766998337e-08,
1.1407478782586943e-08,
7.799952038419558e-09,
5.333502713018058e-09,
3.6471049454669566e-09,
2.4940004563648322e-09,
1.70551347969202e-09,
1.1663324261807554e-09,
7.976210871191926e-10,
5.454773999550763e-10,
3.7304544385265726e-10,
2.55123652632966e-10,
1.744789425625632e-10,
1.1932681701419737e-10,
8.160849280968648e-11])
assert np.allclose(np.array(loss_history), target_loss_history, atol=1e-6)
# + [markdown] id="V8AqQ0n7raQI"
# # Exercício 4
#
# Repita o exercício 3 mas usando uma rede com duas camadas não-lineares:
#
# $a = \sigma(w_1x + b_1)$
#
# $y' = \sigma(w_2a + b_2)$
#
# + id="fkBfLU3Tlhq3"
class Net():
def __init__(self):
self.hidden_layer = NonLinear()
self.output_layer = NonLinear()
def forward(self, x: Tensor):
return self.output_layer.forward(self.hidden_layer.forward(x))
# + id="5AN6PzkylXYR" colab={"base_uri": "https://localhost:8080/"} outputId="90a81c1e-397f-4da2-d4f3-37487b14c34c"
learning_rate = 1.0
model = Net()
optimizer = SGD(parameters=[model.hidden_layer.w, model.hidden_layer.b, model.output_layer.w, model.output_layer.b], learning_rate=learning_rate)
x = Tensor(-5)
y_target = Tensor(0.76)
num_iterations = 50
loss_history = []
for i in range(num_iterations):
# Zera os gradientes dos passo anterior.
optimizer.zero_grad()
# Roda a um passo forward do modelo.
y_pred = model.forward(x)
# Calcula o gradiente do erro, data a predição do modelo.
loss = compute_loss(y_target=y_target, y_pred=y_pred)
# Calcula agora os gradientes de w e b usando a função backward do modelo.
loss.backward()
# Atualiza os pesos w e b usando os seus respectivos gradientes.
optimizer.step()
loss_history.append(loss.data)
print(f'iter:{i}: y_prime: {y_pred.data:.5f}')
# + id="fAPArWHZBF8s"
# Assert do histórico de losses
target_loss_history = np.array([
0.06760000000000001,
0.04816451784326003,
0.03441893949967674,
0.024685869154550014,
0.017779518514339895,
0.012865672147580373,
0.009357930442551227,
0.006843854944228629,
0.005033355153684456,
0.003722486916596324,
0.002767860127525519,
0.002068519037319172,
0.0015531727586461292,
0.001171256605013691,
0.0008867097250423786,
0.0006736562851878449,
0.0005134081578305322,
0.00039237986185759277,
0.00030063198160464033,
0.00023084800404160196,
0.0001776110422089531,
0.00013688907444861002,
0.00010566603751232631,
8.167562040111844e-05,
6.320787765847752e-05,
4.8967839833139685e-05,
3.797151234545809e-05,
2.9468940940422566e-05,
2.2886999002965188e-05,
1.778663376632945e-05,
1.3830774434900419e-05,
1.0760144929813144e-05,
8.37496647215546e-06,
6.521069100328111e-06,
5.07931761304956e-06,
3.957538836299656e-06,
3.0843432785441995e-06,
2.4043861297584576e-06,
1.874725053962448e-06,
1.4620159502394981e-06,
1.1403504552510215e-06,
8.89585959590245e-07,
6.94054335088378e-07,
5.415623658353852e-07,
4.2261721020193424e-07,
3.298256981859764e-07,
2.574280800457942e-07,
2.0093587846657402e-07,
1.568504247743093e-07,
1.2244398229883047e-07
])
assert np.allclose(np.array(loss_history), target_loss_history, atol=1e-6)
# + [markdown] id="YNAx30ZLCZuj"
# # Exercício 5
#
# Repita o exercício 4 mas compartilhando os pesos das duas camadas não-lineares. Mostre que ambas tem os mesmos pesos após o treino.
# + id="M78rgX2OlHWI"
class NetShared():
def __init__(self):
self.hidden_layer = NonLinear()
self.output_layer = NonLinear()
self.output_layer.w = self.hidden_layer.w
self.output_layer.b = self.hidden_layer.b
def forward(self, x: Tensor):
return self.output_layer.forward(self.hidden_layer.forward(x))
# + id="gItHAnBDmPJj" colab={"base_uri": "https://localhost:8080/"} outputId="e17b5024-3883-4006-e449-a5f7e0b2d9e9"
learning_rate = 1.0
model = NetShared()
optimizer = SGD(parameters=[model.hidden_layer.w, model.hidden_layer.b, model.output_layer.w, model.output_layer.b], learning_rate=learning_rate)
x = Tensor(-5)
y_target = Tensor(0.76)
num_iterations = 50
loss_history = []
for i in range(num_iterations):
# Zera os gradientes dos passo anterior.
optimizer.zero_grad()
# Roda a um passo forward do modelo.
y_pred = model.forward(x)
# Calcula o gradiente do erro, data a predição do modelo.
loss = compute_loss(y_target=y_target, y_pred=y_pred)
# Calcula agora os gradientes de w e b usando a função backward do modelo.
loss.backward()
# Atualiza os pesos w e b usando os seus respectivos gradientes.
optimizer.step()
loss_history.append(loss.data)
print(f'iter:{i}: y_prime: {y_pred.data}')
# + id="-wfVgVgUBL2b"
# Assert do histórico de losses
target_loss_history = np.array([
0.06760000000000001,
0.03330943358728514,
0.01812309304377204,
0.010431455731754344,
0.00628328726800519,
0.003921585863693047,
0.002515913769956196,
0.0016490770012327091,
0.001099269875970989,
0.0007426407360579466,
0.0005071214254096055,
0.00034931071712997896,
0.0002423146970980538,
0.00016906818320206488,
0.00011852649897990173,
8.34225019207209e-05,
5.8908072936428374e-05,
4.1711214955750446e-05,
2.9602068987044087e-05,
2.104850477904461e-05,
1.4990519614837506e-05,
1.0690478374361229e-05,
7.632552514629166e-06,
5.454526520113034e-06,
3.901160939771698e-06,
2.7920656777350508e-06,
1.9994311078486844e-06,
1.4325100419623816e-06,
1.0267548557132565e-06,
7.361838049377913e-07,
5.279988583833094e-07,
3.787802854699951e-07,
2.717896235939522e-07,
1.9505429520143487e-07,
1.4000497904948548e-07,
1.0050478927006106e-07,
7.215673640396385e-08,
5.180917660144311e-08,
3.7202327787478815e-08,
2.6715420845967644e-08,
1.9185717920921844e-08,
1.377889958835379e-08,
9.896197179203946e-09,
7.10782660599054e-09,
5.105258647978467e-09,
3.6669857031273956e-09,
2.633962683117349e-09,
1.8919845693984993e-09,
1.3590391851568933e-09,
9.762292271381411e-10
])
assert np.allclose(np.array(loss_history), target_loss_history, atol=1e-6)
# + id="ayTpeISUpZet"
assert model.hidden_layer.w.data == model.output_layer.w.data
assert model.hidden_layer.b.data == model.output_layer.b.data
|
ex03/Guilherme_Pereira/Aula_3_Guilherme_Pereira.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# One idea that we ought to be able to leverage is to create a module (with an accompanying IR interface) that abstracts the Halide code target. Doing this will hopefully simplify code-generation, as well as allow us to dump out "the Halide program" in a form that people unfamiliar with this tensor language can understand and appreciate.
#
# In order to encapsulate some useful interface functionality we, will also put bindings with the NumPy library in this module.
import sys
sys.path.append('../')
sys.path.append('../src/')
from adt import ADT
from adt import memo as ADTmemo
import numpy as np
import ctypes
from halide import halide_type_t, halide_buffer_t, halide_dimension_t
from halide import hw_expr_t, hw_var_t, hw_rdom_t, hw_func_t, hw_img_t, hw_param_t
from halide import C
# # Halide IR
#
# A Halide program is a sequence of statements (stages), each of which either defines or updates a given `func`. All updates to a func must come immediately subsequent to the definition of that func.
#
# At the start of the program, some number of `var` and `rdom` variables may be declared.
#
# The overall program is called a "pipeline." It has zero or more inputs supplied as `param`s (scalars) or `img`s (multi-dimensional arrays). The `img` object is backed by a `halide_buffer_t`, which we will see can be supplied from a NumPy array. The output is likewise backed by a `halide_buffer_t`. In order to support multiple output buffers, we use a `pipeline` object to group those output `func`s.
#
# The Halide primitive type system has `int`, `uint` and `float` with different bit-widths (e.g. 8, 16, 32, 64) and different vector widths (e.g. 1,2,3,4). This too must be reflected in the IR.
# +
binops = {
"+": True,
"-": True,
"*": True,
"/": True,
"==": True,
"<": True,
">": True,
"<=": True,
">=": True,
}
basetypes = {
"f32": True,
"f64": True,
}
for bw in ["8","16","32","64"]:
basetypes["i"+bw] = True
basetypes["u"+bw] = True
HIR = ADT("""
module HIR {
pipeline = Pipeline ( var* vars,
rdom* rdoms,
func* funcs,
param* params,
img* imgs,
stmt* stmts,
func* outputs )
var = Var ( string name )
rdom = RDom ( string name, range* bounds )
param = Param ( string name, type typ )
img = Img ( string name, int ndim, type typ )
func = Func ( string name )
| ImgFunc ( img img )
expr = Const ( object v, type typ )
| Evar ( var v )
| Erdom ( rdom r )
| Eparam ( param p )
| BinOp ( op op, expr lhs, expr rhs )
| Min ( expr lhs, expr rhs )
| Max ( expr lhs, expr rhs )
| Select ( expr pred, expr lhs, expr rhs )
| FAccess ( func f, expr* args )
| BigSum ( rdom r, expr body )
stmt = PureDef ( func f, var* args, expr rhs )
| Update ( func f, expr* args, expr rhs )
range = Range ( expr lo, expr hi )
type = Type ( typbase base, int lanes )
}
""", {
'op': lambda x: x in binops,
'typbase': lambda x: x in basetypes,
})
ADTmemo(HIR,['Type'],{'typbase': lambda x: x})
f32, f64 = HIR.Type('f32',1), HIR.Type('f64',1)
u8, u16, u32, u64 = (HIR.Type('u8',1), HIR.Type('u16',1),
HIR.Type('u32',1), HIR.Type('u64',1))
i8, i16, i32, i64 = (HIR.Type('i8',1), HIR.Type('i16',1),
HIR.Type('i32',1), HIR.Type('i64',1))
# -
# ## Input Short-hand
#
# In order to make the IR easier to input in this notebook, let's create some shorthand.
# +
def _lift_(obj):
if isinstance(obj,HIR.expr):
return obj
if isinstance(obj,HIR.func):
return obj
elif isinstance(obj,HIR.Var):
return HIR.Evar(obj)
elif isinstance(obj,HIR.RDom):
return HIR.Erdom(obj)
elif isinstance(obj,HIR.Param):
return HIR.Eparam(obj)
elif isinstance(obj,HIR.Img):
return HIR.ImgFunc(obj)
elif type(obj) is int:
return HIR.Const(obj,i32)
elif type(obj) is float:
return HIR.Const(obj,f64)
else:
raise TypeError("unrecognized object type")
def _Min(x,y):
return HIR.Min(_lift_(x),_lift_(y))
def _Max(x,y):
return HIR.Max(_lift_(x),_lift_(y))
def _expr_add_(lhs,rhs):
return HIR.BinOp('+',_lift_(lhs),_lift_(rhs))
HIR.expr.__add__ = _expr_add_
HIR.expr.__radd__ = lambda r,l: _expr_add_(l,r)
def _expr_sub_(lhs,rhs):
return HIR.BinOp('-',_lift_(lhs),_lift_(rhs))
HIR.expr.__sub__ = _expr_sub_
HIR.expr.__rsub__ = lambda r,l: _expr_sub_(l,r)
def _expr_mul_(lhs,rhs):
return HIR.BinOp('*',_lift_(lhs),_lift_(rhs))
HIR.expr.__mul__ = _expr_mul_
HIR.expr.__rmul__ = lambda r,l: _expr_mul_(l,r)
def _expr_div_(lhs,rhs):
return HIR.BinOp('/',_lift_(lhs),_lift_(rhs))
HIR.expr.__truediv__ = _expr_div_
HIR.expr.__rtruediv__ = lambda r,l: _expr_div_(l,r)
def _expr_lt_(lhs,rhs):
return HIR.BinOp('<',_lift_(lhs),_lift_(rhs))
HIR.expr.__lt__ = _expr_lt_
HIR.expr.__rlt__ = lambda r,l: _expr_lt_(l,r)
def _expr_gt_(lhs,rhs):
return HIR.BinOp('>',_lift_(lhs),_lift_(rhs))
HIR.expr.__gt__ = _expr_gt_
HIR.expr.__rgt__ = lambda r,l: _expr_gt_(l,r)
def _expr_le_(lhs,rhs):
return HIR.BinOp('<=',_lift_(lhs),_lift_(rhs))
HIR.expr.__le__ = _expr_le_
HIR.expr.__rle__ = lambda r,l: _expr_le_(l,r)
def _expr_ge_(lhs,rhs):
return HIR.BinOp('>=',_lift_(lhs),_lift_(rhs))
HIR.expr.__ge__ = _expr_ge_
HIR.expr.__rge__ = lambda r,l: _expr_ge_(l,r)
# expose arithmetic operators to un-lifted vars, rdoms, params
for t in [HIR.var,HIR.rdom,HIR.param]:
for nm in ['__add__','__sub__','__mul__','__truediv__',
'__radd__','__rsub__','__rmul__','__rtruediv__',
'__lt__','__gt__','__le__','__ge__',
'__rlt__','__rgt__','__rle__','__rge__']:
setattr(t,nm,getattr(HIR.expr,nm))
def _func_getitem_(f,keys):
if not type(keys) is tuple: keys = (keys,)
keys = [ _lift_(k) for k in keys ]
f = _lift_(f)
return HIR.FAccess(f,keys)
HIR.func.__getitem__ = _func_getitem_
HIR.img.__getitem__ = _func_getitem_
# -
# ### Example Halide Programs in the IR
#
# Let's try to write:
# * a 3x3 blur kernel
# * a Laplacian-based energy sum of squares
# * an image gradient output as two separate images for dx and dy
# +
def gen_blur():
lift = _lift_
Min, Max = _Min, _Max
in_img = HIR.Img('in_img', 2, f64)
w, h = HIR.Param('w',i32), HIR.Param('h',i32)
clamp = lambda x,lo,hi: Max( lo, Min( hi, x ) )
x, y = HIR.Var('x'), HIR.Var('y')
f = HIR.Func('f')
blur_x = HIR.Func('blur_x')
blur_y = HIR.Func('blur_y')
stmts = [
HIR.PureDef( f, [x,y], in_img[clamp(x,0,w-1),clamp(y,0,h-1)]),
HIR.PureDef( blur_x, [x,y], (f[x-1,y] + 2.0*f[x,y] + f[x+1,y])/4.0 ),
HIR.PureDef( blur_y, [x,y], (blur_x[x,y-1] + 2.0*blur_x[x,y] + blur_x[x,y+1])/4.0 ),
]
pipeline = HIR.Pipeline(
vars = [x,y],
rdoms = [],
funcs = [f,blur_x,blur_y],
params = [w,h],
imgs = [in_img],
stmts = stmts,
outputs = [blur_y])
return pipeline
blurpipe = gen_blur()
def gen_laplacian():
lift = _lift_
Min, Max = _Min, _Max
f = HIR.Img('f', 2, f64)
w, h = HIR.Param('w',i32), HIR.Param('h',i32)
x = HIR.RDom('x', [HIR.Range(lift(0),lift(w))])
y = HIR.RDom('y', [HIR.Range(lift(0),lift(h))])
result = HIR.Func('result')
dx, dy = HIR.Func('dx'), HIR.Func('dy')
i, j = HIR.Var('i'), HIR.Var('j')
Eq = lambda x,y: HIR.BinOp('==',lift(x),lift(y))
body = ( HIR.Select( Eq(x,w-1), lift(0.0), dx[x,y]*dx[x,y] ) +
HIR.Select( Eq(y,h-1), lift(0.0), dy[x,y]*dy[x,y] ) )
stmts = [
HIR.PureDef(dx, [i,j], f[Min(i+1,w-1),j] - f[i,j]),
HIR.PureDef(dy, [i,j], f[i,Min(j+1,h-1)] - f[i,j]),
HIR.PureDef(result, [i], lift(0.0)),
HIR.Update (result, [lift(0)], HIR.BigSum(x, HIR.BigSum(y, body))),
]
pipeline = HIR.Pipeline(
vars = [i,j],
rdoms = [x,y],
funcs = [result,dx,dy],
params = [w,h],
imgs = [f],
stmts = stmts,
outputs = [result])
return pipeline
laplacepipe = gen_laplacian()
def gen_grad():
lift = _lift_
f = HIR.Img('f', 2, f64)
result = HIR.Func('result')
dx, dy = HIR.Func('dx'), HIR.Func('dy')
i, j = HIR.Var('i'), HIR.Var('j')
stmts = [
HIR.PureDef(dx, [i,j], f[i+1,j] - f[i,j]),
HIR.PureDef(dy, [i,j], f[i,j+1] - f[i,j]),
]
pipeline = HIR.Pipeline(
vars = [i,j],
rdoms = [],
funcs = [dx,dy],
params = [],
imgs = [f],
stmts = stmts,
outputs = [dx,dy])
return pipeline
gradpipe = gen_grad()
# -
# ## Output Format
#
# We can read these pipeline definitions more easily if we present them in a structured output format.
#
#
# +
def _HIR_type_str_rep(t):
if t.lanes > 1: return f"{t.base}v{t.lanes}"
else: return t.base
HIR.type.__str__ = _HIR_type_str_rep
del _HIR_type_str_rep
def _HIR_var_str_rep(v):
return v.name
HIR.var.__str__ = _HIR_var_str_rep
del _HIR_var_str_rep
def _HIR_rdom_str_rep(r):
bds = ']['.join([ f"{rg.lo},{rg.hi}" for rg in r.bounds ])
return f"{r.name}[{bds}]"
HIR.rdom.__str__ = _HIR_rdom_str_rep
del _HIR_rdom_str_rep
def _HIR_param_str_rep(p):
return f"{p.name} : {p.typ}"
HIR.param.__str__ = _HIR_param_str_rep
del _HIR_param_str_rep
def _HIR_img_str_rep(i):
return f"{i.name}({i.ndim}) : {i.typ}"
HIR.img.__str__ = _HIR_img_str_rep
del _HIR_img_str_rep
def _HIR_func_str_rep(f):
if type(f) is HIR.Func: return f.name
elif type(f) is HIR.ImgFunc: return f.img.name
HIR.func.__str__ = _HIR_func_str_rep
del _HIR_func_str_rep
_HIR_op_prec = {
"+" : 30,
"-" : 30,
"*" : 40,
"/" : 40,
"<" : 20,
">" : 20,
"<=" : 20,
">=" : 20,
"==" : 10,
}
def _HIR_expr_str_rep(e,prec=0):
eclass = type(e)
s = "ERROR"
if eclass is HIR.Evar: s = e.v.name
elif eclass is HIR.Erdom: s = e.r.name
elif eclass is HIR.Eparam: s = e.p.name
elif eclass is HIR.Const:
if e.typ is i32 or e.typ is f64:
s = str(e.v)
else:
s = f"({e.v}:{e.typ})"
elif eclass is HIR.BinOp:
op_prec = _HIR_op_prec[e.op]
s = (f"{_HIR_expr_str_rep(e.lhs,op_prec)} {e.op} "
f"{_HIR_expr_str_rep(e.rhs,op_prec+1)}")
if prec > op_prec: s = f"({s})"
elif eclass is HIR.Min or eclass is HIR.Max:
fname = "Min" if eclass is HIR.Min else "Max"
s = f"{fname}({e.lhs},{e.rhs})"
elif eclass is HIR.Select:
s = f"select({e.pred},{e.lhs},{e.rhs})"
elif eclass is HIR.FAccess:
args = ','.join([ str(a) for a in e.args ])
s = f"{e.f}({args})"
elif eclass is HIR.BigSum:
s = f"sum({e.r.name},{e.body})"
return s
HIR.expr.__str__ = _HIR_expr_str_rep
_HIR_expr_str_rep
def _HIR_stmt_str_rep(s):
args = ','.join([ str(a) for a in s.args ])
return f"{s.f}({args}) = {s.rhs}"
HIR.stmt.__str__ = _HIR_stmt_str_rep
del _HIR_stmt_str_rep
def _HIR_pipe_str_rep(p):
vs = '\n '.join([ str(v) for v in p.vars ])
rs = '\n '.join([ str(r) for r in p.rdoms ])
fs = '\n '.join([ str(f) for f in p.funcs ])
ps = '\n '.join([ str(p) for p in p.params ])
imgs = '\n '.join([ str(i) for i in p.imgs ])
stmts = '\n '.join([ str(s) for s in p.stmts ])
outs = '\n '.join([ str(o) for o in p.outputs ])
s = (f"Var {vs}\n"
f"RDom {rs}\n"
f"Func {fs}\n"
f"Param {ps}\n"
f"Img {imgs}\n"
f"Stmt {stmts}\n"
f"Out {outs}")
return s
HIR.pipeline.__str__ = _HIR_pipe_str_rep
del _HIR_pipe_str_rep
# -
# ### Printing Out the Example Programs
print("Blur Pipeline\n----------")
print(blurpipe)
print("\n\nLaplacian Energy Pipeline\n----------")
print(laplacepipe)
print("\n\nGradient Pipeline\n----------")
print(gradpipe)
# ## Executing a Pipeline
#
# We would like some way to execute a pipeline. In general, we may want other ways to execute or compile a pipeline, but for the time being, we will rely on the following ideas.
#
# Every pipeline has some number of `Var`, `RDom`, and `Func` variables. However, by definition these must all be internal to the pipeline. Specifically `Param` and `Img` variables represent external inputs. And then the output funcs represent the returned values.
#
# Therefore we can define a Halide pipeline's compilation to a function as supplying and receiving these specific parameters and buffers. The multi-dimensional buffers will be specified as numpy arrays.
#
# To begin, we must lower all of the pipeline IR nodes into Halide objects, which I will call "compilation" here even though the Halide compiler has not properly been invoked yet.
# +
def _HIR_Type_struct(typ):
if hasattr(typ, '_cached_struct'): return typ._cached_struct
if typ.base[0] == 'f': flag = C.type_float
elif typ.base[0] == 'u': flag = C.type_uint
elif typ.base[0] == 'i': flag = C.type_int
bits = int(typ.base[1:])
typ._cached_struct = halide_type_t(flag,bits,typ.lanes)
return typ._cached_struct
HIR.Type.struct = _HIR_Type_struct
del _HIR_Type_struct
class _HIR_Compilation:
def __init__(self, pipe):
self._pipe = pipe
self._vars = {
v : C.hwrap_new_var(bytes(v.name,'utf-8'))
for v in pipe.vars }
self._params = {
p : C.hwrap_new_param(bytes(p.name,'utf-8'),
p.typ.struct())
for p in pipe.params }
self._imgs = {
i : C.hwrap_new_img(bytes(i.name,'utf-8'),
i.ndim, i.typ.struct())
for i in pipe.imgs }
self._funcs = {
f : C.hwrap_new_func(bytes(f.name,'utf-8'))
for f in pipe.funcs }
self._rdoms = {}
self._exprs = {}
self._stmts = {
s : self.get_stmt(s)
for s in pipe.stmts }
def get_func(self,f):
if f in self._funcs: return self._funcs[f]
else:
assert type(f) is HIR.ImgFunc
f_img = C.hwrap_img_to_func(self._imgs[f.img])
self._funcs[f] = f_img
return f_img
def get_rdom(self,r):
if r in self._rdoms: return self._rdoms[r]
n_bd = len(r.bounds)
bds = []
for rng in r.bounds:
bds.append( self.get_expr(rng.lo) )
bds.append( self.get_expr(rng.hi) )
c_bds = ((n_bd * 2) * hw_expr_t)(*bds)
rd = C.hwrap_new_rdom(bytes(r.name,'utf-8'),
n_bd, c_bds)
self._rdoms[r] = rd
return rd
def get_expr(self,e):
if e in self._exprs: return self._exprs[e]
ee = None
eclass = type(e)
if eclass is HIR.Const:
assert e.typ.lanes == 1
ee = getattr(C, f"hwrap_{e.typ.base}_to_expr")(e.v)
elif eclass is HIR.Evar:
ee = C.hwrap_var_to_expr(self._vars[e.v])
elif eclass is HIR.Erdom:
rr = self.get_rdom(e.r)
ee = C.hwrap_rdom_to_expr(rr)
elif eclass is HIR.Eparam:
ee = C.hwrap_param_to_expr(self._params[e.p])
elif eclass is HIR.BinOp:
if e.op == "+": op_f = C.hwrap_add
elif e.op == "-": op_f = C.hwrap_sub
elif e.op == "*": op_f = C.hwrap_mul
elif e.op == "/": op_f = C.hwrap_div
elif e.op == "==": op_f = C.hwrap_eq
elif e.op == "<": op_f = C.hwrap_lt
elif e.op == ">": op_f = C.hwrap_gt
elif e.op == "<=": op_f = C.hwrap_le
elif e.op == ">=": op_f = C.hwrap_ge
else: assert False, f"unrecognized operator: {e.op}"
ee = op_f(self.get_expr(e.lhs), self.get_expr(e.rhs))
elif eclass is HIR.Min:
ee = C.hwrap_min(self.get_expr(e.lhs), self.get_expr(e.rhs))
elif eclass is HIR.Max:
ee = C.hwrap_max(self.get_expr(e.lhs), self.get_expr(e.rhs))
elif eclass is HIR.Select:
ee = C.hwrap_select(self.get_expr(e.pred),
self.get_expr(e.lhs),
self.get_expr(e.rhs))
elif eclass is HIR.FAccess:
args = [ self.get_expr(a) for a in e.args ]
c_args = (len(args)*hw_expr_t)(*args)
ee = C.hwrap_access_func(self.get_func(e.f),
len(args),c_args)
elif eclass is HIR.BigSum:
r = self.get_rdom(e.r)
ee = C.hwrap_big_sum(r, self.get_expr(e.body))
self._exprs[e] = ee
return ee
def get_stmt(self, s):
f = self.get_func(s.f)
rhs = self.get_expr(s.rhs)
if type(s) is HIR.PureDef:
args = [ self._vars[v] for v in s.args ]
c_args = (len(args)*hw_var_t)(*args)
return C.hwrap_pure_def(f, len(args), c_args, rhs)
elif type(s) is HIR.Update:
args = [ self.get_expr(e) for e in s.args ]
c_args = (len(args)*hw_expr_t)(*args)
return C.hwrap_update(f, len(args), c_args, rhs)
# -
# ### NumPy Bindings
#
# Let's go ahead and include these buffer conversions here. We'll need them to actually execute a pipeline.
def _ndarray_to_halide_buf(a):
def typ_convert(dt):
t = dt.type
# remapping to prevent some pointless errors
if t is float:
t = np.float64 if (sys.float_info.max_exp == 1024) else np.float32
if t is int: t = np.int32
# main case switch
if t is np.int8: return halide_type_t(C.type_int,8,1)
elif t is np.int16: return halide_type_t(C.type_int,16,1)
elif t is np.int32: return halide_type_t(C.type_int,32,1)
elif t is np.int64: return halide_type_t(C.type_int,64,1)
elif t is np.uint8: return halide_type_t(C.type_uint,8,1)
elif t is np.uint16: return halide_type_t(C.type_uint,16,1)
elif t is np.uint32: return halide_type_t(C.type_uint,32,1)
elif t is np.uint64: return halide_type_t(C.type_uint,64,1)
elif t is np.float32: return halide_type_t(C.type_float,32,1)
elif t is np.float64: return halide_type_t(C.type_float,64,1)
else:
raise TypeError(f"unexpected type {t}")
buf = halide_buffer_t()
buf.device = 0
buf.device_interface = None
buf.host = a.ctypes.data_as(ctypes.POINTER(ctypes.c_ubyte))
buf.flags = 0
buf.type = typ_convert(a.dtype)
buf.dimensions = a.ndim
buf.dim = (halide_dimension_t * a.ndim)()
# now loop through and sort out each dimension
for k in range(0,a.ndim):
s = int(a.strides[k] / a.itemsize)
assert a.strides[k] % a.itemsize == 0
buf.dim[k] = halide_dimension_t(0,a.shape[k],s,0)
buf.padding = None
return buf
# Testing that this works.
Av = np.array([[5.,2.,0.],[2.2,0.,4.5],[0.,6.1,3.3]], order='F')
Ahv = _ndarray_to_halide_buf(Av)
Ahv
# ### Execution
#
# In order to invoke Halide's auto-tuner we need to have estimated values for parameters and input images. However, we don't have sufficient data to do that until we have at least one call to the Halide function. Therefore, we must have a special JIT function to apply these estimates on the first invocation
# +
def _HIR_Type_ctype(typ):
if hasattr(typ, '_cached_ctype'): return typ._cached_ctype
if typ.base == 'f32': ct = ctypes.c_float
elif typ.base == 'f64': ct = ctypes.c_double
elif typ.base == 'u8': ct = ctypes.c_uint8
elif typ.base == 'u16': ct = ctypes.c_uint16
elif typ.base == 'u32': ct = ctypes.c_uint32
elif typ.base == 'u64': ct = ctypes.c_uint64
elif typ.base == 'i8': ct = ctypes.c_int8
elif typ.base == 'i16': ct = ctypes.c_int16
elif typ.base == 'i32': ct = ctypes.c_int32
elif typ.base == 'i64': ct = ctypes.c_int64
typ._cached_ctype = ct
return typ._cached_ctype
HIR.Type.ctype = _HIR_Type_ctype
del _HIR_Type_ctype
class _HIR_JIT_Execution(_HIR_Compilation):
def __init__(self, pipe):
super().__init__(pipe)
def _check_args(self, params, imgs, outputs):
if type(params) != list: raise TypeError("expected list of 'params'")
if type(imgs) != list: raise TypeError("expected list of 'imgs'")
if type(outputs)!= list: raise TypeError("expected list of 'outputs'")
n_p = len(self._pipe.params)
n_i = len(self._pipe.imgs)
n_o = len(self._pipe.outputs)
if len(params) != n_p: raise TypeError(f"expected list of {n_p} 'params'")
if len(imgs) != n_i: raise TypeError(f"expected list of {n_i} 'imgs'")
if len(outputs) != n_o: raise TypeError(f"expected list of {n_o} 'outputs'")
def _set_params(self, params):
for k,val in enumerate(params):
p_IR = self._pipe.params[k]
p_obj = self._params[p_IR]
val_ref = ctypes.byref(p_IR.typ.ctype()(val))
C.hwrap_set_param(p_obj,val_ref)
def _jit_compile(self, params, imgs, outputs):
if hasattr(self,'_pipeline_obj'): return
i32 = C.hwrap_i32_to_expr
self._set_params(params)
# estimate input bounds
for k,np_arr in enumerate(imgs):
img_IR = self._pipe.imgs[k]
img_obj = self._imgs[img_IR]
for d_i,d_N in enumerate(np_arr.shape):
C.hwrap_set_img_bound_estimate(img_obj,d_i,i32(0),i32(d_N))
# estimate output bounds
out_fs = []
for k,np_arr in enumerate(outputs):
out_IR = self._pipe.outputs[k]
out_obj = self._funcs[out_IR]
out_fs.append(out_obj)
for d_i,d_N in enumerate(np_arr.shape):
C.hwrap_set_func_bound_estimate(out_obj,d_i,i32(0),i32(d_N))
n_out = len(outputs)
c_fs = (n_out * hw_func_t)(*out_fs)
self._pipeline_obj = C.hwrap_new_pipeline(n_out,c_fs)
C.hwrap_autoschedule_pipeline(self._pipeline_obj)
def _exec(self, params, imgs, outputs):
self._check_args(params,imgs,outputs)
self._jit_compile(params,imgs,outputs)
# bind the arguments
self._set_params(params)
# bind input buffers
for k,np_arr in enumerate(imgs):
h_buf = _ndarray_to_halide_buf(np_arr)
img_obj = self._imgs[self._pipe.imgs[k]]
C.hwrap_set_img(img_obj, ctypes.byref(h_buf))
# bind output buffers and Execute!
outs = [ _ndarray_to_halide_buf(arr) for arr in outputs ]
c_outs = (len(outs)*halide_buffer_t)(*outs)
C.hwrap_realize_pipeline(self._pipeline_obj, len(outs),c_outs)
# -
# In order to make execution easier to invoke on a pipeline, we can augment the Pipeline object with functions directly.
# +
def _HIR_Pipeline_signature(self):
ps = '\n '.join([ str(p) for p in self.params ])
imgs = '\n '.join([ str(i) for i in self.imgs ])
outs = '\n '.join([ str(o) for o in self.outputs ])
s = (f"Param {ps}\n"
f"Img {imgs}\n"
f"Out {outs}")
return s
HIR.Pipeline.signature = _HIR_Pipeline_signature
del _HIR_Pipeline_signature
def _HIR_Pipeline_exec(self,params,imgs,outputs):
if not hasattr(self,'_executor'):
self._executor = _HIR_JIT_Execution(self)
self._executor._exec(params,imgs,outputs)
HIR.Pipeline.exec = _HIR_Pipeline_exec
del _HIR_Pipeline_exec
# -
# ### Testing Execution
#
# First, let's get a couple of test images...
import PIL.Image
# +
def gen_checker_arr(w,h,k):
a = []
for x in range(0,w):
a.append([])
x_1 = (x//k)%2
for y in range(0,h):
y_1 = (y//k)%2
a[x].append( float((x_1+y_1)%2) )
return np.array(a, order='F')
checker = gen_checker_arr(100,100,10)
def gen_ramp_arr(w,h):
a = []
for x in range(0,w):
a.append([])
for y in range(0,h):
a[x].append( float(x+y) )
return np.array(a, order='F')
ramp = gen_ramp_arr(100,100)
Z = np.zeros([100,100], order='F')
# -
display(PIL.Image.fromarray(255*checker).convert("RGB"))
display(PIL.Image.fromarray(ramp).convert("RGB"))
# Now, in order to hold outputs of other sizes, we need the following buffers to be setup
blur_out = np.zeros([100,100], order='F')
energy_out = np.zeros([1], order='F')
grad_x_out = np.zeros([99,100], order='F')
grad_y_out = np.zeros([100,99], order='F')
# We can call the pipelines and visualize results now...
gradpipe.exec([],[ramp],[grad_x_out,grad_y_out])
display(PIL.Image.fromarray(128*grad_x_out).convert("RGB"))
display(PIL.Image.fromarray(128*grad_y_out).convert("RGB"))
gradpipe.exec([],[checker],[grad_x_out,grad_y_out])
display(PIL.Image.fromarray(128*grad_x_out + 128).convert("RGB"))
display(PIL.Image.fromarray(128*grad_y_out + 128).convert("RGB"))
blurpipe.exec([100,100],[ramp],[blur_out])
display(PIL.Image.fromarray(1*blur_out).convert("RGB"))
blurpipe.exec([100,100],[checker],[blur_out])
display(PIL.Image.fromarray(256*blur_out).convert("RGB"))
laplacepipe.exec([100,100],[ramp],[energy_out])
print(energy_out[0])
laplacepipe.exec([100,100],[checker],[energy_out])
print(energy_out[0])
|
notebooks/Halide Target.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Buuuuli/AIPI530/blob/main/test_model.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="PQgmLBWM9ufs"
def test_model(model,test_loader,device):
model = model.to(device)
# Turn autograd off
with torch.no_grad():
# Set the model to evaluation mode
model.eval()
# Set up lists to store true and predicted values
test_preds = []
probability = []
# Calculate the predictions on the test set and add to list
for data in test_loader:
inputs = data[0].to(device)
# Feed inputs through model to get raw scores
logits = model.forward(inputs) #model_resnet # change net to cost_path
# Convert raw scores to probabilities (not necessary since we just care about discrete probs in this case)
probs = F.softmax(logits,dim=1)
# Get discrete predictions using argmax
preds = np.argmax(probs.cpu().numpy(),axis=1)
# Add predictions and actuals to lists
test_preds.extend(preds)
probability.extend(probs)
return test_preds,probability
|
test_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Prepare dataset
# The purpose of this file is to normalize dataset to have same size along the whole dataset in one run.
# This code finds all files from the directory and cuts each of them into smaller pieces of same *length*, optionally with a *stride*. If the piece of a file is shorter than a *length* but still longer than a *minimum length treshold* zeroes at the end of a file are padded (to make the size equal to *length*).
#
# To-do list
#
# **Part 1**
# * [x] find all files in the directory
# * [x] prepare a strategy how to cut files: user gives file length in seconds, but we oparate on array indexes
# * [x] cut sound into pieces
# * [x] apply melspectrogram
# * [x] save files
#
# **Part 2**
# * [ ] Prepare test, validation and training sets with k-fold validation
# ## Create list of all files to cut
# +
# %matplotlib inline
import matplotlib
matplotlib.interactive(False)
matplotlib.use('Agg')
# find all of the files in the directory
import os
import gc
basePath="../data/xeno-canto-dataset-full-all-Countries/"
melsPath= "../data/mels-27class/"
birds=[] # list of all birds
for root, dirs, files in os.walk(basePath):
if root == basePath:
birds=dirs
birds50=[]
flist=[] # list of all files
blist=[] # list of files for one bird
i50=0;
for i, bird in enumerate(birds):
for root, dirs, files in os.walk(basePath+bird):
for file in files:
if file.endswith(".mp3"):
blist.append(os.path.join(root, file))
if len(blist) > 50:
i50 = i50+1;
print(i50, ". Found ", len(blist), ' files for ', bird ,'(',i+1,')')
birds50.append(bird)
flist.append(blist)
blist=[]
print(birds50)
print(root)
# -
# ## Find strategy to cut the file
# We want to cut files to smaller pieces of the desired size (5 seconds in example), and stride of 1 second. Stride tells us how different pieces of files will overlap at each other.
def saveMel(signal, directory):
gc.enable()
# MK_spectrogram modified
N_FFT = 1024 #
HOP_SIZE = 1024 #
N_MELS = 128 # Higher
WIN_SIZE = 1024 #
WINDOW_TYPE = 'hann' #
FEATURE = 'mel' #
FMIN = 1400
fig = plt.figure(1,frameon=False)
fig.set_size_inches(6,6)
ax = plt.Axes(fig, [0., 0., 1., 1.])
ax.set_axis_off()
fig.add_axes(ax)
S = librosa.feature.melspectrogram(y=signal, sr=sr,
n_fft=N_FFT,
hop_length=HOP_SIZE,
n_mels=N_MELS,
htk=True,
fmin=FMIN, # higher limit ##high-pass filter freq.
fmax=sr/2) # AMPLITUDE
librosa.display.specshow(librosa.power_to_db(S**2,ref=np.max), fmin=FMIN) #power = S**2
fig.savefig(directory)
plt.ioff()
#plt.show(block=False)
fig.clf()
ax.cla()
plt.clf()
plt.close('all')
# +
import warnings
warnings.filterwarnings('ignore')
import sys
from tqdm import tqdm_notebook as tqdm
import librosa
import librosa.display
import numpy as np
import matplotlib.pyplot as plt
size = {'desired': 5, # [seconds]
'minimum': 4, # [seconds]
'stride' : 0, # [seconds]
'name': 5 # [number of letters]
} # stride should not be bigger than desired length
print('Number of directories to check and cut: ', len(flist))
#step = (size['desired']-size['stride'])*sr # length of step between two cuts in seconds
step=1
if step>0:
for bird, birdList in enumerate(flist):
print("Processing ",bird,'. ', birds50[bird], "...")
for birdnr, path in tqdm(enumerate(birdList)):
# load the mp3 file
directory=melsPath+str(bird)+birds50[bird][:size['name']]+"/"
if not os.path.exists(directory):
os.makedirs(directory)
if not os.path.exists(directory+path.rsplit('/',1)[1].replace(' ', '')[:-4]+"1_1.png"):
signal, sr = librosa.load(path) # sr = sampling rate
step = (size['desired']-size['stride'])*sr # length of step between two cuts in seconds
nr=0;
for start, end in zip(range(0,len(signal),step),range(size['desired']*sr,len(signal),step)):
# cut file and save each piece
nr=nr+1
# save the file if its length is higher than minimum
if end-start > size['minimum']*sr:
melpath=path.rsplit('/',1)[1]
melpath=directory+melpath.replace(' ', '')[:-4]+str(nr)+"_"+str(nr)+".png"
saveMel(signal[start:end],melpath)
#print('New file...',start/sr,' - ',end/sr)
#print('Start: ',start,'end: ', end, 'length: ', end-start)
pass
else:
print("Error: Stride should be lower than desired length.")
print('Number of files after cutting: ')
# -
# Test
import matplotlib.image as mpimg
ilist=[]
for root, dirs, files in os.walk(melsPath):
print(dirs)
for file in files:
if file.endswith(".png"):
ilist.append(os.path.join(root, file))
img=mpimg.imread(ilist[0])
imgplot = plt.imshow(img)
plt.show()
img=mpimg.imread(ilist[100])
imgplot = plt.imshow(img)
plt.show()
img=mpimg.imread(ilist[1000])
imgplot = plt.imshow(img)
plt.show()
img=mpimg.imread(ilist[40000])
imgplot = plt.imshow(img)
plt.show()
print("Found ",len(ilist)," files")
# +
#print(path)
#os.remove(path)
# -
|
notebooks/AM_prepareData.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import xgboost as xgb
from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn.model_selection import train_test_split
import gc
import math
data_frame = pd.read_pickle("../data/interim/train_data.pkl")
data_frame.primary_use.unique().size
data_frame.site_id.unique().size
data_frame.head()
timestamp = data_frame['timestamp']
#data_frame.drop("timestamp")
timestamp_seconds_of_day = (timestamp.dt.hour * 60 + timestamp.dt.minute) * 60 + timestamp.dt.second
data_frame["time_sin"] = np.sin(2 * np.pi * timestamp_seconds_of_day / 86400)
data_frame["time_cos"] = np.cos(2 * np.pi * timestamp_seconds_of_day / 86400)
data_frame["dayofweek_sin"] = np.sin(2 * np.pi * timestamp.dt.dayofweek / 7)
data_frame["dayofweek_cos"] = np.cos(2 * np.pi * timestamp.dt.dayofweek / 7)
data_frame["dayofyear_sin"] = np.sin(2 * np.pi * timestamp.dt.dayofyear / 366)
data_frame["dayofyear_cos"] = np.cos(2 * np.pi * timestamp.dt.dayofyear / 366)
data_frame.head()
data_frame.sample(100).plot.scatter("time_sin", "time_cos").set_aspect("equal")
data_frame.sample(100).plot.scatter("dayofweek_sin", "dayofweek_cos").set_aspect("equal")
data_frame.sample(100).plot.scatter("dayofyear_sin", "dayofyear_cos").set_aspect("equal")
wind_direction = data_frame['wind_direction']
#data_frame.drop("wind_direction")
data_frame["wind_direction_sin"] = np.sin(2 * np.pi * wind_direction / 360)
data_frame["wind_direction_cos"] = np.cos(2 * np.pi * wind_direction / 360)
data_frame.loc[data_frame["wind_direction"].isna(), ["wind_direction_sin", "wind_direction_cos"]] = 0
data_frame.loc[data_frame["wind_speed"] == 0, ["wind_direction_sin", "wind_direction_cos"]] = 0
data_frame.head()
data_frame["wind_direction"].unique()
data_frame[data_frame["wind_direction"].isna()].head()
data_frame[data_frame["wind_speed"]==0].head()
data_frame.sample(100).plot.scatter("wind_direction_sin", "wind_direction_cos").set_aspect("equal")
|
notebooks/01-au-feature-engineering-playground.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Data from baseballsavant.mlb.com
# + slideshow={"slide_type": "slide"}
import requests
import pandas as pd
import seaborn as sns
from bs4 import BeautifulSoup
import matplotlib.pyplot as plt
# + slideshow={"slide_type": "slide"}
judge = pd.read_csv('judge.csv')
# + slideshow={"slide_type": "slide"}
stanton = pd.read_csv('stanton.csv')
# -
pd.set_option('display.max_columns', None)
# + slideshow={"slide_type": "slide"}
judge.tail(5)
stanton.head()
# +
# All of <NAME>'s batted ball events in 2017
judge_events_2017 = judge[judge['game_date']>'2017-01-01']['events']
print("<NAME> batted ball event totals, 2017:")
print(judge_events_2017.value_counts)
# All of <NAME>'s batted ball events in 2017
stanton_events_2017 = stanton[stanton['game_date']>'2017-01-01']['events']
print("\n<NAME> batted ball event totals, 2017:")
print(stanton_events_2017.value_counts)
# +
judge_stanton_hr = pd.concat([judge_hr, stanton_hr])
sns.boxplot(judge_stanton_hr['release_speed']).set_title('Home Runs, 2015-2017')
# -
# # Data from pybaseball api
pip install pybaseball
from pybaseball import statcast
from pybaseball import playerid_lookup
from pybaseball import statcast_pitcher
playerid_lookup('kershaw', 'clayton')
# # Connection to AWS
# %load_ext sql
# %sql mysql://admin:sql_2020@lmu-sql.cmxyr8kgsxte.us-west-1.rds.amazonaws.com/sql_project
# + language="sql"
# SELECT pitch_type, game_date, release_speed
# FROM judge
# LIMIT 5;
# -
# + [markdown] slideshow={"slide_type": "slide"}
# # Use MLB's Statcast data to compare New York Yankees sluggers <NAME> and <NAME>.
# -
# %load_ext sql
# %sql mysql://admin:sql_2020@lmu-sql.cmxyr8kgsxte.us-west-1.rds.amazonaws.com/sql_project
# + language="sql"
# SELECT pitch_type, game_date, release_speed
# FROM judge
# LIMIT 5;
# + [markdown] slideshow={"slide_type": "slide"}
# # Who is a better hitter?
# + [markdown] slideshow={"slide_type": "subslide"}
# This is an important question to see who contributes more to the team.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Judge's home runs
# + slideshow={"slide_type": "subslide"} language="sql"
# SELECT DISTINCT events, COUNT(events)
# FROM judge
# WHERE game_year = '2017'
# AND events = 'home_run'
# + [markdown] slideshow={"slide_type": "slide"}
# ## Stanton's home runs
# + slideshow={"slide_type": "subslide"} language="sql"
# SELECT DISTINCT events, COUNT(events)
# FROM stanton
# WHERE game_year = '2017'
# AND events = 'home_run'
# + [markdown] slideshow={"slide_type": "slide"}
# Judge and Stanton are similar in a lot of ways, one being that they hit a lot of home runs. Stanton and Judge led baseball in home runs in 2017, with 59 and 52, respectively. These are exceptional totals - the player in third "only" had 45 home runs.
# + [markdown] slideshow={"slide_type": "slide"}
# # All batted ball events
# + [markdown] slideshow={"slide_type": "slide"}
# ## All of <NAME>'s batted ball events in 2017
# + slideshow={"slide_type": "subslide"} language="sql"
# SELECT events, COUNT(*)
# FROM judge
# WHERE year = '2017'
# GROUP BY events
# + [markdown] slideshow={"slide_type": "slide"}
# ## All of <NAME>'s batted ball events in 2017
# + slideshow={"slide_type": "subslide"} language="sql"
# SELECT events, COUNT(*)
# FROM stanton
# WHERE game_year = '2017'
# GROUP BY events
# + [markdown] slideshow={"slide_type": "subslide"}
# Even though their home runs are very similar, the frequencies of other events are quite different.
# +
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
# Load Aaron Judge's Statcast data
judge = pd.read_csv('judge.csv')
# Load Giancarlo Stanton's Statcast data
stanton = pd.read_csv('stanton.csv')
# +
# Filter to include home runs only
judge_hr = judge.loc[judge.events == 'home_run']
stanton_hr = stanton.loc[stanton.events == 'home_run']
# Create a figure with two scatter plots of launch speed vs. launch angle, one for each player's home runs
fig1, axs1 = plt.subplots(ncols=2, sharex=True, sharey=True)
sns.regplot(x=judge_hr.launch_speed, y=judge_hr.launch_angle, fit_reg=False, color='tab:blue', data=judge_hr, ax=axs1[0]).set_title('Aaron Judge\nHome Runs, 2015-2017')
sns.regplot(x=stanton_hr.launch_speed, y=stanton_hr.launch_angle, fit_reg=False, color='tab:blue', data=stanton_hr, ax=axs1[1]).set_title('Giancarlo Stanton\nHome Runs, 2015-2017')
# Create a figure with two KDE plots of launch speed vs. launch angle, one for each player's home runs
fig2, axs2 = plt.subplots(ncols=2, sharex=True, sharey=True)
sns.kdeplot(judge_hr.launch_speed, judge_hr.launch_angle, cmap="Blues", shade=True, shade_lowest=False, ax=axs2[0]).set_title('Aaron Judge\nHome Runs, 2015-2017')
sns.kdeplot(stanton_hr.launch_speed, stanton_hr.launch_angle, cmap="Blues", shade=True, shade_lowest=False, ax=axs2[1]).set_title('Giancarlo Stanton\nHome Runs, 2015-2017');
# + [markdown] slideshow={"slide_type": "slide"}
# # Pitch Type that Produced Home Runs
# + [markdown] slideshow={"slide_type": "subslide"}
# The next question to answer is whqat type of pitches produced home runs.
# + slideshow={"slide_type": "slide"} language="sql"
# SELECT judge.pitch_type AS 'JudgePitchHit', stanton.pitch_type AS 'StantonPitchHit',
# CASE
# WHEN judge.pitch_type = 'FF' THEN 'Fastball'
# WHEN judge.pitch_type = 'FT' THEN 'Fastball'
# WHEN judge.pitch_type = 'CH' THEN 'Off-Speed'
# WHEN judge.pitch_type = 'CU' THEN 'Off-Speed'
# END AS 'JudgePitchType',
# CASE
# WHEN stanton.pitch_type = 'FF' THEN 'Fastball'
# WHEN stanton.pitch_type = 'FT' THEN 'Fastball'
# WHEN stanton.pitch_type = 'FC' THEN 'Fastball'
# WHEN stanton.pitch_type = 'SI' THEN 'Fastball'
# WHEN stanton.pitch_type = 'FS' THEN 'Fastball'
# WHEN stanton.pitch_type = 'CH' THEN 'Off-Speed'
# WHEN stanton.pitch_type = 'CU' THEN 'Off-Speed'
# WHEN stanton.pitch_type = 'SL' THEN 'Off-Speed'
# END AS 'StantonPitchType'
# FROM judge
# JOIN stanton
# ON judge.game_date = stanton.game_date
# WHERE judge.events = 'home_run' AND
# stanton.events = 'home_run'
# LIMIT 20;
# + [markdown] slideshow={"slide_type": "subslide"}
# From looking at this data, one can see that Judge hits home runs mostly off of Four-Steam-Fastballs (FF). Stanton on the other hand, only hits about half of his home runs from four-steam-fastballs. Stantons other home runs are hit from Off-Speed
# types of balls such as Sliders (SL), Curveballs (CU), and Changeup (CH).
# + [markdown] slideshow={"slide_type": "slide"}
# # Home run hitting zone
# + slideshow={"slide_type": "subslide"}
Where home runs are most likely to be hit.
# + slideshow={"slide_type": "slide"} language="sql"
# SELECT DISTINCT zone, COUNT(zone) AS ZoneCount
# FROM judge
# WHERE zone IN
# (
# SELECT zone
# FROM stanton
# )
# AND events = 'home_run'
# GROUP BY zone
# ORDER BY ZoneCount DESC
# + slideshow={"slide_type": "slide"}
from IPython.display import Image
from IPython.core.display import HTML
Image(url= "https://cdn.vox-cdn.com/thumbor/T8PateY9GBdYSFMkZ-XTOX2Ic7k=/0x0:218x217/720x0/filters:focal(0x0:218x217):format(webp):no_upscale()/cdn.vox-cdn.com/uploads/chorus_asset/file/3681132/Zone_Map.0.png")
# + [markdown] slideshow={"slide_type": "subslide"}
# From the table, we can see that home runs are most likely to be hit from zones 5, 6, and 4. From the visual, one can see that this is the middle zone.
# + [markdown] slideshow={"slide_type": "slide"}
# # Release Speed of Ball Hit
# + [markdown] slideshow={"slide_type": "subslide"}
# Another comparison between the two players. What was the release speed of ball that was a home run?
# + slideshow={"slide_type": "slide"} language="sql"
# CREATE VIEW Compare_Release_of_HR AS
# SELECT judge.pitch_type AS 'JudgePitchType', stanton.pitch_type AS 'StantonPitchType', judge.release_speed AS 'JudgeReleaseSpeed', stanton.release_speed AS 'StantonReleaseSpeed'
# FROM judge, stanton
# WHERE judge.events = 'home_run'
# AND stanton.events = 'home_run'
# LIMIT 5;
# + slideshow={"slide_type": "subslide"} language="sql"
# SELECT *
# FROM Compare_Release_of_HR;
# + [markdown] slideshow={"slide_type": "subslide"}
# One can see that Judge is capable of hitting faster balls as home runs. Stanton on the other hand has about an average home run hitting speed of 89.5 miles per hour.
# -
# !jupyter nbconvert presentation.ipynb --to slides --post serve
|
presentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
import os
from glob import glob
from copy import copy
from sklearn.model_selection import train_test_split
from keras.preprocessing.image import ImageDataGenerator
# + _uuid="18c41871453fa8a4ead2604f938b178701883af7"
random_seed = 0
np.random.seed(random_seed)
# + _uuid="a85e72f50cc89d34f868fb2f3954dd8a01591eef"
# !ls -lh ../input
# + _uuid="21a4080a42381fd96230080bae354255282b5a10"
all_data = pd.read_csv('../input/train/train.csv')
list(all_data.columns)
# + _uuid="64703d29f45e6d77bb28d435489f960fba4ec9ec"
pet_data = all_data.set_index('PetID')
image_data = []
for image in glob('../input/train_images/*.jpg'):
basename = os.path.basename(image)
pet_id, _ = basename.rsplit('-')
pet_row = pet_data.loc[pet_id].to_dict()
pet_row['ImageFilename'] = image
pet_row['ImageBasename'] = basename
image_data.append(pet_row)
image_data = pd.DataFrame(image_data)
image_data.head(2)
# -
image_data['AdoptionSpeed']= image_data['AdoptionSpeed'].astype(str)
image_data = image_data.loc[image_data['Type'] == 1]
#image_data_cat = image_data.loc[image_data['Type'] == 2]
# + _uuid="14ba9f9d079e24182cf51e8ba1eba00d5d86ca39"
len(image_data), len(pet_data)
# + _uuid="3e1185d1c46cadb2e479302bd608b207e3883436"
y = image_data['AdoptionSpeed']
test_size = 0.2
validation_size = 0.2
# Split the training data off from leftover (i.e. validation and testing)
# train_test_split(*arrays, **options)
# random_state is the seed used by the random number generator
# data is split in a stratified fashion, using this as the class labels
X_train, X_leftover, y_train, y_leftover = train_test_split(
image_data, y, test_size=test_size, random_state=random_seed,
stratify=y.values # stratify to ensure equal distribution of classes
)
# Determine how much the leftover section should be split to test
test_split = test_size / (test_size + validation_size)
X_validate, X_test, y_validate, y_test = train_test_split(
X_leftover, y_leftover, test_size=test_split, random_state=random_seed,
stratify=y_leftover.values # stratify to ensure equal distribution of classes
)
X_train.shape, X_validate.shape, X_test.shape
# +
#X_train['AdoptionSpeed'].hist(bins=3)
# + _uuid="79e70e70c6b7ccc5f052937fd841d192b4ffb3d3"
train_datagen = ImageDataGenerator(
rescale=1./255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
horizontal_flip=True)
val_datagen = ImageDataGenerator(rescale=1./255)
# + _uuid="89396d68e17b5b1f65c9135a94ad7883e8073c72"
image_data.dtypes
# +
#from imblearn.keras import BalancedBatchGenerator
#from imblearn.under_sampling import NearMiss
#training_generator = BalancedBatchGenerator.flow_from_dataframe(
# X, y, sampler=NearMiss(), batch_size=10, random_state=42)
# -
BATCH_SIZE = 30
# + _uuid="5df1913c0210e2fa52de0e10fc3d2b6150c07b95"
# Generate batches of tensor image data with real-time data augmentation.
# The data will be looped over (in batches).
train_generator = train_datagen.flow_from_dataframe(
X_train.reset_index(), # Need to reset index due to bug in flow_from_dataframe
directory='../input/train_images/',
x_col='ImageBasename',
y_col='AdoptionSpeed',
target_size=(150, 150),
color_mode='rgb',
class_mode='categorical',
batch_size=BATCH_SIZE,
)
val_generator = val_datagen.flow_from_dataframe(
X_validate.reset_index(), # Need to reset index due to bug in flow_from_dataframe
directory='../input/train_images/',
x_col='ImageBasename',
y_col='AdoptionSpeed',
target_size=(150, 150),
color_mode='rgb',
class_mode='categorical',
batch_size= BATCH_SIZE,
)
# -
from collections import Counter
counter = Counter(train_generator.classes)
max_val = float(max(counter.values()))
class_weights = {class_id : max_val/num_images for class_id, num_images in counter.items()}
# +
#X_train
# +
#train_datagen = ImageDataGenerator(
# rescale=1./255)
# +
#train_generator = train_datagen.flow_from_dataframe(
# X_train.reset_index(), # Need to reset index due to bug in flow_from_dataframe
# directory='../input/train_images/',
# x_col='ImageBasename',
# y_col='AdoptionSpeed',
# target_size=(150, 150),
# color_mode='rgb',
# class_mode='categorical',
# batch_size=20)
# + _uuid="71aaf4c1c163258255bb5247aefee57f701e4d7f"
import os
from tensorflow.keras import layers
from tensorflow.keras import Model
# + _uuid="0fdca6f9a762397b5c59a7800e81bb9c2bceccf5"
# !wget --no-check-certificate \
# https://storage.googleapis.com/mledu-datasets/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5 \
# -O /tmp/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5
# + _uuid="6845e990b1c240a5d030242bab1a588b350cdc80"
from tensorflow.keras.applications.inception_v3 import InceptionV3
local_weights_file = '/tmp/inception_v3_weights_tf_dim_ordering_tf_kernels_notop.h5'
pre_trained_model = InceptionV3(
input_shape=(150, 150, 3), include_top=False, weights=None)
pre_trained_model.load_weights(local_weights_file)
# + _uuid="0481c19b0d1b760bd5d27aa54f26ed51bd317611"
for layer in pre_trained_model.layers:
layer.trainable = False
# + _uuid="5ea0997d217ef23e3ab849764ac66ad4814facce"
last_layer = pre_trained_model.get_layer('mixed7')
print ('last layer output shape:', last_layer.output_shape)
last_output = last_layer.output
# +
# import regularizer
from keras.regularizers import l1
# instantiate regularizer
reg = l1(0.001)
# example of l1 norm on activity from a cnn layer
from keras.layers import Conv2D
from keras.regularizers import l1
# -
from keras import regularizers
# + _uuid="1d59fa63f7184be87a7f14362398202eae3f2928"
from tensorflow.keras.optimizers import RMSprop
# Flatten the output layer to 1 dimension
x = layers.Flatten()(last_output)
# Add a fully connected layer with 1,024 hidden units and ReLU activation
x = layers.Dense(512, activation='relu', kernel_regularizer=regularizers.l2(0.01),
activity_regularizer=l1(0.001))(x)
# Add a dropout rate of 0.2
x = layers.Dropout(0.5)(x)
# Add a final sigmoid layer for classification
x = layers.Dense(5, activation='softmax')(x)
# Dropout is a a technique used to tackle Overfitting .
# The Dropout method in keras.layers module takes in a
# float between 0 and 1, which is the fraction of the
# neurons to drop.
# Configure and compile the model
model = Model(pre_trained_model.input, x)
# + _uuid="5dd67d25b0c17c660ef4981112dd17e95ec7d35e"
from tensorflow.keras.optimizers import SGD
unfreeze = False
# Unfreeze all models after "mixed6"
for layer in pre_trained_model.layers:
if unfreeze:
layer.trainable = True
if layer.name == 'mixed6':
unfreeze = True
# As an optimizer, here we will use SGD
# with a very low learning rate (0.00001)
model.compile(loss='categorical_crossentropy',
optimizer=SGD(
lr=0.0001,
momentum=0.9),
metrics=['acc'])
# + _uuid="5501ab895e83da11a8f4b1da45cde93fa41971ab"
history = model.fit_generator(
train_generator,
steps_per_epoch=len(X_train)//BATCH_SIZE,
epochs=100,
validation_data=val_generator,
validation_steps=len(X_validate)//BATCH_SIZE,
workers=4,
class_weight=class_weights,
verbose=1)
# + _uuid="0fe48d5f5df9ed14dd47a74f8c4b221e2c69da5b"
# %matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
# Retrieve a list of accuracy results on training and test data
# sets for each training epoch
acc = history.history['acc']
val_acc = history.history['val_acc']
# Retrieve a list of list results on training and test data
# sets for each training epoch
loss = history.history['loss']
val_loss = history.history['val_loss']
# Get number of epochs
epochs = range(len(acc))
# Plot training and validation accuracy per epoch
plt.plot(epochs, acc)
plt.plot(epochs, val_acc)
plt.title('Training and validation accuracy')
plt.figure()
# Plot training and validation loss per epoch
plt.plot(epochs, loss)
plt.plot(epochs, val_loss)
plt.title('Training and validation loss')
|
image-multi-class-weights.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
root = tkt.Tk() # 윈도우 창 생성
root.title("계산기") # Title 세팅
root.resizable(0,0) # 윈도우 크기 고정
root.wm_attributes("-topmost", 1) # 화면 상단에 유지
#변수 선언
equa = ""
equation = tkt.StringVar()
calculation = tkt.Label(root, textvariable=equation)
equation.set("계산식을 입력하세요 : ")
calculation.grid(row=2, columnspan=8)
def btnPress(num):
global equa
equa = equa + str(num)
def EqualPress():
global equa
total = str(eval(equa))
equation.set(total)
equa = ""
def ClearPress():
global equa
equa = ""
equation.set("")
Button0 = tkt.Button(root, text="0", bg='white',command=lambda: btnPress(0), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button0.grid(row=6, column=2, padx=10, pady=10)
Button1 = tkt.Button(root, text="1", bg='white',command=lambda: btnPress(1), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button1.grid(row=3, column=1, padx=10, pady=10)
Button2 = tkt.Button(root, text="2", bg='white',command=lambda: btnPress(2), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button2.grid(row=3, column=2, padx=10, pady=10)
Button3 = tkt.Button(root, text="3", bg='white',command=lambda: btnPress(3), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button3.grid(row=3, column=3, padx=10, pady=10)
Button4 = tkt.Button(root, text="4", bg='white',command=lambda: btnPress(4), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button4.grid(row=4, column=1, padx=10, pady=10)
Button5 = tkt.Button(root, text="5", bg='white',command=lambda: btnPress(5), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button5.grid(row=4, column=2, padx=10, pady=10)
Button6 = tkt.Button(root, text="6", bg='white',command=lambda: btnPress(6), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button6.grid(row=4, column=3, padx=10, pady=10)
Button7 = tkt.Button(root, text="7", bg='white',command=lambda: btnPress(7), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button7.grid(row=5, column=1, padx=10, pady=10)
Button8 = tkt.Button(root, text="8", bg='white',command=lambda: btnPress(8), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button8.grid(row=5, column=2, padx=10, pady=10)
Button9 = tkt.Button(root, text="9", bg='white',command=lambda: btnPress(9), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Button9.grid(row=5, column=3, padx=10, pady=10)
Plus = tkt.Button(root, text="+", bg='white',command=lambda: btnPress("+"), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Plus.grid(row=3, column=4, padx=10, pady=10)
Minus = tkt.Button(root, text="-", bg='white',command=lambda: btnPress("-"), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Minus.grid(row=4, column=4, padx=10, pady=10)
Multiply = tkt.Button(root, text="*", bg='white',command=lambda: btnPress("*"), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Multiply.grid(row=5, column=4, padx=10, pady=10)
Divide = tkt.Button(root, text="/", bg='white',command=lambda: btnPress("/"), height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Divide.grid(row=6, column=4, padx=10, pady=10)
Equal = tkt.Button(root, text="=", bg='white',command=EqualPress, height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Equal.grid(row=6, column=3, padx=10, pady=10)
Clear = tkt.Button(root, text="C", bg='white',command=ClearPress, height=1, width=7, borderwidth=1, relief=tkt.SOLID)
Clear.grid(row=6, column=1, padx=10, pady=10)
root.mainloop()
# -
|
Calculator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Viewing and analyzing volumetric timeseries data
# ### Load volumetric timeseries data with dask
# +
import dask.array as da
file_name = '../data/LLSM/AOLLSM_m4_560nm.zarr'
data = da.from_zarr(file_name)
# -
data
# ### Create an empty napari viewer
# %gui qt
# +
import napari
from napari.utils import nbscreenshot
viewer = napari.Viewer(axis_labels='tzyx')
nbscreenshot(viewer)
# -
# ## Display the volumetric timeseries
viewer.add_image(data, name='LLSM', multiscale=False, scale=[1, 3, 1, 1],
contrast_limits=[0, 150_000], colormap='magma');
nbscreenshot(viewer)
# ### Add an analyzed layer
# +
from skimage import filters
viewer.add_image(data.map_blocks(filters.sobel), name='sobel', scale=[1, 3, 1, 1],
contrast_limits=[0, 10_000]);
# -
nbscreenshot(viewer)
|
notebooks/dask_4D_LLSM.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import nltk
nltk.download('punkt')
import numpy as np
import pandas as pd
import nltk
from nltk.stem import PorterStemmer
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report,confusion_matrix
import seaborn as sns
from nltk.corpus import stopwords
import matplotlib.pyplot as plt
df = pd.read_csv('/Users/mustafa/Desktop/student age prediction task/reading-age-data.csv', encoding='latin-1')
df=df.rename(columns={'v1': 'Excerpt','v2': 'Book and Page','v3': 'Age'})
df.groupby('Age').describe() #75 percent pe mean, freq mean repetition and unique means 56
df['length'] = df['Excerpt'].apply(len)
df.head()
df_labels = df['Age']
df_labels.head(11)
# MEASURE LEANGTH OF MESSAGES
df['length'] = df['Excerpt'].apply(len)
# SHOW LENGTH IN GRAPHICAL FORM
df.hist(column='length',by='Age',bins=50, figsize=(15,6))
# +
#Data cleaning starts
df['Excerpt'] = df.Excerpt.map(lambda x: x.lower())
df['Excerpt'] = df.Excerpt.str.replace('[^\w\s]', ' ') #remove comma and spaces
# +
df['Excerpt'] = df['Excerpt'].apply(nltk.word_tokenize)
stops = set(stopwords.words("english"))
# -
stemmer = PorterStemmer()
df['Excerpt'] = df['Excerpt'].apply(lambda x: [stemmer.stem(y) for y in x]) #picks prefix and lem converts
show = df['Excerpt']
show.head()
df['Excerpt'] = df['Excerpt'].apply(lambda x: ' '.join(x))
count_vect = CountVectorizer()
counts = count_vect.fit_transform(df['Excerpt']); #count numeric values of tokens
transformer = TfidfTransformer().fit(counts) #transform to numeric values
counts = transformer.fit_transform(counts)
X_train, X_test, y_train, y_test = train_test_split(counts, df['Age'], test_size=0.3, random_state=69) #
from sklearn.tree import DecisionTreeClassifier
from sklearn.naive_bayes import MultinomialNB #works on text
from sklearn.svm import SVC
from sklearn.ensemble import AdaBoostClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=6)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
print(confusion_matrix(y_test, y_pred)) #cant tell properly because of so much age data cause of 28 numeric values
from sklearn.metrics import accuracy_score
print(accuracy_score(y_test, y_pred))
# implementing adabost
ab = AdaBoostClassifier().fit(X_train, y_train)
# +
predicted = ab.predict(X_test)
print(np.mean(predicted == y_test))
# -
# implementing naive bayes
NB = MultinomialNB().fit(X_train, y_train)
predicted = NB.predict(X_test)
print(np.mean(predicted == y_test))
print(confusion_matrix(y_test, predicted))
print(classification_report(y_test,predicted))
# implementing SVM
sv = SVC().fit(X_train, y_train)
predicted = sv.predict(X_test)
print(np.mean(predicted == y_test))
print(confusion_matrix(y_test, predicted))
# +
#print(classification_report(y_test,predicted))
# +
# implementing disession tree
dt = DecisionTreeClassifier().fit(X_train, y_train)
# +
predicted = dt.predict(X_test)
print(np.mean(predicted == y_test))
# -
print(confusion_matrix(y_test, predicted))
my_dataset = pd.read_csv('/Users/mustafa/Desktop/student age prediction task/reading-age-data.csv', encoding='latin-1')
# converting content to lower case
pred = (my_dataset['Excerpt'].str.lower())
# printing predictions made by model
print("prediction: {}". format(classifier.predict(count_vect.transform(pred.values.astype('U')))))
# saving predictions in a variable
my_pred = dt.predict(count_vect.transform(pred.values.astype('U')))
# saving predicted labels in .csv file
my_dataset['autotag'] = my_pred
my_dataset.to_csv('/Users/mustafa/Desktop/student age prediction task/reading-age-data.csv',index = False)
|
age prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jamavato25/Datasciense300/blob/main/Ejercicio_Matriz_4x4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="rESqp3SEu1J_"
import numpy as np
# + colab={"base_uri": "https://localhost:8080/"} id="3tuNRsHJvgmc" outputId="1c512d41-d4f7-4e0a-d91e-d8399175cae6"
m0 = [[2, 4, 5, 7],
[ 8, 3, 1,11],
[14, 6,10,12],
[ 9,13,15,None]]
for p in range(len(m0)) :
for e in range(len(m0[0])):
if m0[p][e]==None:
print(p,e)
q = p
t = e
print("_________________________________")
for x in range (q-1, q+2):
for y in range (t-1, t+2):
if x<4:
if y<4:
print(m0[x][y])
else:
pass
# + colab={"base_uri": "https://localhost:8080/"} id="SFIxb3u2KRgM" outputId="089ad303-f038-4a4d-bdfd-f59ff2bb1e3c"
m1 = [[2, 4, 5, 7],
[10, None, 1, 11],
[14, 6, 10, 8],
[ 9, 12, 15, 3]]
for i in range(len(m1)) :
for j in range(len(m1[0])):
if m1[i][j]==None:
print(i,j)
q = i
t = j
print("_________________________________")
for x in range (q-1, q+2):
for y in range (t-1, t+2):
if x<=4:
if y<=4:
print(m1[x][y])
else:
pass
# + colab={"base_uri": "https://localhost:8080/"} id="SQN7NvD8erqQ" outputId="6aca6a57-4f0f-4584-86ab-871737a69f05"
m2 = [[ 2, 4, 5, 7],
[ 10, 14, 1, 11],
[None, 6, 13, 8],
[ 9, 12, 15, 3]]
for i in range(len(m2)) :
for j in range(len(m2[0])):
if m2[i][j]==None:
print(i,j)
q = i
t = j
print("_________________________________")
for x in range (q-1, q+2):
for y in range (t-1, t+2):
if x>0:
if y<4:
print(m2[x][y])
else:
pass
# + id="jFEd1_K9pzUK"
def busqueda (p):
for i in range(len(p)):
for j in range(len(p[0])):
if p[i][j]==num:
print(i,j)
return(i,j)
# + colab={"base_uri": "https://localhost:8080/", "height": 235} id="XCEW-2v0IAtI" outputId="4608ec18-4683-4079-8734-7982ca425012"
import random
matriz = len[m0]
for i in range(0,4):
matriz [i] = len[m0]
a=""
c=1
for i in range(4):
for j in range(4):
matriz[i][j] = random.randint(1,16)
a+=str(c)+" "
c=c+1
print(a)
a=""
posicion = int(input("\n favor ingresar posicion [1_16]: "))
if(posicion % 4 == 0):
fila= int(posición / 4)-1
columna = 4
else:
fila = int(posicion/4)
columna = int(posicion % 4) - 1
print("\nValor en posicion", posicion, " : ", matriz[fila][columna], " ubicado en la fila: ", fila+1, "y columna:", columna+1)
a=""
for i in range(4):
for j in range(4):
a+=str(matriz[i][j])+" "
print(a)
a=" "
# + [markdown] id="Co5es3WXpzDG"
#
|
Ejercicio_Matriz_4x4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
empty_dictionary = {}
print(type(empty_dictionary))
bio_data = {'Name': '<NAME>', 'Age':35, 'Height':"5.6 ft", 'Hobby': 'Music'}
print(bio_data)
credentials = { 'UserA' : 'wkliopnc' , 'UserB': 98760 , 'UserC' :98760 }
hobby = bio_data['Hobby']
print(hobby)
age = bio_data['Age']
print(age)
age = bio_data.get('Age')
print(age)
profession = bio_data.get('profession','age')
print(profession)
bio_data['Age'] = 36
print(bio_data)
#add a key, val
bio_data['Profession'] = 'Singer'
print(bio_data)
print('Profession' in bio_data)
# +
#get list of keys
print(list(bio_data.keys()))
#get list of values
print(list(bio_data.values()))
# -
new_dictionary = dict(Country='Jamaica', Songs=['One Love','Misty Morning'])
print(new_dictionary)
bio_data.update(new_dictionary)
print(bio_data)
del bio_data['Songs']
print(bio_data)
# +
students_data = { 1:['<NAME>', 24] , 2:['<NAME>',25], 3:['<NAME>', 26], 4:['<NAME>',24], 5:['<NAME>',27]}
print(students_data)
# -
print(len(students_data))
#see all the details of students.
print(list(students_data.values()))
students_data[6] = ['<NAME>', 22]
print(students_data)
del students_data[2]
print(students_data)
print(list(students_data.keys()))
|
1. Python Introductory Course/1. Intro to Python/Dictionaries.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Q#
# language: qsharp
# name: iqsharp
# ---
# # Multi-Qubit Systems
#
# This tutorial introduces you to multi-qubit systems - their representation in mathematical notation and in Q# code, and the concept of entanglement.
#
# If you are not familiar with the [single-qubit systems](../Qubit/Qubit.ipynb), we recommend that you complete that tutorial first.
#
# This tutorial covers the following topics:
# * Vector representation of multi-qubit systems
# * Entangled and separable states
# * Dirac notation
# # Multi-Qubit Systems
#
# In the previous tutorial we discussed the concept of a qubit - the basic building block of a quantum computer.
# A multi-qubit system is a collection of multiple qubits, treated as a single system.
#
# Let's start by examining a system of two classical bits. Each bit can be in two states: $0$ and $1$. Therefore, a system of two bits can be in four different states: $00$, $01$, $10$, and $11$. Generally, a system of $N$ classical bits can be in any of the $2^N$ states.
#
# A system of $N$ qubits can also be in any of the $2^N$ classical states, but, unlike the classical bits, it can also be in a **superposition** of all these states.
#
# Similarly to single-qubit systems, a state of an $N$-qubit system can be represented as a complex vector of size $2^N$:
# $$\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_{2^N-1}\end{bmatrix}$$
# ## Basis States
#
# Similarly to single-qubit systems, multi-qubit systems have their own sets of basis states.
# The computational basis for an $N$-qubit system is a set of $2^N$ vectors, in each of which with one element equals $1$, and the other elements equal $0$.
#
# For example, this is the **computational basis** for a two-qubit system:
#
# $$\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\text{, }
# \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix}\text{, }
# \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}\text{, }
# \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}$$
#
# It is easy to see that these vectors form an orthonormal basis. Note that each of these basis states can be represented as a tensor product of some combination of single-qubit basis states:
#
# <table>
# <col width=200>
# <col width=200>
# <col width=200>
# <col width=200>
# <tr>
# <td style="text-align:center; background-color:white">$\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} =
# \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix}$</td>
# <td style="text-align:center; background-color:white">$\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} =
# \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix}$</td>
# <td style="text-align:center; background-color:white">$\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} =
# \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \end{bmatrix}$</td>
# <td style="text-align:center; background-color:white">$\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} =
# \begin{bmatrix} 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \end{bmatrix}$</td>
# </tr>
# </table>
#
# Any two-qubit system can be expressed as some linear combination of those tensor products of single-qubit basis states.
#
# Similar logic applies to systems of more than two qubits. In general case,
#
# $$\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_{2^N-1} \end{bmatrix} =
# x_0 \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} +
# x_1 \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix} + \dotsb +
# x_{2^N-1} \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix}$$
#
# The coefficients of the basis vectors define how "close" is the system state to the corresponding basis vector.
#
# > Just like with single-qubit systems, there exist other orthonormal bases states for multi-qubit systems. An example for a two-qubit system is the **Bell basis**:
# >
# > $$\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix}\text{, }
# \frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \\ 0 \\ -1 \end{bmatrix}\text{, }
# \frac{1}{\sqrt{2}}\begin{bmatrix} 0 \\ 1 \\ 1 \\ 0 \end{bmatrix}\text{, }
# \frac{1}{\sqrt{2}}\begin{bmatrix} 0 \\ 1 \\ -1 \\ 0 \end{bmatrix}$$
# >
# > You can check that these vectors are normalized, and orthogonal to each other, and that any two-qubit state can be expressed as a linear combination of these vectors. The vectors of Bell basis, however, can not be represented as tensor products of single-qubit basis states.
# # Separable states
#
# Sometimes the state of a multi-qubit system can be separated into the states of individual qubits or smaller subsystems.
# To do this, you would express the vector state of the system as a [tensor product](../LinearAlgebra/LinearAlgebra.ipynb#Tensor-Product) of the vectors representing each individual qubit/subsystem.
# Here is an example for two qubits:
#
# $$\begin{bmatrix} \frac{1}{\sqrt{2}} \\ 0 \\ \frac{1}{\sqrt{2}} \\ 0 \end{bmatrix} =
# \begin{bmatrix} \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} \end{bmatrix} \otimes
# \begin{bmatrix} 1 \\ 0 \end{bmatrix}$$
#
# The states that allow such representation are known as **separable states**.
# ### <span style="color:blue">Exercise 1</span>: Show that the state is separable
#
# $$\frac{1}{2} \begin{bmatrix} 1 \\ i \\ -i \\ 1 \end{bmatrix} =
# \begin{bmatrix} ? \\ ? \end{bmatrix} \otimes \begin{bmatrix} ? \\ ? \end{bmatrix}$$
#
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-1:-Show-that-the-state-is-separable).*
# > Note that finding such representation is not always possible, as you will see in the next exercise.
#
# ### <span style="color:blue">Exercise 2</span>: Is this state separable?
#
# $$\frac{1}{\sqrt{2}}\begin{bmatrix} 1 \\ 0 \\ 0 \\ 1 \end{bmatrix}$$
#
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-2:-Is-this-state-separable?).*
# # Entanglement
#
# As we've just seen, some quantum states are impossible to factor into individual qubit states or even into states of larger subsystems. The states of these qubits are inseparable from one another and must always be considered as part of a larger system - they are **entangled**.
#
# > For example, every state in the Bell basis we saw earlier is an entangled state.
#
# Entanglement is a huge part of what makes quantum computing so powerful.
# It allows us to link the qubits so that they stop behaving like individuals and start behaving like a large, more complex system.
# In entangled systems, measuring one of the qubits modifies the state of the other qubits, and tells us something about their state.
# In the example above, when one of the qubits is measured, we know that the second qubit will end up in the same state.
# This property is used extensively in many quantum algorithms.
# # Dirac Notation
#
# Just like with single qubits, [Dirac notation](../Qubit/Qubit.ipynb#Dirac-Notation) provides a useful shorthand for writing down states of multi-qubit systems.
#
# As we've seen earlier, multi-qubit systems have their own canonical bases, and the basis states can be represented as tensor products of single-qubit basis states. Any multi-qubit system can be represented as a linear combination of these basis states:
#
# $$\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} =
# x_0\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} +
# x_1\begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} +
# x_2\begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} +
# x_3\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} =
# x_0|0\rangle \otimes |0\rangle +
# x_1|0\rangle \otimes |1\rangle +
# x_2|1\rangle \otimes |0\rangle +
# x_3|1\rangle \otimes |1\rangle$$
#
# To simplify this, tensor products of basis states have their own notation:
#
# $$|0\rangle \otimes |0\rangle = |00\rangle \\
# |0\rangle \otimes |1\rangle = |01\rangle \\
# |1\rangle \otimes |0\rangle = |10\rangle \\
# |1\rangle \otimes |1\rangle = |11\rangle$$
#
# $$|0\rangle \otimes |0\rangle \otimes |0\rangle = |000\rangle$$
#
# And so on.
#
# Or, more generally:
#
# $$|i_0\rangle \otimes |i_1\rangle \otimes \dotsb \otimes |i_n\rangle = |i_0i_1...i_n\rangle$$
#
# Using this notation simplifies our example:
#
# $$\begin{bmatrix} x_0 \\ x_1 \\ x_2 \\ x_3 \end{bmatrix} =
# x_0|00\rangle + x_1|01\rangle + x_2|10\rangle + x_3|11\rangle$$
#
# Just like with single qubits, we can put arbitrary symbols within the kets the same way variables are used in algebra.
# Whether a ket represents a single qubit or an entire system depends on the context.
# Some ket symbols have a commonly accepted usage, such as the symbols for the Bell basis:
#
# <table>
# <col width=300>
# <col width=300>
# <tr>
# <td style="text-align:center; background-color:white">$|\Phi^+\rangle = \frac{1}{\sqrt{2}}\big(|00\rangle + |11\rangle\big) \\ |\Phi^-\rangle = \frac{1}{\sqrt{2}}\big(|00\rangle - |11\rangle\big)$</td>
# <td style="text-align:center; background-color:white">$|\Psi^+\rangle = \frac{1}{\sqrt{2}}\big(|01\rangle + |10\rangle\big) \\ |\Psi^-\rangle = \frac{1}{\sqrt{2}}\big(|01\rangle - |10\rangle\big)$</td>
# </tr>
# </table>
# >## Endianness
# >
# > In classical computing, endianness refers to the order of bits (or bytes) when representing numbers in binary. You're probably familiar with the typical way of writing numbers in binary: $0 = 0_2$, $1 = 1_2$, $2 = 10_2$, $3 = 11_2$, $4 = 100_2$, $5 = 101_2$, $6 = 110_2$, etc. This is known as **big-endian format**. In big-endian format, the *most significant* bits come first. For example: $110_2 = 1 \cdot 4 + 1 \cdot 2 + 0 \cdot 1 = 4 + 2 = 6$.
# >
# > There is an alternate way of writing binary numbers - **little-endian format**. In little-endian format, the *least significant* bits come first. For example, $2$ would be written as $01$, $4$ as $001$, and $6$ as $011$. To put it another way, in little endian format, the number is written backwards compared to the big-endian format.
# >
# > In Dirac notation for multi-qubit systems, it's common to see integer numbers within the kets instead of bit sequences. What those numbers mean depends on the context - whether the notation used is big-endian or little-endian.
# >
# > Examples with a 3 qubit system:
# >
# > <table>
# > <tr>
# > <th style="text-align:center; border:1px solid">Integer Ket</th>
# > <td style="text-align:center; border:1px solid">$|0\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|1\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|2\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|3\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|4\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|5\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|6\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|7\rangle$</td>
# > </tr>
# > <tr>
# > <th style="text-align:center; border:1px solid">Big-endian</th>
# > <td style="text-align:center; border:1px solid">$|000\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|001\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|010\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|011\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|100\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|101\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|110\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|111\rangle$</td>
# > </tr>
# > <tr>
# > <th style="text-align:center; border:1px solid">Little-endian</th>
# > <td style="text-align:center; border:1px solid">$|000\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|100\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|010\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|110\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|001\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|101\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|011\rangle$</td>
# > <td style="text-align:center; border:1px solid">$|111\rangle$</td>
# > </tr>
# ></table>
# >
# > Multi-qubit quantum systems that store superpositions of numbers are often referred to as **quantum registers**.
# ### <span style="color:blue">Demo: Multi-qubit systems</span>
#
# This demo shows you how to allocate multiple qubits in Q# and examine their joint state. It uses single-qubit gates for manipulating the individual qubit states - if you need a refresher on them, please see the [corresponding tutorial](../SingleQubitGates/SingleQubitGates.ipynb).
#
# These demos use the function `DumpMachine` to print the state of the quantum simulator.
# If you aren't familiar with the output of this function for single qubits, you should revisit the tutorial on [the concept of a qubit](../Qubit/Qubit.ipynb#Demo:-Examining-Qubit-States-in-Q#).
# When printing the state of multi-qubit systems, this function outputs the same information for each multi-qubit basis state.
# [This tutorial](../VisualizationTools/VisualizationTools.ipynb#Demo:-DumpMachine-for-multi-qubit-systems) explains how `DumpMachine` works for multiple qubits in more detail.
# +
// Run this cell using Ctrl+Enter (⌘+Enter on Mac)
// Then run the next cell to see the output
open Microsoft.Quantum.Diagnostics;
operation MultiQubitSystemsDemo () : Unit {
// This allocates an array of 2 qubits, each of them in state |0⟩.
// The overall state of the system is |00⟩
use qs = Qubit[2];
// X gate changes the first qubit into state |1⟩
// The entire system is now in state |10⟩
X(qs[0]);
Message("System in state |10⟩:");
DumpMachine();
// This changes the second qubit into state |+⟩ = (1/sqrt(2))(|0⟩ + |1⟩).
// The entire system is now in state (1/sqrt(2))(|10⟩ + |11⟩)
H(qs[1]);
Message("System in state (1/sqrt(2))(|10⟩ + |11⟩):");
DumpMachine();
// This changes the first qubit into state |-⟩ = (1/sqrt(2))(|0⟩ - |1⟩)
// The entire system is now in state 0.5(|00⟩ + |01⟩ - |10⟩ - |11⟩)
H(qs[0]);
Message("System in state 0.5(|00⟩ + |01⟩ - |10⟩ - |11⟩):");
DumpMachine();
// You can use DumpRegister to examine the state of specific qubits rather than the entire simulator.
// This prints the state of the first qubit
Message("First qubit (in state |-⟩ = (1/sqrt(2))(|0⟩ - |1⟩):");
DumpRegister((), [qs[0]]);
// The next lines entangle the qubits.
// Don't worry about what exactly they do for now
H(qs[1]);
CNOT(qs[0], qs[1]);
Message("Entangled state 0.5(|00⟩ - |11⟩):");
DumpMachine();
// Since the states of entangled qubits are inseparable,
// it makes no sense to examine only one of them
Message("Let's try to examine one of two entangled qubits on its own...");
DumpRegister((), [qs[0]]);
// This returns the system into state |00⟩
ResetAll(qs);
}
# -
%simulate MultiQubitSystemsDemo
# > You might have noticed that we've been "resetting" the qubits at the end of our demos, i.e., returning them to $|0\rangle$ state. Q# requires you to return your qubits into the $|0\rangle$ state before releasing them at the end of the `using` block.
# > The reason for this is entanglement.
# >
# > Consider running a program on a quantum computer: the number of qubits is very limited, and you want to reuse the released qubits in other parts of the program.
# If they are not in zero state by that time, they can potentially be still entangled with the qubits which are not yet released, thus operations you perform on them can affect the state of other parts of the program, causing erroneous and hard to debug behavior.
# >
# > Resetting the qubits to zero state automatically when they go outside the scope of their using block is dangerous as well: if they were entangled with others, measuring them to reset them can affect the state of the unreleased qubits, and thus change the results of the program - without the developer noticing this.
# >
# > The requirement that the qubits should be in zero state before they can be released aims to remind the developer to double-check that all necessary information has been properly extracted from the qubits, and that they are not entangled with unreleased qubits any more.
# >
# > (An alternative way to break entanglement is to measure qubits; in this case Q# allows to release them regardless of the measurement result. You can learn more about measurements in [this tutorial](../SingleQubitSystemMeasurements/SingleQubitSystemMeasurements.ipynb).)
# In the following exercises you will learn to prepare separable quantum states by manipulating individual qubits.
# You will only need [single-qubit gates](../SingleQubitGates/SingleQubitGates.ipynb) for that.
#
# > In each exercise, you'll be given an array of qubits to manipulate; you can access $i$-th element of the array `qs` as `qs[i]`.
# Array elements are indexed starting with 0, the first array element corresponds to the leftmost qubit in Dirac notation.
# ### <span style="color:blue">Exercise 3</span>: Prepare a basis state
#
# **Input:** A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}$.
#
# **Goal:** Transform the system into the basis state $|11\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}$.
# +
%kata T1_PrepareState1
operation PrepareState1 (qs : Qubit[]) : Unit is Adj+Ctl {
X(qs[0]);
X(qs[1]);
}
# -
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-3:-Prepare-a-basis-state).*
# ### <span style="color:blue">Exercise 4</span>: Prepare a superposition of two basis states
#
# **Input:** A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}$.
#
# **Goal:** Transform the system into the state $\frac{1}{\sqrt2}\big(|00\rangle - |01\rangle\big) = \frac{1}{\sqrt2}\begin{bmatrix} 1 \\ -1 \\ 0 \\ 0 \end{bmatrix}$.
#
# <details>
# <summary><b>Need a hint? Click here</b></summary>
# Represent the target state as a tensor product $|0\rangle \otimes \frac{1}{\sqrt2}\big(|0\rangle - |1\rangle\big) = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \otimes \frac{1}{\sqrt2}\begin{bmatrix} 1 \\ -1 \end{bmatrix}$.
# </details>
# +
%kata T2_PrepareState2
operation PrepareState2 (qs : Qubit[]) : Unit is Adj+Ctl {
X(qs[1]);
H(qs[1]);
}
# -
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-4:-Prepare-a-superposition-of-two-basis-states).*
# ### <span style="color:blue">Exercise 5</span>: Prepare a superposition with real amplitudes
#
# **Input:** A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}$.
#
# **Goal:** Transform the system into the state $\frac{1}{2}\big(|00\rangle - |01\rangle + |10\rangle - |11\rangle\big) = \frac{1}{2}\begin{bmatrix} 1 \\ -1 \\ 1 \\ -1 \end{bmatrix}$.
#
# <details>
# <summary><b>Need a hint? Click here</b></summary>
# Represent the target state as a tensor product $\frac{1}{\sqrt2}\big(|0\rangle + |1\rangle\big) \otimes \frac{1}{\sqrt2}\big(|0\rangle - |1\rangle\big) = \frac{1}{\sqrt2} \begin{bmatrix} 1 \\ 1 \end{bmatrix} \otimes \frac{1}{\sqrt2}\begin{bmatrix} 1 \\ -1 \end{bmatrix}$.
# </details>
# +
%kata T3_PrepareState3
operation PrepareState3 (qs : Qubit[]) : Unit is Adj+Ctl {
H(qs[0]);
X(qs[1]);
H(qs[1]);
}
# -
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-5:-Prepare-a-superposition-with-real-amplitudes).*
# ### <span style="color:blue">Exercise 6</span>: Prepare a superposition with complex amplitudes
#
# **Input:** A two-qubit system in the basis state $|00\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}$.
#
# **Goal:** Transform the system into the state $\frac{1}{2}\big(|00\rangle + e^{i\pi/4}|01\rangle + e^{i\pi/2}|10\rangle + e^{3i\pi/4}|11\rangle\big) = \frac{1}{2}\begin{bmatrix} 1 \\ e^{i\pi/4} \\ e^{i\pi/2} \\ e^{3i\pi/4} \end{bmatrix}$.
#
# <details>
# <summary><b>Need a hint? Click here</b></summary>
# Represent the target state as a tensor product $\frac{1}{\sqrt2}\big(|0\rangle + e^{i\pi/2}|1\rangle\big) \otimes \frac{1}{\sqrt2}\big(|0\rangle + e^{i\pi/4}|1\rangle\big) = \frac{1}{\sqrt2} \begin{bmatrix} 1 \\ e^{i\pi/2} \end{bmatrix} \otimes \frac{1}{\sqrt2}\begin{bmatrix} 1 \\ e^{i\pi/4} \end{bmatrix}$.
# </details>
# +
%kata T4_PrepareState4
operation PrepareState4 (qs : Qubit[]) : Unit is Adj+Ctl {
H(qs[0]);
S(qs[0]);
H(qs[1]);
T(qs[1]);
}
# -
# *Can't come up with a solution? See the explained solution in the [Multi-Qubit Systems Workbook](./Workbook_MultiQubitSystems.ipynb#Exercise-6:-Prepare-a-superposition-with-complex-amplitudes).*
# ## Conclusion
#
# As you've seen in the exercises, you can prepare separable multi-qubit states using only single-qubit gates.
# However, to prepare and manipulate entangled states you'll need more powerful tools.
# In the [next tutorial](../MultiQubitGates/MultiQubitGates.ipynb) you will learn about multi-qubit gates which give you access to all states of multi-qubit systems.
|
tutorials/MultiQubitSystems/MultiQubitSystems.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
step 1: ssh into the cluster using: "ssh -L localhost:8888:localhost:8889 'remote server address' "
step 2: On the remote server ( your cluster ), launch the jupyter notebook: "jupyter notebook --no-browser --port=8889"
#Note: you may need to activate corresponding environement using conda before running jupyter notebook )
step 3: On local machine ( your laptop or desktop ): open the url: http://localhost:8888 from your web browser
# Note In the next step, you will use the token number to log into it.
# +
step 4: After launching jupyter notebook on remote server, there are many output messages. Locate the line that looks like this
http://localhost:8889/?token=<PASSWORD>. copy the line after "token="
# -
step 5: Use this token number to log in the url: http://localhost:8888 on your local machine.
step 6: Now, you can locally use Jupyter notebook hosted by the remote server.
|
tutorial/How-to-launch-jupyter-notebook-from-cluster/How.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Loading S&P 500 data prduced by Airflow DAG `../dags/sp500.py`
import pandas as pd
from pandas_profiling import ProfileReport
# ## Ticker data
# +
# ticker_df = pd.read_parquet("file:../data/sp500/ticker_data/") #TODO how to read whole dir?
# -
ticker_df = pd.read_parquet("file:../data/sp500/ticker_data/Symbol=AAPL/2021-08-12_2021-08-12.snappy.parquet")
ticker_df
# +
# ticker_profile = ProfileReport(ticker_df, title="Pandas Profiling Report", explorative=True)
# ticker_profile.to_notebook_iframe()
# -
# ## finviz news
finviz_df = pd.read_parquet("../data/sp500/news/finviz/Symbol=AAPL/2021-08-12_2021-08-12.snappy.parquet")
finviz_df
# +
# finviz_profile = ProfileReport(finviz_df, title="Pandas Profiling Report", explorative=True)
# finviz_profile.to_notebook_iframe()
# -
# ## NewsAPI news
news_api_df = pd.read_parquet("../data/sp500/news/newsapi/Symbol=AAPL/2021-08-10_2021-08-17.snappy.parquet")
news_api_df
|
notebooks/20210711-load-sp500-data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.10 64-bit (''nlp'': virtualenv)'
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# +
from augmentation import get_augmentations
class Args:
aug = 'barlow'
img_size = 224
barlow = get_augmentations(Args())
# +
from PIL import Image
import numpy as np
import torch
import matplotlib.pyplot as plt
from torchvision import transforms
image_file_path = '/netscratch/saifullah/rvl-cdip-wo-tobacco3842/subset/form/correct/88025296.tif'
image = np.array(Image.open(image_file_path))
# plt.imshow(image, cmap='gray')
# plt.show()
# blurred = ocrodeg.binary_blur(image.astype(np.float32), 1.0, noise=0.01)
# # blotched = ocrodeg.random_blotches(image, 3e-4, 1e-4)
# plt.imshow(blurred, cmap='gray')
# plt.show()
image = torch.tensor(image)
# +
from das.data.transforms.grayscale_to_rgb import GrayScaleToRGB
import random
from PIL import Image, ImageOps, ImageFilter
import ocrodeg
class GaussianBlur(object):
"""Gaussian blur augmentation in SimCLR https://arxiv.org/abs/2002.05709"""
def __init__(self, sigma=[.1, 2.]):
self.sigma = sigma
def __call__(self, x):
sigma = random.uniform(self.sigma[0], self.sigma[1])
x = x.filter(ImageFilter.GaussianBlur(radius=sigma))
return x
class Solarization(object):
def __init__(self, p):
self.p = p
def __call__(self, img):
if random.random() < self.p:
return ImageOps.solarize(img)
else:
return img
# +
import torchvision
from torchvision.transforms import RandomResizedCrop
from torchvision.transforms import functional as F
from torchvision.transforms.functional import InterpolationMode, _interpolation_modes_from_int
import math
class RandomResizedCropCustom(RandomResizedCrop):
@staticmethod
def get_params(img, scale, ratio, region_mask):
"""Get parameters for ``crop`` for a random sized crop.
Args:
img (PIL Image or Tensor): Input image.
scale (list): range of scale of the origin size cropped
ratio (list): range of aspect ratio of the origin aspect ratio cropped
Returns:
tuple: params (i, j, h, w) to be passed to ``crop`` for a random
sized crop.
"""
width, height = F._get_image_size(img)
area = height * width
log_ratio = torch.log(torch.tensor(ratio))
for _ in range(10):
target_area = area * torch.empty(1).uniform_(scale[0], scale[1]).item()
aspect_ratio = torch.exp(
torch.empty(1).uniform_(log_ratio[0], log_ratio[1])
).item()
w = int(round(math.sqrt(target_area * aspect_ratio)))
h = int(round(math.sqrt(target_area / aspect_ratio)))
if 0 < w <= width and 0 < h <= height:
# mask = region_mask[h//2:height-h//2, w//2:width-w//2]
pixel_list = region_mask.nonzero()
p_idx = torch.randint(0, max(1, len(pixel_list)), size=(1, )).item()
i = pixel_list[p_idx][0] - h // 2
j = pixel_list[p_idx][1] - w // 2
i = torch.clip(i, min=0, max=height - h)
j = torch.clip(j, min=0, max=width - w)
return i, j, h, w
# Fallback to central crop
in_ratio = float(width) / float(height)
if in_ratio < min(ratio):
w = width
h = int(round(w / min(ratio)))
elif in_ratio > max(ratio):
h = height
w = int(round(h * max(ratio)))
else: # whole image
w = width
h = height
i = (height - h) // 2
j = (width - w) // 2
return i, j, h, w
def forward(self, img, pixel_list):
"""
Args:
img (PIL Image or Tensor): Image to be cropped and resized.
Returns:
PIL Image or Tensor: Randomly cropped and resized image.
"""
i, j, h, w = self.get_params(img, self.scale, self.ratio, pixel_list)
return F.resized_crop(img, i, j, h, w, self.size, self.interpolation)
def get_black_and_white_regions_mask(image_tensor):
black_and_white_threshold = 0.5
c, h, w = image_tensor.shape
ky = 8
kx = 8
black_and_white_regions_fast = (image_tensor[0].unfold(
0, ky, kx).unfold(1, ky, kx) < black_and_white_threshold).any(dim=2).any(dim=2)
black_and_white_regions_fast = black_and_white_regions_fast.repeat_interleave(
ky, dim=0).repeat_interleave(kx, dim=1)
black_and_white_regions_fast = torchvision.transforms.functional.resize(
black_and_white_regions_fast.unsqueeze(0), [h, w]).squeeze()
return ((black_and_white_regions_fast).float())
class RandomResizedCropThreshold(object):
def __init__(self, img_size):
self.t = RandomResizedCropCustom((img_size,img_size), scale=(0.05, 0.15))
# self.t = transforms.Resize((img_size, img_size))
# self.grid_xy = 4
def __call__(self, img):
region = get_black_and_white_regions_mask(img)
img = self.t(img, region)
return img
# c, h, w = img.shape
# size_y = h // self.grid_xy # patch size
# size_x = w // self.grid_xy # patch stride
# patches = img.unfold(1, size_y, size_y).unfold(2, size_x, size_x)
# patches = patches.reshape(c, self.grid_xy * self.grid_xy, size_y, size_x).permute(1, 0, 2, 3)
# valid_patches = []
# for i in range(patches.shape[0]):
# if len(patches[i][patches[i] < 0.5]) > 0:
# valid_patches.append(self.t(patches[i]))
# return torch.stack(valid_patches)
class Blotches(object):
def __call__(self, img):
if len(img.shape) != 2:
img = img.squeeze()
return torch.from_numpy(ocrodeg.random_blotches(np.array(img), 3e-4, 1e-4)).unsqueeze(0)
class BinaryBlur(object):
def __call__(self, img):
if len(img.shape) != 2:
img = img.squeeze()
return torch.from_numpy(ocrodeg.binary_blur(np.array(img), 0.5)).unsqueeze(0)
class DocumentAugmentations2(object):
def __init__(self, img_size):
self.aug1 = transforms.Compose([
RandomResizedCropThreshold(img_size),
transforms.RandomApply([BinaryBlur()], p=0.5),
transforms.RandomHorizontalFlip(p=0.5),
GrayScaleToRGB(),
transforms.ToPILImage(),
transforms.RandomApply(
[transforms.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1)],
p=0.8
),
transforms.RandomGrayscale(p=0.2),
transforms.RandomApply([GaussianBlur([.1, .5])], p=0.5),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
self.aug2 = transforms.Compose([
RandomResizedCropThreshold(img_size),
transforms.RandomApply([Blotches()], p=0.2),
transforms.RandomApply([BinaryBlur()], p=0.5),
transforms.RandomHorizontalFlip(p=0.5),
GrayScaleToRGB(),
transforms.ToPILImage(),
transforms.RandomApply(
[transforms.ColorJitter(brightness=0.1, contrast=0.1, saturation=0.1, hue=0.1)],
p=0.8
),
transforms.RandomGrayscale(p=0.2),
transforms.RandomApply([GaussianBlur([.1, .5])], p=0.5),
transforms.ToTensor(),
transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
def __call__(self, image):
crops = []
crops.append(self.aug1(image))
crops.append(self.aug2(image))
return crops
doc_augs = DocumentAugmentations2(img_size=224)
# image_file_path = '/netscratch/saifullah/rvl-cdip-wo-tobacco3842/subset/form/correct/88025296.tif'
image_file_path = '/netscratch/saifullah/rvl-cdip-wo-tobacco3842/subset/email/correct/2064207242a.tif'
# image_file_path = '/netscratch/saifullah/rvl-cdip-wo-tobacco3842/subset/invoice/correct/00922031.tif'
for i in range(1):
image = np.array(Image.open(image_file_path))
image = image / 255.
image = torch.tensor(image)
if len(image.shape) == 2:
image = image.unsqueeze(0)
images = doc_augs(image)
for image in images:
plt.imshow(image.permute(1, 2, 0))
plt.show()
|
augmentations_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center> <font size='6' font-weight='bold'> Nettoyage des données </font> </center>
# <center> <i> <NAME>, <NAME>, <NAME>, <NAME>, <NAME> et <NAME> </i> </center>
# + [markdown] toc=true
# <h1>Table of Contents<span class="tocSkip"></span></h1>
# <div class="toc"><ul class="toc-item"><li><span><a href="#Import-des-données" data-toc-modified-id="Import-des-données-1"><span class="toc-item-num">1 </span>Import des données</a></span><ul class="toc-item"><li><span><a href="#Informations-générales" data-toc-modified-id="Informations-générales-1.1"><span class="toc-item-num">1.1 </span>Informations générales</a></span></li><li><span><a href="#Lecture-des-CSV" data-toc-modified-id="Lecture-des-CSV-1.2"><span class="toc-item-num">1.2 </span>Lecture des CSV</a></span></li><li><span><a href="#Filtrage-par-noeud" data-toc-modified-id="Filtrage-par-noeud-1.3"><span class="toc-item-num">1.3 </span>Filtrage par noeud</a></span></li></ul></li><li><span><a href="#Conversion-en-datetime" data-toc-modified-id="Conversion-en-datetime-2"><span class="toc-item-num">2 </span>Conversion en datetime</a></span></li><li><span><a href="#Analyse-et-visualisation-(partie-1)" data-toc-modified-id="Analyse-et-visualisation-(partie-1)-3"><span class="toc-item-num">3 </span>Analyse et visualisation (partie 1)</a></span></li><li><span><a href="#Feature-engineering" data-toc-modified-id="Feature-engineering-4"><span class="toc-item-num">4 </span>Feature engineering</a></span><ul class="toc-item"><li><span><a href="#Categorical-variables" data-toc-modified-id="Categorical-variables-4.1"><span class="toc-item-num">4.1 </span>Categorical variables</a></span></li><li><span><a href="#Features-liées-aux-timestamp" data-toc-modified-id="Features-liées-aux-timestamp-4.2"><span class="toc-item-num">4.2 </span>Features liées aux timestamp</a></span></li><li><span><a href="#Périodes-de-vacances" data-toc-modified-id="Périodes-de-vacances-4.3"><span class="toc-item-num">4.3 </span>Périodes de vacances</a></span></li><li><span><a href="#Confinement" data-toc-modified-id="Confinement-4.4"><span class="toc-item-num">4.4 </span>Confinement</a></span></li><li><span><a href="#Couvre-feu" data-toc-modified-id="Couvre-feu-4.5"><span class="toc-item-num">4.5 </span>Couvre-feu</a></span></li><li><span><a href="#Jours-fériés" data-toc-modified-id="Jours-fériés-4.6"><span class="toc-item-num">4.6 </span>Jours fériés</a></span></li><li><span><a href="#Vacances-scolaires" data-toc-modified-id="Vacances-scolaires-4.7"><span class="toc-item-num">4.7 </span>Vacances scolaires</a></span></li><li><span><a href="#Temps-avant-les-prochaines-grandes-vacances-scolaires" data-toc-modified-id="Temps-avant-les-prochaines-grandes-vacances-scolaires-4.8"><span class="toc-item-num">4.8 </span>Temps avant les prochaines grandes vacances scolaires</a></span></li><li><span><a href="#Données-météorologiques" data-toc-modified-id="Données-météorologiques-4.9"><span class="toc-item-num">4.9 </span>Données météorologiques</a></span></li><li><span><a href="#Moment-de-la-journée" data-toc-modified-id="Moment-de-la-journée-4.10"><span class="toc-item-num">4.10 </span>Moment de la journée</a></span></li></ul></li><li><span><a href="#Analyse-et-visualisation-(partie-2)" data-toc-modified-id="Analyse-et-visualisation-(partie-2)-5"><span class="toc-item-num">5 </span>Analyse et visualisation (partie 2)</a></span></li><li><span><a href="#Export-train-/-dev-/-test" data-toc-modified-id="Export-train-/-dev-/-test-6"><span class="toc-item-num">6 </span>Export train / dev / test</a></span></li><li><span><a href="#3-rues-par-ligne" data-toc-modified-id="3-rues-par-ligne-7"><span class="toc-item-num">7 </span>3 rues par ligne</a></span><ul class="toc-item"><li><span><a href="#Préliminaires" data-toc-modified-id="Préliminaires-7.1"><span class="toc-item-num">7.1 </span>Préliminaires</a></span></li><li><span><a href="#Nettoyage" data-toc-modified-id="Nettoyage-7.2"><span class="toc-item-num">7.2 </span>Nettoyage</a></span></li><li><span><a href="#Export" data-toc-modified-id="Export-7.3"><span class="toc-item-num">7.3 </span>Export</a></span></li></ul></li></ul></div>
# +
import os
import datetime
from functools import reduce
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
# -
# Les données sont enregistrées dans 3 fichiers CSV différents. Elles portent le nom suivant :
data_path = './data'
os.listdir(path=data_path)
list_filenames = ['champs-elysees.csv', 'convention.csv', 'sts.csv']
# # Import des données
# ## Informations générales
# **Les données ont été téléchargées depuis :**
# - https://opendata.paris.fr/explore/dataset/comptages-routiers-permanents/information/?disjunctive.libelle&disjunctive.etat_trafic&disjunctive.libelle_nd_amont&disjunctive.libelle_nd_aval&sort=t_1h
#
# **Lien de la notice d'obtention des features :**
# - https://opendata.paris.fr/api/datasets/1.0/comptages-routiers-permanents/attachments/notice_donnes_trafic_capteurs_permanents_version_20190607_pdf/
#
# **Quelques infos issues du site sur le dataset:**
# >**Données de trafic routier issues des capteurs permanents sur 13 mois glissants en J-1**
# Sur le réseau parisien, la mesure du trafic s’effectue majoritairement par le biais de boucles électromagnétiques implantés dans la chaussée.
# La donnée est produite par la Direction de la Voirie et des déplacements - Service des Déplacements - Poste Central d'Exploitation Lutèce.
# La donnée et les visualisations associées (Tableau, Carte et Dataviz) sont brutes sans aucune interprétation ou analyse. Elles donnent à voir la donnée telle qu'elle est publiée quotidiennement.
# Elles donnent un aperçu du taux d'occupation et du débit sur plus de 3000 tronçons de voies. A elles seules, elles ne permettent pas de caractériser la complexité de la circulation à Paris.
# >
# **Deux types de données sont ainsi élaborés :**
# le taux d’occupation, qui correspond au temps de présence de véhicules sur la boucle en pourcentage d’un intervalle de temps fixe (une heure pour les données fournies). Ainsi, 25% de taux d’occupation sur une heure signifie que des véhicules ont été présents sur la boucle pendant 15 minutes. Le taux fournit une information sur la congestion routière. L’implantation des boucles est pensée de manière à pouvoir déduire, d’une mesure ponctuelle, l’état du trafic sur un arc.
# le débit est le nombre de véhicules ayant passé le point de comptage pendant un intervalle de temps fixe (une heure pour les données fournies).
# L'horodate horaire est effectué en fin de période d'élaboration.
# Par exemple, l’horodate « 2019-01-01 01:00:00 » désigne la période du 1er janvier 2019 à 00h00 au 1er janvier 2019 à 01h00.
# Ainsi, l’observation couplée en un point du taux d’occupation et du débit permet de caractériser le trafic. Cela constitue l’un des fondements de l’ingénierie du trafic, et l’on nomme d’ailleurs cela le « diagramme fondamental ».
# Un débit peut correspondre à deux situations de trafic : fluide ou saturée, d’où la nécessité du taux d’occupation. A titre d’exemple : sur une heure, un débit de 100 véhicules par heure sur un axe habituellement très chargé peut se rencontrer de nuit (trafic fluide) ou bien en heure de pointe (trafic saturé).
# >
# **L’équipement du réseau parisien :**
# Les principaux axes de la Ville de Paris sont équipés de stations de comptage des véhicules et de mesure du taux d’occupation, à des fins à la fois de régulation du trafic et des transports en commun, d’information aux usagers (diffusion sur le site Sytadin), et d’étude.
# Il existe deux types de stations sur le réseau : les stations de mesure du taux d’occupation seul, et des stations à la fois de mesure du taux et de comptage des véhicules.
# Les stations de mesure du taux sont implantées très régulièrement : elles permettent une connaissance fine des conditions de circulation.
# Les stations de débit sont moins nombreuses, et généralement implantées entre les principales intersections. En effet, le débit se conserve généralement sur une section entre deux grands carrefours.
# ## Lecture des CSV
# On regroupera toutes les lignes des 3 CSV dans un même DataFrame. Une colonne filename y a été ajoutée pour facilement avoir l'origine de la ligne à portée de main.
#
# Avant tout, nous allons imputer les NaN avec la méthode du *rolling mean*.
# +
window = 14 # modifier si besoin la taille de la fenêtre
l_df = [pd.read_csv(
os.path.join(data_path, filename),
sep=';',
index_col=0).assign(filename=filename) for filename in list_filenames]
for idx, df in enumerate(l_df):
df = df.sort_values("Date et heure de comptage")
df['Débit horaire'] = df['Débit horaire'].interpolate()
df["Taux d'occupation"] = df["Taux d'occupation"].interpolate()
l_df[idx] = df
# +
df = pd.concat(l_df, ignore_index=True)
df.sample(5)
# -
# Vérification de la non-présence de NaN :
df.isna().sum()
# ## Filtrage par noeud
# On peut déjà drop les identifiants des noeuds et les données liées à la géométrie car ils ne nous serviront pas pour la suite.
# On supprimera aussi
df = df.drop(columns=[
'Identifiant noeud amont', 'Identifiant noeud aval', 'geo_point_2d',
'geo_shape', 'Date debut dispo data', 'Date fin dispo data'
])
# Contient pour chaque fichier CSV un 2-tuple de la forme (noeud_amont, noeud_aval)
dic_noeuds = {
'champs-elysees.csv': ('Av_Champs_Elysees-Washington', 'Av_Champs_Elysees-Berri'),
'convention.csv': ('Lecourbe-Convention', 'Convention-Blomet'),
'sts.csv': ('Sts_Peres-Voltaire', 'Sts_Peres-Universite')
}
# +
list_criteria = []
for key, val in dic_noeuds.items():
criterion = (df['filename']==key) & (df['Libelle noeud amont']==val[0]) & (df['Libelle noeud aval']==val[1])
list_criteria.append(criterion)
criterion_noeuds = reduce(lambda x, y: x | y, list_criteria)
print(f'Taille du df avant filtrage: {len(df)}')
df = df[criterion_noeuds]
print(f'Taille du df après filtrage: {len(df)}')
# -
# On peut désormais drop les libellés.
df = df.drop(columns=['Libelle noeud amont', 'Libelle noeud aval'])
df.head()
df['filename'].unique()
# # Conversion en datetime
df.dtypes
df['Date et heure de comptage']
# ‼️ Il semble y avoir un soucis de timezone pour les capteurs... ‼️
#
# **Hypothèse:** On ca supposer que l'heure UTC est la bonne pour la suite.
def remove_timezone(row):
return row.tz_localize(None)
df['Date et heure de comptage'] = pd.to_datetime(df['Date et heure de comptage'], utc=True)
df['Date et heure de comptage'] = df['Date et heure de comptage'].apply(remove_timezone)
df['Date et heure de comptage']
# On a pour l'instant l'heure UTC. Nous allons nous replacer à l'heure de Paris pour la suite, pour des questions pratiques.
df.dtypes
# On rajoute 1 heure pour revenir à l'heure de Paris.
df['Date et heure de comptage'] = df['Date et heure de comptage'] + pd.DateOffset(hours=1)
df['Date et heure de comptage']
date_begin = df['Date et heure de comptage'].min().strftime('%d/%m/%Y')
date_end = df['Date et heure de comptage'].max().strftime('%d/%m/%Y')
print(f'Première mesure de comptage prise : {date_begin}')
print(f'Dernière mesure de comptage prise : {date_end}')
# # Analyse et visualisation (partie 1)
df[['Débit horaire', "Taux d'occupation"]].describe()
df[['Débit horaire', "Taux d'occupation"]].plot()
sns.violinplot(y='Débit horaire', data=df)
sns.violinplot(y="Taux d'occupation", data=df)
sns.displot(df, x="Taux d'occupation")
# # Feature engineering
# ## Categorical variables
# Ajoutons un *one-hot encoding* pour les variables catégoriques. On n'oubliera cependant pas de passer à un *dummy encoding* avant d'entraîner le modèle pour éviter un problème de dimension. ‼️
df.dtypes
# **Ordinal encoding :**
# Il semble en réalité plus pertinent d'utiliser un *ordinal encoding* pour donner une relation d'ordre à la feature. On se servira pour cela des informations contenues dans la notice.
# <img src="ressources/ordinal_encoding.png" />
df['Etat trafic']
mapper = {'Inconnu': 0, 'Fluide': 1, 'Pré-saturé': 2, 'Saturé': 3, 'Bloqué': 4}
df['Etat trafic'] = df['Etat trafic'].map(mapper)
df.sample(5)
# ## Features liées aux timestamp
# Ajout du jour (sans l'heure) :
df['Date'] = pd.to_datetime(df["Date et heure de comptage"]).dt.date
df.sample(5)
# Ajout du jour de la semaine:
df['Jour de la semaine'] = pd.to_datetime(df["Date et heure de comptage"]).dt.dayofweek
df.sample(5)
# Reste maintenant à one-hot encoder cette variable.
# ‼️ On pensera à drop un des 7 jours pour éviter des problèmes d'overfitting ‼️
# +
df = pd.concat([
df,
pd.get_dummies(df['Jour de la semaine'],
prefix='Jour de la semaine',
drop_first=False)
], axis=1).drop(columns=['Jour de la semaine'])
df.head()
# -
# ## Périodes de vacances
# ## Confinement
# D'après Wikipedia:
# >L'interdiction de déplacement en France, vulgarisée dans les médias par l'expression « confinement de la population » ou « confinement national », est une mesure sanitaire mise en place pour la première fois du 17 mars à 12 h au 11 mai 2020 (55 jours, soit 1 mois et 25 jours), et une deuxième fois à partir du 30 octobre 2020 au 15 décembre 2020 (soit 1 mois et 18 jours), s'insère dans un ensemble de politiques de restrictions de contacts humains et de déplacements en réponse à la pandémie de Covid-19 en France.
# L'objectif est de donner une valeur qui traduit l'intensité du confinement.
#
# Nous allons donc créer une feature `Etat du confinement` qui traduira l'intensité de ce dernier. Elle prendra les valeurs suivantes :
# - 0 -> période avant le 1er confinement
# - 1 -> pas de confinement mais avec expérience du 1er confinement et mesures d'hygiènes renforcées
# - 2 -> confinement assoupli (réouverture des commerces non-essentiels notamment)
# - 3 -> confinement total.
confinement_1 = pd.date_range(start='3/17/2020', end='5/11/2020')
confinement_2 = pd.date_range(start='10/30/2020', end='11/28/2020')
confinement_2_assoupli = pd.date_range(start='11/28/2020', end='12/15/2020')
# +
# create a list of our conditions
conditions = [
(df["Date et heure de comptage"] < confinement_1[0]), # 0
(confinement_1[0] <= df["Date et heure de comptage"]) & (df["Date et heure de comptage"] < confinement_1[-1]), # 3
(confinement_1[-1] <= df["Date et heure de comptage"]) & (df["Date et heure de comptage"] < confinement_2[0]), # 1
(confinement_2[0] <= df["Date et heure de comptage"]) & (df["Date et heure de comptage"] < confinement_2[-1]), # 3
(confinement_2_assoupli[0] <= df["Date et heure de comptage"]) & (df["Date et heure de comptage"] < confinement_2_assoupli[-1]), # 2
(confinement_2_assoupli[-1] <= df["Date et heure de comptage"]) # 1
]
# create a list of the values we want to assign for each condition
values = [0, 3, 1, 3, 2, 1]
# create a new column and use np.select to assign values to it using our lists as arguments
df['Etat du confinement'] = np.select(conditions, values)
df.sample(5)
# -
df['Etat du confinement'].value_counts()
# ## Couvre-feu
couvre_feu_start = pd.Timestamp('10/17/2020')
couvre_feu_start
df['Couvre-feu'] = (couvre_feu_start <= df['Date'])
df.sample(5)
# ## Jours fériés
# Le CSV a été obtenu via le lien suivant :
# - https://www.data.gouv.fr/en/datasets/jours-feries-en-france/
df_feries = pd.read_csv('data/jours_feries_metropole.csv')
df_feries.head()
# On ne garde que les lignes relatives à 2019 ou 2020
df_feries = df_feries[df_feries['annee'].isin(['2019', '2020'])]
df_feries.sample(5)
# +
def get_date(row):
return row.date()
df_feries['date'] = pd.to_datetime(df_feries['date']).apply(get_date)
series_feries = df_feries['date']
# -
df['Jour férié'] = df['Date'].isin(series_feries)
df['Jour férié'].value_counts()
df.head()
# ## Vacances scolaires
# Le CSV a été obtenu via le lien suivant :
# - https://www.data.gouv.fr/en/datasets/le-calendrier-scolaire/
df_vacances = pd.read_csv('data/fr-en-calendrier-scolaire.csv', sep=';')
df_vacances.head()
df_vacances = df_vacances[df_vacances['location'] == 'Paris']
df_vacances.head()
df_vacances = df_vacances[df_vacances['annee_scolaire'].isin(['2019-2020', '2020-2021'])]
df_vacances.head()
# On observe un NaN... Affichons toute le DataFrame comme il n'y a que peu de lignes.
df_vacances
# Le seul NaN ne correpond pas à une date comprise dans notre étude. On peut donc la drop sereinement.
df_vacances = df_vacances[~ df_vacances['end_date'].isna()]
df_vacances
df_vacances.dtypes
# +
df_vacances['start_date'] = pd.to_datetime(df_vacances['start_date'])
df_vacances['end_date'] = pd.to_datetime(df_vacances['end_date'])
df_vacances.dtypes
# -
# On peut maintenant ajouter notre colonne `Vacances scolaires` à notre DataFrame de départ.
# +
def est_pendant_vacances(date):
for index, row_vacances in df_vacances.iterrows():
start = row_vacances['start_date']
end = row_vacances['end_date']
if start < date < end:
return True
else:
pass
return False
df['Vacances scolaires'] = df['Date'].apply(est_pendant_vacances)
df.sample(5)
# -
# ## Temps avant les prochaines grandes vacances scolaires
# Déjà, créons un DataFrame avec uniquement les grandes vacances.
df_grandes_vacances = df_vacances[df_vacances['description'].str.contains('Vacances')]
df_grandes_vacances.head()
# On trie maintenant ce DataFrame par ordre chronologique.
df_grandes_vacances = df_grandes_vacances.sort_values(by=['start_date'])
df_grandes_vacances.head()
# +
# create a list of our conditions
conditions = []
# create a list of the values we want to assign for each condition
values = []
for idx, row in df_grandes_vacances.iterrows():
conditions.append(df["Date et heure de comptage"] < row['start_date'])
values.append(row['start_date'])
df['Date des prochaines vacances scolaires'] = np.select(conditions, values)
df['Date des prochaines vacances scolaires'] = df['Date des prochaines vacances scolaires']
df.sample(5)
# -
df['Temps avant les prochaines vacances scolaires'] = df['Date des prochaines vacances scolaires'] - df['Date et heure de comptage']
df.sample(5)
# ## Données météorologiques
df_weather = pd.read_pickle('data/combined_weather_data_from_2009_to_present.pkl')
df_weather.head()
df_weather.columns
df = df.merge(df_weather, left_on='Date et heure de comptage', right_on='datetime', how='left').drop(columns=['datetime'])
df.head()
# Liste des colonnes à disposition :
df.columns
# ## Moment de la journée
# +
# create a list of our conditions
criterion = (df['sunrise'] <= df["Date et heure de comptage"]) & (df["Date et heure de comptage"] < df['sunset'])
# create a new column and use np.select to assign values to it using our lists as arguments
df['Journée'] = criterion
df.sample(5)
# -
# # Analyse et visualisation (partie 2)
df.columns
corr = df.corr()
mask = np.zeros_like(corr)
mask[np.triu_indices_from(mask)] = True
with sns.axes_style("white"):
plt.figure(figsize=(12,12))
ax = sns.heatmap(corr, mask=mask, vmax=.3, square=True)
# # Export train / dev / test
sep_date = pd.Timestamp('2020/11/23')
sep_date
df_train = df[df['Date et heure de comptage'] < sep_date]
df_test = df[df['Date et heure de comptage'] >= sep_date]
print(f'% train: {len(df_train) / len(df)}')
print(f'% test: {len(df_test) / len(df)}')
df_train.to_pickle('data/df_train.pkl')
df_test.to_pickle('data/df_test.pkl')
# # 3 rues par ligne
# ## Préliminaires
for filename in list_filenames:
print(f'{filename}')
date_begin = df['Date et heure de comptage'][df['filename']==filename].min().strftime('%d/%m/%Y')
date_end = df['Date et heure de comptage'][df['filename']==filename].max().strftime('%d/%m/%Y')
print(f'Première mesure de comptage prise : {date_begin}')
print(f'Dernière mesure de comptage prise : {date_end}')
print(f'len: {len(df[df["filename"]==filename])}')
print()
# ## Nettoyage
# **Objectif :**
# Faire une version du dataframe avec les valeurs des 3 arcs à chaque ligne (et non pas une ligne par arc).
list_filenames
l_df = [df[df['filename']==elt] for elt in list_filenames]
l_df[0].head()
# +
l_cols_original = ['Débit horaire', "Taux d'occupation", "Etat trafic", "Etat arc"]
for idx, (cur_df, filename) in enumerate(zip(l_df, list_filenames)): # we skip the first dataframe
l_cols_new = [filename[:-4] + '_' + elt for elt in l_cols_original]
l_df[idx] = cur_df.rename(columns=dict(zip(l_cols_original, l_cols_new))).drop(columns=['Libelle'])
l_df[0].head()
# +
def concat_reduce(df_1, df_2):
filename = df_2['filename'].iloc[0][:-4]
l_cols_original = ['Débit horaire', "Taux d'occupation", "Etat trafic", "Etat arc"]
l_cols = ['Date et heure de comptage'] + [filename + '_' + elt for elt in l_cols_original]
return df_1.merge(df_2[l_cols], on='Date et heure de comptage')
df_concat = reduce(concat_reduce, l_df)
df_concat = df_concat.sort_values(by='Date et heure de comptage')
df_concat.sample(10)
# -
len(df_concat)
df_concat.columns
# For convenience, we'll know reorder the columns.
# +
columns_new_order = [
'Date et heure de comptage', 'champs-elysees_Débit horaire',
"champs-elysees_Taux d'occupation", 'champs-elysees_Etat trafic',
'champs-elysees_Etat arc', 'convention_Débit horaire',
"convention_Taux d'occupation", 'convention_Etat trafic',
'convention_Etat arc', 'sts_Débit horaire', "sts_Taux d'occupation",
'sts_Etat trafic', 'sts_Etat arc', 'filename', 'Date',
'Jour de la semaine_0', 'Jour de la semaine_1', 'Jour de la semaine_2',
'Jour de la semaine_3', 'Jour de la semaine_4', 'Jour de la semaine_5',
'Jour de la semaine_6', 'Etat du confinement', 'Couvre-feu', 'Jour férié',
'Vacances scolaires', 'Date des prochaines vacances scolaires',
'Temps avant les prochaines vacances scolaires', 'tempC', 'windspeedKmph',
'winddirDegree', 'weatherCode', 'precipMM', 'humidity', 'visibility',
'pressure', 'cloudcover', 'HeatIndexC', 'DewPointC', 'WindChillC',
'WindGustKmph', 'FeelsLikeC', 'hourly_uvIndex', 'maxtempC', 'mintempC',
'avgtempC', 'totalSnow_cm', 'sunHour', 'daily_uvIndex', 'sunrise',
'sunset', 'moon_phase', 'moon_illumination', 'Journée'
]
df_concat = df_concat[columns_new_order]
df_concat.head()
# -
df_concat.columns
# ## Export
# On vérifie qu'on a bien la longueur attendue pour `df_concat`.
len(df_concat) == min([len(df_street) for df_street in l_df])
sep_date = pd.Timestamp('2020/11/23')
sep_date
df_concat_train = df_concat[df_concat['Date et heure de comptage'] < sep_date]
df_concat_test = df_concat[df_concat['Date et heure de comptage'] >= sep_date]
print(f'% train: {len(df_concat_train) / len(df_concat)}')
print(f'% test: {len(df_concat_test) / len(df_concat)}')
df_concat_train.to_pickle('data/df_concat_train.pkl')
df_concat_test.to_pickle('data/df_concat_test.pkl')
|
cleaning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/deejuu/OOP-58002/blob/main/Application_2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="hoNDr8f6UC5w"
# Writte a python program that display your student no. and full name and create a class name OOP_58002
# + colab={"base_uri": "https://localhost:8080/"} id="d79dJmq3T9oJ" outputId="3e716164-aa82-4135-ea58-7e9a05c8c478"
class OOP_58002:
def __init__(self,name,number):
self.name = name
self.number = number
def myFunction(self):
print("My student number is",self.number)
print("My name is",self.name)
OOP_580021= OOP_58002("Tolentino, <NAME>.",202117984)
OOP_580021.myFunction()
|
Application_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
custs = pd.read_csv('./customers.tsv', sep='\t')
custs.head()
plt.rc('font', **{'size' : 14})
fig, axs = plt.subplots(1,3,figsize=(20,10))
for field, idx in zip(['gender', 'income_class', 'relationship_status'], range(3)):
custs[field].value_counts().plot.bar(ax=axs[idx])
custs.plot.scatter(x='age', y='years_as_customer')
|
Data Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import scipy as sp
from scipy import io,integrate,sparse
import matplotlib.pyplot as plt
from matplotlib.lines import Line2D
from lanczos_bin import *
from IPython.display import clear_output
# %load_ext autoreload
# %autoreload 2
# -
plt.rcParams['text.latex.preamble'] = r'\renewcommand{\vec}{\mathbf}'
plt.rc('text', usetex=True)
plt.rc('font', family='serif')
# # weighted CESM vs CESM
#
# Want to illustrate:
# - weighted CESM is unbiased estimator
# - weighted CESM is probability distribution function
# - concentration as $n\to\infty$
nodes = np.array([1,2,3,4])
weights = np.array([.1,.4,.2,.3])
# +
np.random.seed(0) # for reproducibility
fig,axs = plt.subplots(1,3,figsize=(6,1.9),sharey=True,sharex=True)
fig.subplots_adjust(wspace=.1)
axs = axs.flatten()
for j,n in enumerate([100,1000,10000]):
# synthetic example
lam = np.hstack([
np.linspace(0,1,n-n//5-n//5-n//20),
np.linspace(3,4,n//5),
np.linspace(5,8,n//5),
np.linspace(15.8,16,n//20),
])
lam += np.random.randn(n)/10
lam = np.sort(lam)
lam /= np.max(lam)
n_samples = 30
CESM = Distribution()
CESM.from_weights(lam,np.ones(n)/n)
step = n//1000 if n > 1000 else 1 #downsample largest CESMs for plotting
axs[j].step(CESM.get_distr()[0][::step],CESM.get_distr()[1][::step],where='post',color='#E76F51',label='CESM')
axs[j].set_title(f'$n={n}$')
for i in range(n_samples):
v = np.random.randn(n)
v /= np.linalg.norm(v)
wCESM = Distribution()
wCESM.from_weights(lam,v**2)
axs[j].step(*wCESM.get_distr(),where='post',lw=.75,color='#073642',alpha=.2)
legend_elements = [Line2D([0],[0],linestyle='-',color='#073642',\
label=r'$\Phi(\vec{A}_{n})$'),
Line2D([0],[0],linestyle='-',lw=1,color='#073642',alpha=.2,\
label=r'$\Psi(\vec{A}_n,\vec{v}_i)$'),
]
axs[0].set_xticks([0,1])
axs[0].set_yticks([0,.2,.4,.6,.8,1])
axs[0].set_yticklabels([0,'','','','',1])
plt.savefig(f'imgs/WCESMs.pdf',bbox_inches='tight')
|
fig1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Importando dependências
import keras
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import RMSprop
# +
# Carregando os dados de treino e teste
(x_treino, y_treino), (x_teste, y_teste) = mnist.load_data()
# +
# Exibindo como estão os dados
# Quantas imagens para treino?
print("Imagens de Treino:", len(x_treino))
# Quantas imagens para teste?
print("Imagens de Teste:", len(x_teste))
# Qual o formato de uma imagem?
print("Formato da imagem:", x_treino[0].shape)
# O que a imagem x_treino[0] representa?
print("Representação da imagem x_treino[0]:", y_treino[0])
# Como são os dados de uma imagem?
print("Dados da imagem:", x_treino[0])
# +
# Exibindo a imagem
import matplotlib.pyplot as plt
# Configuração para o jupyter notebook exibir a imagem corretamente
# %matplotlib inline
indice = 0
# Se quiser perguntar para o usuário um número de índice:
#indice = int(input("Digite um número válido entre 0 e 59999: "))
print("Essa imagem representa:", y_treino[indice])
plt.imshow(x_treino[indice], cmap=plt.cm.binary)
plt.show()
# +
# Achatando as matrizes de pixels e transformando em uma única lista com valores
quantidade_treino = len(x_treino) # Vai me trazer 60000
quantidade_teste = len(x_teste) # Vai me trazer 10000
tamanho_imagem = x_treino[0].shape # Vai me trazer (28, 28)
tamanho_total = tamanho_imagem[0] * tamanho_imagem[1] # Vai me trazer 784
x_treino = x_treino.reshape(quantidade_treino, tamanho_total)
x_teste = x_teste.reshape(quantidade_teste, tamanho_total)
# +
# Visualizar dados achatados
print("Novo formato dos dados:", x_treino[0].shape)
print(x_treino[0])
# +
# Normalização dos dados
# Converte todos os valores de int8 para float32
x_treino = x_treino.astype('float32')
x_teste = x_teste.astype('float32')
# Valores entre 0 e 255 ficarão entre 0 e 1
x_treino /= 255
x_teste /= 255
# +
# Visualizando os dados normalizados
print("Dados normalizados")
print(x_treino[0])
# +
# Transformando y_treino e y_teste para variáveis categóricas
valores_unicos = set(y_treino) # Irá me trazer os itens únicos: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
qtde_valores_unicos = len(valores_unicos) # Irá me trazer que são 10 itens únicos
print("Quantidade de Valores Únicos em y_treino:", qtde_valores_unicos)
# O que temos em y_treino[0]?
print("y_treino[0] antes:", y_treino[0])
# Transforma 1 em [0, 1, 0, 0, 0, 0, 0, 0, 0], 2 em [0, 0, 1, 0, 0, 0, 0, 0, 0] e assim por diante
y_treino = keras.utils.to_categorical(y_treino, qtde_valores_unicos)
y_teste = keras.utils.to_categorical(y_teste, qtde_valores_unicos)
# Como ficou y_treino[0] depois da transformação?
print("y_treino[0] depois:", y_treino[0])
# +
# Criando o modelo
model = Sequential()
# Primeira hidden layer com 30 neurônios, com função de ativação ReLU
# Na primeira camada, precisamos definir o input shape, que no caso será (784,)
model.add(Dense(30, activation='relu', input_shape=(tamanho_total,)))
# Adicionamos um regularizador. No caso, será um Dropout
model.add(Dropout(0.2))
# Segunda hidden layer com 20 neurônios, com função de ativação ReLU
model.add(Dense(20, activation='relu'))
# Mais um regularizador depois da segunda hidden layer
model.add(Dropout(0.2))
# Finalizamos com a camada de output, com a quantidade de valores únicos (no caso 10) e uma
# função de ativação Softmax
model.add(Dense(qtde_valores_unicos, activation='softmax'))
# Exibimos o resumo do modelo criado
model.summary()
# +
# Compila o modelo criado
model.compile(loss='categorical_crossentropy',
optimizer=RMSprop(),
metrics=['accuracy'])
# +
# Treina o modelo
history = model.fit(x_treino, y_treino,
batch_size=128,
epochs=10,
verbose=1,
validation_data=(x_teste, y_teste))
# +
# Fazendo nossas previsões
indice = 9
# Qual o valor categórico de y_teste[indice]?
print("Valor em y_teste[indice]", y_teste[indice])
# y_teste[indice] irá me trazer [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.], por tanto, deve ser um 7
# Reajustando a imagem em x_teste[indice]
imagem = x_teste[indice].reshape((1, tamanho_total))
# Fazendo minha previsão
prediction = model.predict(imagem) # Irá retornar os valores de cada posição do output
print("Previsão:", prediction)
# Ajustando a previsão para o número real
prediction_class = model.predict_classes(imagem)
print("Previsão (ajustada):", prediction_class)
(x_treino_img, y_treino_img), (x_teste_img, y_teste_img) = mnist.load_data()
plt.imshow(x_teste_img[indice], cmap=plt.cm.binary)
|
Ocean_IA_Deep_14_08_19.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Factorization Machine
# ----
#
# ### Concept
# - Factorization Machine is general predictor like SVM. FM calculate all of pair-wise interaction between variables. So, FM can overcome the situation `cold-start` because of pair-wise vector factorization. It works like latent vector, but break the independence of the interaction parameter by factorizating them. Therefore, this algorithm can have a similar effect to using SVD++ with multiple variables.
# - This Algorithm works well especially in recommender system like e-commerce. Because of the sparsity in implicit data and content meta-information.
# - [Paper is here](https://www.csie.ntu.edu.tw/~b97053/paper/Rendle2010FM.pdf)
# - [My implemented code is here](https://github.com/yoonkt200/ml-theory-python/tree/master/nn-recommender/FM.py)
#
# ### Model Equation
# - Conceptional model equation
#
# $$ \hat{y}(x) = w_0 + \sum_{i=1}^{n}w_i x_i + \sum_{i=1}^{n}\sum_{j=i+1}^{n} <v_i, v_j> x_i x_j $$
#
# $$ <v_i, v_j> = \hat{w}_{ij} $$
#
# - FM have a closed model equation that can be computed in linear time O(kn), but actually O(kmd) because of zero-values.
#
# $$ 0.5\sum_{i=1}^{n}\sum_{j=1}^{n} <v_i, v_j> x_i x_j - 0.5\sum_{i=1}^{n}<v_i, v_i> x_i x_i $$
#
# $$ 0.5(\sum_{i=1}^{n}\sum_{j=1}^{n}\sum_{f=1}^{k} v_{i,f} v_{j,f} x_i x_j - \sum_{i=1}^{n}\sum_{f=1}^{k} v_{i,f} v_{i,f} x_i x_i) $$
#
# $$ 0.5\sum_{f=1}^{k}((\sum_{i=1}^{n} v_i x_i)(\sum_{j=1}^{n} v_j x_j) - \sum_{i=1}^{n} {v_i}^2{x_i}^2) $$
#
# $$ 0.5\sum_{f=1}^{k}((\sum_{i=1}^{n} v_i x_i)^2 - \sum_{i=1}^{n} {v_i}^2{x_i}^2) $$
#
# - Below code is implementation of FM's equation
# + pycharm={"is_executing": false, "name": "#%%\n"}
import numpy as np
# Pre-trained parameters
b = 0.3
w = np.array([0.001, 0.02, 0.009, -0.001])
v = np.array([[0.00516, 0.0212581, 0.150338, 0.22903],
[0.241989, 0.0474224, 0.128744, 0.0995021],
[0.0657265, 0.1858, 0.0223, 0.140097],
[0.145557, 0.202392, 0.14798, 0.127928]])
# Equation of FM model
def inference(data):
num_data = len(data)
scores = np.zeros(num_data)
for n in range(num_data):
feat_idx = data[n][0]
val = np.array(data[n][1])
# linear feature score
linear_feature_score = np.sum(w[feat_idx] * val)
# factorized feature score
vx = v[feat_idx] * (val.reshape(-1, 1))
cross_sum = np.sum(vx, axis=0)
square_sum = np.sum(vx*vx, axis=0)
cross_feature_score = 0.5 * np.sum(np.square(cross_sum) - square_sum)
# Model's equation
scores[n] = b + linear_feature_score + cross_feature_score
# Sigmoid transformation for binary classification
scores = 1.0 / (1.0 + np.exp(-scores))
return scores
# + pycharm={"name": "#%%\n"}
# Inference test for 3 case
data = [[[0, 1, 3], # feature index
[0.33, 1, 1]], # feature value
[[2],
[1]],
[[0, 1, 2, 3],
[0.96, 1, 1, 1]]]
inference(data)
# + [markdown] pycharm={"name": "#%% md\n"}
# ### Learning FM
# - The equation computed in linear time. So we can use SGD with below gradients. And in most cases add L2 Regularization on training model.
#
# $$ 1, \hspace{1cm} if \hspace{0.3cm} \theta \hspace{0.2cm} is \hspace{0.2cm} w_0 $$
#
# $$ x_i, \hspace{1cm} if \hspace{0.3cm} \theta \hspace{0.2cm} is \hspace{0.2cm} w_i $$
#
# $$ x_i \sum_{j=1}^{n} v_{j,f}x_{j} - v_{i,f} {x_i}^2 \hspace{1cm} if \hspace{0.3cm} \theta \hspace{0.2cm} is \hspace{0.2cm} v_{i,f} $$
#
# ### Binary Classification by FM
# - The FM classification model follow this rules.
# - 1. h(x) = add sigmoid function from original h(x)
# - 2. cost function is based on binary-cross entropy(or MLE)
# - 3. parameter has different 3 type : bias(b), linear weight(w), latent weight(v)
# - 4. gradient is based on binary-cross entropy and add FM parameter's gradient (Above `Learning FM chapter`)
#
# $$ h(x) = \hat{y}(x) = sigmoid(0.5\sum_{f=1}^{k}((\sum_{i=1}^{n} v_i x_i)^2 - \sum_{i=1}^{n} {v_i}^2{x_i}^2)) $$
#
# $$ Cost(\Theta) = -1/n()\sum_{i=1}^{n}[y^{(i)}log(h(x^{i})) + (1-y^{(i)})log(1-h(x^{(i)}))] $$
#
# $$ SGD repeat \{ $$
#
# $$ \theta_j = \theta_j - \alpha (h(x^{i})-y^{i}) * Gradient $$
#
# $$ \} $$
|
05-recommender/01-factorization-machine.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
with open("requirement.txt", "w") as f:
f.write("kfp==1.4.0\n")
f.write("numpy\n")
f.write("keras\n")
f.write("tqdm\n")
f.write("config\n")
f.write("sklearn\n")
# !pip install -r requirement.txt --upgrade --user
# +
from typing import NamedTuple
import numpy
def load_data(log_folder:str)->NamedTuple('Outputs', [('start_time_string',str)]):
import numpy as np
import time
import sys
print("import done...")
start = time.time()
data= np.load("triplet-data.npz")
sys.path.append("./")
# from config import img_size, channel, faces_data_dir, FREEZE_LAYERS, classify, facenet_weight_path
# from inception_resnet_v1 import InceptionResNetV1
# from utils import scatter
X_train, X_test = data['arr_0'], data['arr_1']
print(X_train.shape, X_test.shape)
print("Saving data...")
#print(X_train)
#print(X_test)
np.savez_compressed('/persist-log/triplet-data.npz', X_train, X_test)
print('Save complete ...')
start_time_string=str(start) #type is string
return [start_time_string]
def distributed_training_worker1(start_time_string:str)->NamedTuple('Outputs',[('model_path',str)]):
import numpy as np
import sys
import time
import tensorflow as tf
import json
import os
sys.path.append("./")
sys.path.append("/persist-log")
from config import img_size, channel, faces_data_dir, FREEZE_LAYERS, classify, facenet_weight_path
from inception_resnet_v1 import InceptionResNetV1
from itertools import permutations
from tqdm import tqdm
from tensorflow.keras import backend as K
from sklearn.manifold import TSNE
#load data from pvc in the container
data = np.load('/persist-log/triplet-data.npz')
X_train, X_test = data['arr_0'], data['arr_1']
def training_model(in_shape,freeze_layers,weights_path):
def create_base_network(in_dims,freeze_layers,weights_path):
model = InceptionResNetV1(input_shape=in_dims, weights_path=weights_path)
print('layer length: ', len(model.layers))
for layer in model.layers[:freeze_layers]:
layer.trainable = False
for layer in model.layers[freeze_layers:]:
layer.trainable = True
return model
def triplet_loss(y_true,y_pred,alpha=0.4):
total_lenght = y_pred.shape.as_list()[-1]
anchor = y_pred[:, 0:int(total_lenght * 1 / 3)]
positive = y_pred[:, int(total_lenght * 1 / 3):int(total_lenght * 2 / 3)]
negative = y_pred[:, int(total_lenght * 2 / 3):int(total_lenght * 3 / 3)]
# distance between the anchor and the positive
pos_dist = K.sum(K.square(anchor - positive), axis=1)
# distance between the anchor and the negative
neg_dist = K.sum(K.square(anchor - negative), axis=1)
# compute loss
basic_loss = pos_dist - neg_dist + alpha
loss = K.maximum(basic_loss, 0.0)
return loss
# define triplet input layers
anchor_input = tf.keras.layers.Input(in_shape, name='anchor_input')
positive_input = tf.keras.layers.Input(in_shape, name='positive_input')
negative_input = tf.keras.layers.Input(in_shape, name='negative_input')
Shared_DNN = create_base_network(in_shape, freeze_layers, weights_path)
# Shared_DNN.summary()
# encoded inputs
encoded_anchor = Shared_DNN(anchor_input)
encoded_positive = Shared_DNN(positive_input)
encoded_negative = Shared_DNN(negative_input)
# output
merged_vector = tf.keras.layers.concatenate([encoded_anchor, encoded_positive, encoded_negative],axis=-1,name='merged_layer')
model = tf.keras.Model(inputs=[anchor_input, positive_input, negative_input], outputs=merged_vector)
model.compile(
optimizer=adam_optim,
loss=triplet_loss,
)
return model
os.environ['TF_CONFIG'] = json.dumps({'cluster': {'worker': ["pipeline-worker-1:3000","pipeline-worker-2:3000","pipeline-worker-3:3000"]},'task': {'type': 'worker', 'index': 0}})
#os.environ['TF_CONFIG'] = json.dumps({'cluster': {'worker': ["pipeline-worker-1:3000"]},'task': {'type': 'worker', 'index': 0}})
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy(
tf.distribute.experimental.CollectiveCommunication.RING)
NUM_WORKERS = strategy.num_replicas_in_sync
print('=================\r\nWorkers: ' + str(NUM_WORKERS) + '\r\n=================\r\n')
learn_rate = 0.0001 + NUM_WORKERS * 0.00006
adam_optim = tf.keras.optimizers.Adam(lr=learn_rate)
batch_size = 32* NUM_WORKERS
model_path='/persist-log/weight_tfdl.h5'
print(model_path)
callbacks = [tf.keras.callbacks.ModelCheckpoint(model_path, save_weights_only=True, verbose=1)]
#X_train=np.array(X_train)
#print(type(X_train))
with strategy.scope():
Anchor = X_train[:, 0, :].reshape(-1, img_size, img_size, channel)
Positive = X_train[:, 1, :].reshape(-1, img_size, img_size, channel)
Negative = X_train[:, 2, :].reshape(-1, img_size, img_size, channel)
Y_dummy = np.empty(Anchor.shape[0])
model = training_model((img_size, img_size, channel), FREEZE_LAYERS, facenet_weight_path)
model.fit(x=[Anchor, Positive, Negative],
y=Y_dummy,
# Anchor_test = X_test[:, 0, :].reshape(-1, img_size, img_size, channel)
# Positive_test = X_test[:, 1, :].reshape(-1, img_size, img_size, channel)
# Negative_test = X_test[:, 2, :].reshape(-1, img_size, img_size, channel)
# Y_dummy = np.empty(Anchor.shape[0])
# Y_dummy2 = np.empty((Anchor_test.shape[0], 1))
# validation_data=([Anchor_test,Positive_test,Negative_test],Y_dummy2),
# validation_split=0.2,
batch_size=batch_size, # old setting: 32
# steps_per_epoch=(X_train.shape[0] // batch_size) + 1,
epochs=10,
callbacks=callbacks
)
end = time.time()
start_time_float=float(start_time_string)
print('execution time = ', ((end - start_time_float)/60))
return [model_path]
# -
def distributed_training_worker2(start_time_string:str)->NamedTuple('Outputs',[('model_path_work2',str)]):
import numpy as np
import sys
import time
import tensorflow as tf
import json
import os
sys.path.append("./")
sys.path.append("/persist-log")
from config import img_size, channel, faces_data_dir, FREEZE_LAYERS, classify, facenet_weight_path
from inception_resnet_v1 import InceptionResNetV1
from itertools import permutations
from tqdm import tqdm
from tensorflow.keras import backend as K
from sklearn.manifold import TSNE
#load data from pvc in the container
data = np.load('/persist-log/triplet-data.npz')
X_train, X_test = data['arr_0'], data['arr_1']
def training_model(in_shape,freeze_layers,weights_path):
def create_base_network(in_dims,freeze_layers,weights_path):
model = InceptionResNetV1(input_shape=in_dims, weights_path=weights_path)
print('layer length: ', len(model.layers))
for layer in model.layers[:freeze_layers]:
layer.trainable = False
for layer in model.layers[freeze_layers:]:
layer.trainable = True
return model
def triplet_loss(y_true,y_pred,alpha=0.4):
total_lenght = y_pred.shape.as_list()[-1]
anchor = y_pred[:, 0:int(total_lenght * 1 / 3)]
positive = y_pred[:, int(total_lenght * 1 / 3):int(total_lenght * 2 / 3)]
negative = y_pred[:, int(total_lenght * 2 / 3):int(total_lenght * 3 / 3)]
# distance between the anchor and the positive
pos_dist = K.sum(K.square(anchor - positive), axis=1)
# distance between the anchor and the negative
neg_dist = K.sum(K.square(anchor - negative), axis=1)
# compute loss
basic_loss = pos_dist - neg_dist + alpha
loss = K.maximum(basic_loss, 0.0)
return loss
# define triplet input layers
anchor_input = tf.keras.layers.Input(in_shape, name='anchor_input')
positive_input = tf.keras.layers.Input(in_shape, name='positive_input')
negative_input = tf.keras.layers.Input(in_shape, name='negative_input')
Shared_DNN = create_base_network(in_shape, freeze_layers, weights_path)
# Shared_DNN.summary()
# encoded inputs
encoded_anchor = Shared_DNN(anchor_input)
encoded_positive = Shared_DNN(positive_input)
encoded_negative = Shared_DNN(negative_input)
# output
merged_vector = tf.keras.layers.concatenate([encoded_anchor, encoded_positive, encoded_negative],axis=-1,name='merged_layer')
model = tf.keras.Model(inputs=[anchor_input, positive_input, negative_input], outputs=merged_vector)
model.compile(
optimizer=adam_optim,
loss=triplet_loss,
)
return model
os.environ['TF_CONFIG'] = json.dumps({'cluster': {'worker': ["pipeline-worker-1:3000","pipeline-worker-2:3000","pipeline-worker-3:3000"]},'task': {'type': 'worker', 'index': 1}})
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy(
tf.distribute.experimental.CollectiveCommunication.RING)
NUM_WORKERS = strategy.num_replicas_in_sync
print('=================\r\nWorkers: ' + str(NUM_WORKERS) + '\r\n=================\r\n')
learn_rate = 0.0001 + NUM_WORKERS * 0.00006
adam_optim = tf.keras.optimizers.Adam(lr=learn_rate)
batch_size = 32* NUM_WORKERS
model_path_work2='/persist-log/weight_tfdl.h5'
callbacks = [tf.keras.callbacks.ModelCheckpoint(model_path_work2, save_weights_only=True, verbose=1)]
#X_train=np.array(X_train)
#print(type(X_train))
with strategy.scope():
Anchor = X_train[:, 0, :].reshape(-1, img_size, img_size, channel)
Positive = X_train[:, 1, :].reshape(-1, img_size, img_size, channel)
Negative = X_train[:, 2, :].reshape(-1, img_size, img_size, channel)
Y_dummy = np.empty(Anchor.shape[0])
model = training_model((img_size, img_size, channel), FREEZE_LAYERS, facenet_weight_path)
model.fit(x=[Anchor, Positive, Negative],
y=Y_dummy,
# Anchor_test = X_test[:, 0, :].reshape(-1, img_size, img_size, channel)
# Positive_test = X_test[:, 1, :].reshape(-1, img_size, img_size, channel)
# Negative_test = X_test[:, 2, :].reshape(-1, img_size, img_size, channel)
# Y_dummy = np.empty(Anchor.shape[0])
# Y_dummy2 = np.empty((Anchor_test.shape[0], 1))
# validation_data=([Anchor_test,Positive_test,Negative_test],Y_dummy2),
# validation_split=0.2,
batch_size=batch_size, # old setting: 32
# steps_per_epoch=(X_train.shape[0] // batch_size) + 1,
epochs=10,
callbacks=callbacks
)
end = time.time()
start_time_float=float(start_time_string)
print('execution time = ', ((end - start_time_float)/60))
return [model_path_work2]
def distributed_training_worker3(start_time_string:str)->NamedTuple('Outputs',[('model_path_work3',str)]):
import numpy as np
import sys
import time
import tensorflow as tf
import json
import os
sys.path.append("./")
sys.path.append("/persist-log")
from config import img_size, channel, faces_data_dir, FREEZE_LAYERS, classify, facenet_weight_path
from inception_resnet_v1 import InceptionResNetV1
from itertools import permutations
from tqdm import tqdm
from tensorflow.keras import backend as K
from sklearn.manifold import TSNE
#load data from pvc in the container
data = np.load('/persist-log/triplet-data.npz')
X_train, X_test = data['arr_0'], data['arr_1']
def training_model(in_shape,freeze_layers,weights_path):
def create_base_network(in_dims,freeze_layers,weights_path):
model = InceptionResNetV1(input_shape=in_dims, weights_path=weights_path)
print('layer length: ', len(model.layers))
for layer in model.layers[:freeze_layers]:
layer.trainable = False
for layer in model.layers[freeze_layers:]:
layer.trainable = True
return model
def triplet_loss(y_true,y_pred,alpha=0.4):
total_lenght = y_pred.shape.as_list()[-1]
anchor = y_pred[:, 0:int(total_lenght * 1 / 3)]
positive = y_pred[:, int(total_lenght * 1 / 3):int(total_lenght * 2 / 3)]
negative = y_pred[:, int(total_lenght * 2 / 3):int(total_lenght * 3 / 3)]
# distance between the anchor and the positive
pos_dist = K.sum(K.square(anchor - positive), axis=1)
# distance between the anchor and the negative
neg_dist = K.sum(K.square(anchor - negative), axis=1)
# compute loss
basic_loss = pos_dist - neg_dist + alpha
loss = K.maximum(basic_loss, 0.0)
return loss
# define triplet input layers
anchor_input = tf.keras.layers.Input(in_shape, name='anchor_input')
positive_input = tf.keras.layers.Input(in_shape, name='positive_input')
negative_input = tf.keras.layers.Input(in_shape, name='negative_input')
Shared_DNN = create_base_network(in_shape, freeze_layers, weights_path)
# Shared_DNN.summary()
# encoded inputs
encoded_anchor = Shared_DNN(anchor_input)
encoded_positive = Shared_DNN(positive_input)
encoded_negative = Shared_DNN(negative_input)
# output
merged_vector = tf.keras.layers.concatenate([encoded_anchor, encoded_positive, encoded_negative],axis=-1,name='merged_layer')
model = tf.keras.Model(inputs=[anchor_input, positive_input, negative_input], outputs=merged_vector)
model.compile(
optimizer=adam_optim,
loss=triplet_loss,
)
return model
os.environ['TF_CONFIG'] = json.dumps({'cluster': {'worker': ["pipeline-worker-1:3000","pipeline-worker-2:3000","pipeline-worker-3:3000"]},'task': {'type': 'worker', 'index': 2}})
strategy = tf.distribute.experimental.MultiWorkerMirroredStrategy(
tf.distribute.experimental.CollectiveCommunication.RING)
NUM_WORKERS = strategy.num_replicas_in_sync
print('=================\r\nWorkers: ' + str(NUM_WORKERS) + '\r\n=================\r\n')
learn_rate = 0.0001 + NUM_WORKERS * 0.00006
adam_optim = tf.keras.optimizers.Adam(lr=learn_rate)
batch_size = 32* NUM_WORKERS
model_path_work3='/persist-log/weight_tfdl.h5'
callbacks = [tf.keras.callbacks.ModelCheckpoint(model_path_work3, save_weights_only=True, verbose=1)]
#X_train=np.array(X_train)
#print(type(X_train))
with strategy.scope():
Anchor = X_train[:, 0, :].reshape(-1, img_size, img_size, channel)
Positive = X_train[:, 1, :].reshape(-1, img_size, img_size, channel)
Negative = X_train[:, 2, :].reshape(-1, img_size, img_size, channel)
Y_dummy = np.empty(Anchor.shape[0])
model = training_model((img_size, img_size, channel), FREEZE_LAYERS, facenet_weight_path)
model.fit(x=[Anchor, Positive, Negative],
y=Y_dummy,
# Anchor_test = X_test[:, 0, :].reshape(-1, img_size, img_size, channel)
# Positive_test = X_test[:, 1, :].reshape(-1, img_size, img_size, channel)
# Negative_test = X_test[:, 2, :].reshape(-1, img_size, img_size, channel)
# Y_dummy = np.empty(Anchor.shape[0])
# Y_dummy2 = np.empty((Anchor_test.shape[0], 1))
# validation_data=([Anchor_test,Positive_test,Negative_test],Y_dummy2),
# validation_split=0.2,
batch_size=batch_size, # old setting: 32
# steps_per_epoch=(X_train.shape[0] // batch_size) + 1,
epochs=10,
callbacks=callbacks
)
end = time.time()
start_time_float=float(start_time_string)
print('execution time = ', ((end - start_time_float)/60))
return [model_path_work3]
def model_prediction(model_path:str,model_path_work2:str,model_path_work3:str)->NamedTuple('Outputs',[('model_path',str)]):
from os import listdir
from os.path import isfile
import time
import numpy as np
import cv2
from sklearn.manifold import TSNE
from scipy.spatial import distance
import tensorflow as tf
import sys
sys.path.append("./")
sys.path.append("/persist-log")
sys.path.append("/facenet/test")
from img_process import align_image, prewhiten
from triplet_training import create_base_network
from utils import scatter
from config import img_size, channel, classify, FREEZE_LAYERS, facenet_weight_path, faces_data_dir
anchor_input = tf.keras.Input((img_size, img_size, channel,), name='anchor_input')
Shared_DNN = create_base_network((img_size, img_size, channel), FREEZE_LAYERS, facenet_weight_path)
encoded_anchor = Shared_DNN(anchor_input)
model = tf.keras.Model(inputs=anchor_input, outputs=encoded_anchor)
model.load_weights(model_path)
model.summary()
start = time.time()
def l2_normalize(x, axis=-1, epsilon=1e-10):
output = x / np.sqrt(np.maximum(np.sum(np.square(x), axis=axis, keepdims=True), epsilon))
return output
# Acquire embedding from image
def embedding_extractor(img_path):
img = cv2.imread(img_path)
aligned = align_image(img)
#cv2.imwrite("facenet/align/"+"_aligned.jpg", aligned)
if aligned is not None:
aligned = aligned.reshape(-1, img_size, img_size, channel)
embs = l2_normalize(np.concatenate(model.predict(aligned)))
return embs
else:
print(img_path + ' is None')
return None
testset_dir = 'facenet/test/'
items = listdir(testset_dir)
jpgsList = [x for x in items if isfile(testset_dir + x)]
foldersList = [x for x in items if not isfile(testset_dir + x)]
print(jpgsList)
print(foldersList)
acc_total = 0
for i, anch_jpg in enumerate(jpgsList):
anchor_path = testset_dir + anch_jpg
anch_emb = embedding_extractor(anchor_path)
for j, clt_folder in enumerate(foldersList):
clt_path = testset_dir + clt_folder + '/'
clt_jpgs = listdir(clt_path)
#print('anchor_path is :',anchor_path)
#print('clt_jpgs is :',clt_jpgs)
#print('clt_path is :',clt_path)
str = anch_jpg
computeType = 1 if clt_folder == str.replace('.jpg', '') else 0
loss = 0
if computeType == 1:
sum1 = 0
print('==============' + clt_folder + '&' + anch_jpg + '==============')
for k, clt_jpg in enumerate(clt_jpgs):
clt_jpg_path = clt_path + clt_jpg
clt_emb = embedding_extractor(clt_jpg_path)
distanceDiff = distance.euclidean(anch_emb, clt_emb) # calculate the distance
#print('distance = ', distanceDiff)
sum1 = distanceDiff + sum1
loss = loss + 1 if distanceDiff >= 1 else loss
print("sum1", sum1 / 50.0)
print('loss: ', loss)
accuracy = (len(clt_jpgs) - loss) / len(clt_jpgs)
print('accuracy: ', accuracy)
acc_total += accuracy
else:
print('==============' + clt_folder + '&' + anch_jpg + '==============')
sum2 = 0
for k, clt_jpg in enumerate(clt_jpgs):
clt_jpg_path = clt_path + clt_jpg
clt_emb = embedding_extractor(clt_jpg_path)
distanceDiff = distance.euclidean(anch_emb, clt_emb) # calculate the distance
#print('distance = ', distanceDiff)
loss = loss + 1 if distanceDiff < 1 else loss
sum2 = distanceDiff + sum2
print("sum2", sum2 / 50.0)
print('loss: ', loss)
accuracy = (len(clt_jpgs) - loss) / len(clt_jpgs)
print('accuracy: ', accuracy)
acc_total += accuracy
print('--acc_total', acc_total)
acc_mean = acc_total / 81 * 100
print('final acc++------: ', acc_mean)
end = time.time()
print ('execution time', (end - start))
return [model_path]
# +
#serving
def serving(model_path:str, log_folder:str):
from flask import Flask,render_template,url_for,request,redirect,make_response,jsonify
from werkzeug.utils import secure_filename
import os
import cv2
import sys
import time
import base64
import math
from datetime import timedelta
import numpy as np
from os import listdir
from os.path import isfile
from sklearn.manifold import TSNE
from scipy.spatial import distance
import tensorflow as tf
sys.path.append("./")
sys.path.append("/persist-log")
sys.path.append("/templates")
from img_process import align_image, prewhiten
from triplet_training import create_base_network
from utils import scatter
from config import img_size, channel, classify, FREEZE_LAYERS, facenet_weight_path, faces_data_dir
serving_time = time.time
ALLOWED_EXTENSIONS = set(['jpg','JPG'])
def allowed_file(filename):
return '.' in filename and filename.rsplit('.',1)[1] in ALLOWED_EXTENSIONS
def return_img_stream(img_local_path):
img_stream = ''
with open(img_local_path,'rb') as img_f:
img_stream = img_f.read()
img_stream = base64.b64encode(img_stream).decode()
return img_stream
# L2 normalization
def l2_normalize(x, axis=-1, epsilon=1e-10):
output = x / np.sqrt(np.maximum(np.sum(np.square(x), axis=axis, keepdims=True), epsilon))
return output
#--------------------------------------------------------------demo.py
# Acquire embedding from image
def embedding_extractor(img_path,model):
img = cv2.imread(img_path)
aligned = align_image(img)
#cv2.imwrite("facenet/align/"+"_aligned.jpg", aligned)
if aligned is not None:
aligned = aligned.reshape(-1, img_size, img_size, channel)
embs = l2_normalize(np.concatenate(model.predict(aligned)))
return embs
else:
print(img_path + ' is None')
return None
#-------------------------------------------------------------flask
app = Flask(__name__, template_folder="/templates")
app.send_file_max_age_default = timedelta(seconds=1)
@app.route('/upload',methods=['GET','POST'])
def upload():
img_stream = ''
loss = 0
distanceDiffbig = 0
distanceDiffsmall = 0
distance_sum = 0
face = ''
face2 = ''
face3 = ''
acc_mean = 0
distance_low1 = 0
distance_low2 = 0
distance_low3 = 0
distance_show1 = 2
distance_show2 = 2
distance_show3 = 2
if request.method =='POST':
f = request.files['file']
user_input = request.form.get('name')
basepath = os.path.dirname(__file__)
sys.path.append('/facenet/test')
upload_path = os.path.join(basepath,'/facenet/test',secure_filename(f.filename))
print(basepath)
f.save(upload_path)
#start = time.time()
#model_path = '/persist-log/weight_tfdl.h5'
anchor_input = tf.keras.Input((img_size, img_size, channel,), name='anchor_input')
Shared_DNN = create_base_network((img_size, img_size, channel), FREEZE_LAYERS, facenet_weight_path)
encoded_anchor = Shared_DNN(anchor_input)
model = tf.keras.Model(inputs=anchor_input, outputs=encoded_anchor)
model.load_weights(model_path) #/persist-log
model.summary()
testset_dir = 'facenet/test/'
items = listdir(testset_dir)
jpgsList = [x for x in items if isfile(testset_dir + x)]
foldersList = [x for x in items if not isfile(testset_dir + x)]
print(jpgsList)
print(foldersList)
acc_total = 0
img_stream = return_img_stream(upload_path)
for i, anch_jpg in enumerate(jpgsList):
#anchor_path = testset_dir + anch_jpg
anch_emb = embedding_extractor(upload_path,model)
for j, clt_folder in enumerate(foldersList):
clt_path = testset_dir + clt_folder + '/'
clt_jpgs = listdir(clt_path)
str = anch_jpg
print('==============' + clt_folder + '&' + anch_jpg + '==============')
for k, clt_jpg in enumerate(clt_jpgs):
clt_jpg_path = clt_path + clt_jpg
clt_emb = embedding_extractor(clt_jpg_path,model)
distanceDiff = distance.euclidean(anch_emb, clt_emb) # calculate the distance
distance_sum=distance_sum + distanceDiff
if distanceDiff >= 1:
distanceDiffbig = distanceDiffbig + 1
else:
distanceDiffsmall = distanceDiffsmall + 1
if distanceDiffbig >= distanceDiffsmall :
loss = distanceDiffsmall
else:
loss = distanceDiffbig
distance_sum=distance_sum / 16
if distance_sum < distance_show3:
if distance_sum < distance_show2:
if distance_sum < distance_show1:
distance_show1 = distance_sum
distance_low1 = distance_sum
face = clt_folder
else:
distance_low2 = distance_sum
distance_show2 = distance_sum
face2 = clt_folder
else:
distance_show3 = distance_sum
distance_low3 = distance_sum
face3 = clt_folder
else:
distanceDiff = distanceDiff
print('distance sum is:', distance_sum)
print('distanceDiffsmall = ', distanceDiffsmall)
print('distanceDiffbig = ', distanceDiffbig)
print( distanceDiff)
distance_sum = 0
distanceDiffsmall = 0
distanceDiffbig = 0
print('loss: ', loss)
accuracy = (len(clt_jpgs) - loss) / len(clt_jpgs)
acc_total += accuracy
print('face = ', face)
print('The first is:',face,'distance is ',distance_low1)
print('The Second is:',face2,'distance is ',distance_low2)
print('The third is:',face3,'distance is ',distance_low3)
distance_low1 = round(distance_low1,2)
distance_low2 = round(distance_low2,2)
distance_low3 = round(distance_low3,2)
acc_mean = acc_total / 9 * 100
acc_mean = round(acc_mean,2)
print('final acc++------: ', acc_mean)
os.remove(upload_path)
#end = time.time()
#print ('execution time', (end - serving_time))
return render_template('upload.html',img_stream = img_stream, face = face , face2 = face2 , face3 = face3 , distance_low1 = distance_low1, distance_low2 = distance_low2 , distance_low3 = distance_low3, acc_mean = acc_mean )
if __name__ == '__main__':
app.run(host = '127.0.0.1',port=8987,debug=True)
return
# +
import kfp.dsl as dsl
import kfp.components as components
from typing import NamedTuple
import kfp
from kfp import dsl
from kfp.components import func_to_container_op, InputPath, OutputPath
from kubernetes.client.models import V1ContainerPort
@dsl.pipeline(
name='triplet_training pipeline',
description='triplet training test.'
)
def triplet_training_pipeline():
log_folder = '/persist-log'
pvc_name = "triplet-trainaing-pvc"
#label name
name="pod-name"
value1="worker-1" # selector pod-name: worker-1
value2="worker-2" # selector pod-name: worker-2
value3="worker-3" # selector pod-name: worker-3
container_port=3000
#select node
label_name="disktype"
label_value1="worker-1"
label_value2="worker-2"
label_value3="worker-3"
vop = dsl.VolumeOp(
name=pvc_name,
resource_name="newpvc",
storage_class="managed-nfs-storage",
size="30Gi",
modes=dsl.VOLUME_MODE_RWM
)
load_data_op=func_to_container_op(
func=load_data,
base_image="mike0355/k8s-facenet-distributed-training:4",
)
distributed_training_worker1_op=func_to_container_op(
func=distributed_training_worker1,
base_image="mike0355/k8s-facenet-distributed-training:4"
)
distributed_training_worker2_op=func_to_container_op(
func=distributed_training_worker2,
base_image="mike0355/k8s-facenet-distributed-training:4"
)
distributed_training_worker3_op=func_to_container_op(
func=distributed_training_worker3,
base_image="mike0355/k8s-facenet-distributed-training:4"
)
model_prediction_op=func_to_container_op(
func=model_prediction,
base_image="mike0355/k8s-facenet-distributed-training:4"
)
serving_op=func_to_container_op(
func=serving,
base_image="mike0355/k8s-facenet-serving:3"
)
#----------------------------------------------------------task
load_data_task=load_data_op(log_folder).add_pvolumes({
log_folder:vop.volume,
})
distributed_training_worker1_task=distributed_training_worker1_op(load_data_task.outputs['start_time_string']).add_pvolumes({ #woker1
log_folder:vop.volume,
}).add_pod_label(name,value1).add_node_selector_constraint(label_name,label_value1).add_port(V1ContainerPort(container_port=3000,host_port=3000))
distributed_training_worker2_task=distributed_training_worker2_op(load_data_task.outputs['start_time_string']).add_pvolumes({ #woker2
log_folder:vop.volume,
}).add_pod_label(name,value2).add_port(V1ContainerPort(container_port=3000,host_port=3000)).add_node_selector_constraint(label_name,label_value2)
distributed_training_worker3_task=distributed_training_worker3_op(load_data_task.outputs['start_time_string']).add_pvolumes({ #woker3
log_folder:vop.volume,
}).add_pod_label(name,value3).add_port(V1ContainerPort(container_port=3000,host_port=3000)).add_node_selector_constraint(label_name,label_value3)
model_prediction_task=model_prediction_op(distributed_training_worker1_task.outputs['model_path'],distributed_training_worker2_task.outputs['model_path_work2'],
distributed_training_worker3_task.outputs['model_path_work3']).add_pvolumes({
log_folder:vop.volume,
})
serving_task=serving_op(model_prediction_task.outputs['model_path'], log_folder).add_pvolumes({
log_folder:vop.volume,
})
# -
kfp.compiler.Compiler().compile(triplet_training_pipeline, 'distributed-training-1011-final.yaml')
#kfp.compiler.Compiler().compile(triplet_training_pipeline, 'load-data0902.zip')
# +
# -
|
FaceNet-distributed-training/pipeline/k8s_distributed_training_final_version.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="yv8OxUW-aZuw"
# # Data Import and Processing
# + [markdown] id="X1RZkp7AaZuy"
# Datasets are essential to any data science project! The more data you have, the easier it will be to identify relationships between features. However, it is also essential for the datasets to be understood by the computer before you can conduct any data analysis. Thus, the main objective of this exercise is to equip you with the required skills to import and process your dataset before any data analysis or machine learning is conducted.
# + [markdown] id="qo9K9fTeaZuz"
# ## 1. Data Import
# + [markdown] id="JLizB8V8aZu0"
# There are many websites which you can obtain data for free. Some examples of these include Kaggle (https://www.kaggle.com/) and University of California, Irvine (https://archive.ics.uci.edu/ml/datasets.html/) (UCI). We can manually download the datasets and place them in new folders on our computers. However, it may be time consuming to do so. Thus, here is a neat little trick to automate this process! The script is labelled as magic.py. Try it out!
#
# For the script to work, make sure you have the os, wget, pandas and matplotlib library installed in your python virtual environment.
#
# If you encounter an error while running the cell below, please comment out the first line: #%matplotlib qt
# + colab={"base_uri": "https://localhost:8080/"} id="48iAfPyqaZu4" outputId="2467bcd8-1e0b-41d5-f72e-fd5af886b27d" executionInfo={"status": "ok", "timestamp": 1644558834314, "user_tz": -330, "elapsed": 5, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
# #%matplotlib qt
# %run "magic.py"
# + [markdown] id="fkxfjF4paZu9"
# Hooray! You have successfully downloaded the data and plotted a graph without any manual intervention. Without opening the magic.py file, are you able to deduce where the data was downloaded to? The printed statements above will provide some hint!
# + id="ySGOwlZwaZu-" executionInfo={"status": "ok", "timestamp": 1644558876359, "user_tz": -330, "elapsed": 1517, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
# + [markdown] id="q7C9VJ9FaZvB"
# <font color=blue>Bonus: Does the figure look correct? Are you able to explain the negative values and the black lines on the x-axis?</font>
# + id="L3Jq2J_AaZvD" executionInfo={"status": "ok", "timestamp": 1644558876794, "user_tz": -330, "elapsed": 2, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
# + [markdown] id="_ArNZ3QSaZvK"
# ## 1.1 Downloading the Pokemon dataset
# + [markdown] id="lHLWIthfaZvL"
# Now it is time to import a dataset on your own. The dataset to be used will be the Pokemon Image dataset. Please spend some time going through the dataset description before attempting the next set of instructions.
# + colab={"base_uri": "https://localhost:8080/", "height": 329} id="vDNWA2xIdf4D" executionInfo={"status": "error", "timestamp": 1644561855999, "user_tz": -330, "elapsed": 6, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}} outputId="631497bf-c8d8-4d4b-dd3f-e7bf6169d1df"
df = pd.read_csv(r'C:\Users\rakes\Downloads\pokemon.csv')
print(df.head())
# + [markdown] id="arxWPo20aZvN"
# Create a new folder to store the dataset. Write a code below to download the dataset automatically using the urllib.request.urlretrieve function to help you. You can use the code within magic.py as reference.
#
# To access the contents within magic.py, find the magic.py file in the folder. Right-click on it and open it with wordpad.
#
# Use the URL: "http://sl2files.sustainablelivinglab.org/PokeIMG.zip" and save it as "PokeIMG.zip"
#
# <font color=blue>Bonus: Download the data using only 2 lines of code!</font>
# + id="rq7PYkDHaZvP"
# + [markdown] id="azsj1jXnaZvT"
# Well done! We now have our data downloaded! ** Make sure to extract the files from the zip file into the directory!! **
#
#
# We will now access our data and learn some of its features. To do this, let’s explore a Python library called ‘pandas’!
# + [markdown] id="bPTqn9m5aZvU"
# ## 1.2 Introduction to Pandas
# + [markdown] id="SQgW_MizaZvV"
# Pandas is a powerful tool to import datasets. It organises data into an easily processed [dataframe](https://www.datacamp.com/community/tutorials/pandas-tutorial-dataframe-python) which allows for easy statistical analysis.
#
# Read this [article](https://towardsdatascience.com/a-quick-introduction-to-the-pandas-python-library-f1b678f34673) and watch this [video](https://www.youtube.com/watch?v=dcqPhpY7tWk) for a quick introduction to pandas: What they are, what are some applications of pandas, and how you can use it.
#
# Pay careful attention to the part about importing data and viewing data, as we will use some of the functions in our exercises later!
#
# Summarise what you learnt about Pandas in your worksheet.
# - How do you install and use Pandas?
# - What are the common type of files that Pandas is used for?
# - What is a dataframe?
# - How do you access the rows and columns in the dataframe?
# - Name and describe some commonly used Pandas functions.
# + [markdown] id="7xniCy-DaZvW"
# ANSWER:
# - conda install pandas or pip install pandas into the python virtual environment. Remember to import pandas in the notebook.
# - Pandas can be used for both CSV files and Excel spreadsheets.
# - Dataframes are 2D data structures that have rows and columns. Dataframes are similar to how data are presented in Excel spreadsheets.
# - Rows and columns can be accessed through their names or their numbers. For example, dataframe['petal_size'] can be used to access data within the column that is labelled as "petal_size". Alternatively, dataframe.iloc[1] accesses data within the second row of the dataframe.
# - dataframe.head(): Returns the top few rows of the dataframe
# - dataframe.shape: Returns the dimensions of the dataframe (number of rows and columns)
# - dataframe.fillna(): Fills missing values with given values
# - dataframe.describe(): Returns basic statistics of the dataframe
# - dataframe.info(): Returns the type of data within each column
# + [markdown] id="uN8GdTnsaZvX"
# Now, let us use some functions within Pandas to help us access data. The first step is to import Pandas. Try importing pandas as pd.
# + id="yggX5E90aZva" executionInfo={"status": "ok", "timestamp": 1644559245911, "user_tz": -330, "elapsed": 430, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
import numpy as np
# + [markdown] id="ZYYgOLZ9aZvd"
# After importing Pandas, we will now try to read in the Iris Flower dataset. It is currently saved as a Comma Separated Values file (CSV). We will need to understand more about CSV files before we can access the data in them.
# + [markdown] id="7wyyOjwIaZvf"
# ## 1.2.1 Comma Separated Values (CSV) files
# + [markdown] id="bpM7sENlaZvg"
# Datasets are mainly stored in CSV files. CSV files contain data that are separated by comma characters or other characters. For example, a CSV file containing names of people may be stored as John,Mary,Harry,Luke. The comma between the names will tell the computer where to separate one name from the other.
#
# The files usually have a .csv extension but there are files which do not follow this extension. One example will be that of the iris data.
#
# See this [article](https://www.howtogeek.com/348960/what-is-a-csv-file-and-how-do-i-open-it/) to find out more about csv files: What are they? How to access them?
# + id="o5J2moceaZvh" executionInfo={"status": "ok", "timestamp": 1644559271120, "user_tz": -330, "elapsed": 3, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
import pandas as pd
# + [markdown] id="pdkLAJ5CaZvl"
# <font color=blue>Bonus: After understanding the nature of CSV files, how would one check whether the data file is a CSV file? Which python function can be used to do this?</font>
# + id="WPejC5qsaZvm"
# + [markdown] id="YNHvX4LBaZvr"
# ## 1.2.2 Pokemon image dataset
# + [markdown] id="mLOEDjs3aZvs"
# The Iris Flower dataset is a csv file, even though it has the extension .data. Now, open the dataset using the pd.read_csv() function and assign it into a variable df. Then, print out the first 5 rows of the dataframe to see the data attribute. What do you notice?
# + id="JUxizHumaZvt" outputId="c0ce346b-683f-44ed-d462-f2b3b86cb1b4" colab={"base_uri": "https://localhost:8080/", "height": 329} executionInfo={"status": "error", "timestamp": 1644560685287, "user_tz": -330, "elapsed": 7, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
df = pd.read_csv(r'C:\Users\rakes\Downloads\pokemon.csv')
print(df.head())
# + id="h5Fix9XLaZvw" colab={"base_uri": "https://localhost:8080/", "height": 183} executionInfo={"status": "error", "timestamp": 1644078246630, "user_tz": -330, "elapsed": 386, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}} outputId="8baada6c-7e3a-4d01-d4b2-00da3b6ab4d1"
df = pd.read_csv("pokemon.csv")
print(df.head(12))
# + [markdown] id="wupjuXHtaZvz"
# Did you realise the dataframe was missing headers/column names? This happens as the original file does not have header/column names. As such, it is always important to find out more details about the data file before using it. The required header name is 'Name'.
# + [markdown] id="lyt1rLJvaZv-"
# Now, let us try to include the names into the dataframe. It is necessary to read the data into the dataframe again to specify that the data has missing headers. This will allow us to add the names into the dataframe later. Fill in the blank of the missing header.
# + id="5QK2ge6xaZv_" outputId="9f1b48ec-4a15-48a2-a209-ddae96789329" colab={"base_uri": "https://localhost:8080/", "height": 218} executionInfo={"status": "error", "timestamp": 1643890199525, "user_tz": -330, "elapsed": 412, "user": {"displayName": "SE MECH A 05 <NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GjMwdMl6Vx3d1ua_4P8rd6Xm9KwN1FqNyKG-yPk=s64", "userId": "01601407517104806532"}}
#Answer
df = pd.read_csv("pokemon.csv",header=None)
print(df.head(10))
names = []
# + [markdown] id="RPLv342LaZwI"
# With the proper labels, you can now use pandas to obtain basic information (Number of rows and columns, type of data, number of missing values and basic statistics) about the dataset. Use .info() and .describe() to obtain basic information about the dataset!
# + id="6lOAoIHaaZwJ"
# + [markdown] id="Ru8uMMHZaZwN"
# Based on the information obtained, you should note that there are 150 different flowers in the dataset and that there are no missing values in the dataset.
# + [markdown] id="fGS8QqI8aZwO"
# ## You have now mastered the ability to download datasets automatically and import them using Pandas. Additionally, you have also learnt how to use the Pandas functions to obtain basic information about the dataset. Now we will proceed to a class activity where you will have to put all these skills to good use!
|
(2) [Jupyter - Youth] Module 5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # mlbotの初心者向けチュートリアル
#
# この記事ではmlbot(機械学習を使った仮想通貨自動売買ボット)を初心者向けに解説します。
#
# 前提
#
# - 研究の足がかりとなるもの
# - そのままでは儲からない
#
# ### 環境構築方法
#
# https://github.com/richmanbtc/mlbot_tutorial に記載
#
# ### 上級者向けチュートリアル
#
# 以下のチュートリアルも合わせて読むと良いと思います。
#
# - [ハイパーパラメータチューニング](https://github.com/richmanbtc/mlbot_tutorial/blob/master/work/hyper_parameter_tuning.ipynb)
# - [Non-Stationarity Score](https://github.com/richmanbtc/mlbot_tutorial/blob/master/work/non_stationarity_score.ipynb)
# - [p平均法](https://github.com/richmanbtc/mlbot_tutorial/blob/master/work/p_mean.ipynb)
#
# ### 教科書
#
# [Kaggleで勝つデータ分析の技術](https://www.amazon.co.jp/dp/4297108437)を読むと、
# 実践的な機械学習の知識が身につきます。
#
# この本には、Kaggle上位勢が実際に使っている、
# 性能が上がりやすい手法が書かれています。
# コード例もあるので勉強しやすいです。
#
# もし、このチュートリアルがわからない場合は、
# この本を買うと良いと思います。
#
# ## 必要なライブラリのインポート
#
# 以下のコードでは必要なライブラリをインポートしています。
# +
import math
import ccxt
from crypto_data_fetcher.gmo import GmoFetcher
import joblib
import lightgbm as lgb
import matplotlib.pyplot as plt
import numba
import numpy as np
import pandas as pd
from scipy.stats import ttest_1samp
import seaborn as sns
import talib
from sklearn.ensemble import BaggingRegressor
from sklearn.linear_model import RidgeCV
from sklearn.model_selection import cross_val_score, KFold, TimeSeriesSplit
# -
# ## データを用意
#
# 以下のコードでは、例としてGMOコインのBTC/JPYレバレッジ取引の15分足データをohlcv形式で取得しています。
# データ取得用のライブラリ https://github.com/richmanbtc/crypto_data_fetcher を利用しています。
# ライブラリ内ではAPIでデータを取得しています。
#
# https://note.com/btcml/n/nd78671a67792 を利用すると、高速にデータを読み込めます。
#
# ### ohlcv形式
#
# ohlcv形式は、ローソク足と出来高を合わせたデータ形式です。
# Open(始値)、High(高値)、Low(安値)、Close(終値)、Volume(出来高)の頭文字を並べるとohlcvになります。
#
# カラムの意味は以下のようになっています。
#
# - timestamp: 時刻(UTC)
# - op: 始値
# - hi: 高値
# - lo: 低値
# - cl: 終値
# - volume: 出来高
#
# ### 実験データ期間について
#
# コード中のコメントにあるように、実験に使うデータ期間を限定します。
# 理由は、フィッティングを防ぐためです。
#
# 仮想通貨データはサンプル数が少ないので、
# 同じデータで何度も実験をすると、
# 正しくバリデーションしていたとしても
# だんだんとデータにフィッティングしていきます。
#
# 実験に使わないデータを残しておくと、その部分についてはフィッティングを防げます。
# 全期間のデータで実験したときに、
# 実験に使った期間と使わなかった期間でバックテストの傾向が変わらなければ、
# フィッティングの影響は少ないと判断できます。
#
# また、本番用のモデルを学習するときは、
# 全期間のデータを使って学習したほうが良いと思います。
# 精度が上がりやすいからです。
#
# ### 改良ポイント
#
# #### 取引所と取引ペア選び
#
# いろいろな取引所やBTC/JPY以外のペアを試すと良いかもしれません。
# 取引ペアごとに値動きの傾向は変わります。
# 同じペアでも取引所ごとに値動きの傾向は変わります。
#
# #### 時間軸(足の間隔)変更
#
# 時間軸によって値動きの傾向が変わります。
# 学習、バックテスト、検定などにも影響を与えます。
# いろいろな時間軸を試すと良いかもしれません。
#
# 時間軸が短いメリット
#
# - 値動きを予測しやすい
# - サンプル数が多くなり、統計的に有意になりやすい
# - サンプル数が多くなり、学習が成功しやすい
#
# 時間軸が長いメリット
#
# - バックテストと実際の誤差が出づらい (APIや取引所の処理遅延などの影響を受けづらい)
# - 運用資金をスケールさせやすい
# +
memory = joblib.Memory('/tmp/gmo_fetcher_cache', verbose=0)
fetcher = GmoFetcher(memory=memory)
# GMOコインのBTC/JPYレバレッジ取引 ( https://api.coin.z.com/data/trades/BTC_JPY/ )を取得
# 初回ダウンロードは時間がかかる
df = fetcher.fetch_ohlcv(
market='BTC_JPY', # 市場のシンボルを指定
interval_sec=15 * 60, # 足の間隔を秒単位で指定。この場合は15分足
)
# 実験に使うデータ期間を限定する
df = df[df.index < pd.to_datetime('2021-04-01 00:00:00Z')]
display(df)
df.to_pickle('df_ohlcv.pkl')
# -
# ## maker手数料カラムを追加
#
# 以下のコードでは、maker手数料カラム(fee)を追加しています。
# GMOコインは過去に何度か手数料を変更しているので、
# バックテストを正確に行うために、
# 各時刻ごとの手数料が必要です。
# このチュートリアルでは指値(maker)注文しか使わないので、追加するのはmaker手数料だけです。
#
# GMOコインの過去のニュースから、
# 手数料の変更タイミングと変更後の手数料の値を人力で取得し、
# そこから各時刻の手数料を設定しています。
#
# 手数料の変更は定期メンテナンスのときに行われたみたいです。
# 定期メンテナンスの時刻は日本時間の15:00〜16:00です。
# UTCの場合は6:00〜7:00です。
# +
maker_fee_history = [
{
# https://coin.z.com/jp/news/2020/08/6482/
# 変更時刻が記載されていないが、定期メンテナンス後と仮定
'changed_at': '2020/08/05 06:00:00Z',
'maker_fee': -0.00035
},
{
# https://coin.z.com/jp/news/2020/08/6541/
'changed_at': '2020/09/09 06:00:00Z',
'maker_fee': -0.00025
},
{
# https://coin.z.com/jp/news/2020/10/6686/
'changed_at': '2020/11/04 06:00:00Z',
'maker_fee': 0.0
},
]
df = pd.read_pickle('df_ohlcv.pkl')
# 初期の手数料
# https://web.archive.org/web/20180930223704/https://coin.z.com/jp/corp/guide/fees/
df['fee'] = 0.0
for config in maker_fee_history:
df.loc[pd.to_datetime(config['changed_at']) <= df.index, 'fee'] = config['maker_fee']
df['fee'].plot()
plt.title('maker手数料の推移')
plt.show()
display(df)
df.to_pickle('df_ohlcv_with_fee.pkl')
# -
# ## 特徴量エンジニアリング
#
# 以下のコードではテクニカル指標計算ライブラリの[TA-Lib](https://mrjbq7.github.io/ta-lib/)を利用して特徴量を作成しています。
# 特徴量の意味は深く考えていません。
# TA-Libで実装されている特徴量を片っ端から追加しただけです。
# ただし、以下のように気をつけることはあります。
#
# ### 特徴量で気をつけること
#
# #### 未来の情報が含まれないようにする
#
# 未来の情報は本番稼働時には使えません。
# また、未来の情報が含まれると、予測精度が劇的に上がることが多いです。
# 予測精度が劇的に上がったときは、未来の情報が含まれていないか確認すると良いです。
#
# #### どのくらい過去のデータに依存するか?
#
# TRIXなど、指数平均を使うような特徴量は、無限の過去に依存します。
# このことは過去データが全て存在するバックテストでは問題になりづらいですが、
# 本番稼働で問題になります。
# 本番稼働ではボットの計算が遅いと発注が遅れて取引機会を逃すことがあります。
# ボットの計算を速くするためには、
# 過去データを全て取得してから予測値を計算するのでは無く、
# 過去一定の期間、例えば直近一ヶ月のみを取得して計算することをよくやります。
# このときにTRIXなどは計算に誤差が生まれます。
# 誤差は計算に使う期間を長くすれば減ります。
# https://www.ta-lib.org/d_api/ta_setunstableperiod.html も参考になります。
#
# 以下のような対応をします。
# 無限の過去に依存する特徴量は、誤差が十分小さくなるようなデータ期間で計算する。
# 有限の過去に依存する特徴量は、依存する最大長以上のデータ期間で計算する。
#
# ### 改良ポイント
#
# #### 特徴量の改善
#
# いろいろな特徴量を試すと良いと思います。
# TA-Libのようなテクニカル指標以外にも、以下のような特徴量が考えられます。
#
# - 板情報 (Order Book)
# - 価格帯別出来高 (Volume Profile Visible Range, VPVR)
# - オープンインタレスト (Open Interest, OI)
# - 清算 (Liquidation)
# - オンチェーンデータ
# - SNSデータ (単語を含むツイート数や、自然言語処理など)
#
# 上級者向けチュートリアルに記載のrichman non-stationarity scoreが下がるような特徴量を探すのもおすすめです。
#
# 以下のようなTA-Lib以外のライブラリを試すのも良いと思います。
#
# - https://github.com/bukosabino/ta
# +
def calc_features(df):
open = df['op']
high = df['hi']
low = df['lo']
close = df['cl']
volume = df['volume']
orig_columns = df.columns
hilo = (df['hi'] + df['lo']) / 2
df['BBANDS_upperband'], df['BBANDS_middleband'], df['BBANDS_lowerband'] = talib.BBANDS(close, timeperiod=5, nbdevup=2, nbdevdn=2, matype=0)
df['BBANDS_upperband'] -= hilo
df['BBANDS_middleband'] -= hilo
df['BBANDS_lowerband'] -= hilo
df['DEMA'] = talib.DEMA(close, timeperiod=30) - hilo
df['EMA'] = talib.EMA(close, timeperiod=30) - hilo
df['HT_TRENDLINE'] = talib.HT_TRENDLINE(close) - hilo
df['KAMA'] = talib.KAMA(close, timeperiod=30) - hilo
df['MA'] = talib.MA(close, timeperiod=30, matype=0) - hilo
df['MIDPOINT'] = talib.MIDPOINT(close, timeperiod=14) - hilo
df['SMA'] = talib.SMA(close, timeperiod=30) - hilo
df['T3'] = talib.T3(close, timeperiod=5, vfactor=0) - hilo
df['TEMA'] = talib.TEMA(close, timeperiod=30) - hilo
df['TRIMA'] = talib.TRIMA(close, timeperiod=30) - hilo
df['WMA'] = talib.WMA(close, timeperiod=30) - hilo
df['ADX'] = talib.ADX(high, low, close, timeperiod=14)
df['ADXR'] = talib.ADXR(high, low, close, timeperiod=14)
df['APO'] = talib.APO(close, fastperiod=12, slowperiod=26, matype=0)
df['AROON_aroondown'], df['AROON_aroonup'] = talib.AROON(high, low, timeperiod=14)
df['AROONOSC'] = talib.AROONOSC(high, low, timeperiod=14)
df['BOP'] = talib.BOP(open, high, low, close)
df['CCI'] = talib.CCI(high, low, close, timeperiod=14)
df['DX'] = talib.DX(high, low, close, timeperiod=14)
df['MACD_macd'], df['MACD_macdsignal'], df['MACD_macdhist'] = talib.MACD(close, fastperiod=12, slowperiod=26, signalperiod=9)
# skip MACDEXT MACDFIX たぶん同じなので
df['MFI'] = talib.MFI(high, low, close, volume, timeperiod=14)
df['MINUS_DI'] = talib.MINUS_DI(high, low, close, timeperiod=14)
df['MINUS_DM'] = talib.MINUS_DM(high, low, timeperiod=14)
df['MOM'] = talib.MOM(close, timeperiod=10)
df['PLUS_DI'] = talib.PLUS_DI(high, low, close, timeperiod=14)
df['PLUS_DM'] = talib.PLUS_DM(high, low, timeperiod=14)
df['RSI'] = talib.RSI(close, timeperiod=14)
df['STOCH_slowk'], df['STOCH_slowd'] = talib.STOCH(high, low, close, fastk_period=5, slowk_period=3, slowk_matype=0, slowd_period=3, slowd_matype=0)
df['STOCHF_fastk'], df['STOCHF_fastd'] = talib.STOCHF(high, low, close, fastk_period=5, fastd_period=3, fastd_matype=0)
df['STOCHRSI_fastk'], df['STOCHRSI_fastd'] = talib.STOCHRSI(close, timeperiod=14, fastk_period=5, fastd_period=3, fastd_matype=0)
df['TRIX'] = talib.TRIX(close, timeperiod=30)
df['ULTOSC'] = talib.ULTOSC(high, low, close, timeperiod1=7, timeperiod2=14, timeperiod3=28)
df['WILLR'] = talib.WILLR(high, low, close, timeperiod=14)
df['AD'] = talib.AD(high, low, close, volume)
df['ADOSC'] = talib.ADOSC(high, low, close, volume, fastperiod=3, slowperiod=10)
df['OBV'] = talib.OBV(close, volume)
df['ATR'] = talib.ATR(high, low, close, timeperiod=14)
df['NATR'] = talib.NATR(high, low, close, timeperiod=14)
df['TRANGE'] = talib.TRANGE(high, low, close)
df['HT_DCPERIOD'] = talib.HT_DCPERIOD(close)
df['HT_DCPHASE'] = talib.HT_DCPHASE(close)
df['HT_PHASOR_inphase'], df['HT_PHASOR_quadrature'] = talib.HT_PHASOR(close)
df['HT_SINE_sine'], df['HT_SINE_leadsine'] = talib.HT_SINE(close)
df['HT_TRENDMODE'] = talib.HT_TRENDMODE(close)
df['BETA'] = talib.BETA(high, low, timeperiod=5)
df['CORREL'] = talib.CORREL(high, low, timeperiod=30)
df['LINEARREG'] = talib.LINEARREG(close, timeperiod=14) - close
df['LINEARREG_ANGLE'] = talib.LINEARREG_ANGLE(close, timeperiod=14)
df['LINEARREG_INTERCEPT'] = talib.LINEARREG_INTERCEPT(close, timeperiod=14) - close
df['LINEARREG_SLOPE'] = talib.LINEARREG_SLOPE(close, timeperiod=14)
df['STDDEV'] = talib.STDDEV(close, timeperiod=5, nbdev=1)
return df
df = pd.read_pickle('df_ohlcv_with_fee.pkl')
df = df.dropna()
df = calc_features(df)
display(df)
df.to_pickle('df_features.pkl')
# -
# ## 学習に使う特徴量の定義
#
# 以下のコードでは学習に使う特徴量カラムを指定しています。
# 特徴量は私が適当に選んだものです。
# コメントアウトなどでいろいろな組み合わせを試すと良いと思います。
# 特徴量選択もおすすめです。
# Kaggleで勝つデータ分析の技術などで勉強すると良いと思います。
# +
features = sorted([
'ADX',
'ADXR',
'APO',
'AROON_aroondown',
'AROON_aroonup',
'AROONOSC',
'CCI',
'DX',
'MACD_macd',
'MACD_macdsignal',
'MACD_macdhist',
'MFI',
# 'MINUS_DI',
# 'MINUS_DM',
'MOM',
# 'PLUS_DI',
# 'PLUS_DM',
'RSI',
'STOCH_slowk',
'STOCH_slowd',
'STOCHF_fastk',
# 'STOCHRSI_fastd',
'ULTOSC',
'WILLR',
# 'ADOSC',
# 'NATR',
'HT_DCPERIOD',
'HT_DCPHASE',
'HT_PHASOR_inphase',
'HT_PHASOR_quadrature',
'HT_TRENDMODE',
'BETA',
'LINEARREG',
'LINEARREG_ANGLE',
'LINEARREG_INTERCEPT',
'LINEARREG_SLOPE',
'STDDEV',
'BBANDS_upperband',
'BBANDS_middleband',
'BBANDS_lowerband',
'DEMA',
'EMA',
'HT_TRENDLINE',
'KAMA',
'MA',
'MIDPOINT',
'T3',
'TEMA',
'TRIMA',
'WMA',
])
print(features)
# -
# ## 目的変数の計算
#
# 以下のコードでは目的変数(y)を計算しています。
# 目的変数は、機械学習が予測する対象です。
# yと表記されることが多いです。
# 買いはy_buy、売りはy_sellとしています。
#
# 何をyとするかは、いろいろなやり方があります。
# このチュートリアルでは、
# 実際の取引ルールに従ってトレードした場合に得られるリターンをyとしています。
# 指値が約定するかどうかと手数料を考慮してリターンを計算しています。
#
# ### Force Entry Price
#
# Force Entry Priceは買うと決めてから約定するまで指値で追いかけた場合に、実際に約定する価格です。
# 私が独自に定義した用語です。
# fepと略す場合もあります。
# いくらで指値を出すかは外部から与える必要があります。
# entryと名前がついていますが、exitも同じ計算なので区別はないです。
# 以下のコードではcalc_force_entry_priceでForce Entry Priceを計算しています。
# コード中のforce_entry_timeは約定するまでにかかった時間です。
# fetと略す場合もあります。
#
# 具体的には以下のように計算します。
# 詳細はコードを読んでください。
#
# 1. 毎時刻、与えられた指値価格で、指値を出す
# 2. 指値が約定したら、指値をForce Entry Priceとする
# 3. 指値が約定しなかったら、次の時刻へ進み、1へ戻る
#
# ### 実際の取引ルールに従ってトレードした場合に得られるリターン
#
# 具体的には以下のようにyを計算します。買い指値の場合で説明します。売り指値でもほぼ同じです。
# 詳細はコードを読んでください。
#
# 1. 毎時刻、あるルールで計算された指値距離(limit_price_dist)に基づいて、買い指値を出す
# 2. 買い指値が約定しなかった場合のyはゼロとする
# 3. 買い指値が約定した場合、一定時間(horizon)だけ待ってから、Force Entry Priceの執行方法でエグジットする
# 4. エグジット価格 / エントリー価格 - 1 - 2 * feeをyとする
#
# ### 改良のポイント
#
# #### 執行の改善
#
# チュートリアルでは、
# 毎時刻、指値を出すだけの執行を使っていますが、
# 損切りを入れたり、成行注文を使うなど、
# 他の執行方法も試すと良いかもしれません。
#
# #### 指値価格の計算方法
#
# チュートリアルでは、
# ATRを使って指値価格を計算していますが、
# 他の計算方法も試すと良いかもしれません。
#
# ### 参考リンク
#
# https://note.com/btcml/n/n9f730e59848c
#
# +
@numba.njit
def calc_force_entry_price(entry_price=None, lo=None, pips=None):
y = entry_price.copy()
y[:] = np.nan
force_entry_time = entry_price.copy()
force_entry_time[:] = np.nan
for i in range(entry_price.size):
for j in range(i + 1, entry_price.size):
if round(lo[j] / pips) < round(entry_price[j - 1] / pips):
y[i] = entry_price[j - 1]
force_entry_time[i] = j - i
break
return y, force_entry_time
df = pd.read_pickle('df_features.pkl')
# 呼び値 (取引所、取引ペアごとに異なるので、適切に設定してください)
pips = 1
# ATRで指値距離を計算します
limit_price_dist = df['ATR'] * 0.5
limit_price_dist = np.maximum(1, (limit_price_dist / pips).round().fillna(1)) * pips
# 終値から両側にlimit_price_distだけ離れたところに、買い指値と売り指値を出します
df['buy_price'] = df['cl'] - limit_price_dist
df['sell_price'] = df['cl'] + limit_price_dist
# Force Entry Priceの計算
df['buy_fep'], df['buy_fet'] = calc_force_entry_price(
entry_price=df['buy_price'].values,
lo=df['lo'].values,
pips=pips,
)
# calc_force_entry_priceは入力と出力をマイナスにすれば売りに使えます
df['sell_fep'], df['sell_fet'] = calc_force_entry_price(
entry_price=-df['sell_price'].values,
lo=-df['hi'].values, # 売りのときは高値
pips=pips,
)
df['sell_fep'] *= -1
horizon = 1 # エントリーしてからエグジットを始めるまでの待ち時間 (1以上である必要がある)
fee = df['fee'] # maker手数料
# 指値が約定したかどうか (0, 1)
df['buy_executed'] = ((df['buy_price'] / pips).round() > (df['lo'].shift(-1) / pips).round()).astype('float64')
df['sell_executed'] = ((df['sell_price'] / pips).round() < (df['hi'].shift(-1) / pips).round()).astype('float64')
# yを計算
df['y_buy'] = np.where(
df['buy_executed'],
df['sell_fep'].shift(-horizon) / df['buy_price'] - 1 - 2 * fee,
0
)
df['y_sell'] = np.where(
df['sell_executed'],
-(df['buy_fep'].shift(-horizon) / df['sell_price'] - 1) - 2 * fee,
0
)
# バックテストで利用する取引コストを計算
df['buy_cost'] = np.where(
df['buy_executed'],
df['buy_price'] / df['cl'] - 1 + fee,
0
)
df['sell_cost'] = np.where(
df['sell_executed'],
-(df['sell_price'] / df['cl'] - 1) + fee,
0
)
print('約定確率を可視化。時期によって約定確率が大きく変わると良くない。')
df['buy_executed'].rolling(1000).mean().plot(label='買い')
df['sell_executed'].rolling(1000).mean().plot(label='売り')
plt.title('約定確率の推移')
plt.legend(bbox_to_anchor=(1.05, 1))
plt.show()
print('エグジットまでの時間分布を可視化。長すぎるとロングしているだけとかショートしているだけになるので良くない。')
df['buy_fet'].rolling(1000).mean().plot(label='買い')
df['sell_fet'].rolling(1000).mean().plot(label='売り')
plt.title('エグジットまでの平均時間推移')
plt.legend(bbox_to_anchor=(1.2, 1))
plt.show()
df['buy_fet'].hist(alpha=0.3, label='買い')
df['sell_fet'].hist(alpha=0.3, label='売り')
plt.title('エグジットまでの時間分布')
plt.legend(bbox_to_anchor=(1.2, 1))
plt.show()
print('毎時刻、この執行方法でトレードした場合の累積リターン')
df['y_buy'].cumsum().plot(label='買い')
df['y_sell'].cumsum().plot(label='売り')
plt.title('累積リターン')
plt.legend(bbox_to_anchor=(1.05, 1))
plt.show()
df.to_pickle('df_y.pkl')
# -
# ## モデルの学習とOOS予測値計算
#
# 本番稼働時に使うモデルの学習と、OOS(Out-of-sample)予測値の計算を行います。
#
# 基本的なアイデアはy_buy, y_sellを予測し、
# 予測値がプラスのときのみトレードすれば勝てるだろう、
# というものです。
# y_buy, y_sellそれぞれの予測モデルが必要です。
#
# ### 本番用モデルの学習
#
# 本番用モデルはデータ全体で学習させます。
# y_buy、y_sellそれぞれの予測モデルを作り、保存します。
# 保存したモデルはこのチュートリアルでは使いません。
# 本番稼働するときに使います。
#
# ### OOS(Out-of-sample)予測値
#
# Cross Validationを使って、y_buy, y_sellのOOS予測値を計算します。
# OOS予測値はバックテストのために必要です。
#
# Cross Validationはモデルの成績を測る方法の一つです。
# 大まかに言うと、
# 様々な方法でデータを学習データとテストデータに分割し、
# 学習データで学習させたモデルを、
# テストデータで評価するという方法です。
# 詳細は[sklearnのドキュメント](https://scikit-learn.org/stable/modules/cross_validation.html)や、Kaggleで勝つデータ分析の技術を見てください。
#
# OOS予測値は、モデルの学習に使っていないデータ期間でのモデル予測値のことです。
# OOSはOut-of-sampleの略で、サンプル(学習に使ったデータサンプル)の外という意味があります。
# OOSで計算する理由は、条件をなるべく本番と同じにするためです。
# 本番稼働時は、学習に使っていないデータ(未来のデータ)に対処しないといけません。
#
# Cross Validationを使い、
# OOS予測値を計算する関数がmy_cross_val_predictです。
# my_cross_val_predictは、
# [sklearn.model_selection.cross_val_predict](https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_predict.html)とほぼ同じ処理ですが、
# cross_val_predictは入力と出力のサイズが同じでないと使えないので、
# 入力と出力のサイズが異なっていても使えるように、
# 自前で書いています。
# KFoldなら入力と出力のサイズが同じなのでsklearn.model_selection.cross_val_predictを使えますが、
# TimeSeriesSplitでは使えません。
#
# OOS予測値計算の流れは以下のようになります。
#
# 1. 様々な方法(cv_indicies)でデータを学習データ(train_idx)とテストデータ(val_idx)に分割
# 2. 学習データでモデルを学習(fit)
# 3. テストデータでモデル予測値を計算(predict)
# 4. 1に戻り、cv_indiciesの長さ分、繰り返す
#
# 以下のコードでは、y_buy, y_sellのOOS予測値を、それぞれy_pred_buy、y_pred_sellと表記しています。
#
# ### 改良ポイント
#
# #### パージ
#
# このチュートリアルで使う目的変数(y)は、
# 将来のリターンから計算するので、
# 計算に未来のデータが使われています。
# 特徴量の計算には過去のデータが使われています。
# つまり、ある時刻のデータには前後のデータの情報が含まれています。
#
# なので、
# KFoldやTimeSeriesSplitで分割すると、
# テストデータに学習データの情報が混入する可能性があります。
#
# すると、バリデーションとして不適切になります。
# 実際の問題設定と乖離するからです。
# 実際は、将来のデータを学習時に利用することはできません。
#
# これを防ぐために、パージという手法があります。
# 学習データからテストデータに時間的に近いデータを取り除く手法です。
# このチュートリアルでは説明をシンプルにするために、パージを使っていません。
#
# この辺のことは、
# [ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践](https://www.amazon.co.jp/dp/4322134637)
# に詳しく書かれています。
#
# +
df = pd.read_pickle('df_y.pkl')
df = df.dropna()
# モデル (コメントアウトで他モデルも試してみてください)
# model = RidgeCV(alphas=np.logspace(-7, 7, num=20))
model = lgb.LGBMRegressor(n_jobs=-1, random_state=1)
# アンサンブル (コメントアウトを外して性能を比較してみてください)
# model = BaggingRegressor(model, random_state=1, n_jobs=1)
# 本番用モデルの学習 (このチュートリアルでは使わない)
# 実稼働する用のモデルはデータ全体で学習させると良い
model.fit(df[features], df['y_buy'])
joblib.dump(model, 'model_y_buy.xz', compress=True)
model.fit(df[features], df['y_sell'])
joblib.dump(model, 'model_y_sell.xz', compress=True)
# 通常のCV
cv_indicies = list(KFold().split(df))
# ウォークフォワード法
# cv_indicies = list(TimeSeriesSplit().split(df))
# OOS予測値を計算
def my_cross_val_predict(estimator, X, y=None, cv=None):
y_pred = y.copy()
y_pred[:] = np.nan
for train_idx, val_idx in cv:
estimator.fit(X[train_idx], y[train_idx])
y_pred[val_idx] = estimator.predict(X[val_idx])
return y_pred
df['y_pred_buy'] = my_cross_val_predict(model, df[features].values, df['y_buy'].values, cv=cv_indicies)
df['y_pred_sell'] = my_cross_val_predict(model, df[features].values, df['y_sell'].values, cv=cv_indicies)
# 予測値が無い(nan)行をドロップ
df = df.dropna()
print('毎時刻、y_predがプラスのときだけトレードした場合の累積リターン')
df[df['y_pred_buy'] > 0]['y_buy'].cumsum().plot(label='買い')
df[df['y_pred_sell'] > 0]['y_sell'].cumsum().plot(label='売り')
(df['y_buy'] * (df['y_pred_buy'] > 0) + df['y_sell'] * (df['y_pred_sell'] > 0)).cumsum().plot(label='買い+売り')
plt.title('累積リターン')
plt.legend(bbox_to_anchor=(1.05, 1))
plt.show()
df.to_pickle('df_fit.pkl')
# -
# ## バックテストと検定
#
# バックテストと検定(統計的検定)を行います。
#
# ### バックテスト
#
# バックテストとは、
# 過去データに対して、トレードをシミュレーションして、
# どのくらいの成績が出るかを見ることです。
#
# シンプルに考えると、
# y_pred_buyがプラスのときだけy_buyを再現するようなトレードを行い、
# y_pred_sellがプラスのときだけy_sellを再現するようなトレードを行えば、
# 前項の累積リターン(買い+売り)を再現できます。
#
# しかし、これをそのまま再現しようとすると、
# 偶然にも、
# 買い指値のみ約定して、売り指値が約定しないことが続いた場合、
# ポジションがロング側に増えていき、
# レバレッジが上がってしまいます。
# レバレッジが上がると、
# 取引所のレバレッジ制限、ポジションサイズ制限に引っかかったり、
# 急変時にロスカットされる可能性が高まるので、
# 良くないです。
#
# そこで、ポジションサイズが大きくなりすぎないように、
# 以下のようなトレードルールでバックテストします。
# 具体的な計算式はソースコードを見てください。
#
# 1. 現在ポジションがプラスの場合、エグジット用の売り指値を出す
# 2. 現在ポジションがマイナスの場合、エグジット用の買い指値を出す
# 3. 最大ポジションまで余裕があり、y_pred_buyがプラスのとき、エントリー用の買い指値を出す
# 4. 最大ポジションまで余裕があり、y_pred_sellがプラスのとき、エントリー用の売り指値を出す
#
# 私の経験上、
# このルールでトレードすると、
# 前項の累積リターン(買い+売り)とは少し差が出ますが、
# だいたい似たような成績になります。
#
# ### 統計的検定とエラー率
#
# 統計的検定を使うと、
# バックテストで得られた結果が偶然なのかそうでないのかを、
# 見積もれます。
#
# 検定ではエラー率が重要です。
# ここで言うエラー率は、
# False Positive(本当は偶然なのに、偶然ではないと判定されてしまうこと)の確率のことです。
#
# エラー率は低いほど良いです。
# エラー率は100000分の1以下が良いと思います。
# その根拠は次の通りです。
#
# 実験は何度も行います。
# 仮に、実験を1000回行ったとすると、そのうちの一回くらいはFalse Positiveが出てしまうかもしれません。
# そのまま運用したら勝てません。
# もし、エラー率が100000分の1以下であれば、
# 1000回やってもFalse Positiveが出る確率は1%以下です。
# つまり、運用すれば99%以上の確率で勝てるということです。
#
# 厳密には、
# 統計的検定は様々な仮定の上に成り立っており、
# それらの仮定は現実で成り立たなかったりするので、
# 99%以上の確率では勝てないと思います。
# でも、何も根拠が無いよりは勝ちやすいと思います。
#
# ### p平均法
#
# 私が独自に考えた手法です。
#
# トレード成績の検定は、普通はt検定とかを使うと思います。
# [ファイナンス機械学習―金融市場分析を変える機械学習アルゴリズムの理論と実践](https://www.amazon.co.jp/dp/4322134637)で提唱されているPSR(Probabilistic sharpe ratio)やDSR(Deflated sharpe ratio)などもありえます。
#
# これらの手法の問題は、
# リターンの長期的な変化に弱いことです。
# 例えば、3年前はすごいプラスだったけど、直近1年はマイナスで、期間全体で見るとプラスの場合、未来で勝てるか怪しいですが、
# これらの手法を使うと、安定して儲かるとみなされる可能性があります。
# これらの手法はサンプルの順番を考慮しないので、
# 直近1年がマイナスということを、知り得ないからです。
#
# この問題を緩和するためにp平均法を考えました。
# 以下のような手法です。
# 判定に使うp値平均は低いほうが良いです。
#
# 1. リターン時系列をN個の期間に分割
# 2. 各期間でt検定してp値を計算する
# 3. 得られたN個のp値の平均を取る
# 4. p値平均を判定に使う
#
# 詳しく分析できていませんが、
# 一つでも大きいpがあると、
# p値平均が大きくなってしまうので、
# すべての期間で安定して儲かる場合のみ有意になる点が、
# ポイントかなと思います。
#
# p平均法はcalc_p_meanで、
# p平均法のエラー率はcalc_p_mean_type1_error_rateで計算しています。
#
# p平均法の説明は、上級チュートリアルにも書きました。
#
# ### 改良ポイント
#
# #### 含み損によるゼロカットの考慮
#
# 説明をシンプルにするために、
# バックテストで含み損によるゼロカットを考慮していません。
# バックテストのコードを修正すれば対応できると思います。
# レバレッジを決めるヒントになると思います。
#
# ### 注意点
#
# #### バックテストの累積リターン曲線に注目しすぎない
#
# バックテストの累積リターン曲線はあまり見ないほうが良いと思います。
# 理由は、見すぎると検定が妥当ではなくなるからです。
#
# 具体的にどう問題になるかというと、
# 例えば、累積リターン曲線からコロナショックのときに大きくドローダウンすることがわかったとします。
# その情報から、コロナショックで効く特徴量とかを探して対応したら、
# コロナショック時の成績を容易に上げられてしまいます。
# こういうことをすると、テストデータの情報を学習にフィードバックしていることになります。
# テストデータを学習に使ってしまうと、OOS予測値がOOSではなくなるので、
# 検定の妥当性が低下します。
#
# バックテスト結果から多くの情報を得れば得るほど、
# 実験者の脳を経由して、
# 多くのテストデータ情報が学習にフィードバックされてしまいます。
# なのでバックテスト結果からはなるべく情報を得ないほうが良いです。
# 情報を得てしまっても忘れたほうが良いです。
#
# 完全にこういうことを防ぐのは難しいとしても、
# 細かい部分には注目しすぎないほうが良いと思います。
#
# 全体的に右肩上がりだなくらいの情報は読み取るとしても、
# コロナショックのときはどうとか、細かいことは見ないほうが良いと思います。
# 試行錯誤をするときに、そもそもグラフを表示させないのも手です。
#
# p値平均など、検定の結果だけを見るのが良いと思います。
#
# また、
# 上級チュートリアルのハイパーパラメータチューニングで使われているNested-CVを使うのと、
# このような問題を緩和できます。
#
# #### 完全な右肩上がりにこだわりすぎない
#
# 完全な右肩上がりにはこだわりすぎないほうが良いです。
#
# 理由は、利益の絶対額が上がりづらいからです。
# 綺麗な右肩上がりのストラテジーは利益率が高いことが多いですが、
# 利益の絶対額が小さいことが多いです。
# 時間軸が短くないと綺麗な右肩上がりになりづらく、
# 時間軸が短いと利益の絶対額が小さくなりがちだからです。
#
# ほぼ毎日プラスを目指す代わりに、一ヶ月単位でほぼプラスを目指すなど、
# 人によって多少差があると思いますが、慎重になりすぎないのが良いと思います。
#
# +
@numba.njit
def backtest(cl=None, hi=None, lo=None, pips=None,
buy_entry=None, sell_entry=None,
buy_cost=None, sell_cost=None
):
n = cl.size
y = cl.copy() * 0.0
poss = cl.copy() * 0.0
ret = 0.0
pos = 0.0
for i in range(n):
prev_pos = pos
# exit
if buy_cost[i]:
vol = np.maximum(0, -prev_pos)
ret -= buy_cost[i] * vol
pos += vol
if sell_cost[i]:
vol = np.maximum(0, prev_pos)
ret -= sell_cost[i] * vol
pos -= vol
# entry
if buy_entry[i] and buy_cost[i]:
vol = np.minimum(1.0, 1 - prev_pos) * buy_entry[i]
ret -= buy_cost[i] * vol
pos += vol
if sell_entry[i] and sell_cost[i]:
vol = np.minimum(1.0, prev_pos + 1) * sell_entry[i]
ret -= sell_cost[i] * vol
pos -= vol
if i + 1 < n:
ret += pos * (cl[i + 1] / cl[i] - 1)
y[i] = ret
poss[i] = pos
return y, poss
df = pd.read_pickle('df_fit.pkl')
# バックテストで累積リターンと、ポジションを計算
df['cum_ret'], df['poss'] = backtest(
cl=df['cl'].values,
buy_entry=df['y_pred_buy'].values > 0,
sell_entry=df['y_pred_sell'].values > 0,
buy_cost=df['buy_cost'].values,
sell_cost=df['sell_cost'].values,
)
df['cum_ret'].plot()
plt.title('累積リターン')
plt.show()
print('ポジション推移です。変動が細かすぎて青色一色になっていると思います。')
print('ちゃんと全ての期間でトレードが発生しているので、正常です。')
df['poss'].plot()
plt.title('ポジション推移')
plt.show()
print('ポジションの平均の推移です。どちらかに偏りすぎていないかなどを確認できます。')
df['poss'].rolling(1000).mean().plot()
plt.title('ポジション平均の推移')
plt.show()
print('取引量(ポジション差分の絶対値)の累積です。')
print('期間によらず傾きがだいたい同じなので、全ての期間でちゃんとトレードが行われていることがわかります。')
df['poss'].diff(1).abs().dropna().cumsum().plot()
plt.title('取引量の累積')
plt.show()
print('t検定')
x = df['cum_ret'].diff(1).dropna()
t, p = ttest_1samp(x, 0)
print('t値 {}'.format(t))
print('p値 {}'.format(p))
# p平均法 https://note.com/btcml/n/n0d9575882640
def calc_p_mean(x, n):
ps = []
for i in range(n):
x2 = x[i * x.size // n:(i + 1) * x.size // n]
if np.std(x2) == 0:
ps.append(1)
else:
t, p = ttest_1samp(x2, 0)
if t > 0:
ps.append(p)
else:
ps.append(1)
return np.mean(ps)
def calc_p_mean_type1_error_rate(p_mean, n):
return (p_mean * n) ** n / math.factorial(n)
x = df['cum_ret'].diff(1).dropna()
p_mean_n = 5
p_mean = calc_p_mean(x, p_mean_n)
print('p平均法 n = {}'.format(p_mean_n))
print('p平均 {}'.format(p_mean))
print('エラー率 {}'.format(calc_p_mean_type1_error_rate(p_mean, p_mean_n)))
# -
# ## 良い結果が出たバックテスト例
#
# richmanbtcが実際に使っているボットのバックテスト結果。
# 青色はハイパーパラメータチューニングや試行錯誤に使った期間。
# 青色期間とオレンジ色期間をまとめてウォークフォワードでバックテスト。
#
# このように、全期間で右肩上がりになっていると、将来も安定する可能性が高い。
# ハイパーパラメータチューニングや試行錯誤に使わないデータ(オレンジ色)を残しておくと、
# フィッティングしていないかの最終チェックができるので安心。
#
# 
#
# ## 実運用
#
# バックテストで良い結果が出たら、実運用をします。
# このチュートリアルでは説明しませんが、
# 機械学習の難易度と比べたら、
# かんたんに実装できると思います。
# わからない場合は、ネット上にいろいろな人のソースコードが転がっているので、参考にすると良いと思います。
#
# ### 注意点
#
# #### どのくらいポジションサイズを増やせるか?
#
# ポジションサイズが増えると、発注サイズが増えます。
# 発注サイズが増えると、
# 全量約定しなくなったり、
# 自分の大きい注文が板に見えることにより、
# 値動きに影響を与えたりすることがあります。
# そのようなことが起きると、
# 実運用とバックテストが乖離し、
# 成績が劣化する可能性があります。
# それを防ぐために、どのくらいポジションサイズを増やせるか、見積もる必要があります。
#
# GMOコインは約定データが手に入るので、
# 指値で約定する出来高を調べれば、
# どのくらいポジションサイズを増やせるか見積もれます。
# 例えば、買いの指値であれば、指値より安い価格で約定した注文の出来高を調べれば良いです。
#
# 約定データが手に入らない場合は、
# 全体の売買代金に対する自分のボットの売買代金の割合から見積もる方法もあります。
# 15分ごとに発注するボットを例として考えます。
# 1日の売買代金が1000億円だとすると、15分間の売買代金は約10億円と見積もれます。
# 自分のボットの売買代金を全体の1%とすると、
# 15分間で発注可能なのは、10億円 * 0.01 = 1000万円です。
# ドテンする場合は発注サイズは最大でポジションサイズの2倍になるので、
# 可能なポジションサイズは500万円以下と見積もれます。
# ドテンしない場合は1000万円以下です。
#
# #### 一ヶ月で最大いくら稼げるか?
#
# こうして求められた最大ポジションサイズに月次利益率をかけると、
# 一ヶ月で稼げる最大額を見積もれます。
# 例えば、ドテンしない場合で、月次利益率が50%だとすると、500万円です。
#
# 見積もった額が自分が必要な額よりも小さい場合、
# 試行錯誤の結果、もし勝てるようになっても、
# 必要なリターンを得られないので、
# 時間の無駄になります。
# その場合は、
# 早々に取引所、取引ペア、時間軸などを変えたほうが、
# 時間を節約できるかもしれません。
#
# +
# 最大ポジションサイズと月次利益の見積もり例
amount_per_day_jpy = 1000.0 * 10000 * 10000 # 1日の売買代金 1000億円
order_interval_min = 15.0 # 15分間隔で発注
monthly_return = 0.5 # 月次利益率 50%
my_order_ratio = 0.01 # 自分のボットの売買代金割合 1%
max_position_size = amount_per_day_jpy / (24 * 60) * order_interval_min * my_order_ratio
monthly_profit = max_position_size * monthly_return
print('最大ポジションサイズ {}円'.format(max_position_size))
print('月次利益 {}円'.format(monthly_profit))
# -
|
work/long_period/gmo/default/tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Substitution Ciphers
# A substitution cipher is a method of encrypting in which every plaintext character (or group of characters) is replaced with a different ciphertext symbol. The receiver deciphers the text by performing the inverse substitution.
#
# <img src="images/substitution-cipher.png" width=500px>
# <!--  -->
#
# - Substitution can consider single characters (simple substitution cipher) but also group of characters (e.g., pair, triplets, and so on).
# - Alphabet simple substitution Ciphers admits $26!\sim 10^{26}\sim 2^{88}$ possible encoding rules (not easy to try them all). Assuming 1ns for each try, it would take $>10^9$years.
# - However, substitution does not alter the statistics so plaintext can be deduced by analyzing the frequency distribution of the ciphertext.
# +
# %matplotlib widget
import matplotlib.pyplot as plt
import numpy as np
from scipy import io
# -
# ## Caesar Cipher
# The method is named after <NAME>, who used it in his private correspondence. Each letter in the plaintext is replaced by a letter some fixed number of positions down the alphabet.
# - Same characters for plaintext and ciphertext.
# - Very simple encoding rule. Only 26 possibilities!
#
# <img src="images/caesar-cipher.png" width=500px>
# Two easy way to break the cipher:
# - **Brute force**: Since alphabet is 26 letters long only 26 shifts are possible you can try all possibilities and check them all.
# - **Frequency analysis**: Knowing what is the frequency of letters (e.g., in English, letters «e», «t», «a», «i» are more common than others), it is possible to infer what shift was used by oserving the frequency of the characters in the ciphertext.
# ### Decoder
# As first thing, we need to define the decoding procedure.
#
# Decoder needs two pieces of information:
# - the **alphabet**: it may seem trivial but substitution cipher assumes the decoder knows both plain and cipher alphabet. In case of Caesar cipher they are the same so we just need to define one.
# - the **shift** (the key): given the alphabet, the Caesar cipher is completely defined by the shift that must be applied to the plain alphabet to obtain the cipher alphabet.
#
# We choose to implement the decoder as a function that takes the `ciphertext`a and the `shift` as input and returns the `plaintext`. The alphabet is hard-coded in the function.
def caesar_decoding(ciphertext, shift=0):
'''
Decode a ciphertext encrypted with a Caesar Cipher, considering the
26-letter English alphabet.
Parameters
----------
ciphertext: str,
ciphertext to be decoded
shift: int, optional (default=0)
alphabet shift that maps the English alphabet into the cipher alphabet.
Return
------
plaintext: str,
decoded ciphertext.
'''
# define hard-coded 26-letter English alphabet
alphabet = 'abcdefghijklmnopqrstuvwxyz'
# build a dictionary that maps the plain alphabet into the cipher alphabet
cipher_alphabet = alphabet[-shift:] + alphabet[:-shift]
mapping = dict(zip(alphabet, cipher_alphabet))
# iter over each charater of the ciphertext when apply substitution
# characters not in the alphabet are left unchanged
plaintext = ''.join([mapping[char] if char in alphabet else char
for char in ciphertext.lower()])
return plaintext
# +
# code snippet to test the implementation of the decoder
ciphertext = 'lipps!' # 'hello!' encoded with shift=4
plaintext = caesar_decoding(ciphertext, shift=4)
print(ciphertext, '->', plaintext)
# -
# ### Ciphertext
# Then, we need to load the ciphertext stored in the file `ciphertext_caesar.txt`.
#
# We know that:
# - ciphertext contains the text of a [Wikipedia](https://www.wikipedia.org/) page encrypted with a Caesar Cipher.
# - cipher consider the 26-letter English alphabet
# - characters that do not belong to the alphabet (such as numbers and special characters) are left unchanged.
# +
with open('ciphertext_caesar.txt', mode='r', encoding='utf8') as file:
ciphertext = file.read()
# print just first characters
print(ciphertext[:1000])
# -
# ### letters distribution
# A piece of knowledge that can be useful to break a Caesar cipher is the distribution of the alphabet letters in English language. It is stored in `alphabet_distribution.mat`.
#
# The distribution of the letters in English language has been estimated by observing many different Wikipedia pages.
# +
# loading the distribution from .mat file
mdict = io.loadmat('alphabet_distribution.mat', squeeze_me=True)
alphabet = mdict['alphabet']
frequency = mdict['frequency']
# print distribution
for letter, freq in zip(alphabet, frequency):
print(f'{letter}: {freq}')
# -
# plot distribution as bar plot
fig, ax = plt.subplots(figsize=(5,3))
probability = frequency/np.sum(frequency)
ax.bar(alphabet, probability)
ax.set(xlabel='letter', ylabel='probability')
ax.grid(True)
fig.tight_layout()
# plot distribution by sorting letters by frequency in descending order
fig, ax = plt.subplots(figsize=(5,3))
idx = np.argsort(probability)[::-1]
ax.bar(alphabet[idx], probability[idx])
ax.set(xlabel='letter', ylabel='probability')
ax.grid(True)
fig.tight_layout()
# ### Brute Force
# Since alphabet is 26 letters long only 26 shifts are possible you can try all possibilities and check them all.
# try every possible shift and print the corresponding plaintext
for shift in range(len(alphabet)):
plaintext = caesar_decoding(ciphertext, shift=shift)
print(f'{shift:2d} -> {plaintext[:73]}')
# The only shift resulting in a plausible plaintext is `shift`=14.
shift = 14
plaintext = caesar_decoding(ciphertext, shift=shift)
print(plaintext[:1000])
# It make sense!
# #### Fitness Measure
# The first attempt was successful. Each possible shift was tested and the correspondent plaintext was manually analyzed. Information about alphabet distribution was completely ignored.
#
# > Is it possible to use the alphabet distribution to assess the quality of the decoded plaintext?
#
# Yes, it is. We can use a metric that measures how the letter distribution in the decoded plaintext **fit** the actual letter distribution. The *fitness measure* measures how likely a given plaintext is the right one.
#
# Fitness measure $f$ for a given plaintext $\mathcal{P}$ is defined as follow:
# $$ f(\mathcal{P}) = \sum_{a\in \mathcal{P}} a \cdot p_x(a) $$
# where:
# - $a$ represents each single character of the plaintext $\mathcal{P}$
# - $p_x$ identifies the probability distribution of generic letter $x$. Therefore, $p_x(a)$ is the probability to observe the character $a$.
def fitness(text):
''' fitness measure '''
dist = dict(zip(alphabet, probability)) # hard-coded alphabet distribution
measure = np.sum([text.count(char)*dist[char] for char in alphabet])
return measure
# +
# compute fitness for each possible plaintext
fit = np.array([fitness(caesar_decoding(ciphertext, shift=shift))
for shift in range(len(alphabet))])
# get shift with maximum fitness measure
imax = np.argmax(fit)
print(f'best fitness: shift={imax}')
# plot fitness measure for all possible plaintext and mark maximum
fig, ax = plt.subplots(figsize=(5,3))
ax.bar(np.arange(len(alphabet)), fit)
ax.plot(imax, fit[imax], '*', color='C3')
ax.set(xlabel='shift', ylabel='fitness measure')
ax.grid(True)
fig.tight_layout()
# -
# ### Frequency Analysis
# Knowing what is the typical frequency for each letter (e.g., in English, letters «e», «t», «a», «i» are more common than others), it is possible to infer what shift was used to encrypt the plaintext. We just need to oserve the frequency of the characters in the ciphertext and find what shift best match the two distribution.
# +
# computing alphabet distribution on the ciphertext
freq_ciphertext = np.array([ciphertext.count(x) for x in alphabet])
prob_ciphertext = freq_ciphertext/len(ciphertext)
# print letters frequency and estimated probability
for letter, freq, prob in zip(alphabet, freq_ciphertext, prob_ciphertext):
print(f'{letter}: {freq:5d} ({prob:.3f})')
# +
fig, ax = plt.subplots(2, 1, figsize=(5,4))
ax[0].bar(alphabet, probability, label='plaintext')
ax[0].set(xlabel='letter', ylabel='probability')
ax[0].grid(True)
ax[0].legend(loc='upper right')
ax[1].bar(alphabet, prob_ciphertext, label='ciphertext')
ax[1].set(xlabel='letter', ylabel='probability')
ax[1].grid(True)
ax[1].legend(loc='upper right')
fig.tight_layout()
# -
# By comparing the two distribution plots, It is evident that the letter `e` (the most common) is mapped to the letter `s`, `f` to `t` and so on. The shift used by the Caesar cipher is therefore 14.
shift = 14
plaintext = caesar_decoding(ciphertext, shift=shift)
print(plaintext[:1000])
# ## Simple Substitution Cipher
# In a simple substitution cipher, every plaintext character is replaced with a different ciphertext character.
#
# As for Caesar Cipher, plaintext and ciphertext share the same set of characters (the alphabet), but, mapping from plaintext to ciphertext can be any of the $26! \sim 10^{26}\sim 2^{88}$ possibilities
#
# Since nowadays machines cannot explore 26! candidates, **frequency analysis** must be exploited to narrow down their number.
# ### Decoder
# As for Caesar cipher the decoder must know the **alphabet**, but this time a bare shift is not sufficient to define a decoder but there is the need of a **mapping rule** that maps each character of the plaintext to the character of the ciphertext.
#
# Again, we can implement the decoder as a function that takes the `ciphertext`a and the mapping `rule` as input and returns the `plaintext`. The alphabet is hard-coded in the function.
def simple_decoding(ciphertext, rule):
'''
Decode a ciphertext encrypted with a Simple Substitution Cipher,
considering the 26-letter English alphabet.
Parameters
----------
ciphertext: str,
ciphertext to be decoded
rule: dict,
map from cipher alphabet to plaintext alphabet.
Return
------
plaintext: str,
decoded ciphertext.
'''
plaintext = ''.join([rule[char] if char in alphabet else char
for char in ciphertext.lower()])
return plaintext
# ### Ciphertext
# Let us load the ciphertext stored in the file `ciphertext_simple.txt`.
#
# As before, we know that:
# - ciphertext contains the text of a [Wikipedia](https://www.wikipedia.org/) page encrypted with a Simple Substitution Cipher.
# - cipher consider the 26-letter English alphabet
# - characters that do not belong to the alphabet (such as numbers and special characters) are left unchanged.
with open('ciphertext_simple.txt', mode='r', encoding='utf8') as file:
ciphertext = file.read()
print(ciphertext[:1000])
# ### Frequency Analysis
# For reasonably large pieces of text (with enough characters to be statistically relevant), a possible procedure can be:
# - to just replace the most common ciphertext character with the most common character in the plaintext (for English text is `e`).
# - to replace the second most common ciphertext character with the second most common character in the plaintext
# - and so on
text = ''.join(filter(lambda x: x in alphabet, ciphertext))
print(text[:1000])
# +
# computing alphabet distribution on the ciphertext
freq_ciphertext = np.array([text.count(x) for x in alphabet])
prob_ciphertext = freq_ciphertext/len(text)
# print letters frequency and estimated probability
for letter, freq, prob in zip(alphabet, freq_ciphertext, prob_ciphertext):
print(f'{letter}: {freq:5d} ({prob:.3f})')
# +
fig, ax = plt.subplots(2, 1, figsize=(5,4))
ax[0].bar(alphabet, probability, label='plaintext')
ax[0].set(xlabel='letter', ylabel='probability')
ax[0].grid(True)
ax[0].legend(loc='upper right')
ax[1].bar(alphabet, prob_ciphertext, label='ciphertext')
ax[1].set(xlabel='letter', ylabel='probability')
ax[1].grid(True)
ax[1].legend(loc='upper right')
fig.tight_layout()
# -
# Let us plot the two distribution in descending order so that we can match the ciphertext most common character with the one that is most common in a typical Eanglish Wikipedia page.
# +
fig, ax = plt.subplots(2, 1, figsize=(5,4))
idx_plain = np.argsort(probability)[::-1] # sorted indexes for plaintext
ax[0].bar(alphabet[idx_plain], probability[idx_plain], label='plaintext')
ax[0].set(xlabel='letter', ylabel='probability')
ax[0].grid(True)
ax[0].legend(loc='upper right')
idx_cipher = np.argsort(prob_ciphertext)[::-1] # sorted indexes for ciphertext
ax[1].bar(alphabet[idx_cipher], prob_ciphertext[idx_cipher],
label='ciphertext')
ax[1].set(xlabel='letter', ylabel='probability')
ax[1].grid(True)
ax[1].legend(loc='upper right')
fig.tight_layout()
# -
# Let us define our first guess by matching the two distributions.
# +
rule = dict(zip(alphabet[idx_cipher], alphabet[idx_plain]))
# visualize the mapping
idx = np.argsort(list(rule.values()))
print(' plain alphabet:', ''.join(np.array(list(rule.values()))[idx]))
print('cipher alphabet:', ''.join(np.array(list(rule.keys()))[idx]))
# -
plaintext = simple_decoding(ciphertext, rule)
print(plaintext[:700])
# As expected, the first guess is not perfect. However, we can start recognizing some words such as "aprol" as first word inside the parenthesis that probably is a "april". This means that the letter mapped to `o` should be mapped to `i`.
#
# Let us modify the rule and check again.
# +
rule['x'], rule['j'] = 'i', 'o'
# visualize the mapping
idx = np.argsort(list(rule.values()))
print(' plain alphabet:', ''.join(np.array(list(rule.values()))[idx]))
print('cipher alphabet:', ''.join(np.array(list(rule.keys()))[idx]))
# -
plaintext = simple_decoding(ciphertext, rule)
print(plaintext[:700])
# Assuming that inside the parenthesis there is a date, the word "gebrmarf" probably corresponds to "february". This means that `e`, `b`, `r`, `a` are correctly mapped but `g`, `m`, `f` are not.
#
# With this iterative and manual procedure we can get to the final solution.
# +
rule['x'], rule['j'] = 'i', 'o'
rule['i'], rule['o'], rule['s'] = 'f', 'y', 'g'
rule['c'], rule['l'] = 'u', 'm'
rule['e'], rule['j'], rule['f'] = 'n', 't', 'o'
rule['b'], rule['t'] = 'd', 'c'
rule['z'], rule['q'] = 'v', 'k'
rule['p'], rule['u'] = 'x', 'j'
rule['k'], rule['g'] = 'z', 'q'
idx = np.argsort(list(rule.values()))
print(''.join(np.array(list(rule.values()))[idx]))
print(''.join(np.array(list(rule.keys()))[idx]))
# -
plaintext = simple_decoding(ciphertext, rule)
print(plaintext[:1200])
|
2.substitution-cipher/substitution_cipher.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/"} id="VgmaCkAMYtDe" outputId="29d3c487-551d-49ea-f8bd-ed8acc7a18bd"
# !curl -O https://www.robots.ox.ac.uk/~vgg/data/fgvc-aircraft/archives/fgvc-aircraft-2013b.tar.gz
# !tar xzf fgvc-aircraft-2013b.tar.gz
# !mv fgvc-aircraft-2013b dataset
# + [markdown] id="E9KEEr-SqTW1"
# ## Imports
# + id="MpYIMjSYZMLQ"
import pathlib
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from keras.models import Sequential, load_model
from keras.layers import Conv2D, MaxPool2D, Dense, Flatten, Dropout
#from tensorflow.keras.utils import to_categorical
from sklearn.model_selection import train_test_split
from PIL import Image
# + [markdown] id="_x9gNNs-6Q1B"
# ## Constantes
# + id="Dr_2EW33bf-Q"
DATA_DIR = pathlib.Path('dataset/data')
IMAGE_WIDTH = 128
IMAGE_HEIGHT = IMAGE_WIDTH
IMAGE_DEPTH = 3
# + id="feQN_B_oavZQ"
manufacturer_df = pd.read_csv(DATA_DIR / 'images_manufacturer_train.txt', sep=' ',
names=['image_id', 'manufacturer'],
usecols=['image_id', 'manufacturer'], # usecols for v1.4 compatibility
dtype={'image_id': str}, # ids are not int but string
)
# + [markdown] id="wSuWOM9nh-My"
# ## Verify data
# + colab={"base_uri": "https://localhost:8080/"} id="paQqQO1hdch1" outputId="3cfdbf42-0acd-409f-ee7c-9b1c2afdd92e"
manufacturer_df['manufacturer'].value_counts(dropna=False)
# + colab={"base_uri": "https://localhost:8080/"} id="jFiETklBhno9" outputId="4b25fba1-adc3-4b32-d529-98fba2718d96"
manufacturer_df.isna().sum()
# + id="16LEf8A4iTn7"
assert manufacturer_df['image_id'].isna().sum() == 0, "Valeur manquante dans image_id"
assert manufacturer_df['manufacturer'].isna().sum() == 0, "Valeur manquante dans manufacturer"
# + [markdown] id="04de5VNXkcEy"
# ## Deal with N columns
# + id="xLSb__cpoVXp"
# !grep ',' dataset/data/images_manufacturer_train.txt
# + colab={"base_uri": "https://localhost:8080/"} id="7URQG153oo12" outputId="f7097aec-015e-4bc5-d9df-3ba105f1fc64"
# Recherche le caractère T dans le fichier et n'affiche que trois lignes (head -3)
# ! grep 'T' dataset/data/images_manufacturer_train.txt | head -3
# + colab={"base_uri": "https://localhost:8080/"} id="HClFFaszpPZV" outputId="27c72844-9e02-4d7a-ffec-c4fb7fa2d22e"
# wc : compte le nombre d'éléments (-l : ligne, -c : caractère, -w : word)
# ! grep 'T' dataset/data/images_manufacturer_train.txt | wc -l
# + colab={"base_uri": "https://localhost:8080/"} id="ADBAL1zXqHo4" outputId="77cf8152-e68c-4709-d8c9-c9a625d7389d"
# !cut -f 1 -d ' ' dataset/data/images_manufacturer_train.txt | head -3
# + id="nSnzpmQeko8s"
manufacturer_df = pd.read_csv(DATA_DIR / 'images_manufacturer_train.txt', sep='\t',
names=['all'],
dtype={'all': str}, # ids are not int but string
)
# La fonction split() découpe une chaîne de caractères
manufacturer_df['image_id'] = manufacturer_df['all'].apply(lambda x: x.split(' ')[0])
# La fonction '<car>'.join(liste) concatène les éléments de liste en utilisant le séparateur <car>
manufacturer_df['manufacturer'] = manufacturer_df['all'].apply(lambda x: ' '.join(x.split(' ')[1:]))
# + colab={"base_uri": "https://localhost:8080/"} id="wQM4hx9ullxf" outputId="eadfa22e-ec6c-4383-8540-b4c79d5d7732"
manufacturer_df['manufacturer'].unique()
# + id="EPFfKMJ6lnfv" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="39ef8dbc-cccd-4a63-a8f8-a51922eeb2dc"
manufacturer_df.head()
# + id="TTuuD-UC_PkW"
manufacturer_df['path'] = manufacturer_df['image_id'].apply(lambda x: pathlib.Path('dataset/data/images') / (x + '.jpg'))
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="ljXuSBbR_941" outputId="86c838d7-6f9b-4164-cb8a-75ee0af5cb60"
manufacturer_df.head()
# + id="etcQytfyAf3E"
def build_image_database(path):
"""Build a pandas dataframe with target class and access path to images.
Parameters
----------
path (Path): path pattern to read csv file containing images information.
Returns
-------
A pandas dataframe, including target class and path to image.
"""
manufacturer_df = pd.read_csv(path, sep='\t',
names=['all'],
dtype={'all': str}, # ids are not int but string
)
# La fonction split() découpe une chaîne de caractères
manufacturer_df['image_id'] = manufacturer_df['all'].apply(lambda x: x.split(' ')[0])
# La fonction '<car>'.join(liste) concatène les éléments de liste en utilisant le séparateur <car>
manufacturer_df['manufacturer'] = manufacturer_df['all'].apply(lambda x: ' '.join(x.split(' ')[1:]))
# La colonne path contient le chemin d'accès à l'image
manufacturer_df['path'] = manufacturer_df['image_id'].apply(lambda x: pathlib.Path('dataset/data/images') / (x + '.jpg'))
return manufacturer_df
# + [markdown] id="AWytFnec6qv_"
# ## Functions
# + id="IQ-oAOTYF37l"
def build_image_database(path, target):
"""Build a pandas dataframe with target class and access path to images.
Parameters
----------
path (Path): path pattern to read csv file containing images information.
target (str): name of the target column.
Returns
-------
A pandas dataframe, including target class and path to image.
"""
_df = pd.read_csv(path, sep='\t',
names=['all'],
dtype={'all': str}, # ids are not int but string
)
# La fonction split() découpe une chaîne de caractères
_df['image_id'] = _df['all'].apply(lambda x: x.split(' ')[0])
# La fonction '<car>'.join(liste) concatène les éléments de liste en utilisant le séparateur <car>
_df[target] = _df['all'].apply(lambda x: ' '.join(x.split(' ')[1:]))
# La colonne path contient le chemin d'accès à l'image
_df['path'] = _df['image_id'].apply(lambda x: pathlib.Path('dataset/data/images') / (x + '.jpg'))
return _df.drop(columns=['all'])
# + colab={"base_uri": "https://localhost:8080/", "height": 112} id="LMcXHwyMCqpJ" outputId="b7a3fa83-aac2-4164-e36d-53f4b711717a"
build_image_database(DATA_DIR / 'images_manufacturer_train.txt', 'manufacturer').head(2)
# + id="FtSgX-pJEdI9" outputId="8f9b57dd-b739-4876-eaa7-b762fb1e8b50" colab={"base_uri": "https://localhost:8080/", "height": 112}
build_image_database(DATA_DIR / 'images_family_train.txt', 'family').head(2)
# + id="DhlPwxW9HRcB" outputId="fd8a2000-c611-4bc0-92e2-f567e73c1d09" colab={"base_uri": "https://localhost:8080/", "height": 112}
build_image_database(DATA_DIR / 'images_variant_train.txt', 'variant').head(2)
# + [markdown] id="HmguEyg_7BJ5"
# ## Load manufacturer dataset
# + id="DZctwYrfIIFj"
manufacturer_df = build_image_database(DATA_DIR / 'images_manufacturer_train.txt', 'manufacturer')
# + id="xJlsGiBcKi6G" outputId="a85fea55-ec9f-433b-fafd-4562c16f1a67" colab={"base_uri": "https://localhost:8080/", "height": 112}
manufacturer_df.head(2)
# + id="H4Zu_NAQKoJX" outputId="e4e0fed2-b39c-4efe-f287-c72a10e3aa82" colab={"base_uri": "https://localhost:8080/"}
# On récupère un chemin d'accès
manufacturer_df.head(1)['path'].values[0]
# + id="7s4bMDbjKxP4" outputId="49184e3f-8b66-4468-d7b0-67b03749c351" colab={"base_uri": "https://localhost:8080/", "height": 288}
plt.imshow(plt.imread(manufacturer_df.head(1)['path'].values[0]))
# + id="L9csnHVMLBiJ"
# La fonction :
# - prend un df (argument)
# - prend une ligne (row : argument, l'indice de la ligne)
# - prend une colonne (target : argument)
# - elle affiche la classe (la valeur de target) et l'image associée, pour la ligne en argument
def show_image(df, row, target):
"""Show an image from an image database, with the associated class.
Parameters
----------
df (pd.DataFrame): images definition dataframe
row (int): row index in df of image to be displayed
target (str): name of the target column
Returns
-------
None
"""
assert target in df.columns, "Missing target column in dataframe"
assert 'path' in df.columns, "Missing image path in dataframe"
print(df.iloc[row,][target])
plt.imshow(plt.imread(df.iloc[row,]['path']))
return
# + id="i3No6BuUOhgw" outputId="4f8eb6e4-bf6d-4029-a054-683a9b01cab1" colab={"base_uri": "https://localhost:8080/", "height": 288}
show_image(manufacturer_df, 42, 'manufacturer')
# + id="sAwImp5gOu-Q" outputId="3e1887ce-a3d7-4428-e045-52f92eed9912" colab={"base_uri": "https://localhost:8080/", "height": 287}
show_image(build_image_database(DATA_DIR / 'images_family_train.txt', 'family'), 24, 'family')
# + id="p3g-4q2jiWco" outputId="9bb04202-ffdb-4ecb-dc25-3f02e21c9078" colab={"base_uri": "https://localhost:8080/"}
manufacturer_df.shape
# + id="l1D_VDYWjQck" outputId="fd09ee70-8127-42e9-9489-1b3664f64c38" colab={"base_uri": "https://localhost:8080/", "height": 143}
manufacturer_df.head(3)
# + id="W4CW8xBQkFr4" outputId="a1d662fd-9053-4410-9e4f-de422028fd3a" colab={"base_uri": "https://localhost:8080/", "height": 287}
show_image(manufacturer_df, 0, 'manufacturer')
# + id="PDoKu0iVj147" outputId="b2d1dda8-33dc-42e7-c470-3ad16892abc1" colab={"base_uri": "https://localhost:8080/"}
plt.imread(manufacturer_df.head(1)['path'].values[0]).shape
# + id="Z3LPSBorkghq"
manufacturer_df['image_shape'] = manufacturer_df['path'].apply(lambda p: plt.imread(p).shape)
# + id="IgJxYeGJmW9L" outputId="b5fe196c-4399-41c9-cf3d-bd4b5c93e6e9" colab={"base_uri": "https://localhost:8080/"}
# Distribution du nombre de lignes
manufacturer_df['shape'].apply(lambda x: x[0]).value_counts()
# + id="aPQG2nSPnRty" outputId="19ec507f-3bae-4751-9b9a-8a76f21dd90d" colab={"base_uri": "https://localhost:8080/"}
# Distribution du nombre de colonnes
manufacturer_df['shape'].apply(lambda x: x[1]).value_counts()
# + id="0-0LscbxoOzO"
def load_resize_image(path, height, width):
"""Load an image and resize it to the target size.
Parameters
----------
path (Path): access path to image file
height (int): resize image to this height
width (int): resize image to this width
Returns
-------
np.array containing resized image
"""
return np.array(Image.open(path).resize((width, height)))
# + id="UJF-lrhcqdnb" outputId="7f1282df-ce97-42b6-9ac9-581745ae58d0" colab={"base_uri": "https://localhost:8080/"}
manufacturer_df.head(10).apply(lambda r: load_resize_image(r['path'], IMAGE_HEIGHT, IMAGE_WIDTH), axis=1)
# + id="Qk13kDXTrKj-"
manufacturer_df['resized_image'] = manufacturer_df.apply(lambda r: load_resize_image(r['path'], IMAGE_HEIGHT, IMAGE_WIDTH), axis=1)
# + id="nkvC-tvRtlS-" outputId="d60d66b1-f0a7-4613-b715-5efd58bcb49d" colab={"base_uri": "https://localhost:8080/", "height": 287}
plt.imshow(manufacturer_df.iloc[42,]['resized_image'])
# + id="rCEZVyzpb5dU"
def build_classification_model(df: pd.DataFrame, target: str, images: str):
"""Build a TF model using information from target and images columns in dataframe.
Parameters
----------
df (pd.DataFrame): dataframe with target and images columns
target (str): column name for target variable
images (str): column name for images
Returns
-------
TF model built & compiled
"""
nb_classes = df[target].nunique() # Compute number of classes for output layer
size = df[images].iloc[0].shape # Compute images size for input layer
#Building the model
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu', input_shape=size))
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(rate=0.25))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(rate=0.25))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(rate=0.5))
model.add(Dense(nb_classes, activation='softmax')) # output layer with nb_classes
#Compilation of the model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
return model
# + id="lQVky_M3gqWf"
model = build_classification_model(manufacturer_df, 'manufacturer', 'resized_image')
# + id="fKw_haHq-Kvy"
# Calcul du nombre de classes pour dimensionner la couche de sortie
nb_classes = manufacturer_df['manufacturer'].nunique()
# + id="4ybtPDXNTIc5"
#Building the model
model = Sequential()
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu', input_shape=(IMAGE_WIDTH,
IMAGE_HEIGHT,
IMAGE_DEPTH)))
model.add(Conv2D(filters=32, kernel_size=(5,5), activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(rate=0.25))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPool2D(pool_size=(2, 2)))
model.add(Dropout(rate=0.25))
model.add(Flatten())
model.add(Dense(256, activation='relu'))
model.add(Dropout(rate=0.5))
model.add(Dense(nb_classes, activation='softmax')) # Couche de sortie à nb_classes
#Compilation of the model
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
# + colab={"base_uri": "https://localhost:8080/"} id="eG5BDwQg_D58" outputId="59a47bff-690a-4eef-b786-ab0b5cfebcab"
manufacturer_df['manufacturer'].value_counts()
# + colab={"base_uri": "https://localhost:8080/"} id="NaF50pWi_s3S" outputId="5793b4e2-6b39-49a8-ffd3-a3806a4557e5"
manufacturer_df['manufacturer'].astype('category').cat.codes
# + colab={"base_uri": "https://localhost:8080/"} id="oWtMEfQ1Bmse" outputId="133a1696-8f43-4709-8464-81acea63ab0d"
tf.keras.utils.to_categorical(manufacturer_df['manufacturer'].astype('category').cat.codes)
# + id="LsK6DqgsCmfC"
y = tf.keras.utils.to_categorical(manufacturer_df['manufacturer'].astype('category').cat.codes)
# + [markdown] id="ewK5-MgEEZ0z"
# ## Build train & test set
# + id="2BqkQLyuhve0"
def build_x_and_y(df: pd.DataFrame, target: str, images: str):
"""Build x tensor and y tensor for model fitting.
Parameters
----------
df (pd.DataFrame): dataframe containing images and target
target (str): name of target column
images (str): name of images column
Returns
-------
x (np.array): tensor of x values
y (np.array): tensor of y values
"""
x = np.array(df[images].to_list())
y = tf.keras.utils.to_categorical(df[target].astype('category').cat.codes)
return x, y
# + id="Yxf7tPGKkIAo"
# Load train & test dataset
train_df = build_image_database(DATA_DIR / 'images_manufacturer_train.txt', 'manufacturer')
test_df = build_image_database(DATA_DIR / 'images_manufacturer_test.txt', 'manufacturer')
# Load & resize images
train_df['resized_image'] = train_df.apply(lambda r: load_resize_image(r['path'],
IMAGE_HEIGHT, IMAGE_WIDTH),
axis=1)
test_df['resized_image'] = test_df.apply(lambda r: load_resize_image(r['path'],
IMAGE_HEIGHT, IMAGE_WIDTH),
axis=1)
# Build tensors for training & testing
X_train, y_train = build_x_and_y(train_df, 'manufacturer', 'resized_image')
X_test, y_test = build_x_and_y(test_df, 'manufacturer', 'resized_image')
# Build TF classification model
model = build_classification_model(train_df, 'manufacturer', 'resized_image')
# + id="OEJuT6HKDN7u"
X_train, X_test, y_train, y_test = train_test_split(manufacturer_df[['resized_image', 'manufacturer']], y,
test_size=0.2,
stratify=manufacturer_df['manufacturer'])
# + id="VvsSNUKgGgLP"
assert X_train.shape[0] + X_test.shape[0] == manufacturer_df.shape[0]
assert y_train.shape[0] + y_test.shape[0] == y.shape[0]
# + colab={"base_uri": "https://localhost:8080/"} id="A83te1gXHh65" outputId="1095d627-9a25-41c5-e4e6-108ce3a0ca31"
X_train['manufacturer'].value_counts(normalize=True)[:5]
# + colab={"base_uri": "https://localhost:8080/"} id="fGctr9G0H6Fq" outputId="edd0f2d1-f2bc-4368-e3c4-66e35bdbb021"
X_test['manufacturer'].value_counts(normalize=True)[:5]
# + colab={"base_uri": "https://localhost:8080/"} id="6Hfk3ImiINIt" outputId="c860e8af-5af0-4f88-d989-cd23a4fc4526"
print(X_train['resized_image'].shape, X_test['resized_image'].shape)
# + [markdown] id="ssFGdDj5JXqg"
# ## Train model
# + colab={"base_uri": "https://localhost:8080/"} id="DtrDK7n4KOS9" outputId="d7176eb9-463b-4e97-d9ac-206ef6d8c135"
np.array(X_train['resized_image'].to_list()).shape
# + id="k9TMjV0MJKvu"
# %%time
epochs = 5
history = model.fit(np.array(X_train['resized_image'].to_list()), y_train, batch_size=32, epochs=epochs,
validation_data=(np.array(X_test['resized_image'].to_list()), y_test))
# + colab={"base_uri": "https://localhost:8080/"} id="ulL7d8A4DP_e" outputId="b55e9ab7-0164-4378-e176-d36f3234673f"
# https://dpaste.org/VwAF
# A faire une fois pour récupérer les informations sur la TPU
try:
tpu = tf.distribute.cluster_resolver.TPUClusterResolver() # TPU detection
print('Running on TPU ', tpu.cluster_spec().as_dict()['worker'])
except ValueError:
raise BaseException('ERROR: Not connected to a TPU runtime; please see the previous cell in this notebook for instructions!')
tf.config.experimental_connect_to_cluster(tpu)
tf.tpu.experimental.initialize_tpu_system(tpu)
tpu_strategy = tf.distribute.experimental.TPUStrategy(tpu)
# + colab={"base_uri": "https://localhost:8080/"} id="8WTuFANDGb3-" outputId="23ef2230-2f6e-4211-ff67-f2dc20062b92"
with tpu_strategy.scope():
model = build_classification_model(train_df, 'manufacturer', 'resized_image')
model.summary()
# + colab={"base_uri": "https://localhost:8080/"} id="lVxIvoyyKt8U" outputId="020fad50-5b12-4a7c-8961-2af9ad95e2cd"
# Load the TensorBoard notebook extension
# %load_ext tensorboard
import datetime
# !rm -rf ./logs
log_dir = "logs/fit/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
# + colab={"base_uri": "https://localhost:8080/"} id="eIvJu3ewJ3GL" outputId="7f17ef9a-9119-47d0-f3ba-76544c02160f"
# %%time
epochs = 30
history = model.fit(X_train, y_train, batch_size=96, epochs=epochs,
validation_data=(X_test, y_test),
#callbacks=[tensorboard_callback]
)
# + colab={"base_uri": "https://localhost:8080/", "height": 174} id="4kPuwL_vPSnt" outputId="5080b0d3-9dcc-4dae-c449-5d619d5dcaf9"
model.predict_classes(test_df['resized_image'].iloc[10])
# + colab={"base_uri": "https://localhost:8080/"} id="HDCcRnIiai6O" outputId="37360dbd-9b44-4788-f588-a4d55a8408a8"
X_test[10:20].shape
# + colab={"base_uri": "https://localhost:8080/", "height": 288} id="4Zzf54vJdd9Q" outputId="b7675bcb-34e3-40ff-f62d-44a0a58268df"
show_image(test_df, 10, 'manufacturer')
# + colab={"base_uri": "https://localhost:8080/"} id="a2X35pfIaCeU" outputId="c6d67921-cdb8-483e-a046-fa14fe33afa5"
np.argmax(model.predict(X_test[10:20]), axis=1)
# + colab={"base_uri": "https://localhost:8080/", "height": 36} id="0xEmBzMjuZg6" outputId="d66453df-5e75-4a8a-c6f8-9478190bdc62"
train_df['manufacturer'].astype('category').cat.categories
# + id="76prrRLTetiK"
def classify_images(images, model, classes_names=None):
"""Classify images through a TF model.
Parameters
----------
images (np.array): set of images to classify
model (tf.keras.Model): TF/Keras model
classes_names: dictionary with names of classes
Returns
-------
predicted classes
"""
results = model.predict(images) # predict for images
classes = np.argmax(results, axis=1) # argmax returns the index of the max value per row
if classes_names is not None:
classes = np.array(classes_names[classes])
return classes
# + colab={"base_uri": "https://localhost:8080/", "height": 606} id="_53bZQ_Uh2XK" outputId="462606e5-181f-419c-978a-ee3f1bf2cee4"
import seaborn as sns
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(pd.crosstab(np.argmax(y_test, axis=1),
classify_images(X_test, model),
normalize='index'),
cmap='vlag',
ax=ax);
# + colab={"base_uri": "https://localhost:8080/", "height": 727} id="3o1XQSRcxFbj" outputId="25e46dd1-a0b2-4b89-930a-67deb0b95159"
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(pd.crosstab(test_df['manufacturer'],
classify_images(X_test, model, test_df['manufacturer'].astype('category').cat.categories),
normalize='index'),
cmap='vlag',
ax=ax);
# + colab={"base_uri": "https://localhost:8080/", "height": 610} id="IBv-rG8YaclL" outputId="8cb3b289-689e-492e-a880-c410b8a2e8ce"
fig, ax = plt.subplots(figsize=(12, 10))
sns.heatmap(pd.crosstab(np.argmax(y_train, axis=1), classify_images(X_train, model), normalize='index'),
cmap='vlag',
ax=ax);
# + id="LtVvi_x8dS-m"
model.save('model/my_model.h5')
# + colab={"base_uri": "https://localhost:8080/"} id="LRoosGWt1lvR" outputId="1c1aa785-48cb-45c6-c4e4-67fa2c4c1453"
# !ls -lh model
# + id="qFDlro4f1s01"
import datetime
def save_model(model, basename):
"""Save tf/Keras model.
Model file is named model + timestamp.
Parameters
----------
model (tf/Keras model): model to be saved
basename: location to save model file
"""
model.save('{}_{}.h5'.format(basename, datetime.datetime.now().strftime('%Y-%m-%d_%H-%M-%S')))
return
# + id="bm62oHGZ2kiP"
save_model(model, 'model/planes')
# + id="vDKNIF7B2tA0"
reloaded_model = load_model('/content/model/planes_2022-03-18_16-27-37.h5')
# + colab={"base_uri": "https://localhost:8080/"} id="Jzi_rYDI3c8c" outputId="0c72763b-4ffb-402d-f555-fb2f31f86429"
np.argmax(reloaded_model.predict(X_test[10:20]), axis=1)
# + id="R0Nq9w-H3u3T"
|
notebooks/train_classification_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
texte = "je vais en Espagne."
texte_modifie = texte.lower()
texte_modifie = texte.lower()
texte_modifie = texte.capitalize()
texte2 = "Je suis un amis, un vrai, pas un ennemi."
texte2_modifie = texte2.count("n")
texte2_modifie = texte2.find("un")
val = "548"
res = val.isdigit()
print(res)
print(texte2_modifie)
print(texte2.split())
|
15_methodes_chaines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# The MIT License (MIT)<br>
# Copyright (c) 2016,2017 Massachusetts Institute of Technology<br>
#
# Authors: <NAME>, <NAME><br>
# This software has been created in projects supported by the US National<br>
# Science Foundation and NASA (PI: Pankratius)<br>
#
# Permission is hereby granted, free of charge, to any person obtaining a copy<br>
# of this software and associated documentation files (the "Software"), to deal<br>
# in the Software without restriction, including without limitation the rights<br>
# to use, copy, modify, merge, publish, distribute, sublicense, and/or sell<br>
# copies of the Software, and to permit persons to whom the Software is<br>
# furnished to do so, subject to the following conditions:<br>
#
# The above copyright notice and this permission notice shall be included in<br>
# all copies or substantial portions of the Software.<br>
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR<br>
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,<br>
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE<br>
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER<br>
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,<br>
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN<br>
# THE SOFTWARE.<br>
# %matplotlib notebook
import matplotlib.pyplot as plt
# Land hydrology model produced by NASA<br>
# https://grace.jpl.nasa.gov/data/get-data/land-water-content/
from skdaccess.geo.gldas import DataFetcher as GLDAS_DF
from skdaccess.framework.param_class import *
geo_point = AutoList([(38, -117)]) # location in Nevada
gldas_fetcher = GLDAS_DF([geo_point],start_date='2010-01-01',end_date='2014-01-01')
data_wrapper = gldas_fetcher.output() # Get a data wrapper
label, data = next(data_wrapper.getIterator()) # Get GLDAS data
data.head()
plt.plot(data['Equivalent Water Thickness (cm)']);
plt.xticks(rotation=15);
|
skdaccess/examples/Demo_GLDAS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Project: Explore US births since 2000
# ## Introduction to dataset
f = open("US_births_2000-2014.csv", "r")
us_births = f.read()
births_split = us_births.split('\n')
print(births_split[0:10])
# ## Convert data to a list of lists
def read_csv(file):
f = open(file, "r")
string = f.read()
string_list = string.split('\n')
string_list = string_list[1:]
final_list = []
for row in string_list:
int_fields = []
string_fields = row.split(',')
for row in string_fields:
int_fields.append(int(row))
final_list.append(int_fields)
return final_list
us_births_list = read_csv("US_births_2000-2014.csv")
print(us_births_list[0:10])
# ## Calculate the number of births per month
def month_birth(list):
births_per_month = {}
for item in list:
month = item[1]
births = item[4]
if month in births_per_month:
births_per_month[month] += births
else:
births_per_month[month] = births
return births_per_month
us_month_births = month_birth(us_births_list)
print(us_month_births)
# ## Calculate the number of births each day of the week
def day_birth(list):
births_per_day = {}
for item in list:
day = item[3]
births = item[4]
if day in births_per_day:
births_per_day[day] += births
else:
births_per_day[day] = births
return births_per_day
us_days_births = day_birth(us_births_list)
print(us_days_births)
# ## Create a more general function
def general_counts(list, column):
births_per_column = {}
for item in list:
key = item[column]
births = item[4]
if key in births_per_column:
births_per_column[key] += births
else:
births_per_column[key] = births
return births_per_column
us_years_births = general_counts(us_births_list, 0)
print(us_years_births)
|
courses/8. Datasets exploration in Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="mu6YP2e5uFc9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 315} outputId="b0a51b84-9c91-43f1-c51e-969f37c8fa20" executionInfo={"status": "ok", "timestamp": 1583261634776, "user_tz": -60, "elapsed": 7426, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
# !pip install --upgrade tables
# + id="OBd74c--srEB" colab_type="code" colab={}
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# + id="MaGWWoKztDQf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="739f257a-e0ed-4e4e-b9da-0c5991553c30" executionInfo={"status": "ok", "timestamp": 1583261661017, "user_tz": -60, "elapsed": 818, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
# cd "/content/drive/My Drive/Colab Notebooks/dw_matrix_two/dw_matrix_transformacja2/data"
# + id="fQy-2cnftgWm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="e71e0295-9c75-42a9-d02b-7c2e9234f26b" executionInfo={"status": "ok", "timestamp": 1583261666558, "user_tz": -60, "elapsed": 2961, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
df = pd.read_hdf('car.h5')
df.shape
# + id="UYxHu5_Cv9q5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="71605f9c-f19e-4e9d-d5f3-3338ff52b766" executionInfo={"status": "ok", "timestamp": 1583261682983, "user_tz": -60, "elapsed": 1142, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
df.columns.values
# + id="ToZFlE5-wAgj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 284} outputId="9a9ca896-57eb-487d-806e-221c5c2b2ca9" executionInfo={"status": "ok", "timestamp": 1583261797910, "user_tz": -60, "elapsed": 1380, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
df['price_value'].hist(bins=100)
# + id="ewZL2barwXXc" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 185} outputId="67c205f0-9b7c-4178-a520-b890b3cfde54" executionInfo={"status": "ok", "timestamp": 1583261843674, "user_tz": -60, "elapsed": 1220, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
df['price_value'].describe()
# + id="vePNN7lEwnle" colab_type="code" colab={}
def group_and_barplot(feat_groupby, feat_agg='price_value', agg_funcs=[np.median, np.mean, np.size], feat_sort='mean', top=50, subplots=True):
return (
df
.groupby(feat_groupby)[feat_agg]
.agg(agg_funcs)
.sort_values(ascending=False, by=feat_sort)
.head(top)
).plot(kind='bar', figsize=(15, 5), subplots=subplots)
# + id="J6hthCsFxERd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 417} outputId="2c2c8940-4fbe-4de1-fa78-f90402cd5350" executionInfo={"status": "ok", "timestamp": 1583264020454, "user_tz": -60, "elapsed": 2923, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
group_and_barplot('param_marka-pojazdu');
# + id="s_5d1mei488t" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 436} outputId="2e314f63-2908-453f-e7fc-a8e3167ab79f" executionInfo={"status": "ok", "timestamp": 1583264253300, "user_tz": -60, "elapsed": 2303, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
group_and_barplot('param_kraj-pochodzenia', feat_sort='size');
# + id="7viInMZw6AhT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 390} outputId="92797dd2-815a-4399-f034-778e00df3650" executionInfo={"status": "ok", "timestamp": 1583264339917, "user_tz": -60, "elapsed": 2039, "user": {"displayName": "<NAME>", "photoUrl": "https://lh3.googleusercontent.com/a-/AOh14GiO92tdXC0dtCHGzPck6FSst19LWQulze4jUZPPEg=s64", "userId": "11332132132109748705"}}
group_and_barplot('param_kolor');
|
day2_visualization.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Percentage of permanent residence issued to Chinese and Indian nationals in 2015, comparing with the rest of Asia
#
# Data source: [Yearbook of Immigration Statistics 2015, Homeland Security, United States](https://www.dhs.gov/immigration-statistics/yearbook/2015)
# +
import pyexcel as p
base_url = "https://raw.githubusercontent.com/pyexcel/pyexcel-chart/master/"
sheet=p.get_sheet(url=base_url+"fy2015_table3d.xls")
sheet.top()
# -
# Let skip the first three rows because they contain meta data only.
sheet=p.get_sheet(url=base_url+"fy2015_table3d.xls", start_row=3)
sheet.top()
sheet.name_rows_by_column(0)
sheet.row.select(['Region and country of birth','Asia', 'India', 'China, People\'s Republic'])
sheet
sheet.transpose()
sheet
sheet.plot(chart_type='line')
sheet
pie_dict = {}
pie_dict['China'] = sheet['2015', 'China, People\'s Republic']/sheet['2015', 'Asia']
pie_dict['India'] = sheet['2015', 'India']/sheet['2015', 'Asia']
pie_dict['The Rest of Asia'] = 1 - pie_dict['China'] - pie_dict['India']
pie_sheet = p.get_sheet(adict=pie_dict)
pie_sheet
pie_sheet.plot(
chart_type='pie',
legend_at_bottom=True,
title='Percentage of permanent residence issued to Chinese and Indian nationals in 2015, comparing with the rest of Asia'
)
|
notebook/US immigration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# default_exp uniprot_integration
# -
# # UniProt data formatting
# +
#export
import re
import pandas as pd
import numpy as np
# -
# This notebook contains functions to import a uniport annotation file and to format it as pandas dataframe for further usage in alphamap.
#
# The preprocessed uniprot annotation includes information about:
# - __the known preprocessing events__ for proteins, such as signal peptide, transit peptide, propeptide, chain, peptide;
# - information on all available in Uniprot __post translational modificatios__, like modified residues (Phosphorylation, Methylation, Acetylation, etc.), Lipidation, Glycosylation, etc.;
# - information on __sequence similarities__ with other proteins and __the domain(s)__ present in a protein, such as domain, repeat, region, motif, etc.;
# - information on __the secondary and tertiary structure__ of proteins, such as turn, beta strand, helix.
# ## Instructions on how to download a UniProt annotation file
#
# 1. Go to the Uniprot website(https://www.uniprot.org/uniprot/), select the organism of interest in the "Popular organisms" section and click on it.
# 2. Click the "Download" button and select "Text" format.
# 3. Select the "Compressed" radio button and click "Go".
# 4. Unzip the downloaded file and specify the path to this file.
# ## Helper functions
# +
#export
def extract_note(string: str, splitted:bool = False):
"""
Helper function to extract information about note of the protein from Uniprot using regular expression.
Args:
string (str): Uniprot annotation string.
splitted (bool, optional): Flag to allow linebreaks. Default is 'False'.
Returns:
str: Extracted string of the uniprot note section.
"""
if not splitted:
regex = r"\/note=\"(?P<note>.+?)\""
else:
regex = r"\/note=\"(?P<note>.*)"
result = re.findall(regex, string)
return result
def extract_note_end(string: str, has_mark:bool = True):
"""
Helper function to extract information about note of the protein from Uniprot using regular expression.
Args:
string (str): Uniprot annotation string.
has_mark (bool, optional): Flag if end quotation marks are present. Default is 'False'.
Returns:
str: Extracted string of the uniprot note section.
"""
if has_mark:
regex = r"FT\s+(?P<note>.*)\""
else:
regex = r"FT\s+(?P<note>.*)"
result = re.findall(regex, string)
return result
# +
#hide
# write tests for extract_note and extract_note_end functions
def test_extract_note_not_splitted():
string = 'FT /note="Missing (in isoform 2)"'
output = extract_note(string)
assert "Missing (in isoform 2)" == output[0]
def test_extract_note_splitted():
string = 'FT /note="MAAALFVLLGF -> MKQSD'
output = extract_note(string, splitted=True)
assert "MAAALFVLLGF -> MKQSD" == output[0]
def test_extract_note_end_finished():
string = 'FT ASPQER (in isoform 4)"'
output = extract_note_end(string)
assert "ASPQER (in isoform 4)" == output[0]
def test_extract_note_end_not_finished():
string = 'FT ASPQER (in isoform 4)'
output = extract_note_end(string, has_mark=False)
assert "ASPQER (in isoform 4)" == output[0]
test_extract_note_not_splitted()
test_extract_note_splitted()
test_extract_note_end_finished()
test_extract_note_end_not_finished()
# +
#export
def resolve_unclear_position(value: str):
"""
Replace unclear position of the start/end of the modification defined as '?' with -1 and if it's defined as '?N'
or ">N" - by removing the '?'/'>'/'<' signs.
Args:
value (str): Unclear sequence position from uniprot.
Returns:
float: Resolved sequence position.
"""
# if it's "1..?" or "?..345" for start or end -> remove -1 that we can filter later
# if it's "31..?327" or "?31..327" -> remove the question mark
# if it's "<1..106" or "22..>115" -> remove the "<" or ">" signs
if value == '?':
return -1
value = value.replace('?', '').replace('>', '').replace('<', '')
return float(value)
def extract_positions(posit_string: str):
"""
Extract isoform_id(str) and start/end positions(float) of any feature key from the string.
Args:
posit_string (str): Uniprot position string.
Returns:
[str, float, float]: str: Uniprot isoform accession, float: start position, float: end position
"""
isoform = ''
start = end = np.nan
if '..' in posit_string:
start, end = posit_string.split('..')
if ':' in posit_string:
if isinstance(start, str):
isoform, start = start.split(':')
else:
isoform, start = posit_string.split(':')
# in the case when we have only one numeric value as a posit_string
if isinstance(start, float):
start = posit_string
# change the type of start and end into int/float(np.nan)
if isinstance(start, str):
start = resolve_unclear_position(start)
if isinstance(end, str):
end = resolve_unclear_position(end)
return isoform, start, end
# +
#hide
# write tests for extract_positions and resolve_unclear_position functions
def test_extract_positions():
string = '34..65'
isoform, start, end = extract_positions(string)
np.testing.assert_equal(['', 34, 65], [isoform, start, end])
def test_extract_positions_with_isoform():
string = 'P35613-2:195..199'
isoform, start, end = extract_positions(string)
np.testing.assert_equal(['P35613-2', 195, 199], [isoform, start, end])
def test_extract_positions_start_with_isoform():
string = 'Q9C0I9-2:256'
isoform, start, end = extract_positions(string)
np.testing.assert_equal(['Q9C0I9-2', 256, np.nan], [isoform, start, end])
def test_extract_positions_start():
string = '256'
isoform, start, end = extract_positions(string)
np.testing.assert_equal(['', 256, np.nan], [isoform, start, end])
def test_resolve_unclear_position_unknown():
string = '?'
message = f"For unknown position resolve_unclear_position function returns wrong output instead of -1."
assert -1 == resolve_unclear_position(string), message
def test_resolve_unclear_position_unclear():
string1 = '>117'
string2 = '<1'
string3 = '?327'
string4 = '?10'
message = f"For unclear position resolve_unclear_position function returns wrong output."
assert 117 == resolve_unclear_position(string1), message
assert 1 == resolve_unclear_position(string2), message
assert 327 == resolve_unclear_position(string3), message
assert 10 == resolve_unclear_position(string4), message
test_extract_positions()
test_extract_positions_with_isoform()
test_extract_positions_start_with_isoform()
test_extract_positions_start()
test_resolve_unclear_position_unknown()
test_resolve_unclear_position_unclear()
# -
# ## Uniprot preprocessing function
#export
def preprocess_uniprot(path_to_file: str):
"""
A complex complete function to preprocess Uniprot data from specifying the path to a flat text file
to the returning a dataframe containing information about:
- protein_id(str)
- feature(category)
- isoform_id(str)
- start(float)
- end(float)
- note information(str)
Args:
path_to_file (str): Path to a .txt annotation file directly downloaded from uniprot.
Returns:
pd.DataFrame: Dataframe with formatted uniprot annotations for alphamap.
"""
all_data = []
with open(path_to_file) as f:
is_splitted = False
new_instance = False
combined_note = []
line_type = ''
for line in f:
if line.startswith(('AC', 'FT')):
if is_splitted:
# in case when the note information is splitted into several lines
if line.rstrip().endswith('"'):
# if it's the final part of the note
combined_note.extend(extract_note_end(line))
all_data.append([protein_id, feature, isoform, start, end, " ".join(combined_note)])
is_splitted = False
new_instance = False
else:
# if it's the middle part of the note
combined_note.extend(extract_note_end(line, has_mark=False))
elif line.startswith('AC'):
# contains the protein_id information
if line_type != 'AC':
# to prevent a situation when the protein has several AC lines with different names
# in this case we are taking the first name in the first line
protein_id = line.split()[1].replace(';', '')
line_type = 'AC'
elif line.startswith('FT'):
line_type = 'FT'
# contains all modifications/preprocessing events/etc., their positions, notes
data = line.split()
if data[1].isupper() and not data[1].startswith('ECO'):
feature = data[1]
isoform, start, end = extract_positions(data[2])
new_instance = True
else:
if data[1].startswith('/note'):
note = extract_note(line)
if note:
# if note was created > it contains just one line and can be already added to the data
all_data.append([protein_id, feature, isoform, start, end, note[0]])
new_instance = False
else:
# if note is empty > it's splitted into several lines and we create combined_note
combined_note = extract_note(line, splitted=True)
is_splitted = True
else:
if new_instance:
# in case when we don't have any note but need to add other information about instance
all_data.append([protein_id, feature, isoform, start, end, ''])
new_instance = False
# create a dataframe for preprocessed data
uniprot_df = pd.DataFrame(all_data, columns=['protein_id', 'feature', 'isoform_id', 'start', 'end', 'note'])
# change the dtypes of the columns
uniprot_df.feature = uniprot_df.feature.astype('category')
# to filter the instances that don't have a defined start/end position(start=-1 or end=-1)
uniprot_df = uniprot_df[(uniprot_df.start != -1) & (uniprot_df.end != -1)].reset_index(drop=True)
return uniprot_df
# +
#hide
# for testing of the function a text file for P11532 protein was downloaded from the Uniprot
path_to_test_file = '../testdata/P11532_test_file.txt'
def test_preprocess_uniprot():
test_df = preprocess_uniprot(path_to_test_file)
np.testing.assert_equal((167, 6), test_df.shape, err_msg = 'The shape of the returned file is incorrect.')
assert test_df.feature.dtype == 'category', 'The type of the feature column is not a category.'
# to check the cases when protein had no note but had feature, start and end, f.e.
# FT HELIX 14..31
# FT /evidence="ECO:0000244|PDB:1DXX"
np.testing.assert_array_equal(['P11532', 'HELIX', '', 14.0, 31.0, ''],
test_df[(test_df.feature == 'HELIX') & (test_df.start == 14)].values.tolist()[0],
err_msg = "The output for the protein that doesn't have a note but has \
feature information, a start and an end position is incorrect.")
# to check the cases when protein had a note written in one line and doesn't have end, f.e.
# FT MOD_RES 3500
# FT /note="Phosphoserine"
np.testing.assert_array_equal(['P11532', 'MOD_RES', '', 3500.0, np.nan, 'Phosphoserine'],
test_df[(test_df.feature == 'MOD_RES') & (test_df.start == 3500)].values.tolist()[0],
err_msg = "The output for the protein that has the note written in one line \
and doesn't have an end position for the feature is incorrect.")
# to check the cases when protein had a note split into several line, f.e.
# FT VARIANT 3340
# FT /note="C -> Y (in DMD; results in highly reduced protein
# FT levels and expression at the sarcolemma)"
assert 'C -> Y (in DMD; results in highly reduced protein levels and expression at the sarcolemma)' == \
test_df[(test_df.feature == 'VARIANT') & (test_df.start == 3340)]['note'].values[0], \
"The output for the protein that has a note split into several lines is incorrect."
# to check the cases when protein had protein_ids written in several line, f.e.
# AC P11532; A1L0U9; E7EQR9; E7EQS5; E7ESB2; E9PDN1; E9PDN5; F5GZY3; F8VX32;
# AC Q02295; Q14169; Q14170; Q5JYU0; Q6NSJ9; Q7KZ48; Q8N754; Q9UCW3; Q9UCW4;
assert 1 == test_df.protein_id.nunique(), "A preprocess_uniprot function returns a non-unique protein_id."
assert 'P11532' == test_df.protein_id.unique()[0], 'A preprocess_uniprot function returns a wrong protein_id.'
test_preprocess_uniprot()
# -
# ## UniProt feature dictionary
# The following is a dictionary that maps feature names to the feature entries in the processed uniprot annotation file.
#export
uniprot_feature_dict = {
'Chain': 'CHAIN',
'Initiator methionine': 'INIT_MET',
'Peptide': 'PEPTIDE',
'Propeptide': 'PROPEP',
'Signal peptide': 'SIGNAL',
'Transit peptide': 'TRANSIT',
'Cross-link': 'CROSSLNK',
'Disulfide bond': 'DISULFID',
'Glycosylation': 'CARBOHYD',
'Lipidation': 'LIPID',
'Modified residue': 'MOD_RES',
'Coiled coil': 'COILED',
'Compositional bias': 'COMPBIAS',
'Domain': 'DOMAIN',
'Motif': 'MOTIF',
'Region': 'REGION',
'Repeat': 'REPEAT',
'Zinc finger': 'ZN_FING',
'Intramembrane': 'INTRAMEM',
'Topological domain': 'TOPO_DOM',
'Transmembrane': 'TRANSMEM',
'Beta strand': 'STRAND',
'Helix': 'HELIX',
'Turn': 'TURN',
'Active site': 'ACT_SITE',
'Binding site': 'BINDING',
'Calcium binding': 'CA_BIND',
'DNA binding': 'DNA_BIND',
'Metal binding': 'METAL',
'Nucleotide binding': 'NP_BIND',
'Site': 'SITE',
'Non-standard residue': 'NON_STD',
'Non-adjacent residues': 'NON_CONS',
'Non-terminal residue': 'NON_TER',
'Natural variant': 'VARIANT',
'Sequence conflict': 'CONFLICT',
'Alternative sequence': 'VAR_SEQ',
'Sequence uncertainty': 'UNSURE',
'Secondary structure': 'STRUCTURE',
'Mutagenesis': 'MUTAGEN'
}
# +
#hide
###### Export notebook to script ######
# -
#hide
from nbdev.showdoc import *
#hide
from nbdev.export import *
notebook2script()
|
nbs/Uniprot_integration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/iued-uni-heidelberg/DAAD-Training-2021/blob/main/compLingProject104SentenceAlignmentHunalignV04a.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="hhDdKnVbT6Aa"
# # Experiments with alignment tools
# + [markdown] id="iM-SQNgcjh6t"
# resources / corpora:
# https://heibox.uni-heidelberg.de/d/d65daff8341e467c82b1/
#
#
# Instructions are here:
# https://github.com/danielvarga/hunalign
#
# + id="5wTTt2yCTo7U" outputId="efd9383f-a641-4dbf-ad10-cbd8d8147f39" colab={"base_uri": "https://localhost:8080/"}
# !git clone https://github.com/danielvarga/hunalign.git
# + id="ZddMwgW9T5Rj" outputId="e6bf59f0-10da-42c3-abac-8e15eb4c3075" colab={"base_uri": "https://localhost:8080/"}
# %cd hunalign/src/hunalign
# !pwd
# + id="hJbwoRqGVK_O" outputId="1f823488-af86-4ea7-9a94-7789c654524b" colab={"base_uri": "https://localhost:8080/"}
# !make
# + id="fVz4B9KoVW7T"
# %cd /content/hunalign/
# !pwd
# !src/hunalign/hunalign data/hu-en.stem.dic examples/demo.hu.stem examples/demo.en.stem -hand=examples/demo.manual.ladder -text > /tmp/align.txt
# # !less /tmp/align.txt
# + id="aSfCT3TzeYfl" outputId="e2b402a5-74e5-4260-9dc0-259feec0f087" colab={"base_uri": "https://localhost:8080/"}
# !head --lines=20 /tmp/align.txt
# + colab={"base_uri": "https://localhost:8080/"} id="OtZIH64gfTO6" outputId="04d5e83b-e2dd-4077-eee8-93c8ca471e5f"
# %cd /content/
# !pwd
# + id="4C3Lu_yijc-2"
# downloading files - en es
# !wget https://heibox.uni-heidelberg.de/f/dc01904f8f9040a69610/?dl=1
# !mv index.html?dl=1 solar-t01-en-RE01.txt
# !wget https://heibox.uni-heidelberg.de/f/646957ccb3d24f359ed7/?dl=1
# !mv index.html?dl=1 solar-t01-es-RE01.txt
# + id="-irmCMkDjfjK"
# downloading files - en de
# !wget https://heibox.uni-heidelberg.de/f/dc489828a2d642bfba82/?dl=1
# !mv index.html?dl=1 ab-t01-en.txt
# English file
# !wget https://heibox.uni-heidelberg.de/f/e7e542d75d7644d1857d/?dl=1
# !mv index.html?dl=1 ab-t01-de.txt
# Other language files
# + id="S7VB7wPmes6C"
# !head --lines=10 ab-t01-en.txt
# + id="84YR_aNtfmz6"
# !head --lines=10 ab-t01-de.txt
# + id="YbI3WH-WccuO"
# !./hunalign/src/hunalign/hunalign -text -realign -autodict=es2enAutodict.txt ./hunalign/data/null.dic solar-t01-en-RE01.txt solar-t01-es-RE01.txt > solar-t01-en2esAlignment.tsv
# + id="JBo3h8SMdZfv"
# !./hunalign/src/hunalign/hunalign -text -realign -autodict=de2enAutodict.txt ./hunalign/data/null.dic >
# + id="aeeVxY50OtDX" outputId="3593cb60-cec0-4def-cdb2-d3459d4a527a" colab={"base_uri": "https://localhost:8080/"}
# !./hunalign/src/hunalign/hunalign -text -realign -autodict=de2enAutodict.txt ./hunalign/data/null.dic ab-t001-en-fatigue.txt ab-t001-de-fatigue.txt > ab-t001-en2de-fatigue.tsv
# + id="V_gxwlekhkZW"
# # copy dictionaries for editing
# !cp es2enAutodict.txt es2enAutodict.dic
# !cp de2enAutodict.txt de2enAutodict.dic
# + id="yh_I8HhHivWJ"
# you can edit dictionaries and try realigning tests if results are not good, like in this example:
# !./hunalign/src/hunalign/hunalign -text -realign -autodict=es2enAutodict2.txt es2enAutodict.txt solar-t01-en-RE01.txt solar-t01-es-RE01.txt > solar-t01-en2esAlignment2.txt
# + id="4uqIFYZHlaTo"
# %cd /content/
# + [markdown] id="vYPVNJE9naFM"
# # Converting tsv to tmx
# + id="ZzYUz9XineGH"
# change names of files accordingly (input and output)
import re, os, sys
FIn = open('ab-t01-en2de.tsv', 'r')
FOut = open('ab-t01-en2de.tmx', 'w')
SrcLang = 'en'
TgtLang = 'de'
SLineHead = '''<?xml version="1.0" encoding="UTF-8"?>
<!DOCTYPE tmx SYSTEM "tmx14.dtd">
<tmx version="1.4">
<header creationtool="OmegaT" o-tmf="OmegaT TMX" adminlang="EN-US" datatype="plaintext" creationtoolversion="5.7.0_0_8ae1ecfb" segtype="sentence" srclang="en"/>
<body>
'''
SLineEnd = '''
</body>
</tmx>
'''
FOut.write(SLineHead)
for SLine in FIn:
SLine = SLine.strip()
LLine = re.split('\t', SLine)
try:
SSrcLang = LLine[0]
STgtLang = LLine[1]
STuvSLTag = f' <tuv xml:lang="{SrcLang}">'
STuvTLTag = f' <tuv xml:lang="{TgtLang}">'
STuvSL = STuvSLTag + '''\n <seg>''' + SSrcLang + '''</seg>\n''' + ''' </tuv>\n'''
STuvTL = STuvTLTag + '''\n <seg>''' + STgtLang + '''</seg>\n''' + ''' </tuv>\n'''
STuv = ''' <tu>\n''' + STuvSL + STuvTL + ''' </tu>\n'''
FOut.write(STuv)
except:
continue
FOut.write(SLineEnd)
FOut.flush()
|
compLingProject104SentenceAlignmentHunalignV04a.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import gym
import torch as T
import numpy as np
from PIL import Image
# -
device = T.device("cuda:0" if T.cuda.is_available() else "cpu")
class ReplayBuffer:
def __init__(self):
self.memory_actions = []
self.memory_states = []
self.memory_log_probs = []
self.memory_rewards = []
self.is_terminals = []
def clear_memory(self):
del self.memory_actions[:]
del self.memory_states[:]
del self.memory_log_probs[:]
del self.memory_rewards[:]
del self.is_terminals[:]
class ActorCritic(T.nn.Module):
def __init__(self, state_dimension, action_dimension, nb_latent_variables):
super(ActorCritic, self).__init__()
self.action_layer = T.nn.Sequential(
T.nn.Linear(state_dimension, nb_latent_variables),
T.nn.Tanh(),
T.nn.Linear(nb_latent_variables, nb_latent_variables),
T.nn.Tanh(),
T.nn.Linear(nb_latent_variables, action_dimension),
T.nn.Softmax(dim=-1)
)
self.value_layer = T.nn.Sequential(
T.nn.Linear(state_dimension, nb_latent_variables),
T.nn.Tanh(),
T.nn.Linear(nb_latent_variables, nb_latent_variables),
T.nn.Tanh(),
T.nn.Linear(nb_latent_variables, 1)
)
def act(self, state, memory):
state = T.from_numpy(state).float().to(device)
action_probs = self.action_layer(state)
dist = T.distributions.Categorical(action_probs)
action = dist.sample()
memory.memory_states.append(state)
memory.memory_actions.append(action)
memory.memory_log_probs.append(dist.log_prob(action))
return action.item()
def evaluate(self, state, action):
action_probs = self.action_layer(state)
dist = T.distributions.Categorical(action_probs)
action_log_probs = dist.log_prob(action)
dist_entropy = dist.entropy()
state_value = self.value_layer(state)
return action_log_probs, T.squeeze(state_value), dist_entropy
class Agent:
def __init__(
self, state_dimension, action_dimension, nb_latent_variables,
lr, betas, gamma, K_epochs, eps_clip):
self.lr = lr
self.betas = betas
self.gamma = gamma
self.eps_clip = eps_clip
self.K_epochs = K_epochs
self.policy = ActorCritic(
state_dimension,
action_dimension,
nb_latent_variables).to(device)
self.optimizer = T.optim.Adam(
self.policy.parameters(), lr=lr, betas=betas)
self.policy_old = ActorCritic(
state_dimension,
action_dimension,
nb_latent_variables).to(device)
self.policy_old.load_state_dict(self.policy.state_dict())
self.MseLoss = T.nn.MSELoss()
def update(self, memory):
# Monte Carlo estimate
rewards = []
discounted_reward = 0
for reward, is_terminal in \
zip(reversed(memory.memory_rewards), reversed(memory.is_terminals)):
if is_terminal:
discounted_reward = 0
discounted_reward = reward + (self.gamma * discounted_reward)
rewards.insert(0, discounted_reward)
# Normalize
rewards = T.tensor(rewards).to(device)
rewards = (rewards - rewards.mean()) / (rewards.std() + 1e-5)
# Convert to Tensor
old_states = T.stack(memory.memory_states).to(device).detach()
old_actions = T.stack(memory.memory_actions).to(device).detach()
old_log_probs = T.stack(memory.memory_log_probs).to(device).detach()
# Policy Optimization
for _ in range(self.K_epochs):
log_probs, state_values, dist_entropy = self.policy.evaluate(
old_states, old_actions)
# Finding ratio: pi_theta / pi_theta__old
ratios = T.exp(log_probs - old_log_probs.detach())
# Surrogate Loss
advantages = rewards - state_values.detach()
surr1 = ratios * advantages
surr2 = T.clamp(ratios, 1-self.eps_clip, 1+self.eps_clip) * advantages
loss = -T.min(surr1, surr2) + \
0.5*self.MseLoss(state_values, rewards) - 0.01*dist_entropy
# Backpropagation
self.optimizer.zero_grad()
loss.mean().backward()
self.optimizer.step()
# New weights to old policy
self.policy_old.load_state_dict(self.policy.state_dict())
env = gym.make("LunarLander-v2")
np.random.seed(0)
render = True
memory = ReplayBuffer()
agent = Agent(
state_dimension=env.observation_space.shape[0],
action_dimension=4,
nb_latent_variables=64,
lr=0.002,
betas=(0.9, 0.999),
gamma=0.99,
K_epochs=4,
eps_clip=0.2)
agent.policy_old.load_state_dict(T.load("../Exercise11.03/PPO_LunarLander-v2.pth"))
for ep in range(5):
ep_reward = 0
state = env.reset()
for t in range(300):
action = agent.policy_old.act(state, memory)
state, reward, done, _ = env.step(action)
ep_reward += reward
if render:
env.render()
img = env.render(mode = "rgb_array")
img = Image.fromarray(img)
image_dir = "./gif"
if not os.path.exists(image_dir):
os.makedirs(image_dir)
img.save(os.path.join(image_dir, "{}.jpg".format(t)))
if done:
break
print("Episode: {}, Reward: {}".format(ep, int(ep_reward)))
ep_reward = 0
env.close()
|
Chapter11/Activity11.02/Activity11_02.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# # In-Class Coding Lab: Functions
#
# The goals of this lab are to help you to understand:
#
# - How to use Python's built-in functions in the standard library.
# - How to write user-defined functions
# - The benefits of user-defined functions to code reuse and simplicity.
# - How to create a program to use functions to solve a complex idea
#
# We will demonstrate these through the following example:
#
#
# ## The Credit Card Problem
#
# If you're going to do commerce on the web, you're going to support credit cards. But how do you know if a given number is valid? And how do you know which network issued the card?
#
# **Example:** Is `5300023581452982` a valid credit card number?Is it? Visa? MasterCard, Discover? or American Express?
#
# While eventually the card number is validated when you attempt to post a transaction, there's a lot of reasons why you might want to know its valid before the transaction takes place. The most common being just trying to catch an honest key-entry mistake made by your site visitor.
#
# So there are two things we'd like to figure out, for any "potential" card number:
#
# - Who is the issuing network? Visa, MasterCard, Discover or American Express.
# - In the number potentially valid (as opposed to a made up series of digits)?
#
# ### What does the have to do with functions?
#
# If we get this code to work, it seems like it might be useful to re-use it in several other programs we may write in the future. We can do this by writing the code as a **function**. Think of a function as an independent program its own inputs and output. The program is defined under a name so that we can use it simply by calling its name.
#
# **Example:** `n = int("50")` the function `int()` takes the string `"50"` as input and converts it to an `int` value `50` which is then stored in the value `n`.
#
# When you create these credit card functions, we might want to re-use them by placing them in a **Module** which is a file with a collection of functions in it. Furthermore we can take a group of related modules and place them together in a Python **Package**. You install packages on your computer with the `pip` command.
#
# -
# ## Built-In Functions
#
# Let's start by checking out the built-in functions in Python's math library. We use the `dir()` function to list the names of the math library:
#
# +
import math
dir(math)
# -
# If you look through the output, you'll see a `factorial` name. Let's see if it's a function we can use:
help(math.factorial)
# It says it's a built-in function, and requies an integer value (which it referrs to as x, but that value is arbitrary) as an argument. Let's call the function and see if it works:
math.factorial(5) #this is an example of "calling" the function with input 5. The output should be 120
math.factorial(0) # here we call the same function with input 0. The output should be 1.
## Call the factorial function with an input argument of 4. What is the output?
math.factorial(4)
# ## Using functions to print things awesome in Juypter
#
# Up until this point we've used the boring `print()` function for our output. Let's do better. In the `IPython.display` module there are two functions `display()` and `HTML()`. The `display()` function outputs a Python object to the Jupyter notebook. The `HTML()` function creates a Python object from [HTML Markup](https://www.w3schools.com/html/html_intro.asp) as a string.
#
# For example this prints Hello in Heading 1.
#
# +
from IPython.display import display, HTML
print("Exciting:")
display(HTML("<h1>Hello</h1>"))
print("Boring:")
print("Hello")
# -
# Let's keep the example going by writing two of our own functions to print a title and print text as normal, respectively.
#
# Execute this code:
# +
def print_title(text):
'''
This prints text to IPython.display as H1
'''
return display(HTML("<H1>" + text + "</H1>"))
def print_normal(text):
'''
this prints text to IPython.display as normal text
'''
return display(HTML(text))
# -
# Now let's use these two functions in a familiar program!
print_title("Area of a Rectangle")
length = float(input("Enter length: "))
width = float(input("Enter width: "))
area = length * width
print_normal("The area is %.2f" % area)
# ## Let's get back to credit cards....
#
# Now that we know how a bit about **Packages**, **Modules**, and **Functions** let's attempt to write our first function. Let's tackle the easier of our two credit card related problems:
#
# - Who is the issuing network? Visa, MasterCard, Discover or American Express.
#
# This problem can be solved by looking at the first digit of the card number:
#
# - "4" ==> "Visa"
# - "5" ==> "MasterCard"
# - "6" ==> "Discover"
# - "3" ==> "American Express"
#
# So for card number `5300023581452982` the issuer is "MasterCard".
#
# It should be easy to write a program to solve this problem. Here's the algorithm:
#
# ```
# input credit card number into variable card
# get the first digit of the card number (eg. digit = card[0])
# if digit equals "4"
# the card issuer "Visa"
# elif digit equals "5"
# the card issuer "MasterCard"
# elif digit equals "6"
# the card issuer is "Discover"
# elif digit equals "3"
# the card issues is "American Express"
# else
# the issuer is "Invalid"
# print issuer
# ```
#
# ### Now You Try It
#
# Turn the algorithm into python code
card = input("Your credit card number:" )
digit = card[0]
if (digit == "4"):
print("the card issuer is Visa")
elif (digit == "5"):
print("the card issuer is MasterCard")
elif (digit == "6"):
print("the card issuer is Discover")
elif (digit == "3"):
print("the card issuer is American Express")
else:
print("the issuer is invalid")
# **IMPORTANT** Make sure to test your code by running it 5 times. You should test issuer and also the "Invalid Card" case.
#
# ## Introducing the Write - Refactor - Test - Rewrite approach
#
# It would be nice to re-write this code to use a function. This can seem daunting / confusing for beginner programmers, which is why we teach the **Write - Refactor - Test - Rewrite** approach. In this approach you write the ENTIRE PROGRAM and then REWRITE IT to use functions. Yes, it's inefficient, but until you get comfotable thinking "functions first" its the best way to modularize your code with functions. Here's the approach:
#
# 1. Write the code
# 2. Refactor (change the code around) to use a function
# 3. Test the function by calling it
# 4. Rewrite the original code to use the new function.
#
#
# We already did step 1: Write so let's move on to:
#
# ### Step 2: refactor
#
# Let's strip the logic out of the above code to accomplish the task of the function:
#
# - Send into the function as input a credit card number as a `str`
# - Return back from the function as output the issuer of the card as a `str`
#
# To help you out we've written the function stub for you all you need to do is write the function body code.
def CardIssuer(card):
digit = card[0]
if (digit == "4"):
issuer = ("Visa")
elif (digit == "5"):
issuer = ("MasterCard")
elif (digit == "6"):
issuer = ("Discover")
elif (digit == "3"):
issuer = ("American Express")
else:
print("the issuer is invalid")
return issuer
# ### Step 3: Test
#
# You wrote the function, but how do you know it works? The short answer is unless you test it you're guessing.
#
# Testing our function is as simple as calling the function with input values where WE KNOW WHAT TO EXPECT from the output. We then compare that to the ACTUAL value from the called function. If they are the same, then we know the function is working as expected!
#
# Here's some examples:
#
# ```
# WHEN card='40123456789' We EXPECT CardIssuer(card) to return Visa
# WHEN card='50123456789' We EXPECT CardIssuer(card) to return MasterCard
# WHEN card='60123456789' We EXPECT CardIssuer(card) to return Discover
# WHEN card='30123456789' We EXPECT CardIssuer(card) to return American Express
# WHEN card='90123456789' We EXPECT CardIssuer(card) to return Invalid Card
# ```
#
# ### Now you Try it!
#
# Write the tests based on the examples:
# Testing the CardIssuer() function
def CardIssuer(card):
print("WHEN card='40123456789' We EXPECT CardIssuer(card) to return Visa ACTUAL", CardIssuer("40123456789"))
print("WHEN card='50123456789' We EXPECT CardIssuer(card) to return MasterCard ACTUAL", CardIssuer("50123456789"))
print("WHEN card='60123456789' We EXPECT CardIssuer(card) to return Discover ACTUAL", CardIssuer("60123456789"))
print("WHEN card='30123456789' We EXPECT CardIssuer(card) to return American Express", CardIssuer("30123456789"))
print("WHEN card='90123456789' We EXPECT CardIssuer(card) to return Invalid Card", CardIssuer("90123456789"))
# ### Step 4: Rewrite
#
# The final step is to re-write the original program, but use the function instead. The algorithm becomes
#
# ```
# input credit card number into variable card
# call the CardIssuer function with card as input, issuer as output
# print issuer
# ```
#
# ### Now You Try It!
#
card = input("Your credit card number:" )
print("Your card comes from ",CardIssuer(card))
# ## Functions are abstractions. Abstractions are good.
#
#
# Step on the accellerator and the car goes. How does it work? Who cares, it's an abstraction! Functions are the same way. Don't believe me. Consider the Luhn Check Algorithm: https://en.wikipedia.org/wiki/Luhn_algorithm
#
# This nifty little algorithm is used to verify that a sequence of digits is possibly a credit card number (as opposed to just a sequence of numbers). It uses a verfication approach called a **checksum** to as it uses a formula to figure out the validity.
#
# Here's the function which given a card will let you know if it passes the Luhn check:
#
def checkLuhn(card):
total = 0
length = len(card)
parity = length % 2
for i in range(length):
digit = int(card[i])
if i%2 == parity:
digit = digit * 2
if digit > 9:
digit = digit -9
total = total + digit
return total % 10 == 0
# ### Is that a credit card number or the ramblings of a madman?
#
# In order to test the `checkLuhn()` function you need some credit card numbers. (Don't look at me... you ain't gettin' mine!!!!) Not to worry, the internet has you covered. The website: http://www.getcreditcardnumbers.com/ is not some mysterious site on the dark web. It's a site for generating "test" credit card numbers. You can't buy anything with these numbers, but they will pass the Luhn test.
#
# Grab a couple of numbers and test the Luhn function as we did with the `CardIssuer()` function. Write at least to tests like these ones:
#
# ```
# WHEN card='5443713204330437' We EXPECT checkLuhn(card) to return True
# WHEN card='5111111111111111' We EXPECT checkLuhn(card) to return False
# ```
#
card=input("enter card")
checkLuhn(card)
# ## Putting it all together
#
# Finally use our two functions to write the following program. It will ask for a series of credit card numbers, until you enter 'quit' for each number it will output whether it's invalid or if valid name the issuer.
#
#
# Here's the Algorithm:
# ```
# loop
# input a credit card number
# if card = 'quit' stop loop
# if card passes luhn check
# get issuer
# print issuer
# else
# print invalid card
# ```
#
# ### Now You Try It
while True:
card = input("Credit card number: ")
if card == ('quit'):
break
else:
if (checkLuhn(card)):
issuer = CardIssuer(card)
print(issuer)
else:
print("the issuer is invalid")
|
content/lessons/06/Class-Coding-Lab/CCL-Functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jonkrohn/ML-foundations/blob/master/notebooks/2-linear-algebra-ii.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="aTOLgsbN69-P"
# # Linear Algebra II: Matrix Operations
# + [markdown] id="yqUB9FTRAxd-"
# This topic, *Linear Algebra II: Matrix Operations*, builds on the basics of linear algebra. It is essential because these intermediate-level manipulations of tensors lie at the heart of most machine learning approaches and are especially predominant in deep learning.
#
# Through the measured exposition of theory paired with interactive examples, you’ll develop an understanding of how linear algebra is used to solve for unknown values in high-dimensional spaces as well as to reduce the dimensionality of complex spaces. The content covered in this topic is itself foundational for several other topics in the *Machine Learning Foundations* series, especially *Probability & Information Theory* and *Optimization*.
# + [markdown] id="d4tBvI88BheF"
# Over the course of studying this topic, you'll:
#
# * Develop a geometric intuition of what’s going on beneath the hood of machine learning algorithms, including those used for deep learning.
# * Be able to more intimately grasp the details of machine learning papers as well as all of the other subjects that underlie ML, including calculus, statistics, and optimization algorithms.
# * Reduce the dimensionalty of complex spaces down to their most informative elements with techniques such as eigendecomposition, singular value decomposition, and principal component analysis.
# + [markdown] id="Z68nQ0ekCYhF"
# **Note that this Jupyter notebook is not intended to stand alone. It is the companion code to a lecture or to videos from <NAME>'s [Machine Learning Foundations](https://github.com/jonkrohn/ML-foundations) series, which offer detail on the following:**
#
# *Review of Introductory Linear Algebra*
#
# * Modern Linear Algebra Applications
# * Tensors, Vectors, and Norms
# * Matrix Multiplication
# * Matrix Inversion
# * Identity, Diagonal and Orthogonal Matrices
#
# *Segment 2: Eigendecomposition*
#
# * Affine Transformation via Matrix Application
# * Eigenvectors and Eigenvalues
# * Matrix Determinants
# * Matrix Decomposition
# * Applications of Eigendecomposition
#
# *Segment 3: Matrix Operations for Machine Learning*
#
# * Singular Value Decomposition (SVD)
# * The Moore-Penrose Pseudoinverse
# * The Trace Operator
# * Principal Component Analysis (PCA): A Simple Machine Learning Algorithm
# * Resources for Further Study of Linear Algebra
# + [markdown] id="ty8zFJj9j3Ui"
# ## Segment 1: Review of Introductory Linear Algebra
# + id="ixvqsCeFj3Uj"
import numpy as np
import torch
# + [markdown] id="E0LgmflFj3Um"
# ### Vector Transposition
# + colab={"base_uri": "https://localhost:8080/"} id="6enkxzMmLWtm" outputId="11614ad5-3af0-4a91-e243-d5704f9840ea"
x = np.array([25, 2, 5])
x
# + colab={"base_uri": "https://localhost:8080/"} id="apVGqjNCLWtp" outputId="a697c790-88ad-409b-c2d4-b78a84031112"
x.shape
# + colab={"base_uri": "https://localhost:8080/"} id="hvLQEylJj3Un" outputId="d3d92704-7f4a-467f-cd0c-861947c6cb6a"
x = np.array([[25, 2, 5]])
x
# + colab={"base_uri": "https://localhost:8080/"} id="WE7xFVxiLWtu" outputId="de66408e-f7e0-44d3-b099-d958e9cf5885"
x.shape
# + colab={"base_uri": "https://localhost:8080/"} id="D6XtfKZ8j3Ut" outputId="a86b8395-033e-4127-eb6b-0eabee40a197"
x.T
# + colab={"base_uri": "https://localhost:8080/"} id="IN1_aSVQj3Uw" outputId="7c76c511-c7f3-4490-82b2-1f5c9850b6e1"
x.T.shape
# + colab={"base_uri": "https://localhost:8080/"} id="K-_nrgesj3U4" outputId="c284ae79-eb4d-413e-a706-d9e3a1941788"
x_p = torch.tensor([25, 2, 5])
x_p
# + colab={"base_uri": "https://localhost:8080/"} id="X0YuG9Pmj3U6" outputId="35d9e48e-2db1-4d83-e2f7-cf0fa660adb6"
x_p.T
# + colab={"base_uri": "https://localhost:8080/"} id="S_bRLc5wj3U8" outputId="6c1d50d9-8a4c-4b1e-f661-0501f85b13cf"
x_p.view(3, 1) # "view" because we're changing output but not the way x is stored in memory
# + [markdown] id="llPpXVPHj3U_"
# **Return to slides here.**
# + [markdown] id="43tlq2huj3U_"
# ## $L^2$ Norm
# + colab={"base_uri": "https://localhost:8080/"} id="wF1B2qL1j3VA" outputId="bf7c5f86-3118-44ff-d869-0c5122f68f9b"
x
# + colab={"base_uri": "https://localhost:8080/"} id="SW2iYHE8j3VC" outputId="13e3359f-0eed-4d85-de8e-23c58cada736"
(25**2 + 2**2 + 5**2)**(1/2)
# + colab={"base_uri": "https://localhost:8080/"} id="BGiMFU0pj3VE" outputId="150523de-597f-4bdf-ad78-dea7a8111233"
np.linalg.norm(x)
# + [markdown] id="3YBk8ta2j3VI"
# So, if units in this 3-dimensional vector space are meters, then the vector $x$ has a length of 25.6m
# + id="jjS4_w_Rj3VI"
# the following line of code will fail because torch.norm() requires input to be float not integer
# torch.norm(p)
# + colab={"base_uri": "https://localhost:8080/"} id="fgadi8SFj3VK" outputId="f75d2562-1306-44c3-eb15-70c28b54c9d0"
torch.norm(torch.tensor([25, 2, 5.]))
# + [markdown] id="qHti3Xslj3VM"
# **Return to slides here.**
# + [markdown] id="4xDLTPutj3VN"
# ### Matrices
# + colab={"base_uri": "https://localhost:8080/"} id="Fep93KC7j3VN" outputId="903feceb-dd1d-483a-9f4e-0d819fd915a0"
X = np.array([[25, 2], [5, 26], [3, 7]])
X
# + colab={"base_uri": "https://localhost:8080/"} id="S_yMqWdSj3VP" outputId="f5b88777-730f-4ebd-cdfd-0cff71f1c4be"
X.shape
# + colab={"base_uri": "https://localhost:8080/"} id="RDkn2n92j3VX" outputId="1c1126b5-8a0f-4bc8-8649-de06344c8b46"
X_p = torch.tensor([[25, 2], [5, 26], [3, 7]])
X_p
# + colab={"base_uri": "https://localhost:8080/"} id="SzpKBCqKj3VY" outputId="67af8715-9f4f-4a46-a5b0-cce4072fb3a1"
X_p.shape
# + [markdown] id="pC1rWTlVj3Vg"
# ### Matrix Transposition
# + colab={"base_uri": "https://localhost:8080/"} id="srh333wTj3Vg" outputId="924ebdcb-d50f-4485-8973-a4db1d41311b"
X
# + colab={"base_uri": "https://localhost:8080/"} id="e7siMBsRj3Vi" outputId="c08f5fb4-b4bf-433b-bb05-cdf9039d3732"
X.T
# + colab={"base_uri": "https://localhost:8080/"} id="YF3iqTkUj3Vk" outputId="c1c7b592-bcf1-4111-e4c6-0ec18ed3ba63"
X_p.T
# + [markdown] id="mXo5iD5Xj3Vm"
# **Return to slides here.**
# + [markdown] id="loFYZ-pXj3Vm"
# ### Matrix Multiplication
# + [markdown] id="BrHCDYrzj3Vm"
# Scalars are applied to each element of matrix:
# + colab={"base_uri": "https://localhost:8080/"} id="Yf3WIZ6Jj3Vn" outputId="9553f178-bb4f-4a17-c995-c8ed247ee759"
X*3
# + colab={"base_uri": "https://localhost:8080/"} id="Pk-lY78Nj3Vp" outputId="afa1ba2d-8786-42a0-95d9-f29fb7cbe128"
X*3+3
# + colab={"base_uri": "https://localhost:8080/"} id="g_sJ0NI8j3Vq" outputId="cc35cf49-c8a6-48f5-d043-36716840c3af"
X_p*3
# + colab={"base_uri": "https://localhost:8080/"} id="jebPN-iPj3Vs" outputId="54af2b03-f9b9-4fe5-d3af-3a0aa21eca99"
X_p*3+3
# + [markdown] id="-a4o6abYj3Vu"
# Using the multiplication operator on two tensors of the same size in PyTorch (or Numpy or TensorFlow) applies element-wise operations. This is the **Hadamard product** (denoted by the $\odot$ operator, e.g., $A \odot B$) *not* **matrix multiplication**:
# + colab={"base_uri": "https://localhost:8080/"} id="JtRT2V0cj3Vu" outputId="20d4c8ae-10b8-4684-bf35-f9cbc7917621"
A = np.array([[3, 4], [5, 6], [7, 8]])
A
# + colab={"base_uri": "https://localhost:8080/"} id="LLJYG8MIj3Vw" outputId="4f2ed3ee-e73d-4d08-fc86-fc9686e80ae1"
X
# + colab={"base_uri": "https://localhost:8080/"} id="MtXoLfKbj3Vx" outputId="5ec52048-a53c-4a73-f03e-596cd5c07e21"
X * A
# + colab={"base_uri": "https://localhost:8080/"} id="8T09ZO4ij3Vz" outputId="1b4d9009-0f4c-4d10-cba2-12af61170884"
A_p = torch.tensor([[3, 4], [5, 6], [7, 8]])
A_p
# + colab={"base_uri": "https://localhost:8080/"} id="VBadBzQJj3V1" outputId="6de65a38-6ae2-4c64-ebec-646ff6dea1fa"
X_p * A_p
# + [markdown] id="s_4kMhF7j3V4"
# Matrix multiplication with a vector:
# + colab={"base_uri": "https://localhost:8080/"} id="LAJEstCLj3V5" outputId="a5616fd7-6bd4-4db9-8576-d2716b013d2a"
b = np.array([1, 2])
b
# + colab={"base_uri": "https://localhost:8080/"} id="ZOxK6XEXj3V8" outputId="f9dd86f0-9127-4faa-de34-2ca28030bf62"
np.dot(A, b) # even though technically dot products is between 2 vectors
# + colab={"base_uri": "https://localhost:8080/"} id="0Y3Ohltbj3V-" outputId="0c617b79-4a7a-4630-ede3-8d745a805527"
b_p = torch.tensor([1, 2])
b_p
# + colab={"base_uri": "https://localhost:8080/"} id="LioexYZ_j3WB" outputId="3c20aeb2-4d26-4e62-88b1-125d641ca130"
torch.matmul(A_p, b_p)
# + [markdown] id="6Wa5CB28j3WC"
# Matrix multiplication with two matrices:
# + colab={"base_uri": "https://localhost:8080/"} id="a8ZXM-T4j3WD" outputId="ee700c6c-07e0-476e-f158-42db9ab1ba64"
B = np.array([[1, 9], [2, 0]])
B
# + colab={"base_uri": "https://localhost:8080/"} id="xE0DA5Xrj3WF" outputId="9ad4c12f-a24a-45c5-cbd3-0b6ef4d1234e"
np.dot(A, B) # note first column is same as Xb
# + colab={"base_uri": "https://localhost:8080/"} id="bBvYO9jFj3WH" outputId="1e3ad0ac-5970-483b-d3d1-aea14b7eb4ac"
B_p = torch.tensor([[1, 9], [2, 0]])
B_p
# + colab={"base_uri": "https://localhost:8080/"} id="o2nEnn3Mj3WI" outputId="560d96dd-64c1-4f30-ad32-a8d81c33a20b"
torch.matmul(A_p, B_p)
# + [markdown] id="eCFqu8LWj3WJ"
# ### Matrix Inversion
# + colab={"base_uri": "https://localhost:8080/"} id="Hhr16-XVj3WK" outputId="bcd77f90-b2ea-4a56-f17a-e9d5b8f188ab"
X = np.array([[4, 2], [-5, -3]])
X
# + colab={"base_uri": "https://localhost:8080/"} id="FIGmFK9oj3WM" outputId="e1f07c91-957f-4753-b33f-85facd606219"
Xinv = np.linalg.inv(X)
Xinv
# + colab={"base_uri": "https://localhost:8080/"} id="WWEFauNsj3WO" outputId="16432486-a596-4555-b3b9-a760e782e10d"
y = np.array([4, -7])
y
# + colab={"base_uri": "https://localhost:8080/"} id="egKyXcZhj3WR" outputId="dc29ee18-127b-403c-ba23-0facac2527e9"
w = np.dot(Xinv, y)
w
# + [markdown] id="4-QHJQR5LWvF"
# Show that $y = Xw$:
# + colab={"base_uri": "https://localhost:8080/"} id="W-6jEzyRLWvG" outputId="5e5c96af-b77d-4c4b-dd10-5f4a25932f86"
np.dot(X, w)
# + colab={"base_uri": "https://localhost:8080/"} id="jro-lItLj3WT" outputId="0a26156e-3268-4366-c7fc-00ea137a358a"
X_p = torch.tensor([[4, 2], [-5, -3.]]) # note that torch.inverse() requires floats
X_p
# + colab={"base_uri": "https://localhost:8080/"} id="o4HfI57Nj3WW" outputId="a0c775b1-197e-4e2b-99e8-c5028567aa71"
Xinv_p = torch.inverse(X_p)
Xinv_p
# + colab={"base_uri": "https://localhost:8080/"} id="dy88LRcyj3WY" outputId="ea7db28e-9853-4a9b-ee73-cfa07d1788b8"
y_p = torch.tensor([4, -7.])
y_p
# + colab={"base_uri": "https://localhost:8080/"} id="1wB3r-ggj3Wa" outputId="00f64cbf-d79c-4a75-baf2-12488a834342"
w_p = torch.matmul(Xinv_p, y_p)
w_p
# + colab={"base_uri": "https://localhost:8080/"} id="tksRdg5JLWvQ" outputId="6033185b-6249-4a73-e6b0-725a84cde236"
torch.matmul(X_p, w_p)
# + [markdown] id="oWXikiwFj3Wb"
# **Return to slides here.**
# + [markdown] id="R4XpcVX2j3Wc"
# ## Segment 2: Eigendecomposition
# + [markdown] id="2vgT25z9fN_E"
# ### Affine Transformation via Matrix Application
# + [markdown] id="gLjGas2ij3Ws"
# Let's say we have a vector $v$:
# + colab={"base_uri": "https://localhost:8080/"} id="zZvzKGRkj3Ws" outputId="e4948d7d-0202-4e46-f7a3-cfc7e065e5d9"
v = np.array([3, 1])
v
# + [markdown] id="4UlRvHvZj3Wt"
# Let's plot $v$ using my `plot_vectors()` function (which is based on Hadrien Jean's `plotVectors()` function from [this notebook](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/2.7%20Eigendecomposition/2.7%20Eigendecomposition.ipynb), under [MIT license](https://github.com/hadrienj/deepLearningBook-Notes/blob/master/LICENSE)).
# + id="Hl54713Rj3Wt"
import matplotlib.pyplot as plt
# + id="fmyWW7Xvj3Wu"
def plot_vectors(vectors, colors):
"""
Plot one or more vectors in a 2D plane, specifying a color for each.
Arguments
---------
vectors: list of lists or of arrays
Coordinates of the vectors to plot. For example, [[1, 3], [2, 2]]
contains two vectors to plot, [1, 3] and [2, 2].
colors: list
Colors of the vectors. For instance: ['red', 'blue'] will display the
first vector in red and the second in blue.
Example
-------
plot_vectors([[1, 3], [2, 2]], ['red', 'blue'])
plt.xlim(-1, 4)
plt.ylim(-1, 4)
"""
plt.figure()
plt.axvline(x=0, color='lightgray')
plt.axhline(y=0, color='lightgray')
for i in range(len(vectors)):
x = np.concatenate([[0,0],vectors[i]])
plt.quiver([x[0]], [x[1]], [x[2]], [x[3]],
angles='xy', scale_units='xy', scale=1, color=colors[i],)
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="8uP1xgnLj3Wx" outputId="2136da79-aa1d-4f1c-c864-d518b1632540"
plot_vectors([v], ['lightblue'])
plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# + [markdown] id="ydGgh5lRj3Wy"
# "Applying" a matrix to a vector (i.e., performing matrix-vector multiplication) can linearly transform the vector, e.g, rotate it or rescale it.
# + [markdown] id="ReW9fF-sj3Wy"
# The identity matrix, introduced earlier, is the exception that proves the rule: Applying an identity matrix does not transform the vector:
# + colab={"base_uri": "https://localhost:8080/"} id="0riv3SS8j3Wz" outputId="0ae43869-0889-424e-f0b0-d0c31eb45bea"
I = np.array([[1, 0], [0, 1]])
I
# + colab={"base_uri": "https://localhost:8080/"} id="nc7nn6VDj3W0" outputId="2be11f81-4fb8-49b0-c1d9-d28237e8431d"
Iv = np.dot(I, v)
Iv
# + colab={"base_uri": "https://localhost:8080/"} id="AXQBaq2fj3W1" outputId="88366d2a-93b6-4fbb-f11f-e56d71a4b8db"
v == Iv
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="SP81dIksj3W3" outputId="e591e35b-d7ce-4007-8abb-3474a836f4b9"
plot_vectors([Iv], ['blue'])
plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# + [markdown] id="knI50bEJ8UsQ"
# In contrast, consider this matrix (let's call it $E$) that flips vectors over the $x$-axis:
# + id="PTGnNFx48UsR" colab={"base_uri": "https://localhost:8080/"} outputId="d2e52a9c-39f1-4bf1-9523-cf8c0c7cc08e"
E = np.array([[1, 0], [0, -1]])
E
# + id="d6CZbgfT8UsS" colab={"base_uri": "https://localhost:8080/"} outputId="0e65b8c5-40c0-4fc1-f364-575d2a4fb3fe"
Ev = np.dot(E, v)
Ev
# + id="0hDvoi258UsS" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="8c91af12-0cd5-499c-8f09-fd84cf899109"
plot_vectors([v, Ev], ['lightblue', 'blue'])
plt.xlim(-1, 5)
_ = plt.ylim(-3, 3)
# + [markdown] id="cfj26eui8UsS"
# Or, this matrix, $F$, which flips vectors over the $y$-axis:
# + id="E5wijvsi8UsT" colab={"base_uri": "https://localhost:8080/"} outputId="542688c6-9b76-4a05-9e98-0f0d6c19a96c"
F = np.array([[-1, 0], [0, 1]])
F
# + id="P7tQhi2Z8UsT" colab={"base_uri": "https://localhost:8080/"} outputId="98445eb4-f3b3-4afa-d94d-0e7219e004ec"
Fv = np.dot(F, v)
Fv
# + id="xrlgyYFH8UsT" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="52722d15-4e3c-4a35-8ef6-73cdf37ed960"
plot_vectors([v, Fv], ['lightblue', 'blue'])
plt.xlim(-4, 4)
_ = plt.ylim(-1, 5)
# + [markdown] id="bDVVb2Ty8UsT"
# Applying a flipping matrix is an example of an **affine transformation**: a change in geometry that may adjust distances or angles between vectors, but preserves parallelism between them.
#
# In addition to flipping a matrix over an axis (a.k.a., *reflection*), other common affine transformations include:
# * *Scaling* (changing the length of vectors)
# * *Shearing* (example of this on the Mona Lisa coming up shortly)
# * *Rotation*
#
# (See [here](https://stackabuse.com/affine-image-transformations-in-python-with-numpy-pillow-and-opencv/) for an outstanding blog post on affine transformations in Python, including how to apply them to images as well as vectors.)
# + [markdown] id="JcdkCchSj3W4"
# A single matrix can apply multiple affine transforms simultaneously (e.g., flip over an axis and rotate 45 degrees). As an example, let's see what happens when we apply this matrix $A$ to the vector $v$:
# + colab={"base_uri": "https://localhost:8080/"} id="R-EsIE7cj3W4" outputId="c3903fca-b72c-4277-8768-f586ff11f510"
A = np.array([[-1, 4], [2, -2]])
A
# + colab={"base_uri": "https://localhost:8080/"} id="DZ0rxeKTj3W5" outputId="fd61867f-b549-44dc-8a37-b0c7ceb97a9b"
Av = np.dot(A, v)
Av
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="RCAfNJ8hj3W7" outputId="70f81cfe-49c2-4596-e938-8c640f3390bc"
plot_vectors([v, Av], ['lightblue', 'blue'])
plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="7cMA5yMij3W8" outputId="d32f2d9a-9246-4ad0-e000-5417c8f1ab8e"
# Another example of applying A:
v2 = np.array([2, 1])
plot_vectors([v2, np.dot(A, v2)], ['lightgreen', 'green'])
plt.xlim(-1, 5)
_ = plt.ylim(-1, 5)
# + [markdown] id="gRqpCA6qj3W-"
# We can concatenate several vectors together into a matrix (say, $V$), where each column is a separate vector. Then, whatever linear transformations we apply to $V$ will be independently applied to each column (vector):
# + colab={"base_uri": "https://localhost:8080/"} id="dsRo3xPFj3W-" outputId="4304eeb7-e534-4d96-e790-37cce6f4c2bb"
v
# + colab={"base_uri": "https://localhost:8080/"} id="nQDdsKXNj3XA" outputId="d3ed01f9-db60-4616-9d21-23781a454ebc"
# recall that we need to convert array to 2D to transpose into column, e.g.:
np.matrix(v).T
# + id="Zb9cSgjnj3XB"
v3 = np.array([-3, -1]) # mirror image of v over both axes
v4 = np.array([-1, 1])
# + colab={"base_uri": "https://localhost:8080/"} id="EsdcEFXYj3XC" outputId="d2934a39-ce74-47d5-f72c-737c6c52a902"
V = np.concatenate((np.matrix(v).T,
np.matrix(v2).T,
np.matrix(v3).T,
np.matrix(v4).T),
axis=1)
V
# + colab={"base_uri": "https://localhost:8080/"} id="t3CSo0Hrj3XD" outputId="ac2a1403-1fa1-4097-9938-4049c15c834d"
IV = np.dot(I, V)
IV
# + colab={"base_uri": "https://localhost:8080/"} id="a6M61JEWj3XE" outputId="a0a35ad1-2584-46a2-f429-32b8d7c88723"
AV = np.dot(A, V)
AV
# + id="wGmvjr85j3XG"
# function to convert column of matrix to 1D vector:
def vectorfy(mtrx, clmn):
return np.array(mtrx[:,clmn]).reshape(-1)
# + colab={"base_uri": "https://localhost:8080/"} id="L2eQ4w83j3XH" outputId="d5c09731-8d6a-4539-b49a-400c0f00c1f2"
vectorfy(V, 0)
# + colab={"base_uri": "https://localhost:8080/"} id="_o4HOgEwj3XI" outputId="6da61ad6-e365-4d05-d539-0bd04418fbf5"
vectorfy(V, 0) == v
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="btsivNB_j3XK" outputId="a0475146-074d-443b-888f-15956aeb78eb"
plot_vectors([vectorfy(V, 0), vectorfy(V, 1), vectorfy(V, 2), vectorfy(V, 3),
vectorfy(AV, 0), vectorfy(AV, 1), vectorfy(AV, 2), vectorfy(AV, 3)],
['lightblue', 'lightgreen', 'lightgray', 'orange',
'blue', 'green', 'gray', 'red'])
plt.xlim(-4, 6)
_ = plt.ylim(-5, 5)
# + [markdown] id="EFTcb9xkf3vT"
# Now that we can appreciate the linear transformation of vectors by matrices, let's move on to working with eigenvectors and eigenvalues...
#
# **Return to slides here.**
# + [markdown] id="et4bgYFDj3Wr"
# ### Eigenvectors and Eigenvalues
# + [markdown] id="4n31lIDpj3XL"
# An **eigenvector** (*eigen* is German for "typical"; we could translate *eigenvector* to "characteristic vector") is a special vector $v$ such that when it is transformed by some matrix (let's say $A$), the product $Av$ has the exact same direction as $v$.
#
# An **eigenvalue** is a scalar (traditionally represented as $\lambda$) that simply scales the eigenvector $v$ such that the following equation is satisfied:
#
# $Av = \lambda v$
# + [markdown] id="G7zVjpW-j3XL"
# Easiest way to understand this is to work through an example:
# + colab={"base_uri": "https://localhost:8080/"} id="GbXJtk1Ej3XL" outputId="acd1fee7-c1b5-4802-f1d9-c4c45da43a40"
A
# + [markdown] id="0t2JsM6Wj3XN"
# Eigenvectors and eigenvalues can be derived algebraically (e.g., with the [QR algorithm](https://en.wikipedia.org/wiki/QR_algorithm), which was independently developed in the 1950s by both [Vera Kublanovskaya](https://en.wikipedia.org/wiki/Vera_Kublanovskaya) and John Francis), however this is outside scope of the *ML Foundations* series. We'll cheat with NumPy `eig()` method, which returns a tuple of:
#
# * a vector of eigenvalues
# * a matrix of eigenvectors
# + id="CYWmgM7jj3XN"
lambdas, V = np.linalg.eig(A)
# + [markdown] id="OVUp_p6-j3XO"
# The matrix contains as many eigenvectors as there are columns of A:
# + colab={"base_uri": "https://localhost:8080/"} id="7iHlAMa7j3XO" outputId="75314623-6a8f-4287-b353-007b28cc6a3c"
V # each column is a separate eigenvector v
# + [markdown] id="EBSmc2JLj3XP"
# With a corresponding eigenvalue for each eigenvector:
# + colab={"base_uri": "https://localhost:8080/"} id="QYJbCydNj3XP" outputId="684c5f9b-71ae-4ef9-a2be-5f2f85c153f2"
lambdas
# + [markdown] id="OoZPiaBMj3XR"
# Let's confirm that $Av = \lambda v$ for the first eigenvector:
# + colab={"base_uri": "https://localhost:8080/"} id="n1QZ57TJj3XR" outputId="d7a16ced-5d9f-4eff-a72d-80946c0d3b88"
v = V[:,0]
v
# + colab={"base_uri": "https://localhost:8080/"} id="6vwkWMiIj3XV" outputId="52edc4c1-90ea-4d44-b7fa-c969da736616"
lambduh = lambdas[0] # note that "lambda" is reserved term in Python
lambduh
# + colab={"base_uri": "https://localhost:8080/"} id="Leh9n8QBj3XW" outputId="16a28285-ff50-4254-8d8b-3659b5175e07"
Av = np.dot(A, v)
Av
# + colab={"base_uri": "https://localhost:8080/"} id="PROIJU30j3XX" outputId="e50ee151-86e9-4447-e367-efb35d8c5e78"
lambduh * v
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="0bT3vjoQj3XY" outputId="61d76876-3eb2-4b49-bf20-d8d98e090377"
plot_vectors([Av, v], ['blue', 'lightblue'])
plt.xlim(-1, 2)
_ = plt.ylim(-1, 2)
# + [markdown] id="tKQI4691j3XZ"
# And again for the second eigenvector of A:
# + colab={"base_uri": "https://localhost:8080/"} id="riOJuqz3j3XZ" outputId="0272716e-ffd7-4f8c-edcc-91853ce73df5"
v2 = V[:,1]
v2
# + colab={"base_uri": "https://localhost:8080/"} id="QveeHYhDj3Xa" outputId="00f6aa04-7142-418a-9a51-f4730a15807f"
lambda2 = lambdas[1]
lambda2
# + colab={"base_uri": "https://localhost:8080/"} id="TDk1VoVIj3Xb" outputId="04e289f4-088f-4c6f-f81e-d068df12f09e"
Av2 = np.dot(A, v2)
Av2
# + colab={"base_uri": "https://localhost:8080/"} id="smlYxxgpj3Xc" outputId="673979e9-340b-4133-d338-59a160226dad"
lambda2 * v2
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="3IigKHp0j3Xd" outputId="2eb1f8ba-9ea6-4811-b8b0-2aa73d909cf6"
plot_vectors([Av, v, Av2, v2],
['blue', 'lightblue', 'green', 'lightgreen'])
plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
# + [markdown] id="VF9uLWjOj3Xe"
# Using the PyTorch `eig()` method, we can do exactly the same:
# + colab={"base_uri": "https://localhost:8080/"} id="EcJa6w0mj3Xe" outputId="3644237f-e752-4fb8-8b8f-4885a0f16b31"
A
# + colab={"base_uri": "https://localhost:8080/"} id="9WvCqoRij3Xf" outputId="cc7e56c3-8297-4456-be71-8aace5dafe86"
A_p = torch.tensor([[-1, 4], [2, -2.]]) # must be float for PyTorch eig()
A_p
# + id="TE1W1lykjHfW"
lambdas_cplx, V_cplx = torch.linalg.eig(A_p) # outputs complex numbers because real matrices can have complex eigenvectors
# + id="lEIkBb8OjhTk" outputId="209c2388-342a-4117-9d61-93c27b618126" colab={"base_uri": "https://localhost:8080/"}
V_cplx # complex-typed values with "0.j" imaginary part are in fact real numbers
# + id="ycqfObc1pyca" outputId="641e88a4-26c7-4af6-9d0e-d22593b5ab00" colab={"base_uri": "https://localhost:8080/"}
V_p = V_cplx.float()
V_p
# + id="h9_Ri5MGntlz" outputId="258427a0-e318-47d9-f973-a99b1e67f128" colab={"base_uri": "https://localhost:8080/"}
v_p = V_p[:,0]
v_p
# + id="cnjVvGxEqHM6" outputId="846997ef-f166-4af3-8fe0-542b7420a040" colab={"base_uri": "https://localhost:8080/"}
lambdas_cplx
# + id="_7bIBSQuoGVk" outputId="e29e0853-28c2-4d23-fee7-c9677e73b354" colab={"base_uri": "https://localhost:8080/"}
lambdas_p = lambdas_cplx.float()
lambdas_p
# + colab={"base_uri": "https://localhost:8080/"} id="VrYaxNCRj3Xj" outputId="56084ce8-18fa-427c-9924-09844b70a155"
lambda_p = lambdas_p[0]
lambda_p
# + colab={"base_uri": "https://localhost:8080/"} id="SUq1UGH7j3Xl" outputId="2654ae27-e3f5-47c2-be58-2d423f1f4494"
Av_p = torch.matmul(A_p, v_p) # matmul() expects float-typed tensors
Av_p
# + colab={"base_uri": "https://localhost:8080/"} id="co1VNLIej3Xn" outputId="b0f72a7f-f020-428f-de01-8566096010fd"
lambda_p * v_p
# + colab={"base_uri": "https://localhost:8080/"} id="1b47vG92j3Xo" outputId="18e1f0d5-79d3-47b8-9b1d-b0f5e5312c4f"
v2_p = V_p[:,1]
v2_p
# + colab={"base_uri": "https://localhost:8080/"} id="B-evpW17j3Xp" outputId="02bf3935-2f35-48d3-d478-874d5fce786f"
lambda2_p = lambdas_p[1]
lambda2_p
# + colab={"base_uri": "https://localhost:8080/"} id="2d5gjh2sj3Xq" outputId="61f13b16-3549-431e-daa3-cf21a2ee83ca"
Av2_p = torch.matmul(A_p.float(), v2_p.float())
Av2_p
# + colab={"base_uri": "https://localhost:8080/"} id="8-ki3i8dj3Xr" outputId="8fadf2d4-4546-469d-cde0-d88f4873ffdb"
lambda2_p.float() * v2_p.float()
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="s2p8yb_Zj3Xs" outputId="a3512303-e8b5-46a1-fd52-98129161ff21"
plot_vectors([Av_p.numpy(), v_p.numpy(), Av2_p.numpy(), v2_p.numpy()],
['blue', 'lightblue', 'green', 'lightgreen'])
plt.xlim(-1, 4)
_ = plt.ylim(-3, 2)
# + [markdown] id="6-HqwyESj3Xt"
# ### Eigenvectors in >2 Dimensions
# + [markdown] id="M01JPwToj3Xt"
# While plotting gets trickier in higher-dimensional spaces, we can nevertheless find and use eigenvectors with more than two dimensions. Here's a 3D example (there are three dimensions handled over three rows):
# + colab={"base_uri": "https://localhost:8080/"} id="HWsBDEMgj3Xt" outputId="2facbb5a-a032-450a-a315-5a6e68996d28"
X = np.array([[25, 2, 9], [5, 26, -5], [3, 7, -1]])
X
# + id="Y-uUMyRFj3Xv"
lambdas_X, V_X = np.linalg.eig(X)
# + colab={"base_uri": "https://localhost:8080/"} id="virh7GVFj3Xw" outputId="406581f3-928c-4498-bb86-45fefdf6e14d"
V_X # one eigenvector per column of X
# + colab={"base_uri": "https://localhost:8080/"} id="9yHkmEd0j3Xw" outputId="f570a46a-353e-41f1-a9e9-43851a59e9d8"
lambdas_X # a corresponding eigenvalue for each eigenvector
# + [markdown] id="Qp3qPeUxj3Xy"
# Confirm $Xv = \lambda v$ for an example eigenvector:
# + colab={"base_uri": "https://localhost:8080/"} id="dUEfbThhj3Xy" outputId="20aacd11-e2c0-44fc-f4e5-4c4737b8cb0a"
v_X = V_X[:,0]
v_X
# + colab={"base_uri": "https://localhost:8080/"} id="xhnF5asDj3X0" outputId="ae9e4750-8413-46c5-83eb-1a79a9e4995d"
lambda_X = lambdas_X[0]
lambda_X
# + colab={"base_uri": "https://localhost:8080/"} id="K3bA6vRzj3X1" outputId="7622d8fd-5413-4958-e802-5e524efa418b"
np.dot(X, v_X) # matrix multiplication
# + colab={"base_uri": "https://localhost:8080/"} id="UfN3hk0Gj3X2" outputId="39988510-8949-4d0b-8af1-982923a238b6"
lambda_X * v_X
# + [markdown] id="VcjTZv24j3X3"
# **Exercises**:
#
# 1. Use PyTorch to confirm $Xv = \lambda v$ for the first eigenvector of $X$.
# 2. Confirm $Xv = \lambda v$ for the remaining eigenvectors of $X$ (you can use NumPy or PyTorch, whichever you prefer).
# + [markdown] id="5z5AdeHKj3X4"
# **Return to slides here.**
# + [markdown] id="F44cMjS8j3Wc"
# ### 2x2 Matrix Determinants
# + colab={"base_uri": "https://localhost:8080/"} id="GjsXPZEsj3Wc" outputId="fe6a6a5f-036c-4838-8e13-ec8d921ee914"
X = np.array([[4, 2], [-5, -3]])
X
# + colab={"base_uri": "https://localhost:8080/"} id="4tg8BDzOj3We" outputId="cd6589fc-a010-49f2-90d8-6a51e9576a50"
np.linalg.det(X)
# + [markdown] id="87wpY5hUj3Wg"
# **Return to slides here.**
# + colab={"base_uri": "https://localhost:8080/"} id="o5jp6vkNj3Wg" outputId="8d71eb93-7e03-4659-9af3-2dd9f0ecd64d"
N = np.array([[-4, 1], [-8, 2]])
N
# + colab={"base_uri": "https://localhost:8080/"} id="ejdkdN7Lj3Wi" outputId="cbbdd79f-f63e-4315-9c52-442c6743cbbf"
np.linalg.det(N)
# + id="nbIrtcaCj3Wj"
# Uncommenting the following line results in a "singular matrix" error
# Ninv = np.linalg.inv(N)
# + id="kBT5VC5Nj3Wl"
N = torch.tensor([[-4, 1], [-8, 2.]]) # must use float not int
# + colab={"base_uri": "https://localhost:8080/"} id="MQA5g0gGj3Wm" outputId="d05c3b60-1a0e-43e0-cfcc-558b17617fb7"
torch.det(N)
# + [markdown] id="XBIJB7tfj3Wn"
# **Return to slides here.**
# + [markdown] id="rwwoY1k6j3Wn"
# ### Generalizing Determinants
# + colab={"base_uri": "https://localhost:8080/"} id="bqjRKaCaj3Wn" outputId="e0ade6d1-2d9f-45ac-8869-c5103d82f6d5"
X = np.array([[1, 2, 4], [2, -1, 3], [0, 5, 1]])
X
# + colab={"base_uri": "https://localhost:8080/"} id="uimvv39Nj3Wp" outputId="ab87a52f-fa2e-479f-b7c0-71ada9df8a91"
np.linalg.det(X)
# + [markdown] id="hQEG5ad1rmr2"
# **Return to slides here.**
# + [markdown] id="d2MIHl4MLWw0"
# ### Determinants & Eigenvalues
# + colab={"base_uri": "https://localhost:8080/"} id="g0uEEY2qj3X6" outputId="3d6f3bb2-8c99-4bb8-96fc-ddff7a1cb8e0"
lambdas, V = np.linalg.eig(X)
lambdas
# + colab={"base_uri": "https://localhost:8080/"} id="41P8dP9Gj3X8" outputId="13eb549a-c9a3-4177-dcb6-0c0ad1509e94"
np.product(lambdas)
# + [markdown] id="Rf83gqIULWw2"
# **Return to slides here.**
# + [markdown] id="6zNOgq7I62YA"
# Here's $|\text{det}(X)|$ in NumPy:
# + colab={"base_uri": "https://localhost:8080/"} id="a7Bleu07j3X-" outputId="0d8a701b-d685-4b45-d2f4-4e751323f1e1"
np.abs(np.linalg.det(X))
# + [markdown] id="KZQaYZ0q7Zn2"
# Let's use a matrix $B$, which is composed of basis vectors, to explore the impact of applying matrices with varying $|\text{det}(X)|$ values:
# + colab={"base_uri": "https://localhost:8080/"} id="rMPe8LOXj3X_" outputId="348000cf-8843-45aa-f8fa-0a3a485e4779"
B = np.array([[1, 0], [0, 1]])
B
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="zlhnOiNzj3YA" outputId="61573bd9-2620-49b9-88c7-31b02aee8c50"
plot_vectors([vectorfy(B, 0), vectorfy(B, 1)],
['lightblue', 'lightgreen'])
plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
# + [markdown] id="RIkz1gCO7_TW"
# Let's start by applying the matrix $N$ to $B$, recalling from earlier that $N$ is singular:
# + colab={"base_uri": "https://localhost:8080/"} id="Fjpem_6Ij3YB" outputId="a25e3e2d-12c5-4dbf-d3c3-3c0c6a909a0f"
N
# + colab={"base_uri": "https://localhost:8080/"} id="2BhgWTvaj3YC" outputId="7e0e86a9-7ee1-4a3c-a1f5-acfec5845364"
np.linalg.det(N)
# + colab={"base_uri": "https://localhost:8080/"} id="O3XSySPaj3YE" outputId="fa2fbce7-466d-46ec-e854-31293e4e9344"
NB = np.dot(N, B)
NB
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="GLiyz0nxj3YF" outputId="8a076890-a688-4f2d-a9c5-92f438b3b2fc"
plot_vectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(NB, 0), vectorfy(NB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
plt.xlim(-6, 6)
_ = plt.ylim(-9, 3)
# + id="9ErYF2Ss5zZj" colab={"base_uri": "https://localhost:8080/"} outputId="f3480d94-d262-4501-d513-94d79f2bd7e0"
lambdas, V = np.linalg.eig(N)
lambdas
# + [markdown] id="TLwFZuuN8L78"
# Aha! If any one of a matrix's eigenvalues is zero, then the product of the eigenvalues must be zero and the determinant must also be zero.
# + [markdown] id="tT6ZmuaN8cwJ"
# Now let's try applying $I_2$ to $B$:
# + colab={"base_uri": "https://localhost:8080/"} id="mqEkY-8lj3YH" outputId="577168b0-e809-41a2-db9c-1672032b48d1"
I
# + colab={"base_uri": "https://localhost:8080/"} id="zwmKA0wLj3YI" outputId="e0a8ecba-7c93-49e8-dd2c-7a9633f660bf"
np.linalg.det(I)
# + colab={"base_uri": "https://localhost:8080/"} id="xaIq_dUKj3YJ" outputId="61861e02-8c3f-49f5-ab03-32c917e5248c"
IB = np.dot(I, B)
IB
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="8y6svzaLj3YK" outputId="19acbe5a-ce55-4d2c-bc72-7a45cc41b252"
plot_vectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(IB, 0), vectorfy(IB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
# + id="IWkwRV_46T-q" colab={"base_uri": "https://localhost:8080/"} outputId="39bf046d-1161-4887-dd49-4ada23197341"
lambdas, V = np.linalg.eig(I)
lambdas
# + [markdown] id="Dfrv5ipF9Nx3"
# All right, so applying an identity matrix isn't the most exciting operation in the world. Let's now apply this matrix $J$ which is more interesting:
# + colab={"base_uri": "https://localhost:8080/"} id="Xj4bnqVcj3YL" outputId="987e2ce1-72b2-493f-8aeb-8366a5302017"
J = np.array([[-0.5, 0], [0, 2]])
J
# + colab={"base_uri": "https://localhost:8080/"} id="D2ODTOpAj3YM" outputId="b9335a15-225e-4f09-9a3e-0972aecddee1"
np.linalg.det(J)
# + colab={"base_uri": "https://localhost:8080/"} id="3kHJ7Q2Ij3YN" outputId="9bdedc29-6c36-4b00-ad2a-dd8628cdc4ea"
np.abs(np.linalg.det(J))
# + colab={"base_uri": "https://localhost:8080/"} id="ABciINQwj3YO" outputId="0b0f0af3-bd62-43fc-d8cb-961efdfa9b4f"
JB = np.dot(J, B)
JB
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="5nWa22ZNj3YO" outputId="e1149289-9d5f-4f30-806e-d4088d8b8575"
plot_vectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(JB, 0), vectorfy(JB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
# + id="K4GTT7Ja6azt" colab={"base_uri": "https://localhost:8080/"} outputId="0f37faa6-5a11-43b1-8197-177f39f93f29"
lambdas, V = np.linalg.eig(J)
lambdas
# + [markdown] id="b1KENtMQ9g4g"
# Finally, let's apply the matrix $D$, which scales vectors by doubling along both the $x$ and $y$ axes:
# + id="u-OI7xBWj3YQ" colab={"base_uri": "https://localhost:8080/"} outputId="e6541a38-11ac-458a-ec58-cd8d44143f13"
D = I*2
D
# + colab={"base_uri": "https://localhost:8080/"} id="iKoTu9sbj3YR" outputId="c15b37f2-af9c-4b97-aab7-8a04055b0cfc"
np.linalg.det(D)
# + colab={"base_uri": "https://localhost:8080/"} id="kTb0o2Ydj3YS" outputId="294eda68-feda-4538-fbdf-def2a56fa453"
DB = np.dot(D, B)
DB
# + colab={"base_uri": "https://localhost:8080/", "height": 269} id="3J2ou_zSj3YT" outputId="fa18904f-980e-441b-e90a-ceba3d03bb4c"
plot_vectors([vectorfy(B, 0), vectorfy(B, 1), vectorfy(DB, 0), vectorfy(DB, 1)],
['lightblue', 'lightgreen', 'blue', 'green'])
plt.xlim(-1, 3)
_ = plt.ylim(-1, 3)
# + id="kTfi_wGC-QCL" colab={"base_uri": "https://localhost:8080/"} outputId="84a7fc47-74a5-4330-d582-08d18e9d4c5e"
lambdas, V = np.linalg.eig(D)
lambdas
# + [markdown] id="Av0R8fddj3Yb"
# **Return to slides here.**
# + [markdown] id="MXNajp3Ej3Yb"
# ### Eigendecomposition
# + [markdown] id="wQt403xbj3Yb"
# The **eigendecomposition** of some matrix $A$ is
#
# $A = V \Lambda V^{-1}$
#
# Where:
#
# * As in examples above, $V$ is the concatenation of all the eigenvectors of $A$
# * $\Lambda$ (upper-case $\lambda$) is the diagonal matrix diag($\lambda$). Note that the convention is to arrange the lambda values in descending order; as a result, the first eigenvalue (and its associated eigenvector) may be a primary characteristic of the matrix $A$.
# + id="W7LmR3YGj3Yb" colab={"base_uri": "https://localhost:8080/"} outputId="a05b99fd-1f68-4073-f40b-9288f7dffb5b"
# This was used earlier as a matrix X; it has nice clean integer eigenvalues...
A = np.array([[4, 2], [-5, -3]])
A
# + id="37zeBrqhj3Yc"
lambdas, V = np.linalg.eig(A)
# + id="b7LtIIMJj3Yd" colab={"base_uri": "https://localhost:8080/"} outputId="1558c22f-368c-4a1a-894d-8a35a8c163a5"
V
# + id="q1uuRwcdj3Ye" colab={"base_uri": "https://localhost:8080/"} outputId="3cd86242-e4f9-43c5-9786-cc0f3eeb33c2"
Vinv = np.linalg.inv(V)
Vinv
# + id="_InHRuS1j3Yf" colab={"base_uri": "https://localhost:8080/"} outputId="517d12a9-c9a6-46ad-8624-2209e3065f44"
Lambda = np.diag(lambdas)
Lambda
# + [markdown] id="KSBnzTBZj3Yg"
# Confirm that $A = V \Lambda V^{-1}$:
# + id="pG1E3yLYj3Yg" colab={"base_uri": "https://localhost:8080/"} outputId="d0d5f55d-ad40-468e-9b59-b01544169863"
np.dot(V, np.dot(Lambda, Vinv))
# + [markdown] id="JTmKZk8fj3Yh"
# Eigendecomposition is not possible with all matrices. And in some cases where it is possible, the eigendecomposition involves complex numbers instead of straightforward real numbers.
#
# In machine learning, however, we are typically working with real symmetric matrices, which can be conveniently and efficiently decomposed into real-only eigenvectors and real-only eigenvalues. If $A$ is a real symmetric matrix then...
#
# $A = Q \Lambda Q^T$
#
# ...where $Q$ is analogous to $V$ from the previous equation except that it's special because it's an orthogonal matrix.
# + id="GpZLd9Ozj3Yh" colab={"base_uri": "https://localhost:8080/"} outputId="cb9d2c0f-10e2-4a90-a8bc-0f8b9b3030bc"
A = np.array([[2, 1], [1, 2]])
A
# + id="EJOgExEZj3Yj"
lambdas, Q = np.linalg.eig(A)
# + id="9qouDzN5j3Yk" colab={"base_uri": "https://localhost:8080/"} outputId="3d2a6b59-8bf4-411f-dec1-7030e2790cc8"
lambdas
# + id="JZFyXQzkj3Yl" colab={"base_uri": "https://localhost:8080/"} outputId="5f50e622-6b1f-47c4-9ca9-9fa985350c1e"
Lambda = np.diag(lambdas)
Lambda
# + id="BLXaGoVBj3Yl" colab={"base_uri": "https://localhost:8080/"} outputId="31dac6db-a335-4a5f-b30b-a379c9fa34aa"
Q
# + [markdown] id="UnOfuIf7j3Yo"
# Let's confirm $A = Q \Lambda Q^T$:
# + id="k4DukMWJj3Yo" colab={"base_uri": "https://localhost:8080/"} outputId="3f63b1df-262d-4391-8441-a768428e63f2"
np.dot(Q, np.dot(Lambda, Q.T))
# + [markdown] id="_eq_1nssj3Ym"
# (As a quick aside, we can demostrate that $Q$ is an orthogonal matrix because $Q^TQ = QQ^T = I$.)
# + id="TcavBhdEj3Ym" colab={"base_uri": "https://localhost:8080/"} outputId="b70d091a-811d-41cd-a3aa-5df504445da4"
np.dot(Q.T, Q)
# + id="xup113b8j3Yo" colab={"base_uri": "https://localhost:8080/"} outputId="4a2bc99b-af0f-4ebb-83db-1c6c1accc449"
np.dot(Q, Q.T)
# + [markdown] id="fdJaTKnsj3Yp"
# **Exercises**:
#
# 1. Use PyTorch to decompose the matrix $P$ (below) into its components $V$, $\Lambda$, and $V^{-1}$. Confirm that $P = V \Lambda V^{-1}$.
# 2. Use PyTorch to decompose the symmetric matrix $S$ (below) into its components $Q$, $\Lambda$, and $Q^T$. Confirm that $S = Q \Lambda Q^T$.
# + id="_RVUCVlvj3Yp" colab={"base_uri": "https://localhost:8080/"} outputId="ad6a4154-c7ed-4a67-9d70-545c6f014240"
P = torch.tensor([[25, 2, -5], [3, -2, 1], [5, 7, 4.]])
P
# + id="GjKZ_AWLj3Yq" colab={"base_uri": "https://localhost:8080/"} outputId="5ad1a522-fab3-46d3-88eb-ea4bb4a365fc"
S = torch.tensor([[25, 2, -5], [2, -2, 1], [-5, 1, 4.]])
S
# + [markdown] id="1OFq3uGaj3Yq"
# **Return to slides here.**
# + [markdown] id="gKam0tJOj3Yr"
# ## Segment 3: Matrix Operations for ML
# + [markdown] id="j-wbn7omj3Yr"
# ### Singular Value Decomposition (SVD)
# + [markdown] id="x2SHytttj3Yr"
# As on slides, SVD of matrix $A$ is:
#
# $A = UDV^T$
#
# Where:
#
# * $U$ is an orthogonal $m \times m$ matrix; its columns are the **left-singular vectors** of $A$.
# * $V$ is an orthogonal $n \times n$ matrix; its columns are the **right-singular vectors** of $A$.
# * $D$ is a diagonal $m \times n$ matrix; elements along its diagonal are the **singular values** of $A$.
# + id="V7hR4Htdj3Yr" colab={"base_uri": "https://localhost:8080/"} outputId="d97b4830-1135-4d7c-b099-6280f8ab391a"
A = np.array([[-1, 2], [3, -2], [5, 7]])
A
# + id="ihj2XfMQj3Ys"
U, d, VT = np.linalg.svd(A) # V is already transposed
# + id="DUfP2aaTj3Yv" colab={"base_uri": "https://localhost:8080/"} outputId="497735ae-89ea-4525-a040-f1d11d754e29"
U
# + id="s_Fkoarvj3Yw" colab={"base_uri": "https://localhost:8080/"} outputId="5cf1e562-ed64-46dd-c8b1-05388625e4d2"
VT
# + id="wNSRDcfsj3Yx" colab={"base_uri": "https://localhost:8080/"} outputId="19a817f0-0666-4a6c-8f12-5a1d37fefa07"
d
# + id="Lbxh2rYoj3Yy" colab={"base_uri": "https://localhost:8080/"} outputId="2a080caf-492e-4a10-8ac5-7870bbf52ecc"
np.diag(d)
# + [markdown] id="6JN2VA3GNIP5"
# $D$ must have the same dimensions as $A$ for $UDV^T$ matrix multiplication to be possible:
# + id="V47I3B87j3Y0" colab={"base_uri": "https://localhost:8080/"} outputId="52643cfa-80ad-476b-d7da-10a66dd15ad9"
D = np.concatenate((np.diag(d), [[0, 0]]), axis=0)
D
# + id="9euCs5vvj3Y2" colab={"base_uri": "https://localhost:8080/"} outputId="15771a45-e87e-4b9d-8a73-521e89818b2a"
np.dot(U, np.dot(D, VT))
# + [markdown] id="u-WCBOzKj3Y3"
# SVD and eigendecomposition are closely related to each other:
#
# * Left-singular vectors of $A$ = eigenvectors of $AA^T$.
# * Right-singular vectors of $A$ = eigenvectors of $A^TA$.
# * Non-zero singular values of $A$ = square roots of eigenvalues of $AA^T$ = square roots of eigenvalues of $A^TA$
#
# **Exercise**: Using the matrix `P` from the preceding PyTorch exercises, demonstrate that these three SVD-eigendecomposition equations are true.
# + [markdown] id="CWEOMqUUj3Y3"
# ### Image Compression via SVD
# + [markdown] id="XmRvLo_Tj3Y3"
# The section features code adapted from [<NAME>'s](https://gist.github.com/frankcleary/4d2bd178708503b556b0).
# + id="luD8Y98Vj3Y3"
from PIL import Image
# + [markdown] id="thPmYUx4j3Y4"
# Fetch photo of Oboe, a terrier, with the book *Deep Learning Illustrated*:
# + id="bPUItNUVj3Y4" colab={"base_uri": "https://localhost:8080/"} outputId="816b8dd0-5606-4e39-dac4-205dbe012587"
# ! wget https://raw.githubusercontent.com/jonkrohn/DLTFpT/master/notebooks/oboe-with-book.jpg
# + id="6lx_Frl6j3Y6" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="c459e154-20c9-4dc9-e88c-78e83793e7bd"
img = Image.open('oboe-with-book.jpg')
_ = plt.imshow(img)
# + [markdown] id="XYmg1Fa8j3Y6"
# Convert image to grayscale so that we don't have to deal with the complexity of multiple color channels:
# + id="uki3S6w0j3Y7" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="41c10d25-0aed-4e22-b42e-96dd449ac3ab"
imggray = img.convert('LA')
_ = plt.imshow(imggray)
# + [markdown] id="eVwgrA0Jj3Y9"
# Convert data into numpy matrix, which doesn't impact image data:
# + id="wHijyFgUj3Y9" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="5c5a287e-92f0-488d-e7d2-a25d7030eb5b"
imgmat = np.array(list(imggray.getdata(band=0)), float)
imgmat.shape = (imggray.size[1], imggray.size[0])
imgmat = np.matrix(imgmat)
_ = plt.imshow(imgmat, cmap='gray')
# + [markdown] id="x8VCD3lyj3Y-"
# Calculate SVD of the image:
# + id="kbBLn2Csj3Y-"
U, sigma, V = np.linalg.svd(imgmat)
# + [markdown] id="ApybkCdLj3Y-"
# As eigenvalues are arranged in descending order in diag($\lambda$) so too are singular values, by convention, arranged in descending order in $D$ (or, in this code, diag($\sigma$)). Thus, the first left-singular vector of $U$ and first right-singular vector of $V$ may represent the most prominent feature of the image:
# + id="rZTwlhGxj3Y_" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="bbabb61f-17ac-4e73-b1e2-10754c9dc100"
reconstimg = np.matrix(U[:, :1]) * np.diag(sigma[:1]) * np.matrix(V[:1, :])
_ = plt.imshow(reconstimg, cmap='gray')
# + [markdown] id="4p2cEqIoj3Y_"
# Additional singular vectors improve the image quality:
# + id="f5-6LEbij3ZA" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="c0504b84-9b7b-4ee7-86c7-0dcbefdcdc86"
for i in [2, 4, 8, 16, 32, 64]:
reconstimg = np.matrix(U[:, :i]) * np.diag(sigma[:i]) * np.matrix(V[:i, :])
plt.imshow(reconstimg, cmap='gray')
title = "n = %s" % i
plt.title(title)
plt.show()
# + [markdown] id="IjfUJ4wNj3ZA"
# With 64 singular vectors, the image is reconstructed quite well, however the data footprint is much smaller than the original image:
# + id="hXQy4TzCj3ZB" colab={"base_uri": "https://localhost:8080/"} outputId="c8a9c18c-a070-4dbc-9f6b-003492db1f06"
imgmat.shape
# + id="SXJtpYGeLWxz" colab={"base_uri": "https://localhost:8080/"} outputId="7e994526-5509-4ab4-bd1c-0b6f4c2b318c"
full_representation = 4032*3024
full_representation
# + id="vOHZXITLLWx1" colab={"base_uri": "https://localhost:8080/"} outputId="6780de62-ccfd-4936-f0cb-172c2e178db4"
svd64_rep = 64*4032 + 64 + 64*3024
svd64_rep
# + id="YwdA6taLj3ZD" colab={"base_uri": "https://localhost:8080/"} outputId="0dfe0239-d22e-4b54-ca53-3fc07b24ecc8"
svd64_rep/full_representation
# + [markdown] id="_HdtL8p7j3ZD"
# Specifically, the image represented as 64 singular vectors is 3.7% of the size of the original!
#
# Alongside images, we can use singular vectors for dramatic, lossy compression of other types of media files.
# + [markdown] id="lBQnc4uGj3ZE"
# **Return to slides here.**
# + [markdown] id="FEnTYLbBj3ZE"
# ### The Moore-Penrose Pseudoinverse
# + [markdown] id="q4_MX4D5j3ZE"
# Let's calculate the pseudoinverse $A^+$ of some matrix $A$ using the formula from the slides:
#
# $A^+ = VD^+U^T$
# + id="gbbiRcmzj3ZE" colab={"base_uri": "https://localhost:8080/"} outputId="ed37e9e2-23b7-4246-8a19-7b50ced837cf"
A
# + [markdown] id="TFNYVdZ4j3ZF"
# As shown earlier, the NumPy SVD method returns $U$, $d$, and $V^T$:
# + id="I6NjgNbjj3ZF"
U, d, VT = np.linalg.svd(A)
# + id="_sROQTAzj3ZG" colab={"base_uri": "https://localhost:8080/"} outputId="9c13bc75-ea2d-40b6-b775-7236dd699c39"
U
# + id="drDSW-vkj3ZG" colab={"base_uri": "https://localhost:8080/"} outputId="7aacd4f9-ff3d-4d1f-c88e-75c7b2cd3705"
VT
# + id="Sr3jIv4Jj3ZH" colab={"base_uri": "https://localhost:8080/"} outputId="f6cef297-d008-4e8d-a841-56d2d83d75b5"
d
# + [markdown] id="7yalmt19j3ZI"
# To create $D^+$, we first invert the non-zero values of $d$:
# + id="HEvRLwQfj3ZI" colab={"base_uri": "https://localhost:8080/"} outputId="73622be9-d30e-4cd1-ce56-e4d25a3cab1e"
D = np.diag(d)
D
# + id="6O2LADtLj3ZJ" colab={"base_uri": "https://localhost:8080/"} outputId="2cba2b81-e322-46c9-c914-68ec3b84ea39"
1/8.669
# + id="y1ZbYtmIj3ZJ" colab={"base_uri": "https://localhost:8080/"} outputId="5df71298-4522-481a-e7f9-c8d2e57729db"
1/4.104
# + [markdown] id="yO1tNES9j3ZK"
# ...and then we would take the tranpose of the resulting matrix.
#
# Because $D$ is a diagonal matrix, this can, however, be done in a single step by inverting $D$:
# + id="Y0sjcP3Ej3ZK" colab={"base_uri": "https://localhost:8080/"} outputId="8b6588b0-a8a4-4764-f927-e3817e58ff1b"
Dinv = np.linalg.inv(D)
Dinv
# + [markdown] id="PXJnvna-j3ZM"
# $D^+$ must have the same dimensions as $A^T$ in order for $VD^+U^T$ matrix multiplication to be possible:
# + id="Ydq0zJHNRZPy" colab={"base_uri": "https://localhost:8080/"} outputId="389d0c75-984d-4f85-a8a1-e054f3d6d4ca"
Dplus = np.concatenate((Dinv, np.array([[0, 0]]).T), axis=1)
Dplus
# + [markdown] id="zFgtoJUKSRg1"
# (Recall $D$ must have the same dimensions as $A$ for SVD's $UDV^T$, but for MPP $U$ and $V$ have swapped sides around the diagonal matrix.)
# + [markdown] id="6Xt4NYHuj3ZO"
# Now we have everything we need to calculate $A^+$ with $VD^+U^T$:
# + id="ZtWN_wnij3ZO" colab={"base_uri": "https://localhost:8080/"} outputId="14912908-896a-4b0e-c9b1-4bc3e8a17f32"
np.dot(VT.T, np.dot(Dplus, U.T))
# + [markdown] id="3syT7-hCj3ZP"
# Working out this derivation is helpful for understanding how Moore-Penrose pseudoinverses work, but unsurprisingly NumPy is loaded with an existing method `pinv()`:
# + id="fh0nDMeLj3ZP" colab={"base_uri": "https://localhost:8080/"} outputId="9178720c-7e4d-4ea7-98b2-500c5ba24a39"
np.linalg.pinv(A)
# + [markdown] id="xNrIfpAij3ZS"
# **Exercise**
#
# Use the `torch.svd()` method to calculate the pseudoinverse of `A_p`, confirming that your result matches the output of `torch.pinverse(A_p)`:
# + id="W2635vlEj3ZS" colab={"base_uri": "https://localhost:8080/"} outputId="4c185220-c5f8-43b7-b2d0-eac1e437ea89"
A_p = torch.tensor([[-1, 2], [3, -2], [5, 7.]])
A_p
# + id="ZW4SsUOlj3ZT" colab={"base_uri": "https://localhost:8080/"} outputId="c994841a-797e-41d7-ae7a-a480e8d2a58b"
torch.pinverse(A_p)
# + [markdown] id="KlXBgI3Nj3ZT"
# **Return to slides here.**
# + [markdown] id="xMnIqjpfj3ZT"
# For regression problems, we typically have many more cases ($n$, or rows of $X$) than features to predict (columns of $X$). Let's solve a miniature example of such an overdetermined situation.
#
# We have eight data points ($n$ = 8):
# + id="2Ft4PXaTj3ZU"
x1 = [0, 1, 2, 3, 4, 5, 6, 7.] # E.g.: Dosage of drug for treating Alzheimer's disease
y = [1.86, 1.31, .62, .33, .09, -.67, -1.23, -1.37] # E.g.: Patient's "forgetfulness score"
# + id="HaoEgLTzLWyH"
title = 'Clinical Trial'
xlabel = 'Drug dosage (mL)'
ylabel = 'Forgetfulness'
# + id="OiMAISFBj3ZW" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="cc6075ec-253c-4d3c-8cb4-0f648d3fe204"
fig, ax = plt.subplots()
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
_ = ax.scatter(x1, y)
# + [markdown] id="GWZUFeqzj3ZX"
# Although it appears there is only one predictor ($x_1$), our model requires a second one (let's call it $x_0$) in order to allow for a $y$-intercept. Without this second variable, the line we fit to the plot would need to pass through the origin (0, 0). The $y$-intercept is constant across all the points so we can set it equal to `1` across the board:
# + id="RpAIoxydj3ZX" colab={"base_uri": "https://localhost:8080/"} outputId="7d2c3e3e-248e-4d25-c4ef-f07d52b272a3"
x0 = np.ones(8)
x0
# + [markdown] id="_bkwC8Wnj3ZY"
# Concatenate $x_0$ and $x_1$ into a matrix $X$:
# + id="x56TMNFMj3ZY" colab={"base_uri": "https://localhost:8080/"} outputId="1d874fd7-f48a-4810-9d28-29dc75f1b201"
X = np.concatenate((np.matrix(x0).T, np.matrix(x1).T), axis=1)
X
# + [markdown] id="v7TomkyCj3ZY"
# From the slides, we know that we can calculate the weights $w$ using the equation $w = X^+y$:
# + id="iRYhw-N0j3ZZ" colab={"base_uri": "https://localhost:8080/"} outputId="e118518f-cf9b-400a-a833-772ea9143bd7"
w = np.dot(np.linalg.pinv(X), y)
w
# + [markdown] id="N2SoGsRNj3ZZ"
# The first weight corresponds to the $y$-intercept of the line, which is typically denoted as $b$:
# + id="nLvuVmBGj3ZZ" colab={"base_uri": "https://localhost:8080/"} outputId="a0733664-d354-4f4f-843c-e4b5c4e8eb93"
b = np.asarray(w).reshape(-1)[0]
b
# + [markdown] id="96XCC8Z-j3Za"
# While the second weight corresponds to the slope of the line, which is typically denoted as $m$:
# + id="HHTNUSJCj3Za" colab={"base_uri": "https://localhost:8080/"} outputId="c53ca721-51d9-4232-bf5c-0161c8d12a9b"
m = np.asarray(w).reshape(-1)[1]
m
# + [markdown] id="lvGCTZRqj3Zc"
# With the weights we can plot the line to confirm it fits the points:
# + id="q9SAiUyej3Zc" colab={"base_uri": "https://localhost:8080/", "height": 295} outputId="276d5d7c-444c-4638-d008-12fc1b46fed9"
fig, ax = plt.subplots()
plt.title(title)
plt.xlabel(xlabel)
plt.ylabel(ylabel)
ax.scatter(x1, y)
x_min, x_max = ax.get_xlim()
y_at_xmin = m*x_min + b
y_at_xmax = m*x_max + b
ax.set_xlim([x_min, x_max])
_ = ax.plot([x_min, x_max], [y_at_xmin, y_at_xmax], c='C01')
# + [markdown] id="vNJJNtDzSh83"
# **DO NOT return to slides here. Onward!**
# + [markdown] id="rJnSV2afj3Zd"
# ### The Trace Operator
# + [markdown] id="dq9uqorvj3Zd"
# Denoted as Tr($A$). Simply the sum of the diagonal elements of a matrix: $$\sum_i A_{i,i}$$
# + id="vOdkry9ij3Zd" colab={"base_uri": "https://localhost:8080/"} outputId="692f6162-2874-4848-fb46-59f542b0f3a0"
A = np.array([[25, 2], [5, 4]])
A
# + id="zwh8-KTNj3Ze" colab={"base_uri": "https://localhost:8080/"} outputId="7f5c2213-e7ff-439e-9f26-c5ce9bd8845d"
25 + 4
# + id="7LxzUu37j3Zf" colab={"base_uri": "https://localhost:8080/"} outputId="5368b908-74f9-4ede-e6f6-e19bfe3005be"
np.trace(A)
# + [markdown] id="dUeQKrYMj3Zg"
# The trace operator has a number of useful properties that come in handy while rearranging linear algebra equations, e.g.:
#
# * Tr($A$) = Tr($A^T$)
# * Assuming the matrix shapes line up: Tr($ABC$) = Tr($CAB$) = Tr($BCA$)
# + [markdown] id="kuKYTjskj3Zg"
# In particular, the trace operator can provide a convenient way to calculate a matrix's Frobenius norm: $$||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$$
# + [markdown] id="JcqTZnimj3Zg"
# **Exercises**
#
# With the matrix `A_p` provided below:
#
# 1. Use the PyTorch trace method to calculate the trace of `A_p`.
# 2. Use the PyTorch Frobenius norm method and the trace method to demonstrate that $||A||_F = \sqrt{\mathrm{Tr}(AA^\mathrm{T})}$
# + id="rQhYWOFvj3Zg" colab={"base_uri": "https://localhost:8080/"} outputId="8e1a3b14-a944-427d-a239-5349c4988bcc"
A_p
# + [markdown] id="QXuZgAUgj3Zh"
# **Return to slides here.**
# + [markdown] id="1rQOXPyaj3Zh"
# ### Principal Component Analysis
# + [markdown] id="X3_Etgo4j3Zh"
# This PCA example code is adapted from [here](https://jupyter.brynmawr.edu/services/public/dblank/CS371%20Cognitive%20Science/2016-Fall/PCA.ipynb).
# + id="ubl3WdRWj3Zh"
from sklearn import datasets
iris = datasets.load_iris()
# + id="ZE2yvfEbj3Zi" colab={"base_uri": "https://localhost:8080/"} outputId="22481efa-7413-4713-efc6-c3f2965252de"
iris.data.shape
# + id="fa9fcMl2j3Zi" colab={"base_uri": "https://localhost:8080/"} outputId="a58badd2-c61c-4555-a67e-273d9a86a665"
iris.get("feature_names")
# + id="8O9xwrOLj3Zj" colab={"base_uri": "https://localhost:8080/"} outputId="4cbdd710-0b45-46d7-9ca7-f69b0a94bbf8"
iris.data[0:6,:]
# + id="YoodmvRsj3Zj"
from sklearn.decomposition import PCA
# + id="PcJwICbtj3Zk"
pca = PCA(n_components=2)
# + id="bNb6txoIj3Zk"
X = pca.fit_transform(iris.data)
# + id="plS7skQGj3Zl" colab={"base_uri": "https://localhost:8080/"} outputId="3cb1ebcf-3026-407f-b5bb-48a793fb8900"
X.shape
# + id="wC_j-7Xyj3Zl" colab={"base_uri": "https://localhost:8080/"} outputId="e9cfa100-941a-4804-803d-95485f933cf3"
X[0:6,:]
# + id="O_aNxFn5j3Zm" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="827f3462-d784-47d4-a231-4c6b62ee7705"
_ = plt.scatter(X[:, 0], X[:, 1])
# + id="bTck5c93j3Zm" colab={"base_uri": "https://localhost:8080/"} outputId="d9ab042f-fd36-4211-f31f-576a917763d3"
iris.target.shape
# + id="IzGhB6NTj3Zn" colab={"base_uri": "https://localhost:8080/"} outputId="54ab57dc-3cff-49d6-b543-a5cdcc9bc9c0"
iris.target[0:6]
# + id="DQ8oRWsWj3Zn" colab={"base_uri": "https://localhost:8080/"} outputId="20ec84c8-970f-4448-c51b-0297e4b8c51b"
unique_elements, counts_elements = np.unique(iris.target, return_counts=True)
np.asarray((unique_elements, counts_elements))
# + id="VAIoVTYWj3Zo" colab={"base_uri": "https://localhost:8080/"} outputId="8e821e2c-fb38-48c2-e9c9-5919af3e541a"
list(iris.target_names)
# + id="JlZX_2vQj3Zo" colab={"base_uri": "https://localhost:8080/", "height": 269} outputId="b2741dbb-3a32-4b0e-bb4c-84cee47de1fc"
_ = plt.scatter(X[:, 0], X[:, 1], c=iris.target)
# + [markdown] id="w1Y8YA2oj3Zp"
# **Return to slides here.**
|
notebooks/2-linear-algebra-ii.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sqlite3
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import scale
from customplot import *
cnx = sqlite3.connect('database.sqlite')
df = pd.read_sql_query("SELECT * FROM Player_Attributes", cnx)
df.columns
df.describe().transpose()
df.isnull().any().any() ,df.shape
df.isnull().sum(axis=0)
row = df.shape[0]
df = df.dropna()
df.isnull().any().any() , df.shape
row - df.shape[0]
df = df.reindex(np.random.permutation(df.index))
df.head(5)
df.head(5)
df = df.reindex(np.random.permutation(df.index))
df.head(5)
df[:10][['penalties','overall_rating']]
df[:5][['attacking_work_rate','penalties','overall_rating']]
potentialFeatures = ['acceleration','curve','free_kick_accuracy','ball_control','shot_power','stamina']
for f in potentialFeatures:
related = df['overall_rating'].corr(df[f])
print("%s: %f" %(f,related))
cols = ['potential', 'crossing', 'finishing', 'heading_accuracy',
'short_passing', 'volleys', 'dribbling', 'curve', 'free_kick_accuracy',
'long_passing', 'ball_control', 'acceleration', 'sprint_speed',
'agility', 'reactions', 'balance', 'shot_power', 'jumping', 'stamina',
'strength', 'long_shots', 'aggression', 'interceptions', 'positioning',
'vision', 'penalties', 'marking', 'standing_tackle', 'sliding_tackle',
'gk_diving', 'gk_handling', 'gk_kicking', 'gk_positioning',
'gk_reflexes']
correlations = [df['overall_rating'].corr(df[f]) for f in cols]
len(cols), len(correlations)
def plot_dataframe(df,y_label):
color='coral'
fig = plt.gcf()
fig.set_size_inches(20,12)
plt.ylabel(y_label)
ax=df2.correlation.plot(linewidth=3.3, color=color)
ax.set_xticks(df2.index)
ax.set_xticklabels(df2.attributes, rotaion=75);
plt.show()
#
#
# +
# create a function for plotting a dataframe with string columns and numeric values
def plot_dataframe(df, y_label):
color='yellow'
fig = plt.gcf()
fig.set_size_inches(20, 12)
plt.ylabel(y_label)
ax = df2.correlation.plot(linewidth=3.3, color=color)
ax.set_xticks(df2.index)
ax.set_xticklabels(df2.attributes, rotation=75); #Notice the ; (remove it and see what happens !)
plt.show()
# -
df2 = pd.DataFrame({'attributes': cols, 'correlation': correlations})
plot_dataframe(df2, 'Player\'s Overall Rating')
select5features = ['gk_kicking', 'potential', 'marking', 'interceptions', 'standing_tackle']
select5features
df_select = df[select5features].copy(deep=True)
df_select.head()
# +
data = scale(df_select)
# Define number of clusters
noOfClusters = 4
# Train a model
model = KMeans(init='k-means++', n_clusters=noOfClusters, n_init=20).fit(data)
# +
print(90*'_')
print("\nCount of players in each cluster")
print(90*'_')
pd.value_counts(model.labels_, sort=False)
# -
P = pd_centers(featuresUsed=select5features, centers=model.cluster_centers_)
P
# %matplotlib inline
parallel_plot(P)
|
Final Notebook/soccerAnalysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: cflows
# language: python
# name: cflows
# ---
# ## Config
# +
# %load_ext autoreload
# %autoreload 2
from pathlib import Path
from experiment import data_path
model_name = 'sphere-cef-joint'
gen_path = data_path / 'generated' / model_name
# -
# ## Generate data non-uniformly on sphere
# +
from torch.utils.data import DataLoader, random_split
import data
import numpy as np
num_samples = 1000
batch_size = 100
mu = [-1, -1, 0.0]
sigma = [[1,0,0], [0,1,0], [0,0,1]]
data = data.Sphere(
manifold_dim=2,
ambient_dim=3,
size=num_samples,
mu=mu,
sigma=sigma)
# +
from nflows import cef_models
flow = cef_models.SphereCEFlow()
conf_embedding = flow.embedding
backbone = flow.distribution
# -
# ## Train
# Schedule training
# +
import torch.optim as opt
batch_size = 100
optim = opt.Adam(flow.parameters(), lr=0.005)
scheduler = opt.lr_scheduler.MultiStepLR(optim, milestones=[40], gamma=0.5)
def schedule():
'''Yield epoch weights for likelihood and recon loss, respectively'''
for _ in range(45):
yield 10, 10000
scheduler.step()
loader = DataLoader(data, batch_size=batch_size, shuffle=True, num_workers=6)
# +
import matplotlib as mpl
import matplotlib.pyplot as plt
import torch
points = data.points[:num_samples]
# Initialize model
with torch.no_grad():
gen_samples = flow.sample(num_samples)
sample_mid_latent, _ = flow.embedding.forward(points)
sample_recons, _ = flow.embedding.inverse(sample_mid_latent)
# Plot data and recons before training
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
point_plot = ax.scatter(points[:,0].cpu(), points[:,1].cpu(), points[:,2].cpu(),
color='#faab36')
recon_plot = ax.scatter(sample_recons[:,0].cpu(), sample_recons[:,1].cpu(),
sample_recons[:,2].cpu(), color='#249ea0')
ax.auto_scale_xyz([-1.3, 1.3], [-1.3, 1.3], [-1, 1]) # Correct aspect ratio manually
ax.view_init(elev=20, azim=260)
# +
import torch
import torch.nn as nn
from tqdm import tqdm
for epoch, (alpha, beta) in enumerate(schedule()):
# Train for one epoch
flow.train()
progress_bar = tqdm(enumerate(loader))
for batch, point in progress_bar:
optim.zero_grad()
# Compute reconstruction error
with torch.set_grad_enabled(beta > 0):
mid_latent, _ = conf_embedding.forward(point)
reconstruction, log_conf_det = conf_embedding.inverse(mid_latent)
reconstruction_error = torch.mean((point - reconstruction)**2)
# Compute log likelihood
with torch.set_grad_enabled(alpha > 0):
log_pu = backbone.log_prob(mid_latent)
log_likelihood = torch.mean(log_pu - log_conf_det)
# Training step
loss = - alpha*log_likelihood + beta*reconstruction_error
loss.backward()
optim.step()
# Display results
progress_bar.set_description(f'[E{epoch} B{batch}] | loss: {loss: 6.2f} | LL: {log_likelihood:6.2f} '
f'| recon: {reconstruction_error:6.5f} ')
# +
# Plot data and recons
with torch.no_grad():
sample_mid_latent, _ = conf_embedding.forward(points)
sample_recons, _ = conf_embedding.inverse(sample_mid_latent)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
point_plot = ax.scatter(points[:,0], points[:,1], points[:,2], color='#faab36')
recon_plot = ax.scatter(sample_recons[:,0], sample_recons[:,1], sample_recons[:,2],
color='#249ea0')
ax.auto_scale_xyz([-1.3, 1.3], [-1.3, 1.3], [-1, 1]) # Correct aspect ratio manually
ax.view_init(elev=20, azim=260)
# +
# Plot generated samples to gauge density
gen_samples = flow.sample(num_samples).detach()
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
point_plot = ax.scatter(gen_samples[:,0], gen_samples[:,1], gen_samples[:,2], color='#faab36')
ax.auto_scale_xyz([-1.3, 1.3], [-1.3, 1.3], [-1, 1]) # Correct aspect ratio manually
ax.view_init(elev=20, azim=260)
# -
# ## Plot Densities and Samples
# +
from matplotlib.colors import LinearSegmentedColormap
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
rgbs = [(250/255,171/255,54/255),(223/255,220/255,119/255),(217/255,255/255,200/255),
(129/255,208/255,177/255), (36/255,158/255,160/255)] # Custom color scheme
custom_cm = LinearSegmentedColormap.from_list("CEF_colors", rgbs, N=21)
# -
# mkdir figures
# +
# Plot the density of data distribution
from scipy.special import erf
mu_norm = np.linalg.norm(mu)
const = np.exp(-mu_norm**2 / 2) / (2**(5/2) * np.pi**(3/2))
def data_likelihood(x, y, z): # Density for 2d Sphere dataset
t = x*mu[0] + y*mu[1] + z*mu[2]
density = (2 * t) + np.sqrt(2*np.pi) * (t**2 + 1) * np.exp(t**2 / 2) * (1 + erf(t / np.sqrt(2)))
return density * const
def plot_data_density():
# create grid of points on spherical surface
u = np.linspace(0, 2 * np.pi, 240) # azimuthal angle
v = np.linspace(0, np.pi, 120) # polar angle
# create the sphere surface in xyz coordinates
XX = np.outer(np.cos(u), np.sin(v))
YY = np.outer(np.sin(u), np.sin(v))
ZZ = np.outer(np.ones(np.size(u)), np.cos(v))
density_grid_2 = np.zeros_like(XX)
grid_points = np.zeros([len(u), 3], dtype=np.float32)
for i in range(len(v)):
z = np.cos(v[i])
s = np.sin(v[i])
for j in range(len(u)):
x = np.cos(u[j])*s
y = np.sin(u[j])*s
density_grid_2[j, i] = data_likelihood(x, y, z)
# plot density as heatmap. for coloration values should fill (0,1)
heatmap = density_grid_2 / np.max(density_grid_2)
return XX, YY, ZZ, density_grid_2, heatmap
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
XX, YY, ZZ, density_grid_data, heatmap = plot_data_density()
colorbar = cm.ScalarMappable(cmap=custom_cm)
colorbar.set_array(density_grid_data)
plt.colorbar(colorbar, pad=-0.02, fraction=0.026, format='%.2f')
ax.view_init(elev=20, azim=260)
ax.plot_surface(XX, YY, ZZ, cstride=1, rstride=1, facecolors=custom_cm(heatmap))
ax.auto_scale_xyz([-1.15, 1.15], [-1.15, 1.15], [-1, 1]) # Correct aspect ratio manually
ax.set_xticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_yticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_zticks([-1.0, -0.5, 0.0, 0.5, 1.0])
plt.tight_layout(pad=0, w_pad=0)
plt.savefig("figures/sphere-data-density.png", bbox_inches='tight', dpi=300)
plt.show()
# -
# Above should have similar distribution to original data distribution here
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
point_plot = ax.scatter(points[:,0], points[:,1], points[:,2], color='#faab36')
ax.view_init(elev=20, azim=260)
ax.set_xlim(-1.3, 1.3)
ax.set_ylim(-1.3, 1.3)
ax.set_zlim(-1.0, 1.0)
ax.set_xticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_yticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_zticks([-1.0, -0.5, 0.0, 0.5, 1.0])
plt.savefig("figures/sphere-data-samples.png", bbox_inches='tight', dpi=300)
# +
def likelihood_of_point(arr, manifold_model, density_model):
with torch.no_grad():
grid_points = torch.from_numpy(arr)
mid_latent, _ = manifold_model.forward(grid_points)
_, log_conf_det = manifold_model.inverse(mid_latent)
log_pu = density_model.log_prob(mid_latent)
log_likelihood = log_pu - log_conf_det
return torch.exp(log_likelihood).numpy()
def plot_model_density(manifold_model, density_model):
# create grid of points on spherical surface
u = np.linspace(0, 2 * np.pi, 240) # azimuthal angle
v = np.linspace(0, np.pi, 120) # polar angle
# create the sphere surface in xyz coordinates
XX = np.outer(np.cos(u), np.sin(v))
YY = np.outer(np.sin(u), np.sin(v))
ZZ = np.outer(np.ones(np.size(u)), np.cos(v))
density_grid = np.zeros_like(XX)
grid_points = np.zeros([len(u), 3], dtype=np.float32)
for i in range(len(v)):
z = np.cos(v[i])
s = np.sin(v[i])
for j in range(len(u)):
grid_points[j, 0] = np.cos(u[j])*s
grid_points[j, 1] = np.sin(u[j])*s
grid_points[j, 2] = z
# Treat every point in grid as (x, y, z) data_point
# Calculate likelihood from model in batches
density_grid[:, i] = likelihood_of_point(grid_points, manifold_model, density_model)
# plot density as heatmap. for coloration values should fill (0,1)
heatmap = density_grid / np.max(density_grid_data)
return XX, YY, ZZ, density_grid, heatmap
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
XX, YY, ZZ, density_grid, heatmap = plot_model_density(conf_embedding, backbone)
colorbar = cm.ScalarMappable(cmap=custom_cm)
colorbar.set_array(density_grid_data) # Setting to density_grid_data for matching scales
plt.colorbar(colorbar, pad=-0.02, fraction=0.026, format='%.2f')
ax.view_init(elev=20, azim=260)
ax.plot_surface(XX, YY, ZZ, cstride=1, rstride=1, facecolors=custom_cm(heatmap))
ax.auto_scale_xyz([-1.15, 1.15], [-1.15, 1.15], [-1, 1]) # Correct aspect ratio manually
ax.set_xticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_yticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_zticks([-1.0, -0.5, 0.0, 0.5, 1.0])
plt.tight_layout(pad=0, w_pad=0)
plt.savefig("figures/sphere-model-density.png", bbox_inches='tight', dpi=300)
plt.show()
# +
# Replot using trained density model
gen_samples = flow.sample(num_samples).detach()
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection='3d')
gen_plot = ax.scatter(gen_samples[:,0], gen_samples[:,1], gen_samples[:,2], color='#faab36')
ax.view_init(elev=20, azim=260)
ax.set_xlim(-1.3, 1.3)
ax.set_ylim(-1.3, 1.3)
ax.set_zlim(-1.0, 1.0)
ax.set_xticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_yticks([-1.0, -0.5, 0.0, 0.5, 1.0])
ax.set_zticks([-1.0, -0.5, 0.0, 0.5, 1.0])
plt.savefig("figures/sphere-generated-samples.png", dpi=300)
|
experiments/sphere-cef-joint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import k3d
import numpy as np
from ipywidgets import interact, IntSlider
width = height = length = 3
color_map = (0xFF0000, 0x00FF00, 0x0000FF)
voxels = np.ones(width * height * length, dtype=np.uint8).reshape((length, height, width))
obj = k3d.voxels(voxels, color_map)
plot = k3d.plot(voxel_paint_color=2)
plot += obj
@interact(color=IntSlider(value=plot.voxel_paint_color, min=0, max=len(color_map)))
def color(color):
plot.voxel_paint_color = color
plot.display()
# -
obj.voxels.flatten() # initial data
# Edit object (add/remove some voxels)
plot.mode = 'change'
obj.fetch_data('voxels') # this is an async operation
obj.voxels.flatten() # updated data
obj.visible = False
obj.visible = True
|
examples/voxel_edit.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Smart Wearables -- Bonsai Tree Classification on stream data
# ## 1. Introduction & Library Imports
import numpy as np
from sklearn.metrics.classification import accuracy_score, recall_score, f1_score
import scipy.stats as st
import sys
from sklearn.model_selection import train_test_split
from bonsai.base.regtree import RegTree
from bonsai.base.alphatree import AlphaTree
from bonsai.base.c45tree import C45Tree
from bonsai.base.ginitree import GiniTree
from bonsai.base.xgbtree import XGBTree
from bonsai.base.friedmantree import FriedmanTree
from bonsai.ensemble.randomforests import RandomForests
from bonsai.ensemble.paloboost import PaloBoost
from bonsai.ensemble.gbm import GBM
import copy
import sys
import json
import time
# +
import math
from keras import optimizers
from utils import *
from model import *
from keras.utils.np_utils import to_categorical
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
# Setting seed for reproducability
np.random.seed(1234)
PYTHONHASHSEED = 0
from sklearn import preprocessing
from sklearn.metrics import confusion_matrix, recall_score, precision_score
from keras.models import Sequential
from keras.layers import Dense, Dropout, LSTM, Activation
# %matplotlib inline
#import pydot
#import graphviz
#pydot.find_graphviz = lambda: True
import keras
# -
# ## 2. Data Gathering
# +
data_input_file = 'data/FNOW/MHEALTH.npz'
np_load_old = np.load
# modify the default parameters of np.load
np.load = lambda *a,**k: np_load_old(*a, allow_pickle=True, **k)
tmp = np.load(data_input_file)
np.load = np_load_old
# -
X = tmp['X']
X = X[:, 0, :, :]
y = tmp['y']
folds = tmp['folds']
n_class = y.shape[1]
y = np.argmax(y, axis=1)
print('Hancrafted Template 2017 {}'.format(data_input_file))
# ## 3. Feature Engineering
# +
def A(sample):
feat = []
for col in range(0,sample.shape[1]):
average = np.average(sample[:,col])
feat.append(average)
return feat
def SD(sample):
feat = []
for col in range(0, sample.shape[1]):
std = np.std(sample[:, col])
feat.append(std)
return feat
def AAD(sample):
feat = []
for col in range(0, sample.shape[1]):
data = sample[:, col]
add = np.mean(np.absolute(data - np.mean(data)))
feat.append(add)
return feat
def ARA(sample):
#Average Resultant Acceleration[1]:
# Average of the square roots of the sum of the values of each axis squared √(xi^2 + yi^2+ zi^2) over the ED
feat = []
sum_square = 0
sample = np.power(sample, 2)
for col in range(0, sample.shape[1]):
sum_square = sum_square + sample[:, col]
sample = np.sqrt(sum_square)
average = np.average(sample)
feat.append(average)
return feat
def TBP(sample):
from scipy import signal
feat = []
sum_of_time = 0
for col in range(0, sample.shape[1]):
data = sample[:, col]
peaks = signal.find_peaks_cwt(data, np.arange(1,4))
feat.append(peaks)
return feat
def feature_extraction(X):
#Extracts the features, as mentioned by Catal et al. 2015
# Average - A,
# Standard Deviation - SD,
# Average Absolute Difference - AAD,
# Average Resultant Acceleration - ARA(1),
# Time Between Peaks - TBP
X_tmp = []
for sample in X:
features = A(copy.copy(sample))
features = np.hstack((features, A(copy.copy(sample))))
features = np.hstack((features, SD(copy.copy(sample))))
features = np.hstack((features, AAD(copy.copy(sample))))
features = np.hstack((features, ARA(copy.copy(sample))))
#features = np.hstack((features, TBP(sample)))
X_tmp.append(features)
X = np.array(X_tmp)
return X
# -
# ## 4. RegTree
avg_acc = []
avg_recall = []
avg_f1 = []
avg_ttime=[]
avg_ptime=[]
avg_size=[]
for i in range(0, len(folds)):
train_idx = folds[i][0]
test_idx = folds[i][1]
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
#Your train goes here. For instance:
#X_train=X_train.transpose(0,1,2).reshape(X_train.shape[0],-1)
#X_test=X_test.transpose(0,1,2).reshape(X_test.shape[0],-1)
X_train = feature_extraction(X_train)
X_test = feature_extraction(X_test)
method = RegTree(max_depth=8)
t0=time.time()
method.fit(X_train, y_train)
avg_ttime.append(time.time()-t0)
#Your testing goes here. For instance:
t1=time.time()
y_pred = method.predict(X_test)
avg_ptime.append(time.time()-t1)
y_pred=np.round(y_pred,0)
y_pred=y_pred.astype(int)
v=method.dump()
avg_size.append(round(v.__sizeof__()/1024,3))
acc_fold = accuracy_score(y_test, y_pred)
avg_acc.append(acc_fold)
recall_fold = recall_score(y_test, y_pred, average='macro')
avg_recall.append(recall_fold)
f1_fold = f1_score(y_test, y_pred, average='macro')
avg_f1.append(f1_fold)
print('Accuracy[{:.4f}] Recall[{:.4f}] F1[{:.4f}] at fold[{}]'.format(acc_fold, recall_fold, f1_fold ,i))
print('______________________________________________________')
ic_acc = st.t.interval(0.9, len(avg_acc) - 1, loc=np.mean(avg_acc), scale=st.sem(avg_acc))
ic_recall = st.t.interval(0.9, len(avg_recall) - 1, loc=np.mean(avg_recall), scale=st.sem(avg_recall))
ic_f1 = st.t.interval(0.9, len(avg_f1) - 1, loc=np.mean(avg_f1), scale=st.sem(avg_f1))
print('Mean Accuracy[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_acc), ic_acc[0], ic_acc[1]))
print('Mean Recall[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_recall), ic_recall[0], ic_recall[1]))
print('Mean F1[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_f1), ic_f1[0], ic_f1[1]))
print('Mean size[{:.3f}]'.format(np.mean(avg_size)))
print('Mean training time[{:.3f}]'.format(round(np.mean(avg_ttime)*1000,3)))
print('Mean prediction time[{:.3f}]'.format(round(np.mean(avg_ptime)*1000,3)))
# ## 5. XGBTree
avg_acc = []
avg_recall = []
avg_f1 = []
avg_ttime=[]
avg_ptime=[]
avg_size=[]
for i in range(0, len(folds)):
train_idx = folds[i][0]
test_idx = folds[i][1]
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
X_train = feature_extraction(X_train)
X_test = feature_extraction(X_test)
method = XGBTree(max_depth=10,min_samples_split=1,min_samples_leaf=1)
t0=time.time()
method.fit(X_train, y_train)
avg_ttime.append(time.time()-t0)
#Your testing goes here. For instance:
t1=time.time()
y_pred = method.predict(X_test)
avg_ptime.append(time.time()-t1)
y_pred=np.round(y_pred,0)
y_pred=y_pred.astype(int)
v=method.dump()
avg_size.append(round(v.__sizeof__()/1024,3))
acc_fold = accuracy_score(y_test, y_pred)
avg_acc.append(acc_fold)
recall_fold = recall_score(y_test, y_pred, average='macro')
avg_recall.append(recall_fold)
f1_fold = f1_score(y_test, y_pred, average='macro')
avg_f1.append(f1_fold)
print('Accuracy[{:.4f}] Recall[{:.4f}] F1[{:.4f}] at fold[{}]'.format(acc_fold, recall_fold, f1_fold ,i))
print('______________________________________________________')
ic_acc = st.t.interval(0.9, len(avg_acc) - 1, loc=np.mean(avg_acc), scale=st.sem(avg_acc))
ic_recall = st.t.interval(0.9, len(avg_recall) - 1, loc=np.mean(avg_recall), scale=st.sem(avg_recall))
ic_f1 = st.t.interval(0.9, len(avg_f1) - 1, loc=np.mean(avg_f1), scale=st.sem(avg_f1))
print('Mean Accuracy[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_acc), ic_acc[0], ic_acc[1]))
print('Mean Recall[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_recall), ic_recall[0], ic_recall[1]))
print('Mean F1[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_f1), ic_f1[0], ic_f1[1]))
print('Mean size[{:.3f}]'.format(np.mean(avg_size)))
print('Mean training time[{:.3f}]'.format(round(np.mean(avg_ttime)*1000,3)))
print('Mean prediction time[{:.3f}]'.format(round(np.mean(avg_ptime)*1000,3)))
# ## 6. FriedmanTree
avg_acc = []
avg_recall = []
avg_f1 = []
avg_ttime=[]
avg_ptime=[]
avg_size=[]
for i in range(0, len(folds)):
train_idx = folds[i][0]
test_idx = folds[i][1]
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
#Your train goes here. For instance:
#X_train=X_train.transpose(0,1,2).reshape(X_train.shape[0],-1)
#X_test=X_test.transpose(0,1,2).reshape(X_test.shape[0],-1)
X_train = feature_extraction(X_train)
X_test = feature_extraction(X_test)
method = FriedmanTree(max_depth=8,min_samples_split=1,min_samples_leaf=1)
t0=time.time()
method.fit(X_train, y_train)
avg_ttime.append(time.time()-t0)
#Your testing goes here. For instance:
t1=time.time()
y_pred = method.predict(X_test)
avg_ptime.append(time.time()-t1)
y_pred=np.round(y_pred,0)
y_pred=y_pred.astype(int)
v=method.dump()
avg_size.append(round(v.__sizeof__()/1024,3))
acc_fold = accuracy_score(y_test, y_pred)
avg_acc.append(acc_fold)
recall_fold = recall_score(y_test, y_pred, average='macro')
avg_recall.append(recall_fold)
f1_fold = f1_score(y_test, y_pred, average='macro')
avg_f1.append(f1_fold)
print('Accuracy[{:.4f}] Recall[{:.4f}] F1[{:.4f}] at fold[{}]'.format(acc_fold, recall_fold, f1_fold ,i))
print('______________________________________________________')
ic_acc = st.t.interval(0.9, len(avg_acc) - 1, loc=np.mean(avg_acc), scale=st.sem(avg_acc))
ic_recall = st.t.interval(0.9, len(avg_recall) - 1, loc=np.mean(avg_recall), scale=st.sem(avg_recall))
ic_f1 = st.t.interval(0.9, len(avg_f1) - 1, loc=np.mean(avg_f1), scale=st.sem(avg_f1))
print('Mean Accuracy[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_acc), ic_acc[0], ic_acc[1]))
print('Mean Recall[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_recall), ic_recall[0], ic_recall[1]))
print('Mean F1[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_f1), ic_f1[0], ic_f1[1]))
print('Mean size[{:.3f}]'.format(np.mean(avg_size)))
print('Mean training time[{:.3f}]'.format(round(np.mean(avg_ttime)*1000,3)))
print('Mean prediction time[{:.3f}]'.format(round(np.mean(avg_ptime)*1000,3)))
# ## 7. PaloBoost
avg_acc = []
avg_recall = []
avg_f1 = []
avg_ttime=[]
avg_ptime=[]
avg_size=[]
for i in range(0, len(folds)):
train_idx = folds[i][0]
test_idx = folds[i][1]
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
#Your train goes here. For instance:
#X_train=X_train.transpose(0,1,2).reshape(X_train.shape[0],-1)
#X_test=X_test.transpose(0,1,2).reshape(X_test.shape[0],-1)
X_train = feature_extraction(X_train)
X_test = feature_extraction(X_test)
method = PaloBoost(n_estimators=100,max_depth=5)
t0=time.time()
method.fit(X_train, y_train)
avg_ttime.append(time.time()-t0)
#Your testing goes here. For instance:
t1=time.time()
y_pred = method.predict(X_test)
avg_ptime.append(time.time()-t1)
y_pred=np.round(y_pred,0)
y_pred=y_pred.astype(int)
v=method.dump()
avg_size.append(round(v.__sizeof__()/1024,3))
acc_fold = accuracy_score(y_test, y_pred)
avg_acc.append(acc_fold)
recall_fold = recall_score(y_test, y_pred, average='macro')
avg_recall.append(recall_fold)
f1_fold = f1_score(y_test, y_pred, average='macro')
avg_f1.append(f1_fold)
print('Accuracy[{:.4f}] Recall[{:.4f}] F1[{:.4f}] at fold[{}]'.format(acc_fold, recall_fold, f1_fold ,i))
print('______________________________________________________')
ic_acc = st.t.interval(0.9, len(avg_acc) - 1, loc=np.mean(avg_acc), scale=st.sem(avg_acc))
ic_recall = st.t.interval(0.9, len(avg_recall) - 1, loc=np.mean(avg_recall), scale=st.sem(avg_recall))
ic_f1 = st.t.interval(0.9, len(avg_f1) - 1, loc=np.mean(avg_f1), scale=st.sem(avg_f1))
print('Mean Accuracy[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_acc), ic_acc[0], ic_acc[1]))
print('Mean Recall[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_recall), ic_recall[0], ic_recall[1]))
print('Mean F1[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_f1), ic_f1[0], ic_f1[1]))
print('Mean size[{:.3f}]'.format(np.mean(avg_size)))
print('Mean training time[{:.3f}]'.format(round(np.mean(avg_ttime)*1000,3)))
print('Mean prediction time[{:.3f}]'.format(round(np.mean(avg_ptime)*1000,3)))
# ## 8. GBM
avg_acc = []
avg_recall = []
avg_f1 = []
avg_ttime=[]
avg_ptime=[]
avg_size=[]
for i in range(0, len(folds)):
train_idx = folds[i][0]
test_idx = folds[i][1]
X_train, y_train = X[train_idx], y[train_idx]
X_test, y_test = X[test_idx], y[test_idx]
#Your train goes here. For instance:
#X_train=X_train.transpose(0,1,2).reshape(X_train.shape[0],-1)
#X_test=X_test.transpose(0,1,2).reshape(X_test.shape[0],-1)
X_train = feature_extraction(X_train)
X_test = feature_extraction(X_test)
method = GBM(n_estimators=100,max_depth=5)
t0=time.time()
method.fit(X_train, y_train)
avg_ttime.append(time.time()-t0)
#Your testing goes here. For instance:
t1=time.time()
y_pred = method.predict(X_test)
avg_ptime.append(time.time()-t1)
y_pred=np.round(y_pred,0)
y_pred=y_pred.astype(int)
v=method.dump()
avg_size.append(round(v.__sizeof__()/1024,3))
acc_fold = accuracy_score(y_test, y_pred)
avg_acc.append(acc_fold)
recall_fold = recall_score(y_test, y_pred, average='macro')
avg_recall.append(recall_fold)
f1_fold = f1_score(y_test, y_pred, average='macro')
avg_f1.append(f1_fold)
print('Accuracy[{:.4f}] Recall[{:.4f}] F1[{:.4f}] at fold[{}]'.format(acc_fold, recall_fold, f1_fold ,i))
print('______________________________________________________')
ic_acc = st.t.interval(0.9, len(avg_acc) - 1, loc=np.mean(avg_acc), scale=st.sem(avg_acc))
ic_recall = st.t.interval(0.9, len(avg_recall) - 1, loc=np.mean(avg_recall), scale=st.sem(avg_recall))
ic_f1 = st.t.interval(0.9, len(avg_f1) - 1, loc=np.mean(avg_f1), scale=st.sem(avg_f1))
print('Mean Accuracy[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_acc), ic_acc[0], ic_acc[1]))
print('Mean Recall[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_recall), ic_recall[0], ic_recall[1]))
print('Mean F1[{:.4f}] IC [{:.4f}, {:.4f}]'.format(np.mean(avg_f1), ic_f1[0], ic_f1[1]))
print('Mean size[{:.3f}]'.format(np.mean(avg_size)))
print('Mean training time[{:.3f}]'.format(round(np.mean(avg_ttime)*1000,3)))
print('Mean prediction time[{:.3f}]'.format(round(np.mean(avg_ptime)*1000,3)))
# ## 9. Conclusion
# +
from prettytable import PrettyTable
x = PrettyTable()
x.field_names = ["Model", "Mean Accuracy", "Mean Recall", "Mean F1"]
x.add_row(["Reg Tree", 0.9805,0.9775,0.9768])
x.add_row(["XGB Tree", 0.9820, 0.9774, 0.9797])
x.add_row(["Friedman Tree", 0.9798, 0.9753, 0.9763])
x.add_row(["Palo Boost", 0.9671, 0.9673, 0.9674])
x.add_row(["GBM", 0.9731, 0.9702, 0.9709])
y = PrettyTable()
y.field_names = ["Model", "Mean Accuracy", "Mean Recall", "Mean F1"]
y.add_row(["Mean", 97.65, 0, 0])
print(x)
print(y)
# -
|
HAR_FNOW.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6.9 64-bit
# name: python36964bitce553f8d58a746c5874dcf1bfcd11db3
# ---
import numpy as np
import pandas as pd
import cv2
import matplotlib.pyplot as plt
from keras.preprocessing.image import ImageDataGenerator, img_to_array
from PIL import Image
import skimage.io
train_data = pd.read_csv('train_split_v3.txt', header=None, sep=' ', names=['id','image', 'result', 'type1', 'type2'])
train_data.head()
train_data.count()
train_datagen = ImageDataGenerator(
featurewise_center=False,
featurewise_std_normalization=False,
rotation_range=10,
width_shift_range=0.1,
height_shift_range=0.1,
horizontal_flip=True,
brightness_range=(0.9, 1.1),
zoom_range=(0.85, 1.15),
fill_mode='constant',
cval=0.,
)
# !mkdir augmentation
new_train_data = pd.DataFrame(columns=['id','image', 'result', 'type1', 'type2'])
new_train_data.head()
# +
new_train_data = pd.concat([new_train_data,train_data[train_data['result'] == 'normal'].sample(1700, random_state=4)])
new_train_data = pd.concat([new_train_data,train_data[train_data['result'] == 'pneumonia'].sample(1700, random_state=4)])
new_train_data = pd.concat([new_train_data,train_data[train_data['result'] == 'COVID-19']])
new_train_data.head()
# +
import skimage.color
total_augmented = 0
for index, row in train_data[train_data['result'] == 'COVID-19'].iterrows():
img = plt.imread("train/" + row['image'])
img = skimage.color.gray2rgb(img)
img = np.expand_dims(img,axis=0)
i = 0
for batch in train_datagen.flow(img, batch_size=1):
i += 1
if (i % 7) == 0:
break
name = 'agm-' + str(index) +"-"+ str(i) + ".jpg"
new_train_data = new_train_data.append({
"image": name,
"result": "COVID-19"
}, ignore_index = True)
cv2.imwrite("augmentation/" + name, batch[0])
total_augmented += 1
print(total_augmented)
# -
import seaborn as sns
sns.set_style('whitegrid')
plt.figure()
plt.subplots(figsize=(10,5))
grafico=sns.barplot(x=['Treino-Normal','Treino-Pneumonia','Treino-Covid'],
y=[new_train_data[new_train_data['result'] == 'normal'].shape[0],
new_train_data[new_train_data['result'] == 'pneumonia'].shape[0],
new_train_data[new_train_data['result'] == 'COVID-19'].shape[0],
])
grafico.set_title('Data Set')
plt.show()
new_train_data.to_csv("train_split_v3_augmented.csv")
# !mv augmentation/* train/
# !rm augmentation
train_data_augmented = pd.read_csv('train_split_v3_augmented.csv', header=None, sep=',', names=['id','image', 'result', 'type1', 'type2'], na_values='')
train_data_augmented.count()
|
dataset/data_augmentation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CONVERGENCE ANALYSIS
# +
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import scipy.linalg as sl
# the following allows us to plot triangles indicating convergence order
from mpltools import annotation
# font sizes for plots
plt.rcParams['font.size'] = 12
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.sans-serif'] = ['Arial', 'Dejavu Sans']
# -
# ## Comparisons between centres of mass
#
# The aim of this analysis is to compare different variables related to the centre of mass (excluding boundaries particles) when:
# - the resolution changes (i.e. $\Delta x$ changes);
# - the number of elements in the domain changes, keeping the resolution at the same level.
#
# Every simulation was run until $t=3$ and all the measurements were done at that time. The comparison is done with measurements from a "relatively" fine resolution with $\Delta x = 0.05$.
# ### Changes in dx
# ### Position
#
# From the graph below we can see that the length of the position vector from $(0,0)$ to the centre of mass converges with approximately a second order when decreasing $\Delta x$. The same happens for the two components of $x$.
# +
dx = [1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
x0 = [0.4497, 0.2225, 0.5897, 0.4752, 0.2882, 0.195, 0.01, 0.0657, 0.0337, 0.0131]
x1 = [0.2442, 0.257574, 0.09967, 0.133539, 0.180445, 0.08253, 0.00445, 0.00496, 0.00406, 0.00927]
position = [0.46934259, 0.243844642, 0.596482501, 0.485520467, 0.303228784, 0.201874103, 0.000430195, 0.064909365, 0.033934468, 0.01393603]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, x0, 'r.', label='x[0]')
ax1.loglog(dx, x1, 'b.', label='x[1]')
ax1.loglog(dx, position, 'k.', label='position')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to position at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $x$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((2e-1, 5e-3), (2, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_x0 = np.polyfit(np.log(dx[start_fit:]), np.log(x0[start_fit:]), 1)
line_fit_x1 = np.polyfit(np.log(dx[start_fit:]), np.log(x1[start_fit:]), 1)
line_fit_position = np.polyfit(np.log(dx[start_fit:]), np.log(position[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_x0[1]) * dx**(line_fit_x0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_x0[0]))
ax1.loglog(dx, np.exp(line_fit_x1[1]) * dx**(line_fit_x1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_x1[0]))
ax1.loglog(dx, np.exp(line_fit_position[1]) * dx**(line_fit_position[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_position[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Velocity and acceleration
#
# For velocity and acceleration, the convergence analysis does not lead to interesting results. This could be because changes in $\Delta x$ cause changes in the number of particles and therefore a measurement of velocity or acceleration can be randomly closer or not to the finer case. We can however notice that the $y$ component of the velocity seems to improve when increasing the resolution.
# +
dx = [1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
v0 = [0.276369, 0.01603, 0.436959, 0.338715, 0.064444, 0.091879, 0.015315, 0.141082, 0.102803, 0.05358]
v1 = [0.0862017, 0.1729332, 0.1248471, 0.0471538, 0.0965404, 0.0515041, 0.0306607, 0.0070812, 0.0696404, 0.0020615]
velocity = [0.275489869, 0.006787895, 0.429864508, 0.33276521, 0.063371339, 0.092679886, 0.013367576, 0.140504296, 0.10312033, 0.053618518]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, v0, 'r.', label='v[0]')
ax1.loglog(dx, v1, 'b.', label='v[1]')
ax1.loglog(dx, velocity, 'k.', label='velocity')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to velocity at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $v$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((2e-1, 5e-3), (1.5, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_v0 = np.polyfit(np.log(dx[start_fit:]), np.log(v0[start_fit:]), 1)
line_fit_v1 = np.polyfit(np.log(dx[start_fit:]), np.log(v1[start_fit:]), 1)
line_fit_velocity = np.polyfit(np.log(dx[start_fit:]), np.log(velocity[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_v0[1]) * dx**(line_fit_v0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_v0[0]))
ax1.loglog(dx, np.exp(line_fit_v1[1]) * dx**(line_fit_v1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_v1[0]))
ax1.loglog(dx, np.exp(line_fit_velocity[1]) * dx**(line_fit_velocity[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_velocity[0]))
ax1.legend(loc='best', fontsize=14)
# +
dx = [1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
a0 = [0.245874, 0.215933, 0.36783, 0.428153, 0.146128, 0.159833, 0.739793, 0.908353, 0.459523, 0.524283]
a1 = [0.416635, 1.816766, 0.03389, 1.593741, 0.725285, 1.36068, 1.149667, 0.05062, 1.070852, 0.16]
acceleration = [0.483166702, 0.389549087, 0.133801741, 1.062612357, 0.407893651, 0.555520054, 0.032336635, 0.660885506, 0.233783347, 0.229686248]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, a0, 'r.', label='a[0]')
ax1.loglog(dx, a1, 'b.', label='a[1]')
ax1.loglog(dx, acceleration, 'k.', label='acceleration')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to acceleration at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $a$ at $t=3$', fontsize=16)
ax1.grid(True)
#annotation.slope_marker((2e-1, 5e-3), (1.5, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_a0 = np.polyfit(np.log(dx[start_fit:]), np.log(a0[start_fit:]), 1)
line_fit_a1 = np.polyfit(np.log(dx[start_fit:]), np.log(a1[start_fit:]), 1)
line_fit_acceleration = np.polyfit(np.log(dx[start_fit:]), np.log(acceleration[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_a0[1]) * dx**(line_fit_a0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_a0[0]))
ax1.loglog(dx, np.exp(line_fit_a1[1]) * dx**(line_fit_a1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_a1[0]))
ax1.loglog(dx, np.exp(line_fit_acceleration[1]) * dx**(line_fit_acceleration[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_acceleration[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Density (rho) and drho
#
# For this two values the analysis is even worse in terms of results. Since the density is a value related only to the particles, the way we did the analysis was with the values of $rho$ and $drho$ of the closest particle to the center of mass. Of course this measumerent is completely random and does not follow any trend.
# +
dx = [1, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, 0.3, 0.2, 0.1]
rho = [3.64, 4.9, 21.02, 3.11, 6.02, 5.82, 9.24, 2.65, 8.1, 1.11]
drho = [469.8297, 195.6897, 8.0904, 116.0933, 318.0127, 130.8603, 78.2069, 134.5273, 37.9913, 384.2097]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, rho, 'r.', label='rho')
ax1.loglog(dx, drho, 'b.', label='drho')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to density at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $rho$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((2e-1, 2), (0.5, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_rho = np.polyfit(np.log(dx[start_fit:]), np.log(rho[start_fit:]), 1)
line_fit_drho = np.polyfit(np.log(dx[start_fit:]), np.log(drho[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_rho[1]) * dx**(line_fit_rho[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_rho[0]))
ax1.loglog(dx, np.exp(line_fit_drho[1]) * dx**(line_fit_drho[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_drho[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Changes in the number of elements (dx = 0.6)
#
# For this analysis, it seems we are having more interesting results. The position vector and the $x$ value of the center of mass seems to be more accurate for bigger numbers of elements. But all the other measurements, especially for values in the $y$ directions, converge with high orders for domains with less particles. This behaviour can be related to the fact that, when there are lots of particles, with a "not fine" resolution it is harder to produce an accurate result. The smaller the number of particles, the smaller the number of interactions between them. Therefore, with less elements, the simulation is more accurate.
# ### Position
#
# The position analysis is the only one that does not respect this behaviour. The $x$ value and the position vector of the center of mass converge with a higher number of elements. However, the $y$ value has a completely different behaviour, which reflects all the measurements for other variables related to the center of mass.
# +
dx = [387, 419, 480, 539, 575, 639, 697]
x0 = [0.4009, 0.2545, 0.2352, 0.2481, 0.2959, 0.2174, 0.0209]
x1 = [0.000249, 0.176385, 0.11097, 0.01577, 0.27626, 0.04232, 0.21353]
position = [0.400189592, 0.269294316, 0.247663012, 0.247052207, 0.34636264, 0.221084966, 0.082232739]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, x0, 'r.', label='x[0]')
ax1.loglog(dx, x1, 'b.', label='x[1]')
ax1.loglog(dx, position, 'k.', label='position')
ax1.set_xlabel('Number of elements', fontsize=14)
ax1.set_ylabel('Error related to position at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $x$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((5e2, 6e-1), (-2, 1), ax=ax1, size_frac=0.25, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_x0 = np.polyfit(np.log(dx[start_fit:]), np.log(x0[start_fit:]), 1)
line_fit_x1 = np.polyfit(np.log(dx[start_fit:]), np.log(x1[start_fit:]), 1)
line_fit_position = np.polyfit(np.log(dx[start_fit:]), np.log(position[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_x0[1]) * dx**(line_fit_x0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_x0[0]))
ax1.loglog(dx, np.exp(line_fit_x1[1]) * dx**(line_fit_x1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_x1[0]))
ax1.loglog(dx, np.exp(line_fit_position[1]) * dx**(line_fit_position[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_position[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Velocity
#
# For the velocity, both the two components and the velocity vector converge for smaller numbers of elements. However, the $y$ component clearly converges with a way higher order than the other two.
# +
dx = [387, 419, 480, 539, 575, 639, 697]
v0 = [0.24559, 0.038359, 0.052394, 0.074917, 0.1757096, 0.428153, 0.147971]
v1 = [0.0201271, 0.0269, 0.1043279, 0.1070289, 0.563881, 0.3846309, 0.653112]
velocity = [0.244942529, 0.039748991, 0.05397344, 0.119235645, 0.179506958, 0.141367929, 0.246827728]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, v0, 'r.', label='v[0]')
ax1.loglog(dx, v1, 'b.', label='v[1]')
ax1.loglog(dx, velocity, 'k.', label='velocity')
ax1.set_xlabel('Number of elements', fontsize=14)
ax1.set_ylabel('Error related to velocity at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $v$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((5e2, 6e-2), (1.5, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_v0 = np.polyfit(np.log(dx[start_fit:]), np.log(v0[start_fit:]), 1)
line_fit_v1 = np.polyfit(np.log(dx[start_fit:]), np.log(v1[start_fit:]), 1)
line_fit_velocity = np.polyfit(np.log(dx[start_fit:]), np.log(velocity[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_v0[1]) * dx**(line_fit_v0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_v0[0]))
ax1.loglog(dx, np.exp(line_fit_v1[1]) * dx**(line_fit_v1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_v1[0]))
ax1.loglog(dx, np.exp(line_fit_velocity[1]) * dx**(line_fit_velocity[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_velocity[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Acceleration
#
# For the acceleration we have a more homogeneous behaviour for the three variables measured. The order of convergence for the two acceleration components is near to $4$, while the acceleration position has an order a little bit higher than $2$.
# +
dx = [387, 419, 480, 539, 575, 639, 697]
a0 = [0.138904, 0.313395, 0.049519, 0.297072, 1.062487, 0.3812327, 2.38971]
a1 = [0.990654, 0.345567, 0.516946, 1.226236, 2.61143, 5.2834, 2.816911]
acceleration = [0.362030312, 0.174110304, 0.397105949, 0.831850431, 0.38179608, 0.464608143, 1.648051311]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, a0, 'r.', label='a[0]')
ax1.loglog(dx, a1, 'b.', label='a[1]')
ax1.loglog(dx, acceleration, 'k.', label='acceleration')
ax1.set_xlabel('Number of elements', fontsize=14)
ax1.set_ylabel('Error related to acceleration at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $a$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((4e2, 2.3e-1), (2, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_a0 = np.polyfit(np.log(dx[start_fit:]), np.log(a0[start_fit:]), 1)
line_fit_a1 = np.polyfit(np.log(dx[start_fit:]), np.log(a1[start_fit:]), 1)
line_fit_acceleration = np.polyfit(np.log(dx[start_fit:]), np.log(acceleration[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_a0[1]) * dx**(line_fit_a0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_a0[0]))
ax1.loglog(dx, np.exp(line_fit_a1[1]) * dx**(line_fit_a1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_a1[0]))
ax1.loglog(dx, np.exp(line_fit_acceleration[1]) * dx**(line_fit_acceleration[0]), 'k-',
label = 'slope: {:.2f}'.format(line_fit_acceleration[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Density (rho) and drho
#
# Both $rho$ and $drho$ convergence almost with a 5th-order.
# +
dx = [387, 419, 480, 539, 575, 639, 697]
rho = [4.85, 2.08, 4.05, 18.22, 42.57, 41.68, 18.82]
drho = [0.39452, 356.004, 216.818, 245.8217, 372.846, 176.7835, 77.9899]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, rho, 'r.', label='rho')
ax1.loglog(dx, drho, 'b.', label='drho')
ax1.set_xlabel('Number of elements', fontsize=14)
ax1.set_ylabel('Error related to density at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $rho$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((5e2, 2), (5, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_rho = np.polyfit(np.log(dx[start_fit:]), np.log(rho[start_fit:]), 1)
line_fit_drho = np.polyfit(np.log(dx[start_fit:]), np.log(drho[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_rho[1]) * dx**(line_fit_rho[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_rho[0]))
ax1.loglog(dx, np.exp(line_fit_drho[1]) * dx**(line_fit_drho[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_drho[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ## Comparisons between wave peaks
#
# The aim of this analysis is to compare different variables related to the peaks reached when the resolution changes (i.e. $\Delta x$ changes).
#
# Every simulation was run until $t=3$ and all the measurements were done at that time. The comparison is done with measurements from a "relatively" fine resolution with $\Delta x = 0.1$.
# ### Position
#
# Both the $x$ and $y$ value of the peak converge with an almost 2nd-order.
# +
x0_in = 19.610161
x1_in = 4.256377
dx = [1, 0.9, 0.7, 0.6, 0.5]
x0 = [abs(12.795582-x0_in), abs(14.570876-x0_in), abs(17.725793-x0_in), abs(17.725793-x0_in), abs(17.695031-x0_in)]
x1 = [abs(2.886488-x1_in), abs(3.164916-x1_in), abs(3.158486-x1_in), abs(3.158486-x1_in), abs(3.939792-x1_in)]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, x0, 'r.', label='x[0]')
ax1.loglog(dx, x1, 'b.', label='x[1]')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to position at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $x$ at $t=3$', fontsize=16)
ax1.grid(True)
annotation.slope_marker((7e-1, 5e-1), (2, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_x0 = np.polyfit(np.log(dx[start_fit:]), np.log(x0[start_fit:]), 1)
line_fit_x1 = np.polyfit(np.log(dx[start_fit:]), np.log(x1[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_x0[1]) * dx**(line_fit_x0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_x0[0]))
ax1.loglog(dx, np.exp(line_fit_x1[1]) * dx**(line_fit_x1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_x1[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Velocity
#
# Also the $x$ and $y$ components of the velocity converge for a finer resolution. We can however see that the $x$ component does not improve as much as the $y$ component does. As a consequence, improving the resolution does not mean improving a lot the $x$ component of the velocity, but it means to improve a lot the $y$ one (with an order of convergence of almost $4$).
# +
x0_in = 8.441288
x1_in = 1.076729
dx = [1, 0.9, 0.7, 0.6, 0.5]
x0 = [abs(1.070133-x0_in), abs(2.312139-x0_in), abs(0.839408-x0_in), abs(0.839408-x0_in), abs(4.404251-x0_in)]
x1 = [abs(-0.358817-x1_in), abs(0.341137-x1_in), abs(1.004885-x1_in), abs(1.004885-x1_in), abs(0.870988-x1_in)]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, x0, 'r.', label='v[0]')
ax1.loglog(dx, x1, 'b.', label='v[1]')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to velocity at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $v$ at $t=3$', fontsize=16)
ax1.grid(True)
#annotation.slope_marker((7e-1, 5e-1), (2, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_x0 = np.polyfit(np.log(dx[start_fit:]), np.log(x0[start_fit:]), 1)
line_fit_x1 = np.polyfit(np.log(dx[start_fit:]), np.log(x1[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_x0[1]) * dx**(line_fit_x0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_x0[0]))
ax1.loglog(dx, np.exp(line_fit_x1[1]) * dx**(line_fit_x1[0]), 'b-',
label = 'slope: {:.2f}'.format(line_fit_x1[0]))
ax1.legend(loc='best', fontsize=14)
# -
# ### Pressure
#
# The pressure does not change much with a finer resolution. In fact, it even worsens, even if just of a relatively really small amount.
# +
x0_in = 48218.884551
dx = [1, 0.9, 0.7, 0.6, 0.5]
x0 = [abs(14622.275473-x0_in), abs(13870.593406-x0_in), abs(13469.845871-x0_in), abs(13469.845871-x0_in), abs(12521.149787-x0_in)]
fig, ax1 = plt.subplots(1, 1, figsize=(8, 5))
ax1.loglog(dx, x0, 'r.', label='P')
ax1.set_xlabel('$\Delta x$', fontsize=14)
ax1.set_ylabel('Error related to pressure at $t=3$', fontsize=14)
ax1.set_title('Convergence plot for $P$ at $t=3$', fontsize=16)
ax1.grid(True)
#annotation.slope_marker((7e-1, 5e-1), (2, 1), ax=ax1, size_frac=0.23, pad_frac=0.05)
# find best fit linear line to data
start_fit = 0
line_fit_x0 = np.polyfit(np.log(dx[start_fit:]), np.log(x0[start_fit:]), 1)
ax1.loglog(dx, np.exp(line_fit_x0[1]) * dx**(line_fit_x0[0]), 'r-',
label = 'slope: {:.2f}'.format(line_fit_x0[0]))
ax1.legend(loc='best', fontsize=14)
|
Convergence_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={} colab_type="code" id="t64eBMZW1_S5"
pip install category_encoders
# + colab={"base_uri": "https://localhost:8080/", "height": 80} colab_type="code" id="34hh7YYS0G00" outputId="2af10035-5e7f-4591-b730-8bb3f331c1d0"
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn.model_selection import ShuffleSplit
from sklearn.metrics import accuracy_score
from keras.layers import Dense
from keras.models import Sequential
from keras.optimizers import SGD
from matplotlib import pyplot as plt
import matplotlib as mpl
import seaborn as sns
import numpy as np
import pandas as pd
import category_encoders as ce
import os
import pickle
import gc
from tqdm import tqdm
import pickle
from sklearn.svm import SVR
from sklearn.linear_model import LinearRegression
from sklearn import linear_model
from sklearn.neighbors import KNeighborsRegressor
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import ExtraTreesRegressor, GradientBoostingRegressor
from sklearn import ensemble
import xgboost as xgb
# + colab={"base_uri": "https://localhost:8080/", "height": 54} colab_type="code" id="05WtQIF90z9M" outputId="a57a9568-581b-4477-efb8-160ca18b3207"
from google.colab import drive
drive.mount('/content/drive')
# + colab={} colab_type="code" id="sVsYosjT0G1A"
def encode_text_features(encode_decode, data_frame, encoder_isa=None, encoder_mem_type=None):
# Implement Categorical OneHot encoding for ISA and mem-type
if encode_decode == 'encode':
encoder_isa = ce.one_hot.OneHotEncoder(cols=['isa'])
encoder_mem_type = ce.one_hot.OneHotEncoder(cols=['mem-type'])
encoder_isa.fit(data_frame, verbose=1)
df_new1 = encoder_isa.transform(data_frame)
encoder_mem_type.fit(df_new1, verbose=1)
df_new = encoder_mem_type.transform(df_new1)
encoded_data_frame = df_new
else:
df_new1 = encoder_isa.transform(data_frame)
df_new = encoder_mem_type.transform(df_new1)
encoded_data_frame = df_new
return encoded_data_frame, encoder_isa, encoder_mem_type
# + colab={} colab_type="code" id="HwxxEzWA0G1G"
def absolute_percentage_error(Y_test, Y_pred):
error = 0
for i in range(len(Y_test)):
if(Y_test[i]!= 0 ):
error = error + (abs(Y_test[i] - Y_pred[i]))/Y_test[i]
error = error/ len(Y_test)
return error[0]
# + colab={} colab_type="code" id="_QOjg3qU1eo8"
def return_best_param(model, grid, X_train, Y_train):
grid = GridSearchCV(model, grid, refit = True, verbose = 0)
# fitting the model for grid search
tqdm(grid.fit(X_train, Y_train))
print('Found Best Parameters for this model', model)
# print how our model looks after hyper-parameter tuning
return (grid.best_estimator_)
# + [markdown] colab_type="text" id="Edkj6tmx0G1M"
# # Dataset 1 :SHA
# + colab={} colab_type="code" id="npQlrKff0G1O"
def process_all_sha(dataset_path, dataset_name,dataset_name_n,path_for_saving_data):
################## Data Preprocessing ######################
df = pd.read_csv(dataset_path + dataset_name + '.csv')
dfn = pd.read_csv(dataset_path + dataset_name_n + '.csv')
encoded_data_frame, encoder_isa, encoder_mem_type = encode_text_features('encode', df
, encoder_isa = None, encoder_mem_type=None)
encoded_data_frame_n, encoder_isa_n, encoder_mem_type_n = encode_text_features('encode', dfn
, encoder_isa = None, encoder_mem_type=None)
total_data_n = encoded_data_frame_n.drop(columns = ['arch','bus_speed','mem-type_1','mem-type_2','isa_1'])
total_data = encoded_data_frame.drop(columns = ['arch','mem-type_1','mem-type_2','mem-type_3','mem-type_4','isa_1', 'isa_2'])
print(total_data.columns, total_data_n.columns, len(total_data.columns), len(total_data_n.columns))
total_data = total_data.fillna(0)
total_data_n = total_data_n.fillna(0)
X_sim = total_data.drop(columns = ['runtime']).to_numpy()
Y_sim = total_data['runtime'].to_numpy()
X_phy = total_data_n.drop(columns = ['runtime']).to_numpy()
Y_phy = total_data_n['runtime'].to_numpy()
print(X_sim.shape, X_phy.shape, Y_sim.shape, Y_phy.shape)
# Separating Physical data to 10% and 90%
X_train_phy, X_test_phy, Y_train_phy, Y_test_phy = train_test_split(X_phy, Y_phy, test_size = 0.90, random_state = 0)
print(X_train_phy.shape, X_test_phy.shape, Y_train_phy.shape, Y_test_phy.shape)
X_train_sim = np.append(X_sim, X_train_phy,axis = 0)
Y_train_sim = np.append(Y_sim, Y_train_phy,axis = 0)
print(X_train_sim.shape, Y_train_sim.shape, X_test_phy.shape, Y_test_phy.shape)
X_train = X_train_sim
X_test = X_test_phy
Y_train = Y_train_sim
Y_test = Y_test_phy
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
scaler_x = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_x.fit_transform(X_train)
X_test = scaler_x.fit_transform(X_test)
Y_train = np.reshape(Y_train, (len(Y_train),1))
Y_test = np.reshape(Y_test, (len(Y_test),1))
Y_train = scaler_y.fit_transform(Y_train)
Y_test = scaler_y.fit_transform(Y_test)
################## Data Preprocessing ######################
# Put best models here using grid search
# 1. SVR
param_grid_svr = {'C': [0.1, 1, 10, 100, 1000],
# Regularization parameter. The strength of the regularization is inversely proportional to C.
# Must be strictly positive. The penalty is a squared l2 penalty.
'gamma': [1, 0.1, 0.01, 0.001, 0.0001],
# Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
# if gamma='scale' (default) is passed then it uses 1 / (n_features * X.var()) as value of gamma,
# if ‘auto’, uses 1 / n_features.
'kernel': ['rbf']}
model_svr = SVR()
best_svr = return_best_param(model_svr, param_grid_svr, X_train, Y_train)
# 2. LR
param_grid_lr = {'fit_intercept': [True, False],
'normalize' : [True, False],
}
model_lr = LinearRegression()
best_lr = return_best_param(model_lr, param_grid_lr, X_train, Y_train)
# 3. RR
param_grid_rr = {'alpha': [0.1, 1, 10, 100, 1000],
'fit_intercept' : [True, False],
'normalize' :[True, False],
'solver' : ['auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga'],
}
model_rr = linear_model.Ridge()
best_rr = return_best_param(model_rr, param_grid_rr, X_train, Y_train)
# 4. KNN
param_grid_knn = {'n_neighbors': [2, 3, 4, 5, 6, 7, 9, 10, 13, 15],
'weights' : ['uniform', 'distance'],
'p' : [1, 2, 4, 5, 7 ,10]
}
model_knn = KNeighborsRegressor()
best_knn = return_best_param(model_knn, param_grid_knn, X_train, Y_train)
# 5. GPR
param_grid_gpr = {'alpha': [1e-10, 1e-9, 1e-5, 1e-2],
'normalize_y' : [True, False],
}
model_gpr = GaussianProcessRegressor()
best_gpr = return_best_param(model_gpr, param_grid_gpr, X_train, Y_train)
# 6. Decision Tree
param_grid_dt = {'criterion': ['mse','friedman_mse', 'mae'],
'splitter' : ['best', 'random'],
'max_depth': [2,3,4,5,7,9,10,15,20,30 ],
'min_samples_leaf' : [1, 2,3, 4, 5,6, 7],
'max_features' : ['auto', 'sqrt', 'log2'],
}
model_dt = DecisionTreeRegressor()
best_dt = DecisionTreeRegressor(criterion='friedman_mse', max_depth=30,
max_features='log2', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=2, min_samples_split=2,
min_weight_fraction_leaf=0.0, presort=False,
random_state=None, splitter='best')
# return_best_param(model_dt, param_grid_dt, X_train, Y_train)
# 7. Random Forest
param_grid_rf = {'n_estimators' : [10, 50, 100, 200],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'warm_start': ['True', 'False'],
}
model_rf = RandomForestRegressor()
best_rf = RandomForestRegressor(bootstrap=True, criterion='mae', max_depth=3,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=50,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start='False')
# return_best_param(model_rf, param_grid_rf, X_train, Y_train)
# 8. Extra Trees Regressor
param_grid_etr = {'n_estimators' : [10, 50, 100, 200],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'warm_start': ['True', 'False']
}
model_etr = ExtraTreesRegressor()
best_etr = ExtraTreesRegressor(bootstrap=False, criterion='friedman_mse', max_depth=3,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=200, n_jobs=None,
oob_score=False, random_state=42, verbose=0,
warm_start='True')
# return_best_param(model_etr, param_grid_etr, X_train, Y_train)
# 9. GBR
param_grid_gbr = {'n_estimators' : [10, 20, 50, 100],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'loss' : ['ls', 'lad', 'huber', 'quantile'],
}
model_gbr = GradientBoostingRegressor()
best_gbr = ensemble.GradientBoostingRegressor(alpha=0.9, criterion='mse', init=None,
learning_rate=0.1, loss='lad', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=50,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
# return_best_param(model_gbr, param_grid_gbr, X_train, Y_train)
# 10. XGB
param_grid_xgb = {'n_estimators' : [10, 20, 50, 100],
'max_depth': [3,4,5,7,10,15],
'learning_rate' : [0.1, 0.5, 0.01, 0.001, 0.0001]
}
model_xgb = xgb.XGBRegressor()
best_xgb = xgb.XGBRegressor(alpha=10, base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=0.3, gamma=0,
importance_type='gain', learning_rate=0.1, max_delta_step=0,
max_depth=3, min_child_weight=1, missing=None, n_estimators=50,
n_jobs=1, nthread=None, objective='reg:linear', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, validate_parameters=False, verbosity=1)
# return_best_param(model_xgb, param_grid_xgb, X_train, Y_train)
best_models = [best_svr, best_lr, best_rr, best_knn, best_gpr, best_dt, best_rf, best_etr, best_gbr, best_xgb]
best_models_name = ['best_svr', 'best_lr', 'best_rr', 'best_knn', 'best_gpr', 'best_dt', 'best_rf', 'best_etr'
, 'best_gbr', 'best_xgb']
k = 0
df = pd.DataFrame(columns = ['model_name', 'dataset_name', 'r2', 'mape'])
for model in best_models:
model_orig = model
print('Running model number:', k+1, 'with Model Name: ', best_models_name[k])
r2_scores = []
mape_scores = []
fold = 1
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
model_orig.fit(X_train, Y_train)
Y_pred_fold = model_orig.predict(X_test)
Y_test_fold = scaler_y.inverse_transform(Y_test)
Y_pred_fold = scaler_y.inverse_transform(Y_pred_fold)
# print('Accuracy =',accuracy_score(Y_test, Y_pred))
r2_scores.append(r2_score(Y_test_fold, Y_pred_fold))
mape_scores.append(absolute_percentage_error(Y_test_fold, Y_pred_fold))
df = df.append({'model_name': best_models_name[k], 'dataset_name': dataset_name
, 'r2': r2_scores[0], 'mape': mape_scores[0],}, ignore_index=True)
k = k + 1
print(df.head())
df.to_csv('result_transfer_Sim_to_Phy_sha_10' + '.csv')
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="eV5noIsE0G1U" outputId="ae8e09a0-e954-4f79-b279-48460b5f7c85"
dataset_name_n = 'sha_physical'
dataset_name = 'sha_simulated'
dataset_path = '\\Dataset_CSV\\all_datasets\\'
path_for_saving_data = '\\Saved_Models_Data\\TL'
process_all_sha(dataset_path, dataset_name, dataset_name_n, path_for_saving_data)
# -
# # Dataset 2: Dijkstra
# + colab={} colab_type="code" id="nZqqCifDONLp"
def process_all_dijkstra(dataset_path, dataset_name,dataset_name_n,path_for_saving_data):
################## Data Preprocessing ######################
df = pd.read_csv(dataset_path + dataset_name + '.csv')
dfn = pd.read_csv(dataset_path + dataset_name_n + '.csv')
encoded_data_frame, encoder_isa, encoder_mem_type = encode_text_features('encode', df
, encoder_isa = None, encoder_mem_type=None)
encoded_data_frame_n, encoder_isa_n, encoder_mem_type_n = encode_text_features('encode', dfn
, encoder_isa = None, encoder_mem_type=None)
total_data_n = encoded_data_frame_n.drop(columns = ['arch','bus_speed','mem-type_1','mem-type_2','isa_1'])
total_data = encoded_data_frame.drop(columns = ['arch','mem-type_1','mem-type_2','mem-type_3','mem-type_4','isa_1', 'isa_2'])
print(total_data.columns, total_data_n.columns, len(total_data.columns), len(total_data_n.columns))
total_data = total_data.fillna(0)
total_data_n = total_data_n.fillna(0)
X_sim = total_data.drop(columns = ['runtime']).to_numpy()
Y_sim = total_data['runtime'].to_numpy()
X_phy = total_data_n.drop(columns = ['runtime']).to_numpy()
Y_phy = total_data_n['runtime'].to_numpy()
print(X_sim.shape, X_phy.shape, Y_sim.shape, Y_phy.shape)
# Separating Physical data to 10% and 90%
X_train_phy, X_test_phy, Y_train_phy, Y_test_phy = train_test_split(X_phy, Y_phy, test_size = 0.90, random_state = 0)
print(X_train_phy.shape, X_test_phy.shape, Y_train_phy.shape, Y_test_phy.shape)
X_train_sim = np.append(X_sim, X_train_phy,axis = 0)
Y_train_sim = np.append(Y_sim, Y_train_phy,axis = 0)
print(X_train_sim.shape, Y_train_sim.shape, X_test_phy.shape, Y_test_phy.shape)
X_train = X_train_sim
X_test = X_test_phy
Y_train = Y_train_sim
Y_test = Y_test_phy
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
scaler_x = StandardScaler()
scaler_y = StandardScaler()
X_train = scaler_x.fit_transform(X_train)
X_test = scaler_x.fit_transform(X_test)
Y_train = np.reshape(Y_train, (len(Y_train),1))
Y_test = np.reshape(Y_test, (len(Y_test),1))
Y_train = scaler_y.fit_transform(Y_train)
Y_test = scaler_y.fit_transform(Y_test)
################## Data Preprocessing ######################
# Put best models here using grid search
# 1. SVR
param_grid_svr = {'C': [0.1, 1, 10, 100, 1000],
# Regularization parameter. The strength of the regularization is inversely proportional to C.
# Must be strictly positive. The penalty is a squared l2 penalty.
'gamma': [1, 0.1, 0.01, 0.001, 0.0001],
# Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
# if gamma='scale' (default) is passed then it uses 1 / (n_features * X.var()) as value of gamma,
# if ‘auto’, uses 1 / n_features.
'kernel': ['rbf']}
model_svr = SVR()
best_svr = return_best_param(model_svr, param_grid_svr, X_train, Y_train)
# 2. LR
param_grid_lr = {'fit_intercept': [True, False],
'normalize' : [True, False],
}
model_lr = LinearRegression()
best_lr = return_best_param(model_lr, param_grid_lr, X_train, Y_train)
# 3. RR
param_grid_rr = {'alpha': [0.1, 1, 10, 100, 1000],
'fit_intercept' : [True, False],
'normalize' :[True, False],
'solver' : ['auto', 'svd', 'cholesky', 'lsqr', 'sparse_cg', 'sag', 'saga'],
}
model_rr = linear_model.Ridge()
best_rr = return_best_param(model_rr, param_grid_rr, X_train, Y_train)
# 4. KNN
param_grid_knn = {'n_neighbors': [2, 3, 4, 5, 6, 7, 9, 10, 13, 15],
'weights' : ['uniform', 'distance'],
'p' : [1, 2, 4, 5, 7 ,10]
}
model_knn = KNeighborsRegressor()
best_knn = return_best_param(model_knn, param_grid_knn, X_train, Y_train)
# 5. GPR
param_grid_gpr = {'alpha': [1e-10, 1e-9, 1e-5, 1e-2],
'normalize_y' : [True, False],
}
model_gpr = GaussianProcessRegressor()
best_gpr = return_best_param(model_gpr, param_grid_gpr, X_train, Y_train)
# 6. Decision Tree
param_grid_dt = {'criterion': ['mse','friedman_mse', 'mae'],
'splitter' : ['best', 'random'],
'max_depth': [2,3,4,5,7,9,10,15,20,30 ],
'min_samples_leaf' : [1, 2,3, 4, 5,6, 7],
'max_features' : ['auto', 'sqrt', 'log2'],
}
model_dt = DecisionTreeRegressor()
best_dt = DecisionTreeRegressor(criterion='mae', max_depth=20, max_features='auto',
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=6,
min_samples_split=2, min_weight_fraction_leaf=0.0,
presort=False, random_state=None, splitter='best')
# return_best_param(model_dt, param_grid_dt, X_train, Y_train)
# 7. Random Forest
param_grid_rf = {'n_estimators' : [10, 50, 100, 200],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'warm_start': ['True', 'False'],
}
model_rf = RandomForestRegressor()
best_rf = RandomForestRegressor(bootstrap=True, criterion='mae', max_depth=None,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=10,
n_jobs=None, oob_score=False, random_state=None,
verbose=0, warm_start='True')
# return_best_param(model_rf, param_grid_rf, X_train, Y_train)
# 8. Extra Trees Regressor
param_grid_etr = {'n_estimators' : [10, 50, 100, 200],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'warm_start': ['True', 'False']
}
model_etr = ExtraTreesRegressor()
best_etr = ExtraTreesRegressor(bootstrap=False, criterion='mae', max_depth=10,
max_features='auto', max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=50, n_jobs=None,
oob_score=False, random_state=42, verbose=0,
warm_start='True')
# return_best_param(model_etr, param_grid_etr, X_train, Y_train)
# 9. GBR
param_grid_gbr = {'n_estimators' : [10, 20, 50, 100],
'criterion': ['mse','friedman_mse', 'mae'],
'max_depth': [3,4,5,7,10,15, None ],
'loss' : ['ls', 'lad', 'huber', 'quantile'],
}
model_gbr = GradientBoostingRegressor()
best_gbr = ensemble.GradientBoostingRegressor(alpha=0.9, criterion='mse', init=None,
learning_rate=0.1, loss='lad', max_depth=3,
max_features=None, max_leaf_nodes=None,
min_impurity_decrease=0.0, min_impurity_split=None,
min_samples_leaf=1, min_samples_split=2,
min_weight_fraction_leaf=0.0, n_estimators=50,
n_iter_no_change=None, presort='auto',
random_state=42, subsample=1.0, tol=0.0001,
validation_fraction=0.1, verbose=0, warm_start=False)
# return_best_param(model_gbr, param_grid_gbr, X_train, Y_train)
# 10. XGB
param_grid_xgb = {'n_estimators' : [10, 20, 50, 100],
'max_depth': [3,4,5,7,10,15],
'learning_rate' : [0.1, 0.5, 0.01, 0.001, 0.0001]
}
model_xgb = xgb.XGBRegressor()
best_xgb = xgb.XGBRegressor(alpha=10, base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=0.3, gamma=0,
importance_type='gain', learning_rate=0.1, max_delta_step=0,
max_depth=3, min_child_weight=1, missing=None, n_estimators=100,
n_jobs=1, nthread=None, objective='reg:linear', random_state=0,
reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
silent=None, subsample=1, validate_parameters=False, verbosity=1)
# return_best_param(model_xgb, param_grid_xgb, X_train, Y_train)
best_models = [best_svr, best_lr, best_rr, best_knn, best_gpr, best_dt, best_rf, best_etr, best_gbr, best_xgb]
best_models_name = ['best_svr', 'best_lr', 'best_rr', 'best_knn', 'best_gpr', 'best_dt', 'best_rf', 'best_etr'
, 'best_gbr', 'best_xgb']
k = 0
df = pd.DataFrame(columns = ['model_name', 'dataset_name', 'r2', 'mape'])
for model in best_models:
model_orig = model
print('Running model number:', k+1, 'with Model Name: ', best_models_name[k])
r2_scores = []
mape_scores = []
fold = 1
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
model_orig.fit(X_train, Y_train)
Y_pred_fold = model_orig.predict(X_test)
Y_test_fold = scaler_y.inverse_transform(Y_test)
Y_pred_fold = scaler_y.inverse_transform(Y_pred_fold)
# print('Accuracy =',accuracy_score(Y_test, Y_pred))
r2_scores.append(r2_score(Y_test_fold, Y_pred_fold))
mape_scores.append(absolute_percentage_error(Y_test_fold, Y_pred_fold))
df = df.append({'model_name': best_models_name[k], 'dataset_name': dataset_name
, 'r2': r2_scores[0], 'mape': mape_scores[0],}, ignore_index=True)
k = k + 1
print(df.head())
df.to_csv('result_transfer_Sim_to_Phy_dijkstra_10' + '.csv')
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="IMZUd1oKOYvR" outputId="8cc3551a-5cab-4265-83c1-bd767e0753d2"
dataset_name_n = 'dijkstra_physical'
dataset_name = 'dijkstra_simulated'
dataset_path = '\\Dataset_CSV\\all_datasets\\'
path_for_saving_data = '\\Saved_Models_Data\\TL'
process_all_dijkstra(dataset_path, dataset_name, dataset_name_n, path_for_saving_data)
# + colab={} colab_type="code" id="SSTkvfRcTArg"
|
Codes/Transfer Learning/Simulated-To-Physical-Cross-System/.ipynb_checkpoints/All_Models_Sim_to_PHY-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <a href="http://landlab.github.io"><img style="float: left" src="../../landlab_header.png"></a>
# # The deAlmeida Overland Flow Component
# <hr>
# <small>For more Landlab tutorials, click here: <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html</a></small>
# <hr>
# This notebook illustrates running the deAlmeida overland flow component in an extremely simple-minded way on a real topography, then shows it creating a flood sequence along an inclined surface with an oscillating water surface at one end.
#
# First, import what we'll need:
from landlab.components.overland_flow import OverlandFlow
from landlab.plot.imshow import imshow_grid
from landlab.plot.colors import water_colormap
from landlab import RasterModelGrid
from landlab.io.esri_ascii import read_esri_ascii
from matplotlib.pyplot import figure
import numpy as np
from time import time
# %matplotlib inline
# Pick the initial and run conditions
run_time = 100 # duration of run, (s)
h_init = 0.1 # initial thin layer of water (m)
n = 0.01 # roughness coefficient, (s/m^(1/3))
g = 9.8 # gravity (m/s^2)
alpha = 0.7 # time-step factor (nondimensional; from Bates et al., 2010)
u = 0.4 # constant velocity (m/s, de Almeida et al., 2012)
run_time_slices = (10, 50, 100)
# Elapsed time starts at 1 second. This prevents errors when setting our boundary conditions.
elapsed_time = 1.0
# Use Landlab methods to import an ARC ascii grid, and load the data into the field that the component needs to look at to get the data. This loads the elevation data, z, into a "field" in the grid itself, defined on the nodes.
rmg, z = read_esri_ascii('Square_TestBasin.asc')
rmg.add_field('topographic__elevation', z, at='node')
rmg.set_closed_boundaries_at_grid_edges(True, True, True, True)
# We can get at this data with this syntax:
np.all(rmg.at_node['topographic__elevation'] == z)
# Note that the boundary conditions for this grid mainly got handled with the final line of those three, but for the sake of completeness, we should probably manually "open" the outlet. We can find and set the outlet like this:
my_outlet_node = 100 # This DEM was generated using Landlab and the outlet node ID was known
rmg.status_at_node[my_outlet_node] = 1 # 1 is the code for fixed value
# Now initialize a couple more grid fields that the component is going to need:
rmg.add_zeros('surface_water__depth', at='node') # water depth (m)
rmg.at_node['surface_water__depth'] += h_init
# Let's look at our watershed topography
imshow_grid(rmg, 'topographic__elevation')
# Now instantiate the component itself
of = OverlandFlow(
rmg, steep_slopes=True
) #for stability in steeper environments, we set the steep_slopes flag to True
# Now we're going to run the loop that drives the component:
while elapsed_time < run_time:
# First, we calculate our time step.
dt = of.calc_time_step()
# Now, we can generate overland flow.
of.overland_flow()
# Increased elapsed time
print('Elapsed time: ', elapsed_time)
elapsed_time += dt
imshow_grid(rmg, 'surface_water__depth', cmap='Blues')
# Now let's get clever, and run a set of time slices:
elapsed_time = 1.
for t in run_time_slices:
while elapsed_time < t:
# First, we calculate our time step.
dt = of.calc_time_step()
# Now, we can generate overland flow.
of.overland_flow()
# Increased elapsed time
elapsed_time += dt
figure(t)
imshow_grid(rmg, 'surface_water__depth', cmap='Blues')
# ### Click here for more <a href="https://landlab.readthedocs.io/en/latest/user_guide/tutorials.html">Landlab tutorials</a>
|
notebooks/tutorials/overland_flow/overland_flow_driver.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Finite differences in 1D
# We approximate the boundary value problem consisting of the following PDE:
# $$
# -u''(x) + u(x) = f(x), \qquad 0 < x < 1.
# $$
# (This is actually an ODE since the unknown is a function of a single real variable $x$.) This equation is supplemented with Dirichlet boundary conditions
# $$
# u(0) = u(1) = 0
# $$
# at both ends.
#
# The purpose of this notebooks is to quickly illustrate the standard finite difference method for solving this, taking the opportunity to also ensure that we are all on the same page regarding the python prerequisites. Let's begin by importing the `numpy` module.
import numpy as np
# ## Approximating the derivative
#
# It is very easy to understand and implement finite differences. The finite difference approximation of $u(x)$ is a finite sequence $u_i$. Each $u_i$ approximates $u(x_i)$ at a point $x_i$ in the interval $[0, 1]$ where we need the solution. The sequence of points $x_i$ may be thought of a grid or mesh of the domain $[0, 1]$.
#
# To approximate the ODE, we need to approximate derivatives using the grid. The **forward difference** approximation of $d u / dx$ is
# $$
# [D_+u]_i = \frac{ u(x_{i+1}) - u(x_i) }{ h}, \qquad
# u'(x_i) \approx [D_+u]_i.
# $$
# The **backward difference** approximation is
# $$
# [D_-u]_i = \frac{ u(x_{i}) - u(x_{i-1}) }{ h}, \qquad
# u'(x_i) \approx [D_+u]_i.
# $$
# Note that by Taylor's theorem, when $u$ is smooth, both approximate the derivative as $x_{i\pm 1} \to x_i$:
# $$
# \frac{d u }{d x}(x_i) \approx [D_+ u]_i, \qquad \frac{d u }{d x}(x_i) \approx [D_- u]_i.
# $$
# In fact, from calculus tools, you immediately see that both the approximations are $O(h)$ where $h$ is the spacing between the points on a uniform grid.
# ## The finite difference system
#
# For approximating the ODE $-u'' +u = f$, we need to approximate the second derivative, not the first. Obviously there are many ways to combine the above two differences to get an approximation to $u''$,
# $$
# \frac{d }{dx} \frac{d u}{d x} (x_i) \approx [D_\pm D_\pm u]_i.
# $$
# Depending on the choice in $\pm$, we have four possible approximations.
#
# However, some are $O(h^2)$ accurate, while others are only $O(h)$-accurate. (Which?)
#
# The **Central Difference Formula** for approximating the second derivative is
# $$
# \frac{d }{dx} \frac{d u}{d x} (x_i) \approx [D_+D_- u]_i \equiv [D_-D_+ u]_i,
# $$
# which can be alternately written on a uniform grid of mesh size $h$ as
# $$
# \begin{aligned}
# u''(x)
# &
# \approx { u'(x+h/2) - u'(x-h/2) \over h }
# \\
# & \approx { \left(\frac{u(x+h/2+h/2) - u(x+h/2-h/2)}{h}\right) - \left(\frac{u(x-h/2) - u(x-h/2-h/2)}{h} \right)\over h }
# \\
# & \approx {u(x+h) - 2 u(x) + u(x-h)\over h^2}.
# \end{aligned}
# $$
# ## Implementing the finite difference system
#
#
# The **matrix** of the *central second finite difference* operator on a grid of *just* 5 equally spaced points, two of which have zero boundary conditions, can be "made by hand" as a `numpy` array, as follows (save for a factor of $-1/h^2$).
A = np.array([[ 2, -1, 0],
[-1, 2, -1],
[ 0, -1, 2]])
A
# For large number of grid points, we need an automatic way to make this matrix. Numpy provides many ways to create matrices quickly. For example, the `diag` command generates matrices with input entries in the diagonal, superdiagonals, or subdiagonals.
N = 10
2 * np.diag(np.ones(N))
A = 2 * np.diag(np.ones(N)) + \
np.diag(-np.ones(N-1), -1) + \
np.diag(-np.ones(N-1), 1)
A
# This `A` when multiplied by a vector of values of $u/h^2$ gives approximate values of $-u''$. Using this we can approximate the left hand side of the PDE $-u'' + u = f$, as done next.
# ## Solving the difference equation system
#
#
# Adding values of $u$ to the discretization of $-u''$ we obtain the left hand side of the finite difference system. The right hand side just consists of a vector values of $f$ at the grid points.
#
# We solve the finite difference equations using the built-in inverse routine in numpy's `linalg` submodule. (Note the definition of a python function and how we use `@` for numpy's matrix multiplication.)
def solve(f, h):
size = len(f)
A = (1/h**2) * (2 * np.diag(np.ones(size)) + \
np.diag(-np.ones(size-1), -1) +
np.diag(-np.ones(size-1), 1)) + np.eye(size)
return np.linalg.inv(A) @ f
# Now you have an approximate solution to the boundary value problem in the returned vector. Is it any good?
# ## Check for correctness
# **Verification** is a key step while designing and implementing numerical methods.
#
# We will verify that the `solve` function is solving as expected by the **method of manufactured solutions**, which is just a fancy name for the following simple idea: pick your favorite smooth function $u$ satisfying the boundary conditions, then generate the right hand side $f$ that would give your $u$ as the exact solution by applying the differential operator to $u$.
#
# In the check below, I will use
# $$
# u = \sin(x)
# $$
# on an interval $(0, 3\pi)$ so that the zero boundary conditions hold. Then put $f = -u'' + u = 2\sin(x)$. Let's provide this $f$ to `solve` and see whether it outputs an approximation to $u = \sin(x)$.
# An equally spaced grid in an interval is easily made using the `linspace` facility.
np.linspace(0, 3*np.pi, num=10)
# Let's "manufacture" the data $f$ for the manufactured solution $u=\sin(x)$.
N = 30 # the system becomes more expensive to solve for large N
h = 3*np.pi / N
x = np.linspace(0, 3*np.pi, num=N)
f = 2 * np.sin(x)
# One point to note about the boundary points: when we solve, we make sure not to give the end point values in `f` (as the solution there is already determined by the boundary conditions). Restricting $f$ outside of these points is done by **slicing** in numpy (which you should definitely learn if you don't know already) as in `f[1:-1]`.
u = solve(f[1:-1], h)
# For visualizing the solution, we use `matplotlib` module.
import matplotlib.pyplot as plt
plt.plot(u, '.-')
# How can you make sure the end points with the known zero solution values are also included in the final plot? This is again done using slicing.
uu = np.zeros(N)
uu[1:-1] = u
# Let's conclude by comparing the exact solution with the numerical solution by plotting both in the same scene.
plt.plot(uu, '.', label='computed solution')
plt.plot(np.sin(x), ':', label='exact solution', alpha=0.5)
plt.grid(True)
plt.legend();
# Clearly, the `solve` function captured something close to the exact solution.
#
# Going back through this notebook, you can easily change the mesh parameter to make $h$ smaller. Then repeating the above steps, you will see that the discrete solution points gets closer to exact solution curve.
#
# We will proceed to study finite elements. Then, unlike the above, we will think of the discrete solution as a function (and not as a set of discrete values as above). The function will be from a finite-dimensional space (called a finite element space).
|
notebooks/FiniteDifferences1D.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/nvisagan/DS-Unit-1-Sprint-1-Dealing-With-Data/blob/master/module4-makefeatures/LS_DS_114_Make_Features_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="SnDJqBLi0FYW" colab_type="text"
# <img align="left" src="https://lever-client-logos.s3.amazonaws.com/864372b1-534c-480e-acd5-9711f850815c-1524247202159.png" width=200>
# + [markdown] id="W5GjI1z5yNG4" colab_type="text"
# # ASSIGNMENT
#
# - Replicate the lesson code.
#
# - This means that if you haven't followed along already, type out the things that we did in class. Forcing your fingers to hit each key will help you internalize the syntax of what we're doing.
# - [Lambda Learning Method for DS - By <NAME>](https://docs.google.com/document/d/1ubOw9B3Hfip27hF2ZFnW3a3z9xAgrUDRReOEo-FHCVs/edit?usp=sharing)
# - Convert the `term` column from string to integer.
# - Make a column named `loan_status_is_great`. It should contain the integer 1 if `loan_status` is "Current" or "Fully Paid." Else it should contain the integer 0.
#
# - Make `last_pymnt_d_month` and `last_pymnt_d_year` columns.
# + id="AazB4eFwym2p" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="91c2087f-2e7b-494e-f225-4a63a3bb2280"
# Get the Lending Club Data
# !wget https://resources.lendingclub.com/LoanStats_2018Q4.csv.zip
# + id="QY4sbfFIrqDg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="07693eb1-a487-4e5c-fc2c-ef963e54b609"
# Unzip the zipped csv
# !unzip LoanStats_2018Q4.csv.zip
# + id="rjiQqwsRrtr7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 326} outputId="5015fc96-b1ad-45b1-872a-848ec40af10f"
import pandas as pd
# Display Options in Pandas
pd.set_option('display.max.rows', 500)
pd.set_option('display.max.columns', 500)
#Read CSV with Pandas Libraries
df = pd.read_csv('LoanStats_2018Q4.csv', header = 1, skipfooter=2, engine='python')
print(df.shape)
df.head()
# + id="jkfrK6mM5I7r" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="6e113116-c667-4032-cf93-195b5cb41663"
# Sum of Missing Values in columns
df.isnull().sum().sort_values(ascending=False)
# + id="RUkeggqY7Ly0" colab_type="code" colab={}
# Drop the unneeded columns
df = df.drop(columns=['id', 'member_id', 'desc', 'url'], axis='columns')
# + id="SweWuup-70Ur" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="761edeca-557e-4f0b-8606-21f2f7d8a4ca"
# Check type of term column
type(df['term'])
df['term']
# + id="gNtFQYD1-vEy" colab_type="code" colab={}
# Create a stripping function
def remove_month_to_int(string):
return int(string.strip(' months'))
# + id="NKJRBMiD_PEb" colab_type="code" colab={}
#Apply to term
df['term']= df['term'].apply(remove_month_to_int)
# + id="Vw7QS_DwBIAO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="fadeb46b-4263-49d0-e07f-4d60a1aeb494"
df['term']
# + id="sw7foMhoC5oy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 309} outputId="5f4d1089-d952-46be-fba6-ff61968a3e82"
# Create a new dataframe column loan_status_is_great. It should contain the
# integer 1 if loan_status is "Current" or "Fully Paid."
# Else it should contain the integer 0.
df['loan_status_is_great'] = [1 if x in ['Current','Fully Paid'] else 0 for x in df['loan_status']]
df.head()
# + id="wg_y1C1hEhhh" colab_type="code" colab={}
df['last_pymnt_d'] = pd.to_datetime(df['last_pymnt_d'],
infer_datetime_format=True)
# Make last_pymnt_d_month column
df["last_pymnt_d_month"] = df["last_pymnt_d"].dt.month
# + id="6mjqWbszGnGK" colab_type="code" colab={}
# Make last_pymnt_d_year column.
df["last_pymnt_d_year"] = df["last_pymnt_d"].dt.year
# + id="96DHrNH5HWMi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 309} outputId="e4882dbf-1600-4d8d-ce84-cb31b5fb7e04"
df.head()
# + [markdown] colab_type="text" id="L8k0LiHmo5EU"
# # STRETCH OPTIONS
#
# You can do more with the LendingClub or Instacart datasets.
#
# LendingClub options:
# - There's one other column in the dataframe with percent signs. Remove them and convert to floats. You'll need to handle missing values.
# - Modify the `emp_title` column to replace titles with 'Other' if the title is not in the top 20.
# - Take initiatve and work on your own ideas!
#
# Instacart options:
# - Read [Instacart Market Basket Analysis, Winner's Interview: 2nd place, Kazuki Onodera](http://blog.kaggle.com/2017/09/21/instacart-market-basket-analysis-winners-interview-2nd-place-kazuki-onodera/), especially the **Feature Engineering** section. (Can you choose one feature from his bulleted lists, and try to engineer it with pandas code?)
# - Read and replicate parts of [Simple Exploration Notebook - Instacart](https://www.kaggle.com/sudalairajkumar/simple-exploration-notebook-instacart). (It's the Python Notebook with the most upvotes for this Kaggle competition.)
# - Take initiative and work on your own ideas!
# + [markdown] colab_type="text" id="0_7PXF7lpEXg"
# You can uncomment and run the cells below to re-download and extract the Instacart data
# + id="urIePNa0yNG6" colab_type="code" colab={}
# # !wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
# + id="X9zEyu-uyNG8" colab_type="code" colab={}
# # !tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
# + id="Y3IqrhlpyNG-" colab_type="code" colab={}
# # %cd instacart_2017_05_01
|
DS-Unit-1-Sprint-1-Dealing-With-Data-master/module4-makefeatures/LS_DS_114_Make_Features_Assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 讯飞tts的class
#
# 需要使用以json格式写的API才可以初始化。
# ```json
# {
# "key": "3************c77",
# "id": "5*****5a",
# "url": "http://api.xfyun.cn/v1/service/v1/tts"
# }
#
# ```
#
# 调用例子:
# ```python
# with open('API_setup.txt') as json_file:
# api = json.load(json_file)
# a=Speech(api, voice_name="x_yifeng")
# a.save("你好","test.mp3")
# a.play("你好")
# ```
# +
import re
import base64
import json
import time
import hashlib
import urllib.request
import urllib.parse
import json
import subprocess
import os
import string
from io import BytesIO
from pydub import AudioSegment, playback
# +
class Speech:
""" 讯飞TTS """
MAX_SEGMENT_SIZE = 300
MIN_SEGMENT_SIZE = 2
def __init__(self,
api,
voice_name='aisjiuxu',
audio_type="mp3", #音频编码,raw(生成wav)或lame(生成mp3)
speed="60",
volume="100",
pitch="30",
engine_type="aisound",
):
'''要使用api进行初始化'''
self.api=api
self.split_pattern=__class__.split_pattern()
self.audio_type=audio_type
audio_type_dict={"mp3":"lame","wav":"raw"}
self.text='.'
self.Param = {
"auf": "audio/L16;rate=16000", #音频采样率
"aue": {"mp3":"lame","wav":"raw"}[audio_type], #音频编码,raw(生成wav)或lame(生成mp3)
"voice_name": voice_name,
"speed": speed, #语速[0,100]
"volume": volume, #音量[0,100]
"pitch": pitch, #音高[0,100]
"engine_type": engine_type #引擎类型。aisound(普通效果),intp65(中文),intp65_en(英文)
}
# self.Param_b64str=self.construct_base64_str()
def split_pattern():
# cn_punc="!,。?、~@#¥%……&*():;《)《》“”()»〔〕-" #this line is Chinese punctuation
# en_punc=string.punctuation
# useless_chars = frozenset(
# en_punc
# + string.whitespace
# + cn_punc
# )
# split_pattern=re.compile("([\s\S]{"
# +"{},{}".format(__class__.MIN_SEGMENT_SIZE, __class__.MAX_SEGMENT_SIZE)
# + "}[useless_chars|(?!.\d+)|(?!,\d+)])")
split_pattern=re.compile("([\s\S]{"
+"{},{}".format(__class__.MIN_SEGMENT_SIZE, __class__.MAX_SEGMENT_SIZE)
+ "}[,.\n,。|(?!.\d+)|(?!,\d+)])") # 似乎是个bug,有时候会有断句的错误,还是只用逗号句号好了
return split_pattern
def splitText(self,text):
text+="."
s=[]
if len(text)>__class__.MAX_SEGMENT_SIZE:
s+=self.split_pattern.findall(text)
else:
s.append(text)
return s
def construct_base64_str(Param):
# 配置参数编码为base64字符串,过程:字典→明文字符串→utf8编码→base64(bytes)→base64字符串
Param_str = json.dumps(Param) #得到明文字符串
Param_utf8 = Param_str.encode('utf8') #得到utf8编码(bytes类型)
Param_b64 = base64.b64encode(Param_utf8) #得到base64编码(bytes类型)
Param_b64str = Param_b64.decode('utf8') #得到base64字符串
return Param_b64str
def construct_header(api, Param_b64str):
# 构造HTTP请求的头部
time_now = str(int(time.time()))
checksum = (api["key"] + time_now + Param_b64str).encode('utf8')
checksum_md5 = hashlib.md5(checksum).hexdigest()
header = {
"X-Appid": api["id"],
"X-CurTime": time_now,
"X-Param": Param_b64str,
"X-CheckSum": checksum_md5
}
return header
def construct_urlencode_utf8(t):
# 构造HTTP请求Body
body = {
"text": t
}
body_urlencode = urllib.parse.urlencode(body)
body_utf8 = body_urlencode.encode('utf8')
return body_utf8
def getAudioData(self,text):
Param=self.Param
api=self.api
# 发送HTTP POST请求
req = urllib.request.Request(
api["url"],
data=__class__.construct_urlencode_utf8(text),
headers=__class__.construct_header(api, __class__.construct_base64_str(Param)))
response = urllib.request.urlopen(req)
response_head = response.headers['Content-Type']
if(response_head == "text/plain"): #出错,返回错误信息
err_msg=json.loads(response.read().decode('utf8'))
raise UserWarning("讯飞WebAPI错误: {}".format(err_msg["desc"]))
else:
audio_data=response.read()
# 为了方便连接多个语句,此处使用pydub处理获得的数据
if self.Param["aue"]=='lame':
voice = AudioSegment.from_mp3(BytesIO(audio_data))
elif self.Param["aue"]=='raw':
voice = AudioSegment.from_wav(BytesIO(audio_data))
return voice
def play(self, text):
'''play voice'''
for t in self.splitText(text):
playback.play(self.getAudioData(t))
def save(self, text, path):
""" Save audio data to an MP3 file. """
with open(path, "wb") as f:
self.savef(text,f)
def savef(self, text,file):
""" Write audio data into a file object. """
combined = AudioSegment.empty()
for t in self.splitText(text):
combined += self.getAudioData(t)
combined.export(file,
format="mp3",
codec="libmp3lame")
|
xunfei_tts.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Chained Visualizations with Yellowbrick Pipelines
#
# In Yellowbrick, `VisualPipelines` are modeled on Scikit-Learn `Pipelines`, which allow us to chain estimators together in a sane way and use them as a single estimator. This is very useful for models that require a series of extraction, normalization, and transformation steps in advance of prediction. For more about Scikit-Learn Pipelines, check out [this post](http://zacstewart.com/2014/08/05/pipelines-of-featureunions-of-pipelines.html) by <NAME>.
#
# `VisualPipelines` sequentially apply a list of transforms, visualizers, and a final estimator which may be evaluated by additional visualizers. Intermediate steps of the pipeline must be kinds of 'transforms', that is, they must implement `fit` and `transform` methods. The final estimator only needs to implement `fit`.
#
# Any step that implements draw or show methods can be called sequentially directly from the VisualPipeline, allowing multiple visual diagnostics to be generated, displayed, and saved on demand. If `draw` or `show` is not called, the visual pipeline should be equivalent to the simple pipeline to ensure no reduction in performance.
#
# The purpose of the pipeline is to assemble several steps that can be cross-validated together while setting different parameters. These steps can be visually diagnosed by visualizers at every point in the pipeline.
# +
# %matplotlib inline
import os
import sys
# Modify the path
sys.path.append("/Users/rebeccabilbro/Desktop/waves/stuff/yellowbrick")
import requests
import numpy as np
import pandas as pd
import yellowbrick as yb
import matplotlib.pyplot as plt
# -
# ## Fetching the data
# +
## The path to the test data sets
FIXTURES = os.path.join(os.getcwd(), "data")
## Dataset loading mechanisms
datasets = {
"credit": os.path.join(FIXTURES, "credit", "credit.csv"),
"concrete": os.path.join(FIXTURES, "concrete", "concrete.csv"),
"occupancy": os.path.join(FIXTURES, "occupancy", "occupancy.csv"),
"mushroom": os.path.join(FIXTURES, "mushroom", "mushroom.csv"),
}
def load_data(name, download=False):
"""
Loads and wrangles the passed in dataset by name.
If download is specified, this method will download any missing files.
"""
# Get the path from the datasets
path = datasets[name]
# Check if the data exists, otherwise download or raise
if not os.path.exists(path):
if download:
download_all()
else:
raise ValueError((
"'{}' dataset has not been downloaded, "
"use the download.py module to fetch datasets"
).format(name))
# Return the data frame
return pd.read_csv(path)
# -
# Load the classification data set
data = load_data('credit')
# +
# Specify the features of interest
features = [
'limit', 'sex', 'edu', 'married', 'age', 'apr_delay', 'may_delay',
'jun_delay', 'jul_delay', 'aug_delay', 'sep_delay', 'apr_bill', 'may_bill',
'jun_bill', 'jul_bill', 'aug_bill', 'sep_bill', 'apr_pay', 'may_pay', 'jun_pay',
'jul_pay', 'aug_pay', 'sep_pay',
]
classes = ['default', 'paid']
# Extract the numpy arrays from the data frame
X = data[features].as_matrix()
y = data.default.as_matrix()
# +
from yellowbrick.features.rankd import Rank2D
visualizer = Rank2D(features=features, algorithm='covariance')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
# +
from yellowbrick.features.radviz import RadViz
visualizer = RadViz(classes=classes, features=features)
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.show()
# -
# ## Ok now try with `VisualPipeline`
# +
from yellowbrick.pipeline import VisualPipeline
from yellowbrick.features.rankd import Rank2D
from yellowbrick.features.radviz import RadViz
multivisualizer = VisualPipeline([
('rank2d', Rank2D(features=features, algorithm='covariance')),
('radviz', RadViz(classes=classes, features=features)),
])
# -
multivisualizer.fit(X, y)
multivisualizer.transform(X)
multivisualizer.show()
|
examples/rebeccabilbro/pipelines.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/michael-sam/data_analytics/blob/main/eda/visualisation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="2yu1SYsO0rTD"
# # Data visualisation
#
# Created this notebook that used pretty neat techniques for visualizing data.
# + [markdown] id="ImPRxvIG0xBb"
# ## Setup and dataset
# + papermill={"duration": 1.177802, "end_time": "2020-09-13T08:31:15.099426", "exception": false, "start_time": "2020-09-13T08:31:13.921624", "status": "completed"} tags=[] id="RwxpL3PfkY2s"
#import the necessary Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import time
import matplotlib.ticker as ticker
# + papermill={"duration": 0.17356, "end_time": "2020-09-13T08:31:15.313086", "exception": false, "start_time": "2020-09-13T08:31:15.139526", "status": "completed"} tags=[] id="cFnkzC0VkY2u"
df = pd.read_csv('dataset/Superstore_sales.csv')
# + [markdown] id="PnJ8LoT904UC"
# # Data cleaning
# + papermill={"duration": 0.079136, "end_time": "2020-09-13T08:31:15.513129", "exception": false, "start_time": "2020-09-13T08:31:15.433993", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 357} id="tHr0HsJzkY2v" outputId="27cf6745-577c-4e4d-972d-40e253739849"
df.head()
# + papermill={"duration": 0.079024, "end_time": "2020-09-13T08:31:15.634226", "exception": false, "start_time": "2020-09-13T08:31:15.555202", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 297} id="C0E8k4DtkY2x" outputId="735eb1df-d57f-4ab5-9712-abc09d64c06f"
df.describe()
# + papermill={"duration": 0.083657, "end_time": "2020-09-13T08:31:15.760753", "exception": false, "start_time": "2020-09-13T08:31:15.677096", "status": "completed"} tags=[] id="I2vtI15qkY2y"
df.drop('Row ID',axis = 1, inplace = True) #Dropping the Row ID column
df['Order Date'] = pd.to_datetime(df['Order Date'], format='%d/%m/%Y') #convert Order dates to pandas datetime format
df['Ship Date'] = pd.to_datetime(df['Ship Date'], format='%d/%m/%Y') #convert shipping dates to pandas datetime format
# + papermill={"duration": 0.05641, "end_time": "2020-09-13T08:31:15.859293", "exception": false, "start_time": "2020-09-13T08:31:15.802883", "status": "completed"} tags=[] id="pgn6IDKAkY20"
#sorting data by order date
df.sort_values(by=['Order Date'], inplace=True, ascending=True)
# + papermill={"duration": 0.05205, "end_time": "2020-09-13T08:31:15.953423", "exception": false, "start_time": "2020-09-13T08:31:15.901373", "status": "completed"} tags=[] id="m6747wlckY22"
#setting the index to be the date will help us a lot later on
df.set_index("Order Date", inplace = True)
# + [markdown] papermill={"duration": 0.042145, "end_time": "2020-09-13T08:31:16.038329", "exception": false, "start_time": "2020-09-13T08:31:15.996184", "status": "completed"} tags=[] id="SSG6jUKokY23"
# **checking if there is any null data or not**
# + papermill={"duration": 0.069583, "end_time": "2020-09-13T08:31:16.150131", "exception": false, "start_time": "2020-09-13T08:31:16.080548", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/"} id="3435bWRykY24" outputId="bddb5a77-a887-4f05-cc66-d4f0b11477b6"
print(df.isnull().sum())
# + [markdown] papermill={"duration": 0.041889, "end_time": "2020-09-13T08:31:16.240983", "exception": false, "start_time": "2020-09-13T08:31:16.199094", "status": "completed"} tags=[] id="eORdhoh6kY25"
# <b>To handle the null values in postal code. We will not drop them, instead we will add the postal code of respective city.<br>
# 1. we need to find the cities for which the postal code is not mentioned.
# 2. Fill the postal code of the respective city into the postal code column.</b>
# + papermill={"duration": 0.080569, "end_time": "2020-09-13T08:31:16.363827", "exception": false, "start_time": "2020-09-13T08:31:16.283258", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 642} id="jEA420KIkY25" outputId="943e7c0a-f165-4445-cda9-75b1dd4d7632"
df[df['Postal Code'].isnull()]
# + [markdown] papermill={"duration": 0.043102, "end_time": "2020-09-13T08:31:16.450791", "exception": false, "start_time": "2020-09-13T08:31:16.407689", "status": "completed"} tags=[] id="YcqfT_OUkY26"
# **We can see that the postal code is not mentioned only for Burlington city in Vermont state. So, we need to fill the postal code of that city.**
# + papermill={"duration": 0.053693, "end_time": "2020-09-13T08:31:16.548120", "exception": false, "start_time": "2020-09-13T08:31:16.494427", "status": "completed"} tags=[] id="4KzHeGG2kY26"
df['Postal Code'] = df['Postal Code'].fillna(5401) # Postal code for Burlington city
# + papermill={"duration": 0.070275, "end_time": "2020-09-13T08:31:16.662383", "exception": false, "start_time": "2020-09-13T08:31:16.592108", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/"} id="A3vOeYPNkY26" outputId="b5d8a5cf-ce28-4cd2-bb07-cec37d971b4f"
print(df.isnull().sum())
# + [markdown] papermill={"duration": 0.044004, "end_time": "2020-09-13T08:31:16.750580", "exception": false, "start_time": "2020-09-13T08:31:16.706576", "status": "completed"} tags=[] id="dJp_zLsAkY27"
# # Most Valuable customers
#
# The Most Valuable Customers buy more or higher-value products than the average. customer
# + papermill={"duration": 0.067527, "end_time": "2020-09-13T08:31:16.862351", "exception": false, "start_time": "2020-09-13T08:31:16.794824", "status": "completed"} tags=[] id="v8NOnKGTkY27"
Top_customers = df.groupby(["Customer Name"]).sum().sort_values("Sales", ascending=False).head(20) # Sort the Customers as per the sales
Top_customers = Top_customers[["Sales"]].astype(int) # Cast Sales Value as integers
Top_customers.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the customer name into dataframe
# + papermill={"duration": 0.437785, "end_time": "2020-09-13T08:31:17.344795", "exception": false, "start_time": "2020-09-13T08:31:16.907010", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 466} id="HipGixQukY27" outputId="8116660c-2785-4d71-8882-1b6539e13d94"
plt.figure(figsize = (15,5)) # width and height of figure is defined in inches
plt.title("Most Valuable Customers (2015-2019)", fontsize=18)
plt.bar(Top_customers["Customer Name"], Top_customers["Sales"],color= '#99ff99',edgecolor='green', linewidth = 1)
plt.xlabel("Customers",fontsize=15) # x axis shows the customers
plt.ylabel("Revenue",fontsize=15) # y axis shows the Revenue
plt.xticks(fontsize=12, rotation=90)
plt.yticks(fontsize=12)
current_values = plt.gca().get_yticks()
plt.gca().set_yticklabels(['{:,.0f}'.format(x) for x in current_values]) # formatting yticks to thousands separated with commas
for k,v in Top_customers["Sales"].items(): #To show the exact revenue generated on the figure
plt.text(k,v-5000,'$'+ '{:,}'.format(v), fontsize=12,rotation=90,color='k', horizontalalignment='center');
# + [markdown] papermill={"duration": 0.047696, "end_time": "2020-09-13T08:31:17.439710", "exception": false, "start_time": "2020-09-13T08:31:17.392014", "status": "completed"} tags=[] id="fMhBgbIAkY27"
# # Revenue by states
#
# Top 10 States which generated the highest revenue.
# + papermill={"duration": 0.066826, "end_time": "2020-09-13T08:31:17.554027", "exception": false, "start_time": "2020-09-13T08:31:17.487201", "status": "completed"} tags=[] id="ydlZB98LkY28"
Top_states = df.groupby(["State"]).sum().sort_values("Sales", ascending=False).head(20) # Sort the States as per the sales
Top_states = Top_states[["Sales"]].astype(int) # Cast Sales Value as integers
Top_states.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the states into dataframe
# + papermill={"duration": 0.372332, "end_time": "2020-09-13T08:31:17.973131", "exception": false, "start_time": "2020-09-13T08:31:17.600799", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 436} id="QVQowr8ZkY28" outputId="57c6cef0-338b-4b0d-887b-ece0490c6b20"
plt.figure(figsize = (15,5)) # width and height of figure is defined in inches
plt.title("States which generated Highest Revenue (2015-2019)", fontsize=18)
plt.bar(Top_states["State"], Top_states["Sales"],color= '#FF6F61',edgecolor='Red', linewidth = 1)
plt.xlabel("States",fontsize=15) # x axis shows the States
plt.ylabel("Revenue",fontsize=15) # y axis shows the Revenue
plt.xticks(fontsize=12, rotation=90)
plt.yticks(fontsize=12)
current_values = plt.gca().get_yticks()
plt.gca().set_yticklabels(['{:,.0f}'.format(x) for x in current_values]) # formatting yticks to thousands separated with commas
for k,v in Top_states["Sales"].items(): #To show the exact revenue generated on the figure
if v>400000:
plt.text(k,v-150000,'$'+ '{:,}'.format(v), fontsize=12,rotation=90,color='k', horizontalalignment='center');
else:
plt.text(k,v+15000,'$'+ '{:,}'.format(v), fontsize=12,rotation=90,color='k', horizontalalignment='center');
# + [markdown] papermill={"duration": 0.048365, "end_time": "2020-09-13T08:31:18.070798", "exception": false, "start_time": "2020-09-13T08:31:18.022433", "status": "completed"} tags=[] id="PY4FAr1hkY29"
# # Revenue by cities
#
# Top 10 cities which generated the highest revenue.
# + papermill={"duration": 0.069157, "end_time": "2020-09-13T08:31:18.188874", "exception": false, "start_time": "2020-09-13T08:31:18.119717", "status": "completed"} tags=[] id="t-xsIO9zkY29"
Top_cities = df.groupby(["City"]).sum().sort_values("Sales", ascending=False).head(20) # Sort the States as per the sales
Top_cities = Top_cities[["Sales"]].astype(int) # Cast Sales Value as integers
Top_cities.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the cities into the dataframe
# + papermill={"duration": 0.38386, "end_time": "2020-09-13T08:31:18.621720", "exception": false, "start_time": "2020-09-13T08:31:18.237860", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 431} id="hkpeeWKpkY29" outputId="bac59a9d-8ba7-4ec1-a974-a515103f234d"
plt.figure(figsize = (15,5)) # width and height of figure is defined in inches
plt.title("Cities which generated Highest Revenue (2015-2019)", fontsize=18)
plt.bar(Top_cities["City"], Top_cities["Sales"],color= '#95DEE3',edgecolor='blue', linewidth = 1)
plt.xlabel("Cities",fontsize=15) # x axis shows the States
plt.ylabel("Revenue",fontsize=15) # y axis shows the Revenue
plt.xticks(fontsize=12, rotation=90)
plt.yticks(fontsize=12)
current_values = plt.gca().get_yticks()
plt.gca().set_yticklabels(['{:,.0f}'.format(x) for x in current_values]) # formatting yticks to thousands separated with commas
for k,v in Top_cities["Sales"].items(): #To show the exact revenue generated on the figure
if v>250000:
plt.text(k,v-60000,'$'+ '{:,}'.format(v), fontsize=12,rotation=90,color='k', horizontalalignment='center');
else:
plt.text(k,v+15000,'$'+ '{:,}'.format(v), fontsize=12,rotation=90,color='k', horizontalalignment='center');
# + [markdown] papermill={"duration": 0.051213, "end_time": "2020-09-13T08:31:18.725272", "exception": false, "start_time": "2020-09-13T08:31:18.674059", "status": "completed"} tags=[] id="lstgEyvVkY2-"
# # Revenue by categories
# + papermill={"duration": 0.072273, "end_time": "2020-09-13T08:31:18.849100", "exception": false, "start_time": "2020-09-13T08:31:18.776827", "status": "completed"} tags=[] id="66brqy1ykY2-"
Top_category = df.groupby(["Category"]).sum().sort_values("Sales", ascending=False) # Sort the Categories as per the sales
Top_category = Top_category[["Sales"]] # keep only the sales column in the dataframe
total_revenue_category = Top_category["Sales"].sum() # To find the total revenue generated as per category
total_revenue_category = '{:,}'.format(int(total_revenue_category)) # Convert the total_revenue_category from float to int and then to string
total_revenue_category = '$' + total_revenue_category # Adding '$' sign before the Value
Top_category.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the category into the dataframe
# + papermill={"duration": 0.208592, "end_time": "2020-09-13T08:31:19.118375", "exception": false, "start_time": "2020-09-13T08:31:18.909783", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 369} id="yvbzNhELkY2-" outputId="9622c651-83eb-4a1c-d783-52dc882f537d"
plt.rcParams["figure.figsize"] = (13,5) # width and height of figure is defined in inches
plt.rcParams['font.size'] = 12.0 # Font size is defined
plt.rcParams['font.weight'] = 6 # Font weight is defined
# we don't want to look at the percentage distribution in the pie chart. Instead, we want to look at the exact revenue generated by the categories.
def autopct_format(values):
def my_format(pct):
total = sum(values)
val = int(round(pct*total/100.0))
return ' ${v:,}'.format(v=val)
return my_format
colors = ['#BC243C','#FE840E','#C62168'] # Colors are defined for the pie chart
explode = (0.05,0.05,0.05)
fig1, ax1 = plt.subplots()
ax1.pie(Top_category['Sales'], colors = colors, labels=Top_category['Category'], autopct= autopct_format(Top_category['Sales']), startangle=90,explode=explode)
centre_circle = plt.Circle((0,0),0.85,fc='white') # drawing a circle on the pie chart to make it look better
fig = plt.gcf()
fig.gca().add_artist(centre_circle) # Add the circle on the pie chart
# Equal aspect ratio ensures that pie is drawn as a circle
ax1.axis('equal')
# we can look the total revenue generated by all the categories at the center
label = ax1.annotate('Total Revenue \n'+str(total_revenue_category),color = 'black', fontweight = 'bold', xy=(0, 0), fontsize=12, ha="center")
plt.tight_layout()
plt.show()
# + [markdown] papermill={"duration": 0.052401, "end_time": "2020-09-13T08:31:19.224094", "exception": false, "start_time": "2020-09-13T08:31:19.171693", "status": "completed"} tags=[] id="OTEdVWcPkY2_"
# <i><b>Category - Technology</b></i> generated the highest revenue of about <b>$827,426</b><br>
#
# <b>Total Revenue</b> generated by all the categories - <b>$2,261,536</b>
# + [markdown] papermill={"duration": 0.052453, "end_time": "2020-09-13T08:31:19.329303", "exception": false, "start_time": "2020-09-13T08:31:19.276850", "status": "completed"} tags=[] id="Wugq87W4kY2_"
# # Revenue by products
# + papermill={"duration": 0.078016, "end_time": "2020-09-13T08:31:19.460360", "exception": false, "start_time": "2020-09-13T08:31:19.382344", "status": "completed"} tags=[] id="TsZlZ4bnkY2_"
Top_products = df.groupby(["Product Name"]).sum().sort_values("Sales",ascending=False).head(8) # Sort the product names as per the sales
Top_products = Top_products[["Sales"]].round(2) # Round off the Sales Value up to 2 decimal places
Top_products.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the product names into the dataframe
total_revenue_products = Top_products["Sales"].sum() # To find the total revenue generated by all the top products
total_revenue_products = '{:,}'.format(int(total_revenue_products)) # Convert the total_revenue_products from float to int and then to string
total_revenue_products = '$' + total_revenue_products # Adding '$' sign before the Value
# + papermill={"duration": 0.319778, "end_time": "2020-09-13T08:31:19.833295", "exception": false, "start_time": "2020-09-13T08:31:19.513517", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 508} id="2L7c4TyJkY3A" outputId="86423736-e04e-417b-fef6-b5f19834c91b"
plt.rcParams["figure.figsize"] = (13,7) # width and height of figure is defined in inches
plt.rcParams['font.size'] = 12.0 # Font size is defined for the figure
colors = ['#ff9999','#66b3ff','#99ff99','#ffcc99','#55B4B0','#E15D44','#009B77','#B565A7'] # colors are defined for the pie chart
explode = (0.05,0.05,0.05,0.05,0.05,0.05,0.05,0.05)
fig1, ax1 = plt.subplots()
ax1.pie(Top_products['Sales'], colors = colors, labels=Top_products['Product Name'], autopct= autopct_format(Top_products['Sales']), startangle=90,explode=explode)
centre_circle = plt.Circle((0,0),0.80,fc='white') # Draw a circle on the pie chart
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax1.axis('equal')
label = ax1.annotate('Total Revenue \n of these products \n'+str(total_revenue_products),color = 'black',fontweight = 'bold', xy=(0, 0), fontsize=12, ha="center")
plt.tight_layout()
plt.show()
# + [markdown] papermill={"duration": 0.055106, "end_time": "2020-09-13T08:31:19.943844", "exception": false, "start_time": "2020-09-13T08:31:19.888738", "status": "completed"} tags=[] id="WDgS7lCOkY3A"
# We can see that <i><b>Product - Canon imageCLASS 2200 Advanced Copier</b></i> generated the highest revenue of about <b>$61,600</b><br>
#
# <b>Total Revenue</b> generated by all these products - <b>$209,624</b>
# + [markdown] papermill={"duration": 0.05513, "end_time": "2020-09-13T08:31:20.054724", "exception": false, "start_time": "2020-09-13T08:31:19.999594", "status": "completed"} tags=[] id="aXSRwqS8kY3A"
# # Revenue by sub-categories
# + papermill={"duration": 0.081386, "end_time": "2020-09-13T08:31:20.191788", "exception": false, "start_time": "2020-09-13T08:31:20.110402", "status": "completed"} tags=[] id="JSF6xOuXkY3A"
# Sort both category and sub category as per the sales
Top_subcat = df.groupby(['Category','Sub-Category']).sum().sort_values("Sales", ascending=False).head(10)
Top_subcat = Top_subcat[["Sales"]].astype(int) # Cast Sales column to integer data type
Top_subcat = Top_subcat.sort_values("Category") # Sort the values as per Category
Top_subcat.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add both columns into data frame
Top_subcat_1 = Top_subcat.groupby(['Category']).sum() # Calculated the total Sales of all the categories
Top_subcat_1.reset_index(inplace=True) # Reset the index
# + papermill={"duration": 0.259182, "end_time": "2020-09-13T08:31:20.506586", "exception": false, "start_time": "2020-09-13T08:31:20.247404", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 725} id="1TqydA5_kY3B" outputId="e0c8b14e-5dd4-4e2f-96f5-699a5918d640"
plt.rcParams["figure.figsize"] = (15,10) # width and height of figure is defined in inches
fig, ax = plt.subplots()
ax.axis('equal') # Equal aspect ratio ensures that pie is drawn as a circle
width = 0.1
outer_colors = ['#FE840E','#009B77','#BC243C'] # Outer colors of the pie chart
inner_colors = ['Orangered','tomato','coral',"darkturquoise","mediumturquoise","paleturquoise","lightpink","pink","hotpink","deeppink"] # inner colors of the pie chart
pie = ax.pie(Top_subcat_1['Sales'], radius=1, labels=Top_subcat_1['Category'],colors=outer_colors,wedgeprops=dict(edgecolor='w'))
pie2 = ax.pie(Top_subcat['Sales'], radius=1-width, labels=Top_subcat['Sub-Category'],autopct= autopct_format(Top_subcat['Sales']),labeldistance=0.7,colors=inner_colors,wedgeprops=dict(edgecolor='w'), pctdistance=0.53,rotatelabels =True)
# Rotate fractions
# [0] = wedges, [1] = labels, [2] = fractions
fraction_text_list = pie2[2]
for text in fraction_text_list:
text.set_rotation(315) # rotate the autopct values
centre_circle = plt.Circle((0,0),0.6,fc='white') # Draw a circle on the pie chart
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax1.axis('equal')
plt.tight_layout()
plt.show()
# + [markdown] papermill={"duration": 0.059023, "end_time": "2020-09-13T08:31:20.626582", "exception": false, "start_time": "2020-09-13T08:31:20.567559", "status": "completed"} tags=[] id="y3jCCG7jkY3B"
# <i><b>Sub-Category - Phones</b></i> generated the highest revenue of about <b>$327,782</b><br>
# + [markdown] papermill={"duration": 0.05851, "end_time": "2020-09-13T08:31:20.744805", "exception": false, "start_time": "2020-09-13T08:31:20.686295", "status": "completed"} tags=[] id="Ha6qIxyekY3B"
# # Revenue by segments
# + papermill={"duration": 0.077756, "end_time": "2020-09-13T08:31:20.880961", "exception": false, "start_time": "2020-09-13T08:31:20.803205", "status": "completed"} tags=[] id="HZfvAff1kY3B"
Top_segment = df.groupby(["Segment"]).sum().sort_values("Sales", ascending=False) # Sort the segment as per the sales
Top_segment = Top_segment[["Sales"]] # keep only the sales column in the dataframe
Top_segment.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the segment column into the data frame
total_revenue_segement = Top_segment["Sales"].sum() # To find the total revenue generated as per segment
total_revenue_segement = '{:,}'.format(int(total_revenue_segement)) # Convert the total_revenue_segment from float to int and then to string
total_revenue_segement= '$' + total_revenue_segement # Adding '$' sign before the Value
# + papermill={"duration": 0.16457, "end_time": "2020-09-13T08:31:21.104638", "exception": false, "start_time": "2020-09-13T08:31:20.940068", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 365} id="sdAHTAaGkY3C" outputId="584306c3-26d3-4133-ea96-3eb5308d8165"
plt.rcParams["figure.figsize"] = (13,5) # width and height of figure is defined in inches
plt.rcParams['font.size'] = 12.0 # Font size is defined
plt.rcParams['font.weight'] = 6 # Font weight is defined
colors = ['#BC243C','#FE840E','#C62168'] # Colors are defined for the pie chart
explode = (0.06,0.02,0.02)
fig1, ax1 = plt.subplots()
ax1.pie(Top_segment['Sales'], colors = colors, labels=Top_segment['Segment'], autopct= autopct_format(Top_segment['Sales']),startangle=90, wedgeprops=dict(edgecolor='w'))
centre_circle = plt.Circle((0,0),0.84,fc='white') # Draw a circle on the pie chart
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax1.axis('equal')
label = ax1.annotate('Total Revenue \n'+str(total_revenue_segement),color = 'black', fontweight = 'bold', xy=(0, 0), fontsize=12, ha="center")
plt.tight_layout()
plt.show()
# + [markdown] papermill={"duration": 0.06112, "end_time": "2020-09-13T08:31:21.226578", "exception": false, "start_time": "2020-09-13T08:31:21.165458", "status": "completed"} tags=[] id="NUbFtvsOkY3C"
# <i><b>Segment - Consumer</b></i> generated the highest revenue of about <b>$1,148,061</b><br>
#
# <b>Total Revenue</b> generated by all the segments - <b>$2,261,536</b>
# + [markdown] papermill={"duration": 0.060657, "end_time": "2020-09-13T08:31:21.348241", "exception": false, "start_time": "2020-09-13T08:31:21.287584", "status": "completed"} tags=[] id="lMMQWxySkY3C"
# # Revenue by regions
#
# + papermill={"duration": 0.078398, "end_time": "2020-09-13T08:31:21.487486", "exception": false, "start_time": "2020-09-13T08:31:21.409088", "status": "completed"} tags=[] id="wY0Iab_EkY3C"
Top_region = df.groupby(["Region"]).sum().sort_values("Sales", ascending=False) # Sort the Region as per the sales
Top_region = Top_region[["Sales"]].astype(int) # Cast Sales column to integer data type
Top_region.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the Region column into the data frame
# + papermill={"duration": 0.234025, "end_time": "2020-09-13T08:31:21.781888", "exception": false, "start_time": "2020-09-13T08:31:21.547863", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 393} id="_6176wcCkY3C" outputId="f1b90d52-cc46-45f5-8679-dbd1de96943f"
plt.figure(figsize = (10,5)) # width and height of figure is defined in inches
plt.title("Region-wise Revenue Generation", fontsize=18)
plt.bar(Top_region["Region"], Top_region["Sales"],color= '#FF6F61',edgecolor='Red', linewidth = 1)
plt.xlabel("Region",fontsize=15) # x axis shows the Region
plt.ylabel("Revenue",fontsize=15) # y axis show the Revenue generated
plt.xticks(fontsize=12, rotation=90)
plt.yticks(fontsize=12)
for k,v in Top_region["Sales"].items(): #To show the exact revenue generated on the figure
plt.text(k,v-150000,'$'+ '{:,}'.format(v), fontsize=12,color='k', horizontalalignment='center');
# + [markdown] papermill={"duration": 0.06124, "end_time": "2020-09-13T08:31:21.904883", "exception": false, "start_time": "2020-09-13T08:31:21.843643", "status": "completed"} tags=[] id="o5jyymvskY3D"
# <h3>Which shipping mode has the highest sales?</h3>
# + papermill={"duration": 0.081812, "end_time": "2020-09-13T08:31:22.048856", "exception": false, "start_time": "2020-09-13T08:31:21.967044", "status": "completed"} tags=[] id="Jl1NlvkDkY3D"
Top_shipping = df.groupby(["Ship Mode"]).sum().sort_values("Sales", ascending=False) # Sort the Shipping modes as per the sales
Top_shipping = Top_shipping[["Sales"]] # keep only the sales column in the dataframe
Top_shipping.reset_index(inplace=True) # Since we have used groupby, we will have to reset the index to add the Ship Mode column into the data frame
total_revenue_ship = Top_segment["Sales"].sum() # To find the total revenue generated as per shipping mode
total_revenue_ship = '{:,}'.format(int(total_revenue_ship)) # Convert the total_revenue_ship from float to int and then to string
total_revenue_ship = '$' + total_revenue_ship # Adding '$' sign before the Value
# + papermill={"duration": 0.178724, "end_time": "2020-09-13T08:31:22.290090", "exception": false, "start_time": "2020-09-13T08:31:22.111366", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 370} id="-lw_uxmfkY3D" outputId="9f422026-bab7-4368-e93c-8bc4f1eea604"
plt.rcParams["figure.figsize"] = (13,5) # width and height of figure is defined in inches
plt.rcParams['font.size'] = 12.0 # Font size is defined
plt.rcParams['font.weight'] = 6 # Font weight is defined
colors = ['#BC243C','#FE840E','#C62168',"limegreen"] # define colors for the pie chart
fig1, ax1 = plt.subplots()
ax1.pie(Top_shipping['Sales'], colors = colors, labels=Top_shipping['Ship Mode'], autopct= autopct_format(Top_shipping['Sales']), startangle=90, wedgeprops=dict(edgecolor='w'))
centre_circle = plt.Circle((0,0),0.82,fc='white') # Draw a circle on the pie chart
fig = plt.gcf()
fig.gca().add_artist(centre_circle)
# Equal aspect ratio ensures that pie is drawn as a circle
ax1.axis('equal')
label = ax1.annotate('Total Revenue \n'+str(total_revenue_ship),color = 'black', fontweight='bold', xy=(0, 0), fontsize=12, ha="center")
plt.tight_layout()
plt.show()
# + [markdown] papermill={"duration": 0.063561, "end_time": "2020-09-13T08:31:22.417928", "exception": false, "start_time": "2020-09-13T08:31:22.354367", "status": "completed"} tags=[] id="L2CVCffJkY3D"
# <i><b>Shipping mode - Standard Class</b></i> generated the highest revenue of about <b>$1,340,831</b><br>
#
# <b>Total Revenue</b> generated by all the shipping modes - <b>$2,261,536</b>
# + [markdown] papermill={"duration": 0.062981, "end_time": "2020-09-13T08:31:22.544379", "exception": false, "start_time": "2020-09-13T08:31:22.481398", "status": "completed"} tags=[] id="Wn_eb_MIkY3D"
# # Correlation of Features
# Plotting a correlation matrix provides an overview of how the features are related to one another. For a Pandas dataframe, `.corr` provides the Pearson Correlation values of the columns pairwise in that dataframe.
# + papermill={"duration": 0.346862, "end_time": "2020-09-13T08:31:22.955627", "exception": false, "start_time": "2020-09-13T08:31:22.608765", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 466} id="dm95xwTjkY3E" outputId="0ec9199e-e951-4d30-de10-fe1fa37f4442"
df1 = df[['Segment','Sales']]
df_cat = pd.get_dummies(df1)
cor_mat = df_cat.corr()
mask = np.array(cor_mat)
mask[np.tril_indices_from(mask)]=False
fig = plt.gcf()
fig.set_size_inches(20,5)
sns.heatmap(data = cor_mat, mask = mask, square = True, annot = True, cbar = True)
# + papermill={"duration": 0.339075, "end_time": "2020-09-13T08:31:23.359940", "exception": false, "start_time": "2020-09-13T08:31:23.020865", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 483} id="wcFWSVgqkY3E" outputId="0b23f6ca-fa9e-469b-e82a-a9c4b6def9cf"
df1 = df[['Category','Sales']]
df_cat = pd.get_dummies(df1)
cor_mat = df_cat.corr()
mask = np.array(cor_mat)
mask[np.tril_indices_from(mask)]=False
fig = plt.gcf()
fig.set_size_inches(20,5)
sns.heatmap(data = cor_mat, mask = mask, square = True, annot = True, cbar = True)
# + papermill={"duration": 0.367045, "end_time": "2020-09-13T08:31:23.794287", "exception": false, "start_time": "2020-09-13T08:31:23.427242", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 491} id="EER74T8SkY3E" outputId="495a601b-a66c-43fe-b6fe-94e76f836d33"
df1 = df[['Ship Mode','Sales']]
df_cat = pd.get_dummies(df1)
cor_mat = df_cat.corr()
mask = np.array(cor_mat)
mask[np.tril_indices_from(mask)]=False
fig = plt.gcf()
fig.set_size_inches(20,5)
sns.heatmap(data = cor_mat, mask = mask, square = True, annot = True, cbar = True)
# + [markdown] papermill={"duration": 0.095006, "end_time": "2020-09-13T08:31:23.958873", "exception": false, "start_time": "2020-09-13T08:31:23.863867", "status": "completed"} tags=[] id="g5Qj-KURkY3E"
# # Choropleth map
#
# Since the state abbreviation or the latitude and longitude are not given, it is difficult to plot a map. The state abbreviations are added to the respective states and a choropleth map is plotted.
# + papermill={"duration": 0.084549, "end_time": "2020-09-13T08:31:24.112933", "exception": false, "start_time": "2020-09-13T08:31:24.028384", "status": "completed"} tags=[] id="L3xWOlNrkY3E"
state = ['Alabama', 'Arizona' ,'Arkansas', 'California', 'Colorado', 'Connecticut', 'Delaware', 'Florida',
'Georgia', 'Hawaii', 'Idaho', 'Illinois', 'Indiana', 'Iowa', 'Kansas', 'Kentucky', 'Louisiana', 'Maine', 'Maryland',
'Massachusetts', 'Michigan', 'Minnesota', 'Mississippi', 'Missouri', 'Montana','Nebraska', 'Nevada', 'New Hampshire',
'New Jersey', 'New Mexico', 'New York', 'North Carolina', 'North Dakota', 'Ohio', 'Oklahoma', 'Oregon', 'Pennsylvania',
'Rhode Island', 'South Carolina', 'South Dakota', 'Tennessee', 'Texas', 'Utah', 'Vermont', 'Virginia', 'Washington',
'West Virginia', 'Wisconsin','Wyoming']
state_code = ['AL','AZ','AR','CA','CO','CT','DE','FL','GA','HI','ID','IL','IN','IA','KS','KY','LA','ME','MD','MA',
'MI','MN','MS','MO','MT','NE','NV','NH','NJ','NM','NY','NC','ND','OH','OK','OR','PA','RI','SC','SD','TN',
'TX','UT','VT','VA','WA','WV','WI','WY']
# + papermill={"duration": 0.098367, "end_time": "2020-09-13T08:31:24.280645", "exception": false, "start_time": "2020-09-13T08:31:24.182278", "status": "completed"} tags=[] id="rC30rJHIkY3F"
state_df = pd.DataFrame(state, state_code) # Create a dataframe
state_df.reset_index(level=0, inplace=True)
state_df.columns = ['State Code','State']
sales = df.groupby(["State"]).sum().sort_values("Sales", ascending=False)
sales.reset_index(level=0, inplace=True)
sales.drop('Postal Code',1, inplace = True)
sales= sales.sort_values('State', ascending=True)
sales.reset_index(inplace = True)
sales.drop('index',1,inplace = True)
sales.insert(1, 'State Code', state_df['State Code'])
# + papermill={"duration": 0.319553, "end_time": "2020-09-13T08:31:24.669995", "exception": false, "start_time": "2020-09-13T08:31:24.350442", "status": "completed"} tags=[] colab={"base_uri": "https://localhost:8080/", "height": 542} id="YuGHmNAokY3F" outputId="13279653-8b5c-481e-80cc-7a664b4e8702"
import plotly.graph_objects as go
from plotly.offline import init_notebook_mode, plot_mpl
sales['text'] = sales['State']
fig = go.Figure(data=go.Choropleth(
locations=sales['State Code'], # Spatial coordinates
text=sales['text'],
z = sales['Sales'].astype(float), # Data to be color-coded
locationmode = 'USA-states', # set of locations match entries in `locations`
colorscale = 'Reds',
colorbar_title = "Sales",
))
fig.update_layout(
title_text = 'Sales',
geo_scope='usa', # limit map scope to USA
)
fig.show();
# + [markdown] id="ON4WzC_N9Q60"
# Reference: Majority of codes are customized from [Rohit Sahoo,
# EDA Superstore Dataset](https://www.kaggle.com/rohitsahoo/eda-superstore-dataset/data#notebook-container)
# + id="Or3omZCw9SAa"
|
eda/visualisation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: cientista
# language: python
# name: cientista
# ---
# +
from selenium.webdriver import Chrome, ChromeOptions
from selenium.webdriver.chrome.options import Options
from selenium.webdriver.chrome.service import Service
from selenium.webdriver.common.by import By
from pdf2image import convert_from_path
from time import sleep
import requests
import shutil
import os
def purgedir(parent):
for root, dirs, files in os.walk(parent):
for item in files:
filespec = os.path.join(root, item)
os.unlink(filespec)
def inita():
s=Service(r'C:/Users/pdv/chromedriver.exe')
browser = Chrome(service=s)
browser.get('https://www.supermercadosdalben.com.br/ofertas.html')
sleep(3)
body = browser.find_element(By.TAG_NAME, 'body')
img = body.find_elements(By.CLASS_NAME, 'img-responsive ')
img[1].click()
sleep(5)
window_after = browser.window_handles[1]
browser.switch_to.window(window_after)
url = browser.current_url
browser.quit()
response = requests.get(url, stream=True)
with open('C:/Users/pdv/Desktop/selenium-imgs/dalbem.pdf', 'wb') as out_file:
shutil.copyfileobj(response.raw, out_file)
del response
purgedir(f'C:/Users/pdv/Desktop/selenium-imgs/rename')
images = convert_from_path('C:/Users/pdv/Desktop/selenium-imgs/dalbem.pdf',
poppler_path=r'C:\Program Files (x86)\poppler-21.11.0\Library\bin',
output_folder='C:/Users/pdv/Desktop/selenium-imgs/rename',
fmt='PNG')
for i in range(len(images)):
images[i].save('pagina'+ str(i) +'.png', 'PNG')
print('page')
return 1
if __name__ == "__main__":
inita()
# -
|
dalbem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="fI_VRq2nbJBv"
# # Transfer Learning with CNN - <NAME>
# + [markdown] colab_type="text" id="TVxkvIFJbZxF"
# Este documento corresponde a la entrega práctica final de la asignatura de cuarto curso: Computación bioinspirada. Corresponde a la entrega de dificultad media establecida. Trata sobre la realización de una red neuronal convolucional que se ajuste al dataset *CIFAR 10* (de la web: [skymind.ai/wiki/open-datasets](https://skymind.ai/wiki/open-datasets)) para la clasificación de los datos en al menos 4 categorías. Se pide realizar la práctica mediante la técnica de transferencia de aprendizaje.
# + [markdown] colab_type="toc" id="iiDWK93rdS_f"
# >[Transfer Learning with CNN - <NAME>](#scrollTo=fI_VRq2nbJBv)
#
# >>[Planificación del proyecto](#scrollTo=7ge5_Xb5detx)
#
# >>[Parte teórica](#scrollTo=8gtFcyoxih9m)
#
# >>>[¿Qué es una CNN (Convolutional neural network)?](#scrollTo=S4NQhRMGjIHf)
#
# >>>>[¿Qué es una convolución?](#scrollTo=FV3RNt8FsANg)
#
# >>>>[¿Qué es el pooling?](#scrollTo=q8-hdh6213fe)
#
# >>>[¿Qué es la técnica de transferencia de aprendizaje?](#scrollTo=btIngNC08om6)
#
# >>>>[¿Cuándo y cómo afinar? ¿Cómo decidimos qué modelo utilizar?](#scrollTo=Y2TJf6d0GtBN)
#
# >>>[Pero, ¿qué es el overfitting?](#scrollTo=kr7BM_Yf2Be8)
#
# >>>>[¿Cuándo tenemos riesgo de overfitting?](#scrollTo=dQG8JZXY3UgX)
#
# >>>>[¿Cómo prevenir el sobreajuste de datos?](#scrollTo=VJuPnTKt5DLn)
#
# >>>>[¿Técnicas para solucionar el overfitting?](#scrollTo=_Mf5zjlWvy7R)
#
# >>[Parte práctica](#scrollTo=CwYJC2SX6FVP)
#
# >>>[¿Qué modelo se ha escogido?](#scrollTo=1DN0W2pJ6cDZ)
#
# >>>[Análisis de tareas](#scrollTo=rNKudQoJ1V5t)
#
# >>>>[Descarga y almacenamiento del dataset](#scrollTo=dggtw2G23GnV)
#
# >>>>[Entrenamiento del pre-modelo.](#scrollTo=HzjC7SaPeVHi)
#
# >>>>[Entrenamiento del modelo con los pesos pre-entrenados.](#scrollTo=ReBf5Bm9QLyo)
#
# >>>>[Visualización de los resultados obtenidos.](#scrollTo=GBrdnCKDtWkl)
#
# >>>>[Guardado del modelo](#scrollTo=wGTJeG7abbct)
#
# >>[Conclusiones](#scrollTo=B3cuziDLLdxL)
#
#
# + [markdown] colab_type="text" id="7ge5_Xb5detx"
# ## Planificación del proyecto
# + [markdown] colab_type="text" id="kPJ7uQNUdjpv"
# Puesto que este documento es el proyecto final de la asignatura y se consta de un mes para su entrega, es necesario de planificar el transcurso de desarrollo. Para ello se dividirá el documento en: parte teórica y parte práctica. La parte teórica será realizada al inicio de la elaboración y constará de:
#
# * ¿Qué es una CNN (Convolutional neural networks)?
# * ¿Qué es una convolución?
# * ¿Qué es el pooling?
# * ¿Qué es la técnica de transferencia de aprendizaje?
# * ¿Cuándo y cómo afinar? ¿Cómo decidimos qué modelo utilizar?
# * Pero, ¿qué es el overfitting?
# * ¿Cuando tenemos riesgo de overfitting?
# * ¿Cómo prevenir el sobreajuste de datos?
# * ¿Técnicas para solucionar el overfitting?
#
# En la parte práctica se desarrollará la red, ayudándonos de gráficas para ver el correcto funcionamiento de ella. Los puntos que se introducirán se verán más abajo.
# + [markdown] colab_type="text" id="8gtFcyoxih9m"
# ## Parte teórica
# + [markdown] colab_type="text" id="7bQJVDE2isp7"
# Se necesita una guía teórica para poder entender la resolución práctica del proyecto desarrollado más adelante. Por ello, a continuación se detalla los diferentes conceptos que nos van a servir de utilidad para descifrar el código mostrado en la parte teórica.
# + [markdown] colab_type="text" id="S4NQhRMGjIHf"
# ### ¿Qué es una CNN (Convolutional neural network)?
# + [markdown] colab_type="text" id="LAn0ptcmjUY3"
# Una red neuronal convolucional es un tipo de red neuronal artificial donde las neuronas corresponden a campos receptivos de una manera muy similar a las neuronas en la corteza visual primaria de un cerebro biológico. Este tipo de red es una variación de un perceptron multicapa, sin embargo, debido a que su aplicación es realizada en matrices bidimensionales, son muy efectivas para tareas de visión artificial, como en la clasificación y segmentación de imágenes, entre otras aplicaciones.
#
# 
#
# En la imagen anterior tenemos una representación muy básica de lo que es una CNN. Este tipo de red se compone de:
#
# 1. Una capa de entrada (imagen)
# 2. Varias capas alternas de convolución y reducción (pooling).
# 3. Una ANN clasificatoria.
#
# Las redes neuronales convolucionales consisten en múltiples capas de filtros convolucionales de una o más dimensiones. Después de cada capa, por lo general se añade una función para realizar un mapeo causal no-lineal.
#
# Como redes de clasificación, al principio se encuentra la fase de extracción de características, compuesta de neuronas convolucionales y de reducción de muestreo. Al final de la red se encuentran neuronas de perceptron sencillas para realizar la clasificación final sobre las características extraídas. La fase de extracción de características se asemeja al proceso estimulante en las células de la corteza visual. Esta fase se compone de capas alternas de neuronas convolucionales y neuronas de reducción de muestreo. Según progresan los datos a lo largo de esta fase, se disminuye su dimensionalidad, siendo las neuronas en capas lejanas mucho menos sensibles a perturbaciones en los datos de entrada, pero al mismo tiempo siendo estas activadas por características cada vez más complejas.
#
# 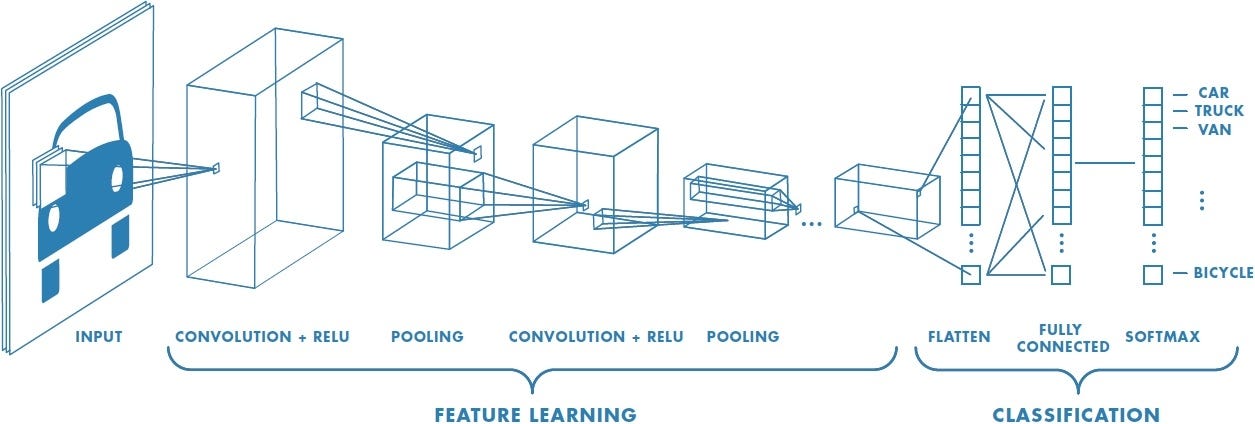
#
# Por lo tanto, tenemos dos conceptos importantes que aprender, qué es una convolución y qué es el pooling.
# + [markdown] colab_type="text" id="FV3RNt8FsANg"
# #### ¿Qué es una convolución?
# + [markdown] colab_type="text" id="HFOZSAZlsNpX"
# Una convolución es la suma ponderada de una región de entrada por una matriz de pesos. Una definición más práctica: "Es el producto matricial para cada pixel de la imagen de entrada". ¿Pero para qué nos sirve la convolución? El operador de convolución tiene el efecto de filtrar la imagen de entrada con un núcleo previamente entrenado. Esto transforma los datos de tal manera que ciertas características (determinadas por la forma del núcleo) se vuelven más dominantes en la imagen de salida al tener estas un valor numérico más alto asignados a los pixeles que las representan. Estos núcleos tienen habilidades de procesamiento de imágenes específicas, como por ejemplo la detección de bordes que se puede realizar con núcleos que resaltan la gradiente en una dirección en particular.
#
# **En resumen, aplicamos la convolución para obtener las características más importantes (según el kernel proporcionado) de la entrada que le pasemos.**
#
# 
# + [markdown] colab_type="text" id="q8-hdh6213fe"
# #### ¿Qué es el pooling?
# + [markdown] colab_type="text" id="soX1EpzJ174P"
# La capa de reducción o pooling se coloca generalmente después de la capa convolucional. **Su utilidad principal radica en la reducción de las dimensiones espaciales (ancho x alto) del volumen de entrada para la siguiente capa convolucional**. No afecta a la dimensión de profundidad del volumen. La operación realizada por esta capa también se llama reducción de muestreo, ya que la reducción de tamaño conduce también a la pérdida de información. Sin embargo, una pérdida de este tipo puede ser beneficioso para la red por dos razones:
#
# * Disminución en el tamaño conduce a una menor sobrecarga de cálculo para las próximas capas de la red.
# * Reducir el overfitting.
#
# Las redes neuronales cuentan con cierta tolerancia a pequeñas perturbaciones en los datos de entrada. Por ejemplo, si dos imágenes casi idénticas (diferenciadas únicamente por un traslado de algunos pixeles lateralmente) se analizan con una red neuronal, el resultado debería de ser esencialmente el mismo. Esto se obtiene, en parte, dado a la reducción de muestreo que ocurre dentro de una red neuronal convolucional. Al reducir la resolución, las mismas características corresponderán a un mayor campo de activación en la imagen de entrada.
#
# Originalmente, las redes neuronales convolucionales utilizaban un proceso de subsampling para llevar a cabo esta operación. Sin embargo, estudio recientes han demostrado que otras operaciones, como por ejemplo max-pooling, son mucho más eficaces en resumir características sobre una región. Además, existe evidencia que este tipo de operación es similar a como la corteza visual puede resumir información internamente.
#
# La operación de max-pooling encuentra el valor máximo entre una ventana de muestra y pasa este valor como resumen de características sobre esa área. Como resultado, el tamaño de los datos se reduce por un factor igual al tamaño de la ventana de muestra sobre la cual se opera.
#
# 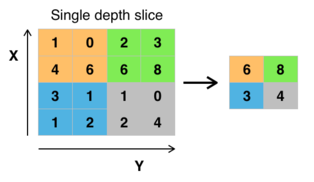
# + [markdown] colab_type="text" id="btIngNC08om6"
# ### ¿Qué es la técnica de transferencia de aprendizaje?
# + [markdown] colab_type="text" id="tc4XRKJH8wuR"
# En la práctica es muy difícil entrenar un modelo desde cero. Esto se debe a que es difícil encontrar conjuntos de datos lo suficientemente grandes como para lograr una buena precisión en las predicciones debido al sobreajuste que sufren las redes neuronales. Aquí es cuando debemos aplicar una técnica conocida como transferencia de conocimiento: Esta se basa en el uso de modelos previamente entrenados (Oquab et al., 2014).
#
# Las redes neuronales convolucionales requieren grandes conjuntos de datos y una gran cantidad de tiempo
# para entrenar. Algunas redes pueden tomar hasta 2-3 semanas a través de múltiples GPU para entrenar.
# La transferencia de aprendizaje es una técnica muy útil que trata de abordar ambos problemas.
# En lugar de entrenar la red desde cero, la transferencia de aprendizaje utiliza un modelo entrenado en un
# conjunto de datos diferente, y lo adapta al problema que estamos tratando de resolver.
#
# Existen dos estrategias para ello:
#
# * *Utilizar el modelo entrenado como un extractor de características fijas*: En esta estrategia, se elimina la
# última capa full-connected del modelo entrenado, congelamos los pesos de las capas restantes, y
# hacemos, a medida, un clasificador de aprendizaje automático en la salida de las capas convolucionales.
# * *Afinar el modelo entrenado*: Partiendo de un modelo entrenado, lo seguimos entrenando con las
# imágenes de nuestro problemas para intentar especializarlo en nuestro objetivo.
#
# En las redes neuronales de las primeras capas obtenemos características de bajo nivel como los bordes para luego, en las capas posteriores, capturar las de alto nivel. Al utilizar modelos previamente entrenados, aprovechamos las características de bajo nivel y resolvemos el problema del sobreajuste. Además, reducimos la carga de entrenamiento que tienen un alto costo computacional para los modelos más complejos.
#
# 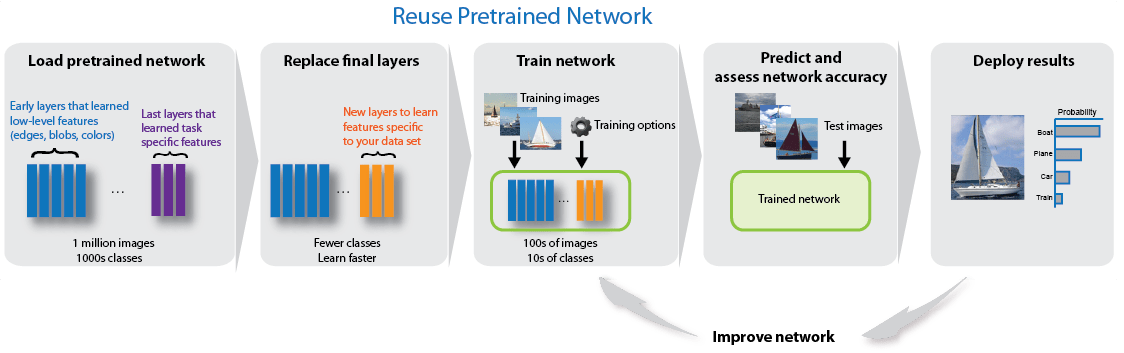
#
#
# + [markdown] colab_type="text" id="Y2TJf6d0GtBN"
# #### ¿Cuándo y cómo afinar? ¿Cómo decidimos qué modelo utilizar?
# + [markdown] colab_type="text" id="ErOZ-fxCG46z"
# Esta es una función de varios factores, pero los dos más importantes son:
# * El tamaño del nuevo conjunto de datos (pequeño o grande)
# * Su similitud con el conjunto de datos original de la red anfitrion.
#
# Teniendo en cuenta que los kernels de la CNN son más genéricos en las capas iniciales y más específicos (del
# conjunto de datos original) en las capas finales, tenemos cuatro escenarios:
#
# 1. **El nuevo conjunto de datos es pequeño y similar al conjunto de datos original**. Debido a que los datos
# son pequeños, no es una buena idea ajustar la CNN debido a problemas de overfitting. Dado que los
# datos son similares a los datos originales, esperamos que los kernels de nivel superior en CNN también
# sean relevantes para este conjunto de datos. Por lo tanto, la mejor idea podría ser entrenar un
# clasificador lineal final adaptado para nuestro caso.
#
# 2. **El nuevo conjunto de datos es grande y similar al conjunto de datos original**. Ya que tenemos más datos,
# si entrenamos la red completa es probable que no generemos overfitting.
#
# 3. **El nuevo conjunto de datos es pequeño y muy diferente del conjunto de datos original**. Como los datos
# son pequeños, es probable que sea mejor entrenar solo un clasificador lineal. Como el conjunto de datos
# es muy diferente, los kernels de capas superiores no van a ser relevantes por lo que vaciar los pesos de
# estos kernels e intentar el entrenamiento es lo más recomendable.
#
# 4. **El nuevo conjunto de datos es grande y muy diferente del conjunto de datos original**. Dado que el
# conjunto de datos es muy grande, podemos entrenar la red desde cero aunque la capas iniciales pueden
# ser provechosas por lo que estos pesos nos pueden venir bien.
# + [markdown] colab_type="text" id="kr7BM_Yf2Be8"
# ### Pero, ¿qué es el overfitting?
# + [markdown] colab_type="text" id="JMx1NNWx2eom"
# El overfitting es el efecto de sobreentrenar un algoritmo de aprendizaje con unos ciertos datos para los que se conoce el resultado deseado. El algoritmo de aprendizaje debe alcanzar un estado en el que será capaz de predecir el resultado en otros casos a partir de lo aprendido con los datos de entrenamiento, generalizando para poder resolver situaciones distintas a las acaecidas durante el entrenamiento. Sin embargo, cuando un sistema se entrena demasiado (se sobreentrena) o se entrena con datos extraños, el algoritmo de aprendizaje puede quedar ajustado a unas características muy específicas de los datos de entrenamiento que no tienen relación causal con la función objetivo. Durante la fase de sobreajuste el éxito al responder las muestras de entrenamiento sigue incrementándose mientras que su actuación con muestras nuevas va empeorando.
#
# 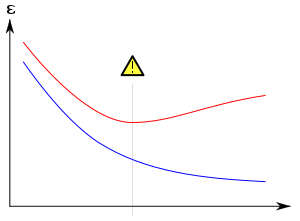
#
# El error de entrenamiento se muestra en azul, mientras que el error de validación se muestra en rojo. Si el error de validación se incrementa mientras que el de entrenamiento decrece puede que se esté produciendo una situación de sobreajuste.
# + [markdown] colab_type="text" id="dQG8JZXY3UgX"
# #### ¿Cuándo tenemos riesgo de overfitting?
# + [markdown] colab_type="text" id="SiFoSr1p3uZp"
# La primera es que debe existir un equilibrio entre la cantidad de datos que tenemos y la complejidad del modelo. En nuestro ejemplo, cuando usamos un modelo con 10 parámetros para describir un problema para el que tenemos 10 datos, el resultado es previsible: vamos a construir un modelo a medida de los datos que tenemos, estamos resolviendo un sistema de ecuaciones con tantas incógnitas como ecuaciones. Dicho de otra manera: si este modelo con 10 parámetros lo hubiésemos ajustado con un total de 100 datos en lugar de 10, seguramente funcionaría mejor que un modelo más básico.
#
# 
# + [markdown] colab_type="text" id="VJuPnTKt5DLn"
# #### ¿Cómo prevenir el sobreajuste de datos?
# + [markdown] colab_type="text" id="9YlKcmCT5NCz"
# Para intentar que estos problemas nos afecten lo menos posible, podemos llevar a cabo diversas acciones.
#
# * **Cantidad mínima de muestras tanto para entrenar el modelo como para validarlo**.
# * **Clases variadas y equilibradas en cantidad**: En caso de aprendizaje supervisado y suponiendo que tenemos que clasificar diversas clases o categorías, es importante que los datos de entrenamiento estén balanceados. Supongamos que tenemos que diferenciar entre manzanas, peras y bananas, debemos tener muchas fotos de las 3 frutas y en cantidades similares. Si tenemos muy pocas fotos de peras, esto afectará en el aprendizaje de nuestro algoritmo para identificar esa fruta.
# * **Conjunto de validación de datos**. Siempre subdividir nuestro conjunto de datos y mantener una porción del mismo “oculto” a nuestra máquina entrenada. Esto nos permitirá obtener una valoración de aciertos/fallos real del modelo y también nos permitirá detectar fácilmente efectos del overfitting /underfitting.
# * **Parameter Tunning o Ajuste de Parámetros**: deberemos experimentar sobre todo dando más/menos “tiempo/iteraciones” al entrenamiento y su aprendizaje hasta encontrar el equilibrio.
# * **Cantidad excesiva de Dimensiones (features), con muchas variantes distintas, sin suficientes muestras**. A veces conviene eliminar o reducir la cantidad de características que utilizaremos para entrenar el modelo. Una herramienta útil para hacerlo es PCA.
# * Podemos caer en overfitting si usamos **capas ocultas en exceso**, ya que haríamos que el modelo memorice las posibles salidas, en vez de ser flexible y adecuar las activaciones a las entradas nuevas.
# + [markdown] colab_type="text" id="_Mf5zjlWvy7R"
# #### ¿Técnicas para solucionar el overfitting?
# + [markdown] colab_type="text" id="C8-7egx7v3AI"
# Para conseguir un modelo que generalice bien es importante prestar atención a la arquitectura empleada.
# La cantidad de capas, la elección de capas, el ajuste de los hiperparámetros y el uso de
# técnicas de prevención de overfitting es esencial.
# Este proceso recibe el nombre de regularización y existen múltiples técnicas para llevarlo a cabo.
# Algunas de las más exitosas son:
# * Data augmentation
# * Regularización de pesos: L1, L2 y elastic net regularization
# * Máximum norm constraints
# * Dropout
# * Early stopping
# + [markdown] colab_type="text" id="CwYJC2SX6FVP"
# ## Parte práctica
# + [markdown] colab_type="text" id="CRe0t0Bv6LAJ"
# Una vez visto todos los conceptos necesarios para poder entender lo descrito a continuación, procedemos a explicar paso a paso el desarrollo del proyecto práctico.
# + [markdown] colab_type="text" id="1DN0W2pJ6cDZ"
# ### ¿Qué modelo se ha escogido?
# + [markdown] colab_type="text" id="d5V_kn1aox9j"
# Keras cuenta con varios modelos pre-entrenados que podemos usar en transfer
# learning:
#
# * Xception
# * VGG16
# * VGG19
# * ResNet50
# * InceptionV3
# * InceptionResNetV2
# * MobileNet
# * DenseNet
# * NASNet
#
# Para escoger qué modelo utilizar debemos ver las características existentes en el dataset proporcionado; se ha escogido el dataset proporcionado en la página [skymind.ai/wiki/open-datasets](https://skymind.ai/wiki/open-datasets); se ha elegido el dataset *CIFAR 10*.
# 
#
# FInalmente, el modelo escogido será ResNet50. La explicación más sencilla posible de su elección son los buenos resultados obtenidos en las primeras pruebas. Una explicación más formada es lo definido anteriormente en la parte teórica: en nuestro caso el conjunto de datos (CIFAR 10) es grande y algo similar a los datos del pre-modelo, coincidiendo algunas clases y teniendo otras similares. Aunque no es el mejor pre-modelo que podemos escoger para este dataset, se intentarán obtener los mejores resultados posibles.
#
#
# 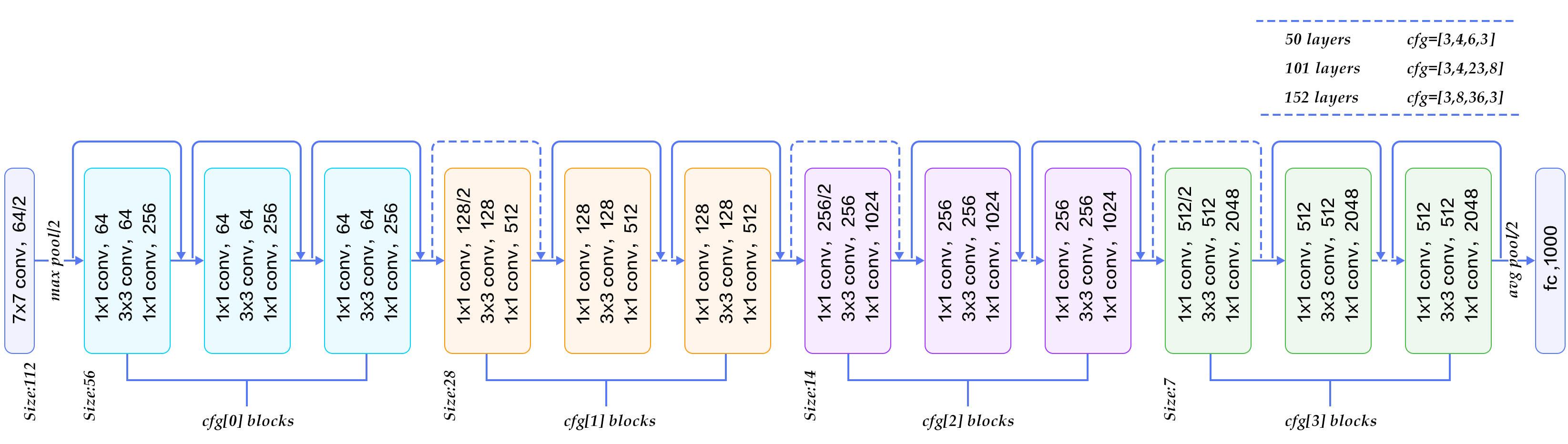
# + [markdown] colab_type="text" id="rNKudQoJ1V5t"
# ### Análisis de tareas
# + [markdown] colab_type="text" id="P8SBpNjB1bRS"
# Para tener una mayor organización en torno a la información del proyecto, definiremos diferentes puntos para encontrar más facilmente en qué posición nos encontramos.
#
# 1. Descarga y almacenamiento del dataset.
# 2. Entrenamiento del pre-modelo.
# 3. Entrenamiento del modelo con los pesos pre-entrenados.
# 4. Visualización de los resultados obtenidos.
# 5. Guardado del modelo
# + [markdown] colab_type="text" id="dggtw2G23GnV"
# #### Descarga y almacenamiento del dataset
# + [markdown] colab_type="text" id="XSWkAKfftQrJ"
# Keras nos ofrece la posibilidad de importar el dataset CIFAR10 de una manera más sencilla. Aunque también existe la posibilidad de descargar los datos mediante la invocación *wget* a la URL de [skymind.ai/wiki/open-datasets](https://skymind.ai/wiki/open-datasets); aunque de este modo (wget) será algo más complejo.
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="v0CnaIqY47bR" outputId="6e269cc4-4dcf-4a65-faa1-efb4da89a7af"
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
# + [markdown] colab_type="text" id="wphabBt8m6Ew"
# Una vez importados, podemos ver el tamaño de las imágenes descargadas; con esto sabremos qué dimensión poner de entrada y si es necesario redimensionarlas.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="y7LjObKlm-1t" outputId="43488f5f-db36-45f2-d1a8-ccacfccf29ee"
import numpy as np
print("Existen {} imágenes de entrenamiento y {} imágenes de test.".format(x_train.shape[0], x_test.shape[0]))
print('Hay {} clases únicas para predecir.'.format(np.unique(y_train).shape[0]))
# + [markdown] colab_type="text" id="bwaf1qzGoHAP"
# Es necesario etiquetar cada salida. Como tenemos 10 clases que clasificar, deberemos etiquetar cada salida con un array de 10 valores; los cuales pueden estar en 0 o 1, sólo puede haber una con el valor positivo (etiqueta correcta).
#
# CIFAR 10 tiene 10 clases para poder clasificarlas, como en el proyecto se nos pide al menos 4, se ha decidido implementar las 10 clases que tenemos disponible.
# + colab={} colab_type="code" id="fRD0B7gGohBm"
from keras.utils import np_utils
y_train = np_utils.to_categorical(y_train, 10)
y_test = np_utils.to_categorical(y_test, 10)
# + [markdown] colab_type="text" id="mGbFVXY1ouTG"
# Finalmente, podemos ver que se han descargado correctamente los datos con la función 'imshow' de la librería matplot.
# + colab={"base_uri": "https://localhost:8080/", "height": 485} colab_type="code" id="wknL-COlo8bz" outputId="34baee4b-d4c2-49ed-8fe5-50d4a1455c0f"
from matplotlib import pyplot as plt
fig = plt.figure(figsize=(10, 10))
for i in range(1, 9):
img = x_train[i-1]
fig.add_subplot(2, 4, i)
plt.imshow(img)
print("Dimensiones de las imágenes: ", x_train.shape[1:])
# + [markdown] colab_type="text" id="HzjC7SaPeVHi"
# #### Entrenamiento del pre-modelo.
# + [markdown] colab_type="text" id="LI7qpLQnqbQ6"
# Una vez descargado el dataset para el proyecto, importaremos el pre-modelo que se va a utilizar.
# + colab={"base_uri": "https://localhost:8080/", "height": 6412} colab_type="code" id="FyGhCR0aqwxL" outputId="cf9e83a8-6c4e-4e00-956c-1cd34bf39311"
from keras.applications.resnet50 import ResNet50
height = 64
width = 64
premodel = ResNet50(weights='imagenet', include_top=False, input_shape=(height, width, 3))
premodel.summary()
# + [markdown] colab_type="text" id="O2SM0l1Fq2uc"
# Como hemos visto en el apartado anterior, las dimensiones de la imagen eran de 32x32x3, y por lo tanto no coincide con las dimensiones de entrada que le hemos asignado al pre-modelo. **Es decir, es necesario que reescalar las dimensiones del dataset.**
#
# Otro punto a definir es la invocación al pre-modelo con el parámetro 'include_top' igual a 'False'. *¿Por qué se hace esto?* El modelo ResNet50 está entrenado con el dataset 'imagenet', y clasifica entre imágenes que no coinciden con el dataset escogido. Por lo que, es necesario que la última capa de la red sea creada para especializarse en las clases de CIFAR10.
# + colab={} colab_type="code" id="0HYbCsdVr2aL"
from scipy.misc import imresize
import numpy as np
def resize(images) :
X = np.zeros((images.shape[0],height,width,3))
for i in range(images.shape[0]):
X[i]= imresize(images[i], (height,width,3), interp='bilinear', mode=None)
return X
x_train_new = x_train.astype('float32')
x_test_new = x_test.astype('float32')
x_train_new = resize(x_train_new)
x_test_new = resize(x_test_new)
# + [markdown] colab_type="text" id="d_p7Ig18URLe"
# Una vez que tenemos las imágenes redimensionadas y normalizadas podremos llamar a la instrucción «predict» que nos devolverá el kernel con dimesión de {H x W x C}. Esto lo hacemos con los vectores: x_train y x_test.
# + colab={} colab_type="code" id="DWQbSYgutbW1"
from keras.applications.resnet50 import preprocess_input
resnet_train_input = preprocess_input(x_train_new)
train_features = premodel.predict(resnet_train_input)
# + [markdown] colab_type="text" id="KTX5xQG3utta"
# Haremos lo mismo con el conjunto de test.
# + colab={} colab_type="code" id="opga7P74u0GS"
resnet_test_input = preprocess_input(x_test_new)
test_features = premodel.predict(resnet_test_input)
# + [markdown] colab_type="text" id="qy6hgEMl-WFx"
# A partir de aquí, tenemos como resultados las imágenes predecidas por el pre-modelo. Estas imágenes en realidad se tratan de los kernels que residen en el interior de ella, puesto que no existe ninguna capa de clasificación (las hemos retirado al invocar el modelo).
# + [markdown] colab_type="text" id="ReBf5Bm9QLyo"
# #### Entrenamiento del modelo con los pesos pre-entrenados.
# + [markdown] colab_type="text" id="dEzu1V91QPJG"
# Una vez que el pre-modelo nos ha dado sus predicciones, crearemos el modelo expecífico para nuestro dataset. Para ello crearemos una ANN, con varias capas densas, y utilizando la técnica de Dropout (para prevenir el overfitting).
# + colab={"base_uri": "https://localhost:8080/", "height": 340} colab_type="code" id="iC2fjrCc_Bwp" outputId="452cb23d-480b-452a-f41d-c4919bc42062"
from keras.layers import Input, GlobalAveragePooling2D, Dense,Dropout
from keras.models import Model, Sequential
model = Sequential()
model.add(GlobalAveragePooling2D(input_shape=train_features.shape[1:]))
model.add(Dense(2048, activation='relu', name='fc1'))
model.add(Dropout(0.3))
model.add(Dense(1024, activation='relu', name='fc2'))
model.add(Dropout(0.3))
model.add(Dense(10, activation='softmax'))
model.summary()
# + [markdown] colab_type="text" id="qox62njM_eEw"
# Puesto que la capa «GlobalAveragePooling2D» es relativamente actual y nueva, se necesita dar una pequeña explicación sobre ella. Entonces, **¿qué hace el Global Average Pool?**
#
# El tamaño del kernel es de dimensiones { H x W }; por lo tanto, toma la media global a través de altura y ancho, y le da un tensor con dimensiones de { 1 x C } para una entrada de { H x W x C }; en resumen, redimensiona el kernel de la última capa que nos llega del pre-modelo en un formato correcto para poder introducir una capa Dense (en nuestro caso se introduciría directamente a la «softmax»). Una vez definido el modelo, procedemos a compilarlo.
#
# Una vez tenemos el modelo creado. Unicamente tenemos que compilarlo y empezar a entrenarlo. Como optimizador se ha escogido el «*sgd*», el cual ha sido elegido debido a su buen funcionamiento a gran escala; es decir, como tenemos aproximadamente unos 6,5 millones de parámetros a entrenar, este optimizador nos viene a la perfección debido a la gran cantidad de actualizaciones que habrá en los parámetros.
# + colab={} colab_type="code" id="c2eeilN0_g5J"
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
# + [markdown] colab_type="text" id="sPlZwpjN_mcU"
# Y por último, terminamos entrenando el modelo y comprobamos si existe overfitting o algún tipo de problema. El tamaño del lote se ha escogido a base de prueba y error; lo mismo para el número de épocas.
# + colab={"base_uri": "https://localhost:8080/", "height": 272} colab_type="code" id="1WduuVpf_ts6" outputId="0f1bb8ca-ef63-43ec-8026-cf77f362ad2f"
history = model.fit(train_features, y_train, batch_size=256, epochs=7, validation_split=0.2, verbose=1, shuffle=True)
# + [markdown] colab_type="text" id="GBrdnCKDtWkl"
# #### Visualización de los resultados obtenidos.
# + [markdown] colab_type="text" id="U77E1odsAOu2"
# Una vez que tenemos el modelo entrenado, podemos ver las gráficas. En este caso, no se percibe la existencia de overfitting; el error de validación y de entrenamiento es muy parejo, y sólo nos haría falta ver el accuracy que puede llegar a conseguir la red.
# + colab={"base_uri": "https://localhost:8080/", "height": 376} colab_type="code" id="FG4xMOQkATHF" outputId="9902188e-c613-452d-edb8-4df5f9ab57ec"
ent_loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(ent_loss) + 1)
plt.plot(epochs, ent_loss, 'b', label='Training')
plt.plot(epochs, val_loss, 'r', label='Validation')
plt.title('Loss of Training and Validation')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + [markdown] colab_type="text" id="K16c6pdqXmFj"
# Finalmente, se puede comprobar el porcentaje de acierto que llega a obtener la red.
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="b259e5CocQPI" outputId="936e0bb2-9a1b-444f-e0eb-b412f69a00c1"
score = model.evaluate(test_features, y_test)
print('Accuracy on the Test Images: ', score[1])
# + [markdown] colab_type="text" id="wGTJeG7abbct"
# #### Guardado del modelo
# + [markdown] colab_type="text" id="rw0gDRErbeBk"
# Una vez que hemos comprobado que nuestro modelo está bien implementado y operable. Podemos pasar al guardado de la topología y de sus pesos. Este guardado irá destinado al disco duro de nuestro ordenador personal, en el cual reside el programa gráfico que se ha implementado.
# + colab={} colab_type="code" id="t196eu8zcBEe"
model.save('model.h5')
# + [markdown] colab_type="text" id="B3cuziDLLdxL"
# ## Conclusiones
# + [markdown] colab_type="text" id="pg59BviQLfbZ"
# Este tipo de técnica es de las más raras que se pueden ver por papers, artículos científicos, etc., pero podemos ver que una ventaja que tiene es la rápidez con la que podemos entrenarla. Los resultados obtenidos no son muy buenos, aunque tampoco malos; el nivel de ajuste llega a ser perfecto, pero el porcentaje de acierto: 77%, es bajo con respecto a lo que puede conseguir la técnica de Transfer Learning.
#
# Aún así, se puede llegar a estar contento con el ajuste conseguido puesto que es la primera red convolucional realizada mediante esta técnica.
|
Transfer Learning with Convolutional Neural Networks - Dificultad media/Transfer Learning with Convolutional Neural Networks - CIFAR10 - Primera parte.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
df = pd.read_csv('data/total.csv')
df.head()
df['datetime'] = df.year.astype('str') + '-' + df.month.astype('str')
df['datetime'] = pd.to_datetime(df.datetime).astype('str')
df['datetime'] = df.datetime.str[:7]
df
df.city.value_counts()
df.groupby('city').agg('count').sort_values('nr').head(55)
df
gemeinden = {
"Ausservillgraten": "Außervillgraten",
"Außervillgraten": "Außervillgraten",
"Buch bei Jenbach": "Buch in Tirol",
"Buch in Tirol": "Buch in Tirol",
"Elbigenalp": "Elbigenalp",
"Elbingenalp": "Elbigenalp",
"Going am Wilden Kaiser": "Going am Wilden Kaiser",
"Going/Wilden Kaiser": "Going am Wilden Kaiser",
"Hopfgarten im Brixenta": "Hopfgarten im Brixental",
"Hopfgarten in Deferegg": "Hopfgarten in Defereggen",
"Hopfgarten/Brixental": "Hopfgarten im Brixental",
"Hopfgarten/Defereggen": "Hopfgarten in Defereggen",
"Nussdorf-Debant": "Nußdorf-Debant",
"Nußdorf-Debant": "Nußdorf-Debant",
"Obernberg": "Obernberg am Brenner",
"Obernberg am Brenner": "Obernberg am Brenner",
"Prägraten": "Prägraten am Großvenediger",
"Prägraten am Großvened": "Prägraten am Großvenediger",
"Scheffau": "Scheffau am Wilden Kaiser",
"Scheffau am Wilden Kai": "Scheffau am Wilden Kaiser",
"Scheffau/Wild.Kaiser": "Scheffau am Wilden Kaiser",
"Schönberg im Stubaital": "Schönberg im Stubaital",
"Schönberg/Stubaital": "Schönberg im Stubaital",
"Silz": "Silz",
"Silz inkl. Kühtai": "Silz",
"St. Anton am Arlberg": "St. Anton am Arlberg",
"St. Jakob in Deferegge": "St. Jakob in Defereggen",
"St. Jakob in Haus": "St. Jakob in Haus",
"St. Johann im Walde": "St. Johann im Walde",
"St. Johann in Tirol": "St. Johann in Tirol",
"St. Leonhard im Pitzta": "St. Leonhard im Pitztal",
"St. Sigmund im Sellrai": "St. Sigmund im Sellrain",
"St. Ulrich am Pillerse": "St. Ulrich am Pillersee",
"St. Veit in Defereggen": "St. Veit in Defereggen",
"St.Anton am Arlberg": "St. Anton am Arlberg",
"St.Jakob in Haus": "St. Jakob in Haus",
"St.Jakob/Defereggen": "St. Jakob in Defereggen",
"St.Johann am Walde": "St. Johann im Walde",
"St.Johann im Walde": "St. Johann im Walde",
"St.Johann in Tirol": "St. Johann in Tirol",
"St.Leonhard/Pitztal": "St. Leonhard im Pitztal",
"St.Sigmund/Sellrain": "St. Sigmund im Sellrain",
"St.Ulrich/Pillersee": "St. Ulrich am Pillersee",
"St.Veit in Defereggen": "St. Veit in Defereggen",
"Steinach": "Steinach am Brenner",
"Steinach am Brenner": "Steinach am Brenner",
"Steinach/Brenner": "Steinach am Brenner",
"Telfes im Stubai": "Telfes im Stubai",
"Telfes im Stubaital": "Telfes im Stubai",
"Weissenbach": "Weißenbach am Lech",
"Weissenbach am Lech": "Weißenbach am Lech",
"Weißenbach am Lech": "Weißenbach am Lech"
}
len(gemeinden)
df['gemeinde'] = df.city.map(gemeinden)
df.head()
df.gemeinde.fillna(df.city, inplace=True)
df
df.city.value_counts()
df.gemeinde.value_counts()
df_2 = df[['gemeinde', 'datetime', 'overnight_stays', 'bezirk']]
df_2.columns = ['Gemeinde', 'Monat', 'Nächtigungen', 'Bezirk']
df_2.reset_index(drop=True, inplace=True)
df_2
df_2
df_2.Bezirk.unique()
bezirke = {
'I': 'Be<NAME>',
'IM': 'Bezirk Imst',
'IL': 'Bezirk Innsbruck-Land',
'KB': 'Bezirk Kitzbühel',
'KU': '<NAME>',
'LA': 'Bez<NAME>',
'LZ': 'Bezirk Lienz',
'RE': '<NAME>',
'SZ': '<NAME>'
}
df_2.Bezirk = df_2.Bezirk.map(bezirke)
df_2
df_2['Bundesland'] = 'Tyrol'
df_2['Staat'] = 'Österreich'
df_2['Kontinent'] = 'Europa'
df_2
plz = pd.read_csv('data/plz_2.csv')
plz
df_2 = pd.merge(df_2, plz, how='inner', on='Gemeinde').drop_duplicates()
df_2.PLZ = df_2.PLZ.astype('str')
df_2.PLZ = df_2.PLZ + ', Österreich'
df_2['City'] = df_2.Gemeinde + ', Austria'
df_2.Gemeinde.value_counts()
df_2
cities = df_2.City.unique()
from geopy.geocoders import Nominatim
geolocator = Nominatim(user_agent="specify_your_app_name_here")
import time
# +
latitudes = []
longitudes = []
for city in cities:
print(city)
location = geolocator.geocode(city)
latitudes.append(location.latitude)
longitudes.append(location.longitude)
time.sleep(0.3)
# -
lat_long = pd.DataFrame()
lat_long['City'] = cities
lat_long['Latitude'] = latitudes
lat_long['Longitude'] = longitudes
lat_long
df_2 = pd.merge(df_2, lat_long, on='City', how='inner')
np.min(df_2.Latitude), np.max(df_2.Latitude)
np.min(df_2.Longitude), np.max(df_2.Longitude)
df_2.to_csv('tirol-nächtigungen-2000-2018.csv', index=False, sep=';')
|
5-mapping-duplicate-municipals.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ML Pipeline Preparation
# Follow the instructions below to help you create your ML pipeline.
# ### 1. Import libraries and load data from database.
# - Import Python libraries
# - Load dataset from database with [`read_sql_table`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_sql_table.html)
# - Define feature and target variables X and Y
# import libraries
import nltk
nltk.download(['punkt', 'wordnet', 'averaged_perceptron_tagger','stopwords'])
import pandas as pd
import numpy as np
import re
import pickle
from sqlalchemy import create_engine
from nltk.tokenize import word_tokenize
from nltk.stem import WordNetLemmatizer
from nltk.corpus import stopwords
from sklearn.multioutput import MultiOutputClassifier
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier, AdaBoostClassifier
from sklearn.metrics import f1_score, classification_report, accuracy_score, make_scorer
from scipy.stats.mstats import gmean
from sklearn.model_selection import GridSearchCV
from sklearn.base import BaseEstimator, TransformerMixin
import warnings
warnings.filterwarnings("ignore")
# load data from database
engine = create_engine('sqlite:///../data/DisasterResponse.db')
df = pd.read_sql_table('messages',engine)
X = df['message']
Y = df.drop(['message','genre','original','id'],axis=1)
Y.columns
# ### 2. Write a tokenization function to process your text data
def tokenize(text):
text = re.sub('[^a-zA-Z0-9]',' ',text)
words = word_tokenize(text)
words = [w for w in words if w not in stopwords.words('english')]
lemmatizer = WordNetLemmatizer()
clean_words = []
for word in words:
clean_word = lemmatizer.lemmatize(word).lower().strip()
clean_words.append(clean_word)
return clean_words
# ### 3. Build a machine learning pipeline
# This machine pipeline should take in the `message` column as input and output classification results on the other 36 categories in the dataset. You may find the [MultiOutputClassifier](http://scikit-learn.org/stable/modules/generated/sklearn.multioutput.MultiOutputClassifier.html) helpful for predicting multiple target variables.
pipeline = Pipeline([
('vect',CountVectorizer(tokenizer=tokenize)),
('tfidf',TfidfTransformer()),
('clf',MultiOutputClassifier(RandomForestClassifier()))
])
# ### 4. Train pipeline
# - Split data into train and test sets
# - Train pipeline
X_train, X_test, y_train, y_test = train_test_split(X,Y)
pipeline.fit(X_train, y_train)
# ### 5. Test your model
# Report the f1 score, precision and recall for each output category of the dataset. You can do this by iterating through the columns and calling sklearn's `classification_report` on each.
y_pred = pipeline.predict(X_test)
category_names = Y.columns
for i in range(len(category_names)):
print('-'*60,'\n',"Category:", category_names[i],"\n", classification_report(y_test.iloc[:, i].values, y_pred[:, i]))
print('Accuracy of',category_names[i], accuracy_score(y_test.iloc[:, i].values, y_pred[:,i]))
def multioutput_f1score(y_true, y_pred):
scores = []
for i in range(Y.shape[1]):
score = f1_score(y_true.iloc[:,i], y_pred[:,i],average='weighted')
scores.append(score)
scores = np.asarray(scores)
score = gmean(scores)
return score
multioutput_f1score(y_test,y_pred)
# ### 6. Improve your model
# Use grid search to find better parameters.
# +
parameters = {
'clf__estimator__n_estimators':[100,200],
'clf__estimator__min_samples_split':[2,3,4],
'clf__estimator__criterion': ['entropy', 'gini']
}
scorer = make_scorer(multioutput_f1score,greater_is_better = True)
cv = GridSearchCV(pipeline,param_grid=parameters,verbose = 2, n_jobs = -1)
cv.fit(X_train, y_train)
# -
# ### 7. Test your model
# Show the accuracy, precision, and recall of the tuned model.
#
# Since this project focuses on code quality, process, and pipelines, there is no minimum performance metric needed to pass. However, make sure to fine tune your models for accuracy, precision and recall to make your project stand out - especially for your portfolio!
cv.best_estimator_
# +
y_pred = cv.best_estimator_.predict(X_test)
multioutput_f1score(y_test,y_pred)
# -
for i in range(len(category_names)):
print('-'*60,'\n',"Category:", category_names[i],"\n", classification_report(y_test.iloc[:, i].values, y_pred[:, i]))
print('Accuracy of',category_names[i], accuracy_score(y_test.iloc[:, i].values, y_pred[:,i]))
# ### 8. Try improving your model further. Here are a few ideas:
# * try other machine learning algorithms
# * add other features besides the TF-IDF
pipeline = Pipeline([
('vect',CountVectorizer(tokenizer=tokenize)),
('tfidf',TfidfTransformer()),
('clf',MultiOutputClassifier(AdaBoostClassifier()))
])
pipeline.fit(X_train, y_train)
y_pred = pipeline.predict(X_test)
multioutput_f1score(y_test,y_pred)
for i in range(len(category_names)):
print('-'*60,'\n',"Category:", category_names[i],"\n", classification_report(y_test.iloc[:, i].values, y_pred[:, i]))
print('Accuracy of',category_names[i], accuracy_score(y_test.iloc[:, i].values, y_pred[:,i]))
# ### 9. Export your model as a pickle file
pickle.dump(pipeline, open('../models/nb_classifier.pkl', "wb"))
# ### 10. Use this notebook to complete `train.py`
# Use the template file attached in the Resources folder to write a script that runs the steps above to create a database and export a model based on a new dataset specified by the user.
|
02 - Disaster Response Pipelines/notebooks/ML Pipeline Preparation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import requests, StringIO, pandas as pd, json, re, matplotlib.pyplot as plt, numpy as np
from pandas.tseries.offsets import *
def get_file_content(credentials):
"""For given credentials, this functions returns a StringIO object containing the file content."""
url1 = ''.join([credentials['auth_url'], '/v3/auth/tokens'])
data = {'auth': {'identity': {'methods': ['password'],
'password': {'user': {'name': credentials['username'],'domain': {'id': credentials['domain_id']},
'password': <PASSWORD>['password']}}}}}
headers1 = {'Content-Type': 'application/json'}
resp1 = requests.post(url=url1, data=json.dumps(data), headers=headers1)
resp1_body = resp1.json()
for e1 in resp1_body['token']['catalog']:
if(e1['type']=='object-store'):
for e2 in e1['endpoints']:
if(e2['interface']=='public'and e2['region']==credentials['region']):
url2 = ''.join([e2['url'],'/', credentials['container'], '/', credentials['filename']])
s_subject_token = resp1.headers['x-subject-token']
headers2 = {'X-Auth-Token': s_subject_token, 'accept': 'application/json'}
resp2 = requests.get(url=url2, headers=headers2)
return StringIO.StringIO(resp2.content)
credentials_1 = {
'auth_url':'https://identity.open.softlayer.com',
'project':'object_storage_0f7215bb_0b9e_4e91_b9b9_8c0d8dfc3f42',
'project_id':'bb4d27f9a6604a00abe42e6c4b9163aa',
'region':'dallas',
'user_id':'886c42d512454815b71f2549b4db1092',
'domain_id':'9d15a5cfdf4a41b183c24f40ed3f9166',
'domain_name':'1137375',
'username':'admin_e4d97a89c034e925c3148f8e7aef1c272f5cf01d',
'password':"""<PASSWORD>.""",
'filename':'Restaurant_Inspection_Scores.csv',
'container':'notebooks',
'tenantId':'s37b-2b9482f211849b-b0681b4f837d'
}
content_string = get_file_content(credentials_1)
restaurant_df = pd.read_csv(content_string)
restaurant_df.head()
restaurant_df.tail()
#sorting restaurants according to inspection date
mask = (restaurant_df['Inspection Date'] > 11/26/2014)
restaurant_df[mask].sort_values(by="Inspection Date",ascending=True)
#query number of violations(score less than 70) in different areas(zip code) for past one year
restaurant_df['Inspection Date'] = pd.to_datetime(restaurant_df['Inspection Date'])
mask = ((restaurant_df['Inspection Date'] > (pd.datetime.today() - pd.DateOffset(years=1)).strftime("%m/%d/%Y")) & (restaurant_df['Inspection Date'] <= pd.datetime.today().strftime("%m/%d/%Y")) & (restaurant_df['Score'] < 70))
temp = restaurant_df[mask].sort_values(by="Score",ascending=True)
restaurant_df1 = temp[['Score','Zip Code']]
restaurant_df1 = pd.DataFrame({'count' : restaurant_df1.groupby(['Zip Code']).size()})
restaurant_df1
# %matplotlib inline
#plot graph to show number of violations(score less than 70) in different areas(zip code) for past one year
zipcode = restaurant_df1.index.map(int)
zipcode_arranged = np.arange(len(zipcode))
count = restaurant_df1.values
plt.figure(figsize=(15,10))
bar_width = 0.5
plt.bar( zipcode_arranged,count, bar_width, color='blue')
plt.xlabel("Zip Code")
plt.ylabel("number of violations")
plt.title("Number of violations in past year for each zip code")
plt.xticks(zipcode_arranged + bar_width, zipcode, rotation=90)
plt.show()
#query number of times the score was less than 60 for different restaurants till date
restaurant_df['Inspection Date'] = pd.to_datetime(restaurant_df['Inspection Date'])
mask = ((restaurant_df['Score'] < 60))
temp = restaurant_df[mask].sort_values(by="Score",ascending=True)
restaurant_df2 = temp[['Score','Restaurant Name']]
restaurant_df2 = pd.DataFrame({'count' : restaurant_df2.groupby(['Restaurant Name']).size()})
restaurant_df2
#graph to plot number of times the score was less than 60 for different restaurants till date
restaurant_name = restaurant_df2.index
restaurant_name_arranged = np.arange(len(restaurant_name))
count = restaurant_df2.values
plt.figure(figsize=(15,10))
bar_width = 0.5
plt.bar( restaurant_name_arranged,count, bar_width, color='blue')
plt.xlabel("restaurant name")
plt.ylabel("number of violations")
plt.title("Number of violations for each restaurant")
plt.xticks(restaurant_name_arranged + bar_width, restaurant_name, rotation=90)
plt.show()
#query number of times a restaurant had 2nd Follow Up inspection
mask = ((restaurant_df['Process Description'] == '2nd Follow Up to 50 - 69'))
restaurant_df3 = temp[['Process Description','Restaurant Name']]
restaurant_df3 = pd.DataFrame({'count' : restaurant_df3.groupby(['Restaurant Name']).size()})
restaurant_df3
#graph to plot number of times a restaurant had 2nd Follow Up inspection
restaurant_name1 = restaurant_df3.index
restaurant_name_arranged1 = np.arange(len(restaurant_name1))
count1 = restaurant_df3.values
plt.figure(figsize=(15,10))
bar_width = 0.5
plt.bar( restaurant_name_arranged1,count1, bar_width, color='blue')
plt.xlabel("restaurant name")
plt.ylabel("number of 2nd Follow Ups")
plt.title("number of times a restaurant had 2nd Follow Up inspection")
plt.xticks(restaurant_name_arranged1 + bar_width, restaurant_name1, rotation=90)
plt.show()
|
Team Assignments/test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# <img src="https://www.microsoft.com/en-us/research/uploads/prod/2020/05/Recomendation.png" width="400">
#
# # Recommendation A/B Testing: Experimentation with Imperfect Compliance
#
# An online business would like to test a new feature or offering of their website and learn its effect on downstream revenue. Furthermore, they would like to know which kind of users respond best to the new version. We call the user-specfic effect a **heterogeneous treatment effect**.
#
# Ideally, the business would run an A/B tests between the old and new versions of the website. However, a direct A/B test might not work because the business cannot force the customers to take the new offering. Measuring the effect in this way will be misleading since not every customer exposed to the new offering will take it.
#
# The business also cannot look directly at existing data as it will be biased: the users who use the latest website features are most likely the ones who are very engaged on the website and hence spend more on the company's products to begin with. Estimating the effect this way would be overly optimistic.
# + [markdown] slideshow={"slide_type": "slide"}
# In this customer scenario walkthough, we show how tools from the [EconML](https://aka.ms/econml) library can still use a direct A/B test and mitigate these shortcomings.
#
# ### Summary
#
# 1. [Background](#Background)
# 2. [Data](#Data)
# 3. [Get Causal Effects with EconML](#Get-Causal-Effects-with-EconML)
# 4. [Understand Treatment Effects with EconML](#Understand-Treatment-Effects-with-EconML)
# 5. [Make Policy Decisions with EconML](#Make-Policy-Decisions-with-EconML)
# 6. [Conclusions](#Conclusions)
# + [markdown] slideshow={"slide_type": "slide"}
# # Background
#
# <img src="https://cdn.pixabay.com/photo/2013/07/13/12/18/boeing-159589_640.png" width="450">
#
# In this scenario, a travel website would like to know whether joining a membership program compels users to spend more time engaging with the website and purchasing more products.
#
# A direct A/B test is infeasible because the website cannot force users to become members. Likewise, the travel company can’t look directly at existing data, comparing members and non-members, because the customers who chose to become members are likely already more engaged than other users.
#
# **Solution:** The company had run an earlier experiment to test the value of a new, faster sign-up process. EconML's IV estimators can exploit this experimental nudge towards membership as an instrument that generates random variation in the likelihood of membership. This is known as an **intent-to-treat** setting: the intention is to give a random group of user the "treatment" (access to the easier sign-up process), but not not all users will actually take it.
#
# EconML's `IntentToTreatDRIV` estimator model takes advantage of the fact that not every customer who was offered the easier sign-up became a member to learn the effect of membership rather than the effect of receiving the quick sign-up.
# + slideshow={"slide_type": "skip"}
# Some imports to get us started
# Utilities
import os
import urllib.request
import numpy as np
import pandas as pd
# Generic ML imports
import lightgbm as lgb
from sklearn.preprocessing import PolynomialFeatures
# EconML imports
from econml.iv.dr import LinearIntentToTreatDRIV
from econml.cate_interpreter import SingleTreeCateInterpreter, \
SingleTreePolicyInterpreter
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] slideshow={"slide_type": "slide"}
# # Data
#
# The data* is comprised of:
# * Features collected in the 28 days prior to the experiment (denoted by the suffix `_pre`)
# * Experiment variables (whether the use was exposed to the easier signup -> the instrument, and whether the user became a member -> the treatment)
# * Variables collected in the 28 days after the experiment (denoted by the suffix `_post`).
#
# Feature Name | Type | Details
# :--- |:--- |:---
# **days_visited_exp_pre** | X | #days a user visits the attractions pages
# **days_visited_free_pre** | X | #days a user visits the website through free channels (e.g. domain direct)
# **days_visited_fs_pre** | X | #days a user visits the flights pages
# **days_visited_hs_pre** | X | #days a user visits the hotels pages
# **days_visited_rs_pre** | X | #days a user visits the restaurants pages
# **days_visited_vrs_pre** | X |#days a user visits the vacation rental pages
# **locale_en_US** | X | whether the user access the website from the US
# **os_type** | X | user's operating system (windows, osx, other)
# **revenue_pre** | X | how much the user spent on the website in the pre-period
# **easier_signup** | Z | whether the user was exposed to the easier signup process
# **became_member** | T | whether the user became a member
# **days_visited_post** | Y | #days a user visits the website in the 28 days after the experiment
#
#
# **To protect the privacy of the travel company's users, the data used in this scenario is synthetically generated and the feature distributions don't correspond to real distributions. However, the feature names have preserved their names and meaning.*
# + slideshow={"slide_type": "skip"}
# Import the sample AB data
file_url = "https://msalicedatapublic.blob.core.windows.net/datasets/RecommendationAB/ab_sample.csv"
ab_data = pd.read_csv(file_url)
# + slideshow={"slide_type": "slide"}
# Data sample
ab_data.head()
# + slideshow={"slide_type": "fragment"}
# Define estimator inputs
Z = ab_data['easier_signup'] # nudge, or instrument
T = ab_data['became_member'] # intervention, or treatment
Y = ab_data['days_visited_post'] # outcome of interest
X_data = ab_data.drop(columns=['easier_signup', 'became_member', 'days_visited_post']) # features
# + [markdown] slideshow={"slide_type": "slide"}
# The data was generated using the following undelying treatment effect function:
#
# $$
# \text{treatment_effect} = 0.2 + 0.3 \cdot \text{days_visited_free_pre} - 0.2 \cdot \text{days_visited_hs_pre} + \text{os_type_osx}
# $$
#
# The interpretation of this is that users who visited the website before the experiment and/or who use an iPhone tend to benefit from the membership program, whereas users who visited the hotels pages tend to be harmed by membership. **This is the relationship we seek to learn from the data.**
# + slideshow={"slide_type": "skip"}
# Define underlying treatment effect function
TE_fn = lambda X: (0.2 + 0.3 * X['days_visited_free_pre'] - 0.2 * X['days_visited_hs_pre'] + X['os_type_osx']).values
true_TE = TE_fn(X_data)
# Define the true coefficients to compare with
true_coefs = np.zeros(X_data.shape[1])
true_coefs[[1, 3, -2]] = [0.3, -0.2, 1]
# + [markdown] slideshow={"slide_type": "slide"}
# # Get Causal Effects with EconML
#
# To learn a linear projection of the treatment effect, we use the `LinearIntentToTreatDRIV` EconML estimator. For a more flexible treatment effect function, use the `IntentToTreatDRIV` estimator instead.
#
# The model requires to define some nuissance models (i.e. models we don't really care about but that matter for the analysis): the model for how the outcome $Y$ depends on the features $X$ (`model_Y_X`) and the model for how the treatment $T$ depends on the instrument $Z$ and features $X$ (`model_T_XZ`). Since we don't have any priors on these models, we use generic boosted tree estimators to learn them.
# + slideshow={"slide_type": "fragment"}
# Define nuissance estimators
lgb_T_XZ_params = {
'objective' : 'binary',
'metric' : 'auc',
'learning_rate': 0.1,
'num_leaves' : 30,
'max_depth' : 5
}
lgb_Y_X_params = {
'metric' : 'rmse',
'learning_rate': 0.1,
'num_leaves' : 30,
'max_depth' : 5
}
model_T_XZ = lgb.LGBMClassifier(**lgb_T_XZ_params)
model_Y_X = lgb.LGBMRegressor(**lgb_Y_X_params)
flexible_model_effect = lgb.LGBMRegressor(**lgb_Y_X_params)
# + slideshow={"slide_type": "slide"}
# Train EconML model
model = LinearIntentToTreatDRIV(
model_Y_X = model_Y_X,
model_T_XZ = model_T_XZ,
flexible_model_effect = flexible_model_effect,
featurizer = PolynomialFeatures(degree=1, include_bias=False)
)
model.fit(Y, T, Z=Z, X=X_data, inference="statsmodels")
# + slideshow={"slide_type": "skip"}
# Compare learned coefficients with true model coefficients
coef_indices = np.arange(model.coef_.shape[0])
# Calculate error bars
coef_error = np.asarray(model.coef__interval()) # 90% confidence interval for coefficients
coef_error[0, :] = model.coef_ - coef_error[0, :]
coef_error[1, :] = coef_error[1, :] - model.coef_
# + slideshow={"slide_type": "fragment"}
plt.errorbar(coef_indices, model.coef_, coef_error, fmt="o", label="Learned coefficients\nand 90% confidence interval")
plt.scatter(coef_indices, true_coefs, color='C1', label="True coefficients")
plt.xticks(coef_indices, X_data.columns, rotation='vertical')
plt.legend()
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# We notice that the coefficients estimates are pretty close to the true coefficients for the linear treatment effect function.
#
# We can also use the `model.summary` function to get point estimates, p-values and confidence intervals. From the table below, we notice that only the **days_visited_free_pre**, **days_visited_hs_pre** and **os_type_osx** features are statistically significant (the confidence interval doesn't contain $0$, p-value < 0.05) for the treatment effect.
# + slideshow={"slide_type": "fragment"}
model.summary()
# + slideshow={"slide_type": "skip"}
test_customers = X_data.iloc[:1000]
true_customer_TE = TE_fn(test_customers)
model_customer_TE = model.effect(test_customers)
# + slideshow={"slide_type": "skip"}
# How close are the predicted treatment effect to the true treatment effects for 1000 users?
plt.scatter(true_customer_TE, model.effect(test_customers), label="Predicted vs True treatment effect")
plt.xlabel("True treatment effect")
plt.ylabel("Predicted treatment effect")
plt.legend()
plt.show()
# + [markdown] slideshow={"slide_type": "slide"}
# # Understand Treatment Effects with EconML
#
# EconML includes interpretability tools to better understand treatment effects. Treatment effects can be complex, but oftentimes we are interested in simple rules that can differentiate between users who respond positively, users who remain neutral and users who respond negatively to the proposed changes.
#
# The EconML `SingleTreeCateInterpreter` provides interperetability by training a single decision tree on the treatment effects outputted by the any of the EconML estimators. In the figure below we can see in dark red users who respond negatively to the membership program and in dark green users who respond positively.
# + slideshow={"slide_type": "fragment"}
intrp = SingleTreeCateInterpreter(include_model_uncertainty=True, max_depth=2, min_samples_leaf=10)
intrp.interpret(model, test_customers)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X_data.columns, fontsize=12)
# + [markdown] slideshow={"slide_type": "slide"}
# # Make Policy Decisions with EconML
#
# Interventions usually have a cost: incetivizing a user to become a member can be costly (e.g by offering a discount). Thus, we would like to know what customers to target to maximize the profit from their increased engagement. This is the **treatment policy**.
#
# The EconML library includes policy interpretability tools such as `SingleTreePolicyInterpreter` that take in a treatment cost and the treatment effects to learn simple rules about which customers to target profitably.
# + slideshow={"slide_type": "fragment"}
intrp = SingleTreePolicyInterpreter(risk_level=0.05, max_depth=2, min_samples_leaf=10)
intrp.interpret(model, test_customers, sample_treatment_costs=0.2)
plt.figure(figsize=(25, 5))
intrp.plot(feature_names=X_data.columns, fontsize=12)
# + [markdown] slideshow={"slide_type": "slide"}
# # Conclusions
#
# In this notebook, we have demonstrated the power of using EconML to:
#
# * Get valid causal insights in seemingly impossible scenarios
# * Intepret the resulting individual-level treatment effects
# * Build policies around the learned effects
#
# To learn more about what EconML can do for you, visit our [website](https://aka.ms/econml), our [GitHub page](https://github.com/microsoft/EconML) or our [documentation](https://econml.azurewebsites.net/).
|
notebooks/CustomerScenarios/Case Study - Recommendation AB Testing at An Online Travel Company.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Notebook used to convert file format from CIAC db dump to a format we can use to generate ML labels
import pandas as pd
df = pd.read_csv('./caic_bc_fx_July142019.csv',
parse_dates=['date', 'date_modified', 'date_issued'],
dtype = {'rating': 'object',
'aspect_elev_0': 'object', 'aspect_elev_1': 'object', 'aspect_elev_2': 'object',
'size_0': 'object', 'size_1': 'object', 'size_2': 'object',
'problem_0': 'object', 'problem_1': 'object', 'problem_2': 'object'})
#1. filter out draft
df = df[df['status']=='published']
df.columns
df.tail()
df['zone_id'].value_counts()
# +
def number_to_danger(num):
if num == '0':
return 'no-data'
elif num == '1':
return 'Low'
elif num == '2':
return 'Moderate'
elif num == '3':
return 'Considerable'
elif num == '4':
return 'High'
elif num == '5':
return 'Extreme'
else:
return 'Unknown-Danger'
# -
df['Day1DangerAboveTreeline'] = df['rating'].str[0].apply(number_to_danger)
df['Day1DangerNearTreeline'] = df['rating'].str[1].apply(number_to_danger)
df['Day1DangerBelowTreeline'] = df['rating'].str[2].apply(number_to_danger)
df['Day2DangerAboveTreeline'] = df['rating'].str[3].apply(number_to_danger)
df['Day2DangerNearTreeline'] = df['rating'].str[4].apply(number_to_danger)
df['Day2DangerBelowTreeline'] = df['rating'].str[5].apply(number_to_danger)
# +
import numpy as np
def num_to_problem(num):
if num == '0':
return 'LooseDry'
elif num == '1':
return 'LooseWet'
elif num == '2':
return 'StormSlabs'
elif num == '3':
return 'WindSlab'
elif num == '4':
return 'PersistentSlab'
elif num == '5':
return 'DeepPersistentSlab'
elif num == '6':
return 'WetSlabs'
elif num == '7':
return 'Cornices'
elif num == '8':
return 'Glide'
else:
raise Exception('Unknown Problem Exception with num: ' + str(num))
def num_to_likelihood(num):
if num == 0:
return '0-unlikely'
elif num == 1:
return '1-possible'
elif num == 2:
return '2-likely'
elif num == 3:
return '3-very likely'
elif num == 4:
return '4-certain'
else:
raise Exception('Unknown Likelihood Exception with num: ' + str(num))
def str_to_maximum_size(s):
if(pd.isna(s)):
return 'no-data'
if s[0] == '1':
return '3-historic'
elif s[1] == '1':
return '2-very large'
elif s[2] == '1':
return '1-large'
elif s[3] == '1':
return '0-small'
else:
raise Exception('Unknown MaximumSize Exception with size: ' + s)
def str_to_minimum_size(s):
if(pd.isna(s)):
return 'no-data'
if s[3] == '1':
return '0-small'
elif s[2] == '1':
return '1-large'
elif s[1] == '1':
return '2-very large'
elif s[0] == '1':
return '3-historic'
else:
raise Exception('Unknown MinimumSize Exception with size: ' + s)
def num_to_region(num):
if num == 0:
return 'Steamboat & Flat Tops'
elif num == 1:
return 'Front Range'
elif num == 2:
return 'Vail & Summit County'
elif num == 3:
return 'Sawatch Range'
elif num == 4:
return 'Aspen'
elif num == 5:
return 'Grand Mesa'
elif num == 6:
return 'Gunnison'
elif num == 7:
return 'Northern San Juan'
elif num == 8:
return 'Southern San Juan'
elif num == 9:
return 'Sangre De Cristo'
elif num == 10: #these three aren't currently used by OAP
return 'Northern'
elif num == 11:
return 'Central'
elif num == 12:
return 'Southern'
else:
raise Exception('Unknown region_id: ' + str(num))
def row_to_avy_problem(row):
num_problems = row['problems']
if pd.isna(num_problems):
return
row['Region'] = num_to_region(row['zone_id'])
for i in range(0, int(num_problems)):
try:
problem_type = num_to_problem(row['problem_' + str(i)])
#print('processing problem type: ' + problem_type)
row[problem_type + '_Likelihood'] = num_to_likelihood(row['likelihood_' + str(i)])
row[problem_type + '_MaximumSize'] = str_to_maximum_size(row['size_' + str(i)])
row[problem_type + '_MinimumSize'] = str_to_minimum_size(row['size_' + str(i)])
if pd.isna(row['aspect_elev_' + str(i)]):
row[problem_type + '_OctagonBelowTreelineNorth'] = 'no-data'
row[problem_type + '_OctagonNearTreelineNorth'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineNorth'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineNorthEast'] = 'no-data'
row[problem_type + '_OctagonNearTreelineNorthEast'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineNorthEast'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineEast'] = 'no-data'
row[problem_type + '_OctagonNearTreelineEast'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineEast'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineSouthEast'] = 'no-data'
row[problem_type + '_OctagonNearTreelineSouthEast'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineSouthEast'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineSouth'] = 'no-data'
row[problem_type + '_OctagonNearTreelineSouth'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineSouth'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineSouthWest'] = 'no-data'
row[problem_type + '_OctagonNearTreelineSouthWest'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineSouthWest'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineWest'] = 'no-data'
row[problem_type + '_OctagonNearTreelineWest'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineWest'] = 'no-data'
row[problem_type + '_OctagonBelowTreelineNorthWest'] = 'no-data'
row[problem_type + '_OctagonNearTreelineNorthWest'] = 'no-data'
row[problem_type + '_OctagonAboveTreelineNorthWest'] = 'no-data'
else:
row[problem_type + '_OctagonBelowTreelineNorth'] = row['aspect_elev_' + str(i)][0]
row[problem_type + '_OctagonNearTreelineNorth'] = row['aspect_elev_' + str(i)][1]
row[problem_type + '_OctagonAboveTreelineNorth'] = row['aspect_elev_' + str(i)][2]
row[problem_type + '_OctagonBelowTreelineNorthEast'] = row['aspect_elev_' + str(i)][3]
row[problem_type + '_OctagonNearTreelineNorthEast'] = row['aspect_elev_' + str(i)][4]
row[problem_type + '_OctagonAboveTreelineNorthEast'] = row['aspect_elev_' + str(i)][5]
row[problem_type + '_OctagonBelowTreelineEast'] = row['aspect_elev_' + str(i)][6]
row[problem_type + '_OctagonNearTreelineEast'] = row['aspect_elev_' + str(i)][7]
row[problem_type + '_OctagonAboveTreelineEast'] = row['aspect_elev_' + str(i)][8]
row[problem_type + '_OctagonBelowTreelineSouthEast'] = row['aspect_elev_' + str(i)][9]
row[problem_type + '_OctagonNearTreelineSouthEast'] = row['aspect_elev_' + str(i)][10]
row[problem_type + '_OctagonAboveTreelineSouthEast'] = row['aspect_elev_' + str(i)][11]
row[problem_type + '_OctagonBelowTreelineSouth'] = row['aspect_elev_' + str(i)][12]
row[problem_type + '_OctagonNearTreelineSouth'] = row['aspect_elev_' + str(i)][13]
row[problem_type + '_OctagonAboveTreelineSouth'] = row['aspect_elev_' + str(i)][14]
row[problem_type + '_OctagonBelowTreelineSouthWest'] = row['aspect_elev_' + str(i)][15]
row[problem_type + '_OctagonNearTreelineSouthWest'] = row['aspect_elev_' + str(i)][16]
row[problem_type + '_OctagonAboveTreelineSouthWest'] = row['aspect_elev_' + str(i)][17]
row[problem_type + '_OctagonBelowTreelineWest'] = row['aspect_elev_' + str(i)][18]
row[problem_type + '_OctagonNearTreelineWest'] = row['aspect_elev_' + str(i)][19]
row[problem_type + '_OctagonAboveTreelineWest'] = row['aspect_elev_' + str(i)][20]
row[problem_type + '_OctagonBelowTreelineNorthWest'] = row['aspect_elev_' + str(i)][21]
row[problem_type + '_OctagonNearTreelineNorthWest'] = row['aspect_elev_' + str(i)][22]
row[problem_type + '_OctagonAboveTreelineNorthWest'] = row['aspect_elev_' + str(i)][23]
except:
print("format exception on bc_avo_fx_id: " + str(row['bc_avo_fx_id']) + ' skipping')
return row
# -
tmp = df.apply(row_to_avy_problem, axis=1)
# +
#tmp.to_csv("tmp.csv")
# +
tmp.rename(columns={'date_issued': 'PublishedDateTime', 'summary': 'Day1DetailedForecast'}, inplace=True)
# -
tmp['ForecastUrl'] = ''
tmp['BottomLineSummary'] = ''
tmp['Day1Warning'] = ''
tmp['Day1WarningEnd'] = ''
tmp['Day1WarningText'] = ''
tmp['Day2DetailedForecast'] = ''
tmp['Day2Warning'] = ''
tmp['Day2WarningEnd'] = ''
tmp['Day2WarningText'] = ''
tmp['SpecialStatement'] = ''
tmp['UnifiedRegion'] = tmp['Region']
# +
tmp['Day1Date'] = tmp['PublishedDateTime'].dt.strftime('%Y%m%d')
# +
#tmp.to_csv("tmp.csv")
# -
#filter to the latest forecast for the date (to remove)
#currently just taking the last forecast for the day but this could be improved to differentiate between updated and new forecasts
#also end of season forecast will be overwritten by placeholder forecast
tmp['maxdate'] = tmp.groupby(['Region', 'Day1Date'])['PublishedDateTime'].transform('max')
tmp['PublishedDateTime'] = pd.to_datetime(tmp['PublishedDateTime'])
tmp['maxdate'] = pd.to_datetime(tmp['maxdate'])
tmp = tmp[tmp['PublishedDateTime'] == tmp['maxdate']]
tmp['Day1Date'].head()
# +
#dump the critical points
#tmp[['Region', 'lat', 'lon']].groupby(['Region', 'lat', 'lon']).max()
# -
#final column list
cols = [
'Region',
'UnifiedRegion',
'PublishedDateTime',
'Day1Date',
'SpecialStatement',
'BottomLineSummary',
'ForecastUrl',
'Day1DangerAboveTreeline',
'Day1DangerNearTreeline',
'Day1DangerBelowTreeline',
'Day1DetailedForecast',
'Day1Warning',
'Day1WarningEnd',
'Day1WarningText',
'Day2DangerAboveTreeline',
'Day2DangerNearTreeline',
'Day2DangerBelowTreeline',
'Day2DetailedForecast',
'Day2Warning',
'Day2WarningEnd',
'Day2WarningText',
'Cornices_Likelihood',
'Cornices_MaximumSize',
'Cornices_MinimumSize',
'Cornices_OctagonAboveTreelineEast',
'Cornices_OctagonAboveTreelineNorth',
'Cornices_OctagonAboveTreelineNorthEast',
'Cornices_OctagonAboveTreelineNorthWest',
'Cornices_OctagonAboveTreelineSouth',
'Cornices_OctagonAboveTreelineSouthEast',
'Cornices_OctagonAboveTreelineSouthWest',
'Cornices_OctagonAboveTreelineWest',
'Cornices_OctagonNearTreelineEast',
'Cornices_OctagonNearTreelineNorth',
'Cornices_OctagonNearTreelineNorthEast',
'Cornices_OctagonNearTreelineNorthWest',
'Cornices_OctagonNearTreelineSouth',
'Cornices_OctagonNearTreelineSouthEast',
'Cornices_OctagonNearTreelineSouthWest',
'Cornices_OctagonNearTreelineWest',
'Cornices_OctagonBelowTreelineEast',
'Cornices_OctagonBelowTreelineNorth',
'Cornices_OctagonBelowTreelineNorthEast',
'Cornices_OctagonBelowTreelineNorthWest',
'Cornices_OctagonBelowTreelineSouth',
'Cornices_OctagonBelowTreelineSouthEast',
'Cornices_OctagonBelowTreelineSouthWest',
'Cornices_OctagonBelowTreelineWest',
'Glide_Likelihood',
'Glide_MaximumSize',
'Glide_MinimumSize',
'Glide_OctagonAboveTreelineEast',
'Glide_OctagonAboveTreelineNorth',
'Glide_OctagonAboveTreelineNorthEast',
'Glide_OctagonAboveTreelineNorthWest',
'Glide_OctagonAboveTreelineSouth',
'Glide_OctagonAboveTreelineSouthEast',
'Glide_OctagonAboveTreelineSouthWest',
'Glide_OctagonAboveTreelineWest',
'Glide_OctagonNearTreelineEast',
'Glide_OctagonNearTreelineNorth',
'Glide_OctagonNearTreelineNorthEast',
'Glide_OctagonNearTreelineNorthWest',
'Glide_OctagonNearTreelineSouth',
'Glide_OctagonNearTreelineSouthEast',
'Glide_OctagonNearTreelineSouthWest',
'Glide_OctagonNearTreelineWest',
'Glide_OctagonBelowTreelineEast',
'Glide_OctagonBelowTreelineNorth',
'Glide_OctagonBelowTreelineNorthEast',
'Glide_OctagonBelowTreelineNorthWest',
'Glide_OctagonBelowTreelineSouth',
'Glide_OctagonBelowTreelineSouthEast',
'Glide_OctagonBelowTreelineSouthWest',
'Glide_OctagonBelowTreelineWest',
'LooseDry_Likelihood',
'LooseDry_MaximumSize',
'LooseDry_MinimumSize',
'LooseDry_OctagonAboveTreelineEast',
'LooseDry_OctagonAboveTreelineNorth',
'LooseDry_OctagonAboveTreelineNorthEast',
'LooseDry_OctagonAboveTreelineNorthWest',
'LooseDry_OctagonAboveTreelineSouth',
'LooseDry_OctagonAboveTreelineSouthEast',
'LooseDry_OctagonAboveTreelineSouthWest',
'LooseDry_OctagonAboveTreelineWest',
'LooseDry_OctagonNearTreelineEast',
'LooseDry_OctagonNearTreelineNorth',
'LooseDry_OctagonNearTreelineNorthEast',
'LooseDry_OctagonNearTreelineNorthWest',
'LooseDry_OctagonNearTreelineSouth',
'LooseDry_OctagonNearTreelineSouthEast',
'LooseDry_OctagonNearTreelineSouthWest',
'LooseDry_OctagonNearTreelineWest',
'LooseDry_OctagonBelowTreelineEast',
'LooseDry_OctagonBelowTreelineNorth',
'LooseDry_OctagonBelowTreelineNorthEast',
'LooseDry_OctagonBelowTreelineNorthWest',
'LooseDry_OctagonBelowTreelineSouth',
'LooseDry_OctagonBelowTreelineSouthEast',
'LooseDry_OctagonBelowTreelineSouthWest',
'LooseDry_OctagonBelowTreelineWest',
'LooseWet_Likelihood',
'LooseWet_MaximumSize',
'LooseWet_MinimumSize',
'LooseWet_OctagonAboveTreelineEast',
'LooseWet_OctagonAboveTreelineNorth',
'LooseWet_OctagonAboveTreelineNorthEast',
'LooseWet_OctagonAboveTreelineNorthWest',
'LooseWet_OctagonAboveTreelineSouth',
'LooseWet_OctagonAboveTreelineSouthEast',
'LooseWet_OctagonAboveTreelineSouthWest',
'LooseWet_OctagonAboveTreelineWest',
'LooseWet_OctagonNearTreelineEast',
'LooseWet_OctagonNearTreelineNorth',
'LooseWet_OctagonNearTreelineNorthEast',
'LooseWet_OctagonNearTreelineNorthWest',
'LooseWet_OctagonNearTreelineSouth',
'LooseWet_OctagonNearTreelineSouthEast',
'LooseWet_OctagonNearTreelineSouthWest',
'LooseWet_OctagonNearTreelineWest',
'LooseWet_OctagonBelowTreelineEast',
'LooseWet_OctagonBelowTreelineNorth',
'LooseWet_OctagonBelowTreelineNorthEast',
'LooseWet_OctagonBelowTreelineNorthWest',
'LooseWet_OctagonBelowTreelineSouth',
'LooseWet_OctagonBelowTreelineSouthEast',
'LooseWet_OctagonBelowTreelineSouthWest',
'LooseWet_OctagonBelowTreelineWest',
'PersistentSlab_Likelihood',
'PersistentSlab_MaximumSize',
'PersistentSlab_MinimumSize',
'PersistentSlab_OctagonAboveTreelineEast',
'PersistentSlab_OctagonAboveTreelineNorth',
'PersistentSlab_OctagonAboveTreelineNorthEast',
'PersistentSlab_OctagonAboveTreelineNorthWest',
'PersistentSlab_OctagonAboveTreelineSouth',
'PersistentSlab_OctagonAboveTreelineSouthEast',
'PersistentSlab_OctagonAboveTreelineSouthWest',
'PersistentSlab_OctagonAboveTreelineWest',
'PersistentSlab_OctagonNearTreelineEast',
'PersistentSlab_OctagonNearTreelineNorth',
'PersistentSlab_OctagonNearTreelineNorthEast',
'PersistentSlab_OctagonNearTreelineNorthWest',
'PersistentSlab_OctagonNearTreelineSouth',
'PersistentSlab_OctagonNearTreelineSouthEast',
'PersistentSlab_OctagonNearTreelineSouthWest',
'PersistentSlab_OctagonNearTreelineWest',
'PersistentSlab_OctagonBelowTreelineEast',
'PersistentSlab_OctagonBelowTreelineNorth',
'PersistentSlab_OctagonBelowTreelineNorthEast',
'PersistentSlab_OctagonBelowTreelineNorthWest',
'PersistentSlab_OctagonBelowTreelineSouth',
'PersistentSlab_OctagonBelowTreelineSouthEast',
'PersistentSlab_OctagonBelowTreelineSouthWest',
'PersistentSlab_OctagonBelowTreelineWest',
'DeepPersistentSlab_Likelihood',
'DeepPersistentSlab_MaximumSize',
'DeepPersistentSlab_MinimumSize',
'DeepPersistentSlab_OctagonAboveTreelineEast',
'DeepPersistentSlab_OctagonAboveTreelineNorth',
'DeepPersistentSlab_OctagonAboveTreelineNorthEast',
'DeepPersistentSlab_OctagonAboveTreelineNorthWest',
'DeepPersistentSlab_OctagonAboveTreelineSouth',
'DeepPersistentSlab_OctagonAboveTreelineSouthEast',
'DeepPersistentSlab_OctagonAboveTreelineSouthWest',
'DeepPersistentSlab_OctagonAboveTreelineWest',
'DeepPersistentSlab_OctagonNearTreelineEast',
'DeepPersistentSlab_OctagonNearTreelineNorth',
'DeepPersistentSlab_OctagonNearTreelineNorthEast',
'DeepPersistentSlab_OctagonNearTreelineNorthWest',
'DeepPersistentSlab_OctagonNearTreelineSouth',
'DeepPersistentSlab_OctagonNearTreelineSouthEast',
'DeepPersistentSlab_OctagonNearTreelineSouthWest',
'DeepPersistentSlab_OctagonNearTreelineWest',
'DeepPersistentSlab_OctagonBelowTreelineEast',
'DeepPersistentSlab_OctagonBelowTreelineNorth',
'DeepPersistentSlab_OctagonBelowTreelineNorthEast',
'DeepPersistentSlab_OctagonBelowTreelineNorthWest',
'DeepPersistentSlab_OctagonBelowTreelineSouth',
'DeepPersistentSlab_OctagonBelowTreelineSouthEast',
'DeepPersistentSlab_OctagonBelowTreelineSouthWest',
'DeepPersistentSlab_OctagonBelowTreelineWest',
'StormSlabs_Likelihood',
'StormSlabs_MaximumSize',
'StormSlabs_MinimumSize',
'StormSlabs_OctagonAboveTreelineEast',
'StormSlabs_OctagonAboveTreelineNorth',
'StormSlabs_OctagonAboveTreelineNorthEast',
'StormSlabs_OctagonAboveTreelineNorthWest',
'StormSlabs_OctagonAboveTreelineSouth',
'StormSlabs_OctagonAboveTreelineSouthEast',
'StormSlabs_OctagonAboveTreelineSouthWest',
'StormSlabs_OctagonAboveTreelineWest',
'StormSlabs_OctagonNearTreelineEast',
'StormSlabs_OctagonNearTreelineNorth',
'StormSlabs_OctagonNearTreelineNorthEast',
'StormSlabs_OctagonNearTreelineNorthWest',
'StormSlabs_OctagonNearTreelineSouth',
'StormSlabs_OctagonNearTreelineSouthEast',
'StormSlabs_OctagonNearTreelineSouthWest',
'StormSlabs_OctagonNearTreelineWest',
'StormSlabs_OctagonBelowTreelineEast',
'StormSlabs_OctagonBelowTreelineNorth',
'StormSlabs_OctagonBelowTreelineNorthEast',
'StormSlabs_OctagonBelowTreelineNorthWest',
'StormSlabs_OctagonBelowTreelineSouth',
'StormSlabs_OctagonBelowTreelineSouthEast',
'StormSlabs_OctagonBelowTreelineSouthWest',
'StormSlabs_OctagonBelowTreelineWest',
'WetSlabs_Likelihood',
'WetSlabs_MaximumSize',
'WetSlabs_MinimumSize',
'WetSlabs_OctagonAboveTreelineEast',
'WetSlabs_OctagonAboveTreelineNorth',
'WetSlabs_OctagonAboveTreelineNorthEast',
'WetSlabs_OctagonAboveTreelineNorthWest',
'WetSlabs_OctagonAboveTreelineSouth',
'WetSlabs_OctagonAboveTreelineSouthEast',
'WetSlabs_OctagonAboveTreelineSouthWest',
'WetSlabs_OctagonAboveTreelineWest',
'WetSlabs_OctagonNearTreelineEast',
'WetSlabs_OctagonNearTreelineNorth',
'WetSlabs_OctagonNearTreelineNorthEast',
'WetSlabs_OctagonNearTreelineNorthWest',
'WetSlabs_OctagonNearTreelineSouth',
'WetSlabs_OctagonNearTreelineSouthEast',
'WetSlabs_OctagonNearTreelineSouthWest',
'WetSlabs_OctagonNearTreelineWest',
'WetSlabs_OctagonBelowTreelineEast',
'WetSlabs_OctagonBelowTreelineNorth',
'WetSlabs_OctagonBelowTreelineNorthEast',
'WetSlabs_OctagonBelowTreelineNorthWest',
'WetSlabs_OctagonBelowTreelineSouth',
'WetSlabs_OctagonBelowTreelineSouthEast',
'WetSlabs_OctagonBelowTreelineSouthWest',
'WetSlabs_OctagonBelowTreelineWest',
'WindSlab_Likelihood',
'WindSlab_MaximumSize',
'WindSlab_MinimumSize',
'WindSlab_OctagonAboveTreelineEast',
'WindSlab_OctagonAboveTreelineNorth',
'WindSlab_OctagonAboveTreelineNorthEast',
'WindSlab_OctagonAboveTreelineNorthWest',
'WindSlab_OctagonAboveTreelineSouth',
'WindSlab_OctagonAboveTreelineSouthEast',
'WindSlab_OctagonAboveTreelineSouthWest',
'WindSlab_OctagonAboveTreelineWest',
'WindSlab_OctagonNearTreelineEast',
'WindSlab_OctagonNearTreelineNorth',
'WindSlab_OctagonNearTreelineNorthEast',
'WindSlab_OctagonNearTreelineNorthWest',
'WindSlab_OctagonNearTreelineSouth',
'WindSlab_OctagonNearTreelineSouthEast',
'WindSlab_OctagonNearTreelineSouthWest',
'WindSlab_OctagonNearTreelineWest',
'WindSlab_OctagonBelowTreelineEast',
'WindSlab_OctagonBelowTreelineNorth',
'WindSlab_OctagonBelowTreelineNorthEast',
'WindSlab_OctagonBelowTreelineNorthWest',
'WindSlab_OctagonBelowTreelineSouth',
'WindSlab_OctagonBelowTreelineSouthEast',
'WindSlab_OctagonBelowTreelineSouthWest',
'WindSlab_OctagonBelowTreelineWest'
]
len(tmp)
finalDf = tmp[cols]
finalDf.replace(np.nan, 'no-data', inplace=True)
finalDf[:20]
finalDf.to_csv('CleanedForecastsCAIC2019.V1.csv', index=False, date_format='%Y%m%d %H:00')
|
Data/ConvertCAIC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# +
# GPU: 32*40 in 9.96s = 128.5/s
# CPU: 32*8 in 10.1s = 25/s
# -
import os
import sys
import numpy as np
import mxnet as mx
from collections import namedtuple
print("OS: ", sys.platform)
print("Python: ", sys.version)
print("Numpy: ", np.__version__)
print("MXNet: ", mx.__version__) # mxnet-cu80mkl
# !cat /proc/cpuinfo | grep processor | wc -l
# !nvidia-smi --query-gpu=gpu_name --format=csv
Batch = namedtuple('Batch', ['data'])
BATCH_SIZE = 32
RESNET_FEATURES = 2048
BATCHES_GPU = 40
BATCHES_CPU = 8
def give_fake_data(batches):
""" Create an array of fake data to run inference on"""
np.random.seed(0)
dta = np.random.rand(BATCH_SIZE*batches, 224, 224, 3).astype(np.float32)
return dta, np.swapaxes(dta, 1, 3)
def yield_mb(X, batchsize):
""" Function yield (complete) mini_batches of data"""
for i in range(len(X)//batchsize):
yield i, X[i*batchsize:(i+1)*batchsize]
# Create batches of fake data
fake_input_data_cl, fake_input_data_cf = give_fake_data(BATCHES_GPU)
print(fake_input_data_cl.shape, fake_input_data_cf.shape)
# Download Resnet weights
path='http://data.mxnet.io/models/imagenet/'
[mx.test_utils.download(path+'resnet/50-layers/resnet-50-symbol.json'),
mx.test_utils.download(path+'resnet/50-layers/resnet-50-0000.params')]
# Load model
sym, arg_params, aux_params = mx.model.load_checkpoint('resnet-50', 0)
# List the last 10 layers
all_layers = sym.get_internals()
print(all_layers.list_outputs()[-10:])
def predict_fn(classifier, data, batchsize):
""" Return features from classifier """
out = np.zeros((len(data), RESNET_FEATURES), np.float32)
for idx, dta in yield_mb(data, batchsize):
classifier.forward(Batch(data=[mx.nd.array(dta)]))
out[idx*batchsize:(idx+1)*batchsize] = classifier.get_outputs()[0].asnumpy().squeeze()
return out
# ## 1. GPU
# Get last layer
fe_sym = all_layers['flatten0_output']
# Initialise GPU
fe_mod = mx.mod.Module(symbol=fe_sym, context=[mx.gpu(0)], label_names=None)
fe_mod.bind(for_training=False, inputs_need_grad=False,
data_shapes=[('data', (BATCH_SIZE,3,224,224))])
fe_mod.set_params(arg_params, aux_params)
cold_start = predict_fn(fe_mod, fake_input_data_cf, BATCH_SIZE)
# %%time
# GPU: 9.96s
features = predict_fn(fe_mod, fake_input_data_cf, BATCH_SIZE)
# ## 2. CPU
# Kill all GPUs ...
os.environ['CUDA_VISIBLE_DEVICES'] = '-1'
# Get last layer
fe_sym = all_layers['flatten0_output']
# Initialise CPU
fe_mod = mx.mod.Module(symbol=fe_sym, context=mx.cpu(), label_names=None)
fe_mod.bind(for_training=False, inputs_need_grad=False,
data_shapes=[('data', (BATCH_SIZE,3,224,224))])
fe_mod.set_params(arg_params, aux_params)
# Create batches of fake data
fake_input_data_cl, fake_input_data_cf = give_fake_data(BATCHES_CPU)
print(fake_input_data_cl.shape, fake_input_data_cf.shape)
cold_start = predict_fn(fe_mod, fake_input_data_cf, BATCH_SIZE)
# %%time
# CPU: 10.1s
features = predict_fn(fe_mod, fake_input_data_cf, BATCH_SIZE)
|
DeepLearningFrameworks/inference/ResNet50-MXNet-mkl.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={"duration": 0.007959, "end_time": "2021-07-01T05:05:58.786651", "exception": false, "start_time": "2021-07-01T05:05:58.778692", "status": "completed"} tags=[]
# Linear Regression with Python
# + [markdown] papermill={"duration": 0.00664, "end_time": "2021-07-01T05:05:58.800472", "exception": false, "start_time": "2021-07-01T05:05:58.793832", "status": "completed"} tags=[]
# Ref :
#
# https://thecleverprogrammer.com/2020/11/27/machine-learning-algorithms-with-python/
#
# https://thecleverprogrammer.com/2020/11/20/linear-regression-with-python/
# + papermill={"duration": 1.306371, "end_time": "2021-07-01T05:06:00.113810", "exception": false, "start_time": "2021-07-01T05:05:58.807439", "status": "completed"} tags=[]
import matplotlib.pylab as plt
import numpy as np
# %matplotlib inline
from sklearn.linear_model import LinearRegression
from sklearn import datasets
# + papermill={"duration": 0.033076, "end_time": "2021-07-01T05:06:00.154082", "exception": false, "start_time": "2021-07-01T05:06:00.121006", "status": "completed"} tags=[]
diabetes = datasets.load_diabetes()
# + papermill={"duration": 0.017371, "end_time": "2021-07-01T05:06:00.178553", "exception": false, "start_time": "2021-07-01T05:06:00.161182", "status": "completed"} tags=[]
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(diabetes.data, diabetes.target, test_size=0.2, random_state=0)
# + papermill={"duration": 0.035585, "end_time": "2021-07-01T05:06:00.221160", "exception": false, "start_time": "2021-07-01T05:06:00.185575", "status": "completed"} tags=[]
# There are three steps to model something with sklearn
# 1. Set up the model
model = LinearRegression()
# 2. Use fit
model.fit(X_train, y_train)
# + papermill={"duration": 0.189571, "end_time": "2021-07-01T05:06:00.418413", "exception": false, "start_time": "2021-07-01T05:06:00.228842", "status": "completed"} tags=[]
y_pred = model.predict(X_test)
plt.plot(y_test, y_pred, '.')
# plot a line, a perfit predict would all fall on this line
x = np.linspace(0, 330, 100)
y = x
plt.plot(x, y)
plt.show()
# + papermill={"duration": 0.007786, "end_time": "2021-07-01T05:06:00.434277", "exception": false, "start_time": "2021-07-01T05:06:00.426491", "status": "completed"} tags=[]
|
linear-regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. An overview of the basic functions of Spark
#
# #### This tutorial covers:
# - Creating RDDs and DataFrames using SparkContext
# - Interoperability between RDDs and DataFrames
# - Multiple rows and multiple column specifications for DataFrames
# - Selecting, editing and renaming columns in dataframes
# - Interoperability between Pandas and Spark dataframes
# - Reading data from a csv
# - Changing Dataframe schemas
# - Filtering & Grouping
# - Other operations
# ## 1.1 Basic Spark Operations
# **We create a RDD by calling sc.parallelize**
# sc = spark context
basic_data = sc.parallelize(["St. Gallen", "Switzerland", 75.000])
# **But we can't read the RDD as such, we must call an action**
basic_data
basic_data.collect() # return all elements as an array to the driver
# ** Other actions we can perform: **
basic_data.first() # get the first item
basic_data.take(2) # get the first two items
basic_data.count() # counts the items in the RDD
# ** Lets create a second dimension to our data by adding a new entry **
data = sc.parallelize([["St. Gallen", "Switzerland", 75000],
["Milan", "Italy", 1330000]])
data
data.first() # now the entire array is returned
# ## 1.2 Spark DataFrames
# #### We can convert our RDD to a Spark DF
# * Different that RDDs, DFs have a schema, where each column has a name and a data type
# * SQL, frequently used in relational databases, is a common way to organize and query the data
# * Schemas are useful, because they allow spark to perform substantially better when calculating the execution plan
# * The DataFrame was called SchemaRDD before Spark v1.3
df = data.toDF()
df
type(df)
# #### Column names are automatically assigned
df.show()
# ## Explicitly defined schemas
# However, schemas will not always be inferred correctly by Spark, especially when reading in external data, where integers might have been saved as string
starting_input = sc.parallelize(["St. Gallen,Switzerland,75000,TRUE,38.9",
"Milan,Italy,1330000,FALSE,45.1",
"London,United Kingdom,8136000,FALSE,33.1",
"New York,USA,8538000,FALSE,35.8"])
starting_input.collect()
parts = starting_input.map(lambda x: x.split(","))
parts.collect()
# #### If we just convert this input to a DF, it will only be read as strings and hinder us from using certain functionalities
regular_conversion = parts.toDF()
regular_conversion.printSchema()
regular_conversion.show()
parts.collect()
# #### Luckily we can explicitly define the schema
# +
from pyspark.sql.types import StructType, StructField, StringType, LongType, BooleanType
from pyspark.sql.types import Row
fields = [StructField('City', StringType(), True),
StructField('Country', StringType(), True),
StructField('Population', LongType(), True),
StructField('In Switzerland', BooleanType(), True),
StructField('Median Age', LongType(), True),
]
# -
# #### Creating dataframes using sc.parallelize() and Row() functions
# * Row functions allow specifying column names for dataframes
# * Depending on which action is called, the output is returned in a different format
#
from pyspark.sql.types import Row
row_rdd = sc.parallelize([Row(id=1,
city="St. Gallen",
country="Switzerland",
population= 75000)])
row_rdd.collect()
# #### Working with multiple rows
row_rdd = sc.parallelize([Row(id=1,
city="St. Gallen",
country="Switzerland",
population= 75000
),
Row(id=2,
city="Milan",
country="Italy",
population= 1330000
),
Row(id=3,
city="London",
country="United Kingdom",
population= 8136000
)])
row_rdd = row_rdd.toDF()
row_rdd.show()
# #### We can now observe differences in the columns of the DF by looking at the schema
row_rdd.printSchema()
# #### We can also apply row names to an existing RDD
# * The map transformation performs a transformation on every element in the RDD
# * In our case we pass an anonymous function (/lamdbda function) to the RDD which is performed on each element
# * Remember: we are never modifying the original RDD but are creating a new one
#
data = sc.parallelize([["St. Gallen", "Switzerland", 75000],
["Milan", "Italy", 1330000],
["London", "United Kingdom", 8136000]])
data
column_names = Row('City', 'Country', 'Population')
cities = data.map(lambda r: column_names(*r))
cities.collect()
cities = cities.toDF()
cities.show()
# #### Extracting specific cells from dataframes
cities.collect()[0][2]
# #### Adding a column
cities = cities.withColumn(
"water consumed p.a.",
cities.Population * 340 * 365 # 340l is the average amount of water consumed per person a day
)
cities.show()
# #### Editing a column name
cities.withColumnRenamed("water consumed p.a.","Water Usage").show()
# #### We can also easily convert a Spark dataframe to a Pandas Dataframe
# * This may be useful if we want to continue working on a small df we extracted from our spark cluster
import pandas
df_pandas = cities.toPandas()
df_pandas
# # 1.3 Reading Data from a CSV
# #### Reading external data as a dataframe
avocado = spark.read\
.format("csv")\
.option("header", "True")\
.load("./data/avocado.csv") # replace by the path on your computer
type(avocado)
# #### How many rows are contained in this dataset?
avocado.count()
# #### Lets take a look at the content
avocado.limit(5).show()
# ### Examining the columns data types
# At the moment all columns are strings
avocado.printSchema()
# #### Converting schema types
# * Let's change the type of one of the columns to a float
# * Notice the change when we print the schema
avocado = avocado.withColumn("Total Volume", avocado["Total Volume"].cast("float"))
avocado = avocado.withColumn("year", avocado["year"].cast("int"))
avocado.printSchema()
# #### We can also examine specific columns
avocado.select('year').show(5)
# #### Or multiple columns
avocado.select("Total Volume","year").show(5)
# #### Unique Values by Column
# What are the distinct values for the region column?
# +
years_included = avocado.select('region')\
.distinct()\
years_included.show(10)
# -
# ## 1.4 Filtering & Aggregations
# Say we only want to use the data from 2018
avocados_2018 = avocado.filter(avocado['year'] == "2018")
avocados_2018.show(5)
# #### Or after a certain year...
avocados_2016_onwards = avocado.filter(avocado['year'] >= 2016 )
avocados_2016_onwards.show(5)
# #### We can also see how many data rows exist for each year
agg_data_years = avocado.groupBy("year").count()
agg_data_years.show()
# ## Aggregations
# * We can use aggregations to collect values on a column
# * "agg" knows avg, max, min, sum, count.
agg_data_years.agg({"year":"avg"}).show()
# +
years_column = avocado.select("year")
years_column.agg({"year":"max"}).show()
# -
years_column.agg({"year":"min"}).show()
years_column.agg({"year":"sum"}).show()
years_column.agg({"year":"count"}).show() # note that we can also do this via years_column.count()
# ## 1.5 Grouping Data
# Lets check how many avocados were sold in each region.
avocados_sold = avocado.groupBy("region").agg({"Total Volume": "sum"})
avocados_sold.show(10)
# #### Changing column names
# The column name automatically assigned isn't very nice, let's change it
avocados_sold = avocados_sold.withColumnRenamed("sum(Total Volume)","avocados sold")
avocados_sold.show()
# #### Calculating columns sums
total_sales = avocados_sold.agg({"avocados sold":"sum"})
total_sales.show()
# Lets extract that number as a variable
total_avocados_sold = total_sales.collect()[0][0]
# ## 1.6 SQL Queries
#
# * Spark allows us to query our data as if it were in a relational database with SQL similar commands
# * Before we can query them, we have register them as SQL tables
# * This can either be done as a temporary table (only available in the current session) or as a global table (available across all sessions)
# * Spark's Catalyst optimmizer makes SQL queries very fast
# #### Register the dataframe as a temporary view
#
# * The view is valid for one session
# * This is required to run SQL commands on the dataframe
avocado.createOrReplaceTempView("avocado_local")
all_records_df = sqlContext.sql('SELECT * FROM avocado_local')
all_records_df.show(5)
sqlContext.sql('SELECT AveragePrice, Date FROM avocado_local').show(5)
sqlContext.sql('SELECT Region, AveragePrice, Date FROM avocado_local where Date == "2015-11-29"').show(5)
# #### Global temporary view
#
# * Temporary view shared across multiple sessions
# * Kept alive till the Spark application terminates
avocado.createGlobalTempView("avocado_global")
# #### Careful: The name of global tables has to be preceded by "global.temp"
sqlContext.sql('SELECT * FROM global_temp.avocado_global').show(5)
# ## 1.7 Ordering
# #### We can order tables directly via a SQL query
regions = spark.sql("SELECT Date, AveragePrice, Region FROM global_temp.avocado_global ORDER BY Region Desc")
regions.show(5)
# #### But watch out that the type of the column is what you were expecting it to be. Integers classified as strings will return unexpected results
prices = spark.sql("SELECT Date, AveragePrice, Region FROM global_temp.avocado_global ORDER BY AveragePrice Desc")
prices.show(5)
# #### We can also order regular spark DFs
avocado_order = avocado.select("Date", "AveragePrice","region" )
avocado_order.show(5)
avocado_order.orderBy(avocado.Date.desc()).show(5)
# # 1.8 Plotting Avocado Revenue
# Lets say we'd want to see how the total revenue for non-organic avocados in Las Vegas of xy has developed over time
avocado.show(5) # our initial data
# #### We only select the columns we are interested in
avocado_ = avocado.select("Date", "AveragePrice", "Total Volume", "type", "region")
# #### We filter for all conventional avocados in one location
avocado_by_region = avocado_.filter((avocado_["region"] == "LasVegas") & (avocado_["type"] == "conventional"))
# #### Create a new column with the revenue
import pyspark.sql.functions as func # we import this package from
avocado_revenue = avocado_by_region.withColumn("revenue", func.round(avocado_by_region.AveragePrice *
avocado_by_region["Total Volume"]))
# #### Convert the date row into timestamp values
#
avocado_revenue = avocado_revenue.withColumn("date", func.to_timestamp(avocado_revenue.Date, 'yyyy-MM-dd'))
# #### Create the plot
# +
import matplotlib as mpl
import matplotlib.pyplot as plt
# %matplotlib inline
x = [x[0] for x in avocado_revenue.toLocalIterator()]
y = [x[5] for x in avocado_revenue.toLocalIterator()]
plt.scatter(x,y)
plt.xticks(x, rotation='vertical')
ax = plt.axes()
ax.xaxis.set_major_locator(plt.MaxNLocator(4))
plt.show()
# -
# #### Looks like the result we were looking for. Lets save it as a csv locally as well
# +
# This command directly saves the rdd. However it creates a folder wherein our csc will be saved. We will use another option
#avocado_revenue.repartition(1).write.csv("/Users/dominiquepaul/xJob/3-Spark/1-Output/data/output", sep=',')
# -
# #### A cleaner solution
avocado_revenue.toPandas().to_csv("/Users/dominiquepaul/xJob/3-Spark/testing/output.csv", index=False)
|
3. Spark Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={"duration": 0.008288, "end_time": "2021-05-20T08:30:20.971629", "exception": false, "start_time": "2021-05-20T08:30:20.963341", "status": "completed"} tags=[]
# # Learning PyTorch: Defining new autograd functions
#
# Source: https://pytorch.org/tutorials/beginner/pytorch_with_examples.html#pytorch-defining-new-autograd-functions
#
#
# Under the hood, each primitive autograd operator is really two functions that operate on Tensors. The `forward` function computes output Tensors from input Tensors. The `backward` function receives the gradient of the output Tensors with respect to some scalar value, and computes the gradient of the input Tensors with respect to that same scalar value.
#
# If `x` is a Tensor that has `x.requires_grad=True` then `x.grad` is another Tensor holding the gradient of `x` with respect to some scalar value.
#
# In PyTorch we can easily define our own autograd operator by defining a subclass of `torch.autograd.Function` and implementing the `forward` and `backward` functions. We can then use our new autograd operator by constructing an instance and calling it like a function, passing Tensors containing input data.
#
# In this example we define our model as  instead of , where  is the Legendre polynomial of degree three.
#
# We write our own custom autograd function for computing forward and backward of , and use it to implement our model.
# + papermill={"duration": 1.151685, "end_time": "2021-05-20T08:30:22.130435", "exception": false, "start_time": "2021-05-20T08:30:20.978750", "status": "completed"} tags=[]
import torch
import math
class LegendrePolynomial3(torch.autograd.Function):
"""
We can implement our own custom autograd Functions by subclassing torch.autograd.Function
and implementing the forward and backward passes which operate on Tensors.
"""
@staticmethod
def forward(ctx, input):
"""
In forward pass we receive a Tensor containing input and return a Tensor containing output.
ctx is a context object that can be used to stash information for backward computation.
You can cache arbitrary objects for use in the backward pass using the
ctx.save_for_backward method.
"""
ctx.save_for_backward(input)
return 0.5 * (5 * input ** 3 - 3 * input)
@staticmethod
def backward(ctx, grad_output):
"""
In backward pass we receive a Tensor containing gradient of the loss with respect to the output,
and we need to compute the gradient of the loss with respect to the input.
"""
input, = ctx.saved_tensors
return grad_output * 1.5 * (5 * input ** 2 - 1)
# + papermill={"duration": 0.020931, "end_time": "2021-05-20T08:30:22.159658", "exception": false, "start_time": "2021-05-20T08:30:22.138727", "status": "completed"} tags=[]
dtype = torch.float
device = torch.device("cpu")
# device = torch.device("cuda:0") # Uncomment this to run on GPU
# + papermill={"duration": 0.080664, "end_time": "2021-05-20T08:30:22.249166", "exception": false, "start_time": "2021-05-20T08:30:22.168502", "status": "completed"} tags=[]
# Create Tensors to hold input and outputs.
# By default, 'requires_grad=False', which indicates that we do not need to
# compute gradients with respect to these Tensors during the backward pass.
x = torch.linspace(-math.pi, math.pi, 2000, device=device, dtype=dtype)
y = torch.sin(x)
# + papermill={"duration": 0.018193, "end_time": "2021-05-20T08:30:22.274599", "exception": false, "start_time": "2021-05-20T08:30:22.256406", "status": "completed"} tags=[]
# Create random Tensors for weights.
# For this example, we need 4 weights: y = a + b * P3(c + d * x),
# these weights need to be initialized not too far from the correct result to ensure convergence.
# Setting 'requires_grad=True' indicates that we want to compute gradients with
# respect to these Tensors during the backward pass.
a = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
b = torch.full((), -1.0, device=device, dtype=dtype, requires_grad=True)
c = torch.full((), 0.0, device=device, dtype=dtype, requires_grad=True)
d = torch.full((), 0.3, device=device, dtype=dtype, requires_grad=True)
# + papermill={"duration": 0.891578, "end_time": "2021-05-20T08:30:23.173305", "exception": false, "start_time": "2021-05-20T08:30:22.281727", "status": "completed"} tags=[]
learning_rate = 5e-6
for t in range(2000):
# To apply our Function, we use Function.apply method. We alias this as 'P3'.
P3 = LegendrePolynomial3.apply
# Forward pass: compute predicted y using operations;
# we compute P3 using our custom autograd operation.
y_pred = a + b * P3(c + d * x)
# Compute and print loss
loss = (y_pred - y).pow(2).sum()
if t % 100 == 99:
print(t, loss.item()) # loss.item() gets the scalar value held in the loss.
# Use autograd to compute the backward pass.
loss.backward()
# Update weights using gradient descent
with torch.no_grad():
a -= learning_rate * a.grad
b -= learning_rate * b.grad
c -= learning_rate * c.grad
d -= learning_rate * d.grad
# Manually zero the gradients after updating weights
a.grad = None
b.grad = None
c.grad = None
d.grad = None
print(f'Result: y = {a.item()} + {b.item()} * P3({c.item()} + {d.item()} x)')
|
learning-pytorch-2-new-autograd-functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/timothyolano/Linear-Algebra-58019/blob/main/Final_Exam.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="KTiAIYgVXAOw"
# #1
#
# + colab={"base_uri": "https://localhost:8080/"} id="9buhnmqnUE36" outputId="ae4099d8-d5be-49b9-89f3-3060cb1a3b05"
import numpy as np
A = np.array([[1, 1, 1],[1, 0, 4],[0, 0, 5]])
print(f'Matrix A:\n {A}')
print()
B = np.array([[89],[89],[95]])
print(f'Matrix B:\n {A}')
C = np.linalg.inv(A).dot(B)
print(f'\nInverse of Matrix A:\n{C}')
# + [markdown] id="DvNZeF66W-us"
# #2
#
# + colab={"base_uri": "https://localhost:8080/"} id="AouEpJv4WA3d" outputId="d820c8f5-6756-475e-8a79-034de2d1f0be"
import numpy as np
A = np.array([[3, -1, 1],[9, 3, -3],[-12, 4, -4]])
print(f'Matrix A:\n {A}')
#as we all know a singular matrix is one with a determinant of zero and thus no inverse. since the given matrix is singular, it has no inverse so we cannot solve it properly.
#to show it's output we can use an alt which is the pseudoinverse(pinv).
pinv_A = np.linalg.pinv(A)
print(f'\nPINV:\n{inv_A}')
print()
B = np.array([[5],[10],[-20]])
print(f'Matrix B:\n {B}')
X = np.dot(pinv_A, B)
print(f'\nDot product:\n{X}')
C = np.dot(A, X)
print(f'\nChecking:\n{C}')
# + [markdown] id="j_lSad5UXCb-"
# #3
# + colab={"base_uri": "https://localhost:8080/"} id="s3N_DfLuFyLX" outputId="b6a14075-be3c-440d-efd2-df9d86e84371"
import numpy as np
from numpy.linalg import eig
a = np.array([[8, 5, -6],[-12, -9, 12],[-3 , -3, 5]])
print(f'\nthe Eigenvalue/s is/are: ')
print(a)
ev,evt = np.linalg.eig(a)
print(f'\nThe Eigenvalue/s is/are: {ev.round()}')
print(f'\nThe Right Eigenvectors are: \n{evt.round()}\n')
|
Final_Exam.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # FFT model training
#
# In this notebook we will train a model based of fast Fourier transform for detection of atrial fibrillation.
# * [Init dataset](#Init-dataset)
# * [Train pipeline](#Train-pipeline)
# * [Show loss and metric on train](#Show-loss-and-metric-on-train)
# * [Make predictions](#Make-predictions)
# ## Init dataset
# For model training we will use the PhysioNet's short single lead ECG recording [database](https://physionet.org/challenge/2017/). To follow the tutorial download the PhysioNet's database.
# +
import sys, os
sys.path.append(os.path.join("..", "..", ".."))
from cardio import EcgDataset
eds = EcgDataset(path="/notebooks/data/ECG/training2017/*.hea", no_ext=True, sort=True)
eds.cv_split(0.8)
# -
# ## Train pipeline
# To train the model we construct a ```train_pipeline```. Within the pipeline we initialize the ```FFTModel``` model with given model_config, initialize variable to store loss, load and preprocesse signals, declare which components of the batch are ```x``` and ```y``` for the model and train the model.
# +
import numpy as np
import cardio.dataset as ds
from cardio.dataset import F, V, B
from cardio.models.fft_model import FFTModel
model_config = {
"input_shape": F(lambda batch: batch.signal[0].shape),
"loss": "binary_crossentropy",
"optimizer": "adam"
}
def make_data(batch, **kwagrs):
return {'x': np.array(list(batch.signal)), 'y': batch.target}
train_pipeline = (ds.Pipeline()
.init_model("dynamic", FFTModel, name="fft_model", config=model_config)
.init_variable("loss_history", init_on_each_run=list)
.load(fmt="wfdb", components=["signal", "meta"])
.load(src="/notebooks/data/ECG/training2017/REFERENCE.csv",
fmt="csv", components="target")
.drop_labels(["~"])
.rename_labels({"N": "NO", "O": "NO"})
.random_resample_signals("normal", loc=300, scale=10)
.drop_short_signals(4000)
.split_signals(3000, 3000)
.binarize_labels()
.apply_transform(np.transpose, axes=[0, 2, 1], src='signal', dst='signal')
.unstack_signals()
.train_model('fft_model', make_data=make_data,
save_to=V("loss_history"), mode="a"))
# -
# Run ```train_pipeline```:
# +
# %env CUDA_VISIBLE_DEVICES=1
fft_trained = (eds.train >> train_pipeline).run(batch_size=300, shuffle=True,
drop_last=True, n_epochs=250, prefetch=0)
# -
# ## Show loss and metric on train
# Now ```fft_trained``` contains trained model and loss history. Method ```get_variable``` allows to get ```loss_history``` and we can plot it:
# +
import pandas as pd
import matplotlib.pyplot as plt
loss = pd.DataFrame(fft_trained.get_variable("loss_history"), columns=["loss"])
loss["avr loss"] = pd.DataFrame(loss).rolling(center=True, window=100).mean()
loss.plot()
plt.show()
# -
# ## Make predictions
# For predictions we create ```predict_pipeline```. It differs from ```train_pipeline``` in several things. We import trained model instead of initializing a new one and apply ```predict_model``` instead of ```train_model``` action. Another difference is that we aggregate predictions on signal segments into the final prediction for the whole signal. Function ```make_pivot``` is responsible for it.
# +
def make_pivot(pipeline, variable_name):
cropes = np.array([x[0] for x in pipeline.get_variable("shapes")])
pos = np.vstack([np.pad(np.cumsum(cropes)[:-1], pad_width=(1, 0), mode='constant'), cropes]).T
labels = np.array(pipeline.get_variable(variable_name))
return np.array([labels[s: s + i].mean(axis=0) for s, i in pos])
predict_pipeline = (ds.Pipeline()
.import_model("fft_model", fft_trained)
.init_variable("true_labels", init_on_each_run=list)
.init_variable("pred_labels", init_on_each_run=list)
.init_variable("shapes", init_on_each_run=list)
.init_variable("pivot_true_labels", init_on_each_run=list)
.init_variable("pivot_pred_labels", init_on_each_run=list)
.load(fmt="wfdb", components=["signal", "meta"])
.load(src="/notebooks/data/ECG/training2017/REFERENCE.csv",
fmt="csv", components="target")
.drop_labels(["~"])
.rename_labels({"N": "NO", "O": "NO"})
.drop_short_signals(4000)
.split_signals(3000, 3000)
.binarize_labels()
.apply_transform(np.transpose, axes=[0, 2, 1], src='signal', dst='signal')
.update_variable("shapes", F(lambda batch: [x.shape for x in batch.signal]), mode='w')
.unstack_signals()
.update_variable("true_labels", B('target'), mode='w')
.predict_model('fft_model', make_data=make_data, save_to=V("pred_labels"), mode="w")
.update_variable("pivot_true_labels", F(lambda batch: make_pivot(batch.pipeline,
'true_labels')), mode='e')
.update_variable("pivot_pred_labels", F(lambda batch: make_pivot(batch.pipeline,
'pred_labels')), mode='e'))
# -
# Run ```predict_pipeline``` on the test part of the dataset:
res_test = (eds.test >> predict_pipeline).run(batch_size=300, shuffle=False, drop_last=False,
n_epochs=1, prefetch=0)
# Consider predicted values and true labels which are stored in ```pivot_pred_labels``` and ```pivot_true_labels```. We get them through ```get_variable``` method and caclulate several classification metrics:
# +
from sklearn.metrics import f1_score
print(f1_score(np.array(res_test.get_variable("pivot_true_labels"))[:, 0],
np.rint(res_test.get_variable("pivot_pred_labels"))[:, 0], average='macro'))
# +
from sklearn.metrics import classification_report
print(classification_report(np.array(res_test.get_variable("pivot_true_labels"))[:, 0],
np.rint(res_test.get_variable("pivot_pred_labels"))[:, 0]))
|
cardio/models/fft_model/fft_model_training.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # TDI Capstone Project, Part 2: Compile NEI data
#
# **Note:** NEI stands for National Emissions Inventory.
#
# **What does this code do?**
# 1. Retrieves NEI emissions estimates for several important pollutants (specified in `poll_codes`: NOx, PM10, PM2.5, PMfine, SO2, SO4, VOC, CO, NH3; years: 20008, 2011, 2014), for all facilities for which the estimates are available (about 75% of major emitters, very few minor emitters). All these estimates are added as columns to a single dataframe.
# 1. Determines the industries of all facilities. Adds the industry to the dataframe as an additional column.
# 1. Determines the three "primary pollutants" for each industry -> the pollutants the industry emitted the most of, relative to the other industries, in 2014. For example, if facilities in industry X emitted 1.5 times more VOCs and 1.2 times more NOx than facilities across all industries, on average, then VOCs would be the industry's primary pollutant. This information is not included in the dataframe.
# 1. Calculates each facility's normalized emissions of those three "primary pollutants." The normalization is performed by dividing the emissions by the mean emissions of that pollutant by all other facilities in the industry, and allows us to compare emissions of different pollutants across industries. These normalized emissions are included in the dataframe.
# 1. Saves the dataframe to a CSV file, so that I can use it later.
# +
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
data_path = './data'
def get_NEI_data(poll_codes,yrs):
def get_facilities_list(file_facilities_icis):
facilities_icis = pd.read_csv(file_facilities_icis,dtype='str')
facilities_icis = facilities_icis[['REGISTRY_ID','NAICS_CODES']].dropna(axis=0,subset=['REGISTRY_ID'])
facilities_icis = facilities_icis[facilities_icis['REGISTRY_ID'].duplicated()==0]
return facilities_icis
def add_NEI_IDs(X,file_program_links_frs):
"""Adds NEI IDs for all facilities (for which NEI IDs are available)."""
program_links = pd.read_csv(file_program_links_frs,dtype='str')
NEI_links = program_links[program_links['PGM_SYS_ACRNM']=='EIS']
NEI_links = NEI_links.rename(columns={'PGM_SYS_ID':'EIS_ID'}).drop('PGM_SYS_ACRNM',axis=1)
X = X.merge(NEI_links,how='left',on='REGISTRY_ID')
return X
def add_emissions_from_yr(X,poll_codes,file_nei,nei_year='2014'):
"""Adds emissions estimates for each pollutant in poll_codes."""
nei = pd.read_csv(file_nei,dtype='str')
cols_for_merge = ['total_emissions']
for code in poll_codes:
for_merge = nei[nei['pollutant_cd']==code][['eis_facility_site_id']+cols_for_merge]
for_merge[cols_for_merge] = for_merge[cols_for_merge].astype(float)
rename_dict = {col:col+':'+code+':'+str(nei_year) for col in cols_for_merge}
for_merge = for_merge.rename(columns=rename_dict)
X = X.merge(for_merge,how='left',left_on='EIS_ID',
right_on='eis_facility_site_id').drop('eis_facility_site_id',axis=1)
return X
# Get list of relevant facilities
file_facilities_icis = os.path.join(data_path,'ICIS-Air_downloads','ICIS-AIR_FACILITIES.csv')
icis_facilities = get_facilities_list(file_facilities_icis)
# Link REGISTRY_ID to NEI_ID
file_program_links_frs = os.path.join(data_path,'frs_downloads','FRS_PROGRAM_LINKS.csv')
icis_facilities = add_NEI_IDs(icis_facilities,file_program_links_frs)
# Add 2014 NEI data
if '2014' in yrs:
file_nei14 = os.path.join(data_path,'NEI_data','2014v2facilities.csv')
icis_facilities = add_emissions_from_yr(icis_facilities,poll_codes,file_nei14,nei_year='2014')
# Add 2011 NEI data
if '2011' in yrs:
file_nei11 = os.path.join(data_path,'NEI_data','2011neiv2_facility.csv')
icis_facilities = add_emissions_from_yr(icis_facilities,poll_codes,file_nei11,nei_year='2011')
# Add 2008 NEI data
if '2008' in yrs:
file_nei08 = os.path.join(data_path,'NEI_data','2008neiv3_facility.csv')
icis_facilities = add_emissions_from_yr(icis_facilities,poll_codes,file_nei08,nei_year='2008')
# Remove duplicates introduced by left joins.
icis_facilities = icis_facilities[icis_facilities['REGISTRY_ID'].duplicated()==False]
return icis_facilities
def add_industry_nei(X):
"""Transformer for adding feature: industry of regulated facility"""
from external_variables import naics_dict
naics_lookup = pd.DataFrame({'FIRST_NAICS':list(naics_dict.keys()),
'FAC_INDUSTRY':list(naics_dict.values())})
X['FIRST_NAICS'] = X['NAICS_CODES'].apply(lambda x: str(x).split(' ')[0][0:2])
X = X.merge(naics_lookup,how='left',on='FIRST_NAICS')
X = X.drop('FIRST_NAICS',axis=1)
X['FAC_INDUSTRY'] = X['FAC_INDUSTRY'].fillna('unknown')
return X
def calc_primary_emissions(nei_data):
"""Function for calculating emissions for the primary pollutants for ALL facilities, normalized by
the mean emissions for all facilities in a given facility's industry.
"""
def get_primary_poll_for_industry(nei_data,yr):
"""Function to get 'primary pollutants' for each industry.
'primary pollutants' are defined as the three pollutants that are highest, relative to the
corss-industry emission values.
"""
# Get mean emissions totals for each pollutant, for each industry.
needed_cols = ['FAC_INDUSTRY']+[col for col in nei_data.columns if '2014' in col]
mean_emiss = nei_data[needed_cols].groupby('FAC_INDUSTRY').mean()
# Norm. emissions of each pollutant by dividing by the mean across all industries. Primary pollutants
# for an industry are the those that have the largest emissoins relative to cross-industry means.
primary_poll = {}
mean_emiss_quant = mean_emiss.copy()
for i,row in mean_emiss_quant.iterrows():
mean_emiss_quant.loc[i,:] = mean_emiss_quant.loc[i,:]/mean_emiss.mean()
primary_poll[i] = {'poll'+str(i+1):name.split(':')[1] for
i,name in enumerate(list(row.nlargest(3).index))}
return primary_poll
def calc_mean_emiss_by_industry(nei_data,years=['2008','2011','2014']):
"""Function for calculating mean emissions of each pollutant, for each industry"""
mean_emiss_by_year = {}
for year in years:
needed_cols = ['FAC_INDUSTRY']+[col for col in nei_data.columns if year in col]
mean_emiss = nei_data[needed_cols].groupby('FAC_INDUSTRY').mean()
mean_emiss_by_year[year] = mean_emiss.rename(columns={col:col.split(':')[1] for col
in mean_emiss.columns})
return mean_emiss_by_year
def add_primary_poll_cols(row,poll_num,year,primary_poll,mean_emiss):
"""Function for calculating emissions for the primary pollutants for a SINGLE facility, normalized by
the emissions for all facilities in the industry.
"""
poll_name = primary_poll[row['FAC_INDUSTRY']]['poll'+str(poll_num)]
poll_val = row[':'.join(['total_emissions',poll_name,year])] / \
mean_emiss[year].loc[row['FAC_INDUSTRY'],poll_name]
return poll_val
primary_poll = get_primary_poll_for_industry(nei_data,'2014')
mean_emiss = calc_mean_emiss_by_industry(nei_data,years=['2008','2011','2014'])
for year in ['2008','2011','2014']:
for poll_num in range(1,4):
new_col = []
for i,row in nei_data.iterrows():
new_col.append(add_primary_poll_cols(row,poll_num,year,primary_poll,mean_emiss))
nei_data['poll'+str(poll_num)+'_'+year] = new_col
print(poll_num)
return nei_data, primary_poll
if __name__=='__main__':
yrs = ['2008','2011','2014']
poll_codes = ['NOX','PM10-PRI','PM25-PRI','PMFINE','SO2','SO4','VOC','CO','NH3']
nei_data = get_NEI_data(poll_codes,yrs)
nei_data = add_industry_nei(nei_data)
nei_data,primary_poll = calc_primary_emissions(nei_data)
nei_data = nei_data[nei_data['REGISTRY_ID'].duplicated()==0]
primary_poll_df = pd.DataFrame(primary_poll)
primary_poll_df.to_csv(os.path.join(data_path,'primary_pollutants_by_industry.csv'))
nei_data.to_csv(os.path.join(data_path,'processed_nei_emissions_by_facility.csv'))
|
notebooks/prepare_nei_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
# %matplotlib inline # for inline plots
x=[1,2,3,4,5,6,7]
y=[50,51,52,48,47,49,46]
plt.xlabel('Day')
plt.ylabel('Temperature')
plt.title('Weather')
plt.plot(x,y,color='green',linewidth=5, linestyle='dotted')
# ### Formatting Stings
# +
plt.xlabel('Day')
plt.ylabel('Temperature')
plt.title('Weather')
plt.plot(x,y,'b+--')
# -
# Same effect as 'b+' format string
plt.plot(x,y,color='blue',marker='+',linestyle='')
# ### Marker Size
plt.plot(x,y,color='blue',marker='+',linestyle='',markersize=20)
# ### Alpha property to control transparency of line chart
plt.plot(x,y,'g<--',alpha=0.5) # alpha can be specified on a scale 0 to 1
|
03_DataVisualization/02_FormattingPlots.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %reset -f
# new
# Import packages
import math
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
# Change matplotlib backend
# %matplotlib notebook
# #%matplotlib inline
# Import slider package
from matplotlib.widgets import Slider
# #%matplotlib widget
# +
# Fermi-Dirac Distribution
def fermi(E: float, E_f: float, T: float) -> float:
k_b = 8.617 * (10**-5) # eV/K
return 1/(np.exp((E - E_f)/(k_b * T)) + 1)
def normdensity(x,mu,sigma):
weight = 1.0 /(sigma * math.sqrt(2.0*math.pi))
argument = ((x - mu)**2)/(2.0*sigma**2)
normdensity = weight*math.exp(-1.0*argument)
return normdensity
def normdist(x,mu,sigma):
argument = (x - mu)/(math.sqrt(2.0)*sigma)
normdist = (1.0 + math.erf(argument))/2.0
return normdist
# -
# General plot parameters
mpl.rcParams['font.family'] = 'Avenir'
mpl.rcParams['font.size'] = 18
mpl.rcParams['axes.linewidth'] = 2
mpl.rcParams['axes.spines.top'] = False
mpl.rcParams['axes.spines.right'] = False
mpl.rcParams['xtick.major.size'] = 10
mpl.rcParams['xtick.major.width'] = 2
mpl.rcParams['ytick.major.size'] = 10
mpl.rcParams['ytick.major.width'] = 2
# Create figure and add axes
fig = plt.figure(figsize=(6, 4))
ax = fig.add_subplot(111)
# Temperature values
#T = np.linspace(100, 1000, 10)
x = np.linspace(-50,50,100)
mu = 0
sigma = 1
y = np.linspace(0,0,100)
z = np.linspace(0,0,100)
# Get colors from coolwarm colormap
colors = plt.get_cmap('coolwarm', 10)
# Plot F-D data
#for i in range(len(T)):
# x = np.linspace(0, 1, 100)
# y = fermi(x, 0.5, T[i])
for i in range(len(x)):
y[i] = normdist(x[i],mu,sigma)
z[i] = normdensity(x[i],mu,sigma)
ax.plot(x, y, color="red", linewidth=2.5)
ax.plot(x, z, color="blue", linewidth=2.5)
# Add legend
labels = ['100 K', '200 K', '300 K', '400 K', '500 K', '600 K',
'700 K', '800 K', '900 K', '1000 K']
ax.legend(labels, bbox_to_anchor=(1.05, -0.1), loc='lower left',
frameon=False, labelspacing=0.2)
# +
# Create figure and add axes
fig = plt.figure(figsize=(6, 4))
# Create main axis
ax = fig.add_subplot(111)
fig.subplots_adjust(bottom=0.2, top=0.75)
# -
# Create axes for sliders
ax_Ef = fig.add_axes([0.3, 0.85, 0.4, 0.05])
ax_Ef.spines['top'].set_visible(True)
ax_Ef.spines['right'].set_visible(True)
ax_T = fig.add_axes([0.3, 0.92, 0.4, 0.05])
ax_T.spines['top'].set_visible(True)
ax_T.spines['right'].set_visible(True)
# Create sliders
s_Ef = Slider(ax=ax_Ef, label='Std. Deviation ', valmin=0.001, valmax=10.0,
valinit=1, valfmt=' %1.1f ', facecolor='#cc7000')
s_T = Slider(ax=ax_T, label='Mean ', valmin=-10, valmax=10,
valinit=0, valfmt='%1.1f ', facecolor='#cc7000')
# +
# Plot default data
#x = np.linspace(-0, 1, 100)
Ef_0 = 0.5
T_0 = 100
#y = fermi(x, Ef_0, T_0)
#f_d, = ax.plot(x, y, linewidth=2.5)
x = np.linspace(-50,50,100)
mu = 0
sigma = 1
for i in range(len(x)):
y[i] = normdist(x[i],mu,sigma)
f_d, = ax.plot(x, y, linewidth=2.5)
# -
# Update values
def update(val):
Ef = s_Ef.val
T = s_T.val
# f_d.set_data(x, fermi(x, Ef, T))
for i in range(len(x)):
y[i] = normdist(x[i],T,Ef)
f_d.set_data(x, y)
fig.canvas.draw_idle()
s_Ef.on_changed(update)
s_T.on_changed(update)
x = np.linspace(-50,50,100)
x
|
site/normal-demonstration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ** This notebook assumes ... **
#
# 1) Basic familiarity with gwsurrogate as covered in basics.ipynb
#
# 2) You've downloaded a non-spinning numerical relativity or EMRI surrogate. To see all available surrogates, check the surrogate repository by doing (from ipython)
#
# ```python
# >>> import gwsurrogate as gws
# >>> gws.catalog.list()
# >>> gws.catalog.pull("NAME OF SURROGATE MODEL TO DOWNLOAD")
# ```
# +
### setup paths used throughout this notebook ###
import sys
path_to_gws = '/home/balzani57/Repo/GitRepos/Codes/gwsurrogate/gwsurrogate/'
sys.path.append(path_to_gws)
# %matplotlib inline
import numpy as np, matplotlib.pyplot as plt
import gwsurrogate as gws
import gwtools
import tqdm
# -
# # Non-spinning surrogate models
#
# This notebook will cover four non-spinning models
#
# A multi-mode NR surrogate covering mass ratios 1 to 10
#
# 1. SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5
#
# A multi-mode EMRI surrogate covering mass ratios 3 to $10^4$
#
# 2. EMRISur1dq1e4.h5
#
# And two multi-mode NR surrogates that are the same physical model as 1, but using a "linear" (affine) representation needed for certain applications
#
# 3. SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0_FastSplined_WithVandermonde.h5
# 4. SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0_FastSplined_WithVandermonde_NewInterface.h5
#
# Models 3 & 4 are covered near the end of this notebook.
#
# Models 1 & 2 use the same code at the beginning part of this notebook -- simply change the model's data file specified in the "load the surrogate data" cell below...
# +
### load the surrogate data ###
#path_to_surrogate = path_to_gws+'surrogate_downloads/SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5'
path_to_surrogate = path_to_gws+'surrogate_downloads/EMRISur1dq1e4.h5'
model = gws.EvaluateSurrogate(path_to_surrogate, ell_m=[(2,2),(3,3)]) # load two m>0 modes only
# -
# # Lesson 1: Simple evaluations
# +
# Evaluate and plot the 2,2 mode.
# By default, the modes are evaluated on the sphere, and negative modes are generated from
# known relationships. So we need to set both options to false to get only the (2,2) mode.
modes, times, hp, hc = model(q=3.7, ell=[2], m=[2], mode_sum=False, fake_neg_modes=False)
print('You have evaluated the (%i,%i) mode'%(modes[0][0],modes[0][1]))
gwtools.plot_pretty(times, [hp, hc],fignum=1)
plt.plot(times,gwtools.amp(hp+1j*hc),'r')
plt.title('The (%i,%i) mode'%(modes[0][0],modes[0][1]))
plt.xlabel('t/M ')
plt.show()
# +
# generating both the (3,3) and (3,-3) modes is easy!
modes, times, hp, hc = model(q=3.7, ell=[3], m=[3], mode_sum=False)
print("Evaluated modes =", modes)
gwtools.plot_pretty(times, [hp[:,0], hc[:,0]],fignum=2)
plt.plot(times,gwtools.amp(hp[:,0]+1j*hc[:,0]),'r')
plt.xlabel('t/M ')
plt.title('The (%i,%i) mode'%(modes[0][0],modes[0][1]))
gwtools.plot_pretty(times, [hp[:,1], hc[:,1]],fignum=3)
plt.plot(times,gwtools.amp(hp[:,1]+1j*hc[:,1]),'r')
plt.title('The (%i,%i) mode'%(modes[1][0],modes[1][1]))
plt.xlabel('t/M ')
plt.show()
# -
# Trying to evaluate a mode which doesn't exist throws a warning
model(q=3.7, ell=[3], m=[2], mode_sum=False, fake_neg_modes=False)
# # Lesson 2: Physical waveforms
# load all the modes
# if using the NR surrogate, the (2,0) mode is excluded by default (See http://arxiv.org/abs/1502.07758 for why)
model = gws.EvaluateSurrogate(path_to_surrogate)
# +
# Evaluate the (2,2) mode for physical input values
M = 115.0 # units of solar masses
q = 4.0
theta = np.pi/3.0
phi = np.pi/3.0
dist = 1.0 # units of megaparsecs
fmin = 1.0 # units of hz
# The surrogate evaluation is NOT long enough to achieve a starting frequency of 1hz
modes,times,hp,hc = model(M=M,q=q,dist=dist,theta=theta,phi=phi,ell=[2],m=[2],mode_sum=False,fake_neg_modes=False,f_low=fmin)
# +
# We'll be safer with 15 hz
fmin = 15
# Lets evaluate the (2,2) and (2,-2) at phi = theta = pi/3 on the sphere
times,hp,hc = model(M=M,q=q,dist=dist,theta=theta,phi=phi,ell=[2],m=[2],f_low=fmin)
gwtools.plot_pretty(times, [hp, hc])
plt.plot(times,gwtools.amp(hp+1j*hc),'r')
plt.xlabel('t (seconds)')
plt.show()
# -
# # Lesson 3: EMRI Surrogate vs NR
#
# Here we repeat the experiment shown in Figure 3 (https://arxiv.org/pdf/1910.10473.pdf) which compares the EMRI surrogate model to Numerical Relativity waveforms in the range q <=10.
#
# Our numerical relativity waveforms will be generated using the NR surrogate model SpEC_q1_10_NoSpin.
# gwtools is installed as a dependency of gwsurrogate -- used for optimization over time and phase shifts
from gwtools.gwtools import modes_list_to_dict, minimize_norm_error, euclidean_norm_sqrd, q_to_nu
from gwtools.mismatch import mathcal_E_error_from_mode_list
# +
# load the emri and NR surrogate models
emri_modes = [(2,2),(2,1),(3,3),(3,1),(3,2),(4,4),(4,2),(4,3),(5,5),(5,3),(5,4)]
path_to_surrogate = gws.__path__[0]+'/surrogate_downloads/SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5'
spec = gws.EvaluateSurrogate(path_to_surrogate, ell_m=emri_modes)
path_to_surrogate = gws.__path__[0]+'/surrogate_downloads/EMRISur1dq1e4.h5'
emri = gws.EvaluateSurrogate(path_to_surrogate) # load two m>0 modes only
# +
# generate a q=8 EMRI and NR waveform -- decide on dimensionless or physical waveforms
q=8
## dimensionless waveforms ##
modes_spec, times_spec, hp_spec, hc_spec = spec(q=q, mode_sum=False, fake_neg_modes=False)
modes_emri, time_emri, hp_emri, hc_emri = emri(q, mode_sum=False, fake_neg_modes=False)
h_spec = hp_spec + 1.0j*hc_spec
h_emri = hp_emri + 1.0j*hc_emri
h_emri = modes_list_to_dict(modes_spec,h_emri)
h_spec = modes_list_to_dict(modes_spec,h_spec)
t_low_adj =5; t_up_adj = 2; # needed for minimization algorithm below
## physical waveforms ##
#M = 115.0 # units of solar masses
#theta = np.pi/3.0; phi = np.pi/3.0
#dist = 1.0 # units of megaparsecs
#fmin = 95.0 # units of hz
#t_low_adj =.2; t_up_adj = .01; # needed for minimization algorithm below
#modes_spec, times_spec, hp_spec, hc_spec = spec(M=M,q=q,dist=dist,theta=theta,phi=phi,\
# ell=[2],m=[2],mode_sum=False,fake_neg_modes=False,\
# f_low=fmin)
#modes_emri, time_emri, hp_emri, hc_emri = emri(M=M,q=q,dist=dist,theta=theta,phi=phi,\
# ell=[2],m=[2],mode_sum=False,fake_neg_modes=False,\
# f_low=fmin,\
# times=times_spec,units='mks') # tests user-defined time grids
#h_spec={}; h_spec[(2,2)] = hp_spec + 1.0j*hc_spec
#h_emri={}; h_emri[(2,2)] = hp_emri + 1.0j*hc_emri
# -
# waveforms have not yet been aligned in time and phase
plt.figure(figsize=(14,4))
plt.plot(time_emri,np.real(h_emri[(2,2)]),label='{2,2} mode - EMRI')
plt.plot(times_spec,np.real(h_spec[(2,2)]),label='{2,2} mode - NR')
plt.xlabel('t',fontsize=12)
plt.ylabel('h(t)',fontsize=12)
plt.legend(fontsize=12)
#plt.savefig('emri_sur_q_%f.png'%q)
#plt.xlim([-3000,200])
#plt.xlim([-1.6,0.1])
plt.show()
## here we minimize the error over time and phase shifts for the (2,2) mode only
[errors_before_min, errors_after_min], [tc, phic], [common_times,h_emri_aligned,h_nr_aligned] = \
minimize_norm_error(time_emri,h_emri[(2,2)],times_spec,h_spec[(2,2)],\
euclidean_norm_sqrd,t_low_adj=t_low_adj,t_up_adj=t_up_adj,method='nelder-mead')
print(errors_before_min)
print(errors_after_min)
print(tc) # time shift needed
print(phic) # phase shift needed
# +
# plot waveforms after minimizations
plt.figure(1)
plt.plot(common_times, np.real(h_nr_aligned),'blue',label='{2,2} mode - NR')
plt.plot(common_times, np.real(h_emri_aligned),'r--',label='{2,2} mode - EMRI')
plt.legend(fontsize=12)
plt.figure(2)
plt.plot(common_times, np.imag(h_nr_aligned),'blue',label='{2,2} mode - NR')
plt.plot(common_times, np.imag(h_emri_aligned),'r--',label='{2,2} mode - EMRI')
plt.legend(fontsize=12)
# -
# # Lesson 4: Linear surrogates
#
# Lessons 1 & 2 considered a nonlinear model: both EMRISur1dq1e4.hdf5 and SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5 prescribes a nonlinear relationship between the strain, h, and the data pieces (the amplitude and phase of each harmonic mode) that are modeled.
#
# We call a surrogate linear if $h_{\ell m}$ if it can be expressed as a linear combination of basis functions
#
# $$h_{\ell m} (t;q) = \sum_{i=1}^n c_{\ell m}^n(q) e_{\ell m}^n(t)$$
#
# Some applications, like the RapidPE pipeline, [benefit from using a linear surrogate model](http://iopscience.iop.org/article/10.1088/1361-6382/aa7649/meta). These surrogates are also typically faster to evaluate.
#
# Here we consider two "linearized" (an admittedly poor modifier) versions of the surrogate SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5. We simply show these models agree with one another, as they should
# reload all modes of the original nonlinear surrogate model, including the (2,0)
path_to_surrogate = path_to_gws+'surrogate_downloads/SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0.h5'
sur = gws.EvaluateSurrogate(path_to_surrogate,excluded=None)
# ### A Linear, fast-spline surrogate using the default gwsurrogate interface
# load the linear, fast-spline surrogate model
path_to_surrogate = "/home/balzani57/Repo/GitRepos/Codes/gwsurrogate/surrogate_downloads/SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0_FastSplined_WithVandermonde.h5"
sur_lin = gws.EvaluateSurrogate(path_to_surrogate,excluded=None)
# +
# check the original surrogate and linear "surrogate-of-a-surrogate" models agree
lm_modes, t, hreal_lin, himag_lin = sur_lin(1.2, mode_sum=False, fake_neg_modes=False)
lm_modes, t, hreal, himag = sur(q=1.2, mode_sum=False, fake_neg_modes=False)
plt.figure(1)
plt.plot(t, hreal[:, 2], 'k', label='Original amp/phase surrogate')
plt.plot(t, np.real(hreal_lin[:, 2]), 'r--', label='spline surrogate-of-a-surrogate')
plt.plot(t, (1000.0)* abs(hreal[:, 2] - np.real(hreal_lin[:, 2])), 'c', label=r'$1000 \times$ error')
plt.legend(frameon=False, loc='upper left')
plt.show()
# and make sure we get the (2, 0) mode as well
lm_modes, t, hreal, himag = sur_lin(1.0, mode_sum=False, fake_neg_modes=False)
print("evaluated (ell, m) modes =",lm_modes)
plt.figure(2)
h22 = hreal[:, 2] + 1.0j * himag[:, 2]
plt.plot(t, h22.real, 'b',label='real part of (2,2)')
plt.plot(t, h22.imag, 'r--',label='imaginary part of (2,2)')
plt.plot(t, np.abs(h22), 'k',label='amplitude of (2,2)')
plt.plot(t, hreal[:, 0], 'c', lw=2,label='real part of (2,0)')
plt.legend(frameon=False, loc='upper left')
plt.show()
# +
# now perform a more complete error analysis
nqtest = 150
qtest = np.linspace(1., 10., nqtest)
def many_h_evals(qvals):
"""evalutate the original surrogate at many mass ratio values"""
h_evals = []
for i in tqdm.trange(len(qvals)):
q = qvals[i]
_, t, hreal, himag = sur(q, mode_sum=False, fake_neg_modes=False)
h_evals.append( hreal + 1.j*himag )
return h_evals
def waveform_norm(h):
return np.sqrt(np.sum(abs(h**2)))
def waveform_error(h1, h2):
return waveform_norm(h1 - h2) / waveform_norm(h1)
def test_spline_surrogate(spline_surrogate, nqtest, h_evals):
qtest = np.linspace(1., 10., nqtest)
errs = []
for i in tqdm.trange(len(qtest)):
q = qtest[i]
h = h_evals[i]
lm_modes, t, hreal, himag = spline_surrogate(q, mode_sum=False, fake_neg_modes=False)
h_spline = hreal + 1.j*himag
#h_spline = np.array([spline_modes[k] for k in lm_modes])
errs.append(waveform_error(h, h_spline))
return np.array(errs)
h_evals = many_h_evals(qtest)
loaded_err = test_spline_surrogate(sur_lin, nqtest, h_evals)
plt.semilogy(qtest, loaded_err, label='error')
# -
# ### Linear, fast-spline surrogate using a new gws interface
# +
# FastTensorSplineSurrogate is a new feature
from gwsurrogate.new import surrogate
loaded_surrogate = surrogate.FastTensorSplineSurrogate()
# ... and we load the linear (spline) surrogate in a different way
path_to_surrogate = '/home/balzani57/Repo/GitRepos/Codes/gwsurrogate/surrogate_downloads/'
loaded_surrogate.load(path_to_surrogate+"SpEC_q1_10_NoSpin_nu5thDegPoly_exclude_2_0_FastSplined_WithVandermonde_NewInterface.h5")
# +
# check the original and linear "surrogate-of-a-surrogate" models agree
h_modes = loaded_surrogate([1.2])
lm_modes, t, hreal, himag = sur(q=1.2, mode_sum=False, fake_neg_modes=False)
plt.plot(t, hreal[:, 2], 'k', label='Original amp/phase surrogate')
plt.plot(t, np.real(h_modes[2, 2]), 'r--', label='spline surrogate-of-a-surrogate')
plt.plot(t, abs(hreal[:, 2] - np.real(h_modes[2, 2])), 'c', label='error')
plt.legend(frameon=False, loc='upper left')
plt.show()
# +
## Compare the linear surrogate using new and original interfaces -- These should be EXACTLY identical
h_modes = loaded_surrogate([10.0])
_, t, hreal, himag = sur_lin(q=10.0, mode_sum=False, fake_neg_modes=False)
h = hreal + 1.j*himag
plt.plot(t, hreal[:, 2], 'k', label='Original amp/phase surrogate')
plt.plot(t, np.real(h_modes[2, 2]), 'r--', label='spline surrogate-of-a-surrogate')
#plt.plot(t, abs(hreal[:, 2] - np.real(h_modes[2, 2])), 'c', label='error')
plt.legend(frameon=False, loc='upper left')
plt.show()
print np.max(abs(hreal[:, 2] - np.real(h_modes[2, 2])))
h_modes = np.array([h_modes[k] for k in lm_modes])
print waveform_error(h_modes, h.T)
# +
# ...and a more complete error analysis
errs = []
nqtest = 100
qtest = np.linspace(1., 10., nqtest)
for i in tqdm.trange(len(qtest)):
q = qtest[i]
h_modes = loaded_surrogate([q])
_, t, hreal, himag = sur_lin(q=q, mode_sum=False, fake_neg_modes=False)
h = hreal + 1.j*himag
h_spline = np.array([h_modes[k] for k in lm_modes])
errs.append(waveform_error(h_spline, h.T))
errs = np.array( errs )
plt.semilogy(qtest, errs, label='error')
# ... Why aren't the errors exactly zero? Its probably due to nudging
# where the end point parameters are not truely identical
# -
|
tutorial/notebooks/nonspinning_nr_emri.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Create photoreduction forcing files
# +
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.basemap import Basemap, cm
import netCDF4 as nc
import xarray as xr
import pickle
# %matplotlib inline
# -
# Photo-enhanced reduction should occur over the euphotic zone depth. For the Canada Basin, Laney et al. (2017) estimated the euphotic zone depth as ~70-110 m based on the 1% light extinction from ITP measurements. Bhatia et al. (2021) estimated the euphotic zone depth in the CAA with a median of 50 m.
# ##### Load files
# ANHA12 grid:
mesh = nc.Dataset('/ocean/brogalla/GEOTRACES/data/ANHA12/ANHA12_mesh1.nc')
tmask = np.array(mesh.variables['tmask'])
land_mask = np.ma.masked_where((tmask[0,:,:,:] > 0.1), tmask[0,:,:,:])
lons = np.array(mesh.variables['nav_lon'])
lats = np.array(mesh.variables['nav_lat'])
mbathy = np.array(mesh.variables['mbathy'])[0,:,:] # bottom depth
# Define euphotic zone depth:
euphotic_depth = np.zeros(lons.shape)
euphotic_depth[:] = 70
euphotic_depth[(mbathy == 43)] = 65
euphotic_depth[(mbathy == 42)] = 60
euphotic_depth[(mbathy == 41)] = 55
euphotic_depth[mbathy <= 40] = 50
# ##### Calculations
# +
fig, ax1, proj1= pickle.load(open('/ocean/brogalla/GEOTRACES/pickles/mn-reference.pickle','rb'))
x, y = proj1(lons, lats)
# Euphotic zone depth:
CB = proj1.contourf(x, y, euphotic_depth, vmin=50, vmax=70, levels=[50,55,60,65,70])
cbaxes = fig.add_axes([0.92, 0.2, 0.04, 0.45])
CBar = plt.colorbar(CB, cax=cbaxes)
CBar.set_label(label='Euphotic zone depth [m]',size=8)
CBar.ax.tick_params(labelsize=8)
# -
# Save file:
# +
file_write = xr.Dataset(
{'euphotic': (("y","x"), euphotic_depth)},
coords = {
"y": np.zeros(2400),
"x": np.zeros(1632),
},
attrs = {
'long_name':'Euphotic zone depth',
'units':'m',
}
)
file_write.to_netcdf('/ocean/brogalla/GEOTRACES/data/euphotic-20210811.nc')
# -
|
forcing/scavenging---euphotic-depth.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Ridge and Lasso Regression
#
# https://openclassrooms.com/fr/courses/4444646-entrainez-un-modele-predictif-lineaire/4507811-tp-comparez-le-comportement-du-lasso-et-de-la-regression-ridge
#
# In this exercice, we will try to compare the pros and cons of Ridge's and Lasso's Regression
#
# The aim is to determine if a patient has the prostate cancer. By determining is rate of lpsa.
#
# We assume the dataset is pure.
#
# Import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.metrics import mean_absolute_error, median_absolute_error, r2_score
from pylab import *
from warnings import simplefilter
# ignore all future warnings
simplefilter(action='ignore', category=FutureWarning)
df = pd.read_csv('data.txt', delimiter='\t')
df.head()
x = df.iloc[:60,1:-3]
x.head()
Y = pd.DataFrame(df["lpsa"])
X = df.drop(labels=["lpsa", "train", "col", "pgg45"], axis=1)
# ## Linear Regression
#
# In order to compare to Ridge's and Lasso's performance, we should firstly estimate the efficiency of the basic linear regression.
LinearRegression_ = LinearRegression()
scores = cross_val_score(LinearRegression_, X, Y, cv=3)
print(scores, " / Moyenne R² : ", scores.mean())
# # Ridge Regression
#
# Ridge Regression is a way to avoid overfitting by regularizing the weight of high coefficient.
# we firstly generate a lot of alphas values in order to get the best one
alphas = np.logspace(-5, 5, 200)
RidgeRegression = RidgeCV(alphas=alphas)
model = RidgeRegression.fit(X, Y)
print("best alpha : {}".format(model.alpha_))
score = model.score(X, Y)
score
# # Lasso Regression
#
# This regression will try to reduce the dimension of our dataset by eliminating some coefficient near of 0. Then it should simplify the model.
LassoRegression = LassoCV(alphas=alphas)
model = LassoRegression.fit(X, list(Y["lpsa"]))
print("best alpha : {}".format(model.alpha_))
score = model.score(X, Y)
score
|
OpenClassRoom/RidgeAndLassoRegression/RidgeAndLassoRegression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="z4vi8tH5xO_x" colab_type="text"
# # Neural Machine Translation Example
# + id="DiQIr4FSloBt" colab_type="code" outputId="7fdf6017-4afe-4f8f-e947-f9eb22586cdc" colab={"base_uri": "https://localhost:8080/", "height": 870}
# Install TensorFlow and also our package via PyPI
# !pip install tensorflow-gpu==2.0.0
# !pip install headliner
# + id="DLWI5oUvJ1St" colab_type="code" outputId="785a297c-a15c-473f-c816-fa7ef18f7797" colab={"base_uri": "https://localhost:8080/", "height": 255}
# Download the German-English sentence pairs
# !wget http://www.manythings.org/anki/deu-eng.zip
# !unzip deu-eng.zip
# + id="kYyOWzeep2lU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 102} outputId="4d4584c8-b6ed-4f40-923c-cbc11a6230ad"
# Create the dataset but only take a subset for faster training
import io
def create_dataset(path, num_examples):
lines = io.open(path, encoding='UTF-8').read().strip().split('\n')
word_pairs = [[w for w in l.split('\t')[:2]] for l in lines[:num_examples]]
return zip(*word_pairs)
eng, ger = create_dataset('deu.txt', 30000)
data = list(zip(eng, ger))
data[:5]
# + id="pPiBB8TCzCVg" colab_type="code" colab={}
# Split the dataset into train and test
from sklearn.model_selection import train_test_split
train, test = train_test_split(data, test_size=100)
# + id="SOz2fIXQz_Kz" colab_type="code" outputId="2a07f18f-7818-4ec5-e14f-c89a5de6ef5c" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# Define the model and train it
from headliner.trainer import Trainer
from headliner.model.summarizer_attention import SummarizerAttention
summarizer = SummarizerAttention(lstm_size=1024, embedding_size=256)
trainer = Trainer(batch_size=64,
steps_per_epoch=100,
steps_to_log=20,
max_output_len=10,
model_save_path='/tmp/summarizer')
trainer.train(summarizer, train, num_epochs=10, val_data=test)
# + id="TKYgDLngooL1" colab_type="code" outputId="e5758b7c-3b75-425f-e07f-496174c2fa27" colab={"base_uri": "https://localhost:8080/", "height": 34}
# Do some prediction
summarizer.predict('How are you?')
|
notebooks/Neural_Machine_Translation_Example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # In Class 20190402
# Learning notebooks and python itk.
import itk
from itkwidgets import view
import numpy as np
from matplotlib import pyplot as plt
InputPixelType = itk.ctype('float')
OutputPixelType = itk.ctype('float')
Dimension = 3
InputImageType = itk.Image[InputPixelType, Dimension]
OutputImageType = itk.Image[OutputPixelType, Dimension]
image_file_name = "data/brainweb165a10f17.mha"
reader1=itk.ImageFileReader[InputImageType].New(FileName=image_file_name)
reader1.Update()
image1 = reader1.GetOutput()
reader2=itk.ImageFileReader[InputImageType].New(FileName=image_file_name)
reader2.Update()
image2 = reader2.GetOutput()
reader3 = itk.ImageFileReader.New(FileName=image_file_name)
reader3.Update()
image3 = reader3.GetOutput()
image4 = itk.image_file_reader(FileName=image_file_name)
image5 = itk.imread(image_file_name)
image6 = itk.imread(image_file_name, InputPixelType)
for i, t in enumerate([image1, image2, image3, image4, image5, image6]):
print("%d: %s" % (i, type(t)))
|
inclass/inclass3-abpwrs/notes/20190402_ClassNotes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
#
# # Diseño de software para cómputo científico
#
# ----
#
# ## Unidad 1: Modelo de objetos de Python
#
# <small><b>Source:</b> <a href="https://dbader.org/blog/python-dunder-methods">https://dbader.org/blog/python-dunder-methods</a></small>
# + [markdown] slideshow={"slide_type": "slide"}
# ### Agenda de la Unidad 1
# ---
#
# - Clase 1:
# - Diferencias entre alto y bajo nivel.
# - Lenguajes dinámicos y estáticos.
#
# - Limbo:
# - Introducción al lenguaje Python.
# - Librerías de cómputo científico.
#
# - Clase Limbo + 1 y Limbo + 2:
# - **Orientación a objetos**, decoradores.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Python Data types
# -----
#
# - Parte de la promesas incumplidas que tengo es explicar por que esto
# -
[1, 2, 3] + [4, 5, 6]
# Funciona distinto de esto
# +
import numpy as np
np.array([1, 2, 3]) + [4, 5, 6]
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Python Data types
# -----
#
# al igual que estas dos cosas
# -
np.array([1, 2, 3]) * 2
[1, 2, 3] * 2
# + [markdown] slideshow={"slide_type": "subslide"}
# ## Python Data types
# -----
# O una de estas directamente no funciona
# -
np.array([1, 2, 3]) + 1
[1, 2, 3] + 1
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# - Por que funciona esto?
# -
len([1, 3])
1 + 17
# +
def foo():
return "hello"
foo() # <<< eso
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Vamos con el ejemplo siple
# -
class HasLen:
def __init__(self, l):
self.l = l
def __len__(self):
return self.l
foo = HasLen(42)
len(foo)
foo.__len__()
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# - En Python, los métodos especiales son un conjunto de métodos predefinidos que se puede usar para enriquecer las clases. Son fáciles de reconocer porque comienzan y terminan con guiones bajos dobles, por ejemplo `__init__` o `__str__`.
#
# - Como es cansador decir *under-under-method-under-under* la comunidad empezo a decirles **dunder** contraccion de *double-under*.
#
# - Los métodos Dunder le permiten emular el comportamiento de los tipos integrados. Por ejemplo, para obtener la longitud de una cadena puede llamar a `len('cadena')`.
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Inicialización
# -
class Account:
"""A simple account class"""
def __init__(self, owner, amount=0):
"""This is the constructor that lets us create
objects from this class.
"""
self.owner = owner
self.amount = amount
self._transactions = []
def add_transaction(self, amount):
if not isinstance(amount, int):
raise ValueError('please use int for amount')
self._transactions.append(amount)
@property
def balance(self):
return self.amount + sum(self._transactions)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Representación
# + slideshow={"slide_type": "-"}
class Account(Account):
def __repr__(self):
return f'{self.__class__.__name__}({self.owner}, {self.amount})'
def __str__(self):
return f'Account of {self.owner} with starting amount: {self.amount}'
# -
acc = Account('bob', 10)
acc # repr(acc)
print(acc) # str(acc)
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Iteración
# -
class Account(Account):
def __len__(self):
return len(self._transactions)
def __getitem__(self, position):
return self._transactions[position]
def __setitem__(self, pos, v):
self._transactions[pos] = v
# +
acc = Account('bob', 10)
acc.add_transaction(20)
acc.add_transaction(-10)
acc.add_transaction(50)
acc.add_transaction(-20)
acc.add_transaction(30)
acc.balance
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Iteración
# -
len(acc)
for t in acc:
print(t)
acc[1]
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Comparación
#
# Los métodos son siempre con `__` al comienzo y al final: `ge, gt, le, lt, eq, ne`
# Pero a partir de `__eq__` y algun otro se pueden completar automaticamente los demas con un decorador.
# +
import functools
@functools.total_ordering
class Account(Account):
# ... (see above)
def __eq__(self, other):
return self.balance == other.balance
def __lt__(self, other):
return self.balance < other.balance
# -
acc2 = Account('tim', 100)
acc2.add_transaction(20)
acc2.add_transaction(40)
acc2.balance
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Comparación
# -
acc2 > acc
acc2 == acc
acc2 >= acc
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Aritmética
#
# Los métodos son siempre con `__` al comienzo y al final: `add, diff, mult, div, pow`, etc.
# -
class Account(Account):
def __add__(self, other):
owner = f"{self.owner} + {other.owner}"
start_amount = self.balance + other.balance
return Account(owner, start_amount)
acc2 = Account("tim", 200)
acc2.balance
acc3 = acc2 + acc
acc3
# + [markdown] slideshow={"slide_type": "subslide"}
# ### Dunders
# ----
#
# Objetos ejecutablles/llamables/callables
# -
class Account(Account):
# ... (see above)
def __call__(self, c):
print('Start amount: {}'.format(self.amount))
print(c)
print('Transactions: ')
for transaction in self:
print(transaction)
print('\nBalance: {}'.format(self.balance))
acc2 = Account("tim", 200)
acc2.add_transaction(10)
acc2.balance
callable(acc2)
acc2("kk")
# + [markdown] slideshow={"slide_type": "subslide"}
# Dunders Final
# -------------
#
# Hay muchos mas magic methods, pero eso se los dejo ver segun haga falta https://rszalski.github.io/magicmethods/
# +
class A:
def __init__(self, nombre):
super().__setattr__("_data", {"nombre": nombre})
def __getattr__(self, n):
return self._data.get(n, "<UNK>")
def __setattr__(self, n, v):
self._data[n] = v
def m(self):
return 43
a =A("tito")
a.nombresx = 1
# -
import sh
sh.pwd()
print(dir(a))
|
legacy/unidad_1/04_OOP_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import seaborn as sns
sns.set()
sns.set(style = "darkgrid")
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
emp_by_type = data_sdh.groupby('IS_SCHNEIDER_EMP')
emp_by_type.first()
pd.crosstab(data_sdh["COMPANY"],data_sdh['IS_SCHNEIDER_EMP'],margins=True)
sns.lineplot(x = "IS_SCHNEIDER_EMP", y = count('FULL_NAME'),data = data_sdh[:10])
|
Untitled20.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Author: <NAME>
# ## Let's Grow More - VIP Internship
# ## Task 1 - Iris Flowers Classification ML Project
# ##### Description --
#
# **The iris flowers dataset contains numeric attributes, and it is perfect for beginners to learn about supervised ML algorithms, mainly how to load and handle data. Also, since this is a small dataset, it can easily fit in memory without requiring special transformations or scaling capabilities.**
#
# **Dataset :** https://bit.ly/3kXTdox
# ### Importing Libraries
# +
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.manifold import TSNE
from warnings import filterwarnings
filterwarnings(action='ignore')
# -
# ### Loading the Dataset
data = pd.read_csv("Iris.csv")
print("Dataset loaded successfully")
# ## Exploring Data
# ### Reading Dataset
data.head()
data.tail()
# ### Data Information
data.shape
data.columns
data.count()
data.Species.unique()
# ### Finding the Number of Clusters
# +
actual_y=data['Species']
x=data.drop(['Id','Species'],axis=1)
x.head()
# +
from sklearn.cluster import KMeans
#Here inertia means Sum of squared distances of samples to their closest cluster center.
number_of_clusters=[2,3,4,5,6,7,8,10]
inertia=[]
for i in number_of_clusters:
kmeans=KMeans(n_clusters=i).fit(x)
inertia.append(kmeans.inertia_)
plt.plot(number_of_clusters,inertia)
plt.title('Number of Clusters',size=20)
plt.grid()
plt.show()
# +
kmeans = KMeans(n_clusters = 3)
y_kmeans = kmeans.fit_predict(x)
# add these predicted y's as column to our dataframe
x['predicted_y']=y_kmeans
# -
kmeans.cluster_centers_
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
ax.axis('equal')
l = ['Versicolor', 'Setosa', 'Virginica']
s = [50,50,50]
ax.pie(s, labels = l,autopct='%1.2f%%')
plt.show()
data.hist()
plt.show()
sns.violinplot(data=data,x="Species", y="PetalWidthCm",palette="rocket")
sns.pairplot(data,hue='Species')
data.plot(kind="scatter", x="SepalLengthCm", y= "SepalWidthCm")
# +
y_mapping={1:'Setosa',2:'versicolour',0:'virginica'}
x['predicted_y']=x['predicted_y'].map(y_mapping)
# -
setosa = x.loc[x.predicted_y == 'Setosa',['SepalLengthCm','SepalWidthCm']]
virginica = x.loc[x.predicted_y == 'virginica',['SepalLengthCm','SepalWidthCm']]
versicolour = x.loc[x.predicted_y == 'versicolour',['SepalLengthCm','SepalWidthCm']]
# +
plt.scatter(setosa['SepalLengthCm'], setosa['SepalWidthCm'], s = 100, c = 'red', label = 'Setosa')
plt.scatter(virginica['SepalLengthCm'], virginica['SepalWidthCm'], s = 100, c = 'blue', label = 'Virginica')
plt.scatter(versicolour['SepalLengthCm'], versicolour['SepalWidthCm'], s = 100, c = 'green', label = 'Versicolour')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:,1], s = 100, c = 'yellow', label = 'Centroids')
plt.legend()
plt.xlabel('SepalLengthCm Feature',size=10)
plt.ylabel('SepalWidthCm Feature',size=10)
plt.title('Clusters with its Centroids',size=20)
plt.grid()
plt.show()
|
TASK 1- Iris Flowers Classification/TASK 1 - Iris Flowers Classification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Python极简入门
# ## 1. 数据类型
# +
# #!/usr/bin/env python
# -*- coding: utf-8 -*-
# -
i = 1
i
f = 1.0
f
f+i
s = "east196"
s
l = [1,2,3,4]
l
l.append(5)
l
d = {"name":"east196","age":18}
d
d["name"]
d["sex"]
d.get("sex")
d.get("sex", "male")
d["sex"] = "male"
d["sex"]
# ## 2. 流程
a = 1
b = 2
a = b
a
i = 10
if i > 0:
print("i>0")
else:
print("i=0 or i<0")
for i in range(10):
print(i)
for i in [1,2,3]:
print("="*i)
# ## 3. 函数
# 可以类比 操作
#
# 例如 装箱操作,输入的是原材料+箱子,输出的是 成品
# +
real_box = "箱子"
real_material = "原材料"
def box_it(box, material):
return "装入{box}的{material}".format(box=box, material=material)
# -
# 只定义一个操作是没有意义的,你还要真的去操作
real = box_it(real_box,real_material)
print(real)
# ## 4. 类
# 可以类比为 人 的这个定义
#
# 人有自身的属性,比如姓名name、年龄age,可以对应类中的属性概念
#
# 同时人有可以执行的操作,比如吃饭eat、睡觉sleep、打豆豆beat_doudou。
class Person():
def __init__(self, name, age):
self.name = name
self.age = age
def eat(self):
print(self.name + " 吃饭")
def sleep(self):
print("%s 睡觉" % self.name)
def beat_doudou(self):
print("{name}打豆豆".format(name=self.name))
# 同样,定义一个类别叫做人,是个抽象的概念
#
# 现实生活中,我们会具体到某一个人,比如east196
east196 = Person(name="east196",age=18)
print(east196)
east196.eat()
east196.sleep()
east196.beat_doudou()
# 和dict的区别?
#
# 可以简单的认为dict代表属性
#
# def的函数代表操作
#
# 对于一个特定的实体,比如说人,在不使用类的情况下可以这样表示
# +
east196 = {"name":"east196","age":18}
def eat(name):
print(name + " 吃饭")
def sleep(name):
print("%s 睡觉" % name)
def beat_doudou(name):
print("{name}打豆豆".format(name=name))
# -
print(east196)
eat(east196["name"])
sleep(east196["name"])
beat_doudou(east196["name"])
# 看起来有点乱是不是?
#
# 再看看class版本的east196,是不是更符合人类思维一点点?
#
# ## 5. 类库
# python的标准库能够满足入门的需求
#
# +
import os
print(os.name) # nt代表是windows
# -
#
# 然而如何应对现实世界的千奇百怪的需求?每个需求都自己从头开始?
#
# 没有那么麻烦!python拥有数以千计的类库,几乎能想的到的产品都可以用python来做
#
# 试试做个模版怎么样?
print("""
大王叫我来巡山
抓个和尚做晚餐
""")
# 发现了没?三个"""开头结尾的字符串是可以内部换行的
s = """
{name}巡山
抓和尚
""".format(name="east196")
print(s)
# 好吧,我有个兄弟叫east197,我们一起巡山?
s = """
{name1}巡山
{name2}巡山
抓和尚
""".format(name1="east196",name2="east197")
print(s)
# 有点丑,但是可以过关的
#
# 但是我还有500个结义弟兄~~~
#
# python内置的这个format可是不支持循环的,写五百个name出来?
#
# 玩不动了吧~~~
#
# 有个叫jinja2的第三方库可以帮你
#
# 在terminal的黑漆漆窗口下输入`pip install jinja2`就可以安装好
# > 如果你需要一个基础功能,多半网上已经有人实现。
#
# python的标准库容量和功能有限,我们需要强大的功能怎么办?
#
# 很多爱好者在[pypi](笙惜)网站上发布了他们自己编写的功能,用pip命令就可以安装。
# +
import jinja2
# 先来5个,要500 弟兄就把range(5) 改成range(500)就好
names = [u"east{i}".format(i=i) for i in range(5)] # 列表推导式
sentence = jinja2.Template(u"""
{% for name in names %}
{{ name }} 巡山
{% endfor %}
抓和尚""").render(names=names)
print(sentence)
# -
|
hello_py.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
# +
class Operator:
def __call__(self, *args, **kwargs):
return self.forward(*args, **kwargs)
def forward(self):
pass
def backward(self):
pass
class Add(Operator):
def forward(self, x, y):
assert isinstance(x, Tensor)
assert isinstance(y, Tensor)
x.outdegree+=1
y.outdegree+=1
x.is_leaf = False
y.is_leaf = False
out = Tensor(x.data + y.data,op=self, in_nodes=[x, y])
return out
def backward(self, in_nodes):
return [np.ones_like(node.data) for node in in_nodes]
class Multipy(Operator):
def forward(self, x, y):
assert isinstance(x, Tensor)
assert isinstance(y, Tensor)
x.outdegree+=1
y.outdegree+=1
x.is_leaf = False
y.is_leaf = False
out = Tensor(x.data * y.data, op=self, in_nodes=[x,y])
return out
def backward(self, in_nodes):
return [in_nodes[1].data.copy(), in_nodes[0].data.copy()]
class Sin(Operator):
def forward(self, x):
assert isinstance(x, Tensor)
x.outdegree += 1
x.is_leaf = False
out = Tensor(np.sin(x.data), op=self, in_nodes=[x])
return out
def backward(self, in_nodes):
return [np.cos(in_nodes[0].data)]
class Log(Operator):
def forward(self, x):
assert isinstance(x, Tensor)
x.outdegree += 1
x.is_leaf = False
out = Tensor(np.log(x.data), op=self, in_nodes=[x])
return out
def backward(self, in_nodes):
return [1/in_nodes[0].data]
class Sub(Operator):
def forward(self, x, y):
assert isinstance(x, Tensor)
assert isinstance(y, Tensor)
x.outdegree+=1
y.outdegree+=1
x.is_leaf = False
y.is_leaf = False
out = Tensor(x.data - y.data,op=self, in_nodes=[x, y])
return out
def backward(self, in_nodes):
x, y = in_nodes
return [np.ones_like(x.data), -1 * np.ones_like(y.data)]
# -
class Tensor:
def __init__(self, data, op=None, in_nodes=None):
assert isinstance(data, np.ndarray)
self.data = data
self.op = op
self.in_nodes = in_nodes
self.grad = np.zeros_like(self.data)
self.is_leaf = True
self.is_root = self.op is None
self.outdegree = 0
def __add__(self, other):
add_op = Add()
return add_op.forward(self, other)
def __mul__(self, other):
mul_op = Multipy()
return mul_op.forward(self, other)
def __sub__(self, other):
sub_op = Sub()
return sub_op.forward(self, other)
def backward(self):
if self.is_leaf:
self.grad = np.ones_like(self.data)
grads = self.op.backward(self.in_nodes)
for i, node in enumerate(self.in_nodes):
node.grad += self.grad * grads[i]
node.outdegree -=1
if not node.is_root and self.outdegree == 0:
node.backward()
def zero_grads(self):
self.grad = np.zeros_like(self.data)
vz = Tensor(np.array([2.]))
v0 = Tensor(np.array([5.]))
v1 = Log()(vz)
v2 = vz*v0
v3 = Sin()(v0)
v4 = v1 + v2
v5 = v4 - v3
v5.data
v5.backward()
vz.grad
v0.grad
|
Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
from tensorflow.contrib import seq2seq
import re
import collections
from tqdm import tqdm
import random
import numpy as np
class Model:
def __init__(self,maxlen=50,
vocabulary_size=20000,
learning_rate=1e-3,
embedding_size = 256):
self.output_size = embedding_size
self.maxlen = maxlen
word_embeddings = tf.Variable(
tf.random_uniform(
[vocabulary_size, embedding_size], -np.sqrt(3), np.sqrt(3)
)
)
self.global_step = tf.get_variable(
"global_step", shape=[], trainable=False,
initializer=tf.initializers.zeros())
self.embeddings = word_embeddings
self.output_layer = tf.layers.Dense(vocabulary_size, name="output_layer")
self.output_layer.build(self.output_size)
self.BEFORE = tf.placeholder(tf.int32,[None,maxlen])
self.INPUT = tf.placeholder(tf.int32,[None,maxlen])
self.AFTER = tf.placeholder(tf.int32,[None,maxlen])
self.batch_size = tf.shape(self.INPUT)[0]
self.get_thought = self.thought(self.INPUT)
self.attention = tf.matmul(
self.get_thought, tf.transpose(self.embeddings), name = 'attention'
)
fw_logits = self.decoder(self.get_thought, self.AFTER)
bw_logits = self.decoder(self.get_thought, self.BEFORE)
self.loss = self.calculate_loss(fw_logits, self.AFTER) + self.calculate_loss(bw_logits, self.BEFORE)
self.optimizer = tf.train.AdamOptimizer(learning_rate).minimize(self.loss)
def get_embedding(self, inputs):
return tf.nn.embedding_lookup(self.embeddings, inputs)
def thought(self, inputs):
encoder_in = self.get_embedding(inputs)
fw_cell = tf.nn.rnn_cell.GRUCell(self.output_size)
bw_cell = tf.nn.rnn_cell.GRUCell(self.output_size)
sequence_length = tf.reduce_sum(tf.sign(inputs), axis=1)
rnn_output = tf.nn.bidirectional_dynamic_rnn(
fw_cell, bw_cell, encoder_in, sequence_length=sequence_length,
dtype=tf.float32)[1]
return sum(rnn_output)
def decoder(self, thought, labels):
main = tf.strided_slice(labels, [0, 0], [self.batch_size, -1], [1, 1])
shifted_labels = tf.concat([tf.fill([self.batch_size, 1], 2), main], 1)
decoder_in = self.get_embedding(shifted_labels)
cell = tf.nn.rnn_cell.GRUCell(self.output_size)
max_seq_lengths = tf.fill([self.batch_size], self.maxlen)
helper = seq2seq.TrainingHelper(
decoder_in, max_seq_lengths, time_major = False
)
decoder = seq2seq.BasicDecoder(cell, helper, thought)
decoder_out = seq2seq.dynamic_decode(decoder)[0].rnn_output
return decoder_out
def calculate_loss(self, outputs, labels):
mask = tf.cast(tf.sign(labels), tf.float32)
logits = self.output_layer(outputs)
return seq2seq.sequence_loss(logits, labels, mask)
# +
def simple_textcleaning(string):
string = re.sub('[^A-Za-z ]+', ' ', string)
return re.sub(r'[ ]+', ' ', string.lower()).strip()
def batch_sequence(sentences, dictionary, maxlen = 50):
np_array = np.zeros((len(sentences), maxlen), dtype = np.int32)
for no_sentence, sentence in enumerate(sentences):
current_no = 0
for no, word in enumerate(sentence.split()[: maxlen - 2]):
np_array[no_sentence, no] = dictionary.get(word, 1)
current_no = no
np_array[no_sentence, current_no + 1] = 3
return np_array
def counter_words(sentences):
word_counter = collections.Counter()
word_list = []
num_lines, num_words = (0, 0)
for i in sentences:
words = re.findall('[\\w\']+|[;:\-\(\)&.,!?"]', i)
word_counter.update(words)
word_list.extend(words)
num_lines += 1
num_words += len(words)
return word_counter, word_list, num_lines, num_words
def build_dict(word_counter, vocab_size = 50000):
count = [['PAD', 0], ['UNK', 1], ['START', 2], ['END', 3]]
count.extend(word_counter.most_common(vocab_size))
dictionary = dict()
for word, _ in count:
dictionary[word] = len(dictionary)
return dictionary, {word: idx for idx, word in dictionary.items()}
def split_by_dot(string):
string = re.sub(
r'(?<!\d)\.(?!\d)',
'SPLITTT',
string.replace('\n', '').replace('/', ' '),
)
string = string.split('SPLITTT')
return [re.sub(r'[ ]+', ' ', sentence).strip() for sentence in string]
# +
contents = []
with open('books/Blood_Born') as fopen:
contents.extend(split_by_dot(fopen.read()))
with open('books/Dark_Thirst') as fopen:
contents.extend(split_by_dot(fopen.read()))
len(contents)
# -
contents = [simple_textcleaning(sentence) for sentence in contents]
contents = [sentence for sentence in contents if len(sentence) > 20]
len(contents)
contents[:5]
maxlen = 50
vocabulary_size = len(set(' '.join(contents).split()))
embedding_size = 256
learning_rate = 1e-3
batch_size = 16
vocabulary_size
# +
from sklearn.utils import shuffle
stride = 1
t_range = int((len(contents) - 3) / stride + 1)
left, middle, right = [], [], []
for i in range(t_range):
slices = contents[i * stride : i * stride + 3]
left.append(slices[0])
middle.append(slices[1])
right.append(slices[2])
left, middle, right = shuffle(left, middle, right)
# -
word_counter, _, _, _ = counter_words(middle)
dictionary, _ = build_dict(word_counter, vocab_size = vocabulary_size)
tf.reset_default_graph()
sess = tf.InteractiveSession()
model = Model(vocabulary_size = len(dictionary), embedding_size = embedding_size)
sess.run(tf.global_variables_initializer())
for i in range(5):
pbar = tqdm(range(0, len(middle), batch_size), desc='train minibatch loop')
for p in pbar:
batch_x = batch_sequence(
middle[i : min(i + batch_size, len(middle))],
dictionary,
maxlen = maxlen,
)
batch_y_before = batch_sequence(
left[i : min(i + batch_size, len(middle))],
dictionary,
maxlen = maxlen,
)
batch_y_after = batch_sequence(
right[i : min(i + batch_size, len(middle))],
dictionary,
maxlen = maxlen,
)
loss, _ = sess.run([model.loss, model.optimizer],
feed_dict = {model.BEFORE: batch_y_before,
model.INPUT: batch_x,
model.AFTER: batch_y_after,})
pbar.set_postfix(cost=loss)
# +
with open('books/Driftas_Quest') as f:
book = f.read()
book = split_by_dot(book)
book = [simple_textcleaning(sentence) for sentence in book]
book = [sentence for sentence in book if len(sentence) > 20][:100]
book_sequences = batch_sequence(book, dictionary, maxlen = maxlen)
encoded, attention = sess.run([model.get_thought, model.attention],feed_dict={model.INPUT:book_sequences})
# +
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin_min
n_clusters = 10
kmeans = KMeans(n_clusters=n_clusters, random_state=0)
kmeans = kmeans.fit(encoded)
avg = []
closest = []
for j in range(n_clusters):
idx = np.where(kmeans.labels_ == j)[0]
avg.append(np.mean(idx))
closest, _ = pairwise_distances_argmin_min(kmeans.cluster_centers_,encoded)
ordering = sorted(range(n_clusters), key=lambda k: avg[k])
print('. '.join([book[closest[idx]] for idx in ordering]))
# -
# ## Important words
indices = np.argsort(attention.mean(axis=0))[::-1]
rev_dictionary = {v:k for k, v in dictionary.items()}
[rev_dictionary[i] for i in indices[:10]]
|
unsupervised-summarization/1.skip-thought.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 3point6
# language: python
# name: 3point6
# ---
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
from IPython.display import Image
np.random.seed(0) #fix seed so everyone has the same result
# Basic Introduction into Conditional Density Estimation
# ---------------------------------------------------
# Welcome to my tutorial that aims to give you a short introduction into the topic of "Conditional Density Estimation" with an application to Photometric Redshift Estimation. We will first start with a short theory introduction and then move towards a practical implementation of a conditional density estimate. This Tutorial closes with an application to LSST photometric redshifts. I will host a general sprint tomorrow where I will work on including the work from a student of Rachel and me (<NAME>) on conditional density estimation with error quantification into the gcr catalogs. The following short introduction is based on the following references and references therein. Some of the following text comes from my thesis that everyone is very welcome to read :-)
#
# Recommended Literature:
# -----------------------
# Bishop (2006): <NAME>. 2006. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, Berlin, Heidelberg.
#
# <NAME>., <NAME>.,, <NAME>. (2001). The Elements of Statistical Learning. New York, NY, USA: Springer New York Inc..
#
# Rau, <NAME> (2017): Photometric redshift estimation for precision cosmology. Dissertation, LMU München: Faculty of Physics
# Regression
# ----------
#
# The basic task of regression it to estimate the functional relationship between a given set of
# inputs x and a target variable $t$. In Fig. 2.3 we illustrate a typical regression setting, where
# the blue points correspond to the data that we want to model. We see that these datapoints
# do not follow an exact functional relationship, but instead have an intrinsic scatter around
# the true function shown in red. The modelling is therefore not restricted to determining this
# function, but also includes the estimation of the predictive distribution $p(t|x)$ of the target
# variable t given the input x.
# In analogy to the discussion in the previous section, we model the conditional distribution
# as a Gaussian, where the mean is given by a polynomial function $y(x, w)$ and the variance $β$
# is assumed to be independent of $x$
#
# $$p(t|x, w, \sigma^2) = \mathcal{N}(t|y(x, w), \sigma^2)$$
#
#
# If we do not have any prior information about the functional form of $y(x, w)$ we can assume
# a very complex function that will adapt to the data. A simple choice could be a polynomial
# model or, more general a linear basis function model
#
# $$y(\mathbf{x}, \mathbf{w}) = \sum_{j = 1}^{M - 1} w_j \phi_j(\mathbf{x}) = \mathbf{w}^{T} \phi(\mathbf{x})$$
#
# where $w = (w_0, . . . , w_{M−1})^T$ is a M dimensional vector of free model parameters, or weights.
#
#
# In the corresponding basis function vector $\boldsymbol{\phi} = (\phi_0, . . . , \phi_{M−1})^T$ we define $\phi_0 = 1$ such, that the first weight is an offset to the function. The basis functions $\boldsymbol{\phi}$ themselves can be e.g.
# linear combinations, polynomial terms or Gaussians that depend on the input x. To give an
# example, consider the case of a single input variable x, where we obtain a polynomial model
# by setting $φ_j(x) = x^j$. The choice of suitable basis functions will strongly depend on the data
# at hand and has to be carefully chosen in advance to reflect our intuition about the data.
# With a linear basis function model for the mean of the conditional distribution, we obtain the
# likelihood as
# $$p(\mathbf{t} | \mathbf{X}, \mathbf{w}, \sigma^2) = \prod_{i = 1}^{N} \mathcal{N}(t_i | y(\mathbf{x}_i, \mathbf{w}), \sigma^2)$$
# where the data D consists of a set of N input variables $X = \{x_i|0 < i \leq N\}$ with their
# associated target values $t = \{t_i | 0 < i \leq N\}$. In analogy to the previous section, we jointly optimize the log-likelihood with respect to the free parameters w of the mean function
# $y(x, w)$ and the variance $\sigma^2$.
#
# There are two sets of parameters in this model: the weights that describe the mean of the conditional distribution and the standard deviation $\sigma$. In this case we assume that the width of the conditional PDF is independent on input positions $\sigma(x) = \sigma$.
#
# The maximum likelihood estimator for the weights and standard deviation are given as
# $$\mathbf{w}_{\rm ML} = (\boldsymbol{\Phi}^{T} \boldsymbol{\Phi})^{-1} \boldsymbol{\Phi}^{T} \mathbf{t}$$
# where $\boldsymbol{\Phi}$ has components $\phi_{n j} = \phi_j(\mathbf{x}_n)$.
# $$\sigma_{\rm ML}^2 = \frac{1}{N} \sum_{i = 1}^{N} \left(t_i - y(\mathbf{x}_i, \mathbf{w}_{\rm ML})\right)^2$$
#
# Of course if we expect a more complicated functional form for the conditional Density we want to make another ansatz e.g. a input dependent variance or a mixture model.
#
# Furthermore instead of simply evaluating the maximum likelihood estimate we often want to quantify the uncertainty in $\mathbf{w}$ or $\sigma$. Depending on the imposed model the typical inference schemes like Variational Inference, MCMC sampling, etc. are available.
Image(filename='cond_pdf.png', width=600)
# Classification
# ----------
#
#
# One of the simplest discrete random
# experiments is the coin toss, where a potentially biased coin is thrown to yield either heads or
# tails. If we parametrize the possible states as $s = {0, 1}$, the probabilities for the individual
# outcomes $p(X = 1) = \mu$ and $p(X = 0) = 1 − \mu$ depend only on the ‘success rate’ $\mu$. The corresponding probability distribution for this process is then given as
#
# $$p(X = s) = \mu^s (1 − µ)^{1−s}$$
#
# For a dataset $\mathcal{D}$, the log-likelihood of the Bernoulli distribution can be obtained
# as
# $$\log{p(\mathcal{D}|\mu)} = \sum_{i = 1}^{N} x_i \log{\left(\mu\right)} + (1 - x_i) \log{\left(1 - \mu\right)}$$
# and we can obtain the maximum likelihood solution for $\mu$ as the sample mean
# $$\mu_{\rm ML} = \frac{1}{N} \sum_{i = 1}^{N} x_i$$
#
# In analogy to the previsouly discussed Regression case we parametrize the free parameter in the log-likelihood using a flexible function. In the case of classification this is the success probability $\mu = y(\mathbf{x}, \mathbf{w})$, that is on the $[0, 1]$ scale
# $$y(\mathbf{x}, \mathbf{w}) = \frac{1}{1 + \exp{\left(- \mathbf{w}^{T} \boldsymbol{\Phi}(\mathbf{x}) \right)}}$$
#
# Again one can apply a optimization scheme to obtain maximum likelihood values for $\mathbf{w}_{\rm ML}$ or inference techniques to obtain posteriors on these parameters.
#
# We finally note that the evaluation of classification methods works slightly different than in the regression case, since class inbalances can lead to misleading results. We will not discuss ML model evaluation in great detail and refer to the literature for a discussion on ROC curves and conceps like purity and completeness.
# Bias-Variance Tradeoff
# -------------
# In order to gain more insights into the tradeoff between model complexity and fitting accuracy,
# Consider the sum of squared error function $p(\mathbf{x}, t)$
#
# $$L = \iint \left(y(\mathbf{x}) - t \right)^2 p(\mathbf{x}, t) dt d\mathbf{x}$$
#
# Applying the variational principle to optimize $y(\mathbf{x})$ and taking the expectation wrt. different datasets we obtain:
#
# $$E_{\mathcal{D}}[L] = (bias)^2 + variance + noise$$
#
# where the different terms are:
#
# $$(bias)^2 = \int \{E_{\mathcal{D}}[\hat{y}(\mathbf{x}; \mathcal{D})] - y(\mathbf{x})\}^2 p(\mathbf{x}) d\mathbf{x} $$
#
# $$variance = \int E_{\mathcal{D}}[\left(\hat{y}(\mathbf{x}; \mathbf{D}) - E_{\mathcal{D}}[\hat{y}(\mathbf{x}; \mathcal{D})]\right)^2] p(\mathbf{x}) \, d\mathbf{x}$$
#
# $$noise = \iint \, (y(\mathbf{x}) - t)^2 p(\mathbf{x}, t)\, d\mathbf{x} dt$$
#
# Here, $y(\mathbf{x})$ denotes the true, unknown, functional form of the conditional mean and $\hat{y}(\mathbf{x}; \mathcal{D})$ and estimate.
#
# The bias term quantifies how well our estimate on average coincides with the
# conditional mean. This term is large, if we select a model that is not complex enough to
# capture the underlying structure in the data and it is small, if we consider complex models.
# The variance does not depend on the true function y(x) and quantifies how strongly
# the fitted models vary between the generated datasets. This variance term is in general large,
# if a too complex model is fitted to a relatively small dataset as shown in the lower left panel of
# the following figure. If the variance contributes significantly to the total error, it is advisable to consider
# less complex models that are more stable and thus have a smaller variance or, even better,
# collect more data. The intrinsic noise does not depend on our estimate yˆ(x; D)
# and represents the irreducible error in the data. We conclude, that in order to optimize
# the complexity of the model, we have to trade-off the bias and variance terms that both
# contribute to the expected sum of squared loss for regression. This can be achieved by varying
# the complexity of the model and subsequently estimating the expected loss on unseen data.
#
# This motivates splitting a dataset into three parts: training, cross-validation and test set. The test set is never used exept once after all prior steps of model training and data preprocessing to evaluate model perfrmance. The training set is used to train the model and the cross validation dataset to calibrate the setup of the ML architecture.
#
Image(filename='bias_variance.png', width=600)
# We illustrate the tradeoff between bias and variance in Figure 2.4, where we estimate an exponential function from the
# underlying data shown in grey using a polynomial model. While the simple linear model (‘Poly
# 1’) is not complex enough to capture the nonlinear structure in the data, adding higher order
# polynomial terms does not always improve the quality of the recovered model, but can instead
# lead to overfitting as shown in the lower left panel for a 10th order polynomial (‘Poly 10’).
# Here the complex model is adapting too tightly to the small amount of available data and
# thus strongly fluctuates around the truth. For this small sample, a quadratic model (‘Poly 2’)
# produces the best fit. Increasing the data sample to $N = 2000$ points, significantly stabilizes
# the high order polynomial, which now perfectly recovers the underlying exponential function.
# This simple experiment demonstrates, that the complexity of the model needs to be balanced
# with the nonlinearity of the data, as well as the number of available data samples. If we have
# more data available, we can increase the model complexity to more accurately capture the
# complex structure in the data. In contrast, if data is sparse, increasing the complexity of the
# fit, can even lead to greater errors than a more simplistic model.
# Lets experiment a bit with model complexity. The following cell contains a simple regression example: we can change the number of samples, the degree of the polynomial and the noise imposed on the response variable. Please feel free to play around to investigate the aforementioned tradeoff between bias and variance.
# +
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from numpy.random import normal
def get_prediction(n_samp, poly_order, noise=0.2):
xlim = np.linspace(0.0, 1.0, num=100)
model = LinearRegression()
x = np.random.uniform(0.0, 1.0, size=n_samp).reshape(-1, 1)
y = np.exp(x[:, 0]) + np.array([normal(0.0, scale=noise) for _ in range(len(x))])
poly = PolynomialFeatures(degree=poly_order)
x_poly_features = poly.fit_transform(x)
model.fit(x_poly_features, y)
x_poly_xlim = poly.fit_transform(xlim.reshape(-1, 1))
return xlim, model.predict(x_poly_xlim), x, y
# -
results_new = get_prediction(100, 10)
plt.plot(results_new[0], results_new[1], color='black')
plt.plot(results_new[2], results_new[3], '.', color='red')
plt.xlabel('x', fontsize=14)
plt.ylabel('y', fontsize=14)
plt.gca().tick_params(axis='both', which='major', labelsize=14)
# Selection Functions and Biases
# --------------------------
# The training data used in a Machine Learning algorithm is representative, if it
# was drawn from the same parent distribution as the test data. In many practical applications
# however, this cannot be guaranteed and we have to consider several effects, that can bias the
# training data. In photometric redshift estimation, often spectroscopic data is used. Obtaining representative spectroscopic samples requires long exposure times, especially at the faint end of the magnitude space. Therefore spectroscopic training samples for photometric redshift estimation are typically incomplete.
#
# Viewed in a simplified manner, there are two types of selection functions that we can face. In the first case the training set has a different distribution in the features, in photoZ estimation colors, than the test set, i.e. the feature variables $x_T$ and target values $t_T$ are biased in terms
# of the marginal distribution $p(x_T)$. This is shown as the grey band in the right plot. In statistics this is often called covariat shift and there are ways to correct for possible biases (e.g. by reweighting). The other possible bias happens if there is an incompleteness in terms of the target values. In spectroscopic redshift estimation this could happen if there is a depletion of high confidence galaxy redshifts as a function of redshift (e.g. because characteristic features of the spectrum shift outside of the spectral range). These selection biases directly affect the conditional distribution $p(t_T |x_T )$ and a correction can be impossible in these cases if there is no physical modelling available. The red band shows in the right panel illustrates this effect.
#
# The left plot illustrates another aspect of photometric redshift estimation in a very simplified manner. Both panels illustrate how the g-r color of an elliptical and SCD galaxy change as as function of distance, or redshift. The left panel illustrates that conditional distributions can be multimodal in color-redshift space. Of course if one uses more colors this will be less extreme, but for broad band photometry there persist mismatches between SED type and redshift. In the context of conditional density estimation this will be manifested in multimodality invalidating the Gaussian assumption. The grey vertical band illustrates here the conditional distribution.
Image(filename='merged_selection_effects.png', width=900)
# Application: Photometric Redshift Estimation
# ---------------------------------------
#
# In the following we will put the learned concepts into practise by implementing a conditional density estimator based on the sklearn package and the Random Forest Classifier, where the classes are given by redshift bins. The Random Forest is a tree based Machine Learning method. A single decision tree partitions the input space (in our case the color space) recursively into binary partitions until each cell contains only galaxies of very similar redshift (or type). A Random Forest trains a number of trees on several resampled, i.e. bootstrapped, datasets.
#
# After the training phase that results in a set of trained decision trees, new data can be run down each tree to give a prediction on each tree. The majority vote of these decision trees wrt. to the class membership is then the final prediction of the Random Forest. For more details on the Random Forest technique we refer to the literature.
#
# We will first require an installation of the sklearn package that contains a suitable Implementation of the Random Forest Classifier.
#
from sklearn.ensemble import RandomForestClassifier
# We will now load in the example dataset that I put into the folder and make some simple plots of the photometry and redshift distributions.
#
#
# This simple test dataset contains the true redshifts and the LSST magnitudes in the filter bands as well as the galaxy id's. We also shuffle the data to avoid any intrinsic corrrelation in the data. This is an important step in the application of a ML algorithm.
# The dataset columns are given as:
#
# | Column | Description || Column | Description
# | --------------- | ----------- || --------------- | ------------
# | 0) galaxy_id | Galaxy Index || 8) mag_r_obs |observed r-band magnitude
# | 1) redshift_true | True Redshift || 9) magerr_r_obs | error observed r-band magnitude
# | 2) ra | Right ascension || 10) mag_i_obs | observed i-band magnitude
# | 3) dec | Declination || 11) magerr_i_obs | error observed i-band magnitude
# | 4) mag_u_obs | observed u-band magnitude || 12) mag_z_obs | observed z-band magnitude
# | 5) magerr_u_obs | error observed u-band magnitude || 13) magerr_z_obs | error observed z-band magnitude
# | 6) mag_g_obs | observed g-band magnitude || 14) mag_y_obs | observed y-band magnitude
# | 7) magerr_g_obs | error observed g-band magnitude || 15) magerr_y_obs |error observed y-band magnitude
#
#
#
#
data = np.loadtxt('datasets/data.dat') # red region in plot is the training set (train)
idx = np.random.choice(len(data), len(data))
data = data[idx, :]
z_data = data[:, 1]
photometry = np.column_stack((data[:, 4], data[:, 6], data[:, 8], data[:, 10], data[:, 12], data[:, 14]))
# Visualizing the Data
# --------------------
#
# Let's visualize the basic properties of the Dataset, i.e. plotting the marginal distribution of the redshift and photometry. In particular we look for outlier populations for example u band dropouts as shown in the boxplots. A particular advantage of the Random Forest prediction is that it is relatively insensitive to outliers, so we do not explicitly deal with these missing values. For other Machine Learning models it is extremely important to think about a strategy to deal with missing values like this.
plt.hist(z_data, 50, normed=True, label='Redshift Distribution')
plt.xlabel('Redshift z', fontsize=14)
plt.ylabel('Number', fontsize=14)
plt.gca().tick_params(axis='both', which='major', labelsize=14)
# +
from matplotlib.pyplot import boxplot
boxplot(photometry, labels=['mag_u_obs', 'mag_g_obs', 'mag_r_obs', 'mag_i_obs',
'mag_z_obs', 'mag_y_obs'])
plt.gca().tick_params(axis='both', which='major', labelsize=14, labelrotation=45)
plt.ylabel('Magnitude Value', fontsize=14)
# +
from matplotlib.pyplot import boxplot
boxplot(photometry[photometry[:, 0] < 90], labels=['mag_u_obs', 'mag_g_obs', 'mag_r_obs', 'mag_i_obs',
'mag_z_obs', 'mag_y_obs'])
plt.gca().tick_params(axis='both', which='major', labelsize=14, labelrotation=45)
plt.ylabel('Magnitude Value', fontsize=14)
# -
# The Conditional Density Estimator
# -------------------------------
#
# The idea of our conditional density estimator is to discretize the redshift and treat these bins as classes in classification. In this way we reframe the regression problem into a classification problem, that allows us to estimate the uncertainty of our predictions in a flexible way without imposing a strict distributional form for the conditional distribution (like the Gaussian discussed earlier).
#
# The simplest way to do this, is to assume a histogram parametrization for the conditional distribution and treat the probability predictions as the histogram bin heights of the conditional distribution. Given a training set, we train a classifier to predict the probability that a galaxies redshift lies in a certain photometric redshift bin. For a given test set, we query all galaxies through the trained model. This results in a vector of probability predictions that can be interpreted as a histogram. The following cell implements a python class that uses the RandomForestClassifier from sklearn to implement this scheme.
#
# +
# Define Machine Learning method
class ClassCond(object):
def __init__(self, classifier, bins):
""" Class that defines the classification based
conditional density estimator
Parameter:
----------
classifier: instance of sklearn.ensemble.RandomForestClassifier
bins: numpy array, z-grid for the classifier
"""
self.bins = bins
self.clf = classifier
def fit(self, X, Y):
""" fit a classification based
conditional density estimator p(Y | X)
Parameter:
----------
X: numpy array (n_samples, n_features), input features
Y: numpy array (n_samples, 1), target variable
"""
self.Y = np.array(Y, dtype=np.double)
grid_Y = np.linspace(np.min(Y), np.max(Y), num=self.bins)
self.delta_z = grid_Y[1:] - grid_Y[:-1]
grid_Y = np.linspace(np.min(Y)-self.delta_z[0]/4, np.max(Y)+self.delta_z[0]/4, num=self.bins)
self.midpoints = grid_Y[:-1] + self.delta_z/2.
self.response_classes = self.get_bin_idx(Y, grid_Y)
#put edge cases in bins in range
self.clf.fit(X=X, y=self.response_classes)
def get_bin_idx(self, zspec, breaks):
list_idx_breaks = []
for el in zspec:
for idx_breaks in range(len(breaks)-1):
if (el > breaks[idx_breaks]) & (el < breaks[idx_breaks+1]):
list_idx_breaks.append(idx_breaks)
return np.array(list_idx_breaks)
def predict(self, X):
""" predict histogram heights of the conditional density for
element with input features X
Parameter:
----------
X: numpy array (n_samples, n_features), input features
Returns:
--------
result: numpy array (len(bins)-1,), histogram heights of the conditional density
"""
#dim of X (ngalaxy, numberofphotometricbands)
prob_vec = self.clf.predict_proba(X)
#dim prob_vec: (ngalaxy, self.bins (number of redshift bins used for discretization))
#normalize the histogram to unit area (p * delta z)
#prob vec is a matrix with each row being a galaxy and each column being a histogram bin height.
result = prob_vec/(self.delta_z[0]) #on the premise that the grid is evenly spaced
return result
def ind_result(self, X):
""" predict histogram heights of the conditional density for
element with input features X
Parameter:
----------
X: numpy array (n_samples, n_features), input features
Returns:
--------
result: numpy array (len(bins)-1,), normalized histogram heights of the conditional density
"""
prob_vec = self.predict(X)
each = sum(self.midpoints * prob_vec *(z_max/(n_bins-1)))
# -
def get_mean(midpoints, pred):
""" Calculate the conditional mean
Parameters:
-----------
midpoints: numpy array (len(bins)-1,), midpoints of the conditional histogram
pred: numpy array (nsamples, len(bins) - 1), array of predicted histogram heights from the conditional distributions
Returns:
--------
list_mean: numpy array (nsamples,), array of the conditional means
"""
list_mean = []
for el in pred:
norm_pz = el/np.trapz(el, model.midpoints)
list_mean.append(np.trapz(model.midpoints*norm_pz, model.midpoints))
return np.array(list_mean)
# Application
# -----------
#
# In the following we will predict conditional distributions for our example dataset. Following the previous discussion we will split the dataset into two parts: for simplicity into a training set and a cross-validation set. We also define a redshift grid that consists of 100 breaks.
# +
#We split the dataset into two disjunct sets
train_data_z = z_data[:5000]
cv_data_z = z_data[5000:]
train_data_photometry = photometry[:5000, :]
cv_data_photometry = photometry[5000:, :]
#Number of Redshift Bins
n_break = 30
#We initialize the Conditional Density Estimator and train the model
model = ClassCond(RandomForestClassifier(n_jobs=2), bins=n_break)
model.fit(train_data_photometry, train_data_z)
# -
pred = model.predict(cv_data_photometry)
pred.shape
plt.plot(list_mean, cv_data_z, '.', ms=1, color='red')
plt.plot(np.linspace(0.0, 3.0), np.linspace(0.0, 3.0), color='black')
plt.xlabel('Photometric Redshift', fontsize=14)
plt.ylabel('True Redshift', fontsize=14)
plt.gca().tick_params(axis='both', which='major', labelsize=14)
# +
idx_pred = 10
plt.plot(model.midpoints, pred[idx_pred, :], color='red', label='Conditional Distribution '+str(idx_pred))
plt.axvline(cv_data_z[idx_pred], color='black', lw=2, label='True Redshift '+str(idx_pred))
plt.xlabel('Redshift z', fontsize=14)
plt.ylabel(r'$p(z | f)$', fontsize=14)
plt.gca().tick_params(axis='both', which='major', labelsize=14)
# -
plt.plot(model.midpoints, np.mean(pred, axis=0), color='red')
plt.hist(cv_data_z, n_break, normed=True, histtype='step', color='black')
plt.xlabel('Redshift z', fontsize=14)
plt.ylabel(r'p(z)', fontsize=14)
plt.gca().tick_params(axis='both', which='major', labelsize=14)
# Lets see how good these results are. The Y1 requirement for LSS and WL science are defined in the uncertainty in the mean sample redshift distribution. For LSS this uncertainty should be below 0.01 and for WL it should be below 0.005. So lets see how good our results are:
print(np.mean(cv_data_z) - np.mean(list_mean))
# A photometric redshift distribution of this accuracy would therefore already meet the LSST Y1 requirements!!! Of course the real situation is much more complicated and it is not possible to achieve reliable redshift estimates using essentially 10 lines of code. In particular we use here a completeley representative training sample, which is unrealistic for LSST, since we will not be able to obtain spectroscopic redshifts at these faint magnitudes.
#
# This example should be seen as a warning in the application and interpretation of conditional density estimates. They often give very quickly seemingly extremly good results. However in practise these results are very seldomly defendable in the presence of sample selection biases and other systematics.
|
ConditionalDensityEstimationTutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Analyize Google Chrome history
#
# Idea and initial code taken from the [Analyzing Browser History Using Python and Pandas](https://applecrazy.github.io/blog/posts/analyzing-browser-hist-using-python/) blogpost by __AppleCrazy__.
# %matplotlib inline
import os
import pandas as pd
import numpy as np
import sqlite3
import shutil
import tempfile
import collections
from pathlib import Path
from IPython.display import display
from urllib.parse import urlparse
import matplotlib.pyplot as plt
import seaborn as sns
sns.set('notebook', style = 'white')
DB_PATH = os.path.join(Path.home(), 'Library/Application Support/Google/Chrome/Default/History')
# ## Retrieve the history from the sqlite database
def get_chrome_history_from_sqlite(db_path, filter_out_invalid_dates = True):
TMP_DATABASE_PATH=tempfile.mktemp()
shutil.copy(db_path, TMP_DATABASE_PATH)
conn = sqlite3.connect(TMP_DATABASE_PATH)
c = conn.cursor()
EXPORT_CMD = "select datetime(last_visit_time/1000000-11644473600,'unixepoch'), url from urls order by last_visit_time desc"
c.execute(EXPORT_CMD)
data = c.fetchall()
df = pd.DataFrame(data, columns = ['datetime', 'url'])
if filter_out_invalid_dates:
df = df[df.datetime != '1601-01-01 00:00:00']
df['domain'] = df.url.apply(lambda x: urlparse(x).netloc)
df['datetime'] = pd.to_datetime(df.datetime)
return df
assert os.path.exists(DB_PATH), 'Chrome sqlite database "{}" does not exist!'.format(DB_PATH)
df = get_chrome_history_from_sqlite(DB_PATH)
# ## Plot the most frequent visited domains
#
# This code is taken from AppleCrazy's blogpost.
# +
def get_domain_visit_counts(data):
# Aggregate domain entries
site_frequencies = data.domain.value_counts().to_frame()
# Make the domain a column
site_frequencies.reset_index(level=0, inplace=True)
# Rename columns to appropriate names
site_frequencies.columns = ['domain', 'count']
return site_frequencies
def plot_domain_visit_counts_as_piechart(site_frequencies, with_labels = True, topN = 20, figsize = (14, 14)):
fig, ax = plt.subplots(figsize=figsize)
ax.set_title('Top {} Sites Visited\n({} visits in total)'.format(topN, site_frequencies['count'].sum()))
pie_data = site_frequencies['count'].head(topN).tolist()
if with_labels:
pie_labels = site_frequencies.apply(lambda x: '{} ({})'.format(x.domain, x['count']), axis = 1).head(topN)
else:
pie_labels = None
ax.pie(pie_data, autopct='%1.1f%%', labels=pie_labels)
return fig, ax
site_frequencies = get_domain_visit_counts(df)
fig, ax = plot_domain_visit_counts_as_piechart(site_frequencies)
# -
# ## Plot the frequency of page visits per hour of the day
fig, ax = plt.subplots(figsize = (20, 6))
df.datetime.dt.hour.value_counts().sort_index(ascending = True).plot(kind = 'bar', ax = ax)
ax.set_title('Visits per hour')
ax.set_xlabel('hour of the day');
# ## Create "clock" plot of visits per time of day
# +
def time_to_angle(t, factor = np.pi / 12):
return (t * factor) % (2 * np.pi)
def time_to_x_y(t, stretch_x = 1, stretch_y = 1):
angle_in_rad = time_to_angle(t)
x, y = np.sin(angle_in_rad), np.cos(angle_in_rad)
return x, y
def datetime_to_angle(x):
return time_to_angle(x.datetime.hour + x.datetime.minute / 60)
df['angle_in_rad'] = df.apply(datetime_to_angle, axis = 1)
df['x'] = np.sin(df.angle_in_rad)
df['y'] = np.cos(df.angle_in_rad)
# +
VARIANCE = 0.3
USE_DOMAIN_COLORS = False
COLOR_MAP_NAME = 'Paired'
def cleanup_axes(ax):
ax.grid('off')
for pos, spine in ax.spines.items(): spine.set_visible(False)
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
def add_variance(x, variance = VARIANCE):
return x + np.random.uniform(low = -variance, high = variance, size=len(df))
df['x_ran'] = add_variance(df.x)
df['y_ran'] = add_variance(df.y)
colors = plt.get_cmap(COLOR_MAP_NAME).colors
num_colors = len(colors)
cmap_domain_2_idx = {domain: colors[idx % num_colors] for idx, domain in enumerate(set(df.domain.values))}
df['domain_color'] = df.domain.apply(lambda domain: cmap_domain_2_idx[domain])
fig, ax = plt.subplots(figsize = (12, 12))
df.plot(kind = 'scatter', x = 'x_ran', y = 'y_ran', ax = ax, s = 2, alpha = 0.6, c = df.domain_color if USE_DOMAIN_COLORS else None)
cleanup_axes(ax)
hour_label_factor = 1.7
for hour in range(24):
x, y = time_to_x_y(hour)
ax.text(x = x / hour_label_factor, y = y / hour_label_factor, s = hour, fontdict={'horizontalalignment': 'center', 'verticalalignment': 'center', 'weight': 'bold', 'size': 16}, color = 'black')
ax.set_title('Page visits per hour')
fig.tight_layout()
fig.savefig('data/visits_per_hour.png')
|
analyze_chrome_history.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import requests
from bs4 import BeautifulSoup
from selenium import webdriver
from time import sleep
import re
html = requests.get('http://www.lawhiskeysociety.com/whiskey-profile/3365/Aberlour-12-Year-Old-Non-Chill-filtered')
soup = BeautifulSoup(html.content, 'lxml')
soup.find('div', {'class': 'titlePopup'}).text
soup.find_all('td', {'class': 'textValuePopup'})
# +
# bottler
print(soup.find_all('td', {'class': 'textValuePopup'})[0].text)
# Age
print(soup.find_all('td', {'class': 'textValuePopup'})[1].text)
# Type
print(soup.find_all('td', {'class': 'textValuePopup'})[2].text)
# Vintage
print(soup.find_all('td', {'class': 'textValuePopup'})[3].text)
# Subtype
print(soup.find_all('td', {'class': 'textValuePopup'})[4].text)
# ABV
print(soup.find_all('td', {'class': 'textValuePopup'})[5].text)
# Region
print(soup.find_all('td', {'class': 'textValuePopup'})[6].text)
# Price
print(soup.find_all('td', {'class': 'textValuePopup'})[7].text)
# Availability
print(soup.find_all('td', {'class': 'textValuePopup'})[8].text)
# -
# username
for i in soup.find_all('td', {'class':'contentCell2Popup', 'width':'40'}):
print(i.text)
# review
for i in soup.find_all('td', {'class':'contentCell2Popup', 'align':'left'}):
print('*****'+i.text)
# letter grade
for i in soup.find_all('td', {'class':'contentCell2Popup'}):
for x in i.find_all('img',{'src':True}):
print(x.attrs['src'])
# ### Test on second url
html = requests.get('http://www.lawhiskeysociety.com/whiskey/3701/Ardmore-2000-Villa-Konthor')
soup = BeautifulSoup(html.content, 'lxml')
soup.find('div', {'class': 'titlePopup'}).text
soup.find_all('td', {'class': 'textValuePopup'})
# +
# bottler
print(soup.find_all('td', {'class': 'textValuePopup'})[0].text)
# Age
print(soup.find_all('td', {'class': 'textValuePopup'})[1].text)
# Type
print(soup.find_all('td', {'class': 'textValuePopup'})[2].text)
# Vintage
print(soup.find_all('td', {'class': 'textValuePopup'})[3].text)
# Subtype
print(soup.find_all('td', {'class': 'textValuePopup'})[4].text)
# ABV
print(soup.find_all('td', {'class': 'textValuePopup'})[5].text)
# Region
print(soup.find_all('td', {'class': 'textValuePopup'})[6].text)
# Price
print(soup.find_all('td', {'class': 'textValuePopup'})[7].text)
# Availability
print(soup.find_all('td', {'class': 'textValuePopup'})[8].text)
# -
# username
for i in soup.find_all('td', {'class':'contentCell2Popup', 'width':'40'}):
print(i.text)
# review
for i in soup.find_all('td', {'class':'contentCell2Popup', 'align':'left'}):
print('*****'+i.text)
# letter grade
for i in soup.find_all('td', {'class':'contentCell2Popup'}):
for x in i.find_all('img',{'src':True}):
print(x.attrs['src'])
# ### Function Creation
import requests
from bs4 import BeautifulSoup
from time import sleep
import re
html = requests.get('http://www.lawhiskeysociety.com/whiskey-profile/3365/Aberlour-12-Year-Old-Non-Chill-filtered')
soup = BeautifulSoup(html.content, 'lxml')
# +
def cleaner(string):
string = re.sub(',', '', string)
string = re.sub(' %', '', string)
string = re.sub('\$', '', string)
return string
grade_grabber = lambda x: re.search('images\/letters\/(.*)_', x).group(1)
# all above stays outside of the function
def get_whiskey_reviews(url):
sleep(2)
html = requests.get(url)
soup = BeautifulSoup(html.content, 'lxml')
w_name = cleaner(soup.find('div', {'class': 'titlePopup'}).text)
bottler = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[0].text)
age = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[1].text)
w_type = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[2].text)
vint = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[3].text)
subt = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[4].text)
abv = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[5].text)
region = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[6].text)
price = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[7].text)
avaib = cleaner(soup.find_all('td', {'class': 'textValuePopup'})[8].text)
username = []
for i in soup.find_all('td', {'class':'contentCell2Popup', 'width':'40'}):
username.append(cleaner(i.text))
grade = []
for i in soup.find_all('td', {'class':'contentCell2Popup'}):
for x in i.find_all('img',{'src':True}):
grade.append(grade_grabber(x.attrs['src']))
review = []
for i in soup.find_all('td', {'class':'contentCell2Popup', 'align':'left'}):
review.append(cleaner(i.text))
for i in range(0,len(username)):
# print(username[i], grade[i], review[i], w_name, bottler, age, w_type, vint, subt, abv, region, price, avaib)
master_list = [username[i], grade[i], review[i], w_name, bottler, age, w_type, vint, subt, abv, region, price, avaib]
with open('./aws_whiskey_reviews.csv', 'a+') as f:
print(','.join(master_list), file=f)
# -
def cleaner(string):
string = re.sub(',', '', string)
string = re.sub(' %', '', string)
string = re.sub('\$', '', string)
return string
cleaner(price)
grade_grabber = lambda x: re.search('images\/letters\/(.*)_', x).group(1)
grade_grabber('images/letters/bminus_thumb.jpg')
# ### Testing
df_whiskey = pd.read_csv('./Scraped_Data/df_whiskey.csv')
# whiskey's reviewed within the past 3.5 year, have greater than an F, and clost less than $1000
df_whiskey['url'][0:2]
df_whiskey['url'][0:2].apply(get_whiskey_reviews)
def get_user_reviews_csv(url):
counter = 0
review_number = 1
for i in range(0,101):
driver.get(f'https://www.beeradvocate.com{url}?view=beer&sort=&start={i*25}')
sleep(2)
beer_page = driver.page_source
beer_page_soup = BeautifulSoup(beer_page, 'lxml')
reviews = beer_page_soup.find_all('div', {'id':'rating_fullview_content_2'})
counter += 1
print(f'{url} -- page {counter}')
for count, review in enumerate(reviews):
score = review.find('span', {'class': 'BAscore_norm'}).text
breakdown = review.find('span', {'class': 'muted'}).text
u_names = review.find('a', {'class':'username'}).text
try:
r_text = review_cleaner(reviews[count].text)
except:
r_text = "No Review"
master_list = [str(review_number), url, score, breakdown, u_names, r_text]
with open('./aws_user_reviews.csv', 'a+') as f:
print(','.join(master_list), file=f)
review_number += 1
sleep(2)
# +
# whiskey's reviewed within the last 3.5 years
# got rid of > $1000, ratings of F, no price
# NAS Year -- no age statment
# OB Bottler -- original bottlings
# -
df_whiskey = pd.read_csv('./Scraped_Data/df_whiskey.csv')
df_whiskey.head()
# +
# grades = {'A': 5, 'A-': 4.75, 'B+': 4.25, 'B': 4, 'B-': 3.75, 'C+': 3.25, 'C': 3, 'C-': 2.75, 'D+': 2.25, 'D': 2, 'D-': 1.75}
# -
grades = {'A': 5, 'A-': 4.5, 'B+': 4.25, 'B': 4, 'B-': 3.5, 'C+': 3.25, 'C': 3, 'C-': 2.5, 'D+': 2.25, 'D': 2, 'D-': 1.5}
df_whiskey['average_rating'].value_counts()
df_whiskey['average_rating'] = df_whiskey['average_rating'].replace(grades)
df_whiskey['personal_rating'] = df_whiskey['personal_rating'].replace(grades)
df_whiskey.head()
|
Scraping/whiskey_Scraper.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import re
import glob
import rarfile, os
from collections import Counter
from collections import defaultdict
from PIL import Image
from datetime import datetime
import shutil
def imshow(*args, **kwargs):
params = dict(cmap=plt.cm.gray, interpolation='nearest')
params.update(kwargs)
plt.imshow(*args, **params)
def rgb2gray(rgb):
return np.dot(rgb[...,:3], [0.299, 0.587, 0.114])
def getDate(filename, split='\\'):
if split in filename:
s = re.findall('\d+', filename.split(split)[-1])[0]
else:
s = re.findall('\d+', filename)[0]
return datetime.strptime(s, '%Y%m%d')
def myround(x, base=2):
return int(base * round(float(x)/base))
# -
# ## Cleaning image directory
# +
directories = Counter()
filenames = sorted(glob.iglob('/Users/ajmendez/data/dilbert/images/*/*'))
bad_filenames = []
for i, filename in enumerate(filenames):
# # First remove sub directories
# origdir,filename = os.path.split(filename)
# dirname = os.path.dirname(origdir)
# shutil.move(os.path.join(origdir,filename), os.path.join(dirname, filename))
# # Filter BW/Color ones
# bwfilename = filename.replace('-colour', '')
# if (filename != bwfilename) and (bwfilename in filenames):
# os.remove(bwfilename)
# continue
# # Remove small copies
# sfilename = filename.replace('-small','')
# if (filename != sfilename) and (sfilename in filenames):
# os.remove(filename)
# continue
# # Files without size
# if os.stat(filename).st_size == 0:
# os.remove(filename)
# print(filename)
gfilename = filename.replace('.gif', '.jpg')
if (filename != gfilename) and (gfilename in filenames):
os.remove(gfilename)
continue
directories[os.path.basename(os.path.dirname(filename))] += 1
directories.most_common(1000)
# -
simplesizes = defaultdict(list)
simpleshapes = defaultdict(list)
filenames = sorted(glob.iglob('/Users/ajmendez/data/dilbert/images/*/*'))
for filename in filenames:
with Image.open(filename) as img:
key = (myround(img.height), myround(img.width))
simplesizes[key].append(filename)
simpleshapes[key].append((img.height, img.width))
sorted(map(lambda x: (x[0], len(x[1])), simplesizes.items()), key=lambda x: -x[-1])[:10]
np.sort()
# +
def plotBox(xmin, xmax, ymin, ymax):
plt.plot([xmin, xmax, xmax, xmin, xmin],
[ymin, ymin, ymax, ymax, ymin], color='r', lw=2)
def threshold(img, thresh=60):
Y = np.zeros(img.shape)+255
Y[img < thresh] = img[img < thresh]
return(Y)
def getOffsets(im, sep=120, axis=1):
m = np.mean(im, axis=axis)
thresh = np.percentile(m, 2)
s = np.std(im, axis=axis)
sthresh = np.percentile(s, 2)
pts = np.where((m<thresh) | (s<sthresh))[0]
lines = np.sort(np.concatenate([[0], pts, [im.shape[i]]]))
delta = np.diff(lines)
offsets = lines[np.where(delta > xm)[0]]
sizes = delta[np.where(delta > xm)[0]]
for offset,size in zip(offsets, sizes):
yield offset, offset+size
def carve(img, nx=120, ny=120, linethresh=None):
Y = threshold(img)
Y = img
ymean = np.mean(Y, axis=1)
linethresh = np.percentile(np.mean(Y, axis=1), 2)
ylines = np.where(np.mean(Y,1)<linethresh)[0]
lines = np.sort(np.concatenate([[0], ylines,[img.shape[0]]]))
deltas = np.diff(lines)
yoffsets = lines[np.where(deltas>ny)[0]]#[::2]
heights = deltas[np.where(deltas>ny)[0]]#[::2]
for yoffset,height in zip(yoffsets, heights):
X = Y[yoffset:yoffset+height,:]
xmean = np.mean(X, axis=0)
xthresh = np.percentile(xmean, 2)
xlines = np.where(xmean < xthresh)[0]
lines = np.sort(np.concatenate([[0], xlines, [img.shape[1]]]))
deltas = np.diff(lines)
xoffsets = lines[np.where(deltas>nx)[0]]#[::2]
widths = deltas[np.where(deltas>nx)[0]]#[::2]
for xoffset, width in zip(xoffsets, widths):
yield xoffset, xoffset+width, yoffset, yoffset+height
# plt.figure(figsize=(12,6))
# imshow(image)
# for box in carve(image):
# plotBox(*box)
# -
def oned(im, xm=120, axis=1):
m = np.mean(im, axis=axis)
plt.plot(m)
thresh = np.percentile(m, 2)
s = np.std(im, axis=axis)
plt.plot(s)
sthresh = np.percentile(s, 2)
plt.axhline(thresh, color='orange')
plt.axhline(thresh, color='red')
pts = np.where((m<thresh) | (s<sthresh))[0]
lines = np.sort(np.concatenate([[0], pts, [im.shape[i]]]))
delta = np.diff(lines)
offsets = lines[np.where(delta > xm)[0]]
heights = delta[np.where(delta > xm)[0]]
for offset, height in zip(offsets, heights):
plt.axvspan(offset, offset+height, zorder=2, color='0.5')
for i, ax in enumerate(plt.subplots(2,1, figsize=(12,6))[1]):
plt.sca(ax)
oned(image, axis=1-i)
nskip = 5000
bad = []
params = {}
for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
# if len(filenames) < 2:
# continue
# if j < 2:
# continue
# if j not in bad:
# continue
key = (height,width)
shapes = simpleshapes[key]
image = np.zeros(np.min(shapes, axis=0))
for i,filename in enumerate(filenames):
if i > nskip:
continue
try:
x = plt.imread(filename)
except Exception as e:
print(e)
print(filename)
continue
if len(x.shape) in [3,4]:
x = rgb2gray(x)
image += x[:image.shape[0],
:image.shape[1]]*1.0/np.min([nskip, len(shapes)])
outfilename = '/Users/ajmendez/data/dilbert/stacks_bad/stack_{:03d}.fig.png'.format(j)
if os.path.exists(outfilename):
continue
outfilename = '/Users/ajmendez/data/dilbert/stacks/stack_{:03d}.png'.format(j)
# plt.imsave(outfilename, image, cmap=plt.cm.gray)
plt.figure(figsize=(12,6))
imshow(image)
params[key] = []
for i,box in enumerate(carve(image)):
plotBox(*box)
params[key].append(box)
plt.title((height,width,len(filenames)))
plt.savefig(outfilename.replace('.png', '.fig.png'))
plt.close()
# break
# # Skip Bad Files
for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
badfilename = '/Users/ajmendez/data/dilbert/stacks_bad/stack_{:03d}.fig.png'.format(j)
if os.path.exists(badfilename):
continue
key = (height,width)
shapes = simpleshapes[key]
image = np.zeros(np.min(shapes, axis=0))
for i,filename in enumerate(filenames):
try:
x = plt.imread(filename)
except Exception as e:
print(e)
print(filename)
continue
if len(x.shape) in [3,4]:
x = rgb2gray(x)
basename = os.path.splitext(os.path.basename(filename))[0]
dirname = os.path.dirname(filename).replace('images', 'panels')
if not os.path.exists(dirname):
os.makedirs(dirname)
for k, box in enumerate(params[key]):
outfilename = os.path.join(dirname,
basename+'.{:02d}.png'.format(k))
xmin,xmax, ymin,ymax = box
im = Image.fromarray(x[ymin:ymax, xmin:xmax].astype(np.uint8))
im.thumbnail((128,128))
im.save(outfilename)
# plt.imsave(outfilename, x[ymin:ymax, xmin:xmax],
# cmap=plt.cm.gray)
# break
# break
# +
w,h = 620,425
heights, widths = map(np.array, zip(*simplesizes.keys()))
d = (widths-w)**2 + (heights-h)**2
ii = np.argmin(d)
plt.plot(widths, heights, '.')
plt.plot(widths[ii], heights[ii], 'og')
plt.plot(w,h, 'sr')
# -
nbad = 0
heights,widths = [],[]
for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
badfilename = '/Users/ajmendez/data/dilbert/stacks_bad/stack_{:03d}.fig.png'.format(j)
if os.path.exists(badfilename):
nbad += len(filenames)
plt.scatter(width,height, s=len(filenames)+5, lw=0, alpha=0.5, color='r')
else:
heights.append(height)
widths.append(width)
plt.scatter(width,height, lw=0, alpha=0.5, color='k')
heights,widths = map(np.array, (heights,widths))
print('{:,d} files are still unprocessed. ~{:0,.0f} panels'.format(nbad, nbad*(3*5/6 + 8*1/6)))
for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
badfilename = '/Users/ajmendez/data/dilbert/stacks_bad/stack_{:03d}.fig.png'.format(j)
if not os.path.exists(badfilename):
continue
shapes = simpleshapes[(height,width)]
image = np.zeros(np.min(shapes, axis=0))
d = (widths-w)**2 + (heights-h)**2
d[(widths<w)&(height<w)] = 1e6
i = np.argmin(d)
key = (heights[i],widths[i])
boxes = params[key]
for i,filename in enumerate(filenames):
try:
x = plt.imread(filename)
except Exception as e:
print(e)
print(filename)
continue
if len(x.shape) in [3,4]:
x = rgb2gray(x)
image += x[:image.shape[0],
:image.shape[1]]*1.0/len(shapes)
outfilename = '/Users/ajmendez/data/dilbert/stacks_nearest/stack_{:03d}.png'.format(j)
dirname = os.path.dirname(outfilename)
if not os.path.exists(dirname):
os.makedirs(dirname)
plt.figure(figsize=(12,6))
imshow(image)
params[key] = []
for i,box in enumerate(carve(image)):
plotBox(*box)
params[key].append(box)
plt.title((height,width,len(filenames)))
plt.savefig(outfilename.replace('.png', '.fig.png'))
plt.close()
# break
for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
badfilename = '/Users/ajmendez/data/dilbert/stacks_bad/stack_{:03d}.fig.png'.format(j)
if not os.path.exists(badfilename):
continue
d = (widths-w)**2 + (heights-h)**2
i = np.argmin(d)
key = (heights[i],widths[i])
boxes = params[key]
shapes = simpleshapes[key]
image = np.zeros(np.min(shapes, axis=0))
for i,filename in enumerate(filenames):
try:
x = plt.imread(filename)
except Exception as e:
print(e)
print(filename)
continue
if len(x.shape) in [3,4]:
x = rgb2gray(x)
basename = os.path.splitext(os.path.basename(filename))[0]
dirname = os.path.dirname(filename).replace('images', 'panels2')
if not os.path.exists(dirname):
os.makedirs(dirname)
for k, box in enumerate(boxes):
outfilename = os.path.join(dirname,
basename+'.{:02d}.png'.format(k))
xmin,xmax, ymin,ymax = box
im = Image.fromarray(x[ymin:ymax, xmin:xmax].astype(np.uint8))
im.thumbnail((128,128))
im.save(outfilename)
# plt.imsave(outfilename, x[ymin:ymax, xmin:xmax],
# cmap=plt.cm.gray)
break
break
# +
# from pprint import pformat, pprint
# +
# pprint(params, width=1000)
# +
# params2 = {}
# for j,((height,width),filenames) in enumerate(sorted(simplesizes.items(), key=lambda x: -len(x[-1]))):
# params2[j] = params[(height,width)]
# +
# pprint(params2, width=1000)
# -
|
notebook/20161124_panels.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + code_folding=[]
### imports
import numpy as np
#import tensorflow.keras as keras
import keras
from matplotlib import pyplot as plt
import os, sys
import copy
import pickle
import sys
sys.path.append(os.path.abspath('../'))
from keras2c import keras2c_main
from keras import backend as K
# -
# layers: bidirectional rnn
# merge with different sizes
# conv3d
# pool3d
# seperable conv
# conv transpose
# depthwise conv
# crop3d
# pad3d
# upsampling1d
# upsampling2d
# upsampling3d
# locally connected 1d
# locally connected 2d
# time distributed
#
#
# im2col for convolution?
# static or const?
# broadcasting sizes for merge layers
# find the common dimension and add them that way?
#
#
#
# common API for all function calls
# figure out max array sizes?
# figure out keras h5 file format
#
#
a = keras.layers.Input((4,5))
b = keras.layers.TimeDistributed(keras.layers.Dense(8))(a)
model = keras.models.Model(a,b)
weights = model.layers[1].get_weights()
weights[0].shape
layer = model.layers[1]
layer.layer.__call__(K.constant(np.ones((layer.input_shape[2:]))[np.newaxis,:]))
layer.get_input_at(0).name.split(':')[0]
layer.__class__.__name__
from keras2c.io_parsing import *
model.inputs[0].name
get_layer_io_names(layer)
inshp = (9, 7, 6, 3)
alpha = 0.5
a = keras.layers.Input(inshp)
b = keras.layers.LeakyReLU(alpha=alpha)(a)
model = keras.models.Model(inputs=a, outputs=b)
model.layers[1].output.name
outputs.shape
# +
def k2c_sub2idx(sub, shape, ndim):
#/* converts from subscript to linear indices in row major order */
idx = 0
temp = 0;
for i in range(ndim):
temp = sub[i];
for j in range(ndim-1,i,-1):
temp *= shape[j]
idx += temp;
return int(idx)
def k2c_idx2sub(idx,shape,ndim):
sub = np.zeros(ndim)
for j in range(ndim-1,-1,-1):
sub[j] = idx % shape[j]
idx = idx // shape[j]
return tuple(sub.astype(int))
def flip(a, axis):
ndim = a.ndim
shp = a.shape
a = a.flatten()
step = 1
reduced_size = 1
for i in shp[axis:]:
reduced_size *= i
threshold = int(reduced_size/2)
jump = int(reduced_size)
k=0
while k<a.size:
sub = list(k2c_idx2sub(k,shp,ndim))
sub[axis] = shp[axis]-sub[axis]-1
idx = k2c_sub2idx(sub,shp,ndim)
temp = a[k]
a[k] = a[idx]
a[idx] = temp
if (k+1) % jump >= threshold:
k = (k + 1 -threshold + jump)
else:
k += step
return a.reshape(shp)
# -
np.random.randint(1,5)
for i in range(10):
ndim = 5 #np.random.randint(1,6)
ax = 0 #np.random.randint(ndim)
shp = (5,10,1,1,1) #tuple(np.random.randint(1,25,ndim))
print(ndim)
print(shp)
a = np.random.random(shp)
b1 = np.flip(a,ax)
b2 = flip(a,ax)
print(np.max(np.abs(b1-b2)))
a
b1
b2
np.max(np.abs(b1-b2))
# + [markdown] heading_collapsed=true
# # # model testing
# + hidden=true
shape1 = (None,5,4,2)
shape2 = (None,5,4,1)
output_shape = list(shape1[:-len(shape2)])
for i, j in zip(shape1[-len(shape2):], shape2):
if i is None or j is None:
output_shape.append(None)
elif i == 1:
output_shape.append(j)
elif j == 1:
output_shape.append(i)
else:
if i != j:
raise ValueError('Operands could not be broadcast '
'together with shapes ' +
str(shape1) + ' ' + str(shape2))
output_shape.append(i)
set([shape1,shape2]) # check if all inputs are the same shape
# + hidden=true
convert_sequential_to_model(model).layers
# + hidden=true
model.layers
# + hidden=true
def convert_sequential_to_model(model):
"""Convert a sequential model to the underlying functional format"""
if type(model).__name__ == 'Sequential':
if hasattr(model, '_inbound_nodes'):
inbound_nodes = model._inbound_nodes
elif hasattr(model, 'inbound_nodes'):
inbound_nodes = model.inbound_nodes
else:
raise ValueError('can not get (_)inbound_nodes from model')
# Since Keras 2.2.0
if model.model == model:
input_layer = keras.layers.Input(batch_shape=model.layers[0].input_shape)
prev_layer = input_layer
for layer in model.layers:
prev_layer = layer(prev_layer)
funcmodel = keras.models.Model([input_layer], [prev_layer])
model = funcmodel
else:
model = model.model
if hasattr(model, '_inbound_nodes'):
model._inbound_nodes = inbound_nodes
elif hasattr(model, 'inbound_nodes'):
model.inbound_nodes = inbound_nodes
assert model.layers
for i in range(len(model.layers)):
if type(model.layers[i]).__name__ in ['Model', 'Sequential']:
model.layers[i] = convert_sequential_to_model(model.layers[i])
return model
|
scratch/scratch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Dependencies and Setup
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
import random
from datetime import datetime
import json
# Import API key
from api_keys import weather_api_key
# Incorporated citipy to determine city based on latitude and longitude
from citipy import citipy
# -
# ### API Call
# +
#url = "http://api.openweathermap.org/data/2.5/weather?q=Minneapolis,US&"
#units = "metric"
#test_url = f"{url}appid={weather_api_key}"
#test_url = query_url + "minneapolis"
#print(test_url)
#FOR HISTORICAL UPON GETTING DATASET
#url = "http://history.openweathermap.org/data/2.5/history/city?"
#test_url = f"{url}q=Minneapolis,US&appid={weather_api_key}"
# +
#response = requests.get(test_url).json()
#print(response)
# +
city = (data[0])
print(city)
# -
# +
weather = weather_des[0]
weather_final = weather['description']
print(weather_final)
# -
# ### Convert Raw Data to DataFrame
#
# +
dict = {"city": city,
"temp": temp,
"humidity": humidity,
"cloud": cloud,
"wind": wind,
"weather description": weather_final
}
print(dict)
# -
df = pd.DataFrame(dict, index=[0])
df
|
.ipynb_checkpoints/Minneapolis Weather-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # <span style="color:brown"> Variational Auto Encoder (VAE)
#
# ### <span style="color:blue"> by <NAME>
#
# Autoencoders are a type of neural network that can be used to learn efficient codings of input data. Given some inputs, the network first applies a series of transformations that map the input data into a lower dimensional space. This part of the network is called the ***encoder***.
#
# Then, the network uses the encoded data to try and recreate the inputs. This part of the network is the ***decoder***. Using the encoder, we can compress data of the type that is understood by the network. However, autoencoders are rarely used for this purpose, as usually there exist hand-crafted algorithms (like jpg-compression) that are more efficient.
#
# Instead, autoencoders have repeatedly been applied to perform de-noising tasks. The encoder receives pictures that have been tampered with noise, and it learns how to reconstruct the original images.
#
# One such application for *autoencoders* is called the **variational autoencoder**. Using variational autoencoders, it’s not only possible to compress data — it’s also possible to generate new objects of the type the autoencoder has seen before.
# + deletable=true editable=true
import sys
import os
import datetime as dt
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] deletable=true editable=true
# ## Load in dataset
# + deletable=true editable=true
from tensorflow.examples.tutorials.mnist import input_data
data = input_data.read_data_sets('datasets/MNIST', one_hot=True)
# + [markdown] deletable=true editable=true
# ## Hyperparameters
# + deletable=true editable=true
# Input
image_size = 28
image_channel = 1
image_size_flat = image_size * image_size * image_channel
image_shape = [image_size, image_size, image_channel]
# Network
keep_prob = 0.8
n_latent = 8
decoder_units = int(32 * image_channel / 2)
# Training
learning_rate=1e-3
batch_size = 24
iterations = 10000
log_step = 100
viz_step = 500
# + [markdown] deletable=true editable=true
# ## Model's placeholders
# + deletable=true editable=true
tf.reset_default_graph()
X = tf.placeholder(tf.float32, shape=[None, image_size_flat], name='X_placeholder')
y = tf.placeholder(tf.float32, shape=[None, image_size_flat], name='y_placeholder')
# + [markdown] deletable=true editable=true
# ### Helpers
# + deletable=true editable=true
def leakyReLU(X, alpha=0.3):
return tf.maximum(X, tf.multiply(X, alpha))
def conv2d(X, filters=64, kernel_size=4, strides=2, padding='SAME', activation=tf.nn.relu, dropout=True):
layer = tf.layers.conv2d(inputs=X, filters=filters, kernel_size=kernel_size,
strides=strides, padding=padding, activation=activation)
if dropout:
layer = tf.nn.dropout(layer, keep_prob=keep_prob)
return layer
def conv2d_transpose(X, filters=64, kernel_size=4, strides=2, padding='SAME', activation=tf.nn.relu, dropout=True):
layer = tf.layers.conv2d_transpose(inputs=X, filters=filters, kernel_size=kernel_size,
strides=strides, padding=padding, activation=activation)
if dropout:
layer = tf.nn.dropout(layer, keep_prob=keep_prob)
return layer
def dense(X, units, activation=leakyReLU):
return tf.layers.dense(inputs=X, units=units, activation=activation)
# + [markdown] deletable=true editable=true
# ## The Encoder
#
# As our inputs are images, it’s most reasonable to apply some convolutional transformations to them. What’s most noteworthy is the fact that we are creating two vectors in our encoder, as the encoder is supposed to create objects following a Gaussian Distribution:
#
# * A vector of means
# * A vector of standard deviations
#
# You will see later how we *“force”* the encoder to make sure it really creates values following a Normal Distribution. The returned values that will be fed to the decoder are the z-values. We will need the mean and standard deviation of our distributions later, when computing losses.
# + deletable=true editable=true
def encoder(X):
with tf.variable_scope('encoder', reuse=None):
X = tf.reshape(X, shape=[-1, image_size, image_size, image_channel])
X = conv2d(X, activation=leakyReLU, dropout=True)
X = conv2d(X, activation=leakyReLU, dropout=True)
X = conv2d(X, strides=1, activation=leakyReLU, dropout=True)
X = tf.contrib.layers.flatten(X)
mean = tf.layers.dense(X, units=n_latent)
stddev = 0.5 * tf.layers.dense(X, units=n_latent) # 0.5 * mean
noise = tf.random_normal(tf.stack([tf.shape(X)[0], n_latent]))
z = mean + tf.multiply(noise, tf.exp(stddev))
return z, mean, stddev
# + [markdown] deletable=true editable=true
# ## The Decoder
#
# The decoder does not care about whether the input values are sampled from some specific distribution that has been defined by us. It simply will try to reconstruct the input images. To this end, we use a series of *transpose convolutions*.
# + deletable=true editable=true
def decoder(z):
with tf.variable_scope('decoder', reuse=None):
X = dense(z, units=decoder_units, activation=leakyReLU)
X = dense(z, units=decoder_units*2, activation=leakyReLU)
shape = X.get_shape()[1].value // 2
reshape_dim = [-1, shape, shape, image_channel]
X = tf.reshape(X, reshape_dim)
X = conv2d_transpose(X, dropout=True)
X = conv2d_transpose(X, strides=1, dropout=True)
X = conv2d_transpose(X, strides=1, dropout=False)
X = tf.contrib.layers.flatten(X)
X = dense(X, units=image_size_flat, activation=tf.nn.sigmoid)
img = tf.reshape(X, [-1, *image_shape])
return img
# + deletable=true editable=true
z, mean, stddev = encoder(X)
img = decoder(z)
print(z)
print(img)
# + [markdown] deletable=true editable=true
#
# + deletable=true editable=true
img_reshape = tf.reshape(img, [-1, image_size_flat])
img_loss = tf.reduce_sum(tf.squared_difference(img_reshape, y), axis=1)
latent_loss = -0.5 * tf.reduce_sum(1.0 + 2.0 * stddev - tf.square(mean) - tf.exp(2.0*stddev), axis=1)
loss = tf.reduce_mean(img_loss + latent_loss)
# rec_loss = tf.reduce_sum(tf.squared_difference(decoded, X), 1)
# kl_term = -0.5 * tf.reduce_sum(1.0 + 2.0 * stddev - tf.square(mean) - tf.exp(2.0 * stddev), 1)
# loss = tf.reduce_mean(rec_loss + kl_term)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
train_step = optimizer.minimize(loss)
# + [markdown] deletable=true editable=true
# ## Tensorflow's `Session`
# + deletable=true editable=true
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)
# + [markdown] deletable=true editable=true
# ### Tensorboard
# + deletable=true editable=true
tensorboard_path = 'tensorboard/'
save_path = 'models/'
logdir = os.path.join(tensorboard_path, 'log')
pretrained = os.path.join(save_path, 'model.ckpt')
saver = tf.train.Saver()
writer = tf.summary.FileWriter(logdir=logdir, graph=sess.graph)
if tf.gfile.Exists(save_path):
if len(os.listdir(save_path)) > 1:
saver.restore(sess=sess, save_path=save_path)
else:
tf.gfile.MakeDirs(save_path)
# + [markdown] deletable=true editable=true
# ## Training
# + deletable=true editable=true
train_start = dt.datetime.now()
for i in range(iterations):
batch = data.train.next_batch(batch_size=batch_size)[0]
feed_dict = {X: batch, y: batch}
sess.run(train_step, feed_dict=feed_dict)
if i % log_step == 0:
_loss, _img_loss, _latent_loss, _mean, _stddev = sess.run([loss, img_loss, latent_loss, mean, stddev], feed_dict=feed_dict)
sys.stdout.write('\rLoss={:.2f}\timg_loss = {:.2f}\tlatent_loss = {:.2f}\tmean = {.2f}\tstddev = {:.2f}\tTime taken = {}'.format(
_loss, _img_loss, _latent_loss, _mean, _stddev, dt.datetime.now() - start_time
))
if i % viz_step == 0:
_reconstruct = sess.run(img, feed_dict=feed_dict)
plt.imshow(np.reshape(batch[0], image_shape), cmap='Greys')
plt.imshow(_reconstruct[0], cmap='Greys')
plt.show()
print()
# + deletable=true editable=true
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 3D Segmentation with UNet
#
# [](https://colab.research.google.com/github/Project-MONAI/MONAI/blob/master/examples/notebooks/unet_segmentation_3d_ignite.ipynb)
# ## Setup environment
# + tags=[]
# %pip install -qU "monai[ignite, nibabel, tensorboard]"
# -
# ## Setup imports
# + tags=[]
# Copyright 2020 MONAI Consortium
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
# http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
import glob
import logging
import os
import shutil
import sys
import tempfile
import IPython
import ignite
import nibabel as nib
import numpy as np
import torch
from monai.config import print_config
from monai.data import ArrayDataset, create_test_image_3d
from monai.handlers import MeanDice, StatsHandler, TensorBoardImageHandler, TensorBoardStatsHandler
from monai.losses import DiceLoss
from monai.networks import predict_segmentation
from monai.networks.nets import UNet
from monai.transforms import (
AddChannel,
Compose,
LoadNifti,
RandSpatialCrop,
Resize,
ScaleIntensity,
ToTensor,
)
from monai.utils import first
print_config()
# -
# ## Setup data directory
#
# You can specify a directory with the `MONAI_DATA_DIRECTORY` environment variable.
# This allows you to save results and reuse downloads.
# If not specified a temporary directory will be used.
# + tags=[]
directory = os.environ.get("MONAI_DATA_DIRECTORY")
root_dir = tempfile.mkdtemp() if directory is None else directory
print(root_dir)
# -
# ## Setup logging
logging.basicConfig(stream=sys.stdout, level=logging.INFO)
# ## Setup demo data
# +
for i in range(40):
im, seg = create_test_image_3d(128, 128, 128, num_seg_classes=1)
n = nib.Nifti1Image(im, np.eye(4))
nib.save(n, os.path.join(root_dir, f"im{i}.nii.gz"))
n = nib.Nifti1Image(seg, np.eye(4))
nib.save(n, os.path.join(root_dir, f"seg{i}.nii.gz"))
images = sorted(glob.glob(os.path.join(root_dir, "im*.nii.gz")))
segs = sorted(glob.glob(os.path.join(root_dir, "seg*.nii.gz")))
# -
# ## Setup transforms, dataset
# + tags=[]
# Define transforms for image and segmentation
imtrans = Compose(
[
LoadNifti(image_only=True),
ScaleIntensity(),
AddChannel(),
RandSpatialCrop((96, 96, 96), random_size=False),
ToTensor(),
]
)
segtrans = Compose(
[
LoadNifti(image_only=True),
AddChannel(),
RandSpatialCrop((96, 96, 96), random_size=False),
ToTensor(),
]
)
# Define nifti dataset, dataloader.
ds = ArrayDataset(images, imtrans, segs, segtrans)
loader = torch.utils.data.DataLoader(
ds, batch_size=10, num_workers=2, pin_memory=torch.cuda.is_available()
)
im, seg = first(loader)
print(im.shape, seg.shape)
# -
# ## Create Model, Loss, Optimizer
# +
# Create UNet, DiceLoss and Adam optimizer.
net = UNet(
dimensions=3,
in_channels=1,
out_channels=1,
channels=(16, 32, 64, 128, 256),
strides=(2, 2, 2, 2),
num_res_units=2,
)
loss = DiceLoss(sigmoid=True)
lr = 1e-3
opt = torch.optim.Adam(net.parameters(), lr)
# -
# ## Create supervised_trainer using ignite
# Create trainer
device = torch.device("cuda:0")
trainer = ignite.engine.create_supervised_trainer(net, opt, loss, device, False)
# ## Setup event handlers for checkpointing and logging
# + tags=[]
# optional section for checkpoint and tensorboard logging
# adding checkpoint handler to save models (network params and optimizer stats) during training
log_dir = os.path.join(root_dir, "logs")
checkpoint_handler = ignite.handlers.ModelCheckpoint(
log_dir, "net", n_saved=10, require_empty=False
)
trainer.add_event_handler(
event_name=ignite.engine.Events.EPOCH_COMPLETED,
handler=checkpoint_handler,
to_save={"net": net, "opt": opt},
)
# StatsHandler prints loss at every iteration and print metrics at every epoch,
# we don't set metrics for trainer here, so just print loss, user can also customize print functions
# and can use output_transform to convert engine.state.output if it's not a loss value
train_stats_handler = StatsHandler(name="trainer")
train_stats_handler.attach(trainer)
# TensorBoardStatsHandler plots loss at every iteration and plots metrics at every epoch, same as StatsHandler
train_tensorboard_stats_handler = TensorBoardStatsHandler(log_dir=log_dir)
train_tensorboard_stats_handler.attach(trainer)
# -
# ## Add Validation every N epochs
# +
# optional section for model validation during training
validation_every_n_epochs = 1
# Set parameters for validation
metric_name = "Mean_Dice"
# add evaluation metric to the evaluator engine
val_metrics = {metric_name: MeanDice(sigmoid=True, to_onehot_y=False)}
# Ignite evaluator expects batch=(img, seg) and returns output=(y_pred, y) at every iteration,
# user can add output_transform to return other values
evaluator = ignite.engine.create_supervised_evaluator(net, val_metrics, device, True)
# create a validation data loader
val_imtrans = Compose(
[LoadNifti(image_only=True), ScaleIntensity(), AddChannel(), Resize((96, 96, 96)), ToTensor()]
)
val_segtrans = Compose([LoadNifti(image_only=True), AddChannel(), Resize((96, 96, 96)), ToTensor()])
val_ds = ArrayDataset(images[-20:], val_imtrans, segs[-20:], val_segtrans)
val_loader = torch.utils.data.DataLoader(
val_ds, batch_size=5, num_workers=8, pin_memory=torch.cuda.is_available()
)
@trainer.on(ignite.engine.Events.EPOCH_COMPLETED(every=validation_every_n_epochs))
def run_validation(engine):
evaluator.run(val_loader)
# Add stats event handler to print validation stats via evaluator
val_stats_handler = StatsHandler(
name="evaluator",
output_transform=lambda x: None, # no need to print loss value, so disable per iteration output
global_epoch_transform=lambda x: trainer.state.epoch, # fetch global epoch number from trainer
)
val_stats_handler.attach(evaluator)
# add handler to record metrics to TensorBoard at every validation epoch
val_tensorboard_stats_handler = TensorBoardStatsHandler(
log_dir=log_dir,
output_transform=lambda x: None, # no need to plot loss value, so disable per iteration output
global_epoch_transform=lambda x: trainer.state.epoch, # fetch global epoch number from trainer
)
val_tensorboard_stats_handler.attach(evaluator)
# add handler to draw the first image and the corresponding label and model output in the last batch
# here we draw the 3D output as GIF format along Depth axis, at every validation epoch
val_tensorboard_image_handler = TensorBoardImageHandler(
log_dir=log_dir,
batch_transform=lambda batch: (batch[0], batch[1]),
output_transform=lambda output: predict_segmentation(output[0]),
global_iter_transform=lambda x: trainer.state.epoch,
)
evaluator.add_event_handler(
event_name=ignite.engine.Events.EPOCH_COMPLETED, handler=val_tensorboard_image_handler,
)
# -
# ## Run training loop
# + tags=[]
# create a training data loader
train_ds = ArrayDataset(images[:20], imtrans, segs[:20], segtrans)
train_loader = torch.utils.data.DataLoader(
train_ds, batch_size=5, shuffle=True, num_workers=8, pin_memory=torch.cuda.is_available(),
)
train_epochs = 5
state = trainer.run(train_loader, train_epochs)
IPython.display.clear_output()
# -
# ## Visualizing Tensorboard logs
# %load_ext tensorboard
# %tensorboard --logdir=log_dir
# Expected training curve on TensorBoard:
# 
# ## Cleanup data directory
#
# Remove directory if a temporary was used.
# + tags=[]
if directory is None:
shutil.rmtree(root_dir)
|
examples/notebooks/unet_segmentation_3d_ignite.ipynb
|