code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: torch
# language: python
# name: torch
# ---
# # Optimal Transport
# +
import os,random
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib as mpl
import matplotlib.pyplot as plt
import sys, os,argparse,pickle
import numpy as np
from sklearn.metrics import accuracy_score, recall_score, f1_score
sys.path.insert(0, '../')
from models.classifier import classifier
from dataProcessing.dataModule import SingleDatasetModule, CrossDatasetModule
from Utils.trainerTL_pl import TLmodel
from pytorch_lightning.loggers import MLFlowLogger
from pytorch_lightning import LightningDataModule, LightningModule, Trainer
from pytorch_lightning.callbacks import EarlyStopping,ModelCheckpoint
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
DATA_DIR = 'C:\\Users\\gcram\\Documents\\Smart Sense\\Datasets\\frankDataset\\'
datasetList = ['Dsads','Ucihar','Uschad','Pamap2']
n_classes = 4
# -
|
experiments/OptimalTransport.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="Tce3stUlHN0L"
# ##### Copyright 2019 The TensorFlow Authors.
# + cellView="form" id="tuOe1ymfHZPu"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] id="qFdPvlXBOdUN"
# # Mixed precision
# + [markdown] id="MfBg1C5NB3X0"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/guide/mixed_precision"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/mixed_precision.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] id="xHxb-dlhMIzW"
# ## Overview
#
# Mixed precision is the use of both 16-bit and 32-bit floating-point types in a model during training to make it run faster and use less memory. By keeping certain parts of the model in the 32-bit types for numeric stability, the model will have a lower step time and train equally as well in terms of the evaluation metrics such as accuracy. This guide describes how to use the Keras mixed precision API to speed up your models. Using this API can improve performance by more than 3 times on modern GPUs and 60% on TPUs.
# + [markdown] id="3vsYi_bv7gS_"
# Today, most models use the float32 dtype, which takes 32 bits of memory. However, there are two lower-precision dtypes, float16 and bfloat16, each which take 16 bits of memory instead. Modern accelerators can run operations faster in the 16-bit dtypes, as they have specialized hardware to run 16-bit computations and 16-bit dtypes can be read from memory faster.
#
# NVIDIA GPUs can run operations in float16 faster than in float32, and TPUs can run operations in bfloat16 faster than float32. Therefore, these lower-precision dtypes should be used whenever possible on those devices. However, variables and a few computations should still be in float32 for numeric reasons so that the model trains to the same quality. The Keras mixed precision API allows you to use a mix of either float16 or bfloat16 with float32, to get the performance benefits from float16/bfloat16 and the numeric stability benefits from float32.
#
# Note: In this guide, the term "numeric stability" refers to how a model's quality is affected by the use of a lower-precision dtype instead of a higher precision dtype. An operation is "numerically unstable" in float16 or bfloat16 if running it in one of those dtypes causes the model to have worse evaluation accuracy or other metrics compared to running the operation in float32.
# + [markdown] id="MUXex9ctTuDB"
# ## Setup
# + id="IqR2PQG4ZaZ0"
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from tensorflow.keras import mixed_precision
# + [markdown] id="814VXqdh8Q0r"
# ## Supported hardware
#
# While mixed precision will run on most hardware, it will only speed up models on recent NVIDIA GPUs and Cloud TPUs. NVIDIA GPUs support using a mix of float16 and float32, while TPUs support a mix of bfloat16 and float32.
#
# Among NVIDIA GPUs, those with compute capability 7.0 or higher will see the greatest performance benefit from mixed precision because they have special hardware units, called Tensor Cores, to accelerate float16 matrix multiplications and convolutions. Older GPUs offer no math performance benefit for using mixed precision, however memory and bandwidth savings can enable some speedups. You can look up the compute capability for your GPU at NVIDIA's [CUDA GPU web page](https://developer.nvidia.com/cuda-gpus). Examples of GPUs that will benefit most from mixed precision include RTX GPUs, the V100, and the A100.
# + [markdown] id="-q2hisD60F0_"
# Note: If running this guide in Google Colab, the GPU runtime typically has a P100 connected. The P100 has compute capability 6.0 and is not expected to show a significant speedup.
#
# You can check your GPU type with the following. The command only exists if the
# NVIDIA drivers are installed, so the following will raise an error otherwise.
# + id="j-Yzg_lfkoa_"
# !nvidia-smi -L
# + [markdown] id="hu_pvZDN0El3"
# All Cloud TPUs support bfloat16.
#
# Even on CPUs and older GPUs, where no speedup is expected, mixed precision APIs can still be used for unit testing, debugging, or just to try out the API. On CPUs, mixed precision will run significantly slower, however.
# + [markdown] id="HNOmvumB-orT"
# ## Setting the dtype policy
# + [markdown] id="54ecYY2Hn16E"
# To use mixed precision in Keras, you need to create a `tf.keras.mixed_precision.Policy`, typically referred to as a *dtype policy*. Dtype policies specify the dtypes layers will run in. In this guide, you will construct a policy from the string `'mixed_float16'` and set it as the global policy. This will cause subsequently created layers to use mixed precision with a mix of float16 and float32.
# + id="x3kElPVH-siO"
policy = mixed_precision.Policy('mixed_float16')
mixed_precision.set_global_policy(policy)
# + [markdown] id="6ids1rT_UM5q"
# For short, you can directly pass a string to `set_global_policy`, which is typically done in practice.
# + id="6a8iNFoBUSqR"
# Equivalent to the two lines above
mixed_precision.set_global_policy('mixed_float16')
# + [markdown] id="oGAMaa0Ho3yk"
# The policy specifies two important aspects of a layer: the dtype the layer's computations are done in, and the dtype of a layer's variables. Above, you created a `mixed_float16` policy (i.e., a `mixed_precision.Policy` created by passing the string `'mixed_float16'` to its constructor). With this policy, layers use float16 computations and float32 variables. Computations are done in float16 for performance, but variables must be kept in float32 for numeric stability. You can directly query these properties of the policy.
# + id="GQRbYm4f8p-k"
print('Compute dtype: %s' % policy.compute_dtype)
print('Variable dtype: %s' % policy.variable_dtype)
# + [markdown] id="MOFEcna28o4T"
# As mentioned before, the `mixed_float16` policy will most significantly improve performance on NVIDIA GPUs with compute capability of at least 7.0. The policy will run on other GPUs and CPUs but may not improve performance. For TPUs, the `mixed_bfloat16` policy should be used instead.
# + [markdown] id="cAHpt128tVpK"
# ## Building the model
# + [markdown] id="nB6ujaR8qMAy"
# Next, let's start building a simple model. Very small toy models typically do not benefit from mixed precision, because overhead from the TensorFlow runtime typically dominates the execution time, making any performance improvement on the GPU negligible. Therefore, let's build two large `Dense` layers with 4096 units each if a GPU is used.
# + id="0DQM24hL_14Q"
inputs = keras.Input(shape=(784,), name='digits')
if tf.config.list_physical_devices('GPU'):
print('The model will run with 4096 units on a GPU')
num_units = 4096
else:
# Use fewer units on CPUs so the model finishes in a reasonable amount of time
print('The model will run with 64 units on a CPU')
num_units = 64
dense1 = layers.Dense(num_units, activation='relu', name='dense_1')
x = dense1(inputs)
dense2 = layers.Dense(num_units, activation='relu', name='dense_2')
x = dense2(x)
# + [markdown] id="2dezdcqnOXHk"
# Each layer has a policy and uses the global policy by default. Each of the `Dense` layers therefore have the `mixed_float16` policy because you set the global policy to `mixed_float16` previously. This will cause the dense layers to do float16 computations and have float32 variables. They cast their inputs to float16 in order to do float16 computations, which causes their outputs to be float16 as a result. Their variables are float32 and will be cast to float16 when the layers are called to avoid errors from dtype mismatches.
# + id="kC58MzP4PEcC"
print(dense1.dtype_policy)
print('x.dtype: %s' % x.dtype.name)
# 'kernel' is dense1's variable
print('dense1.kernel.dtype: %s' % dense1.kernel.dtype.name)
# + [markdown] id="_WAZeqDyqZcb"
# Next, create the output predictions. Normally, you can create the output predictions as follows, but this is not always numerically stable with float16.
# + id="ybBq1JDwNIbz"
# INCORRECT: softmax and model output will be float16, when it should be float32
outputs = layers.Dense(10, activation='softmax', name='predictions')(x)
print('Outputs dtype: %s' % outputs.dtype.name)
# + [markdown] id="D0gSWxc9NN7q"
# A softmax activation at the end of the model should be float32. Because the dtype policy is `mixed_float16`, the softmax activation would normally have a float16 compute dtype and output float16 tensors.
#
# This can be fixed by separating the Dense and softmax layers, and by passing `dtype='float32'` to the softmax layer:
# + id="IGqCGn4BsODw"
# CORRECT: softmax and model output are float32
x = layers.Dense(10, name='dense_logits')(x)
outputs = layers.Activation('softmax', dtype='float32', name='predictions')(x)
print('Outputs dtype: %s' % outputs.dtype.name)
# + [markdown] id="tUdkY_DHsP8i"
# Passing `dtype='float32'` to the softmax layer constructor overrides the layer's dtype policy to be the `float32` policy, which does computations and keeps variables in float32. Equivalently, you could have instead passed `dtype=mixed_precision.Policy('float32')`; layers always convert the dtype argument to a policy. Because the `Activation` layer has no variables, the policy's variable dtype is ignored, but the policy's compute dtype of float32 causes softmax and the model output to be float32.
#
#
# Adding a float16 softmax in the middle of a model is fine, but a softmax at the end of the model should be in float32. The reason is that if the intermediate tensor flowing from the softmax to the loss is float16 or bfloat16, numeric issues may occur.
#
# You can override the dtype of any layer to be float32 by passing `dtype='float32'` if you think it will not be numerically stable with float16 computations. But typically, this is only necessary on the last layer of the model, as most layers have sufficient precision with `mixed_float16` and `mixed_bfloat16`.
#
# Even if the model does not end in a softmax, the outputs should still be float32. While unnecessary for this specific model, the model outputs can be cast to float32 with the following:
# + id="dzVAoLI56jR8"
# The linear activation is an identity function. So this simply casts 'outputs'
# to float32. In this particular case, 'outputs' is already float32 so this is a
# no-op.
outputs = layers.Activation('linear', dtype='float32')(outputs)
# + [markdown] id="tpY4ZP7us5hA"
# Next, finish and compile the model, and generate input data:
# + id="g4OT3Z6kqYAL"
model = keras.Model(inputs=inputs, outputs=outputs)
model.compile(loss='sparse_categorical_crossentropy',
optimizer=keras.optimizers.RMSprop(),
metrics=['accuracy'])
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
# + [markdown] id="0Sm8FJHegVRN"
# This example cast the input data from int8 to float32. You don't cast to float16 since the division by 255 is on the CPU, which runs float16 operations slower than float32 operations. In this case, the performance difference in negligible, but in general you should run input processing math in float32 if it runs on the CPU. The first layer of the model will cast the inputs to float16, as each layer casts floating-point inputs to its compute dtype.
#
# The initial weights of the model are retrieved. This will allow training from scratch again by loading the weights.
# + id="0UYs-u_DgiA5"
initial_weights = model.get_weights()
# + [markdown] id="zlqz6eVKs9aU"
# ## Training the model with Model.fit
#
# Next, train the model:
# + id="hxI7-0ewmC0A"
history = model.fit(x_train, y_train,
batch_size=8192,
epochs=5,
validation_split=0.2)
test_scores = model.evaluate(x_test, y_test, verbose=2)
print('Test loss:', test_scores[0])
print('Test accuracy:', test_scores[1])
# + [markdown] id="MPhJ9OPWt4x5"
# Notice the model prints the time per step in the logs: for example, "25ms/step". The first epoch may be slower as TensorFlow spends some time optimizing the model, but afterwards the time per step should stabilize.
#
# If you are running this guide in Colab, you can compare the performance of mixed precision with float32. To do so, change the policy from `mixed_float16` to `float32` in the "Setting the dtype policy" section, then rerun all the cells up to this point. On GPUs with compute capability 7.X, you should see the time per step significantly increase, indicating mixed precision sped up the model. Make sure to change the policy back to `mixed_float16` and rerun the cells before continuing with the guide.
#
# On GPUs with compute capability of at least 8.0 (Ampere GPUs and above), you likely will see no performance improvement in the toy model in this guide when using mixed precision compared to float32. This is due to the use of [TensorFloat-32](https://www.tensorflow.org/api_docs/python/tf/config/experimental/enable_tensor_float_32_execution), which automatically uses lower precision math in certain float32 ops such as `tf.linalg.matmul`. TensorFloat-32 gives some of the performance advantages of mixed precision when using float32. However, in real-world models, you will still typically see significantly performance improvements from mixed precision due to memory bandwidth savings and ops which TensorFloat-32 does not support.
#
# If running mixed precision on a TPU, you will not see as much of a performance gain compared to running mixed precision on GPUs, especially pre-Ampere GPUs. This is because TPUs do certain ops in bfloat16 under the hood even with the default dtype policy of float32. This is similar to how Ampere GPUs use TensorFloat-32 by default. Compared to Ampere GPUs, TPUs typically see less performance gains with mixed precision on real-world models.
#
# For many real-world models, mixed precision also allows you to double the batch size without running out of memory, as float16 tensors take half the memory. This does not apply however to this toy model, as you can likely run the model in any dtype where each batch consists of the entire MNIST dataset of 60,000 images.
# + [markdown] id="mNKMXlCvHgHb"
# ## Loss scaling
#
# Loss scaling is a technique which `tf.keras.Model.fit` automatically performs with the `mixed_float16` policy to avoid numeric underflow. This section describes what loss scaling is and the next section describes how to use it with a custom training loop.
# + [markdown] id="1xQX62t2ow0g"
# ### Underflow and Overflow
#
# The float16 data type has a narrow dynamic range compared to float32. This means values above $65504$ will overflow to infinity and values below $6.0 \times 10^{-8}$ will underflow to zero. float32 and bfloat16 have a much higher dynamic range so that overflow and underflow are not a problem.
#
# For example:
# + id="CHmXRb-yRWbE"
x = tf.constant(256, dtype='float16')
(x ** 2).numpy() # Overflow
# + id="5unZLhN0RfQM"
x = tf.constant(1e-5, dtype='float16')
(x ** 2).numpy() # Underflow
# + [markdown] id="pUIbhQypRVe_"
# In practice, overflow with float16 rarely occurs. Additionally, underflow also rarely occurs during the forward pass. However, during the backward pass, gradients can underflow to zero. Loss scaling is a technique to prevent this underflow.
# + [markdown] id="FAL5qij_oNqJ"
# ### Loss scaling overview
#
# The basic concept of loss scaling is simple: simply multiply the loss by some large number, say $1024$, and you get the *loss scale* value. This will cause the gradients to scale by $1024$ as well, greatly reducing the chance of underflow. Once the final gradients are computed, divide them by $1024$ to bring them back to their correct values.
#
# The pseudocode for this process is:
#
# ```
# loss_scale = 1024
# loss = model(inputs)
# loss *= loss_scale
# # Assume `grads` are float32. You do not want to divide float16 gradients.
# grads = compute_gradient(loss, model.trainable_variables)
# grads /= loss_scale
# ```
#
# Choosing a loss scale can be tricky. If the loss scale is too low, gradients may still underflow to zero. If too high, the opposite the problem occurs: the gradients may overflow to infinity.
#
# To solve this, TensorFlow dynamically determines the loss scale so you do not have to choose one manually. If you use `tf.keras.Model.fit`, loss scaling is done for you so you do not have to do any extra work. If you use a custom training loop, you must explicitly use the special optimizer wrapper `tf.keras.mixed_precision.LossScaleOptimizer` in order to use loss scaling. This is described in the next section.
#
# + [markdown] id="yqzbn8Ks9Q98"
# ## Training the model with a custom training loop
# + [markdown] id="CRANRZZ69nA7"
# So far, you have trained a Keras model with mixed precision using `tf.keras.Model.fit`. Next, you will use mixed precision with a custom training loop. If you do not already know what a custom training loop is, please read the [Custom training guide](../tutorials/customization/custom_training_walkthrough.ipynb) first.
# + [markdown] id="wXTaM8EEyEuo"
# Running a custom training loop with mixed precision requires two changes over running it in float32:
#
# 1. Build the model with mixed precision (you already did this)
# 2. Explicitly use loss scaling if `mixed_float16` is used.
#
# + [markdown] id="M2zpp7_65mTZ"
# For step (2), you will use the `tf.keras.mixed_precision.LossScaleOptimizer` class, which wraps an optimizer and applies loss scaling. By default, it dynamically determines the loss scale so you do not have to choose one. Construct a `LossScaleOptimizer` as follows.
# + id="ogZN3rIH0vpj"
optimizer = keras.optimizers.RMSprop()
optimizer = mixed_precision.LossScaleOptimizer(optimizer)
# + [markdown] id="FVy5gnBqTE9z"
# If you want, it is possible choose an explicit loss scale or otherwise customize the loss scaling behavior, but it is highly recommended to keep the default loss scaling behavior, as it has been found to work well on all known models. See the `tf.keras.mixed_precision.LossScaleOptimizer` documention if you want to customize the loss scaling behavior.
# + [markdown] id="JZYEr5hA3MXZ"
# Next, define the loss object and the `tf.data.Dataset`s:
# + id="9cE7Mm533hxe"
loss_object = tf.keras.losses.SparseCategoricalCrossentropy()
train_dataset = (tf.data.Dataset.from_tensor_slices((x_train, y_train))
.shuffle(10000).batch(8192))
test_dataset = tf.data.Dataset.from_tensor_slices((x_test, y_test)).batch(8192)
# + [markdown] id="4W0zxrxC3nww"
# Next, define the training step function. You will use two new methods from the loss scale optimizer to scale the loss and unscale the gradients:
#
# - `get_scaled_loss(loss)`: Multiplies the loss by the loss scale
# - `get_unscaled_gradients(gradients)`: Takes in a list of scaled gradients as inputs, and divides each one by the loss scale to unscale them
#
# These functions must be used in order to prevent underflow in the gradients. `LossScaleOptimizer.apply_gradients` will then apply gradients if none of them have `Inf`s or `NaN`s. It will also update the loss scale, halving it if the gradients had `Inf`s or `NaN`s and potentially increasing it otherwise.
# + id="V0vHlust4Rug"
@tf.function
def train_step(x, y):
with tf.GradientTape() as tape:
predictions = model(x)
loss = loss_object(y, predictions)
scaled_loss = optimizer.get_scaled_loss(loss)
scaled_gradients = tape.gradient(scaled_loss, model.trainable_variables)
gradients = optimizer.get_unscaled_gradients(scaled_gradients)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
return loss
# + [markdown] id="rcFxEjia6YPQ"
# The `LossScaleOptimizer` will likely skip the first few steps at the start of training. The loss scale starts out high so that the optimal loss scale can quickly be determined. After a few steps, the loss scale will stabilize and very few steps will be skipped. This process happens automatically and does not affect training quality.
# + [markdown] id="IHIvKKhg4Y-G"
# Now, define the test step:
#
# + id="nyk_xiZf42Tt"
@tf.function
def test_step(x):
return model(x, training=False)
# + [markdown] id="hBs98MZyhBOB"
# Load the initial weights of the model, so you can retrain from scratch:
# + id="jpzOe3WEhFUJ"
model.set_weights(initial_weights)
# + [markdown] id="s9Pi1ADM47Ud"
# Finally, run the custom training loop:
# + id="N274tJ3e4_6t"
for epoch in range(5):
epoch_loss_avg = tf.keras.metrics.Mean()
test_accuracy = tf.keras.metrics.SparseCategoricalAccuracy(
name='test_accuracy')
for x, y in train_dataset:
loss = train_step(x, y)
epoch_loss_avg(loss)
for x, y in test_dataset:
predictions = test_step(x)
test_accuracy.update_state(y, predictions)
print('Epoch {}: loss={}, test accuracy={}'.format(epoch, epoch_loss_avg.result(), test_accuracy.result()))
# + [markdown] id="d7daQKGerOFE"
# ## GPU performance tips
#
# Here are some performance tips when using mixed precision on GPUs.
#
# ### Increasing your batch size
#
# If it doesn't affect model quality, try running with double the batch size when using mixed precision. As float16 tensors use half the memory, this often allows you to double your batch size without running out of memory. Increasing batch size typically increases training throughput, i.e. the training elements per second your model can run on.
#
# ### Ensuring GPU Tensor Cores are used
#
# As mentioned previously, modern NVIDIA GPUs use a special hardware unit called Tensor Cores that can multiply float16 matrices very quickly. However, Tensor Cores requires certain dimensions of tensors to be a multiple of 8. In the examples below, an argument is bold if and only if it needs to be a multiple of 8 for Tensor Cores to be used.
#
# - tf.keras.layers.Dense(**units=64**)
# - tf.keras.layers.Conv2d(**filters=48**, kernel_size=7, stride=3)
# - And similarly for other convolutional layers, such as tf.keras.layers.Conv3d
# - tf.keras.layers.LSTM(**units=64**)
# - And similar for other RNNs, such as tf.keras.layers.GRU
# - tf.keras.Model.fit(epochs=2, **batch_size=128**)
#
# You should try to use Tensor Cores when possible. If you want to learn more, [NVIDIA deep learning performance guide](https://docs.nvidia.com/deeplearning/sdk/dl-performance-guide/index.html) describes the exact requirements for using Tensor Cores as well as other Tensor Core-related performance information.
#
# ### XLA
#
# XLA is a compiler that can further increase mixed precision performance, as well as float32 performance to a lesser extent. Refer to the [XLA guide](https://www.tensorflow.org/xla) for details.
# + [markdown] id="2tFDX8fm6o_3"
# ## Cloud TPU performance tips
#
# As with GPUs, you should try doubling your batch size when using Cloud TPUs because bfloat16 tensors use half the memory. Doubling batch size may increase training throughput.
#
# TPUs do not require any other mixed precision-specific tuning to get optimal performance. They already require the use of XLA. TPUs benefit from having certain dimensions being multiples of $128$, but this applies equally to the float32 type as it does for mixed precision. Check the [Cloud TPU performance guide](https://cloud.google.com/tpu/docs/performance-guide) for general TPU performance tips, which apply to mixed precision as well as float32 tensors.
# + [markdown] id="--wSEU91wO9w"
# ## Summary
#
# - You should use mixed precision if you use TPUs or NVIDIA GPUs with at least compute capability 7.0, as it will improve performance by up to 3x.
# - You can use mixed precision with the following lines:
#
# ```python
# # On TPUs, use 'mixed_bfloat16' instead
# mixed_precision.set_global_policy('mixed_float16')
# ```
#
# * If your model ends in softmax, make sure it is float32. And regardless of what your model ends in, make sure the output is float32.
# * If you use a custom training loop with `mixed_float16`, in addition to the above lines, you need to wrap your optimizer with a `tf.keras.mixed_precision.LossScaleOptimizer`. Then call `optimizer.get_scaled_loss` to scale the loss, and `optimizer.get_unscaled_gradients` to unscale the gradients.
# * Double the training batch size if it does not reduce evaluation accuracy
# * On GPUs, ensure most tensor dimensions are a multiple of $8$ to maximize performance
#
# For an example of mixed precision using the `tf.keras.mixed_precision` API, check [functions and classes related to training performance](https://github.com/tensorflow/models/blob/master/official/modeling/performance.py). Check out the official models, such as [Transformer](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/transformer_encoder_block.py), for details.
#
|
site/en/guide/mixed_precision.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Naive Bayes part-2
# ### Email Spam Detection using Naive Bayes
import pandas as pd
df=pd.read_csv("spam.csv",engine='python',encoding='utf-8',error_bad_lines=False)
df.head()
df.groupby('Category').describe()
df['spam']=df['Category'].apply(lambda x: 1 if x=='spam' else 0)
df.head()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df.Message,df.spam,test_size=0.2)
# ## Vectorizer
# #### Defining number for each unique word
# <img src=nb11.png height=400 width=800>
from sklearn.feature_extraction.text import CountVectorizer
v = CountVectorizer()
X_train_count = v.fit_transform(X_train.values)
X_train_count.toarray()[:2]
# <img src=nb12.png height=800 width=800>
from sklearn.naive_bayes import MultinomialNB
model = MultinomialNB()
model.fit(X_train_count,y_train)
emails = [
'Hey mohan, can we get together to watch footbal game tomorrow?',
'Upto 20% discount on parking, exclusive offer just for you. Dont miss this reward!'
]
emails_count = v.transform(emails) # Beacuse of our model can predict numerical values
model.predict(emails_count)
X_test_count = v.transform(X_test)
model.score(X_test_count, y_test)
# ## sklearn pipeline
from sklearn.pipeline import Pipeline # Defining steps. here two steps
clf = Pipeline([
('vectorizer', CountVectorizer()),
('nb', MultinomialNB())
])
clf.fit(X_train, y_train) # this time, we don't need conversion manually
clf.score(X_test,y_test) # So, we got same result as expected
clf.predict(emails)
|
Machine Learning/14. Naive Bayes 2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # Sketching AutoEncoder with line connectivity prediction
#
# This notebook demonstrates an autoencoder that predicts both a list of 2d points and an approximately binary connection matrix for those points. Lines between each possible pair of points are drawn into separate rasters and these are weighted by the respective weight in the connection matrix before being merged into a single image with a compositing function. Only the encoder network has learnable parameters; the decoder is entirely deterministic, but differentiable.
#
# The network is defined below; the number of points can be configured and we can control whether to allow points to connect to themselves (allowing drawing of single points) or not.
# +
import torch
import torch.nn as nn
try:
from dsketch.raster.disttrans import line_edt2
from dsketch.raster.raster import exp
from dsketch.raster.composite import softor
except:
# !pip install git+https://github.com/jonhare/DifferentiableSketching.git
from dsketch.raster.disttrans import line_edt2
from dsketch.raster.raster import exp
from dsketch.raster.composite import softor
class AE(nn.Module):
def __init__(self, npoints=10, hidden=64, sz=28, allow_points=True):
super(AE, self).__init__()
# build the coordinate grid:
r = torch.linspace(-1, 1, sz)
c = torch.linspace(-1, 1, sz)
grid = torch.meshgrid(r, c)
grid = torch.stack(grid, dim=2)
self.register_buffer("grid", grid)
# if we allow points, we compute the upper-triangular part of the symmetric connection
# matrix including the diagonal. If points are not allowed, we don't need the diagonal values
# as they would be implictly zero
if allow_points:
nlines = int((npoints**2 + npoints) / 2)
else:
nlines = int(npoints * (npoints-1) / 2)
self.coordpairs = torch.combinations(torch.arange(0, npoints, dtype=torch.long), r=2, with_replacement=allow_points)
# shared part of the encoder
self.enc1 = nn.Sequential(
nn.Linear(sz**2, hidden),
nn.ReLU(),
nn.Linear(hidden, hidden),
nn.ReLU())
# second part for computing npoints 2d coordinates (using tanh because we use a -1..1 grid)
self.enc_pts = nn.Sequential(
nn.Linear(hidden, npoints*2),
nn.Tanh())
# second part for computing upper triangular part of the connection matrix
self.enc_con = nn.Sequential(
nn.Linear(hidden, nlines),
nn.Sigmoid())
def forward(self, inp, sigma=7e-3):
# the encoding process will flatten the input and
# push it through the encoder networks
bs = inp.shape[0]
x = inp.view(bs, -1)
z = self.enc1(x)
pts = self.enc_pts(z) #[batch, npoints*2]
pts = pts.view(bs, -1, 2) # expand -> [batch, npoints, 2]
conn = self.enc_con(z) #[batch, nlines]
# compute all valid permuations of line start and end points
lines = torch.stack((pts[:,self.coordpairs[:,0]], pts[:,self.coordpairs[:,1]]), dim=-2) #[batch, nlines, 2, 2]
# Rasterisation steps
# draw the lines (for every input in the batch)
rasters = exp(line_edt2(lines, self.grid), sigma) # -> [batch * nlines, 28, 28]
# weight by the values in the connection matrix
rasters = rasters * conn.view(bs, -1, 1, 1)
# composite
return softor(rasters)
# -
# We'll do a simple test on MNIST and try and train the AE to be able to reconstruct digit images (and of course at the same time perform image vectorisation/autotracing of polylines). Hyperparameters are pretty arbitrary (defaults for Adam; 256 batch size) and the line width is fixed to a value that works well for MNIST.
# +
import matplotlib.pyplot as plt
from torchvision.datasets.mnist import MNIST
from torchvision import transforms
import torchvision
batch_size = 256
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Lambda(lambda x: x.view(28, 28))
])
trainset = torchvision.datasets.MNIST('/tmp', train=True, transform=transform, download=True)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch_size, shuffle=True, num_workers=0)
testset = torchvision.datasets.MNIST('/tmp', train=False, transform=transform, download=True)
testloader = torch.utils.data.DataLoader(testset, batch_size=batch_size, shuffle=False, num_workers=0)
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
model = AE(npoints=6, allow_points=True).to(device)
opt = torch.optim.Adam(model.parameters())
for epoch in range(10):
for images, classes in trainloader:
images = images.to(device)
opt.zero_grad()
out = model(images)
loss = nn.functional.mse_loss(out, images)
loss.backward()
opt.step()
print(loss)
# -
# Finally here's a visualisation of a set of test inputs and their rendered reconstructions:
# +
batch = iter(testloader).next()[0][0:64]
out = model(batch.to(device))
plt.figure()
inputs = torchvision.utils.make_grid(batch.unsqueeze(1))
plt.title("Inputs")
plt.imshow(inputs.permute(1,2,0))
plt.figure()
outputs = torchvision.utils.make_grid(out.detach().cpu().unsqueeze(1))
plt.title("Outputs")
plt.imshow(outputs.permute(1,2,0))
# -
|
samples/MNIST_VectorAE_SimplePolyConnect.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 电影影评情感分析
import warnings
warnings.filterwarnings("ignore")
# +
# 加载数据
import pandas as pd
import os
BANK_PATH = '.'
def load_data(bank_path=BANK_PATH):
csv_path=os.path.join(bank_path, "train_data.csv")
return pd.read_csv(csv_path)
comment_data = load_data()
comment_data
# -
test_data = pd.read_csv('test_data.csv')
test_data.head()
# 我们发现训练样本的label比较平衡
data_com_X = comment_data
data_com_X.label.value_counts()
data_com_X.info()
# +
# 分词
import jieba
# 停用词
stopwords = pd.read_csv("./stopwords.txt"
,index_col=False
,quoting=3
,sep="\t"
,names=['stopword']
,encoding='utf-8') # quoting=3 全不引用
def preprocess_text(content_lines,sentences,category):
for line in content_lines:
try:
segs=jieba.lcut(line)
segs = filter(lambda x:len(x)>1, segs)
segs = filter(lambda x:x not in stopwords, segs)
sentences.append((" ".join(segs), category))
except:
print(line)
continue
data_com_X_1 = data_com_X[data_com_X.label == 1]
data_com_X_0 = data_com_X[data_com_X.label == 0]
sentences=[]
preprocess_text(data_com_X_1.comment.dropna().values.tolist() ,sentences ,'like')
preprocess_text(data_com_X_0.comment.dropna().values.tolist() ,sentences ,'nlike')
# 生成训练集(乱序)
import random
random.shuffle(sentences)
for sentence in sentences[:10]:
print(sentence[0], sentence[1])
# -
test_sentences = []
preprocess_text(test_data.comment.dropna().values.tolist() ,test_sentences ,'like')
test_sentences[0]
# +
import numpy as np
from sklearn.model_selection import StratifiedShuffleSplit
x,y=zip(*sentences)
x_train=x[:32000]
y_train=y[:32000]
x_test = x[32000:]
y_test =y[32000:]
test_set, _ =zip(*test_sentences)
X_all = x_train + x_test + test_set
len_train = len(x_train)
len_val = len(x_test)
tfv = TfidfVectorizer()
tfv.fit(X_all)
X_all = tfv.transform(X_all)
# 恢复成训练集和测试集部分
x_train = X_all[:len_train]
x_test = X_all[len_train:len_train+len_val]
test_set = X_all[len_train+len_val:]
# -
from sklearn.model_selection import StratifiedKFold
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB, BernoulliNB
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score,precision_score
from sklearn.model_selection import cross_val_score
import numpy as np
# model_NB = MultinomialNB()
model_NB = SVC(kernel='linear')
model_NB.fit(x_train, y_train)
res = cross_val_score(model_NB, x_train, y_train, cv=20, scoring='accuracy')
print ("多项式贝叶斯分类器20折交叉验证得分: ", res)
res.mean()
# vec.fit(x_test)
y_pred=model_NB.predict(x_test)
y_pred
print("ACC Score : %f" % accuracy_score(y_test,y_pred))
# 保存结果
result_pd = pd.DataFrame()
result_pd['label'] = model_NB.predict(test_set)
result_pd[result_pd['label'] == 'like'] = 1
result_pd[result_pd['label'] == 'nlike'] = 0
result_pd.to_csv('submit_result.csv', index=False)
|
code/sentiment_analysis/demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### Load Model Class
# This page allows user to load a set of simulation files (including results) from ASCII files or from netcdf file.
#
# The UI will automatically query the directory (or netcdf file) for available results and will
# disable result types that are unavailable. If the projection information is included in the
# netcdf file, it will be loaded into UI and disabled. Otherwise, the user must input projection
# information for ASCII files.
# +
from adhui.adh_model_ui import LoadModel
import panel as pn
pn.extension()
# -
# Instantiate the model loader ui
load_model = LoadModel()
# display the model loader ui
load_model.panel()
adh_mod = load_model._load_data()
adh_mod.pprint()
|
docs/User_Guide/02_Load_Model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.2 64-bit (''.venv'': venv)'
# name: python3
# ---
# # Chef Recipe | How to cook a joke
# > A simple example to learn how to use Chef and it's ingredients
#
# - toc: true
# - badges: true
# - comments: true
# - categories: [recipe, python, jupyter]
# - hide: false
# - image: images/social/jokes.svg
# <!-- - image: images/chart-preview.png -->
# ----
# ## Modules
#
# ### Chef
#
# {% gist 1bc116f05d09e598a1a2dcfbb0e2fc22 chef.py %}
#
# ### Ingredients
#
# {% gist 5c75b7cdea330d15dcd93adbb08648c3 joking.py %}
#
# ## Call graph
#
# 
#
# ----
# ## Configuration
# ### Parameters
gist_user = 'davidefornelli'
gist_chef_id = '1bc116f05d09e598a1a2dcfbb0e2fc22'
gist_ingredients_id = '5c75b7cdea330d15dcd93adbb08648c3'
ingredients_to_import = [
(gist_ingredients_id, 'joking.py')
]
# ## Configure environment
# %pip install httpimport
# ### Import chef
# +
import httpimport
with httpimport.remote_repo(
['chef'],
f"https://gist.githubusercontent.com/{gist_user}/{gist_chef_id}/raw"
):
import chef
# -
# ### Import ingredients
# +
def ingredients_import(ingredients):
for ingredient in ingredients:
mod, package = chef.process_gist_ingredient(
gist_id=ingredient[0],
gist_file=ingredient[1],
gist_user=gist_user
)
globals()[package] = mod
ingredients_import(ingredients=ingredients_to_import)
# -
# ## Tell me a joke
joking.tell_me_a_joke()
|
_notebooks/2021-11-18-nb_chef_recipe_jokes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# # Spring-mass problem: tracking based on range and range rate
#
# Created on 01 January 2018
#
# Example 4.8.2 Spring-mass problem
# pg 216 in Statistical Orbit Determination, Tapley, Born, Schutz.
# pg 271 problem 15
#
# @author: <NAME>
# Import generic libraries
import numpy as np
import math
# Importing what's needed for nice plots.
import matplotlib.pyplot as plt
from matplotlib import rc
rc('font', **{'family': 'serif', 'serif': ['Helvetica']})
rc('text', usetex=True)
params = {'text.latex.preamble' : [r'\usepackage{amsmath}', r'\usepackage{amssymb}']}
plt.rcParams.update(params)
from mpl_toolkits.axes_grid.anchored_artists import AnchoredText
# Object of mass $m$ is connected to two fixed walls by springs with spring constants $k_1$ and $k_2$. The sensor used to measure the range $\rho$ and range-rate $\dot{\rho}$ is located at a point $P$ which is at a height of $h$ on the wall to which spring $k_1$ is attached.
#
# The initial position and velocity of the object are assumed to be $x_0 = 3.0~\mathrm{m}$ and $v_0 = 0.0~\mathrm{m/s}$.
#
# The EOM (Equation of Motion) of the body is given by
# \begin{equation}
# \ddot{x} = - (k_1 + k_2)(x-\bar{x})/m = -\omega^2 (x-\bar{x})
# \end{equation}
# where $x$ is the position of the object, $\bar{x}$ is its static equilibrium position and $\omega$ is the angular frequency. $\bar{x}$ is to 0.
# +
# Parameters for the given problem
k1 = 2.5;
k2 = 3.7;
m = 1.5;
h = 5.4;
x0 = 3.0;
v0 = 0.0;
omega2 = (k1+k2)/m;
omega = math.sqrt(omega2);
# -
# From the EOM, it is inferred that an appropriate choice of state vector is
# \begin{equation}
# \mathbf{X} =
# \begin{bmatrix}
# x \\
# v
# \end{bmatrix}
# \end{equation}
#
# The relationship between position $x$ and velocity $v$ easily leads to a differential equation
# \begin{equation}
# \frac{dx}{dt} = v
# \end{equation}
# while the relationship between velocity and acceleration leads to another DE.
# \begin{equation}
# \frac{dv}{dt} = -\omega^2 x
# \end{equation}
#
# These two DEs lead to:
# \begin{equation}
# \frac{d}{dt}\begin{bmatrix}
# x \\
# v
# \end{bmatrix}
# =
# \begin{bmatrix}
# v \\
# -\omega^2 x
# \end{bmatrix}
# \end{equation}
#
# The state space formulation is thus
# \begin{equation}
# \dot{\mathbf{X}} =
# \begin{bmatrix}
# 0 & 1 \\
# -\omega^2 & 0
# \end{bmatrix}
# \mathbf{X} = \mathbf{A} \mathbf{X}
# \end{equation}
#
# Function fn_A implements $\mathbf{A}$.
#
# An analysis of the state space formulation leads to the state transition matrix $\Phi$ given by
# \begin{equation}
# \Phi =
# \begin{bmatrix}
# \cos (\omega t) & \frac{1}{\omega}\sin (\omega t) \\
# -\omega \sin (\omega t) & \cos (\omega t)
# \end{bmatrix}
# \end{equation}
#
# Check: the determinant of this STM is indeed 1.
#
# Function fn_STM implements the STM.
# The sensor measures the range and range-rate to the object.
# The measurement vector $y$ is related to the state vector $x$ by the measurement function $g$.
# \begin{equation}
# y = \begin{bmatrix}
# \rho \\
# \dot{\rho}
# \end{bmatrix}
# =
# \begin{bmatrix}
# \sqrt{x^2 + h^2}\\
# \frac{xv}/{\rho}
# \end{bmatrix}
# \end{equation}
#
# Functin fn_G implements the measurement function $g$.
#
# Both the range and range-rate are nonlinear functions of the system state. Therefore, the Jacobian matrix of the measurement function needs to be found for inclusion in the nonlinear tracking filter.
# \begin{equation}
# \tilde{\mathbf{H}}(\mathbf{X}) =
# \begin{bmatrix}
# \frac{x}{\rho} & 0 \\
# \big( \frac{v}{\rho} -\frac{x^2 v}{\rho^3} \big) & \frac{x}{\rho}
# \end{bmatrix}
# \end{equation}
#
# This is implemented in function fn_Htilde.
# +
# Define the functions given by the stated equations
def fn_A(x_state,t,omega):
# eqn 4.8.3
A = np.array([[0.,1.],[-omega**2,0.]],dtype=np.float64);
return A
def fn_G(x_state,h):
# eqn 4.8.4
rho = math.sqrt(x_state[0]**2+h**2);
G = np.array([rho,x_state[0]*x_state[1]/rho],dtype=np.float64);
return G
def fn_Htilde(x_state,h):
# Jacobian matrix of G
dx = np.shape(x_state)[0];
x = x_state[0];v=x_state[1];
rhovel = fn_G(x_state,h);
dy=np.shape(rhovel)[0];
rho = rhovel[0];#rhodot=rhovel[1];
Htilde=np.zeros([dy,dx],dtype=np.float64);
Htilde[0,0]=x/rho;
Htilde[1,0]= v/rho - x**2*v/rho**3;
Htilde[1,1]=x/rho;
return Htilde
def fn_STM(t,omega):
stm = np.zeros([2,2],dtype=np.float64);
stm[0,0]=math.cos(omega*t);
stm[0,1]=(1/omega)*math.sin(omega*t);
stm[1,0]=-omega*math.sin(omega*t);
stm[1,1]=math.cos(omega*t);
return stm
# +
# Define the time step and time vector
delta_t = 1.0; # [s]
timevec = np.arange(0.,10.+delta_t,delta_t,dtype=np.float64);
# Dimensionality of the measurement vector
dy = 2; # 2 quantities measured
y_meas = np.zeros([dy,len(timevec)],dtype=np.float64); # array of measurements
# Load measurements
import pandas as pd
dframe = pd.read_excel("sod_book_pg218_table_4_8_1_data.xlsx",sheetname="Sheet1")
dframe = dframe.reset_index()
data_time = dframe['Time'][0:len(timevec)+1]
data_range = dframe['Range'][0:len(timevec)+1]
data_range_rate = dframe['Range rate'][0:len(timevec)+1]
y_meas[0,:] = data_range;
y_meas[1,:] = data_range_rate;
# -
# a priori values
x_nom_ini = np.array([4.,0.2],dtype=np.float64); # a priori state vector
P_ini = np.diag(np.array([1000.,100.],dtype=np.float64)); # a priori covariance matrix
dx = np.shape(x_nom_ini)[0]; # dimensionality of the state vector
delta_x_ini = np.zeros([dx],dtype=np.float64); # a priori perturbation vector
def fn_BatchProcessor(delta_x,xnom,Pnom,timevec,y_meas,R_meas,omega,h):
dy = np.shape(R_meas)[0];
# Total observation matrix
TotalObsvMat = np.linalg.inv(Pnom)#np.zeros([dx,dx],dtype=np.float64);
# total observation vector
TotalObsvVec = np.dot(TotalObsvMat,delta_x)#np.zeros([dx],dtype=np.float64);
# simulated perturbation vector
delta_Y = np.zeros([dy],dtype=np.float64);
Rinv = np.linalg.inv(R_meas);
for index in range(len(timevec)):
stm_nom = fn_STM(timevec[index],omega)
x_state_nom = np.dot(stm_nom,xnom);
H = fn_Htilde(x_state_nom,h)
Hi = np.dot(H,stm_nom);
HiT = np.transpose(Hi);
Ynom = fn_G(x_state_nom,h);
delta_Y = np.subtract(y_meas[:,index],Ynom);
TotalObsvMat = TotalObsvMat + np.dot(HiT,np.dot(Rinv,Hi));
TotalObsvVec = TotalObsvVec + np.dot(HiT,np.dot(Rinv,delta_Y));
S_hat = np.linalg.inv(TotalObsvMat);
delta_x = np.dot(S_hat,TotalObsvVec);
x0_hat = xnom + delta_x;
return x0_hat,delta_x,S_hat
sd_rho = 1.;
sd_rhodot = 1.;
R_meas = np.diag(np.array([sd_rho**2,sd_rhodot**2],dtype=np.float64));
# +
num_iter = 4;
x0_hat = np.zeros([dx,num_iter],dtype=np.float64);
S_hat = np.zeros([dx,dx,num_iter],dtype=np.float64);
obsv_error = np.zeros([dy,num_iter],dtype=np.float64);
xnom_in = x_nom_ini;
Pnom_in = P_ini;
delta_x_in = delta_x_ini;
for i_iter in range (0,num_iter):
x0_hat[:,i_iter],delta_x,S_hat[:,:,i_iter] = fn_BatchProcessor(delta_x_in,xnom_in,Pnom_in,timevec,y_meas,R_meas,omega,h);
xnom_in = x0_hat[:,i_iter];
delta_x_in = delta_x_in - delta_x;
print x0_hat[:,num_iter-1]
print S_hat[:,:,num_iter-1]
sigma_x0 = math.sqrt(S_hat[0,0,num_iter-1]);
sigma_v0 = math.sqrt(S_hat[1,1,num_iter-1]);
sigma_x0v0 = math.sqrt(S_hat[0,1,num_iter-1]);
print sigma_x0
print sigma_v0
print sigma_x0v0
print math.sqrt(S_hat[1,0,num_iter-1]);
# -
# See page 219 in SOD book:
# The state estimate x0_hat[:,num_iter-1] is identical to the estimate in the book.
#
# The standard deviations are identical to those in the book. The correlation coefficient is incorrect.
#
|
examples/spring_mass_problem/Notebook_000_springmassproblem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# + pycharm={"name": "#%%\n"}
# Preprocess data for gene effect (continuous)
from ceres_infer.data import process_data
# +
# Preprocess data for gene effect (continuous)
ext_data = {'dir_datasets': '../data/DepMap/19Q3',
'dir_ceres_datasets': '../data/DepMap/19Q3/Sanger',
'data_name': 'data_sanger',
'fname_gene_effect': 'gene_effect.csv',
'fname_gene_dependency': 'gene_dependency.csv',
'out_name': 'dm_data_sanger',
'out_match_name': 'dm_data_match_sanger'}
preprocess_params = {'useGene_dependency': False,
'dir_out': '../out/20.0925 proc_data/gene_effect/',
'dir_depmap': '../data/DepMap/',
'ext_data':ext_data}
# -
proc = process_data(preprocess_params)
proc.process()
proc.process_new()
proc.process_external(match_samples='q3', shared_only=True)
# + pycharm={"name": "#%%\n"}
# Preprocess data for gene dependency (categorical)
preprocess_params = {'useGene_dependency': True,
'dir_out': '../out/20.0925 proc_data/gene_dependency/',
'dir_depmap': '../data/DepMap/',
'ext_data':ext_data}
proc = process_data(preprocess_params)
proc.process()
proc.process_new()
proc.process_external(match_samples='q3', shared_only=True)
|
notebooks/run01-preprocess_data-Sanger.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # histogram gradient boosting classifier model
#
# faster implementation of gradient boosting classifier
#
# - assume training data in filepath
# + `data/processed/train.csv`
# - assume testing data in filepath
# + `data/processed/test.csv`
# - assume both have same structure:
# + first column is query
# + second column is category
# - assume input strings are 'clean':
# + in lower case
# + punctuation removed (stop words included)
# + words separated by spaces (no padding)
# - output:
# + `models/supportvectormachine/clf_svc.pckl`
# +
import numpy as np
import pandas as pd
import pickle
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier # sklearn 0.21+
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.compose import make_column_transformer
from sklearn import metrics
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.svm import LinearSVC #(setting multi_class=”crammer_singer”)
split_training_data_filepath = '../data/processed/train.csv'
split_testing_data_filepath = '../data/processed/test.csv'
model_filepath = '../models/histogramgradientbosting.pckl'
# -
# fetch training data only:
df_train = pd.read_csv(split_training_data_filepath, index_col=0)
# do not want the class label to be numerical nor ordinal.
# df_train['category'] = pd.Categorical(df_train['category'])
df_train['category'] = pd.Categorical(df_train['category'])
display(df_train.sample(3))
# +
# transform the text field
tfidf = TfidfVectorizer(
# stop_words=stop_words,
strip_accents= 'ascii',
ngram_range=(1,1), # consider unigrams/bigrams/trigrams?
min_df = 4,
max_df = 0.80,
binary=True, # count term occurance in each query only once
)
# column transformer
all_transforms = make_column_transformer(
(tfidf, ['query'])
)
# classify using random forest (resistant to overfitting):
clf_hgbc = HistGradientBoostingClassifier(
max_depth = 8,
max_iter = 20,
tol = 1e-4,
)
pipe = make_pipeline(all_transforms, clf_hgbc)
# -
# %%time
# scores = cross_val_score(pipe, df_train['query'], df_train['category'], cv=10, scoring='accuracy')
# scores = cross_val_score(clf_svc, X, y, cv=5, scoring='f1_macro')
# scores = cross_val_score(clf_svc, X, df_train['category'], cv=2, scoring='accuracy')
# cross_val_score(pipe, df_train['query'], df_train['category'], cv=5, scoring='accuracy')
# print("accuracy: %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
# %%time
X = tfidf.fit_transform(df_train['query']).toarray()
display(X.shape)
X
# %%time
# train model
clf_hgbc.fit(X, df_train['category'])
# leads to out-of-memory errors.
# %%time
# check model
df_test = pd.read_csv(split_testing_data_filepath, index_col=0)
X_test = tfidf.transform(df_test['query'])
print('read in test data', X_test.shape)
y_predicted = clf_hgbc.predict(X_test)
print('computed', len(y_predicted), 'predictions of test data')
print('number of correct test predictions:', sum(y_predicted == df_test['category']))
print('number of incorrect predictions:', sum(y_predicted != df_test['category']))
print('ratio of correct test predictions:', round(sum(y_predicted == df_test['category'])/len(df_test),3))
print('')
|
notebooks/103_hist_gradient_boost.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1> CREAZIONE MODELLO SARIMA ROMANIA
import pandas as pd
df = pd.read_csv('../../csv/nazioni/serie_storica_ro.csv')
df.head()
df['TIME'] = pd.to_datetime(df['TIME'])
df.info()
df=df.set_index('TIME')
df.head()
# <h3>Creazione serie storica dei decessi totali
df = df.groupby(pd.Grouper(freq='M')).sum()
df.head()
ts = df.Value
ts.head()
# +
from datetime import datetime
from datetime import timedelta
start_date = datetime(2015,1,1)
end_date = datetime(2020,9,30)
lim_ts = ts[start_date:end_date]
#visulizzo il grafico
import matplotlib.pyplot as plt
plt.figure(figsize=(12,6))
plt.title('Decessi mensili Romania dal 2016 al 30 settembre 2020', size=22)
plt.plot(lim_ts)
for year in range(start_date.year,end_date.year+1):
plt.axvline(pd.to_datetime(str(year)+'-01-01'), color='k', linestyle='--', alpha=0.5)
# -
# <h3>Decomposizione
# +
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
ts_trend = decomposition.trend #andamento della curva
ts_seasonal = decomposition.seasonal #stagionalità
ts_residual = decomposition.resid #parti rimanenti
plt.subplot(411)
plt.plot(ts,label='original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(ts_trend,label='trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(ts_seasonal,label='seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(ts_residual,label='residual')
plt.legend(loc='best')
plt.tight_layout()
# -
# <h3>Test di stazionarietà
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
#Determing rolling statistics
rolmean = timeseries.rolling(window=365).mean()
rolstd = timeseries.rolling(window=365).std()
#Plot rolling statistics:
plt.plot(timeseries, color='blue',label='Original')
plt.plot(rolmean, color='red', label='Rolling Mean')
plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show()
#Perform Dickey-Fuller test:
print ('Results of Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print (dfoutput)
critical_value = dftest[4]['5%']
test_statistic = dftest[0]
alpha = 1e-3
pvalue = dftest[1]
if pvalue < alpha and test_statistic < critical_value: # null hypothesis: x is non stationary
print("X is stationary")
return True
else:
print("X is not stationary")
return False
test_stationarity(ts)
# <h3>Suddivisione in Train e Test
# <b>Train</b>: da gennaio 2015 a ottobre 2019; <br />
# <b>Test</b>: da ottobre 2019 a dicembre 2019.
from datetime import datetime
train_end = datetime(2019,10,31)
test_end = datetime (2019,12,31)
covid_end = datetime(2020,8,30)
# +
from dateutil.relativedelta import *
tsb = ts[:test_end]
decomposition = seasonal_decompose(tsb, period=12, two_sided=True, extrapolate_trend=1, model='multiplicative')
tsb_trend = decomposition.trend #andamento della curva
tsb_seasonal = decomposition.seasonal #stagionalità
tsb_residual = decomposition.resid #parti rimanenti
tsb_diff = pd.Series(tsb_trend)
d = 0
while test_stationarity(tsb_diff) is False:
tsb_diff = tsb_diff.diff().dropna()
d = d + 1
print(d)
#TEST: dal 01-01-2015 al 31-10-2019
train = tsb[:train_end]
#TRAIN: dal 01-11-2019 al 31-12-2019
test = tsb[train_end + relativedelta(months=+1): test_end]
# -
# <h3>Grafici di Autocorrelazione e Autocorrelazione Parziale
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(ts, lags =12)
plot_pacf(ts, lags =12)
plt.show()
# <h2>Creazione del modello SARIMA sul Train
# +
from statsmodels.tsa.statespace.sarimax import SARIMAX
model = SARIMAX(train, order=(12,0,8))
model_fit = model.fit()
print(model_fit.summary())
# -
# <h4>Verifica della stazionarietà dei residui del modello ottenuto
residuals = model_fit.resid
test_stationarity(residuals)
# +
plt.figure(figsize=(12,6))
plt.title('Confronto valori previsti dal modello con valori reali del Train', size=20)
plt.plot (train.iloc[1:], color='red', label='train values')
plt.plot (model_fit.fittedvalues.iloc[1:], color = 'blue', label='model values')
plt.legend()
plt.show()
# +
conf = model_fit.conf_int()
plt.figure(figsize=(12,6))
plt.title('Intervalli di confidenza del modello', size=20)
plt.plot(conf)
plt.xticks(rotation=45)
plt.show()
# -
# <h3>Predizione del modello sul Test
# +
#inizio e fine predizione
pred_start = test.index[0]
pred_end = test.index[-1]
print(pred_end)
print(pred_start)
# +
#inizio e fine predizione
pred_start = test.index[0]
pred_end = test.index[-1]
#predizione del modello sul test
predictions_test= model_fit.predict(start=pred_start, end=pred_end)
plt.figure(figsize=(12,6))
plt.title('Predizione del modello SARIMA sul Test', size=20)
plt.plot(test, color='red', label='actual')
plt.plot(predictions_test, label='prediction' )
plt.xticks(rotation=45)
plt.legend()
plt.show()
print(predictions_test)
# -
forecast_errors = [test[i]-predictions_test[i] for i in range(len(test))]
print('Forecast Errors: %s' % forecast_errors)
bias = sum(forecast_errors) * 1.0/len(test)
print('Bias: %f' % bias)
from sklearn.metrics import mean_absolute_error
mae = mean_absolute_error(test, predictions_test)
print('MAE: %f' % mae)
from sklearn.metrics import mean_squared_error
mse = mean_squared_error(test, predictions_test)
print('MSE: %f' % mse)
from math import sqrt
rmse = sqrt(mse)
print('RMSE: %f' % rmse)
import numpy as np
from statsmodels.tools.eval_measures import rmse
nrmse = rmse(predictions_test, test)/(np.max(test)-np.min(test))
print('NRMSE: %f'% nrmse)
# <h2>Predizione del modello compreso l'anno 2020
# +
#inizio e fine predizione
start_prediction = ts.index[0]
end_prediction = ts.index[-1]
predictions_tot = model_fit.predict(start=start_prediction, end=end_prediction)
plt.figure(figsize=(12,6))
plt.title('Previsione modello su dati osservati - dal 2015 al 30 settembre 2020', size=20)
plt.plot(ts, color='blue', label='actual')
plt.plot(predictions_tot.iloc[1:], color='red', label='predict')
plt.xticks(rotation=45)
plt.legend(prop={'size': 12})
plt.show()
# -
diff_predictions_tot = (ts - predictions_tot)
plt.figure(figsize=(12,6))
plt.title('Differenza tra i valori osservati e i valori stimati del modello', size=20)
plt.plot(diff_predictions_tot)
plt.show()
diff_predictions_tot['24-02-2020':].sum()
predictions_tot.to_csv('../../csv/pred/predictions_SARIMA_ro.csv')
# <h2>Intervalli di confidenza della previsione totale
forecast = model_fit.get_prediction(start=start_prediction, end=end_prediction)
in_c = forecast.conf_int()
print(forecast.predicted_mean)
print(in_c)
print(forecast.predicted_mean - in_c['lower Value'])
plt.plot(in_c)
plt.show()
upper = in_c['upper Value']
lower = in_c['lower Value']
lower.to_csv('../../csv/lower/predictions_SARIMA_ro_lower.csv')
upper.to_csv('../../csv/upper/predictions_SARIMA_ro_upper.csv')
|
Modulo 5 - Analisi europea/nazioni/Romania/.ipynb_checkpoints/Romania modello SARIMA (mensile)-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/jchen-1122/CLRS/blob/master/stockPrediction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="p3p0tXIsYrXN" colab_type="code" colab={}
# import libraries
import math
import pandas_datareader as web
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense, LSTM
from datetime import date
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
# + [markdown] id="uC-p0KcLoAXQ" colab_type="text"
# # **Stock Prediction using Machine Learning**
#
# This program uses an artificial recurrent neural network called Long Short Term Memory (LSTM) to predict the closing stock price of a corporation of using the past 60 day stock price. **Please enter your desired stock in the cell below.** By default, we are going to analyze the Apple stock (AAPL).
#
# + id="tA0N7U_YqEyv" colab_type="code" colab={}
stock = 'AAPL'
# + [markdown] id="pmjYRdiEqVBb" colab_type="text"
# **Choose a year that your model will start to trained on.** The longer the time frame, the more data the model will train on. However, the more the data, the longer the model will run for and could possibly result in overfitting. Choose wisely! By default, we will look at the stock prices from January 1, 2012.
# + id="UNhoO-fVtIPp" colab_type="code" colab={}
year = 2012
# + id="bleNrf8rZEUz" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 450} outputId="6821d6da-5575-4265-9b8e-ad072e413a22"
def transform_year_to_dt(year):
return str(year) + '-01-01'
# Get the stock quote
df = web.DataReader(stock, data_source='yahoo', start=transform_year_to_dt(year), end=date.today())
# + [markdown] id="mt-Nn4xFuE-O" colab_type="text"
# Below is the current close price history graph of the stock with price as a function of time.
# + id="ZUK_6tPUZlki" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 558} outputId="eec15c3a-a313-4b08-ac5e-36137e57d98e"
# Data visualizaton of closing price history
plt.figure(figsize=(16, 8))
plt.title('Close Price History')
plt.plot(df['Close'])
plt.xlabel('Date', fontsize=18)
plt.ylabel(stock+' Close Price USD ($)', fontsize=18)
plt.show()
# + [markdown] id="TLUc0tKRu4nQ" colab_type="text"
# **Choose the size of your training dataset as a percentage of the total dataset.** Typically, our training dataset size should be larger than our validation and test dataset size. By default, the training dataset length is set to 80% of the entire dataset.
# + id="-tQN3PGGvKYB" colab_type="code" colab={}
training_data_size = 0.8
# + id="iSyZCuT9aDtP" colab_type="code" colab={}
# create a dataframe with only the 'Close' column
data = df.filter(['Close'])
# convert dataframe into numpy array
dataset = data.values
# get number of rows to train the model on
training_data_len = math.ceil(len(dataset) * training_data_size)
# scale/normalize the data
scaler = MinMaxScaler(feature_range=(0,1))
scaled_data = scaler.fit_transform(dataset)
# + [markdown] id="FtriBofpvwl8" colab_type="text"
# Another important component of the training data size is each individual length. How many days are relevant to predicting the price of a stock? 1 month? 3 months? **Choose a time frame that you believe is enough to determine this information in days.** By default we set this to 60 days, or two months.
# + id="2htCy4zwwRln" colab_type="code" colab={}
days = 60
# + id="X5TVdTKwckql" colab_type="code" colab={}
# Create training dataset
# Create the scaled training_data_set
train_data = scaled_data[0: training_data_len, :]
#Split the data into x_train and y_train data sets
x_train = []
y_train = []
for i in range(days, len(train_data)):
x_train.append(train_data[i-days: i, 0])
y_train.append(train_data[i, 0])
# convert the x_train and y_train to numpy arrays
x_train, y_train = np.array(x_train), np.array(y_train)
# reshape the data (LSTM expects 3D)
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1))
# + [markdown] id="59SZYWnewmnA" colab_type="text"
# # **Our Model**
# Our model uses two LSTM layers and two Dense layers. Of course, our model is just one of many possible models that can be used to fit our training data. In practice, LSTM is a valuable tool that is used in many financial modeling contexts. Another customizable feature within each layer is the number of neurons. Again, choosing too few neurons can cause accuracy issues and choosing too many can cause overfitting problems. This logic also applies to the number of layers in our model. The optimal amount of neurons also depends on the dataset size and training data size. **Choose the number of neurons in the LSTM layer.** By default, there are 50 neurons in each layer.
# + id="j9oRtxlfxrg7" colab_type="code" colab={}
neurons = 50
# + id="klNUN4Xjed6Z" colab_type="code" colab={}
# Build LSTM model
model = Sequential()
model.add(LSTM(neurons, return_sequences=True, input_shape=(x_train.shape[1], 1)))
model.add(LSTM(neurons, return_sequences=False))
half_neurons = math.ceil(neurons / 2)
model.add(Dense(half_neurons))
model.add(Dense(1))
# Compile the model
model.compile(optimizer='adam', loss='mean_squared_error')
# + [markdown] id="XM8QdMTbyf_v" colab_type="text"
# After choosing the number of neurons at each layer and compiling the layers into a single model, we can decide how our model fits the data. Batch size refers to the number of training examples in each iteration. Epochs refers to the number of iterations there are. Increasing batch size will decrease the running time and increasing the number of epochs will dramatically increase the running time. Again, the issue of overfitting comes into play, so choose wisely. **Choose the batch_size and epoch numbers.** By default, both are set to 1.
# + id="PullehEpycaU" colab_type="code" colab={}
batch_size = 1
epochs = 1
# + [markdown] id="bOLrqUDjyLzM" colab_type="text"
# # **Train your Data on your Model!**
# You may have to wait a few minutes. The model will be finished running when all epochs are finished iterating.
# + id="cwwUAjDVfrQV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 68} outputId="1e891475-37da-4a91-fd62-ed8771bf1c53"
# Train the model
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs)
# + id="IrHThhz0f2yO" colab_type="code" colab={}
# create the testing dataset
# create a new array containing scaled values from index 1543 to 2003
test_data = scaled_data[training_data_len - days: , :]
# create the datasets x_test and y_test
x_test = []
y_test = dataset[training_data_len:, :]
for i in range(days, len(test_data)):
x_test.append(test_data[i-days:i, 0])
# convert the data to a numpy array
x_test = np.array(x_test)
# reshape the data
x_test = np.reshape(x_test, (x_test.shape[0], x_test.shape[1], 1))
# get the model's predicted price values
predictions = model.predict(x_test)
predictions = scaler.inverse_transform(predictions)
# + [markdown] id="JoW9wJ7Qz5_s" colab_type="text"
# How well did our model do? Below is the root mean squared error. The closer the number is to zero, the better our model fitted. the dataset.
# + id="ZkQtagOkhsrK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="00f72fd6-39b1-4c61-e449-8295525f5d4a"
# get root mean squared error (RMSE)
rmse = np.sqrt(np.mean(predictions - y_test)**2)
rmse
# + [markdown] id="STXIboBP0HzE" colab_type="text"
# In fact, we can show how well our model did by the graph below. The blue region refers to our test data and the right region with two colors shows the actual stock price and the predicted price. How well did your model do?
# + id="lmSZvjpniCxX" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 660} outputId="ee0870e0-2e6a-4f49-b569-ca332b5fc612"
# plot the data
train = data[:training_data_len]
valid = data[training_data_len:]
valid['Predictions'] = predictions
# visualize the data
plt.figure(figsize=(16,8))
plt.title('Model')
plt.xlabel('Date', fontsize=18)
plt.ylabel('Close Price USD ($)', fontsize=18)
plt.plot(train['Close'])
plt.plot(valid[['Close', 'Predictions']])
plt.legend(['Train', 'Actual', 'Predictions'], loc='lower right')
plt.show()
# + id="ZrEn7pqzjex2" colab_type="code" colab={}
# get the quote
quote = web.DataReader(stock, data_source='yahoo', start=transform_year_to_dt(year), end=date.today())
# create a new dataframe
new_df = apple_quote.filter(['Close'])
# get the last 60 day closing price values and convert the dataframe to an array
last_60_days = new_df[-60:].values
# scale the data to be values between 0 and 1
last_60_days_scaled = scaler.transform(last_60_days)
# create an empty list
X_test = []
# append past 60 days
X_test.append(last_60_days_scaled)
# convert the X_test to a numpy array
X_test = np.array(X_test)
# reshape the data
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
# get predicted scaled price
pred_price = model.predict(X_test)
# undo the scaling
pred_price = scaler.inverse_transform(pred_price)
# + [markdown] id="YDWPDkln13nH" colab_type="text"
# Below is a chart that is equivalent to the graph above. The numbers shown on the right column are the model's predicted values and the middle column is the actual closing price. Notice that the chart only contains our test data and not our training data as we only used our model to train with our training data and predict with our testing data.
# + id="_EA-_oq11aRI" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 450} outputId="a43b6273-d214-43b5-f3f4-0c7a0851b977"
valid = valid.rename(columns={"Close": "Actual Closing Price"})
valid
# + [markdown] id="iGJQR_eO2byv" colab_type="text"
# **Feel free to go back and change some of the customizable things like stock, year, batch_size, epochs, etc to fit your data on a different model.**
|
stockPrediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: dev
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Update sklearn to prevent version mismatches
# !pip install sklearn --upgrade
# install joblib. This will be used to save your model.
# Restart your kernel after installing
# !pip install joblib
# +
import pandas as pd
import numpy as np
import warnings
warnings.simplefilter('ignore', FutureWarning)
# -
# # Read the CSV and Perform Basic Data Cleaning
df = pd.read_csv("exoplanet_data.csv")
# Drop the null columns where all values are null
df = df.dropna(axis='columns', how='all')
# Drop the null rows
df = df.dropna()
df.head()
# koi_disposition: y-values. Indicates a candidate planet of interest
# # Select your features (columns)
# Set features. This will also be used as your x values.
selected_features = df[['koi_fpflag_nt', 'koi_fpflag_ss', 'koi_fpflag_ec', 'koi_period', 'koi_period_err1', 'koi_period_err2', 'koi_time0bk', 'koi_time0bk_err1', 'koi_time0bk_err2', 'koi_impact', 'koi_impact_err1', 'koi_impact_err2','koi_duration','koi_duration_err1','koi_duration_err2','koi_depth','koi_depth_err1','koi_depth_err2','koi_prad','koi_prad_err1','koi_prad_err2','koi_teq','koi_insol','koi_insol_err1','koi_insol_err2','koi_model_snr','koi_tce_plnt_num',"koi_steff",'koi_steff_err1','koi_steff_err2','koi_slogg','koi_slogg_err1','koi_slogg_err2',"koi_srad","koi_srad_err1","koi_srad_err2",'ra','dec','koi_kepmag']]
# # Create a Train Test Split
#
# Use `koi_disposition` for the y values
from sklearn.model_selection import train_test_split
# assign data to X and y
X = selected_features
y = df["koi_disposition"]
# use train, test, split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42, stratify=y)
X_train.shape
X_train.head()
# # Pre-processing
#
# Scale the data using the MinMaxScaler and perform some feature selection
# Scale the data
from sklearn.preprocessing import MinMaxScaler
# Scale the model
X_scaler = MinMaxScaler().fit(X_train)
# Transform the training and testing data
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
# Create a Random Forest model
from sklearn.ensemble import RandomForestClassifier
model_RF1 = RandomForestClassifier(n_estimators=300)
model_RF1.fit(X_train_scaled, y_train)
# # Train the Model
#
#
model_RF1_training_score = round(model_RF1.score(X_train_scaled, y_train)*100,3)
base_accuracy = round(model_RF1.score(X_test_scaled, y_test)*100,3)
print(f"Initial Model Training Data Score: {model_RF1_training_score} %")
print(f"Initial Model Testing Data Score: {base_accuracy} %")
# # Feature Selection
# Determine which features we should keep
feature_names = X.columns.tolist()
initial_features = sorted(zip(model_RF1.feature_importances_, feature_names), reverse=True)
# Build a list of the features and rank them from most important to least
ranked_features = pd.DataFrame(initial_features, columns=['Score', 'Feature'])
ranked_features = ranked_features.set_index('Feature')
ranked_features
# Remove any features with a score below 0.015 (an arbitary classification)
selected_features = []
for r in initial_features:
if r[0] > 0.015:
selected_features.append(r[1])
# +
# Use new data for all subsequent models
## Assign new data to X
X_train_select = X_train[selected_features]
X_test_select = X_test[selected_features]
X_scaler = MinMaxScaler().fit(X_train_select)
X_train_scaled = X_scaler.transform(X_train_select)
X_test_scaled = X_scaler.transform(X_test_select)
## Train new model
model_RF2 = RandomForestClassifier(n_estimators=300)
model_RF2.fit(X_train_scaled, y_train)
model_RF2_training_score = round(model_RF2.score(X_train_scaled, y_train)*100,3)
select_features_accuracy = round(model_RF2.score(X_test_scaled, y_test)*100,3)
print(f"Revised Model Training Data Score: {model_RF2_training_score} %")
print(f"Revised Model Testing Data Score: {select_features_accuracy} %")
# -
# # Hyperparameter Tuning
# Use `GridSearchCV` to tune the model's parameters
# Import the GridSearchCV model
from sklearn.model_selection import GridSearchCV
# +
model_RF3 = RandomForestClassifier(random_state=41)
param_grid = {
'n_estimators': [300, 600, 1200, 1400],
'max_features': ['auto', 'sqrt', 'log2'],
'max_depth': [14, 15, 16, 17, 18, None]
}
grid = GridSearchCV(model_RF3, param_grid, cv=5, verbose=3, n_jobs=-1)
# Train the model with GridSearch
_ = grid.fit(X_train_scaled, y_train)
# +
# Tuned parameters
max_features = grid.best_params_['max_features']
n_estimators = grid.best_params_['n_estimators']
max_depth = grid.best_params_['max_depth']
criterion = 'entropy'
# Train the tuned model
tuned_model = RandomForestClassifier(max_features=max_features, n_estimators=n_estimators,
criterion=criterion, max_depth=max_depth, random_state=42)
tuned_model.fit(X_train_scaled, y_train)
model_RF3_training_score = round(tuned_model.score(X_train_scaled, y_train)*100,3)
tuned_accuracy = round(tuned_model.score(X_test_scaled, y_test)*100,3)
print(f"Tuned Model Training Data Score: {model_RF3_training_score} %")
print(f"Tune Model Testing Data Score: {tuned_accuracy} %")
# -
# # Model Predictions
# +
predicted_model = tuned_model.predict(X_test_scaled)
classifications = y_test.unique().tolist()
prediction_actual = {
'Actual': y_test,
'Prediction': predicted_model
}
RF_df = pd.DataFrame(prediction_actual)
RF_df = RF_df.set_index('Actual').reset_index()
RF_df.head(15)
# -
# # Evaluate the Model
evaluated_model = {'Model Type': ['Base Model', 'Selected Features Model', 'Tuned Model'],
'Accuracy': [f"{base_accuracy}%", f"{select_features_accuracy}%", f"{tuned_accuracy}%"]}
evaluated_model_df = pd.DataFrame(evaluated_model)
evaluated_model_df = evaluated_model_df.set_index('Model Type')
evaluated_model_df.to_csv('Resources/RandomForestClassifier_eval.csv')
evaluated_model_df
# # Save the Model
# save your model by updating "your_name" with your name
# and "your_model" with your model variable
# be sure to turn this in to BCS
# if joblib fails to import, try running the command to install in terminal/git-bash
import joblib
filename = 'ml_model_RF.sav'
joblib.dump(tuned_model, filename)
|
model_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import scipy
import matplotlib.pyplot as plt
# -
# Let `X` be a categorical variable, `size`, and `Y` be a continuous variable, `price`.
sample_size = 1000
# # 1. Variable Creation
# #### 1.1 Categoricals
# * `size`: This will be correlated with price. It will not be correlated with color.
# * `color`: This will not be correlated with price or size.
# +
size = np.array([
['XS'] * int(sample_size / 5),
['S'] * int(sample_size / 5),
['M'] * int(sample_size / 5),
['L'] * int(sample_size / 5),
['XL'] * int(sample_size / 5),
]).flatten()
np.unique(size, return_counts=True)
# -
color = np.random.choice(['blue', 'green', 'red', 'orange'], sample_size)
np.unique(color, return_counts=True)
# #### 1.2 Continuous
# * `price`: This will have mutual information with `size`, no mutual information with `weight`
# * `weight`: This will not have mutual information with anything.
np.random.uniform(low=5, high=10)
# +
price_map = {
'XS': lambda x: np.random.uniform(low=10, high=21),
'S': lambda x: np.random.uniform(low=20, high=31),
'M': lambda x: np.random.uniform(low=30, high=41),
'L': lambda x: np.random.uniform(low=40, high=51),
'XL': lambda x: np.random.uniform(low=50, high=60)
}
price = []
for val in size:
price.append(price_map[val](None))
price = np.array(price)
# -
weight = np.random.random(size=sample_size) * 50
# ### 1.3 Expected Test results
# We will need 9 different tests. There are 3 different combinations of rv's that we need to measure mutual information for, and we need to ensure that our estimators can handle no mutual information, some mutual information, and nearly full mutual information. So we will have:
#
# * Categorical vs. Categorical
# * `size` vs. `color` $\rightarrow$ high MI
# * `size` vs. `type` $\rightarrow$ medium MI
# * `size` vs. `color` $\rightarrow$ no MI
# * Continuous vs. Continuous
# * `price` vs. `weight` $\rightarrow$ high MI
# * `price` vs. `weight` $\rightarrow$ medium MI
# * `price` vs. `weight` $\rightarrow$ no MI
# * Continuous vs. Categorical
# * `weight` vs. `type` $\rightarrow$ high MI
# * `price` vs. `weight` $\rightarrow$ medium MI
# * `price` vs. `weight` $\rightarrow$ no MI
# ## 2. `entropy_estimators` package
# +
import warnings
import numpy as np
import numpy.linalg as la
from numpy import log
from scipy.special import digamma
from sklearn.neighbors import BallTree, KDTree
# CONTINUOUS ESTIMATORS
def entropy(x, k=3, base=2):
""" The classic K-L k-nearest neighbor continuous entropy estimator
x should be a list of vectors, e.g. x = [[1.3], [3.7], [5.1], [2.4]]
if x is a one-dimensional scalar and we have four samples
"""
assert k <= len(x) - 1, "Set k smaller than num. samples - 1"
x = np.asarray(x)
n_elements, n_features = x.shape
x = add_noise(x)
tree = build_tree(x)
nn = query_neighbors(tree, x, k)
const = digamma(n_elements) - digamma(k) + n_features * log(2)
return (const + n_features * np.log(nn).mean()) / log(base)
def centropy(x, y, k=3, base=2):
""" The classic K-L k-nearest neighbor continuous entropy estimator for the
entropy of X conditioned on Y.
"""
xy = np.c_[x, y]
entropy_union_xy = entropy(xy, k=k, base=base)
entropy_y = entropy(y, k=k, base=base)
return entropy_union_xy - entropy_y
def tc(xs, k=3, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
entropy_features = [entropy(col, k=k, base=base) for col in xs_columns]
return np.sum(entropy_features) - entropy(xs, k, base)
def ctc(xs, y, k=3, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
centropy_features = [centropy(col, y, k=k, base=base)
for col in xs_columns]
return np.sum(centropy_features) - centropy(xs, y, k, base)
def corex(xs, ys, k=3, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
cmi_features = [mi(col, ys, k=k, base=base) for col in xs_columns]
return np.sum(cmi_features) - mi(xs, ys, k=k, base=base)
def mi(x, y, z=None, k=3, base=2, alpha=0):
""" Mutual information of x and y (conditioned on z if z is not None)
x, y should be a list of vectors, e.g. x = [[1.3], [3.7], [5.1], [2.4]]
if x is a one-dimensional scalar and we have four samples
"""
assert len(x) == len(y), "Arrays should have same length"
assert k <= len(x) - 1, "Set k smaller than num. samples - 1"
x, y = np.asarray(x), np.asarray(y)
x, y = x.reshape(x.shape[0], -1), y.reshape(y.shape[0], -1)
x = add_noise(x)
y = add_noise(y)
points = [x, y]
if z is not None:
z = np.asarray(z)
z = z.reshape(z.shape[0], -1)
points.append(z)
points = np.hstack(points)
# Find nearest neighbors in joint space, p=inf means max-norm
tree = build_tree(points)
dvec = query_neighbors(tree, points, k)
if z is None:
a, b, c, d = avgdigamma(x, dvec), avgdigamma(
y, dvec), digamma(k), digamma(len(x))
if alpha > 0:
d += lnc_correction(tree, points, k, alpha)
else:
xz = np.c_[x, z]
yz = np.c_[y, z]
a, b, c, d = avgdigamma(xz, dvec), avgdigamma(
yz, dvec), avgdigamma(z, dvec), digamma(k)
return (-a - b + c + d) / log(base)
def cmi(x, y, z, k=3, base=2):
""" Mutual information of x and y, conditioned on z
Legacy function. Use mi(x, y, z) directly.
"""
return mi(x, y, z=z, k=k, base=base)
def kldiv(x, xp, k=3, base=2):
""" KL Divergence between p and q for x~p(x), xp~q(x)
x, xp should be a list of vectors, e.g. x = [[1.3], [3.7], [5.1], [2.4]]
if x is a one-dimensional scalar and we have four samples
"""
assert k < min(len(x), len(xp)), "Set k smaller than num. samples - 1"
assert len(x[0]) == len(xp[0]), "Two distributions must have same dim."
x, xp = np.asarray(x), np.asarray(xp)
x, xp = x.reshape(x.shape[0], -1), xp.reshape(xp.shape[0], -1)
d = len(x[0])
n = len(x)
m = len(xp)
const = log(m) - log(n - 1)
tree = build_tree(x)
treep = build_tree(xp)
nn = query_neighbors(tree, x, k)
nnp = query_neighbors(treep, x, k - 1)
return (const + d * (np.log(nnp).mean() - np.log(nn).mean())) / log(base)
def lnc_correction(tree, points, k, alpha):
e = 0
n_sample = points.shape[0]
for point in points:
# Find k-nearest neighbors in joint space, p=inf means max norm
knn = tree.query(point[None, :], k=k+1, return_distance=False)[0]
knn_points = points[knn]
# Substract mean of k-nearest neighbor points
knn_points = knn_points - knn_points[0]
# Calculate covariance matrix of k-nearest neighbor points, obtain eigen vectors
covr = knn_points.T @ knn_points / k
_, v = la.eig(covr)
# Calculate PCA-bounding box using eigen vectors
V_rect = np.log(np.abs(knn_points @ v).max(axis=0)).sum()
# Calculate the volume of original box
log_knn_dist = np.log(np.abs(knn_points).max(axis=0)).sum()
# Perform local non-uniformity checking and update correction term
if V_rect < log_knn_dist + np.log(alpha):
e += (log_knn_dist - V_rect) / n_sample
return e
# DISCRETE ESTIMATORS
def entropyd(sx, base=2):
""" Discrete entropy estimator
sx is a list of samples
"""
unique, count = np.unique(sx, return_counts=True, axis=0)
# Convert to float as otherwise integer division results in all 0 for proba.
proba = count.astype(float) / len(sx)
# Avoid 0 division; remove probabilities == 0.0 (removing them does not change the entropy estimate as 0 * log(1/0) = 0.
proba = proba[proba > 0.0]
return np.sum(proba * np.log(1. / proba)) / log(base)
def midd(x, y, base=2):
""" Discrete mutual information estimator
Given a list of samples which can be any hashable object
"""
assert len(x) == len(y), "Arrays should have same length"
return entropyd(x, base) - centropyd(x, y, base)
def cmidd(x, y, z, base=2):
""" Discrete mutual information estimator
Given a list of samples which can be any hashable object
"""
assert len(x) == len(y) == len(z), "Arrays should have same length"
xz = np.c_[x, z]
yz = np.c_[y, z]
xyz = np.c_[x, y, z]
return entropyd(xz, base) + entropyd(yz, base) - entropyd(xyz, base) - entropyd(z, base)
def centropyd(x, y, base=2):
""" The classic K-L k-nearest neighbor continuous entropy estimator for the
entropy of X conditioned on Y.
"""
xy = np.c_[x, y]
return entropyd(xy, base) - entropyd(y, base)
def tcd(xs, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
entropy_features = [entropyd(col, base=base) for col in xs_columns]
return np.sum(entropy_features) - entropyd(xs, base)
def ctcd(xs, y, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
centropy_features = [centropyd(col, y, base=base) for col in xs_columns]
return np.sum(centropy_features) - centropyd(xs, y, base)
def corexd(xs, ys, base=2):
xs_columns = np.expand_dims(xs, axis=0).T
cmi_features = [midd(col, ys, base=base) for col in xs_columns]
return np.sum(cmi_features) - midd(xs, ys, base)
# MIXED ESTIMATORS
def micd(x, y, k=3, base=2, warning=True):
""" If x is continuous and y is discrete, compute mutual information
"""
assert len(x) == len(y), "Arrays should have same length"
entropy_x = entropy(x, k, base)
y_unique, y_count = np.unique(y, return_counts=True, axis=0)
y_proba = y_count / len(y)
entropy_x_given_y = 0.
for yval, py in zip(y_unique, y_proba):
x_given_y = x[(y == yval).all(axis=1)]
if k <= len(x_given_y) - 1:
entropy_x_given_y += py * entropy(x_given_y, k, base)
else:
if warning:
warnings.warn("Warning, after conditioning, on y={yval} insufficient data. "
"Assuming maximal entropy in this case.".format(yval=yval))
entropy_x_given_y += py * entropy_x
return abs(entropy_x - entropy_x_given_y) # units already applied
def midc(x, y, k=3, base=2, warning=True):
return micd(y, x, k, base, warning)
def centropycd(x, y, k=3, base=2, warning=True):
return entropy(x, base) - micd(x, y, k, base, warning)
def centropydc(x, y, k=3, base=2, warning=True):
return centropycd(y, x, k=k, base=base, warning=warning)
def ctcdc(xs, y, k=3, base=2, warning=True):
xs_columns = np.expand_dims(xs, axis=0).T
centropy_features = [centropydc(
col, y, k=k, base=base, warning=warning) for col in xs_columns]
return np.sum(centropy_features) - centropydc(xs, y, k, base, warning)
def ctccd(xs, y, k=3, base=2, warning=True):
return ctcdc(y, xs, k=k, base=base, warning=warning)
def corexcd(xs, ys, k=3, base=2, warning=True):
return corexdc(ys, xs, k=k, base=base, warning=warning)
def corexdc(xs, ys, k=3, base=2, warning=True):
return tcd(xs, base) - ctcdc(xs, ys, k, base, warning)
# UTILITY FUNCTIONS
def add_noise(x, intens=1e-10):
# small noise to break degeneracy, see doc.
return x + intens * np.random.random_sample(x.shape)
def query_neighbors(tree, x, k):
return tree.query(x, k=k + 1)[0][:, k]
def count_neighbors(tree, x, r):
return tree.query_radius(x, r, count_only=True)
def avgdigamma(points, dvec):
# This part finds number of neighbors in some radius in the marginal space
# returns expectation value of <psi(nx)>
tree = build_tree(points)
dvec = dvec - 1e-15
num_points = count_neighbors(tree, points, dvec)
return np.mean(digamma(num_points))
def build_tree(points):
if points.shape[1] >= 20:
return BallTree(points, metric='chebyshev')
return KDTree(points, metric='chebyshev')
# TESTS
def shuffle_test(measure, x, y, z=False, ns=200, ci=0.95, **kwargs):
""" Shuffle test
Repeatedly shuffle the x-values and then estimate measure(x, y, [z]).
Returns the mean and conf. interval ('ci=0.95' default) over 'ns' runs.
'measure' could me mi, cmi, e.g. Keyword arguments can be passed.
Mutual information and CMI should have a mean near zero.
"""
x_clone = np.copy(x) # A copy that we can shuffle
outputs = []
for i in range(ns):
np.random.shuffle(x_clone)
if z:
outputs.append(measure(x_clone, y, z, **kwargs))
else:
outputs.append(measure(x_clone, y, **kwargs))
outputs.sort()
return np.mean(outputs), (outputs[int((1. - ci) / 2 * ns)], outputs[int((1. + ci) / 2 * ns)])
# -
# #### 2.1
midd(size, color)
mi(price, weight)
np.asmatrix(price).T.shape
np.asmatrix(size).T
micd(np.asmatrix(price).T, np.asmatrix(size).T)
|
notebooks/Math-appendix/information theory/mutual information - entropy estimators package exploration.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pygmt
# First off, let's get the Earth relief data. Note that you have to specify the region if the desired resolution is finer than `05m`.
#
# You can also see the data are stored as an `xarray` object:
region = [-70.8, -66.56, -17.17, -14.42]
grid = pygmt.datasets.load_earth_relief(resolution='01m', region=region)
grid
fig = pygmt.Figure()
fig.grdimage(grid, region=region, projection='M6i', cmap='mby.cpt')
fig.coast(rivers='r/0.7p,cornflowerblue', borders='1/0.7p,,--', water='cornflowerblue', frame=['af', '+t"Lago Titicaca"'])
fig.show()
fig.savefig('titicaca_pygmt.png')
|
SOURCE_DOCS/coloring_topography/titicaca_pygmt.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="LYvAOR2VzHmW"
#
# **Diplomatura en Ciencia de Datos, Aprendizaje Automático y sus Aplicaciones**
#
# **Edición 2021**
#
# ---
#
# # Trabajo práctico entregable - Parte 2
# + id="Xwdfo7z20TUK"
import io
import matplotlib
import matplotlib.pyplot as plt
import numpy
import pandas as pd
import seaborn
seaborn.set_context('talk')
# + [markdown] id="XY2Hl-Ma07Nn"
# ## Lectura del dataset
#
# En la notebook 00 se explican los detalles de la siguiente sección.
# + id="Vviv_sqXdR5W"
url = 'https://cs.famaf.unc.edu.ar/~mteruel/datasets/diplodatos/sysarmy_survey_2020_processed.csv'
df = pd.read_csv(url)
# + colab={"base_uri": "https://localhost:8080/", "height": 297} id="gckNHXXLktJ4" outputId="8a359f96-42c3-442d-b73f-dbd453369435"
df[:3]
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="2lzmzK1NuPNT" outputId="41e0e478-b95b-4dc4-a390-902bd50a8ce3"
df[['profile_gender', 'salary_monthly_NETO']].groupby('profile_gender').describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 203} id="pycKJ5jWkShW" outputId="39835943-cb56-417f-cac7-d7068b0d12f9"
df[df.salary_monthly_NETO > 1000]\
[['profile_gender', 'salary_monthly_NETO']].groupby('profile_gender').describe()
# + id="uZ1GxkLylHx0"
alpha = 0.05
# + id="OfzFpDO-lYxk"
is_man = df.profile_gender == 'Hombre'
groupA = df[(df.salary_monthly_NETO > 1000) & is_man].salary_monthly_NETO
groupB = df[(df.salary_monthly_NETO > 1000) & ~is_man].salary_monthly_NETO
# + [markdown] id="co_0M_ojtmUh"
# ## Ejercicio 1: Estimación
#
# **Consigna:** Calcular una estimación puntual y un intervalo de confianza de nivel (1-alpha) para la resta entre la media del salario Neto para Hombres menos la media del salario Neto para otros géneros(diferencia de las medias entre el grupoA y grupoB).
# ¿Cómo se relaciona este intervalo de confianza con el test de hipótesis?
# + [markdown] id="0fA1RQ0upe6N"
# Estimacion puntual: Resta de las medias.
#
# Lo que vamos a estimar es la resta entre las medias.
#
# Lo que hay que hacer es calcular la media del grupo A y la media del grupo B y restarlas.
#
# el intervalo de confianza se usa calculando con la media y la desviacion. El alpha esta pre-definido
# + id="0fA1RQ0upe6N"
# + [markdown] id="IFi2T7Y6nM92"
# ## Ejercicio 2: Test de hipótesis
#
# + [markdown] id="Rzxe8UYU6EfJ"
#
# ### 2.1 Formalización
#
# Describir formalmente los distintos compenentes de un test de hipótesis para comprobar si la distribución de los salarios es distinta entre los grupos A y B.
#
# **Hipótesis Nula**
#
# $H_0=...$
#
# **Estadístico (Pivote)**
# * Identificar el estadístico
# * Escribir qué distribución tiene bajo $H_0$
#
# + [markdown] id="3Ip_5YdenC8u"
# ### 2.2 P-valor
#
# 1. Calcule el p-valor y decida si rechazar o no la hipótesis nula.
# 2. Interprete el resultado.
# 3. Los dos grupos de nuestra muestra tienen tamaños muy distintos. ¿Esto afecta al tests?
#
# Links útiles:
# * [Test de hipótesis usando scipy](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html)
# * [Test de Welch](http://daniellakens.blogspot.com/2015/01/always-use-welchs-t-test-instead-of.html)
# + [markdown] id="8VxiQr5YrQYR"
# ### [Opcional] 2.3 Potencia del test
#
# Nuestra muestra, ¿era lo suficientemente grande para detectar si existe o no una diferencia entre los grupos?
#
# 1. Utilice la función `tt_ind_solve_power` para calcular el tamaño necesario de la muestra para un poder estadístico de 0.8, 0.9 y 0.95, asumiendo una significancia estadística de 0.05.
# 2. ¿Cómo intepretan el poder estadístico de un test? Dado su conocimiento de dominio sobre los datos, ¿les parece que esta muestra es lo suficientemente grande para ser representativo de la tendencia general? ¿y para utilizarlo en un juicio penal contra una empresa XX por una causa de discriminación?
#
# [Documentación](https://www.statsmodels.org/stable/generated/statsmodels.stats.power.tt_ind_solve_power.html)
#
# NOTA: este análisis debería hacerse ANTES de recolectar los datos.
# + colab={"base_uri": "https://localhost:8080/"} id="_IiqGfo4t6Db" outputId="30acabed-46e2-476d-ec27-fec5823af98c"
from statsmodels.stats.power import tt_ind_solve_power
# + id="LUQ7MA2Apj9x"
effect_size = (groupA.mean() - groupB.mean()) / groupB.std()
# nobs1=None - What we want to know
alpha = 0.05
ratio = len(groupB) / len(groupA)
# + colab={"base_uri": "https://localhost:8080/"} id="cvHcpY-3ty8Q" outputId="52cc1464-e94b-45df-9610-0592399001b9"
tt_ind_solve_power(effect_size=effect_size, alpha=alpha, power=power, ratio=ratio)
# + [markdown] id="useKMdPyMod5"
# ## Ejercicio 3: Comunicación y visualización
#
# **Consigna:** Seleccionen un resultado que les parezca relevante a partir de alguno de los ejercicios del entregable. Diseñe e implemente una comunicación en base a este mensaje, en un archivo PDF.
#
# Elija las palabras y visualización más adecuada para que la comunicación sea entendible, efectiva y se dapte a UNA de las siguientes situaciones:
#
# 1. Una sección en un artículo de difusión a presentar como parte de una organización sin fines de lucro.
# No más de 1 página A4 (o dos si los gráficos son muy grandes).
# 1. Ejemplo: Alguna de las secciones [Los ecosistemas de emprendimiento de América Latina y el Caribe frente al COVID-19: Impactos, necesidades y recomendaciones](https://publications.iadb.org/es/los-ecosistemas-de-emprendimiento-de-america-latina-y-el-caribe-frente-al-covid-19-impactos-necesidades-y-recomendaciones), por ejemplo la sección *2.2. Reacciones de los emprendedores*.
# 2. Ejemplo: Alguna de las secciones de [The state of gender pay gap in 2021](https://www.payscale.com/data/gender-pay-gap?tk=carousel-ps-rc-job)
# 3. Puntos clave:
# 1. Simpleza de los gráficos.
# 2. Comunicación en lenguaje simple a personas que no son necesariamente expertos de dominio.
# 2. Selección de UNA oración sobre la que se hace énfasis.
# 3. No es necesario que mencionen objetivos ni descripciones del conjunto de datos, se supone que eso ya estaría explicado en otras secciones del informe.
#
# 2. Una publicación científica o reporte técnico interno. No más de una página A4:
# 2. Ejemplo: La sección de resultados de [IZA DP No. 12914: The Impact of a Minimum Wage Change on the Distribution of Wages and Household Income](https://www.iza.org/publications/dp/12914/the-impact-of-a-minimum-wage-change-on-the-distribution-of-wages-and-household-income).
# 2. Ejemplo: Alguna de las secciones de [Temporary reduction in daily global CO2 emissions during the COVID-19 forced confinement](https://www.nature.com/articles/s41558-020-0797-x)
# 3. Puntos clave:
# 3. Nivel de detalle técnico requerido. Es necesario justificar la validez del análisis.
# 4. La idea presentada puede ser más compleja. Pueden asumir que la audiencia tiene conocimiento técnico y va a analizar las visualizaciones en detalle.
# 5. Pueden presentar más en detalle las limitaciones del análisis (significancia estadística, etc.)
# 2. No es necesario que mencionen objetivos ni descripciones del conjunto de datos, se supone que eso ya estaría explicado en otras secciones del informe.
#
# 3. Un tweet (o post de LinkedIn) para la cuenta de su empresa consultora que hace análisis de datos. El objetivo es promocionar un análisis de datos abiertos que van a incluir en su portfolio:
# 1. Ejemplo: [Comparación vacunas covid](https://twitter.com/infobeautiful/status/1381577746527236098?s=20)
# 2. Ejemplo: [Tweet del BID](https://twitter.com/el_BID/status/1388508583944507396?s=20). Lo valioso de este tweet es que usaron un único número para transmitir un mensaje. Puede ser algo así, o con un gráfico muy simple.
# 3. Ejemplo: [Cambio climático](https://twitter.com/UNFCCC/status/1387732156190011394?s=20) Es un muy buen ejemplo, excepto que el gráfico no se lee nada y hay que entrar a la publicación original.
# 3. Ejemplo: [¿Cuánto están los programadores en las empresas?](https://www.linkedin.com/posts/denis-rothman-0b034043_tech-career-work-activity-6793861923269054464-gS6y) (No verificamos la veracidad o seriedad de la fuente).
# 4. Puntos clave:
# 1. Su audiencia no va a mirar la visualización por más de unos segundos, y no tiene conocimiento técnico.
# 3. Tienen que incluir además una *breve* descripción de cómo obtuvieron los datos que están presentando, que no entraría en el tweet.
#
# + id="twwYHUztt45L"
|
Entregable_Parte_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Serial Compressible Kolmogorov Flow Solver
#
# ## Objective
# The objective of this notebook is to write a compressible flow solver in a $2n_x\pi\times2n_y\pi$ periodic domain. The flow is forced in the $x$-direction using the Kolmogorov flow forcing:
# $$
# S_u = \sin(n_Ky)
# $$
#
# ## Equations
#
# In compressible flows, the non-dimensional flow variables are:
# * Density $\rho$
# * Velocity $u_i=\left(u_1,u_2\right)^T$ in 2D
# * Temperature $T=(\gamma-1)e-\gamma\frac{Ma^2}{2}u_iu_i$
# * Pressure $p=\rho T$, Perfect gas law is assumed
# * Internal energy $\rho e=\frac{1}{\gamma-1}p+\gamma\frac{Ma^2}{2}\rho u_iu_i$
# * Viscosity: $\mu(T)=T^{0.7}$
#
#
# The compressible flow equations are written in their conservative form:
# $$
# \frac{\partial U_i}{\partial t}=\frac{\partial F^i_x}{\partial x}+\frac{\partial F^i_y}{\partial y}+S_i
# $$
# where the variable vector $U_i$ is defined as
# $$
# U_i=\left(\rho,\rho u_1,\rho u_2,\rho e\right)^T,
# $$
# $$
# S_i=\left(0,\sin(n_Kx_1),0,0\right)^T,
# $$
# and the flux vector is
# $$
# F_i =\left(\begin{array}{l}
# -\rho u_i \\
# -\rho u_iu_1-\frac{1}{\gamma Ma^2}p\delta_{i1}+\frac{\mu(T)}{Re}S_{i1}\\
# -\rho u_iu_2-\frac{1}{\gamma Ma^2}p\delta_{i2}+\frac{\mu(T)}{Re}S_{i2}\\
# -\rho u_i(e+p)+\frac{\mu(T)}{Re}\gamma Ma^2S_{ij}u_j+\frac{\gamma}{\gamma -1}\frac{\mu(T)}{Pr Re}\frac{\partial T}{\partial x_i}
# \end{array}\right)
# $$
#
# where the rate of deformation tensor is
#
# $$
# S_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}-\frac{2}{3}\frac{\partial u_k}{\partial x_k}\delta_{ij}\right)
# $$
#
# The original MacCormack scheme is a popular choice and consists of 2 steps:
# * **Predictor**
# $$
# \left.U_i\right\vert_{m,n}^{(*)}=\left.U_i\right\vert_{m,n}^{(l)}+\frac{\Delta t}{\Delta x}\left(\left.F_i\right\vert^{(l)}_{m+1,n}-\left.F_i\right\vert_{m,n}^{(l)}\right)+\frac{\Delta t}{\Delta y}\left(\left.F_i\right\vert^{(l)}_{m,n+1}-\left.F_i\right\vert_{m,n}^{(l)}\right)
# $$
# * **Corrector**
# $$
# \left.U_i\right\vert_{m,n}^{(l+1)}=\frac{\left.U_i\right\vert_{m,n}^{(*)}+\left.U_i\right\vert_{m,n}^{(l)}}{2}+\frac{\Delta t}{\Delta x}\left(\left.F_i\right\vert^{(*)}_{m,n}-\left.F_i\right\vert_{m-1,n}^{(*)}\right)+\frac{\Delta t}{\Delta y}\left(\left.F_i\right\vert^{(*)}_{m,n}-\left.F_i\right\vert_{m,n-1}^{(*)}\right)
# $$
#
# This scheme is second order in time and space, which can be demonstrated in 1D:
#
# $$
# \left.U_i\right\vert_{m}^{(*)}=\left.U_i\right\vert_{m}^{(l)}+\frac{\Delta t}{\Delta x}\left(\left.F_i\right\vert^{(l)}_{m+1}-\left.F_i\right\vert_{m}^{(l)}\right)
# $$
# $$
# \left.U_i\right\vert_{m}^{(l+1)}=\frac{\left.U_i\right\vert_{m}^{(*)}+\left.U_i\right\vert_{m}^{(l)}}{2}+\frac{\Delta t}{\Delta x}\left(\left.F_i\right\vert^{(*)}_{m}-\left.F_i\right\vert_{m-1}^{(*)}\right)
# $$
#
# The time step must satisfy the Courant Freidrich Levy conditions as well the stability condition for the viscous term:
# $$
# \Delta t\leq \frac{CFL}{\max\left[\frac{\left\vert u\right\vert+c}{\Delta x},\frac{\left\vert v\right\vert+c}{\Delta y}\right]}\text{ with } c=\frac{T}{\gamma Ma^2}
# $$
# and
# $$
# \Delta t \leq\frac{C_{viscous}}{\max\left[\frac{\mu(T)}{Re}\max\left(\frac{1}{\Delta x^2},\frac{1}{\Delta y^2}\right)\right]}
# $$
#
# +
import numpy as np
import matplotlib.pyplot as plt
i_rho = 0; i_rhou = 1; i_rhov = 2; i_rhoe = 3; nrhovars = 4
i_u = 0; i_v = 1; i_p = 2; i_T = 3; i_e = 4; nvars = 5
i_x = 0; i_y = 1
ndims = 2
nfluxes = 4
# +
Re = 10
Ma = 0.5
Pr = 0.7
gamma = 1.4
# lx = ly = 2*np.pi
lx = 4*np.pi
ly = 2*np.pi
# nx = ny = 64
nx = 4096
ny = 2048
dx = lx / nx
dy = ly / ny
ndims = 2
x = np.linspace(dx/2,lx-dx/2,nx)
y = np.linspace(dy/2,ly-dy/2,ny)
X,Y = np.meshgrid(x,y)
X = X.T
Y = Y.T
# -
# ## Definition of variables
#
# * Convervative variables: $U=(\rho,\rho u_x,\rho u_y,\rho e)^T$
# * Raw variables: $q=(u_x,u_y,p,T)^T$
# * Temperature $T=(\gamma-1)e-\gamma\frac{Ma^2}{2}u_iu_i$
# * Pressure $p=\rho T$, Perfect gas law is assumed
# * Internal energy $\rho e=\frac{1}{\gamma-1}p+\gamma\frac{Ma^2}{2}\rho u_iu_i$
# * Viscosity: $\mu(T)=T^{0.7}$
""" Variables"""
def U2q(U):
global gamma,Ma
global i_rho,i_rhou,i_rhov,i_rhoe
global i_u,i_v,i_p,i_T,i_e,nvars
q = np.zeros((nx,ny,nvars))
q[:,:,i_u] = U[:,:,i_rhou]/U[:,:,i_rho]
q[:,:,i_v] = U[:,:,i_rhov]/U[:,:,i_rho]
q[:,:,i_e] = U[:,:,i_rhoe]/U[:,:,i_rho]
q[:,:,i_T] = (gamma - 1)*q[:,:,i_e] - \
gamma*Ma**2*(q[:,:,i_u]**2 + q[:,:,i_v]**2)
q[:,:,i_p] = U[:,:,i_rho]*q[:,:,i_T]
return q
def mu(T):
return np.power(T,0.7)
# +
""" Divergence operators
Dplus_x_option1 calculates the derivative of flux along x
assuming that F has dimensions [:nx,:ny]"""
def Dplus_x_option1(F):
global dx,nx,ny
Dp = np.zeros_like(F)
for j in range(ny):
for i in range(nx-1):
Dp[i,j] = (F[i+1,j] - F[i,j])/dx
# enforce periodicity at i = nx - 1
Dp[nx-1,j] = (F[0,j] - F[nx-1,j])/dx
return Dp
def Dplus_x_option2(F):
global dx,nx,ny
Dp = np.zeros_like(F)
Dp[:nx-1,:] = (F[1:,:] - F[:nx-1,:])/dx
# enforce periodicity at i = nx - 1
Dp[nx-1,:] = (F[0,:] - F[nx-1,:])/dx
return Dp
def Dplus_x(F):
global dx,nx,ny
Dp = np.zeros_like(F)
Dp[:nx-1,:] = (F[1:,:] - F[:nx-1,:])/dx
# enforce periodicity at i = nx - 1
Dp[nx-1,:] = (F[0,:] - F[nx-1,:])/dx
return Dp
def Dminus_x(F):
global dx,nx,ny
Dm = np.zeros_like(F)
Dm[1:,:] = (F[1:,:] - F[:-1,:])/dx
# enforce periodicity at i = nx - 1
Dm[0,:] = (F[0,:] - F[nx-1,:])/dx
return Dm
def Dplus_y(F):
global dy,nx,ny
Dp = np.zeros_like(F)
Dp[:,:ny-1] = (F[:,1:] - F[:,:ny-1])/dy
# enforce periodicity at j = ny - 1
Dp[:,ny-1] = (F[:,0] - F[:,ny-1])/dy
return Dp
def Dminus_y(F):
global dy,nx,ny
Dm = np.zeros_like(F)
Dm[:,1:] = (F[:,1:] - F[:,:-1])/dy
# enforce periodicity at i = nx - 1
Dm[:,0] = (F[:,0] - F[:,ny-1])/dy
return Dm
def grad_vel_tensor(q):
global i_u,i_v,i_x,i_y,dx,dy
global dx,dy,nx,ny,ndims
#grad_vel[i,j,i_vel,i_dim]
grad_vel = np.zeros((nx,ny,ndims,ndims))
# derivative in x = (q[i+1,j,i_vel] - q[i-1,j,i_vel])/(2*dx)
grad_vel[1:-1,:,:,i_x] = (q[2:,:,:] - q[:-2,:,:]) / (2*dx)
# enforce periodicity
grad_vel[0,:,:,i_x] = (q[1,:,:] - q[-1,:,:]) / (2*dx)
grad_vel[-1,:,:,i_x] = (q[0,:,:] - q[-2,:,:]) / (2*dx)
# # derivative in y
grad_vel[:,1:-1,:,i_y] = (q[:,2:,:] - q[:,:-2,:]) / (2*dy)
# #enforce periodicity
grad_vel[:,0,:,i_y] = (q[:,1,:] - q[:,-1,:]) / (2*dy)
grad_vel[:,-1,:,i_y] = (q[:,0,:] - q[:,-2,:]) / (2*dy)
return grad_vel
def Sij_tensor(gradvel):
global i_u,i_v,i_x,i_y,ndims
S = np.zeros_like(gradvel)
div = gradvel[:,:,i_u,i_x] + gradvel[:,:,i_v,i_y]
for j in range(ndims):
for i in range(ndims):
S[:,:,i,j] = 0.5*(gradvel[:,:,i,j] + gradvel[:,:,j,i])
for i in range(ndims):
S[:,:,i,i] -= 2./3.*div
return S
def grad_temperature(T):
global nx,ny,ndims,dx,dy,i_x,i_y
gradT = np.zeros((nx,ny,ndims))
# x-derivative
gradT[1:-1,:,i_x] = (T[2:,:] - T[:-2,:])/(2*dx)
# enforce periodicity
gradT[0,:,i_x] = (T[1,:] - T[-1,:])/(2*dx)
gradT[-1,:,i_x] = (T[0,:] - T[-2,:])/(2*dx)
# y-derivative
gradT[:,1:-1,i_y] = (T[:,2:] - T[:,:-2])/(2*dy)
# enforce periodicity
gradT[:,0,i_y] = (T[:,1] - T[:,-1])/(2*dy)
gradT[:,-1,i_y] = (T[:,0] - T[:,-2])/(2*dy)
return gradT
# -
F = np.sin(X)
q = np.zeros((nx,ny,nvars))
q[:,:,i_u] = np.sin(X)
np.shape(q[:,:,:i_v+1])
grad_vel = grad_vel_tensor(q[:,:,:i_v+1])
S = Sij_tensor(grad_vel)
ndims
# plt.contourf(X,Y,q[:,:,i_u])
# plt.contourf(X[1:-1,:],Y[1:-1,:],(q[2:,:,i_u] - q[:-2,:,i_u]) / (2*dx))
plt.contourf(X,Y,grad_vel[:,:,i_u,i_x])
plt.show()
# # %%timeit
Dp2 = Dplus_x_option2(F)
# +
# F = np.ones((nx,ny))
F = np.sin(X)
plt.contourf(X,Y,F)
plt.show()
Dp2 = Dminus_x(F)
plt.contourf(X,Y,Dp2)
plt.show()
print(np.amax(Dp2),np.amin(Dp2))
plt.plot(x,Dp2[:,0])
plt.plot(x,np.cos(x),'--')
# -
# $$
# F_i =\left(\begin{array}{l}
# -\rho u_i \\
# -\rho u_iu_1-\frac{1}{\gamma Ma^2}p\delta_{i1}+\frac{\mu(T)}{Re}S_{i1}\\
# -\rho u_iu_2-\frac{1}{\gamma Ma^2}p\delta_{i2}+\frac{\mu(T)}{Re}S_{i2}\\
# -\rho u_i(e+p)+\frac{\mu(T)}{Re}\gamma Ma^2S_{ij}u_j+\frac{\gamma}{\gamma -1}\frac{\mu(T)}{Pr Re}\frac{\partial T}{\partial x_i}
# \end{array}\right)
# $$
# $$
# F_x =\left(\begin{array}{l}
# -\rho u_x \\
# -\rho u_xu_x-\frac{1}{\gamma Ma^2}p+\frac{\mu(T)}{Re}S_{xx}\\
# -\rho u_xu_y+\frac{\mu(T)}{Re}S_{xy}\\
# -\rho u_x(e+p)+\frac{\mu(T)}{Re}\gamma Ma^2(S_{xx}u_x+S_{xy}u_y)+\frac{\gamma}{\gamma -1}\frac{\mu(T)}{Pr Re}\frac{\partial T}{\partial x}
# \end{array}\right)
# $$
def Flux(U,q,S,gradT):
global i_rho,i_u,i_v,i_e,i_p,i_T,nfluxes
mu_visc = mu(q[:,:,i_T])
Fx = np.zeros((nx,ny,nfluxes))
Fx[:,:,i_rho] = -U[:,:,i_rhou]
Fx[:,:,i_rhou] = - U[:,:,i_rhou]*q[:,:,i_u] \
- q[:,:,i_p]/(gamma*Ma**2) \
+ mu_visc/Re*S[:,:,i_x,i_x]
Fx[:,:,i_rhov] = - U[:,:,i_rhou]*q[:,:,i_v] \
+ mu_visc/Re*S[:,:,i_x,i_y]
Fx[:,:,i_rhoe] = -U[:,:,i_rhou]*(q[:,:,i_e] + q[:,:,i_p]) \
+mu_visc/Re*gamma*Ma**2* \
(S[:,:,i_x,i_x]*q[:,:,i_x] + S[:,:,i_x,i_y]*q[:,:,i_v]) \
+gamma/(gamma - 1)*mu_visc/(Pr*Re)*gradT[:,:,i_x]
Fy[:,:,i_rho] = -U[:,:,i_rhov]
Fy[:,:,i_rhou] = - U[:,:,i_rhov]*q[:,:,i_u] \
+ mu_visc/Re*S[:,:,i_y,i_x]
Fy[:,:,i_rhov] = - U[:,:,i_rhov]*q[:,:,i_v] \
- q[:,:,i_p]/(gamma*Ma**2) \
+ mu_visc/Re*S[:,:,i_x,i_x]
Fy[:,:,i_rhoe] = -U[:,:,i_rhov]*(q[:,:,i_e] + q[:,:,i_p]) \
+mu_visc/Re*gamma*Ma**2* \
(S[:,:,i_y,i_x]*q[:,:,i_x] + S[:,:,i_y,i_y]*q[:,:,i_v]) \
+gamma/(gamma - 1)*mu_visc/(Pr*Re)*gradT[:,:,i_y]
# $$
# F_x =\left(\begin{array}{l}
# -\rho u_y \\
# -\rho u_yu_x+\frac{\mu(T)}{Re}S_{xx}\\
# -\rho u_yu_y-\frac{1}{\gamma Ma^2}p+\frac{\mu(T)}{Re}S_{xy}\\
# -\rho u_y(e+p)+\frac{\mu(T)}{Re}\gamma Ma^2(S_{yx}u_x+S_{yy}u_y)+\frac{\gamma}{\gamma -1}\frac{\mu(T)}{Pr Re}\frac{\partial T}{\partial y}
# \end{array}\right)
# $$
# ## Assignment
#
# * Perform verification of functions
# * Finish the code.
|
01-Serial-compressible-Kolmogorov-Flow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
"""
Mask R-CNN
Train on the toy Balloon dataset and implement color splash effect.
Copyright (c) 2018 Matterport, Inc.
Licensed under the MIT License (see LICENSE for details)
Written by <NAME>
------------------------------------------------------------
Usage: import the module (see Jupyter notebooks for examples), or run from
the command line as such:
# Train a new model starting from pre-trained COCO weights
python3 balloon.py train --dataset=/path/to/balloon/dataset --weights=coco
# Resume training a model that you had trained earlier
python3 balloon.py train --dataset=/path/to/balloon/dataset --weights=last
# Train a new model starting from ImageNet weights
python3 balloon.py train --dataset=/path/to/balloon/dataset --weights=imagenet
# Apply color splash to an image
python3 balloon.py splash --weights=/path/to/weights/file.h5 --image=<URL or path to file>
# Apply color splash to video using the last weights you trained
python3 balloon.py splash --weights=last --video=<URL or path to file>
"""
import os
import sys
import json
import datetime
import numpy as np
import skimage.draw
import skimage
# Root directory of the project
ROOT_DIR = os.path.abspath("../../")
# Import Mask RCNN
sys.path.append(ROOT_DIR) # To find local version of the library
from mrcnn.config import Config
from mrcnn import model as modellib, utils
# Path to trained weights file
COCO_WEIGHTS_PATH = os.path.join(ROOT_DIR, "mask_rcnn_coco.h5")
# Directory to save logs and model checkpoints, if not provided
# through the command line argument --logs
DEFAULT_LOGS_DIR = os.path.join(ROOT_DIR, "logs")
# -
import skimage
dataset_dir='../../Eye/'
class EyeConfig(Config):
"""Configuration for training on the toy dataset.
Derives from the base Config class and overrides some values.
"""
# Give the configuration a recognizable name
NAME = "Eye"
# We use a GPU with 12GB memory, which can fit two images.
# Adjust down if you use a smaller GPU.
IMAGES_PER_GPU = 1
# Number of classes (including background)
NUM_CLASSES = 1 + 6 # Background + balloon
# Number of training steps per epoch
STEPS_PER_EPOCH = 100
# Skip detections with < 90% confidence
DETECTION_MIN_CONFIDENCE = 0.9
def get_ax(rows=1, cols=1, size=8):
"""Return a Matplotlib Axes array to be used in
all visualizations in the notebook. Provide a
central point to control graph sizes.
Change the default size attribute to control the size
of rendered images
"""
_, ax = plt.subplots(rows, cols, figsize=(size*cols, size*rows))
return ax
# +
annotations=json.load(open('../../Eye/train/via_region_data.json'))
annotations = list(annotations.values()) # don't need the dict keys
# The VIA tool saves images in the JSON even if they don't have any
# annotations. Skip unannotated images.
annotations = [a for a in annotations if a['regions']]
print(len(annotations))
#print(annotations[0])
# -
class EyeDataset(utils.Dataset):
def load_Eye(self, dataset_dir,subset):
"""Load a subset of the Balloon dataset.
dataset_dir: Root directory of the dataset.
subset: Subset to load: train or val
"""
# Add classes. We have only one class to add.
self.add_class("Eye", 1, "OpticDisc")
self.add_class("Eye", 2, "Exudates")
self.add_class("Eye", 3, "Venules")
self.add_class("Eye", 4, "Hemorrhages")
self.add_class("Eye", 5, "Microaneurysms")
self.add_class("Eye", 6, "Arterioles")
# Train or validation dataset?
#assert subset in ["train", "val"]
#dataset_dir = os.path.join(dataset_dir, subset)
# Load annotations
# VGG Image Annotator saves each image in the form:
# { 'filename': '28503151_5b5b7ec140_b.jpg',
# 'regions': {
# '0': {
# 'region_attributes': {},
# 'shape_attributes': {
# 'all_points_x': [...],
# 'all_points_y': [...],
# 'name': 'polygon'}},
# ... more regions ...
# },
# 'size': 100202
# }
# We mostly care about the x and y coordinates of each region
annotations = json.load(open(os.path.join(dataset_dir, subset,"via_region_data.json")))
annotations = list(annotations.values()) # don't need the dict keys
# The VIA tool saves images in the JSON even if they don't have any
# annotations. Skip unannotated images.
annotations = [a for a in annotations if a['regions']]
# Add images
for a in annotations:
# Get the x, y coordinaets of points of the polygons that make up
# the outline of each object instance. There are stores in the
# shape_attributes (see json format above)
polygons = [r['shape_attributes'] for r in a['regions'].values()]
# load_mask() needs the image size to convert polygons to masks.
# Unfortunately, VIA doesn't include it in JSON, so we must read
# the image. This is only managable since the dataset is tiny.
image_path = os.path.join(dataset_dir, subset,a['filename'])
image = skimage.io.imread(image_path)
height, width = image.shape[:2]
ann=[a['regions'][str(i)]['region_attributes']['name'] for i in range(len(a['regions']))]
self.add_image(
"Eye",
image_id=a['filename'], # use file name as a unique image id
path=image_path,
width=width, height=height,
polygons=polygons,
annotations=ann)
def load_mask(self, image_id):
"""Generate instance masks for an image.
Returns:
masks: A bool array of shape [height, width, instance count] with
one mask per instance.
class_ids: a 1D array of class IDs of the instance masks.
"""
# If not a balloon dataset image, delegate to parent class.
image_info = self.image_info[image_id]
if image_info["source"] != "Eye":
return super(self.__class__, self).load_mask(image_id)
# Convert polygons to a bitmap mask of shape
# [height, width, instance_count]
info = self.image_info[image_id]
mask = np.zeros([info["height"], info["width"], len(info["polygons"])],
dtype=np.uint8)
for i, p in enumerate(info["polygons"]):
# # Get indexes of pixels inside the polygon and set them to 1
# rr, cc = skimage.draw.polygon(p['all_points_y'], p['all_points_x'])
# mask[rr, cc, i] = 1
assert p['name'] in ['circle','ellipse','polygon','rect']
if p['name']=='circle':
cy,cx,radius=p['cy'],p['cx'],p['r']
rr,cc=skimage.draw.circle(cy,cx,radius)
if p['name']=='ellipse':
cy,cx,ry,rx=p['cy'],p['cx'],p['ry'],p['rx']
rr,cc=skimage.draw.ellipse(cy,cx,ry,rx)
if p['name']=='polygon':
cy,cx=p['all_points_y'],p['all_points_x']
rr,cc=skimage.draw.polygon(cy,cx)
if p['name']=='rect':
cy,cx,width,height=p['y'],p['x'],p['width'],p['height']
y,x=[cy-height,cy-height,cy+height,cy+height],[cx-width,cx+width,cx-width,cx+width]
rr,cc=skimage.draw.polygon(y,x)
mask[rr,cc,i]=1
labels = info['annotations']
class_ids = np.array([self.class_names.index(s) for s in labels]) # infer train_shape.ipynb
# Return mask, and array of class IDs of each instance. Since we have
# one class ID only, we return an array of 1s
return mask.astype(np.bool), class_ids.astype(np.int32) #np.ones([mask.shape[-1]], dtype=np.int32)
def image_reference(self, image_id):
"""Return the path of the image."""
info = self.image_info[image_id]
if info["source"] == "Eye":
return info["path"]
else:
super(self.__class__, self).image_reference(image_id)
dataset_Eye=EyeDataset()
dataset_Eye.load_Eye(dataset_dir,'train')
dataset_Eye.prepare()
eyeConfig=EyeConfig()
eyeConfig.display()
# +
from mrcnn import utils
import mrcnn.model as modellib
from mrcnn import visualize
from mrcnn.model import log
# %matplotlib inline
# Load and display random samples
image_ids = np.random.choice(dataset_Eye.image_ids, 3)
for image_id in image_ids:
image = dataset_Eye.load_image(image_id)
mask, class_ids = dataset_Eye.load_mask(image_id)
visualize.display_top_masks(image, mask, class_ids, dataset_Eye.class_names,limit=dataset_Eye.num_classes)
# -
print("Image Count: {}".format(len(dataset_Eye.image_ids)))
print("Class Count: {}".format(dataset_Eye.num_classes))
for i, info in enumerate(dataset_Eye.class_info):
print("{:3}. {:50}".format(i, info['name']))
# ## Bounding Boxes
# Rather than using bounding box coordinates provided by the source datasets, we compute the bounding boxes from masks instead. This allows us to handle bounding boxes consistently regardless of the source dataset, and it also makes it easier to resize, rotate, or crop images because we simply generate the bounding boxes from the updates masks rather than computing bounding box transformation for each type of image transformation.
# +
# Load random image and mask.# Load
import random
image_id = random.choice(dataset_Eye.image_ids)
image = dataset_Eye.load_image(image_id)
mask, class_ids = dataset_Eye.load_mask(image_id)
# Compute Bounding box
bbox = utils.extract_bboxes(mask)
# Display image and additional stats
print("image_id ", image_id, dataset_Eye.image_reference(image_id))
log("image", image)
log("mask", mask)
log("class_ids", class_ids)
log("bbox", bbox)
# Display image and instances
visualize.display_instances(image, bbox, mask, class_ids, dataset_Eye.class_names)
# -
# ## Mini mask
# +
from mrcnn.visualize import display_images
image_id = np.random.choice(dataset_Eye.image_ids, 1)[0]
image, image_meta, class_ids, bbox, mask = modellib.load_image_gt(
dataset_Eye, eyeConfig, image_id, use_mini_mask=False)
log("image", image)
log("image_meta", image_meta)
log("class_ids", class_ids)
log("bbox", bbox)
log("mask", mask)
display_images([image]+[mask[:,:,i] for i in range(min(mask.shape[-1], 7))])
# +
def color_splash(image, mask):
"""Apply color splash effect.
image: RGB image [height, width, 3]
mask: instance segmentation mask [height, width, instance count]
Returns result image.
"""
# Make a grayscale copy of the image. The grayscale copy still
# has 3 RGB channels, though.
gray = skimage.color.gray2rgb(skimage.color.rgb2gray(image)) * 255
# Copy color pixels from the original color image where mask is set
if mask.shape[-1] > 0:
# We're treating all instances as one, so collapse the mask into one layer
mask = (np.sum(mask, -1, keepdims=True) >= 1)
splash = np.where(mask, image, gray).astype(np.uint8)
else:
splash = gray.astype(np.uint8)
return splash
def detect_and_color_splash(model, image_path=None, video_path=None):
assert image_path or video_path
# Image or video?
if image_path:
# Run model detection and generate the color splash effect
print("Running on {}".format(args.image))
# Read image
image = skimage.io.imread(args.image)
# Detect objects
r = model.detect([image], verbose=1)[0]
# Color splash
splash = color_splash(image, r['masks'])
# Save output
file_name = "splash_{:%Y%m%dT%H%M%S}.png".format(datetime.datetime.now())
skimage.io.imsave(file_name, splash)
elif video_path:
import cv2
# Video capture
vcapture = cv2.VideoCapture(video_path)
width = int(vcapture.get(cv2.CAP_PROP_FRAME_WIDTH))
height = int(vcapture.get(cv2.CAP_PROP_FRAME_HEIGHT))
fps = vcapture.get(cv2.CAP_PROP_FPS)
# Define codec and create video writer
file_name = "splash_{:%Y%m%dT%H%M%S}.avi".format(datetime.datetime.now())
vwriter = cv2.VideoWriter(file_name,
cv2.VideoWriter_fourcc(*'MJPG'),
fps, (width, height))
count = 0
success = True
while success:
print("frame: ", count)
# Read next image
success, image = vcapture.read()
if success:
# OpenCV returns images as BGR, convert to RGB
image = image[..., ::-1]
# Detect objects
r = model.detect([image], verbose=0)[0]
# Color splash
splash = color_splash(image, r['masks'])
# RGB -> BGR to save image to video
splash = splash[..., ::-1]
# Add image to video writer
vwriter.write(splash)
count += 1
vwriter.release()
print("Saved to ", file_name)
# -
model = modellib.MaskRCNN(mode="training", config=eyeConfig,
model_dir=DEFAULT_LOGS_DIR)
model.load_weights(COCO_WEIGHTS_PATH, by_name=True, exclude=[
"mrcnn_class_logits", "mrcnn_bbox_fc",
"mrcnn_bbox", "mrcnn_mask"])
# ```
# print('training...')
# # Train the head branches
# # Passing layers="heads" freezes all layers except the head
# # layers. You can also pass a regular expression to select
# # which layers to train by name pattern.
# model.train(dataset_Eye, dataset_Eye,
# learning_rate=eyeConfig.LEARNING_RATE,
# epochs=1,
# layers='heads')
# ```
|
samples/shapes/Eye.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Unrestricted Hartee-Fock
#
# The Hartree-Fock method we covered last week is restricted to closed-shell systems in which you have the same amount of $\alpha$ and $\beta$ electrons. This means many systems are not treatable by Restricted Hatree-Fock, such as radicals, bond breaking, and paramagnetic systems.
#
# For Unrestricted Hartree-Fock (UHF), the main difference is that a set of coupled equations are introduced. There are equations for the $\alpha$ electrons and equations for the $\beta$ electrons. Note there is another method for treating open shell systems called Restricted Open-shell Hartree-Fock (ROHF) that we don't cover here.
# ## Some useful resources:
# - Szabo and Ostlund Chapter 3 (for algorithm see section 3.8)
# - [Notes by <NAME>](http://vergil.chemistry.gatech.edu/notes/hf-intro/hf-intro.html)
# - [Psi4Numpy SCF page](https://github.com/psi4/psi4numpy/tree/master/Tutorials/03_Hartree-Fock)
# ## Imports
import numpy as np
import scipy.linalg as spla
import pyscf
from pyscf import gto, scf
import time
# ## The UHF algorithm from Szabo and Ostlund:
# 1. Specify a molecule (coordinates $\{R_A\}$, atomic numbers $\{Z_A\}$, number of $\alpha $ electrons $N_\alpha$ and number of $\beta$ electrons $N_\beta$) and atomic orbital basis $\{\phi_\mu\}$.
# 2. Calculate molecular integrals over AOs ( overlap $S_{\mu\nu}$, core Hamiltonian $H^{\mathrm{core}}_{\mu\nu}$, and 2 electron integrals $(\mu \nu | \lambda \sigma)$ ).
# 3. Make a guess at the original density matrix $P^\alpha$ and $P^\beta$. Where
# $P^\alpha + P^\beta = P^\mathrm{Total}$
# 4. Calculate the intermediate matrix $G^\alpha$ using the density matrix $P^\alpha$ and the two electron integrals $(\mu \nu | \lambda \sigma)$
# 5. Calculate the intermediate matrix $G^\beta$ using the density matrix $P^\beta$ and the two electron integrals $(\mu \nu | \lambda \sigma)$
# 6. Construct the two Fock matrices, one for the $\alpha$ electrons $F^\alpha$ and one for the $\beta$ electrons $F^\beta$. Each is composed from the core Hamiltonian $H^{\mathrm{core}}_{\mu\nu}$ and the respective intermediate matrix $G$.
# 7. Solve the generalized eigenvalue problem for each of the Fock matrices and the overlap matrix $S$ to get orbital energies $\epsilon$ and molecular orbitals $C^\alpha$ and $C^\beta$. \**
# 8. Form a new guess at the density matrices $P^{\mathrm{Total}}$, $P^\alpha$ and $P^\beta$ using $C^\alpha$ and $C^\beta$, respectively.
# 9. Check for convergence. (Are the changes in energy and/or density smaller than some threshold?) If not, return to step 4.
# 10. If converged, use the molecular orbitals $C$, density matrices $P$, and Fock matrix $F$ to calculate observables like the total energy, etc.
#
# \** This can also be solved with the method of orthogonalizing the atomic orbitals as shown in the basic Hartree-Fock approach
# # STEP 1 : Specify the molecule
#
# Note: Modifying charge and multiplicity in water in order to demonstrate UHF capability. If charge is 0 and multiplicity is 1, UHF will be the same as RHF for our water example.
# start timer
start_time = time.time()
# define molecule
mol = pyscf.gto.M(
atom="""O 0.0000000 0.0000000 0.0000000;
H 0.7569685 0.0000000 -0.5858752;
H -0.7569685 0.0000000 -0.5858752""",
basis='sto-3g',
unit = "Ang",
verbose=0,
symmetry=False,
spin = 1,
charge = -1
)
# get number of atomic orbitals
num_ao = mol.nao_nr()
# get number of electrons
num_elec_alpha, num_elec_beta = mol.nelec
num_elec = num_elec_alpha + num_elec_beta
# get nuclear repulsion energy
E_nuc = mol.energy_nuc()
# # STEP 2 : Calculate molecular integrals
#
# Overlap
#
# $$ S_{\mu\nu} = (\mu|\nu) = \int dr \phi^*_{\mu}(r) \phi_{\nu}(r) $$
#
# Kinetic
#
# $$ T_{\mu\nu} = (\mu\left|-\frac{\nabla}{2}\right|\nu) = \int dr \phi^*_{\mu}(r) \left(-\frac{\nabla}{2}\right) \phi_{\nu}(r) $$
#
# Nuclear Attraction
#
# $$ V_{\mu\nu} = (\mu|r^{-1}|\nu) = \int dr \phi^*_{\mu}(r) r^{-1} \phi_{\nu}(r) $$
#
# Form Core Hamiltonian
#
# $$ H^\mathrm{core} = T + V $$
#
# Two electron integrals
#
# $$ (\mu\nu|\lambda\sigma) = \int dr_1 dr_2 \phi^*_{\mu}(r_1) \phi_{\nu}(r_1) r_{12}^{-1} \phi_{\lambda}(r_2) \phi_{\sigma}(r_2) $$
#
# calculate overlap integrals
S = mol.intor('cint1e_ovlp_sph')
# calculate kinetic energy integrals
T = mol.intor('cint1e_kin_sph')
# calculate nuclear attraction integrals
V = mol.intor('cint1e_nuc_sph')
# form core Hamiltonian
H = T + V
# calculate two electron integrals
eri = mol.intor('cint2e_sph',aosym='s8')
# since we are using the 8 fold symmetry of the 2 electron integrals
# the functions below will help us when accessing elements
__idx2_cache = {}
def idx2(i, j):
if (i, j) in __idx2_cache:
return __idx2_cache[i, j]
elif i >= j:
__idx2_cache[i, j] = int(i*(i+1)/2+j)
else:
__idx2_cache[i, j] = int(j*(j+1)/2+i)
return __idx2_cache[i, j]
def idx4(i, j, k, l):
return idx2(idx2(i, j), idx2(k, l))
# # STEP 3 : Core Guess
# +
# AO orthogonalization matrix
A = spla.fractional_matrix_power(S, -0.5)
# Solve the generalized eigenvalue problem
E_orbitals, C = spla.eigh(H,S)
# Compute initial density matrix
D_alpha = np.zeros((num_ao,num_ao))
D_beta = np.zeros((num_ao,num_ao))
for i in range(num_ao):
for j in range(num_ao):
for k in range(num_elec_alpha):
D_alpha[i,j] += C[i,k] * C[j,k]
for k in range(num_elec_beta):
D_beta[i,j] += C[i,k] * C[j,k]
D_total = D_alpha + D_beta
# -
# # STEP 4: DIIS
# [DIIS Theory Overview](https://github.com/shivupa/QMMM_study_group/blob/master/03_advanced_SCF/diis_pyscf.ipynb)
# ### Steps in DIIS Function
# 1. Build B matrix
# 2. Solve the Pulay equation
# 3. Build the DIIS Fock matrix
def diis(F_list, diis_res):
# Build B matrix
dim_B = len(F_list) + 1
B = np.empty((dim_B, dim_B))
B[-1, :] = -1
B[:, -1] = -1
B[-1, -1] = 0
for i in range(len(F_list)):
for j in range(len(F_list)):
B[i, j] = np.einsum('ij,ij->', diis_res[i], diis_res[j])
# Right hand side of Pulay eqn
right = np.zeros(dim_B)
right[-1] = -1
# Solve Pulay for coeffs
cn = np.linalg.solve(B, right)
# Build DIIS Fock
F_diis = np.zeros_like(F_list[0])
for x in range(cn.shape[0] - 1):
F_diis += cn[x] * F_list[x]
return F_diis
# # STEPS 5 - 9 : SCF loop
#
# 5. Calculate the intermediate matrix $G$ using the density matrix $P$ and the two electron integrals $(\mu \nu | \lambda \sigma)$.
#
# $$G^\alpha_{\mu\nu} = \sum_{\lambda\sigma}^{\mathrm{num\_ao}} P^T_{\lambda \sigma}(\mu\nu|\lambda\sigma)-P_{\lambda \sigma}^\alpha(\mu\lambda|\nu\sigma)$$
#
# $$G^\beta_{\mu\nu} = \sum_{\lambda\sigma}^{\mathrm{num\_ao}} P^T_{\lambda \sigma}(\mu\nu|\lambda\sigma)-P_{\lambda \sigma}^\beta(\mu\lambda|\nu\sigma)]$$
#
# 6. Construct the Fock matrix $F$ from the core hamiltonian $H^{\mathrm{core}}_{\mu\nu}$ and the intermediate matrix $G$.
#
# $$F^\alpha\ =\ H^{\mathrm{core}}\ + G^\alpha $$
#
# $$F^\beta\ =\ H^{\mathrm{core}}\ + G^\beta $$
#
# 7. Solve the generalized eigenvalue problem using the Fock matrix $F$ and the overlap matrix $S$ to get orbital energies $\epsilon$ and molecular orbitals.
#
# $$F^\alpha C^\alpha\ =\ SC^\alpha\epsilon^\alpha$$
# $$F^\beta C^\beta\ =\ SC^\beta\epsilon^\beta$$
#
# 8. Form a new guess at the density matrix $P$ using $C$.
#
# $$ P^\alpha_{\mu\nu} = \sum_{i}^{\mathrm{N_\alpha}} C^\alpha_{\mu i} C^\alpha_{\nu i} $$
# $$ P^\beta_{\mu\nu} = \sum_{i}^{\mathrm{N_\beta}} C^\beta_{\mu i} C^\beta_{\nu i} $$
# $$ P^{\mathrm{Total}} = P^\alpha + P^\beta $$
# 9. Check for convergence. (Are the changes in energy and density smaller than some threshold?) If not, return to step 5.
#
# $$ E_{\mathrm{elec}} = \sum^{\mathrm{num\_ao}}_{\mu\nu} P^T_{\mu\nu} H^\mathrm{core}_{\mu\nu} + P^\alpha_{\mu\nu}F^\alpha_{\mu\nu} + P^\beta_{\mu\nu}F^\beta_{\mu\nu} $$
# $$ \Delta E = E_{\mathrm{new}} - E_{\mathrm{old}} $$
# $$ |\Delta P| = \left[ \sum^{\mathrm{num\_ao}}_{\mu\nu} [P^{\mathrm{Total new}}_{\mu\nu} - P_{\mu\nu}^{\mathrm{Total old}}]^2 \right]^{1/2}$$
#
# +
# 2 helper functions for printing during SCF
def print_start_iterations():
print("{:^79}".format("{:>4} {:>11} {:>11} {:>11} {:>11}".format("Iter", "Time(s)", "RMSC DM", "delta E", "E_elec")))
print("{:^79}".format("{:>4} {:>11} {:>11} {:>11} {:>11}".format("****", "*******", "*******", "*******", "******")))
def print_iteration(iteration_num, iteration_start_time, iteration_end_time, iteration_rmsc_dm, iteration_E_diff, E_elec):
print("{:^79}".format("{:>4d} {:>11f} {:>.5E} {:>.5E} {:>11f}".format(iteration_num, iteration_end_time - iteration_start_time, iteration_rmsc_dm, iteration_E_diff, E_elec)))
# Set stopping criteria
iteration_max = 100
convergence_E = 1e-9
convergence_DM = 1e-5
# Loop variables
iteration_num = 0
E_total = 0
E_elec = 0.0
iteration_E_diff = 0.0
iteration_rmsc_dm = 0.0
converged = False
exceeded_iterations = False
# +
# Trial & Residual vector lists
F_list_alpha = []
F_list_beta = []
DIIS_resid_alpha = []
DIIS_resid_beta = []
print("{:^79}".format('=====> Starting SCF Iterations <=====\n'))
print_start_iterations()
while (not converged and not exceeded_iterations):
# Store last iteration and increment counters
iteration_start_time = time.time()
iteration_num += 1
E_elec_last = E_elec
D_total_last = np.copy(D_total)
# Form G matrix
G_alpha = np.zeros((num_ao,num_ao))
G_beta = np.zeros((num_ao,num_ao))
for i in range(num_ao):
for j in range(num_ao):
for k in range(num_ao):
for l in range(num_ao):
G_alpha[i,j] += D_alpha[k,l] * ((2.0*(eri[idx4(i,j,k,l)])) - (eri[idx4(i,k,j,l)]))
G_beta[i,j] += D_beta[k,l] * ((2.0*(eri[idx4(i,j,k,l)])) - (eri[idx4(i,k,j,l)]))
# Build fock matrices
F_alpha = H + G_alpha
F_beta = H + G_beta
# Calculate electronic energy
E_elec = 0.5 * np.sum(np.multiply((D_total), H) + np.multiply(D_alpha, F_alpha) + np.multiply(D_beta, F_beta))
# Build the DIIS AO gradient
diis_r_alpha = A.T @ (F_alpha @ D_alpha @ S - S @ D_alpha @ F_alpha) @ A
diis_r_beta = A.T @ (F_beta @ D_beta @ S - S @ D_beta @ F_beta) @ A
# DIIS RMS
diis_rms = (np.mean(diis_r_alpha**2)**0.5 + np.mean(diis_r_beta**2)**0.5) * 0.5
# Append lists
F_list_alpha.append(F_alpha)
F_list_beta.append(F_beta)
DIIS_resid_alpha.append(diis_r_alpha)
DIIS_resid_beta.append(diis_r_beta)
if iteration_num >=2:
# Preform DIIS to get Fock Matrix
F_alpha = diis(F_list_alpha, DIIS_resid_alpha)
F_beta = diis(F_list_beta, DIIS_resid_beta)
# Compute new guess with F DIIS
E_orbitals_alpha, C_alpha = spla.eigh(F_alpha,S)
E_orbitals_beta, C_beta = spla.eigh(F_beta,S)
D_alpha = np.zeros((num_ao,num_ao))
D_beta = np.zeros((num_ao,num_ao))
for i in range(num_ao):
for j in range(num_ao):
for k in range(num_elec_alpha):
D_alpha[i,j] += C_alpha[i,k] * C_alpha[j,k]
for k in range(num_elec_beta):
D_beta[i,j] += C_beta[i,k] * C_beta[j,k]
D_total = D_alpha + D_beta
# Calculate energy change of iteration
iteration_E_diff = np.abs(E_elec - E_elec_last)
# RMS change of density matrix
iteration_rmsc_dm = np.sqrt(np.sum((D_total - D_total_last)**2))
iteration_end_time = time.time()
print_iteration(iteration_num, iteration_start_time, iteration_end_time, iteration_rmsc_dm, iteration_E_diff, E_elec)
if(np.abs(iteration_E_diff) < convergence_E and iteration_rmsc_dm < convergence_DM):
converged = True
print('\n',"{:^79}".format('=====> SCF Converged <=====\n'))
# calculate total energy
E_total = E_elec + E_nuc
print("{:^79}".format("Total Energy : {:>11f}".format(E_total)))
if(iteration_num == iteration_max):
exceeded_iterations = True
print("{:^79}".format('=====> SCF Exceded Max Iterations <=====\n'))
|
03_advanced_SCF/uhf_diis_pyscf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import shutil, os
import pandas as pd
# +
df = pd.read_csv('instruments.csv')
f = df[270:300]['fname']
f
# -
shutil.copy("clean/"+f[60],"hi")
a = 270
for i in range(0,30):
shutil.copy("clean/"+f[a],"clarinet")
a = a+1
|
test.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.4.0
# language: julia
# name: julia-1.4
# ---
using FileIO
using Plots
using JLD
result = load("normalization3d-test.jld");
plot((result["parameters"][1])["low_line"], marker=:dot)
plot!(result["parameters"][1]["corrected_low_line"], marker=:dot)
s = 2
plot((result["parameters"][s])["mean_line"], marker=:dot)
plot!(result["parameters"][s]["corrected_mean_line"], marker=:dot, ylim=(0, 0.004))
s = 3
plot((result["parameters"][s])["mean_line"], marker=:dot)
plot!(result["parameters"][s]["corrected_mean_line"], marker=:dot, ylim=(0, 0.004))
s = 56
plot((result["parameters"][s])["mean_line"], marker=:dot)
plot!(result["parameters"][s]["corrected_mean_line"], marker=:dot, ylim=(0, 0.01))
# # 结论
# K-means 是有效的,同时没有过拟合。
# 但是拟合的指数函数太直了?
|
notebook/normalization-test-result.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DoWhy-The Causal Story Behind Hotel Booking Cancellations
# 
#
# We consider what factors cause a hotel booking to be cancelled. This analysis is based on a hotel bookings dataset from [<NAME> Nunes (2019)](https://www.sciencedirect.com/science/article/pii/S2352340918315191). On GitHub, the dataset is available at [rfordatascience/tidytuesday](https://github.com/rfordatascience/tidytuesday/blob/master/data/2020/2020-02-11/readme.md).
#
# There can be different reasons for why a booking is cancelled. A customer may have requested something that was not available (e.g., car parking), a customer may have found later that the hotel did not meet their requirements, or a customer may have simply cancelled their entire trip. Some of these like car parking are actionable by the hotel whereas others like trip cancellation are outside the hotel's control. In any case, we would like to better understand which of these factors cause booking cancellations.
#
# The gold standard of finding this out would be to use experiments such as *Randomized Controlled Trials* wherein each customer is randomly assigned to one of the two categories i.e. each customer is either assigned a car parking or not. However, such an experiment can be too costly and also unethical in some cases (for example, a hotel would start losing its reputation if people learn that its randomly assigning people to different level of service).
#
# Can we somehow answer our query using only observational data or data that has been collected in the past?
#
#
# %reload_ext autoreload
# %autoreload 2
# +
# Config dict to set the logging level
import logging.config
DEFAULT_LOGGING = {
'version': 1,
'disable_existing_loggers': False,
'loggers': {
'': {
'level': 'INFO',
},
}
}
logging.config.dictConfig(DEFAULT_LOGGING)
# Disabling warnings output
import warnings
from sklearn.exceptions import DataConversionWarning, ConvergenceWarning
warnings.filterwarnings(action='ignore', category=DataConversionWarning)
warnings.filterwarnings(action='ignore', category=ConvergenceWarning)
warnings.filterwarnings(action='ignore', category=UserWarning)
# #!pip install dowhy
import dowhy
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# -
# ## Data Description
# For a quick glance of the features and their descriptions the reader is referred here.
# https://github.com/rfordatascience/tidytuesday/blob/master/data/2020/2020-02-11/readme.md
dataset = pd.read_csv('https://raw.githubusercontent.com/Sid-darthvader/DoWhy-The-Causal-Story-Behind-Hotel-Booking-Cancellations/master/hotel_bookings.csv')
dataset.head()
dataset.columns
# ## Feature Engineering
#
# Lets create some new and meaningful features so as to reduce the dimensionality of the dataset.
# - **Total Stay** = stays_in_weekend_nights + stays_in_week_nights
# - **Guests** = adults + children + babies
# - **Different_room_assigned** = 1 if reserved_room_type & assigned_room_type are different, 0 otherwise.
# Total stay in nights
dataset['total_stay'] = dataset['stays_in_week_nights']+dataset['stays_in_weekend_nights']
# Total number of guests
dataset['guests'] = dataset['adults']+dataset['children'] +dataset['babies']
# Creating the different_room_assigned feature
dataset['different_room_assigned']=0
slice_indices =dataset['reserved_room_type']!=dataset['assigned_room_type']
dataset.loc[slice_indices,'different_room_assigned']=1
# Deleting older features
dataset = dataset.drop(['stays_in_week_nights','stays_in_weekend_nights','adults','children','babies'
,'reserved_room_type','assigned_room_type'],axis=1)
dataset.columns
# We also remove other columns that either contain NULL values or have too many unique values (e.g., agent ID). We also impute missing values of the `country` column with the most frequent country. We remove `distribution_channel` since it has a high overlap with `market_segment`.
dataset.isnull().sum() # Country,Agent,Company contain 488,16340,112593 missing entries
dataset = dataset.drop(['agent','company'],axis=1)
# Replacing missing countries with most freqently occuring countries
dataset['country']= dataset['country'].fillna(dataset['country'].mode()[0])
dataset = dataset.drop(['reservation_status','reservation_status_date','arrival_date_day_of_month'],axis=1)
dataset = dataset.drop(['arrival_date_year'],axis=1)
dataset = dataset.drop(['distribution_channel'], axis=1)
# Replacing 1 by True and 0 by False for the experiment and outcome variables
dataset['different_room_assigned']= dataset['different_room_assigned'].replace(1,True)
dataset['different_room_assigned']= dataset['different_room_assigned'].replace(0,False)
dataset['is_canceled']= dataset['is_canceled'].replace(1,True)
dataset['is_canceled']= dataset['is_canceled'].replace(0,False)
dataset.dropna(inplace=True)
print(dataset.columns)
dataset.iloc[:, 5:20].head(100)
dataset = dataset[dataset.deposit_type=="No Deposit"]
dataset.groupby(['deposit_type','is_canceled']).count()
dataset_copy = dataset.copy(deep=True)
# ### Calculating Expected Counts
# Since the number of number of cancellations and the number of times a different room was assigned is heavily imbalanced, we first choose 1000 observations at random to see that in how many cases do the variables; *'is_cancelled'* & *'different_room_assigned'* attain the same values. This whole process is then repeated 10000 times and the expected count turns out to be near 50% (i.e. the probability of these two variables attaining the same value at random).
# So statistically speaking, we have no definite conclusion at this stage. Thus assigning rooms different to what a customer had reserved during his booking earlier, may or may not lead to him/her cancelling that booking.
counts_sum=0
for i in range(1,10000):
counts_i = 0
rdf = dataset.sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
counts_sum+= counts_i
counts_sum/10000
# We now consider the scenario when there were no booking changes and recalculate the expected count.
# Expected Count when there are no booking changes
counts_sum=0
for i in range(1,10000):
counts_i = 0
rdf = dataset[dataset["booking_changes"]==0].sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
counts_sum+= counts_i
counts_sum/10000
# In the 2nd case, we take the scenario when there were booking changes(>0) and recalculate the expected count.
# Expected Count when there are booking changes = 66.4%
counts_sum=0
for i in range(1,10000):
counts_i = 0
rdf = dataset[dataset["booking_changes"]>0].sample(1000)
counts_i = rdf[rdf["is_canceled"]== rdf["different_room_assigned"]].shape[0]
counts_sum+= counts_i
counts_sum/10000
# There is definitely some change happening when the number of booking changes are non-zero. So it gives us a hint that *Booking Changes* must be a confounding variable.
#
# But is *Booking Changes* the only confounding variable? What if there were some unobserved confounders, regarding which we have no information(feature) present in our dataset. Would we still be able to make the same claims as before?
# ## Using DoWhy to estimate the causal effect
# ## Step-1. Create a Causal Graph
# Represent your prior knowledge about the predictive modelling problem as a CI graph using assumptions. Don't worry, you need not specify the full graph at this stage. Even a partial graph would be enough and the rest can be figured out by *DoWhy* ;-)
#
# Here are a list of assumptions that have then been translated into a Causal Diagram:-
#
# - *Market Segment* has 2 levels, “TA” refers to the “Travel Agents” and “TO” means “Tour Operators” so it should affect the Lead Time (which is simply the number of days between booking and arrival).
# - *Country* would also play a role in deciding whether a person books early or not (hence more *Lead Time*) and what type of *Meal* a person would prefer.
# - *Lead Time* would definitely affected the number of *Days in Waitlist* (There are lesser chances of finding a reservation if you’re booking late). Additionally, higher *Lead Times* can also lead to *Cancellations*.
# - The number of *Days in Waitlist*, the *Total Stay* in nights and the number of *Guests* might affect whether the booking is cancelled or retained.
# - *Previous Booking Retentions* would affect whether a customer is a *Repeated Guest* or not. Additionally, both of these variables would affect whether the booking get *cancelled* or not (Ex- A customer who has retained his past 5 bookings in the past has a higher chance of retaining this one also. Similarly a person who has been cancelling this booking has a higher chance of repeating the same).
# - *Booking Changes* would affect whether the customer is assigned a *different room* or not which might also lead to *cancellation*.
# - Finally, the number of *Booking Changes* being the only confounder affecting *Treatment* and *Outcome* is highly unlikely and its possible that there might be some *Unobsevered Confounders*, regarding which we have no information being captured in our data.
import pygraphviz
causal_graph = """digraph {
different_room_assigned[label="Different Room Assigned"];
is_canceled[label="Booking Cancelled"];
booking_changes[label="Booking Changes"];
previous_bookings_not_canceled[label="Previous Booking Retentions"];
days_in_waiting_list[label="Days in Waitlist"];
lead_time[label="Lead Time"];
market_segment[label="Market Segment"];
country[label="Country"];
U[label="Unobserved Confounders"];
is_repeated_guest;
total_stay;
guests;
meal;
hotel;
U->different_room_assigned; U->is_canceled;U->required_car_parking_spaces;
market_segment -> lead_time;
lead_time->is_canceled; country -> lead_time;
different_room_assigned -> is_canceled;
country->meal;
lead_time -> days_in_waiting_list;
days_in_waiting_list ->is_canceled;
previous_bookings_not_canceled -> is_canceled;
previous_bookings_not_canceled -> is_repeated_guest;
is_repeated_guest -> is_canceled;
total_stay -> is_canceled;
guests -> is_canceled;
booking_changes -> different_room_assigned; booking_changes -> is_canceled;
hotel -> is_canceled;
required_car_parking_spaces -> is_canceled;
total_of_special_requests -> is_canceled;
country->{hotel, required_car_parking_spaces,total_of_special_requests,is_canceled};
market_segment->{hotel, required_car_parking_spaces,total_of_special_requests,is_canceled};
}"""
# Here the *Treatment* is assigning the same type of room reserved by the customer during Booking. *Outcome* would be whether the booking was cancelled or not.
# *Common Causes* represent the variables that according to us have a causal affect on both *Outcome* and *Treatment*.
# As per our causal assumptions, the 2 variables satisfying this criteria are *Booking Changes* and the *Unobserved Confounders*.
# So if we are not specifying the graph explicitly (Not Recommended!), one can also provide these as parameters in the function mentioned below.
#
# To aid in identification of causal effect, we remove the unobserved confounder node from the graph. (To check, you can use the original graph and run the following code. The `identify_effect` method will find that the effect cannot be identified.)
causal_graph = "\n".join([line for line in causal_graph.splitlines() if not line.startswith("U")])
model= dowhy.CausalModel(
data = dataset,
graph=causal_graph,
treatment='different_room_assigned',
outcome='is_canceled')
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
# ## Step-2. Identify the Causal Effect
# We say that Treatment causes Outcome if changing Treatment leads to a change in Outcome keeping everything else constant.
# Thus in this step, by using properties of the causal graph, we identify the causal effect to be estimated
import statsmodels
model= dowhy.CausalModel(
data = dataset,
graph=causal_graph.replace("\n", " "),
treatment="different_room_assigned",
outcome='is_canceled')
#Identify the causal effect
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
# ## Step-3. Estimate the identified estimand
estimate = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_stratification",target_units="ate")
# ATE = Average Treatment Effect
# ATT = Average Treatment Effect on Treated (i.e. those who were assigned a different room)
# ATC = Average Treatment Effect on Control (i.e. those who were not assigned a different room)
print(estimate)
# The result is surprising. It means that having a different room assigned _decreases_ the chances of a cancellation. There's more to unpack here: is this the correct causal effect? Could it be that different rooms are assigned only when the booked room is unavailable, and therefore assigning a different room has a positive effect on the customer (as opposed to not assigning a room)?
#
# There could also be other mechanisms at play. Perhaps assigning a different room only happens at check-in, and the chances of a cancellation once the customer is already at the hotel are low? In that case, the graph is missing a critical variable on _when_ these events happen. Does `different_room_assigned` happen mostly on the day of the booking? Knowing that variable can help improve the graph and our analysis.
#
# While the associational analysis earlier indicated a positive correlation between `is_canceled` and `different_room_assigned`, estimating the causal effect using DoWhy presents a different picture. It implies that a decision/policy to reduce the number of `different_room_assigned` at hotels may be counter-productive.
#
#
# ## Step-4. Refute results
#
# Note that the causal part does not come from data. It comes from your *assumptions* that lead to *identification*. Data is simply used for statistical *estimation*. Thus it becomes critical to verify whether our assumptions were even correct in the first step or not!
#
# What happens when another common cause exists?
# What happens when the treatment itself was placebo?
# ### Method-1
# **Radom Common Cause:-** *Adds randomly drawn covariates to data and re-runs the analysis to see if the causal estimate changes or not. If our assumption was originally correct then the causal estimate shouldn't change by much.*
refute1_results=model.refute_estimate(identified_estimand, estimate,
method_name="random_common_cause")
print(refute1_results)
# ### Method-2
# **Placebo Treatment Refuter:-** *Randomly assigns any covariate as a treatment and re-runs the analysis. If our assumptions were correct then this newly found out estimate should go to 0.*
refute2_results=model.refute_estimate(identified_estimand, estimate,
method_name="placebo_treatment_refuter")
print(refute2_results)
# ### Method-3
# **Data Subset Refuter:-** *Creates subsets of the data(similar to cross-validation) and checks whether the causal estimates vary across subsets. If our assumptions were correct there shouldn't be much variation.*
refute3_results=model.refute_estimate(identified_estimand, estimate,
method_name="data_subset_refuter")
print(refute3_results)
# We can see that our estimate passes all three refutation tests. This does not prove its correctness, but it increases confidence in the estimate.
|
docs/source/example_notebooks/DoWhy-The Causal Story Behind Hotel Booking Cancellations.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="5U1bPetVYK4G" colab_type="text"
# # Start Tensorflow with starttf
#
# First we need to install tensorflow and check if it works.
# + id="YKRSAMwmWWzn" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
# !pip install tensorflow
import tensorflow as tf
# + id="D7gE9-ECjngu" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}, "base_uri": "https://localhost:8080/", "height": 34.0} outputId="74029654-e99e-4185-c598-3c91f96ef6e2" executionInfo={"status": "ok", "timestamp": 1526144714921.0, "user_tz": -120.0, "elapsed": 593.0, "user": {"displayName": "<NAME>", "photoUrl": "//lh3.googleusercontent.com/-wv0FkQOEnjg/AAAAAAAAAAI/AAAAAAAAAHM/byTo6iipigo/s50-c-k-no/photo.jpg", "userId": "112772895502545919169"}}
print(tf.__version__)
# + [markdown] id="KLjN3csHXFf2" colab_type="text"
# Next let's install starttf and opendatalake
# + id="Y8HotiWuYv1p" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
# !pip uninstall -y starttf
# !pip uninstall -y opendatalake
# !pip install https://github.com/penguinmenac3/starttf/archive/master.zip
# !pip install https://github.com/penguinmenac3/opendatalake/archive/master.zip
# + [markdown] id="as-_GHVsY-LQ" colab_type="text"
# # Starting out
#
# ## Loading a dataset
#
# Let's start by loading a dataset.
# The simplest dataset for beginners is mnist.
# The good thing about mnist is, that you do not need any complex downloading code.
# Simply load it via the opendatalake.
# + id="LNlTt3s5b8g0" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
from opendatalake.classification.mnist import mnist
base_dir = "datasets/mnist"
# Get a generator and its parameters
train_gen, train_gen_params = mnist(base_dir=base_dir, phase="train")
validation_gen, validation_gen_params = mnist(base_dir=base_dir, phase="validation")
# Create a generator to see some images
data = train_gen(train_gen_params)
# + [markdown] id="K-OR1AOQdDbF" colab_type="text"
# Now you have downloaded the dataset and a generator which will output you labels and features.
# Let's inspect some features and labels!
# + id="yjgnNJZWdML9" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}, "base_uri": "https://localhost:8080/", "height": 51.0} outputId="e037bfdd-3406-44da-eb64-b2f3ec80af7c" executionInfo={"status": "ok", "timestamp": 1526144734549.0, "user_tz": -120.0, "elapsed": 515.0, "user": {"displayName": "<NAME>", "photoUrl": "//lh3.googleusercontent.com/-wv0FkQOEnjg/AAAAAAAAAAI/AAAAAAAAAHM/byTo6iipigo/s50-c-k-no/photo.jpg", "userId": "112772895502545919169"}}
features, labels = next(data)
print(features.keys())
print(labels.keys())
# + [markdown] id="PbyB-19rdazt" colab_type="text"
# The image is a numpy array. Let's plot it using matplotlib. The label is one hot encoded probabilities. Using np.argmax you can receive the label of the image.
#
# In the case of mnist the image is a 1d-array with 786 values. However, it actually represents a (28,28) image. So first you have to reshape it using numpy.
#
# The Label is one hot encoded, this means you can use `np.argmax` to retrieve the index at which the one is (aka the label in human readable form).
#
# Finally plot the image using matplotlibs imshow.
# + id="eVREumamdY8d" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}, "base_uri": "https://localhost:8080/", "height": 362.0} outputId="e62cf86f-f488-49a8-896c-357f997da913" executionInfo={"status": "ok", "timestamp": 1526144735191.0, "user_tz": -120.0, "elapsed": 439.0, "user": {"displayName": "<NAME>", "photoUrl": "//lh3.googleusercontent.com/-wv0FkQOEnjg/AAAAAAAAAAI/AAAAAAAAAHM/byTo6iipigo/s50-c-k-no/photo.jpg", "userId": "112772895502545919169"}}
import numpy as np
import matplotlib.pyplot as plt
# Reshape image from (786,) to (28,28)
img = np.reshape(features['image'], (28,28))
number = np.argmax(labels['probs'])
# Plot img with number as title
plt.title("Number: %d" % number)
plt.imshow(img)
plt.show()
# + [markdown] id="_FkCrnqEgz3x" colab_type="text"
# ## Hyperparameters object
#
# We need a hyperparams object to store all hyperparamters we setup for our training. Let's create one where we can add all variables.
# + id="aTkJkkc3g90g" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
from starttf.utils.dict2obj import Dict2Obj
hyper_params = Dict2Obj({})
# + [markdown] id="ImAClLTFfFc1" colab_type="text"
# ## Preparing a training
#
# Before writing a model, loss and everything fancy, you need to prepare your data for training.
#
# In the case of mnist no cleaning or augmentation is required, so we can simply write the data into a tfrecord file.
#
# However, to illustrate how data augmentation could work, we will set the data augmentation steps to 1 manually.
# This involves adding a problem parameter to our hyper parameters.
# + id="y5CfwwFgf_he" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
from starttf.tfrecords.autorecords import write_data
write_data(hyper_params, "tfrecords/mnist/train", train_gen, train_gen_params, 4)
write_data(hyper_params, "tfrecords/mnist/validation", validation_gen, validation_gen_params, 2)
# + [markdown] id="zbYrSStLwzpU" colab_type="text"
# ## Training a model (the easy way)
#
# Now that the data is written into a format that we can efficiently read for training, let's have a look at an easy way to train a model.
#
# First let's create a dict where to gather all hyperparameters for training. Usually you would put that in an extra .json file which can be loaded easily.
# + id="8cw2zI7uyXet" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
hyper_params_dict = {}
# + [markdown] id="JOmUzd22ybaZ" colab_type="text"
# For simplicity we will use a predefined model (we will later see how to write a create model function by ourselves).
#
# This model has a hyperparameter for `dropout_rate`
# + id="lXeNw6YAxNDw" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
from starttf.models.mnist import create_model as mnist_model
# + [markdown] id="6wbIGqcsxXLd" colab_type="text"
# Next we need to define a loss.
#
# The loss glues together our labels and the model.
#
# In the case of mnist it is a simple cross entropy loss.
# + id="h1hHVuwoxVkT" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
def create_loss(model, labels, mode, hyper_params):
"""
Create a cross entropy loss with the loss as the only metric.
:param model: A dictionary containing all output tensors of your model.
:param labels: A dictionary containing all label tensors.
:param mode: tf.estimators.ModeKeys defining if you are in eval or training mode.
:param hyper_params: A hyper parameters object.
:return: All the losses (tensor dict, "loss" is the loss that is used for minimization)
and all the metrics(tensor dict) that should be logged for debugging.
"""
metrics = {}
losses = {}
# Add loss
labels = tf.reshape(labels["probs"], [-1, hyper_params.problem.number_of_categories])
ce = tf.nn.softmax_cross_entropy_with_logits_v2(logits=model["logits"], labels=labels)
loss_op = tf.reduce_mean(ce)
# Add losses to dict. "loss" is the primary loss that is optimized.
losses["loss"] = loss_op
metrics['accuracy'] = tf.metrics.accuracy(labels=labels,
predictions=model["probs"],
name='acc_op')
return losses, metrics
# + [markdown] id="UbGeBGXxxVYd" colab_type="text"
# Now we need to define all our hyperparameters and launch the training.
# + id="dqggqmHNxv3D" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}, "base_uri": "https://localhost:8080/", "height": 410.0} outputId="123341d5-20e1-4f91-fa3c-0040875ca873"
hyper_params = Dict2Obj({
"problem": {
"data_path": "datasets/mnist",
"number_of_categories": 10
},
"train": {
"learning_rate": {
"type": "const",
"start_value": 0.001
},
"optimizer": {
"type": "adam"
},
"batch_size": 64,
"validation_batch_size": 64,
"steps": 20000,
"summary_steps": 50,
"save_checkpoint_steps": 50,
"keep_checkpoint_max": 200,
"checkpoint_path": "checkpoints/mnist",
"tf_records_path": "tfrecords/mnist"
},
"arch": {
"network_name": "MnistNetwork",
"dropout_rate": 0.5
}
})
from starttf.estimators.scientific_estimator import easy_train_and_evaluate
easy_train_and_evaluate(hyper_params, mnist_model, create_loss, inline_plotting=True)
# + [markdown] id="l5vZRDeY5rb8" colab_type="text"
# If you run this code on your native machine, you can visit the checkpoints path and find images there which contain plots of your metrics. In this case the loss.
# + [markdown] id="pjVt8y9mr87M" colab_type="text"
# ## Defining a model
# + [markdown] id="Y-D3lhx_tfah" colab_type="text"
# Next we define a model using those tensors.
# Creating a model works by passing in an input_tensor, mode, and hyper params.
#
# The mode tells the network if it has to run in evaluation, prediction or training mode.
# When in eval mode, we want to resue the weights from the training network.
# Otherwise the network would train and evaluate using different weights.
#
# The Network we want to write is a little bit ispired by vgg just smaller. We have 2 conv layers, a pooling layer, 2 conv layers a pooling layer, dropout in training and finally some fully connected layer before a softmax layer.
# + id="accAmakd0_sf" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
def create_model(input_tensor, mode, hyper_params):
model = {}
with tf.variable_scope('SimpleMnistNetwork') as scope:
# Prepare the inputs
x = tf.reshape(tensor=input_tensor["image"], shape=(-1, 28, 28, 1), name="input")
# First Conv Block
conv1 = tf.layers.conv2d(inputs=x, filters=16, kernel_size=(3, 3), strides=(1, 1), name="conv1",
activation=tf.nn.relu)
conv2 = tf.layers.conv2d(inputs=conv1, filters=32, kernel_size=(3, 3), strides=(1, 1), name="conv2",
activation=tf.nn.relu)
pool2 = tf.layers.max_pooling2d(inputs=conv2, pool_size=(2, 2), strides=(2, 2), name="pool2")
# Second Conv Block
conv3 = tf.layers.conv2d(inputs=pool2, filters=32, kernel_size=(3, 3), strides=(1, 1), name="conv3",
activation=tf.nn.relu)
conv4 = tf.layers.conv2d(inputs=conv3, filters=32, kernel_size=(3, 3), strides=(1, 1), name="conv4",
activation=tf.nn.relu)
pool4 = tf.layers.max_pooling2d(inputs=conv4, pool_size=(2, 2), strides=(2, 2), name="pool4")
if mode == tf.estimator.ModeKeys.TRAIN:
pool4 = tf.layers.dropout(inputs=pool4, rate=hyper_params.arch.dropout_rate, name="drop4")
# Fully Connected Block
probs = tf.layers.flatten(inputs=pool4)
logits = tf.layers.dense(inputs=probs, units=10, activation=None, name="logits")
probs = tf.nn.softmax(logits=logits, name="probs")
# Collect outputs for api of network.
model["pool2"] = pool2
model["pool4"] = pool4
model["logits"] = logits
model["probs"] = probs
return model
# + [markdown] id="pmBR5Vxs1AH9" colab_type="text"
# Now let's train the model again.
# + id="Hvy79ETqtpTm" colab_type="code" colab={"autoexec": {"startup": false, "wait_interval": 0.0}}
easy_train_and_evaluate(hyper_params, create_model, create_loss, inline_plotting=True)
# + [markdown] id="_x5yya7f2HXb" colab_type="text"
# Congratulations!
#
# When you now want to work on a different dataset you have to do basically the same.
# + [markdown] id="WEvh33oA2Mxh" colab_type="text"
# ## How to do that on something else than mnist?
#
# 1. Write a data generator, like the mnist generator we used. (See [mnist here](https://github.com/penguinmenac3/opendatalake/blob/master/opendatalake/classification/mnist.py) or a named folder based loader [here](https://github.com/penguinmenac3/opendatalake/blob/master/opendatalake/classification/named_folders.py))
# ```python
# def threadable_gen(params, stride=1, offset=0, infinite=False):
# # This function cannot be a lambda or pooling does not work.
# # All interactions with the outside world must be via the params object. (agian for pooling to work)
# # yield dicts for features and labels
# ```
# 2. Prepare your data as we have done here using the write_data method. You can optionally pass in a data augmentation, label_preprocessing and feature_preprocessing method if you want to.
# ```python
# def write_data(hyper_params,
# prefix,
# threadable_generator,
# params,
# num_threads,
# preprocess_feature=None,
# preprocess_label=None,
# augment_data=None):
# ```
# 3. Write a model or use a predefined one. There are implementations of common models in starttf.models. You can find vgg16 there for example. If you have an awesome model, consider a pull request at [starttf project on github](https://github.com/penguinmenac3/starttf/)
# ```python
# def create_model(input_tensor, mode, hyper_params):
# # Return a model output tensors dict.
# ```
# 4. Write a loss like we did here to glue together your model and the labels.
# ```python
# def create_loss(model, labels, mode, hyper_params):
# # Return a losses dict (the entry for key "loss" is used for minimization) and metrics dict (like shown in this notebook)
# # If you need some advanced losses, consider using starttf.losses. (alpha balancing, focus loss, mask loss, ...)
# ```
# 5. Use the easy_train_and_evaluate method or write your own training logic. Here we used a train_and_evaluate method, if you need some specific training that it cannot do you can use the source code [here](https://github.com/penguinmenac3/starttf/blob/master/starttf/estimators/scientific_estimator.py) and modify it to your requirements. If it is of general interest and has good code quality, consider pull requesting. ;)
# ```python
# def easy_train_and_evaluate(hyper_params, create_model, create_loss, init_model=None):
# # Init Model is a callback that you can use to initialize your model with pretrained weights just before training starts.
# ```
#
# Stick to those patterns and writing a model for example 3d-detection of vehicles in realtime is done with just as many lines of code as writing an mnist network.
# Trust me on that one. I tried it myself. ;)
|
starttf/examples/mnist_starttf_explanation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Packages
import pandas as pd
import numpy as np
import scipy.stats as stats
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import datetime
import re
# %matplotlib inline
# # Dataset
#prescription from primary care data
scripts = pd.read_csv('../primary_care/gp_scripts.txt', sep = '\t', encoding='ISO-8859-1')
# previous dataset",
records = pd.read_pickle('../primary_care/full_records.pkl')
#bayer prescriptions
prescriptions = pd.read_excel('../primary_care/prescriptions.xlsx')
#drug encodings
drug_lkps = pd.read_excel('../primary_care/all_lkps_maps.xlsx', sheet_name='read_v2_drugs_lkp')
records
# # Prescriptions
prescriptions.columns = ['Antidiabetes', 'Antihyperlipidemic', 'Antihypertensive']
prescription_name = {
'antidiabetes' : {
'names': list(prescriptions['Antidiabetes'][:15])
},
'antihyperlipidemic' : {
'names': list(prescriptions['Antihyperlipidemic'][:6])
},
'antihypertensive' : {
'names': list(prescriptions['Antihypertensive'].values)
},
'all' : {
'names': list(prescriptions['Antidiabetes'][:15])+ list(prescriptions['Antihyperlipidemic'][:6]) + list(prescriptions['Antihypertensive'].values)
}
}
# # patients
patients = list(records['eid'])
len(patients)
relevant_scripts = scripts[scripts['eid'].isin(patients)].reset_index()
relevant_scripts.shape
relevant_scripts.columns
concise_scripts = relevant_scripts[['eid', 'read_2', 'bnf_code', 'dmd_code', 'drug_name', 'quantity']]
concise_scripts['drug_name'] = concise_scripts['drug_name'].str.lower()
prescriptions = list(relevant_scripts.drug_name.unique())
# +
prescriptions_clean = [x.replace("*", "") for x in prescriptions if type(x) == str]
# -
ointments = []
oral = []
intravenous = []
optha = []
ENT = []
equipment = []
alternative = []
supplements = []
unknown = []
accessories = ['bag', 'stocking', 'catheter', 'stockinette',
'dressing', 'suture', 'test', 'tape', 'bandage',
'swab', 'syringe', 'needle', 'ostomy']
transdermal = ['injection', 'vaccine', 'hypodermic', 'inj']
nasal = ['inhaler', 'nasal spray', 'ear', 'inhalation', 'inh']
dermal = ['oint', 'ointment', 'cream', 'lotion', 'crm', 'dermal',
'shampoo', 'wash', 'spray', 'patches', 'gel',
'emollient', 'derm']
supplement = ['shake', 'supplement', 'supplemental', 'vitamin']
ingest = ['tabs', 'tablets', 'tab', 'cap','caps', 'capsule', 'oral']
suppository = ['suppository', 'pessary', 'rectal']
for x in prescriptions_clean:
if type(x) == float:
continue
elif any(i in x for i in ingest):
oral.append(x)
elif any(n in x for n in nasal):
ENT.append(x)
elif any(d in x for d in dermal):
ointments.append(x)
elif any(t in x for t in transdermal):
intravenous.append(x)
elif 'eye' in x:
optha.append(x)
elif any(a in x for a in accessories):
equipment.append(x)
elif any(su in x for su in supplement):
supplements.append(x)
elif any(s in x for s in suppository):
alternative.append(x)
else:
unknown.append(x)
dfnames= ['ENT','ointments', 'intravenous', 'optha', 'equipment', 'oral', 'alternative','supplements', 'unknown']
dfs = [ENT, ointments, intravenous, optha, equipment, oral, alternative, supplements, unknown]
# +
combined = pd.DataFrame(columns = ['prescription', 'proposedcategory'])
def dfmaker(dflist, dfnamelist, resultdf):
for i in range(len(dflist)):
temp = pd.DataFrame(dflist[i], columns = ['prescription'])
temp['proposedcategory'] = dfnamelist[i]
resultdf = resultdf.append(temp)
return resultdf
# -
combined = dfmaker(dfs, dfnames, combined)
a = list(combined.prescription.unique())
[elem for elem in prescriptions_clean if elem not in a ]
combined.shape
combined['group'] = [x.split(" ")[0] if type(x.split(" ")[0]) == str else np.nan for x in combined['prescription']]
len(combined.group.unique())
combined.groupby('group').agg(list)
combined_arranged = combined[['group', 'prescription', 'proposedcategory']]
combined_arranged.to_csv('../primary_care/unique_medications.csv')
oralmed = combined[combined['proposedcategory'] == 'oral']
oralmed.groupby('group').agg(list)
list(combined.group.unique())
relevant_scripts
relevant_scripts[relevant_scripts['drug_name'].str.contains('aspirin') == True]
relevant_scripts.sort_values('bnf_code')
relevant_scripts.sort_values('dmd_code')
relevant_scripts.sort_values('bnf_code').tail(100)
concise_scripts
drug_name_counts = concise_scripts.groupby('drug_name').count()['eid'].reset_index()
concise_scripts = concise_scripts.drop_duplicates('drug_name')
drug_name_counts.columns = ['drug_name', 'counts']
drug_name_counts.counts
unknown_meds = relevant_scripts[relevant_scripts['drug_name'].isnull() == True]
unknown_medsdf = unknown_meds.groupby('read_2').count().drop('index', axis = 1).reset_index()
unknown_medications = unknown_medsdf[['read_2', 'eid']]
unknown_medications.columns = ['read_2', 'count']
unknown_medications
concise_scripts['name'] = [x.split(' ')[0] if type(x) == str else np.nan for x in concise_scripts['drug_name']]
bnf_scripts = concise_scripts[concise_scripts['bnf_code'].isnull() == False].sort_values('bnf_code').reset_index()
drug_name_counts.describe()
bnf = pd.merge(bnf_scripts[['bnf_code', 'drug_name', 'name']], drug_name_counts, on='drug_name', how = "left")
bnf
dmd_scripts = concise_scripts[concise_scripts['dmd_code'].isnull() == False].sort_values('dmd_code').reset_index()
dmd = pd.merge(dmd_scripts[['dmd_code', 'drug_name', 'name']], drug_name_counts, on='drug_name', how = "left")
concise = pd.merge(concise_scripts[['drug_name', 'dmd_code', 'read_2', 'bnf_code', 'name']], drug_name_counts, on='drug_name', how = "left")
with pd.ExcelWriter('../primary_care/medications.xlsx') as writer:
concise.to_excel(writer, sheet_name='all_unique_names')
unknown_medications.to_excel(writer, sheet_name='unknown medications')
bnf.to_excel(writer, sheet_name='bnf_codes')
dmd.to_excel(writer, sheet_name='dmd_codes')
records
bnf
bnf[bnf['bnf_code'].str[0:2] == '10']
bnf[:18575].groupby('bnf_code').sum().shape
bnf[:18575].groupby('bnf_code').sum()['counts'].sum()
bnf[18575:].groupby('bnf_code').sum()['counts'].sum()
dmd['dmd_code_str'] = [str(int(x)) for x in dmd['dmd_code']]
dmd[dmd['dmd_code_str'] != 0].groupby('dmd_code_str').sum().shape
dmd[dmd['dmd_code_str'] != 0].groupby('dmd_code_str').sum()['counts'].sum()
dmd[dmd['dmd_code_str'].str[0:2] == '24']
unknown_medications
|
notebooks/scripts_new.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# https://machinelearningmastery.com/semi-supervised-learning-with-label-propagation/
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# define dataset
X, y = sklearn.datasets.make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, random_state=1)
# split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1, stratify=y)
# split train into labeled and unlabeled
X_train_lab, X_test_unlab, y_train_lab, y_test_unlab = train_test_split(X_train, y_train, test_size=0.50, random_state=1, stratify=y_train)
# summarize training set size
print('Labeled Train Set:', X_train_lab.shape, y_train_lab.shape)
print('Unlabeled Train Set:', X_test_unlab.shape, y_test_unlab.shape)
# summarize test set size
print('Test Set:', X_test.shape, y_test.shape)
# define model
model = LogisticRegression()
# fit model on labeled dataset
model.fit(X_train_lab, y_train_lab)
model.
# make predictions on hold out test set
yhat = model.predict(X_test)
# calculate score for test set
score = accuracy_score(y_test, yhat)
# summarize score
print('Accuracy: %.3f' % (score*100))
from numpy import concatenate
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.semi_supervised import LabelPropagation
# define dataset
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, random_state=1)
# split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1, stratify=y)
# split train into labeled and unlabeled
X_train_lab, X_test_unlab, y_train_lab, y_test_unlab = train_test_split(X_train, y_train, test_size=0.50, random_state=1, stratify=y_train)
# create the training dataset input
X_train_mixed = concatenate((X_train_lab, X_test_unlab))
# create "no label" for unlabeled data
nolabel = [-1 for _ in range(len(y_test_unlab))]
# recombine training dataset labels
y_train_mixed = concatenate((y_train_lab, nolabel))
# define model
model = LabelPropagation()
# fit model on training dataset
model.fit(X_train_mixed, y_train_mixed)
# make predictions on hold out test set
yhat = model.predict(X_test)
# calculate score for test set
score = accuracy_score(y_test, yhat)
# summarize score
print('Accuracy: %.3f' % (score*100))
# evaluate logistic regression fit on label propagation for semi-supervised learning
from numpy import concatenate
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.semi_supervised import LabelPropagation
from sklearn.linear_model import LogisticRegression
# define dataset
X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, random_state=1)
# split into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.50, random_state=1, stratify=y)
# split train into labeled and unlabeled
X_train_lab, X_test_unlab, y_train_lab, y_test_unlab = train_test_split(X_train, y_train, test_size=0.50, random_state=1, stratify=y_train)
# create the training dataset input
X_train_mixed = concatenate((X_train_lab, X_test_unlab))
# create "no label" for unlabeled data
nolabel = [-1 for _ in range(len(y_test_unlab))]
# recombine training dataset labels
y_train_mixed = concatenate((y_train_lab, nolabel))
# define model
model = LabelPropagation()
# fit model on training dataset
model.fit(X_train_mixed, y_train_mixed)
# get labels for entire training dataset data
tran_labels = model.transduction_
# define supervised learning model
model2 = LogisticRegression()
# fit supervised learning model on entire training dataset
model2.fit(X_train_mixed, tran_labels)
# make predictions on hold out test set
yhat = model2.predict(X_test)
# calculate score for test set
score = accuracy_score(y_test, yhat)
# summarize score
print('Accuracy: %.3f' % (score*100))
|
code/semi-supervised.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Read training grid locations from gt10a.shp file and get corresponding band information for the patch from the raster file
# +
from osgeo import gdal
import ogr
import matplotlib.pyplot as plt
import numpy as np
import fiona, random
driver = gdal.GetDriverByName('GTiff')
#rasterFileName = "/home/gadiraju/data/bl-slums/raw-img/MUL_mosaic_415.tif" #path to raster
rasterFileName1 = "/scratch/slums/bl-slums/raw-img/PS_mosaic_415.tif"
dataset1 = gdal.Open(rasterFileName1)
rasterFileName2 = "/scratch/slums/bl-slums/raw-img/PS_mosaic_415_NDBI.tif"
dataset2 = gdal.Open(rasterFileName2)
rasterFileName3 = "/scratch/slums/bl-slums/features/pan/haralick/PAN_mosaic_415-simple-50.tif"
dataset3 = gdal.Open(rasterFileName3)
rasterFileName4 = "/scratch/slums/bl-slums/raw-img/PAN_mosaic_415_edgeDensity.tif"
dataset4 = gdal.Open(rasterFileName4)
vector = fiona.open('/scratch/slums/bl-slums/gt/final-data/gt10e/gt10e.shp')
imggeotrans = dataset1.GetGeoTransform()
coordinates_list = []
count_numbers = [0]*3
#print count_numbers
actual_class = []
train_test = []
ids_list = []
for feat in vector:
curr_class = feat['properties']['Cl']
if curr_class >0:
#print curr_class
coordinates_list.append(feat['geometry']['coordinates'])
count_numbers[curr_class-1]+=1
actual_class.append(curr_class)
train_test.append(feat['properties']['Type'])
ids_list.append(feat['properties']['ID'])
bands1=[]
bands2=[]
bands3=[]
bands4=[]
data_all_bands = []
cols = dataset1.RasterXSize
rows = dataset1.RasterYSize
transform = dataset1.GetGeoTransform()
xOrigin = transform[0]
yOrigin = transform[3]
pixelWidth = transform[1]
pixelHeight = -transform[5]
print xOrigin, yOrigin, pixelWidth, pixelHeight
for i in range(8):
bands1.append(dataset1.GetRasterBand(i+1))
# data_all_bands.append(band.ReadAsArray(0,0,cols,rows).astype(np.float))
bands2.append(dataset2.GetRasterBand(1))
for i in range(8):
bands3.append(dataset3.GetRasterBand(i+1))
bands4.append(dataset4.GetRasterBand(1))
points_list = coordinates_list #list of X,Y coordinates
#points_list = [(756073.458902 , 1456683.91481)]
train_images_list = [[],[],[]]
test_images_list = [[],[],[]]
test_IDs = []
for pt in range(len(points_list)):
if pt%100 == 0 and pt>0:
print 'Finished {} points\n'.format(pt)
point = points_list[pt]
cls = actual_class[pt]
#print point, cls
curr = np.zeros((18,40,40))-1
curr = curr.astype(float)
col = int((point[0] - xOrigin) / pixelWidth)
row = int((yOrigin - point[1] ) / pixelHeight)
for k in range(8):
data = bands1[k].ReadAsArray(col,row,40,40).astype(np.float)
#print data[9,9]
curr[k,:,:] = data
data = bands2[0].ReadAsArray(col,row,40,40).astype(np.float)
curr[8,:,:] = data
for k in range(8):
data = bands3[k].ReadAsArray(col,row,40,40).astype(np.float)
#print data[9,9]
curr[9+k,:,:] = data
data = bands4[0].ReadAsArray(col,row,40,40).astype(np.float)
curr[17,:,:] = data
curr = curr.T
if train_test[pt] == 1:
train_images_list[cls-1].append(curr)
else:
test_images_list[cls-1].append(curr)
test_IDs.append(ids_list[pt])
# +
for k in range(len(train_images_list)):
tmp_Y_1 = np.zeros((len(train_images_list[k]),len(train_images_list)))
#print tmp_Y_1.shape
tmp_Y_1[:,k] = 1
tmp_Y_2 = np.zeros((len(test_images_list[k]),len(test_images_list)))
tmp_Y_2[:,k] = 1
curr_train = train_images_list[k]
curr_train = np.asarray(curr_train)
print 'Curr_train shape ={}'.format(curr_train.shape)
curr_test = np.asarray(test_images_list[k])
print curr_train.shape, curr_test.shape
print curr_test.shape
if k==0:
trainX = curr_train
testX = curr_test
trainY = tmp_Y_1
testY = tmp_Y_2
print trainX.shape, trainY.shape, testX.shape, testY.shape
else:
trainX = np.vstack((trainX, curr_train))
testX = np.vstack((testX, curr_test))
trainY = np.vstack((trainY, tmp_Y_1))
testY = np.vstack((testY, tmp_Y_2))
print trainX.shape, trainY.shape, testX.shape, testY.shape
# -
# ## Save the above files to disk so that we don't need to re-create them many times
# +
import pickle
f = open('/scratch/slums/bl-slums/gt/final-pt-tr-3-X','w')
pickle.dump(trainX,f)
f.close()
f = open('/scratch/slums/bl-slums/gt/final-pt-tr-3-Y','w')
pickle.dump(trainY,f)
f.close()
f = open('/scratch/slums/bl-slums/gt/final-pt-te-3-X','w')
pickle.dump(testX,f)
f.close()
f = open('/scratch/slums/bl-slums/gt/final-pt-te-3-Y','w')
pickle.dump(testY,f)
f.close()
# -
|
patch-based/preprocessing/SimpleNet - Tensorflow - Preprocessing - 3Class.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Likelihood-free inference using Bayesian neural network
from sciope.models.bnn_classifier import BNNModel
from sciope.utilities.priors.uniform_prior import UniformPrior
import numpy as np
import matplotlib.pyplot as plt
# +
import tensorflow as tf
#in case CUDA is causing problems...
tf.config.set_visible_devices([], 'GPU')
# -
# ## MA2 Simulator
def simulator(param, n=100):
"""
Simulate a given parameter combination.
Parameters
----------
param : vector or 1D array
Parameters to simulate (\theta).
n : integer
Time series length
"""
m = len(param)
g = np.random.normal(0, 1, n)
gy = np.random.normal(0, 0.3, n)
y = np.zeros(n)
x = np.zeros(n)
for t in range(0, n):
x[t] += g[t]
for p in range(0, np.minimum(t, m)):
x[t] += g[t - 1 - p] * param[p]
y[t] = x[t] + gy[t]
return np.reshape(y, (1,1,100))
# ## Create synthetic data
obs_data = simulator([0.6,0.2])
obs_data = np.transpose(obs_data, (0,2,1))
plt.plot(obs_data[0])
# ## Define initial prior
# +
parameter_names = ['k1', 'k2']
lower_bounds = [-2, -1]
upper_bounds = [2, 1]
prior = UniformPrior(np.array(lower_bounds), np.array(upper_bounds))
# -
# ## Perform parameter inference using BNN classifier
# +
from sciope.inference.bnn_inference import BNNClassifier
bnn = BNN(obs_data, simulator, prior, num_bins=4)
# -
post = bnn.infer(num_samples=3000, num_rounds=6, chunk_size=10)
# +
import matplotlib.pyplot as plt
def plot_posterior(posterior):
true_params = [0.6, 0.2]
fig, ax = plt.subplots(posterior.shape[1], posterior.shape[1], facecolor = 'w')
for i in range(posterior.shape[1]):
for j in range(posterior.shape[1]):
if i > j:
ax[i,j].axis('off')
else:
if i == j:
ax[i,j].hist(posterior[:,i], bins = 'auto')
ax[i,j].axvline(np.median(posterior[:,i]), color = 'C1')
ax[i,j].axvline(true_params[i])
ax[i,j].set_xlim(lower_bounds[i], upper_bounds[i])
else:
ax[i,j].scatter(posterior[:,j], posterior[:,i])
ax[i,j].scatter(true_params[j], true_params[i], c='red')
ax[i,j].set_ylim(lower_bounds[i], upper_bounds[i])
ax[i,j].set_xlim(lower_bounds[j], upper_bounds[j])
fig.set_size_inches(10,10)
fig.tight_layout()
# -
plot_posterior(post[-1])
# ## Perform parameter inference using BNN Regressor
# Obs. Current implemented version do not perform proposal correction, i.e the ouput will be the proposal posterior.
# Current implementation does not use early stopping
from sciope.inference.bnn_inference import BNNRegressor
bnn = BNNRegressor(obs_data, simulator, prior, verbose=True)
proposal_posterior, samples = bnn.infer(num_samples=1000, num_rounds=6, chunk_size=100)
# +
from tensorflow_probability import distributions as tfd
fig = plt.figure()
x, y = np.mgrid[-2:2:.01, -1:1:.01]
pos = np.dstack((x, y))
rv = tfd.MultivariateNormalTriL(loc=proposal_posterior.m,
scale_tril=tf.linalg.cholesky(proposal_posterior.S))
plt.contourf(x, y, rv.prob(pos))
plt.xlim(-2,2)
plt.ylim(-1,1)
plt.yticks([])
plt.xticks([])
plt.show()
# -
|
examples/inference/MA2/bnn_inference.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "4eaf2778-6876-42ff-8055-522af9e56462"}
# 
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "d41360ba-b76c-4e58-a405-e5afc2e4d05b"}
# # Named Entity Recognition using rules
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "80da0783-173d-4c3a-a460-2346e8319dfa"}
import os
import json
import string
import numpy as np
import pandas as pd
import sparknlp
import sparknlp_jsl
from sparknlp.base import *
from sparknlp.util import *
from sparknlp.annotator import *
from sparknlp_jsl.annotator import *
from sparknlp.pretrained import ResourceDownloader
from pyspark.sql import functions as F
from pyspark.ml import Pipeline, PipelineModel
pd.set_option('max_colwidth', 100)
pd.set_option('display.max_columns', 100)
pd.set_option('display.expand_frame_repr', False)
print('sparknlp_jsl.version : ',sparknlp_jsl.version())
spark
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "b790b392-f666-4fa6-bf76-707e1420d559"}
# ## How it works
#
# This annotator is a kind of RegexMatcher based on a JSON file, that is defined through the parameter `setJsonPath()`
#
# In this JSON file, you define the regex that you want to match along with the information that will output on metadata field.
#
# For example here, you define the name of an entity that will categorize the matches, the regex value and the `matchScope` that will tell the regex whether to make a full match or a partial match
#
# ```
# {
# "entity": "Stage",
# "ruleScope": "sentence",
# "regex": "[cpyrau]?[T][0-9X?][a-z^cpyrau]*",
# "matchScope": "token"
# }
# ```
#
#
# Ignore the `ruleScope` for the moment, it's always at a `sentence` level. Which means find match on each sentence. So, for example for this text:
# ```
# A patient has liver metastases pT1bN0M0 and the T5 primary site may be colon or lung. If the primary site is not clearly identified,
# this case is cT4bcN2M1, Stage Grouping 88. N4 A child T?N3M1 has soft tissue aM3 sarcoma and the staging has been left unstaged.
# Both clinical and pathologic staging would be coded pT1bN0M0 as unstageable cT3cN2.Medications started.
# ```
#
# The expected result will be:
# ```
# val expectedResult = Array("pT1bN0M0", "T5", "cT4bcN2M1", "T?N3M1", "pT1bN0M0", "cT3cN2.Medications")
# val expectedMetadata =
# Array(Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "1"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "2"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "3"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "3")
# )
# ```
#
# Whereas, using a `matchScope` at sub-token level it will output:
#
# ```
# val expectedResult = Array("pT1b", "T5", "cT4bc", "T?", "pT1b", "cT3c")
# val expectedMetadata =
# Array(Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "1"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "2"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "3"),
# Map("field" -> "Stage", "normalized" -> "", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "3")
# )
# ```
#
# The `confidence` value is another feature, which is computed basically using a heuristic approach based on how many matches it has.
#
# To clarify how many matches, this is an example of the JSON file with additional fields that will define the match we want to get
#
# ```
# {
# "entity": "Gender",
# "ruleScope": "sentence",
# "matchScope": "token",
# "prefix": ["birth", "growing", "assessment"],
# "suffix": ["faster", "velocities"],
# "contextLength": 50,
# "context": ["typical", "grows"]
# }
# ```
#
#
# for example, `prefix` and `suffix` refer to the words that are required to be near the word we want to match.
#
# This two work also with `contextLength` that will tell the maximum distance that prefix or suffix words can be away from the word to match, whereas `context` are words that must be immediately after or before the word to match
#
# Now, there is another feature that can be used. The `dictionary` parameter. In this parameter, you define the set of words that you want to match and the word that will replace this match.
#
# For example, with this definition, you are telling `ContextualParser` that when words `woman`, `female`, and `girl` are matched those will be replaced by `female`, whereas `man`, `male`, `boy` and `gentleman` are matched those will be replaced by `male`.
#
# ```
# female woman female girl
# male man male boy gentleman
# ```
#
# So, for example for this text:
#
# ```
# At birth, the typical boy is growing slightly faster than the typical girl, but the velocities become equal at about seven months, and then the girl grows faster until four years. From then until adolescence no differences in velocity can be detected.
# ```
#
# The expected output of the annotator will be:
#
# ```
# val expectedResult = Array("boy", "girl", "girl")
# val expectedMetadata =
# Array(Map("field" -> "Gender", "normalized" -> "male", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Gender", "normalized" -> "female", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"),
# Map("field" -> "Gender", "normalized" -> "female", "confidenceValue" -> "0.13", "hits" -> "regex", "sentence" -> "0"))
# ```
#
# For the `dictionary`, you just need to define a csv or tsv file, where the first element of the row is the normalized word, the other elements will be the values to match. You can define several words and elements to match just by adding another row and you set the path to the file on the parameter `setDictionary`.
#
# The `dictionary` parameter is of the type` ExternalResource` by default the delimiter is `"\t"` you cand set another delimiter if your want according to your dictionary file format.
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "06f81ade-50c5-4a9a-b040-2ad262feecff"}
sample_text = """A 28-year-old female with a history of gestational diabetes mellitus diagnosed eight years prior to
presentation and subsequent type two diabetes mellitus ( T2DM ), one prior episode of HTG-induced pancreatitis
three years prior to presentation , associated with an acute hepatitis , and obesity with a body mass index
( BMI ) of 33.5 kg/m2 , presented with a one-week history of polyuria , polydipsia , poor appetite , and vomiting.
Two weeks prior to presentation , she was treated with a five-day course of amoxicillin for a respiratory tract infection .
She was on metformin , glipizide , and dapagliflozin for T2DM and atorvastatin and gemfibrozil for HTG .
She had been on dapagliflozin for six months at the time of presentation . Physical examination on presentation was
significant for dry oral mucosa ; significantly , her abdominal examination was benign with no tenderness , guarding ,
or rigidity . Pertinent laboratory findings on admission were : serum glucose 111 mg/dl , bicarbonate 18 mmol/l ,
anion gap 20 , creatinine 0.4 mg/dL , triglycerides 508 mg/dL , total cholesterol 122 mg/dL , glycated hemoglobin
( HbA1c ) 10% , and venous pH 7.27 . Serum lipase was normal at 43 U/L . Serum acetone levels could not be assessed
as blood samples kept hemolyzing due to significant lipemia .
The patient was initially admitted for starvation ketosis , as she reported poor oral intake for three days prior
to admission . However , serum chemistry obtained six hours after presentation revealed her glucose was 186 mg/dL ,
the anion gap was still elevated at 21 , serum bicarbonate was 16 mmol/L , triglyceride level peaked at 2050 mg/dL ,
and lipase was 52 U/L .
β-hydroxybutyrate level was obtained and found to be elevated at 5.29 mmol/L - the original sample was centrifuged
and the chylomicron layer removed prior to analysis due to interference from turbidity caused by lipemia again .
The patient was treated with an insulin drip for euDKA and HTG with a reduction in the anion gap to 13 and triglycerides
to 1400 mg/dL , within 24 hours .
Twenty days ago.
Her euDKA was thought to be precipitated by her respiratory tract infection in the setting of SGLT2 inhibitor use .
At birth the typical boy is growing slightly faster than the typical girl, but the velocities become equal at about
seven months, and then the girl grows faster until four years.
From then until adolescence no differences in velocity
can be detected. 21-02-2020
21/04/2020
"""
data = spark.createDataFrame([[sample_text]]).toDF("text").cache()
data.show(truncate = 100)
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "99992201-9bbd-40b3-8bb1-0ac2e9128704"}
# ## Rules
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "312ebe79-ae92-4cbe-98df-0e11842aa47a"}
# !mkdir data
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "78f4dc0b-a4f4-46d4-9b4e-ef6234a272a3"}
gender = '''male,man,male,boy,gentleman,he,him
female,woman,female,girl,lady,old-lady,she,her
neutral,neutral'''
with open('data/gender.csv', 'w') as f:
f.write(gender)
gender = {
"entity": "Gender",
"ruleScope": "sentence",
"completeMatchRegex": "true"
}
import json
with open('data/gender.json', 'w') as f:
json.dump(gender, f)
date = {
"entity": "Date ",
"ruleScope": "sentence",
"regex": "\\d{1,2}[\\/\\-\\:]{1}(\\d{1,2}[\\/\\-\\:]{1}){0,1}\\d{2,4}",
"valuesDefinition":[],
"prefix": [],
"suffix": [],
"contextLength": 150,
"context": []
}
with open('data/date.json', 'w') as f:
json.dump(date, f)
age = {
"entity": "Age",
"ruleScope": "sentence",
"matchScope":"token",
"regex":"\\s*(0?[1-9]|[1-9][0-9]|[1][1-9][1-9]|200){1,2}[\\s-,]+|(?i)\\b(?:zero|ten|eleven|twelve|thirteen|fourteen|fifteen|sixteen|seventeen|eighteen|nineteen|twenty)\\b(?=\\s*year)|\\b(?:(?:one|two|three|four|five|six|seven|eight|nine)? hundred(?:\\sand)?\\s)?(?:(?:twenty|thirty|forty|fifty|sixty|seventy|eighty|ninety)[\\s-]?)?\\b(?:one|two|three|four|five|six|seven|eight|nine)?(?=\\syear)",
"prefix":["age of"],
"suffix": ["-years-old",
"years-old",
"-year-old",
"-months-old",
"-month-old",
"-months-old",
"-day-old",
"-days-old",
"month old",
"days old",
"year old",
"years old",
"years",
"year",
"months",
"old"
],
"contextLength": 25,
"context": [],
"contextException": ["ago"],
"exceptionDistance": 10
}
with open('data/age.json', 'w') as f:
json.dump(age, f)
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "89c8a307-2a6c-4b37-85b5-9ad80fc9ef79"}
# ## Pipeline definition
#
# All rule files from the rule folder are added to the pipeline. They will generate different annotation labels that need to be consolidated.
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "4866ee1f-07ad-4738-8a07-f00af7b43222"}
document_assembler = DocumentAssembler() \
.setInputCol("text") \
.setOutputCol("document")
sentence_detector = SentenceDetector() \
.setInputCols(["document"]) \
.setOutputCol("sentence")
tokenizer = Tokenizer() \
.setInputCols(["sentence"]) \
.setOutputCol("token")
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "abcc3d0d-f63a-41a0-be75-d267f2ce66f7"}
# %sh cd /databricks/driver/data && ls -lt
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "94218ae4-3245-4d85-8cce-b4ab4181cfc2"}
gender_contextual_parser = ContextualParserApproach() \
.setInputCols(["sentence", "token"]) \
.setOutputCol("entity_gender") \
.setJsonPath("/databricks/driver/data/gender.json") \
.setCaseSensitive(False) \
.setContextMatch(False)\
.setDictionary('file:/databricks/driver/data/gender.csv', read_as=ReadAs.TEXT, options={"delimiter":","})\
.setPrefixAndSuffixMatch(False)
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "d6cd0244-0942-4041-87ec-170b9e1994c7"}
age_contextual_parser = ContextualParserApproach() \
.setInputCols(["sentence", "token"]) \
.setOutputCol("entity_age") \
.setJsonPath("/databricks/driver/data/age.json") \
.setCaseSensitive(False) \
.setContextMatch(False)\
.setPrefixAndSuffixMatch(False)
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "c9f9217f-33e5-4859-80f2-0fceb5e6bd63"}
date_contextual_parser = ContextualParserApproach() \
.setInputCols(["sentence", "token"]) \
.setOutputCol("entity_date") \
.setJsonPath("/databricks/driver/data/date.json") \
.setCaseSensitive(False) \
.setContextMatch(False)\
.setPrefixAndSuffixMatch(False)
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "beaffa51-2229-40a8-9b44-99c4d4644c71"}
parserPipeline = Pipeline(stages=[
document_assembler,
sentence_detector,
tokenizer,
gender_contextual_parser,
age_contextual_parser,
date_contextual_parser])
empty_data = spark.createDataFrame([[""]]).toDF("text")
parserModel = parserPipeline.fit(empty_data)
light_model = LightPipeline(parserModel)
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "a0fc6dfd-5e67-45fe-aafa-1c126a2c8927"}
annotations = light_model.fullAnnotate(sample_text)[0]
annotations.keys()
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "f01165bc-7b35-414f-880a-fb8af9c5c231"}
print (annotations['entity_gender'])
print (annotations['entity_age'])
print (annotations['entity_date'])
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "128d5bd0-01a6-42df-9ba8-66dadc7f2386"}
import random
def get_color():
r = lambda: random.randint(100,255)
return '#%02X%02X%02X' % (r(),r(),r())
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "57fc304d-b06e-4761-b5d1-4f00864b6f90"}
ner_chunks = []
label_color = {}
unified_entities = {'entity':[]}
for ent_name in annotations.keys():
if "entity" in ent_name and len(annotations[ent_name])>0:
ner_chunks.append(ent_name)
label = annotations[ent_name][0].metadata['field']
label_color[label] = get_color()
unified_entities['entity'].extend(annotations[ent_name])
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "d78b6d15-fe07-42ee-9343-d75535715768"}
unified_entities['entity'].sort(key=lambda x: x.begin, reverse=False)
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "df3c1589-2064-4666-a421-ec31dc9451b9"}
unified_entities['entity']
# + [markdown] application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "8fd675bf-b2ba-421e-ba96-3fbee864e9ac"}
# ## Highlighting the entites with html
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "9029dc8a-a474-4a1a-b743-2d166ff619d4"}
html_output = ''
pos = 0
for n in unified_entities['entity']:
if pos < n.begin and pos < len(sample_text):
white_text = sample_text[pos:n.begin]
html_output += '<span class="others" style="background-color: white">{}</span>'.format(white_text)
pos = n.end+1
html_output += '<span class="entity-wrapper" style="background-color: {}"><span class="entity-name">{} </span><span class="entity-type">[{}]</span></span>'.format(
label_color[n.metadata['field']],
n.result,
n.metadata['field'])
if pos < len(sample_text):
html_output += '<span class="others" style="background-color: white">{}</span>'.format(sample_text[pos:])
html_output += """</div>"""
# + application/vnd.databricks.v1+cell={"title": "", "showTitle": false, "inputWidgets": {}, "nuid": "6ede0ff2-4710-40fc-9290-59ebe0cc5fb4"}
from IPython.display import HTML
HTML(html_output)
|
tutorials/Certification_Trainings/Healthcare/databricks_notebooks/10. Named Entity Recognition using rules.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# import necessary packages
import os
import matplotlib.pyplot as plt
import geopandas as gpd
from descartes import PolygonPatch
import pandas as pd
import numpy as np
import seaborn as sns
import fiona
import cbsodata
import pyproj
#using data from <NAME> Research, which has been transformed in Excel
factors = pd.read_excel("data/factors.xlsx",decimal=",")
factors.set_index("factor").to_csv("output/factors.csv")
factors
|
Python/Prettig Wonen Factors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %pylab inline
from pandas import read_csv
from pandas import read_table
from pyannote.audio.train.trainer import Trainer
from scipy.signal import convolve, hamming, triang
# +
runs = read_table('examples/reference.txt', delim_whitespace=True,
names=['run', 'max_lr'], index_col='run')
figsize(10, 2 * len(runs))
for r, (run, reference) in enumerate(runs.iterrows()):
result = read_table(f'examples/{run}.csv', delim_whitespace=True, names=['lr', 'loss'])
lrs = np.array(result.lr)
losses = np.array(result.loss)
subplot(len(runs), 1, r+1)
semilogy(lrs, losses, label=f'{run}')
auto_lr = Trainer._choose_lr(10**lrs, losses)
probability = auto_lr['probability']
auto_lr = np.log10(auto_lr['max_lr'])
target_lr = reference.max_lr
if abs(auto_lr - target_lr) > 0.25:
print(f'AutoLR failed for "{run}" (is: {auto_lr:.2f}, should be: {target_lr:.2f})')
xlim(-6, 3);
ylim(np.min(result.loss), np.median(result.loss[:50]) * 1.2);
semilogy([reference.max_lr, reference.max_lr],
[np.min(losses), 1], label='TargetLR')
semilogy([auto_lr, auto_lr], [np.min(losses), 1], label='AutoLR')
legend(loc=3);
if r == 0:
title('loss = f(lr)')
# -
|
scripts/auto_lr/test_auto_lr.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="X4cRE8IbIrIV"
# If you're opening this Notebook on colab, you will probably need to install 🤗 Transformers and 🤗 Datasets as well as other dependencies. Uncomment the following cell and run it.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="MOsHUjgdIrIW" outputId="f84a093e-147f-470e-aad9-80fb51193c8e"
# #! pip install datasets transformers sacrebleu
# + [markdown] id="HFASsisvIrIb"
# If you're opening this notebook locally, make sure your environment has the last version of those libraries installed.
#
# You can find a script version of this notebook to fine-tune your model in a distributed fashion using multiple GPUs or TPUs [here](https://github.com/huggingface/transformers/tree/master/examples/seq2seq).
# + [markdown] id="rEJBSTyZIrIb"
# # Fine-tuning a model on a translation task
# + [markdown] id="kTCFado4IrIc"
# In this notebook, we will see how to fine-tune one of the [🤗 Transformers](https://github.com/huggingface/transformers) model for a translation task. We will use the [WMT dataset](http://www.statmt.org/wmt16/), a machine translation dataset composed from a collection of various sources, including news commentaries and parliament proceedings.
#
# 
#
# We will see how to easily load the dataset for this task using 🤗 Datasets and how to fine-tune a model on it using the `Trainer` API.
# -
model_checkpoint = "Helsinki-NLP/opus-mt-en-ro"
# + [markdown] id="4RRkXuteIrIh"
# This notebook is built to run with any model checkpoint from the [Model Hub](https://huggingface.co/models) as long as that model has a sequence-to-sequence version in the Transformers library. Here we picked the [`Helsinki-NLP/opus-mt-en-ro`](https://huggingface.co/Helsinki-NLP/opus-mt-en-ro) checkpoint.
# + [markdown] id="whPRbBNbIrIl"
# ## Loading the dataset
# + [markdown] id="W7QYTpxXIrIl"
# We will use the [🤗 Datasets](https://github.com/huggingface/datasets) library to download the data and get the metric we need to use for evaluation (to compare our model to the benchmark). This can be easily done with the functions `load_dataset` and `load_metric`. We use the English/Romanian part of the WMT dataset here.
# + id="IreSlFmlIrIm"
from datasets import load_dataset, load_metric
raw_datasets = load_dataset("wmt16", "ro-en")
metric = load_metric("sacrebleu")
# + [markdown] id="RzfPtOMoIrIu"
# The `dataset` object itself is [`DatasetDict`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasetdict), which contains one key for the training, validation and test set:
# + id="GWiVUF0jIrIv" outputId="35e3ea43-f397-4a54-c90c-f2cf8d36873e"
raw_datasets
# + [markdown] id="u3EtYfeHIrIz"
# To access an actual element, you need to select a split first, then give an index:
# + id="X6HrpprwIrIz" outputId="d7670bc0-42e4-4c09-8a6a-5c018ded7d95"
raw_datasets["train"][0]
# + [markdown] id="WHUmphG3IrI3"
# To get a sense of what the data looks like, the following function will show some examples picked randomly in the dataset.
# + id="i3j8APAoIrI3"
import datasets
import random
import pandas as pd
from IPython.display import display, HTML
def show_random_elements(dataset, num_examples=5):
assert num_examples <= len(dataset), "Can't pick more elements than there are in the dataset."
picks = []
for _ in range(num_examples):
pick = random.randint(0, len(dataset)-1)
while pick in picks:
pick = random.randint(0, len(dataset)-1)
picks.append(pick)
df = pd.DataFrame(dataset[picks])
for column, typ in dataset.features.items():
if isinstance(typ, datasets.ClassLabel):
df[column] = df[column].transform(lambda i: typ.names[i])
display(HTML(df.to_html()))
# + id="SZy5tRB_IrI7" outputId="ba8f2124-e485-488f-8c0c-254f34f24f13"
show_random_elements(raw_datasets["train"])
# + [markdown] id="lnjDIuQ3IrI-"
# The metric is an instance of [`datasets.Metric`](https://huggingface.co/docs/datasets/package_reference/main_classes.html#datasets.Metric):
# + id="5o4rUteaIrI_" outputId="18038ef5-554c-45c5-e00a-133b02ec10f1"
metric
# + [markdown] id="jAWdqcUBIrJC"
# You can call its `compute` method with your predictions and labels, which need to be list of decoded strings (list of list for the labels):
# + id="6XN1Rq0aIrJC" outputId="a4405435-a8a9-41ff-9f79-a13077b587c7"
fake_preds = ["hello there", "general kenobi"]
fake_labels = [["hello there"], ["general kenobi"]]
metric.compute(predictions=fake_preds, references=fake_labels)
# + [markdown] id="n9qywopnIrJH"
# ## Preprocessing the data
# + [markdown] id="YVx71GdAIrJH"
# Before we can feed those texts to our model, we need to preprocess them. This is done by a 🤗 Transformers `Tokenizer` which will (as the name indicates) tokenize the inputs (including converting the tokens to their corresponding IDs in the pretrained vocabulary) and put it in a format the model expects, as well as generate the other inputs that model requires.
#
# To do all of this, we instantiate our tokenizer with the `AutoTokenizer.from_pretrained` method, which will ensure:
#
# - we get a tokenizer that corresponds to the model architecture we want to use,
# - we download the vocabulary used when pretraining this specific checkpoint.
#
# That vocabulary will be cached, so it's not downloaded again the next time we run the cell.
# + id="eXNLu_-nIrJI"
from transformers import AutoTokenizer
tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)
# -
# For the mBART tokenizer (like we have here), we need to set the source and target languages (so the texts are preprocessed properly). You can check the language codes [here](https://huggingface.co/facebook/mbart-large-cc25) if you are using this notebook on a different pairs of languages.
if "mbart" in model_checkpoint:
tokenizer.src_lang = "en-XX"
tokenizer.tgt_lang = "ro-RO"
# + [markdown] id="Vl6IidfdIrJK"
# By default, the call above will use one of the fast tokenizers (backed by Rust) from the 🤗 Tokenizers library.
# + [markdown] id="rowT4iCLIrJK"
# You can directly call this tokenizer on one sentence or a pair of sentences:
# + id="a5hBlsrHIrJL" outputId="acdaa98a-a8cd-4a20-89b8-cc26437bbe90"
tokenizer("Hello, this one sentence!")
# + [markdown] id="qo_0B1M2IrJM"
# Depending on the model you selected, you will see different keys in the dictionary returned by the cell above. They don't matter much for what we're doing here (just know they are required by the model we will instantiate later), you can learn more about them in [this tutorial](https://huggingface.co/transformers/preprocessing.html) if you're interested.
#
# Instead of one sentence, we can pass along a list of sentences:
# -
tokenizer(["Hello, this one sentence!", "This is another sentence."])
# To prepare the targets for our model, we need to tokenize them inside the `as_target_tokenizer` context manager. This will make sure the tokenizer uses the special tokens corresponding to the targets:
with tokenizer.as_target_tokenizer():
print(tokenizer(["Hello, this one sentence!", "This is another sentence."]))
# + [markdown] id="2C0hcmp9IrJQ"
# If you are using one of the five T5 checkpoints that require a special prefix to put before the inputs, you should adapt the following cell.
# -
if model_checkpoint in ["t5-small", "t5-base", "t5-larg", "t5-3b", "t5-11b"]:
prefix = "translate English to Romanian: "
else:
prefix = ""
# We can then write the function that will preprocess our samples. We just feed them to the `tokenizer` with the argument `truncation=True`. This will ensure that an input longer that what the model selected can handle will be truncated to the maximum length accepted by the model. The padding will be dealt with later on (in a data collator) so we pad examples to the longest length in the batch and not the whole dataset.
# + id="vc0BSBLIIrJQ"
max_input_length = 128
max_target_length = 128
source_lang = "en"
target_lang = "ro"
def preprocess_function(examples):
inputs = [prefix + ex[source_lang] for ex in examples["translation"]]
targets = [ex[target_lang] for ex in examples["translation"]]
model_inputs = tokenizer(inputs, max_length=max_input_length, truncation=True)
# Setup the tokenizer for targets
with tokenizer.as_target_tokenizer():
labels = tokenizer(targets, max_length=max_target_length, truncation=True)
model_inputs["labels"] = labels["input_ids"]
return model_inputs
# + [markdown] id="0lm8ozrJIrJR"
# This function works with one or several examples. In the case of several examples, the tokenizer will return a list of lists for each key:
# + id="-b70jh26IrJS" outputId="acd3a42d-985b-44ee-9daa-af5d944ce1d9"
preprocess_function(raw_datasets['train'][:2])
# + [markdown] id="zS-6iXTkIrJT"
# To apply this function on all the pairs of sentences in our dataset, we just use the `map` method of our `dataset` object we created earlier. This will apply the function on all the elements of all the splits in `dataset`, so our training, validation and testing data will be preprocessed in one single command.
# + id="DDtsaJeVIrJT" outputId="aa4734bf-4ef5-4437-9948-2c16363da719"
tokenized_datasets = raw_datasets.map(preprocess_function, batched=True)
# + [markdown] id="voWiw8C7IrJV"
# Even better, the results are automatically cached by the 🤗 Datasets library to avoid spending time on this step the next time you run your notebook. The 🤗 Datasets library is normally smart enough to detect when the function you pass to map has changed (and thus requires to not use the cache data). For instance, it will properly detect if you change the task in the first cell and rerun the notebook. 🤗 Datasets warns you when it uses cached files, you can pass `load_from_cache_file=False` in the call to `map` to not use the cached files and force the preprocessing to be applied again.
#
# Note that we passed `batched=True` to encode the texts by batches together. This is to leverage the full benefit of the fast tokenizer we loaded earlier, which will use multi-threading to treat the texts in a batch concurrently.
# + [markdown] id="545PP3o8IrJV"
# ## Fine-tuning the model
# + [markdown] id="FBiW8UpKIrJW"
# Now that our data is ready, we can download the pretrained model and fine-tune it. Since our task is of the sequence-to-sequence kind, we use the `AutoModelForSeq2SeqLM` class. Like with the tokenizer, the `from_pretrained` method will download and cache the model for us.
# + id="TlqNaB8jIrJW" outputId="84916cf3-6e6c-47f3-d081-032ec30a4132"
from transformers import AutoModelForSeq2SeqLM, DataCollatorForSeq2Seq, Seq2SeqTrainingArguments, Seq2SeqTrainer
model = AutoModelForSeq2SeqLM.from_pretrained(model_checkpoint)
# + [markdown] id="CczA5lJlIrJX"
# Note that we don't get a warning like in our classification example. This means we used all the weights of the pretrained model and there is no randomly initialized head in this case.
# + [markdown] id="_N8urzhyIrJY"
# To instantiate a `Seq2SeqTrainer`, we will need to define three more things. The most important is the [`Seq2SeqTrainingArguments`](https://huggingface.co/transformers/main_classes/trainer.html#transformers.Seq2SeqTrainingArguments), which is a class that contains all the attributes to customize the training. It requires one folder name, which will be used to save the checkpoints of the model, and all other arguments are optional:
# + id="Bliy8zgjIrJY"
batch_size = 16
args = Seq2SeqTrainingArguments(
"test-translation",
evaluation_strategy = "epoch",
learning_rate=2e-5,
per_device_train_batch_size=batch_size,
per_device_eval_batch_size=batch_size,
weight_decay=0.01,
save_total_limit=3,
num_train_epochs=1,
predict_with_generate=True,
fp16=True,
)
# + [markdown] id="km3pGVdTIrJc"
# Here we set the evaluation to be done at the end of each epoch, tweak the learning rate, use the `batch_size` defined at the top of the cell and customize the weight decay. Since the `Seq2SeqTrainer` will save the model regularly and our dataset is quite large, we tell it to make three saves maximum. Lastly, we use the `predict_with_generate` option (to properly generate summaries) and activate mixed precision training (to go a bit faster).
#
# Then, we need a special kind of data collator, which will not only pad the inputs to the maximum length in the batch, but also the labels:
# -
data_collator = DataCollatorForSeq2Seq(tokenizer, model=model)
# + [markdown] id="7sZOdRlRIrJd"
# The last thing to define for our `Seq2SeqTrainer` is how to compute the metrics from the predictions. We need to define a function for this, which will just use the `metric` we loaded earlier, and we have to do a bit of pre-processing to decode the predictions into texts:
# + id="UmvbnJ9JIrJd"
import numpy as np
def postprocess_text(preds, labels):
preds = [pred.strip() for pred in preds]
labels = [[label.strip()] for label in labels]
return preds, labels
def compute_metrics(eval_preds):
preds, labels = eval_preds
if isinstance(preds, tuple):
preds = preds[0]
decoded_preds = tokenizer.batch_decode(preds, skip_special_tokens=True)
# Replace -100 in the labels as we can't decode them.
labels = np.where(labels != -100, labels, tokenizer.pad_token_id)
decoded_labels = tokenizer.batch_decode(labels, skip_special_tokens=True)
# Some simple post-processing
decoded_preds, decoded_labels = postprocess_text(decoded_preds, decoded_labels)
result = metric.compute(predictions=decoded_preds, references=decoded_labels)
result = {"bleu": result["score"]}
prediction_lens = [np.count_nonzero(pred != tokenizer.pad_token_id) for pred in preds]
result["gen_len"] = np.mean(prediction_lens)
result = {k: round(v, 4) for k, v in result.items()}
return result
# + [markdown] id="rXuFTAzDIrJe"
# Then we just need to pass all of this along with our datasets to the `Seq2SeqTrainer`:
# + id="imY1oC3SIrJf"
trainer = Seq2SeqTrainer(
model,
args,
train_dataset=tokenized_datasets["train"],
eval_dataset=tokenized_datasets["validation"],
data_collator=data_collator,
tokenizer=tokenizer,
compute_metrics=compute_metrics
)
# + [markdown] id="CdzABDVcIrJg"
# We can now finetune our model by just calling the `train` method:
# + id="uNx5pyRlIrJh" outputId="077e661e-d36c-469b-89b8-7ff7f73541ec"
trainer.train()
# -
# ### Upload your model on the Hub
# Now that you have fine-tuned your model, share it with the community and you'll be able to generate results like the one shown in the first picture of this notebook!
#
# First you have to store your authentication token from the Hugging Face website (sign up [here](https://huggingface.co/join) if you haven't already!) then uncomment the following cell and input your username and password.
# !huggingface-cli login
# Make sure your version of Transformers is at least 4.6.1 since the functionality was introduced in that version:
# +
import transformers
print(transformers.__version__)
# + [markdown] id="wY82caEX3l_i"
# Pick a repository name you like for your model to replace `"my-awesome_model"` and just execute the next cell to upload it to the Hub!
# -
trainer.push_to_hub("my-awesome-model")
# You can now share this model with all your friends, family, favorite pets: they can all load it with the identifier `"your-username/the-name-you-picked"` so for instance:
#
# ```python
# from transformers import AutoModelForSeq2SeqLM
#
# model = AutoModelForSeq2SeqLM.from_pretrained("sgugger/my-awesome-model")
# ```
|
examples/translation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
import statsmodels.api as sm
from sklearn import linear_model
# Load the data into a pandas dataframe
iris = sns.load_dataset("iris")
iris.head()
X = iris[["petal_length"]] #predictor
y = iris["petal_width"] #response
#Linear regression
# Note the swap of X and y
model = sm.OLS(y, X)
results = model.fit()
# Statsmodels gives R-like statistical output
print(results.summary())
# +
#where is the intercept info?
# +
X = iris["petal_length"]
X = np.vander(X, 2) # add a constant row for the intercept
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
# -
# #### Petal_width=0.41-0.36* (petal_length)
X = iris[["petal_length","sepal_length"]] #predictors
y = iris["petal_width"]
# +
#Multiple Linear regression
# Note the swap of X and y
X = iris[["petal_length","sepal_length"]]
X = sm.add_constant(X) # another way to add a constant row for an intercept
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
model = sm.OLS(y, X)
results = model.fit()
# Statsmodels gives R-like statistical output
print(results.summary())
# -
# #### use categorical variables
dummies = pd.get_dummies(iris["species"])
# Add to the original dataframe
iris = pd.concat([iris, dummies], axis=1)#assign numerical values to the different species
iris.head()
# +
X = iris[["petal_length","sepal_length", "setosa", "versicolor", "virginica"]]
X = sm.add_constant(X) # another way to add a constant row for an intercept
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
# +
# you would be inclined to choose the model that had the lower AIC or BIC value
# +
# Fit the linear model using sklearn
#from sklearn import linear_model
model = linear_model.LinearRegression()
results = model.fit(X, y)
# Print the coefficients
print results.intercept_, results.coef_
# -
# # Conditions of linear regression
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns
import statsmodels.api as sm
from sklearn import linear_model
# Load the data into a pandas dataframe
iris = sns.load_dataset("iris")
iris.head()
# +
# Linear relationship between Y and Xs
# -
sns.pairplot(iris[['petal_width', 'petal_length', 'sepal_length']].dropna(how = 'any', axis = 0))
# +
#Multiple Linear regression
#
X = iris[["petal_length","sepal_length"]]
X = sm.add_constant(X) # another way to add a constant row for an intercept
y = iris["petal_width"]
model = sm.OLS(y, X)
results = model.fit()
print(results.summary())
model = sm.OLS(y, X)
results = model.fit()
# Statsmodels gives R-like statistical output
print(results.summary())
# -
# ## Are the residuals normally distributed?
# +
#JB test: test for normal distribution of residuals
## H0: The null hypothesis for the test is that the data are normally distributed (in this case residuals)
# Unfortunately, with small samples the Jarque-Bera test is prone rejecting the null hypothesis–
#that the distribution is normal–when it is in fact true
# -
res = results.resid
sm.qqplot(res)
plt.show()
# +
#Durbin-watson: used for measuring autocorrelation
#pproximately equal to 2(1-r), where r is the sample autocorrelation
#ranges from zero to four, and a value around two suggests that there is no autocorrelation.
#Values greater than two suggest negative correlation, and values less that one suggest positive correlation
# -
# ## Multicollinearity
# +
#condition no.: used for measuring multi-collinearity
# cond no>30 means multi-collinearity
#influences the stability & reliability of coefficents
# -
corr=X.corr() #correlation bw predictors
print(corr)
# ## heteroscedasticity
#
# ### test whether the variance of the errors from a regression is dependent on the values of the independent variables
# ### there should ne relation or pattern between residuals and fitted values, i.e. we want homoscedasticity
# ### breusch-pagan test
# ### h0: null hypothesis of the Breusch-Pagan test is homoscedasticity (= variance does not depend on auxiliary regressors)
import statsmodels.stats.api as sms
from statsmodels.compat import lzip
name = ['Lagrange multiplier statistic', 'p-value',
'f-value', 'f p-value']
test = sms.het_breushpagan(results.resid, results.model.exog)
lzip(name, test)
# +
#reject the null hypothesis that the variance of the residuals is constant and infer that heteroscedasticity is indeed present
# -
# ## Influence Test
#
# ### plot helps us to find influential cases (i.e., subjects) if any. Not all outliers are influential in linear regression analysis
# ### outlying values at the upper right corner or at the lower right corner
from statsmodels.graphics.regressionplots import *
plot_leverage_resid2(results)
influence_plot(results)
# # Logistic regression
# ## binary response variables (Y)- 0 or 1
# ## Xs can be numerical or categorical
# +
# %matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
# -
import numpy as np
import pandas as pd
import statsmodels.api as sm
df = pd.read_csv("trainT.csv") #titanic
df.head(5)
df.shape
df.isnull().sum() #number of nas in a column
df = df[["Survived","Pclass","Age","Fare"]]
df=df.dropna() #drops nas
df.head(7)
plt.figure(figsize=(6,4))
fig, ax = plt.subplots()
df.Survived.value_counts().plot(kind='barh', color="blue", alpha=.65)
ax.set_ylim(-1, len(df.Survived.value_counts()))
plt.title("Survival Breakdown (1 = Survived, 0 = Died)")
sns.factorplot(x="Pclass", y="Fare", hue="Survived", data=df, kind="box")
# +
#formula = 'Survived ~ C(Pclass) + C(Sex) + Age + Fare' #c indicates categorical
# -
y=df[['Survived']]
print(type(y))
x=df[["Pclass","Age","Fare"]]
print(type(x))
# +
# Make the model
logit =sm.Logit(y, x.astype(float)) #import statsmodels.api as sm
# Fit the model
result = logit.fit()
# -
print result.summary()
# +
#log [p/(1-p)] = -.28*Pclass + .0146 * faree -0.01*Age
# +
#how a 1 unit increase or decrease in a variable affects the odds of surviving
#Number of successes:1 failure
# -
# odds
print np.exp(result.params)
# +
#odds that passengers die increase by a factor of 0.98 for each unit change in age.
# +
#prob = odds / (1 + odds) .
#probability of finding someone dead on basis of age = 0.98/(1+0.98)
# +
from patsy import dmatrices
import pandas as pd
from sklearn.linear_model import LogisticRegression
import statsmodels.discrete.discrete_model as sm
# -
df2=pd.read_csv("trainT.csv")
df2.head(7)
df2 = df2[["Survived","Pclass","Sex","Age","Fare"]]
df2.head(6)
df2=df2.dropna()
df2.head(6)
# +
y, X = dmatrices('Survived ~ C(Pclass) + C(Sex) + Age + Fare', df2, return_type = 'dataframe')
#c indicates categorical
# sklearn output
model = LogisticRegression(fit_intercept = False, C = 1e9)
mdl = model.fit(X, y)
model.coef_
# -
logit = sm.Logit(y, X)
logit.fit().params
# Fit the model
result = logit.fit()
print result.summary()
# create a results dictionary to hold our regression results for easy analysis later
results = {}
# +
#http://hamelg.blogspot.co.uk/2015/11/python-for-data-analysis-part-28.html
# +
# create a regression friendly dataframe using patsy's dmatrices function
y,x = dmatrices(formula, data=df, return_type='dataframe')
# instantiate our model
model = sm.Logit(y,x)
# fit our model to the training data
res = model.fit()
# save the result for outputing predictions later
results['Logit'] = [res, formula]
res.summary()
# +
# fare is not statistically significant
# -
formula = 'Survived ~ C(Pclass) + C(Sex) + Age'
# +
results = {}
# create a regression friendly dataframe using patsy's dmatrices function
y,x = dmatrices(formula, data=df, return_type='dataframe')
# instantiate our model
model = sm.Logit(y,x)
# fit our model to the training data
res = model.fit()
# save the result for outputing predictions later
results['Logit'] = [res, formula]
res.summary()
# -
# # Polynomial regression
# +
# %matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
# -
import numpy as np
import pandas as pd
import statsmodels.api as sm
x=np.linspace(-4,4,1500) #1500 sample numbers between -4 and 4
# +
#plot subplots
# -
fig, ((ax1,ax2,ax3),(ax4,ax5,ax6))=plt.subplots(nrows=2,ncols=3) #subplots
ax1.plot(x,x)
ax1.set_title('linear')
ax1.plot(x,x**2)
ax1.set_title('2nd degree')
ax1.plot(x,x**3)
ax1.set_title('3rd degree')
ax1.plot(x,x**4)
ax1.set_title('4th degree')
ax1.plot(x,x**5)
ax1.set_title('5th degree')
ax1.plot(x,x**6)
ax1.set_title('6th degree')
import seaborn as sns
# Load the data into a pandas dataframe
iris = sns.load_dataset("iris")
iris.head()
x=iris.sepal_length
y=iris.petal_length
from sklearn import linear_model
lr= linear_model.LinearRegression()
from sklearn.metrics import r2_score
# +
for deg in [1,2,3,4,5]:
lr.fit(np.vander(x,deg+1),y);
y_lr=lr.predict(np.vander(x,deg+1))
plt.plot(x,y_lr,label='degree'+str(deg));
plt.legend(loc=2);
print r2_score(y,y_lr)
plt.plot(x,y,'ok')
# -
|
section5/StatsMod1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Exercise 2
# This exercise will walk you through the creation of a dictionary.
# 1. First, load the data in the `names.txt` file. This file contains common names of some species. Load this into a list.
# 2. Do the same thing with the `species.txt` file. This file contains chemical formulae for some species.
# 3. Now create a dictionary where the data from `names.txt` are the values and the data from `species.txt` are the keys.
# + You should automate the creation of the dictionary by using a `for` loop
# + The `for` loop should iterate over the representation created by the `zip` function. You can refer to the example around line 32 in Lecture 4 for guidance.
# + **HINT:** Initialize the dictionary by with `my_new_dict = {}` just before executing the `for` loop.
# 4. Access a value from the dictonary and print it to the screen.
#
# **Note:** The same dictionary can be created by executing the following one-liner: `species_dict_2 = dict(zip(species, names))`.
# +
def readlines_to_list(filename):
f = open(filename)
lines = f.readlines()
li_lines = []
for line in lines:
li_lines.append(line.replace('\n', ''))
return li_lines
li_names = readlines_to_list('names.txt')
print(li_names)
li_species = readlines_to_list('species.txt')
print(li_species)
# -
# my redundant way of trying zip and create the dict...
zipped_list = list(zip(li_names, li_species))
my_new_dict_v0 = {}
length = len(li_names)
for item in zipped_list:
my_new_dict_v0[item[1]] = item[0]
print(my_new_dict_v0)
# better way
my_new_dict = {}
for s, name in zip(li_species, li_names):
my_new_dict[s] = name
print(my_new_dict)
print('Accessing my_new_dict with key=H2O: ',my_new_dict['H2O'])
|
lectures/L4/Exercise_2-final.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
sql(
'''
SELECT order_id,
date_format(order_date, '%Y-%m-%d') order_date,
category,
Avg(profit) OVER (PARTITION BY Order_Date) daily_avg_profit
FROM superstore
WHERE order_date BETWEEN (SELECT MIN(order_date) FROM superstore) AND
(SELECT MAX(order_date) FROM superstore)
GROUP BY order_date;
'''
)
|
12_window_function.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
data = pd.read_csv(r'E:\Python\Dataset.csv')
# -
data.head()
y = data.diagnosis
list = ['Unnamed: 32','id','diagnosis']
x = data.drop(list,axis = 1 )
x.head()
import matplotlib.pyplot as plt
# Scatter Plot
# +
# create a figure and axis
fig, ax = plt.subplots()
# scatter the radius_mean against the texture_mean
ax.scatter(data['radius_mean'], data['texture_mean'])
# set a title and labels
ax.set_title('Dataset')
ax.set_xlabel('radius_mean')
ax.set_ylabel('texture_mean')
# -
#we can also plot it by simply using scatter plot
# plotting points as a scatter plot
plt.scatter(data['radius_mean'], data['texture_mean'], label= "stars", color= "green",
marker= "o", s=50)
plt.legend()
# Line Chart
# get columns to plot
columns = data.iloc[:,:7]
# create x data
x = range(0, data.shape[0])
# create figure and axis
fig, ax = plt.subplots()
# plot each column
for column in columns:
ax.plot(x, data[column], label=column)
# set title and legend
ax.set_title('Dataset')
ax.legend()
# Histogram
# create figure and axis
fig, ax = plt.subplots()
# plot histogram
ax.hist(data['radius_mean'])
# set title and labels
ax.set_title('Radius Mean')
ax.set_xlabel('radius_mean')
ax.set_ylabel('texture_mean')
# +
# plotting a histogram
# setting the ranges and no. of intervals
range = (0,30)
bins = 10
plt.hist(data['radius_mean'], bins, range, color = 'blue',
histtype = 'barstacked', rwidth = 0.8)
plt.xlabel('radius_mean')
plt.ylabel('texture_mean')
plt.title('Radius Mean')
plt.show()
# -
# #Bar Chart
#
# +
# create a figure and axis
fig, ax = plt.subplots()
# count the occurrence of each class
data1 = data['radius_mean'].value_counts()
# get x and y data
points = data1.index
frequency = data1.values
# create bar chart
ax.bar(points, frequency)
# set title and labels
ax.set_title('Radius Mean')
ax.set_xlabel('P')
ax.set_ylabel('Frequency')
# -
|
Data Visualisation/Data_visualisation_using_matplotlib.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
x = 0
for filename in os.listdir('DATA/TROPOMI_AER_AI/'):
with open(os.path.join(os.getcwd()+'/DATA/TROPOMI_AER_AI/', filename), 'r') as f: # open in readonly mode
print(filename)
ds = xr.open_dataset(os.path.join(os.getcwd()+'/DATA/TROPOMI_AER_AI/', filename), group='PRODUCT',
engine='netcdf4', decode_coords=True)
df = ds.to_dataframe()
print(x)
if x==0:
frame = df
x = x + 1;
else:
frames = [frame, df]
result = pd.concat(frames)
print(len(result))
frame = result
x = x + 1
# +
import seaborn as sns
import pandas as pd
import geopandas as gpd
import numpy as np
import matplotlib.pyplot as plt
import geopandas as gpd
# %matplotlib inline
import xarray as xr
file_path_2 = 'DATA/TROPOMI_AER_AI/S5P_NRTI_L2__AER_AI_20210218T055230_20210218T055730_17363_01_010400_20210218T062609.nc'
file_path_1 = 'DATA/TROPOMI_AER_AI//S5P_NRTI_L2__AER_AI_20210213T040730_20210213T041230_17291_01_010400_20210213T044042.nc'
ds = xr.open_dataset(file_path_2, group='PRODUCT',
engine='netcdf4', decode_coords=True)
print(ds)
df = ds.to_dataframe()
ds_2 = xr.open_dataset(file_path_1, group='PRODUCT',
engine='netcdf4', decode_coords=True)
print(ds_2)
df_2 = ds_2.to_dataframe()
frames = [df, df_2]
result = pd.concat(frames)
# -
print(len(df))
print(len(df_2))
print(len(result))
# +
# initialize an axis
fig, ax = plt.subplots(figsize=(18,6))
countries = gpd.read_file(
gpd.datasets.get_path("naturalearth_lowres"))
countries.plot(color="lightgrey",ax=ax)
result.plot(x="longitude", y="latitude", kind="scatter",
c="aerosol_index_354_388", colormap="YlOrRd",
ax=ax)
# add grid
ax.grid(b=True, alpha=0.5)
plt.show()
# -
|
Plotting tropomi data.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cs
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: .NET (C#)
// language: C#
// name: .net-csharp
// ---
// [this doc on github](https://github.com/dotnet/interactive/tree/master/samples/notebooks/csharp/Docs)
//
// # Variable Sharing
//
// .NET Interactive enables you to write code in multiple languages within a single notebook and in order to take advantage of those languages' different strengths, you might find it useful to share data between them. By default, .NET Interactive provides [subkernels](https://github.com/dotnet/interactive/blob/master/docs/kernels-overview.md) for three different languages within the same process. You can share variables between .NET subkernels using the `#!share` magic command.
// + language="csharp"
var x = "C# subkernel value";
x
// + language="fsharp"
// #!share --from csharp x
// sprintf "%s, accessed from F# subkernel" x
// -
// Variables are shared by reference for reference types. A consequence of this is that if you share a mutable object, changes to its state will be visible across subkernels:
// + language="fsharp"
// open System.Collections.Generic
//
// let list = List<string>()
// list.Add "Added by F#"
// list
// + language="csharp"
// #!share --from fsharp list
list.Add("Added by C#");
list
// + language="fsharp"
//
// list
// -
// # Direct data entry with `#!value`
//
// It's common to have text that you'd like to use in a notebook. It might be JSON, CSV, XML, or some other format. It might be in a file, in your clipboard, or on the web. The `#!value` magic command is available to make it as easy as possible to get that text into a variable in your notebook. An important thing to know is that `#!value` is an alias to a subkernel designed just to hold values. This means that once you store something in it, you can access it from another subkernel using `#!share`.
//
// There are three ways to use `#!value` to get data into your notebook session:
//
// ### 1. From the clipboard
//
// The simplest way to use `#!value` is to paste some text into the cell. The text will be stored as a string, but unlike using a `string` literal in C#, F#, or PowerShell, there's no need to escape anything.
//
// +
// #!value --name someJson
{
"what": "some JSON",
"why": "to share it with another subkernel"
}
// +
// #!share someJson --from value
using Newtonsoft.Json.Linq;
var jObject = JObject.Parse(someJson);
jObject.ToString()
// -
//
// ### 2. From a file
//
// If the data you want to read into your notebook is stored in a file, you can use `#!value` with the `--from-file` option:
// #!value --from-file data.json --name someJson
// #!share someJson --from value
someJson
//
// ### 3. From a URL
//
// You can pull data into your notebook from a URL as well, using the `--from-url` option.
//
// #!value --from-url https://dot.net --name dn
// #!share --from value dn
display(dn, "text/html");
// ## Specifying a MIME type
//
// Regardless of which of these approaches you use, you can additionally choose to display the value in the notebook at the time of submission by using the `--mime-type` option. This accomplishes a few things. If your notebook frontend knows how to display that mime type, you can see it appropriately formatted:
// +
// #!value --name someJson --mime-type application/json
{
"what": "some JSON",
"why":
[
"to share it with another subkernel",
"to see it in a treeview"
]
}
// -
// This also causes the value to be saved in your `.ipynb` file, something that would not otherwise happen.
//
//
// This also effectively stores the value in your `.ipynb` file, something that would not otherwise happen.
//
// ## Limitations
//
// Variable sharing has some limitations to be aware of. When sharing a variable with a subkernel where its compilation requirements aren't met, for example due to a missing `using` (C#) or `open` (F#) declaration, a custom type defined in the notebook, or a missing assembly reference, `#!share` will fail. This limitation may be lifted in the future but for now, if you want to share variables of types that aren't imported by default, you will have to explicitly run the necessary import code in the destination kernel.
//
// + language="csharp"
public class DefinedInCSharp { }
var csharpInstance = new DefinedInCSharp();
// + language="fsharp"
// #!share --from csharp csharpInstance
// csharpInstance
// -
|
notebooks/polyglot/Variable sharing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # ipymarkup
# Collection of NLP vizualizations for NER and syntax tree markup. Similar to Spacy <a href="https://explosion.ai/demos/displacy">displaCy</a> and <a href="https://explosion.ai/demos/displacy-ent">displaCy ENT</a>.
from ipymarkup.demo import show_table
show_table()
# ## NER
# All NER markup visualization functions have two arguments as input: `text` and `spans`. `spans` are tuples of `start`, `stop` and optional `type`.
# ### `show_span_ascii_markup`
# +
from ipymarkup import show_span_ascii_markup
text = 'В мероприятии примут участие не только российские учёные, но и зарубежные исследователи, в том числе, Крис Хелмбрехт - управляющий директор и совладелец креативного агентства Kollektiv (Германия, США), Ннека Угбома - руководитель проекта Mushroom works (Великобритания), Гергей Ковач - политик и лидер субкультурной партии «Dog with two tails» (Венгрия), Георг Жено - немецкий режиссёр, один из создателей экспериментального театра «Театр.doc», Театра им. Йозефа Бойса (Германия).'
spans = [(102, 116, 'PER'), (186, 194, 'LOC'), (196, 199, 'LOC'), (202, 214, 'PER'), (254, 268, 'LOC'), (271, 283, 'PER'), (324, 342, 'ORG'), (345, 352, 'LOC'), (355, 365, 'PER'), (445, 455, 'ORG'), (456, 468, 'PER'), (470, 478, 'LOC')]
show_span_ascii_markup(text, spans)
# -
# ### `show_span_box_markup`
# +
from ipymarkup import show_span_box_markup
show_span_box_markup(text, spans)
# -
# To assign specific colors use `ipymarkup.palette`:
# +
from ipymarkup.palette import palette, BLUE, RED, GREEN
show_span_box_markup(text, spans, palette=palette(PER=BLUE, ORG=RED, LOC=GREEN))
# -
# ### `show_span_line_markup`
# +
from ipymarkup import show_span_line_markup
spans = [(102, 200, 'PERSON'), (119, 139, 'PERSONPROPERTY'), (142, 200, 'PERSONPROPERTY'), (153, 200, 'ORGANIZATION'), (186, 194, 'GEO'), (196, 199, 'GEO'), (202, 252, 'PERSON'), (217, 252, 'PERSONPROPERTY'), (254, 268, 'GEO'), (296, 353, 'PERSONPROPERTY'), (302, 353, 'ORGANIZATION'), (345, 352, 'GEO'), (355, 385, 'PERSON'), (368, 385, 'PERSONPROPERTY'), (406, 443, 'ORGANIZATION'), (445, 479, 'ORGANIZATION'), (470, 478, 'GEO')]
show_span_line_markup(text, spans)
# -
# To make all colors blue, initialize palette with single color:
show_span_line_markup(text, spans, palette=palette(BLUE))
# ## `show_span_ascii_markup`
show_span_ascii_markup(text, spans)
# ### `spans`
# For convenience `span` objects can be tuples, dicts or objects:
# +
class C(object):
def __init__(self, start, stop, type=None):
self.start = start
self.stop = stop
self.type = type
text = '0123456789'
spans = [
(1, 2), # tuple/list (int, int)
(3, 4, 'b'), # tuple/list (int, int, str)
[5, 6],
C(7, 8),
C(9, 10, 'c') # object with start, stop, type attributes
]
show_span_box_markup(text, spans)
show_span_line_markup(text, spans)
show_span_ascii_markup(text, spans)
# -
# ## Syntax tree
# Syntax tree visualization functions have two arguments as input: `words` and `deps`. `words` are strings, `deps` — list of tuples `source`, `target` and optional `type`.
# ### `show_dep_markup`
# +
from ipymarkup import show_dep_markup
words = ['В', 'советский', 'период', 'времени', 'число', 'ИТ', '-', 'специалистов', 'в', 'Армении', 'составляло', 'около', 'десяти', 'тысяч', '.']
deps = [(2, 0, 'case'), (2, 1, 'amod'), (10, 2, 'obl'), (2, 3, 'nmod'), (10, 4, 'obj'), (7, 5, 'compound'), (5, 6, 'punct'), (4, 7, 'nmod'), (9, 8, 'case'), (4, 9, 'nmod'), (13, 11, 'case'), (13, 12, 'nummod'), (10, 13, 'nsubj'), (10, 14, 'punct')]
show_dep_markup(words, deps)
# -
# ### `show_dep_ascii_markup`
# +
from ipymarkup import show_dep_ascii_markup
words = ['В', 'советский', 'период', 'времени', 'число', 'ИТ', '-', 'специалистов', 'в', 'Армении', 'составляло', 'около', 'десяти', 'тысяч', '.']
deps = [(2, 0, 'case'), (2, 1, 'amod'), (10, 2, 'obl'), (2, 3, 'nmod'), (10, 4, 'obj'), (7, 5, 'compound'), (5, 6, 'punct'), (4, 7, 'nmod'), (9, 8, 'case'), (4, 9, 'nmod'), (13, 11, 'case'), (13, 12, 'nummod'), (10, 13, 'nsubj'), (10, 14, 'punct')]
show_dep_ascii_markup(words, deps)
# -
# ### `deps`
# For convenience `dep` objects can be tuples, dicts or objects. Same as `spans` in NER visualizations:
# +
class C(object):
def __init__(self, source, target, type=None):
self.source = source
self.target = target
self.type = type
words = 'aa bb cc dd ee'.split()
deps = [
(0, 1),
(1, 2, 'b'),
[3, 4],
C(0, 2),
C(1, 3, 'c')
]
show_dep_markup(words, deps)
show_dep_ascii_markup(words, deps)
# -
# ## Cookbook
# ### `format_*` functions
# To use visualizations outside of Jupyter notebook use `format_*` function. For example `show_dep_ascii_markup` has `format_dep_ascii_markup` counterpart that return generator of strings:
# +
from ipymarkup import format_dep_ascii_markup
list(format_dep_ascii_markup(words, deps))
# -
# Same for `show_span_box_markup` and `format_span_box_markup`:
# +
from ipymarkup import format_span_box_markup
list(format_span_box_markup(text, spans))
# -
|
docs.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day 05
#
# Santa needs help figuring out which strings in his text file are naughty or nice.
#
# A nice string is one with all of the following properties:
#
# It contains at least three vowels (aeiou only), like aei, xazegov, or aeiouaeiouaeiou.
# It contains at least one letter that appears twice in a row, like xx, abcdde (dd), or aabbccdd (aa, bb, cc, or dd).
# It does not contain the strings ab, cd, pq, or xy, even if they are part of one of the other requirements.
#
# For example:
#
# ugknbfddgicrmopn is nice because it has at least three vowels (u...i...o...), a double letter (...dd...), and none of the disallowed substrings.
# aaa is nice because it has at least three vowels and a double letter, even though the letters used by different rules overlap.
# jchzalrnumimnmhp is naughty because it has no double letter.
# haegwjzuvuyypxyu is naughty because it contains the string xy.
# dvszwmarrgswjxmb is naughty because it contains only one vowel.
#
# How many strings are nice?
# ## Puzzle 1
# +
import string
VOWELS = "aeiou"
DOUBLES = [2 * _ for _ in string.ascii_lowercase]
FORBIDDEN = ("ab", "cd", "pq", "xy")
def count_vowels(instr:str) -> int:
"""Return count of vowels aeiou in string.
:param instr: input string
"""
return len([_ for _ in instr if _ in VOWELS])
def count_double_letters(instr:str) -> int:
"""Return count of double letters in string.
:param instr: input string
"""
return len([_ for _ in DOUBLES if _ in instr])
def count_forbidden(instr:str) -> int:
"""Return count of forbidden letter combinations.
:param instr: input string
"""
return len([_ for _ in FORBIDDEN if _ in instr])
def naughty_or_nice(instr:str) -> str:
"""Returns naughty or nice status of string.
:param instr: input string
"""
if count_forbidden(instr) or (count_vowels(instr) < 3) or (not count_double_letters(instr)):
return "naughty"
return "nice"
# -
instrs = ("ugknbfddgicrmopn",
"aaa",
"jchzalrnumimnmhp",
"haegwjzuvuyypxyu",
"dvszwmarrgswjxmb")
for instr in instrs:
print(instr, naughty_or_nice(instr))
# ### Solution
with open("day05.txt", "r") as ifh:
results = [naughty_or_nice(_.strip()) for _ in ifh.readlines()]
print(sum([_ == "nice" for _ in results]))
# ## Puzzle 2
#
# Realizing the error of his ways, Santa has switched to a better model of determining whether a string is naughty or nice. None of the old rules apply, as they are all clearly ridiculous.
#
# Now, a nice string is one with all of the following properties:
#
# It contains a pair of any two letters that appears at least twice in the string without overlapping, like xyxy (xy) or aabcdefgaa (aa), but not like aaa (aa, but it overlaps).
# It contains at least one letter which repeats with exactly one letter between them, like xyx, abcdefeghi (efe), or even aaa.
#
# For example:
#
# qjhvhtzxzqqjkmpb is nice because is has a pair that appears twice (qj) and a letter that repeats with exactly one letter between them (zxz).
# xxyxx is nice because it has a pair that appears twice and a letter that repeats with one between, even though the letters used by each rule overlap.
# uurcxstgmygtbstg is naughty because it has a pair (tg) but no repeat with a single letter between them.
# ieodomkazucvgmuy is naughty because it has a repeating letter with one between (odo), but no pair that appears twice.
#
# How many strings are nice under these new rules?
# +
import re
from itertools import permutations
PAIRS = ["%s%s" % _ for _ in permutations(string.ascii_lowercase, 2)] + DOUBLES
TRIPLES = [re.compile(f"{_}.{_}") for _ in string.ascii_lowercase]
def has_two_pairs(instr:str) -> bool:
"""Returns True if string has two non-overlapping pairs of letters
:param instr: input string
"""
paircounts = {pair: instr.count(pair) for pair in PAIRS}
candidates = [re.compile(f"{pair}.*{pair}") for (pair, val) in paircounts.items() if val > 1]
for candidate in candidates:
if re.search(candidate, instr) is not None:
return True
return False
def has_triple(instr:str) -> bool:
"""Returns True if string has repeated letter with one separating letter
:param instr: input string
"""
for triple in TRIPLES:
if re.search(triple, instr) is not None:
return True
return False
def new_naughty_or_nice(instr:str) -> bool:
"""Returns naughty/nice status with updated rules
:param instr: input string
"""
if (not has_two_pairs(instr)) or (not has_triple(instr)):
return "naughty"
return "nice"
# -
instrs = ("qjhvhtzxzqqjkmpb", "xxyxx", "uurcxstgmygtbstg", "ieodomkazucvgmuy")
for instr in instrs:
print(instr, new_naughty_or_nice(instr))
# ### Solution
with open("day05.txt", "r") as ifh:
results = [new_naughty_or_nice(_.strip()) for _ in ifh.readlines()]
print(sum([_ == "nice" for _ in results]))
|
day05.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Multivariate Linear and Logistic Regression with Regularization
# ## Terminology & Symbols
# * Training size (<span style="color:#C63">$m$</span>) - The number of samples we can use for learning
# * Dimensionality (<span style="color:#C63">$d$</span>) - The number of dimensions in the input (feature) space
# * Feature set (<span style="color:#C63">$X$</span>) - An $m \times d$ matrix where every row represents a single feature vector
# * Target (<span style="color:#C63">$y$</span>) - An $m$-vector representing the value we are trying to predict
# * Training set (<span style="color:#C63">$(X,y)$</span>) - The combined matrix of inputs and their associated known target values
# * Test set - An optional set of hold out data used for validation
#
# * Feature weights (<span style="color:#C63">$\theta$</span>) - the free variables in our modeling
# * Hypothesis function (<span style="color:#C63">$h_{\theta}(x)$</span>) - the function/model we are trying to learn by manipulating $\theta$
# * Loss Function (<span style="color:#C63">$J(\theta)$</span>) - the "error" introduced by our method (What we want to minimize)
# + [markdown] heading_collapsed=true
# ## Motivating Problems
# + [markdown] heading_collapsed=true hidden=true
# ### Regression
# + hidden=true
import numpy as np
import matplotlib.pyplot as plt
rng = np.random.RandomState(7)
## Setup training data
def f(x):
""" Magic ground truth function """
return 5./7. *((np.pi)**2 - (np.pi)**2 + - 0 * 4 + x * np.sin(x) + 2*(rng.rand(len(x))-0.5))
# generate full validation set of points
X = np.linspace(0, 10, 100)
# select a subset to act as the training data
rng.shuffle(X)
train_X = np.sort(X[:20])
train_y = f(train_X)
validation_y = f(X)
X = np.sort(X)[:, np.newaxis]
train_X = train_X[:, np.newaxis]
train_y = np.atleast_2d(train_y).T
## Plot the training data
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.legend(loc='lower left')
# + [markdown] heading_collapsed=true hidden=true
# ### Classification
# + hidden=true
## Threshold the regression data
threshold = 3**2
radius_squared = (train_y)**2 + (train_X-5)**2
idxs1 = np.where(radius_squared > threshold)
idxs2 = np.where(radius_squared <= threshold)
## Plot the training data
plt.scatter(train_X[idxs1], train_y[idxs1], color='navy', s=30, marker='x', label="class 1")
plt.scatter(train_X[idxs2], train_y[idxs2], color='orange', s=30, marker='o', label="class 2")
plt.legend(loc='upper left')
plt.show()
# -
# ## Linear Regression
# ### Univariate Linear Regression
# +
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(train_X, train_y)
y = model.predict(X)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y, color='teal', linewidth=lw, label="degree %d" % degree)
# -
# Given a training set consisting of one feature, $x$, and one target, $y$, we want to generate a hypothesis $h$ about the linear relationship between $x$ and $y$:
#
# $y \approx h(x) = a + bx$
#
# The bias ($a$) and feature weight ($b$) can be rolled into a single weight vector i.e., $\mathbf{\theta} = \begin{bmatrix} a \\ b\end{bmatrix}$:
#
# $h_{\theta}(x) = \theta_0 + \theta_1 x$
#
# In vector notation (we implicitly prepend a 1 to every x i.e., $\mathbf{x} = \begin{bmatrix} 1 \\ x\end{bmatrix}$):
#
# $h_{\theta}(x) = \mathbf{\theta}^T\mathbf{x}$
#
# One evaluation metric of the quality of fit is by looking at the **cumulative** squared error/residual:
#
# $J(\theta) = \sum_{i=1}^{m}(h_{\theta}(x_i) - y_i)^2$
#
# By minimizing $J$, we get the "best" model. I could make this an average by adding a $\frac{1}{m}$ out front, but it should be clear that this has no effect on where in weight space the minimum lies (it only squashes or stretches $J(\theta)$.
# +
def compute_cost(X, y, theta):
m = y.shape[1]
J = np.sum((X.dot(theta)-y.T)**2)/2/m
return J
def gradient_descent(X, y, theta, alpha, iterations=100):
X = np.atleast_2d(X)
y = np.atleast_2d(y)
theta = np.atleast_2d(theta)
m = y.shape[1]
J_history = np.zeros(iterations)
for i in range(iterations):
H = X.dot(theta)
loss = H - y.T
gradient = X.T.dot(loss) / m
theta = theta - alpha * gradient
J_history[i] = compute_cost(X, y, theta)
return theta, J_history
##add bias
train_X_bias = np.hstack((np.ones((train_X.shape[0], 1)), train_X))
validation_X = np.hstack((np.ones((X.shape[0], 1)), X))
initial_theta = np.zeros((train_X_bias.shape[1],1))
final_theta, J_history = gradient_descent(train_X_bias, train_y, initial_theta, 0.01, 20)
print(final_theta)
y_predict = np.dot(validation_X,final_theta)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y_predict, color='teal', linewidth=lw)
# -
plt.plot(range(len(J_history)), J_history)
# ### Multivariate Linear Regression
from sklearn.preprocessing import PolynomialFeatures
degree = 25
model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
model.fit(train_X, train_y)
y = model.predict(X)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y, color='yellowgreen', linewidth=lw, label="degree %d" % degree)
plt.gca().set_ylim(-10,10)
# Note, these last two equations do not specify the dimensionality ($d$) of $\theta$ and $x$:
#
# $h_{\theta}(x) = \mathbf{\theta}^T\mathbf{x}$
#
# $J(\theta) = \sum_{i=1}^{m}(h_{\theta}(\mathbf{x_i}) - y_i)^2$
#
# We can adapt our original test case just by adding new parameters: $\mathbf{x} = \begin{bmatrix} 1 \\ x \\ x^2 \\ x^3 \\ x^4 \end{bmatrix}$
#
# The optimum lies where the gradient is zero, we can get there two ways:
#
# 1. Solving the equation analytically
# 2. Solving the equation numerically through iteration
# #### Closed Form Solution of Ordinary Least Squares
# $J(\theta) = \sum_{i=1}^{m}(h_{\theta}(x_i) - y_i)^2$
#
# $J(\theta) = \sum_{i=1}^{m}(\theta^Tx_i - y_i)^2$
#
# The optimum occurs where the gradient is zero:
#
# \begin{align}
# \frac{d J(\theta)}{d\mathbf{\theta}} & = 0 \\
# 2 \sum_{i=1}^{m}\left[\theta^Tx_i - y_i)x_i\right] & = 0 \\
# \sum_{i=1}^{m}\left[(\theta^Tx_i)x_i - y_ix_i\right] & = 0 \\
# \sum_{i=1}^{m}(\theta^Tx_i)x_i & = \sum_{i=1}^{m}y_ix_i \\
# \sum_{i=1}^{m}(x_ix_i^T)\theta & = \sum_{i=1}^{m}y_ix_i \\
# \end{align}
#
# Let $A = \sum_{i=1}^{m}(x_ix_i^T) = \mathbf{X}^T \mathbf{X}$
#
# $b=\sum_{i=1}^{m}y_ix_i$ = $\mathbf{X}^T\mathbf{y}$
#
# \begin{align}
# A\theta & = b \\
# \theta & = A^{-1}b \\
# \theta & = (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T\mathbf{y} \\
# \end{align}
#
# Note, we are inverting $\mathbf{X}^T \mathbf{X}$ which is $m \times m$, i.e., big with lots of data.
#
# #### Gradient Descent
# Recall:
#
# $\frac{d J(\theta)}{d\theta_j} = 2 \sum_{i=1}^{m}\left[\theta^Tx_i - y_i)x_{i,j}\right]$
#
# Represents the gradient of the cost function, so if we want to minimize this, we follow its negative direction.
#
# Algorithm:
#
# > Initialize $\theta_j = \mathbf{0}$ <br>
# > Repeat { <br>
# >> $\theta_j = \theta_j - \alpha\left(\sum_{i=1}^{m}\left[(\theta^Tx_i - y_i)x_{i,j}\right]\right)$ <br>
#
# > } <br>
#
# We saw last week the benefits of stochastic gradient descent where we don't have to use the whole dataset each time to do the update.
# ## Feature Scaling
# + [markdown] heading_collapsed=true
# ### Why?
# + [markdown] hidden=true
# Varied dimension "widths" will pull the gradient descent algorithm in wider directions.
# + [markdown] heading_collapsed=true
# ### How?
# + [markdown] hidden=true
# * Range scaling $\left(\frac{x - x_{min}}{x_{max}- x_{min}}\right)$
# * Z-Score scaling $\left(\frac{x - \mu}{\sigma}\right)$
# + [markdown] heading_collapsed=true
# ## Learning Rate
# + [markdown] hidden=true
# plot # of iterations vs. cost function
# -
# ## Regularization
# $J(\theta) = \sum_{i=1}^{m}(h_{\theta}(\mathbf{x_i}) - y_i)^2 + p(\theta)$
# ### Ridge Regularization
# * $L_2$ penalty term
# * Tikhonov Regularization
#
# $p(\theta) = \lambda \sum_{i=1}^{m}\theta_i^2$
#
#
from sklearn.linear_model import Ridge
degree = 25
model = make_pipeline(PolynomialFeatures(degree), Ridge())
model.fit(train_X, train_y)
y = model.predict(X)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y, color='gold', linewidth=lw, label="degree %d" % degree)
plt.gca().set_ylim(-10,10)
# ### LASSO Regularization
# * $L_1$ penalty term
# * Reduces number of dimensions
# * Good for feature selection
#
# $p(\theta) = \lambda \sum_{i=1}^{m}|\theta_i|$
#
from sklearn.linear_model import Lasso
degree = 300
model = make_pipeline(PolynomialFeatures(degree), Lasso())
model.fit(train_X, train_y)
y = model.predict(X)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y, color='darkorange', linewidth=lw, label="degree %d" % degree)
plt.gca().set_ylim(-10,10)
# ### Elastic Net Regularization
# * Combination $L_1$ and $L_2$ Regularization
#
# $p(\theta) = \lambda_1 \sum_{i=1}^{m}|\theta_i| + \lambda_2 \sum_{i=1}^{m}\theta_i^2$
from sklearn.linear_model import ElasticNet
degree = 25
model = make_pipeline(PolynomialFeatures(degree), ElasticNet())
model.fit(train_X, train_y)
y = model.predict(X)
plt.scatter(train_X, train_y, color='navy', s=30, marker='o', label="training data")
plt.plot(X, y, color='firebrick', linewidth=lw, label="degree %d" % degree)
plt.gca().set_ylim(-10,10)
# ## Logistic Regression
# We then formulate our problem such that we are using the sigmoid function to determine the probability that an input resides in a particular class of data. With multiple classes this turns into a "one-vs.-rest" scheme, thus if there are $k$ classes, there are $k$ instances of logistics regression. The highest prediction is taken as the class for that data point.
# \begin{align}
# h_\theta(x) & = g(\theta^Tx) \\
# z & = \theta^Tx \\
# g(z) & = \frac{1}{1+e^{-z}}\\
# \end{align}
# +
def sigmoid(x):
return 1. / (1 + np.exp(-x))
xx = np.linspace(-10,10,100)
plt.plot(xx, sigmoid(xx))
# -
# We use the sigmoid function to take the discrete output and make it differentiable.
# Our $y$ values are discrete (0 or 1). How do we define a cost function for this?
#
# Existing cost function:
#
# $J(\theta) = \sum_{i=1}^{m}(h_{\theta}(x_i) - y_i)^2$
#
# This will not work as it produces a non-convex $J$.
#
# So, we need a convex cost function that has the following properties:
# * When the correct classification is 1, then a zero cost should be assigned to a value of $h(x)$ = 1
# * When the correct classification is 1, then a maximal cost should be assigned to a value of $h(x)$ = 0
# * When the correct classification is 0, then a zero cost should be assigned to a value of $h(x)$ = 0
# * When the correct classification is 0, then a maximal cost should be assigned to a value of $h(x)$ = 1
#
# Thus, we end up with:
#
# $\text{Cost}(h_\theta(x), y) = $
# \begin{cases}
# -\log(h_\theta(x)), & \text{if } y = 1\\
# -\log(1 - h_\theta(x)), & \text{if } y = 0
# \end{cases}
#
# We can do this more compactly by using the fact that y is discrete:
#
# $\text{Cost}(h, y) = -y\log(h - (1-y)\log(1 - h)$
#
#
# This simplifies the gradient needed for gradient descent:
#
# $
# \frac{d}{d \theta}J(\theta) = \frac{1}{m} \left(-y^Tlog(h) - (1-y)^Tlog(1-h))\right)
# $
# ### Regularized Logistic Regression
|
weeks2&3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.1
# language: julia
# name: julia-1.6
# ---
lines = readlines("input")
dots = split.(filter(x->occursin(",",x), lines), ",")
dots = reduce(hcat, dots) |> x -> parse.(Int,x) |> transpose
fold_instructions = split.(filter(x->occursin("fold",x), lines), " ")
fold_instructions = [split(x[3],"=") for x in fold_instructions]
fold(coord, foldpos) = coord <= foldpos ? coord : 2*foldpos - coord
fold(8,10)
fold(12,10)
fold.(dots[:,1], 655)
mat = [1 2; 2 3; 1 2; 3 4]
unique(mat, dims=1)
function vfold(x, dots)
xs = fold.(dots[:,1], x)
ys = dots[:,2]
return unique(hcat(xs, ys), dims=1)
end
vfold(parse(Int, fold_instructions[1][2]), dots)
# ## Part II
function hfold(y, dots)
ys = fold.(dots[:,2], y)
xs = dots[:,1]
return unique(hcat(xs, ys), dims=1)
end
folded = dots
for inst in fold_instructions
folded = inst[1]=="x" ? vfold(parse(Int,inst[2]),folded) : hfold(parse(Int,inst[2]),folded)
end
maximum(folded,dims=1)
final = zeros(Int, 6,39)
for pos in eachrow(folded)
final[6-pos[2],pos[1]+1] = 1
end
final
using Plots
heatmap(final, aspect_ratio=1)
|
13/13.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img style="float: right;" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOIAAAAjCAYAAACJpNbGAAAABHNCSVQ<KEY>zAAALEgAACxIB0t1+/AAAABR0RVh0Q3JlYXRpb24gVGltZQAzLzcvMTNND4u/AAAAHHRFWHRTb2Z0d2FyZQBBZG9iZSBGaXJld29ya3MgQ1M26LyyjAAACMFJREFUeJztnD1y20gWgD+6nJtzAsPhRqKL3AwqwQdYDpXDZfoEppNNTaWbmD7BUEXmI3EPMFCR2YI1UDQpdAPqBNzgvRZA/BGUZEnk9FeFIgj0z2ugX7/XP+jGer2mLv/8b6d+4Efgf/8KG0+Zn8XyXLx+bgEslqegcfzxSY3Irrx6bgEsFssBWsRGowGufwHAYtq7u+H6fUCOxTTWax4wBAbr+SRqNDKesOv3gN/133sW0yh927j1mucIaFWINl7PJ+OcvMcfW8Bol3iN44+mLIOsTCp3UJFfAETr+WRQcG8EOJpunEnTyDlYzycbeWr5xxq3jOF6PglK8ix9buv5xCsrAzBkMV1l5OwD/aJ4BXzV3+8F9z4gz/hTSbz8cxc84FuNvDc4VIsYA7+qohmGwAnycA194G22YqUYlZxv4vpN4AuwBv4oON5m8k3TVLnK4sYFcRyN86dWvCwnlCvFCeUVvwX8CkSZZ5eWs5mLJWE/VZThBMgpfirPk5J4f1SU4QsQ6LNP4+j9OkSUKdRiGlD87CWe3PcyR5PFdAhc1cz/joOziMoIeVF95GX1EGVY6bWhvsAeZQrm+kON80PDneD6PRbTi4LQpmJfsZieFaR1qXlXURh3y2BaBPyG63sspv0t6e+CKJTrf2YxHe8Qr6z8AXBdGbMoHgCTshgr4AiItfxljenPJGv5roCi+rGVw1TExTTWl99ThRsglfYHUnF7SMv+Bhjn4idxbhFLGiAu6gjXD3LuUBF5VzWi3CoAfMP1kxe7mNYZMT5DLFgf13eAXi3ZtvMOsUb3V3J5/mmqy+/66RbnTC1LFdfIu/kd8Qx2bTQeg2GBTPfiUF1TgHNE0QaIq/JDX9RKr/WBy/V8EhfEHWncWMO2EKV8S7UypYnYdE2r+o8gyj5MHXVYsZh+JnG7A+3LPQxR5g9II/UJ148ockmrybqm2+Qapo6gppwB8J7EM6jqaz8u0lhfkXgB58BKPam6rvEdh2kRARbTMa7/HXEfVqnW8hxxWwE+5+JJRTYd9CM90gxw/XFuMKMo/yTNDzUkLnbr6rCYnuH6N8igQ3CvNPJproDPuH6MKMd4Z5kMUjnrh98tn1if72/Ie729Vzq708L0YV3/HGmgB4iHsjOProhhd1lrEr4zaz/FvM4lolTnqWum/6jKmeuDmFb1jHylNg96hPQbhcU0wPVBXESvQI4W5aNshsK4jeOPhSOcOaThMVb48dhU8m2UlR+29ZHzrqyhLL0EaTROteGt67EYIsT6F1HXC/ikcvS00dl51PRwLaIwQtzCxGWRFnRMkT8v/SyAy8I+iliHJtDUsHHq7imipE42GtJanxdcB6mgQcm9MmKNs1m5F9MI13+n+cXZSEpAeV8mQgZqNkmU/HsuT7kf4PrGhXcK0h1SXv7iPKsJKCrDYvoV17+meMqhiDFlll7GEb4U3iseAf+k7mqksmU9qUoaj73E7TEtol3iZnks7Moai8WylUN3TS0WANbzyYv2rqxFtFheANYi7iGNRoPOrO2QGTQIu8vhU8vSmbWNDAHQD7vLYWfWbgFx2F3ee3FBZ9ZuIgMpTWAQdpeRXm9pPoPOrD3UMCtkQM4BRmF3ubG6ZZdxkOfCWsT9pU96CuX56KfOjeIFVC8Ar8NI0xuyOQJsVkWl8xzptQGPNY/6xFiLuL+0gIu0FVTrNESmbK7C7tLrzNpmPW0EeGF32UyFN19UnCAT4ZHGWWnYqDNrB4jViZBK/kbD9sLuMiBZSD8AVp1Z+0LD/NmZta+BIzOS3pm1xwBhd9kvkeEGUbQeqSmIdHhkXnGs5fIQRUxPV1x0Zm2zMuoq7C69rU/yBWAt4v7iAd86s/ZaDweZP+wBvwBOZ9b2SCrrmPzk+AWizA09j1QxMK4gZumcWKUWMvkdA56mfxN2l7GmHWk6V2F32Qi7yxaIsmnYHvkJ9zEQqAwBotQXwK2m0c+EN/Kk8zPTZiOkIWrp/xNTnpeOtYh7iFauN+k5W+0vXab6UsbyecAw229SxWiG3aVZ7NBCKrGHuneazy2iyBeIuxkjk9UDE1bzOtJ4IzbdwysNN0D6dnf9Rk3/iKSBWOnhUbASSWW+DbvLWM+HKreZ3O/r77gza5u842w6LxFrEfcTj+Jv3mK4q7Co63hE+fI6E94hUaT0cry+XushSuvoNZO2CdsCrlXJHDYVMUIUJso2BmhfL+wuV6rMvVR6AXnS1428XupaE7Hwnrqkg4cMGD0lr3NfpVegrUw1m2sN0+crNirEX1uTqiPbPoyI/QSKKmqA9I9aer+fcR2zxIj7GiMV+EYVIkZc3r5eH2rYI+0vnpBYIE/vGwUCdYM7s3agbqXJu58VIOwug86sfd2ZtSPNKwi7S9PHy4UnscCmXKuUZQRdsqbPwCHp2754pKYnW0akcZBO/x2df29XnvA//6iV8T3TSluBmOQlR+v5JNvaHixlDZRalRZifbZaAg3vIIrkmP6YVu6owI1M9x2r0vVIFCBGXNLS96Ph45IGY2ey6e1DY20UMaLGItUXoIhVvCv5tvDg2MWLqYNaoKBKWe6Z7gBR8OwAzZOyD4poBmtidlwt/gIxw/QHz0+oWKIoj19fRz8p3YOjoV8195F5l31ltZ5PfnluISyW+/IK6SPstRIiH/FaLHvLa2R+6F6f978AVsD7v0vf0HK4vNK9VfbVojSBceP4o/PcglgsD8GMmjaRbRCc1PEQIrbv45nlIfleIrs778XkrcWSZXMcXPZyqbvfxy7ckuyqHJPslJzH9c3We2ZRbx1O/07ziJbDI1FE2Qwp4n4DNzHJhkZF16+3bnwrCmi40U2eWoj7KZvobn7+YtKO1vPJVyyWPSZrER1kNU0TqfienpvlaWZR7oX+3tba6lxcX7MK3tNfo2RlpNc8tthsIFbAKYtpsA+TtRbLNp5/H4/EFXX0MOfbOGUxvbCKaDkEnl8Rq0jc1ayFjhFFjKwiWg6B/wNk+JCXXNBIXQAAAABJRU5ErkJggg==">
# # A Jupyter notebook demonstrating how to run multiple simulations with PCSE/WOFOST
#
# This Jupyter notebook will demonstrate how to implement a loop that can run multiple simulations using PCSE/WOFOST for water-limited conditions. Results are exported to an Excel file.
#
# **Prerequisites for running this notebook**
#
# Several packages need to be installed for running PCSE/WOFOST:
#
# 1. PCSE and its dependencies. See the [PCSE user guide](http://pcse.readthedocs.io/en/stable/installing.html) for more information;
# 2. The `pandas` module for processing and storing WOFOST output;
#
# Finally, you need a working internet connection.
# ## Importing the relevant modules
#
# First the required modules need to be imported. These include the CGMS8 data providers for PCSE as well as other relevant modules.
#
# **Important:** For the example we will assume that data files are in the data directory within the directory where this notebook is located. This will be the case if you downloaded the notebooks from github.
# +
import os, sys
data_dir = os.path.join(os.getcwd(), "data")
import yaml
import pandas as pd
import pcse
from pcse.fileinput import CABOFileReader
from pcse.models import Wofost71_WLP_FD
from pcse.base_classes import ParameterProvider
from pcse.exceptions import WeatherDataProviderError
from pcse.util import WOFOST71SiteDataProvider
from pcse.db import NASAPowerWeatherDataProvider
print("This notebook was built with:")
print("python version: %s " % sys.version)
print("PCSE version: %s" % pcse.__version__)
# -
# ## Setting up the parameters for crop, soil and site
#
# Parameter files for crop and soil were taken from the [WOFOST Control Centre](http://www.wageningenur.nl/en/Expertise-Services/Research-Institutes/alterra/Facilities-Products/Software-and-models/WOFOST/Downloads.htm). These parameter file are in the `CABO` format which can be read the with `CABOFileReader` module.
# ### Crop parameter files
crop_dir = os.path.join(data_dir, 'crop')
crop_files = [CABOFileReader(os.path.join(crop_dir,f)) for f in os.listdir(crop_dir) if f.endswith("CAB")]
# ### Soil parameter files
soil_dir = os.path.join(data_dir, 'soil')
soil_files = [CABOFileReader(os.path.join(soil_dir,f)) for f in os.listdir(soil_dir) if f.startswith("ec")]
# ### Site parameters
# Site parameters are an ancillary class of parameters that are related to a given site. For example, an important parameter is the initial amount of moisture in the soil profile (`WAV`) and the atmospheric CO2 concentration.
sited = WOFOST71SiteDataProvider(WAV=100, CO2=360., SMLIM=0.35)
# ## Agromanagement
# Agromanagement can be defined in a file but often it is easier to define it directly as a string in the YAML format. Because the agromanagement needs to be updated for each year. It can thus be manipulated by string replacement and then parsed by the yaml parser.
#
# Here we define three agromanagement scenarios which define a crop calendar (no state or timed events) with suitable sowing dates for maize, potato and sugar beet in the Netherlands.
# +
agro_maize = """
- {year}-03-01:
CropCalendar:
crop_name: '{crop}'
variety_name: 'maize'
crop_start_date: {year}-04-15
crop_start_type: sowing
crop_end_date:
crop_end_type: maturity
max_duration: 300
TimedEvents: null
StateEvents: null
- {year}-12-01: null
"""
agro_potato = """
- {year}-03-01:
CropCalendar:
crop_name: '{crop}'
variety_name: 'potato'
crop_start_date: {year}-05-01
crop_start_type: sowing
crop_end_date:
crop_end_type: maturity
max_duration: 300
TimedEvents: null
StateEvents: null
- {year}-12-01: null
"""
agro_sugarbeet = """
- {year}-03-01:
CropCalendar:
crop_name: '{crop}'
variety_name: 'sugar_beet'
crop_start_date: {year}-05-01
crop_start_type: sowing
crop_end_date: {year}-10-15
crop_end_type: harvest
max_duration: 300
TimedEvents: null
StateEvents: null
- {year}-12-01: null
"""
agro_templates = [agro_maize, agro_potato, agro_sugarbeet]
# -
# ## Daily weather data
#
# Weather data will be derived from the NASA POWER database which provides weather data at a resolution of 0.5x0.5 degree.
weatherdata = NASAPowerWeatherDataProvider(longitude=5, latitude=52)
print(weatherdata)
# ### Exporting weather data
# Weather data can also be easily exported to a dataframe for further analysis.
df = pd.DataFrame(weatherdata.export()).set_index("DAY")
df.head()
# ## Simulating with WOFOST
#
# ### Implementing the main loop
# The following example implements a loop running over all years, crops and soil types. Daily output for each run is converted to a Pandas DataFrame and written as a separate excel file to an output folder. Summary results from all simulations is written to a separate excel file at the end of the simulation.
# +
# Placeholder for storing summary results
summary_results = []
# Years to simulate
years = range(2004, 2008)
# Loop over crops, soils and years
for cropd, agro in zip(crop_files, agro_templates):
crop_type = cropd['CRPNAM']
for soild in soil_files:
soil_type = soild['SOLNAM']
for year in years:
# String to identify this run
run_id = "{crop}_{soil}_{year}".format(crop=crop_type, soil=soil_type, year=year)
# Set the agromanagement with correct year and crop
agromanagement = yaml.load(agro.format(year=year, crop=crop_type))
# Encapsulate parameters
parameters = ParameterProvider(sitedata=sited, soildata=soild, cropdata=cropd)
# Start WOFOST, run the simulation
try:
wofost = Wofost71_WLP_FD(parameters, weatherdata, agromanagement)
wofost.run_till_terminate()
except WeatherDataProviderError as e:
msg = "Runid '%s' failed because of missing weather data." % run_id
print(msg)
continue
# convert daily output to Pandas DataFrame and store it
df = pd.DataFrame(wofost.get_output()).set_index("day")
fname = os.path.join(data_dir, "output", run_id + ".xls")
df.to_excel(fname)
# Collect summary results
r = wofost.get_summary_output()[0]
r['run_id'] = run_id
summary_results.append(r)
# -
# ### Looking at the summary results
# The summary results output provides a concise overview of the results of all simulations. If you are interested only in the final simulation results it is often more convenient to use the summary results. Moreover, some output (such as the date of anthesis - `DOA`) that is provided in the summary results cannot be easily gathered from the daily output.
# Write the summary results to an excel file
df_summary = pd.DataFrame(summary_results).set_index('run_id')
fname = os.path.join(data_dir, "output", "summary_results.xls")
df_summary.to_excel(fname)
df_summary.head()
# ### Looking at the daily results
# The excel files with the results from the batch simulation in the output folder should look like the figure below. Each excel file provides the results from a combination of crop, soil type and year:
# 
|
04 Running PCSE in batch mode.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %reset -f
# %matplotlib inline
import pyross
import numpy as np
import matplotlib.pyplot as plt
# # Introduction: Forecast for SEAI5R model with stochastic parameters
# In this notebook, we consider the SEAI5R model with UK age structure and contact matrix. **Note that while we consider the UK age structure and contact matrix, the model parameters are not fitted to any data, but rather chosen ad-hoc.**
#
# Based on the results of inference, we calculate a forecast (including 90/10 percentiles), both with and without interventions.
# ### Load age structure, contact matrix, and results from inference
# +
## population and age classes
M=4 ## number of age classes
my_data = np.genfromtxt('../data/age_structures/UK.csv', delimiter=',', skip_header=1)
aM, aF = my_data[:, 1], my_data[:, 2]
Ni0=aM+aF; Ni=np.zeros((M))
# scale the population down to a more manageble level
Ni[0] = (np.sum(Ni0[0:4])).astype('int')
Ni[1] = (np.sum(Ni0[4:8])).astype('int')
Ni[2] = (np.sum(Ni0[8:12])).astype('int')
Ni[3] = (np.sum(Ni0[12:16])).astype('int')
N=np.sum(Ni)
print(N)
fi = Ni/N
# +
# Get individual contact matrices
CH0, CW0, CS0, CO0 = pyross.contactMatrix.UK()
CH = np.zeros((M, M))
CW = np.zeros((M, M))
CS = np.zeros((M, M))
CO = np.zeros((M, M))
for i in range(16):
CH0[i,:] = CH0[i,:]*Ni0[i]
CW0[i,:] = CW0[i,:]*Ni0[i]
CS0[i,:] = CS0[i,:]*Ni0[i]
CO0[i,:] = CO0[i,:]*Ni0[i]
for i in range(M):
for j in range(M):
i1, j1 = i*4, j*4
CH[i,j] = np.sum( CH0[i1:i1+4, j1:j1+4] )/Ni[i]
CW[i,j] = np.sum( CW0[i1:i1+4, j1:j1+4] )/Ni[i]
CS[i,j] = np.sum( CS0[i1:i1+4, j1:j1+4] )/Ni[i]
CO[i,j] = np.sum( CO0[i1:i1+4, j1:j1+4] )/Ni[i]
C = CH + CW + CS +CO
# NOTE: For the inference all population numbers were divided by 5e2. We here assume
# that this does not change the result of the inference!!
N = N#/ 5e2
Ni = Ni #/5e2
# +
pre_intervention_traj = np.load('../inference/pre_intervention_traj_SEAI5R.npy')*5e2
print(np.shape(pre_intervention_traj))
'''
fig,ax = plt.subplots(1,1,figsize=(10,6))
for i,e in enumerate(pre_intervention_traj.T):
ax.plot(e)
plt.show()
plt.close()
''';
# -
# Note that for the plots below, we do not show the actual trajectory used for the inference, but a newly generated "reference trajectory". Since in the scales below the time interval where inference is done (up to time 20 days) is not really resolvable, this does not really change the plots.
#
# **Note that while we consider the UK age structure and contact matrix, the model parameters are not fitted to any data, but rather chosen ad-hoc.**
# +
# Generate longer trajectory, which is used as "reference trajectory"
beta = 0.04 # infection rate
gIa = 1./7 # removal rate of asymptomatic infectives
gIs = 1./7
gIh = 1/14
gIc = 1/14
alpha = 0.2 # fraction of asymptomatic infectives
fsa = 0.8 # the self-isolation parameter
fh = 0.1
gE = 1/5
gA = 1/3
hh = 0.1*np.ones(M) # fraction which goes from Is to hospital
cc = 0.05*np.ones(M) # fraction which goes from hospital to ICU
mm = 0.4*np.ones(M) # mortality from IC
sa = 0 # change in the population, not taken into account by inference at the moment
# initial conditions
E0 = np.array([10]*M)
A0 = np.array([10]*M)
Ia0 = np.array([10]*M)# each age group has asymptomatic infectives
Is0 = np.array([10]*M)# and also symptomatic infectives
Ih0 = np.array([10]*M)
Ic0 = np.array([10]*M)
Im0 = np.array([2]*M)
R0 = np.zeros(M)
S0 = Ni.copy() - (Ia0+Is0+R0+E0+A0+Ih0+Ic0+Im0)
parameters = {'alpha':alpha,'beta':beta, 'gIa':gIa,'gIs':gIs,
'gIh':gIh,'gIc':gIc, 'gE':gE, 'gA':gA,
'fsa':fsa, 'fh':fh,
'sa':sa, 'hh':hh, 'cc':cc, 'mm':mm}
model = pyross.stochastic.SEAI5R(parameters, M, Ni.copy())
#print(Ni)
# the contact structure is independent of time
def contactMatrix(t):
return C
# start simulation
Tf_reference=600; Nf_reference=Tf_reference+1
data_reference=model.simulate(S0, E0, A0, Ia0, Is0, Ih0, Ic0, Im0, contactMatrix, Tf_reference, Nf_reference,
method='tau-leaping',
)
#print(data_reference['X'][30])
'''
fig,ax = plt.subplots(1,1,figsize=(10,6))
for i,e in enumerate(data_reference['X'].T):
ax.plot(e)
plt.show()
plt.close()
''';
# -
# Now we load the means + covariance matrix obtained from inference
# +
means = np.load('../inference/optimal_model_param_SEAI5R.npy')
alpha, beta, gIa, gIs, gE, gA = means
print(means)
hess = np.load('../inference/hessian_SEAI5R.npy')
cov = np.linalg.inv(hess)# * 10.
# these parameters we assume exact
gIh = 1/14
gIc = 1/14
fsa = 0.8 # the self-isolation parameter
fh = 0.1
hh = 0.1*np.ones(M) # fraction which goes from Is to hospital
cc = 0.05*np.ones(M) # fraction which goes from hospital to ICU
mm = 0.4*np.ones(M) # mortality from IC
sa = 0*np.ones(M) # arrival of new susceptibles
# take the values at time 20 days of the reference trajectory as initial condition for the forecast
index_initial_condition = 20
S_0 = data_reference['X'][index_initial_condition,:M]
E_0 = data_reference['X'][index_initial_condition,M:2*M]
A_0 = data_reference['X'][index_initial_condition,2*M:3*M]
Ia_0 = data_reference['X'][index_initial_condition,3*M:4*M]
Is_0 = data_reference['X'][index_initial_condition,4*M:5*M]
Ih_0 = data_reference['X'][index_initial_condition,5*M:6*M]
Ic_0 = data_reference['X'][index_initial_condition,6*M:7*M]
Im_0 = data_reference['X'][index_initial_condition,7*M:8*M]
Ni_0 = data_reference['X'][index_initial_condition,8*M:]
# -
print(cov)
# ## Forecast without interventions
# +
# duration of simulation
Tf_forecast=580; Nf_forecast=Tf_forecast+1;
# the contact structure is independent of time
def contactMatrix(t):
return C
# intantiate model
parameters = {'alpha':alpha,'beta':beta, 'gIa':gIa,'gIs':gIs,
'gIh':gIh,'gIc':gIc, 'gE':gE, 'gA':gA,
'fsa':fsa, 'fh':fh,
'sa':sa,
'hh':hh, 'cc':cc, 'mm':mm,
'cov':cov}
# +
N_samples = 500
output_trajectories = np.zeros([N_samples,M*9,Nf_forecast],dtype=float)
sample_parameters = np.random.multivariate_normal(means, cov, N_samples)
for i in range(N_samples):
print(i,end='\r')
while (sample_parameters[i] < 0).any():
sample_parameters[i] = np.random.multivariate_normal(means, cov)
#
parameters = {'alpha':sample_parameters[i,0],
'beta':sample_parameters[i,1],
'gIa':sample_parameters[i,2],
'gIs':sample_parameters[i,3],
'gE':sample_parameters[i,4],
'gA':sample_parameters[i,5],
'gIh':gIh,'gIc':gIc,
'fsa':fsa,'fh':fh,
'sa':sa,'hh':hh,
'mm':mm,'cc':cc
}
#model = pyross.stochastic.SEAI5R(parameters, M, np.array( Ni.copy(),dtype=float))
model = pyross.deterministic.SEAI5R(parameters, M, np.array( Ni.copy(),dtype=float))
result = model.simulate(S_0, E_0, A_0, Ia_0, Is_0, Ih_0, Ic_0, Im_0,
#events =events,
# contactMatrices=contactMatrices,
contactMatrix=contactMatrix,
Tf=Tf_forecast, Nf=Nf_forecast,
#verbose=True,
# method='tau-leaping'
)
output_trajectories[i] = result['X'].T
# -
trajectories_forecast = output_trajectories
t_forecast = result['t'] + 20
# +
# Plot sum of A, Ia, Is populations
Tf_inference = 20
fontsize=25
ylabel=r'Fraction of infectives'
# Plot total number of symptomatic infectives
cur_trajectories_forecast = np.sum( trajectories_forecast[:,2*M:5*M,:] , axis = 1)
cur_mean_forecast = np.mean( cur_trajectories_forecast, axis=0)
percentile = 10
percentiles_lower = np.percentile(cur_trajectories_forecast,percentile,axis=0)
percentiles_upper = np.percentile(cur_trajectories_forecast,100-percentile,axis=0)
percentiles_median = np.percentile(cur_trajectories_forecast,50,axis=0)
cur_trajectory_underlying = np.sum( data_reference['X'][:,2*M:5*M] ,axis=1 )
#
# Plot trajectories
#
fig, ax = plt.subplots(1,1,figsize=(6,4))
ax.axvspan(0, Tf_inference,
label='Range used for inference',
alpha=0.3, color='dodgerblue')
ax.set_title(r'Inference and forecast',
y=1.05,
fontsize=fontsize)
for i,e in enumerate(cur_trajectories_forecast):
ax.plot(t_forecast,e/N,
alpha=0.15,
lw=3,
)
ax.plot(cur_trajectory_underlying/N,
lw=3,
color='limegreen',
label='Trajectory used for inference')
ax.plot(t_forecast,percentiles_median/N,
alpha=1,ls='--',
color='orange',label='Median',
lw=3)
ax.set_xlim(0,np.max(t_forecast))
ax.set_xlim(0,300)
ax.set_ylabel(ylabel,fontsize=fontsize)
ax.set_xlabel(r'$t$ [days]',fontsize=fontsize)
ax.legend(loc='upper right',bbox_to_anchor=(1.1,1),
fontsize=12)
plt.show()
fig.savefig('SEAI5R_UK_inference_forecasting_0.png',bbox_inches='tight',dpi=100)
fig.savefig('SEAI5R_UK_inference_forecasting_0.jpg',bbox_inches='tight',dpi=300)
plt.close()
# Plot sum of A, Ia, Is populations
Tf_inference = 20
fontsize=25
#
ylabel=r'Fraction of infectives'
#
# Plot total number of symptomatic infectives
cur_trajectories_forecast = np.sum( trajectories_forecast[:,2*M:5*M,:] , axis = 1)
cur_mean_forecast = np.mean( cur_trajectories_forecast, axis=0)
percentile = 10
percentiles_lower = np.percentile(cur_trajectories_forecast,percentile,axis=0)
percentiles_upper = np.percentile(cur_trajectories_forecast,100-percentile,axis=0)
percentiles_median = np.percentile(cur_trajectories_forecast,50,axis=0)
cur_trajectory_underlying = np.sum( data_reference['X'][:,2*M:5*M] ,axis=1 )
#
# Plot trajectories
#
fig, ax = plt.subplots(1,1,figsize=(6,4))
ax.axvspan(0, Tf_inference,
label='Range used for inference',
alpha=0.3, color='dodgerblue')
ax.set_title(r'Inference and forecast',
y=1.05,
fontsize=fontsize)
ax.plot(cur_trajectory_underlying/N,
lw=3,
color='limegreen',
label='Trajectory used for inference')
ax.plot(t_forecast,percentiles_median/N,
alpha=1,ls='--',
color='orange',label='Median',
lw=3)
# remove comments to plot percentiles
ax.fill_between(t_forecast,percentiles_lower/N,
percentiles_upper/N,
alpha=0.3,
lw=2,
label=r'10/90 Percentiles',
color='orange',
)
ax.set_xlim(0,np.max(t_forecast))
ax.set_xlim(0,300)
ax.set_ylabel(ylabel,fontsize=fontsize)
ax.set_xlabel(r'$t$ [days]',fontsize=fontsize)
ax.legend(loc='upper right',bbox_to_anchor=(1.1,1),
fontsize=12)
plt.show()
fig.savefig('SEAI5R_UK_inference_forecasting_1.png',bbox_inches='tight',dpi=100)
fig.savefig('SEAI5R_UK_inference_forecasting_1.jpg',bbox_inches='tight',dpi=300)
plt.close()
# -
# ## Forecast with interventions
# +
output_trajectories_2 = np.zeros([N_samples,M*9,Nf_forecast],dtype=float)
sample_parameters = np.random.multivariate_normal(means, cov, N_samples)
beginning_lockdown_1 = 50
end_lockdown_1 = 150
beginning_lockdown_2 = 180
end_lockdown_2 = 250
def contactMatrix2(t):
if t < beginning_lockdown_1: #or t > 150) and (t < 200):
return C
elif t < end_lockdown_1:
return CH
elif t < beginning_lockdown_2:
return C
elif t < end_lockdown_2:
return CH
else:
return C
for i in range(N_samples):
print(i,end='\r')
while (sample_parameters[i] < 0).any():
sample_parameters[i] = np.random.multivariate_normal(means, cov)
#
parameters = {'alpha':sample_parameters[i,0],
'beta':sample_parameters[i,1],
'gIa':sample_parameters[i,2],
'gIs':sample_parameters[i,3],
'gE':sample_parameters[i,4],
'gA':sample_parameters[i,5],
'gIh':gIh,'gIc':gIc,
'fsa':fsa,'fh':fh,
'sa':sa,'hh':hh,
'mm':mm,'cc':cc
}
#model = pyross.stochastic.SEAI5R(parameters, M, np.array( Ni.copy(),dtype=float))
model = pyross.deterministic.SEAI5R(parameters, M, np.array( Ni.copy(),dtype=float))
result = model.simulate(S_0, E_0, A_0, Ia_0, Is_0, Ih_0, Ic_0, Im_0,
#events =events,
# contactMatrices=contactMatrices,
contactMatrix=contactMatrix2,
Tf=Tf_forecast, Nf=Nf_forecast,
#verbose=True,
#method='tau-leaping'
)
output_trajectories_2[i] = result['X'].T
# -
trajectories_forecast = output_trajectories_2
# +
# Plot sum of A, Ia, Is populations
Tf_inference = 20
fontsize=25
#
ylabel=r'Fraction of infectives'
#
# Plot total number of symptomatic infectives
cur_trajectories_forecast = np.sum( trajectories_forecast[:,2*M:5*M,:] , axis = 1)
cur_mean_forecast = np.mean( cur_trajectories_forecast, axis=0)
percentile = 10
percentiles_lower = np.percentile(cur_trajectories_forecast,percentile,axis=0)
percentiles_upper = np.percentile(cur_trajectories_forecast,100-percentile,axis=0)
percentiles_median = np.percentile(cur_trajectories_forecast,50,axis=0)
#
# Plot trajectories
#
fig, ax = plt.subplots(1,1,figsize=(7,5))
ax.axvspan(0, Tf_inference,
label='Range used for inference',
alpha=0.3, color='dodgerblue')
ax.axvspan(beginning_lockdown_1+Tf_inference,end_lockdown_1+Tf_inference,
label='Lockdown',
alpha=0.1, color='crimson')
ax.axvspan(beginning_lockdown_2+Tf_inference,end_lockdown_2+Tf_inference,
# label='Lockdown',
alpha=0.1, color='crimson')
ax.set_title(r'Inference, forecast, and interventions',
y=1.05,
fontsize=fontsize)
for i,e in enumerate(cur_trajectories_forecast):
ax.plot(t_forecast,e/N,
alpha=0.15,
lw=3,
)
ax.plot(cur_trajectory_underlying/N,
lw=3,
color='limegreen',
label='Trajectory used for inference\n(without interventions)')
ax.plot(t_forecast,percentiles_median/N,
alpha=1,ls='--',
color='orange',label='Median',
lw=3)
ax.set_xlim(0,np.max(t_forecast))
ax.set_ylabel(ylabel,fontsize=fontsize)
ax.set_xlabel(r'$t$ [days]',fontsize=fontsize)
ax.legend(loc='upper right',bbox_to_anchor=(1.,1),
fontsize=12)
ax.set_ylim(-0.005,0.13)
plt.show()
fig.savefig('SEAI5R_UK_inference_forecasting_2.png',bbox_inches='tight',dpi=100)
fig.savefig('SEAI5R_UK_inference_forecasting_2.jpg',bbox_inches='tight',dpi=300)
plt.close()
fig, ax = plt.subplots(1,1,figsize=(7,5))
ax.axvspan(0, Tf_inference,
label='Range used for inference',
alpha=0.3, color='dodgerblue')
ax.axvspan(beginning_lockdown_1+Tf_inference,end_lockdown_1+Tf_inference,
label='Lockdown',
alpha=0.1, color='crimson')
ax.axvspan(beginning_lockdown_2+Tf_inference,end_lockdown_2+Tf_inference,
# label='Lockdown',
alpha=0.1, color='crimson')
ax.set_title(r'Inference, forecast, and interventions',
y=1.05,
fontsize=fontsize)
ax.plot(cur_trajectory_underlying/N,
lw=3,
color='limegreen',
label='Trajectory used for inference\n(without interventions)')
ax.plot(t_forecast,percentiles_median/N,
alpha=1,ls='--',
color='orange',label='Median',
lw=3)
ax.fill_between(t_forecast,percentiles_lower/N,
percentiles_upper/N,
alpha=0.3,
lw=2,
label=r'10/90 Percentiles',
color='orange',
)
ax.set_xlim(0,np.max(t_forecast))
ax.set_ylabel(ylabel,fontsize=fontsize)
ax.set_xlabel(r'$t$ [days]',fontsize=fontsize)
ax.legend(loc='upper right',bbox_to_anchor=(1.,1),
fontsize=12)
ax.set_ylim(-0.005,0.1)
plt.show()
fig.savefig('SEAI5R_UK_inference_forecasting_3.png',bbox_inches='tight',dpi=100)
fig.savefig('SEAI5R_UK_inference_forecasting_3.jpg',bbox_inches='tight',dpi=300)
plt.close()
fig, ax = plt.subplots(1,1,figsize=(7,5))
ax.axvspan(0, Tf_inference,
label='Range used for inference',
alpha=0.3, color='dodgerblue')
ax.axvspan(beginning_lockdown_1+Tf_inference,end_lockdown_1+Tf_inference,
label='Lockdown',
alpha=0.1, color='crimson')
ax.axvspan(beginning_lockdown_2+Tf_inference,end_lockdown_2+Tf_inference,
# label='Lockdown',
alpha=0.1, color='crimson')
ax.set_title(r'Inference, forecast, and interventions',
y=1.05,
fontsize=fontsize)
ax.plot(cur_trajectory_underlying[:21]/N,
lw=3,
color='limegreen',
label='Trajectory used for inference')
ax.plot(t_forecast,percentiles_median/N,
alpha=1,ls='--',
color='orange',label='Median',
lw=3)
ax.fill_between(t_forecast,percentiles_lower/N,
percentiles_upper/N,
alpha=0.3,
lw=2,
label=r'10/90 Percentiles',
color='orange',
)
ax.set_xlim(0,np.max(t_forecast))
ax.set_ylabel(ylabel,fontsize=fontsize)
ax.set_xlabel(r'$t$ [days]',fontsize=fontsize)
ax.legend(loc='upper right',bbox_to_anchor=(1.,1),
fontsize=12)
ax.set_ylim(-0.005,0.1)
plt.show()
fig.savefig('SEAI5R_UK_inference_forecasting_4.png',bbox_inches='tight',dpi=100)
fig.savefig('SEAI5R_UK_inference_forecasting_4.jpg',bbox_inches='tight',dpi=300)
plt.close()
# -
|
examples/forecast/notebooks-to-be-updated/ex13 - SEAI5R - UK- forecasting with interventions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# + [markdown] origin_pos=0
# # Natural Language Processing: Pretraining
# :label:`chap_nlp_pretrain`
#
#
# Humans need to communicate.
# Out of this basic need of the human condition, a vast amount of written text has been generated on an everyday basis.
# Given rich text in social media, chat apps, emails, product reviews, news articles, research papers, and books, it becomes vital to enable computers to understand them to offer assistance or make decisions based on human languages.
#
# *Natural language processing* studies interactions between computers and humans using natural languages.
# In practice, it is very common to use natural language processing techniques to process and analyze text (human natural language) data, such as language models in :numref:`sec_language_model` and machine translation models in :numref:`sec_machine_translation`.
#
# To understand text, we can begin by learning
# its representations.
# Leveraging the existing text sequences
# from large corpora,
# *self-supervised learning*
# has been extensively
# used to pretrain text representations,
# such as by predicting some hidden part of the text
# using some other part of their surrounding text.
# In this way,
# models learn through supervision
# from *massive* text data
# without *expensive* labeling efforts!
#
#
# As we will see in this chapter,
# when treating each word or subword as an individual token,
# the representation of each token can be pretrained
# using word2vec, GloVe, or subword embedding models
# on large corpora.
# After pretraining, representation of each token can be a vector,
# however, it remains the same no matter what the context is.
# For instance, the vector representation of "bank" is the same
# in both
# "go to the bank to deposit some money"
# and
# "go to the bank to sit down".
# Thus, many more recent pretraining models adapt representation of the same token
# to different contexts.
# Among them is BERT, a much deeper self-supervised model based on the transformer encoder.
# In this chapter, we will focus on how to pretrain such representations for text,
# as highlighted in :numref:`fig_nlp-map-pretrain`.
#
# 
# :label:`fig_nlp-map-pretrain`
#
#
# For sight of the big picture,
# :numref:`fig_nlp-map-pretrain` shows that
# the pretrained text representations can be fed to
# a variety of deep learning architectures for different downstream natural language processing applications.
# We will cover them in :numref:`chap_nlp_app`.
#
# :begin_tab:toc
# - [word2vec](word2vec.ipynb)
# - [approx-training](approx-training.ipynb)
# - [word-embedding-dataset](word-embedding-dataset.ipynb)
# - [word2vec-pretraining](word2vec-pretraining.ipynb)
# - [glove](glove.ipynb)
# - [subword-embedding](subword-embedding.ipynb)
# - [similarity-analogy](similarity-analogy.ipynb)
# - [bert](bert.ipynb)
# - [bert-dataset](bert-dataset.ipynb)
# - [bert-pretraining](bert-pretraining.ipynb)
# :end_tab:
#
|
d2l/tensorflow/chapter_natural-language-processing-pretraining/index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# Text provided under a Creative Commons Attribution license, CC-BY. All code is made available under the FSF-approved MIT license. (c) <NAME>, <NAME> 2015. Thanks to NSF for support via CAREER award #1149784.
# -
# [@LorenaABarba](https://twitter.com/LorenaABarba)
# ##### Version 0.12 (August 2015)
# 12 steps to Navier-Stokes
# ======
# ***
# Hello! Welcome to the **12 steps to Navier-Stokes**. This is a practical module that is used in the beginning of an interactive Computational Fluid Dynamics (CFD) course taught by [Prof. <NAME>](http://lorenabarba.com) since Spring 2009 at Boston University. The course assumes only basic programming knowledge (in any language) and of course some foundation in partial differential equations and fluid mechanics. The practical module was inspired by the ideas of Dr. Rio Yokota, who was a post-doc in Barba's lab, and has been refined by Prof. Barba and her students over several semesters teaching the course. The course is taught entirely using Python and students who don't know Python just learn as we work through the module.
#
# This [IPython notebook](http://ipython.org/ipython-doc/stable/interactive/htmlnotebook.html) will lead you through the first step of programming your own Navier-Stokes solver in Python from the ground up. We're going to dive right in. Don't worry if you don't understand everything that's happening at first, we'll cover it in detail as we move forward and you can support your learning with the videos of [<NAME>'s lectures on YouTube](http://www.youtube.com/playlist?list=PL30F4C5ABCE62CB61).
#
# For best results, after you follow this notebook, prepare your own code for Step 1, either as a Python script or in a clean IPython notebook.
#
# To execute this Notebook, we assume you have invoked the notebook server using: `ipython notebook`.
# Step 1: 1-D Linear Convection
# -----
# ***
# The 1-D Linear Convection equation is the simplest, most basic model that can be used to learn something about CFD. It is surprising that this little equation can teach us so much! Here it is:
#
# $$\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0$$
#
# With given initial conditions (understood as a *wave*), the equation represents the propagation of that initial *wave* with speed $c$, without change of shape. Let the initial condition be $u(x,0)=u_0(x)$. Then the exact solution of the equation is $u(x,t)=u_0(x-ct)$.
#
# We discretize this equation in both space and time, using the Forward Difference scheme for the time derivative and the Backward Difference scheme for the space derivative. Consider discretizing the spatial coordinate $x$ into points that we index from $i=0$ to $N$, and stepping in discrete time intervals of size $\Delta t$.
#
# From the definition of a derivative (and simply removing the limit), we know that:
#
# $$\frac{\partial u}{\partial x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x}$$
#
# Our discrete equation, then, is:
#
# $$\frac{u_i^{n+1}-u_i^n}{\Delta t} + c \frac{u_i^n - u_{i-1}^n}{\Delta x} = 0 $$
#
# Where $n$ and $n+1$ are two consecutive steps in time, while $i-1$ and $i$ are two neighboring points of the discretized $x$ coordinate. If there are given initial conditions, then the only unknown in this discretization is $u_i^{n+1}$. We can solve for our unknown to get an equation that allows us to advance in time, as follows:
#
# $$u_i^{n+1} = u_i^n - c \frac{\Delta t}{\Delta x}(u_i^n-u_{i-1}^n)$$
#
# Now let's try implementing this in Python.
#
# We'll start by importing a few libraries to help us out.
#
# * `numpy` is a library that provides a bunch of useful matrix operations akin to MATLAB
# * `matplotlib` is a 2D plotting library that we will use to plot our results
# * `time` and `sys` provide basic timing functions that we'll use to slow down animations for viewing
# Remember: comments in python are denoted by the pound sign
import numpy #here we load numpy
from matplotlib import pyplot #here we load matplotlib
import time, sys #and load some utilities
#this makes matplotlib plots appear in the notebook (instead of a separate window)
# %matplotlib inline
# Now let's define a few variables; we want to define an evenly spaced grid of points within a spatial domain that is 2 units of length wide, i.e., $x_i\in(0,2)$. We'll define a variable `nx`, which will be the number of grid points we want and `dx` will be the distance between any pair of adjacent grid points.
nx = 41 # try changing this number from 41 to 81 and Run All ... what happens?
dx = 2 / (nx-1)
nt = 25 #nt is the number of timesteps we want to calculate
dt = .025 #dt is the amount of time each timestep covers (delta t)
c = 1 #assume wavespeed of c = 1
# We also need to set up our initial conditions. The initial velocity $u_0$ is given as
# $u = 2$ in the interval $0.5 \leq x \leq 1$ and $u = 1$ everywhere else in $(0,2)$ (i.e., a hat function).
#
# Here, we use the function `ones()` defining a `numpy` array which is `nx` elements long with every value equal to 1.
u = numpy.ones(nx) #numpy function ones()
u[int(.5 / dx):int(1 / dx + 1)] = 2 #setting u = 2 between 0.5 and 1 as per our I.C.s
print(u)
# Now let's take a look at those initial conditions using a Matplotlib plot. We've imported the `matplotlib` plotting library `pyplot` and the plotting function is called `plot`, so we'll call `pyplot.plot`. To learn about the myriad possibilities of Matplotlib, explore the [Gallery](http://matplotlib.org/gallery.html) of example plots.
#
# Here, we use the syntax for a simple 2D plot: `plot(x,y)`, where the `x` values are evenly distributed grid points:
pyplot.plot(numpy.linspace(0, 2, nx), u);
# Why doesn't the hat function have perfectly straight sides? Think for a bit.
# Now it's time to implement the discretization of the convection equation using a finite-difference scheme.
#
# For every element of our array `u`, we need to perform the operation $u_i^{n+1} = u_i^n - c \frac{\Delta t}{\Delta x}(u_i^n-u_{i-1}^n)$
#
# We'll store the result in a new (temporary) array `un`, which will be the solution $u$ for the next time-step. We will repeat this operation for as many time-steps as we specify and then we can see how far the wave has convected.
#
# We first initialize our placeholder array `un` to hold the values we calculate for the $n+1$ timestep, using once again the NumPy function `ones()`.
#
# Then, we may think we have two iterative operations: one in space and one in time (we'll learn differently later), so we'll start by nesting one loop inside the other. Note the use of the nifty `range()` function. When we write: `for i in range(1,nx)` we will iterate through the `u` array, but we'll be skipping the first element (the zero-th element). *Why?*
# +
un = numpy.ones(nx) #initialize a temporary array
for n in range(nt): #loop for values of n from 0 to nt, so it will run nt times
un = u.copy() ##copy the existing values of u into un
for i in range(1, nx): ## you can try commenting this line and...
#for i in range(nx): ## ... uncommenting this line and see what happens!
u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])
# -
# **Note**—We will learn later that the code as written above is quite inefficient, and there are better ways to write this, Python-style. But let's carry on.
#
# Now let's try plotting our `u` array after advancing in time.
pyplot.plot(numpy.linspace(0, 2, nx), u);
# OK! So our hat function has definitely moved to the right, but it's no longer a hat. **What's going on?**
# Learn More
# -----
# ***
# For a more thorough explanation of the finite-difference method, including topics like the truncation error, order of convergence and other details, watch **Video Lessons 2 and 3** by Prof. Barba on YouTube.
from IPython.display import YouTubeVideo
YouTubeVideo('iz22_37mMkk')
YouTubeVideo('xq9YTcv-fQg')
# For a careful walk-through of the discretization of the linear convection equation with finite differences (and also the following steps, up to Step 4), watch **Video Lesson 4** by Prof. Barba on YouTube.
YouTubeVideo('y2WaK7_iMRI')
# ## Last but not least
# **Remember** to rewrite Step 1 as a fresh Python script or in *your own* IPython notebook and then experiment by changing the discretization parameters. Once you have done this, you will be ready for [Step 2](./02_Step_2.ipynb).
#
#
# ***
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
# > (The cell above executes the style for this notebook. We modified a style we found on the GitHub of [CamDavidsonPilon](https://github.com/CamDavidsonPilon), [@Cmrn_DP](https://twitter.com/cmrn_dp).)
|
CFDPython/lessons-own/01_Step_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.neighbors import NearestNeighbors, DistanceMetric
import pandas as pd
import numpy as np
# %matplotlib inline
# # Dummy example on short texts
# ## Bag of word model
# list of text documents
text_test = ["This is a test document","this is a second text","and here is a third text", "this is a dum text!"]
# create the transform
vectorizer_test = CountVectorizer()
# tokenize and build vocab
vectorizer_test.fit(text_test)
# summarize
print(vectorizer_test.vocabulary_)
# encode document
vector_test = vectorizer_test.transform(text_test)
# summarize encoded vector
print(vector_test.toarray())
data= pd.DataFrame(vector_test.toarray())
data.columns = vectorizer_test.get_feature_names()
data.head()
# ## TF-IDF of documents
# create the transform
vectorizer_tfidf_test = TfidfVectorizer()
# tokenize and build vocab
vectorizer_tfidf_test.fit(text_test)
# summarize
print(vectorizer_tfidf_test.vocabulary_)
# +
# encode document
vector_tfidf_test = vectorizer_tfidf_test.transform(text_test)
data= pd.DataFrame(vector_tfidf_test.toarray())
data.columns = vectorizer_tfidf_test.get_feature_names()
data.head()
# -
# ## Compute distances between documents
# +
dist = DistanceMetric.get_metric('euclidean')
data= pd.DataFrame(dist.pairwise(vector_tfidf_test.toarray()))
data
# +
dist = DistanceMetric.get_metric('braycurtis')
data= pd.DataFrame(dist.pairwise(vector_tfidf_test.toarray()))
data
# -
# # Using Wikipedia abstracts
# ## Import dataset
# import text documents from wikipedia abstracts
wiki_data=pd.read_csv('new_zeland_people.tsv',delimiter='\t', index_col='name')['abstract']
len(wiki_data)
wiki_data.head()
# ## Compute word counts
# +
name = '<NAME>'
#Extract text for a particular person
text = wiki_data[name]
#Define the count vectorizer that will be used to process the data
count_vectorizer = CountVectorizer()
#Apply this vectorizer to text to get a sparse matrix of counts
count_matrix = count_vectorizer.fit_transform([text])
#Get the names of the features
features = count_vectorizer.get_feature_names()
#Create a series from the sparse matrix
d = pd.Series(count_matrix.toarray().flatten(),
index = features).sort_values(ascending=False)
ax = d[:10].plot(kind='bar', figsize=(10,6), width=.8, fontsize=14, rot=45,
title='<NAME> Wikipedia Article Word Counts')
ax.title.set_size(18)
# -
# ## Compute TF-IDF
# +
#Define the TFIDF vectorizer that will be used to process the data
tfidf_vectorizer = TfidfVectorizer()
#Apply this vectorizer to the full dataset to create normalized vectors
tfidf_matrix = tfidf_vectorizer.fit_transform(wiki_data)
#Get the names of the features
features = tfidf_vectorizer.get_feature_names()
#get the row that contains relevant vector
row = wiki_data.index.get_loc(name)
#Create a series from the sparse matrix
d = pd.Series(tfidf_matrix.getrow(row).toarray().flatten(), index = features).sort_values(ascending=False)
ax = d[:10].plot(kind='bar', title='<NAME> Wikipedia Article Word TF-IDF Values',
figsize=(10,6), width=.8, fontsize=14, rot=45 )
ax.title.set_size(20)
# -
# ## Search the kNN
# +
nbrs = NearestNeighbors(n_neighbors=10, metric='cosine').fit(tfidf_matrix)
distances, indices = nbrs.kneighbors()
def get_closest_neighs(name):
row = wiki_data.index.get_loc(name)
result = pd.DataFrame({'names':wiki_data.iloc[indices[row],].reset_index()['name'],
'distance': distances[row].flatten()})
return result
# -
get_closest_neighs('<NAME>')
# +
# Find the closest neighbors for '<NAME>' using an euclidean metric
# -
# # Metagenomes as text documents
# +
# import the Bray-curtis distance matrix and metagenome description
bc_25bp=pd.read_csv('SIMKA_results/bc_25.csv', header=None)
samples=pd.read_csv('SIMKA_results/metagenomes_description.csv', index_col='ID')['body_site']
samples
# +
# create a 2-NN search for the samples
# +
# Retrieve the two NN for 'sample_6'
|
sprint3_retrieval/sprint3_demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
#directory i.e dataset/IPL2013.csv
ipl_auction_df=pd.read_csv('/Users/jagdishwarbiradar/PycharmProjects/AuctionPrice-Prediction/dataset/IPL2013.csv')
ipl_auction_df.info() # No missing values
# recognize the categorical variables
X_features = ipl_auction_df.columns
print(X_features)
# Encoding Categorical Features by dummy variable
categorical_features =['AGE','COUNTRY','PLAYING ROLE','CAPTAINCY EXP']
ipl_auction_encoded_df = pd.get_dummies(ipl_auction_df[X_features], columns = categorical_features,drop_first=True )
X_features = ipl_auction_encoded_df.columns
X_features
# + pycharm={"name": "#%%\n"}
import sklearn
from sklearn.model_selection import train_test_split
import statsmodels.api as sm
###############################
"""Splitting the dataset into train and Validation """
##spliting data into 80%:20%
X=sm.add_constant(ipl_auction_encoded_df)
Y=ipl_auction_encoded_df['SOLD PRICE']
train_x ,test_x,train_y,test_y=train_test_split(X,Y,train_size=0.8,random_state=42)
print(train_x ,test_x,train_y,test_y)
|
src/Validation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Synthetic Model
# Notebook to generate a set of models.
# #### Import libraries
# +
from IPython.display import Markdown as md
from IPython.display import display as dp
import string as st
import sys
import numpy as np
import matplotlib.pyplot as plt
import cPickle as pickle
import datetime
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d.art3d import Poly3DCollection, Line3DCollection
from fatiando.utils import ang2vec, vec2ang
from fatiando.mesher import Sphere, Prism, PolygonalPrism
from fatiando.gravmag import sphere, prism, polyprism
# -
notebook_name = 'synthetic_model.ipynb'
# #### Importing auxiliary functions
dir_modules = '../../../mypackage'
sys.path.append(dir_modules)
import auxiliary_functions as func
# #### Loading 2D grid properties
with open('data/regular_grid.pickle') as f:
regular = pickle.load(f)
with open('data/airborne_survey.pickle') as f:
airborne = pickle.load(f)
# #### List of saved files
saved_files = []
# ### Observation area
print 'Area limits: \n x_max = %.1f m \n x_min = %.1f m \n y_max = %.1f m \n y_min = %.1f m' % (regular['area'][1], regular['area'][0],regular['area'][3],regular['area'][2])
# ## Regional Field
inc_gf , dec_gf = (-40.,-22.) ## https://geomag.bgs.ac.uk/data_service/models_compass/wmm_calc.html no RJ
# ## Create a model w/ the presence of Remanence Magnetization
model_multi = dict()
# ### main field
model_multi['main_field'] = (inc_gf,dec_gf)
# #### Setting bounds of a polygonal cross-section
# +
% matplotlib notebook
fig = plt.figure(figsize=(9,9), tight_layout=True)
ax = fig.add_subplot(111)
ax.set_title('Click on figure to set any point')
ax.axis([regular['y'].min(), regular['y'].max(), regular['x'].min(), regular['x'].max()])
ax.set_ylabel('x(m)')
ax.set_xlabel('y(m)')
line, = ax.plot([], [])
line.figure.canvas.draw()
x = []
y = []
plotx = []
ploty = []
def pick(event):
if event.inaxes != ax.axes:
return 'It must be any point over de area '
x.append(event.ydata)
y.append(event.xdata)
plotx.append(event.xdata)
ploty.append(event.ydata)
line.set_color('r')
line.set_marker('o')
line.set_linestyle('')
line.set_data(plotx,ploty)
line.figure.canvas.draw()
line.figure.canvas.mpl_connect('button_press_event', pick)
plt.show()
# -
print x
print y
# ## Magnetization Polygonal prism
# +
model_multi['m_Rpp'] = 4.
model_multi['inc_R'] = -25.
model_multi['dec_R'] = 30.
mag_tot_Rpp = ang2vec(model_multi['m_Rpp'],
model_multi['inc_R'],
model_multi['dec_R'])
model_multi['magnetization_pp'] = mag_tot_Rpp
# -
# ### Vertices of a Polygonal prism-1
model_multi['x1_verts'] = [-120.86173387456893, 217.88504245497916, -139.68099922621059, -1005.3672054017161, -2002.788269038715, -3019.0285980273529, -3884.7148042028603, -4204.6423151807649, -3809.4377427962945, -2360.3543107199021, -1494.6681045443956, -666.62042907216983, -120.86173387456893]
model_multi['y1_verts'] = [-1475.5336403581159, -822.01437309183802, -227.90594830431655, -386.33486158098731, -623.97823149599935, -604.17461733641267, -227.90594830431655, -1020.0505146876794, -1594.3553253156206, -1574.5517111560348, -1297.3011129218594, -1396.3191837197774, -1475.5336403581159]
model_multi['z1_top'] = 450.
model_multi['z1_bottom'] = 3150.
model_multi['verts1'] = zip(model_multi['x1_verts'],
model_multi['y1_verts'] )
# ### Creating a polyprism model
model_multi['polygons'] = [PolygonalPrism(model_multi['verts1'],
model_multi['z1_top'],
model_multi['z1_bottom'],
{'magnetization':mag_tot_Rpp})]
# ## Magnetization spheres
# +
model_multi['m_Rs'] = 3.
model_multi['inc_R'] = -25.
model_multi['dec_R'] = 30.
mag_tot_Rs = ang2vec(model_multi['m_Rs'],
model_multi['inc_R'],
model_multi['dec_R'])
model_multi['magnetization_s'] = mag_tot_Rs
# -
# ### Sphere-1
model_multi['xc1'] = 1800.
model_multi['yc1'] = -1800.
model_multi['zc1'] = 1000.
model_multi['radius1'] = 500.
# ### Sphere-2
model_multi['xc2'] = 800.
model_multi['yc2'] = 800.
model_multi['zc2'] = 1000.
model_multi['radius2'] = 500.
# ### Creating a spheres model
model_multi['spheres'] = [Sphere(model_multi['xc1'],
model_multi['yc1'],
model_multi['zc1'],
model_multi['radius1'],
{'magnetization':mag_tot_Rs}),
Sphere(model_multi['xc2'],
model_multi['yc2'],
model_multi['zc2'],
model_multi['radius2'],
{'magnetization':mag_tot_Rs})]
theta = np.linspace(0, 2 * np.pi, 100)
# ## Magnetization of rectangular prisms
# +
model_multi['m_Rp1'] = 1.5
model_multi['inc_R1'] = -25.
model_multi['dec_R1'] = 30.
mag_tot_Rp1 = ang2vec(model_multi['m_Rp1'],
model_multi['inc_R1'],
model_multi['dec_R1'])
model_multi['magnetization_p1'] = mag_tot_Rp1
# +
model_multi['m_Rp2'] = 2.5
model_multi['inc_R2'] = -25.
model_multi['dec_R2'] = 30.
mag_tot_Rp2 = ang2vec(model_multi['m_Rp2'],
model_multi['inc_R2'],
model_multi['dec_R2'])
model_multi['magnetization_p2'] = mag_tot_Rp2
# -
# ## Rectangular prisms
# ### Prism-1
model_multi['x1_max'] = 3200.
model_multi['x1_min'] = 2200.
model_multi['y1_max'] = 3000.
model_multi['y1_min'] = 2300
model_multi['z1_min'] = 150.
model_multi['z1_max'] = 650.
model_multi['x_verts1'] = [model_multi['x1_max'],model_multi['x1_min'],model_multi['x1_min'],model_multi['x1_max'],model_multi['x1_max']]
model_multi['y_verts1'] = [model_multi['y1_max'],model_multi['y1_max'],model_multi['y1_min'],model_multi['y1_min'],model_multi['y1_max']]
# ### Prism-2
model_multi['x2_max'] = -2000.
model_multi['x2_min'] = -2900.
model_multi['y2_max'] = 4000.
model_multi['y2_min'] = 2000.
model_multi['z2_min'] = 500.
model_multi['z2_max'] = 2050.
model_multi['x_verts2'] = [model_multi['x2_max'],model_multi['x2_min'],model_multi['x2_min'],model_multi['x2_max'],model_multi['x2_max']]
model_multi['y_verts2'] = [model_multi['y2_max'],model_multi['y2_max'],model_multi['y2_min'],model_multi['y2_min'],model_multi['y2_max']]
# ### Creating model
model_multi['prisms'] = [Prism(model_multi['x1_min'],model_multi['x1_max'],
model_multi['y1_min'],model_multi['y1_max'],
model_multi['z1_min'],model_multi['z1_max'],
{'magnetization':mag_tot_Rp1}),
Prism(model_multi['x2_min'],model_multi['x2_max'],
model_multi['y2_min'],model_multi['y2_max'],
model_multi['z2_min'],model_multi['z2_max'],
{'magnetization':mag_tot_Rp2})]
# #### Generating .pickle file
now = datetime.datetime.utcnow().strftime('%d %B %Y %H:%M:%S UTC')
model_multi['metadata'] = 'Generated by {name} on {date}'.format(date=now, name=notebook_name)
# +
file_name = 'data/model_multi.pickle'
with open(file_name, 'w') as f:
pickle.dump(model_multi, f)
saved_files.append(file_name)
# -
# ## Visualization of model projection
# +
title_font = 20
bottom_font = 18
saturation_factor = 1.
plt.close('all')
plt.figure(figsize=(9,9), tight_layout=True)
plt.title('Model projection',fontsize=title_font)
plt.plot(model_multi['y1_verts'],model_multi['x1_verts'],
color='k',linestyle='-',linewidth=2)
plt.plot(model_multi['y_verts1'],model_multi['x_verts1'],
color='k',linestyle='-',linewidth=2)
plt.plot(model_multi['y_verts2'],model_multi['x_verts2'],
color='k',linestyle='-',linewidth=2)
plt.plot(model_multi['radius1']*np.sin(theta)+ model_multi['yc1'] ,
model_multi['radius1']*np.cos(theta)+ model_multi['xc1'],
color='k',linestyle='-',linewidth=2)
plt.plot(model_multi['radius2']*np.sin(theta)+ model_multi['yc2'] ,
model_multi['radius2']*np.cos(theta)+ model_multi['xc2'],
color='k',linestyle='-',linewidth=2)
plt.xlabel('y (m)', fontsize = title_font)
plt.ylabel('x (m)', fontsize = title_font)
plt.ylim(np.min(airborne['x']),np.max(airborne['x']))
plt.xlim(np.min(airborne['y']),np.max(airborne['y']))
plt.tick_params(labelsize=15)
file_name = 'figs/model_projection'
plt.savefig(file_name+'.png',dpi=200)
saved_files.append(file_name+'.png')
plt.savefig(file_name+'.eps',dpi=200)
saved_files.append(file_name+'.eps')
plt.show()
# -
# #### Saved files
with open('reports/report_%s.md' % notebook_name[:st.index(notebook_name, '.')], 'w') as q:
q.write('# Saved files \n')
now = datetime.datetime.utcnow().strftime('%d %B %Y %H:%M:%S UTC')
header = 'Generated by {name} on {date}'.format(date=now, name=notebook_name)
q.write('\n\n'+header+'\n\n')
for i, sf in enumerate(saved_files):
print '%d %s' % (i+1,sf)
q.write('* `%s` \n' % (sf))
|
code/notebooks/synthetic_tests/model_multibody_shallow-seated/.ipynb_checkpoints/synthetic_model-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Lab 3 Minimizing Cost
# ## Lab03-3-minimizing_cost_tf_optimizer
import tensorflow as tf
tf.set_random_seed(777)
# training set
X = [1, 2, 3]
Y = [1, 2, 3]
# 잘못된 weight 값을 initial value로 지정
W = tf.Variable(5.0)
# Linear regression model(y_hat) without intercept term
hypothesis = X * W
# cost/loss function(MSE)
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Minimize: Gradient Descent(tf 내장 함수)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)
# Session 객체 생성 및 변수 초기화
sess = tf.Session()
sess.run(tf.global_variables_initializer())
# 100번 최적화시킴
for step in range(100):
print(step, sess.run(W))
sess.run(train) # 0.1의 learning rate으로 다시 optimize 해줌
# +
## 참고
# 최적화할 때 횟수에 따른 W의 변화 plot
import tensorflow as tf
import matplotlib.pyplot as plt
tf.set_random_seed(777)
# training set
X = [1, 2, 3]
Y = [1, 2, 3]
# 잘못된 weight 값을 initial value로 지정
W = tf.Variable(5.0)
# Linear regression model(y_hat) without intercept term
hypothesis = X * W
# cost/loss function(MSE)
cost = tf.reduce_mean(tf.square(hypothesis - Y))
# Minimize: Gradient Descent(tf 내장 함수)
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1)
train = optimizer.minimize(cost)
# Session 객체 생성
sess = tf.Session()
# tf 변수 초기화
sess.run(tf.global_variables_initializer())
step_list = []
W_list = []
# 100번 최적화시킴
for step in range(100):
step_list.append(step)
W_list.append(sess.run(W))
#print(step, sess.run(W))
sess.run(train) # 0.1의 learning rate으로 다시 optimize 해줌
plt.plot(step_list, W_list)
plt.show()
|
Python/tensorflow/DeepLearningZeroToAll/Lab03-3-minimizing_cost_tf_optimizer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import findspark
findspark.init()
import pyspark
# -
sc.stop()
# +
from pyspark import SparkConf, SparkContext
conf = SparkConf().setMaster("local").setAppName("MinTemperatures")
sc = SparkContext(conf = conf)
def parseLine(line):
fields = line.split(',')
stationID = fields[0]
entryType = fields[2]
temperature = float(fields[3]) * 0.1 * (9.0 / 5.0) + 32.0
return (stationID, entryType, temperature)
lines = sc.textFile("file:///D:/Github/Hadoop_Spark_Practice/udemy_pyspark/1800.csv")
# -
lines.foreach(println)
lines.take(10).foreach(println)
parsedLines = lines.map(parseLine) # transfer from line to parsed pairs
parsedLines.collect().foreach(println)
# +
minTemps = parsedLines.filter(lambda x: "TMIN" in x[1]) # only keep the records with TMIN
stationTemps = minTemps.map(lambda x: (x[0], x[2])) # remove x[1]
minTemps = stationTemps.reduceByKey(lambda x, y: min(x,y)) # find the min value
results = minTemps.collect()
for result in results:
print(result[0] + "\t{:.2f}F".format(result[1]))
# -
list(map(lambda x: x*x,[1,2,3]))
|
udemy_pyspark/Notebook_Test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Analysis for Experiment 1
rm(list= ls())
library(dplyr)
library(lme4)
library(lmerTest)
library(BayesFactor)
library(ggplot2)
library(stringr)
# relevant conditions
data.folder <- 'Experiment 1. Connectedness and Common Region'
relevant_conditions <- c('2 masks', '1 mask', '2 masks_connected dots', '1 mask_connected dots')
# ## Analysis of disappearance duration: at least one target is invisible
# +
## reading imported response data
subjective_state_change<- read.csv(file.path(data.folder, 'Experiment1_SubjectiveStateChange.csv'), sep=';')
subjective_state_change <- subjective_state_change %>%
# removing irrelevant conditions
filter(ConditionLabel %in% relevant_conditions) %>%
# extracting presence of individual factors from the condition label
mutate(MasksN= str_sub(ConditionLabel, 1,1),
Connected= ifelse(str_sub(ConditionLabel, -4, -1)=='dots', TRUE, FALSE)) %>%
# making sure that factors are represented as factors
mutate(MasksN = as.factor(MasksN),
Connected = as.factor(Connected)) %>%
# ordering conditions for plotting
mutate(ConditionLabel= factor(ConditionLabel, levels= relevant_conditions))
# +
disappearance.time <- subjective_state_change %>%
group_by(ID, MasksN, Connected) %>%
summarise(time.proportion= sum(Duration[TargetCount<2])/BlockDuration[1])
disappearance.time <- data.frame(disappearance.time)
lm.null <- lme4::lmer(time.proportion ~ 1 + (1|ID), data= disappearance.time, REML= FALSE)
lm.masks <- update(lm.null, .~. + MasksN)
lm.connected <- update(lm.masks, .~. + Connected)
lm.interaction <- update(lm.connected, .~. + MasksN*Connected)
anova(lm.null, lm.masks, lm.connected, lm.interaction)
# -
# seeding random generator to ensure reproducable Bayesian MCMC results
set.seed(111122017)
duration.bayes <- sort(anovaBF(time.proportion ~ MasksN + Connected + ID, data= disappearance.time, whichRandom = 'ID'),
decreasing = TRUE)
duration.bayes
# +
# averages per group
time.per.condition.plot <- subjective_state_change %>%
# computing observer proportion per condition
group_by(ID, ConditionLabel) %>%
summarise(time.proportion= sum(Duration[TargetCount<2])/BlockDuration[1]) %>%
# Adjusting observers' means following Loftus & Masson (1994)
group_by(ID) %>%
mutate(ID.avg= mean(time.proportion)) %>%
ungroup() %>%
mutate(overall.avg= mean(time.proportion)) %>%
mutate(time.adjusted= time.proportion - ID.avg + overall.avg) %>%
# computing group averages per condition
group_by(ConditionLabel) %>%
summarise(time.avg= mean(time.adjusted*100),
time.serr= sd(time.adjusted*100)/sqrt(n()))
# averages per condition x observer for linear mixed models
time.per.condition.lmer <- subjective_state_change %>%
# computing observer proportion per condition
group_by(ID, ConditionLabel) %>%
summarise(time.proportion= sum(Duration[TargetCount<2])/BlockDuration[1])
# comparison to the baseline condition (M3)
duration.lmer <- summary(lmerTest::lmer(time.proportion ~ ConditionLabel + (1|ID), data= time.per.condition.lmer))
duration.lmer
rcontrast<-function(t, df) {
return (sqrt(t^2/(t^2 + df)))
}
coefficients.only <- data.frame(duration.lmer$coefficients)
colnames(coefficients.only) <- c('Estimate', 'Std.Error', 'df', 't.value', 'p.value')
dplyr::mutate(coefficients.only, R.sqr= rcontrast(t.value, df))
# plot
time.plot <- ggplot(data= time.per.condition.plot, aes(x= ConditionLabel, y= time.avg, ymin= time.avg-time.serr, ymax= time.avg+time.serr))+
geom_errorbar(color= 'darkgreen', width=0.3)+
geom_point(color= 'darkgreen', size= 3) +
ylab('Disappearance time [%]') +
ggtitle('Proportion of time when at least one target was invisible')
print(time.plot)
# -
# ## Simultaneity of appearance and disappearance events
# +
results <- read.csv(file.path(data.folder, 'Experiment1_Simultaneity.csv'), sep=';')
results <- results %>%
# removing irrelevant conditions
filter(ConditionLabel %in% relevant_conditions) %>%
# extracting presence of individual factors from the condition label
mutate(MasksN= str_sub(ConditionLabel, 1,1),
Connected= ifelse(str_sub(ConditionLabel, -4, -1)=='dots', TRUE, FALSE)) %>%
# making sure that factors are represented as factors
mutate(MasksN = as.factor(MasksN),
Connected = as.factor(Connected),
Event= as.factor(Event)) %>%
# ordering conditions for plotting
mutate(ConditionLabel= factor(ConditionLabel, levels= relevant_conditions))
# +
sim.events <- results %>%
group_by(ID, Connected, MasksN, Event, ConditionLabel) %>%
summarise(sim.proportion= 100*sum(SimCount>1)/n())
sim.events <- data.frame(sim.events)
lm.null <- lme4::lmer(sim.proportion ~ 1 + (1|ID), data= sim.events, REML= FALSE)
lm.masks <- update(lm.null, .~. + MasksN)
lm.Connected <- update(lm.masks, .~. + Connected)
lm.event <- update(lm.Connected, .~. + Event)
lm.mask.connected <- update(lm.event, .~. + MasksN*Connected)
lm.mask.event <- update(lm.mask.connected, .~. + MasksN*Event)
lm.connected.event <- update(lm.mask.event, .~. + Connected*Event)
lm.full.interaction <- update(lm.connected.event, .~. + MasksN*Connected*Event)
anova(lm.null, lm.masks, lm.Connected, lm.event, lm.mask.connected, lm.mask.event, lm.connected.event, lm.full.interaction)
# -
set.seed(211122017)
sim.bayes <- sort(anovaBF(sim.proportion ~ MasksN+Connected+Event+ID, data= data.frame(sim.events), whichRandom = 'ID'), decreasing = TRUE)
sim.bayes
# As analysis above suggested a significant effect of the event type, looking disappearances (0) and reappearances (1) separately
#
# ### Disappearances
# +
sim.disappearance <- sim.events %>%
filter(Event==0)
lm.null <- lme4::lmer(sim.proportion ~ 1 + (1|ID), data= sim.disappearance, REML= FALSE)
lm.masks <- update(lm.null, .~. + MasksN)
lm.connected <- update(lm.masks, .~. + Connected)
lm.mask.connected <- update(lm.connected, .~. + MasksN*Connected)
anova(lm.null, lm.masks, lm.connected, lm.mask.connected)
set.seed(311122017)
sim.bayes <- sort(anovaBF(sim.proportion ~ MasksN+Connected+ID, data= data.frame(sim.disappearance), whichRandom = 'ID'), decreasing = TRUE)
sim.bayes
# +
# averages per group
sim.per.condition.plot <- sim.disappearance %>%
# Adjusting observers' means following Loftus & Masson (1994)
group_by(ID) %>%
mutate(ID.avg= mean(sim.proportion)) %>%
ungroup() %>%
mutate(overall.avg= mean(sim.proportion)) %>%
mutate(sim.adjusted= sim.proportion - ID.avg + overall.avg) %>%
# computing group averages per condition
group_by(ConditionLabel) %>%
summarise(sim.avg= mean(sim.adjusted),
sim.serr= sd(sim.adjusted)/sqrt(n()))
# comparison to the baseline condition (M3)
sim.lmer <- summary(lmerTest::lmer(sim.proportion ~ ConditionLabel + (1|ID), data= sim.disappearance))
sim.lmer
rcontrast<-function(t, df) {
return (sqrt(t^2/(t^2 + df)))
}
coefficients.only <- data.frame(sim.lmer$coefficients)
colnames(coefficients.only) <- c('Estimate', 'Std.Error', 'df', 't.value', 'p.value')
dplyr::mutate(coefficients.only, R.sqr= rcontrast(t.value, df))
# plot
sim.plot <- ggplot(data= sim.per.condition.plot, aes(x= ConditionLabel, y= sim.avg, ymin= sim.avg-sim.serr, ymax= sim.avg+sim.serr))+
geom_errorbar(color= 'red', width=0.3)+
geom_point(color= 'red', size= 3) +
ylab('Simultaneity [%]') +
ylim(24, 59) +
ggtitle('Simultaneity of disappearance events')
print(sim.plot)
# -
# ### Reappearances
# +
sim.reappearance <- sim.events %>%
filter(Event==1)
lm.null <- lme4::lmer(sim.proportion ~ 1 + (1|ID), data= sim.reappearance, REML= FALSE)
lm.masks <- update(lm.null, .~. + MasksN)
lm.connected <- update(lm.masks, .~. + Connected)
lm.mask.connected <- update(lm.connected, .~. + MasksN*Connected)
anova(lm.null, lm.masks, lm.connected, lm.mask.connected)
set.seed(411122017)
sim.bayes <- sort(anovaBF(sim.proportion ~ MasksN+Connected+ID, data= data.frame(sim.reappearance), whichRandom = 'ID'), decreasing = TRUE)
sim.bayes
# +
# averages per group
sim.per.condition.plot <- sim.reappearance %>%
# Adjusting observers' means following Loftus & Masson (1994)
group_by(ID) %>%
mutate(ID.avg= mean(sim.proportion)) %>%
ungroup() %>%
mutate(overall.avg= mean(sim.proportion)) %>%
mutate(sim.adjusted= sim.proportion - ID.avg + overall.avg) %>%
# computing group averages per condition
group_by(ConditionLabel) %>%
summarise(sim.avg= mean(sim.adjusted),
sim.serr= sd(sim.adjusted)/sqrt(n()))
# comparison to the baseline condition (M3)
sim.lmer <- summary(lmerTest::lmer(sim.proportion ~ ConditionLabel + (1|ID), data= sim.reappearance))
sim.lmer
rcontrast<-function(t, df) {
return (sqrt(t^2/(t^2 + df)))
}
coefficients.only <- data.frame(sim.lmer$coefficients)
colnames(coefficients.only) <- c('Estimate', 'Std.Error', 'df', 't.value', 'p.value')
dplyr::mutate(coefficients.only, R.sqr= rcontrast(t.value, df))
# plot
sim.plot <- ggplot(data= sim.per.condition.plot, aes(x= ConditionLabel, y= sim.avg, ymin= sim.avg-sim.serr, ymax= sim.avg+sim.serr))+
geom_errorbar(color= 'red', width=0.3)+
geom_point(color= 'red', size= 3) +
ylab('Simultaneity [%]') +
ylim(24, 59) +
ggtitle('Simultaneity of reappearance events')
print(sim.plot)
# -
# ## Analysis of disappearance duration: average disappearance across all targets
# +
responses <- read.csv(file.path(data.folder, 'Experiment1_Response.csv'), sep=';')
responses <- responses %>%
# removing irrelevant conditions
filter(ConditionLabel %in% relevant_conditions) %>%
# extracting presence of individual factors from the condition label
mutate(MasksN= str_sub(ConditionLabel, 1,1),
Connected= ifelse(str_sub(ConditionLabel, -4, -1)=='dots', TRUE, FALSE)) %>%
# making sure that factors are represented as factors
mutate(MasksN = as.factor(MasksN),
Connected = as.factor(Connected)) %>%
# ordering conditions for plotting
mutate(ConditionLabel= factor(ConditionLabel, levels= relevant_conditions))
# computing block duration
block.duration <- responses %>%
filter(EventLabel %in% c('Block start', 'Block end')) %>%
group_by(ID, Block) %>%
summarise(Block.Duration= Time[2]-Time[1])
responses <- responses %>%
left_join(block.duration, by = c('ID', 'Block'))
# computing disappearance time
disappearance.across.targets <- responses %>%
# only for real target events
filter(Target %in% c(0, 1)) %>%
# computing disappearance for individual targets
group_by(ID, Block, MasksN, Connected, Target, ConditionLabel) %>%
summarise(disapp.prop = 100*sum(Time[EventLabel=='Released']-Time[EventLabel=='Pressed'])/Block.Duration[1]) %>%
# average across all of them
group_by(ID, Connected, MasksN, ConditionLabel) %>%
summarise(time.proportion = mean(disapp.prop))
disappearance.across.targets <- data.frame(disappearance.across.targets)
# -
lm.null <- lme4::lmer(time.proportion ~ 1 + (1|ID), data= disappearance.across.targets, REML= FALSE)
lm.masks <- update(lm.null, .~. + MasksN)
lm.connected <- update(lm.masks, .~. + Connected)
lm.interaction <- update(lm.connected, .~. + MasksN*Connected)
anova(lm.null, lm.masks, lm.connected, lm.interaction)
set.seed(511122017)
duration.bayes <- sort(anovaBF(time.proportion ~ MasksN + Connected + ID, data= disappearance.across.targets, whichRandom = 'ID'),
decreasing = TRUE)
duration.bayes
# +
# averages per group
time.per.condition.plot <- disappearance.across.targets %>%
# Adjusting observers' means following Loftus & Masson (1994)
group_by(ID) %>%
mutate(ID.avg= mean(time.proportion)) %>%
ungroup() %>%
mutate(overall.avg= mean(time.proportion)) %>%
mutate(time.adjusted= time.proportion - ID.avg + overall.avg) %>%
# computing group averages per condition
group_by(ConditionLabel) %>%
summarise(time.avg= mean(time.adjusted),
time.serr= sd(time.adjusted)/sqrt(n()))
# comparison to the baseline condition (M3)
duration.lmer <- summary(lmerTest::lmer(time.proportion ~ ConditionLabel + (1|ID), data= disappearance.across.targets))
duration.lmer
rcontrast<-function(t, df) {
return (sqrt(t^2/(t^2 + df)))
}
coefficients.only <- data.frame(duration.lmer$coefficients)
colnames(coefficients.only) <- c('Estimate', 'Std.Error', 'df', 't.value', 'p.value')
dplyr::mutate(coefficients.only, R.sqr= rcontrast(t.value, df))
# plot
time.plot <- ggplot(data= time.per.condition.plot, aes(x= ConditionLabel, y= time.avg, ymin= time.avg-time.serr, ymax= time.avg+time.serr))+
geom_errorbar(color= 'darkgreen', width=0.3)+
geom_point(color= 'darkgreen', size= 3) +
ylab('Disappearance time [%]') +
ggtitle('Average proportion of time when targets were invisible')
print(time.plot)
|
Experiment 1. (B) Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import sys
sys.path.append('src')
from sklearn.metrics import classification_report
import pandas as pd
from src.sentiment_classifier import SentimentClassifier
def load_dataset(dataset_path):
df = pd.read_csv(dataset_path)
return df[df['Sentiment'] != 'irrelevant'].reset_index(drop=True)
train_set_path="data/Train.csv"
test_set_path="data/Test.csv"
normalization_lexicon_path="data/normalization-lexicon/emnlp_dict.txt"
train = load_dataset(train_set_path)
test = load_dataset(test_set_path)
# + pycharm={"name": "#%%\n"}
clf = SentimentClassifier(normalization_lexicon_path, start_day_hour=10)
clf.fit(train)
# + pycharm={"name": "#%%\n"}
pred_sent, pred_org = clf.predict_sentiment(test), clf.predict_organization(test)
print('=========== Sentiment prediction report ===========')
print(classification_report(test['Sentiment'], pred_sent))
print('=========== Organization prediction report ===========')
print(classification_report(test['Topic'], pred_org))
# + pycharm={"name": "#%%\n"}
correct_idx = []
for idx, row in test.iterrows():
if row['Sentiment'] == pred_sent[idx]:
correct_idx.append(idx)
correct_test = test.iloc[correct_idx]
correct_test = correct_test.sample(10).reset_index(drop=True)
rates = clf.predict_sentiment(correct_test, get_rate=True)
for idx, row in correct_test.sample(10).iterrows():
print('%s: %.2f' % (row['Sentiment'], rates[idx]))
# + pycharm={"name": "#%%\n"}
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.5 64-bit (''base'': conda)'
# name: python3
# ---
# # Twitter Scraping Using TWINT
#
# Twitter is erratic about giving out developer/API access codes. If you can't get one, we can use twint for scraping instead. As a bonus, we can easily get historical data.
#
# In this script, we'll se the geo coords we want first, for those tweets tagged with geo coords,
# then run the data pull in chunks by year, convert to a dataframe, and save to a csv.
# +
# This notebook calls functions stored in a different notebook - you may need to install
# #!pip install import-ipynb
# then, you may need open and run twitter_scrape_by_twint.ipynb in your IDE or on
# the same running python kernel before running this file
#
# if you make changes to that file, you will need to restart your kernel and maybe your IDE for changes to apply
# +
# necessary imports
import twint
import pandas as pd
import csv
import datetime
import time
import os
# import the more generic scraper function written and stored in the twitter_scrape.ipynb file
import import_ipynb
import twitter_scrape_by_twint
# -
# Main loop function - takes a city and year and sets off the most reliable method to date
# of coazing twint into giving us as many geo-tagged results as possible for that year given
# all the problems and bugs in twint at the time of running.
#
# Known problems discovered and worked around: since/until inconsistent, limit inconsistent but performs best at
# 500, prefers to work backwards from an "until" date, twitter cuts you off if you call it too much
#
# Problems not worked around: 500 limit effectively limits you to 500*365 max per year; overlap between city ranges;
# Twitter sometimes gives you back different results from run to run
def twitter_scrape_by_geo_year(city_name = "niamey", which_year = 2021, use_tor_channel = False):
"""Given a city name and year, scrapes as many tweets as possible with twint and stores them in a csv"""
geo_str = ""
city_name = city_name.lower()
# take the year and reorganize into
target_date_min, target_date_max = get_target_dates_min_and_max(which_year)
# here are the geo coordinates and ranges for a number of major cities in Niger
# the cities were chosen by size and interest
# Diffa and the Lake Chad Basin were left out of this analysis
if city_name == "niamey":
geo_str = "13.5234,2.1167,75km"
elif city_name == "agadez":
geo_str = "16.9701,7.9856,75km"
elif city_name == "tillaberi":
geo_str = "14.2589,1.4671,75km"
elif city_name == "tahoua":
geo_str = "14.8939,5.2639,75km"
elif city_name == "dosso":
geo_str = "13.179,3.2071,75km"
elif city_name == "zinder":
geo_str = "13.804,8.9886,75km"
elif city_name == "maradi":
geo_str = "13.496,7.1081,75km"
else:
raise Exception("city \'{}\' is not recognized".format(city_name))
# instantiate twint
c = twint.Config()
c.Limit = 500
c.Pandas = True
c.Debug = True
c.Count = True
c.Stats = True
c.Hide_output=True
c.Geo = geo_str
c.Until = target_date_max.isoformat()
print("will search {} tweet chunks back from 00:00am {}".format(c.Limit, c.Until))
# if we want to use tor because we're getting locked out
if use_tor_channel == True:
# **optionally** run through the Tor browser
# just start up the main Tor browser and uncommen the below lines
print("using Tor")
c.Proxy_host = "127.0.0.1"
c.Proxy_port = 9150
c.Proxy_type = "socks5"
# let's create a file name in a subdirectory
target_file_name = "./" + city_name.lower() + "_geosearch"
if not os.path.exists(target_file_name):
os.makedirs(target_file_name)
target_file_name = target_file_name + "/" + str(which_year) + "_geo.csv"
# here is where we call the below twint operation in the twitter_scrap file
twitter_scrape.twitter_scrape_given_twint_config(c, target_date_min, target_date_max, target_file_name, city_name)
# # Main run block
# Run this block below to actually conduct the scraping and saving. Generally this will be done one city name and one year at a time. but a loop is provided to run multiple years at a time. Then manually change the year and/or city and run again. One csv file per run. Don't do this too fast or Twitter may refuse, throttle, or alter results.
#
# These runs can take a while. Short pauses are built in to reduce chances of Twitter refusal. Hopefully you only need to run this once, then run once a year after that to get a series of data for later analysis.
# +
target_city = "agadez" # options: "niamey" "agadez" "tillaberi" "tahoua" "dosso" "zinder" "maradi"
use_tor = False
# start at 2010 (there's nothing before that), going up to 2020 in this example
for target_year in range(2010, 2020 + 1, 1):
print("calling scrape for year {}".format(target_year))
twitter_scrape_by_geo_year(target_city, target_year, use_tor)
print("done scraping year {}".format(target_year))
|
twitter_scraping/twitter_scrape_geo_year.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/vinhnemo/fastai_audio/blob/master/notebooks/01.%20Audio%2C%20STFT%2C%20Melspectrograms%20with%20Python.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Eqvp0dR745sN"
# %reload_ext autoreload
# %autoreload 2
# %matplotlib inline
# + id="BsVy0IdT474_" outputId="0ab69764-159f-4b7f-d817-d124c639f4dd" colab={"base_uri": "https://localhost:8080/"}
# @title Mount & Clone
# Imports
import requests
# @markdown Mount GDrive
Gdrive = True # @param {type: 'boolean'}
global path
class MountClone:
def __init__(
self,
Gdrive=False,
repositoryUrl="",
verbose=False):
if Gdrive:
self.mount_drive()
if repositoryUrl:
self.clone_repo(repositoryUrl, verbose)
def __str__(self):
try:
return self.path
except NameError:
return ''
def mount_drive(self):
from google.colab import drive
drive.mount('/content/drive')
self.path = "/content/drive"
def clone_repo(self, repositoryUrl, verbose=False):
response = requests.get(repositoryUrl)
if response.status_code == 200:
print("✔️ Public repository")
# ! cd /content
# ! git clone $repositoryUrl
folder = repositoryUrl.split("/")[-1]
self.path = f"/content/{folder}"
else:
print("❌ Not a public Repository")
if __name__ == "__main__":
path = MountClone(Gdrive=Gdrive)
# + id="DaRY5RJg45sP"
from itertools import islice
from pathlib import Path
from IPython.display import Audio
import librosa
import librosa.display
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.fftpack import fft
from scipy.signal import get_window
# + id="o6m15tpd45sP"
plt.rcParams['figure.figsize'] = (12, 3)
# + id="ZTH8XuuJ6Gui" outputId="0a33f0d9-0e68-4840-f719-9b6260b86169" colab={"base_uri": "https://localhost:8080/"}
# %ll
# + id="T8z7VQgD45sP" outputId="d55558a2-4b26-404f-e2ec-a10076ffd2fd" colab={"base_uri": "https://localhost:8080/", "height": 142}
DATA = Path('/content/drive/MyDrive/Colab Notebooks/freesound-audio-tagging')
AUDIO = DATA/'audio_train'
CSV = DATA/'train.csv'
df = pd.read_csv(CSV)
df.head(3)
# + id="XOWsqoUz45sQ" outputId="46d637a8-2d54-40ad-92cc-3fc796157f1f" colab={"base_uri": "https://localhost:8080/"}
row = df.iloc[1] # saxophone clip
filename = AUDIO / row.fname
# open the audio file
clip, sample_rate = librosa.load(filename, sr=None)
print('Sample Rate {} Hz'.format(sample_rate))
print('Clip Length {:3.2f} seconds'.format(len(clip)/sample_rate))
# + id="F4Gg9NpG45sQ"
three_seconds = sample_rate * 3
clip = clip[:three_seconds]
# + id="PjlGIw8w45sR" outputId="2941ace7-c14c-4d12-f825-b0fb4bf42600" colab={"base_uri": "https://localhost:8080/", "height": 350}
timesteps = np.arange(len(clip)) / sample_rate # in seconds
fig, ax = plt.subplots(2, figsize=(12, 5))
fig.subplots_adjust(hspace=0.5)
# plot the entire clip
ax[0].plot(timesteps, clip)
ax[0].set_xlabel('Time (s)')
ax[0].set_ylabel('Amplitude')
ax[0].set_title('Raw Audio: {} ({} samples)'.format(row.label, len(clip)))
n_fft = 1024 # frame length
start = 45000 # start at a part of the sound thats not silence..
x = clip[start:start+n_fft]
# mark location of frame in the entire signal
ax[0].axvline(start/sample_rate, c='r')
ax[0].axvline((start+n_fft)/sample_rate, c='r')
# plot N samples
ax[1].plot(x)
ax[1].set_xlabel('Samples')
ax[1].set_ylabel('Amplitude')
ax[1].set_title('Raw Audio: {} ({} samples)'.format(row.label, len(x)));
# + id="HmNObiA045sS" outputId="39c63611-5059-4d9f-e383-ec991c447087" colab={"base_uri": "https://localhost:8080/", "height": 75}
Audio(clip, rate=sample_rate)
# + id="WvexGkvt45sS" outputId="75443005-7ebf-434a-a595-7342c912c0ab" colab={"base_uri": "https://localhost:8080/", "height": 157}
window = get_window('hann', n_fft)
wx = x * window
fig, ax = plt.subplots(1, 2, figsize=(16, 2))
ax[0].plot(window)
ax[1].plot(wx);
# + id="Dsjua_ih45sT" outputId="7d5ade2e-2d74-4872-b8a7-703264624ed9" colab={"base_uri": "https://localhost:8080/"}
# Compute (real) FFT on window
X = fft(x, n_fft)
X.shape, X.dtype
# + id="AnK-gvlH45sT" outputId="93078eff-960e-4104-cfb8-7b4b6b51e350" colab={"base_uri": "https://localhost:8080/", "height": 228}
# We only use the first (n_fft/2)+1 numbers of the output, as the second half if redundant
X = X[:n_fft//2+1]
# Convert from rectangular to polar, usually only care about magnitude
X_magnitude, X_phase = librosa.magphase(X)
plt.plot(X_magnitude);
X_magnitude.shape, X_magnitude.dtype
# + id="fu-GnuyC45sT" outputId="3b066f3d-4037-42fa-f95f-35710299080a" colab={"base_uri": "https://localhost:8080/", "height": 214}
# we hear loudness in decibels (on a log scale of amplitude)
X_magnitude_db = librosa.amplitude_to_db(X_magnitude)
plt.plot(X_magnitude_db);
# + id="C_tvwLO345sU" outputId="4c43aef3-72cb-47c1-ec45-6e05e2adf6f2" colab={"base_uri": "https://localhost:8080/", "height": 404}
hop_length = 512
stft = librosa.stft(clip, n_fft=n_fft, hop_length=hop_length)
stft_magnitude, stft_phase = librosa.magphase(stft)
stft_magnitude_db = librosa.amplitude_to_db(stft_magnitude, ref=np.max)
plt.figure(figsize=(12, 6))
librosa.display.specshow(stft_magnitude_db, x_axis='time', y_axis='linear',
sr=sample_rate, hop_length=hop_length)
title = 'n_fft={}, hop_length={}, time_steps={}, fft_bins={} (2D resulting shape: {})'
plt.title(title.format(n_fft, hop_length,
stft_magnitude_db.shape[1],
stft_magnitude_db.shape[0],
stft_magnitude_db.shape));
# + id="1WXrNyBf45sU" outputId="bdeab82a-03df-4aa9-9acd-dc875b7923c7" colab={"base_uri": "https://localhost:8080/", "height": 350}
# number of mel frequency bands
n_mels = 64
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
fmin = 0
fmax = 22050 # sample_rate/2
mel_spec = librosa.feature.melspectrogram(clip, n_fft=n_fft, hop_length=hop_length,
n_mels=n_mels, sr=sample_rate, power=1.0,
fmin=fmin, fmax=fmax)
mel_spec_db = librosa.amplitude_to_db(mel_spec, ref=np.max)
librosa.display.specshow(mel_spec_db, x_axis='time', y_axis='mel',
sr=sample_rate, hop_length=hop_length,
fmin=fmin, fmax=fmax, ax=ax[0])
ax[0].set_title('n_mels=64, fmin=0, fmax=22050')
fmin = 20
fmax = 8000
mel_spec = librosa.feature.melspectrogram(clip, n_fft=n_fft, hop_length=hop_length,
n_mels=n_mels, sr=sample_rate, power=1.0,
fmin=fmin, fmax=fmax)
mel_spec_db = librosa.amplitude_to_db(mel_spec, ref=np.max)
librosa.display.specshow(mel_spec_db, x_axis='time', y_axis='mel',
sr=sample_rate, hop_length=hop_length,
fmin=fmin, fmax=fmax, ax=ax[1])
ax[1].set_title('n_mels=64, fmin=20, fmax=8000')
plt.show()
# + id="lXc4aCQ045sU"
|
notebooks/01. Audio, STFT, Melspectrograms with Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import copy
from difflib import SequenceMatcher
import os
import pandas as pd
from tqdm import tqdm
# <h2>Cargamos libro Excel</h2>
# +
df_main = pd.read_excel('Compilado02.xlsx', engine='openpyxl', sheet_name=None)
for key in df_main.keys():
print(key)
# -
# <h2>Hacemos las comparaciones de nombres</h2>
# +
df_students01 = df_main['alumnas2020'].copy(deep=True)
df_students02 = df_main['alumnas2021'].copy(deep=True)
# This function will help us to compare strings
def similar(a, b):
return SequenceMatcher(None, a, b).ratio()
# This one makes the comparison industrial
def gen_similar(list01, list02):
list_similars = []
for word in list01:
ratio = 0
for spiegel in list02:
if ratio < max(ratio, similar(word, spiegel)):
ratio = similar(word, spiegel)
solution = (word, ratio, spiegel)
list_similars.append(solution)
return(list_similars)
list01 = df_students01['Nombre'].to_list()
list02 = df_students02['Nombre'].to_list()
list_similars = gen_similar(list01, list02)
# -
# <h2>Creamos nuestra columna relacional</h2>
# +
for row in range(df_students02.shape[0]):
name_2021 = df_students02.at[row, 'Nombre']
for i, col in enumerate(['Nombre 2020', 'Name match %']):
value = [entry[i] for entry in list_similars if entry[-1] == name_2021]
if len(value) != 0:
df_students02.at[row, col] = value[0]
dict_final = {'students2020': df_students01, 'students2021': df_students02, 'classes': df_main['clases']}
# Adicionalmente, se guarda el diccionario en formato de libro en Excel
writer = pd.ExcelWriter('test.xlsx', engine='xlsxwriter')
for df_name, df in dict_final.items():
df.to_excel(writer, sheet_name=df_name)
writer.save()
# +
num = 289
den = 2
while den < 100:
if num % den == 0:
print(den, num/den)
break
den += 1
# -
# <h2>Agregamos los nombres del 2021 como llave</h2>
# +
names_2020 = dict_final['students2020']['Nombre'].to_list()
names_2021 = dict_final['students2021']['Nombre'].to_list()
df_2020 = dict_final['students2021'].copy(deep=True)
df_2021 = dict_final['students2021'].copy(deep=True)
df_classes = dict_final['classes'].copy(deep=True)
# We create our new columns with None values for every row
df_classes['name 2020'], df_classes['ratio 2020'], df_classes['email 2020'] = None, None, None
df_classes['name 2021'], df_classes['ratio 2021'], df_classes['email 2021'] = None, None, None
# A list called "cols" is created to order our columns in the future
cols = [col for col in df_classes]
# Through an iteration the best match-ratio gets chosen
for i, row in enumerate(tqdm(range(df_classes.shape[0]))):
name = df_classes.at[row, 'Nombre']
solution_2020, solution_2021 = None, None
ratio_2020, ratio_2021 = 0, 0
for name_2020 in names_2020:
if ratio_2020 < max(ratio_2020, similar(name, name_2020)):
ratio_2020 = similar(name, name_2020)
solution_2020 = name_2020
for name_2021 in names_2021:
if ratio_2021 < max(ratio_2021, similar(name, name_2021)):
ratio_2021 = similar(name, name_2021)
solution_2021 = name_2021
# In this line we finally fill our rows with the corresponding information
df_classes.at[row, 'name 2020'], df_classes.at[row, 'ratio 2020'] = solution_2020, ratio_2020
df_classes.at[row, 'name 2021'], df_classes.at[row, 'ratio 2021'] = solution_2021, ratio_2021
dict_aux = {solution_2020: ('email 2020', df_2020), solution_2021: ('email 2021', df_2021)}
# Agregamos los correos
for key, value in dict_aux.items():
try:
df_classes.at[row, value[0]] = value[1][value[1]['Nombre'] == key]['Mail'].values[0].strip()
except:
pass
# This line orders our dataframe columns as wanted
df_classes = df_classes[[cols[0]] + cols[-6:] + cols[1:-6]]
# Finally, we update our dictionary, generate a new Excel file, and display our edited dataframe
dict_final = {'students2020': df_students01, 'students2021': df_students02, 'classes': df_classes}
writer = pd.ExcelWriter('esperemos_que_funcione.xlsx', engine='xlsxwriter')
for df_name, df in dict_final.items():
df.to_excel(writer, sheet_name=df_name)
writer.save()
display(df_classes)
# -
for key in dict_final.keys():
print(key)
display(dict_final['students2021'])
# <h2>Preparación de la hoja de clases</h2>
# +
df_test = dict_final['classes'].copy(deep=True)
df_2021 = dict_final['students2021'].copy(deep=True)
cols = [col for col in df_test]
df_test['Correos'] = None
for row in range(df_test.shape[0]):
current_row = df_test.loc[row]
name = current_row['name 2021']
# En las siguientes líneas corregimos el error en la fecha del workshop
if (current_row['Grupo'] == 'Workshop') and (current_row['Días'] == 'Sa'):
df_test.at[row, 'Inicio'] = current_row['Inicio'].replace(year=2021)
df_test.at[row, 'Termino'] = current_row['Termino'].replace(year=2021)
# Agregamos los correos
try:
df_test.at[row, 'Correos'] = df_2021[df_2021['Nombre'] == name]['Mail'].values[0].strip()
except:
pass
# Utilizando las columnas dejamos la llave al comienzo
df_test = df_test[[cols[-1]] + ['Correos'] + cols[1:-1] + [cols[0]]]
# Eliminamos los grupos que no iniciaron en 2021, ordenamos por fecha y se borran duplicados
df_test = df_test[(df_test['Inicio'].dt.year == 2021) & (df_test['Grupo'] != 'Workshop')]
df_test = df_test.sort_values(by='Inicio', ascending=False)
#df_test = df_test.drop_duplicates(subset='name 2021', keep='last')
df_test.to_excel('mailing_with_duplicates.xlsx')
display(df_test)
# -
# <h1 align='center'>Hasta aquí código funcional</h1>
# <h2>Comparisons as dictionaries</h2>
# +
df_students01 = df_main['alumnas2020'].copy(deep=True)
df_students02 = df_main['alumnas2021'].copy(deep=True)
def similar(a, b):
return SequenceMatcher(None, a, b).ratio()
def gen_similar(title01, list01, title02, list02, title_ratio):
dict_similars = {title01: [], title_ratio: [], title02: []}
for word in list01:
ratio = 0
for spiegel in list02:
if ratio < max(ratio, similar(word, spiegel)):
ratio = similar(word, spiegel)
solution = {title01: word, title_ratio: ratio, title02: spiegel}
for key in dict_similars.keys():
dict_similars[key].append(solution[key])
return(dict_similars)
list01 = df_students01['Nombre'].to_list()
list02 = df_students02['Nombre'].to_list()
dict_similars = gen_similar('2020 names', list01, '2021 names', list02, '2020 to 2021 names')
# +
df_classes = df_main['clases'].copy(deep=True)
def gen_similar(list01, list02):
list_similars = []
for word in list01:
ratio = 0
for spiegel in list02:
if ratio < max(ratio, similar(word, spiegel)):
ratio = similar(word, spiegel)
solution = (word, ratio, spiegel)
list_similars.append(solution)
return(list_similars)
list01 = df_students02['Nombre'].to_list()
list02 = df_classes['Nombre'].to_list()
list_similars = gen_similar(list01, list02)
print(df_classes['Nombre'][0], list_similars)
for row in range(df_classes.shape[0]):
name_2021 = df_classes.at[row, 'Nombre']
for i, col in enumerate(['Nombre 2021', 'Name match %']):
value = [entry[i] for entry in list_similars if entry[-1] == name_2021]
if len(value) != 0:
df_classes.at[row, col] = value[0]
display(df_classes)
|
Segmentation/Untitled.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: reco_full
# language: python
# name: conda-env-reco_full-py
# ---
# <i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
#
# <i>Licensed under the MIT License.</i>
# # Content-Based Personalization with LightGBM on Spark
#
# This notebook provides a quick example of how to train a [LightGBM](https://github.com/Microsoft/Lightgbm) model on Spark using [MMLSpark](https://github.com/Azure/mmlspark) for a content-based personalization scenario.
#
# We use the [CRITEO dataset](https://www.kaggle.com/c/criteo-display-ad-challenge), a well known dataset of website ads that can be used to optimize the Click-Through Rate (CTR). The dataset consists of a series of numerical and categorical features and a binary label indicating whether the add has been clicked or not.
#
# The model is based on [LightGBM](https://github.com/Microsoft/Lightgbm), which is a gradient boosting framework that uses tree-based learning algorithms. Finally, we take advantage of
# [MMLSpark](https://github.com/Azure/mmlspark) library, which allows LightGBM to be called in a Spark environment and be computed distributely.
#
# This scenario is a good example of **implicit feedback**, where binary labels indicate the interaction between a user and an item. This contrasts with explicit feedback, where the user explicitely rate the content, for example from 1 to 5.
#
# ## Global Settings and Imports
# This notebook can be run in a Spark environment in a DSVM or in Azure Databricks. For more details about the installation process, please refer to the [setup instructions](../../SETUP.md).
#
# **NOTE for Azure Databricks:**
# * A python script is provided to simplify setting up Azure Databricks with the correct dependencies. Run ```python tools/databricks_install.py -h``` for more details.
# * MMLSpark should not be run on a cluster with autoscaling enabled. Disable the flag in the Azure Databricks Cluster configuration before running this notebook.
# +
import os
import sys
import pyspark
from pyspark.ml import PipelineModel
from pyspark.ml.feature import FeatureHasher
import papermill as pm
import scrapbook as sb
from reco_utils.common.spark_utils import start_or_get_spark
from reco_utils.common.notebook_utils import is_databricks
from reco_utils.dataset.criteo import load_spark_df
from reco_utils.dataset.spark_splitters import spark_random_split
# Setup MML Spark
if not is_databricks():
# get the maven coordinates for MML Spark from databricks_install script
from tools.databricks_install import MMLSPARK_INFO
packages = [MMLSPARK_INFO["maven"]["coordinates"]]
repo = MMLSPARK_INFO["maven"].get("repo")
spark = start_or_get_spark(packages=packages, repository=repo)
dbutils = None
print("MMLSpark version: {}".format(MMLSPARK_INFO['maven']['coordinates']))
from mmlspark.train import ComputeModelStatistics
from mmlspark.lightgbm import LightGBMClassifier
print("System version: {}".format(sys.version))
print("PySpark version: {}".format(pyspark.version.__version__))
# + tags=["parameters"]
# Criteo data size, it can be "sample" or "full"
DATA_SIZE = "sample"
# LightGBM parameters
# More details on parameters: https://lightgbm.readthedocs.io/en/latest/Parameters-Tuning.html
NUM_LEAVES = 32
NUM_ITERATIONS = 50
LEARNING_RATE = 0.1
FEATURE_FRACTION = 0.8
EARLY_STOPPING_ROUND = 10
# Model name
MODEL_NAME = 'lightgbm_criteo.mml'
# -
# ## Data Preparation
#
# The [Criteo Display Advertising Challenge](https://www.kaggle.com/c/criteo-display-ad-challenge) (Criteo DAC) dataset is a well-known industry benchmarking dataset for developing CTR prediction models, and is used frequently by research papers. The original dataset contains over 45M rows, but there is also a down-sampled dataset which has 100,000 rows (this can be used by setting `DATA_SIZE = "sample"`). Each row corresponds to a display ad served by Criteo and the first column is indicates whether this ad has been clicked or not.<br><br>
# The dataset contains 1 label column and 39 feature columns, where 13 columns are integer values (int00-int12) and 26 columns are categorical features (cat00-cat25).<br><br>
# What the columns represent is not provided, but for this case we can consider the integer and categorical values as features representing the user and / or item content. The label is binary and is an example of implicit feedback indicating a user's interaction with an item. With this dataset we can demonstrate how to build a model that predicts the probability of a user interacting with an item based on available user and item content features.
#
raw_data = load_spark_df(size=DATA_SIZE, spark=spark, dbutils=dbutils)
# visualize data
raw_data.limit(2).toPandas().head()
# ### Feature Processing
# The feature data provided has many missing values across both integer and categorical feature fields. In addition the categorical features have many distinct values, so effectively cleaning and representing the feature data is an important step prior to training a model.<br><br>
# One of the simplest ways of managing both features that have missing values as well as high cardinality is to use the hashing trick. The [FeatureHasher](http://spark.apache.org/docs/latest/ml-features.html#featurehasher) transformer will pass integer values through and will hash categorical features into a sparse vector of lower dimensionality, which can be used effectively by LightGBM.<br><br>
# First, the dataset is splitted randomly for training and testing and feature processing is applied to each dataset.
raw_train, raw_test = spark_random_split(raw_data, ratio=0.8, seed=42)
columns = [c for c in raw_data.columns if c != 'label']
feature_processor = FeatureHasher(inputCols=columns, outputCol='features')
train = feature_processor.transform(raw_train)
test = feature_processor.transform(raw_test)
# ## Model Training
# In MMLSpark, the LightGBM implementation for binary classification is invoked using the `LightGBMClassifier` class and specifying the objective as `"binary"`. In this instance, the occurrence of positive labels is quite low, so setting the `isUnbalance` flag to true helps account for this imbalance.<br><br>
#
# ### Hyper-parameters
# Below are some of the key [hyper-parameters](https://github.com/Microsoft/LightGBM/blob/master/docs/Parameters-Tuning.rst) for training a LightGBM classifier on Spark:
# - `numLeaves`: the number of leaves in each tree
# - `numIterations`: the number of iterations to apply boosting
# - `learningRate`: the learning rate for training across trees
# - `featureFraction`: the fraction of features used for training a tree
# - `earlyStoppingRound`: round at which early stopping can be applied to avoid overfitting
lgbm = LightGBMClassifier(
labelCol="label",
featuresCol="features",
objective="binary",
isUnbalance=True,
boostingType="gbdt",
boostFromAverage=True,
baggingSeed=42,
numLeaves=NUM_LEAVES,
numIterations=NUM_ITERATIONS,
learningRate=LEARNING_RATE,
featureFraction=FEATURE_FRACTION,
earlyStoppingRound=EARLY_STOPPING_ROUND
)
# ### Model Training and Evaluation
model = lgbm.fit(train)
predictions = model.transform(test)
# +
evaluator = (
ComputeModelStatistics()
.setScoredLabelsCol("prediction")
.setLabelCol("label")
.setEvaluationMetric("AUC")
)
result = evaluator.transform(predictions)
auc = result.select("AUC").collect()[0][0]
result.show()
# -
# Record results with papermill for tests
sb.glue("auc", auc)
# ## Model Saving
# The full pipeline for operating on raw data including feature processing and model prediction can be saved and reloaded for use in another workflow.
# save model
pipeline = PipelineModel(stages=[feature_processor, model])
pipeline.write().overwrite().save(MODEL_NAME)
# cleanup spark instance
if not is_databricks():
spark.stop()
# ## Additional Reading
# \[1\] <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>. 2017. LightGBM: A highly efficient gradient boosting decision tree. In Advances in Neural Information Processing Systems. 3146–3154. https://papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf <br>
# \[2\] MML Spark: https://mmlspark.blob.core.windows.net/website/index.html <br>
#
|
examples/02_model_content_based_filtering/mmlspark_lightgbm_criteo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="oKWhZWV7jwzX"
# # NYC Properties price prediction
# + [markdown] id="6H9Doli9kB70"
# Dataset: [https://www.kaggle.com/new-york-city/nyc-property-sales](https://www.kaggle.com/new-york-city/nyc-property-sales)
# + id="jRgBEsTDkqsn"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import OrdinalEncoder
from xgboost import XGBRegressor
import seaborn as sns
from sklearn.linear_model import LinearRegression
# + id="mHiQygrIlanF" colab={"base_uri": "https://localhost:8080/", "height": 629} outputId="923a50b3-1ccc-48c8-fd9b-83b6d5c8ad87"
path = 'https://raw.githubusercontent.com/absiddik7/Datasets/main/nyc-rolling-sales.csv'
dataset = pd.read_csv(path)
dataset.head()
# + id="L-7wxQAZ9Fx9" colab={"base_uri": "https://localhost:8080/"} outputId="f7640c18-8a9c-4971-d8c4-c5ad220c7d29"
dataset.info()
# + [markdown] id="-eTIQh_GT2Rn"
# #Fix Structural Errors and Data Formatting
# + id="YzgqF-jbUDjm"
dataset.replace(' ',np.nan,inplace=True)
# + [markdown] id="3JlPNeTqj8Qe"
# Here we can see, there are some columns that are mistyped. Let's correct them.
# + id="-8zxq2nGmOJJ"
num_col = ['LAND SQUARE FEET','GROSS SQUARE FEET','SALE PRICE']
for item in num_col:
dataset[item] = pd.to_numeric(dataset[item],errors = 'coerce')
# + id="iWkJAs2eXmSh"
dataset['SALE DATE'] = pd.to_datetime(dataset['SALE DATE'],errors = 'coerce')
# + id="D1blI1AOTGzZ"
categorical_col = ['BOROUGH','TAX CLASS AT PRESENT','BUILDING CLASS AT PRESENT','TAX CLASS AT TIME OF SALE','BUILDING CLASS AT TIME OF SALE']
for item in categorical_col:
dataset[item] = dataset[item].astype('object')
# + id="j7Q8PokXH2JU"
dataset['SALE DATE'] = pd.to_datetime(dataset['SALE DATE'], errors='coerce')
# + [markdown] id="GNaPcRR84fHE"
# Encoding Categorical Values
# + id="eXwTYJrA4mwd"
ordEncoder = OrdinalEncoder()
dataset[['NEIGHBORHOOD','BUILDING CLASS CATEGORY','TAX CLASS AT PRESENT','BUILDING CLASS AT PRESENT','BUILDING CLASS AT TIME OF SALE']] = ordEncoder.fit_transform(dataset[['NEIGHBORHOOD','BUILDING CLASS CATEGORY','TAX CLASS AT PRESENT','BUILDING CLASS AT PRESENT','BUILDING CLASS AT TIME OF SALE']])
# + colab={"base_uri": "https://localhost:8080/", "height": 851} id="ZQ49lx9pP6g1" outputId="366415fe-c366-4256-db2a-9db97eac91c2"
dataset
# + [markdown] id="GAUth9f3Jsz3"
# Separate selling year and month
# + id="0qbLRNiMIXce"
dataset['SALE YEAR'] = pd.DatetimeIndex(dataset['SALE DATE']).year
dataset['SALE MONTH'] = pd.DatetimeIndex(dataset['SALE DATE']).month
# + id="vjUwMTPDUJq_" colab={"base_uri": "https://localhost:8080/", "height": 508} outputId="1658364d-8330-47e5-f021-6bc2e37e5873"
# # copy the dataset to avoid mismanupulation
df_copy = dataset.copy()
df_copy.tail()
# + [markdown] id="_dNRUh_LTaQD"
# # Outliers Handling
# + [markdown] id="WHv0oxBuSoIO"
# SALE PRICE Outliers
# + [markdown] id="T1SJjF0wqlY3"
# As mention in the dataset documentation, sale price 0 indicates the property transfer transactions. So we will remove the 0 values.
# + id="MQtJult5qkip"
dataset.drop(dataset[dataset['SALE PRICE']==0].index,axis=0,inplace=True)
# + id="ZXpK7aV9TioC" colab={"base_uri": "https://localhost:8080/", "height": 410} outputId="3e2c0a07-c31e-46f7-a20c-fc69ac9cdb80"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='SALE PRICE',data=dataset)
plt.title('Sell Price in USD')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="l7-_wOMTZiZJ"
# Find outliers using IQR
# + id="QGVIYrNhcwF4"
def IQR_Calculator(column_name):
Q1 = dataset[column_name].quantile(0.25)
Q3 = dataset[column_name].quantile(0.75)
IQR = Q3-Q1
lower_limit = Q1 - 1.5*IQR
upper_limit = Q3 + 1.5*IQR
outliers_idx = dataset[(dataset[column_name]<lower_limit) | (dataset[column_name]>upper_limit)].index
return outliers_idx
# + id="-8w4hiKbdLrB"
outliers_idx = IQR_Calculator('SALE PRICE')
# + [markdown] id="epxWv8D3_VO_"
# Remove Outliers
# + id="4wJetQH9YFNi"
dataset.drop(outliers_idx,axis=0,inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="h3KGCyucagOc" outputId="19f52b93-3565-4132-c920-aaf939dedba9"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='SALE PRICE',data= dataset)
plt.title('Sell Price in USD')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="m7nQR_bR98sN" outputId="892850be-fd1a-4f01-eef1-c189c4c52f71"
sns.histplot(dataset['SALE PRICE'],kde=True)
plt.title('Sell Price in USD')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="fUrE-XCM2RpO"
# Here we can see, many transaction under 100000 dollar which is seem so cheap and not fair. So we will cosider this as outliers and remove it.
# + id="rj77LBq72O9u"
dataset.drop(dataset[dataset['SALE PRICE']<100000].index,axis=0,inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="HTeYtcH32Oq2" outputId="f4aeded8-1bcb-4ff0-fa8f-bf61e61abbd4"
sns.histplot(dataset['SALE PRICE'],kde=True)
plt.title('Sell Price in USD')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="P-CXoqz9ZnxW"
# LAND SQUARE FEET Outliers
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="CmXyaM6cUvYc" outputId="bc04b93e-e563-44bc-df0b-b207c17270fe"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='LAND SQUARE FEET',data=dataset)
plt.title('LAND SQUARE FEET')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="FL0YrB7Icnka"
# Find outliers using IQR
# + id="dgdmT0hSckE4"
landSqfeet_outliers_idx = IQR_Calculator('LAND SQUARE FEET')
# + [markdown] id="fg3yG2W9fQJx"
# Remove Outliers
# + id="ss802U8ncj55"
dataset.drop(landSqfeet_outliers_idx,axis=0,inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="0W8U1OUCcjrP" outputId="92cad3cc-0143-4755-af0e-25333a88d94b"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='LAND SQUARE FEET',data=dataset)
plt.title('LAND SQUARE FEET')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="Wp-xjjLOcjCH" outputId="856b12b7-8d3f-4bb9-86eb-42785479cda5"
sns.histplot(dataset['LAND SQUARE FEET'])
plt.title('LAND SQUARE FEETD')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="CKoMAVMQiB-A"
# GROSS SQUARE FEET
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="XlXeLHnFh7CG" outputId="14aa28c2-d7c5-4b1d-bafc-9333934ebb4d"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='GROSS SQUARE FEET',data=dataset)
plt.title('GROSS SQUARE FEET')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + [markdown] id="nT9Qjn_R3TsO"
# Find outliers using IQR
# + id="f5DB1wKBiNeu"
grossSqFeet_Outliers_idx = IQR_Calculator('GROSS SQUARE FEET')
# + id="2u3PWkZxiNPe"
dataset.drop(grossSqFeet_Outliers_idx,axis=0,inplace=True)
# + id="0rME7OVkiM9y" colab={"base_uri": "https://localhost:8080/", "height": 410} outputId="4afeb1eb-4299-4c4e-9ce8-58ce6891f475"
sns.set_style('whitegrid')
sns.set(rc = {'figure.figsize':(12,6)})
sns.boxplot(x='GROSS SQUARE FEET',data=dataset)
plt.title('GROSS SQUARE FEET')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 410} id="qDT2dhPm3hdH" outputId="3f48d60e-9395-4376-98ed-c42c9dc8089e"
sns.histplot(dataset['GROSS SQUARE FEET'])
plt.title('GROSS SQUARE FEET')
plt.ticklabel_format(style='plain', axis='x')
plt.show()
# + id="0mSJd-SOXYJx"
# + [markdown] id="EVPH9wr7qBEo"
# Drop rows where LAND SQUARE FEET and GROSS SQUARE FEET are 0.
# + id="2bWmnGQCXX6M"
#zero_idx = dataset[(dataset['LAND SQUARE FEET']==0) & (dataset['GROSS SQUARE FEET']==0)].index
#dataset.drop(zero_idx,axis=0,inplace=True)
# + [markdown] id="hBAiYSAapWdk"
# # Missing Value Handeling
#
# + id="4lUe9PUl86Ef" colab={"base_uri": "https://localhost:8080/"} outputId="cb898cb5-058d-4900-bd57-b89a57a286cd"
dataset.isnull().sum()
# + colab={"base_uri": "https://localhost:8080/"} id="GSmEV6Oa9WVQ" outputId="06df1a5a-7ddd-49cd-fcae-e903d75e7f1e"
round(dataset.isnull().sum()*100/len(dataset),2)
# + colab={"base_uri": "https://localhost:8080/", "height": 578} id="pdCJAFQcsuk5" outputId="ff019b15-9b2f-4342-adaa-89a70ef66b85"
sns.set(rc = {'figure.figsize':(12,6)})
sns.heatmap(dataset.isnull(),cbar=False)
# + colab={"base_uri": "https://localhost:8080/", "height": 354} id="sOGZ9c-Svn46" outputId="907165a4-161f-46e7-cc4e-064dc2869f2b"
nan_col = dataset.columns[dataset.isnull().any()]
data = round(dataset[nan_col].isnull().sum()*100/len(dataset),2)
data.plot(kind='barh')
# + [markdown] id="TErQQYT21u2G"
# Here 100% of BASE-MENT data and around 77% of APARTMENT NUMBER data are missing. It is quite difficult to fill up this amount of data.
# Also, the name: 0 column does not indicate anything exactly. So, we will drop these columns.
# + id="ptY9WsZU_FA5"
dataset.drop(['Unnamed: 0','EASE-MENT','APARTMENT NUMBER'],axis=1,inplace=True,)
# + [markdown] id="vodQpZS_k3SC"
# Drop the row where 'TAX CLASS AT PRESENT' and 'BUILDING CLASS AT PRESENT' are null.
# + id="1wzsZkRmk2Wg"
dataset.dropna(subset=['TAX CLASS AT PRESENT','BUILDING CLASS AT PRESENT'],inplace=True)
# + [markdown] id="A9EXkixAVEhR"
# Drop the row where 'LAND SQUARE FEET', 'GROSS SQUARE FEET' and 'SALE PRICE' both are null.
# + id="e0aDGott9U0Y"
dataset.dropna(subset=['LAND SQUARE FEET','GROSS SQUARE FEET','SALE PRICE'],thresh=1,inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="uAyDlnWHWvxB" outputId="0b41509e-4770-4273-b5c2-97b7af30945e"
nan_col = dataset.columns[dataset.isnull().any()]
round(dataset[nan_col].isnull().sum()*100/len(dataset),2)
# + id="5AeU4oUVNi-o" colab={"base_uri": "https://localhost:8080/", "height": 371} outputId="d765d734-3a08-4e14-ec0b-3aee23dfb6be"
nan_col = dataset.columns[dataset.isnull().any()]
data = round(dataset[nan_col].isnull().sum()*100/len(dataset),2)
data.plot(kind='barh')
# + [markdown] id="nY01OhLMUa3i"
# Remove rows where TOTAL UNITS 0 and SALE PRICE is null.
# + id="tk_Y3TkcOqIR"
zero_units_idx = dataset[(dataset['TOTAL UNITS']==0) & (dataset['SALE PRICE'].isnull())].index
dataset.drop(zero_units_idx,axis=0,inplace=True)
# + [markdown] id="gZIMs1cQWU4W"
# Remove rows where RESIDENTIAL UNITS + COMMERCIAL UNITS is not equal TOTAL UNITS
# + id="Qg2IotydWj1P"
unit_idx = dataset[dataset['RESIDENTIAL UNITS'] + dataset['COMMERCIAL UNITS'] != dataset['TOTAL UNITS']].index
dataset.drop(unit_idx,axis=0,inplace=True)
# + colab={"base_uri": "https://localhost:8080/"} id="7p1shVzT-ZuC" outputId="7944fec1-fc9c-49fc-a740-081a1df65cda"
round(dataset.isnull().sum()*100/len(dataset),2)
# + [markdown] id="xlNeUzn7ATHt"
# ###Fill the missing values with predictions of model
# + [markdown] id="4SEPD_Q7YR3-"
# Create a function for filling the multiple columns missing values
# + id="r4mDUQc9YQ_A"
def fill_nan(column_name,testData,nan_index):
#Training Data
trainData = dataset.dropna()
trainData = trainData.drop(['NEIGHBORHOOD','BUILDING CLASS CATEGORY','ADDRESS','SALE DATE'],axis=1)
#split train and test data
x_train = trainData.drop(column_name,axis=1)
y_train = trainData[column_name]
x_test = testData.drop(column_name,axis=1)
#Build LinearRegression Model
lrModel = LinearRegression()
lrModel.fit(x_train,y_train)
prediction = lrModel.predict(x_test)
#convert prediction values to float
pred_values=[]
for item in prediction:
pred_values.append(format(item,'.1f'))
# fill missing values with the new predicted values
dataset.loc[nan_index,column_name] = pred_values
# + [markdown] id="Cnp__X16Xgrj"
# ####Fill SALE PRICE missing values
# + id="rEMIY3JQAbp7"
testData = dataset[dataset['LAND SQUARE FEET'].notnull() & dataset['GROSS SQUARE FEET'].notnull() & dataset['SALE PRICE'].isnull()]
testData = testData.drop(['NEIGHBORHOOD','BUILDING CLASS CATEGORY','ADDRESS','SALE DATE'],axis=1)
nan_price_idx = testData.index
# + id="UHYMOiggbaAm"
fill_nan('SALE PRICE',testData,nan_price_idx)
# + colab={"base_uri": "https://localhost:8080/"} id="c7JfvsquaQYt" outputId="431b556b-fa8d-4ad0-f2af-9e18a7badaaa"
dataset.isnull().sum()
# + id="6K1TR0dIfjRQ"
dataset.dropna(inplace =True)
# + colab={"base_uri": "https://localhost:8080/", "height": 629} id="rNtBja0NghuL" outputId="980fe5de-aa51-4eb1-9106-f7e6afd1cd89"
dataset.head()
# + [markdown] id="o-sO52bQl41v"
# #Find Feature importance using mutual information
# + id="mtEuietV9daz"
from sklearn.feature_selection import mutual_info_regression
from sklearn.model_selection import train_test_split
# + [markdown] id="YxX9YWxMQm0f"
# Drop unnecessary columns
# + id="hHgXShK7Qkyk"
dataset.drop(['ADDRESS','SALE DATE'],axis=1,inplace=True)
# + id="CqLZt9B7mYHL"
X = dataset.drop('SALE PRICE',axis=1)
y = dataset['SALE PRICE']
# + id="m9k_ABFdnFYd"
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# + id="wIgc_DGK9dJ0" colab={"base_uri": "https://localhost:8080/"} outputId="161d97a8-27fe-49d9-99e0-ec78db6ced92"
mutual_info = mutual_info_regression(X_train,y_train)
mutual_info
# + id="U71R8CGNSGUw" colab={"base_uri": "https://localhost:8080/"} outputId="7f34c15c-57f2-46e0-e5af-f8d73577b39f"
mutual_info = pd.Series(mutual_info)
mutual_info.index = X_train.columns
mutual_info.sort_values(ascending=False)
# + [markdown] id="wPqrTqujTF-c"
# Let's drop the lowest important features
# + id="lwIB45v2cfrP"
df = dataset.drop(['SALE YEAR'],axis=1)
# + colab={"base_uri": "https://localhost:8080/"} id="Is-U7oAmU-gY" outputId="0c38956c-30dd-40c6-8e3f-f5e7230f5ced"
df.info()
# + id="UqHE0h0cVRuB"
df['BOROUGH'] = pd.to_numeric(df['BOROUGH'],errors = 'coerce')
df['SALE PRICE'] = pd.to_numeric(df['SALE PRICE'],errors = 'coerce')
df['TAX CLASS AT TIME OF SALE'] = pd.to_numeric(df['TAX CLASS AT TIME OF SALE'],errors = 'coerce')
# + [markdown] id="DQEAVycwcSs4"
# #Machine Learning Model
# + [markdown] id="m1YPSwyvZJIm"
# We will try 2 Regression Model:
# > Random Forest Regressor
#
# > XGBRegressor
# + id="QsSdDEP-ZpeM"
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
# + id="-yNEba8FZpRE"
rfrModel = RandomForestRegressor()
xgbrModel = XGBRegressor()
# + id="RI0AJnkga0BD"
X = df.drop('SALE PRICE',axis=1)
y = df['SALE PRICE']
# + id="aNLg6f_KgqK0"
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=101)
# + id="jocAP_u3az2E" colab={"base_uri": "https://localhost:8080/"} outputId="b9b3ada9-fc3a-42f5-f1aa-57e363d307c0"
rfrModel.fit(X_train,y_train)
xgbrModel.fit(X_train,y_train)
# + id="zFPIsMt8fI1x"
rfr_pred = rfrModel.predict(X_test)
xgbr_pred = xgbrModel.predict(X_test)
# + [markdown] id="iFiMSVrodGFo"
# ###Evaluating the model
# + [markdown] id="PnvK8NNDeqWi"
# We will evaluate this two model by
#
# > Mean Absolute Error(MAE)
#
# > Mean Square Error(MSE)
#
# > Root Mean Square Error(RMSE)
#
# > R Squared (R2)
#
#
# + id="ifQkIEruPN7q"
from sklearn.metrics import mean_absolute_error,mean_squared_error,r2_score
# + id="2p7d25hBazpF" colab={"base_uri": "https://localhost:8080/"} outputId="87ed8c58-a244-455d-e9e0-ac5cffd3a3d6"
print('RandomForestRegressor')
print('MAE:',mean_absolute_error(y_test,rfr_pred))
print('MSE:',mean_squared_error(y_test,rfr_pred))
print('RMSE:',np.sqrt(mean_absolute_error(y_test,rfr_pred)))
print('R2:',r2_score(y_test,rfr_pred))
# + id="_hwE4tvffCl6" colab={"base_uri": "https://localhost:8080/"} outputId="6654c3c0-48a3-4675-9a23-699c59f6b917"
print('XGBRegressor')
print('MAE:',mean_absolute_error(y_test,xgbr_pred))
print('MSE:',mean_squared_error(y_test,xgbr_pred))
print('RMSE:',np.sqrt(mean_absolute_error(y_test,xgbr_pred)))
print('R2:',r2_score(y_test,xgbr_pred))
# + [markdown] id="4Pd13SyylbEi"
# As we can see the Random Forest Regressor model perform better than XGBoost Regressor model.
# + [markdown] id="_vgpTzCtlvtP"
# ### Hyperparameter Optimizatio for Random Forest Regressor
# + id="GiVPjxyYuObi"
from sklearn.model_selection import RandomizedSearchCV
# + id="R36In_kfreWo" colab={"base_uri": "https://localhost:8080/", "height": 574} outputId="ae3b98a0-69e8-4c96-9076-861f79a19786"
df
# + id="GIKFgS4hP4Oy"
# + id="10rXU51_PE0G"
# + id="Sc3u0Xc4PE3l"
# + id="0mwn2yp7iFgn"
# + id="PZySYVxNsU6Q"
# + id="RXeuPai5zk9h"
# + id="dP2FFFwNja1P"
# + id="ON-6fxW0Qf4t"
# + id="YSigOu-nSO6W"
|
NYC_Property_Price_Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 11장. 레이블되지 않은 데이터 다루기 : 군집 분석
# **아래 링크를 통해 이 노트북을 주피터 노트북 뷰어(nbviewer.jupyter.org)로 보거나 구글 코랩(colab.research.google.com)에서 실행할 수 있습니다.**
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://nbviewer.jupyter.org/github/rickiepark/python-machine-learning-book-2nd-edition/blob/master/code/ch11/ch11.ipynb"><img src="https://jupyter.org/assets/main-logo.svg" width="28" />주피터 노트북 뷰어로 보기</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/rickiepark/python-machine-learning-book-2nd-edition/blob/master/code/ch11/ch11.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
# </td>
# </table>
# `watermark`는 주피터 노트북에 사용하는 파이썬 패키지를 출력하기 위한 유틸리티입니다. `watermark` 패키지를 설치하려면 다음 셀의 주석을 제거한 뒤 실행하세요.
# +
# #!pip install watermark
# -
# %load_ext watermark
# %watermark -u -d -v -p numpy,pandas,matplotlib,scipy,sklearn
# # k-평균 알고리즘을 사용하여 유사한 객체를 그룹핑하기
# ## 사이킷런을 사용한 k-평균 군집
# +
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=150,
n_features=2,
centers=3,
cluster_std=0.5,
shuffle=True,
random_state=0)
# -
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1],
c='white', marker='o', edgecolor='black', s=50)
plt.grid()
plt.tight_layout()
plt.show()
# +
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3,
init='random',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
# -
plt.scatter(X[y_km == 0, 0],
X[y_km == 0, 1],
s=50, c='lightgreen',
marker='s', edgecolor='black',
label='cluster 1')
plt.scatter(X[y_km == 1, 0],
X[y_km == 1, 1],
s=50, c='orange',
marker='o', edgecolor='black',
label='cluster 2')
plt.scatter(X[y_km == 2, 0],
X[y_km == 2, 1],
s=50, c='lightblue',
marker='v', edgecolor='black',
label='cluster 3')
plt.scatter(km.cluster_centers_[:, 0],
km.cluster_centers_[:, 1],
s=250, marker='*',
c='red', edgecolor='black',
label='centroids')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.show()
# ## 엘보우 방법을 사용하여 최적의 클러스터 개수를 찾기
print('왜곡: %.2f' % km.inertia_)
distortions = []
for i in range(1, 11):
km = KMeans(n_clusters=i,
init='k-means++',
n_init=10,
max_iter=300,
random_state=0)
km.fit(X)
distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()
# ## 실루엣 그래프로 군집 품질을 정량화하기
# +
import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
km = KMeans(n_clusters=3,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,
edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()
# -
# 잘못된 클러스터링:
# +
km = KMeans(n_clusters=2,
init='k-means++',
n_init=10,
max_iter=300,
tol=1e-04,
random_state=0)
y_km = km.fit_predict(X)
plt.scatter(X[y_km == 0, 0],
X[y_km == 0, 1],
s=50,
c='lightgreen',
edgecolor='black',
marker='s',
label='cluster 1')
plt.scatter(X[y_km == 1, 0],
X[y_km == 1, 1],
s=50,
c='orange',
edgecolor='black',
marker='o',
label='cluster 2')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
s=250, marker='*', c='red', label='centroids')
plt.legend()
plt.grid()
plt.tight_layout()
plt.show()
# +
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
c_silhouette_vals = silhouette_vals[y_km == c]
c_silhouette_vals.sort()
y_ax_upper += len(c_silhouette_vals)
color = cm.jet(float(i) / n_clusters)
plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,
edgecolor='none', color=color)
yticks.append((y_ax_lower + y_ax_upper) / 2.)
y_ax_lower += len(c_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()
# -
# # 계층적인 트리로 클러스터를 조직화하기
# ## 상향식으로 클러스터 묶기
# +
import pandas as pd
import numpy as np
np.random.seed(123)
variables = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']
X = np.random.random_sample([5, 3])*10
df = pd.DataFrame(X, columns=variables, index=labels)
df
# -
# ## 거리 행렬에서 계층 군집 수행하기
# +
from scipy.spatial.distance import pdist, squareform
row_dist = pd.DataFrame(squareform(pdist(df, metric='euclidean')),
columns=labels,
index=labels)
row_dist
# -
# 함수 설명을 보면 `pdist` 함수에서 계산한 축약된 거리 행렬(상삼각행렬(upper triangular matrix))을 입력 속성으로 사용할 수 있습니다. 아니면 `linkage` 함수에 초기 데이터 배열을 전달하고 `metric='euclidean'` 지표를 매개변수로 사용할 수 있습니다. 앞서 `squareform` 함수로 만든 거리 행렬은 `linkage` 함수가 기대한 값과 다르기 때문에 사용해서는 안됩니다.
# +
# 1. 잘못된 방식: squareform 거리 행렬
from scipy.cluster.hierarchy import linkage
row_clusters = linkage(row_dist, method='complete', metric='euclidean')
pd.DataFrame(row_clusters,
columns=['row label 1', 'row label 2',
'distance', 'no. of items in clust.'],
index=['cluster %d' % (i + 1)
for i in range(row_clusters.shape[0])])
# +
# 2. 올바른 방식: 축약된 거리 행렬
row_clusters = linkage(pdist(df, metric='euclidean'), method='complete')
pd.DataFrame(row_clusters,
columns=['row label 1', 'row label 2',
'distance', 'no. of items in clust.'],
index=['cluster %d' % (i + 1)
for i in range(row_clusters.shape[0])])
# +
# 3. 올바른 방식: 입력 샘플 행렬
row_clusters = linkage(df.values, method='complete', metric='euclidean')
pd.DataFrame(row_clusters,
columns=['row label 1', 'row label 2',
'distance', 'no. of items in clust.'],
index=['cluster %d' % (i + 1)
for i in range(row_clusters.shape[0])])
# +
from scipy.cluster.hierarchy import dendrogram
# 검은색 덴드로그램 만들기 (1/2 부분만)
# from scipy.cluster.hierarchy import set_link_color_palette
# set_link_color_palette(['black'])
row_dendr = dendrogram(row_clusters,
labels=labels,
# 검은색 덴드로그램 만들기 (2/2 부분)
# color_threshold=np.inf
)
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()
# -
# ## 히트맵에 덴드로그램 연결하기
# +
fig = plt.figure(figsize=(8, 8), facecolor='white')
axd = fig.add_axes([0.09, 0.1, 0.2, 0.6])
# 노트: matplotlib < v1.5.1일 때는 use orientation='right'를 사용하세요
row_dendr = dendrogram(row_clusters, orientation='left')
# 군집에 맞게 데이터를 재정렬합니다.
df_rowclust = df.iloc[row_dendr['leaves'][::-1]]
axd.set_xticks([])
axd.set_yticks([])
# 덴드로그램의 축을 제거합니다.
for i in axd.spines.values():
i.set_visible(False)
# 히트맵을 출력합니다.
axm = fig.add_axes([0.23, 0.1, 0.6, 0.6]) # x-위치, y-위치, 너비, 높이
cax = axm.matshow(df_rowclust, interpolation='nearest', cmap='hot_r')
fig.colorbar(cax)
axm.set_xticklabels([''] + list(df_rowclust.columns))
axm.set_yticklabels([''] + list(df_rowclust.index))
plt.show()
# -
# ## 사이킷런에서 병합 군집 적용하기
# +
from sklearn.cluster import AgglomerativeClustering
ac = AgglomerativeClustering(n_clusters=3,
affinity='euclidean',
linkage='complete')
labels = ac.fit_predict(X)
print('클러스터 레이블: %s' % labels)
# -
ac = AgglomerativeClustering(n_clusters=2,
affinity='euclidean',
linkage='complete')
labels = ac.fit_predict(X)
print('클러스터 레이블: %s' % labels)
# # DBSCAN을 사용하여 밀집도가 높은 지역 찾기
# +
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=200, noise=0.05, random_state=0)
plt.scatter(X[:, 0], X[:, 1])
plt.tight_layout()
plt.show()
# -
# K-평균과 계층 군집:
# +
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
km = KMeans(n_clusters=2, random_state=0)
y_km = km.fit_predict(X)
ax1.scatter(X[y_km == 0, 0], X[y_km == 0, 1],
edgecolor='black',
c='lightblue', marker='o', s=40, label='cluster 1')
ax1.scatter(X[y_km == 1, 0], X[y_km == 1, 1],
edgecolor='black',
c='red', marker='s', s=40, label='cluster 2')
ax1.set_title('K-means clustering')
ac = AgglomerativeClustering(n_clusters=2,
affinity='euclidean',
linkage='complete')
y_ac = ac.fit_predict(X)
ax2.scatter(X[y_ac == 0, 0], X[y_ac == 0, 1], c='lightblue',
edgecolor='black',
marker='o', s=40, label='cluster 1')
ax2.scatter(X[y_ac == 1, 0], X[y_ac == 1, 1], c='red',
edgecolor='black',
marker='s', s=40, label='cluster 2')
ax2.set_title('Agglomerative clustering')
plt.legend()
plt.tight_layout()
plt.show()
# -
# DBSCAN:
# +
from sklearn.cluster import DBSCAN
db = DBSCAN(eps=0.2, min_samples=5, metric='euclidean')
y_db = db.fit_predict(X)
plt.scatter(X[y_db == 0, 0], X[y_db == 0, 1],
c='lightblue', marker='o', s=40,
edgecolor='black',
label='cluster 1')
plt.scatter(X[y_db == 1, 0], X[y_db == 1, 1],
c='red', marker='s', s=40,
edgecolor='black',
label='cluster 2')
plt.legend()
plt.tight_layout()
plt.show()
|
code/ch11/ch11.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.11 64-bit (''trading'': conda)'
# name: python3
# ---
import ccxt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
exchange_binance = ccxt.binanceusdm()
exchange_binance_2 = ccxt.binance()
# +
column_name = ['time', 'open', 'high', 'low', 'close', 'volume']
unfi_df = pd.DataFrame(exchange_binance.fetch_ohlcv(symbol='UNFI/USDT', timeframe='4h',limit=500),columns=column_name)['close']
uni_df = pd.DataFrame(exchange_binance.fetch_ohlcv(symbol='UNI/USDT',timeframe='4h',limit=500),columns=column_name)['close']
unfi_df = np.log(unfi_df/unfi_df[0])
uni_df = np.log(uni_df/uni_df[0])
spread = unfi_df - uni_df
unfi_df_logrt = unfi_df.pct_change()
uni_df_logrt = uni_df.pct_change()
# +
defi_df = pd.DataFrame(exchange_binance.fetch_ohlcv(
symbol='DEFI/USDT', timeframe='4h', limit=1000), columns=column_name)['close']
yfii_df = pd.DataFrame(exchange_binance.fetch_ohlcv(
symbol='YFII/USDT', timeframe='4h', limit=1000), columns=column_name)['close']
defi_df = np.log(defi_df/defi_df[0])
yfii_df = np.log(yfii_df/yfii_df[0])
spread_1 = defi_df - yfii_df
#defi_df_logrt = defi_df.pct_change()
#yfii_df_logrt = yfii_df.pct_change()
# +
plt.subplot(2,2,1)
plt.plot(spread_1)
plt.subplot(2,2,2)
plt.plot(defi_df , label = 'DEFI')
plt.plot(yfii_df, label = 'YFII')
plt.legend()
plt.subplot(2,2,3)
plt.plot(spread)
plt.subplot(2,2,4)
plt.plot(unfi_df)
plt.plot(uni_df)
# -
from statsmodels.tsa.stattools import adfuller
adfuller(x=spread)
# +
import statsmodels.api as sm
dfy = uni_df.values
dfx = sm.add_constant(unfi_df.values)
linear = sm.OLS(dfy, dfx)
result = linear.fit()
result.summary()
# +
dfy = defi_df.values
dfx = sm.add_constant(yfii_df.values)
linear = sm.OLS(dfy, dfx)
result = linear.fit()
result.summary()
# +
uni_df = (0.6774)*(unfi_df)+(0.1153)
plt.scatter(unfi_df,uni_df)
plt.plot(unfi_df.values, uni_df.values, color='r')
plt.show()
# +
import statsmodels.api as sm
uni_df_logrt = uni_df_logrt[2:]*0.6774
unfi_df_logrt = unfi_df_logrt[2:]
dfy = uni_df_logrt.values
dfx = sm.add_constant(unfi_df_logrt.values)
linear = sm.OLS(dfy, dfx)
result = linear.fit()
result.summary()
# +
uni_df_logrt = (-0.00145)*(unfi_df_logrt)+(0.0915)
plt.scatter(unfi_df_logrt, uni_df_logrt)
plt.plot(unfi_df_logrt.values, uni_df_logrt.values, color='r')
plt.show()
# +
column_name = ['time', 'open', 'high', 'low', 'close', 'volume']
unfi_df = pd.DataFrame(exchange_binance.fetch_ohlcv(
symbol='BTC/USDT', timeframe='1d', limit=1000), columns=column_name)['close']
uni_df = pd.DataFrame(exchange_binance_2.fetch_ohlcv(
symbol='BTC/USDT', timeframe='1d', limit=1000), columns=column_name)['close']
unfi_df = np.log(unfi_df/unfi_df[0])
uni_df = np.log(uni_df/uni_df[0])
spread = (unfi_df - uni_df)
unfi_df_logrt = unfi_df.pct_change()
uni_df_logrt = uni_df.pct_change()
plt.plot(spread)
# -
|
statistic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Clean up
# !hdfs dfs -rm -r -f /datasets /tmp
# !rm -rf /tmp/hadoop_git_readme*
# !hdfs dfs -expunge
# ## Command line
# !hdfs dfsadmin -report
# !hdfs dfs -ls /
# !hdfs dfs -df -h /
# !hdfs dfs -du -h /
# !hdfs dfs -mkdir /datasets
# !wget -q http://www.gutenberg.org/cache/epub/100/pg100.txt \
# -O ../datasets/shakespeare_all.txt
# +
# !hdfs dfs -put ../datasets/shakespeare_all.txt \
# /datasets/shakespeare_all.txt
# !hdfs dfs -put ../datasets/hadoop_git_readme.txt \
# /datasets/hadoop_git_readme.txt
# -
# !hdfs dfs -ls /datasets
# !hdfs dfs -cat /datasets/hadoop_git_readme.txt | wc -l
# !hdfs dfs -cat \
# hdfs:///datasets/hadoop_git_readme.txt \
# file:///home/vagrant/datasets/hadoop_git_readme.txt | wc -l
# !hdfs dfs -cp /datasets/hadoop_git_readme.txt \
# /datasets/copy_hadoop_git_readme.txt
# !hdfs dfs -rm /datasets/copy_hadoop_git_readme.txt
# !hdfs dfs -expunge
# !hdfs dfs -get /datasets/hadoop_git_readme.txt \
# /tmp/hadoop_git_readme.txt
# !hdfs dfs -tail /datasets/hadoop_git_readme.txt
# ## Snakebite
from snakebite.client import Client
client = Client("localhost", 9000)
client.serverdefaults()
for x in client.ls(['/']):
print x['path']
client.df()
list(client.du(["/"]))
# +
# Note:
# put command is not yet available
# -
for el in client.cat(['/datasets/hadoop_git_readme.txt']):
print el.next().count("\n")
# +
# Note:
# # copy command is not yet available
# -
client.delete(['/datasets/shakespeare_all.txt']).next()
(client
.copyToLocal(['/datasets/hadoop_git_readme.txt'],
'/tmp/hadoop_git_readme_2.txt')
.next())
list(client.mkdir(['/datasets_2']))
list(client.delete(['/datasets*'], recurse=True))
|
projects/advanced/large_scale/ml_hdfs_intro_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/milayacharlieCvSU/OOP-1-1/blob/main/OOP_Concepts_2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Y34qKCP1It0c"
# Classes with Multiple Objects
# + colab={"base_uri": "https://localhost:8080/"} id="QE_2gUo_GrV-" outputId="897a3359-37ab-445b-a6c8-48d11442aee2"
class Birds:
def __init__ (self, bird_name):
self.bird_name = bird_name
def flying_birds(self):
print(f"{self.bird_name} flies above the sky.")
def non_flying_birds(self):
print(f"{self.bird_name} is the national bird of Australia.")
vulture = Birds("Griffon Vulture")
crane = Birds("Common Crane")
emu = Birds("Emu")
vulture.flying_birds()
crane.flying_birds()
emu.non_flying_birds()
# + [markdown] id="1qQa9pzvOBHE"
# Encapsulation (mangling with double underscore)
# + colab={"base_uri": "https://localhost:8080/"} id="JHsA8NYRRdC8" outputId="0e3a1c68-862c-47f3-e29b-56b982fbe79c"
class foo:
def __init__(self, a, b):
self.__a = a
self.__b = b
def add(self):
return self.__a + self.__b
object_foo = foo(3,4)
object_foo.add()
object_foo.a = 6
object_foo.b = 7
object_foo.add()
# + colab={"base_uri": "https://localhost:8080/"} id="1s_YPyMsRvUb" outputId="db32a97a-3724-49f5-f376-cefa81b5cbf3"
class Counter:
def __init__(self):
self.__current = 0
def increment(self):
self.__current += 1
def value(self):
return self.__current
def reset(self):
self.__current = 0
number = Counter()
number.__current = 1
number.increment()
number.increment()
number.increment()
print(number.value())
# + [markdown] id="xaRQEDlSUvo-"
# Inheritance
# + colab={"base_uri": "https://localhost:8080/"} id="OlbRKxkpUwrv" outputId="6bd4ac11-f7ce-47cb-b932-368d34628028"
class Person:
def __init__(self, first_name, surname):
self.first_name = first_name
self.surname = surname
def fullname(self):
print(self.first_name, self.surname)
person = Person("Mam", "Sayo")
person.fullname()
class Teacher(Person):
pass
person2 = Teacher("Ma'am", "Maria")
person2.fullname()
class Student(Person):
pass
person3 = Student("Charlie", "Milaya")
person3.fullname()
# + [markdown] id="9-Zdclz0XbFJ"
# Polymorphism
# + colab={"base_uri": "https://localhost:8080/"} id="FowkGJiPXdVT" outputId="0b80baad-c9a1-4eb5-c6c4-81a5c594e521"
class RegularPolygon:
def __init__(self, side):
self.side = side
class Square(RegularPolygon):
def area(self):
return self.side**2
class EquilateralTriangle(RegularPolygon):
def area(self):
return self.side**2*0.433
obj1 = Square(4)
print(obj1.area())
obj2 = EquilateralTriangle(3)
print(obj2.area())
# + [markdown] id="H1S1xp9FxsDy"
# #### Application 1
# + [markdown] id="bij2MCUkxv6W"
# 1. Create a Python program that displays the name of three students (Student 1, Student 2, Student 3) and their term grades.
# 2. Create a class name Person and attributes - std1, std2, std3, pre, mid, fin
# 3. Compute the average of each term grade using Grade() method.
# 4. Information about student's grade must be hidden from others.
# + colab={"base_uri": "https://localhost:8080/"} id="SKYTL-6Jx041" outputId="bb69b979-4e4a-432f-cd7e-2cd243d9786a"
class Person:
def __init__(self, std, pre, mid, fin):
self.__std = std
self.__pre = pre
self.__mid = mid
self.__fin = fin
def display(self):
print("Student Name : %s" % self.__std)
print("Prefinal Grade : %.2f" % self.__pre)
print("Midtern Grade : %.2f" % self.__mid)
print("Final Grade : %.2f" % self.__fin)
def average_grade(self):
return (self.__pre + self.__mid + self.__fin)/3
std1 = Person("Student 1", 1.50, 1.25, 1.00)
std1.display()
print("Average Grade : %.2f" % std1.average_grade(), end="\n\n")
std2 = Person("Student 2", 1.25, 1.50, 1.25)
std2.display()
print("Average Grade : %.2f" % std2.average_grade(), end="\n\n")
std3 = Person("Student 3", 2.00, 1.50, 1.25)
std3.display()
print("Average Grade : %.2f" % std3.average_grade())
|
OOP_Concepts_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Deck of Cards
#
# > A minimal example of using nbdev to create a python library.
# https://nitinverma78.github.io/deck_of_cards/
# This repo uses code from <NAME>'s ThinkPython2. This file was automatically generated from a Jupyter Notebook using nbdev. To change it you must edit `index.ipynb`
# ## Install
# `pip install -e`
# > There is already a project called deck_of_cards on pypi. This project has no relation to that. This project is an example of how to create python packages with nbdev.
# ## How to use
# Playing cards in python!
from deck_of_cards.deck import Deck
d = Deck()
print(f'Number of playing cards in the deck: {len(d.cards)}')
card = d.pop_card()
print(card)
|
index.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Search Engine Implementation
#
# An implementation of a search engine to rank matching documents according to their relevance to a given search query. The ranking is calculated by using simple term frequency and document frequency measures.
# Let's first import the librarys we will be using.
import os
import math
import numpy as np
import matplotlib.pyplot as plt
# Make a list of all txt files in the path specified
# +
path = 'ACL\\' # notice here that backward slash is replaced with double backward slashes
txtFiles = []
for fileName in os.listdir(path):
if fileName.endswith('.txt'):
txtFiles.append(path+fileName)
print(len(txtFiles),txtFiles[:5])
# -
# Defining a function to take a document as an input and return a list of words in the input document
## function to read text and return list of words
def wordList(doc):
sList=[]
for w in doc.split(" "):
sList.append(w.strip('\n'))
return sList
# A sample text to the functions
sampleText="On July 16, 1969, the Apollo 11 spacecraft launched from the Kennedy Space Center in Florida. Its mission was to go\
where no human being had gone before—the moon! The crew consisted of <NAME>, <NAME>, and <NAME>. The\
spacecraft landed on the moon in the Sea of Tranquility, a basaltic flood plain, on 20--July 1969"
print(wordList(sampleText))
### function to remove puntuation marks from words
# import string.maketrans as textfilter
from string import punctuation as puncs
def removePuncs(wordList):
#print('punctuation marks are: ', puncs)
sList = []
for w in wordList:
word=w.translate(str.maketrans({key: None for key in puncs}))
sList.append(word)
return sList
removePuncs(wordList(sampleText))
### function to calculate term frequency in the doc
def termFrequencyInDoc(wordList):
termFrequency_dic={}
for w in wordList:
if w in termFrequency_dic.keys():
termFrequency_dic[w]+=1
else:
termFrequency_dic[w]=1
return termFrequency_dic
termFrequencyInDoc(removePuncs(wordList(sampleText)))
## function to calculate word Document frequency
def wordDocFre(dicList):
vocan={}
for docDic in dicList:
for w in docDic.keys():
if w in vocan.keys():
vocan[w]+=1
else:
vocan[w]=1
return vocan
# Calculate inverse document using IDF(w) = log [(M+1)/k]
## function takes dictionary returned from wordDocFre functions above and outputs inverse document frequency of each word.
def inverseDocFre(vocan,totalDocs):
invDocFreqDic={}
for key,value in vocan.items():
invDocFreqDic[key] = math.log((totalDocs + 1)/value)
return invDocFreqDic
### function to calculate tf-idf for everyword in doc
def tfidf(docList):
dicList=[]
for i in range(0,len(docList)):
sList = wordList(open(docList[i]).read())
sListWoPuncs = removePuncs(sList)
dicList.append(termFrequencyInDoc(sListWoPuncs))
invDocFreqDic = inverseDocFre(wordDocFre(dicList),len(docList))
tfidf_Dic = []
for tfDic in dicList:
tempDic = {}
for key in tfDic.keys():
tempDic[key] = tfDic[key] * invDocFreqDic[key]
tfidf_Dic.append(tempDic)
return tfidf_Dic, dicList
# #### sorting vocabulary according to IDF-against K (number of documents containing that word) values and plot using matplotlib.pyplot
# <img src="files/images/IDFvsDF.png">
# +
dicList=[]
for i in range(0,len(txtFiles)):
sList = wordList(open(txtFiles[i]).read())
sListWoPuncs = removePuncs(sList)
dicList.append(termFrequencyInDoc(sListWoPuncs))
DocFreqDic = wordDocFre(dicList)
invDocFreqDic = inverseDocFre(DocFreqDic,len(txtFiles))
invDocFreqList = list(invDocFreqDic.values())
plt.plot(sorted(list(DocFreqDic.values()), reverse=True), sorted(list(invDocFreqDic.values())))
plt.title('IDF-K relation')
plt.xlabel('K (Doc Freq)')
plt.ylabel('IDF')
plt.show()
# -
# #### A plot that shows how IDF-K relation changes as base of logarithm changes
# +
legnd = []
for i in range(0,9):
invDocFreqDic={}
for key,value in DocFreqDic.items():
invDocFreqDic[key] = math.log((len(txtFiles) + 1)/value, 10-i)
plt.plot(sorted(list(DocFreqDic.values()), reverse=True), sorted(list(invDocFreqDic.values())))
legnd.append("log base " + str(10-i))
invDocFreqDic={}
for key,value in DocFreqDic.items():
invDocFreqDic[key] = math.log((len(txtFiles) + 1)/value, 0.5)
plt.plot(sorted(list(DocFreqDic.values())), sorted(list(invDocFreqDic.values())))
legnd.append("log base " + str(0.5))
invDocFreqDic={}
for key,value in DocFreqDic.items():
invDocFreqDic[key] = math.log((len(txtFiles) + 1)/value, 0.5)
plt.plot(sorted(list(DocFreqDic.values())), sorted(list(invDocFreqDic.values())))
legnd.append("log base " + str(0.25))
plt.title('IDF-K relation with respect to log base')
plt.xlabel('K (Doc Freq)')
plt.ylabel('IDF')
plt.legend(legnd, loc='upper right')
plt.show
# -
# construct a plot Term Frequency weight transformation such as this one
# <img src="files/images/TFNorm.png">
# +
legnd = []
sList = wordList(open(txtFiles[0]).read())
sListWoPuncs = removePuncs(sList)
x_cwd = termFrequencyInDoc(sListWoPuncs)
plt.plot(sorted(list(x_cwd.values())), sorted(list(x_cwd.values())))
legnd.append("y=x ")
y_tfwd1 = {}
for key in x_cwd.keys():
y_tfwd1[key] = math.log(1+x_cwd[key])
plt.plot(sorted(list(x_cwd.values())), sorted(list(y_tfwd1.values())))
legnd.append("y= log(1+x) ")
y_tfwd2 = {}
for key in x_cwd.keys():
y_tfwd2[key] = math.log(1+math.log(1+x_cwd[key]))
plt.plot(sorted(list(x_cwd.values())), sorted(list(y_tfwd2.values())))
legnd.append("y= log(1 + log(1+x)) ")
y_tfwd3 = {}
for key in x_cwd.keys():
y_tfwd3[key] = 1
plt.plot(sorted(list(x_cwd.values())), sorted(list(y_tfwd3.values())))
legnd.append("0/1 bit vector")
plt.title('Term Frequency transformations')
plt.xlabel('x=c(w,d)')
plt.ylabel('y=TF(w,d)')
plt.legend(legnd, loc='upper right')
plt.ylim(0, 10)
plt.show
# -
# #### construct plot of BM25 as shown here
# <img src="files/images/BM25.png">
# +
legnd = []
sList = wordList(open(txtFiles[0]).read())
sListWoPuncs = removePuncs(sList)
#DocFreqDic
x_cwd = termFrequencyInDoc(sListWoPuncs)
plt.plot(sorted(list(x_cwd.values())), sorted(list(x_cwd.values())))
legnd.append("y=x ")
y_tfwd1 = {}
for key in x_cwd.keys():
y_tfwd1[key] = ((DocFreqDic[key] + 1) * x_cwd[key])/(x_cwd[key] + DocFreqDic[key])
plt.plot(sorted(list(x_cwd.values())), sorted(list(y_tfwd1.values())))
legnd.append("y= (k+1)x / x+k ")
y_tfwd2 = {}
for key in x_cwd.keys():
y_tfwd2[key] = 1
plt.plot(sorted(list(x_cwd.values())), sorted(list(y_tfwd2.values())))
legnd.append("k=0 ")
plt.title('Term Frequency transformations')
plt.xlabel('x=c(w,d)')
plt.ylabel('y=TF(w,d)')
plt.legend(legnd, loc='upper right')
#plt.ylim(0, 10)
plt.show
# -
def tfTransformation(cwd_list):
tfwd = []
for cwd in cwd_list:
temp_dic = {}
for key in cwd.keys():
temp_dic[key] = math.log(1+math.log(1+cwd[key]))
tfwd.append(temp_dic)
return tfwd
def ranking_func(query):
queryList = wordList(query)
queryWoPuncs = removePuncs(queryList)
queryLowerCase = []
for word in queryWoPuncs:
queryLowerCase = word.lower()
cwq = termFrequencyInDoc(queryLowerCase)
cwd_list, tfidf_list = tfidf(txtFiles)
tfwd_list = tfTransformation(cwd_list)
rank_list = []
for i in range (0, len(txtFiles)):
rank = 0
for key in cwq.keys():
try:
rank += cwq[key] * tfwd_list[i][key] * tfidf_list[i][key]
except:
rank = 0
rank_list.append(rank)
doc_index_list = []
for i in range (0,5):
doc_index_list.append(rank_list.index(max(rank_list)))
del rank_list[rank_list.index(max(rank_list))]
for i in range (0,5):
print (txtFiles[doc_index_list[i]])
ranking_func("Text Mining")
|
similarily_ranking.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import fastf1 as ff1
from matplotlib import pyplot as plt
from fastf1 import plotting
plotting.setup_mpl()
# -
# # Variables
# +
directory = '../Telemetry/2021/TUR/Alpine/Qualifying/'
year = 2021
raceNumber = 16
title = 'Turkish GP Q2'
driver1_no_lap = 14
driver2_no_lap = 14
driver1_name = 'OCO'
driver1_fullname = 'Ocon'
driver2_name = 'ALO'
driver2_fullname = 'Alonso'
graphLinediWidth = 0.3
color1 = plotting.TEAM_COLORS['Alpine']
color2 = 'yellow'
# -
# # Loads Session DATA
# +
ff1.Cache.enable_cache('cache')
quali = ff1.get_session(year, raceNumber, 'Q')
laps = quali.load_laps(with_telemetry=True)
# -
# # Initialization
# +
driver1 = laps.pick_driver(driver1_name).pick_wo_box()
driver2 = laps.pick_driver(driver2_name).pick_wo_box()
driver1 = driver1[driver1['LapNumber'] == driver1_no_lap]
driver2 = driver2[driver2['LapNumber'] == driver2_no_lap]
name1 = driver1_fullname
name2 = driver2_fullname
driver1Data = driver1.telemetry
driver2Data = driver2.telemetry
# -
# # Telemetry charts
#
# ## Speed
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['Speed'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['Speed'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("Speed (kph)")
ax.legend(bbox_to_anchor=(0,1),loc=3)
d = driver1.pick_fastest()
d2 = driver2.pick_fastest()
plt.text(-0.05, 1.13, d['LapTime'].total_seconds(),
horizontalalignment='center',
verticalalignment='center',
transform = ax.transAxes)
plt.text(-0.05, 1.06,d2['LapTime'].total_seconds(),
horizontalalignment='center',
verticalalignment='center',
transform = ax.transAxes)
plt.savefig(directory + 'telemetrySpeed.png', dpi=1200)
plt.show()
# -
# ## RMP
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['RPM'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['RPM'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("RPM")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryRPM.png', dpi=1200)
plt.show()
# -
# ## Gear
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['nGear'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['nGear'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("Gear")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryGear.png', dpi=1200)
plt.show()
# -
# ## Throttle Pedal
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['Throttle'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['Throttle'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("Throttle pedal pressure 0-100")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryThrottle.png', dpi=1200)
plt.show()
# -
# ## Brake Pedal
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['Brake'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['Brake'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("Brake pedal pressure 0-100")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryBrake.png', dpi=1200)
plt.show()
# -
# ## DRS Activation
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['DRS'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['DRS'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("DRS indicator")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryDRS.png', dpi=1200)
plt.show()
# -
# # Experimental graphs
# ## Meters travelled per second
# +
fig, ax = plt.subplots()
ax.plot(driver1Data['Distance'], driver1Data['Time'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], driver2Data['Time'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Distance (m)")
ax.set_ylabel("Time")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryTime.png', dpi=1200)
plt.show()
# -
# ## Percentage of the lap completed per second
# ### Sector 1 (limits need to be adjusted for other tracks)
# +
fig, ax = plt.subplots()
driver1Data.add_relative_distance()
driver2Data.add_relative_distance()
print(driver1['Sector1Time'])
sector1Time = 0.0005 * 0.75
plt.ylim(top=0.0005 * 0.75, bottom=0)
plt.xlim(right=0.4)
ax.plot(driver1Data['RelativeDistance'], driver1Data['Time'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['RelativeDistance'], driver2Data['Time'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Relative Distance (% of the lap)")
ax.set_ylabel("Time")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryTimeSector1.png', dpi=1200)
plt.show()
# -
# ### Sector 2 (limits need to be adjusted for other tracks)
# +
fig, ax = plt.subplots()
driver1Data.add_relative_distance()
driver2Data.add_relative_distance()
print(driver1['Sector2Time'])
sector1Time = 0.0005 * 0.75
plt.ylim(bottom=0.0005 * 0.75, top=sector1Time*2)
plt.xlim(left=0.4, right=0.8)
ax.plot(driver1Data['RelativeDistance'], driver1Data['Time'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['RelativeDistance'], driver2Data['Time'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Relative Distance (% of the lap)")
ax.set_ylabel("Time")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryTimeSector2.png', dpi=1200)
plt.show()
# -
# ### Sector 3 (limits need to be adjusted for other tracks)
# +
fig, ax = plt.subplots()
driver1Data.add_relative_distance()
driver2Data.add_relative_distance()
print(driver1['Sector2Time'])
sector1Time = 0.0005 * 0.75
plt.ylim(bottom=sector1Time*2, top=sector1Time*2.65)
plt.xlim(left=0.8, right=1)
ax.plot(driver1Data['RelativeDistance'], driver1Data['Time'], color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['RelativeDistance'], driver2Data['Time'], color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_xlabel("Relative Distance (% of the lap)")
ax.set_ylabel("Time")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryTimeSector3.png', dpi=1200)
plt.show()
# -
# ## time by distance differential
# +
fig, ax = plt.subplots()
driver1Data = driver1.telemetry
driver2Data = driver2.telemetry
dif1 = driver1Data.calculate_differential_distance()
dif2 = driver2Data.calculate_differential_distance()
graphLinediWidth = 0.2
ax.plot(driver1Data['Time'], dif1 , color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Time'], dif2 , color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_ylabel("Differential Distance (m)")
ax.set_xlabel("Time")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryDifferentialTime.png', dpi=1200)
plt.show()
# -
# ## Relation between differential distance and total distance done
# +
fig, ax = plt.subplots()
driver1Data = driver1.telemetry
driver2Data = driver2.telemetry
dif1 = driver1Data.calculate_differential_distance()
dif2 = driver2Data.calculate_differential_distance()
graphLinediWidth = 0.2
ax.plot(driver1Data['Distance'], dif1 , color=color1, linewidth=graphLinediWidth, label=name1)
ax.plot(driver2Data['Distance'], dif2 , color=color2, linewidth=graphLinediWidth, label=name2)
ax.set_title(title)
ax.set_ylabel("Differential Distance (m)")
ax.set_xlabel("Distance")
ax.legend(bbox_to_anchor=(0,1),loc=3)
plt.savefig(directory + 'telemetryDifferentialDistance.png', dpi=1200)
plt.show()
# -
|
Notebooks/.ipynb_checkpoints/Telemetry Qualy-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/JamesHorrex/AI_stock_trading/blob/master/SS_AITrader_JNJ.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="bKT2tX6DtauA" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="fa1e8a12-66f2-46fd-ce37-feadf870c3b5"
# %matplotlib inline
import numpy as np
import tensorflow as tf
print(tf.__version__)
# + id="k2b2DdBskfka" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 314} outputId="00cb26ed-aca4-4377-a78a-f8625fab7556"
# !pip install git+https://github.com/tensorflow/docs
# + id="IYtw7-dbkYiD" colab_type="code" colab={}
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
import tensorflow_docs.modeling
# + id="hDdT5zKLv1rP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 123} outputId="13fb15d6-3369-4e11-9fcb-54c9f1a54aec"
from google.colab import drive
drive.mount('/content/gdrive')
# + id="mAz2vMeqAyTL" colab_type="code" colab={}
import pandas as pd
df=pd.read_csv('gdrive/My Drive/SS_AITrader/JNJ/df_JNJ_20drtn_features.csv')
# + id="I0Qvmpz-BCSt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="afc83f19-e0b7-44b3-d55f-b3d12aa17ade"
df.head()
# + id="1qE_jesFKOpZ" colab_type="code" colab={}
df['timestamp'] = pd.to_datetime(df['timestamp'])
# + id="qTGO7R82NRMH" colab_type="code" colab={}
from_date='2010-01-01'
to_date='2020-01-01'
# + id="Hy0qnGa0NZpz" colab_type="code" colab={}
df = df[pd.to_datetime(from_date) < df['timestamp'] ]
df = df[pd.to_datetime(to_date) > df['timestamp'] ]
# + id="inuuZ7pWKXup" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="f2444359-314d-4733-c495-d7cf429b511c"
df.head()
# + id="cp3Y0aSaO6jD" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="8f2115c6-43b9-417b-c811-ccc956626edb"
df.tail()
# + id="KR7WRpTJaRB4" colab_type="code" colab={}
df.drop(['timestamp'], inplace=True, axis=1)
# + id="Anb_cU4SHzkl" colab_type="code" colab={}
train_dataset = df.sample(frac=0.8,random_state=0)
test_dataset = df.drop(train_dataset.index)
# + id="-Ze7LKS-ak6u" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 312} outputId="f7f37765-ba8d-413f-9b8d-f52fc4e5b38b"
train_dataset.head()
# + id="KyB_Wb9Fav0m" colab_type="code" colab={}
train_labels = train_dataset.pop('labels')
test_labels = test_dataset.pop('labels')
# + id="YumkgVabeud9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 121} outputId="f18e4bce-214f-451b-ae6d-bd45d8b8ea63"
train_labels.head()
# + id="LQpxY8Kjeh9H" colab_type="code" colab={}
from sklearn.utils import compute_class_weight
def get_sample_weights(y):
y = y.astype(int) # compute_class_weight needs int labels
class_weights = compute_class_weight('balanced', np.unique(y), y)
print("real class weights are {}".format(class_weights), np.unique(y))
print("value_counts", np.unique(y, return_counts=True))
sample_weights = y.copy().astype(float)
for i in np.unique(y):
sample_weights[sample_weights == i] = class_weights[i] # if i == 2 else 0.8 * class_weights[i]
# sample_weights = np.where(sample_weights == i, class_weights[int(i)], y_)
return sample_weights
# + id="iXhEiJnO28kQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 259} outputId="0d39ac27-bb8a-4847-a3c1-e9a81ed6af02"
get_sample_weights(train_labels)
# + id="EmTtLI6ufD7f" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="23ea7e33-c965-4ae1-ad31-c47df32671ce"
SAMPLE_WEIGHT=get_sample_weights(train_labels)
# + id="ft6KC349cvWN" colab_type="code" colab={}
train_stats = train_dataset.describe()
train_stats = train_stats.transpose()
# + id="zMEH1r2ya1UM" colab_type="code" colab={}
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
# + id="QZQxTHBAGIJY" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 537} outputId="4e6e7c30-cfb7-439b-9ab2-376b6f380af8"
from sklearn.feature_selection import SelectKBest, f_classif, mutual_info_classif
from operator import itemgetter
k=30
list_features = list(normed_train_data.columns)
select_k_best = SelectKBest(f_classif, k=k)
select_k_best.fit(normed_train_data, train_labels)
selected_features_anova = itemgetter(*select_k_best.get_support(indices=True))(list_features)
selected_features_anova
# + id="UoGj_iK6JdDy" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 537} outputId="25a8325e-6be3-49d1-ac87-74d69657d497"
select_k_best = SelectKBest(mutual_info_classif, k=k)
select_k_best.fit(normed_train_data, train_labels)
selected_features_mic = itemgetter(*select_k_best.get_support(indices=True))(list_features)
selected_features_mic
# + id="VS_4c6YyMHl9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 226} outputId="1f602069-227e-46d6-b2a5-086c0ee63e97"
list_features = list(normed_train_data.columns)
feat_idx = []
for c in selected_features_mic:
feat_idx.append(list_features.index(c))
feat_idx = sorted(feat_idx)
X_train_new=normed_train_data.iloc[:, feat_idx]
X_test_new=normed_test_data.iloc[:, feat_idx]
#kbest=SelectKBest(f_classif, k=10)
#X_train_new = kbest.fit_transform(normed_train_data, train_labels)
#X_test_new = kbest.transform(normed_test_data)
X_test_new.shape
X_test_new.head()
# + id="1Y6IeZLPdDbh" colab_type="code" colab={}
def build_model(hidden_dim,dropout=0.5):
## input layer
inputs=tf.keras.Input(shape=(X_train_new.shape[1],))
h1= tf.keras.layers.Dense(units=hidden_dim,activation='relu')(inputs)
h2= tf.keras.layers.Dropout(dropout)(h1)
h3= tf.keras.layers.Dense(units=hidden_dim*2,activation='relu')(h2)
h4= tf.keras.layers.Dropout(dropout)(h3)
h5= tf.keras.layers.Dense(units=hidden_dim*2,activation='relu')(h4)
h6= tf.keras.layers.Dropout(dropout)(h5)
h7= tf.keras.layers.Dense(units=hidden_dim,activation='relu')(h6)
##output
outputs=tf.keras.layers.Dense(units=2,activation='softmax')(h7)
return tf.keras.Model(inputs=inputs, outputs=outputs)
# + id="YvYU19fefqf7" colab_type="code" colab={}
criterion = tf.keras.losses.sparse_categorical_crossentropy
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
model = build_model(hidden_dim=64)
model.compile(optimizer=optimizer,loss=criterion,metrics=['accuracy'])
# + id="2RjdYWf5gX4x" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 190} outputId="3ec182d0-77f7-4e21-fed6-3a597afe6429"
example_batch = X_train_new[:10]
example_result = model.predict(example_batch)
example_result
# + id="bwsZt86Vg9Fs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="cd99a066-ee67-47f0-99ac-2f42615a61a8"
EPOCHS=200
BATCH_SIZE=20
history = model.fit(
X_train_new, train_labels,
epochs=EPOCHS, batch_size=BATCH_SIZE ,sample_weight=SAMPLE_WEIGHT,shuffle=True,validation_split = 0.2, verbose=1,
callbacks=[tfdocs.modeling.EpochDots()])
# + id="ODHW1NAOqNcK" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 206} outputId="65294990-ba5f-4494-a201-38a6a3492cc5"
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
# + id="Q3-cFZIRrMKd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 362} outputId="5e3e3162-34f2-43fb-cc80-cf67a41fc653"
import matplotlib.pyplot as plt
hist=history.history
fig=plt.figure(figsize=(12,5))
ax=fig.add_subplot(1,2,1)
ax.plot(hist['loss'],lw=3)
ax.plot(hist['val_loss'],lw=3)
ax.set_title('Training & Validation Loss',size=15)
ax.set_xlabel('Epoch',size=15)
ax.tick_params(axis='both',which='major',labelsize=15)
ax=fig.add_subplot(1,2,2)
ax.plot(hist['accuracy'],lw=3)
ax.plot(hist['val_accuracy'],lw=3)
ax.set_title('Training & Validation accuracy',size=15)
ax.set_xlabel('Epoch',size=15)
ax.tick_params(axis='both',which='major',labelsize=15)
plt.show()
# + id="eOahIbKW6AMf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 210} outputId="6fa64ef4-fda8-465c-f60a-59f03a6b090f"
# !pip install shap
# + id="368Jn0vJ6KwX" colab_type="code" colab={}
import shap
explainer = shap.DeepExplainer(model, np.array(X_train_new))
# + id="u9u_3boZEVPn" colab_type="code" colab={}
shap_values = explainer.shap_values(np.array(X_test_new))
# + id="A5xcKTYcExMZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 585} outputId="671656c5-5d0f-4dcd-d0f3-e4b86c4c2c57"
shap.summary_plot(shap_values[1], X_test_new)
# + id="1e2NoPn2Oump" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 415} outputId="d94dc410-be13-42cd-bb2f-3ea6815e86ff"
pred=model.predict(X_test_new)
pred.argmax(axis=1)
# + id="5t5o4NldebYo" colab_type="code" colab={}
from sklearn.metrics import classification_report, confusion_matrix
cm=confusion_matrix(test_labels, pred.argmax(axis=1))
# + id="E2N0EkwSkbPS" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 215} outputId="a55c0dfd-9360-4cf7-f981-8725f0ff8c7a"
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
# + id="BqloAWv8pioM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 69} outputId="038eab52-c528-4181-c7e8-5bd817969c81"
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score, f1_score
print('Precision: %.3f' % precision_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
print('Recall: %.3f' % recall_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
print('F1: %.3f' % f1_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
# + id="f6Kbg7ee6Ddc" colab_type="code" colab={}
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectKBest, chi2
import xgboost as xgb
from sklearn.model_selection import KFold, GridSearchCV
from sklearn.metrics import accuracy_score, make_scorer
# + id="t3dxaKoa6HzT" colab_type="code" colab={}
pipe = Pipeline([
('fs', SelectKBest()),
('clf', xgb.XGBClassifier(objective='binary:logistic'))
])
# + id="YYasVbi56P_Q" colab_type="code" colab={}
search_space = [
{
'clf__n_estimators': [200],
'clf__learning_rate': [0.01, 0.1],
'clf__max_depth': range(3, 10),
'clf__colsample_bytree': [i/10.0 for i in range(1, 3)],
'clf__gamma': [i/10.0 for i in range(3)],
'fs__score_func': [mutual_info_classif,f_classif],
'fs__k': [10,20,25,30],
}
]
# + id="MyjNXlvW7k0f" colab_type="code" colab={}
kfold = KFold(n_splits=5, shuffle=True, random_state=42)
# + id="ytjrsKU77sQB" colab_type="code" colab={}
scoring = {'AUC':'roc_auc', 'Accuracy':make_scorer(accuracy_score)}
# + id="VrXsHFmn7wML" colab_type="code" colab={}
grid = GridSearchCV(
pipe,
param_grid=search_space,
cv=kfold,
scoring=scoring,
refit='AUC',
verbose=1,
n_jobs=-1
)
# + id="Shvo5yEg7303" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 207} outputId="d05c750c-e791-42d1-9428-b0050798fbd6"
model = grid.fit(normed_train_data, train_labels)
# + id="S0MwiyBuOL-z" colab_type="code" colab={}
import pickle
# Dictionary of best parameters
best_pars = grid.best_params_
# Best XGB model that was found based on the metric score you specify
best_model = grid.best_estimator_
# Save model
pickle.dump(grid.best_estimator_, open('gdrive/My Drive/SS_AITrader/JNJ/xgb_JNJ_log_reg.pickle', "wb"))
# + id="lYPYB1GQRn44" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 51} outputId="11b17609-987a-4ff9-9abc-62bc0133dc22"
predict = model.predict(normed_test_data)
print('Best AUC Score: {}'.format(model.best_score_))
print('Accuracy: {}'.format(accuracy_score(test_labels, predict)))
cm=confusion_matrix(test_labels,predict)
# + id="_F-aB0lqS1dx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 215} outputId="6d59bdf9-c55c-45c6-83cf-e46c18e5a7b2"
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
# + id="DNgkOrW_TPMl" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 54} outputId="03dd39ca-5bb3-4e01-dc65-9d1b1c776272"
print(model.best_params_)
# + id="g5_E1028Tx0Q" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="3ee87948-18ab-4fcb-a611-8cfe942814a4"
model = xgb.XGBClassifier(max_depth=8,
objective='binary:logistic',
n_estimators=200,
learning_rate = 0.1,
colsample_bytree= 0.2,
gamma= 0.2)
eval_set = [(X_train_new, train_labels), (X_test_new, test_labels)]
model.fit(X_train_new, train_labels, early_stopping_rounds=15, eval_metric=["error", "logloss"], eval_set=eval_set, verbose=True)
# + id="QSaYf0OGYnBq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="f0f4dc66-749b-4bc2-a96c-a140bba9846d"
# make predictions for test data
y_pred = model.predict(X_test_new)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = accuracy_score(test_labels, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
# + id="Z8D-K6-UZeNJ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 545} outputId="23f2d304-2611-4e78-bcda-304fca07f8be"
from matplotlib import pyplot
results = model.evals_result()
epochs = len(results['validation_0']['error'])
x_axis = range(0, epochs)
# plot log loss
fig, ax = pyplot.subplots()
ax.plot(x_axis, results['validation_0']['logloss'], label='Train')
ax.plot(x_axis, results['validation_1']['logloss'], label='Test')
ax.legend()
pyplot.ylabel('Log Loss')
pyplot.title('XGBoost Log Loss')
pyplot.show()
# plot classification error
fig, ax = pyplot.subplots()
ax.plot(x_axis, results['validation_0']['error'], label='Train')
ax.plot(x_axis, results['validation_1']['error'], label='Test')
ax.legend()
pyplot.ylabel('Classification Error')
pyplot.title('XGBoost Classification Error')
pyplot.show()
# + id="FC9l3_3rdBVp" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="b05607a9-8569-47c8-a987-4dda08e0aba8"
shap_values = shap.TreeExplainer(model).shap_values(X_test_new)
# + id="sCqFjPjzdIyd" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 585} outputId="8b457514-50aa-44a1-819b-87437d06b460"
shap.summary_plot(shap_values, X_test_new)
# + id="9E1paKnoeZWG" colab_type="code" colab={}
predict = model.predict(X_test_new)
cm=confusion_matrix(test_labels,predict)
# + id="_HC4TpNaefH3" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 215} outputId="aecdd284-faea-4ffa-de5f-5b3440dd25b2"
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
|
SS_AITrader_JNJ.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# #%matplotlib inline
# %load_ext autoreload
# %autoreload 2
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import wandb
import time
import random
import copy
from copy import deepcopy
import threading
from train_utils import *
import gym3
from procgen import ProcgenGym3Env
import matplotlib.pyplot as plt
device = 'cuda' if torch.cuda.is_available() else 'cpu'; device
# +
bs = 64
color_lookup = {
'all':[0,1,2,3,4,5,6,7],
'outer':[0,1,6,7],
'inner':[2,3,4,5]
}
backgrounds = ['all', 'outer', 'inner']
roads = ['all', 'outer', 'inner']
backnoises = [0, 100]
configs = []
for bg in backgrounds:
for rd in roads:
for backnoise in backnoises:
config = {
'name':f"bg:{bg} rd:{rd} noise:{backnoise}",
'color_theme': color_lookup[bg],
'color_theme_road':color_lookup[rd],
'background_noise_level':backnoise
}
configs.append(config)
len(configs)
# -
def get_env(config, bs=bs):
return ProcgenGym3Env(num=bs, env_name="testgame", num_levels=100_000, start_level=0,
color_theme=config['color_theme'],
color_theme_road=config['color_theme_road'],
background_noise_level=config['background_noise_level'])
"""config = configs[0]
s = np.array([[.0,.0] for _ in range(bs)], dtype=np.float32)
seq_len = 15
N_IMGS = 4
plt.figure(figsize=(20, 10))
titles=['indist', 'outdist']
for i, title in enumerate(titles):
ax = plt.subplot(1,5, i+1)
env = get_env(title, config)
for i in range(seq_len):
env.act(s)
rew, obs, first = env.observe()
img = obs['rgb']
img = np.concatenate(img[:N_IMGS],0)
info = env.get_info()
plt.imshow(img)
plt.title(f"{config['name']}: {title}")
plt.axis("off")"""
def testdrive(m, use_autopilot, config):
TRAINING_WHEELS_WINDOW = 10
m.eval()
seq_len = 400
bs = 256
val_env = get_env(config, bs=bs)
s = np.array([[.0,.0] for _ in range(bs)], dtype=np.float32)
reward = 0
with torch.no_grad():
for i in range(seq_len):
val_env.act(s)
rew, obs, first = val_env.observe()
reward += rew.sum()
img = obs['rgb']
info = val_env.get_info()
autopilot_control = np.array([[e["autopilot_"+c] for c in control_properties] for e in info])
aux = np.array([[e[a] for a in aux_properties] for e in info])
front = torch.from_numpy(img.astype(np.float32)/255.).unsqueeze(0).permute(0,1,4,2,3).to(device)
aux = torch.from_numpy(aux.astype(np.float32)).unsqueeze(0).to(device)
if use_autopilot or i < TRAINING_WHEELS_WINDOW:
s = autopilot_control
else:
out, _ = m(front, aux, '')
s = out.squeeze(0).squeeze(-1).cpu().numpy()
s = np.clip(s, -5., 5.)
reward /= (bs*seq_len)
val_env.close()
m.train()
return reward
loss_fn = torch.nn.MSELoss().cuda()
def get_model():
m = VizCNN(use_rnn=False).to(device);
opt = torch.optim.Adam(m.parameters(), lr=3e-4)
scaler = torch.cuda.amp.GradScaler()
return m, opt, scaler
# +
def train(config):
m, opt, scaler = get_model()
global bs
dataloader = DataLoader(env=get_env(config, bs=bs), bs=bs, seq_len=200)
m.train()
logger = Logger()
n_updates = 100
counter = 1
log_cadence = 5_000
bptt = 1
while counter < n_updates:
front_container, aux_container, target_container = dataloader.get_chunk()
chunk_len, bs, _, _, _ = front_container.shape
len_ix = 0
while len_ix < chunk_len:
front = front_container[len_ix:len_ix+bptt, :, :, :, :].to(device).half()
aux = aux_container[len_ix:len_ix+bptt, :, :].to(device).half()
target = target_container[len_ix:len_ix+bptt, :, :].to(device).half()
len_ix += bptt*4
with torch.cuda.amp.autocast(): pred, _ = m(front, aux, '')
loss = loss_fn(target, pred)
scaler.scale(loss).backward()
scaler.step(opt)
scaler.update()
opt.zero_grad()
counter += 1
torch.save(m.state_dict(), config['name']+".torch")
dataloader.destroy()
del dataloader, m
# -
for config in configs:
print("training ", config)
train(config)
# +
results = []
for config_test in configs:
m, _, _ = get_model()
baseline_score = testdrive(m, use_autopilot=True, config=config_test)
for config_train in configs:
m.load_state_dict(torch.load(config_train['name']+".torch"))
score = testdrive(m, use_autopilot=False, config=config_test) / baseline_score
result = {'trn_env':config_train['name'],
'test_env':config_test['name'],
'score':score}
results.append(result)
# -
import pandas as pd
df = pd.DataFrame(results)
df.pivot(index='trn_env', columns='test_env', values='score')
|
1_carlita_train_DR_grid.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# # Exercise 1 - Brief introduction to R, Combinatorics
#
# ## <NAME>, <NAME>, <NAME>
#
#
# First we will go through some basics of R and implement functions for computation of different combinatoric selections.
#
# # Brief introduction to R
#
#
# simple arithmetic operations
2+4
5/2
# BEWARE of brackets! Only round ones are used for counting!
# Square and compound have a different function in R.!
(((10+2)*(340-33))-2)/3
# combination number, factorials
choose(10,2)
factorial(4)
# data types ->numeric, character, logical,(complex)
# the class function determines the type of the object
a=2+3
class(a)
b="pismenko"
class(b)
c=(1>3)
class(c)
d=3+1i
class(d)
# ## data structures in R
#
# - vector (column vector)
#
# - factor (special case of vector)
#
# - matrix (matrix with dimensions nxm)
#
# - data.frame (data frame with columns representing diferent types of informations and rows representing single records)
#
# vector definition
a = c(3,4,6,7)
a <- c(3,4,6,7)
a[2]
# other options
rep(1,4) # creates a vector with four ones
seq(1,10,2) # sequence from 1 to 10 with step 2
1:10 # sequence from 1 to 10 with step 1
b=c("A","B","C","D")
b
class(b)
# redefining an object to another type - eg as.vector, as.matrix, as.factor,...
b=as.factor(b)
b
# working with vectors - merging by columns/rows
cbind(a,b)
rbind(a,b)
c(a,b)
# matrix definition
A=matrix(c(3,4,6,7,3,2),nrow=2,ncol=3)
B=matrix(c(3,4,6,7,3,2),nrow=2,ncol=3,byrow=TRUE)
C=matrix(c(3,4,6,7,3,2),nrow=3,ncol=2)
B
B[1,3]
A[1,]
A[,2:3]
# diagonal matrix
diag(4)
diag(4,2)
# matrix operations - pay attention to matrix multiplication -> %*%
A+B
A-B
A*B
A%*%C
|
support_files/en/.ipynb_checkpoints/T1_Rintro-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import json
with open('ms-en/translated-trainset-parliament.json') as fopen:
data = json.load(fopen)
# -
rejected = ['PERTANYAAN-PERTANYAAN JAWAB LISAN', 'PENGGAL KEEMPAT', 'PUSAT JAGAAN BERDAFTAR',
'BILANGAN PUSAT JAGAAN', 'pewan']
# +
selected, reject = [], []
for row in data:
if any([r.lower() in row[0].lower() for r in rejected]):
reject.append(row)
continue
s = row[0]
if (sum(c.isdigit() for c in s) / len(s)) > 0.15:
reject.append(row)
continue
if sum(c.isalpha() for c in s) == 0:
reject.append(row)
continue
selected.append(row)
print(len(selected))
x_parliament, y_parliament = list(zip(*selected))
# +
import random
with open('ms-en/ubuntu-ms-en.json') as fopen:
data = json.load(fopen)
X, Y = list(zip(*data))
X = list(X)
Y = list(Y)
# +
with open('ms-en/qed-ms-en.json') as fopen:
data = json.load(fopen)
x, y = list(zip(*data))
X.extend(x)
Y.extend(y)
# +
with open('ms-en/tanzil-ms-en.json') as fopen:
data = json.load(fopen)
x, y = list(zip(*data))
X.extend(x)
Y.extend(y)
# +
from glob import glob
translated = glob('ms-en/translated*0.json')
translated
# -
for file in translated:
with open(file) as fopen:
data = json.load(fopen)
x, y = list(zip(*data))
X.extend(x)
Y.extend(y)
# +
from tqdm import tqdm
from unidecode import unidecode
import re
def cleaning(string):
string = unidecode(string).replace('\n', ' ').replace('\t', ' ')
string = re.sub(r'[ ]+', ' ', string).strip()
return string
def check(string):
string = re.sub('[^A-Za-z\- ]+', ' ', string)
string = re.sub(r'[ ]+', ' ', string.lower()).strip()
return string
# +
translated = glob('ms-en/*.translate')
x, y = [], []
rejected = ['lexus', 'little', 'lizards', 'lizard']
for t in translated:
if 'rephrase.json' in t:
continue
with open(t) as fopen:
data = json.load(fopen)
count = 0
for no, row in enumerate(data):
splitted = row[0]['text'].split('<>')
splitted_bm = row[1].split('<>')
if len(splitted) != len(splitted_bm):
count += 1
continue
for k in range(len(splitted)):
s = check(splitted[k])
if any([r in s for r in rejected]):
continue
y.append(splitted[k])
x.append(splitted_bm[k])
print(t, count / len(data) * 100)
# -
X.extend(x)
Y.extend(y)
i = random.randint(0, len(x) - 100)
list(zip(x[i: i + 100], y[i: i + 100]))
with open('en-ms/texts.json.translate') as fopen:
news = json.load(fopen)
for i in range(len(news)):
l = news[i][0]
r = news[i][1]
l_len = len(l.split()) / 2 < len(r.split())
r_len = len(r.split()) / 2 < len(l.split())
if l != r and l_len and r_len:
X.append(news[i][1])
Y.append(news[i][0])
for file in glob('en-ms/dataset-*.json.translate')[:6]:
with open(file) as fopen:
news = json.load(fopen)
for i in range(len(news)):
l = news[i][0]
r = news[i][1]
l_len = len(l.split()) / 2 < len(r.split())
r_len = len(r.split()) / 2 < len(l.split())
if l != r and l_len and r_len:
X.append(news[i][1])
Y.append(news[i][0])
# +
filtered_X, filtered_Y = [], []
for i in tqdm(range(len(X))):
X[i] = cleaning(X[i])
Y[i] = cleaning(Y[i])
if len(X[i]) and len(Y[i]):
filtered_X.append(X[i])
filtered_Y.append(Y[i])
# +
count, ids = 0, []
for i in tqdm(range(len(filtered_X))):
if filtered_X[i] == filtered_Y[i]:
count += 1
ids.append(i)
count / len(filtered_X) * 100
# -
uniques = set()
for i in tqdm(range(len(filtered_X))):
s = f'{filtered_X[i]} [EENNDD] {filtered_Y[i]}'
uniques.add(s)
uniques = list(uniques)
len(uniques)
X, Y = [], []
for i in tqdm(range(len(uniques))):
x, y = uniques[i].split(' [EENNDD] ')
xc = check(x)
yc = check(y)
xc_len = len(xc.split()) / 2 > len(yc)
yc_len = len(yc.split()) / 2 > len(xc)
if xc == yc or xc_len or yc_len:
continue
X.append(x)
Y.append(y)
# +
X_len, Y_len = [], []
for i in tqdm(range(len(X))):
X_len.append(len(X[i].split()))
Y_len.append(len(Y[i].split()))
# -
max(X_len), max(Y_len)
# +
import numpy as np
np.argsort(X_len)[::-1][:100]
# -
list(zip(X[-10:], Y[-10:]))
with open('en-ms.json', 'w') as fopen:
json.dump({'left': Y, 'right': X}, fopen)
with open('english-en-ms.txt', 'w') as fopen:
fopen.write('\n'.join(Y))
with open('malay-en-ms.txt', 'w') as fopen:
fopen.write('\n'.join(X))
|
pretrained-model/mass/prepare-dataset-en-ms.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import numpy as np
import seaborn as sns
from scipy import stats
import matplotlib.pyplot as plt
import csv
import random
import copy
import pandas as pd
import ptitprince as pt
# %matplotlib inline
file_path="C:/Users/Zeta/Documents/acou_sommeil_HD_ENS/NB_article_acou-sommeil"
# -
# # Importation des données et mise en forme
# +
#Ouverture du dossier contenant le fichier
os.chdir(file_path)
#Ouverture du fichier csv de données
with open('questionnaires_inclusion_int_finaux.csv', 'rt',encoding="utf8") as csvfile:
spamreader = csv.reader(csvfile, delimiter=';')
dico=[]
for row in spamreader:
dico.append(row)
#Suppression de la ligne de labels
dico=dico[1:]
#Stockage des données dans un dictionnaire organisé
THI_EVAS={}
for elm in dico:
if THI_EVAS.keys().__contains__(elm[0]):
THI_EVAS[elm[0]][0].append(int(elm[3]))
THI_EVAS[elm[0]][1].append(int(elm[1]))
THI_EVAS[elm[0]][2].append(int(elm[2]))
else:
THI_EVAS[elm[0]]=[[int(elm[3])],[int(elm[1])], [int(elm[2])]] #THI puis EVA I puis EVA G
print(THI_EVAS)
# -
# # Tests statistiques
# +
dico_stats={}
# I pour intensité (donc VAS-L), G pour gêne (donc VAS-I)
keys=["THI_incl","THI_int","THI_final","I_incl", "I_int", "I_final", "G_incl", "G_int", "G_final"]
for elm in keys:
dico_stats[elm]=[]
for elm in THI_EVAS:
for i in range(3):
dico_stats[keys[i]].append(THI_EVAS[elm][0][i])
dico_stats[keys[i+3]].append(THI_EVAS[elm][1][i])
dico_stats[keys[i+6]].append(THI_EVAS[elm][2][i])
#les distributions sont prêtes pour les tests stats
print("Questionnaire analysé : THI")
print("Wilcoxon à l'échelle du groupe entre t0 et t1")
print (stats.wilcoxon(dico_stats[keys[0]],dico_stats[keys[1]]))
print("Wilcoxon à l'échelle du groupe entre t1 et t2")
print (stats.wilcoxon(dico_stats[keys[1]],dico_stats[keys[2]]))
print("Wilcoxon à l'échelle du groupe entre t0 et t2")
print (stats.wilcoxon(dico_stats[keys[0]],dico_stats[keys[2]]))
print("")
print("Questionnaire analysé : VAS_L")
print("Wilcoxon à l'échelle du groupe entre t0 et t1")
print (stats.wilcoxon(dico_stats[keys[3]],dico_stats[keys[4]]))
print("Wilcoxon à l'échelle du groupe entre t1 et t2")
print (stats.wilcoxon(dico_stats[keys[4]],dico_stats[keys[5]]))
print("Wilcoxon à l'échelle du groupe entre t0 et t2")
print (stats.wilcoxon(dico_stats[keys[3]],dico_stats[keys[5]]))
print("")
print("Questionnaire analysé : VAS_I")
print("Wilcoxon à l'échelle du groupe entre t0 et t1")
print (stats.wilcoxon(dico_stats[keys[6]],dico_stats[keys[7]]))
print("Wilcoxon à l'échelle du groupe entre t1 et t2")
print (stats.wilcoxon(dico_stats[keys[7]],dico_stats[keys[8]]))
print("Wilcoxon à l'échelle du groupe entre t0 et t2")
print (stats.wilcoxon(dico_stats[keys[6]],dico_stats[keys[8]]))
# -
# ## question : c'est fait en valeurs absolues, mais serait-il interessant de faire cela en pourcentage (fait dans la version brouillon du NB)
# # Affichage classique
# +
means=[]
stds=[]
for elm in dico_stats:
means.append(np.mean(dico_stats[elm]))
stds.append(np.std(dico_stats[elm]))
THI_m = means[:3]
EVA_I_m=means[3:6]
EVA_G_m=means[6:]
THI_s = stds[:3]
EVA_I_s=stds[3:6]
EVA_G_s=stds[6:]
plt.figure()
plt.errorbar(["T0","T1","T2"],THI_m, THI_s)
plt.title("evolutions THI groupe entre t0, t1 et t2")
plt.ylabel("Score THI", fontsize=16)
plt.xlabel("Instant mesure", fontsize=16)
plt.figure()
plt.errorbar(["T0","T1","T2"],EVA_I_m, EVA_I_s)
plt.title("evolutions VAS_L groupe entre t0, t1 et t2")
plt.ylabel("Score VAS-L", fontsize=16)
plt.xlabel("Instant mesure", fontsize=16)
plt.figure()
plt.errorbar(["T0","T1","T2"],EVA_G_m, EVA_G_s)
plt.title("evolutions VAS_I groupe entre t0, t1 et t2")
plt.ylabel("Score VAS-I", fontsize=16)
plt.xlabel("Instant mesure", fontsize=16)
# -
# # Affichage violin plot
# +
def make_me_a_rainbow(columns,title, descrip):
#columns est ddu type [[nom_colonne1, [data1]], [nom_colonne2, [data2],...]]
l=[]
li=[]
for elm in columns:
for eli in elm[1]:
l.append(eli)
li.append(elm[0])
#print(l)
#print(li)
li2=[i for i in range(len(l))]
columns = descrip
df_ = pd.DataFrame(index=li2, columns=columns)
df_ = df_.fillna(0) # with 0s rather than NaNs
data = np.array([li,l]).T
df = pd.DataFrame(data, index=li2, columns=columns)
#print(df)
#adding a red line connecting the groups' mean value (useful for longitudinal data)
dx=columns[0]; dy=columns[1]; ort="v"; pal = "Set2"; sigma = .2
f, ax = plt.subplots(figsize=(7, 5))
ax=pt.RainCloud(x = dx, y = dy, data = df, palette = pal, bw = sigma,
width_viol = .6, ax = ax, orient = ort, jitter=0.08,
pointplot = True, point_size=5)
ax.margins(0.3)
plt.xlabel(dx, fontsize=16)
plt.ylabel(dy, fontsize=16)
plt.title(title, fontsize = 20)
#Affichage THI
datas=[[0, dico_stats[keys[0]]], [1, dico_stats[keys[1]]], [2, dico_stats[keys[2]]]]
make_me_a_rainbow(datas,"Evolution THI groupe entre T0, T1 et T2", ["Instant mesure (T0, T1, T2)", "Score THI"])
#VAS-L
datas=[[0, dico_stats[keys[3]]], [1, dico_stats[keys[4]]], [2, dico_stats[keys[5]]]]
make_me_a_rainbow(datas,"Evolution VAS-L groupe entre T0, T1 et T2", ["Instant mesure (T0, T1, T2)", "Score VAS-L"])
#VAS-I
datas=[[0, dico_stats[keys[6]]], [1, dico_stats[keys[7]]], [2, dico_stats[keys[8]]]]
make_me_a_rainbow(datas,"Evolution VAS-I groupe entre T0, T1 et T2", ["Instant mesure (T0, T1, T2)", "Score VAS-I"])
# -
|
Analyse suivi global patients.ipynb
|
# -*- coding: utf-8 -*-
# <!-- dom:TITLE: Data Analysis and Machine Learning: Support Vector Machines -->
# # Data Analysis and Machine Learning: Support Vector Machines
# <!-- dom:AUTHOR: <NAME> at Department of Physics, University of Oslo & Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University -->
# <!-- Author: -->
# **<NAME>**, Department of Physics, University of Oslo and Department of Physics and Astronomy and National Superconducting Cyclotron Laboratory, Michigan State University
#
# Date: **Nov 9, 2018**
#
# Copyright 1999-2018, <NAME>. Released under CC Attribution-NonCommercial 4.0 license
#
#
#
# ## Support Vector Machines, overarching aims
#
# A Support Vector Machine (SVM) is a very powerful and versatile
# Machine Learning model, capable of performing linear or nonlinear
# classification, regression, and even outlier detection. It is one of
# the most popular models in Machine Learning, and anyone interested in
# Machine Learning should have it in their toolbox. SVMs are
# particularly well suited for classification of complex but small-sized or
# medium-sized datasets.
#
# The case with two well-separated classes only can be understood in an intuitive way in terms of lines in a two-dimensional space separating the two classes (see figure below).
#
# The basic mathematics behind the SVM is however less familiar to most of us.
# It relies on the definition of hyperplanes and the
# definition of a **margin** which separates classes (in case of
# classification problems) of variables. It is also used for regression
# problems.
#
# With SVMs we distinguish between hard margin and soft margins. The
# latter introduces a so-called softening parameter to be discussed
# below. We distinguish also between linear and non-linear
# approaches. The latter are the most frequent ones since it is rather
# unlikely that we can separate classes easily by say straight lines.
#
# **Note: several figures are missing. They will be added shortly. To run the codes, use the jupyter notebook**
#
#
# ## Hyperplanes and all that
#
# The theory behind support vector machines (SVM hereafter) is based on
# the mathematical description of so-called hyperplanes. Let us start
# with a two-dimensional case. This will also allow us to introduce our
# first SVM examples. These will be tailored to the case of two specific
# classes, as displayed in the figure here based on the usage of the petal data.
#
# We assume here that our data set can be well separated into two
# domains, where a straight line does the job in the separating the two
# classes. Here the two classes are represented by either squares or
# circles.
# +
# %matplotlib inline
from sklearn import datasets
from sklearn.svm import SVC, LinearSVC
from sklearn.linear_model import SGDClassifier
from sklearn.preprocessing import StandardScaler
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
C = 5
alpha = 1 / (C * len(X))
lin_clf = LinearSVC(loss="hinge", C=C, random_state=42)
svm_clf = SVC(kernel="linear", C=C)
sgd_clf = SGDClassifier(loss="hinge", learning_rate="constant", eta0=0.001, alpha=alpha,
max_iter=100000, random_state=42)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
lin_clf.fit(X_scaled, y)
svm_clf.fit(X_scaled, y)
sgd_clf.fit(X_scaled, y)
print("LinearSVC: ", lin_clf.intercept_, lin_clf.coef_)
print("SVC: ", svm_clf.intercept_, svm_clf.coef_)
print("SGDClassifier(alpha={:.5f}):".format(sgd_clf.alpha), sgd_clf.intercept_, sgd_clf.coef_)
# Compute the slope and bias of each decision boundary
w1 = -lin_clf.coef_[0, 0]/lin_clf.coef_[0, 1]
b1 = -lin_clf.intercept_[0]/lin_clf.coef_[0, 1]
w2 = -svm_clf.coef_[0, 0]/svm_clf.coef_[0, 1]
b2 = -svm_clf.intercept_[0]/svm_clf.coef_[0, 1]
w3 = -sgd_clf.coef_[0, 0]/sgd_clf.coef_[0, 1]
b3 = -sgd_clf.intercept_[0]/sgd_clf.coef_[0, 1]
# Transform the decision boundary lines back to the original scale
line1 = scaler.inverse_transform([[-10, -10 * w1 + b1], [10, 10 * w1 + b1]])
line2 = scaler.inverse_transform([[-10, -10 * w2 + b2], [10, 10 * w2 + b2]])
line3 = scaler.inverse_transform([[-10, -10 * w3 + b3], [10, 10 * w3 + b3]])
# Plot all three decision boundaries
plt.figure(figsize=(11, 4))
plt.plot(line1[:, 0], line1[:, 1], "k:", label="LinearSVC")
plt.plot(line2[:, 0], line2[:, 1], "b--", linewidth=2, label="SVC")
plt.plot(line3[:, 0], line3[:, 1], "r-", label="SGDClassifier")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs") # label="Iris-Versicolor"
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo") # label="Iris-Setosa"
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper center", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.show()
# -
# ## What is a hyperplane?
#
# The aim of the SVM algorithm is to find a hyperplane in an $p$-dimensional space, where $p$ is the number of features that distinctly classifies the data points.
#
# In a $p$-dimensional space, a hyperplane is what we call an affine subspace of dimension of $p-1$.
# As an example, in two dimension, a hyperplane is simply as straight line while in three dimensions it is
# a two-dimensional subspace, or stated simply, a plane.
#
# In two dimensions, with the variables $x_1$ and $x_2$, the hyperplane is defined as
# $$
# b+w_1x_1+w_2x_2=0,
# $$
# where $b$ is the intercept and $w_1$ and $w_2$ define the elements of a vector orthogonal to the line
# $b+w_1x_1+w_2x_2=0$.
# In two dimensions we define the vectors $\boldsymbol{x} =[x1,x2]$ and $\boldsymbol{w}=[w1,w2]$.
# We can then rewrite the above equation as
# $$
# \boldsymbol{w}^T\boldsymbol{x}+b=0.
# $$
# ## A $p$-dimensional space of features
#
# We limit ourselves to two classes of outputs $y_i$ and assign these classes the values $y_i = \pm 1$.
# In a $p$-dimensional space of say $p$ features we have a hyperplane defines as
# $$
# b+wx_1+w_2x_2+\dots +w_px_p=0.
# $$
# If we define a
# matrix $\boldsymbol{X}=\left[\boldsymbol{x}_1,\boldsymbol{x}_2,\dots, \boldsymbol{x}_p\right]$
# of dimension $n\times p$, where $n$ represents the observations for each feature and each vector $x_i$ is a column vector of the matrix $\boldsymbol{X}$,
# $$
# \boldsymbol{x}_i = \begin{bmatrix} x_{i1} \\ x_{i2} \\ \dots \\ \dots \\ x_{ip} \end{bmatrix}.
# $$
# If the above condition is not met for a given vector $\boldsymbol{x}_i$ we have
# $$
# b+w_1x_{i1}+w_2x_{i2}+\dots +w_px_{ip} >0,
# $$
# if our output $y_i=1$.
# In this case we say that $\boldsymbol{x}_i$ lies on one of the sides of the hyperplane and if
# $$
# b+w_1x_{i1}+w_2x_{i2}+\dots +w_px_{ip} < 0,
# $$
# for the class of observations $y_i=-1$,
# then $\boldsymbol{x}_i$ lies on the other side.
#
# Equivalently, for the two classes of observations we have
# $$
# y_i\left(b+w_1x_{i1}+w_2x_{i2}+\dots +w_px_{ip}\right) > 0.
# $$
# When we try to separate hyperplanes, if it exists, we can use it to construct a natural classifier: a test observation is assigned a given class depending on which side of the hyperplane it is located.
#
# <!-- !split -->
# ## The two-dimensional case
#
# Let us try to develop our intuition about SVMs by limiting ourselves to a two-dimensional
# plane. To separate the two classes of data points, there are many
# possible lines (hyperplanes if you prefer a more strict naming)
# that could be chosen. Our objective is to find a
# plane that has the maximum margin, i.e the maximum distance between
# data points of both classes. Maximizing the margin distance provides
# some reinforcement so that future data points can be classified with
# more confidence.
#
# What a linear classifier attempts to accomplish is to split the
# feature space into two half spaces by placing a hyperplane between the
# data points. This hyperplane will be our decision boundary. All
# points on one side of the plane will belong to class one and all points
# on the other side of the plane will belong to the second class two.
#
# Unfortunately there are many ways in which we can place a hyperplane
# to divide the data. Below is an example of two candidate hyperplanes
# for our data sample.
#
# ## Getting into the details
#
# Let us define the function
# $$
# f(x) = \boldsymbol{w}^T\boldsymbol{x}+b = 0,
# $$
# as the function that determines the line $L$ that separates two classes (our two features), see the figure here.
#
#
# Any point defined by $\boldsymbol{x}_i$ and $\boldsymbol{x}_2$ on the line $L$ will satisfy $\boldsymbol{w}^T(\boldsymbol{x}_1-\boldsymbol{x}_2)=0$.
#
# The signed distance $\delta$ from any point defined by a vector $\boldsymbol{x}$ and a point $\boldsymbol{x}_0$ on the line $L$ is then
# $$
# \delta = \frac{1}{\vert\vert \boldsymbol{w}\vert\vert}(\boldsymbol{w}^T\boldsymbol{x}+b).
# $$
# ## First attempt at a minimization approach
#
# How do we find the parameter $b$ and the vector $\boldsymbol{w}$? What we could
# do is to define a cost function which now contains the set of all
# misclassified points $M$ and attempt to minimize this function
# $$
# C(\boldsymbol{w},b) = -\sum_{i\in M} y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b).
# $$
# We could now for example define all values $y_i =1$ as misclassified in case we have $\boldsymbol{w}^T\boldsymbol{x}_i+b < 0$ and the opposite if we have $y_i=-1$. Taking the derivatives gives us
# $$
# \frac{\partial C}{\partial b} = -\sum_{i\in M} y_i,
# $$
# and
# $$
# \frac{\partial C}{\partial \boldsymbol{w}} = -\sum_{i\in M} y_ix_i.
# $$
# ## Solving the equations
#
# We can now use the Newton-Raphson method or gradient descent to solve the equations
# $$
# b \leftarrow b +\eta \frac{\partial C}{\partial b},
# $$
# and
# $$
# \boldsymbol{w} \leftarrow \boldsymbol{w} +\eta \frac{\partial C}{\partial \boldsymbol{w}},
# $$
# where $\eta$ is our by now well-known learning rate.
#
# There are however problems with this approach, although it looks
# pretty straightforward to implement. In case we separate our data into
# two distinct classes, we may up with many possible lines, as indicated
# in the figure and shown by running the following program. For small
# gaps between the entries, we may also end up needing many iterations
# before the solutions converge and if the data cannot be separated
# properly into two distinct classes, we may not experience a converge
# at all.
#
# ## A better approach
#
# A better approach is rather to try to define a large margin between
# the two classes (if they are well separated from the beginning).
#
# Thus, we wish to find a margin $M$ with $\boldsymbol{w}$ normalized to
# $\vert\vert \boldsymbol{w}\vert\vert =1$ subject to the condition
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \geq M \hspace{0.1cm}\forall i=1,2,\dots, p.
# $$
# All points are thus at a signed distance from the decision boundary defined by the line $L$. The parameters $b$ and $w_1$ and $w_2$ define this line.
#
# We seek thus the largest value $M$ defined by
# $$
# \frac{1}{\vert \vert \boldsymbol{w}\vert\vert}y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \geq M \hspace{0.1cm}\forall i=1,2,\dots, n,
# $$
# or just
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \geq M\vert \vert \boldsymbol{w}\vert\vert \hspace{0.1cm}\forall i.
# $$
# If we scale the equation so that $\vert \vert \boldsymbol{w}\vert\vert = 1/M$, we have to find the minimum of
# $\boldsymbol{w}^T\boldsymbol{w}=\vert \vert \boldsymbol{w}\vert\vert$ (the norm) subject to the condition
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) \geq 1 \hspace{0.1cm}\forall i.
# $$
# We have thus defined our margin as the invers of the norm of $\boldsymbol{w}$. We want to minimize the norm in order to have a as large as possible margin $M$. Before we proceed, we need to remind ourselves about Lagrangian multipliers.
#
# ## A quick reminder on Lagrangian multipliers
#
# Consider a function of three independent variables $f(x,y,z)$ . For the function $f$ to be an
# extreme we have
# $$
# df=0.
# $$
# A necessary and sufficient condition is
# $$
# \frac{\partial f}{\partial x} =\frac{\partial f}{\partial y}=\frac{\partial f}{\partial z}=0,
# $$
# due to
# $$
# df = \frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz.
# $$
# In many problems the variables $x,y,z$ are often subject to constraints (such as those above for the margin)
# so that they are no longer all independent. It is possible at least in principle to use each
# constraint to eliminate one variable
# and to proceed with a new and smaller set of independent varables.
#
# The use of so-called Lagrangian multipliers is an alternative technique when the elimination
# of variables is incovenient or undesirable. Assume that we have an equation of constraint on
# the variables $x,y,z$
# $$
# \phi(x,y,z) = 0,
# $$
# resulting in
# $$
# d\phi = \frac{\partial \phi}{\partial x}dx+\frac{\partial \phi}{\partial y}dy+\frac{\partial \phi}{\partial z}dz =0.
# $$
# Now we cannot set anymore
# $$
# \frac{\partial f}{\partial x} =\frac{\partial f}{\partial y}=\frac{\partial f}{\partial z}=0,
# $$
# if $df=0$ is wanted
# because there are now only two independent variables! Assume $x$ and $y$ are the independent
# variables.
# Then $dz$ is no longer arbitrary.
#
# ## Adding the muliplier
#
# However, we can add to
# $$
# df = \frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy+\frac{\partial f}{\partial z}dz,
# $$
# a multiplum of $d\phi$, viz. $\lambda d\phi$, resulting in
# $$
# df+\lambda d\phi = (\frac{\partial f}{\partial z}+\lambda
# \frac{\partial \phi}{\partial x})dx+(\frac{\partial f}{\partial y}+\lambda\frac{\partial \phi}{\partial y})dy+
# (\frac{\partial f}{\partial z}+\lambda\frac{\partial \phi}{\partial z})dz =0.
# $$
# Our multiplier is chosen so that
# $$
# \frac{\partial f}{\partial z}+\lambda\frac{\partial \phi}{\partial z} =0.
# $$
# We need to remember that we took $dx$ and $dy$ to be arbitrary and thus we must have
# $$
# \frac{\partial f}{\partial x}+\lambda\frac{\partial \phi}{\partial x} =0,
# $$
# and
# $$
# \frac{\partial f}{\partial y}+\lambda\frac{\partial \phi}{\partial y} =0.
# $$
# When all these equations are satisfied, $df=0$. We have four unknowns, $x,y,z$ and
# $\lambda$. Actually we want only $x,y,z$, $\lambda$ needs not to be determined,
# it is therefore often called
# Lagrange's undetermined multiplier.
# If we have a set of constraints $\phi_k$ we have the equations
# $$
# \frac{\partial f}{\partial x_i}+\sum_k\lambda_k\frac{\partial \phi_k}{\partial x_i} =0.
# $$
# ## Setting up the problem
# In order to solve the above problem, we define the following Lagrangian function to be minimized
# $$
# {\cal L}(\lambda,b,\boldsymbol{w})=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}-\sum_{i=1}^n\lambda_i\left[y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)-1\right],
# $$
# where $\lambda_i$ is a so-called Lagrange multiplier subject to the condition $\lambda_i \geq 0$.
#
# Taking the derivatives with respect to $b$ and $\boldsymbol{w}$ we obtain
# $$
# \frac{\partial {\cal L}}{\partial b} = -\sum_{i} \lambda_iy_i=0,
# $$
# and
# $$
# \frac{\partial {\cal L}}{\partial \boldsymbol{w}} = 0 = \boldsymbol{w}-\sum_{i} \lambda_iy_i\boldsymbol{x}_i.
# $$
# Inserting these constraints into the equation for ${\cal L}$ we obtain
# $$
# {\cal L}=\sum_i\lambda_i-\frac{1}{2}\sum_{ij}^n\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j,
# $$
# subject to the constraints $\lambda_i\geq 0$ and $\sum_i\lambda_iy_i=0$.
# We must in addition satisfy the [Karush-Kuhn-Tucker](https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions) (KKT) condition
# $$
# \lambda_i\left[y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) -1\right] \hspace{0.1cm}\forall i.
# $$
# 1. If $\lambda_i > 0$, then $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1$ and we say that $x_i$ is on the boundary.
#
# 2. If $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)> 1$, we say $x_i$ is not on the boundary and we set $\lambda_i=0$.
#
# When $\lambda_i > 0$, the vectors $\boldsymbol{x}_i$ are called support vectors. They are the vectors closest to the line (or hyperplane) and define the margin $M$.
#
# ## The problem to solve
#
# We can rewrite
# $$
# {\cal L}=\sum_i\lambda_i-\frac{1}{2}\sum_{ij}^n\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j,
# $$
# and its constraints in terms of a matrix-vector problem where we minimize w.r.t. $\lambda$ the following problem
# $$
# \frac{1}{2} \boldsymbol{\lambda}^T\begin{bmatrix} y_1y_1\boldsymbol{x}_1^T\boldsymbol{x}_1 & y_1y_2\boldsymbol{x}_1^T\boldsymbol{x}_2 & \dots & \dots & y_1y_n\boldsymbol{x}_1^T\boldsymbol{x}_n \\
# y_2y_1\boldsymbol{x}_2^T\boldsymbol{x}_1 & y_2y_2\boldsymbol{x}_2^T\boldsymbol{x}_2 & \dots & \dots & y_1y_n\boldsymbol{x}_2^T\boldsymbol{x}_n \\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# y_ny_1\boldsymbol{x}_n^T\boldsymbol{x}_1 & y_ny_2\boldsymbol{x}_n^T\boldsymbol{x}_2 & \dots & \dots & y_ny_n\boldsymbol{x}_n^T\boldsymbol{x}_n \\
# \end{bmatrix}\boldsymbol{\lambda}-\mathbb{1}\boldsymbol{\lambda},
# $$
# subject to $\boldsymbol{y}^T\boldsymbol{\lambda}=0$. Here we defined the vectors $\boldsymbol{\lambda} =[\lambda_1,\lambda_2,\dots,\lambda_n]$ and
# $\boldsymbol{y}=[y_1,y_2,\dots,y_n]$.
#
#
# ## The last steps
#
# Solving the above problem, yields the values of $\lambda_i$.
# To find the coefficients of your hyperplane we need simply to compute
# $$
# \boldsymbol{w}=\sum_{i} \lambda_iy_i\boldsymbol{x}_i.
# $$
# With our vector $\boldsymbol{w}$ we can in turn find the value of the intercept $b$ (here in two dimensions) via
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1,
# $$
# resulting in
# $$
# b = \frac{1}{y_i}-\boldsymbol{w}^T\boldsymbol{x}_i,
# $$
# or if we write it out in terms of the support vectors only, with $N_s$ being their number, we have
# $$
# b = \frac{1}{N_s}\sum_{j\in N_s}\left(y_j-\sum_{i=1}^n\lambda_iy_i\boldsymbol{x}_i^T\boldsymbol{x}_j\right).
# $$
# With our hyperplane coefficients we can use our classifier to assign any observation by simply using
# $$
# y_i = \mathrm{sign}(\boldsymbol{w}^T\boldsymbol{x}_i+b).
# $$
# Below we discuss how to find the optimal values of $\lambda_i$. Before we proceed however, we discuss now the so-called soft classifier.
#
# ## A soft classifier
#
# Till now, the margin is strictly defined by the support vectors. This defines what is called a hard classifier, that is the margins are well defined.
#
# Suppose now that classes overlap in feature space, as shown in the
# figure here. One way to deal with this problem before we define the
# so-called **kernel approach**, is to allow a kind of slack in the sense
# that we allow some points to be on the wrong side of the margin.
#
# We introduce thus the so-called **slack** variables $\boldsymbol{\xi} =[\xi_1,x_2,\dots,x_n]$ and
# modify our previous equation
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1,
# $$
# to
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1-\xi_i,
# $$
# with the requirement $\xi_i\geq 0$. The total violation is now $\sum_i\xi$.
# The value $\xi_i$ in the constraint the last constraint corresponds to the amount by which the prediction
# $y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1$ is on the wrong side of its margin. Hence by bounding the sum $\sum_i \xi_i$,
# we bound the total amount by which predictions fall on the wrong side of their margins.
#
# Misclassifications occur when $\xi_i > 1$. Thus bounding the total sum by some value $C$ bounds in turn the total number of
# misclassifications.
#
# ## Soft optmization problem
#
#
# This has in turn the consequences that we change our optmization problem to finding the minimum of
# $$
# {\cal L}=\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}-\sum_{i=1}^n\lambda_i\left[y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)-(1-\xi_)\right]+C\sum_{i=1}^n\xi_i-\sum_{i=1}^n\gamma_i\xi_i,
# $$
# subject to
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b)=1-\xi_i \hspace{0.1cm}\forall i,
# $$
# with the requirement $\xi_i\geq 0$.
#
# Taking the derivatives with respect to $b$ and $\boldsymbol{w}$ we obtain
# $$
# \frac{\partial {\cal L}}{\partial b} = -\sum_{i} \lambda_iy_i=0,
# $$
# and
# $$
# \frac{\partial {\cal L}}{\partial \boldsymbol{w}} = 0 = \boldsymbol{w}-\sum_{i} \lambda_iy_i\boldsymbol{x}_i,
# $$
# and
# $$
# \lambda_i = C-\gamma_i \hspace{0.1cm}\forall i.
# $$
# Inserting these constraints into the equation for ${\cal L}$ we obtain the same equation as before
# $$
# {\cal L}=\sum_i\lambda_i-\frac{1}{2}\sum_{ij}^n\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{x}_j,
# $$
# but now subject to the constraints $\lambda_i\geq 0$, $\sum_i\lambda_iy_i=0$ and $0\leq\lambda_i \leq C$.
# We must in addition satisfy the Karush-Kuhn-Tucker condition which now reads
# 5
# 0
#
# <
# <
# <
# !
# !
# M
# A
# T
# H
# _
# B
# L
# O
# C
# K
# $$
# \gamma_i\xi_i = 0,
# $$
# and
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{x}_i+b) -(1-\xi_) \geq 0 \hspace{0.1cm}\forall i.
# $$
# ## Kernels and non-linearity
#
# The cases we have studied till were all characterized by two classes
# with a close to linear separability. The classifiers we have described
# so far find linear boundaries in our input feature space. It is
# possible to make our procedure more flexible by exploring the feature
# space using other basis expansions such higher-order polynomials,
# wavelets, splines etc.
#
# If our feature space is not easy to separate, as shown in the figure
# here, we can achieve a better separation by introducing more complex
# basis functions. The ideal would be, as shown in the next figure, to, via a specific transformation to
# obtain a separation between the classes which is almost linear.
#
# The change of basis, from $x\rightarrow z=\phi(x)$ leads to the same type of equations to be solved, except that
# we need to introduce for example a polynomial transformation to a two-dimensional training set.
# +
import numpy as np
import os
np.random.seed(42)
# To plot pretty figures
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
from sklearn.svm import SVC
from sklearn import datasets
X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D**2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])
plt.subplots_adjust(right=1)
plt.show()
# -
# ## The equations
#
# Suppose we define a polynomial transformation of degree two only (we continue to live in a plane with $x_i$ and $y_i$ as variables)
# $$
# z = \phi(x_i) =\left(x_i^2, y_i^2, \sqrt{2}x_iy_i\right).
# $$
# With our new basis, the equations we solved earlier are basically the same, that is we have now (without the slack option for simplicity)
# $$
# {\cal L}=\sum_i\lambda_i-\frac{1}{2}\sum_{ij}^n\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{z}_j,
# $$
# subject to the constraints $\lambda_i\geq 0$, $\sum_i\lambda_iy_i=0$, and for the support vectors
# $$
# y_i(\boldsymbol{w}^T\boldsymbol{z}_i+b)= 1 \hspace{0.1cm}\forall i,
# $$
# from which we also find $b$.
# To compute $\boldsymbol{z}_i^T\boldsymbol{z}_j$ we define the kerne $K(\boldsymbol{x}_i,\boldsymbol{x}_j)$ as
# $$
# K(\boldsymbol{x}_i,\boldsymbol{x}_j)=\boldsymbol{z}_i^T\boldsymbol{z}_j= \phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j).
# $$
# For the above example, the kernel reads
# $$
# K(\boldsymbol{x}_i,\boldsymbol{x}_j)=[x_i^2, y_i^2, \sqrt{2}x_iy_i]^T\begin{bmatrix} x_j^2 \\ y_j^2 \\ \sqrt{2}x_jy_j \end{bmatrix}=x_i^2x_j^2+2x_ix_jy_iy_j+y_i^2y_j^2.
# $$
# We note that this is nothing but the dot product of the two original
# vectors $(\boldsymbol{x}_i^T\boldsymbol{x}_j)^2$. Instead of thus computing the
# product in the Lagrangian of $\boldsymbol{z}_i^T\boldsymbol{z}_j$ we simply compute
# the dot product $(\boldsymbol{x}_i^T\boldsymbol{x}_j)^2$. This leads to the so-called
# kernel trick and the result leads to the same as if we went through
# the trouble of performing the transformation
# $(\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j)$ during the SVM calculations.
#
#
# ## The problem to solve
# Using our definition of the kernel We can rewrite again the Lagrangian
# $$
# {\cal L}=\sum_i\lambda_i-\frac{1}{2}\sum_{ij}^n\lambda_i\lambda_jy_iy_j\boldsymbol{x}_i^T\boldsymbol{z}_j,
# $$
# subject to the constraints $\lambda_i\geq 0$, $\sum_i\lambda_iy_i=0$ in terms of a convex optimization problem
# $$
# \frac{1}{2} \boldsymbol{\lambda}^T\begin{bmatrix} y_1y_1K(\boldsymbol{x}_1,\boldsymbol{x}_1) & y_1y_2K(\boldsymbol{x}_1,\boldsymbol{x}_2) & \dots & \dots & y_1y_nK(\boldsymbol{x}_1,\boldsymbol{x}_n) \\
# y_2y_1K(\boldsymbol{x}_2,\boldsymbol{x}_1) & y_2y_2(\boldsymbol{x}_2,\boldsymbol{x}_2) & \dots & \dots & y_1y_nK(\boldsymbol{x}_2,\boldsymbol{x}_n) \\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# y_ny_1K(\boldsymbol{x}_n,\boldsymbol{x}_1) & y_ny_2K(\boldsymbol{x}_n\boldsymbol{x}_2) & \dots & \dots & y_ny_nK(\boldsymbol{x}_n,\boldsymbol{x}_n) \\
# \end{bmatrix}\boldsymbol{\lambda}-\mathbb{1}\boldsymbol{\lambda},
# $$
# subject to $\boldsymbol{y}^T\boldsymbol{\lambda}=0$. Here we defined the vectors $\boldsymbol{\lambda} =[\lambda_1,\lambda_2,\dots,\lambda_n]$ and
# $\boldsymbol{y}=[y_1,y_2,\dots,y_n]$.
# If we add the slack constants this leads to the additional constraint $0\leq \lambda_i \leq C$.
#
# We can rewrite this (see the solutions below) in terms of a convex optimization problem of the type
# $$
# \begin{align*}
# &\mathrm{min}_{\lambda}\hspace{0.2cm} \frac{1}{2}\boldsymbol{\lambda}^T\boldsymbol{P}\boldsymbol{\lambda}+\boldsymbol{q}^T\boldsymbol{\lambda},\\ \nonumber
# &\mathrm{subject\hspace{0.1cm}to} \hspace{0.2cm} \boldsymbol{G}\boldsymbol{\lambda} \preceq \boldsymbol{h} \hspace{0.2cm} \wedge \boldsymbol{A}\boldsymbol{\lambda}=f.
# \end{align*}
# $$
# Below we discuss how to solve these equations. Here we note that the matrix $\boldsymbol{P}$ has matrix elements $p_{ij}=y_iy_jK(\boldsymbol{x}_i,\boldsymbol{x}_j)$.
# Given a kernel $K$ and the targets $y_i$ this matrix is easy to set up. The constraint $\boldsymbol{y}^T\boldsymbol{\lambda}=0$ leads to $f=0$ and $\boldsymbol{A}=\boldsymbol{y}$. How to set up the matrix $\boldsymbol{G}$ is discussed later. Here note that the inequalities $0\leq \lambda_i \leq C$ can be split up into
# $0\leq \lambda_i$ and $\lambda_i \leq C$. These two inequalities define then the matrix $\boldsymbol{G}$ and the vector $\boldsymbol{h}$.
#
#
# ## Different kernels and Mercer's theorem
#
# There are several popular kernels being used. These are
# 1. Linear: $K(\boldsymbol{x},\boldsymbol{y})=\boldsymbol{x}^T\boldsymbol{y}$,
#
# 2. Polynomial: $K(\boldsymbol{x},\boldsymbol{y})=(\boldsymbol{x}^T\boldsymbol{y}+\gamma)^d$,
#
# 3. Gaussian Radial Basis Function: $K(\boldsymbol{x},\boldsymbol{y})=\exp{\left(-\gamma\vert\vert\boldsymbol{x}-\boldsymbol{y}\vert\vert^2\right)}$,
#
# 4. Tanh: $K(\boldsymbol{x},\boldsymbol{y})=\tanh{(\boldsymbol{x}^T\boldsymbol{y}+\gamma)}$,
#
# and many other ones.
#
# An important theorem for us is [Mercer's theorem](https://en.wikipedia.org/wiki/Mercer%27s_theorem).
# The theorem states that if a kernel function $K$ is symmetric, continuous and leads to a positive semi-definite matrix $\boldsymbol{P}$ then
# there exists a function $\phi$ that maps $\boldsymbol{x}_i$ and $\boldsymbol{x}_j$ into another space
# (possibly with much higher dimensions) such that
# $$
# K(\boldsymbol{x}_i,\boldsymbol{x}_j)=\phi(\boldsymbol{x}_i)^T\phi(\boldsymbol{x}_j).
# $$
# So you can use $K$ as a kernel since you know $\phi$ exists, even if
# you don’t know what $\phi$ is.
# Note that some frequently used kernels (such as the Sigmoid kernel) don’t respect all of Mercer’s conditions, yet they generally work
# well in practice.
#
#
# ## The moons example
# +
from __future__ import division, print_function, unicode_literals
import numpy as np
np.random.seed(42)
import matplotlib
import matplotlib.pyplot as plt
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
from sklearn.svm import SVC
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
])
polynomial_svm_clf.fit(X, y)
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
poly_kernel_svm_clf.fit(X, y)
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
plt.figure(figsize=(11, 4))
plt.subplot(121)
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.subplot(122)
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
plt.show()
def gaussian_rbf(x, landmark, gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)
gamma = 0.3
x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)
XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(11, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
xy=(X1D[3, 0], 0),
xytext=(-0.5, 0.20),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$ ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
xy=(XK[3, 0], XK[3, 1]),
xytext=(0.65, 0.50),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
plt.subplots_adjust(right=1)
plt.show()
x1_example = X1D[3, 0]
for landmark in (-2, 1):
k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
print("Phi({}, {}) = {}".format(x1_example, landmark, k))
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
plt.figure(figsize=(11, 7))
for i, svm_clf in enumerate(svm_clfs):
plt.subplot(221 + i)
plot_predictions(svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
plt.show()
# -
# ## Mathematical optimization of convex functions
#
# A mathematical (quadratic) optimization problem, or just optimization problem, has the form
# $$
# \begin{align*}
# &\mathrm{min}_{\lambda}\hspace{0.2cm} \frac{1}{2}\boldsymbol{\lambda}^T\boldsymbol{P}\boldsymbol{\lambda}+\boldsymbol{q}^T\boldsymbol{\lambda},\\ \nonumber
# &\mathrm{subject\hspace{0.1cm}to} \hspace{0.2cm} \boldsymbol{G}\boldsymbol{\lambda} \preceq \boldsymbol{h} \wedge \boldsymbol{A}\boldsymbol{\lambda}=f.
# \end{align*}
# $$
# subject to some constraints for say a selected set $i=1,2,\dots, n$.
# In our case we are optimizing with respect to the Lagrangian multipliers $\lambda_i$, and the
# vector $\boldsymbol{\lambda}=[\lambda_1, \lambda_2,\dots, \lambda_n]$ is the optimization variable we are dealing with.
#
# In our case we are particularly interested in a class of optimization problems called convex optmization problems.
# In our discussion on gradient descent methods we discussed at length the definition of a convex function.
#
# Convex optimization problems play a central role in applied mathematics and we recommend strongly [Boyd and Vandenberghe's text on the topics](http://web.stanford.edu/~boyd/cvxbook/).
#
#
#
# ## How do we solve these problems?
#
# If we use Python as programming language and wish to venture beyond
# **scikit-learn**, **tensorflow** and similar software which makes our
# lives so much easier, we need to dive into the wonderful world of
# quadratic programming. We can, if we wish, solve the minimization
# problem using say standard gradient methods or conjugate gradient
# methods. However, these methods tend to exhibit a rather slow
# converge. So, welcome to the promised land of quadratic programming.
#
# The functions we need are contained in the quadratic programming package **CVXOPT** and we need to import it together with **numpy** as
import numpy
import cvxopt
# This will make our life much easier. You don't need t write your own optimizer.
#
#
# ## A simple example
#
# We remind ourselves about the general problem we want to solve
# $$
# \begin{align*}
# &\mathrm{min}_{x}\hspace{0.2cm} \frac{1}{2}\boldsymbol{x}^T\boldsymbol{P}\boldsymbol{x}+\boldsymbol{q}^T\boldsymbol{x},\\ \nonumber
# &\mathrm{subject\hspace{0.1cm} to} \hspace{0.2cm} \boldsymbol{G}\boldsymbol{x} \preceq \boldsymbol{h} \wedge \boldsymbol{A}\boldsymbol{x}=f.
# \end{align*}
# $$
# Let us show how to perform the optmization using a simple case. Assume we want to optimize the following problem
# $$
# \begin{align*}
# &\mathrm{min}_{x}\hspace{0.2cm} \frac{1}{2}x^2+5x+3y \\ \nonumber
# &\mathrm{subject to} \\ \nonumber
# &x, y \geq 0 \\ \nonumber
# &x+3y \geq 15 \\ \nonumber
# &2x+5y \leq 100 \\ \nonumber
# &3x+4y \leq 80. \\ \nonumber
# \end{align*}
# $$
# The minimization problem can be rewritten in terms of vectors and matrices as (with $x$ and $y$ being the unknowns)
# $$
# \frac{1}{2}\begin{bmatrix} x\\ y \end{bmatrix}^T \begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix}3\\ 4 \end{bmatrix}^T \begin{bmatrix}x \\ y \end{bmatrix}.
# $$
# Similarly, we can now set up the inequalities (we need to change $\geq$ to $\leq$ by multiplying with $-1$ on bot sides) as the following matrix-vector equation
# $$
# \begin{bmatrix} -1 & 0 \\ 0 & -1 \\ -1 & -3 \\ 2 & 5 \\ 3 & 4\end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} \preceq \begin{bmatrix}0 \\ 0\\ -15 \\ 100 \\ 80\end{bmatrix}.
# $$
# We have collapsed all the inequalities into a single matrix $\boldsymbol{G}$. We see also that our matrix
# $$
# \boldsymbol{P} =\begin{bmatrix} 1 & 0\\ 0 & 0 \end{bmatrix}
# $$
# is clearly positive semi-definite (all eigenvalues larger or equal zero).
# Finally, the vector $\boldsymbol{h}$ is defined as
# $$
# \boldsymbol{h} = \begin{bmatrix}0 \\ 0\\ -15 \\ 100 \\ 80\end{bmatrix}.
# $$
# Since we don't have any equalities the matrix $\boldsymbol{A}$ is set to zero
# The following code solves the equations for us
# Import the necessary packages
import numpy
from cvxopt import matrix
from cvxopt import solvers
P = matrix(numpy.diag([1,0]), tc=’d’)
q = matrix(numpy.array([3,4]), tc=’d’)
G = matrix(numpy.array([[-1,0],[0,-1],[-1,-3],[2,5],[3,4]]), tc=’d’)
h = matrix(numpy.array([0,0,-15,100,80]), tc=’d’)
# Construct the QP, invoke solver
sol = solvers.qp(P,q,G,h)
# Extract optimal value and solution
sol[’x’]
sol[’primal objective’]
# ## Back to the more realistic cases
#
# We are now ready to return to our setup of the optmization problem for a more realistic case. Introducint the **slack** parameter $C$ we have
# $$
# \frac{1}{2} \boldsymbol{\lambda}^T\begin{bmatrix} y_1y_1K(\boldsymbol{x}_1,\boldsymbol{x}_1) & y_1y_2K(\boldsymbol{x}_1,\boldsymbol{x}_2) & \dots & \dots & y_1y_nK(\boldsymbol{x}_1,\boldsymbol{x}_n) \\
# y_2y_1K(\boldsymbol{x}_2,\boldsymbol{x}_1) & y_2y_2K(\boldsymbol{x}_2,\boldsymbol{x}_2) & \dots & \dots & y_1y_nK(\boldsymbol{x}_2,\boldsymbol{x}_n) \\
# \dots & \dots & \dots & \dots & \dots \\
# \dots & \dots & \dots & \dots & \dots \\
# y_ny_1K(\boldsymbol{x}_n,\boldsymbol{x}_1) & y_ny_2K(\boldsymbol{x}_n\boldsymbol{x}_2) & \dots & \dots & y_ny_nK(\boldsymbol{x}_n,\boldsymbol{x}_n) \\
# \end{bmatrix}\boldsymbol{\lambda}-\mathbb{I}\boldsymbol{\lambda},
# $$
# subject to $\boldsymbol{y}^T\boldsymbol{\lambda}=0$. Here we defined the vectors $\boldsymbol{\lambda} =[\lambda_1,\lambda_2,\dots,\lambda_n]$ and
# $\boldsymbol{y}=[y_1,y_2,\dots,y_n]$.
# With the slack constants this leads to the additional constraint $0\leq \lambda_i \leq C$.
#
# **code will be added**
#
#
# ## Multiclass problems and regression with SVMs
# This material will be added later.
|
doc/pub/svm/ipynb/svm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.4
# language: julia
# name: julia-0.6
# ---
Pkg.add("Plots")
using Plots
using Base.Dates
gr(legend = false)
# +
dates = Date("2016-09-01"):Month(1):Date("2018-09-01")
xs_labels = [Dates.format(d, "yyyy-uu") for d in dates]
#2018-09-01
xs_month = [1, 16, 17, 18, 19, 20, 21, 22, 24, 25]
ys_rank = [47, 47, 47, 50, 37, 44, 46, 43, 50, 39]
xs = collect(1:length(xs_labels));
ys = Vector{Union{Int64}}()
for i in 1:length(xs)
push!(ys, -10)
end
# +
## rank plot
#
plot(xs, ys, line=(:dot,4), marker=:hex, xlabel="month", ylabel="rank", xticks=(xs, xs_labels), xrotation=90)
scatter!(xs_month, ys_rank)
plot!(xs_month, ys_rank, line=(2, :dot,1, :black ) )
hline!([50], line=(4,:solid,0.15,:green) )
plot!(annotations=(-0.5,50,text("50",:left,8) ))
vline!([1,10], line=(4,:solid,0.5,:blue) )
vline!([1,23], line=(4,:solid,0.5,:blue) )
plot!(annotations=(1, 50+10,text("Release v0.5",:left,8) ))
plot!(annotations=(10,50+10,text("Release V0.6",:left,8) ))
plot!(annotations=(23,50+10,text("Release V1.0",:left,8) ))
yflip!()
ylims!((1,80))
title!("Rank of Julia (TIOBE) ")
# -
# 2018-09-1
xs_month = [1, 15, 16, 17, 18, 19, 20, 21, 22, 24, 25]
ys_rating = [0.196, 0.600, 0.439, 0.226, 0.189, 0.301, 0.195, 0.342, 0.281, 0.156, 0.242];
# +
plot(xs, ys, line=(:dot,4), marker=:hex, xlabel="month", ylabel="ratings(%)", xticks=(xs, xs_labels), xrotation=90)
scatter!(xs_month, ys_rating)
plot!(xs_month, ys_rating, line=(2, :dot,1, :black ) )
#hline!([50], line=(2,:solid,0.5,:blue) )
#plot!(annotations=(3,50+3,text("50",:left,8) ))
vline!([1,10], line=(4,:solid,0.5,:blue) )
vline!([1,23], line=(4,:solid,0.5,:blue) )
plot!(annotations=(1, 0.4,text("Release V0.5",:left,8) ))
plot!(annotations=(10,0.4,text("Release V0.6",:left,8) ))
plot!(annotations=(23,0.4,text("Release V1.0",:left,8) ))
ylims!((0,0.7))
title!("Popularity rating (TIOBE)")
# -
# # ReMonk ranking
# January 2014 62
# June 2014 57
# January 2015 56
# June 2015 52
# January 2016, 51
# June 2016, 52
xs_labels = ["2014-Q1", "2014-Q3", "2015-Q1", "2015-Q3", "2016-Q1", "2016-Q3"]
xs_quater = collect(1:6);
ys_rank = [62, 57, 56, 52, 51, 52]
ys_lb = collect(30:2:65)
ys_labels = [string(v) for v in ys_lb];
plot(xs_quater, ys_rank, line=(:dot,4), marker=:hex, xlabel="Quater", ylabel="Rank",
xticks=(xs_quater, xs_labels), yticks=(ys_lb, ys_labels), xrotation=90)
scatter!(xs_quater, ys_rank)
plot!(xs_quater, ys_rank, line=(2, :dot,1, :black ) )
ylims!((30,65))
yflip!()
title!("Rank of Julia (RedMonk)")
# # Popularity rank on two
# +
xs_labels = ["2013-Q1", "2013-Q3", "2014-Q1", "2014-Q3", "2015-Q1", "2015-Q3", "2016-Q1", "2016-Q3",
"2017-Q1", "2017-Q3", "2018-Q1"]
# 13 14 15 16 17 18
# 0.2 0.3 0.4 0.5 0.6
# 1 2 3 4 5 6 7 8 9 10 11
xs_rank = [22, 43, 41, 53, 54, 52, 54, 54, 69, 75, 75 ]
ys_rank = [20, 32, 22, 28, 34, 37, 41, 40, 37, 39, 50 ];
# +
plot(xs_rank, ys_rank, line=(:dot,1), marker=:hex, xlabel="Popularity Rank on GitHub", ylabel="Popularity Rank on Stack Overflow" )
scatter!(xs_rank, ys_rank)
plot!([0,100], [0,100], line=(:solid,2, 0.5) )
plot!(xs_rank, ys_rank, line=(1, :dot,1, :black ) )
for i in 1:length(xs_labels)
plot!(annotations=(xs_rank[i]+2, ys_rank[i]-2, text(xs_labels[i], :left, 8) ))
end
#version_name = ["v0.2", "v0.3", "v0.4", "v0.5", "v0.6"]
reease_i = [2,4,6,8,9]
scatter!(xs_rank[reease_i], ys_rank[reease_i], color=:yellow)
scatter!([85], [70], color=:yellow)
plot!(annotations=(85, 70+5, text("Legend", :left, 8) ))
plot!(annotations=(85+2, 70, text("major release", :left, 8) ))
xlims!((0, 100))
ylims!((0, 100))
title!("Rank of Julia (RedMonk)")
|
trend_analysis/Julia ranking.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import argparse
from tqdm import tqdm
import os
from PIL import Image
import cv2
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm
# +
st_path = '/home/mist/low-light/imageInPaper/IinPaper-v2/lampicka09/drbnlampicka09.png'
w = 512 ; h = 384
im_sg = Image.open(st_path)
im_sg=im_sg.resize((w,h))
im_sg.show()
im_sg.save(st_path)
|
imageInPaper3/resize.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Model Development V2
# - Final model development
#
# ## Process:
# - Merging Dataframes
# - Multinomial Naive Bayes Classifer
# - Latent Semantic Indexing
# - Clustered using Kmeans
# - Hierarchical Dirichlet Process
# - Latent Semantic Analysis
# +
import csv
import json
import pickle
from pymongo import MongoClient
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
# %matplotlib inline
import nltk
import os
from nltk.corpus import stopwords
from sklearn.utils.extmath import randomized_svd
# gensim
from gensim import corpora, models, similarities, matutils
# sklearn
from sklearn import datasets
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn.neighbors import KNeighborsClassifier
import sklearn.metrics.pairwise as smp
import logging
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
# -
with open('nyt-model-df.pkl', 'rb') as nyt_data:
df = pickle.load(nyt_data)
with open('mag-model-df.pkl', 'rb') as mag_data:
df1 = pickle.load(mag_data)
print('NYT Column Names: %s' % str(list(df.columns)))
print()
print('Magazine Column Names: %s' % str(list(df1.columns)))
# # Merge DataFrames
# select the relevant columns in our ratings dataset
nyt_df = df[['lead_paragraph', 'source']]
mag = df1[['lead_paragraph', 'source']]
# remove the duplicates and drop their index
nyt = nyt_df.drop_duplicates().reset_index(drop=True)
nyt.shape, mag.shape
frames = [nyt, mag]
super_df = pd.concat(frames).reset_index(drop=True)
super_df = super_df.dropna()
docs1 = super_df['lead_paragraph'].dropna()
# +
# create a list of stopwords
stopwords_set = frozenset(stopwords.words('english'))
# Update iterator to remove stopwords
class SentencesIterator(object):
# giving 'stop' a list of stopwords would exclude them
def __init__(self, dirname, stop=None):
self.dirname = dirname
def __iter__(self):
# os.listdr is ALSO a generator
for fname in os.listdir(self.dirname):
for line in open(os.path.join(self.dirname, fname),encoding="latin-1"):
# at each step, gensim needs a list of words
line = line.lower().split()
if stop:
outline = []
for word in line:
if word not in stopwords_set:
outline.append(word)
yield outline
else:
yield line
# -
for doc in docs1:
try:
doc = SentencesIterator(doc.decode("utf8"))
except:
doc = SentencesIterator(doc)
docs = pd.Series.tolist(docs1)
# +
tfidf = TfidfVectorizer(stop_words="english",
token_pattern="\\b[a-zA-Z][a-zA-Z]+\\b",
min_df=10)
tfidf_vecs = tfidf.fit_transform(docs)
# -
# ## BASELINE: Multinomial Naive Bayes Classification
# - language is fundamentally different
# - captures word choice
super_df.shape, tfidf_vecs.shape
# +
# Train/Test split
X_train, X_test, y_train, y_test = train_test_split(tfidf_vecs, super_df['source'], test_size=0.33)
# Train
nb = MultinomialNB()
nb.fit(X_train, y_train)
# Test
nb.score(X_test, y_test)
# -
# # LSI
# +
# terms by docs instead of docs by terms
tfidf_corpus = matutils.Sparse2Corpus(tfidf_vecs.transpose())
# Row indices
id2word = dict((v, k) for k, v in tfidf.vocabulary_.items())
# This is a hack for Python 3!
id2word = corpora.Dictionary.from_corpus(tfidf_corpus,
id2word=id2word)
# +
# Build an LSI space from the input TFIDF matrix, mapping of row id to word, and num_topics
# num_topics is the number of dimensions (k) to reduce to after the SVD
# Analagous to "fit" in sklearn, it primes an LSI space trained to 300-500 dimensions
lsi = models.LsiModel(tfidf_corpus, id2word=id2word, num_topics=300)
# +
# Retrieve vectors for the original tfidf corpus in the LSI space ("transform" in sklearn)
lsi_corpus = lsi[tfidf_corpus] # pass using square brackets
# what are the values given by lsi? (topic distributions)
# ALSO, IT IS LAZY! IT WON'T ACTUALLY DO THE TRANSFORMING COMPUTATION UNTIL ITS CALLED. IT STORES THE INSTRUCTIONS
# Dump the resulting document vectors into a list so we can take a look
doc_vecs = [doc for doc in lsi_corpus]
doc_vecs[0] #print the first document vector for all the words
# -
# Convert the gensim-style corpus vecs to a numpy array for sklearn manipulations
nyt_lsi = matutils.corpus2dense(lsi_corpus, num_terms=300).transpose()
nyt_lsi.shape
lsi.show_topic(0)
# +
# all docs by 300 topic vectors (word vectors)
pd.DataFrame(nyt_lsi).head()
# need to transform by cosine similarity
# look up if I need to change into an LDA corpus
# -
# # Clustering - KMeans
# Convert the gensim-style corpus vecs to a numpy array for sklearn manipulations (back to docs to terms matrix)
nyt_lsi = matutils.corpus2dense(lsi_corpus, num_terms=300).transpose()
nyt_lsi.shape
# +
# Create KMeans.
kmeans = KMeans(n_clusters=3)
# Cluster
nyt_lsi_clusters = kmeans.fit_predict(nyt_lsi)
# -
# Take a look. It likely didn't do cosine distances.
print(nyt_lsi_clusters[0:50])
print("Lead Paragraph: \n" + str(df1.iloc[0:5].lead_paragraph))
# # Did an HDP
# An HDP model is fully unsupervised. It can also determine the ideal number of topics it needs through posterior inference.
hdpmodel = models.HdpModel(corpus=tfidf_corpus, id2word=id2word)
hdpmodel.show_topics()
hdptopics = hdpmodel.show_topics(formatted=False)
lda1 = hdpmodel.suggested_lda_model()
# out of 150 topics, shows top 20 HDP topics
lda1.print_topics()
lda1_corpus = lda1[tfidf_corpus]
nyt_lda1 = matutils.corpus2dense(lda1_corpus, num_terms=150).transpose()
df3 = pd.DataFrame(nyt_lda1)
df3.head()
# take the mean of every word vector! (averaged across all document vectors)
# describes word usage ('meaning') across the body of documents in the nyt corpus
# answers the question: what 'topics' has the nyt been talking about the most over 2005-2015?
df3.mean().sort_values()
# # Do an LDA here
# +
lda = models.LdaModel(corpus=tfidf_corpus, num_topics=20, id2word=id2word, passes=3)
# LDA does not scale super well. It can get you great results on 100,000 docs, but 1000 topics on 10e7 docs and it does a poor job.
# LDA is a good latent feature for unsupervised clustering
# -
# Let's take a look at what happened. Here are the 10 most important words for each of the 3 topics we found:
lda.print_topics()
# +
# Transform the docs from the word space to the topic space (like "transform" in sklearn)
lda_corpus = lda[tfidf_corpus] #corpus is the data
# lists the topic distribution per document:
# list(lda_corpus)
# -
# Store the documents' topic vectors in a list so we can take a peak
lda_docs = [doc for doc in lda_corpus]
# Check out the document vectors in the topic space for the first 15 documents
lda_docs[0:15]
nyt_lda = matutils.corpus2dense(lda_corpus, num_terms=20).transpose()
df3 = pd.DataFrame(nyt_lda)
df3.mean().sort_values(ascending=False).head(10)
# ## Logistic Regression / Random Forest
# - <s>Tried KNN Classifier </s> Destroyed my memory
# - probabilistic classification on a spectrum from nyt to natl enq
# +
# remember to pull in the final article dumps from EC2 instance
|
lab_notebooks/NYT-Magazine Classifier V2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [Root]
# language: python
# name: Python [Root]
# ---
# +
#<NAME>
#the intention is to put both the images from training (primary and
#secondary) and test into .pkl files so that they can be used for the NN
# -
#bring in libraries and stuff
#going to import cPickle and decide later
import _pickle as cpkl
import pickle as pkl
from PIL import Image
import os, os.path
# +
#the intention is to build 2 pickles
#one will be the train dataset primary images and secondary images
#training pickle dataset will be a list object. every element in the
#list object will be a dictionary where the first image is a key (this is the primary image)
#and then the value will be the secondary image (the answer to the key) this association must
#be maintained throughout they system
#one will be the test dataset
# +
#so the first image list is going to be called: test_image_list
#the next layer down (each element of the list) is going to be a dictionary
#that dictionary is going to have 1 key and 1 value
#so:---- a list of dictionaries of one element each
#need to come up with way to iterate and match the ends of the strings before the _mask.tif
#so as stated earlier the plan is to use the primary as the keys and
#the secondary as the values. so f = key and g = val.
#for f in os dir
#if f doesn't end with mask.tif then make the comparison
#otherwise skip f for that iteration because we want to keep f as the key
import copy
train_image_list = []
train_path = '/home/ec2-user/Notebooks/datasets_for_projects/train'
outerloop_count = 0
innerloop_count = 0
for f in os.listdir(train_path):
#sub_train_image_list = []
if not f.endswith('mask.tif'):
for g in os.listdir(train_path):
gString = copy.deepcopy(g)
fString = copy.deepcopy(f)
if gString.endswith('mask.tif') and gString.replace('_mask', '')==fString:
#the -4 indicates that i am slicing the .tif off of the back if the
#file name that is being passed as the key for the dictionary
dictNamef = str.join('', ('subDict',f))
dictNameg = str.join('', ('subDcit',g))
#need to copy the strings so they literal can be used for the dict keys
fStringCopy = copy.deepcopy(dictNamef)
fStringCopy = fStringCopy[0:-4]
gStringCopy = copy.deepcopy(dictNameg)
gStringCopy = gStringCopy[0:-4]
with Image.open(os.path.join(train_path, f)) as imagef:
fStringCopy = {
'pixels': imagef.tobytes(),
'size': imagef.size,
'mode': imagef.mode
}
with Image.open(os.path.join(train_path, g)) as imageg:
gStringCopy = {
'pixels': imageg.tobytes(),
'size': imageg.size,
'mode': imageg.mode
}
imageList = []
imageList.append(fStringCopy)
imageList.append(gStringCopy)
train_image_list.append(imageList)
break
innerloop_count=innerloop_count+1
outerloop_count=outerloop_count+1
# +
#first list is primary images from the training set
train_image_list_primary = []
train_path = '/home/kevin/Datasets/train'
for f in os.listdir(train_path):
if not f.endswith('mask.tif'):
continue
with Image.open(os.path.join(train_path, f)) as image:
imageDict = {
'pixels': image.tobytes(),
'size': image.size,
'mode': image.mode,
}
train_image_list_primary.append(imageDict)
# -
#second list is the secondary images from the training set
train_image_list_secondary = []
#note train_path is the same so no need to redefine
for f in os.listdir(train_path):
if f.endswith('mask.tif'):
with Image.open(os.path.join(train_path, f)) as image:
imageDict = {
'pixels': image.tobytes(),
'size': image.size,
'mode': image.mode
}
train_image_list_secondary.append(imageDict)
# +
#third list will be the test images
test_image_list = []
test_path = '/home/kevin/Datasets/test'
for f in os.listdir(test_path):
if not f.endswith('.tif'):
continue
with Image.open(os.path.join(test_path, f)) as image:
imageDict = {
'pixels': image.tobytes(),
'size': image.size,
'mode': image.mode,
}
test_image_list.append(imageDict)
# +
#now that we have lists with dictionaries conaining all the data,
#we are ready to pickle the lists since they don't contain any of the
#images themselves it should go smoothly
with open('training_P.pkl', 'wb') as f1:
cpkl.dump(train_image_list_primary, f1)
f1.close
# +
#now onto training secondary images:
with open('training_S.pkl', 'wb') as f2:
cpkl.dump(train_image_list_secondary, f2)
f2.close
# +
#lastly lets pickle the testing set of images:
with open('testing.pkl', 'wb') as f3:
cpkl.dump(test_image_list, f3)
f3.close
# -
with open('training2.pkl', 'wb') as f4:
cpkl.dump(train_image_list, f4)
f4.close
# +
#all of the 3 image sets are now all pre-processed and
#pickeled into 3 files
# -
print(os.path.isdir('/home/ec2-user/Notebooks/datasets_for_projects/train'))
|
Pickling_Ultrasound_Data_2nd_approach.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] deletable=true editable=true
# # Artificial Intelligence Engineer Nanodegree - Probabilistic Models
# ## Project: Sign Language Recognition System
# - [Introduction](#intro)
# - [Part 1 Feature Selection](#part1_tutorial)
# - [Tutorial](#part1_tutorial)
# - [Features Submission](#part1_submission)
# - [Features Unittest](#part1_test)
# - [Part 2 Train the models](#part2_tutorial)
# - [Tutorial](#part2_tutorial)
# - [Model Selection Score Submission](#part2_submission)
# - [Model Score Unittest](#part2_test)
# - [Part 3 Build a Recognizer](#part3_tutorial)
# - [Tutorial](#part3_tutorial)
# - [Recognizer Submission](#part3_submission)
# - [Recognizer Unittest](#part3_test)
# - [Part 4 (OPTIONAL) Improve the WER with Language Models](#part4_info)
# + [markdown] deletable=true editable=true
# <a id='intro'></a>
# ## Introduction
# The overall goal of this project is to build a word recognizer for American Sign Language video sequences, demonstrating the power of probabalistic models. In particular, this project employs [hidden Markov models (HMM's)](https://en.wikipedia.org/wiki/Hidden_Markov_model) to analyze a series of measurements taken from videos of American Sign Language (ASL) collected for research (see the [RWTH-BOSTON-104 Database](http://www-i6.informatik.rwth-aachen.de/~dreuw/database-rwth-boston-104.php)). In this video, the right-hand x and y locations are plotted as the speaker signs the sentence.
# [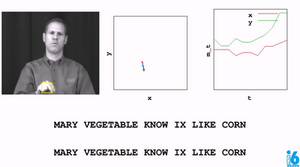](https://drive.google.com/open?id=0B_5qGuFe-wbhUXRuVnNZVnMtam8)
#
# The raw data, train, and test sets are pre-defined. You will derive a variety of feature sets (explored in Part 1), as well as implement three different model selection criterion to determine the optimal number of hidden states for each word model (explored in Part 2). Finally, in Part 3 you will implement the recognizer and compare the effects the different combinations of feature sets and model selection criteria.
#
# At the end of each Part, complete the submission cells with implementations, answer all questions, and pass the unit tests. Then submit the completed notebook for review!
# + [markdown] deletable=true editable=true
# <a id='part1_tutorial'></a>
# ## PART 1: Data
#
# ### Features Tutorial
# ##### Load the initial database
# A data handler designed for this database is provided in the student codebase as the `AslDb` class in the `asl_data` module. This handler creates the initial [pandas](http://pandas.pydata.org/pandas-docs/stable/) dataframe from the corpus of data included in the `data` directory as well as dictionaries suitable for extracting data in a format friendly to the [hmmlearn](https://hmmlearn.readthedocs.io/en/latest/) library. We'll use those to create models in Part 2.
#
# To start, let's set up the initial database and select an example set of features for the training set. At the end of Part 1, you will create additional feature sets for experimentation.
# + deletable=true editable=true
import numpy as np
import pandas as pd
from asl_data import AslDb
asl = AslDb() # initializes the database
asl.df.head() # displays the first five rows of the asl database, indexed by video and frame
# + deletable=true editable=true
asl.df.ix[98,1] # look at the data available for an individual frame
# + [markdown] deletable=true editable=true
# The frame represented by video 98, frame 1 is shown here:
# 
# + [markdown] deletable=true editable=true
# ##### Feature selection for training the model
# The objective of feature selection when training a model is to choose the most relevant variables while keeping the model as simple as possible, thus reducing training time. We can use the raw features already provided or derive our own and add columns to the pandas dataframe `asl.df` for selection. As an example, in the next cell a feature named `'grnd-ry'` is added. This feature is the difference between the right-hand y value and the nose y value, which serves as the "ground" right y value.
# + deletable=true editable=true
asl.df['grnd-ry'] = asl.df['right-y'] - asl.df['nose-y']
asl.df.head() # the new feature 'grnd-ry' is now in the frames dictionary
# + [markdown] deletable=true editable=true
# ##### Try it!
# + deletable=true editable=true
from asl_utils import test_features_tryit
# TODO add df columns for 'grnd-rx', 'grnd-ly', 'grnd-lx' representing differences between hand and nose locations
asl.df['grnd-rx'] = asl.df['right-x'] - asl.df['nose-x']
asl.df['grnd-lx'] = asl.df['left-x'] - asl.df['nose-x']
asl.df['grnd-ly'] = asl.df['left-y'] - asl.df['nose-y']
# test the code
test_features_tryit(asl)
# + deletable=true editable=true
# collect the features into a list
features_ground = ['grnd-rx','grnd-ry','grnd-lx','grnd-ly']
#show a single set of features for a given (video, frame) tuple
[asl.df.ix[98,1][v] for v in features_ground]
# + [markdown] deletable=true editable=true
# ##### Build the training set
# Now that we have a feature list defined, we can pass that list to the `build_training` method to collect the features for all the words in the training set. Each word in the training set has multiple examples from various videos. Below we can see the unique words that have been loaded into the training set:
# + deletable=true editable=true
training = asl.build_training(features_ground)
print("Training words: {}".format(training.words))
# + [markdown] deletable=true editable=true
# The training data in `training` is an object of class `WordsData` defined in the `asl_data` module. in addition to the `words` list, data can be accessed with the `get_all_sequences`, `get_all_Xlengths`, `get_word_sequences`, and `get_word_Xlengths` methods. We need the `get_word_Xlengths` method to train multiple sequences with the `hmmlearn` library. In the following example, notice that there are two lists; the first is a concatenation of all the sequences(the X portion) and the second is a list of the sequence lengths(the Lengths portion).
# + deletable=true editable=true
training.get_word_Xlengths('CHOCOLATE')
# + [markdown] deletable=true editable=true
# ###### More feature sets
# So far we have a simple feature set that is enough to get started modeling. However, we might get better results if we manipulate the raw values a bit more, so we will go ahead and set up some other options now for experimentation later. For example, we could normalize each speaker's range of motion with grouped statistics using [Pandas stats](http://pandas.pydata.org/pandas-docs/stable/api.html#api-dataframe-stats) functions and [pandas groupby](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.groupby.html). Below is an example for finding the means of all speaker subgroups.
# + deletable=true editable=true
df_means = asl.df.groupby('speaker').mean()
df_means
# + [markdown] deletable=true editable=true
# To select a mean that matches by speaker, use the pandas [map](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.map.html) method:
# + deletable=true editable=true
asl.df['left-x-mean'] = asl.df['speaker'].map(df_means['left-x'])
asl.df.head()
# + [markdown] deletable=true editable=true
# ##### Try it!
# + deletable=true editable=true
from asl_utils import test_std_tryit
# TODO Create a dataframe named `df_std` with standard deviations grouped by speaker
df_std = asl.df.groupby('speaker').std()
# test the code
test_std_tryit(df_std)
# + [markdown] deletable=true editable=true
# <a id='part1_submission'></a>
# ### Features Implementation Submission
# Implement four feature sets and answer the question that follows.
# - normalized Cartesian coordinates
# - use *mean* and *standard deviation* statistics and the [standard score](https://en.wikipedia.org/wiki/Standard_score) equation to account for speakers with different heights and arm length
#
# - polar coordinates
# - calculate polar coordinates with [Cartesian to polar equations](https://en.wikipedia.org/wiki/Polar_coordinate_system#Converting_between_polar_and_Cartesian_coordinates)
# - use the [np.arctan2](https://docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.arctan2.html) function and *swap the x and y axes* to move the $0$ to $2\pi$ discontinuity to 12 o'clock instead of 3 o'clock; in other words, the normal break in radians value from $0$ to $2\pi$ occurs directly to the left of the speaker's nose, which may be in the signing area and interfere with results. By swapping the x and y axes, that discontinuity move to directly above the speaker's head, an area not generally used in signing.
#
# - delta difference
# - as described in Thad's lecture, use the difference in values between one frame and the next frames as features
# - pandas [diff method](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.diff.html) and [fillna method](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.fillna.html) will be helpful for this one
#
# - custom features
# - These are your own design; combine techniques used above or come up with something else entirely. We look forward to seeing what you come up with!
# Some ideas to get you started:
# - normalize using a [feature scaling equation](https://en.wikipedia.org/wiki/Feature_scaling)
# - normalize the polar coordinates
# - adding additional deltas
#
# + deletable=true editable=true
# TODO add features for normalized by speaker values of left, right, x, y
# Name these 'norm-rx', 'norm-ry', 'norm-lx', and 'norm-ly'
# using Z-score scaling (X-Xmean)/Xstd
def normalize_speaker_score(col):
mean = asl.df['speaker'].map(df_means[col])
std = asl.df['speaker'].map(df_std[col])
return (asl.df[col] - mean) / std
features_norm = ['norm-rx', 'norm-ry', 'norm-lx','norm-ly']
asl.df['norm-lx'] = normalize_speaker_score('left-x')
asl.df['norm-ly'] = normalize_speaker_score('left-y')
asl.df['norm-rx'] = normalize_speaker_score('right-x')
asl.df['norm-ry'] = normalize_speaker_score('right-y')
# + deletable=true editable=true
# TODO add features for polar coordinate values where the nose is the origin
# Name these 'polar-rr', 'polar-rtheta', 'polar-lr', and 'polar-ltheta'
# Note that 'polar-rr' and 'polar-rtheta' refer to the radius and angle
features_polar = ['polar-rr', 'polar-rtheta', 'polar-lr', 'polar-ltheta']
rx = asl.df['right-x'] - asl.df['nose-x']
ry = asl.df['right-y'] - asl.df['nose-y']
asl.df['polar-rr'] = np.sqrt(rx**2 + ry**2)
asl.df['polar-rtheta'] = np.arctan2(rx, ry)
lx = asl.df['left-x'] - asl.df['nose-x']
ly = asl.df['left-y'] - asl.df['nose-y']
asl.df['polar-lr'] = np.sqrt(lx**2 + ly**2)
asl.df['polar-ltheta'] = np.arctan2(lx, ly)
# + deletable=true editable=true
# TODO add features for left, right, x, y differences by one time step, i.e. the "delta" values discussed in the lecture
# Name these 'delta-rx', 'delta-ry', 'delta-lx', and 'delta-ly'
features_delta = ['delta-rx', 'delta-ry', 'delta-lx', 'delta-ly']
asl.df['delta-lx'] = asl.df['left-x'].diff().fillna(0)
asl.df['delta-ly'] = asl.df['left-y'].diff().fillna(0)
asl.df['delta-rx'] = asl.df['right-x'].diff().fillna(0)
asl.df['delta-ry'] = asl.df['right-y'].diff().fillna(0)
# + deletable=true editable=true
features_polar_norm = ['norm-polar-rr', 'norm-polar-rtheta', 'norm-polar-lr', 'norm-polar-ltheta']
def normalize(col, df):
return (df[col] - df[col].mean()) / df[col].std()
asl.df['norm-polar-rr'] = normalize('polar-rr', asl.df)
asl.df['norm-polar-rtheta'] = normalize('polar-rtheta', asl.df)
asl.df['norm-polar-lr'] = normalize('polar-lr', asl.df)
asl.df['norm-polar-ltheta'] = normalize('polar-ltheta', asl.df)
# + deletable=true editable=true
features_delta_polar_norm = ['delta-norm-polar-rr', 'delta-norm-polar-rtheta', 'delta-norm-polar-lr',
'delta-norm-polar-ltheta']
asl.df['delta-norm-polar-rr'] = asl.df['norm-polar-rr'].diff().fillna(0)
asl.df['delta-norm-polar-rtheta'] = asl.df['norm-polar-rtheta'].diff().fillna(0)
asl.df['delta-norm-polar-lr'] = asl.df['norm-polar-lr'].diff().fillna(0)
asl.df['delta-norm-polar-ltheta'] = asl.df['norm-polar-ltheta'].diff().fillna(0)
# + deletable=true editable=true
features_polar_scaled = ['scaled-polar-rr', 'scaled-polar-rtheta', 'scaled-polar-lr', 'scaled-polar-ltheta']
def min_max_scale(col, df):
feat_min = df[col].min()
feat_max = df[col].max()
return (df[col] - feat_min) / (feat_max - feat_min)
asl.df['scaled-polar-rr'] = min_max_scale('polar-rr', asl.df)
asl.df['scaled-polar-rtheta'] = min_max_scale('polar-rtheta', asl.df)
asl.df['scaled-polar-lr'] = min_max_scale('polar-lr', asl.df)
asl.df['scaled-polar-ltheta'] = min_max_scale('polar-ltheta', asl.df)
# + deletable=true editable=true
features_delta_polar_scaled = ['delta-scaled-polar-rr', 'delta-scaled-polar-rtheta', 'delta-scaled-polar-lr',
'delta-scaled-polar-ltheta']
asl.df['delta-scaled-polar-rr'] = asl.df['scaled-polar-rr'].diff().fillna(0)
asl.df['delta-scaled-polar-rtheta'] = asl.df['scaled-polar-rtheta'].diff().fillna(0)
asl.df['delta-scaled-polar-lr'] = asl.df['scaled-polar-lr'].diff().fillna(0)
asl.df['delta-scaled-polar-ltheta'] = asl.df['scaled-polar-ltheta'].diff().fillna(0)
# + deletable=true editable=true
# TODO add features of your own design, which may be a combination of the above or something else
# Name these whatever you would like
# TODO define a list named 'features_custom' for building the training set
features_custom = features_polar_scaled + features_delta_polar_scaled
features_custom
# + [markdown] deletable=true editable=true
# **Question 1:** What custom features did you choose for the features_custom set and why?
#
# **Answer 1:**
# + [markdown] deletable=true editable=true
# Scaled polar coordinates and their scaled delta values are used as features. Essentially, polar coordinates are differences between the left and right hand positions from the nose transformed into polar coordinate system. The transformation is to ensure 0 to 2$\pi$ continuity in the signing area. These polar coordinate features tell where the hands are in each particular time frame. The difference in polar coordinates between one frame and the next frames can tell how much left and right hands move between one frames to the next. As the transformed polar coordinates and their delta values from one time frame to the next are different in scale, they are transformed into the same scale using min-max scaling such that their relative differences are maintained. This ensures that features with much larger values don't outweigh ones with much smaller values. In addition, scaling also helps machine learning algorithms converge much faster as well.
# + [markdown] deletable=true editable=true
# <a id='part1_test'></a>
# ### Features Unit Testing
# Run the following unit tests as a sanity check on the defined "ground", "norm", "polar", and 'delta"
# feature sets. The test simply looks for some valid values but is not exhaustive. However, the project should not be submitted if these tests don't pass.
# + deletable=true editable=true
import unittest
# import numpy as np
class TestFeatures(unittest.TestCase):
def test_features_ground(self):
sample = (asl.df.ix[98, 1][features_ground]).tolist()
self.assertEqual(sample, [9, 113, -12, 119])
def test_features_norm(self):
sample = (asl.df.ix[98, 1][features_norm]).tolist()
np.testing.assert_almost_equal(sample, [ 1.153, 1.663, -0.891, 0.742], 3)
def test_features_polar(self):
sample = (asl.df.ix[98,1][features_polar]).tolist()
np.testing.assert_almost_equal(sample, [113.3578, 0.0794, 119.603, -0.1005], 3)
def test_features_delta(self):
sample = (asl.df.ix[98, 0][features_delta]).tolist()
self.assertEqual(sample, [0, 0, 0, 0])
sample = (asl.df.ix[98, 18][features_delta]).tolist()
self.assertTrue(sample in [[-16, -5, -2, 4], [-14, -9, 0, 0]], "Sample value found was {}".format(sample))
suite = unittest.TestLoader().loadTestsFromModule(TestFeatures())
unittest.TextTestRunner().run(suite)
# + [markdown] deletable=true editable=true
# <a id='part2_tutorial'></a>
# ## PART 2: Model Selection
# ### Model Selection Tutorial
# The objective of Model Selection is to tune the number of states for each word HMM prior to testing on unseen data. In this section you will explore three methods:
# - Log likelihood using cross-validation folds (CV)
# - Bayesian Information Criterion (BIC)
# - Discriminative Information Criterion (DIC)
# + [markdown] deletable=true editable=true
# ##### Train a single word
# Now that we have built a training set with sequence data, we can "train" models for each word. As a simple starting example, we train a single word using Gaussian hidden Markov models (HMM). By using the `fit` method during training, the [Baum-Welch Expectation-Maximization](https://en.wikipedia.org/wiki/Baum%E2%80%93Welch_algorithm) (EM) algorithm is invoked iteratively to find the best estimate for the model *for the number of hidden states specified* from a group of sample seequences. For this example, we *assume* the correct number of hidden states is 3, but that is just a guess. How do we know what the "best" number of states for training is? We will need to find some model selection technique to choose the best parameter.
# + deletable=true editable=true
import warnings
from hmmlearn.hmm import GaussianHMM
def train_a_word(word, num_hidden_states, features):
warnings.filterwarnings("ignore", category=DeprecationWarning)
training = asl.build_training(features)
X, lengths = training.get_word_Xlengths(word)
model = GaussianHMM(n_components=num_hidden_states, n_iter=1000).fit(X, lengths)
logL = model.score(X, lengths)
return model, logL
demoword = 'BOOK'
model, logL = train_a_word(demoword, 3, features_ground)
print("Number of states trained in model for {} is {}".format(demoword, model.n_components))
print("logL = {}".format(logL))
# + [markdown] deletable=true editable=true
# The HMM model has been trained and information can be pulled from the model, including means and variances for each feature and hidden state. The [log likelihood](http://math.stackexchange.com/questions/892832/why-we-consider-log-likelihood-instead-of-likelihood-in-gaussian-distribution) for any individual sample or group of samples can also be calculated with the `score` method.
# + deletable=true editable=true
def show_model_stats(word, model):
print("Number of states trained in model for {} is {}".format(word, model.n_components))
variance=np.array([np.diag(model.covars_[i]) for i in range(model.n_components)])
for i in range(model.n_components): # for each hidden state
print("hidden state #{}".format(i))
print("mean = ", model.means_[i])
print("variance = ", variance[i])
print()
show_model_stats(demoword, model)
# + [markdown] deletable=true editable=true
# ##### Try it!
# Experiment by changing the feature set, word, and/or num_hidden_states values in the next cell to see changes in values.
# + [markdown] deletable=true editable=true
# ### features_custom
# + deletable=true editable=true
my_testword = 'CHOCOLATE'
model, logL = train_a_word(my_testword, 3, features_custom)
show_model_stats(my_testword, model)
print("logL = {}".format(logL))
# + [markdown] deletable=true editable=true
# ##### Visualize the hidden states
# We can plot the means and variances for each state and feature. Try varying the number of states trained for the HMM model and examine the variances. Are there some models that are "better" than others? How can you tell? We would like to hear what you think in the classroom online.
# + deletable=true editable=true
# %matplotlib inline
# + deletable=true editable=true
import math
from matplotlib import (cm, pyplot as plt, mlab)
def visualize(word, model):
""" visualize the input model for a particular word """
variance=np.array([np.diag(model.covars_[i]) for i in range(model.n_components)])
figures = []
for parm_idx in range(len(model.means_[0])):
xmin = int(min(model.means_[:,parm_idx]) - max(variance[:,parm_idx]))
xmax = int(max(model.means_[:,parm_idx]) + max(variance[:,parm_idx]))
fig, axs = plt.subplots(model.n_components, sharex=True, sharey=False)
colours = cm.rainbow(np.linspace(0, 1, model.n_components))
for i, (ax, colour) in enumerate(zip(axs, colours)):
x = np.linspace(xmin, xmax, 100)
mu = model.means_[i,parm_idx]
sigma = math.sqrt(np.diag(model.covars_[i])[parm_idx])
ax.plot(x, mlab.normpdf(x, mu, sigma), c=colour)
ax.set_title("{} feature {} hidden state #{}".format(word, parm_idx, i))
ax.grid(True)
figures.append(plt)
for p in figures:
p.show()
model, logL = train_a_word(my_testword, 3, features_norm)
visualize(my_testword, model)
# + [markdown] deletable=true editable=true
# ##### ModelSelector class
# Review the `ModelSelector` class from the codebase found in the `my_model_selectors.py` module. It is designed to be a strategy pattern for choosing different model selectors. For the project submission in this section, subclass `SelectorModel` to implement the following model selectors. In other words, you will write your own classes/functions in the `my_model_selectors.py` module and run them from this notebook:
#
# - `SelectorCV `: Log likelihood with CV
# - `SelectorBIC`: BIC
# - `SelectorDIC`: DIC
#
# You will train each word in the training set with a range of values for the number of hidden states, and then score these alternatives with the model selector, choosing the "best" according to each strategy. The simple case of training with a constant value for `n_components` can be called using the provided `SelectorConstant` subclass as follow:
# + deletable=true editable=true
from my_model_selectors import SelectorConstant
training = asl.build_training(features_norm) # Experiment here with different feature sets defined in part 1
word = 'VEGETABLE' # Experiment here with different words
model = SelectorConstant(training.get_all_sequences(), training.get_all_Xlengths(), word, n_constant=3).select()
print("Number of states trained in model for {} is {}".format(word, model.n_components))
# + [markdown] deletable=true editable=true
# ##### Cross-validation folds
# If we simply score the model with the Log Likelihood calculated from the feature sequences it has been trained on, we should expect that more complex models will have higher likelihoods. However, that doesn't tell us which would have a better likelihood score on unseen data. The model will likely be overfit as complexity is added. To estimate which topology model is better using only the training data, we can compare scores using cross-validation. One technique for cross-validation is to break the training set into "folds" and rotate which fold is left out of training. The "left out" fold scored. This gives us a proxy method of finding the best model to use on "unseen data". In the following example, a set of word sequences is broken into three folds using the [scikit-learn Kfold](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.KFold.html) class object. When you implement `SelectorCV`, you will use this technique.
# + deletable=true editable=true
from sklearn.model_selection import KFold
training = asl.build_training(features_ground) # Experiment here with different feature sets
word = 'VEGETABLE' # Experiment here with different words
word_sequences = training.get_word_sequences(word)
split_method = KFold()
for cv_train_idx, cv_test_idx in split_method.split(word_sequences):
print("Train fold indices:{} Test fold indices:{}".format(cv_train_idx, cv_test_idx)) # view indices of the folds
# + [markdown] deletable=true editable=true
# **Tip:** In order to run `hmmlearn` training using the X,lengths tuples on the new folds, subsets must be combined based on the indices given for the folds. A helper utility has been provided in the `asl_utils` module named `combine_sequences` for this purpose.
# + [markdown] deletable=true editable=true
# ##### Scoring models with other criterion
# Scoring model topologies with **BIC** balances fit and complexity within the training set for each word. In the BIC equation, a penalty term penalizes complexity to avoid overfitting, so that it is not necessary to also use cross-validation in the selection process. There are a number of references on the internet for this criterion. These [slides](http://www2.imm.dtu.dk/courses/02433/doc/ch6_slides.pdf) include a formula you may find helpful for your implementation.
#
# The advantages of scoring model topologies with **DIC** over BIC are presented by <NAME> in this [reference](http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.58.6208&rep=rep1&type=pdf) (also found [here](https://pdfs.semanticscholar.org/ed3d/7c4a5f607201f3848d4c02dd9ba17c791fc2.pdf)). DIC scores the discriminant ability of a training set for one word against competing words. Instead of a penalty term for complexity, it provides a penalty if model likelihoods for non-matching words are too similar to model likelihoods for the correct word in the word set.
# + [markdown] deletable=true editable=true
# <a id='part2_submission'></a>
# ### Model Selection Implementation Submission
# Implement `SelectorCV`, `SelectorBIC`, and `SelectorDIC` classes in the `my_model_selectors.py` module. Run the selectors on the following five words. Then answer the questions about your results.
#
# **Tip:** The `hmmlearn` library may not be able to train or score all models. Implement try/except contructs as necessary to eliminate non-viable models from consideration.
# + deletable=true editable=true
words_to_train = ['FISH', 'BOOK', 'VEGETABLE', 'FUTURE', 'JOHN']
import timeit
# this pervents RuntimeWarning: invalid value encountered in true_divide
# from occuring due to division by 0 or nan in hmmlearn
np.seterr(divide='ignore', invalid='ignore')
# + deletable=true editable=true
# autoreload for automatically reloading changes made in my_model_selectors and my_recognizer
# %load_ext autoreload
# %autoreload 2
# + deletable=true editable=true
# TODO: Implement SelectorCV in my_model_selector.py
from my_model_selectors import SelectorCV
training = asl.build_training(features_custom) # Experiment here with different feature sets defined in part 1
sequences = training.get_all_sequences()
Xlengths = training.get_all_Xlengths()
for word in words_to_train:
start = timeit.default_timer()
model = SelectorCV(sequences, Xlengths, word, verbose=False,
min_n_components=2, max_n_components=15, random_state=14).select()
end = timeit.default_timer()-start
if model is not None:
print("Training complete for {} with {} states with time {} seconds".format(word, model.n_components, end))
else:
print("Training failed for {}".format(word))
# + deletable=true editable=true
# TODO: Implement SelectorBIC in module my_model_selectors.py
from my_model_selectors import SelectorBIC
training = asl.build_training(features_custom) # Experiment here with different feature sets defined in part 1
sequences = training.get_all_sequences()
Xlengths = training.get_all_Xlengths()
for word in words_to_train:
start = timeit.default_timer()
model = SelectorBIC(sequences, Xlengths, word,
min_n_components=2, max_n_components=15, random_state=14).select()
end = timeit.default_timer()-start
if model is not None:
print("Training complete for {} with {} states with time {} seconds".format(word, model.n_components, end))
else:
print("Training failed for {}".format(word))
# + deletable=true editable=true
# TODO: Implement SelectorDIC in module my_model_selectors.py
from my_model_selectors import SelectorDIC
training = asl.build_training(features_custom) # Experiment here with different feature sets defined in part 1
sequences = training.get_all_sequences()
Xlengths = training.get_all_Xlengths()
for word in words_to_train:
start = timeit.default_timer()
model = SelectorDIC(sequences, Xlengths, word,
min_n_components=2, max_n_components=15, random_state=14).select()
end = timeit.default_timer()-start
if model is not None:
print("Training complete for {} with {} states with time {} seconds".format(word, model.n_components, end))
else:
print("Training failed for {}".format(word))
# + [markdown] deletable=true editable=true
# **Question 2:** Compare and contrast the possible advantages and disadvantages of the various model selectors implemented.
#
# **Answer 2:**
# + [markdown] deletable=true editable=true
# **Cross validation (CV)** works by splitting samples into K different folds. Each fold takes its turn as a test set for the other K-1 training set. The best model is selected by considering the highest average log likelihood of all the folds. This way the selected model is not sensitive to how the data is split, thus ensuring more generalization ability. It is also simple to interpret. One main disadvantage of this approach is that K number of training is required.
#
# **Bayesian Information Criterion (BIC)** chooses the model which gives the lowest BIC. The BIC formula is *-2 * logL + p * logN* where *logL* is the log likelihood, *p* is the number of parameters, and *N* is the number of data points. As seen in the formula, BIC penalizes the model when adding more complexity(more parameters) to the model. The disadvantage of BIC is that there is no way to know whether the complexity penalty will exactly offset the overfitting property.
#
# **Discriminative Information Criterion (DIC)** chooses the model which gives the highest DIC. Unlike BIC, it takes into account the goal of the model which is classification task. The idea of DIC is that it tries to find model with the highest log likelihood of the original word and low log likelihood of the other words. In other words, DIC aims to penalize if the model underfits.
#
# All in all, I would argue that cross validation is the most effective approach for model selection due to its simplicity and unbiased scoring metric which ultimately maximizes generalization potential.
# + [markdown] deletable=true editable=true
# <a id='part2_test'></a>
# ### Model Selector Unit Testing
# Run the following unit tests as a sanity check on the implemented model selectors. The test simply looks for valid interfaces but is not exhaustive. However, the project should not be submitted if these tests don't pass.
# + deletable=true editable=true
from asl_test_model_selectors import TestSelectors
suite = unittest.TestLoader().loadTestsFromModule(TestSelectors())
unittest.TextTestRunner().run(suite)
# + [markdown] deletable=true editable=true
# <a id='part3_tutorial'></a>
# ## PART 3: Recognizer
# The objective of this section is to "put it all together". Using the four feature sets created and the three model selectors, you will experiment with the models and present your results. Instead of training only five specific words as in the previous section, train the entire set with a feature set and model selector strategy.
# ### Recognizer Tutorial
# ##### Train the full training set
# The following example trains the entire set with the example `features_ground` and `SelectorConstant` features and model selector. Use this pattern for you experimentation and final submission cells.
#
#
# + deletable=true editable=true
from my_model_selectors import SelectorConstant
def train_all_words(features, model_selector):
training = asl.build_training(features) # Experiment here with different feature sets defined in part 1
sequences = training.get_all_sequences()
Xlengths = training.get_all_Xlengths()
model_dict = {}
for word in training.words:
model = model_selector(sequences, Xlengths, word,
n_constant=3).select()
model_dict[word]=model
return model_dict
models = train_all_words(features_ground, SelectorConstant)
print("Number of word models returned = {}".format(len(models)))
# + [markdown] deletable=true editable=true
# ##### Load the test set
# The `build_test` method in `ASLdb` is similar to the `build_training` method already presented, but there are a few differences:
# - the object is type `SinglesData`
# - the internal dictionary keys are the index of the test word rather than the word itself
# - the getter methods are `get_all_sequences`, `get_all_Xlengths`, `get_item_sequences` and `get_item_Xlengths`
# + deletable=true editable=true
test_set = asl.build_test(features_ground)
print("Number of test set items: {}".format(test_set.num_items))
print("Number of test set sentences: {}".format(len(test_set.sentences_index)))
# + [markdown] deletable=true editable=true
# <a id='part3_submission'></a>
# ### Recognizer Implementation Submission
# For the final project submission, students must implement a recognizer following guidance in the `my_recognizer.py` module. Experiment with the four feature sets and the three model selection methods (that's 12 possible combinations). You can add and remove cells for experimentation or run the recognizers locally in some other way during your experiments, but retain the results for your discussion. For submission, you will provide code cells of **only three** interesting combinations for your discussion (see questions below). At least one of these should produce a word error rate of less than 60%, i.e. WER < 0.60 .
#
# **Tip:** The hmmlearn library may not be able to train or score all models. Implement try/except contructs as necessary to eliminate non-viable models from consideration.
# + deletable=true editable=true
# TODO implement the recognize method in my_recognizer
from my_recognizer import recognize
from asl_utils import show_errors
# + [markdown] deletable=true editable=true
# # Evaluation
# + deletable=true editable=true
def show_error_stats(guesses, test_set):
"""Print WER
WER = (S+I+D)/N but we have no insertions or deletions for isolated words so WER = S/N
"""
S = 0
N = len(test_set.wordlist)
num_test_words = len(test_set.wordlist)
if len(guesses) != num_test_words:
print("Size of guesses must equal number of test words ({})!".format(num_test_words))
for word_id in range(num_test_words):
if guesses[word_id] != test_set.wordlist[word_id]:
S += 1
print("**** WER = {}".format(float(S) / float(N)))
print("Total correct: {} out of {}".format(N - S, N))
def evaluate(features):
test_set = asl.build_test(features)
print('Features', features)
for selector in (SelectorCV, SelectorBIC, SelectorDIC):
print('Selector', str(selector))
models = train_all_words(features, selector)
probabilities, guesses = recognize(models, test_set)
show_error_stats(guesses, test_set)
print("==========================================")
# + [markdown] deletable=true editable=true
# ### features_norm
# + deletable=true editable=true
evaluate(features_norm)
# + [markdown] deletable=true editable=true
# ### features_delta
# + deletable=true editable=true
evaluate(features_delta)
# + [markdown] deletable=true editable=true
# ### features_polar
# + deletable=true editable=true
evaluate(features_polar)
# + [markdown] deletable=true editable=true
# ### features_polar_norm
# + deletable=true editable=true
evaluate(features_polar_norm)
# + [markdown] deletable=true editable=true
# ### features_delta_polar_norm
# + deletable=true editable=true
evaluate(features_delta_polar_norm)
# + [markdown] deletable=true editable=true
# ### features_polar_scaled
# + deletable=true editable=true
evaluate(features_polar_scaled)
# + [markdown] deletable=true editable=true
# ### features_delta_polar_scaled
# + deletable=true editable=true
evaluate(features_delta_polar_scaled)
# + [markdown] deletable=true editable=true
# ### features_polar_norm + features_delta_polar_norm
# + deletable=true editable=true
evaluate(features_polar_norm + features_delta_polar_norm)
# + [markdown] deletable=true editable=true
# ### features_custom (features_polar_scaled + features_delta_polar_scaled)
# + deletable=true editable=true
evaluate(features_polar_scaled + features_delta_polar_scaled)
# + deletable=true editable=true
# + [markdown] deletable=true editable=true
# ### (features_custom, SelectorCV)
# + deletable=true editable=true
models = train_all_words(features_custom, SelectorCV)
test_set = asl.build_test(features_custom)
probabilities, guesses = recognize(models, test_set)
show_errors(guesses, test_set)
# + [markdown] deletable=true editable=true
# ### (features_polar_norm + features_delta_polar_norm, SelectorBIC)
# + deletable=true editable=true
models = train_all_words(features_polar_norm + features_delta_polar_norm, SelectorBIC)
test_set = asl.build_test(features_polar_norm + features_delta_polar_norm)
probabilities, guesses = recognize(models, test_set)
show_errors(guesses, test_set)
# + [markdown] deletable=true editable=true
# ### (features_custom, SelectorBIC)
# + deletable=true editable=true
models = train_all_words(features_custom, SelectorBIC)
test_set = asl.build_test(features_custom)
probabilities, guesses = recognize(models, test_set)
show_errors(guesses, test_set)
# + [markdown] deletable=true editable=true
# **Question 3:** Summarize the error results from three combinations of features and model selectors. What was the "best" combination and why? What additional information might we use to improve our WER? For more insight on improving WER, take a look at the introduction to Part 4.
#
# **Answer 3:**
# + [markdown] deletable=true editable=true
# <table>
# <tr>
# <th><center>Feature</center></th><th><center>CV</center></th><th><center>BIC</center></th>
# <th><center>DIC</center></th>
# </tr>
# <tr>
# <td>features_norm</td><td>0.6235</td><td>0.6123</td><td>0.6235</td>
# </tr>
# <tr>
# <td>features_delta</td><td>0.6292</td><td>0.6179</td><td>0.6573</td>
# </tr>
# <tr>
# <td>features_polar</td><td>0.5786</td><td>0.5393</td><td>0.5449</td>
# </tr>
# <tr>
# <td>features_polar_norm</td><td>0.6123</td><td>0.5280</td><td>0.5280</td>
# </tr>
# <tr>
# <td>features_delta_polar_norm</td><td>0.5674</td><td>0.5393</td><td>0.6292</td>
# </tr>
# <tr>
# <td>features_polar_norm + features_delta_polar_norm</td>
# <td><font color="red">0.4943</font></td>
# <td><font color="red">0.4382</font></td>
# <td><font color="red">0.4606</font></td>
# </tr>
# <tr>
# <td>features_polar_scaled</td>
# <td><font color="red">0.4831</td></td>
# <td>0.5393</td>
# <td><font color="red">0.4719</td></td>
# </tr>
# <tr>
# <td>features_delta_polar_scaled</td><td>0.6067</td><td>0.6123</td><td>0.6067</td>
# </tr>
# <tr>
# <td>features_polar_scaled + features_delta_polar_scaled</td>
# <td><font color="red">0.4494</font></td>
# <td><font color="red">0.4662</font></td>
# <td><font color="red">0.4382</font></td>
# </tr>
# </table>
# + [markdown] deletable=true editable=true
# From the table above, it can be clearly seen that the normalized/scaled polar coordinates and its delta features give WER of lower than 0.5 in all model selectors which are better than other features. *features_polar_norm + features_delta_polar_norm* and *features_polar_scaled + features_delta_polar_scaled* both give the best WER at 0.4382 using BIC and DIC respectively. *features_polar_scaled* alone also shows high accuracy with a WER under 0.5 using CV and DIC. This indicates that the combination of normalized/scaled polar and its delta features are good discriminators in ASL classification.
#
# Moreover, the choice of data preprocessing also plays an important role. In this experiment, Z-score standardization and Min-Max scaling are examined. *features_polar_norm* and *features_polar_scaled* are similar in feature but applied different normalization techniques. In this case, Min-Max scaling works better using CV and DIC. In contrast, WERs of *features_delta_polar_norm* and *features_delta_polar_scaled* show Z-score standardization works better except using DIC. In machine learning, normalizing numerical data is considered indispensable especially when input features are in different scale. It ensures that features with much higher values don't dominate ones with much small values and helps machine learning algorithms converge faster as well.
#
# As seen in the table, the best WER is *0.4382* which is achieved by using *features_polar_scaled + features_delta_polar_scaled* and DIC, and *features_polar_norm + features_delta_polar_norm* and BIC. To further improve the accuracy of the model, more sophisticated approches are required. One approach is to take advantage of the language structure for example, rather than training an individual word and recognizing it separately, one can train words that often co-occur together and recognize them at once. Another approach is refered to as n-gram models. It works by recording statistics of co-occuring n words in huge corpus and using these statistics to help bias our recognition based on the expected distribution of the co-occurence of words.
# + [markdown] deletable=true editable=true
# <a id='part3_test'></a>
# ### Recognizer Unit Tests
# Run the following unit tests as a sanity check on the defined recognizer. The test simply looks for some valid values but is not exhaustive. However, the project should not be submitted if these tests don't pass.
# + deletable=true editable=true
from asl_test_recognizer import TestRecognize
suite = unittest.TestLoader().loadTestsFromModule(TestRecognize())
unittest.TextTestRunner().run(suite)
# + [markdown] deletable=true editable=true
# <a id='part4_info'></a>
# ## PART 4: (OPTIONAL) Improve the WER with Language Models
# We've squeezed just about as much as we can out of the model and still only get about 50% of the words right! Surely we can do better than that. Probability to the rescue again in the form of [statistical language models (SLM)](https://en.wikipedia.org/wiki/Language_model). The basic idea is that each word has some probability of occurrence within the set, and some probability that it is adjacent to specific other words. We can use that additional information to make better choices.
#
# ##### Additional reading and resources
# - [Introduction to N-grams (Stanford Jurafsky slides)](https://web.stanford.edu/class/cs124/lec/languagemodeling.pdf)
# - [Speech Recognition Techniques for a Sign Language Recognition System, <NAME> et al](https://www-i6.informatik.rwth-aachen.de/publications/download/154/Dreuw--2007.pdf) see the improved results of applying LM on *this* data!
# - [SLM data for *this* ASL dataset](ftp://wasserstoff.informatik.rwth-aachen.de/pub/rwth-boston-104/lm/)
#
# ##### Optional challenge
# The recognizer you implemented in Part 3 is equivalent to a "0-gram" SLM. Improve the WER with the SLM data provided with the data set in the link above using "1-gram", "2-gram", and/or "3-gram" statistics. The `probabilities` data you've already calculated will be useful and can be turned into a pandas DataFrame if desired (see next cell).
# Good luck! Share your results with the class!
# + deletable=true editable=true
# create a DataFrame of log likelihoods for the test word items
df_probs = pd.DataFrame(data=probabilities)
df_probs.head()
|
asl_recognizer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="gO2BchskQWoH"
# # Домашнее задание 3.
#
# `Keras` и сверточные нейронные сети.
# + [markdown] id="r_L58Kyas0Sl" colab_type="text"
# Задание выполнил(а): Подчезерцев Алексей
# + id="YiHigtNQ2LNu" colab_type="code" colab={}
RANDOM_SEED = 42
# + colab_type="code" id="WmIuIaLEATMn" outputId="8d2e1848-dbef-4722-f340-4fa3971f6caa" executionInfo={"status": "ok", "timestamp": 1572685417626, "user_tz": -180, "elapsed": 3253, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "<KEY>", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 114}
import tensorflow as tf
import keras
from keras import backend as K
# %matplotlib inline
import matplotlib.pyplot as plt
print(tf.__version__)
print(keras.__version__)
# + colab_type="code" id="efsrp4vQfls5" colab={}
def reset_tf_session():
curr_session = tf.get_default_session()
if curr_session is not None:
curr_session.close()
K.clear_session()
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
s = tf.InteractiveSession(config=config)
K.set_session(s)
return s
# + [markdown] colab_type="text" id="HE_SpMQMQm8Y"
# ## Задание 1 — инициализация весов CNN (3 балла).
#
# В этом задании нужно будет исследовать, как выбор функции инициализации весов влияет на обучение CNN.
#
# + [markdown] colab_type="text" id="oIoAOXkJSwbs"
# Продолжим работать с датасетом CIFAR-10.
# + colab_type="code" id="IsuA4kiHA4ff" outputId="23e6bd4f-5077-46bc-c27a-ae3b4b8671bd" executionInfo={"status": "ok", "timestamp": 1572685427287, "user_tz": -180, "elapsed": 12881, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mBbUw_CVz8K3RIunXwSoj-hNZ6f2buYD0JYAcB_=s64", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 85}
from keras.datasets import cifar10
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
NUM_CLASSES = 10
cifar10_classes = ["airplane", "automobile", "bird", "cat", "deer",
"dog", "frog", "horse", "ship", "truck"]
print("Train samples:", x_train.shape, y_train.shape)
print("Test samples:", x_test.shape, y_test.shape)
# нормализуем входные данные
x_train = x_train / 255 - 0.5
x_test = x_test / 255 - 0.5
y_train = keras.utils.to_categorical(y_train, 10)
y_test = keras.utils.to_categorical(y_test, 10)
# + colab_type="code" id="xNl2e8LeftcC" colab={}
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Activation, Dropout
from keras.layers.advanced_activations import LeakyReLU
from keras.models import load_model
# + [markdown] colab_type="text" id="f2vQIUE3UeiE"
# Определим функцию `fit_model` с архитектурой архитектура CNN.
#
# Метод `model.fit` возвращает объект класса `keras.callbacks.History()` — это колбэк, который автоматически применяется ко всем моделям и логирует много чего полезного. В частности логируются значения функции потерь на каждой итерации.
# + [markdown] colab_type="text" id="dDslR6vNZry8"
# **Задание 1.1** (0.5 балла) Добавьте в архитектуру модели инициализацию весов для тех слоев, где она необходима.
#
# + colab_type="code" id="2_Lu7SO3CMid" colab={}
def fit_model(initializer='glorot_normal'):
s = reset_tf_session()
INIT_LR = 5e-3
BATCH_SIZE = 32
EPOCHS = 10
def lr_scheduler(epoch):
return INIT_LR * 0.9 ** epoch
### YOUR CODE HERE
# kernel_initializer=initializer для тех слоев, которым нужна инициализация весов
model = Sequential()
model.add(Conv2D(filters=16, padding='same', kernel_size=(3,3), input_shape=(32,32,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Conv2D(filters=64, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(MaxPooling2D(pool_size=(2,2), padding='same'))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(40, kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Dropout(0.5))
model.add(Dense(10, kernel_initializer=initializer))
model.add(Activation("softmax"))
model.compile(
loss='categorical_crossentropy',
optimizer=keras.optimizers.adamax(lr=INIT_LR),
metrics=['accuracy']
)
history = model.fit(
x_train, y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[keras.callbacks.LearningRateScheduler(lr_scheduler)],
shuffle=True,
verbose=0,
initial_epoch=0
)
# Возвращаем объект класса keras.callbacks.History
return history
# + [markdown] colab_type="text" id="bYkZkghfT4uN"
# **Задание 1.2** (1.5 балла). Обучите модель с разными [функциями инициализации](https://keras.io/initializers/) весов:
# * `Zeros` — веса инициализируются нулями
# * `Constant=0.05` — веса инициализируются константой 0.05
# * `RandomUniform` — веса генерируются равномерно из отрезка [-0.05, 0.05]
# * `glorot_normal` — Xavier initializer из лекций
# * `lecun_uniform`
#
# Добавьте в список `losses` значения функции потерь для каждой функции инициализации, их можно достать из `History`
#
#
# + id="kPBPFSWXyT_u" colab_type="code" outputId="47d00240-3783-4730-9d84-360e9742aaec" executionInfo={"status": "ok", "timestamp": 1572636939139, "user_tz": -180, "elapsed": 924102, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mBbUw_CVz8K3RIunXwSoj-hNZ6f2buYD0JYAcB_=s64", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 541}
losses = []
for initializer in [keras.initializers.Zeros(),
keras.initializers.Constant(value=0.05),
keras.initializers.RandomUniform(minval=-0.05, maxval=0.05, seed=RANDOM_SEED),
keras.initializers.glorot_normal(seed=RANDOM_SEED),
keras.initializers.lecun_uniform(seed=RANDOM_SEED),
]:
history = fit_model(initializer)
losses.append(history.history['loss'])
# + [markdown] colab_type="text" id="wsk8bCEPcOav"
#
# **Задание 1.3** (1 балла). Постройте графики зависимости функций потерь от номера итерации, подпишите их. Прокомментируйте результат.
# + colab_type="code" id="3yqBZIYEAPWZ" outputId="b3340eb4-527c-41dc-fdb6-58bd8f16d16d" executionInfo={"status": "ok", "timestamp": 1572636941086, "user_tz": -180, "elapsed": 1773, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mBbUw_CVz8K3RIunXwSoj-hNZ6f2buYD0JYAcB_=s64", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 458}
labels = ["Zero", "Constant", "RandomUniform", "Glorot normal", "Lecun"]
plt.figure(figsize=[16, 7])
for i,v in enumerate(labels):
plt.plot(losses[i], label=f"{v} init")
plt.title('Зависимость функции потерь от номера итерации и типа инициализации')
plt.legend(loc='best')
plt.xlabel("# итерации")
plt.ylabel("Функция потерь")
plt.show()
# + [markdown] id="XUo1JnPI_T0W" colab_type="text"
# Инициализация 0 не позволяет обучаться слою (производная в точке зануляется).
#
# Другие же показали уменьшение функции потерь при увеличении номера итерации.
# При этом чем более математически обоснован алгоритм, тем меньше потери.
#
# Случайная инициализация весов себя показала заметно лучше, чем с одинаковыми значениями.
# Даже если параметры имеют одинаковые значения, они будут обучаться по-разному (т.к. веса их разные), что приведет к более быстрому и качественному решению.
#
# Glorot normal и Lecun дали почти одинаковые результаты, но lecun немного лучше.
# + [markdown] colab_type="text" id="nellCcusBAZ8"
# ## Задание 2 — CNN для CIFAR-10 с сохранением весов модели (7 баллов)
#
# В этом задании мы модифицируем нейросеть с семинара, чтобы она достигала большего значения `accuracy` и научимся сохранять веса модели в файл во время обучения. Можно использовать только те же слои, которые использовались на семинаре: `Conv2D, MaxPooling2D, LeakyReLU, Dropout, Flatten, Dense`.
# + [markdown] colab_type="text" id="xuVF3c2qJwyx"
# **Задание 2.1** (4 балла). Подберите архитектуру модели так, чтобы значение `accuracy` на тестовой выборке было не менее 85.
# + colab_type="code" id="syKDJPUdCtoI" colab={}
def make_model():
model = Sequential()
initializer = keras.initializers.lecun_uniform(seed=RANDOM_SEED)
model.add(Conv2D(filters=64, padding='same', kernel_size=(3,3), input_shape=(32,32,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Conv2D(filters=64, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(MaxPooling2D(pool_size=(2,2), padding='same'))
model.add(Dropout(0.3))
model.add(Conv2D(filters=128, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Conv2D(filters=128, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(MaxPooling2D(pool_size=(2,2), padding='same'))
model.add(Dropout(0.3))
model.add(Conv2D(filters=256, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Conv2D(filters=256, padding='same', kernel_size=(3,3), kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(MaxPooling2D(pool_size=(2,2), padding='same'))
model.add(Dropout(0.3))
model.add(Flatten())
model.add(Dense(256, kernel_initializer=initializer))
model.add(LeakyReLU(0.1))
model.add(Dropout(0.5))
model.add(Dense(NUM_CLASSES, kernel_initializer=initializer))
model.add(Activation("softmax"))
return model
# + colab_type="code" id="MoZifjkgFdcg" outputId="624b85ef-a3dc-400a-e0c6-e2fcf9011452" executionInfo={"status": "ok", "timestamp": 1572695264612, "user_tz": -180, "elapsed": 1075, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mBbUw_CVz8K3RIunXwSoj-hNZ6f2buYD0JYAcB_=s64", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 969}
s = reset_tf_session()
model = make_model()
model.summary()
# + [markdown] colab_type="text" id="JJLpZQhJGBqL"
# **Задание 2.2** (2 балла). Реализуйте колбэк, который сохраняет модель в `.hdf5` файл и печатает имя файла, в который была сохранена модель. Используйте функцию `model_save`. Строка с именем файла имеет вид `<name>_{0:02d}.hdf5`, отформатируйте ее так, чтобы в имени строки фигурировал номер эпохи.
# + colab_type="code" id="xYjUeuDXGBII" colab={}
class ModelSaveCallback(keras.callbacks.Callback):
def __init__(self, file_name):
super(ModelSaveCallback, self).__init__()
self.file_name = file_name
def on_epoch_end(self, epoch, logs=None):
filename = self.file_name.format(epoch)
keras.models.save_model(self.model, filename)
print(f"Model save into {filename}")
# + [markdown] colab_type="text" id="Svrwkh8ALpHa"
# **Задание 2.3** (1 балл). Реализуйте функцию, которая с помощью `load_model` будет загружать модель из файла.
# + colab_type="code" id="fVD0P5V7M00C" colab={}
def load_from_file(model_filename, last_epoch):
return keras.models.load_model(model_filename.format(last_epoch))
# + colab_type="code" id="zOLb6flQFjCw" outputId="f6eb1ee3-b988-471d-94e4-90b51573b149" executionInfo={"status": "ok", "timestamp": 1572696386233, "user_tz": -180, "elapsed": 1118539, "user": {"displayName": "\u0410\u043b\u0435\u043a\u0441\u0435\u0439 \u041f\u043e\u0434\u0447\u0435\u0437\u0435\u0440\u0446\u0435\u0432", "photoUrl": "https://lh3.googleusercontent.com/a-/AAuE7mBbUw_CVz8K3RIunXwSoj-hNZ6f2buYD0JYAcB_=s64", "userId": "04087359208169148337"}} colab={"base_uri": "https://localhost:8080/", "height": 1000}
INIT_LR = 5e-3
BATCH_SIZE = 32
EPOCHS = 20
model_filename = 'weights_{0:02d}.hdf5'
s = reset_tf_session()
model = make_model()
model.compile(
loss='categorical_crossentropy',
optimizer=keras.optimizers.adamax(lr=INIT_LR),
metrics=['accuracy']
)
def lr_scheduler(epoch):
return INIT_LR * 0.9 ** epoch
# в случае, если обучение было прервано, можно загрузить модель из файла,
# соответствующего последней эпохе, за которую есть сохраненные веса
# model = load_from_file(model_filename, 4)
history = model.fit(
x_train, y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=[keras.callbacks.LearningRateScheduler(lr_scheduler),
# не забудьте передать сюда ModelSaveCallback
ModelSaveCallback(model_filename)
],
validation_data=(x_test, y_test),
shuffle=True,
verbose=1,
initial_epoch=0
)
# + [markdown] id="MSSlpNhFDLO2" colab_type="text"
# Необходимый результат был достигнут на 11 эпохе, далее модель продолжала обучаться и улучшать качество.
#
# По данным экспериментов, предшествующих получению данного результата, хорошо себя показала группа слоев из двух Conv2D с LeakyReLU после каждого из них с последующим MaxPooling2D и Dropout. Две таких группы было мало для получения хорошего качества, а четыре - уже много. Наибольшее влияние производил параметр количества фильтров в слое Conv2D.
|
introduction_to_deep_learning/hw_03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/Ciiku-Kihara/SANITATION-IMPROVEMENT-PROJECT/blob/main/THE_SANITATION_INFRASTRUCTURE_IMPROVEMENT_PROJECT_notebook.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="Lp86qxr8RMnj"
# ## **1. LOADING DATASET**
# + id="akNIwrsMRfCY"
#import the Numpy library
import pandas as pd
#import pandas library
import numpy as np
#import matplotlib
import matplotlib.pyplot as plt
# + id="oLaUicmdRibG" colab={"base_uri": "https://localhost:8080/", "height": 551} outputId="0a2e8028-2f7f-4362-d468-839e172f84b8"
#Loading dataset
#preview first five entries to ensure the table has been loaded correctly
#
sanitation_by_district = pd.read_csv('sanitation_by_district.csv')
sanitation_by_district.head(5)
# + [markdown] id="Gd3QWSqsdXSh"
# ##**2. DATA UNDERSTANDING**
# + id="yFNJf60RSyPk" colab={"base_uri": "https://localhost:8080/"} outputId="7406c637-4db1-4a47-e011-84db7ada600e"
#Preview info on dataset
#
sanitation_by_district.info()
# + id="8_CsDk-4S15C" colab={"base_uri": "https://localhost:8080/"} outputId="0b1ed788-9b4e-4671-b1fa-c6792c37563f"
#View the columns in our dataset
#
sanitation_by_district.columns
# + colab={"base_uri": "https://localhost:8080/"} id="VbB6cxyOS-dY" outputId="f80ff0cb-a715-4084-f8ef-fcbb062fd8c9"
#View the dimensions of dataset
#i.e how many columns and rows are in our dataset
#
sanitation_by_district.shape
# + id="d9CyJsA9TCvN" colab={"base_uri": "https://localhost:8080/", "height": 304} outputId="bab26965-7fea-4b84-a602-e7b177bbef1d"
#Preview general statistics about data
#
sanitation_by_district.describe()
# + [markdown] id="rkysu_oPTJ0b"
# ##**3. DATA PREPARATION.**
# + [markdown] id="Xd2kSQ-fvygM"
# #**3.1. Data Cleaning.**
# + [markdown] id="bGor4N-2v8F6"
# # 3.1a) Validity of data
# + id="Q1P-O9CbTKp1" colab={"base_uri": "https://localhost:8080/", "height": 266} outputId="54ead252-0b9e-451c-9616-de2bdfdac007"
#Dropping irrelevant columns
#
sanitation_by_district.drop(['MTEF', 'MTP', 'Longtitude', 'Latitude', 'Location', 'OBJECTID','Census_Table'], axis = 1, inplace = True)
sanitation_by_district.head(5)
# + id="JXkVClFHUaDs" colab={"base_uri": "https://localhost:8080/", "height": 447} outputId="5242af31-9577-47da-9f64-4a9c89da31a4"
#Preview the first 10 rows the remaining columns in our data set
#
sanitation_by_district.head(10)
# + id="-NVzcr6nVAb2" colab={"base_uri": "https://localhost:8080/", "height": 266} outputId="c23bc330-7c1d-4869-c4e6-86ffe39f993f"
#resetting index
#
sanitation_by_district.reset_index(drop=True)
sanitation_by_district.head(5)
# + id="YXv6YZAEVjH3" colab={"base_uri": "https://localhost:8080/", "height": 506} outputId="a77b9061-7694-4b8b-832f-4a8a3a5fe362"
#clearing any white space in the columns data
#
sanitation_by_district.columns = sanitation_by_district.columns.str.strip()
sanitation_by_district
# + [markdown] id="IHKvkRrzWuNM"
# # 3.1b) Completeness of data.
# + colab={"base_uri": "https://localhost:8080/"} id="bhk6dXnfWvH8" outputId="81d2c51c-540a-455b-d54d-47e0a6d8fe2b"
#checking for the existence of any null values
#
sanitation_by_district.isnull().sum()
# + id="mGFoqv-xbOB7" colab={"base_uri": "https://localhost:8080/", "height": 522} outputId="530e0e1e-7f37-4455-fab4-82851cd22e8a"
#Dropping the rows with null values
#
sanitation_by_district_1 = sanitation_by_district.dropna()
sanitation_by_district_1
# The entire rows were dropped because majority of the entries in those rows
# were null values or zeros
# + id="i8bwHNJydB3J"
#resetting index
#
sanitation_by_district_1.reset_index(inplace=True)
# + id="VfI9tCUNdR0k" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="f365767b-680a-4329-8104-42b92881e7fd"
#previewing dataset
#
sanitation_by_district_1.head(5)
# + colab={"base_uri": "https://localhost:8080/", "height": 522} id="QqCfy9u8SQat" outputId="b44843d3-7d9d-433a-bc7f-960bbe12a99e"
#dropping irrelevant column
#
sanitation_by_district_1.pop('index')
sanitation_by_district_1
# + [markdown] id="k8gkm6jAdkyG"
# # 3.1c) Consistency of data.
# + colab={"base_uri": "https://localhost:8080/"} id="CyI-YeTUdlgd" outputId="3681de09-eb5a-413f-872a-9b4d459e04c9"
#checking if there is any existence of duplicates in the data file
#And dropping if any exists
#
sanitation_by_district_1.duplicated().values.any()
# + id="8L0pWsefeXV0"
# There are no duplicates in the file
# + [markdown] id="akYqSDf0eg9J"
# # 3.1d) Uniformity of data.
# + id="xx03R6cqej1B" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="4389e0e6-3df6-49bd-c7e6-076cfc8b3baa"
#fix column names and turn them to lower case
#remove the white space in between the names
#
sanitation_by_district_1.columns = sanitation_by_district_1.columns.str.replace(' ','_').str.lower()
sanitation_by_district_1=sanitation_by_district_1.rename(columns={'_district':'district'})
sanitation_by_district_1.head(5)
# + [markdown] id="jeR3V9gNe9tI"
# ##**3.2.IMPORTING CLEANED DATASET.**
# + id="34litWK9fHkp" colab={"base_uri": "https://localhost:8080/", "height": 282} outputId="edb37972-68fb-4943-95a4-abc5a81e445e"
#
sanitation_by_district_1.to_csv('sanitation_by_district_1')
sanitation_by_district_1.head()
# + id="1EmxtaJGfdlP" colab={"base_uri": "https://localhost:8080/", "height": 522} outputId="83bd0fe8-b949-475e-ea19-d419100ad8bd"
#Loading the new dataset and resetting the index values
#
Sanitation_in_Kenya = pd.read_csv('sanitation_by_district_1')
Sanitation_in_Kenya.head(5)
Sanitation_in_Kenya.reset_index(inplace=True)
Sanitation_in_Kenya.head(5)
Sanitation_in_Kenya.drop(['index','Unnamed: 0'], axis = 1, inplace = True)
Sanitation_in_Kenya
# + [markdown] id="KRS5jvm--mPZ"
# ## **4. ANALYSIS**
# + [markdown] id="RY2fDUKIfOM0"
# #4a) Find the least and most popular form of sanitation in the country
# + id="O5MTVp8j40qJ" colab={"base_uri": "https://localhost:8080/"} outputId="fe3a918c-e601-4923-c4cf-86de7f379924"
#Finding the most popular and least popular form of Sanitation across the country
#First combining the different columns on sanitation categories into one list
Household_Sanitation_Categories = ["no_of_households_with_main_sewer", "no_of_households_with_septic_tank",
"no_of_households_with_cess_pool", "no_of_households_with_vip_pit_latrine",
"no_of_households_with_pit_latrine_covered/uncovered",
"no_of_households_with_bucket", "no_of_households_with_bush",
"no_of_households_with_other"]
#Determining the popularity of the different forms of sanitation in descending order
Popular = Sanitation_in_Kenya[Household_Sanitation_Categories].sum().sort_values(ascending=False)
Popular
#From the order we can determine the most and least popular form of sanitation
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="2GDjPWIrHbH7" outputId="6234e2a4-cc71-44ea-b07a-25f68b9cc3d1"
## A bar graph to show the differences in least and most popular forms of sanitation
# in the country
Popular = Popular.to_frame().reset_index()
Popular.columns = ['Form of Sanitation', 'Number of households']
Popular
x = Popular['Form of Sanitation']
y = Popular['Number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.barh(x,y)
plt.xlabel("Form of Sanitation")
plt.ylabel("Number of households")
plt.title("Number of Households per Form of Sanitation")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="3LWsZVunIZVe" outputId="30a6b539-b6f7-4b47-b9a8-0d9c1f672010"
# Different forms of sanitation in the country ordered by percentage
(Sanitation_in_Kenya[Household_Sanitation_Categories].sum()/Sanitation_in_Kenya.households.sum()*100).sort_values(ascending=False)
# + colab={"base_uri": "https://localhost:8080/"} id="QJVb2CDFOnZe" outputId="5b236276-0492-4797-e782-a1fbeef956a0"
# Determining total number of households in urban areas
urban = Sanitation_in_Kenya.loc[Sanitation_in_Kenya['rural/urban'] == 'Urban' ]
urban
total_urban = urban['households'].sum()
total_urban
# + colab={"base_uri": "https://localhost:8080/"} id="5rqnzqhkPTXR" outputId="a585e777-15f7-4401-f959-0699ef09053a"
# Determining total number of households in rural areas
rural = Sanitation_in_Kenya.loc[Sanitation_in_Kenya['rural/urban'] == 'Rural' ]
rural
total_rural = rural['households'].sum()
total_rural
# + [markdown] id="-coDZQzAfltP"
# # 4b) Find the least and most common form of sanitation in urban areas
# + colab={"base_uri": "https://localhost:8080/"} id="rc9YkUOkPcGq" outputId="babfb7cf-97da-434f-ddca-b6669037482d"
# Different forms of sanitation in urban areas ordered by percentage
urban_category_proportion = ((urban[Household_Sanitation_Categories].sum())/total_urban * 100).sort_values(ascending = False)
urban_category_proportion
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="t7ZFEz-BpXkC" outputId="d0151746-fe41-4e4c-fa08-4c63a66356bc"
#Creating a bar graph of the different sanitation category percentanges in urban areas
urban = urban_category_proportion.to_frame().reset_index()
urban.columns = ['Form of Sanitation', 'Percentage']
urban
x = urban['Form of Sanitation']
y = urban['Percentage']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.barh(x,y)
plt.xlabel("Percentage of total households")
plt.ylabel("Form of sanitation")
plt.title("Number of Households per Form of Sanitation in urban areas")
plt.show()
# + [markdown] id="fXbGaMm5f_gR"
# # 4c) Find the least and most common form of sanitation in rural areas
# + colab={"base_uri": "https://localhost:8080/"} id="dLY1vW14o-dL" outputId="da7ce6d1-ec3a-4113-e948-6029348cefb8"
# Different forms of sanitation in rural areas ordered by percentage
rural_category_proportion = ((rural[Household_Sanitation_Categories].sum())/total_rural * 100).sort_values(ascending = False)
rural_category_proportion
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="XV-bQEXgumfL" outputId="bd8859eb-65dc-4e09-94e7-7aec890ae655"
#Creating a bar graph of the different sanitation category percentanges in rural areas
#Creating a bar graph of the different sanitation category percentanges in urban areas
rural = rural_category_proportion.to_frame().reset_index()
rural.columns = ['Form of Sanitation', 'Percentage']
rural
x = rural['Form of Sanitation']
y = rural['Percentage']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.barh(x,y)
plt.xlabel("Percentage of total households")
plt.ylabel("Form of sanitation")
plt.title("Number of Households per Form of Sanitation in rural areas")
plt.show()
# + [markdown] id="LiGPJSN8gLlV"
# # 4d) Determining the most and least popular form of sanitation per county
#
# + colab={"base_uri": "https://localhost:8080/", "height": 264} id="q70uNYfWBUm3" outputId="6b1682a2-3964-44fc-a15e-34d996255b23"
#Determining the most and least popular form of sanitation per county
#First creating a dataframe to reflect the county and different sanitation categories
Household_Sanitation_Categories_county = Sanitation_in_Kenya[['county',"no_of_households_with_main_sewer", "no_of_households_with_septic_tank",
"no_of_households_with_cess_pool", "no_of_households_with_vip_pit_latrine",
"no_of_households_with_pit_latrine_covered/uncovered",
"no_of_households_with_bucket", "no_of_households_with_bush",
"no_of_households_with_other"]]
Household_Sanitation_Categories_county
#Finding the sum of each category per county(grouped by county)
Sum = Household_Sanitation_Categories_county.groupby('county').sum()
Sum.head()
#The most popular and least popular forms of sanitation per county determined in the next cells
# + colab={"base_uri": "https://localhost:8080/"} id="5geliEFfMdPZ" outputId="01f0266a-98c9-429d-affd-3a8b0ef773b4"
#Finding the least popular form of sanitation per county
Sum.idxmin(axis=1)
# + colab={"base_uri": "https://localhost:8080/"} id="MNGYns4hM6LI" outputId="2bec78f7-121c-47f7-eb83-b9209a5e9e73"
#Finding the most popular form of sanitation per county
Sum.idxmax(axis=1)
# + [markdown] id="LL4LTpWxgaeI"
# # 4e) Determining districts and counties with high number of households using bushes
# + id="ajWNX-YoFx3T" colab={"base_uri": "https://localhost:8080/", "height": 347} outputId="087fc4a2-83df-4ed9-eeb7-dcc49ae8386b"
#Finding the top ten districts with highest number of households using bushes
Top_ten_districts_bush = Sanitation_in_Kenya[['district','no_of_households_with_bush']].sort_values('no_of_households_with_bush',ascending=False).head(10)
Top_ten_districts_bush
# + id="qpCc7T0gPhRv" colab={"base_uri": "https://localhost:8080/"} outputId="8f794dd2-88ad-41ae-87d1-82cc2ba4492a"
#Finding the top 10 counties with the highest number of households using bushes
Top_ten_county_bush = Sanitation_in_Kenya.groupby(['county']).no_of_households_with_bush.sum().sort_values(ascending=False).head(10)
Top_ten_county_bush
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="ckN-X1JZlrhz" outputId="9a6447a0-3258-4344-c01d-87ece07fd55b"
# Plotting a graph for top 10 counties with households using bushes
bush = Top_ten_county_bush.to_frame().reset_index()
bush
bush.columns = ['county', 'number of households']
bush
x = bush['county']
y = bush['number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.bar(x, y, color ='blue',width = 0.4)
plt.xlabel("Counties")
plt.ylabel("Number of households")
plt.title("Top 10 counties using bushes")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="LOusVDYEGiwM" outputId="adb44651-3e06-411b-ddcf-2b8add54aa96"
#Finding whether the top ten districts with highest number of households are in
#the top ten counties with largest number of households using bushes
#First finding which counties the districts belong to and output displayed below
for ind in Top_ten_districts_bush.index:
A = Sanitation_in_Kenya['district'][ind]
B = Sanitation_in_Kenya['county'][ind]
print(A,'-',B)
#Checking whether these counties are part of the ones displayed in top 10
#as the counties with highest number of households using bushes and we find it is the case as displayed below as 'True'
if B in Top_ten_county_bush:
print("True")
else:
print("False")
# + [markdown] id="_2Uzvj2Jg2Fp"
# # 4f) Determining the districts and counties with high number of households using buckets
# + colab={"base_uri": "https://localhost:8080/", "height": 347} id="2sISzqSWyZ_2" outputId="f62f495d-996b-4481-a000-1469cb91f8cc"
#Determine the top 10 districts with highest and number of households using buckets
Top_ten_districts_bucket = Sanitation_in_Kenya[['district','no_of_households_with_bucket']].sort_values('no_of_households_with_bucket',ascending=False).head(10)
Top_ten_districts_bucket
# + colab={"base_uri": "https://localhost:8080/"} id="3uYsQOzQy55v" outputId="f5a5931c-87f3-4617-ab27-3fd9c257f344"
#Finding the top 10 counties with the highest number of households using buckets
Top_ten_county_bucket = Sanitation_in_Kenya.groupby(['county']).no_of_households_with_bucket.sum().sort_values(ascending=False).head(10)
Top_ten_county_bucket
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="fkvHwqIRndy_" outputId="7e158c6f-4f17-4c50-8c54-dd3aca48e2c9"
# Plotting a graph for top 10 counties with households using buckets
bucket = Top_ten_county_bucket.to_frame().reset_index()
bucket
bucket.columns = ['county', 'number of households']
bucket
x = bucket['county']
y = bucket['number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.bar(x, y, color ='blue',width = 0.4)
plt.xlabel("Counties")
plt.ylabel("Number of households")
plt.title("Top 10 counties using buckets")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="DU0vWIr-kUvG" outputId="97252e83-81bb-45ef-81d6-61c49fddab46"
#Finding whether the top ten districts with highest number of households are in
#the top ten counties with largest number of households using buckets
#First finding which counties the districts belong to and output displayed below
for ind in Top_ten_districts_bucket.index:
A = Sanitation_in_Kenya['district'][ind]
B = Sanitation_in_Kenya['county'][ind]
print(A,'-',B)
#Checking whether these counties are part of the ones displayed in top 10
#as the counties with highest number of households using buckets and we find it is the case as displayed below as 'False'
if B in Top_ten_county_bucket:
print("True")
else:
print("False")
#Kirinyaga county is not part of the top ten counties with highest number of counties using bushes
#but one of its districts is in Top ten districts with highest number of households using buckets
# + [markdown] id="ExtBjZ3fhRtp"
# # 4g) Determining areas least and most connected to the main sewer
# + colab={"base_uri": "https://localhost:8080/"} id="rlEUiC9JsGjY" outputId="a2afdeb4-f63e-49ba-8a9e-72bc306fd751"
#Finding counties with highest and lowest number of households connected to main sewer
Sanitation_in_Kenya.groupby(['county']).no_of_households_with_main_sewer.sum().sort_values(ascending=False)
# + colab={"base_uri": "https://localhost:8080/"} id="cEHWqieotOOb" outputId="f79dc5c0-e414-4be1-bbdc-01c824d95a38"
# Top ten counties connected to main sewer
country_sewer = Sanitation_in_Kenya.groupby(['county']).no_of_households_with_main_sewer.sum().sort_values(ascending=False).head(10)
country_sewer
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="TEHC76xRth9W" outputId="6259fbbb-9688-42c7-9e03-de2aa75a51df"
# Plotting a graph for top 10 counties with households connected to main sewer in the country
country_sewer = country_sewer.to_frame().reset_index()
country_sewer
country_sewer.columns = ['county', 'number of households']
country_sewer
x = country_sewer['county']
y = country_sewer['number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.bar(x, y, color ='blue',width = 0.4)
plt.xlabel("Counties")
plt.ylabel("Number of households")
plt.title("Top 10 counties connected to main sewer")
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 195} id="rl426u-SyIJI" outputId="c404fb4a-70c4-4e1c-d9ef-17349081aade"
#Finding districts in urban areas with highest number of households connected to main sewer
urban[['district','rural/urban','no_of_households_with_main_sewer']].sort_values('no_of_households_with_main_sewer',ascending=False).head()
# + colab={"base_uri": "https://localhost:8080/"} id="vdM9vFPdAMAg" outputId="b9cbc7af-b252-439b-c5a1-82514af8800f"
#Finding counties in urban areas with highest and lowest number of households connected to main sewer
urban.groupby('county').no_of_households_with_main_sewer.sum().sort_values(ascending=False)
# + colab={"base_uri": "https://localhost:8080/"} id="zFUJgzdhuxRC" outputId="023cbb80-3d7b-4fa7-d094-c2c4acf04721"
# Top 10 counties connected to sewers in urban areas
urban_sewer = urban.groupby('county').no_of_households_with_main_sewer.sum().sort_values(ascending=False).head(10)
urban_sewer
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="iTgSVTjewtcE" outputId="47c43617-4623-4c88-8422-b9b34c5ab8e6"
# Plotting a graph for top 10 counties with households connected to main sewer in urban areas
urban_sewer = urban_sewer.to_frame().reset_index()
urban_sewer
urban_sewer.columns = ['county', 'number of households']
urban_sewer
x = urban_sewer['county']
y = urban_sewer['number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.bar(x, y, color ='blue',width = 0.4)
plt.xlabel("Counties")
plt.ylabel("Number of households")
plt.title("Top 10 counties connected to main sewer in urban areas")
plt.show()
# + colab={"base_uri": "https://localhost:8080/"} id="PFLOpy2ax2Vo" outputId="1742534f-e0e2-4655-f9ae-fc0e6d1f6b9d"
# Determining percentage of urban households connected to the main sewers
(urban['no_of_households_with_main_sewer'].sum()/total_urban) * 100
# + colab={"base_uri": "https://localhost:8080/", "height": 195} id="lo_wZsHF0EID" outputId="860805b8-3737-421e-e85f-108516c86ab3"
#Finding districts in rural areas with highest number of households connected to main sewer
rural[['district','rural/urban','no_of_households_with_main_sewer']].sort_values('no_of_households_with_main_sewer',ascending=False).head()
# + colab={"base_uri": "https://localhost:8080/"} id="JldQEuz-0Kjp" outputId="8e3e5023-6aa0-40bc-bcd1-16d277a482a0"
#Finding counties in rural areas with highest and lowest number of households connected to main sewer
rural.groupby('county').no_of_households_with_main_sewer.sum().sort_values(ascending=False)
# + colab={"base_uri": "https://localhost:8080/"} id="Lr1JN1XyxfAM" outputId="19e367c7-544e-4438-d9b5-6ec57ee9ddfb"
# Top 10 counties with households connected to main sewer in rural areas
rural_sewer = rural.groupby('county').no_of_households_with_main_sewer.sum().sort_values(ascending=False).head(10)
rural_sewer
# + colab={"base_uri": "https://localhost:8080/", "height": 350} id="uw8HZvllx-sB" outputId="e7bff2eb-bd43-43ec-c49a-3ba8a6507cf8"
# Plotting a graph for top 10 counties with households connected to main sewer in urban areas
rural_sewer = rural_sewer.to_frame().reset_index()
rural_sewer
rural_sewer.columns = ['county', 'number of households']
rural_sewer
x = rural_sewer['county']
y = rural_sewer['number of households']
fig = plt.figure(figsize = (10, 5))
# creating the bar plot
plt.bar(x, y, color ='blue',width = 0.4)
plt.xlabel("Counties")
plt.ylabel("Number of households")
plt.title("Top 10 counties connected to main sewer in rural areas")
plt.show()
# + id="I_tj19TCezzL" colab={"base_uri": "https://localhost:8080/"} outputId="0f7a3720-206f-4a37-8fa0-f9fb312efc28"
#Determining percentage of rural households connected to the main sewers
(rural['no_of_households_with_main_sewer'].sum() / total_rural)*100
|
THE_SANITATION_INFRASTRUCTURE_IMPROVEMENT_PROJECT_notebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Fundamental Concepts
#
# **Gather Business Requirements**
#
# Before starting a data modelling effort the team needs to:
#
# 1. define objectives of the business based on KPIs, issues, decision making & analytics needs.
# 2. capture data behaviour from source system experts, including performing high-level data profiling
# **Dimensional Modelling Design Process**
#
# The four steps are:
#
# 1. Select the business process
# A business process is the operational activity performed by the organisation. They generate or capture performance metrics that translate to facts in a fact table. Most fact tables focus on the results of one business process.
#
# 2. Declare the grain
# The grain establishes exactly what a single row in a single fact table represents. This is selected before choosing dimensions or facts because every dimension or fact must be consistent with the grain. Atomic grain is the lowest level at which data is captured by a given business process.
#
# 3. Identify the dimensions
# Dimensions provide the descriptive (who, what where, when, why, how) context surrounding a business process event or step. These descriptive attributes are used to filter / slice & dice data. A dimension should be single-valued when joined with its associated fact table. They are the entry point to most business analysis, and hence drive greatly the user's BI experience.
#
# 4. Identify the facts
# Facts are used for measurements that result from the business process. Each fact row has a one-to-one relationship to a measurement event as described by the fact table's grain. Hence, a fact table corresponds to a physical, observable event, not the demands of a particular report. Within a fact table, only facts consistent with the declared grain are allowed.
#
# **Star Schemas and OLAP cubes**
#
# Star schemas are dimensional structures deployed in a RDBMS that consist of fact tables linked to associated dimension tables via primary / foreign key relationships. An online analytical processing (OLAP) cube is a dimensional structure implemented in a multi-dimensional database. It is equivalent to a relationsal star schema. An OLAP cube contains dimensional attributes and facts, but is accessed through languages with more analytic capabilities than SQL. OLAP cubes are part of these basic techniques because an OLAP cube is often the final step in the deployment of a Data Warehouse / Business Intelligence system, or may exist as an aggregate structure based on a more atomic relational star schema.
# **Grace Extensions to Dimensional Modelling**
#
# Dimensional models are resilient when data relationships change. All changes should be implemented such that no query needs to change, and the results of the queries don't change too.
#
# - **FACT** : Facts consistent with the grain of an existing fact table can be added by creating new columns
# - **DIMENSION** : Attributes can be added to an existing dimension table by creating new columns
# - **GRAIN**: The grain of a fact table can be made more atomic by adding attributes to the existing dimension table, and then restating the fact table at a lower grain, being careful to preserve the existing column names in the fact & dimension tables
|
notebooks/kimball/chap01-fundamental-concepts.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Q-Learning in the GridWorld environment
# Q-learning was an early RL breakthrough when it was developed by <NAME> for his [PhD thesis](http://www.cs.rhul.ac.uk/~chrisw/thesis.html) in 1989. It introduces incremental dynamic programming to control an MDP without knowing or modeling the transition and reward matrices that we used for value and policy iteration in the previous section. A convergence proof followed three years later by [Watkins and Dayan](http://www.gatsby.ucl.ac.uk/~dayan/papers/wd92.html).
#
# Q-learning directly optimizes the action-value function, q, to approximate q*. The learning proceeds off-policy, that is, the algorithm does not need to select actions based on the policy that's implied by the value function alone. However, convergence requires that all state-action pairs continue to be updated throughout the training process. A straightforward way to ensure this is by using an ε-greedy policy.
# The Q-learning algorithm keeps improving a state-action value function after random initialization for a given number of episodes. At each time step, it chooses an action based on an ε-greedy policy, and uses a learning rate, α, to update the value function, as follows:
# $$Q(S_t, A_t)\leftarrow Q(S_t, A_t) + \alpha\left[R_{t_1}+\gamma \max_a Q(S_{t+1},,a) − Q(S_t, A_t)\right]$$
# Note that the algorithm does not compute expected values because it does know the transition probabilities. It learns the Q function from the rewards produced by the ε-greedy policy and its current estimate of the value function for the next state.
#
# The use of the estimated value function to improve this estimate is called bootstrapping. The Q-learning algorithm is part of the TD learning algorithms. TD learning does not wait until receiving the final reward for an episode. Instead, it updates its estimates using the values of intermediate states that are closer to the final reward. In this case, the intermediate state is one time step ahead.
# The notebook demonstrates how to build a Q-learning agent using the 3 x 4 grid of states from the Dynamic Programmimg [example](01_gridworld_dynamic_programming.ipynb).
# ## Imports & Settings
# +
# %matplotlib inline
from pathlib import Path
from time import process_time
import numpy as np
import pandas as pd
from mdptoolbox import mdp
from itertools import product
import gym
# -
# ## Set up Gridworld
# We first create our small gridworld as in the Dynamic Programmimg [example](01_gridworld_dynamic_programming.ipynb).
# ### States, Actions and Rewards
grid_size = (3, 4)
blocked_cell = (1, 1)
baseline_reward = -0.02
absorbing_cells = {(0, 3): 1, (1, 3): -1}
actions = ['L', 'U', 'R', 'D']
num_actions = len(actions)
probs = [.1, .8, .1, 0]
to_1d = lambda x: np.ravel_multi_index(x, grid_size)
to_2d = lambda x: np.unravel_index(x, grid_size)
num_states = np.product(grid_size)
cells = list(np.ndindex(grid_size))
states = list(range(len(cells)))
cell_state = dict(zip(cells, states))
state_cell= dict(zip(states, cells))
absorbing_states = {to_1d(s):r for s, r in absorbing_cells.items()}
blocked_state = to_1d(blocked_cell)
state_rewards = np.full(num_states, baseline_reward)
state_rewards[blocked_state] = 0
for state, reward in absorbing_states.items():
state_rewards[state] = reward
action_outcomes = {}
for i, action in enumerate(actions):
probs_ = dict(zip([actions[j % 4] for j in range(i, num_actions + i)], probs))
action_outcomes[actions[(i + 1) % 4]] = probs_
action_outcomes
# ### Transition Matrix
def get_new_cell(state, move):
cell = to_2d(state)
if actions[move] == 'U':
return cell[0] - 1, cell[1]
elif actions[move] == 'D':
return cell[0] + 1, cell[1]
elif actions[move] == 'R':
return cell[0], cell[1] + 1
elif actions[move] == 'L':
return cell[0], cell[1] - 1
state_rewards
def update_transitions_and_rewards(state, action, outcome):
if state in absorbing_states.keys() or state == blocked_state:
transitions[action, state, state] = 1
else:
new_cell = get_new_cell(state, outcome)
p = action_outcomes[actions[action]][actions[outcome]]
if new_cell not in cells or new_cell == blocked_cell:
transitions[action, state, state] += p
rewards[action, state, state] = baseline_reward
else:
new_state= to_1d(new_cell)
transitions[action, state, new_state] = p
rewards[action, state, new_state] = state_rewards[new_state]
rewards = np.zeros(shape=(num_actions, num_states, num_states))
transitions = np.zeros((num_actions, num_states, num_states))
actions_ = list(range(num_actions))
for action, outcome, state in product(actions_, actions_, states):
update_transitions_and_rewards(state, action, outcome)
rewards.shape, transitions.shape
# ## Q-Learning
# We will train the agent for 2,500 episodes, use a learning rate of α= 0.1, and an ε=0.05 for the ε-greedy policy
max_episodes = 2500
alpha = .1
epsilon = .05
gamma = .99
# Then, we will randomly initialize the state-action value function as a NumPy array with the dimensions of [number of states and number of actions]:
Q = np.random.rand(num_states, num_actions)
skip_states = list(absorbing_states.keys())+[blocked_state]
Q[skip_states] = 0
# The algorithm generates 2,500 episodes that start at a random location and proceed according to the ε-greedy policy until termination, updating the value function according to the Q-learning rule:
start = process_time()
for episode in range(max_episodes):
state = np.random.choice([s for s in states if s not in skip_states])
while not state in absorbing_states.keys():
if np.random.rand() < epsilon:
action = np.random.choice(num_actions)
else:
action = np.argmax(Q[state])
next_state = np.random.choice(states, p=transitions[action, state])
reward = rewards[action, state, next_state]
Q[state, action] += alpha * (reward + gamma * np.max(Q[next_state])-Q[state, action])
state = next_state
process_time() - start
# The episodes take 0.6 seconds and converge to a value function fairly close to the result of the value iteration example from the previous section.
pd.DataFrame(np.argmax(Q, 1).reshape(grid_size)).replace(dict(enumerate(actions)))
pd.DataFrame(np.max(Q, 1).reshape(grid_size))
# ## PyMDPToolbox
# ### Q Learning
# +
start = process_time()
ql = mdp.QLearning(transitions=transitions,
reward=rewards,
discount=gamma,
n_iter=int(1e6))
ql.run()
f'Time: {process_time()-start:.4f}'
# -
policy = np.asarray([actions[i] for i in ql.policy])
pd.DataFrame(policy.reshape(grid_size))
value = np.asarray(ql.V).reshape(grid_size)
pd.DataFrame(value)
|
Chapter21/02_gridworld_q_learning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
from collections import namedtuple
from typing import List
NameLine = namedtuple("NameLine", ["name", "sex", "count"])
def name_lines_for_year(year: int) -> List[NameLine]:
if not (1880 <= year <= 2019):
raise ValueError("Year out of range.")
with open(f"./data/yob{year}.txt", "r") as f:
lines: List[str] = f.readlines()
name_lines = [NameLine(*line.strip().split(",")) for line in lines]
return name_lines
x = name_lines_for_year(1990)
x[:10]
last_fourty_years = list(range(2020-40, 2020))
name_lines_fourty_years = [ nl for year in last_fourty_years for nl in name_lines_for_year(year)]
name_lines_fourty_years[:10]
len(name_lines_fourty_years)
len([name for name in name_lines_fourty_years if name.sex == 'F'])
female_names = {} # {"name" : {year: count, year: count}}
for year in last_fourty_years:
for current in name_lines_for_year(year):
if current.sex != "F":
continue
name = current.name
to_update = female_names.get(name, {})
to_update[year] = current.count
female_names[name] = to_update
list(female_names.keys())[:10]
female_totals = {name: sum(map(int, x.values())) for name, x in female_names.items()}
list(female_totals.items())[:10]
top_names = sorted([ (count,name) for name, count in female_totals.items()], reverse=True)
top_names[:10]
with open("top2000f-last40.txt", "w") as f:
for count, name in top_names[:2000]:
f.write(f"{name}\n")
with open("src/namelist.tsx", "w") as f:
f.write(f"const names = [\n")
for count, name in top_names[:2000]:
f.write(f' "{name}",\n')
f.write("];\n")
f.write("export default names;\n")
|
NamesManipulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Chunk Wrangling
#
# #### This is the process of wrangling through the data we have and bring out insights available so that this can be used to next delete the unwanted columns and rows so we can have a lower sized and inly the exact required data
#
#
# ### Importing the libraries
import pandas as pd
import numpy as np
# ### Reading dataset to a dataframe
# +
df_chunk = pd.read_csv("../dataset/combined.csv",nrows=1000)
# initial dataset has around 36 lakh rows so for easy wrangling to understand about the unwanted columns we take a chunk of dataset.
# -
# ### Wrangling data
df = df_chunk.copy()
df.head()
df.columns
# +
df.shape
# for understanding structure of dataset
# -
df.info()
df.columns
df.flgs
df.state
df.ltime.value_counts()
df.seq
df.drop(['pkSeqID', 'stime', 'flgs', 'flgs_number','proto', 'proto_number',
'saddr', 'sport', 'daddr', 'dport','state','seq','ltime','subcategory','category'], axis=1, inplace=True)
df.columns
df.shape
df.describe()
df.info()
# ## Insights from chuncked dataset:
# 1.We only require upto 31 features out of the 46 we have for moachine learning classification.
#
# 2.We can see that pkSeqID(sequence id), stime(Record start time), flgs(flag represting letter), flg number,proto,port number, saddr(ip of sender), sport(port of sender), daddr(ip of receiver), dport(ip of receiver),state(we already have state number),seq(Argus sequence number and not required), ltime(record time and not required), subcategory, category (not required as we will later filter it out with 1 and 0 for DDoS alone).These are the basic features captured by wireshark.
#
# 3.The columns from 29 to 42 are extracted flow based features from the initial columns.
#
# 4.Since we only want DDoS we need to remove all other kinds of attacks except normal and DDoS from the Category column of dataset.
#
# 5.Since there is lot of data it is better to use Google colab for data manipulation step on the complete dataset which has around 36 lakh packets.
|
Data chunk wrangling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#hide
#skip
! [ -e /content ] && pip install -Uqq fastai # upgrade fastai on colab
# +
#default_exp callback.mixup
# -
#export
from fastai.basics import *
from torch.distributions.beta import Beta
#hide
from nbdev.showdoc import *
from fastai.test_utils import *
# # MixUp and Friends
#
# > Callbacks that can apply the MixUp (and variants) data augmentation to your training
from fastai.vision.all import *
#export
def reduce_loss(loss, reduction='mean'):
"Reduce the loss based on `reduction`"
return loss.mean() if reduction == 'mean' else loss.sum() if reduction == 'sum' else loss
#export
class MixHandler(Callback):
"A handler class for implementing `MixUp` style scheduling"
run_valid = False
def __init__(self, alpha=0.5):
self.distrib = Beta(tensor(alpha), tensor(alpha))
def before_train(self):
self.stack_y = getattr(self.learn.loss_func, 'y_int', False)
if self.stack_y: self.old_lf,self.learn.loss_func = self.learn.loss_func,self.lf
def after_train(self):
if self.stack_y: self.learn.loss_func = self.old_lf
def after_cancel_train(self):
self.after_train()
def after_cancel_fit(self):
self.after_train()
def lf(self, pred, *yb):
if not self.training: return self.old_lf(pred, *yb)
with NoneReduce(self.old_lf) as lf:
loss = torch.lerp(lf(pred,*self.yb1), lf(pred,*yb), self.lam)
return reduce_loss(loss, getattr(self.old_lf, 'reduction', 'mean'))
# Most `Mix` variants will perform the data augmentation on the batch, so to implement your `Mix` you should adjust the `before_batch` event with however your training regiment requires. Also if a different loss function is needed, you should adjust the `lf` as well.
# ## MixUp -
#export
class MixUp(MixHandler):
"Implementation of https://arxiv.org/abs/1710.09412"
def __init__(self, alpha=.4): super().__init__(alpha)
def before_batch(self):
lam = self.distrib.sample((self.y.size(0),)).squeeze().to(self.x.device)
lam = torch.stack([lam, 1-lam], 1)
self.lam = lam.max(1)[0]
shuffle = torch.randperm(self.y.size(0)).to(self.x.device)
xb1,self.yb1 = tuple(L(self.xb).itemgot(shuffle)),tuple(L(self.yb).itemgot(shuffle))
nx_dims = len(self.x.size())
self.learn.xb = tuple(L(xb1,self.xb).map_zip(torch.lerp,weight=unsqueeze(self.lam, n=nx_dims-1)))
if not self.stack_y:
ny_dims = len(self.y.size())
self.learn.yb = tuple(L(self.yb1,self.yb).map_zip(torch.lerp,weight=unsqueeze(self.lam, n=ny_dims-1)))
# First we'll look at a very minimalistic example to show how our data is being generated with the `PETS` dataset:
path = untar_data(URLs.PETS)
pat = r'([^/]+)_\d+.*$'
fnames = get_image_files(path/'images')
item_tfms = [Resize(256, method='crop')]
batch_tfms = [*aug_transforms(size=224), Normalize.from_stats(*imagenet_stats)]
dls = ImageDataLoaders.from_name_re(path, fnames, pat, bs=64, item_tfms=item_tfms,
batch_tfms=batch_tfms)
# We can examine the results of our `Callback` by grabbing our data during `fit` at `before_batch` like so:
# +
mixup = MixUp(1.)
with Learner(dls, nn.Linear(3,4), loss_func=CrossEntropyLossFlat(), cbs=mixup) as learn:
learn.epoch,learn.training = 0,True
learn.dl = dls.train
b = dls.one_batch()
learn._split(b)
learn('before_train')
learn('before_batch')
_,axs = plt.subplots(3,3, figsize=(9,9))
dls.show_batch(b=(mixup.x,mixup.y), ctxs=axs.flatten())
# -
#hide
test_ne(b[0], mixup.x)
test_eq(b[1], mixup.y)
# We can see that every so often an image gets "mixed" with another.
#
# How do we train? You can pass the `Callback` either to `Learner` directly or to `cbs` in your fit function:
#slow
learn = vision_learner(dls, resnet18, loss_func=CrossEntropyLossFlat(), metrics=[error_rate])
learn.fit_one_cycle(1, cbs=mixup)
# ## CutMix -
#export
class CutMix(MixHandler):
"Implementation of https://arxiv.org/abs/1905.04899"
def __init__(self, alpha=1.): super().__init__(alpha)
def before_batch(self):
bs, _, H, W = self.x.size()
self.lam = self.distrib.sample((1,)).to(self.x.device)
shuffle = torch.randperm(bs).to(self.x.device)
xb1,self.yb1 = self.x[shuffle], tuple((self.y[shuffle],))
x1, y1, x2, y2 = self.rand_bbox(W, H, self.lam)
self.learn.xb[0][..., y1:y2, x1:x2] = xb1[..., y1:y2, x1:x2]
self.lam = (1 - ((x2-x1)*(y2-y1))/float(W*H))
if not self.stack_y:
ny_dims = len(self.y.size())
self.learn.yb = tuple(L(self.yb1,self.yb).map_zip(torch.lerp,weight=unsqueeze(self.lam, n=ny_dims-1)))
def rand_bbox(self, W, H, lam):
cut_rat = torch.sqrt(1. - lam).to(self.x.device)
cut_w = torch.round(W * cut_rat).type(torch.long).to(self.x.device)
cut_h = torch.round(H * cut_rat).type(torch.long).to(self.x.device)
# uniform
cx = torch.randint(0, W, (1,)).to(self.x.device)
cy = torch.randint(0, H, (1,)).to(self.x.device)
x1 = torch.clamp(cx - cut_w // 2, 0, W)
y1 = torch.clamp(cy - cut_h // 2, 0, H)
x2 = torch.clamp(cx + cut_w // 2, 0, W)
y2 = torch.clamp(cy + cut_h // 2, 0, H)
return x1, y1, x2, y2
# Similar to `MixUp`, `CutMix` will cut a random box out of two images and swap them together. We can look at a few examples below:
# +
cutmix = CutMix(1.)
with Learner(dls, nn.Linear(3,4), loss_func=CrossEntropyLossFlat(), cbs=cutmix) as learn:
learn.epoch,learn.training = 0,True
learn.dl = dls.train
b = dls.one_batch()
learn._split(b)
learn('before_train')
learn('before_batch')
_,axs = plt.subplots(3,3, figsize=(9,9))
dls.show_batch(b=(cutmix.x,cutmix.y), ctxs=axs.flatten())
# -
# We train with it in the exact same way as well
#slow
learn = vision_learner(dls, resnet18, loss_func=CrossEntropyLossFlat(), metrics=[accuracy, error_rate])
learn.fit_one_cycle(1, cbs=cutmix)
# # Export -
#hide
from nbdev.export import notebook2script
notebook2script()
|
nbs/19_callback.mixup.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: innvestigate
# language: python
# name: innvestigate
# ---
# # Analyzing with iNNvestigate
# **iNNvestigate** got created to make analyzing neural network's predictions easy! The library should help the user to focus on research and development by providing implemented analysis methods and facilitating rapid development of new methods. In this notebook we will show you how to use **iNNvestigate** and for a better understanding we recommend to read [iNNvestigate neural networks!](https://jmlr.org/papers/v20/18-540.html) first! How to use **iNNvestigate** you can read in this notebook: [Developing with iNNvestigate](introduction_development.ipynb)
#
# -----
#
# **The intention behind iNNvestigate is to make it easy to use analysis methods, but it is not to explain the underlying concepts and assumptions. Please, read the according publication(s) when using a certain method and when publishing please cite the according paper(s) (as well as the [iNNvestigate paper](https://jmlr.org/papers/v20/18-540.html)). Thank you!** You can find most related publication in [iNNvestigate neural networks!](https://jmlr.org/papers/v20/18-540.html) and in the README file.
#
# ### Analysis methods
#
# The field of analyizing neural network's predictions is about gaining insights how and why a potentially complex network gave as output a certain value or choose a certain class over others. This is often called interpretability or explanation of neural networks. We just call it analyzing a neural network's prediction to be as neutral as possible and to leave any conclusions to the user.
#
# Most methods have in common that they analyze the input features w.r.t. a specific neuron's output. Which insights a method reveals about this output can be grouped into (see [Learning how to explain: PatternNet and PatternAttribution](https://arxiv.org/abs/1705.05598)):
#
# * **function:** analyzing the operations the network function uses to extract or compute the output. E.g., how would changing an input feature change the output.
# * **signal:** analyzing the components of the input that cause the output. E.g., which parts of an input image or which directions of an input are used to determine the output.
# * **attribution:** attributing the "importance" of input features for the output. E.g., how much would changing an input feature change the output.
#
# ----
#
# In this notebook we will introduce methods for each of these categories and along show how to use different features of **iNNvestigate**, namely how to:
#
# * analyze a prediction.
# * train an analyzer.
# * analyze a prediction w.r.t to a specific output neuron.
#
# Let's dive right into it!
# ### Run on Colab
# > Colab uses per default tensorflow 1.15 which was not used for development of `iNNvestigate`
# > Switch to colab GPU runtime for performance
#
# <table align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/albermax/innvestigate/blob/master/examples/notebooks/introduction.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# </table>
#
#
import os
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 1.x
IS_COLAB = True
if not os.path.exists('/content/innvestigate'):
# !git clone https://github.com/albermax/innvestigate.git
# !pip install /content/innvestigate --no-deps
# %cd /content/innvestigate/examples/notebooks
except Exception:
IS_COLAB = False
#
# ### Training a network
#
# To analyze a network, we need a network! As a base for **iNNvestigate** we chose the Keras deep learning library, because it is easy to use and allows to inspect build models.
#
# In this first piece of code we import all the necessary modules:
import warnings
warnings.simplefilter('ignore')
# +
# %matplotlib inline
import imp
import matplotlib.pyplot as plot
import numpy as np
import os
import keras
import keras.backend
import keras.layers
import keras.models
import keras.utils
import innvestigate
import innvestigate.utils as iutils
# Use utility libraries to focus on relevant iNNvestigate routines.
mnistutils = imp.load_source("utils_mnist", "../utils_mnist.py")
# -
innvestigate.__version__
# to load the data:
# +
# Load data
# returns x_train, y_train, x_test, y_test as numpy.ndarray
data_not_preprocessed = mnistutils.fetch_data()
# Create preprocessing functions
input_range = [-1, 1]
preprocess, revert_preprocessing = mnistutils.create_preprocessing_f(data_not_preprocessed[0], input_range)
# Preprocess data
data = (
preprocess(data_not_preprocessed[0]), keras.utils.to_categorical(data_not_preprocessed[1], 10),
preprocess(data_not_preprocessed[2]), keras.utils.to_categorical(data_not_preprocessed[3], 10),
)
if keras.backend.image_data_format == "channels_first":
input_shape = (1, 28, 28)
else:
input_shape = (28, 28, 1)
# -
# and to now create and train a CNN model:
# +
model = keras.models.Sequential([
keras.layers.Conv2D(32, (3, 3), activation="relu", input_shape=input_shape),
keras.layers.Conv2D(64, (3, 3), activation="relu"),
keras.layers.MaxPooling2D((2, 2)),
keras.layers.Flatten(),
keras.layers.Dense(512, activation="relu"),
keras.layers.Dense(10, activation="softmax"),
])
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
model.fit(data[0], data[1], epochs=20, batch_size=128)
scores = model.evaluate(data[2], data[3], batch_size=128)
print("Scores on test set: loss=%s accuracy=%s" % tuple(scores))
# -
# ## Analyzing a predicition
#
# Let's first choose an image to analyze:
# +
# Choosing a test image for the tutorial:
image = data[2][7:8]
plot.imshow(image.squeeze(), cmap='gray', interpolation='nearest')
plot.show()
# -
# In this first part we show how to create and use an analyzer. To do so we use an analyzer from *function* category, namely the gradient. The gradient shows how the linearized network function reacts on changes of a single feature.
#
# This is simply done by passing the model without a softmax to the analyzer class:
# +
# Stripping the softmax activation from the model
model_wo_sm = iutils.keras.graph.model_wo_softmax(model)
# Creating an analyzer
gradient_analyzer = innvestigate.analyzer.Gradient(model_wo_sm)
# Applying the analyzer
analysis = gradient_analyzer.analyze(image)
# Displaying the gradient
plot.imshow(analysis.squeeze(), cmap='seismic', interpolation='nearest')
plot.show()
# -
# For convience there is a function that creates an analyzer for you. It passes all the parameter on to the class instantiation:
# +
# Creating an analyzer
gradient_analyzer = innvestigate.create_analyzer("gradient", model_wo_sm)
# Applying the analyzer
analysis = gradient_analyzer.analyze(image)
# Displaying the gradient
plot.imshow(analysis.squeeze(), cmap='seismic', interpolation='nearest')
plot.show()
# -
# To emphasize different compontents of the analysis many people use instead of the "plain" gradient the absolute value or the square of it. With the gradient analyzer this can be done specifying additional parameters when creating the analyzer:
# Creating a parameterized analyzer
abs_gradient_analyzer = innvestigate.create_analyzer("gradient", model_wo_sm, postprocess="abs")
square_gradient_analyzer = innvestigate.create_analyzer("gradient", model_wo_sm, postprocess="square")
# Similar other analyzers can be parameterized.
#
# Now we visualize the result by projecting the gradient into a gray-color-image:
# +
# Applying the analyzers
abs_analysis = abs_gradient_analyzer.analyze(image)
square_analysis = square_gradient_analyzer.analyze(image)
# Displaying the analyses, use gray map as there no negative values anymore
plot.imshow(abs_analysis.squeeze(), cmap='gray', interpolation='nearest')
plot.show()
plot.imshow(square_analysis.squeeze(), cmap='gray', interpolation='nearest')
plot.show()
# -
# ## Training an analyzer
#
# Some analyzers are data-dependent and need to be trained. In **iNNvestigate** this realized with a SKLearn-like interface. In the next piece of code we train the method PatternNet that analyzes the *signal*:
# +
# Creating an analyzer
patternnet_analyzer = innvestigate.create_analyzer("pattern.net", model_wo_sm, pattern_type="relu")
# Train (or adapt) the analyzer to the training data
patternnet_analyzer.fit(data[0], verbose=True)
# Applying the analyzer
analysis = patternnet_analyzer.analyze(image)
# -
# And visualize it:
# Displaying the signal (projected back into input space)
plot.imshow(analysis.squeeze()/np.abs(analysis).max(), cmap="gray", interpolation="nearest")
plot.show()
# ## Choosing the output neuron
#
# In the previous examples we always analyzed the output of the neuron with the highest activation. In the next one we show how one can choose the neuron to analyze:
# Creating an analyzer and set neuron_selection_mode to "index"
inputXgradient_analyzer = innvestigate.create_analyzer("input_t_gradient", model_wo_sm,
neuron_selection_mode="index")
# The gradient\*input analyzer is an example from the *attribution* category and we visualize it by means of a colored heatmap to highlight positive and negative attributions:
for neuron_index in range(10):
print("Analysis w.r.t. to neuron", neuron_index)
# Applying the analyzer and pass that we want
analysis = inputXgradient_analyzer.analyze(image, neuron_index)
# Displaying the gradient
plot.imshow(analysis.squeeze(), cmap='seismic', interpolation='nearest')
plot.show()
# ## Additional resources
#
# If you would like to learn more we have more notebooks for you, for example: [Comparing methods on MNIST](mnist_method_comparison.ipynb), [Comparing methods on ImageNet](imagenet_method_comparison.ipynb) and [Comparing networks on ImageNet](imagenet_network_comparison.ipynb)
#
# If you want to know more about how to use the API of **iNNvestigate** look into: [Developing with iNNvestigate](introduction_development.ipynb)
|
lib/innvestigate/examples/notebooks/introduction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import os
from glob import glob
from pprint import pprint
import json
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection
from matplotlib.colors import ListedColormap, BoundaryNorm
import matplotlib.pyplot as plt
import cellcycle.PlottingTools as plottingTools
from cellcycle.ParameterSet import ParameterSet
import cellcycle.DataStorage as dataStorage
import cellcycle.DataAnalysis as dataAnalysis
import cellcycle.MakeDataframe as makeDataframe
from cellcycle import mainClass
# -
indx = 10
file_path_input_params_json = '../../input_params.json'
input_param_dict = mainClass.extract_variables_from_input_params_json(file_path_input_params_json)
root_path = input_param_dict["DATA_FOLDER_PATH"]
simulation_location = 'SI/S15_titration_switch_combined_vary_n_sites/time_traces_low_growth_rate'
file_path = os.path.join(root_path, simulation_location)
print('file_path', file_path)
parameter_path = os.path.join(file_path, 'parameter_set.csv')
print('parameter_path', parameter_path)
# # Make data frame from time traces
# +
data_frame = makeDataframe.make_dataframe(file_path)
data_frame = data_frame.sort_values(by=['n_c_max_0'])
time_traces_data_frame = pd.read_hdf(data_frame['path_dataset'].iloc[indx], key='dataset_time_traces')
v_init_data_frame = pd.read_hdf(data_frame['path_dataset'].iloc[indx], key='dataset_init_events')
v_init = v_init_data_frame.iloc[10]['v_init']
v_init_per_ori = v_init_data_frame.iloc[10]['v_init_per_ori']
t_init_list = v_init_data_frame['t_init'].to_numpy()
v_d_data_frame = pd.read_hdf(data_frame['path_dataset'].iloc[indx], key='dataset_div_events')
data_frame
# +
time = np.array(time_traces_data_frame["time"])
volume = np.array(time_traces_data_frame["volume"])
n_ori = np.array(time_traces_data_frame["n_ori"])
active_fraction = np.array(time_traces_data_frame["active_fraction"])
free_conc = np.array(time_traces_data_frame["free_conc"])
print(time.size)
cycle_0 = 6
cycle_f = 9
t_0 = time[volume==v_d_data_frame['v_b'][cycle_0]]
indx_0 = np.where(time==t_0)[0][0]
t_f = time[volume==v_d_data_frame['v_b'][cycle_f]]
indx_f = np.where(time==t_f)[0][0]+20
print(indx_0, indx_f)
n_ori_cut = n_ori[indx_0:indx_f]
time_cut = time[indx_0:indx_f]
volume_cut = volume[indx_0:indx_f]
active_fraction_cut = active_fraction[indx_0:indx_f]
free_conc_cut = free_conc[indx_0:indx_f]
t_init_list_cut_1 = t_init_list[t_init_list>t_0]
t_init_list_cut = t_init_list_cut_1[t_init_list_cut_1<t_f]
t_b = t_init_list + data_frame.iloc[indx]['t_CD']
t_b_cut_1 = t_b[t_b<t_f]
t_b_cut = t_b_cut_1[t_b_cut_1>t_0]
print(t_init_list_cut, t_b_cut)
# -
# # Color definitions
pinkish_red = (247 / 255, 109 / 255, 109 / 255)
green = (0 / 255, 133 / 255, 86 / 255)
dark_blue = (36 / 255, 49 / 255, 94 / 255)
light_blue = (168 / 255, 209 / 255, 231 / 255)
darker_light_blue = (112 / 255, 157 / 255, 182 / 255)
blue = (55 / 255, 71 / 255, 133 / 255)
yellow = (247 / 255, 233 / 255, 160 / 255)
# # Plot four figures
# +
label_list = [r'$V(t)$', r'$[D]_{\rm T, f}(t)$', r'$f(t)$', r'$[D]_{\rm ATP, f}(t)$']
x_axes_list = [time_cut, time_cut, time_cut, time_cut]
y_axes_list = [volume_cut, free_conc_cut, active_fraction_cut, free_conc_cut * active_fraction_cut]
color_list = [green, dark_blue, darker_light_blue, pinkish_red]
fig, ax = plt.subplots(4, figsize=(3.2,4))
plt.xlabel(r'time [$\tau_{\rm d}$]')
y_min_list = [0,0,0,0]
y_max_list = [1, 1.2, 1.2, 1.2]
doubling_time = 1/data_frame.iloc[indx]['doubling_rate']
print(1/doubling_time)
print('number of titration sites per origin:', data_frame.iloc[indx]['n_c_max_0'])
for item in range(0, len(label_list)):
ax[item].set_ylabel(label_list[item])
ax[item].plot(x_axes_list[item], y_axes_list[item], color=color_list[item])
ax[item].set_ylim(ymin=0)
ax[item].tick_params(
axis='x', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
bottom=False, # ticks along the bottom edge are off
top=False, # ticks along the top edge are off
labelbottom=False) # labels along the bottom edge are off
ax[item].spines["top"].set_visible(False)
ax[item].spines["right"].set_visible(False)
ax[item].margins(0)
for t_div in t_b_cut:
ax[item].axvline(x=t_div,
ymin=y_min_list[item],
ymax=y_max_list[item],
c="black",
zorder=0,
linewidth=0.8,
clip_on=False)
for t_init in t_init_list_cut:
ax[item].axvline(x=t_init,
ymin=y_min_list[item],
ymax=y_max_list[item],
c="black",
zorder=0,
linewidth=0.8,
linestyle='--',
clip_on=False)
ax[0].set_yticks([0, v_init])
# ax[0].set(ylim=(0, v_init+0.01))
ax[0].set_yticklabels(['0',r'$v^\ast$'])
ax[0].get_yticklabels()[1].set_color(green)
ax[0].axhline(y=v_init, color=green, linestyle='--')
ax[1].axhline(y=data_frame.iloc[0]['michaelis_const_initiator'], color=color_list[1], linestyle='--')
ax[1].set_yticks([0, data_frame.iloc[0]['michaelis_const_initiator']])
ax[1].set_yticklabels([0, r'$K_{\rm D}$'])
ax[1].get_yticklabels()[1].set_color(color_list[1])
ax[1].set(ylim=(0,data_frame.iloc[0]['michaelis_const_initiator']*1.15))
# ax[2].axhline(y=data_frame.iloc[0]['frac_init'], color=pinkish_red, linestyle='--')
ax[2].set_yticks([0, 0.5, 1])
ax[2].set_yticklabels(['0', '0.5', '1'])
ax[3].set_yticks([0, data_frame.iloc[0]['critical_free_active_conc']])
ax[3].set_yticklabels(['0',r'$[D]_{\rm ATP, f}^\ast$'])
ax[3].get_yticklabels()[1].set_color(color_list[3])
ax[3].axhline(y=data_frame.iloc[0]['critical_free_active_conc'], color=color_list[3], linestyle='--')
ax[3].tick_params(bottom=True, labelbottom=True)
ax[3].tick_params(axis='x', colors='black')
ax[3].set_xticks([time_cut[0],
time_cut[0]+ doubling_time,
time_cut[0]+ 2*doubling_time,
time_cut[0]+ 3*doubling_time
])
ax[3].set_xticklabels(['0', '1', '2', '3'])
plt.savefig(file_path + '/S11_titration_switch_combined_'+str(indx)+'.pdf', format='pdf',bbox_inches='tight')
# -
#
|
notebooks/SI/S15_vary_n_time_traces_low.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data Cleaning
# ### Dataset
# <br>
# Source: https://archive.ics.uci.edu/ml/datasets/Online+Retail
# <br>
# <br>
# - InvoiceNo: Invoice number. Nominal, a 6-digit integral number uniquely assigned to each transaction. <br>
# - If this code starts with letter 'c', it indicates a cancellation.<br>
# - StockCode: Product (item) code. Nominal, a 5-digit integral number uniquely assigned to each distinct product.<br>
# - Description: Product (item) name. Nominal.<br>
# - Quantity: The quantities of each product (item) per transaction. Numeric.<br>
# - InvoiceDate: Invice Date and time. Numeric, the day and time when each transaction was generated.<br>
# - UnitPrice: Unit price. Numeric, Product price per unit in sterling.<br>
# - CustomerID: Customer number. Nominal, a 5-digit integral number uniquely assigned to each customer.<br>
# - Country: Country name. Nominal, the name of the country where each customer resides.<br>
# <br>
# <br>
import os
import pandas as pd
import matplotlib.pyplot as plt
os.chdir(r'D:\Data\Projects\Business Analytics\E-Commerce Data')
pd.set_option('display.float_format', lambda x: '%.3f' % x)
from warnings import filterwarnings
filterwarnings('ignore')
df_ = pd.read_csv('e-commerce data.csv', encoding = 'ISO-8859-1')
print(df_.shape)
df_.head()
# ### Missing Values
missing = pd.DataFrame(df_.isnull().sum()).rename(columns = {0: 'total'})
missing['percent'] = missing['total'] / len(df_)*100
#missing = missing[missing.total != 0]
missing.sort_values('percent', ascending = False)
# There is no way to obtain the missing values from CustomerID or Description,
# so the rows will be dropped
df = df_.dropna(how='any')
# ### Duplicates
df.loc[df.duplicated(), :].shape
# There are 5225 duplicates
df = df.drop_duplicates(subset = ['InvoiceNo', 'StockCode', 'Description', 'Quantity', 'InvoiceDate',
'UnitPrice', 'CustomerID', 'Country'])
# ### Datatypes
df.dtypes.sort_values()
df.InvoiceDate = pd.to_datetime(df.InvoiceDate)
# Transformation via int to get rid of decimals
df.CustomerID = df.CustomerID.astype('int64').astype('str')
# Removal of punctuation
df.Description = df.Description.str.replace(',', ' ')
# +
# Save clean dataset
# df.to_csv('dfclean.csv', sep=',', encoding='utf-8', index=False)
|
01_CustomerSegmentation_Cleaning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: kaggle
# language: python
# name: kaggle
# ---
# ## <NAME> Manufacturing
#
# > Can you cut the time a Mercedes-Benz spends on the test bench?
# +
# Python and data manipulation stuff
import operator
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import xgboost as xgb
import lightgbm as lgb
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import TheilSenRegressor
from sklearn.linear_model import Ridge
from sklearn.svm import SVR
from sklearn.linear_model import ElasticNet
from sklearn.ensemble import ExtraTreesRegressor
from sklearn.model_selection import KFold
from sklearn.preprocessing import LabelEncoder
from sklearn.manifold import TSNE
from sklearn.metrics import r2_score
from sklearn.decomposition import PCA, FastICA
from sklearn.random_projection import GaussianRandomProjection
from sklearn.random_projection import SparseRandomProjection
from sklearn.decomposition import TruncatedSVD
# -
# ### EDA
#
# The EDA analysis started based on this public kernels (Thanks a lot for this sharing):
#
# * https://www.kaggle.com/headsortails/mercedas-2-feature-interactions
# * https://www.kaggle.com/sudalairajkumar/simple-exploration-notebook-mercedes
# * https://www.kaggle.com/headsortails/mercedas-update2-intrinsic-noise
#
# ## Helpers
# K-Fold helper
def kfold_validate(clf, X, y, k_folds = 5):
acc = []
rtimes = 5
rstate = [420, 123, 456, 678, 666]
for it in range(rtimes):
count = 0
kf = KFold(n_splits=k_folds, shuffle = True, random_state=rstate[it])
for train_idx, test_idx in kf.split(X):
count += 1
# Separe training and test in the Training set for k-Fold
fold_Xtrain, fold_Xtest = X[train_idx], X[test_idx]
fold_ytrain, fold_ytest = y[train_idx], y[test_idx]
# Train
clf.fit(fold_Xtrain, fold_ytrain)
pred = clf.predict(fold_Xtest)
accuracy = r2_score(fold_ytest, pred)
acc.append(accuracy)
print("Fold: %s of % s | iter: %s => r2_score = %s" %(count, k_folds, it, accuracy))
print("\nR2_score statistics:")
print("Mean = %s%%" % '{0:.5f}'.format(np.mean(acc)))
print("STD = %s%%" % '{0:.5f}'.format(np.std(acc)))
# K-Fold helper
def kfold_validate_keras(clf, X, y, k_folds = 5):
acc = []
rtimes = 5
rstate = [420, 123, 456, 678, 666]
for it in range(rtimes):
count = 0
kf = KFold(n_splits=k_folds, shuffle = True, random_state=rstate[it])
for train_idx, test_idx in kf.split(X):
count += 1
# Separe training and test in the Training set for k-Fold
fold_Xtrain, fold_Xtest = X[train_idx], X[test_idx]
fold_ytrain, fold_ytest = y[train_idx], y[test_idx]
# Train
clf.fit(fold_Xtrain,fold_ytrain, epochs=250,
validation_data=(fold_Xtest, fold_ytest))
pred = clf.predict(fold_Xtest)
accuracy = r2_score(fold_ytest, pred)
acc.append(accuracy)
print("Fold: %s of % s | iter: %s => r2_score = %s" %(count, k_folds, it, accuracy))
print("\nR2_score statistics:")
print("Mean = %s%%" % '{0:.5f}'.format(np.mean(acc)))
print("STD = %s%%" % '{0:.5f}'.format(np.std(acc)))
# https://www.kaggle.com/eikedehling/stack-of-svm-elasticnet-xgboost-rf-0-55
class Ensemble(object):
def __init__(self, n_splits, stacker, base_models):
self.n_splits = n_splits
self.stacker = stacker
self.base_models = base_models
def fit_predict(self, X, y, T):
X = np.array(X)
y = np.array(y).ravel()
T = np.array(T)
folds = list(KFold(n_splits=self.n_splits, shuffle=True, random_state=1024).split(X, y))
S_train = np.zeros((X.shape[0], len(self.base_models)))
S_test = np.zeros((T.shape[0], len(self.base_models)))
acc = []
for i, clf in enumerate(self.base_models):
S_test_i = np.zeros((T.shape[0], self.n_splits))
for j, (train_idx, test_idx) in enumerate(folds):
X_train = X[train_idx]
y_train = y[train_idx]
X_holdout = X[test_idx]
y_holdout = y[test_idx]
clf.fit(X_train, y_train)
y_pred = clf.predict(X_holdout)[:]
accuracy = r2_score(y_holdout, y_pred)
print ("Model %d fold %d score %f" % (i, j, accuracy))
acc.append(accuracy)
S_train[test_idx, i] = y_pred
S_test_i[:, j] = clf.predict(T)[:]
S_test[:, i] = S_test_i.mean(axis=1)
print("\nR2_score statistics for Models:")
print("Mean = %s%%" % '{0:.5f}'.format(np.mean(acc)))
print("STD = %s%%" % '{0:.5f}'.format(np.std(acc)))
print("\nStarting kFold for stacked models")
kfold_validate(self.stacker, S_train, y)
# Train on all data
self.stacker.fit(S_train, y)
res = self.stacker.predict(S_test)[:]
return res
# Test validation helper
def lb_probing(pred):
probing = pd.read_csv('data/lb_probing.csv')
values = []
for idp in probing.id:
values.append(pred.y[pred.ID == idp].values[0])
print('lb probing score = %s' % r2_score(probing.y, np.array(values)))
# ## Aproach 1: Several models and stacking
# ### Read the data
df_train = pd.read_csv('data/train.csv')
df_test = pd.read_csv('data/test.csv')
# +
# Insert probed data
probing = pd.read_csv('data/lb_probing.csv')
for idp in probing.id:
n_row = df_test[df_test.ID == idp]
n_row['y'] = list(probing[probing.id == idp]['y'])
df_train = pd.concat([df_train, n_row], axis=0)
# -
# ### Feature Engineering and Data Cleaning
# +
# Get the mean for y across repeated rows
filter_col = list(df_train.columns)
filter_col.remove('ID')
filter_col.remove('y')
repeated = df_train[df_train.duplicated(subset=filter_col, keep=False)]
mean_repeated = repeated.groupby(filter_col, as_index=False).mean()
# Remove repeated rows
print(df_train.shape)
filter_col = list(df_train.columns)
filter_col.remove('ID')
filter_col.remove('y')
df_train.drop_duplicates(subset=filter_col, keep=False, inplace=True)
print(df_train.shape)
# Merge with filtered rows
df_train = pd.concat([df_train, mean_repeated], axis=0)
print(df_train.shape)
# Magic feature from Cro-Magnon
uniquex0 = list(df_train['X0'].unique())
dict_meanx0 = {}
df_train['meanx0'] = df_train.y
df_test['meanx0'] = np.repeat(np.median(df_train.y), len(df_test))
for x in uniquex0:
meanx0 = np.median(df_train['y'][df_train['X0'] == x])
dict_meanx0[x] = meanx0
df_train['meanx0'][df_train['X0'] == x] = meanx0
df_test['meanx0'][df_test['X0'] == x] = meanx0
# group train and test
num_train = len(df_train)
df_all = pd.concat([df_train, df_test], axis=0)
df_all = df_all.reset_index()
# Get the object features
obj_features = []
int_features = []
for c in df_all.columns:
if df_all[c].dtype == 'object':
obj_features.append(c)
else:
int_features.append(c)
# One-Hot Encoding
for cc in obj_features:
dummies = pd.get_dummies(df_all[cc])
dummies = dummies.add_prefix("{}#".format(cc))
df_all.drop(cc, axis=1, inplace=True)
df_all = df_all.join(dummies)
df_train = df_all[:num_train]
df_test = df_all[num_train:].drop(['y'], axis=1)
x_train = df_train.drop(['ID', 'y'], axis=1).as_matrix()
y_train = df_train.filter('y').as_matrix()
x_test = df_test.drop(['ID'], axis=1).as_matrix()
id_test = df_test['ID'].apply(int)
# -
# ### Modeling
# +
# XGBoost 1
xgb_params_1 = {
'learning_rate': 0.01,
'n_estimators': 1024,
'max_depth':3,
'subsample': 1,
'colsample_bytree':0.5,
'reg_alpha':0.5,
'reg_lambda':0.5
}
xgb_clf_1 = xgb.XGBRegressor(**xgb_params_1)
#if cross_validate:
# kfold_validate(xgb_clf, x_train, y_train)
# Fit in all data and use on test
#xgb_clf.fit(x_train, y_train)
#xgb_pred = xgb_clf.predict(x_test)
#result = pd.DataFrame({'ID': id_test, 'y': xgb_pred})
#lb_probing(result)
# +
# XGBoost 2
xgb_params_2 = {
'learning_rate': 0.01,
'n_estimators': 4096,
'max_depth':5,
'subsample': 1,
'colsample_bytree':0.5,
'reg_alpha':0.5,
'reg_lambda':0.5
}
xgb_clf_2 = xgb.XGBRegressor(**xgb_params_2)
# +
# LightGBM 1
gbm_params_1 = {
'objective': 'regression',
'metric': 'rmse',
'boosting': 'gbdt',
'num_leaves': 256,
'learning_rate': 0.01,
'n_estimators': 500,
'feature_fraction': 0.9,
'bagging_fraction': 0.8,
'bagging_freq': 5,
'n_jobs': -1,
'num_rounds': 2000,
'max_depth': 15,
}
gbm_clf_1 = lgb.LGBMRegressor(**gbm_params_1)
# +
# LightGBM 2
gbm_params_2 = {
'objective': 'regression',
'metric': 'rmse',
'boosting': 'gbdt',
'num_leaves': 512,
'learning_rate': 0.01,
'n_estimators': 2500,
'feature_fraction': 0.9,
'bagging_fraction': 0.8,
'bagging_freq': 5,
'n_jobs': -1,
'num_rounds': 5000,
'max_depth': 15,
}
gbm_clf_2 = lgb.LGBMRegressor(**gbm_params_2)
# +
# Random Forest
rf_params = {
'n_estimators': 256,
'n_jobs':-1
}
rf_clf = RandomForestRegressor(**rf_params)
# +
# Extra Trees 1
et_params_1 = {
'n_estimators': 64,
'max_depth': 8,
'n_jobs': 4
}
et_clf_1 = ExtraTreesRegressor(**et_params_1)
# +
# Extra Trees 2
et_params_2 = {
'n_estimators': 256,
'n_jobs': 4
}
et_clf_2 = ExtraTreesRegressor(**et_params_2)
# +
# Ridge
ridge_params = {
'alpha': 100,
'normalize':False,
'solver':'auto'
}
ridge_clf = Ridge(**ridge_params)
# -
x_train.shape
# +
# Stacked approach
stack = Ensemble(n_splits=5,
stacker=ElasticNet(l1_ratio=0.1, alpha=1.4),
base_models=(xgb_clf_1, xgb_clf_2, gbm_clf_1,
gbm_clf_2, rf_clf, et_clf_1))
pred_app1 = stack.fit_predict(x_train, y_train, x_test)
approach1 = pd.DataFrame({'ID': id_test, 'y': pred_app1})
approach1.to_csv('approach1.csv', index=False)
lb_probing(approach1)
# -
# ## Approach 2: Deep Learning
from keras.models import Sequential
from keras.layers import Dense, Dropout, BatchNormalization, Activation
from keras.wrappers.scikit_learn import KerasRegressor
from keras.callbacks import EarlyStopping
from keras import backend as K
def r2_keras(y_true, y_pred):
SS_res = K.sum(K.square(y_true - y_pred))
SS_tot = K.sum(K.square(y_true - K.mean(y_true)))
return (1 - SS_res/(SS_tot + K.epsilon()))
# First arch: Smaller NN
def smallNN(input_dims = 581):
model = Sequential()
#input layer
model.add(Dense(input_dims, input_dim=input_dims))
model.add(BatchNormalization())
model.add(Activation('relu'))
model.add(Dropout(0.25))
# hidden layers
model.add(Dense(input_dims))
model.add(BatchNormalization())
model.add(Activation('tanh'))
model.add(Dropout(0.25))
model.add(Dense(input_dims//2))
model.add(BatchNormalization())
model.add(Activation('tanh'))
model.add(Dropout(0.25))
model.add(Dense(input_dims//4, activation='tanh'))
# output layer (y_pred)
model.add(Dense(1, activation='linear'))
# compile this model
model.compile(loss='mean_squared_error',
optimizer='adam',
metrics=[r2_keras])
return model
# +
small_nn_clf = KerasRegressor(
build_fn=smallNN,
nb_epoch=300,
batch_size=128,
verbose=1)
# Fit in all data and use on test
small_nn_clf.fit(x_train, y_train, epochs=500, verbose=0)
small_nn_pred = small_nn_clf.predict(x_test, verbose=0)
result = pd.DataFrame({'ID': id_test, 'y': small_nn_pred})
lb_probing(result)
# -
# ## Approach 3: Clustering
features = ['X118', 'X127','X47','X315','X311','X179',
'X314','X232','X29','X263','X261']
y_clip = np.clip(df_train['y'].values, a_min=None, a_max=130)
tsne = TSNE(random_state=2016,perplexity=50,verbose=2)
x = tsne.fit_transform(pd.concat([df_train.filter(features),df_test.filter(features)]))
cm = plt.cm.get_cmap('RdYlBu')
plt.figure(figsize=(12,10))
cb = plt.scatter(x[:df_train.shape[0],0],x[:df_train.shape[0],1], c=y_clip, cmap=cm, marker='o', s=15, label='train')
plt.colorbar(cb)
plt.legend(prop={'size':15})
plt.title('t-SNE embedding of train data', fontsize=20)
plt.show()
# +
from sklearn.cluster import KMeans
kmeans_params = {
'n_clusters': 4,
'init': 'k-means++',
'max_iter': 300,
'n_jobs': -1,
'algorithm':'auto',
'random_state': 420
}
kmeans = KMeans(**kmeans_params).fit(x[:num_train])
train_pred = kmeans.predict(x[:num_train])
test_pred = kmeans.predict(x[num_train:])
# -
df_train['cluster'] = train_pred
df_test['cluster'] = test_pred
# +
# @TODO
# -
# Average all models
average = pd.DataFrame({'ID': id_test, 'y': .35*small_nn_pred + .65*pred_app1})
average.to_csv('finalEnsemble.csv', index=False)
lb_probing(average)
# ## Experiments results
#
# In this cell I will try to report all the tries that I did.
#
# ### Raw data
#
# | Features | Mean & STD CV 5-Fold | LB Probing |
# | :-------------- |:-------------:| :-----|
# | XGBoost using Label encoder | Mean = 0.56434%, STD = 0.05999% | 0.435572281085 |
# | LightGBM using Label encoder | Mean = 0.55672%, STD = 0.06136% | 0.671859646279 |
# | XGBoost using One Hot Encoding | Mean = 0.56819%, STD = 0.05853% | 0.463080164631 |
# | LightGBM using One Hot Encoding | Mean = 0.56586%, STD = 0.06029% | 0.624736134116 |
#
#
# ### Removing the Y outlier
#
# The problem with removing the outlier is that it represents a great information and is useful for some data in test set. Local CV improves but LBprobing will decrease. *"The one who can predict outliers will win this competition"*
#
# | Features | Mean & STD CV 5-Fold | LB Probing |
# | :-------------- |:-------------:| :-----|
# | XGBoost using One Hot Encoding | Mean = 0.59033%, STD = 0.02744% | 0.41257467562 |
# | LightGBM using One Hot Encoding | Mean = 0.58706%, STD = 0.02747% | 0.4969397011976 |
#
# ### Removing Columns with zero variance
#
# Trying this approach but we wont use
#
# | Features | Mean & STD CV 5-Fold | LB Probing |
# | :-------------- |:-------------:| :-----|
# | XGBoost using One Hot Encoding | Mean = 0.56744%, STD = 0.05776% | 0.456847306399 |
# | LightGBM using One Hot Encoding | Mean = 0.56567%, STD = 0.06012% | 0.621702756209 |
#
# ### Removing Repeated Rows
#
# Seems to improve LGB but not XGBoost
#
# | Features | Mean & STD CV 5-Fold | LB Probing |
# | :-------------- |:-------------:| :-----|
# | XGBoost using One Hot Encoding | Mean = 0.57143%, STD = 0.06449% | 0.461810565188 |
# | LightGBM using One Hot Encoding | Mean = 0.57197%, STD = 0.06900% | 0.596767729737 |
#
# ### Using feature from Cro-Magnon
#
# | Features | Mean & STD CV 5-Fold | LB Probing |
# | :-------------- |:-------------:| :-----|
# | XGBoost using One Hot Encoding | Mean = 0.57010%, STD = 0.06372% | 0.455551275766 |
# | LightGBM using One Hot Encoding | Mean = 0.57447%, STD = 0.06785% | 0.610080074095 |
#
# ### Start Stacking
#
# Advice:
# ```
# |-- 2 or 3 GBMs (one with low depth, one with medium and one with high)
# |-- 1 or 2 Random Forests (again as diverse as possible–one low depth, one high)
# |-- 1 or 2 NNs (one deeper, one smaller)
# |-- 1 linear model
# ```
|
competitions/mercedes-manufacturing/mercedesEDA.ipynb
|
# ---
# jupyter:
# jupytext:
# split_at_heading: true
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#export
from fastai.basics import *
from fastai.callback.progress import *
from fastai.text.data import TensorText
from fastai.tabular.all import TabularDataLoaders, Tabular
from fastai.callback.hook import total_params
#hide
from nbdev.showdoc import *
# +
#default_exp callback.wandb
# -
# # Wandb
#
# > Integration with [Weights & Biases](https://docs.wandb.com/library/integrations/fastai)
# First thing first, you need to install wandb with
# ```
# pip install wandb
# ```
# Create a free account then run
# ```
# wandb login
# ```
# in your terminal. Follow the link to get an API token that you will need to paste, then you're all set!
#export
import wandb
from wandb.wandb_config import ConfigError
#export
class WandbCallback(Callback):
"Saves model topology, losses & metrics"
toward_end,remove_on_fetch,run_after = True,True,FetchPredsCallback
# Record if watch has been called previously (even in another instance)
_wandb_watch_called = False
def __init__(self, log="gradients", log_preds=True, log_model=True, log_dataset=False, dataset_name=None, valid_dl=None, n_preds=36, seed=12345):
# Check if wandb.init has been called
if wandb.run is None:
raise ValueError('You must call wandb.init() before WandbCallback()')
# W&B log step
self._wandb_step = wandb.run.step - 1 # -1 except if the run has previously logged data (incremented at each batch)
self._wandb_epoch = 0 if not(wandb.run.step) else math.ceil(wandb.run.summary['epoch']) # continue to next epoch
store_attr(self, 'log,log_preds,log_model,log_dataset,dataset_name,valid_dl,n_preds,seed')
def before_fit(self):
"Call watch method to log model topology, gradients & weights"
self.run = not hasattr(self.learn, 'lr_finder') and not hasattr(self, "gather_preds") and rank_distrib()==0
if not self.run: return
# Log config parameters
log_config = self.learn.gather_args()
_format_config(log_config)
try:
wandb.config.update(log_config, allow_val_change=True)
except Exception as e:
print(f'WandbCallback could not log config parameters -> {e}')
if not WandbCallback._wandb_watch_called:
WandbCallback._wandb_watch_called = True
# Logs model topology and optionally gradients and weights
wandb.watch(self.learn.model, log=self.log)
# log dataset
assert isinstance(self.log_dataset, (str, Path, bool)), 'log_dataset must be a path or a boolean'
if self.log_dataset is True:
if Path(self.dls.path) == Path('.'):
print('WandbCallback could not retrieve the dataset path, please provide it explicitly to "log_dataset"')
self.log_dataset = False
else:
self.log_dataset = self.dls.path
if self.log_dataset:
self.log_dataset = Path(self.log_dataset)
assert self.log_dataset.is_dir(), f'log_dataset must be a valid directory: {self.log_dataset}'
metadata = {'path relative to learner': os.path.relpath(self.log_dataset, self.learn.path)}
log_dataset(path=self.log_dataset, name=self.dataset_name, metadata=metadata)
# log model
if self.log_model and not hasattr(self, 'save_model'):
print('WandbCallback requires use of "SaveModelCallback" to log best model')
self.log_model = False
if self.log_preds:
try:
if not self.valid_dl:
#Initializes the batch watched
wandbRandom = random.Random(self.seed) # For repeatability
self.n_preds = min(self.n_preds, len(self.dls.valid_ds))
idxs = wandbRandom.sample(range(len(self.dls.valid_ds)), self.n_preds)
if isinstance(self.dls, TabularDataLoaders):
test_items = getattr(self.dls.valid_ds.items, 'iloc', self.dls.valid_ds.items)[idxs]
self.valid_dl = self.dls.test_dl(test_items, with_labels=True, process=False)
else:
test_items = [getattr(self.dls.valid_ds.items, 'iloc', self.dls.valid_ds.items)[i] for i in idxs]
self.valid_dl = self.dls.test_dl(test_items, with_labels=True)
self.learn.add_cb(FetchPredsCallback(dl=self.valid_dl, with_input=True, with_decoded=True))
except Exception as e:
self.log_preds = False
print(f'WandbCallback was not able to prepare a DataLoader for logging prediction samples -> {e}')
def after_batch(self):
"Log hyper-parameters and training loss"
if self.training:
self._wandb_step += 1
self._wandb_epoch += 1/self.n_iter
hypers = {f'{k}_{i}':v for i,h in enumerate(self.opt.hypers) for k,v in h.items()}
wandb.log({'epoch': self._wandb_epoch, 'train_loss': to_detach(self.smooth_loss.clone()), 'raw_loss': to_detach(self.loss.clone()), **hypers}, step=self._wandb_step)
def after_epoch(self):
"Log validation loss and custom metrics & log prediction samples"
# Correct any epoch rounding error and overwrite value
self._wandb_epoch = round(self._wandb_epoch)
wandb.log({'epoch': self._wandb_epoch}, step=self._wandb_step)
# Log sample predictions
if self.log_preds:
try:
inp,preds,targs,out = self.learn.fetch_preds.preds
b = tuplify(inp) + tuplify(targs)
x,y,its,outs = self.valid_dl.show_results(b, out, show=False, max_n=self.n_preds)
wandb.log(wandb_process(x, y, its, outs), step=self._wandb_step)
except Exception as e:
self.log_preds = False
print(f'WandbCallback was not able to get prediction samples -> {e}')
wandb.log({n:s for n,s in zip(self.recorder.metric_names, self.recorder.log) if n not in ['train_loss', 'epoch', 'time']}, step=self._wandb_step)
def after_fit(self):
if self.log_model:
if self.save_model.last_saved_path is None:
print('WandbCallback could not retrieve a model to upload')
else:
metadata = {n:s for n,s in zip(self.recorder.metric_names, self.recorder.log) if n not in ['train_loss', 'epoch', 'time']}
log_model(self.save_model.last_saved_path, metadata=metadata)
self.run = True
if self.log_preds: self.remove_cb(FetchPredsCallback)
wandb.log({}) # ensure sync of last step
# Optionally logs weights and or gradients depending on `log` (can be "gradients", "parameters", "all" or None), sample predictions if ` log_preds=True` that will come from `valid_dl` or a random sample pf the validation set (determined by `seed`). `n_preds` are logged in this case.
#
# If used in combination with `SaveModelCallback`, the best model is saved as well (can be deactivated with `log_model=False`).
#
# Datasets can also be tracked:
# * if `log_dataset` is `True`, tracked folder is retrieved from `learn.dls.path`
# * `log_dataset` can explicitly be set to the folder to track
# * the name of the dataset can explicitly be given through `dataset_name`, otherwise it is set to the folder name
# * *Note: the subfolder "models" is always ignored*
#
# For custom scenarios, you can also manually use functions `log_dataset` and `log_model` to respectively log your own datasets and models.
#export
def _make_plt(img):
"Make plot to image resolution"
# from https://stackoverflow.com/a/13714915
my_dpi = 100
fig = plt.figure(frameon=False, dpi=my_dpi)
h, w = img.shape[:2]
fig.set_size_inches(w / my_dpi, h / my_dpi)
ax = plt.Axes(fig, [0., 0., 1., 1.])
ax.set_axis_off()
fig.add_axes(ax)
return fig, ax
#export
def _format_config(log_config):
"Format config parameters before logging them"
for k,v in log_config.items():
if callable(v):
if hasattr(v,'__qualname__') and hasattr(v,'__module__'): log_config[k] = f'{v.__module__}.{v.__qualname__}'
else: log_config[k] = str(v)
if isinstance(v, slice): log_config[k] = dict(slice_start=v.start, slice_step=v.step, slice_stop=v.stop)
#export
def _format_metadata(metadata):
"Format metadata associated to artifacts"
for k,v in metadata.items(): metadata[k] = str(v)
#export
def log_dataset(path, name=None, metadata={}):
"Log dataset folder"
# Check if wandb.init has been called in case datasets are logged manually
if wandb.run is None:
raise ValueError('You must call wandb.init() before log_dataset()')
path = Path(path)
if not path.is_dir():
raise f'path must be a valid directory: {path}'
name = ifnone(name, path.name)
_format_metadata(metadata)
artifact_dataset = wandb.Artifact(name=name, type='dataset', description='raw dataset', metadata=metadata)
# log everything except "models" folder
for p in path.ls():
if p.is_dir():
if p.name != 'models': artifact_dataset.add_dir(str(p.resolve()), name=p.name)
else: artifact_dataset.add_file(str(p.resolve()))
wandb.run.use_artifact(artifact_dataset)
#export
def log_model(path, name=None, metadata={}):
"Log model file"
if wandb.run is None:
raise ValueError('You must call wandb.init() before log_model()')
path = Path(path)
if not path.is_file():
raise f'path must be a valid file: {path}'
name = ifnone(name, f'run-{wandb.run.id}-model')
_format_metadata(metadata)
artifact_model = wandb.Artifact(name=name, type='model', description='trained model', metadata=metadata)
artifact_model.add_file(str(path.resolve()))
wandb.run.log_artifact(artifact_model)
#export
@typedispatch
def wandb_process(x:TensorImage, y, samples, outs):
"Process `sample` and `out` depending on the type of `x/y`"
res_input, res_pred, res_label = [],[],[]
for s,o in zip(samples, outs):
img = s[0].permute(1,2,0)
res_input.append(wandb.Image(img, caption='Input data'))
for t, capt, res in ((o[0], "Prediction", res_pred), (s[1], "Ground Truth", res_label)):
fig, ax = _make_plt(img)
# Superimpose label or prediction to input image
ax = img.show(ctx=ax)
ax = t.show(ctx=ax)
res.append(wandb.Image(fig, caption=capt))
plt.close(fig)
return {"Inputs":res_input, "Predictions":res_pred, "Ground Truth":res_label}
#export
@typedispatch
def wandb_process(x:TensorImage, y:(TensorCategory,TensorMultiCategory), samples, outs):
return {"Prediction Samples": [wandb.Image(s[0].permute(1,2,0), caption=f'Ground Truth: {s[1]}\nPrediction: {o[0]}')
for s,o in zip(samples,outs)]}
#export
@typedispatch
def wandb_process(x:TensorImage, y:TensorMask, samples, outs):
res = []
class_labels = {i:f'{c}' for i,c in enumerate(y.get_meta('codes'))} if y.get_meta('codes') is not None else None
for s,o in zip(samples, outs):
img = s[0].permute(1,2,0)
masks = {}
for t, capt in ((o[0], "Prediction"), (s[1], "Ground Truth")):
masks[capt] = {'mask_data':t.numpy().astype(np.uint8)}
if class_labels: masks[capt]['class_labels'] = class_labels
res.append(wandb.Image(img, masks=masks))
return {"Prediction Samples":res}
#export
@typedispatch
def wandb_process(x:TensorText, y:(TensorCategory,TensorMultiCategory), samples, outs):
data = [[s[0], s[1], o[0]] for s,o in zip(samples,outs)]
return {"Prediction Samples": wandb.Table(data=data, columns=["Text", "Target", "Prediction"])}
#export
@typedispatch
def wandb_process(x:Tabular, y:Tabular, samples, outs):
df = x.all_cols
for n in x.y_names: df[n+'_pred'] = y[n].values
return {"Prediction Samples": wandb.Table(dataframe=df)}
# ## Example of use:
#
# Once your have defined your `Learner`, before you call to `fit` or `fit_one_cycle`, you need to initialize wandb:
# ```
# import wandb
# wandb.init()
# ```
# To use Weights & Biases without an account, you can call `wandb.init(anonymous='allow')`.
#
# Then you add the callback to your `learner` or call to `fit` methods, potentially with `SaveModelCallback` if you want to save the best model:
# ```
# from fastai.callback.wandb import *
#
# # To log only during one training phase
# learn.fit(..., cbs=WandbCallback())
#
# # To log continuously for all training phases
# learn = learner(..., cbs=WandbCallback())
# ```
# Datasets and models can be tracked through the callback or directly through `log_model` and `log_dataset` functions.
#
# For more details, refer to [W&B documentation](https://docs.wandb.com/library/integrations/fastai).
# +
#hide
#slow
from fastai.vision.all import *
path = untar_data(URLs.MNIST_TINY)
items = get_image_files(path)
tds = Datasets(items, [PILImageBW.create, [parent_label, Categorize()]], splits=GrandparentSplitter()(items))
dls = tds.dataloaders(after_item=[ToTensor(), IntToFloatTensor()])
os.environ['WANDB_MODE'] = 'dryrun' # run offline
wandb.init(anonymous='allow')
learn = cnn_learner(dls, resnet18, loss_func=CrossEntropyLossFlat(), cbs=WandbCallback(log_model=False))
learn.fit(1)
# add more data from a new learner on same run
learn = cnn_learner(dls, resnet18, loss_func=CrossEntropyLossFlat(), cbs=WandbCallback(log_model=False))
learn.fit(1, lr=slice(0.05))
# -
#export
_all_ = ['wandb_process']
# ## Export -
#hide
from nbdev.export import *
notebook2script()
|
nbs/70_callback.wandb.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import nltk
import numpy as np
import torch
from nltk.tokenize import RegexpTokenizer
from nltk.stem import WordNetLemmatizer
from nltk.corpus import stopwords
from torch.utils.data import Dataset, DataLoader
from torch.nn.functional import pad
BATCH_SIZE = 64
# -
# read GloVe
# citation: https://stackoverflow.com/questions/37793118/load-pretrained-glove-vectors-in-python
def loadGloveModel(File):
print("Loading Glove Model")
with open(File, 'r', encoding='utf-8') as f:
gloveModel = {}
for line in f:
splitLines = line.split()
word = splitLines[0]
wordEmbedding = np.array([float(value) for value in splitLines[1:]])
gloveModel[word] = wordEmbedding
print(len(gloveModel)," words loaded!")
return gloveModel
# read movie reviews data
# tokenize -> lowercase -> remove stopwords -> lemmatize
def get_movie_reviews_data(path, data_type = "train"):
tokenizer = RegexpTokenizer(r'\w+')
lemmatizer = WordNetLemmatizer()
english_stopwords = stopwords.words('english')
if data_type == "train":
with open(path) as f:
lines = list(f.readlines())[1:]
sentences = [line.split('\t')[2] for line in lines]
labels = [int(line.split('\t')[3]) for line in lines]
tokenized_sentences = [[lemmatizer.lemmatize(token.lower()) for token in tokenizer.tokenize(sentence) if token.lower() in word2vec_dict and token.lower() not in english_stopwords] for sentence in sentences]
zipped = [(x, y) for x, y in zip(tokenized_sentences, labels) if x != []]
tokenized_sentences = [x for x, y in zipped]
labels = [y for x, y in zipped]
return tokenized_sentences, labels
elif data_type == "test":
with open(path) as f:
lines = list(f.readlines())[1:]
sentences = [line.split('\t')[2] for line in lines]
tokenized_sentences = [[lemmatizer.lemmatize(token.lower()) for token in tokenizer.tokenize(sentence) if token.lower() in word2vec_dict and token.lower() not in english_stopwords] for sentence in sentences]
tokenized_sentences = [x for x in tokenized_sentences if x != []]
return tokenized_sentences, None
# get embeddings
def get_embeddings(tokenized_sentences, word2vec_dict):
return [np.array([word2vec_dict[word] for word in x]) for x in tokenized_sentences]
# custom Dataset class
class MovieReviewsData(Dataset):
def __init__(self, X, Y = None):
self.maxlen = max(len(x) for x in X)
self.X = [pad(torch.FloatTensor(x), (0, 0, 0, self.maxlen - len(x))) for x in X]
if Y is not None:
self.Y = torch.LongTensor(Y)
else:
self.Y = None
def __len__(self):
return len(self.X)
def __getitem__(self, idx):
if self.Y is not None:
return self.X[idx], self.Y[idx]
else:
return self.X[idx]
# load data
word2vec_dict = loadGloveModel('glove.42B.300d/glove.42B.300d.txt')
train_tokenized_sentences, train_Y = get_movie_reviews_data("sentiment-analysis-on-movie-reviews/train.tsv", "train")
test_tokenized_sentences, _ = get_movie_reviews_data("sentiment-analysis-on-movie-reviews/test.tsv", "test")
train_X = get_embeddings(train_tokenized_sentences, word2vec_dict)
test_X = get_embeddings(test_tokenized_sentences, word2vec_dict)
np.save('train_X.npy', train_X)
np.save('train_Y.npy', train_Y)
np.save('test_X.npy', test_X)
train_dataset = MovieReviewsData(train_X, train_Y)
test_dataset = MovieReviewsData(test_X)
train_loader = DataLoader(train_dataset, shuffle = True, batch_size = BATCH_SIZE)
test_loader = DataLoader(test_dataset, shuffle = False, batch_size = BATCH_SIZE)
|
process_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# ### The following are steps in using this module
# First import the classifier and numpy.
import SVMClassifier as SVMC
import numpy as np
# Let's setup some data to feed into the SVM. A good day and an extremely bad day. The required features in order are: day length (hrs), average temperature (F), average humidity, max windspeed (mph), average windspeed (mph), max windgust (mph), precipitation (in). The first row is on a sunshine day, and the second row is a stormy day.
days = np.array([[11, 80, 80, 7, 3, 10, 0.], [8, 30, 50, 50, 30, 50, 1.]])
days.shape
# We see that days has the required shape to fit into SVMC. Great! Now to use it:
SVMC.predictOutage(days)
# The classifier is telling us, for the sunny day, it's classifiying the day as 0, which is a case when there are only 0 - 2 outages. On the other hand, for the stormy day, it's classifying the day as 2, which is a case when there are 8 or more outages.
#
# We can also predict the probabilities of each classification using the predictOutageProba function:
SVMC.predictOutageProba(days)
# For the sunny day, there is a 96% chance that the day is of type 0, i.e. 0 - 2 outages.
# For the stormy day, there is a 49% chance that the day is of type 2, i.e. more than 8 outages.
#
# #### Caution:
# The predictOutage function does not use the probabilities of the predictOutageProba function to make it's decision. The predictOutageProba function uses a pairwise correlation algorithm. Therefore they are not guaranteed to be consistent with each other, i.e. classification with the highest probability by predictOutageProba may not be the classification chosen by predictOutage. For more information please go to https://www.csie.ntu.edu.tw/~cjlin/libsvm/
|
PowerOutagePredictor/SVM/Example use of SVMClassifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload 2
# + pycharm={"name": "#%%\n"}
import pandas as pd
# + pycharm={"name": "#%%\n"}
# configure
dissimilar_path = "s3://familysearch-names/processed/tree-hr-given-dissimilar.csv.gz"
nickname_path = "s3://familysearch-names/processed/tree-hr-nicknames.csv.gz"
# + pycharm={"name": "#%%\n"}
df = pd.read_csv(dissimilar_path)
# + pycharm={"name": "#%%\n"}
df
# + pycharm={"name": "#%%\n"}
df.to_csv(nickname_path, columns=["name", "alt_name"], header=False, index=False)
# + pycharm={"name": "#%%\n"}
|
notebooks/41_generate_nicknames.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# (item_response_nba)=
# # NBA Foul Analysis with Item Response Theory
#
# :::{post} Apr 17, 2022
# :tags: hierarchical model, case study, generalized linear model
# :category: intermediate, tutorial
# :author: <NAME>, <NAME>
# :::
# +
import os
import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pymc as pm
# %matplotlib inline
print(f"Running on PyMC v{pm.__version__}")
# -
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)
az.style.use("arviz-darkgrid")
# ## Introduction
# This tutorial shows an application of Bayesian Item Response Theory {cite:p}`fox2010bayesian` to NBA basketball foul calls data using PyMC. Based on Austin Rochford's blogpost [NBA Foul Calls and Bayesian Item Response Theory](https://www.austinrochford.com/posts/2017-04-04-nba-irt.html).
#
# ### Motivation
# Our scenario is that we observe a binary outcome (a foul being called or not) from an interaction (a basketball play) of two agents with two different roles (the player committing the alleged foul and the player disadvantaged in the play). Moreover, each committing or disadvantaged agent is an individual which might be observed several times (say LeBron James observed committing a foul in more than one play). Then it might be that not only the agent's role, but also the abilities of the single individual player contribute to the observed outcome. And so we'd like to __estimate the contribution to the observed outcome of each individual's (latent) ability as a committing or disadvantaged agent.__ This would allow us, for example, to rank players from more to less effective, quantify uncertainty in this ranking and discover extra hierarchical structures involved in foul calls. All pretty useful stuff!
#
#
# So how can we study this common and complex __multi-agent interaction__ scenario, with __hierarchical__ structures between more than a thousand individuals?
#
# Despite the scenario's overwhelming complexity, Bayesian Item Response Theory combined with modern powerful statistical software allows for quite elegant and effective modeling options. One of these options employs a {term}`Generalized Linear Model` called [Rasch model](https://en.wikipedia.org/wiki/Rasch_model), which we now discuss in more detail.
#
#
# ### Rasch Model
# We sourced our data from the official [NBA Last Two Minutes Reports](https://official.nba.com/2020-21-nba-officiating-last-two-minute-reports/) with game data between 2015 to 2021. In this dataset, each row `k` is one play involving two players (the committing and the disadvantaged) where a foul has been either called or not. So we model the probability `p_k` that a referee calls a foul in play `k` as a function of the players involved. Hence we define two latent variables for each player, namely:
# - `theta`: which estimates the player's ability to have a foul called when disadvantaged, and
# - `b`: which estimates the player's ability to have a foul not called when committing.
#
# Note that the higher these player's parameters, the better the outcome for the player's team. These two parameters are then estimated using a standard Rasch model, by assuming the log-odds-ratio of `p_k` equals `theta-b` for the corresponding players involved in play `k`. Also, we place hierarchical hyperpriors on all `theta`'s and all `b`'s to account for shared abilities between players and largely different numbers of observations for different players.
#
#
# ### Discussion
# Our analysis gives an estimate of the latent skills `theta` and `b` for each player in terms of posterior distributions. We analyze this outcome in three ways.
#
# We first display the role of shared hyperpriors, by showing how posteriors of players with little observations are drawn to the league average.
#
# Secondly, we rank the posteriors by their mean to view best and worst committing and disadvantaged players, and observe that several players still rank in the top 10 of the same model estimated in [Austin Rochford blogpost](https://www.austinrochford.com/posts/2017-04-04-nba-irt.html) on different data.
#
# Thirdly, we show how we spot that grouping payers by their position is likely to be an informative extra hierarchical layer to introduce in our model, and leave this as an exercise for the interested reader. Let us conclude by mentioning that this opportunity of easily adding informed hierarchical structure to a model is one of the features that makes Bayesian modelling very flexible and powerful for quantifying uncertainty in scenarios where introducing (or discovering) problem-specific knowledge is crucial.
#
#
# The analysis in this notebook is performed in four main steps:
#
# 1. Data collection and processing.
# 2. Definition and instantiation of the Rasch model.
# 3. Posterior sampling and convergence checks.
# 4. Analysis of the posterior results.
#
# ## Data collection and processing
# We first import data from the original data set, which can be found at [this URL](https://raw.githubusercontent.com/polygraph-cool/last-two-minute-report/32f1c43dfa06c2e7652cc51ea65758007f2a1a01/output/all_games.csv). Each row corresponds to a play between the NBA seasons 2015-16 and 2020-21. We imported only five columns, namely
# - `committing`: the name of the committing player in the play.
# - `disadvantaged`: the name of the disadvantaged player in the play.
# - `decision`: the reviewed decision of the play, which can take four values, namely:
# - `CNC`: correct noncall, `INC`: incorrect noncall, `IC`: incorrect call, `CC`: correct call.
# - `committing_position`: the position of the committing player which can take values
# - `G`: guard, `F`: forward, `C`: center, `G-F`, `F-G`, `F-C`, `C-F`.
# - `disadvantaged_position`: the position of the disadvantaged player, with possible values as above.
#
# We note that we already removed from the original dataset the plays where less than two players are involved (for example travel calls or clock violations). Also, the original dataset does not contain information on the players' position, which we added ourselves.
# + tags=[]
try:
df_orig = pd.read_csv(os.path.join("..", "data", "item_response_nba.csv"), index_col=0)
except FileNotFoundError:
df_orig = pd.read_csv(pm.get_data("item_response_nba.csv"), index_col=0)
df_orig.head()
# -
# We now process our data in three steps:
# 1. We create a dataframe `df` by removing the position information from `df_orig`, and we create a dataframe `df_position` collecting all players with the respective position. (This last dataframe will not be used until the very end of the notebook.)
# 2. We add a column to `df`, called `foul_called`, that assigns 1 to a play if a foul was called, and 0 otherwise.
# 3. We assign IDs to committing and disadvantaged players and use this indexing to identify the respective players in each observed play.
#
# Finally, we display the head of our main dataframe `df` along with some basic statistics.
# + tags=[]
# 1. Construct df and df_position
df = df_orig[["committing", "disadvantaged", "decision"]]
df_position = pd.concat(
[
df_orig.groupby("committing").committing_position.first(),
df_orig.groupby("disadvantaged").disadvantaged_position.first(),
]
).to_frame()
df_position = df_position[~df_position.index.duplicated(keep="first")]
df_position.index.name = "player"
df_position.columns = ["position"]
# 2. Create the binary foul_called variable
def foul_called(decision):
"""Correct and incorrect noncalls (CNC and INC) take value 0.
Correct and incorrect calls (CC and IC) take value 1.
"""
out = 0
if (decision == "CC") | (decision == "IC"):
out = 1
return out
df = df.assign(foul_called=lambda df: df["decision"].apply(foul_called))
# 3 We index observed calls by committing and disadvantaged players
committing_observed, committing = pd.factorize(df.committing, sort=True)
disadvantaged_observed, disadvantaged = pd.factorize(df.disadvantaged, sort=True)
df.index.name = "play_id"
# Display of main dataframe with some statistics
print(f"Number of observed plays: {len(df)}")
print(f"Number of disadvanteged players: {len(disadvantaged)}")
print(f"Number of committing players: {len(committing)}")
print(f"Global probability of a foul being called: " f"{100*round(df.foul_called.mean(),3)}%\n\n")
df.head()
# + [markdown] tags=[]
# ## Item Response Model
#
# ### Model definition
#
# We denote by:
# - $N_d$ and $N_c$ the number of disadvantaged and committing players, respectively,
# - $K$ the number of plays,
# - $k$ a play,
# - $y_k$ the observed call/noncall in play $k$,
# - $p_k$ the probability of a foul being called in play $k$,
# - $i(k)$ the disadvantaged player in play $k$, and by
# - $j(k)$ the committing player in play $k$.
#
# We assume that each disadvantaged player is described by the latent variable:
# - $\theta_i$ for $i=1,2,...,N_d$,
#
# and each committing player is described by the latent variable:
# - $b_j$ for $j=1,2,...,N_c$.
#
# Then we model each observation $y_k$ as the result of an independent Bernoulli trial with probability $p_k$, where
#
# $$
# p_k =\text{sigmoid}(\eta_k)=\left(1+e^{-\eta_k}\right)^{-1},\quad\text{with}\quad \eta_k=\theta_{i(k)}-b_{j(k)},
# $$
#
# for $k=1,2,...,K$, by defining (via a [non-centered parametrisation](https://twiecki.io/blog/2017/02/08/bayesian-hierchical-non-centered/))
#
# \begin{align*}
# \theta_{i}&= \sigma_\theta\Delta_{\theta,i}+\mu_\theta\sim \text{Normal}(\mu_\theta,\sigma_\theta^2), &i=1,2,...,N_d,\\
# b_{j}&= \sigma_b\Delta_{b,j}\sim \text{Normal}(0,\sigma_b^2), &j=1,2,...,N_c,
# \end{align*}
#
# with priors/hyperpriors
#
# \begin{align*}
# \Delta_{\theta,i}&\sim \text{Normal}(0,1), &i=1,2,...,N_d,\\
# \Delta_{b,j}&\sim \text{Normal}(0,1), &j=1,2,...,N_c,\\
# \mu_\theta&\sim \text{Normal}(0,100),\\
# \sigma_\theta &\sim \text{HalfCauchy}(2.5),\\
# \sigma_b &\sim \text{HalfCauchy}(2.5).
# \end{align*}
#
# Note that $p_k$ is always dependent on $\mu_\theta,\,\sigma_\theta$ and $\sigma_b$ ("pooled priors") and also depends on the actual players involved in the play due to $\Delta_{\theta,i}$ and $\Delta_{b,j}$ ("unpooled priors"). This means our model features partial pooling. Morover, note that we do not pool $\theta$'s with $b$'s, hence assuming these skills are independent even for the same player. Also, note that we normalised the mean of $b_{j}$ to zero.
#
# Finally, notice how we worked backwards from our data to construct this model. This is a very natural way to construct a model, allowing us to quickly see how each variable connects to others and their intuition. Meanwhile, when instantiating the model below, the construction goes in the opposite direction, i.e. starting from priors and moving up to the observations.
#
# ### PyMC implementation
# We now implement the model above in PyMC. Note that, to easily keep track of the players (as we have hundreds of them being both committing and disadvantaged), we make use of the `coords` argument for {class}`pymc.Model`. (For tutorials on this functionality see the notebook {ref}`data_container` or [this blogpost](https://oriolabrilpla.cat/python/arviz/pymc3/xarray/2020/09/22/pymc3-arviz.html).) We choose our priors to be the same as in [Austin Rochford's post](https://www.austinrochford.com/posts/2017-04-04-nba-irt.html), to make the comparison consistent.
# +
coords = {"disadvantaged": disadvantaged, "committing": committing}
with pm.Model(coords=coords) as model:
# Data
foul_called_observed = pm.Data("foul_called_observed", df.foul_called, mutable=False)
# Hyperpriors
mu_theta = pm.Normal("mu_theta", 0.0, 100.0)
sigma_theta = pm.HalfCauchy("sigma_theta", 2.5)
sigma_b = pm.HalfCauchy("sigma_b", 2.5)
# Priors
Delta_theta = pm.Normal("Delta_theta", 0.0, 1.0, dims="disadvantaged")
Delta_b = pm.Normal("Delta_b", 0.0, 1.0, dims="committing")
# Deterministic
theta = pm.Deterministic("theta", Delta_theta * sigma_theta + mu_theta, dims="disadvantaged")
b = pm.Deterministic("b", Delta_b * sigma_b, dims="committing")
eta = pm.Deterministic("eta", theta[disadvantaged_observed] - b[committing_observed])
# Likelihood
y = pm.Bernoulli("y", logit_p=eta, observed=foul_called_observed)
# -
# We now plot our model to show the hierarchical structure (and the non-centered parametrisation) on the variables `theta` and `b`.
# + tags=[]
pm.model_to_graphviz(model)
# -
# ## Sampling and convergence
#
# We now sample from our Rasch model.
with model:
trace = pm.sample(1000, tune=1500, random_seed=RANDOM_SEED)
# We plot below the energy difference of the obtained trace. Also, we assume our sampler has converged as it passed all automatic PyMC convergence checks.
az.plot_energy(trace);
# ## Posterior analysis
# ### Visualisation of partial pooling
# Our first check is to plot
# - y: the difference between the raw mean probability (from the data) and the posterior mean probability for each disadvantaged and committing player
# - x: as a function of the number of observations per disadvantaged and committing player.
#
# These plots show, as expected, that the hierarchical structure of our model tends to estimate posteriors towards the global mean for players with a low amount of observations.
# + tags=[]
# Global posterior means of μ_theta and μ_b
mu_theta_mean, mu_b_mean = trace.posterior["mu_theta"].mean(), 0
# Raw mean from data of each disadvantaged player
disadvantaged_raw_mean = df.groupby("disadvantaged")["foul_called"].mean()
# Raw mean from data of each committing player
committing_raw_mean = df.groupby("committing")["foul_called"].mean()
# Posterior mean of each disadvantaged player
disadvantaged_posterior_mean = (
1 / (1 + np.exp(-trace.posterior["theta"].mean(dim=["chain", "draw"]))).to_pandas()
)
# Posterior mean of each committing player
committing_posterior_mean = (
1
/ (1 + np.exp(-(mu_theta_mean - trace.posterior["b"].mean(dim=["chain", "draw"])))).to_pandas()
)
# Compute difference of raw and posterior mean for each
# disadvantaged and committing player
def diff(a, b):
return a - b
df_disadvantaged = pd.DataFrame(
disadvantaged_raw_mean.combine(disadvantaged_posterior_mean, diff),
columns=["Raw - posterior mean"],
)
df_committing = pd.DataFrame(
committing_raw_mean.combine(committing_posterior_mean, diff), columns=["Raw - posterior mean"]
)
# Add the number of observations for each disadvantaged and committing player
df_disadvantaged = df_disadvantaged.assign(obs_disadvantaged=df["disadvantaged"].value_counts())
df_committing = df_committing.assign(obs_committing=df["committing"].value_counts())
# Plot the difference between raw and posterior means as a function of
# the number of observations
fig, (ax1, ax2) = plt.subplots(1, 2, sharey=True)
fig.suptitle(
"Difference of raw and posterior mean of player's foul call probability as "
"\na function of the player's number of observations\n",
fontsize=15,
)
ax1.scatter(data=df_disadvantaged, x="obs_disadvantaged", y="Raw - posterior mean", s=7, marker="o")
ax1.set_title("theta")
ax1.set_ylabel("Raw mean - posterior mean")
ax1.set_xlabel("obs_disadvantaged")
ax2.scatter(data=df_committing, x="obs_committing", y="Raw - posterior mean", s=7)
ax2.set_title("b")
ax2.set_xlabel("obs_committing")
plt.show()
# -
# ### Top and bottom committing and disadvantaged players
# As we successfully estimated the skills of disadvantaged (`theta`) and committing (`b`) players, we can finally check which players perform better and worse in our model.
# So we now plot our posteriors using forest plots. We plot the 10 top and bottom players ranked with respect to the latent skill `theta` and `b`, respectively.
# +
def order_posterior(inferencedata, var, bottom_bool):
xarray_ = inferencedata.posterior[var].mean(dim=["chain", "draw"])
return xarray_.sortby(xarray_, ascending=bottom_bool)
top_theta, bottom_theta = (
order_posterior(trace, "theta", False),
order_posterior(trace, "theta", True),
)
top_b, bottom_b = (order_posterior(trace, "b", False), order_posterior(trace, "b", True))
amount = 10 # How many top players we want to display in each cathegory
fig = plt.figure(figsize=(17, 14))
fig.suptitle(
"\nPosterior estimates for top and bottom disadvantaged (theta) and "
"committing (b) players \n(94% HDI)\n",
fontsize=25,
)
theta_top_ax = fig.add_subplot(221)
b_top_ax = fig.add_subplot(222)
theta_bottom_ax = fig.add_subplot(223, sharex=theta_top_ax)
b_bottom_ax = fig.add_subplot(224, sharex=b_top_ax)
# theta: plot top
az.plot_forest(
trace,
var_names=["theta"],
combined=True,
coords={"disadvantaged": top_theta["disadvantaged"][:amount]},
ax=theta_top_ax,
labeller=az.labels.NoVarLabeller(),
)
theta_top_ax.set_title(f"theta: top {amount}")
theta_top_ax.set_xlabel("theta\n")
theta_top_ax.set_xlim(xmin=-2.5, xmax=0.1)
theta_top_ax.vlines(mu_theta_mean, -1, amount, "k", "--", label=("League average"))
theta_top_ax.legend(loc=2)
# theta: plot bottom
az.plot_forest(
trace,
var_names=["theta"],
colors="blue",
combined=True,
coords={"disadvantaged": bottom_theta["disadvantaged"][:amount]},
ax=theta_bottom_ax,
labeller=az.labels.NoVarLabeller(),
)
theta_bottom_ax.set_title(f"theta: bottom {amount}")
theta_bottom_ax.set_xlabel("theta")
theta_bottom_ax.vlines(mu_theta_mean, -1, amount, "k", "--", label=("League average"))
theta_bottom_ax.legend(loc=2)
# b: plot top
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": top_b["committing"][:amount]},
ax=b_top_ax,
labeller=az.labels.NoVarLabeller(),
)
b_top_ax.set_title(f"b: top {amount}")
b_top_ax.set_xlabel("b\n")
b_top_ax.set_xlim(xmin=-1.5, xmax=1.5)
b_top_ax.vlines(0, -1, amount, "k", "--", label="League average")
b_top_ax.legend(loc=2)
# b: plot bottom
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": bottom_b["committing"][:amount]},
ax=b_bottom_ax,
labeller=az.labels.NoVarLabeller(),
)
b_bottom_ax.set_title(f"b: bottom {amount}")
b_bottom_ax.set_xlabel("b")
b_bottom_ax.vlines(0, -1, amount, "k", "--", label="League average")
b_bottom_ax.legend(loc=2)
plt.show();
# -
# By visiting [Austin Rochford post](https://www.austinrochford.com/posts/2017-04-04-nba-irt.html) and checking the analogous table for the Rasch model there (which uses data from the 2016-17 season), the reader can see that several top players in both skills are still in the top 10 with our larger data set (covering seasons 2015-16 to 2020-21).
# + [markdown] tags=[]
# ### Discovering extra hierarchical structure
#
# A natural question to ask is whether players skilled as disadvantaged players (i.e. players with high `theta`) are also likely to be skilled as committing players (i.e. with high `b`), and the other way around. So, the next two plots show the `theta` (resp. `b`) score for the top players with respect to `b` ( resp.`theta`).
# +
amount = 20 # How many top players we want to display
top_theta_players = top_theta["disadvantaged"][:amount].values
top_b_players = top_b["committing"][:amount].values
top_theta_in_committing = set(committing).intersection(set(top_theta_players))
top_b_in_disadvantaged = set(disadvantaged).intersection(set(top_b_players))
if (len(top_theta_in_committing) < amount) | (len(top_b_in_disadvantaged) < amount):
print(
f"Some players in the top {amount} for theta (or b) do not have observations for b (or theta).\n",
"Plot not shown",
)
else:
fig = plt.figure(figsize=(17, 14))
fig.suptitle(
"\nScores as committing (b) for best disadvantaged (theta) players"
" and vice versa"
"\n(94% HDI)\n",
fontsize=25,
)
b_top_theta = fig.add_subplot(121)
theta_top_b = fig.add_subplot(122)
az.plot_forest(
trace,
var_names=["b"],
colors="blue",
combined=True,
coords={"committing": top_theta_players},
figsize=(7, 7),
ax=b_top_theta,
labeller=az.labels.NoVarLabeller(),
)
b_top_theta.set_title(f"\nb score for top {amount} in theta\n (94% HDI)\n\n", fontsize=17)
b_top_theta.set_xlabel("b")
b_top_theta.vlines(mu_b_mean, -1, amount, color="k", ls="--", label="League average")
b_top_theta.legend(loc="upper right", bbox_to_anchor=(0.46, 1.05))
az.plot_forest(
trace,
var_names=["theta"],
colors="blue",
combined=True,
coords={"disadvantaged": top_b_players},
figsize=(7, 7),
ax=theta_top_b,
labeller=az.labels.NoVarLabeller(),
)
theta_top_b.set_title(f"\ntheta score for top {amount} in b\n (94% HDI)\n\n", fontsize=17)
theta_top_b.set_xlabel("theta")
theta_top_b.vlines(mu_theta_mean, -1, amount, color="k", ls="--", label="League average")
theta_top_b.legend(loc="upper right", bbox_to_anchor=(0.46, 1.05));
# -
# These plots suggest that scoring high in `theta` does not correlate with high or low scores in `b`. Moreover, with a little knowledge of NBA basketball, one can visually note that a higher score in `b` is expected from players playing center or forward rather than guards or point guards.
# Given the last observation, we decide to plot a histogram for the occurrence of different positions for top disadvantaged (`theta`) and committing (`b`) players. Interestingly, we see below that the largest share of best disadvantaged players are guards, meanwhile, the largest share of best committing players are centers (and at the same time a very small share of guards).
# + tags=[]
amount = 50 # How many top players we want to display
top_theta_players = top_theta["disadvantaged"][:amount].values
top_b_players = top_b["committing"][:amount].values
positions = ["C", "C-F", "F-C", "F", "G-F", "G"]
# Histogram of positions of top disadvantaged players
fig = plt.figure(figsize=(8, 6))
top_theta_position = fig.add_subplot(121)
df_position.loc[df_position.index.isin(top_theta_players)].position.value_counts().loc[
positions
].plot.bar(ax=top_theta_position, color="orange", label="theta")
top_theta_position.set_title(f"Positions of top {amount} disadvantaged (theta)\n", fontsize=12)
top_theta_position.legend(loc="upper left")
# Histogram of positions of top committing players
top_b_position = fig.add_subplot(122, sharey=top_theta_position)
df_position.loc[df_position.index.isin(top_b_players)].position.value_counts().loc[
positions
].plot.bar(ax=top_b_position, label="b")
top_b_position.set_title(f"Positions of top {amount} committing (b)\n", fontsize=12)
top_b_position.legend(loc="upper right");
# -
# The histograms above suggest that it might be appropriate to add a hierarchical layer to our model. Namely, group disadvantaged and committing players by the respective positions to account for the role of position in evaluating the latent skills `theta` and `b`. This can be done in our Rasch model by imposing mean and variance hyperpriors for each player grouped by the positions, which is left as an exercise for the reader. To this end, notice that the dataframe `df_orig` is set up precisely to add this hierarchical structure. Have fun!
#
# A warm thank you goes to [<NAME>](https://github.com/ericmjl) for many useful comments that improved this notebook.
# + [markdown] tags=[]
# ## Authors
#
# * Adapted from Austin Rochford's [blogpost on NBA Foul Calls and Bayesian Item Response Theory](https://www.austinrochford.com/posts/2017-04-04-nba-irt.html) by [<NAME>](https://github.com/ltoniazzi) on 3 Jul 2021 ([PR181](https://github.com/pymc-devs/pymc-examples/pull/181))
# * Re-executed by [<NAME>](https://github.com/michaelosthege) on 10 Jan 2022 ([PR266](https://github.com/pymc-devs/pymc-examples/pull/266))
# * Updated by [<NAME>](https://github.com/ltoniazzi) on 25 Apr 2022 ([PR309](https://github.com/pymc-devs/pymc-examples/pull/309))
# -
# ## References
#
# :::{bibliography}
# :filter: docname in docnames
# :::
# ## Watermark
# + tags=[]
# %load_ext watermark
# %watermark -n -u -v -iv -w -p aesara,aeppl,xarray
# -
# :::{include} ../page_footer.md
# :::
|
examples/case_studies/item_response_nba.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Email from Python demo
#
# This notebook is based on [<NAME>'s video](https://www.youtube.com/watch?v=JRCJ6RtE3xU&t=751s).
#
# His video and work is gratefully acknowledged.
#
# First we need to setup an App password in gmail, see his video for how to do that.
#
# Next we need to set up an environment variable to hide the password and not use is in plain text in the app, see his [video](https://www.youtube.com/watch?v=5iWhQWVXosU) on that topic.
#
# ### Import libraries, environment variables and input files
#
# _environment variables and files are listed in a `enviro.py` file that is ignored by `.gitignore`_
import os
import smtplib
import imghdr
from email.message import EmailMessage
from enviro import gmail_login, gmail_pwd, email, email2, file01, image_list, csv_files
# ### Initialize variables
# +
# Login credentials to send emails from
login = gmail_login
password = <PASSWORD>
# Target email addresses
email_01 = email
email_02 = email2
# a single file to send
single_file = file01
# a list of images to send
file_list = image_list
# a list of data files to send
data_files = csv_files
# -
# ### SMTP protocol
#
# First a real example.
#
# **Note that the lines that actually send the emails are commented out to avoid sending emails each time the notebook is run.**
with smtplib.SMTP('smtp.gmail.com', 587) as smtp:
smtp.ehlo()
smtp.starttls()
smtp.ehlo()
smtp.login(login, password)
subject = 'Simple SMTP protocol'
body = 'This is a test email'
msg = f'Subject: {subject}\n\n{body}'
# the next line will send an actual email
#smtp.sendmail(login, email, msg)
# Next the same code using a localhost for testing purposes:
#
# - open a terminal
#
# start a debug mail server
#
# - `python -m smtpd -c DebuggingServer -n localhost:1025`
#
with smtplib.SMTP('localhost', 1025) as smtp:
subject = 'Debugging Server'
body = 'This is a test email'
msg = f'Subject: {subject}\n\n{body}'
smtp.sendmail(login, email_01, msg)
# ### Sending emails more simply
# +
msg = EmailMessage()
msg['Subject'] = 'test email using EmailMessage() Class'
msg['From'] = login
msg['To'] = email_01
msg.set_content('This is a test email')
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
# ### Adding single attachement
# +
msg = EmailMessage()
msg['Subject'] = 'Test a single attachment (image)'
msg['From'] = login
msg['To'] = email_01
msg.set_content('File attached..')
with open(single_file, 'rb') as f:
file_data = f.read()
file_type = imghdr.what(f.name)
file_name = f.name
msg.add_attachment(file_data, maintype='image', subtype=file_type, filename=file_name)
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
# ### Adding mulitple attachements
#
# #### Images
# +
msg = EmailMessage()
msg['Subject'] = 'test multiple attachements (images)'
msg['From'] = login
msg['To'] = email_01
msg.set_content('File attached..')
image_files = file_list
for image in image_files:
file = '../../data/' + image
with open(file, 'rb') as f:
file_data = f.read()
file_type = imghdr.what(f.name)
file_name = f.name
msg.add_attachment(file_data, maintype='image', subtype=file_type, filename=file_name)
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
# #### Image files and generic bag of bytes type - i.e. generic data file
# +
msg = EmailMessage()
msg['Subject'] = 'test mulitple attachements (images and generic types)'
msg['From'] = login
msg['To'] = email_01
msg.set_content('File attached..')
image_files = file_list
data_files = data_files
for image in image_files:
file = '../../data/' + image
with open(file, 'rb') as f:
file_data = f.read()
file_type = imghdr.what(f.name)
file_name = f.name
msg.add_attachment(file_data, maintype='image', subtype=file_type, filename=file_name)
for data_file in data_files:
file = '../../data/' + data_file
with open(file, 'rb') as f:
file_data = f.read()
file_name = f.name
msg.add_attachment(file_data, maintype='application', subtype='octet-stream', filename=file_name)
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
# ### Sending emails to multiple recipients
# +
contacts = [email_01, email_02]
msg = EmailMessage()
msg['Subject'] = 'test multiple recipents'
msg['From'] = login
msg['To'] = contacts
msg.set_content('File attached..')
image_files = file_list
for image in image_files:
file = '../../data/' + image
with open(file, 'rb') as f:
file_data = f.read()
file_type = imghdr.what(f.name)
file_name = f.name
msg.add_attachment(file_data, maintype='image', subtype=file_type, filename=file_name)
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
# ### Sending HTML
# +
msg = EmailMessage()
msg['Subject'] = 'test HTML email'
msg['From'] = login
msg['To'] = email_01
msg.set_content('This is a plain text sample email.')
msg.add_alternative("""\
<!DOCTYPE html>
<html>
<body>
<h1 style="color:SlateGray;">This is an HTML Email!</h1>
</body>
</html>
""", subtype='html')
with smtplib.SMTP_SSL('smtp.gmail.com', 465) as smtp:
smtp.login(login, password)
# the next line will send an actual email
#smtp.send_message(msg)
# -
|
scripts/demos/Email_from_python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
def read_search_strings(file_path='search_strings.csv'):
'''
Reads from csv from file_path
:return: pandas DataFrame of the csv
'''
df = pd.read_csv(file_path, header=0, sep=',', encoding='latin1')
return df
df = read_search_strings()
# +
def cleanup_categoryid(df):
'''
Assigns new category id starting from 1.
** This function modifies df **
:return: dictionary[key] = categroyId
'''
i = 0
category_dict = dict()
for j, row in df.iterrows():
category = row[3]
if not category in category_dict.keys():
i += 1
category_dict[category] = i
df.at[j, 'categoryId'] = i
else:
df.at[j, 'categoryId'] = i
return category_dict
print(cleanup_categoryid(df))
df[100:200]
df
# +
from sklearn.model_selection import train_test_split
def data_split(df, train=0.65, valid=0.15, test=0.20):
"""
split data into training, validation, and test sets
:param df: the data set
:param train: percentage of training data
:param valid: percentage of validation data
:param test: percentage of test data
:return: X_train, X_valid, X_test, Y_train, Y_valid, Y_test
"""
# instantiate variables
column_headers = list(df.columns.values)
X_train = pd.DataFrame()
X_valid = pd.DataFrame()
X_test = pd.DataFrame()
Y_train = pd.DataFrame()
Y_valid = pd.DataFrame()
Y_test = pd.DataFrame()
id_num = df['categoryId'].nunique()
for i in range(1, id_num+1):
x_category_df = df.loc[df['categoryId'] == i]['item_title']
y_category_df = df.loc[df['categoryId'] == i]['categoryId']
x_category_train_valid, x_category_test, y_category_train_valid, y_category_test = \
train_test_split(x_category_df, y_category_df, test_size=test)
x_category_train, x_category_valid, y_category_train, y_category_valid = \
train_test_split(x_category_train_valid, y_category_train_valid, train_size=train/(train+valid))
X_train = pd.concat([X_train, x_category_train], axis=0)
X_valid = pd.concat([X_valid, x_category_valid], axis=0)
X_test = pd.concat([X_test, x_category_test], axis=0)
Y_train = pd.concat([Y_train, y_category_train], axis=0)
Y_valid = pd.concat([Y_valid, y_category_valid], axis=0)
Y_test = pd.concat([Y_test, y_category_test], axis=0)
return X_train, X_valid, X_test, Y_train, Y_valid, Y_test
data_split(df)
# -
|
notebooks/data_cleaner.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Content:<br>
#
# * [1. Resampling - dimensionality reductions](#resampl)
# * [2. Features extraction steps](#featuresextractionsteps)
# +
import os
from os.path import isdir, join
from pathlib import Path
import pandas as pd
# Math
import numpy as np
from scipy.fftpack import fft
from scipy import signal
from scipy.io import wavfile
import librosa
from sklearn.decomposition import PCA
# Visualization
import matplotlib.pyplot as plt
import seaborn as sns
import IPython.display as ipd
import librosa.display
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
import pandas as pd
# %matplotlib inline
# +
import sys
sys.path.insert(1, '../../')
from libs.utils import *
from libs.functions import *
# -
train_audio_path = '../../../_inputs/raw/train/audio/'
#
# + _cell_guid="02126a6d-dd84-4f0a-88eb-ed9ff46a9bdf" _uuid="76266716e7df45a83073fb2964218c85b36d31cb"
filename = '/yes/0a7c2a8d_nohash_0.wav'
# sample_rate, samples = wavfile.read(str(train_audio_path) + filename)
samples, sample_rate = librosa.load(str(train_audio_path)+filename)
# + [markdown] _cell_guid="a7715152-3866-48dd-8bbb-31a72e9aa9bf" _uuid="3bc26d76ea9f627c4d476ff8e9523f37d0668bbf"
# Define a function that calculates spectrogram.
#
# Note, that we are taking logarithm of spectrogram values. It will make our plot much more clear, moreover, it is strictly connected to the way people hear.
# We need to assure that there are no 0 values as input to logarithm.
# + [markdown] _cell_guid="f081f185-336a-429d-ba71-c0d2337c35ae" _uuid="e8f5fa497bbd2b3f5e7dbb9fa20d59d9773309a1"
# ## 1. Resampling - dimensionality reduction
# <a id="resampl"></a>
#
# Another way to reduce the dimensionality of our data is to resample recordings.
#
# You can hear that the recording don't sound very natural, because they are sampled with 16k frequency, and we usually hear much more. However, [the most speech related frequencies are presented in smaller band](https://en.wikipedia.org/wiki/Voice_frequency). That's why you can still understand another person talking to the telephone, where GSM signal is sampled to 8000 Hz.
#
# Summarizing, we could resample our dataset to 8k. We will discard some information that shouldn't be important, and we'll reduce size of the data.
#
# We have to remember that it can be risky, because this is a competition, and sometimes very small difference in performance wins, so we don't want to lost anything. On the other hand, first experiments can be done much faster with smaller training size.
#
# We'll need to calculate FFT (Fast Fourier Transform).
#
# + [markdown] _cell_guid="0fc3b446-d19e-4cd2-b1d6-3cf58ff332bf" _uuid="665e57b4652493e6d3b61ba2b7e70967170e7900"
# Let's read some recording, resample it, and listen. We can also compare FFT, Notice, that there is almost no information above 4000 Hz in original signal.
# + _cell_guid="919e85ca-7769-4214-a1d7-5eaa74a32b19" _uuid="b8fdb36dc4fce089ea5a3c3dcc27f65625232e34"
filename = '/yes/0a7c2a8d_nohash_0.wav'
new_sample_rate = 8000
sample_rate, samples = wavfile.read(str(train_audio_path) + filename)
resampled = signal.resample(samples, int(new_sample_rate/sample_rate * samples.shape[0]))
# + _cell_guid="13f397f1-cd5d-4f0f-846a-0edd9f58bcff" _uuid="afa8138a2ae7888ade44713fb5f8451f9c9e7f02"
ipd.Audio(samples, rate=sample_rate)
# + _cell_guid="5ab11b21-9528-47fa-8ff0-244b1d0c94b3" _uuid="3f600c9414ab5cef205c814ba16a356d4121790b"
ipd.Audio(resampled, rate=new_sample_rate)
# + [markdown] _cell_guid="37da8174-e6aa-463d-bef7-c8b20c6ca513" _uuid="96380594085d818693b959307d371e95f727f03b"
# Almost no difference!
# + _cell_guid="baed6102-3c75-4f16-85d7-723d8a084b9a" _uuid="4448038dfa22ec582cde229346cb1ba309c76b9f"
xf, vals = custom_fft(samples, sample_rate)
plt.figure(figsize=(12, 4))
plt.title('FFT of recording sampled with ' + str(sample_rate) + ' Hz')
plt.plot(xf, vals)
plt.xlabel('Frequency')
plt.grid()
plt.show()
# + _cell_guid="3cc1a49a-4cd4-49ed-83c8-f2437062f8be" _uuid="88953237ea59d13e9647813bef06a911f06f0e61"
xf, vals = custom_fft(resampled, new_sample_rate)
plt.figure(figsize=(12, 4))
plt.title('FFT of recording sampled with ' + str(new_sample_rate) + ' Hz')
plt.plot(xf, vals)
plt.xlabel('Frequency')
plt.grid()
plt.show()
# + [markdown] _cell_guid="592ffc6a-edda-4b08-9419-d3462599da5c" _uuid="152c1b14d7a7b57d7ab4fb0bd52e38564406cb92"
# This is how we reduced dataset size twice!
# + [markdown] _cell_guid="f98fe35d-2d56-4153-b054-0882bd2e58ce" _uuid="57fe8c6a25753e2eb46285bc8d725d20182c1421"
# ## 2. Features extraction steps
# <a id="featuresextractionsteps"></a>
#
# I would propose the feature extraction algorithm like that:
# 1. Resampling
# 2. *VAD*
# 3. Maybe padding with 0 to make signals be equal length
# 4. Log spectrogram (or *MFCC*, or *PLP*)
# 5. Features normalization with *mean* and *std*
# 6. Stacking of a given number of frames to get temporal information
#
# It's a pity it can't be done in notebook. It has not much sense to write things from zero, and everything is ready to take, but in packages, that can not be imported in Kernels.
# -
|
FinalProject_SpeechRecognition/src/eda/additional/2. Resampling and Feature Extraction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
import numpy
# %matplotlib inline
def scurve(x, x0, dx):
"""Returns 0 for x<x0 or x>x+dx, and a cubic in between."""
s = numpy.minimum(1, numpy.maximum(0, (x-x0)/dx))
return (3 - 2*s)*( s*s )
def itau(ytau,taud,ys):
"""Returns a profile tau(ys) that uses s-curves between node,valuesa ytau,taud"""
taus = 0.*ys
ks = 0
for i in range(len(ys)):
y = ys[i]
if y>=ytau[ks+1]:
ks=min(len(ytau)-2,ks+1)
taus[i] = taud[ks] + ( taud[ks+1] - taud[ks]) * scurve(y, ytau[ks], ytau[ks+1]-ytau[ks])
return taus
ytau,taud = [-70,-45,-15,0,15,45,70], [0,.2,-0.1,-.02,-.1,.1,0]
ys = numpy.linspace(-70,70,100)
tau = itau(ytau, taud, ys)
plt.plot(ytau,taud,'x')
plt.plot(ys, tau)
plt.xlim(-70,70);
plt.xlabel('Latitude ($^\circ$N)');
plt.ylabel(r'$\tau$ (Pa)');
plt.grid();
|
docs/Wind profile.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## TRIERES showcase
# ### Case study: Give an input string to FPGA and get the upper-case string from FPGA
# ### You don't need FPGA knowledge, just basic Python syntax !!!
# 
#
# Assuming that the FPGA is already flashed
# Configure the Python path to look for FPGA aceleration library
import time
import sys
import os
snap_action_sw=os.environ['SNAP_ROOT'] + "/actions/hls_helloworld_python/sw"
sys.path.append(snap_action_sw)
# Import the FPGA accelerator library
import snap_helloworld_python
input = "Hello world. This is my first OpenCAPI TriEres experience with Python. It's extremely fun"
# Currently we reserve space on host for output (can also be done in library)
fpga_output = "11111111111111111111111111111111111111111111111111111111111111111111111111111111111111"
# Execute the FPGA accelerator as a Python function
# +
start_fpga = time.time()
out, fpga_output = snap_helloworld_python.uppercase(input)
done_fpga = time.time()
elapsed_fpga = done_fpga - start_fpga
# -
print("Output from FPGA:"+fpga_output)
# +
start_cpu = time.time()
cpu_output=input.upper()
done_cpu = time.time()
print("Output from CPU :"+cpu_output)
elapsed_cpu = done_cpu - start_cpu
# -
print("FPGA time = "+'{0:.10f}'.format(elapsed_fpga)+"\nCPU time = "+'{0:.10f}'.format(elapsed_cpu))
|
actions/hls_helloworld_python/sw/trieres_helloworld.ipynb
|
# ---
# title: This is a Knowledge Template Header
# authors:
# - sally_smarts
# - wesley_wisdom
# tags:
# - knowledge
# - example
# created_at: 2016-06-29
# updated_at: 2016-06-30
# tldr: This is short description of the content and findings of the post.
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# *NOTE: In the TL,DR, optimize for **clarity** and **comprehensiveness**. The goal is to convey the post with the least amount of friction, especially since ipython/beakers require much more scrolling than blog posts. Make the reader get a correct understanding of the post's takeaway, and the points supporting that takeaway without having to strain through paragraphs and tons of prose. Bullet points are great here, but are up to you. Try to avoid academic paper style abstracts.*
#
# - Having a specific title will help avoid having someone browse posts and only finding vague, similar sounding titles
# - Having an itemized, short, and clear tl,dr will help readers understand your content
# - Setting the reader's context with a motivation section makes someone understand how to judge your choices
# - Visualizations that can stand alone, via legends, labels, and captions are more understandable and powerful
#
# ### Motivation
# *NOTE: optimize in this section for **context setting**, as specifically as you can. For instance, this post is generally a set of standards for work in the repo. The specific motivation is to have least friction to current workflow while being able to painlessly aggregate it later.*
#
# The knowledge repo was created to consolidate research work that is currently scattered in emails, blogposts, and presentations, so that people didn't redo their work.
# ### This Section Says Exactly This Takeaway
# +
import pandas as pd
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
# %matplotlib inline
x = np.linspace(0, 3*np.pi, 500)
plot_df = pd.DataFrame()
plot_df["x"] = x
plot_df["y"] = np.sin(x**2)
plot_df.plot('x', 'y',
color='lightblue',
figsize=(15,10))
plt.title("Put enough labeling in your graph to be understood on its own", size=25)
plt.xlabel('you definitely need axis labels', size=20)
plt.ylabel('both of them', size=20)
# -
# *NOTE: in graphs, optimize for being able to **stand alone**. When aggregating and putting things in presentations, you won't have to recreate and add code to each plot to make it understandable without the entire post around it. Will it be understandable without several paragraphs?*
# ### Putting Big Bold Headers with Clear Takeaways Will Help Us Aggregate Later
# ### Appendix
# Put all the stuff here that is not necessary for supporting the points above. Good place for documentation without distraction.
|
knowledgerepos/test.kp/orig_src/test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# [View in Colaboratory](https://colab.research.google.com/github/raahatg21/Digit-Recognition-MNIST-Dataset-with-Keras/blob/master/MNIST_2.ipynb)
# + [markdown] id="14inq5rRYQnE" colab_type="text"
# # MNIST Dataset: Image Classification
# + [markdown] id="bViIm4_-X1AM" colab_type="text"
# **Using Convulution Neural Network trained from scratch. 99.15% Validation Accuracy. 99.14% Test Accuracy.**
# + id="DxCxYcyvYPlp" colab_type="code" colab={}
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot')
# + id="Y1yOTJQCYYjB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="ac2b260f-e63d-41fd-c0b3-2ff903869cec"
from keras.datasets import mnist
from keras import models
from keras import layers
from keras.utils import to_categorical
# + id="Xosgi2XOYtxB" colab_type="code" colab={}
# Importing the MNIST data that comes preloaded with Keras
(train_data, train_labels), (test_data, test_labels) = mnist.load_data()
# + id="2BNzRkODY0u2" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="44f97880-bdc4-4cd0-d201-935b2a438ccf"
train_data.shape, train_labels.shape
# + id="ok1ThhAdZl3E" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e3c4f986-4c62-4397-9f02-cac29eea9eab"
test_data.shape, test_labels.shape
# + id="IaxkwwqFY5SR" colab_type="code" colab={}
# Preprocessing the Data
train_data = train_data.reshape((60000, 28, 28, 1))
train_data = train_data.astype('float32')/255
test_data = test_data.reshape((10000, 28, 28, 1))
test_data = test_data.astype('float32')/255
# + id="iFupp9NvZhuV" colab_type="code" colab={}
# Preprocessing the Labels
train_labels = to_categorical(train_labels, num_classes = 10)
test_labels = to_categorical(test_labels, num_classes = 10)
# + id="69NrozUaZ-tn" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="b000f6df-d528-42cc-a868-e26dcfc56ea0"
# As an example
train_labels[1], test_labels[4]
# + id="IEfMrkPqaE9s" colab_type="code" colab={}
# Validation Split (First 10,000 samples of Training Set)
partial_train_data = train_data[10000:]
partial_train_labels = train_labels[10000:]
val_data = train_data[:10000]
val_labels = train_labels[:10000]
# + id="AQjUb973adW5" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 121} outputId="66c77903-6ca8-4ed4-892a-590505d273d1"
partial_train_data.shape, partial_train_labels.shape, val_data.shape, val_labels.shape, test_data.shape, test_labels.shape
# + id="UCf6BfZMatXX" colab_type="code" colab={}
# Building the Model (Convnet of 3 Pairs of Conv2D-MaxPool layers and 2 Dense layers. Dropout is also used to fight overfitting.)
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation = 'relu', input_shape = (28, 28, 1)))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Dropout(0.5))
model.add(layers.Conv2D(64, (3, 3), activation = 'relu'))
model.add(layers.MaxPooling2D(2, 2))
model.add(layers.Dropout(0.5))
model.add(layers.Conv2D(64, (3, 3), activation = 'relu'))
model.add(layers.Flatten())
model.add(layers.Dense(128, activation = 'relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(10, activation = 'softmax'))
# + id="bOPPad-mdOQ7" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 521} outputId="80dedbe2-39a8-453e-bad4-6ac5172302f3"
model.summary()
# + id="1jDqwKkpdP7c" colab_type="code" colab={}
# Compiling the Model
model.compile(optimizer = 'rmsprop', loss = 'categorical_crossentropy', metrics = ['acc'])
# + id="GA3iXGOhdd9v" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 729} outputId="c1167b24-e755-4bf7-d81c-bff7d5827165"
# Training
history = model.fit(partial_train_data, partial_train_labels, epochs = 20, batch_size = 128, validation_data = (val_data, val_labels), verbose = 2)
# + id="tPq8bsfCdv8L" colab_type="code" colab={}
loss = history.history['loss']
val_loss = history.history['val_loss']
acc = history.history['acc']
val_acc = history.history['val_acc']
# + id="-ByGc-F0gn_W" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 363} outputId="766fd52f-9100-4c0f-a1e3-966158d2b5c5"
# Plotting Training and Validation Loss
epochs = range(1, 21)
plt.plot(epochs, loss, 'ko', label = 'Training Loss')
plt.plot(epochs, val_loss, 'k', label = 'Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
# + id="pSDQ2KSbg-zr" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 363} outputId="9f03cbab-02fa-4166-d83e-e507a6edf3ab"
# Plotting Training and Validation Accuracy
plt.plot(epochs, acc, 'yo', label = 'Training Accuracy')
plt.plot(epochs, val_acc, 'y', label = 'Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()
# + id="8d6QMvUYhS3v" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 52} outputId="78c8d176-411e-4b62-ed63-4bcae12015e9"
# Evaluating on Test Data
test_loss, test_acc = model.evaluate(test_data, test_labels)
test_loss, test_acc
|
MNIST_9914.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
'''
Control Flow
'''
# +
# Variable
age = 21
# if Statement
if age > 18:
print('Eligible to vote')
# +
# Variable
age = 15
# if Statement
if age > 18:
print('Eligible to vote')
else:
print('Not eligible to vote')
# +
# Variable
x = 21
# if, elif and else Statement
if x < 0:
print('x is negative')
elif x % 2:
print('x is positive and odd')
else:
print('x is even and non-negative')
|
01 Introduction to Python/03_control Flow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import geopandas as gpd
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
from cartopy.feature import ShapelyFeature
import cartopy.crs as ccrs
import matplotlib.patches as mpatches
import plotly.graph_objects as go
import pandas as pd
import plotly.express as px
# +
# generate matplotlib handles to create a legend of the features we put in our map.
def generate_handles(labels, colors, edge='k', alpha=1):
lc = len(colors) # get the length of the color list
handles = []
for i in range(len(labels)):
handles.append(mpatches.Rectangle((0, 0), 1, 1, facecolor=colors[i % lc], edgecolor=edge, alpha=alpha))
return handles
plt.ion()
# -
# +
# load the outline of Northern Ireland and Ireland
outline = gpd.read_file('data_files/Simplified_Shapes/Ireland.shp')
outline = outline.to_crs(epsg=2158)
#load datasets for display on map
water = gpd.read_file('data_files/Files_for_analysis/water_per_county.shp')
water = water.to_crs(epsg=2158)
counties = gpd.read_file('data_files/Files_for_analysis/Ire_Counties.shp')
counties = counties.to_crs(epsg=2158)
center_counties = gpd.read_file('data_files/Simplified_Shapes/Counties_Center_pts.shp')
#center_counties = center_counties.to_crs(epsg=2158)
# -
water
# +
counties
# +
#shp_file = geopandas.read_file('myshpfile.shp')
#shp_file.to_file('myshpfile.geojson', driver='GeoJSON')
water = gpd.read_file('data_files/Files_for_analysis/water_per_county.shp')
#water = water.to_crs(epsg=2158)
#water.to_file('data_files/Files_for_analysis/county_water.geojson', driver='GeoJSON')
# +
#county_water = gpd.read_file('data_files/Files_for_analysis/county_water.geojson')
#print (county_water.head())
# +
fig, ax = plt.subplots(1, figsize=(12, 18))
# to make a nice colorbar that stays in line with our map, use these lines:
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1, axes_class=plt.Axes)
ax = water.plot(column='sum_area_s', ax=ax, vmin=0, vmax=275, cmap='bone_r', edgecolor='k',
legend=True, cax=cax, legend_kwds={'label': 'Total Area of Waterbodies in sq km'})
#Switch off the bounding box drawn round the map so it looks a bit tidier
ax.axis('off');
# -
fig.savefig('Total area of inland water per county in ireland.png', dpi=300, bbox_inches='tight')
# +
#
|
ipynb/Create_chloropleth_map_of_water_area_per_county.ipynb
|