code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Practice Session 08: Connected components and k-core decomposition
# In this session we will use [NetworkX](https://networkx.github.io/) to compute the number of connected components and the size of the largest connected component on a graph. We will use the [Star Wars graph](https://github.com/evelinag/StarWars-social-network/tree/master/networks).
#
# The dataset is contained in this input file that you will find in our [data](https://github.com/chatox/networks-science-course/tree/master/practicum/data) directory:
# * ``starwars.graphml``: co-occurence of characters in scenes in the Star Wars saga in [GraphML](http://graphml.graphdrawing.org/) format.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# # 1. The Star Wars graph
# The following code just loads the *Star Wars* graph into variable *g*. Leave as-is.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
import io
import networkx as nx
import matplotlib.pyplot as plt
import random
import numpy as np
INPUT_GRAPH_FILENAME = "starwars.graphml"
# +
# Read the graph in GraphML format
g_in = nx.read_graphml(INPUT_GRAPH_FILENAME)
# Re-label the nodes so they use the 'name' as label
g_relabeled = nx.relabel.relabel_nodes(g_in, dict(g_raw.nodes(data='name')))
# Convert the graph to undirected
g = g_relabeled.to_undirected()
# +
# Create a plot of 20x10
plt.figure(figsize=(20,10))
# Layout the nodes using a spring model
nx.draw_spring(g, with_labels=True)
# Display
_ = plt.show()
# -
# <font size="+1" color="red">Replace this cell with a brief commentary indicating the number of nodes (g.number_of_nodes()), edges (g.number_of_edges()), and connected components (by visual inspection) in the Star Wars graph.</font>
# # 2. Removing a fraction of edges
# The following function, `remove_fraction_edges(g, p)` returns a new graph which is a copy of *g* in which a fraction *p* of edges have been removed.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
def remove_fraction_edges(g_in, p):
# Check input is within bounds
if p < 0.0 or p > 1.0:
raise ValueError
# Create a copy of the input graph
g_out = g_in.copy()
# Decide how many edges should be in the output graph
target_num_edges = int((1.0-p) * g_in.number_of_edges())
# While there are more edges than desired
while g_out.number_of_edges() > target_num_edges:
# Remove one random edge
edge = random.choice(list(g_out.edges()))
g_out.remove_edge(edge[0], edge[1])
# Return the resulting graph
return g_out
# Use `remove_fraction_edges(g, p)` to create three graphs named *g10*, *g50*, and *g90* that should contain 10%, 50%, and 90% of the edges in the original graph. Then, plot those three graphs.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+1" color="red">Replace this cell with code to create g10, g50, g90 as described above, and to plot these three graphs.</font>
# <font size="+1" color="red">Replace this cell with a brief commentary of what you observe in these three graphs with respect to the number of connected components, the number of singletons, and the size of the largest connected components.</font>
# # 3. Number of connected components
# Next, we will write some code to count the number of connected components.
#
# This code will be structured around two functions: `assign_component` and `assign_component_recursive`.
#
# The function `assign_component` takes as input a graph *g*, and returns a dictionary that maps every node in *g* to a positive integer indicating its connected component number. The `assign_component` function should do the following:
#
# 1. Create an empty dictionary `node2componentid`
# 1. Start with `componentid = 1`
# 1. Iterate through all the nodes in the graph: `for node in g.nodes()`
# 1. For each `node` that is not in the `node2componentid` dictionary (i.e., `if node not in node2componentid`), call `assign_component_recursive`, incrementing *componentid* by 1 in each call
# 1. Return the `node2componentid` dictionary.
#
# The function `assign_component_recursive` takes the following arguments:
#
# 1. A graph *g*
# 1. A dictionary *node2componentid*
# 1. A starting node *starting_node*
# 1. A number *component_id*
#
# The function should do the following:
#
# 1. Set `node2componentid[starting_node] = component_id`.
# 1. For each neighbor in `g.neighbors(starting_node)`, if that neighbor is not in the `node2componentid` dictionary, call the function `assign_recursive(g, node2componentid, neighbor, componentid)`.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+1" color="red">Replace this cell with code for "assign_component_recursive" and "assign_component".</font>
# The code below returns the number of connected components. Leave as-is.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
def count_connected_components(g):
# Call the function to assign each node to a connected component
node2componentid = assign_component(g)
# Count the number of distinct values in this assignment
return len(set(node2componentid.values()))
# The code below computes how many connected components are in graphs in which 0%, 2%, 4%, ..., 98% of the edges are removed. Leave as-is.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# +
components_per_fraction = {}
for p in np.arange(0.0, 1.02, 0.02):
reduced_graph = remove_fraction_edges(g, p)
connected_components = count_connected_components(reduced_graph)
components_per_fraction[p] = connected_components
# -
# Create a plot in which in the x axis is the fraction of removed edges, and in the y axis the number of connected components as a fraction of the maximum number of connected components possible in the graph. Hence, both the x-axis and the y-axis should go from 0.0 to 1.0. Include labels in both axes. A basic plot is obtained as follows.
#
# ```python
# x_vals = sorted(components_per_fraction.keys())
# y_vals = [components_per_fraction[x]/g.number_of_nodes() for x in x_vals]
# plt.plot(x_vals, y_vals, ...)
# ```
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+1" color="red">Replace this cell with code to create the described graph.</font>
# <font size="+1" color="red">Replace this cell with a brief commentary with what you observe on this graph. Do you see a linear trend, or something else?</font>
# # 4. Largest connected component
# Write a function `size_largest_connected_component` to compute the size of the largest connected component on a graph. Basically you need to call `assign_component` and then iterate through the nodes, counting how many times you see each *componentid*, and returning the maximum of this.
#
# To obtain the maximum value on a dictionary, e.g., *component_sizes*, you can use `np.max(list(component_sizes.values()))`
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
def largest_connected_component(g):
node2componentid = assign_component(g)
component_sizes = {}
for (node,componentid) in node2componentid.items():
if componentid not in component_sizes:
component_sizes[componentid] = 0
component_sizes[componentid] += 1
return np.max(list(component_sizes.values()))
# <font size="+1" color="red">Replace this cell with code for "size_largest_connected_component".</font>
# Next, use the `size_largest_connected_component` function to obtain data to create a plot. In this plot, in the x axis there should be the fraction of removed nodes and in the y axis the size of the largest connected component as a fraction of the total number of nodes. Both axis should go from 0.0 to 1.0; remember to label the axes.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+1" color="red">Replace this cell with code to generate the requested graph.</font>
# <font size="+1" color="red">Replace this cell with a brief commentary on what you observe on this graph. Do you see a linear trend? Is there an inflection point? How many edges do you need to remove for the largest connected component to be, say, 80% of the nodes?</font>
# # 5. K-core decomposition
# Now we will perform a k-core decomposition, using the following auxiliary functions, which you can leave as-is.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# +
def get_max_degree(g):
degree_sequence = [x[1] for x in g.degree()]
return(max(degree_sequence))
def nodes_with_degree_less_or_equal_than(g, degree):
nodes = []
for node in g.nodes():
if g.degree(node) <= degree:
nodes.append(node)
return nodes
# -
# Complete the code for function `kcore_decomposition(g)`; to use this function, you do `node_to_kcore = kcore_decomposition(g)`.
#
# ```python
# def kcore_decomposition(graph):
# ''' Perform a k-core decomposition of the given graph
# '''
# g = graph.copy()
# max_degree = get_max_degree(g)
#
# node_to_level = {}
# for level in range(1, max_degree + 1):
#
# while True:
# # Obtain the list of nodes with degree <= level
# nodes_in_level = nodes_with_degree_less_or_equal_than(g, level)
#
# # Check if this list is empty
# if len(nodes_in_level) == 0:
# # TO-DO: implement (one line)
#
# # If the list is not empty, assign the nodes to the
# # corresponding level and remove the node
# for node in nodes_in_level:
# # TO-DO: implement this (two lines)
#
# return(node_to_level)
# ```
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+1" color="red">Replace this cell with your code for "kcore_decomposition"</font>
# <font size="+1" color="red">Replace this cell with code to list the nodes in the deepest k-core in the graph, and in the second deepest k-core.</font>
# <font size="+1" color="red">Replace this cell with a brief commentary on the type of characters you find in these k-cores.</font>
# # Deliver (individually)
#
# A .zip file containing:
#
# * This notebook.
#
#
# ## Extra points available
#
# For extra points and extra learning (+2, so your maximum grade can be a 12 in this assignment), note that in our graphs for the number of connected components and size of largest connected component, the line is not smooth. This is because there are random variations as the removal of edges is random every time. To fix this, you will need to repeat each experiment, e.g., 100 times, and plot the average line. For extra points, replace the graphs of number of connected components and size of largest connected component with an average of multiple experimental runs.
#
# **Note:** if you go for the extra points, add ``<font size="+2" color="blue">Additional results: multiple experiments per graph</font>`` at the top of your notebook.
#
# <font size="-1" color="gray">(Remove this cell when delivering.)</font>
# <font size="+2" color="#003300">I hereby declare that, except for the code provided by the course instructors, all of my code, report, and figures were produced by myself.</font>
|
practicum/OLD-ps08_components_k_cores.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="0phJzvmTrLJG"
# !pip uninstall tensorflow keras
# + id="WWaJcRwBrPGt"
# !pip install tensorflow==1.14 keras==2.1.2
# + id="cbW9mpFbrRlb"
# !git clone https://github.com/deepanrajm/deep_learning.git
# + id="BNYik2L5nJdY"
from keras.models import Sequential
from keras.layers import Dense, Dropout, LSTM
from keras.callbacks import LambdaCallback
import numpy as np
from pathlib import Path
# + id="r0MWFfw0rkyr"
# Load the training data
source_data = Path("deep_learning/Generate_Text/sherlock_holmes.txt").read_text()
text = source_data.lower()
# + id="cai3crD2rv2M"
# Create a list of unique characters in the data
chars = sorted(list(set(text)))
chars_to_numbers = dict((c, i) for i, c in enumerate(chars))
numbers_to_chars = dict((i, c) for i, c in enumerate(chars))
# Split the text into 40-character sequences
sequence_length = 40
# Capture both each 40-character sequence and the 41-st character that we want to predict
training_sequences = []
training_sequences_next_character = []
# + id="OzsqevDarxkk"
# Loop over training text, skipping 40 characters forward on each loop
for i in range(0, len(text) - sequence_length, 40):
# Grab the 40-character sequence as the X value
training_sequences.append(text[i: i + sequence_length])
# Grab the 41st character as the Y value to predict
training_sequences_next_character.append(text[i + sequence_length])
# + id="bNG-Ly6Dry_M"
# Convert letters to numbers to make training more efficient
X = np.zeros((len(training_sequences), sequence_length, len(chars)), dtype=np.bool)
y = np.zeros((len(training_sequences), len(chars)), dtype=np.bool)
for i, sentence in enumerate(training_sequences):
for t, char in enumerate(sentence):
X[i, t, chars_to_numbers[char]] = 1
y[i, chars_to_numbers[training_sequences_next_character[i]]] = 1
# + id="iKQWfwucr1mz"
def generate_new_text(epoch, _):
seed_text = "when you have eliminated the impossible,"
new_text = ""
# Generate 1000 characters of new text
for i in range(1000):
# Encode the seed text as an array of numbers the same way our training data is encoded
x_pred = np.zeros((1, sequence_length, len(chars)))
for t, char in enumerate(seed_text):
x_pred[0, t, chars_to_numbers[char]] = 1.
# Predict which letter is most likely to come next
predicted_letter_prob = model.predict(x_pred, verbose=0)[0]
# Uncomment these lines to control the amount of randomness.
# # Lower values make the model less random
# randomness = 0.6
# Hack to prevent sum of predictions from adding up to over 1.0 due to floating point precision issues
predicted_letter_prob *= 0.99
# Using the letter probabilities as weights, choose the next letter randomly
next_index = np.argmax(np.random.multinomial(1, predicted_letter_prob, 1))
# Look up the letter itself from it's index number
next_char = numbers_to_chars[next_index]
# Add the new letter to our new text.
new_text += next_char
# Update the seed text by dropping the first letter and adding the new letter.
# This is so we can predict the next letter in the sequence.
seed_text = seed_text[1:] + next_char
# Print the new text we generated
print(new_text)
# + id="4A6cLVOhr57D"
# Set up the model
model = Sequential()
model.add(LSTM(128, input_shape=(sequence_length, len(chars)), return_sequences=True))
model.add(LSTM(128))
model.add(Dropout(0.5))
model.add(Dense(len(chars), activation='softmax'))
model.compile(
loss='categorical_crossentropy',
optimizer="adam"
)
# Train the model
model.fit(
X,
y,
batch_size=128,
epochs=1,
verbose=2,
callbacks=[LambdaCallback(on_epoch_end=generate_new_text)]
)
|
Generate_Text/Text_Generate.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # An introduction to Logistic Regression
#
# This notebook is a brief explanation of how we can build a linear Machine Learning model in Python using [scikit-learn](http://scikit-learn.org). If you are unfamiliar with Logistic Regression, you can start by reading on [Wikipedia](https://en.wikipedia.org/wiki/Logistic_regression), or watch this very interesting series of [videos](https://www.youtube.com/watch?v=-la3q9d7AKQ) to get you up to speed.
#
# This example is built on the dataset provided for the [Kaggle competition](https://www.kaggle.com/c/titanic) "Titanic: Machine Learning for disaster". We are basically given information on the people who were on board, and we must build a model to predict what sort of people would have a better chance of survival ([spoiler](https://en.wikipedia.org/wiki/Women_and_children_first)).
#
# This is a classic example of a binary classification problem, since there are only two possible outcomes for each person. Logistic Regression is a popular choice because of its simplicity, and it can be accurate enough in certain situations. In this example, we will use this method to predict whether a person will survive or not based on their age, sex and the class of their ticket. So... let's do it.
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set(style="white")
# +
# Importing the dataset
dataset = pd.read_csv('../Data/train_titanic.csv')
dataset = dataset[dataset['Age'].notnull()]
cat_cols = ['Sex' ]
dataset = pd.get_dummies(dataset, columns = cat_cols)
X = dataset[['Pclass','Age','Sex_male']].values
y = dataset['Survived'].values
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X = scaler.fit_transform(X)
# -
import pyspark
from pyspark.sql import SparkSession
from pyspark.mllib.classification import LabeledPoint
from pyspark import SparkContext
sc = SparkContext.getOrCreate()
spark = SparkSession(sc)
# +
df = dataset[['Pclass','Age','Sex_male','Survived']]
s_df = spark.createDataFrame(df)
train_df, test_df = s_df.randomSplit([.8,.2],seed=1234)
train_dataset = train_df.rdd.map(lambda x: LabeledPoint(x[3], x[:3])).collect()
test_dataset = test_df.rdd.map(lambda x: LabeledPoint(x[3], x[:3])).collect()
# -
train_df.head(2)
# +
#from pyspark.mllib.classification import LogisticRegressionWithLBFGS
#from pyspark.mllib.regression import LabeledPoint
# Build the model
#model = LogisticRegressionWithLBFGS.train(sc.parallelize(train_dataset))
# +
from pyspark.ml.classification import LogisticRegression
from pyspark.ml.feature import VectorAssembler
vecAssembler = VectorAssembler(inputCols=["Age", "Sex_male", "Pclass"], outputCol="features")
train_datavector = vecAssembler.transform(train_df)
test_datavector = vecAssembler.transform(test_df)
# +
from pyspark.ml.feature import StandardScaler
scaler = StandardScaler(inputCol="features", outputCol="scaledFeatures",
withStd=True, withMean=False)
# Compute summary statistics by fitting the StandardScaler
scalerModel = scaler.fit(train_datavector)
# Normalize each feature to have unit standard deviation.
train_datav_scaled = scalerModel.transform(train_datavector)
test_datav_scaled = scalerModel.transform(test_datavector)
# +
lr = LogisticRegression(featuresCol="scaledFeatures",labelCol="Survived")
# Fit the model
lrModel = lr.fit(train_datav_scaled )
predictions = lrModel.transform(test_datav_scaled)
# -
# ### Training set and Test set
# Kaggle gives us a test set, but for this example we'd rather split it ourselves so we can visualize how the model is performing. We will keep 80% of the data in the training set.
# ### Feature scaling
# We apply feature scaling to normalize the range of each variable. This ensures that each feature contributes approximately the same to the distances computed in the objective function. Note that both the training and the test set must be scaled.
# ### Fitting Logistic Regression to the Training set
# Once the data is clean and ready, we can build the classifier and fit it to the training data.
# ### Predicting on the test set
# Once the model has learned from the training data, we can make predictions on the test data using predict.
# ### Assessing the model's performance
# There are several ways to assess how good our predictions are. One of them is the [confusion matrix](http://www.dataschool.io/simple-guide-to-confusion-matrix-terminology/). This will quickly let us see how many good and bad predictions the model is making. Alternatively, we can use the accuracy score, which gives us the ratio of correctly classified samples.
predictions_df.head()
# +
# Transformations to pandas
predictions_df = predictions.toPandas()
predictions_df = predictions_df[['scaledFeatures', 'Survived','prediction']]
predictions_df[['Age','Sex_male','Pclass']] = pd.DataFrame(predictions_df.scaledFeatures.values.tolist(), index= predictions_df.index)
predictions_df = predictions_df.drop(['scaledFeatures'],axis=1)
predictions_df.prediction = predictions_df.prediction.astype(int)
predictions_df.head(5)
X_test = predictions_df[['Pclass','Age','Sex_male']].values
y_test = predictions_df['Survived'].values
y_pred = predictions_df['prediction'].values
# +
from sklearn.metrics import accuracy_score
import numpy as np
acc_score = accuracy_score(np.array(predictions_df['Survived']),np.array(predictions_df['prediction']))
print acc_score
# -
# ### Bananas!
# So we have built a model with a fairly good accuracy (circa 85%). I am sure we can do better, but we can be proud of these numbers with a linear model that uses only three features.
# ## Visualizing our results
# We have used the accuracy score to assess our model's performance. This is very useful, but plotting the results is a more exciting way of looking at our work. So let's do that. We will first plot the predicted results, together with the decision boundary.
#
# The decision boundary separates our vector space in two regions (for the two possible outcomes in this case study, died or survived). Since we have three features, and we are using a linear model, the decision boundary is a plane that we can visualize on a 3-dimensional plot.
# Data transformations
#
X_test
# We need to reorder
# +
x_surf = np.linspace(np.min(X_test[:,0]), np.max(X_test[:,0]), 10) # generate a mesh
y_surf = np.linspace(np.min(X_test[:,1]), np.max(X_test[:,1]),10)
x_surf, y_surf = np.meshgrid(x_surf, y_surf)
z_surf = -(lrModel.intercept + lrModel.coefficients[0]*x_surf + lrModel.coefficients[1]*y_surf)/lrModel.coefficients[2]
# +
from mpl_toolkits.mplot3d import axes3d
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111, projection='3d')
died = np.where(y_pred==0)[0]
survived = np.where(y_pred==1)[0]
p=ax.scatter(xs = X_test[died,0], ys =X_test[died,1], zs=X_test[died,2],
zdir='z', s=20, c='red',label = 'Died')
p=ax.scatter(xs = X_test[survived,0], ys =X_test[survived,1], zs=X_test[survived,2],
zdir='z', s=20, c='blue',label = 'Survived')
ax.set_xlabel('Class')
ax.set_ylabel('Age')
ax.set_zlabel('Sex')
ax.legend()
ax.set_title('Model Predictions')
ax.zaxis.set_ticks(np.unique(X_test[:,2]))
ax.zaxis.set_ticklabels(['Female','Male'])
ax.xaxis.set_ticks(np.unique(X_test[:,0]))
ax.xaxis.set_ticklabels(['1','2','3'])
ax.plot_surface(x_surf, y_surf,
z_surf,
rstride=1,
cstride=1,
color='None',
alpha = 0.4)
plt.show()
# -
# ## Visualizing our results (II)
# Since we know what our model is predicting on each side of the decision boundary, we can color the points using the actual data. This will let us visualize where our model is failing.
# +
from mpl_toolkits.mplot3d import axes3d
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111, projection='3d')
died = np.where(y_test==0)[0]
survived = np.where(y_test==1)[0]
p=ax.scatter(xs = X_test[died,0], ys =X_test[died,1], zs=X_test[died,2],
zdir='z', s=20, c='red',label = 'Died')
p=ax.scatter(xs = X_test[survived,0], ys =X_test[survived,1], zs=X_test[survived,2],
zdir='z', s=20, c='blue',label = 'Survived')
ax.set_xlabel('Class')
ax.set_ylabel('Age')
ax.set_zlabel('Sex')
ax.legend()
ax.set_title('Actual Data')
ax.zaxis.set_ticks(np.unique(X_test[:,2]))
ax.zaxis.set_ticklabels(['Female','Male'])
ax.xaxis.set_ticks(np.unique(X_test[:,0]))
ax.xaxis.set_ticklabels(['1','2','3'])
ax.plot_surface(x_surf, y_surf,
z_surf,
rstride=1,
cstride=1,
color='None',
alpha = 0.4)
plt.show()
# -
# ### And...
#
# that's it! I hope you liked it. Please get in touch if you have any suggestions or comments.
|
LogisticRegression2/LogisticRegressionTitanic_Spark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <img src="http://akhavanpour.ir/notebook/images/srttu.gif" alt="SRTTU" style="width: 150px;"/>
#
# [](https://notebooks.azure.com/import/gh/Alireza-Akhavan/class.vision)
import cv2
import numpy as np
# +
img = cv2.imread('./images/color.png')
B, G, R = cv2.split(img)
height, width, channels = img.shape
zeros = np.zeros([height,width], dtype = "uint8")
red = cv2.merge([zeros, zeros, R])
green = cv2.merge([zeros, G, zeros])
blue = cv2.merge([B, zeros, zeros])
cv2.imshow("Original", img)
cv2.imshow("Red", red)
cv2.imshow("Green", green)
cv2.imshow("Blue", blue)
cv2.waitKey(0)
cv2.destroyAllWindows()
# -
# <div class="alert alert-block alert-info">
# <div style="direction:rtl;text-align:right;font-family:B Lotus, B Nazanin, Tahoma"> دانشگاه تربیت دبیر شهید رجایی<br>مباحث ویژه - آشنایی با بینایی کامپیوتر<br>علیرضا اخوان پور<br>96-97<br>
# </div>
# <a href="https://www.srttu.edu/">SRTTU.edu</a> - <a href="http://class.vision">Class.Vision</a> - <a href="http://AkhavanPour.ir">AkhavanPour.ir</a>
# </div>
|
03-extra.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <table align="left" width="100%"> <tr>
# <td style="background-color:#ffffff;">
# <a href="http://qworld.lu.lv" target="_blank"><img src="../images/qworld.jpg" width="35%" align="left"> </a></td>
# <td style="background-color:#ffffff;vertical-align:bottom;text-align:right;">
# prepared by <NAME> (<a href="http://qworld.lu.lv/index.php/qlatvia/" target="_blank">QLatvia</a>)
# </td>
# </tr></table>
# <table width="100%"><tr><td style="color:#bbbbbb;background-color:#ffffff;font-size:11px;font-style:italic;text-align:right;">This cell contains some macros. If there is a problem with displaying mathematical formulas, please run this cell to load these macros. </td></tr></table>
# $ \newcommand{\bra}[1]{\langle #1|} $
# $ \newcommand{\ket}[1]{|#1\rangle} $
# $ \newcommand{\braket}[2]{\langle #1|#2\rangle} $
# $ \newcommand{\dot}[2]{ #1 \cdot #2} $
# $ \newcommand{\biginner}[2]{\left\langle #1,#2\right\rangle} $
# $ \newcommand{\mymatrix}[2]{\left( \begin{array}{#1} #2\end{array} \right)} $
# $ \newcommand{\myvector}[1]{\mymatrix{c}{#1}} $
# $ \newcommand{\myrvector}[1]{\mymatrix{r}{#1}} $
# $ \newcommand{\mypar}[1]{\left( #1 \right)} $
# $ \newcommand{\mybigpar}[1]{ \Big( #1 \Big)} $
# $ \newcommand{\sqrttwo}{\frac{1}{\sqrt{2}}} $
# $ \newcommand{\dsqrttwo}{\dfrac{1}{\sqrt{2}}} $
# $ \newcommand{\onehalf}{\frac{1}{2}} $
# $ \newcommand{\donehalf}{\dfrac{1}{2}} $
# $ \newcommand{\hadamard}{ \mymatrix{rr}{ \sqrttwo & \sqrttwo \\ \sqrttwo & -\sqrttwo }} $
# $ \newcommand{\vzero}{\myvector{1\\0}} $
# $ \newcommand{\vone}{\myvector{0\\1}} $
# $ \newcommand{\stateplus}{\myvector{ \sqrttwo \\ \sqrttwo } } $
# $ \newcommand{\stateminus}{ \myrvector{ \sqrttwo \\ -\sqrttwo } } $
# $ \newcommand{\myarray}[2]{ \begin{array}{#1}#2\end{array}} $
# $ \newcommand{\X}{ \mymatrix{cc}{0 & 1 \\ 1 & 0} } $
# $ \newcommand{\Z}{ \mymatrix{rr}{1 & 0 \\ 0 & -1} } $
# $ \newcommand{\Htwo}{ \mymatrix{rrrr}{ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} \\ \frac{1}{2} & -\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} } } $
# $ \newcommand{\CNOT}{ \mymatrix{cccc}{1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0} } $
# $ \newcommand{\norm}[1]{ \left\lVert #1 \right\rVert } $
# $ \newcommand{\pstate}[1]{ \lceil \mspace{-1mu} #1 \mspace{-1.5mu} \rfloor } $
# $ \newcommand{\Y}{ \mymatrix{rr}{0 & -i \\ i & 0} } $ $ \newcommand{\S}{ \mymatrix{rr}{1 & 0 \\ 0 & i} } $
# $ \newcommand{\T}{ \mymatrix{rr}{1 & 0 \\ 0 & e^{i \frac{pi}{4}}} } $
# $ \newcommand{\Sdg}{ \mymatrix{rr}{1 & 0 \\ 0 & -i} } $
# $ \newcommand{\Tdg}{ \mymatrix{rr}{1 & 0 \\ 0 & e^{-i \frac{pi}{4}}} } $
# <h1> Bloch sphere </h1>
# In the previous notebook, we visualized the state of a qubit $\ket{\psi} = \cos{\frac{\theta}{2}} \ket{0} + e^{i\phi} \sin{\frac{\theta}{2}} \ket{1}$ by separatly drawing angles $\frac{\theta}{2}$ and $\phi$. Bloch sphere geometrically represents the state of a qubit with both angles giving a vector from the center of a unit sphere (sphere with radius equal to one unit) to the surface of the sphere. Two angles precisely determine the point, at which the vector is pointing. The only exception is when $\ket{\psi} = \ket{0}$ or $\ket{\psi} = \ket{1}$ - in that case for any angle $\phi$ it will be the same point on the surface. Note that we don't take into account the global phase. To summarize:
# <ul>
# <li>Bloch sphere as a geometrical object covers all possible states of a single qubit (upto global phase);</li>
# <li>Each point on the surface of the Bloch sphere represents state of a qubit.</li>
# </ul>
# Here we can see how the Bloch sphere looks like:
#
# <img src="../images/bloch_sphere.png" width="40%">
# The Bloch sphere as 3D object has three axes. States on the opposite ends of each axis are orthogonal (in fact, any two states on the opposite sides of a Bloch sphere are orthogonal.).
# - On the poles of the z-axis there are states $\ket{0}$ and $\ket{1}$.
#
# - The angle $\theta$ shows how far the state is from state $\ket{0}$.
#
# - The angle $\phi$ shows the local phase, that is how much the state is "rotated" around z-axis.
#
# - Poles of the x-axis represent the states $\frac{1}{\sqrt{2}} (\ket{0} + \ket{1})$ and $\frac{1}{\sqrt{2}} (\ket{0} - \ket{1})$ and they differ by a local phase of $\phi = \pi$.
#
# - Poles of the y-axis represent the states $\frac{1}{\sqrt{2}} (\ket{0} + i\ket{1})$ and $\frac{1}{\sqrt{2}} (\ket{0} - i\ket{1})$ and they differ by a local phase of $\phi = \pi$..
# Starting from $\frac{1}{\sqrt{2}} (\ket{0} + \ket{1})$ and changing the phase in each step by $\frac{\pi}{2}$ we reach the states $\frac{1}{\sqrt{2}} (\ket{0} + i \ket{1})$, $\frac{1}{\sqrt{2}} (\ket{0} - \ket{1})$, $\frac{1}{\sqrt{2}} (\ket{0} - i \ket{1})$, or, if we show the local phase in Euler form, then we have $\frac{1}{\sqrt{2}} (\ket{0} + e^{i \cdot 0} \ket{1})$, $\frac{1}{\sqrt{2}} (\ket{0} + e^{i \cdot \frac{\pi}{2}} \ket{1})$, $\frac{1}{\sqrt{2}} (\ket{0} + e^{i \cdot \pi} \ket{1})$, $\frac{1}{\sqrt{2}} (\ket{0} + e^{i \cdot \frac{3 \pi}{2}} \ket{1})$.
# # <h2> Understanding the angles </h2>
#
# Geometrically we are used to perceive two orthogonal states as the ones that have angle of 90 degrees ($\frac{\pi}{2}$) between them. This worked quite well when we represented quantum state with real-valued amplitudes in the 2D-plane. As now you know, angle $\theta$ is responsible for the real part of the amplitudes, and shows how "far" the state is from the state $\ket{0}$. Let's take a look at general quantum state
#
# $$
# \ket{\psi} = \cos{\frac{\theta}{2}} \ket{0} + e^{i\phi} \sin{\frac{\theta}{2}} \ket{1},
# $$
#
# where $0 \leq \theta \leq \pi$ and $0 \leq \phi < 2\pi$, and focus only on the case with real-valued amplitudes. In that case we have $\phi = 0$:
#
# $$
# \ket{\psi} = \cos{\frac{\theta}{2}} \ket{0} + \sin{\frac{\theta}{2}} \ket{1}.
# $$
# Note that the angle provided to $\cos$ and $\sin$ functions lie in interval $[0, \frac{\pi}{2}]$, which gives us the first quadrant of a unit circle on the 2D plane. For example, when we have $\theta = \frac{\pi}{2}$, we have angle of 45 degrees, and so our state looks in the following way:
#
# <img src="../images/real_45_degree_state.png" width="20%">
# While visually we have angle $\frac{\theta}{2}$ from the state $\ket{0}$ on a 2D-plane, on a Bloch sphere we have angle $\theta$ from the state $\ket{0}$, and so orthogonal state $\ket{1}$ is located 180 degrees ($\pi$ radians) away from the state $\ket{0}$.
# On a Bloch sphere it is easier to first find the geometrical position of the state on an equator (as if $\theta = \frac{\pi}{2}$). The angle $\phi$ begins the rotation from the state $\frac{1}{\sqrt{2}} (\ket{0} + \ket{1})$. When you find the position of the state on an equator, then you can easily find the right position that takes into account also the angle $\theta$.
# <h2> Visualization of the state </h2>
#
# To visualize the state $\ket{\psi} = \cos{\frac{\theta}{2}} \ket{0} + e^{i\phi} \sin{\frac{\theta}{2}} \ket{1}$ on a Bloch sphere, we need to take the following coordinates:
# <ul>
# <li>$x = \sin \theta \cos \phi$</li>
# <li>$y = \sin \theta \sin \phi$</li>
# <li>$z = \cos \theta$.</li>
# </ul>
#
# Let's visualize the state $\ket{\psi} = \cos{\frac{\pi}{4}} \ket{0} + e^{i \frac{4\pi}{3}} \sin{\frac{\pi}{4}} \ket{1}$, where we have $\theta = \frac{\pi}{2}$ and $\phi = \frac{4\pi}{3}$. In this case our coordinates will be:
# <ul>
# <li>$x = -\frac{1}{2}$</li>
# <li>$y = -\frac{\sqrt{3}}{2}$</li>
# <li>$z = 0$.</li>
# </ul>
# +
from qiskit.visualization import plot_bloch_vector, bloch
from matplotlib.pyplot import text
from math import pi, cos, sin
from qutip import *
# angles that represent our state
theta = pi/2
phi = 4*pi/3
# calculating the coordinates
x = sin(theta)*cos(phi)
y = sin(theta)*sin(phi)
z = cos(theta)
# preparing the sphere
sphere = bloch
sphere.Bloch
b = Bloch()
# preparing the lables
b.ylpos = [1.1, -1.2]
b.xlabel = ['$\\left|0\\right>+\\left|1\\right>$', '$\\left|0\\right>-\\left|1\\right>$']
b.ylabel = ['$\\left|0\\right>+i\\left|1\\right>$', '$\\left|0\\right>-i\\left|1\\right>$']
# first 6 drawn vectors will be blue, the 7th - red
b.vector_color = ['b','b','b','b','b','b','r']
# drawing vectors of orthogonal states (most popular bases), note the coordinates of vectors,
# they correspond to the according states.
b.add_vectors([[0,0,1],[0,0,-1],[0,1,0],[0,-1,0],[1,0,0],[-1,0,0]])
# drawing our state (as 7th vector)
b.add_vectors([x,y,z])
# showing the Bloch sphere with all that we have prepared
b.show()
# -
# <h3> Task 1 </h3>
#
# Play around with the code above to draw different states by changing $\theta$ and $\phi$. Can you manage to draw two different states on the same Bloch sphere?
# <h3> Task 2 </h3>
#
# Implement a function in Python that takes quantum state $\cos{\frac{\theta}{2}} \ket{0} + e^{i\phi} \sin{\frac{\theta}{2}} \ket{1}$ as two numbers $\frac{\theta}{2}$ and $\phi$ and draws this state on a Bloch sphere. You can use the code from the above example.
#
# your solution is here
#
# <a href="C07_Bloch_Sphere_Solutions.ipynb#task2">click for our solution</a>
# <h3> Task 3 (optional) </h3>
#
# Extend the function from Task 2 by allowing it to accept more than one state. Try to use different colors for different states.
#
# Test it with the states $\cos{\frac{\pi/2}{2}} \ket{0} + e^{i\frac{\pi}{2}} \sin{\frac{\pi/2}{2}} \ket{1}$ and $\cos{\frac{\pi/3}{2}} \ket{0} + e^{i\pi} \sin{\frac{\pi/3}{2}} \ket{1}$.
#
# your solution is here
#
# <a href="C07_Bloch_Sphere_Solutions.ipynb#task3">click for our solution</a>
|
silver/C07_Bloch_Sphere.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="-XxqkeqNEI0D" colab_type="code" colab={}
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv('bitcoin_usd.csv')
# + id="7xOlBxPtEY69" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="af56243a-def6-4341-a673-7559937241b4"
df
# + id="Gc3rnvcKEcM9" colab_type="code" colab={}
df=df.drop(labels=['_id','time'],axis=1)
# + id="cwVmHiMgpWZi" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 265} outputId="def4087a-c44b-4472-94c8-e7cded4ebd8f"
plt.plot(df)
plt.show()
# + id="sQJ0qF8ypy_-" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 764} outputId="18a1fcad-4415-43b7-ace3-08c7ae7bbea7"
import seaborn as sns
sns.pairplot(df)
# + id="6_-v9pBJqPHC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 166} outputId="66b276c4-1018-4710-fda8-af42b2118df7"
df.corr()
# + id="dyCzCQYFqXHL" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 286} outputId="a401e675-345c-4436-9b22-2f8eaca1c00f"
sns.heatmap(df.corr())
# + id="s4GD0gR5Ek2v" colab_type="code" colab={}
y = df['high']
# + id="kQm6vA2LE65W" colab_type="code" colab={}
y = np.array(y)
# + id="6oeGt-xZE_Xw" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="19e68be5-6bb2-485a-83bd-7406d22f56eb"
y
# + id="N7uVmjySFKaS" colab_type="code" colab={}
df=df.drop(labels=['high'],axis=1)
# + id="V7LtE9EiFOTu" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 402} outputId="bee957b8-3e27-4619-99a2-c1fb97b44fe1"
df
# + id="aYdTPayHFXOq" colab_type="code" colab={}
X = np.array(df)
# + id="kcPDck6OFrVv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 134} outputId="38650018-2d32-42eb-8a82-f1d648f1f95e"
X
# + id="8C3jsjevHvA-" colab_type="code" colab={}
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
X1=scaler.fit_transform(X.reshape(-1,3))
# + id="CVUcqLipH4yF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 134} outputId="0f34f337-6f88-4ece-c970-f2312ed59645"
X1
# + id="J59fUqbgJ35j" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="3abf0a9f-8744-4ccb-f39b-d00bfad8fc0b"
X1.shape
# + id="rFTAcBukL0Tl" colab_type="code" colab={}
n_features = 1
X1 = X1.reshape((X1.shape[0], X1.shape[1], n_features))
# + id="aoWMed2SNldN" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="177331a2-274e-493c-87e0-631f58c28e74"
X1.shape
# + id="gpOA28NsKgjV" colab_type="code" colab={}
from sklearn.preprocessing import MinMaxScaler
scaler=MinMaxScaler(feature_range=(0,1))
y1=scaler.fit_transform(y.reshape(-1,1))
# + id="AZyv5Mj0KpJk" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 134} outputId="5845a531-a6dc-4696-ebd0-50379f454ae2"
y1
# + id="X5LpywAiLvSq" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="e5ce7b8d-e687-458e-ec33-3d2668d2ec1a"
y1.shape
# + id="FDYZxZHrGCVG" colab_type="code" colab={}
# Importing the library
from sklearn.model_selection import train_test_split
# + id="JAfK2L7yGDTw" colab_type="code" colab={}
#Splitting the data
X_train, X_test, y_train, y_test = train_test_split(X1, y1, test_size=0.2)
# + id="LfE7f5_FNH3D" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 67} outputId="9cb2043a-28c9-48c7-8b1b-b8ce0b7a3897"
print(X_train.shape), print(y_train.shape)
# + id="0z0doE-vNIjG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 67} outputId="9aa00adb-8b4c-482f-a608-2efbb36fbd2d"
print(X_test.shape), print(y_test.shape)
# + id="bltK0qQvOTgr" colab_type="code" colab={}
### Create the Stacked LSTM model
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM,GRU
import time
# + [markdown] id="lWXYDjLmaHeJ" colab_type="text"
# # **GRU**
# + id="6K9PFWcaaKXR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="be987dfc-7108-4829-918b-d5db92c5f492"
# define model1 GRU
sg_time = time.time()
model1 = Sequential()
model1.add(GRU(100, activation='linear', return_sequences=True, input_shape=(3, 1)))
model1.add(GRU(50, activation='linear'))
model1.add(Dense(1))
model1.compile(optimizer='adam', loss='mse')
# fit model
model1.fit(X_train, y_train, epochs=100, verbose=1)
eg_time = time.time()
print("Execution Time: ",eg_time-sg_time)
# + id="rwEVgkYcaNPo" colab_type="code" colab={}
### Lets Do the prediction and check performance metrics
train_predict=model1.predict(X_train)
test_predict=model1.predict(X_test)
# + id="WPd64lhuaQSg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="fef201ca-d9d4-44d4-ec32-bcae1bb245e9"
### Calculate MSE performance metrics
import math
from sklearn.metrics import mean_squared_error
mean_squared_error(y_train,train_predict)
# + id="F_0Wm3qraQyU" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="83e1d67e-b6db-420c-88f2-f41604d5cf88"
### Calculate MSE performance metrics
import math
from sklearn.metrics import mean_squared_error
mse1 = mean_squared_error(y_test,test_predict)
mse1
# + id="t1wsAjgBaX3d" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="5769ba6d-bb39-48f5-d5d5-51533a609062"
### Calculate r2 performance metrics
import math
from sklearn.metrics import r2_score
r1 = r2_score(y_test,test_predict)
r1
# + [markdown] id="GL1v5n1PaCcG" colab_type="text"
# # **LSTM**
# + id="OyYvj7SYNLEm" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="38257005-e349-4873-b1bf-476e49404529"
# define model2 LSTM
sl_time = time.time()
model2 = Sequential()
model2.add(LSTM(100, activation='linear', return_sequences=True, input_shape=(3, 1)))
model2.add(LSTM(50, activation='linear'))
model2.add(Dense(1))
model2.compile(optimizer='adam', loss='mse')
# fit model
model2.fit(X_train, y_train, epochs=100, verbose=1)
el_time = time.time()
print("Execution time: ", el_time-sl_time)
# + id="sLLERlBsNLDz" colab_type="code" colab={}
### Lets Do the prediction and check performance metrics
train_predict=model2.predict(X_train)
test_predict=model2.predict(X_test)
# + id="JjSVQorMPGdM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="1a3b781c-3204-4789-8121-d30fc4b70497"
### Calculate MSE performance metrics
import math
from sklearn.metrics import mean_squared_error
mean_squared_error(y_train,train_predict)
# + id="AI23yCRRPM77" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="79d26606-cb8a-4d9f-e716-164f9a41d45a"
### Calculate MSE performance metrics
import math
from sklearn.metrics import mean_squared_error
mse2 = mean_squared_error(y_test,test_predict)
mse2
# + id="4-xr7-MQRoPs" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 34} outputId="5ed9ce3f-a3fe-4e03-f72f-bcaea96fbeee"
### Calculate r2 performance metrics
import math
from sklearn.metrics import r2_score
r2 = r2_score(y_test,test_predict)
r2
# + id="1wggQ-yYid5Z" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 265} outputId="1145cf18-a1ac-4886-96ac-f8b7b2818442"
# plot
plt.plot(scaler.inverse_transform(y_test))
plt.plot(scaler.inverse_transform(test_predict))
plt.xlim(200,300)
plt.show()
# + id="EUMNwXZDbHpW" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 106} outputId="7c5eb375-fce3-4661-a294-976d1a2f7a1c"
df_model = pd.DataFrame({'Model_Applied': ['GRU', 'LSTM'], 'MSE': [mse1, mse2], 'R2': [r1, r2],
'Execution Time': [eg_time - sg_time, el_time - sl_time]})
df_model
|
prediction/Deep_Learning_Models.ipynb
|
% ---
% jupyter:
% jupytext:
% text_representation:
% extension: .m
% format_name: light
% format_version: '1.5'
% jupytext_version: 1.14.4
% kernelspec:
% display_name: Matlab
% language: matlab
% name: matlab_kernel
% ---
% # Machine learning in critical care tutorial
%
% This tutorial guides you through using support vector machines (SVM) to build a mortality prediction model. The tutorial requires LIBSVM, a package used to train SVMs, and the dataset 'MLCCData.mat', which contains features and outcomes for a set of ICU patients from MIMIC-III.
% First add libsvm to the path and set some useful variables for plotting.
% +
% Path variables which are necessary
addpath([pwd filesep 'libsvm']);
addpath(pwd);
% Some variables used to make pretty plots
col = [0.9047 0.1918 0.1988
0.2941 0.5447 0.7494
0.3718 0.7176 0.3612
1.0000 0.5482 0.1000
0.4550 0.4946 0.4722
0.6859 0.4035 0.2412
0.9718 0.5553 0.7741
0.5313 0.3359 0.6523];
col = repmat(col,2,1);
col_fill = col;
col(9:end,:) = 0; % when plotting > 8 items, we make the outline black
marker = {'d','+','o','x','>','s','<','+','^'};
marker = repmat(marker,1,2);
ms = 12;
% -
% Double check that we have LIBSVM installed with the appropriate mex file.
% +
svm_path = which('svmtrain');
fprintf('\n');
if strfind(lower(svm_path),'.mex') > 0
fprintf('The path for svmtrain is: %s\n',svm_path);
fprintf('libsvm is loaded properly! Carry on!\n');
else
fprintf('Could not find LIBSVM. Make sure it''s added to the path.\n');
end
% -
% ## Loading other datasets
%
% If you do not have the ICU dataset, you have the option of doing this tutorial with fisher iris using the below code:
%
% ```
% % Option 1. This loads fisher iris instead of the ICU data
% load fisheriris;
% X = meas(:,1:3);
% X_header = {'Sepal length','Sepal width','Petal length'};
% y = double(strcmp(species,'virginica')==1);
% clear meas species;
% ```
%
% Alternatively, you can use your own dataset by directly querying an SQLite instance of the database as follows:
%
% ```
% % Option 2. Extract the patient data using the query from your assignment
% % Run the following to connect to the database
%
% % STEP 1: Tell Matlab where the driver is
% javaclasspath('sqlite-jdbc-3.8.11.2.jar') % use this for SQLite
%
% % STEP 2: Connect to the Database
% if exist('conn','var') != 1
% conn = database('','','',...
% 'org.sqlite.JDBC',['jdbc:sqlite:' pwd filesep 'data' filesep 'mimiciii_v1_3_demo.sqlite']);
% end
%
% % Option 2 (continued). Extract the patient data using the query from your assignment
% % At the moment this query is long, and takes ~5 minutes
% setdbprefs('DataReturnFormat','dataset')
% query = makeQuery('mlcc1-problem-set-solutions.sql');
% data = fetch(conn,query);
%
% % now convert data to a cell array
% data = dataset2cell(data);
%
% % we can get the column names from the first row of the 'data' variable
% header = data(1,:);
% header{2} = 'OUTCOME';
% header = regexprep(header,'_',''); % remove underscores
% data = data(2:end,:);
%
% % MATLAB sometimes reads 'null' instead of NaN
% data(cellfun(@isstr, data) & cellfun(@(x) strcmp(x,'null'), data)) = {NaN};
%
% % MATLAB sometimes has blank cells which should be NaN
% data(cellfun(@isempty, data)) = {NaN};
%
% % Convert the data into a matrix of numbers
% % This is a MATLAB data type thing - we can't do math with cell arrays
% data = cell2mat(data);
%
% X = data(:,3:5);
% X_header = header(3:5);
% y = data(:,2);
% ```
%
% This tutorial uses a pre-prepared mat file for simplicity.
% +
% (Option 3) Load the ICU data from the .mat file provided
% Loads in 'X', 'X_header', and 'y' variables
load('MLCCData.mat');
idxData = ismember(header,{'Age','HeartRateMin','GCSMin'});
X = data(:,idxData);
X_header = header(idxData);
y = data(:,2);
X_header
% +
% Data will have at least three columns:
% ICUSTAY_ID, OUTCOME, AGE
% the following loops display the data nicely
W = 5; % the maximum number of columns to print at one time
for o=1:floor(size(data,2)/W)
idxColumn = (o-1)*W + 1 : o*W;
if idxColumn(end) > size(data,2)
idxColumn = idxColumn(1):size(data,2);
end
fprintf('%12s\t',header{idxColumn});
fprintf('\n');
for n=1:5
for m=idxColumn
fprintf('%12g\t',data(n, m));
end
fprintf('\n');
end
fprintf('\n');
end
% +
% Before we train a model - let's inspect the data
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
figure(1); clf; hold all;
plot3(X(idxTarget,1),X(idxTarget,2),X(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:)...
,'MarkerSize',10,'LineWidth',2);
plot3(X(~idxTarget,1),X(~idxTarget,2),X(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:)...
,'MarkerSize',10,'LineWidth',2);
grid on;
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
% change the angle of the view to help inspection
set(gca,'view',[45 25]);
% 1) What do you see that is notable?
% ANSWER: for the ICU data...
% there are ages ~ 300, these are de-identified ages
% -
% Correct the erroneous ages
% Hint: the median age of patients > 89 is 91.6.
X( X(:,1) > 89, 1 ) = 91.6;
% +
% Inspect the data correction
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
figure(1); clf; hold all;
plot3(X(idxTarget,1),X(idxTarget,2),X(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:)...
,'MarkerSize',10,'LineWidth',2);
plot3(X(~idxTarget,1),X(~idxTarget,2),X(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:)...
,'MarkerSize',10,'LineWidth',2);
grid on;
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
% change the angle of the view to help inspection
set(gca,'view',[45 25]);
% 1) What do you see that is notable?
% ANSWER: for the ICU data...
% patients with a minimum heart rate of 0 appear more likely to die
% patients with "extreme" data (outside the massive blob in the middle) seem more likely to die
% +
% Normalize the data!
% First get the column wise mean and the column wise standard deviation
mu = nanmean(X, 1);
sigma = nanstd(X, [], 1);
% Now subtract each element of mu from each column of X
X = bsxfun(@minus, X, mu);
X = bsxfun(@rdivide, X, sigma);
% -
% We will be using libsvm. If you call svmtrain on its own, it lists the options available
svmtrain;
% +
% Using LIBSVM, train an SVM classifier with a linear kernel
model_linear = svmtrain(y, X, '-t 0');
% Atypically, LIBSVM receives options as a single string in the fourth input
% e.g. '-v 1 -b 1 -g 0.5 -c 1'
% Apply the classifier to the data set
pred = svmpredict(y, X, model_linear);
% -
% We can interpret the above output. The code only ran for 1 iteration.
% The objective function, "obj", is NaN.
% We have 0 support vectors (nSV).
%
% There's clearly a bug! What have we forgotten?
X(1:20,:)
% Looks like there is some missing data (not a number, or 'NaN') - when the code tries to do math with these missing values, it returns NaN. Imagine you try to calculate how far away NaN is from your current position - the result would be NaN.
%
% The SVM asks the question: "is this point above the hyperplane I'm learning or below the hyperplane I'm learning?". (Recall that a 'hyperplane' is just a high dimensional line). The idea is that we want all 'o' to be above the hyperplane and all 'x' to be below the hyperplane (i.e. we want to separate our data). But if we ask if 'NaN' is above or below the hyperplane, we just get 'NaN'. Then, when it sums across all points to see how many 'o' are above the plane, it also returns 'NaN'. This breaks the algorithm and it stops trying to optimize the separating plane.
% Make sure we impute a value for missing data, otherwise the models can't train
X( isnan(X) ) = 0;
% since we've normalized the data to have 0 mean, imputing 0 is equivalent to imputing the mean
X(1:20,:)
% Great, now let's try to find the hyperplane that best separates the data using our SVM.
% +
% Using LIBSVM, train an SVM classifier with a linear kernel
model_linear = svmtrain(y, X, '-t 0');
% Atypically, LIBSVM receives options as a single string in the fourth input
% e.g. '-v 1 -b 1 -g 0.5 -c 1'
% Apply the classifier to the data set
pred = svmpredict(y, X, model_linear);
% +
figure(1); clf; hold all;
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
% We would like to plot the original data because it's in units we understand (e.g. age in years)
% we can un-normalize the data for plotting:
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
plot3(X_orig(idxTarget,1),X_orig(idxTarget,2),X_orig(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(~idxTarget,1),X_orig(~idxTarget,2),X_orig(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(pred==1,1),X_orig(pred==1,2),X_orig(pred==1,3),...
'Linestyle','none','Marker','o',...
'MarkerFaceColor','none','MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2,...
'HandleVisibility','off');
grid on;
xi = -3:0.25:3;
yi = -3:0.25:3;
% plot the hyperplane
w = model_linear.SVs' * model_linear.sv_coef;
b = model_linear.rho;
[XX,YY] = meshgrid(xi,yi);
ZZ=(b - w(1) * XX - w(2) * YY)/w(3);
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
mesh(XX,YY,ZZ,'EdgeColor',col(5,:),'FaceColor','none');
%legend({'Died in hospital','Survived'},'FontSize',16);
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% -
% There is a word for this separating hyperplane: bad. It's so far away from our data it simply classifies everything as 0, or 'below the hyperplane'. This is not a very useful classifier - it's simply predicting all patients will survive. The question is, why is this happening?
fprintf('Number of patients who die: %g.\n',sum(y==1));
fprintf('Number of patients who live: %g.\n',sum(y==0));
% The answer lies in the class balance: we have almost 3 times as many patients who live compared to patients who die. The optimization algorithm will never make a perfect boundary: it has to determine a balance between misclassifying patients who survive and misclassifying patients who die. The simplest solution is just to say everyone survives. How do we fix this?
%
% A common approach in machine learning for the unbalanced class problem is to either:
% 1. Subsample the bigger class (i.e. only use 1524 of our 4893 surviving patients)
% 2. Upsample the smaller class (i.e. copy the 1524 non-surviving patients until we have 4893)
%
% We will try the first approach.
% +
N0 = sum(y==0);
N1 = sum(y==1);
% we randomly pick 0s so that we don't accidentally pick a biased subset
% for example, if X was sorted by age, we would only get young people by selecting the first N1 rows
% if you know X isn't sorted, then this is an excessive step
% still, it's safer to randomize the indices we select just incase!
rng(777,'twister'); % ensure we always get the same random numbers
[~,idxRandomize] = sort(rand(N0,1));
idxKeep = find(y==0); % find all the negative outcomes
idxKeep = idxKeep(idxRandomize(1:N1)); % pick a random N1 negative outcomes
idxKeep = [find(y==1);idxKeep]; % add in the positive outcomes
idxKeep = sort(idxKeep); % probably not needed but it's cleaner
% -
X_train = X(idxKeep,:);
y_train = y(idxKeep);
% +
% Using LIBSVM, train an SVM classifier with a linear kernel
model_linear = svmtrain(y_train, X_train, '-t 0');
% Atypically, LIBSVM receives options as a single string in the fourth input
% e.g. '-v 1 -b 1 -g 0.5 -c 1'
% Apply the classifier to the data set
% Note, we can apply the predictions to *all* the data, instead of just our training set
[pred,acc,dist] = svmpredict(y, X, model_linear);
% -
% Our accuracy has actually *decreased* from 76% to 66.9%. This is because our classifier is actually trying now: while this classifier may have lower accuracy, it may have better performance in metrics which more appropriately factor in the unbalanced classes.
%
% Note also that we have two other outputs:
% * 'acc' - the accuracy of the model
% * 'dist' - the distance of each observation point to the hyperplane
%
% Let's look at the distance measure.
[pred(45:50),dist(45:50),y(45:50)]
% Note that LIBSVM outputs negative distances for positive cases and positive distances for negative cases. When we later try to calculate the AUROC, we need to rank the predictions in ascending order. It will be much more convenient to do this if LIBSVM instead assigned positive distances for positive cases and negative distances for negative cases (also it makes more intuitive sense).
%
% LIBSVM assigns the first row of the training data to positive distances - therefore, in order to to ensure positive cases get positive distances, we just need to put a positive case as the first row.
% +
idx1 = find(y_train==1,1);
idxTemp = 1:numel(y_train);
% create an index to ensure the first observation in the data is a positive outcome
idxTemp(1) = idx1;
idxTemp(idx1) = 1;
X_train = X_train(idxTemp,:);
y_train = y_train(idxTemp);
% retrain the RBF and linear SVM
model_linear = svmtrain(y_train, X_train, '-t 0 -q');
model_rbf = svmtrain(y_train, X_train, '-t 2 -q');
% Apply the classifier to the data set
[pred,acc,dist] = svmpredict(y, X, model_rbf, '-q');
% look at a random set of predictions
[pred(45:50),dist(45:50),y(45:50)]
% -
% Because we ensured the first training observation was a positive case (i.e. the first row in `X_train` corresponded to a 1 in `y_train`), LIBSVM now attempts to classify positive cases as `1`. Hurray! This is just a technical detail and it saves us the effort of having to invert the distances when we try to use them later to calculate the AUROC.
%
% Note also we used the '-q' option to make LIBSVM quiet.
% +
% Evaluate the model qualitatively
figure(1); clf; hold all;
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
% We would like to plot the original data because it's in units we understand (e.g. age in years)
% we can un-normalize the data for plotting:
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
plot3(X_orig(idxTarget,1),X_orig(idxTarget,2),X_orig(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(~idxTarget,1),X_orig(~idxTarget,2),X_orig(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(pred==1,1),X_orig(pred==1,2),X_orig(pred==1,3),...
'Linestyle','none','Marker','o',...
'MarkerFaceColor','none','MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2,...
'HandleVisibility','off');
grid on;
xi = -3:0.25:3;
yi = -3:0.25:3;
% plot the hyperplane
w = model_linear.SVs' * model_linear.sv_coef;
b = model_linear.rho;
[XX,YY] = meshgrid(xi,yi);
ZZ=(b - w(1) * XX - w(2) * YY)/w(3);
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
mesh(XX,YY,ZZ,'EdgeColor',col(5,:),'FaceColor','none');
legend({'Died in hospital','Survived'},'FontSize',16);
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% -
% Much better! The hyperplane has picked somewhere in the middle of GCS to separate the data. GCS stands for Glasgow Coma Scale: it is a measure of a patient's neurological status. A value of 3 is equivalent to a coma, and a value of 15 is equivalent to normal neurological function. Our classifier has learned this, and now predicts that patients in a coma are more likely to die.
% +
% Evaluate the model quantitatively
% First, we calculate the four "operating point" statistics
TP = sum( pred == 1 & y == 1 );
FP = sum( pred == 0 & y == 1 );
TN = sum( pred == 0 & y == 0 );
FN = sum( pred == 1 & y == 0 );
% Now we create the confusion matrix
cm = [TP, FP;
TN, FN]
% +
% We can also create the sensitivity/specificity measures
fprintf('\n');
fprintf('Sensitivity: %6.2f%%\n', 100 * TP / (TP+FN));
fprintf('Specificity: %6.2f%%\n', 100 * TN / (TN+FP));
fprintf('PPV: %6.2f%%\n', 100 * TP / (TP + FP));
fprintf('NPV: %6.2f%%\n', 100 * TN / (TN+FN));
fprintf('\n');
% all together
fprintf('%6g\t%6g\t%10.2f%% \n', cm(1,1), cm(1,2), 100 * TP / (TP + FP));
fprintf('%6g\t%6g\t%10.2f%% \n', cm(2,1), cm(2,2), 100 * TN / (TN+FN));
fprintf('%5.2f%%\t%5.2f%%\t%10.2f%% \n', 100 * TP / (TP+FN), 100 * TN / (TN+FP), 100 * (TP+TN)/(TP+TN+FP+FN));
% -
% For patients who die, our model detects 35.46% of them. Not the most sensitive of classifiers.
%
% Furthermore, for patients who our model predicts to die, 61.02% actually die.
% +
% Now let's try with an RBF kernel
% This is LIBSVM's most flexible kernel
% We specify it as '-t 2'
% train the model
model_rbf = svmtrain(y_train, X_train, '-t 2');
% Apply the classifier to the data set
[pred,acc,dist] = svmpredict(y, X, model_rbf);
% +
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
% plot the model and the data
figure(1); clf; hold all;
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
plot3(X_orig(idxTarget,1),X_orig(idxTarget,2),X_orig(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(~idxTarget,1),X_orig(~idxTarget,2),X_orig(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(pred==1,1),X_orig(pred==1,2),X_orig(pred==1,3),...
'Linestyle','none','Marker','o',...
'MarkerFaceColor','none','MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2,...
'HandleVisibility','off');
grid on;
% reapply the SVM to a grid of all possible values
xi=-5:0.25:5;
yi=-5:0.25:5;
zi=-5:0.25:5;
[XX,YY,ZZ] = meshgrid(xi,yi,zi);
tmpdat = [XX(:),YY(:),ZZ(:)];
[grid_pred,grid_acc,VV] = svmpredict(zeros(size(tmpdat,1),1), tmpdat, model_rbf, '-q');
VV = reshape(VV,length(yi),length(xi),length(zi));
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
% plot the new hyperplane
h3=patch(isosurface(XX,YY,ZZ,VV,0));
set(h3,'facecolor','none','edgecolor',col(5,:));
% standard info for the plot
%legend({'Died in hospital','Survived'},'FontSize',16);
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% -
% We see this hyperplane is a lot more flexible. It can be hard to interpret what's above and what's below - we can add in another isosurface which is much "closer" to what the SVM believes to be patients who died.
% +
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
% plot the model and the data
figure(1); clf; hold all;
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
plot3(X_orig(idxTarget,1),X_orig(idxTarget,2),X_orig(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(~idxTarget,1),X_orig(~idxTarget,2),X_orig(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(pred==1,1),X_orig(pred==1,2),X_orig(pred==1,3),...
'Linestyle','none','Marker','o',...
'MarkerFaceColor','none','MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2,...
'HandleVisibility','off');
grid on;
% reapply the SVM to a grid of all possible values
xi=-5:0.25:5;
yi=-5:0.25:5;
zi=-5:0.25:5;
[XX,YY,ZZ] = meshgrid(xi,yi,zi);
tmpdat = [XX(:),YY(:),ZZ(:)];
[grid_pred,grid_acc,VV] = svmpredict(zeros(size(tmpdat,1),1), tmpdat, model_rbf, '-q');
VV = reshape(VV,length(yi),length(xi),length(zi));
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
% plot the hyperplane
h3=patch(isosurface(XX,YY,ZZ,VV,0));
set(h3,'facecolor','none','edgecolor',col(5,:));
% plot the hyperplane closer to positive outcomes
% note the SVM is treating positive outcomes as "below" the hyperplane, which is why we look for -1
h3=patch(isosurface(XX,YY,ZZ,VV,-1));
set(h3,'facecolor','none','edgecolor',col(4,:));
% standard info for the plot
%legend({'Died in hospital','Survived'},'FontSize',16);
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% +
% Evaluate the model quantitatively
% First, we calculate the four "operating point" statistics
TP = sum( pred == 1 & y == 1 );
FP = sum( pred == 0 & y == 1 );
TN = sum( pred == 0 & y == 0 );
FN = sum( pred == 1 & y == 0 );
% Now we create the confusion matrix
cm = [TP, FP;
FN, TN]
% +
% We can also create the sensitivity/specificity measures
fprintf('\n');
fprintf('Sensitivity: %6.2f%%\n', 100 * TP / (TP+FN));
fprintf('Specificity: %6.2f%%\n', 100 * TN / (TN+FP));
fprintf('PPV: %6.2f%%\n', 100 * TP / (TP + FP));
fprintf('NPV: %6.2f%%\n', 100 * TN / (TN+FN));
fprintf('\n');
% all together
fprintf('%6g\t%6g\t%10.2f%% \n', cm(1,1), cm(1,2), 100 * TP / (TP + FP));
fprintf('%6g\t%6g\t%10.2f%% \n', cm(2,1), cm(2,2), 100 * TN / (TN+FN));
fprintf('%5.2f%%\t%5.2f%%\t%10.2f%% \n', 100 * TP / (TP+FN), 100 * TN / (TN+FP), 100 * (TP+TN)/(TP+TN+FP+FN));
% +
% Directly compare the RBF model with the linear model
pred_linear = svmpredict(y, X, model_linear, '-q');
pred_rbf = svmpredict(y, X, model_rbf, '-q');
TP_l = sum( pred_linear == 1 & y == 1 );
FP_l = sum( pred_linear == 0 & y == 1 );
TN_l = sum( pred_linear == 0 & y == 0 );
FN_l = sum( pred_linear == 1 & y == 0 );
TP_r = sum( pred_rbf == 1 & y == 1 );
FP_r = sum( pred_rbf == 0 & y == 1 );
TN_r = sum( pred_rbf == 0 & y == 0 );
FN_r = sum( pred_rbf == 1 & y == 0 );
fprintf('Linear\tRBF\n');
fprintf('%4.2f%%\t%4.2f%%\tAccuracy\n', 100 * (TP_l+TN_l) / (TP_l+FN_l+TN_l+FP_l), 100 * (TP_r+TN_r) / (TP_r+FN_r+TN_r+FP_r));
fprintf('%4.2f%%\t%4.2f%%\tSensitivity\n', 100 * TP_l / (TP_l+FN_l), 100 * TP_r / (TP_r+FN_r));
fprintf('%6.2f%%\t%4.2f%%\tSpecificity\n', 100 * TN_l / (TN_l+FP_l), 100 * TN_r / (TN_r+FP_r));
fprintf('%6.2f%%\t%4.2f%%\tPPV\n', 100 * TP_l / (TP_l + FP_l), 100 * TP_r / (TP_r + FP_r));
fprintf('%6.2f%%\t%4.2f%%\tNPV\n', 100 * TN_l / (TN_l+FN_l), 100 * TN_r / (TN_r+FN_r));
% -
% It's hard to tell which is better - RBF has higher sensitivity, specificity, PPV, but lower accuracy and NPV. Of course, we have to remember that accuracy is still not the best measure due to the imbalanced class problem. Let's look at the area under the receiver operator characteristic curve (AUROC). This is a useful measure which summarizes the operating point statistics over all operating points.
% +
N_POS = sum(y==1);
N_NEG = sum(y==0);
[pred_linear,~,dist_linear] = svmpredict(y, X, model_linear, '-q');
[pred_rbf,~,dist_rbf] = svmpredict(y, X, model_rbf, '-q');
[~,idxSort] = sort(dist_rbf,1,'ascend');
y_rbf=y(idxSort);
idxNegative = y_rbf==0;
%=== Count the number of negative targets below each element
auc_rbf = cumsum(idxNegative,1);
%=== Only get positive targets
auc_rbf = auc_rbf(~idxNegative);
auc_rbf = sum(auc_rbf,1); %=== count number who are negative
auc_rbf = auc_rbf./(N_POS * N_NEG);
[~,idxSort] = sort(dist_linear,1,'ascend');
y_linear=y(idxSort);
idxNegative = y_linear==0;
%=== Count the number of negative targets below each element
auc_linear = cumsum(idxNegative,1);
%=== Only get positive targets
auc_linear = auc_linear(~idxNegative);
auc_linear = sum(auc_linear,1); %=== count number who are negative
auc_linear = auc_linear./(N_POS * N_NEG);
clear y_linear y_rbf;
[auc_rbf, auc_linear]
% -
% Looks like the AUROC for our RBF classifier is better! It's also nice to look at the ROC curve graphically, which helps interpret the value.
% +
% Plot the RBF model and the linear model ROC curves
% We have a subfunction, 'calcRoc', which calculates the x and y values for the ROC
[roc_l_x, roc_l_y] = calcRoc(dist_linear, y);
[roc_r_x, roc_r_y] = calcRoc(dist_rbf, y);
figure(1); clf; hold all;
plot(roc_r_x, roc_r_y, '--','Color',col(1,:));
plot(roc_l_x, roc_l_y, '.-','Color',col(2,:));
legend('RBF kernel','Linear kernel');
xlabel('1 - Specificity');
ylabel('Sensitivity');
% +
% Specify parameters in the RBF kernel
% The RBF kernel has some parameters of its own: gamma and capacity
% Let's set these to a different value then their defaults
gamma = 2;
capacity = 1;
% train the model
model_rbf_param = svmtrain(y_train, X_train, ['-t 2 -c ' num2str(2^(capacity)) ' -g ' num2str(2^(gamma))]);
[pred_rbf_param,~,dist_rbf_param] = svmpredict(y, X, model_rbf_param);
% +
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
% plot the model and the data
figure(1); clf; hold all;
idxTarget = y == 1; % note: '=' defines a number, '==' compares two variables
plot3(X_orig(idxTarget,1),X_orig(idxTarget,2),X_orig(idxTarget,3),...
'Linestyle','none','Marker','x',...
'MarkerFaceColor',col(1,:),'MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(~idxTarget,1),X_orig(~idxTarget,2),X_orig(~idxTarget,3),...
'Linestyle','none','Marker','+',...
'MarkerFaceColor',col(2,:),'MarkerEdgeColor',col(2,:),...
'MarkerSize',10,'LineWidth',2);
plot3(X_orig(pred==1,1),X_orig(pred==1,2),X_orig(pred==1,3),...
'Linestyle','none','Marker','o',...
'MarkerFaceColor','none','MarkerEdgeColor',col(1,:),...
'MarkerSize',10,'LineWidth',2,...
'HandleVisibility','off');
grid on;
% reapply the SVM to a grid of all possible values
xi=-5:0.25:5;
yi=-5:0.25:5;
zi=-5:0.25:5;
[XX,YY,ZZ] = meshgrid(xi,yi,zi);
tmpdat = [XX(:),YY(:),ZZ(:)];
[grid_pred,grid_acc,VV] = svmpredict(zeros(size(tmpdat,1),1), tmpdat, model_rbf_param, '-q');
VV = reshape(VV,length(yi),length(xi),length(zi));
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
% plot the hyperplane
h3=patch(isosurface(XX,YY,ZZ,VV,0));
set(h3,'facecolor','none','edgecolor',col(5,:));
% plot the hyperplane closer to positive outcomes
% note the SVM is treating positive outcomes as "below" the hyperplane, which is why we look for -1
h3=patch(isosurface(XX,YY,ZZ,VV,-1));
set(h3,'facecolor','none','edgecolor',col(4,:));
% standard info for the plot
%legend({'Died in hospital','Survived'},'FontSize',16);
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% +
[pred_rbf_param,~,dist_rbf_param] = svmpredict(y, X, model_rbf_param, '-q');
%=== Sensitivity (true positive rate)
[roc_rp_x, roc_rp_y, auc_rbf_param] = calcRoc(dist_rbf_param, y);
figure(1); clf; hold all;
plot(roc_r_x, roc_r_y, '--','Color',col(1,:));
plot(roc_rp_x, roc_rp_y, '.-','Color',col(3,:));
legend('RBF kernel','RBF kernel - higher gamma','Location','SouthEast');
xlabel('1 - Specificity');
ylabel('Sensitivity');
[auc_rbf, auc_rbf_param]
% -
% Great! Our parameter tweaking has improved the AUROC. Let's see how much better we can make our model!
% +
% change gamma to improve the model
gamma = 10; % N.B. keep this as an integer as we exponentiate with it
capacity = 1;
% train the model
model_rbf_opt = svmtrain(y_train, X_train, ['-q -t 2 -c ' num2str(2^(capacity)) ' -g ' num2str(2^(gamma))]);
[pred_rbf_opt,~,dist_rbf_opt] = svmpredict(y, X, model_rbf_opt, '-q');
[roc_ro_x, roc_ro_y, auc_rbf_opt] = calcRoc(dist_rbf_opt, y);
figure(1); clf; hold all;
plot(roc_r_x, roc_r_y, '--','Color',col(1,:));
plot(roc_rp_x, roc_rp_y, '.-','Color',col(3,:));
plot(roc_ro_x, roc_ro_y, '.-','Color',col(4,:));
legend('RBF kernel','RBF kernel - higher gamma','RBF kernel - very high gamma', 'Location','SouthEast');
xlabel('1 - Specificity');
ylabel('Sensitivity');
auc_rbf_opt
% -
% Almost perfect AUROC! Awesome! Have we solved mortality prediction? Probably not yet :)
%
% The issue here is we are evaluating the model on the *same data* that we develop it on. SVMs are flexible enough that they can "memorize" the data they have trained on - that is, they create a set of rules such as "if the age is 82, the heart rate is 40, and the gcs is 7, then the patient died". This set of rules is intuitively too specific - the fact thate one patient died with these exact values does not imply that all future patients will too. We would call our model "overfit" - it is memorizing the exact details of our training data rather then estimating a more generalizable model. The best way to assess if a model is overfit is to test it on new, never before seen data. To do this, we simply split our data into two sets: one for training and one for testing.
% +
rng(625,'twister'); % set the seed so that everyone gets the same train/test sets
idxTrain = rand(size(X,1),1) > 0.5; % randomly assign training data
X_train = X(idxTrain,:);
y_train = y(idxTrain); % note that the first row is positive so LIBSVM will assign positive distances to positive cases
X_test = X(~idxTrain,:);
y_test = y(~idxTrain);
% +
% Now we can train the model on the training data, and evaluate it on the test data
% We retrain all three models to compare the performances
% The original linear model
model_linear = svmtrain(y_train, X_train, '-q -t 0');
% The original RBF model
model_rbf = svmtrain(y_train, X_train, '-q -t 2');
% The RBF model with very high gamma
gamma = 10;
capacity = 1;
model_rbfopt = svmtrain(y_train, X_train, ['-q -t 2 -c ' num2str(2^(capacity)) ' -g ' num2str(2^(gamma))]);
% +
% Evaluate the models on the training set
[pred_linear_tr,~,dist_linear_tr] = svmpredict(y_train, X_train, model_linear);
[ pred_rbf_tr,~,dist_rbf_tr] = svmpredict(y_train, X_train, model_rbf);
[pred_rbfopt_tr,~,dist_rbfopt_tr] = svmpredict(y_train, X_train, model_rbfopt);
% Evaluate the models on the test set
[pred_linear_test,~,dist_linear_test] = svmpredict(y_test, X_test, model_linear);
[pred_rbf_test,~,dist_rbf_test] = svmpredict(y_test, X_test, model_rbf);
[pred_rbfopt_test,~,dist_rbfopt_test] = svmpredict(y_test, X_test, model_rbfopt);
% +
% Plot their AUROCs on the training set as dashed lines, and on the test set as solid lines
[roc_linear_tr_x, roc_linear_tr_y, auroc_linear_tr] = calcRoc(dist_linear_tr, y_train);
[ roc_rbf_tr_x, roc_rbf_tr_y, auroc_rbf_tr] = calcRoc( dist_rbf_tr, y_train);
[roc_rbfopt_tr_x, roc_rbfopt_tr_y, auroc_rbf_opt_tr] = calcRoc(dist_rbfopt_tr, y_train);
[roc_linear_test_x, roc_linear_test_y, auroc_linear_test] = calcRoc(dist_linear_test, y_test);
[ roc_rbf_test_x, roc_rbf_test_y, auroc_rbf_test] = calcRoc( dist_rbf_test, y_test);
[roc_rbfopt_test_x, roc_rbfopt_test_y, auroc_rbf_opt_test] = calcRoc(dist_rbfopt_test, y_test);
figure(1); clf; hold all;
plot(roc_linear_tr_x, roc_linear_tr_y, '--','Color',col(1,:));
plot(roc_rbf_tr_x, roc_rbf_tr_y, '--','Color',col(3,:));
plot(roc_rbfopt_tr_x, roc_rbfopt_tr_y, '--','Color',col(4,:));
plot(roc_linear_test_x, roc_linear_test_y, '-','Color',col(1,:));
plot(roc_rbf_test_x, roc_rbf_test_y, '-','Color',col(3,:));
plot(roc_rbfopt_test_x, roc_rbfopt_test_y, '-','Color',col(4,:));
legend('Linear kernel','RBF kernel','RBF kernel - very high gamma', 'Location','SouthEast');
xlabel('1 - Specificity');
ylabel('Sensitivity');
{ 'Data', 'Linear','RBF','RBF with high gamma';
'train', auroc_linear_tr, auroc_rbf_tr, auroc_rbf_opt_tr;
'test', auroc_linear_test, auroc_rbf_test, auroc_rbf_opt_test }
% -
% Above has given us a lot of information. The training set performances are the dashed lines, while the test set performances are the solid lines.
%
% * The linear SVM has about equivalent performance on train and test sets - since the model is not very flexible (sometimes called "low variance"), it doesn't overfit as easily. This is true in general - there is a balance between flexible models and overfitting
% * The RBF model performs better than the linear model, and while the training set performance is slightly better than the test set performance (in general you would expect this), it has not overfit, in that the test set performance is not significantly worse than we would expect
% * The RBF model with very high gamma has overfit - the training set peformance is *much* higher than the test set performance. The training set performance implies that we should have perfect classification - but the truth is much worse, with a test set AUROC of 0.60.
%
% We can visualize *just* the hyperplane of the high gamma RBF to visualize the overfitting.
% +
X_orig = bsxfun(@times, X, sigma);
X_orig = bsxfun(@plus, X_orig, mu);
% plot only the model hyperplane
figure(1); clf; hold all;
% create a grid of values in the main region of interest
xi=-3:0.1:3;
yi=-3:0.1:3;
zi=-3:0.1:3;
[XX,YY,ZZ] = meshgrid(xi,yi,zi);
tmpdat = [XX(:),YY(:),ZZ(:)];
% apply the SVM to this grid
[grid_pred,grid_acc,VV] = svmpredict(zeros(size(tmpdat,1),1), tmpdat, model_rbfopt, '-q');
% reshape the predictions into a 3 dimensions
VV = reshape(VV,length(yi),length(xi),length(zi));
XX = XX*sigma(1) + mu(1);
YY = YY*sigma(2) + mu(2);
ZZ = ZZ*sigma(3) + mu(3);
% plot the separating hyperplane
h3=patch(isosurface(XX,YY,ZZ,VV,0));
set(h3,'facecolor','none','edgecolor',col(5,:));
% standard info for the plot
xlabel(X_header{1},'FontSize',16);
ylabel(X_header{2},'FontSize',16);
zlabel(X_header{3},'FontSize',16);
set(gca,'view',[-127 10]);
% -
% Here we can see that the hyperplane is hundreds of tiny grey dots. By setting a high gamma, we have set the hyperplane to be very close to each training point (technically, to each support vector). As a result, the separating boundary is simply a circle around each training point - clearly not a very generalizable model!
%
% To pick the best gamma and capacity, we are going to learn a very important concept in machine learning: cross-validation. By now it's clear that using a validation set to periodically check how well our model is doing is a good idea. Note I called it a validation set: this is slightly different than a test set. A test set is used *once* at the end of all model development when you want to publish the results. A validation set is used repeatedly during model development to give you an idea of how the model would likely perform on the test set.
%
% Cross-validation in particular aims to solve the following trade-off:
%
% 1. Bigger validation sets result in better estimates of performance
% 2. Bigger validation sets result in smaller training sets and (usually) worse performance
%
% The technique involves splitting the training set into subsets, or folds. You then train a model using data from all but one fold, and subsequently evaluate the model on that fold. Repeat this process for every fold that you have and voila - cross-validation! Let's try it out.
% +
K = 5; % how many folds
[~,idxSplit] = sort(rand(size(X_train,1),1));
idxSplit = mod(idxSplit,K) + 1;
auroc = zeros(1,K);
for k=1:K
idxDevelop = idxSplit ~= k;
idxValidate = idxSplit == k;
model = svmtrain(y_train(idxDevelop), X_train(idxDevelop,:), '-q -t 2');
[pred,~,dist] = svmpredict(y_train(idxValidate), X_train(idxValidate,:), model);
if (pred(1) == 0 && dist(1) > 0) || (pred(1) == 1 && dist(1) < 0)
% flip the sign of dist to ensure that the AUROC is calculated properly
% the AUROC expects predictions of 1 to be assigned increasing distances
dist = -dist;
end
[~, ~, auroc(k)] = calcRoc(dist, y_train(idxValidate));
end
auroc
% -
% As we can see, we get some variation in the AUROC - each validation set is slightly different - and each AUROC is a noisy estimate of the true performance because we have a limited number of observations.
%
% Cross-validation is often used to tune hyperparameters of a model. Hyperparameters are the same as parameters, except they control how the model is trained. For example, gamma and capacity are hyperparameters, and control how big the circles are and how many errors we allow the model to make.
%
% These values are very important - and we can use cross-validation to set them to better values than the default. How we do this is simple - we try a bunch of values, and those which work best in cross-validation are the ones we pick. This is called a grid search.
% +
% set the pseudo random number generator seed so our results are consistent
rng(90210,'twister');
K = 5; % how many folds
[~,idxSplit] = sort(rand(size(X_train,1),1));
idxSplit = mod(idxSplit,K) + 1;
gamma_grid = -5:5:5;
capacity_grid = -5:5:5;
G = numel(gamma_grid);
C = numel(capacity_grid);
auroc = zeros(G,C,K);
for c=1:C
for g=1:G
for k=1:K
idxDevelop = idxSplit ~= k;
idxValidate = idxSplit == k;
gamma = gamma_grid(g);
capacity = capacity_grid(c);
model = svmtrain(y_train(idxDevelop), X_train(idxDevelop,:), ['-q -t 2 -g ' num2str(2^gamma) ' -c ' num2str(2^capacity)]);
[pred,~,dist] = svmpredict(y_train(idxValidate), X_train(idxValidate,:), model, '-q');
if (pred(1) == 0 && dist(1) > 0) || (pred(1) == 1 && dist(1) < 0)
% flip the sign of dist to ensure that the AUROC is calculated properly
% the AUROC expects predictions of 1 to be assigned increasing distances
dist = -dist;
end
[~, ~, auroc(g,c,k)] = calcRoc(dist, y_train(idxValidate));
end
end
end
% it's easiest to look at the mean AUROC across all the folds, rather than all 5
mean(auroc,3)
% -
% We can see that some values are better than others. We're looking for a maximum somewhere in these values. Grid search is a lot like mountain climbing - you keep going until you find the peak. We'll just pick the values which gave us the best performance here - in practice you would probably make this grid bigger with smaller step sizes to get better hyperparameters.
%
% It looks like the 1st row (gamma = -5) and 3rd column (capacity = 5) have the best performance. These will be the hyperparameters we select for our final model.
% +
gamma = -5;
capacity = 5;
model_rbfcv = svmtrain(y_train, X_train, ['-q -t 2 -g ' num2str(2^gamma) ' -c ' num2str(2^capacity)]);
[~,~,dist_rbfcv_tr] = svmpredict(y_train, X_train, model_rbfcv, '-q');
[~,~,dist_rbfcv_test] = svmpredict( y_test, X_test, model_rbfcv, '-q');
[roc_rbfcv_tr_x, roc_rbfcv_tr_y, auroc_rbfcv_tr] = calcRoc(dist_rbfcv_tr, y_train);
[roc_rbfcv_test_x, roc_rbfcv_test_y, auroc_rbfcv_test] = calcRoc(dist_rbfcv_test, y_test);
figure(1); clf; hold all;
plot(roc_rbf_test_x, roc_rbf_test_y, '-','Color',col(3,:));
plot(roc_rbfcv_test_x, roc_rbfcv_test_y, '-','Color',col(6,:));
legend('RBF kernel','RBF kernel - cross-validation', 'Location','SouthEast');
xlabel('1 - Specificity');
ylabel('Sensitivity');
% -
% We can see that with relatively little effort we've eeked out some extra performance in our model, essentially for free. This is the power of cross-validation. We could likely improve the model more, but the time needed to do the grid search would become longer (changing gamma and capacity to very large or very small values can drastically increase the SVM training time). This is the main drawback of cross-validation - it takes time.
% With your new skills in hand, you're ready to practice on your own! Try the following exercises on the *full* dataset, not just the three features we've examined.
%
% 1. Train an SVM using cross-validation to pick capacity and gamma
% 2. Train a logistic regression model
% 4. Train a random forest
%
% Don't worry about using cross-validation for the logistic regression and random forest models.
% +
% Prepare the data for model development
rng(128301,'twister');
X = data(:,3:end);
y = data(:,2);
% set aside 30% of the data for final testing
idxTest = rand(size(data,1),1) > 0.7;
X_test = X(idxTest,:);
y_test = y(idxTest);
X_train = X(~idxTest,:);
y_train = y(~idxTest);
% remember to pick a balanced subset!
N0 = sum(y_train==0);
N1 = sum(y_train==1);
[~,idxRandomize] = sort(rand(N0,1));
idxKeep = find(y_train==0); % find all the negative outcomes
idxKeep = idxKeep(idxRandomize(1:N1)); % pick a random N1 negative outcomes
idxKeep = [find(y_train==1);idxKeep]; % add in the positive outcomes
idxKeep = sort(idxKeep); % probably not needed but it's cleaner
X_train = X_train(idxKeep,:);
y_train = y_train(idxKeep);
% +
% Train an SVM using all you've learned!
% don't forget to normalize the data and impute the mean for missing values
% -
% Train a logistic regression model
help glmfit; % used to train the model, look at 'binomial'
help glmval; % used to make predictions, look at 'logit'
% Train a random forest
help treebagger;
|
mlcc/lab2-intro-ml/mlcc2_svm_workshop.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import tarfile
import urllib
DOWNLOAD_ROOT = "https://raw.githubusercontent.com/ageron/handson-ml2/master/"
HOUSING_PATH = os.path.join("datasets", "housing")
HOUSING_URL = DOWNLOAD_ROOT + "datasets/housing/housing.tgz"
def fetch_housing_data(housing_url=HOUSING_URL, housing_path=HOUSING_PATH):
os.makedirs(housing_path, exist_ok=True)
tgz_path = os.path.join(housing_path, "housing.tgz")
urllib.request.urlretrieve(housing_url, tgz_path)
housing_tgz = tarfile.open(tgz_path)
housing_tgz.extractall(path=housing_path)
housing_tgz.close()
# +
import pandas as pd
def load_housing_data(housing_path = HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
# -
housing = load_housing_data()
housing.head()
housing.info()
housing["ocean_proximity"].value_counts()
housing.describe()
# %matplotlib inline
import matplotlib.pyplot as plt
housing.hist(bins=50, figsize=(20,15))
plt.show()
# +
import numpy as np
def split_train_test(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
# -
train_set, test_set = split_train_test(housing, 0.2)
len(train_set)
len(test_set)
# +
from zlib import crc32
def test_set_check(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio *2**32
def split_train_test_by_id(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: test_set_check(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
# +
#housing_with_id = housing.reset_index()
#housing_with_id["id"] = housing["longitude"] * 1000 + housing["latitude"]
#train_set, test_set = split_train_test_by_id(housing_with_id,0.2,"id")
# +
from sklearn.model_selection import train_test_split
train_set, test_set = train_test_split(housing, test_size = 0.2, random_state= 42)
# -
housing["income_cat"] = pd.cut(housing["median_income"], bins = [0,1.5, 3.0, 4.5, 6., np.inf], labels = [1,2,3,4,5])
# +
housing["income_cat"].hist()
# +
from sklearn.model_selection import StratifiedShuffleSplit
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(housing, housing["income_cat"]):
strat_train_set = housing.loc[train_index]
strat_test_set = housing.loc[test_index]
# +
strat_test_set["income_cat"].value_counts() / len(strat_test_set)
# -
for set_ in (strat_train_set, strat_test_set):
set_.drop("income_cat", axis = 1, inplace = True)
# +
housing = strat_train_set.copy()
# -
housing.plot(kind = "scatter", x = "longitude", y = "latitude")
housing.plot(kind = "scatter", x = "longitude", y = "latitude", alpha = 0.1)
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population", figsize=(10,7),
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)
plt.legend()
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)
# +
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms", "housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12,8))
# -
housing.plot(kind="scatter", x="median_income", y="median_house_value",
alpha=0.1)
housing["rooms_per_household"] = housing["total_rooms"]/housing["households"]
housing["bedrooms_per_room"] = housing["total_bedrooms"]/housing["total_rooms"]
housing["population_per_household"]=housing["population"]/housing["households"]
corr_matrix = housing.corr()
corr_matrix["median_house_value"].sort_values(ascending = False)
housing = strat_train_set.drop("median_house_value", axis = 1)
housing_labels = strat_train_set["median_house_value"].copy()
# +
#housing.dropna(subset=["total_bedrooms"])
# option 1
#housing.drop("total_bedrooms", axis=1)
# option 2
#median = housing["total_bedrooms"].median() # option 3
#housing["total_bedrooms"].fillna(median, inplace=True)
# +
from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy = "median")
# -
housing_num = housing.drop("ocean_proximity", axis = 1)
imputer.fit(housing_num)
housing_num.head()
housing_num.info()
# +
imputer.statistics_
# -
housing_num.median().values
X = imputer.transform(housing_num)
housing_tr = pd.DataFrame(X, columns = housing_num.columns, index = housing_num.index)
imputer.strategy
housing_cat = housing[["ocean_proximity"]]
housing_cat.head(10)
from sklearn.preprocessing import OrdinalEncoder
ordinal_encoder = OrdinalEncoder()
housing_cat_encoded = ordinal_encoder.fit_transform(housing_cat)
housing_cat_encoded[:10]
ordinal_encoder.categories_
from sklearn.preprocessing import OneHotEncoder
cat_encoder = OneHotEncoder()
housing_cat_1hot = cat_encoder.fit_transform(housing_cat)
housing_cat_1hot
housing_cat_1hot.toarray()
cat_encoder.categories_
# +
from sklearn.base import BaseEstimator, TransformerMixin
rooms_ix, bedrooms_ix, population_ix, households_ix= 3,4,5,6
class CombinedAttributesAdder(BaseEstimator, TransformerMixin):
def __init__(self, add_bedrooms_per_room = True):
self.add_bedrooms_per_room = add_bedrooms_per_room
def fit(self, X, y = None):
return self
def transform(self, X):
rooms_per_household = X[:, rooms_ix] / X[:, households_ix]
population_per_household = X[:, population_ix] / X[:, households_ix]
if self.add_bedrooms_per_room:
bedrooms_per_room = X[:, bedrooms_ix] / X[:, rooms_ix]
return np.c_[X, rooms_per_household, population_per_household, bedrooms_per_room]
else:
return np.c_[X, rooms_per_household, population_per_household]
attr_adder = CombinedAttributesAdder(add_bedrooms_per_room = False)
housing_extra_attribs = attr_adder.transform(housing.values)
# +
# normalization: (value -min) / (max - min)
# in Scikit-Learn we use MinMaxScaler for this normalization
#Standardization: (value -mean) / mean deviation
# in Scikit-Learn we use StandardScaler
# +
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy = "median")),
('attribs_adder', CombinedAttributesAdder()),
('std_scaler', StandardScaler()),
])
housing_num_tr = num_pipeline.fit_transform(housing_num)
# +
from sklearn.compose import ColumnTransformer
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(), cat_attribs),
])
housing_prepared = full_pipeline.fit_transform(housing)
# +
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(housing_prepared, housing_labels)
# -
some_data = housing.iloc[:5]
some_labels = housing_labels.iloc[:5]
some_data_prepared = full_pipeline.transform(some_data)
print("Predictions:", lin_reg.predict(some_data_prepared))
print("Labels:", list(some_labels))
from sklearn.metrics import mean_squared_error
housing_predictions = lin_reg.predict(housing_prepared)
lin_mse = mean_squared_error(housing_labels, housing_predictions)
lin_rmse = np.sqrt(lin_mse)
lin_rmse
from sklearn.tree import DecisionTreeRegressor
tree_reg = DecisionTreeRegressor()
tree_reg.fit(housing_prepared, housing_labels)
housing_predictions = tree_reg.predict(housing_prepared)
tree_mse = mean_squared_error(housing_labels, housing_predictions)
tree_rmse = np.sqrt(tree_mse)
tree_rmse
# +
# Oh God, I can't believe that the error is 0.0 coz this is currently impossible
# thanks to Albert. There is no model possible without error(of course for real life data,not dummy data)
# +
from sklearn.model_selection import cross_val_score
scores = cross_val_score( tree_reg, housing_prepared, housing_labels,
scoring= "neg_mean_squared_error", cv= 10)
tree_rmse_scores = np.sqrt(-scores)
# -
def display_scores(scores):
print("Scores:", scores)
print("Mean:", scores.mean())
print("Standard deviation:", scores.std())
display_scores(tree_rmse_scores)
lin_scores = cross_val_score(lin_reg, housing_prepared, housing_labels,
scoring= "neg_mean_squared_error", cv = 10)
lin_rmse_scores = np.sqrt(-lin_scores)
display_scores(lin_rmse_scores)
# +
#RandomForestRegressor : also known as Ensemble Learning
from sklearn.ensemble import RandomForestRegressor
forest_reg = RandomForestRegressor()
forest_reg.fit(housing_prepared, housing_labels)
housing_predictions = forest_reg.predict(housing_prepared)
forest_mse = mean_squared_error(housing_labels, housing_predictions)
forest_rmse = np.sqrt(forest_mse)
forest_rmse
# +
from sklearn.model_selection import cross_val_score
forest_scores = cross_val_score(forest_reg, housing_prepared, housing_labels,
scoring="neg_mean_squared_error", cv= 10)
forest_rmse_scores = np.sqrt(-forest_scores)
display_scores(forest_rmse_scores)
# -
scores = cross_val_score(lin_reg, housing_prepared, housing_labels, scoring="neg_mean_squared_error", cv=10)
pd.Series(np.sqrt(-scores)).describe()
# +
from sklearn.svm import SVR
svm_reg = SVR(kernel="linear")
svm_reg.fit(housing_prepared, housing_labels)
housing_predictions = svm_reg.predict(housing_prepared)
svm_mse = mean_squared_error(housing_labels, housing_predictions)
svm_rmse = np.sqrt(svm_mse)
svm_rmse
# +
from sklearn.model_selection import GridSearchCV
param_grid = [
{'n_estimators': [3, 10, 30], 'max_features': [2, 4, 6, 8]},
{'bootstrap': [False], 'n_estimators': [3, 10], 'max_features': [2, 3, 4]},
]
forest_reg = RandomForestRegressor()
grid_search = GridSearchCV(forest_reg, param_grid, cv=5,
scoring='neg_mean_squared_error',
return_train_score=True)
grid_search.fit(housing_prepared, housing_labels)
# -
grid_search.best_params_
grid_search.best_estimator_
cvres = grid_search.cv_results_
for mean_score, params in zip(cvres["mean_test_score"], cvres["params"]):
print(np.sqrt(-mean_score), params)
feature_importances = grid_search.best_estimator_.feature_importances_
feature_importances
extra_attribs = ["rooms_per_hhold", "pop_per_hhold", "bedrooms_per_room"]
cat_encoder = full_pipeline.named_transformers_["cat"]
cat_one_hot_attribs = list(cat_encoder.categories_[0])
attributes = num_attribs + extra_attribs + cat_one_hot_attribs
sorted(zip(feature_importances, attributes), reverse=True)
# +
final_model = grid_search.best_estimator_
X_test = strat_test_set.drop("median_house_value", axis = 1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
# -
from scipy import stats
confidence = 0.95
squared_errors = ( final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc = squared_errors.mean(),
scale = stats.sem(squared_errors)))
|
Regression/Housing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="-l_C63VlP1iu" outputId="926b41c7-8ca6-4127-efa8-c4e09f5bc7ac"
# !pip install simpletransformers
# !pip install datasets
# + colab={"base_uri": "https://localhost:8080/"} id="MDGFLNurQRlf" outputId="db7b98d5-6bec-4fc2-8b44-9222bdab0d0c"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="n5stsLYnRoSD" outputId="5cc75003-4963-44d5-950d-374512921cbf"
# !tar -zxvf /content/drive/MyDrive/Models/model_with_key.tar.gz
# + id="YVq_455HSMdi"
from simpletransformers.t5 import T5Model
# + id="5UusJ5ROSTVV"
t5_model_directory = "outputs/best_model"
# + id="ESpKcW58SvJk"
# class for generating question
class QuestionGenerator():
def __init__(self):
''' Initializes the class to generate a MCQ given a context and an answer '''
self.model = T5Model("t5", t5_model_directory)
def get_processed_input(self, context, key):
''' Returns processed input with the required tokens '''
return 'generate_question: {0} answer: {1}'.format(context, key)
def get_predictions(self, context, key):
''' Generates the question from the context '''
to_predict = [self.get_processed_input(context, key)]
predictions = self.model.predict(to_predict)
if len(predictions) == 1:
return predictions[0]
else:
raise Exception('Not able to generate')
def get_mcq(self, context, key):
''' Call this method to get the final MCQ for the provided context and key '''
question = self.get_predictions(context, key)
return question
# + id="i_S0r6TaTqUq"
# class for generating answers
from transformers import T5ForConditionalGeneration, T5Tokenizer
class AnswerGenerator():
def __init__(self):
base_model = 't5-base'
self.tokenizer = T5Tokenizer.from_pretrained(base_model)
self.model = T5ForConditionalGeneration.from_pretrained(base_model)
def get_answer_for_question(self, question, context):
input = 'question: %s context: %s' % (question, context)
features = self.tokenizer(input, return_tensors='pt')
input_ids = features['input_ids']
attention_mask = features['attention_mask']
outcome = self.model.generate(input_ids = input_ids, attention_mask = attention_mask, max_length=255)
answer = self.tokenizer.decode(outcome[0]).replace('<pad>', '').replace('</s>', '').strip()
return answer
# + id="V0vXVlfqU7EX"
import pandas as pd
# + colab={"base_uri": "https://localhost:8080/", "height": 199, "referenced_widgets": ["b922548ca17c4973a97cf8429920b250", "a70b432316394c989f1abbb8775902b0", "499a817fcfc24464bd1c2b53e4b10979", "5eef2843203b4edbb196ac3780b0e943", "<KEY>", "<KEY>", "<KEY>", "f0fe851817b64e068f4745259c9d34fb", "e7c3e62907ed42698280ca8f05eb2852", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "59a7e79fb2ab4afdaccc7d7260feaa4b", "<KEY>", "<KEY>", "<KEY>", "d78458792b2d4cf7a7ddd8b697a947f7", "<KEY>", "<KEY>", "<KEY>", "<KEY>", "242b853b9d7143068438cec1e63e0d39", "f170eca8d6b04166ae232d62a2a4ae87", "<KEY>", "5b620f069e304e97a3416c6dd88fa126", "8a609d0ca92e4de38e687d0001a402bb", "a10680c5cc5a49b9931105789adf2273", "<KEY>", "e8013d3fa88b41838ac614f104eaa9a2", "ad73d3e6787f461987de3408f3b30fa6", "<KEY>", "<KEY>", "<KEY>", "b4084d2adf1e4945bde11c812c94fdee", "a7ad80a7da474e8997cbe6ff7954744d", "d3a43ca2a6814f6dbbf650982d9bcbb4", "da68a932c7ad40b1aa6ec3df945a15b4", "5ada05308408422686934f89e7e66d1c", "<KEY>", "bb6d8a920161411fa35b25a05ecc99c1", "99ea263620784c9884fd05f07eed8b1c", "4a10204c54e54dec95ea6512e33095a3", "<KEY>", "<KEY>", "eaf82f8e06484b938b90ba3869cce696", "<KEY>", "9365c7c033ec4c01aec77390f583a274", "<KEY>", "f0f6723541ca47c6af09371f3a530eab", "<KEY>", "91a91c5273344113a45c741370ec153e", "<KEY>", "<KEY>", "<KEY>", "f1941ac48d12408fa1cafe48ec4506d4", "381d38ad03974a298b8aa3a501f20437", "<KEY>", "<KEY>", "<KEY>", "01f8502d2fe849489dc5392776e25975", "<KEY>", "3bab5b51d8ab43ee8544cf150610f1f7", "8d2e9f455cd04ced829b3edbea1025f6", "<KEY>"]} id="T9CXe03zVS3Y" outputId="3d9a1f62-c106-45cf-adba-49ddb81cc26d"
# loading dataset
from datasets import load_dataset
raw_datasets = load_dataset('squad')
# + id="-rFNu7xoVCa2"
# Preprocessing validation dataset and preparing list of dictionary for evaluation
validation_list = list()
for i in range(len(raw_datasets['validation'])):
new_record = dict()
new_record['context'] = raw_datasets['validation'][i]['context']
new_record['answer'] = raw_datasets['validation'][i]['answers']['text'][0]
validation_list.append(new_record)
# + id="OWJJkbyfVPRR"
# Evaluation technique
# Generate question using our trained t5 model
# Feed the question to t5-base model
# compare the t5-base model answer with input key to our t5 model
class Evaluate():
def __init__(self):
self.ques_generator = QuestionGenerator()
self.ans_generator = AnswerGenerator()
def eval(self):
correct = 0
for record in validation_list[:100]:
context = record['context']
key = record['answer']
question = self.ques_generator.get_mcq(context, key)
answer = self.ans_generator.get_answer_for_question(question, context)
if key == answer:
correct += 1
return correct
# + id="XBJ_o6MUXani"
correct_preds = Evaluate().eval()
# + colab={"base_uri": "https://localhost:8080/"} id="_IupXxQwYjWt" outputId="4ea42f5e-97bc-4beb-ec01-cba8c8dec7ca"
correct_preds
# + id="hr3MqBB0d-v6"
|
evaluation/Evalution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: dev
# language: python
# name: dev
# ---
# +
import warnings
import pandas as pd
from datetime import datetime
from datetime import date
import sqlalchemy as sql
from pathlib import Path
warnings.filterwarnings('ignore') # Hide warnings
#Library - Project3
import CryptoDownloadData as coinData
import CryptoPerfSummary as coinAnalytic
#DataBase Tables
# Database connection string
crypto_data_connection_string = 'sqlite:///./Reference/crypto.db'
# Database engine
crypto_data_engine = sql.create_engine(crypto_data_connection_string, echo=True)
'COINBASE_100' #CoinList - symbols
'ETF_LIST' #Sample ETF
'CRYPTO_PX_HISTORY' #Crypto PX History
# If need to repopulate database sqllite, please set refresh = True
refresh = False
# -
# Download all price history for Coin List 100 into CRYPTO_PX_HISTORY
# If need to rerun, please change refresh = True
if refresh == True:
coinData.create_coinlist100
coinData.create_sampleETF
coinData.drop_table('CRYPTO_PX_HISTORY')
start_date = datetime(2015, 1, 1)
end_date = datetime.today()
coinData.download_px_data_from_COINBASE_100(start_date, end_date)
# Pull Price by Name
px_history_df = coinData.get_px_history('ETH')
display(px_history_df.head())
display(px_history_df.tail())
# Get Price History Marix by Period - Sharpe and 30d roll beta, annual return
t_date = datetime(2022, 2, 21)
px_matrix = coinAnalytic.get_crypto_hist_martix_summary(t_date)
display(px_matrix.dropna().head())
#Get SMA, HIGH, LOW, RS RATING
t_date = datetime(2022, 2, 21)
px_strat = coinAnalytic.get_crypto_px_strat(t_date)
display(px_strat)
#Our 3 ETF Sample -
#file_path = Path('./Reference/sampleETF.csv')
#coinData.create_index_from_csv(file_path, 'ETF_LIST')
#coinData.create_sampleETF
sql_query = """
SELECT * FROM ETF_LIST"""
etf_list= pd.read_sql_query(sql_query, crypto_data_connection_string)
etf_summary = etf_list.merge(px_strat, left_on='symbol', right_on='symbol').groupby(['ETF','symbol']).mean().sort_values(by=['ETF','rank'])
etf_summary
#3 Portfolios - Return analysis
perf_summary = etf_list.merge(px_matrix, left_on='symbol', right_on='symbol').groupby(['ETF','symbol']).mean().sort_values(by=['ETF','rank'])
perf_summary
|
.ipynb_checkpoints/CryptoAnalyzer-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/AnikaZN/DS-Unit-1-Sprint-3-Statistical-Tests-and-Experiments/blob/master/Anika_Nacey_DS_Unit_1_Sprint_Challenge_3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="NooAiTdnafkz" colab_type="text"
# # Data Science Unit 1 Sprint Challenge 3
#
# ## Exploring Data, Testing Hypotheses
#
# In this sprint challenge you will look at a dataset of people being approved or rejected for credit.
#
# https://archive.ics.uci.edu/ml/datasets/Credit+Approval
#
# Data Set Information: This file concerns credit card applications. All attribute names and values have been changed to meaningless symbols to protect confidentiality of the data. This dataset is interesting because there is a good mix of attributes -- continuous, nominal with small numbers of values, and nominal with larger numbers of values. There are also a few missing values.
#
# Attribute Information:
# - A1: b, a.
# - A2: continuous.
# - A3: continuous.
# - A4: u, y, l, t.
# - A5: g, p, gg.
# - A6: c, d, cc, i, j, k, m, r, q, w, x, e, aa, ff.
# - A7: v, h, bb, j, n, z, dd, ff, o.
# - A8: continuous.
# - A9: t, f.
# - A10: t, f.
# - A11: continuous.
# - A12: t, f.
# - A13: g, p, s.
# - A14: continuous.
# - A15: continuous.
# - A16: +,- (class attribute)
#
# Yes, most of that doesn't mean anything. A16 (the class attribute) is the most interesting, as it separates the 307 approved cases from the 383 rejected cases. The remaining variables have been obfuscated for privacy - a challenge you may have to deal with in your data science career.
#
# Sprint challenges are evaluated based on satisfactory completion of each part. It is suggested you work through it in order, getting each aspect reasonably working, before trying to deeply explore, iterate, or refine any given step. Once you get to the end, if you want to go back and improve things, go for it!
# + [markdown] id="5wch6ksCbJtZ" colab_type="text"
# ## Part 1 - Load and validate the data
#
# - Load the data as a `pandas` data frame.
# - Validate that it has the appropriate number of observations (you can check the raw file, and also read the dataset description from UCI).
# - UCI says there should be missing data - check, and if necessary change the data so pandas recognizes it as na
# - Make sure that the loaded features are of the types described above (continuous values should be treated as float), and correct as necessary
#
# This is review, but skills that you'll use at the start of any data exploration. Further, you may have to do some investigation to figure out which file to load from - that is part of the puzzle.
# + id="Q79xDLckzibS" colab_type="code" outputId="70011068-14f0-4d9b-97a2-8b5da5df3a09" colab={"base_uri": "https://localhost:8080/", "height": 195}
import pandas as pd
import numpy as np
credit = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/credit-screening/crx.data')
credit.columns = ['A1', 'A2', 'A3', 'A4', 'A5', 'A6', 'A7', 'A8', 'A9', 'A10', 'A11', 'A12', 'A13', 'A14', 'A15', 'A16']
credit.head()
# + id="0eBZls1T0ipO" colab_type="code" outputId="654dd1fb-0dcb-49f7-f734-c740b456b9a9" colab={"base_uri": "https://localhost:8080/", "height": 34}
credit.shape
# + id="at76n0wG0msC" colab_type="code" outputId="e8943fd3-6a3e-4b95-9a36-e2e0997671b0" colab={"base_uri": "https://localhost:8080/", "height": 84}
credit['A1'].value_counts()
# + id="AuIp709R1KAU" colab_type="code" outputId="af5c5515-d11d-4b4c-b6da-016874304bfb" colab={"base_uri": "https://localhost:8080/", "height": 67}
credit.replace('?', np.NaN, inplace=True)
credit['A1'].value_counts()
# + id="h0YHTYkx2KUv" colab_type="code" outputId="b4de696b-c4bf-451b-c8ad-f060aa1368d2" colab={"base_uri": "https://localhost:8080/", "height": 302}
credit.isnull().sum()
# + id="Juow5gqr2TY_" colab_type="code" outputId="e35c8484-f347-45dc-a479-735f7a33f618" colab={"base_uri": "https://localhost:8080/", "height": 302}
clean_credit = credit.fillna(method='bfill')
clean_credit.isnull().sum()
# + id="EL1tCMDH3pFV" colab_type="code" outputId="9137040d-d4f6-42f2-fd42-bc1d22502f7a" colab={"base_uri": "https://localhost:8080/", "height": 284}
clean_credit.describe()
# + id="OsL5aF3C39-n" colab_type="code" outputId="7a656ca6-23fd-43aa-d97b-49bad6814f2d" colab={"base_uri": "https://localhost:8080/", "height": 302}
clean_credit.dtypes
#should be 2, 3, 8, 11, 14, 15 as float/int
#what's up with 2 and 14?
# + id="jbu7ZCE46JdO" colab_type="code" outputId="a27029d5-a782-41e5-a31d-26dd15b10a4b" colab={"base_uri": "https://localhost:8080/", "height": 302}
#fixed it
clean_credit['A2'] = pd.to_numeric(clean_credit['A2'], errors='coerce')
clean_credit['A14'] = pd.to_numeric(clean_credit['A14'], errors='coerce')
clean_credit.dtypes
# + [markdown] id="G7rLytbrO38L" colab_type="text"
# ## Part 2 - Exploring data, Testing hypotheses
#
# The only thing we really know about this data is that A16 is the class label. Besides that, we have 6 continuous (float) features and 9 categorical features.
#
# Explore the data: you can use whatever approach (tables, utility functions, visualizations) to get an impression of the distributions and relationships of the variables. In general, your goal is to understand how the features are different when grouped by the two class labels (`+` and `-`).
#
# For the 6 continuous features, how are they different when split between the two class labels? Choose two features to run t-tests (again split by class label) - specifically, select one feature that is *extremely* different between the classes, and another feature that is notably less different (though perhaps still "statistically significantly" different). You may have to explore more than two features to do this.
#
# For the categorical features, explore by creating "cross tabs" (aka [contingency tables](https://en.wikipedia.org/wiki/Contingency_table)) between them and the class label, and apply the Chi-squared test to them. [pandas.crosstab](http://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.crosstab.html) can create contingency tables, and [scipy.stats.chi2_contingency](https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html) can calculate the Chi-squared statistic for them.
#
# There are 9 categorical features - as with the t-test, try to find one where the Chi-squared test returns an extreme result (rejecting the null that the data are independent), and one where it is less extreme.
#
# **NOTE** - "less extreme" just means smaller test statistic/larger p-value. Even the least extreme differences may be strongly statistically significant.
#
# Your *main* goal is the hypothesis tests, so don't spend too much time on the exploration/visualization piece. That is just a means to an end - use simple visualizations, such as boxplots or a scatter matrix (both built in to pandas), to get a feel for the overall distribution of the variables.
#
# This is challenging, so manage your time and aim for a baseline of at least running two t-tests and two Chi-squared tests before polishing. And don't forget to answer the questions in part 3, even if your results in this part aren't what you want them to be.
# + [markdown] id="aKXmKcgEMWZR" colab_type="text"
# # **Exploration/Visualization**
# + id="w7grXrsB9qxG" colab_type="code" colab={}
import seaborn as sns
# + id="_nqcgc0yzm68" colab_type="code" colab={}
positive = clean_credit[clean_credit['A16'] == '+']
negative = clean_credit[clean_credit['A16'] == '-']
# + id="OzoQNu-c7PO9" colab_type="code" outputId="996743a5-cfcd-4c1e-b328-6aac44c21b21" colab={"base_uri": "https://localhost:8080/", "height": 34}
print(positive.shape, negative.shape)
# + id="8iVR4F677pmP" colab_type="code" outputId="6207b969-8563-4c2c-b214-8e9fd74175ad" colab={"base_uri": "https://localhost:8080/", "height": 284}
positive.describe()
#notice: all means are higher except A14
#actually, all values (excluding count, min, max) increase slightly except in A14 column
# + id="00QVXBc-7jj8" colab_type="code" outputId="fd9530da-54de-4583-c577-8635d960a6cf" colab={"base_uri": "https://localhost:8080/", "height": 284}
clean_credit.describe()
# + id="TyKuVzue8NyR" colab_type="code" outputId="1596cfc7-c8b7-4601-9af8-d7ed6b328ed3" colab={"base_uri": "https://localhost:8080/", "height": 284}
negative.describe()
#all values which increase in 'positive' decrease here
#A14 is, again, the only column which behaves differently
# + id="4D7Rpf999mF1" colab_type="code" colab={}
sns.pairplot(clean_credit)
# + id="UrKqh4ooAUOe" colab_type="code" colab={}
sns.pairplot(positive)
#there doesn't seem to be a significant difference in the shape of the data when
#it's divided like this
# + [markdown] id="99G28fxaL-Ap" colab_type="text"
# # **Continuous Variables**
#
# T-tests
#
# 'A11' and 'A14' were found to have the most and least extreme variability, respectively.
# + id="d8edMlHxJVs1" colab_type="code" colab={}
from scipy.stats import ttest_ind, ttest_ind_from_stats, ttest_rel
import matplotlib.pyplot as plt
from matplotlib import style
# + id="wGUHCpVUH08r" colab_type="code" colab={}
#pretty different
pos1 = positive['A11']
neg1 = negative['A11']
# + id="bDnEWQptH3uk" colab_type="code" outputId="85971cc6-da61-4b68-9cc4-3b58ae8cf49e" colab={"base_uri": "https://localhost:8080/", "height": 34}
statistic, pvalue = ttest_ind(pos1, neg1)
print(statistic, pvalue)
# + id="oZgPSCeFIJLj" colab_type="code" outputId="ea5568c5-c211-437c-d1a5-07a7a875dd64" colab={"base_uri": "https://localhost:8080/", "height": 283}
sns.distplot(pos1, color='b')
sns.distplot(neg1, color='r');
# + id="EGwqPJLdK2bj" colab_type="code" colab={}
#not that different
pos2 = positive['A14']
neg2 = negative['A14']
# + id="phhGg0reK8NG" colab_type="code" outputId="8c4097d7-5bbd-426f-b62c-5a145d165935" colab={"base_uri": "https://localhost:8080/", "height": 34}
statistic, pvalue = ttest_ind(pos2, neg2)
print(statistic, pvalue)
#note that with this pvalue we would still reject the null
# + id="_61Z8ugxK950" colab_type="code" outputId="bf9b52db-d6a9-4221-d646-87019c96960c" colab={"base_uri": "https://localhost:8080/", "height": 283}
sns.distplot(pos2, color='b')
sns.distplot(neg2, color='r');
# + id="CI-t5sOFI8MK" colab_type="code" colab={}
#showing my math/documentation for all variables
#2 pvalue 1.0951732421111643e-05
#3 pvalue 3.490724496507552e-08
#8 pvalue 3.188202861884123e-18
#11 pvalue 6.519842491876911e-29 - pretty low, good contender
#14 pvalue 0.005540253842441208 - pretty high
#15 pvalue 3.296216085672561e-06
#select one feature that is extremely different between the classes
#A11 pvalue 6.519842491876911e-29
#another feature that is notably less different
#A14 pvalue 0.005540253842441208
# + [markdown] id="X1J2qIsOMIKb" colab_type="text"
# # **Categorical Variables**
#
# Chi-squared tests
#
# 'A9' and 'A1' were found to have the most and least extreme variability, respectively.
# + id="J359adBvBnsO" colab_type="code" outputId="026fda08-0117-4777-b419-a9df5ffa3222" colab={"base_uri": "https://localhost:8080/", "height": 166}
#pretty different
a9 = pd.crosstab(clean_credit['A9'], clean_credit['A16'], margins = True)
a9
# + id="_8iIkXgYBLnA" colab_type="code" outputId="65301b3c-5afe-4fd9-f871-1ea7be013135" colab={"base_uri": "https://localhost:8080/", "height": 118}
from scipy.stats import chi2_contingency
chi2, p, df, expect = chi2_contingency(a9)
print(f'chi2 stat: {chi2}')
print(f'p-value: {p}')
print(f'df: {df}')
print(f'expected freq: {expect}')
# + id="mE16gdm2IU6Y" colab_type="code" outputId="7a06af93-b295-4742-b793-afd853c2fd31" colab={"base_uri": "https://localhost:8080/", "height": 166}
#not that different
a1 = pd.crosstab(clean_credit['A1'], clean_credit['A16'], margins = True)
a1
# + id="yMso2p1aIeOG" colab_type="code" outputId="9520d1c3-61f9-4398-b73e-1ce5f6c3f944" colab={"base_uri": "https://localhost:8080/", "height": 118}
from scipy.stats import chi2_contingency
chi2, p, df, expect = chi2_contingency(a1)
print(f'chi2 stat: {chi2}')
print(f'p-value: {p}')
print(f'df: {df}')
print(f'expected freq: {expect}')
#note that with this pvalue we would definitely not reject the null
# + id="vilZeexKB1qT" colab_type="code" colab={}
#showing my math/documentation for all variables
#1 p-value: 0.9872222913209711 - this might be the highest p-value I've ever seen
#4 p-value: 9.965375635414722e-05 - weird that this is identical to 5?
#5 p-value: 9.965375635414722e-05
#6 p-value: 5.467419618036717e-10
#7 p-value: 0.00030302914591835153
#9 p-value: 4.975990430471328e-76 - WOW
#10 p-value: 3.78352963294971e-30 - lol only the thirtieth power you're not impressive
#12 p-value: 0.944007059793183
#13 p-value: 0.16630944958702243
#select one feature that is extremely different between the classes
#A9 p-value: 4.975990430471328e-76
#another feature that is notably less different
#A1 p-value: 0.9872222913209711
# + [markdown] id="ZM8JckA2bgnp" colab_type="text"
# ## Part 3 - Analysis and Interpretation
#
# Now that you've looked at the data, answer the following questions:
#
# - Interpret and explain the two t-tests you ran - what do they tell you about the relationships between the continuous features you selected and the class labels?
# - Interpret and explain the two Chi-squared tests you ran - what do they tell you about the relationships between the categorical features you selected and the class labels?
# - What was the most challenging part of this sprint challenge?
#
# Answer with text, but feel free to intersperse example code/results or refer to it from earlier.
# + [markdown] id="LIozLDNG2Uhu" colab_type="text"
# **T-tests**
#
# The t-tests were interesting, because the highest pvalue the data produced was less than 0.05, meaning we would reject the null hypothesis for any of the continuous variables. Hence, it wouldn't be unreasonable to assume that the 'A16' column does have a statistically significant relationship with all of the 6 variables represented here.
#
#
# **Chi-squared tests**
#
# The chi-squared test looked at all 9 categorical variables, and found that 3 of them had fairly high p-values, meaning we would not reject the null hypothesis for all 3 of these (33% of the variables represented in this category!). However, for the remaining 6 variables where we reject the null hypothesis, two of those variables (A9 and A10) had tiny p-values, with a power of e-76 and e-30, respectively. This indicates some pretty huge relationships between these variables and the 'A16' column, and these are definitely factors I would want to explore further and possibly use as predictive variables.
#
#
# **Challenge**
#
# I have a hard time knowing what to visualize to explore the data that way before I start running tests. It helps that the statistical testing actually makes more sense to me and I feel like I learn the most from it., but I still think that learning to visualize a more basic understanding of the way the data acts wouldn't be a bad thing at all, and it is a skill I need to work on.
|
Anika_Nacey_DS_Unit_1_Sprint_Challenge_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Basic core
# This module contains all the basic functions we need in other modules of the fastai library (split with [`torch_core`](/torch_core.html#torch_core) that contains the ones requiring pytorch). Its documentation can easily be skipped at a first read, unless you want to know what a given function does.
# + hide_input=true
from fastai.gen_doc.nbdoc import *
from fastai.core import *
# -
# ## Global constants
# `default_cpus = min(16, num_cpus())` <div style="text-align: right"><a href="https://github.com/fastai/fastai/blob/master/fastai/core.py#L45">[source]</a></div>
# ## Check functions
# + hide_input=true
show_doc(ifnone)
# + hide_input=true
show_doc(is_listy)
# -
# Check if `x` is a `Collection`.
# + hide_input=true
show_doc(is_tuple)
# -
# Check if `x` is a `tuple`.
# ## Collection related functions
# + hide_input=true
show_doc(arrays_split)
# + hide_input=true
show_doc(extract_kwargs)
# + hide_input=true
show_doc(idx_dict)
# -
# Create a dictionary value to index from `a`.
idx_dict(['a','b','c'])
# + hide_input=true
show_doc(listify)
# + hide_input=true
show_doc(random_split)
# + hide_input=true
show_doc(series2cat)
# + hide_input=true
show_doc(uniqueify)
# -
# Return the unique elements in `x`.
# ## Files management and downloads
# + hide_input=true
show_doc(download_url)
# + hide_input=true
show_doc(find_classes)
# + hide_input=true
show_doc(join_path)
# + hide_input=true
show_doc(join_paths)
# + hide_input=true
show_doc(loadtxt_str)
# + hide_input=true
show_doc(save_texts)
# -
# ## Others
# + hide_input=true
show_doc(ItemBase, title_level=3)
# + hide_input=true
show_doc(camel2snake)
# -
# Format `name` by removing capital letters from a class-style name and separates the subwords with underscores.
camel2snake('DeviceDataLoader')
# + hide_input=true
show_doc(even_mults)
# + hide_input=true
show_doc(noop)
# -
# Return `x`.
# + hide_input=true
show_doc(num_cpus)
# + hide_input=true
show_doc(partition)
# + hide_input=true
show_doc(partition_by_cores)
# -
# ## Undocumented Methods - Methods moved below this line will intentionally be hidden
# ## New Methods - Please document or move to the undocumented section
# + hide_input=true
show_doc(range_of)
# -
#
# + hide_input=true
show_doc(to_int)
# -
#
# + hide_input=true
show_doc(arange_of)
# -
#
|
docs_src/core.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
# %matplotlib inline
import pandas as pd
import numpy as np
import cv2
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from termcolor import colored
face_cascade = cv2.CascadeClassifier('/home/mckc/Downloads/opencv-2.4.13/data/haarcascades_GPU/haarcascade_frontalface_default.xml')
# +
#Reading the image data into numpy
def rgb2gray(rgb):
return np.dot(rgb[:,:,:], [0.299, 0.587, 0.114])
def load_data():
import pandas as pd
import numpy as np
from PIL import Image
train = pd.read_csv('/home/mckc/Images/train.csv')
test = pd.read_csv('/home/mckc/Images/test.csv')
print 'the training data shape is ',train.shape
print 'the test data shape is ', test.shape
X_tr = np.zeros((1,1944,2592),dtype=np.uint8)
for i in train.values[:,0]:
image = rgb2gray(np.array(Image.open(i))).astype(np.uint8).reshape(1,1944,2592)
# print X_tr.shape,image.shape
X_tr = np.vstack((X_tr,image))
Y_tr = train.values[:,1]
X_tr = X_tr[1:,:,:]
X_ts = np.zeros((1,1944,2592),dtype=np.uint8)
for i in test.values[:,0]:
image = rgb2gray(np.array(Image.open(i))).astype(np.uint8).reshape(1,1944,2592)
X_ts = np.vstack((X_ts,image))
Y_ts = test.values[:,1]
X_ts = X_ts[1:,:,:]
print 'the training file shape',X_tr.shape,Y_tr.shape
print 'the testing file shape',X_ts.shape,Y_ts.shape
return X_tr,X_ts,Y_tr,Y_ts
# -
def simulate(X,Y):
import scipy as sp
from scipy import misc
complete = np.zeros((1,1944,2592),dtype=np.uint8)
Y_complete = []
for i in range(len(X)):
complete = np.vstack((complete,X[i,:,:].reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = 5).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = 10).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = 15).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = -5).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = -15).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(X[i,:,:], angle = -10).reshape(1,1944,2592)))
rotated = np.fliplr(X[i,:,:])
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = 5).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = 10).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = 15).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = -5).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = -10).reshape(1,1944,2592)))
complete = np.vstack((complete,sp.misc.imrotate(rotated, angle = -15).reshape(1,1944,2592)))
complete = np.vstack((complete,rotated.reshape(1,1944,2592)))
Y_complete = np.append(Y_complete,([Y[i]]*14))
if i % 10==0:
print colored((float(i)/len(X)*100 ,' Percentage complete'),'green')
complete = complete[1:,:,:]
return complete,Y_complete
def extract_faces(X_tr,Y_tr):
from skimage.transform import resize
import time
start_time = time.clock()
all_faces = np.zeros((1,96,96),dtype=np.uint8)
missing = []
multiple = []
Y= []
for i in range(len(X_tr)):
faces = face_cascade.detectMultiScale(X_tr[i,:,:],scaleFactor=1.3,minNeighbors=5,minSize=(70, 70))
n_faces = len(faces)
if n_faces is 1:
for (x,y,w,h) in faces:
fac = np.array(X_tr[i,:,:])[y:(y+h),x:(x+h)]
out = (resize(fac,(96,96))).reshape((1,96,96))
all_faces = np.vstack((all_faces,out))
Y = np.append(Y,Y_tr[i])
else:
if n_faces > 1:
#print ('There are multiple faces for index %d and with length %d' % (i , n_faces))
missing = np.append(missing,i)
#all_faces = np.vstack((all_faces,np.zeros((1,96,96),dtype=np.uint8)))
else:
#print ('The face is missing for index %d' %i)
multiple = np.append(multiple,i)
if i % 50==0:
print colored((float(i)/len(X_tr)*100 ,' Percentage complete'), 'green')
all_faces = all_faces[1:,:,:]
print all_faces.shape
print time.clock() - start_time, "seconds"
return all_faces,missing,multiple,Y
X_tr,X_tst,Y_tr,Y_tst = load_data()
import time
start_time = time.clock()
X_train,Y_train = simulate(X_tr,Y_tr)
print X_train.shape,Y_train.shape
print time.clock() - start_time, "seconds"
X,missing,multiple,Y = extract_faces(X_train[:,:,:],Y_train)
X_test,missing_test,multiple_test,Y_test = extract_faces(X_tst,Y_tst)
def Save_data(X,Y):
for i in range(len(X)):
file_name = '/home/mckc/imagees/'+Y[i]+'_'+str(i)+'.npy'
np.save(file_name,X[i,:,:])
def load():
import os
import numpy as np
files = os.listdir('/home/mckc/imagees/')
X = []
Y = []
for i in files:
X = np.append(X,np.load(i))
index = i.index('_')
Y = np.append(Y,i[:index])
return X,Y
from PIL import Image
image = np.array(Image.open(train.values[3,0]))
plt.imshow(X_tr[1,:,:], cmap = cm.Greys_r)
plt.show()
# +
# get row number
def rgb2gray(rgb):
return np.dot(rgb[:,:,:], [0.299, 0.587, 0.114])
gray = rgb2gray(image).astype(np.uint8)
gray.shape
plt.imshow(gray, cmap = plt.get_cmap('gray'))
plt.show()
# +
faces = face_cascade.detectMultiScale(
gray,
scaleFactor=1.3,
minNeighbors=6,
minSize=(40, 40))
print "Found {0} faces!".format(len(faces))
for (x,y,w,h) in faces:
fac = np.array(gray)[y:(y+h),x:(x+h)]
plt.imshow(fac,cmap=plt.get_cmap('gray'))
# +
#Normalising
X = X -0.5
X_test = X_test - 0.5
print X.mean(),X_test.mean()
# -
X.mean()
map, Y_number = np.unique(Y, return_inverse=True)
Y_test_numer = np.unique(Y_test, return_inverse=True)[1]
print map,X.dtype
print len(X),len(Y_number),X.shape
X = X.astype(np.float16)
X_test = X_test.astype(np.float16)
# +
import lasagne
#from lasagne.layers.cuda_convnet import Conv2DCCLayer as Conv2DLayer
#from lasagne.layers.cuda_convnet import MaxPool2DCCLayer as MaxPool2DLayer
from lasagne import layers
from lasagne.objectives import categorical_crossentropy
from lasagne.updates import nesterov_momentum
from nolearn.lasagne import BatchIterator,visualize,NeuralNet
Conv2DLayer = layers.Conv2DLayer
MaxPool2DLayer = layers.MaxPool2DLayer
net = NeuralNet(
layers=[
('input', layers.InputLayer),
('conv1', Conv2DLayer),
('pool1', MaxPool2DLayer),
('dropout1', layers.DropoutLayer),
('conv2', Conv2DLayer),
('pool2', MaxPool2DLayer),
('dropout2', layers.DropoutLayer),
('conv3', Conv2DLayer),
('pool3', MaxPool2DLayer),
('dropout3', layers.DropoutLayer),
('hidden4', layers.DenseLayer),
('dropout4', layers.DropoutLayer),
('hidden5', layers.DenseLayer),
('output', layers.DenseLayer),
],
input_shape=(None, 1, 96, 96),
conv1_num_filters=32, conv1_filter_size=(3, 3), pool1_pool_size=(2, 2),
dropout1_p=0.1,
conv2_num_filters=64, conv2_filter_size=(2, 2), pool2_pool_size=(2, 2),
dropout2_p=0.2,
conv3_num_filters=128, conv3_filter_size=(2, 2), pool3_pool_size=(2, 2),
dropout3_p=0.3,
hidden4_num_units=1000,
dropout4_p=0.5,
hidden5_num_units=1000,
output_nonlinearity=lasagne.nonlinearities.softmax,
output_num_units=2,
update = nesterov_momentum,
update_learning_rate=0.001,
update_momentum=0.9,
max_epochs=500,
verbose=1,
)
net.fit(X.reshape(-1,1,96,96), Y_number.astype(np.uint8))
# -
predicted = net.predict((X_test.reshape(-1,1,96,96)))
def names(x): return map(x)
# +
predicted_names = []
for i in predicted:
predicted_names = np.append(predicted_names,map[i])
from sklearn.metrics import confusion_matrix
confusion_matrix(Y_test, predicted_names)
# -
from sklearn.metrics import confusion_matrix
confusion_matrix(Y_test, predicted_names)
# +
# %%capture
from keras.models import Sequential
from keras.layers import Dense, Activation
from keras import backend as K
from keras.optimizers import Adam,SGD
from keras.utils import np_utils
Y_Keras = np_utils.to_categorical(Y_number, 2)
# Create first network with Keras
from keras.models import Sequential
from keras.layers import Dense, Activation,Dropout
model = Sequential()
model.add(Dense(1000, input_dim=9216,activation='relu'))
model.add(Dense(2,activation='softmax'))
sgd = SGD(lr=0.001, decay=1e-6, momentum=0.9, nesterov=True)
# Compile model
model.compile(loss='categorical_crossentropy', optimizer='sgd', metrics=['accuracy'])
import time
model.fit(X.reshape(-1,9216), Y_Keras, nb_epoch=100, batch_size=5,verbose=1,
validation_data=(X_test.reshape(-1,9216), np_utils.to_categorical(Y_test_numer, 2)))
time.sleep(1)
# -
X_normal = X.reshape(-1,9216)
X_test_normal = X_test.reshape(-1,9216)
from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(verbose=1,n_jobs=-1)
clf.fit(X_normal,Y_number)
Y_logictic= clf.predict(X_test.reshape(-1,9216))
from sklearn.cross_validation import cross_val_score
score = cross_val_score(clf,X_normal,Y_number)
score
# +
predicted_names = []
for i in Y_logictic:
predicted_names = np.append(predicted_names,map[i])
from sklearn.metrics import confusion_matrix
confusion_matrix(Y_test, predicted_names)
# -
plt.imshow(clf.coef_.reshape(96,96),cmap=cm.Greys_r)
from sklearn.ensemble import RandomForestClassifier
from sklearn.cross_validation import cross_val_score
scores = list()
scores_std = list()
n_trees = [10, 50, 150,250,500]
for n_tree in n_trees:
print(n_tree)
recognizer = RandomForestClassifier(n_tree,verbose=0,oob_score=True,n_jobs=5)
score = cross_val_score(recognizer, X_normal, Y_number)
scores.append(np.mean(score))
scores_std.append(np.std(score))
# +
sc_array = np.array(scores)
std_array = np.array(scores_std)
print('Score: ', sc_array)
print('Std : ', std_array)
plt.figure(figsize=(4,3))
plt.plot(n_trees, scores)
plt.plot(n_trees, sc_array + std_array, 'b--')
plt.plot(n_trees, sc_array - std_array, 'b--')
plt.ylabel('CV score')
plt.xlabel('# of trees')
#plt.savefig('cv_trees.png')
plt.show()
# -
recognizer = RandomForestClassifier(n_tree,verbose=1,oob_score=True,n_jobs=5)
recognizer.fit(X_normal,Y_number)
importances = recognizer.feature_importances_
importance_image = importances.reshape(96,96)
#plt.figure(figsize=(7,7))
plt.imshow(importance_image,cmap=cm.Greys_r)
plt.imshow(X_normal[1,:].reshape(96,96),cmap=cm.Greys_r)
plt.imshow(X_normal[700,:].reshape(96,96),cm.Greys_r)
# +
jpgfile = Image.open("/home/mckc/Downloads/1.jpg")
grey = rgb2gray(np.array(jpgfile))
faces = face_cascade.detectMultiScale(grey.astype(np.uint8),scaleFactor=1.1,minNeighbors=3,minSize=(30, 30))
print faces
for (x,y,w,h) in faces:
fac = np.array(grey[y:(y+h),x:(x+h)])
out = resize(fac,(96,96))
plt.imshow(out,cmap=cm.Greys_r)
from sklearn.ensemble import RandomForestClassifier
recognizer = RandomForestClassifier(500,verbose=0,oob_score=True,n_jobs=5)
recognizer.fit(X_normal,Y_number)
trial = out.astype(np.float64)
print 'Linear Regression Value',map[clf.predict(trial.reshape(-1,9216))]
print 'Random Forest Value',map[recognizer.predict(trial.reshape(-1,9216))]
print 'Lasagne Value',map[recognizer.predict(trial.reshape(-1,1,96,96))]
print 'Keras Value',map[recognizer.predict(trial.reshape(-1,1,96,96))]
# +
jpgfile = Image.open("/home/mckc/Downloads/2.jpg")
grey = rgb2gray(np.array(jpgfile))
faces = face_cascade.detectMultiScale(grey.astype(np.uint8),scaleFactor=1.1,minNeighbors=3,minSize=(30, 30))
print faces
for (x,y,w,h) in faces:
fac = np.array(grey[y:(y+h),x:(x+h)])
out = resize(fac,(96,96))
plt.imshow(out,cmap=cm.Greys_r)
from sklearn.ensemble import RandomForestClassifier
recognizer = RandomForestClassifier(500,verbose=0,oob_score=True,n_jobs=5)
recognizer.fit(X_normal,Y_number)
trial = out.astype(np.float64)
print 'Linear Regression Value',map[clf.predict(trial.reshape(-1,9216))]
print 'Random Forest Value',map[recognizer.predict(trial.reshape(-1,9216))]
print 'Lasagne Value',map[recognizer.predict(trial.reshape(-1,1,96,96))]
print 'Keras Value',map[recognizer.predict(trial.reshape(-1,1,96,96))]
|
Training/Two Class Problem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. install/ check we have installed pandas
# run this if you does not have pandas
# alternatively you can pip install -r requirements.txt
# !pip install pandas
import pandas as pd
#check the pandas versions. We were using 1.0.4
pd.__version__
# # 2. read and write to csv (and may be excels)
#
# Let's read the pokemon.csv
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html
#load the pokemon data, note that we have lot's of options for read_csv, check the docs
pokemon_df = pd.read_csv("data/pokemon.csv", index_col=0, dtype={"Generation": 'object'})
# Let's have a look
pokemon_df
# we can also check the data type
pokemon_df.dtypes
# to sample only the first 30 rows
pokemon_sample = pokemon_df.head(30)
pokemon_sample.to_csv("data/pokemon_sample.csv")
# # 3. talk about what is DataFrame and Series
#
# 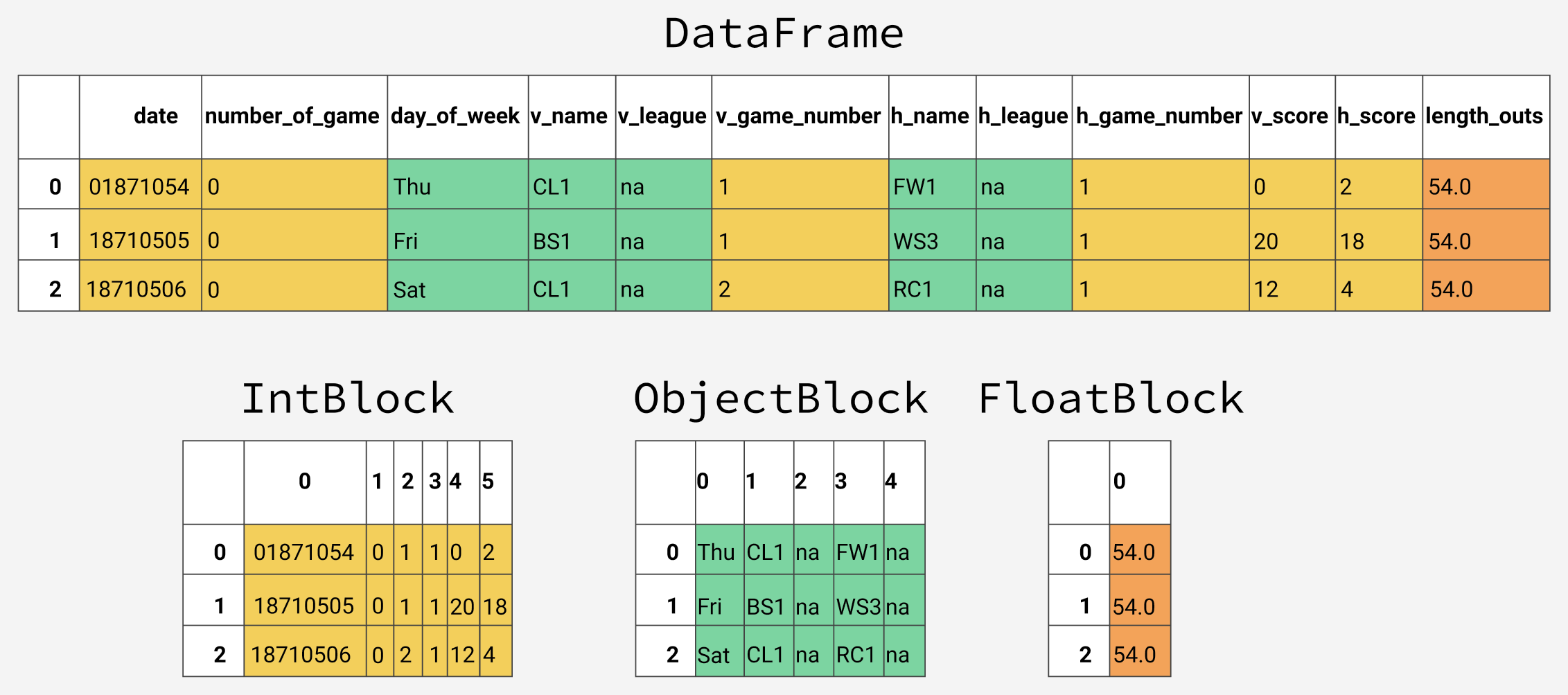
# There's lots of stuff in a pandas DataFrame
dir(pokemon_df)
pokemon_df.columns
pokemon_df.index
pokemon_df.values
# # 4. head and tail and slicing dfs (and play around with columns and indexes)
pokemon_df.head()
pokemon_df.tail()
# putting a list in [] after a DataFrame will create a DataFrame with only those columns (in order)
# pitting a str (column name) will give you that Series (like df.col)
pokemon_df[["Name","Generation","Type 1"]]
# trick to reorder your table (make sure you reasigned the DataFrame, for demo we don't)
pokemon_col = list(pokemon_df.columns)
pokemon_col.sort()
pokemon_df[pokemon_col]
# we kept the DataFrame "untouched"
pokemon_df
# using .loc to get a slice of the DataFrame (think about cutting a cake)
# note that loc refers to the "Index" that we set and the columns names
pokemon_df.loc[711,["Name","Type 1"]]
# .iloc on the other hands, is refering to an "absolute coordinates" that starts form 0
pokemon_df.iloc[711,0]
# # 5. changing data types
#
# https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.astype.html
# first check what datatypes we have
pokemon_df.dtypes
# using astype to change to any types (details check the docs)
pokemon_df.astype({"Generation": "int64"}).dtypes
|
pandas1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.3 64-bit (conda)
# name: python38364bitconda3a4ba74f1f034c57b5fc0285448d66cc
# ---
# +
from functools import partial
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
from scipy.stats import lognorm, norm
# -
# source: https://bmjopen.bmj.com/content/bmjopen/10/8/e039652.full.pdf
#
# "Based on available evidence, we find that the incubation period distribution may be modelled with a lognormal distribution with pooled mu and sigma parameters of 1.63 (1.51, 1.75) and 0.50 (0.45, 0.55), respectively."
#
# +
xs = np.linspace(-1, 8)
cdf_func = partial(lognorm.cdf, loc=1.63, s=0.5)
cdf_ys = cdf_func(x=xs)
def midpoint_with_p_mass(upper, lower=None, color="blue"):
old_cdf = 0 if lower is None else cdf_func(lower)
# do not move because cdf_func(5) could be > 0!
lower = 0 if lower is None else lower
prob_mass = round(cdf_func(upper) - old_cdf, 2)
midpoint = round(0.5 * (upper + lower))
label = f"bin midpoint: {midpoint}, probability mass: {prob_mass}"
plt.axvline(midpoint, label=label, color=color)
return prob_mass
fig, ax = plt.subplots(figsize=(5, 5))
sns.lineplot(
xs,
cdf_ys,
label=r"lognormal cdf with $\mu$ 1.63 and $\sigma$ 0.5",
color="#547482",
linewidth=2.5,
)
p1 = midpoint_with_p_mass(2.5, None, color="#C87259")
p2 = midpoint_with_p_mass(3, 2.5, color="#C2D8C2")
p3 = midpoint_with_p_mass(4, 3, color="#F1B05D")
p4 = midpoint_with_p_mass(8, 4, color="#818662")
lgd = plt.legend(frameon=False, bbox_to_anchor=(0.8, -0.2))
plt.title("COVID-19 Incubation Period\nacc. to McAloon et al. (2020)")
sns.despine()
plt.tight_layout()
plt.savefig("incubation_period.png", bbox_inches="tight", bbox_extra_artists=(lgd,))
p1 + p2 + p3 + p4
# -
|
docs/source/_static/images/make_incubation_period.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
# +
#Import the Data set
df = pd.read_csv("car data.csv")
# -
df.head()
df.isnull().sum()
# +
#Unique values of Categorical Variable
print(df['Fuel_Type'].unique())
print(df['Seller_Type'].unique())
print(df['Transmission'].unique())
print(df['Owner'].unique())
# -
#checking the Null values
df.isnull().sum()
df.describe().T
# +
#Year feature is present : need to get the " how old the car which is nothing but subtract from current year"
#Car name is not required : Hence we should be dropping that
df.columns
# -
final_df = df[['Year', 'Selling_Price', 'Present_Price', 'Kms_Driven',
'Fuel_Type', 'Seller_Type', 'Transmission', 'Owner']]
final_df.head()
# +
# Need to create a the current Year
final_df['current_year'] = 2021
# -
final_df
# +
#How old the car : Current year - year : add with new feature : say : no_years
final_df['no_years'] = final_df['current_year']- final_df['Year']
# -
final_df.columns
#Drop the year and current year columns as not required now
final_df.drop(['Year','current_year'],axis= 1, inplace = True)
final_df.head()
final_df.isnull().sum()
# +
#One hot encoding , drop_first : To remove dummy variable Trap
final_df = pd.get_dummies(final_df,drop_first =True)
#Why dropping the first column for one hot encoding
# CNG <NAME>
# 1 0 0
# 0 1 0
# 0 0 1
# But if we drop the CNG :
# CNG <NAME>
# 0 0 0
# 0 1 0
# 0 0 1
# Please think : if all values are Zero , then it would be represent the CNG by default, no need for one hot encoding
# for that column , hence we drop generally one column , : to remove dummy variable Trap ,drop the first the column for one
# hot enconding
# -
final_df
# +
# now need to check the cotrrelation
final_df.corr()
# -
# corr :
import seaborn as sns
#Heat map
from matplotlib import pyplot as plt
plt.figure(figsize= (20,20))
sns.heatmap(final_df.corr(),cmap ='cool')
sns.pairplot(final_df)
corrmat=final_df.corr()
top_corr_features=corrmat.index
plt.figure(figsize=(20,20))
#plot heat map
g=sns.heatmap(final_df[top_corr_features].corr(),annot=True,cmap="RdYlGn")
#print(corrmat)
final_df.head()
# +
#sellinmg price is the dependent variable : thats need to be calculated
# Separate the independent and dependent vaiable
x_df = final_df.iloc[:,1:]# just avoid sellling_price
y_df = final_df.iloc[:,0]
# -
y_df
x_df
# +
#Feature importance
from sklearn.ensemble import ExtraTreesRegressor
model = ExtraTreesRegressor()
test = model.fit(x_df,y_df)
# -
model.feature_importances_
fea_imp = pd.Series(model.feature_importances_,index = x_df.columns)
fea_imp.nlargest(8).plot(kind = 'bar')
# +
#model preparation :
# first train test split
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x_df,y_df,test_size = 0.3,random_state= 22)
# -
x_train.head()
# + active=""
#
# -
y_train.head()
x_df.shape
# +
# randomforest
from sklearn.ensemble import RandomForestRegressor
model = RandomForestRegressor()
# -
model.fit(x_train,y_train)
rf_pre =model.predict(x_test)
from sklearn import metrics
import numpy as np
print('MAE:', metrics.mean_absolute_error(y_test, rf_pre))
print('MSE:', metrics.mean_squared_error(y_test, rf_pre))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, rf_pre)))
diff = rf_pre - y_test
sns.distplot(diff)
sns.scatterplot(y_test, rf_pre)
#by using randomizedSearchCv to get the best hypeparameter
#Randomized Search CV
import numpy as np
# Number of trees in random forest
n_estimators = [int(x) for x in np.linspace(start = 100, stop = 1200, num = 12)]
# Number of features to consider at every split
max_features = ['auto', 'sqrt']
# Maximum number of levels in tree
max_depth = [int(x) for x in np.linspace(5, 30, num = 6)]
# max_depth.append(None)
# Minimum number of samples required to split a node
min_samples_split = [2, 5, 10, 15, 100]
# Minimum number of samples required at each leaf node
min_samples_leaf = [1, 2, 5, 10]
# +
# Create the random grid
random_grid = {'n_estimators': n_estimators,
'max_features': max_features,
'max_depth': max_depth,
'min_samples_split': min_samples_split,
'min_samples_leaf': min_samples_leaf}
print(random_grid)
# -
from sklearn.model_selection import RandomizedSearchCV
rf_1 = RandomForestRegressor()
rf_1.fit(x_train, y_train)
rf_1.predict(x_test)
y_test
# Random search of parameters, using 3 fold cross validation,
# search across 100 different combinations
rf_random = RandomizedSearchCV(estimator = rf_1, param_distributions = random_grid,scoring='neg_mean_squared_error', n_iter = 10, cv = 5, verbose=2, random_state=42, n_jobs = 1)
rf_random.fit(x_train,y_train)
pred_1=rf_random.predict(x_test)
sns.scatterplot(pred_1,y_test)
rf_random.best_score_
from sklearn import metrics
print('MAE:', metrics.mean_absolute_error(y_test, pred_1))
print('MSE:', metrics.mean_squared_error(y_test, pred_1))
print('RMSE:', np.sqrt(metrics.mean_squared_error(y_test, pred_1)))
# +
import pickle
file = open("car_pred_random_forest_regre.pkl",'wb')
pickle.dump(rf_random,file)
# -
|
Car.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/satoru2001/Twitter_Sentiment_Analysis/blob/master/Twitter_Sentiment_analysis.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="-3sPa5dI-fm1" colab_type="text"
# # Import Data
# + id="YZFjEZkXmutC" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 233} outputId="643906eb-a05e-43ce-aef2-601fe10172e9"
# !wget --no-check-certificate \
# http://cs.stanford.edu/people/alecmgo/trainingandtestdata.zip \
# -O /tmp/SentimentAnalysis.zip
# + [markdown] id="ofl2xrfD-mD4" colab_type="text"
# # Import Libraries
# + id="c-l4u35emmmz" colab_type="code" colab={}
import tensorflow as tf
import pandas as pd
import numpy as np
import csv
import random
import matplotlib.pyplot as plt
from bs4 import BeautifulSoup
import re
import os, sys, codecs,zipfile
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.utils import to_categorical
from tensorflow.keras import regularizers
# + [markdown] id="UIYLaAdL-q6S" colab_type="text"
# # UnZip the File to /tmp
# + id="STMTqdsIncUm" colab_type="code" colab={}
local_ref = '/tmp/SentimentAnalysis.zip'
zip_ref= zipfile.ZipFile(local_ref,'r')
zip_ref.extractall('/tmp')
zip_ref.close()
# + [markdown] id="4tHWywv6-3XB" colab_type="text"
# # Stopwords
# - stop words are the words in a sentence which doesnot/have less impact on the sentiment of a sentence
# - I took it from [here](https://github.com/Yoast/YoastSEO.js/blob/develop/src/config/stopwords.js)
# + id="rIpCVwZc9Sg-" colab_type="code" colab={}
stopwords = [ "a", "about", "above", "after", "again", "against", "all", "am", "an", "and", "any", "are", "as", "at", "be", "because", "been", "before", "being", "below", "between", "both", "but", "by", "could", "did", "do", "does", "doing", "down", "during", "each", "few", "for", "from", "further", "had", "has", "have", "having", "he", "he'd", "he'll", "he's", "her", "here", "here's", "hers", "herself", "him", "himself", "his", "how", "how's", "i", "i'd", "i'll", "i'm", "i've", "if", "in", "into", "is", "it", "it's", "its", "itself", "let's", "me", "more", "most", "my", "myself", "nor", "of", "on", "once", "only", "or", "other", "ought", "our", "ours", "ourselves", "out", "over", "own", "same", "she", "she'd", "she'll", "she's", "should", "so", "some", "such", "than", "that", "that's", "the", "their", "theirs", "them", "themselves", "then", "there", "there's", "these", "they", "they'd", "they'll", "they're", "they've", "this", "those", "through", "to", "too", "under", "until", "up", "very", "was", "we", "we'd", "we'll", "we're", "we've", "were", "what", "what's", "when", "when's", "where", "where's", "which", "while", "who", "who's", "whom", "why", "why's", "with", "would", "you", "you'd", "you'll", "you're", "you've", "your", "yours", "yourself", "yourselves" ]
# + [markdown] id="Lzzf9stSA4XQ" colab_type="text"
# # Reading data from csv
# + id="iW_Qa8v0mtOp" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="0de5cfec-e450-4c65-ed6d-57f53dcf579c"
cols = ['sentiment','id','date','query_string','user','text']
df = pd.read_csv('/tmp/training.1600000.processed.noemoticon.csv',header=None, names=cols,encoding = 'latin-1')
df.head()
# + [markdown] id="6cKavBraA8r6" colab_type="text"
# # Dropping unwanted Columns
# + id="tu8aq1Dx1LG_" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 179} outputId="c25c3a63-f528-48ff-d6a5-36a65b0215c1"
df.drop(['id','date','query_string','user'],axis =1,inplace=True)
print(df.head())
df.sentiment.value_counts()
# + id="CeE8FT5K20ij" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 204} outputId="60537740-daf5-4ced-87ef-f3116531e70e"
df[df.sentiment==4].head()
# + [markdown] id="-MZ7OMYVBLFU" colab_type="text"
# # Checking the Length's of Sentences
# - as twitter has a charecter limit of 140(during this data set) getting >350 means we need to clean data
# + id="rI_olHD323TR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 320} outputId="1301ff65-13d2-4cf0-eea1-30830903c5c7"
df['pre_clean_length'] = [len(txt) for txt in df.text]
fig, ax = plt.subplots(figsize=(5, 5))
plt.boxplot(df.pre_clean_length)
plt.show()
# + [markdown] id="5TxGdS71BgMN" colab_type="text"
# # Lets See the Data that has charecter_length > 140
# + id="873twITZ4Z5W" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 419} outputId="4f953807-e89b-44ec-d1ed-c5f8b8578f1e"
df[df.pre_clean_length>140]
# + [markdown] id="0v2pPcZwBwXZ" colab_type="text"
# # From here onwards we see the different cleaning techniques that we are going to apply on text
#
# ## Cleaning the Html data like "e -> '
# + id="cS_nVLjv8A7l" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 53} outputId="54d95278-471e-4be5-93eb-22e6b5c71e08"
print(df.text[213])
html_cleaned = BeautifulSoup(df.text[213],'lxml')
html_cleaned.get_text()
# + [markdown] id="GwT7XNCODjoQ" colab_type="text"
# ## Removing @usernames
# + id="1G16Mbn4-HWT" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 53} outputId="07f420db-5fbd-4fbb-ea97-ad5b70d3611e"
print(df.text[343])
re.sub(r'@[A-Za-z0-9]+','',df.text[343])
# + [markdown] id="RaVSXhoaDpRr" colab_type="text"
# ## Removing URL's
# + id="4j2NsTHZ_Myx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 53} outputId="77a5115a-88d8-43da-be9e-f640dad84b1e"
print(df.text[0])
re.sub('https?://[A-Za-z0-9./]+','',df.text[0])
# + [markdown] id="WKo1PSL9Dxiy" colab_type="text"
# ## Removing Bom's
# + id="bpTk6qWR_rIW" colab_type="code" colab={}
training = df.text[226]
training = training.replace('�','')
# + id="arl9IgUKP0xP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 35} outputId="65dfa5bd-c282-4178-e4b2-053c6f7db017"
print(training)
# + [markdown] id="BOltP0SRD5_x" colab_type="text"
# # Combining all the above cleaning layers with stop word remover
# + id="DowgvdZPZ4PM" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="41015f36-359a-4e20-dd47-e76a1eb1baca"
tokenizer = Tokenizer()
def tweet_cleaner(t):
soup = BeautifulSoup(t,'lxml')
souped = soup.get_text()
clean_1 = re.sub(r' @[A-Za-z0-9]+ | https?://[A-Za-z0-9./]+','',souped)
try:
clean_2 = clean_1.replace('�','')
except:
clean_2 = clean_1
letters_only = re.sub("[^a-zA-Z]",' ',clean_2)
lower_case = letters_only.lower()
final_clean = re.sub('\s+',' ',lower_case)
final_result = ' '.join([word for word in final_clean.split() if word not in stopwords])
return final_result.strip()
test_result = []
testing = df.text[:100]
for i in testing:
test_result.append(tweet_cleaner(i))
test_result
# + [markdown] id="3b6KcSK0Go2z" colab_type="text"
# # Applying the Cleaner filter to our Tweets
# ## It will take ~10 minutes
# + id="7BhUMuXfKUDQ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="cb5ec6d5-3bbf-44e2-ce5a-b897be88c4e9"
print("Cleaning and parsing the tweets..\n")
clean_tweet_texts = []
for i in range(len(df.text)):
clean_tweet_texts.append(tweet_cleaner(df.text[i]))
if (i%10000)==0:
print (str(i)+'Tweets Completed')
# + [markdown] id="p-osEktOG2lS" colab_type="text"
# # Saving it to a .csv file for further use
# + id="kZoge5jaNvoE" colab_type="code" colab={}
clean_df = pd.DataFrame(clean_tweet_texts,columns=['text'])
clean_df['value'] = df.sentiment
clean_df.to_csv('clean_tweet.csv',encoding='utf-8')
# + [markdown] id="pF1tVqHdsI0D" colab_type="text"
# # Designing and Training our model
# We load the pretrained Glove word Embeddings
# + id="i0j8-YeFRgd4" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 377} outputId="d1da10ba-27d4-428d-a67e-3076f404c0a5"
# !wget --no-check-certificate \
# http://nlp.stanford.edu/data/glove.twitter.27B.zip \
# -O /tmp/glove_twitter.zip
# + [markdown] id="YhA66gV5HXC0" colab_type="text"
# # Unzipping
# + id="gtJaTnIaUgVf" colab_type="code" colab={}
loc_ref = '/tmp/glove_twitter.zip'
zip_ref= zipfile.ZipFile(loc_ref,'r')
zip_ref.extractall('/tmp')
zip_ref.close()
# + [markdown] id="0gzmBp1HHTqs" colab_type="text"
# # Defining Variables
# + id="ukhMOxp8P3lK" colab_type="code" colab={}
embedding_dim = 100
max_len = 20
trunc_type = 'post'
padding_type = 'post'
oov_token = "<oov>"
test_portion = 0.1
corpus = []
num_sentences = 0
# + [markdown] id="Rf7n0nXBHdNd" colab_type="text"
# # Reading from CSV we created above
# + id="ulgDKGdikBOt" colab_type="code" colab={}
with open('clean_tweet.csv') as csvfile:
reader = csv.reader(csvfile,delimiter=',')
next(reader)
for row in reader:
list_item = []
list_item.append(row[1])
if row[2]=='0':
list_item.append(0)
else:
list_item.append(1)
num_sentences+=1
corpus.append(list_item)
# + id="-vVeiyeokBRx" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="ed212a37-b264-4e2f-86b5-331fa694b7c8"
print(num_sentences)
print(len(corpus))
print(corpus[0])
# + [markdown] id="C7nm407KHlJ-" colab_type="text"
# # Tokenizing,Splitting and saperating Sentences and labels
# + id="m7PALOTlspSX" colab_type="code" colab={}
sentences = []
labels = []
random.shuffle(corpus)
for i in range(num_sentences):
sentences.append(corpus[i][0])
labels.append(corpus[i][1])
tokenizer = Tokenizer()
tokenizer.fit_on_texts(sentences)
word_index = tokenizer.word_index
vocab_size = len(word_index)
sequences = tokenizer.texts_to_sequences(sentences)
padding = pad_sequences(sequences,maxlen=max_len,padding = padding_type,truncating=trunc_type)
split = int(num_sentences*test_portion)
train_seq = padding[split:]
train_label = labels[split:]
test_seq = padding[:split]
test_label = labels[:split]
# + id="UFFrnv5xvNcZ" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 71} outputId="f17dacc7-7dbb-45e8-88a3-b2935624c7a8"
print(vocab_size)
print(word_index['shoulda'])
print(len(test_label))
# + [markdown] id="HP3RhR7sIL3v" colab_type="text"
# # Extracting 100 dimension embedded matrix from Glove and creating a word,vector Dictionary
# + id="r4qXVFnbcG-E" colab_type="code" colab={}
embeddings_index = {}
with open('/tmp/glove.twitter.27B.100d.txt') as f:
for line in f:
values = line.split()
word = values[0]
if word.isalpha():
embeddings_index[word] = np.array(values[1:],dtype='float32')
# + [markdown] id="kvDp-LG5H6wR" colab_type="text"
# # Converting Tokanized sentences to embedded matrix
# + id="hC-0idlNhETW" colab_type="code" colab={}
embedding_matrix = np.zeros((vocab_size+1,embedding_dim))
for word ,i in word_index.items():
embedding_vector = embeddings_index.get(word)
if embedding_vector is not None:
embedding_matrix[i] = embedding_vector
# + [markdown] id="ax9mjvvaIICP" colab_type="text"
# # Model
# + id="xlDIrdubwvgg" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 935} outputId="a1661695-5dae-43a6-bc17-7641d741625d"
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size+1,embedding_dim,input_length=max_len,
weights=[embedding_matrix],trainable=False),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Conv1D(64,3,activation='relu'),
tf.keras.layers.MaxPooling1D(3),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Conv1D(64,3,activation='relu'),
tf.keras.layers.MaxPooling1D(3),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64,return_sequences=True)),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Bidirectional(tf.keras.layers.LSTM(64)),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(32,activation='relu'),
tf.keras.layers.BatchNormalization(),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(1, activation='sigmoid')
])
print(model.summary())
# + id="bX8EjYUFyuLv" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 197} outputId="960e051d-7d29-4c81-eac7-ee008eb1ee6c"
from tensorflow.keras.backend import clear_session
clear_session()
train_sent = np.array(train_seq)
train_lab = np.array(train_label)
valid_sent = np.array(test_seq)
valid_lab = np.array(test_label)
model.compile(loss = 'binary_crossentropy',optimizer = 'adam',metrics=['accuracy'])
num_epochs = 5
history = model.fit(train_sent, train_lab, epochs=num_epochs, verbose=1,validation_data=(valid_sent,valid_lab))
# + id="v7xqlt-u52Pt" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 53} outputId="d212b601-22fd-4b1e-dce2-d03ae49113f7"
model.evaluate(valid_sent,valid_lab)
# + [markdown] id="HM4x92ehIzLZ" colab_type="text"
# # Plot the curves
# + id="uUMfaHZvJP6B" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 609} outputId="daf95dd8-68e8-41ea-e6dc-a75ba70befc5"
acc = history.history['accuracy']
val_acc = history.history['val_accuracy']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.plot(epochs, acc, 'r')
plt.plot(epochs, val_acc, 'b')
plt.title('Training and validation accuracy')
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend(["Accuracy", "Validation Accuracy"])
plt.figure()
plt.plot(epochs, loss, 'r')
plt.plot(epochs, val_loss, 'b')
plt.title('Training and validation loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.legend(["Loss", "Validation Loss"])
plt.figure()
# + id="zNsrhQJCdGLF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 53} outputId="8aaf0cee-c884-434e-fcc8-dbed3b37b25f"
y_pred = model.predict(valid_sent)
y_pred = y_pred.flatten()
for i in range(len(y_pred)):
if y_pred[i]>=0.5:
y_pred[i]=1
else:
y_pred[i]=0
y_pred = np.array(y_pred,dtype = 'int')
y_truth = valid_lab.flatten()
print(y_pred[:10])
print(y_truth[:10])
# + [markdown] id="CRasUNK5NOCX" colab_type="text"
# # Confusion Matrix
# + id="CLEYNKEENNur" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 89} outputId="e49f1a2c-84c0-4d66-f877-9d498489034a"
from sklearn.metrics import classification_report, confusion_matrix,f1_score
cnf_matrix = confusion_matrix(y_truth,y_pred)
score = f1_score(y_truth,y_pred)
print('Confusion Matrix:')
print(cnf_matrix)
print('F1 Score:'+str(score))
# + id="urDQXmSLdJmr" colab_type="code" colab={}
|
Twitter_Sentiment_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/KOdin2/machine_learning/blob/main/Extra_trees_assessment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="kA8DSbFA4HCN"
# # Extra trees
# + id="v9GmNtOheAuq"
import matplotlib.pyplot as plt
import numpy as np
import io
import pandas as pd
import sklearn
import csv
#####
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import StratifiedKFold
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import f1_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score, recall_score
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import GridSearchCV
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
# + colab={"resources": {"http://localhost:8080/nbextensions/google.colab/files.js": {"data": "<KEY>", "ok": true, "headers": [["content-type", "application/javascript"]], "status": 200, "status_text": ""}}, "base_uri": "https://localhost:8080/", "height": 348} id="DOLCNaj8eLnw" outputId="f71a4483-00de-4832-aeef-d1f2941e0dec"
from google.colab import files
uploaded = files.upload()
# + [markdown] id="zXLnjg8sRn8S"
# Best measurements to use for classification are:
#
# precision,
# recall,
# accuracy,
# f1,
# roc_auc
#
# + id="Xcacs_-Qj9jy"
def testing_combination_arrays(max_varible):
varible_combinations = []
b = 1
for value in range(0, max_varible):
varible_combinations.append(int(b) )
b+=1
return varible_combinations
def calculate_cross_validation_value(y_train):
arr = y_train.to_numpy()
bin_arr = np.bincount(arr)
return bin_arr.min()
# + id="tzSWN1xihqF_"
#@title Grid search with a given x and y and combination of varible. Also number of cv fold cross validation
def grid_search_RF_function(x_train, y_train, Varible_list_1 , number_of_cv_folds):
best_model_details =[]
#create mdoel
Algorithm = "Extra trees"
model = ExtraTreesClassifier(random_state=0)
min_max = MinMaxScaler()
#Create a pipline, which first will train on max and min and then transform the output
pipe = Pipeline(steps = [
("min_max" , min_max ),
("model" , model )
])
#Set up parameter grid
param_grid = [
{'model__n_estimators': Varible_list_1}
]
#scoring_type can be used to choose what method to compare the models on
scoring_type = 'f1'
grid_search = GridSearchCV(estimator= pipe, param_grid= param_grid, cv= number_of_cv_folds , scoring=scoring_type, return_train_score=True, n_jobs=-1)
grid_search.fit(X= x_train, y= y_train)
#Aquire best parameter for model
best_paramater = grid_search.best_params_
print("[INFO] Best parameter: " + str(best_paramater))
#find best score and round to 4dp
best_accuracy = round(grid_search.best_score_,4)
print("[INFO] Best score: " + str(best_accuracy))
#Append results to
best_model_details.append([ Algorithm,
scoring_type,
best_accuracy,
best_paramater['model__n_estimators'],
str(number_of_cv_folds),
])
return best_model_details, best_paramater
# + id="6aI6HQo9elIc"
def graph_important_features(model, x_train_df):
print("Feature importances via feature_importances_ for Random Forest")
importance = np.abs(model.feature_importances_)
feature_names = np.array(x_train_df.columns)
f, ax = plt.subplots(figsize=(30,5))
plt.bar(height=importance, x=feature_names, )
plt.xticks(rotation='vertical', fontsize = 16)
plt.yticks(fontsize = 16)
plt.xlabel("Feature", fontsize = 20)
plt.ylabel("Gini importance", fontsize = 20)
plt.show()
# + id="F2_pnMoZlrEM"
def reduce_input(x_train, y_train, number_of_cv_folds, best_paramater, x_train_df):
end_of_reduction = False
#create the best best model and fit with data to see inputs used
#create mdoel
Algorithm = "Extra trees"
model = ExtraTreesClassifier(random_state=0,n_estimators = best_paramater['model__n_estimators'])
min_max = MinMaxScaler()
pipe = Pipeline(steps = [
("min_max" , min_max ),
("model" , model )
])
pipe = pipe.fit(x_train, y_train)
bad_input = []
#Aquire the festes that are important
Feature_importance = model.feature_importances_
#copy dataframe so values can be removed
updated_x_train = x_train_df.copy()
a = 0
#Every feauture which has 0 value is removed
for value in Feature_importance:
if(value == 0):
bad_input.append(x_train_df.columns[a])
a+=1
print("[INFO] Number of removed inputs: " + str(len(bad_input)))
if(len(bad_input)==0):
print("[INFO] Inputs can not be further reduced!")
end_of_reduction = True
for value in bad_input:
updated_x_train = updated_x_train.drop([value], axis='columns')
updated_x_train_df = updated_x_train.copy()
#### Plot results of important features
graph_important_features(model, x_train_df)
return end_of_reduction, updated_x_train_df, updated_x_train_df
def best_model_test(x_train, y_train, number_of_cv_folds, best_paramater, best_results, x_train_df):
model_check = []
#create mdoel
Algorithm = "Extra trees"
model = ExtraTreesClassifier(random_state=0,n_estimators = best_paramater['model__n_estimators'])
min_max = MinMaxScaler()
pipe = Pipeline(steps = [
("min_max" , min_max ),
("model" , model )
])
y_train_pred = cross_val_predict(pipe, x_train, y_train, cv=number_of_cv_folds)
conf = confusion_matrix(y_train, y_train_pred)
print(conf)
f1 = round(f1_score(y_train, y_train_pred), 4)
precision = round(precision_score(y_train, y_train_pred), 4)
recall = round(recall_score(y_train, y_train_pred), 4)
print("F1 score\tPurity\t\tRecovery")
print(str(f1) + "\t\t" + str(precision) + "\t\t" + str(recall) + "\n\n")
model_check.append([f1, precision, recall, conf, len(x_train.columns), str(number_of_cv_folds)])
return model_check
# + id="91WPaYXJCgeh"
header = ["Algorithm", "Scoring type", "Score", "Number of esitmators", "Cross-validation setting"]
model_check_header = ["f1", "Purity", "Recovery", "Confusion matrix", "Number of inputs", "Cross-validation setting"]
best_features_header = ["Imporant Features"]
# + id="9R-WrbaweMll" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="f1fb1210-fa87-4d33-e713-7ca3e537f0f4"
best_results = []
model_check = []
best_features = []
print("[INFO] CODE START: Extra trees")
for key in uploaded:
best_model_list = []
best_features = []
reduction_mode = False
print("\n\nFile uploaded: " +str(key))
loaded_file = pd.read_csv(io.BytesIO(uploaded[key]))
x_train_df = loaded_file.drop(['Label'], axis='columns')
x_train = x_train_df.copy()
y_train = loaded_file.Label
#calcualte the largest possible cross validation
number_of_cv_folds = StratifiedKFold(calculate_cross_validation_value(y_train))
print("[INFO] Number of CV folds: " + str(number_of_cv_folds))
#Calualte the all feature combinations and create list for vaible combinations
n_estitmators_var = testing_combination_arrays(50)
print("[INFO] N_estimators combinations: " + str(n_estitmators_var))
while(reduction_mode==False):
#Perform grid search for Random Forest
print("[INFO] Finding best model parameters with reduced x_train")
best_model_details, best_paramater = grid_search_RF_function(x_train, y_train, n_estitmators_var, number_of_cv_folds)
best_model_list.append(best_model_details)
#Reduce input data
print("[INFO] Reducing input data based on best model")
reduction_mode, x_train, x_train_df = reduce_input(x_train, y_train, number_of_cv_folds, best_paramater, x_train_df)
best_features.append(x_train_df.columns)
print("[INFO] Input reduced to lowest combination. Aquiring best parameters and testing model")
best_model_details, best_paramater = grid_search_RF_function(x_train, y_train, n_estitmators_var, number_of_cv_folds)
best_model_list.append(best_model_details)
model_check = best_model_test(x_train, y_train, number_of_cv_folds, best_paramater, best_results, x_train_df)
with open(str(key) + '_extra_trees' + '.csv', 'w', newline='') as file:
writer = csv.writer(file)
writer.writerow(header)
writer.writerows(best_model_list)
writer.writerow(model_check_header)
writer.writerows(model_check)
writer.writerow(best_features_header)
writer.writerows(best_features)
files.download(str(key) + '_extra_trees' + '.csv')
|
Extra_trees_assessment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Finite element solver for an elastic rod
# We create in this notebook a simple finite element solver for a linear elastic rod using continuous, piecewise linear finite elements.
#
# We will use NumPy to perform the simulations, and Matplotlib to visualise the results, so we first import the NumPy and Matplotlib modules:
import numpy as np
# %matplotlib inline
import matplotlib.pyplot as plt
# We will also use [ipywidgets](https://ipywidgets.readthedocs.io) (interactive widgets), so you will to make sure that are installed (ipywidgets is installed on the Azure notebook service).
# ## A first solver
# ### Elastic parameters
# For our elastic rod, we define the Young's modulus $E$ and the cross-sectional area $A$. Both are assumed constant.
E = 100.0
A = 1.0
# ### Distributed load
# We now define the distributed load $f$. We will use a function that takes the coordinate $x$ as an argument so we possibly define loading terms that vary with position.
def distributed_load(x):
return 1.0
# ### Create a mesh
# We will create a mesh of length $L$ with a prescribed number of cells (elements) $n_{\text{cells}}$. For linear elements, the number of nodes $n_{\text{nodes}}$ is equal to $n_{\text{cells}} + 1$.
L = 10.0
n_cells = 30
n_nodes = n_cells + 1
# To create a mesh from 0 to $L$ with equal size cells (elements) we will use the NumPy function `linspace` to generate an array of equally spaced points on the interval $[0, L]$.
mesh = np.linspace(0.0, L, n_nodes)
# Matplotlib can be used to visualise the mesh:
plt.xlabel('$x$')
plt.title('finite element mesh')
plt.plot(mesh, [0]*len(mesh), 'ro-');
# ### A simple finite element solver
# We have already defined our domain (the mesh) and the constitutive parameters ($E$ and $A$). We now need to build the global stiffness matrix $\boldsymbol{K}$ and the global right-hand side vector $\boldsymbol{b}$, after which we can solve $\boldsymbol{K} \boldsymbol{a} = \boldsymbol{b}$ to get the nodal degrees-of-freedom $\boldsymbol{a}$.
# #### Create stiffness matrix $\boldsymbol{K}$
# We create the global stiffness matrix by computing the element matrix $\boldsymbol{k}_{e}$ (which is constant since $A$, $E$ and the cell size are constant in our case), and then looping over all cells and adding their contribution to the global matrix.
# ##### Element stiffness matrix $\boldsymbol{k}_{e}$
# The element stiffness matrix for a linear element of length $l$ and constant $AE$ is
#
# $$
# \boldsymbol{k}_{e}
# = \frac{EA}{l}
# \begin{bmatrix}
# 1 & -1 \\ -1 & 1
# \end{bmatrix}
# $$
#
# Our mesh has constant cells size, so we can compute $\boldsymbol{k}_{e}$ just once:
l = L/n_cells
k_e = (E*A/l)*np.array([[1, -1], [-1, 1]])
print(k_e)
# ##### Assemble global stiffness matrix
# To build the global stiffness matrix $\boldsymbol{K}$, we first create an empty $n_{\text{nodes}} \times n_{\text{nodes}}$ matrix:
K = np.zeros((n_nodes, n_nodes))
# Next, we loop over each cell and add the cell contribution $\boldsymbol{k}_{e}$ to the the global matrix $\boldsymbol{K}$. This is known as *assembly*.
for element in range(n_cells):
K[element:element + 2, element:element + 2] += k_e
# #### Create RHS vector $\boldsymbol{b}$
# We create the global RHS vector $\boldsymbol{b}$ by computing the cell RHS $\boldsymbol{b}_{e}$ cell-by-cell, and adding this to the global RHS vector. We allow the distributed load $f$ to vary with position, which is why we cannot compute it just once. For simplicity we will integrate the local RHS using the midpoint rule. This is exact if $f$ is constant, and is otherwise approximate.
#
# We first create an empty global RHS vector:
b = np.zeros(n_nodes)
# We now loop over each cell and compute $\int_{x_{i}}^{x_{i+1}} N_{1} f dx$ and $\int_{x_{i}}^{x_{i+1}} N_{2} f dx$ for each cell, and add the contribution to the global RHS vector:
for element in range(n_cells):
# Get cell length and midpoint
l = mesh[element + 1] - mesh[element]
x_mid = (mesh[element + 1] + mesh[element])/2.0
# Evaluate loading term
f = distributed_load(x_mid)
# Compute and add RHS contributions
b[element:element + 2] += 0.5*l*f
# #### Apply Dirichet (displacement) boundary condition
# We're almost ready to solve a finite element problem, but we would get into trouble if we tried to solve $\boldsymbol{K} \boldsymbol{a} = \boldsymbol{b}$ using the above stiffness matrix because it is singular (you can verify this by computing the determinant with `np.linalg.det(K)`). The system is singular because we have not applied a Dirichlet boundary condition, hence there is a rigid body translation mode in the system.
#
# We impose the boundary condition $u = 0$ and $x=0$ by zeroing the first row and column of the matrix, placing a one on the first diagonal entry and setting the first entry on the RHS to zero. It should be clear algebraically that this will ensure that the first degree of freedom is equal to zero when we solve the system.
# +
# Zero first row and first column
K[0, :] = 0.0
K[:, 0] = 0.0
# Place one on the diagonal of K and zero in the first entry on the RHS
K[0, 0] = 1.0
b[0] = 0.0
# -
# #### Solve system of equations
# We can now solve the finite element system $\boldsymbol{K}$:
u = np.linalg.solve(K, b)
# #### Visualising the solution
# We now plot the solution:
plt.xlabel('$x$')
plt.ylabel('$u$')
plt.title('Finite element solution for the elastic bar')
plt.plot(mesh, u, 'ro-');
# ## A more programmatic approach
# We now present a finite element solver that is very similar the one above, but we now provide a programming interface so we can reuse a function to explore different loading functions and different levels of refinement of the mesh.
def solver(L, f, n_cells, quad_degree=3):
"A simple finite element solver for a 1D bar"
# Crarte mesh and compute cell size
n_nodes = n_cells + 1
mesh = np.linspace(0.0, L, n_nodes)
l = L/n_cells
# Compute locall stiffness matrix
k_e = (E*A/l)*np.array([[1, -1], [-1, 1]])
# Assemble global stiffnes matrix
K = np.zeros((n_nodes, n_nodes))
for element in range(n_cells):
K[element:element + 2, element:element + 2] += k_e
# Use NumPy to get quadrature points and weights
quad_points, quad_weights = np.polynomial.legendre.leggauss(quad_degree)
# Assemble RHS using Gauss quadrature
b = np.zeros(n_nodes)
for element in range(n_cells):
# Get cell midpoint
x_mid = (mesh[element + 1] + mesh[element])/2.0
# Loop over quadrature points
for zeta, weight in zip(quad_points, quad_weights):
# Compute coordinate of point
x = x_mid + zeta*l/2.0
# Evaluate loading term
f_load = f(x)
# Quadrature weight
w = weight*(l/2.0)
# Compute RHS contributions
N = 0.5 - zeta/2.0
b[element] += w*N*f_load
N = 0.5 + zeta/2.0
b[element + 1] += w*N*f_load
# Apply boundary condition
K[0, :], K[:, 0], K[0, 0] = 0.0, 0.0, 1.0
b[0] = 0.0
return np.linalg.solve(K, b), mesh
# We want to see how the solution changes with mesh refinement for some loading function. To set $f = \sin(x)$, we create a function:
def f_sine(x):
return np.sin(x)
# We now compute solutions for four increasingly fine meshes and store the mesh and the computed displacement field. We pass the domain length (`L`), the function for computing the loading (`f_sine`) and the number cells in the mesh (`n`):
meshes = [3, 5, 10, 20]
solutions = [solver(L, f_sine, n) for n in meshes]
# Plotting the solutions on the same graph:
plt.xlabel('$x$')
plt.ylabel('$u$')
plt.title('Finite element solution for the elastic bar')
for u, mesh in solutions:
plt.plot(mesh, u, 'o-', label=str(len(mesh)-1) + ' cells');
plt.legend(loc='upper left');
# We can see that the solutions get closer as the mesh is refined.
#
# **Exercise** Experiment with your own loading function, and compare the computed results to an analytical solution.
# ### Interactive solver
#
# We can make an interactive solver, where you can change the number of cells via a slider and see how the solution changes. We will use a high-order quadrature scheme to keep the integration error small on the coarse meshes,
#
# You need to run this notebook in a Jupyter session to see and use the slider.
# +
from ipywidgets import widgets
from ipywidgets import interact
# Compute reference solution with 100 cells
u_ref, mesh_ref = solver(L, f_sine, 100)
@interact(num_cells=widgets.IntSlider(min=1, max=10, value=1, description='number of cells'))
def plot(num_cells=5):
plt.xlabel('$x$')
plt.ylabel('$u$')
plt.title('Finite element solution for the elastic bar')
u, mesh = solver(L, f_sine, num_cells, quad_degree=6)
plt.plot(mesh_ref, u_ref, '--', color='k', label='reference solution');
plt.plot(mesh, u, 'o-', label=str(len(mesh)-1) + ' cells');
plt.legend(loc='upper left');
|
02-elastic_bar_linear_fem.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Extracting runs from one DB file to another
#
# This notebook shows how to use the `extract_runs_into_db` function to extract runs from a database (DB) file (the source DB) into another DB file (the target DB). If the target DB does not exist, it will be created. The runs are **NOT** removed from the original DB file; they are copied over.
#
# ## Setup
#
# Let us set up a DB file with some runs in it.
# +
import os
import numpy as np
from qcodes.dataset.database_extract_runs import extract_runs_into_db
from qcodes.dataset.experiment_container import Experiment, load_experiment_by_name
from qcodes.tests.instrument_mocks import DummyInstrument
from qcodes.dataset.measurements import Measurement
from qcodes import Station
# The following function is imported and used here only for the sake
# of explicitness. As a qcodes user, please, consider this function
# private to qcodes which means its name, behavior, and location may
# change without notice between qcodes versions.
from qcodes.dataset.sqlite.database import connect
# -
source_path = os.path.join(os.getcwd(), 'extract_runs_notebook_source.db')
target_path = os.path.join(os.getcwd(), 'extract_runs_notebook_target.db')
source_conn = connect(source_path)
target_conn = connect(target_path)
# +
exp = Experiment(name='extract_runs_experiment',
sample_name='no_sample',
conn=source_conn)
my_inst = DummyInstrument('my_inst', gates=['voltage', 'current'])
station = Station(my_inst)
# +
meas = Measurement(exp=exp)
meas.register_parameter(my_inst.voltage)
meas.register_parameter(my_inst.current, setpoints=(my_inst.voltage,))
#Add 10 runs with gradually more and more data
for run_id in range(1, 11):
with meas.run() as datasaver:
for step, noise in enumerate(np.random.randn(run_id)):
datasaver.add_result((my_inst.voltage, step),
(my_inst.current, noise))
# -
# ## Extraction
#
# Now let us extract runs 3 and 7 into our desired target DB file. All runs must come from the same experiment. To extract runs from different experiments, one may call the function several times.
#
# The function will look in the target DB to see if an experiment with matching attributes already exists. If not, such an experiment is created.
extract_runs_into_db(source_path, target_path, 3, 7)
target_exp = load_experiment_by_name(name='extract_runs_experiment', conn=target_conn)
target_exp
# The last number printed in each line is the number of data points. As expected, we get 3 and 7.
#
# Note that the runs will have different `run_id`s in the new database. Their GUIDs are, however, the same (as they must be).
exp.data_set(3).guid
target_exp.data_set(1).guid
# Furthermore, note that the original `run_id` preserved as `captured_run_id`. We will demonstrate below how to look up data via the `captured_run_id`.
target_exp.data_set(1).captured_run_id
# ## Merging data from 2 databases
# There are occasions where it is convenient to combine data from several databases.
# Let's first demonstrate this by creating some new experiments in another db file.
extra_source_path = os.path.join(os.getcwd(), 'extract_runs_notebook_source_aux.db')
source_extra_conn = connect(extra_source_path)
exp = Experiment(name='extract_runs_experiment_aux',
sample_name='no_sample',
conn=source_extra_conn)
# +
meas = Measurement(exp=exp)
meas.register_parameter(my_inst.current)
meas.register_parameter(my_inst.voltage, setpoints=(my_inst.current,))
#Add 10 runs with gradually more and more data
for run_id in range(1, 11):
with meas.run() as datasaver:
for step, noise in enumerate(np.random.randn(run_id)):
datasaver.add_result((my_inst.current, step),
(my_inst.voltage, noise))
# -
exp.data_set(3).guid
extract_runs_into_db(extra_source_path, target_path, 1, 3)
target_exp_aux = load_experiment_by_name(name='extract_runs_experiment_aux', conn=target_conn)
# The GUID should be preserved.
target_exp_aux.data_set(2).guid
# And the original `run_id` is preserved as `captured_run_id`
target_exp_aux.data_set(2).captured_run_id
# ## Uniquely identifying and loading runs
#
# As runs move from one database to the other, uniquely identifying a run becomes non-trivial.
# Note how we now have 2 runs in the same DB sharing the same `captured_run_id`. This means that `captured_run_id` is **not** a unique key. We can demonstrate that `captured_run_id` is not unique by looking up the `GUID`s that match this `captured_run_id`.
from qcodes.dataset.sqlite.queries import get_guids_from_run_spec
from qcodes.dataset.data_set import load_by_guid, load_by_run_spec
guids = get_guids_from_run_spec(target_conn, captured_run_id=3)
guids
load_by_guid(guids[0], conn=target_conn)
load_by_guid(guids[1], conn=target_conn)
# To enable loading of runs that may share the same `captured_run_id`, the function `load_by_run_data` is supplied.
# This function takes one or more optional sets of metadata. If more than one run matching this information is found the metadata of the matching runs is printed and an error is raised. It is now possible to suply more information to the function to uniquely identify a specific run.
try:
load_by_run_spec(captured_run_id=3,
conn=target_conn)
except NameError:
print("Caught a NameError")
# To single out one of these two runs, we can thus specify the `experiment_name`:
load_by_run_spec(captured_run_id=3,
experiment_name='extract_runs_experiment_aux',
conn=target_conn)
|
docs/examples/DataSet/Extracting-runs-from-one-DB-file-to-another.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#there are 83 red geysers in the original list, 51 of which can be found in MaNGA-HI data
file='joined_table.fits'
from astropy.io import fits
hdul = fits.open(file)
hdul.info()
hdu = hdul[1]
hdr0 = hdul[0].header
hdr = hdul[1].header
data = hdu.data
#data.columns
#print((data.columns))
# +
#there are 65 red geysers
afile='allredgeys.fits'
ahdul = fits.open(afile)
ahdul.info()
ahdu = ahdul[1]
ahdr = ahdul[0].header
ahdr = ahdul[1].header
adata = ahdu.data
#data.columns
#print((data.columns))
# +
from astropy.io import ascii
tblgeysers1='uniqredgeys.txt'
tbl=ascii.read(tblgeysers1,delimiter='\s', names=('mangaid', 'plate', 'ifudsgn', 'objra', 'objdec'))
tbl
# -
import numpy as np
mask=(data['logMHI'] > -999) & (data['Z']<0.05)
detx=data['NSA_ELPETRO_MASS'][mask]
#sel=data['logMHI']>-999
dety=(10**(data['logMHI'][mask]))/(detx)
print(len(dety))
mask2=(data['LOGHILIM200KMS'] > -999) & (data['Z']<0.05)
nondetx=data['NSA_ELPETRO_MASS'][mask2]
nondety=(10**(data['LOGHILIM200KMS'][mask2]))/(nondetx)
print(len(nondety))
import matplotlib.pyplot as plt
plt.figure(figsize=(5,5))
plt.scatter(detx, dety, label='detections', color='red', marker='x')
plt.scatter(nondetx, nondety,label='non-detections', color='green', marker='o' )
plt.xscale('log')
plt.yscale('log')
plt.xlabel("log $M_* [M_o]$")
plt.ylabel("log $M_{HI}/M_*$")
plt.legend(loc='lower left')
plt.savefig('Red_Geyser_Mass_plot.png')
plt.title("Red Geyser $M_{HI}/M_*$ vs $M_*$")
# +
#drphi-control is drpall + mangahi without red geyser sample
drphi = 'drphi.fits'
hdul1 = fits.open(drphi)
data1 = hdul1[1].data
#hdul1.info()
hdu = hdul1[1]
hdr0 = hdul1[0].header
hdr = hdul1[1].header
data1.columns
print(len(data1['MANGAID_1']))
# -
'''
Each galaxy has 7 entries, corresponding
to FUV, NUV, u, g, r, i, z magnitudes. E.g.,
'''
#print(data1['nsa_elpetro_absmag'][0])
'''So to get an NUV-r color (for example) for all galaxies:'''
NUV_r = data1['NSA_ELPETRO_ABSMAG'][:,1] - data1['NSA_ELPETRO_ABSMAG'][:,4]
NUV_r2=NUV_r>5
print(len(NUV_r))
# +
from astropy.table import Column, Table, vstack
bb = Column(NUV_r, name='NUV_r')
bb1=np.array(bb)
print(len(bb1))
with fits.open('drphi.fits') as hdul2:
orig_table = hdul2[1].data
orig_cols = orig_table.columns
new_cols = fits.ColDefs([
fits.Column(array=bb1, name='NUV_r', format='D')])
hdu2 = fits.BinTableHDU.from_columns(orig_cols + new_cols)
#hdu2.writeto('newtable.fits')
# +
#drpall + mangahi with additional NUV_r column, no red geysers
complete = 'newtable2.fits'
hdul3 = fits.open(complete)
data2 = hdul3[1].data
#hdul3.info()
hdu3 = hdul3[1]
hdr01 = hdul3[0].header
hdr11 = hdul3[1].header
#data2.columns
print(len(data2['plateifu_1_2']))
# -
#mask complete table to hide NUV_r < 5 and z > 0.05
mask3= (data2['NUV_r'] > 5) & (data2['nsa_elpetro_mass_2'] > 1) & (data2['Z_2'] < 0.05)#get rid of any 0 entries for mass
datas=data2[mask3]
print('There are',len(datas['nsa_elpetro_mass_2']),'galaxies in the drpall file with NUV-r > 5 and z < 0.05)')
#print('There are 34 galaxies in drpall file that have z > 0.05, for a total of 827 with NUV-r > 5.')
# ## I think ideally, I should've removed the red geyser sample from datas right here, before looking for control sample.
# +
from astropy.table import Table
control_inds = np.array([]) #we'll save the indices of your control galaxes here
dm=0.1
for mass in np.log10(data['nsa_elpetro_mass']):
#find the indices of galaxies which satisfy your criteria
sel_control = np.where((np.log10(datas['nsa_elpetro_mass_2']) > (mass-0.1)) & (np.log10(datas['nsa_elpetro_mass_2']) < (mass+0.1)))
#(you could add NUV-r > 5 reqiurement as well here )
sel_control = sel_control[0]
control_inds=np.concatenate([control_inds,sel_control])
res=[]
[res.append(x) for x in control_inds if x not in res] #getting rid of redundancies in indices
hmm=np.array(res) #turn list into array
print('The indices of the control galaxies:', len(res),'. I don"t know if the fact that this output is 50 less than 749 is a coincidence or not.')
# +
t=Table(datas) #attempting to apply index slicing
t.add_index('nsa_elpetro_mass_2')
res2=list(map(int, res))
control=t[res2]
print(control)
control.write('controlll-take-22.fits', overwrite=True) #export this control table that still has some red geysers in it
cntrl = 'controlll-take-22.fits'
hdul6 = fits.open(cntrl)
data6 = hdul6[1].data
hdu6 = hdul6[1]
hdr6 = hdul6[0].header
hdr6 = hdul6[1].header
# +
#I'm pretty sure this cell is obsolete
last='control-geysers3.fits'
#hdul7 = fits.open(last)
#hdul7.info()
#data7 is the final control group without any of the red geyser sample, even though TOPCAT matching only removed 44 galaxies from controlll-take-3
#hdu7 = hdul7[1]
#hdr7 = hdul7[0].header
#hdr7 = hdul7[1].header
#data7 = hdu7.data
#print(len(data7['nsa_elpetro_mass_1']))
# -
#detections
mask7=(data6['LOGMHI_2'] > -999) & (data6['Z_2'] < 0.05)
mask10=(data6['LOGMHI_2'] < -999) & (data6['LOGHILIM200KMS_2'] > -999)
#print(len(data6['nsa_elpetro_mass_2'][mask10]))
xdetx=data6['nsa_elpetro_mass_2'][mask7]
ydety=(10**(data6['LOGMHI_2'][mask7]))/(xdetx)
print('Number of detected control galaxies =',len(xdetx))
#one galaxy (8082-6101) is neither non-detection nor detection
#nondetections
mask8=(data6['LOGHILIM200KMS_2'] > -999) & (data6['Z_2'] < 0.05)
xnondetx=data6['nsa_elpetro_mass_2'][mask8]
ynondety=(10**(data6['LOGHILIM200KMS_2'][mask8]))/(xnondetx)
print('Number of non-detected control galaxies =',len(xnondetx))
#print('Number of detected control galaxies =',len(ynondety))
import matplotlib.pyplot as plt
plt.figure(figsize=(8,8))
#ax = fig.add_axes([0.1, 0.1, 0.6, 0.75])
plt.scatter(xdetx, ydety, label='control detections', color='darkslategrey', marker='x',s=30)
plt.scatter(xnondetx, ynondety,label='control non-detections', color='silver', marker='o', s=30)
plt.scatter(detx,dety, label='geyser detections', color= 'fuchsia', marker='x', s=50)
plt.scatter(nondetx, nondety, label= 'geyser non-detections', color='red', marker='o', s=40)
plt.xscale('log')
plt.yscale('log')
plt.xlabel("log $M_* [M_o]$", fontsize=15)
plt.ylabel("log $M_{HI}/M_*$",fontsize=15)
plt.legend(loc='lower left', fontsize=15)
plt.savefig('all_mass_plot.png', bbox_inches='tight')
plt.title("Control Group and Geyser Sample $M_{HI}/M_*$ vs $M_*$", fontsize=15)
# +
#combine red geyser table (data) with control sample table (controlll-take-22.fits)
file2='all-finall.fits'
hdul8 = fits.open(file2)
hdul8.info()
hdu8 = hdul8[1]
hdr08 = hdul8[0].header
hdr8 = hdul8[1].header
alldata = hdu8.data
# -
#make column for detection
hip = np.array(alldata['LOGMHI'])
sel = (alldata['LOGMHI'] > -999)
sel = np.multiply(sel, 1)
print(sel)
#import sys
#np.set_printoptions(threshold=sys.maxsize)
#print(sel)
#print(alldata['LOGMHI'])
# +
#make column for sample
bet=alldata['NUV_r']
bet[np.isnan(bet)] = 0
sel2 = bet > 0
sel2 = np.multiply(sel2, 1)
#where_are_NaNs = isnan(alldata['NUV_r'])
#alldata['NUV_r'][where_are_NaNs] = 0
bet[np.isnan(bet)] = 0
print(sel2)
# -
#make new column for MHI/M* take two
ratio = np.zeros(len(alldata))
nondetections = alldata['LOGHILIM200KMS'] > -999
detections = (nondetections == False)
ratio[nondetections] = (10**alldata['LOGHILIM200KMS'][nondetections])/(alldata['nsa_elpetro_mass'][nondetections])
ratio[detections] = (10**alldata['LOGMHI'][detections])/(alldata['nsa_elpetro_mass'][detections])
print(len(ratio))
# +
#table for Dave M*, MHI/M*, detection (1=True, 0=False), and sample (1=red geyser, 0=control)
tebl=Table()
tebl['MANGAID'] = alldata['MANGAID_1']
tebl['M*'] = alldata['nsa_elpetro_mass']
tebl['MHI/M*'] = ratio
tebl['Detection (0=non)'] = sel
tebl['Sample (0=red geyser)'] = sel2
tebl.remove_row(195)
tebl.show_in_notebook()
# -
tebl.write('stattable2.fits', format='fits')
|
red geyser 1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# #### New to Plotly?
# Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
# <br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
# <br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
# #### Version Check
# Plotly's python package is updated frequently. Run `pip install plotly --upgrade` to use the latest version.
import plotly
plotly.__version__
# #### Basic Bar Chart
# +
import plotly.plotly as py
import plotly.graph_objs as go
data = [go.Bar(
x=['giraffes', 'orangutans', 'monkeys'],
y=[20, 14, 23]
)]
py.iplot(data, filename='basic-bar')
# -
# #### Grouped Bar Chart
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace1 = go.Bar(
x=['giraffes', 'orangutans', 'monkeys'],
y=[20, 14, 23],
name='SF Zoo'
)
trace2 = go.Bar(
x=['giraffes', 'orangutans', 'monkeys'],
y=[12, 18, 29],
name='LA Zoo'
)
data = [trace1, trace2]
layout = go.Layout(
barmode='group'
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='grouped-bar')
# -
# ### Stacked Bar Chart
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace1 = go.Bar(
x=['giraffes', 'orangutans', 'monkeys'],
y=[20, 14, 23],
name='SF Zoo'
)
trace2 = go.Bar(
x=['giraffes', 'orangutans', 'monkeys'],
y=[12, 18, 29],
name='LA Zoo'
)
data = [trace1, trace2]
layout = go.Layout(
barmode='stack'
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='stacked-bar')
# -
# ### Bar Chart with Hover Text
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Bar(
x=['Product A', 'Product B', 'Product C'],
y=[20, 14, 23],
text=['27% market share', '24% market share', '19% market share'],
marker=dict(
color='rgb(158,202,225)',
line=dict(
color='rgb(8,48,107)',
width=1.5,
)
),
opacity=0.6
)
data = [trace0]
layout = go.Layout(
title='January 2013 Sales Report',
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='text-hover-bar')
# -
# ### Bar Chart with Direct Labels
# +
import plotly.plotly as py
import plotly.graph_objs as go
x = ['Product A', 'Product B', 'Product C']
y = [20, 14, 23]
data = [go.Bar(
x=x,
y=y,
text=y,
textposition = 'auto',
marker=dict(
color='rgb(158,202,225)',
line=dict(
color='rgb(8,48,107)',
width=1.5),
),
opacity=0.6
)]
py.iplot(data, filename='bar-direct-labels')
# -
# ### Grouped Bar Chart with Direct Labels
# +
import plotly.plotly as py
import plotly.graph_objs as go
x = ['Product A', 'Product B', 'Product C']
y = [20, 14, 23]
y2 = [16,12,27]
trace1 = go.Bar(
x=x,
y=y,
text=y,
textposition = 'auto',
marker=dict(
color='rgb(158,202,225)',
line=dict(
color='rgb(8,48,107)',
width=1.5),
),
opacity=0.6
)
trace2 = go.Bar(
x=x,
y=y2,
text=y2,
textposition = 'auto',
marker=dict(
color='rgb(58,200,225)',
line=dict(
color='rgb(8,48,107)',
width=1.5),
),
opacity=0.6
)
data = [trace1,trace2]
py.iplot(data, filename='grouped-bar-direct-labels')
# -
# ### Rotated Bar Chart Labels
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Bar(
x=['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'],
y=[20, 14, 25, 16, 18, 22, 19, 15, 12, 16, 14, 17],
name='Primary Product',
marker=dict(
color='rgb(49,130,189)'
)
)
trace1 = go.Bar(
x=['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
'Jul', 'Aug', 'Sep', 'Oct', 'Nov', 'Dec'],
y=[19, 14, 22, 14, 16, 19, 15, 14, 10, 12, 12, 16],
name='Secondary Product',
marker=dict(
color='rgb(204,204,204)',
)
)
data = [trace0, trace1]
layout = go.Layout(
xaxis=dict(tickangle=-45),
barmode='group',
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='angled-text-bar')
# -
# ### Customizing Individual Bar Colors
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Bar(
x=['Feature A', 'Feature B', 'Feature C',
'Feature D', 'Feature E'],
y=[20, 14, 23, 25, 22],
marker=dict(
color=['rgba(204,204,204,1)', 'rgba(222,45,38,0.8)',
'rgba(204,204,204,1)', 'rgba(204,204,204,1)',
'rgba(204,204,204,1)']),
)
data = [trace0]
layout = go.Layout(
title='Least Used Feature',
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='color-bar')
# -
# ### Customizing Individual Bar Widths
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace0 = go.Bar(
x=[1, 2, 3, 5.5, 10],
y=[10, 8, 6, 4, 2],
width = [0.8, 0.8, 0.8, 3.5, 4]
)
data = [trace0]
fig = go.Figure(data=data)
py.iplot(fig, filename='width-bar')
# -
# ### Customizing Individual Bar Base
# +
import plotly.plotly as py
import plotly.graph_objs as go
data = [
go.Bar(
x = ['2016','2017','2018'],
y = [500,600,700],
base = [-500,-600,-700],
marker = dict(
color = 'red'
),
name = 'expenses'
),
go.Bar(
x = ['2016','2017','2018'],
y = [300,400,700],
base = 0,
marker = dict(
color = 'blue'
),
name = 'revenue'
)
]
fig = go.Figure(data=data)
py.iplot(fig, filename='base-bar')
# -
# ### Colored and Styled Bar Chart
# +
import plotly.plotly as py
import plotly.graph_objs as go
trace1 = go.Bar(
x=[1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003,
2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012],
y=[219, 146, 112, 127, 124, 180, 236, 207, 236, 263,
350, 430, 474, 526, 488, 537, 500, 439],
name='Rest of world',
marker=dict(
color='rgb(55, 83, 109)'
)
)
trace2 = go.Bar(
x=[1995, 1996, 1997, 1998, 1999, 2000, 2001, 2002, 2003,
2004, 2005, 2006, 2007, 2008, 2009, 2010, 2011, 2012],
y=[16, 13, 10, 11, 28, 37, 43, 55, 56, 88, 105, 156, 270,
299, 340, 403, 549, 499],
name='China',
marker=dict(
color='rgb(26, 118, 255)'
)
)
data = [trace1, trace2]
layout = go.Layout(
title='US Export of Plastic Scrap',
xaxis=dict(
tickfont=dict(
size=14,
color='rgb(107, 107, 107)'
)
),
yaxis=dict(
title='USD (millions)',
titlefont=dict(
size=16,
color='rgb(107, 107, 107)'
),
tickfont=dict(
size=14,
color='rgb(107, 107, 107)'
)
),
legend=dict(
x=0,
y=1.0,
bgcolor='rgba(255, 255, 255, 0)',
bordercolor='rgba(255, 255, 255, 0)'
),
barmode='group',
bargap=0.15,
bargroupgap=0.1
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='style-bar')
# -
# ### Waterfall Bar Chart
# +
import plotly.plotly as py
import plotly.graph_objs as go
x_data = ['Product<br>Revenue', 'Services<br>Revenue',
'Total<br>Revenue', 'Fixed<br>Costs',
'Variable<br>Costs', 'Total<br>Costs', 'Total']
y_data = [400, 660, 660, 590, 400, 400, 340]
text = ['$430K', '$260K', '$690K', '$-120K', '$-200K', '$-320K', '$370K']
# Base
trace0 = go.Bar(
x=x_data,
y=[0, 430, 0, 570, 370, 370, 0],
marker=dict(
color='rgba(1,1,1, 0.0)',
)
)
# Revenue
trace1 = go.Bar(
x=x_data,
y=[430, 260, 690, 0, 0, 0, 0],
marker=dict(
color='rgba(55, 128, 191, 0.7)',
line=dict(
color='rgba(55, 128, 191, 1.0)',
width=2,
)
)
)
# Costs
trace2 = go.Bar(
x=x_data,
y=[0, 0, 0, 120, 200, 320, 0],
marker=dict(
color='rgba(219, 64, 82, 0.7)',
line=dict(
color='rgba(219, 64, 82, 1.0)',
width=2,
)
)
)
# Profit
trace3 = go.Bar(
x=x_data,
y=[0, 0, 0, 0, 0, 0, 370],
marker=dict(
color='rgba(50, 171, 96, 0.7)',
line=dict(
color='rgba(50, 171, 96, 1.0)',
width=2,
)
)
)
data = [trace0, trace1, trace2, trace3]
layout = go.Layout(
title='Annual Profit- 2015',
barmode='stack',
paper_bgcolor='rgba(245, 246, 249, 1)',
plot_bgcolor='rgba(245, 246, 249, 1)',
showlegend=False
)
annotations = []
for i in range(0, 7):
annotations.append(dict(x=x_data[i], y=y_data[i], text=text[i],
font=dict(family='Arial', size=14,
color='rgba(245, 246, 249, 1)'),
showarrow=False,))
layout['annotations'] = annotations
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='waterfall-bar-profit')
# -
# ### Bar Chart with Relative Barmode
# +
x = [1, 2, 3, 4]
trace1 = {
'x': x,
'y': [1, 4, 9, 16],
'name': 'Trace1',
'type': 'bar'
};
trace2 = {
'x': x,
'y': [6, -8, -4.5, 8],
'name': 'Trace2',
'type': 'bar'
};
trace3 = {
'x': x,
'y': [-15, -3, 4.5, -8],
'name': 'Trace3',
'type': 'bar'
}
trace4 = {
'x': x,
'y': [-1, 3, -3, -4],
'name': 'Trace4',
'type': 'bar'
}
data = [trace1, trace2, trace3, trace4];
layout = {
'xaxis': {'title': 'X axis'},
'yaxis': {'title': 'Y axis'},
'barmode': 'relative',
'title': 'Relative Barmode'
};
py.iplot({'data': data, 'layout': layout}, filename='barmode-relative')
# -
# ### Horizontal Bar Charts
# See examples of horizontal bar charts [here](https://plot.ly/python/horizontal-bar-charts/).
# ### Dash Example
from IPython.display import IFrame
IFrame(src= "https://dash-simple-apps.plotly.host/dash-barplot/", width="100%", height="650px", frameBorder="0")
# Find the dash app source code [here](https://github.com/plotly/simple-example-chart-apps/tree/master/barplot).
# ### Reference
# See https://plot.ly/python/reference/#bar for more information and chart attribute options!
# +
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
# ! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'bars.ipynb', 'python/bar-charts/', 'Python Bar Charts | plotly',
'How to make Bar Charts in Python with Plotly.',
title = 'Bar Charts | plotly',
name = 'Bar Charts',
thumbnail='thumbnail/bar.jpg', language='python',
page_type='example_index', has_thumbnail='true', display_as='basic', order=4,
ipynb= '~notebook_demo/186')
|
_posts/python/basic/bar/bars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
from cyjs import *
from IPython.display import display, HTML
from pandas import *
display(HTML(data="""<style>
div#notebook-container { width: 95%; }
div#menubar-container { width: 65%; }
div#maintoolbar-container { width: 99%; }
</style>"""))
from igraph import *
nodeFile = "nodes.tsv"
edgeFile = "edges.tsv"
nodeAttributesFile = "geneExpression.tsv"
edgeAttributesFile = "edgeFlux.tsv"
tblNodes = read_csv(nodeFile, sep="\t")
tblEdges = read_csv(edgeFile, sep="\t")
tblGeneExpression = read_csv(nodeAttributesFile, sep="\t")
tblEdgeFlux = read_csv(edgeAttributesFile, sep="\t")
nodeNames = tblNodes['name'].tolist()
nodeTypes = tblNodes['type'].tolist()
g = Graph(directed=True)
g.add_vertices(nodeNames)
g.vs['type'] = nodeTypes
sources = tblEdges['source'].tolist()
targets = tblEdges['target'].tolist()
edgeTypes = tblEdges['edgeType'].tolist()
g.add_edges(zip(tblEdges['source'].tolist(), tblEdges['target'].tolist()))
g.es['edgeType'] = edgeTypes
cy = cyjs()
display(cy)
cy.deleteGraph()
cy.addGraph(g)
kkLayout = g.layout("kk")
cy.setPosition(kkLayout)
cy.fit(100)
cy.setHeight(900)
sourceNodes = tblEdgeFlux["source"].tolist()
targetNodes = tblEdgeFlux["target"].tolist()
edgeTypes = tblEdgeFlux["edgeType"].tolist()
cy.loadStyleFile("style.js")
for condition in ["cond1", "cond2", "cond3"]:
values = tblEdgeFlux[condition].tolist()
cy.setEdgeAttributes(g, "flux", sourceNodes, targetNodes, edgeTypes, values)
time.sleep(2)
nodes = tblGeneExpression["name"].tolist()
values = tblGeneExpression["expression"].tolist()
cy.setNodeAttributes(g, "expression", nodes, values)
|
cyjs-jupyter/examples/smallNetwork/smallNetwork.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # E-distance with high-dimensional data
#
# - sample from gaussian distributions of different means to showcase this distance measure
# - ask Anurag whether he can find the generators listed in Table 1 so we can do a more powerful comparison analysis
import numpy as np
from scipy.stats import multivariate_normal
from dcor import energy_distance
import sys
sys.path.append('../modules')
from graphpaper import GraphPaper
# %reload_ext autoreload
# %autoreload 2
# %matplotlib inline
# see bottom of https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.multivariate_normal.html
# export
samples_1 = multivariate_normal.rvs(mean=[0, 0, 0], cov=10, size=500, random_state=1)
samples_2 = multivariate_normal.rvs(mean=[10, 10, 10], cov=10, size=500, random_state=1)
samples_3 = multivariate_normal.rvs(mean=[20, 20, 20], cov=10, size=500, random_state=1)
paper = GraphPaper(height=5, width=5, nrows=1, ncols=1)
paper.scatter_3d(1, xs=samples_1[:,0], ys=samples_1[:,1], zs=samples_1[:,2], dot_size=0.5, label='from guassian 1', color='red')
paper.scatter_3d(1, xs=samples_2[:,0], ys=samples_2[:,1], zs=samples_2[:,2], dot_size=0.5, label='from guassian 2', color='green', overlay=True)
paper.scatter_3d(1, xs=samples_3[:,0], ys=samples_3[:,1], zs=samples_3[:,2], dot_size=0.5, label='from guassian 3', color='blue', overlay=True)
paper.show(legend=True, grid_for_all=True)
# see https://dcor.readthedocs.io/en/latest/functions/dcor.energy_distance.html#dcor.energy_distance
print('gaussian 1 to 2:', energy_distance(samples_1, samples_2))
print('gaussian 2 to 3:', energy_distance(samples_2, samples_3))
print('gaussian 1 to 3:', energy_distance(samples_1, samples_3))
|
demos/e-distance-demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import torch
x = torch.ones(2, 2, requires_grad=True)
x
x.data
x.grad
x.grad_fn
y = x + 2
y
y.grad_fn
z = y * y * 3
out = z.mean()
out
x.grad
a = torch.randn(2, 2)
a = ((a * 3) / (a - 1))
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
a.requires_grad_(True)
print(a.requires_grad)
b = (a * a).sum()
print(b.grad_fn)
out.backward()
print(x.grad)
x
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
y.backward(torch.ones(2, 2), retain_graph=True)
x.grad
z = y * y
z
gradient = torch.randn(2, 2)
y.backward(gradient)
x.grad
# +
print(x.requires_grad)
print((x**2).requires_grad)
with torch.no_grad():
print((x**2).requires_grad)
# -
|
src/pytorch for former torch users - autograd.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # FMR standard problem
# ## Problem specification
# We choose a cuboidal thin film permalloy sample measuring $120 \times 120 \times 10 \,\text{nm}^{3}$. The choice of a cuboid is important as it ensures that the finite difference method employed by OOMMF does not introduce errors due to irregular boundaries that cannot be discretized well. We choose the thin film geometry to be thin enough so that the variation of magnetization dynamics along the out-of-film direction can be neglected. Material parameters based on permalloy are:
#
# Exchange energy constant $A = 1.3 \times 10^{-11} \,\text{J/m}$,
#
# Magnetisation saturation $M_\text{s} = 8 \times 10^{5} \,\text{A/m}$,
#
# Gilbert damping $\alpha = 0.008$.
#
# An external magnetic bias field with magnitude $80 \,\text{kA/m}$ is applied along the direction $e = (1, 0.715, 0)$.
#
# We choose the external magnetic field direction slightly off the sample diagonal in order to break the system’s symmetry and thus avoid degenerate eigenmodes. First, we initialize the system with a uniform out-of-plane magnetization $m_{0} = (0, 0, 1)$. We relax the system using the Steepest Descent method. We refer to this stage of simulation as the relaxation stage, and its final relaxed magnetization configuration is saved to serve as the initial configuration for the next dynamic stage.
#
# In the next step (dynamic stage), a simulation is started using the equilibrium magnetisation configuration from the relaxation stage as the initial configuration. Now, the direction of an external magnetic field is altered to $e = (1, 0.7, 0)$. This simulation stage runs for $T = 10 \,\text{ns}$ while the (average and spatially resolved) magnetization $M(t)$ is recorded every $\Delta t = 5 \,\text{ps}$. The Gilbert damping in this dynamic simulation stage is $\alpha = 0.008$.
#
# Details of this standard problem specification can be found in Ref. 1.
# +
import numpy as np
import matplotlib.pyplot as plt
import scipy.fftpack
import scipy.signal
# %matplotlib inline
import fidimag
Lx = Ly = 120 # nm
Lz = 10 # nm
dx = dy = dz = 5 # nm
nx = int(Lx/dx)
ny = int(Ly/dy)
nz = int(Lz/dz)
A = 1.3e-11 # J/m
Ms = 8e5 # A/m
alpha = 0.008
B_mag = 80e3 # A / m
B_axis = np.array([1.0, 0.715, 0.0])
B = B_mag * B_axis / np.linalg.norm(B_axis)
m_init = np.array([0, 0, 1])
t_init = 5e-9
# -
# We create and relax the system.
# +
#NBVAL_IGNORE_OUTPUT
mesh = fidimag.common.CuboidMesh(nx=nx, ny=ny, nz=nz,
dx=dx, dy=dy, dz=dz,
unit_length=1e-9)
sim = fidimag.micro.Sim(mesh, name='relax', driver='steepest_descent')
sim.driver.alpha = 1.0
sim.set_Ms(Ms)
sim.set_m(m_init)
sim.add(fidimag.micro.UniformExchange(A))
sim.add(fidimag.micro.Demag())
sim.add(fidimag.micro.Zeeman(B))
sim.driver.minimise(stopping_dm=1e-7, max_steps=20000)
np.save('m_relax.npy', sim.spin)
# -
# We can now plot the $z$ slice of magnetisation.
fidimag.common.plot(sim, component='all')
# # Dynamic stage
#
# In the dynamic stage, we change the field, 'shocking' the system, and allow the system to evolve in time. This can be thought about in the same way as plucking a guitar string and exciting different modes of the string.
# +
Nsteps = 2001 # Number of steps in dynamic stage
# Change the external field
B_axis = np.array([1.0, 0.7, 0.0])
B = B_mag * B_axis / np.linalg.norm(B_axis)
mesh = fidimag.common.CuboidMesh(nx=nx, ny=ny, nz=nz,
dx=dx, dy=dy, dz=dz,
unit_length=1e-9)
sim = fidimag.micro.Sim(mesh, name='dynamic', driver='llg')
sim.driver.alpha = 1.0
sim.set_Ms(Ms)
sim.set_m(np.load('m_relax.npy'))
sim.add(fidimag.micro.UniformExchange(A))
sim.add(fidimag.micro.Demag())
sim.add(fidimag.micro.Zeeman(B))
sim.get_interaction('Zeeman').update_field(B)
sim.driver.alpha = alpha
ts = np.linspace(0, 10e-9, Nsteps)
# -
#NBVAL_IGNORE_OUTPUT
for i, t in enumerate(ts):
if i % 50 == 0:
print('Step {}, t = {}'.format(i, t))
sim.driver.run_until(t)
sim.save_m()
sim.save_vtk()
# # Postprocessing
#
# We read in the data files and compute the spatially averaged power spectral density, which shows the distribution of power in the excited modes.
m_0 = np.load('m_relax.npy')
mxs = []
mys = []
mzs = []
for i in range(Nsteps):
m = np.load('dynamic_npys/m_{}.npy'.format(i)) - m_0
mxs.append(np.mean(m[0::3]))
mys.append(np.mean(m[1::3]))
mzs.append(np.mean(m[2::3]))
plt.figure(figsize=(8, 6))
plt.plot(ts, mxs)
plt.xlabel('t (ns)')
plt.ylabel('mx average')
plt.grid()
# +
import scipy.fftpack
psd = np.log10(np.abs(scipy.fftpack.fft(mxs))**2 + \
np.abs(scipy.fftpack.fft(mys))**2 + \
np.abs(scipy.fftpack.fft(mzs))**2)
f_axis = scipy.fftpack.fftfreq(Nsteps, d=20e-9/4000)
plt.plot(f_axis/1e9, psd)
plt.xlim([0, 40])
plt.grid()
plt.xlabel('f (GHz)')
plt.ylabel('Psa (a.u.)')
peakind = scipy.signal.find_peaks(psd, width=2)[0]
plt.plot(f_axis/1e9, psd)
plt.scatter(f_axis[peakind]/1e9, psd[peakind])
plt.xlim([0, 50])
# -
print("Lowest frequency peak = {} GHz".format(f_axis[peakind[0]]/1e9))
|
doc/user_guide/ipynb/ferromagnetic-resonance-stdprob.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Problem Statement:
#
# ### RBI Cash demand forecasting using time series.
#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
from pandas import datetime
from sklearn.metrics import mean_squared_error
df= pd.read_excel('RBI.xlsx')
df['Date']= pd.to_datetime(df['Date'])
df.set_index('Date', inplace=True)
df.head()
df.tail()
df.describe()
#Plotting the original data
df.plot(kind= 'line', figsize=(16,6))
plt.show()
# +
#Decomposing to check the seasonality, trend and residuals
df1 = df['Value']
import statsmodels.tsa.seasonal as sts
decomposition = sts.seasonal_decompose(df1,model='multiplicative', period=7) #freq
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
plt.subplot(411)
df1.plot(kind="line",figsize=(10,6),label='Original')
plt.subplot(412)
trend.plot(kind="line",figsize=(10,6),label='trend')
plt.legend(loc='best')
plt.subplot(413)
seasonal.plot(kind="line",figsize=(10,6),label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
residual.plot(kind="line",figsize=(10,6),label='Residuals')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# -
# Here we can see dual seasonality i.e, we have weekly as well as monthly seasonality. However, we see a overall constant trend.
# +
# Testing For Stationarity using Dickeyfuller Test
from statsmodels.tsa.stattools import adfuller
# -
stationarity_test= adfuller(df)
stationarity_test
# +
#Ho: It is non stationary
#H1: It is stationary
def adfuller_test(value):
result=adfuller(value)
labels = ['ADF Test Statistic','p-value','Lags Used','Number of Observations Used']
for value,label in zip(result,labels):
print(label+' : '+ str(value) )
if result[1] <= 0.05:
print("Strong evidence against the null hypothesis(Ho), reject the null hypothesis. Data is stationary")
else:
print("Weak evidence against null hypothesis, indicating it is non-stationary ")
# -
adfuller_test(df)
#Plotting ACF and PACF to get the value of parameter p and q
import statsmodels.api as sm
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
fig= plt.figure(figsize=(15,5))
ax1= fig.add_subplot(211)
fig= sm.graphics.tsa.plot_acf(df['Value'], ax= ax1)
ax2= fig.add_subplot(212)
fig= sm.graphics.tsa.plot_pacf(df['Value'], ax= ax2)
plt.show()
df.shape
print(10)
#Splitting data into train and test
train= df['Value'][0:107]
test= df['Value'][107:]
# # Model 1
# #### Moving Average Method
time1 = df['Value']
moving_avg =time1.rolling(7).mean()
df.plot(kind="line",figsize=(15,5))
moving_avg.plot(kind="line",figsize=(15,5),color='red')
plt.show()
forecast_1= moving_avg.tail(14)
print('RMSE : ', np.sqrt(mean_squared_error(test, forecast_1)))
train.plot(kind="line",figsize=(10,5),legend=True, label='Train')
test.plot(kind="line",figsize=(10,5),legend=True, color='black', label='Test')
forecast_1.plot(kind="line",figsize=(10,5),color='orange',legend=True,label='Forecast')
plt.show()
# # Model 2
# #### SARIMAX (1,0,1), (1,0,1,7)
# +
# Here the data is stationary and has seasonality so I have applied Seasonal ARIMA model,
#I have taken the value of parameter based on the plotted ACF and PACF graph.
# -
model_2= sm.tsa.statespace.SARIMAX(train, order= (1, 0, 1),seasonal_order= (1, 0, 1, 7))
model_2= model_2.fit()
model_2.summary()
forecast_2= model_2.forecast(14)
train.plot(kind="line",figsize=(10,5),legend=True, label='Train')
test.plot(kind="line",figsize=(10,5),legend=True, color='black', label='Test')
forecast_2.plot(kind="line",figsize=(10,5),color='orange',legend=True,label='Forecast')
plt.show()
print('RMSE : ', np.sqrt(mean_squared_error(test, forecast_2[0:14])))
# # Model 3
# #### SARIMAX Auto Arima
# +
# Using Auto arima to get the optimized value of p,d,q
from pmdarima import auto_arima
# +
model_3 = auto_arima(train, start_p=0, start_q=0, d=0,
max_p=3, max_q=3, m=7,
start_P=0, start_Q=0, max_P=2, max_Q=2, seasonal=True,
D=0, trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=True
)
model_3.fit(train)
forecast_3 = model_3.predict(n_periods=len(test))
forecast_3 = pd.DataFrame(forecast_3,index = test.index,columns=['Prediction'])
#plot the predictions for validation set
plt.figure(figsize=(10,5))
plt.plot(train, label='Train')
plt.plot(test, label='Test')
plt.plot(forecast_3, label='Prediction', color='black')
plt.show()
# -
print('RMSE : ', np.sqrt(mean_squared_error(test, forecast_3[0:14])))
# +
#Dataframe with actual test value and forecasted values of Model 1, Model 2 and Model 3
prediction_df= pd.DataFrame()
prediction_df['Actual_Value']= test
prediction_df['Forecast_1']= forecast_1[0:14].round(2)
prediction_df['Forecast_2']= forecast_2[0:14].round(2)
prediction_df['Forecast_3']= forecast_3.round(2)
prediction_df.tail(7)
# -
# # Model 4
# ### Using FB Phrophet
|
RBI_TimeSeries.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd, numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import lzma,json
f=lzma.open("ep/ep_meps_current.json.xz")
#http://parltrack.euwiki.org/dumps/ep_meps_current.json.xz
members=json.loads(f.read())
f=lzma.open("ep/ep_votes.json.xz")
#http://parltrack.euwiki.org/dumps/ep_votes.json.xz
votes=json.loads(f.read())
countries=['Hungary','Romania']
eu={}
parties={}
groups={}
names={}
for j in members:
z='Constituencies'
w='Groups'
if z in j:
if j[z][0]['country'] in countries:
if j[z][0]['country'] not in eu:eu[j[z][0]['country']]={}
eu[j[z][0]['country']][j['UserID']]=j
names[j['Name']['full']]=j
for i in j[z]:
if type(i['party'])==str:
party=i['party']
else:
party=i['party'][0]
party=str(party)
start=int(str(i['start'])[:4])
end=int(str(i['end'])[:4])
if end==9999:
end=2019
if party not in parties:
parties[party]={'min':9999,'max':0}
parties[party]['min']=min(start,parties[party]['min'])
parties[party]['max']=max(end,parties[party]['max'])
if w in j:
for i in j[w]:
party=i['Organization']
party=str(party)
if type(i['groupid'])==str:
code=i['groupid']
else:
code=i['groupid'][0]
start=int(str(i['start'])[:4])
end=int(str(i['end'])[:4])
if end==9999:
end=2019
if party not in groups:
groups[party]={'min':9999,'max':0}
groups[party]['min']=min(start,groups[party]['min'])
groups[party]['max']=max(end,groups[party]['max'])
groups[party]['code']=code
groups
parties
def party_normalizer(party):
if party in ['ALDE','ELDR']: return 'ALDE'
elif party in ['ITS','ENF']: return 'ENF'
elif party in ['NA','NI',['NA', 'NI']]: return 'N/A'
elif party in ['PPE','PPE-DE']: return 'PPE'
elif party in ['S&D','PSE']: return 'S&D'
elif party in ['-','Independent']: return 'N/A'
elif party in ['ALDE Romania','Partidul Conservator','Partidul Puterii Umaniste']: return 'ALDE RO'
elif party in ['Demokratikus Koalíció']: return 'DK'
elif party in ['Együtt 2014 - Párbeszéd Magyarországért']:return 'Együtt PM'
elif party in ['Fidesz-Magyar Polgári Szövetség',
'Fidesz-Magyar Polgári Szövetség-Keresztény Demokrata Néppárt',
'Fidesz-Magyar Polgári Szövetség-Kereszténydemokrata Néppárt',
'Kereszténydemokrata Néppárt']:return 'FIDESZ-KDNP'
elif party in ['Forumul Democrat al Germanitor din România']: return 'FDGR'
elif party in ['Jobbik Magyarországért Mozgalom']:return 'Jobbik'
elif party in ['Lehet Más A Politika']:return 'LMP'
elif party in ['Magyar Demokrata Fórum','Modern Magyarország Mozgalom',
'Szabad Demokraták Szövetsége']: return 'Egyéb'
elif party in ['Magyar Szocialista Párt']: return 'MSZP'
elif party in ['Partidul Democrat','Partidul Democrat-Liberal','Partidul Naţional Liberal',
'Partidul Liberal Democrat','PNL']: return'PNL'
elif party in ['Partidul Mișcarea Populară']: return 'PMP'
elif party in ['Partidul Naţional Ţaranesc Creştin Democrat']:return 'PNȚCD'
elif party in ['Partidul România Mare']:return 'PRM'
elif party in ['Partidul Social Democrat','Partidul Social Democrat + Partidul Conservator']:return 'PSD'
elif party in ['Romániai Magyar Demokrata Szövetség',
'Uniunea Democrată Maghiară din România']:return 'UDMR'
elif party in ['Uniunea Națională pentru Progresul României']: return 'UNPR'
else: return party
def get_allegiance(allegiance,voteid,outcome,name):
if voteid not in allegiance:
allegiance[voteid]={'title':j['title'],'url':j['url'],'ts':j['ts']}
if outcome not in allegiance[voteid]:
allegiance[voteid][outcome]=[]
allegiance[voteid][outcome].append(name)
return allegiance
eu_allegiance={}
eu_vt={}
for country in countries:
hu=eu[country]
hu_allegiance={}
hu_vt={}
for j in votes:
ts=j['ts']
year=str(ts)[:4]
if year not in hu_vt:hu_vt[year]=[]
if year not in hu_allegiance:hu_allegiance[year]={'name':{},'group':{},'party':{}}
if j['title'] not in ["Modification de l'ordre du jour"]:
for outcome in ['For','Against']:
if outcome in j:
for group in j[outcome]['groups']:
for i in group['votes']:
if i['ep_id'] in hu:
dummy={}
dummy['vote']=j['voteid']
dummy['party']='-'
for k in hu[i['ep_id']]['Constituencies']:
if k['start']<ts<k['end']:
dummy['party']=k['party']
dummy['name']=hu[i['ep_id']]['Name']['full']
dummy['outcome']=outcome
dummy['group']=group['group']
dummy['party']=party_normalizer(dummy['party'])
dummy['group']=party_normalizer(dummy['group'])
dummy['title']=j['title']
dummy['url']=j['url']
dummy['ts']=ts
dummy['year']=year
hu_vt[year].append(dummy)
for allegiance_type in ['name','group','party']:
hu_allegiance[year][allegiance_type]=\
get_allegiance(hu_allegiance[year][allegiance_type],j['voteid'],
outcome,dummy[allegiance_type])
eu_allegiance[country]=hu_allegiance
eu_vt[country]=hu_vt
print(country)
# Allegiance
def get_allegiance_matrix(key,vt,allegiance):
allegiance_matrix={}
initvote={'Same':0,'Opposite':0,'Total':0}
for j1 in vt:
outcome=j1['outcome']
name1=j1[key]
if name1 not in allegiance_matrix:allegiance_matrix[name1]={}
if outcome=='For':
for name2 in allegiance[j1['vote']]['For']:
if name2 not in allegiance_matrix[name1]:
allegiance_matrix[name1][name2]=dict(initvote)
allegiance_matrix[name1][name2]['Total']+=1
allegiance_matrix[name1][name2]['Same']+=1
if 'Against' in allegiance[j1['vote']]:
for name2 in allegiance[j1['vote']]['Against']:
if name2 not in allegiance_matrix[name1]:
allegiance_matrix[name1][name2]=dict(initvote)
allegiance_matrix[name1][name2]['Total']+=1
allegiance_matrix[name1][name2]['Opposite']+=1
elif outcome=='Against':
for name2 in allegiance[j1['vote']]['Against']:
if name2 not in allegiance_matrix[name1]:
allegiance_matrix[name1][name2]=dict(initvote)
allegiance_matrix[name1][name2]['Total']+=1
allegiance_matrix[name1][name2]['Same']+=1
if 'For' in allegiance[j1['vote']]:
for name2 in allegiance[j1['vote']]['For']:
if name2 not in allegiance_matrix[name1]:
allegiance_matrix[name1][name2]=dict(initvote)
allegiance_matrix[name1][name2]['Total']+=1
allegiance_matrix[name1][name2]['Opposite']+=1
for j in allegiance_matrix:
for i in allegiance_matrix[j]:
allegiance_matrix[j][i]['Same_perc']=np.round(allegiance_matrix[j][i]['Same']/allegiance_matrix[j][i]['Total'],3)
allegiance_matrix[j][i]['Opposite_perc']=np.round(allegiance_matrix[j][i]['Opposite']/allegiance_matrix[j][i]['Total'],3)
return allegiance_matrix
eu_allegiance_matrix={}
for country in countries:
for year in sorted(eu_vt[country]):
for allegiance_type1 in ['name','group','party']:
for allegiance_type2 in ['name','group','party']:
dummy=get_allegiance_matrix(allegiance_type1,eu_vt[country][year],
eu_allegiance[country][year][allegiance_type2])
if dummy!={}:
if country not in eu_allegiance_matrix:eu_allegiance_matrix[country]={}
if year not in eu_allegiance_matrix[country]:eu_allegiance_matrix[country][year]={}
if allegiance_type1 not in eu_allegiance_matrix[country][year]:
eu_allegiance_matrix[country][year][allegiance_type1]={}
if allegiance_type2 not in eu_allegiance_matrix[country][year][allegiance_type1]:
eu_allegiance_matrix[country][year][allegiance_type1][allegiance_type2]={}
eu_allegiance_matrix[country][year][allegiance_type1][allegiance_type2]=dummy
print(country,year)
open('ep/export/json/eu_allegiance_matrix.json','w').write(json.dumps(eu_allegiance_matrix))
# Listify dictionary
eu_allegiance_list=[]
for country in sorted(eu_allegiance_matrix):
for year in sorted(eu_allegiance_matrix[country]):
for allegiance_type1 in sorted(eu_allegiance_matrix[country][year]):
for allegiance_type2 in sorted(eu_allegiance_matrix[country][year][allegiance_type1]):
for name1 in sorted(eu_allegiance_matrix[country][year][allegiance_type1][allegiance_type2]):
for name2 in sorted(eu_allegiance_matrix[country][year][allegiance_type1][allegiance_type2][name1]):
dummy={'country':country,
'year':year,
'allegiance_type1':allegiance_type1,
'allegiance_type2':allegiance_type2,
'name1':name1,
'name2':name2}
for key in sorted(eu_allegiance_matrix[country][year][allegiance_type1][allegiance_type2][name1][name2]):
dummy[key]=eu_allegiance_matrix[country][year]\
[allegiance_type1][allegiance_type2][name1][name2][key]
eu_allegiance_list.append(dummy)
open('ep/export/json/eu_allegiance_list.json','w').write(json.dumps(eu_allegiance_list))
(pd.DataFrame(eu_allegiance_matrix['Hungary']['2018']['name']['name']['<NAME>']).\
T['Same_perc']-0).sort_values(ascending=False).plot(kind='bar',figsize=(15,9))
# Clusterings
from scipy.cluster.hierarchy import dendrogram, linkage
import numpy as np
def dict_2_matrix(matrix,key,party_labels=False):
labels=sorted(matrix)
slabels=[]
for i in range(len(labels)):
label=labels[i]
if label in names:
if party_labels:
party=party_normalizer(names[label]['Constituencies'][0]['party'])
group=party_normalizer(names[label]['Groups'][0]['groupid'])
slabels.append(str(label)+' | '+str(party)+' | '+str(group))
else:
slabels.append(label)
else:
slabels.append(label)
#extend to square matrix
inner_keys=matrix[sorted(matrix)[0]]
inner_keys=sorted(inner_keys[sorted(inner_keys)[0]])
for name1 in labels:
for name2 in labels:
if name2 not in matrix[name1]:
matrix[name1][name2]={i:0 for i in inner_keys}
return np.array([[matrix[name1][name2][key] for name2 in sorted(matrix[name1])] for name1 in labels]),slabels
def dendro(matrix,th=1000,key='Same_perc',party_labels=False):
X,labelList=dict_2_matrix(matrix,key,party_labels)
linked = linkage(X, 'ward')
plt.figure(figsize=(14, 7))
dendrogram(linked,
orientation='right',
labels=labelList,
p=4,
#truncate_mode='lastp',
#show_contracted=True,
color_threshold=th,
distance_sort='descending',
show_leaf_counts=True)
ax=plt.gca()
plt.setp(ax.get_xticklabels(), rotation=90, fontsize=9)
plt.show()
dendro(eu_allegiance_matrix['Hungary']['2016']['name']['name'],3000,'Same',True)
dendro(eu_allegiance_matrix['Romania']['2017']['name']['name'],5000,'Same',True)
# Matrix to chord
from scipy import sparse
def matrix_2_chord(matrix,labels):
row, col = np.where(matrix)
coo = np.rec.fromarrays([row, col, matrix[row, col]], names='row col value'.split())
coo = coo.tolist()
coo_labeled=[[labels[i[0]],labels[i[1]],i[2]] for i in coo if labels[i[0]]!=labels[i[1]]]
df=pd.DataFrame(coo_labeled)
return df
dfs=[]
for country in countries:
for year in sorted(eu_allegiance_matrix[country]):
for name1 in sorted(eu_allegiance_matrix[country][year]):
for name2 in sorted(eu_allegiance_matrix[country][year][name1]):
try:
matrix,labels=dict_2_matrix(eu_allegiance_matrix[country][year][name1][name2],'Same')
df=matrix_2_chord(matrix,labels)
df['zscore'] = (df[2] - df[2].mean())/df[2].std(ddof=0)
df['minmax']=(df[2] - df[2].min()) / (df[2].max() - df[2].min())
df=df[df['minmax']>0]
df['country']=country
df['year']=year
df['name1']=name1
df['name2']=name2
dfs.append(df)
except: pass
print(country,year)
dfs=pd.concat(dfs)
dfs.to_excel('ep/export/pandas/eu_allegiance_matrix.xlsx')
dfs
|
ep/archive/ep-solo_countries.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # The basic interface for remote computation with IPython
# A Client is the low-level object which manages your connection to the various Schedulers and the Hub.
# Everything you do passes through one of these objects, either indirectly or directly.
#
# It has an `ids` property, which is always an up-to-date list of the integer engine IDs currently available.
# +
import os,sys,time
import numpy
from IPython import parallel
rc = parallel.Client()
# -
rc.ids
# The most basic function of the **Client** is to create the **View** objects,
# which are the interfaces for actual communication with the engines.
#
# There are two basic models for working with engines. Let's start with the simplest case for remote execution, a DirectView of one engine:
e0 = rc[0] # index-access of a client gives us a DirectView
e0.block = True # let's start synchronous
e0
# It's all about:
#
# ```python
# view.apply(f, *args, **kwargs)
# ```
# We want the interface for remote and parallel execution to be as natural as possible.
# And what's the most natural unit of execution? Code! Simply define a function,
# just as you would use locally, and instead of calling it, pass it to `view.apply()`,
# with the remaining arguments just as you would have passed them to the function.
# +
def get_norms(A, levels=[2]):
"""get all the requested norms for an array"""
norms = {}
for level in levels:
norms[level] = numpy.linalg.norm(A, level)
return norms
A = numpy.random.random(1024)
get_norms(A, levels=[1,2,3,numpy.inf])
# -
#
# To call this remotely, simply replace '`get_norms(`' with '`e0.apply(get_norms,`'. This replacement is generally true for turning local execution into remote.
#
# Note that this will probably raise a `NameError` on numpy:
e0.apply(get_norms, A, levels=[1,2,3,numpy.inf])
# The simplest way to import numpy is to do:
e0.execute("import numpy")
# But if you want to simultaneously import modules locally and globally, you can use `view.sync_imports()`:
with e0.sync_imports():
import numpy
e0.apply(get_norms, A, levels=[1,2,3,numpy.inf])
# Functions don’t have to be interactively defined, you can use module functions as well:
e0.apply(numpy.linalg.norm, A, 2)
# ### execute and run
# You can also run files or strings with `run` and `execute`
# respectively.
#
# For instance, I have a script `myscript.py` that defines a function
# `mysquare`:
#
# ```python
# import math
# import numpy
# import sys
#
# a=5
#
# def mysquare(x):
# return x*x
# ```
#
# I can run that remotely, just like I can locally with `%run`, and then I
# will have `mysquare()`, and any imports and globals from the script in the
# engine's namespace:
# %pycat myscript.py
e0.run("myscript.py")
e0.execute("b=mysquare(a)")
e0['a']
e0['b']
# ## Working with the engine namespace
#
# The namespace on the engine is accessible to your functions as
# `globals`. So if you want to work with values that persist in the engine namespace, you just use
# global variables.
# +
def inc_a(increment):
global a
a += increment
print(" %2i" % e0['a'])
e0.apply(inc_a, 5)
print(" + 5")
print(" = %2i" % e0['a'])
# -
# And just like the rest of Python, you don’t have to specify global variables if you aren’t assigning to them:
# +
def mul_by_a(b):
return a*b
e0.apply(mul_by_a, 10)
# -
# If you want to do multiple actions on data, you obviously don’t want to send it every time. For this, we have a `Reference` class. A Reference is just a wrapper for an identifier that gets unserialized by pulling the corresponding object out of the engine namespace.
# +
def is_it_a(b):
return a is b
e0.apply(is_it_a, 5)
# -
e0.apply(is_it_a, parallel.Reference('a'))
# `parallel.Reference` is useful to avoid repeated data movement.
# ## Moving data around
#
# In addition to calling functions and executing code on engines, you can
# transfer Python objects to and from your IPython session and the
# engines. In IPython, these operations are called `push` (sending an
# object to the engines) and `pull` (getting an object from the
# engines).
#
# push takes a dictionary, used to update the remote namespace:
e0.push(dict(a=1.03234, b=3453))
# pull takes one or more keys:
e0.pull('a')
e0.pull(('b','a'))
# ### Dictionary interface
# treating a DirectView like a dictionary results in push/pull operations:
e0['a'] = range(5)
e0.execute('b = a[::-1]')
e0['b']
# `get()` and `update()` work as well.
# ### Exercise: Remote matrix operations
# Can you get the eigenvalues (`numpy.linalg.eigvals` and norms (`numpy.linalg.norm`) of an array that's already on e0:
A = np.random.random((16,16))
A = A.dot(A.T)
e0['A'] = A
np.linalg.eigvals(A)
np.linalg.norm(A, 2)
# # Asynchronous execution
#
# We have covered the basic methods for running code remotely, but we have been using `block=True`. We can also do non-blocking execution.
e0.block = False
# In non-blocking mode, `apply` submits the command to be executed and
# then returns a `AsyncResult` object immediately. The `AsyncResult`
# object gives you a way of getting a result at a later time through its
# `get()` method.
#
# The AsyncResult object provides a superset of the interface in [`multiprocessing.pool.AsyncResult`](http://docs.python.org/library/multiprocessing#multiprocessing.pool.AsyncResult).
# See the official Python documentation for more.
def wait(t):
import time
tic = time.time()
time.sleep(t)
return time.time()-tic
ar = e0.apply(wait, 10)
ar
# `ar.ready()` tells us if the result is ready
ar.ready()
# `ar.get()` blocks until the result is ready, or a timeout is reached, if one is specified
# %time ar.get(1)
# %time ar.get()
# For convenience, you can set block for a single call with the extra sync/async methods:
e0.apply_sync(os.getpid)
ar = e0.apply_async(os.getpid)
ar
ar.get()
ar.metadata
# Now that we have the basic interface covered, we can really get going [in Parallel](Multiplexing.ipynb).
|
IPython-parallel-tutorial/tutorial/Remote Execution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="vLF409jI94Dg"
# # MATH 452: Final Project
#
# Remark:
#
# Please upload your solutions for this project to Canvas with a file named "Final_Project_yourname.ipynb".
# + [markdown] colab_type="text" id="l2ENBj8Nz3kg"
# =================================================================================================================
# + [markdown] colab_type="text" id="XUx4g1oZ94Di"
# ## Problem 1 [20%]:
#
# Consider the following linear system
#
# \begin{equation}\label{matrix}
# A\ast u =f,
# \end{equation}
# or equivalently $u=\arg\min \frac{1}{2} (A* v,v)_F-(f,v)_F$, where $(f,v)_F =\sum\limits_{i,j=1}^{n}f_{i,j}v_{i,j}$ is the Frobenius inner product.
# Here $\ast$ represents a convolution with one channel, stride one and zero padding one. The convolution kernel $A$ is given by
# $$
# A=\begin{bmatrix} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{bmatrix},~~
# $$
# the solution $ u \in \mathbb{R}^{n\times n} $, and the RHS $ f\in \mathbb{R}^{n\times n}$ is given by $f_{i,j}=\dfrac{1}{(n+1)^2}.$
#
#
# ### Tasks:
# Set $J=4$, $n=2^J-1$ and the number of iterations $M=100$. Use the gradient descent method and the multigrid method to solve the above problem with a random initial guess $u^0$. Let $u_{GD}$ and $u_{MG}$ denote the solutions obtained by gradient descent and multigrid respectively.
#
# * [5%] Plot the surface of solution $u_{GD}$ and $u_{MG}$.
#
# * [10%] Define error $e_{GD}^m = \|A * u^{m}_{GD}- f\|_F=\sqrt{\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} |(A * u^{m}_{GD}- f)_{i,j}}|^2 $ for $m=0,1,2,3,...,M$. Similarly, we define the multigrid error $e_{MG}^m$. Plot the errors $e_{GD}^m$ and $e_{MG}^m$ as a function of the iteration $m$ (your x-axis is $m$ and your y-axis is the error). Put both plots together in the same figure.
#
# * [5%] Find the minimal $m_1$ for which $e^{m_1}_{GD} <10^{-5}$ and the minimal $m_2$ for which $e^{m_2}_{MG} <10^{-5}$, and report the computational time for each method. Note that $m_1$ or $m_2$ may be greater than $M=100$, in this case you will have to run more iterations.
# -
# ### Remark:
#
# Below are examples of using gradient descent and multigrid iterations for M-times
# * #### For gradient descent method with $\eta=\frac{1}{8}$, you need to write a code:
#
# Given initial guess $u^0$
# $$
# \begin{align}
# &\text{for } m = 1,2,...,M\\
# &~~~~\text{for } i,j = 1: n\\
# &~~~~~~~~u_{i,j}^{m} = u_{i,j}^{m-1}-\eta(f_{i,j}-(A\ast u^{m-1})_{i,j})\\
# &~~~~\text{endfor}\\
# &\text{endfor}
# \end{align}
# $$
#
# * #### For multigrid method, we have provided the framework code in F02_MultigridandMgNet.ipynb:
#
# Given initial guess $u^0$
# $$
# \begin{align}
# &\text{for } m = 1,2,...,M\\
# &~~~~u^{m} = MG1(u^{m-1},f, J, \nu)\\
# &\text{endfor}
# \end{align}
# $$
# + [markdown] colab_type="text" id="T0S78NQv94Dj"
# =================================================================================================================
# + [markdown] colab_type="text" id="cczmyGLc94Dk"
# ## Problem 2 [50%]:
#
# Use SGD with momentum and weight decay to train MgNet on the Cifar10 dataset. Use 120 epochs, set the initial learning rate to 0.1, momentum to 0.9, weight decay to 0.0005, and divide the learning rate by 10 every 30 epochs. (The code to do this has been provided.) Let $b_i$ denote the test accuracy of the model after $i$ epochs, and let $b^*$ = $\max_i(b_i)$ be the best test accuracy attained during training.
#
#
# ### Tasks:
# * [30%] Train MgNet with the following three sets of hyper-parameters (As a reminder, the hyper-parameters of MgNet are $\nu$, the number of iterations of each layer, $c_u$, the number of channels for $u$, and $c_f$, the number of channels for $f$.):
#
# (1) $\nu=$[1,1,1,1], $c_u=c_f=64$.
#
# (2) $\nu=$[2,2,2,2], $c_u=c_f=64$.
#
# (3) $\nu=$[2,2,2,2], $c_u=c_f=64$, try to improve the test accuracy by implementing MgNet with $S^{l,i}$, which means different iterations in the same layer do not share the same $S^{l}$.
#
#
# * For each numerical experiment above, print the results with the following format:
#
# "Epoch: i, Learning rate: lr$_i$, Training accuracy: $a_i$, Test accuracy: $b_i$"
#
# where $i=1,2,3,...$ means the $i$-th epoch, $a_i$ and $b_i$ are the training accuracy and test accuracy computed at the end of $i$-th epoch, and lr$_i$ is the learning rate of $i$-th epoch.
#
#
# * [10%] For each numerical experiment above, plot the test accuracy against the epoch count, i.e. the x-axis is the number of epochs $i$ and y-axis is the test accuracy $b_i$. An example plot is shown in the next cell.
#
#
# * [10%] Calculate the number of parameters that each of the above models has. Discuss why the number of parameters is different (or the same) for each of the models.
#
# + colab={} colab_type="code" id="damSuh2H94Dl" outputId="62fd266b-438c-4242-b5ae-27f6fdb71a09"
from IPython.display import Image
Image(filename='plot_sample_code.png')
# + colab={} colab_type="code" id="4ykEsSuw94Dp"
# You can calculate the number of parameters of my_model by:
model_size = sum(param.numel() for param in my_model.parameters())
# + [markdown] colab_type="text" id="_hbaPslU94Du"
# =================================================================================================================
# + [markdown] colab_type="text" id="yFzRMwsB94Dv"
# ## Problem 3 [25 %]:
#
# Try to improve the MgNet Accuracy by increasing the number of channels. (We use the same notation as in the previous problem.) Double the number of channels to $c_u=c_f=128$ and try different $\nu$ to maximize the test accuracy.
#
# ### Tasks:
# * [20%] Report $b^{*}$, $\nu$ and the number of parameters of your model for each of the experiments you run.
# * [5%] For the best experiment, plot the test accuracy against the epoch count, i.e. the x-axis is the number of epochs $i$ and y-axis is the test accuracy $b_i$. (Same as for the previous problem.)
# + colab={} colab_type="code" id="h07KdcUz94Dv"
# You can calculate the number of parameters of my_model by:
model_size = sum(param.numel() for param in my_model.parameters())
# + [markdown] colab_type="text" id="8NqbTlxG94D0"
# =================================================================================================================
# + [markdown] colab_type="text" id="BGI1VtYL94D0"
# ## Problem 4 [5%]:
#
# Continue testing larger MgNet models (i.e. increase the number of channels) to maximize the test accuracy. (Again, we use the same notation as in problem 2.)
#
# ### Tasks:
#
# # + [5%] Try different training strategies and MgNet architectures with the goal of achieving $b^*>$ 95%. Hint: you can tune the number of epochs, the learning rate schedule, $c_u$, $c_f$, $\nu$, try different $S^{l,i}$ in the same layer $l$, etc...
# + [markdown] colab_type="text" id="YeIdHNAx94D1"
# =================================================================================================================
|
_build/html/_sources/Module6/Final_Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
import numpy as np
import matplotlib as mpl
import IPython.display as display
import PIL.Image
from tensorflow.keras.preprocessing import image
import cv2
dimage=cv2.imread('clg.jpg')
# +
def deprocess(img):
img = 255*(img + 1.0)/2.0
return tf.cast(img, tf.uint8)
# Display an image
def show(img):
display.display(PIL.Image.fromarray(np.array(img)))
# -
cv2.imshow("flight",dimage)
cv2.waitKey(0)
cv2.destroyAllWindows()
base_model = tf.keras.applications.InceptionV3(include_top=False, weights='imagenet')
names=['mixed3','mixed5']
layers=[base_model.get_layer(name).output for name in names]
dream_model=tf.keras.Model(inputs=base_model.input,outputs=layers)
def calculate_loss(img,model):
img_batch=tf.expand_dims(img,axis=0)
layer_activations=model(img_batch)
if len(layer_activations)==1:
layer_activations=[layer_activations]
losses=[]
for activation in layer_activations:
loss=tf.math.reduce_mean(activation)
losses.append(loss)
return tf.reduce_sum(losses)
class Deepdream(tf.Module):
def __init__(self,model):
self.model=model
@tf.function(
input_signature=(
tf.TensorSpec(shape=[None,None,3], dtype=tf.float32),
tf.TensorSpec(shape=[], dtype=tf.int32),
tf.TensorSpec(shape=[], dtype=tf.float32),)
)
def __call__(self,img,steps,step_size):
print("Tracing the loss")
loss=tf.constant(0.0)
for n in tf.range(steps):
with tf.GradientTape() as tape:
tape.watch(img)
loss=calculate_loss(img,self.model)
gradients=tape.gradient(loss,img)
gradients /= tf.math.reduce_std(gradients) + 1e-8
img=img+gradients*step_size
img=tf.clip_by_value(img,-1,1)
return loss,img
deepdream=Deepdream(dream_model)
# +
def run_deepdream(img,steps=100,step_size=0.01):
img=tf.keras.applications.inception_v3.preprocess_input(img)
img=tf.convert_to_tensor(img)
step_size = tf.convert_to_tensor(step_size)
steps_remaining = steps
step = 0
while steps_remaining:
if steps_remaining>100:
run_steps = tf.constant(100)
else:
run_steps = tf.constant(steps_remaining)
steps_remaining -= run_steps
step += run_steps
loss,img=deepdream(img,run_steps,tf.constant(step_size))
#display.clear_output(wait=True)
show(deprocess(img))
print("Step {}, loss {}".format(step, loss))
result = deprocess(img)
#display.clear_output(wait=True)
show(result)
return result
# -
dreamimage=run_deepdream(img=dimage,steps=500,step_size=0.01)
|
Generative adversarial networks/Deep dream using Inception/Deep dream basic.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] tags=[]
# # Wprowadzenie do Pythona cz. 1
#
# +
# komentarz
# wyrażenia arytmetyczne
print(2+2*23**2)
print((12+1.2)/232**3)
# zmienne
a = 4 # mg/mL <- jednostka jako komentarz
b = 4.562871
c = 3.4e-1 # =3.4x10^-1 = 0.34 <- notacja naukowa
print(a,b,c)
# +
# zmienne - działania
d = a+b+c
print(d)
# +
# formatowanie liczb przy wyświetlaniu wyników:
print("{:.2f}".format(d))
print("{:.4f}".format(d))
print("{:.2e}".format(d))
# to samo w jednej linijce
print("{:.2f} {:.4f} {:.2e}".format(d,d,d))
# +
# Napisać skrypt obliczający stężenie procentowe, znając ms=5 i mr=100
# -
import numpy as np
# +
# funkcje matematyczne
print(np.exp(1))
print(np.log10(100))
print(np.log(100))
# -
|
lekcja1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## 範例重點
# * 學習如何在 keras 中加入 BatchNorm
# * 知道有無 BN 對訓練的影響
# * 比較 BN 在不同 batch size 下的效果
# +
import os
from tensorflow import keras
# 本範例不需使用 GPU, 將 GPU 設定為 "無"
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
# -
train, test = keras.datasets.cifar10.load_data()
# +
## 資料前處理
def preproc_x(x, flatten=True):
x = x / 255.
if flatten:
x = x.reshape((len(x), -1))
return x
def preproc_y(y, num_classes=10):
if y.shape[-1] == 1:
y = keras.utils.to_categorical(y, num_classes)
return y
# +
x_train, y_train = train
x_test, y_test = test
# 資料前處理 - X 標準化
x_train = preproc_x(x_train)
x_test = preproc_x(x_test)
# 資料前處理 -Y 轉成 onehot
y_train = preproc_y(y_train)
y_test = preproc_y(y_test)
# +
from tensorflow.keras.layers import BatchNormalization
"""
建立神經網路,並加入 BN layer
"""
#def build_mlp(input_shape, output_units=10, num_neurons=[512, 256, 128]):
def build_mlp(input_shape, output_units=10, num_neurons=[256, 128, 64]):
input_layer = keras.layers.Input(input_shape)
for i, n_units in enumerate(num_neurons):
if i == 0:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(input_layer)
x = BatchNormalization()(x)
else:
x = keras.layers.Dense(units=n_units,
activation="relu",
name="hidden_layer"+str(i+1))(x)
x = BatchNormalization()(x)
out = keras.layers.Dense(units=output_units, activation="softmax", name="output")(x)
model = keras.models.Model(inputs=[input_layer], outputs=[out])
return model
# -
## 超參數設定
LEARNING_RATE = 1e-3
EPOCHS = 30 # 50
BATCH_SIZE = 1024
MOMENTUM = 0.95
# +
model = build_mlp(input_shape=x_train.shape[1:])
model.summary()
optimizer = keras.optimizers.SGD(lr=LEARNING_RATE, nesterov=True, momentum=MOMENTUM)
model.compile(loss="categorical_crossentropy", metrics=["accuracy"], optimizer=optimizer)
model.fit(x_train, y_train,
epochs=EPOCHS,
batch_size=BATCH_SIZE,
validation_data=(x_test, y_test),
shuffle=True)
# -
# Collect results
train_loss = model.history.history["loss"]
valid_loss = model.history.history["val_loss"]
train_acc = model.history.history["accuracy"]
valid_acc = model.history.history["val_accuracy"]
# +
import matplotlib.pyplot as plt
# %matplotlib inline
plt.plot(range(len(train_loss)), train_loss, label="train loss")
plt.plot(range(len(valid_loss)), valid_loss, label="valid loss")
plt.legend()
plt.title("Loss")
plt.show()
plt.plot(range(len(train_acc)), train_acc, label="train accuracy")
plt.plot(range(len(valid_acc)), valid_acc, label="valid accuracy")
plt.legend()
plt.title("Accuracy")
plt.show()
# -
# ## Work
# 1. 試比較有 BN 在 Batch_size = 2, 16, 32, 128, 256 下的差異
# 2. 請嘗試將 BN 放在 Activation 之前,並比較訓練結果
# 3. 請於 BN 放在 Input Layer 後,並比較結果
|
2nd-ML100Days/homework/D-083/Day083_BatchNorm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 範例
# 接下來的程式碼會示範如何定義一個簡單的 CNN model
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
# +
# 使用 colab 環境的同學請執行以下程式碼
# # %tensorflow_version 1.x # 確保 colob 中使用的 tensorflow 是 1.x 版本而不是 tensorflow 2
# import tensorflow as tf
# print(tf.__version__)
# import os
# from google.colab import drive
# drive.mount('/content/gdrive') # 將 google drive 掛載在 colob,
# # %cd 'gdrive/My Drive'
# os.system("mkdir cupoy_cv_part4") # 可以自己改路徑
# # %cd cupoy_cv_part4 # 可以自己改路徑
# -
# 讀取資料集以及做前處理的函數
def load_data(dirname):
# 讀取 csv 文件
data = pd.read_csv(dirname)
# 過濾有缺失值的 row
data = data.dropna()
# 將圖片像素值讀取為 numpy array 的形態
data['Image'] = data['Image'].apply(lambda img: np.fromstring(img, sep=' ')).values
# 單獨把圖像 array 抽取出來
imgs = np.vstack(data['Image'].values)/255
# reshape 為 96 x 96
imgs = imgs.reshape(data.shape[0], 96, 96)
# 轉換為 float
imgs = imgs.astype(np.float32)
# 提取坐標的部分
points = data[data.columns[:-1]].values
# 轉換為 float
points = points.astype(np.float32)
# normalize 坐標值到 [-0.5, 0.5]
points = points/96 - 0.5
return imgs, points
# 讀取資料
imgs_train, points_train = load_data(dirname = 'training.csv')
print("圖像資料:", imgs_train.shape, "\n關鍵點資料:", points_train.shape)
from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense, Dropout
# 回傳定義好的 model 的函數
def get_model():
# 定義人臉關鍵點檢測網路
model = Sequential()
# 定義神經網路的輸入
model.add(Conv2D(filters=16, kernel_size=3, activation='relu', input_shape=(96, 96, 1)))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=32, kernel_size=3, activation='relu'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=64, kernel_size=3, activation='relu'))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=128, kernel_size=3, activation='relu'))
model.add(MaxPooling2D(pool_size=2))
model.add(Flatten())
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
model.add(Dense(512, activation='relu'))
model.add(Dropout(0.2))
# 最後輸出 30 維的向量,也就是 15 個關鍵點的值
model.add(Dense(30))
return model
model = get_model()
# 配置 loss funtion 和 optimizer
model.compile(loss='mean_squared_error', optimizer='adam')
# 印出網路結構
model.summary()
from keras.callbacks import ModelCheckpoint, History
# model checkpoint
checkpoint = ModelCheckpoint('best_weights.h5', verbose=1, save_best_only=True)
hist = History()
# training the model
hist_model = model.fit(imgs_train.reshape(-1, 96, 96, 1),
points_train,
validation_split=0.2, batch_size=64, callbacks=[checkpoint, hist],
shuffle=True, epochs=150, verbose=1)
# save the model weights
model.save_weights('weights.h5')
# save the model
model.save('model.h5')
# loss 值的圖
plt.title('Optimizer : Adam', fontsize=10)
plt.ylabel('Loss', fontsize=16)
plt.plot(hist_model.history['loss'], color='b', label='Training Loss')
plt.plot(hist_model.history['val_loss'], color='r', label='Validation Loss')
plt.legend(loc='upper right')
# ### 觀察 model 在 testing 上的結果
# 讀取測試資料集
imgs_test, _ = load_data(dirname = 'test.csv')
# 在灰階圖像上畫關鍵點的函數
def plot_keypoints(img, points):
plt.imshow(img, cmap='gray')
for i in range(0,30,2):
plt.scatter((points[i] + 0.5)*96, (points[i+1]+0.5)*96, color='red')
# +
fig = plt.figure(figsize=(15,15))
# 在測試集圖片上用剛剛訓練好的模型做關鍵點的預測
points_test = model.predict(imgs_test.reshape(imgs_test.shape[0], 96, 96, 1))
for i in range(16):
ax = fig.add_subplot(4, 4, i + 1, xticks=[], yticks=[])
plot_keypoints(imgs_test[i], np.squeeze(points_test[i]))
# -
# 目前為止,大致可以觀察到,直接使用簡單的模型以及訓練方式在這組數據上應該可以在訓練集和測試集上都得到一個還不錯的結果,說明這組資料其實不會很難。
# ### 作業
# 請嘗試使用 flip (左右翻轉) 來做 augmentation 以降低人臉關鍵點檢測的 loss
#
# Note: 圖像 flip 之後,groundtruth 的關鍵點也要跟著 flip 哦
#
#
#
model_with_augment = get_model()
model_with_augment.compile(loss='mean_squared_error', optimizer='adam')
# +
# Your code
|
Day44/Day44_train_facial_keypoint_Sample.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Python statistics essential training - 03_04_twovariables
# Standard imports
import numpy as np
import scipy.stats
import pandas as pd
# +
import matplotlib
import matplotlib.pyplot as pp
from IPython import display
from ipywidgets import interact, widgets
# %matplotlib inline
# -
import re
import mailbox
import csv
gapminder = pd.read_csv('gapminder.csv')
gapminder.info()
italy = gapminder.query('country == "Italy"')
italy.head()
italy.plot.scatter("year", "population")
gapminder.query('country == "India"').plot.scatter("year","population")
italy.plot.scatter("year", "gdp_per_day", logy=True)
italy.plot.scatter("gdp_per_day", "life_expectancy", logx=True)
# +
size = np.where(italy.year % 10 == 0,30,2)
italy.plot.scatter("gdp_per_day", "life_expectancy", logx=True, s=size)
# +
data = gapminder.query('(country == "Italy") or (country == "United States")')
size = np.where(data.year % 10 == 0,30,2)
color = np.where(data.country == 'Italy','blue','orange')
data.plot.scatter("gdp_per_day", "life_expectancy", logx=True, s=size, c=color)
# +
data = gapminder.query('(country == "China") or (country == "United States")')
size = np.where(data.year % 10 == 0,30,2)
color = np.where(data.country == 'China','red','orange')
ax = data.plot.scatter("gdp_per_day", "life_expectancy", logx=True, s=size, c=color)
data[data.country == 'China'].plot.line(x='gdp_per_day',y='life_expectancy',ax=ax)
# -
|
Statistics Python Essential Training - Linkedin Learning/2). Visualizing and Describing Data/03_04/03_04_twovariables_end.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# <a href="https://colab.research.google.com/github/codeforhk/python_course/blob/master/py_class_4.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="E_I6QftesBvW"
#
#
# <img src="https://www.codefor.hk/wp-content/themes/DC_CUSTOM_THEME/img/logo-code-for-hk-logo.svg" height="150" width="150" align="center"/>
# <h1><center>Code For Hong Kong - Python class 4</center></h1>
# <h6><center>Written by <NAME></center></h6>
# + [markdown] colab_type="text" id="hffP3JWisQfH"
# # 8.0.0 Recap
# + [markdown] colab_type="text" id="ZC25o1Z7q-Ai"
# ### Review 8.0.0 Concepts
# + [markdown] colab_type="text" id="FltYBhLarQmO"
# - while/ for loop
# - functions
# + [markdown] colab_type="text" id="0pQGnkwGqwII"
# ### Homework 8.0.0 - Hangman
#
# https://github.com/codeforhk/python_course/blob/master/py_class_2_Hangman_Breakdown.ipynb
# + [markdown] colab_type="text" id="ryxxpOnEEhwu"
# # 9.0.0 Final Exam
# + [markdown] colab_type="text" id="3WsDmZFpEhw4"
# ### Exam Rule
#
#
# - Do not search on the internet for answers
# - You have 60 mins to complete it
# - There will be 30 questions of MC & 3 coding questions
# - You will need to complete all of the questions
# - 2 points given for each multiple choice question
# - 10 points for first coding question, 15 points for the last 2 coding questions
#
# ### Exam Grades
# - 75/100 Distinction
# - 60/100 Merit
# - 40/100 Pass
# - 10/100 Attended
#
#
# Exam link below. Please wait for instructions before starting your exams.
# + [markdown] colab_type="text" id="CoEwMdGloFit"
# # 10.0.0 Practical Python Packages & Skills
# + [markdown] colab_type="text" id="46gq-Fmnck1J"
# ## 10.1.0 File system
#
# + colab={} colab_type="code" id="P8VZaP0EHdob"
#very important package you can import
import os
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="_Estw_kiVJ9t" outputId="41ca6eed-deb4-4b24-d636-68ceb1a15c45"
#get current working directory
os.getcwd()
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="cxRs3BOtIHUc" outputId="b6a84ca8-156d-4edb-e638-f150ca4e5f2d"
#list out all the file in your directory
os.listdir()
# + colab={} colab_type="code" id="PAox06RYIONA"
#change working directory
os.chdir('/home')
# + colab={} colab_type="code" id="OoE3dTm5IQwY"
# + [markdown] colab_type="text" id="nbRxeRf7HvTp"
# ## 10.2.0 Pandas - Spreadsheet related
# + [markdown] colab_type="text" id="QngPW2JbONF4"
# 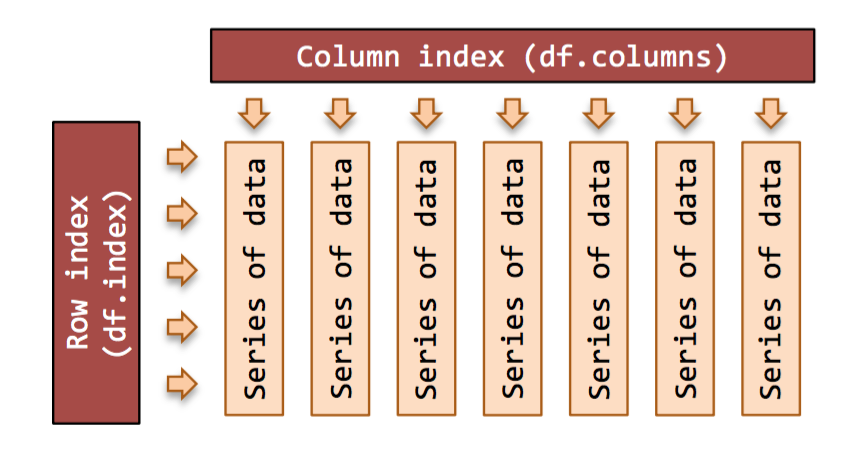
# + [markdown] colab_type="text" id="faYQDHldPLTV"
# 
# + [markdown] colab_type="text" id="LHlq_KkuQcpf"
# 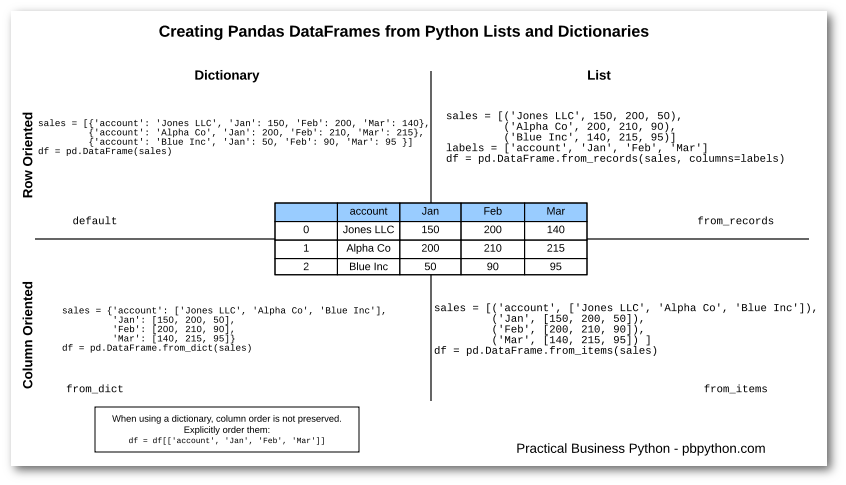
# + colab={} colab_type="code" id="kxQHde8BIUic"
import pandas as pd
# + [markdown] colab_type="text" id="LYuWdGAYQPjv"
# ## 10.3.0 Summary of basic pandas function
# + [markdown] colab_type="text" id="sNZSxGdSNSfE"
# ### 10.3.1 To Create a dataframe
# + colab={} colab_type="code" id="ouCGT40gNSfG"
import pandas as pd
df = pd.DataFrame({'A':[1,2,3]})
# + colab={} colab_type="code" id="iuJleWD7NSfI" outputId="727985bb-1efe-4de1-ab41-a14196c632d8"
df
# + colab={} colab_type="code" id="9CkqxVE8NSfQ"
df.index = ['a','b','c']
# + colab={} colab_type="code" id="i1p3vUmhNSfU" outputId="1bbe9e4b-69c3-471b-83b8-039ef200d2b4"
df
# + colab={} colab_type="code" id="Pu-LrBLyNSfZ" outputId="9bd50c61-efea-4b6d-a9f2-ab317060a9fa"
import pandas as pd
df = pd.DataFrame({'A':[1,2,3],'B':['a','b','c']})
df
# + [markdown] colab_type="text" id="ykV0Cfx6NSfc"
# ...or read from some other source
# + colab={} colab_type="code" id="wZTF6t9JNSfe"
url = 'https://raw.githubusercontent.com/miga101/course-DSML-101/master/pandas_class/diamonds.csv'
df2 = pd.read_csv(url)
# + [markdown] colab_type="text" id="vCp80o6jQDPY"
# ### 10.3.2 To select a subset of dataframe
# + [markdown] colab_type="text" id="bWawQ-6BQDPa"
# You can select a column by square bracket, column names
# + colab={} colab_type="code" id="8Nat2xUeQDPa" outputId="d04c2f45-1bbb-4ae0-a885-d150f75bd43c"
df
# + colab={} colab_type="code" id="q4aqDaK-QDPd" outputId="f85e2fff-3b8e-4c6f-b388-06acaa0a10d1"
df['B']
# + colab={} colab_type="code" id="qq3iecvQQDPh" outputId="abb6d3be-b3c2-4c8a-8ef2-6589fed58f80"
df['A']
# + colab={} colab_type="code" id="SrSOGehwQDPk" outputId="ca1ea952-6ca4-4205-e62c-880ec4331f15"
#e.g to select a column called A
df.A
df['A']
# + [markdown] colab_type="text" id="zTju9wZdQDPm"
# You can use "columns" list all the columns
# + colab={} colab_type="code" id="9ZvvpiqpQDPn"
df.columns = ['patrick','data']
# + colab={} colab_type="code" id="f-HiD3W-QDPt" outputId="9d03c8a3-51c4-436f-fd98-2689390e3e1a"
df.columns
df.columns = ['A','B']
df
# + [markdown] colab_type="text" id="I3CPmtseQDPy"
# Or, you can use "loc" to select a subset of the dataframe
# + colab={} colab_type="code" id="6WVCIOrvQDP1" outputId="56ea7052-7136-4ff3-cb53-a6f358568951"
df.loc[]
# + colab={} colab_type="code" id="qK4K07RTQDP5"
df.loc[2,'B'] = 'patrick'
# + colab={} colab_type="code" id="NVF53Na7QDP8" outputId="89d20ec6-6a59-4f33-e958-31b053b144a4"
df
# + [markdown] colab_type="text" id="JAEHcmHnQDQA"
# Or, you can use "iloc" to use index to select a subset of the dataframe
# + colab={} colab_type="code" id="0r4rm23FQDQB" outputId="452b3ad0-fee7-4d79-ae15-ad20021adc59"
df.iloc[2,0]
# + [markdown] colab_type="text" id="0Hm0tjizQDQC"
# ### 10.3.3 Manipulating the dataset
# + [markdown] colab_type="text" id="bwKi1yGBQDQD"
# ##### simply use a new column name to add a column
# + colab={} colab_type="code" id="xK_3lJ34QDQF" outputId="bb15eb76-9d99-439b-d873-23f5a0c91456"
df['C'] = [0.1,0.2,0.3]
df
# + colab={} colab_type="code" id="HAah4tkLQDQJ"
df['C'] = [0.1,0.2,0.4]
# + colab={} colab_type="code" id="z2h9sjyBQDQP" outputId="a2b14b79-a821-4b62-8cb4-c377b5f16ade"
# IMPORTANT
df['C'].apply(lambda x: x*4)
# + colab={} colab_type="code" id="3URjakEQQDQT" outputId="0ef796d5-efbd-4ca2-d48c-2a771b595451"
df
# + colab={} colab_type="code" id="qHJA15zyQDQU" outputId="16de4d93-291a-4dce-e5b4-a5ef592174f4"
df['C'] = [0.1,0.2,0.3]
df
# + [markdown] colab_type="text" id="nh5p4kKeQDQX"
# ##### Use apply to manipulate a column
# + colab={} colab_type="code" id="mtWyZtlLQDQY"
df['C'] = [i*2 for i in df['C']]
# + colab={} colab_type="code" id="gyNiyjGxQDQa" outputId="00c26dae-4d55-4e36-a0c5-57d819a45be8"
df
# + colab={} colab_type="code" id="RmDOXGWzQDQc"
df['C'] = df['C'].apply(lambda x: x*2)
# + colab={} colab_type="code" id="_HMoHrw3QDQe" outputId="a788e9d9-20c8-4b21-d618-bfa998aba9d5"
df
# + colab={} colab_type="code" id="e6vG3K8jQDQg" outputId="c04b1611-1b04-4b60-b3b0-8604bdcf0857"
df['C'] = df['C'].apply(lambda x: x*2)
df
# + [markdown] colab_type="text" id="rqV5jRvoQDQi"
# ##### Use 'drop' to drop a column
# + colab={} colab_type="code" id="cECvaBu1QDQi"
df = df.drop(['C'], axis = 1)
# + colab={} colab_type="code" id="6OjLTaUzQDQk" outputId="13447729-18d3-40f2-d271-0cd07370bc12"
df
# + colab={} colab_type="code" id="6hm8yDGlQDQl"
df = df.drop(['B', 'C'], axis=1)
# + colab={} colab_type="code" id="zpu1D-LLQDQn" outputId="d934a675-724b-40a8-e8f0-e03b08e754cd"
df
# + [markdown] colab_type="text" id="8IjOROoeQDQt"
# ##### Use 'drop' to drop a row
# + colab={} colab_type="code" id="9BRwA_FkQDQu"
df['Flora'] = 1
# + colab={} colab_type="code" id="rNnJYEK_QDQx" outputId="91ce7c06-9330-4ee7-e32d-9eb37b027ac1"
df.drop([1,2], axis = 0)
# + colab={} colab_type="code" id="8vg3O4gbQDQz" outputId="27f657f9-579c-409d-825e-4401adbc095a"
df.drop([1,2], axis=0)
# + [markdown] colab_type="text" id="6JoDBReZQDQ2"
# ### 10.3.4 Exploring the dataset
# + [markdown] colab_type="text" id="SgcznxvVQDQ2"
# ###### Use head and tail to quickly peek the dataset
# + [markdown] colab_type="text" id="7LtUqF2GT2dD"
#
# + colab={} colab_type="code" id="Gt4jVqkfQDQ3"
df = pd.DataFrame({'A':[1,2,3,4,5], 'B':[1,2,3,4,5]})
# + colab={} colab_type="code" id="rgPqjUyZQDQ4" outputId="b5604abf-9ef8-4f6e-dabb-eeced477467d"
df.tail(2)
# + colab={} colab_type="code" id="uiqlDqCOQDQ7" outputId="880c1461-5eef-4320-bdcb-942818197408"
df.head(2) #shows the top 2 rows
df.tail(2) #shows the last 2 rows
# + [markdown] colab_type="text" id="dd-z-79fQDQ9"
# ###### Use shape, info & describe to quickly understand the size/data type of the dataset
# + colab={} colab_type="code" id="vL--Xg7VQDQ9" outputId="053be1cd-8a57-4a83-9583-9695151e8427"
df.shape
# + colab={} colab_type="code" id="8FtZanSXQDRA" outputId="0d07e9a3-f379-4145-d571-6b540400ad1d"
df.info()
# + colab={} colab_type="code" id="n8VcIrsYQDRD" outputId="32483026-82a8-49c1-95da-ad9dab786b7a"
df.shape
df.info()
df.describe()
# + [markdown] colab_type="text" id="g5FQU663SwDE"
# ## 10.4.0 Advance pandas technique
# + [markdown] colab_type="text" id="2zR8CHNqNSjo"
# ### 10.4.1 Reading Data
#
#
#
# - To create a DataFrame out of common Python data structures, we can pass a dictionary of lists to the DataFrame constructor.
# - Using the columns parameter allows us to tell the constructor how we'd like the columns ordered. By default, the DataFrame constructor will order the columns alphabetically (though this isn't the case when reading from a file - more on that next).
# + [markdown] colab_type="text" id="ieM14ryhNSjp"
# ### 10.4.2 CSV file extraction - Reading data online with a valid url link:
# + [markdown] colab_type="text" id="dUx32oUYNSjq"
# - With this example we will learn how to access online real data (e.g. stock market)
# - Let's get this dataset from a website location, providing a valid link. In this example we are using real Tesla's prices.
# + colab={} colab_type="code" id="PxpDCyT_NSjx" outputId="60d917bc-3470-4c1c-e27a-17b44d3d1bee"
url = "https://raw.githubusercontent.com/miga101/course-DSML-101/master/pandas_class/TSLA.csv"
tesla = pd.read_csv(url, index_col=0, parse_dates=True) # index_col = 0, means that we want date to be our index
# parse_dates=True, means we let Panda to "understand" the date format for us
tesla
# + [markdown] colab_type="text" id="MOLe0E7YNSj0"
# Plotting using pandas
# + colab={} colab_type="code" id="2j4ce0_INSj0" outputId="8645200d-d554-44cf-a925-9006f08e6c9e"
tesla.shape
# + colab={} colab_type="code" id="kS-TPrrVNSj1" outputId="a87ea990-6666-4a3b-f5a6-9deb71fe0ad2"
import matplotlib.pyplot as plt
tesla.plot(y = ['Adj Close','High','Low'])
plt.show()
# + colab={} colab_type="code" id="7108hQHVNSj3" outputId="96ad9280-8b59-4fe9-c2b0-1c55ef1ef7d8"
import matplotlib.pyplot as plt
tesla.plot(y=['Adj Close','Volume']) # plotting by indicating which column we want the values from...
plt.show()
# #pd.plot?
# + colab={} colab_type="code" id="xe30koJNNSj4" outputId="6a5b94f7-55eb-4d30-9456-c86a8346540f"
import matplotlib.pyplot as plt
tesla.plot(y=['Adj Close','Open']) # plotting by indicating which column we want the values from...
plt.show()
# + colab={} colab_type="code" id="mJ_F4ZUqNSj5" outputId="cecc46d6-be5c-4372-aae9-ee84ace17fd3"
tesla[tesla.index>'2017-08-30'].plot(y=['Adj Close','Open'])
plt.show()
# + colab={} colab_type="code" id="-6HN_ocqNSj6" outputId="751b9018-12e8-46f0-8a00-b5f96172dacd"
tesla['Close'].mean() # getting the mean by just calling the mean function
# + colab={} colab_type="code" id="t2dY88-JNSj7" outputId="ad10e668-47df-49af-973b-4155380621da"
tesla.describe() # the describe function will give us a statistical summary
# + [markdown] colab_type="text" id="Erw4VAK2NSj8"
# #### Exercise 10.4.3 - read the csv from the link
# + [markdown] colab_type="text" id="rGrale6nNSj8"
# - Read the csv using pandas
# - Peek into the data by only viewing the first few lines. How would you do that?
# + colab={} colab_type="code" id="CYy7hMjoNSj8" outputId="53fe6d35-2496-4285-c33f-b03b3e57146d"
import pandas as pd
# another example, list of countries
url_c = "https://raw.githubusercontent.com/cs109/2014_data/master/countries.csv"
# Your code here
df = pd.read_csv(url_c)
df.head(5)
# + [markdown] colab_type="text" id="ruEsKkhCNSj9"
# ### 10.4.4 - Build your own Pandas dataframe
# + [markdown] colab_type="text" id="XEGexPZINSj-"
# - Below is how to build the dataframe structure using a dictionary - which is just a combination of lists
# + colab={} colab_type="code" id="Gq-RQTLWNSj-" outputId="f2ffa4a3-b4a6-4283-89b7-c5b7d101080f"
data = {'year': [2010, 2011, 2012, 2011, 2012, 2010, 2011, 2012],
'team': ['Bears', 'Bears', 'Bears', 'Packers', 'Packers', 'Lions', 'Lions', 'Lions'],
'wins': [11, 8, 10, 15, 11, 6, 10, 4],
'losses': [5, 8, 6, 1, 5, 10, 6, 12]}
football = pd.DataFrame(data, columns=['year', 'team', 'wins', 'losses'])
football
# + [markdown] colab_type="text" id="EztC9iTwNSj_"
# ### 10.4.5 - Build your pandas dataframe using list
# + [markdown] colab_type="text" id="8DuwReH5NSj_"
# Back to our hangman example. Let's say I want to build a dataframe, with all the words used in hangman game, and an extra column counting all the len of words. How would I do it?
# + colab={} colab_type="code" id="I0_p_qQ5NSkA" outputId="3c6bc6ba-fe23-40a2-e201-84e01f8845a3"
word_list = ["stick","john","pencil","rubber","glove","quick","brown","fox","jumps","over"
,"lazy","dog","manner","house","food","brain","history","love","peace",
"object"]
df = pd.DataFrame(word_list, columns = ['words'] )
df['word_count'] = df['words'].apply(lambda x: len(x))
df
# + [markdown] colab_type="text" id="hwIswl-WNSkB"
# ### 10.4.6 Dataset from a local CSV file.
#
# Reading a CSV is as simple as calling the read_csv function. By default, the read_csv function expects the column separator to be a comma, but you can change that using the sep parameter.
# + colab={} colab_type="code" id="j0vEY33ANSkB" outputId="f5ad8730-6c31-464e-950e-00f499563e91"
import os
os.getcwd()
os.listdir()
# + colab={} colab_type="code" id="8XjFez-_NSkC"
df = pd.read_csv('football.csv')
# + colab={} colab_type="code" id="-HOIUuLuNSkC"
df.to_csv('df.csv')
# + colab={} colab_type="code" id="UgXL3Vg8NSkD"
football.to_csv('df.csv')
# + colab={} colab_type="code" id="TcjRUvntNSkE"
# First, write the dataframe to a local hard drive
football.to_csv('football.csv')
# + colab={} colab_type="code" id="ZQD9b4ToNSkE" outputId="f6ab1ea7-9de7-44cb-e18e-c5b17bff6350"
pd.read_csv('df.csv')
# + colab={} colab_type="code" id="E074U2Q-NSkF" outputId="8986e873-0964-463d-a301-44d3d6d8bad5"
from_csv = pd.read_csv('football.csv')
from_csv.head(2)
# + colab={} colab_type="code" id="ApTGKEJkNSkI" outputId="e23a37ee-92b2-42f9-b50c-1be3b95c0f51"
# this is the DataFrame we created from a dictionary earlier
football.head()
# + [markdown] colab_type="text" id="8HuCQ0JxNSkL"
# ### 10.4.7 Exporting our data to excel
# + colab={} colab_type="code" id="_4SZIGbmNSkL"
# since our index on the football DataFrame is meaningless, let's not write it
#import openpyxl
#football.to_excel('football.xlsx', index=False)
# + colab={} colab_type="code" id="n3v5ukxkNSkM"
# delete the old DataFrame
del football
# + colab={} colab_type="code" id="BJtKeHfqNSkO"
# read from Excel
football = pd.read_excel('football.xlsx', 'Sheet1')
football
# + colab={} colab_type="code" id="1OeL5Y_cSZba"
# + [markdown] colab_type="text" id="STd1VSJUNSkQ"
# ## 10.5.0 Webscrapping using pandas
#
# Use read_html & read_table to get information off the internet
# + colab={} colab_type="code" id="mGBblvYmNSkR"
#pip install pandas
#pip install lxml
#sudo pip3 install html5lib
#pip install BeautifulSoup4
# + colab={"base_uri": "https://localhost:8080/", "height": 669} colab_type="code" id="3SPK9CsGNSkS" outputId="dd12b24e-2fb8-47cb-e692-25496d0274b8"
import pandas as pd
import html5lib
url='http://www.skysports.com/premier-league-table'
epltable = pd.read_html(url)
epltable[0]
# + colab={} colab_type="code" id="xSJUhzPeNSke" outputId="17769e89-64c6-481d-a437-500cc8f93e2c"
url = 'https://raw.github.com/gjreda/best-sandwiches/master/data/best-sandwiches-geocode.tsv'
# fetch the text from the URL and read it into a DataFrame
from_url = pd.read_table(url, sep='\t')
from_url.head(3)
# + [markdown] colab_type="text" id="9EXfFkWbNSkh"
# #### Exercise 10.5.1 Download from internet
# - Try to download all US states using pandas, and save it do an object called "us"
# + colab={} colab_type="code" id="cu4eS1dtNSkh"
import pandas as pd
url = 'https://simple.wikipedia.org/wiki/List_of_U.S._states'
# + colab={} colab_type="code" id="4Lq0kkntNSkj" outputId="92cfbb49-d8c0-48a6-b6b8-8e1092a691fb"
states
# + [markdown] colab_type="text" id="7PtyVLz_NSkk"
# - Try to make the below table a 'human readable' pandas table
# + colab={} colab_type="code" id="GDu18FKzNSkm"
url = 'https://redirect.viglink.com/?format=go&jsonp=vglnk_150580104072412&key=949efb41171ac6ec1bf7f206d57e90b8&libId=j7r70ik301021u9s000DAfhsh97p2&loc=https%3A%2F%2Fwww.r-bloggers.com%2Fgetting-data-from-an-online-source%2F&v=1&out=https%3A%2F%2Fsakai.unc.edu%2Faccess%2Fcontent%2Fgroup%2F3d1eb92e-7848-4f55-90c3-7c72a54e7e43%2Fpublic%2Fdata%2Fbycatch.csv&ref=https%3A%2F%2Fwww.google.com.hk%2F&title=Getting%20Data%20From%20An%20Online%20Source%20%7C%20R-bloggers&txt=https%3A%2F%2Fsakai.unc.edu%2Faccess%2Fcontent%2Fgroup%2F3d1eb92e-7848-4f55-90c3-7c72a54e7e43%2Fpublic%2Fdata%2Fbycatch.csv'
# fetch the text from the URL and read it into a DataFrame
#fom_url = pd.read_table(url, sep = ',')
#from_url
# + colab={} colab_type="code" id="0yXqcGW0NSko" outputId="4ae6f38d-b3c5-495c-b621-6e1bdedf618b"
# another, list of countries
url="https://raw.githubusercontent.com/cs109/2014_data/master/countries.csv"
countries = pd.read_csv(url)
countries.Region.value_counts()
# + [markdown] colab_type="text" id="0F9igBiHRxop"
# ## 10.4.0 Send Email using python
# + colab={} colab_type="code" id="10v8mRNBR2_1"
#import hashlib, binascii
import smtplib
def send_email( user, pwd, recipient, subject, body):
FROM = user
TO = recipient if type(recipient) is list else [recipient]
SUBJECT = subject
TEXT = body
# Prepare actual message
message = """From: %s\nTo: %s\nSubject: %s\n\n%s
""" % (FROM, ", ".join(TO), SUBJECT, TEXT)
try:
server = smtplib.SMTP("smtp.gmail.com", 587)
server.ehlo()
server.starttls()
server.login(user, pwd)
server.sendmail(FROM, TO, message)
server.close()
print('successfully sent the mail')
except:
print("failed to send mail")
# + colab={} colab_type="code" id="lvNRkeGKR2sy"
send_email('<EMAIL>',pwd,['<EMAIL>','<EMAIL>'],'hello','nonosense')
# + [markdown] colab_type="text" id="XDlwiz5JNOnp"
# ## 10.5.0 Web scraping using python
# + [markdown] colab_type="text" id="AW03fB4vWIl9"
# 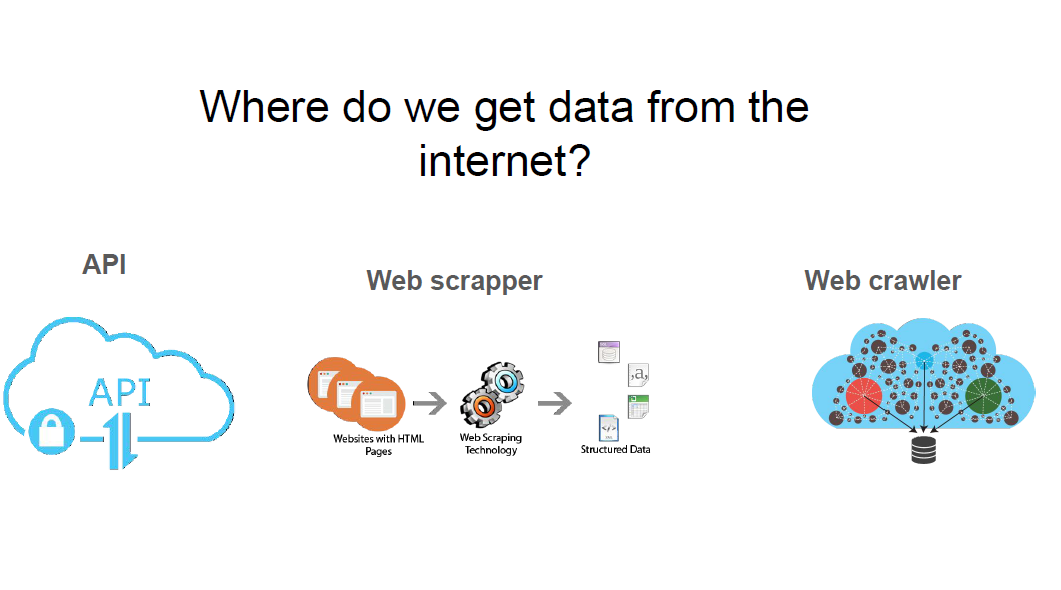
# + [markdown] colab_type="text" id="qE3LOzOOWU-r"
# 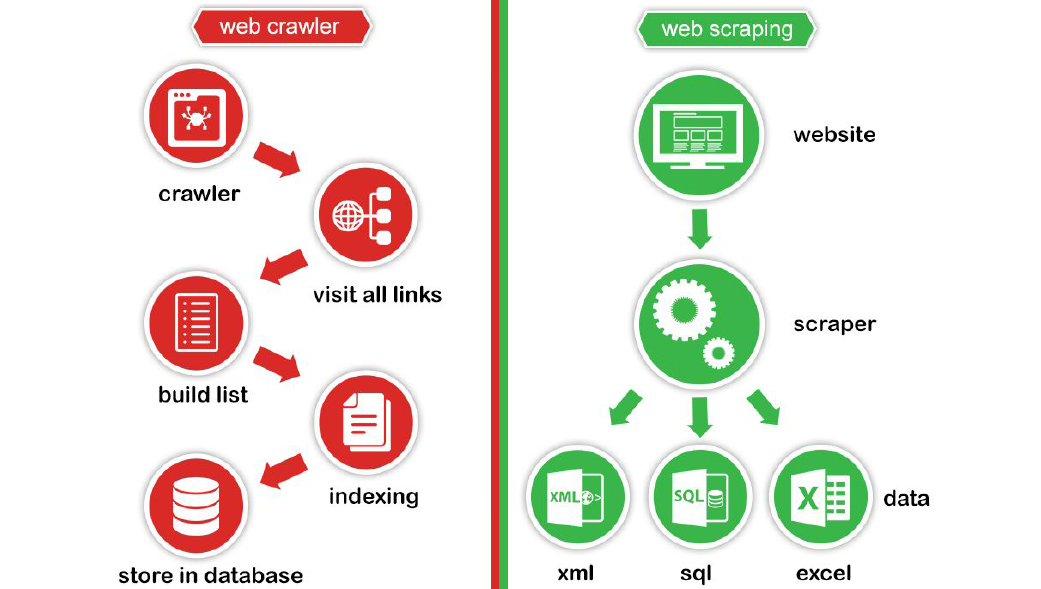
# + [markdown] colab_type="text" id="WzjGIzE1WYT3"
# 
# + [markdown] colab_type="text" id="HnVDWCpkNOnq"
# ### 10.5.1 Requests
# + [markdown] colab_type="text" id="Oe_9yKiKNOnr"
# Import the ibrary
# + colab={} colab_type="code" id="iXyY4mYBNOns"
import requests
# + [markdown] colab_type="text" id="yW1hv9jXNOnx"
# using requests.get()
# + colab={} colab_type="code" id="ukaK1oAKNOny"
r = requests.get('https://en.wikipedia.org/wiki/Machine_learning')
# + colab={} colab_type="code" id="fV6h6UKGNOn9" outputId="457b2b25-c630-49fa-ab7f-7e8a81fd5336"
r
# + [markdown] colab_type="text" id="pz7-3RxwNOoB"
# use r.content to find the content
# + colab={} colab_type="code" id="Sl1H_NsuNOoC"
#r.content
# + [markdown] colab_type="text" id="tAERCx9sNOoI"
# Alternatively, use r.text to find the content
# + [markdown] colab_type="text" id="yFPwZbTONOoR"
# ### 10.5.2 Beautiful Soup
# + [markdown] colab_type="text" id="dO-OCc1ANOoS"
# import the library
# + colab={} colab_type="code" id="loURNX6bNOoT"
from bs4 import BeautifulSoup as bs
# + [markdown] colab_type="text" id="flKUOpTrNOoZ"
# Beautiful soup is to give the web site some meaningful structure
# + colab={} colab_type="code" id="bZfASzp_NOoa"
soup = bs(r.content,'lxml')
# + [markdown] colab_type="text" id="RHN3By6yNOof"
# Use soup.find to find one element
# + colab={} colab_type="code" id="1OOKUUN2NOog" outputId="0ecbba64-a0d8-414b-aae1-c8db991d4006"
soup.find('p')
# + [markdown] colab_type="text" id="-9jWwIJKNOoj"
# use "text" to get pure text
# + colab={} colab_type="code" id="pKWYsZnJNOol" outputId="97a5d86f-25dc-4e45-afb3-a42c28154548"
soup.find('p').text
# + [markdown] colab_type="text" id="bGrcSJT6NOop"
# Use soup.find_all to find more than one outcome
# + colab={} colab_type="code" id="p9ilfkMxNOoq"
l = soup.find_all('p')
# + [markdown] colab_type="text" id="fz9m_QZ0YiqA"
#
# + colab={} colab_type="code" id="cXgI3clPNOot"
# + colab={} colab_type="code" id="1JqKSLBsNOo3" outputId="c67a518d-3c8e-4913-9392-c70ca6c5a0e8"
for i in l:
print(i.text)
# + colab={} colab_type="code" id="qPywJA1kNOpA" outputId="dfb279f6-dff9-47f2-fdea-330bb6e38acd"
l = soup.find_all('p')
l[:2]
# + [markdown] colab_type="text" id="sKm5C6qXNOpW"
# Use class to find specific element
# + colab={} colab_type="code" id="rHzU3DVBNOpY" outputId="38b7f676-73d5-43a2-f379-d3d19f2031bc"
soup.find('span', class_ = 'mw-headline').text
# + colab={} colab_type="code" id="uYacJR_BNOpd" outputId="636607ac-b4a7-4278-c534-b0eba757c806"
soup.find('span', class_ = 'mw-headline')
# + [markdown] colab_type="text" id="d__bX1wCNOph"
# Or use a combination of what we just learn to find more complex stuff
# + colab={} colab_type="code" id="zWHtRen9NOph"
content = soup.find('div', id = 'content')
# + colab={} colab_type="code" id="Z5VylaAENOpj" outputId="41762cca-dac2-489a-aff1-4d1889e2d20d"
content.find('div', id = 'siteNotice')
# + colab={} colab_type="code" id="r3fOzWRaNOpn" outputId="3788a534-986c-41a9-e514-3d04c644761a"
first_level = soup.find('div', id = 'mw-navigation')
first_level
# + colab={} colab_type="code" id="7m4ZWjEJNOp4" outputId="ab559a2c-1b8f-4a68-9a6c-d71e2fae4c9e"
first_level.find('h3')
# + [markdown] colab_type="text" id="O5XXBCcdZ76r"
# ### 10.5.3 Some practical example of web scraping
#
# + colab={} colab_type="code" id="MzLo--rXaFxS"
def google_news(keyword, start, end):
return('https://www.google.com.hk/search?q='+keyword+'&safe=off&source=lnt&tbs=cdr%3A1%2Ccd_min%3A'+str(start)+'%2F1%2F2017%2Ccd_max%3A'+str(end)+'%2F1%2F2017&tbm=nws')
def get_google_header(keyword, start_month):
url = google_news(keyword,start_month,start_month+1)
r = requests.get(url).content
soup = bs(r,'lxml')
google_news_header = [a.find('h3').text for a in soup.find_all('div', class_ = 'g')]
return google_news_header
# + colab={"base_uri": "https://localhost:8080/", "height": 54} colab_type="code" id="iqMHzOhpX1QU" outputId="b4a37e05-6251-4231-d4d4-c5cd3b2f5994"
google_news('football',1,2)
# + colab={"base_uri": "https://localhost:8080/", "height": 187} colab_type="code" id="P5SocXq0X06S" outputId="541ed78f-d31e-4c41-ff70-66ff2a26eef2"
get_google_header('korea', 1)
# + colab={} colab_type="code" id="w-8P6HC6XzB2"
import requests
from bs4 import BeautifulSoup as bs
import pandas as pd
url = 'https://www.yelp.com/search?find_desc=Restaurants&find_loc=Hong+Kong&start=0'
r = requests.get(url)
soup = bs(r.content,'lxml')
all_restaurants = soup.find_all('li', class_ = 'regular-search-result')
all_name = [i.find('a', class_ = 'biz-name js-analytics-click').text for i in all_restaurants]
all_review = [i.find('span', class_ = 'review-count rating-qualifier').text for i in all_restaurants]
all_links = [i.find('a', class_ = 'biz-name js-analytics-click')['href'] for i in all_restaurants]
all_address = [i.find('address') for i in all_restaurants]
all_ratings = [i.find('span', class_ = 'business-attribute price-range').text for i in all_restaurants]
all_cusin = [i.find('span', class_ = 'category-str-list').text for i in all_restaurants]
df = pd.DataFrame({'name':all_name, 'review':all_review,'address':all_address,'ratings':all_ratings, 'links':all_links,'type': all_cusin})
# + [markdown] colab_type="text" id="LV_V1C6mY72L"
# # 11.0.0 Advanced technique in dictionaries
#
# + [markdown] colab_type="text" id="tFi5v9bMan0o"
# ## 11.1.0 How to count values in a dictionary?
# + [markdown] colab_type="text" id="HKAZNqjWauym"
# https://stackoverflow.com/questions/50637701/counting-values-in-an-employee-dictionary-database-in-python
# + colab={"base_uri": "https://localhost:8080/", "height": 51} colab_type="code" id="9VvO2u4_bXiE" outputId="97566a7b-7c6d-4238-a1ec-d4f218db096b"
employee_list = [{
'name': 'John',
'empID': '102',
'dpt': 'tech',
'title': 'programmer',
'salary': '75'
}, {
'name': 'Jane',
'empID': '202',
'dpt': 'tech',
'title': 'programmer',
'salary': '80'
}, {
'name': 'Joe',
'empID': '303',
'dpt': 'accounting',
'title': 'accountant',
'salary': '85'
}]
department_to_count = dict()
for employee in employee_list:
department = employee["dpt"]
if department not in department_to_count:
department_to_count[department] = 0
department_to_count[department] += 1
for department, employee_count in department_to_count.items():
print("Department {} has {} employees".format(department,
employee_count))
# + [markdown] colab_type="text" id="MtBGp32tav0T"
# ## 11.2.0 How to sort value in a dictionary?
# + [markdown] colab_type="text" id="qG0qW-pca2fC"
# https://stackoverflow.com/questions/72899/how-do-i-sort-a-list-of-dictionaries-by-a-value-of-the-dictionary?rq=1
# + [markdown] colab_type="text" id="SZmThPPWa3kC"
# ## 11.3.0 How to merge two dictionaries?
# + [markdown] colab_type="text" id="Jl45TtAga9JL"
# https://stackoverflow.com/questions/38987/how-to-merge-two-dictionaries-in-a-single-expression?rq=1
#
# + colab={} colab_type="code" id="RF7lJTFva8us"
def merge_two_dicts(x, y):
"""Given two dicts, merge them into a new dict as a shallow copy."""
z = x.copy()
z.update(y)
return z
# + [markdown] colab_type="text" id="WEHAMKYKa-i1"
# ## 11.4.0 How to work with keys in dictionaries?
# + [markdown] colab_type="text" id="GK-HWkylbC2-"
# https://stackoverflow.com/questions/1602934/check-if-a-given-key-already-exists-in-a-dictionary?rq=1
#
# https://stackoverflow.com/questions/1024847/add-new-keys-to-a-dictionary?rq=1
# + colab={} colab_type="code" id="LYr1ebq2b0JL"
d = {'key':'value'}
print(d)
# {'key': 'value'}
d['mynewkey'] = 'mynewvalue'
print(d)
# {'mynewkey': 'mynewvalue', 'key': 'value'}
# + [markdown] colab_type="text" id="T_Yoqc93bH0S"
# ## 11.5.0 more advanced technique with dictionaries
#
# https://stackoverflow.com/questions/20374415/how-to-construct-a-dictionary-from-two-dictionaries-in-python?noredirect=1&lq=1
#
# https://stackoverflow.com/questions/209840/convert-two-lists-into-a-dictionary-in-python?rq=1
# + colab={} colab_type="code" id="GszK0ZXrb5wb"
keys = ('name', 'age', 'food')
values = ('Monty', 42, 'spam')
new_dict = dict(zip(keys, values))
|
2020-01-beginner/course-material/py_class_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Register and pair for a single movie
#
# First, provide root and movie names.
## specify file paths related to movie registration
root = '../data/'
movie_name = '2018-01-16_GSC_L4_L4440_RNAi'
## import necessary packages and utility functions
import sys
sys.path.append('../src/')
from utils import *
from registration_utils import *
import os
import pickle
# ## Module 1: movie registration
## register
register_movie(root, movie_name, pad=True)
# ## Module 3: track pair classification
# Specify file paths related to track pairing, if different from above
# +
root = '../data/'
movie_name = '2018-01-16_GSC_L4_L4440_RNAi'
## specify file paths related to track pairing
model_path = '../src/myModel.sav'
# +
originalMovie = '{}/{}/{}.tif'.format(root,movie_name,movie_name)
registeredXML = '{}/{}/r_{}.xml'.format(root,movie_name,movie_name)
out_folder ='{}/{}/'.format(root,movie_name)
out_csv='{}/r_{}.txt'.format(out_folder,movie_name)
out_coords = '{}/r_{}_coords.txt'.format(out_folder,movie_name)
out_cellid = '{}/r_{}_cellIDs.txt'.format(out_folder,movie_name)
## load classifier
model = pickle.load(open(model_path, 'rb'))
## pair the tracks
pair(model,registeredXML,originalMovie,out_folder,out_csv,
maxdist=11,mindist=4,maxcongdist=4,minoverlap=10)
spots2coords(out_csv,out_coords,out_cellid)
# -
|
notebooks/singlemovie.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
import numpy as np
import json
from keras.models import Model
from keras.layers import Input
from keras.layers import Convolution2D, MaxPooling2D, AveragePooling2D, BatchNormalization, merge
from keras import backend as K
def format_decimal(arr, places=8):
return [round(x * 10**places) / 10**places for x in arr]
# ### pipeline 17
# +
data_in_shape = (8, 8, 2)
input_layer_0 = Input(shape=data_in_shape)
branch_0 = Convolution2D(4, 3, 3, activation='relu', border_mode='valid', subsample=(1, 1), dim_ordering='tf', bias=True)(input_layer_0)
input_layer_1 = Input(shape=data_in_shape)
branch_1 = Convolution2D(4, 3, 3, activation='relu', border_mode='valid', subsample=(1, 1), dim_ordering='tf', bias=True)(input_layer_1)
output_layer = merge([branch_0, branch_1], mode='concat')
model = Model(input=[input_layer_0, input_layer_1], output=output_layer)
data_in = []
for i in range(2):
np.random.seed(18000 + i)
data_in.append(np.expand_dims(2 * np.random.random(data_in_shape) - 1, axis=0))
# set weights to random (use seed for reproducibility)
weights = []
for i, w in enumerate(model.get_weights()):
np.random.seed(18000 + i)
weights.append(2 * np.random.random(w.shape) - 1)
model.set_weights(weights)
result = model.predict(data_in)
print({
'inputs': [{'data': format_decimal(data_in[i].ravel().tolist()), 'shape': list(data_in_shape)} for i in range(2)],
'weights': [{'data': format_decimal(weights[i].ravel().tolist()), 'shape': list(weights[i].shape)} for i in range(len(weights))],
'expected': {'data': format_decimal(result[0].ravel().tolist()), 'shape': list(result[0].shape)}
})
# -
|
notebooks/pipeline/pipeline_17.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# 
#
# Pandas est le package de prédilection pour traiter des données structurées.
#
# Pandas est basé sur 2 structures extrêmement liées les Series et le DataFrame.
#
# Ces deux structures permettent de traiter des données sous forme de tableaux indexés.
#
# Les classes de Pandas utilisent des classes de Numpy, il est donc possible d'utiliser les fonctions universelles de Numpy sur les objets Pandas.
# + slideshow={"slide_type": "subslide"}
# on importe pandas avec :
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# + [markdown] slideshow={"slide_type": "slide"}
# # Les Series de Pandas
#
# - Les Series sont indexées, c'est leur avantage sur les arrays de NumPy
# - On peut utiliser les fonctions `.values` et `.index` pour voir les différentes parties de chaque Series
# - On définit une Series par `pd.Series([,], index=['','',])`
# - On peut appeler un élément avec `ma_serie['France']`
# - On peut aussi faire des conditions :
# ```python
# ma_serie[ma_serie>5000000]
# ```
# ```
# 'France' in ma_serie
# ```
# - Les objets Series peuvent être transformés en dictionnaires en utilisant :
# `.to_dict()`
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Définir un objet Series comprenant la population de 5 pays puis afficher les pays ayant une population > 50’000’000.
#
# -
ser_pop = pd.Series([70,8,300,1200],index=["France","Suisse","USA","Chine"])
ser_pop
# extraire un individu
ser_pop["France"]
# extraire un individu par position
ser_pop.iloc[0]
# extraire les pays avec moins de 50M
ser_pop[ser_pop<50]
# + [markdown] slideshow={"slide_type": "subslide"}
# # D'autres opérations sur les objets series
#
# - Pour définir le nom de la Series, on utilise `.name`
# - Pour définir le titre de la colonne des observations, on utilise `.index.name`
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Définir les noms de l’objet et de la colonne des pays pour la Series précédente
#
# -
ser_pop.name = "Populations"
ser_pop.index.name = "Pays"
ser_pop
# + [markdown] slideshow={"slide_type": "subslide"}
# # Les données manquantes
#
# Dans pandas, les données manquantes sont identifiés avec les fonctions de Numpy (`np.nan`). On a d'autres fonctions telles que :
# + slideshow={"slide_type": "fragment"}
pd.isna(pd.Series([2,np.nan,4],index=['a','b','c']))
# + slideshow={"slide_type": "fragment"}
pd.notna(pd.Series([2,np.nan,4],index=['a','b','c']))
# + [markdown] slideshow={"slide_type": "slide"}
# # Les dates avec pandas
#
# - Python possède un module datetime qui permet de gérer facilement des dates
# - Pandas permet d'appliquer les opérations sur les dates aux Series et aux DataFrame
# - Le format es dates Python est `YYYY-MM-DD HH:MM:SS`
#
# - On peut générer des dates avec la fonction `pd.date_range()` avec différente fréquences `freq=`
# - On peut utiliser ces dates comme index dans un DataFrame ou dans un objet Series
# - On peut changer la fréquence en utilisant `.asfreq()`
# - Pour transformer une chaine de caractère en date, on utilise `pd.to_datetime()` avec l’option `dayfirst=True` si on est dans le cas français
# -On pourra aussi spécifier un format pour accélérer le processus `%Y%m%d`
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Créez un objet Series et ajoutez des dates partant du 3 octobre 2017 par jour jusqu’à aujourd’hui. Afficher le résultat dans un graphique (on utilisera la méthode `.plot()`
# + slideshow={"slide_type": "fragment"}
import datetime
dates = pd.date_range(start="2017-10-03",end=datetime.date.today(),freq="d")
ser_date = pd.Series(np.random.randn(len(dates)),index=dates)
ser_date.plot()
plt.savefig("mon_graphique.jpg")
# + [markdown] slideshow={"slide_type": "slide"}
# # Le DataFrame
#
# - Les DataFrame sont des objets très souples pouvant être construits de différentes façon
# - On peut les construire en récupérant des données copier / coller, où directement sur Internet, ou en entrant les valeurs manuellement
#
#
# - Les DataFrame se rapprochent des dictionnaires et on peut construire ces objets en utilisant `DataFrame(dico)`
# - De nombreux détails sur la création des DataFrame se trouve sur ce site :
#
# <http://pandas.pydata.org/pandas-docs/dev/generated/pandas.DataFrame.html>
#
# + [markdown] slideshow={"slide_type": "subslide"}
# # Construction de DataFrame
#
# On peut simplement construire un DataFrame avec le classe pd.DataFrame() à partir de différentes structures :
# + slideshow={"slide_type": "fragment"}
frame1=pd.DataFrame(np.random.randn(10).reshape(5,2),
index=["obs_"+str(i) for i in range(5)],
columns=["col_"+str(i) for i in range(2)])
frame1
# + [markdown] slideshow={"slide_type": "subslide"}
# # Opérations sur les DataFrame
#
# On peut afficher le nom des colonnes :
# + slideshow={"slide_type": "fragment"}
print(frame1.columns)
# + [markdown] slideshow={"slide_type": "fragment"}
# On peut accéder à une colonne avec :
# - `frame1.col_0` : attention au cas de nom de colonnes avec des espaces...
# - `frame1['col_0']`
#
# On peut accéder à une cellule avec :
# - `frame1.loc['obs1','col_0']` : on utilise les index et le nom des colonnes
# - `frame1.iloc[1,0]` : on utilise les positions dans le DataFrame
#
# + [markdown] slideshow={"slide_type": "subslide"}
# # Options de visualisation et de résumé
#
# Pour afficher les 3 premières lignes, on peut utiliser :
#
# + slideshow={"slide_type": "fragment"}
frame1.head(3)
# + [markdown] slideshow={"slide_type": "subslide"}
# Pour afficher un résumé du DF :
# + slideshow={"slide_type": "fragment"}
frame1.info()
# + [markdown] slideshow={"slide_type": "slide"}
# # Importer des données externes
#
# Pandas est l'outil le plus efficace pour importer des données externes, il prend en charge de nombreux formats dont csv, Excel, SQL, SAS...
#
#
# ## Importation de données avec Pandas
#
# Quel que soit le type de fichier, Pandas possède une fonction :
# ```python
# frame=pd.read_...('chemin_du_fichier/nom_du_fichier',...)
# ```
# Pour écrire un DataFrame dans un fichier, on utilise :
# ```python
# frame.to_...('chemin_du_fichier/nom_du_fichier',...)
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Importer un fichier `.csv` avec `pd.read_csv()`. On utilisera le fichier "./data/airbnb.csv"
# -
airbnb = pd.read_csv("./data/airbnb.csv")
airbnb.head()
airbnb.info(verbose=1)
# extraire une colonne
airbnb["price"]
# + [markdown] slideshow={"slide_type": "subslide"}
# # D'autres types de données
#
# ## JSON
# Les objets JSON ressemblent à des dictionnaires.
#
# On utilise le module `json` puis la fonction `json.loads()` pour transformer une entrée JSON en objet json
#
# ## HTML
# On utilise `pd.read_html(url)`. Cet fonction est basée sur les packages `beautifulsoup` et `html5lib`
#
# Cette fonction renvoie une liste de DataFrame qui représentent tous les DataFrame de la page. On ira ensuite chercher l'élément qui nous intéresse avec `frame_list[0]`
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Importez un tableau en html depuis la page <http://www.fdic.gov/bank/individual/failed/banklist.html>
# -
bank = pd.read_html("http://www.fdic.gov/bank/individual/failed/banklist.html")
bank[0]
# + [markdown] slideshow={"slide_type": "subslide"}
# # Importer depuis Excel
#
# On a deux approches pour Excel :
# - On peut utiliser `pd.read_excel()`
# - On peut utiliser la classe `pd.ExcelFile()`
#
# Dans ce cas, on utilise :
# ```python
# xlsfile=pd.ExcelFile('fichier.xlsx')
# xlsfile.parse('Sheet1')
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Importez un fichier Excel avec les deux approches, on utilisera : `credit2.xlsx` et `ville.xls`
# -
credit2 = pd.read_excel("./data/credit2.xlsx")
credit2.head()
ville_excel = pd.ExcelFile("./data/ville.xls")
nom_feuille = ville_excel.sheet_names[0]
nom_feuille
frame_ville = ville_excel.parse(nom_feuille)
frame_ville.columns
# +
import matplotlib.pyplot as plt
plt.scatter(" Longitude "," Latitude ",data=frame_ville, s=0.5)
# + [markdown] slideshow={"slide_type": "subslide"}
# # Importer des données SQL
#
# Pandas possède une fonction `read_sql()` qui permet d’importer directement des bases de données ou des queries dans des DataFrame
#
# Il faut tout de même un connecteur pour accéder aux bases de données
#
# Pour mettre en place ce connecteur, on utlise le package SQLAlchemy.
#
# Suivant le type de base de données, on utilisera différents codes mais la structure du code est toujours la même
# + slideshow={"slide_type": "subslide"}
# on importe l'outil de connexion
from sqlalchemy import create_engine
# + [markdown] slideshow={"slide_type": "fragment"}
# On crée une connexion
# ```python
# connexion=create_engine("sqlite:///(...).sqlite")
# ```
# + [markdown] slideshow={"slide_type": "fragment"}
# On utlise une des fonctions de Pandas pour charger les données
# ```python
# requete="""select ... from ..."""
# frame_sql=pd.read_sql_query(requete,connexion)
# ```
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercices :**
#
# Importez la base de données SQLite salaries et récupérez la table Salaries dans un DataFrame
# +
connexion=create_engine("sqlite:///./data/Salaries.sqlite")
requete="""select * from salaries"""
frame_sql=pd.read_sql_query(requete,connexion)
# -
frame_sql.head()
# # Importer des données SAS
#
# On peut utiliser `pd.read_sas`
# **Exercice :**
# Importez le fichier SAS se trouvant dans le répertoire `./data/`
frame_sas = pd.read_sas("./data/bce_uai.sas7bdat",encoding='ISO-8859-1')
frame_sas["PATRONYME_UAI"].value_counts()
frame_sas.info()
frame_sas.columns
# + [markdown] slideshow={"slide_type": "slide"}
# # Les tris avec Pandas
#
# Pour effectuer des tris, on utilise :
# - `.sort_index()` pour le tri des index
# - `.sort_values()` pour le tri des données
# - `.rank()` affiche le rang des observations
#
# Il peut y avoir plusieurs tris dans la même opération. Dans ce cas, on utilise des listes de colonnes :
# ```python
# frame.sort_values(["col_1","col_2"])
# ```
# -
# **Exercice :**
# Trier les logements airbnb par prix
# convertir la colonne price en numérique
# enlever le $
airbnb["price_num"] = pd.to_numeric(airbnb["price"].str[1:].str.replace(",",""))
#pd.to_numeric()
airbnb.sort_values("price_num",ascending=True)
# + [markdown] slideshow={"slide_type": "slide"}
# # Les statistiques simples
#
# Les Dataframe possèdent de nombreuses méthodes pour calculer des statistiques simples :
# - `.sum(axis=0)` permet de faire une somme par colonne
# - `.sum(axis=1)` permet de faire une somme par ligne
# - `.min()` et `.max()` donnent le minimum par colonne
# - `.idxmin()` et `.idxmax()` donnent l’index du minimum et du maximum
# - `.describe()` affiche un tableau de statistiques descriptives par colonne
# - `.corr()` pour calculer la corrélation entre les colonnes
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Obtenir les différentes statistiques descriptives pour les données AirBnB.
#
# Pn peut s'intéresser à la colonne `Price` (attention des prétraitements sont nécessaires)
#
# -
np.mean(airbnb["price_num"])
airbnb["price_num"].mean()
# + [markdown] slideshow={"slide_type": "slide"}
# # Le traitement des données manquantes
#
# - Les données manquantes sont identifiées par `NaN`
#
#
# - `.dropna()` permet de retirer les données manquantes dans un objet Series et l’ensemble d’une ligne dans le cas d’un DataFrame
# - Pour éliminer par colonne, on utilise `.dropna(axis=1)`
# - Remplacer toutes les données manquantes `.fillna(valeur)`
#
# -
airbnb["price_num"].fillna(airbnb["price_num"].median())
# + [markdown] slideshow={"slide_type": "slide"}
# # Les jointures avec Pandas
#
# On veut joindre des jeux de données en utilisant des clés (variables communes)
#
# - `pd.merge()` permet de joindre deux DataFrame, on utilise comme options `on='key'`
#
# - On peut utiliser comme option `how=`, on peut avoir :
# - `left` dans ce cas, on garde le jeu de données à gauche et pour les données de droite des valeurs manquantes sont ajoutées.
# - `outer`, on garde toutes les valeurs des deux jeux de données
# - ...
#
# - On peut avoir plusieurs clés et faire une jointure sur les deux clés `on=['key1','key2']`
#
# Pour plus de détails : <http://pandas.pydata.org/pandas-docs/dev/generated/pandas.DataFrame.merge.html>
#
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Joindre deux dataframes (credit1 et credit2).
#
# -
credit1 = pd.read_csv("./data/credit1.txt",sep="\t")
credit_global = pd.merge(credit1,credit2,on = "Customer_ID")
# + [markdown] slideshow={"slide_type": "slide"}
# # Gestion des duplications
#
# - On utilise `.duplicated()` ou `.drop_duplicates()` dans le cas où on désire effacer les lignes se répétant
#
#
# - On peut se concentrer sur une seule variables en entrant directement le nom de la variable. Dans ce cas, c’est la première apparition qui compte. Si on veut prendre la dernière apparition, on utilise l’option `keep="last"`. On pourra avoir :
# ```python
# frame1.drop_duplicates(["col_0","col_1"],keep="last")
# ```
# + [markdown] slideshow={"slide_type": "slide"}
# # Discrétisation
#
# Pour discrétiser, on utilise la fonction `pd.cut()`, on va définir une liste de points pour discrétiser et on entre cette liste comme second paramètre de la fonction.
#
# Une fois discrétisé, on peut afficher les modalités obtenues en utilisant `.categories`
#
# On peut aussi compter les occurrence en utilisant `pd.value_counts()`
#
# Il est aussi possible d’entrer le nombre de segments comme second paramètre
#
# On utilisera aussi `qcut()`
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Créez une variable dans le dataframe AirBnB pour obtenir des niveaux de prix.
#
# -
airbnb["price_disc"] = pd.cut(airbnb["price_num"],bins=4)
airbnb["price_disc2"] = pd.cut(airbnb["price_num"],bins= [0,50,100,500,airbnb["price_num"].max()])
airbnb["price_disc3"] = pd.qcut(airbnb["price_num"],4)
airbnb["price_disc3"].value_counts().sort_index()
# + [markdown] slideshow={"slide_type": "slide"}
# # Les tableaux croisés avec Pandas
#
# Les DataFrame possèdent des méthodes pour générer des tableaux croisés, notamment :
# ```python
# frame1.pivot_table()
# ```
# Cette méthode permet de gérer de nombreux cas avec des fonctions standards et sur mesure.
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# Afficher un tableau Pivot pour les données AirBnB. On croise `cancellation_policy` et `room_type` et on regarde la moyenne des prix.
# -
airbnb.pivot_table(values = ["price_num","review_scores_value"],
index = "room_type", columns = "cancellation_policy",
aggfunc=['median',"mean"])
# + [markdown] slideshow={"slide_type": "slide"}
# # L'utilisation de GroupBy sur des DataFrame
#
# - `.groupby` permet de rassembler des observations en fonction d’une variable dite de groupe
#
#
# - Par exemple, `frame.groupby('X').mean()` donnera les moyennes par groupes de `X`
#
#
# - On peut aussi utiliser `.size()` pour connaître la taille des groupes et utiliser d’autres fonctions (`.sum()`)
#
#
# - On peut effectuer de nombreuses opérations de traitement avec le groupby
#
# + [markdown] slideshow={"slide_type": "subslide"}
# **Exercice :**
#
# - Données sur les salaires
#
#
# - On utilise le `groupby()` pour rassembler les types d’emploi
#
#
# - Et on calcule des statistiques pour chaque type
#
#
# On peut utiliser la méthode `.agg()` avec par exemple `'mean'` comme paramètre
#
# On utilise aussi fréquemment la méthode `.apply()` combinée à une fonction lambda
# -
salaries_group = frame_sql.groupby("JobTitle")
salaries_group["TotalPay"].mean().sort_values(ascending=False)
salaries_group["TotalPay"].agg(["mean","count"]).sort_values("count",ascending=False)
# Essayez d'utiliser une fonction lambda sur le groupby
salaries_group["TotalPay"].apply(lambda x : x.max()-x.min()).sort_values(ascending=False)
def diff(x):
return x.max()-x.min()
salaries_group["TotalPay"].apply(diff).sort_values(ascending=False)
|
05_pandas.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Using Variational Autoencoder to Generate Faces
# In this example, we are going to use VAE to generate faces. The dataset we are going to use is [CelebA](http://mmlab.ie.cuhk.edu.hk/projects/CelebA.html). The dataset consists of more than 200K celebrity face images. You have to download the Align&Cropped Images from the above website to run this example.
# +
from bigdl.nn.layer import *
from bigdl.nn.criterion import *
from bigdl.optim.optimizer import *
from bigdl.dataset import mnist
import datetime as dt
from glob import glob
import os
import scipy.misc
import numpy as np
from utils import *
image_size = 148
Z_DIM = 128
ENCODER_FILTER_NUM = 32
#download the data CelebA, and may repalce with your own data path
DATA_PATH = os.getenv("ANALYTICS_ZOO_HOME") + "/apps/variational-autoencoder/img_align_celeba"
from zoo.common.nncontext import *
sc = init_nncontext("Variational Autoencoder Example")
sc.addFile(os.getenv("ANALYTICS_ZOO_HOME")+"/apps/variational-autoencoder/utils.py")
# -
# ## Define the Model
# Here, we define a slightly more complicate CNN networks using convolution, batchnorm, and leakyRelu.
# +
def conv_bn_lrelu(in_channels, out_channles, kw=4, kh=4, sw=2, sh=2, pw=-1, ph=-1):
model = Sequential()
model.add(SpatialConvolution(in_channels, out_channles, kw, kh, sw, sh, pw, ph))
model.add(SpatialBatchNormalization(out_channles))
model.add(LeakyReLU(0.2))
return model
def upsample_conv_bn_lrelu(in_channels, out_channles, out_width, out_height, kw=3, kh=3, sw=1, sh=1, pw=-1, ph=-1):
model = Sequential()
model.add(ResizeBilinear(out_width, out_height))
model.add(SpatialConvolution(in_channels, out_channles, kw, kh, sw, sh, pw, ph))
model.add(SpatialBatchNormalization(out_channles))
model.add(LeakyReLU(0.2))
return model
# -
def get_encoder_cnn():
input0 = Input()
#CONV
conv1 = conv_bn_lrelu(3, ENCODER_FILTER_NUM)(input0) # 32 * 32 * 32
conv2 = conv_bn_lrelu(ENCODER_FILTER_NUM, ENCODER_FILTER_NUM * 2)(conv1) # 16 * 16 * 64
conv3 = conv_bn_lrelu(ENCODER_FILTER_NUM * 2, ENCODER_FILTER_NUM * 4)(conv2) # 8 * 8 * 128
conv4 = conv_bn_lrelu(ENCODER_FILTER_NUM * 4, ENCODER_FILTER_NUM * 8)(conv3) # 4 * 4 * 256
view = View([4*4*ENCODER_FILTER_NUM*8])(conv4)
inter = Linear(4*4*ENCODER_FILTER_NUM*8, 2048)(view)
inter = BatchNormalization(2048)(inter)
inter = ReLU()(inter)
# fully connected to generate mean and log-variance
mean = Linear(2048, Z_DIM)(inter)
log_variance = Linear(2048, Z_DIM)(inter)
model = Model([input0], [mean, log_variance])
return model
def get_decoder_cnn():
input0 = Input()
linear = Linear(Z_DIM, 2048)(input0)
linear = Linear(2048, 4*4*ENCODER_FILTER_NUM * 8)(linear)
reshape = Reshape([ENCODER_FILTER_NUM * 8, 4, 4])(linear)
bn = SpatialBatchNormalization(ENCODER_FILTER_NUM * 8)(reshape)
# upsampling
up1 = upsample_conv_bn_lrelu(ENCODER_FILTER_NUM*8, ENCODER_FILTER_NUM*4, 8, 8)(bn) # 8 * 8 * 128
up2 = upsample_conv_bn_lrelu(ENCODER_FILTER_NUM*4, ENCODER_FILTER_NUM*2, 16, 16)(up1) # 16 * 16 * 64
up3 = upsample_conv_bn_lrelu(ENCODER_FILTER_NUM*2, ENCODER_FILTER_NUM, 32, 32)(up2) # 32 * 32 * 32
up4 = upsample_conv_bn_lrelu(ENCODER_FILTER_NUM, 3, 64, 64)(up3) # 64 * 64 * 3
output = Sigmoid()(up4)
model = Model([input0], [output])
return model
def get_autoencoder_cnn():
input0 = Input()
encoder = get_encoder_cnn()(input0)
sampler = GaussianSampler()(encoder)
decoder_model = get_decoder_cnn()
decoder = decoder_model(sampler)
model = Model([input0], [encoder, decoder])
return model, decoder_model
model, decoder = get_autoencoder_cnn()
# ## Load the Dataset
def get_data():
data_files = glob(os.path.join(DATA_PATH, "*.jpg"))
rdd_train_images = sc.parallelize(data_files[:100000]) \
.map(lambda path: inverse_transform(get_image(path, image_size)).transpose(2, 0, 1))
rdd_train_sample = rdd_train_images.map(lambda img: Sample.from_ndarray(img, [np.array(0.0), img]))
return rdd_train_sample
# +
train_data = get_data()
# -
# ## Define the Training Objective
criterion = ParallelCriterion()
criterion.add(KLDCriterion(), 1.0) # You may want to twick this parameter
criterion.add(BCECriterion(size_average=False), 1.0 / 64)
# ## Define the Optimizer
# +
batch_size = 100
# Create an Optimizer
optimizer = Optimizer(
model=model,
training_rdd=train_data,
criterion=criterion,
optim_method=Adam(0.001, beta1=0.5),
end_trigger=MaxEpoch(1),
batch_size=batch_size)
app_name='vea-'+dt.datetime.now().strftime("%Y%m%d-%H%M%S")
train_summary = TrainSummary(log_dir='/tmp/vae',
app_name=app_name)
train_summary.set_summary_trigger("LearningRate", SeveralIteration(10))
train_summary.set_summary_trigger("Parameters", EveryEpoch())
optimizer.set_train_summary(train_summary)
print ("saving logs to ",app_name)
# -
# ## Spin Up the Training
# This could take a while. It took about 2 hours on a desktop with a intel i7-6700 cpu and 40GB java heap memory. You can reduce the training time by using less data (some changes in the "Load the Dataset" section), but the performce may not as good.
redire_spark_logs()
show_bigdl_info_logs()
# +
def gen_image_row():
decoder.evaluate()
return np.column_stack([decoder.forward(np.random.randn(1, Z_DIM)).reshape(3, 64,64).transpose(1, 2, 0) for s in range(8)])
def gen_image():
return np.row_stack([gen_image_row() for i in range(8)])
# -
for i in range(1, 6):
optimizer.set_end_when(MaxEpoch(i))
trained_model = optimizer.optimize()
image = gen_image()
if not os.path.exists("./images"):
os.makedirs("./images")
if not os.path.exists("./models"):
os.makedirs("./models")
# you may change the following directory accordingly and make sure the directory
# you are writing to exists
scipy.misc.imsave("./images/image_%s.png" % i , image)
decoder.saveModel("./models/decoder_%s.model" % i, over_write = True)
# +
import matplotlib
matplotlib.use('Agg')
# %pylab inline
import numpy as np
import datetime as dt
import matplotlib.pyplot as plt
# +
loss = np.array(train_summary.read_scalar("Loss"))
plt.figure(figsize = (12,12))
plt.plot(loss[:,0],loss[:,1],label='loss')
plt.xlim(0,loss.shape[0]+10)
plt.grid(True)
plt.title("loss")
# -
# ## Random Sample Some Images
from matplotlib.pyplot import imshow
img = gen_image()
imshow(img)
|
apps/variational-autoencoder/using_variational_autoencoder_to_generate_faces.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="v1CUZ0dkOo_F"
# ##### Copyright 2019 The TensorFlow Authors.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# + cellView="form" colab={} colab_type="code" id="qmkj-80IHxnd"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="_xnMOsbqHz61"
# # Pix2Pix
# + [markdown] colab_type="text" id="Ds4o1h4WHz9U"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/beta/tutorials/generative/pix2pix"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# <td>
# <a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/r2/tutorials/generative/pix2pix.ipynb"><img src="https://www.tensorflow.org/images/download_logo_32px.png" />Download notebook</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="ITZuApL56Mny"
# This notebook demonstrates image to image translation using conditional GAN's, as described in [Image-to-Image Translation with Conditional Adversarial Networks](https://arxiv.org/abs/1611.07004). Using this technique we can colorize black and white photos, convert google maps to google earth, etc. Here, we convert building facades to real buildings.
#
# In example, we will use the [CMP Facade Database](http://cmp.felk.cvut.cz/~tylecr1/facade/), helpfully provided by the [Center for Machine Perception](http://cmp.felk.cvut.cz/) at the [Czech Technical University in Prague](https://www.cvut.cz/). To keep our example short, we will use a preprocessed [copy](https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets/) of this dataset, created by the authors of the [paper](https://arxiv.org/abs/1611.07004) above.
#
# Each epoch takes around 15 seconds on a single V100 GPU.
#
# Below is the output generated after training the model for 200 epochs.
#
# 
# 
# + [markdown] colab_type="text" id="e1_Y75QXJS6h"
# ## Import TensorFlow and other libraries
# + colab={} colab_type="code" id="YfIk2es3hJEd"
from __future__ import absolute_import, division, print_function, unicode_literals
try:
# # %tensorflow_version only exists in Colab.
# %tensorflow_version 2.x
except Exception:
pass
import tensorflow as tf
import os
import time
import matplotlib.pyplot as plt
from IPython.display import clear_output
# + [markdown] colab_type="text" id="iYn4MdZnKCey"
# ## Load the dataset
#
# You can download this dataset and similar datasets from [here](https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets). As mentioned in the [paper](https://arxiv.org/abs/1611.07004) we apply random jittering and mirroring to the training dataset.
#
# * In random jittering, the image is resized to `286 x 286` and then randomly cropped to `256 x 256`
# * In random mirroring, the image is randomly flipped horizontally i.e left to right.
# + colab={} colab_type="code" id="Kn-k8kTXuAlv"
_URL = 'https://people.eecs.berkeley.edu/~tinghuiz/projects/pix2pix/datasets/facades.tar.gz'
path_to_zip = tf.keras.utils.get_file('facades.tar.gz',
origin=_URL,
extract=True)
PATH = os.path.join(os.path.dirname(path_to_zip), 'facades/')
# + colab={} colab_type="code" id="2CbTEt448b4R"
BUFFER_SIZE = 400
BATCH_SIZE = 1
IMG_WIDTH = 256
IMG_HEIGHT = 256
# + colab={} colab_type="code" id="aO9ZAGH5K3SY"
def load(image_file):
image = tf.io.read_file(image_file)
image = tf.image.decode_jpeg(image)
w = tf.shape(image)[1]
w = w // 2
real_image = image[:, :w, :]
input_image = image[:, w:, :]
input_image = tf.cast(input_image, tf.float32)
real_image = tf.cast(real_image, tf.float32)
return input_image, real_image
# + colab={} colab_type="code" id="4OLHMpsQ5aOv"
inp, re = load(PATH+'train/100.jpg')
# casting to int for matplotlib to show the image
plt.figure()
plt.imshow(inp/255.0)
plt.figure()
plt.imshow(re/255.0)
# + colab={} colab_type="code" id="rwwYQpu9FzDu"
def resize(input_image, real_image, height, width):
input_image = tf.image.resize(input_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
real_image = tf.image.resize(real_image, [height, width],
method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
return input_image, real_image
# + colab={} colab_type="code" id="Yn3IwqhiIszt"
def random_crop(input_image, real_image):
stacked_image = tf.stack([input_image, real_image], axis=0)
cropped_image = tf.image.random_crop(
stacked_image, size=[2, IMG_HEIGHT, IMG_WIDTH, 3])
return cropped_image[0], cropped_image[1]
# + colab={} colab_type="code" id="muhR2cgbLKWW"
# normalizing the images to [-1, 1]
def normalize(input_image, real_image):
input_image = (input_image / 127.5) - 1
real_image = (real_image / 127.5) - 1
return input_image, real_image
# + colab={} colab_type="code" id="fVQOjcPVLrUc"
@tf.function()
def random_jitter(input_image, real_image):
# resizing to 286 x 286 x 3
input_image, real_image = resize(input_image, real_image, 286, 286)
# randomly cropping to 256 x 256 x 3
input_image, real_image = random_crop(input_image, real_image)
if tf.random.uniform(()) > 0.5:
# random mirroring
input_image = tf.image.flip_left_right(input_image)
real_image = tf.image.flip_left_right(real_image)
return input_image, real_image
# + colab={} colab_type="code" id="n0OGdi6D92kM"
# As you can see in the images below
# that they are going through random jittering
# Random jittering as described in the paper is to
# 1. Resize an image to bigger height and width
# 2. Randomnly crop to the original size
# 3. Randomnly flip the image horizontally
plt.figure(figsize=(6, 6))
for i in range(4):
rj_inp, rj_re = random_jitter(inp, re)
plt.subplot(2, 2, i+1)
plt.imshow(rj_inp/255.0)
plt.axis('off')
plt.show()
# + colab={} colab_type="code" id="tyaP4hLJ8b4W"
def load_image_train(image_file):
input_image, real_image = load(image_file)
input_image, real_image = random_jitter(input_image, real_image)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
# + colab={} colab_type="code" id="VB3Z6D_zKSru"
def load_image_test(image_file):
input_image, real_image = load(image_file)
input_image, real_image = resize(input_image, real_image,
IMG_HEIGHT, IMG_WIDTH)
input_image, real_image = normalize(input_image, real_image)
return input_image, real_image
# + [markdown] colab_type="text" id="PIGN6ouoQxt3"
# ## Input Pipeline
# + colab={} colab_type="code" id="SQHmYSmk8b4b"
train_dataset = tf.data.Dataset.list_files(PATH+'train/*.jpg')
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
train_dataset = train_dataset.map(load_image_train,
num_parallel_calls=tf.data.experimental.AUTOTUNE)
train_dataset = train_dataset.batch(1)
# + colab={} colab_type="code" id="MS9J0yA58b4g"
test_dataset = tf.data.Dataset.list_files(PATH+'test/*.jpg')
# shuffling so that for every epoch a different image is generated
# to predict and display the progress of our model.
train_dataset = train_dataset.shuffle(BUFFER_SIZE)
test_dataset = test_dataset.map(load_image_test)
test_dataset = test_dataset.batch(1)
# + [markdown] colab_type="text" id="THY-sZMiQ4UV"
# ## Build the Generator
# * The architecture of generator is a modified U-Net.
# * Each block in the encoder is (Conv -> Batchnorm -> Leaky ReLU)
# * Each block in the decoder is (Transposed Conv -> Batchnorm -> Dropout(applied to the first 3 blocks) -> ReLU)
# * There are skip connections between the encoder and decoder (as in U-Net).
#
#
# + colab={} colab_type="code" id="tqqvWxlw8b4l"
OUTPUT_CHANNELS = 3
# + colab={} colab_type="code" id="3R09ATE_SH9P"
def downsample(filters, size, apply_batchnorm=True):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2D(filters, size, strides=2, padding='same',
kernel_initializer=initializer, use_bias=False))
if apply_batchnorm:
result.add(tf.keras.layers.BatchNormalization())
result.add(tf.keras.layers.LeakyReLU())
return result
# + colab={} colab_type="code" id="a6_uCZCppTh7"
down_model = downsample(3, 4)
down_result = down_model(tf.expand_dims(inp, 0))
print (down_result.shape)
# + colab={} colab_type="code" id="nhgDsHClSQzP"
def upsample(filters, size, apply_dropout=False):
initializer = tf.random_normal_initializer(0., 0.02)
result = tf.keras.Sequential()
result.add(
tf.keras.layers.Conv2DTranspose(filters, size, strides=2,
padding='same',
kernel_initializer=initializer,
use_bias=False))
result.add(tf.keras.layers.BatchNormalization())
if apply_dropout:
result.add(tf.keras.layers.Dropout(0.5))
result.add(tf.keras.layers.ReLU())
return result
# + colab={} colab_type="code" id="mz-ahSdsq0Oc"
up_model = upsample(3, 4)
up_result = up_model(down_result)
print (up_result.shape)
# + colab={} colab_type="code" id="lFPI4Nu-8b4q"
def Generator():
down_stack = [
downsample(64, 4, apply_batchnorm=False), # (bs, 128, 128, 64)
downsample(128, 4), # (bs, 64, 64, 128)
downsample(256, 4), # (bs, 32, 32, 256)
downsample(512, 4), # (bs, 16, 16, 512)
downsample(512, 4), # (bs, 8, 8, 512)
downsample(512, 4), # (bs, 4, 4, 512)
downsample(512, 4), # (bs, 2, 2, 512)
downsample(512, 4), # (bs, 1, 1, 512)
]
up_stack = [
upsample(512, 4, apply_dropout=True), # (bs, 2, 2, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 4, 4, 1024)
upsample(512, 4, apply_dropout=True), # (bs, 8, 8, 1024)
upsample(512, 4), # (bs, 16, 16, 1024)
upsample(256, 4), # (bs, 32, 32, 512)
upsample(128, 4), # (bs, 64, 64, 256)
upsample(64, 4), # (bs, 128, 128, 128)
]
initializer = tf.random_normal_initializer(0., 0.02)
last = tf.keras.layers.Conv2DTranspose(OUTPUT_CHANNELS, 4,
strides=2,
padding='same',
kernel_initializer=initializer,
activation='tanh') # (bs, 256, 256, 3)
concat = tf.keras.layers.Concatenate()
inputs = tf.keras.layers.Input(shape=[None,None,3])
x = inputs
# Downsampling through the model
skips = []
for down in down_stack:
x = down(x)
skips.append(x)
skips = reversed(skips[:-1])
# Upsampling and establishing the skip connections
for up, skip in zip(up_stack, skips):
x = up(x)
x = concat([x, skip])
x = last(x)
return tf.keras.Model(inputs=inputs, outputs=x)
# + colab={} colab_type="code" id="U1N1_obwtdQH"
generator = Generator()
gen_output = generator(inp[tf.newaxis,...], training=False)
plt.imshow(gen_output[0,...])
# + [markdown] colab_type="text" id="ZTKZfoaoEF22"
# ## Build the Discriminator
# * The Discriminator is a PatchGAN.
# * Each block in the discriminator is (Conv -> BatchNorm -> Leaky ReLU)
# * The shape of the output after the last layer is (batch_size, 30, 30, 1)
# * Each 30x30 patch of the output classifies a 70x70 portion of the input image (such an architecture is called a PatchGAN).
# * Discriminator receives 2 inputs.
# * Input image and the target image, which it should classify as real.
# * Input image and the generated image (output of generator), which it should classify as fake.
# * We concatenate these 2 inputs together in the code (`tf.concat([inp, tar], axis=-1)`)
# + colab={} colab_type="code" id="ll6aNeQx8b4v"
def Discriminator():
initializer = tf.random_normal_initializer(0., 0.02)
inp = tf.keras.layers.Input(shape=[None, None, 3], name='input_image')
tar = tf.keras.layers.Input(shape=[None, None, 3], name='target_image')
x = tf.keras.layers.concatenate([inp, tar]) # (bs, 256, 256, channels*2)
down1 = downsample(64, 4, False)(x) # (bs, 128, 128, 64)
down2 = downsample(128, 4)(down1) # (bs, 64, 64, 128)
down3 = downsample(256, 4)(down2) # (bs, 32, 32, 256)
zero_pad1 = tf.keras.layers.ZeroPadding2D()(down3) # (bs, 34, 34, 256)
conv = tf.keras.layers.Conv2D(512, 4, strides=1,
kernel_initializer=initializer,
use_bias=False)(zero_pad1) # (bs, 31, 31, 512)
batchnorm1 = tf.keras.layers.BatchNormalization()(conv)
leaky_relu = tf.keras.layers.LeakyReLU()(batchnorm1)
zero_pad2 = tf.keras.layers.ZeroPadding2D()(leaky_relu) # (bs, 33, 33, 512)
last = tf.keras.layers.Conv2D(1, 4, strides=1,
kernel_initializer=initializer)(zero_pad2) # (bs, 30, 30, 1)
return tf.keras.Model(inputs=[inp, tar], outputs=last)
# + colab={} colab_type="code" id="gDkA05NE6QMs"
discriminator = Discriminator()
disc_out = discriminator([inp[tf.newaxis,...], gen_output], training=False)
plt.imshow(disc_out[0,...,-1], vmin=-20, vmax=20, cmap='RdBu_r')
plt.colorbar()
# + [markdown] colab_type="text" id="-ede4p2YELFa"
# To learn more about the architecture and the hyperparameters you can refer the [paper](https://arxiv.org/abs/1611.07004).
# + [markdown] colab_type="text" id="0FMYgY_mPfTi"
# ## Define the loss functions and the optimizer
#
# * **Discriminator loss**
# * The discriminator loss function takes 2 inputs; **real images, generated images**
# * real_loss is a sigmoid cross entropy loss of the **real images** and an **array of ones(since these are the real images)**
# * generated_loss is a sigmoid cross entropy loss of the **generated images** and an **array of zeros(since these are the fake images)**
# * Then the total_loss is the sum of real_loss and the generated_loss
#
# * **Generator loss**
# * It is a sigmoid cross entropy loss of the generated images and an **array of ones**.
# * The [paper](https://arxiv.org/abs/1611.07004) also includes L1 loss which is MAE (mean absolute error) between the generated image and the target image.
# * This allows the generated image to become structurally similar to the target image.
# * The formula to calculate the total generator loss = gan_loss + LAMBDA * l1_loss, where LAMBDA = 100. This value was decided by the authors of the [paper](https://arxiv.org/abs/1611.07004).
# + colab={} colab_type="code" id="cyhxTuvJyIHV"
LAMBDA = 100
# + colab={} colab_type="code" id="Q1Xbz5OaLj5C"
loss_object = tf.keras.losses.BinaryCrossentropy(from_logits=True)
# + colab={} colab_type="code" id="wkMNfBWlT-PV"
def discriminator_loss(disc_real_output, disc_generated_output):
real_loss = loss_object(tf.ones_like(disc_real_output), disc_real_output)
generated_loss = loss_object(tf.zeros_like(disc_generated_output), disc_generated_output)
total_disc_loss = real_loss + generated_loss
return total_disc_loss
# + colab={} colab_type="code" id="90BIcCKcDMxz"
def generator_loss(disc_generated_output, gen_output, target):
gan_loss = loss_object(tf.ones_like(disc_generated_output), disc_generated_output)
# mean absolute error
l1_loss = tf.reduce_mean(tf.abs(target - gen_output))
total_gen_loss = gan_loss + (LAMBDA * l1_loss)
return total_gen_loss
# + colab={} colab_type="code" id="iWCn_PVdEJZ7"
generator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
discriminator_optimizer = tf.keras.optimizers.Adam(2e-4, beta_1=0.5)
# + [markdown] colab_type="text" id="aKUZnDiqQrAh"
# ## Checkpoints (Object-based saving)
# + colab={} colab_type="code" id="WJnftd5sQsv6"
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt")
checkpoint = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
# + [markdown] colab_type="text" id="Rw1fkAczTQYh"
# ## Training
#
# * We start by iterating over the dataset
# * The generator gets the input image and we get a generated output.
# * The discriminator receives the input_image and the generated image as the first input. The second input is the input_image and the target_image.
# * Next, we calculate the generator and the discriminator loss.
# * Then, we calculate the gradients of loss with respect to both the generator and the discriminator variables(inputs) and apply those to the optimizer.
# * This entire procedure is shown in the images below.
#
# 
#
#
# ---
#
#
# 
#
# ## Generate Images
#
# * After training, its time to generate some images!
# * We pass images from the test dataset to the generator.
# * The generator will then translate the input image into the output we expect.
# * Last step is to plot the predictions and **voila!**
# + colab={} colab_type="code" id="NS2GWywBbAWo"
EPOCHS = 150
# + colab={} colab_type="code" id="RmdVsmvhPxyy"
def generate_images(model, test_input, tar):
# the training=True is intentional here since
# we want the batch statistics while running the model
# on the test dataset. If we use training=False, we will get
# the accumulated statistics learned from the training dataset
# (which we don't want)
prediction = model(test_input, training=True)
plt.figure(figsize=(15,15))
display_list = [test_input[0], tar[0], prediction[0]]
title = ['Input Image', 'Ground Truth', 'Predicted Image']
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(title[i])
# getting the pixel values between [0, 1] to plot it.
plt.imshow(display_list[i] * 0.5 + 0.5)
plt.axis('off')
plt.show()
# + colab={} colab_type="code" id="KBKUV2sKXDbY"
@tf.function
def train_step(input_image, target):
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
gen_output = generator(input_image, training=True)
disc_real_output = discriminator([input_image, target], training=True)
disc_generated_output = discriminator([input_image, gen_output], training=True)
gen_loss = generator_loss(disc_generated_output, gen_output, target)
disc_loss = discriminator_loss(disc_real_output, disc_generated_output)
generator_gradients = gen_tape.gradient(gen_loss,
generator.trainable_variables)
discriminator_gradients = disc_tape.gradient(disc_loss,
discriminator.trainable_variables)
generator_optimizer.apply_gradients(zip(generator_gradients,
generator.trainable_variables))
discriminator_optimizer.apply_gradients(zip(discriminator_gradients,
discriminator.trainable_variables))
# + colab={} colab_type="code" id="2M7LmLtGEMQJ"
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for input_image, target in dataset:
train_step(input_image, target)
clear_output(wait=True)
for inp, tar in test_dataset.take(1):
generate_images(generator, inp, tar)
# saving (checkpoint) the model every 20 epochs
if (epoch + 1) % 20 == 0:
checkpoint.save(file_prefix = checkpoint_prefix)
print ('Time taken for epoch {} is {} sec\n'.format(epoch + 1,
time.time()-start))
# + colab={} colab_type="code" id="a1zZmKmvOH85"
train(train_dataset, EPOCHS)
# + [markdown] colab_type="text" id="kz80bY3aQ1VZ"
# ## Restore the latest checkpoint and test
# + colab={} colab_type="code" id="HSSm4kfvJiqv"
# !ls {checkpoint_dir}
# + colab={} colab_type="code" id="4t4x69adQ5xb"
# restoring the latest checkpoint in checkpoint_dir
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
# + [markdown] colab_type="text" id="1RGysMU_BZhx"
# ## Generate using test dataset
# + colab={} colab_type="code" id="<KEY>"
# Run the trained model on the entire test dataset
for inp, tar in test_dataset.take(5):
generate_images(generator, inp, tar)
|
site/en/r2/tutorials/generative/pix2pix.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# +
import pandas as pd
import numpy as np
import matplotlib.pylab as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.ar_model import AR
from sklearn.metrics import r2_score
# %matplotlib inline
plt.rcParams['figure.figsize']=(20,10)
plt.style.use('ggplot')
# -
sales_data = pd.read_csv('retail_sales.csv')
sales_data['date']=pd.to_datetime(sales_data['date'])
sales_data.set_index('date', inplace=True)
sales_data.head()
sales_data.plot()
decomposed = seasonal_decompose(sales_data['sales'], model='additive')
x =decomposed.plot() #See note below about this
sales_data['stationary']=sales_data['sales'].diff()
sales_data.head()
sales_data['stationary'].plot()
decomposed = seasonal_decompose(sales_data['stationary'].dropna(), model='additive')
x =decomposed.plot() #See note below about this
pd.tools.plotting.lag_plot(sales_data['sales'])
# +
pd.tools.plotting.autocorrelation_plot(sales_data['sales'])
# -
sales_data['sales'].corr(sales_data['sales'].shift(12))
# +
#create train/test datasets
X = sales_data['stationary'].dropna()
train_data = X[1:len(X)-12]
test_data = X[X[len(X)-12:]]
# -
#train the autoregression model
model = AR(train_data)
model_fitted = model.fit()
print('The lag value chose is: %s' % model_fitted.k_ar)
print('The coefficients of the model are:\n %s' % model_fitted.params)
# +
# make predictions
predictions = model_fitted.predict(
start=len(train_data),
end=len(train_data) + len(test_data)-1,
dynamic=False)
# create a comparison dataframe
compare_df = pd.concat(
[sales_data['stationary'].tail(12),
predictions], axis=1).rename(
columns={'stationary': 'actual', 0:'predicted'})
# -
compare_df
compare_df.plot()
r2 = r2_score(sales_data['stationary'].tail(12), predictions)
r2
|
04-other-analysis/Autoregression_retail_sales.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# +
import os
import numpy as np
import matplotlib.pyplot as plt
plt.rcdefaults()
from matplotlib.lines import Line2D
from matplotlib.patches import Rectangle
from matplotlib.patches import Circle
NumDots = 4
NumConvMax = 8
NumFcMax = 20
White = 1.
Light = 0.7
Medium = 0.5
Dark = 0.3
Darker = 0.15
Black = 0.
def add_layer(patches, colors, size=(24, 24), num=5,
top_left=[0, 0],
loc_diff=[3, -3],
):
# add a rectangle
top_left = np.array(top_left)
loc_diff = np.array(loc_diff)
loc_start = top_left - np.array([0, size[0]])
for ind in range(num):
patches.append(Rectangle(loc_start + ind * loc_diff, size[1], size[0]))
if ind % 2:
colors.append(Medium)
else:
colors.append(Light)
def add_layer_with_omission(patches, colors, size=(24, 24),
num=5, num_max=8,
num_dots=4,
top_left=[0, 0],
loc_diff=[3, -3],
):
# add a rectangle
top_left = np.array(top_left)
loc_diff = np.array(loc_diff)
loc_start = top_left - np.array([0, size[0]])
this_num = min(num, num_max)
start_omit = (this_num - num_dots) // 2
end_omit = this_num - start_omit
start_omit -= 1
for ind in range(this_num):
if (num > num_max) and (start_omit < ind < end_omit):
omit = True
else:
omit = False
if omit:
patches.append(
Circle(loc_start + ind * loc_diff + np.array(size) / 2, 0.5))
else:
patches.append(Rectangle(loc_start + ind * loc_diff,
size[1], size[0]))
if omit:
colors.append(Black)
elif ind % 2:
colors.append(Medium)
else:
colors.append(Light)
def add_mapping(patches, colors, start_ratio, end_ratio, patch_size, ind_bgn,
top_left_list, loc_diff_list, num_show_list, size_list):
start_loc = top_left_list[ind_bgn] \
+ (num_show_list[ind_bgn] - 1) * np.array(loc_diff_list[ind_bgn]) \
+ np.array([start_ratio[0] * (size_list[ind_bgn][1] - patch_size[1]),
- start_ratio[1] * (size_list[ind_bgn][0] - patch_size[0])]
)
end_loc = top_left_list[ind_bgn + 1] \
+ (num_show_list[ind_bgn + 1] - 1) * np.array(
loc_diff_list[ind_bgn + 1]) \
+ np.array([end_ratio[0] * size_list[ind_bgn + 1][1],
- end_ratio[1] * size_list[ind_bgn + 1][0]])
patches.append(Rectangle(start_loc, patch_size[1], -patch_size[0]))
colors.append(Dark)
patches.append(Line2D([start_loc[0], end_loc[0]],
[start_loc[1], end_loc[1]]))
colors.append(Darker)
patches.append(Line2D([start_loc[0] + patch_size[1], end_loc[0]],
[start_loc[1], end_loc[1]]))
colors.append(Darker)
patches.append(Line2D([start_loc[0], end_loc[0]],
[start_loc[1] - patch_size[0], end_loc[1]]))
colors.append(Darker)
patches.append(Line2D([start_loc[0] + patch_size[1], end_loc[0]],
[start_loc[1] - patch_size[0], end_loc[1]]))
colors.append(Darker)
def label(xy, text, xy_off=[0, 4]):
plt.text(xy[0] + xy_off[0], xy[1] + xy_off[1], text,
family='sans-serif', size=8)
if __name__ == '__main__':
fc_unit_size = 2
layer_width = 40
flag_omit = True
patches = []
colors = []
fig, ax = plt.subplots()
############################
# conv layers
size_list = [(32, 32), (18, 18), (10, 10), (6, 6), (4, 4)]
num_list = [3, 32, 32, 48, 48]
x_diff_list = [0, layer_width, layer_width, layer_width, layer_width]
text_list = ['Inputs'] + ['Feature\nmaps'] * (len(size_list) - 1)
loc_diff_list = [[3, -3]] * len(size_list)
num_show_list = list(map(min, num_list, [NumConvMax] * len(num_list)))
top_left_list = np.c_[np.cumsum(x_diff_list), np.zeros(len(x_diff_list))]
for ind in range(len(size_list)):
if flag_omit:
add_layer_with_omission(patches, colors, size=size_list[ind],
num=num_list[ind],
num_max=NumConvMax,
num_dots=NumDots,
top_left=top_left_list[ind],
loc_diff=loc_diff_list[ind])
else:
add_layer(patches, colors, size=size_list[ind],
num=num_show_list[ind],
top_left=top_left_list[ind], loc_diff=loc_diff_list[ind])
label(top_left_list[ind], text_list[ind] + '\n{}@{}x{}'.format(
num_list[ind], size_list[ind][0], size_list[ind][1]))
############################
# in between layers
start_ratio_list = [[0.4, 0.5], [0.4, 0.8], [0.4, 0.5], [0.4, 0.8]]
end_ratio_list = [[0.4, 0.5], [0.4, 0.8], [0.4, 0.5], [0.4, 0.8]]
patch_size_list = [(3, 3), (2, 2), (3, 3), (2, 2)]
ind_bgn_list = range(len(patch_size_list))
text_list = ['Convolution', 'Max-pooling', 'Convolution', 'Max-pooling']
for ind in range(len(patch_size_list)):
add_mapping(
patches, colors, start_ratio_list[ind], end_ratio_list[ind],
patch_size_list[ind], ind,
top_left_list, loc_diff_list, num_show_list, size_list)
label(top_left_list[ind], text_list[ind] + '\n{}x{} kernel'.format(
patch_size_list[ind][0], patch_size_list[ind][1]), xy_off=[26, -65]
)
############################
# fully connected layers
size_list = [(fc_unit_size, fc_unit_size)] * 3
num_list = [768, 500, 2]
num_show_list = list(map(min, num_list, [NumFcMax] * len(num_list)))
x_diff_list = [sum(x_diff_list) + layer_width, layer_width, layer_width]
top_left_list = np.c_[np.cumsum(x_diff_list), np.zeros(len(x_diff_list))]
loc_diff_list = [[fc_unit_size, -fc_unit_size]] * len(top_left_list)
text_list = ['Hidden\nunits'] * (len(size_list) - 1) + ['Outputs']
for ind in range(len(size_list)):
if flag_omit:
add_layer_with_omission(patches, colors, size=size_list[ind],
num=num_list[ind],
num_max=NumFcMax,
num_dots=NumDots,
top_left=top_left_list[ind],
loc_diff=loc_diff_list[ind])
else:
add_layer(patches, colors, size=size_list[ind],
num=num_show_list[ind],
top_left=top_left_list[ind],
loc_diff=loc_diff_list[ind])
label(top_left_list[ind], text_list[ind] + '\n{}'.format(
num_list[ind]))
text_list = ['Flatten\n', 'Fully\nconnected', 'Fully\nconnected']
for ind in range(len(size_list)):
label(top_left_list[ind], text_list[ind], xy_off=[-10, -65])
############################
for patch, color in zip(patches, colors):
patch.set_color(color * np.ones(3))
if isinstance(patch, Line2D):
ax.add_line(patch)
else:
patch.set_edgecolor(Black * np.ones(3))
ax.add_patch(patch)
plt.tight_layout()
plt.axis('equal')
plt.axis('off')
plt.show()
fig.set_size_inches(8, 2.5)
fig_dir = './'
fig_ext = '.png'
fig.savefig(os.path.join(fig_dir, 'convnet_fig' + fig_ext),
bbox_inches='tight', pad_inches=0)
# -
|
Architecture_Visual.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Imports for gplearn and pydotplus in order to see graph view
# +
from IPython.display import Image
import pydotplus
from gplearn.genetic import SymbolicRegressor
from gplearn.fitness import make_fitness
# +
#--Import the required libraries--
import math
import random
import matplotlib.pyplot as plt
import numpy as np
#--debug mode to report on evaluation of tree--
debug_eval = False
# -
# # Import Scipy generic dataset
# * Number of Instances:506
# * Number of Attributes:13
# * Attribute Information (in order):
#
# <li>CRIM per capita crime rate by town</li>
# <li>ZN proportion of residential land zoned for lots over 25,000 sq.ft.</li>
# <li>INDUS proportion of non-retail business acres per town</li>
# <li>CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)</li>
# <li>NOX nitric oxides concentration (parts per 10 million)</li>
# <li>RM average number of rooms per dwelling</li>
# <li>AGE proportion of owner-occupied units built prior to 1940</li>
# <li>DIS weighted distances to five Boston employment centres</li>
# <li>RAD index of accessibility to radial highways</li>
# <li>TAX full-value property-tax rate per \\$10,000</li>
# <li>PTRATIO pupil-teacher ratio by town</li>
# <li>B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town</li>
# <li>LSTAT \\% lower status of the population</li>
# <li>MEDV Median value of owner-occupied homes in $1000’s</li>
# +
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
#load the data from the default data set, and split it into a tuple
data = load_boston(return_X_y = True)
#what percent of our data do we want to use to validate
split_percent = 0.2
train_x, test_x, train_y, test_y = train_test_split(*data, test_size = split_percent, random_state = 0)
#print out the shapes for clarity
print("Shapes:\n data_x:{}\n data_y:{}\n train_x:{}\n test_x:{}\n train_y:{}\n test_y:{}"
.format(data[0].shape,data[1].shape,train_x.shape,test_x.shape,train_y.shape,test_y.shape))
# -
# # Symbolic regression with grid search
#
from sklearn.model_selection import GridSearchCV
est_gp = SymbolicRegressor()
parameters = {'function_set': [('add', 'sub', 'mul', 'div'), ('add', 'sub', 'mul', 'div',
'sqrt', 'log', 'abs', 'neg', 'inv','max', 'min')],
'init_depth': [(2, 6),(3,7)],
'max_samples': [1.0,0.9],
'p_crossover': [0.9,0.8],
'p_hoist_mutation': [0.01,0.05],
'p_point_mutation': [0.01,0.02],
'random_state': [0],
'tournament_size': [20,10,30],
'verbose': [1],
'warm_start': [False]}
#This part sets up the symbolic regressor
clf = GridSearchCV(est_gp, parameters, cv=5,n_jobs = -1, verbose = 1)
#This part runs it on our data
clf.fit(train_x, train_y)
clf.best_params_
# # Scoring
#
print(clf.best_estimator_._program)
clf.best_estimator_.score(test_x,test_y)
graph = pydotplus.graphviz.graph_from_dot_data(clf.best_estimator_._program.export_graphviz())
Image(graph.create_png())
|
SunspotSymbolicRegression-WithGridSearch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (Jupyter - cellregmap)
# language: python
# name: cellregmap_notebook
# ---
import scanpy as sc
import pandas as pd
import xarray as xr
import matplotlib.pyplot as plt
# my_file = "/share/ScratchGeneral/anncuo/OneK1K/expression_objects/sce2.h5ad"
my_file = "/share/ScratchGeneral/anncuo/OneK1K/expression_objects/sce22.h5ad"
adata = sc.read(my_file)
adata
adata.obs
adata.var.index
sc.pp.log1p(adata)
adata.raw.X.shape
mat = adata.raw.X.todense()
mat_df = pd.DataFrame(data=mat.T, index=adata.raw.var.index, columns=adata.obs.index)
mat_df.head()
gene_name = 'AC002472.1'
phenotype = xr.DataArray(mat_df.values, dims=["trait", "cell"], coords={"trait": mat_df.index.values, "cell": mat_df.columns.values})
phenotype
y = phenotype.sel(trait=gene_name)
(y == 0).astype(int).sum()/len(y)
plt.hist(y)
plt.show()
n_genes = adata.raw.X.shape[1]
n_genes
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)==1:
n = n+1
# print("All zeroes, skipping gene")
n
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)>0.99:
n = n+1
# print("Over 99 percent zeroes, skipping gene")
n
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)>0.95:
n = n+1
# print("Over 95 percent zeroes, skipping gene")
n
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)>0.9:
n = n+1
# print("Over 90 percent zeroes, skipping gene")
n
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)>0.8:
n = n+1
# print("Over 80 percent zeroes, skipping gene")
n
n = 0
for i in range(n_genes):
y = mat[:,i]
if (y == 0).astype(int).sum()/len(y)>0.7:
n = n+1
# print("Over 70 percent zeroes, skipping gene")
n
import matplotlib.pyplot as plt
i = 10
y = mat[:,i]
plt.hist(y)
plt.show()
adata.X.shape
gene = "HES4"
adata[:, ['HES4']].X.shape
# +
## test difference in computation time
### 1: for each chr make pandas dataframe with cells and gene names, create csv files, open then select gene
### 2: like 1 but turning csv into pkl
### 3: directly open anndata, extract expression for the selected gene - still somehow make sure correct cells + order
# -
import time
# +
############## option 1 (csv)
# -
start_time = time.time()
mat_df.to_csv("/share/ScratchGeneral/anncuo/OneK1K/expression_objects/phenotype_chr22.csv")
print("--- %s seconds ---" % (time.time() - start_time))
### option 1
start_time = time.time()
mat_df = pd.read_csv("/share/ScratchGeneral/anncuo/OneK1K/expression_objects/phenotype_chr22.csv")
# turn into xr array
phenotype = xr.DataArray(mat_df.values, dims=["trait", "cell"], coords={"trait": mat_df.index.values, "cell": mat_df.columns.values})
# select gene
y = phenotype.sel(trait=gene_name)
print("--- %s seconds ---" % (time.time() - start_time))
# +
############## option 2 (pkl)
# -
start_time = time.time()
csv_filename = "/share/ScratchGeneral/anncuo/OneK1K/expression_objects/phenotype_chr22.csv"
pkl_filename = csv_filename + ".pkl"
mat_df.to_pickle(pkl_filename)
print("--- %s seconds ---" % (time.time() - start_time))s
### option 2
start_time = time.time()
mat_df = pd.read_pickle(pkl_filename)
# turn into xr array
phenotype = xr.DataArray(mat_df.values, dims=["trait", "cell"], coords={"trait": mat_df.index.values, "cell": mat_df.columns.values})
# select gene
y = phenotype.sel(trait=gene_name)
print("--- %s seconds ---" % (time.time() - start_time))
# +
############## option 3 (anndata)
# -
### option 3
start_time = time.time()
# open anndata
adata = sc.read(my_file)
# sparse to dense
mat = adata.raw.X.todense()
# make pandas dataframe
mat_df = pd.DataFrame(data=mat.T, index=adata.raw.var.index, columns=adata.obs.index)
# turn into xr array
phenotype = xr.DataArray(mat_df.values, dims=["trait", "cell"], coords={"trait": mat_df.index.values, "cell": mat_df.columns.values})
# select gene
y = phenotype.sel(trait=gene_name)
print("--- %s seconds ---" % (time.time() - start_time))
input_files_dir = "/share/ScratchGeneral/anncuo/OneK1K/input_files_CellRegMap/"
# C_file = input_files_dir+"PCs.csv"
C_file = input_files_dir+"PCs_Bcells.csv"
start_time = time.time()
C = pd.read_csv(C_file, index_col = 0)
print("--- %s seconds ---" % (time.time() - start_time))
start_time = time.time()
pkl_filename = C_file + ".pkl"
C.to_pickle(pkl_filename)
print("--- %s seconds ---" % (time.time() - start_time))
start_time = time.time()
C_pkl = pd.read_pickle(pkl_filename)
print("--- %s seconds ---" % (time.time() - start_time))
|
notebooks/open_scanpy_objects.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import gc
# # 1. generate file with count of meter_reading equals 0
# count meter_reading equals 0 per site_id, timestamp and meter
# +
# %%time
train_df3= pd.read_csv("train.csv")
building_df = pd.read_csv("building_metadata.csv")
train_df3 = train_df3.merge(building_df[['site_id', 'building_id']], on='building_id', how='left')
toto = train_df3.groupby(['site_id','timestamp', 'meter']).meter_reading.transform(lambda x: x[x.eq(0)].size)
train_df3['cnt_tmp_meter_siteid'] = toto
train_df3.to_feather('train_with_cnt_per_tmp_meter.feather')
# -
# # 2. generate file with hot encoding of meters per building
# a table listing all the building with 4 columns corresponding to the 4 meters. if the building has a partical meter, the value is 1 else it is 0.
# +
# %%time
train_df= pd.read_csv("train.csv")
train_df = train_df.set_index(['building_id', 'meter', 'timestamp'])
train_df = train_df.unstack(1)
train_df.fillna(-1)
train_df2 = train_df
train_df2.columns = ['meter_reading_0','meter_reading_1','meter_reading_2','meter_reading_3',]
train_df2.reset_index(inplace=True)
for col in ['meter_reading_0','meter_reading_1','meter_reading_2','meter_reading_3',]:
train_df2[col].loc[~train_df2[col].isnull()]=1
train_df2[col].loc[train_df2[col].isnull()]=0
del train_df2['timestamp']
train_df3 = train_df2.drop_duplicates(subset=['building_id', 'meter_reading_0','meter_reading_1','meter_reading_2','meter_reading_3',], keep="last").reset_index(drop=True)
train_df3['meter_reading_0'] = train_df3.groupby('building_id')['meter_reading_0'].transform(max)
train_df3['meter_reading_1'] = train_df3.groupby('building_id')['meter_reading_1'].transform(max)
train_df3['meter_reading_2'] = train_df3.groupby('building_id')['meter_reading_2'].transform(max)
train_df3['meter_reading_3'] = train_df3.groupby('building_id')['meter_reading_3'].transform(max)
train_df3 = train_df3.drop_duplicates(subset=['building_id', 'meter_reading_0','meter_reading_1','meter_reading_2','meter_reading_3',], keep="last").reset_index(drop=True)
train_df3.to_feather('building_all_meters.feather')
# -
# # 3. cleanup train dataset to remove "vertical lines"
# in his kernel, Ganfear shows the raw data https://www.kaggle.com/ganfear/missing-data-and-zeros-visualized and visualize when the target (meter_reading) is missing or 0. We can clearly see that there are some vertical blue lines: these lines most likely mean that the 0s were added and it is even more likely that they were added when these vertical lines happen on several meters, at the same time and the same site. The goal of the code below is to remove most of them.
# Note: a single groupby takes 3.5 hours to be calculated.
# +
# %%time
building_df = pd.read_csv("building_metadata.csv")
train = pd.read_csv("train.csv")
building_df['cnt_building_per_site'] = building_df.groupby(['site_id']).building_id.transform(lambda x: x.size)
train = train.merge(building_df[['building_id', 'cnt_building_per_site', 'site_id']], on='building_id', how='left')
print('starting')
train['cnt_mreadEQ0_per_tmp_site'] = train.groupby(['timestamp','site_id']).meter_reading.transform(lambda x: x[x.eq(0)].size)
print('done 1')
train['cnt_mreadEQ0_per_tmp_site_building'] = train.groupby(['timestamp','site_id','building_id']).meter_reading.transform(lambda x: x[x.eq(0)].size)
print('done 2')
train['sum_meter_reading'] = train.groupby(['building_id', 'meter']).meter_reading.transform('sum')
print('done 3')
print(train.shape)
df_train2 = pd.read_feather('train_with_cnt_per_tmp_meter.feather')
train['cnt_tmp_meter_siteid'] = df_train2.cnt_tmp_meter_siteid ### groupby('site_id','timestamp', 'meter') x[x.eq(0)].size)
del df_train2
# +
print(train.shape)
train = train.query('not (building_id <= 104 & meter == 0 & timestamp <= "2016-05-21")')
print(train.shape)
train = train[~(((train.cnt_mreadEQ0_per_tmp_site_building>2) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.cnt_mreadEQ0_per_tmp_site_building==2) & (train.meter_reading==0) & (train.meter==0)))]
print(train.shape)
train = train[~(((train.site_id==5) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.site_id==6) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.site_id==8) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.site_id==9) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.site_id==14) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[~(((train.site_id==15) &(train.cnt_tmp_meter_siteid/train.cnt_building_per_site>.35) & (train.meter_reading==0)))]
print(train.shape)
train = train[['building_id', 'meter', 'timestamp', 'meter_reading']].reset_index(drop=True)
train.to_feather('train_cleanup_001.feather')
# -
# # 4. clean up datasets (train & test)
#
# ####### code extracted from https://www.kaggle.com/purist1024/ashrae-simple-data-cleanup-lb-1-08-no-leaks
# +
def make_is_bad_zero(Xy_subset, min_interval=48, summer_start=3000, summer_end=7500):
"""Helper routine for 'find_bad_zeros'.
This operates upon a single dataframe produced by 'groupby'. We expect an
additional column 'meter_id' which is a duplicate of 'meter' because groupby
eliminates the original one."""
meter = Xy_subset.meter_id.iloc[0]
is_zero = Xy_subset.meter_reading == 0
if meter == 0:
# Electrical meters should never be zero. Keep all zero-readings in this table so that
# they will all be dropped in the train set.
return is_zero
transitions = (is_zero != is_zero.shift(1))
all_sequence_ids = transitions.cumsum()
ids = all_sequence_ids[is_zero].rename("ids")
if meter in [2, 3]:
# It's normal for steam and hotwater to be turned off during the summer
keep = set(ids[(Xy_subset.timestamp < summer_start) |
(Xy_subset.timestamp > summer_end)].unique())
is_bad = ids.isin(keep) & (ids.map(ids.value_counts()) >= min_interval)
elif meter == 1:
time_ids = ids.to_frame().join(Xy_subset.timestamp).set_index("timestamp").ids
is_bad = ids.map(ids.value_counts()) >= min_interval
# Cold water may be turned off during the winter
jan_id = time_ids.get(0, False)
dec_id = time_ids.get(8283, False)
if (jan_id and dec_id and jan_id == time_ids.get(500, False) and
dec_id == time_ids.get(8783, False)):
is_bad = is_bad & (~(ids.isin(set([jan_id, dec_id]))))
else:
raise Exception(f"Unexpected meter type: {meter}")
result = is_zero.copy()
result.update(is_bad)
return result
def find_bad_zeros(X, y):
"""Returns an Index object containing only the rows which should be deleted."""
Xy = X.assign(meter_reading=y, meter_id=X.meter)
is_bad_zero = Xy.groupby(["building_id", "meter"]).apply(make_is_bad_zero)
return is_bad_zero[is_bad_zero].index.droplevel([0, 1])
# -
# `find_bad_sitezero` identifies the "known-bad" electrical readings from the first 141 days of the data for site 0 (i.e. UCF).
def find_bad_sitezero(X):
"""Returns indices of bad rows from the early days of Site 0 (UCF)."""
return X[(X.timestamp < 3378) & (X.site_id == 0) & (X.meter == 0)].index
# `find_bad_building1099` identifies the most absurdly high readings from building 1099. These are orders of magnitude higher than all data, and have been emperically seen in LB probes to be harmful outliers.
def find_bad_building1099(X, y):
"""Returns indices of bad rows (with absurdly high readings) from building 1099."""
return X[(X.building_id == 1099) & (X.meter == 2) & (y > 3e4)].index
# Finally, `find_bad_rows` combines all of the above together to allow you to do a one-line cleanup of your data.
def find_bad_rows(X, y):
return find_bad_zeros(X, y).union(find_bad_sitezero(X)).union(find_bad_building1099(X, y))
# +
from meteocalc import Temp, dew_point, heat_index, wind_chill, feels_like
def c2f(T):
return T * 9 / 5. + 32
def windchill(T, v):
return (10*v**.5 - v +10.5) * (33 - T)
def prepareweather(df):
df['RH'] = 100 - 5 * (df['air_temperature']-df['dew_temperature'])
# df['RH_above50'] = (df['RH'] > 50).astype(int)
df['heat'] = df.apply(lambda x: heat_index(c2f(x.air_temperature), x.RH).c, axis=1)
df['windchill'] = df.apply(lambda x: windchill(x.air_temperature, x.wind_speed), axis=1)
df['feellike'] = df.apply(lambda x: feels_like(c2f(x.air_temperature), x.RH, x.wind_speed*2.237).c, axis=1)
return df
def add_lag_feature(weather_df, window=3):
group_df = weather_df.groupby('site_id')
cols = ['air_temperature', 'dew_temperature', 'heat', 'windchill', 'feellike']
rolled = group_df[cols].rolling(window=window, min_periods=0)
lag_mean = rolled.mean().reset_index().astype(np.float32)
lag_max = rolled.max().reset_index().astype(np.float16)
lag_min = rolled.min().reset_index().astype(np.float16)
lag_std = rolled.std().reset_index().astype(np.float16)
for col in cols:
weather_df[f'{col}_mean_lag{window}'] = lag_mean[col]
# weather_df[f'{col}_max_lag{window}'] = lag_max[col]
# weather_df[f'{col}_min_lag{window}'] = lag_min[col]
# weather_df[f'{col}_std_lag{window}'] = lag_std[col]
def fill_weather_dataset(weather_df):
# Find Missing Dates
time_format = "%Y-%m-%d %H:%M:%S"
start_date = datetime.datetime.strptime(weather_df['timestamp'].min(),time_format)
end_date = datetime.datetime.strptime(weather_df['timestamp'].max(),time_format)
total_hours = int(((end_date - start_date).total_seconds() + 3600) / 3600)
hours_list = [(end_date - datetime.timedelta(hours=x)).strftime(time_format) for x in range(total_hours)]
missing_hours = []
for site_id in range(16):
site_hours = np.array(weather_df[weather_df['site_id'] == site_id]['timestamp'])
new_rows = pd.DataFrame(np.setdiff1d(hours_list,site_hours),columns=['timestamp'])
new_rows['site_id'] = site_id
weather_df = pd.concat([weather_df,new_rows])
weather_df = weather_df.reset_index(drop=True)
# for col in weather_df.columns:
# if col != 'timestamp':
# if weather_df[col].isna().sum():
# weather_df['na_'+col] = weather_df[col].isna().astype(int)
# weather_df['weath_na_total'] = weather_df.isna().sum(axis=1)
# Add new Features
weather_df["datetime"] = pd.to_datetime(weather_df["timestamp"])
weather_df["day"] = weather_df["datetime"].dt.day
weather_df["week"] = weather_df["datetime"].dt.week
weather_df["month"] = weather_df["datetime"].dt.month
# Reset Index for Fast Update
weather_df = weather_df.set_index(['site_id','day','month'])
air_temperature_filler = pd.DataFrame(weather_df.groupby(['site_id','day','month'])['air_temperature'].mean(),columns=["air_temperature"])
weather_df.update(air_temperature_filler,overwrite=False)
# Step 1
cloud_coverage_filler = weather_df.groupby(['site_id','day','month'])['cloud_coverage'].mean()
# Step 2
cloud_coverage_filler = pd.DataFrame(cloud_coverage_filler.fillna(method='ffill'),columns=["cloud_coverage"])
weather_df.update(cloud_coverage_filler,overwrite=False)
due_temperature_filler = pd.DataFrame(weather_df.groupby(['site_id','day','month'])['dew_temperature'].mean(),columns=["dew_temperature"])
weather_df.update(due_temperature_filler,overwrite=False)
# Step 1
sea_level_filler = weather_df.groupby(['site_id','day','month'])['sea_level_pressure'].mean()
# Step 2
sea_level_filler = pd.DataFrame(sea_level_filler.fillna(method='ffill'),columns=['sea_level_pressure'])
weather_df.update(sea_level_filler,overwrite=False)
wind_direction_filler = pd.DataFrame(weather_df.groupby(['site_id','day','month'])['wind_direction'].mean(),columns=['wind_direction'])
weather_df.update(wind_direction_filler,overwrite=False)
wind_speed_filler = pd.DataFrame(weather_df.groupby(['site_id','day','month'])['wind_speed'].mean(),columns=['wind_speed'])
weather_df.update(wind_speed_filler,overwrite=False)
# Step 1
precip_depth_filler = weather_df.groupby(['site_id','day','month'])['precip_depth_1_hr'].mean()
# Step 2
precip_depth_filler = pd.DataFrame(precip_depth_filler.fillna(method='ffill'),columns=['precip_depth_1_hr'])
weather_df.update(precip_depth_filler,overwrite=False)
weather_df = weather_df.reset_index()
weather_df = weather_df.drop(['datetime','day','week','month'],axis=1)
weather_df = timestamp_align(weather_df)
print('add heat, RH...')
weather_df = prepareweather(weather_df)
print('add lag features')
add_lag_feature(weather_df, window=3)
return weather_df
# Original code from https://www.kaggle.com/gemartin/load-data-reduce-memory-usage by @gemartin
from pandas.api.types import is_datetime64_any_dtype as is_datetime
from pandas.api.types import is_categorical_dtype
def reduce_mem_usage(df, use_float16=False):
"""
Iterate through all the columns of a dataframe and modify the data type to reduce memory usage.
"""
start_mem = df.memory_usage().sum() / 1024**2
print("Memory usage of dataframe is {:.2f} MB".format(start_mem))
for col in df.columns:
if is_datetime(df[col]) or is_categorical_dtype(df[col]):
continue
col_type = df[col].dtype
if col_type != object:
c_min = df[col].min()
c_max = df[col].max()
if str(col_type)[:3] == "int":
if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
df[col] = df[col].astype(np.int8)
elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
df[col] = df[col].astype(np.int16)
elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
df[col] = df[col].astype(np.int32)
elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
df[col] = df[col].astype(np.int64)
else:
if use_float16 and c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
df[col] = df[col].astype(np.float16)
elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
df[col] = df[col].astype(np.float32)
else:
df[col] = df[col].astype(np.float64)
else:
df[col] = df[col].astype("category")
end_mem = df.memory_usage().sum() / 1024**2
print("Memory usage after optimization is: {:.2f} MB".format(end_mem))
print("Decreased by {:.1f}%".format(100 * (start_mem - end_mem) / start_mem))
return df
def features_engineering(df):
# Sort by timestamp
df.sort_values("timestamp")
df.reset_index(drop=True)
# Add more features
df["timestamp"] = pd.to_datetime(df["timestamp"],format="%Y-%m-%d %H:%M:%S")
df["hour"] = df["timestamp"].dt.hour
df["month"] = df["timestamp"].dt.month
df["weekday"] = df["timestamp"].dt.weekday
# # Remove Unused Columns
# drop = ['sea_level_pressure", "wind_direction", "wind_speed", "precip_depth_1_hr"]
# df = df.drop(drop, axis=1)
gc.collect()
return df
def building_features(building_meta_df):
building_addfeatures = pd.read_feather('building_all_meters.feather')
for col in building_meta_df.columns:
if col != 'timestamp':
if building_meta_df[col].isna().sum():
building_meta_df['na_'+col] = building_meta_df[col].isna().astype(int)
building_meta_df['build_na_total'] = building_meta_df.isna().sum(axis=1)
building_meta_df = pd.concat([building_meta_df,
building_addfeatures[['meter_reading_0', 'meter_reading_1',
'meter_reading_2', 'meter_reading_3']]], axis=1)
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
building_meta_df.primary_use = le.fit_transform(building_meta_df.primary_use)
building_meta_df['cnt_building_per_site'] = building_meta_df.groupby(['site_id']).building_id.transform(lambda x: x.size)
building_meta_df['cnt_building_per_site_prim'] = building_meta_df.groupby(['site_id', 'primary_use']).building_id.transform(lambda x: x.size)
building_meta_df['sqr_mean_per_site'] = building_meta_df.groupby(['site_id', ]).square_feet.transform('median')
building_meta_df['sqr_mean_per_prim_site'] = building_meta_df.groupby(['site_id', 'primary_use']).square_feet.transform('median')
return building_meta_df
# +
import pandas as pd
import numpy as np
import os, gc
import warnings
from lightgbm import LGBMRegressor
from sklearn.base import BaseEstimator, RegressorMixin, clone
from sklearn.metrics import mean_squared_log_error
pd.set_option("max_columns", 500)
def input_file(file):
path = f"./{file}"
if not os.path.exists(path): return path + ".gz"
return path
def compress_dataframe(df):
result = df.copy()
for col in result.columns:
col_data = result[col]
dn = col_data.dtype.name
if dn == "object":
result[col] = pd.to_numeric(col_data.astype("category").cat.codes, downcast="integer")
elif dn == "bool":
result[col] = col_data.astype("int8")
elif dn.startswith("int") or (col_data.round() == col_data).all():
result[col] = pd.to_numeric(col_data, downcast="integer")
else:
result[col] = pd.to_numeric(col_data, downcast='float')
return result
def read_train():
df = pd.read_feather("./train_cleanup_001.feather")
dft = pd.read_csv('test.csv')
# df = features_engineering(df) ###############################
df.timestamp = (pd.to_datetime(df["timestamp"]) - pd.to_datetime("2016-01-01")).dt.total_seconds() // 3600
return compress_dataframe(df)
def read_building_metadata():
df = pd.read_csv(input_file("building_metadata.csv"))
df = building_features(df)
df = compress_dataframe(df).fillna(-1).set_index("building_id")
return df
site_GMT_offsets = [-5, 0, -7, -5, -8, 0, -5, -5, -5, -6, -7, -5, 0, -6, -5, -5]
def read_weather_train(fix_timestamps=True, interpolate_na=True, add_na_indicators=True):
df = pd.read_csv(input_file("weather_train.csv"), parse_dates=["timestamp"])
################
print('add heat, RH...')
df = prepareweather(df)
print('add lag features')
add_lag_feature(df, window=3)
#################
df.timestamp = (df.timestamp - pd.to_datetime("2016-01-01")).dt.total_seconds() // 3600
if fix_timestamps:
GMT_offset_map = {site: offset for site, offset in enumerate(site_GMT_offsets)}
df.timestamp = df.timestamp + df.site_id.map(GMT_offset_map)
if interpolate_na:
site_dfs = []
for site_id in df.site_id.unique():
# Make sure that we include all possible hours so that we can interpolate evenly
site_df = df[df.site_id == site_id].set_index("timestamp").reindex(range(8784))
site_df.site_id = site_id
for col in [c for c in site_df.columns if c != "site_id"]:
if add_na_indicators: site_df[f"had_{col}"] = ~site_df[col].isna()
site_df[col] = site_df[col].interpolate(limit_direction='both', method='linear')
# Some sites are completely missing some columns, so use this fallback
site_df[col] = site_df[col].fillna(df[col].median())
site_dfs.append(site_df)
df = pd.concat(site_dfs).reset_index() # make timestamp back into a regular column
elif add_na_indicators:
for col in df.columns:
if df[col].isna().any(): df[f"had_{col}"] = ~df[col].isna()
return compress_dataframe(df).set_index(["site_id", "timestamp"])
def combined_train_data(fix_timestamps=True, interpolate_na=True, add_na_indicators=True):
Xy = compress_dataframe(read_train().join(read_building_metadata(), on="building_id").join(
read_weather_train(fix_timestamps, interpolate_na, add_na_indicators),
on=["site_id", "timestamp"]).fillna(-1))
return Xy.drop(columns=["meter_reading"]), Xy.meter_reading
def _add_time_features(X):
return X.assign(tm_day_of_week=((X.timestamp // 24) % 7), tm_hour_of_day=(X.timestamp % 24))
# +
def read_test():
df = pd.read_csv(input_file("test.csv"), parse_dates=["timestamp"])
df.timestamp = (df.timestamp - pd.to_datetime("2016-01-01")).dt.total_seconds() // 3600
return compress_dataframe(df).set_index("row_id")
def read_weather_test(fix_timestamps=True, interpolate_na=True, add_na_indicators=True):
df = pd.read_csv(input_file("weather_test.csv"), parse_dates=["timestamp"])
###############
print('add heat, RH...')
df = prepareweather(df)
print('add lag features')
add_lag_feature(df, window=3)
##############
df.timestamp = (df.timestamp - pd.to_datetime("2016-01-01")).dt.total_seconds() // 3600
if fix_timestamps:
GMT_offset_map = {site: offset for site, offset in enumerate(site_GMT_offsets)}
df.timestamp = df.timestamp + df.site_id.map(GMT_offset_map)
if interpolate_na:
site_dfs = []
for site_id in df.site_id.unique():
# Make sure that we include all possible hours so that we can interpolate evenly
site_df = df[df.site_id == site_id].set_index("timestamp").reindex(range(8784, 26304))
site_df.site_id = site_id
for col in [c for c in site_df.columns if c != "site_id"]:
if add_na_indicators: site_df[f"had_{col}"] = ~site_df[col].isna()
site_df[col] = site_df[col].interpolate(limit_direction='both', method='linear')
# Some sites are completely missing some columns, so use this fallback
site_df[col] = site_df[col].fillna(df[col].median())
site_dfs.append(site_df)
df = pd.concat(site_dfs).reset_index() # make timestamp back into a regular column
elif add_na_indicators:
for col in df.columns:
if df[col].isna().any(): df[f"had_{col}"] = ~df[col].isna()
return compress_dataframe(df).set_index(["site_id", "timestamp"])
def combined_test_data(fix_timestamps=True, interpolate_na=True, add_na_indicators=True):
X = compress_dataframe(read_test().join(read_building_metadata(), on="building_id").join(
read_weather_test(fix_timestamps, interpolate_na, add_na_indicators),
on=["site_id", "timestamp"]).fillna(-1))
return X
# +
X, y = combined_train_data()
bad_rows = find_bad_rows(X, y)
pd.Series(bad_rows.sort_values()).to_csv("rows_to_drop.csv", header=False, index=False)
# -
categorical_columns = [
"building_id", "meter", "site_id", "primary_use", "had_air_temperature", "had_cloud_coverage","had_dew_temperature", "had_precip_depth_1_hr", "had_sea_level_pressure", "had_wind_direction","had_wind_speed", "tm_day_of_week", "tm_hour_of_day"
]
# +
dropcol = []
categorical_columns = [f for f in categorical_columns if f not in dropcol]
# -
X.columns
# +
X = X.drop(index=bad_rows)
y = y.reindex_like(X)
# Additional preprocessing
X = compress_dataframe(_add_time_features(X))
X = X.drop(dropcol, axis=1) # Raw timestamp doesn't help when prediction
y = np.log1p(y)
# -
y
XX = X.copy()
XX['meter_reading'] = y.values
XX.reset_index(drop=True, inplace=True)
XX.to_feather('train_simple_cleanup.feather')
Xt = combined_test_data()
Xt = compress_dataframe(_add_time_features(Xt))
Xt = Xt.drop(dropcol, axis=1) # Raw timestamp doesn't help when prediction
Xt = Xt.reset_index()
Xt.to_feather('test_simple_cleanup.feather')
|
solutions/rank-3/generate_datasets.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cs
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: .NET (C#)
// language: C#
// name: .net-csharp
// ---
// # Welcome Spokane .NET User Group!
// +
//Not explicitly needed
#r "System.CommandLine"
//Other NuGet packages: #r "nuget:<package name>"
using System.CommandLine;
using System.CommandLine.Builder;
using System.CommandLine.Parsing;
using System.CommandLine.Invocation;
using System.CommandLine.IO;
using System.IO;
public enum OutputType
{
Unknown,
Json,
Csv,
Yaml
}
// +
var rootCommand = new RootCommand()
{
new Option<FileInfo>("--input-file", "The file to convert"),
new Option<DirectoryInfo>("--output-directory", "The output directory to covert files into."),
new Option<OutputType>("--output-type", () => OutputType.Yaml, "The conversion type.")
};
rootCommand.Handler = CommandHandler.Create<FileInfo, DirectoryInfo, OutputType, IConsole>(Handler);
static void Handler(FileInfo inputFile, DirectoryInfo outputDirectory, OutputType outputType, IConsole console)
{
console.Out.Write("Invoked Handler");
console.Out.Write($" Input File: {inputFile?.FullName}");
console.Out.Write($" Ouput Directory: {outputDirectory?.FullName}");
console.Out.Write($" Output Type: {outputType}");
}
rootCommand.Invoke("--help");
rootCommand.Invoke("--output-type Csv");
rootCommand.Invoke("--input-file ./file1 --output-directory ./output --output-type Csv");
// +
//Aliases
var rootCommand = new RootCommand()
{
new Option<FileInfo>(new[] {"--input-file", "-i"}, "The file to convert"),
new Option<DirectoryInfo>(new[] {"--output-directory", "-o"}, "The output directory to covert files into."),
new Option<OutputType>(new[] {"--output-type", "-t"}, () => OutputType.Yaml, "The conversion type.")
};
rootCommand.Handler = CommandHandler.Create<FileInfo, DirectoryInfo, OutputType, IConsole>(Handler);
rootCommand.Invoke("--help");
// +
//Model binding
public class ConversionOptions
{
public FileInfo InputFile { get; set; }
public DirectoryInfo OutputDirectory { get; set; }
public OutputType OutputType { get; set; }
}
public record ConversionOptions (
FileInfo InputFile,
DirectoryInfo OutputDirectory,
OutputType OutputType)
{ }
var rootCommand = new RootCommand()
{
new Option<FileInfo>(new[] {"--input-file", "-i"}, "The file to convert"),
new Option<DirectoryInfo>(new[] {"--output-directory", "-o"}, "The output directory to covert files into."),
new Option<OutputType>(new[] {"--output-type", "-t"}, () => OutputType.Yaml, "The conversion type.")
};
rootCommand.Handler = CommandHandler.Create<ConversionOptions, IConsole>(Handler);
static void Handler(ConversionOptions options, IConsole console)
=> console.Out.Write($"Invoked Model Binding Handler: {options}");
rootCommand.Invoke("-i file -o output -t Csv");
// +
// Parse delegates
var rootCommand = new RootCommand()
{
new Option<int>(new[] {"--num-spaces"}, (ArgumentResult argumentResult) => {
string token = argumentResult.Tokens.FirstOrDefault()?.Value;
return token switch {
"one" => 1,
"two" => 2,
"three" => 3,
_ => 4
};
}),
};
rootCommand.Handler = CommandHandler.Create<int, IConsole>(Handler);
static void Handler(int numSpaces, IConsole console)
=> console.Out.Write($"Num Spaces: {numSpaces}");
rootCommand.Invoke("--num-spaces three");
// +
// Custom suggestions
var rootCommand = new RootCommand()
{
new Option<int>(new[] {"--num-spaces"}, (ArgumentResult argumentResult) => {
string token = argumentResult.Tokens.FirstOrDefault()?.Value;
return token switch {
"one" => 1,
"two" => 2,
"three" => 3,
_ => 4
};
})
.AddSuggestions("three", "two", "one"),
};
rootCommand.Parse("--num-spaces t").GetSuggestions()
|
2021.04.13-System.CommandLine/SystemCommandLineSamples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6.8 64-bit
# name: python3
# ---
# +
#loading packages & dependencies
#When the %pylab magic function is entered at the IPython prompt, it triggers the import of various modules within Matplotlib.
from gplearn.genetic import SymbolicRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.utils.random import check_random_state
import matplotlib.pyplot as plt
import numpy as np
# +
# Ground truth
x0 = np.arange(-1, 1, .1)
x1 = np.arange(-1, 1, .1)
x0, x1 = np.meshgrid(x0, x1)
y_truth = x0**2 - x1**2 + x1 - 1 #true function
ax = plt.figure().gca(projection='3d')
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_xticks(np.arange(-1, 1.01, .5))
ax.set_yticks(np.arange(-1, 1.01, .5))
surf = ax.plot_surface(x0, x1, y_truth, rstride=1, cstride=1, color='red', alpha=0.4)
plt.show()
# +
rng = check_random_state(0)
# Training samples
X_train = rng.uniform(-1, 1, 100).reshape(50, 2)
y_train = X_train[:, 0]**2 - X_train[:, 1]**2 + X_train[:, 1] - 1
# Testing samples
X_test = rng.uniform(-1, 1, 100).reshape(50, 2)
y_test = X_test[:, 0]**2 - X_test[:, 1]**2 + X_test[:, 1] - 1
# -
est_gp = SymbolicRegressor(population_size=5000, #the number of programs in each generation
generations=30, stopping_criteria=0.01, #The required metric value required in order to stop evolution early.
p_hoist_mutation=0.05, #0.05, The probability of performing hoist mutation on a tournament winner. Hoist mutation takes the winner of a tournament and selects a random subtree from it. A random subtree of that subtree is then selected and this is ‘hoisted’ into the original subtrees location to form an offspring in the next generation. This method helps to control bloat.
p_crossover=0.7, p_subtree_mutation=0.1,
p_point_mutation=0.1,
max_samples=0.9, verbose=1,
parsimony_coefficient=0.01, random_state=0)
est_gp.fit(X_train, y_train)
print(est_gp._program)
est_tree = DecisionTreeRegressor()
est_tree.fit(X_train, y_train)
est_rf = RandomForestRegressor(n_estimators=10)
est_rf.fit(X_train, y_train)
# +
y_gp = est_gp.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
score_gp = est_gp.score(X_test, y_test)
y_tree = est_tree.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
score_tree = est_tree.score(X_test, y_test)
y_rf = est_rf.predict(np.c_[x0.ravel(), x1.ravel()]).reshape(x0.shape)
score_rf = est_rf.score(X_test, y_test)
fig = plt.figure(figsize=(12, 10))
for i, (y, score, title) in enumerate([(y_truth, None, "Ground Truth"),
(y_gp, score_gp, "SymbolicRegressor"),
(y_tree, score_tree, "DecisionTreeRegressor"),
(y_rf, score_rf, "RandomForestRegressor")]):
ax = fig.add_subplot(2, 2, i+1, projection='3d')
ax.set_xlim(-1, 1)
ax.set_ylim(-1, 1)
ax.set_xticks(np.arange(-1, 1.01, .5))
ax.set_yticks(np.arange(-1, 1.01, .5))
surf = ax.plot_surface(x0, x1, y, rstride=1, cstride=1, color='red', alpha=0.4)
points = ax.scatter(X_train[:, 0], X_train[:, 1], y_train)
if score is not None:
score = ax.text(-.7, 0.1, .1, "$R^2 =\/ %.6f$" % score, 'x', fontsize=14)
plt.title(title)
plt.show()
|
05-Mathematic-Implementation/DS-RegressrionTechniques/RegressionTechniquesComparision.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Analyzing Portfolio Risk and Return
#
# In this Challenge, you'll assume the role of a quantitative analyst for a FinTech investing platform. This platform aims to offer clients a one-stop online investment solution for their retirement portfolios that’s both inexpensive and high quality. (Think about [Wealthfront](https://www.wealthfront.com/) or [Betterment](https://www.betterment.com/)). To keep the costs low, the firm uses algorithms to build each client's portfolio. The algorithms choose from various investment styles and options.
#
# You've been tasked with evaluating four new investment options for inclusion in the client portfolios. Legendary fund and hedge-fund managers run all four selections. (People sometimes refer to these managers as **whales**, because of the large amount of money that they manage). You’ll need to determine the fund with the most investment potential based on key risk-management metrics: the daily returns, standard deviations, Sharpe ratios, and betas.
#
# ## Instructions
#
# ### Import the Data
#
# Use the `whale_analysis.ipynb` file to complete the following steps:
#
# 1. Import the required libraries and dependencies.
#
# 2. Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
#
# 3. Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
#
# ### Analyze the Performance
#
# Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents. To do so, complete the following steps:
#
# 1. Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 2. Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
#
# 3. Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 4. Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
#
# ### Analyze the Volatility
#
# Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots. To do so, complete the following steps:
#
# 1. Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 2. Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# > **Hint** Save this new DataFrame—the one that contains the data for just the four fund portfolios. You’ll use it throughout the analysis.
#
# 3. Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
#
# ### Analyze the Risk
#
# Evaluate the risk profile of each portfolio by using the standard deviation and the beta. To do so, complete the following steps:
#
# 1. Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
#
# 2. Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
#
# 3. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 4. Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 5. Answer the following three questions:
#
# * Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
#
# * Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
#
# * Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
#
# ### Analyze the Risk-Return Profile
#
# To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio. To do so, complete the following steps:
#
# 1. Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
#
# 2. Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
#
# 3. Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# 4. Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
#
# #### Diversify the Portfolio
#
# Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options. To start your analysis, complete the following step:
#
# * Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
#
# Next, for each of the two portfolios that you chose, complete the following steps:
#
# 1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
#
# 2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
#
# 3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
#
# 4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
#
# Finally, answer the following two questions:
#
# * Which of the two portfolios seem more sensitive to movements in the S&P 500?
#
# * Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
#
# ### Import the Data
# #### Step 1: Import the required libraries and dependencies.
# Import the required libraries and dependencies
# YOUR CODE HERE
import pandas as pd
from pathlib import Path
import numpy as np
# %matplotlib inline
# #### Step 2: Use the `read_csv` function and the `Path` module to read the `whale_navs.csv` file into a Pandas DataFrame. Be sure to create a `DateTimeIndex`. Review the first five rows of the DataFrame by using the `head` function.
# +
# Import the data by reading in the CSV file and setting the DatetimeIndex
# Review the first 5 rows of the DataFrame
# YOUR CODE HERE
whale_funds_with_sp500_df = pd.read_csv(
Path("./Resources/whale_navs.csv"),
index_col="date",
parse_dates=True,
infer_datetime_format=True
)
# Review the 'tech_df' DataFrame with both the head & tail functions
display(whale_funds_with_sp500_df.head())
display(whale_funds_with_sp500_df.tail())
# -
# #### Step 3: Use the Pandas `pct_change` function together with `dropna` to create the daily returns DataFrame. Base this DataFrame on the NAV prices of the four portfolios and on the closing price of the S&P 500 Index. Review the first five rows of the daily returns DataFrame.
# +
# Prepare for the analysis by converting the dataframe of NAVs and prices to daily returns
# Drop any rows with all missing values
whale_funds_with_sp500_daily_returns_df = whale_funds_with_sp500_df.pct_change().dropna()
# Review the first five rows of the daily returns DataFrame.
# YOUR CODE HERE
whale_funds_with_sp500_daily_returns_df.head()
# -
# ---
# ## Quantative Analysis
#
# The analysis has several components: performance, volatility, risk, risk-return profile, and portfolio diversification. You’ll analyze each component one at a time.
# ### Analyze the Performance
#
# Analyze the data to determine if any of the portfolios outperform the broader stock market, which the S&P 500 represents.
# #### Step 1: Use the default Pandas `plot` function to visualize the daily return data of the four fund portfolios and the S&P 500. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Plot the daily return data of the 4 funds and the S&P 500
# Inclue a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_with_sp500_daily_returns_df.plot(
figsize = (15,10),
title = "Daily Return of 4 Whale Funds and S&P 500"
)
# #### Step 2: Use the Pandas `cumprod` function to calculate the cumulative returns for the four fund portfolios and the S&P 500. Review the last five rows of the cumulative returns DataFrame by using the Pandas `tail` function.
# +
# Calculate and plot the cumulative returns of the 4 fund portfolios and the S&P 500
# Review the last 5 rows of the cumulative returns DataFrame
# YOUR CODE HERE
#Review 4.1.6
#Notice: For calculating the excess returns, we need to - 1 at the end of the calculating cumulative returns equation
# But here, since we just need to calculate the cumulative returns, so we do not need to - 1
whale_funds_with_sp500_cumulative_returns_df = (1 + whale_funds_with_sp500_daily_returns_df).cumprod()
whale_funds_with_sp500_cumulative_returns_df.tail()
# -
# #### Step 3: Use the default Pandas `plot` to visualize the cumulative return values for the four funds and the S&P 500 over time. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Visualize the cumulative returns using the Pandas plot function
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_with_sp500_cumulative_returns_df.plot(
figsize = (15,10),
title = "Cumulative Returns of 4 Whale Funds and S&P 500"
)
# #### Step 4: Answer the following question: Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
# **Question** Based on the cumulative return data and the visualization, do any of the four fund portfolios outperform the S&P 500 Index?
#
# **Answer** # No, none of them outperform the S&P 500 Index since the mid of 2016 to Sep. 2020.
# ---
# ### Analyze the Volatility
#
# Analyze the volatility of each of the four fund portfolios and of the S&P 500 Index by using box plots.
# #### Step 1: Use the Pandas `plot` function and the `kind="box"` parameter to visualize the daily return data for each of the four portfolios and for the S&P 500 in a box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Use the daily return data to create box plots to visualize the volatility of the 4 funds and the S&P 500
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_with_sp500_daily_returns_df.plot(
kind = "box",
figsize = (15,10),
title = "Box Chart of 4 Whale Funds And S&P 500"
)
# #### Step 2: Use the Pandas `drop` function to create a new DataFrame that contains the data for just the four fund portfolios by dropping the S&P 500 column. Visualize the daily return data for just the four fund portfolios by using another box plot. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# +
# Create a new DataFrame containing only the 4 fund portfolios by dropping the S&P 500 column from the DataFrame
# Create box plots to reflect the return data for only the 4 fund portfolios
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
#Box Chart for volatility, and std means risk
whale_funds_without_sp500_df = whale_funds_with_sp500_df.drop(columns = ["S&P 500"])
whale_funds_without_sp500_df.plot(
kind = "box",
figsize = (15,10),
title = "Box Chart of 4 Whale Funds"
)
# -
# #### Step 3: Answer the following question: Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
# **Question** Based on the box plot visualization of just the four fund portfolios, which fund was the most volatile (with the greatest spread) and which was the least volatile (with the smallest spread)?
#
# **Answer** # Berkshire Hathaway portfolio is the most volatile fund, and Paulson & Co. portfolio is the least volatile fund.
# ---
# ### Analyze the Risk
#
# Evaluate the risk profile of each portfolio by using the standard deviation and the beta.
# #### Step 1: Use the Pandas `std` function to calculate the standard deviation for each of the four portfolios and for the S&P 500. Review the standard deviation calculations, sorted from smallest to largest.
# +
# Calculate and sort the standard deviation for all 4 portfolios and the S&P 500
# Review the standard deviations sorted smallest to largest
# YOUR CODE HERE
#Review 4.2.3
standard_deviation = whale_funds_with_sp500_daily_returns_df.std()
standard_deviation_sorted = standard_deviation.sort_values()
standard_deviation_sorted
# -
# #### Step 2: Calculate the annualized standard deviation for each of the four portfolios and for the S&P 500. To do that, multiply the standard deviation by the square root of the number of trading days. Use 252 for that number.
# +
# Calculate and sort the annualized standard deviation (252 trading days) of the 4 portfolios and the S&P 500
# Review the annual standard deviations smallest to largest
# YOUR CODE HERE
annualized_standard_deviation = standard_deviation * np.sqrt(252)
annualized_standard_deviation.sort_values()
# -
# #### Step 3: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of the four fund portfolios and of the S&P 500 index. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# +
# Using the daily returns DataFrame and a 21-day rolling window,
# plot the rolling standard deviation of the 4 portfolios and the S&P 500
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_with_sp500_rolling_21_std = whale_funds_with_sp500_daily_returns_df.rolling(window=21).std()
whale_funds_with_sp500_rolling_21_std.plot(
figsize = (15,10),
title = "Rolling 21-DAY Std Dev of 4 Whale Portfolios and S&P 500"
)
# -
# #### Step 4: Use the daily returns DataFrame and a 21-day rolling window to plot the rolling standard deviations of only the four fund portfolios. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# +
# Using the daily return data and a 21-day rolling window, plot the rolling standard deviation of just the 4 portfolios.
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_without_sp500_daily_returns_df = whale_funds_without_sp500_df.pct_change().dropna()
whale_funds_without_sp500_rolling_21_std = whale_funds_without_sp500_daily_returns_df.rolling(window=21).std()
whale_funds_without_sp500_rolling_21_std.plot(
figsize = (15,10),
title = "Rolling 21-DAY Std Dev of 4 Whale Portfolios"
)
# -
# #### Step 5: Answer the following three questions:
#
# 1. Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
#
# 2. Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
#
# 3. Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
# **Question 1** Based on the annualized standard deviation, which portfolios pose more risk than the S&P 500?
#
# **Answer 1** # None of four portfolios pose more risk than S&P 500 for the most of time in the recent 5 years.
# **Question 2** Based on the rolling metrics, does the risk of each portfolio increase at the same time that the risk of the S&P 500 increases?
#
# **Answer 2** # Yes, sometimes but not always. For example, during 2017 - 2018, each portfolio has its own performance and does not frequently become more riskier as the risk of S&P 500 increases. But since 2019 to 2020, the risk of each portfolio seems to increase as the risk of the S&P 500 increases. COVID-19 strike to the market might play a major role here.
# **Question 3** Based on the rolling standard deviations of only the four fund portfolios, which portfolio poses the most risk? Does this change over time?
#
# **Answer 3** # Berkshire Hathaway portfolio poses the most risk since 2020. And yes, it changes over time; for example, in the first half year of 2016, Soros fund management poses the most risk.
# ---
# ### Analyze the Risk-Return Profile
#
# To determine the overall risk of an asset or portfolio, quantitative analysts and investment managers consider not only its risk metrics but also its risk-return profile. After all, if you have two portfolios that each offer a 10% return but one has less risk, you’d probably invest in the smaller-risk portfolio. For this reason, you need to consider the Sharpe ratios for each portfolio.
# #### Step 1: Use the daily return DataFrame to calculate the annualized average return data for the four fund portfolios and for the S&P 500. Use 252 for the number of trading days. Review the annualized average returns, sorted from lowest to highest.
# +
# Calculate the annual average return data for the four fund portfolios and the S&P 500
# Use 252 as the number of trading days in the year
# Review the annual average returns sorted from lowest to highest
# YOUR CODE HERE
#Review 4.2.5
year_trading_days = 252
annual_average_whale_funds_with_sp500 = whale_funds_with_sp500_daily_returns_df.mean() * year_trading_days
annual_average_whale_funds_with_sp500.sort_values()
# -
# #### Step 2: Calculate the Sharpe ratios for the four fund portfolios and for the S&P 500. To do that, divide the annualized average return by the annualized standard deviation for each. Review the resulting Sharpe ratios, sorted from lowest to highest.
# +
# Calculate the annualized Sharpe Ratios for each of the 4 portfolios and the S&P 500.
# Review the Sharpe ratios sorted lowest to highest
# YOUR CODE HERE
annual_standard_deviation = whale_funds_with_sp500_daily_returns_df.std() * np.sqrt(year_trading_days)
whale_funds_with_sp500_sharpe_ratio = annual_average_whale_funds_with_sp500 / annual_standard_deviation
whale_funds_with_sp500_sharpe_ratio.sort_values()
# -
# #### Step 3: Visualize the Sharpe ratios for the four funds and for the S&P 500 in a bar chart. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Visualize the Sharpe ratios as a bar chart
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
whale_funds_with_sp500_sharpe_ratio.plot(
kind = "bar",
figsize = (15,10),
title = "Bar Chart of Sharpe Ratios of 4 Funds and S&P 500"
)
# #### Step 4: Answer the following question: Which of the four portfolios offers the best risk-return profile? Which offers the worst?
# **Question** Which of the four portfolios offers the best risk-return profile? Which offers the worst?
#
# **Answer** # Berkshire Hathaway offers the best risk-return profile, whereas Paulson & Co Inc offers the worst.
# ---
# ### Diversify the Portfolio
#
# Your analysis is nearing completion. Now, you need to evaluate how the portfolios react relative to the broader market. Based on your analysis so far, choose two portfolios that you’re most likely to recommend as investment options.
# #### Use the Pandas `var` function to calculate the variance of the S&P 500 by using a 60-day rolling window. Visualize the last five rows of the variance of the S&P 500.
# +
# Calculate the variance of the S&P 500 using a rolling 60-day window.
# YOUR CODE HERE
market_rolling_60_variance = whale_funds_with_sp500_daily_returns_df["S&P 500"].rolling(window=60).var()
market_rolling_60_variance.tail()
# -
# #### For each of the two portfolios that you chose, complete the following steps:
#
# 1. Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
#
# 2. Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
#
# 3. Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
#
# 4. Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# ##### Portfolio 1 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
# +
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
# YOUR CODE HERE
BRK_rolling_60_covariance = whale_funds_with_sp500_daily_returns_df['BERKSHIRE HATHAWAY INC'].rolling(window=60).cov(whale_funds_with_sp500_daily_returns_df['S&P 500'])
BRK_rolling_60_covariance.tail()
# -
# ##### Portfolio 1 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
# +
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
# YOUR CODE HERE
BRK_rolling_60_beta = BRK_rolling_60_covariance / market_rolling_60_variance
BRK_rolling_60_beta.tail()
# -
# ##### Portfolio 1 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
# Calculate the average of the 60-day rolling beta
# YOUR CODE HERE
BRK_rolling_60_beta_mean = BRK_rolling_60_beta.mean()
BRK_rolling_60_beta_mean
# ##### Portfolio 1 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Plot the rolling beta
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
BRK_rolling_60_beta.plot(
figsize = (15,10),
title = "Berkshire Hathaway Portfolio 60-DAY Rolling Average Beta "
)
# ##### Portfolio 2 - Step 1: Using the 60-day rolling window, the daily return data, and the S&P 500 returns, calculate the covariance. Review the last five rows of the covariance of the portfolio.
# +
# Calculate the covariance using a 60-day rolling window
# Review the last five rows of the covariance data
# YOUR CODE HERE
TIGER_rolling_60_covariance = whale_funds_with_sp500_daily_returns_df['TIGER GLOBAL MANAGEMENT LLC'].rolling(window=60).cov(whale_funds_with_sp500_daily_returns_df['S&P 500'])
TIGER_rolling_60_covariance.tail()
# -
# ##### Portfolio 2 - Step 2: Calculate the beta of the portfolio. To do that, divide the covariance of the portfolio by the variance of the S&P 500.
# +
# Calculate the beta based on the 60-day rolling covariance compared to the market (S&P 500)
# Review the last five rows of the beta information
# YOUR CODE HERE
TIGER_rolling_60_beta = TIGER_rolling_60_covariance / market_rolling_60_variance
TIGER_rolling_60_beta.tail()
# -
# ##### Portfolio 2 - Step 3: Use the Pandas `mean` function to calculate the average value of the 60-day rolling beta of the portfolio.
# Calculate the average of the 60-day rolling beta
# YOUR CODE HERE
TIGER_rolling_60_beta_mean = TIGER_rolling_60_beta.mean()
TIGER_rolling_60_beta_mean
# ##### Portfolio 2 - Step 4: Plot the 60-day rolling beta. Be sure to include the `title` parameter, and adjust the figure size if necessary.
# Plot the rolling beta
# Include a title parameter and adjust the figure size
# YOUR CODE HERE
TIGER_rolling_60_beta.plot(
figsize = (15,10),
title = "Tiger Management Portfolio 60-DAY Rolling Average Beta "
)
# +
# Calculate the rolling 60-day beta of Portfolio 3:
PAUL_rolling_60_covariance = whale_funds_with_sp500_daily_returns_df['PAULSON & CO.INC.'].rolling(window=60).cov(whale_funds_with_sp500_daily_returns_df['S&P 500'])
PAUL_rolling_60_beta = PAUL_rolling_60_covariance / market_rolling_60_variance
PAUL_rolling_60_beta_mean = PAUL_rolling_60_beta.mean()
PAUL_rolling_60_beta_mean
# +
# Calculate the rolling 60-day beta of Portfolio 4:
SOROS_rolling_60_covariance = whale_funds_with_sp500_daily_returns_df['SOROS FUND MANAGEMENT LLC'].rolling(window=60).cov(whale_funds_with_sp500_daily_returns_df['S&P 500'])
SOROS_rolling_60_beta = SOROS_rolling_60_covariance / market_rolling_60_variance
SOROS_rolling_60_beta_mean = SOROS_rolling_60_beta.mean()
SOROS_rolling_60_beta_mean
# -
# **Question 1** Which of the two portfolios seem more sensitive to movements in the S&P 500?
#
# **Answer 1** # TIGER_rolling_60_beta_mean is 0.03093, SOROS_rolling_60_beta_mean is 0.06862, BRK_rolling_60_beta_mean is 0.22149, PAUL_rolling_60_beta_mean is 0.07767. Therefore, Berkshire Hathaway and Paulson portfolio are more sensitive to the movements in the S&P 500, since they have the highest betas than the other two portfolios.
#
# **Question 2** Which of the two portfolios do you recommend for inclusion in your firm’s suite of fund offerings?
#
# **Answer 2** # I recommend Berkshire Hathaway and Tiger Global Management portfolio since these two have the highest Sharpe ratios among 4 portfolios.
# ---
|
Module_4_Challenge_Files/Starter_Code/risk_return_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %pylab inline
from solveMDP import *
Vgrid = np.load("richLow.npy")
matplotlib.rcParams['figure.figsize'] = [16, 8]
plt.rcParams.update({'font.size': 15})
# +
# total number of agents
num = 10000
'''
x = [w,ab,s,e,o,z]
x = [5,0, 0,0,0,0]
'''
from jax import random
from quantecon import MarkovChain
# number of economies and each economy has 100 agents
numEcon = 100
numAgents = 100
mc = MarkovChain(Ps)
econStates = mc.simulate(ts_length=T_max-T_min,init=0,num_reps=numEcon)
econStates = jnp.array(econStates,dtype = int)
@partial(jit, static_argnums=(0,))
def transition_real(t,a,x, s_prime):
'''
Input:
x = [w,ab,s,e,o,z] single action
x = [0,1, 2,3,4,5]
a = [c,b,k,h,action] single state
a = [0,1,2,3,4]
Output:
w_next
ab_next
s_next
e_next
o_next
z_next
prob_next
'''
s = jnp.array(x[2], dtype = jnp.int8)
e = jnp.array(x[3], dtype = jnp.int8)
# actions taken
b = a[1]
k = a[2]
action = a[4]
w_next = ((1+r_b[s])*b + (1+r_k[s_prime])*k).repeat(nE)
ab_next = (1-x[4])*(t*(action == 1)).repeat(nE) + x[4]*(x[1]*jnp.ones(nE))
s_next = s_prime.repeat(nE)
e_next = jnp.array([e,(1-e)])
z_next = x[5]*jnp.ones(nE) + ((1-x[5]) * (k > 0)).repeat(nE)
# job status changing probability and econ state transition probability
pe = Pe[s, e]
prob_next = jnp.array([1-pe, pe])
# owner
o_next_own = (x[4] - action).repeat(nE)
# renter
o_next_rent = action.repeat(nE)
o_next = x[4] * o_next_own + (1-x[4]) * o_next_rent
return jnp.column_stack((w_next,ab_next,s_next,e_next,o_next,z_next,prob_next))
def simulation(key):
initE = random.choice(a = nE, p=E_distribution, key = key)
initS = random.choice(a = nS, p=S_distribution, key = key)
x = [5, 0, initS, initE, 0, 0]
path = []
move = []
# first 100 agents are in the 1st economy and second 100 agents are in the 2nd economy
econ = econStates[key.sum()//numAgents,:]
for t in range(T_min, T_max):
_, key = random.split(key)
if t == T_max-1:
_,a = V_solve(t,Vgrid[:,:,:,:,:,:,t],x)
else:
_,a = V_solve(t,Vgrid[:,:,:,:,:,:,t+1],x)
xp = transition_real(t,a,x, econ[t])
p = xp[:,-1]
x_next = xp[:,:-1]
path.append(x)
move.append(a)
x = x_next[random.choice(a = nE, p=p, key = key)]
path.append(x)
return jnp.array(path), jnp.array(move)
# -
# %%time
# simulation part
keys = vmap(random.PRNGKey)(jnp.arange(num))
Paths, Moves = vmap(simulation)(keys)
# + tags=[]
# x = [w,ab,s,e,o,z]
# x = [0,1, 2,3,4,5]
ws = Paths[:,:,0].T
ab = Paths[:,:,1].T
ss = Paths[:,:,2].T
es = Paths[:,:,3].T
os = Paths[:,:,4].T
zs = Paths[:,:,5].T
cs = Moves[:,:,0].T
bs = Moves[:,:,1].T
ks = Moves[:,:,2].T
hs = Moves[:,:,3].T
ms = Ms[jnp.append(jnp.array([0]),jnp.arange(T_max)).reshape(-1,1) - jnp.array(ab, dtype = jnp.int8)]*os
# -
plt.plot(range(20, T_max + 21),jnp.mean(zs,axis = 1), label = "experience")
plt.title("The mean values of simulation")
plt.plot(range(20, T_max + 21),jnp.mean(ws + H*pt*os - ms,axis = 1), label = "wealth + home equity")
plt.plot(range(20, T_max + 21),jnp.mean(H*pt*os - ms,axis = 1), label = "home equity")
plt.plot(range(20, T_max + 21),jnp.mean(ws,axis = 1), label = "wealth")
plt.plot(range(20, T_max + 20),jnp.mean(cs,axis = 1), label = "consumption")
plt.plot(range(20, T_max + 20),jnp.mean(bs,axis = 1), label = "bond")
plt.plot(range(20, T_max + 20),jnp.mean(ks,axis = 1), label = "stock")
plt.legend()
plt.title("housing consumption")
plt.plot(range(20, T_max + 20),(hs).mean(axis = 1), label = "housing")
plt.title("housing consumption for renting peole")
plt.plot(hs[:, jnp.where(os.sum(axis = 0) == 0)[0]].mean(axis = 1), label = "housing")
plt.title("house ownership percentage in the population")
plt.plot(range(20, T_max + 21),(os).mean(axis = 1), label = "owning")
# agent number, x = [w,n,m,s,e,o]
agentNum = 35
plt.plot(range(20, T_max + 21),(ws + os*(H*pt - ms))[:,agentNum], label = "wealth + home equity")
plt.plot(range(20, T_max + 21),ms[:,agentNum], label = "mortgage")
plt.plot(range(20, T_max + 20),cs[:,agentNum], label = "consumption")
plt.plot(range(20, T_max + 20),bs[:,agentNum], label = "bond")
plt.plot(range(20, T_max + 20),ks[:,agentNum], label = "stock")
plt.plot(range(20, T_max + 21),os[:,agentNum]*100, label = "ownership", color = "k")
plt.legend()
# agent selling time collection
agentTime = []
for t in range(30):
if ((os[t,:] == 0) & (os[t+1,:] == 1)).sum()>0:
for agentNum in jnp.where((os[t,:] == 0) & (os[t+1,:] == 1))[0]:
agentTime.append([t, agentNum])
agentTime = jnp.array(agentTime)
# agent selling time collection
agentHold = []
for t in range(30):
if ((os[t,:] == 0) & (os[t+1,:] == 0)).sum()>0:
for agentNum in jnp.where((os[t,:] == 0) & (os[t+1,:] == 0))[0]:
agentHold.append([t, agentNum])
agentHold = jnp.array(agentHold)
plt.title("weath level for buyer and renter")
www = (os*(ws+H*pt - ms)).sum(axis = 1)/(os).sum(axis = 1)
for age in range(30):
buyer = agentTime[agentTime[:,0] == age]
renter = agentHold[agentHold[:,0] == age]
plt.scatter(age, ws[buyer[:,0], buyer[:,1]].mean(),color = "b")
plt.scatter(age, www[age], color = "green")
plt.scatter(age, ws[renter[:,0], renter[:,1]].mean(),color = "r")
plt.title("employement status for buyer and renter")
for age in range(31):
buyer = agentTime[agentTime[:,0] == age]
renter = agentHold[agentHold[:,0] == age]
plt.scatter(age, es[buyer[:,0], buyer[:,1]].mean(),color = "b")
plt.scatter(age, es[renter[:,0], renter[:,1]].mean(),color = "r")
# At every age
plt.title("Stock Investment Percentage")
plt.plot((os[:T_max,:]*ks/(ks+bs)).sum(axis = 1)/os[:T_max,:].sum(axis = 1), label = "owner")
plt.plot(((1-os[:T_max,:])*ks/(ks+bs)).sum(axis = 1)/(1-os)[:T_max,:].sum(axis = 1), label = "renter")
plt.legend()
# At every age
plt.title("Stock Investment Amount")
plt.plot((os[:T_max,:]*ks).sum(axis = 1)/os[:T_max,:].sum(axis = 1), label = "owner")
plt.plot(((1-os[:T_max,:])*ks).sum(axis = 1)/(1-os)[:T_max,:].sum(axis = 1), label = "renter")
plt.legend()
|
20211003/simulation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DL0110EN-SkillsNetwork/Template/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# <h1>Neural Networks More Hidden Neutrons</h1>
#
# <h2>Objective</h2><ul><li> How to create complex Neural Network in pytorch.</li></ul>
#
# <h2>Table of Contents</h2>
#
# <ul>
# <li><a href="https://#Prep">Preperation</a></li>
# <li><a href="https://#Data">Get Our Data</a></li>
# <li><a href="https://#Train">Define the Neural Network, Optimizer, and Train the Model</a></li>
# </ul>
# <p>Estimated Time Needed: <strong>25 min</strong></p>
#
# <hr>
#
# <h2 id="Prep">Preparation</h2>
#
# We'll need to import the following libraries for this lab.
#
import torch
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
# Define the plotting functions.
#
def get_hist(model,data_set):
activations=model.activation(data_set.x)
for i,activation in enumerate(activations):
plt.hist(activation.numpy(),4,density=True)
plt.title("Activation layer " + str(i+1))
plt.xlabel("Activation")
plt.xlabel("Activation")
plt.legend()
plt.show()
def PlotStuff(X,Y,model=None,leg=False):
plt.plot(X[Y==0].numpy(),Y[Y==0].numpy(),'or',label='training points y=0 ' )
plt.plot(X[Y==1].numpy(),Y[Y==1].numpy(),'ob',label='training points y=1 ' )
if model!=None:
plt.plot(X.numpy(),model(X).detach().numpy(),label='neral network ')
plt.legend()
plt.show()
# <h2 id="Data">Get Our Data</h2>
#
# Define the class to get our dataset.
#
# +
class Data(Dataset):
def __init__(self):
self.x=torch.linspace(-20, 20, 100).view(-1,1)
self.y=torch.zeros(self.x.shape[0])
self.y[(self.x[:,0]>-10)& (self.x[:,0]<-5)]=1
self.y[(self.x[:,0]>5)& (self.x[:,0]<10)]=1
self.y=self.y.view(-1,1)
self.len=self.x.shape[0]
def __getitem__(self,index):
return self.x[index],self.y[index]
def __len__(self):
return self.len
# -
# <h2 id="Train">Define the Neural Network, Optimizer and Train the Model</h2>
#
# Define the class for creating our model.
#
class Net(nn.Module):
def __init__(self,D_in,H,D_out):
super(Net,self).__init__()
self.linear1=nn.Linear(D_in,H)
self.linear2=nn.Linear(H,D_out)
def forward(self,x):
x=torch.sigmoid(self.linear1(x))
x=torch.sigmoid(self.linear2(x))
return x
# Create the function to train our model, which accumulate lost for each iteration to obtain the cost.
#
def train(data_set,model,criterion, train_loader, optimizer, epochs=5,plot_number=10):
cost=[]
for epoch in range(epochs):
total=0
for x,y in train_loader:
optimizer.zero_grad()
yhat=model(x)
loss=criterion(yhat,y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total+=loss.item()
if epoch%plot_number==0:
PlotStuff(data_set.x,data_set.y,model)
cost.append(total)
plt.figure()
plt.plot(cost)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.show()
return cost
data_set=Data()
PlotStuff(data_set.x,data_set.y,leg=False)
# Create our model with 9
# neurons in the hidden layer. And then create a BCE loss and an Adam optimizer.
#
torch.manual_seed(0)
model=Net(1,9,1)
learning_rate=0.1
criterion=nn.BCELoss()
optimizer=torch.optim.Adam(model.parameters(), lr=learning_rate)
train_loader=DataLoader(dataset=data_set,batch_size=100)
COST=train(data_set,model,criterion, train_loader, optimizer, epochs=600,plot_number=200)
# + active=""
# # this is for exercises
# model= torch.nn.Sequential(
# torch.nn.Linear(1, 6),
# torch.nn.Sigmoid(),
# torch.nn.Linear(6,1),
# torch.nn.Sigmoid()
#
# )
# -
plt.plot(COST)
# <a href="https://dataplatform.cloud.ibm.com/registration/stepone?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01&context=cpdaas&apps=data_science_experience%2Cwatson_machine_learning"><img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DL0110EN-SkillsNetwork/Template/module%201/images/Watson_Studio.png"/></a>
#
# <h2>About the Authors:</h2>
#
# <a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
#
# Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/jiahui-mavis-zhou-a4537814a?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/fanjiang0619/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/yi-leng-yao-84451275/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/sacchitchadha/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>
#
# ## Change Log
#
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# | ----------------- | ------- | ---------- | ----------------------------------------------------------- |
# | 2020-09-23 | 2.0 | Shubham | Migrated Lab to Markdown and added to course repo in GitLab |
#
# ## <h3 align="center"> © IBM Corporation 2020. All rights reserved. <h3/>
#
|
4. Deep Neural Networks with PyTorch/4. Softmax Rergresstion/4. multiple_neurons.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Consensus Signatures
#
# A consensus signature can be defined as a perturbation-specific summary profile acquired by aggregating replicate level information.
#
#
# #### Level 5 - Replicate-consensus signatures (MODZ)
# L1000 experiments are typically done in 3 or more biological replicates. We derive a consensus replicate signature by applying the
# moderated z-score (MODZ) procedure as follows. First, a pairwise Spearman correlation matrix is computed between the replicate
# signatures in the space of landmark genes with trivial self-correlations being ignored (set to 0). Then, weights for each replicate are
# computed as the sum of its correlations to the other replicates, normalized such that all weights sum to 1. Finally, the consensus
# signature is given by the linear combination of the replicate signatures with the coefficients set to the weights. This procedure serves
# to mitigate the effects of uncorrelated or outlier replicates, and can be thought of as a ‘de-noised’ representation of the given
# experiment’s transcriptional consequences.
# [Subramanian et al 2017](https://www.cell.com/action/showPdf?pii=S0092-8674%2817%2931309-0)
#
#
# ### we have expression values of 978 landmark genes for each signature id (sig_id)
#
#
#
#
# ### The goal here:
# - is to determine the median score of each MOA (Mechanism of action) per dose based on taking the median of the correlation values between compounds of the same MOA.
#
#
# ### Note:
#
# To calculate the median score for each of the two level-5 (rank and Modz) data, this notebook will have to be ran twice for each.
import os
import requests
import pickle
import argparse
import pandas as pd
import numpy as np
import re
from os import walk
from collections import Counter
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
import random
sns.set_style("darkgrid")
import shutil
from statistics import median
import cmapPy.pandasGEXpress.parse_gct as pg
from cmapPy.pandasGEXpress.parse import parse
from io import BytesIO
from urllib.request import urlopen
from zipfile import ZipFile
# ### - Download L1000 Dataset
data_dir = os.getcwd() ##current_dir
zipurl = "https://ndownloader.figshare.com/articles/13181966/versions/1"
def download_L1000_data(data_dir, zipurl):
"""
Download L1000 data from figshare and extract
the zipped files into a directory
"""
if not os.path.exists(data_dir):
os.mkdir(data_dir)
with urlopen(zipurl) as zipresp:
with ZipFile(BytesIO(zipresp.read())) as zfile:
zfile.extractall(data_dir)
download_L1000_data(data_dir, zipurl)
os.listdir(data_dir) ##files in L1000 downloaded dataset
# ### Mechanism of actions (MOAs) - Alignment of L1000 and Cell Painting MOAs
#
# - Align the **L1000 pert_info meta_data** with the **Cell-painting meta_data** based on **broad id** and then further fill in some null values in cell painting MOA column with corresponding L1000 MOAs of the same broad sample id and do the same thing for the L1000 data, then take the L1000 moas as the one that will be used for further analysis (because it has the most distinct MOAs).
cp_moa_dataset = "https://github.com/broadinstitute/lincs-cell-painting/blob/master/metadata/moa\
/repurposing_info_external_moa_map_resolved.tsv?raw=true"
def merge_align_moa(data_dir, cp_moa_link):
"""
This function aligns L1000 MOAs with the cell painting MOAs
and further fill null MOAs in one of the them (cell painting or L1000)
with another, so far they are of the same broad sample ID.
The function outputs aligned L1000 MOA metadata dataframe,
that will be used for further analysis.
params:
data_dir: directory that contains L1000 files
cp_moa_link: github link to cell painting MOA metadata information .csv file
Returns:
df_pertinfo: dataframe with aligned L1000 MOA metadata pertubation information.
"""
df_pertinfo_5 = pd.read_csv(os.path.join(data_dir, 'REP.A_A549_pert_info.txt'), delimiter = "\t")
df_moa_cp = pd.read_csv(cp_moa_link, sep="\t")
df_pertinfo_5 = df_pertinfo_5[['pert_id', 'pert_iname', 'moa']].copy()
df_moa_cp = df_moa_cp[['broad_id', 'pert_iname', 'moa']].copy()
df_pertinfo_5.rename(columns={"pert_id": "broad_id", "pert_iname": "pert_iname_L1000", "moa": "moa_L1000"}, inplace = True)
df_moa_cp.rename(columns={"pert_iname": "pert_iname_cell_painting", "moa": "moa_cell_painting"}, inplace = True)
df_pertinfo = pd.merge(df_pertinfo_5, df_moa_cp, on=['broad_id'], how = 'left')
##fill NaNs in columns - moa_L1000, pert_iname_L1000, with corresponding values in cell_painting and VICE VERSA
df_pertinfo['moa_L1000'].fillna(value=df_pertinfo['moa_cell_painting'], inplace=True)
df_pertinfo['moa_cell_painting'].fillna(value=df_pertinfo['moa_L1000'], inplace=True)
df_pertinfo['pert_iname_cell_painting'].fillna(value=df_pertinfo['pert_iname_L1000'], inplace=True)
for col in ['pert_iname_L1000', 'moa_L1000', 'pert_iname_cell_painting', 'moa_cell_painting']:
df_pertinfo[col] = df_pertinfo[col].apply(lambda x: x.lower())
df_pertinfo.rename(columns={"broad_id": "pert_id", "pert_iname_L1000": "pert_iname",
"moa_L1000": "moa"}, inplace = True)
df_pertinfo.drop(['pert_iname_cell_painting', 'moa_cell_painting'], axis = 1, inplace = True)
return df_pertinfo
df_pert_info = merge_align_moa(data_dir, cp_moa_dataset)
df_pert_info.shape
def construct_lvl5_df(data_dir, consensus_lvl5_file, df_pertinfo):
"""
This function returns L1000 level-5 dataframe with samples
that consist of expression values of 978 landmark genes with some
additional metadata information.
params:
data_dir: directory that contains all L1000 files
consensus_lvl5_file: L1000 level-5 (.gctx) file
df_pertinfo: dataframe with aligned L1000 MOA metadata pertubation information.
Returns:
lvl5_data: L1000 level-5 dataframe consisting of expression
values of 978 landmark genes and metadata information.
"""
lvl5_data = parse(os.path.join(data_dir, consensus_lvl5_file))
df_metalvl_5 = pd.read_csv(os.path.join(data_dir, 'col_meta_level_5_REP.A_A549_only_n9482.txt'), delimiter = "\t")
lvl5_data.data_df.rename_axis(None, inplace = True)
lvl5_data = lvl5_data.data_df.T
lvl5_data.rename_axis(None, inplace = True)
df_meta_features = df_metalvl_5[['sig_id', 'pert_id', 'pert_idose']].copy()
df_meta_features['dose'] = df_meta_features['pert_idose'].map({'-666' : 0, '0.04 uM' : 1, '0.12 uM' : 2, '0.37 uM' : 3,
'1.11 uM' : 4, '3.33 uM' : 5, '10 uM' : 6, '20 uM' : 7})
df_meta_features = pd.merge(df_meta_features, df_pertinfo, on='pert_id')
lvl5_data.reset_index(inplace = True)
lvl5_data.rename(columns={"index": "sig_id"}, inplace = True)
lvl5_data = pd.merge(lvl5_data, df_meta_features, on='sig_id')
return lvl5_data
# L1000 LEVEL 5 Data:
#
# - 'level_5_modz_n9482x978.gctx',
# - 'level_5_rank_n9482x978.gctx'
df_lvl5 = construct_lvl5_df(data_dir, 'level_5_modz_n9482x978.gctx', df_pert_info)
df_lvl5.shape
# ### - Remove highly correlated landmark genes and samples with Null MOAs
def feature_selection(df_data):
"""
Perform feature selection by dropping columns with null MOAs values,
and highly correlated landmark genes from the data.
params:
df_data: L1000 level-5 dataframe
Returns:
df_data: refined L1000 level-5 dataframe
"""
df_data_genes = df_data.drop(['pert_id', 'dose', 'pert_iname', 'moa', 'sig_id'], axis = 1).copy()
df_data_corr = df_data_genes.corr(method = 'spearman')
drop_cols = []
n_cols = len(df_data_corr.columns)
for i in range(n_cols):
for k in range(i+1, n_cols):
val = df_data_corr.iloc[k, i]
col = df_data_corr.columns[i]
if abs(val) >= 0.8:
drop_cols.append(col)
df_data.drop(set(drop_cols), axis = 1, inplace = True)
df_data.drop(df_data[df_data['moa'].isnull()].index).reset_index(drop = True, inplace = True)
return df_data
df_lvl5 = feature_selection(df_lvl5)
df_lvl5.shape
# ### - Get the median scores for the MOAs based on the correlation values of cpds in the same MOAs
def get_median_score(moa_list, df_dose, df_cpd_agg):
"""
Get the correlation values between compounds of each MOA,
then calculate the median of these correlation values
and assign it as the "median score" of the MOA.
params:
moa_list: list of distinct moas for a particular dose
df_dose: merged consensus and moa dataframe of a partcular dose
df_dose_corr: merged consensus and moa dataframe of compound correlations of a particular dose
Returns:
moa_med_score: Dict with moa as the keys, and their median scores as the values
moa_cpds: Dict with moa as the keys, and the list of moa for each moa as the values
"""
moa_cpds = {}
moa_median_score = {}
for moa in moa_list:
cpds = df_dose['pert_iname'][df_dose['moa'] == moa].unique().tolist()
moa_cpds[moa] = cpds
##taking correlation btw cpds for each MOA
df_cpds = df_cpd_agg.loc[cpds]
cpds_corr = df_cpds.T.corr(method = 'spearman').values
if len(cpds_corr) == 1:
median_val = 1
else:
median_val = median(list(cpds_corr[np.triu_indices(len(cpds_corr), k = 1)]))
moa_median_score[moa] = median_val
return moa_median_score, moa_cpds
def check_moa(moa_med_score, moa_cpds, df_moa):
"""
Check if all distinct moas in the moa_consensus dataframe (df_moa)
are in moa_med_score & moa_cpd, if not add them as keys and give them
a null value as the size for moa_med_score and also as values for moa_cpds.
params:
moa_med_score: Dict with moa as the keys, and their median scores as the values
moa_cpds: Dict with moa as the keys, and the list of moa for each moa as the values
data_moa: merged consensus and moa df with moas
Returns:
moa_med_score: Dict with moa as the keys, and their median scores as the values
moa_cpds: Dict with moa as the keys, and the list of moa for each moa as the values
"""
moa_list = df_moa['moa'].unique().tolist()
moa_keys = moa_med_score.keys()
for moa in moa_list:
if moa not in moa_keys:
moa_med_score[moa] = np.nan
moa_cpds[moa] = np.nan
return moa_med_score, moa_cpds
def get_moa_medianscores(df_moa):
"""
Generate a dataframe of distinct moas with their median scores and
corresponding list of compounds for different doses.
params:
df_moa: merged consensus and moa dataframe
Returns:
df_moa_med_score: dataframe of distinct moas with their corresponding median scores
and list of compounds for all doses.
"""
dose_list = list(set(df_moa['dose'].unique().tolist()))[1:]
for dose in dose_list:
df_dose = df_moa[df_moa['dose'] == dose].copy()
df_cpd_agg = df_dose.groupby(['pert_iname']).agg(['mean'])
df_cpd_agg.columns = df_cpd_agg.columns.droplevel(1)
df_cpd_agg.rename_axis(None, axis=0, inplace = True)
df_cpd_agg.drop(['dose'], axis = 1, inplace = True)
dose_moa_list = df_dose['moa'].unique().tolist()
#get the median of the corr values of the cpds for each MOA
dose_moa_med_score, dose_moa_cpds = get_median_score(dose_moa_list, df_dose, df_cpd_agg)
#check if all moa in the df_moa is present in the dose_moa
dose_moa_med_score, dose_moa_cpds = check_moa(dose_moa_med_score, dose_moa_cpds, df_moa)
sorted_moa_med_score = {key:value for key, value in sorted(dose_moa_med_score.items(), key=lambda item: item[0])}
sorted_dose_cpds = {key:value for key, value in sorted(dose_moa_cpds.items(), key=lambda item: item[0])}
if dose == 1:
df_moa_med_score = pd.DataFrame.from_dict(sorted_moa_med_score, orient='index', columns = ['dose_1'])
else:
df_moa_med_score['dose_' + str(dose)] = sorted_moa_med_score.values()
df_moa_med_score['moa_cpds_dose_' + str(dose)] = list(sorted_dose_cpds.values())
return df_moa_med_score
df_moa_median_scores = get_moa_medianscores(df_lvl5)
df_moa_median_scores.shape
# ### - Exclude MOAs with median score 1 and only null values and also columns with only null values
#
# #### The reason why we are excluding MOAs with median value == 1, is because they have only ONE compound and as a result the median correlation value will be just 1, and there will not be differences in values btw different doses.
def exclude_moa(df_moa_med_score):
"""
Exclude MOAs with median score 1 and columns with only null values.
params:
df_moa_med_score: dataframe of distinct moas with their corresponding median scores
and list of compounds for all doses.
Returns:
df_moa_medians: dataframe of distinct moas with NO median values/scores of 1
and their corresponding list of compounds for all doses.
"""
moa_with_med_index = []
for moa in df_moa_med_score.index.tolist():
moa_values = df_moa_med_score.loc[moa]
if all(y != 1.0 for y in moa_values):
moa_with_med_index.append(moa)
df_moa_medians = df_moa_med_score.loc[moa_with_med_index]
null_columns = [col for col in df_moa_medians.columns
if all(df_moa_medians[col].isnull())]
null_moas = [moa for moa in df_moa_medians.index
if all(df_moa_medians.loc[moa].isnull())]
df_moa_medians.drop(null_columns, axis = 1, inplace = True)
df_moa_medians.drop(null_moas, axis = 0, inplace = True)
return df_moa_medians
df_moa_medn_scores = exclude_moa(df_moa_median_scores)
df_moa_medn_scores.isnull().sum()
df_moa_medn_scores.shape
def seperate_cpds_values(df_moa_medians):
"""
Seperate the list of compunds columns from the median values columns in
moa_median_dataframe
params:
df_moa_medians: dataframe of distinct moas with NO median scores of 1
and their corresponding list of compounds for all doses.
Returns:
df_moa_cpds: dataframe of distinct moas with only their corresponding
list of compounds for all doses.
df_moa_values: dataframe of distinct moas with only their median scores for all doses.
"""
dose_cols = [col for col in df_moa_medians.columns.tolist()
if (col.startswith("dose_"))]
df_moa_cpds = df_moa_medians.drop(dose_cols, axis = 1)
df_moa_values = df_moa_medians.loc[:, dose_cols].copy()
df_moa_values = df_moa_values.reset_index().rename(columns={"index": "moa"})
df_moa_cpds = df_moa_cpds.reset_index().rename(columns={"index": "moa"})
return df_moa_cpds, df_moa_values
df_moa_cpds, df_moa_vals = seperate_cpds_values(df_moa_medn_scores)
def get_moa_size(df_moa_cpds, df_moa_values):
"""
This function computes the number of compunds in each MOA
i.e. moa_size and returns dataframe including the moa_size column
params:
df_moa_cpds: dataframe of distinct moas with only their corresponding
list of compounds for all doses.
df_moa_values: dataframe of distinct moas with only their median scores for all doses.
Returns:
df_moa_cpds: dataframe of distinct moas with only their corresponding
list of compounds for all doses including moa_size column.
df_moa_values: dataframe of distinct moas with only their median scores
including moa_size column for all doses.
"""
df_moa_cpd_copy = df_moa_cpds.set_index('moa').rename_axis(None, axis=0).copy()
num_col = len(df_moa_cpd_copy.columns)
moa_count = {}
for moa in df_moa_cpd_copy.index:
col_sum = 0
for col in df_moa_cpd_copy.columns:
col_sum += len(df_moa_cpd_copy.loc[moa, col])
moa_count[moa] = round(col_sum/num_col)
df_moa_cpds['moa_size'] = moa_count.values()
df_moa_values['moa_size'] = moa_count.values()
return df_moa_cpds, df_moa_values
df_moa_cpds, df_moa_vals = get_moa_size(df_moa_cpds, df_moa_vals)
df_moa_cpds.head()
df_moa_vals.head(10)
def check_moas_cpds_doses(df_moa_cpds):
"""
check if moas have the same compounds in all doses,
and return the moas that don't have the same numbers of compounds.
params:
df_moa_cpds: dataframe of distinct moas with only their corresponding
list of compounds for all doses.
Returns:
df_moa_not_equals_cpds: dataframe of moas that don't have the same numbers of
compounds in all doses.
"""
df_moa_cpds = df_moa_cpds.set_index('moa').rename_axis(None, axis=0).copy()
df_moa_cpds.drop(['moa_size'], axis=1, inplace = True)
moas_with_no_equal_cpds = [moa for moa in df_moa_cpds.index
for num in range(len(df_moa_cpds.columns) - 1)
if not ((df_moa_cpds.loc[moa, df_moa_cpds.columns[num]])
== (df_moa_cpds.loc[moa, df_moa_cpds.columns[num+1]]))]
df_moa_not_equals_cpds = df_moa_cpds.loc[set(moas_with_no_equal_cpds)]
return df_moa_not_equals_cpds
data_moa_not_equals_cpds = check_moas_cpds_doses(df_moa_cpds) ##MOAs with not the same cpds in all doses
data_moa_not_equals_cpds.shape
# ### - MOAS that do not have the same number of/same compounds in all Doses
for moa in data_moa_not_equals_cpds.index:
print(moa)
for idx, cols in enumerate(data_moa_not_equals_cpds.columns):
print('Dose ' + str(idx+1) +':', data_moa_not_equals_cpds.loc[moa, cols])
print('\n')
# ### - Save dataframes to .csv files
def conv_list_to_str_cols(df_moa_cpds):
"""This function convert columns values that are lists to strings"""
moa_cpd_cols = [col for col in df_moa_cpds.columns.tolist()
if (col.startswith("moa_cpds_"))]
df_moa_cpds_nw = df_moa_cpds.copy()
for col in moa_cpd_cols:
df_moa_cpds_nw[col] = df_moa_cpds_nw[col].apply(lambda row: ';'.join(map(str, row)))
return df_moa_cpds_nw
def save_to_csv(df, path, file_name):
"""saves moa dataframes to csv"""
if not os.path.exists(path):
os.mkdir(path)
df.to_csv(os.path.join(path, file_name), index = False)
save_to_csv(df_lvl5, 'moa_sizes_consensus_datasets', 'modz_level5_data.csv')
save_to_csv(df_moa_vals, 'moa_sizes_consensus_datasets', 'modz_moa_median_scores.csv')
save_to_csv(conv_list_to_str_cols(df_moa_cpds), 'moa_sizes_consensus_datasets', 'L1000_moa_compounds.csv')
|
1.Data-exploration/Consensus/L1000/L1000_moas_median_scores_calculation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import molsysmt as msm
molecular_system = msm.convert('1tcd.mmtf')
msm.info(molecular_system, target='atom', indices=[7,8,9,10,11,12])
msm.info(molecular_system, target='atom', selection='group.index==6')
msm.info(molecular_system, target='group', indices=[20,21,22,23])
msm.info(molecular_system, target='component', selection='molecule.type!="water"')
msm.info(molecular_system, target='chain')
msm.info(molecular_system, target='component', selection='molecule.type!="water"')
msm.info(molecular_system, target='molecule', selection='molecule.type!="water"')
msm.info(molecular_system, target='entity')
msm.info(molecular_system)
|
sandbox/Test_MolSysMT_Info.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Deep Learning Explained
#
# # Module 5 - Lab - Optimization for Neural Network Training
#
# ## 1.0 Introduction
#
# Deep neural networks are trained by **learning** a set of weights. The optimal weights are learned by **minimizing the loss function** for the neural network. This minimization is performed using an **optimization algorithm**. Thus, optimization algorithms are an essential component in your neural network tool box.
#
# In this lesson you will become familiar with the basic optimization algorithms used to train deep neural networks, along with their pitfalls. The nonlinear nature of neural networks leads to several serious problems with local gradients. As a result of the multiple nonlinearities the local gradient can exhibit complex behavior. Further, the local gradient can be quite different from the larger-scale global behavior of the loss function gradient.
#
# The high dimensionality of the neural network training optimization problems makes detailed understanding of optimization behavior extremely difficult. There is one dimension for each model weight (parameter). Thus, the optimization is performed over a non-linear surface with millions of dimensions. Despite several decades of research, much of the measurable progress has been based on empirical experience rather than theory.
#
# ### 1.1 Local convergence of optimization algorithms
#
# In an ideal case, a minimization problem is **convex**. By convex, we mean that the gradient always points in the direction of the **global minimum** of the loss function. Unfortunately, with nonlinear optimization problems, like neural network training, there is no guarantee that the minimization problem is convex. Further the loss function can have multiple **local minimum**.
#
# The foregoing not withstanding, the minimum of the loss function will at least be convex locally. To understand the behavior of a loss function around a minimum we can expand it as a second order Taylor series of the change in the weights from optimization step $l$ to $l+1$:
#
# $$J(W^{(l+1)}) = J(W^{(l)}) + (W^{(l+1)} - W^{(l)})\vec{g} + \frac{1}{2}(W^{(l+1)} - W^{(l)})^T H (W^{(l+1)} - W^{(l)}) $$
#
# where,
# $W^{(l)}$ is the tensor of weights at step $l$,
# $\vec{g}$ is the gradient vector,
# $H$ is the **Hessian** matrix.
#
# The Hessian is a matrix of second partial derivatives. You can think of the Hessian as being the rate of change of the gradient or the gradient of the gradient. For a vector gradient $f(\vec{x})$ the Hessian is:
#
# $$H \big(f(\vec{x}) \big) = \begin{bmatrix}
# \frac{\partial^2 f(\vec{x})}{\partial x^2_1} &
# \frac{\partial^2 f(\vec{x})}{\partial x_2 \partial x_1} &
# \cdots &
# \frac{\partial^2 f(\vec{x})}{\partial x_n \partial x_1}\\
# \frac{\partial^2 f(\vec{x})}{\partial x_1 \partial x_2} &
# \frac{\partial^2 f(\vec{x})}{\partial x^2_2} &
# \cdots &
# \frac{\partial^2 f(\vec{x})}{\partial x_1 \partial x_n}\\
# \vdots & \vdots & \vdots & \vdots \\
# \frac{\partial^2 f(\vec{x})}{\partial x_1 \partial x_n} &
# \frac{\partial^2 f(\vec{x})}{\partial x_2 \partial x_n} &
# \cdots &
# \frac{\partial^2 f(\vec{x})}{\partial x^2_n}
# \end{bmatrix}$$
#
# The Hessian has several useful properties.
#
# - The Hessian is symmetric, since $\frac{\partial^2 f(\vec{x})}{\partial x_1 \partial x_2} = \frac{\partial^2 f(\vec{x})}{\partial x_2 \partial x_1}$.
# - If the eigenvalues of the Hessian are all positive, the curvature of the gradient is upward, indicating a minimum point in $f(\vec{x})$. The optimization is convex, at least locally. In this case we say the Hessian is **positive definite**.
# - If the eigenvalues of the Hessian are all negative, the curvature of the gradient is downward, indicating and maximum point in $f(\vec{x})$. In this case we say the Hessian is **negative definite**.
# - A Hessian with mixed sign eigenvalues indicates gradient with upward curvature in some dimensions and downward curvature in other dimensions. This situation with mixed curvature is known as a **saddle point**.
# - For a Gaussian process the Hessian is the inverse of the covariance matrix. The eigenvalues of each matrix are just the inverse of the other.
#
# For a step size $\alpha$ we can rewrite the first equation as:
#
# $$J(W^{(l)}- \alpha \vec{g}) = J(W^{(l)}) - \alpha \vec{g}^T \vec{g} + \frac{1}{2} \alpha^2 \vec{g}^T H \vec{g}$$
#
# The minimum point of $J(W^{(l)}- \alpha \vec{g})$ occurs were the gradient is zero in all dimensions. This is evident from the fact that at this point:
# $$J(W^{(l)}) = J(W^{(l)}- \alpha \vec{g})$$
#
# From this point no further reduction in the loss function is possible. The optimal step size for the quadratic approximation is then:
#
# $$\alpha^* = \frac{\vec{g}^T \vec{g}}{\vec{g}^T H \vec{g}}$$
#
# But, what happens if the Hessian is not well behaved? One measure of 'behavior' for a Hessian is the **condition number**:
#
# $$\kappa(H) = \frac{|\lambda_{max}(H)|}{|\lambda_{min}(H)|}$$
#
# where,
# $|\lambda_{max}(H)|$ is the absolute value of the largest eigenvalue of H.
# $|\lambda_{min}(H)|$ is the absolute value of the smallest eigenvalue of H.
#
# The condition number of the Hessian has serious implications for the rate of convergence of optimization algorithms. If the condition number is small, the Hessian is well conditioned and the gradient has similar scale in all dimensions. This happy situation leads to rapid convergence. An ideal condition number is close to 1.
#
# However, if the Hessian is **ill-conditioned**, having a large condition number, the scale of the gradient will be quite different in different dimensions. An optimization algorithm will converge quickly along eigenvector directions corresponding to large eigenvalues. However, convergence will be slow along the direction of eigenvectors with small eigenvalues. This situation has been described as slowly meandering down a long narrow valley. In fact, for real-world stochastic problems (e.g. noisy data), the optimization algorithm may not converge at all along some eigenvector directions!
# ### 1.2 Multimodal loss function and global optimization
#
# The nonlinear nature of the hidden layers can lead to loss functions with significant local structure in a high dimensional space. Given this complexity, it is quite possible there are local minimum, local maximum, or saddle points. In general, there is no guarantee that the global minimum of the objective function can ever be found.
#
# In the early days of neural network research it was generally thought that loss function minimization got 'stuck' at local minimum or saddle points. However, recent experience indicates that this may not be the case. In many real-world cases, the training loss function continues to decrease with epochs. If the optimization algorithm were stuck, this could not be the case. We have explored this behavior in previous lessons.
#
# Continued convergence of the optimization process does not mean that convergence will be rapid. Empirical experience indicates that slow convergence is a common problem. This situation occurs when the Hessian of the loss function is ill-conditioned.
# ### 1.3 Vanishing and exploding gradients
#
# Some common pitfalls of deep neural network loss functions are **vanishing gradients** and **exploding gradients**. Vanishing gradients arise when multiple small gradients are encountered in backpropagation. Exploding gradients arise when rapid changes in the loss function, sometimes referred to as **cliffs**, are encountered in the loss function.
#
# A deep linear model analogy can aid in understanding vanishing gradients. In this simple model each layer has the same weights, represented by the tensor $W$. We can compute an eigenvalue-eigenvector decomposition of $W$:
#
# $$W = Q \Lambda Q^T$$
# where,
# $Q$ is the unitary eigenvector matrix,
# $\Lambda$ is the diagonal matrix of eigenvalues.
#
# At the nth layer a signal entering the top of the network will be weighted by $W^n$ which we can write:
#
# $$W^n = \big( Q \Lambda Q^T \big)^n = Q \Lambda^n Q^T$$
#
# In order to have a stable network all the eigenvalues must be less than 1. Therefore $\Lambda^T$ is a diagonal matrix of increasingly small numbers as $n$ increases. The net effect is that gradients from deep in the networks can be exponentially smaller than from shallow layers. When the backpropagation is applied, the gradient effectively vanishes toward 0.
#
# Exploding gradients arise from sudden changes in curvature of the loss function. Encountering these 'cliffs' results in a gradient descent algorithm overshooting the minimum point, sometimes by an extreme amount. The Hessian represents the curvature of the loss function or the rate of change of the gradient. The eigen-decomposition of the Hessian:
#
# $$H(J(W)) = Q \Lambda Q^T = Q diag(\lambda) Q^T$$
#
# Consider what happens when the loss function has high local curvature. At one optimization step, the eigenvalues $diag(\lambda)$ are all small and well behaved. The Hessian has a small condition number. At the next step the eigenvalues can become enormous (much greater than 1), since the curvature of the loss function is changing so rapidly. Since only some eigenvalues grow large, the condition number becomes extremely large. This leads to the exploding gradient!
#
# Fortunately, there is a simple solution the exploding gradient problem, **gradient clipping**. As the name implies, gradient clipping is nothing more than imposing a hard maximum constraint on the gradient. In practice, this simple algorithm has proven to be quite effective.
#
# ***
# **Note:** All optimizers in Keras have parameters to clip individual weights or the norm of the gradient.
# ***
# ### 1.4 Flat spots
#
# With complex loss function it is common to have regions that are **flat**. These reasons are often called **plateaus**. In other words, areas with negligible gradient. These regions can result in extremely slow learning. There are a number of solutions for this problems. The learning rate can be increased or momentum can be used. These approaches are discussed later in this lesson.
#
# ****
# **Note:** Keras has a callback that can be used to take action when slow learning is encountered.
# ****
# ## 2.0 Batch gradient descent for backpropagation
#
# Recall, that we train neural networks using the **backpropagation** algorithm. The backpropagation algorithm requires several components:
#
# 1. A **loss function** to measure how well our representation matches the function we are trying to learn.
# 2. A method to propagate changes in the representation (weights) through the complex network For this we will use the **chain rule of calculus** to compute **gradients** of the representation. In the general case, this process requires using automatic differentiation methods.
# 3. An **optimization algorithm** that uses the gradients to minimize the loss function.
#
# The backpropagration algorithm learns the optimal weights for the neural network by taking small steps in the direction of the **local gradient**. By *local gradient* we mean the gradient of $J(W)$ computed at each set of weights $W$ as the algorithm proceeds.
#
# Once we have the gradient of the loss function we can update the tensor of weights using the formulation below.
#
# $$W_{t+1} = W_t + \alpha \nabla_{W} J(W_t) $$
# where
# $W_t = $ the tensor of weights or model parameters at step $t$.
# $\alpha\ = $ step size or learning rate.
# $J(W) = $ loss function given the weights.
# $\nabla_{W} J(W) = $ gradient of $J$ with respect to the weights $W$.
#
# It should be evident that the back propagation algorithm is a form of gradient descent. The weights are updated in small steps following the local gradient of $J(W)$ down hill. At the **termination condition** $J(W)$ should be at or very near the minimum possible value.
#
#
# ### 2.1 Compuational example
#
# The basic idea is simple, but actually optimizing a complex neural network is another matter altogether. To demonstrate the concept, we will work on a very simple 2-d problem. The loss function in this case is the mean square error (MSE). So, in effect, the minimum MSE is the same as the maximum likelihood (MLE) solution.
#
# The loss function for a Gaussian process is:
#
# $$J(\hat{x}) = \frac{1}{N} \sum_{i = 1}^{N} \big( \vec{x}_i - \hat{x} \big)^2$$
#
# where;
# $x = $ the sample data, which is a 2d tensor in this case of dimension $N x 2$ where $N$ is the number of samples,
# $\hat{x} = $ the vector of means we want to estimate.
#
# We can compute the gradient for each dimension of as follows:
#
# $$\frac{ \partial \hat{x}}{ \partial x_j} = \frac{2}{N} \sum_{i = 1}^{N} \big( x_{ij} - \tilde{x}_j \big)$$
#
# where,
# $x_j = $ the jth dimension of $\vec{x}$,
# $x_{ij} = $ the ith component of the jth dimension of $\vec{x}$,
# $\tilde{x}_i = $ is the current estimate of ith component of $\hat{x}$.
#
# Execute the code in the cell below to load the packages required to execute the rest of this notebook.
# +
import keras
from keras.datasets import mnist
import keras.utils.np_utils as ku
import keras.models as models
import keras.layers as layers
from keras import regularizers
from keras.layers import Dropout
from keras import optimizers
import numpy as np
import numpy.random as nr
from tensorflow import set_random_seed
import numpy.linalg as nll
import sklearn.model_selection as ms
import time
import matplotlib.pyplot as plt
import math
# %matplotlib inline
# -
# The code in the cell below simulates a bivariate Normal distribution with high covariance between the two dimensions. Execute this code.
# +
cov = np.array([[1.0, 0.99], [0.99, 1.0]])
mean = np.array([1.0, 2.0])
nr.seed(9911)
sample = nr.multivariate_normal(mean, cov, 1000)
sample.shape
# -
# As already mentioned, for a Gaussian process, the covariance matrix is the inverse of the Hessian. This means that both matrices have the same condition number. The code in the cell below computes and displays the eigenvalues of the covariance matrix and the condition number. Execute this code and examine the result.
eigenvalues = nll.eig(cov)[0]
print('Eigenvalues = ' + str(eigenvalues))
print('The condition number = ' + str(eigenvalues[0]/eigenvalues[1]))
# The covariance matrix has a high condition number. This optimization problem will deliberately strain the algorithms.
#
# ****
# **Note:** In a real-world problem, this condition number can be improved by simple Z-Score scaling. However, for the purpose of demonstration we will skip this step.
# ****
#
# Next, execute the code in the cell below to plot the simulated data and examine the result.
plt.scatter(sample[:,0], sample[:,1])
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.title('Sample data')
# With the simulated data prepared, it is time to try gradient descent! The code in the cell below implements a basic **batch gradient descent** algorithm. This algorithm is considered batch gradient descent since all of the cases are used to compute each update of the gradient.
#
# The work is done in the `while` loop. The termination condition is the l2 norm of the gradient is less than a set value or the maximum number of iterations has been executed. The learning rate is fixed for each optimization step. An array is output at the end that gives the path history of the optimizer.
#
# Execute this code and examine the result.
# +
def compute_gradient(x, estimate):
mult = 2.0/x.shape[0]
diff = np.subtract(x, estimate)
return mult * np.sum(diff, axis = 0)
def grad_descent(x, estimate, lr, stopping, max_its = 100):
out = estimate
out = out.reshape((1,2))
err = 10000000.0 ## starting criteria for graident metric
i = 1
while(err > stopping and i < max_its):
grad = compute_gradient(x, estimate)
estimate = estimate + lr * grad
out = np.append(out, estimate.reshape((1,2)))
err = np.std(grad)
i = i + 1
out = out.reshape((i, 2))
print('Number of iterations = ' + str(i))
print('Final gradient value = ' + str(np.std(grad)))
print('MLE = ' + str(out[i-1:]))
return out
lr = 0.1
stopping = 0.01
start = np.array([0.0,0.0])
steps = grad_descent(sample, start, lr, stopping)
# -
# The optimizer appears to have converged to reasonable values in a small number of steps. The MLE can be compared to the location values used in the simulation, $\{1.0, 2.0 \}$.
#
# Next execute the code in the cell below to visualize the trajectory taken by the optimizer. The red points in the plot show the solutions found at each step of the gradient descent algorithm.
# +
def plot_descent(x, steps):
plt.scatter(x[:,0], x[:,1])
plt.scatter(steps[:,0], steps[:,1], color = 'red')
plot_descent(sample, steps)
# -
# The path of convergence looks good. You can see that the rate of convergence of each optimization step decreases as the algorithm approaches convergence. This is expected, since the gradient is decreasing as the optimizer converges.
# ************************
# **Exercise 1:** All gradient dsecent algorithms are sensitive to the learning rate. Now, you will investigate the effect of using an aggressive, or large, learning rate. In the cell below, create and execute the code to apply the gradient descent algorithm with a learning rate of 0.9 and plot the result. Make sure you set a `numpy.random` seed of 9777.
# +
nr.seed(9777)
lr = 0.9
start = np.array([0.0,0.0])
steps = grad_descent(sample, start, lr, stopping, max_its = 1000)
plot_descent(sample, steps)
# -
# Next, you will try a very small learning rate. In the cell below create and execute the code to apply the gradient descent algorithm with a learning rate of 0.01. Use the argument `max_its = 1000` to ensure the algorithm converges. Make sure you set a numpy.random seed of 8888.
# +
nr.seed(8888)
lr = 0.01
start = np.array([0.0,0.0])
steps = grad_descent(sample, start, lr, stopping, max_its = 1000)
plot_descent(sample, steps)
# -
# Notice the differences in convergence properties of the batch gradient descent algorithm and compare them to the algorithm with learning rate of 0.1
# ## 3.0 Stochastic gradient descent
#
# The **stochastic gradient descent (SGD)** algorithm (Nemirovshi and Yudin, 1978) is the workhorse of deep neural network training. As opposed to batch gradient descent, SGD computes the expected gradient using a **mini-batch** Bernoulli sampled from the full set of cases. Mini-batch optimization is often referred to as **online optimization** since the optimizer algorithm can update the solution as cases arrive.
#
# The basic idea of stochastic optimization is using a Bernoulli random sample of the data to estimate the **expected value** of the weights. The weight update for SGD then becomes:
#
# $$W_{t+1} = W_t + \alpha\ E_{\hat{p}data}\Big[ \nabla_{W} J(W_t) \Big]$$
#
# where,
# $E_{\hat{p}data} \big[ \big]$ is the expected value of the gradient given the Bernoulli sample of the data $\hat{p}data$.
#
# Since the SGD algorithm works on mini-batches, it is highly scalable when compared to the batch gradient descent. The later must keep all cases in memory.
#
# Choosing batch size can require some tuning. If the batch is too small, the gradient estimate will be poor. Further, hardware resources will not be fully utilized. Large batches require significant memory. Further, large batches can slow down the computation of each gradient step.
#
# Empirically, SGD has good convergence properties. This behavior seems to arise since the mini-batch samples provide a better exploration of the loss function space. It seems to be the case that the variations in the gradient from one mini-batch sample to another help the algorithm escape from saddle points or other areas of the loss function with poor convergence properties. In fact, for very large datasets, the SGD algorithm often converges before the first pass through the data is completed.
#
# The pseudo code for the SGD algorithm is:
#
# `Random_sort(cases)
# while(grad > stopping_criteria):
# mini-batch = sample_next_n(cases)
# grad = compute_expected_grad(mini_batch)
# weights = update_weights(weights, grad)`
#
# Notice that if the sampling continues for more than one cycle through the cases, the samples are biased. In practice, this small bias does not seem to mater much.
# ### 3.1 Example of basic SGD
#
# The code in the cell below implements a basic SGD algorithm. The code is nearly identical to the batch gradient descent function. The only difference is the Bernoulli sampling using `numpy.random.choice`.
#
# Execute this code and examine the result.
# +
def sgd(x, estimate, lr, stopping, batch_size = 10, max_its = 100):
out = estimate
out = out.reshape((1,2))
err = 10000000.0 #
# starting criteria for graident metric
i = 1
indx = range(x.shape[0])
while((err > stopping) and (i < max_its)):
sample_idx = nr.choice(indx, batch_size)
grad = compute_gradient(x[sample_idx,:], estimate)
estimate = estimate + lr * grad
out = np.append(out, estimate.reshape((1,2)))
err = np.std(grad)
i = i + 1
out = out.reshape((i, 2))
print('Number of iterations = ' + str(i))
print('Final gradient value = ' + str(np.std(grad)))
print('MLE = ' + str(out[i-1:]))
return out
nr.seed(7788)
lr = 0.1
stopping = 0.01
#start = np.array([5.0,-1.0])
start = np.array([0.0,0.0])
steps = sgd(sample, start, lr, stopping)
# -
# The SGD algorithm converges to nearly the same result in a similar number of steps as the batch gradient descent algorithm. Using mini-batches has not changed the result significantly.
#
# Next, execute the code in the cell below to visualize the optimization trajectory. The red points in the plot show the solutions found using each mini-batch in the steps of the SGD algorithm.
plot_descent(sample, steps)
# Compare the trajectory of the SGD optimizer to the batch gradient descent optimizer. In appears that th SGD optimizer converges faster initially, but then seems to wander a bit near convergence. This makes sense, since the expected gradient from the small mini-batches is likely to be noisier than the batch gradient.
# *********
# **Exercise 2:** The mini-batch size is a hyperparameter of all stochastic gradient descent algorithms. Selecting an appropriate mini-batch size can effect both convergence and computational performance. To explore this effect, in the code below repeat the the SGD calculation using a mini-batch size of 1. Set a `numpy.random` seed of 9944.
nr.seed(9944)
# Compare these results to those with a larger mini-batch size. Notice that the differences are subtle, as in general SGD is fairly insensitive to mini-batch size.
# ### 3.2 Adding momentum to SGD
#
# With a poorly conditioned loss function, SGD is known to 'zig-zag' back and forth as the optimizer moves toward convergence. This problem can be severe in some case, leading to many wasted optimization steps that provide only minimal reduction in the loss function at best. To overcome this problem, in 1988 paper Rummelhart, et. al., proposed adding a **momentum** term to the gradient update.
#
# Recall from Newtonian mechanics that $momentum = m \cdot v$, where $m$ is the mass and
#
# $v$ is the velocity
#
# If we assume that $m = 1$ then momentum is the same as velocity. The model weight update then becomes a weighted sum of velocity (momentum) and the gradient:
#
# $$v^{(l)} = momentum \cdot v^{(l - 1)} + lr \cdot \nabla_{W} J(W^{(l)})\\
# W^{(l+1)} = W^{(l)} + v^{(l)}$$
# where,
# $v^{(l)}$ is the velocity at step $l$,
# $momentum$ is the momentum multiplier,
# $lr$ is the learning rate.
#
# The code in the cell below implements a basic version of the SGD algorithm with momentum. The algorithm is identical to ordinary SGD except for the update of the weight estimate.
#
# Execute this code and examine the result.
# +
def sgd_momentum(x, estimate, lr, stopping, momentum, batch_size = 8, max_its = 100):
out = estimate
out = out.reshape((1,2))
v = np.zeros((1, x.shape[1]))
err = 10000000.0 ## starting criteria for graident metric
i = 1
indx = range(x.shape[0])
while((err > stopping) and (i < max_its)):
sample_idx = nr.choice(indx, batch_size)
grad = compute_gradient(x[sample_idx,:], estimate)
v = momentum * v + lr * grad
estimate = estimate + v
out = np.append(out, estimate.reshape((1,2)))
err = np.std(grad)
i = i + 1
out = out.reshape((i, 2))
print('Number of iterations = ' + str(i))
print('Final gradient value = ' + str(np.std(grad)))
print('MLE = ' + str(out[i-1:]))
return out
nr.seed(2288)
lr = 0.1
stopping = 0.01
#start = np.array([5.0,-1.0])
start = np.array([0.0,0.0])
momentum = 0.1
steps = sgd_momentum(sample, start, lr, stopping, momentum)
# -
# These results are nearly identical to those obtained for the basic SGD algorithm. Given the convex nature of the problem, this is not terribly surprising.
#
# Now, execute the code below to display and examine the trajectory of the optimization algorithm.
plot_descent(sample, steps)
# This result is largely the same as for the basic SGD algorithm.
# ### 3.3 SGD with Keras
#
# Keras has an extensive library of optimizers, including a full-featured SGD method. The Keras website has somewhat sparse [documentation on the available optimizers](https://keras.io/optimizers/), with references for some of the algorithms.
#
# As a first step before trying out the Keras SGD optimizer we need to create test and training data set in the form of numpy arrays. Execute the code in the cell below that does just this.
indx = range(sample.shape[0])
nr.seed(9988)
set_random_seed(5566)
indx = ms.train_test_split(indx, test_size = 100)
x_train = np.ravel(sample[indx[0],[0]])
y_train = np.ravel(sample[indx[0],[0]])
x_test = np.ravel(sample[indx[1],[1]])
y_test = np.ravel(sample[indx[1],[1]])
# With the data prepared we can get to work with training and testing the neural network model with the SGD optimizer. To create a problem where a neural network can be applied, we will solve the regression problem for the simulated data we have been using.
#
# The SGD optimizer in Keras has a number of arguments, including:
# - learning rate: `lr`,
# - gradient clipping: `clipnorm`,
# - decay rate: `decay`,
# - momentum: `momentum`.
#
# Examine the code below for details. Execute the code and examine the results.
# +
def plot_loss(history):
'''Function to plot the loss vs. epoch'''
train_loss = history.history['loss']
test_loss = history.history['val_loss']
x = list(range(1, len(test_loss) + 1))
plt.plot(x, test_loss, color = 'red', label = 'Test loss')
plt.plot(x, train_loss, label = 'Training loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss vs. Epoch')
plt.legend()
## First define the layers of the regression model.
nn = models.Sequential()
nn.add(layers.Dense(128, activation = 'relu', input_shape = (1, ),
kernel_regularizer=regularizers.l2(0.01)))
nn.add(Dropout(0.5))
nn.add(layers.Dense(128, activation = 'relu',
kernel_regularizer=regularizers.l2(0.01)))
nn.add(layers.Dense(1))
## Define the SGD optimizer
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.5, nesterov=False)
## The optimizer is used at the compile stage
nn.compile(optimizer = sgd, loss = 'mse', metrics = ['mae'])
## Define the callback list
filepath = 'my_model_file.hdf5' # define where the model is saved
callbacks_list = [
keras.callbacks.EarlyStopping(
monitor = 'val_loss', # Use accuracy to monitor the model
patience = 1 # Stop after one step with lower accuracy
),
keras.callbacks.ModelCheckpoint(
filepath = filepath, # file where the checkpoint is saved
monitor = 'val_loss', # Don't overwrite the saved model unless val_loss is worse
save_best_only = True # Only save model if it is the best
)
]
## Now fit the model
nr.seed(7658)
set_random_seed(5555)
start = time.time() ## Get the system time at strat of execution
history = nn.fit(x_train, y_train,
epochs = 40, batch_size = 1,
validation_data = (x_test, y_test),
callbacks = callbacks_list, # Call backs argument here
verbose = 0)
end = time.time() ## Get the system time at the end of execution
## Execution time is the difference between the end and start times
print('Execution time = ' + str(end - start))
## Visualize the outcome
plot_loss(history)
# -
# Notice that training loss continues to decrease even after test loss increases. This is a commonly observed behavior when training neural networks. The optimizer continues to reduce the training loss, even after the model is over-fit.
#
# We should check that the learned model actually makes sense. The code in the cell below predicts score values for the test dataset, prints the RMSE and plots the result. Execute this code and examine the outcome.
# +
def plot_reg(x, y_score, y):
ax = plt.figure(figsize=(6, 6)).gca() # define axis
## Get the data in plot order
xy = sorted(zip(x,y_score))
x = [x for x, _ in xy]
y_score = [y for _, y in xy]
## Plot the result
plt.plot(x, y_score, c = 'red')
plt.scatter(x, y)
predicted = nn.predict(x_test)
plot_reg(x_test, predicted, y_test)
print(np.std(predicted - y_test))
# -
# These results seem reasonable given the data.
# +
## First define the layers of the regression model.
nn = models.Sequential()
nn.add(layers.Dense(128, activation = 'relu', input_shape = (1, ),
kernel_regularizer=regularizers.l2(0.01)))
nn.add(Dropout(0.5))
nn.add(layers.Dense(128, activation = 'relu',
kernel_regularizer=regularizers.l2(0.01)))
nn.add(layers.Dense(1))
## Define the SGD optimizer
sgd = optimizers.SGD(lr=0.01, decay=1e-6, momentum=0.005, nesterov=False)
## The optimizer is used at the compile stage
nn.compile(optimizer = sgd, loss = 'mse', metrics = ['mae'])
## Now fit the model
nr.seed(5555)
set_random_seed(5577)
start = time.time() ## Get the system time at strat of execution
history = nn.fit(x_train, y_train,
epochs = 40, batch_size = 1,
validation_data = (x_test, y_test),
callbacks = callbacks_list, # Call backs argument here
verbose = 0)
end = time.time() ## Get the system time at the end of execution
## Execution time is the difference between the end and start times
print('Execution time = ' + str(end - start))
## Visualize the outcome
plot_loss(history)
# -
predicted = nn.predict(x_test)
plot_reg(x_test, predicted, y_test)
print(np.std(predicted - y_test))
# ## 4.0 Adaptive gradient descent algorithms
#
# Up until now, we have been worked with algorithms with constant learning rates. In many cases, the gradient of the loss function will change multiple times before convergence is achieved. For example, the gradient may decrease and then increase again. In these cases, a constant learning rate results in slow convergence. There are several possible approaches to changing learning rates of optimization algorithms.
#
# One simple approach is use **learning rate decay**. The learning rate decays from a starting value and decreases as the optimization proceeds. This approach is effective in cases where the gradient decreases fairly steadily as the optimization proceeds. The lower learning rate reduces the chance that the algorithm over-shoots the optimum point and then wanders around with slow convergence. We have seen this behavior in the foregoing SGD examples.
#
# The second approach is to use algorithms with an **adaptive learning rate**. As the name implies, adaptive learning rate algorithms change their rate of convergence depending on the gradient. Ideally, the learning rate should increase when plateaus and poorly conditioned areas of the loss function are encountered. The learning rate should decrease when the gradient of the loss function is better behaved. In practice, these ideals are hard to achieve and researchers have created many algorithms using various heuristics to adapt learning rate.
# ### 4.1 An example of adaptive learning, Adam
#
# The Adam algorithm (Kingma and Ba, 2014) uses a fairly complicated set of heuristics to adapt the learning rate. Adam uses both first and second order momentum measures. Second order momentum is analogous to kinetic energy in Newtonian mechanics. Further, Adam incorporates exponential decay in both momentum measures to ensure that more recent values dominate the learning rate updates.
#
# The code in the cell below implements a basic version of Adam. Examine this code for details, execute this code and check the results.
# +
def adam(x, estimate, lr, stopping, momentum, ke, batch_size = 32, max_its = 1000):
out = estimate
out = out.reshape((1,2))
s = np.zeros((1, x.shape[1]))
r = np.zeros((1, x.shape[1]))
grad_norm = 10000000.0 ## starting criteria for graident metric
i = 1
indx = range(x.shape[0])
while((grad_norm > stopping) and (i < max_its)):
sample_idx = nr.choice(indx, batch_size)
grad = compute_gradient(x[sample_idx,:], estimate)
s = momentum * s + (momentum - 1.0) * grad
s_tilde = s/(1 - momentum**i)
r = ke * r + (ke - 1.0) * np.multiply(grad, grad)
r_tilde = np.sqrt(np.abs(r/(1 - ke**i)))
delta = np.array([lr* ss/(rr + 0.000001) for ss, rr in zip(s_tilde, r_tilde)])
estimate = estimate - delta
out = np.append(out, estimate.reshape((1,2)))
grad_norm = np.std(grad)
i = i + 1
out = out.reshape((i, 2))
print('Number of iterations = ' + str(i))
print('Final gradient value = ' + str(np.std(grad)))
print('MLE = ' + str(out[i-1:]))
return out
nr.seed(5789)
lr = 0.1
stopping = 0.01
#start = np.array([5.0,-1.0])
start = np.array([0.0,0.0])
momentum = 0.1
ke = 0.1
steps = adam(sample, start, lr, stopping, momentum, ke)
# -
# These results are not too different from the SGD algorithms.
#
# Now, execute the code below and examine the results.
plot_descent(sample, steps)
# The trajectory of the Adam optimizer is considerably different than SGD. Notice how the trajectory 'zig-zags' toward convergence. This is likely the result of the poor conditioning of the problem.
# ***********
# **Exercise 3:** The value of so called kinetic energy hyperparameter must be determined. To explore the effect of changing this hyperparameter you will try a larger value. In the cell below create the code to compute the optimization and display the results using a kinetic energy value of 0.99. Set a `numpy.random` seed of 66789.
nr.seed(66789)
# Notice the difference between the convergence of the model with the two values of kinetic energy parameters.
# ### 4.2 Adaptive optimization with Keras
#
# Now, let's try adaptive optimization with Keras. We will use one of the mostly widely used adaptive algorithms, RMSprop (Hinton, 2012). Like Adam, RMSprop accumulates a measure of the squared gradient to change the learning rate. An exponential decay is applied to the accumulated squared gradient to ensure that more recent experience dominates the learning rate.
#
# Examine the code below for details. Execute the code and examine the results.
# +
## First define the regression model.
nn = models.Sequential()
nn.add(layers.Dense(128, activation = 'relu', input_shape = (1, ),
kernel_regularizer=regularizers.l2(1.0)))
nn.add(layers.Dense(128, activation = 'relu',
kernel_regularizer=regularizers.l2(1.0)))
nn.add(layers.Dense(1))
## Define the RMS optimizer
RMS = optimizers.RMSprop(lr=0.01)
nn.compile(optimizer = RMS, loss = 'mse', metrics = ['mae'])
## Now fit the model
nr.seed(9778)
start = time.time() # The time as execution start
history = nn.fit(x_train, y_train,
epochs = 40, batch_size = 1,
validation_data = (x_test, y_test),
callbacks = callbacks_list, # Call backs argument here
verbose = 0)
end = time.time() # Time at execution endf
print('Execution time = ' + str(end - start))
## Visualize the outcome
plot_loss(history)
# -
# Notice that RMSprop converges in fewer epochs than SGD for this situation. The same type of over-fitting of the model is also evident.
#
# Once again, we should check that the learned model actually makes sense. The code in the cell below predicts score values for the test dataset, prints the RMSE and plots the result. Execute this code and examine the outcome.
predicted = nn.predict(x_test)
plot_reg(x_test, predicted, y_test)
print(np.std(predicted - y_test))
# This result is similar to the one achieved with SGD, but perhaps a bit better and faster.
# ## 5.0 Weight initial values
#
# When training deep neural networks the initial values chosen for the weights can have a significant effect on the results. If weights are all set to the same initial value several possible problems will arise:
# - Some of the weights may be linearly dependent. In this case, some weights will change together during training and not be correctly learned.
# - Some weights will become **stuck** at the initial value and are never learned. This is special case of the first problem, for the most part.
#
# Fortunately, the solution to this problem is simple; **randomize** the starting values of the weights. This process is sometimes referred to as adding **fuzz** to the initial weights. A number of schemes have been tried. For example, initial weight values can be drawn from a Gaussian or Normal distribution. In practice, drawing the initial values from a Uniform distribution works as well as any other scheme.
# ## 6.0 Image Classification with Keras
#
# Now, it is your turn to construct and evaluate an image classifier using the Adam optimizer in Keras.
#
# The code in the cell below loads and imports the data set, along with defining one of the performance evaluation charts. Execute this code.
# +
from keras.optimizers import Adam
from keras.datasets import mnist
from keras.layers import Dropout
def plot_accuracy(history):
train_acc = history.history['acc']
test_acc = history.history['val_acc']
x = list(range(1, len(test_acc) + 1))
plt.plot(x, test_acc, color = 'red', label = 'test accuracy')
plt.plot(x, train_acc, label = 'training accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.title('Accuracy vs. Epoch')
plt.legend(loc='lower right')
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28*28)).astype('float32')/255
train_labels = ku.to_categorical(train_labels)
test_images = test_images.reshape((10000, 28*28)).astype('float32')/255
test_labels = ku.to_categorical(test_labels)
# -
# In the cell below, you will create the code to construct a Keras with the following specification:
#
# 1. Set a `numpy.random` seed of 5577.
# 2. Set a Tensorflow random seed 7799 with the `set_random_seed` function.
# 2. Define a sequential model.
# 3. Add a dense hidden layer with 512 units, using ReLU activation. Remember to define the input shape.
# 4. Add a 0.5 `Dropout` layer.
# 5. Add a dense hidden layer with 512 units, using ReLU activation, and l2 regularization with parameter of 10.0.
# 6. Add an output layer with 10 units (one for each digit category) and softmax activation.
# 7. Print a summary of your model.
# 8. Define an optimizer object using the Adam optimizer, with `decay = 0.005`. This argument determines the rate of change of the learning rate.
# 9. Compile your model using the optimizer object, `categorical_crossentropy` for the loss and `accuracy` as the metric.
# 10. Fit the model using 20 `epochs` and a `batch_size` of 128. Save the results to a history object. Don't forget to include the `validation_data`.
#
# *****************
# **Hint:** Refer to the Introduction to Keras lab for some examples of creating, executing and evaluating Keras models.
#
# *********************
# **Note:** You can find detailed documentation for the [Keras Adam optimizer here.](https://keras.io/optimizers/).
# +
nr.seed(5577)
set_random_seed(7799)
# -
# Compare these results the ones you obtained from the regularized model with the `rmsprop` optimizer in the Introduction to Keras lab.
#
# In the cell below create and execute the code to plot the loss history for the training of your neural network model.
plot_loss(history)
# Finally, in the cell below, create and execute the code to plot the accuracy history from training your neural network model.
plot_accuracy(history)
# Examine the results from training your model and compare them to those you obtained from the regularized model using the `rmsprop` optimizer in the Introduction to Keras lab.
#
# Also, note the slow convergence of this model. We have limited the training to 20 epochs in the interest of limiting computing time. It is likely that many more epochs are required to complete the training.
|
Module5/OptimizatonForDeepNetworks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
class TicTacToe:
def __init__(self):
self.N = 3 #: 정방행렬의 변 길이
self.map = [['E' for _ in range(self.N)] for _ in range(self.N)] # E: 빈 공간(Empty)
# [['E', 'E', 'E'], ['E', 'E', 'E'], ['E', 'E', 'E']]
self.map_index_description = [h*self.N + w for h in range(self.N) for w in range(self.N)]
self.player_types = ('X', 'O') # 선공: X, 후공: O
self.global_step = 0
self.win_reward = 1.0
self.defeat_reward = -1.0
self.draw_reward = 0.0
self.player_result = {'X': self.draw_reward, 'O': self.draw_reward}
self.done = False
#game.reset()
def reset(self):
self.map = [['E' for _ in range(self.N)] for _ in range(self.N)]
self.global_step = 0
self.player_result = {'X': self.draw_reward, 'O': self.draw_reward}
self.done = False
return self.map
# game.step(0~8)
def step(self, action):
action_coord_h, action_coord_w = self.transform_action(action)
if self.global_step % 2 == 0:
current_player_idx = 0
other_player_idx = 1
else:
current_player_idx = 1
other_player_idx = 0
current_player_type = self.player_types[current_player_idx]
other_player_type = self.player_types[other_player_idx]
# 현재 플레이어가 착수를 할 위치가 가능한 곳인가?
if self.map[action_coord_h][action_coord_w] == 'E':
self.map[action_coord_h][action_coord_w] = current_player_type
# 승부의 결과?
if self.is_win(current_player_type): # 현재 플레이어 승리
self.player_result[current_player_type] = self.win_reward
self.player_result[other_player_type] = self.defeat_reward
self.done = True
elif self.is_full(): # 무승부
self.done = True
else:
pass
else: # 현재 플레이어 패배
self.player_result[current_player_type] = self.defeat_reward
self.player_result[other_player_type] = self.win_reward
self.done = True
self.global_step += 1
return self.map, self.player_result, self.done
def transform_action(self, action):
return divmod(action, self.N)
def is_win(self, current_player_type):
vertical_win = [True for _ in range(self.N)]
horizontal_win = [True for _ in range(self.N)]
diagonal_win = [True for _ in range(2)]
for h in range(self.N):
for w in range(self.N):
# 가로, 세로
if self.map[h][w] != current_player_type:
vertical_win[h] = False
horizontal_win[w] = False
else:
pass
# 왼 대각
if h == w and self.map[h][w] != current_player_type:
diagonal_win[0] = False
# 오른 대각
rotated_w = abs(w - (self.N - 1))
if h == rotated_w and self.map[h][w] != current_player_type:
diagonal_win[1] = False
if any(vertical_win) or any(horizontal_win) or any(diagonal_win):
return True
else:
return False
def is_full(self):
for h in range(self.N):
for w in range(self.N):
if self.map[h][w] == 'E':
return False
else:
pass
return True
def print_description(self):
print("** Initial NxN Tic-tac-toe Map **")
self.print_current_map()
print("** Action Indexes **")
for idx, des in enumerate(self.map_index_description):
print(des, end=' ')
if (idx + 1) % self.N == 0:
print('\n', end='')
def print_current_map(self):
for h in range(self.N):
for w in range(self.N):
print(self.map[h][w], end=' ')
print('\n', end='')
print()
# Fill this function
def match_prediction(self):
# X: 현재 플레이어
# return value (이긴다: 1 무승부: 0 진다: -1)
# print("'X'의 최대 결과는 '승리'입니다.")
# print("'O'의 최대 결과는 '패배'입니다.")
# print("현재 플레이어의 최대 결과는 패배입니다.")
print("현재 착수할 플레이어가 이긴다고 확신이 드는가? Yes or No")
if __name__ == '__main__':
game = TicTacToe()
game.print_description()
game.reset()
done = False
while not done:
print()
# Do it.
# game.match_prediction()
action = int(input('Select action please: '))
if not(game.map_index_description[0] <= action <= game.map_index_description[-1]):
done = True
print("Error: You entered the wrong number.")
continue
# step(action)
_, player_result, done = game.step(action)
game.print_current_map()
if done:
for player, result in player_result.items():
if result == game.win_reward:
player_result[player] = 'win'
elif result == game.defeat_reward:
player_result[player] = 'defeat'
else:
player_result[player] = 'draw'
print(player_result)
# -
|
python3.6/Tic-tac-toe.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import numpy
import theano.tensor as T
from theano import function
x=T.dscalar('x')
y=T.dscalar('y')
z=x+y
f=function([x,y],z)
f(2,3)
numpy.allclose(f(16.3,12.1),28.4)
# +
a=T.vector()
b=T.vector()
out=a**2+b**2+2*a*b
f=function([a,b],out)
print(f([0,1,2],[0,1,2]))
# -
|
Lisa Lab tutorials/Theano Basics/ Basic Tutorial-1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# author=cxf
# date=2020-8-8
# file for filter and merge samples from run1 and run2
import numpy as np
import pandas as pd
# get cutoff
df_90_r1 = pd.read_csv('../1.cutoff_setting/run1/90_result.txt', index_col=0)
df_95_r1 = pd.read_csv('../1.cutoff_setting/run1/95_result.txt', index_col=0)
df_99_r1 = pd.read_csv('../1.cutoff_setting/run1/99_result.txt', index_col=0)
df_90_r2 = pd.read_csv('../1.cutoff_setting/run2/90_result.txt', index_col=0)
df_95_r2 = pd.read_csv('../1.cutoff_setting/run2/95_result.txt', index_col=0)
df_99_r2 = pd.read_csv('../1.cutoff_setting/run2/99_result.txt', index_col=0)
# remove samples whose least error rate does not meet criterion
df_90_r1 = df_90_r1[df_99_r1['max_num'] != 0]
df_95_r1 = df_95_r1[df_99_r1['max_num'] != 0]
df_99_r1 = df_99_r1[df_99_r1['max_num'] != 0]
df_90_r2 = df_90_r2[df_99_r2['max_num'] != 0]
df_95_r2 = df_95_r2[df_99_r2['max_num'] != 0]
df_99_r2 = df_99_r2[df_99_r2['max_num'] != 0]
# merge inputs and outputs of model
df_all_output = pd.concat([df_90_r1, df_95_r1, df_99_r1,
df_90_r2, df_95_r2, df_99_r2
])
# only retain features users can provide to model and cutoff we expected
pick_list = ['precise','max_cutoff']
df_all_output=df_all_output[pick_list]
df_all_output.to_csv('train_data_run1_run2.csv')
# -
print(df_all_output)
|
model_training/2.extract_features/1.filter_and_merge_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import tensorflow as tf
from tensorflow import keras
import tensorflow as tf
physical_devices = tf.config.list_physical_devices('GPU')
tf.config.experimental.set_memory_growth(physical_devices[0], True)
print(physical_devices)
# From https://www.tensorflow.org/api_docs/python/tf/nn/conv2d
#
# Given an input tensor of shape batch_shape + [in_height, in_width, in_channels] and a filter / kernel tensor of shape [filter_height, filter_width, in_channels, out_channels], this op performs the following:
#
# Flattens the filter to a 2-D matrix with shape [filter_height * filter_width * in_channels, output_channels].
#
# Extracts image patches from the input tensor to form a virtual tensor of shape [batch, out_height, out_width, filter_height * filter_width * in_channels].
#
# For each patch, right-multiplies the filter matrix and the image patch vector.
class spectralConv2D(keras.layers.Layer):
def __init__(self, filters = 32,kernel_size=(3,3),strides=(1, 1), padding='VALID',activation=tf.nn.relu,input_shape=None):
# Initialization
super(spectralConv2D, self).__init__()
assert len(kernel_size) > 1 , "Please input the Kernel Size as a 2D tuple"
self.strides = strides
self.padding = padding
self.filters = filters
self.kernel_size = kernel_size
self.activation = activation
def build(self, input_shape):
# Initialize Filters
# Assuming Input_shape is channels_last
kernel_shape = [self.kernel_size[0],self.kernel_size[1],input_shape[3],self.filters]
self.kernel_real = self.add_weight( shape=kernel_shape,
initializer="glorot_uniform",
trainable=True)
self.kernel_imag = self.add_weight( shape=kernel_shape,
initializer="glorot_uniform",
trainable=True)
self.bias = self.add_weight(shape=(self.filters,), initializer="zeros", trainable=True)
def call(self, inputs):
print(self.kernel_real)
kernel = tf.complex(self.kernel_real,self.kernel_imag)
spatial_kernel = tf.signal.ifft2d(kernel)
spatial_kernel=tf.abs(spatial_kernel)
convolution_output = tf.nn.convolution(
inputs,
spatial_kernel,
strides=list(self.strides),
padding=self.padding
)
convolution_output = tf.nn.bias_add(convolution_output, self.bias)
if self.activation is not None:
convolution_output= self.activation(convolution_output)
return convolution_output
# +
# CIFAR10 Dataset
from modules.utils import load_data
X_train, y_train = load_data(mode='train')
num_training = 49000
num_validation = 1000
X_val = X_train[-num_validation:, :]
y_val = y_train[-num_validation:]
X_train = X_train[:num_training, :]
y_train = y_train[:num_training]
# Preprocessing: subtract the mean value across every dimension for training data, and reshape it to be RGB size
mean_image = np.mean(X_train, axis=0)
X_train = X_train.astype(np.float32) - mean_image.astype(np.float32)
X_val = X_val.astype(np.float32) - mean_image
X_train = X_train.reshape(-1,3,32,32).transpose(0,2,3,1) / 255
X_val = X_val.reshape(-1,3,32,32).transpose(0,2,3,1) / 255
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
# -
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Conv2D,ReLU,GlobalAveragePooling2D,Softmax,Flatten,Dense #, , AveragePooling2D, MaxPooling2D,,
from tensorflow.keras import Model,Input
model = Sequential()
model.add(spectralConv2D(32, (3,3),input_shape=X_train.shape[1:]))
model.add(spectralConv2D(64, (3,3)))
model.add(spectralConv2D(128, (3,3)))
model.add(spectralConv2D(94, (3,3)))
model.add(Flatten())
model.add(Dense(128))
model.add(Dense(10,activation="softmax"))
model.compile(
optimizer= tf.keras.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x=X_train, y=y_train,
batch_size=128,
epochs=5,
validation_data=(X_val, y_val)
)
model.summary()
|
src/spectralParameterization-Notebooks/2.1Spectral_Representation_ConvolutionLayer-test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import os
import re
import time
from gensim.models import Word2Vec
from tqdm import tqdm
# -
replies_df = pd.read_csv('./replies_df.csv')
# +
import nltk
from nltk.stem import PorterStemmer, WordNetLemmatizer
from nltk.tokenize import sent_tokenize, word_tokenize
from nltk.corpus import stopwords
# from wordcloud import STOPWORDS
def get_stopwords():
# stop = set(STOPWORDS)
stop = stopwords.words('english')
custom_words_sen = 'really, like, way, much , still, but, find, need, you, many, lot, always, say, could, well, even, the'
custom_words = custom_words_sen.split(', ')
custom_stop = stop + custom_words
return custom_stop
# +
def preprocess_news(df=replies_df,lowercase=False):
corpus=[]
stem=PorterStemmer()
lem=WordNetLemmatizer()
stop = get_stopwords()
for threads in replies_df['reply']:
if lowercase == True:
words=[str.lower(w) for w in word_tokenize(threads) if (w not in stop)]
else:
words=[w for w in word_tokenize(threads) if (w not in stop)]
words=[lem.lemmatize(w) for w in words if len(w)>2]
corpus.append(words)
return corpus
corpus_lowercase =preprocess_news(replies_df, True)
# -
print(corpus_lowercase[:2])
# +
# https://www.kaggle.com/chewzy/tutorial-how-to-train-your-custom-word-embedding
model = Word2Vec(sentences=corpus_lowercase, min_count=1,size= 50,workers=3, window =3, sg = 1)
# -
len(model.wv.vocab.keys())
print(model.wv.vocab.keys())
model.wv.vector_size
model.wv.get_vector('speed')
model.wv.most_similar('ten05')
model.wv.most_similar('speed')
model.wv.most_similar('fast')
model.wv.most_similar('tenergy')
model.wv.most_similar('h3-50')
model.wv.most_similar('rubber')
model.wv.save_word2vec_format('custom_word2vec.txt')
# * not useful at all
# # tsne
# +
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
def display_closestwords_tsnescatterplot(model, word, size):
arr = np.empty((0,size), dtype='f')
word_labels = [word]
word_vector = model.wv
close_words = word_vector.similar_by_word(word)
arr = np.append(arr, np.array([word_vector[word]]), axis=0)
for wrd_score in close_words:
wrd_vector = word_vector[wrd_score[0]]
word_labels.append(wrd_score[0])
arr = np.append(arr, np.array([wrd_vector]), axis=0)
tsne = TSNE(n_components=2, random_state=0)
np.set_printoptions(suppress=True)
Y = tsne.fit_transform(arr)
x_coords = Y[:, 0]
y_coords = Y[:, 1]
plt.scatter(x_coords, y_coords)
for label, x, y in zip(word_labels, x_coords, y_coords):
plt.annotate(label, xy=(x, y), xytext=(0, 0), textcoords='offset points')
plt.xlim(x_coords.min()+0.00005, x_coords.max()+0.00005)
plt.ylim(y_coords.min()+0.00005, y_coords.max()+0.00005)
plt.show()
# -
display_closestwords_tsnescatterplot(model, 'rubber', 50)
|
EDA/.ipynb_checkpoints/similar_words_by_word2vec_or_tsne-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 更多字符串和特殊方法
# - 前面我们已经学了类,在Python中还有一些特殊的方法起着非常重要的作用,这里会介绍一些特殊的方法和运算符的重载,以及使用特殊方法设计类
# ## str 类
# - 一个str对象是不可变的,也就是说,一旦创建了这个字符串,那么它的内容在认为不改变的情况下是不会变的
# - s1 = str()
# - s2 = str('welcome to Python')
# ## 创建两个对象,分别观察两者id
# - id为Python内存地址
id(a)
# ## 处理字符串的函数
# - len
# - max
# - min
# - 字符串一切是按照ASCII码值进行比较
length = len("fuliqiong")#常用在检索
print(length)
# ## 下角标运算符 []
# - 一个字符串是一个字符序列,可以通过索引进行访问
# - 观察字符串是否是一个可迭代序列 \__iter__
#索引从0开始
#最大是4,取5是越界!
#索引去负数是从后取,从-1开始
c = 'hhhh'
c[0]
c = 'hei ha hei'
c[5]
i = 0
while i<5:
c = 'Joker'
c[i]
print(c[i])
i += 1
# ## 切片 [start: end]
# - start 默认值为0
# - end 默认值为-1
# 1.翻转[::-1]
# 2.步长为正,strat<end
# 3.步长为负,反
a = "jhsajhjdh nsndsndkaxd skjdks"
a[::2]
a[::]
a = '<EMAIL>'
i = 0
while 1:
ord
print(a[:ord=])
ord('a')
if new_line[-1] == '@':
a = ord(new_line[2])
if 96<=a<=122:
break
print(new_line[:-1])
def sousuo(index):
path='/Users/Lenovo/Desktop/Python/mail.txt'
with open(file=path,mode='r') as f:
for i in range(1000):
line = f.readline()
a=new_line.find('175832')
if a==0:
print("ok")
else:
break
sousuo(9)
# ## 链接运算符 + 和复制运算符 *
# - \+ 链接多个字符串,同时''.join()也是
# - \* 复制多个字符串
''.join('hh')
# ## in 和 not in 运算符
# - in :判断某个字符是否在字符串内
# - not in :判断某个字符是否不在字符串内
# - 返回的是布尔值
# ## 比较字符串
# - ==, !=, >=, <=, >, <
# - 依照ASCII码值进行比较
# ## 测试字符串
# 
# - 注意:
# > - isalnum() 中是不能包含空格,否则会返回False
a=bool(0)
print(a)
class mima:
def __init__(self,shuru):
self.shuru = shuru
print("*",shuru)
def changdu(self):
chang = len(self.shuru)
if chang!=8:
print("密码不能小于8位")
def zimu(self):
xiao = islower(self.shuru)
da = isupper(self.shru)
return xiao,da
def shuzi(self):
s = isalnum(self.shuru)
return s
m = mima(178562)
m.shuzi()
# ## 搜索子串
# 
b = '额额东阿及VC名称数量骗我额可'
b.find('东')
# ## 转换字符串
# 
# ## 删除字符串
# 
# ## 格式化字符串
# 
a ="*" * 5
b ="*".rjust(3)
print(a,b)
# ## EP:
# - 1
# 
# - 2
# 随机参数100个数字,将www.baidu.com/?page=进行拼接
# ## Python高级使用方法 -- 字符串
# - 我们经常使用的方法实际上就是调用Python的运算重载
# 
# # Homework
# - 1
# 
moren = 666666666
a = input("请按照ddd-dd-dddd输入社会安全号码:")
b = a.replace('-','')
if b == moren:
print('Valid SSN')
else:
print('InValid SSN')
# - 2
# 
def zifuchuan(str1='',str2=''):
if str2.find(str1) != -1:
print('第一个字符串是第二个字符串的子串')
else:
print('我可去你的吧')
zifuchuan(str1='4544',str2='44')
zifuchuan(str1='dd',str2='4dd4')
str1 = 'sdf44'
str2 = '44'
str2.find(str1)
# - 3
# 
password = input('>>')
n1 = 0
n2 = 1
if len(password) <= 8:
print('invalid password')
else:
for i in password:
if i.isalnum():
n1 += 1
if i.isdigit():
n2 += 1
if n1 == 0:
print('invalid password')
if n2 <= 2:
print('invalid password')
else:
print('valid password')
# - 4
# 
def countLetters(s=''):
count_ = 0
for i in s:
if i.isalpha():
count_ += 1
print(count_)
countLetters(s='522dsfcxcds5')
# - 5
# 
def getNumber(uppercaseLetter = input('>>')):
N = []
for i in uppercaseLetter:
if 97 <= ord(i) <= 99:
i = 2
N.append(i)
elif 100 <= ord(i) <= 102:
i = 3
N.append(i)
elif 103 <= ord(i) <= 105:
i = 4
N.append(i)
elif 106 <= ord(i) <= 108:
i = 5
N.append(i)
elif 109 <= ord(i) <= 111:
i = 6
N.append(i)
elif 112 <= ord(i) <= 115:
i = 7
N.append(i)
elif 116 <= ord(i) <= 118:
i = 8
N.append(i)
elif 119 <= ord(i) <= 122:
i = 9
N.append(i)
print(N)
# - 6
# 
def reverse(s = ''):
print(s)
print(s[::-1])
reverse(s = 'jszhdja5533553')
# - 7
# 
# - 8
# 
# - 9
# 
|
7.24.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#import dependencies
from bs4 import BeautifulSoup as bs
import requests
from splinter import Browser
import pandas as pd
import time
# +
news = "https://mars.nasa.gov/news/"
image = "https://www.jpl.nasa.gov/spaceimages/?search=&category=Mars"
weather = "https://twitter.com/marswxreport?lang=en"
facts = "https://space-facts.com/mars/"
hemi = "https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars"
# -
#news web title/text scrapping
response = requests.get(news)
web = bs(response.text, 'html.parser')
web
news_title = web.find('div', class_ = "content_title").text
news_title
news_p = web.find('div', class_ = "rollover_description_inner").text
news_p
|
mission_to_mars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 数据归一化
import numpy as np
import matplotlib.pyplot as plt
# ### 最值归一化
from sklearn import datasets
iris = datasets.load_iris()
x = iris.data
y = iris.target
from sklearn.model_selection import train_test_split
x_train,x_test, y_train,y_test = train_test_split(x, y, test_size = 0.2, random_state=666)
# ### scikit-learn StandardScaler
from sklearn.preprocessing import StandardScaler
standard_scaler = StandardScaler()
standard_scaler.fit(x_train)
standard_scaler.mean_
standard_scaler.scale_
x_train_standard = standard_scaler.transform(x_train)
x_test_standard = standard_scaler.transform(x_test)
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors=3)
knn_clf.fit(x_train_standard, y_train)
knn_clf.score(x_test_standard, y_test)
|
data/scaling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.4.5
# language: julia
# name: julia-0.4
# ---
using Plots;
gadfly();
include("../fdtd/update.jl");
include("../fdtd/sources.jl");
include("../fdtd/boundaries.jl");
using update;
using sources;
# +
#Global parameters
size = 400;
endTime = 4000;
num_snaps = 100;
snap_step = div(endTime, num_snaps);
# Incident
inc_pos = 100;
# Material
n1 = 2;
n2 = 2;
eps1 = n1^2;
wavelength = round(Integer, size / 5);
q_wavelength = round(Integer, wavelength * n1 / n2 / 2);
n2 = (wavelength * n1) / (q_wavelength * 2.);
eps2 = n2^2;
#Grid
# Magnetic
hy = zeros(size-1);
mu = ones(size-1);
chyh = ones(size);
chye = ones(size);
# Electric
ez = zeros(size);
eps = ones(size) * eps1;
cezh = ones(size);
ceze = ones(size);
#for i in 110:170
# eps[i] = eps1;
#end
for i in div(size, 2):div(size, 2)+q_wavelength-1
# eps[i] = eps2;
end
rightBound = boundaries.setup_first_order_abc(eps, mu, size, true)
leftBound = boundaries.setup_first_order_abc(eps, mu, 1, false)
# output params
ez_snapshot = Array{Any}(num_snaps);
hy_snapshot = Array{Any}(num_snaps);
# +
# Time steps
for time in 1:endTime
# Incident
ez_inc = sin(2*pi/(wavelength) * (time-1))*exp(-3000/time);
hy_inc = sin(2*pi/(wavelength) * (time-2))*exp(-3000/time);
#
# Magnetic
#
# Interior update
update.update_magnetic_field!(ez, hy, mu, chyh, chye);
# TFSF
hy[inc_pos-1] -= hy_inc / globals.imp0;
#
# Electric
#
# Interior update
update.update_electric_field!(ez, hy, eps, cezh, ceze);
# ABC
boundaries.first_order_diff_abc!(ez, leftBound)
boundaries.first_order_diff_abc!(ez, rightBound)
# TFSF
ez[inc_pos] += ez_inc / sqrt( eps[inc_pos] * mu[inc_pos])
# Snapshots for animation
if mod(time, snap_step) == 0
ez_snapshot[div(time,snap_step)] = (time, copy(ez))
hy_snapshot[div(time,snap_step)] = (time, copy(hy).*globals.imp0)
end
end
# +
anim = Animation()
for i = 1:num_snaps
p = plot(1:size, ez_snapshot[i][2], lab="Ez")
time = ez_snapshot[i][1]
plot!(ann=[(0.8*size, 1.5, "time =$time")])
plot!([size/2, size/2], [-2, 2])
plot!([size/2+q_wavelength, size/2+q_wavelength], [-2, 2])
plot!(xlims=(1, size), ylims=(-2, 2))
frame(anim, p)
end
gif(anim, "./Task3/Half_Wavelength_Reflection_TFSF.gif", fps=15)
# -
plot(1:inc_pos-2, ez[1:inc_pos-2])
plot!(xlims=(1, inc_pos-2), ylims=(maximum(ez[1:inc_pos-2]),minimum(ez[1:inc_pos-2])))
maximum(abs(ez[1:inc_pos-2]))
|
tasks/Task3_Zero_Reflection_TFSF.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Run ExtractPhyloWGSResults.py and Rscripts/ProcessBSCITEResults.R.
from sklearn.metrics.cluster import adjusted_rand_score
from sklearn.metrics.cluster import adjusted_mutual_info_score
from sklearn.metrics.cluster import v_measure_score
import pandas as pd
import numpy as np
import os
data_path = "/Users/seonghwanjun/data/cell-line/bulk/OV2295/genotype/"
import sklearn
sklearn.__version__
# +
gt = pd.read_csv("/Users/seonghwanjun/data/cell-line/bulk/OV2295/genotype/gt.txt", header=0, sep=" ")
valid_clone_names = ["A_B_C_D_E_F_G_H_I", "A_B_C_D", "A_B", "C_D", "A", "B", "C", "D", "E_F_G_H_I", "E_F", "E", "F"]
# Evaluate the ancestral metric.
# Get the true ancestral metric: not many SNVs, just do a plain double for loops.
snv_count = gt.shape[0]
A = np.zeros(shape = (snv_count, snv_count))
for i in range(snv_count):
clone_i = set(gt.iloc[i]["CloneName"].split("_"))
for j in range(snv_count):
clone_j = set(gt.iloc[j]["CloneName"].split("_"))
if clone_i != clone_j and clone_j.issubset(clone_i):
A[i,j] = 1
idx = np.array(np.where(gt["CloneName"].isin(valid_clone_names)))[0]
valid_idx = np.ix_(idx, idx)
A0 = A[valid_idx]
# +
# Our method.
rep_count = 20
metrics = np.zeros([rep_count, 4])
for rep in range(rep_count):
rep_path = "/Users/seonghwanjun/data/cell-line/bulk/OV2295/genotype/results/rep" + str(rep)
predicted = pd.read_csv(rep_path + "/joint/tree0/cluster_labels.tsv", header=None, sep="\t", names=["ID", "CloneName"])
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
ancestral_matrix = pd.read_csv(rep_path + "/joint/tree0/ancestral_matrix.csv", header=None)
ancestral_matrix = np.asarray(ancestral_matrix)
ancestral_matrix_0 = ancestral_matrix[valid_idx]
metrics[rep,0] = v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,1] = adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,2] = adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,3] = np.mean(np.abs(ancestral_matrix_0 - A0))
# V-measure, adjusted rand score, adjusted mutual info, ancestral metric.
print(metrics.mean(0))
print(metrics.std(0))
# +
# PhyloSub.
metrics = np.zeros([rep_count, 4])
for rep in range(rep_count):
rep_path = "/Users/seonghwanjun/data/cell-line/bulk/OV2295/genotype/bulk_only/rep" + str(rep)
predicted = pd.read_csv(rep_path + "/joint/tree0/cluster_labels.tsv", header=None, sep="\t", names=["ID", "CloneName"])
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
ancestral_matrix = pd.read_csv(rep_path + "/joint/tree0/ancestral_matrix.csv", header=None)
ancestral_matrix = np.asarray(ancestral_matrix)
ancestral_matrix_0 = ancestral_matrix[valid_idx]
metrics[rep,0] = v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,1] = adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,2] = adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"])
metrics[rep,3] = np.mean(np.abs(ancestral_matrix_0 - A0))
# V-measure, adjusted rand score, adjusted mutual info, ancestral metric.
print(metrics.mean(0))
print(metrics.std(0))
# +
# ddClone
pred_path = os.path.join(data_path, "ddClone")
predicted = pd.read_table(os.path.join(pred_path, "results.txt"), sep=" ")
predicted.columns=["ID", "phi", "CloneName"]
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
print(v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
# +
# B-SCITE:
pred_path = os.path.join(data_path, "B-SCITE")
clustering_prediction_file = os.path.join(pred_path, "results.txt")
predicted = pd.read_table(clustering_prediction_file, sep=" ")
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
# Read the ancestral matrix line-by-line.
with open(os.path.join(pred_path, "bscite.matrices"), "r") as f:
line = f.readline()
mutation_count = int(line.split()[1])
f.readline()
A = []
for _ in range(mutation_count):
line = f.readline()
A.append(line.split())
A = np.asarray(A, dtype=int)
A = A[valid_idx]
print(v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(np.mean(np.abs(A - A0)))
# +
# Compute the metrics on Canopy.
clustering_file = os.path.join(data_path, "canopy", "predicted.csv")
ancestral_matrix_file = os.path.join(data_path, "canopy", "ancestral_matrix.csv")
predicted = pd.read_csv(clustering_file)
predicted.columns=["ID", "CloneName"]
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
ancestral_matrix = np.asarray(pd.read_table(ancestral_matrix_file, header=None, sep=" "))
ancestral_matrix = ancestral_matrix[valid_idx]
print(v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(np.mean(np.abs(ancestral_matrix - A0)))
# +
# PhyloWGS:
clustering_file = os.path.join(data_path, "phylowgs", "clustering.txt")
ancestral_matrix_file = os.path.join(data_path, "phylowgs", "ancestral_matrix.txt")
predicted = pd.read_table(clustering_file, header=None, names=["ID", "CloneName"], sep=" ")
ancestral_matrix = np.asarray(pd.read_table(ancestral_matrix_file, header=None, sep=" "))
tbl_join = predicted.join(gt, lsuffix='_caller', rsuffix='_other')
ret = tbl_join[tbl_join["CloneName_other"].isnull() == False]
ret_valid = tbl_join[tbl_join["CloneName_other"].isin(valid_clone_names)]
print(v_measure_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_rand_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(adjusted_mutual_info_score(ret_valid["CloneName_other"], ret_valid["CloneName_caller"]))
print(np.mean(np.abs(A0 - ancestral_matrix[valid_idx])))
|
notebook/HGSOC/OV2295_SS3_Evaluation.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .r
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: R
# language: R
# name: ir
# ---
# +
options(warn=-1)
shhh <- suppressPackageStartupMessages # It's a library, so shhh!
shhh(library(gplots))
library(qgraph)
shhh(library(tidyverse))
library("RColorBrewer")
options(warn=0)
# -
data <- read.csv(url("http://cardsorting.net/tutorials/25.csv"))
head(data)
data <- data[, -c(1:6)]# delete columns 1 through 6
data <- data[,-ncol(data)]
head(data)
data <- data.frame(data)
hist(as.numeric(unlist(data)), labels=c(0,1))
distances = dist(t(data), method="euclidean")
heatmap.2(as.matrix(distances), symkey=FALSE, density.info="none", trace="none", dendrogram ="row")
# e)
qgraph(1/distances, layout='spring', vsize=3, theme='Hollywood')
# +
# Obtenemos las tarjetas más relacionadas entre sí
min_distance <- min(distances)
cat("Min distance between cards:", min_distance, "\n")
cat("Cards with higher similarity:\n")
min_indexes <- which(as.matrix(distances)==min_distance, arr.ind=TRUE)
names = colnames(data)
correlated_pairs <- data.frame(Item1=character(), Item2=character())
for (row in 1:nrow(min_indexes)) {
new_row <- data.frame(names[min_indexes[row, "row"]],
names[min_indexes[row, "col"]])
names(new_row) <- c("Item1", "Item2")
correlated_pairs <- rbind(correlated_pairs, new_row)
}
correlated_pairs
|
P3/p3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="L9OiyQHo3YhE"
import pandas as pd
# + id="xM4nKtiR3xe-"
df = pd.read_csv("USA_cars_datasets.csv")
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="9plDgqp94Bge" outputId="388d20ae-1166-46ca-e445-6ffd087f2545"
df.head()
# + id="yCS2DGZQ4FBn"
del df['Unnamed: 0']
del df['vin']
del df['lot']
del df['condition']
# + colab={"base_uri": "https://localhost:8080/", "height": 204} id="zwmBgz_O5x_A" outputId="1e1f0167-9743-4e06-c5c3-705c1dbb2693"
df.head()
# + colab={"base_uri": "https://localhost:8080/"} id="m3qVsA0ZB-Tk" outputId="bcc7565b-ff76-41f8-e1cd-a739eced3dc0"
df['country'].unique()
# + colab={"base_uri": "https://localhost:8080/", "height": 266} id="uvceWJA5BTf-" outputId="fabb8858-a5d8-4bfa-c9b5-fea8eb7fc75d"
df[df['country'] == ' canada']
# + id="0P1IsQskBTiO"
# + id="fk5cgg0oAOIR"
# + colab={"base_uri": "https://localhost:8080/"} id="_J_v5qvB-lyT" outputId="fd652c72-f392-4062-a7cc-c044a2ef80c0"
# + colab={"base_uri": "https://localhost:8080/"} id="mMpaWszG-bRH" outputId="a740a4ce-fdf0-43a0-d2bd-8007363311bd"
for country in df['country'].unique():
print(country , len(df[df['country'] == country]))
# + colab={"base_uri": "https://localhost:8080/"} id="42V_2-eQ-K5y" outputId="a33ecd0e-00b1-4293-e39d-792235845421"
for year in df['year'].unique():
print(year , len(df[df['year'] == year]))
# + colab={"base_uri": "https://localhost:8080/"} id="J-2DB-iu504B" outputId="e98115a8-356c-4b70-f6b7-4af99b9e058c"
for model in df['model'].unique():
print(model , len(df[df['model'] == model]))
# + colab={"base_uri": "https://localhost:8080/"} id="4ueu-6DB6HZC" outputId="0ad194c9-e9dc-4fb5-e5ac-694497ca2a14"
for brand in df['brand'].unique():
print(brand , len(df[df['brand'] == brand]))
# + colab={"base_uri": "https://localhost:8080/"} id="OouobKKa7MQo" outputId="0a8d51e5-369e-481d-a64b-dcae6001faf2"
df['year'].unique()
# + colab={"base_uri": "https://localhost:8080/"} id="wSgmZf7m8DFX" outputId="b0594600-fe58-45f1-dcf3-bb26bdaf20ac"
df['title_status'].unique()
# + colab={"base_uri": "https://localhost:8080/"} id="DpF_ufgW8QYh" outputId="dbcd5a77-d208-4d6f-fe96-21da01a14700"
df['color'].unique()
# + id="7NZpF46n8ZRK"
|
US Cars Dataset/US_Cars_Analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Boolean Assigmnet
a = True #Declare a boolean value and store it in a variable.
print(type(a)) #Check the type and print the id of the same.
print(id(a))
# +
x , y = bool(6), bool(6) #Take one boolean value between 0 - 256.#Assign it to two different variables.
print(id(x)) #Check the id of both the variables.
print(id(y))
#Object Reusability Concept #It should come same. Check why?
# +
#Arithmatic Operations on boolean data
r , s = True , False #Take two different boolean values.#Store them in two different variables.
sum = r + s #Find sum of both values
diff = r - s #Find differce between them
pro = r * s #Find the product of both.
t = s / r #Fnd value after dividing first value with second value
w = s % r #Find the remainder after dividing first value with second value
#Cant do for boolean #Find the quotient after dividing first value with second value
f = r ** s #Find the result of first value to the power of second value.
print(bool(sum)) #True
print(bool(diff)) #True
print(bool(pro)) #False
print(bool(t)) #False
print(bool(w)) #False
print(bool(f)) #True
#print(type(sum),type(r))
#print(Addition is bool(sum)) --Why this is giving False
#diff = x.difference(y)-- This will not work 'bool' object has no attribute 'difference'
#Division = You cannot divide by modulo by-- Zero ZeroDivisionError: division by zer
# -
# #Comparison Operators on boolean values
#
# A , B = True , False #Take two different boolean values.#Store them in two different variables.
# OP1 = A > B #Compare these two values with below operator:-
# OP2 = A < B #less than, '<'
# OP3 = A >= B #Greater than or equal to, '>='
# OP4 = A <= B #Less than or equal to, '<='
#
# print(type(OP1))
# print(type(OP2))
# print(type(OP3))
# print(type(OP4))
# #Observe their output(return type should be boolean)
#
# +
#Equality Operator
C , D = True , False #Take two different boolean values.#Store them in two different variables.
print ( C == D) #Equuate them using equality operator (==, !=)
print ( C != D) #Observe the output(return type should be boolean)
# +
#Logical operators
#Observe the output of below code #Cross check the output manually
print(True and True) #----------->Output is True
print(False and True) #----------->Output is False
print(True and False) #----------->Output is False
print(False and False) #----------->Output is False
print(True or True) #----------->Output is True
print(False or True) #----------->Output is True
print(True or False) #----------->Output is True
print(False or False) #----------->Output is False
print(not True) #----------->Output is False
print(not False) #----------->Output is True
# +
#Bitwise Operators #Do below operations on the values provided below:-
#Bitwise and(&)
print(True & False)
print(True & True)
print(False & False)
print(False & False)
#Bitwise or(|) -----> True, False -------> Output is True
print(True | False)
print(True | True)
print(False | False)
print(False | False)
#Bitwise(^) -----> True, False -------> Output is True
print(True ^ False)
print(True ^ True)
print(False ^ False)
print(False ^ False)
#Bitwise negation(~) ------> True -------> Output is -2
print(~False)
print(~True)
#Bitwise left shift -----> True,2 -------> Output is 4
print(True << 2)
#Bitwise right shift ----------> True,2 -------> Output is 0
print(True >> 2)
#Cross check the output manually
# +
#What is the output of expression inside print statement. Cross check before running the program.
a = True
b = True
print(a is b) #True or False? #
print(a is not b) #True or False?
a = False
b = False
print(a is b) #True or False?
print(a is not b) #True or False?
# +
#Membership operation
#in, not in are two membership operators and it returns boolean value
print(True in [10,10.20,10+20j,'Python', True])
print(False in (10,10.20,10+20j,'Python', False))
print(True in {1,2,3, True})
print(True in {True:100, False:200, True:300})
print(False in {True:100, False:200, True:300})
|
Amrita/Boolean_Assisgment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pyplot import figure
import datetime
dataset = pd.read_csv("sheet1.csv")
dataset = dataset.tail(8)
dataset.info()
dataset.head()
new_ym = [datetime.datetime.strptime(string, '%Y/%m') for string in dataset['year_month']]
dataset['year_month'] = new_ym
dataset.info()
# +
x = dataset.year_month
y_VIP = dataset.vip_aov
y_regular = dataset.regular_aov
figure(figsize=(8, 6), dpi=80)
plt.title('VIP_aov versus regular_aov')
plt.plot(x, y_VIP, color = 'r', label = 'VIP_aov')
plt.plot(x, y_regular, color = 'b', label = 'regular_aov')
plt.legend(['VIP_aov','regular_aov'])
plt.xlabel('Year-Month')
plt.ylabel('Average Order Volume')
plt.grid(True)
|
.ipynb_checkpoints/Untitled-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import spiceypy
import math
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl
mpl.rcParams['figure.figsize'] = (26.0, 26.0)
spiceypy.furnsh('/Users/mcosta/ROSETTA/kernels/mk/ROS_OPS_LOCAL.TM')
# +
et = spiceypy.utc2et('2007-02-24T19:10:32.834')
sensor_name = 'ROS_NAVCAM-A'
sensor_id = spiceypy.bodn2c(sensor_name)
(shape, frame, bsight, vectors, bounds) = spiceypy.getfov(sensor_id, 100)
print(vectors, bounds)
# +
nx, ny = (1024, 1024)
x = np.linspace(bounds[0][0], bounds[2][0], nx)
y = np.linspace(bounds[0][1], bounds[2][1], ny)
xv, yv = np.meshgrid(x, y)
phase_matrix = np.zeros((1024, 1024))
emissn_matrix = np.zeros((1024, 1024))
libsight = []
for i, x in enumerate(xv):
for j, y in enumerate(yv):
ibsight = [x[i], y[j], bsight[2]]
libsight.append(ibsight)
try:
(spoint, trgepc, srfvec ) = spiceypy.sincpt('ELLIPSOID', 'MARS', et, 'IAU_MARS', 'NONE', 'ROSETTA', frame, ibsight)
(trgepc, srfvec, phase, solar, emissn) = spiceypy.ilumin('ELLIPSOID', 'MARS', et, 'IAU_MARS', 'NONE', 'ROSETTA', spoint)
emissn_matrix[i,j] = emissn
phase_matrix[i,j] = phase
except:
pass
emissn_matrix[i,j] = 0
phase_matrix[i,j] = math.pi
# -
plt.pcolor(xv, yv, emissn_matrix)
plt.pcolor(xv, yv, phase_matrix)
spiceypy.furnsh('/Users/mcosta/ExoMars2016/kernels/dsk/mars_m129_mol_v01.bds')
# +
nx, ny = (1024, 1024)
x = np.linspace(bounds[0][0], bounds[2][0], nx)
y = np.linspace(bounds[0][1], bounds[2][1], ny)
xv, yv = np.meshgrid(x, y)
phase_matrix = np.zeros((1024, 1024))
emissn_matrix = np.zeros((1024, 1024))
libsight = []
for i, x in enumerate(xv):
for j, y in enumerate(yv):
ibsight = [x[i], y[j], bsight[2]]
libsight.append(ibsight)
try:
(spoint, trgepc, srfvec ) = spiceypy.sincpt('DSK/UNPRIORITIZED', 'MARS', et, 'IAU_MARS', 'NONE', 'ROSETTA', frame, ibsight)
(trgepc, srfvec, phase, solar, emissn) = spiceypy.ilumin('DSK/UNPRIORITIZED', 'MARS', et, 'IAU_MARS', 'NONE', 'ROSETTA', spoint)
emissn_matrix[i,j] = emissn
phase_matrix[i,j] = phase
print(emissn)
except:
pass
emissn_matrix[i,j] = 0
phase_matrix[i,j] = math.pi
# -
plt.pcolor(xv, yv, emissn_matrix)
plt.pcolor(xv, yv, phase_matrix)
|
spiops/test/.ipynb_checkpoints/spirec_sketch-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Introduction librairies sklearn, pandas
# - Pandas : manipuler des fichiers csv (tableaux excel), faire des statistiques descriptives (moyenne variance, mediane,histogramme)
# - Sklearn : Librairie orienté machine learning. Simplifie les taches récurentes, telles que séparer les données, créer un modèle, entraîner un modèle.
#
#
# La librairie "pandas" est destinée à utiliser des fichiers csv sous python de manière naturelle. Les fichiers csv sont représentés par un "DataFrame". C'est un objet python sur lesquels on peut effectuer les opérations les plus courantes (calculer la moyenne d'une colonne, etc.)
# # Importer les données
# Afficher les colonnes :
import pandas
import matplotlib.pyplot as plt
df=pandas.read_csv("housing.csv")
df.columns
# Le "Boston data frame" a 506 lignes and 14 colonnes.
#
# - crim taux de criminalité par ville
#
# - zn proportion de résidences ( lots > 25,000 sq.ft.)
#
# - indus proportion de zone industrielle par ville
#
# - chas 1 si une rivière passe, 0 sinon
#
# - nox nitrogen oxides concentration (pollution).
#
# - rm nombre moyen de chambres par habitation
#
# - age proportion de maisons occupées construites avant 1940.
#
# - dis distance moyenne (pondérée) des 5 centres d'emplois de Boston.
#
# - rad indice d'accés au périph
#
# - tax taxe d'habitation pour \$10,000.
#
# - ptratio taux de "pupil-teacher" par ville (?).
#
# - black 1000(Bk - 0.63)^2 ou Bk est la proportion d'afro-américain par ville (base de donnée US)
#
# - lstat pourcentage de personnes en dessous du seuil de pauvreté (lower status).
#
# # Outils de visualisation
# ## Aperçu des données
df.head()
df.info()
# # Visualisation des données : Statistiques descriptives
# Avec pandas et l'objet "Dataframe", il est facile de visualiser la distribution des variables présentes dans notre jeu de donnée
df.hist(figsize=(30,10))
# ## Selectionner une colone
age = df.age
print(age)
# ## statistiques sur une colonne
#
max_age=age.max()
min_age=age.min()
median_age=age.median()
print(max_age,min_age,median_age)
# ## inspecter la colonne rad
# - que constatez-vous?
# - décrire medv en fonction de rad
# rad est une colonne catégorielle et non numérique !!
df.rad.value_counts()
df.groupby('rad')['medv'].mean()
# ## Visualiser l'impact d'une variable sur une autre
# - Faire le scatter plot de crim contre medv
df.plot.scatter(x="crim", y="medv",alpha=0.5)
# - proposer une visualisation pour décrire medv en fonction de rad
df.groupby('rad')['medv'].mean().plot(kind='barh')
df.boxplot(column='medv', by ='rad')
# A faire : essayer de trouver d'autres variables importantes qui pourraient expliquer medv
# # Partie 2
#
# # Séparer sous la forme (X,Y)
y=df["medv"] # la variable a prédire
x=df.drop('medv', axis=1) # enlever la variable à prédire des prédicteurs
print("la taille de mon jeu de donnée est {}. Je cherche à expliquer le prix de vente d'une maison à partir de {} variables".format(x.shape[0],x.shape[1]))
x=x.fillna(-1) # valeurs manquantes
y=y.fillna(-1) # valeurs manquantes
# # Création du jeu d'entrainement et du jeu de test
# Nous devons maintenant découper notre jeu d'entrainement. Pour cela, j'utilise la fonction train_test_split fournie par sklearn. Le paramètre test_size me permet de choisir la proportion de mon jeu de test. En règle général, cette valeur est comprise entre 0.2 et 0.3.
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(x,y,test_size=0.2)
# # Création d'un modèle (regréssion lineaire)
# Nous allons maintenant essayer d'expliquer la variable y (le prix de la maison) en fonction des variables x. Le modèle est de la forme : $$y=A*x+b$$
# $$ Prix=\beta_{CRIM}*X_{CRIM}+\beta_{ZN}*X_{ZN}+\beta_{INDUS}*X_{INDUS}+...$$
# Où les coefficients du vecteur A seront ceux qui "expliquent" le mieux les données. Par exemple, on pourrait faire l'hypothèse que la variable "CRIM" (taux de criminalité de la zone) a un impact négatif sur le prix des maisons. On peut prévoir un coefficient négatif devant cette variable.
# +
import sklearn.linear_model
model=sklearn.linear_model.LinearRegression()
model.fit(X_train,Y_train) # Attention ! Il ne faut surtout pas mettre les données de test dans la fonction fit
# -
for i in range(len(x.columns)):
print(x.columns[i], model.coef_[i])
# -Interpréter la valeur de ces coefficients. Sont ils crédibles ?
for i in range(len(x.columns)):
print("Le coefficient de {} est {}".format(df.columns[i],model.coef_[i]))
# # Evaluation du modèle
# Comment savoir si notre modèle est bon ou pas ? Il faut un critère de comparaison. Par exemple l'écart quadratique moyen pour une regression, le taux de bonnes prédictions pour une classification
from sklearn.metrics import mean_squared_error,mean_absolute_error
prediction_train=model.predict(X_train)
erreur_train=mean_squared_error(Y_train,prediction_train)
print(erreur_train)
# Et sur le jeu d'entrainement ?
prediction_test=model.predict(X_test)
erreur_test=mean_squared_error(Y_test,prediction_test)
print(erreur_test)
# L'objectif est le suivant : avoir la plus petite erreur possible sur le jeu d'entrainement.
#
# ### Interpréter l'erreur
# cette erreur est elle acceptable ? Notre modèle est il bon ? Nous avons ici considéré l'erreur moyenne au carré, peut être qu'il faut scorer le modèle avec une erreur plus compréhensible.
erreur_train=mean_absolute_error(Y_test,prediction_test)
print(erreur_train)
# La contrainte est la suivante : avoir une erreur similaire sur le jeu de test (contrôle d'overfitting)
# # Visualisation des résultats
import matplotlib.pyplot as plt
erreurs=Y_test-prediction_test
plt.figure()
plt.hist(erreurs, bins=50)
plt.show()
# - Analyser l'histogramme des erreurs
|
formation/TP-01-Python pour Data Scientists/ml_housing-Correction.ipynb
|
(* -*- coding: utf-8 -*-
(* --- *)
(* jupyter: *)
(* jupytext: *)
(* text_representation: *)
(* extension: .ml *)
(* format_name: light *)
(* format_version: '1.5' *)
(* jupytext_version: 1.14.4 *)
(* kernelspec: *)
(* display_name: OCaml *)
(* language: ocaml *)
(* name: iocaml *)
(* --- *)
(* + [markdown] deletable=true editable=true
(* <h1> Salle de devoir surveillé </h1> *)
(* *)
(* <h2> Présentation </h2> *)
(* *)
(* Pour un devoir surveillé, $n$ élèves doivent s'assoir dans une salle avec $n$ tables à leurs noms. Les élèves n'ont pas regardé le plan de la salle et s'assoient au hasard dans la salle. Quelle est la probabilité qu'aucun élève ne se soit assis à la bonne place ? *)
(* *)
(* Au hasard signifie exactement ceci: les élèves discutent debout en étant répartis de façon quelconque dans la salle. Chaque élève est à une plus courte distance d'une des tables et, pour chaque table, cette distance la plus courte correspond à un élève distinct. A l'instant de la sonnerie, tous les élèves s'assoient, en même temps, à la table dont ils sont la plus proche. *)
(* *)
(* Remarque: il peut être intéressant de résoudre le problème généralisé ci-dessous pour répondre au problème original. *)
(* *)
(* <h3>Problème généralisé</h3> *)
(* *)
(* On considère la généralisation suivante. *)
(* *)
(* Le surveillant ne connaît pas les élèves. *)
(* *)
(* $k$ élèves, qui n'ont pas révisé, envoient un élève d'une autre classe à leur place pour faire le devoir surveillé. (On suppose que les $k$ remplaçants ne sont pas des homonymes des $k$ élèves qui se sont fait remplacés). *)
(* *)
(* Il y aura toujours $n$ élèves dans la salle mais $k$ d'entre eux n'ont pas leur véritable nom inscrit sur le plan de la salle (et pour cause !). *)
(* *)
(* On reprend le problème précédent où les $n$ élèves s'installent au hasard sans regarder le plan de classe. Les $k$ remplaçants sont forcément à une place qui n'est pas à leur véritable nom. *)
(* *)
(* On note $p_{n,k}$ la probabilité qu'aucun élève ne se soit assis à la place correspondant à son véritable nom lorsqu'il y a $k$ remplaçants parmi les $n$ élèves. *)
(* *)
(* Calculer $p_{n,k}$ par récurrence. *)
(* *)
(* Remarque: $p_{n,0}$ correspond au problème original. *)
(* *)
(* <h3> Solution </h3> *)
(* *)
(* S'il n'y a qu'un élève ($n=1$) et qu'il ne s'est pas fait remplacé ($k=0$), alors celui-ci est forcément à la bonne place: $p_{1,0}=0$. *)
(* *)
(* Si $n=1$ et $k=1$, alors le remplaçant ne peut pas être à une place qui correspond à son véritable nom: $p_{1,1}=1$. *)
(* *)
(* On considère le problème original ($n\neq0,k=0$). Pour un élève $A$ donné (qui ne s'est pas fait remplacé), la probabilité qu'il s'assoit à une place qui n'est pas la sienne est: $\frac{n-1}{n}$. Si $A$ a pris la place de l'élève $B$, $B$ est obligé de s'assoir à une place qui n'est pas la sienne. $B$ est dans la même situation qu'un remplaçant. On se retrouve avec le problème généralisé $n'=n-1$ et $k'=1$. D'où: $p_{n,0}=\frac{n-1}n.p_{n-1,1}$ pour $n>1$. *)
(* *)
(* Par exemple, pour $n=2$, on a: $p_{2,0}=\frac{1}{2}.p_{1,1}=\frac{1}{2}$ (une chance sur 2 que $A$ et $B$ s'installent à leur table respective, une chance sur 2 qu'ils aient échangé leurs tables). *)
(* *)
(* On considère le problème généralisé avec $k\geq1$. Pour un remplaçant $A$ donné: *)
(* La probabilité qu'il s'assoit à la place d'un des $k$ élèves qui s'est fait remplacé est $\frac kn$ (y compris l'élève qu'il était lui-même censé remplacer). Une fois $A$ assis, on est ramené au problème $n'=n-1$ (un élève de moins) et $k'=k-1$ (un remplaçant de moins). *)
(* La probabilité qu'il s'assoit à la place d'un des $n-k$ élèves qui ne s'est pas fait remplacé est $\frac{n-k}n$. Dans ce dernier cas, l'élève $B$, dont $A$ a pris la place, est obligé de s'assoir à une place qui n'est pas la sienne comme un remplaçant. Une fois $A$ assis, on est ramené au problème $n'=n-1$ (un élève de moins) et $k'=k$ (autant de remplaçants puisque $A$ a été remplacé par $B$). *)
(* Finalement, on a: $p_{n,k}=\frac{k}{n}.p_{n-1,k-1}+\frac{n-k}{n}.p_{n-1,k}$ pour $n>1$ et $n\geq k>0$ *)
(* *)
(* + deletable=true editable=true
open Random;;
Random.self_init;;
(* + deletable=true editable=true
let range debut fin =
let rec loop i acc =
if i = fin then List.rev acc else
loop (i+1) (i::acc) in
loop debut [];;
(* + deletable=true editable=true
let shuffle d =
let nd = List.map (fun c -> (Random.bits (), c)) d in
let sond = List.sort compare nd in
List.map snd sond
(* + deletable=true editable=true
let tirage n =
let liste=shuffle (range 0 n) in
let rec aucun_a_sa_place i liste =
match liste with
|[]-> true
|hd::tl -> if hd=i then false else aucun_a_sa_place (i+1) tl in
aucun_a_sa_place 0 liste;;
let simulation nbre_eleves nbre_simul =
let rec loop num_simul aucun_a_sa_place =
if num_simul = nbre_simul then float_of_int aucun_a_sa_place/.(float_of_int nbre_simul) else
if tirage nbre_eleves then loop (num_simul+1) (aucun_a_sa_place+1)
else loop (num_simul+1) aucun_a_sa_place in
loop 0 0;;
(* + deletable=true editable=true
let rec proba =
let cache = Hashtbl.create 10 in
begin fun (n,k) ->
try Hashtbl.find cache (n,k)
with Not_found -> begin
let calc (n,k) = match (n,k) with
|(1,1) -> 1. (*1 personne; 1 substitut*)
|(1,0) -> 0.
|(n,k) when n=k -> 1.
|(n,0) -> float_of_int(n-1)*.proba(n-1,1)/.(float_of_int n)
| _ -> (float_of_int k*.proba(n-1,k-1)+.float_of_int(n-k)*.proba(n-1,k))/.(float_of_int n) in
let res = calc(n,k) in
Hashtbl.add cache (n,k) res; res
end
end
(* + deletable=true editable=true
for n =2 to 20 do
print_int n;print_string " ";print_float (proba(n,0));print_newline();
done;
(* + deletable=true editable=true
let liste_n = range 2 20;;
(* + deletable=true editable=true
let liste_proba = List.map (fun n-> proba(n,0)) liste_n;;
(* + deletable=true editable=true
let liste_simul = List.map (fun n-> simulation n 50000) liste_n;;
(* + deletable=true editable=true
#use "topfind";;
#require "plplot";;
open Plplot;;
module P = Plot;;
let couleurs_list = [[ 0;255;255;255]; (*`white*)
[ 1; 0; 0; 0]; (*`black*)
[ 2; 0; 0;255]; (*`blue*)
[ 3;255; 0; 0]; (*`red*)
[ 4;165; 42; 42]; (*`brown*)
[ 5; 0; 0; 0]; [ 6; 0; 0; 0]; [ 7; 0; 0; 0]; [ 8; 0; 0; 0]; [ 9; 0; 0; 0];
[10;200;200;200]; (*`gray*)
[11; 0;255;255]; (*`light_blue*)
[12; 0;255; 0]; (*`green*)
[13;255;255; 0]; (*`yellow*)
[14;255; 0;255]; (*`pink*)
[15;160; 0;213]; (*`purple*) ]
let rec loop couleurs_list = match couleurs_list with
| [n;r;g;b]::tl -> plscol0 n r g b; loop tl
| _ -> ();;
let couleurs = (fun () -> plscolbg 255 255 255; loop couleurs_list)
let initialisation filename xmin xmax ymin ymax =
P.init (xmin, ymin) (xmax, ymax) `greedy (`svg `core) ~filename:(filename^".svg") ~pre:couleurs
let xlabel texte = P.text_outside `black (`bottom 0.5) 3. texte
let ylabel texte = P.text_outside `black (`left 0.5) 5. texte
let label texte_x texte_y titre = P.label texte_x texte_y titre
(* + deletable=true editable=true
let xs = Array.of_list (List.map float_of_int liste_n) in
let ys = Array.of_list liste_proba in
let ys' = Array.of_list liste_simul in
let p = initialisation "graph" 2. 20. 0.3 0.55 in
P.plot ~stream:p [P.lines `green xs ys; P.lines `blue xs ys';
xlabel "nombre d'eleves"; ylabel "probabilité qu'aucun élève ne soit à sa place";
P.legend [[P.line_legend "simulation" `blue];
[P.line_legend "théorie" `green]]];
P.finish ~stream:p ();;
(* + [markdown] deletable=true editable=true
(* <img src="./graph.svg" width=750 /> *)
(* + deletable=true editable=true
|
Salle_devoir_surveille/Salle_devoir_surveille_OCaml_solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Face Generation Demo
#
# This notebook demonstrates face generation process of the
# method described in the paper "PixelCNN Models with Auxiliary Variables for Natural Image Generation":
# http://proceedings.mlr.press/v70/kolesnikov17a.html
# +
import tensorflow as tf
# Load tensorflow utils and models
import utils
# Fix random seed for reproducable results
tf.set_random_seed(1)
# Load visualization libraries
import pylab
import matplotlib.pyplot as plt
from IPython import display
# %matplotlib inline
import numpy as np
import scipy.ndimage as nd
import cPickle
import os
# -
# ## Set global parameters
# +
# Computational mode. 'gpu' mode is recommended, 'cpu' mode can be quite slow.
mode = 'gpu' # or 'cpu' is possible
# List of GPUs to use
gpu_list = [0]
num_gpus = len(gpu_list)
# Number of pyramid layers
num_pyramid_layers = 5
# Number of pyramid layers to generate (up to 5)
num_pyramid_layers_to_generate = 5
# Batch size
batch_size_per_gpu = 4
batch_size = batch_size_per_gpu * num_gpus
# -
# ## Building the Pyramid PixelCNN Network
# +
with tf.variable_scope('Resnet') as scope:
# Create placeholder for images, which should be generated
images = tf.placeholder(shape=[batch_size, None, None, 3], dtype=tf.float32)
# Build multi-scale image pyramid
images_pyramid = utils.get_pyramid(images, num_pyramid_layers - 1)
pyramid_embeddings = []
pyramid_predicted_images = []
# Each iterations creates one Pyramid layer
for layer_i in range(num_pyramid_layers):
with tf.variable_scope('scale%d' % layer_i) as scope:
images_current = images_pyramid[layer_i]
images_prev = images_pyramid[layer_i + 1]
# Technical step needed to properly create variables ####
tf.GLOBAL['init'] = True
_ = utils.PyramidPixelCNN(images_current, images_prev)
tf.GLOBAL['init'] = False
scope.reuse_variables()
##########################################################
images_current_gpu_parts = tf.split(images_current, num_gpus, 0)
images_prev_gpu_parts = (tf.split(images_prev, num_gpus, 0)
if images_prev is not None
else [None] * num_gpus)
predicted_images = []
embeddings = []
for i, gpu_i in enumerate(gpu_list):
with tf.device('/gpu:%i' % gpu_i if mode == 'gpu' else '/cpu:0'):
# Build tensorflow model for one super-resolution step
p, e = utils.PyramidPixelCNN(images_current_gpu_parts[i],
images_prev_gpu_parts[i])
predicted_images.append(p)
embeddings.append(e)
pyramid_predicted_images.append(predicted_images)
pyramid_embeddings.append(embeddings)
# Create Tensorflow expression to sample from the predicted pixel distributions
variance = tf.placeholder(shape=[], dtype=tf.float32)
samples = [utils.sample_from_discretized_mix_logistic(tf.concat([pp for pp in p], 0), variance)
for p in pyramid_predicted_images]
# -
# ## This function implements sequential pixel-wise sampling for a given pyramid layer
def sample_from_model_at_layer(layer_i, image_prev_layer, sess, change_variance=0.0):
# Infer resolution for the current layer
resolution = 2 ** (int(np.log2(128)) - layer_i)
if image_prev_layer is not None:
x_gen = nd.zoom(image_prev_layer, (1, 2, 2, 1), order=0)
else:
x_gen = np.zeros((batch_size, resolution, resolution, 3))
# Compute embedding of the image from the previous pyramid layer
if pyramid_embeddings[layer_i][0] is not None:
embedding_current = sess.run(pyramid_embeddings[layer_i],
{images_pyramid[layer_i + 1]: image_prev_layer})
else:
embedding_current = None
# Create figure to visualize sampling preocess
f = plt.figure(figsize=(24, 8))
# Run cycle over every pixel in the image
for yi in range(resolution):
for xi in range(resolution):
FOV = 16
if x_gen.shape[1] <= FOV:
x_feed = x_gen
y_sample = yi
x_sample = xi
embedding_feed = embedding_current
else:
cut_y, cut_x = 0, 0
y_sample = yi
x_sample = xi
if yi >= FOV:
cut_y = yi - FOV + 1
y_sample = -1
if xi >= FOV / 2:
cut_x = xi - FOV / 2
x_sample = FOV / 2
x_feed = x_gen[:, cut_y:cut_y + FOV, cut_x:cut_x + FOV, :]
embedding_feed = [e[:, cut_y:cut_y + FOV, cut_x:cut_x + FOV, :] for e in embedding_current]
# Sample new pixel
feed = {images_pyramid[layer_i]: x_feed, variance: change_variance}
if embedding_current is not None:
[feed.update({pyramid_embeddings[layer_i][i]: r}) for i, r in enumerate(embedding_feed)]
new_pixel = sess.run(samples[layer_i], feed)
# Update current image
x_gen[:, yi, xi, :] = new_pixel[:, y_sample, x_sample, :]
# Add green pixel to simplify tracking of sampling process
if (xi + 1) < resolution:
x_gen[:, yi, xi + 1, :] = np.array([0, 1.0, 0])[None]
elif (yi + 1) < resolution:
x_gen[:, yi + 1, 0, :] = np.array([0, 1.0, 0])[None]
# Visualize current image ###################################
# Set frequency of updates
freq_update = {4: 3, 3: 20, 2: 70, 1: 70}
if (yi * resolution + xi) % freq_update[layer_i] == 0:
# Plot images
for i in range(batch_size):
ax = f.add_subplot(1, batch_size, i + 1)
ax.imshow(utils.unprepro(x_gen[i]).astype('uint8'), interpolation='nearest')
ax.axis('off')
display.display(plt.gcf())
display.clear_output(wait=True)
plt.clf()
###############################################################
# Plot final samples
for i in range(batch_size):
ax = f.add_subplot(1, batch_size, i + 1)
ax.imshow(utils.unprepro(x_gen[i]).astype('uint8'))
ax.axis('off')
return x_gen
# +
# Retrieve pretrained model
if not os.path.exists('model.pickle'):
import urllib
model_file = urllib.URLopener()
print('Downloading the pretrained model...')
model_file.retrieve("https://pub.ist.ac.at/~akolesnikov/files/model.pickle", "model.pickle")
print('Finished')
inits = utils.get_weight_initializer(dict(cPickle.load(open('model.pickle'))))
# -
# ### variance_change is a crucial parameter, which controls variance of the sampled pixels
# Negative values of this variable artifically reduce variance of the predicted pixel distribution and lead to better perceptual quality
variance_change = -10
# # Create tensorflow session and run the computaitons
with tf.Session() as sess:
# Load pretrained weights
sess.run(inits)
# Produce samples
image_list = [None]
for layer_i in range(num_pyramid_layers_to_generate):
sample = sample_from_model_at_layer(num_pyramid_layers - layer_i - 1,
image_list[-1], sess, variance_change)
image_list.append(sample)
image_list = image_list[1:]
# ### Try higher variance
variance_change = 0.0
with tf.Session() as sess:
sess.run(inits)
image_list = [None]
for layer_i in range(num_pyramid_layers_to_generate):
sample = sample_from_model_at_layer(num_pyramid_layers - layer_i - 1,
image_list[-1], sess, variance_change)
image_list.append(sample)
image_list = image_list[1:]
|
demo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="AMNG35yV9_5d" outputId="882405f5-2b1b-47f7-ea75-3dd4d326bcc2"
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge/master/data/'
# !pip install category_encoders==2.*
# !pip install pandas-profiling==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
# -
# # Importing relevant libraries.
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
import category_encoders as ce
from sklearn.model_selection import RandomizedSearchCV
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import accuracy_score
from scipy.stats import randint
from sklearn.preprocessing import StandardScaler, MinMaxScaler
import pandas as pd
import numpy as np
import random
# # creating pandas dataframes and cleaning up the data + feature engineering
# + colab={} colab_type="code" id="-SAM20NV-DPw"
# creating elementary pandas dataframes
import pandas as pd
from sklearn.model_selection import train_test_split
test_features = pd.read_csv('test_features.csv')
train_features = pd.read_csv('train_features.csv')
train_labels = pd.read_csv('train_labels.csv')
sample_submission = pd.read_csv('sample_submission.csv')
# + colab={} colab_type="code" id="wt3ARb_XkjA5"
# In order to create a new feature such that the date recorded is in simple date_time format.
train_features['date_recorded'] = pd.to_datetime(train_features['date_recorded'], infer_datetime_format=True)
test_features['date_recorded'] = pd.to_datetime(test_features['date_recorded'], infer_datetime_format=True)
# creating a new feature wpp
train_features['wpp'] = train_features['amount_tsh']/train_features['population']
test_features['wpp'] = test_features['amount_tsh']/test_features['population']
# cleaning up the NaN and nonesense values
train_features['wpp'] = train_features['wpp'].replace([np.inf, -np.inf], np.nan)
test_features['wpp'] = test_features['wpp'].replace([np.inf, -np.inf], np.nan)
# + colab={} colab_type="code" id="Jo3o0FGPakNR"
# checks to see if there are any 0 values in construction year, and checks NaNs values in wpp.
def feature_eng_zeros(G):
G['construction'] = G['construction_year'] != 0
G['wpp'] = G['wpp'].replace(np.nan, 0)
return G
# running the feature engineering function on the test and train features
train_features = feature_eng_zeros(train_features)
test_features = feature_eng_zeros(test_features)
# + colab={"base_uri": "https://localhost:8080/", "height": 104} colab_type="code" id="a4P8XgHBk56w" outputId="2bda77d2-a21f-4ae3-e449-a6d51e4b8f79"
# cconverts each individual datetime feature into a string, such that the model as can use it.
def feature_eng_convertDT(N):
N['year'] = N['date_recorded'].dt.year
N['month'] = N['date_recorded'].dt.month
N['week'] = N['date_recorded'].dt.week
N['age'] = N['year'] -N['construction_year']
N['age'].loc[N['age'] == N['year']] = 0
N['date_recorded'] = N['date_recorded'].astype(str)
return N
# running the function on the above.
train_features = feature_eng_convertDT(train_features)
test_features = feature_eng_convertDT(test_features)
# + colab={} colab_type="code" id="zVG9wnrDlB30"
# creating a function such that any NaN values get changed over to a random value and not means
# the lambda function functions such that it replaces it with a random values within that particular column.
def NaNFiller(X):
X['public_meeting'] = X['public_meeting'].fillna(lambda x: random.choice(X[X['public_meeting'] != np.nan])['public_meeting'])
X['permit'] = X['permit'].fillna(lambda x: random.choice(X[X['permit'] != np.nan])['permit'])
X['age'] = X['age'].replace(0, round(X['age'].mean()))
X['gps_height'] = X['gps_height'].replace(0, round(X['gps_height'].mean()))
X['funder']= X['funder'].fillna('other')
return X
# Running the NaNFillers function on the train_features.
train_features = NaNFiller(train_features)
test_features = NaNFiller(test_features)
# + colab={} colab_type="code" id="kcAhrMNNmmu2"
# defining a function, such that it drops on each function for train_features, test_features, train_labels.
def drip_drop_columns(X):
drop_cols = ['quantity_group','construction_year','recorded_by','id','num_private',
'amount_tsh', 'wpt_name','subvillage','management_group']
X = X.drop(columns= drop_cols)
return X
# dropping the columsn using hte function.
train_features = drip_drop_columns(train_features)
test_features = drip_drop_columns(test_features)
train_labels = train_labels.drop(columns='id')
# -
# # doing test train split split to begin model testing
#
# ordinal encoding + MinMaxScaler instead of StandardScaler.
# + colab={} colab_type="code" id="_tj8kgkQndxn"
# doing a test train split to begin parsing the columns.
X_train, X_val, y_train, y_val = train_test_split(train_features,train_labels, random_state=42, test_size=.2)
X_test = test_features
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="rik4AKHTanDN" outputId="b1747248-fc01-4053-da7f-ed9aafa81b02"
train_features.shape, test_features.shape
# + colab={} colab_type="code" id="miYmlluvpXcY"
# using ordinal encoder as the encoder.
encoder = ce.OrdinalEncoder()
# Fit & Transform
X_train = encoder.fit_transform(X_train)
# sestting the columns to then be scaled.
cont_columns = ['population', 'gps_height', 'week', 'month', 'year', 'age']
# better scaler than the standard scaler --> as it changes the outlier.
scaled = MinMaxScaler()
X_train[cont_columns] = scaled.fit_transform(X_train[cont_columns])
# -
# # code that will use all your CPUs.
# + colab={"base_uri": "https://localhost:8080/", "height": 228} colab_type="code" id="VZFXBk_9pZj3" outputId="16beaf40-f3ab-485b-841a-7cf2ab3a4445"
# making a dictionary for the param_distribution of the model
p_dist = {
'n_estimators': [325],
'max_depth': [20]
}
# Instantiating the model and inputting inside the randomized search CV.
model = RandomForestClassifier(n_jobs=-1, criterion="entropy")
# Randomized search CV.
search = RandomizedSearchCV(
estimator=model,
param_distributions=p_dist,
scoring='accuracy',
n_iter=10,
n_jobs=-1,
cv=20,
verbose=4,
return_train_score=True,
)
# fitting t o the training data.
search.fit(X_train, y_train)
print('Training Accuracy Score:', search.best_score_)
# + colab={} colab_type="code" id="oBcBqXatpfiE"
# encoding and transforming the X_val
X_val = encoder.transform(X_val)
# scaling and fiting the continous columns.
X_val[cont_columns] = scaled.fit_transform(X_val[cont_columns])
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="TB2eLwF-rPyC" outputId="2afb96f1-baad-4840-db46-52fa09122330"
# checking the score after scaling and fitting continous columsn.
best = search.best_estimator_
y_pred = best.predict(X_val)
print('Validation Set Accuracy Score:', accuracy_score(y_val, y_pred))
# + colab={} colab_type="code" id="yIV3srSnmMW0"
# getting X_test ready for making submission y_pred_test
best = search.best_estimator_
X_test = encoder.transform(X_test)
# scaling and fitting the y_pred test before exporting/
X_test[cont_columns] = scaled.fit_transform(X_test[cont_columns])
y_pred_test = best.predict(X_test)
# -
# # scoring and accuracy:
from sklearn.metrics import plot_confusion_matrix
plot_confusion_matrix(search, X_val, y_val,
values_format='.0f', xticks_rotation='vertical', cmap='Blues')
# +
from sklearn.metrics import classification_report
print(classification_report(y_val, y_pred))
# -
import seaborn as sns
y_pred_proba = search.predict_proba(X_val)[:, 1]
sns.distplot(y_pred_proba)
from sklearn.metrics import roc_auc_score
roc_auc_score(y_val, y_pred_proba, multi_class='ovr')
# # making the submission_files
# + colab={} colab_type="code" id="cf4dNmhArbLF"
submission = sample_submission.copy()
submission['status_group'] = y_pred_test
submission.to_csv('Submission_Kush_ensemble_8.csv', index=False)
# -
|
KushRawal_Kaggle_Lambda - Copy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
import os,glob
from matplotlib import pyplot as plt
# Joey's code but modified to do any number of topics
# # run a random forest on these words and see how well it can identify labels
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
glob.glob('third*.json')
df = pd.read_json('third_encoded_LDA_with_topics.json')
#get the feature columns: those that start with 'key_word:'
feat = [x for x in df.columns if x[:9] == 'key_word:']
len(feat)
# # choose two topics to classify
topics = ['hope','home','missionary work']
sizes = []
for topic in topics:
temp = df.loc[df[topic] == 1].shape[0]
sizes.append(temp)
print('the topic',topic,'has',temp,'talks associated')
# make an even dataset
resized_dfs = []
for topic in topics:
resized = df.loc[df[topic] == 1].iloc[:np.array(sizes).min()].copy()
resized_dfs.append(resized)
print(resized.shape[0], end=' ')
new = pd.concat(resized_dfs)
new.shape
# # are there any instances that are both topics
topic_sum = sum(new[topic] for topic in topics)
remove_ind = new[topic_sum > 1].index
if len(remove_ind) > 0:
print(len(remove_ind))
new.drop(index=remove_ind,inplace=True)
# # reduce the feature to where only these talks have these words so there is a one in each column
# get all the features
b = new
all_key_words = set()
for i in range(b.shape[0]):
all_key_words = all_key_words.union(set(b.iloc[i]['words']))
new_feat = ['key_word:' + word for word in all_key_words]
print(len(new_feat))
# # PREDICT WHETHER THE TALK IS HOME
# # test train split
X = new[new_feat].copy()
print('the target variable is:',topics[0])
y = sum(new[topic]*i for i, topic in enumerate(topics)) #new[topics[0]]
print(y) #I think this is right
print('X.shape',X.shape)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)
for obj in [X_train, X_test, y_train, y_test]:
print(obj.shape)
# +
# X_train
# -
# # RUN THE MODEL
clf = RandomForestClassifier(n_estimators=10
,n_jobs=-1
,oob_score=True)
clf = clf.fit(X_train, y_train)
clf.score(X_train, y_train)
#mean accuracy
clf.score(X_test,y_test)
clf.predict_proba(X_test)
# # IF IT'S STRUGGLING THEN TRY NORMALIZING FEATURES
importances = pd.Series({new_feat[i].replace('key_word:',''):importance for i, importance in enumerate(clf.feature_importances_) if importance > 0})
importances.sort_values(inplace=True, ascending=False)
importances[:20]
importances[19::-1].plot(kind='barh')
plt.title("Random Forest Classifier importances")
plt.tight_layout()
plt.savefig("rfc_importances.png", dpi=128)
plt.show()
|
analysis/supervised learning on lda with RF - 02.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ### Movies for Along Shelf Flux
# +
#KRM
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import matplotlib as mpl
# #%matplotlib inline
from math import *
import scipy.io
import scipy as spy
from netCDF4 import Dataset
import pylab as pl
import os
import sys
import seaborn as sns
# +
lib_path = os.path.abspath('../../Building_canyon/BuildCanyon/PythonModulesMITgcm') # Add absolute path to my python scripts
sys.path.append(lib_path)
import ReadOutTools_MITgcm as rout
# +
def vTracAlong(Mask,V,zlim=30, ylim=230):
'''MaskC : mask corresponding to '''
mask_expand2 = np.expand_dims(Mask[:zlim,ylim,:],0)
mask_expand2 = mask_expand2 + np.zeros(V[:,:zlim,ylim,:].shape)
VTRACbox= np.ma.masked_array(V[:,:zlim,ylim,:],mask = mask_expand2)
return(VTRACbox)
# +
NoCCanyonGrid='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run07/gridGlob.nc'
NoCCanyonGridOut = Dataset(NoCCanyonGrid)
NoCCanyonState='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run07/stateGlob.nc'
NoCCanyonStateOut = Dataset(NoCCanyonState)
FluxTR01NoC = '/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run07/FluxTR01Glob.nc'
NoCFluxOut = Dataset(FluxTR01NoC)
CanyonGrid='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/gridGlob.nc' # this has a canyon but calling it no canyon to use old code
CanyonGridOut = Dataset(CanyonGrid)
CanyonState='/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/stateGlob.nc'
CanyonStateOut = Dataset(CanyonState)
FluxTR01 = '/ocean/kramosmu/MITgcm/TracerExperiments/CNTDIFF/run03/FluxTR01Glob.nc'
FluxOut = Dataset(FluxTR01)
# +
#for dimobj in CanyonStateOut.variables.values():
# print dimobj
# +
# General input
nx = 360
ny = 360
nz = 90
nt = 19 # t dimension size
z = CanyonStateOut.variables['Z']
Time = CanyonStateOut.variables['T']
xc = rout.getField(CanyonGrid, 'XC') # x coords tracer cells
yc = rout.getField(CanyonGrid, 'YC') # y coords tracer cells
bathy = rout.getField(CanyonGrid, 'Depth')
hFacC = rout.getField(CanyonGrid, 'HFacC')
MaskC = rout.getMask(CanyonGrid, 'HFacC')
MaskCNoC = rout.getMask(NoCCanyonGrid, 'HFacC')
# +
VTR = rout.getField(FluxTR01,'VTRAC01') #
UTR = rout.getField(FluxTR01,'UTRAC01') #
UTRAC,VTRAC = rout.unstagger(UTR, VTR)
VTR = rout.getField(FluxTR01NoC,'VTRAC01') #
UTR = rout.getField(FluxTR01NoC,'UTRAC01') #
UTRACNoC,VTRACNoC = rout.unstagger(UTR, VTR)
#WTRAC = rout.getField(FluxTR01,'ADVrTr01') #
#WTRACNoC = rout.getField(FluxTR01NoC,'ADVrTr01') #
# -
CSbase = vTracAlong(MaskC,VTRAC,zlim=30,ylim=230)*1000.0
CSbaseNoC = vTracAlong(MaskCNoC,VTRACNoC,zlim=30,ylim=230)*1000.0
Anom = (CSbase-CSbaseNoC)
# +
minT = CSbase.min()
maxT = CSbase.max()
minTNoC = CSbaseNoC.min()
maxTNoC = CSbaseNoC.max()
minTAnom = Anom.min()
maxTAnom = Anom.max()
print(minT, maxT)
print(minTNoC, maxTNoC)
print(minTAnom,maxTAnom)
# -
import matplotlib.animation as animation
# +
sns.set()
sns.set_style('white')
sns.set_context("talk")
#divmap = sns.diverging_palette(255, 100, l=60, n=7, center="dark", as_cmap=True)
# +
def Plot1(t,ax1):
ax1.clear()
csU = np.linspace(-maxT,maxT,num=31)
Base = ax1.contourf(xc[230,:], z[:30],CSbase[t,:,:],csU,cmap='RdYlGn')
if t == 1:
cbar=plt.colorbar(Base,ax=ax1,ticks=[np.arange(-maxT,maxT,250)])
cbar.set_label('$ mol \cdot m /l \cdot s$')
#CS = ax1.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax1.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax1.set_xlabel('Along-shore distance [km]')
ax1.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax1.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax1.set_ylabel('Depth [m]')
ax1.set_title('Base case - Cross-shore transport at day %0.1f' %(t/2.0+0.5))
def Plot2(t,ax2):
ax2.clear()
csU = np.linspace(-maxTNoC,maxTNoC,num=31)
Base = ax2.contourf(xc[230,:], z[:30],CSbaseNoC[t,:,:],csU,cmap='RdYlGn')
if t == 1:
cbar=plt.colorbar(Base,ax=ax2,ticks=[np.arange(-maxTNoC,maxTNoC,100)])
cbar.set_label('$mol \cdot m /l \cdot s$')
#CS = ax1.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax2.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax2.set_xlabel('Along-shore distance [km]')
ax2.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax2.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax2.set_ylabel('Depth [m]')
ax2.set_title('No canyon case')
def Plot3(t,ax3):
ax3.clear()
csU = np.linspace(minTAnom,-minTAnom,num=31)
Base = ax3.contourf(xc[230,:], z[:30],Anom[t,:,:],csU,cmap='RdYlBu')
if t == 1:
cbar=plt.colorbar(Base,ax=ax3,ticks=[np.arange(minTAnom,-minTAnom,250)])
cbar.set_label('$mol \cdot m /l \cdot s$')
#CS = ax3.contour(yc[100:-1,200],z[:58],Uplot[:58,100:]/Umax,csU2,colors='k',linewidths=[0.75] )
ax3.set_axis_bgcolor((205/255.0, 201/255.0, 201/255.0))
ax3.set_xlabel('Along-shore distance [km]')
ax3.set_xticks([10000,20000,30000,40000,50000,60000,70000,80000,90000,100000,110000,120000])
ax3.set_xticklabels(['10','20','30','40', '50', '60', '70', '80','90','100','110','120'])
ax3.set_ylabel('Depth [m]')
ax3.set_title('Difference')
# +
## Animation
#N=5
xslice=180
yslice=235
zslice= 29 # shelf break index
zslice2= 23
#Empty figures
fig,((ax1),(ax2),(ax3)) = plt.subplots(3, 1)
#Initial image
def init():
Plot1(0,ax1)
Plot2(0,ax2)
Plot3(0,ax3)
plt.tight_layout()
#return[ax1,ax2,ax3,ax4,ax5,ax6,ax7,ax8,ax9]
def animate(tt):
Plot1(tt,ax1)
Plot2(tt,ax2)
Plot3(tt,ax3)
plt.tight_layout()
#The animation function (max frames=47)
anim = animation.FuncAnimation(fig, animate, init_func=init,frames=18, interval = 200,blit=False, repeat=False)
##A line that makes it all work
mywriter = animation.FFMpegWriter()
##Save in current folder
anim.save('TransportAlongTr01_Base_and_NoC.mp4',writer=mywriter,fps=0.2, dpi = 200, bitrate = 1000000, codec = "libx264")
plt.show()
# +
# -
|
MoviesNotebooks/MoviesTransportAlongShelf.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 27, "hidden": true, "row": 0, "width": 12}, "report_default": {"hidden": false}}}}
# # BMI565 - Bioinformatics Programming & Scripting
#
# ## Interactive Data Visualizations with Ipython Widgets
#
# ### Table of Contents
#
# 1. [Introduction](#Introduction)
# * Dependencies
# * Installation
# * Setup
# 2. [Ipython Widgets](#Ipython-Widgets)
# * Some Basic Widgets
# * Widgets To Filter
# * Widgets To Select
# * Creating Interactivity
# * Custom Widgets
# 3. [Motivational Example: Malignant or Benign?](#Motivational-Example:-Malignant-or-Benign?)
# * Load Data into Pandas
# * Initializing & Re-Rendering Visualizations
# * Bringing It All Together
# 4. [In-Class Exercises](#In---Class-Exercises)
# 5. [Resources](#Resources)
#
# ### Introduction
#
# During the course of an exploratory data analysis (EDA) we often generate numerous data visualizations, which we may describe conceptually as *exploratory data visualizations*. Once our EDA is complete and we have conducted our principle analyses, we'll have hopefully gained a handful of insights that we find valuable and would like to communicate to a larger audience of our peers or perhaps even the general public. As with an EDA, the communication of results is often greatly facilitated by visualization – often, just a handful of plots and a paragraph can powerfully distill major findings.
#
# With that in mind, once we have the results of our study, the purpose of data visualization shifts from **exploratory** to **explanatory**. For the latter, the basic approach is often to select a few plots from the EDA that highlight the core findings of a study. Occasionally, however, the additional step of generating bespoke explanatory visualizations that are illustrative of specific findings is necessary.
#
# Interactivity can be used to create compelling explanatory visualizations that invite viewers to explore the results themselves through their web browser or desktop. By making visualizations interactive, we can both improve the quality of a visualization in terms of it's ability to engage a viewer while also making the visualization more informative.
#
# To read a discussion of the distinction between exploratory and explanatory data analysis, see this [blog post](http://www.storytellingwithdata.com/blog/2014/04/exploratory-vs-explanatory-analysis).
#
# #### Dependencies
#
# The following dependencies are required to run this notebook. Note that the version numbers are primarily for reference; exact library versions are unlikely to be required.
#
# 1. Python
# * Python 2.7 or 3.x
# 2. Python Libraries
# * Jupyter 1.0.0
# * Pandas 0.20.3
# * Numpy 1.13.1
# * Ipywidgets 7.0.0
# * Widgetsnbextension 3.0.2
# * MplD3 0.3
# 3. Data
# * <a href="https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)" target="_blank">UCI Machine Learning Repository Data</a>
# * `./data/wdbc.csv`
#
# #### Installation
# If you don't have the above libraries installed, use `conda` to install the packages, or run the following commands in your terminal.
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 8, "hidden": false, "row": 114, "width": 12}, "report_default": {"hidden": false}}}}
# ```bash
# pip3 install pandas==0.20.3 # Pandas (Introduces DataFrame data structure, similar to R)
# pip3 install jupyter==1.0.0 # Jupyter Notebook
# pip3 install ipywidgets==7.0.0 # Ipywidgets
# pip3 install widgetsnbextension==3.0.2 # Notebook Widgets Extension
# pip3 install mpld3==0.3 # MplD3 (renders matplotlib plots using D3.js)
# jupyter nbextension enable --py --sys-prefix widgetsnbextension # Ipywidgets - Extension Setup Step
# ```
# *Use `pip` instead of `pip3` if using Python 2.7*
#
# #### Setup
# If you only have Python 2.7 installed, you should be able to run this notebook with the Python 2.7 kernel as well.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 110, "width": 12}, "report_default": {"hidden": true}}}}
# Render Plots Inline
# %matplotlib notebook
# Imports: Standard Library
import re as Rgx
import math as Math
import os as OS
from __future__ import print_function
# Imports: Third Party
import pandas as Pandas
import numpy as Numpy
import matplotlib.pyplot as Plot
import mpld3 as D3
import statsmodels as Stats
from ipywidgets import widgets, interact
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 122, "width": 12}, "report_default": {"hidden": false}}}}
# ### Ipython Widgets
#
# Ipython widgets provide a way to introduce interactivity into notebooks. The widgets are implemented with HTML (structure), CSS (styling), and JavaScript (action) and encapsulate specific UI functionalities. Below is a list of all the widget classes available, along with the base class they inherit from:
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 25, "hidden": false, "row": 85, "width": 12}, "report_default": {"hidden": false}}}}
for widget in widgets.Widget.widget_types.items():
print("%s%s"% (widget[1].__name__.ljust(24), widget[1].__bases__[0].__name__))
# -
# We can think of certain widgets as being amenable to certain types of manipulation of a data model. For example:
#
# * **Button** and **Radio Button** widgets can be used to toggle a visualization feature, such as an optional regression line on a scatter plot
# * **Slider** and **Ranged Slider** widgets can be used to filter values or date ranges
# * **Toggle** and **Dropdown** widgets can be used to select specific data columns or datasets.
# * **Image** and **HTML** widgets can be used to build out user interfaces
#
# There are also specialized widgets, such as color pickers and date pickers, which can offer a user more granular control of how a visualization is rendered and data is selected.
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 32, "width": 12}, "report_default": {"hidden": false}}}}
# #### Some Basic Widgets
#
# ##### <span style="color: gray">The Button Widget</span>
#
# Each widget takes a set of initialization arguments that vary by widget type – ([see documentation for each widget here](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20List.html)). The most basic example is perhaps a simple button element:
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 69, "width": 12}, "report_default": {"hidden": false}}}}
button = widgets.Button(
description = "I'm a Button! Click me!"
)
button
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 73, "width": 12}, "report_default": {"hidden": false}}}}
# Looks great, but what does it do? Nothing. Let's fix that:
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 77, "width": 12}, "report_default": {"hidden": false}}}}
# Define a Function for The Button to Trigger
def makeAnAnimalSound (element):
import random
sounds = ["moo", "squawk", "cacaw", "woof", "oink", "rawr", "meow", "bark"]
print("%s\t" % random.sample(sounds, 1)[0], element)
button.on_click(makeAnAnimalSound)
button
# -
# This is a special case of binding a function to a widget – the button widget has a method `on_click()` that allows for a function to be triggered when it is clicked.
#
# ##### <span style="color: gray">The Toggle Button Widget</span>
#
# If you need to both set and unset a variable, you can use the toggle button widget.
button = widgets.ToggleButton(
value=False,
description="Activate!",
button_style='info' # 'success', 'info', 'warning', 'danger' or ''
)
# Add Interaction
action = interact(lambda x: print(x), x = button)
# ##### <span style="color: gray">The Checkbox Widget</span>
#
# Basically just another `ToggleButton` widget.
checkbox = widgets.Checkbox(
value=True,
description='Please don\'t check me'
)
# Add Interaction
action = interact(lambda x: print(x), x = checkbox)
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 61, "width": 12}, "report_default": {"hidden": false}}}}
# #### Widgets To Filter
#
# You can use sliders to filter both integer, float, or categorical data types. Below is an example of an integer slider.
#
# ##### <span style="color: gray">The Integer Slider Widget</span>
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 4, "height": 4, "hidden": false, "row": 57, "width": 4}, "report_default": {"hidden": false}}}}
slider = widgets.IntSlider(
value = 0,
min = -10,
max = 10,
step = 1,
description = "Do you like octopi?",
disabled = False,
continuous_update = True,
orientation = "horizontal",
readout = True
)
# Add Interaction
action = interact(lambda x: print(x), x = slider)
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 8, "height": 4, "hidden": false, "row": 57, "width": 4}, "report_default": {"hidden": false}}}}
# ##### <span style="color: gray">The Range Slider Widget</span>
# Both integer and float variants of the range slider are available.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 81, "width": 12}, "report_default": {"hidden": false}}}}
slider = widgets.FloatRangeSlider(
value=[5, 7.5],
min=0,
max=10.0,
step=0.1,
description='How Big is The Fish?',
disabled=False,
continuous_update=True,
orientation='horizontal',
readout=True,
slider_color='white',
color='black'
)
slider
# -
# ##### <span style="color: gray">An Example Filter Interaction</span>
# +
# Create a Random Numpy Array With 40 Values
array = Numpy.sort(Numpy.random.randint(0, 100, size = 40))
print(array)
# Define Range Slider Widget
slider = widgets.FloatRangeSlider(
value=[25, 75],
min=0,
max=100,
step=1,
description='Focus BMI Range:',
continuous_update=True,
orientation='horizontal',
slider_color='white',
color='black'
)
# Add Interaction – Filter Array Values by Range Values
action = interact(lambda x: array[Numpy.logical_and(array >= x[0], array <= x[1])], x = slider)
# -
# #### Widgets To Select
#
# ##### <span style="color: gray">The Dropdown Widget</span>
# The classic dropdown.
# +
# Genres & Their Data Values
genres = {
'Rock' : 1,
'Indie' : 2,
'Hip Hop' : 3,
'Rap' : 4,
'Folk' : 5,
'Country' : 6,
'Bluegrass' : 7,
'Classical' : 8,
'Silence' : 9
}
# Reverse To Data Value : Genre Key
reverse = { value : key for key, value in genres.items()}
# Initialize DropDown
dropdown = widgets.Dropdown(
options=genres,
value=1,
description="I'd Rather Listen To:",
)
# Add Interaction
action = interact(lambda x: print("Index: %d\tGenre: %s" % (x, reverse[x])), x = dropdown)
# -
# ##### <span style="color: gray">The Multi Select Widget</span>
# For when you would like to allow the selection of combinations.
multiselect = widgets.SelectMultiple(
options=['Breakfast', 'Second Breakfast', 'Brunch', 'Lunch', 'Dinner', 'Second Dinner', 'Dessert All Day'],
value=['Breakfast', 'Brunch', 'Lunch', 'Dinner', 'Second Dinner'],
description='I Will Have...'
)
# Add Interaction
action = interact(lambda x: print(x), x = multiselect)
# ##### <span style="color: gray">The Tabs Widget</span>
# +
# Import OrderedDict To Ensure Alphabetical Ordering of Tabs
from collections import OrderedDict
labels = OrderedDict(
(
('A', 'Alice'),
('B', 'Bob'),
('C', 'Charlie'),
('D', 'Diane')
)
)
tab = widgets.Tab()
# Set Names to Labels
tab.children = [widgets.Label(value) for key, value in labels.items()]
for i, key in enumerate(labels.keys()):
tab.set_title(i, key)
tab
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 126, "width": 12}, "report_default": {"hidden": false}}}}
# ##### <span style="color: gray">The Toggle Buttons Widget</span>
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 130, "width": 12}, "report_default": {"hidden": false}}}}
toggle = widgets.ToggleButtons(
options = ["bpm", "bmi", "systolic", "diastolic"],
description = 'Filter:',
disabled = False,
button_style='info', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
icon='check'
)
# Add Interaction
action = interact(lambda x: print(x), x = toggle)
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 36, "width": 12}, "report_default": {"hidden": false}}}}
# #### Using `interact` for Basic Interactivity
# Often times, we're only concerned with the specific data from an interaction. In those cases, we can use the `interact` method, which allows us to work with the widget data directly. As seen above, we pass to the `interact` method two parameters: a simple `lambda` function, which returns the value passed to it, and a widget that the lambda function will be bound to. Of course, we can customize the `lambda` function to, say, reverse and capitalize the string data value retrieved from a `ToggleButtons` widget:
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"hidden": true}, "report_default": {"hidden": true}}}}
# An Inline Function To Print A Reversed & Capitalized String
reverseAndCapitalize = lambda x: "%s >>> %s" % (x, x[::-1].upper())
toggle = interact(reverseAndCapitalize, x = widgets.ToggleButtons(
options = ["bpm", "bmi", "systolic", "diastolic"],
description = 'Filter:',
disabled = False,
button_style='info', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
icon='check'
))
# -
# #### More Advanced Interactivity
# Widget interactivity is powered by JavaScript's [event loop architecture](https://developer.mozilla.org/en-US/docs/Web/JavaScript/EventLoop). While most widgets can use the simple `interact` method to retrieve values, we can also use the `observe` method to bind more complex callback functions to a widget and access additional event context. While the additional context can be useful in some instances, the high-level nature of ipython widgets makes these instances few and far between.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 134, "width": 12}, "report_default": {"hidden": false}}}}
# A Simple DataFrame
df = Pandas.DataFrame({
"bpm": [121, 118, 133],
"bmi": [23.1, 27.1, 22.7],
"systolic": [131, 103, 114],
"diastolic": [67, 82, 93]
})
# Initialize A Toggle Buttons Widget
toggle = widgets.ToggleButtons(
options = ["bpm", "bmi", "systolic", "diastolic"],
description = 'Filter:',
disabled = False,
button_style='info', # 'success', 'info', 'warning', 'danger' or ''
tooltip='Description',
icon='check'
)
# Define A Function That Uses The Widget Interaction Data
def callback (data):
if "new" in data.keys():
print(df[data["new"]], "\n")
# Call Widget's observe Method, Passing Callback Function as Parameter
toggle.observe(callback, names = 'value')
toggle
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 7, "hidden": false, "row": 40, "width": 12}, "report_default": {"hidden": false}}}}
# Above, we defined a function called `callback`, which checks for a new filter value and, if it exists, uses it to select and print the corresponding column of the `df` DataFrame. We then pass this 'callback function' as a parameter to the `observe` method, along with an indication that we'd like the observe method to pass the `value` from the interaction. In doing this, we bind the `ToggleButtons widget` to `callback`. This architecture is not common in Python, but is the bread and butter of event-based programming in JavaScript (and many other asynchronous languages). To see more about events, see their [documentation](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20Events.html).
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 47, "width": 12}, "report_default": {"hidden": false}}}}
# #### Custom Widgets
#
# If you find that none of the above widgets suit your needs, the `ipywidgets` API also enables the development of [custom widgets](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20Custom.html). Before embarking down this road, its worthwhile to build an understanding of how `ipywidgets` work as it is a bit more involved – here's an [excellent tutorial](https://ipywidgets.readthedocs.io/en/stable/examples/Widget%20Low%20Level.html) that focuses on just that.
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": true, "row": 0, "width": 12}, "report_default": {"hidden": false}}}}
# ### Motivational Example: Malignant Versus Benign
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 10, "hidden": false, "row": 13, "width": 12}, "report_default": {"hidden": false}}}}
# Widgets enable us to build UI that allow for the interactive exploration of data sets and their visualization. To illustrate this, we'll use a dataset with 30 (continuous) breast cancer imaging features and a (categorical) dependent variable of `diagnosis` with two factor levels (malignant or benign).
#
# The original data along with descriptions of each feature can be found on the <a href="https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+(Diagnostic)" target="_blank">UCI Machine Learning Repository</a> website.
#
# #### Load Data into Pandas
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 9, "hidden": false, "row": 23, "width": 12}, "report_default": {"hidden": false}}}}
# Read in Data & See Head
data = Pandas.read_csv(OS.getcwd() + "/data/wdbc.csv").drop(["id", "Unnamed: 32"], axis = 1)
data.head()
# Lets Make Our Visualization Look Like ggplot
Plot.style.use('ggplot')
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 6, "hidden": false, "row": 51, "width": 12}, "report_default": {"hidden": false}}}}
# #### Initializing & Re-Rendering a Visualization
#
# To generate interactive data visualizations with Matplotlib, we can look at the visualization component as having two basic pieces:
# * Initialization – Where we setup the basics of the plot and `show` it.
# * Updating – Where we update the data and any associated axes, legends, labels, etc.
#
# Below is an example of a very basic initialization method.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 147, "width": 12}, "report_default": {"hidden": true}}}}
def initPlot (groups, dependent, independent):
"""
Method to initialize a plot, returns fig & axis, Returns Figure & Axis Objects.
"""
# Structure Data for Matplotlib
keys, structuredData = [], []
for key, group in groups:
keys.append(key)
structuredData.append(group[independent])
# Setup Plot Figure & Axis
fig = Plot.figure(figsize = (8, 6))
axis = fig.add_subplot(111)
# Set Labels
axis.set_xlabel(dependent)
axis.set_ylabel(independent)
# Set X Axis Ticks
axis.set_xticks([1, 2])
axis.set_xticklabels(keys)
# Generate Violin Plot
axis.violinplot(structuredData)
Plot.show(fig)
return fig, axis
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 151, "width": 12}, "report_default": {"hidden": false}}}}
# And the update function, notice the call to `Plot.cla()`, which clears the `axis` object and avoids plots rendering on top of eachother.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 155, "width": 12}, "report_default": {"hidden": true}}}}
def updatePlot (groups, dependent, independent, fig, axis):
"""
Method to Render a Plot with a Pandas DataFrame, No Return Value.
"""
# Important – Clear Plot Axis
Plot.cla()
# Structure Data for Matplotlib
keys, structuredData = [], []
for key, group in groups:
keys.append(key)
structuredData.append(group[independent])
# Update Labels
axis.set_xlabel(dependent)
axis.set_ylabel(independent)
# Update X Axis Ticks
axis.set_xticks([1, 2])
axis.set_xticklabels(keys)
# Update Title
Plot.title("Distribution of %s by %s" % (independent, dependent))
# Generate Violin Plot
axis.violinplot(structuredData, showmeans = True)
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 65, "width": 12}, "report_default": {"hidden": false}}}}
# #### Bringing It All Together
#
# You may have noticed earlier that we imported a library called `mpld3`. Before rendering the interactive plot, we'll initialize this library to enable [D3.js](https://d3js.org) to handle the rendering of the plot. One of the benefits of doing so is that the plot generated by `mpld3` will be sharper than a standard `matplotlib` plot. This is because D3 by default renders the plot in scalable vector graphics (SVG, an XML-based format) rather than painting each pixel (i.e. rasterization, like a photo).
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 13, "hidden": false, "row": 0, "width": 11}, "report_default": {"hidden": false}}}}
# Before Plotting, We Need to Enable D3 in The Notebook
D3.enable_notebook()
# Prettify Column Names - Replace Underscores with Spaces and Capitalize the First Letter of Each Word
data.columns = [" ".join([word[0].upper() + word[1:] for word in col.split("_")]) for col in data.columns]
# Filter Columns
filterCols = list(data.columns.drop('Diagnosis'))[0:5]
# Group Data by Diagnosis
groups = data.groupby("Diagnosis")
# Initialize Plot
fig, axis = initPlot(groups, "Diagnosis", filterCols[0])
# Create Filter Toggle
filters = widgets.ToggleButtons(
options = filterCols,
description = 'Filter:',
disabled = False,
button_style='info',
tooltip='Feature',
icon='check'
)
# Bind ToggleButtons Widget Events to Rendering Function
interact(lambda x: updatePlot(groups, "Diagnosis", x, fig, axis), x = filters)
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 57, "width": 4}, "report_default": {"hidden": false}}}}
# ### In-Class Excercises
# 1. Using the available dataset, create an interactive plot that visualizes `Perimeter Mean` by `Radius Mean`. Allow the user to select samples by their `Diagnosis` using a `dropdown` widget.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": true, "row": 0, "width": 12}, "report_default": {"hidden": true}}}}
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 12, "hidden": false, "row": 159, "width": 12}, "report_default": {"hidden": false}}}}
# 2. Create a similar plot to Exercise 1 that visualizes data for both `Diagnosis` (malignant and benign). Allow the user to filter this data by a value range using a `rangeslider` widget.
# + extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": true, "row": 0, "width": 12}, "report_default": {"hidden": true}}}}
# + [markdown] extensions={"jupyter_dashboards": {"version": 1, "views": {"grid_default": {"col": 0, "height": 4, "hidden": false, "row": 171, "width": 12}, "report_default": {"hidden": false}}}}
# ### Resources
# * [ipywidgets Documentation](https://ipywidgets.readthedocs.io/en/stable/user_guide.html)
# * [mpld3](https://mpld3.github.io)
# * [Explanatory v. Exploratory Data Analysis Blog Post](http://www.storytellingwithdata.com/blog/2014/04/exploratory-vs-explanatory-analysis)
|
BMI565_Data_Visualization_&_Interactivity_with_Ipython_Widgets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="TCXpDyvdn_XX"
# # Multi-View Composition
#
# When visualizing a number of different data fields, we might be tempted to use as many visual encoding channels as we can: `x`, `y`, `color`, `size`, `shape`, and so on. However, as the number of encoding channels increases, a chart can rapidly become cluttered and difficult to read. An alternative to "over-loading" a single chart is to instead _compose multiple charts_ in a way that facilitates rapid comparisons.
#
# In this notebook, we will examine a variety of operations for _multi-view composition_:
#
# - _layer_: place compatible charts directly on top of each other,
# - _facet_: partition data into multiple charts, organized in rows or columns,
# - _concatenate_: position arbitrary charts within a shared layout, and
# - _repeat_: take a base chart specification and apply it to multiple data fields.
#
# We'll then look at how these operations form a _view composition algebra_, in which the operations can be combined to build a variety of complex multi-view displays.
#
# _This notebook is part of the [data visualization curriculum](https://github.com/uwdata/visualization-curriculum)._
# + colab={} colab_type="code" id="dIig-LFMn1DY"
import pandas as pd
import altair as alt
# + [markdown] colab_type="text" id="gaYNlguioJYK"
# ## Weather Data
#
# We will be visualizing weather statistics for the U.S. cities of Seattle and New York. Let's load the dataset and peek at the first and last 10 rows:
# + colab={} colab_type="code" id="r3obq-Ksn8W5"
weather = 'https://cdn.jsdelivr.net/npm/vega-datasets@1/data/weather.csv'
# + colab={"base_uri": "https://localhost:8080/", "height": 359} colab_type="code" id="NFKYk5waoSVd" outputId="49003cdc-647a-4a87-8c9b-293b3f7e153f"
df = pd.read_csv(weather)
df.head(10)
# + colab={"base_uri": "https://localhost:8080/", "height": 359} colab_type="code" id="myLKf7LWS2T4" outputId="d72e8414-f30b-47e8-8ac4-dde69462dbf4"
df.tail(10)
# + [markdown] colab_type="text" id="TKyMsDCoPxiC"
# We will create multi-view displays to examine weather within and across the cities.
# + [markdown] colab_type="text" id="KicCeq0Gpm_j"
# ## Layer
# -
# One of the most common ways of combining multiple charts is to *layer* marks on top of each other. If the underlying scale domains are compatible, we can merge them to form _shared axes_. If either of the `x` or `y` encodings is not compatible, we might instead create a _dual-axis chart_, which overlays marks using separate scales and axes.
# + [markdown] colab_type="text" id="Jc4hle6Npoij"
# ### Shared Axes
# + [markdown] colab_type="text" id="nChT_olsQ8vX"
# Let's start by plotting the minimum and maximum average temperatures per month:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="iwgqOsfoyVe_" outputId="77cb9541-dc66-45ac-f06f-7d05ed093534"
alt.Chart(weather).mark_area().encode(
alt.X('month(date):T'),
alt.Y('average(temp_max):Q'),
alt.Y2('average(temp_min):Q')
)
# + [markdown] colab_type="text" id="Bl1XIaeqSrzl"
# _The plot shows us temperature ranges for each month over the entirety of our data. However, this is pretty misleading as it aggregates the measurements for both Seattle and New York!_
#
# Let's subdivide the data by location using a color encoding, while also adjusting the mark opacity to accommodate overlapping areas:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="PbNkncWsRKrV" outputId="fb6da544-e1e7-477e-fedc-e1f0a3dc61b4"
alt.Chart(weather).mark_area(opacity=0.3).encode(
alt.X('month(date):T'),
alt.Y('average(temp_max):Q'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
# + [markdown] colab_type="text" id="j30cu2YmTW8g"
# _We can see that Seattle is more temperate: warmer in the winter, and cooler in the summer._
#
# In this case we've created a layered chart without any special features by simply subdividing the area marks by color. While the chart above shows us the temperature ranges, we might also want to emphasize the middle of the range.
#
# Let's create a line chart showing the average temperature midpoint. We'll use a `calculate` transform to compute the midpoints between the minimum and maximum daily temperatures:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="zHfuCUbyzW7q" outputId="257e2570-49f0-4502-aebb-b8b28aae3897"
alt.Chart(weather).mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
# + [markdown] colab_type="text" id="fQ8IMV3IUfYg"
# _Aside_: note the use of `+datum.temp_min` within the calculate transform. As we are loading the data directly from a CSV file without any special parsing instructions, the temperature values may be internally represented as string values. Adding the `+` in front of the value forces it to be treated as a number.
#
# We'd now like to combine these charts by layering the midpoint lines over the range areas. Using the syntax `chart1 + chart2`, we can specify that we want a new layered chart in which `chart1` is the first layer and `chart2` is a second layer drawn on top:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="DLOAw_LBzcuW" outputId="dc6a8c55-45cf-4029-fa68-29ea0214589e"
tempMinMax = alt.Chart(weather).mark_area(opacity=0.3).encode(
alt.X('month(date):T'),
alt.Y('average(temp_max):Q'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
tempMid = alt.Chart(weather).mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
tempMinMax + tempMid
# + [markdown] colab_type="text" id="CrA84n7W2mUi"
# _Now we have a multi-layer plot! However, the y-axis title (though informative) has become a bit long and unruly..._
#
# Let's customize our axes to clean up the plot. If we set a custom axis title within one of the layers, it will automatically be used as a shared axis title for all the layers:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="LUyPrsgf2N-R" outputId="b261942a-7c09-4aab-c296-c0516e6343b6"
tempMinMax = alt.Chart(weather).mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature °C'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
tempMid = alt.Chart(weather).mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
tempMinMax + tempMid
# + [markdown] colab_type="text" id="jb405Vkd3dFh"
# _What happens if both layers have custom axis titles? Modify the code above to find out..._
#
# Above used the `+` operator, a convenient shorthand for Altair's `layer` method. We can generate an identical layered chart using the `layer` method directly:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="aPnJVekc5iOE" outputId="07beb43c-9dd8-4cbc-9bb0-4fda3216ace8"
alt.layer(tempMinMax, tempMid)
# + [markdown] colab_type="text" id="_QwjqCdm6crv"
# Note that the order of inputs to a layer matters, as subsequent layers will be drawn on top of earlier layers. _Try swapping the order of the charts in the cells above. What happens? (Hint: look closely at the color of the `line` marks.)_
# + [markdown] colab_type="text" id="WzJf0GAe1pug"
# ### Dual-Axis Charts
# + [markdown] colab_type="text" id="C5hcdEdPZddR"
# _Seattle has a reputation as a rainy city. Is that deserved?_
#
# Let's look at precipitation alongside temperature to learn more. First let's create a base plot the shows average monthly precipitation in Seattle:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="kD70HRtQaN-e" outputId="f98c00a3-a8a6-485f-d61d-7ea40bcb6f97"
alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_line(
interpolate='monotone',
stroke='grey'
).encode(
alt.X('month(date):T', title=None),
alt.Y('average(precipitation):Q', title='Precipitation')
)
# + [markdown] colab_type="text" id="nlcsyvEwaZjm"
# To facilitate comparison with the temperature data, let's create a new layered chart. Here's what happens if we try to layer the charts as we did earlier:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="eezzWWPR1tJ6" outputId="f22513cc-d5b7-4c7f-9e95-f73ff3dec020"
tempMinMax = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature °C'),
alt.Y2('average(temp_min):Q')
)
precip = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_line(
interpolate='monotone',
stroke='grey'
).encode(
alt.X('month(date):T'),
alt.Y('average(precipitation):Q', title='Precipitation')
)
alt.layer(tempMinMax, precip)
# + [markdown] colab_type="text" id="jaRBJcj8bGsY"
# _The precipitation values use a much smaller range of the y-axis then the temperatures!_
#
# By default, layered charts use a *shared domain*: the values for the x-axis or y-axis are combined across all the layers to determine a shared extent. This default behavior assumes that the layered values have the same units. However, this doesn't hold up for this example, as we are combining temperature values (degrees Celsius) with precipitation values (inches)!
#
# If we want to use different y-axis scales, we need to specify how we want Altair to *resolve* the data across layers. In this case, we want to resolve the y-axis `scale` domains to be `independent` rather than use a `shared` domain. The `Chart` object produced by a layer operator includes a `resolve_scale` method with which we can specify the desired resolution:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="c2ZZBtzecCff" outputId="770e1942-479c-4ac4-bbac-94b853c39239"
tempMinMax = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature °C'),
alt.Y2('average(temp_min):Q')
)
precip = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_line(
interpolate='monotone',
stroke='grey'
).encode(
alt.X('month(date):T'),
alt.Y('average(precipitation):Q', title='Precipitation')
)
alt.layer(tempMinMax, precip).resolve_scale(y='independent')
# + [markdown] colab_type="text" id="tZ7Pkv4GdG2f"
# _We can now see that autumn is the rainiest season in Seattle (peaking in November), complemented by dry summers._
#
# You may have noticed some redundancy in our plot specifications above: both use the same dataset and the same filter to look at Seattle only. If you want, you can streamline the code a bit by providing the data and filter transform to the top-level layered chart. The individual layers will then inherit the data if they don't have their own data definitions:
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="3XY7hQQrarSk" outputId="7360b4b6-1b15-4bc8-87f4-79d40bf6152f"
tempMinMax = alt.Chart().mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature °C'),
alt.Y2('average(temp_min):Q')
)
precip = alt.Chart().mark_line(
interpolate='monotone',
stroke='grey'
).encode(
alt.X('month(date):T'),
alt.Y('average(precipitation):Q', title='Precipitation')
)
alt.layer(tempMinMax, precip, data=weather).transform_filter(
'datum.location == "Seattle"'
).resolve_scale(y='independent')
# -
# While dual-axis charts can be useful, _they are often prone to misinterpretation_, as the different units and axis scales may be incommensurate. As is feasible, you might consider transformations that map different data fields to shared units, for example showing [quantiles](https://en.wikipedia.org/wiki/Quantile) or relative percentage change.
# + [markdown] colab_type="text" id="2IefKqajprJd"
# ## Facet
# + [markdown] colab_type="text" id="eyadekmFptag"
# *Faceting* involves subdividing a dataset into groups and creating a separate plot for each group. In earlier notebooks, we learned how to create faceted charts using the `row` and `column` encoding channels. We'll first review those channels and then show how they are instances of the more general `facet` operator.
#
# Let's start with a basic histogram of maximum temperature values in Seattle:
# + colab={"base_uri": "https://localhost:8080/", "height": 372} colab_type="code" id="sYjs5JvDcZ6R" outputId="c25f5b7a-ca1f-465b-fa1d-416f3a304f2b"
alt.Chart(weather).mark_bar().transform_filter(
'datum.location == "Seattle"'
).encode(
alt.X('temp_max:Q', bin=True, title='Temperature (°C)'),
alt.Y('count():Q')
)
# + [markdown] colab_type="text" id="Za775__ccf4e"
# _How does this temperature profile change based on the weather of a given day – that is, whether there was drizzle, fog, rain, snow, or sun?_
#
# Let's use the `column` encoding channel to facet the data by weather type. We can also use `color` as a redundant encoding, using a customized color range:
# + colab={"base_uri": "https://localhost:8080/", "height": 271} colab_type="code" id="Q88OIqK5tm35" outputId="68b98e04-57c1-4ed4-960e-5919d0f597a4"
colors = alt.Scale(
domain=['drizzle', 'fog', 'rain', 'snow', 'sun'],
range=['#aec7e8', '#c7c7c7', '#1f77b4', '#9467bd', '#e7ba52']
)
alt.Chart(weather).mark_bar().transform_filter(
'datum.location == "Seattle"'
).encode(
alt.X('temp_max:Q', bin=True, title='Temperature (°C)'),
alt.Y('count():Q'),
alt.Color('weather:N', scale=colors),
alt.Column('weather:N')
).properties(
width=150,
height=150
)
# + [markdown] colab_type="text" id="lNspGpzQdlI8"
# _Unsurprisingly, those rare snow days center on the coldest temperatures, followed by rainy and foggy days. Sunny days are warmer and, despite Seattle stereotypes, are the most plentiful. Though as any Seattleite can tell you, the drizzle occasionally comes, no matter the temperature!_
# + [markdown] colab_type="text" id="PxQ1VwQjXJZt"
# In addition to `row` and `column` encoding channels *within* a chart definition, we can take a basic chart definition and apply faceting using an explicit `facet` operator.
#
# Let's recreate the chart above, but this time using `facet`. We start with the same basic histogram definition, but remove the data source, filter transform, and column channel. We can then invoke the `facet` method, passing in the data and specifying that we should facet into columns according to the `weather` field. The `facet` method accepts both `row` and `column` arguments. The two can be used together to create a 2D grid of faceted plots.
#
# Finally we include our filter transform, applying it to the top-level faceted chart. While we could apply the filter transform to the histogram definition as before, that is slightly less efficient. Rather than filter out "New York" values within each facet cell, applying the filter to the faceted chart lets Vega-Lite know that we can filter out those values up front, prior to the facet subdivision.
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="zbH63h3VWoxB" outputId="c0a8bcd2-08ec-4496-f572-7e476e7cb643"
colors = alt.Scale(
domain=['drizzle', 'fog', 'rain', 'snow', 'sun'],
range=['#aec7e8', '#c7c7c7', '#1f77b4', '#9467bd', '#e7ba52']
)
alt.Chart().mark_bar().encode(
alt.X('temp_max:Q', bin=True, title='Temperature (°C)'),
alt.Y('count():Q'),
alt.Color('weather:N', scale=colors)
).properties(
width=150,
height=150
).facet(
data=weather,
column='weather:N'
).transform_filter(
'datum.location == "Seattle"'
)
# + [markdown] colab_type="text" id="p-2HTw75YmxV"
# Given all the extra code above, why would we want to use an explicit `facet` operator? For basic charts, we should certainly use the `column` or `row` encoding channels if we can. However, using the `facet` operator explicitly is useful if we want to facet composed views, such as layered charts.
#
# Let's revisit our layered temperature plots from earlier. Instead of plotting data for New York and Seattle in the same plot, let's break them up into separate facets. The individual chart definitions are nearly the same as before: one area chart and one line chart. The only difference is that this time we won't pass the data directly to the chart constructors; we'll wait and pass it to the facet operator later. We can layer the charts much as before, then invoke `facet` on the layered chart object, passing in the data and specifying `column` facets based on the `location` field:
# + colab={"base_uri": "https://localhost:8080/", "height": 404} colab_type="code" id="DXPaA6CylJQE" outputId="29cd36bb-babc-4b4b-8820-75175feb7d23"
tempMinMax = alt.Chart().mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature (°C)'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
tempMid = alt.Chart().mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
alt.layer(tempMinMax, tempMid).facet(
data=weather,
column='location:N'
)
# + [markdown] colab_type="text" id="dH3laH2hZ_Er"
# The faceted charts we have seen so far use the same axis scale domains across the facet cells. This default of using *shared* scales and axes helps aid accurate comparison of values. However, in some cases you may wish to scale each chart independently, for example if the range of values in the cells differs significantly.
#
# Similar to layered charts, faceted charts also support _resolving_ to independent scales or axes across plots. Let's see what happens if we call the `resolve_axis` method to request `independent` y-axes:
# + colab={"base_uri": "https://localhost:8080/", "height": 35} colab_type="code" id="tdkplJytl4vh" outputId="602817e3-0824-44ef-dc5a-3e2ced485cfa"
tempMinMax = alt.Chart().mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature (°C)'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
tempMid = alt.Chart().mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
alt.layer(tempMinMax, tempMid).facet(
data=weather,
column='location:N'
).resolve_axis(y='independent')
# + [markdown] colab_type="text" id="J9UK1nYKa2hM"
# _The chart above looks largely unchanged, but the plot for Seattle now includes its own axis._
#
# What if we instead call `resolve_scale` to resolve the underlying scale domains?
# + colab={"base_uri": "https://localhost:8080/", "height": 416} colab_type="code" id="VjRyVRVfbCll" outputId="3b140df2-76f9-4f6d-df74-b38cb7d6e9f5"
tempMinMax = alt.Chart().mark_area(opacity=0.3).encode(
alt.X('month(date):T', title=None, axis=alt.Axis(format='%b')),
alt.Y('average(temp_max):Q', title='Avg. Temperature (°C)'),
alt.Y2('average(temp_min):Q'),
alt.Color('location:N')
)
tempMid = alt.Chart().mark_line().transform_calculate(
temp_mid='(+datum.temp_min + +datum.temp_max) / 2'
).encode(
alt.X('month(date):T'),
alt.Y('average(temp_mid):Q'),
alt.Color('location:N')
)
alt.layer(tempMinMax, tempMid).facet(
data=weather,
column='location:N'
).resolve_scale(y='independent')
# + [markdown] colab_type="text" id="m6snDsbnbFho"
# _Now we see facet cells with different axis scale domains. In this case, using independent scales seems like a bad idea! The domains aren't very different, and one might be fooled into thinking that New York and Seattle have similar maximum summer temperatures._
#
# To borrow a cliché: just because you *can* do something, doesn't mean you *should*...
# + [markdown] colab_type="text" id="sDyHxrLXpubO"
# ## Concatenate
# + [markdown] colab_type="text" id="kq4iE1w9pxMl"
# Faceting creates [small multiple](https://en.wikipedia.org/wiki/Small_multiple) plots that show separate subdivisions of the data. However, we might wish to create a multi-view display with different views of the *same* dataset (not subsets) or views involving *different* datasets.
#
# Altair provides *concatenation* operators to combine arbitrary charts into a composed chart. The `hconcat` operator (shorthand `|` ) performs horizontal concatenation, while the `vconcat` operator (shorthand `&`) performs vertical concatenation.
# + [markdown] colab_type="text" id="c_w_BsgFhta8"
# Let's start with a basic line chart showing the average maximum temperature per month for both New York and Seattle, much like we've seen before:
# + colab={"base_uri": "https://localhost:8080/", "height": 355} colab_type="code" id="KAkDG69Xhnr_" outputId="d97fa576-5791-4912-cf3a-934d12c685d4"
alt.Chart(weather).mark_line().encode(
alt.X('month(date):T', title=None),
alt.Y('average(temp_max):Q'),
color='location:N'
)
# + [markdown] colab_type="text" id="6-6CLOxgh88q"
# _What if we want to compare not just temperature over time, but also precipitation and wind levels?_
#
# Let's create a concatenated chart consisting of three plots. We'll start by defining a "base" chart definition that contains all the aspects that should be shared by our three plots. We can then modify this base chart to create customized variants, with different y-axis encodings for the `temp_max`, `precipitation`, and `wind` fields. We can then concatenate them using the pipe (`|`) shorthand operator:
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" id="crZTVb-FpHDk" outputId="6394136a-5be8-45b4-f610-744cf4cf70cb"
base = alt.Chart(weather).mark_line().encode(
alt.X('month(date):T', title=None),
color='location:N'
).properties(
width=240,
height=180
)
temp = base.encode(alt.Y('average(temp_max):Q'))
precip = base.encode(alt.Y('average(precipitation):Q'))
wind = base.encode(alt.Y('average(wind):Q'))
temp | precip | wind
# + [markdown] colab_type="text" id="YyJN3OIdinC-"
# Alternatively, we could use the more explicit `alt.hconcat()` method in lieu of the pipe `|` operator. _Try rewriting the code above to use `hconcat` instead._
#
# Vertical concatenation works similarly to horizontal concatenation. _Using the `&` operator (or `alt.vconcat` method), modify the code to use a vertical ordering instead of a horizontal ordering._
#
# Finally, note that horizontal and vertical concatenation can be combined. _What happens if you write something like `(temp | precip) & wind`?_
#
# _Aside_: Note the importance of those parentheses... what happens if you remove them? Keep in mind that these overloaded operators are still subject to [Python's operator precendence rules](https://docs.python.org/3/reference/expressions.html#operator-precedence), and so vertical concatenation with `&` will take precedence over horizontal concatenation with `|`!
#
# As we will revisit later, concatenation operators let you combine any and all charts into a multi-view dashboard!
# + [markdown] colab_type="text" id="Dmt0ai7NpyJp"
# ## Repeat
# + [markdown] colab_type="text" id="thajPm3Mp0yV"
# The concatenation operators above are quite general, allowing arbitrary charts to be composed. Nevertheless, the example above was still a bit verbose: we have three very similar charts, yet have to define them separately and then concatenate them.
#
# For cases where only one or two variables are changing, the `repeat` operator provides a convenient shortcut for creating multiple charts. Given a *template* specification with some free variables, the repeat operator will then create a chart for each specified assignment to those variables.
#
# Let's recreate our concatenation example above using the `repeat` operator. The only aspect that changes across charts is the choice of data field for the `y` encoding channel. To create a template specification, we can use the *repeater variable* `alt.repeat('column')` as our y-axis field. This code simply states that we want to use the variable assigned to the `column` repeater, which organizes repeated charts in a horizontal direction. (As the repeater provides the field name only, we have to specify the field data type separately as `type='quantitative'`.)
#
# We then invoke the `repeat` method, passing in data field names for each column:
# + colab={"base_uri": "https://localhost:8080/", "height": 357} colab_type="code" id="Pp3X3Aa0oc28" outputId="3c27963c-cd25-42a5-ef61-99e22f4508e5"
alt.Chart(weather).mark_line().encode(
alt.X('month(date):T',title=None),
alt.Y(alt.repeat('column'), aggregate='average', type='quantitative'),
color='location:N'
).properties(
width=240,
height=180
).repeat(
column=['temp_max', 'precipitation', 'wind']
)
# + [markdown] colab_type="text" id="WeO93wdcm-kl"
# Repetition is supported for both columns and rows. _What happens if you modify the code above to use `row` instead of `column`?_
#
# We can also use `row` and `column` repetition together! One common visualization for exploratory data analysis is the [scatter plot matrix (or SPLOM)](https://en.wikipedia.org/wiki/Scatter_plot#Scatterplot_matrices). Given a collection of variables to inspect, a SPLOM provides a grid of all pairwise plots of those variables, allowing us to assess potential associations.
#
# Let's use the `repeat` operator to create a SPLOM for the `temp_max`, `precipitation`, and `wind` fields. We first create our template specification, with repeater variables for both the x- and y-axis data fields. We then invoke `repeat`, passing in arrays of field names to use for both `row` and `column`. Altair will then generate the [cross product (or, Cartesian product)](https://en.wikipedia.org/wiki/Cartesian_product) to create the full space of repeated charts:
# + colab={"base_uri": "https://localhost:8080/", "height": 630} colab_type="code" id="pEzPoVN_mtJr" outputId="e0589555-41c5-4cb4-dd78-7653ecc841b9"
alt.Chart().mark_point(filled=True, size=15, opacity=0.5).encode(
alt.X(alt.repeat('column'), type='quantitative'),
alt.Y(alt.repeat('row'), type='quantitative')
).properties(
width=150,
height=150
).repeat(
data=weather,
row=['temp_max', 'precipitation', 'wind'],
column=['wind', 'precipitation', 'temp_max']
).transform_filter(
'datum.location == "Seattle"'
)
# + [markdown] colab_type="text" id="zwemGUsXp1m8"
# _Looking at these plots, there does not appear to be a strong association between precipitation and wind, though we do see that extreme wind and precipitation events occur in similar temperature ranges (~5-15° C). However, this observation is not particularly surprising: if we revisit our histogram at the beginning of the facet section, we can plainly see that the days with maximum temperatures in the range of 5-15° C are the most commonly occurring._
#
# *Modify the code above to get a better understanding of chart repetition. Try adding another variable (`temp_min`) to the SPLOM. What happens if you rearrange the order of the field names in either the `row` or `column` parameters for the `repeat` operator?*
#
# _Finally, to really appreciate what the `repeat` operator provides, take a moment to imagine how you might recreate the SPLOM above using only `hconcat` and `vconcat`!_
# + [markdown] colab_type="text" id="bNGvvh6dp2Ba"
# ## A View Composition Algebra
# + [markdown] colab_type="text" id="MxKKfCjX44Dn"
# Together, the composition operators `layer`, `facet`, `concat`, and `repeat` form a *view composition algebra*: the various operators can be combined to construct a variety of multi-view visualizations.
#
# As an example, let's start with two basic charts: a histogram and a simple line (a single `rule` mark) showing a global average.
# + colab={"base_uri": "https://localhost:8080/", "height": 331} colab_type="code" id="JG_OLPpR5yUN" outputId="6776832d-c756-4936-e40d-954c18d3630b"
basic1 = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_bar().encode(
alt.X('month(date):O'),
alt.Y('average(temp_max):Q')
)
basic2 = alt.Chart(weather).transform_filter(
'datum.location == "Seattle"'
).mark_rule(stroke='firebrick').encode(
alt.Y('average(temp_max):Q')
)
basic1 | basic2
# + [markdown] colab_type="text" id="w2LRQzyi6SVs"
# We can then combine the two charts using a `layer` operator, and then `repeat` that layered chart to show histograms with overlaid averages for multiple fields:
# + colab={"base_uri": "https://localhost:8080/", "height": 181} colab_type="code" id="oi06I8yk0EUj" outputId="8f74c396-ae7d-462f-a156-427c14eda87f"
alt.layer(
alt.Chart().mark_bar().encode(
alt.X('month(date):O', title='Month'),
alt.Y(alt.repeat('column'), aggregate='average', type='quantitative')
),
alt.Chart().mark_rule(stroke='firebrick').encode(
alt.Y(alt.repeat('column'), aggregate='average', type='quantitative')
)
).properties(
width=200,
height=150
).repeat(
data=weather,
column=['temp_max', 'precipitation', 'wind']
).transform_filter(
'datum.location == "Seattle"'
)
# + [markdown] colab_type="text" id="cjW4vHVtp8mP"
# Focusing only on the multi-view composition operators, the model for the visualization above is:
#
# ```
# repeat(column=[...])
# |- layer
# |- basic1
# |- basic2
# ```
#
# Now let's explore how we can apply *all* the operators within a final [dashboard](https://en.wikipedia.org/wiki/Dashboard_%28business%29) that provides an overview of Seattle weather. We'll combine the SPLOM and faceted histogram displays from earlier sections with the repeated histograms above:
# +
splom = alt.Chart().mark_point(filled=True, size=15, opacity=0.5).encode(
alt.X(alt.repeat('column'), type='quantitative'),
alt.Y(alt.repeat('row'), type='quantitative')
).properties(
width=125,
height=125
).repeat(
row=['temp_max', 'precipitation', 'wind'],
column=['wind', 'precipitation', 'temp_max']
)
dateHist = alt.layer(
alt.Chart().mark_bar().encode(
alt.X('month(date):O', title='Month'),
alt.Y(alt.repeat('row'), aggregate='average', type='quantitative')
),
alt.Chart().mark_rule(stroke='firebrick').encode(
alt.Y(alt.repeat('row'), aggregate='average', type='quantitative')
)
).properties(
width=175,
height=125
).repeat(
row=['temp_max', 'precipitation', 'wind']
)
tempHist = alt.Chart(weather).mark_bar().encode(
alt.X('temp_max:Q', bin=True, title='Temperature (°C)'),
alt.Y('count():Q'),
alt.Color('weather:N', scale=alt.Scale(
domain=['drizzle', 'fog', 'rain', 'snow', 'sun'],
range=['#aec7e8', '#c7c7c7', '#1f77b4', '#9467bd', '#e7ba52']
))
).properties(
width=115,
height=100
).facet(
column='weather:N'
)
alt.vconcat(
alt.hconcat(splom, dateHist),
tempHist,
data=weather,
title='Seattle Weather Dashboard'
).transform_filter(
'datum.location == "Seattle"'
).resolve_legend(
color='independent'
).configure_axis(
labelAngle=0
)
# + [markdown] colab_type="text" id="2KeY0T5G79KO"
# The full composition model for this dashboard is:
#
# ```
# vconcat
# |- hconcat
# | |- repeat(row=[...], column=[...])
# | | |- splom base chart
# | |- repeat(row=[...])
# | |- layer
# | |- dateHist base chart 1
# | |- dateHist base chart 2
# |- facet(column='weather')
# |- tempHist base chart
# ```
#
# _Phew!_ The dashboard also includes a few customizations to improve the layout:
#
# - We adjust chart `width` and `height` properties to assist alignment and ensure the full visualization fits on the screen.
# - We add `resolve_legend(color='independent')` to ensure the color legend is associated directly with the colored histograms by temperature. Otherwise, the legend will resolve to the dashboard as a whole.
# - We use `configure_axis(labelAngle=0)` to ensure that no axis labels are rotated. This helps to ensure proper alignment among the scatter plots in the SPLOM and the histograms by month on the right.
#
# _Try removing or modifying any of these adjustments and see how the dashboard layout responds!_
#
# This dashboard can be reused to show data for other locations or from other datasets. _Update the dashboard to show weather patterns for New York instead of Seattle._
# + [markdown] colab_type="text" id="NZzvXj7c4BpD"
# ## Summary
#
# For more details on multi-view composition, including control over sub-plot spacing and header labels, see the [Altair Compound Charts documentation](https://altair-viz.github.io/user_guide/compound_charts.html).
#
# Now that we've seen how to compose multiple views, we're ready to put them into action. In addition to statically presenting data, multiple views can enable interactive multi-dimensional exploration. For example, using _linked selections_ we can highlight points in one view to see corresponding values highlight in other views.
#
# In the next notebook, we'll examine how to author *interactive selections* for both individual plots and multi-view compositions.
|
altair_view_composition.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:unidata-python-workshop]
# language: python
# name: conda-env-unidata-python-workshop-py
# ---
# <div style="width:1000 px">
#
# <div style="float:left; width:98 px; height:98px;">
# <img src="https://www.unidata.ucar.edu/images/logos/netcdf-150x150.png" alt="netCDF Logo" style="height: 98px;">
# </div>
#
# <div style="float:right; width:98 px; height:98px;">
# <img src="https://raw.githubusercontent.com/Unidata/MetPy/master/metpy/plots/_static/unidata_150x150.png" alt="Unidata Logo" style="height: 98px;">
# </div>
#
# <div style="text-align:center;">
# <h1>NetCDF and CF: The Basics</h1>
# </div>
#
# <div style="clear:both"></div>
# </div>
#
# <hr style="height:2px;">
#
# ### Overview
#
# This workshop will teach some of the basics of Climate and Forecasting metadata for netCDF data files with some hands-on work available in Jupyter Notebooks using Python. Along with introduction to netCDF and CF, we will introduce the CF data model and discuss some netCDF implementation details to consider when deciding how to write data with CF and netCDF. We will cover gridded data as well as in situ data (stations, soundings, etc.) and touch on storing geometries data in CF.
#
# This assumes a basic understanding of netCDF.
#
# ### Outline
# 1. <a href="#gridded">Gridded Data</a>
# 1. <a href="#obs">Observation Data</a>
# 1. <a href="#exercises">Exercises</a>
# 1. <a href="#references">References</a>
# <a name="gridded"></a>
# ## Gridded Data
# Let's say we're working with some numerical weather forecast model output. Let's walk through the steps necessary to store this data in netCDF, using the Climate and Forecasting metadata conventions to ensure that our data are available to as many tools as possible.
#
# To start, let's assume the following about our data:
# * It corresponds to forecast three dimensional temperature at several times
# * The native coordinate system of the model is on a regular grid that represents the Earth on a Lambert conformal projection.
#
# We'll also go ahead and generate some arrays of data below to get started:
# +
# Import some useful Python tools
from datetime import datetime, timedelta
import numpy as np
# Twelve hours of hourly output starting at 22Z today
start = datetime.utcnow().replace(hour=22, minute=0, second=0, microsecond=0)
times = np.array([start + timedelta(hours=h) for h in range(13)])
# 3km spacing in x and y
x = np.arange(-150, 153, 3)
y = np.arange(-100, 100, 3)
# Standard pressure levels in hPa
press = np.array([1000, 925, 850, 700, 500, 300, 250])
temps = np.random.randn(times.size, press.size, y.size, x.size)
# -
# ### Creating the file and dimensions
#
# The first step is to create a new file and set up the shared dimensions we'll be using in the file. We'll be using the netCDF4-python library to do all of the requisite netCDF API calls.
from netCDF4 import Dataset
nc = Dataset('forecast_model.nc', 'w', format='NETCDF4_CLASSIC', diskless=True)
# We're going to start by adding some global attribute metadata. These are recommendations from the standard (not required), but they're easy to add and help users keep the data straight, so let's go ahead and do it.
nc.Conventions = 'CF-1.7'
nc.title = 'Forecast model run'
nc.institution = 'Unidata'
nc.source = 'WRF-1.5'
nc.history = str(datetime.utcnow()) + ' Python'
nc.references = ''
nc.comment = ''
# At this point, this is the CDL representation of this dataset:
# ```
# netcdf forecast_model {
# attributes:
# :Conventions = "CF-1.7" ;
# :title = "Forecast model run" ;
# :institution = "Unidata" ;
# :source = "WRF-1.5" ;
# :history = "2019-07-16 02:21:52.005718 Python" ;
# :references = "" ;
# :comment = "" ;
# }
# ```
# Next, before adding variables to the file to define each of the data fields in this file, we need to define the dimensions that exist in this data set. We set each of `x`, `y`, and `pressure` to the size of the corresponding array. We set `forecast_time` to be an "unlimited" dimension, which allows the dataset to grow along that dimension if we write additional data to it later.
nc.createDimension('forecast_time', None)
nc.createDimension('x', x.size)
nc.createDimension('y', y.size)
nc.createDimension('pressure', press.size)
nc
# The CDL representation now shows our dimensions:
# ```
# netcdf forecast_model {
# dimensions:
# forecast_time = UNLIMITED (currently 13) ;
# x = 101 ;
# y = 67 ;
# pressure = 7 ;
# attributes:
# :Conventions = "CF-1.7" ;
# :title = "Forecast model run" ;
# :institution = "Unidata" ;
# :source = "WRF-1.5" ;
# :history = "2019-07-16 02:21:52.005718 Python" ;
# :references = "" ;
# :comment = "" ;
# }
# ```
# ### Creating and filling a variable
# So far, all we've done is outlined basic information about our dataset: broad metadata and the dimensions of our dataset. Now we create a variable to hold one particular data field for our dataset, in this case the forecast air temperature. When defining this variable, we specify the datatype for the values being stored, the relevant dimensions, as well as enable optional compression.
temps_var = nc.createVariable('Temperature', datatype=np.float32,
dimensions=('forecast_time', 'pressure', 'y', 'x'),
zlib=True)
# Now that we have the variable, we tell python to write our array of data to it.
temps_var[:] = temps
temps_var
# If instead we wanted to write data sporadically, like once per time step, we could do that instead (though the for loop below might actually be at a higher level in the program:
next_slice = 0
for temp_slice in temps:
temps_var[next_slice] = temp_slice
next_slice += 1
# At this point, this is the CDL representation of our dataset:
# ```
# netcdf forecast_model {
# dimensions:
# forecast_time = UNLIMITED (currently 13) ;
# x = 101 ;
# y = 67 ;
# pressure = 7 ;
# variables:
# float Temperature(forecast_time, pressure, y, x) ;
# attributes:
# :Conventions = "CF-1.7" ;
# :title = "Forecast model run" ;
# :institution = "Unidata" ;
# :source = "WRF-1.5" ;
# :history = "2019-07-16 02:21:52.005718 Python" ;
# :references = "" ;
# :comment = "" ;
# }
# ```
# We can also add attributes to this variable to define metadata. The CF conventions require a `units` attribute to be set for all variables that represent a dimensional quantity. The value of this attribute needs to be parsable by the UDUNITS library. Here we set it to a value of `'Kelvin'`. We also set the standard (optional) attributes of `long_name` and `standard_name`. The former contains a longer description of the variable, while the latter comes from a controlled vocabulary in the CF conventions. This allows users of data to understand, in a standard fashion, what a variable represents. If we had missing values, we could also set the `missing_value` attribute to an appropriate value.
# > **NASA Dataset Interoperability Recommendations:**
# >
# > Section 2.2 - Include Basic CF Attributes
# >
# > Include where applicable: `units`, `long_name`, `standard_name`, `valid_min` / `valid_max`, `scale_factor` / `add_offset` and others.
temps_var.units = 'Kelvin'
temps_var.standard_name = 'air_temperature'
temps_var.long_name = 'Forecast air temperature'
temps_var.missing_value = -9999
temps_var
# The resulting CDL (truncated to the variables only) looks like:
# ```
# variables:
# float Temperature(forecast_time, pressure, y, x) ;
# Temperature:units = "Kelvin" ;
# Temperature:standard_name = "air_temperature" ;
# Temperature:long_name = "Forecast air temperature" ;
# Temperature:missing_value = -9999.0 ;
# ```
# ### Coordinate variables
# To properly orient our data in time and space, we need to go beyond dimensions (which define common sizes and alignment) and include values along these dimensions, which are called "Coordinate Variables". Generally, these are defined by creating a one dimensional variable with the same name as the respective dimension.
#
# To start, we define variables which define our `x` and `y` coordinate values. These variables include `standard_name`s which allow associating them with projections (more on this later) as well as an optional `axis` attribute to make clear what standard direction this coordinate refers to.
# +
x_var = nc.createVariable('x', np.float32, ('x',))
x_var[:] = x
x_var.units = 'km'
x_var.axis = 'X' # Optional
x_var.standard_name = 'projection_x_coordinate'
x_var.long_name = 'x-coordinate in projected coordinate system'
y_var = nc.createVariable('y', np.float32, ('y',))
y_var[:] = y
y_var.units = 'km'
y_var.axis = 'Y' # Optional
y_var.standard_name = 'projection_y_coordinate'
y_var.long_name = 'y-coordinate in projected coordinate system'
# -
# We also define a coordinate variable `pressure` to reference our data in the vertical dimension. The `standard_name` of `'air_pressure'` is sufficient to identify this coordinate variable as the vertical axis, but let's go ahead and specify the `axis` as well. We also specify the attribute `positive` to indicate whether the variable increases when going up or down. In the case of pressure, this is technically optional.
press_var = nc.createVariable('pressure', np.float32, ('pressure',))
press_var[:] = press
press_var.units = 'hPa'
press_var.axis = 'Z' # Optional
press_var.standard_name = 'air_pressure'
press_var.positive = 'down' # Optional
# Time coordinates must contain a `units` attribute with a string value with a form similar to `'seconds since 2019-01-06 12:00:00.00'`. 'seconds', 'minutes', 'hours', and 'days' are the most commonly used units for time. Due to the variable length of months and years, they are not recommended.
#
# Before we can write data, we need to first need to convert our list of Python `datetime` instances to numeric values. We can use the `cftime` library to make this easy to convert using the unit string as defined above.
from cftime import date2num
time_units = 'hours since {:%Y-%m-%d 00:00}'.format(times[0])
time_vals = date2num(times, time_units)
time_vals
# Now we can create the `forecast_time` variable just as we did before for the other coordinate variables:
time_var = nc.createVariable('forecast_time', np.int32, ('forecast_time',))
time_var[:] = time_vals
time_var.units = time_units
time_var.axis = 'T' # Optional
time_var.standard_name = 'time' # Optional
time_var.long_name = 'time'
# The CDL representation of the variables now contains much more information:
# ```
# dimensions:
# forecast_time = UNLIMITED (currently 13) ;
# x = 101 ;
# y = 67 ;
# pressure = 7 ;
# variables:
# float x(x) ;
# x:units = "km" ;
# x:axis = "X" ;
# x:standard_name = "projection_x_coordinate" ;
# x:long_name = "x-coordinate in projected coordinate system" ;
# float y(y) ;
# y:units = "km" ;
# y:axis = "Y" ;
# y:standard_name = "projection_y_coordinate" ;
# y:long_name = "y-coordinate in projected coordinate system" ;
# float pressure(pressure) ;
# pressure:units = "hPa" ;
# pressure:axis = "Z" ;
# pressure:standard_name = "air_pressure" ;
# pressure:positive = "down" ;
# float forecast_time(forecast_time) ;
# forecast_time:units = "hours since 2019-07-16 00:00" ;
# forecast_time:axis = "T" ;
# forecast_time:standard_name = "time" ;
# forecast_time:long_name = "time" ;
# float Temperature(forecast_time, pressure, y, x) ;
# Temperature:units = "Kelvin" ;
# Temperature:standard_name = "air_temperature" ;
# Temperature:long_name = "Forecast air temperature" ;
# Temperature:missing_value = -9999.0 ;
# ```
# ### Auxilliary Coordinates
# Our data are still not CF-compliant because they do not contain latitude and longitude information, which is needed to properly locate the data. To solve this, we need to add variables with latitude and longitude. These are called "auxillary coordinate variables", not because they are extra, but because they are not simple one dimensional variables.
#
# Below, we first generate longitude and latitude values from our projected coordinates using the `pyproj` library.
from pyproj import Proj
X, Y = np.meshgrid(x, y)
lcc = Proj({'proj':'lcc', 'lon_0':-105, 'lat_0':40, 'a':6371000.,
'lat_1':25})
lon, lat = lcc(X * 1000, Y * 1000, inverse=True)
# Now we can create the needed variables. Both are dimensioned on `y` and `x` and are two-dimensional. The longitude variable is identified as actually containing such information by its required units of `'degrees_east'`, as well as the optional `'longitude'` `standard_name` attribute. The case is the same for latitude, except the units are `'degrees_north'` and the `standard_name` is `'latitude'`.
# +
lon_var = nc.createVariable('lon', np.float64, ('y', 'x'))
lon_var[:] = lon
lon_var.units = 'degrees_east'
lon_var.standard_name = 'longitude' # Optional
lon_var.long_name = 'longitude'
lat_var = nc.createVariable('lat', np.float64, ('y', 'x'))
lat_var[:] = lat
lat_var.units = 'degrees_north'
lat_var.standard_name = 'latitude' # Optional
lat_var.long_name = 'latitude'
# -
# With the variables created, we identify these variables as containing coordinates for the `Temperature` variable by setting the `coordinates` value to a space-separated list of the names of the auxilliary coordinate variables:
temps_var.coordinates = 'lon lat'
# This yields the following CDL:
# ```
# double lon(y, x);
# lon:units = "degrees_east";
# lon:long_name = "longitude coordinate";
# lon:standard_name = "longitude";
# double lat(y, x);
# lat:units = "degrees_north";
# lat:long_name = "latitude coordinate";
# lat:standard_name = "latitude";
# float Temperature(time, y, x);
# Temperature:units = "Kelvin" ;
# Temperature:standard_name = "air_temperature" ;
# Temperature:long_name = "Forecast air temperature" ;
# Temperature:missing_value = -9999.0 ;
# Temperature:coordinates = "lon lat";
# ```
# ### Coordinate System Information
# With our data specified on a Lambert conformal projected grid, it would be good to include this information in our metadata. We can do this using a "grid mapping" variable. This uses a dummy scalar variable as a namespace for holding all of the required information. Relevant variables then reference the dummy variable with their `grid_mapping` attribute.
#
# Below we create a variable and set it up for a Lambert conformal conic projection on a spherical earth. The `grid_mapping_name` attribute describes which of the CF-supported grid mappings we are specifying. The names of additional attributes vary between the mappings.
proj_var = nc.createVariable('lambert_projection', np.int32, ())
proj_var.grid_mapping_name = 'lambert_conformal_conic'
proj_var.standard_parallel = 25.
proj_var.latitude_of_projection_origin = 40.
proj_var.longitude_of_central_meridian = -105.
proj_var.semi_major_axis = 6371000.0
proj_var
# Now that we created the variable, all that's left is to set the `grid_mapping` attribute on our `Temperature` variable to the name of our dummy variable:
temps_var.grid_mapping = 'lambert_projection' # or proj_var.name
# This yields the CDL:
# ```
# variables:
# int lambert_projection ;
# lambert_projection:grid_mapping_name = "lambert_conformal_conic ;
# lambert_projection:standard_parallel = 25.0 ;
# lambert_projection:latitude_of_projection_origin = 40.0 ;
# lambert_projection:longitude_of_central_meridian = -105.0 ;
# lambert_projection:semi_major_axis = 6371000.0 ;
# float Temperature(forecast_time, pressure, y, x) ;
# Temperature:units = "Kelvin" ;
# Temperature:standard_name = "air_temperature" ;
# Temperature:long_name = "Forecast air temperature" ;
# Temperature:missing_value = -9999.0 ;
# Temperature:coordinates = "lon lat" ;
# Temperature:grid_mapping = "lambert_projection" ;
# ```
# ### Cell Bounds
#
# > **NASA Dataset Interoperability Recommendations:**
# >
# > Section 2.3 - Use CF “bounds” attributes
# >
# > CF conventions state: “When gridded data does not represent the point values of a field but instead represents some characteristic of the field within cells of finite ‘volume,’ a complete description of the variable should include metadata that describes the domain or extent of each cell, and the characteristic of the field that the cell values represent.”
#
# For example, if a rain guage is read every 3 hours but only dumped every six hours, it might look like this
#
# ```
# netcdf precip_bucket_bounds {
# dimensions:
# lat = 12 ;
# lon = 19 ;
# time = 8 ;
# tbv = 2;
# variables:
# float lat(lat) ;
# float lon(lon) ;
# float time(time) ;
# time:units = "hours since 2019-07-12 00:00:00.00";
# time:bounds = "time_bounds" ;
# float time_bounds(time,tbv)
# float precip(time, lat, lon) ;
# precip:units = "inches" ;
# data:
# time = 3, 6, 9, 12, 15, 18, 21, 24;
# time_bounds = 0, 3, 0, 6, 6, 9, 6, 12, 12, 15, 12, 18, 18, 21, 18, 24;
# }
# ```
#
# So the time coordinate looks like
# ```
# |---X
# |-------X
# |---X
# |-------X
# |---X
# |-------X
# |---X
# |-------X
# 0 3 6 9 12 15 18 21 24
# ```
# <a name="obs"></a>
# ## Observational Data
#
# So far we've focused on how to handle storing data that are arranged in a grid. What about observation data? The CF conventions describe this as conventions for Discrete Sampling Geometeries (DSG).
#
# For data that are regularly sampled (say, all at the same heights) this is straightforward. First, let's define some sample profile data, all at a few heights less than 1000m:
lons = np.array([-97.1, -105, -80])
lats = np.array([35.25, 40, 27])
heights = np.linspace(10, 1000, 10)
temps = np.random.randn(lats.size, heights.size)
stids = ['KBOU', 'KOUN', 'KJUP']
# ### Creation and basic setup
# First we create a new file and define some dimensions. Since this is profile data, heights will be one dimension. We use station as our other dimension. We also set the global `featureType` attribute to `'profile'` to indicate that this file holds "an ordered set of data points along a vertical line at a fixed horizontal position and fixed time". We also add a dimension to assist in storing our string station ids.
nc.close()
nc = Dataset('obs_data.nc', 'w', format='NETCDF4_CLASSIC', diskless=True)
nc.createDimension('station', lats.size)
nc.createDimension('heights', heights.size)
nc.createDimension('str_len', 4)
nc.Conventions = 'CF-1.7'
nc.featureType = 'profile'
nc
# Which gives this CDL:
# ```
# netcdf obs_data {
# dimensions:
# station = 3 ;
# heights = 10 ;
# str_len = 4 ;
# attributes:
# :Conventions = "CF-1.7" ;
# :featureType = "profile" ;
# }
# ```
# We can create our coordinates with:
# +
lon_var = nc.createVariable('lon', np.float64, ('station',))
lon_var.units = 'degrees_east'
lon_var.standard_name = 'longitude'
lat_var = nc.createVariable('lat', np.float64, ('station',))
lat_var.units = 'degrees_north'
lat_var.standard_name = 'latitude'
# -
# The standard refers to these as "instance variables" because each one refers to an instance of a feature. From here we can create our `height` coordinate variable:
heights_var = nc.createVariable('heights', np.float32, ('heights',))
heights_var.units = 'meters'
heights_var.standard_name = 'altitude'
heights_var.positive = 'up'
heights_var[:] = heights
# ### Station IDs
# Now we can also write our station IDs to a variable. This is a 2D variable, but one of the dimensions is simply there to facilitate treating strings as character arrays. We also assign this an attribute `cf_role` with a value of `'profile_id'` to facilitate software to identify individual profiles:
stid_var = nc.createVariable('stid', 'c', ('station', 'str_len'))
stid_var.cf_role = 'profile_id'
stid_var.long_name = 'Station identifier'
stid_var[:] = stids
# Now our CDL looks like:
# ```
# netcdf obs_data {
# dimensions:
# station = 3 ;
# heights = 10 ;
# str_len = 4 ;
# variables:
# double lon(station) ;
# lon:units = "degrees_east" ;
# lon:standard_name = "longitude" ;
# double lat(station) ;
# lat:units = "degrees_north" ;
# lat:standard_name = "latitude" ;
# float heights(heights) ;
# heights:units = "meters" ;
# heights:standard_name = "altitude";
# heights:positive = "up" ;
# char stid(station, str_len) ;
# stid:cf_role = "profile_id" ;
# stid:long_name = "Station identifier" ;
# attributes:
# :Conventions = "CF-1.7" ;
# :featureType = "profile" ;
# }
# ```
# ### Writing the field
# Now all that's left is to write our profile data, which looks fairly standard. We also add a scalar variable for the time at which these profiles were captured:
# +
time_var = nc.createVariable('time', np.float32, ())
time_var.units = 'minutes since 2019-07-16 17:00'
time_var.standard_name = 'time'
time_var[:] = [5.]
temp_var = nc.createVariable('temperature', np.float32, ('station', 'heights'))
temp_var.units = 'celsius'
temp_var.standard_name = 'air_temperature'
temp_var.coordinates = 'lon lat heights time'
# -
# Note the use of the `coordinates` attribute to store the names of the auxilliary coordinate variables since they're all dimensioned on `station` and not proper coordinate variables. This yields the CDL for the variables:
# ```
# variables:
# double lon(station) ;
# lon:units = "degrees_east" ;
# lon:standard_name = "longitude" ;
# double lat(station) ;
# lat:units = "degrees_north" ;
# lat:standard_name = "latitude" ;
# float heights(heights) ;
# heights:units = "meters" ;
# heights:standard_name = "altitude";
# heights:positive = "up" ;
# char stid(station, str_len) ;
# stid:cf_role = "profile_id" ;
# stid:long_name = "Station identifier" ;
# float time ;
# time:units = "minutes since 2019-07-16 17:00" ;
# time:standard_name = "time" ;
# float temperature(station, heights) ;
# temperature:units = "celsius" ;
# temperature:standard_name = "air_temperature" ;
# temperature:coordinates = "lon lat heights time" ;
# ```
#
# These standards for storing DSG extend to time series, trajectories, and combinations of them. They also can extend for differing amounts of data per feature using ragged arrays. For more information see the [main document](http://cfconventions.org/Data/cf-conventions/cf-conventions-1.7/cf-conventions.html#discrete-sampling-geometries) or the [annotated DSG examples](http://cfconventions.org/Data/cf-conventions/cf-conventions-1.7/cf-conventions.html#appendix-examples-discrete-geometries).
# <a name="exercises"></a>
# ## Exercises
# 1. Create another 3D variable representing relative humidity
# 2. Createa another variable for surface precipitation
# <a name="references"></a>
# ## References
#
# - See CF Conventions doc ([1.7](http://cfconventions.org/Data/cf-conventions/cf-conventions-1.7/cf-conventions.html))
# - See <NAME>'s old [CF presentation](http://cfconventions.org/Data/cf-documents/overview/viewgraphs.pdf)
# - See [CF presentation](https://docs.google.com/presentation/d/1OImxWBNxyj-zdreIarH5GSIuDyREGB62rDah19g6M94/edit#) I gave at Oct 2018 nc training workshop
# - See NASA ESDS “Dataset Interoperability Recommendations for Earth Science” ([web page](https://earthdata.nasa.gov/user-resources/standards-and-references/dataset-interoperability-recommendations-for-earth-science))
# - See CF Data Model (cfdm) python package [tutorial](https://ncas-cms.github.io/cfdm/tutorial.html)
# - See <NAME>'s cfgeom python package (GitHub [repo](https://github.com/twhiteaker/CFGeom))([tutorial]( https://twhiteaker.github.io/CFGeom/tutorial.html))
|
notebooks/CF Conventions/NetCDF and CF - The Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:alert]
# language: python
# name: conda-env-alert-py
# ---
# # Pipeline without Text Clustering
# +
# General Import
import re
import math
import string
import numpy as np
import pandas as pd
from scipy.sparse import hstack
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics.pairwise import cosine_distances
import gensim.downloader as api
from nltk.tokenize import word_tokenize
import spacy
from spacy.lang.en.stop_words import STOP_WORDS
# +
# Starting point
import os
import sys
from pathlib import Path
PATH_HOME = Path.home()
PATH_PROJ = Path.cwd()
PATH_DATA = PATH_PROJ
sys.path.append(str(PATH_PROJ))
# -
# ## load data
# TRAIN
df_train = pd.read_csv('data2.csv')
df_train.dropna(inplace=True)
print(df_train.shape)
df_train.head(2)
# rename dataframe
df_train = df_train.rename(columns={'Intent': 'intent', 'Questions': 'query'})
df_train = df_train[['intent', 'query']]
df_train.head(2)
# TEST
df_test = pd.read_csv('uat_data_intent.csv')
df_test.dropna(inplace=True)
print(df_test.shape)
df_test.head(2)
df_test['correct_google'] = np.where(df_test['User Clicked intent'] == df_test['Google-intent'], 1, 0)
df_test.head()
# rename dataframe
df_test = df_test.rename(columns={'User Clicked intent': 'intent', 'Question': 'query'})
df_test = df_test[['intent', 'query']]
df_test.head(2)
# ## Utilities
def clean_text(text):
""" Basic text cleaning
1. lowercase
2. remove special characters
"""
text = text.lower()
text = re.sub(r'[^a-z0-9\s]', '', text)
return text
def nltk_tokenize(text):
""" tokenize text using NLTK and join back as sentence"""
# import nltk
# nltk.download('punkt')
return ' '.join(word_tokenize(text))
# +
# Function for spacy tokenizer
# Create our list of punctuation marks
punctuations = string.punctuation
# Create our list of stopwords
nlp = spacy.load('en_core_web_lg')
stop_words = spacy.lang.en.stop_words.STOP_WORDS
# Creating our tokenizer function
def spacy_tokenizer(sentence):
# Creating our token object, which is used to create documents with linguistic annotations.
mytokens = nlp(sentence)
# Lemmatizing each token and converting each token into lowercase
mytokens = [ word.lemma_.lower().strip() if word.lemma_ != "-PRON-" else word.lower_ for word in mytokens ]
# Removing stop words
mytokens = [ word for word in mytokens if word not in stop_words and word not in punctuations ]
# return preprocessed list of tokens
return mytokens
# -
# ## Pipeline
# +
# preprocessing questions
df_train['query'] = df_train['query'].apply(clean_text)
df_train['query'] = df_train['query'].apply(nltk_tokenize)
df_train['query'] = df_train['query'].apply(lambda x:' '.join([token.lemma_ for token in nlp(x) if token.lemma_ not in stop_words]))
df_train['query'] = df_train['query'].str.lower()
# preprocessing test as well
df_test['query'] = df_test['query'].apply(clean_text)
df_test['query'] = df_test['query'].apply(nltk_tokenize)
df_test['query'] = df_test['query'].apply(lambda x:' '.join([token.lemma_ for token in nlp(x) if token.lemma_ not in stop_words]))
df_test['query'] = df_test['query'].str.lower()
# -
df_train.head(2)
df_test.head(2)
intent_list = df_train.intent.unique().tolist()
intent_list[:2]
intents = intent_list.copy()
intent2index = {v: i for (i, v) in enumerate(intents)}
index2intent = {y:x for x,y in intent2index.items()}
test_intent_list = df_test.intent.unique().tolist()
set(intent_list) == set(test_intent_list)
import warnings
warnings.filterwarnings("ignore")
# TEST
try:
word2vec
except NameError:
word2vec = api.load("word2vec-google-news-300")
def get_keywords(intent_list, stop_words):
""" Get list of keywords from intent """
keywords = []
for intent in list(set(intent_list)):
keywords.extend(intent.strip().split(' '))
keyword_list = list(set(keywords))
keyword_list = [i.lower() for i in keyword_list if i.lower() not in stop_words]
keyword_list.append('nsip')
keyword_list_lemma = []
text = nlp(' '.join([w for w in keyword_list]))
for token in text:
keyword_list_lemma.append(token.lemma_)
return keyword_list_lemma
keyword_list_lemma = get_keywords(intent_list, stop_words=STOP_WORDS)
def get_nlp_features(df, keyword_list_lemma):
""" Get keyword features from dataframe """
data = df.copy()
data['lemma'] = data['query'].apply(lambda x:' '.join([token.lemma_ for token in nlp(x) if token.lemma_ not in stop_words]))
data['keyword'] = data['lemma'].apply(lambda x: list(set([token.lemma_ for token in nlp(x) if token.lemma_ in keyword_list_lemma])))
data['noun'] = data['query'].apply(lambda x: list(set([token.lemma_ for token in nlp(x) if token.pos_ in ['NOUN','PROPN'] and token.lemma_ not in stop_words])))
data['verb'] = data['query'].apply(lambda x: list(set([token.lemma_ for token in nlp(x) if token.pos_ in ['VERB'] and token.lemma_ not in stop_words])))
data['noun'] = data['noun'].apply(lambda x: ' '.join([w for w in x]))
data['verb'] = data['verb'].apply(lambda x: ' '.join([w for w in x]))
data['keyword'] = data['keyword'].apply(lambda x: ' '.join([w for w in x]))
return data
df_train = get_nlp_features(df_train, keyword_list_lemma)
df_train['target'] = df_train['intent'].apply(lambda x: intent2index[x])
df_train.head(2)
df_test = get_nlp_features(df_test, keyword_list_lemma)
df_test['target'] = df_test['intent'].apply(lambda x: intent2index[x])
df_test.head(2)
countvector_cols = ['lemma', 'keyword', 'noun', 'verb']
def get_train_test(df_train, df_test, feature_cols):
""" split dataset, get X_train, X_test, y_train, y_test """
X_train = df_train[feature_cols]
# print(X_train.head(1))
y_train = df_train['target']
# print(y_train.head(1))
X_test = df_test[feature_cols]
y_test = df_test['target']
# print(X_test.head(1))
# print(y_test.head(1))
return X_train, y_train, X_test, y_test
X_train, y_train, X_test, y_test = get_train_test(df_train, df_test, feature_cols=countvector_cols)
def add_nlp_to_x(X_train, X_test):
""" Add NLP features to input X """
v_lemma = TfidfVectorizer()
x_train_lemma = v_lemma.fit_transform(X_train['lemma'])
x_test_lemma = v_lemma.transform(X_test['lemma'])
vocab_lemma = dict(v_lemma.vocabulary_)
v_keyword = TfidfVectorizer()
x_train_keyword = v_keyword.fit_transform(X_train['keyword'])
x_test_keyword = v_keyword.transform(X_test['keyword'])
vocab_keyword = dict(v_keyword.vocabulary_)
v_noun = TfidfVectorizer()
x_train_noun = v_noun.fit_transform(X_train['noun'])
x_test_noun = v_noun.transform(X_test['noun'])
vocab_noun = dict(v_noun.vocabulary_)
v_verb = TfidfVectorizer()
x_train_verb = v_verb.fit_transform(X_train['verb'])
x_test_verb = v_verb.transform(X_test['verb'])
vocab_verb = dict(v_verb.vocabulary_)
# combine all features
x_train_combined = hstack((x_train_lemma,
x_train_keyword,
x_train_noun,
x_train_verb),format='csr')
x_train_combined_columns= v_lemma.get_feature_names()+\
v_keyword.get_feature_names()+\
v_noun.get_feature_names()+\
v_verb.get_feature_names()
x_test_combined = hstack((x_test_lemma,
x_test_keyword,
x_test_noun,
x_test_verb), format='csr')
x_test_combined_columns = v_lemma.get_feature_names()+\
v_keyword.get_feature_names()+\
v_noun.get_feature_names()+\
v_verb.get_feature_names()
x_train_combined = pd.DataFrame(x_train_combined.toarray())
x_train_combined.columns = x_train_combined_columns
x_test_combined = pd.DataFrame(x_test_combined.toarray())
x_test_combined.columns = x_test_combined_columns
return x_train_combined, x_test_combined, v_lemma, v_keyword, v_noun, v_verb
x_train_combined, x_test_combined, v_lemma, v_keyword, v_noun, v_verb = add_nlp_to_x(X_train, X_test)
# build classifier
clf = RandomForestClassifier(max_depth=50, n_estimators=1000)
clf.fit(x_train_combined, y_train)
probs = clf.predict_proba(x_test_combined)
best_3 = pd.DataFrame(np.argsort(probs, axis=1)[:,-3:],columns=['top3','top2','top1'])
best_3['top1'] = clf.classes_[best_3['top1']]
best_3['top2'] = clf.classes_[best_3['top2']]
best_3['top3'] = clf.classes_[best_3['top3']]
result = pd.concat([best_3.reset_index(drop=True),
pd.DataFrame(y_test).reset_index(drop=True),
X_test[countvector_cols].reset_index(drop=True)], axis=1)
score_1 = result[result['top1'] == result['target']].shape[0] / result.shape[0]
score_2 = result[(result['top1'] == result['target']) | (result['top2'] == result['target'])].shape[0] / result.shape[0]
score_3 = result[(result['top1'] == result['target']) | (result['top2'] == result['target'])| (result['top3'] == result['target'])].shape[0] / result.shape[0]
print('Accuracy for top 1 clustering + classifier result is {:.1%}'.format(score_1))
print('Accuracy for top 2 clustering + classifier result is {:.1%}'.format(score_2))
print('Accuracy for top 3 clustering + classifier result is {:.1%}'.format(score_3))
# ## Save vectors
import pickle
# save the model to disk
model_filename = 'RFClassifier2.pkl'
pickle.dump(clf, open(model_filename, 'wb'))
# save vectorizer
with open('TFIDFVectorizer_lemma2.pkl', 'wb') as f:
pickle.dump(v_lemma, f)
with open('TFIDFVectorizer_keyword2.pkl', 'wb') as f:
pickle.dump(v_keyword, f)
with open('TFIDFVectorizer_noun2.pkl', 'wb') as f:
pickle.dump(v_noun, f)
with open('TFIDFVectorizer_verb2.pkl', 'wb') as f:
pickle.dump(v_verb, f)
# save necessary variables
with open('intent_list2.pkl', 'wb') as f:
pickle.dump(intent_list, f)
with open('intent2index2.pkl', 'wb') as f:
pickle.dump(intent2index, f)
with open('keyword_list_lemma2.pkl', 'wb') as f:
pickle.dump(keyword_list_lemma, f)
|
07-Pipeline_without_clustering.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # Load your own MXNet BERT model
//
// In the previous [example](https://github.com/awslabs/djl/blob/master/jupyter/BERTQA.ipynb), you run BERT inference with the model from Model Zoo. You can also load the model on your own pre-trained BERT and use custom classes as the input and output.
//
// In general, the MXNet BERT model requires these three inputs:
//
// - word indices: The index of each word in a sentence
// - word types: The type index of the word.
// - valid length: The actual length of the question and resource document tokens
//
// We will dive deep into these details later.
// ## Preparation
//
// This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
// There are dependencies we will use.
// +
// // %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
// %maven ai.djl:api:0.8.0
// %maven ai.djl.mxnet:mxnet-engine:0.8.0
// %maven ai.djl.mxnet:mxnet-model-zoo:0.8.0
// %maven org.slf4j:slf4j-api:1.7.26
// %maven org.slf4j:slf4j-simple:1.7.26
// %maven net.java.dev.jna:jna:5.3.0
// See https://github.com/awslabs/djl/blob/master/mxnet/mxnet-engine/README.md
// for more MXNet library selection options
// %maven ai.djl.mxnet:mxnet-native-auto:1.7.0-backport
// -
// ### Import java packages
// +
import java.io.*;
import java.nio.file.*;
import java.util.*;
import java.util.stream.*;
import ai.djl.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.inference.*;
import ai.djl.translate.*;
import ai.djl.training.util.*;
import ai.djl.repository.zoo.*;
import ai.djl.modality.nlp.*;
import ai.djl.modality.nlp.qa.*;
import ai.djl.mxnet.zoo.nlp.qa.*;
import ai.djl.modality.nlp.bert.*;
// -
// **Reuse the previous input**
// +
var question = "When did BBC Japan start broadcasting?";
var resourceDocument = "BBC Japan was a general entertainment Channel.\n" +
"Which operated between December 2004 and April 2006.\n" +
"It ceased operations after its Japanese distributor folded.";
QAInput input = new QAInput(question, resourceDocument);
// -
// ## Dive deep into Translator
//
// Inference in deep learning is the process of predicting the output for a given input based on a pre-defined model.
// DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
// output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
//
// 
//
// The red block ("Images") in the workflow is the input that DJL expects from you. The green block ("Images
// bounding box") is the output that you expect. Because DJL does not know which input to expect and which output format that you prefer, DJL provides the `Translator` interface so you can define your own
// input and output.
//
// The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
// component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
// input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
// `Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
// format.
// ### Pre-processing
//
// Now, you need to convert the sentences into tokens. We provide a powerful tool `BertTokenizer` that you can use to convert questions and answers into tokens, and batchify your sequence together. Once you have properly formatted tokens, you can use `Vocabulary` to map your token to BERT index.
//
// The following code block demonstrates tokenizing the question and answer defined earlier into BERT-formatted tokens.
// +
var tokenizer = new BertTokenizer();
List<String> tokenQ = tokenizer.tokenize(question.toLowerCase());
List<String> tokenA = tokenizer.tokenize(resourceDocument.toLowerCase());
System.out.println("Question Token: " + tokenQ);
System.out.println("Answer Token: " + tokenA);
// -
// `BertTokenizer` can also help you batchify questions and resource documents together by calling `encode()`.
// The output contains information that BERT ingests.
//
// - getTokens: It returns a list of strings, including the question, resource document and special word to let the model tell which part is the question and which part is the resource document. Because MXNet BERT was trained with a fixed sequence length, you see the `[PAD]` in the tokens as well.
// - getTokenTypes: It returns a list of type indices of the word to indicate the location of the resource document. All Questions will be labelled with 0 and all resource documents will be labelled with 1.
//
// [Question tokens...DocResourceTokens...padding tokens] => [000000...11111....0000]
//
//
// - getValidLength: It returns the actual length of the question and tokens, which are required by MXNet BERT.
// - getAttentionMask: It returns the mask for the model to indicate which part should be paid attention to and which part is the padding. It is required by PyTorch BERT.
//
// [Question tokens...DocResourceTokens...padding tokens] => [111111...11111....0000]
//
// MXNet BERT was trained with fixed sequence length 384, so we need to pass that in when we encode the question and resource doc.
BertToken token = tokenizer.encode(question.toLowerCase(), resourceDocument.toLowerCase(), 384);
System.out.println("Encoded tokens: " + token.getTokens());
System.out.println("Encoded token type: " + token.getTokenTypes());
System.out.println("Valid length: " + token.getValidLength());
// Normally, words and sentences are represented as indices instead of tokens for training.
// They typically work like a vector in a n-dimensional space. In this case, you need to map them into indices.
// DJL provides `Vocabulary` to take care of you vocabulary mapping.
//
// Assume your vocab.json is of the following format
// ```
// {'token_to_idx':{'"slots": 19832,...}, 'idx_to_token':["[UNK]", "[PAD]", ...]}
// ```
// We provide the `vocab.json` from our pre-trained BERT for demonstration.
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/mxnet/bertqa/vocab.json", "build/mxnet/bertqa/vocab.json", new ProgressBar());
var file = Paths.get("build/mxnet/bertqa/vocab.json");
var inputStream = Files.newInputStream(file);
var vocabulary = MxBertVocabulary.parse(inputStream);
// You can easily convert the token to the index using `vocabulary.getIndex(token)` and the other way around using `vocabulary.getToken(index)`.
long index = vocabulary.getIndex("car");
String token = vocabulary.getToken(2482);
System.out.println("The index of the car is " + index);
System.out.println("The token of the index 2482 is " + token);
// To properly convert them into `float[]` for `NDArray` creation, use the following helper function:
/**
* Convert a List of Number to float array.
*
* @param list the list to be converted
* @return float array
*/
public static float[] toFloatArray(List<? extends Number> list) {
float[] ret = new float[list.size()];
int idx = 0;
for (Number n : list) {
ret[idx++] = n.floatValue();
}
return ret;
}
// Now that you have everything you need, you can create an NDList and populate all of the inputs you formatted earlier. You're done with pre-processing!
//
// #### Construct `Translator`
//
// You need to do this processing within an implementation of the `Translator` interface. `Translator` is designed to do pre-processing and post-processing. You must define the input and output objects. It contains the following two override classes:
// - `public NDList processInput(TranslatorContext ctx, I)`
// - `public String processOutput(TranslatorContext ctx, O)`
//
// Every translator takes in input and returns output in the form of generic objects. In this case, the translator takes input in the form of `QAInput` (I) and returns output as a `String` (O). `QAInput` is just an object that holds questions and answer; We have prepared the Input class for you.
// Armed with the needed knowledge, you can write an implementation of the `Translator` interface. `BertTranslator` uses the code snippets explained previously to implement the `processInput`method. For more information, see [`NDManager`](https://javadoc.io/static/ai.djl/api/0.8.0/index.html?ai/djl/ndarray/NDManager.html).
//
// ```
// manager.create(Number[] data, Shape)
// manager.create(Number[] data)
// ```
//
// The `Shape` for `data0` and `data1` is sequence_length. For `data2` the `Shape` is just 1.
public class BertTranslator implements Translator<QAInput, String> {
private List<String> tokens;
@Override
public Batchifier getBatchifier() {
return null;
}
@Override
public NDList processInput(TranslatorContext ctx, QAInput input) throws IOException {
var inputStream = Files.newInputStream(Paths.get("build/mxnet/bertqa/vocab.json"));
Vocabulary vocabulary = MxBertVocabulary.parse(inputStream);
BertTokenizer tokenizer = new BertTokenizer();
BertToken token =
tokenizer.encode(
input.getQuestion().toLowerCase(),
input.getParagraph().toLowerCase(),
384);
// get the encoded tokens that would be used in precessOutput
tokens = token.getTokens();
// map the tokens(String) to indices(long)
List<Long> indices =
token.getTokens().stream().map(vocabulary::getIndex).collect(Collectors.toList());
float[] indexesFloat = toFloatArray(indices);
float[] types = toFloatArray(token.getTokenTypes());
int validLength = token.getValidLength();
NDManager manager = ctx.getNDManager();
NDArray data0 = manager.create(indexesFloat);
data0.setName("data0");
NDArray data1 = manager.create(types);
data1.setName("data1");
NDArray data2 = manager.create(new float[] {validLength});
data2.setName("data2");
return new NDList(data0, data1, data2);
}
@Override
public String processOutput(TranslatorContext ctx, NDList list) {
NDArray array = list.singletonOrThrow();
NDList output = array.split(2, 2);
// Get the formatted logits result
NDArray startLogits = output.get(0).reshape(new Shape(1, -1));
NDArray endLogits = output.get(1).reshape(new Shape(1, -1));
int startIdx = (int) startLogits.argMax(1).getLong();
int endIdx = (int) endLogits.argMax(1).getLong();
return tokens.subList(startIdx, endIdx + 1).toString();
}
}
// Congrats! You have created your first Translator! We have pre-filled the `processOutput()` function to process the `NDList` and return it in a desired format. `processInput()` and `processOutput()` offer the flexibility to get the predictions from the model in any format you desire.
//
// With the Translator implemented, you need to bring up the predictor that uses your `Translator` to start making predictions. You can find the usage for `Predictor` in the [Predictor Javadoc](https://javadoc.io/static/ai.djl/api/0.8.0/index.html?ai/djl/inference/Predictor.html). Create a translator and use the `question` and `resourceDocument` provided previously.
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/mxnet/bertqa/0.0.1/static_bert_qa-symbol.json", "build/mxnet/bertqa/bertqa-symbol.json", new ProgressBar());
DownloadUtils.download("https://djl-ai.s3.amazonaws.com/mlrepo/model/nlp/question_answer/ai/djl/mxnet/bertqa/0.0.1/static_bert_qa-0002.params.gz", "build/mxnet/bertqa/bertqa-0000.params", new ProgressBar());
// +
BertTranslator translator = new BertTranslator();
Criteria<QAInput, String> criteria = Criteria.builder()
.setTypes(QAInput.class, String.class)
.optModelUrls("build/mxnet/bertqa/") // Search for models in the build/mxnet/bert folder
.optTranslator(translator)
.optProgress(new ProgressBar()).build();
ZooModel model = ModelZoo.loadModel(criteria);
// +
String predictResult = null;
QAInput input = new QAInput(question, resourceDocument);
// Create a Predictor and use it to predict the output
try (Predictor<QAInput, String> predictor = model.newPredictor(translator)) {
predictResult = predictor.predict(input);
}
System.out.println(question);
System.out.println(predictResult);
// -
// Based on the input, the following result will be shown:
// ```
// [december, 2004]
// ```
// That's it!
//
// You can try with more questions and answers. Here are the samples:
//
// **Answer Material**
//
// The Normans (Norman: Nourmands; French: Normands; Latin: Normanni) were the people who in the 10th and 11th centuries gave their name to Normandy, a region in France. They were descended from Norse ("Norman" comes from "Norseman") raiders and pirates from Denmark, Iceland and Norway who, under their leader Rollo, agreed to swear fealty to King Charles III of West Francia. Through generations of assimilation and mixing with the native Frankish and Roman-Gaulish populations, their descendants would gradually merge with the Carolingian-based cultures of West Francia. The distinct cultural and ethnic identity of the Normans emerged initially in the first half of the 10th century, and it continued to evolve over the succeeding centuries.
//
//
// **Question**
//
// Q: When were the Normans in Normandy?
// A: 10th and 11th centuries
//
// Q: In what country is Normandy located?
// A: france
//
// For the full source code,see the [DJL repo](https://github.com/awslabs/djl/blob/master/examples/src/main/java/ai/djl/examples/inference/BertQaInference.java) and translator implementation [MXNet](https://github.com/awslabs/djl/blob/master/mxnet/mxnet-model-zoo/src/main/java/ai/djl/mxnet/zoo/nlp/qa/MxBertQATranslator.java) [PyTorch](https://github.com/awslabs/djl/blob/master/pytorch/pytorch-model-zoo/src/main/java/ai/djl/pytorch/zoo/nlp/qa/PtBertQATranslator.java).
|
jupyter/mxnet/load_your_own_mxnet_bert.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.1
# language: julia
# name: julia-1.6
# ---
# ## <center> Slice in a volume bounded by an isosurface<br><br>Brain slice </center>
# A 3D array stores the values of a scalar field defined on a volume. We illustrate how is defined a slice in the sub-volume bounded by an isosurface, without visualizing the isosurface.
#
# We are using the same data file, `MNI152.npy`, as in the notebook `13-Isosurface-Marching-Cube-Meshing_jl.ipynb`
# Hence, here is drawn a slice in the brain illustrated in that notebook.
using PlotlyJS
using NPZ
include("src/plotlyju.jl");
# +
brain_vol = npzread("data/MNI152.npy");
m, n, p= size(brain_vol)
x = 1:m
y = 1:n
z = 1:p
X = [xi for xi in x, yi in y, zi in z]
Y = [yi for xi in x, yi in y, zi in z]
Z = [zi for xi in x, yi in y, zi in z];
pl_brain = [[0.0, "#4a4b66"], #custom colorscale for brain, derived from Matplotlib bone
[0.125, "#5d617d"],
[0.25, "#707b8f"],
[0.375, "#8294a1"],
[0.5, "#94aeb4"],
[0.625, "#aac5c7"],
[0.75, "#c5dada"],
[0.875, "#e2eded"],
[1.0, "#ffffff"]];
isosurf = isosurface(surface_show=false, surface_count=1,
colorscale=pl_brain,
showscale=false,
x=vec(X),
y=vec(Y),
z=vec(Z),
value=vec(brain_vol),
slices=attr(x= attr(show=true,
fill= 1.0,
locations= [43])),
isomin= 0,
isomax= maximum(brain_vol))
layout= Layout(width=500,
height=500,
scene=attr(camera=attr(eye=attr(x=1.48, y=1.48, z=0.6)),
#xaxis=attr(visible=false),
#yaxis=attr(visible=false),
#zaxis=attr(visible=false),
aspectmode="data"),
margin=attr(t=10, r=0, b=8, l=0))
pl = Plot(isosurf, layout, style=plotlyju)
# -
# 
# Animation: successive x-slices.
# 
|
16-Brain-slice.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
def total_1(m,n):
i=0
k=n-m
while i < k :
i=i+1
m=n-k+m+i
return m
m=int(input('请输入第一个整数,以回车结束。'))
n=int(input('请输入第二个整数,以回车结束。')
print('最终结果是: ',total_1(m,n))
# +
def birth(birth_month,birth_day):
if birth_month==12:
if birth_day>21:
print('您是摩羯座')
else:
print('你是射手座')
if birth_month==11:
if bitrh_day>22:
print('你是射手座')
else:
print('你是天蝎座')
if birth_month==10:
if birth_day>23:
print('您是天蝎座')
else:
print('您是天秤座')
if birth_month==9:
if birth_day>22:
print('您是天秤座')
else:
print('您是处女座')
if birth_month==8:
if bitrh_day>22:
print('您是处女座')
else:
print('您是狮子座')
if birth_month==7:
if birth_day>22:
print('您是狮子座')
else:
print('您是巨蟹座')
if birth_month==6:
if birth_day>22:
print('你是巨蟹座')
else:
print('您是双子座')
if birth_month==5:
if birth_day>20:
print('您是双子座')
else:
print('您是金牛座')
if birth_month==4:
if birth_day>19:
print('您是金牛座')
else:
print('您是白羊座')
if birth_month==3:
if birth_day>20:
print('您是白羊座')
else:
print('您是双鱼座')
if birth_month==2:
if birth_day>18:
print('您是双鱼座')
else:
print('您是水瓶座')
if birth_month==1:
if birth_day>19:
print('您是水瓶座')
else:
print('您是摩羯座')
name=input('请输入您的姓名,以回车结束')
print('Hello',name)
birth_month=int(input('请输入您的出生月份,以回车结束'))
birth_day=int(input('请输入您的出生日期,以回车结束'))
birth(birth_month,birth_day)
# -
some_string=input('请输入一个单数单词')
if some_string=='photo'or some_string=='piano':
print('在词尾加s')
elif some_string.endswith('s')or some_string.endswith('x')or some_string.endswith('o')or some_string.endswith('sh')or some_string.endswith('ch'):
print('在词尾加es')
elif some_string.endswith('y'):
print('变y为i加es')
elif some_string.endswith('f')or some_string.endswith('fe'):
print('变f或fe为v,再加es')
else:
print('在词尾加s')
# +
def compute(some_string):
if some_string=='photo'or some_string=='piano':
print('在词尾加s')
elif some_string.endswith('s')or some_string.endswith('x')or some_string.endswith('o')or some_string.endswith('sh')or some_string.endswith('ch'):
print('在词尾加es')
elif some_string.endswith('y'):
print('变y为i加es')
elif some_string.endswith('f')or some_string.endswith('fe'):
print('变f或fe为v,再加es')
else:
print('在词尾加s')
some_string=input('请输入一个单数单词')
compute(some_string)
# -
|
chapter2/homework/computer/3-29/201611690535(1).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "slide"}
# # Introduction to Data Science
# # Activity for Lecture 9: Linear Regression 1
# *COMP 5360 / MATH 4100, University of Utah, http://datasciencecourse.net/*
#
# Name:
#
# Email:
#
# UID:
#
# + [markdown] slideshow={"slide_type": "slide"}
# ## Class exercise: amphetamine and appetite
#
# Amphetamine is a drug that suppresses appetite. In a study of this effect, a pharmocologist randomly allocated 24 rats to three treatment groups to receive an injection of amphetamine at one of two dosage levels (2.5 mg/kg or 5.0 mg/kg), or an injection of saline solution (0 mg/kg). She measured the amount of food consumed by each animal (in gm/kg) in the 3-hour period following injection. The results (gm of food consumed per kg of body weight) are shown below.
#
# +
# imports and setup
import scipy as sc
import numpy as np
import pandas as pd
import statsmodels.formula.api as sm
from sklearn import linear_model
import matplotlib.pyplot as plt
# %matplotlib inline
plt.rcParams['figure.figsize'] = (10, 6)
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
# Experiment results:
food_consump_dose0 = [112.6, 102.1, 90.2, 81.5, 105.6, 93.0, 106.6, 108.3]
food_consump_dose2p5 = [73.3, 84.8, 67.3, 55.3, 80.7, 90.0, 75.5, 77.1]
food_consump_dose5 = [38.5, 81.3, 57.1, 62.3, 51.5, 48.3, 42.7, 57.9]
# -
# ## Activity 1: Scatterplot and Linear Regression
#
# **Exercise:** Make a scatter plot with dose as the $x$-variable and food consumption as the $y$ variable. Then run a linear regression on the data using the 'ols' function from the statsmodels python library to relate the variables by
#
# $$
# \text{Food Consumption} = \beta_0 + \beta_1 \text{Dose}.
# $$
#
# What is the resulting linear equation? What is the $R^2$ value? Do you think the variables have a strong linear relationship? Add the line to your scatter plot.
#
# your code goes here
# **Your answer goes here:**
# + [markdown] slideshow={"slide_type": "slide"}
# ## Activity 2: Residuals
#
# The regression in Activity 1 is in fact valid even though the predictor $x$ only has 3 distinct values; for each fixed value of $x$, the researcher collected a random sample of $y$ values.
#
# However, one assumption which is made by simple linear regression is that the residuals have an approximately normal distribution.
#
# **Exercise:** Compute the residuals for the above regression and make a normal probability plot of the residuals. Do you think they are approximately normally distributed?
#
#
# + slideshow={"slide_type": "-"}
# your code goes here
# + [markdown] slideshow={"slide_type": "-"}
# **Your answer goes here:**
#
# -
|
09-LinearRegression1/09-LinearRegression1_Activity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Telecom churn - Case study
# Team members:
# Anuprabha and <NAME>
# #### Business objective :
# 1.Find customers who are likely to churn
# 2.Identity churn features
# #### steps followed:
# 1. data processing
# 2. Driving new feature and tagging customers
# 3. exploratory data analysis
# 4. Random forest - to find feature importance
# 5. Feature scaling
# 6. smote
# 7. PCA (with smote and without smote)
# 8. model building (with smote and without smote)
# Logistic regression , Decision tree ,Random forest , Adaboost , Gradientboost
# 9. Model comparison
# +
#import lib
import pandas as pd
import numpy as np
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', None)
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from imblearn.combine import SMOTETomek
from collections import Counter
from sklearn.preprocessing import MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.decomposition import IncrementalPCA
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.model_selection import RandomizedSearchCV
from sklearn.metrics import accuracy_score, f1_score, classification_report,precision_score,recall_score,confusion_matrix, roc_auc_score, roc_curve
# -
df = pd.read_csv('telecom_churn_data.csv')
df.head()
df.shape
df.info(verbose=True, null_counts=True)
# # 1. data processing
# +
# Rename month to code
df.rename(columns={'jun_vbc_3g':'vbc_3g_6','jul_vbc_3g':'vbc_3g_7','aug_vbc_3g':'vbc_3g_8',
'sep_vbc_3g':'vbc_3g_9'},inplace=True)
# -
# #### Drop date columns
# drop all date columns
date_drop = [x for x in df.columns if 'date' in x]
date_drop
df = df.drop(date_drop,axis=1)
df.shape
# ### missing value tratment
# getting percentage of null value
null_col=round(100*df.isnull().sum()/len(df.index),2)
null_col[null_col!=0].sort_values()
# +
# checking missing values for month 8 or any
df.loc[df.night_pck_user_8.isnull()&df.total_rech_data_8.isnull() & df.max_rech_data_8.isnull()&df.count_rech_2g_8.isnull(),['count_rech_2g_8','total_rech_data_8','max_rech_data_8','night_pck_user_8']].head()
# -
# - From above it is observed that .There is a pattern in missing values. some values are
# missing altogether as the customer didnot recharge .
# - so impute all missing values with zero.
#
# +
# Impute zero
df.fillna(0, inplace=True)
# -
# check missing values again
null_col=round(100*df.isnull().sum()/len(df.index),2)
null_col[null_col!=0]
# #### Drop columns :
# Below columns can be dropped
#
# - mobile number
# - total_rech_data_6 = count_rech_2g_6 + count_rech_3g_6
# so drop count_reach_2g and 3g for all 4 months
#
df = df.drop(['mobile_number',
'count_rech_2g_6','count_rech_2g_7','count_rech_2g_8','count_rech_2g_9',
'count_rech_3g_6','count_rech_3g_7','count_rech_3g_8','count_rech_3g_9' ],axis=1)
# ### Unique values
#
# Drop columns which have more than 95% same information content.
uni_col=[] # list of columns with unique value
for i in df.columns:
x = df[i].value_counts(normalize=True).max()
if(x>=.95):
print(i," :",x)
uni_col.append(i)
uni_col
df = df.drop(uni_col,axis=1)
df.shape
# change negative values in ARPU to -1
df['arpu_6']=df.arpu_6.apply(lambda x:x if x>0 else -1)
df['arpu_7']=df.arpu_7.apply(lambda x:x if x>0 else -1)
df['arpu_8']=df.arpu_8.apply(lambda x:x if x>0 else -1)
df['arpu_9']=df.arpu_9.apply(lambda x:x if x>0 else -1)
# ## New feature
#
# - total data recharge--> amt_data_rech = total_rech_data * av_rech_amt_data
# - total call recharge---> total_rech_amt -> given
# - total amount = total data recharge + total call recharge
# - find 70 th percentile and filter high value customer
# +
# find average of recharge amount of 6&7 and find 70th percentile
# add new columns for recharge +data recharge
df['total_amt_6'] = df['total_rech_amt_6']+ (df['total_rech_data_6']*df['av_rech_amt_data_6'])
df['total_amt_7'] = df['total_rech_amt_7']+ (df['total_rech_data_7']*df['av_rech_amt_data_7'])
# mean recharge amount of first 2 months
df['avg_rech_amt_good'] = df[['total_amt_6','total_amt_7']].mean(axis=1)
# +
# filter high value customers
df= df[df['avg_rech_amt_good']>=(df['avg_rech_amt_good'].quantile(.7))]
# -
df.shape
df.avg_rech_amt_good.describe()
df.avg_rech_amt_good.quantile(.997)
# #### Remove outliers
# +
# filter outliers from high value customers
df= df[df['avg_rech_amt_good']<(df['avg_rech_amt_good'].quantile(.997))]
# -
df.shape
# ## Tag churners
# Tag the churned customers (churn=1, else 0) based on the fourth month as follows:
# Those who have not made any calls (either incoming or outgoing) AND have not used mobile internet even once in the churn phase.
#
# • total_ic_mou_9
# • total_og_mou_9
# • vol_2g_mb_9
# • vol_3g_mb_9
#
# +
# churn target variable 1-churn
df['churn'] = df.apply(lambda x:1 if (x.total_ic_mou_9==0) and (x.total_og_mou_9==0) and
(x.vol_2g_mb_9==0) and (x.vol_3g_mb_9==0) else 0 ,axis=1)
# -
df.churn.value_counts()*100 / len(df.index)
# #### remove attributes of the churn phase
# remove all the columns of 9th month
churn_mnth = [x for x in df.columns if '9' in x]
churn_mnth
df = df.drop(churn_mnth,axis=1)
df.shape
# # 3. EDA
# +
# function - plots
def distplot_numeric(data, columns):
for column in columns:
sns.distplot(data[column])
plt.show()
def barchart_wrt_churn(data, columns):
for column in columns:
sns.barplot(x='churn', y=column, data=data)
plt.show()
def boxplot_wrt_churn(data, columns):
for column in columns:
sns.boxplot(x='churn', y=column, data=data)
plt.show()
plt.figure(figsize=(5, 5))
# -
# ### Univariate analysis:
distplot_numeric(df, ['arpu_6','loc_og_t2t_mou_6','std_og_t2t_mou_6', 'onnet_mou_6', 'offnet_mou_6',
'arpu_7','loc_og_t2t_mou_7','std_og_t2t_mou_7', 'onnet_mou_7', 'offnet_mou_7'])
# ### Bivariate analysis:
barchart_wrt_churn(df, ['arpu_6','loc_og_t2t_mou_6','std_og_t2t_mou_6', 'onnet_mou_6', 'offnet_mou_6', 'arpu_7',
'loc_og_t2t_mou_7','std_og_t2t_mou_7', 'onnet_mou_7', 'offnet_mou_7'])
boxplot_wrt_churn(df, ['aon', 'arpu_6', 'total_amt_6','total_amt_7', 'avg_rech_amt_good'])
# +
#churn
f, ax = plt.subplots(1, 2, figsize=(16,8))
colors = ["#228B22", "#FF6347"]
labels ="No Churn", "Churn"
plt.suptitle('Information on Churn', fontsize=20)
df["churn"].value_counts().plot.pie(explode=[0,0.25], autopct='%1.2f%%', ax=ax[0], shadow=True, colors=colors,
labels=labels, fontsize=12, startangle=70)
ax[0].set_ylabel('% of Condition of Churn', fontsize=14)
sns.barplot(x="fb_user_6", y="churn", hue="churn", data=df, estimator=lambda x: len(x) / len(df) * 100)
# -
# # Train & Test split
# +
# Putting feature variable to X
X = df.drop(['churn'],axis=1)
# Putting response variable to y
y = df['churn']
# -
# Splitting the data into train and test
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7,test_size=0.3,random_state=100)
X_train.shape
X_test.shape
# # Feature importance
# #### Random forest before smote- to find feature importance
#
# +
rf = RandomForestClassifier()
params_rf={'max_depth': [5, 10, 20],
'min_samples_split': [5, 10, 20],
'max_features': [5,10],
'n_estimators': [10, 30, 50],
'min_samples_leaf': [2, 5, 10],
'bootstrap': [True, False]
}
model_rf = RandomizedSearchCV(rf, params_rf, cv=3,n_iter = 100, random_state=42, n_jobs=-1, verbose=2)
model_rf.fit(X_train, y_train)
model_rf.best_params_
# +
# random forest best fit model creation
model_rf = RandomForestClassifier(n_estimators=30,
max_depth=20,
min_samples_split=10,
max_features = 5,
criterion='entropy',
oob_score=True)
model_rf.fit(X_train, y_train)
# -
# Extract feature importances
feature_importance_rf = pd.DataFrame({'feature': list(X_train.columns),
'importance': model_rf.feature_importances_})
feature_importance_rf.sort_values(by=['importance'],ascending=False,inplace=True)
plt.figure(figsize=(10,8))
plt.barh(feature_importance_rf['feature'].iloc[:25,],width=feature_importance_rf['importance'].iloc[:25,])
plt.title('The top 25 important variables from Random Forest are ')
plt.show()
# ## Feature Standardisation
#
# +
#create an object
scaler = MinMaxScaler()
# -
# without smote
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# ## SMOTE Sampling
# smote is done only on train set.
# +
print('Before Sampling')
print(Counter(y))
oversample = SMOTETomek(random_state=42)
X_train_sm ,y_train_sm = oversample.fit_resample(X_train,y_train)
print('After Sampling')
print(Counter(y_train_sm))
# -
y_train_sm.shape
y_train.shape
# # PCA
# Dimentionality reduction
# ### 1. PCA without smote
pca = PCA(random_state=42)
pca.fit(X_train)
# +
#pca.explained_variance_ratio_
# -
var_cumu = np.cumsum(pca.explained_variance_ratio_)
# +
fig = plt.figure(figsize=[7,5])
plt.plot(var_cumu)
plt.ylabel("Cumulative variance explained without smote")
plt.show()
# -
# 50 components can be taken.
pca_final = IncrementalPCA(n_components=50)
# PCA without smote
X_train_pca = pca_final.fit_transform(X_train)
X_train_pca.shape
# PCA without smote
X_test_pca = pca_final.transform(X_test)
X_test_pca.shape
# ### 2.PCA with Smote
pca_sm = PCA(random_state=42)
pca_sm.fit(X_train_sm)
var_cumu_sm = np.cumsum(pca_sm.explained_variance_ratio_)
# +
fig = plt.figure(figsize=[10,6])
plt.plot(var_cumu_sm)
plt.ylabel("Cumulative variance explained with smote")
plt.show()
# -
pca_sm_final = IncrementalPCA(n_components=50)
# PCA with smote
X_train_pca_sm = pca_sm_final.fit_transform(X_train_sm)
X_train_pca_sm.shape
# PCA with smote
X_test_pca_sm = pca_sm_final.transform(X_test)
X_test_pca_sm.shape
# # Model building:
# Build models with and without PCA and compare.
# variables for model comparison
model = []
sample = []
precision_train = []
precision_test = []
recall_train = []
recall_test = []
F1score_train = []
F1score_test = []
AUCROC_train = []
AUCROC_test = []
# +
# Function for finding performance metrics
def evaluation(churn_model, X_train,y_train,X_test, y_test, algo=None, sampling=None):
# Train predicion
y_prob_train=churn_model.predict_proba(X_train)
y_pred_train=churn_model.predict(X_train)
print('Train Score:')
print('Confusion Matrix')
print('='*60)
print(confusion_matrix(y_train,y_pred_train),"\n")
print('Classification Report')
print('='*60)
print(classification_report(y_train,y_pred_train),"\n")
print('AUC-ROC = ',roc_auc_score(y_train, y_prob_train[:,1]))
print('recall = ',recall_score(y_train,y_pred_train),"\n")
print('#'*60)
#list to compare different models
model.append(algo)
sample.append(sampling)
precision_train.append(precision_score(y_train,y_pred_train))
recall_train.append(recall_score(y_train,y_pred_train))
F1score_train.append(f1_score(y_train,y_pred_train))
AUCROC_train.append(roc_auc_score(y_train, y_prob_train[:,1]))
# Test prediction
y_prob_test=churn_model.predict_proba(X_test)
y_pred_test=churn_model.predict(X_test)
print('Test Score:')
print('Confusion Matrix')
print('='*60)
print(confusion_matrix(y_test,y_pred_test),"\n")
print('Classification Report')
print('='*60)
print(classification_report(y_test,y_pred_test),"\n")
print('AUC-ROC=',roc_auc_score(y_test, y_prob_test[:,1]))
print('recall = ',recall_score(y_test,y_pred_test),"\n")
#list to compare different models
precision_test.append(precision_score(y_test,y_pred_test))
recall_test.append(recall_score(y_test,y_pred_test))
F1score_test.append(f1_score(y_test,y_pred_test))
AUCROC_test.append(roc_auc_score(y_test, y_prob_test[:,1]))
# -
# ## model 1- Logistic regression - without smote
# +
log=LogisticRegression()
params={'C':[10, 1, 0.5, 0.1],'penalty':['l1','l2'],'class_weight':['balanced']}
# Create grid search using 4-fold cross validation
model_LR = GridSearchCV(log, params, cv=4, scoring='roc_auc', n_jobs=-1)
model_LR.fit(X_train_pca, y_train)
model_LR.best_estimator_
# -
evaluation(model_LR, X_train_pca, y_train, X_test_pca, y_test, 'Logitic Regression', 'without smote')
# ## model 2 - logistic regression with smote
model_LR.fit(X_train_pca_sm, y_train_sm)
evaluation(model_LR, X_train_pca_sm,y_train_sm,X_test_pca_sm, y_test, 'Logitic Regression', 'with smote')
# ## model 3 - Decision tree without smote
# +
dt = DecisionTreeClassifier(random_state=42)
params_tree = {
'max_depth': [2,5,10,15],
'min_samples_split' : [5,10,15,20],
'min_samples_leaf': [3,5,8],
}
model_tree = GridSearchCV(estimator=dt,
param_grid=params_tree,
cv=3, n_jobs=-1, verbose=2, scoring = "roc_auc")
model_tree.fit(X_train_pca,y_train)
model_tree.best_estimator_
# -
# ### Decision tree with best hyperparameters
dt_best = DecisionTreeClassifier(max_depth=5,
min_samples_leaf=3,
min_samples_split=5,
random_state=42)
dt_best.fit(X_train_pca,y_train)
evaluation(dt_best, X_train_pca, y_train, X_test_pca, y_test, 'Decision Tree', 'without smote')
# ## model 4 - Decision tree with smote
model_tree.fit(X_train_pca_sm,y_train_sm)
model_tree.best_estimator_
# ### Decision tree (smote) with best hyperparameters
dt_best_sm = DecisionTreeClassifier(max_depth=15,
min_samples_leaf=8,
min_samples_split=20,
random_state=42)
dt_best_sm.fit(X_train_pca_sm,y_train_sm)
evaluation(dt_best_sm, X_train_pca_sm,y_train_sm,X_test_pca_sm, y_test, 'Decision Tree', 'with smote')
# ## model 5 - Random forest without smote
# +
rf = RandomForestClassifier()
params_rf={'max_depth': [5, 10, 20],
'min_samples_leaf': [5, 10, 20],
'max_features': [5,10],
'n_estimators': [10, 30, 50]
}
model_rf = RandomizedSearchCV(rf, params_rf, cv=3,n_iter = 100, random_state=42, n_jobs=-1, verbose=2)
model_rf.fit(X_train_pca, y_train)
model_rf.best_estimator_
# -
# ### Best fit Random forest without smote
rf_best = RandomForestClassifier(max_depth=20,
max_features=10,
min_samples_leaf=5,
n_estimators=50,bootstrap = True)
rf_best.fit(X_train_pca, y_train)
evaluation(rf_best, X_train_pca, y_train, X_test_pca, y_test, 'Random Forest', 'without smote')
# ## model 6 - Random forest with smote
model_rf.fit(X_train_pca_sm,y_train_sm)
model_rf.best_estimator_
# #### Best fit Random forest with smote
rf_best_sm = RandomForestClassifier(max_depth=20,
max_features=10,
min_samples_leaf=5,
n_estimators=50,bootstrap = True)
rf_best_sm.fit(X_train_pca_sm, y_train_sm)
evaluation(rf_best_sm,X_train_pca_sm,y_train_sm, X_test_pca_sm, y_test, 'Random Forest', 'with smote')
# ## model 7 - AdaBoost without smote
# +
#learning rate is the hyperparameter
lr = [0.05,0.01, 0.1, 0.25, 0.5, 0.75, 1]
#decision tree with depth=1 are referred as decision stumps
d_tree=DecisionTreeClassifier(criterion='entropy',max_depth=1)
parameters_table=[]
#choosing hyper parameters (learning rate)
for i in lr:
model_ada = AdaBoostClassifier( learning_rate=i,
base_estimator=d_tree,
random_state=100)
model_ada.fit(X_train_pca, y_train)
accuracy_training=round(model_ada.score(X_train_pca, y_train),2)
accuracy_validation=round(model_ada.score(X_test_pca, y_test),2)
parameters_table.append([i,accuracy_training,accuracy_validation])
# +
hyper_param_df=pd.DataFrame(parameters_table).reset_index().rename(columns={0:'learning_rate',
1:'training_accuracy',
2:'validaton_accuracy'})
hyper_param_df
# -
# ### Best fit Adaboost without smote
# +
ada_best=AdaBoostClassifier( learning_rate=0.5,
base_estimator=d_tree,
random_state=100)
ada_best.fit(X_train_pca,y_train)
# -
evaluation(ada_best, X_train_pca, y_train, X_test_pca, y_test, 'AdaBoosting', 'without smote')
# ## model 8 - AdaBoost with smote
parameters_table=[]
#choosing hyper parameters (learning rate)
for i in lr:
model_ada = AdaBoostClassifier( learning_rate=i,
base_estimator=d_tree,
random_state=100)
model_ada.fit(X_train_pca_sm, y_train_sm)
accuracy_training=round(model_ada.score(X_train_pca_sm, y_train_sm),2)
accuracy_validation=round(model_ada.score(X_test_pca_sm, y_test),2)
parameters_table.append([i,accuracy_training,accuracy_validation])
# +
hyper_param_df=pd.DataFrame(parameters_table).reset_index().rename(columns={0:'learning_rate',
1:'training_accuracy',
2:'validaton_accuracy'})
hyper_param_df
# -
# ### Best fit Adaboost with smote
# +
ada_best_sm=AdaBoostClassifier( learning_rate=0.5,
base_estimator=d_tree,
random_state=100)
ada_best_sm.fit(X_train_pca_sm,y_train_sm)
# -
evaluation(ada_best_sm, X_train_pca_sm, y_train_sm, X_test_pca_sm, y_test, 'AdaBoosting', 'with smote')
# ## model 9 - GradientBoost without smote
# +
lr = [ 0.05, 0.01,0.1, 0.25, 0.5, 0.75, 1]
parameters_table=[]
for i in lr:
model_gb = GradientBoostingClassifier(n_estimators=20, learning_rate =i,
max_features=5, max_depth=2,random_state=42)
model_gb.fit(X_train_pca, y_train)
accuracy_training=round(model_gb.score(X_train_pca, y_train),2)
accuracy_validation=round(model_gb.score(X_test_pca, y_test),2)
parameters_table.append([i,accuracy_training,accuracy_validation])
hyper_param_df=pd.DataFrame(parameters_table).reset_index().rename(columns={0:'learning_rate',
1:'training_accuracy',
2:'validaton_accuracy'})
hyper_param_df
# -
# ### best fit GradientBoost without smote
# +
best_gb = GradientBoostingClassifier(n_estimators=20,
learning_rate=0.5,
max_features=5,
max_depth=2,
random_state=42)
best_gb.fit(X_train_pca, y_train)
# -
evaluation(best_gb, X_train_pca, y_train, X_test_pca, y_test, 'GradientBoosting', 'without smote')
# ## model 10 - GradientBoost with smote
# +
lr = [ 0.05, 0.01,0.1, 0.25, 0.5, 0.75, 1]
parameters_table=[]
for i in lr:
model_gb = GradientBoostingClassifier(n_estimators=20, learning_rate =i,
max_features=5, max_depth=2,random_state=42)
model_gb.fit(X_train_pca_sm, y_train_sm)
accuracy_training=round(model_gb.score(X_train_pca_sm, y_train_sm),2)
accuracy_validation=round(model_gb.score(X_test_pca_sm, y_test),2)
parameters_table.append([i,accuracy_training,accuracy_validation])
hyper_param_df=pd.DataFrame(parameters_table).reset_index().rename(columns={0:'learning_rate',
1:'training_accuracy',
2:'validaton_accuracy'})
hyper_param_df
# -
# ### Best fit GradientBoost with smote
# +
best_gb_sm = GradientBoostingClassifier(n_estimators=20,
learning_rate=0.5,
max_features=5,
max_depth=2,
random_state=42)
best_gb_sm.fit(X_train_pca_sm, y_train_sm)
# -
evaluation(best_gb_sm, X_train_pca_sm, y_train_sm, X_test_pca_sm, y_test, 'GradientBoosting', 'with smote')
# # Model comparison:
# Models are compared with without smote.
eval_df = pd.DataFrame({'model':model,
'resample':sample,
'precision_train':precision_train,
'recall_train':recall_train,
'f1-score_train':F1score_train,
'AUC-ROC_train':AUCROC_train,
'precision_test':precision_test,
'recall_test':recall_test,
'f1-score_test':F1score_test,
'AUC-ROC_test':AUCROC_test})
eval_df
# Models performed well after smote.
# ### Best models after smote:
# 1. logisic Regression:
# train -> recall = 0.85 , auc-roc= 0.90
# test -> recall = 0.84 , auc-roc= 0.90
# 2. Adaboosting:
# train -> recall = 0.82 , auc-roc= 0.89
# test -> recall = 0.80 , auc-roc= 0.88
# ## Important churn predictors:
# Found before performing pca.
plt.figure(figsize=(10,8))
plt.barh(feature_importance_rf['feature'].iloc[:25,],width=feature_importance_rf['importance'].iloc[:25,])
plt.title('The top 25 important variables from Random Forest are ')
plt.show()
# - most of the top predictors are related to the 'action' phase (third month) of the customer lifecycle.
# #### strategies to manage churn:
# 1.free local and std mou
# 2.reducing recharge amount
# 3.Discounts on data packs
# 4.Improvement on roaming services
#
|
telecom_churn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # CNN for Classification
# ---
# In this and the next notebook, we define **and train** a CNN to classify images from the [Fashion-MNIST database](https://github.com/zalandoresearch/fashion-mnist).
#
# We are providing two solutions to show you how different network structures and training strategies can affect the performance and accuracy of a CNN. This first solution will be a simple CNN with two convolutional layers.
#
# Please note that this is just one possible solution out of many!
# ### Load the [data](http://pytorch.org/docs/master/torchvision/datasets.html)
#
# In this cell, we load in both **training and test** datasets from the FashionMNIST class.
# +
# our basic libraries
import torch
import torchvision
# data loading and transforming
from torchvision.datasets import FashionMNIST
from torch.utils.data import DataLoader
from torchvision import transforms
# The output of torchvision datasets are PILImage images of range [0, 1].
# We transform them to Tensors for input into a CNN
## Define a transform to read the data in as a tensor
data_transform = transforms.ToTensor()
# choose the training and test datasets
train_data = FashionMNIST(root='./data', train=True,
download=True, transform=data_transform)
test_data = FashionMNIST(root='./data', train=False,
download=True, transform=data_transform)
# Print out some stats about the training and test data
print('Train data, number of images: ', len(train_data))
print('Test data, number of images: ', len(test_data))
# +
# prepare data loaders, set the batch_size
## TODO: you can try changing the batch_size to be larger or smaller
## when you get to training your network, see how batch_size affects the loss
batch_size = 20
train_loader = DataLoader(train_data, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_data, batch_size=batch_size, shuffle=True)
# specify the image classes
classes = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
# -
# ### Visualize some training data
#
# This cell iterates over the training dataset, loading a random batch of image/label data, using `dataiter.next()`. It then plots the batch of images and labels in a `2 x batch_size/2` grid.
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# obtain one batch of training images
dataiter = iter(train_loader)
images, labels = dataiter.next()
images = images.numpy()
# plot the images in the batch, along with the corresponding labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(batch_size):
ax = fig.add_subplot(2, batch_size/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title(classes[labels[idx]])
# -
# ### Define the network architecture
#
# The various layers that make up any neural network are documented, [here](http://pytorch.org/docs/master/nn.html). For a convolutional neural network, we'll use a simple series of layers:
# * Convolutional layers
# * Maxpooling layers
# * Fully-connected (linear) layers
#
# You are also encouraged to look at adding [dropout layers](http://pytorch.org/docs/stable/nn.html#dropout) to avoid overfitting this data.
#
# ---
#
# To define a neural network in PyTorch, you define the layers of a model in the function `__init__` and define the feedforward behavior of a network that employs those initialized layers in the function `forward`, which takes in an input image tensor, `x`. The structure of this Net class is shown below and left for you to fill in.
#
# Note: During training, PyTorch will be able to perform backpropagation by keeping track of the network's feedforward behavior and using autograd to calculate the update to the weights in the network.
#
# #### Define the Layers in ` __init__`
# As a reminder, a conv/pool layer may be defined like this (in `__init__`):
# ```
# # 1 input image channel (for grayscale images), 32 output channels/feature maps, 3x3 square convolution kernel
# self.conv1 = nn.Conv2d(1, 32, 3)
#
# # maxpool that uses a square window of kernel_size=2, stride=2
# self.pool = nn.MaxPool2d(2, 2)
# ```
#
# #### Refer to Layers in `forward`
# Then referred to in the `forward` function like this, in which the conv1 layer has a ReLu activation applied to it before maxpooling is applied:
# ```
# x = self.pool(F.relu(self.conv1(x)))
# ```
#
# You must place any layers with trainable weights, such as convolutional layers, in the `__init__` function and refer to them in the `forward` function; any layers or functions that always behave in the same way, such as a pre-defined activation function, may appear *only* in the `forward` function. In practice, you'll often see conv/pool layers defined in `__init__` and activations defined in `forward`.
#
# #### Convolutional layer
# The first convolution layer has been defined for you, it takes in a 1 channel (grayscale) image and outputs 10 feature maps as output, after convolving the image with 3x3 filters.
#
# #### Flattening
#
# Recall that to move from the output of a convolutional/pooling layer to a linear layer, you must first flatten your extracted features into a vector. If you've used the deep learning library, Keras, you may have seen this done by `Flatten()`, and in PyTorch you can flatten an input `x` with `x = x.view(x.size(0), -1)`.
#
# ### TODO: Define the rest of the layers
#
# It will be up to you to define the other layers in this network; we have some recommendations, but you may change the architecture and parameters as you see fit.
#
# Recommendations/tips:
# * Use at least two convolutional layers
# * Your output must be a linear layer with 10 outputs (for the 10 classes of clothing)
# * Use a dropout layer to avoid overfitting
#
# ### A note on output size
#
# For any convolutional layer, the output feature maps will have the specified depth (a depth of 10 for 10 filters in a convolutional layer) and the dimensions of the produced feature maps (width/height) can be computed as the _input image_ width/height, W, minus the filter size, F, divided by the stride, S, all + 1. The equation looks like: `output_dim = (W-F)/S + 1`, for an assumed padding size of 0. You can find a derivation of this formula, [here](http://cs231n.github.io/convolutional-networks/#conv).
#
# For a pool layer with a size 2 and stride 2, the output dimension will be reduced by a factor of 2. Read the comments in the code below to see the output size for each layer.
# +
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel (grayscale), 10 output channels/feature maps
# 3x3 square convolution kernel
## output size = (W-F)/S +1 = (28-3)/1 +1 = 26
# the output Tensor for one image, will have the dimensions: (10, 26, 26)
# after one pool layer, this becomes (10, 13, 13)
self.conv1 = nn.Conv2d(1, 10, 3)
# maxpool layer
# pool with kernel_size=2, stride=2
self.pool = nn.MaxPool2d(2, 2)
# second conv layer: 10 inputs, 20 outputs, 3x3 conv
## output size = (W-F)/S +1 = (13-3)/1 +1 = 11
# the output tensor will have dimensions: (20, 11, 11)
# after another pool layer this becomes (20, 5, 5); 5.5 is rounded down
self.conv2 = nn.Conv2d(10, 20, 3)
# 20 outputs * the 5*5 filtered/pooled map size
# 10 output channels (for the 10 classes)
self.fc1 = nn.Linear(20*5*5, 10)
# define the feedforward behavior
def forward(self, x):
# two conv/relu + pool layers
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
# prep for linear layer
# flatten the inputs into a vector
x = x.view(x.size(0), -1)
# one linear layer
x = self.fc1(x)
# a softmax layer to convert the 10 outputs into a distribution of class scores
x = F.log_softmax(x, dim=1)
# final output
return x
# instantiate and print your Net
net = Net()
print(net)
# -
# ### TODO: Specify the loss function and optimizer
#
# Learn more about [loss functions](http://pytorch.org/docs/master/nn.html#loss-functions) and [optimizers](http://pytorch.org/docs/master/optim.html) in the online documentation.
#
# Note that for a classification problem like this, one typically uses cross entropy loss, which can be defined in code like: `criterion = nn.CrossEntropyLoss()`; cross entropy loss combines `softmax` and `NLL loss` so, alternatively (as in this example), you may see NLL Loss being used when the output of our Net is a distribution of class scores.
#
# PyTorch also includes some standard stochastic optimizers like stochastic gradient descent and Adam. You're encouraged to try different optimizers and see how your model responds to these choices as it trains.
#
# +
import torch.optim as optim
## TODO: specify loss function
# cross entropy loss combines softmax and nn.NLLLoss() in one single class.
criterion = nn.NLLLoss()
## TODO: specify optimizer
# stochastic gradient descent with a small learning rate
optimizer = optim.SGD(net.parameters(), lr=0.001)
# -
# ### A note on accuracy
#
# It's interesting to look at the accuracy of your network **before and after** training. This way you can really see that your network has learned something. In the next cell, let's see what the accuracy of an untrained network is (we expect it to be around 10% which is the same accuracy as just guessing for all 10 classes).
# +
# Calculate accuracy before training
correct = 0
total = 0
# Iterate through test dataset
for images, labels in test_loader:
# forward pass to get outputs
# the outputs are a series of class scores
outputs = net(images)
# get the predicted class from the maximum value in the output-list of class scores
_, predicted = torch.max(outputs.data, 1)
# count up total number of correct labels
# for which the predicted and true labels are equal
total += labels.size(0)
correct += (predicted == labels).sum()
# calculate the accuracy
# to convert `correct` from a Tensor into a scalar, use .item()
accuracy = 100.0 * correct.item() / total
# print it out!
print('Accuracy before training: ', accuracy)
# -
# ### Train the Network
#
# Below, we've defined a `train` function that takes in a number of epochs to train for.
# * The number of epochs is how many times a network will cycle through the entire training dataset.
# * Inside the epoch loop, we loop over the training dataset in batches; recording the loss every 1000 batches.
#
# Here are the steps that this training function performs as it iterates over the training dataset:
#
# 1. Zero's the gradients to prepare for a forward pass
# 2. Passes the input through the network (forward pass)
# 3. Computes the loss (how far is the predicted classes are from the correct labels)
# 4. Propagates gradients back into the network’s parameters (backward pass)
# 5. Updates the weights (parameter update)
# 6. Prints out the calculated loss
#
#
def train(n_epochs):
loss_over_time = [] # to track the loss as the network trains
for epoch in range(n_epochs): # loop over the dataset multiple times
running_loss = 0.0
for batch_i, data in enumerate(train_loader):
# get the input images and their corresponding labels
inputs, labels = data
# zero the parameter (weight) gradients
optimizer.zero_grad()
# forward pass to get outputs
outputs = net(inputs)
# calculate the loss
loss = criterion(outputs, labels)
# backward pass to calculate the parameter gradients
loss.backward()
# update the parameters
optimizer.step()
# print loss statistics
# to convert loss into a scalar and add it to running_loss, we use .item()
running_loss += loss.item()
if batch_i % 1000 == 999: # print every 1000 batches
avg_loss = running_loss/1000
# record and print the avg loss over the 1000 batches
loss_over_time.append(avg_loss)
print('Epoch: {}, Batch: {}, Avg. Loss: {}'.format(epoch + 1, batch_i+1, avg_loss))
running_loss = 0.0
print('Finished Training')
return loss_over_time
# +
# define the number of epochs to train for
n_epochs = 30 # start small to see if your model works, initially
# call train and record the loss over time
training_loss = train(n_epochs)
# -
# ## Visualizing the loss
#
# A good indication of how much your network is learning as it trains is the loss over time. In this example, we printed and recorded the average loss for each 1000 batches and for each epoch. Let's plot it and see how the loss decreases (or doesn't) over time.
#
# In this case, you can see that it takes a little bit for a big initial loss decrease, and the loss is flattening out over time.
# visualize the loss as the network trained
plt.plot(training_loss)
plt.xlabel('1000\'s of batches')
plt.ylabel('loss')
plt.ylim(0, 2.5) # consistent scale
plt.show()
# ### Test the Trained Network
#
# Once you are satisfied with how the loss of your model has decreased, there is one last step: test!
#
# You must test your trained model on a previously unseen dataset to see if it generalizes well and can accurately classify this new dataset. For FashionMNIST, which contains many pre-processed training images, a good model should reach **greater than 85% accuracy** on this test dataset. If you are not reaching this value, try training for a larger number of epochs, tweaking your hyperparameters, or adding/subtracting layers from your CNN.
# +
# initialize tensor and lists to monitor test loss and accuracy
test_loss = torch.zeros(1)
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
# set the module to evaluation mode
net.eval()
for batch_i, data in enumerate(test_loader):
# get the input images and their corresponding labels
inputs, labels = data
# forward pass to get outputs
outputs = net(inputs)
# calculate the loss
loss = criterion(outputs, labels)
# update average test loss
test_loss = test_loss + ((torch.ones(1) / (batch_i + 1)) * (loss.data - test_loss))
# get the predicted class from the maximum value in the output-list of class scores
_, predicted = torch.max(outputs.data, 1)
# compare predictions to true label
# this creates a `correct` Tensor that holds the number of correctly classified images in a batch
correct = np.squeeze(predicted.eq(labels.data.view_as(predicted)))
# calculate test accuracy for *each* object class
# we get the scalar value of correct items for a class, by calling `correct[i].item()`
for i in range(batch_size):
label = labels.data[i]
class_correct[label] += correct[i].item()
class_total[label] += 1
print('Test Loss: {:.6f}\n'.format(test_loss.numpy()[0]))
for i in range(10):
if class_total[i] > 0:
print('Test Accuracy of %5s: %2d%% (%2d/%2d)' % (
classes[i], 100 * class_correct[i] / class_total[i],
np.sum(class_correct[i]), np.sum(class_total[i])))
else:
print('Test Accuracy of %5s: N/A (no training examples)' % (classes[i]))
print('\nTest Accuracy (Overall): %2d%% (%2d/%2d)' % (
100. * np.sum(class_correct) / np.sum(class_total),
np.sum(class_correct), np.sum(class_total)))
# -
# ### Visualize sample test results
#
# Format: predicted class (true class)
# +
# obtain one batch of test images
dataiter = iter(test_loader)
images, labels = dataiter.next()
# get predictions
preds = np.squeeze(net(images).data.max(1, keepdim=True)[1].numpy())
images = images.numpy()
# plot the images in the batch, along with predicted and true labels
fig = plt.figure(figsize=(25, 4))
for idx in np.arange(batch_size):
ax = fig.add_subplot(2, batch_size/2, idx+1, xticks=[], yticks=[])
ax.imshow(np.squeeze(images[idx]), cmap='gray')
ax.set_title("{} ({})".format(classes[preds[idx]], classes[labels[idx]]),
color=("green" if preds[idx]==labels[idx] else "red"))
# -
# ### Question: What are some weaknesses of your model? (And how might you improve these in future iterations.)
# **Answer**: This model performs well on everything but shirts and pullovers (0% accuracy); it looks like this incorrectly classifies most of those as a coat which has a similar overall shape. Because it performs well on everything but hese two classes, I suspect this model is overfitting ceratin classes at the cost of generalization. I suspect that this accuracy could be improved by adding some dropout layers to aoid overfitting.
# +
# Saving the model
model_dir = 'saved_models/'
model_name = 'fashion_net_simple.pt'
# after training, save your model parameters in the dir 'saved_models'
# when you're ready, un-comment the line below
torch.save(net.state_dict(), model_dir+model_name)
# -
|
Intro-To-Computer-Vision-1/1_5_CNN_Layers/4_2. Classify FashionMNIST, solution 1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import sys
import numpy as np
import math
import ceo
import matplotlib.pyplot as plt
import IPython
# %matplotlib inline
# +
# Telescope parameters
D = 25.5
# WFS parameters
nLenslet = 25 # number of sub-apertures across the pupil
n = 16 # number of pixels per subaperture
detectorRes = 2*n*nLenslet/2
nPx = n*nLenslet+1
print "pupil sampling: %d pixel"%nPx
print "detector resolution: %d pixel"%detectorRes
# number of Guide Stars and position
N_GS = 3 # NUMBER of GSs
alpha =6*60. # radius of circle where GSs are located [in arcsec]
zenith_angle = np.ones(N_GS)*alpha*math.pi/180/3600 # in radians
azimuth_angle = np.arange(N_GS)*360.0/N_GS # in degrees
# Initialize GS, WFS, SPS, and GMT objects
gs = ceo.Source("I",zenith=zenith_angle,azimuth=azimuth_angle*math.pi/180,
rays_box_size=D,rays_box_sampling=nPx,rays_origin=[0.0,0.0,25])
wfs = ceo.ShackHartmann(nLenslet, n, D/nLenslet,N_PX_IMAGE=2*n,BIN_IMAGE=2,N_GS=N_GS)
gmt = ceo.GMT_MX(D,nPx)
ps = ceo.IdealSegmentPistonSensor(gmt, gs)
# Initialize on-axis GS for performance evaluation
ongs = ceo.Source("I",zenith=0.,azimuth=0., rays_box_size=D,rays_box_sampling=nPx,rays_origin=[0.0,0.0,25])
# -
# Calibrate WFS slope null vector
gs.reset()
gmt.reset() # Telescope perfectly phased
gmt.propagate(gs)
wfs.calibrate(gs,0.8)
plt.imshow(wfs.flux.host(shape=(nLenslet*3,nLenslet)).T,interpolation='none')
# +
# Calibrate SPS reference vector (corresponding to field-dependent aberrations)
gs.reset()
gmt.reset()
gmt.propagate(gs)
ph_fda = gs.phase.host(units='micron').T
SPSmeas_ref = ps.piston(gs, segment='edge')
fig, ax = plt.subplots()
fig.set_size_inches(20,5)
fig.suptitle('Field-dependent aberrations', fontsize=20)
imm = ax.imshow(ph_fda, interpolation='None')
fig.colorbar(imm, orientation='horizontal', shrink=0.6)
# -
# Calibrate M2 segment TT Interaction Matrix and Reconstructor
TTstroke = 25e-3 #arcsec
gmt.reset()
D_M2_TT = gmt.calibrate(wfs, gs, mirror="M2", mode="segment tip-tilt", stroke=TTstroke*math.pi/180/3600)
R_M2_TT = np.linalg.pinv(D_M2_TT)
R_M2_TT.shape
# Calibrate Idealized Segment Piston Sensor Interaction Matrix and Reconstructor
PSstroke = 200e-9 #m
gmt.reset()
D_M1_PS = gmt.calibrate(ps, gs, mirror="M1", mode="segment piston", stroke=PSstroke, segment='edge')
R_M1_PS = np.linalg.pinv(D_M1_PS)
R_M1_PS.shape
plt.pcolor(D_M1_PS)
# ### Close-loop correction with conventional calibrations
# The correction comprises:
#
# 1) M2 segment tip-tilt (sensed with 3 SH WFS)
#
# 2) M1 segment piston (sensed with 3 SPS)
#
# Note: If you introduce a segment tip-tilt on M1 it will be compensated by M2, and therefore a Field-Dependent Segment Piston (FDSP) will be created. This FDSP will be seen by the 3 SPS and will try to compensate for it, introducing additional errors!
# + active=""
# ##### Reset before starting
# gs.reset()
# gmt.reset()
# + active=""
# ##### Apply a known Tilt to a particular segment on M1
# M1RotVec = np.array([ #arcsec
# [0,0,0] ,
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0]]) * math.pi/180/3600
#
# ##### Apply a know segment piston/translation to a particular segment on M1
# M1TrVec = np.array([ # meters surf
# [0,0,500e-9],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0]])
#
# for idx in range(7): gmt.M1.update(origin=M1TrVec[idx,:], euler_angles=M1RotVec[idx,:], idx=idx+1)
#
# ##### Apply a known Tilt to a particular segment on M2
# M2RotVec = np.array([ #arcsec
# [0,0,0] ,
# [0,0,0],
# [0,50e-3,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0]]) * math.pi/180/3600
#
# ##### Apply a know segment piston/translation to a particular segment on M2
# M2TrVec = np.array([ # meters surf
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,0],
# [0,0,300e-9],
# [50e-6,0,0],
# [0,0,0]])
#
# for idx in range(7): gmt.M2.update(origin=M2TrVec[idx,:], euler_angles=M2RotVec[idx,:], idx=idx+1)
#
# ongs.reset()
# gmt.propagate(ongs)
# plt.imshow(ongs.phase.host(units='nm'),interpolation='None')
# plt.colorbar()
# + active=""
# ##### Close the loop !!!!!
# f, ax = plt.subplots()
# f.set_size_inches(6,8)
# niter = 10
# rmsval = np.zeros(niter)
# myTTest1 = np.zeros((7,2))
# myPSest1 = np.zeros(6)
# for ii in range(niter):
# gs.reset()
# ongs.reset()
# gmt.propagate(gs)
# gmt.propagate(ongs)
# rmsval[ii] = ongs.wavefront.rms()
# ####### visualization
# if ii > 0: clb.remove()
# h = ax.imshow(ongs.phase.host(units='micron'),interpolation='None')
# clb = f.colorbar(h, ax=ax, shrink=0.6)
# clb.set_label('um')
# IPython.display.clear_output(wait=True)
# IPython.display.display(f)
# ####### segment TT correction
# wfs.reset()
# wfs.analyze(gs)
# slopevec = wfs.valid_slopes.host().ravel()
# myTTest1 += np.dot(R_M2_TT, slopevec).reshape((7,2))
# M2RotCor = np.zeros((7,3))
# M2RotCor[:,0:2] = myTTest1
# M2RotVec1 = M2RotVec - M2RotCor
# for idx in range(7): gmt.M2.update(origin=M2TrVec[idx,:], euler_angles=M2RotVec1[idx,:], idx=idx+1)
# ####### segment Piston correction
# SPSmeas = ps.piston(gs, segment='edge') - SPSmeas_ref
# myPSest1 += np.dot(R_M1_PS, SPSmeas.ravel())
# M1TrCor = np.zeros((7,3))
# M1TrCor[0:6,2] = myPSest1
# M1TrVec1 = M1TrVec - M1TrCor
# for idx in range(7): gmt.M1.update(origin=M1TrVec1[idx,:], euler_angles=M1RotVec[idx,:], idx=idx+1)
# plt.close()
# + active=""
# plt.semilogy(rmsval*1e9)
# plt.grid()
# plt.xlabel('iteration')
# plt.ylabel('nm wf rms')
# print myTTest1*180*3600/math.pi*1e3
# print myPSest1*1e9
# + active=""
# rmsval*1e9
# -
# ### Close loop correction with Brian's FDSP calibrations
# The correction comprises:
#
# 1) M2 segment tip-tilt (sensed with 3 SH WFS)
#
# 2) FDSP (sensed with 3 SPS)
#
# 3) M1 segment piston (sensed with 3 SPS)
#
#
# Calibrate FDSP Interaction Matrix and Reconstructor
TTstroke = 50e-3 #arcsec
gmt.reset()
D_FDSP = gmt.calibrate(ps, gs, mirror="M1", mode="FDSP", stroke=TTstroke*math.pi/180/3600, segment='edge',
agws=wfs, recmat=R_M2_TT)
R_FDSP = np.linalg.pinv(D_FDSP)
R_FDSP.shape
plt.pcolor(D_FDSP)
##### Combine Interaction Matrices of M1 segment piston AND FDSP.
D_PIST = np.concatenate((D_M1_PS, D_FDSP), axis=1)
R_PIST = np.linalg.pinv(D_PIST)
print R_PIST.shape
plt.pcolor(D_PIST)
plt.colorbar()
##### Reset before starting
gs.reset()
gmt.reset()
# +
##### Apply a known Tilt to a particular segment on M1
M1RotVec = np.array([ #arcsec
[0,0,0] ,
[0,0,0],
[0,0,0],
[0,0,0],
[0,50e-3,0],
[0,0,0],
[0,0,0]]) * math.pi/180/3600
##### Apply a know segment piston/translation to a particular segment on M1
M1TrVec = np.array([ # meters surf
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,1e-6],
[0,0,0]])
for idx in range(7): gmt.M1.update(origin=M1TrVec[idx,:].tolist(), euler_angles=M1RotVec[idx,:].tolist(), idx=idx+1)
##### Apply a known Tilt to a particular segment on M2
M2RotVec = np.array([ #arcsec
[0,0,0] ,
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0]]) * math.pi/180/3600
##### Apply a know segment piston/translation to a particular segment on M2
M2TrVec = np.array([ # meters surf
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0],
[0,0,0]])
for idx in range(7): gmt.M2.update(origin=M2TrVec[idx,:].tolist(), euler_angles=M2RotVec[idx,:].tolist(), idx=idx+1)
ongs.reset()
gmt.propagate(ongs)
plt.imshow(ongs.phase.host(units='nm'),interpolation='None')
plt.colorbar()
# -
##### Close the loop !!!!!
f, ax = plt.subplots()
f.set_size_inches(6,8)
niter = 4
TTniter = 10
rmsval = np.zeros(niter*TTniter)
myTTest1 = np.zeros((7,2))
myPSest1 = np.zeros(6)
myFDSPest1 = np.zeros((6,2)) #6x M1 segment tip-tilt
for ii in range(niter):
for jj in range(TTniter):
ongs.reset()
gmt.propagate(ongs)
rmsval[ii*TTniter+jj] = ongs.wavefront.rms()
#---- visualization
if ii*TTniter+jj > 0: clb.remove()
h = ax.imshow(ongs.phase.host(units='micron'),interpolation='None')
clb = f.colorbar(h, ax=ax, shrink=0.6)
clb.set_label('um')
IPython.display.clear_output(wait=True)
IPython.display.display(f)
#---- segment TT correction
gs.reset()
gmt.propagate(gs)
wfs.reset()
wfs.analyze(gs)
slopevec = wfs.valid_slopes.host().ravel()
myTTest1 += np.dot(R_M2_TT, slopevec).reshape((7,2))
M2RotCor = np.zeros((7,3))
M2RotCor[:,0:2] = myTTest1
M2RotVec1 = M2RotVec - M2RotCor
for idx in range(7): gmt.M2.update(origin=M2TrVec[idx,:].tolist(),
euler_angles=M2RotVec1[idx,:].tolist(), idx=idx+1)
####### FDSP and segment piston correction
gs.reset()
gmt.propagate(gs)
PISTmeas = ps.piston(gs, segment='edge') - SPSmeas_ref
myPISTest1 = np.dot(R_PIST, PISTmeas.ravel())
#--- segment piston
myPSest1 += myPISTest1[0:6]
M1TrCor = np.zeros((7,3))
M1TrCor[0:6,2] = myPSest1
M1TrVec1 = M1TrVec - M1TrCor
#--- FDSP
myFDSPest1 += myPISTest1[6:].reshape((6,2))
M1RotCor = np.zeros((7,3))
M1RotCor[0:6,0:2] = myFDSPest1
M1RotVec1 = M1RotVec - M1RotCor
for idx in range(7): gmt.M1.update(origin=M1TrVec1[idx,:].tolist(),
euler_angles=M1RotVec1[idx,:].tolist(), idx=idx+1)
"""
####### FDSP correction only
gs.reset()
gmt.propagate(gs)
FDSPmeas = ps.piston(gs, segment='edge') - SPSmeas_ref
myFDSPest1 += np.dot(R_FDSP, FDSPmeas.ravel()).reshape((6,2))
M1RotCor = np.zeros((7,3))
M1RotCor[0:6,0:2] = myFDSPest1
M1RotVec1 = M1RotVec - M1RotCor
for idx in range(7): gmt.M1.update(origin=M1TrVec[idx,:].tolist(),
euler_angles=M1RotVec1[idx,:].tolist(), idx=idx+1)
####### segment Piston correction only
gs.reset()
gmt.propagate(gs)
SPSmeas = ps.piston(gs, segment='edge') - SPSmeas_ref
myPSest1 += np.dot(R_M1_PS, SPSmeas.ravel())
M1TrCor = np.zeros((7,3))
M1TrCor[0:6,2] = myPSest1
M1TrVec1 = M1TrVec - M1TrCor
for idx in range(7): gmt.M1.update(origin=M1TrVec1[idx,:].tolist(),
euler_angles=M1RotVec[idx,:].tolist(), idx=idx+1)
"""
plt.close()
plt.semilogy(rmsval*1e9)
plt.grid()
plt.xlabel('iteration')
plt.ylabel('nm wf rms')
print 'segment tip-tilt'
print myTTest1*180*3600/math.pi*1e3
print 'segment piston'
print myPSest1*1e9
print 'FDSP'
print myFDSPest1*180*3600/math.pi*1e3
rmsval*1e9
|
notebooks/FDSP_control.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
os.environ['CUDA_VISIBLE_DEVICES'] = ''
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# -
import numpy as np
import json
import tensorflow as tf
import itertools
import collections
import re
import random
import sentencepiece as spm
from tqdm import tqdm
import xlnet_utils as squad_utils
# +
from prepro_utils import preprocess_text, encode_ids
sp_model = spm.SentencePieceProcessor()
sp_model.Load('sp10m.cased.v9.model')
# +
import tensorflow as tf
import logging
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
tf.get_logger().setLevel(logging.ERROR)
tf.autograph.set_verbosity(1)
# +
train_file = '/home/husein/pure-text/ms-train-2.0.json'
train_examples = squad_utils.read_squad_examples(
input_file=train_file, is_training=True)
len(train_examples)
# +
test_file = '/home/husein/pure-text/ms-dev-2.0.json'
test_examples = squad_utils.read_squad_examples(
input_file=test_file, is_training=False)
len(test_examples)
# +
max_seq_length = 512
doc_stride = 128
max_query_length = 64
train_features = squad_utils.convert_examples_to_features(
examples=train_examples,
sp_model=sp_model,
max_seq_length=max_seq_length,
doc_stride=doc_stride,
max_query_length=max_query_length,
is_training=True)
# -
test_features = squad_utils.convert_examples_to_features(
examples=test_examples,
sp_model=sp_model,
max_seq_length=max_seq_length,
doc_stride=doc_stride,
max_query_length=max_query_length,
is_training=False)
# +
import pickle
with open('xlnet-squad-train.pkl', 'wb') as fopen:
pickle.dump([train_features, train_examples], fopen)
with open('xlnet-squad-test.pkl', 'wb') as fopen:
pickle.dump([test_features, test_examples], fopen)
# -
|
session/squad/prepare-squad-dataset-xlnet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# + [markdown] origin_pos=0
# # 概率
# :label:`sec_prob`
#
# 简单地说,机器学习就是做出预测。
#
# 根据病人的临床病史,我们可能想预测他们在下一年心脏病发作的*概率*。
# 在飞机喷气发动机的异常检测中,我们想要评估一组发动机读数为正常运行情况的概率有多大。
# 在强化学习中,我们希望智能体(agent)能在一个环境中智能地行动。
# 这意味着我们需要考虑在每种可行的行为下获得高奖励的概率。
# 当我们建立推荐系统时,我们也需要考虑概率。
# 例如,假设我们为一家大型在线书店工作,我们可能希望估计某些用户购买特定图书的概率。
# 为此,我们需要使用概率学。
# 有完整的课程、专业、论文、职业、甚至院系,都致力于概率学的工作。
# 所以很自然地,我们在这部分的目标不是教授你整个科目。
# 相反,我们希望教给你在基础的概率知识,使你能够开始构建你的第一个深度学习模型,
# 以便你可以开始自己探索它。
#
# 现在让我们更认真地考虑第一个例子:根据照片区分猫和狗。
# 这听起来可能很简单,但对于机器却可能是一个艰巨的挑战。
# 首先,问题的难度可能取决于图像的分辨率。
#
# 
# :width:`300px`
# :label:`fig_cat_dog`
#
# 如 :numref:`fig_cat_dog`所示,虽然人类很容易以$160 \times 160$像素的分辨率识别猫和狗,
# 但它在$40\times40$像素上变得具有挑战性,而且在$10 \times 10$像素下几乎是不可能的。
# 换句话说,我们在很远的距离(从而降低分辨率)区分猫和狗的能力可能会变为猜测。
# 概率给了我们一种正式的途径来说明我们的确定性水平。
# 如果我们完全肯定图像是一只猫,我们说标签$y$是"猫"的*概率*,表示为$P(y=$"猫"$)$等于$1$。
# 如果我们没有证据表明$y=$“猫”或$y=$“狗”,那么我们可以说这两种可能性是相等的,
# 即$P(y=$"猫"$)=P(y=$"狗"$)=0.5$。
# 如果我们不十分确定图像描绘的是一只猫,我们可以将概率赋值为$0.5<P(y=$"猫"$)<1$。
#
# 现在考虑第二个例子:给出一些天气监测数据,我们想预测明天北京下雨的概率。
# 如果是夏天,下雨的概率是0.5。
#
# 在这两种情况下,我们都不确定结果,但这两种情况之间有一个关键区别。
# 在第一种情况中,图像实际上是狗或猫二选一。
# 在第二种情况下,结果实际上是一个随机的事件。
# 因此,概率是一种灵活的语言,用于说明我们的确定程度,并且它可以有效地应用于广泛的领域中。
#
# ## 基本概率论
#
# 假设我们掷骰子,想知道看到1的几率有多大,而不是看到另一个数字。
# 如果骰子是公平的,那么所有六个结果$\{1, \ldots, 6\}$都有相同的可能发生,
# 因此我们可以说$1$发生的概率为$\frac{1}{6}$。
#
# 然而现实生活中,对于我们从工厂收到的真实骰子,我们需要检查它是否有瑕疵。
# 检查骰子的唯一方法是多次投掷并记录结果。
# 对于每个骰子,我们将观察到$\{1, \ldots, 6\}$中的一个值。
# 对于每个值,一种自然的方法是将它出现的次数除以投掷的总次数,
# 即此*事件*(event)概率的*估计值*。
# *大数定律*(law of large numbers)告诉我们:
# 随着投掷次数的增加,这个估计值会越来越接近真实的潜在概率。
# 让我们用代码试一试!
#
# 首先,我们导入必要的软件包。
#
# + origin_pos=1 tab=["mxnet"]
# %matplotlib inline
import random
from mxnet import np, npx
from d2l import mxnet as d2l
npx.set_np()
# + [markdown] origin_pos=4
# 在统计学中,我们把从概率分布中抽取样本的过程称为*抽样*(sampling)。
# 笼统来说,可以把*分布*(distribution)看作是对事件的概率分配,
# 稍后我们将给出的更正式定义。
# 将概率分配给一些离散选择的分布称为*多项分布*(multinomial distribution)。
#
# 为了抽取一个样本,即掷骰子,我们只需传入一个概率向量。
# 输出是另一个相同长度的向量:它在索引$i$处的值是采样结果中$i$出现的次数。
#
# + origin_pos=5 tab=["mxnet"]
fair_probs = [1.0 / 6] * 6
np.random.multinomial(1, fair_probs)
# + [markdown] origin_pos=8
# 在估计一个骰子的公平性时,我们希望从同一分布中生成多个样本。
# 如果用Python的for循环来完成这个任务,速度会慢得惊人。
# 因此我们使用深度学习框架的函数同时抽取多个样本,得到我们想要的任意形状的独立样本数组。
#
# + origin_pos=9 tab=["mxnet"]
np.random.multinomial(10, fair_probs)
# + [markdown] origin_pos=12
# 现在我们知道如何对骰子进行采样,我们可以模拟1000次投掷。
# 然后,我们可以统计1000次投掷后,每个数字被投中了多少次。
# 具体来说,我们计算相对频率,以作为真实概率的估计。
#
# + origin_pos=13 tab=["mxnet"]
counts = np.random.multinomial(1000, fair_probs).astype(np.float32)
counts / 1000
# + [markdown] origin_pos=16
# 因为我们是从一个公平的骰子中生成的数据,我们知道每个结果都有真实的概率$\frac{1}{6}$,
# 大约是$0.167$,所以上面输出的估计值看起来不错。
#
# 我们也可以看到这些概率如何随着时间的推移收敛到真实概率。
# 让我们进行500组实验,每组抽取10个样本。
#
# + origin_pos=17 tab=["mxnet"]
counts = np.random.multinomial(10, fair_probs, size=500)
cum_counts = counts.astype(np.float32).cumsum(axis=0)
estimates = cum_counts / cum_counts.sum(axis=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates[:, i].asnumpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();
# + [markdown] origin_pos=20
# 每条实线对应于骰子的6个值中的一个,并给出骰子在每组实验后出现值的估计概率。
# 当我们通过更多的实验获得更多的数据时,这$6$条实体曲线向真实概率收敛。
#
# ### 概率论公理
#
# 在处理骰子掷出时,我们将集合$\mathcal{S} = \{1, 2, 3, 4, 5, 6\}$
# 称为*样本空间*(sample space)或*结果空间*(outcome space),
# 其中每个元素都是*结果*(outcome)。
# *事件*(event)是一组给定样本空间的随机结果。
# 例如,“看到$5$”($\{5\}$)和“看到奇数”($\{1, 3, 5\}$)都是掷出骰子的有效事件。
# 注意,如果一个随机实验的结果在$\mathcal{A}$中,则事件$\mathcal{A}$已经发生。
# 也就是说,如果投掷出$3$点,因为$3 \in \{1, 3, 5\}$,我们可以说,“看到奇数”的事件发生了。
#
# *概率*(probability)可以被认为是将集合映射到真实值的函数。
# 在给定的样本空间$\mathcal{S}$中,事件$\mathcal{A}$的概率,
# 表示为$P(\mathcal{A})$,满足以下属性:
#
# * 对于任意事件$\mathcal{A}$,其概率从不会是负数,即$P(\mathcal{A}) \geq 0$;
# * 整个样本空间的概率为$1$,即$P(\mathcal{S}) = 1$;
# * 对于*互斥*(mutually exclusive)事件(对于所有$i \neq j$都有$\mathcal{A}_i \cap \mathcal{A}_j = \emptyset$)的任意一个可数序列$\mathcal{A}_1, \mathcal{A}_2, \ldots$,序列中任意一个事件发生的概率等于它们各自发生的概率之和,即$P(\bigcup_{i=1}^{\infty} \mathcal{A}_i) = \sum_{i=1}^{\infty} P(\mathcal{A}_i)$。
#
# 以上也是概率论的公理,由科尔莫戈罗夫于1933年提出。
# 有了这个公理系统,我们可以避免任何关于随机性的哲学争论;
# 相反,我们可以用数学语言严格地推理。
# 例如,假设事件$\mathcal{A}_1$为整个样本空间,
# 且当所有$i > 1$时的$\mathcal{A}_i = \emptyset$,
# 那么我们可以证明$P(\emptyset) = 0$,即不可能发生事件的概率是$0$。
#
# ### 随机变量
#
# 在我们掷骰子的随机实验中,我们引入了*随机变量*(random variable)的概念。
# 随机变量几乎可以是任何数量,并且它可以在随机实验的一组可能性中取一个值。
# 考虑一个随机变量$X$,其值在掷骰子的样本空间$\mathcal{S}=\{1,2,3,4,5,6\}$中。
# 我们可以将事件“看到一个$5$”表示为$\{X=5\}$或$X=5$,
# 其概率表示为$P(\{X=5\})$或$P(X=5)$。
# 通过$P(X=a)$,我们区分了随机变量$X$和$X$可以采取的值(例如$a$)。
# 然而,这可能会导致繁琐的表示。
# 为了简化符号,一方面,我们可以将$P(X)$表示为随机变量$X$上的*分布*(distribution):
# 分布告诉我们$X$获得某一值的概率。
# 另一方面,我们可以简单用$P(a)$表示随机变量取值$a$的概率。
# 由于概率论中的事件是来自样本空间的一组结果,因此我们可以为随机变量指定值的可取范围。
# 例如,$P(1 \leq X \leq 3)$表示事件$\{1 \leq X \leq 3\}$,
# 即$\{X = 1, 2, \text{or}, 3\}$的概率。
# 等价地,$P(1 \leq X \leq 3)$表示随机变量$X$从$\{1, 2, 3\}$中取值的概率。
#
# 请注意,*离散*(discrete)随机变量(如骰子的每一面)
# 和*连续*(continuous)随机变量(如人的体重和身高)之间存在微妙的区别。
# 现实生活中,测量两个人是否具有完全相同的身高没有太大意义。
# 如果我们进行足够精确的测量,你会发现这个星球上没有两个人具有完全相同的身高。
# 在这种情况下,询问某人的身高是否落入给定的区间,比如是否在1.79米和1.81米之间更有意义。
# 在这些情况下,我们将这个看到某个数值的可能性量化为*密度*(density)。
# 高度恰好为1.80米的概率为0,但密度不是0。
# 在任何两个不同高度之间的区间,我们都有非零的概率。
# 在本节的其余部分中,我们将考虑离散空间中的概率。
# 对于连续随机变量的概率,你可以参考深度学习数学附录中[随机变量](https://d2l.ai/chapter_appendix-mathematics-for-deep-learning/random-variables.html)
# 的一节。
#
# ## 处理多个随机变量
#
# 很多时候,我们会考虑多个随机变量。
# 比如,我们可能需要对疾病和症状之间的关系进行建模。
# 给定一个疾病和一个症状,比如“流感”和“咳嗽”,以某个概率存在或不存在于某个患者身上。
# 我们需要估计这些概率以及概率之间的关系,以便我们可以运用我们的推断来实现更好的医疗服务。
#
# 再举一个更复杂的例子:图像包含数百万像素,因此有数百万个随机变量。
# 在许多情况下,图像会附带一个*标签*(label),标识图像中的对象。
# 我们也可以将标签视为一个随机变量。
# 我们甚至可以将所有元数据视为随机变量,例如位置、时间、光圈、焦距、ISO、对焦距离和相机类型。
# 所有这些都是联合发生的随机变量。
# 当我们处理多个随机变量时,会有若干个变量是我们感兴趣的。
#
# ### 联合概率
#
# 第一个被称为*联合概率*(joint probability)$P(A=a,B=b)$。
# 给定任意值$a$和$b$,联合概率可以回答:$A=a$和$B=b$同时满足的概率是多少?
# 请注意,对于任何$a$和$b$的取值,$P(A = a, B=b) \leq P(A=a)$。
# 这点是确定的,因为要同时发生$A=a$和$B=b$,$A=a$就必须发生,$B=b$也必须发生(反之亦然)。因此,$A=a$和$B=b$同时发生的可能性不大于$A=a$或是$B=b$单独发生的可能性。
#
# ### 条件概率
#
# 联合概率的不等式带给我们一个有趣的比率:
# $0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1$。
# 我们称这个比率为*条件概率*(conditional probability),
# 并用$P(B=b \mid A=a)$表示它:它是$B=b$的概率,前提是$A=a$已发生。
#
# ### 贝叶斯定理
#
# 使用条件概率的定义,我们可以得出统计学中最有用的方程之一:
# *Bayes定理*(Bayes' theorem)。
# 根据*乘法法则*(multiplication rule )可得到$P(A, B) = P(B \mid A) P(A)$。
# 根据对称性,可得到$P(A, B) = P(A \mid B) P(B)$。
# 假设$P(B)>0$,求解其中一个条件变量,我们得到
#
# $$P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}.$$
#
# 请注意,这里我们使用紧凑的表示法:
# 其中$P(A, B)$是一个*联合分布*(joint distribution),
# $P(A \mid B)$是一个*条件分布*(conditional distribution)。
# 这种分布可以在给定值$A = a, B=b$上进行求值。
#
# ### 边际化
#
# 为了能进行事件概率求和,我们需要*求和法则*(sum rule),
# 即$B$的概率相当于计算$A$的所有可能选择,并将所有选择的联合概率聚合在一起:
#
# $$P(B) = \sum_{A} P(A, B),$$
#
# 这也称为*边际化*(marginalization)。
# 边际化结果的概率或分布称为*边际概率*(marginal probability)
# 或*边际分布*(marginal distribution)。
#
# ### 独立性
#
# 另一个有用属性是*依赖*(dependence)与*独立*(independence)。
# 如果两个随机变量$A$和$B$是独立的,意味着事件$A$的发生跟$B$事件的发生无关。
# 在这种情况下,统计学家通常将这一点表述为$A \perp B$。
# 根据贝叶斯定理,马上就能同样得到$P(A \mid B) = P(A)$。
# 在所有其他情况下,我们称$A$和$B$依赖。
# 比如,两次连续抛出一个骰子的事件是相互独立的。
# 相比之下,灯开关的位置和房间的亮度并不是(因为可能存在灯泡坏掉、电源故障,或者开关故障)。
#
# 由于$P(A \mid B) = \frac{P(A, B)}{P(B)} = P(A)$等价于$P(A, B) = P(A)P(B)$,
# 因此两个随机变量是独立的,当且仅当两个随机变量的联合分布是其各自分布的乘积。
# 同样地,给定另一个随机变量$C$时,两个随机变量$A$和$B$是*条件独立的*(conditionally independent),
# 当且仅当$P(A, B \mid C) = P(A \mid C)P(B \mid C)$。
# 这个情况表示为$A \perp B \mid C$。
#
# ### 应用
# :label:`subsec_probability_hiv_app`
#
# 我们实战演练一下!
# 假设一个医生对患者进行艾滋病病毒(HIV)测试。
# 这个测试是相当准确的,如果患者健康但测试显示他患病,这个概率只有1%;
# 如果患者真正感染HIV,它永远不会检测不出。
# 我们使用$D_1$来表示诊断结果(如果阳性,则为$1$,如果阴性,则为$0$),
# $H$来表示感染艾滋病病毒的状态(如果阳性,则为$1$,如果阴性,则为$0$)。
# 在 :numref:`conditional_prob_D1`中列出了这样的条件概率。
#
# :条件概率为$P(D_1 \mid H)$
#
# | 条件概率 | $H=1$ | $H=0$ |
# |---|---|---|
# |$P(D_1 = 1 \mid H)$| 1 | 0.01 |
# |$P(D_1 = 0 \mid H)$| 0 | 0.99 |
# :label:`conditional_prob_D1`
#
# 请注意,每列的加和都是1(但每行的加和不是),因为条件概率需要总和为1,就像概率一样。
# 让我们计算如果测试出来呈阳性,患者感染HIV的概率,即$P(H = 1 \mid D_1 = 1)$。
# 显然,这将取决于疾病有多常见,因为它会影响错误警报的数量。
# 假设人口总体是相当健康的,例如,$P(H=1) = 0.0015$。
# 为了应用贝叶斯定理,我们需要运用边际化和乘法法则来确定
#
# $$\begin{aligned}
# &P(D_1 = 1) \\
# =& P(D_1=1, H=0) + P(D_1=1, H=1) \\
# =& P(D_1=1 \mid H=0) P(H=0) + P(D_1=1 \mid H=1) P(H=1) \\
# =& 0.011485.
# \end{aligned}
# $$
#
# 因此,我们得到
#
# $$\begin{aligned}
# &P(H = 1 \mid D_1 = 1)\\ =& \frac{P(D_1=1 \mid H=1) P(H=1)}{P(D_1=1)} \\ =& 0.1306 \end{aligned}.$$
#
# 换句话说,尽管使用了非常准确的测试,患者实际上患有艾滋病的几率只有13.06%。
# 正如我们所看到的,概率可能是违反直觉的。
#
# 患者在收到这样可怕的消息后应该怎么办?
# 很可能,患者会要求医生进行另一次测试来确定病情。
# 第二个测试具有不同的特性,它不如第一个测试那么精确,
# 如 :numref:`conditional_prob_D2`所示。
#
# :条件概率为$P(D_2 \mid H)$
#
# | 条件概率 | $H=1$ | $H=0$ |
# |---|---|---|
# |$P(D_2 = 1 \mid H)$| 0.98 | 0.03 |
# |$P(D_2 = 0 \mid H)$| 0.02 | 0.97 |
# :label:`conditional_prob_D2`
#
# 不幸的是,第二次测试也显示阳性。让我们通过假设条件独立性来计算出应用Bayes定理的必要概率:
#
# $$\begin{aligned}
# &P(D_1 = 1, D_2 = 1 \mid H = 0) \\
# =& P(D_1 = 1 \mid H = 0) P(D_2 = 1 \mid H = 0) \\
# =& 0.0003,
# \end{aligned}
# $$
#
# $$\begin{aligned}
# &P(D_1 = 1, D_2 = 1 \mid H = 1) \\
# =& P(D_1 = 1 \mid H = 1) P(D_2 = 1 \mid H = 1) \\
# =& 0.98.
# \end{aligned}
# $$
#
# 现在我们可以应用边际化和乘法规则:
#
# $$\begin{aligned}
# &P(D_1 = 1, D_2 = 1) \\
# =& P(D_1 = 1, D_2 = 1, H = 0) + P(D_1 = 1, D_2 = 1, H = 1) \\
# =& P(D_1 = 1, D_2 = 1 \mid H = 0)P(H=0) + P(D_1 = 1, D_2 = 1 \mid H = 1)P(H=1)\\
# =& 0.00176955.
# \end{aligned}
# $$
#
# 最后,鉴于存在两次阳性检测,患者患有艾滋病的概率为
#
# $$\begin{aligned}
# &P(H = 1 \mid D_1 = 1, D_2 = 1)\\
# =& \frac{P(D_1 = 1, D_2 = 1 \mid H=1) P(H=1)}{P(D_1 = 1, D_2 = 1)} \\
# =& 0.8307.
# \end{aligned}
# $$
#
# 也就是说,第二次测试使我们能够对患病的情况获得更高的信心。
# 尽管第二次检验比第一次检验的准确性要低得多,但它仍然显著提高我们的预测概率。
#
# ## 期望和方差
#
# 为了概括概率分布的关键特征,我们需要一些测量方法。
# 一个随机变量$X$的*期望*(expectation,或平均值(average))表示为
#
# $$E[X] = \sum_{x} x P(X = x).$$
#
# 当函数$f(x)$的输入是从分布$P$中抽取的随机变量时,$f(x)$的期望值为
#
# $$E_{x \sim P}[f(x)] = \sum_x f(x) P(x).$$
#
# 在许多情况下,我们希望衡量随机变量$X$与其期望值的偏置。这可以通过方差来量化
#
# $$\mathrm{Var}[X] = E\left[(X - E[X])^2\right] =
# E[X^2] - E[X]^2.$$
#
# 方差的平方根被称为*标准差*(standared deviation)。
# 随机变量函数的方差衡量的是:当从该随机变量分布中采样不同值$x$时,
# 函数值偏离该函数的期望的程度:
#
# $$\mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right].$$
#
# ## 小结
#
# * 我们可以从概率分布中采样。
# * 我们可以使用联合分布、条件分布、Bayes定理、边缘化和独立性假设来分析多个随机变量。
# * 期望和方差为概率分布的关键特征的概括提供了实用的度量形式。
#
# ## 练习
#
# 1. 进行$m=500$组实验,每组抽取$n=10$个样本。改变$m$和$n$,观察和分析实验结果。
# 2. 给定两个概率为$P(\mathcal{A})$和$P(\mathcal{B})$的事件,计算$P(\mathcal{A} \cup \mathcal{B})$和$P(\mathcal{A} \cap \mathcal{B})$的上限和下限。(提示:使用[友元图](https://en.wikipedia.org/wiki/Venn_diagram)来展示这些情况。)
# 3. 假设我们有一系列随机变量,例如$A$、$B$和$C$,其中$B$只依赖于$A$,而$C$只依赖于$B$,你能简化联合概率$P(A, B, C)$吗?(提示:这是一个[马尔可夫链](https://en.wikipedia.org/wiki/Markov_chain)。)
# 4. 在 :numref:`subsec_probability_hiv_app`中,第一个测试更准确。为什么不运行第一个测试两次,而是同时运行第一个和第二个测试?
#
# + [markdown] origin_pos=21 tab=["mxnet"]
# [Discussions](https://discuss.d2l.ai/t/1761)
#
|
d2l/mxnet/chapter_preliminaries/probability.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="CzfwhS6KNKKH" executionInfo={"status": "ok", "timestamp": 1606005484625, "user_tz": -60, "elapsed": 995, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}}
import tensorflow as tf
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.layers import Embedding, LSTM, Dense, Dropout, Bidirectional
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.models import Sequential
from tensorflow.keras.optimizers import Adam
import numpy as np
# + colab={"base_uri": "https://localhost:8080/"} id="Yj_I6Zr7pVsl" executionInfo={"status": "ok", "timestamp": 1606000574488, "user_tz": -60, "elapsed": 4228, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="6971d19b-402b-4144-b1ed-03e1a026d7c8"
from google.colab import drive
drive.mount('/content/drive')
# + colab={"base_uri": "https://localhost:8080/"} id="utYZLQaGNNDM" executionInfo={"status": "ok", "timestamp": 1606005940687, "user_tz": -60, "elapsed": 978, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="8c32ed2a-607c-4e5f-b048-92d230594999"
to_exclude = '!"#$%&—.()*+-/;<=>@[\\]^_`{|}~\t,\'\n|'
tokenizer = Tokenizer(filters = to_exclude)
text = open('/content/drive/MyDrive/DSpraktikum/data/emily-together.txt').read()
text = text.replace('—', ' ') # pridane aby odstranilo dlhe -
corpus = text.lower().split("\n")
tokenizer.fit_on_texts(corpus)
total_words = len(tokenizer.word_index) + 1
print(tokenizer.word_index)
print(total_words)
print(corpus)
# + id="soPGVheskaQP" executionInfo={"status": "ok", "timestamp": 1606005942922, "user_tz": -60, "elapsed": 1074, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}}
input_sequences = []
for line in corpus:
token_list = tokenizer.texts_to_sequences([line])[0]
for i in range(1, len(token_list)):
n_gram_sequence = token_list[:i+1]
input_sequences.append(n_gram_sequence)
# pad sequences
max_sequence_len = max([len(x) for x in input_sequences])
input_sequences = np.array(pad_sequences(input_sequences, maxlen=max_sequence_len, padding='pre'))
# create predictors and label
xs, labels = input_sequences[:,:-1],input_sequences[:,-1]
ys = tf.keras.utils.to_categorical(labels, num_classes=total_words)
# + id="w9vH8Y59ajYL" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606006132991, "user_tz": -60, "elapsed": 190671, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="95d675fd-f58d-4b83-f6ba-b456a707e90c"
model = Sequential()
model.add(Embedding(total_words, 256, input_length=max_sequence_len-1))
model.add(Bidirectional(LSTM(256)))
model.add(Dense(total_words, activation='softmax'))
adam = Adam(lr=0.01)
model.compile(loss='categorical_crossentropy', optimizer=adam, metrics=['accuracy'])
#earlystop = EarlyStopping(monitor='val_loss', min_delta=0, patience=5, verbose=0, mode='auto')
history = model.fit(xs, ys, epochs=50, verbose=1, batch_size=256)
#print model.summary()
print(model)
# + id="3YXGelKThoTT" executionInfo={"status": "ok", "timestamp": 1606006134909, "user_tz": -60, "elapsed": 473, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}}
import matplotlib.pyplot as plt
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.show()
# + id="poeprYK8h-c7" colab={"base_uri": "https://localhost:8080/", "height": 279} executionInfo={"status": "ok", "timestamp": 1606006143686, "user_tz": -60, "elapsed": 526, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="f705bb0f-39d3-4752-c282-ec98dd749648"
plot_graphs(history, 'loss')
# + id="6Vc6PHgxa6Hm" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606006152441, "user_tz": -60, "elapsed": 2557, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="e14968e9-5f9b-4de5-8dc4-0c342f715f50"
seed_text = "truth"
next_words = 50
for _ in range(next_words):
token_list = tokenizer.texts_to_sequences([seed_text])[0]
token_list = pad_sequences([token_list], maxlen=max_sequence_len-1, padding='pre')
predicted = model.predict_classes(token_list, verbose=0)
output_word = ""
for word, index in tokenizer.word_index.items():
if index == predicted:
output_word = word
break
seed_text += " " + output_word
print(seed_text)
# + id="2WPdYJqN0D_D" colab={"base_uri": "https://localhost:8080/"} executionInfo={"status": "ok", "timestamp": 1606006328178, "user_tz": -60, "elapsed": 11285, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17486802797856736994"}} outputId="705284c3-a8a3-4437-9c81-e16db37704ac"
model.save('/content/drive/MyDrive/DSpraktikum/model1')
# + id="uy3akAYKbiy3"
|
assignment_07/poetrybywords.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Atividade Integradora
import findspark as fs
from pyspark.sql import SparkSession
from pyspark.sql.types import *
from pyspark.sql import functions as f
from pyspark.sql.window import Window
from pyspark.ml.feature import StopWordsRemover
import pandas as pd
import seaborn as sns
sns.set(style="ticks", palette="pastel")
import os
from wordcloud import WordCloud, ImageColorGenerator
import matplotlib.pyplot as plt
# %matplotlib inline
spark_location='/Users/vivi/server/spark' # Set your own
java8_location= '/Library/Java/JavaVirtualMachines/jdk1.8.0_251.jdk/Contents/Home/' # Set your own
os.environ['JAVA_HOME'] = java8_location
fs.init(spark_home=spark_location)
datapath = 'data'
files = sorted(os.listdir(datapath))
files
# !head data/yelp_academic_dataset_review.json
spark = SparkSession.builder \
.master('local[*]') \
.appName('Integradora Yelp') \
.config("spark.ui.port", "4060") \
.getOrCreate()
sc = spark.sparkContext
spark#.stop()
# ## Bases
usr_raw = spark.read.json(datapath+'/yelp_academic_dataset_user.json')
rv_raw = spark.read.json(datapath+'/yelp_academic_dataset_review.json')
bz_raw = spark.read.json(datapath+'/yelp_academic_dataset_business.json')
tp_raw = spark.read.json(datapath+'/yelp_academic_dataset_tip.json')
bz_raw.printSchema()
bz_raw.select('attributes').show()
tp_raw.show()
bz_raw.createOrReplaceTempView('bz')
rv_raw.createOrReplaceTempView('rv')
usr_raw.createOrReplaceTempView('usr')
tp_raw.createOrReplaceTempView('tp')
print(spark.catalog.listTables())
bz_raw.columns
usr_raw.columns
rv_raw.columns
tp_raw.columns
# ## Joins
# Juntando as informações de reviews, estabelecimentos da cidade escolhidas e usuários que frequentam esses estabelecimentos.
# - Reviews + Business
base = spark.sql("""
SELECT A.*,
B.address,
B.categories,
B.city,
B.hours,
B.is_open,
B.latitude,
B.longitude,
B.name AS name_bz,
B.postal_code,
B.review_count,
B.stars AS stars_bz,
B.state
FROM rv as A
LEFT JOIN bz as B
ON A.business_id = B.business_id
WHERE B.city = 'Toronto'
AND B.state = 'ON'
AND B.review_count > 20
""")
base.show(5)
base.createOrReplaceTempView('base')
# - Contagem da quantidade de linhas para garantir que a integridade do dataset ser mantém ao longo do processamento.
#linhas na base de reviews + business
spark.sql('''
SELECT Count(*)
FROM base
''').show()
# - (Reviews + Business) + Users
# + jupyter={"source_hidden": true}
base1 = spark.sql("""
SELECT A.*,
B.average_stars AS stars_usr,
B.compliment_cool,
B.compliment_cute,
B.compliment_funny,
B.compliment_hot,
B.compliment_list,
B.compliment_more,
B.compliment_note,
B.compliment_photos,
B.compliment_plain,
B.compliment_profile,
B.compliment_writer,
B.cool AS cool_usr,
B.elite AS elite_usr,
B.fans,
B.friends,
B.funny AS funny_usr,
B.name AS name_usr,
B.review_count AS review_count_usr,
B.useful AS useful_usr,
B.yelping_since
FROM base as A
LEFT JOIN usr as B
ON A.user_id = B.user_id
""")
# -
base1.createOrReplaceTempView('base1')
#linhas na base de reviews + business + users
spark.sql('''
SELECT Count(*)
FROM base1
''').show()
aux = spark.sql('''
SELECT user_id, city, yelping_since,
COUNT(review_id) AS city_review_counter,
review_count_usr
FROM base1
GROUP BY user_id, review_count_usr, city, yelping_since
ORDER BY city_review_counter DESC
''')
aux.createOrReplaceTempView('aux')
aux.show()
# Aparentemente os usuários fazem reviews em estabelecimentos não só em Toronto. Para incluir essa informação no modelo, será criada uma variável com a relação entre as quantidade de reviews do usuário na cidade pela quantidade total de reviews do usuário.
# - Média de reviews por usuário na cidade e total
spark.sql('''
SELECT AVG(city_review_counter),
AVG(review_count_usr)
FROM aux
''').show()
# - Remoção de usuários com apenas 1 review na cidade
base2 = spark.sql('''
SELECT A.*,
B.city_review_counter,
(B.city_review_counter/B.review_count_usr) AS city_review_ratio
FROM base1 as A
LEFT JOIN aux as B
ON A.user_id = B.user_id
WHERE B.city_review_counter > 1
''')
base2.createOrReplaceTempView('base2')
#linhas na base de reviews + business + users
spark.sql('''
SELECT Count(*)
FROM base2
''').show()
# - Classificação das avaliações em Boa (1 - maior do que 4) e Ruim ou inexistente (0 - menor do que 4).
base3 = spark.sql("""
SELECT *,
(CASE WHEN stars >=4 THEN 1 ELSE 0 END) as class_rv,
(CASE WHEN stars_bz >=4 THEN 1 ELSE 0 END) as class_bz,
(CASE WHEN stars_usr >=4 THEN 1 ELSE 0 END) as class_usr
FROM base2
""")
base3.columns
base3.createOrReplaceTempView('base3')
spark.sql('''
SELECT Count(*)
FROM base2
''').show()
# - Base + Tips
spark.sql('''
SELECT business_id, user_id,
count(text) AS tips_counter,
sum(compliment_count) as total_compliments
FROM tp
GROUP BY business_id, user_id
ORDER BY total_compliments DESC
''').show()
base4 = spark.sql('''
SELECT A.*,
IFNULL(B.compliment_count,0) AS compliment_count_tip,
IFNULL(B.text,'') AS tip
FROM base3 as A
LEFT JOIN tp as B
ON (A.user_id = B.user_id AND A.business_id = B.business_id)
''')
base4.select('business_id', 'user_id','tip','compliment_count_tip').show()
base4.select('text','tip').show()
# ## Tratamento de texto
def word_clean(sdf,col,new_col):
rv1 = sdf.withColumn(new_col,f.regexp_replace(f.col(col), "'d", " would"))
rv2 = rv1.withColumn(new_col,f.regexp_replace(f.col(new_col), "'ve", " have"))
rv3 = rv2.withColumn(new_col,f.regexp_replace(f.col(new_col), "'s", " is"))
rv4 = rv3.withColumn(new_col,f.regexp_replace(f.col(new_col), "'re", " are"))
rv5 = rv4.withColumn(new_col,f.regexp_replace(f.col(new_col), "n't", " not"))
rv6 = rv5.withColumn(new_col,f.regexp_replace(f.col(new_col), '\W+', " "))
rv7 = rv6.withColumn(new_col,f.lower(f.col(new_col)))
return rv7
base5 = word_clean(base4,'text','text_clean')
base6 = word_clean(base5,'tip','tip_clean')
base6.select('text_clean','tip_clean').show()
# - Contagem de amigos de cada usuário
base7 = base6.withColumn('friends_counter', f.size(f.split(f.col('friends'),',')))
base7.createOrReplaceTempView('base7')
base8 = spark.sql('''
SELECT *,
(CASE WHEN friends = 'None' THEN 0 ELSE friends_counter END) as friends_count
FROM base7
''')
df = base8.select('friends','friends_counter','friends_count').limit(10).toPandas()
df.dtypes
df
base8.select('friends','friends_counter','friends_count').show()
# Concatenando review e tip
base9 = base8.withColumn('review_tip', f.concat(f.col('text_clean'),f.lit(' '), f.col('tip_clean')))
base9.columns
base9.select('text_clean','tip_clean','review_tip','stars','compliment_count_tip','funny','cool').show()
base9.createOrReplaceTempView('base9')
spark.sql('''
SELECT stars, count(tip_clean) as tip_counter
FROM base9
GROUP BY stars
ORDER BY tip_counter DESC
''').show()
base10 = base9.withColumn('id',f.row_number())
# + jupyter={"outputs_hidden": true}
base10.select('id','review_id','stars').show()
# -
# - Remoção de colunas que não serão utilizadas na primeira modelagem
base_final = base10.drop('friends','friends_counter','name_usr','city','review_id', 'address','state', 'hours','text_clean','text','tip','tip_clean','elite_usr')
base_final.columns
# - Gravar base final em csv
base_final.limit(50000).write \
.format('csv') \
.mode('overwrite') \
.option('sep', ',') \
.option('header', True) \
.save('output/yelp.csv')
# ## Base para modelo de tópicos
words = base_final.select('review_id','user_id','business_id','categories','stars','review_tip')
words2 = words.withColumn('category', f.explode(f.split(f.col('categories'),', ')))
words3 = words2.drop('categories')
words3.show()
# +
#words4 = words3.withColumn('word', f.explode(f.split(f.col('review_tip'),' ')))
# -
words3.write \
.format('csv') \
.mode('overwrite') \
.option('sep', ',') \
.option('header', True) \
.save('output/yelp_words.csv')
# # Matriz de distâncias
# - Preparação para criação de matriz de distâncias baseada na nota de cada avaliação.
dist1 = base_final.select('user_id','categories','stars')
dist1.show()
dist2 = dist1.withColumn('category', f.explode(f.split(f.col('categories'),', ')))
dist2.show()
dist2.createOrReplaceTempView('dist')
# - Quantidade de usuários e estabelecimentos
spark.sql('''
SELECT Count(DISTINCT user_id)
FROM dist
''').show()
spark.sql('''
SELECT Count(DISTINCT categories)
FROM dist
''').show()
spark.sql('''
SELECT Count(DISTINCT category)
FROM dist
''').show()
# - Aumentando o limite máximo de coluna de acordo com o número de estabelecimentos
# +
#spark.conf.set('spark.sql.pivotMaxValues', u'21000')
# -
dist3 = dist2.groupBy("user_id").pivot("category").mean("stars")
dist4 = dist3.fillna(0)
# + jupyter={"outputs_hidden": true}
dist4.show()
# -
dist4.write \
.format('csv') \
.mode('overwrite') \
.option('sep', ',') \
.option('header', True) \
.save('output/yelp_dist.csv')
|
hist/Processamento Yelp 02jul.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Mixed precision training
# This module allows the forward and backward passes of your neural net to be done in fp16 (also known as *half precision*). This is particularly important if you have an NVIDIA GPU with [tensor cores](https://www.nvidia.com/en-us/data-center/tensorcore/), since it can speed up your training by 200% or more.
# + hide_input=true
from fastai.gen_doc.nbdoc import *
from fastai.callbacks.fp16 import *
from fastai.vision import *
# -
# ## Overview
# To train your model in mixed precision you just have to call [`Learner.to_fp16`](/train.html#to_fp16), which converts the model and modifies the existing [`Learner`](/basic_train.html#Learner) to add [`MixedPrecision`](/callbacks.fp16.html#MixedPrecision).
# + hide_input=true
show_doc(Learner.to_fp16)
# -
# For example:
path = untar_data(URLs.MNIST_SAMPLE)
data = ImageDataBunch.from_folder(path)
model = simple_cnn((3,16,16,2))
learn = Learner(data, model, metrics=[accuracy]).to_fp16()
learn.fit_one_cycle(1)
# Details about mixed precision training are available in [NVIDIA's documentation](https://docs.nvidia.com/deeplearning/sdk/mixed-precision-training/index.html). We will just summarize the basics here.
#
# The only parameter you may want to tweak is `loss_scale`. This is used to scale the loss up, so that it doesn't underflow fp16, leading to loss of accuracy (this is reversed for the final gradient calculation after converting back to fp32). Generally the default `512` works well, however. You can also enable or disable the flattening of the master parameter tensor with `flat_master=True`, however in our testing the different is negligible.
#
# Internally, the callback ensures that all model parameters (except batchnorm layers, which require fp32) are converted to fp16, and an fp32 copy is also saved. The fp32 copy (the `master` parameters) is what is used for actually updating with the optimizer; the fp16 parameters are used for calculating gradients. This helps avoid underflow with small learning rates.
#
# All of this is implemented by the following Callback.
# + hide_input=true
show_doc(MixedPrecision)
# -
# ### Callback methods
# You don't have to call the following functions yourself - they're called by fastai's [`Callback`](/callback.html#Callback) system automatically to enable the class's functionality.
# + hide_input=true
show_doc(MixedPrecision.on_backward_begin)
# + hide_input=true
show_doc(MixedPrecision.on_backward_end)
# + hide_input=true
show_doc(MixedPrecision.on_loss_begin)
# + hide_input=true
show_doc(MixedPrecision.on_step_end)
# + hide_input=true
show_doc(MixedPrecision.on_train_begin)
|
docs_src/callbacks.fp16.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/ninonlack/QM2-group-7-/blob/main/Untitled13.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="zZxo-YNJoCfY"
import matplotlib.pyplot as plt
import pandas as pd
import pylab
# %matplotlib inline
pylab.rcParams['figure.figsize'] = (30., 15.)
# + id="esfvOCTood-l" outputId="68b9a576-6cc4-49e7-d275-f172d4b6d4d3" colab={"base_uri": "https://localhost:8080/", "height": 202}
covidcase_path = "/content/statesvscovidcasesdatasheet.csv"
covidcase = pd.read_csv(covidcase_path)
covidcase.head()
# + id="GIoCFvk0orvl" outputId="806cc209-0c8c-46a8-e8e5-da75efe0e0ae" colab={"base_uri": "https://localhost:8080/"}
covidcase['State'].is_unique
# + id="7Tb9UFVgtuWJ" outputId="ee20cb81-e1b7-41d2-b70c-13df570326be" colab={"base_uri": "https://localhost:8080/"}
covidcase = pd.read_csv('/content/statesvscovidcasesdatasheet.csv', index_col='State')
print(covidcase)
# + id="geMXfUcDt-_Q" outputId="4683ae59-03a3-4fb7-e2db-d2e8ad74cb42" colab={"base_uri": "https://localhost:8080/", "height": 465}
covidcase.plot()
# + id="0YHGNBOVuR4Z" outputId="706fd007-c686-4391-f0dd-666dafd42f41" colab={"base_uri": "https://localhost:8080/", "height": 508}
covidcase.plot(kind='bar')
|
Untitled13.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import cv2
import numpy as np
from tqdm import tqdm
from time import time
import matplotlib.pyplot as plt
from scipy.signal import medfilt
PIXELS = 16
RADIUS = 300
HORIZONTAL_BORDER = 30
file_name = '../data/small-shaky-5.avi'
cap = cv2.VideoCapture(file_name)
frame_rate = int(cap.get(cv2.CAP_PROP_FPS))
frame_width = int(cap.get(cv2.CAP_PROP_FRAME_WIDTH))
frame_height = int(cap.get(cv2.CAP_PROP_FRAME_HEIGHT))
frame_count = int(cap.get(cv2.CAP_PROP_FRAME_COUNT))
def point_transform(H, pt):
"""
@param: H is homography matrix of dimension (3x3)
@param: pt is the (x, y) point to be transformed
Return:
returns a transformed point ptrans = H*pt.
"""
a = H[0,0]*pt[0] + H[0,1]*pt[1] + H[0,2]
b = H[1,0]*pt[0] + H[1,1]*pt[1] + H[1,2]
c = H[2,0]*pt[0] + H[2,1]*pt[1] + H[2,2]
return [a/c, b/c]
def motion_propagate(old_points, new_points, old_frame):
"""
@param: old_points are points in old_frame that are
matched feature points with new_frame
@param: new_points are points in new_frame that are
matched feature points with old_frame
@param: old_frame is the frame to which
motion mesh needs to be obtained
@param: H is the homography between old and new points
Return:
returns a motion mesh in x-direction
and y-direction for old_frame
"""
# spreads motion over the mesh for the old_frame
x_motion = {}; y_motion = {};
cols, rows = old_frame.shape[1]/PIXELS, old_frame.shape[0]/PIXELS
# pre-warping with global homography
H, _ = cv2.findHomography(old_points, new_points, cv2.RANSAC)
for i in range(rows):
for j in range(cols):
pt = [PIXELS*j, PIXELS*i]
ptrans = point_transform(H, pt)
x_motion[i, j] = pt[0]-ptrans[0]
y_motion[i, j] = pt[1]-ptrans[1]
# disturbute feature motion vectors
temp_x_motion = {}; temp_y_motion = {}
for i in range(rows):
for j in range(cols):
vertex = [PIXELS*j, PIXELS*i]
for pt, st in zip(old_points, new_points):
# velocity = point - feature point match in next frame
# dst = sqrt((vertex[0]-st[0])**2+(vertex[1]-st[1])**2)
# velocity = point - feature point in current frame
dst = np.sqrt((vertex[0]-pt[0])**2+(vertex[1]-pt[1])**2)
if dst < RADIUS:
ptrans = point_transform(H, pt)
try:
temp_x_motion[i, j].append(st[0]-ptrans[0])
except:
temp_x_motion[i, j] = [st[0]-ptrans[0]]
try:
temp_y_motion[i, j].append(st[1]-ptrans[1])
except:
temp_y_motion[i, j] = [st[1]-ptrans[1]]
# apply median filter (f-1) on obtained motion for each vertex
x_motion_mesh = np.zeros((rows, cols), dtype=float)
y_motion_mesh = np.zeros((rows, cols), dtype=float)
for key in x_motion.keys():
try:
temp_x_motion[key].sort()
x_motion_mesh[key] = x_motion[key]+temp_x_motion[key][len(temp_x_motion[key])/2]
except KeyError:
x_motion_mesh[key] = x_motion[key]
try:
temp_y_motion[key].sort()
y_motion_mesh[key] = y_motion[key]+temp_y_motion[key][len(temp_y_motion[key])/2]
except KeyError:
y_motion_mesh[key] = y_motion[key]
# apply second median filter (f-2) over the motion mesh for outliers
x_motion_mesh = medfilt(x_motion_mesh, kernel_size=[3, 3])
y_motion_mesh = medfilt(y_motion_mesh, kernel_size=[3, 3])
return x_motion_mesh, y_motion_mesh
def generate_vertex_profiles(x_paths, y_paths, x_motion_mesh, y_motion_mesh):
"""
@param: x_paths is vertex profiles along x-direction
@param: y_paths is vertex profiles along y_direction
@param: x_motion_mesh is obtained motion mesh along
x-direction from motion_propogate()
@param: y_motion_mesh is obtained motion mesh along
y-direction from motion_propogate()
Returns:
returns updated x_paths, y_paths with new
x_motion_mesh, y_motion_mesh added to the
last x_paths, y_paths
"""
new_x_path = x_paths[:, :, -1] + x_motion_mesh
new_y_path = y_paths[:, :, -1] + y_motion_mesh
x_paths = np.concatenate((x_paths, np.expand_dims(new_x_path, axis=2)), axis=2)
y_paths = np.concatenate((y_paths, np.expand_dims(new_y_path, axis=2)), axis=2)
return x_paths, y_paths
def gauss(t, r, window_size):
"""
@param: window_size is the size of window over which gaussian to be applied
@param: t is the index of current point
@param: r is the index of point in window
Return:
returns spacial guassian weights over a window size
"""
return np.exp((-9*(r-t)**2)/window_size**2)
def optimize_path(c, iterations=100, window_size=6):
"""
@param: c is original camera trajectory
@param: window_size is the hyper-parameter for the smoothness term
Returns:
returns an optimized gaussian smooth camera trajectory
"""
lambda_t = 100
p = np.empty_like(c)
W = np.zeros((c.shape[2], c.shape[2]))
for t in range(W.shape[0]):
for r in range(-window_size/2, window_size/2+1):
if t+r < 0 or t+r >= W.shape[1] or r == 0:
continue
W[t, t+r] = gauss(t, t+r, window_size)
gamma = 1+lambda_t*np.dot(W, np.ones((c.shape[2],)))
bar = tqdm(total=c.shape[0]*c.shape[1])
for i in range(c.shape[0]):
for j in range(c.shape[1]):
P = np.asarray(c[i, j, :])
for iteration in range(iterations):
P = np.divide(c[i, j, :]+lambda_t*np.dot(W, P), gamma)
p[i, j, :] = np.asarray(P)
bar.update(1)
bar.close()
return p
def mesh_warp_frame(frame, x_motion_mesh, y_motion_mesh):
"""
@param: frame is the current frame
@param: x_motion_mesh is the motion_mesh to
be warped on frame along x-direction
@param: y_motion_mesh is the motion mesh to
be warped on frame along y-direction
Returns:
returns a mesh warped frame according
to given motion meshes x_motion_mesh,
y_motion_mesh
"""
# define handles on mesh in x-direction
map_x = np.zeros((frame.shape[0], frame.shape[1]), np.float32)
# define handles on mesh in y-direction
map_y = np.zeros((frame.shape[0], frame.shape[1]), np.float32)
for i in range(x_motion_mesh.shape[0]-1):
for j in range(x_motion_mesh.shape[1]-1):
src = [[j*PIXELS, i*PIXELS],
[j*PIXELS, (i+1)*PIXELS],
[(j+1)*PIXELS, i*PIXELS],
[(j+1)*PIXELS, (i+1)*PIXELS]]
src = np.asarray(src)
dst = [[j*PIXELS+x_motion_mesh[i, j], i*PIXELS+y_motion_mesh[i, j]],
[j*PIXELS+x_motion_mesh[i+1, j], (i+1)*PIXELS+y_motion_mesh[i+1, j]],
[(j+1)*PIXELS+x_motion_mesh[i, j+1], i*PIXELS+y_motion_mesh[i, j+1]],
[(j+1)*PIXELS+x_motion_mesh[i+1, j+1], (i+1)*PIXELS+y_motion_mesh[i+1, j+1]]]
dst = np.asarray(dst)
H, _ = cv2.findHomography(src, dst, cv2.RANSAC)
for k in range(PIXELS*i, PIXELS*(i+1)):
for l in range(PIXELS*j, PIXELS*(j+1)):
x = H[0, 0]*l+H[0, 1]*k+H[0, 2]
y = H[1, 0]*l+H[1, 1]*k+H[1, 2]
w = H[2, 0]*l+H[2, 1]*k+H[2, 2]
if not w == 0:
x = x/(w*1.0); y = y/(w*1.0)
else:
x = l; y = k
map_x[k, l] = x
map_y[k, l] = y
# repeat motion vectors for remaining frame in y-direction
for i in range(PIXELS*x_motion_mesh.shape[0], map_x.shape[0]):
map_x[i, :] = map_x[PIXELS*x_motion_mesh.shape[0]-1, :]
map_y[i, :] = map_y[PIXELS*x_motion_mesh.shape[0]-1, :]
# repeat motion vectors for remaining frame in x-direction
for j in range(PIXELS*x_motion_mesh.shape[1], map_x.shape[1]):
map_x[:, j] = map_x[:, PIXELS*x_motion_mesh.shape[0]-1]
map_y[:, j] = map_y[:, PIXELS*x_motion_mesh.shape[0]-1]
# deforms mesh
new_frame = cv2.remap(frame, map_x, map_y, interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT)
return new_frame
# +
start_time = time()
# generate stabilized video
fourcc = cv2.VideoWriter_fourcc(*'XVID')
out = cv2.VideoWriter('../stable.avi', fourcc, frame_rate, (2*frame_width, frame_height))
# params for ShiTomasi corner detection
feature_params = dict( maxCorners = 1000,
qualityLevel = 0.3,
minDistance = 7,
blockSize = 7 )
# Parameters for lucas kanade optical flow
lk_params = dict( winSize = (15, 15),
maxLevel = 2,
criteria = (cv2.TERM_CRITERIA_EPS | cv2.TERM_CRITERIA_COUNT, 20, 0.03))
# Take first frame
cap.set(cv2.CAP_PROP_POS_FRAMES, 0)
ret, old_frame = cap.read()
old_gray = cv2.cvtColor(old_frame, cv2.COLOR_BGR2GRAY)
# preserve aspect ratio
VERTICAL_BORDER = (HORIZONTAL_BORDER*old_gray.shape[1])/old_gray.shape[0]
# +
# motion meshes in x-direction and y-direction
x_motion_meshes = []; y_motion_meshes = []
# path parameters
x_paths = np.zeros((old_frame.shape[0]/PIXELS, old_frame.shape[1]/PIXELS, 1))
y_paths = np.zeros((old_frame.shape[0]/PIXELS, old_frame.shape[1]/PIXELS, 1))
frame_num = 1
bar = tqdm(total=frame_count)
while frame_num < frame_count:
# processing frames
ret, frame = cap.read()
frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
# find corners in it
p0 = cv2.goodFeaturesToTrack(old_gray, mask = None, **feature_params)
# calculate optical flow
p1, st, err = cv2.calcOpticalFlowPyrLK(old_gray, frame_gray, p0, None, **lk_params)
# Select good points
good_new = p1[st==1]
good_old = p0[st==1]
# estimate motion mesh for old_frame
x_motion_mesh, y_motion_mesh = motion_propagate(good_old, good_new, frame)
try:
x_motion_meshes = np.concatenate((x_motion_meshes, np.expand_dims(x_motion_mesh, axis=2)), axis=2)
y_motion_meshes = np.concatenate((y_motion_meshes, np.expand_dims(y_motion_mesh, axis=2)), axis=2)
except:
x_motion_meshes = np.expand_dims(x_motion_mesh, axis=2)
y_motion_meshes = np.expand_dims(y_motion_mesh, axis=2)
# generate vertex profiles
x_paths, y_paths = generate_vertex_profiles(x_paths, y_paths, x_motion_mesh, y_motion_mesh)
# updates frames
bar.update(1)
frame_num += 1
old_frame = frame.copy()
old_gray = frame_gray.copy()
bar.close()
# -
# optimize for smooth vertex profiles
optimization = time()
sx_paths = optimize_path(x_paths)
sy_paths = optimize_path(y_paths)
print 'Time Taken: ', time()-optimization
# plot some vertex profiles
for i in range(0, x_paths.shape[0]):
for j in range(0, x_paths.shape[1], 10):
plt.plot(x_paths[i, j, :])
plt.plot(sx_paths[i, j, :])
plt.savefig('../results/paths/'+str(i)+'_'+str(j)+'.png')
plt.clf()
# U = P-C
x_motion_meshes = np.concatenate((x_motion_meshes, np.expand_dims(x_motion_meshes[:, :, -1], axis=2)), axis=2)
y_motion_meshes = np.concatenate((y_motion_meshes, np.expand_dims(y_motion_meshes[:, :, -1], axis=2)), axis=2)
new_x_motion_meshes = sx_paths-x_paths
new_y_motion_meshes = sy_paths-y_paths
r = 3
frame_num = 0
bar = tqdm(total=frame_count)
cap.set(cv2.CAP_PROP_POS_FRAMES, 0)
while frame_num < frame_count:
try:
# reconstruct from frames
ret, frame = cap.read()
x_motion_mesh = x_motion_meshes[:, :, frame_num]
y_motion_mesh = y_motion_meshes[:, :, frame_num]
new_x_motion_mesh = new_x_motion_meshes[:, :, frame_num]
new_y_motion_mesh = new_y_motion_meshes[:, :, frame_num]
# mesh warping
new_frame = mesh_warp_frame(frame, new_x_motion_mesh, new_y_motion_mesh)
new_frame = new_frame[HORIZONTAL_BORDER:-HORIZONTAL_BORDER, VERTICAL_BORDER:-VERTICAL_BORDER, :]
new_frame = cv2.resize(new_frame, (frame.shape[1], frame.shape[0]), interpolation=cv2.INTER_CUBIC)
output = np.concatenate((frame, new_frame), axis=1)
out.write(output)
# draw old motion vectors
for i in range(x_motion_mesh.shape[0]):
for j in range(x_motion_mesh.shape[1]):
theta = np.arctan2(y_motion_mesh[i, j], x_motion_mesh[i, j])
cv2.line(frame, (j*PIXELS, i*PIXELS), (int(j*PIXELS+r*np.cos(theta)), int(i*PIXELS+r*np.sin(theta))), 1)
cv2.imwrite('../results/old_motion_vectors/'+str(frame_num)+'.jpg', frame)
# draw new motion vectors
for i in range(new_x_motion_mesh.shape[0]):
for j in range(new_x_motion_mesh.shape[1]):
theta = np.arctan2(new_y_motion_mesh[i, j], new_x_motion_mesh[i, j])
cv2.line(new_frame, (j*PIXELS, i*PIXELS), (int(j*PIXELS+r*np.cos(theta)), int(i*PIXELS+r*np.sin(theta))), 1)
cv2.imwrite('../results/new_motion_vectors/'+str(frame_num)+'.jpg', new_frame)
frame_num += 1
bar.update(1)
except:
break
bar.close()
cap.release()
out.release()
print 'Time elapsed: ', str(time()-start_time)
|
src/mesh_flow.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Dataquest Guided Project: Profitable App Profiles for the App Store and Google Play Markets
# <NAME> ([levcb](www.github.com/levcb))
#
# This project identifies mobile app profiles that are profitable in the App Store and Google Play markets. This project provides data insights intended to facilitate data-driven decisions about app characteristics for a hypothetical company building free apps. Accordingly, this hypothetical company's main source of revenue is in-app ads, meaning that the revenue for a given app is driven primarily by its number of users.
#
# Two datasets are used here: one containing data about approximately 10,000 Android apps from Google Play, and another containing data about approximately 7,000 iOS apps from the App Store.
# We'll start by opening and exploring the two datasets. The below function prints rows in a readable way.
def explore_data(dataset, start, end, rows_and_columns=False):
# define section of dataset to explore
dataset_slice = dataset[start:end]
# print each row in selected slice
for row in dataset_slice:
print(row)
# insert line break to improve readability
print('\n')
# if rows_and_columns parameter set to True, print numbers of rows and columns
if rows_and_columns:
print("Number of rows: ", len(dataset))
print("Number of columns: ", len(dataset[0]))
# Next, we'll open each dataset.
# +
from csv import reader
# open Apple Store dataset
ios_data = list(reader(open('AppleStore.csv')))
# separate header row from data rows
ios_header = ios_data[0]
ios_data = ios_data[1:]
# open Google Play dataset
android_data = list(reader(open('googleplaystore.csv')))
# separate header row from data rows
android_header = android_data[0]
android_data = android_data[1:]
# -
# Now that we've opened the datasets, we'll use our `explore_data` function to explore them. The below cells print the first few rows and the number of columns and rows in each dataset.
# print first three rows and number of rows and columns in iOS dataset
explore_data(ios_data, 0, 3, True)
# print first three rows and number of rows and columns in Android dataset
explore_data(android_data, 0, 3, True)
# Now we'll print the column headings for each dataset to help us identify which columns will be most useful for our purposes. (To make this data more comprehensible, I've created tables providing the iOS and Android column names and descriptions.)
print(ios_header)
print(android_header)
# ### iOS
# | Column Name | Description |
# |--------------------|-----------------------------------------------|
# | `id` | App ID |
# | `track_name` | App name |
# | `size_bytes` | Size (in bytes) |
# | `currency` | Currency type |
# | `price` | Price amount |
# | `rating_count_tot` | User rating counts (for all versions) |
# | `rating_count_ver` | User rating counts (for current version) |
# | `user_rating` | Average user rating (for all versions) |
# | `user_rating_ver` | Average user rating (for current version) |
# | `ver` | Latest version code |
# | `cont_rating` | Content rating |
# | `prime_genre` | Primary genre |
# | `sup_devices.num` | Number of supporting devices |
# | `ipadSc_urls.num` | Number of screenshots shown for display |
# | `lang.num` | Number of supported languages |
# | `vpp_lic` | Whether VPP device-based licensing is enabled |
# ### Android
# | Column Name | Description |
# |--------------------|------------------------------------------------------|
# | `App` | App name |
# | `Category` | Category the app belongs to |
# | `Rating` | Overall user rating of the app |
# | `Reviews` | Number of user reviews for the app |
# | `Size` | Size of the app |
# | `Installs` | Number of user downloads/installs |
# | `Type` | Paid or free |
# | `Price` | Price of the app |
# | `Content Rating` | Age group the app is targeted at |
# | `Genres` | Genres an app belongs to in addition to its category |
#
# Before beginning our analysis, we'll remove any incorrect or duplicate data, any non–English language apps, and any apps that aren't free (as we're only interested in English apps that are free to download).
#
# Other users have found that the Google Play dataset has a mistake in row 10472:
print(android_data[10472])
# The `Category` value (`android_data[10472][8]`) is missing from this entry, which causes a column shift.
#
# In the next code cell, we'll delete this row to remove the problem data from our dataset.
del android_data[10472]
# Now, if we print `android_data[10472]` again, we'll see that the problem row has been deleted:
print(android_data[10472])
# The Google Play dataset also has some duplicate entries. Below, we'll define a function that finds duplicate apps and unique apps in a given dataset. We'll then use that function to find the number of duplicate and unique Android apps in our dataset as well as a few examples of each.
# +
def find_duplicates(dataset):
duplicate_apps = []
unique_apps = []
# loop through dataset, add app to duplicate list if multiples found
for app in dataset:
name = app[0]
if name in unique_apps:
duplicate_apps.append(name)
else:
unique_apps.append(name)
return [duplicate_apps, unique_apps]
android_duplicates = find_duplicates(android_data)
# print total duplicate and unique apps along with examples for Android dataset
print("Number of duplicate Android apps: ", len(android_duplicates[0]))
print("Examples of duplicate Android apps: ", android_duplicates[0][5:10])
print("Number of unique Android apps: ", len(android_duplicates[1]))
print("Examples of unique Android apps: ", android_duplicates[1][0:5])
# -
# We can see this duplicate data by creating a function to print duplicate rows, then calling it for one of the duplicate apps we identified above (Slack) to show that there are multiple entries for Slack in our dataset.
# +
def list_duplicates(app_name, dataset):
# loop through dataset, print all entries for a given app
for app in dataset:
name = app[0]
if name == app_name:
print(app)
list_duplicates('Slack', android_data)
# -
# By running the `find_duplicates()` function on the dataset for iOS apps, we can see that there are no duplicates in the iOS dataset.
ios_duplicates = find_duplicates(ios_data)
# print total duplicate and unique apps along with examples for iOS dataset
print("Number of duplicate iOS apps: ", len(ios_duplicates[0]))
print("Examples of duplicate iOS apps: ", ios_duplicates[0][0:4])
print("Number of unique iOS apps: ", len(ios_duplicates[1]))
print("Examples of unique iOS apps: ", ios_duplicates[1][0:4])
# Now we'll remove the duplicates from the Google Play dataset by keeping only the most recent entry for each duplicated app. We'll do this by finding the entry with the highest number of user reviews (found in the `Reviews` column of the dataset at index `[3]`). To continue with our example of Slack, this means that we'll want the Slack entry with 51,510 user reviews, rather than the entry with 51,507 user reviews.
#
# We'll start by creating a dictionary called `reviews_max` that contains the names of all apps in the dataset as keys and their highest number of user reviews as values.
reviews_max = {}
for app in android_data:
# loop through Android dataset to create dictionary
name = app[0]
# convert number of reviews to float
n_reviews = float(app[3])
if (name in reviews_max and reviews_max[name] < n_reviews) or name not in reviews_max:
reviews_max[name] = n_reviews
# Now, we'll test whether everything went as expected by finding the length of the `reviews_max` dictionary (which should be 9,659, the same as the number of unique Android apps) and the number of user reviews for Slack (which should be 51,510).
print(len(reviews_max))
print(reviews_max['Slack'])
# As shown above, everything ran as expected. Now we'll use the dictionary we created to remove duplicate rows from our Android dataset.
android_clean = []
already_added = []
# loop through dataset to create a dataset free of duplicates
for app in android_data:
name = app[0]
# convert number of reviews to float
n_reviews = float(app[3])
if n_reviews == reviews_max[name] and name not in already_added:
android_clean.append(app)
already_added.append(name)
# Below, we'll check the length of the `android_clean` dataset to confirm that our clean dataset has a length of 9,659.
print(len(android_clean))
# Having confirmed the correct link, we'll now define a function that confirms whether an app name has more than three characters that aren't common English characters. If so, we'll conclude that that app likely isn't in English (returning `False`).
# +
def is_english(string):
non_english_chars = 0
# use Unicode code point of a given character to determine whether it is a common
# English character. Values above 127 are non-standard characters
for char in string:
if ord(char) > 127: non_english_chars += 1
# if more than three non-standard characters, app is likely not in English
if non_english_chars > 3: return False
return True
print(is_english('Instagram'))
print(is_english('爱奇艺PPS -《欢乐颂2》电视剧热播'))
print(is_english('Docs To Go™ Free Office Suite'))
print(is_english('Instachat 😜'))
# -
# Now, we'll define a function to loop through our datasets to collect all the English-language apps in each dataset and compile them into lists.
# +
def find_english(dataset, name):
english_apps = []
for row in dataset:
if is_english(row[name]):
english_apps.append(row)
return english_apps
english_ios = find_english(ios_data, 1)
english_android = find_english(android_data, 0)
# compare numbers of apps in English-language subsets and full datasets
print(len(english_ios), len(english_android))
print(len(ios_data), len(android_data))
# -
# Next, we'll follow a similar procedure to identify free apps. As before, we'll loop through each dataset, append free apps to a list, and
# +
def find_free(dataset, price):
free_apps = []
for row in dataset:
# prices stored as '0.0' in iOS dataset and '0' in Android dataset
if row[price] == '0.0' or row[price] == '0':
free_apps.append(row)
return free_apps
free_ios = find_free(english_ios, 4)
free_android = find_free(english_android, 7)
# compare numbers of apps in free subsets and full datasets
print(len(free_ios), len(free_android))
print(len(ios_data), len(android_data))
# -
# Our validation strategy for an app idea has three steps:
# 1. Build a minimal Android version of the app and add it to the Google Play Store.
# 2. If the app receives a good response from users, we develop it further.
# 3. If the app is profitable after six months, we build an iOS version of the app and add it to the App Store.
#
# Ideally, we want to find apps that will be profitable in both markets.
#
# Next, we'll inspect each dataset and identify the columns that could be used to generate frequency tables to determine the most common genres in each market. For iOS, that appears to be the `prime_genre` column (index `12`), while for the Android dataset, the relevant columns appear to be `Category` (index `1`) and `Genres` (index `9`).
# In the below cell, we'll define two functions. We can use the first function (`freq_table()`) to create a frequency table of the genres in each dataset, and we can use the second (`display_table()`) to make that frequency table more interpretable. Specifically, the `display_table()` function saves each key–value pair as a tuple, adds each tuple to a list, sorts that list in descending order, and presents the information in a readable format.
# +
def freq_table(dataset, index):
table = {}
total = 0
for row in dataset:
total += 1
value = row[index]
if value in table:
table[value] += 1
else:
table[value] = 1
table_percentages = {}
for key in table:
# calculate percentage and round to two digits
percentage = round((table[key] / total) * 100, 2)
table_percentages[key] = percentage
return table_percentages
def display_table(dataset, index):
table = freq_table(dataset, index)
table_display = []
for key in table:
key_val_as_tuple = (table[key], key)
table_display.append(key_val_as_tuple)
table_sorted = sorted(table_display, reverse = True)
for entry in table_sorted:
print(entry[1], ':', entry[0])
# -
# The most common iOS genre by far is games (58.16%), followed by entertainment (7.88%). Other genres are all less than 5%, and most are less than 3%. The majority of apps appear to be designed for entertainment purposes (e.g., games, social networking, music) rather than practical purposes (e.g., education, utilities, productivity).
#
# Based on the above, it seems that games are the most popular type of app on the App Store. However, that doesn't necessarily mean that they're the most profitable or have the most users. On the contrary, it might be better to develop an app in a less crowded category to minimize competition and increase the chances that our app will show up in users' searches; we'll need more information to determine the most profitable app profile.
display_table(free_ios, 11)
# The Android dataset differentiates between category (the broader group of apps to which a given app belongs) and genre (a more niche, specific description of the app's type). The most common Android category is family (17.67%), followed by games (10.59%). Other categories are all less than 8%, and most are less than 4%. The most common genre, however, is tools (7.63%), followed by entertainment (6.0%). Other genres are all roughly 5% or less, and many are less than 1%.
#
# As with the iOS data, we'll need more information to determine the most profitable app profile, but in comparison with the App Store market, the categories and genres in the Android Market seem to be much more evenly distributed. There is no dominant genre, and there's a more even spread of entertainment and practical apps.
display_table(free_android, 1)
display_table(free_android, 9)
# Below, we'll create a frequency table for the free iOS app genres. We'll then calculate the average ratings for each genre.
genres_ios = freq_table(free_ios, 11)
for genre in genres_ios:
total = 0
len_genre = 0
for row in free_ios:
genre_app = row[11]
if genre_app == genre:
user_ratings = float(row[5])
total += user_ratings
len_genre += 1
# round to even number, add comma separators for readability
avg_ratings = "{:,}".format(round((total / len_genre), 0))
print(genre, avg_ratings)
# The genres with the greatest number of average user ratings are navigation (*n* = 86,090), reference (*n* = 74,942), and social networking (*n* = 71,548). Games, despite being the most common genre, have only 22,789 average user ratings.
#
# It's likely safe to assume that the high averages for navigation and social networking are due to huge, highly popular apps like Google Maps, Waze, Facebook, and Twitter. Since competing with such dominant apps is a pretty challenging task, it may be a better idea to select a more moderately rated genre like reference, weather, or music. The market for these apps is less crowded, and the apps within them seem to amass a decently high number of user ratings.
# Next, we'll follow the same procedure for the Android dataset.
categories_android = freq_table(free_android, 1)
for category in categories_android:
total = 0
len_category = 0
for row in free_android:
category_app = row[1]
if category_app == category:
installs = row[5]
# strip non-numeric characters and convert to float
installs = installs.replace('+', '')
installs = installs.replace(',', '')
installs = float(installs)
total += installs
len_category += 1
# round to even number, add comma separators for readability
avg_installs = "{:,}".format(round((total / len_category), 0))
print(category, avg_installs)
# The categories with the greatest number of average user ratings are communication (*n* = 90,935,672), social (*n* = 48,184,459), and video players (*n* = 36,599,010). As above, we can probably assume that the high averages for these apps are for very popular apps like WhatsApp, Messenger, Facebook, and YouTube. The next most popular categories include game (*n* = 33,111,303), photography (*n* = 32,321,374), and entertainment (*n* = 19,516,735).
#
# Cross-referencing with our results for the iOS store, and keeping in mind our goal of developing an app that could be popular in both markets, we might consider developing an app in the music, books and reference, or photo and video category.
|
Guided Project–Profitable App Profiles for the App Store and Google Play Markets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/klavna/age-frindly-busan/blob/main/Untitled1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="8sLf20L0gMFs"
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="Lh7yL-XGizFI" outputId="b187223b-f65a-428f-f17a-e9fef6ff5c24"
train = pd.read_csv('/content/sample_data/california_housing_train.csv')
test = pd.read_csv('/content/sample_data/california_housing_test.csv')
train.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 206} id="xeFxEq8MjgwC" outputId="e5d1f12e-ba3d-4f49-c83d-6c820763b566"
test.head()
# + colab={"base_uri": "https://localhost:8080/", "height": 364} id="w9ONby3djkxn" outputId="04fbb22b-cef4-41b1-a043-52eadc57efb4"
train.describe()
# + colab={"base_uri": "https://localhost:8080/", "height": 771} id="HezA1iaqjolF" outputId="b6df5cec-303e-42ef-fa79-b76cd6c80953"
train.hist(figsize=(15,13), grid=False, bins=50)
plt.show()
# + id="zxq4zGjij0MI"
correlation = train.corr()
# + colab={"base_uri": "https://localhost:8080/", "height": 691} id="-jVEP_Rpj64c" outputId="210e768f-5e75-48ec-c40d-a15b585d9de3"
plt.figure(figsize=(10,10))
sns.heatmap(correlation, annot=True)
plt.show()
|
Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# <i>Copyright (c) Microsoft Corporation. All rights reserved.</i>
#
# <i>Licensed under the MIT License.</i>
# # Apply Diversity Metrics
# ## -- Compare ALS and Random Recommenders on MovieLens (PySpark)
#
# In this notebook, we demonstrate how to evaluate a recommender using metrics other than commonly used rating/ranking metrics.
#
# Such metrics include:
# - Coverage - We use following two metrics defined by \[Shani and Gunawardana\]:
#
# - (1) catalog_coverage, which measures the proportion of items that get recommended from the item catalog;
# - (2) distributional_coverage, which measures how equally different items are recommended in the recommendations to all users.
#
# - Novelty - A more novel item indicates it is less popular, i.e. it gets recommended less frequently.
# We use the definition of novelty from \[Castells et al.\]
#
# - Diversity - The dissimilarity of items being recommended.
# We use a definition based on _intralist similarity_ by \[Zhang et al.]
#
# - Serendipity - The "unusualness" or "surprise" of recommendations to a user.
# We use a definition based on cosine similarity by \[Zhang et al.]
#
# We evaluate the results obtained with two approaches: using the ALS recommender algorithm vs. a baseline of random recommendations.
# - Matrix factorization by [ALS](https://spark.apache.org/docs/latest/api/python/_modules/pyspark/ml/recommendation.html#ALS) (Alternating Least Squares) is a well known collaborative filtering algorithm.
# - We also define a process which randomly recommends unseen items to each user.
# - We show two options to calculate item-item similarity: (1) based on item co-occurrence count; and (2) based on item feature vectors.
#
# The comparision results show that the ALS recommender outperforms the random recommender on ranking metrics (Precision@k, Recall@k, NDCG@k, and Mean average precision), while the random recommender outperforms ALS recommender on diversity metrics. This is because ALS is optimized for estimating the item rating as accurate as possible, therefore it performs well on accuracy metrics including rating and ranking metrics. As a side effect, the items being recommended tend to be popular items, which are the items mostly sold or viewed. It leaves the [long-tail items](https://github.com/microsoft/recommenders/blob/main/GLOSSARY.md) having less chance to get introduced to the users. This is the reason why ALS is not performing as well as a random recommender on diversity metrics.
#
# From the algorithmic point of view, items in the tail suffer from the cold-start problem, making them hard for recommendation systems to use. However, from the business point of view, oftentimes the items in the tail can be highly profitable, since, depending on supply, business can apply a higher margin to them. Recommendation systems that optimize metrics like novelty and diversity, can help to find users willing to get these long tail items. Usually there is a trade-off between one type of metric vs. another. One should decide which set of metrics to optimize based on business scenarios.
# **Coverage**
#
# We define _catalog coverage_ as the proportion of items showing in all users’ recommendations:
# $$
# \textrm{CatalogCoverage} = \frac{|N_r|}{|N_t|}
# $$
# where $N_r$ denotes the set of items in the recommendations (`reco_df` in the code below) and $N_t$ the set of items in the historical data (`train_df`).
#
# _Distributional coverage_ measures how equally different items are recommended to users when a particular recommender system is used.
# If $p(i|R)$ denotes the probability that item $i$ is observed among all recommendation lists, we define distributional coverage as
# $$
# \textrm{DistributionalCoverage} = -\sum_{i \in N_t} p(i|R) \log_2 p(i)
# $$
# where
# $$
# p(i|R) = \frac{|M_r (i)|}{|\textrm{reco_df}|}
# $$
# and $M_r (i)$ denotes the users who are recommended item $i$.
#
#
# **Diversity**
#
# Diversity represents the variety present in a list of recommendations.
# _Intra-List Similarity_ aggregates the pairwise similarity of all items in a set. A recommendation list with groups of very similar items will score a high intra-list similarity. Lower intra-list similarity indicates higher diversity.
# To measure similarity between any two items we use _cosine similarity_:
# $$
# \textrm{Cosine Similarity}(i,j)= \frac{|M_t^{l(i,j)}|} {\sqrt{|M_t^{l(i)}|} \sqrt{|M_t^{l(j)}|} }
# $$
# where $M_t^{l(i)}$ denotes the set of users who liked item $i$ and $M_t^{l(i,j)}$ the users who liked both $i$ and $j$.
# Intra-list similarity is then defined as
# $$
# \textrm{IL} = \frac{1}{|M|} \sum_{u \in M} \frac{1}{\binom{N_r(u)}{2}} \sum_{i,j \in N_r (u),\, i<j} \textrm{Cosine Similarity}(i,j)
# $$
# where $M$ is the set of users and $N_r(u)$ the set of recommendations for user $u$. Finally, diversity is defined as
# $$
# \textrm{diversity} = 1 - \textrm{IL}
# $$
#
#
# **Novelty**
#
# The novelty of an item is inverse to its _popularity_. If $p(i)$ represents the probability that item $i$ is observed (or known, interacted with etc.) by users, then
# $$
# p(i) = \frac{|M_t (i)|} {|\textrm{train_df}|}
# $$
# where $M_t (i)$ is the set of users who have interacted with item $i$ in the historical data.
#
# The novelty of an item is then defined as
# $$
# \textrm{novelty}(i) = -\log_2 p(i)
# $$
# and the novelty of the recommendations across all users is defined as
# $$
# \textrm{novelty} = \sum_{i \in N_r} \frac{|M_r (i)|}{|\textrm{reco_df}|} \textrm{novelty}(i)
# $$
#
# **Serendipity**
#
# Serendipity represents the “unusualness” or “surprise” of recommendations. Unlike novelty, serendipity encompasses the semantic content of items and can be imagined as the distance between recommended items and their expected contents (Zhang et al.) Lower cosine similarity indicates lower expectedness and higher serendipity.
# We define the expectedness of an unseen item $i$ for user $u$ as the average similarity between every already seen item $j$ in the historical data and $i$:
# $$
# \textrm{expectedness}(i|u) = \frac{1}{|N_t (u)|} \sum_{j \in N_t (u)} \textrm{Cosine Similarity}(i,j)
# $$
# The serendipity of item $i$ is (1 - expectedness) multiplied by _relevance_, where relevance indicates whether the item turns out to be liked by the user or not. For example, in a binary scenario, if an item in `reco_df` is liked (purchased, clicked) in `test_df`, its relevance equals one, otherwise it equals zero. Aggregating over all users and items, the overall
# serendipity is defined as
# $$
# \textrm{serendipity} = \frac{1}{|M|} \sum_{u \in M_r}
# \frac{1}{|N_r (u)|} \sum_{i \in N_r (u)} \big(1 - \textrm{expectedness}(i|u) \big) \, \textrm{relevance}(i)
# $$
#
# **Note**: This notebook requires a PySpark environment to run properly. Please follow the steps in [SETUP.md](https://github.com/Microsoft/Recommenders/blob/master/SETUP.md#dependencies-setup) to install the PySpark environment.
# +
# set the environment path to find Recommenders
# %load_ext autoreload
# %autoreload 2
import sys
import pyspark
from pyspark.ml.recommendation import ALS
import pyspark.sql.functions as F
from pyspark.sql.types import FloatType, IntegerType, LongType, StructType, StructField
from pyspark.ml.feature import Tokenizer, StopWordsRemover
from pyspark.ml.feature import HashingTF, CountVectorizer, VectorAssembler
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
from recommenders.utils.timer import Timer
from recommenders.datasets import movielens
from recommenders.datasets.spark_splitters import spark_random_split
from recommenders.evaluation.spark_evaluation import SparkRankingEvaluation, SparkDiversityEvaluation
from recommenders.utils.spark_utils import start_or_get_spark
from pyspark.sql.window import Window
import pyspark.sql.functions as F
import numpy as np
import pandas as pd
print("System version: {}".format(sys.version))
print("Spark version: {}".format(pyspark.__version__))
# -
#
# Set the default parameters.
# + tags=["parameters"]
# top k items to recommend
TOP_K = 10
# Select MovieLens data size: 100k, 1m, 10m, or 20m
MOVIELENS_DATA_SIZE = '100k'
# user, item column names
COL_USER="UserId"
COL_ITEM="MovieId"
COL_RATING="Rating"
COL_TITLE="Title"
COL_GENRE="Genre"
# -
# ### 1. Set up Spark context
#
# The following settings work well for debugging locally on VM - change when running on a cluster. We set up a giant single executor with many threads and specify memory cap.
# +
# the following settings work well for debugging locally on VM - change when running on a cluster
# set up a giant single executor with many threads and specify memory cap
spark = start_or_get_spark("ALS PySpark", memory="16g")
spark.conf.set("spark.sql.analyzer.failAmbiguousSelfJoin", "false")
spark.conf.set("spark.sql.crossJoin.enabled", "true")
# -
# ### 2. Download the MovieLens dataset
# +
# Note: The DataFrame-based API for ALS currently only supports integers for user and item ids.
schema = StructType(
(
StructField(COL_USER, IntegerType()),
StructField(COL_ITEM, IntegerType()),
StructField(COL_RATING, FloatType()),
StructField("Timestamp", LongType()),
)
)
data = movielens.load_spark_df(spark, size=MOVIELENS_DATA_SIZE, schema=schema, title_col=COL_TITLE, genres_col=COL_GENRE)
data.show()
# -
# #### Split the data using the Spark random splitter provided in utilities
train_df, test_df = spark_random_split(data.select(COL_USER, COL_ITEM, COL_RATING), ratio=0.75, seed=123)
print ("N train_df", train_df.cache().count())
print ("N test_df", test_df.cache().count())
# #### Get all possible user-item pairs
# Note: We assume that training data contains all users and all catalog items.
users = train_df.select(COL_USER).distinct()
items = train_df.select(COL_ITEM).distinct()
user_item = users.crossJoin(items)
# ### 3. Train the ALS model on the training data, and get the top-k recommendations for our testing data
#
# To predict movie ratings, we use the rating data in the training set as users' explicit feedback. The hyperparameters used in building the model are referenced from [here](http://mymedialite.net/examples/datasets.html). We do not constrain the latent factors (`nonnegative = False`) in order to allow for both positive and negative preferences towards movies.
# Timing will vary depending on the machine being used to train.
# +
header = {
"userCol": COL_USER,
"itemCol": COL_ITEM,
"ratingCol": COL_RATING,
}
als = ALS(
rank=10,
maxIter=15,
implicitPrefs=False,
regParam=0.05,
coldStartStrategy='drop',
nonnegative=False,
seed=42,
**header
)
# +
with Timer() as train_time:
model = als.fit(train_df)
print("Took {} seconds for training.".format(train_time.interval))
# -
# In the movie recommendation use case, recommending movies that have been rated by the users does not make sense. Therefore, the rated movies are removed from the recommended items.
#
# In order to achieve this, we recommend all movies to all users, and then remove the user-movie pairs that exist in the training dataset.
# +
# Score all user-item pairs
dfs_pred = model.transform(user_item)
# Remove seen items.
dfs_pred_exclude_train = dfs_pred.alias("pred").join(
train_df.alias("train"),
(dfs_pred[COL_USER] == train_df[COL_USER]) & (dfs_pred[COL_ITEM] == train_df[COL_ITEM]),
how='outer'
)
top_all = dfs_pred_exclude_train.filter(dfs_pred_exclude_train["train.Rating"].isNull()) \
.select('pred.' + COL_USER, 'pred.' + COL_ITEM, 'pred.' + "prediction")
print(top_all.count())
window = Window.partitionBy(COL_USER).orderBy(F.col("prediction").desc())
top_k_reco = top_all.select("*", F.row_number().over(window).alias("rank")).filter(F.col("rank") <= TOP_K).drop("rank")
print(top_k_reco.count())
# -
# ### 4. Random Recommender
#
# We define a recommender which randomly recommends unseen items to each user.
# +
# random recommender
window = Window.partitionBy(COL_USER).orderBy(F.rand())
# randomly generated recommendations for each user
pred_df = (
train_df
# join training data with all possible user-item pairs (seen in training)
.join(user_item,
on=[COL_USER, COL_ITEM],
how="right"
)
# get user-item pairs that were not seen in the training data
.filter(F.col(COL_RATING).isNull())
# count items for each user (randomly sorting them)
.withColumn("score", F.row_number().over(window))
# get the top k items per user
.filter(F.col("score") <= TOP_K)
.drop(COL_RATING)
)
# -
# ### 5. ALS vs Random Recommenders Performance Comparison
# +
def get_ranking_results(ranking_eval):
metrics = {
"Precision@k": ranking_eval.precision_at_k(),
"Recall@k": ranking_eval.recall_at_k(),
"NDCG@k": ranking_eval.ndcg_at_k(),
"Mean average precision": ranking_eval.map_at_k()
}
return metrics
def get_diversity_results(diversity_eval):
metrics = {
"catalog_coverage":diversity_eval.catalog_coverage(),
"distributional_coverage":diversity_eval.distributional_coverage(),
"novelty": diversity_eval.novelty(),
"diversity": diversity_eval.diversity(),
"serendipity": diversity_eval.serendipity()
}
return metrics
# -
def generate_summary(data, algo, k, ranking_metrics, diversity_metrics):
summary = {"Data": data, "Algo": algo, "K": k}
if ranking_metrics is None:
ranking_metrics = {
"Precision@k": np.nan,
"Recall@k": np.nan,
"nDCG@k": np.nan,
"MAP": np.nan,
}
summary.update(ranking_metrics)
summary.update(diversity_metrics)
return summary
# #### ALS Recommender Performance Results
# +
als_ranking_eval = SparkRankingEvaluation(
test_df,
top_all,
k = TOP_K,
col_user=COL_USER,
col_item=COL_ITEM,
col_rating=COL_RATING,
col_prediction="prediction",
relevancy_method="top_k"
)
als_ranking_metrics = get_ranking_results(als_ranking_eval)
# +
als_diversity_eval = SparkDiversityEvaluation(
train_df = train_df,
reco_df = top_k_reco,
col_user = COL_USER,
col_item = COL_ITEM
)
als_diversity_metrics = get_diversity_results(als_diversity_eval)
# -
als_results = generate_summary(MOVIELENS_DATA_SIZE, "als", TOP_K, als_ranking_metrics, als_diversity_metrics)
# #### Random Recommender Performance Results
# +
random_ranking_eval = SparkRankingEvaluation(
test_df,
pred_df,
col_user=COL_USER,
col_item=COL_ITEM,
col_rating=COL_RATING,
col_prediction="score",
k=TOP_K,
)
random_ranking_metrics = get_ranking_results(random_ranking_eval)
# +
random_diversity_eval = SparkDiversityEvaluation(
train_df = train_df,
reco_df = pred_df,
col_user = COL_USER,
col_item = COL_ITEM
)
random_diversity_metrics = get_diversity_results(random_diversity_eval)
# -
random_results = generate_summary(MOVIELENS_DATA_SIZE, "random", TOP_K, random_ranking_metrics, random_diversity_metrics)
# #### Result Comparison
# +
cols = ["Data", "Algo", "K", "Precision@k", "Recall@k", "NDCG@k", "Mean average precision","catalog_coverage", "distributional_coverage","novelty", "diversity", "serendipity" ]
df_results = pd.DataFrame(columns=cols)
df_results.loc[1] = als_results
df_results.loc[2] = random_results
# -
df_results
# #### Conclusion
# The comparision results show that the ALS recommender outperforms the random recommender on ranking metrics (Precision@k, Recall@k, NDCG@k, and Mean average precision), while the random recommender outperforms ALS recommender on diversity metrics. This is because ALS is optimized for estimating the item rating as accurate as possible, therefore it performs well on accuracy metrics including rating and ranking metrics. As a side effect, the items being recommended tend to be popular items, which are the items mostly sold or viewed. It leaves the long-tail less popular items having less chance to get introduced to the users. This is the reason why ALS is not performing as well as a random recommender on diversity metrics.
# ### 6. Calculate diversity metrics using item feature vector based item-item similarity
# In the above section we calculate diversity metrics using item co-occurrence count based item-item similarity. In the scenarios when item features are available, we may want to calculate item-item similarity based on item feature vectors. In this section, we show how to calculate diversity metrics using item feature vector based item-item similarity.
# Get movie features "title" and "genres"
movies = (
data.groupBy(COL_ITEM, COL_TITLE, COL_GENRE).count()
.na.drop() # remove rows with null values
.withColumn(COL_GENRE, F.split(F.col(COL_GENRE), "\|")) # convert to array of genres
.withColumn(COL_TITLE, F.regexp_replace(F.col(COL_TITLE), "[\(),:^0-9]", "")) # remove year from title
.drop("count") # remove unused columns
)
# +
# tokenize "title" column
title_tokenizer = Tokenizer(inputCol=COL_TITLE, outputCol="title_words")
tokenized_data = title_tokenizer.transform(movies)
# remove stop words
remover = StopWordsRemover(inputCol="title_words", outputCol="text")
clean_data = remover.transform(tokenized_data).drop(COL_TITLE, "title_words")
# +
# convert text input into feature vectors
# step 1: perform HashingTF on column "text"
text_hasher = HashingTF(inputCol="text", outputCol="text_features", numFeatures=1024)
hashed_data = text_hasher.transform(clean_data)
# step 2: fit a CountVectorizerModel from column "genres".
count_vectorizer = CountVectorizer(inputCol=COL_GENRE, outputCol="genres_features")
count_vectorizer_model = count_vectorizer.fit(hashed_data)
vectorized_data = count_vectorizer_model.transform(hashed_data)
# step 3: assemble features into a single vector
assembler = VectorAssembler(
inputCols=["text_features", "genres_features"],
outputCol="features",
)
feature_data = assembler.transform(vectorized_data).select(COL_ITEM, "features")
feature_data.show(10, False)
# -
# The *features* column is represented with a SparseVector object. For example, in the feature vector (1043,[128,544,1025],[1.0,1.0,1.0]), 1043 is the vector length, indicating the vector consisting of 1043 item features. The values at index positions 128,544,1025 are 1.0, and the values at other positions are all 0.
# +
als_eval = SparkDiversityEvaluation(
train_df = train_df,
reco_df = top_k_reco,
item_feature_df = feature_data,
item_sim_measure="item_feature_vector",
col_user = COL_USER,
col_item = COL_ITEM
)
als_diversity=als_eval.diversity()
als_serendipity=als_eval.serendipity()
print(als_diversity)
print(als_serendipity)
# +
random_eval = SparkDiversityEvaluation(
train_df = train_df,
reco_df = pred_df,
item_feature_df = feature_data,
item_sim_measure="item_feature_vector",
col_user = COL_USER,
col_item = COL_ITEM
)
random_diversity=random_eval.diversity()
random_serendipity=random_eval.serendipity()
print(random_diversity)
print(random_serendipity)
# -
# It's interesting that the value of diversity and serendipity changes when using different item-item similarity calculation approach, for both ALS algorithm and random recommender. The diversity and serendipity of random recommender are still higher than ALS algorithm.
# ### References
# The metric definitions / formulations are based on the following references:
# - <NAME>, <NAME>, and <NAME>, Novelty and diversity metrics for recommender systems: choice, discovery and relevance, ECIR 2011
# - <NAME> and <NAME>, Evaluating recommendation systems, Recommender Systems Handbook pp. 257-297, 2010.
# - <NAME>, Serendipity: Accuracy’s unpopular best friend in recommender Systems, eugeneyan.com, April 2020
# - <NAME>, <NAME>, <NAME> and <NAME>, Auralist: introducing serendipity into music recommendation, WSDM 2012
#
# cleanup spark instance
spark.stop()
|
examples/03_evaluate/als_movielens_diversity_metrics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + active=""
# ## Characteristics of New Housing
#
# This page provides national, annual data on the characteristics of new privately-owned residential structures, such as square footage, number of bedrooms and bathrooms, type of wall material, and sales prices. Many characteristics are available at the region level. https://www.census.gov/construction/chars/
#
# ### Data Sources
# - InputFiles : https://www.census.gov/construction/chars/microdata.html
#
# ### Changes
# - 12-29-2018 : Started project
#
#
# ### Key Versions
# pandas = '0.23.4'
# numpy = '1.15.4'
# requests = '2.19.1'
# -
import pandas as pd
from pathlib import Path
from datetime import datetime
import zipfile
import requests
import io
import glob
import numpy as np
import feather
# ### File Locations
today = datetime.today()
in_file = Path.cwd() / "data" / "raw" / "FILE1"
in_directory = Path.cwd() / "data" / "raw"
summary_file = Path.cwd() / "data" / "processed" / f"summary_{today:%b-%d-%Y}.feather"
# ### Load Data from URL Sources
#
# Main Page for where to manually download this files.
# https://www.census.gov/construction/chars/microdata.html
# +
file_names = ['soc17.zip','soc16.zip','soc15.zip','soc14.zip','soc13.zip',
'soc12.zip','soc11.zip','soc10.zip','soc09.zip','soc08.zip',
'soc07.zip','soc06.zip','soc05.zip','soc04.zip','soc03.zip',
'soc02.zip','soc01.zip','soc00.zip','soc99.zip']
for file in file_names:
fileName = 'soc17.zip'
source_url = 'https://www.census.gov/construction/chars/xls/%s' % file
in_file = Path.cwd() / "data" / "raw" / file.split('.')[0]
r = requests.get(source_url)
z = zipfile.ZipFile(io.BytesIO(r.content))
z.extractall(in_file)
del in_file
# -
#Compliments: http://pbpython.com/excel-file-combine.html
all_data = pd.DataFrame()
for f in glob.glob("./data/raw/*/*.xls"):
#print (f.split('/')[-2])
df = pd.read_excel(f)
df['FILENAME'] = f.split('/')[-2]
all_data = all_data.append(df,ignore_index=True, sort=False)
all_data.describe()
all_data.head()
# ### Column Cleanup
# - Rename the columns for consistency; they are all acronyms.
# +
cols_to_rename = {'ACS': 'CentralAir',
'AGER': 'RestrictedAge',
'ASSOC': 'HomeOwnerAssociation',
'BASE': 'FoundationType',
'CAT': 'BuildReason',
'CLOS': 'ClosingCostsInc',
'CON': 'CondominiumProject',
'DECK': 'Deck',
'DET': 'HouseDesign',
'DIV': 'CensusDivision',
'FINC': 'FinancingType',
'FNBS': 'FinishedBasement',
'FOYER': 'TwoStoryFoyer',
'FRAME': 'FramingMaterial',
'GAR': 'Garage',
'HEAT': 'HeatingSystemPrimary',
'HEAT2': 'HeatingSystemSecondary',
'LNDR': 'LaundryLocation',
'METRO': 'InMetroArea',
'MFGS': 'ConstructionMethod',
'PATI': 'Patio',
'PRCH': 'Porch',
'SEWER': 'SewerType',
'STOR': 'Stories',
'WALS': 'ExteriorWallsGtrTwo',
'WAL1': 'ExteriorMaterialsPrimary',
'WAL2': 'ExteriorMaterialsSecondary',
'WATER': 'WaterSupply',
'AREA': 'LotSizeSQFT',
'BEDR': 'Bedrooms',
'COMP': 'CompletionDate',
'FNSQ': 'FinishedBasementSQFT',
'FFNSQ': 'FinishedBasementFinalSQFT',
'FPLS': 'Fireplaces',
'FULB': 'BathroomsFull',
'HAFB': 'BathroomsHalf',
'LOTV': 'LotValue',
'PVALU': 'PermitValue',
'SALE': 'SaleDate',
'FSQFS': 'FootageFinalSQFT',
'STRT': 'StartDate',
'CONPR': 'PriceContract',
'SLPR': 'PriceSales',
'SQFS': 'FootagePrelimSQFT',
'WEIGHT': 'SurveyWieght',
'FUEL': 'HeatingSystemFuelPrimary',
'FUEL2': 'HeatingSystemFuelSecondary',
'FCONPR': 'PriceContractAtCompletion',
'FSLPR': 'PriceSalesAtCompletion',
'AUTH': 'PermitAuthorizationDate',
}
drop_columns = [ 'AREA_F',
'FNSQ_F',
'FFNSQ_F',
'SLPR_F',
'FSLPR_F',
'CONPR_F',
'FCONPR_F',
'LOTV_F',
'SQFS_F',
'FSQFS_F',
'PVALU_F',
'ID']
all_data.rename(columns=cols_to_rename, inplace=True)
all_data.drop(columns=drop_columns, axis=1, errors='ignore', inplace=True)
# -
# ### Clean up each columns descriptions.
# +
#Central Conditioning
# 1 = yes, 2=no, 0=unknown
all_data.loc[all_data['CentralAir']==1,'CentralAir']='Yes'
all_data.loc[all_data['CentralAir']==2,'CentralAir']='No'
all_data.loc[all_data['CentralAir']==0,'CentralAir']= np.nan
all_data['CentralAir'] = all_data['CentralAir'].astype('category')
all_data.CentralAir.value_counts(dropna=False)
# +
#Age Restrictions
#Will this house be in a development that is age‐ restricted?
#1 = Yes
#2 = No
#Age‐restricted developments are intended for occupancy by persons of a specific age group,
#usually 55 and older or 62 and older. Not applicable prior to 2009 files
column = 'RestrictedAge'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Community Association
column = 'HomeOwnerAssociation'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Foundation Type
#“Other” includes raised supports, earthen, and other foundation
#types.
column = 'FoundationType'
all_data.loc[all_data[column]==1,column]='Basement'
all_data.loc[all_data[column]==2,column]='Crawl Space'
all_data.loc[all_data[column]==3,column]='Slab'
all_data.loc[all_data[column]==4,column]='Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Catageroy Type: BuildReason
#Beginning with the file for 2017, houses that are built
#for rent will be included in the "1‐Built for Sale/Sold"
#category rather than being shown separately.
column = 'BuildReason'
all_data.loc[all_data[column]==1,column]='SaleOrRent'
all_data.loc[all_data[column]==2,column]='Contractor'
all_data.loc[all_data[column]==3,column]='Owner'
all_data.loc[all_data[column]==4,column]='Rent'
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Condominium
#Applies only to houses built for sale/sold.
column = 'CondominiumProject'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Deck
# 1 = yes, 2=no, 0=unknown
column = 'Deck'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data.Deck.value_counts(dropna=False)
# +
#Design of House
#1 = Detached
#2 = Attached
#0 = Not reported
column = 'HouseDesign'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Division (Census)
#1 = New England
#2 = Middle Atlantic
#3 = East North Central 4 = West North Central 5 = South Atlantic
#6 = East South Central 7 = West South Central 8 = Mountain
#9 = Pacific
column = 'CensusDivision'
all_data.loc[all_data[column]==1,column]='New England'
all_data.loc[all_data[column]==2,column]='Middle Atlantic'
all_data.loc[all_data[column]==3,column]='East North Central'
all_data.loc[all_data[column]==4,column]='West North Central'
all_data.loc[all_data[column]==5,column]='South Atlantic'
all_data.loc[all_data[column]==6,column]='East South Central'
all_data.loc[all_data[column]==7,column]='West South Central'
all_data.loc[all_data[column]==8,column]='Mountain'
all_data.loc[all_data[column]==9,column]= 'Pacific'
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Type of Financiing
#01 = Conventional 02 = FHA
#03 = VA
#04 = Cash
#05 = Other financing 00 = Not reported
#“Other” includes Rural Housing Service, cash, Habitat for Humanity, loan from an individual,
#State or local government mortgage‐backed bonds and other types of financing.
#Applies only to houses sold, contractor‐built houses and owner‐built houses.
column = 'FinancingType'
all_data.loc[all_data[column]==1,column]='Conventional'
all_data.loc[all_data[column]==2,column]='FHA'
all_data.loc[all_data[column]==3,column]= 'VA'
all_data.loc[all_data[column]==4,column]= 'Cash'
all_data.loc[all_data[column]==5,column]= 'Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Finished Basement
#1 = Yes
#2 = No
#0 = Not reported
# Applies only to houses reporting a full or partial basement.
column = 'FinishedBasement'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
#for those with basement foundations; determine if it wasn't reported
mapper = (all_data[column]==0) & (all_data['FoundationType']=='Basement')
all_data.loc[mapper,column]= np.nan
#else classify as No; i.e. they don't have a findished basement in
#slab foundation homes.
mapper = (all_data[column]==0) & (all_data['FoundationType']!='Basement')
all_data.loc[mapper,column]= 'No'
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Two Story Foyer
#1 = Yes
#2 = No
#0 = Not reported
column = 'HouseDesign'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Frame Material
#1 = Wood
#2 = Steel
#3 = Concrete/masonry other than contret fomrs
#4 = insulated contrete forms (or SIP)
#0 = Not reported
column = 'FramingMaterial'
all_data.loc[all_data[column]==1,column]='Wood'
all_data.loc[all_data[column]==2,column]='Steel'
all_data.loc[all_data[column]==3,column]='ConcreteMasonry'
all_data.loc[all_data[column]==4,column]='InsulatedConcreteForm'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Parking
#1 = 1 car garage
#2 = 2 car garage
#3 = 3 or more car garage 4 = Other
#0 = Not reported
#“Other” includes carport, other off‐street parking (including a driveway with no garage
#or carport), and other parking facilities.
column = 'Garage'
all_data.loc[all_data[column]==1,column]='1Car'
all_data.loc[all_data[column]==2,column]='2Car'
all_data.loc[all_data[column]==3,column]='3orMoreCar'
all_data.loc[all_data[column]==4,column]='Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Primary Heat
#01 = Air‐source or ground‐source heat pump
#02 = Forced‐air furnace without heat pump
#03 = Hot water or steam system
#04 = Other or no heat
#00 = Not reported
#“Other” includes electric baseboard or wall panels, fireplace with
#insert, stove that burns coal or wood, non‐portable room heater that
#burns liquid fuel and is connected to a flue, vent, or chimney,
#passive solar system, other heat sources, and no heat.
column = 'HeatingSystemPrimary'
all_data.loc[all_data[column]==1,column]='AirOrGroundHeatPump'
all_data.loc[all_data[column]==2,column]='ForcedAirNoHeatPump'
all_data.loc[all_data[column]==3,column]='HotWaterOrSteam'
all_data.loc[all_data[column]==4,column]='OtherOrNone'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Secondary Heat
#01 = Air‐source or ground‐source heat pump
#02 = Forced‐air furnace without heat pump
#03 = Hot water or steam system
#04 = Other
#00 = Not reported OR No second heating
#“Other” includes electric baseboard or wall panels, fireplace with
#insert, stove that burns coal or wood, non‐portable room heater that
#burns liquid fuel and is connected to a flue, vent, or chimney,
#passive solar system, other heat sources, and no heat.
column = 'HeatingSystemSecondary'
all_data.loc[all_data[column]==1,column]='AirOrGroundHeatPump'
all_data.loc[all_data[column]==2,column]='ForcedAirNoHeatPump'
all_data.loc[all_data[column]==3,column]='HotWaterOrSteam'
all_data.loc[all_data[column]==4,column]='Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Laundry Location
#1 = In the basement
#2 = On the first floor
#3 = On the second or higher floor 4 = In the garage or carport
#5 = No connection planned
#6 = Multiple locations
#0 = Not reported
#“Other” includes electric baseboard or wall panels, fireplace with
#insert, stove that burns coal or wood, non‐portable room heater that
#burns liquid fuel and is connected to a flue, vent, or chimney,
#passive solar system, other heat sources, and no heat.
column = 'LaundryLocation'
all_data.loc[all_data[column]==1,column]='Basement'
all_data.loc[all_data[column]==2,column]='FirstFloor'
all_data.loc[all_data[column]==3,column]='SecondFloorOrHigher'
all_data.loc[all_data[column]==4,column]='Garage'
all_data.loc[all_data[column]==5,column]='NoConnection'
all_data.loc[all_data[column]==6,column]='MultipleLocations'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Metro Area
#1 = Located in Metro Area
#2 = Non in an Metro Area
column = 'InMetroArea'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Construction Type
#1 = Modular
#2 = Panelized / Precut 3 = Site‐built
#0 = Not reported
column = 'ConstructionMethod'
all_data.loc[all_data[column]==1,column]='Modular'
all_data.loc[all_data[column]==2,column]='Panelized'
all_data.loc[all_data[column]==3,column]='SiteBuilt'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Patio
#1 = Yes
#2 = No
column = 'Patio'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Porch
#1 = Yes
#2 = No
column = 'Porch'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Sewer Type
#1 = Public Sewer
#2 = Septic
#3 = Other
column = 'SewerType'
all_data.loc[all_data[column]==1,column]='PublicSewer'
all_data.loc[all_data[column]==2,column]='Septic'
all_data.loc[all_data[column]==3,column]='Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Stories
#1 = 1 story
#2 = 2 stories (including 11⁄2 stories)
#3 = 3 stories or more
#0 = Not reported
column = 'Stories'
all_data.loc[all_data[column]==1,column]=1
all_data.loc[all_data[column]==2,column]=2
all_data.loc[all_data[column]==3,column]=3
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Primary Exterior Wall Materials
#01 = Wood or wood products
#02 = Brick or brick veneer
#03 = Aluminum siding (not covered with vinyl)
#04 = Stucco
#05 = Vinyl siding (inc. vinyl‐covered aluminum)
#06 = Concrete block (not including stucco)
#07 = Stone, rock, or other stone materials
#08 = Fiber cement siding
#09 = Other
#00 = Not reported
#Beginning with the file for 2008,
#Aluminum siding is also included with “09‐Other”
#rather than being shown separately.
column = 'ExteriorMaterialsPrimary'
all_data.loc[all_data[column]==1,column]='Wood'
all_data.loc[all_data[column]==2,column]='Brick'
all_data.loc[all_data[column]==3,column]='Aluminum'
all_data.loc[all_data[column]==4,column]='Stucco'
all_data.loc[all_data[column]==5,column]='Vinyl'
all_data.loc[all_data[column]==6,column]='ConcreteBlock'
all_data.loc[all_data[column]==7,column]='Aluminum'
all_data.loc[all_data[column]==8,column]='FiberCement'
all_data.loc[all_data[column]==9,column]='Other'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Secondary Exterior Wall Materials
#01 = Wood or wood products
#02 = Brick or brick veneer
#03 = Aluminum siding (not covered with vinyl)
#04 = Stucco
#05 = Vinyl siding (inc. vinyl‐covered aluminum)
#06 = Concrete block (not including stucco)
#07 = Stone, rock, or other stone materials
#08 = Fiber cement siding
#09 = Other
#00 = Not reported
#In files for years prior to 2009, WAL2 is “10” for houses
# with no secondary wall material (those with WALS=”2”).
#Beginning with the file for 2009, houses with WALS=”2” have WAL2=”00”.
column = 'ExteriorMaterialsSecondary'
all_data.loc[all_data[column]==1,column]='Wood'
all_data.loc[all_data[column]==2,column]='Brick'
all_data.loc[all_data[column]==3,column]='Aluminum'
all_data.loc[all_data[column]==4,column]='Stucco'
all_data.loc[all_data[column]==5,column]='Vinyl'
all_data.loc[all_data[column]==6,column]='ConcreteBlock'
all_data.loc[all_data[column]==7,column]='Aluminum'
all_data.loc[all_data[column]==8,column]='FiberCement'
all_data.loc[all_data[column]==9,column]='Other'
all_data.loc[all_data[column]==10,column]=np.nan
all_data.loc[all_data[column]==0,column]= np.nan
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Secondary Walls?
#1 = Yes
#2 = No
column = 'ExteriorWallsGtrTwo'
all_data.loc[all_data[column]==1,column]='Yes'
all_data.loc[all_data[column]==2,column]='No'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Water Type
#1 = Public water (inc. community or shared well)
#2 = Individual well
#3 = Other
#0 = Not reported
column = 'WaterSupply'
all_data.loc[all_data[column]==1,column]='Public'
all_data.loc[all_data[column]==2,column]='Well'
all_data.loc[all_data[column]==3,column]='Other'
all_data.loc[all_data[column]=='',column]=np.nan
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Area
#For all houses, values less than 2,000 were changed to 2,000.
#For houses built for sale/sold and houses built for rent,
#all values greater than 87,120 were changed to 87,120.
#For houses that are contractor‐built and owner‐built,
#all values greater than 435,600 were changed to 435,600.
column = 'LotSizeSQFT'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column].value_counts(dropna=False)
# +
#Bedrooms
#1 = 1 story
#2 = 2 stories (including 11⁄2 stories)
#3 = 3 stories or more
#0 = Not reported
column = 'Bedrooms'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column].value_counts(dropna=False)
# +
#Completion Date
#0= Not Completed as of survey date.
column = 'CompletionDate'
all_data.loc[all_data[column]==0,column]= pd.NaT
all_data[column] = pd.to_datetime(all_data[column], format='%Y%m', errors='ignore')
# +
#Final Square Foot Area of Finished Basement at Completion
#Applies only to houses with a full or partial finished basement
#and reporting square foot areas of house (unchanged) and finished
#basement. Values not allowed to exceed 50% or be less than 5% of #
#area of house. Values outside those limits changed to those limits.
column = 'FinishedBasementFinalSQFT'
#all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Fireplaces Walls?
#0= None
#1 = 1
#2 = 2 or more
#9 = not reported
column = 'Fireplaces'
all_data.loc[all_data[column]==9,column]= np.nan
all_data[column].value_counts(dropna=False)
# +
#Full Bath
#1 = 1 bathroom or less
#2 = 2 bathrooms
#3 = 3 bathrooms
#4 = 4 bathrooms or more 9 = Not reported
column = 'BathroomsFull'
all_data.loc[all_data[column]==9,column]= np.nan
all_data[column].value_counts(dropna=False)
# +
#Half Bath
#0 = 0 half bathroom
#1 = 1 half bathrooms
#2 =2 half bathrooms or more
#9 = Not reported
column = 'BathroomsHalf'
all_data.loc[all_data[column]==9,column]= np.nan
all_data[column].value_counts(dropna=False)
# +
#Lot Value Bath
#0 = Not applicable or not reported.
column = 'LotValue'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Lot Value Bath
#0 = Not applicable or not reported.
column = 'PermitValue'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Sale Date
#0= Not Completed as of survey date.
column = 'SaleDate'
all_data.loc[all_data[column]==0,column]= pd.NaT
all_data[column] = pd.to_datetime(all_data[column], format='%Y%m', errors='ignore')
# +
#Final Square Foot Area of House at Completion
#
column = 'FootageFinalSQFT'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Start Date
#0= Not Completed as of survey date.
column = 'StartDate'
all_data.loc[all_data[column]==0,column]= pd.NaT
all_data[column] = pd.to_datetime(all_data[column], format='%Y%m', errors='ignore')
# +
#Contract Price
#Applies only to contractor‐built houses. Within each division,
#top 3% and bottom 1% of all reported values were changed to those
#limits.
#Unchanged values less than $15,000 were changed to $15,000.
column = 'PriceContract'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Sales Price
#Sales price at the time the first sales contract was signed or
#deposit made; includes the price of the improved lot
#Applies only to houses sold. Within each division, top 3% and
#bottom 1% of all reported values were changed to those limits.
#Unchanged values less than $15,000 were changed to $15,000.
column = 'PriceSales'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Square Foot Area of House (Prelim)
#
column = 'FootagePrelimSQFT'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Weight
#Number of housing units represented by this sample case.
column = 'SurveyWieght'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Primary Space Heating Fuel
#01 = Electricity
#02 = Nat Gas
#03 = Bottled or Liquified Gas (incl Propane)
#04 = Oil (heating/kerosene)
#05 = Other or no heat
#00 = Not reported
#“Other” includes wood, pellets, solar, coal, and other fuels.
#In the files for 2008 and 2009, Bottled gas is included
#with “02‐Natural gas” rather than being shown separately.
column = 'HeatingSystemFuelPrimary'
all_data.loc[all_data[column]==1,column]='Electricity'
all_data.loc[all_data[column]==2,column]='Nat Gas'
all_data.loc[all_data[column]==3,column]='BottledLiquid'
all_data.loc[all_data[column]==4,column]='Oil'
all_data.loc[all_data[column]==5,column]='OtherOrNone'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Primary Space Heating Fuel
#01 = Electricity
#02 = Nat Gas
#03 = Bottled or Liquified Gas (incl Propane)
#04 = Oil (heating/kerosene)
#05 = Other or no heat
#00 = Not reported
#“Other” includes wood, pellets, solar, coal, and other fuels.
#In the files for 2008 and 2009, Bottled gas is included
#with “02‐Natural gas” rather than being shown separately.
column = 'HeatingSystemFuelSecondary'
all_data.loc[all_data[column]==1,column]='Electricity'
all_data.loc[all_data[column]==2,column]='Nat Gas'
all_data.loc[all_data[column]==3,column]='BottledLiquid'
all_data.loc[all_data[column]==4,column]='Oil'
all_data.loc[all_data[column]==5,column]='OtherOrNone'
all_data.loc[all_data[column]==0,column]= np.nan
all_data[column] = all_data[column].astype('category')
all_data[column].value_counts(dropna=False)
# +
#Final Contract Price at Completion
#Final contract price reported at the time the house was completed;
#whole dollars to nearest $100.
#0 = Not applicable or not reported
#Applies only to contractor‐built houses. Within each division,
#top 3% and bottom 1% of all reported values were changed to those
#limits. Unchanged values less than $15,000 were changed to $15,000.
column = 'PriceContractAtCompletion'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#FFinal Sales Price at Completion
#Final sales price reported at the time the house was completed;
#whole dollars to nearest $100.
#0 = Not applicable or not reported
column = 'PriceSalesAtCompletion'
all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#Permit Authorization Date
#When was this house authorized by a building permit?
#Usually the month the building permit for the house was issued,
#but can vary based on the availability of permits for sampling for
#SOC. Set to the start date if the house is in an area where permits
#are not required or if the start date was before the issuance of
#the final building permit.
column = 'PermitAuthorizationDate'
all_data.loc[all_data[column]==0,column]= pd.NaT
all_data[column] = pd.to_datetime(all_data[column], format='%Y%m', errors='ignore')
#all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# +
#File Name
column = 'FILENAME'
all_data[column] = all_data[column].astype('category')
#all_data.loc[all_data[column]==0,column]= np.nan
#all_data[column].value_counts(dropna=False)
# -
# ### Check Data Types
# Most the data is catagory, number or datetime. There should be no
# objects if we have done our job correctly!
all_data.dtypes == 'object'
# ### Data Manipulation
# +
#Could put in this section log transform of the larger values b
# but that would only be applicable to machine modeling if that is
# what someone would like to do in the future.
# -
# ### Save output file into processed directory
#
# Save a file in the processed directory that is cleaned properly. It will be read in and used later for further analysis.
#
# Other options besides pickle include:
# - feather
# - msgpack
# - parquet
feather.write_dataframe(all_data, summary_file)
#df = feather.read_dataframe(path)
|
1-Data_Prep.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <h1>Reboot: Box-Plots for Education Competition</h1>
# My resolution for the project based on the "Machine Learning with Experts: School Budgets" course by <a href='datacamp.com'>DataCamp</a>
# <h2> 1. Import Libraries </h2>
# +
#ignore warnings
import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from warnings import warn
# -
# <h2> 2. Load Data </h2>
#
# The data has been loaded from the <a href='https://www.drivendata.org/competitions/46/box-plots-for-education-reboot/page/85/'>DrivenData Competition</a>.
#
# Firstly, we will use the training set of data.
# +
df = pd.read_csv('TrainingData.csv', index_col=0)
df.head()
# -
df.shape
# <h2> 3. Implement Essential Functions </h2>
# The multi-class log-loss, multi-class train-test split functions were taken from the https://github.com/datacamp/course-resources-ml-with-experts-budget repository by DataCamp and represented in the aforesaid course.
#
# +
BOX_PLOTS_COLUMN_INDICES = [list(range(37)),
list(range(37, 48)),
list(range(48, 51)),
list(range(51, 76)),
list(range(76, 79)),
list(range(79, 82)),
list(range(82, 87)),
list(range(87, 96)),
list(range(96, 104))]
def multi_multi_log_loss(predicted,
actual,
class_column_indices=BOX_PLOTS_COLUMN_INDICES,
eps=1e-15):
""" Multi class version of Logarithmic Loss metric as implemented on
DrivenData.org
"""
class_scores = np.ones(len(class_column_indices), dtype=np.float64)
# calculate log loss for each set of columns that belong to a class:
for k, this_class_indices in enumerate(class_column_indices):
# get just the columns for this class
preds_k = predicted[:, this_class_indices].astype(np.float64)
# normalize so probabilities sum to one (unless sum is zero, then we clip)
preds_k /= np.clip(preds_k.sum(axis=1).reshape(-1, 1), eps, np.inf)
actual_k = actual[:, this_class_indices]
# shrink predictions so
y_hats = np.clip(preds_k, eps, 1 - eps)
sum_logs = np.sum(actual_k * np.log(y_hats))
class_scores[k] = (-1.0 / actual.shape[0]) * sum_logs
return np.average(class_scores)
# +
def multilabel_sample(y, size=1000, min_count=5, seed=None):
""" Takes a matrix of binary labels `y` and returns
the indices for a sample of size `size` if
`size` > 1 or `size` * len(y) if size =< 1.
The sample is guaranteed to have > `min_count` of
each label.
"""
try:
if (np.unique(y).astype(int) != np.array([0, 1])).all():
raise ValueError()
except (TypeError, ValueError):
raise ValueError('multilabel_sample only works with binary indicator matrices')
if (y.sum(axis=0) < min_count).any():
raise ValueError('Some classes do not have enough examples. Change min_count if necessary.')
if size <= 1:
size = np.floor(y.shape[0] * size)
if y.shape[1] * min_count > size:
msg = "Size less than number of columns * min_count, returning {} items instead of {}."
warn(msg.format(y.shape[1] * min_count, size))
size = y.shape[1] * min_count
rng = np.random.RandomState(seed if seed is not None else np.random.randint(1))
if isinstance(y, pd.DataFrame):
choices = y.index
y = y.values
else:
choices = np.arange(y.shape[0])
sample_idxs = np.array([], dtype=choices.dtype)
# first, guarantee > min_count of each label
for j in range(y.shape[1]):
label_choices = choices[y[:, j] == 1]
label_idxs_sampled = rng.choice(label_choices, size=min_count, replace=False)
sample_idxs = np.concatenate([label_idxs_sampled, sample_idxs])
sample_idxs = np.unique(sample_idxs)
# now that we have at least min_count of each, we can just random sample
sample_count = int(size - sample_idxs.shape[0])
# get sample_count indices from remaining choices
remaining_choices = np.setdiff1d(choices, sample_idxs)
remaining_sampled = rng.choice(remaining_choices,
size=sample_count,
replace=False)
return np.concatenate([sample_idxs, remaining_sampled])
def multilabel_train_test_split(X, Y, size, min_count=5, seed=None):
""" Takes a features matrix `X` and a label matrix `Y` and
returns (X_train, X_test, Y_train, Y_test) where all
classes in Y are represented at least `min_count` times.
"""
index = Y.index if isinstance(Y, pd.DataFrame) else np.arange(Y.shape[0])
test_set_idxs = multilabel_sample(Y, size=size, min_count=min_count, seed=seed)
train_set_idxs = np.setdiff1d(index, test_set_idxs)
test_set_mask = index.isin(test_set_idxs)
train_set_mask = ~test_set_mask
return (X[train_set_mask], X[test_set_mask], Y[train_set_mask], Y[test_set_mask])
# -
# <h2> 4. Reshape and Split the Data </h2>
#
# I will create encode the given labels and split the training data to evaluate my algorithm.
# +
#labels need to be predicted by the description of the contest
LABELS = ['Function',
'Use',
'Sharing',
'Reporting',
'Student_Type',
'Position_Type',
'Object_Type',
'Pre_K',
'Operating_Status']
#other labels
NON_LABELS = [c for c in df.columns if c not in LABELS]
dummy_labels = pd.get_dummies(df[LABELS])
X_train, X_test, y_train, y_test = multilabel_train_test_split(df[NON_LABELS],
dummy_labels,
0.2,
seed=43)
# -
# <h2> 5. Preprocess the Data </h2>
#
# Hereby I will define functions retrieving and transforming both text and numeric data and concatenating them into one set. Also for convenience I will convert my logloss function into sklearn metric.
# +
NUMERIC_COLUMNS = df.columns[df.dtypes.values == 'float'].values.tolist()
# function merging all text values in a row
def combine_text_columns(data_frame, to_drop=NUMERIC_COLUMNS + LABELS):
""" Takes the dataset as read in, drops the non-feature, non-text columns and
then combines all of the text columns into a single vector that has all of
the text for a row.
:param data_frame: The data as read in with read_csv (no preprocessing necessary)
:param to_drop (optional): Removes the numeric and label columns by default.
"""
# drop non-text columns that are in the df
to_drop = set(to_drop) & set(data_frame.columns.tolist())
text_data = data_frame.drop(to_drop, axis=1)
# replace nans with blanks
text_data.fillna("", inplace=True)
# joins all of the text items in a row (axis=1)
# with a space in between
return text_data.apply(lambda x: " ".join(x), axis=1)
# +
from sklearn.preprocessing import FunctionTransformer
get_text_data = FunctionTransformer(combine_text_columns, validate=False)
get_numeric_data = FunctionTransformer(lambda x: x[NUMERIC_COLUMNS], validate=False)
# +
from sklearn.metrics.scorer import make_scorer
log_loss_scorer = make_scorer(multi_multi_log_loss)
# -
# <h2> 6. Make Pipeline </h2>
#
# In this step I will train my pipeline model, which will use logistic regression.
# +
from sklearn.feature_selection import chi2, SelectKBest
from sklearn.pipeline import Pipeline, FeatureUnion
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import PolynomialFeatures
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.multiclass import OneVsRestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import MaxAbsScaler
TOKENS_ALPHANUMERIC = '[A-Za-z0-9]+(?=\\s+)'
# +
# %%time
# set a reasonable number of features before adding interactions
chi_k = 1000
# create the pipeline object
pl = Pipeline([
('union', FeatureUnion(
transformer_list = [
('numeric_features', Pipeline([
('selector', get_numeric_data),
('imputer', SimpleImputer()) # get rid of missing values
])),
('text_features', Pipeline([
('selector', get_text_data),
('vectorizer', HashingVectorizer(token_pattern=TOKENS_ALPHANUMERIC,
norm=None, binary=False, alternate_sign=False,
ngram_range=(1, 2))), #transform text data in numerical
('dim_red', SelectKBest(chi2, chi_k)) #select 1000 best features
]))
]
)),
('int', PolynomialFeatures(degree=2)), #take into account combination of features
('scale', MaxAbsScaler()), #scale all the features
('clf', OneVsRestClassifier(LogisticRegression()))
])
# fit the pipeline to our training data
pl.fit(X_train, y_train.values)
# print the score of our trained pipeline on our test set
print("Logloss score of trained pipeline: ", log_loss_scorer(pl, X_test, y_test.values))
# -
# <h2> 7. Make Predictions </h2>
#
# Right here I will use my model on the testing set and create predction file.
# +
# Load holdout data
holdout = pd.read_csv('TestData.csv', index_col=0)
# Make predictions
predictions = pl.predict_proba(holdout)
# Format correctly in new DataFrame: prediction_df
prediction_df = pd.DataFrame(columns=pd.get_dummies(df[LABELS], prefix_sep='__').columns,
index=holdout.index,
data=predictions)
prediction_df = prediction_df[prediction_df.columns.sort_values()]
# Save prediction_df to csv called "predictions.csv"
prediction_df.to_csv("predictions.csv")
# -
# The Logistic Regression with selecting 1000 best features showed 0.7733 logloss in the private score and currently ranked 58th among 1585 others. With wiping off the limit on the feature number the result can be even more tremendous.
|
Box-Plots for Education.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/lisatwyw/data-gym/blob/master/gspread_demo.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + id="Lb7ZoNMM2_nH" colab_type="code" colab={}
from google.colab import auth
auth.authenticate_user()
import gspread
from oauth2client.client import GoogleCredentials
gc = gspread.authorize(GoogleCredentials.get_application_default())
# + [markdown] id="_e1tPrKS3r_T" colab_type="text"
# # Import data from demo spreadsheet ("AirBnB open data") #
# + id="_Y5DXy3j3xc5" colab_type="code" colab={}
url2='https://docs.google.com/spreadsheets/d/1YTD0pxdGTGAzM8IiWDfLL4AZPjrFRN-vpGUiLQWOtoI/edit#gid=1512387781'
gc2= gspread.authorize(GoogleCredentials.get_application_default())
wb2= gc2.open_by_url(url2)
sheet = wb2.worksheet('AB_NYC_2019')
# + id="gQDz6Cl55vxG" colab_type="code" colab={}
import pandas as pd
import matplotlib.pyplot as plt
data = sheet.get_all_values()
df = pd.DataFrame( data )
# + id="w-PuSUBD69qj" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 551} outputId="43ea7fe9-17f2-42b0-a65c-61a4cd56f545"
df.head().transpose()
|
demo/gsheet_demo.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6 with Spark
# language: python3
# name: python36
# ---
# # Data analysis with Python, Apache Spark, and PixieDust
# ***
#
# In this notebook you will:
#
# * analyze customer demographics, such as, age, gender, income, and location
# * combine that data with sales data to examine trends for product categories, transaction types, and product popularity
# * load data from GitHub as well as from a public open data set
# * cleanse, shape, and enrich the data, and then visualize the data with the PixieDust library
#
# Don't worry! PixieDust charts don't require coding.
#
# By the end of the notebook, you will understand how to combine data to gain insights about which customers you might target to increase sales.
# <a id="toc"></a>
# ## Table of contents
#
# #### [Setup](#Setup)
# [Load data into the notebook](#Load-data-into-the-notebook)
# #### [Explore customer demographics](#part1)
# [Prepare the customer data set](#Prepare-the-customer-data-set)<br>
# [Visualize customer demographics and locations](#Visualize-customer-demographics-and-locations)<br>
#
# #### [Summary and next steps](#summary)
# ## Setup
# You need to import libraries and load the customer data into this notebook.
# Import the necessary libraries:
import pixiedust
import pyspark.sql.functions as func
import pyspark.sql.types as types
import re
import json
import os
import requests
# **If you get any errors or if a package is out of date:**
#
# * uncomment the lines in the next cell (remove the `#`)
# * restart the kernel (from the Kernel menu at the top of the notebook)
# * reload the browser page
# * run the cell above, and continue with the notebook
# +
#!pip install pixiedust --upgrade
# -
# ### Load data into the notebook
#
# The data file contains both the customer demographic data that you'll analyzed in Part 1, and the sales transaction data for Part 2.
#
# With `pixiedust.sampleData()` you can load csv data from any url. The below loads the data in a Spark DataFrame.
#
# > In case you wondered, this works with Pandas as well, just add `forcePandas = True` to load data in a Pandas DataFrame. *But do not add this to the below cell as in this notebook you will use Spark.*
raw_df = pixiedust.sampleData('https://raw.githubusercontent.com/IBMCodeLondon/localcart-workshop/master/data/customers_orders1_opt.csv')
raw_df
# [Back to Table of Contents](#toc)
# <a id="part1"></a>
# # Explore customer demographics
# In this part of the notebook, you will prepare the customer data and then start learning about your customers by creating multiple charts and maps.
# ## Prepare the customer data set
# Create a new Spark DataFrame with only the data you need and then cleanse and enrich the data.
#
# Extract the columns that you are interested in, remove duplicate customers, and add a column for aggregations:
# +
# Extract the customer information from the data set
customer_df = raw_df.select("CUST_ID",
"CUSTNAME",
"ADDRESS1",
"ADDRESS2",
"CITY",
"POSTAL_CODE",
"POSTAL_CODE_PLUS4",
"STATE",
"COUNTRY_CODE",
"EMAIL_ADDRESS",
"PHONE_NUMBER",
"AGE",
"GenderCode",
"GENERATION",
"NATIONALITY",
"NATIONAL_ID",
"DRIVER_LICENSE").dropDuplicates()
customer_df.printSchema()
# -
# Notice that the data type of the AGE column is currently a string. Convert the AGE column to a numeric data type so you can run calculations on customer age.
# +
# ---------------------------------------
# Cleanse age (enforce numeric data type)
# ---------------------------------------
def getNumericVal(col):
"""
input: pyspark.sql.types.Column
output: the numeric value represented by col or None
"""
try:
return int(col)
except ValueError:
# age-33
match = re.match('^age\-(\d+)$', col)
if match:
try:
return int(match.group(1))
except ValueError:
return None
return None
toNumericValUDF = func.udf(lambda c: getNumericVal(c), types.IntegerType())
customer_df = customer_df.withColumn("AGE", toNumericValUDF(customer_df["AGE"]))
customer_df
# -
customer_df.show(5)
# The GenderCode column contains salutations instead of gender values. Derive the gender information for each customer based on the salutation and rename the GenderCode column to GENDER.
# +
# ------------------------------
# Derive gender from salutation
# ------------------------------
def deriveGender(col):
""" input: pyspark.sql.types.Column
output: "male", "female" or "unknown"
"""
if col in ['Mr.', 'Master.']:
return 'male'
elif col in ['Mrs.', 'Miss.']:
return 'female'
else:
return 'unknown';
deriveGenderUDF = func.udf(lambda c: deriveGender(c), types.StringType())
customer_df = customer_df.withColumn("GENDER", deriveGenderUDF(customer_df["GenderCode"]))
customer_df.cache()
# -
# ## Explore the customer data set
#
# Instead of exploring the data with `.printSchema()` and `.show()` you can quickly explore data sets using PixieDust'. Invoke the `display()` command and click the table icon to review the schema and preview the data. Customize the options to display only a subset of the fields or rows or apply a filter (by clicking the funnel icon).
# + pixiedust={"displayParams": {"filter": "{\"regex\": \"false\", \"field\": \"AGE\", \"case_matter\": \"false\", \"value\": \"30\", \"constraint\": \"None\"}", "handlerId": "tableView", "no_margin": "true", "rowCount": "200"}}
display(customer_df)
# -
# [Back to Table of Contents](#toc)
# ## Visualize customer demographics and locations
#
# Now you are ready to explore the customer base. Using simple charts, you can quickly see these characteristics:
# * Customer demographics (gender and age)
# * Customer locations (city, state, and country)
#
# You will create charts with the PixieDust library:
#
# - [View customers by gender in a pie chart](#View-customers-by-gender-in-a-pie-chart)
# - [View customers by generation in a bar chart](#View-customers-by-generation-in-a-bar-chart)
# - [View customers by age in a histogram chart](#View-customers-by-age-in-a-histogram-chart)
# - [View specific information with a filter function](#View-specific-information-with-a-filter-function)
# - [View customer density by location with a map](#View-customer-density-by-location-with-a-map)
# ### View customers by gender in a pie chart
#
# Run the `display()` command and then configure the graph to show the percentages of male and female customers:
#
# 1. Run the next cell. The PixieDust interactive widget appears.
# 1. Click the chart button and choose **Pie Chart**. The chart options tool appears.
# 1. In the chart options, drag `GENDER` into the **Keys** box.
# 1. In the **Aggregation** field, choose **COUNT**.
# 1. Increase the **# of Rows to Display** to a very large number to display all data.
# 1. Click **OK**. The pie chart appears.
#
# If you want to make further changes, click **Options** to return to the chart options tool.
# + pixiedust={"displayParams": {"aggregation": "COUNT", "handlerId": "pieChart", "keyFields": "GENDER", "rowCount": "10000000"}}
display(customer_df)
# -
# [Back to Table of Contents](#toc)
# ### View customers by generation in a bar chart
# Look at how many customers you have per "generation."
#
# Run the next cell and configure the graph:
# 1. Choose **Bar Chart** as the chart type and configure the chart options as instructed below.
# 2. Put `GENERATION` into the **Keys** box.
# 3. Set **aggregation** to `COUNT`.
# 1. Increase the **# of Rows to Display** to a very large number to display all data.
# 4. Click **OK**
# 4. Change the **Renderer** at the top right of the chart to explore different visualisations.
# 4. You can use clustering to group customers, for example by geographic location. To group generations by country, select `COUNTRY_CODE` from the **Cluster by** list from the menu on the left of the chart.
# + pixiedust={"displayParams": {"aggregation": "COUNT", "clusterby": "COUNTRY_CODE", "handlerId": "barChart", "keyFields": "GENERATION", "rendererId": "bokeh", "rowCount": "10000000"}}
display(customer_df)
# -
# [Back to Table of Contents](#toc)
# ### View customers by age in a histogram chart
# A generation is a broad age range. You can look at a smaller age range with a histogram chart. A histogram is like a bar chart except each bar represents a range of numbers, called a bin. You can customize the size of the age range by adjusting the bin size. The more bins you specify, the smaller the age range.
#
# Run the next cell and configure the graph:
# 1. Choose **Histogram** as the chart type.
# 2. Put `AGE` into the **Values** box.
# 1. Increase the **# of Rows to Display** to a very large number to display all data.
# 1. Click **OK**.
# 3. Use the **Bin count** slider to specify the number of the bins. Try starting with 40.
# + pixiedust={"displayParams": {"chartsize": "66", "handlerId": "histogram", "rendererId": "bokeh", "rowCount": "1000000", "valueFields": "AGE"}}
display(customer_df)
# -
# [Back to Table of Contents](#toc)
# PixieDust supports basic filtering to make it easy to analyse data subsets. For example, to view the age distribution for a specific gender configure the chart as follows:
#
# 1. Choose `Histogram` as the chart type.
# 2. Put `AGE` into the **Values** box and click OK.
# 3. Click the filter button (looking like a funnel), and choose **GENDER** as field and `female` as value, and click `Apply`.
#
# The filter is only applied to the working data set and does not modify the input `customer_df`.
#
# + pixiedust={"displayParams": {"filter": "{\"field\": \"GENDER\", \"constraint\": \"None\", \"value\": \"female\", \"case_matter\": \"false\", \"regex\": \"false\"}", "handlerId": "histogram", "no_margin": "true", "valueFields": "AGE"}}
display(customer_df)
# -
# You can also filter by location. For example, the following command creates a new DataFrame that filters for customers from the USA:
condition = "COUNTRY_CODE = 'US'"
us_customer_df = customer_df.filter(condition)
# You can pivot your analysis perspective based on aspects that are of interest to you by choosing different keys and clusters.
#
# Create a bar chart and cluster the data.
#
# Run the next cell and configure the graph:
# 1. Choose **Bar chart** as the chart type.
# 2. Put `COUNTRY_CODE` into the **Keys** box.
# 4. Set Aggregation to **COUNT**.
# 5. Click **OK**. The chart displays the number of US customers.
# 6. From the **Cluster By** list, choose **GENDER**. The chart shows the number of customers by gender.
# + pixiedust={"displayParams": {"aggregation": "COUNT", "clusterby": "GENDER", "handlerId": "barChart", "keyFields": "COUNTRY_CODE"}}
display(us_customer_df)
# -
# Now try to cluster the customers by state.
#
# A bar chart isn't the best way to show geographic location!
# [Back to Table of Contents](#toc)
# ### View customer density by location with a map
# Maps are a much better way to view location data than other chart types.
#
# Visualize customer density by US state with a map.
#
# Run the next cell and configure the graph:
# 1. Choose **Map** as the chart type.
# 2. Put `STATE` into the **Keys** box.
# 4. Set Aggregation to **COUNT**.
# 5. Click **OK**. The map displays the number of US customers.
# 6. From the **Renderer** list, choose **brunel**.
#
# > PixieDust supports three map renderers: brunel, [mapbox](https://www.mapbox.com/) and Google. Note that the Mapbox renderer and the Google renderer require an API key or access token and supported features vary by renderer.
#
# 7. You can explore more about customers in each state by changing the aggregation method, for example look at customer age ranges (avg, minimum, and maximum) by state. Simply Change the aggregation function to `AVG`, `MIN`, or `MAX` and choose `AGE` as value.
#
# + pixiedust={"displayParams": {"handlerId": "mapView", "keyFields": "STATE", "mapboxtoken": "<KEY>", "valueFields": "CUST_ID"}}
display(us_customer_df)
# -
# [Back to Table of Contents](#toc)
# ### View data using matplotlib
#
# PixieDust is a great tool for quick visualisations, but using the Python visualisation packages directly gives you more control over the charts you create. Below is a simple example of what you can do with matplotlib.
#
#
# +
# without this the plots would be opened in a new window (not browser)
# with this instruction plots will be included in the notebook
%matplotlib inline
import matplotlib.pyplot as plt
# -
# Internally PixieDust converts the data to a Pandas DataFrame as this is what most visualisation packages use. So let's do the same here:
df = customer_df.toPandas()
df.head()
# The default plot is a line chart:
df['AGE'].plot();
# To create a plot that makes more sense for this data have a look at the [documentation](https://pandas.pydata.org/pandas-docs/stable/user_guide/visualization.html) for all options. A histogram might work better. Go ahead and change the number of bins until you think the number of bins looks right:
df['AGE'].plot.hist(bins=8);
# Change the size of the plot with `figsize`:
df['AGE'].plot.hist(bins=15,figsize=(10,5));
# The below plot shows only the womens age:
df['AGE'][df['GENDER']=='female'].plot.hist(bins=15,figsize=(10,5));
# To add the men, simply repeat the plot command with a different selection of the data:
df['AGE'][df['GENDER']=='female'].plot.hist(bins=15,figsize=(10,5));
df['AGE'][df['GENDER']=='male'].plot.hist(bins=15,figsize=(10,5));
# The above plot is difficult to read as the histograms overlap. You can fix this by changing the colours and making them transparant. To add a legend each histogram needs to be assigned to an object `ax` that is used to create a legend:
ax = df['AGE'][df['GENDER']=='female'].plot.hist(
bins=15,figsize=(10,5),alpha=0.5,color='#1A4D3B');
ax = df['AGE'][df['GENDER']=='male'].plot.hist(
bins=15,figsize=(10,5),alpha=0.5,color='#4D1A39');
ax.legend(['female','male']);
# It is easy to change pretty much everything as in the below code. This was the ugliest I could come up with. Can you make it worse?
df['AGE'].plot.hist(
bins=15,
title="Age",
legend=False,
fontsize=14,
grid=False,
linestyle='--',
edgecolor='black',
color='darkred',
linewidth=3);
# You can use `groupby()` in combination with a bar plot to visualize average age by country:
country = df['AGE'].groupby(df['COUNTRY_CODE']).mean()
ax=country.plot.bar();
ax.set_ylabel('Age');
# [Back to Table of Contents](#toc)
#
# Copyright © 2017, 2018 IBM. This notebook and its source code are released under the terms of the MIT License.
|
notebooks/part-1-analyze-customer-data.ipynb
|