code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
class Solution:
def validate_IPv4(self, IP: str) -> str:
nums = IP.split('.')
for x in nums:
# Validate integer in range (0, 255):
# 1. length of chunk is between 1 and 3
if len(x) == 0 or len(x) > 3:
return "Neither"
# 2. no extra leading zeros
# 3. only digits are allowed
# 4. less than 255
if x[0] == '0' and len(x) != 1 or not x.isdigit() or int(x) > 255:
return "Neither"
return "IPv4"
def validate_IPv6(self, IP: str) -> str:
nums = IP.split(':')
hexdigits = '0123456789abcdefABCDEF'
for x in nums:
# Validate hexadecimal in range (0, 2**16):
# 1. at least one and not more than 4 hexdigits in one chunk
# 2. only hexdigits are allowed: 0-9, a-f, A-F
if len(x) == 0 or len(x) > 4 or not all(c in hexdigits for c in x):
return "Neither"
return "IPv6"
def validIPAddress(self, IP: str) -> str:
if IP.count('.') == 3:
return self.validate_IPv4(IP)
elif IP.count(':') == 7:
return self.validate_IPv6(IP)
else:
return "Neither"
def valid_ipv4(ip):
#Length of the chunk is betweeen 1 and 3
nums=ip.split('.')
for x in nums:
#length of chunk is between 0 and 3
if len(x) == 0 or len(x) >3:
return False
#1.no extra leading zero, 2. only digits are allowed 3. less than 255
if x[0] == '0' and len(x) != 1 or not x.isdigit() or int(x) > 255:
return False
return True
print(valid_ipv4("192.168.127.12"))
|
array_strings/ipynb/.ipynb_checkpoints/valid_ipv4-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + code_folding=[]
# Standard imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# %matplotlib inline
import os
import sys
import re
import glob
import suftware as su
from scipy.stats import norm
from scipy.stats import poisson
e = np.exp(1)
pi = np.pi
def pseudo_log(x,base=e):
return np.log(x+.5)/np.log(base)
# +
in_dir = '/Users/jkinney/Dropbox/15_mpathic/20_mpathic_redo/20.08.16_mpsa_raw_data'
out_dir = '20.08.16_mpsa_data'
# Get in-file
in_file = f'{in_dir}/results.brca2_9nt_lib1_rep1.txt'
# Determine name of sample
m = re.match(".*/results.(?P<locus>[^_]+)_9nt_(?P<librep>.+).txt",in_file)
locus = m.groupdict()['locus']
librep = m.groupdict()['librep']
name = f'{locus}_{librep}'
# Set parameters
min_ct_per_bc=1
min_num_barcodes=10
num_resamps=100
min_sigma=1E-2
report_every=10
estimate_mi=True
# Create dict to record statistics
stats_dict = {}
# Load file
in_df = pd.read_csv(in_file, delimiter='\t', index_col=0)
print(f'Processing {in_file}')
# Remove extraneous columns
del in_df['mis_ct']
del in_df['lib_ct']
in_df.head()
# +
# Marginalize by splice site
data_df = in_df.groupby('ss').sum()
data_df.reset_index(inplace=True)
# Remove indices with tot_ct < 10
ix = data_df['tot_ct'] >= 10
data_df = data_df[ix]
# Sort by tot_ct
data_df.sort_values(by='tot_ct', inplace=True, ascending=False)
data_df.reset_index(inplace=True, drop=True)
# Make sequences RNA
data_df['ss'] = [ss.replace('T','U') for ss in data_df['ss']]
# Rename columns
data_df.rename(columns={'ss':'x'}, inplace=True)
# Compute y
i_n = data_df['tot_ct']
o_n = data_df['ex_ct']
y_n = np.log10((o_n+1)/(i_n+1))
data_df['y'] = y_n
# Assign to training and test sets
data_df = data_df[['tot_ct', 'ex_ct', 'y', 'x']]
# Preview dataframe
N = len(data_df)
print(f'N: {N}')
data_df.head()
# -
|
mavenn/development/20.10.13_prepare_mpsa_data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import random
import tensorflow as tf
import shutil
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
config = tf.compat.v1.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.compat.v1.InteractiveSession(config=config)
# -
def create_model():
model = keras.models.Sequential([
keras.layers.Conv2D(128, (3,3), activation='relu', input_shape=(150, 150, 3)),
keras.layers.MaxPooling2D(2,2),
keras.layers.Conv2D(64, (3,3), activation='relu'),
keras.layers.MaxPooling2D(2,2),
keras.layers.Conv2D(32, (3,3), activation='relu'),
keras.layers.MaxPooling2D(2,2),
keras.layers.Flatten(),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=RMSprop(lr=0.001), loss='binary_crossentropy', metrics=['acc'])
return model
def gen_data():
training_datagen = ImageDataGenerator(
rescale=1/255,
rotation_range=40,
width_shift_range=0.2,
height_shift_range=0.2,
shear_range=0.2,
zoom_range=0.2,
fill_mode='nearest'
)
validation_datagen = ImageDataGenerator(
rescale=1/255
)
training_generator = training_datagen.flow_from_directory(
'cat-dog-dataset/train',
target_size=(150, 150),
batch_size=32,
class_mode='binary'
)
validation_generator = validation_datagen.flow_from_directory(
'cat-dog-dataset/val',
target_size=(150, 150),
batch_size=32,
class_mode='binary'
)
return training_generator, validation_generator
callback = EarlyStopping(monitor='loss', patience=5)
training_generator, validation_generator = gen_data()
model = create_model()
history = model.fit(
training_generator,
epochs=30,
validation_data=validation_generator,
callbacks=[callback],
verbose=1
)
model.save('cats-dogs-model.h5')
# +
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.figure(figsize=(10, 6))
plt.plot(epochs, acc, 'r', label='Training Accuracy')
plt.plot(epochs, val_acc, 'b', label='Validation Accuracy')
plt.plot(epochs, loss, 'g', label='Training Loss')
plt.plot(epochs, val_loss, 'y', label='Validation Loss')
plt.title('Traing and Validation, Accuracy and Loss')
plt.legend(loc=0)
plt.show()
# -
|
Deep_Learning/Early_Stopping.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.8.5 64-bit
# name: python3
# ---
# # SpaceX EDX SQL Server
# ## Objectives
#
# Writing and executing SQL queries to solve the questions being asked.
#
# #### The dataset used to be queried can be found below.
#
# In many cases the dataset to be analyzed is available as a .CSV (comma separated values) file, perhaps on the internet. Click on the link below to download and save the dataset (.CSV file):
#
# <a href="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_2/data/Spacex.csv?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01" target="_blank">SpaceX DataSet</a>
#
#
# ### Connect to the database
#
# Let us first load the SQL extension and establish a connection with the database
#
# As <code> IBM's DB2 guidelines on this notebook doesnt work </code> I will implement the SQL queries using my normal Microsoft SQL Server instance using my own library <code> 'sqlserver' </code> for other info on my libary visit https://github.com/ADGVLOGS/pythonsqlserverclass
#
# !pip install sqlserver
# ### Initialization
#
# the .sqlserver() object parameters stands for
# (ip,portnumber,databasename,username,password)
import sqlserver as ss
db = ss.sqlserver('localhost','1433','SpaceX','admin','admin')
# #### Display the names of the unique launch sites in the space mission
#
db.GetRecordsOfColumn('select DISTINCT Launch_Site from tblSpaceX','Launch_Site')
# #### Display 5 records where launch sites begin with the string 'KSC'
#
# +
import pyodbc
import pandas as pd
import numpy as np
conn = pyodbc.connect('Driver={SQL Server};'
'Server=localhost;'
'Database=SpaceX;'
'User ID=admin;Password=<PASSWORD>;')
cursor = conn.cursor()
cursor.execute("select TOP 5 * from tblSpaceX WHERE Launch_Site LIKE 'KSC%'")
columns = [column[0] for column in cursor.description]
results = []
for row in cursor.fetchall():
results.append(dict(zip(columns, row)))
df = pd.DataFrame.from_dict(results)
df
# -
# #### Display the total payload mass carried by boosters launched by NASA (CRS)
#
TPM = db.GetRecordsOfColumn("select SUM(PAYLOAD_MASS_KG_) TotalPayloadMass from tblSpaceX where Customer = 'NASA (CRS)'",'TotalPayloadMass')
ndf= pd.DataFrame(TPM)
ndf.columns = ['Total Payload Mass']
ndf
# #### Display average payload mass carried by booster version F9 v1.1
#
APM = db.GetRecordsOfColumn("select AVG(PAYLOAD_MASS_KG_) AveragePayloadMass from tblSpaceX where Booster_Version = 'F9 v1.1'",'AveragePayloadMass')
ndf= pd.DataFrame(APM)
ndf.columns = ['Average Payload Mass']
ndf
# #### List the date where the succesful landing outcome in drone ship was acheived.
#
SLO = db.GetRecordsOfColumn("select MIN(Date) SLO from tblSpaceX where Landing_Outcome = 'Success (drone ship)'",'SLO')
ndf= pd.DataFrame(SLO)
ndf.columns = ['Date which first Successful landing outcome in drone ship was acheived.']
ndf
# #### List the names of the boosters which have success in ground pad and have payload mass greater than 4000 but less than 6000
#
SLO = db.GetRecordsOfColumn("select Booster_Version from tblSpaceX where Landing_Outcome = 'Success (ground pad)' AND Payload_MASS_KG_ > 4000 AND Payload_MASS_KG_ < 6000",'Booster_Version')
ndf= pd.DataFrame(SLO)
ndf.columns = ['Date which first Successful landing outcome in drone ship was acheived.']
ndf
# #### List the total number of successful and failure mission outcomes
#
# +
conn = pyodbc.connect('Driver={SQL Server};'
'Server=localhost;'
'Database=SpaceX;'
'User ID=admin;Password=<PASSWORD>;')
cursor = conn.cursor()
cursor.execute("SELECT(SELECT Count(Mission_Outcome) from tblSpaceX where Mission_Outcome LIKE '%Success%') as Successful_Mission_Outcomes,(SELECT Count(Mission_Outcome) from tblSpaceX where Mission_Outcome LIKE '%Failure%') as Failure_Mission_Outcomes")
columns = [column[0] for column in cursor.description]
results = []
for row in cursor.fetchall():
results.append(dict(zip(columns, row)))
df = pd.DataFrame.from_dict(results)
df
# -
# #### List the names of the booster_versions which have carried the maximum payload mass. Use a subquery
#
# +
conn = pyodbc.connect('Driver={SQL Server};'
'Server=localhost;'
'Database=SpaceX;'
'User ID=admin;Password=<PASSWORD>;')
cursor = conn.cursor()
cursor.execute("SELECT DISTINCT Booster_Version, MAX(PAYLOAD_MASS_KG_) AS [Maximum Payload Mass] FROM tblSpaceX GROUP BY Booster_Version ORDER BY [Maximum Payload Mass] DESC")
columns = [column[0] for column in cursor.description]
results = []
for row in cursor.fetchall():
results.append(dict(zip(columns, row)))
df = pd.DataFrame.from_dict(results)
df
# -
# #### List the records which will display the month names, succesful landing_outcomes in ground pad ,booster versions, launch_site for the months in year 2017
#
# +
conn = pyodbc.connect('Driver={SQL Server};'
'Server=localhost;'
'Database=SpaceX;'
'User ID=admin;Password=<PASSWORD>;')
cursor = conn.cursor()
cursor.execute("SELECT DateName( month , DateAdd( month , MONTH(CONVERT(date,Date, 105)) , 0 ) - 1 ) as Month, Booster_Version, Launch_Site, Landing_Outcome FROM tblSpaceX WHERE (Landing_Outcome LIKE N'%Success%') AND YEAR(CONVERT(date,Date, 105)) = '2017'")
columns = [column[0] for column in cursor.description]
results = []
for row in cursor.fetchall():
results.append(dict(zip(columns, row)))
df = pd.DataFrame.from_dict(results)
df
# -
# #### Rank the count of successful landing_outcomes between the date 2010-06-04 and 2017-03-20 in descending order.
#
# +
sl = db.GetRecordsOfColumn("SELECT COUNT(Landing_Outcome) AS sl FROM dbo.tblSpaceX WHERE (Landing_Outcome LIKE '%Success%') AND (Date >'04-06-2010') AND (Date < '20-03-2017')",'sl')
ndf= pd.DataFrame(sl)
ndf.columns = ['Successful Landing Outcomes Between 2010-06-04 and 2017-03-20']
ndf
# -
# ### Author : <NAME>
|
EDA SQL.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # EPR data processing
#
# An example user-defined function for processing EPR data with the DNPLab package.
#
# For the function below the call would look something like,
#
#
"""
lsobject = ls.start(
parent_directory,
skip=[".DSC", ".YGF", ".par"], # otherwise duplicates
classifiers=["max_loc", "frequency"],
function=process_EPR.proc_epr,
function_args={},
)
lsobject.drive()
"""
# parent_directory contains Bruker EPR data. Add patterns, skip, date searching, etc.
# according to the lsframe docs. The function_args are empty in this case. Since DTA
# and spc files come with companion DSC, YGF, or par files and DNPLab uses any of these,
# skip these files to avoid duplicates.
# Import DNPLab and any other packages that may be needed for your function,
#
#
import dnplab as dnp
import numpy as np
# The function accepts a path to an EPR spectrum file and returns the field value where the spectrum is maximum and the frequency. The function returns zeros where errors are encountered.
#
#
def proc_epr(path, args):
try:
data = dnp.dnpImport.load(path)
if len(data.dims) == 1 and "frequency" in data.attrs.keys():
return [
np.argmax(data.values, axis=0) / len(data.values),
data.attrs["frequency"],
]
else:
return [0, 0]
except:
return [0, 0]
|
docs/source/auto_examples/process_EPR.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. Data Collection
# #### 따로 추가할 데이터가 있으면 여기서 wget 하거나 jupyter 자체에서 파일 upload 가능
# !ls
# !cat 0.data/SampleList.sh
# !ls 0.data/
# !ls 1.Fastq_dump/
# # 2. Run the Pipeline
# ### 다음과 같은 과정으로 진행되는 Snakemake pipeline 작성
# #### 1. Trimmomatic으로 Read Quality Control 및 Adapter 제거
# #### 2. Bowtie2로 Reference Mapping
# #### 3. Picard tool로 BAM 파일 processing (PCR duplicate 제거, Paired end read 보정)
# #### 4. GATK pipeline으로 Variant Calling (InDel local realign, base quality recalibration, haplotypecaller)
# #### 5. GATK pipeline으로 SNP 추출 및 Quality Filtering (QUAL, QD, MQ, FS 필터링)
# #### 6. VCFtools로 최종적인 SNP filtering (Missing Genotype, MAF, Read depth)
# !cat Snakefile
# !snakemake --allowed-rules renameFinalVCF
# !snakemake --rulegraph > rule.txt
# !dot -Tpng rule.txt > rule.png
from IPython.display import Image
Image("rule.png")
# # 3. VCF에서 MySQL DB 연동
# #### 각 loci의 위치 정보 및 alternative allele의 수와 같은 데이터를 그대로 보존하기 위하여 VCF에서 바로 MySQL DB로 변환
# ### 3.1. MySQL DB 연결
import pymysql
conn = pymysql.connect(host="localhost", user="hs0517", password="<PASSWORD>", db="2018_BI3_hs0517", charset="utf8")
curs = conn.cursor()
curs.execute("SHOW DATABASES;")
print("Current DB :", curs.fetchall())
curs.execute("SHOW TABLES;")
print("Tables on DB :", curs.fetchall())
# ### 3.2. SNP table 생성
# #### DB 내 table은 다음과 같은 schema로 구성됨
#
# #### 1. metadata : SRA entry, Sample name, sex, population으로 구성
# #### 2. genotype : SRA entry, chromosome, position, number of alternative alleles(AAcount)로 구성
sql = """
CREATE TABLE IF NOT EXISTS metadata
(
SRA_entry VARCHAR(40) NOT NULL,
Sample_name VARCHAR(40) NOT NULL,
Sex VARCHAR(10),
Population VARCHAR(10) NOT NULL,
PRIMARY KEY(SRA_entry)
);
"""
curs.execute(sql)
conn.commit()
sql = """
CREATE TABLE IF NOT EXISTS genotype
(
Chrom INT UNSIGNED,
POS INT UNSIGNED,
Ref CHAR(1),
Alt CHAR(1)
);
"""
curs.execute(sql)
conn.commit()
# ### 3.3. DB 내용 채우기
# #### metadata 채우기
import pandas as pd
#Sample Metadata
df = pd.DataFrame({"name":["NA11995", "NA12004", "NA07056", "NA12156", "NA12815", "NA18531", "NA18527", "NA18618", "NA18640", "NA18525", "NA18939", "NA18957", "NA18992", "NA18941", "NA18998"],
"sex":["Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female", "Female"],
"population":["CEU", "CEU", "CEU", "CEU", "CEU", "CHB", "CHB", "CHB", "CHB", "CHB", "JPT", "JPT", "JPT", "JPT", "JPT"],
"sra":["SRR766010", "SRR766059", "SRR764718", "SRR764691", "SRR716646", "SRR715903", "SRR718069", "SRR707197", "SRR701476", "SRR715904", "SRR766031", "SRR768534", "SRR716428", "SRR766029", "SRR766013"]})
for idx, row in df.iterrows():
# sra, name, sex, population
sql = "INSERT IGNORE INTO metadata VALUES(\"{}\",\"{}\",\"{}\",\"{}\");".format(row[3], row[0], row[1], row[2])
curs.execute(sql)
conn.commit()
# #### VCF 파싱해서 genotype table 채우기
from pysam import VariantFile
VCFfile = VariantFile("6.VCF/final.vcf")
# #### Sample에 대한 column 만들어주기
for sample in VCFfile.header.samples:
sql = "ALTER TABLE genotype ADD COLUMN {} INT;".format(sample)
curs.execute(sql)
conn.commit()
curs.execute("DESCRIBE genotype;")
print(curs.fetchall())
for row in VCFfile.fetch():
sex_chrom = {"X":23, "Y":24}
if (row.chrom not in [str(i) for i in range(1, 23)]) and (row.chrom not in sex_chrom): continue
chrom = sex_chrom[row.chrom] if row.chrom in sex_chrom else row.chrom
pos = row.pos
AAcount = {}
for sample in VCFfile.header.samples:
AAcount[sample] = row.samples[sample]["GT"].count(1)
# Chrom, Pos, Ref, Alt, Sample1, Sample2, ...
sql = "INSERT IGNORE INTO genotype (Chrom, POS, Ref, Alt, " + ",".join([sample for sample in VCFfile.header.samples]) + ")" + \
" VALUES({},{},\"{}\",\"{}\",".format(chrom, pos, row.ref, row.alts[0]) + \
",".join([str(AAcount[sample]) for sample in VCFfile.header.samples]) + ");"
curs.execute(sql)
conn.commit()
curs.execute("select distinct Chrom from genotype;")
print(curs.fetchall())
# ### 3.4. schema visualize 하여 확인
# !java -jar schemaSpy_5.0.0.jar -t mysql -u hs0517 -p SNP -host localhost -db 2018_BI3_hs0517 -o ./7.DBschema -dp /usr/share/java/mysql-connector-java.jar
# # 4. PCA
# ### 조건에 따라 다른 Fasta를 만들 수 있도록 Query (Chrom, Pos, Sample 등)
# #### MySQL table에 Query를 보내 0, 1, 2 coding된 데이터를 얻어옴
TargetSRA = ['SRR701476', 'SRR707197', 'SRR715903', 'SRR715904', 'SRR716428', 'SRR716646', 'SRR718069', \
'SRR764691', 'SRR764718', 'SRR766010', 'SRR766013', 'SRR766029', 'SRR766031', 'SRR766059', 'SRR768534']
TargetChrom = [1, 2]
TargetPos = [(1, 100000000), (5000000, 20000000)]
# +
GenoMatrix = pd.DataFrame(columns=TargetSRA)
for Chrom in TargetChrom:
for Pos in TargetPos:
# By ascending order of POS
curs.execute("select {} from genotype where Chrom={} AND POS>{} AND POS<{} ORDER BY POS;".format(",".join(TargetSRA), Chrom, Pos[0], Pos[1]))
sample_genotype = curs.fetchall()
for i in range(len(GenoMatrix.index), len(sample_genotype)):
GenoMatrix.loc[i] = list(sample_genotype[i])
# -
GenoMatrix.head
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
pca = PCA(n_components=5)
pca.fit(GenoMatrix)
pca.components_
# ### PVE (Percentage of Variance Explained)
print('explained variance ratio (first five components): %s'
% str(pca.explained_variance_ratio_))
# ### Figure
import seaborn as sns
pc_df = pd.DataFrame(pca.components_.transpose(),
columns = ['PC1', 'PC2','PC3','PC4', 'PC5'])
sns.lmplot( x="PC1", y="PC2",
data=pc_df,
fit_reg=False,
legend=True,
scatter_kws={"s": 80}) # specify the point size
# # 5. MySQL에서 Fasta 포맷으로 추출
# #### Fasta 작성 시 몇가지 정보 손실이 불가피
# #### 대표적으로 Chromosome, Position 등의 정보가 손실됨
curs.execute("select sra_entry from metadata;")
SRA_entry = [SRA_name[0] for SRA_name in curs.fetchall()]
SRA_entry
# ### 조건에 따라 다른 Fasta를 만들 수 있도록 Query (Chrom, Pos, Sample 등)
TargetSRA = ['SRR701476', 'SRR707197', 'SRR715903', 'SRR715904', 'SRR716428', 'SRR716646', 'SRR718069', \
'SRR764691', 'SRR764718', 'SRR766010', 'SRR766013', 'SRR766029', 'SRR766031', 'SRR766059', 'SRR768534']
TargetChrom = [1]
TargetPos = [(1, 100000000)]
# +
SRASequence = {}
for Chrom in TargetChrom:
for Pos in TargetPos:
for SRA in TargetSRA:
# By ascending order of POS
curs.execute("select Ref, Alt, {} from genotype where Chrom={} AND POS>{} AND POS<{} ORDER BY POS;".format(SRA, Chrom, Pos[0], Pos[1]))
sample_genotype = curs.fetchall()
SRASequence.setdefault(SRA, "")
for locus in sample_genotype:
SRASequence[SRA] += locus[0] if locus[2] == 0 else locus[1]
# +
outFastaName = "8.Fasta/SNPseq.fa"
with open(outFastaName, "w") as outfile:
for SRA in SRASequence:
print(">", SRA, sep="", file=outfile)
print(SRASequence[SRA], file=outfile)
# -
# # 6. Phylogenetic 분석
# ### 6.1. FastTree ML tree with bootstrap value
# #### 6.1.1. Fasta 포맷에서 Phylip 및 nexus 포맷으로 변경 (bootstrap하기 위해)
# +
import sys, os, glob
def Read_fasta_sequence(sFname):
Infile = open(sFname, "r")
Out_dic = {}
for sLine in Infile:
if sLine.startswith(">"):
sSample = sLine.strip()[1:]
Out_dic.setdefault(sSample, "")
else:
Out_dic[sSample] += sLine.strip()
Infile.close()
return Out_dic
def Fasta_to_phylip(sFname, Seq_dic):
Sample_list = sorted(Seq_dic.keys())
nSeq_length = len(Seq_dic[Sample_list[0]])
Outfile = open(sFname.replace(".fa",".phylip"), "w")
Outfile.write(str(len(Sample_list))+" "+str(nSeq_length)+"\n")
for i in range(0, nSeq_length, 100):
for sSample in Sample_list:
sTemp_seq = Seq_dic[sSample][i:i+100]
sTemp_list = [sTemp_seq[j:j+20] for j in range(0, len(sTemp_seq), 20)]
if i==0:
Outfile.write(sSample.ljust(15, " ")+" ".join(sTemp_list)+"\n")
else:
Outfile.write(" "*15+" ".join(sTemp_list)+"\n")
Outfile.write("\n")
Outfile.close()
def Fasta_to_nexus(sFname, Seq_dic):
Sample_list = sorted(Seq_dic.keys())
nSeq_length = len(Seq_dic[Sample_list[0]])
Outfile = open(sFname.replace(".fa",".nexus"), "w")
Outfile.write("#NEXUS"+"\n"\
"BEGIN DATA;"+"\n"\
"dimensions ntax="+str(len(Sample_list))+" nchar="+str(nSeq_length)+";"+"\n"\
"format missing=?"+"\n"\
"symbols=\"ABCDEFGHIKLMNPQRSTUVWXYZ\""+"\n"\
"interleave datatype=DNA gap= -;"+"\n"+"\n"\
"matrix"+"\n")
for i in range(0, nSeq_length, 100):
for sSample in Sample_list:
sTemp_seq = Seq_dic[sSample][i:i+100]
sTemp_list = [sTemp_seq[j:j+20] for j in range(0, len(sTemp_seq), 20)]
Outfile.write(sSample.ljust(15, " ")+" ".join(sTemp_list)+"\n")
Outfile.write("\n")
Outfile.write(";"+"\n")
Outfile.write("END;"+"\n")
sFlist = ["8.Fasta/SNPseq.fa"]
#print sFlist
for i in sFlist:
#print i
Seq_dic = Read_fasta_sequence(i)
Fasta_to_phylip(i, Seq_dic)
Fasta_to_nexus(i, Seq_dic)
# -
# #### 6.1.2. FastTree 실행 (bootstrap 100)
# !./FastTreeMP -n 100 < 8.Fasta/SNPseq.phylip > 9.FastTree/TreeOut
# #### 6.1.3. FigTree로 Visualization
# !java -jar FigTree_v1.4.3/lib/figtree.jar -graphic PNG -width 320 -height 320 9.FastTree/TreeOut 9.FastTree/TreeOut.png
Image("9.FastTree/TreeOut.png")
# ### 6.2. RAxML ML tree with bootstrap value
# #### 6.2.1. RAxML run
# !standard-RAxML/raxmlHPC-PTHREADS-SSE3 -T 24 -m GTRCAT -s 8.Fasta/SNPseq.phylip -n TreeOut --bootstop-perms=100 -p 9
# !mv RAxML*TreeOut 10.RAxML
# #### 6.2.2. FigTree로 Visualization
# !java -jar FigTree_v1.4.3/lib/figtree.jar -graphic PNG -width 320 -height 320 10.RAxML/RAxML_result.TreeOut 10.RAxML/TreeOut.png
Image("10.RAxML/TreeOut.png")
# ### 6.3. Phylip NJ tree with bootstrap value
# #### 6.3.1. Seqboot
# !printf '8.Fasta/SNPseq.phylip\nY\n9\n' | phylip seqboot
# !mv outfile 11.Phylip/seqbootOutfile
# #### 6.3.2. DNAdist
# !printf '11.Phylip/seqbootOutfile\nD\nT\n4\nM\nD\n100\nY\n' | phylip dnadist
# !mv outfile 11.Phylip/dnadistOutfile
# #### 6.3.3. Neighbor
# !printf '11.Phylip/dnadistOutfile\nM\n100\n9\nY\n' | phylip neighbor
# !mv outtree 11.Phylip/neighborOuttree
# !mv outfile 11.Phylip/neighborOutfile
# #### 6.3.4. Consense
# !printf '11.Phylip/neighborOuttree\nY\n' | phylip consense
# !mv outtree 11.Phylip/consenseTree
# !mv outfile 11.Phylip/consenseFile
# #### 6.3.5. FigTree로 Visualization
# !java -jar FigTree_v1.4.3/lib/figtree.jar -graphic PNG -width 320 -height 320 11.Phylip/neighborOuttree 11.Phylip/TreeOut.png
Image("11.Phylip/TreeOut.png")
|
.ipynb_checkpoints/SNP_pipeline-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .sos
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: SoS
# language: sos
# name: sos
# ---
# + [markdown] kernel="SoS" tags=[]
# # Error handling
# + [markdown] kernel="SoS" tags=[]
# * **Difficulty level**: easy
# * **Time need to lean**: 10 minutes or less
# * **Key points**:
# * Option `-e` specifies how sos handled runtime options
# * `-e default` terminates the current step (and branch), but allowes other branches to complete.
# * `-e ignore` ignores errors and allow current and other branches to complete.
# * `-e abort` terminates the current and all running steps immediately.
# + [markdown] kernel="SoS" tags=[]
# Runtime errors happen from time to time. Depending on the nature of errors you can terminate the entire workflow brutally, gentaly, or ignore all errors.
# + [markdown] kernel="SoS" tags=[]
# ## Four error handling modes
# + [markdown] kernel="SoS" tags=[]
# Let us assume that an error happens at a substep of step, and we need to decide
#
# 1. Should running steps or substeps be terminates immediately.
# 2. Should the rest of the substeps of the failing step be executed if they have not been submitted.
# 3. Should the unaffected branches of the DAG be executed while allowing the branch with failed step to terminate.
# 4. Should SoS try to execute the steps after the failed step.
#
# The choices to these questions are controlled by the following error modes, specified with option `-e` to command `sos run` (or magics `%run` etc in SoS Notebook):
#
# | mode | running substeps | pending substeps | following steps | unaffected branches | exit status |
# | -- | --| -- | -- | -- | -- |
# | **`default`** | allow complete | allow complete | canceled | allow complete | failed |
# | **`ignore`** | allow complete | allow complete | allow complete | allow complete | success |
# | **`abort`** | aborted | canceled | canceled | canceled | failed |
# + [markdown] kernel="SoS" tags=[]
# Let us use the following example workflow to demonstrate the different modes. In this workflow,
#
# 1. Step `10` has three substeps that are executed in parallel for 2 seconds. The second substep will generate an error at the end of the step.
# 2. Step `20` follows step `10` and will execute three substeps for 2 seconds.
# 3. Step `30` has `input: None` so it will start at the same time as step `10`. It is supposed to sleep 3 seconds.
# 4. Step `40` will be executed after step `30` for 1 second.
# + kernel="SoS" tags=[]
# %save -f test_error_mode.sos
[global]
import time
[10]
input: for_each=dict(i=range(3))
print(f'Substep 10.{_index} started')
time.sleep(2)
fail_if(i==1, 'Substep terminated')
print(f'Substep 10.{_index} completed')
[20]
print(f'Substep 20.{_index} started')
time.sleep(2)
print(f'Substep 20.{_index} completed')
[30]
input: None
print(f'Step 30 started')
time.sleep(3)
print(f'Step 30 completed')
[40]
print(f'Step 40 started')
time.sleep(1)
print(f'Step 40 completed')
# + [markdown] kernel="SoS" tags=[]
# The execution of this workflow in different error handling modes are depicated as follows:
#
# <p align="center">
# <img src="https://vatlab.github.io/sos-docs/doc/media/error_handling.png" width="800px">
# </p>
# + [markdown] kernel="SoS" tags=[]
# ## `default` error mode
# + kernel="SoS" tags=[]
!sos run test_error_mode -v0
# + [markdown] kernel="SoS" tags=[]
# In the `default` error-handling mode, three substeps of step 10 and step 30 are started at the same time. After substep 10.1 failed, step 10 is stopped, but step 30 is allowed to completed, followed by step 40 because it is independent of step 10. Step 20 is canceled due to the error from step 10.
# + [markdown] kernel="SoS" tags=[]
# ## `ignore` error mode
# + kernel="SoS" tags=[]
!sos run test_error_mode -e ignore -v0
# + [markdown] kernel="SoS" tags=[]
# In the `ignore` error-handling mode, three substeps of step 10 and step 30 are started at the same time. After substep 10.1 failed, it produces an `step_output` with an invalid substep. The workflow continues to execute. The substep `20.1` is not executed, but the rest of two substeps are executed successfully. The other branch of the DAG (steps `30` and `40`) are not affected by the error. The workflow is considered to be executed successfully in the end despite of the error.
# + [markdown] kernel="SoS" tags=[]
# ## `abort` error mode
# + kernel="SoS" tags=[]
!sos run test_error_mode -e abort -v0
# + [markdown] kernel="SoS" tags=[]
# In the `abort` error-handling mode, three substeps of step 10 and step 30 are started at the same time. After substep 10.1 failed, it stops step 10, as well as the step 30 which are still running. Steps 20 and 40 are cancelled as well.
|
src/user_guide/error_handling.ipynb
|
# ##### Copyright 2021 Google LLC.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
#
# # steel_mill_slab_sat
# <table align="left">
# <td>
# <a href="https://colab.research.google.com/github/google/or-tools/blob/master/examples/notebook/examples/steel_mill_slab_sat.ipynb"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/colab_32px.png"/>Run in Google Colab</a>
# </td>
# <td>
# <a href="https://github.com/google/or-tools/blob/master/examples/python/steel_mill_slab_sat.py"><img src="https://raw.githubusercontent.com/google/or-tools/master/tools/github_32px.png"/>View source on GitHub</a>
# </td>
# </table>
# First, you must install [ortools](https://pypi.org/project/ortools/) package in this colab.
# !pip install ortools
# +
# #!/usr/bin/env python3
# Copyright 2010-2021 Google LLC
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
"""Solves the Stell Mill Slab problem with 4 different techniques."""
# overloaded sum() clashes with pytype.
# pytype: disable=wrong-arg-types
import collections
import time
from absl import app
from absl import flags
from ortools.linear_solver import pywraplp
from ortools.sat.python import cp_model
FLAGS = flags.FLAGS
flags.DEFINE_integer('problem', 2, 'Problem id to solve.')
flags.DEFINE_boolean('break_symmetries', True,
'Break symmetries between equivalent orders.')
flags.DEFINE_string(
'solver', 'mip_column', 'Method used to solve: sat, sat_table, sat_column, '
'mip_column.')
def build_problem(problem_id):
"""Build problem data."""
if problem_id == 0:
capacities = [
0, 12, 14, 17, 18, 19, 20, 23, 24, 25, 26, 27, 28, 29, 30, 32, 35,
39, 42, 43, 44
]
num_colors = 88
num_slabs = 111
orders = [
(4, 1), # (size, color)
(22, 2),
(9, 3),
(5, 4),
(8, 5),
(3, 6),
(3, 4),
(4, 7),
(7, 4),
(7, 8),
(3, 6),
(2, 6),
(2, 4),
(8, 9),
(5, 10),
(7, 11),
(4, 7),
(7, 11),
(5, 10),
(7, 11),
(8, 9),
(3, 1),
(25, 12),
(14, 13),
(3, 6),
(22, 14),
(19, 15),
(19, 15),
(22, 16),
(22, 17),
(22, 18),
(20, 19),
(22, 20),
(5, 21),
(4, 22),
(10, 23),
(26, 24),
(17, 25),
(20, 26),
(16, 27),
(10, 28),
(19, 29),
(10, 30),
(10, 31),
(23, 32),
(22, 33),
(26, 34),
(27, 35),
(22, 36),
(27, 37),
(22, 38),
(22, 39),
(13, 40),
(14, 41),
(16, 27),
(26, 34),
(26, 42),
(27, 35),
(22, 36),
(20, 43),
(26, 24),
(22, 44),
(13, 45),
(19, 46),
(20, 47),
(16, 48),
(15, 49),
(17, 50),
(10, 28),
(20, 51),
(5, 52),
(26, 24),
(19, 53),
(15, 54),
(10, 55),
(10, 56),
(13, 57),
(13, 58),
(13, 59),
(12, 60),
(12, 61),
(18, 62),
(10, 63),
(18, 64),
(16, 65),
(20, 66),
(12, 67),
(6, 68),
(6, 68),
(15, 69),
(15, 70),
(15, 70),
(21, 71),
(30, 72),
(30, 73),
(30, 74),
(30, 75),
(23, 76),
(15, 77),
(15, 78),
(27, 79),
(27, 80),
(27, 81),
(27, 82),
(27, 83),
(27, 84),
(27, 79),
(27, 85),
(27, 86),
(10, 87),
(3, 88)
]
elif problem_id == 1:
capacities = [0, 17, 44]
num_colors = 23
num_slabs = 30
orders = [
(4, 1), # (size, color)
(22, 2),
(9, 3),
(5, 4),
(8, 5),
(3, 6),
(3, 4),
(4, 7),
(7, 4),
(7, 8),
(3, 6),
(2, 6),
(2, 4),
(8, 9),
(5, 10),
(7, 11),
(4, 7),
(7, 11),
(5, 10),
(7, 11),
(8, 9),
(3, 1),
(25, 12),
(14, 13),
(3, 6),
(22, 14),
(19, 15),
(19, 15),
(22, 16),
(22, 17),
(22, 18),
(20, 19),
(22, 20),
(5, 21),
(4, 22),
(10, 23)
]
elif problem_id == 2:
capacities = [0, 17, 44]
num_colors = 15
num_slabs = 20
orders = [
(4, 1), # (size, color)
(22, 2),
(9, 3),
(5, 4),
(8, 5),
(3, 6),
(3, 4),
(4, 7),
(7, 4),
(7, 8),
(3, 6),
(2, 6),
(2, 4),
(8, 9),
(5, 10),
(7, 11),
(4, 7),
(7, 11),
(5, 10),
(7, 11),
(8, 9),
(3, 1),
(25, 12),
(14, 13),
(3, 6),
(22, 14),
(19, 15),
(19, 15)
]
elif problem_id == 3:
capacities = [0, 17, 44]
num_colors = 8
num_slabs = 10
orders = [
(4, 1), # (size, color)
(22, 2),
(9, 3),
(5, 4),
(8, 5),
(3, 6),
(3, 4),
(4, 7),
(7, 4),
(7, 8),
(3, 6)
]
return (num_slabs, capacities, num_colors, orders)
class SteelMillSlabSolutionPrinter(cp_model.CpSolverSolutionCallback):
"""Print intermediate solutions."""
def __init__(self, orders, assign, load, loss):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__orders = orders
self.__assign = assign
self.__load = load
self.__loss = loss
self.__solution_count = 0
self.__all_orders = range(len(orders))
self.__all_slabs = range(len(assign[0]))
self.__start_time = time.time()
def on_solution_callback(self):
"""Called on each new solution."""
current_time = time.time()
objective = sum(self.Value(l) for l in self.__loss)
print('Solution %i, time = %f s, objective = %i' %
(self.__solution_count, current_time - self.__start_time,
objective))
self.__solution_count += 1
orders_in_slab = [[
o for o in self.__all_orders if self.Value(self.__assign[o][s])
] for s in self.__all_slabs]
for s in self.__all_slabs:
if orders_in_slab[s]:
line = ' - slab %i, load = %i, loss = %i, orders = [' % (
s, self.Value(self.__load[s]), self.Value(self.__loss[s]))
for o in orders_in_slab[s]:
line += '#%i(w%i, c%i) ' % (o, self.__orders[o][0],
self.__orders[o][1])
line += ']'
print(line)
def steel_mill_slab(problem, break_symmetries):
"""Solves the Steel Mill Slab Problem."""
### Load problem.
(num_slabs, capacities, num_colors, orders) = build_problem(problem)
num_orders = len(orders)
num_capacities = len(capacities)
all_slabs = range(num_slabs)
all_colors = range(num_colors)
all_orders = range(len(orders))
print('Solving steel mill with %i orders, %i slabs, and %i capacities' %
(num_orders, num_slabs, num_capacities - 1))
# Compute auxiliary data.
widths = [x[0] for x in orders]
colors = [x[1] for x in orders]
max_capacity = max(capacities)
loss_array = [
min(x for x in capacities if x >= c) - c for c in range(max_capacity +
1)
]
max_loss = max(loss_array)
orders_per_color = [
[o for o in all_orders if colors[o] == c + 1] for c in all_colors
]
unique_color_orders = [
o for o in all_orders if len(orders_per_color[colors[o] - 1]) == 1
]
### Model problem.
# Create the model and the decision variables.
model = cp_model.CpModel()
assign = [[
model.NewBoolVar('assign_%i_to_slab_%i' % (o, s)) for s in all_slabs
] for o in all_orders]
loads = [
model.NewIntVar(0, max_capacity, 'load_of_slab_%i' % s)
for s in all_slabs
]
color_is_in_slab = [[
model.NewBoolVar('color_%i_in_slab_%i' % (c + 1, s)) for c in all_colors
] for s in all_slabs]
# Compute load of all slabs.
for s in all_slabs:
model.Add(sum(assign[o][s] * widths[o] for o in all_orders) == loads[s])
# Orders are assigned to one slab.
for o in all_orders:
model.AddExactlyOne(assign[o])
# Redundant constraint (sum of loads == sum of widths).
model.Add(sum(loads) == sum(widths))
# Link present_colors and assign.
for c in all_colors:
for s in all_slabs:
for o in orders_per_color[c]:
model.AddImplication(assign[o][s], color_is_in_slab[s][c])
model.AddImplication(color_is_in_slab[s][c].Not(),
assign[o][s].Not())
# At most two colors per slab.
for s in all_slabs:
model.Add(sum(color_is_in_slab[s]) <= 2)
# Project previous constraint on unique_color_orders
for s in all_slabs:
model.Add(sum(assign[o][s] for o in unique_color_orders) <= 2)
# Symmetry breaking.
for s in range(num_slabs - 1):
model.Add(loads[s] >= loads[s + 1])
# Collect equivalent orders.
width_to_unique_color_order = {}
ordered_equivalent_orders = []
for c in all_colors:
colored_orders = orders_per_color[c]
if not colored_orders:
continue
if len(colored_orders) == 1:
o = colored_orders[0]
w = widths[o]
if w not in width_to_unique_color_order:
width_to_unique_color_order[w] = [o]
else:
width_to_unique_color_order[w].append(o)
else:
local_width_to_order = {}
for o in colored_orders:
w = widths[o]
if w not in local_width_to_order:
local_width_to_order[w] = []
local_width_to_order[w].append(o)
for w, os in local_width_to_order.items():
if len(os) > 1:
for p in range(len(os) - 1):
ordered_equivalent_orders.append((os[p], os[p + 1]))
for w, os in width_to_unique_color_order.items():
if len(os) > 1:
for p in range(len(os) - 1):
ordered_equivalent_orders.append((os[p], os[p + 1]))
# Create position variables if there are symmetries to be broken.
if break_symmetries and ordered_equivalent_orders:
print(' - creating %i symmetry breaking constraints' %
len(ordered_equivalent_orders))
positions = {}
for p in ordered_equivalent_orders:
if p[0] not in positions:
positions[p[0]] = model.NewIntVar(0, num_slabs - 1,
'position_of_slab_%i' % p[0])
model.AddMapDomain(positions[p[0]], assign[p[0]])
if p[1] not in positions:
positions[p[1]] = model.NewIntVar(0, num_slabs - 1,
'position_of_slab_%i' % p[1])
model.AddMapDomain(positions[p[1]], assign[p[1]])
# Finally add the symmetry breaking constraint.
model.Add(positions[p[0]] <= positions[p[1]])
# Objective.
obj = model.NewIntVar(0, num_slabs * max_loss, 'obj')
losses = [model.NewIntVar(0, max_loss, 'loss_%i' % s) for s in all_slabs]
for s in all_slabs:
model.AddElement(loads[s], loss_array, losses[s])
model.Add(obj == sum(losses))
model.Minimize(obj)
### Solve model.
solver = cp_model.CpSolver()
solver.parameters.num_search_workers = 8
objective_printer = cp_model.ObjectiveSolutionPrinter()
status = solver.Solve(model, objective_printer)
### Output the solution.
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
print(
'Loss = %i, time = %f s, %i conflicts' %
(solver.ObjectiveValue(), solver.WallTime(), solver.NumConflicts()))
else:
print('No solution')
def collect_valid_slabs_dp(capacities, colors, widths, loss_array):
"""Collect valid columns (assign, loss) for one slab."""
start_time = time.time()
max_capacity = max(capacities)
valid_assignment = collections.namedtuple('valid_assignment',
'orders load colors')
all_valid_assignments = [valid_assignment(orders=[], load=0, colors=[])]
for order_id in range(len(colors)):
new_width = widths[order_id]
new_color = colors[order_id]
new_assignments = []
for assignment in all_valid_assignments:
if assignment.load + new_width > max_capacity:
continue
new_colors = list(assignment.colors)
if new_color not in new_colors:
new_colors.append(new_color)
if len(new_colors) > 2:
continue
new_assignment = valid_assignment(orders=assignment.orders +
[order_id],
load=assignment.load + new_width,
colors=new_colors)
new_assignments.append(new_assignment)
all_valid_assignments.extend(new_assignments)
print('%i assignments created in %.2f s' %
(len(all_valid_assignments), time.time() - start_time))
tuples = []
for assignment in all_valid_assignments:
solution = [0 for _ in range(len(colors))]
for i in assignment.orders:
solution[i] = 1
solution.append(loss_array[assignment.load])
solution.append(assignment.load)
tuples.append(solution)
return tuples
def steel_mill_slab_with_valid_slabs(problem, break_symmetries):
"""Solves the Steel Mill Slab Problem."""
### Load problem.
(num_slabs, capacities, num_colors, orders) = build_problem(problem)
num_orders = len(orders)
num_capacities = len(capacities)
all_slabs = range(num_slabs)
all_colors = range(num_colors)
all_orders = range(len(orders))
print('Solving steel mill with %i orders, %i slabs, and %i capacities' %
(num_orders, num_slabs, num_capacities - 1))
# Compute auxiliary data.
widths = [x[0] for x in orders]
colors = [x[1] for x in orders]
max_capacity = max(capacities)
loss_array = [
min(x for x in capacities if x >= c) - c for c in range(max_capacity +
1)
]
max_loss = max(loss_array)
### Model problem.
# Create the model and the decision variables.
model = cp_model.CpModel()
assign = [[
model.NewBoolVar('assign_%i_to_slab_%i' % (o, s)) for s in all_slabs
] for o in all_orders]
loads = [model.NewIntVar(0, max_capacity, 'load_%i' % s) for s in all_slabs]
losses = [model.NewIntVar(0, max_loss, 'loss_%i' % s) for s in all_slabs]
unsorted_valid_slabs = collect_valid_slabs_dp(capacities, colors, widths,
loss_array)
# Sort slab by descending load/loss. Remove duplicates.
valid_slabs = sorted(unsorted_valid_slabs,
key=lambda c: 1000 * c[-1] + c[-2])
for s in all_slabs:
model.AddAllowedAssignments([assign[o][s] for o in all_orders] +
[losses[s], loads[s]], valid_slabs)
# Orders are assigned to one slab.
for o in all_orders:
model.AddExactlyOne(assign[o])
# Redundant constraint (sum of loads == sum of widths).
model.Add(sum(loads) == sum(widths))
# Symmetry breaking.
for s in range(num_slabs - 1):
model.Add(loads[s] >= loads[s + 1])
# Collect equivalent orders.
if break_symmetries:
print('Breaking symmetries')
width_to_unique_color_order = {}
ordered_equivalent_orders = []
orders_per_color = [
[o for o in all_orders if colors[o] == c + 1] for c in all_colors
]
for c in all_colors:
colored_orders = orders_per_color[c]
if not colored_orders:
continue
if len(colored_orders) == 1:
o = colored_orders[0]
w = widths[o]
if w not in width_to_unique_color_order:
width_to_unique_color_order[w] = [o]
else:
width_to_unique_color_order[w].append(o)
else:
local_width_to_order = {}
for o in colored_orders:
w = widths[o]
if w not in local_width_to_order:
local_width_to_order[w] = []
local_width_to_order[w].append(o)
for w, os in local_width_to_order.items():
if len(os) > 1:
for p in range(len(os) - 1):
ordered_equivalent_orders.append((os[p], os[p + 1]))
for w, os in width_to_unique_color_order.items():
if len(os) > 1:
for p in range(len(os) - 1):
ordered_equivalent_orders.append((os[p], os[p + 1]))
# Create position variables if there are symmetries to be broken.
if ordered_equivalent_orders:
print(' - creating %i symmetry breaking constraints' %
len(ordered_equivalent_orders))
positions = {}
for p in ordered_equivalent_orders:
if p[0] not in positions:
positions[p[0]] = model.NewIntVar(
0, num_slabs - 1, 'position_of_slab_%i' % p[0])
model.AddMapDomain(positions[p[0]], assign[p[0]])
if p[1] not in positions:
positions[p[1]] = model.NewIntVar(
0, num_slabs - 1, 'position_of_slab_%i' % p[1])
model.AddMapDomain(positions[p[1]], assign[p[1]])
# Finally add the symmetry breaking constraint.
model.Add(positions[p[0]] <= positions[p[1]])
# Objective.
model.Minimize(sum(losses))
print('Model created')
### Solve model.
solver = cp_model.CpSolver()
solver.num_search_workers = 8
solution_printer = SteelMillSlabSolutionPrinter(orders, assign, loads,
losses)
status = solver.Solve(model, solution_printer)
### Output the solution.
if status == cp_model.OPTIMAL:
print(
'Loss = %i, time = %.2f s, %i conflicts' %
(solver.ObjectiveValue(), solver.WallTime(), solver.NumConflicts()))
else:
print('No solution')
def steel_mill_slab_with_column_generation(problem):
"""Solves the Steel Mill Slab Problem."""
### Load problem.
(num_slabs, capacities, _, orders) = build_problem(problem)
num_orders = len(orders)
num_capacities = len(capacities)
all_orders = range(len(orders))
print('Solving steel mill with %i orders, %i slabs, and %i capacities' %
(num_orders, num_slabs, num_capacities - 1))
# Compute auxiliary data.
widths = [x[0] for x in orders]
colors = [x[1] for x in orders]
max_capacity = max(capacities)
loss_array = [
min(x for x in capacities if x >= c) - c for c in range(max_capacity +
1)
]
### Model problem.
# Generate all valid slabs (columns)
unsorted_valid_slabs = collect_valid_slabs_dp(capacities, colors, widths,
loss_array)
# Sort slab by descending load/loss. Remove duplicates.
valid_slabs = sorted(unsorted_valid_slabs,
key=lambda c: 1000 * c[-1] + c[-2])
all_valid_slabs = range(len(valid_slabs))
# create model and decision variables.
model = cp_model.CpModel()
selected = [model.NewBoolVar('selected_%i' % i) for i in all_valid_slabs]
for order_id in all_orders:
model.Add(
sum(selected[i]
for i, slab in enumerate(valid_slabs)
if slab[order_id]) == 1)
# Redundant constraint (sum of loads == sum of widths).
model.Add(
sum(selected[i] * valid_slabs[i][-1]
for i in all_valid_slabs) == sum(widths))
# Objective.
model.Minimize(
sum(selected[i] * valid_slabs[i][-2] for i in all_valid_slabs))
print('Model created')
### Solve model.
solver = cp_model.CpSolver()
solver.parameters.num_search_workers = 8
solver.parameters.log_search_progress = True
solution_printer = cp_model.ObjectiveSolutionPrinter()
status = solver.Solve(model, solution_printer)
### Output the solution.
if status in (cp_model.OPTIMAL, cp_model.FEASIBLE):
print(
'Loss = %i, time = %.2f s, %i conflicts' %
(solver.ObjectiveValue(), solver.WallTime(), solver.NumConflicts()))
else:
print('No solution')
def steel_mill_slab_with_mip_column_generation(problem):
"""Solves the Steel Mill Slab Problem."""
### Load problem.
(num_slabs, capacities, _, orders) = build_problem(problem)
num_orders = len(orders)
num_capacities = len(capacities)
all_orders = range(len(orders))
print('Solving steel mill with %i orders, %i slabs, and %i capacities' %
(num_orders, num_slabs, num_capacities - 1))
# Compute auxiliary data.
widths = [x[0] for x in orders]
colors = [x[1] for x in orders]
max_capacity = max(capacities)
loss_array = [
min(x for x in capacities if x >= c) - c for c in range(max_capacity +
1)
]
### Model problem.
# Generate all valid slabs (columns)
unsorted_valid_slabs = collect_valid_slabs_dp(capacities, colors, widths,
loss_array)
# Sort slab by descending load/loss. Remove duplicates.
valid_slabs = sorted(unsorted_valid_slabs,
key=lambda c: 1000 * c[-1] + c[-2])
all_valid_slabs = range(len(valid_slabs))
# create model and decision variables.
start_time = time.time()
solver = pywraplp.Solver('Steel',
pywraplp.Solver.SCIP_MIXED_INTEGER_PROGRAMMING)
selected = [
solver.IntVar(0.0, 1.0, 'selected_%i' % i) for i in all_valid_slabs
]
for order in all_orders:
solver.Add(
sum(selected[i]
for i in all_valid_slabs
if valid_slabs[i][order]) == 1)
# Redundant constraint (sum of loads == sum of widths).
solver.Add(
sum(selected[i] * valid_slabs[i][-1]
for i in all_valid_slabs) == sum(widths))
# Objective.
solver.Minimize(
sum(selected[i] * valid_slabs[i][-2] for i in all_valid_slabs))
status = solver.Solve()
### Output the solution.
if status == pywraplp.Solver.OPTIMAL:
print('Objective value = %f found in %.2f s' %
(solver.Objective().Value(), time.time() - start_time))
else:
print('No solution')
if FLAGS.solver == 'sat':
steel_mill_slab(FLAGS.problem, FLAGS.break_symmetries)
elif FLAGS.solver == 'sat_table':
steel_mill_slab_with_valid_slabs(FLAGS.problem, FLAGS.break_symmetries)
elif FLAGS.solver == 'sat_column':
steel_mill_slab_with_column_generation(FLAGS.problem)
else: # 'mip_column'
steel_mill_slab_with_mip_column_generation(FLAGS.problem)
|
examples/notebook/examples/steel_mill_slab_sat.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Advanced Lane Finding Project
#
# The goals / steps of this project are the following:
#
# * Compute the camera calibration matrix and distortion coefficients given a set of chessboard images.
# * Apply a distortion correction to raw images.
# * Use color transforms, gradients, etc., to create a thresholded binary image.
# * Apply a perspective transform to rectify binary image ("birds-eye view").
# * Detect lane pixels and fit to find the lane boundary.
# * Determine the curvature of the lane and vehicle position with respect to center.
# * Warp the detected lane boundaries back onto the original image.
# * Output visual display of the lane boundaries and numerical estimation of lane curvature and vehicle position.
#
# ---
# ## First, I'll compute the camera calibration using chessboard images
# +
import pickle
import os
import numpy as np
import cv2
import glob
import matplotlib.pyplot as plt
# %matplotlib qt
def camera_calibration():
global img_size
nx = 9 # TODO: enter the number of inside corners in x
ny = 6 # TODO: enter the number of inside corners in y
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((nx*ny, 3), np.float32)
objp[:, :2] = np.mgrid[0:nx, 0:ny].T.reshape(-1, 2)
# Arrays to store object points and image points from all the images.
objpoints = [] # 3d points in real world space
imgpoints = [] # 2d points in image plane.
# Make a list of calibration images
images = glob.glob('./camera_cal/calibration*.jpg')
# Step through the list and search for chessboard corners
for fname in images:
img = cv2.imread(fname)
img_size = img.shape
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# Find the chessboard corners
ret, corners = cv2.findChessboardCorners(gray, (nx, ny), None)
# If found, add object points, image points
if ret:
objpoints.append(objp)
imgpoints.append(corners)
# Draw and display the corners
img = cv2.drawChessboardCorners(img, (nx, ny), corners, ret)
print(fname)
cv2.imshow('Img', img)
cv2.waitKey(500)
cv2.destroyAllWindows()
# Takes an image, object points, and image points performs the camera calibration
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, img_size[:2], None, None)
if ret: # Save camera calibration parameters
dist_pickle = {'mtx': mtx, 'dist': dist, 'rvecs': rvecs, 'tvecs': tvecs}
pickle.dump(dist_pickle, open('mtx_dist_pickle.p', 'wb'))
print('Save parameters')
# distortion-corrected image
for img_name in os.listdir('test_images/'):
image = cv2.imread('test_images/' + img_name)
# Undistorting the image:
img_undist = cv2.undistort(image, mtx, dist, None, mtx)
cv2.imshow('img_name', img_undist)
print('name:', img_name)
cv2.imwrite('test_images_result/' + img_name, img_undist)
cv2.waitKey(1000)
cv2.destroyAllWindows()
# Display
image = cv2.imread('camera_cal/calibration1.jpg')
img_undist = cv2.undistort(image, mtx, dist, None, mtx)
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 9))
f.tight_layout()
ax1.imshow(image)
ax1.set_title('Original Image', fontsize=20)
ax2.imshow(img_undist)
ax2.set_title('Undistorted Image', fontsize=20)
plt.subplots_adjust(left=0., right=1, top=0.9, bottom=0.)
print("Undistorted Finish")
camera_calibration()
# -
# ## And so on and so forth...
# +
#1. Provide an example of a distortion-corrected image.
# -
|
examples/example.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 特徴量エンジニアリング概要
# ## 本プロジェクトの目的
#
# 機械学習のパフォーマンス改善に向けて重要な特徴量エンジニアリングの手法を,実装例を交えて紹介する.
# 主に特徴量エンジニアリングについて述べるが,一部特徴量選択についても触れる.
# ## 特徴量エンジニアリングとは
#
# 機械学習における特徴量とは,分析対象を測定することが可能な変数を指す.データセットでは特徴量は列として表記されることが多い.
#
# データセットに含める特徴量の質が,機械学習モデルの精度に影響し,ひいては機械学習を活用する場合に得るインサイトの質に大きく影響する.
#
# データセットの質を改善する為に,特徴量選択や特徴量エンジニアリングが実施される.
# 特徴量選択は分析対象に関連する特徴量に重点を置き,無関係な特徴量を取り除くプロセスを指す.特徴量エンジニアリングは,既存の特徴量をもとに新たな特徴量を構築してデータセットに追加することを指す.
# ## 特徴量選択と特徴量エンジニアリングの具体例
#
# 特徴エンジニアリングの手法の詳細は他のNotebookに記載するが,本節では特徴量選択と特徴量エンジニアリングの違いを説明する為の具体例を示す.
#
# データセットはFlood Modeling Datasetを使用し,論文[Time Series Extrinsic Regression](https://arxiv.org/abs/2006.12672)のSVR Optimisedの条件に対してtsfreshによる特徴量選択及び特徴量エンジニアリングを試行する.
#
# 学習パラメータは論文通り,下記パラメータに対して3-Folds Cross ValidationのGridSearchのベストモデルを採用する.
#
# |Parameters|Values|
# |:--|:--|
# |Kernel|RBF, Sigmoid|
# |gamma|0.001, 0.01, 0.1, 1|
# |C|0.1, 1, 10, 100|
#
# ### 実装例
# --- ローカルモジュールの更新を自動で読み込む ---
# %load_ext autoreload
# %autoreload 2
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
from sklearn.metrics import mean_squared_error
from sklearn.metrics import make_scorer
from tsfresh import extract_features
from tsfresh import select_features
from tsfresh.feature_selection.significance_tests import target_real_feature_real_test
from lib.dataloader.flood_modeling import load_flood_modeling
# #### データセットダウンロード
if (not os.path.exists("flood_modeling_datasets")):
# !mkdir -p "flood_modeling_datasets" ; \
# cd flood_modeling_datasets ; \
# wget "https://zenodo.org/record/3902694/files/FloodModeling1_TEST.ts" ; \
# wget "https://zenodo.org/record/3902694/files/FloodModeling1_TRAIN.ts" ; \
# ls
else:
print('[INFO] Dataset flood_modeling_datasets is already exist')
# +
train_ts = os.path.join('flood_modeling_datasets', 'FloodModeling1_TRAIN.ts')
test_ts = os.path.join('flood_modeling_datasets', 'FloodModeling1_TEST.ts')
x_train, y_train, x_test, y_test = load_flood_modeling(train_ts, test_ts)
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)
# -
# #### 3-Flods Cross ValidationとGridSearchでモデルを学習する
# +
def rmse(y_true, y_pred):
rmse = np.sqrt(mean_squared_error(y_true, y_pred))
return rmse
params = {
'kernel': ['rbf', 'sigmoid'],
'gamma': [0.001, 0.01, 0.1, 1],
'C': [0.1, 1, 10, 100]
}
model_svr = GridSearchCV(
svm.SVR(),
params,
cv=KFold(n_splits=3, shuffle=True, random_state=1234),
scoring=make_scorer(rmse, greater_is_better=False))
model_svr.fit(x_train, y_train)
print('[INFO] Best params: {}'.format(model_svr.best_params_))
print('[INFO] Best score: {}'.format(-model_svr.best_score_))
# -
# #### テストデータで評価
prediction = model_svr.predict(x_test)
print(rmse(y_test, prediction))
# 論文[Time Series Extrinsic Regression](https://arxiv.org/abs/2006.12672)の実験結果がRMSE=0.05なので,再現できた.
# #### tsfreshで時系列データから特徴量を抽出(特徴量エンジニアリング)して学習
#
# tsfreshを用いて特徴量を抽出する為に,時系列データを整然データに整形する.
df_x_train = pd.DataFrame(x_train.T)
df_x_train_melt = df_x_train.melt(var_name='sample', value_name='A')
print(df_x_train_melt.shape)
df_x_train_melt.head()
df_x_train_melt_ef = extract_features(df_x_train_melt, column_id='sample')
print(df_x_train_melt_ef.shape)
df_x_train_melt_ef.dropna(axis=1, inplace=True)
print(df_x_train_melt_ef.shape)
df_x_train_melt_ef.head()
df_x_test = pd.DataFrame(x_test.T)
df_x_test_melt = df_x_test.melt(var_name='sample', value_name='A')
print(df_x_test_melt.shape)
df_x_test_melt.head()
df_x_test_melt_ef = extract_features(df_x_test_melt, column_id='sample')
print(df_x_test_melt_ef.shape)
df_x_test_melt_ef.dropna(axis=1, inplace=True)
print(df_x_test_melt_ef.shape)
df_x_test_melt_ef.head()
(df_x_train_melt_ef.columns == df_x_test_melt_ef.columns).all()
# 時系列データ266sampleから787種の特徴量を抽出し,NaNを除去し最終的に775種の特徴量が得られた.
# 得られた特徴量の統計量は下記の通り.
df_x_train_melt_ef.describe()
# これらの特徴量を用いて,モデルを学習する.
# +
model_svr = GridSearchCV(
svm.SVR(),
params,
cv=KFold(n_splits=3, shuffle=True, random_state=1234),
scoring=make_scorer(rmse, greater_is_better=False))
model_svr.fit(df_x_train_melt_ef, y_train)
print('[INFO] Best params: {}'.format(model_svr.best_params_))
print('[INFO] Best score: {}'.format(-model_svr.best_score_))
# -
prediction = model_svr.predict(df_x_test_melt_ef)
print(rmse(y_test, prediction))
# tsfreshで抽出した特徴量で学習すると,RMSE=0.67で論文の0.05よりも悪化した.
# 統計的仮説検定によりp値を算出し,慣習に倣い,0.01を閾値とする場合と0.05を閾値とする場合を試行する.
#
# 特徴量選択は,[tsfresh.feature_selection.selection.select_features](https://tsfresh.readthedocs.io/en/latest/api/tsfresh.feature_selection.html#module-tsfresh.feature_selection.selection)を用いる.
# #### 特徴量を選択して学習
df_x_train_melt_ef_under005 = select_features(df_x_train_melt_ef, y_train, fdr_level=0.05, ml_task='regression')
print(df_x_train_melt_ef_under005.shape)
df_x_train_melt_ef_under005.head()
df_x_train_melt_ef_under001 = select_features(df_x_train_melt_ef, y_train, fdr_level=0.01, ml_task='regression')
print(df_x_train_melt_ef_under001.shape)
df_x_train_melt_ef_under001.head()
# +
df_x_test_melt_ef_under001 = df_x_test_melt_ef[df_x_train_melt_ef_under001.columns]
model_svr = GridSearchCV(
svm.SVR(),
params,
cv=KFold(n_splits=3, shuffle=True, random_state=1234),
scoring=make_scorer(rmse, greater_is_better=False))
model_svr.fit(df_x_train_melt_ef_under001, y_train)
print('[INFO] Best params: {}'.format(model_svr.best_params_))
print('[INFO] Best score: {}'.format(-model_svr.best_score_))
prediction = model_svr.predict(df_x_test_melt_ef_under001)
print(rmse(y_test, prediction))
# +
df_x_test_melt_ef_under005 = df_x_test_melt_ef[df_x_train_melt_ef_under005.columns]
model_svr = GridSearchCV(
svm.SVR(),
params,
cv=KFold(n_splits=3, shuffle=True, random_state=1234),
scoring=make_scorer(rmse, greater_is_better=False))
model_svr.fit(df_x_train_melt_ef_under005, y_train)
print('[INFO] Best params: {}'.format(model_svr.best_params_))
print('[INFO] Best score: {}'.format(-model_svr.best_score_))
prediction = model_svr.predict(df_x_test_melt_ef_under005)
print(rmse(y_test, prediction))
# -
# ## Reference
#
# * [特徴量変数](https://www.datarobot.com/jp/wiki/feature/)
# * [特徴量の選択](https://www.datarobot.com/jp/wiki/feature-selection/)
# * [特徴量エンジニアリング](https://www.datarobot.com/jp/wiki/feature-engineering/)
# * [データインサイト](https://www.datarobot.com/jp/wiki/insights/)
# * [Awesome Public Datasets](https://github.com/awesomedata/awesome-public-datasets)
# * [Feature-Engineeringのリンク集めてみた](https://qiita.com/squash/items/667f8cda16c76448b0f4)
# * [DataFrameで特徴量作るのめんどくさ過ぎる。。featuretoolsを使って自動生成したろ](https://qiita.com/Hyperion13fleet/items/4eaca365f28049fe11c7)
# * [時系列データから自動で特徴抽出するライブラリ tsfresh](https://qiita.com/yuko1658/items/871df86f99a9134cc9ef)
# * [特徴量選択のまとめ](https://qiita.com/shimopino/items/5fee7504c7acf044a521)
# * [機械学習で特徴量を正しく選択する方法](https://rightcode.co.jp/blog/information-technology/feature-selection-right-choice)
# * [特徴選択とは?機械学習の予測精度を改善させる必殺技「特徴選択」を理解しよう](https://www.codexa.net/feature-selection-methods/)
# * [Human Activity Recognition Using Smartphones Data Set](https://archive.ics.uci.edu/ml/datasets/human+activity+recognition+using+smartphones)
# * [Human Activity Recognition using Smartphone](https://arxiv.org/abs/1401.8212)
# * [Human Activity Analysis and Recognition from
# Smartphones using Machine Learning Techniques](https://arxiv.org/abs/2103.16490)
# * [Human Activity Recognition using Machine Learning](https://github.com/sushantdhumak/Human-Activity-Recognition-with-Smartphones)
# * [How to Choose a Feature Selection Method For Machine Learning](https://machinelearningmastery.com/feature-selection-with-real-and-categorical-data/)
# * [統計分析を理解しよう-よく使われている統計分析方法の概要-](https://www.nli-research.co.jp/report/detail/id=61928?site=nli)
# * [Monash, UEA & UCR Time Series Extrinsic Regression Repository](http://tseregression.org/)
# * [Flood Modeling Dataset 1](https://zenodo.org/record/3902694#.YTQjG50zaUk)
# * [Flood Modeling Dataset 2](https://zenodo.org/record/3902696#.YTQktZ0zaUk)
# * [Flood Modeling Dataset 3](https://zenodo.org/record/3902698#.YTQktZ0zaUk)
# * [Monash University, UEA, UCR Time Series Extrinsic Regression Archive](https://arxiv.org/abs/2006.10996)
# * [Time Series Extrinsic Regression](https://arxiv.org/abs/2006.12672)
# * [ChangWeiTan/TS-Extrinsic-Regression](https://github.com/ChangWeiTan/TS-Extrinsic-Regression)
# * [製造業:センサデータを機械学習に使う](https://www.datarobot.com/jp/blog/use_manufacturing_sensor_data_for_machine_learning/)
# * [tsfresh](https://tsfresh.readthedocs.io/en/latest/index.html)
# * [大規模データの解析における問題点](https://www.mbsj.jp/admins/ethics_and_edu/PNE/5_article.pdf)
|
python/feature_engineering/00_Overview.ipynb
|
# ---
# jupyter:
# jupytext:
# formats: python_scripts//py:percent,notebooks//ipynb
# text_representation:
# extension: .py
# format_name: percent
# format_version: '1.3'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %% [markdown]
# # Exercise 01
# The goal is to write an exhaustive search to find the best parameters
# combination maximizing the model performance
# %%
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OrdinalEncoder
from sklearn.model_selection import RandomizedSearchCV
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
# This line is currently required to import HistGradientBoostingClassifier
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
from scipy.stats import expon, uniform
from scipy.stats import randint
df = pd.read_csv(
"https://www.openml.org/data/get_csv/1595261/adult-census.csv")
# Or use the local copy:
# df = pd.read_csv('../datasets/adult-census.csv')
target_name = "class"
target = df[target_name].to_numpy()
data = df.drop(columns=target_name)
df_train, df_test, target_train, target_test = train_test_split(
data, target, random_state=42)
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OrdinalEncoder
categorical_columns = [
'workclass', 'education', 'marital-status', 'occupation',
'relationship', 'race', 'native-country', 'sex']
categories = [data[column].unique()
for column in data[categorical_columns]]
categorical_preprocessor = OrdinalEncoder(categories=categories)
preprocessor = ColumnTransformer(
[('cat-preprocessor', categorical_preprocessor, categorical_columns)],
remainder='passthrough', sparse_threshold=0)
from sklearn.experimental import enable_hist_gradient_boosting
from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.pipeline import make_pipeline
model = make_pipeline(
preprocessor, HistGradientBoostingClassifier(random_state=42))
# %% [markdown]
# TODO: write your solution here
#
# Use the previously defined model (called `model`) and using two nested `for`
# loops, make a search of the best combinations of the `learning_rate` and
# `max_leaf_nodes` parameters. In this regard, you will need to train and test
# the model by setting the parameters. The evaluation of the model should be
# performed using `cross_val_score`. We can propose to define the following
# parameters search:
# - `learning_rate` for the values 0.01, 0.1, and 1;
# - `max_leaf_nodes` for the values 5, 25, 45.
|
Day_2_Machine_Learning_Python/04_basic_parameters_tuning_exercise_01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %matplotlib inline
#
# # Scaling the regularization parameter for SVCs
#
#
# The following example illustrates the effect of scaling the
# regularization parameter when using `svm` for
# `classification <svm_classification>`.
# For SVC classification, we are interested in a risk minimization for the
# equation:
#
#
# \begin{align}C \sum_{i=1, n} \mathcal{L} (f(x_i), y_i) + \Omega (w)\end{align}
#
# where
#
# - $C$ is used to set the amount of regularization
# - $\mathcal{L}$ is a `loss` function of our samples
# and our model parameters.
# - $\Omega$ is a `penalty` function of our model parameters
#
# If we consider the loss function to be the individual error per
# sample, then the data-fit term, or the sum of the error for each sample, will
# increase as we add more samples. The penalization term, however, will not
# increase.
#
# When using, for example, `cross validation <cross_validation>`, to
# set the amount of regularization with `C`, there will be a
# different amount of samples between the main problem and the smaller problems
# within the folds of the cross validation.
#
# Since our loss function is dependent on the amount of samples, the latter
# will influence the selected value of `C`.
# The question that arises is `How do we optimally adjust C to
# account for the different amount of training samples?`
#
# The figures below are used to illustrate the effect of scaling our
# `C` to compensate for the change in the number of samples, in the
# case of using an `l1` penalty, as well as the `l2` penalty.
#
# l1-penalty case
# -----------------
# In the `l1` case, theory says that prediction consistency
# (i.e. that under given hypothesis, the estimator
# learned predicts as well as a model knowing the true distribution)
# is not possible because of the bias of the `l1`. It does say, however,
# that model consistency, in terms of finding the right set of non-zero
# parameters as well as their signs, can be achieved by scaling
# `C1`.
#
# l2-penalty case
# -----------------
# The theory says that in order to achieve prediction consistency, the
# penalty parameter should be kept constant
# as the number of samples grow.
#
# Simulations
# ------------
#
# The two figures below plot the values of `C` on the `x-axis` and the
# corresponding cross-validation scores on the `y-axis`, for several different
# fractions of a generated data-set.
#
# In the `l1` penalty case, the cross-validation-error correlates best with
# the test-error, when scaling our `C` with the number of samples, `n`,
# which can be seen in the first figure.
#
# For the `l2` penalty case, the best result comes from the case where `C`
# is not scaled.
#
# .. topic:: Note:
#
# Two separate datasets are used for the two different plots. The reason
# behind this is the `l1` case works better on sparse data, while `l2`
# is better suited to the non-sparse case.
#
#
# +
print(__doc__)
# Author: <NAME> <<EMAIL>>
# <NAME> <<EMAIL>>
# License: BSD 3 clause
import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import LinearSVC
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import GridSearchCV
from sklearn.utils import check_random_state
from sklearn import datasets
rnd = check_random_state(1)
# set up dataset
n_samples = 100
n_features = 300
# l1 data (only 5 informative features)
X_1, y_1 = datasets.make_classification(n_samples=n_samples,
n_features=n_features, n_informative=5,
random_state=1)
# l2 data: non sparse, but less features
y_2 = np.sign(.5 - rnd.rand(n_samples))
X_2 = rnd.randn(n_samples, n_features // 5) + y_2[:, np.newaxis]
X_2 += 5 * rnd.randn(n_samples, n_features // 5)
clf_sets = [(LinearSVC(penalty='l1', loss='squared_hinge', dual=False,
tol=1e-3),
np.logspace(-2.3, -1.3, 10), X_1, y_1),
(LinearSVC(penalty='l2', loss='squared_hinge', dual=True,
tol=1e-4),
np.logspace(-4.5, -2, 10), X_2, y_2)]
colors = ['navy', 'cyan', 'darkorange']
lw = 2
for clf, cs, X, y in clf_sets:
# set up the plot for each regressor
fig, axes = plt.subplots(nrows=2, sharey=True, figsize=(9, 10))
for k, train_size in enumerate(np.linspace(0.3, 0.7, 3)[::-1]):
param_grid = dict(C=cs)
# To get nice curve, we need a large number of iterations to
# reduce the variance
grid = GridSearchCV(clf, refit=False, param_grid=param_grid,
cv=ShuffleSplit(train_size=train_size,
test_size=.3,
n_splits=250, random_state=1))
grid.fit(X, y)
scores = grid.cv_results_['mean_test_score']
scales = [(1, 'No scaling'),
((n_samples * train_size), '1/n_samples'),
]
for ax, (scaler, name) in zip(axes, scales):
ax.set_xlabel('C')
ax.set_ylabel('CV Score')
grid_cs = cs * float(scaler) # scale the C's
ax.semilogx(grid_cs, scores, label="fraction %.2f" %
train_size, color=colors[k], lw=lw)
ax.set_title('scaling=%s, penalty=%s, loss=%s' %
(name, clf.penalty, clf.loss))
plt.legend(loc="best")
plt.show()
|
01 Machine Learning/scikit_examples_jupyter/svm/plot_svm_scale_c.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Summary
#
# **Airbnb listings in Melbourne city**
#
# Detailed listings data for Melbourne
# The data behind the Inside Airbnb site is sourced from publicly available information from the Airbnb site.
#
# [Dataset source](http://insideairbnb.com/get-the-data.html)
#
# **Stats**
#
# * 22,909 listings
# * 14,849 unique hosts
# * 14,599 listings for "whole apartment"
# * 9,090 unique hosts for "whole apartment"
#
#
# * 30 neighbourhoods
# * 485 cities
# * 538 streets
#
#
# * bathrooms: min 0.5, max 14, median 1
# * bedrooms: min 0, max 16, median 2
# * price: expressed in dollars min 0, max 999, avg. 180
#
# # Goals
#
# This analysis will explore the dataset provided by [insideairbnb.com](http://insideairbnb.com/index.html).
#
# The goal here is to get this cleaned up a little and into Elasticsearch where we'll explore further.
#
# ## Thanks to the Elastic Machine Learning team for the work this example is based on :)!
import pandas as pd
import numpy as np
import json
import csv
from elasticsearch import helpers, Elasticsearch
import requests
import re
import os
df = pd.read_csv("listings.csv")
# You can ignore the DType warning the line above may produce.
df = df[["id",
"host_id",
"street",
"neighbourhood_cleansed",
"city",
"state",
"zipcode",
"country",
"latitude",
"longitude",
"property_type",
"room_type",
"bathrooms",
"bedrooms",
"square_feet",
"price",
"number_of_reviews"]]
df.head()
# ## Cleaning and pre-processing
#
# **Set the number of bedrooms to 1 in case it's a NaN
# and the number of bathroom to 1 if it's either a NaN or 0**
df["bedrooms"].replace(np.nan, 1, inplace=True)
df["bathrooms"].replace(np.nan, 1, inplace=True)
df["bathrooms"].replace(0, 1, inplace=True)
# **Cleaning the `price` field and changing its type to float**
reg = "\$([0-9]*)(\.|\,){1,1}.*"
df["price"] = df["price"].apply(lambda x: re.search(reg, x).group(1))
df["price"] = df["price"].astype("float")
# ## Stats
print(f"Number of listings: {len(df)}")
print(f"Number of hosts: {len(df.groupby('host_id'))}")
# **Now we'll focus on "whole apartment" listings only, filtering out the ones with shared/private bedrooms**
entire_place = df[(df["room_type"]=="Entire home/apt")]
entire_place = entire_place.drop('room_type', axis=1)
print(f"Number of listings: {len(entire_place)}")
print(f"Number of hosts: {len(entire_place.groupby('host_id'))}")
# **The number of states is > 1**
# **Looking at the data we can see that the field contains different variation of 'Victoria' and other terms. Let's replace the state value for each entry with the unique term'Victoria'**
print(f"Number of unique states: {len(entire_place['state'].unique())}")
print(entire_place["state"].unique())
entire_place["state"] = "Victoria"
print(f"Number of unique cities: {len(entire_place['city'].unique())}")
print(f"Number of unique neighbourhood: {len(entire_place['neighbourhood_cleansed'].unique())}")
print(f"Number of unique street: {len(entire_place['street'].unique())}")
# ### Recording the cleaned data to disk
cleaned_file = f"cleaned_melbourne_listings.csv"
entire_place.to_csv(cleaned_file, header=False, index=False)
# ## Putting the data in Elasticsearch - mappings and indexing
mappings = {
"settings" : {
"number_of_shards" : 1
},
"mappings" : {
"properties" : {
"listing_id" : {"type" : "keyword"},
"host_id" : {"type" : "keyword"},
"street" : {"type" : "keyword"},
"neighbourhood" : {"type" : "keyword"},
"city" : {"type" : "keyword"},
"state" : {"type" : "keyword"},
"zipcode" : {"type" : "keyword"},
"country" : {"type" : "keyword"},
"location" : {"type": "geo_point"},
"property_type" : {"type" : "keyword"},
"bathrooms" : {"type" : "float"},
"bedrooms" : {"type" : "float"},
"price" : {"type" : "float"},
"number_of_reviews" : {"type" : "integer"}
}
}
}
INDEX_NAME = 'airbnb_melbourne'
def get_data():
with open(cleaned_file, mode='r') as csv_file:
csv_reader = csv.DictReader(csv_file,
fieldnames=["listing_id", "host_id", "street",
"neighbourhood", "city", "state",
"zipcode", "country", "latitude",
"longitude", "property_type",
"bathrooms", "bedrooms", "square_feet",
"price", "number_of_reviews"])
for i in csv_reader:
i["location"] = {"lat": i["latitude"], "lon": i["longitude"]}
del i["latitude"]
del i["longitude"]
yield {
"_index": INDEX_NAME,
"_source": i
}
# ### Use Elastic Cloud
es = Elasticsearch(
[os.environ['ELASTIC_CLOUD_ES_ENDPOINT']],
http_auth=('elastic', os.environ['ELASTIC_CLOUD_PASSWORD']),
scheme="https",
port=443,
)
es.indices.delete(INDEX_NAME, ignore=[400, 404]) # to reset
es.indices.create(INDEX_NAME, mappings)
helpers.bulk(es, get_data())
# now show the creation of the Kibana Index Pattern and explain what it's for
# # Retrieve data from Elasticsearch into pandas
q = {"query": {"match_all": {}}, "size": 1000}
results = helpers.scan(es, query=q, index="stkilda")
processed = []
for r in results:
r['_source']['price_avg'] = r['_source']['price']['avg']
del r['_source']['price']
processed.append(r['_source'])
df = pd.DataFrame.from_dict(processed)
df
|
Elastic Intro to Data Science - Airbnb Melbourne.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import matplotlib.pyplot as plt
# %matplotlib inline
# +
# numpy tensors
import numpy as np
N, D_in, H, D_out = 64, 1000, 100, 10
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
learning_rate = 1e-6
for t in range(500):
# forward pass: compute predicted y
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
# loss
loss = np.square(y_pred - y).sum()
print('Loss at round {}: {}'.format(t, loss))
# backprop: compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
# update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
# +
# pytorch tensors
import torch
dtype = torch.float
device = torch.device('cpu')
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)
w1 = torch.randn(D_in, H, device=device, dtype=dtype)
w2 = torch.randn(H, D_out, device=device, dtype=dtype)
learning_rate = 1e-6
for t in range(500):
# forward pass: compute predicted y
h = x.mm(w1)
h_relu = h.clamp(min=0)
y_pred = h_relu.mm(w2)
# loss
loss = (y_pred - y).pow(2).sum().item()
print('Loss at round {}: {}'.format(t, loss))
# backprop: compute gradients of w1 and w2 with respect to loss
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.t().mm(grad_y_pred)
grad_h_relu = grad_y_pred.mm(w2.t())
grad_h = grad_h_relu.clone()
grad_h[h < 0] = 0
grad_w1 = x.t().mm(grad_h)
# update weights
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
# +
# autograd
dtype = torch.float
device = torch.device('cpu')
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)
w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)
w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)
learning_rate = 1e-6
for t in range(500):
# forward pass: compute predicted y
y_pred = x.mm(w1).clamp(min=0).mm(w2)
# loss
loss = (y_pred - y).pow(2).sum()
print('Loss at round {}: {}'.format(t, loss.item()))
# backprop: compute gradients of w1 and w2 with respect to loss
loss.backward()
# update weights
with torch.no_grad():
w1 -= learning_rate * w1.grad
w2 -= learning_rate * w2.grad
w1.grad.zero_()
w2.grad.zero_()
# +
# define new autograd functions
class MyReLU(torch.autograd.Function):
@staticmethod
def forward(ctx, input):
ctx.save_for_backward(input)
return input.clamp(min=0)
@staticmethod
def backward(ctx, grad_output):
input, = ctx.saved_tensors
grad_input = grad_output.clone()
grad_input[input < 0] = 0
return grad_input
dtype = torch.float
device = torch.device('cpu')
N, D_in, H, D_out = 64, 1000, 100, 10
x = torch.randn(N, D_in, device=device, dtype=dtype)
y = torch.randn(N, D_out, device=device, dtype=dtype)
w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True)
w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True)
learning_rate = 1e-6
for t in range(500):
relu = MyReLU.apply
# forward pass: compute predicted y
y_pred = relu(x.mm(w1)).mm(w2)
# loss
loss = (y_pred - y).pow(2).sum()
print('Loss at round {}: {}'.format(t, loss.item()))
# backprop: compute gradients of w1 and w2 with respect to loss
loss.backward()
# update weights
with torch.no_grad():
w1 -= learning_rate * w1.grad
w2 -= learning_rate * w2.grad
w1.grad.zero_()
w2.grad.zero_()
# +
# tensorflow static graph
import tensorflow as tf
N, D_in, H, D_out = 64, 1000, 100, 10
x = tf.placeholder(tf.float32, shape=(None, D_in))
y = tf.placeholder(tf.float32, shape=(None, D_out))
w1 = tf.Variable(tf.random_normal((D_in, H)))
w2 = tf.Variable(tf.random_normal((H, D_out)))
h = tf.matmul(x, w1)
h_relu = tf.maximum(h, tf.zeros(1))
y_pred = tf.matmul(h_relu, w2)
loss = tf.reduce_sum((y - y_pred) ** 2.0)
grad_w1, grad_w2 = tf.gradients(loss, [w1, w2])
learning_rate = 1e-6
new_w1 = w1.assign(w1 - learning_rate * grad_w1)
new_w2 = w2.assign(w2 - learning_rate * grad_w2)
with tf.Session() as session:
session.run(tf.global_variables_initializer())
x_value = np.random.randn(N, D_in)
y_value = np.random.randn(N, D_out)
for _ in range(500):
loss_value, _, _ = session.run([loss, new_w1, new_w2], feed_dict={x: x_value, y: y_value})
print(loss_value)
# +
# pytorch nn
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
torch.nn.ReLU(),
torch.nn.Linear(H, D_out))
learning_rate = 1e-4
for i in range(500):
# forward
y_pred = model(x)
# get loss
criterion = torch.nn.MSELoss(size_average=False)
loss = criterion(y_pred, y)
print('{} loss in round {}'.format(loss.item(), i))
# zero gradients
model.zero_grad()
# backward
loss.backward()
# update weights
with torch.no_grad():
for param in model.parameters():
param -= learning_rate * param.grad
# +
# pytorch optim
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
model = torch.nn.Sequential(torch.nn.Linear(D_in, H),
torch.nn.ReLU(),
torch.nn.Linear(H, D_out))
learning_rate = 1e-4
optimizer = torch.optim.Adam(lr=learning_rate, params=model.parameters())
for i in range(500):
# forward
y_pred = model(x)
# get loss
criterion = torch.nn.MSELoss(size_average=False)
loss = criterion(y_pred, y)
print('{} loss in round {}'.format(loss.item(), i))
# zero gradients
optimizer.zero_grad()
# backward
loss.backward()
# update weights
optimizer.step()
# +
# pytorch custom nn modules
class TwoLayerNet(torch.nn.Module):
def __init__(self, D_in, H, D_out):
super(TwoLayerNet, self).__init__()
self.l1 = torch.nn.Linear(D_in, H)
self.r = torch.nn.ReLU()
self.l2 = torch.nn.Linear(H, D_out)
def forward(self, x):
x = self.l1(x)
x = self.r(x)
x = self.l2(x)
return x
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
model = TwoLayerNet(D_in, H, D_out)
learning_rate = 1e-4
optimizer = torch.optim.Adam(lr=learning_rate, params=model.parameters())
for i in range(500):
# forward
y_pred = model(x)
# get loss
criterion = torch.nn.MSELoss(size_average=False)
loss = criterion(y_pred, y)
print('{} loss in round {}'.format(loss.item(), i))
# zero gradients
optimizer.zero_grad()
# backward
loss.backward()
# update weights
optimizer.step()
# +
# pytorch dynamic graphs
import random
class TwoLayerNet(torch.nn.Module):
def __init__(self, D_in, H, D_out):
super(TwoLayerNet, self).__init__()
self.l1 = torch.nn.Linear(D_in, H)
self.r = torch.nn.ReLU()
self.l2 = torch.nn.Linear(H, D_out)
self.hidden = torch.nn.Linear(H, H)
def forward(self, x):
x = self.l1(x)
x = self.r(x)
for _ in range(random.randint(0, 3)):
x = self.hidden(x)
x = self.r(x)
x = self.l2(x)
return x
N, D_in, H, D_out = 64, 1000, 100, 10
# Create random Tensors to hold inputs and outputs
x = torch.randn(N, D_in)
y = torch.randn(N, D_out)
model = TwoLayerNet(D_in, H, D_out)
learning_rate = 1e-4
optimizer = torch.optim.Adam(lr=learning_rate, params=model.parameters())
for i in range(500):
# forward
y_pred = model(x)
# get loss
criterion = torch.nn.MSELoss(size_average=False)
loss = criterion(y_pred, y)
print('{} loss in round {}'.format(loss.item(), i))
# zero gradients
optimizer.zero_grad()
# backward
loss.backward()
# update weights
optimizer.step()
# -
|
Learning PyTorch with Examples/Learning PyTorch with Examples.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="dXI5CtHBzo8e"
# # 🛠 02 Neural network classification with TensorFlow Exercises
#
# 1. Play with neural networks in the [TensorFlow Playground](https://playground.tensorflow.org/) for 10-minutes. Especially try different values of the learning, what happens when you decrease it? What happens when you increase it?
# 2. Replicate the model pictured in the [TensorFlow Playground diagram](https://playground.tensorflow.org/#activation=relu&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.001®ularizationRate=0&noise=0&networkShape=6,6,6,6,6&seed=0.51287&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false®ularization_hide=true&discretize_hide=true®ularizationRate_hide=true&percTrainData_hide=true&dataset_hide=true&problem_hide=true&noise_hide=true&batchSize_hide=true) below using TensorFlow code. Compile it using the Adam optimizer, binary crossentropy loss and accuracy metric. Once it's compiled check a summary of the model.
# 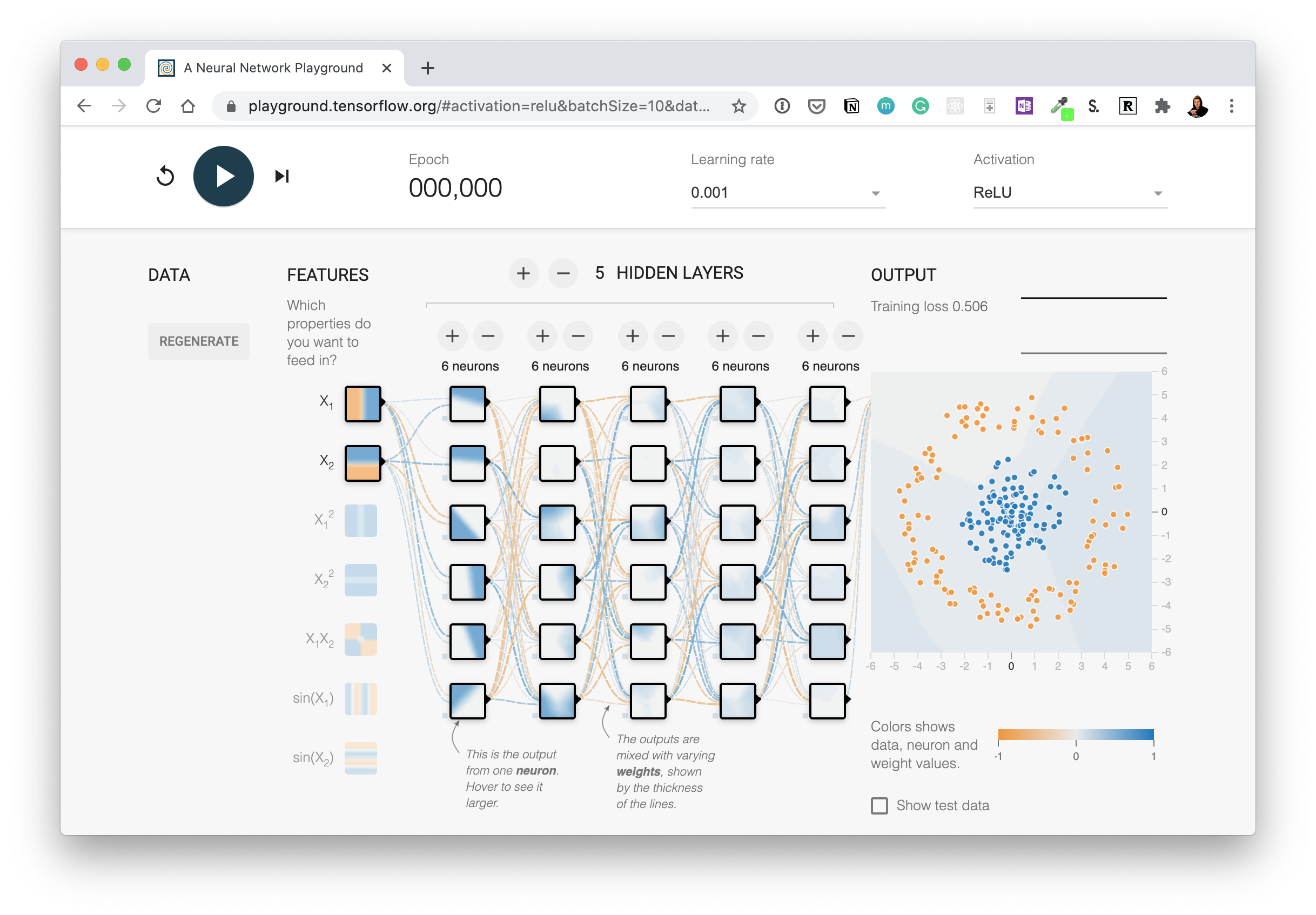
# *Try this network out for yourself on the [TensorFlow Playground website](https://playground.tensorflow.org/#activation=relu&batchSize=10&dataset=circle®Dataset=reg-plane&learningRate=0.001®ularizationRate=0&noise=0&networkShape=6,6,6,6,6&seed=0.51287&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false®ularization_hide=true&discretize_hide=true®ularizationRate_hide=true&percTrainData_hide=true&dataset_hide=true&problem_hide=true&noise_hide=true&batchSize_hide=true). Hint: there are 5 hidden layers but the output layer isn't pictured, you'll have to decide what the output layer should be based on the input data.*
# 3. Create a classification dataset using Scikit-Learn's [`make_moons()`](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_moons.html) function, visualize it and then build a model to fit it at over 85% accuracy.
# 4. Create a function (or write code) to visualize multiple image predictions for the fashion MNIST at the same time. Plot at least three different images and their prediciton labels at the same time. Hint: see the [classifcation tutorial in the TensorFlow documentation](https://www.tensorflow.org/tutorials/keras/classification) for ideas.
# 5. Recreate [TensorFlow's](https://www.tensorflow.org/api_docs/python/tf/keras/activations/softmax) [softmax activation function](https://en.wikipedia.org/wiki/Softmax_function) in your own code. Make sure it can accept a tensor and return that tensor after having the softmax function applied to it.
# 6. Train a model to get 88%+ accuracy on the fashion MNIST test set. Plot a confusion matrix to see the results after.
# 7. Make a function to show an image of a certain class of the fashion MNIST dataset and make a prediction on it. For example, plot 3 images of the `T-shirt` class with their predictions.
#
# + [markdown] id="TIgc4d2uUoR1"
# ## 3. Create a classification dataset using Scikit-Learn's [`make_moons()`](https://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_moons.html) function, visualize it and then build a model to fit it at over 85% accuracy.
# + id="uMgVqyt-zsHU"
from sklearn.datasets import make_moons
# Create classification dataset
X,y = make_moons(n_samples=1000,
noise=0.03,
random_state=42)
# + colab={"base_uri": "https://localhost:8080/"} id="qYDi6cQST_R_" outputId="8f48209f-fe1b-4bc5-a791-699c6423fc95"
# Check features
X
# + colab={"base_uri": "https://localhost:8080/"} id="OsSkWu78Vesr" outputId="a89711e7-1d01-4c0b-f214-574c11c27d88"
# Check labels
y
# + colab={"base_uri": "https://localhost:8080/", "height": 419} id="XVV4jzcYVh7A" outputId="e89ebd6a-1057-4ef6-f90d-5e83170c33b7"
# Visualize it in dataframes
import pandas as pd
moon_face = pd.DataFrame({"X0":X[:,0],"X1":X[:,1],"label":y})
moon_face
# + colab={"base_uri": "https://localhost:8080/", "height": 265} id="5vLLdzyJs_eS" outputId="d5e4e486-a50d-4437-9d27-0a023ca59608"
# Visualize with a plot
import matplotlib.pyplot as plt
plt.scatter(X[:,0],X[:,1],c=y,cmap=plt.cm.RdYlBu);
# + colab={"base_uri": "https://localhost:8080/", "height": 35} id="nVoU_uK6t3Fm" outputId="3995852f-5f22-4ec8-cd24-5c6f8c647e18"
# import tensorflow
import tensorflow as tf
tf.__version__
# + colab={"base_uri": "https://localhost:8080/"} id="7FRWjTthtXlq" outputId="8169c4eb-f79a-4c7e-aa47-f7bf5c694451"
# Build a model
# Set random seed
tf.random.set_seed(42)
# Create model
model_1 = tf.keras.Sequential([
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(1,activation="sigmoid")
])
# Compile model
model_1.compile(loss="binary_crossentropy",
optimizer=tf.keras.optimizers.Adam(lr=0.001),
metrics=["accuracy"])
# Fit model
history = model_1.fit(X,y,epochs=150)
# + colab={"base_uri": "https://localhost:8080/"} id="YowbnXXbtx15" outputId="e81d3625-dd06-4334-e593-1a7277bce0d7"
# Evaluate
model_1.evaluate(X,y)
# + id="jrIUJIYYvXbV"
import numpy as np
def plot_decision_boundary(model,X,y):
"""
Plots the decision boundary created by a model predicting on X
"""
# Define the axis boundaries of the plot and create a meshgrid
x_min,x_max = X[:,0].min() - 0.1, X[:,0].max() + 0.1
y_min,y_max = X[:,1].min() - 0.1, X[:,1].max() + 0.1
xx, yy = np.meshgrid(np.linspace(x_min,x_max,100),
np.linspace(y_min,y_max,100))
# Create X values (we're going to make predictions on these)
x_in = np.c_[xx.ravel(),yy.ravel()] # stack 2D array together
# Make predictions
y_pred = model.predict(x_in)
# Check for multi-class
if len(y_pred[0]) > 1:
print("doing multiclass classification")
# We have to reshape our prediction to get them ready for plot
y_pred = np.argmax(y_pred,axis=1).reshape(xx.shape)
else:
print("doing binarry classification")
y_pred = np.round(y_pred).reshape(xx.shape)
# Plot the decision boundary
plt.contourf(xx,yy,y_pred,cmap=plt.cm.RdYlBu,alpha=0.7)
plt.scatter(X[:,0],X[:,1],c=y,s=40,cmap=plt.cm.RdYlBu)
plt.xlim(xx.min(),xx.max())
plt.ylim(yy.min(),yy.max())
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="ea3Jiof_vxjR" outputId="c93d1aab-5197-43e1-fbe5-a8c991784616"
plot_decision_boundary(model_1,X,y)
# + [markdown] id="gd89MZVJwifF"
# ## 4. Create a function (or write code) to visualize multiple image predictions for the fashion MNIST at the same time. Plot at least three different images and their prediciton labels at the same time.
# + colab={"base_uri": "https://localhost:8080/"} id="9MnsqxITwh88" outputId="c6c8967d-7838-46a9-cdb0-e81ccc282c43"
# Loading fashion MNIST dataset
fashion_mnist = tf.keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# + id="1d6n3uy1vy5-"
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat','Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
# + id="e7dnnukKPEoH"
# Plot multiple random images and their prediction labels
import random
def random_images_and_labels():
plt.figure(figsize=(7,7))
for i in range(4):
ax = plt.subplot(2,2,i+1)
rand_index = random.choice(range(len(train_images)))
plt.imshow(train_images[rand_index],cmap=plt.cm.binary)
plt.title(class_names[train_labels[rand_index]])
plt.axis(False)
# + colab={"base_uri": "https://localhost:8080/", "height": 427} id="I0zVt6thP4Bj" outputId="ce7430b0-98af-41db-a52a-736177f6c216"
random_images_and_labels()
# + [markdown] id="b0kK1JLZRECG"
# ## 5. Recreate [TensorFlow's](https://www.tensorflow.org/api_docs/python/tf/keras/activations/softmax) [softmax activation function](https://en.wikipedia.org/wiki/Softmax_function) in your own code. Make sure it can accept a tensor and return that tensor after having the softmax function applied to it.
# + id="Sg1QKD-kP5nq"
# Normalize data
train_images_norm = train_images / 255.0
test_images_norm = test_images / 225.0
# + colab={"base_uri": "https://localhost:8080/"} id="zm00Q_O_R3Zx" outputId="e449b67b-86eb-4d7c-bfed-ba7ae09ca9cd"
# Model for normalized data
# Set seed
tf.random.set_seed(42)
# Create model
model_2 = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28,28)),
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(10,activation="softmax")
])
# Compile model
model_2.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(),
metrics=["accuracy"])
# Fit model
history = model_2.fit(train_images_norm,
train_labels,
epochs=10,
validation_data=(test_images_norm,test_labels))
# + [markdown] id="b9XDDiD6TlNZ"
# ## 6. Train a model to get 88%+ accuracy on the fashion MNIST test set. Plot a confusion matrix to see the results after.
# + colab={"base_uri": "https://localhost:8080/"} id="azlSeT-yTUPj" outputId="8d62fc30-376a-4e1c-97d9-e37b8cf8ec6d"
# Set seed
tf.random.set_seed(42)
# Create model
model_3 = tf.keras.Sequential([
tf.keras.layers.Flatten(input_shape=(28,28)),
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(4,activation="relu"),
tf.keras.layers.Dense(10,activation="softmax")
])
# Compile model
model_3.compile(loss=tf.keras.losses.SparseCategoricalCrossentropy(),
optimizer=tf.keras.optimizers.Adam(lr=0.001),
metrics=["accuracy"])
# Fit model
history = model_3.fit(train_images_norm,
train_labels,
epochs=100,
validation_data=(test_images_norm,test_labels))
# + id="_gYqOmMEXb8H"
# Confusion matrix plot
import itertools
from sklearn.metrics import confusion_matrix
def make_confusion_matrix(y_true,y_pred,classes=None,figsize=(10,10),text_size=15):
# Create the confusion matrix
cm = confusion_matrix(y_true,y_pred)
cm_norm = cm.astype("float") / cm.sum(axis=1)[:,np.newaxis] # normalize our confusion matrix
n_classes = cm.shape[0]
# Let's prettify it
fig,ax = plt.subplots(figsize=figsize)
# Create a matrix plot
cax = ax.matshow(cm,cmap=plt.cm.Blues)
fig.colorbar(cax)
# Set labels to be classes
if classes:
labels = classes
else:
labels = np.arange(cm.shape[0])
# Label the axes
ax.set(title="Confusion Matrix",
xlabel="Predicted Label",
ylabel="True Label",
xticks=np.arange(n_classes),
yticks=np.arange(n_classes),
xticklabels=labels,
yticklabels=labels)
# Set x-axis labels to bottom
ax.xaxis.set_label_position("bottom")
ax.xaxis.tick_bottom()
# Adjust label size
ax.yaxis.label.set_size(text_size)
ax.xaxis.label.set_size(text_size)
ax.title.set_size(text_size)
# Set threshold for different colors
threshold = (cm.max() + cm.min()) /2.
# Plot the text on each cell
for i,j in itertools.product(range(cm.shape[0]),range(cm.shape[1])):
plt.text(j,i,f"{cm[i,j]} ({cm_norm[i,j]*100:.1f}%)",
horizontalalignment="center",
color="white" if cm[i,j] > threshold else "black",
size=text_size)
# + id="D2qZGN69bVOT"
# Make some predictions with our model
y_probs = model_3.predict(test_images_norm)
# Convert all of the prediction probabilities into integers
y_preds = y_probs.argmax(axis=1)
# + colab={"base_uri": "https://localhost:8080/", "height": 852} id="fg7halAJbuZp" outputId="e3141293-14a2-45f3-a82a-7c86640978ad"
make_confusion_matrix(y_true=test_labels,
y_pred=y_preds,
classes=class_names,
figsize=(15,15),
text_size=10)
# + [markdown] id="pmmtv7GUcflb"
#
# ## 7. Make a function to show an image of a certain class of the fashion MNIST dataset and make a prediction on it. For example, plot 3 images of the `T-shirt` class with their predictions.
# + id="2RaXcrstceXi"
# Function to show image of a certain class
def plot_random_image(model,images,true_labels,classes):
"""
Picks a random image, plots it and labels it with a prediction and truth label.
"""
# Set up random integer
i = random.randint(0,len(images))
# Create predictions and targets
target_image = images[i]
pred_probs = model.predict(target_image.reshape(1,28,28))
pred_label = classes[pred_probs.argmax()]
true_label = classes[true_labels[i]]
# Plot the image
plt.imshow(target_image,cmap=plt.cm.binary)
# Change the color of the titles depending on if the prediction is right or wrong
if pred_label == true_label:
color = "green"
else:
color = "red"
# Add xlabel information (prediction/true label)
plt.xlabel("Pred: {} {:2.0f}% (True: {})".format(pred_label,
100*tf.reduce_max(pred_probs),
true_label),
color=color)
# + id="PFX5vMP1byhO" colab={"base_uri": "https://localhost:8080/", "height": 279} outputId="91d88e73-5db2-4a8e-ce59-d4e2a6e902cb"
plot_random_image(model=model_3,
images=test_images_norm,
true_labels=test_labels,
classes=class_names)
# + colab={"base_uri": "https://localhost:8080/", "height": 279} id="WMQftYGb32Q0" outputId="062b312b-e2b4-4006-f813-4f878c32ed0d"
plot_random_image(model=model_3,
images=test_images_norm,
true_labels=test_labels,
classes=class_names)
# + colab={"base_uri": "https://localhost:8080/", "height": 279} id="9vBt2WVT32oc" outputId="51327f32-0795-4a9c-9734-28cf4d1b939c"
plot_random_image(model=model_3,
images=test_images_norm,
true_labels=test_labels,
classes=class_names)
# + id="k96Dzv2533BF"
|
TensorFlow/02_neural_network_classification_with_tensorflow_exercise.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Dependencies
# + _kg_hide-input=true
# # !pip install --quiet efficientnet
# !pip install --quiet image-classifiers
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _kg_hide-input=true _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
import warnings, json, re, glob, math
from scripts_step_lr_schedulers import *
from melanoma_utility_scripts import *
from kaggle_datasets import KaggleDatasets
from sklearn.model_selection import KFold
import tensorflow.keras.layers as L
import tensorflow.keras.backend as K
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from tensorflow.keras import optimizers, layers, metrics, losses, Model
# import efficientnet.tfkeras as efn
from classification_models.tfkeras import Classifiers
SEED = 0
seed_everything(SEED)
warnings.filterwarnings("ignore")
# -
# ## TPU configuration
# + _kg_hide-input=true
strategy, tpu = set_up_strategy()
print("REPLICAS: ", strategy.num_replicas_in_sync)
AUTO = tf.data.experimental.AUTOTUNE
# -
# # Model parameters
# + _kg_hide-input=true
# base_model_path = '/kaggle/input/efficientnet/'
dataset_path = 'melanoma-256x256'
config = {
"HEIGHT": 256,
"WIDTH": 256,
"CHANNELS": 3,
"BATCH_SIZE": 256,
"EPOCHS": 30,
"LEARNING_RATE": 3e-4,
"ES_PATIENCE": 10,
"N_FOLDS": 5,
# "BASE_MODEL_PATH": base_model_path + 'efficientnet-b3_weights_tf_dim_ordering_tf_kernels_autoaugment_notop.h5',
"BASE_MODEL_PATH": 'imagenet',
"DATASET_PATH": dataset_path
}
with open('config.json', 'w') as json_file:
json.dump(json.loads(json.dumps(config)), json_file)
config
# -
# # Load data
# + _kg_hide-input=true
database_base_path = '/kaggle/input/siim-isic-melanoma-classification/'
k_fold = pd.read_csv(database_base_path + 'train.csv')
test = pd.read_csv(database_base_path + 'test.csv')
print('Train samples: %d' % len(k_fold))
display(k_fold.head())
print(f'Test samples: {len(test)}')
display(test.head())
GCS_PATH = KaggleDatasets().get_gcs_path(dataset_path)
TRAINING_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/train*.tfrec')
TEST_FILENAMES = tf.io.gfile.glob(GCS_PATH + '/test*.tfrec')
# -
# # Augmentations
def data_augment(image, label):
p_spatial = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_spatial2 = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_rotate = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
p_crop = tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
### Spatial-level transforms
if p_spatial >= .2: # flips
image['input_image'] = tf.image.random_flip_left_right(image['input_image'])
image['input_image'] = tf.image.random_flip_up_down(image['input_image'])
if p_spatial >= .7:
image['input_image'] = tf.image.transpose(image['input_image'])
if p_rotate >= .8: # rotate 270º
image['input_image'] = tf.image.rot90(image['input_image'], k=3)
elif p_rotate >= .6: # rotate 180º
image['input_image'] = tf.image.rot90(image['input_image'], k=2)
elif p_rotate >= .4: # rotate 90º
image['input_image'] = tf.image.rot90(image['input_image'], k=1)
if p_spatial2 >= .7: # random rotation range 0º to 45º
image['input_image'] = transform_rotation(image['input_image'], config['HEIGHT'])
if p_crop >= .6: # crops
if p_crop >= .95:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.7), int(config['WIDTH']*.7), config['CHANNELS']])
elif p_crop >= .85:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.8), int(config['WIDTH']*.8), config['CHANNELS']])
elif p_crop >= .7:
image['input_image'] = tf.image.random_crop(image['input_image'], size=[int(config['HEIGHT']*.9), int(config['WIDTH']*.9), config['CHANNELS']])
else:
image['input_image'] = tf.image.central_crop(image['input_image'], central_fraction=.6)
image['input_image'] = tf.image.resize(image['input_image'], size=[config['HEIGHT'], config['WIDTH']])
return image, label
# ## Auxiliary functions
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _kg_hide-input=true _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
# Datasets utility functions
def read_labeled_tfrecord(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, LABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
label = tf.cast(example['target'], tf.float32)
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
data['diagnosis'] = tf.cast(tf.one_hot(example['diagnosis'], 10), tf.int32)
return {'input_image': image, 'input_meta': data}, label # returns a dataset of (image, data, label)
def read_labeled_tfrecord_eval(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, LABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
label = tf.cast(example['target'], tf.float32)
image_name = example['image_name']
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
data['diagnosis'] = tf.cast(tf.one_hot(example['diagnosis'], 10), tf.int32)
return {'input_image': image, 'input_meta': data}, label, image_name # returns a dataset of (image, data, label, image_name)
def load_dataset(filenames, ordered=False, buffer_size=-1):
ignore_order = tf.data.Options()
if not ordered:
ignore_order.experimental_deterministic = False # disable order, increase speed
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.with_options(ignore_order) # uses data as soon as it streams in, rather than in its original order
dataset = dataset.map(read_labeled_tfrecord, num_parallel_calls=buffer_size)
return dataset # returns a dataset of (image, data, label)
def load_dataset_eval(filenames, buffer_size=-1):
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.map(read_labeled_tfrecord_eval, num_parallel_calls=buffer_size)
return dataset # returns a dataset of (image, data, label, image_name)
def get_training_dataset(filenames, batch_size, buffer_size=-1):
dataset = load_dataset(filenames, ordered=False, buffer_size=buffer_size)
dataset = dataset.map(data_augment, num_parallel_calls=AUTO)
dataset = dataset.repeat() # the training dataset must repeat for several epochs
dataset = dataset.shuffle(2048)
dataset = dataset.batch(batch_size, drop_remainder=True) # slighly faster with fixed tensor sizes
dataset = dataset.prefetch(buffer_size) # prefetch next batch while training (autotune prefetch buffer size)
return dataset
def get_validation_dataset(filenames, ordered=True, repeated=False, batch_size=32, buffer_size=-1):
dataset = load_dataset(filenames, ordered=ordered, buffer_size=buffer_size)
if repeated:
dataset = dataset.repeat()
dataset = dataset.shuffle(2048)
dataset = dataset.batch(batch_size, drop_remainder=repeated)
dataset = dataset.prefetch(buffer_size)
return dataset
def get_eval_dataset(filenames, batch_size=32, buffer_size=-1):
dataset = load_dataset_eval(filenames, buffer_size=buffer_size)
dataset = dataset.batch(batch_size, drop_remainder=False)
dataset = dataset.prefetch(buffer_size)
return dataset
# Test function
def read_unlabeled_tfrecord(example, height=config['HEIGHT'], width=config['WIDTH'], channels=config['CHANNELS']):
example = tf.io.parse_single_example(example, UNLABELED_TFREC_FORMAT)
image = decode_image(example['image'], height, width, channels)
image_name = example['image_name']
# meta features
data = {}
data['patient_id'] = tf.cast(example['patient_id'], tf.int32)
data['sex'] = tf.cast(example['sex'], tf.int32)
data['age_approx'] = tf.cast(example['age_approx'], tf.int32)
data['anatom_site_general_challenge'] = tf.cast(tf.one_hot(example['anatom_site_general_challenge'], 7), tf.int32)
return {'input_image': image, 'input_tabular': data}, image_name # returns a dataset of (image, data, image_name)
def load_dataset_test(filenames, buffer_size=-1):
dataset = tf.data.TFRecordDataset(filenames, num_parallel_reads=buffer_size) # automatically interleaves reads from multiple files
dataset = dataset.map(read_unlabeled_tfrecord, num_parallel_calls=buffer_size)
# returns a dataset of (image, data, label, image_name) pairs if labeled=True or (image, data, image_name) pairs if labeled=False
return dataset
def get_test_dataset(filenames, batch_size=32, buffer_size=-1):
dataset = load_dataset_test(filenames, buffer_size=buffer_size)
dataset = dataset.batch(batch_size, drop_remainder=False)
dataset = dataset.prefetch(buffer_size)
return dataset
# Advanced augmentations
def transform_rotation(image, height):
# input image - is one image of size [dim,dim,3] not a batch of [b,dim,dim,3]
# output - image randomly rotated
DIM = height
XDIM = DIM%2 #fix for size 331
rotation = 45. * tf.random.uniform([1], minval=0, maxval=1, dtype='float32')
# CONVERT DEGREES TO RADIANS
rotation = math.pi * rotation / 180.
# ROTATION MATRIX
c1 = tf.math.cos(rotation)
s1 = tf.math.sin(rotation)
one = tf.constant([1] ,dtype='float32')
zero = tf.constant([0], dtype='float32')
rotation_matrix = tf.reshape( tf.concat([c1,s1,zero, -s1,c1,zero, zero,zero,one],axis=0), [3, 3] )
# LIST DESTINATION PIXEL INDICES
x = tf.repeat( tf.range(DIM//2,-DIM//2,-1), DIM )
y = tf.tile( tf.range(-DIM//2,DIM//2),[DIM] )
z = tf.ones([DIM*DIM],dtype='int32')
idx = tf.stack( [x,y,z] )
# ROTATE DESTINATION PIXELS ONTO ORIGIN PIXELS
idx2 = K.dot(rotation_matrix,tf.cast(idx,dtype='float32'))
idx2 = K.cast(idx2,dtype='int32')
idx2 = K.clip(idx2,-DIM//2+XDIM+1,DIM//2)
# FIND ORIGIN PIXEL VALUES
idx3 = tf.stack( [DIM//2-idx2[0,], DIM//2-1+idx2[1,]] )
d = tf.gather_nd(image, tf.transpose(idx3))
return tf.reshape(d,[DIM, DIM, 3])
# -
# ## Learning rate scheduler
# + _kg_hide-input=true
lr_min = 1e-6
lr_start = 0
lr_max = config['LEARNING_RATE']
step_size = 26880 // config['BATCH_SIZE'] #(len(k_fold[k_fold[f'fold_{fold_n}'] == 'train']) * 2) // config['BATCH_SIZE']
total_steps = config['EPOCHS'] * step_size
hold_max_steps = 0
warmup_steps = step_size * 5
rng = [i for i in range(0, total_steps, step_size)]
y = [linear_schedule_with_warmup(tf.cast(x, tf.float32), total_steps=total_steps,
warmup_steps=warmup_steps, hold_max_steps=hold_max_steps,
lr_start=lr_start, lr_max=lr_max, lr_min=lr_min) for x in rng]
sns.set(style="whitegrid")
fig, ax = plt.subplots(figsize=(20, 6))
plt.plot(rng, y)
print("Learning rate schedule: {:.3g} to {:.3g} to {:.3g}".format(y[0], max(y), y[-1]))
# -
# # Model
def model_fn(input_shape):
input_image = L.Input(shape=input_shape, name='input_image')
BaseModel, preprocess_input = Classifiers.get('resnet50')
base_model = BaseModel(input_shape=input_shape,
weights=config['BASE_MODEL_PATH'],
include_top=False)
x = base_model(input_image)
x = L.GlobalAveragePooling2D()(x)
output = L.Dense(1, activation='sigmoid')(x)
model = Model(inputs=input_image, outputs=output)
return model
# # Training
# + _kg_hide-input=true _kg_hide-output=true
eval_dataset = get_eval_dataset(TRAINING_FILENAMES, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
image_names = next(iter(eval_dataset.unbatch().map(lambda data, label, image_name: image_name).batch(len(k_fold)))).numpy().astype('U')
image_data = eval_dataset.map(lambda data, label, image_name: data)
history_list = []
kfold = KFold(config['N_FOLDS'], shuffle=True, random_state=SEED)
for n_fold, (trn_idx, val_idx) in enumerate(kfold.split(TRAINING_FILENAMES)):
n_fold +=1
print('\nFOLD: %d' % (n_fold))
tf.tpu.experimental.initialize_tpu_system(tpu)
# K.clear_session()
### Data
train_filenames = np.array(TRAINING_FILENAMES)[trn_idx]
valid_filenames = np.array(TRAINING_FILENAMES)[val_idx]
train_size = count_data_items(train_filenames)
step_size = train_size // config['BATCH_SIZE']
# Train model
model_path = 'model_fold_%d.h5' % (n_fold)
es = EarlyStopping(monitor='val_loss', mode='min', patience=config['ES_PATIENCE'],
restore_best_weights=True, verbose=1)
checkpoint = ModelCheckpoint(model_path, monitor='val_loss', mode='min',
save_best_only=True, save_weights_only=True)
with strategy.scope():
model = model_fn((config['HEIGHT'], config['WIDTH'], config['CHANNELS']))
lr = lambda: linear_schedule_with_warmup(tf.cast(optimizer.iterations, tf.float32),
total_steps=total_steps, warmup_steps=warmup_steps,
hold_max_steps=hold_max_steps, lr_start=lr_start,
lr_max=lr_max, lr_min=lr_min)
optimizer = optimizers.Adam(learning_rate=lr)
model.compile(optimizer, loss=losses.BinaryCrossentropy(label_smoothing=0.05),
metrics=[metrics.AUC()])
history = model.fit(get_training_dataset(train_filenames, batch_size=config['BATCH_SIZE'], buffer_size=AUTO),
validation_data=get_validation_dataset(valid_filenames, ordered=True, repeated=False,
batch_size=config['BATCH_SIZE'], buffer_size=AUTO),
epochs=config['EPOCHS'],
steps_per_epoch=step_size,
callbacks=[checkpoint, es],
verbose=2).history
history_list.append(history)
# Make predictions
preds = model.predict(image_data)
name_preds = dict(zip(image_names, preds.reshape(len(preds))))
k_fold[f'pred_fold_{n_fold}'] = k_fold.apply(lambda x: name_preds[x['image_name']], axis=1)
valid_filenames = np.array(TRAINING_FILENAMES)[val_idx]
valid_dataset = get_eval_dataset(valid_filenames, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
valid_image_names = next(iter(valid_dataset.unbatch().map(lambda data, label, image_name: image_name).batch(count_data_items(valid_filenames)))).numpy().astype('U')
k_fold[f'fold_{n_fold}'] = k_fold.apply(lambda x: 'validation' if x['image_name'] in valid_image_names else 'train', axis=1)
# -
# ## Model loss graph
# + _kg_hide-input=true
for n_fold in range(config['N_FOLDS']):
print(f'Fold: {n_fold}')
plot_metrics(history_list[n_fold])
# -
# ## Model loss graph aggregated
# + _kg_hide-input=true
plot_metrics_agg(history_list, config['N_FOLDS'])
# -
# # Model evaluation
# + _kg_hide-input=true
display(evaluate_model(k_fold, config['N_FOLDS']).style.applymap(color_map))
# -
# # Model evaluation by Subset
# + _kg_hide-input=true
display(evaluate_model_Subset(k_fold, config['N_FOLDS']).style.applymap(color_map))
# -
# # Confusion matrix
# + _kg_hide-input=true
for n_fold in range(config['N_FOLDS']):
n_fold += 1
pred_col = f'pred_fold_{n_fold}'
train_set = k_fold[k_fold[f'fold_{n_fold}'] == 'train']
valid_set = k_fold[k_fold[f'fold_{n_fold}'] == 'validation']
print(f'Fold: {n_fold}')
plot_confusion_matrix(train_set['target'], np.round(train_set[pred_col]),
valid_set['target'], np.round(valid_set[pred_col]))
# -
# # Visualize predictions
# + _kg_hide-input=true
k_fold['pred'] = 0
for n_fold in range(config['N_FOLDS']):
n_fold +=1
k_fold['pred'] += k_fold[f'pred_fold_{n_fold}'] / config['N_FOLDS']
print('Top 10 samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].head(10))
print('Top 10 positive samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].query('target == 1').head(10))
print('Top 10 predicted positive samples')
display(k_fold[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'diagnosis',
'target', 'pred'] + [c for c in k_fold.columns if (c.startswith('pred_fold'))]].query('pred > .5').head(10))
print('Label/prediction distribution')
print(f"Train positive labels: {len(k_fold[k_fold['target'] > .5])}")
print(f"Train positive predictions: {len(k_fold[k_fold['pred'] > .5])}")
# -
# # Make predictions
# + _kg_hide-input=true
model_path_list = glob.glob('/kaggle/working/' + '*.h5')
n_models = len(model_path_list)
model_path_list.sort()
print(f'{n_models} Models to predict:')
print(*model_path_list, sep='\n')
# + _kg_hide-input=true
test_dataset = get_test_dataset(TEST_FILENAMES, batch_size=config['BATCH_SIZE'], buffer_size=AUTO)
NUM_TEST_IMAGES = len(test)
test_preds = np.zeros((NUM_TEST_IMAGES, 1))
for model_path in model_path_list:
tf.tpu.experimental.initialize_tpu_system(tpu)
# K.clear_session()
print(model_path)
model = model_fn((config['HEIGHT'], config['WIDTH'], config['CHANNELS']))
model.load_weights(model_path)
test_preds += model.predict(test_dataset) / n_models
image_names = next(iter(test_dataset.unbatch().map(lambda data, image_name: image_name).batch(NUM_TEST_IMAGES))).numpy().astype('U')
name_preds = dict(zip(image_names, test_preds.reshape(len(test_preds))))
test['target'] = test.apply(lambda x: name_preds[x['image_name']], axis=1)
# -
# # Visualize test predictions
# + _kg_hide-input=true
print(f"Test predictions {len(test[test['target'] > .5])}|{len(test[test['target'] <= .5])}")
print('Top 10 samples')
display(test[['image_name', 'sex', 'age_approx','anatom_site_general_challenge','target'] +
[c for c in test.columns if (c.startswith('pred_fold'))]].head(10))
print('Top 10 positive samples')
display(test[['image_name', 'sex', 'age_approx','anatom_site_general_challenge', 'target'] +
[c for c in test.columns if (c.startswith('pred_fold'))]].query('target > .5').head(10))
# -
# # Test set predictions
# + _kg_hide-input=true
submission = pd.read_csv(database_base_path + 'sample_submission.csv')
submission['target'] = test['target']
submission.to_csv('submission.csv', index=False)
display(submission.head(10))
display(submission.describe())
|
Model backlog/Train/18-melanoma-5fold-resnet50-imagenet.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Double Q Learning
#
# In this notebook, we will implement Double Q Learning algorithm to play Hill Climbing.
#
# ## Step 1: Import the libraries
import time
import random
import gym
import numpy as np
import matplotlib.pyplot as plt
from collections import namedtuple, deque
# ## Step 2: Create our environment
env = gym.make('MountainCar-v0')
env._max_episode_steps = 1000
env.seed(1)
# ## Step 3: Viewing our Enviroment
# Execute the code cell below to play Cartpole with a random policy.
print("The size of state is: ", env.observation_space.shape)
print("No. of Actions: ", env.action_space.n)
env.reset()
plt.figure()
plt.imshow(env.render(mode='rgb_array'))
env.close()
plt.title('Original Frame')
plt.show()
def random_play():
env.reset()
while True:
env.render(mode='rgb_array')
action = env.action_space.sample()
state, reward, done, _ = env.step(action)
if done:
env.close()
break
random_play()
# ## Step 4: Creating State Preprocess Function
# +
pos_space = np.linspace(-1.2, 0.6, 12)
vel_space = np.linspace(-0.07, 0.07, 20)
def get_state(state):
pos, vel = state
pos_bin = np.digitize(pos, pos_space)
vel_bin = np.digitize(vel, vel_space)
return (pos_bin, vel_bin)
# -
# ## Step 6: Creating out agent
# +
GAMMA = 0.99 # discount factor
LR = .1 # learning rate
class Agent():
def __init__(self, p_size = 12, v_size = 20, action_size = 3):
self.action_space = list(range(0, action_size))
# Intilizing state
self.states = []
for p in range(p_size + 1):
for v in range(v_size + 1):
self.states.append((p, v))
# Iitliazing Q
self.Q1 = {}
for s in self.states:
for a in self.action_space:
self.Q1[s, a] = 0
self.Q2 = {}
for s in self.states:
for a in self.action_space:
self.Q2[s, a] = 0
def act(self, state, eps=.0):
"""Returns actions for given state as per action value function."""
state = get_state(state)
values = np.array([(self.Q1[state, a] + self.Q2[state, a]) for a in self.action_space])
action = np.argmax(values)
g_action = np.random.choice(self.action_space) if np.random.random() < eps else action
return g_action
def act_state(self, state, Q1, Q2):
values = np.array([(Q1[state, a] + Q2[state, a]) for a in self.action_space])
action = np.argmax(values)
return action
def step(self, s, a, ns, r):
s = get_state(s)
ns = get_state(ns)
na = 0
rand = np.random.random()
if rand < 0.5:
na = self.act_state(ns, self.Q1, self.Q1)
self.Q1[s, a] = self.Q1[s, a] + LR * (r + (GAMMA * self.Q2[ns, na]) - self.Q1[s, a])
else:
na = self.act_state(ns, self.Q2, self.Q2)
self.Q2[s, a] = self.Q2[s, a] + LR * (r + (GAMMA * self.Q1[ns, na]) - self.Q2[s, a])
# -
# ## Step 7: Watching untrained agent play
# +
agent = Agent(p_size=12, v_size=20, action_size= 3)
# watch an untrained agent
state = env.reset()
for j in range(200):
action = agent.act(state, 0.5)
env.render()
next_state, reward, done, _ = env.step(action)
state = next_state
if done:
break
env.close()
# -
# ## Step 8: Loading Agent
# +
start_epoch = 0
eps_start = 1.0
scores = []
scores_window = deque(maxlen=100)
# To Load checkpoint uncomment code
# checkpoint = np.load('mountain_climb_doubleq.npy', allow_pickle=True)
# agent.Q1 = checkpoint[()]['Q1']
# agent.Q2 = checkpoint[()]['Q2']
# scores = checkpoint[()]['scores']
# eps_start = checkpoint[()]['eps_start']
# start_epoch = len(scores)
# index = 1
# for i in reversed(scores):
# scores_window.append(i)
# if index == 100:
# break
# index += 1
# -
# ## Step 9: Train the Agent with DQN
def train(n_episodes=50000, eps_end=0.01):
global eps_start
eps = eps_start
for i_episode in range(start_epoch+1, n_episodes+1):
state = env.reset()
score = 0
while True:
action = agent.act(state, eps)
next_state, reward, done, _ = env.step(action)
agent.step(state, action, next_state, reward)
score += reward
state = next_state
if done:
break
eps = eps - 2/n_episodes if eps > eps_end else eps_end # decrease epsilon
scores_window.append(score) # save most recent score
scores.append(score) # save most recent score
eps_start = eps
print('\rEpisode {}\tAverage Score: {:.2f}\tEpsilion: {:.2f}'.format(i_episode, np.mean(scores_window), eps), end="")
if i_episode % 1000 == 0:
print('\rEpisode {}\tAverage Score: {:.2f}\tEpsilion: {:.2f}'.format(i_episode, np.mean(scores_window), eps))
if np.mean(scores_window) > -120:
print("Enviroment Solved")
return scores
scores = train()
# plot the scores
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(np.arange(len(scores)), scores)
plt.ylabel('Score')
plt.xlabel('Episode #')
plt.show()
# +
# watch an trained agent
state = env.reset()
score = 0
for j in range(200):
env.render()
action = agent.act(state)
state, reward, done, _ = env.step(action)
score += reward
if done:
print("Your total score is: ", score)
break
env.close()
# -
data = {
"Q1": agent.Q1,
"Q2": agent.Q2,
"scores": scores,
"eps_start": eps_start
}
np.save("mountain_climb_doubleq.npy", data)
|
notes/03_temporal_difference/mountain_climb_double_qlearning.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: python3
# language: python
# name: python3
# ---
# ## Meta-Learning with the Rank-Weighted GP Ensemble (RGPE)
#
# BoTorch is designed in to be model-agnostic and only requries that a model conform to a minimal interface. This tutorial walks through an example of implementing the rank-weighted Gaussian process ensemble (RGPE) [Feurer, Letham, Bakshy ICML 2018 AutoML Workshop] and using the RGPE in BoTorch to do meta-learning across related optimization tasks.
#
# * Original paper: https://arxiv.org/pdf/1802.02219.pdf
# +
import torch
import math
from torch import Tensor
torch.manual_seed(29)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
dtype = torch.double
# -
# ### Toy Problem
# * We consider optimizing the following 1-D synthetic function
# $$f(x, s_i) = \frac{1}{10}\bigg(x-1\bigg)\bigg(\sin(x+s_i)+\frac{1}{10}\bigg)$$
# where
# $$s_i = \frac{(i+9)\pi}{8}$$
# is a task-dependent shift parameter and $i$ is the task index $i \in [1, t]$.
#
# * In this tutorial, we will consider the scenario where we have collected data from 5 prior tasks (referred to as base tasks), which with a different task dependent shift parameter $s_i$.
#
# * The goal now is use meta-learning to improve sample efficiency when optimizing a 6th task.
# #### Toy Problem Setup
#
# First let's define a function for compute the shift parameter $s_i$ and set the shift amount for the target task.
# +
NUM_BASE_TASKS = 5
def task_shift(task):
"""
Fetch shift amount for task.
"""
return math.pi * (task + 9) / 8.0
# set shift for target task
TARGET_SHIFT = math.pi
# -
# Then, let's define our function $f(x, s_i)$ and set bounds on $x$.
# +
BOUNDS = torch.tensor([[-10.0], [10.0]], dtype=dtype, device=device)
def f(X: Tensor, shift: float = TARGET_SHIFT) -> Tensor:
"""
Torch-compatible objective function for the target_task
"""
f_X = 0.1*(X-1) * (torch.sin(X + shift) + 0.1)
return f_X
# -
# #### Sample training data for prior base tasks
# We sample data from a Sobol sequence to help ensure numerical stability when using a small amount of 1-D data. Sobol sequences help prevent us from sampling a bunch of training points that are close together.
# +
from botorch.utils.sampling import draw_sobol_samples
from botorch.utils.transforms import normalize, unnormalize
# Sample data for each base task
data_by_task = {}
for task in range(NUM_BASE_TASKS):
num_training_points = torch.randint(low=15, high=26, size=(1,)).item()
# draw points from a sobol sequence
raw_x = draw_sobol_samples(bounds=BOUNDS, n=num_training_points, q=1, seed=task+5397923).squeeze(1)
# get observed values
f_x = f(raw_x, task_shift(task))
train_y = f_x + 0.05*torch.randn_like(f_x)
# store training data
data_by_task[task] = {
# scale x to [0, 1]
'train_x': normalize(raw_x, bounds=BOUNDS),
'train_y': train_y,
}
# -
# #### Let's plot the base tasks and the target task function along with the observed points
# +
from matplotlib import pyplot as plt
# %matplotlib inline
fig, ax = plt.subplots(1, 1, figsize=(12, 8))
x = torch.linspace(-10,10,51)
for task in data_by_task:
# plot true function and observed values for base runs
t = ax.plot(
unnormalize(data_by_task[task]['train_x'], bounds=BOUNDS).cpu().numpy(),
data_by_task[task]['train_y'].cpu().numpy(),
'.',
markersize=10,
label=f"Observed task {task}",
)
ax.plot(
x.detach().numpy(),
f(x, task_shift(task)).cpu().numpy(),
label=f"Base task {task}",
color=t[0].get_color(),
)
# plot true target function
ax.plot(
x.detach().numpy(),
f(x, TARGET_SHIFT).detach().numpy(),
'--',
label="Target task",
)
ax.legend(loc="lower right", fontsize=10)
plt.tight_layout()
# -
# ### Fit base task models
# First, let's define a helper function to fit a SingleTaskGP with an inferred noise level given training data.
# +
from gpytorch.mlls import ExactMarginalLogLikelihood
from botorch.models import SingleTaskGP
from botorch.fit import fit_gpytorch_model
def get_fitted_model(train_X: Tensor, train_Y: Tensor) -> SingleTaskGP:
"""
Fit SingleTaskGP with torch.optim.Adam.
"""
model = SingleTaskGP(train_X, train_Y)
mll = ExactMarginalLogLikelihood(model.likelihood, model).to(train_X)
fit_gpytorch_model(mll)
return model
# -
# #### Now let's fit a SingleTaskGP for each base task
# Fit base model
base_model_list = []
for task in range(NUM_BASE_TASKS):
print(f"Fitting base model {task}")
model = get_fitted_model(data_by_task[task]['train_x'], data_by_task[task]['train_y'])
base_model_list.append(model)
# ### Implement the RGPE
#
# The main idea of the RGPE is to estimate the target function as weighted sum of the target model and the base models:
# $$\bar f(\mathbf x | \mathcal D) =
# \sum_{i=1}^{t} w_if^i(\mathbf x |\mathcal D_i)$$
# Importantly, the ensemble model is also a GP:
# $$\bar f(\mathbf x | \mathcal D) \sim \mathcal N\bigg(\sum_{i=1}^{t} w_i\mu_i(\mathbf x), \sum_{i=1}^{t}w_i^2\sigma_i^2\bigg)$$
#
# The weights $w_i$ for model $i$ are based on the the ranking loss between a draw from the model's posterior and the targets. Specifically, the ranking loss for model $i$ is:
# $$\mathcal L(f^i, \mathcal D_t) = \sum_{j=1}^{n_t}\sum_{k=1}^{n_t}\mathbb 1\bigg[\bigg(f^i\big(\mathbf x^t_j\big) < f^i\big(\mathbf x_k^t\big)\bigg)\oplus \big(y_j^t < y_k^t\big)\bigg]$$
# where $\oplus$ is exclusive-or.
#
# The loss for the target model is computing using leave-one-out cross-validation (LOOCV) and is given by:
# $$\mathcal L(f^t, \mathcal D_t) = \sum_{j=1}^{n_t}\sum_{k=1}^{n_t}\mathbb 1\bigg[\bigg(f^t_{-j}\big(\mathbf x^t_j\big) < f^t_{-j}\big(\mathbf x_k^t\big)\bigg)\oplus \big(y_j^t < y_k^t\big)\bigg]$$
# where $f^t_{-j}$ model fitted to all data from the target task except training example $j$.
#
# The weights are then computed as:
# $$w_i = \frac{1}{S}\sum_{s=1}^S\mathbb 1\big(i = \text{argmin}_{i'}l_{i', s}\big)$$
def roll_col(X: Tensor, shift: int) -> Tensor:
"""
Rotate columns to right by shift.
"""
return torch.cat((X[:, -shift:], X[:, :-shift]), dim=1)
def compute_ranking_loss(f_samps: Tensor, target_y: Tensor) -> Tensor:
"""
Compute ranking loss for each sample from the posterior over target points.
Args:
f_samps: `n_samples x n`-dim tensor of samples
target_y: `n x 1`-dim tensor of targets
Returns:
Tensor: `n_samples`-dim tensor containing the ranking loss across each sample
"""
y_stack = target_y.squeeze(-1).expand(f_samps.shape)
rank_loss = torch.zeros(f_samps.shape[0], dtype=torch.long, device=target_y.device)
for i in range(1,target_y.shape[0]):
rank_loss += torch.sum(
(roll_col(f_samps, i) < f_samps) ^ (roll_col(y_stack, i) < y_stack),
dim=1
)
return rank_loss
# Defin a function to do use LOOCV to fit `n` independent GPs (using batch mode) and sample from their posterior at their respective test point. Note one deviation from the original paper is that the kernel hyperparameters are refit for each fold of the LOOCV, whereas the paper uses kernel hyperparameters from the original target model fit on all data points.
#
# Check out the [gpytorch batch mode fitting tutorial](https://github.com/cornellius-gp/gpytorch/blob/master/examples/01_Simple_GP_Regression/Simple_Batch_Mode_GP_Regression.ipynb) for more info on batch mode GPs.
def get_target_model_loocv_sample_preds(train_x: Tensor, train_y: Tensor, num_samples: int) -> Tensor:
"""
Use LOOCV to fit `b=n` independent GPs using batch mode and sample from
their independent posteriors.
Args:
train_x: `n x d` tensor of training points
train_y: `n x 1` tensor of training targets
num_sample: number of mc samples to draw
Return: `num_samples x n`-dim tensor of samples for each target point from the corresponding GP
(which was training without that point).
"""
batch_size = len(train_x)
masks = torch.eye(len(train_x), dtype=torch.uint8)
train_x_cv = torch.stack([train_x[~m] for m in masks])
train_y_cv = torch.stack([train_y[~m] for m in masks])
test_x_cv = torch.stack([train_x[m] for m in masks])
test_y_cv = torch.stack([train_y[m] for m in masks])
model = get_fitted_model(train_x_cv, train_y_cv)
with torch.no_grad():
# test_x_cv here is `n (batch dimension) x 1 (num points) x 1 (num dimensions)`.
posterior = model.posterior(test_x_cv)
# Since we have a batch mode gp and model.posterior always returns an output dimension,
# the output from `posterior.sample()` here `num_samples x n x 1 x 1`, so let's squeeze
# the last two dimensions.
return posterior.sample(sample_shape=torch.Size([num_samples])).squeeze(-1).squeeze(-1)
# +
from typing import List
def compute_rank_weights(
train_x: Tensor,
train_y: Tensor,
base_models: List[SingleTaskGP],
num_samples: int
) -> Tensor:
"""
Compute ranking weights for each base model and the target model (using
LOOCV for the target model). Note: This implementation does not currently
address weight dilution, since we only have a small number of base models.
Args:
train_x: `n x d` tensor of training points (for target task)
train_y: `n` tensor of training targets (for target task)
base_models: list of `n_t` base models
num_samples: number of mc samples
Returns:
Tensor: `n_t`-dim tensor with the ranking weight for each model
"""
ranking_losses = []
# compute ranking loss for each base model
for task in range(len(base_models)):
model = base_models[task]
# compute posterior over training points for target task
posterior = model.posterior(train_x)
f_samps = posterior.sample(sample_shape=torch.Size((num_samples,))).squeeze(-1).squeeze(-1)
# compute and save ranking loss
ranking_losses.append(compute_ranking_loss(f_samps, train_y))
# compute ranking loss for target model using LOOCV
f_samps = get_target_model_loocv_sample_preds(train_x, train_y, num_samples)
ranking_losses.append(compute_ranking_loss(f_samps, train_y))
ranking_loss_tensor = torch.stack(ranking_losses)
# compute best model (minimum ranking loss) for each sample
best_models = torch.argmin(ranking_loss_tensor, dim=0)
# compute proportion of samples for which each model is best
rank_weights = best_models.bincount(minlength=len(ranking_losses)).type_as(train_x)/num_samples
return rank_weights
# +
from botorch.models.gpytorch import GPyTorchModel
from gpytorch.models import GP
from gpytorch.distributions import MultivariateNormal
from gpytorch.likelihoods import LikelihoodList
from torch.nn import ModuleList
class RGPE(GP, GPyTorchModel):
"""
Rank-weighted GP ensemble. Note: this class inherits from GPyTorchModel which provides an
interface for GPyTorch models in botorch.
"""
def __init__(self, models: List[SingleTaskGP], weights: Tensor) -> None:
super().__init__()
self.models = ModuleList(models)
for m in models:
if not hasattr(m, "likelihood"):
raise ValueError(
"RGPE currently only supports models that have a likelihood (e.g. ExactGPs)"
)
self.likelihood = LikelihoodList(*[m.likelihood for m in models])
self.weights = weights
self.to(dtype=weights.dtype, device=weights.device)
def forward(self, x: Tensor) -> MultivariateNormal:
# compute posterior for each model
posteriors = [model.posterior(x) for model in self.models]
weighted_means = []
weighted_covars = []
# filter model with zero weights
# weights on covariance matrices are weight**2
non_zero_weight_indices = (self.weights**2 > 0).nonzero()
non_zero_weights = self.weights[non_zero_weight_indices]
# re-normalize
non_zero_weights /= non_zero_weights.sum()
for non_zero_weight_idx in range(non_zero_weight_indices.shape[0]):
raw_idx = non_zero_weight_indices[non_zero_weight_idx].item()
posterior = posteriors[raw_idx]
weight = non_zero_weights[non_zero_weight_idx]
weighted_means.append(weight * posterior.mean.squeeze(-1))
# Use lazy covariance matrix
weighted_covars.append(posterior.mvn.lazy_covariance_matrix * weight**2)
# set mean and covariance to be the rank-weighted sum the means and covariances of the
# base models and target model
mean_x = torch.sum(torch.stack(weighted_means), dim=0)
covar_x = gpytorch.lazy.PsdSumLazyTensor(*weighted_covars)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
# -
# ### Optimize target function using RGPE + MC-based qEI
# +
from botorch.acquisition.monte_carlo import qExpectedImprovement
from botorch.sampling.samplers import SobolQMCNormalSampler
from botorch.optim.optimize import optimize_acqf
# suppress GPyTorch warnings about adding jitter
import warnings
warnings.filterwarnings("ignore", "^.*jitter.*", category=RuntimeWarning)
best_rgpe_all = []
best_random_all = []
best_vanilla_ei_all = []
N_BATCH = 5
INNER_OPTIMIZER_LOOPS = 15
NUM_POSTERIOR_SAMPLES = 10
RANDOM_INITIALIZATION_SIZE = 4
N_TRIALS = 20
MC_SAMPLES = 1000
N_RESTART_CANDIDATES = 100
N_RESTARTS = 5
Q_BATCH_SIZE = 1
# Average over multiple trials
for trial in range(N_TRIALS):
print(f"Trial {trial + 1} of {N_TRIALS}")
best_rgpe = []
best_random = []
best_vanilla_ei = []
# Initial random observations
raw_x = draw_sobol_samples(bounds=BOUNDS, n=RANDOM_INITIALIZATION_SIZE, q=1, seed=trial).squeeze(1)
train_x = normalize(raw_x, bounds=BOUNDS)
train_y = f(train_x)
vanilla_ei_train_x = train_x.clone()
vanilla_ei_train_y = train_y.clone()
# keep track of the best observed point at each iteration
best_value = train_y.max().item()
best_rgpe.append(best_value)
best_random.append(best_value)
vanilla_ei_best_value = best_value
best_vanilla_ei.append(vanilla_ei_best_value)
# Run N_BATCH rounds of BayesOpt after the initial random batch
for iteration in range(N_BATCH):
target_model = get_fitted_model(train_x, train_y)
model_list = base_model_list + [target_model]
rank_weights = compute_rank_weights(train_x, train_y, base_model_list, NUM_POSTERIOR_SAMPLES)
# create model and acquisition function
rgpe_model = RGPE(model_list, rank_weights)
sampler_qei = SobolQMCNormalSampler(num_samples=MC_SAMPLES)
qEI = qExpectedImprovement(model=model, best_f=best_value)
# optimize
candidate, _ = optimize_acqf(
acq_function=qEI,
bounds=torch.tensor([[0.],[1.]], dtype=dtype, device=device),
q=Q_BATCH_SIZE,
num_restarts=N_RESTARTS,
raw_samples=N_RESTART_CANDIDATES,
)
# fetch the new values
new_x = candidate.detach()
new_y = f(unnormalize(new_x, bounds=BOUNDS))
# update training points
train_x = torch.cat((train_x, new_x))
train_y = torch.cat((train_y, new_y))
random_candidate = torch.rand(1, dtype=dtype, device=device)
next_random_best = f(unnormalize(random_candidate, bounds=BOUNDS)).max().item()
best_random.append(max(best_random[-1], next_random_best))
# get the new best observed value
best_value = train_y.max().item()
best_rgpe.append(best_value)
# Run Vanilla EI for comparison
vanilla_ei_model = get_fitted_model(vanilla_ei_train_x, vanilla_ei_train_y)
vanilla_ei_sampler = SobolQMCNormalSampler(num_samples=MC_SAMPLES)
vanilla_qEI = qExpectedImprovement(
model=vanilla_ei_model,
best_f=vanilla_ei_best_value,
sampler=vanilla_ei_sampler,
)
vanilla_ei_candidate, _ = optimize_acqf(
acq_function=vanilla_qEI,
bounds=torch.tensor([[0.],[1.]], dtype=dtype, device=device),
q=Q_BATCH_SIZE,
num_restarts=N_RESTARTS,
raw_samples=N_RESTART_CANDIDATES,
)
# fetch the new values
vanilla_ei_new_x = vanilla_ei_candidate.detach()
vanilla_ei_new_y = f(unnormalize(vanilla_ei_new_x, bounds=BOUNDS))
# update training points
vanilla_ei_train_x = torch.cat([vanilla_ei_train_x, vanilla_ei_new_x])
vanilla_ei_train_y = torch.cat([vanilla_ei_train_y, vanilla_ei_new_y])
# get the new best observed value
vanilla_ei_best_value = vanilla_ei_train_y.max().item()
best_vanilla_ei.append(vanilla_ei_best_value)
best_rgpe_all.append(best_rgpe)
best_random_all.append(best_random)
best_vanilla_ei_all.append(best_vanilla_ei)
# -
# #### Plot best observed value vs iteration
# +
import numpy as np
best_rgpe_all = np.array(best_rgpe_all)
best_random_all = np.array(best_random_all)
best_vanilla_ei_all = np.array(best_vanilla_ei_all)
x = range(RANDOM_INITIALIZATION_SIZE, RANDOM_INITIALIZATION_SIZE + N_BATCH + 1)
fig, ax = plt.subplots(1, 1, figsize=(10, 6))
# Plot RGPE - EI
ax.errorbar(
x,
best_rgpe_all.mean(axis=0),
yerr=1.96 * best_rgpe_all.std(axis=0) / math.sqrt(N_TRIALS),
label="RGPE - EI",
linewidth=3,
capsize=5,
capthick=3,
)
# Plot SingleTaskGP - EI
ax.errorbar(
x,
best_vanilla_ei_all.mean(axis=0),
yerr=1.96 * best_vanilla_ei_all.std(axis=0) / math.sqrt(N_TRIALS),
label="SingleTaskGP - EI",
linewidth=3,
capsize=5,
capthick=3,
)
# Plot Random
ax.errorbar(
x,
best_random_all.mean(axis=0),
yerr= 1.96 * best_random_all.std(axis=0) / math.sqrt(N_TRIALS),
label="Random",
linewidth=3,
capsize=5,
capthick=3,
)
ax.set_ylim(bottom=0)
ax.set_xlabel('Iteration', fontsize=12)
ax.set_ylabel('Best Observed Value', fontsize=12)
ax.set_title('Best Observed Value by Iteration', fontsize=12)
ax.legend(loc="lower right", fontsize=10)
plt.tight_layout()
# -
|
tutorials/meta_learning_with_rgpe.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: DESI master custom
# language: python
# name: desi-master-custom
# ---
# # Imports
# +
import os, sys
import numpy as np
import healpy
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.signal import medfilt
from astropy.table import Table, vstack, join
from astropy.io import fits
import desispec.io
from desispec.interpolation import resample_flux
from desispec.resolution import Resolution
from desispec.spectra import Spectra
from desisim.templates import BGS, ELG
from desisim.scripts.quickspectra import sim_spectra
from desisim.io import read_basis_templates
from redrock.external.desi import rrdesi
import redrock.templates
import redrock.results
from redrock.external import desi
import time
# %matplotlib inline
sns.set(context='talk', palette='Dark2', style='ticks')
# -
# # Analysis
# +
# Read data into astropy tables
# Read in Truth Data
truthdata = Table.read(os.path.join(os.getcwd(), '..', 'lenssource-truth.fits'))
# Read in lens+source zbest
zbest_lens = Table.read(os.path.join(os.getcwd(), '..', 'lenssource-zbest.fits'))
# Read in shortened truth data
truthdata_ELG = Table.read(os.path.join(os.getcwd(), '..', 'source-truth.fits'))
# Read in source zbest
zbest_source = Table.read(os.path.join(os.getcwd(), '..', 'source-zbest.fits'))
# +
# Plot of true redshift vs redrock redshift
lensdiff = truthdata['LENS_Z'] - zbest_lens['Z']
srcdiff = truthdata_ELG['SOURCE_Z'] - zbest_source['Z']
srcsucc = np.where((np.abs(srcdiff) < 0.003) & (zbest_source['ZWARN'] == 0))[0]
lenssucc = np.where((np.abs(lensdiff) < 0.003) & (zbest_lens['ZWARN'] == 0))[0]
srcfail = np.where((np.abs(srcdiff) > 0.003) | (zbest_source['ZWARN'] != 0))[0]
lensfail = np.where((np.abs(lensdiff) > 0.003) | (zbest_lens['ZWARN'] != 0))[0]
fig, (lens, src) = plt.subplots(1,2, figsize=(16,6), sharey=False)
lens.plot(truthdata['LENS_Z'], zbest_lens['Z'], ',', label='Lens Redshifts')
lens.plot([0, max(truthdata['LENS_Z'])], [0, max(truthdata['LENS_Z'])], '--', lw=1, label='Measured Z = True Z \nw/Success={:.1f}%'.format(len(lenssucc)/len(lensdiff)*100))
lens.legend()
lens.set_xlabel('True Redshift')
lens.set_ylabel('Measured Redshift')
lens.set_ylim(0, max(truthdata['LENS_Z']))
src.plot(truthdata_ELG['SOURCE_Z'], zbest_source['Z'], ',', label='Source Redshifts')
src.plot([0, max(truthdata_ELG['SOURCE_Z'])], [0, max(truthdata_ELG['SOURCE_Z'])], '--', lw=1, label='Measured Z = True Z \nw/Success={:.1f}%'.format(len(srcsucc)/len(srcdiff)*100))
src.legend()
src.set_xlabel('True Redshift')
src.set_ylim(0, max(truthdata_ELG['SOURCE_Z']))
# +
# Plot of BGS delta redshift vs. flux ratio
lensfail = np.where((np.abs(lensdiff) > 0.003) | (zbest_lens['ZWARN'] != 0))[0]
fig, (ax1, ax2) = plt.subplots(1,2,figsize=(18,6))
ax1.plot(truthdata['FRATIO'], lensdiff, ',', label='BGS')
ax1.set_xlabel('Flux Ratio')
ax1.set_ylabel('True Z - Measured Z')
ax1.plot(truthdata['FRATIO'][lensfail], lensdiff[lensfail], 'rX', label='BGS Failures')
#ax1.title('Difference in BGS Redshift vs. Flux Ratio')
ax2.plot(truthdata['FRATIO'], lensdiff, ',')
ax2.set_xlabel('Flux Ratio')
ax2.set_ylim(-5e-4, 5e-4)
ax1.legend()
# +
# Function to bin ELG redshift data
def ELGz_hist(data, deltaFratio, minFratio, maxFratio, squareroot=False):
if squareroot:
bins = np.arange(np.sqrt(minFratio), np.sqrt(maxFratio), deltaFratio)**2 #+ deltaFratio/2
else:
bins = np.arange(minFratio, maxFratio, deltaFratio) #+ deltaFratio/2
hist, _ = np.histogram(data, bins=len(bins), range=(bins.min(), bins.max()))
return hist, bins
def plt_fraction_secure(key, minF, maxF, deltaF, xlabel=None, twinaxis=False, ax=None, squared=False):
from scipy.stats import poisson
if xlabel is None:
xlabel = key.lower()
ELGsucc = np.where((np.abs(srcdiff) < 0.003) & (zbest_source['ZWARN'] == 0))[0]
if squared:
Hist, bins = ELGz_hist(truthdata_ELG[key], minFratio=minF, maxFratio=maxF, deltaFratio=deltaF, squareroot=True)
Hist_good, _ = ELGz_hist(truthdata_ELG[key][ELGsucc], minFratio=minF, maxFratio=maxF, deltaFratio=deltaF, squareroot=True)
else:
Hist, bins = ELGz_hist(truthdata_ELG[key], minFratio=minF, maxFratio=maxF, deltaFratio=deltaF)
Hist_good, _ = ELGz_hist(truthdata_ELG[key][ELGsucc], minFratio=minF, maxFratio=maxF, deltaFratio=deltaF)
good = np.where(Hist != 0)[0]
if not ax:
fig, ax = plt.subplots(1,1,figsize=(9,6))
if twinaxis:
axtwin = ax.twinx()
axtwin.plot(truthdata_ELG[key], srcdiff, 'X', color='dodgerblue', alpha=0.8, label='ELG delta Z')
axtwin.set_ylabel('source delta z')
axtwin.legend(loc='lower left')
Ntot = Hist[good]
Nsuccess = Hist_good[good]
alphas = [1, 0.5, 0.25]
for i, sigma in enumerate([0.68, 0.95, 0.997]):
tot_lower, tot_upper = poisson.interval(sigma, Ntot)
succ_lower, succ_upper = poisson.interval(sigma, Nsuccess)
fraction = Nsuccess / Ntot
frac_lower = fraction * np.sqrt((succ_lower*0 / Ntot)**2 + (tot_lower / Ntot)**2)
frac_upper = fraction * np.sqrt((succ_upper*0 / Ntot)**2 + (tot_upper / Ntot)**2)
frac_upper[frac_upper>=1] = 1
ax.fill_between(bins[good], frac_lower, frac_upper, edgecolor='dimgrey', facecolor='lightblue',
lw=2, label='{}% Confidence Interval'.format(sigma*100), alpha=alphas[i])
#ax.plot(bins[good], fraction, '--', color='dimgrey')
ax.set_xlabel('{}'.format(xlabel))
ax.set_ylabel('Fraction of Secure Source Redshifts')
ax.legend()
# +
# Plot of histogram ratio of ELG outputs
minF = min(truthdata_ELG['FRATIO'])
maxF = max(truthdata_ELG['FRATIO'])
num = len(truthdata_ELG['FRATIO'])
deltaF = 0.04 #(maxF-minF)/(num)
fig, ax = plt.subplots(1,1,figsize=(9,6))
plt_fraction_secure('FRATIO', minF, maxF, deltaF, xlabel='Ratio of Source Flux to Lens Flux', squared=True, ax=ax)
ax.legend(loc='lower right')
plt.savefig('Fratio_plot.png', dpi=300)
# +
# Plot of secure redshifts vs. source mag
key = 'SOURCE_MAG'
minF = min(truthdata_ELG[key])
maxF = max(truthdata_ELG[key])
num = len(truthdata_ELG[key])
deltaF = .2 #(maxF-minF)/(num)
plt_fraction_secure(key, minF, maxF, deltaF, xlabel='Source r-Band Magnitude')
plt.savefig('sourceMag_plot.png', dpi=300)
# +
# Plot of secure redshifts vs. lens mag
key = 'LENS_MAG'
minF = min(truthdata_ELG[key])
maxF = max(truthdata_ELG[key])
num = len(truthdata_ELG[key])
deltaF = 0.1 #(maxF-minF)/(num)
fig, ax = plt.subplots(1,1,figsize=(9,6))
plt_fraction_secure(key, minF, maxF, deltaF, xlabel='Lens Magnitude', ax=ax)
ax.set_xlim(18,20)
# +
# Plot of secure redshifts vs. source redshift
key = 'SOURCE_Z'
minF = min(truthdata_ELG[key])
maxF = max(truthdata_ELG[key])
num = len(truthdata_ELG[key])
deltaF = 0.1 #(maxF-minF)/(num)
plt_fraction_secure(key, minF, maxF, deltaF, xlabel='Source Redshift')
# +
# Plot of secure redshifts vs. lens redshift
key = 'LENS_Z'
minF = min(truthdata_ELG[key])
maxF = max(truthdata_ELG[key])
num = len(truthdata_ELG[key])
deltaF = 0.06 #(maxF-minF)/(num)
plt_fraction_secure(key, minF, maxF, deltaF, xlabel='Lens Redshift')
# +
# Get flux and wave data
chunk = 0 # Change to chunk that you want to look at spectra in
combflux = fits.getdata(os.path.join(os.getcwd(), '..', 'lenssource-truth.fits'), 'FLUX')
combwave = fits.getdata(os.path.join(os.getcwd(), '..', 'lenssource-truth.fits'), 'WAVE')
BGSflux = fits.getdata(os.path.join(os.getcwd(), '..', 'lenssource-truth.fits'), 'BGSFLUX')
ELGflux = fits.getdata(os.path.join(os.getcwd(), '..', 'lenssource-truth.fits'), 'ELGFLUX')
spectra = desispec.io.read_spectra(os.path.join(os.getcwd(), '..', 'lenssource-spectra-chunk00{}.fits'.format(chunk)))
# +
# Plot spectra
## Top panel is source and lens
## Observed Noiseless Spectrum
## Observed Noisy Spectrum
## No Title but put magnitude in legend
nperchunk=500 #make this equal to your nperchunk, or the number of simulations per chunk
specnum=spec+chunk*nperchunk
spec = 11 # 0-500, if there are more than 500 spectra, change the chunk variable
fig, (E, B, N) = plt.subplots(3,1,figsize=(12,12), sharey=False, sharex=True)
E.plot(combwave, ELGflux[specnum], label='Source @ z={:.4f} & r={:.2f}'.format(truthdata['SOURCE_Z'][specnum], truthdata['SOURCE_MAG'][specnum]))
E.plot(combwave, BGSflux[specnum], label='Lens @ z={:.4f} & r={:.2f}'.format(truthdata['LENS_Z'][specnum], truthdata['LENS_MAG'][specnum]))
#E.plot(combwave, combflux[specnum], label='Combined Spectra', alpha=0.5)
E.legend(fontsize='x-small')
#E.set_ylabel('Flux')
#E.set_title('Flux Ratio: {:.2f}'.format(truthdata['FRATIO'][specnum]))
B.plot(combwave, combflux[specnum], label='Noiseless Combined Spectra')
B.legend()
B.set_ylabel('Flux [$10^{-17} erg s^{-1} cm^{-2} \AA^{-1}$]')
N.set_xlabel('Wavelength [$\AA$]')
for band in spectra.bands:
N.plot(spectra.wave[band], spectra.flux[band][spec], alpha=0.7)
N.plot(combwave, combflux[specnum], color='k', linewidth=1.1, label='Noisy Combined Spectra')
N.set_ylim(min(combflux[specnum]) - 25, max(combflux[specnum]) + 25)
N.legend()
fig.savefig('sampleSpectra.png', dpi=300)
# -
|
py/speclens_analysis.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="p78j872pOKTZ"
# # CAP 5768 - Data Science - Dr. Marques - Fall 2019
#
# <NAME>
# + [markdown] colab_type="text" id="NYmNMHGLOKTa"
# ## Assignment 2: Exploratory data analysis
# + [markdown] colab_type="text" id="9UMnsRndOKTb"
# ### Goals
#
# - To increase familiarity with the Python "data science stack" (NumPy, Pandas, Matplotlib).
# - To explore (manipulate, summarize, and visualize) datasets.
# - To improve the ability to write Python code to answer questions and test hypotheses based on the contents of those datasets.
# + [markdown] colab_type="text" id="B0rEAT7MOKTb"
# ### Instructions
#
# - This assignment is structured in three parts, using a different dataset for each part.
# - For each part, there will be some Python code to be written and questions to be answered.
# - At the end, you should export your notebook to PDF format; it will "automagically" become your report.
# - Submit the report (PDF), notebook (.ipynb file), and (optionally) link to the "live" version of your solution on Google Colaboratory via Canvas.
# - The total number of points is 154 (plus up to 85 bonus points), distributed as follows: Part 1 (58+ pts), Part 2 (28+ pts), Part 3 (43+ pts), and Conclusions (25 pts).
# + [markdown] colab_type="text" id="qiufouQn6OD9"
# ### Important
#
# - It is OK to attempt the bonus points, but please **do not overdo it!**
# - Remember: this is an exercise in performing exploratory data analysis; expanding (and practicing) your knowledge of Python, Jupyter notebooks, Numpy, Pandas, and Matplotlib; and writing code to test hypotheses and answer questions based on the available data (and associated summary statistics).
# - This is not (yet) the time to do sophisticated statistical analysis, train ML models, etc.
# - You must **organize your data files in the proper folders** for the code to work.
# + [markdown] colab_type="text" id="fiXV2xUI7lUZ"
# -------------------
# ## Part 1: The MovieLens 1M dataset
#
# This is a dataset of movie ratings data collected from users of MovieLens in the late 1990s and early 2000s. The data provide movie ratings, movie metadata, and demographic data about the users. Such data is often of interest in the development of recommendation systems based on machine learning algorithms.
#
# The MovieLens 1M dataset contains ~1 million ratings collected from ~6,000 users on ~4,000 movies. It's spread across three tables: _ratings_, _user information_, and _movie information_. After extracting the data from the ZIP file (available on Canvas), we can load each table into a pandas DataFrame object using the Python code below.
#
# See:
# https://grouplens.org/datasets/movielens/ for additional information.
# +
# Imports
import numpy as np
import pandas as pd
from pandas import DataFrame, Series
# %matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import pearsonr
# -
# Before running the cell below, make sure that you have downloaded the movielens.zip file from Canvas, unzipped it, and placed its contents under the 'data' folder.
#
# <img src="notebook_images/movielens_path.png" width="500" align="left">
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="4dkSabDG5gjc" outputId="3c3cdd00-171e-4e91-9bcc-67f79eceeb70"
import pandas as pd
# Make display smaller
pd.options.display.max_rows = 10
unames = ['user_id', 'gender', 'age', 'occupation', 'zip']
users = pd.read_table('data/movielens/users.dat', sep='::',
header=None, names=unames, engine='python')
rnames = ['user_id', 'movie_id', 'rating', 'timestamp']
ratings = pd.read_table('data/movielens/ratings.dat', sep='::',
header=None, names=rnames, engine='python')
mnames = ['movie_id', 'title', 'genres']
movies = pd.read_table('data/movielens/movies.dat', sep='::',
header=None, names=mnames, engine='python')
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # Your turn! (24 points, i.e., 6 pts each)
#
# Write Python code to answer the following questions (make sure the messages displayed by your code are complete and descriptive enough):
# 1. How many users are stored in the _users_ table and what information is stored for each user?
# 2. How many movies are stored in the _movies_ table and what information is stored for each movie?
# 3. How many ratings are stored in the _ratings_ table and what information is stored for each rating?
# 4. How are users, the movies each user has rated, and the rating related?
#
# *Note*: ages and occupations are coded as integers indicating _groups_ described in the dataset’s README file.
# +
# Uncomment to see details of the movies datasets
# # !cat 'data/movielens/README'
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# -
# ### How many users are stored in the users table and what information is stored for each user?
# + colab={} colab_type="code" id="d4jcQfb2AIub"
len(users)
# -
users.dtypes
users.head()
users.gender.unique()
users.occupation.unique()
# There are 6,040 users. For each one of them the dataset has:
#
# * `user_id`: a unique id, stored as an integer.
# * `gender`: a character that identifies the user's gender - possible values are `F` and `M`.
# * `age`: user's age range, coded as explained in the _README_ file, stored as an integer.
# * `occupation`: user's occupation, coded as an integer.
# * `zip`: user's ZIP code, stored as a string.
#
# ### How many movies are stored in the movies table and what information is stored for each movie?
len(movies)
movies.dtypes
movies.head()
# There are 3,883 movies. For each movie the dataset has:
#
# * `movie_id`: a unique id, stored as an integer.
# * `title`: a string with the movie title and year.
# * `genres`: all genres for the movie, separated by `|`.
# ### How many ratings are stored in the ratings table and what information is stored for each rating?
len(ratings)
ratings.dtypes
ratings.head()
ratings.rating.unique()
# There are 1,000,209 ratings. For each rating the dataset has:
#
# * `user_id`: the id of the user who rated the movie.
# * `movied_id`: the id of the rated movie.
# * `rating`: the user rating, in a range from 1 to 5, as an integer.
# * `timestamp`: seconds since midnight Coordinated Universal Time (UTC) of January 1, 1970 ([source](http://files.grouplens.org/datasets/movielens/ml-20m-README.html)).
#
# ### How are users, the movies each user has rated, and the rating related?
# They are related by their id fields, `user_id` and `movie_id`.
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # Your turn! (24 points, i.e., 6 pts each)
#
# Write Python code to answer the following questions (make sure the messages displayed by your code are complete and descriptive enough):
# 5. What is the occupation that maps to most of the users? Plot a bar chart of the occupation counts and report the size of the largest bin.
# 6. What percentage of users are 50 years old or older? Plot a pie chart showing all percentages (per age group) and report the requested value.
# 7. Which movie received the highest number of ratings (and how were such ratings distributed)?
# 8. What is the average rating for all movies/users?
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# + [markdown] colab_type="text" id="YxJNmDgn-PyW"
# (ENTER YOUR ANSWERS HERE)
# + [markdown] colab={} colab_type="code" id="d4jcQfb2AIub"
# ### 5. What is the occupation that maps to most of the users? Plot a bar chart of the occupation counts and report the size of the largest bin.
#
# Most of the time we are interested in asnwering questions, e.g. "what is the most frequent occupation". Therefore we will graph them in sorted order.
#
# We also translate the coded occupation into the occupation name, as defined in the README file for the dataset.
# +
# Table comes from information in the README file
occupation_names = { 'occupation' : {
0: 'other', 1: 'academic/educator', 2: 'artist',
3: 'clerical/admin', 4: 'college/grad student',
5: 'customer service', 6: 'doctor/health care',
7: 'executive/managerial', 8: 'farmer', 9: 'homemaker',
10: 'K-12 student', 11: 'lawyer', 12: 'programmer',
13: 'retired', 14: 'sales/marketing', 15: 'scientist',
16: 'self-employed', 17: 'technician/engineer',
18: 'tradesman/craftsman', 19: 'unemployed', 20: 'writer'}}
users.replace(occupation_names, inplace=True)
# -
occupation_by_users = users.groupby('occupation')['user_id'] \
.count().sort_values(ascending=False)
print('Occupation with most users: {}, with {} users'.format(
occupation_by_users.index[0], occupation_by_users.iloc[0]))
# +
def format_graph(ax):
# Remove box around the graph
for s in ('right', 'left', 'top', 'bottom'):
ax.spines[s].set_visible(False)
# Remove all tick marks
plt.tick_params(bottom=False, top=False, left=False, right=False)
def formatted_barh_graph(df, title):
ax = df.plot.barh(title=title)
format_graph(ax)
# Show a vertical grid to help size the bars
ax.grid(axis='x', alpha=0.4)
# And now, nitpicking (zero can be inferred)
ax.xaxis.get_major_ticks()[0].label1.set_visible(False)
title = 'Number of users by occupation ({:,} users)'.format(len(users))
formatted_barh_graph(occupation_by_users, title)
# -
# ### 6. What percentage of users are 50 years old or older? Plot a pie chart showing all percentages (per age group) and report the requested value.
# According to the README file:
#
# > Age is chosen from the following ranges:
# >
# > * 1: "Under 18"
# > * 18: "18-24"
# > * 25: "25-34"
# > * 35: "35-44"
# > * 45: "45-49"
# > * 50: "50-55"
# > * 56: "56+"
#
# Thus "50 years old or older" encompasses two groups, "50" and "56".
fifty_or_older = users.eval('(age == 50) | (age == 56)')
c = len(users[fifty_or_older])
print('There are {} ({:.2f}%) users who are 50 years old or older'
.format(c, c/len(users)*100))
users.groupby('age').count()['user_id'].plot(
kind='pie', autopct='%1.1f%%', title='Users by age group');
# ### 7. Which movie received the highest number of ratings (and how were such ratings distributed)?
highest_number_ratings = ratings.groupby('movie_id')['rating'] \
.count().sort_values(ascending=False).index[0]
movies[movies['movie_id'] == highest_number_ratings]
# +
# calculate absolute number of ratings for that movie, by rating
num_ratings = pd.DataFrame(
ratings[ratings['movie_id'] == highest_number_ratings] \
.groupby('rating')['user_id'].count())
# calculate percentage (distribution) for each rating
num_ratings['percentage'] = num_ratings['user_id'] / num_ratings['user_id'].sum() * 100
# Print and graph
display(num_ratings)
num_ratings['user_id'].plot(kind='pie', autopct='%1.1f%%',
title='Distribution of ratings')
# -
# ### 8. What is the average rating for all movies/users?
print('The average rating for all movies/users: {:.1f}'
.format(ratings['rating'].sum() / len(ratings)))
# -------------------
# We will use the Python code below to merge all three tables into a unified data frame.
data = pd.merge(pd.merge(ratings, users), movies)
data.head()
# The Python code below will show the top 10 films among female viewers (and, for comparison's sake, the ratings for those movies by male viewers) in decreasing order (highest rated movie on top).
# Build pivot table
mean_ratings = data.pivot_table('rating', index='title',
columns='gender', aggfunc='mean')
display(mean_ratings[:3])
# Group ratings by title
ratings_by_title = data.groupby('title').size()
#display(ratings_by_title.index)
display(ratings_by_title[:3])
# Select only movies with 250 ratings or more
active_titles = ratings_by_title.index[ratings_by_title >= 250]
display(active_titles[:3])
# Select rows on the index
mean_ratings = mean_ratings.loc[active_titles]
display(mean_ratings[:3])
# Fix naming inconsistency
mean_ratings = mean_ratings.rename(index={'Seven Samurai (The Magnificent Seven) (Shichinin no samurai) (1954)':
'Seven Samurai (Shichinin no samurai) (1954)'})
top_female_ratings = mean_ratings.sort_values(by='F', ascending=False)
top_female_ratings.head(10)
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # Your turn! (10 points, i.e., 5 pts each)
#
# Modify the Python code to:
# 9. Display the top 10 favorite movies among male viewers, selecting only movies with 250 ratings or more.
# 10. Display the top 10 favorite movies among young viewers (17 years old or younger), selecting only movies with 300 ratings or more.
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# + [markdown] colab={} colab_type="code" id="d4jcQfb2AIub"
# ### 9. Display the top 10 favorite movies among male viewers, selecting only movies with 250 ratings or more.
# -
mean_ratings.sort_values(by='M', ascending=False).head(10)
# ### 10. Display the top 10 favorite movies among young viewers (17 years old or younger), selecting only movies with 300 ratings or more.
# According to the README file:
#
# > Age is chosen from the following ranges:
# >
# > * 1: "Under 18"
# Note that the "top 10 favorite" movies may end up being more than ten movies, once we account for rating ties. That is what happened in this case. There are 17 movies in the "top 10 favorite" list because of ties in ratings.
# +
age_mean_ratings = data.pivot_table('rating', index='title',
columns='age', aggfunc='mean')
# Select movies with 300 ratings or more
ratings_by_title = data.groupby('title').size()
active_titles = ratings_by_title.index[ratings_by_title >= 300]
age_mean_ratings = age_mean_ratings.loc[active_titles]
# Select ratings for young viewers
young_mean_ratings = age_mean_ratings[1]
# Account for possible ties: get the top ten rating values
top_ten_ratings = young_mean_ratings.sort_values(
ascending=False).unique()[:10]
# Show all movies that fall into the "top 10 ratings" range
with pd.option_context('display.max_rows', None):
print(young_mean_ratings[young_mean_ratings >= top_ten_ratings[-1]] \
.sort_values(ascending=False))
# -
# Precocious these youngsters seem to be... Or perhaps the lesson here is "don't trust in self-identified data" (who knows what the actual age is of those users).
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # BONUS! (up to 20 points)
#
# Write Python code to display the most divisive movies (selecting only movies with 250 ratings or more), i.e.:
# - The top 10 movies with the greatest rating difference so that we can see which ones were preferred by women.
# - The top 10 movies with the greatest rating difference in the opposite direction (sign) so that we can see which ones were preferred by men.
#
# Hint/Convention: ``mean_ratings['diff'] = mean_ratings['M'] - mean_ratings['F']``
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# + [markdown] colab={} colab_type="code" id="d4jcQfb2AIub"
# ### The top 10 movies with the greatest rating difference so that we can see which ones were preferred by women.
# -
# mean_ratings was created above, with movies that have 250 ratings or more
mean_ratings['Preferred by F'] = mean_ratings['F'] - mean_ratings['M']
pref_by_women = mean_ratings.sort_values(by='Preferred by F', ascending=False)[:10]
pref_by_women
# Visualize it: show the rating differences in a full rating scale, to visualize how far apart they actually are ([based on this post](https://www.machinelearningplus.com/plots/top-50-matplotlib-visualizations-the-master-plots-python/#17.-Dot-Plot)).
# +
import matplotlib.patches as mpatches
def plot_ratings_difference(df):
F_COLOR, M_COLOR = 'firebrick', 'midnightblue'
fig, ax = plt.subplots()
ax.hlines(y=df.index, xmin=1, xmax=5, color='gray', alpha=0.7,
linewidth=0.8)
ax.scatter(y=df.index, x=df.F, s=75, color=F_COLOR, alpha=0.7)
ax.scatter(y=df.index, x=df.M, s=75, color=M_COLOR, alpha=0.7)
format_graph(ax)
plt.gca().invert_yaxis()
plt.xticks([1, 2, 3, 4, 5]);
ax.xaxis.set_ticks_position('top')
# Manually add the legend
plt.legend(loc='upper right', bbox_to_anchor=(1.25, 1),
handles=[mpatches.Patch(color=F_COLOR, label='Women'),
mpatches.Patch(color=M_COLOR, label='Men')])
plot_ratings_difference(pref_by_women)
# -
# ### The top 10 movies with the greatest rating difference in the opposite direction (sign) so that we can see which ones were preferred by men.
pref_by_men = mean_ratings.sort_values(by='Preferred by F', ascending=True)[:10]
pref_by_men
plot_ratings_difference(pref_by_men)
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # BONUS! (up to 10 points)
#
# Write Python code to display the top 10 movies (with 250 ratings or more) that elicited the most disagreement among viewers, independent of gender identification.
#
# Hint: Disagreement can be measured by the _variance_ or _standard deviation_ of the ratings.
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# + [markdown] colab={} colab_type="code" id="d4jcQfb2AIub"
# ### Write Python code to display the top 10 movies (with 250 ratings or more) that elicited the most disagreement among viewers, independent of gender identification.
# -
# Step 1: count how many votes each movie received in the 1-5 rating scale. This gives the raw disagreement count.
total_ratings = data.pivot_table('user_id', index='title',
columns='rating', aggfunc='count')
total_ratings.head(3)
# Step 2: Change the raw counts into ratios, to normalize by number of reviewers. Otherwise movies with more reviewers would naturally have higher disagreement, just by having larger numbers in the calculations we will do later.
# +
sum_ratings = total_ratings.sum(axis=1)
for c in total_ratings.columns:
total_ratings[c] /= sum_ratings
# Check that we normalized correctly
assert(np.allclose(total_ratings.sum(axis=1), 1))
total_ratings.head(3)
# -
# Step 3: Calculate a _disagreement measure_. We will use `std()` for that.
total_ratings['disagreement'] = total_ratings.std(axis=1)
total_ratings.head(3)
# Step 4: Filter by number of reviewers, sort and display results
# Note that we want the movies with the lowest standard deviation. That means the ratings are more evenly spread in the rating scale, indicating reviewers do not agree on a rating. High standard deviation happens when one of the ratings receives most of the votes, indicating consensus.
#
# The ratings are shown in a heatmap, using [Pandas styling](https://pandas.pydata.org/pandas-docs/stable/user_guide/style.html). The heatmap was chosen to visualize how close the ratings are (resulting in a low standard deviation). The closeness of ratings shows up in the heatmap as cells (in the same row) having similar colors.
#
#
# To accomplish that:
#
# 1. `low` and `high` were set to match the 0-100% scale of the overal distribution of ratings. If they are not set, the heatmap would color based on values on the table, breaking the visualization.
# 1. The heatmap uses a sequential colormap, to further highlight how close they are (as opposed to a diverging colormap - see more in [this Matplotlib tutorial](https://matplotlib.org/3.1.0/tutorials/colors/colormaps.html)).
# +
total_ratings = total_ratings.loc[active_titles]
top_ten_disagreements = total_ratings.sort_values(
by='disagreement', ascending=True).head(10)
top_ten_disagreements.style.format('{:.3f}') \
.background_gradient(subset=[1,2,3,4,5], cmap='binary',
axis='columns', low=0, high=1)
# -
# The next cell is used to export to PDF. Styled Pandas DataFrames are not exported to PDF. The cell below shows a .png saved from the cell above. The .png is exported correctly to PDF.
# 
# Contrast with the "agreement" heatmap below, showing the top 10 movies for which users gave similar ratings. Cells in a row bounce between light and dark colors, without other shades in between.
total_ratings.sort_values(
by='disagreement', ascending=True).tail(10) \
.style.format('{:.3f}') \
.background_gradient(subset=[1,2,3,4,5], cmap='binary',
axis='columns', low=0, high=1)
# The next cell is used to export to PDF. Styled Pandas DataFrames are not exported to PDF. The cell below shows a .png saved from the cell above. The .png is exported correctly to PDF.
# 
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # BONUS! (up to 10 points)
#
# Write Python code to answer the question:
# What is the most popular movie genre?
# Plot a bar chart of the genre counts and report the size of the largest bin.
#
# Hint: use the original **movies** data frame, _before_ the merge!
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# -
# With thanks to [this Stackoverflow answer](https://stackoverflow.com/a/52133059/336802) for pointing to the Pandas [`get_dummies` function](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.get_dummies.html).
#
# This is done in two steps:
#
# 1. `get_dummies()` splits the genres into columns ([hot-encodes](https://en.wikipedia.org/wiki/One-hot) them).
# 1. `sum()` adds all the 1s that `get_dummies()` created.
#
# Although we can do it all in one line, we will do in steps to understand it better.
# Step 1: split the genres into hot-encoded columns
genres = movies.genres.str.get_dummies()
genres.head(3)
# Step 2: count each genre and sort them so the chart looks better.
genres = genres.sum().sort_values()
genres.head(3)
# Step 3: plot the genres and customize the graph to increase information/pixels ratio.
title = 'Number of movies by genre ({:,} movies)'.format(len(movies))
formatted_barh_graph(genres, title)
# The largest category, as requested in the question.
print('The largest movie category is {}, with {:,} movies'
.format(genres.tail(1).index[0],genres[-1]))
# + [markdown] colab_type="text" id="ivz9CfpTOKTc"
# ------------
# ## Part 2: Titanic
# + [markdown] colab_type="text" id="F0XHAppiOKTc"
# In this part we'll use the dataset of passengers on the *Titanic*, available through the Seaborn library.
#
# See https://www.kaggle.com/c/titanic/data for codebook and additional information.
# +
# To validate the certificate when downloading
# see https://stackoverflow.com/a/60671292
import ssl
ssl._create_default_https_context = ssl._create_unverified_context
titanic = sns.load_dataset('titanic')
# -
titanic.head()
# + [markdown] colab_type="text" id="TTEVu2FjOKTq"
# ## Questions 11-14 (16 points total, i.e. 4 pts each)
#
# Look at the Python code below and answer the following questions (expressing the amounts in absolute terms):
#
# 11. How many female passengers did not survive (regardless of their class)?
# 12. How many first class female passengers did not survive?
# 13. How many male passengers did not survive (regardless of their class)?
# 14. How many third class male passengers did not survive?
# -
titanic.pivot_table('survived', index='sex', columns='class', margins=True)
sns.catplot(x="sex", y="survived", hue="class", kind="bar", data=titanic);
# + [markdown] colab_type="text" id="dv-bu9a77Zit"
# ## Solution
# + [markdown] colab_type="text" id="eOLyQdlcOKTq"
# ### 11. How many female passengers did not survive (regardless of their class)?
# +
def genre_died(genre):
return (titanic['sex'] == genre) & (titanic['survived'] == 0)
print('{} female passangers did not survive'.format(
len(titanic[genre_died('female')])))
# -
# ### 12. How many first class female passengers did not survive?
print('{} first class female passengers did not survive'.format(
len(titanic[genre_died('female') & (titanic['class'] == 'First')])))
# ### 13. How many male passengers did not survive (regardless of their class)?
print('{} male passangers did not survive'.format(
len(titanic[genre_died('male')])))
# ### 14. How many third class male passengers did not survive?
print('{} third class male passengers did not survive'.format(
len(titanic[genre_died('male') & (titanic['class'] == 'Third')])))
# + [markdown] colab_type="text" id="BbUZtqu7OKTl"
# ## Your turn! (12 points, i.e., 4 pts each)
#
# Write Python code to answer the following questions (make sure the messages displayed by your code are complete and descriptive enough):
#
# 15. How many passengers (absolute number) were there per deck/class?
#
# (**Hint**: The plot below shows how decks and classes were related and provides a visual estimate.)
# 16. How many passengers (absolute number) in Deck A survived?
# 17. How many passengers (absolute number) in Deck E survived and what was the breakdown (in Deck E) per class?
#
# 
# + [markdown] colab_type="text" id="eWDwcuiz7Wiz"
# ## Solution
# + [markdown] colab={} colab_type="code" id="ZZqA7kEWOKTl"
# ### 15. How many passengers (absolute number) were there per deck/class?
# -
# First we need to fix the missing deck entries. Because it is a category, we need to expand the category with a value that represents "missing".
# https://stackoverflow.com/a/36193135
titanic.deck = titanic.deck.cat.add_categories(['Unknown'])
titanic.deck.fillna('Unknown', inplace=True)
# With that in place, we can find the counts with the pivot table. We could `count` on different columns to get the number of passagers, so we picked a column that does not have `NaN` (or we would have to deal with that first).
# Aggregate by `count` to consider all passengers (survivors or not)
# To show only survivors (survived=1), aggregate by `sum`
titanic.pivot_table('survived', index='deck', columns='class',
aggfunc='count', margins=True, fill_value='')
# ### 16. How many passengers (absolute number) in Deck A survived?
print('{} passengers in deck A survived'
.format(len(titanic.query('(deck == "A") & (survived == 1)'))))
# ### 17. How many passengers (absolute number) in Deck E survived and what was the breakdown (in Deck E) per class?
titanic[titanic['deck'] == 'E'].pivot_table(
'survived', index='class', aggfunc='sum', margins=True)
# Why `aggfunc('sum')` works here: `survived` is an integer with 0 or 1 as value. Summing up that column is the same as counting survivors (the 1s).
# + [markdown] colab_type="text" id="QtjTzR09-PyS"
# # BONUS! (up to 20 points)
#
# Write Python code to answer the following questions (using percentage values):
# - How many women traveling alone did not survive?
# - How many men 35 years old or younger did not survive?
# - What was the average fare per class?
# + [markdown] colab_type="text" id="BTExQawjAIuU"
# ## Solution
# -
# ### How many women traveling alone did not survive?
# + colab={} colab_type="code" id="d4jcQfb2AIub"
print('{} women travelling alone did not survive'
.format(len(titanic.query('(sex == "female") & alone & (survived == 0)'))))
# -
# ### How many men 35 years old or younger did not survive?
print('{} men 35 years old or younger did not survive'
.format(len(titanic.query('(sex == "male") & (age <= 35) & (survived == 0)'))))
# ### What was the average fare per class?
# Two solutions, for comparison.
titanic.groupby('class')['fare'].mean()
# aggregration by `mean` is the default
titanic.pivot_table('fare', index='class')
# + [markdown] colab_type="text" id="ivz9CfpTOKTc"
# ------------
# ## Part 3: US Baby Names 1880–2018
# + [markdown] colab_type="text" id="F0XHAppiOKTc"
# The United States Social Security Administration (SSA) has made available data on the frequency of baby names from 1880 through the present. These plain text data files, one per year, contain the total number of births for each sex/name combination. The raw archive of these files can be obtained from http://www.ssa.gov/oact/babynames/limits.html.
#
# After downloading the 'National data' file _names.zip_ and unzipping it, you will have a directory containing a series of files like _yob1880.txt_ through _yob2018.txt_. We need to do some data wrangling to load this dataset (see code below).
# -
# For your convenience, I have made the _names.zip_ file available on Canvas.
# Before running the cell below, make sure that you have downloaded it, unzipped it, and placed its contents under the 'data' folder.
#
# <img src="notebook_images/births_path.png" width="500" align="left">
# +
years = range(1880, 2019)
pieces = []
columns = ['name', 'sex', 'births']
for year in years:
path = 'data/names/yob%d.txt' % year
frame = pd.read_csv(path, names=columns)
frame['year'] = year
pieces.append(frame)
# Concatenate everything into a single DataFrame
names = pd.concat(pieces, ignore_index=True)
# -
names
# + [markdown] colab_type="text" id="KurMrocpOKTo"
# ## Your turn! (25 points)
#
# Write Python code to compute the number of baby boys and baby girls born each year and display the two line plots over time.
#
# Hint: Start by aggregating the data at the year and sex level using ``groupby`` or ``pivot_table``.
#
# Your plot should look like this:
#
# 
# + [markdown] colab_type="text" id="5jY56oY97Yvp"
# ## Solution
# + colab={} colab_type="code" id="A4QFk_ktOKTo"
ax = names.pivot_table('births', index='year', columns='sex', aggfunc='sum') \
.plot(title='Total births by sex and year')
ax.grid(alpha=0.3)
# + [markdown] colab_type="text" id="YNr4O_tHOKTn"
# -------------
# ## Analyzing Naming Trends
#
# Suppose we're interested in analyzing the Top 1000 most popular baby names per year.
#
# We will do so by following these steps:
# 1. Insert a column _prop_ with the fraction of babies given each name relative to the total number of births. A prop value of 0.02 would indicate that 2 out of every 100 babies were given a particular name in a given year.
# 2. Group the data by year and sex, then add the new column to each group.
# 3. Extract a subset of the data (the top 1,000 names for each sex/year combination). This is yet another group operation.
# 4. Split the Top 1,000 names into the boy and girl portions.
# 5. Build a pivot table of the total number of births by year and name.
#
# Finally, we will plot the absolute number of babies named 'John', 'Noah', 'Madison', or 'Lorraine' over time.
# -
def add_prop(group):
group['prop'] = group.births / group.births.sum()
return group
names = names.groupby(['year', 'sex']).apply(add_prop)
names
# Sanity check (all percentages should add up to 1, i.e., 100%)
names.groupby(['year', 'sex']).prop.sum()
def get_top1000(group):
return group.sort_values(by='births', ascending=False)[:1000]
grouped = names.groupby(['year', 'sex'])
top1000 = grouped.apply(get_top1000)
# Drop the group index, not needed
top1000.reset_index(inplace=True, drop=True)
top1000
boys = top1000[top1000.sex == 'M']
girls = top1000[top1000.sex == 'F']
total_births = top1000.pivot_table('births', index='year',
columns='name',
aggfunc=sum)
total_births.info()
total_births
subset = total_births[['John', 'Noah', 'Madison', 'Lorraine']]
ax = subset.plot(subplots=True, figsize=(12, 10), grid=False,
title="Number of births per year")
# ax = subset.plot(subplots=True, figsize=(12, 10), grid=False,
# title="Number of births per year", ylim=(0,0.1))
# + [markdown] colab_type="text" id="TTEVu2FjOKTq"
# --------------
# # BONUS! (up to 25 points)
#
# Write Python code to test the hypothesis:
#
# H1: There has been an increase in naming diversity over time.
#
# Hint: Compute a metric that consists of the number of distinct names, taken in order of popularity from highest to lowest, in the top 50% of births, and plot that metric over time.
#
# Your plot should look like this:
#
# 
# + [markdown] colab_type="text" id="dv-bu9a77Zit"
# ## Solution
# -
# ### _Diversity_ as "more names are being used"
# This is the simplest possible measure of name diversity: more names are being used over time.
#
# The graph shows that the number of unique names increased rapidly until the early 2000s. After that it started to decrease (more pronouncedly for girl names). By this metric, name diversity greatly increased during the 20<sup>th</sup> century, but in the 21<sup>st</sup> century it is decreasing.
names_by_year = names.pivot_table('name', index='year', columns='sex',
aggfunc='count', fill_value=0)
names_by_year.plot(title='Unique names');
# ### _Diversity_ as "more names in the top 50% births"
# Another way to look at diversity is to inspect the names responsible for 50% of total number of births.
#
# We will inspect them in two ways:
#
# 1. The absolute number of names
# 1. The percentage of names
# The graph below shows the total number of names accounting for 50% of the number of births.
#
# It shows that in general name diversity is growing over time, with a few declines, but generally trending up.
# +
def get_count_top_half(group):
# Our dataset is already sorted by number of births, but we should
# be defensive and not assume that, or the cumsum code will break
group = group.sort_values(by='prop', ascending=False)
return len(group[group['prop'].cumsum() <= 0.5])
# Count of births in the top half of total births
count_top_50_births = names.groupby(['year', 'sex']).apply(get_count_top_half)
# Move genre to a column, in preparation to plot it
count_top_50_births = count_top_50_births.unstack()
count_top_50_births.plot(
title='Number of names in the top half number of births');
# -
# The next graphs looks at the same metric, but now in relative terms. They graph the number of names accounting for 50% and 99% of the births.
#
# They show that the proportion of names accouting for 50% and 99% of the births declined until the 1980s (50%) and 1960s (99%), increasing diversity (less concentration of names). After that the proportion started to rise again, decreasing diversity. In other words, although we are using more names in absolute numbers (previous graph), we are picking from a smaller subset of all names used in a given year (picking from a large subset, but a smaller percentage than previous years - therefore, in that sense, decreasing diversity).
# +
q = 0.5
def get_prop_top_pct(group):
# Our dataset is already sorted by number of births, but we should
# be defensive and not assume that, or the cumsum code will break
group = group.sort_values(by='prop', ascending=False)
return len(group[group['prop'].cumsum() <= q]) / len(group)
def graph_pct_names(pct, ticks_value):
global q
q = pct
# Proportion of births in the top % of total births
top_pct_births = names.groupby(['year', 'sex']).apply(get_prop_top_pct)
# Move genre to a column, in preparation to plot it
top_pct_births = top_pct_births.unstack()
top_pct_births.plot(
title='% of names in the top {:.0f}% number of births'.format(pct*100))
# Make the ticks more readable (match the graph title)
ticks_text = ['{:.0f}%'.format(x*100) for x in ticks_value]
plt.yticks(ticks_value, ticks_text);
graph_pct_names(0.5, [0.01, 0.02, 0.03, 0.04])
graph_pct_names(0.99, [0.4, 0.8, 1])
# + [markdown] colab_type="text" id="YNr4O_tHOKTn"
# -------------
# ## Boy names that became girl names (and vice versa)
#
# Next, let's look at baby names that were more popular with one sex earlier in the sample but have switched to the opposite sex over the years. One example is the name Lesley or Leslie (or other possible, less common, spelling variations).
#
# We will do so by following these steps:
# 1. Go back to the top1000 DataFrame and compute a list of names occurring in the dataset starting with “lesl”.
# 2. Filter down to just those names and sum births grouped by name to see the relative frequencies.
# 3. Aggregate by sex and year and normalize within year.
# 4. Plot the breakdown by sex over time.
# -
all_names = pd.Series(top1000.name.unique())
lesley_like = all_names[all_names.str.lower().str.contains('lesl')]
lesley_like
filtered = top1000[top1000.name.isin(lesley_like)]
filtered.groupby('name').births.sum()
table = filtered.pivot_table('births', index='year',
columns='sex', aggfunc='sum')
table = table.div(table.sum(1), axis=0)
fig = plt.figure()
table.plot(style={'M': 'b-', 'F': 'r--'})
# + [markdown] colab_type="text" id="KsQUHbQXOKTt"
# ---------------------
#
# Now it's time for you to come up with a different hypotheses, which we will call H2. **Be creative!**
#
# Example: The name 'Reese' has been more prevalent among baby girls than baby boys since 2000.
# + [markdown] colab_type="text" id="IDUa4m4hOKTu"
# ## Your turn! (28 points)
#
# Write Python code to test hypothesis H2 (and some text to explain whether it was confirmed or not).
# + [markdown] colab_type="text" id="X2zRCH0R7bG1"
# ## Solution
# -
# According to [Wikipedia's article "Naming in the United States"](https://en.wikipedia.org/wiki/Naming_in_the_United_States#Gender):
#
# > Gender name usage also plays a role in the way parents view names. It is not uncommon for American parents to give girls names that have traditionally been used for boys. Boys, on the other hand, are almost never given feminine names. Names like Ashley, Sidney, Aubrey, and Avery originated as boys' names. Traditionally masculine or androgynous names that are used widely for girls have a tendency to be abandoned by the parents of boys and develop an almost entirely female usage
#
# Given that statement, the hypothesis we will test is:
#
# **H2: Once a predominantly boy name is adopted by 50% or more of girls, within one generation ([about 30 years](https://en.wikipedia.org/wiki/Generation)) it will become almost exclusively (over 80%) a girl name.**
#
# We will use the list of names mentioned in the Wikipedia article (Ashley, Sidney, Aubrey, and Avery) to test the hypothesis.
# + colab={} colab_type="code" id="IfCLnKp-OKTv"
def plot_name(name):
this_name = names[names['name'] == name]
# Count by year/sex
table = this_name.pivot_table('births', index='year',
columns='sex', aggfunc='sum')
# Change count to proportion F/M in each year
table = table.div(table.sum(axis='columns'), axis='rows')
# Plot the proportions
ax = table.plot(title=name, label='')
# Format the graph to help analyze the hypothesis
# 1. Mark the 50% and 80% levels we are using in the hypothesis
ax.axhspan(0.5, 0.8, alpha=0.1, color='green')
# 2. Show only those labels to draw even more attention to them
# And remove the tick marks from those label to clean up a bit
plt.yticks([0.5, 0.8, 1.0], ['50%', '80%', '100%'])
plt.tick_params(left=False)
# 3. Remove the boxes (noise, most of the time)
# Leave bottom line to "ground" the graph
ax.spines['right'].set_visible(False)
ax.spines['left'].set_visible(False)
ax.spines['top'].set_visible(False)
# 4. Move years to the top, remove obvious "years" label
# The eyes now hit the year more quickly, making the
# purpose of the x axis clearer from the start
ax.xaxis.set_ticks_position('top')
ax.xaxis.set_label_text('')
# Point to the years when the thresholds were crossed
# (we may not have the upper threshold in some cases)
def draw_arrow(pct):
crossed_pct = table[table['F'] >= pct]
if (len(crossed_pct) > 0):
year = crossed_pct.index[0]
ap = dict(arrowstyle='->', connectionstyle='angle3',
alpha=0.7)
bbox = dict(boxstyle='round', fc='white', ec='white',
alpha=0.6)
ax.annotate('{:.0f}% in {}'.format(pct*100, year),
xy=(year, pct), xytext=(year-40, pct-0.1),
arrowprops=ap, bbox=bbox)
draw_arrow(0.5)
draw_arrow(0.8)
for name in ('Ashley', 'Sidney', 'Aubrey', 'Avery'):
plot_name(name)
# -
# **Conclusion**: H2 is false. We found one example, Sidney, where the name was not adopted by over 80% of girls (although it is still in the thirty-year window, it is unlikely it will revert the trend shown in the graph). However, even with Sidney not quite following the same pattern, we can say that H2 is a good predictor for a boy name becoming a girl name in a relatively short amount of time, once it is used as a girl name by half of the births.
# + [markdown] colab_type="text" id="GLi0m9uuKkpD"
# ## Conclusions (25 points)
#
# Write your conclusions and make sure to address the issues below:
# - What have you learned from this assignment?
# - Which parts were the most fun, time-consuming, enlightening, tedious?
# - What would you do if you had an additional week to work on this?
# + [markdown] colab_type="text" id="tmRWLHo5K99F"
# ## Solution
# + [markdown] colab_type="text" id="ug_U9rd3K99G"
# ### What have you learned from this assignment?
# -
# * `pivot_table` - before this assignment, I used `groupby` for these types of problems. Now I have a better understanding of pivot tables.
# * `query` - before this assignment, I used traditional filtering. `query()` is cleaner, thus easier to follow and to maintain.
# * Got a bit better in cleaning up graphs (removing boxes, making grids less prominent, etc.). Used in one example so far (the movie genres horizontal bar graph), but getting more confident in the APIs to try in other graphs in the future.
# ### Which parts were the most fun, time-consuming, enlightening, tedious?
# Fun:
#
# * Exploring data with graphs continue to be fun :)
# * Learning how to customize graphs also continues to be fun and educational
#
# Enlightening:
#
# * The power of `pivot_table`
# * The cleaness of `query`
# * Defining "diversity" is harder than it looks
#
#
# Tedious:
#
# * None
# ### What would you do if you had an additional week to work on this?
# * Investigate when `query()` is slower than traditional filtering. The textbook has some general statements, but no specific guidelines.
# * Try `pivot_table` even more. I struggle to define what should be the main variable, the index and the columns in a few cases. I would like for that to come more naturally to me, i.e. first visualize I want to get done, then effortlessly translate that into the different pieces of the `pivot_table` API.
|
assignment2/CAP5768_Assignment2_cgarbin.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# 
# # QuestDB Tutorial for Python
# ## Getting Started
#
# To get started, you'll need a few things installed and set up. This should be quick.
#
# 1. QuestDB: To install Questdb you can see [Installation](https://questdb.io/getstarted) for complete instructions in case you want to use Docker, or `brew` on MacOS, but the easiest way is to download the binaries and run it directly. Instructions for that are [Here](https://questdb.io/docs/guideBinaries).
# 2. Jupyter Notebooks: That's what this is. To run it, you should:
# 1. make **sure** you are running Python 3.x and _not_ Python 2.7. If you're in doubt, `python --version` will tell you.
# 2. install Jupyter Notebooks with `pip3 install --upgrade ipython jupyter`
# 3. make sure that the libraries we use in this tutorial are also installed with `pip3 install requests urlib matplotlib pandas`
# 4. clone this repository (`git clone https://github.com/davidgs/QuestNotebook`)
# 5. in the repository directory run `jupyter notebook`
#
# That will get you right back to a page like this that is interactive, allowing you to run the code and interact with the database yourself.
#
# If you get errors like `ModuleNotFoundError: No module named 'requests'` for any of the libraries you installed above, double-check to make sure that you are actually using Python 3.x `jupytper --path` will let you know if Jupyter is using 2.7 or 3.x
# ## Create A Database
#
# We will need someplace to store our data, so let's create a test database where we can put some random data.
#
# We will create a simple table with 5 columns, one of which is a `timestamp`
#
# The Create operation in QuestDB appends records to bottom of a table. If the table has a designated `timestamp`, new record timestamps must be superior or equal to the latest timestamp. Attempts to add a timestamp in middle of a table will result in a timestamp out of order error.
#
# * `cust_id` is the customer identifier. It uniquely identifies customer.
# * `balance_ccy` balance currency. We use `SYMBOL` here to avoid storing text against each record to save space and increase database performance.
# * `balance` is the current balance for customer and currency tuple.
# * `inactive` is used to flag deleted records.
# * `timestamp` timestamp in microseconds of the record. Note that if you receive the timestamp data as a string, it could also be inserted using `to_timestamp`.
#
# This should return a `200` status the first time you run it. If you run it more than once, subsequent runs will return `400` because the database already exists.
# +
import requests
import urllib.parse as par
q = 'create table balances'\
'(cust_id int,'\
' balance_ccy char,'\
'balance double,'\
'inactive boolean,'\
'timestamp timestamp)'\
'timestamp(timestamp)'
r = requests.get("http://localhost:9000/exec?query=" + q)
print(r.status_code)
# -
# ## Generate some Data
#
# Since we have a new setup, we should add some data to QuestDB so that we can have something to query. We will add some random data, for now.
#
# You can re-run this section as many times as you want to add 100 entries at a time, or simply change the `range(100)` to add as many datapoints as you wish.
#
# +
import requests
import random
from datetime import datetime
success = 0
fail = 0
currency = ["$", "€", "£", "¥"]
random.seed()
for x in range(1000):
cust = random.randint(20, 42)
cur = random.choice(currency)
bal = round(random.uniform(10.45, 235.15), 2)
act = bool(random.getrandbits(1))
query = "insert into balances values("\
+ str(cust) + ",'"\
+ cur + "'," \
+ str(bal) + "," \
+ str(act) + ",systimestamp())"
r = requests.get("http://localhost:9000/exec?query=" + query)
if r.status_code == 200:
success += 1
else:
fail += 1
print("Rows inserted: " + str(success))
if fail > 0:
print("Rows Failed: " + str(fail))
# -
# ## Query Data from QuestDB
#
# Now that we have data available, let's try querying some of it to see what we get back!
# +
import requests
import io
r = requests.get("http://localhost:9000/exp?query=select * from balances")
rawData = r.text
print(rawData)
# -
# ## Read the content into Pandas Dataframe
#
# So you'll notice that the returned data is just a massive `csv` string. If you'd rather have `json` data, then you would change the endpoint to `http://localhost:9000/exec ...` But since we're going to use Pandas to frame our data, we'll stick with `csv`.
#
# We are also telling pandas to parse the `timestamp` field as a date. This is important since we're dealing with Time Series data.
# +
import pandas as pd
pData = pd.read_csv(io.StringIO(rawData), parse_dates=['timestamp'])
print(pData)
# -
# ## Narrow the search
#
# That's just getting us *all* the data, but let's narrow the search using some SQL clauses. Let's look for a specific `cust_id` and only balances of that customer that are in $s. We are also only interested in times the customer was `active` Since this is SQL, you can make this query as simple, or as complex, as you'd like.
#
# Since all of the data was generated randomly, this exact query may return no results, so you may have to adjust the `cust_id` below until you get results back.
#
# ***Note:** The query string _must_ be URL-encoded before it is sent.
# +
import urllib.parse
q = "select cust_id,"\
" balance,"\
" balance_ccy,"\
" inactive,"\
" timestamp"\
" from balances"\
" where cust_id = 26"\
" and balance_ccy = '$'"\
" and not inactive"
query = urllib.parse.quote(q)
r = requests.get("http://localhost:9000/exp?query=" + query)
queryData = r.content
rawData = pd.read_csv(io.StringIO(queryData.decode('utf-8')), parse_dates=['timestamp'])
print(rawData)
# -
# ## Plot the data
#
# We will use `matplotlib` to plot the data
# +
from matplotlib import pyplot as plt
rawData.plot("timestamp", ["balance"], subplots=True)
# -
# ## Clean up
#
# Now we will clean everything up for the next time.
r = requests.get("http://localhost:9000/exec?query=drop table balances")
if r.status_code == 200:
print("Database Table dropped")
else:
print("Database Table not Dropped: " + str(r.status_code))
|
QuestNotebook.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
file="NIS_radar.txt"
#file="NIS_lidar.txt"
nis=loadtxt(file, dtype=float, delimiter="/n", unpack=False)
x = np.array(range(1,nis.shape[0]+1))
plt.plot(x, nis)
plt.title('Radar NIS')
plt.show()
# -
|
NIS_output/.ipynb_checkpoints/NIS Visualization-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2 (SageMath)
# language: python
# name: python2
# ---
# # CW 2
# <NAME>
# #COORD.PY
#
# (a) Create a function coord_for(n, a=0, b=1) that takes three parameters: n is the integer number of intervals, a is the interval left endpoint, and b is the interval right endpoint. Note that the endpoints a and b are keyword parameters with default values of 0 and 1, respectively. To generate the coordinates, start with an empty list, then use a for loop and append each equally spaced x coordinate to the list. Return the completed list.
#
# (b) Create a function coord_while(n, a=0, b=1) that does the same thing as in (a), but uses a while loop instead of a for loop
#
# (c) Create a function coord_comp(n, a=0, b=1) that does the same thing as in (a), but uses a list comprehension instead of a for loop.
#
# +
def coord_for(n, a, b):
h=(b-a)/n
for_list = []
for i in range (n+1):
list.append(a+i*h)
return list
def coord_while(n, a, b):
h=(b-a)/n
while_list = []
while ((a+i) <= b):
while_list.append(a)
a = a+h
return while_list
def coord_comp(n, a, b):
h=(b-a)/n
comp_list = [(a+(i*h)) for i in range (n+1)]
return comp_list
if _name_ == "_main_":
n = (input("interval number: ")
a = (input("lower bound: ")
b = (input("upper bound: ")
for_list = coord_for(n, a, b)
while_list = coord_while(n, a, b)
comp_list = coord_comp(n, a, b)
print("for loop: ", for_list)
print("while loop: ", while_list)
print("list comprehension: ", comp_list)
# -
# #FIBS.PY
#
# (a) Create a function fibs(n) that takes one positive integer parameter n and returns a list of the first n Fibonacci numbers.
#
# (b) Create a function fib_generator() that returns a generator (i.e., using the yield keyword instead of return) for the next Fibonacci number, starting with the number . Done correctly, the following code should return the list [1,1,2,3,5]
#
# +
def fibonacci(n):
fib_list = []
a=0
b=1
while n > 0:
fib_list.append(b)
a, b = b, a+b
n = n-1
return (fib_list)
def fibs_generator():
a, b = 0, 1
while True:
yield b
a, b = b, a+b
if __name__ == "__main__":
n = input("n value: ")
print(fibonacci(n))
g = fibs_generator()
fibs_list = [next(g) for _ in range(5)]
print(fibslist)
# -
# #CONVERGE.PY
#
# (a) Create a function compute_sum(tol=1e-2) that returns the value of the sum. The keyword parameter tol specifies a tolerance. Stop the summation when the next term of the sum would be smaller than this tolerance.
#
# (b) Show to what value does the sum converges as you let the tolerance become smaller and smaller.
#
# +
def compute_sum(tol):
k = 1
conv_sum = 0
term = (1/k**2)
while tol < term:
term = (1/k**2)
conv_sum += term
k += 1
return conv_sum
if __name__=="__main__":
convergence = compute_sum(tol=1e-2)
print("If tol is 1e-2, sum converges at", convergence)
smaller_tol = (compute_sum(tol=1e-10))
print("If tol is 1e-10, sum converges at", smaller_tol)
|
cw2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# 6.5. Pooling
# 6.5.1. Maximum Pooling and Average Pooling
import torch
from torch import nn
from d2l import torch as d2l
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
# Y: output(after X is max pooled)
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i:i + p_h, j:j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i:i + p_h, j:j + p_w].mean()
return Y
# -
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))
pool2d(X, (2, 2), 'avg')
# 6.5.2. Padding and Stride
# tensor X whose shape has four dimensions, where the number of examples (batch size) and number of channels are both 1
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X
# default: the stride and pooling window have the same size
pool2d = nn.MaxPool2d(3) # both are 3x3
pool2d(X)
# the stride and padding can be manually specified
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
# soecify an arbitrary rectangular pooling window and specify the padding and stride for height and width, respectively
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)
# 6.5.3. Multiple Channels
# torch.cat(tensors, dim=0, *, out=None) → Tensor
# => concatenates the given sequence of seq tensors in the given dimension. All tensors must either have the same shape (except in the concatenating dimension) or be empty.
# tensors (sequence of Tensors) – any python sequence of tensors of the same type
# dim (int, optional) – the dimension over which the tensors are concatenated
X = torch.cat((X, X + 1), 1)
X
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
|
eunice012716/Week3/ch6/6.5/example_ch6_5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from IPython.display import HTML
css_file = './custom.css'
HTML(open(css_file, "r").read())
# # Gradient Descent
#
# © 2018 <NAME>
# ## 1. Definition
#
# Gradient Descent is a generic optimization algorithm used to find optimal solutions (maximum or minimum). It can be used to minimize a given cost function of a Machine Learning algorithm, for instance.
#
# It works by tweaking a set of parameters, performing incremental changes to them at every step, gradually converging to the solution (or not!).
#
# The key is the ***incremental changes*** of the parameters. How does it know if it should ***increase*** or ***decrease*** a given parameter? How does it know ***how much*** to change?
#
# This is what the ***partial derivative*** is used for. It determines how much the ***cost function changes*** if ***one parameter changes a little bit***.
#
# If we want to know ***how much*** $J(w_1, w_2) \\ $ ***changes*** when we ***modify*** the value of $w_1 \ $ ***a bit***, we have the ***partial derivative of*** $J(w_1, w_2) \\ $ ***with respect to*** $w_1 \ $:
#
# $$
# \frac{\partial{J(w_1, w_2)}}{\partial{w_1}}
# $$
#
# The same holds for $w_2$:
#
# $$
# \frac{\partial{J(w_1, w_2)}}{\partial{w_2}}
# $$
#
# So, ***gradient descent*** will compute ***partial derivatives with respect to every weight*** (and the ***bias*** too!)
#
# Then it will ***update each weight*** using its corresponding ***partial derivative*** and a ***multiplying factor*** $\eta$ which is known as the ***learning rate***.
#
# $$
# w_1 = w_1 - \eta \frac{\partial{J(w_1, w_2)}}{\partial{w_1}}
# $$
#
# ***IMPORTANT***:
# - The ***learning rate*** is the ***single most important hyper-parameter*** to tune when you are using ***Deep Learning*** models!
# - If it is ***too small***, convergence to the solution will be ***extremely slow***, but if it is ***too big***, you may end up ***not converging at all***. You will understand these mechanisms in the ***interactive example*** and the ***experiment***.
#
# 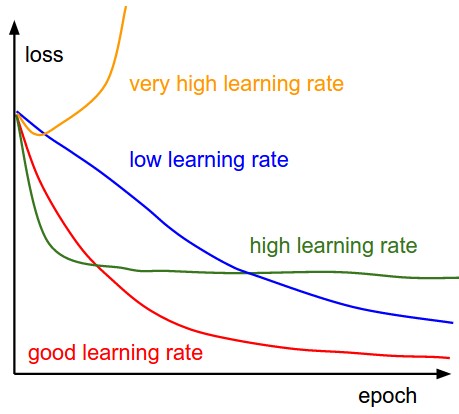
# <center>Source: CS231n CNN for Visual Recognition</center>
#
# After ***updating all weights***, it restarts the process, ***re-evaluating the partial derivatives using the updated weights*** and ***updating all weights one more time***, and so on and so forth!
#
# That is just it! No rocket science, it is quite simple, actually!
#
# But ***partial derivatives*** can be a bit intimidating, so let's go through an interactive example!
from intuitiveml.optimizer.GradientDescent import *
vb = VBox(build_figure_deriv())
vb.layout.align_items = 'center'
vb
# Click the ***Step*** button once. It will show you vectors: ***red*** and ***gray***.
#
# The ***red*** vector is our ***update*** to the weight.
#
# The ***gray*** vector shows ***how much the cost changes*** given our update.
#
# If you divide their ***lengths***, gray over red, it will give you the ***approximate partial derivative***.
#
# The ***update*** itself equals the ***partial derivative*** times the ***learning rate***.
#
# Change the ***learning rate*** to 0.25. If you click the ***Step*** button once again, you should see a much bigger update.
#
# #### Exercises:
#
# 1. Now, choose a different learning rate, reset the plot and follow some steps. Observe the path it traces and check if it hits the minimum. Try different learning rates, see what happens if you choose a really big value for it.
#
#
# 2. Then, change the function to a ***Non-convex*** and set the learning rate to the minimum before following some steps. Where does it converge to? Try resetting and observing its path. Does it reach the global minimum? Try different learning rates and see what happens then.
# ### 1.2 Types of Gradient Descent
#
# There are 3 types of Gradient Descent, depending on the number of samples it uses to compute the partial derivatives.
#
# #### 1.2.1 Batch
#
# It uses ***all data points*** to compute the partial derivatives and, therefore, its path towards the solution is stable, yet it is going to be ***very slow*** on large datasets.
#
# #### 1.2.2 Stochastic
#
# It uses a ***single data point*** to compute the partial derivative and, because of it, it is ***very fast***, but its path towards the solution is going to be ***erratic*** and ***jumpy***.
#
# #### 1.2.3 Mini-Batch
#
# It uses ***some data points*** to compute the partial derivative and it is a compromise between ***stability*** and ***speed***. Its size is a ***hyper-parameter*** on its own, although a value of 32 (and other powers of 2) are commonly used.
# ## 2. Experiment
#
# Time to try it yourself!
#
# There are two parameters, x1 and x2, and we're using Gradient Descent to try to reach the ***minimum*** indicated by the ***star***.
#
# The dataset has only 50 data points.
#
# The controls below allow you to:
# - adjust the learning rate
# - scale the features x1 and x2
# - set the number of epochs (steps)
# - batch size (since the dataset has 50 points, a size of 64 means using ***all*** points)
# - starting point for x1 and x2 (initialization)
#
# Use the controls to play with different configurations and answer the questions below.
x1, x2, y = data()
mygd = plotGradientDescent(x1, x2, y)
vb = VBox(build_figure(mygd))
vb.layout.align_items = 'center'
vb
# #### Questions
#
# 1. ***Without scaling features***, start with the ***learning rate at minimum***:
# - change the batch size - try ***stochastic***, ***batch*** and ***mini-batch*** sizes - what happens to the trajectory? Why?
# - keeping ***maximum batch size***, increase ***learning rate*** to 0.000562 (three notches) - what happens to the trajectory? Why?
# - now reduce gradually ***batch size*** - what happens to the trajectory? Why?
# - go back to ***maximum batch size*** and, this time, increase ***learning rate*** a bit further- what happens to the trajectory? Why?
# - experiment with different settings (yet ***no scaling***), including initial values ***x1*** and ***x2*** and try to get as close as possible to the ***minimum*** - how hard is it?
# - what was the ***largest learning rate*** you manage to use succesfully?
#
#
# 2. Check ***Scale Features*** - what happened to the surface (cost)? What about its level (look at the scale)?
#
#
# 3. ***Using scaled features***, answer the same items as in ***question 1***.
#
#
# 4. How do you compare the ***performance*** of gradient descent with and without ***scaling***? Why did this happen? (think about the partial derivatives with respect to each feature, especially without scaling)
# 1.) With SGD the trajectory is very jumpy but ends closest to the minimum. With BGD the trajectory is the smoothest but ends not as close to the minimum as SGD. MBGD yields something in between. At lr = 0.000562 and BGD the trajectory overshoots. With MBGD it gets worse with decreasing MB. With an even higher lr the trajectory overshoots even more. It is relatively hard to approach the minimum, high number of epochs seems to be required. LR around 0.001 max.
#
# 2.) The cost shrinked dramatically from 2K-12K to 20-70.
#
# 3.) SGD and MBGD end closer to minimum than BGD. Smoothness improved for all of them. At lr = 0.000562 and BGD the trajectory gets closer to minimum. With smaller batch sitze the trajectory gets worse, being very jumpy with < 4. With MBGD it gets worse with decreasing MB but still usable up to a high learning rate (depends on the init I think). Was easier to reach minimum, even with max. learning rate.
#
# 4.) Performance is better with scaling, probably because with scaling we made the cost function more symmetrically hence easier to optimize.
#
# Reasons for SGD and MBGD get closer to goal is higher number of steps compared to GD.
# ## 3. More Resources
#
# [Gradient descent, how neural networks learn](https://www.youtube.com/watch?v=IHZwWFHWa-w)
#
# [Intro to optimization in deep learning: Gradient Descent](https://blog.paperspace.com/intro-to-optimization-in-deep-learning-gradient-descent/)
#
# [Stochastic Gradient Descent with momentum](https://towardsdatascience.com/stochastic-gradient-descent-with-momentum-a84097641a5d)
#
# [An overview of gradient descent optimization algorithms](http://ruder.io/optimizing-gradient-descent/)
#
# [Why Momentum Really Works](https://distill.pub/2017/momentum/)
# #### This material is copyright <NAME> and made available under the Creative Commons Attribution (CC-BY) license ([link](https://creativecommons.org/licenses/by/4.0/)).
#
# #### Code is also made available under the MIT License ([link](https://opensource.org/licenses/MIT)).
from IPython.display import HTML
HTML('''<script>
function code_toggle() {
if (code_shown){
$('div.input').hide('500');
$('#toggleButton').val('Show Code')
} else {
$('div.input').show('500');
$('#toggleButton').val('Hide Code')
}
code_shown = !code_shown
}
$( document ).ready(function(){
code_shown=false;
$('div.input').hide()
});
</script>
<form action="javascript:code_toggle()"><input type="submit" id="toggleButton" value="Show Code"></form>''')
|
6. Gradient Descent.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6
# language: python
# name: python36
# ---
# Copyright (c) Microsoft Corporation. All rights reserved.
#
# Licensed under the MIT License.
# 
# # Automated Machine Learning
# _**Classification of credit card fraudulent transactions with local run **_
#
# ## Contents
# 1. [Introduction](#Introduction)
# 1. [Setup](#Setup)
# 1. [Train](#Train)
# 1. [Results](#Results)
# 1. [Test](#Tests)
# 1. [Explanation](#Explanation)
# 1. [Acknowledgements](#Acknowledgements)
# ## Introduction
#
# In this example we use the associated credit card dataset to showcase how you can use AutoML for a simple classification problem. The goal is to predict if a credit card transaction is considered a fraudulent charge.
#
# This notebook is using the local machine compute to train the model.
#
# If you are using an Azure Machine Learning Compute Instance, you are all set. Otherwise, go through the [configuration](../../../configuration.ipynb) notebook first if you haven't already to establish your connection to the AzureML Workspace.
#
# In this notebook you will learn how to:
# 1. Create an experiment using an existing workspace.
# 2. Configure AutoML using `AutoMLConfig`.
# 3. Train the model.
# 4. Explore the results.
# 5. Test the fitted model.
# 6. Explore any model's explanation and explore feature importance in azure portal.
# 7. Create an AKS cluster, deploy the webservice of AutoML scoring model and the explainer model to the AKS and consume the web service.
# ## Setup
#
# As part of the setup you have already created an Azure ML `Workspace` object. For Automated ML you will need to create an `Experiment` object, which is a named object in a `Workspace` used to run experiments.
# +
import logging
from matplotlib import pyplot as plt
import pandas as pd
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.core.dataset import Dataset
from azureml.train.automl import AutoMLConfig
from azureml.explain.model._internal.explanation_client import ExplanationClient
# -
# This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
print("This notebook was created using version 1.9.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
# +
ws = Workspace.from_config()
# choose a name for experiment
experiment_name = 'automl-classification-ccard-local'
experiment=Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
# -
# ### Load Data
#
# Load the credit card dataset from a csv file containing both training features and labels. The features are inputs to the model, while the training labels represent the expected output of the model. Next, we'll split the data using random_split and extract the training data for the model.
data = "https://automlsamplenotebookdata.blob.core.windows.net/automl-sample-notebook-data/creditcard.csv"
dataset = Dataset.Tabular.from_delimited_files(data)
training_data, validation_data = dataset.random_split(percentage=0.8, seed=223)
label_column_name = 'Class'
# ## Train
#
# Instantiate a AutoMLConfig object. This defines the settings and data used to run the experiment.
#
# |Property|Description|
# |-|-|
# |**task**|classification or regression|
# |**primary_metric**|This is the metric that you want to optimize. Classification supports the following primary metrics: <br><i>accuracy</i><br><i>AUC_weighted</i><br><i>average_precision_score_weighted</i><br><i>norm_macro_recall</i><br><i>precision_score_weighted</i>|
# |**enable_early_stopping**|Stop the run if the metric score is not showing improvement.|
# |**n_cross_validations**|Number of cross validation splits.|
# |**training_data**|Input dataset, containing both features and label column.|
# |**label_column_name**|The name of the label column.|
#
# **_You can find more information about primary metrics_** [here](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-configure-auto-train#primary-metric)
# +
automl_settings = {
"n_cross_validations": 3,
"primary_metric": 'average_precision_score_weighted',
"experiment_timeout_hours": 0.25, # This is a time limit for testing purposes, remove it for real use cases, this will drastically limit ability to find the best model possible
"verbosity": logging.INFO,
"enable_stack_ensemble": False
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
training_data = training_data,
label_column_name = label_column_name,
**automl_settings
)
# -
# Call the `submit` method on the experiment object and pass the run configuration. Depending on the data and the number of iterations this can run for a while.
# In this example, we specify `show_output = True` to print currently running iterations to the console.
local_run = experiment.submit(automl_config, show_output = True)
# +
# If you need to retrieve a run that already started, use the following code
#from azureml.train.automl.run import AutoMLRun
#local_run = AutoMLRun(experiment = experiment, run_id = '<replace with your run id>')
# -
local_run
# ## Results
# #### Widget for Monitoring Runs
#
# The widget will first report a "loading" status while running the first iteration. After completing the first iteration, an auto-updating graph and table will be shown. The widget will refresh once per minute, so you should see the graph update as child runs complete.
#
# **Note:** The widget displays a link at the bottom. Use this link to open a web interface to explore the individual run details
from azureml.widgets import RunDetails
RunDetails(local_run).show()
# ### Analyze results
#
# #### Retrieve the Best Model
#
# Below we select the best pipeline from our iterations. The `get_output` method on `automl_classifier` returns the best run and the fitted model for the last invocation. Overloads on `get_output` allow you to retrieve the best run and fitted model for *any* logged metric or for a particular *iteration*.
best_run, fitted_model = local_run.get_output()
fitted_model
# #### Print the properties of the model
# The fitted_model is a python object and you can read the different properties of the object.
#
# ## Tests
#
# Now that the model is trained, split the data in the same way the data was split for training (The difference here is the data is being split locally) and then run the test data through the trained model to get the predicted values.
# convert the test data to dataframe
X_test_df = validation_data.drop_columns(columns=[label_column_name]).to_pandas_dataframe()
y_test_df = validation_data.keep_columns(columns=[label_column_name], validate=True).to_pandas_dataframe()
# call the predict functions on the model
y_pred = fitted_model.predict(X_test_df)
y_pred
# ### Calculate metrics for the prediction
#
# Now visualize the data on a scatter plot to show what our truth (actual) values are compared to the predicted values
# from the trained model that was returned.
# +
from sklearn.metrics import confusion_matrix
import numpy as np
import itertools
cf =confusion_matrix(y_test_df.values,y_pred)
plt.imshow(cf,cmap=plt.cm.Blues,interpolation='nearest')
plt.colorbar()
plt.title('Confusion Matrix')
plt.xlabel('Predicted')
plt.ylabel('Actual')
class_labels = ['False','True']
tick_marks = np.arange(len(class_labels))
plt.xticks(tick_marks,class_labels)
plt.yticks([-0.5,0,1,1.5],['','False','True',''])
# plotting text value inside cells
thresh = cf.max() / 2.
for i,j in itertools.product(range(cf.shape[0]),range(cf.shape[1])):
plt.text(j,i,format(cf[i,j],'d'),horizontalalignment='center',color='white' if cf[i,j] >thresh else 'black')
plt.show()
# -
# ## Explanation
# In this section, we will show how to compute model explanations and visualize the explanations using azureml-explain-model package. We will also show how to run the automl model and the explainer model through deploying an AKS web service.
#
# Besides retrieving an existing model explanation for an AutoML model, you can also explain your AutoML model with different test data. The following steps will allow you to compute and visualize engineered feature importance based on your test data.
#
# ### Run the explanation
# #### Download engineered feature importance from artifact store
# You can use ExplanationClient to download the engineered feature explanations from the artifact store of the best_run. You can also use azure portal url to view the dash board visualization of the feature importance values of the engineered features.
client = ExplanationClient.from_run(best_run)
engineered_explanations = client.download_model_explanation(raw=False)
print(engineered_explanations.get_feature_importance_dict())
print("You can visualize the engineered explanations under the 'Explanations (preview)' tab in the AutoML run at:-\n" + best_run.get_portal_url())
# #### Retrieve any other AutoML model from training
automl_run, fitted_model = local_run.get_output(metric='accuracy')
# #### Setup the model explanations for AutoML models
# The fitted_model can generate the following which will be used for getting the engineered explanations using automl_setup_model_explanations:-
#
# 1. Featurized data from train samples/test samples
# 2. Gather engineered name lists
# 3. Find the classes in your labeled column in classification scenarios
#
# The automl_explainer_setup_obj contains all the structures from above list.
X_train = training_data.drop_columns(columns=[label_column_name])
y_train = training_data.keep_columns(columns=[label_column_name], validate=True)
X_test = validation_data.drop_columns(columns=[label_column_name])
# +
from azureml.train.automl.runtime.automl_explain_utilities import automl_setup_model_explanations
automl_explainer_setup_obj = automl_setup_model_explanations(fitted_model, X=X_train,
X_test=X_test, y=y_train,
task='classification')
# -
# #### Initialize the Mimic Explainer for feature importance
# For explaining the AutoML models, use the MimicWrapper from azureml.explain.model package. The MimicWrapper can be initialized with fields in automl_explainer_setup_obj, your workspace and a surrogate model to explain the AutoML model (fitted_model here). The MimicWrapper also takes the automl_run object where engineered explanations will be uploaded.
from azureml.explain.model.mimic_wrapper import MimicWrapper
explainer = MimicWrapper(ws, automl_explainer_setup_obj.automl_estimator,
explainable_model=automl_explainer_setup_obj.surrogate_model,
init_dataset=automl_explainer_setup_obj.X_transform, run=automl_run,
features=automl_explainer_setup_obj.engineered_feature_names,
feature_maps=[automl_explainer_setup_obj.feature_map],
classes=automl_explainer_setup_obj.classes,
explainer_kwargs=automl_explainer_setup_obj.surrogate_model_params)
# #### Use Mimic Explainer for computing and visualizing engineered feature importance
# The explain() method in MimicWrapper can be called with the transformed test samples to get the feature importance for the generated engineered features. You can also use azure portal url to view the dash board visualization of the feature importance values of the engineered features.
# Compute the engineered explanations
engineered_explanations = explainer.explain(['local', 'global'], eval_dataset=automl_explainer_setup_obj.X_test_transform)
print(engineered_explanations.get_feature_importance_dict())
print("You can visualize the engineered explanations under the 'Explanations (preview)' tab in the AutoML run at:-\n" + automl_run.get_portal_url())
# #### Initialize the scoring Explainer, save and upload it for later use in scoring explanation
# +
from azureml.explain.model.scoring.scoring_explainer import TreeScoringExplainer
import joblib
# Initialize the ScoringExplainer
scoring_explainer = TreeScoringExplainer(explainer.explainer, feature_maps=[automl_explainer_setup_obj.feature_map])
# Pickle scoring explainer locally to './scoring_explainer.pkl'
scoring_explainer_file_name = 'scoring_explainer.pkl'
with open(scoring_explainer_file_name, 'wb') as stream:
joblib.dump(scoring_explainer, stream)
# Upload the scoring explainer to the automl run
automl_run.upload_file('outputs/scoring_explainer.pkl', scoring_explainer_file_name)
# -
# ### Deploying the scoring and explainer models to a web service to Azure Kubernetes Service (AKS)
#
# We use the TreeScoringExplainer from azureml.explain.model package to create the scoring explainer which will be used to compute the raw and engineered feature importances at the inference time. In the cell below, we register the AutoML model and the scoring explainer with the Model Management Service.
# Register trained automl model present in the 'outputs' folder in the artifacts
original_model = automl_run.register_model(model_name='automl_model',
model_path='outputs/model.pkl')
scoring_explainer_model = automl_run.register_model(model_name='scoring_explainer',
model_path='outputs/scoring_explainer.pkl')
# #### Create the conda dependencies for setting up the service
#
# We need to create the conda dependencies comprising of the azureml-explain-model, azureml-train-automl and azureml-defaults packages.
# +
from azureml.automl.core.shared import constants
from azureml.core.environment import Environment
automl_run.download_file(constants.CONDA_ENV_FILE_PATH, 'myenv.yml')
myenv = Environment.from_conda_specification(name="myenv", file_path="myenv.yml")
myenv
# -
# #### Write the Entry Script
# Write the script that will be used to predict on your model
# +
# %%writefile score.py
import numpy as np
import pandas as pd
import os
import pickle
import azureml.train.automl
import azureml.explain.model
from azureml.train.automl.runtime.automl_explain_utilities import AutoMLExplainerSetupClass, \
automl_setup_model_explanations
import joblib
from azureml.core.model import Model
def init():
global automl_model
global scoring_explainer
# Retrieve the path to the model file using the model name
# Assume original model is named original_prediction_model
automl_model_path = Model.get_model_path('automl_model')
scoring_explainer_path = Model.get_model_path('scoring_explainer')
automl_model = joblib.load(automl_model_path)
scoring_explainer = joblib.load(scoring_explainer_path)
def run(raw_data):
data = pd.read_json(raw_data, orient='records')
# Make prediction
predictions = automl_model.predict(data)
# Setup for inferencing explanations
automl_explainer_setup_obj = automl_setup_model_explanations(automl_model,
X_test=data, task='classification')
# Retrieve model explanations for engineered explanations
engineered_local_importance_values = scoring_explainer.explain(automl_explainer_setup_obj.X_test_transform)
# You can return any data type as long as it is JSON-serializable
return {'predictions': predictions.tolist(),
'engineered_local_importance_values': engineered_local_importance_values}
# -
# #### Create the InferenceConfig
# Create the inference config that will be used when deploying the model
# +
from azureml.core.model import InferenceConfig
inf_config = InferenceConfig(entry_script='score.py', environment=myenv)
# -
# #### Provision the AKS Cluster
# This is a one time setup. You can reuse this cluster for multiple deployments after it has been created. If you delete the cluster or the resource group that contains it, then you would have to recreate it.
# +
from azureml.core.compute import ComputeTarget, AksCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your cluster.
aks_name = 'scoring-explain'
# Verify that cluster does not exist already
try:
aks_target = ComputeTarget(workspace=ws, name=aks_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
prov_config = AksCompute.provisioning_configuration(vm_size='STANDARD_D3_V2')
aks_target = ComputeTarget.create(workspace=ws,
name=aks_name,
provisioning_configuration=prov_config)
aks_target.wait_for_completion(show_output=True)
# -
# #### Deploy web service to AKS
# +
# Set the web service configuration (using default here)
from azureml.core.webservice import AksWebservice
from azureml.core.model import Model
aks_config = AksWebservice.deploy_configuration()
# +
aks_service_name ='model-scoring-local-aks'
aks_service = Model.deploy(workspace=ws,
name=aks_service_name,
models=[scoring_explainer_model, original_model],
inference_config=inf_config,
deployment_config=aks_config,
deployment_target=aks_target)
aks_service.wait_for_deployment(show_output = True)
print(aks_service.state)
# -
# #### View the service logs
aks_service.get_logs()
# #### Consume the web service using run method to do the scoring and explanation of scoring.
# We test the web sevice by passing data. Run() method retrieves API keys behind the scenes to make sure that call is authenticated.
# +
# Serialize the first row of the test data into json
X_test_json = X_test_df[:1].to_json(orient='records')
print(X_test_json)
# Call the service to get the predictions and the engineered and raw explanations
output = aks_service.run(X_test_json)
# Print the predicted value
print('predictions:\n{}\n'.format(output['predictions']))
# Print the engineered feature importances for the predicted value
print('engineered_local_importance_values:\n{}\n'.format(output['engineered_local_importance_values']))
# -
# #### Clean up
# Delete the service.
aks_service.delete()
# ## Acknowledgements
# This Credit Card fraud Detection dataset is made available under the Open Database License: http://opendatacommons.org/licenses/odbl/1.0/. Any rights in individual contents of the database are licensed under the Database Contents License: http://opendatacommons.org/licenses/dbcl/1.0/ and is available at: https://www.kaggle.com/mlg-ulb/creditcardfraud
#
#
# The dataset has been collected and analysed during a research collaboration of Worldline and the Machine Learning Group (http://mlg.ulb.ac.be) of ULB (Université Libre de Bruxelles) on big data mining and fraud detection. More details on current and past projects on related topics are available on https://www.researchgate.net/project/Fraud-detection-5 and the page of the DefeatFraud project
# Please cite the following works:
# • <NAME>, <NAME>, <NAME> and <NAME>. Calibrating Probability with Undersampling for Unbalanced Classification. In Symposium on Computational Intelligence and Data Mining (CIDM), IEEE, 2015
# • <NAME>, Andrea; <NAME>; <NAME>, Yann-Ael; <NAME>; <NAME>. Learned lessons in credit card fraud detection from a practitioner perspective, Expert systems with applications,41,10,4915-4928,2014, Pergamon
# • <NAME>, Andrea; <NAME>; <NAME>; <NAME>; <NAME>. Credit card fraud detection: a realistic modeling and a novel learning strategy, IEEE transactions on neural networks and learning systems,29,8,3784-3797,2018,IEEE
# o <NAME>, Andrea Adaptive Machine learning for credit card fraud detection ULB MLG PhD thesis (supervised by <NAME>)
# • <NAME>; <NAME>, Andrea; <NAME>, Yann-Aël; <NAME>; <NAME>; <NAME>. Scarff: a scalable framework for streaming credit card fraud detection with Spark, Information fusion,41, 182-194,2018,Elsevier
# • <NAME>; <NAME>, Yann-Aël; <NAME>; <NAME>. Streaming active learning strategies for real-life credit card fraud detection: assessment and visualization, International Journal of Data Science and Analytics, 5,4,285-300,2018,Springer International Publishing
|
how-to-use-azureml/automated-machine-learning/local-run-classification-credit-card-fraud/auto-ml-classification-credit-card-fraud-local.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Image Analysis with the Computer Vision Service
#
# <p style='text-align:center'><img src='./images/computer_vision.jpg' alt='A robot holding a picture'/></p>
#
# *Computer Vision* is a branch of artificial intelligence (AI) that explores the development of AI systems that can "see" the world, either in real-time through a camera or by analyzing images and video. This is made possible by the fact that digital images are essentially just arrays of numeric pixel values, and we can use those pixel values as *features* to train machine learning models that can classify images, detect discrete objects in an image, and even generate text-based summaries of a photographs.
#
# ## Use the Computer Vision Cognitive Service
#
# Microsoft Azure includes a number of *cognitive services* that encapsulate common AI functions, including some that can help you build computer vision solutions.
#
# The *Computer Vision* cognitive service provides an obvious starting point for our exploration of computer vision in Azure. It uses pre-trained machine learning models to analyze images and extract information about them.
#
# For example, suppose Northwind Traders has decided to implement a "smart store", in which AI services monitor the store to identify customers requiring assistance, and direct employees to help them. By using the Computer Vision service, images taken by cameras throughout the store can be analyzed to provide meaningful descriptions of what they depict.
#
# ### Create a Cognitive Services Resource
#
# Let's start by creating a **Cognitive Services** resource in your Azure subscription:
#
# 1. In another browser tab, open the Azure portal at https://portal.azure.com, signing in with your Microsoft account.
# 2. Click the **+Create a resource** button, search for *Cognitive Services*, and create a **Cognitive Services** resource with the following settings:
# - **Name**: *Enter a unique name*.
# - **Subscription**: *Your Azure subscription*.
# - **Location**: *Choose any available region*:
# - **Pricing tier**: S0
# - **Resource group**: *Create a resource group with a unique name*.
# 3. Wait for deployment to complete. Then go to your cognitive services resource, and on the **Overview** page, click the link to manage the keys for the service. You will need the endpoint and keys to connect to your cognitive services resource from client applications.
#
# ### Get the Key and Endpoint for your Cognitive Services resource
#
# To use your cognitive services resource, client applications need its endpoint and authentication key:
#
# 1. In the Azure portal, on the **Keys and Endpoint** page for your cognitive service resource, copy the **Key1** for your resource and paste it in the code below, replacing **YOUR_COG_KEY**.
# 2. Copy the **endpoint** for your resource and and paste it in the code below, replacing **YOUR_COG_ENDPOINT**.
# 3. Run the code in the cell below by clicking its green <span style="color:green">▷</span> button.
# +
cog_key = 'YOUR_COG_KEY'
cog_endpoint = 'YOUR_COG_ENDPOINT'
print('Ready to use cognitive services at {} using key {}'.format(cog_endpoint, cog_key))
# -
# Now that you've set up the key and endpoint, you can use the custom vision service to analyze an image.
#
# Run the following cell to get a description for an image in the */data/vision/store_cam1.jpg* file.
from azure.cognitiveservices.vision.computervision import ComputerVisionClient
from msrest.authentication import CognitiveServicesCredentials
from python_code import vision
import os
# %matplotlib inline
# +
# Get the path to an image file
image_path = os.path.join('data', 'vision', 'workplace.jpg')
# Get a client for the computer vision service
computervision_client = ComputerVisionClient(cog_endpoint, CognitiveServicesCredentials(cog_key))
# Get a description from the computer vision service
image_stream = open(image_path, "rb")
description = computervision_client.describe_image_in_stream(image_stream)
# Display image and caption (code in helper_scripts/vision.py)
vision.show_image_caption(image_path, description)
# -
# That seems reasonably accurate.
#
# Let's try another image.
# +
# Get the path to an image file
image_path = os.path.join('data', 'vision', 'store_cam2.jpg')
# Get a description from the computer vision service
image_stream = open(image_path, "rb")
description = computervision_client.describe_image_in_stream(image_stream)
# Display image and caption (code in helper_scripts/vision.py)
vision.show_image_caption(image_path, description)
# -
# ## Identify the important aspects of the image
#
# Sometimes there would just be a need to understand what are the key focus areas on the image. We can use the object detection service to do so.
#
# Run the following code to analyze an image of a shopper.
# +
# Get the path to an image file
image_path = os.path.join('data', 'vision', 'store_cam1.jpg')
# Specify the features we want to analyze
features = ['Description', 'Tags', 'Adult', 'Objects', 'Faces', 'Brands']
# Get an analysis from the computer vision service
image_stream = open(image_path, "rb")
analysis = computervision_client.detect_objects_in_stream(image_stream, visual_features=features)
# Show the bounding boxes of the image (code in python_code/vision.py)
vision.show_bounding_boxes(image_path, analysis)
# -
# Again, the suggested caption seems to be pretty accurate.
#
# ## Analyze image features
#
# So far, you've used the Computer Vision service to generate a descriptive caption for a couple of images; but there's much more you can do. The Computer Vision service provides analysis capabilities that can extract detailed information like:
#
# - The locations of common types of object detected in the image.
# - Location gender, and approximate age of human faces in the image.
# - Whether the image contains any 'adult', 'racy', or 'gory' content.
# - Relevant tags that could be associated with the image in a database to make it easy to find.
#
# Run the following code to analyze an image of a shopper.
# +
# Get the path to an image file
image_path = os.path.join('data', 'vision', 'store_cam1.jpg')
# Specify the features we want to analyze
features = ['Description', 'Tags', 'Adult', 'Objects', 'Faces']
# Get an analysis from the computer vision service
image_stream = open(image_path, "rb")
analysis = computervision_client.analyze_image_in_stream(image_stream, visual_features=features)
# Show the results of analysis (code in helper_scripts/vision.py)
vision.show_image_analysis(image_path, analysis)
# -
# ## Learn More
#
# In addition to the capabilities you've explored in this notebook, the Computer Vision cognitive service includes the ability to:
#
# - Identify celebrities in images.
# - Detect brand logos in an image.
# - Perform optical character recognition (OCR) to read text in an image.
#
# To learn more about the Computer Vision cognitive service, see the [Computer Vision documentation](https://docs.microsoft.com/azure/cognitive-services/computer-vision/)
#
|
Labs/vision/01a - Image Analysis with Computer Vision.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Download** (right-click, save target as ...) this page as a jupyterlab notebook from:
#
# [Laboratory 0](https://atomickitty.ddns.net/engr-1330-webroot/8-Labs/Lab00/Lab00.ipynb)
#
# ___
#
# ## Submitting your laboratory.
#
# Replace the missing items below
#
# **LAST NAME, FIRST NAME**
#
# **R00000000**
#
# ENGR 1330 Laboratory 0
#
# then
#
# - run all cells (laboratory instructor will show how)
# - export notebook as PDF (if nbconvert error, then export as html, use html2pdf online converter)
# - upload your pdf to the Blackboard server to hand in your completed laboratory
# # <font color=darkblue>Laboratory 0: Yes, That's how we count in python!</font>
#
#
# Counting, is our most fundamental arithmetic construct. Where it start matters.
#
# At Harvard they start at (0) zero [https://www.youtube.com/watch?v=jjqgP9dpD1k&t=12s](https://www.youtube.com/watch?v=jjqgP9dpD1k&t=12s), at MIT they start at (1) one [https://www.youtube.com/watch?v=3zTO3LEY-cM](https://www.youtube.com/watch?v=3zTO3LEY-cM), and the rest of us are a bit (pun intended) confused!
#
# Well python developers decided to start at Zero, hence laboratory 0 - our beginning.
#
# Our goal is to get a working JupyterLab/Notebook environment on your laptop.
# ## This "document" is a Jupyter Notebook; the medium that we will be using throughout the semester.
# ___
#
# ## How do you get here?
#
# We suggest, recommend (demand?) you install Anaconda on your laptop. The remainder of this lab meeting is to get your Anaconda install started and maybe even completed. If you started before lab, you may be in good shape.
#
#  <br>
#
# There are online services that allow you create, modify, and export Jupyter notebooks. However, to have this on your local machines (computers), you can install [Anaconda](https://www.anaconda.com/products/individual). Anaconda is a package of different software suites/launchers including "Jupyter Notebook".
#
# You can find videos on how to install Anaconda on your devices on BlackBoard:
# - Go to [Anaconda.com](https://www.anaconda.com/products/individual)
# - Scroll down to the bottom of the page or click on products > individual edition
# - Download the correct version for your operating system: Windows, MacOS, and Linux; and possibly hardware - This may take a while depending on your connection speed
# - Once the installer file is downloaded, run it and install Anaconda on your machine.
# - Anaconda requires almost 3 GB of free space
# - Install it in a separate folder- Preferably on a drive with lots of free memory!
# - BE PATIENT!- It will take a while.
#
# **MacOS and Windows are x86-64 architecture. Chromebooks, Apple M1/M2, Raspberry Pi are arm64 architecture**
# ___
# **To Download A Visual Guide On Installing ANACONDA** ,right-click, and download (save) this file:
#
# [ANACONDA Install Help](https://atomickitty.ddns.net/engr-1330-webroot/8-Labs/Lab00/Anaconda%20Install.pptx)
#
# ___
#
# ## Lab Exercise 1
# The classic hello world script!
print('hello YOUR NAME HERE') # activate and run this cell
# ## Lab Exercise 2
# Identify the cell types below:
# +
# I am what kind of cell? == Code
# -
# # I am what kind of cell? == Markdown
# + active=""
# # I am what kind of cell? == Raw
# -
# ## Readings
#
# <NAME>. (2021) *Jupyter Notebook: An Introduction*, [https://realpython.com/jupyter-notebook-introduction/](https://realpython.com/jupyter-notebook-introduction/)
|
8-Labs/Lab00/dev_src/Lab00-WS.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import Cell_BLAST as cb
import utils
os.environ["CUDA_VISIBLE_DEVICES"] = utils.pick_gpu_lowest_memory()
cb.config.RANDOM_SEED = 0
cb.config.N_JOBS = 4
fixed_model_kwargs = dict(
latent_dim=10, cat_dim=20,
epoch=500, patience=20
)
cb.__version__
# ---
# # Mouse
# ## Quake_Smart-seq2_Diaphragm
quake_smart_seq2_diaphragm = cb.data.ExprDataSet.read_dataset("../../Datasets/data/Quake_Smart-seq2_Diaphragm/data.h5")
utils.peek(quake_smart_seq2_diaphragm, "build/diaphragm/Quake_Smart-seq2_Diaphragm")
quake_smart_seq2_diaphragm.obs.head()
quake_smart_seq2_diaphragm.obs["cluster"] = "cluster_" + quake_smart_seq2_diaphragm.obs["cluster"].astype(int).astype(str)
quake_smart_seq2_diaphragm.obs.dtypes
#opt_model_kwargs = dict(batch_effect="donor")
quake_smart_seq2_diaphragm_model = cb.directi.fit_DIRECTi(
quake_smart_seq2_diaphragm, quake_smart_seq2_diaphragm.uns["seurat_genes"],
**fixed_model_kwargs #**opt_model_kwargs
)
quake_smart_seq2_diaphragm.latent = quake_smart_seq2_diaphragm_model.inference(quake_smart_seq2_diaphragm)
ax = quake_smart_seq2_diaphragm.visualize_latent("cell_ontology_class", scatter_kws=dict(rasterized=True))
ax.get_figure().savefig("build/diaphragm/Quake_Smart-seq2_Diaphragm/cell_ontology_class.svg", dpi=utils.DPI, bbox_inches="tight")
ax = quake_smart_seq2_diaphragm.visualize_latent("cell_type1", scatter_kws=dict(rasterized=True))
ax.get_figure().savefig("build/diaphragm/Quake_Smart-seq2_Diaphragm/cell_type1.svg", dpi=utils.DPI, bbox_inches="tight")
ax = quake_smart_seq2_diaphragm.visualize_latent("cluster", scatter_kws=dict(rasterized=True))
ax.get_figure().savefig("build/diaphragm/Quake_Smart-seq2_Diaphragm/cluster.svg", dpi=utils.DPI, bbox_inches="tight")
ax = quake_smart_seq2_diaphragm.visualize_latent("donor", scatter_kws=dict(rasterized=True))
ax.get_figure().savefig("build/diaphragm/Quake_Smart-seq2_Diaphragm/donor.svg", dpi=utils.DPI, bbox_inches="tight")
ax = quake_smart_seq2_diaphragm.visualize_latent("gender", scatter_kws=dict(rasterized=True))
ax.get_figure().savefig("build/diaphragm/Quake_Smart-seq2_Diaphragm/gender.svg", dpi=utils.DPI, bbox_inches="tight")
quake_smart_seq2_diaphragm.write_dataset("build/diaphragm/Quake_Smart-seq2_Diaphragm/Quake_Smart-seq2_Diaphragm.h5")
# %%capture capio
quake_smart_seq2_diaphragm_models = [quake_smart_seq2_diaphragm_model]
opt_model_kwargs = dict(batch_effect="donor")
for i in range(1, cb.config.N_JOBS):
print("==== Model %d ====" % i)
quake_smart_seq2_diaphragm_models.append(cb.directi.fit_DIRECTi(
quake_smart_seq2_diaphragm, quake_smart_seq2_diaphragm.uns["seurat_genes"],
**fixed_model_kwargs, **opt_model_kwargs,
random_seed=i
))
quake_smart_seq2_diaphragm_blast = cb.blast.BLAST(
quake_smart_seq2_diaphragm_models, quake_smart_seq2_diaphragm,
)
quake_smart_seq2_diaphragm_blast.save("build/diaphragm/Quake_Smart-seq2_Diaphragm")
with open("build/diaphragm/Quake_Smart-seq2_Diaphragm/stdout.txt", "w") as f:
f.write(capio.stdout)
with open("build/diaphragm/Quake_Smart-seq2_Diaphragm/stderr.txt", "w") as f:
f.write(capio.stderr)
utils.self_projection(quake_smart_seq2_diaphragm_blast, "build/diaphragm/Quake_Smart-seq2_Diaphragm")
# %%writefile build/diaphragm/Quake_Smart-seq2_Diaphragm/predictable.txt
cell_ontology_class
cell_type1
cluster
|
Notebooks/Database/diaphragm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
import numpy as np
import scipy.optimize as opti
# %matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
sns.set_context('poster')
from scipy.interpolate import griddata
from scipy.interpolate import rbf
from scipy.interpolate import LinearNDInterpolator
import cPickle as pickle
from datetime import datetime
import os
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
import sys
sys.path.append('/Users/vonderlinden2/rsx_analysis/writing_to_vtk/source')
import structured_3d_vtk as struc_3d
reload(struc_3d)
# +
spatial_increment = 0.001
x_min, x_max = -0.028, 0.025
y_min, y_max = -0.043, 0.039
z_min, z_max = 0.249, 0.249
bounds = ((x_min, x_max), (y_min, y_max), (z_min, z_max))
x_coord = np.linspace(x_min, x_max, np.ceil((x_max-x_min)/spatial_increment))
y_coord = np.linspace(y_min, y_max, np.ceil((y_max-y_min)/spatial_increment))
mesh = np.meshgrid(x_coord, y_coord, indexing='ij')
grid_points = np.dstack(map(np.ravel, mesh))[0]
# -
bx_measurements = struc_3d.read_idl('bx', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
# # Interpolate linearly
# +
today = datetime.today()
today = today.strftime('%Y-%m-%d')
file_path = '../output/' + today + '/B_z0249_'
out_dir = '../output/' + today
try:
os.makedirs(out_dir)
except:
pass
ending = '.npz'
bx_measurements = struc_3d.read_idl('bx', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
by_measurements = struc_3d.read_idl('by', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
bz_measurements = struc_3d.read_idl('bz', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
for plane in [0.249, 0.302, 0.357, 0.416]:
bx_measurements[plane] = struc_3d.average_duplicate_points(bx_measurements[plane])
by_measurements[plane] = struc_3d.average_duplicate_points(by_measurements[plane])
bz_measurements[plane] = struc_3d.average_duplicate_points(bz_measurements[plane])
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
interpolated_vectors = []
for time_point in xrange(len(direction_measurements[0][0.249]['a_out'])):
print time_point
points = []
values = []
for measurements in direction_measurements:
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points.append(points_direction)
values.append(values_direction)
points[0] = np.delete(points[0], 2, axis=1)
points[1] = np.delete(points[1], 2, axis=1)
points[2] = np.delete(points[2], 2, axis=1)
interpolated_vector = struc_3d.interpolate_vector(grid_points, points, values)
#interpolated_vector = struc_3d.add_vacuum_field(interpolated_vector)
assert np.sum(np.isnan(interpolated_vector[0])) == 0
assert np.sum(np.isnan(interpolated_vector[1])) == 0
assert np.sum(np.isnan(interpolated_vector[2])) == 0
sizes = (np.unique(grid_points[:, 0]).size,
np.unique(grid_points[:, 1]).size)
grid_swapped = np.swapaxes(grid_points, 0, 1)
grid_x = np.resize(grid_swapped[0], (sizes[0], sizes[1]))
grid_y = np.resize(grid_swapped[1], (sizes[0], sizes[1]))
grid = np.asarray([grid_x, grid_y])
interpolated_vector = np.asarray(interpolated_vector)
vector_swapped = np.swapaxes(interpolated_vector, 0, 1)
vector_x = np.resize(vector_swapped[:, 0], (sizes[0], sizes[1]))
vector_y = np.resize(vector_swapped[:, 1], (sizes[0], sizes[1]))
vector = np.asarray([vector_x, vector_y])
interpolated_vectors.append(vector)
np.savez(file_path + str(time_point).zfill(4) + ending,
b=vector,
grid=grid)
# +
today = datetime.today()
today = today.strftime('%Y-%m-%d')
file_path = '../output/' + today + '/B_z0249_'
out_dir = '../output/' + today
try:
os.makedirs(out_dir)
except:
pass
ending = '.p'
bx_measurements = struc_3d.read_idl('bx', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
by_measurements = struc_3d.read_idl('by', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
bz_measurements = struc_3d.read_idl('bz', data_path='../../comprehensive_3d_plot/output/2016-08-12/')
for plane in [0.249, 0.302, 0.357, 0.416]:
bx_measurements[plane] = struc_3d.average_duplicate_points(bx_measurements[plane])
by_measurements[plane] = struc_3d.average_duplicate_points(by_measurements[plane])
bz_measurements[plane] = struc_3d.average_duplicate_points(bz_measurements[plane])
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
interpolators = []
for time_point in xrange(250):
print time_point
points = []
values = []
for measurements in direction_measurements:
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points.append(points_direction)
values.append(values_direction)
points[0] = np.delete(points[0], 2, axis=1)
points[1] = np.delete(points[1], 2, axis=1)
points[2] = np.delete(points[2], 2, axis=1)
interpolator_x = LinearNDInterpolator(points[0], values[0])
interpolator_y = LinearNDInterpolator(points[1], values[1])
interpolator_z = LinearNDInterpolator(points[2], values[2])
pickle.dump(interpolator_x, open(file_path + 'x_' + str(time_point).zfill(4) + ending, 'wb'))
pickle.dump(interpolator_y, open(file_path + 'y_' + str(time_point).zfill(4) + ending, 'wb'))
pickle.dump(interpolator_z, open(file_path + 'z_' + str(time_point).zfill(4) + ending, 'wb'))
# -
# # Examine grid ordering
# +
file_path = '../output/2016-07-03/B_z0249_'
ending = '.npz'
bx_measurements = struc_3d.read_idl('bx')
by_measurements = struc_3d.read_idl('by')
bz_measurements = struc_3d.read_idl('bz')
for plane in [0.249, 0.302, 0.357, 0.416]:
bx_measurements[plane] = struc_3d.average_duplicate_points(bx_measurements[plane])
by_measurements[plane] = struc_3d.average_duplicate_points(by_measurements[plane])
bz_measurements[plane] = struc_3d.average_duplicate_points(bz_measurements[plane])
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
time_point=0
points = []
values = []
measurements = bx_measurements
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points = points_direction
values = values_direction
points = np.delete(points, 2, axis=1)
interpolated_scalar = struc_3d.interpolate_scalar(grid_points, points, values)
#interpolated_vector = struc_3d.add_vacuum_field(interpolated_vector)
assert np.sum(np.isnan(interpolated_scalar)) == 0
sizes = (np.unique(grid_points[:, 0]).size,
np.unique(grid_points[:, 1]).size)
grid_swapped = np.swapaxes(grid_points, 0, 1)
grid_x = np.resize(grid_swapped[0], (sizes[0], sizes[1]))
grid_y = np.resize(grid_swapped[1], (sizes[0], sizes[1]))
grid = np.asarray([grid_x, grid_y])
interpolated_scalar = np.asarray(interpolated_scalar)
scalar = np.resize(interpolated_scalar, (sizes[0], sizes[1]))
# -
scalar
interpolated_scalar
grid_points
grid[1][0][2]
scalar[0][2]
scalar[0][1] - scalar[0][0]
scalar[0][1]
np.diff(scalar, axis=1)
np.diff(scalar, axis=0)
np.gradient(scalar)[0]
np.gradient(scalar)[1]
scalar[1, 0] - scalar[0,0]
# # Interpolate cubic with C-T method
# +
file_path = '../output/2016-07-03/B_z0249_cubic'
ending = '.npz'
bx_measurements = struc_3d.read_idl('bx')
by_measurements = struc_3d.read_idl('by')
bz_measurements = struc_3d.read_idl('bz')
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
interpolated_vectors = []
for time_point in xrange(21):
print time_point
points = []
values = []
for measurements in direction_measurements:
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points.append(points_direction)
values.append(values_direction)
points[0] = np.delete(points[0], 2, axis=1)
points[1] = np.delete(points[1], 2, axis=1)
points[2] = np.delete(points[2], 2, axis=1)
interpolated_vector = struc_3d.interpolate_vector(grid_points, points, values, method='cubic')
#interpolated_vector = struc_3d.add_vacuum_field(interpolated_vector)
assert np.sum(np.isnan(interpolated_vector[0])) == 0
assert np.sum(np.isnan(interpolated_vector[1])) == 0
assert np.sum(np.isnan(interpolated_vector[2])) == 0
sizes = (np.unique(grid_points[:, 0]).size,
np.unique(grid_points[:, 1]).size)
grid_swapped = np.swapaxes(grid_points, 0, 1)
grid_x = np.resize(grid_swapped[0], (sizes[0], sizes[1]))
grid_y = np.resize(grid_swapped[1], (sizes[0], sizes[1]))
grid = np.asarray([grid_x, grid_y])
interpolated_vector = np.asarray(interpolated_vector)
vector_swapped = np.swapaxes(interpolated_vector, 0, 1)
vector_x = np.resize(vector_swapped[:, 0], (sizes[0], sizes[1]))
vector_y = np.resize(vector_swapped[:, 1], (sizes[0], sizes[1]))
vector = np.asarray([vector_x, vector_y])
interpolated_vectors.append(vector)
np.savez(file_path + str(time_point).zfill(4) + ending,
b=vector,
grid=grid)
# -
# # Use radial basis functions
from scipy.interpolate import Rbf
def average_duplicate_points(data_dict):
data_dict['x_out'] = data_dict['x_out'].astype('float64')
data_dict['y_out'] = data_dict['y_out'].astype('float64')
data_dict['a_out'] = data_dict['a_out'].astype('float64')
time_points = data_dict['a_out'].shape[0]
data = {}
for idx in xrange(data_dict['x_out'].size):
location = (data_dict['x_out'][idx], data_dict['y_out'][idx])
if location in data.keys():
data[location] = np.column_stack((data[location], data_dict['a_out'][:, idx]))
else:
data[location] = data_dict['a_out'][:, idx]
unique_data_dict = {'x_out': [],
'y_out': [],
'a_out': [],
'std': []}
for location in data.keys():
if data[location][0].size > 1:
unique_data_dict['std'].append(data[location].std(axis=1, ddof=1))
unique_data_dict['a_out'].append(data[location].mean(axis=1))
else:
unique_data_dict['std'].append(np.zeros(time_points))
unique_data_dict['a_out'].append(data[location])
unique_data_dict['x_out'].append(location[0])
unique_data_dict['y_out'].append(location[1])
unique_data_dict['x_out'] = np.asarray(unique_data_dict['x_out'])
unique_data_dict['y_out'] = np.asarray(unique_data_dict['y_out'])
test = np.asarray(unique_data_dict['a_out'])
unique_data_dict['a_out'] = np.hsplit(np.asarray(unique_data_dict['a_out']), time_points)
unique_data_dict['delays'] = data_dict['delays']
return unique_data_dict
bx_measurements.keys()
# +
file_path = '../output/2016-07-03/B_z0249_rbf_thin_plate_'
ending = '.npz'
bx_measurements = struc_3d.read_idl('bx')
by_measurements = struc_3d.read_idl('by')
bz_measurements = struc_3d.read_idl('bz')
bx_measurements[0.249] = average_duplicate_points(bx_measurements[0.249])
by_measurements[0.249] = average_duplicate_points(by_measurements[0.249])
bz_measurements[0.249] = average_duplicate_points(bz_measurements[0.249])
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
interpolated_vectors = []
for time_point in xrange(21):
print time_point
points = []
values = []
for measurements in direction_measurements:
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points.append(points_direction)
values.append(values_direction)
points[0] = np.delete(points[0], 2, axis=1)
points[1] = np.delete(points[1], 2, axis=1)
points[2] = np.delete(points[2], 2, axis=1)
rbf_func_x = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='thin_plate')
rbf_func_y = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='thin_plate')
rbf_func_z = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='thin_plate')
interpolated_vector[0] = rbf_func_x(grid_points[:, 0], grid_points[:, 1])
interpolated_vector[1] = rbf_func_y(grid_points[:, 0], grid_points[:, 1])
interpolated_vector[2] = rbf_func_z(grid_points[:, 0], grid_points[:, 1])
assert np.sum(np.isnan(interpolated_vector[0])) == 0
assert np.sum(np.isnan(interpolated_vector[1])) == 0
assert np.sum(np.isnan(interpolated_vector[2])) == 0
sizes = (np.unique(grid_points[:, 0]).size,
np.unique(grid_points[:, 1]).size)
grid_swapped = np.swapaxes(grid_points, 0, 1)
grid_x = np.resize(grid_swapped[0], (sizes[0], sizes[1]))
grid_y = np.resize(grid_swapped[1], (sizes[0], sizes[1]))
grid = np.asarray([grid_x, grid_y])
interpolated_vector = np.asarray(interpolated_vector)
vector_swapped = np.swapaxes(interpolated_vector, 0, 1)
vector_x = np.resize(vector_swapped[:, 0], (sizes[0], sizes[1]))
vector_y = np.resize(vector_swapped[:, 1], (sizes[0], sizes[1]))
vector = np.asarray([vector_x, vector_y])
interpolated_vectors.append(vector)
np.savez(file_path + str(time_point).zfill(4) + ending,
b=vector,
grid=grid)
# +
file_path = '../output/2016-07-03/B_z0249_rbf_cubic_'
ending = '.npz'
bx_measurements = struc_3d.read_idl('bx')
by_measurements = struc_3d.read_idl('by')
bz_measurements = struc_3d.read_idl('bz')
bx_measurements[0.249] = average_duplicate_points(bx_measurements[0.249])
by_measurements[0.249] = average_duplicate_points(by_measurements[0.249])
bz_measurements[0.249] = average_duplicate_points(bz_measurements[0.249])
direction_measurements = [bx_measurements, by_measurements, bz_measurements]
interpolated_vectors = []
for time_point in xrange(21):
print time_point
points = []
values = []
for measurements in direction_measurements:
(points_direction,
values_direction) = struc_3d.read_points_from_measurement_dict(measurements,
time_point,
[0.249])
points.append(points_direction)
values.append(values_direction)
points[0] = np.delete(points[0], 2, axis=1)
points[1] = np.delete(points[1], 2, axis=1)
points[2] = np.delete(points[2], 2, axis=1)
rbf_func_x = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='cubic')
rbf_func_y = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='cubic')
rbf_func_z = Rbf(points[0][:, 0], points[0][:, 1], values[0], function='cubic')
interpolated_vector[0] = rbf_func_x(grid_points[:, 0], grid_points[:, 1])
interpolated_vector[1] = rbf_func_y(grid_points[:, 0], grid_points[:, 1])
interpolated_vector[2] = rbf_func_z(grid_points[:, 0], grid_points[:, 1])
assert np.sum(np.isnan(interpolated_vector[0])) == 0
assert np.sum(np.isnan(interpolated_vector[1])) == 0
assert np.sum(np.isnan(interpolated_vector[2])) == 0
sizes = (np.unique(grid_points[:, 0]).size,
np.unique(grid_points[:, 1]).size)
grid_swapped = np.swapaxes(grid_points, 0, 1)
grid_x = np.resize(grid_swapped[0], (sizes[0], sizes[1]))
grid_y = np.resize(grid_swapped[1], (sizes[0], sizes[1]))
grid = np.asarray([grid_x, grid_y])
interpolated_vector = np.asarray(interpolated_vector)
vector_swapped = np.swapaxes(interpolated_vector, 0, 1)
vector_x = np.resize(vector_swapped[:, 0], (sizes[0], sizes[1]))
vector_y = np.resize(vector_swapped[:, 1], (sizes[0], sizes[1]))
vector = np.asarray([vector_x, vector_y])
interpolated_vectors.append(vector)
np.savez(file_path + str(time_point).zfill(4) + ending,
b=vector,
grid=grid)
|
centroid_fitting/interpolate_full_0249_plane_for_centroid_fitting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # k-nearest neighbors
#
# Only use the already imported libraries `numpy` and `matplotlib.pyplot` for the assignment. Do not import any other library.
# +
import matplotlib.pyplot as plt
import numpy as np
def load_iris_dataset():
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
return X, y
X, y = load_iris_dataset()
# -
# ## Task 1: Visualization and Preprocessing
#
# 1) Explain the content of the dataset in few words. What are the input features? What is the classification target? Check out: [https://en.wikipedia.org/wiki/Iris_flower_data_set](https://en.wikipedia.org/wiki/Iris_flower_data_set).
#
# The dataset contains a set of 150 records under four features
# - sepal length
# - sepal width
# - petal length
# - petal width
#
# The dataset contains 3 different classification targets
# - Iris setosa - 0
# - Iris versicolor - 1
# - Iris virginica - 2
# 2) Compute and print the following statistics about the dataset:
# - Number of samples
# - Number of samples per class
# - Mean and standard deviation for each input feature
#
# +
classes=["Iris setosa","Iris versicolor","Iris virginica"]
features=["sepal length","sepal width","petal length","petal width"]
np.random.seed(0)
n_samples=X.shape[0]
n_samples_class=np.zeros(len(classes))
for i in y:
n_samples_class[0]+=1 if i==0 else 0
n_samples_class[1]+=1 if i==1 else 0
n_samples_class[2]+=1 if i==2 else 0
mean=np.mean(X,axis=0)
std=np.std(X,axis=0)
print("The number of samples: %i"%n_samples)
for i, c in enumerate(n_samples_class):
print("The number of samples per class %s: %i"%(classes[i],c))
for i,v in enumerate(zip(mean,std)):
print("The mean and standard deviation of %s feature: (%f,%f)"%(features[i],v[0],v[1]))
# -
# 3) Visualize the variables Sepal length and Petal length in a scatter plot (Sepal length on the x-axis, petal length on the y-axis). Color each point of the plot according to its class.
classes_indx=["Iris setosa: 0","Iris versicolor: 1","Iris virginica: 2"]
fig, ax=plt.subplots()
scatter=ax.scatter(X[:,0], X[:,2], c=y)
handles, _ = scatter.legend_elements()
ax.legend(handles,classes_indx,loc="lower right",title="Classes")
ax.set_xlabel('Sepal length')
ax.set_ylabel('petal length')
ax.set_title('Sepal length vs Petal length')
plt.show()
# 4) Split the dataset randomly into training and test data. 70% of data should be used for training and 30% should be used for testing. Implement the function `train_test_split`. Do not modify the interface of the function.
def train_test_split(X, y):
"""
Returns X_train, X_test, y_train, y_test,
where X_train and X_test are the input features of the training and test set,
and y_train and y_test are the class labels of the training and test set.
"""
choice = np.random.choice(range(X.shape[0]), size=(int(0.7*X.shape[0]),), replace=False)
ind = np.zeros(X.shape[0], dtype=bool)
ind[choice] = True
X_train=X[ind == True,:]
X_test=X[ind == False,:]
y_train=y[ind == True,]
y_test=y[ind == False,]
return X_train, X_test, y_train, y_test
X_train, X_test, y_train, y_test = train_test_split(X, y)
assert (X_train.shape[0] + X_test.shape[0]) == X.shape[0]
assert (y_train.shape[0] + y_test.shape[0]) == y.shape[0]
assert X_train.shape[1] == X_test.shape[1]
# 5) kNN uses a distance measure to identify close neighbors. If the input features are not of the same scale, the distance is not as meaningful, which can negatively impact classification performance. Perform min-max scaling (i.e. scale the values of the input features in such a way that their range is from 0 to 1) on the training and test data. Remember that you should only use information from the training data to perform the scaling on both data sets.
X_test=(X_test-np.min(X_train,axis=0))/(np.max(X_train,axis=0)-np.min(X_train,axis=0))
X_train=(X_train-np.min(X_train,axis=0))/(np.max(X_train,axis=0)-np.min(X_train,axis=0))
# ## Task 2: k-nearest neighbors
#
# **For B.Sc. Data Science:**
# Implement the kNN algorithm with uniform weighting and arbitrary `k`. Fill out the `predict` method of class `KNearestNeighborsClassifier`.
#
# Use Euclidean distance to determine the nearest neighbors.
# You can ignore the optional parameter `distance_metric`, which is provided as a field in the kNN class.
#
# **For everyone else:**
# Implement the kNN algorithm with distance-based weighting and arbitrary `k`.
# Fill out the `predict` method of class `KNearestNeighborsClassifier`.
#
# The parameter `distance_metric` will either contain the string `uniform` or a function. If the value is `uniform`, the classifier should use the Euclidean distance for determining nearest neighbors and uniform weighting. If the value is a function, the classifier should use the function as distance metric and perform distance-weighted classification. An example distance metric is provided with `euclidean_distance`.
# +
class KNearestNeighbors(object):
def __init__(self, k, distance_metric='uniform'):
self.k = k
self.distance_metric = distance_metric
def fit(self, X, y):
"""
This functions saves the training data to be used during the prediction.
"""
self.X = X
self.y = y
def predict(self, X):
"""
Returns a vector of shape (n,) if X has shape (n,d),
where n is the number of samples and d is the number of features.
"""
y_pred=[]
for x in X:
if self.distance_metric=='uniform':
distance=np.array([euclidean_distance(x,data_point) for data_point in self.X])
else:
distance=np.array([self.distance_metric(x,data_point) for data_point in self.X])
ind=np.argsort(distance)
y_predicted = self.y[ind[0:self.k]]
if self.distance_metric=='uniform':
weights=np.array([1.0/self.k for _ in range(self.k)])
else:
inv_distance=1.0/(distance[ind[0:self.k]]+1e-8)
inv_distance_sum=np.sum(inv_distance)
weights=inv_distance/inv_distance_sum
y_pred.append(np.bincount(y_predicted, weights=weights).argmax())
return np.array(y_pred)
def euclidean_distance(x1, x2):
"""
Given vectors x1 and x2 with shape (n,) returns distance between vectors as float.
"""
return np.sqrt(np.sum((x1 - x2)*(x1 - x2)))
# -
# ## Task 3: Evaluation
#
# 1) Implement functions to compute precision, recall and F1-score. `y_pred` and `y_true` are the vectors of predicted and true class labels respectively with shape `(n,)`, where `n` is the number of samples. Each function should return a float containing the corresponding score.
# +
def precision(y_pred, y_true):
true_positive=np.zeros(len(classes))
for pred, true in zip(y_pred,y_true):
true_positive[true]+=1 if pred == true else 0
counts_pred=np.array([np.count_nonzero(y_pred == data_point) for data_point in [0,1,2]])
precision = np.divide(true_positive, counts_pred)
if precision.any() == np.nan:
precision = np.divide(true_positive, counts_pred+1e-12)
return np.mean(precision)
def recall(y_pred, y_true):
true_positive=np.zeros(len(classes))
for pred, true in zip(y_pred,y_true):
true_positive[true]+=1 if pred == true else 0
counts_true=np.array([np.count_nonzero(y_true == data_point) for data_point in [0,1,2]])
recall = np.divide(true_positive, counts_true)
if recall.any() == np.nan:
recall = np.divide(true_positive, counts_true+1e-12)
return np.mean(recall)
def f1score(y_pred, y_true):
p = precision(y_pred, y_true)
r = recall(y_pred, y_true)
return (2*r*p)/(r+p)
# -
# 2) Evaluate the performance of kNN with uniform weighting on the Iris dataset for `k=1,3,5`. Train each of the `3` classifiers on the training data from Task 1. Perform the predictions on both the training and test data. Then compute precision, recall, and F1-score for each model and for both training and test data. Print all scores per model. What do you observe?
#
# **For all students other than B.Sc. Data Science:**
# Evaluate the kNN classifier with Euclidean distance-weighting. Compare the performance to uniform-weighting. How does the performance change compared to uniform weighting for each `k`?
# +
import time
start=time.time()
for k in [1,3,5]:
KNN=KNearestNeighbors(k=k,distance_metric='uniform')
KNN.fit(X_train,y_train)
y_pred=KNN.predict(X_train)
print('uniform classifier with k ={}'.format(k))
print('\tprecision for training data : {}'.format(precision(y_pred,y_train)))
print('\trecall for training data : {}'.format(recall(y_pred,y_train)))
print('\tf1 score for training data : {}'.format(f1score(y_pred,y_train)))
y_pred=KNN.predict(X_test)
print('\tprecision for test data : {}'.format(precision(y_pred,y_test)))
print('\trecall for test data : {}'.format(recall(y_pred,y_test)))
print('\tf1 score for test data : {}'.format(f1score(y_pred,y_test)))
KNN=KNearestNeighbors(k=k,distance_metric=euclidean_distance)
KNN.fit(X_train,y_train)
y_pred=KNN.predict(X_train)
print('distance weighted classifier with k ={}'.format(k))
print('\tprecision for training data : {}'.format(precision(y_pred,y_train)))
print('\trecall for training data : {}'.format(recall(y_pred,y_train)))
print('\tf1 score for training data : {}'.format(f1score(y_pred,y_train)))
y_pred=KNN.predict(X_test)
print('\tprecision for test data : {}'.format(precision(y_pred,y_test)))
print('\trecall for test data : {}'.format(recall(y_pred,y_test)))
print('\tf1 score for test data : {}'.format(f1score(y_pred,y_test)))
print(time.time()-start)
# -
# ==> *Write your observations here and report your results.* (double klick here to edit)
# 3) Explain why kNN with `k=1` achieves perfect results on the training data. Why is it not the best model?
# ==> *Write your response here.* (double klick here to edit)
|
k-nearest neighbors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:tensorflow]
# language: python
# name: conda-env-tensorflow-py
# ---
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib inline
gate_size=64
corr=[]
data=np.load('bach_g64.npy')
data=data[:2]
'''
for i in range(len(data)):
for j in range(len(data)):
for m in range(len(data[i])-gate_size):
seqa=data[i][m:m+gate_size]
for n in range(len(data[j])-gate_size):
seqb=data[j][n:n+gate_size]
corr.append(np.correlate(seqa,seqb))
if len(np.correlate(seqa,seqb))!=1:
print(i,j,m,n)
break
'''
for i in range(len(data)):
for j in range(len(data)):
for m in range(len(data[i])-gate_size):
seqa=data[i][m:m+gate_size]
corr.append(np.correlate(seqa,data[j]))
data[0][0:0+gate_size].shape
data[0][288:288+gate_size].shape
len(data[0]-gate_size)
len(corr)
len(data[0])
len(data[1])
np.correlate([1, 2, 3], [0, 1, 0.5, 0, 0])
len(data)
means=[]
for pieces in corr:
means.append(np.mean(pieces))
np.mean(np.array(means))
def corr_two_seq(seq1,seq2,gate_size):
corr=[]
for m in range(len(seq1)-gate_size):
seqa=seq1[m:m+gate_size]
corr.append(np.correlate(seqa,seq2))
return corr
def mean_corr(corr):
means=[]
for pieces in corr:
means.append(np.mean(pieces))
return np.mean(np.array(means))
def mean_corr_normalize(corr):
means=[]
for pieces in corr:
pieces=pieces/np.max(pieces)
means.append(np.mean(pieces))
return np.mean(np.array(means))
data=np.load('bach_g64.npy')
bach1=data[0]
bach2=data[1]
data=np.load('jazz_g64.npy')
jazz1=data[0]
jazz2=data[1]
corr_bach=corr_two_seq(bach1,bach2,64)
mean_corr(corr_bach)
corr_bj=corr_two_seq(bach1,jazz1,64)
mean_corr(corr_bj)
mean_corr_normalize(corr_bj)
mean_corr_normalize(corr_bach)
def combine(seq1,seq2,gate_size):
corr=corr_two_seq(seq1,seq2,gate_size)
return mean_corr_normalize(corr)
combine(jazz2,jazz1,64)
np.correlate([1, 2, 3], [0, 1, 0.5,0])
np.cov([1, 2, 3], [0, 1, 0.5])
np.cov([1, 2, 3], [0, 2, 1])
data_jazz=np.load('jazz_g64.npy')[:100]
data_bach=np.load('bach_g64.npy')[:100]
i=0
s=0
for jazz_piece in data_jazz:
for bach_piece in data_bach:
s+=combine(jazz_piece,bach_piece,64)
i+=1
print(s/i)
i=0
s=0
for jazz_piece in data_bach:
for bach_piece in data_bach:
s+=combine(jazz_piece,bach_piece,64)
i+=1
print(s/i)
i=0
s=0
for jazz_piece in data_jazz:
for bach_piece in data_jazz:
s+=combine(jazz_piece,bach_piece,64)
i+=1
print(s/i)
bach1_g=bach1[100:100+gate_size]
cor=np.correlate(bach1_g,bach1)
plt.plot(cor)
plt.plot(cor[::-1])
plt.plot(cor/np.max(cor))
np.sum(cor/np.max(cor))
cor=np.correlate(bach1_g,jazz1)
plt.plot(cor[::-1])
jazz1
cor[::-1][100]
np.correlate(bach1_g,bach1[0:0+gate_size])
import numpy as np
from matplotlib import pyplot as plt
import time
import multiprocessing
# %matplotlib inline
# +
def corr_two_seq(seq1,seq2,gate_size):
corr=[]
for m in range(len(seq1)-gate_size):
seqa=seq1[m:m+gate_size]
corr.append(np.correlate(seqa,seq2))
return corr
def mean_corr_normalize(corr):
means=[]
for pieces in corr:
pieces=pieces/np.max(pieces)
means.append(np.mean(pieces))
return np.mean(np.array(means))
def combine(seq1,seq2,gate_size):
corr=corr_two_seq(seq1,seq2,gate_size)
return mean_corr_normalize(corr)
def cor_score(data_1,data_2,num):
i = 0
s = 0
for piece1 in data_1:
for piece2 in data_2:
s += combine(piece1, piece2, 64)
i += 1
s = s / i
return s
'''
def multi_corr(func,arg1,arg2,data_span,thread_amount):
threads = []
n=0
for i in range(thread_amount):
threads.append(threading.Thread
( target=func, args=(copy.deepcopy(arg1[n:n+data_span]),
copy.deepcopy(arg2[n:n+data_span]), i) ))
n+=data_span
return threads
'''
def elapsed(sec):
if sec<60:
return str(sec) + " sec"
elif sec<(60*60):
return str(sec/60) + " min"
else:
return str(sec/(60*60)) + " hr"
# -
data_jazz=np.load('jazz_g64.npy')
data_bach=np.load('bach_g64.npy')
num_threads=16
data_jazz=np.load('jazz_g64_notes.npy')
data_bach=np.load('bach_g64_notes.npy')
plt.plot(data_bach[0])
plt.plot(data_bach[8])
data_bach_m=np.load('bach_g64.npy')
plt.plot(data_bach_m[8])
|
Genre classify/Correlation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import pickle
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
# %load_ext tensorboard
import datetime
from tensorflow.keras.utils import to_categorical
filename = "../../Datasets/CHD/heart.csv"
df = pd.read_csv(filename)
df.head()
# +
initializer0 = keras.initializers.RandomUniform(minval = 0, maxval =0.005)
initializer1 = keras.initializers.RandomUniform(minval = 0, maxval =0.005)
initializer2 = keras.initializers.RandomUniform(minval = -2, maxval =1)
class Diffact(keras.layers.Layer):
def __init__(self):
super(Diffact, self).__init__()
self.k0 = self.add_weight(name='k0', shape = (), initializer=initializer0, trainable=True)
self.k1 = self.add_weight(name='k1', shape = (), initializer=initializer1, trainable=True)
self.k2 = self.add_weight(name='k2', shape = (), initializer=initializer2, trainable=True)
def call(self, inputs):
return self.k0 + tf.multiply(inputs, self.k1) + tf.multiply(tf.multiply(inputs,inputs), self.k2)
# -
#Change the column names for better understanding
df.columns = ['age', 'sex', 'chest_pain_type', 'resting_blood_pressure', 'cholesterol', 'fasting_blood_sugar', 'rest_ecg', 'max_heart_rate_achieved',
'exercise_induced_angina', 'st_depression', 'st_slope', 'num_major_vessels', 'thalassemia', 'target']
#Finding the shape of the dataframe
df.shape
# Describing the Dataframe
df.describe()
#Finding information of dataframe
df.info()
#Finding the missing values. In this dataframe there is no missing value.
df.isnull().sum()
# Select the columns to use for prediction in the neural network
X= df.drop('target',axis=1)
Y=df['target']
print (X.shape, Y.shape, df.columns)
Y=np.array(Y)
Y=to_categorical(Y)
# +
from sklearn.model_selection import StratifiedKFold, cross_val_score, KFold, train_test_split
from sklearn.preprocessing import LabelEncoder, StandardScaler, MinMaxScaler
# split data into train, test
X_train,X_test,y_train,y_test = train_test_split(X,Y,test_size=0.3,random_state=39, shuffle=True)
#kipping y since value already 1 or 0
# encoder = LabelEncoder()
# encoder.fit(Y)
# encoded_Y = encoder.transform(Y)
# normalize data
scaler = MinMaxScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_train = pd.DataFrame(X_train_scaled)
X_test_scaled = scaler.fit_transform(X_test)
X_test = pd.DataFrame(X_test_scaled)
print (X_train.shape, y_train.shape)
print (X_test.shape, y_test.shape)
print (df.columns)
# -
# create model with fully connected layers with dropout regulation
model = Sequential()
model.add(layers.Dense(25, input_dim=13))
diffact = Diffact()
model.add(diffact)
model.add(layers.Dropout(0.1))
model.add(layers.Dense(2, activation = 'softmax'))
#model.add(diffact)
model.summary()
# +
batch_size = 5
epochs = 100
model.compile(loss="categorical_crossentropy", optimizer=keras.optimizers.Adam(lr=0.001), metrics=["accuracy"])
log_dir = "heartlogs/smallk2/" + datetime.datetime.now().strftime("%Y%m%d-%H%M%S")
tensorboard_callback = tf.keras.callbacks.TensorBoard(log_dir=log_dir, histogram_freq=1)
model.fit(X_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.33 ,callbacks=[tensorboard_callback], verbose=1)
# -
score = model.evaluate(X_test, y_test, verbose=0)
print("Test loss:", score[0])
print("Test accuracy:", score[1])
print("AF coefficients (weights) {}".format(diffact.get_weights()))
# %tensorboard --logdir heartlogs/smallk2 --port=8042
|
Models/CHD/Diffact-keras-noncv-heart.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # In this script, I Experiment with the Cifar-10 dataset. Moreover, I will transfer the AANN modifications to conv-deconv autoencoder architecture.
# -------------------------------------------------------------------------------------------------------------------
# ### Technology used: Tensorflow-core
# +
# packages used for machine learning
import tensorflow as tf
# packages used for processing:
from six.moves import cPickle as pickle # for reading the data
import matplotlib.pyplot as plt # for visualization
import numpy as np
from sklearn.preprocessing import OneHotEncoder # for encoding the labels in one hot form
# for operating system related stuff
import os
import sys # for memory usage of objects
from subprocess import check_output
# to plot the images inline
# %matplotlib inline
# +
# Input data files are available in the "../Data/" directory.
def exec_command(cmd):
'''
function to execute a shell command and see it's
output in the python console
@params
cmd = the command to be executed along with the arguments
ex: ['ls', '../input']
'''
print(check_output(cmd).decode("utf8"))
# -
# check the structure of the project directory
exec_command(['ls', '../..'])
# +
''' Set the constants for the script '''
# various paths of the files
data_path = "../../Data/cifar-10" # the data path
train_meta = os.path.join(data_path, "batches.meta")
idea = "IDEA_1"
base_model_path = '../../Models'
idea_model_path = os.path.join(base_model_path, idea)
# constant values:
size = 32 # the images of size 32 x 32
channels = 3 # RGB channels
highest_pixel_value = 255.0 # 8 bits for every channel. So, max value is 255
no_of_epochs = 100 # No. of epochs to run
no_of_batches = 5 # There are 5 batches in the dataset
checkpoint_factor = 5 # save the model after every 5 steps (epochs)
num_classes = 10 # There are 10 different classes in the dataset
k_size = 5 # all kernels are 5x5
n_hidden_neurons_in_fc_layers = 512
representation_vector_length = 128 # length of the mid_level representation vector
batch_size = 128 # we look at 5000 images at a time
# -
# check the contents inside the data folder
exec_command(['ls', data_path])
# function to unPickle a file:
def unpickle(file):
'''
This function takes the file path and unPickles the file acquired from it
@Param file: the string path of the file
@return: The dict object unPickled from the file
'''
import cPickle
with open(file, 'rb') as fo:
dict = cPickle.load(fo)
return dict
# ### Let's check the contents of the batches.meta file
# +
meta_data = unpickle(train_meta)
# check it's contents
meta_data
# -
# ### Let's read and display some of the images from the dataset along with their labels
# +
train_batch_preliminary = unpickle(os.path.join(data_path, "data_batch_3"))
# check it's contents
train_batch_preliminary.keys()
# +
# Extract the first 3 images from the dataset
preliminary_data = train_batch_preliminary['data'].reshape((len(train_batch_preliminary['data']), 32, 32, 3),
order='F')
preliminary_labels = train_batch_preliminary['labels']
# view some of the data:
preliminary_data[33, :10, :10, 2] #(10 x 10) data of blue channel of 33rd image
# -
# check a few values of the labels of the dataset
preliminary_labels[:10]
for _ in range(3):
random_index = np.random.randint(preliminary_data.shape[0])
plt.figure().suptitle("Random Image from the dataset: %s" %(meta_data['label_names'][preliminary_labels[random_index]]))
plt.imshow(preliminary_data[random_index], interpolation='none')
# ### The images look blurred out because they are very low resolution images (32 x 32) pixels only.
#
# ## It can be seen that the images in the original dataset are skewed. So, we will have to rotate them by 90 degrees clockwise
# +
# let's try using the numpy.rot90 method for this:
random_index = np.random.randint(preliminary_data.shape[0])
plt.figure().suptitle("Random Image from the dataset: %s" %(meta_data['label_names'][preliminary_labels[random_index]]))
plt.imshow(np.rot90(preliminary_data[random_index], axes=(1, 0)), interpolation='none'); # suppress the unnecessary
# output
# -
# This works. So, now we can create a function to put all this together. This function would take the batch pickle file and create the data suitable for feeding it off to a convolutional neural network.
# The batch generator function:
def generateBatch(batchFile):
'''
The function to generate a batch of data suitable for performing the convNet operations on it
@param batchFile -> the path of the input batchfile
@return batch: (data, labels) -> the processed data.
'''
# unpickle the batch file:
data_dict = unpickle(batchFile)
# extract the data and labels from this dictionary
unprocessed_data = data_dict['data']
integer_labels = np.array(data_dict['labels']) # labels in integer form
# reshape and rotate the data
data = unprocessed_data.reshape((len(unprocessed_data), size, size, channels), order='F')
processed_data = np.array(map(lambda x: np.rot90(x, axes=(1, 0)), data))
# normalize the images by dividing all the pixels by 255
processed_data = processed_data.astype(np.float32) / highest_pixel_value
# encode the labels in one-hot encoded form
# we use the sklearn.preprocessing package for doing this
encoder = OneHotEncoder(sparse=False)
encoded_labels = np.array(encoder.fit_transform(integer_labels.reshape(len(integer_labels), 1)))
# return the processed data and the encoded_labels:
return (processed_data, encoded_labels)
# ### Time to test this function
# +
# load the batch no. 1 and check if it works correctly.
batch_data, batch_labels = generateBatch(os.path.join(data_path, "data_batch_1"))
print (batch_data.shape, batch_labels.shape)
# batch_data[0, :12, :12, 2]
# +
# extract one image from the data and display it
randomIndex = np.random.randint(batch_data.shape[0])
randomImage = batch_data[randomIndex]
print "Random image shape: " + str(randomImage.shape)
print "Random image dataType" + str(randomImage.dtype)
print "\n\ncheck if the data has been properly normalized"
print randomImage[:3, :3, 0]
# Visualize the random image from the dataset
plt.figure()
plt.imshow(randomImage, interpolation='none'); # suppress the unnecessary
# -
# Alright! So, the data extraction module is setup. Let's move on to the actual model building and training.
# # Define the computation graph. This uses a conv-deconv network for the ANN concept
# ### define the placeholders for the computations:
# point to reset the graph:
tf.reset_default_graph()
with tf.variable_scope("Placeholders"):
tf_input = tf.placeholder(tf.float32, shape=(None, size, size, channels), name="inputs")
# add an image summary for the tf_input
tf_input_summary = tf.summary.image("Input_images", tf_input)
tf_labels = tf.placeholder(tf.float32, shape=(None, num_classes), name="labels")
# this is to send in the representation vector tweaked by us to generate images that we want
tf_representation_vector = tf.placeholder(tf.float32, shape=(None, num_classes), name="representation")
# print all these tensors to check if they have been correctly defined
tf_input, tf_labels, tf_representation_vector
# all look good
# ### define the kernel and bias variables used for the computation. I am defining them separately instead of using the layers api from the latest tensorflow because I am going to use the same weights while deconvolving the representations (Use of tied weights).
with tf.variable_scope("Weights_and_biases"):
# special b0 for the input images to be added when performing the backward computations
b0 = tf.get_variable("b0", shape=(1, size, size, channels), dtype=tf.float32,
initializer=tf.zeros_initializer())
# normal kernel weights and biases
w1 = tf.get_variable("W1", shape=(k_size, k_size, channels, 4), dtype=tf.float32,
initializer=tf.truncated_normal_initializer())
b1 = tf.get_variable("b1", shape=(1, 16, 16, 4), dtype=tf.float32,
initializer=tf.zeros_initializer())
w2 = tf.get_variable("W2", shape=(k_size, k_size, 4, 8), dtype=tf.float32,
initializer=tf.truncated_normal_initializer())
b2 = tf.get_variable("b2", shape=(1, 8, 8, 8), dtype=tf.float32,
initializer=tf.zeros_initializer())
w3 = tf.get_variable("W3", shape=(k_size, k_size, 8, 16), dtype=tf.float32,
initializer=tf.truncated_normal_initializer())
b3 = tf.get_variable("b3", shape=(1, 4, 4, 16), dtype=tf.float32,
initializer=tf.zeros_initializer())
w4 = tf.get_variable("W4", shape=(k_size, k_size, 16, 32), dtype=tf.float32,
initializer=tf.truncated_normal_initializer())
b4 = tf.get_variable("b4", shape=(1, 2, 2, 32), dtype=tf.float32,
initializer=tf.zeros_initializer())
# two more weights and biases for the final fully connected layers
w_fc1 = tf.get_variable("W_fc1", shape=(representation_vector_length, n_hidden_neurons_in_fc_layers),
dtype=tf.float32, initializer=tf.contrib.layers.xavier_initializer())
b_fc1 = tf.get_variable("b_fc1", shape=(1, n_hidden_neurons_in_fc_layers), dtype=tf.float32,
initializer=tf.zeros_initializer())
w_fc2 = tf.get_variable("W_fc2", shape=(n_hidden_neurons_in_fc_layers, num_classes), dtype=tf.float32,
initializer=tf.contrib.layers.xavier_initializer())
b_fc2 = tf.get_variable("b_fc2", shape=(1, num_classes), dtype=tf.float32,
initializer=tf.zeros_initializer())
# ### define the forward computations
# define a function for the forward_computations (named as encode)
def encode(inp):
'''
** Note this function uses globally defined filter and bias weights
** activation function used is tf.abs! (AANN idea)
Function to encode the given input images into the final num_classes-dimensional representation vector
@param
inp => tensor corresponding to batch of input images
@return => tensor of shape [batch_size x num_classes]
'''
stride_pattern = [1, 2, 2, 1] # define the stride pattern to halve the image everytime
padding_pattern = "SAME" # padding pattern for the conv layers
# define the convolution layers:
z1 = tf.nn.conv2d(inp, w1, stride_pattern, padding_pattern) + b1
a1 = tf.abs(z1)
z2 = tf.nn.conv2d(a1, w2, stride_pattern, padding_pattern) + b2
a2 = tf.abs(z2)
z3 = tf.nn.conv2d(a2, w3, stride_pattern, padding_pattern) + b3
a3 = tf.abs(z3)
z4 = tf.nn.conv2d(a3, w4, stride_pattern, padding_pattern) + b4
a4 = tf.abs(z4)
# reshape the a4 activation map:
fc_inp = tf.reshape(a4, shape=(-1, representation_vector_length))
assert fc_inp.shape[-1] == representation_vector_length, "mid_level_representation_vector isn't 128 dimensional"
# define the fully connected layers:
z_fc1 = tf.matmul(fc_inp, w_fc1) + b_fc1
a_fc1 = tf.abs(z_fc1)
z_fc2 = tf.matmul(a_fc1, w_fc2) + b_fc2
a_fc2 = tf.abs(z_fc2)
assert a_fc2.shape[-1] == num_classes, "final_representation_vector isn't 10 dimensional"
# if everything is fine, return the final activation vectors:
return a_fc2, tf.shape(a1), tf.shape(a2), tf.shape(a3)
with tf.variable_scope("Encoder"):
y_, sha1, sha2, sha3 = encode(tf_input)
# check the type of y_
print y_
# looks good alright!
# ### define the backward computations
def decode(inp, sha1, sha2, sha3):
'''
** Note this function uses globally defined filter and bias weights
** activation function used is tf.abs! (AANN idea)
Function to decode the given input representation vector into
the size - dimensional images that should be as close as possible
@param
inp => tensor corresponding to batch of representation vectors
@return => tensor of shape [batch_size x size x size x channels]
'''
stride_pattern = [1, 2, 2, 1] # define the stride pattern to halve the image everytime
padding_pattern = "SAME" # padding pattern for the conv layers
# define the backward pass through the fully connected layers:
z_b_1 = tf.matmul(inp, tf.transpose(w_fc2)) + b_fc1
a_b_1 = tf.abs(z_b_1)
z_b_2 = tf.matmul(a_b_1, tf.transpose(w_fc1)) + tf.reshape(b4, shape=(1, -1))
a_b_2 = tf.abs(z_b_2)
assert a_b_2.shape[-1] == representation_vector_length, "reverse_pass: vector not 128 dimensional"
# reshape the vector into a feature map:
dconv_in = tf.reshape(a_b_2, shape=(-1, 2, 2, 32)) # reshape into 2x2 maps
# define the deconvolution operations
z_b_dconv_1 = tf.nn.conv2d_transpose(dconv_in, w4, sha3,
stride_pattern, padding_pattern) + b3
a_b_dconv_1 = tf.abs(z_b_dconv_1)
z_b_dconv_2 = tf.nn.conv2d_transpose(a_b_dconv_1, w3, sha2,
stride_pattern, padding_pattern) + b2
a_b_dconv_2 = tf.abs(z_b_dconv_2)
z_b_dconv_3 = tf.nn.conv2d_transpose(a_b_dconv_2, w2, sha1,
stride_pattern, padding_pattern) + b1
a_b_dconv_3 = tf.abs(z_b_dconv_3)
z_b_dconv_4 = tf.nn.conv2d_transpose(a_b_dconv_3, w1, tf.shape(tf_input),
stride_pattern, padding_pattern) + b0
a_b_dconv_4 = tf.abs(z_b_dconv_4)
# return the final computed image:
return a_b_dconv_4
with tf.variable_scope("Decoder"):
x_ = decode(y_, sha1, sha2, sha3)
# add the image summary for the x_ tensor
x__summary = tf.summary.image("Network_generated_image", x_)
# check if the x_ is a good tensor
print x_
# looks good
# define the decoder predictions:
with tf.variable_scope("Decoder_predictions"):
generated_image = decode(tf_representation_vector, sha1, sha2, sha3)
# check sanity of the generated_image
print generated_image
# looks good! :)
# +
# define the predictions generated by the network in the forward direction:
def direction_cosines(vector):
'''
function to calculate the direction cosines of the given batch of input vectors
@param
vector => activations tensor
@return => the direction cosines of x
'''
sqr = tf.square(vector)
div_val = tf.sqrt(tf.reduce_sum(sqr, axis=1, keep_dims=True))
# return the direction cosines of the vector:
return vector / div_val
# use this function to define the predictions:
with tf.variable_scope("Predictions"):
predictions = direction_cosines(y_)
# -
predictions
# ## Time to define the costs:
# ### Forward cost:
with tf.variable_scope("Forward_cost"):
fwd_cost = tf.reduce_mean(tf.abs(predictions - tf_labels))
# add scalar summary for the fwd_cost
fwd_cost_summary = tf.summary.scalar("Forward_cost", fwd_cost)
# ### Backward cost:
with tf.variable_scope("Backward_cost"):
bwd_cost = tf.reduce_mean(tf.abs(x_ - tf_input))
# add a scalar summary for the bwd_cost
bwd_cost_summary = tf.summary.scalar("Backward_cost", bwd_cost)
# ## Define the final cost and the training step:
with tf.variable_scope("Final_cost"):
cost = fwd_cost + bwd_cost
# add a scalar summary
cost_summary = tf.summary.scalar("Final_cost", cost)
with tf.variable_scope("Trainer"):
optimizer = tf.train.AdamOptimizer(learning_rate=0.01)
train_step = optimizer.minimize(cost) # minimize the final cost
# ## Perform the init and summary errands:
with tf.variable_scope("Errands"):
init = tf.global_variables_initializer()
all_summaries = tf.summary.merge_all()
# # Create a tensorboard writer and visualize this graph before starting the training loop
model_path = os.path.join(idea_model_path, "Model_cifar_4")
# ## Now, let's write the session code to run this computation graph and perform the training
# +
'''
WARNING WARNING WARNING!!! This is the main training cell. Since, the data used for this task is CIFAR-10,
This cell will take a really really long time on low-end machines. It will however not crash your pc, since
I have bootstrapped the training in such a way that it loads a small chunk of data at a time to train.
It took me around 5hrs to execute this cell entirely.
'''
with tf.Session() as sess:
tensorboard_writer = tf.summary.FileWriter(logdir=model_path, graph=sess.graph)
saver = tf.train.Saver(max_to_keep=2)
if(os.path.isfile(os.path.join(model_path, "checkpoint"))):
# load the weights from the model1
# instead of global variable initializer, restore the graph:
saver.restore(sess, tf.train.latest_checkpoint(model_path))
else:
# initialize all the variables
sess.run(tf.global_variables_initializer())
g_step = 158000
for ep in range(400, 500): # epochs loop
print "epoch: " + str(ep + 1)
print "================================================================================================="
print "================================================================================================="
for batch_n in range(no_of_batches): # batches loop
# generate the batch images and labels
batch_images, batch_labels = generateBatch(os.path.join(data_path, "data_batch_" + str(batch_n + 1)))
min_batch_size = batch_size
print "current_batch: " + str(batch_n + 1)
for index in range(int(np.ceil(float(len(batch_images)) / min_batch_size))):
start = index * min_batch_size
end = start + min_batch_size
minX = batch_images[start: end]; minY = batch_labels[start: end]
_, loss = sess.run([train_step, cost], feed_dict={tf_input: minX, tf_labels: minY})
if(index % 35 ==0):
print('range:{} loss= {}'.format((start, end), loss))
g_step += 1
print "\n=========================================================================================\n"
if((ep + 1) % checkpoint_factor == 0 or ep == 0):
# calculate the summaries:
sums = sess.run(all_summaries, feed_dict={tf_input: minX, tf_labels: minY})
# add the summaries to the fileWriter
tensorboard_writer.add_summary(sums, global_step = g_step)
# save the model trained so far:
saver.save(sess, os.path.join(model_path, "model_cifar_4"), global_step = (ep + 1))
print "================================================================================================="
print "================================================================================================="
# -
g_step
|
Scripts/IDEA_1/Experimentation_with_cifar-10_Model_4.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="zdMgfG7GMF_R"
# <center>
# <h1> Transformer TTS: A Text-to-Speech Transformer in TensorFlow 2 </h1>
# <h2> Audio synthesis with Autoregressive Transformer TTS and WaveRNN Vocoder</h2>
# </center>
#
# ## Autoregressive Model
# + colab={"base_uri": "https://localhost:8080/", "height": 225} colab_type="code" id="JQ5YuFPAxXUy" outputId="c8bfbd19-832a-4d91-9d08-f33246a5a853"
# Clone the Transformer TTS and WaveRNN repos
# !git clone https://github.com/as-ideas/TransformerTTS.git
# !git clone https://github.com/fatchord/WaveRNN
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="9bIzkIGjMRwm" outputId="35af5cfc-f104-4a15-8e23-703a341c6acc"
# Install requirements
# !apt-get install -y espeak
# !pip install -r TransformerTTS/requirements.txt
# + colab={"base_uri": "https://localhost:8080/", "height": 555} colab_type="code" id="v4hwKfrqajaX" outputId="d56164ed-5d67-4718-cb6b-08cbeabd5612"
# Download the pre-trained weights
# ! wget https://public-asai-dl-models.s3.eu-central-1.amazonaws.com/TransformerTTS/ljspeech_wavernn_autoregressive_transformer.zip
# ! unzip ljspeech_wavernn_autoregressive_transformer.zip
# + colab={} colab_type="code" id="t687IVuoajac"
# Set up the paths
from pathlib import Path
WaveRNN_path = 'WaveRNN/'
TTS_path = 'TransformerTTS/'
config_path = Path('ljspeech_wavernn_autoregressive_transformer/wavernn')
import sys
sys.path.append(TTS_path)
# + colab={"base_uri": "https://localhost:8080/", "height": 69} colab_type="code" id="LucwkAK1yEVq" outputId="dd72de8c-0806-42db-93e7-7b876d1e1dd5"
# Load pretrained models
from utils.config_manager import ConfigManager
from utils.audio import Audio
import IPython.display as ipd
config_loader = ConfigManager(str(config_path), model_kind='autoregressive')
audio = Audio(config_loader.config)
model = config_loader.load_model(str(config_path / 'autoregressive_weights/ckpt-40'))
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="UcoAeUDdajak" outputId="d1be75fc-b5b5-46b5-8f79-c898f2cdcac2"
# Synthesize text
sentence = 'Scientists at the CERN laboratory, say that they have discovered a new particle.'
out = model.predict(sentence)
# + colab={"base_uri": "https://localhost:8080/", "height": 62} colab_type="code" id="KpsLMKvkajao" outputId="b4e4c6ee-ae50-4b86-db49-5f8b8788d064"
# Convert spectrogram to wav (with griffin lim)
wav = audio.reconstruct_waveform(out['mel'].numpy().T)
ipd.display(ipd.Audio(wav, rate=config_loader.config['sampling_rate']))
# + colab={} colab_type="code" id="xDho7I1Cajat"
# Normalize for WaveRNN
mel = (out['mel'].numpy().T+4.)/8.
# + [markdown] colab_type="text" id="eZJo81viVus-"
# ### WaveRNN
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="5oQhgBhUPB9C" outputId="fcb8214c-6a36-4449-c1ab-dd7030727f89"
# Do some sys cleaning and imports
sys.path.remove(TTS_path)
sys.modules.pop('utils')
# + colab={} colab_type="code" id="WjIuQALHTr-R"
sys.path.append(WaveRNN_path)
from utils.dsp import hp
from models.fatchord_version import WaveRNN
import torch
import numpy as np
WaveRNN_path = Path(WaveRNN_path)
# + colab={"base_uri": "https://localhost:8080/", "height": 52} colab_type="code" id="dptoYzL1XFAr" outputId="694f5bc0-76e4-498b-c1d3-c0cb0b062704"
# Unzip the pretrained model
# !unzip WaveRNN/pretrained/ljspeech.wavernn.mol.800k.zip -d WaveRNN/pretrained/
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="rKixR97aTtwX" outputId="bbf21044-5094-44c5-8038-8185c068db09"
# Load pretrained model
hp.configure(WaveRNN_path / 'hparams.py') # Load hparams from file
if torch.cuda.is_available():
device = torch.device('cuda')
else:
device = torch.device('cpu')
model = WaveRNN(rnn_dims=hp.voc_rnn_dims,
fc_dims=hp.voc_fc_dims,
bits=hp.bits,
pad=hp.voc_pad,
upsample_factors=hp.voc_upsample_factors,
feat_dims=hp.num_mels,
compute_dims=hp.voc_compute_dims,
res_out_dims=hp.voc_res_out_dims,
res_blocks=hp.voc_res_blocks,
hop_length=hp.hop_length,
sample_rate=hp.sample_rate,
mode=hp.voc_mode).to(device)
model.load(str(WaveRNN_path / 'pretrained/latest_weights.pyt'))
# + colab={} colab_type="code" id="mPF7TrqDOE8S"
# Ignore some TF warnings
import tensorflow as tf
tf.get_logger().setLevel('ERROR')
# + colab={"base_uri": "https://localhost:8080/", "height": 34} colab_type="code" id="EVkdFQeRUGQ-" outputId="74bc7f04-1db5-4c5d-8c65-0e585c63bdaf"
# Generate sample with pre-trained WaveRNN vocoder
batch_pred = True # False is slower but possibly better
_ = model.generate(mel.clip(0,1)[np.newaxis,:,:], 'scientists.wav', batch_pred, 11_000, hp.voc_overlap, hp.mu_law)
# + colab={"base_uri": "https://localhost:8080/", "height": 62} colab_type="code" id="vQYaZawLXTJI" outputId="f18063b9-6b56-49bc-cc53-f13b25c3efb6"
# Load wav file
ipd.display(ipd.Audio('scientists.wav'))
|
notebooks/synthesize_autoregressive_wavernn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Title
#
# **Exercise: B.1 - Simple Multi-linear Regression**
#
# # Description
# The aim of this exercise is to understand how to use multi regression. Here we will observe the difference in MSE for each model as the predictors change.
#
# # Instructions:
# - Read the file Advertisement.csv as a dataframe.
# - For each instance of the predictor combination, form a model. For example, if you have 2 predictors, A and B, you will end up getting 3 models - one with only A, one with only B and one with both A and B.
# - Split the data into train and test sets
# - Compute the MSE of each model
# - Print the Predictor - MSE value pair.
#
#
# # Hints:
#
# <a href="https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_csv.html" target="_blank">pd.read_csv(filename)</a> : Returns a pandas dataframe containing the data and labels from the file data
#
# <a href="http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.normalize.html" target="_blank">sklearn.preprocessing.normalize()</a> : Scales input vectors individually to unit norm (vector length).
#
# <a href="https://numpy.org/doc/stable/reference/generated/numpy.interp.html" target="_blank">np.interp()</a> : Returns one-dimensional linear interpolation
#
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html" target="_blank">sklearn.train_test_split()</a> : Splits the data into random train and test subsets
#
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html" target="_blank">sklearn.LinearRegression()</a> : LinearRegression fits a linear model
#
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression.fit" target="_blank">sklearn.fit()</a> : Fits the linear model to the training data
#
# <a href="https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression.predict" target="_blank">sklearn.predict()</a> : Predict using the linear model.
#
#
# Note: This exercise is **auto-graded and you can try multiple attempts.**
# !pip install prettytable
#import necessary libraries
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.metrics import mean_squared_error
from prettytable import PrettyTable
# ### Reading the dataset
#Read the file "Advertising.csv"
df = pd.read_csv("Advertising.csv")
#Take a quick look at the data to list all the predictors
df.head()
# ### Create different multi predictor models
# +
### edTest(test_mse) ###
#List to store the MSE values
mse_list = []
#List of all predictor combinations to fit the curve
cols = [['TV'],['Radio'],['Newspaper'],['TV','Radio'],['TV','Newspaper'],['Radio','Newspaper'],['TV','Radio','Newspaper']]
for i in cols:
#Set each of the predictors from the previous list as x
x = df[i]
#"Sales" column is the reponse variable
y = df["Sales"]
#Splitting the data into train-test sets with 80% training data and 20% testing data.
#Set random_state as 0
xtrain, xtest, ytrain, ytest = train_test_split(x, y, train_size=0.8, random_state=42)
#Create a LinearRegression object and fit the model
lreg = LinearRegression()
lreg.fit(xtrain, ytrain)
#Predict the response variable for the test set
y_pred= lreg.predict(xtest)
#Compute the MSE
MSE = mean_squared_error(ytest, y_pred)
#Append the MSE to the list
mse_list.append(MSE)
# -
# ### Display the MSE with predictor combinations
# +
t = PrettyTable(['Predictors', 'MSE'])
#Loop to display the predictor combinations along with the MSE value of the corresponding model
for i in range(len(mse_list)):
t.add_row([cols[i],mse_list[i]])
print(t)
# -
# ### Comment on the trend of MSE values with changing predictor(s) combinations.
# * Min MSE is with predictors TV and Radio, while the max is with Radio only
# *
|
content/lectures/lecture06/notebook/s2-exa1-challenge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Множества
#
# **Множеством** называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
#
# $x \in X(\in - принадлежит)$
#
# Конечные множества можно задать перчеслением всех элементов:
#
# $X = \{x1, x2, x3, ...\}$
#
# или заданием правила формирования множества:
#
# $X = \{n \in N \mid n < 100\}$
#
# Есть специальное множество, которое содержет ни одного элемента:
#
# $\emptyset - пустое \ множество$
#
# Если множество A полностью входит в множество B то записывается это:
#
# $ A \subset B $
#
# ## Числовые множества
#
# * Натуральные числа - $ \mathbb{N} = \{1,2,3,4,5,...\}$
# * Целые числа - $\mathbb{Z} = \{0, \pm 1, \pm 2, \pm 3, \pm 4, ...\}$
# * Рациональные числа - $\mathbb{Q} = \frac{p}{q} \mid p \in \mathbb{Z} \ and \ q \in \mathbb{N}$
# * Действительные числа: рациональные и ирациональные - $\mathbb{R}$
#
# 
#
# ## Логика и кванторы
#
# * $\forall$ - **квантор общности**, для всех
# * $\exists$ - **квантор существования**, существует
# * $\exists!$ - **квантор существования и единственности**, существует и единственный
# * $\nexists$ - **квантор не существования**, не существует
# * $\implies$ - **импликация** если ..., то ...
# * $\iff$ - равносильность утверждения
# * $:$ - такой что
#
# $\forall x : \left| x \right| <2 \implies x^2<4$
#
#
# ## Операции над множествами
#
# * Равенство (A=B). Два множества равны, если они состоят из одних и тех же элементов
# * Объеденение ($A \cup B$). $A \cup B = C \ \{ \forall c \in C : c \in A \ or \ c \in B \} $
# * Пересечение ($A \cap B$). $A \cap B = C \ \{ \forall c \in C : c \in A \ and \ c \in B \} $
# * Разность ($A \setminus B$). $A \setminus B = C \ \{ \forall c \in C : c \in A \ and \ c \notin B \} $
# * Дополнение ($\neg A$). $\neg A = C \ \{ \forall c \in C : c \notin A\}$
# * Декартово произведение $A \times B$. упорядоченная комбинация пар $(x,y) \mid x \in A \ and \ y \in B$
#
#
# 
# 
# 
#
# ### Свойства
# * $A \cup B = B \cup A$
# * $(A \cup B) \cup C = A \cup (B \cup C)$
# * $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
# * $\neg (A \cup B) = \neg A \cap \neg B$
# * $A \setminus B = A \cap \neg B$
#
# ## Мощность множества
# Мощность множества, кардинальное число множества (лат. cardinalis ← cardo «главное обстоятельство; основа; сердце») — характеристика множеств (в том числе бесконечных), обобщающая понятие количества (числа) элементов конечного множества.
#
# В основе этого понятия лежат естественные представления о сравнении множеств.
#
# **Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.**
#
a = {1,2,3}
b = {0,2,3,4}
print('Difference', a.difference(b))
print('Intersection', a.intersection(b))
print('IsDisjoint', a.isdisjoint(b))
print('IsSubset', a.issubset(b))
print('Union', a.union(b))
# # Функции и отображения
#
# Отображение множества во множество – это **правило**, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто **функцией**
#
# Предположим функция f отображает элементы из множества X в множество Y.
#
# $f: X \to Y$
#
# Множество D называется областью определения $x \in D(f)$, а множество E областью значений $y \in E(f)$, а сама функция задается в виде:
#
# $f(x) = y$
#
# 
#
# Графиком функции называется пары чисел:
#
# $G = \{ (x, f(x)) \in X \times Y \mid x \in X \}$
#
# ## Свойства функции
# * Непрерывность, малые изменения её аргумента приводят к малым изменениям её значения, иначе функция терпит разрыв
# * Гладкость функции
# * Экстремумы
# * Выпуклость
#
# 
# 
# 
# 
#
#
# +
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
def function(x):
return np.sin(x)
x = np.arange(0, 10, 0.2)
print('x:', x)
y = function(x)
print('y:', y)
plt.plot(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Sin')
plt.grid(True)
plt.show()
# +
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
# Make data.
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
# Plot the surface with face colors taken from the array we made.
surf = ax.plot_surface(X, Y, Z, linewidth=0)
# Customize the z axis.
ax.set_zlim(-1, 1)
plt.show()
# -
|
module_002_math/lesson_001_sets_and_functions/tutorials_sources/Sets and functions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Desafio 4
#
# Neste desafio, vamos praticar um pouco sobre testes de hipóteses. Utilizaremos o _data set_ [2016 Olympics in Rio de Janeiro](https://www.kaggle.com/rio2016/olympic-games/), que contém dados sobre os atletas das Olimpíadas de 2016 no Rio de Janeiro.
#
# Esse _data set_ conta com informações gerais sobre 11538 atletas como nome, nacionalidade, altura, peso e esporte praticado. Estaremos especialmente interessados nas variáveis numéricas altura (`height`) e peso (`weight`). As análises feitas aqui são parte de uma Análise Exploratória de Dados (EDA).
#
# > Obs.: Por favor, não modifique o nome das funções de resposta.
# ## _Setup_ geral
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as sct
import seaborn as sns
# +
# # %matplotlib inline
from IPython.core.pylabtools import figsize
from statsmodels.graphics.gofplots import qqplot
figsize(12, 8)
sns.set()
# -
athletes = pd.read_csv("athletes.csv")
def get_sample(df, col_name, n=100, seed=42):
"""Get a sample from a column of a dataframe.
It drops any numpy.nan entries before sampling. The sampling
is performed without replacement.
Example of numpydoc for those who haven't seen yet.
Parameters
----------
df : pandas.DataFrame
Source dataframe.
col_name : str
Name of the column to be sampled.
n : int
Sample size. Default is 100.
seed : int
Random seed. Default is 42.
Returns
-------
pandas.Series
Sample of size n from dataframe's column.
"""
np.random.seed(seed)
random_idx = np.random.choice(df[col_name].dropna().index, size=n, replace=False)
return df.loc[random_idx, col_name]
# ## Inicia sua análise a partir daqui
athletes.shape
athletes.describe()
# ## Questão 1
#
# Considerando uma amostra de tamanho 3000 da coluna `height` obtida com a função `get_sample()`, execute o teste de normalidade de Shapiro-Wilk com a função `scipy.stats.shapiro()`. Podemos afirmar que as alturas são normalmente distribuídas com base nesse teste (ao nível de significância de 5%)? Responda com um boolean (`True` ou `False`).
height_sample_3000 = get_sample(df=athletes, col_name='height', n=3000)
def check_normality(statistic, p_value, alpha=0.05):
print('Statistics=%.3f, p_value=%.3f' % (statistic, p_value))
if p_value <= alpha:
seems_normal = False
print('Sample does not look Gaussian (reject H0)')
else:
seems_normal = True
print('Sample looks Gaussian (fail to reject H0)')
return seems_normal
def q1():
statistic, p_value = sct.shapiro(height_sample_3000)
print("Shapiro-Wilk Normality Test")
return check_normality(statistic, p_value)
# Test
q1()
# __Para refletir__:
#
# * Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
# * Plote o qq-plot para essa variável e a analise.
# * Existe algum nível de significância razoável que nos dê outro resultado no teste? (Não faça isso na prática. Isso é chamado _p-value hacking_, e não é legal).
def plot_dist_qq_box(variable_to_plot, fit_legend='normal_fit'):
fig, axes = plt.subplots(2, 2)
l1 = sns.distplot(variable_to_plot, fit=sct.norm, kde=False, ax=axes[0,0])
l2= sns.boxplot(variable_to_plot, orient='v' , ax=axes[0,1])
l3 = qqplot(variable_to_plot, line='s', ax=axes[1,0])
l4 = sns.distplot(variable_to_plot, fit=sct.norm, hist=False, kde_kws={"shade": True}, ax=axes[1,1])
axes[0,0].legend((fit_legend,'distribution'))
axes[1,0].legend(('distribution',fit_legend))
axes[1,1].legend((fit_legend,'kde_gaussian'));
plot_dist_qq_box(height_sample_3000)
# ## Questão 2
#
# Repita o mesmo procedimento acima, mas agora utilizando o teste de normalidade de Jarque-Bera através da função `scipy.stats.jarque_bera()`. Agora podemos afirmar que as alturas são normalmente distribuídas (ao nível de significância de 5%)? Responda com um boolean (`True` ou `False`).
def q2():
statistic, p_value = sct.jarque_bera(height_sample_3000)
print("Jarque-Bera Normality Test")
return check_normality(statistic, p_value)
#Test
q2()
def anderson_darling_normality_test(result):
print('Statistic: %.3f' % result.statistic)
p = 0
is_normal = True
for i in range(len(result.critical_values)):
sl, cv = result.significance_level[i], result.critical_values[i]
if result.statistic < result.critical_values[i]:
print('%.3f: %.3f, data looks normal (fail to reject H0)' % (sl, cv))
else:
print('%.3f: %.3f, data does not look normal (reject H0)' % (sl, cv))
is_normal = False
plt.scatter(result.significance_level,result.critical_values)
plt.xlabel('Significance Level')
plt.ylabel('Critical Values')
plt.title("Anderson-Darling Normality Test")
return is_normal
# +
def print_check_normality_multiple_tests(data):
# Shapiro-Wilk
print("Shapiro-Wilk Normality Test")
statistic, p_value = sct.shapiro(data)
is_normal_shapiro_wilk = check_normality(statistic, p_value)
# Jarque-Bera
print("\nJarque-Bera Normality Test")
statistic, p_value = sct.jarque_bera(data)
is_normal_jarque_bera = check_normality(statistic, p_value)
# D'Agostino-Pearson or D'Agostino K^2
# check skew: pushed left or right (asymmetry)
# check kurtosis: how much is in the tail
print("\nD'Agostino-Pearson Normality Test")
statistic, p_value = sct.normaltest(data)
check_normality(statistic, p_value)
is_normal_dagostino_pearson = check_normality(statistic, p_value)
# Anderson-Darling
print("\nAnderson-Darling Normality Test")
result = sct.anderson(data, dist='norm')
anderson_darling_normality_test(result)
is_normal_anderson_darling = check_normality(statistic, p_value)
is_normal = {"Method": ["Shapiro-Wilk", "Jarque-Bera", "D'Agostino-Pearson", "Anderson-Darling"],
'Is_Normal': [is_normal_shapiro_wilk, is_normal_jarque_bera,
is_normal_dagostino_pearson, is_normal_anderson_darling]
}
return pd.DataFrame(data=is_normal)
# -
# __Para refletir__:
#
# * Esse resultado faz sentido?
print_check_normality_multiple_tests(height_sample_3000)
# ## Questão 3
#
# Considerando agora uma amostra de tamanho 3000 da coluna `weight` obtida com a função `get_sample()`. Faça o teste de normalidade de D'Agostino-Pearson utilizando a função `scipy.stats.normaltest()`. Podemos afirmar que os pesos vêm de uma distribuição normal ao nível de significância de 5%? Responda com um boolean (`True` ou `False`).
weight_sample_3000 = get_sample(df=athletes, col_name='weight', n=3000)
def q3():
statistic, p_value = sct.normaltest(weight_sample_3000)
print("D'Agostino-Pearson Normality Test")
return check_normality(statistic, p_value)
#Test
q3()
# __Para refletir__:
#
# * Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
# * Um _box plot_ também poderia ajudar a entender a resposta.
plot_dist_qq_box(weight_sample_3000)
print_check_normality_multiple_tests(weight_sample_3000)
# ## Questão 4
#
# Realize uma transformação logarítmica em na amostra de `weight` da questão 3 e repita o mesmo procedimento. Podemos afirmar a normalidade da variável transformada ao nível de significância de 5%? Responda com um boolean (`True` ou `False`).
log_weight_sample_3000 = np.log(weight_sample_3000)
def q4():
statistic, p_value = sct.normaltest(log_weight_sample_3000)
print("D'Agostino-Pearson Log-Normality Test")
return check_normality(statistic, p_value)
#test
q4()
plot_dist_qq_box(log_weight_sample_3000, fit_legend='lognormal_fit')
print("IMPORTANT NOTE:")
print("Since your sample was transformed to log")
print("Interpret normal as LOGnormal and normality as LOG-Normality \n")
print_check_normality_multiple_tests(log_weight_sample_3000)
# __Para refletir__:
#
# * Plote o histograma dessa variável (com, por exemplo, `bins=25`). A forma do gráfico e o resultado do teste são condizentes? Por que?
# * Você esperava um resultado diferente agora?
# > __Para as questão 5 6 e 7 a seguir considere todos testes efetuados ao nível de significância de 5%__.
athletes.columns
athletes['nationality'].value_counts()
bra = athletes.loc[athletes['nationality']=='BRA']
bra.head()
# ## Questão 5
#
# Obtenha todos atletas brasileiros, norte-americanos e canadenses em `DataFrame`s chamados `bra`, `usa` e `can`,respectivamente. Realize um teste de hipóteses para comparação das médias das alturas (`height`) para amostras independentes e variâncias diferentes com a função `scipy.stats.ttest_ind()` entre `bra` e `usa`. Podemos afirmar que as médias são estatisticamente iguais? Responda com um boolean (`True` ou `False`).
# bra = athletes.loc[athletes['nationality']=='BRA']
usa = athletes.loc[athletes['nationality']=='USA']
can = athletes.loc[athletes['nationality']=='CAN']
def check_equal_means(statistic, p_value, alpha=0.05):
print('Statistics=%.3f, p_value=%.3f' % (statistic, p_value))
if p_value <= alpha/2:
means_seems_equal = False
print('Sample means not look equal (reject H0)')
else:
means_seems_equal = True
print('Sample means look equal (fail to reject H0)')
return means_seems_equal
def q5():
statistic, p_value = sct.ttest_ind(bra['height'].dropna(), usa['height'].dropna(), equal_var=False)
return check_equal_means(statistic, p_value)
# Teste
q5()
# ## Questão 6
#
# Repita o procedimento da questão 5, mas agora entre as alturas de `bra` e `can`. Podemos afimar agora que as médias são estatisticamente iguais? Reponda com um boolean (`True` ou `False`).
def q6():
statistic, p_value = sct.ttest_ind(bra['height'].dropna(), can['height'].dropna(), equal_var=False)
return check_equal_means(statistic, p_value)
# Teste
q6()
# ## Questão 7
#
# Repita o procedimento da questão 6, mas agora entre as alturas de `usa` e `can`. Qual o valor do p-valor retornado? Responda como um único escalar arredondado para oito casas decimais.
def q7():
statistic, p_value = sct.ttest_ind(usa['height'].dropna(), can['height'].dropna(), equal_var=False)
check_equal_means(statistic, p_value)
return p_value.round(8)
# Teste
q7()
# __Para refletir__:
#
# * O resultado faz sentido?
# * Você consegue interpretar esse p-valor?
# * Você consegue chegar a esse valor de p-valor a partir da variável de estatística?
plot_dist_qq_box(bra['height'].dropna())
plot_dist_qq_box(can['height'].dropna())
plot_dist_qq_box(usa['height'].dropna())
df = pd.DataFrame([bra['height'].dropna().describe(),
can['height'].dropna().describe(),
usa['height'].dropna().describe()]).T
df.columns = ["BRA", "CAN", "USA"]
df.round(3)
plt.hist(can['height'].dropna(), bins=25, alpha=0.5, label='CAN')
plt.hist(usa['height'].dropna(), bins=25, alpha=0.5, label='USA')
plt.legend(loc='upper right')
plt.show()
plt.hist(can['height'].dropna(), bins=25, alpha=0.5, label='CAN')
plt.hist(bra['height'].dropna(), bins=25, alpha=0.5, label='BRA')
plt.legend(loc='upper right')
plt.show()
plt.hist(usa['height'].dropna(), bins=25, alpha=0.5, label='USA')
plt.hist(bra['height'].dropna(), bins=25, alpha=0.5, label='BRA')
plt.legend(loc='upper right')
plt.show()
# +
# #!pip install geopandas
# -
import geopandas
world = geopandas.read_file(geopandas.datasets.get_path('naturalearth_lowres'))
|
data-science-2/main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.10.0 64-bit (''ml_ds'': conda)'
# language: python
# name: python3100jvsc74a57bd09907773c5fbc3da3f849db7e3d9d122f144cb20adabd0bc445cd27fe6fafa12d
# ---
# ## Get the data
# +
import os
import tarfile
import urllib.request
DOWNLOAD_ROOT = "http://spamassassin.apache.org/old/publiccorpus/"
HAM_URL = DOWNLOAD_ROOT + "20030228_easy_ham.tar.bz2"
SPAM_URL = DOWNLOAD_ROOT + "20030228_spam.tar.bz2"
SPAM_PATH = os.path.join("datasets", "spam")
def fetch_spam_data(ham_url=HAM_URL, spam_url=SPAM_URL, spam_path=SPAM_PATH):
if not os.path.isdir(spam_path):
os.makedirs(spam_path)
for filename, url in (("ham.tar.bz2", ham_url), ("spam.tar.bz2", spam_url)):
path = os.path.join(spam_path, filename)
if not os.path.isfile(path):
urllib.request.urlretrieve(url, path)
tar_bz2_file = tarfile.open(path)
tar_bz2_file.extractall(path=spam_path)
tar_bz2_file.close()
# -
fetch_spam_data()
# +
# Let's load the emails
HAM_DIR = os.path.join(SPAM_PATH, "easy_ham")
SPAM_DIR = os.path.join(SPAM_PATH, "spam")
ham_filenames = [name for name in sorted(os.listdir(HAM_DIR)) if len(name) > 20]
spam_filenames = [name for name in sorted(os.listdir(SPAM_DIR)) if len(name) > 20]
# -
len(ham_filenames)
len(spam_filenames)
# +
# Let's use Python's internal email module to parse the emails
import email
import email.policy
def load_email(is_spam, filename, spam_path=SPAM_PATH):
directory = "spam" if is_spam else "easy_ham"
with open(os.path.join(spam_path, directory, filename), "rb") as f:
return email.parser.BytesParser(policy=email.policy.default).parse(f)
# -
ham_emails = [load_email(is_spam=False, filename=name) for name in ham_filenames]
spam_emails = [load_email(is_spam=True, filename=name) for name in spam_filenames]
# ## Explore the Data
# +
# Let's look at how the parsed email looks to get a feel for the data
print(ham_emails[1].get_content().strip())
# -
print(spam_emails[6].get_content().strip())
# ### Email Structures
# +
# Some emails can have pictures and attachments so let's see the types
def get_email_structure(email):
if isinstance(email, str):
return email
payload = email.get_payload()
if isinstance(payload, list):
return "multipart({})".format(", ".join([
get_email_structure(sub_email)
for sub_email in payload
]))
else:
return email.get_content_type()
# +
from collections import Counter
def structures_counter(emails):
structures = Counter()
for email in emails:
structure = get_email_structure(email)
structures[structure] += 1
return structures
# -
structures_counter(ham_emails).most_common()
structures_counter(spam_emails).most_common()
# ### Email Headers
for header, value in spam_emails[0].items():
print(header,":",value)
# +
# Let's look at the Subject header
spam_emails[0]["Subject"]
# -
# ## Split the data for training and testing
# +
import numpy as np
from sklearn.model_selection import train_test_split
X = np.array(ham_emails + spam_emails, dtype=object)
y = np.array([0] * len(ham_emails) + [1] * len(spam_emails))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# -
y_train
# Okay, let's start writing the preprocessing functions. First, we will need a function to convert HTML to plain text. Arguably the best way to do this would be to use the great [BeautifulSoup](https://www.crummy.com/software/BeautifulSoup/) library, but I would like to avoid adding another dependency to this project, so let's hack a quick & dirty solution using regular expressions (at the risk of [un̨ho͞ly radiańcé destro҉ying all enli̍̈́̂̈́ghtenment](https://stackoverflow.com/a/1732454/38626)). The following function first drops the `<head>` section, then converts all `<a>` tags to the word HYPERLINK, then it gets rid of all HTML tags, leaving only the plain text. For readability, it also replaces multiple newlines with single newlines, and finally it unescapes html entities (such as `>` or ` `):
# +
import re
from html import unescape
def html_to_plain_text(html):
text = re.sub('<head.*?>.*?</head>', '', html, flags=re.M | re.S | re.I)
text = re.sub('<a\s.*?>', ' HYPERLINK ', text, flags=re.M | re.S | re.I)
text = re.sub('<.*?>', '', text, flags=re.M | re.S)
text = re.sub(r'(\s*\n)+', '\n', text, flags=re.M | re.S)
return unescape(text)
# +
# Let's see the function in action
html_spam_emails = [email for email in X_train[y_train==1]
if get_email_structure(email) == "text/html"]
sample_html_spam = html_spam_emails[7]
print(sample_html_spam.get_content().strip()[:1000], "...")
# -
print(html_to_plain_text(sample_html_spam.get_content())[:1000], "...")
# +
# Let's build a function that takes the email as an input and returns the content in plain text
def email_to_text(email):
html = None
for part in email.walk():
ctype = part.get_content_type()
if not ctype in ("text/plain", "text/html"):
continue
try:
content = part.get_content()
except: # in case of encoding issues
content = str(part.get_payload())
if ctype == "text/plain":
return content
else:
html = content
if html:
return html_to_plain_text(html)
# -
print(email_to_text(sample_html_spam)[:10000], "...")
# +
# Let's use NLTK (Natural Language Toolkit) for some stemming
try:
import nltk
stemmer = nltk.PorterStemmer()
for word in ("Computations", "Computation", "Computing", "Computed", "Compute", "Compulsive"):
print(word, "=>", stemmer.stem(word))
except ImportError:
print("Error: stemming requires the NLTK module.")
stemmer = None
# -
try:
import urlextract # may require an Internet connection to download root domain names
url_extractor = urlextract.URLExtract()
print(url_extractor.find_urls("Will it detect github.com and https://youtu.be/7Pq-S557XQU?t=3m32s"))
except ImportError:
print("Error: replacing URLs requires the urlextract module.")
url_extractor = None
# Let's put all this together into a transformer that we will use to convert emails to word counters. Note that we split sentences into words using Python's `split()` method, which uses whitespaces for word boundaries.
# +
from sklearn.base import BaseEstimator, TransformerMixin
class EmailToWordCounterTransformer(BaseEstimator, TransformerMixin):
def __init__(self, strip_headers=True, lower_case=True, remove_punctuation=True,
replace_urls=True, replace_numbers=True, stemming=True):
self.strip_headers = strip_headers
self.lower_case = lower_case
self.remove_punctuation = remove_punctuation
self.replace_urls = replace_urls
self.replace_numbers = replace_numbers
self.stemming = stemming
def fit(self, X, y=None):
return self
def transform(self, X, y=None):
X_transformed = []
for email in X:
text = email_to_text(email) or ""
if self.lower_case:
text = text.lower()
if self.replace_urls and url_extractor is not None:
urls = list(set(url_extractor.find_urls(text)))
urls.sort(key=lambda url: len(url), reverse=True)
for url in urls:
text = text.replace(url, " URL ")
if self.replace_numbers:
text = re.sub(r'\d+(?:\.\d*)?(?:[eE][+-]?\d+)?', 'NUMBER', text)
if self.remove_punctuation:
text = re.sub(r'\W+', ' ', text, flags=re.M)
word_counts = Counter(text.split())
if self.stemming and stemmer is not None:
stemmed_word_counts = Counter()
for word, count in word_counts.items():
stemmed_word = stemmer.stem(word)
stemmed_word_counts[stemmed_word] += count
word_counts = stemmed_word_counts
X_transformed.append(word_counts)
return np.array(X_transformed)
# -
X_few = X_train[:3]
X_few_wordcounts = EmailToWordCounterTransformer().fit_transform(X_few)
X_few_wordcounts
# Now we have the word counts, and we need to convert them to vectors. For this, we will build another transformer whose `fit()` method will build the vocabulary (an ordered list of the most common words) and whose `transform()` method will use the vocabulary to convert word counts to vectors. The output is a sparse matrix.
# +
from scipy.sparse import csr_matrix
class WordCounterToVectorTransformer(BaseEstimator, TransformerMixin):
def __init__(self, vocabulary_size=1000):
self.vocabulary_size = vocabulary_size
def fit(self, X, y=None):
total_count = Counter()
for word_count in X:
for word, count in word_count.items():
total_count[word] += min(count, 10)
most_common = total_count.most_common()[:self.vocabulary_size]
self.vocabulary_ = {word: index + 1 for index, (word, count) in enumerate(most_common)}
return self
def transform(self, X, y=None):
rows = []
cols = []
data = []
for row, word_count in enumerate(X):
for word, count in word_count.items():
rows.append(row)
cols.append(self.vocabulary_.get(word, 0))
data.append(count)
return csr_matrix((data, (rows, cols)), shape=(len(X), self.vocabulary_size + 1))
# -
vocab_transformer = WordCounterToVectorTransformer(vocabulary_size=10)
X_few_vectors = vocab_transformer.fit_transform(X_few_wordcounts)
X_few_vectors
X_few_vectors.toarray()
# What does this matrix mean? Well, the 99 in the second row, first column, means that the second email contains 99 words that are not part of the vocabulary. The 11 next to it means that the first word in the vocabulary is present 11 times in this email. The 9 next to it means that the second word is present 9 times, and so on. You can look at the vocabulary to know which words we are talking about. The first word is "the", the second word is "of", etc.
vocab_transformer.vocabulary_
# ## Train the data
# +
from sklearn.pipeline import Pipeline
preprocess_pipeline = Pipeline([
("email_to_wordcount", EmailToWordCounterTransformer()),
("wordcount_to_vector", WordCounterToVectorTransformer()),
])
X_train_transformed = preprocess_pipeline.fit_transform(X_train)
# +
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import cross_val_score
log_clf = LogisticRegression(solver="lbfgs", max_iter=1000, random_state=42)
score = cross_val_score(log_clf, X_train_transformed, y_train, cv=3, verbose=3)
score.mean()
# +
from sklearn.metrics import precision_score, recall_score
X_test_transformed = preprocess_pipeline.transform(X_test)
log_clf = LogisticRegression(solver="lbfgs", max_iter=1000, random_state=42)
log_clf.fit(X_train_transformed, y_train)
y_pred = log_clf.predict(X_test_transformed)
print("Precision: {:.2f}%".format(100 * precision_score(y_test, y_pred)))
print("Recall: {:.2f}%".format(100 * recall_score(y_test, y_pred)))
# -
|
Spam Detection.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# Erasmus+ ICCT project (2018-1-SI01-KA203-047081)
# Toggle cell visibility
from IPython.display import HTML
tag = HTML('''<script>
code_show=true;
function code_toggle() {
if (code_show){
$('div.input').hide()
} else {
$('div.input').show()
}
code_show = !code_show
}
$( document ).ready(code_toggle);
</script>
Toggle cell visibility <a href="javascript:code_toggle()">here</a>.''')
display(tag)
# Hide the code completely
# from IPython.display import HTML
# tag = HTML('''<style>
# div.input {
# display:none;
# }
# </style>''')
# display(tag)
# -
# %matplotlib notebook
import pylab
import matplotlib.pyplot as plt
import math
import sympy as sym
import numpy as np
import ipywidgets as widgets
import control as control
import math as math
from ipywidgets import interact
from IPython.display import Latex, display, Markdown
# + [markdown] lang="it"
# ## Linearizzazione di una funzione
#
# ### Introduzione
#
# > La linearizzazione è definita come un processo per trovare un'approssimazione lineare di una funzione in un certo punto. L'approssimazione lineare di una funzione è ottenuta dall'espansione di Taylor attorno al punto di interesse in cui vengono mantenuti solo i primi due termini. La linearizzazione è un metodo efficace per approssimare l'uscita di una funzione $y=f(x)$ a qualsiasi $x=x_0+\Delta x$ in base al valore e alla pendenza della funzione in $x=x_0$, dato che $f(x)$ è differenziabile in $[x_0,x_0+\Delta x]$ (o $[x_0+\Delta x,x_0]$) e che $x_0$ è vicino a $x_0+\Delta x$. In breve, la linearizzazione approssima l'uscita di una funzione vicino a $x=x_0$. (fonte: [Wikipedia] (https://en.wikipedia.org/wiki/Linearization))
#
# In questo esempio, la linearizzazione è definita come:
#
# \begin{equation}
# f(x)\approx f(x_0)+f^{\prime}(x_0) \cdot (x-x_0),
# \end{equation}
#
# dove $f^{\prime}=\frac{f(x_0+h)-f(x_0)}{h}$ ($h$ è impostato su $0.01$ per calcolare la derivata).
#
# La funzione gradino (unitaria) è definita come:
#
# \begin{equation}
# u(x) =
# \begin{cases}
# 0; & \text{$x<0$}\\
# 1; & \text{$x\geq0$}
# \end{cases},
# \end{equation}
#
# mentre la funzione rampa (unitaria):
#
# \begin{equation}
# r(x) =
# \begin{cases}
# 0; & \text{$x<0$}\\
# x; & \text{$x\geq0$}
# \end{cases}.
# \end{equation}
#
# ---
#
# ### Come usare questo notebook?
# Sposta lo slider per modificare il valore di $x_0$, ovvero il valore di $x$ in corrispondenza del quale si desidera linearizzare la funzione.
# +
# sinus, step, ramp, x^2, sqrt(x)
functionSelect = widgets.ToggleButtons(
options=[('sinusoide', 0), ('gradino', 1), ('rampa', 2), ('parabola', 3), ('radice quadrata', 4)],
description='Seleziona: ')
fig = plt.figure(num='Linearizzazione di una funzione')
fig.set_size_inches((9.8, 3))
fig.set_tight_layout(True)
f1 = fig.add_subplot(1, 1, 1)
f1.grid(which='both', axis='both', color='lightgray')
f1.set_xlabel('$x$')
f1.set_ylabel('$f(x)$')
f1.axhline(0,Color='black',linewidth=0.5)
f1.axvline(0,Color='black',linewidth=0.5)
func_plot, = f1.plot([],[])
tang_plot, = f1.plot([],[])
point_plot, = f1.plot([],[])
f1.set_xlim((-5,5))
f1.set_ylim((-6,6))
def create_draw_functions(x0,index):
x=np.linspace(-5,5,1001)
h=0.001 # equal to \Delta x
global func_plot, tang_plot, point_plot
if index==0:
y=np.sin(x)
fprime=(np.sin(x0+h)-np.sin(x0))/h
tang=np.sin(x0)+fprime*(x-x0)
fx0=np.sin(x0)
elif index==1:
y=np.zeros(1001)
y[510:1001]=1
elif index==2:
y=np.zeros(1001)
y[500:1001]=np.linspace(0,5,501)
elif index==3:
y=x*x
fprime=((x0+h)*(x0+h)-(x0*x0))/h
tang=x0*x0+fprime*(x-x0)
fx0=x0*x0
elif index==4:
x1=np.linspace(0,5,500)
y=np.sqrt(x1)
if x0>=0:
fprime=(np.sqrt(x0+h)-np.sqrt(x0))/h
tang=np.sqrt(x0)+fprime*(x-x0)
fx0=np.sqrt(x0)
f1.lines.remove(func_plot)
f1.lines.remove(tang_plot)
f1.lines.remove(point_plot)
if index == 0:
func_plot, = f1.plot(x,y,label='$f(x)=sin(x)$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,fx0,'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif index == 1: # in case of the unit step function
if x0==0:
func_plot, = f1.step(x,y,label='$f(x)=u(x)$',color='C0')
tang_plot, = f1.plot([],[])
point_plot, = f1.plot([],[])
f1.text(0.1,1.3,'La linearizzazione in $x_0=0$ non è possibile!',fontsize=14)
elif x0<0:
tang=np.zeros(1001)
func_plot, = f1.step(x,y,label='$f(x)=u(x)$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,[0],'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif x0>0:
tang=np.ones(1001)
func_plot, = f1.step(x,y,label='$f(x)=u(x)$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,[1],'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif index==2: # in case of the ramp
if x0<0:
tang=np.zeros(1001)
func_plot, = f1.plot(x,y,label='$f(x)=R(x)$',color='C0')
tang_plot, = f1.plot(x,np.zeros(1001),'--r',label='tangente')
point_plot, = f1.plot(x0,[0],'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif x0>=0:
tang=x
func_plot, = f1.plot(x,y,label='$f(x)=R(x)$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,x0,'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif index==3:
func_plot, = f1.plot(x,y,label='$f(x)=x^2$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,fx0,'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
elif index==4: #in case of the square root function
if x0<0:
for txt in f1.texts:
txt.set_visible(False)
func_plot, = f1.plot(x1,y,label='$f(x)=\sqrt{x}$',color='C0')
tang_plot, = f1.plot([],[])
point_plot, = f1.plot([],[])
f1.text(-4.9,1.3,'La radice quadrata non è definita per $x<0$!',fontsize=14)
else:
func_plot, = f1.plot(x1,y,label='$f(x)=\sqrt{x}$',color='C0')
tang_plot, = f1.plot(x,tang,'--r',label='tangente')
point_plot, = f1.plot(x0,fx0,'om',label='$x_0$')
for txt in f1.texts:
txt.set_visible(False)
if (index==1) and x0==0 or (index==4 and x0<0):
display(Markdown('Guarda i commenti sulla figura.'))
else:
k=round(((tang[-1]-tang[0])/(x[-1]-x[0])),3)
n=round(((tang[-1]-k*x[-1])),3)
display(Markdown('Equazione della tangente: $y=%.3fx+%.3f$.'%(k,n)))
f1.legend()
f1.relim()
f1.relim()
f1.autoscale_view()
f1.autoscale_view()
x0_slider = widgets.FloatSlider(value=1, min=-5, max=5, step=0.2, description='$x_0$',
continuous_update=True, layout=widgets.Layout(width='auto', flex='5 5 auto'),readout_format='.1f')
input_data = widgets.interactive_output(create_draw_functions, {'x0':x0_slider, 'index':functionSelect})
def update_sliders(index):
global x0_slider
x0val = [0.5, 0.5, 1, 1, 5, 10]
x0slider.value = x0val[index]
input_data2 = widgets.interactive_output(update_sliders, {'index':functionSelect})
display(functionSelect)
display(x0_slider,input_data)
# display(Markdown("The system can be represented as $f(x)=5$ for small excursions of x about x0."))
|
ICCT_it/examples/02/.ipynb_checkpoints/TD-05-Linearizzazione-di-una-funzione-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# + [markdown] pycharm={"name": "#%% md\n"}
# # livelossplot example: PyTorch
#
# Last update: `livelossplot 0.5.0`. For code and documentation, see [livelossplot GitHub repository](https://github.com/stared/livelossplot).
#
# <a href="https://colab.research.google.com/github/stared/livelossplot/blob/master/examples/pytorch.ipynb" target="_parent">
# <img src="https://colab.research.google.com/assets/colab-badge.svg"/>
# </a>
# + pycharm={"name": "#%%\n"}
# !pip install livelossplot --quiet
# + pycharm={"is_executing": false}
import numpy as np
from sklearn.model_selection import train_test_split
import torch
from torch import nn
from torch import optim
from torch.utils.data import TensorDataset, DataLoader
from livelossplot import PlotLosses
# + pycharm={"is_executing": false}
base_string = "()()" + (32 - 4) * " "
def shuffle_string(s):
indices = np.arange(len(s), dtype='uint8')
np.random.shuffle(indices)
return "".join(base_string[i] for i in indices)
def is_correct(seq):
open_brackets = 0
val = {"(": 1, " ": 0, ")": -1}
for c in seq:
open_brackets += val[c]
if open_brackets < 0:
return False
return open_brackets == 0
char2id = {" ": 0, "(": 1, ")": 2}
def generate_pairs(size):
X = np.zeros((size, 3, len(base_string)), dtype='float32')
Y = np.zeros((size), dtype='int64')
for i in range(size):
s = shuffle_string(base_string)
Y[i] = int(is_correct(s))
for j, c in enumerate(s):
X[i, char2id[c], j] = 1.
return X, Y
def generate_train_test_pairs(size):
X, Y = generate_pairs(size)
return train_test_split(X, Y, test_size=0.25, random_state=42)
# + pycharm={"is_executing": false}
x = shuffle_string(base_string)
print(x, "- correct" if is_correct(x) else "- incorrect")
# + pycharm={"is_executing": false}
X_train, X_test, Y_train, Y_test = generate_train_test_pairs(1000)
trainloader = DataLoader(TensorDataset(torch.from_numpy(X_train), torch.from_numpy(Y_train)),
batch_size=32, shuffle=True)
testloader = DataLoader(TensorDataset(torch.from_numpy(X_test), torch.from_numpy(Y_test)),
batch_size=32, shuffle=False)
dataloaders = {
"train": trainloader,
"validation": testloader
}
# + pycharm={"is_executing": false}
class Recurrent(nn.Module):
def __init__(self, rnn_size):
super(Recurrent, self).__init__()
self.gru = nn.GRU(input_size=3, hidden_size=rnn_size)
self.fc = nn.Linear(rnn_size, 2)
def forward(self, x):
x = x.permute(2, 0, 1)
output, hidden = self.gru(x)
return self.fc(hidden.squeeze(0))
# + pycharm={"is_executing": false}
# train on cuda if available
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
def train_model(model, criterion, optimizer, num_epochs=10):
liveloss = PlotLosses()
model = model.to(device)
for epoch in range(num_epochs):
logs = {}
for phase in ['train', 'validation']:
if phase == 'train':
model.train()
else:
model.eval()
running_loss = 0.0
running_corrects = 0
for inputs, labels in dataloaders[phase]:
inputs = inputs.to(device)
labels = labels.to(device)
outputs = model(inputs)
loss = criterion(outputs, labels)
if phase == 'train':
optimizer.zero_grad()
loss.backward()
optimizer.step()
_, preds = torch.max(outputs, 1)
running_loss += loss.detach() * inputs.size(0)
running_corrects += torch.sum(preds == labels.data)
epoch_loss = running_loss / len(dataloaders[phase].dataset)
epoch_acc = running_corrects.float() / len(dataloaders[phase].dataset)
prefix = ''
if phase == 'validation':
prefix = 'val_'
logs[prefix + 'log loss'] = epoch_loss.item()
logs[prefix + 'accuracy'] = epoch_acc.item()
liveloss.update(logs)
liveloss.send()
# + pycharm={"is_executing": false}
model = Recurrent(8)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
# + pycharm={"is_executing": false, "name": "#%%\n"}
train_model(model, criterion, optimizer, num_epochs=20)
|
examples/pytorch.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/echiyembekeza/DS-Unit-1-Sprint-1-Dealing-With-Data/blob/master/LS_DS_124_Make_features.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] colab_type="text" id="qacqiXogluN_"
# _Lambda School Data Science_
#
# # Make features
#
# Objectives
# - understand the purpose of feature engineering
# - work with strings in pandas
# - work with dates and times in pandas
#
# Links
# - [Feature Engineering](https://en.wikipedia.org/wiki/Feature_engineering)
# - Python Data Science Handbook
# - [Chapter 3.10](https://jakevdp.github.io/PythonDataScienceHandbook/03.10-working-with-strings.html), Vectorized String Operations
# - [Chapter 3.11](https://jakevdp.github.io/PythonDataScienceHandbook/03.11-working-with-time-series.html), Working with Time Series
# + [markdown] colab_type="text" id="iSGiSktAoWIx"
# ## Get LendingClub data
#
# [Source](https://www.lendingclub.com/info/download-data.action)
# + id="KL_Culn3HWjW" colab_type="code" outputId="91c930a5-6a86-4c63-af0e-0f2f776c8dad" colab={"base_uri": "https://localhost:8080/", "height": 63}
# ! ls
# + colab_type="code" id="2ugxlWXimoHn" outputId="5ea0fbe7-293a-4a62-e235-417109fbda47" colab={"base_uri": "https://localhost:8080/", "height": 1000}
# !wget https://resources.lendingclub.com/LoanStats_2018Q4.csv.zip
# + colab_type="code" id="-4sk6qPgmpmN" outputId="0471590b-211e-49e3-c220-ef9f00a9fca7" colab={"base_uri": "https://localhost:8080/", "height": 63}
# !unzip LoanStats_2018Q4.csv.zip [n]
# + colab_type="code" id="seh5oNE1nD0X" outputId="e1de9332-9a04-48da-d922-e961258e4b9f" colab={"base_uri": "https://localhost:8080/", "height": 276}
# !head LoanStats_2018Q4.csv
# + [markdown] colab_type="text" id="3nAIRCZdofrY"
# ## Load LendingClub data
#
# pandas documentation
# - [`read_csv`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_csv.html)
# - [`options.display`](https://pandas.pydata.org/pandas-docs/stable/options.html#available-options)
# + id="reUUacYMHWj9" colab_type="code" colab={}
import pandas as pd
# + colab_type="code" id="3-8Vn3y6ooBC" outputId="45ee0a11-4b9d-443c-ab57-4bce75c89363" colab={"base_uri": "https://localhost:8080/", "height": 3281}
pd.read_csv(filepath_or_buffer='LoanStats_2018Q4.csv')
# + id="Cg5h6bj_HWkC" colab_type="code" colab={}
# pd.read_csv?
# + id="Qt3JxtcKHWkH" colab_type="code" outputId="88f4e3bd-53e6-4401-dd80-43cfc0d0e4fe" colab={"base_uri": "https://localhost:8080/", "height": 392}
df = pd.read_csv(sep=',', filepath_or_buffer='LoanStats_2018Q4.csv', skiprows=1, skipfooter=2)
df.head()
# + id="JQi86PvfHWkK" colab_type="code" colab={}
df.tail()
# + id="D692m-02HWkP" colab_type="code" colab={}
df.shape
# + id="jtQxullAHWkS" colab_type="code" colab={}
df.describe()
# + id="VpNIGiY7HWkY" colab_type="code" colab={}
df.info()
# + id="I6IDypXbHWkc" colab_type="code" colab={}
df.dtypes.value_counts()
# + id="f6o_KH1AHWke" colab_type="code" colab={}
df.shape[0]
# + id="MI_LQ7LPHWkh" colab_type="code" colab={}
# %timeit df.shape[0]
# + id="AwdsqxnEHWkl" colab_type="code" colab={}
df.isnull().sum(axis=0).sort_values()
# + [markdown] colab_type="text" id="1b5_hMTio2Ly"
# ## Work with strings
# + [markdown] id="ZwLej1seHWkr" colab_type="text"
# For machine learning, we usually want to replace strings with numbers.
#
# We can get info about which columns have a datatype of "object" (strings)
# + colab_type="code" id="WOL7QPVNo3F4" colab={}
df.dtypes
# + id="-CS9n_CFHWkt" colab_type="code" colab={}
df['int_rate'].head()
# + [markdown] id="4er_-FnZHWkw" colab_type="text"
# ### Convert `int_rate`
#
# Define a function to remove percent signs from strings and convert to floats
# + id="np9822LeHWkw" colab_type="code" colab={}
'10.33%'[:-1]
# + id="UWCY8QL0HWk0" colab_type="code" colab={}
def strip_percent(x_str):
return float(x_str.strip('%')) # x_str[-1]
# + [markdown] id="DGGjx45qHWk4" colab_type="text"
# Apply the function to the `int_rate` column
# + id="pR5qLtkZHWk4" colab_type="code" colab={}
df['int_rate'] = df['int_rate'].apply(strip_percent)
df['int_rate'].head()
# + [markdown] id="o3f-mHHqHWk7" colab_type="text"
# ### Clean `emp_title`
#
# Look at top 20 titles
# + id="2O10LbWCHWk7" colab_type="code" colab={}
df['emp_title'].head(n=10)
# + [markdown] id="Yj48cn7VHWk-" colab_type="text"
# How often is `emp_title` null?
# + id="fMRfnTVPHWk_" colab_type="code" colab={}
df['emp_title'].value_counts(dropna=False).head(20)
# + [markdown] id="MKkFkhfwHWlC" colab_type="text"
# Clean the title and handle missing values
# + id="Oe58AM01HWlC" colab_type="code" colab={}
df['emp_title'].isnull().sum()
# + id="sbXX5vqsHWlF" colab_type="code" colab={}
import numpy as np
type(np.NaN)
# + id="41xHc3ayHWlJ" colab_type="code" colab={}
def clean_title(title):
if isinstance(title, str):
return title.strip().lower()
else:
return 'unknown'
# + id="oBK6PQauHWlM" colab_type="code" colab={}
df['emp_title'] = df['emp_title'].apply(clean_title)
df['emp_title'].head()
# + id="2TqMsvzwHWlN" colab_type="code" colab={}
df['emp_title'].value_counts(dropna=False).head(20)
# + [markdown] id="hY7i_OnZHWlP" colab_type="text"
# ### Create `emp_title_manager`
#
# pandas documentation: [`str.contains`](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.str.contains.html)
# + id="RUZbQ0dcHWlQ" colab_type="code" colab={}
df['emp_title'].str.contains('manager').head()
# + id="ZZCoWRNlHWlS" colab_type="code" colab={}
df['emp_title_manager'] = df['emp_title'].str.contains('manager')
df['emp_title_manager'].sample(10)
# + id="VAzTmpZbHWlT" colab_type="code" colab={}
df.to_csv('tmp.csv', index=False)
# + id="4315B8z4HWlU" colab_type="code" colab={}
df['emp_title'].nunique()
# + id="ZYMcJJbZHWlX" colab_type="code" colab={}
idx_manager = df['emp_title_manager'] == True
df_managers = df[idx_manager]
df_managers.shape
# + id="tbaH_-c_HWla" colab_type="code" colab={}
idx_nonmanager = df['emp_title_manager'] == False
df_nonmanagers = df[idx_nonmanager]
df_nonmanagers.shape
# + id="enc3ZUayHWlc" colab_type="code" colab={}
del df_2
# + id="8A7YkyPZHWld" colab_type="code" colab={}
del df
# + id="dPInkxEEHWle" colab_type="code" colab={}
print(df_managers['int_rate'].mean(), df_nonmanagers['int_rate'].mean())
# + id="c48xTIqYHWlh" colab_type="code" colab={}
print(df_managers['int_rate'].std(), df_nonmanagers['int_rate'].std())
# + id="44dRCdHxHWlj" colab_type="code" colab={}
# %matplotlib inline
# + id="GdvLXST4HWlk" colab_type="code" colab={}
df_managers['int_rate'].hist()
# + id="yw6SoA55HWlm" colab_type="code" colab={}
df_nonmanagers['int_rate'].hist()
# + id="u49Xri3YHWlp" colab_type="code" colab={}
# + [markdown] colab_type="text" id="s8BcCY6so3by"
# ## Work with dates
# + [markdown] id="vm_hZMa5HWlq" colab_type="text"
# pandas documentation
# - [to_datetime](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.to_datetime.html)
# - [Time/Date Components](https://pandas.pydata.org/pandas-docs/stable/timeseries.html#time-date-components) "You can access these properties via the `.dt` accessor"
# + colab_type="code" id="kNrKxOTeo4W3" colab={}
df_nonmanagers['issue_d'].head()
# + id="--EpyYxYHWls" colab_type="code" colab={}
df_nonmanagers['issue_d'] = pd.to_datetime(df_nonmanagers['issue_d'])
df_nonmanagers['issue_d'].head()
# + id="udXHFFMZHWlu" colab_type="code" colab={}
df_nonmanagers['issue_year'] = df_nonmanagers['issue_d'].dt.year
df_nonmanagers['issue_month'] = df_nonmanagers['issue_d'].dt.month
df_nonmanagers[['issue_year', 'issue_month']].head()
# + id="YAJI93W0HWlv" colab_type="code" colab={}
# + [markdown] id="DwqYLEmwHWlw" colab_type="text"
# # ASSIGNMENT
#
# - Replicate the lesson code.
#
# - Convert the `term` column from string to integer.
#
# - Make a column named `loan_status_is_great`. It should contain the integer 1 if `loan_status` is "Current" or "Fully Paid." Else it should contain the integer 0.
#
# - Make `last_pymnt_d_month` and `last_pymnt_d_year` columns.
# + id="uMweoz-2KktZ" colab_type="code" outputId="ecb46880-cb28-447e-f719-d03e2982abc8" colab={"base_uri": "https://localhost:8080/", "height": 358}
#We already have the file imported that we will be using
#we named the dataframe df
df.head()
# + id="9Ega9XVraVH3" colab_type="code" outputId="6dbcebe8-a7f0-4ce7-e3eb-82476e0fce79" colab={"base_uri": "https://localhost:8080/", "height": 1071}
#Convert the term column from string to integer.
#We need to call the 'term' column
df['term'] #this shows that the column has values that are str not integers
#having the 'months' at the end makes this a string
# + id="4seyjVP4dAsd" colab_type="code" outputId="c9413319-ce27-44f8-d37f-9589dd459fcd" colab={"base_uri": "https://localhost:8080/", "height": 1071}
#let's try something different
#use a func
def strip_months(term_str):
return float(term_str.strip('months'))
#we need to change this column from a str to int
df_term = df['term'].apply(strip_months)
df_term
# + id="omitHBFFeQFl" colab_type="code" outputId="ccc55d7a-2ab3-4559-c814-c94f19ce923a" colab={"base_uri": "https://localhost:8080/", "height": 1071}
##Next question:
#Make a column named loan_status_is_great.
#It should contain the integer 1 if loan_status is "Current" or "Fully Paid."
#Else it should contain the integer 0.
df['loan_status']#shows us what we have
# + id="ntBKDdk2f_RG" colab_type="code" outputId="5e8cf438-9f55-4f1f-e0b8-7086272369f6" colab={"base_uri": "https://localhost:8080/", "height": 1071}
#make a new column with the name 'loan_status_is_great'
#df['loan_status'] = df['loan_status'].str.contains('Current','Fully Paid')#this returns a bool
col_loan = {True:1, False:0}
df['loan_status_is_great'] = df['loan_status'].replace(col_loan)
df['loan_status_is_great']
# + id="zgFzurIBpVqW" colab_type="code" outputId="ee134909-c1b9-4401-da85-af5213a408bc" colab={"base_uri": "https://localhost:8080/", "height": 1071}
#Make last_pymnt_d_month and last_pymnt_d_year columns
df['last_pymnt_d']
# + id="OE-YrXwNp4Px" colab_type="code" outputId="feb591dc-cdd9-480b-c40f-bd1cac9a6706" colab={"base_uri": "https://localhost:8080/", "height": 669}
df['last_pymnt_d'] = pd.to_datetime(df['last_pymnt_d'])
df['last_pymnt_d'].head
df['last_pymnt_d_month'] = df['last_pymnt_d'].dt.month
df['last_pymnt_d_year'] = df['last_pymnt_d'].dt.year
df[['last_pymnt_d_month', 'last_pymnt_d_year']].head()
# + id="YMB-nm9Hrnye" colab_type="code" outputId="5f92e1d9-db79-4b39-fef2-fdcd924cfa7b" colab={"base_uri": "https://localhost:8080/", "height": 153}
df['last_pymnt_d_month'].value_counts()
# + [markdown] colab_type="text" id="L8k0LiHmo5EU"
# # STRETCH OPTIONS
#
# You can do more with the LendingClub or Instacart datasets.
#
# LendingClub options:
# - There's one other column in the dataframe with percent signs. Remove them and convert to floats. You'll need to handle missing values.
# - Modify the `emp_title` column to replace titles with 'Other' if the title is not in the top 20.
# - Take initiatve and work on your own ideas!
#
# Instacart options:
# - Read [Instacart Market Basket Analysis, Winner's Interview: 2nd place, Kazuki Onodera](http://blog.kaggle.com/2017/09/21/instacart-market-basket-analysis-winners-interview-2nd-place-kazuki-onodera/), especially the **Feature Engineering** section. (Can you choose one feature from his bulleted lists, and try to engineer it with pandas code?)
# - Read and replicate parts of [Simple Exploration Notebook - Instacart](https://www.kaggle.com/sudalairajkumar/simple-exploration-notebook-instacart). (It's the Python Notebook with the most upvotes for this Kaggle competition.)
# - Take initiative and work on your own ideas!
# + [markdown] colab_type="text" id="0_7PXF7lpEXg"
# You can uncomment and run the cells below to re-download and extract the Instacart data
# + id="82rVoYX2HWlx" colab_type="code" colab={}
# # !wget https://s3.amazonaws.com/instacart-datasets/instacart_online_grocery_shopping_2017_05_01.tar.gz
# + id="MYNVDAf7HWly" colab_type="code" colab={}
# # !tar --gunzip --extract --verbose --file=instacart_online_grocery_shopping_2017_05_01.tar.gz
# + id="mm7QaiXpHWly" colab_type="code" colab={}
# # %cd instacart_2017_05_01
|
LS_DS_124_Make_features.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DyNetworkX Tutorial – Plotting Dynamic Betweenness Centrality
#
# The objective of this tutorial is to showcase a typical use case of DyNetworkX.
# We will be using the Enron dataset, a preview of the data file can be seen below.
# Enron dataset will be downloaded to current directory if not already present. (Size: 2 MB)
# +
import os
import urllib
import datetime
file_path = "execs.email.linesnum"
if not os.path.exists(file_path):
print("Downloading Enron dataset from http://www.cis.jhu.edu/~parky/Enron/execs.email.linesnum ...")
urllib.request.urlretrieve("http://www.cis.jhu.edu/~parky/Enron/execs.email.linesnum", file_path)
print("Download complete.")
lines = []
with open(file_path, "r") as file:
for line in file:
t, u, v = line.split(" ")
if int(t) > 315522000:
lines.append(line)
with open(file_path, "w") as file:
for line in lines:
file.write(line)
# -
# ### Loading Data into DyNetworkX
#
# Loading data a text file using the function `dnx.ImpulseGraph.load_from_txt`.
# Make sure to specify necessary arguments such as `delimiter`, `timestamptype`, and `order`.
#
# Comparing the output of the new ImpulseGraph, it is possible to verify the data set is correctly imported. (Note: order not guaranteed)
# +
import dynetworkx as dnx
impulseG = dnx.ImpulseGraph.load_from_txt("execs.email.linesnum", delimiter=" ",
timestamptype=int, order=('t', 'v', 'u'))
print(impulseG.edges()[:5])
# -
# ### Converting between different graph types
#
# Traditionally working with dynamic networks, it is commmon to flatten the temporal dimension by binning data into smaller static graphs called snapshots. This behavior is replicated by the DynetworkX class `SnapshotGraph`.
# By using the argument `length_of_snapshots`, it is possible to specify the desired length of each snapshot to 1 year (converted to seconds to match the data set).
# +
snapshots = impulseG.to_snapshots(length_of_snapshots=31536000)
first_timestamp = impulseG.interval()[0]
snapshotG = dnx.SnapshotGraph()
i = 0
for snapshot in snapshots:
snapshotG.add_snapshot(graph=snapshot, start=31536000*i + first_timestamp,
end=31536000*(i+1) + first_timestamp)
i += 1
# -
# ### Calculating Dynamic Betweenness Centrality
#
# `compute_network_statistic` returns a list, each item in the list refers to each snapshot in the SnapshotGraph. The specified method is applied to each snapshot in the graph, passing additional arguments if present.
# The first snapshot can be seen below.
# +
from networkx.algorithms.centrality import betweenness_centrality
centrality_list = snapshotG.compute_network_statistic(betweenness_centrality)
centrality_sorted = []
unique_nodes = set()
snapshot_list = snapshotG.get()
for snapshot in snapshot_list:
for node in snapshot.nodes():
unique_nodes.add(node)
for snapshot in centrality_list:
centrality_sorted.append(sorted(snapshot.items(), key=lambda x: x[1], reverse=True)+
[(float("NaN"), float("NaN"))]*(len(unique_nodes)-len(snapshot)))
print("{:10s}{:10s}{:10s}{:10s}{:10s}{:10s}{:10s}{:10s}".format(
"Node", "Year 1", "Node", "Year 2", "Node", "Year 3", "Node", "Year 4"))
for i in range(len(unique_nodes)):
print("{:<10.0f}{:0.3f}\
{:<10.0f}{:0.3f}\
{:<10.0f}{:0.3f}\
{:<10.0f}{:0.3f}".format(
*centrality_sorted[0][i], *centrality_sorted[1][i],
*centrality_sorted[2][i], *centrality_sorted[3][i]))
# -
# ### Formatting Data
#
# From this point forward, we are done using DyNetworkX.
# We will finish the objective by getting ready our data to plot.
# +
min_max = []
for i in range(len(centrality_list)):
min_value = float("inf")
max_value = float("-inf")
for value in centrality_list[i].values():
min_value = min(min_value, value)
max_value = max(max_value, value)
min_max.append((min_value, max_value))
snapshot_list = snapshotG.get()
colors = []
for i in range(len(snapshot_list)):
colors.append([])
for node in snapshot_list[i]:
color_value = 0.75*(centrality_list[i][node] - min_max[i][0]) / (min_max[i][1] - min_max[i][0])
colors[i].append((1-color_value, 1-color_value, 1))
# -
# ### Plotting Dynamic Betweenness Centrality
#
# Finally, plot the betweenness centrality over time using Matplotlib.animation.
# +
import matplotlib.pyplot as plt
import networkx as nx
from matplotlib import animation
def update(i, colors, pos, snapshot_list, ax):
ax.clear()
ax.set_xlim([-1.1, 1.1])
ax.set_ylim([-1.1, 1.1])
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
nx.draw_networkx(snapshot_list[i], pos=pos, font_size=16, node_size=900, edgecolors="#000000",
node_color=colors[i], ax=ax)
ax.set_title(f"Year {i+1}", fontsize=24)
fig, ax = plt.subplots(figsize=(20, 20))
staticG = nx.Graph()
for snapshot in snapshotG:
for u, v in snapshot.edges():
staticG.add_edge(u, v)
pos = nx.spring_layout(staticG, k=1)
anim = animation.FuncAnimation(fig, update, frames=len(snapshot_list), interval=5000,
fargs=(colors, pos, snapshot_list, ax))
anim.save('betweenness.gif', writer='pillow')
# +
fig, ax = plt.subplots(figsize=(10, 10))
for node in [169, 125, 82, 105]:
centrality = [0]*4
for i in range(4):
if node in centrality_list[i]:
centrality[i] = centrality_list[i][node]
plt.plot(range(4), centrality, label=node)
plt.xticks(ticks=range(4), labels=[1, 2, 3, 4])
plt.ylabel("Betweenness Centrality", fontsize=16)
plt.xlabel("Year", fontsize=16)
plt.legend()
plt.show()
# -
|
betweenness-centrality.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import gachon_autograder_client as g_autograder
EMAIL = "#TESTYOURMAIL"
PASSWORD = <PASSWORD>"
ASSIGNMENT_NAME = "nb_test"
g_autograder.get_assignment(EMAIL, PASSWORD, ASSIGNMENT_NAME)
|
assignment/get_assignment.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# https://www.youtube.com/watch?v=G4UVJoGFAv0
# +
import sys
import nltk
import sklearn
import numpy
import pandas
print('Python : {}'.format(sys.version))
print('NLTK : {}'.format(nltk.__version__))
print('sklearn : {}'.format(sklearn.__version__))
print('Numpy: {}'.format(numpy.__version__))
print('pandas : {}'.format(pandas.__version__))
# -
# # 1. Load the Data
# +
import pandas as pd
import numpy as np
#load the dataset of sms message
df = pd.read_table('SMSSpamCollection',header=None, encoding='utf-8')
# -
df.head()
df.info()
classes = df[0]
classes.value_counts()
# # 2. Preprocessing the Data
# +
#convert class label to binary value 0 = ham, 1 = spam
from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()
Y = encoder.fit_transform(classes)
print(Y[:10])
# +
#Store the sms message Data
text_messages = df[1]
print(test_messages[:10])
# -
# ## 2.1 Reguler Expression
# - ^ Matches the starting position within the string. In line-based tools, it matches the starting position of any line.
# - . Matches any single character (many applications exclude newlines, and exactly which characters are considered newlines is flavor-, - - --- character-encoding-, and platform-specific, but it is safe to assume that the line feed character is included). Within POSIX bracket expressions, the dot character matches a literal dot. For example, a.c matches "abc", etc., but [a.c] matches only "a", ".", or "c".
# - [ ]A bracket expression. Matches a single character that is contained within the brackets. For example, [abc] matches "a", "b", or "c". [a-z] specifies a range which matches any lowercase letter from "a" to "z". These forms can be mixed: [abcx-z] matches "a", "b", "c", "x", "y", or "z", as does [a-cx-z].
#
# - The - character is treated as a literal character if it is the last or the first (after the ^, if present) character within the brackets: [abc-], [-abc]. Note that backslash escapes are not allowed. The ] character can be included in a bracket expression if it is the first (after the ^) character: []abc].
# - [^ ] Matches a single character that is not contained within the brackets. For example, [^abc] matches any character other than "a", "b", or "c". [^a-z] matches any single character that is not a lowercase letter from "a" to "z". Likewise, literal characters and ranges can be mixed.
# - $ Matches the ending position of the string or the position just before a string-ending newline. In line-based tools, it matches the ending position of any line.
# - ( ) Defines a marked subexpression. The string matched within the parentheses can be recalled later (see the next entry, \n). A marked subexpression is also called a block or capturing group. BRE mode requires \( \).
# - \n Matches what the nth marked subexpression matched, where n is a digit from 1 to 9. This construct is vaguely defined in the POSIX.2 standard. Some tools allow referencing more than nine capturing groups.
# - * Matches the preceding element zero or more times. For example, ab*c matches "ac", "abc", "abbbc", etc. [xyz]* matches "", "x", "y", "z", "zx", "zyx", "xyzzy", and so on. (ab)* matches "", "ab", "abab", "ababab", and so on.
# - {m,n} Matches the preceding element at least m and not more than n times. For example, a{3,5} matches only "aaa", "aaaa", and "aaaaa". This is not found in a few older instances of regexes. BRE mode requires \{m,n\}.
# +
# use reguler expression to replace a email addresses, urls, phonenumber others number, symbol
#replace email addres with 'emailaddr'
processed = text_messages.str.replace(r'^.+@[^\.].*\.[a-z]{2,}$', 'emailaddr')
#replace urls with webaddresses
processed = processed.str.replace(r'^http\://[a-zA-Z0-9\-\.]+\.[a-zA-Z]{2,3}(/\S*)?$', 'webaddresses')
#replace money symbol with 'moneysymb'
processed = processed.str.replace(r'£|\$', 'moneysymb')
#replace 10 digit phoe number with 'phone number'
processed = processed.str.replace(r'^\(?[\d]{3}\)?[\s-]?[\d]{3}[\s-]?[\d]{4}$', 'phonenumber')
#replace normal number with number
processed = processed.str.replace(r'^\d+(\,\d+)?', 'numbr')
# +
#remove punctuation
processed = processed.str.replace(r'[^\w\d\s]', ' ')
#replace whitespace between terms with a sigle space
processed = processed.str.replace(r'\s+', ' ')
#removing leading and trailing whitespaces
processed = processed.str.replace(r'^\s+|\s+?$', '')
# -
#change word to lower case - Hello, HELLO, hello are all same word!
processed = processed.str.lower()
print(processed)
# +
#remove stop words from text messsage
nltk.download('stopwords')
from nltk.corpus import stopwords
stop_words = set(stopwords.words('english'))
processed = processed.apply(lambda x: ' '.join(term for term in x.split() if term not in stop_words))
# +
#remove word stems using a Porter Stemmer
ps = nltk.PorterStemmer()
processed = processed.apply(lambda x: ' '.join(ps.stem(term) for term in x.split()))
# -
print(processed)
# +
nltk.download('punkt')
from nltk.tokenize import word_tokenize
#creating a bag-of-words
all_words =[]
for message in processed:
words = word_tokenize(message)
for w in words:
all_words.append(w)
all_words = nltk.FreqDist(all_words)
# -
#print the total number words and the 15 most common word
print('Number of words : {}'.format(len(all_words)))
print('Most common Words : {}'.format(all_words.most_common(15)))
#use the 1500 most common words as features
words_features = list(all_words.keys())[:1500]
# +
# define a find_features function
def find_features(message):
words = word_tokenize(message)
features = {}
for word in words_features:
features[word] = (word in words)
return features
#Lets see an example
features =find_features(processed[0])
for key, value in features.items():
if value == True:
print(key)
# +
#features
# +
#find features for all messages
messages = zip(processed, Y)
#define a seed for reproducibality
seed = 1
np.random.seed = seed
# np.random.shuffle(messages)
#call findfind_features function for each SMS Messases
featursets = [(find_features(text), label) for (text, label) in messages]
# +
#split training and test dataset using sklearn
from sklearn import model_selection
training, testing = model_selection.train_test_split(featursets, test_size=0.25, random_state = seed)
# -
print('Training : {}'.format(len(training)))
print('Testing : {}'.format(len(testing)))
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression, SGDClassifier
from sklearn.naive_bayes import MultinomialNB
from sklearn.svm import SVC
from sklearn.metrics import classification_report, accuracy_score, confusion_matrix
# +
#Define model to train
names = ['K Nearest Neighbors', 'Decision Tree', 'Random Forest', 'Logistic Regression', 'SGD Classifier', 'Naive Bayes', 'SVM Lenier']
classifiers = [
KNeighborsClassifier(),
DecisionTreeClassifier(),
RandomForestClassifier(),
LogisticRegression(),
SGDClassifier(max_iter=100),
MultinomialNB(),
SVC(kernel = 'linear')
]
models = zip(names, classifiers)
print(models)
# +
#wrap model in NLTK
from nltk.classify.scikitlearn import SklearnClassifier
for name, model in models:
nltk_model = SklearnClassifier(model)
nltk.model.train(training)
accuracy = nltk.classify.accuracy(nltk_model, testing) * 100
print('{} : Accuracy : {}'. format(name, ac))
# +
# Ensemble methods - Voting classifier
from sklearn.ensemble import VotingClassifier
names = ["K Nearest Neighbors", "Decision Tree", "Random Forest", "Logistic Regression", "SGD Classifier",
"Naive Bayes", "SVM Linear"]
classifiers = [
KNeighborsClassifier(),
DecisionTreeClassifier(),
RandomForestClassifier(),
LogisticRegression(),
SGDClassifier(max_iter = 100),
MultinomialNB(),
SVC(kernel = 'linear')
]
models = zip(names, classifiers)
for name, model in models:
nltk_ensemble = SklearnClassifier(model)
nltk_ensemble.train(training)
accuracy = nltk.classify.accuracy(nltk_ensemble, testing)*100
print("Voting Classifier: Accuracy: {}".format(accuracy))
# +
#make class label prediction for testing set
txt_features, labels = zip(*testing)
prediction = nltk_ensemble.classify_many(txt_features)
# +
#print classification report
print(classification_report(labels, prediction))
pd.DataFrame(
confusion_matrix(labels, prediction),
index =[['actual','actual'],['ham','Spam']],
columns = [['predicted','predicted'],['ham','Spam']])
# -
cross = 1199 + 172
all = 1199 + 9 + 13 + 172
result = cross/all
result
|
text_clasification.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DoWhy: Interpreters for Causal Estimators
#
# This is a quick introduction to the use of interpreters in the DoWhy causal inference library.
# We will load in a sample dataset, use different methods for estimating the causal effect of a (pre-specified)treatment variable on a (pre-specified) outcome variable and demonstrate how to interpret the obtained results.
#
# First, let us add the required path for Python to find the DoWhy code and load all required packages
# %load_ext autoreload
# %autoreload 2
# +
import numpy as np
import pandas as pd
import logging
import dowhy
from dowhy import CausalModel
import dowhy.datasets
# -
# Now, let us load a dataset. For simplicity, we simulate a dataset with linear relationships between common causes and treatment, and common causes and outcome.
#
# Beta is the true causal effect.
data = dowhy.datasets.linear_dataset(beta=1,
num_common_causes=5,
num_instruments = 2,
num_treatments=1,
num_discrete_common_causes=1,
num_samples=10000,
treatment_is_binary=True,
outcome_is_binary=False)
df = data["df"]
print(df[df.v0==True].shape[0])
df
# Note that we are using a pandas dataframe to load the data.
# ## Identifying the causal estimand
# We now input a causal graph in the GML graph format.
# With graph
model=CausalModel(
data = df,
treatment=data["treatment_name"],
outcome=data["outcome_name"],
graph=data["gml_graph"],
instruments=data["instrument_names"]
)
model.view_model()
from IPython.display import Image, display
display(Image(filename="causal_model.png"))
# We get a causal graph. Now identification and estimation is done.
identified_estimand = model.identify_effect(proceed_when_unidentifiable=True)
print(identified_estimand)
# ## Method 1: Propensity Score Stratification
#
# We will be using propensity scores to stratify units in the data.
causal_estimate_strat = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_stratification",
target_units="att")
print(causal_estimate_strat)
print("Causal Estimate is " + str(causal_estimate_strat.value))
# ### Textual Interpreter
#
# The textual Interpreter describes (in words) the effect of unit change in the treatment variable on the outcome variable.
# Textual Interpreter
interpretation = causal_estimate_strat.interpret(method_name="textual_effect_interpreter")
# ### Visual Interpreter
#
# The visual interpreter plots the change in the standardized mean difference (SMD) before and after Propensity Score based adjustment of the dataset. The formula for SMD is given below.
#
#
# $SMD = \frac{\bar X_{1} - \bar X_{2}}{\sqrt{(S_{1}^{2} + S_{2}^{2})/2}}$
#
# Here, $\bar X_{1}$ and $\bar X_{2}$ are the sample mean for the treated and control groups.
#
# Visual Interpreter
interpretation = causal_estimate_strat.interpret(method_name="propensity_balance_interpreter")
# This plot shows how the SMD decreases from the unadjusted to the stratified units.
# ## Method 2: Propensity Score Matching
#
# We will be using propensity scores to match units in the data.
causal_estimate_match = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_matching",
target_units="atc")
print(causal_estimate_match)
print("Causal Estimate is " + str(causal_estimate_match.value))
# Textual Interpreter
interpretation = causal_estimate_match.interpret(method_name="textual_effect_interpreter")
# Cannot use propensity balance interpretor here since the interpreter method only supports propensity score stratification estimator.
# ## Method 3: Weighting
#
# We will be using (inverse) propensity scores to assign weights to units in the data. DoWhy supports a few different weighting schemes:
# 1. Vanilla Inverse Propensity Score weighting (IPS) (weighting_scheme="ips_weight")
# 2. Self-normalized IPS weighting (also known as the Hajek estimator) (weighting_scheme="ips_normalized_weight")
# 3. Stabilized IPS weighting (weighting_scheme = "ips_stabilized_weight")
causal_estimate_ipw = model.estimate_effect(identified_estimand,
method_name="backdoor.propensity_score_weighting",
target_units = "ate",
method_params={"weighting_scheme":"ips_weight"})
print(causal_estimate_ipw)
print("Causal Estimate is " + str(causal_estimate_ipw.value))
# Textual Interpreter
interpretation = causal_estimate_ipw.interpret(method_name="textual_effect_interpreter")
interpretation = causal_estimate_ipw.interpret(method_name="confounder_distribution_interpreter", fig_size=(8,8), font_size=12, var_name='W4', var_type='discrete')
|
docs/source/example_notebooks/dowhy_interpreter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
# <script>
# window.dataLayer = window.dataLayer || [];
# function gtag(){dataLayer.push(arguments);}
# gtag('js', new Date());
#
# gtag('config', 'UA-59152712-8');
# </script>
#
# # Tutorial-IllinoisGRMHD: postpostinitial__set_symmetries__copy_timelevels.C
#
# ## Authors: <NAME> & <NAME>
#
# <font color='red'>**This module is currently under development**</font>
#
# ## In this tutorial module we explain tasks that are performed just after the initial data has been set up. This module will likely be absorbed by another one once we finish documenting the code.
#
# ### Required and recommended citations:
#
# * **(Required)** <NAME>., <NAME>., <NAME>., <NAME>., and <NAME>. L. IllinoisGRMHD: an open-source, user-friendly GRMHD code for dynamical spacetimes. Class. Quantum Grav. 32 (2015) 175009. ([arxiv:1501.07276](http://arxiv.org/abs/1501.07276)).
# * **(Required)** <NAME>., <NAME>., <NAME>., <NAME>. Primitive Variable Solvers for Conservative General Relativistic Magnetohydrodynamics. Astrophysical Journal, 641, 626 (2006) ([astro-ph/0512420](https://arxiv.org/abs/astro-ph/0512420)).
# * **(Recommended)** <NAME>., <NAME>., <NAME>. An efficient shock-capturing central-type scheme for multidimensional relativistic flows - II. Magnetohydrodynamics. A&A 400 (2) 397-413 (2003). DOI: 10.1051/0004-6361:20021641 ([astro-ph/0210618](https://arxiv.org/abs/astro-ph/0210618)).
# <a id='toc'></a>
#
# # Table of Contents
# $$\label{toc}$$
#
# This module is organized as follows
#
# 0. [Step 0](#src_dir): **Source directory creation**
# 1. [Step 1](#introduction): **Introduction**
# 1. [Step 2](#postpostinitial__set_symmetries__copy_timelevels__c): **`postpostinitial__set_symmetries__copy_timelevels.C`**
# 1. [Step n-1](#code_validation): **Code validation**
# 1. [Step n](#latex_pdf_output): **Output this notebook to $\LaTeX$-formatted PDF file**
# <a id='src_dir'></a>
#
# # Step 0: Source directory creation \[Back to [top](#toc)\]
# $$\label{src_dir}$$
#
# We will now use the [cmdline_helper.py NRPy+ module](Tutorial-Tutorial-cmdline_helper.ipynb) to create the source directory within the `IllinoisGRMHD` NRPy+ directory, if it does not exist yet.
# +
# Step 0: Creation of the IllinoisGRMHD source directory
# Step 0a: Add NRPy's directory to the path
# https://stackoverflow.com/questions/16780014/import-file-from-parent-directory
import os,sys
nrpy_dir_path = os.path.join("..","..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
# Step 0b: Load up cmdline_helper and create the directory
import cmdline_helper as cmd
IGM_src_dir_path = os.path.join("..","src")
cmd.mkdir(IGM_src_dir_path)
# Step 0c: Create the output file path
outfile_path__postpostinitial__set_symmetries__copy_timelevels__C = os.path.join(IGM_src_dir_path,"postpostinitial__set_symmetries__copy_timelevels.C")
# -
# <a id='introduction'></a>
#
# # Step 1: Introduction \[Back to [top](#toc)\]
# $$\label{introduction}$$
# <a id='postpostinitial__set_symmetries__copy_timelevels__c'></a>
#
# # Step 2: `postpostinitial__set_symmetries__copy_timelevels.C` \[Back to [top](#toc)\]
# $$\label{postpostinitial__set_symmetries__copy_timelevels__c}$$
# +
# %%writefile $outfile_path__postpostinitial__set_symmetries__copy_timelevels__C
//-------------------------------------------------
// Stuff to run right after initial data is set up
//-------------------------------------------------
#include "cctk.h"
#include <cstdio>
#include <cstdlib>
#include "cctk_Arguments.h"
#include "cctk_Functions.h"
#include "cctk_Parameters.h"
#include "Symmetry.h"
#include "IllinoisGRMHD_headers.h"
#include "IllinoisGRMHD_EoS_lowlevel_functs.C"
extern "C" void IllinoisGRMHD_PostPostInitial_Set_Symmetries__Copy_Timelevels(CCTK_ARGUMENTS) {
DECLARE_CCTK_ARGUMENTS;
DECLARE_CCTK_PARAMETERS;
/**********************************
* Piecewise Polytropic EOS Patch *
* Printing the EOS table *
**********************************/
/*
* The short piece of code below takes care
* of initializing the EOS parameters.
* Please refer to the "inlined_functions.C"
* source file for the documentation on the
* function.
*/
eos_struct eos;
initialize_EOS_struct_from_input(eos);
/* For diagnostic and user convenience purposes, we print
* out the EOS parameters (rho_ppoly_tab, K_ppoly_tab,
* and Gamma_ppoly_tab) at t=0.
*/
if(cctk_iteration==0 && (int)GetRefinementLevel(cctkGH)==0) { print_EOS_table(eos); }
if(Gamma_th<0)
CCTK_VError(VERR_DEF_PARAMS,"ERROR. Default Gamma_th (=-1) detected. You must set Gamma_th to the appropriate value in your initial data thorn, or your .par file!\n");
//For emfields, we assume that you've set Bx, By, Bz (the UN-tilded B^i's)
// or Ax, Ay, Az (if using constrained transport scheme of Del Zanna)
if(CCTK_EQUALS(Symmetry,"equatorial")) {
// SET SYMMETRY GHOSTZONES ON ALL CONSERVATIVE AND PRIMIIVE VARIABLES!
int ierr;
ierr=CartSymGN(cctkGH,"IllinoisGRMHD::grmhd_conservatives"); if(ierr!=0) CCTK_VError(VERR_DEF_PARAMS,"Microsoft error code #1874109358120048. Grep it in the source code");
ierr=CartSymGN(cctkGH,"IllinoisGRMHD::grmhd_primitives_allbutBi"); if(ierr!=0) CCTK_VError(VERR_DEF_PARAMS,"Microsoft error code #1874109358120049. Grep it in the source code");
// Finish up by setting symmetry ghostzones on Bx, By, Bz, and their staggered variants.
CCTK_REAL gridfunc_syms_Bx[3] = {-1, 1,-Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Bx , gridfunc_syms_Bx,0,0,0);
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Bx_stagger, gridfunc_syms_Bx,1,0,0);
CCTK_REAL gridfunc_syms_By[3] = { 1,-1,-Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, By , gridfunc_syms_Bx,0,0,0);
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, By_stagger, gridfunc_syms_By,0,1,0);
CCTK_REAL gridfunc_syms_Bz[3] = { 1, 1, Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Bz , gridfunc_syms_Bz,0,0,0);
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Bz_stagger, gridfunc_syms_Bz,0,0,1);
CCTK_REAL gridfunc_syms_psi6phi[3] = { 1, 1, 1};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z,psi6phi , gridfunc_syms_psi6phi,1,1,1);
CCTK_REAL gridfunc_syms_Ax[3] = {-1, 1, Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Ax , gridfunc_syms_Ax,0,1,1);
CCTK_REAL gridfunc_syms_Ay[3] = { 1,-1, Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Ay , gridfunc_syms_Ay,1,0,1);
CCTK_REAL gridfunc_syms_Az[3] = { 1, 1,-Sym_Bz};
IllinoisGRMHD_set_symmetry_gzs_staggered(cctkGH,cctk_lsh,x,y,z, Az , gridfunc_syms_Az,1,1,0);
}
//------------------------------------------------------------------
// FILL _p AND _p_p TIMELEVELS. Probably don't need to do this if
// Carpet::init_fill_timelevels=yes and
// MoL::initial_data_is_crap = yes
// NOTE: We don't fill metric data here.
// FIXME: Do we really need this?
#pragma omp parallel for
for(int k=0;k<cctk_lsh[2];k++) for(int j=0;j<cctk_lsh[1];j++) for(int i=0;i<cctk_lsh[0];i++) {
int index = CCTK_GFINDEX3D(cctkGH,i,j,k);
rho_star_p[index] = rho_star[index];
tau_p[index] = tau[index];
mhd_st_x_p[index] = mhd_st_x[index];
mhd_st_y_p[index] = mhd_st_y[index];
mhd_st_z_p[index] = mhd_st_z[index];
psi6phi_p[index] = psi6phi[index];
Ax_p[index] = Ax[index];
Ay_p[index] = Ay[index];
Az_p[index] = Az[index];
rho_star_p_p[index] = rho_star[index];
tau_p_p[index] = tau[index];
mhd_st_x_p_p[index] = mhd_st_x[index];
mhd_st_y_p_p[index] = mhd_st_y[index];
mhd_st_z_p_p[index] = mhd_st_z[index];
psi6phi_p_p[index] = psi6phi[index];
Ax_p_p[index] = Ax[index];
Ay_p_p[index] = Ay[index];
Az_p_p[index] = Az[index];
}
}
# -
# <a id='code_validation'></a>
#
# # Step n-1: Code validation \[Back to [top](#toc)\]
# $$\label{code_validation}$$
#
# First we download the original `IllinoisGRMHD` source code and then compare it to the source code generated by this tutorial notebook.
# +
# Verify if the code generated by this tutorial module
# matches the original IllinoisGRMHD source code
# First download the original IllinoisGRMHD source code
import urllib
from os import path
original_IGM_file_url = "https://bitbucket.org/zach_etienne/wvuthorns/raw/5611b2f0b17135538c9d9d17c7da062abe0401b6/IllinoisGRMHD/src/postpostinitial__set_symmetries__copy_timelevels.C"
original_IGM_file_name = "postpostinitial__set_symmetries__copy_timelevels-original.C"
original_IGM_file_path = os.path.join(IGM_src_dir_path,original_IGM_file_name)
# Then download the original IllinoisGRMHD source code
# We try it here in a couple of ways in an attempt to keep
# the code more portable
try:
original_IGM_file_code = urllib.request.urlopen(original_IGM_file_url).read().decode("utf-8")
# Write down the file the original IllinoisGRMHD source code
with open(original_IGM_file_path,"w") as file:
file.write(original_IGM_file_code)
except:
try:
original_IGM_file_code = urllib.urlopen(original_IGM_file_url).read().decode("utf-8")
# Write down the file the original IllinoisGRMHD source code
with open(original_IGM_file_path,"w") as file:
file.write(original_IGM_file_code)
except:
# If all else fails, hope wget does the job
# !wget -O $original_IGM_file_path $original_IGM_file_url
# Perform validation
# Validation__postpostinitial__set_symmetries__copy_timelevels__C = !diff $original_IGM_file_path $outfile_path__postpostinitial__set_symmetries__copy_timelevels__C
if Validation__postpostinitial__set_symmetries__copy_timelevels__C == []:
# If the validation passes, we do not need to store the original IGM source code file
# !rm $original_IGM_file_path
print("Validation test for postpostinitial__set_symmetries__copy_timelevels.C: PASSED!")
else:
# If the validation fails, we keep the original IGM source code file
print("Validation test for postpostinitial__set_symmetries__copy_timelevels.C: FAILED!")
# We also print out the difference between the code generated
# in this tutorial module and the original IGM source code
print("Diff:")
for diff_line in Validation__postpostinitial__set_symmetries__copy_timelevels__C:
print(diff_line)
# -
# <a id='latex_pdf_output'></a>
#
# # Step n: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
# $$\label{latex_pdf_output}$$
#
# The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
# [Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.pdf](Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means).
latex_nrpy_style_path = os.path.join(nrpy_dir_path,"latex_nrpy_style.tplx")
# #!jupyter nbconvert --to latex --template $latex_nrpy_style_path --log-level='WARN' Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.ipynb
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.tex
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.tex
# #!pdflatex -interaction=batchmode Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.tex
# !rm -f Tut*.out Tut*.aux Tut*.log
|
IllinoisGRMHD/doc/Tutorial-IllinoisGRMHD__postpostinitial__set_symmetries__copy_timelevels.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Exercise 3.3
# ## Checkerboard
#
# Open the Tensorflow Playground (www.playground.tensorflow.org) and select on the left the checkerboard pattern as the data basis.
#
# The data is taken from a two-dimensional probability distribution and is represented by the value pairs $x_1$ and $x_2$. The regions $x1$, $x_2 > 0$ and $x_1$, $x_2 < 0$ are shown by one color. For value pairs with $x_1 > 0$, $x_2 < 0$ and $x_1 < 0$, $x_2 > 0$, the regions are indicated by a different color.
#
# In features, select the two independent variables $x_1$ and $x_2$ and start the network training. The network learns that $x_1$ and $x_2$ are for these data not independent variables, but are taken from the probability distribution of the checkerboard pattern.
#
# [](https://playground.tensorflow.org/#activation=relu&batchSize=10&dataset=xor®Dataset=reg-plane&learningRate=0.03®ularizationRate=0&noise=0&networkShape=4,2&seed=0.20784&showTestData=false&discretize=false&percTrainData=50&x=true&y=true&xTimesY=false&xSquared=false&ySquared=false&cosX=false&sinX=false&cosY=false&sinY=false&collectStats=false&problem=classification&initZero=false&hideText=false)
#
# ## Tasks
# 1. Try various settings for the number of layers and neurons using `ReLU` as activation function. What is the smallest network that gives a good fit result?
# 2. What do you observe when training networks with the same settings multiple times? Explain your observations.
# 3. Try additional input features: Which one is most helpful?
#
|
Exercise_03_3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] toc-hr-collapsed=true
# # Validation of frc_eia923
# This notebook runs sanity checks on the Fuel Receipts and Costs data that are reported in EIA Form 923. These are the same tests which are run by the frc_eia923 validation tests by PyTest. The notebook and visualizations are meant to be used as a diagnostic tool, to help understand what's wrong when the PyTest based data validations fail for some reason.
# -
# %load_ext autoreload
# %autoreload 2
import sys
import pandas as pd
import sqlalchemy as sa
import pudl
import warnings
import logging
logger = logging.getLogger()
logger.setLevel(logging.INFO)
handler = logging.StreamHandler(stream=sys.stdout)
formatter = logging.Formatter('%(message)s')
handler.setFormatter(formatter)
logger.handlers = [handler]
import matplotlib.pyplot as plt
import matplotlib as mpl
# %matplotlib inline
plt.style.use('ggplot')
mpl.rcParams['figure.figsize'] = (10,4)
mpl.rcParams['figure.dpi'] = 150
pd.options.display.max_columns = 56
pudl_settings = pudl.workspace.setup.get_defaults()
ferc1_engine = sa.create_engine(pudl_settings['ferc1_db'])
pudl_engine = sa.create_engine(pudl_settings['pudl_db'])
pudl_settings
# ## Get the original EIA 923 data
# First we pull the original (post-ETL) EIA 923 data out of the database. We will use the values in this dataset as a baseline for checking that latter aggregated data and derived values remain valid. We will also eyeball these values here to make sure they are within the expected range. This may take a minute or two depending on the speed of your machine.
pudl_out_orig = pudl.output.pudltabl.PudlTabl(pudl_engine, freq=None)
frc_eia923_orig = pudl_out_orig.frc_eia923()
# + [markdown] toc-hr-collapsed=false
# # Validation Against Fixed Bounds
# Some of the variables reported in this table have a fixed range of reasonable values, like the heat content per unit of a given fuel type. These varaibles can be tested for validity against external standards directly. In general we have two kinds of tests in this section:
# * **Tails:** are the exteme values too extreme? Typically, this is at the 5% and 95% level, but depending on the distribution, sometimes other thresholds are used.
# * **Middle:** Is the central value of the distribution where it should be?
# -
# ## Coal Heat Content (bounds)
# Need to update this for more detailed fuel enumeration...
# +
# pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_coal_heat_content)
# -
# ## Oil Heat Content (bounds)
# Need to update this for more detailed fuel enumeration...
# +
# pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_oil_heat_content)
# -
# ## Natural Gas Heat Content (bounds)
# Need to update this for more detailed fuel enumeration...
# +
# pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_gas_heat_content)
# -
# ## Coal Ash Content (bounds)
pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_coal_ash_content)
# ## Coal Sulfur Content (bounds)
pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_coal_sulfur_content)
# ## Coal Mercury Content (bounds)
pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_coal_mercury_content)
# ## Coal Moisture Content (bounds)
pudl.validate.plot_vs_bounds(frc_eia923_orig, pudl.validate.frc_eia923_coal_moisture_content)
# # Validating Historical Distributions
# As a sanity check of the testing process itself, we can check to see whether the entire historical distribution has attributes that place it within the extremes of a historical subsampling of the distribution. In this case, we sample each historical year, and look at the range of values taken on by some quantile, and see whether the same quantile for the whole of the dataset fits within that range
pudl.validate.plot_vs_self(frc_eia923_orig, pudl.validate.frc_eia923_self)
# # Validate Monthly Aggregation
# It's possible that the distribution will change as a function of aggregation, or we might make an error in the aggregation process. These tests check that a collection of quantiles for the original and the data aggregated by month have internally consistent values.
pudl_out_month = pudl.output.pudltabl.PudlTabl(pudl_engine, freq="MS")
frc_eia923_month = pudl_out_month.frc_eia923()
pudl.validate.plot_vs_agg(frc_eia923_orig, frc_eia923_month, pudl.validate.frc_eia923_agg)
# # Validate Annual Aggregation
# It's possible that the distribution will change as a function of aggregation, or we might make an error in the aggregation process. These tests check that a collection of quantiles for the original and the data aggregated by year have internally consistent values.
pudl_out_year = pudl.output.pudltabl.PudlTabl(pudl_engine, freq="AS")
frc_eia923_year = pudl_out_year.frc_eia923()
pudl.validate.plot_vs_agg(frc_eia923_orig, frc_eia923_year, pudl.validate.frc_eia923_agg)
|
test/validate/notebooks/validate_frc_eia923.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from scvi.dataset import LoomDataset, CsvDataset, Dataset10X, AnnDataset
import urllib.request
import os
tenx = CsvDataset("CellBench_sce10x_qc.csv.gz", save_path="data/", compression="gzip", new_n_genes=600)
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# %matplotlib inline
from scvi.models import *
from scvi.inference import UnsupervisedTrainer
n_epochs_all = None
save_path = 'data/'
n_epochs=400 if n_epochs_all is None else n_epochs_all
lr=1e-2
use_batches=False
use_cuda=False
vae = VAE(tenx.nb_genes, n_batch=tenx.n_batches * use_batches)
trainer = UnsupervisedTrainer(vae,
tenx,
train_size=0.75,
use_cuda=use_cuda,
frequency=5)
trainer.train(n_epochs=n_epochs, lr=lr)
ll_train_set = trainer.history["ll_train_set"]
ll_test_set = trainer.history["ll_test_set"]
x = np.linspace(0,500,(len(ll_train_set)))
plt.plot(x, ll_train_set)
plt.plot(x, ll_test_set)
plt.ylim(0,20000)
plt.show()
n_samples_tsne = 1000
trainer.train_set.show_t_sne(n_samples=n_samples_tsne, color_by='labels')
import pandas as pd
labels = pd.read_csv("data/CellBench_sce10x_qc_cols.csv.gz", header=0, index_col=0)
labels
labels.values
cell_types = np.unique(labels)
dir(trainer)
dir(vae)
help(vae.state_dict)
final_state = vae.state_dict()
import torch
torch.save(final_state, "scvi-stuffnthings.pkl")
|
scvi-stuffnthings.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
a = np.array([5,6,9]) #1-dimesnional array
a2 = np.array([[1,2,3],[4,5,6],[7,8,9]]) # 2-dimensional array
a[0]
a2[2,0]
# # Properties
# ## ndim
a.ndim
a2.ndim
# ## itemsize
a.itemsize
a2.itemsize
# ## dtype
a.dtype
a2.dtype
# ## change datatype of element
a3 = np.array([11,22,33], dtype=np.float64) #changing data type
a3.dtype
# ## size
a
a.size
a2
a2.size
# ## shape
a.shape
a2.shape
a3 = np.array([[1,2],[3,4],[5,6]], dtype=complex)
a3
a3.dtype
# ## Zeros()
np.zeros((3,3))
# ## Ones()
np.ones((3,3))
# ## arange()
np.arange(1,5)
np.arange(1,5,2) # with step
# ## linspace()
np.linspace(1,5,10) # to generate linearly spaced 10 number from 1 to 5
# ## reshape()
a3 = np.array([[1,2],[3,4],[5,6]])
a3.shape
a3.reshape(2,3)
a3.reshape(1,6)
a3.reshape(6,1)
a2.reshape(9,1)
# ## ravel()
a2.ravel() # to flat N-Dimensional Array to flat array or 1-D Array
a3.ravel()
a3 # ravel property don't touch/alter the original array to store the 1D array we have captured in new variable as below
a4 = a3.ravel()
a4
# ## min() & max()
a2.min()
a2.max()
# ## sum()
a2.sum()
# ### axis
a2
a2.sum(axis=0)
a2.sum(axis=1)
# ## sqrt()
a2
np.sqrt(a2)
# ## std()
np.std(a2) # standard deviation of a2
# ## basic maths operation
a_1 = np.array([[1,2],[3,4]])
a_2 = np.array([[5,6],[7,8]])
a_1
a_2
a_1 + a_2
a_1 - a_2
a_1 * a_2
a_1 / a_2
# ## matrix dot product
a_1.dot(a_2)
|
NumPy/Operation on NumPy Array.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="78HE8FLsKN9Q"
# In this post, I take an in-depth look at word embeddings produced by Google's BERT and show you how to get started with BERT by producing your own word embeddings.
#
# This post is presented in two forms--as a blog post [here](http://mccormickml.com/2019/05/14/BERT-word-embeddings-tutorial/) and as a Colab notebook [here](https://colab.research.google.com/drive/1ZQvuAVwA3IjybezQOXnrXMGAnMyZRuPU).
# The content is identical in both, but:
#
# * The blog post format may be easier to read, and includes a comments section for discussion.
# * The Colab Notebook will allow you to run the code and inspect it as you read through.
#
# + [markdown] colab_type="text" id="dYapTjoYa0kO"
# # Introduction
#
#
# + [markdown] colab_type="text" id="c8HDKzBai5dL"
# ### History
#
# 2018 was a breakthrough year in NLP. Transfer learning, particularly models like Allen AI's ELMO, OpenAI's Open-GPT, and Google's BERT allowed researchers to smash multiple benchmarks with minimal task-specific fine-tuning and provided the rest of the NLP community with pretrained models that could easily (with less data and less compute time) be fine-tuned and implemented to produce state of the art results. Unfortunately, for many starting out in NLP and even for some experienced practicioners, the theory and practical application of these powerful models is still not well understood.
#
# ### What is BERT?
#
# BERT (Bidirectional Encoder Representations from Transformers), released in late 2018, is the model we will use in this tutorial to provide readers with a better understanding of and practical guidance for using transfer learning models in NLP. BERT is a method of pretraining language representations that was used to create models that NLP practicioners can then download and use for free. You can either use these models to extract high quality language features from your text data, or you can fine-tune these models on a specific task (classification, entity recognition, question answering, etc.) with your own data to produce state of the art predictions.
#
# ### Why BERT embeddings?
#
# In this tutorial, we will use BERT to extract features, namely word and sentence embedding vectors, from text data. What can we do with these word and sentence embedding vectors? First, these embeddings are useful for keyword/search expansion, semantic search and information retrieval. For example, if you want to match customer questions or searches against already answered questions or well documented searches, these representations will help you accuratley retrieve results matching the customer's intent and contextual meaning, even if there's no keyword or phrase overlap.
#
# Second, and perhaps more importantly, these vectors are used as high-quality feature inputs to downstream models. NLP models such as LSTMs or CNNs require inputs in the form of numerical vectors, and this typically means translating features like the vocabulary and parts of speech into numerical representations. In the past, words have been represented either as uniquely indexed values (one-hot encoding), or more helpfully as neural word embeddings where vocabulary words are matched against the fixed-length feature embeddings that result from models like Word2Vec or Fasttext. BERT offers an advantage over models like Word2Vec, because while each word has a fixed representation under Word2Vec regardless of the context within which the word appears, BERT produces word representations that are dynamically informed by the words around them. For example, given two sentences:
#
# "The man was accused of robbing a bank."
# "The man went fishing by the bank of the river."
#
# Word2Vec would produce the same word embedding for the word "bank" in both sentences, while under BERT the word embedding for "bank" would be different for each sentence. Aside from capturing obvious differences like polysemy, the context-informed word embeddings capture other forms of information that result in more accurate feature representations, which in turn results in better model performance.
#
# From an educational standpoint, a close examination of BERT word embeddings is a good way to get your feet wet with BERT and its family of transfer learning models, and sets us up with some practical knowledge and context to better understand the inner details of the model in later tutorials.
#
# Onward!
# + [markdown] colab_type="text" id="ah9KDju5i1tw"
# ### Install and Import
# + [markdown] colab_type="text" id="eCdqJCtQN52l"
# Install the pytorch interface for BERT by Hugging Face. (This library contains interfaces for other pretrained language models like OpenAI's GPT and GPT-2.) We've selected the pytorch interface because it strikes a nice balance between the high-level APIs (which are easy to use but don't provide insight into how things work) and tensorflow code (which contains lots of details but often sidetracks us into lessons about tensorflow, when the purpose here is BERT!).
#
# If you're running this code on Google Colab, you will have to install this library each time you reconnect; the following cell will take care of that for you.
# + [markdown] colab_type="text" id="JSXImOxMPdNg"
# Now let's import pytorch, the pretrained BERT model, and a BERT tokenizer. We'll explain the BERT model in detail in a later tutorial, but this is the pre-trained model released by Google that ran for many, many hours on Wikipedia and [Book Corpus](https://arxiv.org/pdf/1506.06724.pdf), a dataset containing +10,000 books of different genres. This model is responsible (with a little modification) for beating NLP benchmarks across a range of tasks. Google released a few variations of BERT models, but the one we'll use here is the smaller of the two available sizes ("base" and "large") and ignores casing, hence "uncased.""
# + id="pht7hk_zwJCf" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 691} outputId="970fd770-cf55-4162-aa43-376cc48f01a6" executionInfo={"status": "ok", "timestamp": 1571920339934, "user_tz": -540, "elapsed": 11169, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
pip install transformers
# + colab_type="code" id="lJEnBJ3gHTsQ" colab={}
#import torch
#from pytorch_pretrained_bert import BertTokenizer, BertModel, BertForMaskedLM
import torch
from transformers import BertTokenizer, BertModel
# OPTIONAL: if you want to have more information on what's happening, activate the logger as follows
# import logging
#logging.basicConfig(level=logging.INFO)
import matplotlib.pyplot as plt
# %matplotlib inline
# + colab_type="code" outputId="6d7e829c-4a60-4dac-ffcf-e17b04e67964" id="tqXAMcXGwAMr" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571920345245, "user_tz": -540, "elapsed": 5260, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# Load pre-trained model tokenizer (vocabulary)
tokenizer = BertTokenizer.from_pretrained('bert-base-uncased', do_lower_case=True)
# + [markdown] colab_type="text" id="Tlv3VlPnKKHN"
# ## Input Formatting
# Because BERT is a pretrained model that expects input data in a specific format, we will need:
#
# - special tokens to mark the beginning ([CLS]) and separation/end of sentences ([SEP])
# - tokens that conforms with the fixed vocabulary used in BERT
# - token IDs from BERT's tokenizer
# - mask IDs to indicate which elements in the sequence are tokens and which are padding elements
# - segment IDs used to distinguish different sentences
# - positional embeddings used to show token position within the sequence
#
# Luckily, this interface takes care of some of these input specifications for us so we will only have to manually create a few of them (we'll revisit the other inputs in another tutorial).
#
#
#
# + [markdown] colab_type="text" id="diVtyCJCurxJ"
# ###Special Tokens
# BERT can take as input either one or two sentences, and expects special tokens to mark the beginning and end of each one:
#
# **2 Sentence Input**:
#
# [CLS] the man went to the store [SEP] he bought a gallon of milk [SEP]
#
# **1 Sentence Input**:
#
# [CLS] the man went to the store [SEP]
# + colab_type="code" id="VVJDXVZRJF13" colab={}
example = "Here is the sentence I want embeddings for."
# + [markdown] colab_type="text" id="QTQfNx6MKTbb"
# We've imported a BERT-specific tokenizer, let's take a look at the output:
# + [markdown] colab_type="text" id="3gsyrAwYvBfC"
# ###Tokenization
# + id="-LIzuS6WwANF" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="439b49fe-e98c-424c-aadf-4f334dc409a2" executionInfo={"status": "ok", "timestamp": 1571920371041, "user_tz": -540, "elapsed": 934, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print(tokenizer.tokenize(example))
# + [markdown] colab_type="text" id="Q51eN4KAkbIJ"
# Notice how the word "embeddings" is represented:
#
# ['em', '##bed', '##ding', '##s']
#
# The original word has been split into smaller subwords and characters. The two hash signs preceding some of these subwords are just our tokenizer's way to denote that this subword or character is part of a larger word and preceded by another subword. So, for example, the '##bed' token is separate from the 'bed' token; the first is used whenever the subword 'bed' occurs within a larger word and the second is used explicitly for when the standalone token 'thing you sleep on' occurs.
#
# Why does it look this way? This is because the BERT tokenizer was created with a WordPiece model. This model greedily creates a fixed-size vocabulary of individual characters, subwords, and words that best fits our language data. Since the vocabulary limit size of our BERT tokenizer model is 30,000, the WordPiece model generated a vocabulary that contains all English characters plus the ~30,000 most common words and subwords found in the English language corpus the model is trained on. This vocabulary contains four things:
#
# 1. Whole words
# 2. Subwords occuring at the front of a word or in isolation ("em" as in "embeddings" is assigned the same vector as the standalone sequence of characters "em" as in "go get em" )
# 3. Subwords not at the front of a word, which are preceded by '##' to denote this case
# 4. Individual characters
#
# To tokenize a word under this model, the tokenizer first checks if the whole word is in the vocabulary. If not, it tries to break the word into the largest possible subwords contained in the vocabulary, and as a last resort will decompose the word into individual characters. Note that because of this, we can always represent a word as, at the very least, the collection of its individual characters.
#
# As a result, rather than assigning out of vocabulary words to a catch-all token like 'OOV' or 'UNK,' words that are not in the vocabulary are decomposed into subword and character tokens that we can then generate embeddings for.
#
# So, rather than assigning "embeddings" and every other out of vocabulary word to an overloaded unknown vocabulary token, we split it into subword tokens ['em', '##bed', '##ding', '##s'] that will retain some of the contextual meaning of the original word. We can even average these subword embedding vectors to generate an approximate vector for the original word.
#
#
# (For more information about WordPiece, see the [original paper](https://static.googleusercontent.com/media/research.google.com/en//pubs/archive/37842.pdf) and further disucssion in Google's [Neural Machine Translation System](https://arxiv.org/pdf/1609.08144.pdf).)
#
#
# + [markdown] colab_type="text" id="jp5zXAPBVp82"
# Here are some examples of the tokens contained in our vocabulary. Tokens beginning with two hashes are subwords or individual characters.
# + id="yKgC-RX9wANR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="a5cca30f-22c2-4db4-a3b5-fed3011b5ba5" executionInfo={"status": "ok", "timestamp": 1571920372368, "user_tz": -540, "elapsed": 1405, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
len(tokenizer.vocab)
# + colab_type="code" id="1z1SzuTrqx-7" outputId="7f68719a-1a36-43ae-8c8c-1cf9e226781e" colab={"base_uri": "https://localhost:8080/", "height": 391} executionInfo={"status": "ok", "timestamp": 1571920372383, "user_tz": -540, "elapsed": 748, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
list(tokenizer.vocab.keys())[5000:5020]
# + colab_type="code" outputId="008dc8ec-a4dd-4045-8ca8-37c1623d04c7" id="T5tBxqHDwANf" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571920376316, "user_tz": -540, "elapsed": 1647, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
text = "After stealing money from the bank vault, the bank robber was seen fishing on the Mississippi river bank."
marked_text = "[CLS] " + text + " [SEP]"
print (marked_text)
# + colab_type="code" id="Pg0P9rFxJwwp" outputId="dc4415b9-0d75-4a60-8661-e47aa188cf8b" colab={"base_uri": "https://localhost:8080/", "height": 75} executionInfo={"status": "ok", "timestamp": 1571920423659, "user_tz": -540, "elapsed": 1754, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
tokenized_text = tokenizer.tokenize(marked_text)
print(tokenized_text)
print(len(tokenized_text))
# + [markdown] colab_type="text" id="HoF3LC47VgBb"
# Next, we need to call the tokenizer to match the tokens agains their indices in the tokenizer vocabulary:
# + colab_type="code" id="XYjcYJuXoAQx" outputId="126dceb8-3405-48b3-e9bf-eb07e1b1c11b" colab={"base_uri": "https://localhost:8080/", "height": 428} executionInfo={"status": "ok", "timestamp": 1571920424126, "user_tz": -540, "elapsed": 669, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
indexed_tokens = tokenizer.convert_tokens_to_ids(tokenized_text)
for tup in zip(tokenized_text, indexed_tokens):
print (tup)
# + [markdown] colab_type="text" id="if6C_iCULU60"
# ###Segment ID
# BERT is trained on and expects sentence pairs, using 1s and 0s to distinguish between the two sentences. That is, for each token in "tokenized_text," we must specify which sentence it belongs to: sentence 0 (a series of 0s) or sentence 1 (a series of 1s). For our purposes, single-sentence inputs only require a series of 1s, so we will create a vector of 1s for each token in our input sentence.
#
# If you want to process two sentences, assign each word in the first sentence plus the '[SEP]' token a 0, and all tokens of the second sentence a 1.
# + colab_type="code" id="u_jEkVKxJMc0" outputId="d6c10e62-e297-4df0-a79a-e37b9010ee2f" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571920457611, "user_tz": -540, "elapsed": 1136, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
segments_ids = [1] * len(tokenized_text)
print (segments_ids)
# + [markdown] colab_type="text" id="c-nY9LASLr2L"
# ##Running our Example
# Next we need to convert our data to torch tensors and call the BERT model. The BERT PyTorch interface requires that the data be in torch tensors rather than Python lists, so we convert the lists here - this does not change the shape or the data.
#
# model.eval() puts our model in evaluation mode as opposed to training mode. In this case, evaluation mode turns off dropout regularization which is used in training.
#
# Calling `from_pretrained` will fetch the model from the internet. When we load the `bert-base-uncased`, we see the definition of the model printed in the logging. The model is a deep neural network with 12 layers! Explaining the layers and their functions is outside the scope of this post, and you can skip over this output for now.
# + colab_type="code" id="E_t4cM6KLc98" colab={}
# Convert inputs to PyTorch tensors
tokens_tensor = torch.tensor([indexed_tokens])
segments_tensors = torch.tensor([segments_ids])
# + colab_type="code" outputId="590def29-7f39-4414-903c-7edaf9d1671a" id="6SwEE4KlwAOB" colab={"base_uri": "https://localhost:8080/", "height": 1000} executionInfo={"status": "ok", "timestamp": 1571920561907, "user_tz": -540, "elapsed": 6266, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# Load pre-trained model (weights)
model = BertModel.from_pretrained('bert-base-uncased', output_hidden_states=True) # 동일하게 가져옴
# Put the model in "evaluation" mode, meaning feed-forward operation.
model.eval()
# + id="jx9lqFfewAOG" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="bd243ac7-4e9a-4bc8-992a-a19ea8387d57" executionInfo={"status": "ok", "timestamp": 1571920705961, "user_tz": -540, "elapsed": 2953, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# If you have a GPU, put everything on cuda
tokens_tensor = tokens_tensor.to('cuda')
segments_tensors = segments_tensors.to('cuda')
model.to('cuda')
# 리니어가 안붙은 버트 값
# + [markdown] colab_type="text" id="G4Qa5KkkM2Aq"
# Next, let's fetch the hidden states of the network.
#
# torch.no_grad deactivates the gradient calculations, saves memory, and speeds up computation (we don't need gradients or backpropagation since we're just running a forward pass).
#
# + colab_type="code" id="nN0QTZwiMzeq" colab={}
# Predict hidden states features for each layer
with torch.no_grad():
_, _, encoded_layers = model(tokens_tensor, segments_tensors)
# + [markdown] colab_type="text" id="UeQNEFbUgMSf"
# ## Output
# The full set of hidden states for this model, stored in the object `encoded_layers`, is a little dizzying. This object has four dimensions, in the following order:
#
# 1. The layer number (12 layers) -Not anymore . it is the last hidden states
# 2. The batch number (1 sentence)
# 3. The word / token number (22 tokens in our sentence)
# 4. The hidden unit / feature number (768 features)
#
# That’s 202,752 unique values just to represent our one sentence!
#
# The second dimension, the batch size, is used when submitting multiple sentences to the model at once; here, though, we just have one example sentence.
# + colab_type="code" id="eI_uxiW7eRWA" outputId="f1e8caea-cc26-4416-f8ed-bd2f351637ec" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571920773510, "user_tz": -540, "elapsed": 1059, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Number of total layers (embedding layer + hidden layers) :", len(encoded_layers))
layer_i = 1
# + colab_type="code" outputId="8eb024c5-5894-4e6e-e764-8b9c53bd37e2" id="BQ-TpbYwwAOc" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1571920775447, "user_tz": -540, "elapsed": 1034, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Number of batches:", len(encoded_layers[layer_i]))
batch_i = 0
print ("Number of tokens:", len(encoded_layers[layer_i][batch_i]))
token_i = 0
# + colab_type="code" outputId="6069aaa0-4028-4e3a-aae5-d8bf186d14bd" id="WyISJb_LwAOg" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571920780837, "user_tz": -540, "elapsed": 1334, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Number of hidden units:", len(encoded_layers[layer_i][batch_i][token_i]))
# + id="Q8qGcD9Tx-q9" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="7b989943-d7f5-434c-c6e6-fe469c0cf3aa" executionInfo={"status": "ok", "timestamp": 1571920827764, "user_tz": -540, "elapsed": 1163, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
len(encoded_layers[-1][0][0])
# + [markdown] colab_type="text" id="6Uc_S_hmOWe7"
# Let's take a quick look at the range of values for a given layer and token.
#
# You'll find that the range is fairly similar for all layers and tokens, with the majority of values falling between \[-2, 2\], and a small smattering of values around -10.
# + colab_type="code" id="-UF_OAO-S1sP" outputId="1ed79edc-f9d4-4bb4-e2f0-3b9cc891d549" colab={"base_uri": "https://localhost:8080/", "height": 595} executionInfo={"status": "ok", "timestamp": 1571920856504, "user_tz": -540, "elapsed": 3219, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# For the 5th token in our sentence, select its feature values from layer 5.
# For the 5th token in our sentence, select its feature values from layer 5.
token_i = 5
layer_i = 5
vec = encoded_layers[layer_i][batch_i][token_i]
vec = vec.cpu()
# Plot the values as a histogram to show their distribution.
plt.figure(figsize=(10,10))
plt.hist(vec, bins=200)
plt.show()
# + [markdown] colab_type="text" id="LX5XxGyeMuGw"
# Grouping the values by layer makes sense for the model, but for our purposes we want it grouped by token.
#
# The following code just reshapes the values so that we have them in the form:
#
# ```
# [# tokens, # layers, # features]
# ```
# + colab_type="code" id="bamFT4uXMmO6" outputId="1e51e3b0-53ff-4c51-e669-961a10c0995b" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1571920909695, "user_tz": -540, "elapsed": 1191, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# Convert the hidden state embeddings into single token vectors
# Holds the list of 12 layer embeddings for each token
# Will have the shape: [# tokens, # layers, # features]
token_embeddings = []
# For each token in the sentence...
for token_i in range(len(tokenized_text)):
# Holds 12 layers of hidden states for each token
hidden_layers = []
# For each of the 12 layers...
for layer_i in range(len(encoded_layers)-1):
layer_i= layer_i+1
# Lookup the vector for `token_i` in `layer_i`
vec = encoded_layers[layer_i][batch_i][token_i]
hidden_layers.append(vec)
token_embeddings.append(hidden_layers)
# Sanity check the dimensions:
print ("Number of tokens in sequence:", len(token_embeddings))
print ("Number of layers per token:", len(token_embeddings[0]))
# + [markdown] colab_type="text" id="Ey5RhOQ7NGtz"
# ## Creating word and sentence vectors from hidden states
#
# Now, what do we do with these hidden states? We would like to get individual vectors for each of our tokens, or perhaps a single vector representation of the whole sentence, but for each token of our input we have 12 separate vectors each of length 768.
#
# In order to get the individual vectors we will need to combine some of the layer vectors...but which layer or combination of layers provides the best representation? The BERT authors tested this by feeding different vector combinations as input features to a BiLSTM used on a named entity recognition task and observing the resulting F1 scores.
#
# (Image from [<NAME>](http://jalammar.github.io/illustrated-bert/)'s blog)
#
#
# 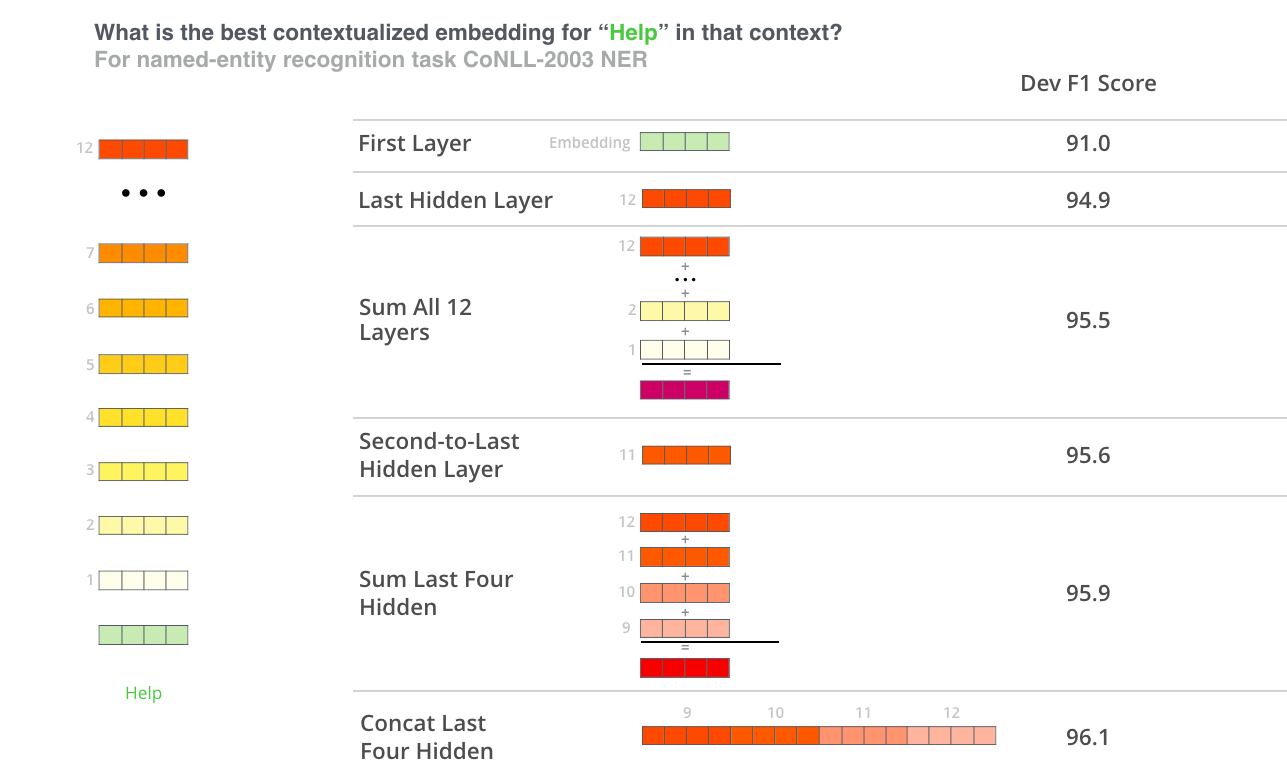
#
# While concatenation of the last four layers produced the best results on this specific task, many of the other methods come in a close second and in general it is advisable to test different versions for your specific application: results may vary.
#
# This is partially demonstrated by noting that the different layers of BERT encode very different kinds of information, so the appropriate pooling strategy will change depending on the application because different layers encode different kinds of information. Hanxiao's discussion of this topic is relevant, as are their experiments looking at the PCA visualizations of different layers trained on a news dataset and observing the differences in the four class separations from different pooling strategies:
#
# (Images from [Hanxiao's](https://github.com/hanxiao/bert-as-service) BERT-as-a-service)
#
# 
# 
#
# The upshot being that, again**, the correct pooling strategy (mean, max, concatenation, etc.) and layers used (last four, all, last layer, etc.) is dependent on the application**. This discussion of pooling strategies applies both to entire sentence embeddings and individual ELMO-like token embeddings.
#
#
#
#
#
#
# + [markdown] colab_type="text" id="76TdtFH8NM9q"
# ### Word Vectors
#
# To give you some examples, let's create word vectors two ways.
#
# First, let's **concatenate** the last four layers, giving us a single word vector per token. Each vector will have length `4 x 768 = 3,072`.
# + id="ZBeFIQ64wAO1" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="e14cb066-b56f-4a4f-9a6e-636061a2daca" executionInfo={"status": "ok", "timestamp": 1571921013992, "user_tz": -540, "elapsed": 1356, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
len(token_embeddings)
# + colab_type="code" id="pv42h9jANMRf" outputId="b737bbf1-a99f-4d8f-d4a2-2bc69b34b411" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571921044508, "user_tz": -540, "elapsed": 1861, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# Stores the token vectors, with shape [22 x 3,072]
token_vecs_cat = []
# For each token in the sentence... 각 토큰마다 4번째 레이어까지 concat
for token in token_embeddings:
# Concatenate the vectors (that is, append them together) from the last
# four layers.
# Each layer vector is 768 values, so `cat_vec` is length 3,072.
cat_vec = torch.cat((token[-1], token[-2], token[-3], token[-4]), 0)
# Use `cat_vec` to represent `token`.
token_vecs_cat.append(cat_vec)
print ('Shape is: %d x %d' % (len(token_vecs_cat), len(token_vecs_cat[0])))
#각각 3072개의 벡터를 가지고 있음
# + [markdown] colab_type="text" id="VnWaByfelM-e"
# As an alternative method, let's try creating the word vectors by **summing** together the last four layers.
# + colab_type="code" id="j4DKDtFwiF0S" outputId="43a01638-7cab-4811-c873-6e5a8a101925" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571921101606, "user_tz": -540, "elapsed": 1764, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
# Stores the token vectors, with shape [22 x 768]
token_vecs_sum = []
# For each token in the sentence...
for token in token_embeddings:
# Sum the vectors from the last four layers.
sum_vec = torch.sum(torch.stack(token)[-4:], 0) # 썸 벡터를 만들고
# Use `sum_vec` to represent `token`.
token_vecs_sum.append(sum_vec)
print ('Shape is: %d x %d' % (len(token_vecs_sum), len(token_vecs_sum[0]))) # 768차원을 가짐
# + [markdown] colab_type="text" id="mQaco6jRLkXn"
# ### Sentence Vectors
#
# To get a single vector for our entire sentence we have multiple application-dependent strategieis, but a simple approach is to average the second to last hiden layer of each token producing a single 768 length vector.
#
#
# + id="puqryc0ywAPB" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 36} outputId="90dafabd-b4c3-4047-fc63-b67045673354" executionInfo={"status": "ok", "timestamp": 1571921123262, "user_tz": -540, "elapsed": 1544, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
encoded_layers[-1].shape # 마지막 레이어를 가져옴
# + colab_type="code" id="Zn0n2S-FWZih" colab={}
sentence_embedding = torch.mean(encoded_layers[-1], 1) # 768차원을 다 더해서 센텐스 벡터를 구하기도 함
# + colab_type="code" id="MQv0FL8VWadn" outputId="e145a22e-93c7-4f1d-ae96-48348537592a" colab={"base_uri": "https://localhost:8080/", "height": 55} executionInfo={"status": "ok", "timestamp": 1571921160373, "user_tz": -540, "elapsed": 2054, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Our final sentence embedding vector of shape:"), sentence_embedding[-1].shape[0]
# + [markdown] colab_type="text" id="TqYcrAipfE3E"
# ### Confirming contextually dependent vectors
#
# To confirm that the value of these vectors are in fact contextually dependent, let's take a look at the output from the following sentence (if you want to try this out you'll have to run this example separately from the top by replacing our original sentence with the following sentence):
# + colab_type="code" id="kS4WoXyUfAPc" outputId="4d7c75d4-eab5-4764-d747-8d8f05c9b397" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571921171397, "user_tz": -540, "elapsed": 2056, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print (text)
# + colab_type="code" id="DNiRsEh9cmWz" outputId="ab2f1c10-7f0d-4e0e-d488-031af4f134c5" colab={"base_uri": "https://localhost:8080/", "height": 428} executionInfo={"status": "ok", "timestamp": 1571921171398, "user_tz": -540, "elapsed": 1902, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
for i,x in enumerate(tokenized_text):
print (i,x)
# + id="rY0GAJrWwAPR" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 55} outputId="bd932d52-8040-40ba-d5c4-0b95d2aeaa93" executionInfo={"status": "ok", "timestamp": 1571921174462, "user_tz": -540, "elapsed": 915, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print(len(token_vecs_sum))
print(len(token_vecs_sum[10]))
# + colab_type="code" id="x47-g2QcdXqQ" outputId="941f780b-601c-4573-c34b-415b02d6bbbb" colab={"base_uri": "https://localhost:8080/", "height": 92} executionInfo={"status": "ok", "timestamp": 1571921182205, "user_tz": -540, "elapsed": 2175, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("First fifteen values of 'bank' as in 'bank robber':")
token_vecs_sum[10][:15] # 15개까지만 봄
# + colab_type="code" id="mvhaWPa-7IN_" outputId="6e4b0216-8f9a-413d-9561-0d65747a9f2e" colab={"base_uri": "https://localhost:8080/", "height": 92} executionInfo={"status": "ok", "timestamp": 1571921217244, "user_tz": -540, "elapsed": 1651, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("First fifteen values of 'bank' as in 'bank vault':") # bank와 abk vault 는 유사함
token_vecs_sum[6][:15]
# + colab_type="code" id="F1KLUm3Tddbs" outputId="598462f2-2c39-41a9-bb9f-e4eb89ec84e8" colab={"base_uri": "https://localhost:8080/", "height": 92} executionInfo={"status": "ok", "timestamp": 1571921228744, "user_tz": -540, "elapsed": 1536, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("First fifteen values of 'bank' as in 'river bank':") # bank와 river bank는 다름
token_vecs_sum[19][:15]
# + [markdown] colab_type="text" id="Ca2TCQ_G7SM3"
# As we can see, these are all different vectors and they should be; although the word 'bank' is the same, in each case of our sentence it has different meanings, sometimes very different meanings.
#
# We have three different uses of "bank" in this sentence, two of which should be almost identical. Let's check the cosine similarity to see if this is the case:
# + [markdown] id="ujeqFVArwAPb" colab_type="text"
# * 10 : 'bank' as in 'bank robber'
# * 6 : 'bank' as in 'bank vault'
# * 19 : 'bank' as in 'riber bank'
# + colab_type="code" id="eYXUwiG0yhBS" colab={}
from sklearn.metrics.pairwise import cosine_similarity
# Compare "bank" as in "bank robber" to "bank" as in "bank vault" 같은 bank
same_bank = cosine_similarity(token_vecs_sum[10].cpu().reshape(1,-1), token_vecs_sum[6].cpu().reshape(1,-1))[0][0]
# Compare "bank" as in "bank robber" to "bank" as in "river bank" 다른 bank
different_bank = cosine_similarity(token_vecs_sum[10].cpu().reshape(1,-1), token_vecs_sum[19].cpu().reshape(1,-1))[0][0]
# + colab_type="code" id="dbb2lDDHzyc2" outputId="58dc3649-9c31-4672-9995-5a3054a03721" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571921273991, "user_tz": -540, "elapsed": 1896, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Similarity of 'bank' as in 'bank robber' to 'bank' as in 'bank vault':", same_bank) # 같은 뱅크
# + colab_type="code" id="EpWD0kEp6yoY" outputId="70e6aa77-317b-4a00-bac3-143383ffcacf" colab={"base_uri": "https://localhost:8080/", "height": 36} executionInfo={"status": "ok", "timestamp": 1571921277485, "user_tz": -540, "elapsed": 1394, "user": {"displayName": "<NAME>", "photoUrl": "", "userId": "17894343361302588769"}}
print ("Similarity of 'bank' as in 'bank robber' to 'bank' as in 'river bank':", different_bank) # 다른 뱅크
# + [markdown] colab_type="text" id="ONLJ36JfPuqf"
# ## Other: special tokens, OOV words, and similarity metrics
#
# ### Special tokens
#
# It should be noted that although the** "[CLS]"** acts as an "aggregate representation" for classification tasks, this is not the best choice for a high quality sentence embedding vector. [According to](https://github.com/google-research/bert/issues/164) BERT author <NAME>: "*I'm not sure what these vectors are, since BERT does not generate meaningful sentence vectors. It seems that this is is doing average pooling over the word tokens to get a sentence vector, but we never suggested that this will generate meaningful sentence representations*."
#
# (However, the [CLS] token does become meaningful if the model has been fine-tuned, where the last hidden layer of this token is used as the "sentence vector" for sequence classification.)
#
# ### Out of vocabulary words
#
# For** out of vocabulary words** that are composed of multiple sentence and character-level embeddings, there is a further issue of how best to recover this embedding. Averaging the embeddings is the most straightforward solution (one that is relied upon in similar embedding models with subword vocabularies like fasttext), but summation of subword embeddings and simply taking the last token embedding (remember that the vectors are context sensitive) are acceptable alternative strategies.
#
# ### Similarity metrics
#
# It is worth noting that word-level **similarity comparisons** are not appropriate with BERT embeddings because these embeddings are contextually dependent, meaning that the word vector changes depending on the sentence it appears in. This allows wonderful things like polysemy so that e.g. your representation encodes river "bank" and not a financial institution "bank", but makes direct word-to-word similarity comparisons less valuable. However, for sentence embeddings similarity comparison is still valid such that one can query, for example, a single sentence against a dataset of other sentences in order to find the most similar. Depending on the similarity metric used, the resulting similarity values will be less informative than the relative ranking of similarity outputs since many similarity metrics make assumptions about the vector space (equally-weighted dimensions, for example) that do not hold for our 768-dimensional vector space.
#
# + [markdown] colab_type="text" id="0unZ2xh4QDap"
# ## Implementations
#
# You can use the code in this notebook as the foundation of your own application to extract BERT features from text. However, official [tensorflow](https://github.com/google-research/bert/blob/master/extract_features.py) and well-regarded [pytorch](https://github.com/huggingface/pytorch-pretrained-BERT/blob/master/examples/extract_features.py) implementations already exist that do this for you. Additionally, [bert-as-a-service](https://github.com/hanxiao/bert-as-service) is an excellent tool designed specifically for running this task with high performance, and is the one I would recommend for production applications. The author has taken great care in the tool's implementation and provides excellent documentation (some of which was used to help create this tutorial) to help users understand the more nuanced details the user faces, like resource management and pooling strategy.
|
4-2_BERT_Word_Embeddings_TransformerVersion.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 0.6.2
# language: julia
# name: julia-0.6
# ---
using BayesNets
roCwAB = HermitianMatrix([
0,1/2,1/2, #A=0, B=0
0,0,1, #A=0, B=1
0,1,0, #A=0, B=2
0,0,1, #A=1, B=0
1/2,0,1/2, #A=1, B=1
1,0,0, #A=1, B=2
0,1,0, #A=2, B=0
1,0,0, #A=2, B=1
1/2,1/2,0 #A=2, B=2
]); #
dmcpd = DiscreteQCPD(:c, [:a, :b], [3,3], 3, roCwAB)
using QI
aoper = ketbra(0,0,3)
boper = ketbra(1,1,3)
ass = Assignment(:a=>aoper, :b => boper)
ass[:a]
raw_matrix = dmcpd(ass)
typeof(raw_matrix)
# Notice that I'm calling the constructor of `DiscreteQPD` with a Matrix instead - I can do that, because, there is a convert method implemented between Matrix and HermitianMatrix.
DiscreteQCPD(:c, [:a, :b], [3,3], 3, raw_matrix)
AcausalStructure()
|
doc/developed_so_far.ipynb
|
# ### The `labelFormat` parameter in `geomText()`
#
# The `labelFormat` parameter specifies template for transforming value of the `label` aesthetic to a string.
#
# To learn more about formatting templates see: [Formatting](https://github.com/JetBrains/lets-plot-kotlin/blob/master/docs/formats.md).
%useLatestDescriptors
%use lets-plot
val df = mapOf<String, Any>(
"y" to (0 until 5),
"z" to listOf(1.0/3, 12.5/7, -22.5/11, 2.5/7, 31.67/1.77),
"s" to listOf("one", "two", "three", "four", "five"))
// Floating point numbers without formatting.
letsPlot(df) + geomText {y = "y"; label = "z"}
// Floating point numbers with formatting.
letsPlot(df) + geomText(labelFormat = ".3f") {y = "y"; label = "z"; }
// Floating point numbers as percentage formatting.
letsPlot(df) + geomText(labelFormat = ".1%") {y = "y"; label = "z"; }
// Number format as a part of a string pattern.
letsPlot(df) + geomText(labelFormat = "Ttl: \${.2f} (B)") {y = "y"; label = "z"; }
// String pattern without value formatting. "{}"
letsPlot(df) + geomText(labelFormat = "--{}--") {y = "y"; label = "s"; }
|
docs/examples/jupyter-notebooks/label_format.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.8.3 64-bit (''base'': conda)'
# language: python
# name: python383jvsc74a57bd00b64f3f517ef2f38123c9b9d844dc7ba7aeffcc4559b7061ceea5f8a66fe5b86
# ---
# + [markdown] _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5" _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19"
# # About this kernel
#
# # + eca_nfnet_l0
# # + ArcFace
# # + Mish() activation
# # + Ranger (RAdam + Lookahead) optimizer
# # + margin = 0.9
# -
# ## Imports
# +
import sys
sys.path.append('../input/shopee-competition-utils')
sys.path.insert(0,'../input/pytorch-image-models')
# +
import numpy as np
import pandas as pd
import torch
from torch import nn
from torch.nn import Parameter
from torch.nn import functional as F
from torch.utils.data import Dataset, DataLoader
import albumentations
from albumentations.pytorch.transforms import ToTensorV2
from custom_scheduler import ShopeeScheduler
from custom_activation import replace_activations, Mish
from custom_optimizer import Ranger
from loss_module import ArcMarginProduct
import math
import cv2
import timm
import os
import random
import gc
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import GroupKFold
from sklearn.neighbors import NearestNeighbors
from tqdm.notebook import tqdm
# -
# ## Config
class CFG:
DATA_DIR = '../input/shopee-product-matching/train_images'
TRAIN_CSV = '../input/shopee-product-matching/train.csv'
# data augmentation
IMG_SIZE = 512
MEAN = [0.485, 0.456, 0.406]
STD = [0.229, 0.224, 0.225]
SEED = 2021
# data split
N_SPLITS = 5
TEST_FOLD = 0
VALID_FOLD = 1
EPOCHS = 8
BATCH_SIZE = 8
NUM_WORKERS = 4
DEVICE = 'cuda:3'
CLASSES = 6609
SCALE = 30
MARGIN = 0.9
MODEL_NAME = 'eca_nfnet_l0'
MODEL_PATH = f'{MODEL_NAME}_arc_face_epoch_{EPOCHS}_bs_{BATCH_SIZE}_margin_{MARGIN}.pt'
FC_DIM = 512
SCHEDULER_PARAMS = {
"lr_start": 1e-5,
"lr_max": 1e-5 * 32,
"lr_min": 1e-6,
"lr_ramp_ep": 5,
"lr_sus_ep": 0,
"lr_decay": 0.8,
}
# ## Augmentations
# +
def get_train_transforms():
return albumentations.Compose(
[
albumentations.Resize(CFG.IMG_SIZE,CFG.IMG_SIZE,always_apply=True),
albumentations.HorizontalFlip(p=0.5),
albumentations.VerticalFlip(p=0.5),
albumentations.Rotate(limit=120, p=0.8),
albumentations.RandomBrightness(limit=(0.09, 0.6), p=0.5),
albumentations.Normalize(mean=CFG.MEAN, std=CFG.STD),
ToTensorV2(p=1.0),
]
)
def get_valid_transforms():
return albumentations.Compose(
[
albumentations.Resize(CFG.IMG_SIZE,CFG.IMG_SIZE,always_apply=True),
albumentations.Normalize(mean=CFG.MEAN, std=CFG.STD),
ToTensorV2(p=1.0)
]
)
def get_test_transforms():
return albumentations.Compose(
[
albumentations.Resize(CFG.IMG_SIZE,CFG.IMG_SIZE,always_apply=True),
albumentations.Normalize(mean=CFG.MEAN, std=CFG.STD),
ToTensorV2(p=1.0)
]
)
# -
# ## Reproducibility
# +
def seed_everything(seed):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed)
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = True # set True to be faster
seed_everything(CFG.SEED)
# -
# ## Dataset
class ShopeeDataset(torch.utils.data.Dataset):
"""for training
"""
def __init__(self,df, transform = None):
self.df = df
self.root_dir = CFG.DATA_DIR
self.transform = transform
def __len__(self):
return len(self.df)
def __getitem__(self,idx):
row = self.df.iloc[idx]
img_path = os.path.join(self.root_dir,row.image)
image = cv2.imread(img_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
label = row.label_group
if self.transform:
augmented = self.transform(image=image)
image = augmented['image']
return {
'image' : image,
'label' : torch.tensor(label).long()
}
class ShopeeImageDataset(torch.utils.data.Dataset):
"""for validating and test
"""
def __init__(self,df, transform = None):
self.df = df
self.root_dir = CFG.DATA_DIR
self.transform = transform
def __len__(self):
return len(self.df)
def __getitem__(self,idx):
row = self.df.iloc[idx]
img_path = os.path.join(self.root_dir,row.image)
image = cv2.imread(img_path)
image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
label = row.label_group
if self.transform:
augmented = self.transform(image=image)
image = augmented['image']
return image,torch.tensor(1)
class ShopeeModel(nn.Module):
def __init__(
self,
n_classes = CFG.CLASSES,
model_name = CFG.MODEL_NAME,
fc_dim = CFG.FC_DIM,
margin = CFG.MARGIN,
scale = CFG.SCALE,
use_fc = True,
pretrained = True):
super(ShopeeModel,self).__init__()
print('Building Model Backbone for {} model'.format(model_name))
self.backbone = timm.create_model(model_name, pretrained=pretrained)
if 'efficientnet' in model_name:
final_in_features = self.backbone.classifier.in_features
self.backbone.classifier = nn.Identity()
self.backbone.global_pool = nn.Identity()
elif 'resnet' in model_name:
final_in_features = self.backbone.fc.in_features
self.backbone.fc = nn.Identity()
self.backbone.global_pool = nn.Identity()
elif 'resnext' in model_name:
final_in_features = self.backbone.fc.in_features
self.backbone.fc = nn.Identity()
self.backbone.global_pool = nn.Identity()
elif 'nfnet' in model_name:
final_in_features = self.backbone.head.fc.in_features
self.backbone.head.fc = nn.Identity()
self.backbone.head.global_pool = nn.Identity()
self.pooling = nn.AdaptiveAvgPool2d(1)
self.use_fc = use_fc
if use_fc:
self.dropout = nn.Dropout(p=0.0)
self.fc = nn.Linear(final_in_features, fc_dim)
self.bn = nn.BatchNorm1d(fc_dim)
self._init_params()
final_in_features = fc_dim
self.final = ArcMarginProduct(final_in_features,
n_classes,
s=scale,
m=margin)
def _init_params(self):
nn.init.xavier_normal_(self.fc.weight)
nn.init.constant_(self.fc.bias, 0)
nn.init.constant_(self.bn.weight, 1)
nn.init.constant_(self.bn.bias, 0)
def forward(self, image, label):
feature = self.extract_feat(image)
logits = self.final(feature,label)
return logits
def extract_feat(self, x):
batch_size = x.shape[0]
x = self.backbone(x)
x = self.pooling(x).view(batch_size, -1)
if self.use_fc:
x = self.dropout(x)
x = self.fc(x)
x = self.bn(x)
return x
# ## ArcMarginProduct
class ArcMarginProduct(nn.Module):
r"""Implement of large margin arc distance: :
Args:
in_features: size of each input sample
out_features: size of each output sample
s: norm of input feature
m: margin
cos(theta + m)
"""
def __init__(self, in_features, out_features, s=30.0, m=0.50, easy_margin=False, ls_eps=0.0):
super(ArcMarginProduct, self).__init__()
self.in_features = in_features
self.out_features = out_features
self.s = s
self.m = m
self.ls_eps = ls_eps # label smoothing
self.weight = Parameter(torch.FloatTensor(out_features, in_features))
nn.init.xavier_uniform_(self.weight)
self.easy_margin = easy_margin
self.cos_m = math.cos(m)
self.sin_m = math.sin(m)
self.th = math.cos(math.pi - m)
self.mm = math.sin(math.pi - m) * m
def forward(self, input, label):
# --------------------------- cos(theta) & phi(theta) ---------------------------
cosine = F.linear(F.normalize(input), F.normalize(self.weight))
sine = torch.sqrt(1.0 - torch.pow(cosine, 2))
phi = cosine * self.cos_m - sine * self.sin_m
if self.easy_margin:
phi = torch.where(cosine > 0, phi, cosine)
else:
phi = torch.where(cosine > self.th, phi, cosine - self.mm)
# --------------------------- convert label to one-hot ---------------------------
# one_hot = torch.zeros(cosine.size(), requires_grad=True, device='cuda')
one_hot = torch.zeros(cosine.size(), device=CFG.DEVICE)
one_hot.scatter_(1, label.view(-1, 1).long(), 1)
if self.ls_eps > 0:
one_hot = (1 - self.ls_eps) * one_hot + self.ls_eps / self.out_features
# -------------torch.where(out_i = {x_i if condition_i else y_i) -------------
output = (one_hot * phi) + ((1.0 - one_hot) * cosine)
output *= self.s
return output, nn.CrossEntropyLoss()(output,label)
# ## Engine
# +
def train_fn(model, data_loader, optimizer, scheduler, i):
model.train()
fin_loss = 0.0
tk = tqdm(data_loader, desc = "Epoch" + " [TRAIN] " + str(i+1))
for t,data in enumerate(tk):
for k,v in data.items():
data[k] = v.to(CFG.DEVICE)
optimizer.zero_grad()
_, loss = model(**data)
loss.backward()
optimizer.step()
fin_loss += loss.item()
tk.set_postfix({'loss' : '%.6f' %float(fin_loss/(t+1)), 'LR' : optimizer.param_groups[0]['lr']})
scheduler.step()
return fin_loss / len(data_loader)
def eval_fn(model, data_loader, i):
model.eval()
fin_loss = 0.0
tk = tqdm(data_loader, desc = "Epoch" + " [VALID] " + str(i+1))
with torch.no_grad():
for t,data in enumerate(tk):
for k,v in data.items():
data[k] = v.to(CFG.DEVICE)
_, loss = model(**data)
fin_loss += loss.item()
tk.set_postfix({'loss' : '%.6f' %float(fin_loss/(t+1))})
return fin_loss / len(data_loader)
# -
def read_dataset():
df = pd.read_csv(CFG.TRAIN_CSV)
df['matches'] = df.label_group.map(df.groupby('label_group').posting_id.agg('unique').to_dict())
df['matches'] = df['matches'].apply(lambda x: ' '.join(x))
gkf = GroupKFold(n_splits=CFG.N_SPLITS)
df['fold'] = -1
for i, (train_idx, valid_idx) in enumerate(gkf.split(X=df, groups=df['label_group'])):
df.loc[valid_idx, 'fold'] = i
labelencoder= LabelEncoder()
df['label_group'] = labelencoder.fit_transform(df['label_group'])
train_df = df[df['fold']!=CFG.TEST_FOLD].reset_index(drop=True)
train_df = train_df[train_df['fold']!=CFG.VALID_FOLD].reset_index(drop=True)
valid_df = df[df['fold']==CFG.VALID_FOLD].reset_index(drop=True)
test_df = df[df['fold']==CFG.TEST_FOLD].reset_index(drop=True)
train_df['label_group'] = labelencoder.fit_transform(train_df['label_group'])
return train_df, valid_df, test_df
# +
def precision_score(y_true, y_pred):
y_true = y_true.apply(lambda x: set(x.split()))
y_pred = y_pred.apply(lambda x: set(x.split()))
intersection = np.array([len(x[0] & x[1]) for x in zip(y_true, y_pred)])
len_y_pred = y_pred.apply(lambda x: len(x)).values
precision = intersection / len_y_pred
return precision
def recall_score(y_true, y_pred):
y_true = y_true.apply(lambda x: set(x.split()))
y_pred = y_pred.apply(lambda x: set(x.split()))
intersection = np.array([len(x[0] & x[1]) for x in zip(y_true, y_pred)])
len_y_true = y_true.apply(lambda x: len(x)).values
recall = intersection / len_y_true
return recall
def f1_score(y_true, y_pred):
y_true = y_true.apply(lambda x: set(x.split()))
y_pred = y_pred.apply(lambda x: set(x.split()))
intersection = np.array([len(x[0] & x[1]) for x in zip(y_true, y_pred)])
len_y_pred = y_pred.apply(lambda x: len(x)).values
len_y_true = y_true.apply(lambda x: len(x)).values
f1 = 2 * intersection / (len_y_pred + len_y_true)
return f1
# -
def get_valid_embeddings(df, model):
model.eval()
image_dataset = ShopeeImageDataset(df,transform=get_valid_transforms())
image_loader = torch.utils.data.DataLoader(
image_dataset,
batch_size=CFG.BATCH_SIZE,
pin_memory=True,
num_workers = CFG.NUM_WORKERS,
drop_last=False
)
embeds = []
with torch.no_grad():
for img,label in tqdm(image_loader):
img = img.to(CFG.DEVICE)
label = label.to(CFG.DEVICE)
feat,_ = model(img,label)
image_embeddings = feat.detach().cpu().numpy()
embeds.append(image_embeddings)
del model
image_embeddings = np.concatenate(embeds)
print(f'Our image embeddings shape is {image_embeddings.shape}')
del embeds
gc.collect()
return image_embeddings
def get_valid_neighbors(df, embeddings, KNN = 50, threshold = 0.36):
model = NearestNeighbors(n_neighbors = KNN, metric = 'cosine')
model.fit(embeddings)
distances, indices = model.kneighbors(embeddings)
predictions = []
for k in range(embeddings.shape[0]):
idx = np.where(distances[k,] < threshold)[0]
ids = indices[k,idx]
posting_ids = ' '.join(df['posting_id'].iloc[ids].values)
predictions.append(posting_ids)
df['pred_matches'] = predictions
df['f1'] = f1_score(df['matches'], df['pred_matches'])
df['recall'] = recall_score(df['matches'], df['pred_matches'])
df['precision'] = precision_score(df['matches'], df['pred_matches'])
del model, distances, indices
gc.collect()
return df, predictions
# # Training
# +
def run_training():
train_df, valid_df, test_df = read_dataset()
train_dataset = ShopeeDataset(train_df, transform = get_train_transforms())
train_dataloader = torch.utils.data.DataLoader(
train_dataset,
batch_size = CFG.BATCH_SIZE,
pin_memory = True,
num_workers = CFG.NUM_WORKERS,
shuffle = True,
drop_last = True
)
print(train_df['label_group'].nunique())
model = ShopeeModel()
model = replace_activations(model, torch.nn.SiLU, Mish())
model.to(CFG.DEVICE)
optimizer = Ranger(model.parameters(), lr = CFG.SCHEDULER_PARAMS['lr_start'])
#optimizer = torch.optim.Adam(model.parameters(), lr = config.SCHEDULER_PARAMS['lr_start'])
scheduler = ShopeeScheduler(optimizer,**CFG.SCHEDULER_PARAMS)
best_valid_f1 = 0.
for i in range(CFG.EPOCHS):
avg_loss_train = train_fn(model, train_dataloader, optimizer, scheduler, i)
valid_embeddings = get_valid_embeddings(valid_df, model)
valid_df, valid_predictions = get_valid_neighbors(valid_df, valid_embeddings)
valid_f1 = valid_df.f1.mean()
valid_recall = valid_df.recall.mean()
valid_precision = valid_df.precision.mean()
print(f'Valid f1 score = {valid_f1}, recall = {valid_recall}, precision = {valid_precision}')
if valid_f1 > best_valid_f1:
best_valid_f1 = valid_f1
print('Valid f1 score improved, model saved')
torch.save(model.state_dict(),CFG.MODEL_PATH)
run_training()
# -
def get_test_embeddings(test_df):
model = ShopeeModel()
model.eval()
model = replace_activations(model, torch.nn.SiLU, Mish())
model.load_state_dict(torch.load(CFG.MODEL_PATH))
model = model.to(CFG.DEVICE)
image_dataset = ShopeeImageDataset(test_df,transform=get_test_transforms())
image_loader = torch.utils.data.DataLoader(
image_dataset,
batch_size=CFG.BATCH_SIZE,
pin_memory=True,
num_workers = CFG.NUM_WORKERS,
drop_last=False
)
embeds = []
with torch.no_grad():
for img,label in tqdm(image_loader):
img = img.cuda()
label = label.cuda()
feat,_ = model(img,label)
image_embeddings = feat.detach().cpu().numpy()
embeds.append(image_embeddings)
del model
image_embeddings = np.concatenate(embeds)
print(f'Our image embeddings shape is {image_embeddings.shape}')
del embeds
gc.collect()
return image_embeddings
# ## Best threshold Search
# +
train_df, valid_df, test_df = read_dataset()
print("Searching best threshold...")
search_space = np.arange(10, 50, 1)
model = ShopeeModel()
model.eval()
model = replace_activations(model, torch.nn.SiLU, Mish())
model.load_state_dict(torch.load(CFG.MODEL_PATH))
model = model.to(CFG.DEVICE)
valid_embeddings = get_valid_embeddings(valid_df, model)
best_f1_valid = 0.
best_threshold = 0.
for i in search_space:
threshold = i / 100
valid_df, valid_predictions = get_valid_neighbors(valid_df, valid_embeddings, threshold=threshold)
valid_f1 = valid_df.f1.mean()
valid_recall = valid_df.recall.mean()
valid_precision = valid_df.precision.mean()
print(f"threshold = {threshold} -> f1 score = {valid_f1}, recall = {valid_recall}, precision = {valid_precision}")
if (valid_f1 > best_f1_valid):
best_f1_valid = valid_f1
best_threshold = threshold
print("Best threshold =", best_threshold)
print("Best f1 score =", best_f1_valid)
BEST_THRESHOLD = best_threshold
# +
print("Searching best knn...")
search_space = np.arange(10, 50, 2)
best_f1_valid = 0.
best_knn = 0
for knn in search_space:
valid_df, valid_predictions = get_valid_neighbors(valid_df, valid_embeddings, KNN=knn, threshold=BEST_THRESHOLD)
valid_f1 = valid_df.f1.mean()
valid_recall = valid_df.recall.mean()
valid_precision = valid_df.precision.mean()
print(f"knn = {knn} -> f1 score = {valid_f1}, recall = {valid_recall}, precision = {valid_precision}")
if (valid_f1 > best_f1_valid):
best_f1_valid = valid_f1
best_knn = knn
print("Best knn =", best_knn)
print("Best f1 score =", best_f1_valid)
BEST_KNN = best_knn
# +
test_embeddings = get_valid_embeddings(test_df,model)
test_df, test_predictions = get_valid_neighbors(test_df, test_embeddings, KNN = BEST_KNN, threshold = BEST_THRESHOLD)
test_f1 = test_df.f1.mean()
test_recall = test_df.recall.mean()
test_precision = test_df.precision.mean()
print(f'Test f1 score = {test_f1}, recall = {test_recall}, precision = {test_precision}')
# -
|
notebook/arcface-eca-nfnet-l0-margin-0.9.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/yogesh0609/Letsupgrade_python/blob/master/Assignment_Day_9.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="_YxRX-ZRoxWz" colab_type="text"
# Assignment 1
# + id="VqM3f8wloyoK" colab_type="code" colab={}
import unittest
def is_prime(number):
"""Return True if *number* is prime."""
for element in range(number):
if number % element == 0:
return False
return True
class PrimesTestCase(unittest.TestCase):
"""Tests for `primes.py`."""
def test_is_five_prime(self):
"""Is five successfully determined to be prime?"""
self.assertTrue(is_prime(5))
if __name__ == '__main__':
unittest.main()
# + [markdown] id="GZGSOVU5oy97" colab_type="text"
# Assignment 2
# + id="uBcMpPS_ozLO" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 243} outputId="d1618f42-2f5e-4bb1-806c-e5ee8deb0cdd"
def isArmstrong():
for num in range(1, 1001):
order = len(str(num))
sum = 0
temp = num
while temp > 0:
digit = temp % 10
sum += digit ** order
temp //= 10
if num == sum:
yield(num)
for i in isArmstrong():
print(i)
|
Assignment_Day_9.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.6.3
# language: julia
# name: julia-1.6
# ---
# # Julia Workshop
# ### "Hello World"
println("Hello World")
# ### Operators
println(7+8) #Add
println(3-5) #Substract
println(6*3) #Multiply
println(55/11) #Divide
println(13/2) #Divide
println(5^2) #Power
println(5%2) #Remainder
# ### Numeric Comparison Operators
println(500 == 500)
println(500 == 501)
println(500 != 500)
println(100 == 100.0)
println(100 < 200)
println(-5 <= -5)
# ### Variables
# +
#Case Sensitive: student_name and Student_name are not the same
#Names have to start with an underscore or letter or certain unicode characters
#Variables can contain digits or special characters but should not begin with them
#Operators can also be named to use variable
student_name = "Julia"
student_age = 15
student_gpa = 2.5
last_name = "Smith"
println(student_name)
println(typeof(student_age))
println(typeof(student_gpa))
# -
# ### Strings
# +
s = "Julia is a great language"
b = """Julia says, "Hi". """
student_name = "Julia"
last_name = "Smith"
println(b)
println(s[end])
println(s[begin])
println("$student_name$last_name")
# -
# ### Insert Variables Into A String
student_name = "Julia"
student_gpa = 2.5
println("The student's name is $student_name and her gpa is $student_gpa.")
# ## Data Structures
# ### Tuples
# +
#Immutable
students = ("Ally","Julia","Bob")
println(students)
println(students[2:end])
#Another type of tuple
tupl = ((1,2),(3,4))
println(tupl[1])
println(tupl[1][2])
# -
# ### Named Tuples
# +
#Keys with tuples
coord = (x1 = (1,1), x2 = (-1,-1), x3 = (0,0) )
println(coord.x2) #use .
#Combining two named tuples
new_coord = (x3 = (5,1), x4 = (-6,-1), x5 = (3,0) )
merge(coord,new_coord)
# -
# ### Dictionaries
contacts = Dict("Phone" => "678-459-8431", "Address" => "324 Bermont Point")
println(contacts)
#Search for a key
haskey(contacts, "Address")
# +
#add to a dictionary
contacts["Zip"] = "30005"
println(contacts)
#remove from a dictionary
#Delete an element from a dictionary
pop!(contacts,"Phone")
println(contacts)
# -
# ### Arrays
#Index starts at 1
a = [1,3,2,4,5,6]
println(a[3])
println(a[end])
println(4 in a)
println(findfirst(isequal(2),a))
println(size(a))
println(length(a))
#called maximum and minimum instead of min and max
println(maximum(a))
println(minimum(a))
println(a *3)
# ### Creating arrays using comprehensions and generators
square_array = [n^2 for n in 1:8]
println(square_array)
# ### Creating arrays with different types
empty_arr = Int64[]
different_type = [15,"Julia",3.95]
println(empty_arr)
println(different_type)
# ### Collect Function
#Create an array using range objects is collect()
println(collect(1.5:10.5)) #Step Size 1
println(collect(0:2:16)) #Step Size 2
# ### Creating 2-D Arrays
[n *m for n in 1:8, m in 1:8]
# ### Populating An Array
#Populating an array of zeros
zero = zeros(4,5)
zero
#Populating an array with ones
ones(4,5)
#m*n matrix of normally distributed random numbers with mean=0 and standard deviation = 1
rnorm_arr = rand(4,5)
# ### Accessing Contents of an 2D Array
println(rnorm_arr[3,2])
println(getindex(rnorm_arr,3,2))
# ### Adding and Removing Elements from an array
v = collect(1:7)
push!(v,8) #add at the end
pushfirst!(v,8) #add at the front
splice!(v,2:1,[10,11]) #add at a given index
println(v)
println(pop!(v)) #remove last element of an array
println(v)
println(popfirst!(v))# remove first element of an array
println(v)
println(splice!(v,2)) #remove the second element of an array
println(v)
# ### You can even store functions in an array!
math_functions = [sin,cos,tan]
for i in math_functions
println(i(0))
end''''';;;;;
|
workshops/w10/JULIA_Workshop_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Load the Pandas libraries with alias 'pd'
import pandas as pd
import numpy as np
import seaborn as sns
import statsmodels.formula.api as smf
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
import matplotlib.pyplot as plt
happiness = pd.read_csv("happiness.csv")
happiness.head()
# a simple histogram
happiness.score.hist()
# basic statistics in pandas
happiness.score.describe()
happiness.investment.describe()
# scatterplot
f, ax = plt.subplots(figsize=(6.5, 6.5))
happiness.plot.scatter('investment', 'score', alpha=0.15,ax=ax)
|
chadgoldberg9/Project.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
import requests
from dotenv import find_dotenv, load_dotenv
import pandas as pd
load_dotenv(find_dotenv())
# +
## NVE
# -
NVE_URL = os.environ.get('NVE_URL')
data = requests.get(NVE_URL).json()
sorted_data = sorted(data, key=lambda x: x["dato_Id"])
df = pd.DataFrame.from_dict(sorted_data)
df.set_index("dato_Id", inplace=True)
df.index = pd.to_datetime(df.index)
df = df[df['omrType'] == 'NO']
df.head()
df.to_csv('../data/interim/nve.csv')
# +
## System Price Nordic
# -
data = pd.read_excel('../data/raw/Nordic Hydro Balance 1990_wk 41 2016_FC.xlsx', sheet_name='Hydro vs spot price', header=1)
data.head()
data = data[[data.columns[0], 'System price [SYS] in [EUR/MWh]']]
data.rename(columns={data.columns[0]: 'date'}, inplace=True)
data.dropna(inplace=True)
data['date'] = data['date'].astype(int)
data['date'] = pd.to_datetime(data['date'].astype(str) + '1', format='%Y%W%w')
data.set_index('date', inplace=True)
data.plot()
data.to_csv('../data/interim/system_price.csv')
# +
## Swedish filling level
# -
data = pd.read_excel('../data/raw/Mag_2000-_SE.2015-.xlsx', sheet_name='1950-', header=2, index_col='Vecka')
data.head()
data.to_csv('../data/interim/sweden.csv')
[149, 378, 2, 360, 7, 290, 637, 203, 204, 225, 422, 601]
|
notebooks/01-tlr-dataset_test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
## Mission to Mars
# -
# Dependencies
from bs4 import BeautifulSoup as bs
from pprint import pprint
from splinter import Browser
import pandas as pd
# Windows executable path
executable_path = {'executable_path': '/Users/klsom/Downloads/chromedriver'}
b = Browser('chrome', **executable_path, headless=False)
# +
# Mac executable path
# executable_path = {'executable_path': '/usr/local/bin/chromedriver'}
# b = Browser('chrome', **executable_path, headless=False)
# +
## NASA Mars News
# +
mars_url = 'https://mars.nasa.gov/news/'
b.visit(mars_url)
# BS object
html = b.html
mars_bs = bs(html, 'lxml')
# -
# Scrape the first article title
news_title = mars_bs.find('div', class_='content_title').text
news_title
# Scrape the first article teaser paragraph text
news_p = mars_bs.find('div', class_='article_teaser_body').text
news_p
# +
## JPL Mars Space Images - Featured Image
# -
image_url = 'https://www.jpl.nasa.gov/spaceimages/?search=&category=Mars'
b.visit(image_url)
# Go to 'FULL IMAGE'
b.click_link_by_partial_text('FULL IMAGE')
# Go to 'more info'
b.click_link_by_partial_text('more info')
# BS object
html = b.html
image_bs = bs(html, 'lxml')
# Scrape the URL
feat_img_url = image_bs.find('figure', class_='lede').a['href']
feat_img_full_url = f'https://www.jpl.nasa.gov{feat_img_url}'
feat_img_full_url
# +
## Mars Weather
# -
# Windows executable path
executable_path = {'executable_path': '/Users/klsom/Downloads/chromedriver'}
b = Browser('chrome', **executable_path, headless=False)
tweet_url = 'https://twitter.com/marswxreport?lang=en'
b.visit(tweet_url)
# BS object
html = b.html
tweet_bs = bs(html, 'lxml')
# Scrape the tweet
mars_weather = tweet_bs.find('p', class_='TweetTextSize').text
mars_weather
# +
## Mars Facts
# -
facts_url = 'https://space-facts.com/mars/'
tables = pd.read_html(facts_url)
# Scrape the table of Mars facts
mars_facts_df = tables[0]
mars_facts_df.columns = ['Property', 'Value']
mars_facts_df
# Convert to HTML table string
mars_facts_df.to_html()
# +
## Mars Hemispheres
# -
# Windows executable path
executable_path = {'executable_path': '/Users/klsom/Downloads/chromedriver'}
b = Browser('chrome', **executable_path, headless=False)
hemisphere_url = 'https://astrogeology.usgs.gov/search/results?q=hemisphere+enhanced&k1=target&v1=Mars'
b.visit(hemisphere_url)
# BS object
html = b.html
hemisphere_bs = bs(html, 'lxml')
# +
hemisphere_image_urls = []
# Get a list of all hemispheres
links = b.find_by_css('a.product-item h3')
for item in range(len(links)):
hemisphere = {}
# Find element on each loop
b.find_by_css('a.product-item h3')[item].click()
# Find sample image anchor tag & extract <href>
sample_element = b.find_link_by_text('Sample').first
hemisphere['img_url'] = sample_element['href']
# Get hemisphere title
hemisphere['title'] = b.find_by_css('h2.title').text
# Append to list
hemisphere_image_urls.append(hemisphere)
# Navigate back
b.back()
# -
hemisphere_image_urls
# +
# Populate a list of the hemispheres with links
hemisphere_strings = []
links = hemisphere_bs.find_all('h3')
for hemisphere in links:
hemisphere_strings.append(hemisphere.text)
hemisphere_strings
# +
# Create list for hemisphere image urls
hemisphere_image_urls = []
# Loop through the hemisphere links to obtain the images
for hemisphere in hemisphere_strings:
# Create a dictionary for hemisphere info
hemisphere_dict = {}
# Click on the link with the corresponding text
b.click_link_by_partial_text(hemisphere)
# Scrape the image url string and store into the dictionary
hemisphere_dict['img_url'] = b.find_by_text('Sample')['href']
hemisphere_dict['title'] = hemisphere
hemisphere_image_urls.append(hemisphere_dict)
pprint(hemisphere_image_urls)
# Click the 'Back' button
b.click_link_by_partial_text('Back')
|
Web-Scraping-Challenge/missing_to_mars.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import cv2
import numpy as np
from keras.models import load_model
from statistics import mode
from utils.datasets import get_labels
from utils.inference import detect_faces
from utils.inference import draw_text
from utils.inference import draw_bounding_box
from utils.inference import apply_offsets
from utils.inference import load_detection_model
from utils.preprocessor import preprocess_input
USE_WEBCAM = False # If false, loads video file source
# parameters for loading data and images
emotion_model_path = 'models/emotion_model.hdf5'
emotion_labels = get_labels('fer2013')
# hyper-parameters for bounding boxes shape
frame_window = 10
emotion_offsets = (20, 40)
# loading models
face_cascade = cv2.CascadeClassifier('models/haarcascade_frontalface_default.xml')
emotion_classifier = load_model(emotion_model_path)
# getting input model shapes for inference
emotion_target_size = emotion_classifier.input_shape[1:3]
# starting lists for calculating modes
emotion_window = []
import time
import os
cwd = os.getcwd()
cwd
smile_count=0
# +
height = 768
width = 1280
# height, width, number of channels in image
outter_rect_ix = int(0.15*width)
outter_rect_iy = int(0.96*height)
outter_rect_jx = int(0.85*width)
outter_rect_jy = int(0.94*height)
inner_rect_ix = outter_rect_ix
inner_rect_iy = outter_rect_iy
inner_rect_jx = range(outter_rect_ix,outter_rect_jx)
inner_rect_jy = outter_rect_jy
# -
inner_rect_jx[2]
outter_rect_jx
len(inner_rect_jx)
# +
# Select video or webcam feed
pause_flag = 0
cap = None
if (USE_WEBCAM == True):
cap = cv2.VideoCapture(0) # Webcam source
else:
cap = cv2.VideoCapture('demo/Happy_Face.mp4') # Video file source
cv2.namedWindow('window_frame')
t0=time.time()
t1=time.time()
print_count=0
while cap.isOpened(): # True:
ret, bgr_image = cap.read()
#bgr_image = video_capture.read()[1]
gray_image = cv2.cvtColor(bgr_image, cv2.COLOR_BGR2GRAY)
rgb_image = cv2.cvtColor(bgr_image, cv2.COLOR_BGR2RGB)
faces = face_cascade.detectMultiScale(gray_image, scaleFactor=1.1, minNeighbors=5,
minSize=(30, 30), flags=cv2.CASCADE_SCALE_IMAGE)
for face_coordinates in faces:
x1, x2, y1, y2 = apply_offsets(face_coordinates, emotion_offsets)
gray_face = gray_image[y1:y2, x1:x2]
try:
gray_face = cv2.resize(gray_face, (emotion_target_size))
except:
continue
gray_face = preprocess_input(gray_face, True)
gray_face = np.expand_dims(gray_face, 0)
gray_face = np.expand_dims(gray_face, -1)
emotion_prediction = emotion_classifier.predict(gray_face)
emotion_probability = np.max(emotion_prediction)
emotion_label_arg = np.argmax(emotion_prediction)
emotion_text = emotion_labels[emotion_label_arg]
emotion_window.append(emotion_text)
if len(emotion_window) > frame_window:
emotion_window.pop(0)
try:
emotion_mode = mode(emotion_window)
except:
continue
if emotion_text == 'angry':
color = emotion_probability * np.asarray((255, 0, 0))
elif emotion_text == 'sad':
color = emotion_probability * np.asarray((0, 0, 255))
elif emotion_text == 'happy':
color = emotion_probability * np.asarray((255, 255, 0))
elif emotion_text == 'surprise':
color = emotion_probability * np.asarray((0, 255, 255))
else:
color = emotion_probability * np.asarray((0, 255, 0))
color = color.astype(int)
color = color.tolist()
e_p = str(round(emotion_probability*100,2))
draw_bounding_box(face_coordinates, rgb_image, color)
draw_text(face_coordinates, rgb_image, emotion_mode+" "+e_p+"%",
color, 0, -45, 0.5, 1)
bgr_image = cv2.cvtColor(rgb_image, cv2.COLOR_RGB2BGR)
try:
if (emotion_text =='happy'):
if (smile_count >= (len(inner_rect_jx)-15)):
cv2.imwrite('dump/image{}'.format(print_count)+'.jpg',bgr_image)
font = cv2.FONT_HERSHEY_SIMPLEX
#cv2.putText(bgr_image,'Saving Pic!',(int(width/2)-100,int(height/2)), font, 5, (255,255,255), 5, cv2.LINE_AA)
print_count +=1
smile_count = 0
pause_flag=1
smile_count +=10
except Exception as e:
continue
cv2.rectangle(bgr_image,(outter_rect_ix,outter_rect_iy),(outter_rect_jx,outter_rect_jy),(0,255,255),3)
cv2.rectangle(bgr_image,(inner_rect_ix,inner_rect_iy),(inner_rect_jx[smile_count],inner_rect_jy),(0,255,0),-1)
cv2.imshow('window_frame', bgr_image)
if (pause_flag ==1):
time.sleep(5)
pause_flag=0
if cv2.waitKey(1) & 0xFF == ord('q'):
break
cap.release()
cv2.destroyAllWindows()
# -
bgr_image
import cv2
import numpy as np
from keras.models import load_model
from statistics import mode
from utils.datasets import get_labels
from utils.inference import detect_faces
from utils.inference import draw_text
from utils.inference import draw_bounding_box
from utils.inference import apply_offsets
from utils.inference import load_detection_model
from utils.preprocessor import preprocess_input
# +
img = cv2.imread('demo/image1.jpg')
dimensions = img.shape
# height, width, number of channels in image
height = img.shape[0]
width = img.shape[1]
channels = img.shape[2]
# -
height
width
outter_rect_ix = int(0.15*width)
outter_rect_iy = int(.96*height)
outter_rect_jx = int(.85*width)
outter_rect_jy = int(0.94*height)
# +
#outter_rect_ix = int(0.95*width)
#outter_rect_iy = int(0.96*height)
#outter_rect_jx = int(.97*width)
#outter_rect_jy = int(.04*height)
# -
inner_rect_ix = outter_rect_ix
inner_rect_iy = outter_rect_iy
inner_rect_jx = int(.85*outter_rect_jx)
inner_rect_jy = outter_rect_jy
cv2.rectangle(img,(outter_rect_ix,outter_rect_iy),(outter_rect_jx,outter_rect_jy),(0,255,255),3)
cv2.rectangle(img,(inner_rect_ix,inner_rect_iy),(inner_rect_jx,inner_rect_jy),(0,255,0),-1)
cv2.imshow('window_frame', img)
cv2.waitKey(0)
cv2.destroyAllWindows()
cv2.destroyAllWindows()
|
Untitled-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %run NB_Header.ipynb # Load general libs
# ## 0. Data exploration
# +
df_raw_data = pd.read_csv('sample_data.csv')
display(df_raw_data.shape)
ds_dtypes = df_raw_data.dtypes
ds_dtypes.sort_values()
df_raw_data._get_numeric_data().dtypes #drop non-numeric cols
ds_dtypes[ds_dtypes=="float64"].index.tolist()
df_raw_data.describe(include='all')# .transpose() #['count']
# -
df_raw_data[df_raw_data.art.isna()]
# + [markdown] heading_collapsed=true
# ### Variance scan
# + hidden=true
from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold()
# + hidden=true
thres_var = 1E-4 # (0.01%)
features = ds_dtypes[ds_dtypes=="float64"].index.tolist()
sel_var_thres = selector.fit(df_raw_data[features])
# sorted(zip(features,sel_var_thres.variances_), key=lambda x: x[1])
# features_selected = [feat for feat, var in zip(features, sel_var_thres.variances_) if var >= thres_var]
# + hidden=true
# Low variance features may consider to drop. Yet need to check on their business meaning/importance
thres_var = 0.05
for feat, var in zip(features, sel_var_thres.variances_):
if var < thres_var:
print('{}\t{:.3f}'.format(feat, var))
# -
# ### Multicollinearity check
# +
from statsmodels.stats.outliers_influence import variance_inflation_factor
def calc_vif(X):
vif = pd.DataFrame()
vif["feature"] = X.columns
vif["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
return(vif)
l_keep = ['n_area', 'n_completes', 'n_clicks', 'n_session'] # 'n_act',
calc_vif(df_raw_data[l_keep].dropna())
# -
calc_vif(df_raw_data._get_numeric_data().dropna().drop(['parentid','userid','free_trial','tot_ts_mins'],axis=1))
# Colinearity - bivariate
df_raw_data._get_numeric_data().dropna().drop(['parentid','userid','free_trial'],axis=1).corr()
# ### Two sample means null hypothesis test
# + https://www.analyticsvidhya.com/blog/2020/06/statistics-analytics-hypothesis-testing-z-test-t-test/
# + https://machinelearningmastery.com/chi-squared-test-for-machine-learning/
# * Z-test to approximate t-test (n_sample > 30)
from scipy.stats import norm, t
ds_r1 = df_raw_data[df_raw_data.userid.isin(ds_returner)][attr]
ds_r1 = np.log(ds_r1[ds_r1>0])
ds_r2 = df_raw_data[~df_raw_data.userid.isin(ds_returner)][attr]
ds_r2 = np.log(ds_r2[ds_r2>0])
t_score = (ds_r1.mean() - ds_r2.mean())/np.sqrt(ds_r1.var()/ds_r1.size+ds_r2.var()/ds_r2.size)
p_value = norm.sf(abs(t_score))*2 #for two-sided p-value z test approx
# p_value = t.sf(abs(t_score), min(ds_r1.size, df_r2.size))*2 #for two-sided p-value t test with min(r1,r2) as dof
# * Chi square (distrbution free) frequency test
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.chi2_contingency.html
# +
# chi-squared test with similar proportions
from scipy.stats import chi2_contingency
# contingency table
table = [[10, 20, 30],
[6, 9, 17]]
print(table)
stat, p, dof, expected = chi2_contingency(table)
# interpret test-statistic
from scipy.stats import chi2
prob = 0.95
critical = chi2.ppf(prob, dof)
# -
# * Power analysis
# + code_folding=[]
# https://en.wikipedia.org/wiki/Power_of_a_test
# In the context of binary classification, the power of a test is called its statistical sensitivity,
# its true positive rate (1 - alpha), or its probability of detection for avoiding type I error.
# -
# ### Pre-processing & data standardization
# + [markdown] heading_collapsed=true
# #### Using pandas
# + code_folding=[] hidden=true
# Separate model feature inputs into categorical and numeric types
l_category = ds_dtypes[ds_dtypes=='object'].index.tolist()
l_category.remove('which_day')
print('Category input -', l_category)
l_numeric = [f for f in ds_dtypes[ds_dtypes!='object'].index if f not in ['parentid','userid','postal_code']]
print('Numeric input -', l_numeric)
# + code_folding=[] hidden=true
# Apply one-hot conversion to categorical features and combine numeric features
response = 'is_returner'
df_dataset = df_raw_data[[response]+l_numeric]
df_dataset['free_trial'] = df_dataset['free_trial'].astype(int)
df_dataset = pd.concat([df_dataset, pd.get_dummies(df_raw_data[l_category], prefix=l_category)],axis=1)
# for cat in l_category:
# df_dataset = pd.concat([df_dataset, pd.get_dummies(df_raw_data[cat], prefix=cat)],axis=1)
features = df_dataset.columns[1:].tolist()
df_dataset.fillna(0, inplace=True)
# + hidden=true
# Get quantile counts
df_data.fillna('NA', inplace=True)
ds_biznm = df_data.businessname.value_counts()
ds_biznm.quantile(q=np.arange(0.9,1,0.01))
# + hidden=true
# Bin operation
l_binsz=[0,1000,10_000,100_000,1_000_000,10_000_000,100_000_000,1_000_000_000]
df_raw_data.loc[:,'jval_bin'] = pd.cut(df_raw_data['job_value'].replace('NA',None), l_binsz, \
include_lowest=True, labels=list(range(0,len(l_binsz)-1)))
df_raw_data.jval_bin.value_counts()
# + [markdown] heading_collapsed=true
# #### Using sklearn libs
# + code_folding=[] hidden=true
# https://imbalanced-learn.readthedocs.io/en/stable/auto_examples/applications/porto_seguro_keras_under_sampling.html
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import OneHotEncoder
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import FunctionTransformer
from sklearn.impute import SimpleImputer
def convert_float64(X):
return X.astype(np.float64)
# + code_folding=[] hidden=true
numerical_columns = [name for name in X_train.columns
if '_calc_' in name and '_bin' not in name]
numerical_pipeline = make_pipeline(
FunctionTransformer(func=convert_float64, validate=False),
StandardScaler())
categorical_columns = [name for name in X_train.columns
if '_cat' in name]
categorical_pipeline = make_pipeline(
SimpleImputer(missing_values=-1, strategy='most_frequent'),
OneHotEncoder(categories='auto'))
preprocessor = ColumnTransformer(
[('numerical_preprocessing', numerical_pipeline, numerical_columns),
('categorical_preprocessing', categorical_pipeline, categorical_columns)],
remainder='drop')
# -
# ## 1. Data modeling
# + [markdown] heading_collapsed=true
# ### Plotting library
# + code_folding=[] hidden=true
# Load graph libs
# %matplotlib inline
# import matplotlib
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.ticker import AutoMinorLocator, FuncFormatter
import ptitprince as pt
# + hidden=true
# Matplotlib df
ax = plt.subplot()
# performance_all(y_test, pred, pred_dnn, ax, color='r')
ax.plot([0,1], [0,1], color='k', linestyle='--', linewidth=1.0, label = 'y=x')
ax.legend(loc='lower right');
# + hidden=true
# https://plotly.com/python/px-arguments/#input-data-as-pandas-dataframes
import plotly.express as px
df = px.data.iris()
# Use directly Columns as argument. You can use tab completion for this!
# fig = px.scatter(df, x=df.sepal_length, y=df.sepal_width, color=df.speciess, size=df.petal_length)
fig = px.scatter(df, x=df.sepal_length, y=[df.sepal_width, df.petal_width])
# fig = px.line(df, x="year", y="lifeExp", color='country')
fig.show()
# + hidden=true
# https://plotly.com/python/line-charts/#line-plot-with-goscatter
import plotly.graph_objects as go
# Create traces
fig = go.Figure()
fig.add_trace(go.Scatter(x=fpr, y=tpr, mode='lines', line=dict(color='red'),
name="ACC: {:.2f} AUC: {:.2f} REC: {:.2f}".format(acc, auc, rec)))
# fig.add_trace(go.Scatter(x=random_x, y=random_y1,
# mode='lines+markers',
# name='lines+markers'))
# fig.add_trace(go.Scatter(x=random_x, y=random_y2,
# mode='markers', name='markers'))
fig.update_layout(
showlegend = True,
title = dict(text='ROC Curve', x=0.42, y=0.9, xanchor='center', yanchor='top'),
xaxis_title = "FPR",
yaxis_title = "TPR",
legend_title = "Model ",
# font=dict(
# family="Courier New, monospace",
# size=18,
# color="RebeccaPurple"
# )
# xaxis = dict(
# tickmode = 'array',
# tickvals = df_summ_metric.index,
# ),
# xaxis_tickformat = '%d %b (%a)'
)
fig.show()
# + hidden=true
# Raincloud Plot for normal distribution - var: ATTR
plt.rcParams.update({'font.size': 12, 'figure.figsize': (15, 8)})
ax = pt.RainCloud(x='User Type',y=f'{attr.upper()} mins', alpha=0.75, pointplot=True,
data = df_attr.stack().rename(f'{attr.upper()} mins').reset_index().rename(
columns={'level_1':'User Type'}), orient='h')
ax.xaxis.set_minor_locator(AutoMinorLocator(5))
ax.grid(True, ls=(0, (5, 5)), drawstyle='steps')
ax.set_xlim(0, 80);
# + [markdown] heading_collapsed=true
# ### Interactive display
# + code_folding=[] hidden=true
# Interactive widget
import ipywidgets as widgets
from ipywidgets import interact, interact_manual
# + code_folding=[] hidden=true
# Decorator with function
@interact(ptype=df_LH_summ.index, attr=l_keep, logScale=[False,True])
def plot_interactive(ptype, attr, logScale):
# # ptype = 'RSFR'
# df_LH_attr = df_LH[df_LH.property_type==ptype].reset_index(drop=True)
# df_others_attr = df_others[df_others.property_type==ptype].reset_index(drop=True)
# # attr = 'loan_amount'
# ds1 = df_LH_attr[attr]
# ds2 = df_others_attr[attr]
# if logScale:
# df_attr = pd.DataFrame({'LendingHome':np.log10(ds1), 'Others':np.log10(ds2)})
# else:
# df_attr = pd.DataFrame({'LendingHome':ds1, 'Others':ds2})
# # df_attr.head(3)
# # Raincloud Plot for distribution - var: ATTR
# ax = pt.RainCloud(x='Lender Type',y=f'{attr.upper()}', alpha=0.75, pointplot=True,
# data = df_attr.stack().rename(f'{attr.upper()}').reset_index().rename(
# columns={'level_1':'Lender Type'}), orient='h')
# ax.xaxis.set_minor_locator(AutoMinorLocator(5))
# ax.grid(True, ls=(0, (5, 5)), drawstyle='steps')
# if not logScale:
# ax.set_xlim(df_attr.Others.quantile(q=0.01), df_attr.Others.quantile(q=0.99))
# + [markdown] heading_collapsed=true
# ### Clustering technique
# + hidden=true
# Load Kmean clustering lib
from sklearn.cluster import KMeans
# Load Gaussian mixture model library
from sklearn import mixture
# + hidden=true
# Perform clustering: Gaussian Mix Modeling (GMM) with selected non-trivial features
l_cluster = []
df_cluster = df_dataset[[response]]
X = df_dataset.drop(columns=[response]+list(set(features) - set(feature_score.keys())))
for n_center in range(3,7):
cls = f'n_cluster_{n_center}'
l_cluster.append(cls)
# print('Number of center to cluster: {}'.format(n_center), flush=True)
# cmodel = KMeans(n_clusters=n_center, random_state=777)
cmodel = mixture.GaussianMixture(n_components=n_center, random_state=777)
print('Number of gaussian component to cluster: {}'.format(n_center), flush=True)
cmodel.fit(X) # go fitting
df_cluster.loc[:, cls] = cmodel.predict(X)+1 # classify each user
# User count and return rate summary for each cluster
# display(get_ret_rate(df_cluster, cls, response))
# + [markdown] heading_collapsed=true
# ### Imbalance dataset - oversampling vs. undersampling
# https://imbalanced-learn.readthedocs.io/en/stable/introduction.html
# + hidden=true
from collections import Counter
from imblearn.over_sampling import RandomOverSampler
from imblearn.under_sampling import RandomUnderSampler
# instantiating over and under sampler
over = RandomOverSampler(sampling_strategy=0.5)
under = RandomUnderSampler(sampling_strategy=0.8)
X = df_data[features]
y = df_data[response]
# first performing oversampling to minority class
X_over, y_over = over.fit_resample(X, y)
print(f"Oversampled: {Counter(y_over)}")
# Oversampled: Counter({0: 9844, 1: 4922})
# now to comine under sampling
X_combined_sampling, y_combined_sampling = under.fit_resample(X_over, y_over)
print(f"Combined Random Sampling: {Counter(y_combined_sampling)}")
# Combined Random Sampling: Counter({0: 6152, 1: 4922})
# + [markdown] heading_collapsed=true
# ### Split dataset and k-fold for cross-validation
# + hidden=true
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
df_dataset[features], df_dataset[response], test_size=0.15, random_state=777)
# + hidden=true
X_train = df_dataset[features]
y_train = df_dataset[response]
# + hidden=true
kf = KFold(n_splits=10, shuffle=True, random_state=777)
for train_idx, valid_idx in kf.split(y_train):
pass
# + hidden=true
skf = StratifiedKFold(n_splits=10, random_state=777, shuffle=True)
for train_idx, valid_idx in skf.split(X_train, y_train):
# Prepare train and valid set
X_train_np = X_train.iloc[train_idx].values
y_train_np = y_train.iloc[train_idx].values
X_valid_np = X_train.iloc[valid_idx].values
y_valid_np = y_train.iloc[valid_idx].values
# X_local_train = preprocessor.fit_transform(X_train.iloc[train_idx])
# y_local_train = y_train.iloc[train_idx].values.ravel()
# X_local_test = preprocessor.transform(X_train.iloc[valid_idx])
# y_local_test = y_train.iloc[valid_idx].values.ravel()
# + hidden=true
# Model training setup
best_model = None
best_model_perf = {'ACC':0, 'REC':0}
acc_train, rec_train, _ = model_performance(model, X_train_np, y_train_np, 'Train')
acc_valid, rec_valid, _ = model_performance(model, X_valid_np, y_valid_np, 'Valid')
# check if better model
# acc_avg, rec_avg = 0.5*(acc_train+acc_valid), 0.5*(rec_train+rec_valid)
# if acc_avg > best_model_perf['ACC'] and rec_avg > best_model_perf['REC']:
if acc_valid > best_model_perf['ACC'] and rec_valid > best_model_perf['REC']:
print('Found better model.')
best_model = model
best_model_perf = {'ACC':acc_valid, 'REC':rec_valid, 'fold':fold_indx}
# best_model.save_model('ml-xgb-best_model.xgb')
print(f'Best model trained with performance at fold {best_model_perf["fold"]}:')
model_performance(model, X_train.values, y_train.values, 'Overall');
# + [markdown] heading_collapsed=true
# ### Linear Regression
# + hidden=true
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(X, y)
# + [markdown] heading_collapsed=true
# ### Logistic Regression
# + hidden=true
from sklearn.linear_model import LogisticRegression
clf_lr = LogisticRegression(random_state=777)
clf_lr.fit(X_train, y_train)
# + hidden=true
# feature coeff bar plot
l_sorted = sorted(zip(features_selected, clf_lr.coef_[0]), key=lambda x: x[1],reverse=True)
def plot_feature_importance(l_sorted, sig_lvl=1):
plt.rcParams["figure.figsize"] = [15, 6]
x_feat = [feat for feat, coef in l_sorted if abs(coef) > sig_lvl]
y_feat = [coef for feat, coef in l_sorted if abs(coef) > sig_lvl]
plt.bar(range(len(x_feat)), y_feat, align='center')
_ = plt.xticks(range(len(x_feat)), x_feat, rotation=30)
# + [markdown] heading_collapsed=true
# ### XGBoost Model
# https://towardsdatascience.com/catboost-vs-light-gbm-vs-xgboost-5f93620723db
# + hidden=true
import xgboost
from xgboost import XGBClassifier # XGBRegressor
clf = XGBClassifier(n_jobs=2, learning_rate=0.25, random_state=777, n_estimators=200) #silent=False,
model = clf.fit(X_train_local, y_train_local, \
eval_set=[(X_valid_local, y_valid_local)], \
early_stopping_rounds=10, verbose=False)
# xgb_model= None) # if not best_model else best_model.get_booster())
# + hidden=true
from collections import OrderedDict
feature_score = OrderedDict()
# Select features with non-trivial impact to the model (threshold=1)
for k,v in sorted(best_model.get_booster().get_fscore().items(), key=lambda x:x[1], reverse=True):
if v > 1:
feat = features[int(k[1:])]
print(f'{k} - {feat} - {v}')
feature_score[feat] = v
# xgboost.plot_importance(best_model, max_num_features=10);
# + [markdown] heading_collapsed=true
# ### DNN - Tensorflow
# + hidden=true
# Create DNN model using keras
input_vecs = Input(shape=(len(features),))
nn = layers.Dropout(0.5)(layers.Dense(128, activation='relu')(input_vecs))
nn = layers.BatchNormalization()(nn)
nn = layers.Dropout(0.5)(layers.Dense(64, activation='relu')(nn))
nn = layers.BatchNormalization()(nn)
nn = layers.Dense(16, activation='relu')(nn)
nn = layers.BatchNormalization()(nn)
nn = layers.Dense(4, activation='relu')(nn)
result = layers.Dense(2, activation='softmax')(nn)
# result = layers.Dense(1, activation='linear')(nn) # tanh
init_model = models.Model(input_vecs, result)
init_model.compile(optimizer='adam', loss='categorical_crossentropy')
# init_model.compile(optimizer='adam', loss='mean_squared_error')
# + hidden=true
# Go training!
best_model.fit(X_train_np, y_train_np, epochs=200, verbose=2,
validation_data= (X_valid_np, y_valid_np), # class_weight={0:1, 1:2},
batch_size=128,
callbacks= [EarlyStopping(patience=4, verbose=1, mode='min', restore_best_weights=True)])
# -
# ### DNN - pyTorch
# + code_folding=[]
# PyTorch libs
import torch
import torch.nn as nn
# import torchvision
# import torchvision.transforms as transforms
import logging
# https://github.com/wavepak/torchsample.git
from torchsample.modules import ModuleTrainer
from torchsample.callbacks import EarlyStopping, ReduceLROnPlateau
# + code_folding=[1, 21]
class DNN(nn.Module):
def __init__(self, input_size):
super(DNN, self).__init__()
self.reluAct = nn.ReLU()
self.dropOut = nn.Dropout(0.5)
self.batchNorm_il = nn.BatchNorm1d(512)
self.batchNorm_h1 = nn.BatchNorm1d(256)
self.batchNorm_h2 = nn.BatchNorm1d(64)
self.batchNorm_h3 = nn.BatchNorm1d(16)
self.logSoftAct = nn.LogSoftmax(dim=1)
# self.softAct = nn.Softmax()
# self.sigmoid = nn.Sigmoid()
self.input_layer = nn.Linear(input_size, 512) # equivalent to Dense in keras
self.hidden_layer1 = nn.Linear(512, 256)
self.hidden_layer2 = nn.Linear(256, 64)
self.hidden_layer3 = nn.Linear(64, 16)
self.hidden_layer4 = nn.Linear(16, 4)
self.output_layer = nn.Linear(4, 2)
def forward(self, x):
clsf = self.input_layer(x)
clsf = self.dropOut(self.reluAct(clsf))
clsf = self.batchNorm_il(clsf)
clsf = self.hidden_layer1(clsf)
clsf = self.dropOut(self.reluAct(clsf))
clsf = self.batchNorm_h1(clsf)
clsf = self.hidden_layer2(clsf)
clsf = self.reluAct(clsf)
clsf = self.batchNorm_h2(clsf)
clsf = self.hidden_layer3(clsf)
clsf = self.reluAct(clsf)
clsf = self.batchNorm_h3(clsf)
clsf = self.hidden_layer4(clsf)
clsf = self.reluAct(clsf)
clsf = self.output_layer(clsf)
clsf = self.logSoftAct(clsf)
return clsf
def create_logger(self, logname='logger'):
logger = logging.getLogger()
fh = logging.FileHandler(logname+'.log')
fh.setFormatter(logging.Formatter('%(asctime)s - %(levelname)s: %(message)s', '[%Y-%m-%d %H:%M:%S]'))
logger.setLevel(logging.INFO)
logger.addHandler(fh)
return logging
# +
# https://github.com/ncullen93/torchsample/blob/master/examples/mnist_loader_example.py
model = DNN(len(features))
trainer = ModuleTrainer(model)
callbacks = [EarlyStopping(monitor='val_loss', patience=5),
ReduceLROnPlateau(factor=0.5, patience=3)]
# Negative Log Likelihood Loss (nll_loss)
# https://pytorch.org/docs/master/nn.functional.html#torch.nn.functional.nll_loss
trainer.compile(optimizer='adam', loss='nll_loss', callbacks=callbacks)
# -
# Go training!
best_model.model.train()
best_model.fit(X_train_ts, y_train_ts, val_data=(X_valid_ts, y_valid_ts), shuffle=True,
num_epoch=200, batch_size=bsize, verbose=1)
# + [markdown] heading_collapsed=true
# ### Time series
# + hidden=true
from statsmodels.tsa.stattools import adfuller
def test_stationarity(timeseries):
rolmean = timeseries.rolling(window=30).mean()
rolstd = timeseries.rolling(window=30).std()
plt.figure(figsize=(14,5))
sns.despine(left=True)
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label = 'Rolling Std')
plt.legend(loc='best'); plt.title('Rolling Mean & Standard Deviation')
plt.show()
print ('<Results of Dickey-Fuller Test>')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4],
index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print(dfoutput)
# df1=df.resample(freq='D', how=np.mean)
# test_stationarity(df1.Spend.dropna())
# test_stationarity(df1[‘Spend’].diff(1).dropna())
# + hidden=true
# ACF and PACF plots
# from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.figure()
plt.subplot(211)
plot_acf(series, ax=plt.gca())
plt.subplot(212)
plot_pacf(series, ax=plt.gca())
plt.show()
# + hidden=true
import statsmodels.api as sm
fit1 = sm.tsa.statespace.SARIMAX(train.Spend, order=(7, 1, 2), seasonal_order=(0, 1, 2, 7)).fit(use_boxcox=True)
test['SARIMA'] = fit1.predict(start="2019-07-23", end="2019-09-23", dynamic=True)
plt.figure(figsize=(16, 8))
plt.plot(train['Spend'], label='Train')
plt.plot(test['Spend'], label='Test')
plt.plot(test['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()
# + hidden=true
# Hot-Winters’ additive model
from statsmodels.tsa.api import ExponentialSmoothing
fit1 = ExponentialSmoothing(np.asarray(train['Spend']) ,seasonal_periods=7 ,trend='add', seasonal='add').fit(use_boxcox=True)
test['Holt_Winter'] = fit1.forecast(len(test))
plt.figure(figsize=(16,8))
plt.plot( train['Spend'], label='Train')
plt.plot(test['Spend'], label='Test')
plt.plot(test['Holt_Winter'], label='Holt_Winter')
plt.legend(loc='best')
plt.show()
# -
# ## 2. Model Evaluation
# Regression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
def model_performance(model, X, y, dlabel):
# Evalute model performance on dataset
pred = model.predict(X)
r2 = r2_score(y, pred)
rmse = np.sqrt(mean_squared_error(y, pred))
mae = mean_absolute_error(y, pred)
print(f'{dlabel} R2: {r2:.2f}\tRMSE: {rmse:.2f}\tMAE: {mae:.2f}')
return r2, rmse, mae
# Classification
from sklearn.metrics import accuracy_score, roc_auc_score, recall_score, confusion_matrix, roc_curve # binary
def model_performance(model, X, y, dlabel):
# Evalute model performance on dataset
pred = model.predict(X)
acc = accuracy_score(y, pred)
auc = roc_auc_score(y, pred)
rec = recall_score(y, pred)
print(f'{dlabel} ACC: {acc:.2f}\tREC: {rec:.2f}\tAUC: {auc:.2f}')
return acc, auc, rec
fpr, tpr, thr = roc_curve(y, pred_prob[:,1], pos_label=1)
ax.plot(fpr, tpr, color, label="ACC: {:.2f} AUC: {:.2f} REC: {:.2f}".format(acc, auc, rec))
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
confusion_matrix(y_test, clf.predict(X_test)) # tn, fp, fn, tp
# Multiclass case
acc = accuracy_score(y, np.argmax(pred, axis=1))
auc = roc_auc_score(pd.get_dummies(y), pred, multi_class='ovr', average='micro')
rec = recall_score(y, np.argmax(pred, axis=1), average='macro', labels=[0,1])
|
Data_science_toolkits.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
# %matplotlib inline
import pandas
data = pandas.read_csv('gapminder.csv', index_col='country')
years = data.columns.str.strip('gdpPercap_')
data.columns = years.astype(int)
data.loc['Australia'].plot()
|
gapminder.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.7 64-bit
# language: python
# name: python3
# ---
# +
from matplotlib import pyplot as plt
import cv2, cv2 as cv
img_names = [ "lenna.png", "camera_man.png", "messi.png", ]
# 서브 챠트 생성
chart_idx = 0
fig, charts = plt.subplots( 1, len(img_names), figsize=(18, 17) )
charts = charts.ravel()
for idx, img_name in enumerate(img_names) :
chart = charts[ idx ]
title = img_name.split( "." )[0]
img = cv.imread( f"./image/{img_name}", 0 )
chart.imshow( img, cmap='gray' )
chart.set_title( title )
chart.set_xlabel( f"size = {img.shape}")
pass
plt.show()
# +
print( "Hello..." )
import numpy as np, time, cv2, cv2 as cv, math
from matplotlib import pyplot as plt
print( "Import done.\n" )
def polar(theta):
return 1.0*np.cos(theta) + 1.0j*np.sin(theta)
pass
facts = {}
facts[0] = 1.0
def factorial(n):
if n in facts :
return facts[n]
else :
f = n * factorial(n - 1)
facts[n] = f
return f
pass
pass
poly_coeffs = {}
def poly_coeff(m, n, l) :
key = f"{<KEY>
if key in poly_coeffs :
return poly_coeffs[ key ]
else :
poly_coeff = (-1.0)**m * factorial(n-m) / ( factorial(m) * factorial((n - 2*m + l) // 2) * factorial((n - 2*m - l) // 2) )
poly_coeffs[ key ] = poly_coeff
return poly_coeff
pass
pass # -- poly_coeff
def zernike_poly(Y, X, N, L):
y, x = Y[0], X[0]
vxy = np.zeros(Y.size, dtype=complex)
for index, (x, y) in enumerate( zip(X,Y) ):
vnl = 0.
for M in range( int( (N-L)//2 + 1 ) ):
vnl += poly_coeff( M, N, L ) * ( np.sqrt(x*x + y*y)**(N - 2*M) * polar( L*np.arctan2(y,x) ) )
#vnl += (-1.0)**m * factorial(n-m) / ( factorial(m) * factorial((n - 2*m + l) // 2) * factorial((n - 2*m - l) // 2) ) * \
# ( sqrt(x*x + y*y)**(n - 2*m) * polar(1.0, l*atan2(y,x)) )
pass
vxy[index] = vnl
pass
return vxy
pass # -- zernike_poly
def zernike_reconstruct(img, T, K = 1, hdr = "" ):
# image scale up
shape = img.shape
height = shape[0] ; width = shape[1]
img = cv2.resize( img, (width*K, height*K), interpolation= cv2.INTER_LINEAR)
shape = img.shape
rows, cols = shape
radius = min( rows, cols )/2.0
radius = math.sqrt( rows*rows + cols*cols )/2.0
print( f"{hdr} radius = {radius}" )
idx = np.ones(img.shape)
y, x = np.where(idx > 0)
#p = img[y, x].ravel()
p = img.ravel()
yn = ( (y - rows/2.0)/radius ).ravel()
xn = ( (x - cols/2.0)/radius ).ravel()
k = (np.sqrt(xn**2 + yn**2) <= 1.)
frac_center = np.array(p[k], np.double)
yn = yn[k]
xn = xn[k]
frac_center = frac_center.ravel()
# In the discrete case,
# the normalization factor is not pi but the number of pixels within the unit disk
npix = float(frac_center.size)
reconstr = np.zeros(img.size, dtype=complex)
accum = np.zeros(yn.size, dtype=complex)
for n in range( T + 1 ):
for l in range( n + 1 ):
if (n-l)%2 == 0:
# get the zernike polynomial
vxy = zernike_poly(yn, xn, float(n), float(l))
# project the image onto the polynomial and calculate the moment
a = sum(frac_center * np.conjugate(vxy)) * (n + 1)/npix
# reconstruct
accum += a * vxy
pass
pass
pass
reconstr[k] = accum
return reconstr
pass # -- zernike_reconstruct
# img_reconst
def img_reconst(img_name) :
Ts = [ 10, 20, 30, 40 ]
Ks = [ 1, 3, 5 ]
# 서브 챠트 생성
chart_idx = 0
fig, charts = plt.subplots( len(Ts), len(Ks), figsize=(18, 18) )
charts = charts.ravel()
# 이미지 읽기
img = cv.imread( f"./image/{img_name}.png", 0 )
shape = img.shape
width = 100
if shape[1] > width :
img = cv2.resize( img, (width, shape[0]*width//shape[1]), interpolation= cv2.INTER_LINEAR)
pass
cv2.imwrite( f"./temp/{img_name}_{0:02d}_{0:02d}_org.png", img )
img_org = img
height = img.shape[0]; width = img.shape[1]
chart_idx = 0
for t_idx, T in enumerate( Ts ) :
for k_idx, K in enumerate( Ks ) :
# image reconstruct
hdr = f"{img_name} : T = {T}, K = {K}"
start_time = time.time()
reconst = zernike_reconstruct( img, T, K, hdr )
reconst = reconst.reshape( [height*K, width*K] )
img_conv = reconst.real.astype( np.uint8 )
img_conv = cv2.resize( img_conv, (width, height), interpolation= cv2.INTER_LINEAR)
print( f"{hdr} img_con size = {img_conv.shape}" )
elapsed = (time.time() - start_time)
print( f"{hdr} time elapsed = {elapsed:.1f}" )
# psnr
img_diff = img_conv.astype( np.float64 ) - img_org.astype( np.float64 )
gmax = np.max( img_diff ) + 0.0 # 복원된 이미지의 회색조 최대값
mse = np.sum( np.square( img_diff )/img_diff.size ) + 0.0
psnr = 10.0*math.log10(gmax*gmax/mse)
cv2.imwrite( f"./temp/{img_name}_{T:02d}_{K:02d}_{psnr:.2f}.png", img_conv )
# show image
chart = charts[ chart_idx ]
title = f"{hdr}, elapsed={elapsed:.1f}"
chart.imshow( img_conv, cmap='gray' )
chart.set_title( title )
chart.set_xlabel( f"psnr = {psnr:.2f}" )
chart_idx += 1
print( "*"*80 )
pass
print( "#"*80 )
pass
fig.tight_layout()
plt.show()
pass # -- img_reconst
img_names = [ "lenna", "camera_man", "messi" ]
img_names = [ "camera_man", "messi" ]
img_names = [ "f", "lenna", ]
img_names = [ "f" ]
for img_name in img_names :
img_reconst( img_name )
pass
print( "\nGood bye!.")
|
MyZernike.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Soluzione per la Maze Challenge
# # Studenti: *<NAME> / <NAME>*
# ## Quest 1-2-3
# La prima Quest richiedeva l'esplorazione del labirinto sfruttando il file `mazeClient.py` con delle utility pronte messe a disposizione. Si noti che dalla risoluzione della Quest 1 derivano facilmente la risoluzione della Quest 2 e 3 (che riguardano semplicemente la raccolta di informazioni durante l'esplorazione).
#
# ### Analisi
# Richiedendo l'output del comando *GET_STATE*, si ottiene qualcosa del genere:
#
# `{'userX': 14, 'userY': 12, 'userVal': 32, 'Neighbors': [{'x': 14, 'y': 13, 'val': 71}]}`
#
# Analizzandolo, si è capito che:
# * userX: indice di riga;
# * userY: indice di colonna;
# * userVal: rappresentazione numerica del colore della cella;
# * Neighbors: lista delle celle circostanti.
#
# Si è notato inoltre che *Neighbors* contiene anche le celle diagonalmente vicine, che non sono però raggiungibile mediante un comando di quelli proposti e che andranno perciò tralasciate.
#
# ### Progettazione
# In base all'analisi fatta, il labirinto è facilmente trattabile come un grafo non orientato. Tra gli algoritmi basilari e più conosciuti per l'esplorazione, ce ne sono 2:
# * Esplorazione in ampiezza (BFS): va scartata perché con la lista dei comandi resa disponibile non è possibile spostarsi in un solo passaggio a degli indici stabiliti;
# * Esplorazione in profondità (DFS): fattibile, poiché ad ogni passaggio ci si sposta unicamente in celle vicine.
#
# Per cui si è scelto di esplorare il labirinto scrivendo una funzione DFS opportunatamente modificata. Si è implementata una versione ricorsiva per maggiore chiarezza e compattezza del codice (i labirinti generati sono comunque molto piccoli, per cui il rischio di esaurire la memoria è praticamente nullo).
#
# Una versione iterativa dell'algoritmo è stata inizialmente pensata e scritta tramite pseudocodice, che riportiamo di seguito per completezza e future migliorie:
# ```
# - Scegli un vicino NON visitato:
# - Vai dal vicino
# - Altrimenti (nessun vicino ok):
# - Controlla se puoi andare back
# - Vai back
# - Altrimenti (sono tornato all'origine):
# - Termina
# ```
#
# ### Codice
# Si è scelto di creare una classe `Maze` contenente tutti i metodi per l'esplorazione del labirinto e conseguente raccolta dati.
# Per esplorare il labirinto, basta creare un oggetto di tipo `Maze`. Verrà richiamato il metodo `__init__()` che inizializzerà le variabili dove verranno salvate le statistiche (in vari formati per comodità), esplorerà il primo nodo e chiamerà la funzione `dfs_visit()` per esplorare il resto del labirinto a partire dal primo nodo. Nello specifico le variabili per la raccolta delle statistiche sono:
# * **visited**: una lista che contiene i nodi esattamente come vengono restituiti dal server (utili per il plotting della mappa);
# * **colors_x** e **colors_y**: dei dizionari che contengono per ogni x e per ogni y le occorrenze di ogni colore (utile per il plotting della distribuzione dei colori rispetto alle x e alle y;
# * **colors_count**: un dizionario che contiene il numero di occorrenze di ogni colore (utile per le Quest 2-3).
# +
from mazeClient import send_command
from mazeClient import Commands as command
import json
import pickle
from time import sleep
class Maze():
"""
Class that contains methods to solve the maze
"""
def __init__(self):
# Initialize variables used to collect data from maze
# visited = map representation
# colors_xy = distribution of colors on x,y axes
# colors_count = count of each color present in the map
self.visited = []
self.colors_x = {}
self.colors_y = {}
self.colors_count = {
'red': 0,
'green': 0,
'blue': 0,
'white': 0
}
# Initialize map to better manage colors
self.c_map = {
82: 'red',
71: 'green',
66: 'blue',
32: 'white'
}
# Visit the root (starting position)
curr_node = self.get_dict(send_command(command.GET_STATE))
self.visited.append({
'x': curr_node['userX'],
'y': curr_node['userY'],
'val': curr_node['userVal']
})
# Explore the maze
self.dfs_visit(curr_node, command.GET_STATE)
def get_dict(self, data: bytes):
"""
Parse data and returns a dictionary (more usable)
"""
return json.loads(data.decode('ascii'))
def get_inverse_command(self, cmd: "mazeClient.Commands"):
"""
Returns the "Go Back" command
"""
cmd_map = {
command.MOVE_LEFT: command.MOVE_RIGHT,
command.MOVE_RIGHT: command.MOVE_LEFT,
command.MOVE_UP: command.MOVE_DOWN,
command.MOVE_DOWN: command.MOVE_UP,
command.GET_STATE: command.GET_STATE
}
return cmd_map[cmd]
def get_command_from_pos(self, org: dict, dst: dict) -> "mazeClient.Commands":
"""
Return command to let you move from org to dst
"""
diff_x = org['userX'] - dst['x']
diff_y = org['userY'] - dst['y']
if diff_x == 1:
return command.MOVE_DOWN
elif diff_x == -1:
return command.MOVE_UP
elif diff_y == 1:
return command.MOVE_RIGHT
elif diff_y == -1:
return command.MOVE_LEFT
return command.GET_STATE # Bad usage
def get_reachable_neighbors(self, v: dict):
"""
Returns valid neighbors (excludes the diagonal ones)
"""
tmp = []
for el in v["Neighbors"]:
if (el["x"] - v["userX"] == 0) or (el["y"] - v["userY"] == 0):
tmp.append(el)
return tmp
def visit_node(self, node: dict):
"""
Visit a node and save informations about it
"""
# Extract data from node
node_x = node['x']
node_y = node['y']
node_color = self.c_map[node['val']]
# Save informations
self.visited.append(node)
self.colors_count[node_color] += 1
self.colors_x.setdefault(node_x, {
'red': 0,
'green': 0,
'blue': 0,
'white': 0
})[node_color] += 1
self.colors_y.setdefault(node_y, {
'red': 0,
'green': 0,
'blue': 0,
'white': 0
})[node_color] += 1
def dfs_visit(self, v: dict, last_cmd: str):
"""
DFS Algorithm to explore the maze
"""
for u in self.get_reachable_neighbors(v):
if u not in self.visited:
# Visit the neighbor
self.visit_node(u)
# Move to neighbor
cmd = self.get_command_from_pos(v, u)
u = self.get_dict(send_command(cmd))
#sleep(0.5)
# Visit from that neighbor
self.dfs_visit(u, cmd)
# Move back, no more valid neighbors
send_command(self.get_inverse_command(last_cmd))
#sleep(0.5)
# -
# ## Quest 4, 5 (and extra 3); Advanced Quest 1, 2
# Per risolvere le Quest 4, 5 si è utilizzata la libreria **matplotlib**, utilizzando i dati raccolti durante l'esplorazione del labirinto. Si è deciso inoltre di fare un passo in più rispetto a quanto richiesto della Quest 3, plottando anche un istogramma relativo alla distribuzione dei colori in tutta la mappa.
# Si noti che le funzioni presentate di seguito sono state poste in un file a parte (`stats.py`) per fare ordine.
# Import for plotting operations
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
# ### `plot_map()`
# Visualizza il plot di una matrice che rappresenta la mappa del labirinto. Si è scelto di utilizzare la funzione di matplotlib [mathshow()](https://matplotlib.org/3.2.1/api/_as_gen/matplotlib.pyplot.matshow.html).
#
# Per rappresentare con dei colori personalizzati la matrice, si è effettuato un mapping dei colori a partire dagli interi restituiti dal server, per poi far effettuare un secondo mapping a matplotlib per l'assegnazione vera e propria dei colori.
#
# Si noti che il calcolo dei valori minimi e massimi è stato scritto in maniera poco efficiente per favorire la leggibilità e compattezza del codice.
def plot_map(visited: list):
"""
Plots the map constructing a matrix.
Remember that x = row index, y = column index.
"""
# Colors mapping for matshow library method
colors_map = {82: 1, 71: 2, 66: 3, 32: 4}
cmap = ListedColormap(['k', 'r', 'g', 'b', 'w'])
# Get the coordinates max and min
x_min = min(visited, key=lambda el:el['x'])['x']
x_max = max(visited, key=lambda el:el['x'])['x']
y_min = min(visited, key=lambda el:el['y'])['y']
y_max = max(visited, key=lambda el:el['y'])['y']
matrix_plt = np.zeros((x_max - x_min + 1, y_max - y_min + 1))
for el in visited:
matrix_plt[
x_max - el["x"],
y_max - el["y"]
] = colors_map[el["val"]]
# Plotting the matrix
plt.matshow(matrix_plt, cmap=cmap)
plt.suptitle('Maze representation')
plt.xticks(range(0, y_max-y_min+1, 2), range(y_max, y_min-1, -2))
plt.yticks(range(0, x_max-x_min+1, 2), range(x_max, x_min-1, -2))
plt.show()
# ### `plot_colors_dist()`
# Visualizza un istogramma rappresentante la distribuzione dei colori nella mappa. Si è scelto di utilizzare la funzione di matplotlib [bar()](https://matplotlib.org/3.2.1/api/_as_gen/matplotlib.pyplot.bar.html).
#
# Si noti che viene anche calcolato il numero di celle totali presenti nella mappa, come richiesto dalla Quest 2.
def plot_colors_dist(nodes_count: dict):
"""
Additional plot that shows colors distribution in the map (not requested by any quest)
"""
# Prepare data
names = list(nodes_count.keys())
values = list(nodes_count.values())
colors = ['0.5', 'r', 'g', 'b']
total_cells = sum(nodes_count.values())
# Plot
fig, ax = plt.subplots()
fig.suptitle(f"Colors distribution (total cells: {total_cells})")
rects = ax.bar(names, values, color=colors, align='center')
# Attach a text label above each bar in rects, displaying its height
for rect in rects:
height = rect.get_height()
ax.annotate('{}'.format(height),
xy=(rect.get_x() + rect.get_width() / 2, height),
xytext=(0, 1), # 1 points vertical offset
textcoords="offset points",
ha='center', va='bottom')
plt.show()
# ### `plot_colors_xy_dist()`
# Visualizza il plot delle distribuzioni dei colori rispetto alle x ed alle y. Si è scelto di utilizzare la funzione di matplotlib [bar()](https://matplotlib.org/3.2.1/api/_as_gen/matplotlib.pyplot.bar.html).
#
# Sono state create delle procedure interne per evitare ridondanza nel codice e aumentarne la leggibilità. Nello specifico:
# * `preprocess_data_hist()`: prepara i dati per essere utilizzati da matplotlib;
# * `plot_axes()`: visualizza con un grafico a barre la distribuzione dei colori. Si noti che in particolare questa funzione viene richiamata 2 volte, per permettere il confronto delle distribuzioni tra il vecchio labirinto ed il corrente.
def plot_colors_xy_dist(maze: "Maze", past_maze: "Maze"):
"""
Plot a grouped bar chart that represents colors distribution on x and y
"""
def preprocess_data_hist(colors_xy: tuple):
"""
Internal function that preprocess data for matplotlib
"""
colors_x, colors_y = colors_xy
x_label = []
x_red = []
x_green = []
x_blue = []
x_white = []
y_label = []
y_red = []
y_green = []
y_blue = []
y_white = []
for key in sorted(colors_x):
x_label.append(key)
x_red.append(colors_x[key]["red"])
x_green.append(colors_x[key]["green"])
x_blue.append(colors_x[key]["blue"])
x_white.append(colors_x[key]["white"])
for key in sorted(colors_y):
y_label.append(key)
y_red.append(colors_y[key]["red"])
y_green.append(colors_y[key]["green"])
y_blue.append(colors_y[key]["blue"])
y_white.append(colors_y[key]["white"])
return x_label, x_red, x_green, x_blue, x_white, y_label, y_red, y_green, y_blue, y_white
def plot_axes(ax1, ax2, colors_xy, label="", width=0.2):
"""
Internal function that plots colors distribution on given axes
Width is used to determine the width of each bar
"""
# Preprocess data
x_label, x_red, x_green, x_blue, x_white, y_label, y_red, y_green, y_blue, y_white = preprocess_data_hist(colors_xy)
# Prepare bars for colors x distribution
x = np.arange(len(x_label))
ax1.bar(x - 3*width/2, x_red, width, label='Red', color="red")
ax1.bar(x - width/2, x_green, width, label='Green', color="green")
ax1.bar(x + width/2, x_blue, width, label='Blue', color="blue")
ax1.bar(x + 3*width/2, x_white, width, label='White', color="grey")
# Add some text for labels, title and custom x-axis tick labels, etc.
ax1.set_ylabel('Frequency')
ax1.set_title(label + "X (rows)")
ax1.set_xticks(x)
ax1.set_xticklabels(x_label)
# Prepare bars for colors y distribution
y = np.arange(len(y_label)) # the label locations
ax2.bar(y - 3*width/2, y_red, width, label='Red', color="red")
ax2.bar(y - width/2, y_green, width, label='Green', color="green")
ax2.bar(y + width/2, y_blue, width, label='Blue', color="blue")
ax2.bar(y + 3*width/2, y_white, width, label='White', color="grey")
# Add some text for labels, title and custom x-axis tick labels, etc.
ax2.set_ylabel('Frequency')
ax2.set_title(label + "Y (cols)")
ax2.set_xticks(y)
ax2.set_xticklabels(y_label)
# Create figure, axes and then plot
if past_maze:
fig, ((ax11, ax12), (ax21, ax22)) = plt.subplots(2,2)
plot_axes(ax21, ax22, (past_maze.colors_x, past_maze.colors_y), label="PAST maze color distribution on ")
else:
fig, (ax11, ax12) = plt.subplots(1,2)
fig.set_size_inches(12, 8)
plot_axes(ax11, ax12, (maze.colors_x, maze.colors_y), label="CURRENT maze color distribution on ")
plt.show()
# ### Main
# Di seguito il codice principale del programma. Si noti che per risolvere l'Advanced Quest 2, si è scelto di salvare l'oggetto *maze* in un file **pickle**. Questo è utilizzato per fare una comparazione tra la distribuzione dei colori del labirinto della precedente esecuzione e di quello della corrente esecuzione.
# +
# Explore the Maze (Quests 1-2-3)
maze = Maze()
# Get data of past map (if they exist)
try:
with open('past_maze.pickle', 'rb') as f:
past_maze = pickle.load(f)
except FileNotFoundError:
past_maze = None
# Plot statistics of the maze (Quests 3-4-5, Advanced Quest 2)
plot_colors_dist(maze.colors_count)
plot_colors_xy_dist(maze, past_maze)
plot_map(maze.visited)
# Save current map (Part of Advanced Quest 2)
with open('past_maze.pickle', 'wb') as f:
pickle.dump(maze, f)
# -
# ## Advanced Quest 3
#
# Per l'ultima quest, si è creato un file a parte (`client_controller.py`). Si è utilizzata la libreria **pynput** per l'acquisizione dell'input.
#
# Si è scelto di usare i tasti 'WASD' per muoversi nel labirinto, in quanto le frecce direzionali vengono già prese in input dal server se la finestra è attiva, rendendo totalmente inutile implementarne il supporto.
#
# Si noti inoltre che si è anche scelto di rendere disponibile la pressione del tasto 'E' per ottenere le informazioni sul nodo corrente.
# +
# -*- coding: utf-8 -*-
from mazeClient import Commands as command
from mazeClient import send_command
from pynput import keyboard
def on_press(key):
"""
Listen for input and move if any of 'WASD' is pressed
Exit if any other key is pressed
"""
# Not a valid key pressed?
if not hasattr(key, 'char'):
return False
if not key.char in keycode_map:
return False
# Map keycode to action and execute action
action = keycode_map[key.char]
res = send_command(action)
# Just some print to let user have some feedback
if action == command.GET_STATE:
print(res)
else:
print(action)
if __name__ == "__main__":
# Initialize mapping variable
keycode_map = {
'w': command.MOVE_UP,
'a': command.MOVE_LEFT,
's': command.MOVE_DOWN,
'd': command.MOVE_RIGHT,
'e': command.GET_STATE
}
print("INSTRUCTIONS:\n\tWASD -> Move around the maze;\n\tE -> GET STATE;\n\tAny other Key: QUIT")
# Collect events until released
with keyboard.Listener(on_press=on_press) as listener:
listener.join()
|
mazeChallenge/antoniostrippoli_lucamoroni/report.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Noise Magnitude vs Coefficient Estimate Error
#
# Tests the effect of Gaussian white noise on the estimated coefficients
# +
# %load_ext autoreload
# %autoreload 2
# Import Python packages
import pickle
# Package Imports
from sindy_bvp import SINDyBVP
from sindy_bvp.differentiators import PolyInterp
from sindy_bvp.library_builders import NoiseMaker
# -
# Set file to load and stem for saving
load_stem = "./data/S3-P2-"
save_stem = "./data/Fig4a-S3-"
# +
# %%time
# Set a range of noise magnitudes to test
noise_magnitudes = [0.001, 0.005, 0.01, 0.02, 0.03, 0.04, 0.05, 0.075, 0.10]
# Since the data is noisy, we'll use a Polynomial Interpolation derivative method
poly = PolyInterp(diff_order=2, width=20, degree=5)
# Create an empty
results_list = []
print("Completed:", end=" ")
for noise_mag in noise_magnitudes:
# Initialize NoiseMaker, which adds noise then filters noisy signal
nm = NoiseMaker(noise_magnitude=noise_mag,
gaussian_filter_sigma=None)
# Initialize SINDyBVP object
sbvp = SINDyBVP(file_stem = load_stem,
num_trials = 200,
differentiator = poly,
outcome_var = 'd^{2}u/dx^{2}',
noisemaker = nm,
known_vars = None,
dep_var_name = 'u',
ind_var_name = 'x')
# Execute the optimization
coeffs, plotter = sbvp.sindy_bvp()
print(coeffs.keys())
# Compute the S-L coeffs with Plotter analysis tool
plotter.compute_sl_coeffs()
# gather the learned coefficients and relevant metrics
# And place into the results_list
results_list.append({'noise_mag': noise_mag,
'loss': min(sbvp.groupreg.Losses),
'p': plotter.inferred_phi,
'q': plotter.inferred_q,
'coeffs': coeffs})
print(noise_mag, end=" | ")
# -
## Pickle the results
pickle.dump(results_list, open(save_stem+"results.pickle", "wb"))
|
Fig 4a Data - Noise vs Error - Sys3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from config import password
import pandas as pd
import psycopg2
from sqlalchemy import create_engine
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
psycopg2.connect(f"dbname=postgres user=postgres host=localhost password={password} port=5432")
engine=create_engine(f"postgresql+psycopg2://postgres:{password}@localhost:5432/postgres")
conn=engine.connect()
conn
# # ETL Project
# In this project, I analyzed the Premier League Soccer players’ 2020-2021 salary and goals per season to determine which offensive players ('forwards') were overpaid.
#
# Note, each soccer team is made up of a combination of forwards, midfielders, defenders, and keepers. This study only focuses on forwards, whose main task is scoring goals. Additionally, this study does not consider factors such as total playing time, assists, dribbles, and defensive contributions, among other metrics that would provide a more complete assessment of a player’s value and overall contribution to the team.
# # Extraction
# Two tables were extracted from the Premier League webpage for the 2020-2021 soccer season to obtain players' goals stats and players' salaries.
#
# I saved the data as csv files in resources as 'PLGoalsWeb' and 'PLSalaryWeb.'
#
# # Transformation
# I noticed that there were differences in players' names spelling within the two tables. Given the small sample size, I manually normalized the names across both files. Additionally, I removed the currency symbols from the 'PLSalaryWeb'file for ease of use; and added a column called 'position'to the same. I also deleted data related to penalties from the 'PLGoalsWeb' file's 'Goals' column. Lastly, I selected and saved needed and formatted columns as "PLGoals.csv" and "PLSalary.csv."
# # Load
# In PostgreSQL, I created a database ("postgres") and two tables, "plgoals" and "plsalary." I imported the formatted csv files into the tables/database.
# # Analysis
# For analysis and data visualization purposes, I utilized Pandas to import SQL queries from PostgreSQL PGadmin.
#
# I. Position of the League's Highest Paid Player
#
# Prior to determining the cost efficiency of forwards, which is the focus of this project, I was interested in finding out the position of the highest paid player in the league. Such an analysis would confirm the assumption that a forward is usually the highest paid player in the league by virtue of his main task which is to score goals.
#
# Firstly, I joined the 'plgoals' and 'plsalary' tables. The merged tables would reflect the columns needed to define the main variable ('costpergoal').
costpergoal=pd.read_sql('SELECT plgoals.player, goals, avgvalue, position FROM plgoals RIGHT JOIN plsalary ON plgoals.player = plsalary.player ORDER BY Goals DESC;', conn)
print(costpergoal.head(10))
# Secondly, I filtered the data to obtain top highest paid player per position, as displayed below.
highestpaid=costpergoal.loc[costpergoal.groupby('position')['avgvalue'].nlargest(1).index.get_level_values(1)]
highestpaid
# Lastly, I created a bar chart that compares the highest paid players per position, including forwards, midfielders, defenders, and keepers. The bar chart reflected the filtered result and confirmed the assumption by illustrating that <NAME>, a forward, is indeed the league's highest paid player.
x=highestpaid['player']
y=highestpaid['avgvalue']
plt.bar(x,y)
plt.title('Highest Paid by Position')
plt.ylabel('Players by Salary (in millions)')
plt.xticks(rotation=90)
plt.show();
# II. Top Ten Least Cost-Efficient Forwards
#
# To determine the top ten least cost-efficient offensive players in the league, I joined the 'plgoals' and 'plsalary' tables. The merged table included the following columns: player, goals, avgvalue, position. I created an additional column ('costpergoal') by dividing the player's annual salary ('avgvalue') by the total numbers of goals scored during the season ('goals'). Thereafter, I filtered the table to only obtain results relevant to forwards ('position'). To ensure the top ten least cost-efficient forwards were displayed first, I ordered the data by position (i.e., to display forwards only) and by total number of goals not equal to O. Any division by 0 is undefined and would result in an error in PostgreSQL.
costpergoal=pd.read_sql("SELECT plgoals.player, goals, avgvalue, position, (avgvalue/goals) AS CostPerGoal FROM plgoals RIGHT JOIN plsalary ON plgoals.player = plsalary.player WHERE plsalary.position = 'Forward' AND plgoals.goals <> 0 ORDER BY CostPerGoal DESC", conn)
print(costpergoal.head(10))
# As displayed above, the initially displayed top ten players appeared on duplicate rows in some cases. Additionally, some well-know and historically strongly performing forwards appeared to have a small number of total goals. Both cases were results of players being traded from or to another league during the season. To account for such discrepancies, only the first instance of each player was kept, and other duplicate rows were dropped. The first instance was sufficient for the analysis because salary data remained constant across duplicate instances. Likewise, the query was filtered to only apply to forwards who had scored more than one goal during the season.
costpergoal=costpergoal.drop(costpergoal.index[[0,1]])
costpergoal=costpergoal.drop_duplicates(subset='player', keep='first').head(10)
costpergoal
# Per the chart below, the top ten overpaid offensive players ('forwards') in the 2020-2021 Premier League season were: <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, Raheem Sterling, <NAME>, and <NAME>. These ten players are overpaid because their performance (i.e., goal scoring stats) does not justify the annual salary they receive.
#
# Furthermore, when compared to the chart outlining the highest paid player per position, the chart displaying the top ten forwards by cost per goal provides an interesting finding. <NAME> who is the league's most expensive player is not the least cost-efficient forward. Although his performance does not justify his annual salary, he still performs better than three well-known and expensive forwards.
x=costpergoal['player']
y=costpergoal['costpergoal']
plt.bar(x,y)
plt.title('Top Ten Forwards by Cost per Goal')
plt.ylabel('Cost per Goal (in millions)')
plt.xticks(rotation=90)
plt.show();
# # Conclusion
# This project primarily sought to determine which offensive players ('forwards') were overpaid in the Premier League 2020-2021 season. Accordingly, the project provided results of the top ten least cost-efficient forward in the league.
|
Premier League Soccer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Basic Feature Engineering
#
# Analysis by <NAME>
# These notes build a preliminary pipeline for extracting statistical features from the wrangled images.
#
# More specifically, there will be 4 features, namely the first __ cumulants of the pixel values. This is computed via the unbiased estimator from `scipy.stats.kstat`:
#
# https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.kstat.html
#
# Note that this essentially ignores the geometric aspects of the images.
#
import xarray as xr
import numpy as np
from sklearn.base import BaseEstimator, TransformerMixin
from sklearn.pipeline import FeatureUnion, Pipeline
from scipy.stats import kstat
def load_netcdf(filepath):
X = xr.open_dataarray(filepath).values
X = X.reshape(X.shape[0], -1)
return X
filepath = '../../data/clean_data/train_data/X_64_L_clean_train.nc'
X = load_netcdf(filepath)
X.shape
class cumulants_extractor(BaseEstimator, TransformerMixin):
'''
returns a numpy array of all k-th cumulants less than
highest_cumulant (which must be less than 4)
'''
def __init__(self, highest_cumulant):
self.highest_cumulant = highest_cumulant
def fit(self, X, y = None):
return self
def get_cumulants(self, v):
kstats = np.array([kstat(data = v, n = k)
for k in range(1, self.highest_cumulant + 1)])
return kstats
def transform(self, X):
cumulants = np.apply_along_axis(func1d = self.get_cumulants,
axis = 1,
arr = X,
)
return cumulants
c_extractor = cumulants_extractor(highest_cumulant = 4)
features = c_extractor.transform(X)
features.shape
# ## Quick Test
def cumulants_normal_test(cumulants_extractor):
'''
tests with standard normal distribution whose cumulants are
0, 1, 0, 0,
'''
X = np.random.normal(0, 1, (2, 10**4))
return cumulants_extractor.transform(X)
cumulants_normal_test(c_extractor)
|
develop/2020-5-12-jpm-cumulant-transformer/2020-5-12-jpm-cumulant-transformer.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .cs
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: .NET (C#)
// language: C#
// name: .net-csharp
// ---
// +
public class Example
{
public string Id { get; set; }
}
var querySource = new List<Example>().AsQueryable();
var query = querySource
.Where(e => e.Id.StartsWith("a"))
.Select(e => new { CapturedId = e.Id })
.OrderBy(anonType => anonType.CapturedId)
.Take(5);
display(query.ToString());
// -
#r "nuget:ExpressionPowerTools.Core,0.9.4-alpha"
// +
using ExpressionPowerTools.Core.Extensions;
var tree = query.AsEnumerableExpression();
display(tree.ToString());
// +
using System.Linq.Expressions;
var take = tree.MethodsWithName(nameof(Queryable.Take))
.SelectMany(m => m.AsEnumerable().ConstantsOfType<int>())
.First().Value;
display(take);
// +
var skip = query.HasFragment(q => q.Skip(5));
var take5 = query.HasFragment(q => q.Take(5));
var take10 = query.HasFragment(q => q.Take(10));
display(new [] { (nameof(skip), skip), (nameof(take5), take5), (nameof(take10), take10) });
// +
var query1 = querySource
.Where(e => e.Id.StartsWith("a"))
.Select(e => new { CapturedId = e.Id })
.OrderBy(anonType => anonType.CapturedId)
.Take(6);
var query2 = querySource
.Where(e => e.Id.StartsWith("b"))
.Select(e => new { CapturedId = e.Id })
.OrderBy(anonType => anonType.CapturedId)
.Take(5);
var query3 = querySource
.Where(e => e.Id.StartsWith("a"))
.Select(e => new { CapturedId = e.Id })
.OrderBy(anonType => anonType.CapturedId)
.Take(5);
var query1eq = query1.IsEquivalentTo(query);
var query2eq = query2.IsEquivalentTo(query);
var query3eq = query3.IsEquivalentTo(query);
display(new [] { (nameof(query1eq), query1eq), (nameof(query2eq), query2eq), (nameof(query3eq), query3eq) });
|
docs/notebooks/displayiqueryable.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import pandas as pd
import pickle
# +
import pickle
f = open('/home/henry/Insight/Yogee/Datasets/Model_dataset/ModelDf.pckl', 'rb')
ModelDf = pickle.load(f)
f.close()
# -
ModelDf2017 = ModelDf[ModelDf['year'] == 2017]
StudioCount = ModelDf2017['TotalStudio'].values
import matplotlib.pyplot as plt
plt.hist(StudioCount, bins=[0,1,2,3,4,5])
#plt.title("Number of new yoga studios (zipcode, year)")
plt.xlabel('Number of new studios')
plt.ylabel('Zipcode Count')
plt.xticks([.5,1.5,2.5,3.5,4.5], ['0','1','2','3','4'])
plt.show()
plt.rcParams.update({'font.size': 16})
# +
Years = np.array([2011,2012,2013,2014,2015,2016,2017])
Years = Years.astype(int)
YearCount = np.zeros(np.shape(Years))
for i in range(0,np.shape(Years)[0]):
ModelDfyear = ModelDf[ModelDf['year'] == Years[i]]
NewCount = ModelDfyear['NewStudio'].values
YearCount[i] = np.sum(NewCount)
plt.plot(YearCount)
#plt.title("New studio openings")
plt.xlabel('Year')
plt.ylabel('Number of new studios')
plt.xticks([0,1,2,3,4,5,6], ['2011','2012','2013','2014','2015','2016','2017'])
plt.show()
plt.rcParams.update({'font.size': 16})
# -
ModelDfyear.shape[0]
|
Studio Number by Zipcode.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
from bokeh.plotting import figure, output_notebook, show
from bokeh.models import ColumnDataSource, CustomJS
output_notebook()
# -
x = [2, 3, 5, 6, 8, 7]
y = [6, 4, 3, 8, 7, 5]
p = figure(width=400, height=400, tools="hover", toolbar_location=None, title='Hovering over point:')
cr = p.circle(x, y, color='olive', radius=1, alpha=0.4, hover_color='olive', hover_alpha=1.0)
# +
callback = CustomJS(args={'title': p.title}, code="""
const indices = cb_data.index.indices;
title.text = 'Hovering over points: ' + indices
""")
p.hover.tooltips=None
p.hover.callback=callback
# -
show(p)
|
examples/howto/Hover callback.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/cateto/python4NLP/blob/main/ml-lec/Logistic_Classification_5_1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="jU_A9sv82QGB"
# ## Linear Regression
# * Hypothesis
# * Cost
# * Gradient descent
#
# ## Classification
# ex) Spam Detection ==> Spam(1), Ham(0) [ Binary Classfication, 0, 1 encoding ] <br/>
# ex2) tumor ==> malignant tumor(1), benign tumor(0)
# <br/>
# ex3) stock ==> Sell(1), Buy(0)
#
# ## Logistic Regression의 cost함수
# cost(W) = 1/m ∑ c(H(x), y) <br/>
# c(H(x), y) = -log H(x) : y = 1 <br/>
# = -log(1-H(x)) : y = 0
#
#
# #### log함수 1일때 0, 0일때 무한히 증가
# + id="6Pt_MWBe1T7q" colab={"base_uri": "https://localhost:8080/"} outputId="e0180639-a500-4a07-e971-ab0234cb8ac3"
# Lab 5 Logistic Regression Classifier
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()
tf.set_random_seed(777) # for reproducibility
x_data = [[1, 2],
[2, 3],
[3, 1],
[4, 3],
[5, 3],
[6, 2]]
y_data = [[0],
[0],
[0],
[1],
[1],
[1]]
# + id="1FPCVGPd-f2U"
X = tf.placeholder(tf.float32, shape=[None, 2])
Y = tf.placeholder(tf.float32, shape=[None, 1])
# + colab={"base_uri": "https://localhost:8080/"} id="ArC6txOV_JRm" outputId="2ca92b12-c907-44fb-a125-44ecbedff375"
W = tf.Variable(tf.random_normal([2,1]), name="weight")
b = tf.Variable(tf.random_normal([1]), name="bias")
print(W)
print(b)
# + id="drJe2C8i_b_N"
hypothesis = tf.sigmoid(tf.matmul(X,W)+b)
# + id="Vrp9bNpP_maV"
cost = -tf.reduce_mean(Y*tf.log(hypothesis)+ (1-Y)*tf.log(1-hypothesis))
# + id="b0GM2nWB_4li"
train = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(cost)
# + id="3RRKNrNP_89h"
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))
# + colab={"base_uri": "https://localhost:8080/"} id="Sz96kcpXAlMT" outputId="d0b907c1-a06b-47aa-979c-666a1e2b95dd"
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(11000):
cost_val, _ = sess.run([cost, train], feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, cost_val)
h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data})
print("\n hypothesis:", h, "\nCorrect(Y):", c, "\nAccuracy: ", a)
# + id="zRJ5_sZhBqSq"
|
ml-lec/Logistic_Classification_5_1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: U4-S1-NLP (Python3)
# name: u4-s1-nlp
# ---
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import json
import os
import requests
import urllib.request
import urllib
def qcewCreateDataRows(csv):
dataRows = []
try: dataLines = csv.decode().split('\r\n')
except er: dataLines = csv.split('\r\n');
for row in dataLines:
dataRows.append(row.split(','))
return dataRows
def qcewGetAreaData(year,qtr,area):
urlPath = "http://data.bls.gov/cew/data/api/[YEAR]/[QTR]/area/[AREA].csv"
urlPath = urlPath.replace("[YEAR]",year)
urlPath = urlPath.replace("[QTR]",qtr.lower())
urlPath = urlPath.replace("[AREA]",area.upper())
httpStream = urllib.request.urlopen(urlPath)
csv = httpStream.read()
httpStream.close()
return qcewCreateDataRows(csv)
def qcewGetIndustryData(year,qtr,industry):
urlPath = "http://data.bls.gov/cew/data/api/[YEAR]/[QTR]/industry/[IND].csv"
urlPath = urlPath.replace("[YEAR]",year)
urlPath = urlPath.replace("[QTR]",qtr.lower())
urlPath = urlPath.replace("[IND]",industry)
httpStream = urllib.request.urlopen(urlPath)
csv = httpStream.read()
httpStream.close()
return qcewCreateDataRows(csv)
def qcewGetSizeData(year,size):
urlPath = "http://data.bls.gov/cew/data/api/[YEAR]/1/size/[SIZE].csv"
urlPath = urlPath.replace("[YEAR]",year)
urlPath = urlPath.replace("[SIZE]",size)
httpStream = urllib.request.urlopen(urlPath)
csv = httpStream.read()
httpStream.close()
return qcewCreateDataRows(csv)
Michigan_Data = qcewGetAreaData("2015","1","26000")
Auto_Manufacturing = qcewGetIndustryData("2015","1","3361")
SizeData = qcewGetSizeData("2015","6")
# + tags=[]
print(Michigan_Data[5][2])
# + tags=[]
# prints the area_fips in row 1.
# remember row zero contains field names
print(Auto_Manufacturing[1][0])
# + tags=[]
# prints the own_code in row 1.
# remember row zero contains field names
print(SizeData[1][1])
# -
# + tags=[]
pip install -U blsconnect
# -
api_key = '<KEY>'
# +
from blsconnect import RequestBLS, bls_search
MY_API_KEY = '<KEY>'
bls = RequestBLS(key=MY_API_KEY)
# Get seasonally-adjusted unemployment rates for Florida, Georgia, and all U.S.
series_names = bls_search(data="U3",
state=["FL", "GA", "NY", "NJ", "US"],
sa=True)
df = bls.series(series_names,
start_year=2010,
end_year=2019)
df.head()
# -
df.rename(columns={"LASST120000000000003": "Florida"})
import requests
import json
import prettytable
headers = {'Content-type': 'application/json'}
data = json.dumps({"seriesid": ['CUUR0000SA0','SUUR0000SA0'],"startyear":"2011", "endyear":"2014"})
p = requests.post('https://api.bls.gov/publicAPI/v2/timeseries/data/', data=data, headers=headers)
json_data = json.loads(p.text)
for series in json_data['Results']['series']:
x=prettytable.PrettyTable(["series id","year","period","value","footnotes"])
seriesId = series['seriesID']
for item in series['data']:
year = item['year']
period = item['period']
value = item['value']
footnotes=""
for footnote in item['footnotes']:
if footnote:
footnotes = footnotes + footnote['text'] + ','
if 'M01' <= period <= 'M12':
x.add_row([seriesId,year,period,value,footnotes[0:-1]])
output = open(seriesId + '.txt','w')
output.write (x.get_string())
output.close()
|
notebooks/bls.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
corpus = pd.read_csv("corpus_JHE.csv")
#print(corpus['text'][0])
print(corpus.shape)
n = corpus.shape[0]
#prints the size of the csv file, the first number is the number of the documents
print(n)
# Function to print top words of LDA ()
def print_top_words(model, feature_names, n_top_words):
for index, topic in enumerate(model.components_):
message = "\nTopic #{}:".format(index)
message += " ".join([feature_names[i] for i in topic.argsort()[:-n_top_words - 1 :-1]])
print(message)
print("="*70)
#transform texts into word-vectors
from sklearn.feature_extraction.text import CountVectorizer
# Storing the entire training text in a list
text = list(corpus.text.values)
#these are imposrant parameter settings,
#max_df=0.5 means that each token (word) can appear in at most 50% of the documents,
#min_df=0.05 means that each token needs to appear in minimum 5% of the documents)
tf_vectorizer = CountVectorizer(max_df=0.5, min_df=0.05)
# tokenize and build vocab
tf_vectorizer.fit(text)
#print(tf_vectorizer.vocabulary_)
# encode document
tf = tf_vectorizer.transform(text)
# summarize encoded vector
#print(tf.shape)
#print(tf.toarray())
#tf
# +
#plotting a histogram of the most frequent words
import numpy as np
# Plotly imports
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
feature_names = tf_vectorizer.get_feature_names()
count_vec = np.asarray(tf.sum(axis=0)).ravel()
zipped = list(zip(feature_names, count_vec))
x, y = (list(x) for x in zip(*sorted(zipped, key=lambda x: x[1], reverse=True)))
# Now I want to extract out on the top 15 and bottom 15 words
Y = np.concatenate([y[0:15], y[-16:-1]])
X = np.concatenate([x[0:15], x[-16:-1]])
# Plotting the Plot.ly plot for the Top 50 word frequencies
data = [go.Bar(
x = x[0:50],
y = y[0:50],
marker= dict(colorscale='Jet',
color = y[0:50]
),
text='Word counts'
)]
layout = go.Layout(
title='Top 50 Word frequencies after Preprocessing'
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='basic-bar')
# Plotting the Plot.ly plot for the Top 50 word frequencies
data = [go.Bar(
x = x[-100:],
y = y[-100:],
marker= dict(colorscale='Portland',
color = y[-100:]
),
text='Word counts'
)]
layout = go.Layout(
title='Bottom 100 Word frequencies after Preprocessing'
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig, filename='basic-bar')
# -
# the actual topic modeling is here
#from collections import Counter
#from scipy.misc import imread
from sklearn.feature_extraction.text import TfidfVectorizer, CountVectorizer
from sklearn.decomposition import NMF, LatentDirichletAllocation
from matplotlib import pyplot as plt
# #%matplotlib inline
import base64
import numpy as np
import pandas as pd
# n_components=10 -- the number of topics (clusters), change this to get another number of topcis
# random_state = 1981 -- this is a random seed in order to have the results reproducible, otherwise,
# since the algorithm has random components, the topics may vary slightly from iteration to iteration,
# and particularly the order in which topics are displayed may vary)
lda_model = LatentDirichletAllocation(n_components=10, max_iter=5,
learning_method = 'online',
learning_offset = 50.,
random_state = 1981)
#fit the topic model
lda_model.fit(tf)
# Log Likelyhood: Higher the better
print("Log Likelihood: ", lda_model.score(tf))
# Perplexity: Lower the better. Perplexity = exp(-1. * log-likelihood per word)
print("Perplexity: ", lda_model.perplexity(tf))
# See model parameters
print(lda_model.get_params())
n_top_words = 30
print("\nTopics in LDA model: ")
tf_feature_names = tf_vectorizer.get_feature_names()
print_top_words(lda_model, tf_feature_names, n_top_words)
# +
from wordcloud import WordCloud
# Generate a word cloud image for given topic
# most important words for each topic
vocab = tf_feature_names
def draw_word_cloud(index):
imp_words_topic=""
comp=lda_model.components_[index]
vocab_comp = zip(vocab, comp)
sorted_words = sorted(vocab_comp, key= lambda x:x[1], reverse=True)[:50]
for word in sorted_words:
imp_words_topic=imp_words_topic+" "+word[0]
wordcloud = WordCloud(width=600, height=400).generate(imp_words_topic)
plt.figure( figsize=(5,5))
plt.imshow(wordcloud)
plt.axis("off")
plt.tight_layout()
plt.show()
#change the numbers from 0 to 9 to see all word clouds one-by-one
draw_word_cloud(9)
# -
#print maximum topic of a document
doc_topic = lda_model.transform(tf)
for n in range(doc_topic.shape[0]):
topic_most_pr = doc_topic[n].argmax()
#print("doc: {} topic: {}\n".format(n,topic_most_pr))
n = tf.shape[0]
print(n)
# Create Document — Topic Matrix
lda_output = lda_model.transform(tf)
print(lda_output.shape)
# column names
topicnames = ["Topic" + str(i) for i in range(lda_model.n_components)]
# index names
docnames = ["Doc" + str(i) for i in range(n)]
# Make the pandas dataframe
df_document_topic = pd.DataFrame(np.round(lda_output, 2), columns=topicnames, index=docnames)
# Get dominant topic for each document
dominant_topic = np.argmax(df_document_topic.values, axis=1)
df_document_topic["dominant_topic"] = dominant_topic
df_document_topic["eid"] = corpus.eid.values
df_document_topic["pii"] = corpus.pii.values
#saving document-topic matrix for further analysis
df_document_topic.to_csv('dominant_topics.csv',index=False)
# saving a topic-keyword matrix as a csv for further analysis
df_topic_keywords = pd.DataFrame(lda_model.components_)
# Assign Column and Index
df_topic_keywords.columns = tf_vectorizer.get_feature_names()
df_topic_keywords.index = topicnames
df_topic_keywords.to_csv('topics_keywords.csv',index=True)
print(df_topic_keywords.shape)
# +
# sentiment classification, write sentiment scores to csv
#(columns in output csv: neg -- fraction of negative sentiment per document,
#neu -- fraction of neutral sentiment per document,
#pos - fraction of positive sentiment per document,
#compound -- overall polarity score which I am not using in the analysis,
#eid and pii -- unique identifiers of the articles)
from nltk.sentiment import SentimentIntensityAnalyzer
import nltk
nltk.download('vader_lexicon')
sia = SentimentIntensityAnalyzer()
for x in range(n):
sen = sia.polarity_scores(corpus.text.values[x])
df = pd.DataFrame([sen])
df['eid'] = corpus.eid.values[x]
df['pii'] = corpus.pii.values[x]
if x==0:
sen_all = df
else:
frames = [sen_all, df]
sen_all = pd.concat(frames)
sen_all.to_csv('sentiments.csv',index=False)
# -
|
3_topic_modeling/.ipynb_checkpoints/run3_analyze-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # split datasets
# version: 1
#
# info:
# - split json into train.json, val.json and test.json
#
# ### WARNING: splitbyimages is not ideal (use splitbyannotations) -> because you can fail to have all the classes in train (or val,or test). This was done, because some datasets like tao are missing annotations and images
#
#
# author: <NAME>
from annotate_v5 import *
import platform
import numpy as np
import time
import pandas as pd
from IPython.display import Image, display
import copy
import os
from shutil import copyfile
import matplotlib.pyplot as plt
from matplotlib.image import imread
from matplotlib.patches import Rectangle
import random
#Define root dir dependent on OS
rdir='D:/external_datasets/MOLA/annotations/'
if str(platform.platform()).find('linux')>-1: rdir=rdir.replace('D:/','/mnt/d/')
print('OS: {}'.format(platform.platform()))
print('root dir: {}'.format(rdir))
# ## 1. Init vars
train=70
val=20
test=100-(train+val)
injsonfile='coco2017_reorder_cleanclass.json'
infilename=injsonfile.split('.')[0]
# init json
molajson = json.load(open(rdir+injsonfile))
for k in molajson:
print(k, len(molajson[k]))
# ## 2. Import ids
# #### #NOTE: work with ids and index so you can use numpy for faster operations
# categories id
cats=[]
catids=[]
for c in molajson['categories']:
catids.append(c['id'])
cats.append(c['name'])
#print(cats)
# images filepath and id
imgs=[]
imgids=[]
for c in molajson['images']:
imgs.append(c['file_name'])
imgids.append(c['id'])
# annotations category_id
ann_catids=[]
ann_ids=[]
ann_imgids=[]
for an in tqdm(molajson['annotations']):
ann_catids.append(an['category_id'])
ann_ids.append(an['id'])
ann_imgids.append(an['image_id'])
print(len(ann_ids))
#TEST dupplicates v1 - slow
# duplicates_l=list(set([x for x in ann_ids if ann_ids.count(x) > 1])) # duplicates l
#TEST dupplicates v2 - fast
#from collections import Counter
#duplicates_l=[item for item, count in Counter(ann_ids).items() if count > 1]
#TEST duplicates v3 -faster
u, c = np.unique(np.array(ann_ids), return_counts=True)
duplicates_l= u[c > 1].tolist()
print(len(duplicates_l))
# ## 3. split by images
# #QUESTION Seeded random or not?
# +
#init
train_imgids=[]
val_imgids=[]
test_imgids=[]
#size
train_size=len(imgids) * train // 100 #floor division
val_size=len(imgids) * val // 100
test_size=len(imgids) * test // 100
#select images
random.shuffle(imgids)
train_imgids.extend(imgids[:train_size])
val_imgids.extend(imgids[train_size+1:train_size+val_size-1])
test_imgids.extend(imgids[train_size+val_size+1:train_size+val_size+test_size])
print((len(train_imgids)/len(imgids))*100)
print((len(val_imgids)/len(imgids))*100)
print((len(test_imgids)/len(imgids))*100)
# +
ann_catids_np=np.array(ann_catids)
train_ann_catidx=[]
val_ann_catidx=[]
test_ann_catidx=[]
for imgid in tqdm(train_imgids):
ann_idx_np = np.where(ann_catids_np==imgid)[0] #annotation index of ids
if not ann_idx_np.any(): continue
train_ann_catidx.extend(ann_idx_np.tolist())
for imgid in tqdm(val_imgids):
ann_idx_np = np.where(ann_catids_np==imgid)[0] #annotation index of ids
if not ann_idx_np.any(): continue
val_ann_catidx.extend(ann_idx_np.tolist())
for imgid in tqdm(test_imgids):
ann_idx_np = np.where(ann_catids_np==imgid)[0] #annotation index of ids
if not ann_idx_np.any(): continue
test_ann_catidx.extend(ann_idx_np.tolist())
print((len(train_ann_catidx)/len(ann_catids))*100)
print((len(val_ann_catidx)/len(ann_catids))*100)
print((len(test_ann_catidx)/len(ann_catids))*100)
# -
l_dup=[train_ann_catidx, val_ann_catidx,test_ann_catidx ]
for i in l_dup:
print('original: ', len(i))
u, c = np.unique(np.array(i), return_counts=True)
duplicates_l= u[c > 1].tolist()
print('duplicate: ',len(duplicates_l))
# ### 4. Save splited jsons
percent_idx=[train_ann_catidx,val_ann_catidx, test_ann_catidx]
percent_names=['train', 'val', 'test']
newjson=copy.copy(molajson)
annotations=copy.copy(molajson['annotations'])
for i, percent_i in enumerate(tqdm(percent_idx)):
#get new annotations
newjson['annotations']=[annotations[index] for index in percent_i]
# save
print('\n >> SAVING {}...'.format(percent_names[i]))
outpath=rdir+'splitimg_{}/'.format(infilename)
assure_path_exists(outpath)
outjsonfile=outpath+'{}.json'.format(percent_names[i]) #rdir+'{}_{}.json'.format(percent_names[i],infilename)
with open(outjsonfile, 'w') as f:
json.dump(newjson, f)
print("JSON SAVED : {} \n".format(outjsonfile))
for k in molajson:
print(k, len(newjson[k]))
# ### 5. TEST SPLIT ANNOTATIONS DUPLICATES
injsonfile='mola_mix_aggressive.json'
outjsonfile=rdir+'split_{}/'.format(infilename)+'test.json'
# init json
molajson = json.load(open(outjsonfile))
for k in molajson:
print(k, len(molajson[k]))
# +
# annotations category_id
ann_ids=[]
for an in tqdm(molajson['annotations']):
ann_ids.append(an['id'])
print(len(ann_ids))
#TEST duplicates v3 -faster
u, c = np.unique(np.array(ann_ids), return_counts=True)
duplicates_l= u[c > 1].tolist()
print(len(duplicates_l))
# -
|
splitbyimages_v1.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .scala
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Scala
// language: scala
// name: scala
// ---
import $ivy.`io.github.siddhartha-gadgil::provingground-core-jvm:0.1.1-SNAPSHOT`
// ## Symbolic Algebra for natural numbers
//
// To efficiently manipulate expressions in natural numbers, or more generally rings (and fields), proving-ground has special HoTT types wrapping scala types that are Rings, Rigs, Fields etc in the _spire_ library. As a consequence:
//
// * Symbolic expressions that are equal become _definitionally_ equal, i.e., equal as scala objects.
// * We define recursion which expands for (sums with) literals
// * Expressions involving literals and variables are simplified as much as possible.
//
// The ring of natural numbers is an object NatRing. This has
//
// * a HoTT type _NatTyp_,
// * a scala type _Nat_
// * a scala representation
// * a (spire) ring structure on the underlying terms.
import provingground._, induction._, scalahott._
import NatRing._
val n = "n" :: NatTyp
val m = "m" :: NatTyp
val k = "k" :: NatTyp
// Spire implicits let us use the addition and multiplication operations.
import spire.math._
import spire.algebra._
import spire.implicits._
// ### Addition and multiplication
//
// A sum gives a SigmaTerm, which only stores a set of terms being added.
n + m
(n + m) + n
// Addition is commutative and associative, even when it involves repeated terms.
n + m == m + n
(n + m) + k == n + (m + k)
(n + n) + m == (n + m) + n
// Similarly, multiplication is commutative and associative, and distributes over addition. Multiplication gives Pi-terms with parameter a map to exponents.
n * m == m * n
n * (m * k)
(n * m) * k
n * (m + k)
n *(m + k) == (n * m) + (n * k)
n + 1
1 + n
(1 + n) + 2
n * n
// ### Symbolic definitions
//
// We can use the expressions from these functions in lambdas. For this we need correct substitution.
import HoTT._
val fn = lmbda(n)(n * n)
fn(3)
fn(k)
// ### Recursive definitions
//
// We can define a function f recursively on natural numbers, given the value f(0) and given f(n+1) as a (curryed) function of (n+1) and f(n). This expands for literals.
val m = lmbda(n)(prod(n + 1))
val factorial = Rec(1: Nat, m)
factorial(3)
factorial(5)
factorial(n)
val g = lmbda(k)(factorial(k * k))
g(3)
factorial(9)
// ### Simplifying recursive functions
//
// If we apply a recursive function to a sum n+k with k a literal (say k = 2), then the result simplifies as much as possible by expanding tail recursively in the literal.
factorial(n + 1)
val fn = lmbda(n)(factorial(n + 1))
fn(1)
fn(4)
(n + 2) * (n + 1)
(3 * n) * n
n * (n * n)
(n * k) * k
k * (n * k)
(n * n) * n
factorial(n + 2)
// **Recursive expansion:** We see an example of expansion as much as possible.
val func = lmbda(n)(factorial(n+ 2))
func(3)
func(k) == factorial(k) * (k + 2) * (k + 1)
1 + 2
findFactor(Literal(2), Literal(4))
findDivisibilty(Literal(2), Literal(4))
findDivisibilty(Literal(2), Literal(4)).map(_.typ)
findFactor(n *2, n* 4)
findFactor(n * 2, n * 2 * k)
findFactor(n * k, n * n * k)
findFactor(n * 2, n * 4 * k)
findFactor(n * 2, n * 7 * k)
findFactor(n * 2, n * 4 * k) == Some(k * 2)
findDivisibilty(n * 2, n * 4 * k)
divides(Literal(2))(Literal(3))
findDivisibilty(2, 4)
findDifference(n+ 4, n + 2)
findDifference(4, 2)
findDifferenceFlip(4, 2)
findLEQ(2, 4)
LEQ.unapply(leq(n)(k))
LEQ.unapply(leq(Literal(2))(Literal(4)))
val sg = leq(Literal(2))(Literal(4))
findDifference(n + 2, 2)
val x = NatTyp.Var
val eqn = sg.fibers(x).asInstanceOf[IdentityTyp[Nat]]
eqn.dom == NatTyp
eqn.lhs
findDifference(eqn.lhs, x)
x + 2
findDifference(x + 2, 2)
eqn.lhs == x + 2
findDifference(x + 2, x)
DIV.unapply(divides(n)(k))
divides(n)(k)
findFactor(n * k, n)
findFactor(k, n * k)
DIV.unapply(divides(n)(Literal(7)))
|
notes/NaturalNumbers-SymbolicAlgebra.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="hX4n9TsbGw-f"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="0nbI5DtDGw-i"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="9TnJztDZGw-n"
# # Text classification with an RNN
# + [markdown] colab_type="text" id="AfN3bMR5Gw-o"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/alpha/tutorials/sequences/text_classification_using_rnn"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/r2/tutorials/sequences/text_classification_using_rnn.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/r2/tutorials/sequences/text_classification_using_rnn.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="lUWearf0Gw-p"
# This text classification tutorial trains a [recurrent neural network](https://developers.google.com/machine-learning/glossary/#recurrent_neural_network) on the [IMDB large movie review dataset](http://ai.stanford.edu/~amaas/data/sentiment/) for sentiment analysis.
# + colab={} colab_type="code" id="z682XYsrjkY9"
from __future__ import absolute_import, division, print_function
# !pip install tf-nightly-2.0-preview
import tensorflow as tf
print(tf.__version__)
# + [markdown] colab_type="text" id="1rXHa-w9JZhb"
# Import `matplotlib` and create a helper function to plot graphs:
# + colab={} colab_type="code" id="Mp1Z7P9pYRSK"
import matplotlib.pyplot as plt
def plot_graphs(history, string):
plt.plot(history.history[string])
plt.plot(history.history['val_'+string])
plt.xlabel("Epochs")
plt.ylabel(string)
plt.legend([string, 'val_'+string])
plt.show()
# + [markdown] colab_type="text" id="pRmMubr0jrE2"
# ## Download the data
#
# The IMDB large movie review dataset is a *binary classification* dataset—all the reviews have either a *positive* or *negative* sentiment.
# + colab={} colab_type="code" id="zdLG384BYOb3"
imdb = tf.keras.datasets.imdb
(train_data, train_labels), (test_data, test_labels) = imdb.load_data(num_words=5000)
# + [markdown] colab_type="text" id="BEnNBnbm3PbC"
# ## Format Data
# + colab={} colab_type="code" id="yAxOs_dVYPIb"
# A dictionary mapping words to an integer index
word_index = imdb.get_word_index()
# The first indices are reserved
word_index = {k:(v+3) for k,v in word_index.items()}
word_index["<PAD>"] = 0
word_index["<START>"] = 1
word_index["<UNK>"] = 2 # unknown
word_index["<UNUSED>"] = 3
# Mapping of value -> key
index_word = dict([(value, key) for (key, value) in word_index.items()])
# + colab={} colab_type="code" id="22-iQXLJYRPi"
def decode_review(text):
return ' '.join([index_word.get(i, '?') for i in text])
# pad the data to a fixed length
train_data = tf.keras.preprocessing.sequence.pad_sequences(train_data,
value=word_index["<PAD>"],
padding='post',
maxlen=256)
test_data = tf.keras.preprocessing.sequence.pad_sequences(test_data,
value=word_index["<PAD>"],
padding='post',
maxlen=256)
# + colab={} colab_type="code" id="sZN3Q8yek_XW"
len(train_data[0]), len(test_data[0])
# + colab={} colab_type="code" id="RxMo8-NykfU1"
decode_review(train_data[0])
# + [markdown] colab_type="text" id="NLjQiKq5lE2u"
# ## Create an input data pipeline
#
# Create the training and validation sets with `tf.data.Dataset`.
# + colab={} colab_type="code" id="dDsCaZCDYZgm"
BUFFER_SIZE = len(train_data)
BATCH_SIZE = 64
# + colab={} colab_type="code" id="sUy4XLJmYRUx"
# creating the training and validation sets
vocab_size = 5000
x_val = train_data[:10000]
x_train = train_data[10000:]
y_val = train_labels[:10000]
y_train = train_labels[10000:]
# + colab={} colab_type="code" id="0-ndxS_tYcNb"
train_dataset = tf.data.Dataset.from_tensor_slices(
(x_train, y_train)).repeat().shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
val_dataset = tf.data.Dataset.from_tensor_slices((x_val, y_val)).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices((test_data, test_labels)).batch(BATCH_SIZE)
# + [markdown] colab_type="text" id="bjUqGVBxGw-t"
# ## Create the model
# + [markdown] colab_type="text" id="bgs6nnSTGw-t"
# Build a `tf.keras.Sequential` model and start with an embedding layer. An embedding layer stores one vector per word. When called, it converts the sequences of word indices to sequences of vectors. These vectors are trainable. After training (on enough data), words with similar meanings often have similar vectors.
#
# This index-lookup is much more efficient than the equivalent operation of passing a one-hot encoded vector through a `tf.keras.layers.Dense` layer.
#
# A recurrent neural network (RNN) processes sequence input by iterating through the elements. RNNs pass the outputs from one timestep to their input—and then to the next. Long short term memory (LSTM) is shown here followed by three dense layers:
# + colab={} colab_type="code" id="LwfoBkmRYcP3"
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, 100),
tf.keras.layers.LSTM(64),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# + [markdown] colab_type="text" id="sRI776ZcH3Tf"
# Compile the Keras model to configure the training process:
# + colab={} colab_type="code" id="kj2xei41YZjC"
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
# + [markdown] colab_type="text" id="zIwH3nto596k"
# ## Train the model
# + colab={} colab_type="code" id="hw86wWS4YgR2"
history = model.fit(train_dataset, epochs=10,
steps_per_epoch=len(x_train)//BATCH_SIZE,
validation_data=test_dataset,
validation_steps=len(x_val)//BATCH_SIZE)
# + colab={} colab_type="code" id="BaNbXi43YgUT"
test_loss, test_acc = model.evaluate(test_dataset,
steps=len(test_data)//BATCH_SIZE)
print('Test Loss: {}'.format(test_loss))
print('Test Accuracy: {}'.format(test_acc))
# + colab={} colab_type="code" id="ZfIVoxiNmKBF"
plot_graphs(history, 'accuracy')
# + colab={} colab_type="code" id="IUzgkqnhmKD2"
plot_graphs(history, 'loss')
# + [markdown] colab_type="text" id="7g1evcaRpTKm"
# ## Stack two or more LSTM layers
#
# Keras recurrent layers have two available modes that are controlled by the `return_sequences` constructor argument:
#
# * Return either the full sequences of successive outputs for each timestep (a 3D tensor of shape `(batch_size, timesteps, output_features)`).
# * Return only the last output for each input sequence (a 2D tensor of shape (batch_size, output_features)).
#
# The `tf.keras.layers.Bidirectional` wrapper can also be used with an LSTM layer. This propagates the input forward and backwards through the RNN layer and then concatenates the output. This helps the RNN to learn long range dependencies.
# + colab={} colab_type="code" id="jo1jjO3vn0jo"
model = tf.keras.Sequential([
tf.keras.layers.Embedding(vocab_size, 100),
tf.keras.layers.LSTM(64, return_sequences=True),
tf.keras.layers.LSTM(32),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(64, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
# + colab={} colab_type="code" id="hEPV5jVGp-is"
model.compile(loss='binary_crossentropy',
optimizer='adam',
metrics=['accuracy'])
# + colab={} colab_type="code" id="LeSE-YjdqAeN"
history = model.fit(train_dataset, epochs=10,
steps_per_epoch=len(x_train)//BATCH_SIZE,
validation_data=test_dataset,
validation_steps=len(x_val)//BATCH_SIZE)
# + colab={} colab_type="code" id="_LdwilM1qPM3"
test_loss, test_acc = model.evaluate(test_dataset, steps=len(test_data)//BATCH_SIZE)
print('Test Loss: {}'.format(test_loss))
print('Test Accuracy: {}'.format(test_acc))
# + colab={} colab_type="code" id="_YYub0EDtwCu"
plot_graphs(history, 'accuracy')
# + colab={} colab_type="code" id="DPV3Nn9xtwFM"
plot_graphs(history, 'loss')
# + [markdown] colab_type="text" id="9xvpE3BaGw_V"
# Check out other existing recurrent layers such as [GRU layers](https://www.tensorflow.org/api_docs/python/tf/keras/layers/GRU).
|
site/en/r2/tutorials/sequences/text_classification_rnn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
# +
data = pd.read_csv('../data/english_to_latex.csv')
data.shape
# -
data.head()
# +
# Prompt Engineerings
from transformers import GPT2Tokenizer
MODEL = 'distilgpt2'
tokenizer = GPT2Tokenizer.from_pretrained(MODEL)
tokenizer.pad_token = tokenizer.eos_token
#add two prompts, one for each task
CONVERSION_PROMPT = 'Task\n' # LaTeX conversion task
CONVERSION_TOKEN = 'LaTeX:'
# +
# This is our "training prompt" that we want GPT2 to recognize and learn
training_examples = f'{CONVERSION_PROMPT}English: ' + data['English'] + '\n' + CONVERSION_TOKEN + ' ' + data['LaTeX'].astype(str)
print(training_examples[0])
# +
task_df = pd.DataFrame({'text': training_examples})
task_df.shape
# -
from datasets import Dataset
data = Dataset.from_pandas(task_df)
data
# +
MAX_TOKENS = task_df['text'].apply(lambda x: len(tokenizer(x)['input_ids'])).max() + 5
MAX_TOKENS
# +
# tokenizer created input_ids and attention_mask as output
def tokenize_function(examples):
output = tokenizer(examples['text'], add_special_tokens=True, max_length=MAX_TOKENS,
truncation=True,padding='max_length')
output['labels'] = output["input_ids"]
# -100 is a reserved value to ignore these tokens when calculating the loss
output["labels"] = [[-100 if x == tokenizer.pad_token_id else x for x in y] for y in output["labels"]]
return output
data = data.map(
tokenize_function,
batched=True,
)
print(data)
# +
data.set_format(type="python", columns=["input_ids", "attention_mask", "labels"])
data = data.train_test_split(test_size=0.10, shuffle=True, seed=0)
print(data)
# -
tokenizer.decode(data['train'][0]['input_ids'])
tokenizer.decode([c for c in data['train'][0]['labels'] if c != -100])
# +
from transformers import Trainer, TrainingArguments
from transformers import GPT2LMHeadModel
model = GPT2LMHeadModel.from_pretrained(MODEL)
# +
# Note the batch size of 4 to make sure we have multiple steps per epoch. This generally speeds up training
training_args = TrainingArguments(
output_dir="./english_to_latex", #The output directory
overwrite_output_dir=True, #overwrite the content of the output directory
num_train_epochs=15, # number of training epochs
per_device_train_batch_size=4, # batch size for training
per_device_eval_batch_size=4, # batch size for evaluation
load_best_model_at_end=True,
warmup_steps=len(data['train']) // 5, # number of warmup steps for learning rate scheduler,
weight_decay = 0.05,
logging_steps=1,
log_level='info',
evaluation_strategy='epoch',
save_strategy='epoch'
)
trainer = Trainer(
model=model,
args=training_args,
train_dataset=data['train'],
eval_dataset=data['test'],
)
# -
trainer.evaluate()
trainer.train()
trainer.evaluate()
trainer.save_model()
# Load our finetuned model
loaded_model = GPT2LMHeadModel.from_pretrained('./english_to_latex')
# +
text_sample = 'f of x equals integral from 1 to inf of x'
conversion_text_sample = f'{CONVERSION_PROMPT}English: {text_sample}\n{CONVERSION_TOKEN}'
print(conversion_text_sample)
# +
encoded_input = tokenizer(conversion_text_sample, return_tensors='pt')
print(
tokenizer.decode(loaded_model.generate(
input_ids=encoded_input['input_ids'],
num_beams=3,
max_length=MAX_TOKENS,
temperature=1,
top_k=10,
early_stopping=True
)[0]))
|
latex_gpt2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#
# * https://re-thought.com/pandas-value_counts/
import pandas as pd
pd.to_datetime('2020-09-21 2:30pm')
pd.options.display.max_rows = 150
# In pandas, a single point in time is represented as a Timestamp.
pd.to_datetime('09/21/2020')
type(pd.to_datetime('09/01/2020', dayfirst = True))
# If we supply a list or array of strings as input to to_datetime(),
# it returns a sequence of date/time values in a DatetimeIndex object,
# which is the core data structure that powers much of pandas time series functionality.
pd.to_datetime(['2018-05-05', '7/1/1997', 'Mar 31, 1995'])
# +
# The data type datetime64[ns] indicates that the underlying data is stored as 64-bit
# integers, in units of nanoseconds (ns). This data structure allows pandas to
# compactly store large sequences of date/time values and efficiently perform
# vectorized operations using NumPy datetime64 arrays
# +
# If we’re dealing with a sequence of strings all in the same date/time format,
# we can explicitly specify it with the format parameter.
# We use the format codes %m (numeric month), %d (day of month), and
# # %y (2-digit year) to specify the format.
pd.to_datetime(['12/25/19', '8/23/17', '12/15/12'], format='%m/%d/%y')
# -
# ## Open Power Systems Data
#
# In this tutorial, we’ll be working with daily time series of Open Power System Data (OPSD) for Germany, which has been rapidly expanding its renewable energy production in recent years. The data set includes country-wide totals of electricity consumption, wind power production, and solar power production for 2006-2017.
#
# Electricity production and consumption are reported as daily totals in gigawatt-hours (GWh). The columns of the data file are:
#
# * Date — The date (yyyy-mm-dd format)
# * Consumption — Electricity consumption in GWh
# * Wind — Wind power production in GWh
# * Solar — Solar power production in GWh
# * Wind+Solar — Sum of wind and solar power production in GWh
#
# We will explore how electricity consumption and production in Germany have varied over time, using pandas time series tools to answer questions such as:
#
# * When is electricity consumption typically highest and lowest?
# * How do wind and solar power production vary with seasons of the year?
# * What are the long-term trends in electricity consumption, solar power, and wind power?
# * How do wind and solar power production compare with electricity consumption, and how has this ratio changed over time?
opsd_daily = pd.read_csv('opsd_germany_daily.csv', index_col=0, parse_dates=True)
opsd_daily.shape
opsd_daily.loc['2012-01', 'Consumption']
opsd_daily.dtypes
# +
# Add columns with year, month, and weekday name
# opsd_daily['Year'] = opsd_daily.index.year
# opsd_daily['Month'] = opsd_daily.index.month
# opsd_daily['Weekday Name'] = opsd_daily.index.weekday_name
# -
opsd_daily.loc['2017-08-10']
opsd_daily.loc['2017'].resample('M').ohlc()
opsd_monthly = opsd_daily[['Consumption', 'Wind', 'Solar']].resample('M').sum(min_count = 28)
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(opsd_monthly['Consumption'], color = 'black', label = 'Consumption')
opsd_monthly[['Wind', 'Solar']].plot.area(ax = ax, linewidth = 0)
ax.xaxis.set_major_locator(
# ### Rolling windows
#
# Rolling window operations are another important transformation for time series data. Similar to downsampling, rolling windows split the data into time windows and and the data in each window is aggregated with a function such as mean(), median(), sum(), etc.
#
# Let’s use the rolling() method to compute the 7-day rolling mean of our daily data. We use the center=True argument to label each window at its midpoint
cities = pd.read_html('wikipedia_data.html')[1]
cities=cities.iloc[:-1,[0,3,5,6,7,8]]
cities.explode('NFL')
# +
orchestra_dict = {'City': ['Los Angeles Philharmonic',
'Chicago Symphony Orchestra',
'San Francisco Symphony Orchestra',
'Boston Symphony Orchestra',
'New York Philharmonic',
'National Symphony Orchestra',
'Philadelphia Orchestra',
'Cleveland Orchestra',
'Pittsburgh Symphony Orchestra',
'Cincinnati Symphony Orchestra'],
'Base_Pay_2015': [153400, 151320, 150454,
142896, 141113, 136136,
128700, 127504, 107117,103500]}
orchestra = pd.DataFrame.from_dict(orchestra_dict)
# -
# ## Time comparison
#
# # %%timeit module
import numpy as np
xarray = np.random.rand(1000, 10)
xlist = xarray.tolist()
xdf = pd.DataFrame(xarray)
# +
def some_calc1(x):
if x > 0.1:
return 1
elif x > 0.01:
return 10 * x
elif x > 0:
return 2 * x + 0.03
else:
return 0
def some_calc2(x):
return (x > 0.1) * 1 + \
((x > 0.01) & (x <= 0.04)) * x * 10.0 + \
((x > 0) & (x <= 0.01)) * (x * 2 + 0.03) + \
0.0
# -
@np.vectorize
def some_calcs1_vec(x):
if x > 0.1:
return 1
elif x > 0.01:
return 10 * x
elif x > 0:
return 2 * x + 0.03
else:
return 0
# %timeit array1 = some_calcs1_vec(xarray)
# %timeit array2 = some_calc2(xarray)
# %timeit z1 = some_calcs1_vec(xdf)
# %timeit z2 = some_calc2(xdf)
# +
# The applymap() function is used to apply a function to a Dataframe elementwise.
# This method applies a function that accepts and returns a scalar to every element
# of a DataFrame.
# DataFrame.applymap(self, func)
# %timeit df1 = xdf.applymap(some_calc1)
# %timeit df2 = xdf.applymap(some_calc2)
# -
# %timeit z1 = xdf.apply(some_calcs1_vec, axis = 0)
# #%timeit z2 = xdf.apply(some_calc2, axis = 0)
# %timeit z3 = xdf.apply(some_calcs1_vec, axis = 1)
# #%timeit z4 = xdf.apply(some_calc2, axis = 1)
xdf.applymap(lambda x: len(str(x)))
# +
import numpy as np
import csv
def sigmoid(x):
return 1.0/(1+np.exp(-x))
def cost(x,y,th):
pro = sigmoid(np.dot(x,th))
result = sum(-y * np.log(pro) - (1-y) * np.log(1-pro))
result = result/len(x) #len: number of feature rows
return result
def gradient(x,y,th):
xTrans = x.transpose()
sig = sigmoid(np.dot(x,th))
grad = np.dot(xTrans, ( sig - y ))
grad = grad / len(x) #len: number of feature rows
return grad
def hessian(x,y,th):
xTrans = x.transpose()
sig = sigmoid(np.dot(x,th))
result = (1.0/len(x) * np.dot(xTrans, x) * np.diag(sig) * np.diag(1 - sig) )
return result
def updateTh(x,y,th):
hessianInv = np.linalg.inv(hessian(x,y,th))
grad = gradient(x,y,th)
th = th - np.dot(hessianInv, grad)
return th
m = 80 #number of x rows
x = np.ones([m,3])
y = np.empty([m,1], dtype = int)
th = np.zeros([3,1])
hessianResult = np.identity(3) #identity 3x3
# -
hessianResult
def hessian(self, X, Y, ld):
xTrans = x.transpose()
sig = sigmoid(np.dot(x, self.theta))
# +
def mklbl(prefix, n):
return ["%s%s" % (prefix, i) for i in range(n)]
miindex = pd.MultiIndex.from_product([mklbl('A', 4),
mklbl('B', 2),
mklbl('C', 4),
mklbl('D', 2)])
micolumns = pd.MultiIndex.from_tuples([('a', 'foo'), ('a', 'bar'),
('b', 'foo'), ('b', 'bah')],
names=['lvl0', 'lvl1'])
dfmi = pd.DataFrame(np.arange(len(miindex) * len(micolumns))
.reshape((len(miindex), len(micolumns))),
index=miindex,
columns=micolumns).sort_index().sort_index(axis=1)
dfmi
# -
dfmi.unstack(level = 0).unstack(level = 0).unstack(level = 0)
# df.update()
df = pd.DataFrame({'A': ['a', 'b', 'c'],
'B': ['x', 'y', 'z']})
#new_df = pd.DataFrame({'B': ['d', 'e', 'f', 'g', 'h', 'i']})
new_df = pd.DataFrame({'B':[100, np.nan, 6, 6]})
df.update(new_df)
new_column = pd.Series(['d', 'e'], name = 'B', index = [0, 2])
new_column
df.update(new_column)
# df.value_counts()
df = pd.DataFrame({'num_legs': [2, 4, 4, 6],
'num_wings': [2, 0, 0, 0]},
index=['falcon', 'dog', 'cat', 'ant'])
df['num_legs'].value_counts(ascending = True, normalize = True)
import random
import string
pd.DataFrame({'char': [''.join(random.choice(string.ascii_lowercase)) for i in range(10)],
'char2': [''.join(random.choice(string.ascii_lowercase)) for i in range(10)]})
[''.join(random.choice(string.ascii_lowercase)) for i in range(10)]
|
SIADS_505/office_hours/Week4_Office_Hour_Prep.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Spark DF - Basics
#
# Let's start off with the fundamentals of Spark DataFrame. The functionality in this tutorial has been adapted from
# <NAME>. Find out more here:
# - https://changhsinlee.com/pyspark-dataframe-basics/
#
# Objective: In this exercise, you'll understand more about DataFrames, how to start a spark session, and carry out some basic data exploration, manipulation and aggregation.
#
# What is a DataFrame? A DataFrame is a Dataset organized into named columns. It is conceptually equivalent to a table in a relational database or a data frame in R/Python, but with richer optimizations under the hood. Find more information here: https://spark.apache.org/docs/latest/sql-programming-guide.html
#
# What is a Spark Session? It provides a single point of entry to interact with Spark's underlying functionality, which allows us to simply program Spark with DataFrame/Dataset APIs. A new Spark Session must be started in each of our notebooks.
# Section must be included at the beginning of each new notebook. Remember to change the app name.
# If you're using VirtualBox, change the below to '/home/user/spark-2.1.1-bin-hadoop2.7'
import findspark
findspark.init('/home/ubuntu/spark-2.1.1-bin-hadoop2.7')
import pyspark
from pyspark.sql import SparkSession
spark = SparkSession.builder.appName('basics').getOrCreate()
# Let's read in the data. If you open the dataset, you'll find that each column has a header. We specify that by stating that header=True.
# To make our lives easier, we can also use 'inferSchema' when importing CSVs. This automatically detects data types.
# If you would like to manually change data types, refer to this article: https://medium.com/@mrpowers/adding-structtype-columns-to-spark-dataframes-b44125409803
df = spark.read.csv('Datasets/dataframe_dataset.csv',header=True,inferSchema=True)
# ## Basic Data Exploration
# Now that we've started the session and imported the data, let's explore the data.
# The show method allows you visualise DataFrames in a tabular format.
df.show()
# This dataset was originally from Kaggle (https://www.kaggle.com/rouseguy/bankbalanced/data). It's used to predict whether or not a client will subscribe to a term deposit (deposit column) if called by the banks call centre reps. You'll be using a simplified version of the original dataset throughout the DataFrame tutorials, and the full dataset in the binomial logistic regression machine learning exercise too.
# +
# Print schema allows us to visualise the data structure at a high level.
df.printSchema()
# We can also use head to print a specific amount of rows, so we can get a better understanding of the data points.
# Note that we have to specify 'print' depending on the method we're using. Otherwise it may not show up!
print(df.head(1))
# -
# We can use the describe method get some general statistics on our data too.
df.describe().show()
# From this, you may realise that we should have excluded the non-integer columns. But there is one interesting fact about this table. Martial has a count of 95 and Balance has a count of 96, while the others have a count of 100. Looks like there may be some missing data. We'll handle this in the upcoming data cleaning exercise.
# Let's select the columns that are integers, and use the describe method again.
# We see that the average age is 41. The average bank account balance is $1,074.
# And they spoke to call centre reps for approx. 931 seconds on average.
df.select('age', 'balance', 'duration').describe().show()
# ## Basic Data Manipulation
# The code above shows you how to simply select columns, but there's much more that PySpark can do! Let's dig deeper into data manipulation.
# +
# Let's select the balance column and assign it to a variable.
bal_col = df.select('balance')
# We can then use the show method on that variable.
bal_col.show()
# +
# We can also add columns and manipulate the DataFrame. Let's times balance by 10, and add the output to a new column.
df.withColumn('balance_times_10',df['balance']*10).show()
# Question: If we print the df DataFrame again, why is the 'balance_times_10 column' missing?
df.show()
# +
# Let's try out some additional DataFrame methods.
# How would we identify individuals with a balance above $5,000? Using filter!
df.filter("balance > 5000").show()
# We can also use more advanced filters. For example, let's see the jobs of people with over $2,500 in their bank account.
df.filter("balance > 2500").select('job','balance').show()
# -
# What if we wanted to identify those that were under 40 and had over $2,500 in their account?
# We can use multiple conditions.
df.filter("balance > 2500 AND age < 40").select('age','job','balance').show()
# ## Basic Data Aggregation
# On top of filtering, we can also group/aggregate data. Let's see how that works.
df.groupBy('job').mean().show()
# What just happened? Our dataset was grouped by job title (technician, management, etc.) and the average age, balance and duration for each job was calculated. Why only these three? Because mean() automatically filters out any non-numeric features. But in most cases, it's good practice to sort. Let's see how that's done.
# +
# To simplify things, let's split this into two steps. First, let's create a variable then order by age.
# Careful when using show()! Otherwise the variable type will change and you won't be able to order it.
group_job_df = df.groupBy('job').mean()
# Note that we have to use 'avg(age)' instead of age. Why? Because when you use mean(), it changes the feature's name (as you can see below).
print("Sorted by Age")
group_job_df.orderBy('avg(age)').show()
# Let's see what this looks like in one line.
print("Sorted by Balance")
df.groupBy('job').mean().orderBy('avg(balance)').show()
# -
# ## Cleaning Up
# While the data may be accurate, it's still not necessarily appropriate in a professional context. Let's make a few adjustments to make it more appealing.
# +
from pyspark.sql.functions import format_number, col
# Let's start off with this. Just grouping by job and presenting the mean.
group_job_df = df.groupBy('job').mean()
group_job_df.show()
# Now that we've calculated the mean, the values for blue-collar and technician are extremely long.
# We can use format_number to reduce the total amount of decimals.
# The number two represents the amount of decimals we want to be displayed.
group_job_df = group_job_df.select('job',
format_number('avg(age)',2),
format_number('avg(balance)',2),
format_number('avg(duration)',2))
group_job_df.show()
# But now the column names look quite unprofessional. We can assign an alias to rename each of them.
group_job_df = group_job_df.select(col('job').alias('Job Category'),
col('format_number(avg(age), 2)').alias('Average Age'),
col('format_number(avg(balance), 2)').alias('Average Balance'),
col('format_number(avg(duration), 2)').alias('Average Duration'))
group_job_df.show()
# Finally, let's sort the DataFrame by age.
group_job_df = group_job_df.orderBy('Average Age')
print('Average Age, Balance and Duration by Job Category')
group_job_df.show()
# -
# ## Great job on finishing!
#
# Let's go over a few additional key takeaways:
# - You should understand why group_job_df was reassigned each time.
# - Also, you should know that using pyspark.sql.functions is not the only way of achieving such tasks. You could use a different package, function or method (check out the documentation, or click here: https://stackoverflow.com/questions/34077353/how-to-change-dataframe-column-names-in-pyspark)
# - Finally, you should realise that the PySpark API allows you to fully utilise the Python programming language. You don't have to be explicit like in the code example above - that was for the sake of simplicity. If you're comfortable with programming, try using a loop to make repetitive work faster and simpler.
|
Spark DF - Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="3n3ltmfnrqpi" outputId="a2d4f52a-2fb7-4668-f5f0-fe862aab8eb0" papermill={"duration": 1.489571, "end_time": "2020-09-19T06:26:57.168979", "exception": false, "start_time": "2020-09-19T06:26:55.679408", "status": "completed"} tags=[]
# <center>
# <img src="https://gitlab.com/ibm/skills-network/courses/placeholder101/-/raw/master/labs/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# -
# # **Launch Sites Locations Analysis with Folium**
#
# Estimated time needed: **40** minutes
#
# The launch success rate may depend on many factors such as payload mass, orbit type, and so on. It may also depend on the location and proximities of a launch site, i.e., the initial position of rocket trajectories. Finding an optimal location for building a launch site certainly involves many factors and hopefully we could discover some of the factors by analyzing the existing launch site locations.
#
# In the previous exploratory data analysis labs, you have visualized the SpaceX launch dataset using `matplotlib` and `seaborn` and discovered some preliminary correlations between the launch site and success rates. In this lab, you will be performing more interactive visual analytics using `Folium`.
#
# ## Objectives
#
# This lab contains the following tasks:
#
# * **TASK 1:** Mark all launch sites on a map
# * **TASK 2:** Mark the success/failed launches for each site on the map
# * **TASK 3:** Calculate the distances between a launch site to its proximities
#
# After completed the above tasks, you should be able to find some geographical patterns about launch sites.
#
# Let's first import required Python packages for this lab:
#
# !pip3 install folium
# !pip3 install wget
import folium
import wget
import pandas as pd
# Import folium MarkerCluster plugin
from folium.plugins import MarkerCluster
# Import folium MousePosition plugin
from folium.plugins import MousePosition
# Import folium DivIcon plugin
from folium.features import DivIcon
# If you need to refresh your memory about folium, you may download and refer to this previous folium lab:
#
# [Generating Maps with Python](https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module\_3/DV0101EN-3-5-1-Generating-Maps-in-Python-py-v2.0.ipynb)
#
# ## Task 1: Mark all launch sites on a map
#
# First, let's try to add each site's location on a map using site's latitude and longitude coordinates
#
# The following dataset with the name `spacex_launch_geo.csv` is an augmented dataset with latitude and longitude added for each site.
#
# Download and read the `spacex_launch_geo.csv`
spacex_csv_file = wget.download('https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/datasets/spacex_launch_geo.csv')
spacex_df=pd.read_csv(spacex_csv_file)
spacex_df.head()
# Now, you can take a look at what are the coordinates for each site.
#
# Select relevant sub-columns: `Launch Site`, `Lat(Latitude)`, `Long(Longitude)`, `class`
spacex_df = spacex_df[['Launch Site', 'Lat', 'Long', 'class']]
launch_sites_df = spacex_df.groupby(['Launch Site'], as_index=False).first()
launch_sites_df = launch_sites_df[['Launch Site', 'Lat', 'Long']]
launch_sites_df
# Above coordinates are just plain numbers that can not give you any intuitive insights about where are those launch sites. If you are very good at geography, you can interpret those numbers directly in your mind. If not, that's fine too. Let's visualize those locations by pinning them on a map.
#
# We first need to create a folium `Map` object, with an initial center location to be NASA Johnson Space Center at Houston, Texas.
#
# Start location is NASA Johnson Space Center
nasa_coordinate = [29.559684888503615, -95.0830971930759]
site_map = folium.Map(location=nasa_coordinate, zoom_start=10)
# We could use `folium.Circle` to add a highlighted circle area with a text label on a specific coordinate. For example,
#
# Create a blue circle at NASA Johnson Space Center's coordinate with a popup label showing its name
circle = folium.Circle(nasa_coordinate, radius=1000, color='#d35400', fill=True).add_child(folium.Popup('NASA Johnson Space Center'))
# Create a blue circle at NASA Johnson Space Center's coordinate with a icon showing its name
marker = folium.map.Marker(
nasa_coordinate,
# Create an icon as a text label
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'NASA JSC',
)
)
site_map.add_child(circle)
site_map.add_child(marker)
# and you should find a small yellow circle near the city of Houston and you can zoom-in to see a larger circle.
#
# Now, let's add a circle for each launch site in data frame `launch_sites`
#
# *TODO:* Create and add `folium.Circle` and `folium.Marker` for each launch site on the site map
#
# An example of folium.Circle:
#
# `folium.Circle(coordinate, radius=1000, color='#000000', fill=True).add_child(folium.Popup(...))`
#
# An example of folium.Marker:
#
# `folium.map.Marker(coordinate, icon=DivIcon(icon_size=(20,20),icon_anchor=(0,0), html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'label', ))`
#
launch_sites_df
nasa_coordinate
# +
# Initial the map
site_map = folium.Map(location=nasa_coordinate, zoom_start=4.2)
# For each launch site, add a Circle object based on its coordinate (Lat, Long) values. In addition, add Launch site name as a popup label
LC_40_coordinate = []
SLC_40_coordinate = []
LC_39A_coordinate = []
SLC_4E_coordinate = []
#Create the coordinate lists for each launch site
LC_40_coordinate.append(launch_sites_df.iloc[0][1])
LC_40_coordinate.append(launch_sites_df.iloc[0][2])
SLC_40_coordinate.append(launch_sites_df.iloc[1][1])
SLC_40_coordinate.append(launch_sites_df.iloc[1][2])
LC_39A_coordinate.append(launch_sites_df.iloc[2][1])
LC_39A_coordinate.append(launch_sites_df.iloc[2][2])
SLC_4E_coordinate.append(launch_sites_df.iloc[3][1])
SLC_4E_coordinate.append(launch_sites_df.iloc[3][2])
circle1 = folium.Circle(LC_40_coordinate, radius=1000, color='#000000', fill=True).add_child(folium.Popup('CCAFS LC-40'))
circle2 = folium.Circle(SLC_40_coordinate, radius=1000, color='#000000', fill=True).add_child(folium.Popup('CCAFS SLC-40'))
circle3 = folium.Circle(LC_39A_coordinate, radius=1000, color='#000000', fill=True).add_child(folium.Popup('KSC LC-39A'))
circle4 = folium.Circle(SLC_4E_coordinate, radius=1000, color='#000000', fill=True).add_child(folium.Popup('VAFB SLC-4E'))
marker1 = folium.map.Marker(
LC_40_coordinate,
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'LC-40',
)
)
marker2 = folium.map.Marker(
SLC_40_coordinate,
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'SLC-40',
)
)
marker3 = folium.map.Marker(
LC_39A_coordinate,
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'LC-39A',
)
)
marker4 = folium.map.Marker(
SLC_4E_coordinate,
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % 'SLC-4E',
)
)
site_map.add_child(circle1)
site_map.add_child(circle2)
site_map.add_child(circle3)
site_map.add_child(circle4)
site_map.add_child(marker1)
site_map.add_child(marker2)
site_map.add_child(marker3)
site_map.add_child(marker4)
# -
# The generated map with marked launch sites should look similar to the following:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/launch_site_markers.png" />
# </center>
#
# Now, you can explore the map by zoom-in/out the marked areas
# , and try to answer the following questions:
#
# * Are all launch sites in proximity to the Equator line?
# * Are all launch sites in very close proximity to the coast?
#
# Also please try to explain your findings.
#
# # Task 2: Mark the success/failed launches for each site on the map
#
# Next, let's try to enhance the map by adding the launch outcomes for each site, and see which sites have high success rates.
# Recall that data frame spacex_df has detailed launch records, and the `class` column indicates if this launch was successful or not
#
spacex_df.tail(10)
# Next, let's create markers for all launch records.
# If a launch was successful `(class=1)`, then we use a green marker and if a launch was failed, we use a red marker `(class=0)`
#
# Note that a launch only happens in one of the four launch sites, which means many launch records will have the exact same coordinate. Marker clusters can be a good way to simplify a map containing many markers having the same coordinate.
#
# Let's first create a `MarkerCluster` object
#
# + id="wP9PVUZ7Jfjt" outputId="6a3b8164-940c-4b93-9f3d-c655c4a0c683" papermill={"duration": 0.904519, "end_time": "2020-09-19T06:27:38.357041", "exception": false, "start_time": "2020-09-19T06:27:37.452522", "status": "completed"} tags=[]
marker_cluster = MarkerCluster()
# -
# *TODO:* Create a new column in `launch_sites` dataframe called `marker_color` to store the marker colors based on the `class` value
#
# +
# Apply a function to check the value of `class` column
# If class=1, marker_color value will be green
# If class=0, marker_color value will be red
launch_sites = spacex_df
mark_color = launch_sites['class'].apply(lambda x: 'green' if x == 1 else 'red')
launch_sites['marker_color'] = mark_color
launch_sites
# +
# Function to assign color to launch outcome
def assign_marker_color(launch_outcome):
if launch_outcome == 1:
return 'green'
else:
return 'red'
spacex_df['marker_color'] = spacex_df['class'].apply(assign_marker_color)
spacex_df.tail(10)
# -
# *TODO:* For each launch result in `spacex_df` data frame, add a `folium.Marker` to `marker_cluster`
#
# +
# Add marker_cluster to current site_map
site_map.add_child(marker_cluster)
# for each row in spacex_df data frame
# create a Marker object with its coordinate
# and customize the Marker's icon property to indicate if this launch was successed or failed,
# e.g., icon=folium.Icon(color='white', icon_color=row['marker_color']
for index, record in spacex_df.iterrows():
# TODO: Create and add a Marker cluster to the site map
marker = folium.Marker(location = [record['Lat'], record['Long']], icon=folium.Icon(color='white', icon_color=record['marker_color']))
marker_cluster.add_child(marker)
site_map
# -
# Your updated map may look like the following screenshots:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/launch_site_marker_cluster.png" />
# </center>
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/launch_site_marker_cluster_zoomed.png" />
# </center>
#
# From the color-labeled markers in marker clusters, you should be able to easily identify which launch sites have relatively high success rates.
#
# # TASK 3: Calculate the distances between a launch site to its proximities
#
# Next, we need to explore and analyze the proximities of launch sites.
#
# Let's first add a `MousePosition` on the map to get coordinate for a mouse over a point on the map. As such, while you are exploring the map, you can easily find the coordinates of any points of interests (such as railway)
#
# +
# Add Mouse Position to get the coordinate (Lat, Long) for a mouse over on the map
formatter = "function(num) {return L.Util.formatNum(num, 5);};"
mouse_position = MousePosition(
position='topright',
separator=' Long: ',
empty_string='NaN',
lng_first=False,
num_digits=20,
prefix='Lat:',
lat_formatter=formatter,
lng_formatter=formatter,
)
site_map.add_child(mouse_position)
site_map
# -
# Now zoom in to a launch site and explore its proximity to see if you can easily find any railway, highway, coastline, etc. Move your mouse to these points and mark down their coordinates (shown on the top-left) in order to the distance to the launch site.
#
# You can calculate the distance between two points on the map based on their `Lat` and `Long` values using the following method:
#
# +
from math import sin, cos, sqrt, atan2, radians
def calculate_distance(lat1, lon1, lat2, lon2):
# approximate radius of earth in km
R = 6373.0
lat1 = radians(lat1)
lon1 = radians(lon1)
lat2 = radians(lat2)
lon2 = radians(lon2)
dlon = lon2 - lon1
dlat = lat2 - lat1
a = sin(dlat / 2)**2 + cos(lat1) * cos(lat2) * sin(dlon / 2)**2
c = 2 * atan2(sqrt(a), sqrt(1 - a))
distance = R * c
return distance
# -
# *TODO:* Mark down a point on the closest coastline using MousePosition and calculate the distance between the coastline point and the launch site.
#
# +
# find coordinate of the closet coastline
# e.g.,: Lat: 28.56367 Lon: -80.57163
# distance_coastline = calculate_distance(launch_site_lat, launch_site_lon, coastline_lat, coastline_lon)
#coordinate from 39A to Cuba
cuba_coord = [21.8615, -79.98047]
distance_cuba = calculate_distance(launch_sites_df.iloc[2][1],launch_sites_df.iloc[2][2], cuba_coord[0], cuba_coord[1])
distance_cuba
# -
# *TODO:* After obtained its coordinate, create a `folium.Marker` to show the distance
#
# Create and add a folium.Marker on your selected closest coastline point on the map
# Display the distance between coastline point and launch site using the icon property
# for example
distance_marker = folium.Marker(
cuba_coord,
icon=DivIcon(
icon_size=(20,20),
icon_anchor=(0,0),
html='<div style="font-size: 12; color:#d35400;"><b>%s</b></div>' % "{:10.2f} KM".format(distance_cuba),
)
)
# *TODO:* Draw a `PolyLine` between a launch site to the selected coastline point
#
# Create a `folium.PolyLine` object using the coastline coordinates and launch site coordinate
points = [(21.8615, -79.98047), (launch_sites_df.iloc[2][1],launch_sites_df.iloc[2][2])]
lines=folium.PolyLine(locations=points, weight=3)
site_map.add_child(lines)
# Your updated map with distance line should look like the following screenshot:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/launch_site_marker_distance.png" />
# </center>
#
# *TODO:* Similarly, you can draw a line betwee a launch site to its closest city, railway, highway, etc. You need to use `MousePosition` to find the their coordinates on the map first
#
# A railway map symbol may look like this:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/railway.png" />
# </center>
#
# A highway map symbol may look like this:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/highway.png" />
# </center>
#
# A city map symbol may look like this:
#
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBM-DS0321EN-SkillsNetwork/labs/module_3/images/city.png" />
# </center>
#
# +
# Create a marker with distance to a closest city, railway, highway, etc.
# Draw a line between the marker to the launch site
#Launch site to the nearest Airport
points1 = [(launch_sites_df.iloc[3][1], launch_sites_df.iloc[3][2]), (34.66542, -120.46717)]
lines=folium.PolyLine(locations=points1, weight=3)
site_map.add_child(lines)
# +
#lines=folium.PolyLine(locations=points, weight=1)
#site_map.add_child(lines)
# +
#lines=folium.PolyLine(locations=points, weight=1)
#site_map.add_child(lines)
# -
# After you plot distance lines to the proximities, you can answer the following questions easily:
#
# * Are launch sites in close proximity to railways?
# * Are launch sites in close proximity to highways?
# * Are launch sites in close proximity to coastline?
# * Do launch sites keep certain distance away from cities?
#
# Also please try to explain your findings.
#
# # Next Steps:
#
# Now you have discovered many interesting insights related to the launch sites' location using folium, in a very interactive way. Next, you will need to build a dashboard using Ploty Dash on detailed launch records.
#
# ## Authors
#
# [<NAME>](https://www.linkedin.com/in/yan-luo-96288783/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDS0321ENSkillsNetwork26802033-2021-01-01)
#
# ### Other Contributors
#
# <NAME>
#
# ## Change Log
#
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# | ----------------- | ------- | ---------- | --------------------------- |
# | 2021-05-26 | 1.0 | Yan | Created the initial version |
#
# Copyright © 2021 IBM Corporation. All rights reserved.
#
|
Launch Site Interactive Analysis with Folium.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.9.4 64-bit
# name: python394jvsc74a57bd02951d919548ae18de2df5ded62b9a6d18db65d3b5a4ffaab87b83029c7c31e33
# ---
# + [markdown] id="VwK5-9FIB-lu" colab_type="text"
# # Natural Language Processing
# + [markdown] id="X1kiO9kACE6s" colab_type="text"
# ## Importing the libraries
# + id="7QG7sxmoCIvN" colab_type="code" colab={}
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# + [markdown] id="wTfaCIzdCLPA" colab_type="text"
# ## Importing the dataset
# + id="UCK6vQ5QCQJe" colab_type="code" colab={}
dataset = pd.read_csv('Restaurant_Reviews.tsv', delimiter = '\t', quoting = 3)
# + [markdown] id="Qekztq71CixT" colab_type="text"
# ## Cleaning the texts
# -
import re
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer #used fr stemming the word
corpus = []
for i in range(0, dataset.shape[0]):
review = re.sub('[^a-zA-Z]', ' ', dataset['Review'][i])
review = review.split()
ps = PorterStemmer()
all_stopwords = stopwords.words('english')
all_stopwords.remove('not')
review = [ps.stem(word) for word in review if not word in set(all_stopwords)]
review = ' '.join(review)
corpus.append(review)
# + tags=[]
print(corpus)
# + [markdown] id="CLqmAkANCp1-" colab_type="text"
# ## Creating the Bag of Words model
# +
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer(max_features= 1600)
X = cv.fit_transform(corpus).toarray()
y = dataset.iloc[:, -1].values
# -
print(len(X[0]))
# + [markdown] id="DH_VjgPzC2cd" colab_type="text"
# ## Splitting the dataset into the Training set and Test set
# -
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size= .2, random_state = 0)
# + [markdown] id="VkIq23vEDIPt" colab_type="text"
# ## Training the Naive Bayes model on the Training set
# -
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
# classifier = GaussianNB()
classifier = RandomForestClassifier(n_estimators=1000, criterion='entropy')
# classifier = SVC(kernel='rbf')
# classifier = LogisticRegression()
classifier.fit(X_train, y_train)
# + [markdown] id="1JaRM7zXDWUy" colab_type="text"
# ## Predicting the Test set results
# -
y_pred = classifier.predict(X_test)
print(np.concatenate((y_pred.reshape(len(y_pred),1), y_test.reshape(len(y_test),1)),1))
# + [markdown] id="xoMltea5Dir1" colab_type="text"
# ## Making the Confusion Matrix
# -
from sklearn.metrics import confusion_matrix, accuracy_score
cm = confusion_matrix(y_test, y_pred)
print(cm)
accuracy_score(y_test, y_pred)
|
Natural Language Processing/Bag of Word/natural_language_processing.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="nibpbUnTsxTd"
# ##### Copyright 2018 The TensorFlow Authors.
# + colab={} colab_type="code" id="tXAbWHtqs1Y2"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="HTgMAvQq-PU_"
# # Ragged Tensors
#
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://www.tensorflow.org/guide/ragged_tensors"><img src="https://www.tensorflow.org/images/tf_logo_32px.png" />View on TensorFlow.org</a>
# </td>
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/en/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />Run in Google Colab</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/en/guide/ragged_tensors.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />View source on GitHub</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="cDIUjj07-rQg"
# ## Setup
# + colab={} colab_type="code" id="XqYjyKB-un-b"
# !pip install tf-nightly
# + colab={} colab_type="code" id="KKvdSorS-pDD"
from __future__ import absolute_import, division, print_function
import math
import tensorflow as tf
tf.enable_eager_execution()
# + [markdown] colab_type="text" id="pxi0m_yf-te5"
# ## Overview
#
# Your data comes in many shapes; your tensors should too.
# *Ragged tensors* are the TensorFlow equivalent of nested variable-length
# lists. They make it easy to store and process data with non-uniform shapes,
# including:
#
# * Variable-length features, such as the set of actors in a movie.
# * Batches of variable-length sequential inputs, such as sentences or video
# clips.
# * Hierarchical inputs, such as text documents that are subdivided into
# sections, paragraphs, sentences, and words.
# * Individual fields in structured inputs, such as protocol buffers.
#
# ### What you can do with a ragged tensor
#
# Ragged tensors are supported by more than a hundred TensorFlow operations,
# including math operations (such as `tf.add` and `tf.reduce_mean`), array operations
# (such as `tf.concat` and `tf.tile`), string manipulation ops (such as
# `tf.substr`), and many others:
#
# + colab={} colab_type="code" id="vGmJGSf_-PVB"
digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))
# + [markdown] colab_type="text" id="Pt-5OIc8-PVG"
# There are also a number of methods and operations that are
# specific to ragged tensors, including factory methods, conversion methods,
# and value-mapping operations.
# For a list of supported ops, see the `tf.ragged` package
# documentation.
#
# As with normal tensors, you can use Python-style indexing to access specific
# slices of a ragged tensor. For more information, see the section on
# **Indexing** below.
# + colab={} colab_type="code" id="n8YMKXpI-PVH"
print(digits[0]) # First row
# + colab={} colab_type="code" id="Awi8i9q5_DuX"
print(digits[:, :2]) # First two values in each row.
# + colab={} colab_type="code" id="sXgQtTcgHHMR"
print(digits[:, -2:]) # Last two values in each row.
# + [markdown] colab_type="text" id="6FU5T_-8-PVK"
# And just like normal tensors, you can use Python arithmetic and comparison
# operators to perform elementwise operations. For more information, see the section on
# **Overloaded Operators** below.
# + colab={} colab_type="code" id="2tdUEtb7-PVL"
print(digits + 3)
# + colab={} colab_type="code" id="X-bxG0nc_Nmf"
print(digits + tf.ragged.constant([[1, 2, 3, 4], [], [5, 6, 7], [8], []]))
# + [markdown] colab_type="text" id="2tsw8mN0ESIT"
# If you need to perform an elementwise transformation to the values of a `RaggedTensor`, you can use `tf.ragged.map_flat_values`, which takes a function plus one or more arguments, and applies the function to transform the `RaggedTensor`'s values.
# + colab={} colab_type="code" id="pvt5URbdEt-D"
times_two_plus_one = lambda x: x * 2 + 1
print(tf.ragged.map_flat_values(times_two_plus_one, digits))
# + [markdown] colab_type="text" id="7M5RHOgp-PVN"
# ### Constructing a ragged tensor
#
# The simplest way to construct a ragged tensor is using
# `tf.ragged.constant`, which builds the
# `RaggedTensor` corresponding to a given nested Python `list`:
# + colab={} colab_type="code" id="yhgKMozw-PVP"
sentences = tf.ragged.constant([
["Let's", "build", "some", "ragged", "tensors", "!"],
["We", "can", "use", "tf.ragged.constant", "."]])
print(sentences)
# + colab={} colab_type="code" id="TW1g7eE2ee8M"
paragraphs = tf.ragged.constant([
[['I', 'have', 'a', 'cat'], ['His', 'name', 'is', 'Mat']],
[['Do', 'you', 'want', 'to', 'come', 'visit'], ["I'm", 'free', 'tomorrow']],
])
print(paragraphs)
# + [markdown] colab_type="text" id="SPLn5xHn-PVR"
# Ragged tensors can also be constructed by pairing flat *values* tensors with
# *row-partitioning* tensors indicating how those values should be divided into
# rows, using factory classmethods such as `tf.RaggedTensor.from_value_rowids`,
# `tf.RaggedTensor.from_row_lengths`, and
# `tf.RaggedTensor.from_row_splits`.
#
# #### `tf.RaggedTensor.from_value_rowids`
# If you know which row each value belongs in, then you can build a `RaggedTensor` using a `value_rowids` row-partitioning tensor:
#
# 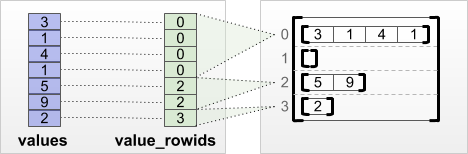
# + colab={} colab_type="code" id="SEvcPUcl-PVS"
print(tf.RaggedTensor.from_value_rowids(
values=[3, 1, 4, 1, 5, 9, 2, 6],
value_rowids=[0, 0, 0, 0, 2, 2, 2, 3]))
# + [markdown] colab_type="text" id="RBQh8sYc-PVV"
# #### `tf.RaggedTensor.from_row_lengths`
#
# If you know how long each row is, then you can use a `row_lengths` row-partitioning tensor:
#
# 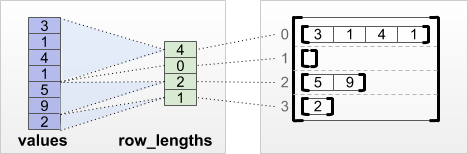
# + colab={} colab_type="code" id="LBY81WXl-PVW"
print(tf.RaggedTensor.from_row_lengths(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_lengths=[4, 0, 3, 1]))
# + [markdown] colab_type="text" id="8p5V8_Iu-PVa"
# #### `tf.RaggedTensor.from_row_splits`
#
# If you know the index where each row starts and ends, then you can use a `row_splits` row-partitioning tensor:
#
# 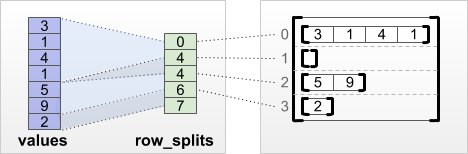
# + colab={} colab_type="code" id="FwizuqZI-PVb"
print(tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2, 6],
row_splits=[0, 4, 4, 7, 8]))
# + [markdown] colab_type="text" id="E-9imo8DhwuA"
# See the `tf.RaggedTensor` class documentation for a full list of factory methods.
# + [markdown] colab_type="text" id="YQAOsT1_-PVg"
# ### What you can store in a ragged tensor
#
# As with normal `Tensor`s, the values in a `RaggedTensor` must all have the same
# type; and the values must all be at the same nesting depth (the *rank* of the
# tensor):
# + colab={} colab_type="code" id="SqbPBd_w-PVi"
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]])) # ok: type=string, rank=2
# + colab={} colab_type="code" id="83ZCSJnQAWAf"
print(tf.ragged.constant([[[1, 2], [3]], [[4, 5]]])) # ok: type=int32, rank=3
# + colab={} colab_type="code" id="ewA3cISdDfmP"
try:
tf.ragged.constant([["one", "two"], [3, 4]]) # bad: multiple types
except ValueError as exception:
print(exception)
# + colab={} colab_type="code" id="EOWIlVidDl-n"
try:
tf.ragged.constant(["A", ["B", "C"]]) # bad: multiple nesting depths
except ValueError as exception:
print(exception)
# + [markdown] colab_type="text" id="nhHMFhSp-PVq"
# ### Example use case
#
# The following example demonstrates how `RaggedTensor`s can be used to construct
# and combine unigram and bigram embeddings for a batch of variable-length
# queries, using special markers for the beginning and end of each sentence.
# For more details on the ops used in this example, see the `tf.ragged` package documentation.
# + colab={} colab_type="code" id="ZBs_V7e--PVr"
queries = tf.ragged.constant([['Who', 'is', 'Dan', 'Smith'],
['Pause'],
['Will', 'it', 'rain', 'later', 'today']])
# Create an embedding table.
num_buckets = 1024
embedding_size = 4
embedding_table = tf.Variable(
tf.truncated_normal([num_buckets, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
# Look up the embedding for each word.
word_buckets = tf.strings.to_hash_bucket_fast(queries, num_buckets)
word_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, word_buckets) # ①
# Add markers to the beginning and end of each sentence.
marker = tf.fill([queries.nrows(), 1], '#')
padded = tf.concat([marker, queries, marker], axis=1) # ②
# Build word bigrams & look up embeddings.
bigrams = tf.string_join([padded[:, :-1], padded[:, 1:]], separator='+') # ③
bigram_buckets = tf.strings.to_hash_bucket_fast(bigrams, num_buckets)
bigram_embeddings = tf.ragged.map_flat_values(
tf.nn.embedding_lookup, embedding_table, bigram_buckets) # ④
# Find the average embedding for each sentence
all_embeddings = tf.concat([word_embeddings, bigram_embeddings], axis=1) # ⑤
avg_embedding = tf.reduce_mean(all_embeddings, axis=1) # ⑥
print(avg_embedding)
# + [markdown] colab_type="text" id="Y_lE_LAVcWQH"
# 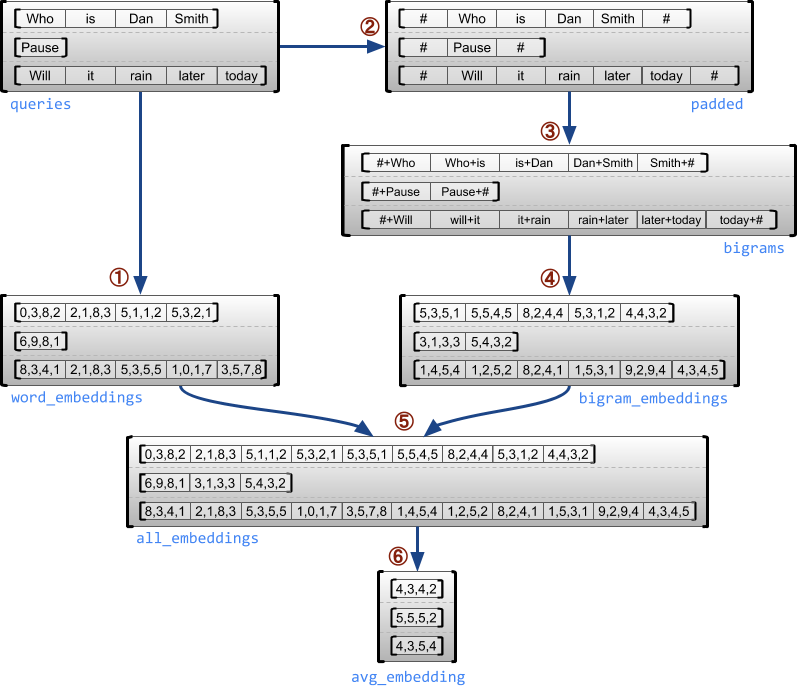
# + [markdown] colab_type="text" id="An_k0pX1-PVt"
# ## Ragged tensors: definitions
#
# ### Ragged and uniform dimensions
#
# A *ragged tensor* is a tensor with one or more *ragged dimensions*,
# which are dimensions whose slices may have different lengths. For example, the
# inner (column) dimension of `rt=[[3, 1, 4, 1], [], [5, 9, 2], [6], []]` is
# ragged, since the column slices (`rt[0, :]`, ..., `rt[4, :]`) have different
# lengths. Dimensions whose slices all have the same length are called *uniform
# dimensions*.
#
# The outermost dimension of a ragged tensor is always uniform, since it consists
# of a single slice (and so there is no possibility for differing slice lengths).
# In addition to the uniform outermost dimension, ragged tensors may also have
# uniform inner dimensions. For example, we might store the word embeddings for
# each word in a batch of sentences using a ragged tensor with shape
# `[num_sentences, (num_words), embedding_size]`, where the parentheses around
# `(num_words)` indicate that the dimension is ragged.
#
# 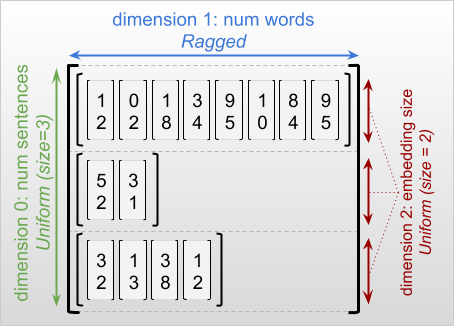
#
# Ragged tensors may have multiple ragged dimensions. For example, we could store
# a batch of structured text documents using a tensor with shape `[num_documents,
# (num_paragraphs), (num_sentences), (num_words)]` (where again parentheses are
# used to indicate ragged dimensions).
#
# #### Ragged tensor shape restrictions
#
# The shape of a ragged tensor is currently restricted to have the following form:
#
# * A single uniform dimension
# * Followed by one or more ragged dimensions
# * Followed by zero or more uniform dimensions.
#
# Note: These restrictions are a consequence of the current implementation, and we
# may relax them in the future.
#
# ### Rank and ragged rank
#
# The total number of dimensions in a ragged tensor is called its ***rank***, and
# the number of ragged dimensions in a ragged tensor is called its ***ragged
# rank***. In graph execution mode (i.e., non-eager mode), a tensor's ragged rank
# is fixed at creation time: it can't depend
# on runtime values, and can't vary dynamically for different session runs.
# A ***potentially ragged tensor*** is a value that might be
# either a `tf.Tensor` or a `tf.RaggedTensor`. The
# ragged rank of a `tf.Tensor` is defined to be zero.
#
# ### RaggedTensor shapes
#
# When describing the shape of a RaggedTensor, ragged dimensions are indicated by
# enclosing them in parentheses. For example, as we saw above, the shape of a 3-D
# RaggedTensor that stores word embeddings for each word in a batch of sentences
# can be written as `[num_sentences, (num_words), embedding_size]`.
# The `RaggedTensor.shape` attribute returns a `tf.TensorShape` for a
# ragged tensor, where ragged dimensions have size `None`:
#
# + colab={} colab_type="code" id="M2Wzx4JEIvmb"
tf.ragged.constant([["Hi"], ["How", "are", "you"]]).shape
# + [markdown] colab_type="text" id="G9tfJOeFlijE"
# The method `tf.RaggedTensor.bounding_shape` can be used to find a tight
# bounding shape for a given `RaggedTensor`:
# + colab={} colab_type="code" id="5DHaqXHxlWi0"
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]).bounding_shape())
# + [markdown] colab_type="text" id="V8e7x95UcLS6"
# ## Ragged vs sparse tensors
#
# A ragged tensor should *not* be thought of as a type of sparse tensor, but
# rather as a dense tensor with an irregular shape.
#
# As an illustrative example, consider how array operations such as `concat`,
# `stack`, and `tile` are defined for ragged vs. sparse tensors. Concatenating
# ragged tensors joins each row to form a single row with the combined length:
#
# 
#
# + colab={} colab_type="code" id="ush7IGUWLXIn"
ragged_x = tf.ragged.constant([["John"], ["a", "big", "dog"], ["my", "cat"]])
ragged_y = tf.ragged.constant([["fell", "asleep"], ["barked"], ["is", "fuzzy"]])
print(tf.concat([ragged_x, ragged_y], axis=1))
# + [markdown] colab_type="text" id="pvQzZG8zMoWa"
#
# But concatenating sparse tensors is equivalent to concatenating the corresponding dense tensors,
# as illustrated by the following example (where Ø indicates missing values):
#
# 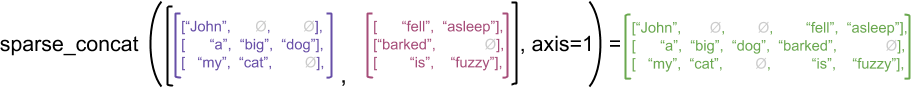
#
# + colab={} colab_type="code" id="eTIhGayQL0gI"
sparse_x = ragged_x.to_sparse()
sparse_y = ragged_y.to_sparse()
sparse_result = tf.sparse.concat(sp_inputs=[sparse_x, sparse_y], axis=1)
print(tf.sparse.to_dense(sparse_result, ''))
# + [markdown] colab_type="text" id="Vl8eQN8pMuYx"
# For another example of why this distinction is important, consider the
# definition of “the mean value of each row” for an op such as `tf.reduce_mean`.
# For a ragged tensor, the mean value for a row is the sum of the
# row’s values divided by the row’s width.
# But for a sparse tensor, the mean value for a row is the sum of the
# row’s values divided by the sparse tensor’s overall width (which is
# greater than or equal to the width of the longest row).
#
# + [markdown] colab_type="text" id="cRcHzS6pcHYC"
# ## Overloaded operators
#
# The `RaggedTensor` class overloads the standard Python arithmetic and comparison
# operators, making it easy to perform basic elementwise math:
# + colab={} colab_type="code" id="skScd37P-PVu"
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
y = tf.ragged.constant([[1, 1], [2], [3, 3, 3]])
print(x + y)
# + [markdown] colab_type="text" id="XEGgbZHV-PVw"
# Since the overloaded operators perform elementwise computations, the inputs to
# all binary operations must have the same shape, or be broadcastable to the same
# shape. In the simplest broadcasting case, a single scalar is combined
# elementwise with each value in a ragged tensor:
# + colab={} colab_type="code" id="IYybEEWc-PVx"
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
print(x + 3)
# + [markdown] colab_type="text" id="okGb9dIi-PVz"
# For a discussion of more advanced cases, see the section on
# **Broadcasting**.
#
# Ragged tensors overload the same set of operators as normal `Tensor`s: the unary
# operators `-`, `~`, and `abs()`; and the binary operators `+`, `-`, `*`, `/`,
# `//`, `%`, `**`, `&`, `|`, `^`, `<`, `<=`, `>`, and `>=`. Note that, as with
# standard `Tensor`s, binary `==` is not overloaded; you can use
# `tf.equal()` to check elementwise equality.
# + [markdown] colab_type="text" id="f2anbs6ZnFtl"
# ## Indexing
#
# Ragged tensors support Python-style indexing, including multidimensional
# indexing and slicing. The following examples demonstrate ragged tensor indexing
# with a 2-D and a 3-D ragged tensor.
#
# ### Indexing a 2-D ragged tensor with 1 ragged dimension
# + colab={} colab_type="code" id="MbSRZRDz-PV1"
queries = tf.ragged.constant(
[['Who', 'is', 'George', 'Washington'],
['What', 'is', 'the', 'weather', 'tomorrow'],
['Goodnight']])
print(queries[1])
# + colab={} colab_type="code" id="EFfjZV7YA3UH"
print(queries[1, 2]) # A single word
# + colab={} colab_type="code" id="VISRPQSdA3xn"
print(queries[1:]) # Everything but the first row
# + colab={} colab_type="code" id="J1PpSyKQBMng"
print(queries[:, :3]) # The first 3 words of each query
# + colab={} colab_type="code" id="ixrhHmJBeidy"
print(queries[:, -2:]) # The last 2 words of each query
# + [markdown] colab_type="text" id="cnOP6Vza-PV4"
# ### Indexing a 3-D ragged tensor with 2 ragged dimensions
# + colab={} colab_type="code" id="8VbqbKcE-PV6"
rt = tf.ragged.constant([[[1, 2, 3], [4]],
[[5], [], [6]],
[[7]],
[[8, 9], [10]]])
# + colab={} colab_type="code" id="f9WPVWf4grVp"
print(rt[1]) # Second row (2-D RaggedTensor)
# + colab={} colab_type="code" id="ad8FGJoABjQH"
print(rt[3, 0]) # First element of fourth row (1-D Tensor)
# + colab={} colab_type="code" id="MPPr-a-bBjFE"
print(rt[:, 1:3]) # Items 1-3 of each row (3-D RaggedTensor)
# + colab={} colab_type="code" id="6SIDeoIUBi4z"
print(rt[:, -1:]) # Last item of each row (3-D RaggedTensor)
# + [markdown] colab_type="text" id="_d3nBh1GnWvU"
# `RaggedTensor`s supports multidimensional indexing and slicing, with one
# restriction: indexing into a ragged dimension is not allowed. This case is
# problematic because the indicated value may exist in some rows but not others.
# In such cases, it's not obvious whether we should (1) raise an `IndexError`; (2)
# use a default value; or (3) skip that value and return a tensor with fewer rows
# than we started with. Following the
# [guiding principles of Python](https://www.python.org/dev/peps/pep-0020/)
# ("In the face
# of ambiguity, refuse the temptation to guess" ), we currently disallow this
# operation.
# + [markdown] colab_type="text" id="IsWKETULAJbN"
# ## Tensor Type Conversion
#
# The `RaggedTensor` class defines methods that can be used to convert
# between `RaggedTensor`s and `tf.Tensor`s or `tf.SparseTensors`:
# + colab={} colab_type="code" id="INnfmZGcBoU_"
ragged_sentences = tf.ragged.constant([
['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])
print(ragged_sentences.to_tensor(default_value=''))
# + colab={} colab_type="code" id="41WAZLXNnbwH"
print(ragged_sentences.to_sparse())
# + colab={} colab_type="code" id="-rfiyYqne8QN"
x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))
# + colab={} colab_type="code" id="S8MkYo2hfVhj"
st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
values=['a', 'b', 'c'],
dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))
# + [markdown] colab_type="text" id="qx025sNMkAHH"
# ## Evaluating ragged tensors
#
# ### Eager execution
#
# In eager execution mode, ragged tensors are evaluated immediately. To access the
# values they contain, you can:
#
# * Use the
# `tf.RaggedTensor.to_list()`
# method, which converts the ragged tensor to a Python `list`.
# + colab={} colab_type="code" id="uMm1WMkc-PV_"
rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print(rt.to_list())
# + [markdown] colab_type="text" id="SrizmqTc-PWC"
# * Use Python indexing. If the tensor piece you select contains no ragged
# dimensions, then it will be returned as an `EagerTensor`. You can then use
# the `numpy()` method to access the value directly.
# + colab={} colab_type="code" id="HpRHhfLe-PWD"
print(rt[1].numpy())
# + [markdown] colab_type="text" id="sNlpI2fR-PWF"
# * Decompose the ragged tensor into its components, using the
# `tf.RaggedTensor.values`
# and
# `tf.RaggedTensor.row_splits`
# properties, or row-paritioning methods such as `tf.RaggedTensor.row_lengths()`
# and `tf.RaggedTensor.value_rowids()`.
# + colab={} colab_type="code" id="yTckrLdB-PWG"
print(rt.values)
# + colab={} colab_type="code" id="B8OnG9NzCEnv"
print(rt.row_splits)
# + [markdown] colab_type="text" id="6tG3kBAo-PWI"
# ### Graph execution
#
# In graph execution mode, ragged tensors can be evaluated using `session.run()`,
# just like standard tensors.
# + colab={} colab_type="code" id="aDhVIrIs-PWJ"
with tf.Session() as session:
rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
rt_value = session.run(rt)
# + [markdown] colab_type="text" id="0-K5pqwJ-PWL"
# The resulting value will be a
# `tf.ragged.RaggedTensorValue`
# instance. To access the values contained in a `RaggedTensorValue`, you can:
#
# * Use the
# `tf.ragged.RaggedTensorValue.to_list()`
# method, which converts the `RaggedTensorValue` to a Python `list`.
# + colab={} colab_type="code" id="R2U3WZf8-PWM"
print(rt_value.to_list())
# + [markdown] colab_type="text" id="4x4b7DpY-PWO"
# * Decompose the ragged tensor into its components, using the
# `tf.ragged.RaggedTensorValue.values`
# and
# `tf.ragged.RaggedTensorValue.row_splits`
# properties.
# + colab={} colab_type="code" id="RtREVSPB-PWO"
print(rt_value.values)
# + colab={} colab_type="code" id="9BIpKNBnCmjV"
print(rt_value.row_splits)
# + colab={} colab_type="code" id="qEmnOr01Cdl3"
tf.enable_eager_execution() # Resume eager execution mode.
# + [markdown] colab_type="text" id="EdljbNPq-PWS"
# ### Broadcasting
#
# Broadcasting is the process of making tensors with different shapes have
# compatible shapes for elementwise operations. For more background on
# broadcasting, see:
#
# * [Numpy: Broadcasting](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
# * `tf.broadcast_dynamic_shape`
# * `tf.broadcast_to`
#
# The basic steps for broadcasting two inputs `x` and `y` to have compatible
# shapes are:
#
# 1. If `x` and `y` do not have the same number of dimensions, then add outer
# dimensions (with size 1) until they do.
#
# 2. For each dimension where `x` and `y` have different sizes:
#
# * If `x` or `y` have size `1` in dimension `d`, then repeat its values
# across dimension `d` to match the other input's size.
#
# * Otherwise, raise an exception (`x` and `y` are not broadcast
# compatible).
# + [markdown] colab_type="text" id="-S2hOUWx-PWU"
# Where the size of a tensor in a uniform dimension is a single number (the size
# of slices across that dimension); and the size of a tensor in a ragged dimension
# is a list of slice lengths (for all slices across that dimension).
#
# #### Broadcasting examples
# + colab={} colab_type="code" id="0n095XdR-PWU"
# x (2D ragged): 2 x (num_rows)
# y (scalar)
# result (2D ragged): 2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)
# + colab={} colab_type="code" id="0SVYk5AP-PWW"
# x (2d ragged): 3 x (num_rows)
# y (2d tensor): 3 x 1
# Result (2d ragged): 3 x (num_rows)
x = tf.ragged.constant(
[[10, 87, 12],
[19, 53],
[12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)
# + colab={} colab_type="code" id="MsfBMD80s8Ux"
# x (3d ragged): 2 x (r1) x 2
# y (2d ragged): 1 x 1
# Result (3d ragged): 2 x (r1) x 2
x = tf.ragged.constant(
[[[1, 2], [3, 4], [5, 6]],
[[7, 8]]],
ragged_rank=1)
y = tf.constant([[10]])
print(x + y)
# + colab={} colab_type="code" id="rEj5QVfnva0t"
# x (3d ragged): 2 x (r1) x (r2) x 1
# y (1d tensor): 3
# Result (3d ragged): 2 x (r1) x (r2) x 3
x = tf.ragged.constant(
[
[
[[1], [2]],
[],
[[3]],
[[4]],
],
[
[[5], [6]],
[[7]]
]
],
ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)
# + [markdown] colab_type="text" id="uennZ64Aqftb"
# Here are some examples of shapes that do not broadcast:
# + colab={} colab_type="code" id="UpI0FlfL4Eim"
# x (2d ragged): 3 x (r1)
# y (2d tensor): 3 x 4 # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# + colab={} colab_type="code" id="qGq1zOT4zMoc"
# x (2d ragged): 3 x (r1)
# y (2d ragged): 3 x (r2) # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# + colab={} colab_type="code" id="CvLae5vMqeji"
# x (3d ragged): 3 x (r1) x 2
# y (3d ragged): 3 x (r1) x 3 # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
[[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
[[7, 8, 0], [9, 10, 0]]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# + [markdown] colab_type="text" id="m0wQkLfV-PWa"
# ## RaggedTensor encoding
#
# Ragged tensors are encoded using the `RaggedTensor` class. Internally, each
# `RaggedTensor` consists of:
#
# * A `values` tensor, which concatenates the variable-length rows into a
# flattened list.
# * A `row_splits` vector, which indicates how those flattened values are
# divided into rows. In particular, the values for row `rt[i]` are stored in
# the slice `rt.values[rt.row_splits[i]:rt.row_splits[i+1]]`.
#
# 
#
#
# + colab={} colab_type="code" id="MrLgMu0gPuo-"
rt = tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2],
row_splits=[0, 4, 4, 6, 7])
print(rt)
# + [markdown] colab_type="text" id="bpB7xKoUPtU6"
# ### Multiple ragged dimensions
#
# A ragged tensor with multiple ragged dimensions is encoded by using a nested
# `RaggedTensor` for the `values` tensor. Each nested `RaggedTensor` adds a single
# ragged dimension.
#
# 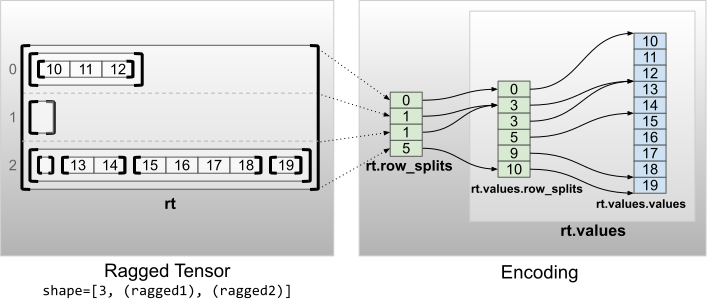
# + colab={} colab_type="code" id="yy3IGT2a-PWb"
rt = tf.RaggedTensor.from_row_splits(
values=tf.RaggedTensor.from_row_splits(
values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
row_splits=[0, 3, 3, 5, 9, 10]),
row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
# + [markdown] colab_type="text" id="5HqEEDzk-PWc"
# The factory function `tf.RaggedTensor.from_nested_row_splits` may be used to construct a
# RaggedTensor with multiple ragged dimensions directly, by providing a list of
# `row_splits` tensors:
# + colab={} colab_type="code" id="AKYhtFcT-PWd"
rt = tf.RaggedTensor.from_nested_row_splits(
flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)
# + [markdown] colab_type="text" id="uba2EnAY-PWf"
# ### Uniform Inner Dimensions
#
# Ragged tensors with uniform inner dimensions are encoded by using a
# multidimensional `tf.Tensor` for `values`.
#
# 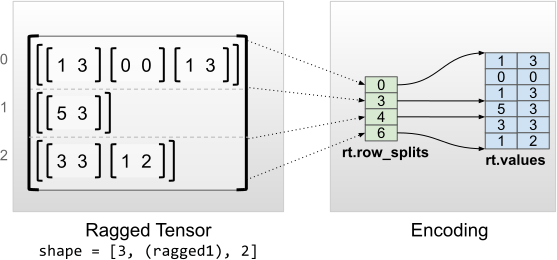
# + colab={} colab_type="code" id="z2sHwHdy-PWg"
rt = tf.RaggedTensor.from_row_splits(
values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of ragged dimensions: {}".format(rt.ragged_rank))
# + [markdown] colab_type="text" id="8yYaNrgX-PWh"
# ### Alternative row-partitioning schemes
#
# The `RaggedTensor` class uses `row_splits` as the primary mechanism to store
# information about how the values are partitioned into rows. However,
# `RaggedTensor` also provides support for four alternative row-partitioning
# schemes, which can be more convenient to use depending on how your data is
# formatted. Internally, `RaggedTensor` uses these additional schemes to improve
# efficiency in some contexts.
#
# <dl>
# <dt>Row lengths</dt>
# <dd>`row_lengths` is a vector with shape `[nrows]`, which specifies the
# length of each row.</dd>
#
# <dt>Row starts</dt>
# <dd>`row_starts` is a vector with shape `[nrows]`, which specifies the start
# offset of each row. Equivalent to `row_splits[:-1]`.</dd>
#
# <dt>Row limits</dt>
# <dd>`row_limits` is a vector with shape `[nrows]`, which specifies the stop
# offset of each row. Equivalent to `row_splits[1:]`.</dd>
#
# <dt>Row indices and number of rows</dt>
# <dd>`value_rowids` is a vector with shape `[nvals]`, corresponding
# one-to-one with values, which specifies each value's row index. In
# particular, the row `rt[row]` consists of the values `rt.values[j]` where
# `value_rowids[j]==row`. \
# `nrows` is an integer that specifies the number of rows in the
# `RaggedTensor`. In particular, `nrows` is used to indicate trailing empty
# rows.</dd>
# </dl>
#
# For example, the following ragged tensors are equivalent:
# + colab={} colab_type="code" id="4TH6XoQ8-PWh"
values = [3, 1, 4, 1, 5, 9, 2, 6]
print(tf.RaggedTensor.from_row_splits(values, row_splits=[0, 4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_row_lengths(values, row_lengths=[4, 0, 3, 1, 0]))
print(tf.RaggedTensor.from_row_starts(values, row_starts=[0, 4, 4, 7, 8]))
print(tf.RaggedTensor.from_row_limits(values, row_limits=[4, 4, 7, 8, 8]))
print(tf.RaggedTensor.from_value_rowids(
values, value_rowids=[0, 0, 0, 0, 2, 2, 2, 3], nrows=5))
# + [markdown] colab_type="text" id="ZGRrpwxjsOGr"
# The RaggedTensor class defines methods which can be used to construct
# each of these row-partitioning tensors.
# + colab={} colab_type="code" id="fIdn-hUBsoSj"
rt = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
print(" values: {}".format(rt.values))
print(" row_splits: {}".format(rt.row_splits))
print(" row_lengths: {}".format(rt.row_lengths()))
print(" row_starts: {}".format(rt.row_starts()))
print(" row_limits: {}".format(rt.row_limits()))
print("value_rowids: {}".format(rt.value_rowids()))
# + [markdown] colab_type="text" id="2r9XUpLUsdOa"
# (Note that `tf.RaggedTensor.values` and `tf.RaggedTensors.row_splits` are properties, while the remaining row-partitioning accessors are all methods. This reflects the fact that the `row_splits` are the primary underlying representation, and the other row-partitioning tensors must be computed.)
# + [markdown] colab_type="text" id="NBX15kEr-PWi"
# Some of the advantages and disadvantages of the different row-partitioning
# schemes are:
#
# # + **Efficient indexing**:
# The `row_splits`, `row_starts`, and `row_limits` schemes all enable
# constant-time indexing into ragged tensors. The `value_rowids` and
# `row_lengths` schemes do not.
#
# # + **Small encoding size**:
# The `value_rowids` scheme is more efficient when storing ragged tensors that
# have a large number of empty rows, since the size of the tensor depends only
# on the total number of values. On the other hand, the other four encodings
# are more efficient when storing ragged tensors with longer rows, since they
# require only one scalar value for each row.
#
# # + **Efficient concatenation**:
# The `row_lengths` scheme is more efficient when concatenating ragged
# tensors, since row lengths do not change when two tensors are concatenated
# together (but row splits and row indices do).
#
# # + **Compatibility**:
# The `value_rowids` scheme matches the
# [segmentation](../api_guides/python/math_ops.md#Segmentation)
# format used by operations such as `tf.segment_sum`. The `row_limits` scheme
# matches the format used by ops such as `tf.sequence_mask`.
|
site/en/guide/ragged_tensors.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="YTNn4zzAJWhA"
# # Operations on Word Vectors
#
# Welcome to your first assignment of Week 2, Course 5 of the Deep Learning Specialization!
#
# Because word embeddings are very computationally expensive to train, most ML practitioners will load a pre-trained set of embeddings. In this notebook you'll try your hand at loading, measuring similarity between, and modifying pre-trained embeddings.
#
# **After this assignment you'll be able to**:
#
# * Explain how word embeddings capture relationships between words
# * Load pre-trained word vectors
# * Measure similarity between word vectors using cosine similarity
# * Use word embeddings to solve word analogy problems such as Man is to Woman as King is to ______.
#
# At the end of this notebook you'll have a chance to try an optional exercise, where you'll modify word embeddings to reduce their gender bias. Reducing bias is an important consideration in ML, so you're encouraged to take this challenge!
# -
# ## Table of Contents
#
# - [Packages](#0)
# - [1 - Load the Word Vectors](#1)
# - [2 - Embedding Vectors Versus One-Hot Vectors](#2)
# - [3 - Cosine Similarity](#3)
# - [Exercise 1 - cosine_similarity](#ex-1)
# - [4 - Word Analogy Task](#4)
# - [Exercise 2 - complete_analogy](#ex-2)
# - [5 - Debiasing Word Vectors (OPTIONAL/UNGRADED)](#5)
# - [5.1 - Neutralize Bias for Non-Gender Specific Words](#5-1)
# - [Exercise 3 - neutralize](#ex-3)
# - [5.2 - Equalization Algorithm for Gender-Specific Words](#5-2)
# - [Exercise 4 - equalize](#ex-4)
# - [6 - References](#6)
# + [markdown] id="ZNlGgfN1JWhL"
# <a name='0'></a>
# ## Packages
#
# Let's get started! Run the following cell to load the packages you'll need.
# + id="cWEywjgpJWhM" outputId="6b0b856a-d05d-4a6d-ba94-01d247254f20"
import numpy as np
from w2v_utils import *
# + [markdown] id="D-CfRQ86JWhN"
# <a name='1'></a>
# ## 1 - Load the Word Vectors
#
# For this assignment, you'll use 50-dimensional GloVe vectors to represent words.
# Run the following cell to load the `word_to_vec_map`.
# + id="xCsAgH3dJWhO"
words, word_to_vec_map = read_glove_vecs('data/glove.6B.50d.txt')
# + [markdown] id="cF9bim0eJWhO"
# You've loaded:
# - `words`: set of words in the vocabulary.
# - `word_to_vec_map`: dictionary mapping words to their GloVe vector representation.
#
# <a name='2'></a>
# ## 2 - Embedding Vectors Versus One-Hot Vectors
# Recall from the lesson videos that one-hot vectors don't do a good job of capturing the level of similarity between words. This is because every one-hot vector has the same Euclidean distance from any other one-hot vector.
#
# Embedding vectors, such as GloVe vectors, provide much more useful information about the meaning of individual words.
# Now, see how you can use GloVe vectors to measure the similarity between two words!
# + [markdown] id="xZBg2QwSJWhO"
# <a name='3'></a>
# ## 3 - Cosine Similarity
#
# To measure the similarity between two words, you need a way to measure the degree of similarity between two embedding vectors for the two words. Given two vectors $u$ and $v$, cosine similarity is defined as follows:
#
# $$\text{CosineSimilarity(u, v)} = \frac {u \cdot v} {||u||_2 ||v||_2} = cos(\theta) \tag{1}$$
#
# * $u \cdot v$ is the dot product (or inner product) of two vectors
# * $||u||_2$ is the norm (or length) of the vector $u$
# * $\theta$ is the angle between $u$ and $v$.
# * The cosine similarity depends on the angle between $u$ and $v$.
# * If $u$ and $v$ are very similar, their cosine similarity will be close to 1.
# * If they are dissimilar, the cosine similarity will take a smaller value.
#
# <img src="images/cosine_sim.png" style="width:800px;height:250px;">
# <caption><center><font color='purple'><b>Figure 1</b>: The cosine of the angle between two vectors is a measure of their similarity.</font></center></caption>
#
# <a name='ex-1'></a>
# ### Exercise 1 - cosine_similarity
#
# Implement the function `cosine_similarity()` to evaluate the similarity between word vectors.
#
# **Reminder**: The norm of $u$ is defined as $ ||u||_2 = \sqrt{\sum_{i=1}^{n} u_i^2}$
#
# #### Additional Hints
# * You may find [np.dot](https://numpy.org/doc/stable/reference/generated/numpy.dot.html), [np.sum](https://numpy.org/doc/stable/reference/generated/numpy.sum.html), or [np.sqrt](https://numpy.org/doc/stable/reference/generated/numpy.sqrt.html) useful depending upon the implementation that you choose.
# + id="mNjuTQ5JJWhP"
# UNQ_C1 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: cosine_similarity
def cosine_similarity(u, v):
"""
Cosine similarity reflects the degree of similarity between u and v
Arguments:
u -- a word vector of shape (n,)
v -- a word vector of shape (n,)
Returns:
cosine_similarity -- the cosine similarity between u and v defined by the formula above.
"""
# Special case. Consider the case u = [0, 0], v=[0, 0]
if np.all(u == v):
return 1
### START CODE HERE ###
# Compute the dot product between u and v (≈1 line)
dot = np.dot(u, v)
# Compute the L2 norm of u (≈1 line)
norm_u = np.sqrt(np.sum(u**2))
# Compute the L2 norm of v (≈1 line)
norm_v = np.sqrt(np.sum(v**2))
# Avoid division by 0
if np.isclose(norm_u * norm_v, 0, atol=1e-32):
return 0
# Compute the cosine similarity defined by formula (1) (≈1 line)
cosine_similarity = dot / (norm_u * norm_v)
### END CODE HERE ###
return cosine_similarity
# + colab={"base_uri": "https://localhost:8080/"} id="nqH8_-3BJWhP" outputId="9454fe42-80ca-4b40-ea23-69ebac038fae"
# START SKIP FOR GRADING
father = word_to_vec_map["father"]
mother = word_to_vec_map["mother"]
ball = word_to_vec_map["ball"]
crocodile = word_to_vec_map["crocodile"]
france = word_to_vec_map["france"]
italy = word_to_vec_map["italy"]
paris = word_to_vec_map["paris"]
rome = word_to_vec_map["rome"]
print("cosine_similarity(father, mother) = ", cosine_similarity(father, mother))
print("cosine_similarity(ball, crocodile) = ",cosine_similarity(ball, crocodile))
print("cosine_similarity(france - paris, rome - italy) = ",cosine_similarity(france - paris, rome - italy))
# END SKIP FOR GRADING
# PUBLIC TESTS
def cosine_similarity_test(target):
a = np.random.uniform(-10, 10, 10)
b = np.random.uniform(-10, 10, 10)
c = np.random.uniform(-1, 1, 23)
assert np.isclose(cosine_similarity(a, a), 1), "cosine_similarity(a, a) must be 1"
assert np.isclose(cosine_similarity((c >= 0) * 1, (c < 0) * 1), 0), "cosine_similarity(a, not(a)) must be 0"
assert np.isclose(cosine_similarity(a, -a), -1), "cosine_similarity(a, -a) must be -1"
assert np.isclose(cosine_similarity(a, b), cosine_similarity(a * 2, b * 4)), "cosine_similarity must be scale-independent. You must divide by the product of the norms of each input"
print("\033[92mAll test passed!")
cosine_similarity_test(cosine_similarity)
# + [markdown] id="FX8fHEBxJWhQ"
# #### Try different words!
#
# After you get the correct expected output, please feel free to modify the inputs and measure the cosine similarity between other pairs of words! Playing around with the cosine similarity of other inputs will give you a better sense of how word vectors behave.
# + [markdown] id="63Pjp_QSJWhQ"
# <a name='4'></a>
# ## 4 - Word Analogy Task
#
# * In the word analogy task, complete this sentence:
# <font color='brown'>"*a* is to *b* as *c* is to **____**"</font>.
#
# * An example is:
# <font color='brown'> '*man* is to *woman* as *king* is to *queen*' </font>.
#
# * You're trying to find a word *d*, such that the associated word vectors $e_a, e_b, e_c, e_d$ are related in the following manner:
# $e_b - e_a \approx e_d - e_c$
# * Measure the similarity between $e_b - e_a$ and $e_d - e_c$ using cosine similarity.
#
# <a name='ex-2'></a>
# ### Exercise 2 - complete_analogy
#
# Complete the code below to perform word analogies!
# + id="kGBV3yoQJWhS"
# UNQ_C2 (UNIQUE CELL IDENTIFIER, DO NOT EDIT)
# GRADED FUNCTION: complete_analogy
def complete_analogy(word_a, word_b, word_c, word_to_vec_map):
"""
Performs the word analogy task as explained above: a is to b as c is to ____.
Arguments:
word_a -- a word, string
word_b -- a word, string
word_c -- a word, string
word_to_vec_map -- dictionary that maps words to their corresponding vectors.
Returns:
best_word -- the word such that v_b - v_a is close to v_best_word - v_c, as measured by cosine similarity
"""
# convert words to lowercase
word_a, word_b, word_c = word_a.lower(), word_b.lower(), word_c.lower()
### START CODE HERE ###
# Get the word embeddings e_a, e_b and e_c (≈1-3 lines)
e_a, e_b, e_c = map(lambda x: word_to_vec_map.get(x), [word_a, word_b, word_c])
### END CODE HERE ###
words = word_to_vec_map.keys()
max_cosine_sim = -100 # Initialize max_cosine_sim to a large negative number
best_word = None # Initialize best_word with None, it will help keep track of the word to output
# loop over the whole word vector set
for w in words:
# to avoid best_word being the input word, skip the input word_c
# skip word_c from query
if w == word_c:
continue
### START CODE HERE ###
# Compute cosine similarity between the vector (e_b - e_a) and the vector ((w's vector representation) - e_c) (≈1 line)
cosine_sim = cosine_similarity(e_a - e_b, e_c - word_to_vec_map[w])
# If the cosine_sim is more than the max_cosine_sim seen so far,
# then: set the new max_cosine_sim to the current cosine_sim and the best_word to the current word (≈3 lines)
if cosine_sim > max_cosine_sim:
max_cosine_sim = cosine_sim
best_word = w
### END CODE HERE ###
return best_word
# +
# PUBLIC TEST
def complete_analogy_test(target):
a = [3, 3] # Center at a
a_nw = [2, 4] # North-West oriented vector from a
a_s = [3, 2] # South oriented vector from a
c = [-2, 1] # Center at c
# Create a controlled word to vec map
word_to_vec_map = {'a': a,
'synonym_of_a': a,
'a_nw': a_nw,
'a_s': a_s,
'c': c,
'c_n': [-2, 2], # N
'c_ne': [-1, 2], # NE
'c_e': [-1, 1], # E
'c_se': [-1, 0], # SE
'c_s': [-2, 0], # S
'c_sw': [-3, 0], # SW
'c_w': [-3, 1], # W
'c_nw': [-3, 2] # NW
}
# Convert lists to np.arrays
for key in word_to_vec_map.keys():
word_to_vec_map[key] = np.array(word_to_vec_map[key])
assert(target('a', 'a_nw', 'c', word_to_vec_map) == 'c_nw')
assert(target('a', 'a_s', 'c', word_to_vec_map) == 'c_s')
assert(target('a', 'synonym_of_a', 'c', word_to_vec_map) != 'c'), "Best word cannot be input query"
assert(target('a', 'c', 'a', word_to_vec_map) == 'c')
print("\033[92mAll tests passed")
complete_analogy_test(complete_analogy)
# + [markdown] id="vnJJ_2sQJWhT"
# Run the cell below to test your code. Patience, young grasshopper...this may take 1-2 minutes.
# +
# START SKIP FOR GRADING
triads_to_try = [('italy', 'italian', 'spain'), ('india', 'delhi', 'japan'), ('man', 'woman', 'boy'), ('small', 'smaller', 'large')]
for triad in triads_to_try:
print ('{} -> {} :: {} -> {}'.format( *triad, complete_analogy(*triad, word_to_vec_map)))
# END SKIP FOR GRADING
# + [markdown] id="41Ozkp_-JWhV"
# Once you get the output, try modifying the input cells above to test your own analogies.
#
# **Hint**: Try to find some other analogy pairs that will work, along with some others where the algorithm doesn't give the right answer:
# * For example, you can try small->smaller as big->?
# -
# ## Congratulations!
#
# You've come to the end of the graded portion of the assignment. By now, you've:
#
# * Loaded some pre-trained word vectors
# * Measured the similarity between word vectors using cosine similarity
# * Used word embeddings to solve word analogy problems such as Man is to Woman as King is to __.
#
# Cosine similarity is a relatively simple and intuitive, yet powerful, method you can use to capture nuanced relationships between words. These exercises should be helpful to you in explaining how it works, and applying it to your own projects!
# + [markdown] id="3nK_lD7mJWhV"
# <font color='blue'>
# <b>What you should remember</b>:
#
# - Cosine similarity is a good way to compare the similarity between pairs of word vectors.
# - Note that L2 (Euclidean) distance also works.
# - For NLP applications, using a pre-trained set of word vectors is often a great way to get started. </font>
#
# Even though you've finished the graded portion, please take a look at the rest of this notebook to learn about debiasing word vectors.
# + [markdown] id="HMRD25MuJWhW"
# <a name='5'></a>
# ## 5 - Debiasing Word Vectors (OPTIONAL/UNGRADED)
# + [markdown] id="9Q1w3ZpEJWhW"
# In the following exercise, you'll examine gender biases that can be reflected in a word embedding, and explore algorithms for reducing the bias. In addition to learning about the topic of debiasing, this exercise will also help hone your intuition about what word vectors are doing. This section involves a bit of linear algebra, though you can certainly complete it without being an expert! Go ahead and give it a shot. This portion of the notebook is optional and is not graded...so just have fun and explore.
#
# First, see how the GloVe word embeddings relate to gender. You'll begin by computing a vector $g = e_{woman}-e_{man}$, where $e_{woman}$ represents the word vector corresponding to the word *woman*, and $e_{man}$ corresponds to the word vector corresponding to the word *man*. The resulting vector $g$ roughly encodes the concept of "gender".
#
# You might get a more accurate representation if you compute $g_1 = e_{mother}-e_{father}$, $g_2 = e_{girl}-e_{boy}$, etc. and average over them, but just using $e_{woman}-e_{man}$ will give good enough results for now.
#
# + id="_qpU-C3KJWhW"
g = word_to_vec_map['woman'] - word_to_vec_map['man']
print(g)
# + [markdown] id="ORIvi0s1JWhX"
# Now, consider the cosine similarity of different words with $g$. What does a positive value of similarity mean, versus a negative cosine similarity?
# + id="TgqV6pDxJWhX"
print ('List of names and their similarities with constructed vector:')
# girls and boys name
name_list = ['john', 'marie', 'sophie', 'ronaldo', 'priya', 'rahul', 'danielle', 'reza', 'katy', 'yasmin']
for w in name_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
# + [markdown] id="YLELp0LJJWhY"
# As you can see, female first names tend to have a positive cosine similarity with our constructed vector $g$, while male first names tend to have a negative cosine similarity. This is not surprising, and the result seems acceptable.
#
# Now try with some other words:
# + id="wgadfCaGJWhY"
print('Other words and their similarities:')
word_list = ['lipstick', 'guns', 'science', 'arts', 'literature', 'warrior','doctor', 'tree', 'receptionist',
'technology', 'fashion', 'teacher', 'engineer', 'pilot', 'computer', 'singer', 'cook', 'chef', 'italian',
'indian', 'nation', 'atom', 'wood', 'almond']
for w in word_list:
print (w, cosine_similarity(word_to_vec_map[w], g))
# + [markdown] id="YUzfNtq4JWhY"
# Do you notice anything surprising? It is astonishing how these results reflect certain unhealthy gender stereotypes. For example, we see “computer” is negative and is closer in value to male first names, while “literature” is positive and is closer to female first names. Ouch!
#
# You'll see below how to reduce the bias of these vectors, using an algorithm due to [Boliukbasi et al., 2016](https://arxiv.org/abs/1607.06520). Note that some word pairs such as "actor"/"actress" or "grandmother"/"grandfather" should remain gender-specific, while other words such as "receptionist" or "technology" should be neutralized, i.e. not be gender-related. You'll have to treat these two types of words differently when debiasing.
#
# <a name='5-1'></a>
# ### 5.1 - Neutralize Bias for Non-Gender Specific Words
#
# The figure below should help you visualize what neutralizing does. If you're using a 50-dimensional word embedding, the 50 dimensional space can be split into two parts: The bias-direction $g$, and the remaining 49 dimensions, which is called $g_{\perp}$ here. In linear algebra, we say that the 49-dimensional $g_{\perp}$ is perpendicular (or "orthogonal") to $g$, meaning it is at 90 degrees to $g$. The neutralization step takes a vector such as $e_{receptionist}$ and zeros out the component in the direction of $g$, giving us $e_{receptionist}^{debiased}$.
#
# Even though $g_{\perp}$ is 49-dimensional, given the limitations of what you can draw on a 2D screen, it's illustrated using a 1-dimensional axis below.
#
# <img src="images/neutral.png" style="width:800px;height:300px;">
# <caption><center><font color='purple'><b>Figure 2</b>: The word vector for "receptionist" represented before and after applying the neutralize operation.</font> </center></caption>
#
# <a name='ex-3'></a>
# ### Exercise 3 - neutralize
#
# Implement `neutralize()` to remove the bias of words such as "receptionist" or "scientist."
#
# Given an input embedding $e$, you can use the following formulas to compute $e^{debiased}$:
#
# $$e^{bias\_component} = \frac{e \cdot g}{||g||_2^2} * g\tag{2}$$
# $$e^{debiased} = e - e^{bias\_component}\tag{3}$$
#
# If you are an expert in linear algebra, you may recognize $e^{bias\_component}$ as the projection of $e$ onto the direction $g$. If you're not an expert in linear algebra, don't worry about this. ;)
#
# <!--
# **Reminder**: a vector $u$ can be split into two parts: its projection over a vector-axis $v_B$ and its projection over the axis orthogonal to $v$:
# $$u = u_B + u_{\perp}$$
# where : $u_B = $ and $ u_{\perp} = u - u_B $
# !-->
# + id="79Pk0QDhJWhZ"
def neutralize(word, g, word_to_vec_map):
"""
Removes the bias of "word" by projecting it on the space orthogonal to the bias axis.
This function ensures that gender neutral words are zero in the gender subspace.
Arguments:
word -- string indicating the word to debias
g -- numpy-array of shape (50,), corresponding to the bias axis (such as gender)
word_to_vec_map -- dictionary mapping words to their corresponding vectors.
Returns:
e_debiased -- neutralized word vector representation of the input "word"
"""
### START CODE HERE ###
# Select word vector representation of "word". Use word_to_vec_map. (≈ 1 line)
e = word_to_vec_map[word]
# Compute e_biascomponent using the formula given above. (≈ 1 line)
e_biascomponent = ((np.dot(e, g))/(np.linalg.norm(g))**2)*g
# Neutralize e by subtracting e_biascomponent from it
# e_debiased should be equal to its orthogonal projection. (≈ 1 line)
e_debiased = e - e_biascomponent
### END CODE HERE ###
return e_debiased
# + id="6PgkxwxXJWhZ"
e = "receptionist"
print("cosine similarity between " + e + " and g, before neutralizing: ", cosine_similarity(word_to_vec_map["receptionist"], g))
e_debiased = neutralize("receptionist", g, word_to_vec_map)
print("cosine similarity between " + e + " and g, after neutralizing: ", cosine_similarity(e_debiased, g))
# +
abc = np.ndarray((3))
cba = np.ndarray((3))
print(abc, abc.shape, cba, cba.shape)
print(abc * cba)
print(np.dot(abc, cba))
print(np.multiply(abc, cba))
print(abc @ cba)
# + [markdown] id="Da--RZGIJWha"
# **Expected Output**: The second result is essentially 0, up to numerical rounding (on the order of $10^{-17}$).
#
#
# <table>
# <tr>
# <td>
# <b>cosine similarity between receptionist and g, before neutralizing:</b> :
# </td>
# <td>
# 0.330779417506
# </td>
# </tr>
# <tr>
# <td>
# <b>cosine similarity between receptionist and g, after neutralizing</b> :
# </td>
# <td>
# -4.442232511624783e-17
# </tr>
# </table>
# + [markdown] id="ciATgxwLJWha"
# <a name='5-2'></a>
# ### 5.2 - Equalization Algorithm for Gender-Specific Words
#
# Next, let's see how debiasing can also be applied to word pairs such as "actress" and "actor." Equalization is applied to pairs of words that you might want to have differ only through the gender property. As a concrete example, suppose that "actress" is closer to "babysit" than "actor." By applying neutralization to "babysit," you can reduce the gender stereotype associated with babysitting. But this still does not guarantee that "actor" and "actress" are equidistant from "babysit." The equalization algorithm takes care of this.
#
# The key idea behind equalization is to make sure that a particular pair of words are equidistant from the 49-dimensional $g_\perp$. The equalization step also ensures that the two equalized steps are now the same distance from $e_{receptionist}^{debiased}$, or from any other work that has been neutralized. Visually, this is how equalization works:
#
# <img src="images/equalize10.png" style="width:800px;height:400px;">
#
#
# The derivation of the linear algebra to do this is a bit more complex. (See Bolukbasi et al., 2016 in the References for details.) Here are the key equations:
#
#
# $$ \mu = \frac{e_{w1} + e_{w2}}{2}\tag{4}$$
#
# $$ \mu_{B} = \frac {\mu \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
# \tag{5}$$
#
# $$\mu_{\perp} = \mu - \mu_{B} \tag{6}$$
#
# $$ e_{w1B} = \frac {e_{w1} \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
# \tag{7}$$
# $$ e_{w2B} = \frac {e_{w2} \cdot \text{bias_axis}}{||\text{bias_axis}||_2^2} *\text{bias_axis}
# \tag{8}$$
#
#
# $$e_{w1B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w1B}} - \mu_B} {||(e_{w1} - \mu_{\perp}) - \mu_B||_2} \tag{9}$$
#
#
# $$e_{w2B}^{corrected} = \sqrt{ |{1 - ||\mu_{\perp} ||^2_2} |} * \frac{e_{\text{w2B}} - \mu_B} {||(e_{w2} - \mu_{\perp}) - \mu_B||_2} \tag{10}$$
#
# $$e_1 = e_{w1B}^{corrected} + \mu_{\perp} \tag{11}$$
# $$e_2 = e_{w2B}^{corrected} + \mu_{\perp} \tag{12}$$
#
#
# <a name='ex-4'></a>
# ### Exercise 4 - equalize
#
# Implement the `equalize()` function below.
#
# Use the equations above to get the final equalized version of the pair of words. Good luck!
#
# **Hint**
# - Use [np.linalg.norm](https://numpy.org/doc/stable/reference/generated/numpy.linalg.norm.html)
# + id="aBhxJtGIJWha"
def equalize(pair, bias_axis, word_to_vec_map):
"""
Debias gender specific words by following the equalize method described in the figure above.
Arguments:
pair -- pair of strings of gender specific words to debias, e.g. ("actress", "actor")
bias_axis -- numpy-array of shape (50,), vector corresponding to the bias axis, e.g. gender
word_to_vec_map -- dictionary mapping words to their corresponding vectors
Returns
e_1 -- word vector corresponding to the first word
e_2 -- word vector corresponding to the second word
"""
### START CODE HERE ###
# Step 1: Select word vector representation of "word". Use word_to_vec_map. (≈ 2 lines)
w1, w2 = pair
e_w1, e_w2 = word_to_vec_map[w1], word_to_vec_map[w2]
# Step 2: Compute the mean of e_w1 and e_w2 (≈ 1 line)
mu = (e_w1 + e_w2) / 2
# Step 3: Compute the projections of mu over the bias axis and the orthogonal axis (≈ 2 lines)
mu_B = (np.dot(mu, bias_axis) / np.linalg.norm(bias_axis)**2) * bias_axis
mu_orth = mu - mu_B
# Step 4: Use equations (7) and (8) to compute e_w1B and e_w2B (≈2 lines)
e_w1B = (np.dot(e_w1, bias_axis) / np.linalg.norm(bias_axis)**2) * bias_axis
e_w2B = (np.dot(e_w2, bias_axis) / np.linalg.norm(bias_axis)**2) * bias_axis
# Step 5: Adjust the Bias part of e_w1B and e_w2B using the formulas (9) and (10) given above (≈2 lines)
corrected_e_w1B = np.sqrt(np.abs(1-np.linalg.norm(mu_orth)**2)) * ((e_w1B - mu_B) / np.linalg.norm((e_w1 - mu_orth) - mu_B))
corrected_e_w2B = np.sqrt(np.abs(1-np.linalg.norm(mu_orth)**2)) * ((e_w2B - mu_B) / np.linalg.norm((e_w2 - mu_orth) - mu_B))
# Step 6: Debias by equalizing e1 and e2 to the sum of their corrected projections (≈2 lines)
e1 = corrected_e_w1B + mu_orth
e2 = corrected_e_w2B + mu_orth
### END CODE HERE ###
return e1, e2
# + id="P405J5ZSJWhb"
print("cosine similarities before equalizing:")
print("cosine_similarity(word_to_vec_map[\"man\"], gender) = ", cosine_similarity(word_to_vec_map["man"], g))
print("cosine_similarity(word_to_vec_map[\"woman\"], gender) = ", cosine_similarity(word_to_vec_map["woman"], g))
print()
e1, e2 = equalize(("man", "woman"), g, word_to_vec_map)
print("cosine similarities after equalizing:")
print("cosine_similarity(e1, gender) = ", cosine_similarity(e1, g))
print("cosine_similarity(e2, gender) = ", cosine_similarity(e2, g))
# + [markdown] id="5cNhiOEaJWhb"
# **Expected Output**:
#
# cosine similarities before equalizing:
# <table>
# <tr>
# <td>
# <b>cosine_similarity(word_to_vec_map["man"], gender)</b> =
# </td>
# <td>
# -0.117110957653
# </td>
# </tr>
# <tr>
# <td>
# <b>cosine_similarity(word_to_vec_map["woman"], gender)</b> =
# </td>
# <td>
# 0.356666188463
# </td>
# </tr>
# </table>
#
# cosine similarities after equalizing:
# <table>
# <tr>
# <td>
# <b>cosine_similarity(e1, gender)</b> =
# </td>
# <td>
# -0.942653373599985
# </td>
# </tr>
# <tr>
# <td>
# <b>cosine_similarity(e2, gender)</b> =
# </td>
# <td>
# 0.9231551731025899
# </td>
# </tr>
# </table>
# + [markdown] id="mXi96ToSJWhc"
# Go ahead and play with the input words in the cell above, to apply equalization to other pairs of words.
#
# Hint: Try...
#
# These debiasing algorithms are very helpful for reducing bias, but aren't perfect and don't eliminate all traces of bias. For example, one weakness of this implementation was that the bias direction $g$ was defined using only the pair of words _woman_ and _man_. As discussed earlier, if $g$ were defined by computing $g_1 = e_{woman} - e_{man}$; $g_2 = e_{mother} - e_{father}$; $g_3 = e_{girl} - e_{boy}$; and so on and averaging over them, you would obtain a better estimate of the "gender" dimension in the 50 dimensional word embedding space. Feel free to play with these types of variants as well!
# + [markdown] id="DDjEdbzuJWhd"
# ### Congratulations!
#
# You have come to the end of both graded and ungraded portions of this notebook, and have seen several of the ways that word vectors can be applied and modified. Great work pushing your knowledge in the areas of neutralizing and equalizing word vectors! See you next time.
# + [markdown] id="FY2ZhorNJWhd"
# <a name='6'></a>
# ## 6 - References
#
# - The debiasing algorithm is from Bolukbasi et al., 2016, [Man is to Computer Programmer as Woman is to
# Homemaker? Debiasing Word Embeddings](https://papers.nips.cc/paper/6228-man-is-to-computer-programmer-as-woman-is-to-homemaker-debiasing-word-embeddings.pdf)
# - The GloVe word embeddings were due to <NAME>, <NAME>, and <NAME>. (https://nlp.stanford.edu/projects/glove/)
#
# -
|
course_5_sequence_models/week_2/Operations_on_word_vectors_v2a.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# # Layers and Blocks
#
# :label:`chapter_model_construction`
#
#
#
#
# When we first started talking about neural networks,
# we introduced linear models with a single output.
# Here, the entire model consists of just a single neuron.
# By itself, a single neuron takes some set of inputs,
# generates a corresponding (*scalar*) output,
# and has a set of associated parameters that can be updated
# to optimize some objective function of interest.
# Then, once we started thinking about networks with multiple outputs,
# we leveraged vectorized arithmetic,
# we showed how we could use linear algebra
# to efficiently express an entire *layer* of neurons.
# Layers too expect some inputs, generate corresponding outputs,
# and are described by a set of tunable parameters.
#
# When we worked through softmax regression,
# a single *layer* was itself *the model*.
# However, when we subsequently introduced multilayer perceptrons,
# we developed models consisting of multiple layers.
# One interesting property of multilayer neural networks
# is that the *entire model* and its *constituent layers*
# share the same basic structure.
# The model takes the true inputs (as stated in the problem formulation),
# outputs predictions of the true outputs,
# and possesses parameters (the combined set of all parameters from all layers)
# Likewise any individual constituent layer in a multilayer perceptron
# ingests inputs (supplied by the previous layer)
# generates outputs (which form the inputs to the subsequent layer),
# and possesses a set of tunable parameters
# tht are updated with respect to the ultimate objective
# (using the signal that flows backwards through the subsequent layer).
#
# While you might think that neurons, layers, and models
# give us enough abstractions to go about our business,
# it turns out that we'll often want to express our model
# in terms of a components that are large than an indivudal layer.
# For example, when designing models, like ResNet-152,
# which possess hundreds (152, thus the name) of layers,
# implementing the network one layer at a time can grow tedious.
# Moreover, this concern is not just hypothetical---such deep networks
# dominate numerous application areas, especally when training data is abundant.
# For example the ResNet architecture mentioned above ([He et al.](https://www.cv-foundation.org/openaccess/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf))
# won the 2015 ImageNet and COCO computer vision compeititions
# for both recognition and detection.
# Deep networks with many layers arranged into components
# with various repeating patterns are now ubiquitous in other domains
# including natural language processing and speech.
#
# To facilitate the implementation of networks consisting of components
# of arbitrary complecity, we introduce a new flexible concept:
# a neural network *block*.
# A block could describe a single neuron,
# a high-dimensional layer,
# or an arbitrarily-complex component consisting of multiple layers.
# From a software development, a `Block` is a class.
# Any subclass of `Block` must define a method called `forward`
# that transforms its input into output,
# and must store any necessary parameters.
# Note that some Blocks do not require any parameters at all!
# Finally a `Block` must possess a `backward` method,
# for purposes of calculating gradients.
# Fortunately, due to some behind-the-scenes magic
# supplied by the autograd `autograd` package
# (introduced in :numref:`chapter_preliminaries`)
# when defining our own `Block` typically requires
# only that we worry about parameters and the `forward` function.
#
#
# One benefit of working with the `Block` abstraction is that
# they can be combined into larger artifacts, often recursively,
# e.g., as illustrated in the following diagram:
#
# 
#
#
# By defining code to generate Blocks of arbitrary complexity on demand,
# we can write surprisingly compact code
# and still implement complex neural networks.
#
# To begin, we revisit the Blocks that played a role
# in our implementation of the multilayer perceptron
# (:numref:`chapter_mlp_gluon`).
# The following code generates a network
# with one fully-connected hidden layer containing 256 units
# followed by a ReLU activation,
# and then another fully-connected layer
# consisting of 10 units (with no activation function).
# Because there are no more layers,
# this last 10-unit layer is regarded as the *output layer*
# and its outputs are also the model's output.
# + attributes={"classes": [], "id": "", "n": "1"}
from mxnet import np, npx
from mxnet.gluon import nn
npx.set_np()
x = np.random.uniform(size=(2, 20))
net = nn.Sequential()
net.add(nn.Dense(256, activation='relu'))
net.add(nn.Dense(10))
net.initialize()
net(x)
# -
# In this example, as in previous chapters,
# our model consists of an object returned by the `nn.Sequential` constructor.
# After instantiating a `nn.Sequential` and storing the `net` variable,
# we repeatedly called its `.add()` method,
# appending layers in the order that they should be executed.
# We suspect that you might have already understood *more or less*
# what was going on here the first time you saw this code.
# You may even have understood it well enough
# to modify the code and design your own networks.
# However, the details regarding
# what exactly happens inside `nn.Sequential`
# have remained mysterious so far.
#
# In short, `nn.Sequential` just defines a special kind of Block.
# Specifically, an `nn.Sequential` maintains a list of constitutent `Blocks`,
# stored in a particular order.
# You might think of `nnSequential` as your first meta-Block.
# The `add` method simply facilitates
# the addition of each successive `Block` to the list.
# Note that each our layers are instances of the `Dense` class
# which is itself a subclass of `Block`.
# The `forward` function is also remarkably simple:
# it chains each Block in the list together,
# passing the output of each as the input to the next.
#
# Note that until now, we have been invoking our models
# via the construction `net(X)` to obtain their outputs.
# This is actually just shorthand for `net.forward(X)`,
# a slick Python trick achieved via the Block class's `__call__` function.
#
#
# Before we dive in to implementing our own custom `Block`,
# we briefly summarize the basic functionality that each `Block` must perform the following duties:
#
# 1. Ingest input data as arguments to its `forward` function.
# 1. Generate an output via the value returned by its `forward` function. Note that the output may have a different shape from the input. For example, the first Dense layer in our model above ingests an input of arbitrary dimension but returns an output of dimension 256.
# 1. Calculate the gradient of its output with respect to its input, which can be accessed via its `backward` method. Typically this happens automatically.
# 1. Store and provide access to those parameters necessary to execute the `forward` computation.
# 1. Initialize these parameters as needed.
#
# ## A Custom Block
#
# Perhaps the easiest way to develop intuition about how `nn.Block` works
# is to just dive right in and implement one ourselves.
# In the following snippet, instead of relying on `nn.Sequential`,
# we just code up a Block from scratch that implements a multilayer perceptron with one hidden layer, 256 hidden nodes, and 10 outputs.
#
# Our `MLP` class below inherits the `Block` class.
# While we rely on some predefined methods in the parent class,
# we need to supply our own `__init__` and `forward` functions
# to uniquely define the behavior of our model.
# + attributes={"classes": [], "id": "", "n": "1"}
from mxnet.gluon import nn
class MLP(nn.Block):
# Declare a layer with model parameters. Here, we declare two fully
# connected layers
def __init__(self, **kwargs):
# Call the constructor of the MLP parent class Block to perform the
# necessary initialization. In this way, other function parameters can
# also be specified when constructing an instance, such as the model
# parameter, params, described in the following sections
super(MLP, self).__init__(**kwargs)
self.hidden = nn.Dense(256, activation='relu') # Hidden layer
self.output = nn.Dense(10) # Output layer
# Define the forward computation of the model, that is, how to return the
# required model output based on the input x
def forward(self, x):
return self.output(self.hidden(x))
# -
# This code may be easiest to understand by working backwards from `forward`.
# Note that the `forward` method takes as input `x`.
# The forward method first evaluates `self.hidden(x)`
# to produce the hidden representation, passing this output
# as the input to the output layer `self.output( ... )`.
#
# The constituent layers of each `MLP` must be instance-level variables.
# After all, if we instantiated two such models `net1` and `net2`
# and trained them on different data,
# we would expect them to them to represent two different learned models.
#
# The `__init__` method is the most natural place to instantiate the layers
# that we subsequently invoke on each call to the `forward` method.
# Note that before getting on with the interesting parts,
# our customized `__init__` method must invoke the parent class's
# init method: `super(MLP, self).__init__(**kwargs)`
# to save us from reimplementing boilerplate code applicable to most Blocks.
# Then, all that's left is to instantiate our two `Dense` layers,
# assigning them to `self.hidden` and `self.output`, respectively.
# Again note that when dealing with standard functionality like this,
# we don't have to worry about backpropagation,
# since the `backward` method is generated for us automatically.
# The same goes for the `initialize` method.
# Let's try this out:
# + attributes={"classes": [], "id": "", "n": "2"}
net = MLP()
net.initialize()
net(x)
# -
# As we argued earlier, the primary virtue of the `Block` abstraction
# is its versatility.
# We can subclass `Block` to create layers
# (such as the `Dense` class provided by Gluon),
# entire models (such as the `MLP` class implemented above),
# or various components of intermediate complexity,
# a pattern that we will lean on heavily throughout
# the next chapters on convolutinoal neural networks.
#
#
# ## The Sequential Block
#
# As we described earlier, the `Sequential` class itself
# is also just a subclass of `Block`,
# designed specifically for daisy-chaining other Blocks together.
# All we need to do to implement our own `MySequential` block
# is to define a few convenience functions:
# 1. An `add` method for appending Blocks one by one to a list.
# 2. A `forward` method to pass inputs through the chain of Blocks
# (in the order of addition).
#
# The following `MySequential` class delivers the same functionality
# as Gluon's default Sequential class:
# + attributes={"classes": [], "id": "", "n": "3"}
class MySequential(nn.Block):
def __init__(self, **kwargs):
super(MySequential, self).__init__(**kwargs)
def add(self, block):
# Here, block is an instance of a Block subclass, and we assume it has
# a unique name. We save it in the member variable _children of the
# Block class, and its type is OrderedDict. When the MySequential
# instance calls the initialize function, the system automatically
# initializes all members of _children
self._children[block.name] = block
def forward(self, x):
# OrderedDict guarantees that members will be traversed in the order
# they were added
for block in self._children.values():
x = block(x)
return x
# -
# At its core is the `add` method. It adds any block to the ordered dictionary of children. These are then executed in sequence when forward propagation is invoked. Let's see what the MLP looks like now.
# + attributes={"classes": [], "id": "", "n": "4"}
net = MySequential()
net.add(nn.Dense(256, activation='relu'))
net.add(nn.Dense(10))
net.initialize()
net(x)
# -
# Indeed, it can be observed that the use of the `MySequential` class is no different from the use of the Sequential class described in :numref:`chapter_mlp_gluon`.
#
#
# ## Blocks with Code
#
# Although the Sequential class can make model construction easier, and you do not need to define the `forward` method, directly inheriting the Block class can greatly expand the flexibility of model construction. In particular, we will use Python's control flow within the forward method. While we're at it, we need to introduce another concept, that of the *constant* parameter. These are parameters that are not used when invoking backprop. This sounds very abstract but here's what's really going on. Assume that we have some function
#
# $$f(\mathbf{x},\mathbf{w}) = 3 \cdot \mathbf{w}^\top \mathbf{x}.$$
#
# In this case 3 is a constant parameter. We could change 3 to something else, say $c$ via
#
# $$f(\mathbf{x},\mathbf{w}) = c \cdot \mathbf{w}^\top \mathbf{x}.$$
#
# Nothing has really changed, except that we can adjust the value of $c$. It is still a constant as far as $\mathbf{w}$ and $\mathbf{x}$ are concerned. However, since Gluon doesn't know about this beforehand, it's worth while to give it a hand (this makes the code go faster, too, since we're not sending the Gluon engine on a wild goose chase after a parameter that doesn't change). `get_constant` is the method that can be used to accomplish this. Let's see what this looks like in practice.
# + attributes={"classes": [], "id": "", "n": "5"}
class FancyMLP(nn.Block):
def __init__(self, **kwargs):
super(FancyMLP, self).__init__(**kwargs)
# Random weight parameters created with the get_constant are not
# iterated during training (i.e. constant parameters)
self.rand_weight = self.params.get_constant(
'rand_weight', np.random.uniform(size=(20, 20)))
self.dense = nn.Dense(20, activation='relu')
def forward(self, x):
x = self.dense(x)
# Use the constant parameters created, as well as the relu and dot functions
x = npx.relu(np.dot(x, self.rand_weight.data()) + 1)
# Reuse the fully connected layer. This is equivalent to sharing
# parameters with two fully connected layers
x = self.dense(x)
# Here in Control flow, we need to call asscalar to return the scalar
# for comparison
while np.abs(x).sum() > 1:
x /= 2
if np.abs(x).sum() < 0.8:
x *= 10
return x.sum()
# -
# In this `FancyMLP` model, we used constant weight `Rand_weight` (note that it is not a model parameter), performed a matrix multiplication operation (`np.dot<`), and reused the *same* `Dense` layer. Note that this is very different from using two dense layers with different sets of parameters. Instead, we used the same network twice. Quite often in deep networks one also says that the parameters are *tied* when one wants to express that multiple parts of a network share the same parameters. Let's see what happens if we construct it and feed data through it.
# + attributes={"classes": [], "id": "", "n": "6"}
net = FancyMLP()
net.initialize()
net(x)
# -
# There's no reason why we couldn't mix and match these ways of build a network. Obviously the example below resembles more a chimera, or less charitably, a [Rube Goldberg Machine](https://en.wikipedia.org/wiki/Rube_Goldberg_machine). That said, it combines examples for building a block from individual blocks, which in turn, may be blocks themselves. Furthermore, we can even combine multiple strategies inside the same forward function. To demonstrate this, here's the network.
# + attributes={"classes": [], "id": "", "n": "7"}
class NestMLP(nn.Block):
def __init__(self, **kwargs):
super(NestMLP, self).__init__(**kwargs)
self.net = nn.Sequential()
self.net.add(nn.Dense(64, activation='relu'),
nn.Dense(32, activation='relu'))
self.dense = nn.Dense(16, activation='relu')
def forward(self, x):
return self.dense(self.net(x))
chimera = nn.Sequential()
chimera.add(NestMLP(), nn.Dense(20), FancyMLP())
chimera.initialize()
chimera(x)
# -
# ## Compilation
#
# The avid reader is probably starting to worry about the efficiency of this. After all, we have lots of dictionary lookups, code execution, and lots of other Pythonic things going on in what is supposed to be a high performance deep learning library. The problems of Python's [Global Interpreter Lock](https://wiki.python.org/moin/GlobalInterpreterLock) are well known. In the context of deep learning it means that we have a super fast GPU (or multiple of them) which might have to wait until a puny single CPU core running Python gets a chance to tell it what to do next. This is clearly awful and there are many ways around it. The best way to speed up Python is by avoiding it altogether.
#
# Gluon does this by allowing for Hybridization (:numref:`chapter_hybridize`). In it, the Python
# interpreter executes the block the first time it's invoked. The Gluon runtime
# records what is happening and the next time around it short circuits any calls
# to Python. This can accelerate things considerably in some cases but care needs
# to be taken with control flow. We suggest that the interested reader skip
# forward to the section covering hybridization and compilation after finishing
# the current chapter.
#
#
# ## Summary
#
# * Layers are blocks
# * Many layers can be a block
# * Many blocks can be a block
# * Code can be a block
# * Blocks take are of a lot of housekeeping, such as parameter initialization, backprop and related issues.
# * Sequential concatenations of layers and blocks are handled by the eponymous `Sequential` block.
#
# ## Exercises
#
# 1. What kind of error message will you get when calling an `__init__` method whose parent class not in the `__init__` function of the parent class?
# 1. What kinds of problems will occur if you remove the `asscalar` function in the `FancyMLP` class?
# 1. What kinds of problems will occur if you change `self.net` defined by the Sequential instance in the `NestMLP` class to `self.net = [nn.Dense(64, activation='relu'), nn. Dense(32, activation='relu')]`?
# 1. Implement a block that takes two blocks as an argument, say `net1` and `net2` and returns the concatenated output of both networks in the forward pass (this is also called a parallel block).
# 1. Assume that you want to concatenate multiple instances of the same network. Implement a factory function that generates multiple instances of the same block and build a larger network from it.
#
# ## Scan the QR Code to [Discuss](https://discuss.mxnet.io/t/2325)
#
# 
|
5 deep-learning-computation/model-construction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python
# language: python3
# name: python3
# ---
# # Exercise List from Labels
#
#
# <a id='exercise-0'></a>
# **Exercise 1**
#
# This is an exercise from the `exercise_list_labels` file
# ## The exercise list
#
# This is an exercise list containing exercises `other_file` and `pyfun_functions_2`
#
#
# <a id='exerciselist-0'></a>
# **Exercise 1**
#
# This is an exercise from the `exercise_list_labels` file
#
# ([*back to text*](#exercise-0))
#
# **Question 3**
#
# I'm a function with a label and a different title
#
# Define a function named `var` that takes a list (call it `x`) and
# computes the variance. This function should use the mean function that we
# defined earlier.
#
# Hint: $ \text{variance} = \frac{1}{N} \sum_i (x_i - \text{mean}(x))^2 $
# + hide-output=false
# your code here
# -
# ([*back to text*](exercises.ipynb#exercise-2))
# ## One more exercise
#
#
# <a id='exerciselist-1'></a>
# **Exercise 4 (exercises)**
#
# This is another function with a label
#
# - and
# - *a*
# - **list**!
#
#
# ([*back to text*](exercises.ipynb#exercise-3))
|
tests/base/ipynb/exercise_list_labels.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Solutions: nearest neighbors computation
#
# This notebook contains practical exercise to manipulate the $k$ nearest neighbors of a particular observation under study, the so called **kNN aglorithm**, standing for *k Nearest Neighbor*.
#
# ## Import and pseudo-datasets
# +
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
# %matplotlib inline
import warnings
warnings.filterwarnings("ignore")
# -
# Plot settings
mpl.rcParams['legend.frameon'] = False
mpl.rcParams['legend.fontsize'] = 'xx-large'
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['axes.titlesize'] = 18
mpl.rcParams['axes.labelsize'] = 18
mpl.rcParams['lines.linewidth'] = 2.5
mpl.rcParams['figure.figsize'] = (10, 7)
# The following piece of code create two reference dataset (*training*) containing 1 million observation, each observation consist of 25 variables (or *features*). For the purpose of the exercise, we use gaussian numbers with a mean of -3.5 and +3.5 for training dataset 1 and 2 respectively (both having a RMS of 5).
# Generation of two (training) datasets of 10e6 observations contanining 25 features each
Nobs = 1000000
trainX1 = 5.0*np.random.randn(Nobs,25) - 3.5
trainX2 = 5.0*np.random.randn(Nobs,25) + 3.5
# Since our training dataset is known, it can be useful to consider labels associated to each event. This label is the property we might want to predict for a new, unknown observation. We decide to label `trainX1` with `1` and `trainX2` with `2`:
# Create the target (or label for each dataset)
trainY1 = np.zeros(Nobs)+1
trainY2 = np.zeros(Nobs)+2
# ## Quick data inspection
#
# Plot and compare the distribution of the first variables for `trainX1` and `trainX2`
# Plotting the distributions of the first feature
plt.hist(trainX1[:, 0], bins=100, alpha=0.3, label='Population 1')
plt.hist(trainX2[:, 0], bins=100, alpha=0.3, label='Population 2')
plt.xlabel('Variable 1')
plt.ylabel('Events')
plt.legend();
# ## Nearest neighbors of a new observation `obs`
obs = np.random.randn(25)
print(obs)
# ### Merge the two datasets `X` and `Y`
#
# The idea is to manipulate a single array `trainX` for the features regardless of the type of data (1 or 2), while keeping track of the label with a single `trainY` array:
trainX = np.concatenate([trainX1, trainX2])
trainY = np.concatenate([trainY1, trainY2])
# ### Compute the distance between `obs` and the global dataset
#
# Using broadcasting and vectorized operation, compute the euclidien distance in the 25 dimension space between the unknown observation and every point of the global dataset (containing both data of type 1 and 2).
distances = np.sum((trainX-obs)**2, axis=1)**0.5
print(distances[:2])
# ### Sort the distances to have the nearest points first
#
# In this question, we want to sort distances by increasing order (to later take only the $k$ first ones), and the associated type of neighbors (1 or 2).
#
# **HINT:** this can be done using the function `np.argsort()`.
# +
# Get the point indices by increasing distances
sorted_points = np.argsort(distances)
# Get the sorted distances
sdistances = distances[sorted_points]
# Get the corresponding data type
sorted_trainY = trainY[sorted_points]
# -
# ### Vizualize the observation and its neighbors in a 2D projection
#
# We would like to vizualize the observation and its 100 nearest neighbors in the 2D projection of the two first features. Produce a scatter plot showing the observation and the 100 nearest neighbors with different color for different types, and markersize depending on the 2D distance.
#
# **HINT:** one can use fancy indexing, considering that `sorted_points[:100]` is the indices of the 100 nearest neighbors.
# +
# Plot observation
xobs, yobs = obs[0], obs[1]
plt.scatter(xobs, yobs, color='black', alpha=0.9, s=100, zorder=3, label='Observation')
# Get the index of the k=100 first neighbors
idx = sorted_points[:100]
# Get data category, x and y values for those NN
typeNN, xNN, yNN = trainY[idx], trainX[idx, 0], trainX[idx, 1]
# Compute markersize depending on the 2D distances
dNN = np.sqrt( (xNN-xobs)**2 + (yNN-yobs)**2 )
markersize = 20*(np.max(dNN) - dNN)
# Get type 1 and type 2 data
type1, type2 = typeNN==1, typeNN==2
# Plot the result
plt.scatter(xNN[type1], yNN[type1], alpha=0.5, s=markersize[type1], label='Type 1 neighbor')
plt.scatter(xNN[type2], yNN[type2], alpha=0.5, s=markersize[type2], label='Type 2 neighbor')
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.legend();
# -
# ### Count the number of nearest neighbors of type 1 and type 2
#
# We would like to consider the k nearest neighbors, and count the fraction of type 1 and type 2 data (to later be able to say if our unknown observation is more likely to be of type 1 or 2). Of course, if we consider the whole training points (`k=Nobs`), there will be `Nobs` points of type 1 and `Nobs` points of type 2. This is why it is interesting to compute the number of type 1 and type 2 neihbors *as a function of k*. We will consider all k values from 1 to 500.
#
# **HINT:** the function `np.cumsum()` might be useful.
# +
# Get the number of neighbor type 1 and type 2 among the k nearest neighbor
Nb1 = np.cumsum(sorted_trainY==1)
Nb2 = np.cumsum(sorted_trainY==2)
# Consider only the k values from 1 to 500
Nb1 = Nb1[:500]
Nb2 = Nb2[:500]
# -
# Plot the number of neighbors of type 1 and type 2 as a function of $k$
plt.plot(Nb1, label='sample 1')
plt.plot(Nb2, label='sample 2')
plt.ylabel('Number of k Nearst Neighbor')
plt.xlabel('k')
plt.legend();
# ### Create a function `get_kNN_obs()` doing all this at once
#
# We want now to have a function taking in argument an observation, a training sample trainX and a target trainY *with an arbitray number of type of data*, which returns the number of nearest neighbors up to kmax for each data type (formated into a list). In other words, we want a function returning `[N1, N2, ... Nj]`, where `Ni` is numpy 1D array of shape `(kmax,)` containing the number of neighbor of type `i` among the `k` nearest neighbors -- up to `kmax`.
# +
def get_kNN_obs(obs, trainX, trainY, kmax=500):
'''
Compute the number of nearest neighbors (up to kmax) of an
observation `obs` with a training sample `trainX` labled
with `trainY`.
return [N1, N2, ... Nj] (list of neighbors number for each k<kmax)
where Ni is a numpy 1D array of shape (kmax,) containing the number
of neighbor of type i in the k nearest neighbors.
'''
# Compute distances
r = np.sum((trainX-obs)**2, axis=1)**(0.5)
# Sort the distances
sorted_NN = np.argsort(r)
sorted_trainY = trainY[sorted_NN]
# Get a list of unique of labels
labels = np.unique(trainY)
# Loop over labels and count the number of nearest neighbors
res = [np.cumsum(sorted_trainY==l)[:kmax] for l in labels]
# Return the array of number of nearest neighbor
return res
def plot_kNN(kNN_array):
for i, kNN in enumerate(kNN_array):
plt.plot(kNN, label='Sample {}'.format(i+1))
plt.ylabel('Number of k Nearst Neighbors')
plt.xlabel('k')
plt.legend()
return
# -
# Plot one observation
kNN = get_kNN_obs(obs, trainX, trainY, kmax=100)
plot_kNN(kNN)
# ## Nearest neighbors of a new set of unknown observations `testX`
#
# ### Preparing the proper broadcasting
#
# In this part, we want to repeat the operation previously made for one observation, on an entire dataset. This is possible using broadcasting. What is the proper re-shaping in order to get an array of shape `(Nobs, Ntrain, Nvar)` from two arrays of shape `(Nobs, Nvar)` and `(Ntrain, Nvar)`?
#
# **HINT:** we can use the `a.reshape()` to add an *empty axis* at the right position.
d1 = np.random.randn(10, 3)
t1 = np.random.randn(5, 3)
# t1+d1 will crash with "could not be broadcast together with shapes (5,3) (10,3)"
# ### Generalize `get_kNN_obs()` to run over a dataset
#
# Here, we want a function returning `[N1, N2, ... Nj]`, where `Ni` is numpy *2D array* of shape `(Nobs, kmax)` containing the number of neighbor of type `i` among the `k` nearest neighbors - up to `kmax` - for each observation.
def get_kNN_data(dataX, trainX, trainY, kmax=500):
'''
Compute the number of nearest neighbors (up to kmax) of an
observation `o` for two sample `d1` and `d2`.
return N1, N2 (array of neighbors in data1 and data2 in the kmax nearest ones)
'''
# Get some numbers (o must be a 2D array)
nd, nv = dataX.shape[0], dataX.shape[1]
nt = trainX.shape[0]
# Prepare proper broadcasting
trainX = trainX.reshape(1, nt, nv)
dataX = dataX.reshape(nd, 1, nv)
# Compute distances
r = np.sum((trainX-dataX)**2, axis=2)**(0.5)
# Sort the distances along distances
sorted_NN = np.argsort(r, axis=1)
sorted_trainY = trainY[sorted_NN]
# Get the list of unique labels
labels = np.unique(sorted_trainY)
# Loop over labels and count the number of nearest neighbors
res = [np.cumsum(sorted_trainY==l, axis=1)[:, :kmax] for l in labels]
# Return the array of number of nearest neighbor
return res
# ### Generation of unknown pseudo-data
# Generate pseudo data like data1 and data2
data_obs_like1 = 3*np.random.randn(10000, 25) - 2.5
data_obs_like2 = 3*np.random.randn(10000, 25) + 2.5
# ### Memory limit - lazy *v.s* eager learner
#
# This algorithm needs to loop over all training observation for each unknown observation. This is called a *lazy learner*, as opposed to the *eager learner* which can be evaluated for each unknown observation without the training sample. This might causes trouble in case of large dataset
# This will crash with a memory error
get_kNN_data(data_obs_like1, trainX, trainY)
# Write a function `kNNprediction(dataX, trainX, trainY, k, ntrain)` which takes only `ntrain` events of the training sample (equally sampled in the array, *i.e.* **not** the first `ntrain` elements of the training sample) and run the kNN computation.
#
# **HINT:** it's recommanded to remain below a size of 1000000. Since our unknown dataset are have 10000 observations, it's better to not considere more than few 1000 training events.
def run_get_kNN(dataX, trainX, trainY, k=100, ntrain=1000):
ntot = trainX.shape[0]
s = int(ntot/ntrain)
small_trainX, small_trainY = trainX[::s], trainY[::s]
return get_kNN_data(dataX, small_trainX, small_trainY, k)
# Call this function on both `data_obs_like1` and `data_obs_like2` and plot the fraction of k nearest neibghors of type 1 for each unknown dataset. Compare how the discriminative power changes with $k$.
# Compute the number of kNN for training1, training2
kmax = 500
obs1_N1, obs1_N2 = run_get_kNN(data_obs_like1, trainX, trainY, k=kmax)
obs2_N1, obs2_N2 = run_get_kNN(data_obs_like2, trainX, trainY, k=kmax)
# +
style = {'bins': np.linspace(0, 1, 50), 'alpha': 0.5}
plt.figure(figsize=(20, 5))
plt.subplot(131)
plt.hist(obs1_N1[:, -1]/kmax, **style, label='Data1_like observations')
plt.hist(obs2_N1[:, -1]/kmax, **style, label='Data2_like observations');
plt.xlabel('Fraction of data1 neighbors')
plt.title('$k_{max}=500$')
plt.legend();
plt.subplot(132)
plt.hist(obs1_N1[:, 200]/200, **style, label='Data1_like observations')
plt.hist(obs2_N1[:, 200]/200, **style, label='Data2_like observations');
plt.xlabel('Fraction of data1 neighbors')
plt.title('$k_{max}=200$')
plt.legend();
plt.subplot(133)
plt.hist(obs1_N1[:, 50]/50, **style, label='Data1_like observations')
plt.hist(obs2_N1[:, 50]/50, **style, label='Data2_like observations');
plt.xlabel('Fraction of data1 neighbors')
plt.title('$k_{max}=50$')
plt.legend();
# -
# ## Computing the nearest neighbors with many categories
#
# ### Generation of a training dataset with 5 types of data
#
# We first create a more complex dataset contanining 5 different populations stored in `trainX_ndata`, with five different averages. The associated labels are in `trainY_ndata`.
Nobs = 10000
mulist = [-5, -2, 0, 2, 5]
dlist = [5.0*np.random.randn(Nobs,25)+mu for mu in mulist]
llist = [np.zeros(Nobs)+i for i in np.arange(len(mulist))]
trainX_ndata = np.concatenate(dlist)
trainY_ndata = np.concatenate(llist)
# ### Number of neighbor of each population
#
# The goal here is to have a function which return the number of neighbors for each population among the $k$ nearest neighbors. In otherwords, we want the composition of the $k$ nearest neighbors.
#
# **HINT:** Since the number and the nature of label is *a priori* unknown, it might be convenient to store the information into a dictionnary `{label: n_kNN_label}`
def get_kNN_composition(dataX, trainX, trainY, k=500):
'''
Compute the number of nearest neighbors (up to k) on a data sample
`d` for a traning sample `t` and its label `l`.
return {label: nNNlabel}
'''
# Sanity checks
if dataX.ndim != 2:
raise NameError('Data must be a 2D array')
if trainX.shape[0] != trainY.shape[0]:
raise NameError('Training dataset and label must have the same size')
if dataX.shape[1] != trainX.shape[1]:
raise NameError('Test and training dataset must have the same number of features')
# Get some numbers (o must be a 2D array)
nd, nv = dataX.shape[0], dataX.shape[1]
nt = trainX.shape[0]
# Prepare proper broadcasting
t = trainX.reshape( 1, nt, nv)
d = dataX.reshape(nd, 1, nv)
# Compute distances
r = np.sum((d-t)**2, axis=2)**(0.5)
# Sort the distances along distances
sorted_NN = np.argsort(r, axis=1)
sorted_trainY = trainY[sorted_NN]
# Get the list of unique labels
labels = np.unique(sorted_trainY)
# Count the number of neighbor of each label around each observation
Nlabel_dict = {label: np.count_nonzero(sorted_trainY[:, :k]==label, axis=1) for label in labels}
# Return the array of number of nearest neighbor
return Nlabel_dict
# ### Behaviour on two different unknown pseud-data
#
# We first generate two sample of pseudo-unknown pseudo-dataset which look like population 1 and population 3.
# Generate pseudo data like data1 and data2
data_obs_pop1 = 3*np.random.randn(10000, 25) - 2
data_obs_pop3 = 3*np.random.randn(10000, 25) + 2
# Write a function `plot_kNN_composition(k)` which plots the number of neighbors of each population among the $k$ nearest neighbors, for the two above pseudo-datasets.
def plot_kNN_composition(k):
# Run the kNN and get the composition
ntrain, n = 1000, trainX_ndata.shape[0]
step = int(n/ntrain)
kNN_data1 = get_kNN_composition(data_obs_pop1, trainX_ndata[::step], trainY_ndata[::step], k=k)
kNN_data2 = get_kNN_composition(data_obs_pop3, trainX_ndata[::step], trainY_ndata[::step], k=k)
# Plotting style and figure
plot_style = {'alpha': 0.5, 'bins': np.linspace(-0.5, k+0.5, k+2), 'log': True}
plt.figure(figsize=(20, 7))
# Plotting the results
plt.subplot(121)
for p, v in kNN_data1.items():
plt.hist(v, label='population {:.0f}'.format(p), **plot_style)
plt.title('Data 1-like, k={}'.format(k))
plt.legend()
plt.subplot(122)
for p, v in kNN_data2.items():
plt.hist(v, label='population {:.0f}'.format(p), **plot_style)
plt.title('Data 3-like, k={}'.format(k))
plt.legend()
return
plot_kNN_composition(k=10)
plot_kNN_composition(k=50)
plot_kNN_composition(k=100)
|
solutions/3-NearestNeighborAlgo-solution.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# %pylab inline
# %cd ../data
# # 1
df = pd.read_csv("bicycle.csv")
df.head()
# # 2
# i.
df['Total'] = df['Fremont Bridge East Sidewalk'] + df['Fremont Bridge West Sidewalk']
df['Date'] = pd.to_datetime(df['Date'], format = "%m/%d/%Y %I:%M:%S %p")
# ii.
df['Hour'] = pd.DatetimeIndex(df['Date']).hour
# iii.
df['Year'] = pd.DatetimeIndex(df['Date']).year
df.head()
# # 3
df2016 = df[df['Year'] == 2016]
df2016.head()
# # 4
len(df2016[df2016['Hour'] == 11])
group = df2016.groupby(by = 'Hour').sum()
group['Total'].plot.bar()
# # 5
a = df.groupby(by = 'Hour').mean()
a
a[a['Total'] == a['Total'].max()]
# On average, the busiest hour of the day is 5 PM.
|
analysis/Homework1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/cindyhfls/NMA_DL_2021_project/blob/main/project_group_OkapisJohnV3.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="pg0Ta9TfMBDc"
#
# To-do:
# * hyperparameter tuning
# * make train its own function?
# * simple correlations
#
#
# + [markdown] id="idt_5qF9ogSJ"
# _____________
# # Preprocessing
# + id="SHRR0PV20BqZ"
#@title Import matplotlib and set defaults
from matplotlib import rcParams
from matplotlib import pyplot as plt
import torch
import copy
from torch.utils.data import Dataset, DataLoader
from torchvision import transforms, utils
import numpy as np
import math
import torch.nn as nn
import torch.nn.functional as F
from matplotlib import pyplot as plt
from torch.utils.data.dataloader import default_collate
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
rcParams['figure.figsize'] = [20, 4]
rcParams['font.size'] =15
rcParams['axes.spines.top'] = False
rcParams['axes.spines.right'] = False
rcParams['figure.autolayout'] = True
# + id="MWiCcZ2Xz44h"
# Data Loading
#@title Data retrieval
import os, requests
fname = []
for j in range(3):
fname.append('steinmetz_part%d.npz'%j)
url = ["https://osf.io/agvxh/download"]
url.append("https://osf.io/uv3mw/download")
url.append("https://osf.io/ehmw2/download")
for j in range(len(url)):
if not os.path.isfile(fname[j]):
try:
r = requests.get(url[j])
except requests.ConnectionError:
print("!!! Failed to download data !!!")
else:
if r.status_code != requests.codes.ok:
print("!!! Failed to download data !!!")
else:
with open(fname[j], "wb") as fid:
fid.write(r.content)
alldat = np.array([])
for j in range(len(fname)):
alldat = np.hstack((alldat, np.load('steinmetz_part%d.npz'%j, allow_pickle=True)['dat']))
# + colab={"base_uri": "https://localhost:8080/"} id="zP4xE0-30qRG" outputId="d59a82b7-8dc9-4e1c-977b-93930227e30b"
#@title Print Keys
print(alldat[0].keys())
# + id="me2qABA1PzIZ"
# @title Set random seed
# @markdown Executing `set_seed(seed=seed)` you are setting the seed
# for DL its critical to set the random seed so that students can have a
# baseline to compare their results to expected results.
# Read more here: https://pytorch.org/docs/stable/notes/randomness.html
# Call `set_seed` function in the exercises to ensure reproducibility.
import random
import torch
def set_seed(seed=None, seed_torch=True):
if seed is None:
seed = np.random.choice(2 ** 32)
random.seed(seed)
np.random.seed(seed)
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed)
torch.cuda.manual_seed(seed)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
print(f'Random seed {seed} has been set.')
# In case that `DataLoader` is used
def seed_worker(worker_id):
worker_seed = torch.initial_seed() % 2**32
np.random.seed(worker_seed)
random.seed(worker_seed)
# + id="jyNZF8eu2GJa"
#@title Define Steinmetz Class
class SteinmetzSession:
data = []
binSize = 10
nTrials = []
nNeurons = []
trialLen = 0
trimStart = "trialStart"
trimEnd = "trialEnd"
def __init__(self, dataIn):
self.data = copy.deepcopy(dataIn)
dims1 = np.shape(dataIn['spks'])
self.nTrials = dims1[1]
self.nNeurons = dims1[0]
self.trialLen = dims1[2]
def binData(self, binSizeIn): # Inputs: data, scalar for binning. Combines binSizeIn bins together to bin data smaller Ex. binSizeIn of 5 on the original dataset combines every 5 10 ms bins into one 50 ms bin across all trials.
varsToRebinSum = ['spks']
varsToRebinMean = ['wheel', 'pupil']
spikes = self.data['spks']
histVec = range(0,self.trialLen+1, binSizeIn)
spikesBin = np.zeros((self.nNeurons, self.nTrials, len(histVec)))
print(histVec)
for trial in range(self.nTrials):
spikes1 = np.squeeze(spikes[:,trial,:])
for time1 in range(len(histVec)-1):
spikesBin[:,trial, time1] = np.sum(spikes1[:, histVec[time1]:histVec[time1+1]-1], axis=1)
spikesBin = spikesBin[:,:,:-1]
self.data['spks'] = spikesBin
self.trialLen = len(histVec) -1
self.binSize = self.binSize*binSizeIn
s = "Binned spikes, turning a " + repr(np.shape(spikes)) + " matrix into a " + repr(np.shape(spikesBin)) + " matrix"
print(s)
def plotTrial(self, trialNum): # Basic function to plot the firing rate during a single trial. Used for debugging trimming and binning
plt.imshow(np.squeeze(self.data['spks'][:,trialNum,:]), cmap='gray_r', aspect = 'auto')
plt.colorbar()
plt.xlabel("Time (bins)")
plt.ylabel("Neuron #")
def realign_data_to_movement(self,length_time_in_ms): # input has to be n * nTrials * nbins
align_time_in_bins = np.round(self.data['response_time']/self.binSize*1000)+ int(500/self.binSize) # has to add 0.5 s because the first 0.5 s is pre-stimulus
length_time_in_bins = int(length_time_in_ms/self.binSize)
validtrials = self.data['response']!=0
maxtime = self.trialLen
newshape = (self.nNeurons,self.nTrials)
newshape+=(length_time_in_bins,)
newdata = np.empty(newshape)
for count,align_time_curr_trial in enumerate(align_time_in_bins):
if (validtrials[count]==0)|(align_time_curr_trial+length_time_in_bins>maxtime) :
validtrials[count] = 0
else:
newdata[:,count,:]= self.data['spks'][:,count,int(align_time_curr_trial):int(align_time_curr_trial)+length_time_in_bins]
# newdata = newdata[:,validtrials,:]
self.data['spks'] = newdata
# self.validtrials = validtrials
print('spikes aligned to movement, returning validtrials')
return validtrials
def get_areas(self):
print(set(list(self.data['brain_area'])))
def extractROI(self, region): #### extract neurons from single region
rmrt=list(np.where(self.data['brain_area']!=region))[0]
print(f' removing data from {len(rmrt)} neurons not contained in {region} ')
self.data['spks']=np.delete(self.data['spks'],rmrt,axis=0)
neur=len(self.data['spks'])
print(f'neurons remaining in trial {neur}')
self.data['brain_area']=np.delete(self.data['brain_area'],rmrt,axis=0)
self.data['ccf']=np.delete(self.data['ccf'],rmrt,axis=0)
def FlattenTs(self):
self.data['spks']=np.hstack(self.data['spks'][:])
def removeTrialAvgFR(self):
mFR = self.data['spks'].mean(1)
mFR = np.expand_dims(mFR, 1).repeat(self.data['spks'].shape[1],axis = 1)
print(np.shape(self.data['spks']))
print(np.shape(mFR))
self.data['spks'] = self.data['spks'].astype(float)
self.data['spks'] -= mFR
def permdims(self):
return torch.permute(torch.tensor(self.data['spks']),(2,1,0))
def smoothFR(self, smoothingWidth):# TODO: Smooth the data and save it back to the data structure
return 0
# + id="tIeFNLI66MDc"
#@title Set up Dataset
### dataset definition
class NeuronDataset(Dataset):
def __init__(self, X, Y):
self.X = X
self.Y = Y
def __len__(self):
return len(self.Y)
def __getitem__(self, idx):
dataP = self.Y[idx]
data = self.X[idx]
sample = {"X": data, "Y": dataP}
return sample
# + colab={"base_uri": "https://localhost:8080/", "height": 956} id="S4PaVL2Y7-fW" outputId="66716752-e2aa-4056-e965-6ca88d6bf29a"
#@title get input for network from session 31
s31=SteinmetzSession(alldat[30])
validtrials = s31.realign_data_to_movement(500) # get 500 ms from movement time,
# cannot get realign and binning to work the same time =[
nTr = np.argwhere(validtrials) # since the other trials were defaulted to a zero value, only plot the valid trials
## plot a trial
plt.figure()
s31.plotTrial(nTr[1])
plt.title('All')
### print areas
s31.get_areas()
# s31.FlattenTs()
MO = copy.deepcopy(s31)
###remove all neurons not in motor cortex
MO.extractROI('MOs')
### plot a trial from motor neuron
plt.figure()
MO.plotTrial(nTr[1])
plt.title('MOs')
### permute the trials
MOdata = MO.permdims().float().to(device)
MOdata = MOdata[:,validtrials,:]
print(MOdata.shape)
TH = copy.deepcopy(s31)
###remove all neurons not in motor cortex
TH.extractROI('TH')
### plot a trial from motor neuron
plt.figure()
TH.plotTrial(nTr[1])
plt.title('TH')
THdata = TH.permdims().float().to(device)
THdata = THdata[:,validtrials,:]
print(THdata.shape)
# + colab={"base_uri": "https://localhost:8080/"} id="Ushslg7nBH6_" outputId="0ddeb2bc-db27-4d67-b9d2-6634425e896a"
#@title get indices for trials (split into ~60%, 30%,10%)
N = MOdata.shape[1]
np.random.seed(42)
ii = torch.randperm(N).tolist()
idx_train = ii[:math.floor(0.6*N)]
idx_val = ii[math.floor(0.6*N):math.floor(0.9*N)]
idx_test = ii[math.floor(0.9*N):]
print(N)
# + id="zkiaD2O9preO"
#@title split into train, test and validation set
x0_train = THdata[:,idx_train,:]
x0_val = THdata[:,idx_val,:]
x0_test = THdata[:,idx_test,:]
x1_train = MOdata[:,idx_train,:]
x1_val = MOdata[:,idx_val,:]
x1_test = MOdata[:,idx_test,:]
# + [markdown] id="1TdDGTtCoM1-"
# ------
# # DataLoader (skip for now), compatibility issue
# + id="3Ju90wuxV1ix"
#@title Split Dataset and Create Data Loaders
# need to make trial first so do batches in trials
batchsz= 20
ND=NeuronDataset(MOdata[:,idx_train,:],MOdata[:,idx_train,:])
DL_Train = DataLoader(ND, batch_size=batchsz)
ND=NeuronDataset(MOdata[:,idx_val,:],MOdata[:,idx_val,:])
DL_Val = DataLoader(ND, batch_size=batchsz)
ND=NeuronDataset(MOdata[:,idx_test,:],MOdata[:,idx_test,:])
DL_Test = DataLoader(ND, batch_size=batchsz)
# + id="O93Dp7s5wT3m" colab={"base_uri": "https://localhost:8080/"} outputId="c558e6ca-93c4-4cd4-8661-68b9ac238a3b"
#### check that the data loader is iterating correctly
print('\nFirst iteration of data set: ', next(iter(DL_Train)), '\n')
print('Length of data set: ', len(DL_Train), '\n')
# + colab={"base_uri": "https://localhost:8080/"} id="MqPRIteEztuq" outputId="06441acd-8aaf-4e63-9ea1-3ef15481170e"
# time * trial * neuron
next(iter(DL_Train))['X'].shape
next(iter(DL_Train))['Y'].shape
# + [markdown] id="CblqpOHboWXe"
# ---------
# # Model
# + id="44BcPW_GuSMC"
class Net(nn.Module): # our model
def __init__(self, ncomp, NN1, NN2, bidi=True):
super(Net, self).__init__()
# play with some of the options in the RNN!
self.rnn1 = nn.RNN(NN1, ncomp, num_layers = 1, dropout = 0, # MO
bidirectional = bidi, nonlinearity = 'tanh')
self.rnn2 = nn.RNN(NN2,ncomp,num_layers = 1, dropout = 0, bidirectional = bidi, nonlinearity = 'tanh') #TH
if bidi == True:
self.fclatent = nn.Linear(ncomp*2,ncomp*2)
else:
self.fclatent = nn.Linear(ncomp,ncomp)
self.fc = nn.Linear(ncomp,NN1)
def forward(self, x0,x1):
y2 = self.rnn2(x0)[0] # ncomp TH
y = self.rnn1(x1)[0] # ncomp MOs
y += self.fclatent(y2) # ncomp MOs with projection of latent TH components
if self.rnn1.bidirectional:
# if the rnn is bidirectional, it concatenates the activations from the forward and backward pass
# we want to add them instead, so as to enforce the latents to match between the forward and backward pass
q = (y[:, :, :ncomp] + y[:, :, ncomp:])/2
else:
q = y
# the softplus function is just like a relu but it's smoothed out so we can't predict 0
# if we predict 0 and there was a spike, that's an instant Inf in the Poisson log-likelihood which leads to failure
z = F.softplus(self.fc(q), 10)
return z, q
# + colab={"base_uri": "https://localhost:8080/"} id="SeFQk7Kex5WQ" outputId="c061bbc9-0825-4d14-f6e4-c6721665af3c"
#@title Set input/hyperparameters here:
ncomp = 10
NN1 = MOdata.shape[2]
print(NN1)
NN2 = THdata.shape[2]
print(NN2)
learning_rate_start = 0.002
# + colab={"base_uri": "https://localhost:8080/"} id="Qrz-ONFcwXh7" outputId="459c4ff1-001d-4505-b34c-1b3c6e34d1f6"
#@title first the basic network with MO => MO (no external input)
net_baseline = Net(ncomp, NN1, NN2, bidi = True).to(device)
net_baseline.fclatent.weight.data[:] = 0 # fixed weights =0 so the TH input is not considered
net_baseline.fclatent.bias.data[:] = 0
net_baseline.fclatent.weight.requires_grad = False
net_baseline.fclatent.bias.requires_grad = False
# special thing: we initialize the biases of the last layer in the neural network
# we set them as the mean firing rates of the neurons.
# this should make the initial predictions close to the mean, because the latents don't contribute much
net_baseline.fc.bias.data[:] = MOdata.mean((0,1))
# we set up the optimizer later in the training loop
print(net_baseline)
# + id="2P1qGp0xrIf5" colab={"base_uri": "https://localhost:8080/"} outputId="286977d8-9e94-476b-f5c9-3e91ce130065"
#@title train net_baseline
'''
you can keep re-running this cell if you think the cost might decrease further
x1_train = input we are predicting (MOs)
x0_train = input from other areas (e.g. TH)
'''
# we define the Poisson log-likelihood loss
def Poisson_loss(lam, spk):
return lam - spk * torch.log(lam)
optimizer = torch.optim.Adam(net_baseline.parameters(), lr=learning_rate_start)
set_seed(seed=2021)
niter = 1000
training_cost = []
val_cost = []
for k in range(niter):
### training
optimizer.zero_grad()
# the network outputs the single-neuron prediction and the latents
z, y = net_baseline(x0_train,x1_train)
# our log-likelihood cost
cost = Poisson_loss(z, x1_train).mean()
# train the network as usual
cost.backward()
optimizer.step()
training_cost.append(cost.item())
### test on validation data
z_val,_ = net_baseline(x0_val,x1_val)
cost = Poisson_loss(z_val, x1_val).mean()
val_cost.append(cost.item())
if k % 100 == 0:
print(f'iteration {k}, cost {cost.item():.4f}')
# + id="5QLSmrzerkYl" colab={"base_uri": "https://localhost:8080/", "height": 250} outputId="43e2c482-26e9-456e-f557-7235f450cd8c"
#@title Plot training progress
plt.plot(training_cost,'b')
plt.plot(val_cost,'r')
plt.hlines(np.min(training_cost),0,niter,'b',linestyles = '--')
plt.hlines(np.min(val_cost),0,niter,'r',linestyles = '--')
plt.legend(['training cost','validation cost','min training cost','min validation cost'])
plt.title('Training cost over epochs')
plt.ylabel('cost')
plt.xlabel('epochs')
# + colab={"base_uri": "https://localhost:8080/", "height": 988} id="zasQt3A-Nilm" outputId="5e790c3c-7e4e-4e8f-c34d-fb8fd04ae3cb"
#@title Plot performance on training data
rpred = z.detach().cpu().numpy()
rates = x1_train
nTr = 5
nNeuron = 0
plt.figure(figsize=(10, 6))
plt.plot(rates[:,nTr, nNeuron])
plt.plot(rpred[:,nTr, nNeuron])
plt.legend(['spikes', 'rates (predicted)'])
plt.title(f'training set Trial {nTr}, Neuron {nNeuron}')
plt.show()
plt.figure(figsize = (12, 8))
plt.subplot(121)
plt.imshow(rates[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'True rates (training set trial {nTr})')
plt.subplot(122)
plt.imshow(rpred[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'Inferred rates (training set trial {nTr})')
plt.show()
# + id="lIEBSZ__tcX0" colab={"base_uri": "https://localhost:8080/", "height": 988} outputId="82ceaf3b-30e0-48e5-b5e4-7527ce4ccbbc"
#@title Performance on validation data
rpred = z_val.detach().cpu().numpy()
rates = x1_val
nTr = 5
nNeuron = 160
plt.figure(figsize=(10, 6))
plt.plot(rates[:,nTr, nNeuron])
plt.plot(rpred[:,nTr, nNeuron])
plt.legend(['spikes', 'rates (predicted)'])
plt.title(f'validation set Trial {nTr}, Neuron {nNeuron}')
plt.show()
plt.figure(figsize = (12, 8))
plt.subplot(121)
plt.imshow(rates[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'True rates (validation set trial {nTr})')
plt.subplot(122)
plt.imshow(rpred[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'Inferred rates (validation set trial {nTr})')
plt.show()
# + id="sB7CqS2NiX4Y"
# save model (first on colab environment but you can download it, see <https://neptune.ai/blog/google-colab-dealing-with-files>)
PATH = 'steinmetz_model_baseline.pt'
torch.save(net_baseline.state_dict(), PATH)
del net_baseline
# + [markdown] id="mB1zaljtiwVA"
# # to prevent further training net_baseline, we are going to start from loading the model directly from now on.
# + id="mRE5Zbvsio2S" colab={"base_uri": "https://localhost:8080/"} outputId="fad002a7-a826-421b-d17f-28f7ae6cecca"
# load saved model
net_baseline = Net(ncomp, NN1, NN2, bidi = True).to(device)
net_baseline.load_state_dict(torch.load('steinmetz_model_baseline.pt'))
# + colab={"base_uri": "https://localhost:8080/"} id="F1pAhkMGwded" outputId="6fc6116a-2391-45ca-ba47-70789058b2ce"
# after training the baseline network, get the weights of rnn1 and freeze it
net_withinput = copy.deepcopy(net_baseline)
net_withinput.fclatent.weight.requires_grad = True
net_withinput.fclatent.bias.requires_grad = True
# # set weight initalization to random
net_withinput.fclatent.reset_parameters()
net_withinput.rnn1.weight_ih_l0.requires_grad = False
net_withinput.rnn1.weight_hh_l0.requires_grad = False
net_withinput.rnn1.bias_ih_l0.requires_grad = False
net_withinput.rnn1.bias_hh_l0.requires_grad = False
net_withinput.rnn1.weight_ih_l0_reverse.requires_grad = False
net_withinput.rnn1.weight_hh_l0_reverse.requires_grad = False
net_withinput.rnn1.bias_ih_l0_reverse.requires_grad = False
net_withinput.rnn1.bias_hh_l0_reverse.requires_grad = False
print(net_withinput)
# + id="SLTgv4h0t4Nv" colab={"base_uri": "https://localhost:8080/"} outputId="f669394b-3c32-4ab5-9cfc-45a2abcb65a9"
#@title train net_withinput
'''
you can keep re-running this cell if you think the cost might decrease further
x1_train = input we are predicting (MOs)
x0_train = input from other areas (e.g. TH)
'''
# we define the Poisson log-likelihood loss
# def Poisson_loss(lam, spk):
# return lam - spk * torch.log(lam)
loss = nn.MSELoss()
optimizer = torch.optim.Adam(net_withinput.parameters(), lr=learning_rate_start) # this is very important
set_seed(seed=2021)
niter = 1000
training_cost = []
val_cost = []
for k in range(niter):
### training
optimizer.zero_grad()
# the network outputs the single-neuron prediction and the latents
z, y = net_withinput(x0_train,x1_train)
# our log-likelihood cost
cost = loss(z, x1_train).mean()
# train the network as usual
cost.backward()
optimizer.step()
training_cost.append(cost.item())
### test on validation data
z_val,_ = net_withinput(x0_val,x1_val)
cost = loss(z_val, x1_val).mean()
val_cost.append(cost.item())
if k % 100 == 0:
print(f'iteration {k}, cost {cost.item():.4f}')
# + id="rS2ZTu2KvXXb" colab={"base_uri": "https://localhost:8080/", "height": 290} outputId="e780ce98-0688-4b31-c158-116a9fbfebe3"
#@title Plot training progress
plt.plot(training_cost,'b')
plt.plot(val_cost,'r')
plt.hlines(np.min(training_cost),0,niter,'b',linestyles = '--')
plt.hlines(np.min(val_cost),0,niter,'r',linestyles = '--')
plt.legend(['training cost','validation cost','min training cost','min validation cost'])
plt.title('Training cost over epochs')
plt.ylabel('cost')
plt.xlabel('epochs')
# + id="fK34xhVbu4VV" colab={"base_uri": "https://localhost:8080/", "height": 988} outputId="14fb96ff-d81e-4a91-a051-8967caee1dce"
#@title Plot performance on training data
rpred = z.detach().cpu().numpy()
rates = x1_train
nTr = 2
nNeuron = 0
plt.figure(figsize=(10, 6))
plt.plot(rates[:,nTr, nNeuron])
plt.plot(rpred[:,nTr, nNeuron])
plt.legend(['spikes', 'rates (predicted)'])
plt.title(f'Trial {nTr}, Neuron {nNeuron}')
plt.show()
plt.figure(figsize = (12, 8))
plt.subplot(121)
plt.imshow(rates[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'True rates (trial {nTr})')
plt.subplot(122)
plt.imshow(rpred[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'Inferred rates (trial {nTr})')
plt.show()
# + id="DR5FKVmEvWh7" colab={"base_uri": "https://localhost:8080/", "height": 988} outputId="c85ae0bb-d660-48da-ea48-52f84df04305"
#@title Performance on validation data
rpred = z_val.detach().cpu().numpy()
rates = x1_val
nTr = 2
nNeuron = 0
plt.figure(figsize=(10, 6))
plt.plot(rates[:,nTr, nNeuron])
plt.plot(rpred[:,nTr, nNeuron])
plt.legend(['spikes', 'rates (predicted)'])
plt.title(f'Trial {nTr}, Neuron {nNeuron}')
plt.show()
plt.figure(figsize = (12, 8))
plt.subplot(121)
plt.imshow(rates[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'True rates (trial {nTr})')
plt.subplot(122)
plt.imshow(rpred[:, nTr, :].T, cmap='gray_r')
plt.xlabel('Time (ms)')
plt.ylabel('Cell #')
plt.title(f'Inferred rates (trial {nTr})')
plt.show()
# + [markdown] id="eA3Q8CRLfqbm"
# #compare with just training the previous network for another 100 epochs
# + colab={"base_uri": "https://localhost:8080/"} id="w4lRfQpofqbp" outputId="d94212d3-3794-49c1-fc6d-7c7192c0fba9"
#@title train net_baseline
'''
you can keep re-running this cell if you think the cost might decrease further
x1_train = input we are predicting (MOs)
x0_train = input from other areas (e.g. TH)
'''
# we define the Poisson log-likelihood loss
# def Poisson_loss(lam, spk):
# return lam - spk * torch.log(lam)
loss = nn.MSELoss()
optimizer = torch.optim.Adam(net_baseline.parameters(), lr=learning_rate_start)
set_seed(seed=2021)
niter = 100
training_cost = []
val_cost = []
for k in range(niter):
### training
optimizer.zero_grad()
# the network outputs the single-neuron prediction and the latents
z, y = net_baseline(x0_train,x1_train)
cost = loss(z,x1_train).mean()
# # our log-likelihood cost
# cost = Poisson_loss(z, x1_train).mean()
# train the network as usual
cost.backward()
optimizer.step()
training_cost.append(cost.item())
### test on validation data
z_val,_ = net_baseline(x0_val,x1_val)
cost = loss(z_val,x1_val).mean()
# cost = Poisson_loss(z_val, x1_val).mean()
val_cost.append(cost.item())
if k % 100 == 0:
print(f'iteration {k}, cost {cost.item():.4f}')
# + colab={"base_uri": "https://localhost:8080/", "height": 302} id="YLHeN4mxfqbq" outputId="4f31d8c2-da25-4f41-b60f-a9e41e97e98c"
#@title Plot training progress
plt.plot(training_cost,'b')
plt.plot(val_cost,'r')
plt.hlines(np.min(training_cost),0,niter,'b',linestyles = '--')
plt.hlines(np.min(val_cost),0,niter,'r',linestyles = '--')
plt.legend(['training cost','validation cost','min training cost','min validation cost'])
plt.title('Training cost over epochs')
plt.ylabel('cost')
plt.xlabel('epochs')
# + id="V_IYDqvRheqa" colab={"base_uri": "https://localhost:8080/"} outputId="3a0e2f26-1124-4dab-e772-03dc704d5590"
#@title what if we don't freeze the weights
# after training the baseline network, get the weights of rnn1 and freeze it
net_withinput2 = copy.deepcopy(net_baseline)
net_withinput2.fclatent.weight.requires_grad = True
net_withinput2.fclatent.bias.requires_grad = True
# # set weight initalization to random
net_withinput2.fclatent.reset_parameters()
print(net_withinput2)
# + id="dXEPLyXMh1h8" colab={"base_uri": "https://localhost:8080/"} outputId="d31ec457-718c-4b99-9a4d-a2e1067a1bd4"
#@title train the input model without freezing weights
'''
you can keep re-running this cell if you think the cost might decrease further
x1_train = input we are predicting (MOs)
x0_train = input from other areas (e.g. TH)
'''
# we define the Poisson log-likelihood loss
# def Poisson_loss(lam, spk):
# return lam - spk * torch.log(lam)
loss = nn.MSELoss()
optimizer = torch.optim.Adam(net_withinput2.parameters(), lr=learning_rate_start)
set_seed(seed=2021)
niter = 1000
training_cost = []
val_cost = []
for k in range(niter):
### training
optimizer.zero_grad()
# the network outputs the single-neuron prediction and the latents
z, y = net_withinput2(x0_train,x1_train)
cost = loss(z,x1_train).mean()
# # our log-likelihood cost
# cost = Poisson_loss(z, x1_train).mean()
# train the network as usual
cost.backward()
optimizer.step()
training_cost.append(cost.item())
### test on validation data
z_val,_ = net_withinput2(x0_val,x1_val)
cost = loss(z_val,x1_val).mean()
# cost = Poisson_loss(z_val, x1_val).mean()
val_cost.append(cost.item())
if k % 100 == 0:
print(f'iteration {k}, cost {cost.item():.4f}')
# + id="eTYQXfXClbYq" colab={"base_uri": "https://localhost:8080/", "height": 302} outputId="6d431b4f-6f27-4ced-bdc8-a903f55eb3e7"
#@title Plot training progress
plt.plot(training_cost,'b')
plt.plot(val_cost,'r')
plt.hlines(np.min(training_cost),0,niter,'b',linestyles = '--')
plt.hlines(np.min(val_cost),0,niter,'r',linestyles = '--')
plt.legend(['training cost','validation cost','min training cost','min validation cost'])
plt.title('Training cost over epochs')
plt.ylabel('cost')
plt.xlabel('epochs')
# + [markdown] id="8XRIIHV8rRxo"
# --------------------- The end -------------------
#
# + [markdown] id="2mlyk4z-rZtS"
# --------------------------
# # Below are some old stuff
# + id="5V9llXOYsNzI"
for (idx, batch) in enumerate(DL_DS):
pass
# print(idx, 'X:', batch['X'])
# + id="cHZuIqCsDb7o"
# + colab={"base_uri": "https://localhost:8080/", "height": 134} id="iONxRXblKYHy" outputId="c9a74295-17ed-4e04-b0eb-8142a190dac6"
#Parameters
params = {'batch_size': 64,
'shuffle': True,
'num_workers': 6}
max_epochs = 100
# Datasets
partition = # IDs
labels = # Labels
# Generators
training_set = Dataset(partition['train'], labels)
training_generator = torch.utils.data.DataLoader(training_set, **params)
validation_set = Dataset(partition['validation'], labels)
validation_generator = torch.utils.data.DataLoader(validation_set, **params)
# + colab={"base_uri": "https://localhost:8080/"} id="k9bBuzK7QfF4" outputId="015a37d6-a32c-4a8b-a97a-3853bf85b157"
import torch
# @title Set device (GPU or CPU). Execute `set_device()`
# inform the user if the notebook uses GPU or CPU.
def set_device():
device = "cuda" if torch.cuda.is_available() else "cpu"
if device != "cuda":
print("WARNING: For this notebook to perform best, "
"if possible, in the menu under `Runtime` -> "
"`Change runtime type.` select `GPU` ")
else:
print("GPU is enabled in this notebook.")
return device
device = set_device()
# + id="Zu2mW21QlTVQ" colab={"base_uri": "https://localhost:8080/", "height": 438} outputId="5afea644-e8f3-43a6-dfae-e1baa3405687"
# set the seed
np.random.seed(42)
# 100 trials is typical of neural data
ntrials = 100
# we simulate 200 neurons
NN = 200
# we will pretend like every "bin" is 10ms, so the trial length is 2500ms
NT = 250
# let's use 10 latent components
ncomp = 10
# this is the recurrent dynamics matrix, which we made diagonal for simplicity
# values have to be smaller than 1 for stability
A0 = np.diag(.8 + .2 * np.random.rand(ncomp,))
# this is the projection matrix from components to neurons
C0 = .025 * np.random.randn(ncomp, NN)
# We generate the dynamics of the low-d system. We initialize the latent state.
# start by initializing the latents
y = 2 * np.random.randn(ncomp)
latents = np.zeros((NT, ntrials, ncomp))
# we run the dynamics forward and add noise (or "innovations") at each timestep
for t in range(NT):
y = y @ A0 + np.random.randn(ntrials, ncomp)
latents[t] = y
# we now project the latents to the neuron space and threshold to generate firing rates
rates = np.maximum(0, latents @ C0)
# now we draw poisson counts to simulate the number of spikes a neuron fires randomly
x = np.random.poisson(rates)
x0 = torch.from_numpy(x[:, :, :200]).to(device).float()
x1 = torch.from_numpy(x[:, :, 200:]).to(device).float()
x0 = torch.permute(x0, (2,1,0))
x0 = np.reshape(x0, (-1,200))
x1 = torch.permute(x1, (2,1,0))
x1 = np.reshape(x1, (-1,200))
print(x1.shape)
# + id="Or4Zk6X4fN19"
import torch
import torch.nn as nn
import torchvision
class AE(nn.Module):
def __init__(self, **kwargs):
super().__init__()
self.encoder_hidden_layer = nn.Linear(
in_features=kwargs["input_shape"], out_features=128
)
self.encoder_output_layer = nn.Linear(
in_features=128, out_features=128
)
self.decoder_hidden_layer = nn.Linear(
in_features=128, out_features=128
)
self.decoder_output_layer = nn.Linear(
in_features=128, out_features=kwargs["input_shape"]
)
def forward(self, features):
activation = self.encoder_hidden_layer(features)
activation = torch.relu(activation)
code = self.encoder_output_layer(activation)
code = torch.relu(code)
activation = self.decoder_hidden_layer(code)
activation = torch.relu(activation)
activation = self.decoder_output_layer(activation)
reconstructed = torch.relu(activation)
return reconstructed
# + colab={"base_uri": "https://localhost:8080/"} id="dJzSEFcff0JT" outputId="a96a0355-f8db-4a02-c161-1ba281a51712"
# use gpu if available
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(np.shape(x0))
# create a model from `AE` autoencoder class
# load it to the specified device, either gpu or cpu
model = AE(input_shape=200).to(device)
# create an optimizer object
# Adam optimizer with learning rate 1e-3
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
# mean-squared error loss
criterion = nn.MSELoss()
# + colab={"base_uri": "https://localhost:8080/"} id="TMxo8WqsgeLn" outputId="02361a98-19d1-4ed7-f50d-6945e58c0b6e"
# + colab={"base_uri": "https://localhost:8080/"} id="b2TmwgcKiYEQ" outputId="9a185142-a4f4-40c5-802f-1ea14b453bb0"
# + colab={"base_uri": "https://localhost:8080/"} id="vNBGqLl1gI50" outputId="61c3c8f3-72f3-40e5-b779-710771ffcb17"
epochs = 100
for epoch in range(epochs):
loss = 0
# reshape mini-batch data to [N, 784] matrix
# load it to the active device
# reset the gradients back to zero
# PyTorch accumulates gradients on subsequent backward passes
optimizer.zero_grad()
# compute reconstructions
print(type(x0))
outputs = model(x0)
# compute training reconstruction loss
train_loss = criterion(outputs, x0)
# compute accumulated gradients
train_loss.backward()
# perform parameter update based on current gradients
optimizer.step()
# add the mini-batch training loss to epoch loss
loss += train_loss.item()
# display the epoch training loss
print("epoch : {}/{}, loss = {:.6f}".format(epoch + 1, epochs, loss))
# + colab={"base_uri": "https://localhost:8080/", "height": 287} id="YIWKAdEiUP9S" outputId="fbf59953-8291-4a42-de89-60735593f5db"
s1.plotTrial(1)
# + colab={"base_uri": "https://localhost:8080/", "height": 324} id="rGn5L_PjQ8H2" outputId="07180641-2003-4a73-dc85-53186d06f681"
s1.binData(10)
s1.plotTrial(1)
|
project_group_OkapisJohnV3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: matplotlib-challenge
# language: python
# name: python3
# ---
# +
# Dependencies and Setup
# %matplotlib inline
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import os
# Hide warning messages in notebook
import warnings
warnings.filterwarnings('ignore')
# File to Load (Remember to Change These)
mouse_data = os.path.join ( "data", "mouse_drug_data.csv")
clinical_data = os.path.join ("data", "clinicaltrial_data.csv")
df1 = pd.read_csv(mouse_data)
df2 = pd.read_csv(clinical_data)
# Read the Mouse and Drug Data and the Clinical Trial Data
# Combine the data into a single dataset
# Display the data table for preview
# -
df3 = pd.merge(left=df2,right=df1, how='outer', left_on='Mouse ID', right_on='Mouse ID')
df3.head().style.format(
{"Tumor Volume (mm3)":"{:.1f}"})
# ## Tumor Response to Treatment
# Store the Mean Tumor Volume Data Grouped by Drug and Timepoint
# Convert to DataFrame
# Preview DataFrame
agg_df3 = df3.groupby(["Drug","Timepoint"]).agg({"Tumor Volume (mm3)":["mean"]}).reset_index()
agg_df3.columns = list(map(''.join, agg_df3.columns.values))
agg_df3 = agg_df3.rename(columns={"Tumor Volume (mm3)mean": "Tumor Volume (mm3)"})
agg_df3.head()
# Store the Standard Error of Tumor Volumes Grouped by Drug and Timepoint
# Convert to DataFrame
# Preview DataFrame
agg_df4 = df3.groupby(["Drug","Timepoint"]).agg({"Tumor Volume (mm3)":["sem"]}).reset_index()
agg_df4.columns = list(map(''.join, agg_df4.columns.values))
agg_df4 = agg_df4.rename(columns={"Tumor Volume (mm3)sem": "Tumor Volume (mm3)"})
agg_df4.head()
# Minor Data Munging to Re-Format the Data Frames
# Preview that Reformatting worked
pivot_df3 = pd.pivot_table(agg_df3, values='Tumor Volume (mm3)', index=['Timepoint'], columns=['Drug'])
pivot_df3.head()
pivot_df4 = pd.pivot_table(agg_df4, values='Tumor Volume (mm3)', index=['Timepoint'], columns=['Drug'])
pivot_df4.head()
# Generate the Plot (with Error Bars)
# Save the Figure
pivot_df3[["Placebo","Capomulin", "Infubinol", "Ketapril"]]\
.plot(kind='line', figsize = (15, 9), grid=True,
yerr = pivot_df4, marker='o', linestyle="--")
plt.title("Tumor response to Treatment")
plt.xlabel('Time (Days)')
plt.ylabel('Tumor Volume (mm3)')
plt.legend(loc='upper left')
plt.savefig("Tumor response to Treatment BG.png")
plt.show()
# ## Metastatic Response to Treatment
# Store the Mean Met. Site Data Grouped by Drug and Timepoint
# Convert to DataFrame
# Preview DataFrame
agg_df5 = df3.groupby(["Drug","Timepoint"]).agg({"Metastatic Sites":["mean"]}).reset_index()
agg_df5.columns = list(map(''.join, agg_df5.columns.values))
agg_df5 = agg_df5.rename(columns={"Metastatic Sitesmean": "Metastatic Sites"})
agg_df5.head()
# Store the Standard Error associated with Met. Sites Grouped by Drug and Timepoint
# Convert to DataFrame
# Preview DataFrame
agg_df6 = df3.groupby(["Drug","Timepoint"]).agg({"Metastatic Sites":["sem"]}).reset_index()
agg_df6.columns = list(map(''.join, agg_df5.columns.values))
agg_df6 = agg_df6.rename(columns={"Metastatic Sitessem": "Metastatic Sites"})
agg_df6.head()
# Minor Data Munging to Re-Format the Data Frames
# Preview that Reformatting worked
pivot_df5 = pd.pivot_table(agg_df5, values='Metastatic Sites', index=['Timepoint'], columns=['Drug'])
pivot_df5.head()
pivot_df6 = pd.pivot_table(agg_df6, values='Metastatic Sites', index=['Timepoint'], columns=['Drug'])
pivot_df6.head()
# Generate the Plot (with Error Bars)
# Save the Figure
# Show the Figure
pivot_df5[["Placebo","Capomulin", "Infubinol", "Ketapril"]]\
.plot(kind='line', figsize = (15, 9),
yerr = pivot_df6, marker='o', linestyle="dotted")
plt.title("Metastatic Spread During Treatment")
plt.xlabel('Treatment Duration (Days)')
plt.ylabel('Metastatic Sites')
plt.legend(loc='upper left')
plt.grid(axis='y')
plt.xticks(np.arange(0, 50, step=10))
plt.savefig("Metastatic Spread During Treatment.png")
plt.show()
# ## Survival Rates
# Store the Count of Mice Grouped by Drug and Timepoint (W can pass any metric)
# Convert to DataFrame
# Preview DataFrame
agg_df7 = df3.groupby(["Drug","Timepoint"]).agg({"Mouse ID":["count"]}).reset_index()
agg_df7.columns = list(map(''.join, agg_df7.columns.values))
agg_df7 = agg_df7.rename(columns={"Mouse IDcount": "Mouse Count"})
agg_df7.head()
# Minor Data Munging to Re-Format the Data Frames
# Preview the Data Frame
pivot_df7 = pd.pivot_table(agg_df7, values='Mouse Count', index=['Timepoint'], columns=['Drug'])
pivot_df7.head()
# +
pivot_df8 = pivot_df7.loc[0,:]
for column in pivot_df7:
pivot_df7[column] = pivot_df7[column] / pivot_df8[column] * 100
pivot_df7.round()
# -
# Generate the Plot (Accounting for percentages)
# Save the Figure
# Show the Figure
pivot_df7.plot(kind='line', figsize = (15, 9), grid=True,
yerr = pivot_df6, marker='o', linestyle="dotted")
plt.title("Survival During Treatment")
plt.xlabel('Time (Days)')
plt.ylabel('Survival Rate (%)')
plt.legend(loc='upper right')
plt.xticks(np.arange(0, 50, step=10))
plt.savefig("Survival During Treatment.png")
plt.show()
# ## Summary Bar Graph
# +
# Calculate the percent changes for each drug
# Display the data to confirm
# -
percent_change_df = ((pivot_df3.iloc[-1] - pivot_df3.iloc[0]) / pivot_df3.iloc[0]) * 100
percent_change_df
# Store all Relevant Percent Changes into a Tuple
# Splice the data between passing and failing drugs
# Orient widths. Add labels, tick marks, etc.
# Use functions to label the percentages of changes
# Call functions to implement the function calls
# Save the Figure
# Show the Figure
percent_change_df[["Capomulin", "Infubinol", "Ketapril", "Placebo"]]\
.plot(kind="bar", figsize = (15, 9), title ="Tumor change Over 45 Day Treatment",
color = ['g', 'r', 'r', 'r'], grid=True, align='edge', width=1)
plt.ylabel("% Tumor Volume Change")
plt.xlabel("Drugs")
plt.grid(linestyle='dotted')
plt.yticks(np.arange(-20, 60, step=20))
plt.text(0.4,-10,'-19%', color='white')
plt.text(1.5,10,'46%', color='white')
plt.text(2.5,10,'57%', color='white')
plt.text(3.5,10,'51%', color='white')
plt.savefig("Tumor change Over 45 Day Treatment.png")
plt.show()
|
Pymaceuticals/HW_pymaceuticals.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab_type="code"
# !pip install autokeras
# + [markdown] colab_type="text"
# ## A Simple Example
# The first step is to prepare your data. Here we use the [California housing
# dataset](https://scikit-learn.org/stable/datasets/index.html#california-housing-dataset) as an example.
#
# + colab_type="code"
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.datasets import fetch_california_housing
import autokeras as ak
house_dataset = fetch_california_housing()
df = pd.DataFrame(
np.concatenate(
(house_dataset.data, house_dataset.target.reshape(-1, 1)), axis=1
),
columns=house_dataset.feature_names + ["Price"],
)
train_size = int(df.shape[0] * 0.9)
df[:train_size].to_csv("train.csv", index=False)
df[train_size:].to_csv("eval.csv", index=False)
train_file_path = "train.csv"
test_file_path = "eval.csv"
# + [markdown] colab_type="text"
# The second step is to run the
# [StructuredDataRegressor](/structured_data_regressor).
# As a quick demo, we set epochs to 10.
# You can also leave the epochs unspecified for an adaptive number of epochs.
#
# + colab_type="code"
# Initialize the structured data regressor.
reg = ak.StructuredDataRegressor(
overwrite=True, max_trials=3
) # It tries 3 different models.
# Feed the structured data regressor with training data.
reg.fit(
# The path to the train.csv file.
train_file_path,
# The name of the label column.
"Price",
epochs=10,
)
# Predict with the best model.
predicted_y = reg.predict(test_file_path)
# Evaluate the best model with testing data.
print(reg.evaluate(test_file_path, "Price"))
# + [markdown] colab_type="text"
# ## Data Format
# The AutoKeras StructuredDataRegressor is quite flexible for the data format.
#
# The example above shows how to use the CSV files directly. Besides CSV files, it also
# supports numpy.ndarray, pandas.DataFrame or [tf.data.Dataset](
# https://www.tensorflow.org/api_docs/python/tf/data/Dataset?version=stable). The data should be
# two-dimensional with numerical or categorical values.
#
# For the regression targets, it should be a vector of numerical values.
# AutoKeras accepts numpy.ndarray, pandas.DataFrame, or pandas.Series.
#
# The following examples show how the data can be prepared with numpy.ndarray,
# pandas.DataFrame, and tensorflow.data.Dataset.
#
# + colab_type="code"
import numpy as np
import pandas as pd
# x_train as pandas.DataFrame, y_train as pandas.Series
x_train = pd.read_csv(train_file_path)
print(type(x_train)) # pandas.DataFrame
y_train = x_train.pop("Price")
print(type(y_train)) # pandas.Series
# You can also use pandas.DataFrame for y_train.
y_train = pd.DataFrame(y_train)
print(type(y_train)) # pandas.DataFrame
# You can also use numpy.ndarray for x_train and y_train.
x_train = x_train.to_numpy()
y_train = y_train.to_numpy()
print(type(x_train)) # numpy.ndarray
print(type(y_train)) # numpy.ndarray
# Preparing testing data.
x_test = pd.read_csv(test_file_path)
y_test = x_test.pop("Price")
# It tries 10 different models.
reg = ak.StructuredDataRegressor(max_trials=3, overwrite=True)
# Feed the structured data regressor with training data.
reg.fit(x_train, y_train, epochs=10)
# Predict with the best model.
predicted_y = reg.predict(x_test)
# Evaluate the best model with testing data.
print(reg.evaluate(x_test, y_test))
# + [markdown] colab_type="text"
# The following code shows how to convert numpy.ndarray to tf.data.Dataset.
#
# + colab_type="code"
train_set = tf.data.Dataset.from_tensor_slices((x_train, y_train))
test_set = tf.data.Dataset.from_tensor_slices((x_test, y_test))
reg = ak.StructuredDataRegressor(max_trials=3, overwrite=True)
# Feed the tensorflow Dataset to the regressor.
reg.fit(train_set, epochs=10)
# Predict with the best model.
predicted_y = reg.predict(test_set)
# Evaluate the best model with testing data.
print(reg.evaluate(test_set))
# + [markdown] colab_type="text"
# You can also specify the column names and types for the data as follows.
# The `column_names` is optional if the training data already have the column names, e.g.
# pandas.DataFrame, CSV file.
# Any column, whose type is not specified will be inferred from the training data.
#
# + colab_type="code"
# Initialize the structured data regressor.
reg = ak.StructuredDataRegressor(
column_names=[
"MedInc",
"HouseAge",
"AveRooms",
"AveBedrms",
"Population",
"AveOccup",
"Latitude",
"Longitude",
],
column_types={"MedInc": "numerical", "Latitude": "numerical"},
max_trials=10, # It tries 10 different models.
overwrite=True,
)
# + [markdown] colab_type="text"
# ## Validation Data
# By default, AutoKeras use the last 20% of training data as validation data.
# As shown in the example below, you can use `validation_split` to specify the percentage.
#
# + colab_type="code"
reg.fit(
x_train,
y_train,
# Split the training data and use the last 15% as validation data.
validation_split=0.15,
epochs=10,
)
# + [markdown] colab_type="text"
# You can also use your own validation set
# instead of splitting it from the training data with `validation_data`.
#
# + colab_type="code"
split = 500
x_val = x_train[split:]
y_val = y_train[split:]
x_train = x_train[:split]
y_train = y_train[:split]
reg.fit(
x_train,
y_train,
# Use your own validation set.
validation_data=(x_val, y_val),
epochs=10,
)
# + [markdown] colab_type="text"
# ## Customized Search Space
# For advanced users, you may customize your search space by using
# [AutoModel](/auto_model/#automodel-class) instead of
# [StructuredDataRegressor](/structured_data_regressor). You can configure the
# [StructuredDataBlock](/block/#structureddatablock-class) for some high-level
# configurations, e.g., `categorical_encoding` for whether to use the
# [CategoricalToNumerical](/block/#categoricaltonumerical-class). You can also do not specify these
# arguments, which would leave the different choices to be tuned automatically. See
# the following example for detail.
#
# + colab_type="code"
import autokeras as ak
input_node = ak.StructuredDataInput()
output_node = ak.StructuredDataBlock(categorical_encoding=True)(input_node)
output_node = ak.RegressionHead()(output_node)
reg = ak.AutoModel(
inputs=input_node, outputs=output_node, overwrite=True, max_trials=3
)
reg.fit(x_train, y_train, epochs=10)
# + [markdown] colab_type="text"
# The usage of [AutoModel](/auto_model/#automodel-class) is similar to the
# [functional API](https://www.tensorflow.org/guide/keras/functional) of Keras.
# Basically, you are building a graph, whose edges are blocks and the nodes are intermediate outputs of blocks.
# To add an edge from `input_node` to `output_node` with
# `output_node = ak.[some_block]([block_args])(input_node)`.
#
# You can even also use more fine grained blocks to customize the search space even
# further. See the following example.
#
# + colab_type="code"
import autokeras as ak
input_node = ak.StructuredDataInput()
output_node = ak.CategoricalToNumerical()(input_node)
output_node = ak.DenseBlock()(output_node)
output_node = ak.RegressionHead()(output_node)
reg = ak.AutoModel(
inputs=input_node, outputs=output_node, max_trials=3, overwrite=True
)
reg.fit(x_train, y_train, epochs=10)
# + [markdown] colab_type="text"
# You can also export the best model found by AutoKeras as a Keras Model.
#
# + colab_type="code"
model = reg.export_model()
model.summary()
# numpy array in object (mixed type) is not supported.
# you need convert it to unicode or float first.
model.predict(x_train)
# + [markdown] colab_type="text"
# ## Reference
# [StructuredDataRegressor](/structured_data_regressor),
# [AutoModel](/auto_model/#automodel-class),
# [StructuredDataBlock](/block/#structureddatablock-class),
# [DenseBlock](/block/#denseblock-class),
# [StructuredDataInput](/node/#structureddatainput-class),
# [RegressionHead](/block/#regressionhead-class),
# [CategoricalToNumerical](/block/#categoricaltonumerical-class).
#
|
docs/ipynb/structured_data_regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + slideshow={"slide_type": "skip"}
from IPython.core.display import display, HTML
display(HTML("<style>.container { width:100% !important; }</style>"))
# + [markdown] slideshow={"slide_type": "slide"}
# # AWS Kinesis - Python + Spark
# + [markdown] slideshow={"slide_type": "slide"}
# * Pre-requisites
# * Introduction
# * Installation
# * CLI - useage
# + [markdown] slideshow={"slide_type": "slide"}
# ## Pre-requisites
# -
# * AWS Account
# * Your own IAM role
# * Python3 installed on system
# + [markdown] slideshow={"slide_type": "slide"}
# ## Introduction
# -
# AWS Kinesis is a **managed streaming service** by Amazon. It has 3 modules:
# * Create streaming server using **Kinesis Data Stream** and ingest from various producers
# * After ingesting data from producers persist to storage like S3, Redshit Spectrum, Dynamo DB or other datbase in AWS using **firehose**
# * Perform real-time analytics on the stream using **Kinesis SQL Analytics**.
#
# Additioanlly these **Kinesis Data Modules** can be connected to other AWS servies such as EMR etc for other downstream applications.
#
# + [markdown] slideshow={"slide_type": "slide"}
# 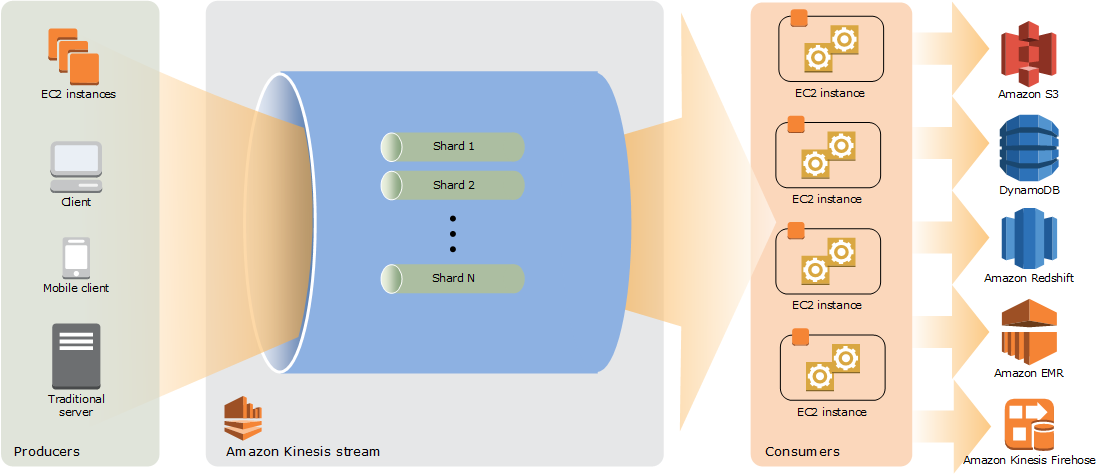
# + [markdown] slideshow={"slide_type": "slide"}
# ## Installation
# -
# #### Step 1: Install boto3 library to interact with AWS from python
# + slideshow={"slide_type": "-"}
sudo pip3 install --upgrade boto3
# -
# #### Step 2: Install AWS CLI library to interact with AWS form console
sudo pip3 install --upgrade awscli
# + [markdown] slideshow={"slide_type": "slide"}
# ## What exactly is Kinesis Data Stream?
#
# * Think of Kinesis Data Stream as a computer(s) into which you can write data and someone else can read that data.
# * For example,
#
# Consider Dublin Bus :
#
# The buses **produce** their location information using GPS and send it to **computer(s)** located in AWS's datacenter.
#
# Then we can **consume** it from there for analytics purpose and extract the ETA for each bus stop.
# + [markdown] slideshow={"slide_type": "slide"}
# ## Exercsise 1 - Create Kinesis Stream
#
# We will create a stream called **taxi_fleet_stream**. We can use AWS CLI or Python for this purpose, both ways are show below!
# + [markdown] slideshow={"slide_type": "slide"}
# ### Create stream with AWS CLI
#
# We will create an AWS Kinesis Data Stream to store the data which we will recieive from the bus(s). Takes about 30 sec to create the stream!
# -
## create stream
# !aws kinesis create-stream --stream-name 'taxi_fleet_stream' --shard-count 1
## list stream
# !aws kinesis list-streams
# describe stream
# !aws kinesis describe-stream --stream-name 'taxi_fleet_stream'
## destroy stream
# !aws kinesis delete-stream --stream-name "taxi_fleet_stream"
# + [markdown] slideshow={"slide_type": "slide"}
# ### Create stream with python
#
# We will create an AWS Kinesis Data Stream using python boto3
# +
import boto3
kinesis_client = boto3.client('kinesis', region_name='eu-west-1')
# create stream
kinesis_client.create_stream(StreamName='taxi_fleet_stream',ShardCount=1)
## If stream already exists, then you will get a "ResourceInUseException"
# + slideshow={"slide_type": "-"}
# list stream
kinesis_client.list_streams()
# -
# destory stream
kinesis_client.delete_stream(StreamName = 'taxi_fleet_stream')
# + [markdown] slideshow={"slide_type": "slide"}
# ### Exercise 2 - Create Producer
#
# The taxi will generate its own carID, fuel level, timestamp as data. We will use python for creating a producer.
#
# Before sending the data we generated, we must create it to a **record**
# Each Record should have 2 attributes, data and partiton key
# Data : The JSON Dump of the data taht you want to send
# PartitonKey : String to indicate on which shard this record is sumbitted
# + [markdown] slideshow={"slide_type": "slide"}
# 
# + slideshow={"slide_type": "slide"}
from pprint import pprint
import boto3
import json
import random
import time
from datetime import datetime
# initialize client
kinesis_client = boto3.client('kinesis', region_name='eu-west-1')
# generate the data we want to send
data = {
"time" : str(datetime.now()),
"car_id" : 1,
"fuel" : random.randint(1, 100)
}
# convert it to record
record = {}
record['Data'] = json.dumps(data)
record['PartitionKey'] = str(data['car_id'])
pprint(record)
# + [markdown] slideshow={"slide_type": "slide"}
# After you send the record a sequence number is assigned automatically by Kinesis. It is unique for each record
# -
# send data to kinesis - put record
response = kinesis_client.put_record(**record, StreamName='taxi_fleet_stream')
pprint(response)
# + [markdown] slideshow={"slide_type": "slide"}
# We will generate this record every 1 second and send it
# + slideshow={"slide_type": "-"}
record = {}
## send data every 1 second
while True:
## create the data we want to send
data = {
"time" : str(datetime.now()),
"car_id" : 1,
"fuel" : random.randint(1, 100)
}
# convert it to record
record['Data'] = json.dumps(data)
record['PartitionKey'] = str(data['car_id'])
## send the record
response = kinesis_client.put_record(**record,StreamName='taxi_fleet_stream')
pprint(record)
print("\n\n")
pprint(response)
print("\n====================\n")
record = {}
## sleep for 1 second - then send next record
time.sleep(1)
# + slideshow={"slide_type": "slide"}
## check payload size
import sys
print ("Estimated size: " + str(sys.getsizeof(record) / 1024) + "KB")
# -
# But Sending small chunks of data every 1 second is very expensive, AWS Kinesis charges you for every 1 Million PUT requests (**Each PUT request is defined as record of size 25KB or less**).
#
# In out case, we have a record size of 0.28125 KB, which is counted as 1 PUT request, as it is less that 25KB.
#
# You can see that if we have 1000s of taxis sending data every second of such small size, then we will quickly eat up our 1 Million **PUT request** Limit. We will explore another option called **put_records()**, whcih allows us to aggregate records and send them as a batch!
#
# Note : If a single record was of say 40KB, then it would count as 2 PUT request and so on!
# + [markdown] slideshow={"slide_type": "slide"}
# ### put_records() - Send more than 1 record
# -
## send data when we have 10 records,
RECORD_LIMIT = 10
record_set = [] # holds all 10 records
record = {}
while True:
## create the data we want to send
data = {
"time" : str(datetime.now()),
"car_id" : 1,
"fuel" : random.randint(1, 100)
}
# convert it to record
record['Data'] = json.dumps(data)
record['PartitionKey'] = str(data['car_id'])
record
## send the data as a batch, send them togather
if(len(record_set) == RECORD_LIMIT):
response = kinesis_client.put_records(StreamName='taxi_fleet_stream',
Records = record_set
)
pprint(record_set)
print("\n\n")
pprint(response)
print("\n====================\n")
record_set = [] #clear payload_set
record_set.append(record)
record = {} # clear record
## sleep for 1 second - then generate next record
time.sleep(1)
# + [markdown] slideshow={"slide_type": "slide"}
# * Each put_records() call can support up to 500 records in the record_set().
# * Each record should have its own partionon key specified as its own part.
# * Each record in the request can be as large as 1 MB, up to a limit of 5 MB for the entire request, including partition keys.
#
# Explicitely mention the Data and Partiton key for each record
# + [markdown] slideshow={"slide_type": "slide"}
# ### Exercise 3 : Create Consumer
#
# We will create a consumer in python who will read this data from kinesis
# +
import boto3
from pprint import pprint
import json
from datetime import datetime
import time
# intitalize client
kinesis_client = boto3.client('kinesis', region_name='eu-west-1')
response = kinesis_client.describe_stream(StreamName='taxi_fleet_stream')
pprint(response)
# # pprint(response)
# my_shard_id = response['StreamDescription']['Shards'][0]['ShardId']
# shard_iterator = kinesis_client.get_shard_iterator(StreamName=my_stream_name,
# ShardId=my_shard_id,
# ShardIteratorType='LATEST')
# my_shard_iterator = shard_iterator['ShardIterator']
# record_response = kinesis_client.get_records(ShardIterator=my_shard_iterator)
# while 'NextShardIterator' in record_response:
# record_response = kinesis_client.get_records(ShardIterator=record_response['NextShardIterator'])
# if(len(record_response['Records'])!= 0):
# [print(record_response['Records'])
# print("\n\n\n")
# time.sleep(1)
# -
kinesis_client.describe_stream(st my_stream_name)
|
aws_kinesis/aws kinesis tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Abbreviation in Wind
#
# > Incomplete list of abbreviations used in wind.
# ## AEP (Annual Energy Production)
# [aep-part-1-capacity-and-more](https://www.windspire.ch/blog/2017/6/22/aep-part-1-capacity-and-more)
|
01_abbreviation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas, networkx as nx
import matplotlib.pyplot as plt
import json
# Load node properties
fo = open('./traces/nodes.out', 'r')
data = fo.read()
fo.close()
dataset = json.loads(data)
locations = {}
for row in dataset['items']:
if row['archi'] == 'm3:at86rf231' and row['x'] != ' ':
addr = int(row['network_address'].split('.')[0].split('-')[1])
#locations[addr] = (float(row['x']), float(row['y']), float(row['z']))
locations[addr] = (float(row['x']), float(row['y']))
locations[97]
# Import Node Ids and corresponding IPv6 addresses
addr = pandas.read_csv('./traces/addr-2019-01JAN-29-1.cap',
sep='[ ;:/-]',
header=None,
usecols=[2,23],
names=['node_id', 'ipv6_addr'],
engine='python')
addr['node_id'] = addr['node_id'].convert_objects(convert_numeric=True)
addr = addr.drop_duplicates(subset=['node_id'], keep="first").sort_values(by=['node_id'])
addr.set_index('node_id')
# Build a look-up dictionary
ipv6 = {}
for index, row in addr.iterrows():
ipv6[row['ipv6_addr']] = row['node_id']
# Import RPL parents for each node
rpl = pandas.read_csv('./traces/rpl-2019-01JAN-29-1.cap',
sep='[ ;:/-]',
header=None,
usecols=[2,11],
names=['node_id', 'rpl_parent'],
engine='python')
rpl['node_id'] = rpl['node_id'].convert_objects(convert_numeric=True)
rpl = rpl.drop_duplicates(subset=['node_id', 'rpl_parent'], keep="first").sort_values(by=['node_id'])
rpl.set_index('node_id')
# Create a network
G = nx.DiGraph()
for index, row in addr.iterrows():
G.add_node(row['node_id'], addr=row['ipv6_addr'], loc=locations.get(row['node_id'], (0,0,0)))
G.node[row['node_id']]['id'] = str(row['node_id'])
G.node[row['node_id']]['color'] = 'blue'
G.node[row['node_id']]['addr'] = row['ipv6_addr']
G.node[row['node_id']]['loc'] = locations.get(row['node_id'], (0,0,0))
G.node[252]['color'] = 'red'
for index, row in rpl.iterrows():
if row['rpl_parent'] in ipv6 and row['node_id'] in G.nodes() and ipv6[row['rpl_parent']] in G.nodes():
G.add_edge(row['node_id'], ipv6[row['rpl_parent']])
plt.clf()
nx.draw_networkx_nodes(G, pos=nx.get_node_attributes(G,'loc'), node_shape='.', node_color=list(nx.get_node_attributes(G,'color').values()), alpha=0.3)
nx.draw_networkx_labels(G, pos=nx.get_node_attributes(G,'loc'), labels=nx.get_node_attributes(G,'id'))
nx.draw_networkx_edges(G, pos=nx.get_node_attributes(G,'loc'))
plt.show()
|
module/data/iot-lab/iot-lab-36nodes/NetworkLayout.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] tags=[]
# # NeXus classes
#
# ## Overview
#
# NeXus provides a substantial number of [base class definitions](https://manual.nexusformat.org/classes/base_classes/index.html#base-class-definitions).
# At this point scippnexus supports only a very limited number of these.
# Furthermore, not all features of each class definition are implemented.
# The class of a group is read from the group's `'NX_class'` attribute.
#
# The following table gives an overview of supported classes.
# There are roughly two categories of classes, those that contain data and can be read as a `scipp.DataArray` (for example NXdata), and those that mostly serve as groups for nested classes (for example NXentry containing NXdata):
# -
# NeXus class | read as | comment | NeXus specification
# :--- |:--- |:--- |:---
# [NXdata](../generated/classes/scippnexus.NXdata.rst) | scipp.DataArray | [example below](#NXdata) | [link](https://manual.nexusformat.org/classes/base_classes/NXdata.html)
# [NXdetector](../generated/classes/scippnexus.NXdetector.rst) | scipp.DataArray | [example below](#NXdetector) | [link](https://manual.nexusformat.org/classes/base_classes/NXdetector.html)
# [NXdisk_chopper](../generated/classes/scippnexus.NXdisk_chopper.rst) | scipp.Dataset |very incomplete support| [link](https://manual.nexusformat.org/classes/base_classes/NXdisk_chopper.html)
# [NXentry](../generated/classes/scippnexus.NXentry.rst) | — | [generic group-like](#Base-class:-NXobject) | [link](https://manual.nexusformat.org/classes/base_classes/NXentry.html)
# [NXevent_data](../generated/classes/scippnexus.NXevent_data.rst) | scipp.DataArray | [example below](#NXevent_data) | [link](https://manual.nexusformat.org/classes/base_classes/NXevent_data.html)
# [NXinstrument](../generated/classes/scippnexus.NXinstrument.rst) | — | [generic group-like](#Base-class:-NXobject) | [link](https://manual.nexusformat.org/classes/base_classes/NXinstrument.html)
# [NXlog](../generated/classes/scippnexus.NXlog.rst) | scipp.DataArray | [example below](#NXlog) | [link](https://manual.nexusformat.org/classes/base_classes/NXlog.html)
# [NXmonitor](../generated/classes/scippnexus.NXmonitor.rst) | scipp.DataArray | [example below](#NXmonitor) | [link](https://manual.nexusformat.org/classes/base_classes/NXmonitor.html)
# [NXroot](../generated/classes/scippnexus.NXroot.rst) | — | [generic group-like](#Base-class:-NXobject) | [link](https://manual.nexusformat.org/classes/base_classes/NXroot.html)
# [NXsample](../generated/classes/scippnexus.NXsample.rst) | scipp.Dataset |very incomplete support| [link](https://manual.nexusformat.org/classes/base_classes/NXsample.html)
# [NXsource](../generated/classes/scippnexus.NXsource.rst) | scipp.Dataset |very incomplete support| [link](https://manual.nexusformat.org/classes/base_classes/NXsource.html)
# [NXtransformations](../generated/classes/scippnexus.NXtransformations.rst) | — | [generic group-like](#Base-class:-NXobject) | [link](https://manual.nexusformat.org/classes/base_classes/NXtransformations.html)
# + [markdown] tags=[]
# For the examples below we use a file from the scippnexus sample data:
# -
from scippnexus import data
filename = data.get_path('PG3_4844_event.nxs')
import scippnexus as snx
f = snx.File(filename)
# + [markdown] tags=[]
# ## Base class: NXobject
#
# Base of all other NeXus classes.
# Provides a generic group-like interface.
# That is, this is equivalent to a dictionary of fields and/or other groups.
#
# NeXus classes that group other information but cannot be read as a data array or dataset provide this interface.
# + [markdown] tags=[]
# ## NXdata
#
# Provides multi-dimensional labeled data.
# See the NeXus format [NXdata base class definition](https://manual.nexusformat.org/classes/base_classes/NXdata.html) for details.
# Can be read as a data array using slicing syntax.
#
# Example:
# -
data = f['entry/bank103']
data
data['x_pixel_offset', :10]
# + [markdown] tags=[]
# ## NXdetector
#
# Provides data for a detector.
# See the NeXus format [NXdetector base class definition](https://manual.nexusformat.org/classes/base_classes/NXdetector.html) for details.
# Can be read as a data array using slicing syntax.
# The underlying data may be dense data or event data.
#
# Example:
# -
detector = f['entry/instrument/bank102']
detector
detector[...]
# If the underlying data is event data, the underlying event data can be selected using the special `select_events` property.
# For example, we can select the first 1000 pulses and load data for all pixels:
detector.select_events['pulse', :1000][...]
# <div class="alert alert-info">
# <b>Note:</b>
#
# Selecting a range of events allows for loading only a potentially very small section of the underlying event data and can thus be very fast.
#
# In contrast, e.g., selecting a small range of pixels in presence of underlying event data is *not* fast, since the events for all pixels are stored in the order as they arrive in the acquisition system and the entire [NXevent_data](#NXevent_data) group must be loaded.
#
# </div>
# + [markdown] tags=[]
# ## NXevent_data
#
# Provides event data in raw format as produced by the acquisition system, i.e., not grouped into detector pixels.
# See the NeXus format [NXevent_data base class definition](https://manual.nexusformat.org/classes/base_classes/NXevent_data.html) for details.
# Can be read as a data array using slicing syntax.
#
# Example:
# -
event_data = f['entry/bank102_events']
event_data[...]
# In some cases the event data fields may be contained directly within an [NXdetector](#NXdetector).
# The event data can also be accessed from there:
f['entry/instrument/bank102'].events[...]
# + [markdown] tags=[]
# ## NXlog
#
# Provides a time-series log.
# See the NeXus format [NXlog base class definition](https://manual.nexusformat.org/classes/base_classes/NXlog.html) for details.
# Can be read as a data array using slicing syntax.
#
# Example:
# -
proton_charge = f['/entry/DASlogs/proton_charge']
proton_charge
proton_charge[...]
# + [markdown] tags=[]
# ## NXmonitor
#
# Provides data for a beam monitor.
# See the NeXus format [NXmonitor base class definition](https://manual.nexusformat.org/classes/base_classes/NXmonitor.html) for details.
# Can be read as a data array using slicing syntax.
#
# Example:
# -
monitor = f['entry/monitor1']
monitor[...]
|
docs/user-guide/nexus-classes.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Regression in Python
#
# ***
# This is a very quick run-through of some basic statistical concepts, adapted from [Lab 4 in Harvard's CS109](https://github.com/cs109/2015lab4) course. Please feel free to try the original lab if you're feeling ambitious :-) The CS109 git repository also has the solutions if you're stuck.
#
# * Linear Regression Models
# * Prediction using linear regression
# * Some re-sampling methods
# * Train-Test splits
# * Cross Validation
#
# Linear regression is used to model and predict continuous outcomes while logistic regression is used to model binary outcomes. We'll see some examples of linear regression as well as Train-test splits.
#
#
# The packages we'll cover are: `statsmodels`, `seaborn`, and `scikit-learn`. While we don't explicitly teach `statsmodels` and `seaborn` in the Springboard workshop, those are great libraries to know.
# ***
# <img width=600 height=300 src="https://imgs.xkcd.com/comics/sustainable.png"/>
# ***
# +
# special IPython command to prepare the notebook for matplotlib and other libraries
# %pylab inline
import numpy as np
import pandas as pd
import scipy.stats as stats
import matplotlib.pyplot as plt
import sklearn
import seaborn as sns
# special matplotlib argument for improved plots
from matplotlib import rcParams
sns.set_style("whitegrid")
sns.set_context("poster")
# -
# ***
# # Part 1: Linear Regression
# ### Purpose of linear regression
# ***
# <div class="span5 alert alert-info">
#
# <p> Given a dataset $X$ and $Y$, linear regression can be used to: </p>
# <ul>
# <li> Build a <b>predictive model</b> to predict future values of $X_i$ without a $Y$ value. </li>
# <li> Model the <b>strength of the relationship</b> between each dependent variable $X_i$ and $Y$</li>
# <ul>
# <li> Sometimes not all $X_i$ will have a relationship with $Y$</li>
# <li> Need to figure out which $X_i$ contributes most information to determine $Y$ </li>
# </ul>
# <li>Linear regression is used in so many applications that I won't warrant this with examples. It is in many cases, the first pass prediction algorithm for continuous outcomes. </li>
# </ul>
# </div>
#
# ### A brief recap (feel free to skip if you don't care about the math)
# ***
#
# [Linear Regression](http://en.wikipedia.org/wiki/Linear_regression) is a method to model the relationship between a set of independent variables $X$ (also knowns as explanatory variables, features, predictors) and a dependent variable $Y$. This method assumes the relationship between each predictor $X$ is linearly related to the dependent variable $Y$.
#
# $$ Y = \beta_0 + \beta_1 X + \epsilon$$
#
# where $\epsilon$ is considered as an unobservable random variable that adds noise to the linear relationship. This is the simplest form of linear regression (one variable), we'll call this the simple model.
#
# * $\beta_0$ is the intercept of the linear model
#
# * Multiple linear regression is when you have more than one independent variable
# * $X_1$, $X_2$, $X_3$, $\ldots$
#
# $$ Y = \beta_0 + \beta_1 X_1 + \ldots + \beta_p X_p + \epsilon$$
#
# * Back to the simple model. The model in linear regression is the *conditional mean* of $Y$ given the values in $X$ is expressed a linear function.
#
# $$ y = f(x) = E(Y | X = x)$$
#
# 
# http://www.learner.org/courses/againstallodds/about/glossary.html
#
# * The goal is to estimate the coefficients (e.g. $\beta_0$ and $\beta_1$). We represent the estimates of the coefficients with a "hat" on top of the letter.
#
# $$ \hat{\beta}_0, \hat{\beta}_1 $$
#
# * Once you estimate the coefficients $\hat{\beta}_0$ and $\hat{\beta}_1$, you can use these to predict new values of $Y$
#
# $$\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1$$
#
#
# * How do you estimate the coefficients?
# * There are many ways to fit a linear regression model
# * The method called **least squares** is one of the most common methods
# * We will discuss least squares today
#
# #### Estimating $\hat\beta$: Least squares
# ***
# [Least squares](http://en.wikipedia.org/wiki/Least_squares) is a method that can estimate the coefficients of a linear model by minimizing the difference between the following:
#
# $$ S = \sum_{i=1}^N r_i = \sum_{i=1}^N (y_i - (\beta_0 + \beta_1 x_i))^2 $$
#
# where $N$ is the number of observations.
#
# * We will not go into the mathematical details, but the least squares estimates $\hat{\beta}_0$ and $\hat{\beta}_1$ minimize the sum of the squared residuals $r_i = y_i - (\beta_0 + \beta_1 x_i)$ in the model (i.e. makes the difference between the observed $y_i$ and linear model $\beta_0 + \beta_1 x_i$ as small as possible).
#
# The solution can be written in compact matrix notation as
#
# $$\hat\beta = (X^T X)^{-1}X^T Y$$
#
# We wanted to show you this in case you remember linear algebra, in order for this solution to exist we need $X^T X$ to be invertible. Of course this requires a few extra assumptions, $X$ must be full rank so that $X^T X$ is invertible, etc. **This is important for us because this means that having redundant features in our regression models will lead to poorly fitting (and unstable) models.** We'll see an implementation of this in the extra linear regression example.
#
# **Note**: The "hat" means it is an estimate of the coefficient.
# ***
# # Part 2: Boston Housing Data Set
#
# The [Boston Housing data set](https://archive.ics.uci.edu/ml/datasets/Housing) contains information about the housing values in suburbs of Boston. This dataset was originally taken from the StatLib library which is maintained at Carnegie Mellon University and is now available on the UCI Machine Learning Repository.
#
#
# ## Load the Boston Housing data set from `sklearn`
# ***
#
# This data set is available in the [sklearn](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_boston.html#sklearn.datasets.load_boston) python module which is how we will access it today.
from sklearn.datasets import load_boston
boston = load_boston()
boston.keys()
boston.data.shape
# Print column names
print(boston.feature_names)
# Print description of Boston housing data set
print(boston.DESCR)
# Now let's explore the data set itself.
bos = pd.DataFrame(boston.data)
bos.head()
# There are no column names in the DataFrame. Let's add those.
bos.columns = boston.feature_names
bos.head()
# Now we have a pandas DataFrame called `bos` containing all the data we want to use to predict Boston Housing prices. Let's create a variable called `PRICE` which will contain the prices. This information is contained in the `target` data.
print(boston.target.shape)
bos['PRICE'] = boston.target
bos.head()
# ## EDA and Summary Statistics
# ***
#
# Let's explore this data set. First we use `describe()` to get basic summary statistics for each of the columns.
bos.describe()
# ### Scatter plots
# ***
#
# Let's look at some scatter plots for three variables: 'CRIM', 'RM' and 'PTRATIO'.
#
# What kind of relationship do you see? e.g. positive, negative? linear? non-linear?
plt.scatter(bos.CRIM, bos.PRICE)
plt.xlabel("Per capita crime rate by town (CRIM)")
plt.ylabel("Housing Price")
plt.title("Relationship between CRIM and Price")
# **Your turn**: Create scatter plots between *RM* and *PRICE*, and *PTRATIO* and *PRICE*. What do you notice?
#your turn: scatter plot between *RM* and *PRICE*
plt.scatter(bos.RM, bos.PRICE)
plt.xlabel("Number of rooms per dwelling (RM)")
plt.ylabel("Housing Price")
plt.title("Relationship between RM and Price")
#your turn: scatter plot between *PTRATIO* and *PRICE*
plt.scatter(bos.PTRATIO, bos.PRICE)
plt.xlabel("Pupil-teacher ratio (PTRATIO)")
plt.ylabel("Housing Price")
plt.title("Relationship between PTRATIO and Price")
# **Your turn**: What are some other numeric variables of interest? Plot scatter plots with these variables and *PRICE*.
#your turn: create some other scatter plots
plt.scatter(bos.DIS, bos.PRICE)
plt.xlabel("Weighted distance to employment centres (DIS)")
plt.ylabel("Housing Price")
plt.title("Relationship between DIS and Price")
# ### Scatter Plots using Seaborn
# ***
#
# [Seaborn](https://stanford.edu/~mwaskom/software/seaborn/) is a cool Python plotting library built on top of matplotlib. It provides convenient syntax and shortcuts for many common types of plots, along with better-looking defaults.
#
# We can also use [seaborn regplot](https://stanford.edu/~mwaskom/software/seaborn/tutorial/regression.html#functions-to-draw-linear-regression-models) for the scatterplot above. This provides automatic linear regression fits (useful for data exploration later on). Here's one example below.
sns.regplot(y="PRICE", x="RM", data=bos, fit_reg = True)
# ### Histograms
# ***
#
# Histograms are a useful way to visually summarize the statistical properties of numeric variables. They can give you an idea of the mean and the spread of the variables as well as outliers.
plt.hist(bos.CRIM, bins=50)
plt.title("CRIM")
plt.xlabel("Crime rate per capita")
plt.ylabel("Frequency")
plt.show()
# **Your turn**: Plot separate histograms and one for *RM*, one for *PTRATIO*. Any interesting observations?
#your turn
plt.hist(bos.RM, bins=40)
plt.title("RM")
plt.xlabel("Average number of rooms")
plt.ylabel("Frequency")
plt.show()
plt.hist(bos.PTRATIO, bins=20)
plt.title("PTRATIO")
plt.xlabel("Pupil-teacher ratio")
plt.ylabel("Frequency")
plt.show()
# ## Linear regression with Boston housing data example
# ***
#
# Here,
#
# $Y$ = boston housing prices (also called "target" data in python)
#
# and
#
# $X$ = all the other features (or independent variables)
#
# which we will use to fit a linear regression model and predict Boston housing prices. We will use the least squares method as the way to estimate the coefficients.
# We'll use two ways of fitting a linear regression. We recommend the first but the second is also powerful in its features.
# ### Fitting Linear Regression using `statsmodels`
# ***
# [Statsmodels](http://statsmodels.sourceforge.net/) is a great Python library for a lot of basic and inferential statistics. It also provides basic regression functions using an R-like syntax, so it's commonly used by statisticians. While we don't cover statsmodels officially in the Data Science Intensive, it's a good library to have in your toolbox. Here's a quick example of what you could do with it.
# Import regression modules
# ols - stands for Ordinary least squares, we'll use this
import statsmodels.api as sm
from statsmodels.formula.api import ols
# statsmodels works nicely with pandas dataframes
# The thing inside the "quotes" is called a formula, a bit on that below
m = ols('PRICE ~ RM',bos).fit()
print(m.summary())
# #### Interpreting coefficients
#
# There is a ton of information in this output. But we'll concentrate on the coefficient table (middle table). We can interpret the `RM` coefficient (9.1021) by first noticing that the p-value (under `P>|t|`) is so small, basically zero. We can interpret the coefficient as, if we compare two groups of towns, one where the average number of rooms is say $5$ and the other group is the same except that they all have $6$ rooms. For these two groups the average difference in house prices is about $9.1$ (in thousands) so about $\$9,100$ difference. The confidence interval fives us a range of plausible values for this difference, about ($\$8,279, \$9,925$), deffinitely not chump change.
# #### `statsmodels` formulas
# ***
# This formula notation will seem familiar to `R` users, but will take some getting used to for people coming from other languages or are new to statistics.
#
# The formula gives instruction for a general structure for a regression call. For `statsmodels` (`ols` or `logit`) calls you need to have a Pandas dataframe with column names that you will add to your formula. In the below example you need a pandas data frame that includes the columns named (`Outcome`, `X1`,`X2`, ...), bbut you don't need to build a new dataframe for every regression. Use the same dataframe with all these things in it. The structure is very simple:
#
# `Outcome ~ X1`
#
# But of course we want to to be able to handle more complex models, for example multiple regression is doone like this:
#
# `Outcome ~ X1 + X2 + X3`
#
# This is the very basic structure but it should be enough to get you through the homework. Things can get much more complex, for a quick run-down of further uses see the `statsmodels` [help page](http://statsmodels.sourceforge.net/devel/example_formulas.html).
#
# Let's see how our model actually fit our data. We can see below that there is a ceiling effect, we should probably look into that. Also, for large values of $Y$ we get underpredictions, most predictions are below the 45-degree gridlines.
# **Your turn:** Create a scatterpot between the predicted prices, available in `m.fittedvalues` and the original prices. How does the plot look?
# your turn
plt.scatter(m.fittedvalues, bos.PRICE)
plt.xlabel("Predicted Price")
plt.ylabel("Housing Price")
plt.title("Relationship between Predicted and Actual Price")
# ### Fitting Linear Regression using `sklearn`
#
# +
from sklearn.linear_model import LinearRegression
X = bos.drop('PRICE', axis = 1)
# This creates a LinearRegression object
lm = LinearRegression()
lm
# -
# #### What can you do with a LinearRegression object?
# ***
# Check out the scikit-learn [docs here](http://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html). We have listed the main functions here.
# Main functions | Description
# --- | ---
# `lm.fit()` | Fit a linear model
# `lm.predit()` | Predict Y using the linear model with estimated coefficients
# `lm.score()` | Returns the coefficient of determination (R^2). *A measure of how well observed outcomes are replicated by the model, as the proportion of total variation of outcomes explained by the model*
# #### What output can you get?
# +
# Look inside lm object
# lm.fit(X=X, y=bos.PRICE)
# -
# Output | Description
# --- | ---
# `lm.coef_` | Estimated coefficients
# `lm.intercept_` | Estimated intercept
# ### Fit a linear model
# ***
#
# The `lm.fit()` function estimates the coefficients the linear regression using least squares.
# Use all 13 predictors to fit linear regression model
lm.fit(X, bos.PRICE)
# **Your turn:** How would you change the model to not fit an intercept term? Would you recommend not having an intercept?
#
# ### Estimated intercept and coefficients
#
# Let's look at the estimated coefficients from the linear model using `1m.intercept_` and `lm.coef_`.
#
# After we have fit our linear regression model using the least squares method, we want to see what are the estimates of our coefficients $\beta_0$, $\beta_1$, ..., $\beta_{13}$:
#
# $$ \hat{\beta}_0, \hat{\beta}_1, \ldots, \hat{\beta}_{13} $$
#
#
print('Estimated intercept coefficient:', lm.intercept_)
print('Number of coefficients:', len(lm.coef_))
# The coefficients
pd.DataFrame(list(zip(X.columns, lm.coef_)), columns = ['features', 'estimatedCoefficients'])
# ### Predict Prices
#
# We can calculate the predicted prices ($\hat{Y}_i$) using `lm.predict`.
#
# $$ \hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_1 + \ldots \hat{\beta}_{13} X_{13} $$
# first five predicted prices
lm.predict(X)[0:5]
# **Your turn:**
#
# * Histogram: Plot a histogram of all the predicted prices
# * Scatter Plot: Let's plot the true prices compared to the predicted prices to see they disagree (we did this with `statsmodels` before).
# your turn
plt.hist(lm.predict(X))
plt.title("Predicted Prices")
plt.xlabel("Predicted Prices")
plt.ylabel("Frequency")
plt.show()
plt.scatter(lm.predict(X), bos.PRICE)
plt.xlabel("Predicted Price")
plt.ylabel("Housing Price")
plt.title("Relationship between Predicted and Actual Price")
# ### Residual sum of squares
#
# Let's calculate the residual sum of squares
#
# $$ S = \sum_{i=1}^N r_i = \sum_{i=1}^N (y_i - (\beta_0 + \beta_1 x_i))^2 $$
print(np.sum((bos.PRICE - lm.predict(X)) ** 2))
# #### Mean squared error
# ***
# This is simple the mean of the residual sum of squares.
#
# **Your turn:** Calculate the mean squared error and print it.
#your turn
mse = ((bos.PRICE - lm.predict(X)) ** 2).mean()
print(mse)
# ## Relationship between `PTRATIO` and housing price
# ***
#
# Try fitting a linear regression model using only the 'PTRATIO' (pupil-teacher ratio by town)
#
# Calculate the mean squared error.
#
lm = LinearRegression()
lm.fit(X[['PTRATIO']], bos.PRICE)
msePTRATIO = np.mean((bos.PRICE - lm.predict(X[['PTRATIO']])) ** 2)
print(msePTRATIO)
# We can also plot the fitted linear regression line.
# +
plt.scatter(bos.PTRATIO, bos.PRICE)
plt.xlabel("Pupil-to-Teacher Ratio (PTRATIO)")
plt.ylabel("Housing Price")
plt.title("Relationship between PTRATIO and Price")
plt.plot(bos.PTRATIO, lm.predict(X[['PTRATIO']]), color='blue', linewidth=3)
plt.show()
# -
# # Your turn
# ***
#
# Try fitting a linear regression model using three independent variables
#
# 1. 'CRIM' (per capita crime rate by town)
# 2. 'RM' (average number of rooms per dwelling)
# 3. 'PTRATIO' (pupil-teacher ratio by town)
#
# Calculate the mean squared error.
lm = LinearRegression()
lm.fit(X[['CRIM', 'RM', 'PTRATIO']], bos.PRICE)
mse2 = np.mean((bos.PRICE - lm.predict(X[['CRIM', 'RM', 'PTRATIO']])) ** 2)
print(mse2)
#
# ## Other important things to think about when fitting a linear regression model
# ***
# <div class="span5 alert alert-danger">
# <ul>
# <li>**Linearity**. The dependent variable $Y$ is a linear combination of the regression coefficients and the independent variables $X$. </li>
# <li>**Constant standard deviation**. The SD of the dependent variable $Y$ should be constant for different values of X.
# <ul>
# <li>e.g. PTRATIO
# </ul>
# </li>
# <li> **Normal distribution for errors**. The $\epsilon$ term we discussed at the beginning are assumed to be normally distributed.
# $$ \epsilon_i \sim N(0, \sigma^2)$$
# Sometimes the distributions of responses $Y$ may not be normally distributed at any given value of $X$. e.g. skewed positively or negatively. </li>
# <li> **Independent errors**. The observations are assumed to be obtained independently.
# <ul>
# <li>e.g. Observations across time may be correlated
# </ul>
# </li>
# </ul>
#
# </div>
#
# # Part 3: Training and Test Data sets
#
# ### Purpose of splitting data into Training/testing sets
# ***
# <div class="span5 alert alert-info">
#
# <p> Let's stick to the linear regression example: </p>
# <ul>
# <li> We built our model with the requirement that the model fit the data well. </li>
# <li> As a side-effect, the model will fit <b>THIS</b> dataset well. What about new data? </li>
# <ul>
# <li> We wanted the model for predictions, right?</li>
# </ul>
# <li> One simple solution, leave out some data (for <b>testing</b>) and <b>train</b> the model on the rest </li>
# <li> This also leads directly to the idea of cross-validation, next section. </li>
# </ul>
# </div>
#
# ***
#
# One way of doing this is you can create training and testing data sets manually.
X_train = X[:-50]
X_test = X[-50:]
Y_train = bos.PRICE[:-50]
Y_test = bos.PRICE[-50:]
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)
# Another way, is to split the data into random train and test subsets using the function `train_test_split` in `sklearn.cross_validation`. Here's the [documentation](http://scikit-learn.org/stable/modules/generated/sklearn.cross_validation.train_test_split.html).
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(
X, bos.PRICE, test_size=0.33, random_state = 5)
print(X_train.shape)
print(X_test.shape)
print(Y_train.shape)
print(Y_test.shape)
# **Your turn:** Let's build a linear regression model using our new training data sets.
#
# * Fit a linear regression model to the training set
# * Predict the output on the test set
lm = LinearRegression()
lm.fit(X_train, Y_train)# your turn
lm.predict(X_test)
# **Your turn:**
#
# Calculate the mean squared error
#
# * using just the test data
# * using just the training data
#
# Are they pretty similar or very different? What does that mean?
print(np.mean((Y_train - lm.predict(X_train)) ** 2))
print(np.mean((Y_test - lm.predict(X_test)) ** 2))
# #### Residual plots
plt.scatter(lm.predict(X_train), lm.predict(X_train) - Y_train, c='b', s=40, alpha=0.5)
plt.scatter(lm.predict(X_test), lm.predict(X_test) - Y_test, c='g', s=40)
plt.hlines(y = 0, xmin=0, xmax = 50)
plt.title('Residual Plot using training (blue) and test (green) data')
plt.ylabel('Residuals')
# **Your turn:** Do you think this linear regression model generalizes well on the test data?
# ### K-fold Cross-validation as an extension of this idea
# ***
# <div class="span5 alert alert-info">
#
# <p> A simple extension of the Test/train split is called K-fold cross-validation. </p>
#
# <p> Here's the procedure:</p>
# <ul>
# <li> randomly assign your $n$ samples to one of $K$ groups. They'll each have about $n/k$ samples</li>
# <li> For each group $k$: </li>
# <ul>
# <li> Fit the model (e.g. run regression) on all data excluding the $k^{th}$ group</li>
# <li> Use the model to predict the outcomes in group $k$</li>
# <li> Calculate your prediction error for each observation in $k^{th}$ group (e.g. $(Y_i - \hat{Y}_i)^2$ for regression, $\mathbb{1}(Y_i = \hat{Y}_i)$ for logistic regression). </li>
# </ul>
# <li> Calculate the average prediction error across all samples $Err_{CV} = \frac{1}{n}\sum_{i=1}^n (Y_i - \hat{Y}_i)^2$ </li>
# </ul>
# </div>
#
# ***
#
# Luckily you don't have to do this entire process all by hand (``for`` loops, etc.) every single time, ``sci-kit learn`` has a very nice implementation of this, have a look at the [documentation](http://scikit-learn.org/stable/modules/cross_validation.html).
# **Your turn (extra credit):** Implement K-Fold cross-validation using the procedure above and Boston Housing data set using $K=4$. How does the average prediction error compare to the train-test split above?
|
linear_regression/Mini_Project_Linear_Regression.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Before your start:
# - Read the README.md file
# - Comment as much as you can and use the resources (README.md file)
# - Happy learning!
# +
# Libraries
# -
# # Challenge 1 - Index Functions
#
# In this challenge, we will practice the advanced functions introduced in the lesson. However, before we start, we will load and evaluate our dataset.
#
# Load the dataset from Ironhack's database:
# * db: `admissions predict`
# * table: `admissions predict`
# +
# your code here
# -
# Remove trailing spaces at the end of the column names if there are any.
#
# +
# your code here
# -
# Let's evaluate the dataset by looking at the `head` function.
# +
# your code here
# -
# Before beginning to work with this dataset and evaluating graduate admissions data, we will verify that there is no missing data in the dataset. Do this in the cell below.
# +
# your code here
# -
# Interestingly, there is a column that uniquely identifies the applicants. This column is the serial number column. Instead of having our own index, we should make this column our index. Do this in the cell below. Keep the column in the dataframe in addition to making it an index.
# +
# your code here
# -
# Turns out that `GRE Score` and `CGPA` also uniquely identify the data. Show this in the cell below.
# +
# your code here
# -
# Replace the index with an index comprised of two columns - `GRE Score` and `CGPA`. Remove the columns from the dataset as well. Make sure to use `inplace=True`.
# Now change the index back to a sequence starting at zero using the `reset_index` function. Make sure to use `inplace=True`.
# +
# your code here
# -
# # Challenge 2 - Advanced Functions
#
# In this part of the lab, we would like to test complex conditions on the entire dataset at once. Let's start by finding the number of rows where the CGPA is higher than 9 and the student has conducted research.
# +
# your code here
# -
# Now return all the rows where the CGPA is greater than 9 and the SOP score is less than 3.5. Find the mean chance of admit for these applicants.
# +
# your code here
# -
# We would like to create a deciding factor column for each student. We standardize several columns and then pick the most important factor from a lookup table. If the standardized value is above 0.8, the student will be accepted.
#
# We will start by creating a standardized column for `CGPA`, `GRE Score` and `LOR`. We will name these columns `CGPA_std`, `GRE_std`, and `LOR_std` respecively.
#
# Recall that standardizing a column is done by subtracting the mean of the column from all observations in the column and then dividing each observation in the column by the column's standard deviation.
#
# In the cell below, write a standardization function (a function that takes a column as input and returns a standardized column as output). Make sure to use the `numpy` versions of mean and standard deviation.
def standardize(col):
"""
This function takes a column from a dataframe
and returns a standardized column by subtracting the column's mean
and dividing by the column's standard deviation.
"""
# your code here
# Now create the standardized columns `CGPA_std`, `GRE_std`, and `LOR_std` and add them to the `admissions` dataframe.
# +
# your code here
# -
# We will generate the decision choice at random using the code below. Please run the cell.
# Libraries
from random import choices
# +
std_columns = ['CGPA_std', 'GRE_std', 'LOR_std']
decision_choice = choices(std_columns, k=admissions.shape[0])
# -
# Now create the deciding column using the `lookup` function. The lookup column is `decision_choice` found above. Call the column resulting from the lookup function `deciding_column` and add it to the `admissions` dataframe.
# +
# your code here
# -
# Create a column called `decision` in the `admissions` dataframe. Assign 1 to this column if the value of `deciding_column` is greater than 0.8 and 0 otherwise.
# +
# your code here
# -
# How many applicants will be accepted to the program using the decision column? Compute the result below.
# +
# your code here
# -
# # Challenge 3 - Method Chaining
#
# To increase our coding efficiency, let's make a number of changes to our dataframe in one line of code.
#
# In the cell below, remove all non character symbols from the column names, replace all spaces in column names to underscores, and change all upper case characters to lower case. Assign these new column values to `admissions.columns`.
# +
# your code here
# -
# In the cell below, give all student with a university rating of 4 or higher a 10 point boost on their GRE score and split the column into 4 bins using the `cut` function. Assign this new score to the variable `adjusted_gre`.
# +
# your code here
|
module-2/Advanced-Pandas/your-code/.ipynb_checkpoints/main-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import torch
# # Neural Networks
# * El uso de funciones de activacion no lineares como la diferencia clave entre modelos lineales
# * Los diferentes tipos de funciones de activacion
# * El modulo `nn` de PyTorch que contiene los bloques para construir NNs
# * Resolver un problema simple de un _fit_ lineal con una NN
# ## Neuronas artificiales
#
# * Neural networks: entidades matematicas capaces de representar funciones complicadas a traves de una composicion de funciones mas simples.
# * Originalmente inspiradas por la forma en la que funciona nuestro cerebro.
# * El bloque de construccion basico es una neurona:
# * Esencialmente una transformacion linear del input (e.g. multiplicacion del input por un numero, el _weight_, y la suma de una constante, el _bias_.
# * Seguido por la aplicacion de una funcion no lineal (referida como la funcion de activacion)
# * $o = f(w x + b)$
# * x es nuestro input, w el _weight_ y b el _bias_. $f$ es la funcion de activacion.
# * x puede ser un escalar o un vector de valores, w puede ser un escalar o una matriz, mientras que b es un escalar o un vector.
# * La expresion $o = f(w x + b)$ es una capa de neuronas, ya que representa varias neuronas a traves de los _weights_ y _bias_ multidimensionales
# $x_1 = f(w_0 x_0 + b_0)$
#
# $x_2 = f(w_1 x_1 + b_1)$
#
# $...$
#
# $y = f(w_n x_n + b_n)$
# ### **dibujos**
# ## Funciones de activacion
# * Nuestro modelo anterior ya tenia una operacion lineal. Eso era el modelo entero.
# * El rol de la funcion de activacion es concentrar los _outputs_ de la operacion lineal precedente a un rango dado.
# * Si queremos asignar un _score_ al output del modelo necesitamos limitar el rango de numeros posibles para ese _score_
# * `float32`
# * $\sum wx + b$
# ### Que opciones tenemos?
# * Una opcion seria ponerle un limite a los valores del _output_.
# * Cualquier cosa debajo de cero seria cero
# * cualquier cosa arriba de 10 seria 10
# * `torch.nn.Hardtanh`
# +
import math
math.tanh(-2.2) # camion
# -
math.tanh(0.1) # oso
math.tanh(2.5) # perro
# 
# * Hay muchas funciones de activacion.
# * Por definicion, las funciones de activacion:
# * Son no lineales. Aplicaciones repetidas de $wx+b$ sin una funcion de activacion resultan en una polinomial. La no linealidad permite a la red aproximar funciones mas complejas.
# * Son diferenciables, para poder calcular las gradientes a traves de ellas. Discontinuidades de punto como en `Hatdtanh` o `ReLU` son validas.
# * Sin esto, las redes caen a ser polinomiales complicadas o dificiles de entrenar.
# * Adicionalmente, las funciones:
# * Tienen al menos un rango sensible, donde cambios no triviales en el input resultan en cambio no trivial correspondiente en el output
# * Tienen al menos un rango no sensible (o saturado), donde cambios al input resultan en poco o ningun cambio en el output.
# * Por utlimo, las fuciones de activacion tienen al menos una de estas:
# * Un limite inferior que se aproxima (o se encuentra) mientras el input tiende a negativo infinito.
# * Un limite superior similar pero inverso para positivo infinito.
# * Dado lo que sabemos de como funciona back-propagation
# * Sabemos que los errores se van a propagar hacia atras a traves de la activacion de manera mas efectiva cuando los inputs se encuentran dentro del rango de respuesta.
# * Por otro lado, los errores no van a afectar a las neuornas para cuales el _input_ esta saturado debido a que la gradiente estara cercana a cero.
# ### En conclusion
#
# * En una red hecha de unidades lineales + activaciones, cuando recibe diferentes _inputs_:
# * diferentes unidades van a responder en diferentes rangos para los mismos inputs
# * los errores asociados a esos inputs van a afectar a las neuronas operancio en el rango sensible, dejando a las otras unidades mas o menos igual en el proceso de aprendizaje.
# * Juntar muchas operaciones lineales + unidades de activacion en paralelo y apilandolas una sobre otra nos provee un objeto matematico capaz de aproximar funciones complicadas.
# * Diferentes combinaciones de unidades van a responder a inputs en diferentes rangos
# * Esos parametros son relativamente faciles de optimizar a traves de SGD
# ### Dibujo graficas computacionales separadas
# +
import torch.nn as nn
linear_model = nn.Linear(1, 1)
linear_model(val_t_un)
# -
# Todas las subclases de `nn.Module` tienen un metodo `call` definido. Esto permite crear una instancia de `nn.Linear` y llamarla como si fuera una funcion.
#
# Llamar una instancia de `nn.Module` con un conjunto de argumetnos termina llamando un metodo llamado `forward` con esos mismos argumentos
# ### Implementacion de `Module.call`
#
# (simplificado para claridad)
def __call__(self, *input, **kwargs):
for hook in self._forward_pre_hooks.values():
hook(self, input)
result = self.forward(*input, **kwargs)
for hook in self._forward_hooks.values():
hook_result = hook(self, input, result)
# ...
for hook in self._backward_hooks.values():
# ...
return result
# ### De regreso al modelo lineal
# +
import torch.nn as nn
linear_model = nn.Linear(1, 1)
linear_model(val_t_un)
# -
# `nn.Linear` acepta tres argumentos:
# * el numero de input features: size del input = 1
# * numero de output features: size del outpu = 1
# * si incluye un bias o no (por default es `True`)
linear_model.weight
linear_model.bias
x = torch.ones(1)
linear_model(x)
# * Nuestro modelo toma un input y produce un output
# * `nn.Module` y sus subclases estan diseniados para hacer eso sobre multiples muestras al mismo tiempo
# * Para acomodar multiples muestras los modulos esperan que la dimension 0 del input sea el numero de muestras en un _batch_
# * Cualquier module en `nn` esta hecho para producir outputs para un _batch_ de multiples inputs al mismo tiempo.
# * B x Nin
# * B es el tamanio del _batch_
# * Nin el numero de input features
x = torch.ones(10, 1)
linear_model(x)
# Para un dataset de imagenes:
# * BxCxHxW
t_c.size()
# +
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0] # Temperatura en grados celsios
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4] # Unidades desconocidas
t_c = torch.tensor(t_c).unsqueeze(1) # Agregamos una dimension para tener B x N_inputs
t_u = torch.tensor(t_u).unsqueeze(1) # Agregamos una dimension para tener B x N_inputs
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]
val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]
train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u
# +
import torch.nn as nn
import torch.optim as optim
params_old = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate_old = 1e-1
optimizer_old = optim.Adam([params_old], lr=learning_rate_old)
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(
linear_model.parameters(), # reemplazamos [params] con este metodo
lr=1e-2)
# -
# ### linear_model.parameters()
list(linear_model.parameters())
def training_loop(model, n_epochs, optimizer, loss_fn, train_x, val_x, train_y, val_y):
loss_val = []
loss_train = []
for epoch in range(1, n_epochs + 1):
train_t_p = model(train_x) # ya no tenemos que pasar los params
train_loss = loss_fn(train_t_p, train_y)
loss_train.append(train_loss)
with torch.no_grad(): # todos los args requires_grad=False
val_t_p = model(val_x)
val_loss = loss_fn(val_t_p, val_y)
loss_val.append(val_loss)
optimizer.zero_grad()
train_loss.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {train_loss}, Validation loss {val_loss}")
# +
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
training_loop(
n_epochs=3000,
optimizer=optimizer,
model=linear_model,
loss_fn=nn.MSELoss(), # Ya no estamos usando nuestra loss function hecha a mano
train_x = train_t_un,
val_x = val_t_un,
train_y = train_t_c,
val_y = val_t_c)
print()
print(linear_model.weight)
print(linear_model.bias)
# -
# ## Finalmente un Neural Network
# * Ultimo paso: reemplazar nuestro modelo lineal
# * No va a ser mejor
# * Lo unico que vamos a cambiar va a ser el modelo
# * Un simple NN:
# * Una capa lineal
# * Activacion
# * "hidden layers"
# +
seq_model = nn.Sequential(
nn.Linear(1, 13), # El 13 es arbitrario
nn.Tanh(),
nn.Linear(13, 1) # Este 13 debe hacer match con el primero
)
seq_model
# -
# * El resultado final es un modelo que toma los inputs esperados por el primer modulo (_layer_)
# * Pasa los outputs intermedios al resto de los modulos
# * Produce un output retornado por el ultimo modulo
[param.size() for param in seq_model.parameters()]
# * Estos son los parametros que el optimizador va a recibir
# * Al llamar `backward()` todos los parametros se van a llenar con su `grad`
# * El optimizador va a actualizar el valor de `grad` durante `optimizer.step()`
for name, param in seq_model.named_parameters():
print(name, param.size())
# +
from collections import OrderedDict
named_seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 8)),
('hidden_activation', nn.Tanh()),
('output_linear', nn.Linear(8, 1))
]))
seq_model
# -
for name, param in named_seq_model.named_parameters():
print(name, param.size())
named_seq_model.output_linear.bias
# Util para inspeccionar parametros o sus gradientes.
# +
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3)
training_loop(
n_epochs=5000,
optimizer=optimizer,
model=seq_model,
loss_fn=nn.MSELoss(), # Ya no estamos usando nuestra loss function hecha a mano
train_x = train_t_un,
val_x = val_t_un,
train_y = train_t_c,
val_y = val_t_c)
print('output', seq_model(val_t_un))
print('answer', val_t_c)
print('hidden', seq_model.hidden_linear.weight.grad)
start = torch.cuda.Event(enable_timing=True)
end = torch.cuda.Event(enable_timing=True)
start.record()
z = x + y
end.record()
# Waits for everything to finish running
torch.cuda.synchronize()
print(start.elapsed_time(end))
# -
# Tambien podemos evaluar el modelo en toda la data y ver que tan diferente es de una linea:
# +
from matplotlib import pyplot as plt
t_range = torch.arange(20., 90.).unsqueeze(1)
fig = plt.figure(dpi=600)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
plt.show()
# -
# ## Subclassing nn.Module
#
# * sublcassing `nn.Module` nos da mucha mas flexibilidad.
# * La interface especifica que como minimo debemos definir un metodo `forward` para la subclase
# * `forward` toma el input al model y regresa el output
# * Si usamos las operaciones de `torch`, `autograd` se encarga de hacer el `backward` pass de forma automatica
#
# * Normalmente vamos a definir los submodulos que usamos en el metodo `forward` en el constructor
# * Esto permite que sean llamados en `forward` y que puedan mantener sus parametros a durante la existencia de nuestro modulo
# +
class SubclassModel(nn.Module):
def __init__(self):
super().__init__()
self.hidden_linear = nn.Linear(1, 13)
self.hidden_activation = nn.Tanh()
self.output_linear = nn.Linear(13, 1)
def forward(self, input):
hidden_t = self.hidden_linear(input)
activated_t = self.hidden_activation(hidden_t)
#activated_t = self.hidden_activation(hidden_t) if random.random() > 0.5 else hidden_t
output_t = self.output_linear(activated_t)
return output_t
subclass_model = SubclassModel()
subclass_model
# -
# * Nos permite manipular los outputs de forma directa y transformarlo en un tensor BxN
# * Dejamos la dimension de batch como -1 ya que no sabemos cuantos inputs van a venir por batch
# * Asignar una instancia de `nn.Module` a un atributo en un `nn.Module` registra el modulo como un submodulo.
# * Permite a `Net` acceso a los `parameters` de sus submodulos sin necesidad de hacerlo manualmente
numel_list = [p.numel() for p in subclass_model.parameters()]
sum(numel_list), numel_list
# **Lo que paso**
#
# * `parameters()` investiga todos los submodulos asignados como atributos del constructor y llama `parameters` de forma recursiva.
# * Al accesar su atributo `grad`, el cual va a ser llenado por el `autograd`, el optimizador va a saber como cambiar los parametros para minimizar el _loss_
for type_str, model in [('seq', seq_model), ('named_seq', named_seq_model), ('subclass', subclass_model)]:
print(type_str)
for name_str, param in model.named_parameters():
print("{:21} {:19} {}".format(name_str, str(param.shape), param.numel()))
print()
# +
class SubclassFunctionalModel(nn.Module):
def __init__(self):
super().__init__()
self.hidden_linear = nn.Linear(1, 14)
self.output_linear = nn.Linear(14, 1)
def forward(self, input):
hidden_t = self.hidden_linear(input)
activated_t = torch.tanh(hidden_t)
output_t = self.output_linear(activated_t)
return output_t
func_model = SubclassFunctionalModel()
func_model
# -
# ## Ejercicios
# * Experimenten con el numero de neuronas en el modelo al igual que el learning rate.
# * Que cambios resultan en un output mas lineal del modelo?
# * Pueden hacer que el modelo haga un overfit obvio de la data?
#
# * Cargen la [data de vinos blancos](https://archive.ics.uci.edu/ml/datasets/wine+quality) y creen un modelo con el numero apropiado de inputs
# * Cuanto tarda en entrenar comparado al dataset que hemos estado usando?
# * Pueden explicar que factores contribuyen a los tiempos de entrenamiento?
# * Pueden hacer que el _loss_ disminuya?
# * Intenten graficar la data
# +
import time
start = time.time()
seq_model = nn.Sequential(
nn.Linear(1, 3000),
nn.Tanh(),
nn.Linear(3000, 1) #
)
optimizer = optim.SGD(seq_model.parameters(), lr=1e-4)
training_loop(
n_epochs=9000,
optimizer=optimizer,
model=seq_model,
loss_fn=nn.MSELoss(), # Se utiliza la función pytorch, no la generada manualmente
train_x = train_t_un,
val_x = val_t_un,
train_y = train_t_c,
val_y = val_t_c)
end = time.time()
print(end - start)
# -
# # Experimentando con el numero de neuronas en el modelo al igual que el learning rate.
# ### Que cambios resultan en un output mas lineal del modelo?
#
# A un mayor número de repeticiones y neuronas la función de perdida reduce su tamaño, para lo cual se le atribuye mayor exactitud a un aumento del número de neuronas. Un numero de learning rate muy pequeño puede no implicar mejoras significativas, sin embargo el mejor resultado en la función loss se observa en el nivel 1e-4 debido a que cualquier denotación mayor no implicaba un aporte al modelo.
#
#
#
# ### Pueden hacer que el modelo haga un overfit obvio de la data?
#
# Un overfit obvio se puede generar al crear demasiadas neuronas y al fijar el learning rate en el monto más alto permitido
#
# +
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# -
whine_df = pd.read_csv("winequality-white.csv", sep=";")
whine_df.head()
# +
corr = whine_df.corr()
corr
# -
X = whine_df['alcohol']
y = whine_df['quality']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=42)
# +
X_train = np.array(X_train)
X_test = np.array(X_test)
y_train = np.array(y_train)
y_test = np.array(y_test)
X_train = torch.tensor(X_train).unsqueeze(1)
X_test = torch.tensor(X_test).unsqueeze(1)
y_train = torch.tensor(y_train).unsqueeze(1)
y_test = torch.tensor(y_test).unsqueeze(1)
# +
import time
start = time.time()
seq_model = nn.Sequential(
nn.Linear(1, 1000),
nn.Tanh(),
nn.Linear(1000, 1)
)
optimizer = optim.SGD(seq_model.parameters(), lr=1e-4)
n_epochs=5000
training_loop(
n_epochs=n_epochs,
optimizer=optimizer,
model=seq_model,
loss_fn=nn.MSELoss(),
train_x = X_train.float(),
val_x = X_test.float(),
train_y = y_train.float(),
val_y = y_test.float())
end = time.time()
print(end - start)
# -
# ## Cuanto tarda en entrenar comparado al dataset que hemos estado usando?
#
# #### Este dataset considerablemente toma más tiempo en entrenarse, se utilizo la función time.time para evaluar el tiempo elapsado y principalmente puedo atribuirlo al número de datos implicados en este set y la exactitud requerida. El primero modelo se entreno en 11 segundos mientras que el segundo demostro 422 segundos
#
#
# ## Pueden explicar que factores contribuyen a los tiempos de entrenamiento?
#
# #### Los factores que explican el tiempo de entrenamiento son el numero de neuronas implicado en la red neuronal predominantemente, el tamaño del learning rate planteado y el número de repeticiones o epochs. Todas estas variables implican un aumento en la exactitud.
#
# ## Pueden hacer que el loss disminuya?
#
# #### Al involucrar en el modelo las variables más correlacionadas como el alcohol para predecir la calidad del vino se reduce la función de perdida, al igual que al aumentar el learning rate al máximo disponible.
#
# ## Intenten graficar la data
#
# !jupyter nbconvert --to script Juarez_Boris_Tarea4_neural_networks.ipynb
pip install visdom
# +
t_p = model(t_u, *params)
fig = plt.figure(dpi=1000)
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_u.numpy(), t_p.detach().numpy())
# -
|
lectures/Juarez_Boris_Tarea4_neural_networks.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import os
titanic_api
_s
cript_file = os.path.join(os.path.pardir, 'src', 'models', 'titanic_api.py')
# +
# %%writefile $titanic_api_script_file
from flask import Flask, request
import pandas as pd
import numpy as np
import json
import pickle
import os
app = Flask(__name__)
model_path = os.path.join(os.path.pardir, os.path.pardir, 'models')
model_file_path = os.path.join(model_path, 'lf_model.pkl')
scaler_file_path = os.path.join(model_path, 'lf_scaler.pkl')
with open(model_file_path, 'rb') as model_file:
model = pickle.load(model_file)
with open(scaler_file_path, 'rb') as scaler_file:
scaler = pickle.load(scaler_file)
columns = [
u'Age', u'Fare', u'FamilySize', u'IsMother', u'IsMale', u'Deck_A', u'Deck_B'\
u'Deck_C', u'Deck_D', u'Deck_E', u'Deck_F', u'Deck_G', u'Deck_Z', u'Pclass_1',\
u'Pclass_2', u'Pclass_3', u'Title_Lady', u'Title_Master', u'Title_Miss', u'Title_Mr',\
u'Title_Mrs', u'Title_Officer', u'Title_Sir', u'Fare_Bin_very_low', u'Fare_Bin_low',\
u'Fare_Bin_very_high', u'Fare_Bin_high', u'Embarked_C', u'Embarked_Q', u'Embarked_S',\
u'AgeState_Adult', u'Agestate_Child'
]
@app.route('/api', methods=['POST'])
def make_prediction():
data = json.dumps(request.get_json(force=True))
df = pd.read_json(data)
passenger_ids = df['PassengerId'].ravel()
actuals = df['Survived'].ravel()
X = df.columns.to_numpy(dtype='float')
X_scaled = scaler.transform(X)
predictions = model.predict(X_scaled)
res = pd.DataFrame({'PassengerId': passenger_ids, 'Predicted': predictions, 'Actual': actuals})
return res.to_json()
if __name__ == "__main__":
app.run(port=10001, debug=True)
# -
|
notebooks/titanic_api.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
ir = pd.read_csv("../data/raw/iris.data")
ir.head()
ir.describe()
ir.info()
ir.columns
ir.count()
ir["Iris-setosa"]
ir.rename(columns={'Iris-setosa':'Iris type'}, inplace=True)
ir.head()
ir.info()
# We changed the name of the last column to "Iris type", since there were 2 type of values.
|
notebooks/Iris.ipynb
|