code
stringlengths 38
801k
| repo_path
stringlengths 6
263
|
|---|---|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Django Shell-Plus
# language: python
# name: django_extensions
# ---
import csv, re
#count current objects in Book
len(Book.objects.all())
file = "data/zotero/CBAB.csv"
with open(file, 'r', encoding ='utf-8') as data:
reader = csv.reader(data)
datalist = list(reader)
failed = []
saved = []
for row in datalist[1:]:
if row[2] != "":
NewBook = Book(zoterokey = row[0],
item_type = row[1],
author = row[3],
title = row[4],
publication_title = row[5],
short_title = row[21],
place = row[27],
publication_year = row[2])
try:
NewBook.save()
saved.append(row)
except:
failed.append(row)
else:
NewBook = Book(zoterokey = row[0],
item_type = row[1],
author = row[3],
title = row[4],
publication_title = row[5],
short_title = row[21],
place = row[27])
try:
NewBook.save()
saved.append(row)
except:
failed.append(row)
print('saved: {} objects \nfailed: {} objects'.format(len(saved), len(failed)))
# +
# delete all Book-objects:
#Book.objects.all().delete()
# -
|
zoteroExport_to_MySQL.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# Virtually everyone has had an online experience where a website makes personalized recommendations in hopes of future sales or ongoing traffic. Amazon tells you “Customers Who Bought This Item Also Bought”, Udemy tells you “Students Who Viewed This Course Also Viewed”. And Netflix awarded a $1 million prize to a developer team in 2009, for an algorithm that increased the accuracy of the company’s recommendation system by 10 percent.
#
# Without further ado, if you want to learn how to build a recommender system from scratch, let’s get started.
# ## The Data
# Book-Crossings(http://www2.informatik.uni-freiburg.de/~cziegler/BX/) is a book rating dataset compiled by <NAME>. It contains 1.1 million ratings of 270,000 books by 90,000 users. The ratings are on a scale from 1 to 10.
#
# The data consists of three tables: ratings, books info, and users info. I downloaded these three tables from here (http://www2.informatik.uni-freiburg.de/~cziegler/BX/).
#Importing all the required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#reading the data files
books = pd.read_csv('BX-CSV-Dump/BX-Books.csv', sep=';', error_bad_lines=False, encoding="latin-1")
books.columns = ['ISBN', 'bookTitle', 'bookAuthor', 'yearOfPublication', 'publisher', 'imageUrlS', 'imageUrlM', 'imageUrlL']
users = pd.read_csv('BX-CSV-Dump/BX-Users.csv', sep=';', error_bad_lines=False, encoding="latin-1")
users.columns = ['userID', 'Location', 'Age']
ratings = pd.read_csv('BX-CSV-Dump/BX-Book-Ratings.csv', sep=';', error_bad_lines=False, encoding="latin-1")
ratings.columns = ['userID', 'ISBN', 'bookRating']
# ### Ratings data
#
# The ratings data set provides a list of ratings that users have given to books. It includes 1,149,780 records and 3 fields: userID, ISBN, and bookRating.
print(ratings.shape)
print(list(ratings.columns))
ratings.head(10)
# ### Ratings distribution
#
# The ratings are very unevenly distributed, and the vast majority of ratings are 0.
plt.rc("font", size=15)
ratings.bookRating.value_counts(sort=False).plot(kind='bar')
plt.title('Rating Distribution\n')
plt.xlabel('Rating')
plt.ylabel('Count')
plt.savefig('system1.png', bbox_inches='tight')
plt.show()
# ### Books data
#
# The books dataset provides book details. It includes 271,360 records and 8 fields: ISBN, book title, book author, publisher and so on.
print(books.shape)
print(list(books.columns))
books.head(10)
# ### Users data
#
# This dataset provides the user demographic information. It includes 278,858 records and 3 fields: user id, location, and age.
print(users.shape)
print(list(users.columns))
users.head(10)
# ### Age distribution
#
# Maximum active users are among those in their 20–30s.
users.Age.hist(bins=[0, 10, 20, 30, 40, 50, 100])
plt.title('Age Distribution\n')
plt.xlabel('Age')
plt.ylabel('Count')
plt.savefig('system2.png', bbox_inches='tight')
plt.show()
# ## Recommendations based on rating counts
rating_count = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].count())
rating_count.sort_values('bookRating', ascending=False).head()
# The book with ISBN “0971880107” received the most rating counts.
# Let’s find out what book it is, and what books are in the top 5
most_rated_books = pd.DataFrame(['0971880107', '0316666343', '0385504209', '0060928336', '0312195516'], index=np.arange(5), columns = ['ISBN'])
most_rated_books_summary = pd.merge(most_rated_books, books, on='ISBN')
most_rated_books_summary
# The book that received the most rating counts in this data set is <NAME>’s “Wild Animus”. And there is something in common among these five books that received the most rating counts — they are all novels. The recommender suggests that novels are popular and likely receive more ratings. And if someone likes “The Lovely Bones: A Novel”, we should probably also recommend to him(or her) “Wild Animus”.
# ## Recommendations based on correlations
# We use Pearsons’R correlation coefficient to measure the linear correlation between two variables, in our case, the ratings for two books.
#
# First, we need to find out the average rating, and the number of ratings each book received.
average_rating = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].mean())
average_rating['ratingCount'] = pd.DataFrame(ratings.groupby('ISBN')['bookRating'].count())
average_rating.sort_values('ratingCount', ascending=False).head()
# Observations: In this data set, the book that received the most rating counts was not highly rated at all. As a result, if we were to use recommendations based on rating counts, we would definitely make mistakes here. So, we need to have a better system.
# #### To ensure statistical significance, users with less than 200 ratings, and books with less than 100 ratings are excluded
counts1 = ratings['userID'].value_counts()
ratings = ratings[ratings['userID'].isin(counts1[counts1 >= 200].index)]
counts = ratings['bookRating'].value_counts()
ratings = ratings[ratings['bookRating'].isin(counts[counts >= 100].index)]
# ### Rating matrix
# We convert the ratings table to a 2D matrix. The matrix will be sparse because not every user rated every book.
ratings_pivot = ratings.pivot(index='userID', columns='ISBN').bookRating
userID = ratings_pivot.index
ISBN = ratings_pivot.columns
print(ratings_pivot.shape)
ratings_pivot.head()
# Let’s find out which books are correlated with the 2nd most rated book “The Lovely Bones: A Novel”.
bones_ratings = ratings_pivot['0316666343']
similar_to_bones = ratings_pivot.corrwith(bones_ratings)
corr_bones = pd.DataFrame(similar_to_bones, columns=['pearsonR'])
corr_bones.dropna(inplace=True)
corr_summary = corr_bones.join(average_rating['ratingCount'])
corr_summary[corr_summary['ratingCount']>=300].sort_values('pearsonR', ascending=False).head(10)
# We obtained the books’ ISBNs, but we need to find out the titles of the books to see whether they make sense.
books_corr_to_bones = pd.DataFrame(['0312291639', '0316601950', '0446610038', '0446672211', '0385265700', '0345342968', '0060930535', '0375707972', '0684872153'],
index=np.arange(9), columns=['ISBN'])
corr_books = pd.merge(books_corr_to_bones, books, on='ISBN')
corr_books
# Let’s select three books from the above highly correlated list to examine: <b>“The Nanny Diaries: A Novel”, “The Pilot’s Wife: A Novel” and “Where the Heart is”</b>.
#
# <b>“The Nanny Diaries”</b> satirizes upper-class Manhattan society as seen through the eyes of their children’s caregivers.
#
# Written by the same author as <b>“The Lovely Bones”, “The Pilot’s Wife”</b> is the third novel in Shreve’s informal trilogy to be set in a large beach house on the New Hampshire coast that used to be a convent.
#
# <b>“Where the Heart Is”</b> dramatizes in detail the tribulations of lower-income and foster children in the United States.
#
# These three books sound like they would be highly correlated with <b>“The Lovely Bones”</b>. It seems our correlation recommender system is working.
# ## Collaborative Filtering Using k-Nearest Neighbors (kNN)
# kNN is a machine learning algorithm to find clusters of similar users based on common book ratings, and make predictions using the average rating of top-k nearest neighbors. For example, we first present ratings in a matrix with the matrix having one row for each item (book) and one column for each user, like so:
# 
# We then find the k item that has the most similar user engagement vectors. In this case, Nearest Neighbors of item id 5= [7, 4, 8, …]. Now, let’s implement kNN into our book recommender system.
#
# Starting from the original data set, we will be only looking at the popular books. In order to find out which books are popular, we combine books data with ratings data.
combine_book_rating = pd.merge(ratings, books, on='ISBN')
columns = ['yearOfPublication', 'publisher', 'bookAuthor', 'imageUrlS', 'imageUrlM', 'imageUrlL']
combine_book_rating = combine_book_rating.drop(columns, axis=1)
combine_book_rating.head()
# We then group by book titles and create a new column for total rating count.
# +
combine_book_rating = combine_book_rating.dropna(axis = 0, subset = ['bookTitle'])
book_ratingCount = (combine_book_rating.
groupby(by = ['bookTitle'])['bookRating'].
count().
reset_index().
rename(columns = {'bookRating': 'totalRatingCount'})
[['bookTitle', 'totalRatingCount']]
)
book_ratingCount.head()
# -
# We combine the rating data with the total rating count data, this gives us exactly what we need to find out which books are popular and filter out lesser-known books.
rating_with_totalRatingCount = combine_book_rating.merge(book_ratingCount, left_on = 'bookTitle', right_on = 'bookTitle', how = 'left')
rating_with_totalRatingCount.head()
# Let’s look at the statistics of total rating count:
pd.set_option('display.float_format', lambda x: '%.3f' % x)
print(book_ratingCount['totalRatingCount'].describe())
# The median book has been rated only once. Let’s look at the top of the distribution:
print(book_ratingCount['totalRatingCount'].quantile(np.arange(.9, 1, .01)))
# About 1% of the books received 50 or more ratings. Because we have so many books in our data, we will limit it to the top 1%, and this will give us 2713 unique books.
popularity_threshold = 50
rating_popular_book = rating_with_totalRatingCount.query('totalRatingCount >= @popularity_threshold')
rating_popular_book.head()
# #### Filter to users in US and Canada only
#
# In order to improve computing speed, and not run into the “MemoryError” issue, I will limit our user data to those in the US and Canada. And then combine user data with the rating data and total rating count data.
# +
combined = rating_popular_book.merge(users, left_on = 'userID', right_on = 'userID', how = 'left')
us_canada_user_rating = combined[combined['Location'].str.contains("usa|canada")]
us_canada_user_rating=us_canada_user_rating.drop('Age', axis=1)
us_canada_user_rating.head()
# -
# #### Implementing kNN
#
# We convert our table to a 2D matrix, and fill the missing values with zeros (since we will calculate distances between rating vectors). We then transform the values(ratings) of the matrix dataframe into a scipy sparse matrix for more efficient calculations.
# #### Finding the Nearest Neighbors
# We use unsupervised algorithms with sklearn.neighbors. The algorithm we use to compute the nearest neighbors is “brute”, and we specify “metric=cosine” so that the algorithm will calculate the cosine similarity between rating vectors. Finally, we fit the model.
# +
us_canada_user_rating = us_canada_user_rating.drop_duplicates(['userID', 'bookTitle'])
us_canada_user_rating_pivot = us_canada_user_rating.pivot(index = 'bookTitle', columns = 'userID', values = 'bookRating').fillna(0)
from scipy.sparse import csr_matrix
us_canada_user_rating_matrix = csr_matrix(us_canada_user_rating_pivot.values)
from sklearn.neighbors import NearestNeighbors
model_knn = NearestNeighbors(metric = 'cosine', algorithm = 'brute')
model_knn.fit(us_canada_user_rating_matrix)
# -
# #### Test our model and make some recommendations:
# In this step, the kNN algorithm measures distance to determine the “closeness” of instances. It then classifies an instance by finding its nearest neighbors, and picks the most popular class among the neighbors.
# +
query_index = np.random.choice(us_canada_user_rating_pivot.shape[0])
distances, indices = model_knn.kneighbors(us_canada_user_rating_pivot.iloc[query_index, :].values.reshape(1, -1), n_neighbors = 6)
for i in range(0, len(distances.flatten())):
if i == 0:
print('Recommendations for {0}:\n'.format(us_canada_user_rating_pivot.index[query_index]))
else:
print('{0}: {1}, with distance of {2}:'.format(i, us_canada_user_rating_pivot.index[indices.flatten()[i]], distances.flatten()[i]))
# -
# Perfect! <NAME> Novels definitely should be recommended, one after another.
# ### Collaborative Filtering Using Matrix Factorization
# 
# Matrix Factorization is simply a mathematical tool for playing around with matrices. The Matrix Factorization techniques are usually more effective, because they allow users to discover the latent (hidden)features underlying the interactions between users and items (books).
#
# We use singular value decomposition (SVD) — one of the Matrix Factorization models for identifying latent factors.
#
# Similar with kNN, we convert our USA Canada user rating table into a 2D matrix (called a utility matrix here) and fill the missing values with zeros.
us_canada_user_rating_pivot2 = us_canada_user_rating.pivot(index = 'userID', columns = 'bookTitle', values = 'bookRating').fillna(0)
us_canada_user_rating_pivot2.head()
# We then transpose this utility matrix, so that the bookTitles become rows and userIDs become columns. After using TruncatedSVD to decompose it, we fit it into the model for dimensionality reduction. This compression happened on the dataframe’s columns since we must preserve the book titles. We choose n_components = 12 for just 12 latent variables, and you can see, our data’s dimensions have been reduced significantly from 40017 X 2442 to 746 X 12.
us_canada_user_rating_pivot2.shape
X = us_canada_user_rating_pivot2.values.T
X.shape
# +
import sklearn
from sklearn.decomposition import TruncatedSVD
SVD = TruncatedSVD(n_components=12, random_state=17)
matrix = SVD.fit_transform(X)
matrix.shape
# -
# We calculate the Pearson’s R correlation coefficient for every book pair in our final matrix. To compare this with the results from kNN, we pick the same book “Two for the DoughThe Green Mile: Coffey’s Hands (Green Mile Series)” to find the books that have high correlation coefficients (between 0.9 and 1.0) with it.
import warnings
warnings.filterwarnings("ignore",category =RuntimeWarning)
corr = np.corrcoef(matrix)
corr.shape
us_canada_book_title = us_canada_user_rating_pivot2.columns
us_canada_book_list = list(us_canada_book_title)
coffey_hands = us_canada_book_list.index("Two for the Dough")
print(coffey_hands)
corr_coffey_hands = corr[coffey_hands]
#corr_coffey_hands
list(us_canada_book_title[(corr_coffey_hands>0.9)])
|
Book Recommender System.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Estimation of the CTA point source sensitivity
# ## Introduction
#
# This notebook explains how to estimate the CTA sensitivity for a point-like IRF at a fixed zenith angle and fixed offset using the full containement IRFs distributed for the CTA 1DC. The significativity is computed for a 1D analysis (On-OFF regions) and the LiMa formula.
#
# We use here an approximate approach with an energy dependent integration radius to take into account the variation of the PSF. We will first determine the 1D IRFs including a containment correction.
#
# We will be using the following Gammapy class:
#
# * [gammapy.spectrum.SensitivityEstimator](https://docs.gammapy.org/dev/api/gammapy.spectrum.SensitivityEstimator.html)
# ## Setup
# As usual, we'll start with some setup ...
# %matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import astropy.units as u
from astropy.coordinates import Angle
from gammapy.irf import load_cta_irfs
from gammapy.spectrum import SensitivityEstimator, CountsSpectrum
# ## Define analysis region and energy binning
#
# Here we assume a source at 0.7 degree from pointing position. We perform a simple energy independent extraction for now with a radius of 0.1 degree.
# +
offset = Angle("0.5 deg")
energy_reco = np.logspace(-1.8, 1.5, 20) * u.TeV
energy_true = np.logspace(-2, 2, 100) * u.TeV
# -
# ## Load IRFs
#
# We extract the 1D IRFs from the full 3D IRFs provided by CTA.
filename = (
"$GAMMAPY_DATA/cta-1dc/caldb/data/cta/1dc/bcf/South_z20_50h/irf_file.fits"
)
irfs = load_cta_irfs(filename)
arf = irfs["aeff"].to_effective_area_table(offset, energy=energy_true)
rmf = irfs["edisp"].to_energy_dispersion(
offset, e_true=energy_true, e_reco=energy_reco
)
psf = irfs["psf"].to_energy_dependent_table_psf(theta=offset)
# ## Determine energy dependent integration radius
#
# Here we will determine an integration radius that varies with the energy to ensure a constant fraction of flux enclosure (e.g. 68%). We then apply the fraction to the effective area table.
#
# By doing so we implicitly assume that energy dispersion has a neglible effect. This should be valid for large enough energy reco bins as long as the bias in the energy estimation is close to zero.
containment = 0.68
energy = np.sqrt(energy_reco[1:] * energy_reco[:-1])
on_radii = psf.containment_radius(energy=energy, fraction=containment)
solid_angles = 2 * np.pi * (1 - np.cos(on_radii)) * u.sr
arf.data.data *= containment
# ## Estimate background
#
# We now provide a workaround to estimate the background from the tabulated IRF in the energy bins we consider.
bkg_data = irfs["bkg"].evaluate_integrate(
fov_lon=0 * u.deg, fov_lat=offset, energy_reco=energy_reco
)
bkg = CountsSpectrum(
energy_reco[:-1], energy_reco[1:], data=(bkg_data * solid_angles)
)
# ## Compute sensitivity
#
# We impose a minimal number of expected signal counts of 5 per bin and a minimal significance of 3 per bin. We assume an alpha of 0.2 (ratio between ON and OFF area).
# We then run the sensitivity estimator.
sensitivity_estimator = SensitivityEstimator(
arf=arf, rmf=rmf, bkg=bkg, livetime="5h", gamma_min=5, sigma=3, alpha=0.2
)
sensitivity_table = sensitivity_estimator.run()
# ## Results
#
# The results are given as an Astropy table. A column criterion allows to distinguish bins where the significance is limited by the signal statistical significance from bins where the sensitivity is limited by the number of signal counts.
# This is visible in the plot below.
# Show the results table
sensitivity_table
# +
# Save it to file (could use e.g. format of CSV or ECSV or FITS)
# sensitivity_table.write('sensitivity.ecsv', format='ascii.ecsv')
# +
# Plot the sensitivity curve
t = sensitivity_estimator.results_table
is_s = t["criterion"] == "significance"
plt.plot(
t["energy"][is_s],
t["e2dnde"][is_s],
"s-",
color="red",
label="significance",
)
is_g = t["criterion"] == "gamma"
plt.plot(
t["energy"][is_g], t["e2dnde"][is_g], "*-", color="blue", label="gamma"
)
plt.loglog()
plt.xlabel("Energy ({})".format(t["energy"].unit))
plt.ylabel("Sensitivity ({})".format(t["e2dnde"].unit))
plt.legend();
# -
# We add some control plots showing the expected number of background counts per bin and the ON region size cut (here the 68% containment radius of the PSF).
# +
# Plot expected number of counts for signal and background
fig, ax1 = plt.subplots()
# ax1.plot( t["energy"], t["excess"],"o-", color="red", label="signal")
ax1.plot(
t["energy"], t["background"], "o-", color="black", label="blackground"
)
ax1.loglog()
ax1.set_xlabel("Energy ({})".format(t["energy"].unit))
ax1.set_ylabel("Expected number of bkg counts")
ax2 = ax1.twinx()
ax2.set_ylabel("ON region radius ({})".format(on_radii.unit), color="red")
ax2.semilogy(t["energy"], on_radii, color="red", label="PSF68")
ax2.tick_params(axis="y", labelcolor="red")
ax2.set_ylim(0.01, 0.5)
# -
# ## Exercises
#
# * Also compute the sensitivity for a 20 hour observation
# * Compare how the sensitivity differs between 5 and 20 hours by plotting the ratio as a function of energy.
|
tutorials/cta_sensitivity.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python (herschelhelp_internal)
# language: python
# name: helpint
# ---
# # ELAIS-N2 - Merging HELP data products
#
# This notebook merges the various HELP data products on ELAIS-N2.
#
# It is first used to create a catalogue that will be used for SED fitting by CIGALE by merging the optical master list, the photo-z and the XID+ far infrared fluxes. Then, this notebook is used to incorporate the CIGALE physical parameter estimations and generate the final HELP data product on the field.
from herschelhelp_internal import git_version
print("This notebook was run with herschelhelp_internal version: \n{}".format(git_version()))
import datetime
print("This notebook was executed on: \n{}".format(datetime.datetime.now()))
# +
import numpy as np
from astropy.table import Column, MaskedColumn, Table, join, vstack
from herschelhelp.filters import get_filter_meta_table
from herschelhelp_internal.utils import add_column_meta
filter_mean_lambda = {
item['filter_id']: item['mean_wavelength'] for item in
get_filter_meta_table()
}
# +
# Set this to true to produce only the catalogue for CIGALE and to false
# to continue and merge the CIGALE results too.
FIRST_RUN_FOR_CIGALE = True
SUFFIX = '20180218'
# -
# # Reading the masterlist, XID+, and photo-z catalogues
# +
# Master list
ml = Table.read(
"../../dmu1/dmu1_ml_ELAIS-N2/data/master_catalogue_elais-n2_{}.fits".format(SUFFIX))
ml.meta = None
# +
# # XID+ MIPS24
# xid_mips24 = Table.read("../../dmu26/dmu26_XID+MIPS_CDFS-SWIRE/data/"
# "dmu26_XID+MIPS_CDFS-SWIRE_cat_20170901.fits")
# xid_mips24.meta = None
# # Adding the error column
# xid_mips24.add_column(Column(
# data=np.max([xid_mips24['FErr_MIPS_24_u'] - xid_mips24['F_MIPS_24'],
# xid_mips24['F_MIPS_24'] - xid_mips24['FErr_MIPS_24_l']],
# axis=0),
# name="ferr_mips_24"
# ))
# xid_mips24['F_MIPS_24'].name = "f_mips_24"
# xid_mips24 = xid_mips24['help_id', 'f_mips_24', 'ferr_mips_24', 'flag_mips_24']
# +
# # XID+ PACS
# xid_pacs = Table.read("../../dmu26/dmu26_XID+PACS_CDFS-SWIRE/data/"
# "dmu26_XID+PACS_CDFS-SWIRE_cat_20171019.fits")
# xid_pacs.meta = None
# # Convert from mJy to μJy
# for col in ["F_PACS_100", "FErr_PACS_100_u", "FErr_PACS_100_l",
# "F_PACS_160", "FErr_PACS_160_u", "FErr_PACS_160_l"]:
# xid_pacs[col] *= 1000
# xid_pacs.add_column(Column(
# data=np.max([xid_pacs['FErr_PACS_100_u'] - xid_pacs['F_PACS_100'],
# xid_pacs['F_PACS_100'] - xid_pacs['FErr_PACS_100_l']],
# axis=0),
# name="ferr_pacs_green"
# ))
# xid_pacs['F_PACS_100'].name = "f_pacs_green"
# xid_pacs['flag_PACS_100'].name = "flag_pacs_green"
# xid_pacs.add_column(Column(
# data=np.max([xid_pacs['FErr_PACS_160_u'] - xid_pacs['F_PACS_160'],
# xid_pacs['F_PACS_160'] - xid_pacs['FErr_PACS_160_l']],
# axis=0),
# name="ferr_pacs_red"
# ))
# xid_pacs['F_PACS_160'].name = "f_pacs_red"
# xid_pacs['flag_PACS_160'].name = "flag_pacs_red"
# xid_pacs = xid_pacs['help_id', 'f_pacs_green', 'ferr_pacs_green',
# 'flag_pacs_green', 'f_pacs_red', 'ferr_pacs_red',
# 'flag_pacs_red']
# +
# # XID+ SPIRE
# xid_spire = Table.read("../../dmu26/dmu26_XID+SPIRE_CDFS-SWIRE/data/"
# "dmu26_XID+SPIRE_CDFS-SWIRE_cat_20170919.fits")
# xid_spire.meta = None
# xid_spire['HELP_ID'].name = "help_id"
# # Convert from mJy to μJy
# for col in ["F_SPIRE_250", "FErr_SPIRE_250_u", "FErr_SPIRE_250_l",
# "F_SPIRE_350", "FErr_SPIRE_350_u", "FErr_SPIRE_350_l",
# "F_SPIRE_500", "FErr_SPIRE_500_u", "FErr_SPIRE_500_l"]:
# xid_spire[col] *= 1000
# xid_spire.add_column(Column(
# data=np.max([xid_spire['FErr_SPIRE_250_u'] - xid_spire['F_SPIRE_250'],
# xid_spire['F_SPIRE_250'] - xid_spire['FErr_SPIRE_250_l']],
# axis=0),
# name="ferr_spire_250"
# ))
# xid_spire['F_SPIRE_250'].name = "f_spire_250"
# xid_spire.add_column(Column(
# data=np.max([xid_spire['FErr_SPIRE_350_u'] - xid_spire['F_SPIRE_350'],
# xid_spire['F_SPIRE_350'] - xid_spire['FErr_SPIRE_350_l']],
# axis=0),
# name="ferr_spire_350"
# ))
# xid_spire['F_SPIRE_350'].name = "f_spire_350"
# xid_spire.add_column(Column(
# data=np.max([xid_spire['FErr_SPIRE_500_u'] - xid_spire['F_SPIRE_500'],
# xid_spire['F_SPIRE_500'] - xid_spire['FErr_SPIRE_500_l']],
# axis=0),
# name="ferr_spire_500"
# ))
# xid_spire['F_SPIRE_500'].name = "f_spire_500"
# xid_spire = xid_spire['help_id',
# 'f_spire_250', 'ferr_spire_250', 'flag_spire_250',
# 'f_spire_350', 'ferr_spire_350', 'flag_spire_350',
# 'f_spire_500', 'ferr_spire_500', 'flag_spire_500']
# +
# Photo-z
#photoz = Table.read("../../dmu24/dmu24_/data/")
#photoz.meta = None
#photoz = photoz['help_id', 'z1_median']
#photoz['z1_median'].name = 'redshift'
#photoz['redshift'][photoz['redshift'] < 0] = np.nan # -99 used for missing values
# +
# Temp spec-z
ml['zspec'][ml['zspec'] < 0] = np.nan # -99 used for missing values
# -
# Flags
flags = Table.read("../../dmu6/dmu6_v_ELAIS-N2/data/elais-n2_20180218_flags.fits")
# # Merging
# +
# merged_table = join(ml, xid_mips24, join_type='left')
# # Fill values
# for col in xid_mips24.colnames:
# if col.startswith("f_") or col.startswith("ferr_"):
# merged_table[col].fill_value = np.nan
# elif col.startswith("flag_"):
# merged_table[col].fill_value = False
# merged_table = merged_table.filled()
# +
# merged_table = join(merged_table, xid_pacs, join_type='left')
# # Fill values
# for col in xid_pacs.colnames:
# if col.startswith("f_") or col.startswith("ferr_"):
# merged_table[col].fill_value = np.nan
# elif col.startswith("flag_"):
# merged_table[col].fill_value = False
# merged_table = merged_table.filled()
# +
# merged_table = join(merged_table, xid_spire, join_type='left')
# # Fill values
# for col in xid_spire.colnames:
# if col.startswith("f_") or col.startswith("ferr_"):
# merged_table[col].fill_value = np.nan
# elif col.startswith("flag_"):
# merged_table[col].fill_value = False
# merged_table = merged_table.filled()
# +
#merged_table = join(merged_table, photoz, join_type='left')
# Fill values
#merged_table['redshift'].fill_value = np.nan
#merged_table = merged_table.filled()
# -
merged_table = ml
# +
for col in flags.colnames:
if 'flag' in col:
try:
merged_table.remove_column(col)
except KeyError:
print("Column: {} not in masterlist.".format(col))
merged_table = join(merged_table, flags, join_type='left')
# Fill values
for col in merged_table.colnames:
if 'flag' in col:
merged_table[col].fill_value = False
merged_table = merged_table.filled()
# -
# # Saving the catalogue for CIGALE (first run)
if FIRST_RUN_FOR_CIGALE:
# Sorting the columns
bands_tot = [col[2:] for col in merged_table.colnames
if col.startswith('f_') and not col.startswith('f_ap')]
bands_ap = [col[5:] for col in merged_table.colnames
if col.startswith('f_ap_') ]
bands = list(set(bands_tot) | set(bands_ap))
bands.sort(key=lambda x: filter_mean_lambda[x])
columns = ['help_id', 'field', 'ra', 'dec', 'hp_idx', 'ebv', #'redshift',
'zspec']
for band in bands:
for col_tpl in ['f_{}', 'ferr_{}', 'f_ap_{}', 'ferr_ap_{}',
'm_{}', 'merr_{}', 'm_ap_{}', 'merr_ap_{}',
'flag_{}']:
colname = col_tpl.format(band)
if colname in merged_table.colnames:
columns.append(colname)
columns += ['stellarity', 'stellarity_origin', 'flag_cleaned',
'flag_merged', 'flag_gaia', 'flag_optnir_obs',
'flag_optnir_det', 'zspec_qual', 'zspec_association_flag']
# Check that we did not forget any column
# assert set(columns) == set(merged_table.colnames)
print(set(columns) - set(merged_table.colnames))
print( set(merged_table.colnames) - set(columns) )
merged_table = add_column_meta(merged_table, '../columns.yml')
merged_table[columns].write("data/ELAIS-N2_{}_cigale.fits".format(SUFFIX), overwrite=True)
# # Merging CIGALE outputs
#
# We merge the CIGALE outputs to the main catalogue. The CIGALE products provides several χ² with associated thresholds. For simplicity, we convert these two values to flags.
if not FIRST_RUN_FOR_CIGALE:
# Cigale outputs
cigale = Table.read("../../dmu28/dmu28_CDFS-SWIRE/data/HELP_final_results.fits")
cigale['id'].name = "help_id"
# We convert the various Chi2 and threshold to flags
flag_cigale_opt = cigale["UVoptIR_OPTchi2"] <= cigale["UVoptIR_OPTchi2_threshold"]
flag_cigale_ir = cigale["UVoptIR_IRchi2"] <= cigale["UVoptIR_IRchi2_threshold"]
flag_cigale = (
(cigale["UVoptIR_best.reduced_chi_square"]
<= cigale["UVoptIR_best.reduced_chi_square_threshold"]) &
flag_cigale_opt & flag_cigale_ir)
flag_cigale_ironly = cigale["IRonly_IRchi2"] <= cigale["IRonly_IRchi2_threshold"]
cigale.add_columns([
MaskedColumn(flag_cigale, "flag_cigale",
dtype=int, fill_value=-1),
MaskedColumn(flag_cigale_opt, "flag_cigale_opt",
dtype=int, fill_value=-1),
MaskedColumn(flag_cigale_ir, "flag_cigale_ir",
dtype=int, fill_value=-1),
MaskedColumn(flag_cigale_ironly, "flag_cigale_ironly",
dtype=int, fill_value=-1)
])
cigale['UVoptIR_bayes.stellar.m_star'].name = "cigale_mstar"
cigale['UVoptIR_bayes.stellar.m_star_err'].name = "cigale_mstar_err"
cigale['UVoptIR_bayes.sfh.sfr10Myrs'].name = "cigale_sfr"
cigale['UVoptIR_bayes.sfh.sfr10Myrs_err'].name = "cigale_sfr_err"
cigale['UVoptIR_bayes.dust.luminosity'].name = "cigale_dustlumin"
cigale['UVoptIR_bayes.dust.luminosity_err'].name = "cigale_dustlumin_err"
cigale['IR_bayes.dust.luminosity'].name = "cigale_dustlumin_ironly"
cigale['IR_bayes.dust.luminosity_err'].name = "cigale_dustlumin_ironly_err"
cigale = cigale['help_id', 'cigale_mstar', 'cigale_mstar_err', 'cigale_sfr',
'cigale_sfr_err', 'cigale_dustlumin', 'cigale_dustlumin_err',
'cigale_dustlumin_ironly', 'cigale_dustlumin_ironly_err',
'flag_cigale', 'flag_cigale_opt', 'flag_cigale_ir',
'flag_cigale_ironly']
if not FIRST_RUN_FOR_CIGALE:
merged_table = join(merged_table, cigale, join_type='left')
# Fill values
for col in cigale.colnames:
if col.startswith("cigale_"):
merged_table[col].fill_value = np.nan
elif col.startswith("flag_"):
merged_table[col].fill_value = -1
merged_table = merged_table.filled()
# # Sorting columns
#
# We sort the columns by increasing band wavelength.
if not FIRST_RUN_FOR_CIGALE:
bands = [col[2:] for col in merged_table.colnames
if col.startswith('f_') and not col.startswith('f_ap')]
bands.sort(key=lambda x: filter_mean_lambda[x])
if not FIRST_RUN_FOR_CIGALE:
columns = ['help_id', 'field', 'ra', 'dec', 'hp_idx', 'ebv', 'redshift', 'zspec']
for band in bands:
for col_tpl in ['f_{}', 'ferr_{}', 'f_ap_{}', 'ferr_ap_{}',
'm_{}', 'merr_{}', 'm_ap_{}', 'merr_ap_{}',
'flag_{}']:
colname = col_tpl.format(band)
if colname in merged_table.colnames:
columns.append(colname)
columns += ['cigale_mstar', 'cigale_mstar_err', 'cigale_sfr', 'cigale_sfr_err',
'cigale_dustlumin', 'cigale_dustlumin_err', 'cigale_dustlumin_ironly',
'cigale_dustlumin_ironly_err', 'flag_cigale', 'flag_cigale_opt',
'flag_cigale_ir', 'flag_cigale_ironly', 'stellarity',
'stellarity_origin', 'flag_cleaned', 'flag_merged', 'flag_gaia',
'flag_optnir_obs', 'flag_optnir_det', 'zspec_qual',
'zspec_association_flag']
if not FIRST_RUN_FOR_CIGALE:
# Check that we did not forget any column
assert set(columns) == set(merged_table.colnames)
# # Saving
if not FIRST_RUN_FOR_CIGALE:
merged_table = add_column_meta(merged_table, '../columns.yml')
merged_table[columns].write("data/CDFS-SWIRE.fits", overwrite=True)
|
dmu32/dmu32_ELAIS-N2/ELAIS-N2_catalogue_merging.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Alternating Line Current
# ## Import modules
# +
import os
import numpy as np
import KUEM as EM
import matplotlib.pyplot as plt
plt.close("all")
# -
# ## Setup constants and settings
# +
# Constants for J
Current = 1
Frequency = 2
# Grid constants
N = np.array([49, 49, 1], dtype = int)
delta_x = np.array([2, 2, 2])
x0 = np.array([-1, -1, -1])
Boundaries = [["closed", "closed"], ["closed", "closed"], "periodic"]
# Evaluation constants
StaticsExact = True
DynamicsExact = True
Progress = 5
approx_n = 0.1
# Video constants
FPS = 30
Speed = 0.2
Delta_t = 5
TimeConstant = 5
Steps = int(FPS / Speed * Delta_t)
SubSteps = int(np.ceil(TimeConstant * Delta_t * np.max(N / delta_x) / Steps))
dt = Delta_t / (Steps * SubSteps)
# Plotting settings
PlotScalar = True
PlotContour = False
PlotVector = True
PlotStreams = False
StreamDensity = 2
StreamLength = 1
ContourLevels = 10
ContourLim = (0, 0.15)
# File names
FilePos = "AlternatingLineCurrent/"
Name_B_2D = "ExAlternatingLineCurrentB_2D.avi"
Name_A_2D = "ExAlternatingLineCurrentA_2D.avi"
Name_B_1D = "ExAlternatingLineCurrentB_1D.avi"
Name_A_1D = "ExAlternatingLineCurrentA_1D.avi"
Save = True
# -
# ## Create the J function
# Define the current
def J(dx, N, x0, c, mu0):
# Create grid
Grid = np.zeros(tuple(N) + (4,))
# Add in the current, normalising so the current is the same no matter the grid size
Grid[int(N[0] / 2), int(N[1] / 2), :, 3] = Current / (dx[0] * dx[1])
# Turn into a vector
J_Vector = EM.to_vector(Grid, N)
# Return the vector
def get_J(t):
return J_Vector * np.sin(2 * np.pi * Frequency * t)
return get_J
# ## Setup the simulation
# Setup the simulation
Sim = EM.sim(N, delta_x = delta_x, x0 = x0, approx_n = approx_n, dt = dt, J = J, boundaries = Boundaries)
# ## Define the samplers
# +
# Set clim
max_val_A = 0.3
max_val_B = 2.5
clim_A = np.array([-max_val_A, max_val_A])
clim_B = np.array([-max_val_B, max_val_B])
# Define hat vectors
x_hat = np.array([1, 0, 0])
y_hat = np.array([0, 1, 0])
hat = np.array([0, 0, 1])
B_hat = np.array([0, -1, 0])
# Define the resolutions
Res_scalar = 1000
Res_vector = 30
Res_line = 1000
# Define extents
extent = [0, delta_x[0], 0, delta_x[1]]
PointsSize = np.array([delta_x[0], delta_x[1]])
x_vals = np.linspace(0, delta_x[0] / 2, Res_line)
# Get grid points
Points_scalar = EM.sample_points_plane(x_hat, y_hat, np.array([0, 0, 0]), PointsSize, np.array([Res_scalar, Res_scalar]))
Points_vector = EM.sample_points_plane(x_hat, y_hat, np.array([0, 0, 0]), PointsSize, np.array([Res_vector, Res_vector]))
Points_line = EM.sample_points_line(np.array([0, 0, 0]), np.array([delta_x[0] / 2, 0, 0]), Res_line)
# Setup samplers
Sampler_B_2D = EM.sampler_B_vector(Sim, Points_vector, x_hat, y_hat)
Sampler_A_2D = EM.sampler_A_scalar(Sim, Points_scalar, hat = hat)
Sampler_B_1D = EM.sampler_B_line(Sim, Points_line, x = x_vals, hat = B_hat)
Sampler_A_1D = EM.sampler_A_line(Sim, Points_line, x = x_vals, hat = hat)
# -
# ## Simulate
# +
# Solve the statics problem
print("Solving starting conditions")
StaticTime = Sim.solve(exact = StaticsExact, progress = Progress)
print(f"Solved starting conditions in {StaticTime:.2g} s")
# Solve the dynamics
print("Solving dynamics")
DynamicTime = Sim.dynamics(Steps, SubSteps, exact = DynamicsExact, progress = Progress)
print(f"Solved dynamics in {DynamicTime:.2g} s")
# -
# ## Create videos
# +
# Create folder
if Save is True and not os.path.exists(FilePos):
os.mkdir(FilePos)
# Save the videos
if Save is True:
print("Creating videos, this may take a while")
Sampler_B_2D.make_video(FilePos + Name_B_2D, FPS = FPS, extent = extent, clim = clim_B, density = StreamDensity, length = StreamLength, use_vector = PlotVector, use_streams = PlotStreams)
print(f"Created video {Name_B_2D}")
Sampler_A_2D.make_video(FilePos + Name_A_2D, FPS = FPS, extent = extent, clim = clim_A, contour_lim = ContourLim, levels = ContourLevels, use_scalar = PlotScalar, use_contour = PlotContour)
print(f"Created video {Name_A_2D}")
Sampler_B_1D.make_video(FilePos + Name_B_1D, FPS = FPS, ylim = clim_B)
print(f"Created video {Name_B_1D}")
Sampler_A_1D.make_video(FilePos + Name_A_1D, FPS = FPS, ylim = clim_A)
print(f"Created video {Name_A_1D}")
|
Examples/ExAlternatingLineCurrent.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **Download** (right-click, save target as ...) this page as a jupyterlab notebook from: [Lab5](http://172.16.31.10/engr-1330-webroot/8-Labs/Lab05/Lab05.ipynb)
#
# ___
# # <font color=darkred>Laboratory 5: Sequence, Selection, and Repetition - Oh My! </font>
#
# **LAST NAME, FIRST NAME**
#
# **R00000000**
#
# ENGR 1330 Laboratory 5 - In-Lab
# Preamble script block to identify host, user, and kernel
import sys
# ! hostname
# ! whoami
print(sys.executable)
print(sys.version)
print(sys.version_info)
# ## Sequence
#
# Our first structure is sequential. To belabor the concept we will compute a short list of cubes, by cubing each element in a list and placing it into another list. The example below is dumb, but useful to introduce repetition later in the lab.
#
# First an unusual cell, used to reset a notebook - it will clear the workspace. Here we use it so the notebook will work the same for everyone (at least at first).
# reset this notebook
# %reset -f
# do a manual kernel restart to get the execution count to restart at one
AList = [0.0,1.0,2.0,3.0,4.0] # Create a list of floats
BList = [] #empty list to accept values
position = -1 # set position pointer to -1
position = position + 1 # increment position
BList.append(pow(AList[position],3)) # append to BList to build list of cubes
position = position + 1
BList.append(pow(AList[position],3))
position = position + 1
BList.append(pow(AList[position],3))
position = position + 1
BList.append(pow(AList[position],3))
position = position + 1
BList.append(pow(AList[position],3))
print(BList)
# ### Selection
#
# Our next structure is selection, illustrated by a simple example
#
# A council member will not be allowed to vote on an ordinance if his/her attendence at council meetings is less than 75%.
# Take the following inputs from the user:
#
# 1. Number of council meetings held.
# 2. Number of council meetings attended.
#
# Compute the percentage of meetings attended
#
# $$\%_{attended} = \frac{Meetings_{attended}}{Meetings_{total}}*100$$
#
# Use the result to decide whether the council member will be allowed to vote or not.
# use our simple I/O methods to obtain council persons name
council_name = str(input('enter council person name'))
# use our simple I/O methods to obtain meeting count
meetings_total = int(input('How many meetings since last vote?'))
# use our simple I/O methods to obtain meetings attended
prompt_string = 'How many meetings did ' + council_name + ' attend? '
meetings_attended = int(input(prompt_string))
# compute percent_attendence
percent_attend = 100.0*(meetings_attended/meetings_total) #the 100.0 forces float
# select and make eligibility report
if percent_attend < 75:
print('Council person ',council_name,' attended ',percent_attend,' percent of meetings and is NOT eligible to vote')
else:
print('Council person ',council_name,' attended ',percent_attend,' percent of meetings and is eligible to vote')
# ## <font color=purple>Repetition (Loops)</font>
# - Controlled repetition
# - Structured FOR Loop
# - Structured WHILE Loop
# ### <font color=purple>Count controlled repetition</font>
# 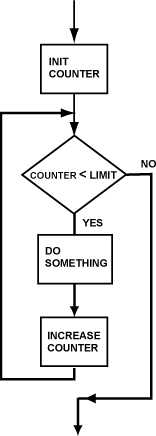 <br>
#
# Count-controlled repetition is also called definite repetition because the number of repetitions is known before the loop begins executing.
# When we do not know in advance the number of times we want to execute a statement, we cannot use count-controlled repetition.
# In such an instance, we would use sentinel-controlled repetition.
#
# A count-controlled repetition will exit after running a certain number of times.
# The count is kept in a variable called an index or counter.
# When the index reaches a certain value (the loop bound) the loop will end.
#
# Count-controlled repetition requires
#
# * control variable (or loop counter)
# * initial value of the control variable
# * increment (or decrement) by which the control variable is modified each iteration through the loop
# * condition that tests for the final value of the control variable
#
# We can use both `for` and `while` loops, for count controlled repetition, but the `for` loop in combination with the `range()` function is more common.
#
# #### Structured `FOR` loop
# We have seen the for loop already, but we will formally introduce it here. The `for` loop executes a block of code repeatedly until the condition in the `for` statement is no longer true.
#
# #### Looping through an iterable
# An iterable is anything that can be looped over - typically a list, string, or tuple.
# The syntax for looping through an iterable is illustrated by an example.
#
# First a generic syntax
#
# for a in iterable:
# print(a)
#
# Notice the colon `:` and the indentation.
# Now a specific example:
# ___
# ### Example: A Loop to Begin With!
#
# Make a list with "Walter", "Jesse", "Gus, "Hank". Then, write a loop that prints all the elements of your lisk.
# +
# # set a list
# BB = ["Walter","Jesse","Gus","Hank"]
# # loop thru the list
# for AllStrings in BB:
# print(AllStrings)
# -
# ___
# #### The `range()` function to create an iterable
#
# The `range(begin,end,increment)` function will create an iterable starting at a value of begin, in steps defined by increment (`begin += increment`), ending at `end`.
#
# So a generic syntax becomes
#
# for a in range(begin,end,increment):
# print(a)
#
# The example that follows is count-controlled repetition (increment skip if greater)
# +
# # set a list
# BB = ["Walter","Jesse","Gus","Hank"]
# # loop thru the list
# for i in range(0,4,1): # Change the numbers, what happens?
# print(BB[i])
# -
# ___
# ### Example: That's odd!
#
# Write a loop to print all the odd numbers between 0 and 10.
# +
# # For loop with range
# for x in range(1,10,2): # a sequence from 2 to 5 with steps of 1
# print(x)
# -
# ___
# ### <font color=purple>Sentinel-controlled repetition</font>
# 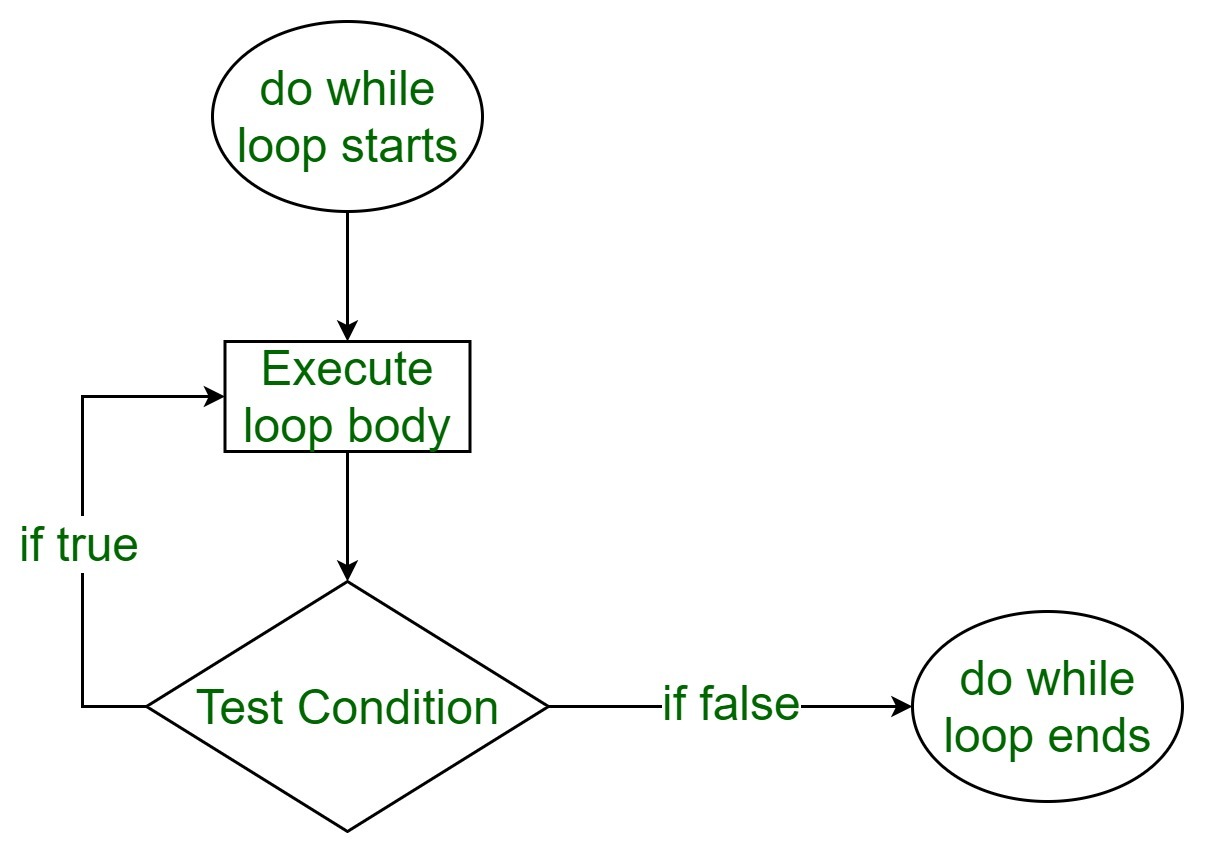 <br>
#
# When loop control is based on the value of what we are processing, sentinel-controlled repetition is used.
# Sentinel-controlled repetition is also called indefinite repetition because it is not known in advance how many times the loop will be executed.
#
#
# <!-- <br>-->
#
# It is a repetition procedure for solving a problem by using a sentinel value (also called a signal value, a dummy value or a flag value) to indicate "end of process".
# The sentinel value itself need not be a part of the processed data.
#
# One common example of using sentinel-controlled repetition is when we are processing data from a file and we do not know in advance when we would reach the end of the file.
#
# We can use both `for` and `while` loops, for __Sentinel__ controlled repetition, but the `while` loop is more common.
#
# #### Structured `WHILE` loop
# The `while` loop repeats a block of instructions inside the loop while a condition remainsvtrue.
#
# First a generic syntax
#
# while condition is true:
# execute a
# execute b
# ....
#
# Notice our friend, the colon `:` and the indentation again.
# +
# # set a counter
# counter = 5
# # while loop
# while counter > 0:
# print("Counter = ",counter)
# counter = counter -1
# -
# > The while loop structure just depicted is a "decrement, skip if equal" in lower level languages. The next structure, also a while loop is an "increment, skip if greater" structure.
# # set a counter
# counter = 0
# # while loop
# while counter <= 5: # change this line to: while counter <= 5: what happens?
# print ("Counter = ",counter)
# counter = counter +1 # change this line to: counter +=1 what happens?
# Beware, its easy to create an infinite loop with this structure. The lab instructor will do so, and illustrate how to regain control of your computer when you do.
# ___
# ### <font color=purple>Nested Repetition | Loops within Loops</font>
#
# <!--  <br> -->
#
#
# > Round like a circle in a spiral, like a wheel within a wheel <br>
# Never ending or beginning on an ever spinning reel <br>
# Like a snowball down a mountain, or a carnival balloon <br>
# Like a carousel that's turning running rings around the moon <br>
# Like a clock whose hands are sweeping past the minutes of its face <br>
# And the world is like an apple whirling silently in space <br>
# Like the circles that you find in the windmills of your mind! <br>
# <br>
# ***Windmills of Your Mind lyrics © Sony/ATV Music Publishing LLC, BMG Rights Management*** <br>
# ***Songwriters: <NAME> / <NAME> / <NAME>*** <br>
# ***Recommended versions: <NAME> | <NAME> | <NAME>*** <br>
# "Like the circles that you find in the windmills of your mind", Nested repetition is when a control structure is placed inside of the body or main part of another control structure.
#
# #### `break` to exit out of a loop
#
# Sometimes you may want to exit the loop when a certain condition different from the counting
# condition is met. Perhaps you are looping through a list and want to exit when you find the
# first element in the list that matches some criterion. The break keyword is useful for such
# an operation.
# For example run the following program:
# +
# #
# j = 0
# for i in range(0,5,1):
# j += 2
# print ("i = ",i,"j = ",j)
# if j == 6:
# break
# +
# # One Small Change
# j = 0
# for i in range(0,5,1):
# j += 2
# print( "i = ",i,"j = ",j)
# if j == 7:
# break
# -
# In the first case, the for loop only executes 3 times before the condition j == 6 is TRUE and the loop is exited.
# In the second case, j == 7 never happens so the loop completes all its anticipated traverses.
#
# In both cases an `if` statement was used within a for loop. Such "mixed" control structures
# are quite common (and pretty necessary).
# A `while` loop contained within a `for` loop, with several `if` statements would be very common and such a structure is called __nested control.__
# There is typically an upper limit to nesting but the limit is pretty large - easily in the
# hundreds. It depends on the language and the system architecture ; suffice to say it is not
# a practical limit except possibly for general-domain AI applications.
# <hr>
# We can also do mundane activities and leverage loops, arithmetic, and format codes to make useful tables like
#
# ### Example: Cosines in the loop!
#
# Write a loop to print a table of the cosines of numbers between 0 and 0.01 with steps of 0.001.
# +
# import math # package that contains cosine
# print(" Cosines ")
# print(" x ","|"," cos(x) ")
# print("--------|--------")
# for i in range(0,100,1):
# x = float(i)*0.001
# print("%.3f" % x, " |", " %.4f " % math.cos(x)) # note the format code and the placeholder % and syntax of using package
# -
# ___
# ### Example: Getting the hang of it!
#
# Write a Python script that takes a real input value (a float) for x and returns the y
# value according to the rules below
#
# \begin{gather}
# y = x~for~0 <= x < 1 \\
# y = x^2~for~1 <= x < 2 \\
# y = x + 2~for~2 <= x < 3 \\
# \end{gather}
#
# Test the script with x values of 0.0, 1.0, 1.1, and 2.1. <br>
# add functionality to **automaticaly** populate the table below:
#
# |x|y(x)|
# |---:|---:|
# |0.0| |
# |1.0| |
# |2.0| |
# |3.0| |
# |4.0| |
# |5.0| |
# +
# userInput = input('Enter enter a float') #ask for user's input
# x = float(userInput)
# print("x:", x)
# if x >= 0 and x < 1:
# y = x
# print("y is equal to",y)
# elif x >= 1 and x < 2:
# y = x*x
# print("y is equal to",y)
# else:
# y = x+2
# print("y is equal to",y)
# +
# without pretty table
# print("---x---","|","---y---")
# print("--------|--------")
# for x in range(0,6,1):
# if x >= 0 and x < 1:
# y = x
# print("%4.f" % x, " |", " %4.f " % y)
# elif x >= 1 and x < 2:
# y = x*x
# print("%4.f" % x, " |", " %4.f " % y)
# else:
# y = x+2
# print("%4.f" % x, " |", " %4.f " % y)
# +
# # with pretty table
# from prettytable import PrettyTable #Required to create tables
# t = PrettyTable(['x', 'y']) #Define an empty table
# for x in range(0,6,1):
# if x >= 0 and x < 1:
# y = x
# print("for x equal to", x, ", y is equal to",y)
# t.add_row([x, y]) #will add a row to the table "t"
# elif x >= 1 and x < 2:
# y = x*x
# print("for x equal to", x, ", y is equal to",y)
# t.add_row([x, y])
# else:
# y = x+2
# print("for x equal to", x, ", y is equal to",y)
# t.add_row([x, y])
# print(t)
# -
# ___
# #### The `continue` statement
# The continue instruction skips the block of code after it is executed for that iteration, and continues with the loop traverse
# It is
# best illustrated by an example.
# +
# j = 0
# for i in range(0,5,1):
# j += 2
# print ("\n i = ", i , ", j = ", j) #here the \n is a newline command
# if j == 6:
# continue
# else:
# print(" this message will be skipped over if j = 6 ") # still within the loop, so the skip is implemented
# #When j ==6 the line after the continue keyword is not printed.
# #Other than that one difference the rest of the script runs normally.
# -
# ___
# #### The `try`, `except` structure
#
# An important control structure (and a pretty cool one for error trapping) is the `try`, `except`
# statement.
#
# The statement controls how the program proceeds when an error occurs in an instruction.
# The structure is really useful to trap likely errors (divide by zero, wrong kind of input)
# yet let the program keep running or at least issue a meaningful message to the user.
#
# The syntax is:
#
# try:
# do something
# except:
# do something else if ``do something'' returns an error
#
# Here is a really simple, but hugely important example:
# +
#MyErrorTrap.py
# x = 12.
# y = 12.
# while y >= -12.: # sentinel controlled repetition
# try:
# print ("x = ", x, "y = ", y, "x/y = ", x/y)
# except:
# print ("error divide by zero")
# y -= 1
# -
# So this silly code starts with x fixed at a value of 12, and y starting at 12 and decreasing by
# 1 until y equals -1. The code returns the ratio of x to y and at one point y is equal to zero
# and the division would be undefined. By trapping the error the code can issue us a measure
# and keep running.
#
# Modify the script as shown below,Run, and see what happens
# +
#NoErrorTrap.py
# x = 12.
# y = 12.
# while y >= -12.: # sentinel controlled repetition
# print ("x = ", x, "y = ", y, "x/y = ", x/y)
# y -= 1
# -
# ___
# ## Readings
#
# *Here are some great reads on this topic:*
# - "Python for Loop" available at [https://www.programiz.com/python-programming/for-loop/](https://www.programiz.com/python-programming/for-loop/)<br>
# - "Python "for" Loops (Definite Iteration)" by <NAME> available at [https://realpython.com/python-for-loop/](https://realpython.com/python-for-loop/) <br>
# - "Python "while" Loops (Indefinite Iteration)" by <NAME> available at [https://realpython.com/python-while-loop/](https://realpython.com/python-while-loop/) <br>
# - "loops in python" available at [https://www.geeksforgeeks.org/loops-in-python/ ](https://www.geeksforgeeks.org/loops-in-python/) <br>
# - "Python Exceptions: An Introduction" by <NAME> available at [https://realpython.com/python-exceptions/](https://realpython.com/python-exceptions/) <br>
#
# *Here are some great videos on these topics:*
# - "Python For Loops - Python Tutorial for Absolute Beginners" by Programming with Mosh available at [https://www.youtube.com/watch?v=94UHCEmprCY](https://www.youtube.com/watch?v=94UHCEmprCY) <br>
# - "Python Tutorial for Beginners 7: Loops and Iterations - For/While Loops" by <NAME> available at [https://www.youtube.com/watch?v=6iF8Xb7Z3wQ](https://www.youtube.com/watch?v=6iF8Xb7Z3wQ) <br>
# - "Python 3 Programming Tutorial - For loop" by sentdex available at [https://www.youtube.com/watch?v=xtXexPSfcZg ](https://www.youtube.com/watch?v=xtXexPSfcZg) <br><br>
|
8-Labs/Lab05/dev_src/Lab05-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import os
import csv
import time
import pickle
import warnings
import numpy as np
import pandas as pd
from src.fABBA_test import fABBA
from src.ABBA import ABBA
from src.mydefaults import mydefaults
from collections import defaultdict
from tslearn.metrics import dtw as dtw
warnings.filterwarnings('ignore')
datadir = 'UCRArchive_2018/'
tol = [0.05*i for i in range(1,11)]
ts_count = 0
for root, dirs, files in os.walk(datadir):
for file in files:
if file.endswith('tsv'):
with open(os.path.join(root, file)) as f:
content = f.readlines()
ts_count += len(content)
print('Number of time series:', ts_count)
alphas = [0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9]
sorting_methods = ['2-norm']
for sortname in sorting_methods:
print('\n sorting method:', sortname)
D_fABBA_2 = len(alphas)*ts_count*[np.NaN]
D_fABBA_DTW = len(alphas)*ts_count*[np.NaN]
D_fABBA_time = len(alphas)*ts_count*[np.NaN]
alphalist = len(alphas)*ts_count*[np.NaN]
countlist = len(alphas)*ts_count*[np.NaN]
ts_name = len(alphas)*ts_count*[''] # time series name for debugging
tol_used = len(alphas)*ts_count*[np.NaN] # Store tol used
csymbolicNum = len(alphas)*ts_count*[np.NaN] # Store amount of symbols
cpiecesNum = len(alphas)*ts_count*[np.NaN] # Store amount of pieces after compression
ctsname = len(alphas)*ts_count*['']
index = 0
for root, dirs, files in os.walk(datadir):
for file in files:
if file.endswith('tsv'):
print(' file:', file)
with open(os.path.join(root, file)) as tsvfile:
tsvfile = csv.reader(tsvfile, delimiter='\t')
for ind, column in enumerate(tsvfile):
for alpha in alphas:
# print('alpha:' + str(alpha) + ' file:', file)
ts_name[index] += str(file) + '_' + str(ind)
ts = [float(i) for i in column]
ts = np.array(ts[1:])
ts = ts[~np.isnan(ts)]
norm_ts = (ts - np.mean(ts))
std = np.std(norm_ts, ddof=1)
std = std if std > np.finfo(float).eps else 1
norm_ts /= std
if len(norm_ts) < 100:
break
tol_index = 0
CompressionTolHigh = False
for tol_index in range(len(tol)):
abba = ABBA(tol=tol[tol_index], verbose=0)
pieces = abba.compress(norm_ts)
ABBA_len = len(pieces)
if ABBA_len <= len(norm_ts)/5:
tol_used[index] = tol[tol_index]
break
elif tol_index == len(tol)-1:
CompressionTolHigh = True
if CompressionTolHigh:
continue # uniform to performance profiles test!
fabba = fABBA(verbose=0, alpha=alpha, scl=1, sorting=sortname)
st = time.time()
symbolic_tsf = fabba.digitize(pieces[:,:2])
ed = time.time()
time_fabba = ed - st
symbolnum = len(set(symbolic_tsf))
csymbolicNum[index] = symbolnum
cpiecesNum[index] = len(pieces)
ctsname[index] = str(file) + '_' + str(ind)
ts_fABBA = fabba.inverse_transform(symbolic_tsf, norm_ts[0])
D_fABBA_2[index] = np.linalg.norm(norm_ts - ts_fABBA)
D_fABBA_DTW[index] = dtw(norm_ts, ts_fABBA)
D_fABBA_time[index] = time_fabba
alphalist[index] = alpha
countlist[index] = fabba.nr_dist
index += 1
Datastore = pd.DataFrame(columns=['ts name', 'number of pieces',
'number of symbols', 'tol', 'fABBA_2',
'fABBA_DTW', 'fABBA_time', 'alpha'])
Datastore["ts name"] = ctsname
Datastore["number of pieces"] = cpiecesNum
Datastore["number of symbols"] = csymbolicNum
Datastore["tol"] = tol_used
Datastore["fABBA_2"] = D_fABBA_2
Datastore["fABBA_DTW"] = D_fABBA_DTW
Datastore["fABBA_time"] = D_fABBA_time
Datastore["alpha"] = alphalist
Datastore["count"] = countlist
Datastore.to_csv('results/count_rate'+sortname+'.csv',index=False)
# -
|
exp/count_rate_2norm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="GNkzTFfynsmV" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 1000} outputId="8c419f94-3d61-4fe1-e733-43b3ae9c28f0"
# !pip install -U tensorflow
# + id="56XEQOGknrAk" colab_type="code" outputId="332db93d-fe68-4753-8f64-5dd86563b0ce" colab={"base_uri": "https://localhost:8080/", "height": 34}
import tensorflow as tf
print(tf.__version__)
# + id="sLl52leVp5wU" colab_type="code" colab={}
import numpy as np
import matplotlib.pyplot as plt
def plot_series(time, series, format="-", start=0, end=None):
plt.plot(time[start:end], series[start:end], format)
plt.xlabel("Time")
plt.ylabel("Value")
plt.grid(True)
# + id="tP7oqUdkk0gY" colab_type="code" outputId="77159534-adf8-478b-a5c6-5a8086e4b9c5" colab={"base_uri": "https://localhost:8080/", "height": 228}
# !wget --no-check-certificate \
# https://storage.googleapis.com/laurencemoroney-blog.appspot.com/Sunspots.csv \
# -O /tmp/sunspots.csv
# + id="NcG9r1eClbTh" colab_type="code" outputId="b4592520-3d6f-4882-d807-2880f036856f" colab={"base_uri": "https://localhost:8080/", "height": 388}
import csv
time_step = []
sunspots = []
with open('/tmp/sunspots.csv') as csvfile:
reader = csv.reader(csvfile, delimiter=',')
next(reader)
for row in reader:
sunspots.append(float(row[2]))
time_step.append(int(row[0]))
series = np.array(sunspots)
time = np.array(time_step)
plt.figure(figsize=(10, 6))
plot_series(time, series)
# + id="L92YRw_IpCFG" colab_type="code" colab={}
split_time = 3000
time_train = time[:split_time]
x_train = series[:split_time]
time_valid = time[split_time:]
x_valid = series[split_time:]
window_size = 60
batch_size = 32
shuffle_buffer_size = 1000
# + id="lJwUUZscnG38" colab_type="code" colab={}
def windowed_dataset(series, window_size, batch_size, shuffle_buffer):
dataset = tf.data.Dataset.from_tensor_slices(series)
dataset = dataset.window(window_size + 1, shift=1, drop_remainder=True)
dataset = dataset.flat_map(lambda window: window.batch(window_size + 1))
dataset = dataset.shuffle(shuffle_buffer).map(lambda window: (window[:-1], window[-1]))
dataset = dataset.batch(batch_size).prefetch(1)
return dataset
# + id="AclfYY3Mn6Ph" colab_type="code" outputId="6e853f39-8d48-411c-d42e-697d764545bf" colab={"base_uri": "https://localhost:8080/", "height": 106}
dataset = windowed_dataset(x_train, window_size, batch_size, shuffle_buffer_size)
model = tf.keras.models.Sequential([
tf.keras.layers.Dense(20, input_shape=[window_size], activation="relu"),
tf.keras.layers.Dense(10, activation="relu"),
tf.keras.layers.Dense(1)
])
model.compile(loss="mse", optimizer=tf.keras.optimizers.SGD(lr=1e-7, momentum=0.9))
model.fit(dataset,epochs=100,verbose=0)
# + id="GaC6NNMRp0lb" colab_type="code" outputId="c9e06a20-f6c2-4b2c-97c0-b7e8520b9b1e" colab={"base_uri": "https://localhost:8080/", "height": 388}
forecast=[]
for time in range(len(series) - window_size):
forecast.append(model.predict(series[time:time + window_size][np.newaxis]))
forecast = forecast[split_time-window_size:]
results = np.array(forecast)[:, 0, 0]
plt.figure(figsize=(10, 6))
plot_series(time_valid, x_valid)
plot_series(time_valid, results)
# + id="13XrorC5wQoE" colab_type="code" outputId="55cc5244-c090-4711-c053-5aa4690876fd" colab={"base_uri": "https://localhost:8080/", "height": 167}
tf.keras.metrics.mean_absolute_error(x_valid, results).numpy()
# + id="xLUj4WMr3bF1" colab_type="code" colab={}
|
python/coursera_python/DL_AI_LM/4/4/.ipynb_checkpoints/S+P_Week_4_Lesson_1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Discover emerging trends
# In this notebook, we analyze the trends of Stack Overflow questions. In particular, we are finding the percentage of new questions tagged from four popular Python data science libraries: matplotlib, numpy, scikit-learn, and pandas.
#
# The data was retrieved from Stack Overflow's handy data explorer [using this query](http://data.stackexchange.com/stackoverflow/query/767327/select-all-posts-from-a-single-tag).
#
# We use pandas stacked area plot, by quarter, the percentage of new questions added to stack overflow from those four libraries.
# +
import pandas as pd
# %matplotlib inline
# -
import glob
dfs = [pd.read_csv(file_name, parse_dates=['creationdate'])
for file_name in glob.glob('../data/stackoverflow/*.csv')]
df = pd.concat(dfs)
df.head()
df.groupby([pd.Grouper(key='creationdate', freq='QS'), 'tagname']) \
.size() \
.unstack('tagname', fill_value=0) \
.pipe(lambda x: x.div(x.sum(1), axis=0)) \
.plot(kind='area', figsize=(12,6), title='Percentage of New Stack Overflow Questions') \
.legend(loc='upper left')
# Pandas has grown the fastest
|
Pandas Tricks/Emerging Stack Overflow Trends.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + id="EbrFD1vMR_qS"
import tensorflow as tf
import os
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings("ignore")
from sklearn import preprocessing
from sklearn.preprocessing import MinMaxScaler, StandardScaler
import matplotlib.pyplot as plt
#https://colab.research.google.com/drive/1b3CUJuDOmPmNdZFH3LQDmt5F0K3FZhqD?usp=sharing
# + colab={"base_uri": "https://localhost:8080/", "height": 644} id="RRVN-4QOSKAx" outputId="0fae4e16-1266-4d53-81fe-2ef0c08efb66"
df = pd.read_excel("preparedData.xlsx")
# -
df.index = pd.to_datetime(df['date'], format='%d-%m-%Y')
df[:26]
df.drop(columns=['reproduction_rate', 'new_tests', 'positive_rate',
'tests_per_case', 'total_vaccinations', 'people_vaccinated',
'people_fully_vaccinated', 'total_boosters', 'new_vaccinations',
'stringency_index', 'population', 'population_density', 'median_age',
'aged_65_older', 'aged_70_older', 'gdp_per_capita', 'extreme_poverty',
'cardiovasc_death_rate', 'diabetes_prevalence', 'female_smokers',
'male_smokers', 'life_expectancy', 'human_development_index',
'covid: (Ireland)', 'COVID-19 testing: (Ireland)',
'COVID-19 rapid antigen test: (Ireland)',
'Health Service Executive: (Ireland)', 'Vaccination: (Ireland)',
'book covid test: (Ireland)_x', 'how many covid cases today: (Ireland)',
'pcr covid test: (Ireland)', 'close contact covid: (Ireland)',
'book a covid test: (Ireland)', 'vaccination centre: (Ireland)',
'pharmacy near me: (Ireland)',
'Treatment and management of COVID-19: (Ireland)',
'Hand sanitizer: (Ireland)', 'Face mask: (Ireland)',
'book covid test: (Ireland)_y', 'covid test dublin: (Ireland)',
'covid test centre: (Ireland)', 'hse covid vaccine: (Ireland)',
'hse vaccine portal: (Ireland)', 'hse portal vaccine: (Ireland)',
'pcr test hse: (Ireland)', 'hse covid test: (Ireland)',
'hse vaccine registration: (Ireland)',
'how long will it take to vaccinate ireland: (Ireland)'], inplace=True)
# + colab={"base_uri": "https://localhost:8080/", "height": 289} id="3fWZ3nYxS3oe" outputId="bde8d1c4-df76-49fc-d5f2-869e042c7c9e"
cases = df['new_cases_smoothed']
plt.title("COVID-19 Cases in Ireland")
cases.plot()
plt.savefig("New Cases.jpg", bbox_inches='tight')
# + id="bY2yEu2QTBXP"
def df_to_X_y(df, window_size=5):
df_as_np = df.to_numpy()
X = []
y = []
for i in range(len(df_as_np)-window_size):
row = [[a] for a in df_as_np[i:i+window_size]]
X.append(row)
label = df_as_np[i+window_size]
y.append(label)
return np.array(X), np.array(y)
# + colab={"base_uri": "https://localhost:8080/"} id="qhGUH0NoV9Zq" outputId="3775d432-2dbe-4046-a355-b8fa9dcd9ca1"
WINDOW_SIZE = 5
X, y = df_to_X_y(cases, WINDOW_SIZE)
X.shape, y.shape
# + colab={"base_uri": "https://localhost:8080/"} id="Vsy2-BjnWMhB" outputId="f20d3567-88c0-4d28-8fbb-38b7193f4ab4"
X_train, y_train = X[:490], y[:490]
X_val, y_val = X[490:630], y[490:630]
X_test, y_test = X[630:], y[630:]
X_train.shape, y_train.shape, X_val.shape, y_val.shape, X_test.shape, y_test.shape
# + colab={"base_uri": "https://localhost:8080/"} id="4jZz4ZjpW217" outputId="6bf1a2da-db28-44c9-ea3e-89612832e203"
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import *
from tensorflow.keras.callbacks import ModelCheckpoint
from tensorflow.keras.losses import MeanSquaredError
from tensorflow.keras.metrics import RootMeanSquaredError
from tensorflow.keras.optimizers import Adam
model1 = Sequential()
model1.add(InputLayer((5, 1)))
model1.add(LSTM(64))
model1.add(Dense(8, 'relu'))
model1.add(Dense(1, 'linear'))
model1.summary()
# + id="5jMK7auDXwEr"
cp1 = ModelCheckpoint('model1/', save_best_only=True)
model1.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="CWeSakSwYLtr" outputId="5307480e-0540-44f3-f3fb-1a5ec0a3adef"
model1.fit(X_train, y_train, validation_data=(X_val, y_val), epochs=10, callbacks=[cp1])
# + id="vdaqGHG4YZkN"
from tensorflow.keras.models import load_model
model1 = load_model('model1/')
# + colab={"base_uri": "https://localhost:8080/", "height": 420} id="byObmr8CZRhp" outputId="00bd6717-cff6-4e3c-a708-89e503e01bdb"
train_predictions = model1.predict(X_train).flatten()
train_results = pd.DataFrame(data={'Train Predictions':train_predictions, 'Actuals':y_train})
train_results
# + colab={"base_uri": "https://localhost:8080/", "height": 286} id="KTqY8r6_Zpev" outputId="cfd490b8-668c-4b58-ec0b-6b79620f3ac3"
import matplotlib.pyplot as plt
plt.plot(train_results['Train Predictions'][50:100])
plt.plot(train_results['Actuals'][50:100])
# + colab={"base_uri": "https://localhost:8080/", "height": 420} id="vuY5nmGYZ8ix" outputId="0cf2414b-fdbf-40d7-a277-90d29814b3dc"
val_predictions = model1.predict(X_val).flatten()
val_results = pd.DataFrame(data={'Val Predictions':val_predictions, 'Actuals':y_val})
val_results
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="6MlctzuuaQww" outputId="7147a4ca-90a3-4c2d-ae2b-76fe40a2ff0b"
plt.plot(val_results['Val Predictions'][:100])
plt.plot(val_results['Actuals'][:100])
# + colab={"base_uri": "https://localhost:8080/", "height": 420} id="5O59Q8MTaRN7" outputId="4e55d8f6-c9ad-4349-9da7-e937b5ade6ae"
test_predictions = model1.predict(X_test).flatten()
test_results = pd.DataFrame(data={'Test Predictions':test_predictions, 'Actuals':y_test})
test_results
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="m8UzGIfEaW-P" outputId="85be190b-81ac-4223-be21-cdc0f67e592f"
plt.plot(test_results['Test Predictions'][:100])
plt.plot(test_results['Actuals'][:100])
# + id="nWdZkoPo-MZM"
# Part 2
# + id="XFf7bCFlctu8"
from sklearn.metrics import mean_squared_error as mse
def plot_predictions1(model, X, y, start=0, end=100):
predictions = model.predict(X).flatten()
df = pd.DataFrame(data={'Predictions':predictions, 'Actuals':y})
plt.plot(df['Predictions'][start:end])
plt.plot(df['Actuals'][start:end])
return df, mse(y, predictions)
# + colab={"base_uri": "https://localhost:8080/", "height": 511} id="pdabyyStdavq" outputId="e07aa785-101b-462b-81e8-35581ce0812f"
plot_predictions1(model1, X_test, y_test)
# + colab={"base_uri": "https://localhost:8080/"} id="K6KDLXc3dg3x" outputId="eaddf43a-5f36-46ef-8e95-6a0870ae8b4f"
model2 = Sequential()
model2.add(InputLayer((5, 1)))
model2.add(Conv1D(64, kernel_size=2))
model2.add(Flatten())
model2.add(Dense(8, 'relu'))
model2.add(Dense(1, 'linear'))
model2.summary()
# + id="YoGw3DQeeTES"
cp2 = ModelCheckpoint('model2/', save_best_only=True)
model2.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="fUe56iajetZe" outputId="db7d44ec-e162-4e66-a3ba-1162c04fde63"
model2.fit(X_train, y_train, validation_data=(X_val, y_val), epochs=10, callbacks=[cp2])
# + colab={"base_uri": "https://localhost:8080/"} id="_0mmRGP8exPo" outputId="6851ddb2-a5b5-405b-c3fe-68c4233c7df2"
model3 = Sequential()
model3.add(InputLayer((5, 1)))
model3.add(GRU(64))
model3.add(Dense(8, 'relu'))
model3.add(Dense(1, 'linear'))
model3.summary()
# + id="WbQzFWjXfa2i"
cp3 = ModelCheckpoint('model3/', save_best_only=True)
model3.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="BzB6BUOQfivn" outputId="1f282be0-2d44-46a9-be3f-c448b98daf81"
model3.fit(X_train, y_train, validation_data=(X_val, y_val), epochs=10, callbacks=[cp3])
# -
df2 = pd.read_excel("preparedData.xlsx")
date_time = pd.to_datetime(df.pop('date'), format='%d-%m-%Y')
# + id="Db8BJQONjbAT"
def df_to_X_y2(df2, window_size=6):
df_as_np = df.to_numpy()
X = []
y = []
for i in range(len(df_as_np)-window_size):
row = [r for r in df_as_np[i:i+window_size]]
X.append(row)
label = df_as_np[i+window_size][0]
y.append(label)
return np.array(X), np.array(y)
# + colab={"base_uri": "https://localhost:8080/"} id="eJhF1cIDleQ1" outputId="f571aa4c-d18c-41ef-d9c2-652ab09f9b3b"
X1, y1 = df_to_X_y2(df)
X1.shape, y1.shape
# + colab={"base_uri": "https://localhost:8080/"} id="FMOArQgyoTnq" outputId="405a6dfd-4335-4d27-de23-a2fed6e08f24"
X_train1, y_train1 = X1[:490], y1[:490]
X_val1, y_val1 = X1[490:630], y1[490:630]
X_test1, y_test1 = X1[630:], y1[630:]
X_train1.shape, y_train1.shape, X_val1.shape, y_val1.shape, X_test1.shape, y_test1.shape
# + id="887KpvYwpkZq"
temp_training_mean = np.mean(X_train1[:, :, 0])
temp_training_std = np.std(X_train1[:, :, 0])
def preprocess(X):
X[:, :, 0] = (X[:, :, 0] - temp_training_mean) / temp_training_std
return X
# + id="z-Kaf4KTqSEV"
preprocess(X_train1)
preprocess(X_val1)
preprocess(X_test1)
# + colab={"base_uri": "https://localhost:8080/"} id="NpFVgXYJqbt8" outputId="4696c3ab-a8cb-45e1-c691-faed44ba0086"
model4 = Sequential()
model4.add(InputLayer((6, 1)))
model4.add(LSTM(64))
model4.add(Dense(8, 'relu'))
model4.add(Dense(1, 'linear'))
model4.summary()
# + id="3RD8D_SXqkk8"
cp4 = ModelCheckpoint('model4/', save_best_only=True)
model4.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="GB5aik6bqogC" outputId="cfabcd42-c96b-4336-a89e-e51352dd6d8b"
model4.fit(X_train1, y_train1, validation_data=(X_val1, y_val1), epochs=10, callbacks=[cp4])
# + colab={"base_uri": "https://localhost:8080/", "height": 511} id="FmwshpETs-jE" outputId="f9ea03ff-6d06-4ed5-cd59-5199bfdecc15"
plot_predictions1(model4, X_test1, y_test1)
# + colab={"base_uri": "https://localhost:8080/", "height": 236} id="FpOwEbBttY8C" outputId="04c3daf4-fbc8-41ac-a69f-cc7ee32ed5df"
p_temp_df = pd.concat([df['new_cases_smoothed'], df2], axis=1)
p_temp_df.head()
# + id="7EViSFyntz9j"
def df_to_X_y3(df, window_size=7):
df_as_np = df.to_numpy()
X = []
y = []
for i in range(len(df_as_np)-window_size):
row = [r for r in df_as_np[i:i+window_size]]
X.append(row)
label = [df_as_np[i+window_size][0], df_as_np[i+window_size][1]]
y.append(label)
return np.array(X), np.array(y)
# + colab={"base_uri": "https://localhost:8080/"} id="M6iv-AUQuJdX" outputId="c5d6aafb-a91e-4d2e-fd07-90734fcad509"
X3, y3 = df_to_X_y3(p_temp_df)
X3.shape, y3.shape
# + colab={"base_uri": "https://localhost:8080/"} id="JAaiWt0buKa4" outputId="9e431fbf-f8b8-4dc4-932b-d3242d2ab266"
X3_train, y3_train = X3[:60000], y3[:60000]
X3_val, y3_val = X3[60000:65000], y3[60000:65000]
X3_test, y3_test = X3[65000:], y3[65000:]
X3_train.shape, y3_train.shape, X3_val.shape, y3_val.shape, X3_test.shape, y3_test.shape
# + id="Y-1iWv_AuKSk"
p_training_mean3 = np.mean(X3_train[:, :, 0])
p_training_std3 = np.std(X3_train[:, :, 0])
temp_training_mean3 = np.mean(X3_train[:, :, 1])
temp_training_std3 = np.std(X3_train[:, :, 1])
def preprocess3(X):
X[:, :, 0] = (X[:, :, 0] - p_training_mean3) / p_training_std3
X[:, :, 1] = (X[:, :, 1] - temp_training_mean3) / temp_training_std3
def preprocess_output3(y):
y[:, 0] = (y[:, 0] - p_training_mean3) / p_training_std3
y[:, 1] = (y[:, 1] - temp_training_mean3) / temp_training_std3
return y
# + id="tA3BDAuluKHO"
preprocess3(X3_train)
preprocess3(X3_val)
preprocess3(X3_test)
# + colab={"base_uri": "https://localhost:8080/"} id="nyxUc20CuJ4p" outputId="5803e53d-5ae0-4c72-ca26-9adf51b577b7"
preprocess_output3(y3_train)
preprocess_output3(y3_val)
preprocess_output3(y3_test)
# + colab={"base_uri": "https://localhost:8080/"} id="czHWSE2Uv4Br" outputId="7b192759-b752-4f24-9f24-cf3a089ce7df"
model5 = Sequential()
model5.add(InputLayer((7, 6)))
model5.add(LSTM(64))
model5.add(Dense(8, 'relu'))
model5.add(Dense(2, 'linear'))
model5.summary()
# + id="HY4LnQYxwDI2"
cp5 = ModelCheckpoint('model5/', save_best_only=True)
model5.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="pR6NEXeSwF6J" outputId="63d8ef64-7125-40e9-d3ba-6e0895617e86"
model5.fit(X3_train, y3_train, validation_data=(X3_val, y3_val), epochs=10, callbacks=[cp5])
# + id="AzIN93E2xRjE"
def plot_predictions2(model, X, y, start=0, end=100):
predictions = model.predict(X)
p_preds, temp_preds = predictions[:, 0], predictions[:, 1]
p_actuals, temp_actuals = y[:, 0], y[:, 1]
df = pd.DataFrame(data={'Temperature Predictions': temp_preds,
'Temperature Actuals':temp_actuals,
'Pressure Predictions': p_preds,
'Pressure Actuals': p_actuals
})
plt.plot(df['Temperature Predictions'][start:end])
plt.plot(df['Temperature Actuals'][start:end])
plt.plot(df['Pressure Predictions'][start:end])
plt.plot(df['Pressure Actuals'][start:end])
return df[start:end]
# + colab={"base_uri": "https://localhost:8080/", "height": 668} id="QzXcewu_zy2k" outputId="0f520f7f-6aa3-4079-edf5-4c5ff4626258"
plot_predictions2(model5, X3_test, y3_test)
# + id="hplJkJvI0fTf"
def postprocess_temp(arr):
arr = (arr*temp_training_std3) + temp_training_mean3
return arr
def postprocess_p(arr):
arr = (arr*p_training_std3) + p_training_mean3
return arr
# + id="Jcmk5ZB21PDe"
def plot_predictions2(model, X, y, start=0, end=100):
predictions = model.predict(X)
p_preds, temp_preds = postprocess_p(predictions[:, 0]), postprocess_temp(predictions[:, 1])
p_actuals, temp_actuals = postprocess_p(y[:, 0]), postprocess_temp(y[:, 1])
df = pd.DataFrame(data={'Temperature Predictions': temp_preds,
'Temperature Actuals':temp_actuals,
'Pressure Predictions': p_preds,
'Pressure Actuals': p_actuals
})
plt.plot(df['Temperature Predictions'][start:end])
plt.plot(df['Temperature Actuals'][start:end])
plt.plot(df['Pressure Predictions'][start:end])
plt.plot(df['Pressure Actuals'][start:end])
return df[start:end]
# + colab={"base_uri": "https://localhost:8080/", "height": 668} id="WdYOQkIN1gAK" outputId="fd51ff85-2f41-4ca2-ed7c-583bc1a318f7"
post_processed_df = plot_predictions2(model5, X3_test, y3_test)
post_processed_df
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="9m_fSfOq1ohj" outputId="7e6d97f7-49fd-4996-8c18-54cffff1d65d"
start, end = 0, 100
plt.plot(post_processed_df['Temperature Predictions'][start:end])
plt.plot(post_processed_df['Temperature Actuals'][start:end])
# + colab={"base_uri": "https://localhost:8080/", "height": 282} id="ORffwf-e125j" outputId="91467aa7-ff80-498a-b713-98e3762a988d"
plt.plot(post_processed_df['Pressure Predictions'][start:end])
plt.plot(post_processed_df['Pressure Actuals'][start:end])
# + colab={"base_uri": "https://localhost:8080/"} id="GmwCnsUj2B8A" outputId="475af39f-a4f9-40cd-bcfe-ce080d8539f1"
model6 = Sequential()
model6.add(InputLayer((7, 6)))
model6.add(LSTM(32, return_sequences=True))
model6.add(LSTM(64))
model6.add(Dense(8, 'relu'))
model6.add(Dense(2, 'linear'))
model6.summary()
# + id="cWepnsFE2Tnl"
cp6 = ModelCheckpoint('model6/', save_best_only=True)
model6.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/", "height": 367} id="7XnlR3om2aiA" outputId="404ce81e-7255-4c09-9e43-12057dc4d980"
model6.fit(X3_train, y3_train, validation_data=(X3_val, y3_val), epochs=10, callbacks=[cp6])
# + colab={"base_uri": "https://localhost:8080/"} id="Fy6pKacl2bOW" outputId="fb3aad92-2323-421e-bc68-956bc39107f3"
model7 = Sequential()
model7.add(InputLayer((7, 6)))
model7.add(Conv1D(64, kernel_size=2, activation='relu'))
model7.add(Flatten())
model7.add(Dense(8, 'relu'))
model7.add(Dense(2, 'linear'))
model7.summary()
cp7 = ModelCheckpoint('model6/', save_best_only=True)
model7.compile(loss=MeanSquaredError(), optimizer=Adam(learning_rate=0.0001), metrics=[RootMeanSquaredError()])
# + colab={"base_uri": "https://localhost:8080/"} id="xMRDXuFY27JA" outputId="54fa8a3f-ae81-4567-a40a-7652a7ec274f"
model7.fit(X3_train, y3_train, validation_data=(X3_val, y3_val), epochs=10, callbacks=[cp7])
|
Code/Simon/Rough Work/Copy_of_LSTM_Time_Series_Forecasting.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + id="Txm4070zi-DP" colab_type="code" colab={"base_uri": "https://localhost:8080/", "height": 0} outputId="46f776b0-d893-46e7-bbe7-58a4a8fb2a0c" executionInfo={"status": "ok", "timestamp": 1581446348958, "user_tz": -60, "elapsed": 670, "user": {"displayName": "Bogumi\u014<NAME>", "photoUrl": "", "userId": "06989668266749762580"}}
print("Hello World")
# + id="2rDFRFwKjCgk" colab_type="code" colab={}
|
HelloGithub.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Project 5: Visualizing the Gender Gap in college degrees
# +
# %matplotlib inline
import pandas as pd
import matplotlib.pyplot as plt
women_degrees = pd.read_csv('percent-bachelors-degrees-women-usa.csv')
cb_dark_blue = (0/255,107/255,164/255)
cb_orange = (255/255, 128/255, 14/255)
stem_cats = ['Engineering', 'Computer Science', 'Psychology', 'Biology', 'Physical Sciences', 'Math and Statistics']
lib_arts_cats = ['Foreign Languages', 'English', 'Communications and Journalism', 'Art and Performance', 'Social Sciences and History']
other_cats = ['Health Professions', 'Public Administration', 'Education', 'Agriculture','Business', 'Architecture']
fig = plt.figure(figsize=(18, 3))
for sp in range(0,6):
ax = fig.add_subplot(1,6,sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[sp]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[sp]], c=cb_orange, label='Men', linewidth=3)
ax.spines["right"].set_visible(False)
ax.spines["left"].set_visible(False)
ax.spines["top"].set_visible(False)
ax.spines["bottom"].set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0,100)
ax.set_title(stem_cats[sp])
ax.tick_params(bottom="off", top="off", left="off", right="off")
if sp == 0:
ax.text(2005, 87, 'Men')
ax.text(2002, 8, 'Women')
elif sp == 5:
ax.text(2005, 62, 'Men')
ax.text(2001, 35, 'Women')
plt.show()
# -
# ## Comparing with all degree categories
# +
stem_cats = ['Engineering', 'Computer Science', 'Psychology', 'Biology', 'Physical Sciences', 'Math and Statistics']
lib_arts_cats = ['Foreign Languages', 'English', 'Communications and Journalism', 'Art and Performance', 'Social Sciences and History']
other_cats = ['Health Professions', 'Public Administration', 'Education', 'Agriculture','Business', 'Architecture']
# -
# +
fig = plt.figure(figsize= (16, 20))
#Generating the first column, the stem category degrees
for sp in range(0, 18,3):
cat_index = int(sp/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[cat_index]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[cat_index]], c=cb_orange, label='Men', linewidth=3)
for key, spines in ax.spines.items():
spines.set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0, 100)
ax.set_title(stem_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right = 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
#Generating the second column, the liberal art degrees
for sp in range(1,16, 3):
cat_index = int((sp-1)/3)
ax = fig.add_subplot(6, 3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[lib_arts_cats[cat_index]], c = cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[lib_arts_cats[cat_index]], c= cb_orange, label = 'Men', linewidth =3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968, 2011)
ax.set_title(lib_arts_cats[cat_index])
ax.tick_params(bottom='off', top = 'off', left ='off', right = 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
#Generating the third column, the other degrees
for sp in range(2, 20, 3):
cat_index = int((sp-2)/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[other_cats[cat_index]], c= cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[other_cats[cat_index]],c= cb_orange, label ='Men', linewidth = 3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968,2011)
ax.set_title(other_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right= 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
# -
# ## Hiding the x-axis labels
# +
#In this part of code, we are hidding the bottommost labels in order to avoid text overlapping
fig = plt.figure(figsize= (16, 20))
#Generating the first column, the stem category degrees
for sp in range(0, 18,3):
cat_index = int(sp/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[cat_index]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[cat_index]], c=cb_orange, label='Men', linewidth=3)
for key, spines in ax.spines.items():
spines.set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0, 100)
ax.set_title(stem_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right = 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the second column, the liberal art degrees
for sp in range(1,16, 3):
cat_index = int((sp-1)/3)
ax = fig.add_subplot(6, 3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[lib_arts_cats[cat_index]], c = cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[lib_arts_cats[cat_index]], c= cb_orange, label = 'Men', linewidth =3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968, 2011)
ax.set_title(lib_arts_cats[cat_index])
ax.tick_params(bottom='off', top = 'off', left ='off', right = 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the third column, the other degrees
for sp in range(2, 20, 3):
cat_index = int((sp-2)/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[other_cats[cat_index]], c= cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[other_cats[cat_index]],c= cb_orange, label ='Men', linewidth = 3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968,2011)
ax.set_title(other_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right= 'off')
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
# -
# ## Reducing the cluttering and simplify the y-axis
# +
fig = plt.figure(figsize= (16, 20))
#Generating the first column, the stem category degrees
for sp in range(0, 18,3):
cat_index = int(sp/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[cat_index]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[cat_index]], c=cb_orange, label='Men', linewidth=3)
for key, spines in ax.spines.items():
spines.set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0, 100)
ax.set_title(stem_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right = 'off')
ax.set_yticks([0,100])
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the second column, the liberal art degrees
for sp in range(1,16, 3):
cat_index = int((sp-1)/3)
ax = fig.add_subplot(6, 3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[lib_arts_cats[cat_index]], c = cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[lib_arts_cats[cat_index]], c= cb_orange, label = 'Men', linewidth =3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968, 2011)
ax.set_title(lib_arts_cats[cat_index])
ax.tick_params(bottom='off', top = 'off', left ='off', right = 'off')
ax.set_yticks([0,100])
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the third column, the other degrees
for sp in range(2, 20, 3):
cat_index = int((sp-2)/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[other_cats[cat_index]], c= cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[other_cats[cat_index]],c= cb_orange, label ='Men', linewidth = 3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968,2011)
ax.set_title(other_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right= 'off')
ax.set_yticks([0,100])
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
# -
# ## Generating a horizontal line
# +
fig = plt.figure(figsize= (16, 20))
#Generating the first column, the stem category degrees
for sp in range(0, 18,3):
cat_index = int(sp/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[cat_index]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[cat_index]], c=cb_orange, label='Men', linewidth=3)
for key, spines in ax.spines.items():
spines.set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0, 100)
ax.set_title(stem_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right = 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the second column, the liberal art degrees
for sp in range(1,16, 3):
cat_index = int((sp-1)/3)
ax = fig.add_subplot(6, 3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[lib_arts_cats[cat_index]], c = cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[lib_arts_cats[cat_index]], c= cb_orange, label = 'Men', linewidth =3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968, 2011)
ax.set_title(lib_arts_cats[cat_index])
ax.tick_params(bottom='off', top = 'off', left ='off', right = 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
#alpha is the transparency of the horizontal line, 50 is the y-axis position
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the third column, the other degrees
for sp in range(2, 20, 3):
cat_index = int((sp-2)/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[other_cats[cat_index]], c= cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[other_cats[cat_index]],c= cb_orange, label ='Men', linewidth = 3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968,2011)
ax.set_title(other_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right= 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
# -
# ## Save the plot
# +
fig = plt.figure(figsize= (16, 20))
#Generating the first column, the stem category degrees
for sp in range(0, 18,3):
cat_index = int(sp/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[stem_cats[cat_index]], c=cb_dark_blue, label='Women', linewidth=3)
ax.plot(women_degrees['Year'], 100-women_degrees[stem_cats[cat_index]], c=cb_orange, label='Men', linewidth=3)
for key, spines in ax.spines.items():
spines.set_visible(False)
ax.set_xlim(1968, 2011)
ax.set_ylim(0, 100)
ax.set_title(stem_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right = 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the second column, the liberal art degrees
for sp in range(1,16, 3):
cat_index = int((sp-1)/3)
ax = fig.add_subplot(6, 3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[lib_arts_cats[cat_index]], c = cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[lib_arts_cats[cat_index]], c= cb_orange, label = 'Men', linewidth =3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968, 2011)
ax.set_title(lib_arts_cats[cat_index])
ax.tick_params(bottom='off', top = 'off', left ='off', right = 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
#alpha is the transparency of the horizontal line, 50 is the y-axis position
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Generating the third column, the other degrees
for sp in range(2, 20, 3):
cat_index = int((sp-2)/3)
ax = fig.add_subplot(6,3, sp+1)
ax.plot(women_degrees['Year'], women_degrees[other_cats[cat_index]], c= cb_dark_blue, label = 'Women', linewidth =3)
ax.plot(women_degrees['Year'], 100-women_degrees[other_cats[cat_index]],c= cb_orange, label ='Men', linewidth = 3)
for key, spine in ax.spines.items():
spine.set_visible(False)
ax.set_ylim(0,100)
ax.set_xlim(1968,2011)
ax.set_title(other_cats[cat_index])
ax.tick_params(bottom = 'off', top = 'off', left = 'off', right= 'off')
ax.set_yticks([0,100])
ax.axhline(50,c=(171/255, 171/255, 171/255), alpha=0.3)
if cat_index == 0:
ax.text(2003, 85, 'Women')
ax.text(2005, 10, 'Men')
elif cat_index == 5:
ax.text(2005, 87, 'Men')
ax.text(2003, 7, 'Women')
ax.tick_params(labelbottom = 'on')
#Plot saving has to be done before the plt.show()
plt.savefig('gender_degrees.png')
plt.show()
|
Project 5: Visualizing The Gender Gap In College Degrees/Basics.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] colab_type="text" id="view-in-github"
# [](https://colab.research.google.com/github/davemlz/eemont/blob/master/docs/tutorials/002-Sentinel-2-Image-Collection-Scaling.ipynb)
# [](https://studiolab.sagemaker.aws/import/github/davemlz/eemont/blob/master/docs/tutorials/002-Sentinel-2-Image-Collection-Scaling.ipynb)
# [](https://pccompute.westeurope.cloudapp.azure.com/compute/hub/user-redirect/git-pull?repo=https://github.com/davemlz/eemont&urlpath=lab/tree/eemont/docs/tutorials/002-Sentinel-2-Image-Collection-Scaling.ipynb&branch=master)
# + [markdown] id="jZEthLln92Ep"
# # Scaling a Sentinel-2 Image Collection
# _Tutorial created by **<NAME>**_: [GitHub](https://github.com/davemlz) | [Twitter](https://twitter.com/dmlmont)
#
# - GitHub Repo: [https://github.com/davemlz/eemont](https://github.com/davemlz/eemont)
# - PyPI link: [https://pypi.org/project/eemont/](https://pypi.org/project/eemont/)
# - Conda-forge: [https://anaconda.org/conda-forge/eemont](https://anaconda.org/conda-forge/eemont)
# - Documentation: [https://eemont.readthedocs.io/](https://eemont.readthedocs.io/)
# - More tutorials: [https://github.com/davemlz/eemont/tree/master/docs/tutorials](https://github.com/davemlz/eemont/tree/master/docs/tutorials)
# + [markdown] id="CD7h0hbi92Er"
# ## Let's start!
# + [markdown] id="E0rc6Cya92Es"
# If required, please uncomment:
# + id="NYzyvKtk92Es"
# #!pip install eemont
# #!pip install geemap
# + [markdown] id="x3Rm3qt_92Et"
# Import the required packges.
# + id="H0C9S_Hh92Et"
import ee, eemont, geemap
# + [markdown] id="k1sdX2p592Eu"
# Authenticate and Initialize Earth Engine and geemap.
# + id="7QDXqVwy8Oef"
Map = geemap.Map()
# + [markdown] id="rhUlnVbq92Ey"
# Example point of interest to filter the image collection.
# + id="ctBHy0dx92Ey"
point = ee.Geometry.Point([-75.92, 2.86])
# + [markdown] id="FYguKZh892Ey"
# Get and filter the Sentinel-2 Surface Reflectance image collection and filter it by region and time.
# + id="sBmM9kZn92Ez"
S2 = (ee.ImageCollection('COPERNICUS/S2_SR')
.filterBounds(point)
.filterDate('2020-01-01','2021-01-01'))
# + [markdown] id="cQJMPJVS92Ez"
# ## Image Scaling
# As you might know, most images in Google Earth Engine are scaled in order to fit the int datatype. To get the original values, scalars must be multiplied. This scaling changes with bands, and for the supported platforms, all bands are scaled using the `scaleAndOffset()` method, that is an extended method provided by the `eemont` package.
# + id="d4aNNSuq92E0"
S2a = S2.scaleAndOffset()
# + [markdown] id="y-icVo8S8AY0"
# The `scaleAndOffset()` method does not require any additional argument, as it identifies the platform and scales the whole image collection.
# + [markdown] id="sOi-jAd_92E5"
# ## Visualization
# + [markdown] id="1JgG9LhO92E5"
# Set the visualization parameters.
# + id="ja17rT6g92E6"
rgbUnscaled = {'min':0, 'max':3000, 'bands':['B4','B3','B2']}
rgbScaled = {'min':0, 'max':0.3, 'bands':['B4','B3','B2']}
# + [markdown] id="dyccJWBu92E6"
# Use geemap to display results.
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} id="9ODWuQeb92E6" outputId="b585417e-ba56-480b-a6c7-2f5402a770f6"
Map.centerObject(point,10)
Map.addLayer(S2.first(),rgbUnscaled,'Unscaled RGB')
Map.addLayer(S2a.first(),rgbScaled,'Scaled RGB')
Map
|
docs/tutorials/002-Sentinel-2-Image-Collection-Scaling.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.7.4 64-bit (conda)
# metadata:
# interpreter:
# hash: b080221bbfcc22139d6f403b5aa156ef25a7f222d4aca0a73dd8f558f29b42b4
# name: python3
# ---
# 1. Import Libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as pyplot
import seaborn as sns
pd.options.display.max_columns = None
# 2. Get the data
cdc = pd.read_csv(r"C:\Users\sanjiv\Documents\Datasets\Kaggle\cdc\Nutrition__Physical_Activity__and_Obesity_-_Behavioral_Risk_Factor_Surveillance_System.csv")
cdc.head(1)
cdc.shape
cdc.columns
cdc.isnull().mean().sort_values(ascending=False) #> 0.25
cdc["ClassID"].value_counts()
|
Projects/CDC/CDC.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from rxntools.reaction import ChemicalReaction
from rxntools.template import ReactionTemplate
from rxntools.smiles import CombineMols
import rdkit.Chem.AllChem as Chem
# # Example 1
rs = 'Cl.[CH3:43][CH2:42][S:44](=[O:45])(=[O:46])Cl.[CH3:39][N:14]([C:15](=[O:16])[N:17]([CH3:18])[C@@H:19]1[CH2:20][N:21]([C:31](=[O:32])[CH:33]2[CH2:34][CH2:35][NH:36][CH2:37][CH2:38]2)[CH2:22][C@H:23]1[c:24]1[cH:25][cH:26][c:27]([F:30])[cH:28][cH:29]1)[c:6]1[cH:7][c:8]([C:10]([F:11])([F:12])[F:13])[cH:9][c:4]([C:3]([F:40])([F:41])[F:2])[cH:5]1>>[CH3:43][CH2:42][S:44](=[O:45])(=[O:46])[N:36]1[CH2:35][CH2:34][CH:33]([C:31](=[O:32])[N:21]2[CH2:22][C@@H:23]([c:24]3[cH:29][cH:28][c:27]([F:30])[cH:26][cH:25]3)[C@H:19]([N:17]([CH3:18])[C:15](=[O:16])[N:14]([CH3:39])[c:6]3[cH:7][c:8]([C:10]([F:12])([F:11])[F:13])[cH:9][c:4]([C:3]([F:40])([F:2])[F:41])[cH:5]3)[CH2:20]2)[CH2:38][CH2:37]1'
print(rs)
# load ChemicalReaction object from rxntools good smarts
cr = ChemicalReaction(rs)
good_smarts = cr.Smarts
cr = ChemicalReaction(good_smarts)
cr.Check()
cr.rxn
# chirality error when extract reaction template.
cr.ExtractTemplate()
# # Example 2
# The reaction with symmetric reactants, the same atom map number exists more than once is considered bad reaction smarts in rxntools.
rs = 'CCN(CC)CC.[CH3:16][C:15]([CH3:17])([CH3:18])[O:14][C:12](=[O:13])O[C:12](=[O:13])[O:14][C:15]([CH3:16])([CH3:17])[CH3:18].[NH2:11][CH2:10][CH2:9][n:6]1[cH:7][cH:8][c:4]([N+:1](=[O:2])[O-:3])[n:5]1>ClCCl>[CH3:16][C:15]([CH3:17])([CH3:18])[O:14][C:12](=[O:13])[NH:11][CH2:10][CH2:9][n:6]1[cH:7][cH:8][c:4]([N+:1](=[O:2])[O-:3])[n:5]1'
print(rs)
# load ChemicalReaction object from rxntools good smarts
cr = ChemicalReaction(rs)
good_smarts = cr.Smarts
cr = ChemicalReaction(good_smarts)
cr.Check()
Chem.Draw.MolToImage(cr.reactants[0], size=(300,300))
# # Example 3
# Absolute chirality changed. Example in Figure 1 of Rdchiral paper.
rs = '[CH3:1][CH2:2][O].[O:3][C:4](=[O:5])[C:6][C@H:7]([CH3:8])[CH2:9][C:10](=[O:11])[O:12][CH3:13]>>[CH3:1][CH2:2][O:3][C:4](=[O:5])[C:6][C@H:7]([CH3:8])[CH2:9][C:10](=[O:11])[O:12][CH3:13]'
print(rs)
# load ChemicalReaction object from rxntools good smarts
cr = ChemicalReaction(rs)
good_smarts = cr.Smarts
cr = ChemicalReaction(good_smarts)
cr.Check()
cr.rxn
Chem.MolFromSmiles(cr.reactants_SMILES)
Chem.MolFromSmiles(cr.products_SMILES)
# chirality error when extract reaction template.
cr.ExtractTemplate()
# # Example 4
# Chiral reaction template. Example in TOC figure of Rdchiral paper. The reaction smarts extracted directly get correct chirality when applying it to reactants.
rs = '[CH3:1][CH2:2][CH2:3][C@H:4]([CH3:5])[Br:6]>>[CH3:1][CH2:2][CH2:3][C@@H:4]([CH3:5])[I:6]'
print(rs)
# load ChemicalReaction object from rxntools good smarts
cr = ChemicalReaction(rs)
good_smarts = cr.Smarts
cr = ChemicalReaction(good_smarts)
cr.Check()
cr.rxn
Chem.MolFromSmiles(cr.reactants_SMILES)
Chem.MolFromSmiles(cr.products_SMILES)
# chirality error when extract reaction template.
cr.ExtractTemplate()
|
notebook/2. Examples of special chemical reaction smarts..ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.6 - AzureML
# language: python
# name: python3-azureml
# ---
# +
import os
import shutil
from azureml.core.workspace import Workspace
from azureml.core.environment import Environment
from azureml.core import Experiment, ScriptRunConfig
from azureml.train.estimator import Estimator
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
from azureml.train.dnn import PyTorch
from azureml.core.conda_dependencies import CondaDependencies
ws = Workspace.from_config()
# myenv = Environment.get(workspace=ws, name="AzureML-PyTorch-1.1-GPU")
pytenv = Environment(name="myenv")
# myenv.save_to_directory('pytenv', overwrite=False)
# -
# pytenv = Environment.load_from_directory('pytenv')
conda_dep = CondaDependencies().create(python_version='3.6')
conda_dep.add_pip_package("olefile==0.4.6") #add this first
# conda_dep.add_channel('deepchem')
# conda_dep.add_channel('omnia')
conda_dep.add_channel('conda-forge')
conda_dep.add_channel('rdkit')
# conda_dep.add_channel('pytorch')
# conda_dep.add_conda_package("deepchem-gpu=2.1.0")
# conda_dep.add_conda_package("astor")
conda_dep.add_conda_package("torchvision")
conda_dep.add_conda_package("pytorch")
conda_dep.add_conda_package("cudatoolkit=10.1")
conda_dep.add_pip_package("astor==0.8.1")
# conda_dep.add_conda_package("olefile==0.46")
pytenv.python.conda_dependencies=conda_dep
# +
from azureml.train.dnn import PyTorch
compute_target = "amlcompute"
script_params = {
'--num_epochs': 30,
'--output_dir': './outputs'}
estimator = PyTorch(source_directory=project_folder,
script_params=script_params,
compute_target=compute_target,
entry_script='pytorch_train.py',
use_gpu=True,
pip_packages=['pillow==5.4.1'])
# -
# +
project_folder = './train-main'
os.makedirs(project_folder, exist_ok=True)
experiment_name = 'synbio-train6'
experiment = Experiment(name=experiment_name,workspace = ws)
# -
runconfig = ScriptRunConfig(source_directory=project_folder, script="train.py")
runconfig.run_config.target = "gpu-compute"
runconfig.run_config.environment = pytenv
run = experiment.submit(config=runconfig)
run.wait_for_completion(show_output=True)
import PyTorch
from rdkit import Chem
|
synbiolic-azure-train/trainer.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# -
dataset = pd.read_csv('../datasets/cleveland.csv', header = None)
dataset.columns = ['age', 'sex', 'cp', 'trestbps', 'chol','fbs', 'restecg', 'thalach', 'exang', 'oldpeak',
'slope', 'ca', 'thal', 'target']
dataset.head()
# Find the empty value in a column
dataset.isnull().sum()
# Change the value target from 0, 1, 2, 3, 4 to 0 or 1. In other word simplify the dataset whether the patient have a heart disease or not
dataset['target'] = dataset['target'].map({0: 0, 1: 1, 2: 1, 3: 1, 4: 1})
# Fill the empty value in thal column with sum method
dataset['thal'] = dataset['thal'].fillna(dataset['thal'].mean())
# Fill the empty value in thal column with sum method
dataset['ca'] = dataset['ca'].fillna(dataset['ca'].mean())
# EDA
# Age
plt.figure(figsize = (16, 8))
sns.countplot(x = 'age', data = dataset, hue = 'target', palette = 'pastel')
# Gender
gender = dataset['sex'].map({0: 'female', 1: 'male'})
plt.figure(figsize = (16, 8))
sns.countplot(x = gender ,hue = dataset['target'], palette = 'pastel')
# <h3>Maximum Heart Rate vs Age</h3>
#
# From the scatter plot below, we can say that most of the patient age between 50 to 60 have a higher chance getting a CVD
# +
plt.figure(figsize = (16, 10))
sns.scatterplot(x = 'age', y = 'thalach', data = dataset, hue = 'target', palette = 'pastel', s = 95)
plt.ylabel('maximum heart rate')
# -
# Export Cleaned Dataset
dataset.to_csv('../datasets/cleaned_cleveland.csv', index = False)
# <h3>Data Pre-processing</h3>
# Split the dataset into train and test
from sklearn.model_selection import train_test_split
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 0)
# Apply standard scaler
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# Import KNN from SKLearn
from sklearn.neighbors import KNeighborsClassifier
# Finding the best K Value
# +
error_rate = []
for i in range(1,40):
knn = KNeighborsClassifier(n_neighbors = i)
knn.fit(X_train,y_train)
pred_i = knn.predict(X_test)
error_rate.append(np.mean(pred_i != y_test))
# -
plt.figure(figsize=(10,6))
plt.plot(range(1,40),error_rate,color = 'red', linestyle = 'dashed', marker = 'o', markersize = 10)
plt.xlabel('K Value')
plt.ylabel('Error Rate')
# Applying KNN to the dataset
classifier = KNeighborsClassifier(n_neighbors = 21)
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
# Accuracy of the prediction
from sklearn.metrics import classification_report, confusion_matrix
print(confusion_matrix(y_test, y_pred))
print(classification_report(y_test, y_pred))
# Decision Tree
#
from sklearn.tree import DecisionTreeClassifier
dtree = DecisionTreeClassifier()
dtree.fit(X_train, y_train)
from IPython.display import Image
from sklearn import tree
import pydotplus
features = list(dataset.drop('target', axis = 1))
features
dot_data = tree.export_graphviz(dtree, out_file = None, feature_names = features)
graph = pydotplus.graph_from_dot_data(dot_data)
Image(graph.create_png())
|
classification/.ipynb_checkpoints/Exploratory Data Analysis-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
from IPython.display import Image
# # CNTK 106: Part A - Time series prediction with LSTM (Basics)
#
# This tutorial demonstrates how to use CNTK to predict future values in a time series using LSTMs.
#
# **Goal**
#
# We use simulated data set of a continuous function (in our case a [sine wave](https://en.wikipedia.org/wiki/Sine)). From `N` previous values of the $y = sin(t)$ function where $y$ is the observed amplitude signal at time $t$, we will predict `M` values of $y$ for the corresponding future time points.
# Figure 1
Image(url="http://www.cntk.ai/jup/sinewave.jpg")
# In this tutorial we will use [LSTM](https://en.wikipedia.org/wiki/Long_short-term_memory) to implement our model. LSTMs are well suited for this task because their ability to learn from experience. For details on how LSTMs work, see [this excellent post](http://colah.github.io/posts/2015-08-Understanding-LSTMs).
#
# In this tutorial we will have following sub-sections:
# - Simulated data generation
# - LSTM network modeling
# - Model training and evaluation
#
# This model works for lots real world data. In part A of this tutorial we use a simple sin(x) function and in part B of the tutorial (currently in development) we will use real data from IOT device and try to predict daily output of solar panel.
# Using CNTK we can easily express our model:
# +
import math
from matplotlib import pyplot as plt
import numpy as np
import os
import pandas as pd
import time
import cntk as C
import cntk.axis
from cntk.layers import Dense, Dropout, Recurrence
# %matplotlib inline
# -
# ### Select the notebook runtime environment devices / settings
#
# Set the device to cpu / gpu for the test environment. If you have both CPU and GPU on your machine, you can optionally switch the devices. By default we choose the best available device.
# Select the right target device when this notebook is being tested:
if 'TEST_DEVICE' in os.environ:
import cntk
if os.environ['TEST_DEVICE'] == 'cpu':
C.device.try_set_default_device(C.device.cpu())
else:
C.device.try_set_default_device(C.device.gpu(0))
# There are two run modes:
# - *Fast mode*: `isFast` is set to `True`. This is the default mode for the notebooks, which means we train for fewer iterations or train / test on limited data. This ensures functional correctness of the notebook though the models produced are far from what a completed training would produce.
#
# - *Slow mode*: We recommend the user to set this flag to `False` once the user has gained familiarity with the notebook content and wants to gain insight from running the notebooks for a longer period with different parameters for training.
isFast = True
# ## Data generation
#
# We need a few helper methods to generate the simulated sine wave data. Let `N` and `M` be a ordered set of past values and future (desired predicted values) of the sine wave, respectively.
#
# - **`generate_data()`**
#
# > In this tutorial, we sample `N` consecutive values of the `sin` function as the input to the model and try to predict future values that is `M` steps away from the last observed value in the input model. We generate multiple such instances of the input signal (by sampling from `sin` function) each of size `N` and the corresponding desired output as our training data. Assuming $k$ = batch size, `generate_data` function produces the $X$ and corresponding $L$ data and returns numpy arrays of the following shape:
#
# > The input set ($X$) to the lstm: $$ X = [\{y_{11}, y_{12}, \cdots , y_{1N}\},
# \{y_{21}, y_{22}, \cdots, y_{2N}\}, \cdots,
# \{y_{k1}, y_{k2}, \cdots, y_{kN}\}]
# $$
# > In the above samples $y_{i,j}$, represents the observed function value for the $i^{th}$ batch and $j^{th}$ time point within the time window of $N$ points.
#
# The desired output ($L$) with `M` steps in the future: $$ L = [ \{y_{1,N+M}\},
# \{y_{2,N+M}\}, \cdots, \{y_{k,N+M}\}]$$
#
# > Note: `k` is a function of the length of the time series and the number of windows of size `N` one can have for the time series.
#
# - **`split_data()`**
#
# > As the name suggests, `split_data` function will split the data into training, validation and test sets.
def split_data(data, val_size=0.1, test_size=0.1):
"""
splits np.array into training, validation and test
"""
pos_test = int(len(data) * (1 - test_size))
pos_val = int(len(data[:pos_test]) * (1 - val_size))
train, val, test = data[:pos_val], data[pos_val:pos_test], data[pos_test:]
return {"train": train, "val": val, "test": test}
def generate_data(fct, x, time_steps, time_shift):
"""
generate sequences to feed to rnn for fct(x)
"""
data = fct(x)
if not isinstance(data, pd.DataFrame):
data = pd.DataFrame(dict(a = data[0:len(data) - time_shift],
b = data[time_shift:]))
rnn_x = []
for i in range(len(data) - time_steps):
rnn_x.append(data['a'].iloc[i: i + time_steps].as_matrix())
rnn_x = np.array(rnn_x)
# Reshape or rearrange the data from row to columns
# to be compatible with the input needed by the LSTM model
# which expects 1 float per time point in a given batch
rnn_x = rnn_x.reshape(rnn_x.shape + (1,))
rnn_y = data['b'].values
# Reshape or rearrange the data from row to columns
# to match the input shape
rnn_y = rnn_y.reshape(rnn_y.shape + (1,))
return split_data(rnn_x), split_data(rnn_y)
# Let us generate and visualize the generated data
# +
N = 5 # input: N subsequent values
M = 5 # output: predict 1 value M steps ahead
X, Y = generate_data(np.sin, np.linspace(0, 100, 10000, dtype=np.float32), N, M)
f, a = plt.subplots(3, 1, figsize=(12, 8))
for j, ds in enumerate(["train", "val", "test"]):
a[j].plot(Y[ds], label=ds + ' raw');
[i.legend() for i in a];
# -
# ## Network modeling
#
# We setup our network with 1 LSTM cell for each input. We have N inputs and each input is a value in our continues function. The N outputs from the LSTM are the input into a dense layer that produces a single output.
# Between LSTM and dense layer we insert a dropout layer that randomly drops 20% of the values coming the LSTM to prevent overfitting the model to the training dataset. We want use use the dropout layer during training but when using the model to make predictions we don't want to drop values.
# 
def create_model(x):
"""Create the model for time series prediction"""
with C.layers.default_options(initial_state = 0.1):
m = C.layers.Recurrence(C.layers.LSTM(N))(x)
m = C.ops.sequence.last(m)
m = C.layers.Dropout(0.2)(m)
m = cntk.layers.Dense(1)(m)
return m
# ## Training the network
# We define the `next_batch()` iterator that produces batches we can feed to the training function.
# Note that because CNTK supports variable sequence length, we must feed the batches as list of sequences. This is a convenience function to generate small batches of data often referred to as minibatch.
def next_batch(x, y, ds):
"""get the next batch to process"""
def as_batch(data, start, count):
part = []
for i in range(start, start + count):
part.append(data[i])
return np.array(part)
for i in range(0, len(x[ds])-BATCH_SIZE, BATCH_SIZE):
yield as_batch(x[ds], i, BATCH_SIZE), as_batch(y[ds], i, BATCH_SIZE)
# Setup everything else we need for training the model: define user specified training parameters, define inputs, outputs, model and the optimizer.
# +
# Training parameters
TRAINING_STEPS = 10000
BATCH_SIZE = 100
EPOCHS = 20 if isFast else 100
# -
# **Key Insight**
#
# There are some key learnings when [working with sequences](https://www.cntk.ai/pythondocs/sequence.html) in LSTM networks. A brief recap:
#
# CNTK inputs, outputs and parameters are organized as tensors. Each tensor has a rank: A scalar is a tensor of rank 0, a vector is a tensor of rank 1, a matrix is a tensor of rank 2, and so on. We refer to these different dimensions as axes.
#
# Every CNTK tensor has some static axes and some dynamic axes. The static axes have the same length throughout the life of the network. The dynamic axes are like static axes in that they define a meaningful grouping of the numbers contained in the tensor but:
# - their length can vary from instance to instance,
# - their length is typically not known before each minibatch is presented, and
# - they may be ordered.
#
# In CNTK the axis over which you run a recurrence is dynamic and thus its dimensions are unknown at the time you define your variable. Thus the input variable only lists the shapes of the static axes. Since our inputs are a sequence of one dimensional numbers we specify the input as
#
# > `C.sequence.input(1)`
#
# The `N` instances of the observed `sin` function output and the corresponding batch are implicitly represented in the dynamic axis as shown below in the form of defaults.
#
# > ```
# x_axes = [C.Axis.default_batch_axis(), C.Axis.default_dynamic_axis()]
# C.input(1, dynamic_axes=x_axes)
# ```
# The reader should be aware of the meaning of the default parameters. Specifiying the dynamic axes enables the recurrence engine handle the time sequence data in the expected order. Please take time to understand how to work with both static and dynamic axes in CNTK as described [here](https://www.cntk.ai/pythondocs/sequence.html).
# +
# input sequences
x = C.sequence.input(1)
# create the model
z = create_model(x)
# expected output (label), also the dynamic axes of the model output
# is specified as the model of the label input
l = C.input(1, dynamic_axes=z.dynamic_axes, name="y")
# the learning rate
learning_rate = 0.001
lr_schedule = C.learning_rate_schedule(learning_rate, C.UnitType.minibatch)
# loss function
loss = C.squared_error(z, l)
# use squared error to determine error for now
error = C.squared_error(z, l)
# use adam optimizer
momentum_time_constant = C.momentum_as_time_constant_schedule(BATCH_SIZE / -math.log(0.9))
learner = C.fsadagrad(z.parameters,
lr = lr_schedule,
momentum = momentum_time_constant,
unit_gain = True)
trainer = C.Trainer(z, (loss, error), [learner])
# -
# We are ready to train. 100 epochs should yield acceptable results.
# +
# train
loss_summary = []
start = time.time()
for epoch in range(0, EPOCHS):
for x1, y1 in next_batch(X, Y, "train"):
trainer.train_minibatch({x: x1, l: y1})
if epoch % (EPOCHS / 10) == 0:
training_loss = trainer.previous_minibatch_loss_average
loss_summary.append(training_loss)
print("epoch: {}, loss: {:.5f}".format(epoch, training_loss))
print("training took {0:.1f} sec".format(time.time() - start))
# -
# A look how the loss function shows how well the model is converging
plt.plot(loss_summary, label='training loss');
# Normally we would validate the training on the data that we set aside for validation but since the input data is small we can run validattion on all parts of the dataset.
# validate
def get_mse(X,Y,labeltxt):
result = 0.0
for x1, y1 in next_batch(X, Y, labeltxt):
eval_error = trainer.test_minibatch({x : x1, l : y1})
result += eval_error
return result/len(X[labeltxt])
# Print the train and validation errors
for labeltxt in ["train", "val"]:
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
# Print validate and test error
labeltxt = "test"
print("mse for {}: {:.6f}".format(labeltxt, get_mse(X, Y, labeltxt)))
# Since we used a simple sin(x) function we should expect that the errors are the same for train, validation and test sets. For real datasets that will be different of course. We also plot the expected output (Y) and the prediction our model made to shows how well the simple LSTM approach worked.
# predict
f, a = plt.subplots(3, 1, figsize = (12, 8))
for j, ds in enumerate(["train", "val", "test"]):
results = []
for x1, y1 in next_batch(X, Y, ds):
pred = z.eval({x: x1})
results.extend(pred[:, 0])
a[j].plot(Y[ds], label = ds + ' raw');
a[j].plot(results, label = ds + ' predicted');
[i.legend() for i in a];
# Not perfect but close enough, considering the simplicity of the model.
#
# Here we used a simple sin wave but you can tinker yourself and try other time series data. `generate_data()` allows you to pass in a dataframe with 'a' and 'b' columns instead of a function.
#
# To improve results, we could train with more data points, let the model train for more epochs or improve on the model itself.
|
Tutorials/CNTK_106A_LSTM_Timeseries_with_Simulated_Data.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import random
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import typing as T
import re
import numpy as np
from dataclasses import dataclass
from shared import bootstrap_accuracy, bootstrap_auc, dataset_local_path, simple_boxplot
RAND = 123456
random.seed(RAND)
# Using 'pandas' to load data now:
df: pd.DataFrame = pd.read_json(
dataset_local_path("lit-wiki-2020.jsonl.gz"), lines=True
)
# +
# Regular expresssions to grab parts of the text:
WORDS = re.compile(r"(\w+)")
NUMBERS = re.compile(r"(\d+)")
def extract_features(row):
"""
Given the title and body of a Wikipedia article,
extract features that might be of use to the 'is literary' task.
Return named features in a dictionary.
"""
title = row["title"].lower()
body = row["body"]
new_features: T.Dict[str, T.Any] = {}
words = WORDS.findall(body)
numbers = [int(x) for x in NUMBERS.findall(body)]
new_features = {
"disambig": "disambiguation" in title,
"page_rank": row["page_rank"],
"length": len(words),
# "18xx": sum(1 for x in numbers if 1800 < x <= 1900),
"list_of": title.startswith('list of'),
}
if len(numbers) > 0:
new_features["mean_n"] = np.mean(numbers)
new_features["std_n"] = np.std(numbers)
return new_features
# right now each entry of the dataframe is a dictionary; json_normalize flattenst hat for us.
designed_f = pd.json_normalize(df.apply(extract_features, axis="columns"))
# -
print(designed_f.loc[11])
for i in range(len(df['title'])):
if 'List of' in df['title'][i]:
print(i)
|
Untitled1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 35
# language: python
# name: python35
# ---
# +
""" Convert hyde asc rasters to geotiff
-------------------------------------------------------------------------------
Author: <NAME>
Date: 20190722
Kernel: python35
Docker: rutgerhofste/gisdocker:ubuntu16.04
"""
SCRIPT_NAME = "Y2019M07D22_RH_Hyde_Convert_Geotiff_V01"
OUTPUT_VERSION = 1
S3_INPUT_PATH = "s3://wri-projects/Aqueduct30/rawData/Hyde/hyde3.2/baseline/unzipped/"
ec2_input_path = "/volumes/data/{}/input_V{:02.0f}/".format(SCRIPT_NAME,OUTPUT_VERSION)
ec2_output_path = "/volumes/data/{}/output_V{:02.0f}/".format(SCRIPT_NAME,OUTPUT_VERSION)
s3_output_path = "s3://wri-projects/Aqueduct30/processData/{}/output_V{:02.0f}/".format(SCRIPT_NAME,OUTPUT_VERSION)
gcs_output_path = "gs://aqueduct30_v01/{}/output_V{:02.0f}/".format(SCRIPT_NAME,OUTPUT_VERSION)
print(gcs_output_path,s3_output_path)
# -
import time, datetime, sys
dateString = time.strftime("Y%YM%mD%d")
timeString = time.strftime("UTC %H:%M")
start = datetime.datetime.now()
print(dateString,timeString)
sys.version
# +
# #!rm -r {ec2_input_path}
# !rm -r {ec2_output_path}
# !mkdir -p {ec2_input_path}
# !mkdir -p {ec2_output_path}
# -
import os
import rasterio
from tqdm import tqdm
# !aws s3 sync {S3_INPUT_PATH} {ec2_input_path}
paths = []
for root, dirs, files in os.walk(ec2_input_path):
for file in files:
if file.endswith(".asc"):
paths.append(os.path.join(root, file))
def raster_to_geotiff(src_path,dst_path):
""" Opens a rasterio single band raster and
converts to LZW compressed geotiff.
dType and projection are preserved.
Args:
src_path(string): input file path.
dst_path(string): output file path.
"""
with rasterio.open(src_path) as src:
profile = src.profile
profile.update(nodata=-9999,
compress='lzw')
if src.crs is None:
crs = rasterio.crs.CRS.from_dict(init='epsg:4326')
else:
crs = src.crs
with rasterio.open(
dst_path,
'w',
driver='GTiff',
height=src.height,
width=src.width,
count=1,
dtype=src.dtypes[0],
crs=crs,
nodata = src.nodata,
transform=src.transform,
) as dst:
dst.write(src.read(1), 1)
return dst_path
for path in tqdm(paths):
input_filename = path.split("/")[-1]
base_filename, input_extension = input_filename.split(".")
output_filename = base_filename + ".tif"
output_path = ec2_output_path + output_filename
raster_to_geotiff(path,output_path)
# !gsutil -m cp -r \
# {ec2_output_path} \
# {gcs_output_path}
# !aws s3 cp --recursive {ec2_output_path} {s3_output_path}
end = datetime.datetime.now()
elapsed = end - start
print(elapsed)
|
scripts/Y2019M07D22_RH_Hyde_Convert_Geotiff_V01.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Shows a significant performance difference between in-memory and persistent caches, but profiling shows that the time is actually absorbed by expanding expressions???
# Must be related to ordering...
# +
from datetime import datetime
import json
import logging
logging.basicConfig(level=logging.INFO)
import pandas as pd
from split_query.core import default
from split_query.decorators import (
dataset, cache_persistent, cache_inmemory,
remote_parameters, range_parameter, tag_parameter)
@dataset(
name='Mock',
attributes=['datetime', 'hourly_count', 'sensor'])
# @cache_inmemory()
@cache_persistent('benchmark')
@remote_parameters(
range_parameter(
'datetime', key_lower='from_dt', key_upper='to_dt',
round_down=lambda dt: datetime(dt.year, 1, 1, 0, 0, 0),
offset=lambda dt: datetime(dt.year + 1, 1, 1, 0, 0, 0)),
tag_parameter('sensor', single=True))
class Dataset(object):
''' This docstring will be displayed in the dataset object repr. '''
def get(self, from_dt, to_dt, sensor):
assert from_dt == datetime(from_dt.year, 1, 1, 0, 0, 0)
assert to_dt == datetime(from_dt.year + 1, 1, 1, 0, 0, 0)
where = '(sensor = {}) and (year = {})'.format(sensor, from_dt.year)
logging.info('QUERY: {}'.format(where))
return pd.DataFrame(dict(
datetime=pd.date_range(from_dt, to_dt),
sensor=sensor, hourly_count=1))
# +
dataset = Dataset()
dataset.clear_cache()
for start_year in [2017, 2015, 2014, 2013, 2012]:
logging.info('START {}'.format(start_year))
logging.info('RESULT\n' + repr(dataset[
dataset.datetime.between(datetime(start_year, 2, 3), datetime(2017, 10, 3)) &
dataset.sensor.isin(['Town Hall (West)', 'Southbank'])].get(
).groupby('sensor').datetime.agg(['min', 'max', 'count'])))
# -
def run(start_year):
''' This is a good follow up query to test performance once a complicated
cache structure has been built up. Make sure caching of algorithm results
is disabled. '''
return dataset[
dataset.datetime.between(datetime(start_year, 2, 3), datetime(2017, 10, 3)) &
dataset.sensor.isin(['Town Hall (West)', 'Southbank'])].get(
).groupby('sensor').datetime.agg(['min', 'max', 'count'])
run(2012)
with open('path_persistent.json', 'w') as outfile:
json.dump(dataset.backend.tracking, outfile, default=default)
|
benchmarks/cache_performance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#import modules
import SimpleITK as sitk
from platipy.imaging.visualisation.tools import ImageVisualiser
from platipy.imaging.utils.tools import get_com
import matplotlib.pyplot as plt
import numpy as np
# %matplotlib notebook
from platipy.imaging.visualisation.tools import ImageVisualiser
from platipy.imaging.registration.registration import (
initial_registration,
fast_symmetric_forces_demons_registration,
transform_propagation,
apply_field
)
# +
#breast=sitk.ReadImage("/home/alicja/Downloads/Segmentation.nii.gz") #right breast
breast=sitk.ReadImage("contralateral_segmentation.nii.gz")
pat_no="14"
timept="5"
filenameB50T_1="WES_014_5_20190121_MR_RESOLVE_DIFF_TRA_SPAIR_P2_RE_B50T_RESOLVE_DIFF_TRA_SPAIR_P2_TRACEW_6.nii.gz"
filenameB800T_1="WES_014_5_20190121_MR_RESOLVE_DIFF_TRA_SPAIR_P2_RE_B800T_RESOLVE_DIFF_TRA_SPAIR_P2_TRACEW_6.nii.gz"
filenameT2w_1="WES_014_5_20190121_MR_T2_TSE_TRA_SPAIR_TSE2D1_11_T2_TSE_TRA_SPAIR_3.nii.gz"
filenameMPE_1="max_img_WES_0" +pat_no+"_"+timept+".nii.gz"
WES_1_B50T=sitk.ReadImage("/home/alicja/Documents/WES_0" + pat_no + "/IMAGES/" +filenameB50T_1)
WES_1_B800T=sitk.ReadImage("/home/alicja/Documents/WES_0" + pat_no + "/IMAGES/" +filenameB800T_1)
WES_1_T2w=sitk.ReadImage("/home/alicja/Documents/WES_0" + pat_no + "/IMAGES/" +filenameT2w_1)
WES_1_MPE=sitk.ReadImage(filenameMPE_1)
WES_010_4_B50T=sitk.ReadImage("/home/alicja/Documents/WES_010/IMAGES/WES_010_4_20180829_MR_EP2D_DIFF_TRA_SPAIR_ZOOMIT_EZ_B50T_EP2D_DIFF_TRA_SPAIR_ZOOMIT_TRACEW_DFC_MIX_5.nii.gz")
# +
image_to_0_rigid, tfm_to_0_rigid = initial_registration(
WES_1_B50T,
WES_010_4_B50T,
options={
'shrink_factors': [8,4],
'smooth_sigmas': [0,0],
'sampling_rate': 0.5,
'final_interp': 2,
'metric': 'mean_squares',
'optimiser': 'gradient_descent_line_search',
'number_of_iterations': 25},
reg_method='Rigid')
image_to_0_dir, tfm_to_0_dir = fast_symmetric_forces_demons_registration(
WES_1_B50T,
image_to_0_rigid,
resolution_staging=[4,2],
iteration_staging=[10,10]
)
breast_to_0_rigid = transform_propagation(
WES_1_B50T,
breast,
tfm_to_0_rigid,
structure=True
)
breast_to_0_dir = apply_field(
breast_to_0_rigid,
tfm_to_0_dir,
structure=True
)
# -
vis = ImageVisualiser(WES_1_B50T, axis='z', cut=get_com(breast_to_0_dir), window=[0, 500])
vis.add_contour(breast_to_0_dir, name='BREAST', color='g')
fig = vis.show()
breast_contour_dilate=sitk.BinaryDilate(breast_to_0_dir, (2,2,2))
vis = ImageVisualiser(WES_1_B50T, axis='z', cut=get_com(breast_to_0_dir), window=[0, 500])
vis.add_contour(breast_contour_dilate, name='BREAST', color='g')
fig = vis.show()
masked_breast = sitk.Mask(WES_1_B50T, breast_contour_dilate)
# +
values = sitk.GetArrayViewFromImage(masked_breast).flatten()
fig, ax = plt.subplots(1,1)
ax.hist(values, bins=np.linspace(1,1500,50), histtype='stepfilled', lw=2)
ax.grid()
ax.set_axisbelow(True)
ax.set_xlabel('Intensity')
ax.set_ylabel('Frequency')
fig.show()
# -
def estimate_tumour_vol(img_mri, lowerthreshold=300, upperthreshold=5000, hole_size=1):
label_threshold = sitk.BinaryThreshold(img_mri, lowerThreshold=lowerthreshold, upperThreshold=upperthreshold)
label_threshold_cc = sitk.RelabelComponent(sitk.ConnectedComponent(label_threshold))
label_threshold_cc_x = (label_threshold_cc==1)
label_threshold_cc_x_f = sitk.BinaryMorphologicalClosing(label_threshold_cc_x, (hole_size,hole_size,hole_size))
return(label_threshold_cc_x_f)
# +
image_mri=WES_1_B50T
arr_mri = sitk.GetArrayFromImage(image_mri)
arr_mri[:,:,:arr_mri.shape[2]//2] = 0 #if laterality is L
image_mri_masked=sitk.GetImageFromArray(arr_mri)
image_mri_masked.CopyInformation(image_mri)
label_threshold_cc_x_f=estimate_tumour_vol(image_mri_masked, lowerthreshold=820, upperthreshold=5000, hole_size=1)
sitk.WriteImage(label_threshold_cc_x_f,"test_label_threshold_0" + pat_no + "_" +timept +"_B50T_hist.nii.gz")
# +
masked_breast = sitk.Mask(WES_1_B800T, breast_contour_dilate)
values = sitk.GetArrayViewFromImage(masked_breast).flatten()
fig, ax = plt.subplots(1,1)
ax.hist(values, bins=np.linspace(1,950,50), histtype='stepfilled', lw=2)
ax.grid()
ax.set_axisbelow(True)
ax.set_xlabel('Intensity')
ax.set_ylabel('Frequency')
fig.show()
# +
image_mri=WES_1_B800T
arr_mri = sitk.GetArrayFromImage(image_mri)
arr_mri[:,:,:arr_mri.shape[2]//2] = 0 #if lat is L
arr_mri[:,(arr_mri.shape[1]//3)*2-20:,:]=0
arr_mri[:,:,230:]=0
image_mri_masked=sitk.GetImageFromArray(arr_mri)
image_mri_masked.CopyInformation(image_mri)
label_threshold_cc_x_f=estimate_tumour_vol(image_mri_masked, lowerthreshold=540, upperthreshold=5000, hole_size=1)
sitk.WriteImage(label_threshold_cc_x_f,"test_label_threshold_0" + pat_no + "_" +timept +"_B800T_hist.nii.gz")
# +
WES_1_T2w=sitk.Resample(WES_1_T2w,WES_1_B50T)
masked_breast = sitk.Mask(WES_1_T2w, breast_contour_dilate)
values = sitk.GetArrayViewFromImage(masked_breast).flatten()
fig, ax = plt.subplots(1,1)
ax.hist(values, bins=np.linspace(1,350,50), histtype='stepfilled', lw=2)
ax.grid()
ax.set_axisbelow(True)
ax.set_xlabel('Intensity')
ax.set_ylabel('Frequency')
fig.show()
# +
image_mri=WES_1_T2w
arr_mri = sitk.GetArrayFromImage(image_mri)
arr_mri[:,:,:arr_mri.shape[2]//2] = 0 #if lat is L
arr_mri[20:,:,:]=0
image_mri_masked=sitk.GetImageFromArray(arr_mri)
image_mri_masked.CopyInformation(image_mri)
label_threshold_cc_x_f=estimate_tumour_vol(image_mri_masked, lowerthreshold=235, upperthreshold=5000, hole_size=1)
sitk.WriteImage(label_threshold_cc_x_f,"test_label_threshold_0" + pat_no + "_" +timept +"_T2w_hist.nii.gz")
# +
WES_1_MPE=sitk.Resample(WES_1_MPE,WES_1_B50T)
masked_breast = sitk.Mask(WES_1_MPE, breast_contour_dilate)
values = sitk.GetArrayViewFromImage(masked_breast).flatten()
fig, ax = plt.subplots(1,1)
ax.hist(values, bins=np.linspace(1,350,50), histtype='stepfilled', lw=2)
ax.grid()
ax.set_axisbelow(True)
ax.set_xlabel('Intensity')
ax.set_ylabel('Frequency')
fig.show()
# +
image_mri=WES_1_MPE
arr_mri = sitk.GetArrayFromImage(image_mri)
arr_mri[:,:,:arr_mri.shape[2]//2] = 0 #if lat is L
arr_mri[:,:,:182] = 0
arr_mri[:,:,232:]=0
image_mri_masked=sitk.GetImageFromArray(arr_mri)
image_mri_masked.CopyInformation(image_mri)
label_threshold_cc_x_f=estimate_tumour_vol(image_mri_masked, lowerthreshold=160, upperthreshold=5000, hole_size=1)
sitk.WriteImage(label_threshold_cc_x_f,"test_label_threshold_0" + pat_no + "_" +timept +"_MPE_hist.nii.gz")
# +
#add segs
seg_B50T=sitk.ReadImage("test_label_threshold_0" + pat_no + "_" +timept +"_B50T_hist.nii.gz")
seg_B800T=sitk.ReadImage("test_label_threshold_0" + pat_no + "_" +timept +"_B800T_hist.nii.gz")
seg_T2=sitk.ReadImage("test_label_threshold_0" + pat_no + "_" +timept +"_T2w_hist.nii.gz")
seg_MPE=sitk.ReadImage("test_label_threshold_0" + pat_no + "_" +timept +"_MPE_hist.nii.gz")
seg_B50T=sitk.Resample(seg_B50T,seg_T2)
seg_B800T=sitk.Resample(seg_B800T,seg_T2)
seg_MPE=sitk.Resample(seg_MPE,seg_T2)
new_seg_T2=sitk.LabelMapToBinary(sitk.Cast(seg_T2, sitk.sitkLabelUInt8))
new_seg_B50T=sitk.LabelMapToBinary(sitk.Cast(seg_B50T, sitk.sitkLabelUInt8))
new_seg_B800T=sitk.LabelMapToBinary(sitk.Cast(seg_B800T, sitk.sitkLabelUInt8))
new_seg_MPE=sitk.LabelMapToBinary(sitk.Cast(seg_MPE, sitk.sitkLabelUInt8))
new_TRACE_seg=(new_seg_B50T+new_seg_B800T)/2
new_seg_1=(sitk.Cast(new_seg_T2,sitk.sitkFloat64)+sitk.Cast(new_TRACE_seg,sitk.sitkFloat64)+sitk.Cast(new_seg_MPE,sitk.sitkFloat64))
vis=ImageVisualiser(new_seg_1, cut=get_com(new_seg_1), window=[0,3])
fig=vis.show()
# +
new_seg_1_1=sitk.BinaryThreshold(new_seg_1, lowerThreshold=2)
vis=ImageVisualiser(new_seg_1_1, cut=get_com(new_seg_1), window=[0,1])
fig=vis.show()
# -
sitk.WriteImage(new_seg_1_1,"new_seg_0"+pat_no+"_"+timept+"_mri.nii.gz")
# +
#Checking for volume decrease
tp1="4"
tp2="5"
#tp3=
#volumes
img1=sitk.ReadImage("new_seg_0"+pat_no+"_"+tp1+"_mri.nii.gz")
img2=sitk.ReadImage("new_seg_0"+pat_no+"_"+tp2+"_mri.nii.gz")
#img3=sitk.ReadImage("new_seg_0"+pat_no+"_"+tp3+"_mri.nii.gz")
arr1=sitk.GetArrayFromImage(img1)
arr2=sitk.GetArrayFromImage(img2)
#arr3=sitk.GetArrayFromImage(img3)
vol1=np.sum(arr1==1)
vol2=np.sum(arr2==1)
#vol3=np.sum(arr3==1)
print(vol1, vol2) #, vol3)
# -
|
Old MRI segmentation code/Hist-seg-WES_014_5.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] papermill={} tags=[]
# <img width="10%" alt="Naas" src="https://landen.imgix.net/jtci2pxwjczr/assets/5ice39g4.png?w=160"/>
# + [markdown] papermill={} tags=[]
# # Plaid - Get transactions
# <a href="https://app.naas.ai/user-redirect/naas/downloader?url=https://raw.githubusercontent.com/jupyter-naas/awesome-notebooks/master/Plaid/Plaid_Get_transactions.ipynb" target="_parent"><img src="https://naasai-public.s3.eu-west-3.amazonaws.com/open_in_naas.svg"/></a>
# + [markdown] papermill={} tags=[]
# **Tags:** #plaid #bank #transactions #snippet #finance #dataframe
# + [markdown] papermill={} tags=["naas"]
# **Author:** [<NAME>](https://www.linkedin.com/in/martindonadieu/)
# + [markdown] papermill={} tags=[]
# ## Input
# + [markdown] papermill={} tags=[]
# ### Install packages
# + papermill={} tags=[]
pip install plaid-python
# + [markdown] papermill={} tags=[]
# ### Create account here :
# https://plaid.com/
#
#
# + [markdown] papermill={} tags=[]
# ### Import libraries
# + papermill={} tags=[]
import os
import plaid
import naas
import IPython.core.display
import uuid
import json
# + [markdown] papermill={} tags=[]
# ### Config your variables
# + papermill={} tags=[]
PLAID_CLIENT_ID = "*************"
PLAID_SECRET = "*************"
PLAID_ENV = 'sandbox'
PLAID_PRODUCTS = ['transactions']
PLAID_COUNTRY_CODES = ['FR']
start_transaction = "2020-09-01"
end_transaction = "2020-10-01"
# + [markdown] papermill={} tags=[]
# ## Model
# + [markdown] papermill={} tags=[]
# ### Connect to plaid
# + papermill={} tags=[]
client = plaid.Client(client_id=PLAID_CLIENT_ID,
secret=PLAID_SECRET,
environment=PLAID_ENV)
# + papermill={} tags=[]
def create_link_token():
response = client.LinkToken.create(
{
'user': {
# This should correspond to a unique id for the current user.
'client_user_id': 'user-id',
},
'client_name': "Plaid Quickstart",
'products': PLAID_PRODUCTS,
'country_codes': PLAID_COUNTRY_CODES,
'language': "en",
'redirect_uri': None,
}
)
return response
# + papermill={} tags=[]
token = create_link_token()
token
# + [markdown] papermill={} tags=[]
# ### Use Naas callback to get the plaid OAuth token
# + papermill={} tags=[]
cb_url = naas.callback.add()
# + [markdown] papermill={} tags=[]
# ### Select Bank connection
# + papermill={} tags=[]
uid = uuid.uuid4().hex
iframe = """
<head>
<script src="https://cdn.plaid.com/link/v2/stable/link-initialize.js"></script>
</head>
<script>
const handler_{uid} = Plaid.create({
token: '{GENERATED_LINK_TOKEN}',
onSuccess: (public_token, metadata) => {
const xhr = new XMLHttpRequest();
xhr.open("POST", "{CALLBACK_URL}", true);
xhr.setRequestHeader('Content-Type', 'application/json');
xhr.send(JSON.stringify({
public_token: public_token
}));
}
});
handler_{uid}.open();
</script>
"""
iframe = iframe.replace('{uid}', uid)
iframe = iframe.replace('{CALLBACK_URL}', cb_url.get('url'))
iframe = iframe.replace('{GENERATED_LINK_TOKEN}', token.get('link_token'))
IPython.core.display.display(IPython.core.display.HTML(iframe))
# + [markdown] papermill={} tags=[]
# ### Get back plaid token
# + papermill={} tags=[]
cb_data = naas.callback.get(cb_url.get('uuid'))
cb_data = json.loads(cb_data)
public_token = cb_data.get("public_token")
public_token
# + [markdown] papermill={} tags=[]
# ### Exange token
# + papermill={} tags=[]
exchange_response = client.Item.public_token.exchange(public_token)
access_token = exchange_response['access_token']
item_id = exchange_response['item_id']
# + [markdown] papermill={} tags=[]
# ## Output
# + [markdown] papermill={} tags=[]
# ### Show transactions
# + papermill={} tags=[]
response = client.Transactions.get(access_token,
start_date=start_transaction,
end_date=end_transaction)
transactions = response['transactions']
while len(transactions) < response['total_transactions']:
response = client.Transactions.get(access_token,
start_date=start,
end_date=end,
offset=len(transactions)
)
transactions.extend(response['transactions'])
transaction_df = pd.DataFrame.from_records(transactions)
transaction_df
# + [markdown] papermill={} tags=[]
# ### Save as csv
# + papermill={} tags=[]
transaction_df.to_csv('transactions.csv')
# + [markdown] papermill={} tags=[]
# #### If you need more data check the api doc
# https://plaid.com/docs/
|
Plaid/Plaid_Get_transactions.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: conda_mxnet_p36
# language: python
# name: conda_mxnet_p36
# ---
# # IoT Greengrass image classification model training and retraining
#
# 1. [Part 1: initial training](#Part-1:-Initial-Training)
# 1. [Prerequisites and preprocessing](#Prequisites-and-Preprocessing)
# 1. [Permissions and environment variables](#Permissions-and-environment-variables)
# 2. [Data preparation](#Data-preparation)
# 3. [Create S3 folders for field data](#Create-S3-folders-for-field-data)
# 2. [Training parameters](#Training-parameters)
# 3. [Training](#Training)
# 2. [Part 2: Retraining the model](#Part-2:-Retraining-the-model)
# 1. [Data preparation](#data-preparation)
# 2. [Retraining](#Retraining)
#
#
# Welcome to the "Machine learning at the edge - using and retraining image classification with AWS IoT Greengrass" notebook. This should serve as a resource alongside the blog post. This notebook will walk you through step by step how to:
# 1. Configure a model for image classification using the [Caltech-256 dataset](http://www.vision.caltech.edu/Image_Datasets/Caltech256/).
# 2. Retrain a model with images you capture on your IoT Greengrass core device.
#
# Both of these correspond to parts 1 and 2 of the blog post.
#
# *Note: This notebook is a modified version of Amazon SageMaker's image classification sample notebook. Please refer to the SageMaker example notebooks for more details about using the service.*
# ## Part 1: Initial training
#
# ### Prequisites and preprocessing
#
# #### Permissions and environment variables
#
# Here we set up the linkage and authentication to AWS services. There are three parts to this:
# * The roles used to give learning and hosting access to your data. This will automatically be obtained from the role used to start the notebook
# * The S3 bucket that you want to use for training and model data
# * The Amazon sagemaker image classification docker image which need not be changed
# +
# %%time
import boto3
import sagemaker
from sagemaker import get_execution_role
from sagemaker.amazon.amazon_estimator import get_image_uri
role = get_execution_role()
print(role)
sess = sagemaker.Session()
bucket=sess.default_bucket()
print(bucket)
training_image = get_image_uri(boto3.Session().region_name, 'image-classification')
# -
# #### Data preparation
# The Caltech 256 dataset consists of images from 257 categories (the last one being a clutter category) and has 30k images with a minimum of 80 images and a maximum of about 800 images per category.
#
# We will leverage a subset of the Caltech dataset for our example (beer-mug, wine-bottle, coffee-mug, soda-can, and clutter). The following will download the full dataset, extract the subset of categories, and create our model in the [lst format](https://mxnet.incubator.apache.org/how_to/recordio.html?highlight=im2rec) (content type: application/x-image).
#
# A .lst file is a tab-separated file with three columns that contains a list of image files. The first column specifies the image index, the second column specifies the class label index for the image, and the third column specifies the relative path of the image file. The image index in the first column should be unique across all of the images. Here we make an image list file using the [im2rec](https://github.com/apache/incubator-mxnet/blob/master/tools/im2rec.py) tool from MXNet. In order to train with the lst format interface, passing the lst file for both training and validation in the appropriate format is mandatory.
# +
import os
import urllib.request
def download(url):
filename = url.split("/")[-1]
if not os.path.exists(filename):
urllib.request.urlretrieve(url, filename)
# Caltech-256 image files
download('http://www.vision.caltech.edu/Image_Datasets/Caltech256/256_ObjectCategories.tar')
# !tar -xf 256_ObjectCategories.tar
# Tool for creating lst file
download('https://raw.githubusercontent.com/apache/incubator-mxnet/master/tools/im2rec.py')
# + language="bash"
#
# # Extract the subset of categories used for this example. We
# # will only need beer-mug, coffee-mug, wine-bottle, soda-can
#
# # Clean up any existing folders left behind by previous runs
# rm -rf category_subset
# rm -rf caltech_256_train_60
#
# # Re indexes the given folders and sub image files. This
# # will be useful when we add more data and/or more
# # classes during model retraining
# reindex_categories() {
# folder_index=0
# for category_folder in $1/*; do
# category_name=`basename $category_folder | cut -d'.' -f2`
# new_folder_index=`printf '%03d' $folder_index`
# new_folder_name='category_subset/'$new_folder_index'.'$category_name
# mv $category_folder $new_folder_name
# image_index=0
# for image_file in $new_folder_name/*; do
# new_image_name=`printf '%04d' $image_index`
# new_image_name=$new_folder_index'_'$new_image_name'.jpg'
# mv $image_file $new_folder_name/$new_image_name
# ((image_index++))
# done
# ((folder_index++))
# done
# }
#
# mkdir -p category_subset
#
# # The caltech dataset is properly formatted for 257 categories. We will
# # only be using 4 for our example. Copy the 4 categories to a new folder
# # and rename them to have the proper indicies in their names - i.e
# # 010.beer-mug -> 000.beer-mug (and sub files)
# # 041.coffee-mug -> 001.coffee-mug (and sub files)
# cp -r 256_ObjectCategories/010.beer-mug/. category_subset/beer-mug/
# cp -r 256_ObjectCategories/041.coffee-mug/. category_subset/coffee-mug/
# cp -r 256_ObjectCategories/195.soda-can/. category_subset/soda-can/
# cp -r 256_ObjectCategories/246.wine-bottle/. category_subset/wine-bottle/
# cp -r 256_ObjectCategories/257.clutter/. category_subset/clutter/
# reindex_categories category_subset
#
# # Take 60 images from each category and put them in a folder
# # dedicated to training images. Use the remaining images in
# # each folder for validation.
# mkdir -p caltech_256_train_60
# for i in category_subset/*; do
# c=`basename $i`
# mkdir -p caltech_256_train_60/$c
# for j in `ls $i/*.jpg | shuf | head -n 60`; do
# mv $j caltech_256_train_60/$c/
# done
# done
#
# python im2rec.py --list --recursive caltech-256-60-train caltech_256_train_60/
# python im2rec.py --list --recursive caltech-256-60-val category_subset/
# -
# A sample of the lst file we created can be viewed by running below.
# !head -n 15 ./caltech-256-60-val.lst > example.lst
f = open('example.lst','r')
lst_content = f.read()
print(lst_content)
# Once we have the data available in the correct format for training, the next step is to upload the image and .lst file to your S3 bucket.
# Four channels: train, validation, train_lst, and validation_lst
s3train = 's3://{}/image-classification/train/'.format(bucket)
s3validation = 's3://{}/image-classification/validation/'.format(bucket)
s3train_lst = 's3://{}/image-classification/train_lst/'.format(bucket)
s3validation_lst = 's3://{}/image-classification/validation_lst/'.format(bucket)
# +
# upload the image files to train and validation channels
# !aws s3 cp caltech_256_train_60 $s3train --recursive --quiet
# !aws s3 cp category_subset $s3validation --recursive --quiet
# upload the lst files to train_lst and validation_lst channels
# !aws s3 cp caltech-256-60-train.lst $s3train_lst --quiet
# !aws s3 cp caltech-256-60-val.lst $s3validation_lst --quiet
# -
# ### Create S3 folders for field data
# In part 2 we will collect data in the field. These images start as unlabeled in the raw_field_data folder in the S3 bucket. You can label these images by moving them to the correct folders in the /labeled_field_data folder. The following cell creates placeholders for these folders.
# +
# Folders for S3 field data
s3fielddata = 's3://{}/image-classification/labeled_field_data/'.format(bucket)
# Set up for retraining. empty.tmp is added to each bucket to allow us to create
# a visible folder in S3.
# !mkdir -p field_data/beer-mug && touch field_data/beer-mug/empty.tmp
# !mkdir -p field_data/coffee-mug && touch field_data/coffee-mug/empty.tmp
# !mkdir -p field_data/soda-can && touch field_data/soda-can/empty.tmp
# !mkdir -p field_data/wine-bottle && touch field_data/wine-bottle/empty.tmp
# !mkdir -p field_data/clutter && touch field_data/clutter/empty.tmp
# !aws s3 cp --recursive field_data $s3fielddata
# -
# ### Training parameters
# The following parameters are defined below to configure our training job. These values are consumed in the following section when the training_params object is constructed.
# + isConfigCell=true
# The algorithm supports multiple network depth (number of layers). They are 18, 34, 50,
#101, 152 and 200. For this training, we will use 18 layers.
num_layers = 18
# The input image dimensions,'num_channels, height, width', for the network. It should be
# no larger than the actual image size. The number of channels should be same as the actual
# image.
image_shape = "3,224,224"
# This is the total number of training samples. It is set to 300 (60 samples * 5 categories)
num_training_samples = 300
# This is the number of output classes for the new dataset: beer-mug, clutter, coffee-mug, wine-bottle, soda-can,
num_classes = 5
# The number of training samples used for each mini batch. In distributed training, the
# number of training samples used per batch will be N * mini_batch_size where N is the number
# of hosts on which training is run.
mini_batch_size = 128
# Number of training epochs.
epochs = 6
# Learning rate for training.
learning_rate = 0.01
# Report the top-k accuracy during training.
top_k = 5
# Resize the image before using it for training. The images are resized so that the shortest
# side is of this parameter. If the parameter is not set, then the training data is used as
# such without resizing.
resize = 256
# period to store model parameters (in number of epochs), in this case, we will save parameters
# from epoch 2, 4, and 6
checkpoint_frequency = 2
# Since we are using transfer learning, we set use_pretrained_model to 1 so that weights can be
# initialized with pre-trained weights. We aren't using a large number of input samples. Therefore,
# we can benefit from using transfer learning to leverage pre-trained weights that have been
# collected on a much larger dataset.
# See: https://docs.aws.amazon.com/sagemaker/latest/dg/IC-HowItWorks.html
use_pretrained_model = 1
# -
# ### Training
# Below creates three functions that will support the configuration and execution of our training jobs throughout the rest of this notebook (initial training and retraining).
# +
# %%time
import time
import boto3
from time import gmtime, strftime
s3 = boto3.client('s3')
sagemaker = boto3.client(service_name='sagemaker')
JOB_NAME_PREFIX = 'greengrass-imageclassification-training'
def create_unique_job_name():
'''
Creates a job name in the following format:
greengrass-imageclassification-training-[year]-[month]-[day]-[hour]-[minute]-[second]
'''
timestamp = time.strftime('-%Y-%m-%d-%H-%M-%S', time.gmtime())
job_name = JOB_NAME_PREFIX + timestamp
return job_name
def create_training_params(unique_job_name):
'''
Constructs training parameters for the train function
below.
'''
training_params = \
{
# specify the training docker image
"AlgorithmSpecification": {
"TrainingImage": training_image,
"TrainingInputMode": "File"
},
"RoleArn": role,
"OutputDataConfig": {
"S3OutputPath": 's3://{}/{}/output'.format(bucket, JOB_NAME_PREFIX)
},
"ResourceConfig": {
"InstanceCount": 1,
"InstanceType": "ml.p2.xlarge",
"VolumeSizeInGB": 50
},
"TrainingJobName": unique_job_name,
"HyperParameters": {
"image_shape": image_shape,
"num_layers": str(num_layers),
"num_training_samples": str(num_training_samples),
"num_classes": str(num_classes),
"mini_batch_size": str(mini_batch_size),
"epochs": str(epochs),
"learning_rate": str(learning_rate),
"top_k": str(top_k),
"resize": str(resize),
"checkpoint_frequency": str(checkpoint_frequency),
"use_pretrained_model": str(use_pretrained_model)
},
"StoppingCondition": {
"MaxRuntimeInSeconds": 360000
},
#Training data should be inside a subdirectory called "train"
#Validation data should be inside a subdirectory called "validation"
#The algorithm currently only supports fullyreplicated model (where data is copied onto each machine)
"InputDataConfig": [
{
"ChannelName": "train",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": s3train,
"S3DataDistributionType": "FullyReplicated"
}
},
"ContentType": "application/x-image",
"CompressionType": "None"
},
{
"ChannelName": "validation",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": s3validation,
"S3DataDistributionType": "FullyReplicated"
}
},
"ContentType": "application/x-image",
"CompressionType": "None"
},
{
"ChannelName": "train_lst",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": s3train_lst,
"S3DataDistributionType": "FullyReplicated"
}
},
"ContentType": "application/x-image",
"CompressionType": "None"
},
{
"ChannelName": "validation_lst",
"DataSource": {
"S3DataSource": {
"S3DataType": "S3Prefix",
"S3Uri": s3validation_lst,
"S3DataDistributionType": "FullyReplicated"
}
},
"ContentType": "application/x-image",
"CompressionType": "None"
}
]
}
return training_params
def train(job_name, training_params):
'''
Creates a training job, job_name, configured with
training_params.
'''
# create the Amazon SageMaker training job
sagemaker.create_training_job(**training_params)
# confirm that the training job has started
status = sagemaker.describe_training_job(TrainingJobName=job_name)['TrainingJobStatus']
print('Training job current status: {}'.format(status))
try:
# wait for the job to finish and report the ending status
sagemaker.get_waiter('training_job_completed_or_stopped').wait(TrainingJobName=job_name)
training_info = sagemaker.describe_training_job(TrainingJobName=job_name)
status = training_info['TrainingJobStatus']
print("Training job ended with status: " + status)
except:
print('Training failed to start')
# if exception is raised, that means it has failed
message = sagemaker.describe_training_job(TrainingJobName=job_name)['FailureReason']
print('Training failed with the following error: {}'.format(message))
# +
# Create a training job and execute
initial_training_job_name = create_unique_job_name()
initial_training_params = create_training_params(initial_training_job_name)
print('Training job name: {}'.format(initial_training_job_name))
train(initial_training_job_name, initial_training_params)
# -
# You can monitor the status of the training job by running the code below. You can also view information about and the status of a training job using the AWS SageMaker console. Just click on the "Jobs" tab.
training_info = sagemaker.describe_training_job(TrainingJobName=initial_training_job_name)
status = training_info['TrainingJobStatus']
print("Training job ended with status: " + status)
print(training_info)
# If you see the message,
#
# > `Training job ended with status: Completed`
#
# then that means training sucessfully completed and the output model was stored in the output path specified by `training_params['OutputDataConfig']`.
# ***This is the end of Part 1. Please return to the blog post and continue from there.***
# ## Part 2: Retraining the model
#
# At this point we have an IoT Greengrass core device capable of capturing images, performing inference, and uploading results to S3. In part 2, we will retrain our model to use the new data captured in the field using our IoT Greengrass core device.
#
# Note, in this example we will be creating a new model with a combination of our original and new training data. Alternatively iterative training can be used. See the [SageMaker Image Classification Algorithm Documentation](https://docs.aws.amazon.com/sagemaker/latest/dg/image-classification.html) for more details.
# ### Data preparation
# In this step we will access our S3 bucket and pull down the training data collected in the field. We will add this data to our original dataset and regenerate our training/validation image files.
# +
# sync s3 labeled field data with local fieldData folder
# !aws s3 sync $s3fielddata ./field_data
# remove empty.tmp from the local field_data folder
# !rm -f field_data/beer-mug/empty.tmp
# !rm -f field_data/coffee-mug/empty.tmp
# !rm -f field_data/soda-can/empty.tmp
# !rm -f field_data/wine-bottle/empty.tmp
# !rm -f field_data/clutter/empty.tmp
# + language="bash"
# # Re indexes the given folders and sub image files. This
# # will be useful when we add more data and/or more
# # classes during model retraining
# reindex_categories() {
# folder_index=0
# for category_folder in $1/*; do
# category_name=`basename $category_folder | cut -d'.' -f2`
# new_folder_index=`printf '%03d' $folder_index`
# new_folder_name='category_subset/'$new_folder_index'.'$category_name
# mv $category_folder $new_folder_name
# image_index=0
# for image_file in $new_folder_name/*; do
# new_image_name=`printf '%04d' $image_index`
# new_image_name=$new_folder_index'_'$new_image_name'.jpg'
# mv $image_file $new_folder_name/$new_image_name
# ((image_index++))
# done
# ((folder_index++))
# done
# }
#
# # Clean up any existing folders left behind by previous runs
# rm -rf category_subset
# rm -rf caltech_256_train_60
#
# # Copy over category subset again
# mkdir -p category_subset
# cp -r 256_ObjectCategories/010.beer-mug/. category_subset/beer-mug/
# cp -r 256_ObjectCategories/041.coffee-mug/. category_subset/coffee-mug/
# cp -r 256_ObjectCategories/195.soda-can/. category_subset/soda-can/
# cp -r 256_ObjectCategories/246.wine-bottle/. category_subset/wine-bottle/
# cp -r 256_ObjectCategories/257.clutter/. category_subset/clutter/
#
# # Copy contents of field data into category subset
# cp -r field_data/beer-mug/. category_subset/beer-mug/
# cp -r field_data/coffee-mug/. category_subset/coffee-mug/
# cp -r field_data/soda-can/. category_subset/soda-can/
# cp -r field_data/wine-bottle/. category_subset/wine-bottle/
# cp -r field_data/clutter/. category_subset/clutter/
#
# reindex_categories category_subset
#
# # Take 60 images from each category and put them in a folder
# # dedicated to training images. Use the remaining images in
# # each folder for validation.
# mkdir -p caltech_256_train_60
# for i in category_subset/*; do
# c=`basename $i`
# mkdir -p caltech_256_train_60/$c
# for j in `ls $i/*.jpg | shuf | head -n 60`; do
# mv $j caltech_256_train_60/$c/
# done
# done
#
# python im2rec.py --list --recursive caltech-256-60-train caltech_256_train_60/
# python im2rec.py --list --recursive caltech-256-60-val category_subset/
# +
# cleanup existing training data in S3
# !aws s3 rm $s3train
# !aws s3 rm $s3validation
# !aws s3 rm $s3train_lst
# !aws s3 rm $s3validation_lst
# upload the image files to train and validation channels
# !aws s3 cp caltech_256_train_60 $s3train --recursive
# !aws s3 cp category_subset $s3validation --recursive
# upload the lst files to train_lst and validation_lst channels
# !aws s3 cp caltech-256-60-train.lst $s3train_lst
# !aws s3 cp caltech-256-60-val.lst $s3validation_lst
# -
# ### Retraining
# Create a new training job and execute
re_training_job_name = create_unique_job_name()
re_training_params = create_training_params(re_training_job_name)
print('Training job name: {}'.format(re_training_job_name))
print('\nInput Data Location: {}'.format(re_training_params['InputDataConfig'][0]['DataSource']['S3DataSource']))
train(re_training_job_name, re_training_params)
# The code in this section can be rerun at any time to generate a new model using the field data uploaded to S3.
#
# **Return to the blog post to continue!**
|
iot-blog/image-classification-connector-and-feedback/notebook/greengrass-image-classification-blog.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # **Income Prediction**
#
# **Objective :** Explore and implement **Principal Component Analysis** - a **Dimensionality Reduction** technique with Logistic Regression, to determine whether a person makes over 50K a year.
#
# For this project we will be using the following UCI dataset- https://archive.ics.uci.edu/ml/datasets/Adult
#
# Here are the features represented through columns :
# <br>
#
# **Input variables**
# <br>
# 1 - age
# <br>
# 2 - workclass
# <br>
# 3 - fnlwgt
# <br>
# 4 - education
# <br>
# 5 - education-num
# <br>
# 6 - marital-status
# <br>
# 7 - occupation
# <br>
# 8 - relationship
# <br>
# 9 - race
# <br>
# 10 - sex
# <br>
# 11 - capital-gain
# <br>
# 12 - capital-loss
# <br>
# 13 - hours-per-week
# <br>
# 14 - native-country
# <br>
#
#
#
# **Output/Target Variable**
# <br>
# 15 - income
# - (>)50K
# - (<=)50K
#
# ## Table of Contents
#
# - Import Python libraries
# - Import dataset
# - Exploratory data analysis
# - Split data into training and test set
# - Feature engineering
# - Feature scaling
# - Logistic regression model with all features
# - Logistic Regression with PCA
# - Select right number of dimensions
# - Plot explained variance ratio with number of dimensions
# - Conclusion
#
#
# ## Import Python libraries
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
#import numpy
#import pandas
#import libraries for plotting
#ignore warnings
# -
# ## Import dataset
#
# Use pandas to read adult.csv as a dataframe called adult
# ## Exploratory Data Analysis
# ### Check shape of dataset
# <br>
# Use .shape() method
# How many instances and attributes are present in the dataset?
# ### Preview Dataset
# <br>
# Use head() method
# ### View summary of dataframe
# <br>
# Use info() method
# Summary of the dataset shows that there are no missing values. But the preview shows that the dataset contains values coded as `?`. So, we will encode `?` as NaN values.
# ### Encode `?` as `NaNs`
# ### Again check the summary of dataframe
# Which variables contain missing values?
# <br>
# What is the datatype of these variables?
# <br>
# We will impute the missing values with the most frequent value - the mode.
# ### Impute missing values with mode
# ### Check again for missing values
# Verify that there are no missing values in the dataset.
# ### Setting feature vector and target variable
# +
#Set the 'income' column to y
#Drop the 'income' column from the dataframe and set the remaining dataframe to X
# -
# ## Split data into separate training and test set
# +
#Import train_test_split
#Split the data set into training data and testing data in a 7:3 ratio
# -
# ## Feature Engineering
# ### Encode categorical variables
# +
#Import LabelEncoder from sklearn
#Create a list named 'categorical' of all the categorical features in X
#Build a for loop that traverses through the list 'categorical' that you created above.
#For each iteration of the loop,
#Create an instance of LabelEncoder named 'encoder'
#Use .fit_transform method to fit encoder to current feature in X_train and X_test
# -
# ## Feature Scaling
# +
#Import StandardScaler
#Create an instance named 'scaler'
#Use .fit_transform method to scale ALL features in X_train and X_test
# -
# ## Logistic Regression model with all features
# +
#Import LogisticRegression
#Import import accuracy_score from sklearn.metrics
#Create an instance of LogisticRegression() called logreg and fit it to the training data.
#Create predictions from the test set and name the result y_pred
#print out the accuracy score for LogisticRegression
# -
# ## Logistic Regression with PCA
#
# Scikit-Learn's PCA class implements PCA algorithm using the code below. Before diving deep, we will explain another important concept called explained variance ratio.
#
#
# ### Explained Variance Ratio
#
# A very useful piece of information is the **explained variance ratio** of each principal component. It is available via the `explained_variance_ratio_ ` variable. It indicates the proportion of the dataset’s variance that lies along the axis of each principal component.
#
# Now, let's get to the PCA implementation.
#
# +
#Import PCA from sklearn.decomposition
#Create an instance named 'pca'
#Use .fit_transform method to fit pca to X_train
#Use pca.explained_variance_ratio_ to find out feature-wise proportion of the dataset’s variance
# -
# **Observations**
#
# - Approximately what % of variance is explained by the first 13 variables?
#
# - How much variance is explained by the last variable? Can we assume that it carries little information?
#
# - Let's now drop it, train the model again and calculate the accuracy.
#
#
# ### Logistic Regression with first 13 features
# +
#Set the 'income' column to y
#Drop the 'income' and 'native.country' columns from the dataframe and set the remaining dataframe to X
#Split the data set into training data and testing data in a 7:3 ratio
#Create a list named 'categorical' of all the categorical features in our newly created X
#Build a for loop that traverses through the list 'categorical' that you created above.
#For each iteration of the loop,
#Create an instance of LabelEncoder named 'encoder'
#Use .fit_transform method to fit encoder to current feature in X_train and X_test
#Use .fit_transform method to scale ALL features in X_train and X_test
#Create an instance of LogisticRegression() called logreg and fit it to the training data.
#Create predictions from the test set and name the result y_pred
#print out the accuracy score for LogisticRegression
# -
# ### Comment
#
# - What is the change in accuracy of our model?
#
# - Now, consider the last two features. Approximately what % of variance is explained by them, combined?
#
# - Let's drop them both, train the model again and calculate the accuracy.
#
# ### Logistic Regression with first 12 features
# +
#Set the 'income' column to y
#Drop the 'income','native.country', 'hours.per.week' columns from the dataframe and set the remaining dataframe to X
#Split the data set into training data and testing data in a 7:3 ratio
#Create a list named 'categorical' of all the categorical features in our newly created X
#Build a for loop that traverses through the list 'categorical' that you created above.
#For each iteration of the loop,
#Create an instance of LabelEncoder named 'encoder'
#Use .fit_transform method to fit encoder to current feature in X_train and X_test
#Use .fit_transform method to scale ALL features in X_train and X_test
#Create an instance of LogisticRegression() called logreg and fit it to the training data.
#Create predictions from the test set and name the result y_pred
#print out the accuracy score for LogisticRegression
# -
# ### Comment
#
# - What is the change in accuracy of our model, if it is trained with 12 features?
#
# - Lastly, we will take the last three features combined. Approximately what % of variance is explained by them?
#
# - Let's repeat the process, drop these features, train the model again and calculate the accuracy.
#
# ### Logistic Regression with first 11 features
# +
#Set the 'income' column to y
#Drop the 'income','native.country','hours.per.week','capital.loss' columns from the dataframe and set the remaining dataframe to X
#Split the data set into training data and testing data in a 7:3 ratio
#Create a list named 'categorical' of all the categorical features in our newly created X
#Build a for loop that traverses through the list 'categorical' that you created above.
#For each iteration of the loop,
#Create an instance of LabelEncoder named 'encoder'
#Use .fit_transform method to fit encoder to current feature in X_train and X_test
#Use .fit_transform method to scale ALL features in X_train and X_test
#Create an instance of LogisticRegression() called logreg and fit it to the training data.
#Create predictions from the test set and name the result y_pred
#print out the accuracy score for LogisticRegression
# -
# ### Comment
#
# - Has the accuracy increased or decreased if we drop the last three features?
#
# - Our aim is to maximize the accuracy. When did we get the highest accuracy?
# ## Select right number of dimensions
#
# - The above process works well if the number of dimensions are small.
#
# - But, it is quite cumbersome if we have large number of dimensions.
#
# - In that case, a better approach is to compute the number of dimensions that can explain significantly large portion of the variance.
#
# - The following code computes PCA without reducing dimensionality, then computes the minimum number of dimensions required to preserve 90% of the training set variance.
# +
#Set the 'income' column to y
#Drop the 'income' column from the dataframe and set the remaining dataframe to X
#Split the data set into training data and testing data in a 7:3 ratio
#Create a list named 'categorical' of all the categorical features in X
#Build a for loop that traverses through the list 'categorical' that you created above.
#For each iteration of the loop,
#Create an instance of LabelEncoder named 'encoder'
#Use .fit_transform method to fit encoder to current feature in X_train
#Use .fit_transform method to scale ALL features in X_train
#Create an instance of PCA named 'pca'
#Use .fit_transform method to fit pca to X_train
cumsum = np.cumsum(pca.explained_variance_ratio_)
dim = np.argmax(cumsum >= 0.90) + 1
print('The number of dimensions required to preserve 90% of variance is',dim)
# -
# ### Comment
#
# - With the required number of dimensions found, we can then set number of dimensions to `dim` and run PCA again.
#
# - With the number of dimensions set to `dim`, we can then calculate the required accuracy.
# ## Plot explained variance ratio with number of dimensions
#
# - An alternative option is to plot the explained variance as a function of the number of dimensions.
#
# - In the plot, we should look for an elbow where the explained variance stops growing fast.
#
# - This can be thought of as the intrinsic dimensionality of the dataset.
#
# - Now, we will plot cumulative explained variance ratio with number of components to show how variance ratio varies with number of components.
plt.figure(figsize=(8,6))
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlim(0,14,1)
plt.xlabel('Number of components')
plt.ylabel('Cumulative explained variance')
plt.show()
# ### Comment
#
# According to the above plot, how many components explain around 90% of variance?
# ## Conclusion
#
# - In this project, we discussed Principal Component Analysis – the most popular dimensionality reduction technique.
# - We demonstrated PCA implementation with Logistic Regression on the adult dataset.
# - Maximum accuracy was first found through a manual feature selection process.
# - As expected, the number of dimensions required to preserve 90 % of variance matched.
# - Finally, we plotted the explained variance ratio with number of dimensions. The graph confirmed our findings.
#
|
Income Prediction/Income Prediction.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="OzG-MRwD8HgI" outputId="27821ee5-c0c7-430e-e532-05caa599b621"
# For the 'InstanceNormalization' layer
# !pip install --upgrade tensorflow_addons
# For the dataset
# !pip install --upgrade tensorflow_datasets
# + colab={} colab_type="code" id="eWBg9-PI8SZG"
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
from tensorflow.keras.initializers import RandomNormal
from tensorflow.keras.layers import (Activation, Concatenate, Conv2D,
Conv2DTranspose, Input, LeakyReLU)
from tensorflow.keras.losses import BinaryCrossentropy
from tensorflow.keras.models import Model, Sequential
from tensorflow.keras.optimizers import Adam
from tensorflow_addons.layers import InstanceNormalization
import tensorflow_datasets as tfds
# %matplotlib inline
# + colab={"base_uri": "https://localhost:8080/", "height": 309} colab_type="code" id="B6M8YY-58Sb6" outputId="bc246112-8e3c-4660-8bc4-b7451e7ae296"
# Load dataset
data, metadata = tfds.load('cycle_gan/monet2photo', with_info=True, as_supervised=True)
train_x, train_y, test_x, test_y = data['trainA'], data['trainB'], data['testA'], data['testB']
# + colab={} colab_type="code" id="tq1rsy-o8SeN"
# Settings
epochs = 50
LAMBDA = 10
img_rows, img_cols, channels = 256, 256, 3
weight_initializer = RandomNormal(stddev=0.02)
gen_g_optimizer = gen_f_optimizer = Adam(lr=0.0002, beta_1=0.5)
dis_x_optimizer = dis_y_optimizer = Adam(lr=0.0002, beta_1=0.5)
# + colab={} colab_type="code" id="Hq6Knn_C8SgY"
# Normalize images to [-1, 1] and reshape
def preprocess_image(image, _):
return tf.reshape(tf.cast(tf.image.resize(image, (int(img_rows), int(img_cols))), tf.float32) / 127.5 - 1, (1, img_rows, img_cols, channels))
# + colab={} colab_type="code" id="wrrpsmCE8SjE"
# Map the normalization onto the dataset
train_x = train_x.map(preprocess_image)
train_y = train_y.map(preprocess_image)
test_x = test_x.map(preprocess_image)
test_y = test_y.map(preprocess_image)
# + colab={} colab_type="code" id="MZG9um_J8SmD"
# "Ck denotes a 4 × 4 Convolution-InstanceNorm-LeakyReLU layer with k filters and stride 2
def Ck(input, k, use_instancenorm=True):
block = Conv2D(k, (4, 4), strides=2, padding='same', kernel_initializer=weight_initializer)(input)
if use_instancenorm:
block = InstanceNormalization(axis=-1)(block)
block = LeakyReLU(0.2)(block)
return block
# C64, C128, C256, C512
def discriminator():
dis_input = Input(shape=(img_rows, img_cols, channels))
d = Ck(dis_input, 64, False)
d = Ck(d, 128)
d = Ck(d, 256)
d = Ck(d, 512)
d = Conv2D(1, (4, 4), padding='same', kernel_initializer=weight_initializer)(d)
return Model(dis_input, d)
# + colab={} colab_type="code" id="ByAGo-Uc8SoS"
# "dk denotes a 3×3 Convolution-InstanceNorm-ReLU with k filters and stride 2"
def dk(k, use_instancenorm=True):
block = Sequential()
block.add(Conv2D(k, (3, 3), strides=2, padding='same', kernel_initializer=weight_initializer))
if use_instancenorm:
block.add(InstanceNormalization(axis=-1))
block.add(Activation('relu'))
return block
# "uk denotes a 3×3 fractional-strided-ConvolutionInstanceNorm-ReLU layer with k filters and stride ½"
def uk(k):
block = Sequential()
block.add(Conv2DTranspose(k, (3, 3), strides=2, padding='same', kernel_initializer=weight_initializer))
block.add(InstanceNormalization(axis=-1))
block.add(Activation('relu'))
return block
def generator():
gen_input = Input(shape=(img_rows, img_cols, channels))
# Layers for the encoder part of the model
encoder_layers = [
dk(64, False),
dk(128),
dk(256),
dk(512),
dk(512),
dk(512),
dk(512),
dk(512)
]
# Layers for the decoder part of the model
decoder_layers = [
uk(512),
uk(512),
uk(512),
uk(512),
uk(256),
uk(128),
uk(64)
]
gen = gen_input
# Add all the encoder layers, and keep track of them for skip connections
skips = []
for layer in encoder_layers:
gen = layer(gen)
skips.append(gen)
skips = skips[::-1][1:] # Reverse for looping and get rid of the layer that directly connects to decoder
# Add all the decoder layers and skip connections
for skip_layer, layer in zip(skips, decoder_layers):
gen = layer(gen)
gen = Concatenate()([gen, skip_layer])
# Final layer
gen = Conv2DTranspose(channels, (3, 3), strides=2, padding='same', kernel_initializer=weight_initializer, activation='tanh')(gen)
# Compose model
return Model(gen_input, gen)
# + colab={} colab_type="code" id="7ZZOaJKkIAT2"
# Define the models
generator_g = generator()
generator_f = generator()
discriminator_x = discriminator()
discriminator_y = discriminator()
# + colab={} colab_type="code" id="8s-DdUc68Sqs"
# Losses
loss = BinaryCrossentropy(from_logits=True)
# Measures how close to one real images are rated, and how close to zero fake images are rated
def discriminator_loss(real, generated):
# Multiplied by 0.5 so that it will train at half-speed
return (loss(tf.ones_like(real), real) + loss(tf.zeros_like(generated), generated)) * 0.5
# Measures how real the discriminator believes the fake image is
def gen_loss(validity):
return loss(tf.ones_like(validity), validity)
# Measures similarity of two images. Used for cycle and identity loss
def image_similarity(image1, image2):
return tf.reduce_mean(tf.abs(image1 - image2))
# + colab={} colab_type="code" id="WYUJS3CF8Ss7"
@tf.function
def step(real_x, real_y):
with tf.GradientTape(persistent=True) as tape:
# Setup Dy loss
fake_y = generator_g(real_x, training=True)
gen_g_validity = discriminator_y(fake_y, training=True)
dis_y_loss = discriminator_loss(discriminator_y(real_y, training=True), gen_g_validity)
with tape.stop_recording():
discriminator_y_gradients = tape.gradient(dis_y_loss, discriminator_y.trainable_variables)
dis_y_optimizer.apply_gradients(zip(discriminator_y_gradients, discriminator_y.trainable_variables))
# Setup Dx loss
fake_x = generator_f(real_y, training=True)
gen_f_validity = discriminator_x(fake_x, training=True)
dis_x_loss = discriminator_loss(discriminator_x(real_x, training=True), gen_f_validity)
with tape.stop_recording():
discriminator_x_gradients = tape.gradient(dis_x_loss, discriminator_x.trainable_variables)
dis_x_optimizer.apply_gradients(zip(discriminator_x_gradients, discriminator_x.trainable_variables))
# Setup adversarial losses
gen_g_adv_loss = gen_loss(gen_g_validity)
gen_f_adv_loss = gen_loss(gen_f_validity)
# Setup cycle losses
cyc_x = generator_f(fake_y, training=True)
cyc_x_loss = image_similarity(real_x, cyc_x)
cyc_y = generator_g(fake_x, training=True)
cyc_y_loss = image_similarity(real_y, cyc_y)
# Setup identity losses
id_x = generator_f(real_x, training=True)
id_x_loss = image_similarity(real_x, id_x)
id_y = generator_g(real_y, training=True)
id_y_loss = image_similarity(real_y, id_y)
# Finalize generator losses and calc gradients
gen_g_loss = gen_g_adv_loss + (cyc_x_loss + cyc_y_loss) * LAMBDA + id_y_loss * 0.5*LAMBDA
gen_f_loss = gen_f_adv_loss + (cyc_x_loss + cyc_y_loss) * LAMBDA + id_x_loss * 0.5*LAMBDA
with tape.stop_recording():
generator_g_gradients = tape.gradient(gen_g_loss, generator_g.trainable_variables)
gen_g_optimizer.apply_gradients(zip(generator_g_gradients, generator_g.trainable_variables))
generator_f_gradients = tape.gradient(gen_f_loss, generator_f.trainable_variables)
gen_f_optimizer.apply_gradients(zip(generator_f_gradients, generator_f.trainable_variables))
# + colab={} colab_type="code" id="uO62UsfgFYn1"
def generate_images():
# Sample images
x = next(iter(test_x.shuffle(1000))).numpy()
y = next(iter(test_y.shuffle(1000))).numpy()
# Get predictions for those images
y_hat = generator_g.predict(x.reshape((1, img_rows, img_cols, channels)))
x_hat = generator_f.predict(y.reshape((1, img_rows, img_cols, channels)))
plt.figure(figsize=(12, 12))
images = [x[0], y_hat[0], y[0], x_hat[0]]
for i in range(4):
plt.subplot(2, 2, i+1)
plt.imshow(images[i] * 0.5 + 0.5)
plt.axis('off')
plt.tight_layout()
plt.show()
# + colab={"base_uri": "https://localhost:8080/", "height": 1000} colab_type="code" id="gPM73sAi8Svs" outputId="519b49ca-51aa-478c-8d6f-bfaeeaec731f"
# Manually loop through epochs
for epoch in range(epochs):
print('Epoch: {}'.format(epoch))
start = time.time()
# Each batch
for k, (real_x, real_y) in enumerate(tf.data.Dataset.zip((train_x, train_y))):
if k % 100 == 0: print(k)
# Train step
step(tf.reshape(real_x, (1, img_rows, img_cols, channels)), tf.reshape(real_y, (1, img_rows, img_cols, channels)))
# View progress
generate_images()
print('Time taken: {}'.format(time.time() - start))
# + colab={} colab_type="code" id="NxvtP4Zn8Sxp"
for _ in range(10):
generate_images()
# + colab={} colab_type="code" id="eYSCjiD68Sz_"
generator_g.save('generator_g.h5')
generator_f.save('generator_f.h5')
discriminator_x.save('discriminator_x.h5')
discriminator_y.save('discriminator_y.h5')
|
pytorch_tutorials/dqn/cyclegan/cyclegan.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # DAT210x - Programming with Python for DS
# ## Module5- Lab10
# +
import numpy as np
import pandas as pd
from sklearn.utils.validation import check_random_state
import scipy.io.wavfile as wavfile
# -
# Good Luck! Heh.
# ### About Audio
# Samples are Observations. Each audio file will is a single sample in our dataset.
#
# Find more information about [Audio Samples here](https://en.wikipedia.org/wiki/Sampling_(signal_processing)).
#
# Each .wav file is actually just a bunch of numeric samples, "sampled" from the analog signal. Sampling is a type of discretization. When we mention 'samples', we mean observations. When we mention 'audio samples', we mean the actually "features" of the audio file.
#
# The goal of this lab is to use multi-target, linear regression to generate by extrapolation, the missing portion of the test audio file.
#
# Each one audio_sample features will be the output of an equation, which is a function of the provided portion of the audio_samples:
#
# missing_samples = f(provided_samples)
#
# You can experiment with how much of the audio you want to chop off and have the computer generate using the Provided_Portion parameter.
# Play with this. This is how much of the audio file will be provided, in percent. The remaining percent of the file will be generated via linear extrapolation.
Provided_Portion = 0.25
# ### The Assignment
# You have to download the dataset (audio files) from the website: https://github.com/Jakobovski/free-spoken-digit-dataset
# Start by creating a regular Python List called `zero`:
# +
# .. your code here ..
# -
# Loop through the dataset and load up all 50 of the `0_jackson*.wav` files using the `wavfile.read()` method: https://docs.scipy.org/doc/scipy-0.14.0/reference/generated/scipy.io.wavfile.read.html Be careful! `.read()` returns a tuple and you're only interested in the audio data, and not sample_rate at this point. Inside your for loop, simply append the loaded audio data into your Python list `zero`:
# +
# .. your code here ..
# -
# Just for a second, convert zero into a DataFrame. When you do so, set the `dtype` to `np.int16`, since the input audio files are 16 bits per sample. If you don't know how to do this, read up on the docs here: http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html
#
# Since these audio clips are unfortunately not length-normalized, we're going to have to just hard chop them to all be the same length. Since Pandas would have inserted NANs at any spot to make zero a perfectly rectangular [n_observed_samples, n_audio_samples] array, do a `dropna` on the Y axis here. Then, convert one back into an NDArray using `yourarrayname.values`:
# +
# .. your code here ..
# -
# It's important to know how (many audio_samples samples) long the data is now.
#
# `zero` is currently shaped like `[n_samples, n_audio_samples]`, so get the `n_audio_samples` count and store it in a variable called `n_audio_samples`:
# +
# .. your code here ..
# -
# Create your linear regression model here and store it in a variable called `model`. Don't actually train or do anything else with it yet:
# +
# .. your code here ..
# -
# There are 50 takes of each clip. You want to pull out just one of them, randomly, and that one will NOT be used in the training of your model. In other words, the one file we'll be testing / scoring on will be an unseen sample, independent to the rest of your training set:
# +
# Leave this line alone until you've submitted your lab:
rng = check_random_state(7)
random_idx = rng.randint(zero.shape[0])
test = zero[random_idx]
train = np.delete(zero, [random_idx], axis=0)
# -
# Print out the shape of `train`, and the shape of `test`.
#
# `train` will be shaped: `[n_samples, n_audio_samples]`, where `n_audio_samples` are the 'features' of the audio file
#
# `test` will be shaped `[n_audio_features]`, since it is a single sample (audio file, e.g. observation).
# +
# .. your code here ..
# -
# The test data will have two parts, `X_test` and `y_test`.
#
# `X_test` is going to be the first portion of the test audio file, which we will be providing the computer as input.
#
# `y_test`, the "label" if you will, is going to be the remaining portion of the audio file. Like such, the computer will use linear regression to derive the missing portion of the sound file based off of the training data its received!
#
# Let's save the original `test` clip, the one you're about to delete half of, to the current directory so that you can compare it to the 'patched' clip once you've generated it. You should have already got the `sample_rate` when you were loading up the .wav files:
wavfile.write('Original Test Clip.wav', sample_rate, test)
# Prepare the TEST data by creating a slice called `X_test`. It should have `Provided_Portion` * `n_audio_samples` audio sample features, taken from your test audio file, currently stored in variable `test`. In other words, grab the FIRST `Provided_Portion` * `n_audio_samples` audio features from `test` and store it in `X_test`. This should be accomplished using indexing:
# +
# .. your code here ..
# -
# If the first `Provided_Portion` * `n_audio_samples` features were stored in `X_test`, then we need to also grab the _remaining_ audio features and store them in `y_test`. With the remaining features stored in there, we will be able to R^2 "score" how well our algorithm did in completing the sound file.
# +
# .. your code here ..
# -
# Duplicate the same process for `X_train`, `y_train`. The only differences being:
#
# 1. Your will be getting your audio data from `train` instead of from `test`
# 2. Remember the shape of `train` that you printed out earlier? You want to do this slicing but for ALL samples (observations). For each observation, you want to slice the first `Provided_Portion` * `n_audio_samples` audio features into `X_train`, and the remaining go into `y_test`. All of this should be doable using regular indexing in two lines of code:
# +
# .. your code here ..
# -
# SciKit-Learn gets 'angry' if you don't supply your training data in the form of a 2D dataframe shaped like `[n_samples, n_features]`.
#
# So if you only have one SAMPLE, such as is our case with `X_test`, and `y_test`, then by calling `.reshape(1, -1)`, you can turn `[n_features]` into `[1, n_features]` in order to appease SciKit-Learn.
#
# On the other hand, if you only have one FEATURE, you can alternatively call `.reshape(-1, 1)` on your data to turn `[n_samples]` into `[n_samples, 1]`.
#
# Reshape X_test and y_test as [1, n_features]:
# +
# .. your code here ..
# -
# Fit your model using your training data and label:
# +
# .. your code here ..
# -
# Use your model to predict the `label` of `X_test`. Store the resulting prediction in a variable called `y_test_prediction`:
# +
# .. your code here ..
# -
# SciKit-Learn will use float64 to generate your predictions so let's take those values back to int16, which is what our .wav files expect:
y_test_prediction = y_test_prediction.astype(dtype=np.int16)
# Score how well your prediction would do for some good laughs, by passing in your test data and test label `y_test`:
# +
# .. your code here ..
# -
print("Extrapolation R^2 Score: ", score)
# Let's take the first `Provided_Portion` portion of the test clip, the part you fed into your linear regression model. Then, stitch that together with the 'abomination' the predictor model generated for you and then save the completed audio clip:
completed_clip = np.hstack((X_test, y_test_prediction))
wavfile.write('Extrapolated Clip.wav', sample_rate, completed_clip[0])
# Congrats on making it to the end of this crazy lab and module =) !
|
Module5/.ipynb_checkpoints/Module5 - Lab10-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + papermill={"duration": 5.415113, "end_time": "2019-08-20T16:10:29.616901", "exception": false, "start_time": "2019-08-20T16:10:24.201788", "status": "completed"} tags=[]
import seaborn as sns
import pandas as pd
import numpy as np
import altair as alt
from markdown import markdown
from IPython.display import Markdown
from ipywidgets.widgets import HTML, Tab
from ipywidgets import widgets
from datetime import timedelta
from matplotlib import pyplot as plt
import os.path as op
from mod import load_data, alt_theme
# + papermill={"duration": 0.278174, "end_time": "2019-08-20T16:10:30.200964", "exception": false, "start_time": "2019-08-20T16:10:29.922790", "status": "completed"} tags=[]
def author_url(author):
return f"https://github.com/{author}"
# + papermill={"duration": 0.170958, "end_time": "2019-08-20T16:10:30.516749", "exception": false, "start_time": "2019-08-20T16:10:30.345791", "status": "completed"} tags=["parameters", "hide_input"]
# Parameters
fmt_date = "{:%Y-%m-%d}"
n_days = 90
start_date = fmt_date.format(pd.datetime.today() - timedelta(days=n_days))
end_date = fmt_date.format(pd.datetime.today())
renderer = "jupyterlab"
github_orgs = ["jupyterhub", "jupyter", "jupyterlab", "jupyter-widgets", "ipython", "binder-examples", "nteract"]
# + papermill={"duration": 0.163233, "end_time": "2019-08-20T16:10:30.822315", "exception": false, "start_time": "2019-08-20T16:10:30.659082", "status": "completed"} tags=["injected-parameters"]
# Parameters
renderer = "kaggle"
start_date = "2019-01-01"
end_date = "2019-02-01"
# + papermill={"duration": 15.64268, "end_time": "2019-08-20T16:10:46.608589", "exception": false, "start_time": "2019-08-20T16:10:30.965909", "status": "completed"} tags=[]
comments, issues, prs = load_data('../data/')
bot_names = pd.read_csv('bot_names.csv')['names'].tolist()
comments = comments.query('author not in @bot_names').drop_duplicates()
issues = issues.query('author not in @bot_names').drop_duplicates()
prs = prs.query('author not in @bot_names').drop_duplicates()
# + papermill={"duration": 0.658588, "end_time": "2019-08-20T16:10:47.543894", "exception": false, "start_time": "2019-08-20T16:10:46.885306", "status": "completed"} tags=[]
# Only keep the dates we want
comments = comments.query('updatedAt > @start_date and updatedAt < @end_date')
issues = issues.query('updatedAt > @start_date and updatedAt < @end_date')
prs = prs.query('updatedAt > @start_date and updatedAt < @end_date')
# + papermill={"duration": 0.373727, "end_time": "2019-08-20T16:10:48.207495", "exception": false, "start_time": "2019-08-20T16:10:47.833768", "status": "completed"} tags=[]
alt.renderers.enable(renderer);
alt.themes.register('my_theme', alt_theme)
alt.themes.enable("my_theme")
# + papermill={"duration": 0.343005, "end_time": "2019-08-20T16:10:48.832807", "exception": false, "start_time": "2019-08-20T16:10:48.489802", "status": "completed"} tags=[]
# Information about out time window
time_delta = pd.to_datetime(end_date) - pd.to_datetime(start_date)
n_days = time_delta.days
# Information about the data we loaded
github_orgs = comments['org'].unique()
# + [markdown] papermill={"duration": 0.2804, "end_time": "2019-08-20T16:10:49.430281", "exception": false, "start_time": "2019-08-20T16:10:49.149881", "status": "completed"} tags=[]
# # GitHub activity
#
# Jupyter also has lots of activity across GitHub repositories. The following sections contain
# overviews of recent activity across the following GitHub organizations:
# + papermill={"duration": 0.300088, "end_time": "2019-08-20T16:10:49.993714", "exception": false, "start_time": "2019-08-20T16:10:49.693626", "status": "completed"} tags=[]
# Define colors we'll use for GitHub membership
author_types = ['MEMBER', 'CONTRIBUTOR', 'COLLABORATOR', "NONE"]
author_palette = sns.palettes.blend_palette(["lightgrey", "lightgreen", "darkgreen"], 4)
author_colors = ["rgb({}, {}, {}, {})".format(*(ii*256)) for ii in author_palette]
author_color_dict = {key: val for key, val in zip(author_types, author_palette)}
# + papermill={"duration": 0.315499, "end_time": "2019-08-20T16:10:50.618931", "exception": false, "start_time": "2019-08-20T16:10:50.303432", "status": "completed"} tags=["hide_input"]
orgs_md = []
for org in github_orgs:
orgs_md.append(f'* [github.com/{org}](https://github.com/{org})')
Markdown('\n'.join(orgs_md))
# + papermill={"duration": 0.346711, "end_time": "2019-08-20T16:10:51.220518", "exception": false, "start_time": "2019-08-20T16:10:50.873807", "status": "completed"} tags=["hide_input"]
Markdown(f"Showing GitHub activity from **{start_date}** to **{end_date}**")
# + [markdown] papermill={"duration": 0.321124, "end_time": "2019-08-20T16:10:51.812793", "exception": false, "start_time": "2019-08-20T16:10:51.491669", "status": "completed"} tags=[]
# ## List of all contributors per organization
#
# First, we'll list each contributor that has contributed to each organization in the last several days.
# Contributions to open source projects are diverse, and involve much more than just contributing code and
# code review. Thanks to everybody in the Jupyter communities for all that they do.
# + papermill={"duration": 1.700777, "end_time": "2019-08-20T16:10:53.784049", "exception": false, "start_time": "2019-08-20T16:10:52.083272", "status": "completed"} tags=[]
n_plot = 5
tabs = widgets.Tab(children=[])
for ii, org in enumerate(github_orgs):
authors_comments = comments.query('org == @org')['author']
authors_prs = prs.query('org == @org')['author']
unique_participants = np.unique(np.hstack([authors_comments.values, authors_prs.values]).astype(str)).tolist()
unique_participants.sort(key=lambda a: a.lower())
all_participants = [f"[{participant}](https://github.com/{participant})" for participant in unique_participants]
participants_md = " | ".join(all_participants)
md_html = HTML("<center>{}</center>".format(markdown(participants_md)))
children = list(tabs.children)
children.append(md_html)
tabs.children = tuple(children)
tabs.set_title(ii, org)
display(Markdown(f"All participants across issues and pull requests in each org in the last {n_days} days"))
display(tabs)
# + [markdown] papermill={"duration": 0.331272, "end_time": "2019-08-20T16:10:54.410232", "exception": false, "start_time": "2019-08-20T16:10:54.078960", "status": "completed"} tags=[] toc-hr-collapsed=false
# ## Merged Pull requests
#
# Here's an analysis of **merged pull requests** across each of the repositories in the Jupyter
# ecosystem.
# + papermill={"duration": 0.335393, "end_time": "2019-08-20T16:10:55.030669", "exception": false, "start_time": "2019-08-20T16:10:54.695276", "status": "completed"} tags=[]
merged = prs.query('state == "MERGED" and closedAt > @start_date and closedAt < @end_date')
# + papermill={"duration": 0.570672, "end_time": "2019-08-20T16:10:55.903580", "exception": false, "start_time": "2019-08-20T16:10:55.332908", "status": "completed"} tags=["hide_input"]
prs_by_repo = merged.groupby(['org', 'repo']).count()['author'].reset_index().sort_values(['org', 'author'], ascending=False)
alt.Chart(data=prs_by_repo, title=f"Merged PRs in the last {n_days} days").mark_bar().encode(
x=alt.X('repo', sort=prs_by_repo['repo'].values.tolist()),
y='author',
color='org'
)
# + [markdown] papermill={"duration": 0.290464, "end_time": "2019-08-20T16:10:56.490276", "exception": false, "start_time": "2019-08-20T16:10:56.199812", "status": "completed"} tags=[]
# ### A list of merged PRs by project
#
# Below is a tabbed readout of recently-merged PRs. Check out the title to get an idea for what they
# implemented, and be sure to thank the PR author for their hard work!
# + papermill={"duration": 2.45034, "end_time": "2019-08-20T16:10:59.272653", "exception": false, "start_time": "2019-08-20T16:10:56.822313", "status": "completed"} tags=["hide_input"]
tabs = widgets.Tab(children=[])
merged_by = {}
pr_by = {}
for ii, (org, idata) in enumerate(merged.groupby('org')):
issue_md = []
issue_md.append(f"#### Closed PRs for org: `{org}`")
issue_md.append("")
for (org, repo), prs in idata.groupby(['org', 'repo']):
issue_md.append(f"##### [{org}/{repo}](https://github.com/{org}/{repo})")
for _, pr in prs.iterrows():
user_name = pr['author']
user_url = author_url(user_name)
pr_number = pr['number']
pr_html = pr['url']
pr_title = pr['title']
pr_closedby = pr['mergedBy']
pr_closedby_url = f"https://github.com/{pr_closedby}"
if user_name not in pr_by:
pr_by[user_name] = 1
else:
pr_by[user_name] += 1
if pr_closedby not in merged_by:
merged_by[pr_closedby] = 1
else:
merged_by[pr_closedby] += 1
text = f"* [(#{pr_number})]({pr_html}): _{pr_title}_ by **[@{user_name}]({user_url})** merged by **[@{pr_closedby}]({pr_closedby_url})**"
issue_md.append(text)
issue_md.append('')
markdown_html = markdown('\n'.join(issue_md))
children = list(tabs.children)
children.append(HTML(markdown_html))
tabs.children = tuple(children)
tabs.set_title(ii, org)
tabs
# + [markdown] papermill={"duration": 0.335825, "end_time": "2019-08-20T16:10:59.839889", "exception": false, "start_time": "2019-08-20T16:10:59.504064", "status": "completed"} tags=[]
# ### Authoring and merging stats by repository
#
# Let's see who has been doing most of the PR authoring and merging. The PR author is generally the
# person that implemented a change in the repository (code, documentation, etc). The PR merger is
# the person that "pressed the green button" and got the change into the main codebase.
# + papermill={"duration": 0.235152, "end_time": "2019-08-20T16:11:00.339384", "exception": false, "start_time": "2019-08-20T16:11:00.104232", "status": "completed"} tags=[]
# Prep our merging DF
merged_by_repo = merged.groupby(['org', 'repo', 'author'], as_index=False).agg({'id': 'count', 'authorAssociation': 'first'}).rename(columns={'id': "authored", 'author': 'username'})
closed_by_repo = merged.groupby(['org', 'repo', 'mergedBy']).count()['id'].reset_index().rename(columns={'id': "closed", "mergedBy": "username"})
# + papermill={"duration": 1.089312, "end_time": "2019-08-20T16:11:01.707053", "exception": false, "start_time": "2019-08-20T16:11:00.617741", "status": "completed"} tags=[]
n_plot = 50
charts = []
for ii, (iorg, idata) in enumerate(merged_by_repo.replace(np.nan, 0).groupby(['org'])):
title = f"PR authors for {iorg} in the last {n_days} days"
idata = idata.groupby('username', as_index=False).agg({'authored': 'sum', 'authorAssociation': 'first'})
idata = idata.sort_values('authored', ascending=False).head(n_plot)
ch = alt.Chart(data=idata, width=1000, title=title).mark_bar().encode(
x='username',
y='authored',
color=alt.Color('authorAssociation', scale=alt.Scale(domain=author_types, range=author_colors))
)
charts.append(ch)
alt.hconcat(*charts)
# + papermill={"duration": 0.863324, "end_time": "2019-08-20T16:11:02.879643", "exception": false, "start_time": "2019-08-20T16:11:02.016319", "status": "completed"} tags=[]
charts = []
for ii, (iorg, idata) in enumerate(closed_by_repo.replace(np.nan, 0).groupby(['org'])):
title = f"Merges for {iorg} in the last {n_days} days"
ch = alt.Chart(data=idata, width=1000, title=title).mark_bar().encode(
x='username',
y='closed',
)
charts.append(ch)
alt.hconcat(*charts)
# + [markdown] papermill={"duration": 0.376737, "end_time": "2019-08-20T16:11:03.594285", "exception": false, "start_time": "2019-08-20T16:11:03.217548", "status": "completed"} tags=[]
# ## Issues
#
# Issues are **conversations** that happen on our GitHub repositories. Here's an
# analysis of issues across the Jupyter organizations.
# + papermill={"duration": 0.233808, "end_time": "2019-08-20T16:11:04.221314", "exception": false, "start_time": "2019-08-20T16:11:03.987506", "status": "completed"} tags=[]
created = issues.query('state == "OPEN" and createdAt > @start_date and createdAt < @end_date')
closed = issues.query('state == "CLOSED" and closedAt > @start_date and closedAt < @end_date')
# + papermill={"duration": 0.286511, "end_time": "2019-08-20T16:11:04.677207", "exception": false, "start_time": "2019-08-20T16:11:04.390696", "status": "completed"} tags=["hide_input"]
created_counts = created.groupby(['org', 'repo']).count()['number'].reset_index()
created_counts['org/repo'] = created_counts.apply(lambda a: a['org'] + '/' + a['repo'], axis=1)
sorted_vals = created_counts.sort_values(['org', 'number'], ascending=False)['repo'].values
alt.Chart(data=created_counts, title=f"Issues created in the last {n_days} days").mark_bar().encode(
x=alt.X('repo', sort=alt.Sort(sorted_vals.tolist())),
y='number',
color='org',
)
# + papermill={"duration": 0.547228, "end_time": "2019-08-20T16:11:05.385468", "exception": false, "start_time": "2019-08-20T16:11:04.838240", "status": "completed"} tags=["hide_input"]
closed_counts = closed.groupby(['org', 'repo']).count()['number'].reset_index()
closed_counts['org/repo'] = closed_counts.apply(lambda a: a['org'] + '/' + a['repo'], axis=1)
sorted_vals = closed_counts.sort_values(['org', 'number'], ascending=False)['repo'].values
alt.Chart(data=closed_counts, title=f"Issues closed in the last {n_days} days").mark_bar().encode(
x=alt.X('repo', sort=alt.Sort(sorted_vals.tolist())),
y='number',
color='org',
)
# + papermill={"duration": 0.520374, "end_time": "2019-08-20T16:11:06.284542", "exception": false, "start_time": "2019-08-20T16:11:05.764168", "status": "completed"} tags=[]
created_closed = pd.merge(created_counts.rename(columns={'number': 'created'}).drop(columns='org/repo'),
closed_counts.rename(columns={'number': 'closed'}).drop(columns='org/repo'),
on=['org', 'repo'], how='outer')
created_closed = pd.melt(created_closed, id_vars=['org', 'repo'], var_name="kind", value_name="count").replace(np.nan, 0)
# + papermill={"duration": 1.49955, "end_time": "2019-08-20T16:11:08.154180", "exception": false, "start_time": "2019-08-20T16:11:06.654630", "status": "completed"} tags=[]
charts = []
for org in github_orgs:
# Pick the top 10 repositories
this_issues = created_closed.query('org == @org')
top_repos = this_issues.groupby(['repo']).sum().sort_values(by='count', ascending=False).head(10).index
ch = alt.Chart(this_issues.query('repo in @top_repos'), width=120).mark_bar().encode(
x=alt.X("kind", axis=alt.Axis(labelFontSize=15, title="")),
y=alt.Y('count', axis=alt.Axis(titleFontSize=15, labelFontSize=12)),
color='kind',
column=alt.Column("repo", header=alt.Header(title=f"Issue activity, last {n_days} days for {org}", titleFontSize=15, labelFontSize=12))
)
charts.append(ch)
alt.hconcat(*charts)
# + papermill={"duration": 0.542847, "end_time": "2019-08-20T16:11:09.061804", "exception": false, "start_time": "2019-08-20T16:11:08.518957", "status": "completed"} tags=[]
# Set to datetime
for kind in ['createdAt', 'closedAt']:
closed.loc[:, kind] = pd.to_datetime(closed[kind])
closed.loc[:, 'time_open'] = closed['closedAt'] - closed['createdAt']
closed.loc[:, 'time_open'] = closed['time_open'].dt.total_seconds()
# + papermill={"duration": 0.66877, "end_time": "2019-08-20T16:11:10.104012", "exception": false, "start_time": "2019-08-20T16:11:09.435242", "status": "completed"} tags=[]
time_open = closed.groupby(['org', 'repo']).agg({'time_open': 'median'}).reset_index()
time_open['time_open'] = time_open['time_open'] / (60 * 60 * 24)
time_open['org/repo'] = time_open.apply(lambda a: a['org'] + '/' + a['repo'], axis=1)
sorted_vals = time_open.sort_values(['org', 'time_open'], ascending=False)['repo'].values
alt.Chart(data=time_open, title=f"Time to close for issues closed in the last {n_days} days").mark_bar().encode(
x=alt.X('repo', sort=alt.Sort(sorted_vals.tolist())),
y=alt.Y('time_open', title="Median Days Open"),
color='org',
)
# + [markdown] papermill={"duration": 0.46466, "end_time": "2019-08-20T16:11:10.963347", "exception": false, "start_time": "2019-08-20T16:11:10.498687", "status": "completed"} tags=[]
# ### A list of recent issues
#
# Below is a list of issues with recent activity in each repository. If they seem of interest
# to you, click on their links and jump in to participate!
# + papermill={"duration": 0.49504, "end_time": "2019-08-20T16:11:11.924875", "exception": false, "start_time": "2019-08-20T16:11:11.429835", "status": "completed"} tags=[]
# Add comment count data to issues and PRs
comment_counts = (
comments
.query("createdAt > @start_date and createdAt < @end_date")
.groupby(['org', 'repo', 'issue_id'])
.count().iloc[:, 0].to_frame()
)
comment_counts.columns = ['n_comments']
comment_counts = comment_counts.reset_index()
# + papermill={"duration": 5.000712, "end_time": "2019-08-20T16:11:17.285259", "exception": false, "start_time": "2019-08-20T16:11:12.284547", "status": "completed"} tags=["hide_input"] toc-hr-collapsed=false
n_plot = 5
tabs = widgets.Tab(children=[])
for ii, (org, idata) in enumerate(comment_counts.groupby('org')):
issue_md = []
issue_md.append(f"#### {org}")
issue_md.append("")
for repo, i_issues in idata.groupby('repo'):
issue_md.append(f"##### [{org}/{repo}](https://github.com/{org}/{repo})")
top_issues = i_issues.sort_values('n_comments', ascending=False).head(n_plot)
top_issue_list = pd.merge(issues, top_issues, left_on=['org', 'repo', 'number'], right_on=['org', 'repo', 'issue_id'])
for _, issue in top_issue_list.sort_values('n_comments', ascending=False).head(n_plot).iterrows():
user_name = issue['author']
user_url = author_url(user_name)
issue_number = issue['number']
issue_html = issue['url']
issue_title = issue['title']
text = f"* [(#{issue_number})]({issue_html}): _{issue_title}_ by **[@{user_name}]({user_url})**"
issue_md.append(text)
issue_md.append('')
md_html = HTML(markdown('\n'.join(issue_md)))
children = list(tabs.children)
children.append(HTML(markdown('\n'.join(issue_md))))
tabs.children = tuple(children)
tabs.set_title(ii, org)
display(Markdown(f"Here are the top {n_plot} active issues in each repository in the last {n_days} days"))
display(tabs)
# + [markdown] papermill={"duration": 0.390047, "end_time": "2019-08-20T16:11:18.037375", "exception": false, "start_time": "2019-08-20T16:11:17.647328", "status": "completed"} tags=[]
# ## Commenters across repositories
#
# These are commenters across all issues and pull requests in the last several days.
# These are colored by the commenter's association with the organization. For information
# about what these associations mean, [see this StackOverflow post](https://stackoverflow.com/a/28866914/1927102).
# + papermill={"duration": 0.397805, "end_time": "2019-08-20T16:11:18.843731", "exception": false, "start_time": "2019-08-20T16:11:18.445926", "status": "completed"} tags=[]
commentors = (
comments
.query("createdAt > @start_date and createdAt < @end_date")
.groupby(['org', 'repo', 'author', 'authorAssociation'])
.count().rename(columns={'id': 'count'})['count']
.reset_index()
.sort_values(['org', 'count'], ascending=False)
)
# + papermill={"duration": 1.291841, "end_time": "2019-08-20T16:11:20.551376", "exception": false, "start_time": "2019-08-20T16:11:19.259535", "status": "completed"} tags=[]
n_plot = 50
charts = []
for ii, (iorg, idata) in enumerate(commentors.groupby(['org'])):
title = f"Top {n_plot} commentors for {iorg} in the last {n_days} days"
idata = idata.groupby('author', as_index=False).agg({'count': 'sum', 'authorAssociation': 'first'})
idata = idata.sort_values('count', ascending=False).head(n_plot)
ch = alt.Chart(data=idata.head(n_plot), width=1000, title=title).mark_bar().encode(
x='author',
y='count',
color=alt.Color('authorAssociation', scale=alt.Scale(domain=author_types, range=author_colors))
)
charts.append(ch)
alt.hconcat(*charts)
# + [markdown] papermill={"duration": 0.251606, "end_time": "2019-08-20T16:11:21.160348", "exception": false, "start_time": "2019-08-20T16:11:20.908742", "status": "completed"} tags=[]
# ## First responders
#
# First responders are the first people to respond to a new issue in one of the repositories.
# The following plots show first responders for recently-created issues.
# + papermill={"duration": 8.269099, "end_time": "2019-08-20T16:11:29.843609", "exception": false, "start_time": "2019-08-20T16:11:21.574510", "status": "completed"} tags=[]
first_comments = []
for (org, repo, issue_id), i_comments in comments.groupby(['org', 'repo', 'issue_id']):
ix_min = pd.to_datetime(i_comments['createdAt']).idxmin()
first_comment = i_comments.loc[ix_min]
if isinstance(first_comment, pd.DataFrame):
first_comment = first_comment.iloc[0]
first_comments.append(first_comment)
first_comments = pd.concat(first_comments, axis=1).T
# + papermill={"duration": 0.271457, "end_time": "2019-08-20T16:11:30.590496", "exception": false, "start_time": "2019-08-20T16:11:30.319039", "status": "completed"} tags=[]
first_responder_counts = first_comments.groupby(['org', 'author', 'authorAssociation'], as_index=False).\
count().rename(columns={'id': 'n_first_responses'}).sort_values(['org', 'n_first_responses'], ascending=False)
# + papermill={"duration": 0.642854, "end_time": "2019-08-20T16:11:31.439328", "exception": false, "start_time": "2019-08-20T16:11:30.796474", "status": "completed"} tags=[]
n_plot = 50
charts = []
for ii, (iorg, idata) in enumerate(first_responder_counts.groupby(['org'])):
title = f"Top {n_plot} first responders for {iorg} in the last {n_days} days"
idata = idata.groupby('author', as_index=False).agg({'n_first_responses': 'sum', 'authorAssociation': 'first'})
idata = idata.sort_values('n_first_responses', ascending=False).head(n_plot)
ch = alt.Chart(data=idata.head(n_plot), width=1000, title=title).mark_bar().encode(
x='author',
y='n_first_responses',
color=alt.Color('authorAssociation', scale=alt.Scale(domain=author_types, range=author_colors))
)
charts.append(ch)
alt.hconcat(*charts)
# + papermill={"duration": 0.445858, "end_time": "2019-08-20T16:11:32.123456", "exception": false, "start_time": "2019-08-20T16:11:31.677598", "status": "completed"} tags=[] language="html"
# <script src="https://cdn.rawgit.com/parente/4c3e6936d0d7a46fd071/raw/65b816fb9bdd3c28b4ddf3af602bfd6015486383/code_toggle.js"></script>
|
reports/monthly/2019-01-01_2019-02-01/github.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # NumPy and Matplotlib examples
# First import NumPy and Matplotlib:
# %pylab inline
import numpy as np
# Now we show some very basic examples of how they can be used.
a = np.random.uniform(size=(100,100))
a.shape
# + tags=["remove_cell"]
evs = np.linalg.eigvals(a)
# + tags=["remove_output"]
evs.shape
# -
# Here is a cell that has both text and PNG output:
# + tags=["remove_input"]
hist(evs.real)
# + [markdown] tags=["remove_cell"]
# This cell is just markdown testing whether an ASCIIDoc quirk is caught and whether [header links are rendered](#numpy-and-matplotlib-examples) even if they [don't resolve correctly now](#NumPy-and-Matplotlib-examples).
#
# one *test* two *tests*. three *tests*
# -
# Make sure markdown parser doesn't crash with empty Latex formulas blocks
# $$ $$
# \[\]
# $$
|
nbconvert/exporters/tests/files/notebook2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# ## Runs cross-instance quantitative analysis
# +
import dense_correspondence_manipulation.utils.utils as utils
import os
utils.add_dense_correspondence_to_python_path()
utils.set_cuda_visible_devices([1])
from dense_correspondence.evaluation.evaluation import DenseCorrespondenceEvaluation, DenseCorrespondenceEvaluationPlotter
from dense_correspondence.dataset.spartan_dataset_masked import SpartanDataset
import logging
logging.basicConfig(level=logging.INFO)
import pandas as pd
import numpy as np
import time
# -
eval_config_filename = os.path.join(utils.getDenseCorrespondenceSourceDir(), 'config', 'dense_correspondence',
'evaluation',
'evaluation.yaml')
eval_config = utils.getDictFromYamlFilename(eval_config_filename)
dce = DenseCorrespondenceEvaluation(eval_config)
# +
network_to_evaluate = 'shoes_actually_iterative'
cross_instance_labels = 'evaluation_labeled_data/shoe_annotated_keypoints.yaml'
full_path_cross_instance_labels = os.path.join(utils.getPdcPath(),cross_instance_labels)
network_path = eval_config["networks"][network_to_evaluate]["path_to_network_params"]
cross_instance_output_dir = os.path.join(os.path.dirname(utils.getDenseCorrespondenceSourceDir()),os.path.dirname(network_path),"analysis","cross_instance")
print cross_instance_output_dir
if not os.path.isdir(cross_instance_output_dir):
os.makedirs(cross_instance_output_dir)
cross_instance_csv = os.path.join(cross_instance_output_dir, "data.csv")
# -
import time
start = time.time()
df = dce.evaluate_single_network_cross_instance(network_to_evaluate, full_path_cross_instance_labels)
print "took", time.time() - start, "seconds"
print cross_instance_csv
df.to_csv(cross_instance_csv)
DCEP = DenseCorrespondenceEvaluationPlotter
fig_axes = DCEP.run_on_single_dataframe(cross_instance_csv, label=network_to_evaluate, save=False)
# +
folder_name = "2018-10-15"
path_to_nets = os.path.join("code/data_volume/pdc/trained_models", folder_name)
path_to_nets = utils.convert_to_absolute_path(path_to_nets)
all_nets = sorted(os.listdir(path_to_nets))
nets_to_plot = []
nets_list = ["shoes_progress_actually_iterative_23", "shoes_3"]
for net in nets_list:
nets_to_plot.append(os.path.join(folder_name,net))
# +
import matplotlib.pyplot as plt
dc_source_dir = utils.getDenseCorrespondenceSourceDir()
network_name = nets_to_plot[0]
path_to_csv = os.path.join(dc_source_dir, "data_volume", "pdc", "trained_models", network_name, "analysis/cross_instance/data.csv")
fig_axes = DCEP.run_on_single_dataframe(path_to_csv, label=network_name, save=False)
for network_name in nets_to_plot[1:]:
path_to_csv = os.path.join(dc_source_dir, "data_volume", "pdc", "trained_models", network_name, "analysis/cross_instance/data.csv")
fig_axes = DCEP.run_on_single_dataframe(path_to_csv, label=network_name, previous_fig_axes=fig_axes, save=False)
_, axes = fig_axes
axes[0].set_title("Cross instance")
plt.show()
# -
|
dense_correspondence/evaluation/evaluation_quantitative_cross_instance.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [default]
# language: python
# name: python3
# ---
# # Easier to find PySpark
# !pwd
# +
# !pip install findspark
# !pip install py4j
import findspark
findspark.init()
from pyspark import SparkContext, SparkConf
# -
# # Set .bashrc
# + active=""
# export SPARK_HOME="/usr/lib/spark"
# export PYSPARK_SUBMIT_ARGS="--master local[2] pyspark-shell"
# -
# # SPARK!!!!
try:
conf = SparkConf().setAppName("test")
sc = SparkContext(conf=conf)
except:
pass
print(sc)
with open('repo_py_docs.txt', 'r') as f:
print(f.readline())
test = sc.textFile('repo_py_docs.txt')
test.count()
# # Import Data
with open('credentials/aws.csv', 'r') as infile:
_ = infile.readline()
username, access_key, secret_key = infile.readline().replace('"', '').split(',')
#dataFile = ("s3n://{0}:{1}@github-spark/repo_py_docs.txt".format(access_key, secret_key))
dataFile = "s3n://{0}:{1}@github-spark/repo_py_docs.txt".format(access_key,secret_key)
# +
import boto
import boto.s3.connection
conn = boto.connect_s3(
aws_access_key_id = access_key,
aws_secret_access_key = secret_key,
host = 's3.amazonaws.com',
is_secure=False, # uncomment if you are not using ssl
calling_format = boto.s3.connection.OrdinaryCallingFormat(),
)
# -
bkt = conn.get_bucket('github-spark', validate=False)
f = bkt.get_key('repo_py_docs.txt', validate=False)
test = sc.textFile("https://s3.amazonaws.com/github-spark/repo_py_docs.txt")
import os
def fetch_data(s3key):
"""
Fetch data with the given s3 key and pass along the contents as a string.
:param s3key: An s3 key path string.
:return: A tuple (file_name, data) where data is the contents of the
file in a string. Note that if the file is compressed the string will
contain the compressed data which will have to be unzipped using the
gzip package.
"""
conn = boto.connect_s3(
aws_access_key_id = access_key,
aws_secret_access_key = secret_key,
host = 's3.amazonaws.com',
#is_secure=False, # uncomment if you are not using ssl
calling_format = boto.s3.connection.OrdinaryCallingFormat(),
)
b = conn.get_bucket('github-spark', validate=False)
k = b.get_key(s3key, validate=False)
data = k.get_contents_as_string()
conn.close()
# I use basename() to get just the file name itself
return os.path.basename(s3key), data
fetch_data('repo_py_docs.txt')
|
spark.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Deeper dive into pcolormesh()
#
# ## Synopsis
#
# - An examination of how pcolormesh expects cell boundaries, and what happens when the cell boundaries are _not_ used.
import matplotlib.pyplot as plt
import xarray
import numpy
import cartopy
# ## Some test data
#
# We'll make up some simple data to examine how pcolormesh works.
#
# - The mesh will be in longitude-latitude coordinates.
# - The mesh will be irregularly spaced along each coordinate direction.
# - There will be 6x4 data values in 6x4 cells.
# - vlon, vlat will be the 1D coordinates of cell boundaries.
# - Think "V" for vertex.
# - clon, clat will be the 1D coordinates of the cell centers, where the notionally data resides.
# - Think "C" for cell center.
# Irregularly space vertex longitudes
vlon = numpy.cumsum([0,60,60,60,45,45,90])-180
# Irregularly space vertex latitudes
vlat = numpy.cumsum([0,45,45,30,60])-90
# Cell centers defined using finite volume interpretation, i.e. middle of cell based on cell bounds
clon = (vlon[:-1]+vlon[1:])/2 # Longitudes of column centers
clat = (vlat[:-1]+vlat[1:])/2 # Latitudes of row centers
# Some arbitrary data to plot
CLON2d, CLAT2d = numpy.meshgrid(clon, clat)
data = (1+numpy.sin(numpy.pi*CLON2d/180)+(0.5-CLAT2d/180)**2)/3
del CLAT2d, CLON2d
# ## Simple pcolormesh via matplotlib.pyplot
#
# First will use the pcolormesh directly from matplotlib.pyplot.
# +
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.pcolormesh(clon, clat, data, vmin=0, vmax=1);
plt.title('1a) plt.pcolormesh(clon, clat, data)');
plt.subplot(122)
plt.pcolormesh(vlon, vlat, data, vmin=0, vmax=1);
plt.title('1b) plt.pcolormesh(vlon, vlat, data)');
plt.tight_layout()
# -
# There should be 6x4 cells of data showing.
#
# - Panel 1a shows only 5x3 values. Moreover, the locations of the cells are wrong.
# - The domain spans from -180<x<180 and -90<y<90 but the figure shows significantly less of the domain.
# - The interface between the 3rd and 4th columns should be at x=0, but is off to the right. Similarly the boundary between the 2nd and 3rd rows should be at y=0 but it to far north. All cell boundaries are wrong.
# - Panel 1b correctly shows 6x4 cells with correctly placed boundaries.
#
# ## pcolormesh via cartopy
#
# Now let's use cartopy to make the plot.
#
# To use cartopy, you declare the projection you wish to use in the visualization in the axes (i.e. where I use `plt.subplot()` below). When you call pcolormesh for those axes (i.e. with `ax.pcolormesh()`) you normally specify the nature of the coordinates for the data with `transform=`. Since most ESMs provide geographic coordinates then you tend to use `transform=cartopy.crs.PlateCarree()`.
# +
plt.figure(figsize=(10,4))
ax = plt.subplot(121, projection=cartopy.crs.PlateCarree())
ax.pcolormesh(clon, clat, data, transform=cartopy.crs.PlateCarree(), vmin=0, vmax=1);
gl = ax.gridlines(draw_labels=True); gl.xlabels_top,gl.ylabels_right = False,False
gl.xformatter,gl.yformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER, cartopy.mpl.gridliner.LATITUDE_FORMATTER
plt.title('2a) ax.pcolormesh(clon, clat, data)');
ax = plt.subplot(122, projection=cartopy.crs.PlateCarree())
ax.pcolormesh(vlon, vlat, data, transform=cartopy.crs.PlateCarree(), vmin=0, vmax=1);
gl = ax.gridlines(draw_labels=True); gl.xlabels_top,gl.ylabels_right = False,False
gl.xformatter,gl.yformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER, cartopy.mpl.gridliner.LATITUDE_FORMATTER
plt.title('2b) ax.pcolormesh(vlon, vlat, data)');
plt.tight_layout()
# -
# Apart from some handy decoartion of the plot (labels), the behavior for `ax.pcolormesh()` is no different than for `plt.pcolormesh()`:
#
# - Panel 2a shows the wrong number of cells, with the wrong cell bondaries, and does not fill the domain.
# - Panel 2b is drawn correctly.
#
# ## pcolormesh via xarray
#
# Now to examine how pcolormesh behaves for an xarray `DataSet` (or `DataArray`) we need to define a Dataset. Here, I'm indicating that vlon and vlat could also be coordinates.
ds = xarray.Dataset({'data': (['clat', 'clon'], data)},
coords={
'clon': (['clon'], clon),
'clat': (['clat'], clat),
'vlon': (['vlon'], vlon),
'vlat': (['vlat'], vlat),
}
)
ds
# Here's see what happens when we use the `.plot()` method and the `.pcolormesh()` method on a cartopy created axes:
# +
plt.figure(figsize=(10,4))
plt.subplot(121)
ds.data.plot();
plt.title('3a) ds.data.plot()')
ax = plt.subplot(122, projection=cartopy.crs.PlateCarree())
ds.data.plot(transform=cartopy.crs.PlateCarree(), vmin=0, vmax=1);
gl = ax.gridlines(draw_labels=True); gl.xlabels_top,gl.ylabels_right = False,False
gl.xformatter,gl.yformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER, cartopy.mpl.gridliner.LATITUDE_FORMATTER
plt.title('3b ds.data.plot() with cartopy axes')
plt.tight_layout()
# -
# Good and bad news!
#
# - On the up side, there are 6x4 cells shown in both panels (3a and 3b).
# - On the down side, the cell boundaries are not in the correct locations.
# - Also, more of the domain is shown than for 1a or 2a but the domain is still not completely filled.
#
# What has happened here is that the good folks behind xarray, knowing that pcolormesh expects cell boundary locations, have calculated the cell boundaries from the cell-center coordinates. It's better than ignoring the problem but unfortunately only gives the correct result for a uniformly spaced mesh.
#
# At this time, I'm unaware of a clean fix for this using xarray so calling `plt.pcolormesh()` with explicit reference to the the cell boundaries, rather than using the help `.plot()` function, seems like the only way to get a correct plot.
# +
# It would be nice if something like this worked...
# ds.data.plot.pcolormesh(x='vlon',y='vlat',infer_intervals=False)
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.pcolormesh(ds.vlon, ds.vlat, ds.data, vmin=0, vmax=1);
plt.title('4a) plt.pcolormesh(ds.vlon, ds.lat, ds.data)');
ax = plt.subplot(122, projection=cartopy.crs.PlateCarree())
plt.pcolormesh(ds.vlon, ds.vlat, ds.data, vmin=0, vmax=1, transform=cartopy.crs.PlateCarree());
gl = ax.gridlines(draw_labels=True); gl.xlabels_top,gl.ylabels_right = False,False
gl.xformatter,gl.yformatter = cartopy.mpl.gridliner.LONGITUDE_FORMATTER, cartopy.mpl.gridliner.LATITUDE_FORMATTER
plt.title('4b) plt.pcolormesh() + cartopy');
# -
# ## Summary
#
# - We've seen that plotting with pcolormesh only gives the wrong right results when the cell boundary coordinates are provided.
# - When data coordinate are used (i.e. not cell boundaries):
# - not all data is plotted;
# - location of data is wrong.
# - The xarray helper function, `.plot()`, plots all the data but not necessarily in the right location
# - xarray `.plot()` is still better than raw pcolormesh.
|
8-Deeper-dive-into-pcolormesh.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# [Home Page](../Start_Here.ipynb)
#      
#      
#      
#      
#    
# [Next Notebook](CNN's.ipynb)
# # CNN Primer and Keras 101
#
# In this notebook you will be introduced to the concept of a convolutional neural network (CNN) and implement one using Keras. This notebook is designed as a starting point for absolute beginners to deep learning.
#
# **Contents of this notebook:**
#
# - [How a deep learning project is planned](#Machine-Learning-Pipeline)
# - [Wrapping things up with an example (classification)](#Wrapping-Things-up-with-an-Example)
# - [Fully connected networks](#Image-Classification-on-types-of-Clothes)
#
#
# **By the end of this notebook the participant will:**
#
# - Understand machine learning pipelines
# - Write a deep learning classifier and train it
#
# **We will be building a _multi-class classifier_ to classify images of clothing into their respective classes.**
# ## Machine Learning Pipeline
#
# During the bootcamp we will be making use of the following concepts to help us understand how a machine learning (ML) project should be planned and executed:
#
# 1. **Data**: To start any ML project we need data which is pre-processed and can be fed into the network.
# 2. **Task**: There are many possible tasks in the field of ML; we need to make sure we understand and define the problem statement accurately.
# 3. **Model**: We need to build our model, which is neither too deep (requiring a lot of computational power) nor too small (preventing it from learning the important features).
# 4. **Loss**: Out of the many _loss functions_ that can be defined, we need to carefully choose one which is suitable for the task we are about to carry out.
# 5. **Learning**: There are a variety of _optimisers_, each with their advantages and disadvantages. We must choose one which is suitable for our task and train our model using some suitably chosen hyperparameters.
# 6. **Evaluation**: We must determine if our model has learned the features properly by analysing how it performs on data it has not previously seen.
# **Here we will be building a _multi-class classifier_ to classify images of clothing into their respective classes.**
#
# We will follow the pipeline presented above to complete the example.
#
# ## Image classification on types of clothes
#
# #### Step 1: Data
#
# We will be using the **Fashion MNIST** dataset, which is a very popular introductory dataset in deep learning. This dataset contains 70,000 grayscale images in 10 categories. The images show individual articles of clothing at low resolution (28 by 28 pixels).
#
# <img src="images/fashion-mnist.png" alt="Fashion MNIST sprite" width="600">
#
# *Source: https://www.tensorflow.org/tutorials/keras/classification*
# +
# Import Necessary Libraries
from __future__ import absolute_import, division, print_function, unicode_literals
# TensorFlow and tf.keras
import tensorflow as tf
from tensorflow import keras
# Helper libraries
import numpy as np
import matplotlib.pyplot as plt
print(tf.__version__)
# +
# Let's Import the Dataset
fashion_mnist = keras.datasets.fashion_mnist
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
# -
# Loading the dataset returns four NumPy arrays:
#
# * The `train_images` and `train_labels` arrays are the *training set*—the data the model uses to learn.
# * The model is tested against the *test set*, the `test_images`, and `test_labels` arrays.
#
# The images are 28x28 NumPy arrays, with pixel values ranging from 0 to 255. The *labels* are an array of integers, ranging from 0 to 9. These correspond to the *class* of clothing the image represents:
#
# <table>
# <tr>
# <th>Label</th>
# <th>Class</th>
# </tr>
# <tr>
# <td>0</td>
# <td>T-shirt/top</td>
# </tr>
# <tr>
# <td>1</td>
# <td>Trouser</td>
# </tr>
# <tr>
# <td>2</td>
# <td>Pullover</td>
# </tr>
# <tr>
# <td>3</td>
# <td>Dress</td>
# </tr>
# <tr>
# <td>4</td>
# <td>Coat</td>
# </tr>
# <tr>
# <td>5</td>
# <td>Sandal</td>
# </tr>
# <tr>
# <td>6</td>
# <td>Shirt</td>
# </tr>
# <tr>
# <td>7</td>
# <td>Sneaker</td>
# </tr>
# <tr>
# <td>8</td>
# <td>Bag</td>
# </tr>
# <tr>
# <td>9</td>
# <td>Ankle boot</td>
# </tr>
# </table>
#
# Each image is mapped to a single label. Since the *class names* are not included with the dataset, let us store them in an array so that we can use them later when plotting the images:
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
# ## Understanding the Data
# +
# Print array size of training dataset
print("Size of Training Images: " + str(train_images.shape))
# Print array size of labels
print("Size of Training Labels: " + str(train_labels.shape))
# Print array size of test dataset
print("Size of Test Images: " + str(test_images.shape))
# Print array size of labels
print("Size of Test Labels: " + str(test_labels.shape))
# Let's see how our outputs look
print("Training Set Labels: " + str(train_labels))
# Data in the test dataset
print("Test Set Labels: " + str(test_labels))
# -
# ## Data Preprocessing
#
plt.figure()
plt.imshow(train_images[0])
plt.colorbar()
plt.grid(False)
plt.show()
# The image pixel values range from 0 to 255. Let us now normalise the data range from 0 - 255 to 0 - 1 in both the *Train* and *Test* set. This normalisation of pixels helps us by optimizing the process where the gradients are computed.
train_images = train_images / 255.0
test_images = test_images / 255.0
# Let's print to verify whether the data is of the correct format.
plt.figure(figsize=(10,10))
for i in range(25):
plt.subplot(5,5,i+1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(train_images[i], cmap=plt.cm.binary)
plt.xlabel(class_names[train_labels[i]])
plt.show()
# ## Defining our Model
#
# Our model has three layers:
#
# - 784 input features (28 * 28)
# - 128 nodes in the hidden layer (feel free to experiment with this value)
# - 10 output nodes to denote the class
#
# We will implement this model in Keras (TensorFlow's high-level API for machine learning).
#
from tensorflow.keras import backend as K
K.clear_session()
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
# The first layer in this network, `tf.keras.layers.Flatten`, transforms the format of the images from a two-dimensional array (of 28 by 28 pixels) to a one-dimensional array (of 28 * 28 = 784 pixels). Think of this layer as unstacking rows of pixels in the image and lining them up. This layer has no parameters to learn; it only reformats the data.
#
# After the pixels are flattened, the network consists of a sequence of two `tf.keras.layers.Dense` layers. These are densely connected, or fully connected, neural layers. The first `Dense` layer has 128 nodes (or neurons). The second (and last) layer is a 10-node *softmax* layer that returns an array of 10 probability scores that sum to 1. Each node contains a score that indicates the probability that the current image belongs to one of the 10 classes.
#
# ### Compile the model
#
# Before the model is ready for training, it needs a few more settings. These are added during the model's *compile* step:
#
# * *Loss function* —This measures how accurate the model is during training. You want to minimize this function to "steer" the model in the right direction.
# * *Optimizer* —This is how the model is updated based on the data it sees and its loss function.
# * *Metrics* —Used to monitor the training and testing steps. The following example uses *accuracy*, the fraction of the images that are correctly classified.
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
# ## Train the model
#
# Training the neural network model requires the following steps:
#
# 1. Feed the training data to the model. In this example, the training data is in the `train_images` and `train_labels` arrays.
# 2. The model learns to associate images and labels.
# 3. You ask the model to make predictions about a test set—in this example, the `test_images` array. Verify that the predictions match the labels from the `test_labels` array.
#
# To start training, call the `model.fit` method—so called because it "fits" the model to the training data:
model.fit(train_images, train_labels, epochs=5)
# ## Evaluate accuracy
#
# Next, compare how the model performs on the test dataset:
# +
# Evaluating the model using the test dataset
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print('\nTest accuracy:', test_acc)
# -
# We get an accuracy of 87% on the test dataset, which is less than the 89% we got during the training phase. This problem in machine learning is called overfitting.
#
# ## Exercise
#
# Try adding more dense layers to the network above and observe the change in accuracy.
#
# ## Important:
# <mark>Shut down the kernel before clicking on “Next Notebook” to free up the GPU memory.</mark>
#
#
# ## Licensing
# This material is released by NVIDIA Corporation under the Creative Commons Attribution 4.0 International (CC BY 4.0)
# [Home Page](../Start_Here.ipynb)
#      
#      
#      
#      
#    
# [Next Notebook](CNN's.ipynb)
|
hpc_ai/ai_science_cfd/English/python/jupyter_notebook/Intro_to_DL/Part_2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.6.8 64-bit (''venv-perceptual-sim2'': virtualenv)'
# language: python
# name: python36864bitvenvperceptualsim2virtualenv04c3fa8e29ed4e2aa1227ebee311e9b1
# ---
import torch
import os
import sys
import re
from shutil import copyfile
import numpy as np
# # Transitions weights of model tined on the 2AFC dataset to the loss provider.
def params_remove_prefix(params):
old_keys = list(params.keys())
for k in old_keys:
params[k[4:]] = params[k]
params.pop(k)
return params
# +
weight_dirs = os.listdir('./checkpoints/')
weight_dirs.remove('.gitignore')
for weight_dir in weight_dirs:
path=os.path.join('./checkpoints/', weight_dir, 'latest_net_.pth')
state_dict = torch.load(path, map_location='cpu')
if not('pnet_lin' in weight_dir):
state_dict = params_remove_prefix(state_dict)
torch.save(state_dict, os.path.join('../loss/weights', weight_dir + '.pth'))
|
src/perceptual_sim_training/transition_weights.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# <center>
# <img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DL0110EN-SkillsNetwork/Template/module%201/images/IDSNlogo.png" width="300" alt="cognitiveclass.ai logo" />
# </center>
#
# <h1>Torch Tensors in 1D</h1>
#
# <h2>Objective</h2><ul><li> How tensor operations work in pytorch.</li></ul>
#
# <h2>Table of Contents</h2>
#
# <p>In this lab, you will learn the basics of tensor operations. Tensors are an essential part of PyTorch; there are complex mathematical objects in and of themselves. Fortunately, most of the intricacies are not necessary. In this section, you will compare them to vectors and numpy arrays.</p>
# <ul>
# <li><a href="https://#Types_Shape">Types and Shape</a></li>
# <li><a href="https://#Index_Slice">Indexing and Slicing</a></li>
# <li><a href="https://#Tensor_Func">Tensor Functions</a></li>
# <li><a href="https://#Tensor_Op">Tensor Operations</a></li>
# <li><a href="https://#Device_Op">Device_Op Operations</a></li>
# </ul>
#
# <p>Estimated Time Needed: <b>25 min</b></p>
# <hr>
#
# <h2>Preparation</h2>
#
# Import the following libraries that you'll use for this lab:
#
# + jupyter={"outputs_hidden": true}
# These are the libraries will be used for this lab.
import torch
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
# -
# Check PyTorch version:
#
# + jupyter={"outputs_hidden": true}
torch.__version__
# -
# This is the function for plotting diagrams. You will use this function to plot the vectors in Coordinate system.
#
# + jupyter={"outputs_hidden": false}
# Plot vecotrs, please keep the parameters in the same length
# @param: Vectors = [{"vector": vector variable, "name": name of vector, "color": color of the vector on diagram}]
def plotVec(vectors):
ax = plt.axes()
# For loop to draw the vectors
for vec in vectors:
ax.arrow(0, 0, *vec["vector"], head_width = 0.05,color = vec["color"], head_length = 0.1)
plt.text(*(vec["vector"] + 0.1), vec["name"])
plt.ylim(-2,2)
plt.xlim(-2,2)
# -
# <!--Empty Space for separating topics-->
#
# <h2 id="Types_Shape">Types and Shape</h2>
#
# You can find the type of the following list of integers <i>\[0, 1, 2, 3, 4]</i> by applying the constructor <code>torch.tensor()</code>:
#
# + jupyter={"outputs_hidden": false}
# Convert a integer list with length 5 to a tensor
ints_to_tensor = torch.tensor([0, 1, 2, 3, 4])
print("The dtype of tensor object after converting it to tensor: ", ints_to_tensor.dtype)
print("The type of tensor object after converting it to tensor: ", ints_to_tensor.type())
# -
# As a result, the integer list has been converted to a long tensor.
#
# The Python type is still <code>torch.Tensor</code>:
#
type(ints_to_tensor)
# <!--Empty Space for separate topics-->
#
# You can find the type of this float list <i>\[0.0, 1.0, 2.0, 3.0, 4.0]</i> by applying the method <code>torch.tensor()</code>:
#
# + jupyter={"outputs_hidden": false}
# Convert a float list with length 5 to a tensor
floats_to_tensor = torch.tensor([0.0, 1.0, 2.0, 3.0, 4.0])
print("The dtype of tensor object after converting it to tensor: ", floats_to_tensor.dtype)
print("The type of tensor object after converting it to tensor: ", floats_to_tensor.type())
# -
# The float list is converted to a float tensor.
#
# +
list_floats=[0.0, 1.0, 2.0, 3.0, 4.0]
floats_int_tensor=torch.tensor(list_floats,dtype=torch.int64)
# -
print("The dtype of tensor object is: ", floats_int_tensor.dtype)
print("The type of tensor object is: ", floats_int_tensor.type())
# <b>Note: The elements in the list that will be converted to tensor must have the same type.</b>
#
# <!--Empty Space for separating topics-->
#
# From the previous examples, you see that <code>torch.tensor()</code> converts the list to the tensor type, which is similar to the original list type. However, what if you want to convert the list to a certain tensor type? <code>torch</code> contains the methods required to do this conversion. The following code converts an integer list to float tensor:
#
# +
# Convert a integer list with length 5 to float tensor
new_float_tensor = torch.FloatTensor([0, 1, 2, 3, 4])
new_float_tensor.type()
print("The type of the new_float_tensor:", new_float_tensor.type())
# -
new_float_tensor = torch.FloatTensor([0, 1, 2, 3, 4])
# <!--Empty Space for separating topics-->
#
# You can also convert an existing tensor object (<code><i>tensor_obj</i></code>) to another tensor type. Convert the integer tensor to a float tensor:
#
# +
# Another method to convert the integer list to float tensor
old_int_tensor = torch.tensor([0, 1, 2, 3, 4])
new_float_tensor = old_int_tensor.type(torch.FloatTensor)
print("The type of the new_float_tensor:", new_float_tensor.type())
# -
# <!--Empty Space for separating topics-->
#
# The <code><i>tensor_obj</i>.size()</code> helps you to find out the size of the <code><i>tensor_obj</i></code>.
# The <code><i>tensor_obj</i>.ndimension()</code> shows the dimension of the tensor object.
#
# +
# Introduce the tensor_obj.size() & tensor_ndimension.size() methods
print("The size of the new_float_tensor: ", new_float_tensor.size())
print("The dimension of the new_float_tensor: ",new_float_tensor.ndimension())
# -
# <!--Empty Space for separating topics-->
#
# The <code><i>tensor_obj</i>.view(<i>row, column</i>)</code> is used for reshaping a tensor object.<br>
#
# What if you have a tensor object with <code>torch.Size(\[5])</code> as a <code>new_float_tensor</code> as shown in the previous example?<br>
# After you execute <code>new_float_tensor.view(5, 1)</code>, the size of <code>new_float_tensor</code> will be <code>torch.Size(\[5, 1])</code>.<br>
# This means that the tensor object <code>new_float_tensor</code> has been reshaped from a one-dimensional tensor object with 5 elements to a two-dimensional tensor object with 5 rows and 1 column.
#
# +
# Introduce the tensor_obj.view(row, column) method
twoD_float_tensor = new_float_tensor.view(5, 1)
print("Original Size: ", new_float_tensor)
print("Size after view method", twoD_float_tensor)
# -
# Note that the original size is 5. The tensor after reshaping becomes a 5X1 tensor analog to a column vector.
#
# <b>Note: The number of elements in a tensor must remain constant after applying view.</b>
#
# <!--Empty Space for separating topics-->
#
# What if you have a tensor with dynamic size but you want to reshape it? You can use <b>-1</b> to do just that.
#
# +
# Introduce the use of -1 in tensor_obj.view(row, column) method
twoD_float_tensor = new_float_tensor.view(-1, 1)
print("Original Size: ", new_float_tensor)
print("Size after view method", twoD_float_tensor)
# -
# You get the same result as the previous example. The <b>-1</b> can represent any size. However, be careful because you can set only one argument as <b>-1</b>.
#
# <!--Empty Space for separating topics-->
#
# You can also convert a <b>numpy</b> array to a <b>tensor</b>, for example:
#
# +
# Convert a numpy array to a tensor
numpy_array = np.array([0.0, 1.0, 2.0, 3.0, 4.0])
new_tensor = torch.from_numpy(numpy_array)
print("The dtype of new tensor: ", new_tensor.dtype)
print("The type of new tensor: ", new_tensor.type())
# -
# <!--Empty Space for separating topics-->
#
# Converting a <b>tensor</b> to a <b>numpy</b> is also supported in PyTorch. The syntax is shown below:
#
# +
# Convert a tensor to a numpy array
back_to_numpy = new_tensor.numpy()
print("The numpy array from tensor: ", back_to_numpy)
print("The dtype of numpy array: ", back_to_numpy.dtype)
# -
# <code>back_to_numpy</code> and <code>new_tensor</code> still point to <code>numpy_array</code>. As a result if we change <code>numpy_array</code> both <code>back_to_numpy</code> and <code>new_tensor</code> will change. For example if we set all the elements in <code>numpy_array</code> to zeros, <code>back_to_numpy</code> and <code> new_tensor</code> will follow suit.
#
# Set all elements in numpy array to zero
numpy_array[:] = 0
print("The new tensor points to numpy_array : ", new_tensor)
print("and back to numpy array points to the tensor: ", back_to_numpy)
# <!--Empty Space for separating topics-->
#
# <b>Pandas Series</b> can also be converted by using the numpy array that is stored in <code>pandas_series.values</code>. Note that <code>pandas_series</code> can be any pandas_series object.
#
# +
# Convert a panda series to a tensor
pandas_series=pd.Series([0.1, 2, 0.3, 10.1])
new_tensor=torch.from_numpy(pandas_series.values)
print("The new tensor from numpy array: ", new_tensor)
print("The dtype of new tensor: ", new_tensor.dtype)
print("The type of new tensor: ", new_tensor.type())
# -
# consider the following tensor
#
this_tensor=torch.tensor([0,1, 2,3])
# The method <code>item()</code> returns the value of this tensor as a standard Python number. This only works for one element.
#
# +
this_tensor=torch.tensor([0,1, 2,3])
print("the first item is given by",this_tensor[0].item(),"the first tensor value is given by ",this_tensor[0])
print("the second item is given by",this_tensor[1].item(),"the second tensor value is given by ",this_tensor[1])
print("the third item is given by",this_tensor[2].item(),"the third tensor value is given by ",this_tensor[2])
# -
# we can use the method <code> tolist()</code> to return a list
#
# +
torch_to_list=this_tensor.tolist()
print('tensor:', this_tensor,"\nlist:",torch_to_list)
# -
# <!--Empty Space for separating topics-->
#
# <h3>Practice</h3>
#
# Try to convert <code>your_tensor</code> to a 1X5 tensor.
#
# +
# Practice: convert the following tensor to a tensor object with 1 row and 5 columns
your_tensor = torch.tensor([1, 2, 3, 4, 5])
# -
# Double-click <b>here</b> for the solution.
#
# <!--
# your_new_tensor = your_tensor.view(1, 5)
# print("Original Size: ", your_tensor)
# print("Size after view method", your_new_tensor)
# -->
#
# <!--Empty Space for separating topics-->
#
# <h2 id="Index_Slice">Indexing and Slicing</h2>
#
# In Python, <b>the index starts with 0</b>. Therefore, the last index will always be 1 less than the length of the tensor object.
# You can access the value on a certain index by using the square bracket, for example:
#
# +
# A tensor for showing how the indexs work on tensors
index_tensor = torch.tensor([0, 1, 2, 3, 4])
print("The value on index 0:",index_tensor[0])
print("The value on index 1:",index_tensor[1])
print("The value on index 2:",index_tensor[2])
print("The value on index 3:",index_tensor[3])
print("The value on index 4:",index_tensor[4])
# -
# <b>Note that the <code>index_tensor\[5]</code> will create an error.</b>
#
# <!--Empty Space for separating topics-->
#
# The index is shown in the following figure:
#
# <img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter%201/idex_1.png" width="500" alt="Python Index" />
#
# <!--Empty Space for separating topics-->
#
# Now, you'll see how to change the values on certain indexes.
#
# Suppose you have a tensor as shown here:
#
# + jupyter={"outputs_hidden": false}
# A tensor for showing how to change value according to the index
tensor_sample = torch.tensor([20, 1, 2, 3, 4])
# -
# Assign the value on index 0 as 100:
#
# + jupyter={"outputs_hidden": false}
# Change the value on the index 0 to 100
print("Inital value on index 0:", tensor_sample[0])
tensor_sample[0] = 100
print("Modified tensor:", tensor_sample)
# -
# As you can see, the value on index 0 changes. Change the value on index 4 to 0:
#
# + jupyter={"outputs_hidden": false}
# Change the value on the index 4 to 0
print("Inital value on index 4:", tensor_sample[4])
tensor_sample[4] = 0
print("Modified tensor:", tensor_sample)
# -
# The value on index 4 turns to 0.
#
# <!--Empty Space for separating topics-->
#
# If you are familiar with Python, you know that there is a feature called slicing on a list. Tensors support the same feature.
#
# Get the subset of <code>tensor_sample</code>. The subset should contain the values in <code>tensor_sample</code> from index 1 to index 3.
#
# + jupyter={"outputs_hidden": false}
# Slice tensor_sample
subset_tensor_sample = tensor_sample[1:4]
print("Original tensor sample: ", tensor_sample)
print("The subset of tensor sample:", subset_tensor_sample)
# -
# As a result, the <code>subset_tensor_sample</code> returned only the values on index 1, index 2, and index 3. Then, it stored them in a <code>subset_tensor_sample</code>.
#
# <b>Note: The number on the left side of the colon represents the index of the first value. The number on the right side of the colon is always 1 larger than the index of the last value. For example, <code>tensor_sample\[1:4]</code> means you get values from the index 1 to index 3 <i>(4-1)</i></b>.
#
# <!--Empty Space for separating topics-->
#
# As for assigning values to the certain index, you can also assign the value to the slices:
#
# Change the value of <code>tensor_sample</code> from index 3 to index 4:
#
# +
# Change the values on index 3 and index 4
print("Inital value on index 3 and index 4:", tensor_sample[3:5])
tensor_sample[3:5] = torch.tensor([300.0, 400.0])
print("Modified tensor:", tensor_sample)
# -
# The values on both index 3 and index 4 were changed. The values on other indexes remain the same.
#
# <!--Empty Space for separating topics-->
#
# You can also use a variable to contain the selected indexes and pass that variable to a tensor slice operation as a parameter, for example:
#
# + jupyter={"outputs_hidden": true}
# Using variable to contain the selected index, and pass it to slice operation
selected_indexes = [3, 4]
subset_tensor_sample = tensor_sample[selected_indexes]
print("The inital tensor_sample", tensor_sample)
print("The subset of tensor_sample with the values on index 3 and 4: ", subset_tensor_sample)
# -
# <!--Empty Space for separating topics-->
#
# You can also assign one value to the selected indexes by using the variable. For example, assign 100,000 to all the <code>selected_indexes</code>:
#
# + jupyter={"outputs_hidden": false}
#Using variable to assign the value to the selected indexes
print("The inital tensor_sample", tensor_sample)
selected_indexes = [1, 3]
tensor_sample[selected_indexes] = 100000
print("Modified tensor with one value: ", tensor_sample)
# -
# The values on index 1 and index 3 were changed to 100,000. Others remain the same.
#
# <b>Note: You can use only one value for the assignment.</b>
#
# <!--Empty Space for separating topics-->
#
# <h3>Practice</h3>
#
# Try to change the values on index 3, 4, 7 of the following tensor to 0.
#
# +
# Practice: Change the values on index 3, 4, 7 to 0
practice_tensor = torch.tensor([2, 7, 3, 4, 6, 2, 3, 1, 2])
# -
# Double-click <b>here</b> for the solution.
#
# <!--
# selected_indexes = [3, 4, 7]
# practice_tensor[selected_indexes] = 0
# print("New Practice Tensor: ", practice_tensor)
# -->
#
# <!--Empty Space for separating topics-->
#
# <h2 id="Tensor_Func">Tensor Functions</h2>
#
# For this section, you'll work with some methods that you can apply to tensor objects.
#
# <h3>Mean and Standard Deviation</h3>
#
# You'll review the mean and standard deviation methods first. They are two basic statistical methods.
#
# <!--Empty Space for separating topics-->
#
# Create a tensor with values <i>\[1.0, -1, 1, -1]</i>:
#
# + jupyter={"outputs_hidden": true}
# Sample tensor for mathmatic calculation methods on tensor
math_tensor = torch.tensor([1.0, -1.0, 1, -1])
print("Tensor example: ", math_tensor)
# -
# <!--Empty Space for separating topics-->
#
# Here is the mean method:
#
# + jupyter={"outputs_hidden": false}
#Calculate the mean for math_tensor
mean = math_tensor.mean()
print("The mean of math_tensor: ", mean)
# -
# <!--Empty Space for separating topics-->
#
# The standard deviation can also be calculated by using <code><i>tensor_obj</i>.std()</code>:
#
# + jupyter={"outputs_hidden": false}
#Calculate the standard deviation for math_tensor
standard_deviation = math_tensor.std()
print("The standard deviation of math_tensor: ", standard_deviation)
# -
# <!--Empty Space for separating topics-->
#
# <h3>Max and Min</h3>
#
# Now, you'll review another two useful methods: <code><i>tensor_obj</i>.max()</code> and <code><i>tensor_obj</i>.min()</code>. These two methods are used for finding the maximum value and the minimum value in the tensor.
#
# <!--Empty Space for separating topics-->
#
# Create a <code>max_min_tensor</code>:
#
# + jupyter={"outputs_hidden": false}
# Sample for introducing max and min methods
max_min_tensor = torch.tensor([1, 1, 3, 5, 5])
print("Tensor example: ", max_min_tensor)
# -
# <b>Note: There are two minimum numbers as 1 and two maximum numbers as 5 in the tensor. Can you guess how PyTorch is going to deal with the duplicates?</b>
#
# <!--Empty Space for separating topics-->
#
# Apply <code><i>tensor_obj</i>.max()</code> on <code>max_min_tensor</code>:
#
# + jupyter={"outputs_hidden": false}
# Method for finding the maximum value in the tensor
max_val = max_min_tensor.max()
print("Maximum number in the tensor: ", max_val)
# -
# The answer is <code>tensor(5)</code>. Therefore, the method <code><i>tensor_obj</i>.max()</code> is grabbing the maximum value but not the elements that contain the maximum value in the tensor.
#
max_min_tensor.max()
# <!--Empty Space for separating topics-->
#
# Use <code><i>tensor_obj</i>.min()</code> on <code>max_min_tensor</code>:
#
# + jupyter={"outputs_hidden": false}
# Method for finding the minimum value in the tensor
min_val = max_min_tensor.min()
print("Minimum number in the tensor: ", min_val)
# -
# The answer is <code>tensor(1)</code>. Therefore, the method <code><i>tensor_obj</i>.min()</code> is grabbing the minimum value but not the elements that contain the minimum value in the tensor.
#
# <!--Empty Space for separating topics-->
#
# <h3>Sin</h3>
#
# Sin is the trigonometric function of an angle. Again, you will not be introducedvto any mathematic functions. You'll focus on Python.
#
# <!--Empty Space for separating topics-->
#
# Create a tensor with 0, π/2 and π. Then, apply the sin function on the tensor. Notice here that the <code>sin()</code> is not a method of tensor object but is a function of torch:
#
# + jupyter={"outputs_hidden": false}
# Method for calculating the sin result of each element in the tensor
pi_tensor = torch.tensor([0, np.pi/2, np.pi])
sin = torch.sin(pi_tensor)
print("The sin result of pi_tensor: ", sin)
# -
# The resultant tensor <code>sin</code> contains the result of the <code>sin</code> function applied to each element in the <code>pi_tensor</code>.<br>
# This is different from the previous methods. For <code><i>tensor_obj</i>.mean()</code>, <code><i>tensor_obj</i>.std()</code>, <code><i>tensor_obj</i>.max()</code>, and <code><i>tensor_obj</i>.min()</code>, the result is a tensor with only one number because these are aggregate methods.<br>
# However, the <code>torch.sin()</code> is not. Therefore, the resultant tensors have the same length as the input tensor.
#
# <!--Empty Space for separating topics-->
#
# <h3>Create Tensor by <code>torch.linspace()</code></h3>
#
# A useful function for plotting mathematical functions is <code>torch.linspace()</code>. <code>torch.linspace()</code> returns evenly spaced numbers over a specified interval. You specify the starting point of the sequence and the ending point of the sequence. The parameter <code>steps</code> indicates the number of samples to generate. Now, you'll work with <code>steps = 5</code>.
#
# + jupyter={"outputs_hidden": false}
# First try on using linspace to create tensor
len_5_tensor = torch.linspace(-2, 2, steps = 5)
print ("First Try on linspace", len_5_tensor)
# -
# <!--Empty Space for separating topics-->
#
# Assign <code>steps</code> with 9:
#
# + jupyter={"outputs_hidden": false}
# Second try on using linspace to create tensor
len_9_tensor = torch.linspace(-2, 2, steps = 9)
print ("Second Try on linspace", len_9_tensor)
# -
# <!--Empty Space for separating topics-->
#
# Use both <code>torch.linspace()</code> and <code>torch.sin()</code> to construct a tensor that contains the 100 sin result in range from 0 (0 degree) to 2π (360 degree):
#
# + jupyter={"outputs_hidden": false}
# Construct the tensor within 0 to 360 degree
pi_tensor = torch.linspace(0, 2*np.pi, 100)
sin_result = torch.sin(pi_tensor)
# -
# Plot the result to get a clearer picture. You must cast the tensor to a numpy array before plotting it.
#
# + jupyter={"outputs_hidden": false}
# Plot sin_result
plt.plot(pi_tensor.numpy(), sin_result.numpy())
# -
# If you know the trigonometric function, you will notice this is the diagram of the sin result in the range 0 to 360 degrees.
#
# <!--Empty Space for separating topics-->
#
# <h3>Practice</h3>
#
# Construct a tensor with 25 steps in the range 0 to π/2. Print out the Maximum and Minimum number. Also, plot a graph showing the diagram that shows the result.
#
# +
# Practice: Create your tensor, print max and min number, plot the sin result diagram
# Type your code here
# -
# Double-click <b>here</b> for the solution.
#
# <!--
# pi_tensor = torch.linspace(0, np.pi/2, 100)
# print("Max Number: ", pi_tensor.max())
# print("Min Number", pi_tensor.min())
# sin_result = torch.sin(pi_tensor)
# plt.plot(pi_tensor.numpy(), sin_result.numpy())
# -->
#
# <!--Empty Space for separating topics-->
#
# <h2 id="Tensor_Op">Tensor Operations</h2>
#
# In the following section, you'll work with operations that you can apply to a tensor.
#
# <!--Empty Space for separating topics-->
#
# <h3>Tensor Addition</h3>
#
# You can perform addition between two tensors.
#
# Create a tensor <code>u</code> with 1 dimension and 2 elements. Then, create another tensor <code>v</code> with the same number of dimensions and the same number of elements:
#
# + jupyter={"outputs_hidden": false}
# Create two sample tensors
u = torch.tensor([1, 0])
v = torch.tensor([0, 1])
# -
# Add <code>u</code> and <code>v</code> together:
#
# + jupyter={"outputs_hidden": false}
# Add u and v
w = u + v
print("The result tensor: ", w)
# -
# The result is <code>tensor(\[1, 1])</code>. The behavior is <i>\[1 + 0, 0 + 1]</i>.
#
# Plot the result to to get a clearer picture.
#
# + jupyter={"outputs_hidden": false}
# Plot u, v, w
plotVec([
{"vector": u.numpy(), "name": 'u', "color": 'r'},
{"vector": v.numpy(), "name": 'v', "color": 'b'},
{"vector": w.numpy(), "name": 'w', "color": 'g'}
])
# -
# <!--Empty Space for separating topics-->
#
# <h3>Try</h3>
#
# Implement the tensor subtraction with <code>u</code> and <code>v</code> as u-v.
#
# + jupyter={"outputs_hidden": false}
# Try by yourself to get a result of u-v
u = torch.tensor([1, 0])
v = torch.tensor([0, 1])
# -
# Double-click <b>here</b> for the solution.
#
# <!--
# print("The result tensor: ", u-v)
# -->
#
# Tensors must be of the same data type to perform addition as well as other operations.If you uncomment the following code and try to run it you will get an error as the two tensors are of two different data types. **NOTE This lab was created on a older PyTorch version so in the current version we are using this is possible and will produce a float64 tensor.**
#
# +
#torch.tensor([1,2,3],dtype=torch.int64)+torch.tensor([1,2,3],dtype=torch.float64)
# -
# <!--Empty Space for separating topics-->
#
# You can add a scalar to the tensor. Use <code>u</code> as the sample tensor:
#
# +
# tensor + scalar
u = torch.tensor([1, 2, 3, -1])
v = u + 1
print ("Addition Result: ", v)
# -
# The result is simply adding 1 to each element in tensor <code>u</code> as shown in the following image:
#
# <img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter%201/brodcasting.gif" width = "500" alt="tensor addition" />
#
# <!--Empty Space for separating topics-->
#
# <h3>Tensor Multiplication </h3>
#
# Now, you'll review the multiplication between a tensor and a scalar.
#
# Create a tensor with value <code>\[1, 2]</code> and then multiply it by 2:
#
# + jupyter={"outputs_hidden": false}
# tensor * scalar
u = torch.tensor([1, 2])
v = 2 * u
print("The result of 2 * u: ", v)
# -
# The result is <code>tensor(\[2, 4])</code>, so the code <code>2 \* u</code> multiplies each element in the tensor by 2. This is how you get the product between a vector or matrix and a scalar in linear algebra.
#
# <!--Empty Space for separating topics-->
#
# You can use multiplication between two tensors.
#
# Create two tensors <code>u</code> and <code>v</code> and then multiply them together:
#
# + jupyter={"outputs_hidden": false}
# tensor * tensor
u = torch.tensor([1, 2])
v = torch.tensor([3, 2])
w = u * v
print ("The result of u * v", w)
# -
# The result is simply <code>tensor(\[3, 4])</code>. This result is achieved by multiplying every element in <code>u</code> with the corresponding element in the same position <code>v</code>, which is similar to <i>\[1 \* 3, 2 \* 2]</i>.
#
# <!--Empty Space for separating topics-->
#
# <h3>Dot Product</h3>
#
# The dot product is a special operation for a vector that you can use in Torch.
#
# Here is the dot product of the two tensors <code>u</code> and <code>v</code>:
#
# +
# Calculate dot product of u, v
u = torch.tensor([1, 2])
v = torch.tensor([3, 2])
print("Dot Product of u, v:", torch.dot(u,v))
# -
# The result is <code>tensor(7)</code>. The function is <i>1 x 3 + 2 x 2 = 7</i>.
#
# <!--Empty Space for separating topics-->
#
# <h3>Practice</h3>
#
# Convert the list <i>\[-1, 1]</i> and <i>\[1, 1]</i> to tensors <code>u</code> and <code>v</code>. Then, plot the tensor <code>u</code> and <code>v</code> as a vector by using the function <code>plotVec</code> and find the dot product:
#
# + jupyter={"outputs_hidden": false}
# Practice: calculate the dot product of u and v, and plot out two vectors
# Type your code here
# -
# Double-click <b>here</b> for the solution.
#
# <!--
# u= torch.tensor([-1, 1])
# v= torch.tensor([1, 1])
# plotVec([
# {"vector": u.numpy(), "name": 'u', "color": 'r'},
# {"vector": v.numpy(), "name": 'v', "color": 'b'}
# ])
# print("The Dot Product is",np.dot(u, v))
# -->
#
# <!--Empty Space for separating topics-->
#
# See <a href="https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01">Broadcasting</a> for more information on numpy that is similar to PyTorch.
#
# <a href="https://dataplatform.cloud.ibm.com/registration/stepone?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01&context=cpdaas&apps=data_science_experience%2Cwatson_machine_learning"><img src="https://cf-courses-data.s3.us.cloud-object-storage.appdomain.cloud/IBMDeveloperSkillsNetwork-DL0110EN-SkillsNetwork/Template/module%201/images/Watson_Studio.png"/></a>
#
# <h2>About the Authors:</h2>
#
# <a href="https://www.linkedin.com/in/joseph-s-50398b136/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
#
# Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>, <a href="https://www.linkedin.com/in/jiahui-mavis-zhou-a4537814a?utm_medium=Exinfluencer&utm_source=Exinfluencer&utm_content=000026UJ&utm_term=10006555&utm_id=NA-SkillsNetwork-Channel-SkillsNetworkCoursesIBMDeveloperSkillsNetworkDL0110ENSkillsNetwork20647811-2021-01-01"><NAME></a>
#
# ## Change Log
#
# | Date (YYYY-MM-DD) | Version | Changed By | Change Description |
# | ----------------- | ------- | ---------- | ----------------------------------------------------------- |
# | 2020-09-21 | 2.0 | Shubham | Migrated Lab to Markdown and added to course repo in GitLab |
#
# <hr>
#
# ## <h3 align="center"> © IBM Corporation 2020. All rights reserved. <h3/>
#
|
Deep Neural Networks with PyTorch/Week 1/1.1_1Dtensors_v2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#In this Question, I have implemented Multinomial Naive Bayes from Scratch
import pandas as pd
import numpy as np
import re
from unidecode import unidecode
# -
def remove_html(text):
html_pattern = re.compile('<.*?>')
return html_pattern.sub(r'', text)
#This function is used to preprocess strings in Abstract for the arxiv dataset
def preprocess_string(str_arg):
str_arg=re.sub('[^a-z\s]+',' ',str_arg,flags=re.IGNORECASE)
str_arg=re.sub('(\s+)',' ',str_arg)
str_arg=str_arg.lower()
str_arg = unidecode(str_arg)
str_arg = remove_html(str_arg)
return str_arg
class NaiveBayes:
def __init__(self):
#Just initializing the object here, nothing to do
pass
def addToBow(self,example,dict_index):
#Algorithm - I am storing counts of all words as per Category Index in BoW
example=example[0] #This is because the Example will have the shape - (1,)
for token_word in example.split(): #for every word in preprocessed example
considered_dict = self.bow_dicts[dict_index]
intVal = 0
if token_word in considered_dict:
intVal = considered_dict[token_word]
self.bow_dicts[dict_index][token_word] = intVal + 1
else:
self.bow_dicts[dict_index][token_word] = 1
def train(self,dataset,labels):
self.examples=dataset
self.labels=labels
self.classes = np.unique(labels)
bag_of_word_list = []
for index in range(self.classes.shape[0]):
bag_of_word_list.append(dict())
self.bow_dicts = np.array(bag_of_word_list) #We want to return 0 if value does not exist
#For Bag of Words, we have one Dictionary for Every Category
self.examples=np.array(self.examples)
self.labels=np.array(self.labels)
#constructing BoW for each category
for cat_index,cat in enumerate(self.classes):
np.apply_along_axis(self.addToBow, 1, pd.DataFrame(self.examples[self.labels==cat]),cat_index) #I am creating the BoW for each class
prob_classes=np.empty(self.classes.shape[0])
all_words=[]
cat_word_counts=np.empty(self.classes.shape[0])
for cat_index,cat in enumerate(self.classes):
#Calculating prior probability p(c) for each class
#For our particular dataset, we will observe that the prior values are the same after computation
number_of_label_rows = self.labels.shape[0]
number_of_rows_each_class = np.sum(self.labels==cat)
prob_classes[cat_index]=float(number_of_rows_each_class/number_of_label_rows)
#Calculating total counts of all the words of each class
count=np.asarray(list(self.bow_dicts[cat_index].values()))
cat_word_counts[cat_index]=np.sum(count)+1
#get all words of this category
all_words+=self.bow_dicts[cat_index].keys()
#combine all words of every category & make them unique to get vocabulary -V- of entire training set
self.vocab=np.unique(np.array(all_words))
self.vocab_length=self.vocab.shape[0]
#computing denominator array (which we use later)
denoms_array = []
for cat_index,cat in enumerate(self.classes):
denoms_array.append(cat_word_counts[cat_index]+self.vocab_length+1)
denoms = np.asarray(denoms_array) #We typecast
#Storing BoW, Probability and Denom for each category (in this order):
arr_new = []
for cat_index,cat in enumerate(self.classes):
arr_new.append([self.bow_dicts[cat_index],prob_classes[cat_index],denoms[cat_index]])
self.cats_info = np.array(arr_new)
def getExampleProb(self,test_example):
likelihood_prob=np.zeros(self.classes.shape[0]) #to store probability w.r.t each class
post_prob=np.zeros(self.classes.shape[0])
#finding probability w.r.t each class of the given test example
for cat_index,cat in enumerate(self.classes):
for test_token in test_example.split():
word_map = self.cats_info[cat_index][0]
if test_token in word_map:
c_val = self.cats_info[cat_index][0].get(test_token)
else:
c_val = 0 #Take 0 if value is absent
test_token_counts=c_val+1 #If we don't add +1, we are going to run into Log0 or undefined statements
denominator_values_arr = self.cats_info[cat_index][2]
test_token_prob=float(test_token_counts/denominator_values_arr)
likelihood_prob[cat_index]=likelihood_prob[cat_index]+np.log10(test_token_prob) #log stops underflow
for cat_index,cat in enumerate(self.classes):
post_prob[cat_index]=likelihood_prob[cat_index]+np.log10(self.cats_info[cat_index][1])
return post_prob
def test(self,test_set):
predictions=[]
for example in test_set:
post_prob=self.getExampleProb(example)
predictions.append(self.classes[np.argmax(post_prob)])
return np.array(predictions)
train_df = pd.read_csv('E:/kaggle1/train.csv') #Please Replace here
# +
#I am dropping duplicates if there are any
train_df=train_df.drop_duplicates()
#Preprocess the string
train_df['Abstract'] = train_df['Abstract'].apply(preprocess_string)
#Preprocess some more!
train_df['Abstract'] = train_df['Abstract'].apply(lambda x: x.replace('>', ''))
# +
#Forming the DataSets
#80-20 Split
total_rows = train_df.shape[0]
eighty_p = 80/100 * total_rows
remaining = total_rows - eighty_p
X_training = train_df['Abstract'][0:int(eighty_p)]
X_testing = train_df['Abstract'][int(eighty_p):]
Y_Training = train_df['Category'][0:int(eighty_p)]
Y_Testing = train_df['Category'][int(eighty_p):]
# -
nb=NaiveBayes() #instantiate a NB class object
nb.train(X_training,Y_Training) #start tarining by calling the train function
pclasses=nb.test(X_testing) #get predcitions for test set
#check how many predcitions actually match original test labels
test_acc=np.sum(pclasses==Y_Testing)/float(Y_Testing.shape[0])
print ("Test Set Examples: ",Y_Testing.shape[0])
print ("Test Set Accuracy: ",test_acc*100,"%")
# +
#Reference I used code and guidance from while coding the class:
#1. https://towardsdatascience.com/unfolding-na%C3%AFve-bayes-from-scratch-2e86dcae4b01
#2. https://machinelearningmastery.com/naive-bayes-classifier-scratch-python/
#3. https://github.com/aishajv/Unfolding-Naive-Bayes-from-Scratch/blob/master/%23%20Unfolding%20Na%C3%AFve%20Bayes%20from%20Scratch!%20Take-2%20%F0%9F%8E%AC.ipynb
# +
#Now, let us run this against a CSV that can work in Kaggle
# -
test_df = pd.read_csv('E:/kaggle1/test.csv')
# +
#WE MUST apply the same preprocessing to the test dataframe. Otherwise we are making a grave mistake and might get worse predictions.
#I am dropping duplicates if there are any
test_df=test_df.drop_duplicates()
#Preprocess the string
test_df['Abstract'] = test_df['Abstract'].apply(preprocess_string)
#Preprocess some more!
test_df['Abstract'] = test_df['Abstract'].apply(lambda x: x.replace('>', ''))
# -
testFrame = test_df['Abstract']
pclasses2=nb.test(testFrame)
pclasses2
df_final_preds = pd.DataFrame(pclasses2)
df_final_preds = df_final_preds.rename(columns={0: "Category"})
df_final_preds["Id"] = df_final_preds.index
columns_titles = ["Id","Category"]
df_final_preds=df_final_preds.reindex(columns=columns_titles)
df_final_preds.to_csv("C:/kaggleMultiNB", index = False) #Generates File. It can be used to submit on Kaggle
# +
#Note: To improve performance, we can train on the whole dataset instead of 80%.
# -
|
KaggleQuestionNumber4 (1).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 2
# language: python
# name: python2
# ---
# # Преобразование Фурье
# ## Дискретное преобразование Фурье
# Дискретное преобразование Фурье (Discrete Fourier Transform) — это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. Дискретное преобразование Фурье требует в качестве входа дискретную функцию. Такие функции часто создаются путём дискретизации (выборки значений из непрерывных функций). Дискретные преобразования Фурье помогают решать дифференциальные уравнения в частных производных и выполнять такие операции, как свёртки. Дискретные преобразования Фурье также активно используются в статистике, при анализе временных рядов.
# ### Формулы преобразований
#
#
# *Прямое преобразование:*
# $$
# X_{k}=\sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N}kn}, k=0,\dots, N-1 \tag{1}
# $$
#
# Обратное преобразование:
# $$
# x_{k}=\frac{1}{N}\sum_{k=0}^{N-1} X_n e^{\frac{2\pi i}{N}kn}, k=0,\dots, N-1 \tag{2}
# $$
# где $N$ — количество значений дискретного сигнала; $x_n, n = 0, \dots, N − 1$ — измеренные значения сигнала (в дискретных временных точках с номерами $n = 0, \dots, N − 1$ , которые являются входными данными для прямого преобразования и выходными для обратного; $X_k , k = 0 ,\dots , N − 1$ — $N$ комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал; являются выходными данными для прямого преобразования и входными для обратного; поскольку амплитуды комплексные, то по ним можно вычислить одновременно и модуль и фазу.
#
# Тогда
#
# $|X_{n}|$ — обычная (вещественная) амплитуда $k$-го синусоидального сигнала;
#
# $arg ( X_n )$ — фаза $n$-го косинусоидального сигнала (аргумент комплексного числа);
#
# $n$ — индекс частоты. Частота $n$-го сигнала равна $\frac{n}{T}$, $T$ — период времени, в течение которого брались входные данные.
#
# Из последнего видно, что преобразование раскладывает сигнал на косинусоидальные составляющие (которые называются гармониками) с частотами от $N$ колебаний за период до одного колебания за период. Поскольку частота дискретизации сама по себе равна $N$ отсчётов за период, то высокочастотные составляющие не могут быть корректно отображены — возникает муаровый эффект. Это приводит к тому, что вторая половина из $N$ комплексных амплитуд, фактически, является зеркальным отображением первой и не несёт дополнительной информации.
# +
def dft(x, inv=False):
X=np.empty_like(x, dtype=np.complex128)
N=len(x)
i=1j
for k in range(N):
S=0+0.*i
for n in range(N):
omega=2*np.pi/N*k*n
if not inv:
omega=-omega
S=S+(np.cos(omega)+np.sin(omega)*i)*x[n]
if inv: S=S/N
X[k]=S
return X
import numpy as np
import matplotlib.pyplot as pl
# %matplotlib inline
pl.rcParams["figure.figsize"] = (15,7)
omega=2*np.pi
dt=0.7
t=np.arange(0, 480, dt)
x=np.cos(t*omega/10+1)+np.cos(t*omega/40+np.pi/2)
N=len(x)
X= dft(x)
nu=np.arange(N)/dt/N
np.seterr(divide='ignore')
T=1/nu
fig = pl.figure()
ax = fig.add_subplot(3,1,1)
pl.plot(t,x)
pl.grid()
ax = fig.add_subplot(3,1,2)
A=np.sqrt(np.real(X)**2+np.imag(X)**2)/N
pl.semilogy(T[0:N//2], A[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10) )
pl.grid()
P=np.arctan2(np.imag(X),np.real(X))
ax = fig.add_subplot(3,1,3)
pl.plot(T[0:N//2], P[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10) )
pl.grid()
pl.show()
# -
# ### Обратное преобразование Фурье
X= dft(x, inv=True)
pl.rcParams["figure.figsize"] = (15,2)
_=pl.plot(t,x)
pl.grid()
# ## Быстрое преобразование Фурье
# Из соотношения (1) следует, что если последовательность ${x_k}$ является комплексной, то при прямом вычислении требуется $N^2$ комплексных умножений и сложений. Основная идея БПФ состоит в том, чтобы исходную последовательность разбить на две более короткие последовательности, ДПФ которых могут быть скомбинированы таким образом, чтобы объединение их дало исходную $N$ точечную ДПФ. Так, например, если $N$ четное, то исходную последовательность можно разбить на две $N/2$ точечные последовательности, то для вычисления $N$ точечную ДПФ потребуется $N^2/2$ комплексных умножений, т.е. в двое меньше, чем раньше. Эту операцию можно повторить, если $N/2$ является четным.
# ### Алгоритм БПФ с прореживанием по времени
# Считаем, что $N$ равно степени $2$-ки. Введем две последовательности $x_{1,n}$ и $x_{2,n}$, состоящие из четных и нечетных членов $x_n$:
# $$
# x_{1,n}=x_{2n},
# $$
# $$
# x_{2,n}=х_{2n+1}, n=0,\dots, N/2-1 \tag{3}
# $$
#
# Для удобства можно ввести определение поворотного множителя:
# $$
# W_N^{nk}=e^{\frac{\pm 2 \pi i kn}{N}}.
# $$
#
def W(k,N, n=1):
return np.exp(-2*np.pi*1j*k*n/N)
# Легко показать, что $W_N^{nk}$ является периодичной функцией с периодом $N$., т.е.
# $$
# W_N^{(n+mN)(k+lN)} = W_N^{kn}, l,m = 0,\pm 1, \dots \tag{4}
# $$
pl.rcParams["figure.figsize"] = (15,4)
k = range(100)
w = [W(ki, 20) for ki in k]
pl.subplot(2,1,1)
pl.plot(k,np.real(w))
pl.subplot(2,1,2)
_=pl.plot(k,np.imag(w))
# $$
# X_k=\sum_{n=0, чет.}^{N-1} x_n W_N^{nk}+\sum_{n=0, нечет.}^{N-1} x_n W_N^{nk}=\sum_{n=0}^{N/2-1} x_{2n} W_N^{2nk}+\sum_{n=0}^{N/2-1} x_{2n+1} W_N^{(2n+1)k} \tag{5}
# $$
# Выражение (5) получилось из (1), где отделены слагаемые с четными номерами от слагаемых с нечетными номерами исходной последовательности. Заметим, что $W_N^2=W_{N/2}$ , перепишем (5) с учетом (3) в виде
# $$
# X_k = \sum_{n=0}^{N/2-1} x_{1,n} W_{N/2}^{nk} + W_N^k \sum_{n=0}^{N/2-1} x_{2,n} W_{N/2}^{nk} \tag{6}
# $$
# или
# $$
# X_k=X_{1,k}+W_N^k X_{2,k} \tag{7}
# $$
# где $X_{1,k}, X_{2,k}$ равны $N/2$ точечному ДПФ последовательностей $x_{1,n}$ и $x_{2,n}$ соответственно.
# Из (7) следует, что $N$ точечное ДПФ может быть разложено на два $N/2$ точечных ДПФ, результаты которых объединяются согласно (7). Если бы $N/2$ точечное ДПФ вычислялось бы обычным образом, то потребовалось $N2/2+N$ комплексных умножений. При больших $N$ (когда $N^2/2 >> N$) это позволяет сократить вычисления на 50%.
# +
def dft2(x):
N=len(x)
if N % 2 > 0:
raise ValueError("Количество отсчетов должно быть четным!")
x1=x[::2] #четные
x2=x[1::2] #нечетные
X1 = dft(x1)
X2 = dft(x2)
return [X1[k]+W(k,N)*X2[k]for k in range(N/2)]
import timeit
x2 = x[:500]
t1 = timeit.timeit('dft(x2)',
setup="from __main__ import dft, x2",
number=1)
print(t1)
t2 = timeit.timeit('dft2(x2)',
setup="from __main__ import dft2, x2",
number=1)
print(t2)
# -
# Можно сравнить результаты двух преобразований, чтобы убедится в том, что они идентичны:
X=dft2(x)
A=np.abs(X)
P=np.angle(X)
N=len(x)
nu=np.arange(N)/dt/N
T=1/nu
pl.subplot(2,1,1)
pl.semilogy(T[0:N//2], A[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10))
pl.grid()
pl.subplot(2,1,2)
pl.plot(T[0:N//2], P[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10))
pl.grid()
# Поскольку $X_k$ определено при $0\leq k \lt N, а X_{1,k}, X_{2,k}$ при $0 \leq k\lt N/2$, необходимо доопределить (7) при $k\gt N/2$. Сделаем это следующим образом, используя периодичность ДПФ и тот факт, что $W_N^{k+N/2} = e^-\frac{j2\pi (k+N/2)}{N} =e^-\frac{j2\pi k}{N}e^{-j\pi} =-W_N^k$
# $$
# X_k=
# \begin{cases}
# X_{1,k}+W_N^kX_{2,k}, 0\leq k \leq N/2-1 \\
# X_{1,k-N/2}+W_N^{k-N/2}X_{2,k-N/2}, N/2\leq k \leq N
# \tag{8}
# \end{cases}
# $$
# Выражение (8) описывает получение $N$ -точечного Фурье преобразования из двух $N/2$ точечных Фурье. Видно, что для получения каждого коэффициента Фурье $X(k)$ необходимо выполнить одно умножение и одно сложение (или вычитание).
#
# Здесь необходимо пояснить, почему выполняется только $N/2$ умножений на каждом шаге, а не $N$ умножений? Необходимо рассмотреть выражение (8). Запишем вычисление $X_0$ и $X_{N/2}$.
# $$
# X_0=X_{1,0}=W_N^0X_{2,0}\\
# X_{N/2}=X_{1,N/2-N/2}-W_N^{N/2-N/2}X_{2,N/2-N/2}=X_1,0-W_N^0X_{2,0} \tag{9}
# $$
# Как видно из (9) $X_0$ и $X_{N/2}$ вычисляются почти одинаково, за исключением того, что в $X_{0}$ надо сложить, а в $X_{N/2}$ отнять одно и тоже произведение. Это произведение можно посчитать один раз, а затем добавить и отнять к и от $X_{1,0}$ для получения соответственно $X_{0}$ и $X_{N/2}$. Таким образом, чтобы вычислить два коэффициента Фурье, необходимо вычислить только одно произведение.
#
# Если мы продолжим разбиение последовательности на две последовательности и применим тот же механизм, то мы еще в два раза уменьшим количество умножений. Таким образом, на каждом шаге мы выполняем $N/2$ умножений, а таких шагов $\log_2N$. Число умножений равно $\frac{Nlog_2N}{2}$, что значительно меньше $N^2$ (при $N=1024$ число умножений меньше в 100 раз).
# Рассмотрим на примере 8-ми точечной последовательности, т.е. $N=8$. Выражение (8) можно иллюстрировать схемой (рис. 1):
#
# <img src="./files3/fft.png">
# Рис. 1. <NAME> для вычисления БПФ (здесь стрелка вверх означает сложение, линия, направленная вниз - вычитание).
#
# Описанный алгоритм известен как простой алгоритм Кули-Тьюки или Быстрое преобразование Фурье (БПФ).
# +
def fft(x):
N=len(x)
if N % 2 > 0:
raise ValueError("Количество отсчетов должно быть степенью 2-ки")
Y1=[]
Y2=[]
if N == 2: #условие окончания рекурсии
return [x[0]+x[1], x[0]-x[1]]
else:
x1=x[::2] #четные
x2=x[1::2] #нечетные
X1 = fft(x1)
X2 = fft(x2)
for k in range(N/2):
tmp=W(k,N)*X2[k]
Y1.append(X1[k]+ tmp)
Y2.append(X1[k]- tmp)
return Y1+Y2 #объединение двух списков
xp2 = x[:512]
t1 = timeit.timeit('dft(xp2)',
setup="from __main__ import dft, xp2",
number=1)
print(t1)
t2 = timeit.timeit('fft(xp2)',
setup="from __main__ import fft, xp2",
number=1)
print(t2)
# -
# При $N=2$ выполяется операция которая носит название "бабочка":
# $$
# X_0=x_0+x_1, \\
# X_1=x_0-x_1,
# $$
# т.к. при $k=0$, $W_N^0 = 1$.
# Можно снова сравнить результаты двух преобразований, чтобы убедится в том, что они идентичны:
pl.rcParams["figure.figsize"] = (15,4)
X=dft(xp2)
A=np.abs(X)
P=np.angle(X)
N=len(xp2)
nu=np.arange(N)/dt/N
T=1/nu
pl.subplot(2,1,1)
pl.semilogy(T[0:N//2], A[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10))
pl.grid()
pl.subplot(2,1,2)
pl.plot(T[0:N//2], P[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10) )
pl.grid()
pl.rcParams["figure.figsize"] = (15,4)
X=fft(xp2)
A=np.abs(X)
P=np.angle(X)
N=len(xp2)
nu=np.arange(N)/dt/N
T=1/nu
pl.subplot(2,1,1)
pl.semilogy(T[0:N//2], A[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10))
pl.grid()
pl.subplot(2,1,2)
pl.plot(T[0:N//2], P[0:N//2])
pl.xlim([0, 100])
pl.xticks(np.arange(0,100,step=10) )
pl.grid()
# ## Задания для самостоятельной работы
# 1. Реализуйте алгоритм БПФ с прореживанием по частоте (см. <ftp://ftp.iait.kg/DSP/dsp_pract_7.doc>).
# 2. Выполните исследование зависимости времени выполнения от количества отсчетов для алгоритмов ДПФ и БПФ и постройте графики.
# 3. Реализуйте алгоритм БПФ без использования рекурсии.
# 4. Реализуйте обратное БПФ.
|
pract3.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Batch Normalization – Lesson
#
# 1. [What is it?](#theory)
# 2. [What are it's benefits?](#benefits)
# 3. [How do we add it to a network?](#implementation_1)
# 4. [Let's see it work!](#demos)
# 5. [What are you hiding?](#implementation_2)
#
# # What is Batch Normalization?<a id='theory'></a>
#
# Batch normalization was introduced in <NAME> and <NAME>'s 2015 paper [Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift](https://arxiv.org/pdf/1502.03167.pdf). The idea is that, instead of just normalizing the inputs to the network, we normalize the inputs to _layers within_ the network. It's called "batch" normalization because during training, we normalize each layer's inputs by using the mean and variance of the values in the current mini-batch.
#
# Why might this help? Well, we know that normalizing the inputs to a _network_ helps the network learn. But a network is a series of layers, where the output of one layer becomes the input to another. That means we can think of any layer in a neural network as the _first_ layer of a smaller network.
#
# For example, imagine a 3 layer network. Instead of just thinking of it as a single network with inputs, layers, and outputs, think of the output of layer 1 as the input to a two layer network. This two layer network would consist of layers 2 and 3 in our original network.
#
# Likewise, the output of layer 2 can be thought of as the input to a single layer network, consisting only of layer 3.
#
# When you think of it like that - as a series of neural networks feeding into each other - then it's easy to imagine how normalizing the inputs to each layer would help. It's just like normalizing the inputs to any other neural network, but you're doing it at every layer (sub-network).
#
# Beyond the intuitive reasons, there are good mathematical reasons why it helps the network learn better, too. It helps combat what the authors call _internal covariate shift_. This discussion is best handled [in the paper](https://arxiv.org/pdf/1502.03167.pdf) and in [Deep Learning](http://www.deeplearningbook.org) a book you can read online written by <NAME>, <NAME>, and <NAME>. Specifically, check out the batch normalization section of [Chapter 8: Optimization for Training Deep Models](http://www.deeplearningbook.org/contents/optimization.html).
# # Benefits of Batch Normalization<a id="benefits"></a>
#
# Batch normalization optimizes network training. It has been shown to have several benefits:
# 1. **Networks train faster** – Each training _iteration_ will actually be slower because of the extra calculations during the forward pass and the additional hyperparameters to train during back propagation. However, it should converge much more quickly, so training should be faster overall.
# 2. **Allows higher learning rates** – Gradient descent usually requires small learning rates for the network to converge. And as networks get deeper, their gradients get smaller during back propagation so they require even more iterations. Using batch normalization allows us to use much higher learning rates, which further increases the speed at which networks train.
# 3. **Makes weights easier to initialize** – Weight initialization can be difficult, and it's even more difficult when creating deeper networks. Batch normalization seems to allow us to be much less careful about choosing our initial starting weights.
# 4. **Makes more activation functions viable** – Some activation functions do not work well in some situations. Sigmoids lose their gradient pretty quickly, which means they can't be used in deep networks. And ReLUs often die out during training, where they stop learning completely, so we need to be careful about the range of values fed into them. Because batch normalization regulates the values going into each activation function, non-linearlities that don't seem to work well in deep networks actually become viable again.
# 5. **Simplifies the creation of deeper networks** – Because of the first 4 items listed above, it is easier to build and faster to train deeper neural networks when using batch normalization. And it's been shown that deeper networks generally produce better results, so that's great.
# 6. **Provides a bit of regularlization** – Batch normalization adds a little noise to your network. In some cases, such as in Inception modules, batch normalization has been shown to work as well as dropout. But in general, consider batch normalization as a bit of extra regularization, possibly allowing you to reduce some of the dropout you might add to a network.
# 7. **May give better results overall** – Some tests seem to show batch normalization actually improves the training results. However, it's really an optimization to help train faster, so you shouldn't think of it as a way to make your network better. But since it lets you train networks faster, that means you can iterate over more designs more quickly. It also lets you build deeper networks, which are usually better. So when you factor in everything, you're probably going to end up with better results if you build your networks with batch normalization.
# # Batch Normalization in TensorFlow<a id="implementation_1"></a>
#
# This section of the notebook shows you one way to add batch normalization to a neural network built in TensorFlow.
#
# The following cell imports the packages we need in the notebook and loads the MNIST dataset to use in our experiments. However, the `tensorflow` package contains all the code you'll actually need for batch normalization.
# +
# Import necessary packages
import tensorflow as tf
import tqdm
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# Import MNIST data so we have something for our experiments
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# -
# ### Neural network classes for testing
#
# The following class, `NeuralNet`, allows us to create identical neural networks with and without batch normalization. The code is heavily documented, but there is also some additional discussion later. You do not need to read through it all before going through the rest of the notebook, but the comments within the code blocks may answer some of your questions.
#
# *About the code:*
# >This class is not meant to represent TensorFlow best practices – the design choices made here are to support the discussion related to batch normalization.
#
# >It's also important to note that we use the well-known MNIST data for these examples, but the networks we create are not meant to be good for performing handwritten character recognition. We chose this network architecture because it is similar to the one used in the original paper, which is complex enough to demonstrate some of the benefits of batch normalization while still being fast to train.
class NeuralNet:
def __init__(self, initial_weights, activation_fn, use_batch_norm):
"""
Initializes this object, creating a TensorFlow graph using the given parameters.
:param initial_weights: list of NumPy arrays or Tensors
Initial values for the weights for every layer in the network. We pass these in
so we can create multiple networks with the same starting weights to eliminate
training differences caused by random initialization differences.
The number of items in the list defines the number of layers in the network,
and the shapes of the items in the list define the number of nodes in each layer.
e.g. Passing in 3 matrices of shape (784, 256), (256, 100), and (100, 10) would
create a network with 784 inputs going into a hidden layer with 256 nodes,
followed by a hidden layer with 100 nodes, followed by an output layer with 10 nodes.
:param activation_fn: Callable
The function used for the output of each hidden layer. The network will use the same
activation function on every hidden layer and no activate function on the output layer.
e.g. Pass tf.nn.relu to use ReLU activations on your hidden layers.
:param use_batch_norm: bool
Pass True to create a network that uses batch normalization; False otherwise
Note: this network will not use batch normalization on layers that do not have an
activation function.
"""
# Keep track of whether or not this network uses batch normalization.
self.use_batch_norm = use_batch_norm
self.name = "With Batch Norm" if use_batch_norm else "Without Batch Norm"
# Batch normalization needs to do different calculations during training and inference,
# so we use this placeholder to tell the graph which behavior to use.
self.is_training = tf.placeholder(tf.bool, name="is_training")
# This list is just for keeping track of data we want to plot later.
# It doesn't actually have anything to do with neural nets or batch normalization.
self.training_accuracies = []
# Create the network graph, but it will not actually have any real values until after you
# call train or test
self.build_network(initial_weights, activation_fn)
def build_network(self, initial_weights, activation_fn):
"""
Build the graph. The graph still needs to be trained via the `train` method.
:param initial_weights: list of NumPy arrays or Tensors
See __init__ for description.
:param activation_fn: Callable
See __init__ for description.
"""
self.input_layer = tf.placeholder(tf.float32, [None, initial_weights[0].shape[0]])
layer_in = self.input_layer
for weights in initial_weights[:-1]:
layer_in = self.fully_connected(layer_in, weights, activation_fn)
self.output_layer = self.fully_connected(layer_in, initial_weights[-1])
def fully_connected(self, layer_in, initial_weights, activation_fn=None):
"""
Creates a standard, fully connected layer. Its number of inputs and outputs will be
defined by the shape of `initial_weights`, and its starting weight values will be
taken directly from that same parameter. If `self.use_batch_norm` is True, this
layer will include batch normalization, otherwise it will not.
:param layer_in: Tensor
The Tensor that feeds into this layer. It's either the input to the network or the output
of a previous layer.
:param initial_weights: NumPy array or Tensor
Initial values for this layer's weights. The shape defines the number of nodes in the layer.
e.g. Passing in 3 matrix of shape (784, 256) would create a layer with 784 inputs and 256
outputs.
:param activation_fn: Callable or None (default None)
The non-linearity used for the output of the layer. If None, this layer will not include
batch normalization, regardless of the value of `self.use_batch_norm`.
e.g. Pass tf.nn.relu to use ReLU activations on your hidden layers.
"""
# Since this class supports both options, only use batch normalization when
# requested. However, do not use it on the final layer, which we identify
# by its lack of an activation function.
if self.use_batch_norm and activation_fn:
# Batch normalization uses weights as usual, but does NOT add a bias term. This is because
# its calculations include gamma and beta variables that make the bias term unnecessary.
# (See later in the notebook for more details.)
weights = tf.Variable(initial_weights)
linear_output = tf.matmul(layer_in, weights)
# Apply batch normalization to the linear combination of the inputs and weights
batch_normalized_output = tf.layers.batch_normalization(linear_output, training=self.is_training)
# Now apply the activation function, *after* the normalization.
return activation_fn(batch_normalized_output)
else:
# When not using batch normalization, create a standard layer that multiplies
# the inputs and weights, adds a bias, and optionally passes the result
# through an activation function.
weights = tf.Variable(initial_weights)
biases = tf.Variable(tf.zeros([initial_weights.shape[-1]]))
linear_output = tf.add(tf.matmul(layer_in, weights), biases)
return linear_output if not activation_fn else activation_fn(linear_output)
def train(self, session, learning_rate, training_batches, batches_per_sample, save_model_as=None):
"""
Trains the model on the MNIST training dataset.
:param session: Session
Used to run training graph operations.
:param learning_rate: float
Learning rate used during gradient descent.
:param training_batches: int
Number of batches to train.
:param batches_per_sample: int
How many batches to train before sampling the validation accuracy.
:param save_model_as: string or None (default None)
Name to use if you want to save the trained model.
"""
# This placeholder will store the target labels for each mini batch
labels = tf.placeholder(tf.float32, [None, 10])
# Define loss and optimizer
cross_entropy = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(labels=labels, logits=self.output_layer))
# Define operations for testing
correct_prediction = tf.equal(tf.argmax(self.output_layer, 1), tf.argmax(labels, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
if self.use_batch_norm:
# If we don't include the update ops as dependencies on the train step, the
# tf.layers.batch_normalization layers won't update their population statistics,
# which will cause the model to fail at inference time
with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
else:
train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
# Train for the appropriate number of batches. (tqdm is only for a nice timing display)
for i in tqdm.tqdm(range(training_batches)):
# We use batches of 60 just because the original paper did. You can use any size batch you like.
batch_xs, batch_ys = mnist.train.next_batch(60)
session.run(train_step, feed_dict={self.input_layer: batch_xs,
labels: batch_ys,
self.is_training: True})
# Periodically test accuracy against the 5k validation images and store it for plotting later.
if i % batches_per_sample == 0:
test_accuracy = session.run(accuracy, feed_dict={self.input_layer: mnist.validation.images,
labels: mnist.validation.labels,
self.is_training: False})
self.training_accuracies.append(test_accuracy)
# After training, report accuracy against test data
test_accuracy = session.run(accuracy, feed_dict={self.input_layer: mnist.validation.images,
labels: mnist.validation.labels,
self.is_training: False})
print('{}: After training, final accuracy on validation set = {}'.format(self.name, test_accuracy))
# If you want to use this model later for inference instead of having to retrain it,
# just construct it with the same parameters and then pass this file to the 'test' function
if save_model_as:
tf.train.Saver().save(session, save_model_as)
def test(self, session, test_training_accuracy=False, include_individual_predictions=False, restore_from=None):
"""
Trains a trained model on the MNIST testing dataset.
:param session: Session
Used to run the testing graph operations.
:param test_training_accuracy: bool (default False)
If True, perform inference with batch normalization using batch mean and variance;
if False, perform inference with batch normalization using estimated population mean and variance.
Note: in real life, *always* perform inference using the population mean and variance.
This parameter exists just to support demonstrating what happens if you don't.
:param include_individual_predictions: bool (default True)
This function always performs an accuracy test against the entire test set. But if this parameter
is True, it performs an extra test, doing 200 predictions one at a time, and displays the results
and accuracy.
:param restore_from: string or None (default None)
Name of a saved model if you want to test with previously saved weights.
"""
# This placeholder will store the true labels for each mini batch
labels = tf.placeholder(tf.float32, [None, 10])
# Define operations for testing
correct_prediction = tf.equal(tf.argmax(self.output_layer, 1), tf.argmax(labels, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
# If provided, restore from a previously saved model
if restore_from:
tf.train.Saver().restore(session, restore_from)
# Test against all of the MNIST test data
test_accuracy = session.run(accuracy, feed_dict={self.input_layer: mnist.test.images,
labels: mnist.test.labels,
self.is_training: test_training_accuracy})
print('-'*75)
print('{}: Accuracy on full test set = {}'.format(self.name, test_accuracy))
# If requested, perform tests predicting individual values rather than batches
if include_individual_predictions:
predictions = []
correct = 0
# Do 200 predictions, 1 at a time
for i in range(200):
# This is a normal prediction using an individual test case. However, notice
# we pass `test_training_accuracy` to `feed_dict` as the value for `self.is_training`.
# Remember that will tell it whether it should use the batch mean & variance or
# the population estimates that were calucated while training the model.
pred, corr = session.run([tf.arg_max(self.output_layer,1), accuracy],
feed_dict={self.input_layer: [mnist.test.images[i]],
labels: [mnist.test.labels[i]],
self.is_training: test_training_accuracy})
correct += corr
predictions.append(pred[0])
print("200 Predictions:", predictions)
print("Accuracy on 200 samples:", correct/200)
# There are quite a few comments in the code, so those should answer most of your questions. However, let's take a look at the most important lines.
#
# We add batch normalization to layers inside the `fully_connected` function. Here are some important points about that code:
# 1. Layers with batch normalization do not include a bias term.
# 2. We use TensorFlow's [`tf.layers.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization) function to handle the math. (We show lower-level ways to do this [later in the notebook](#implementation_2).)
# 3. We tell `tf.layers.batch_normalization` whether or not the network is training. This is an important step we'll talk about later.
# 4. We add the normalization **before** calling the activation function.
#
# In addition to that code, the training step is wrapped in the following `with` statement:
# ```python
# with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
# ```
# This line actually works in conjunction with the `training` parameter we pass to `tf.layers.batch_normalization`. Without it, TensorFlow's batch normalization layer will not operate correctly during inference.
#
# Finally, whenever we train the network or perform inference, we use the `feed_dict` to set `self.is_training` to `True` or `False`, respectively, like in the following line:
# ```python
# session.run(train_step, feed_dict={self.input_layer: batch_xs,
# labels: batch_ys,
# self.is_training: True})
# ```
# We'll go into more details later, but next we want to show some experiments that use this code and test networks with and without batch normalization.
# # Batch Normalization Demos<a id='demos'></a>
# This section of the notebook trains various networks with and without batch normalization to demonstrate some of the benefits mentioned earlier.
#
# We'd like to thank the author of this blog post [Implementing Batch Normalization in TensorFlow](http://r2rt.com/implementing-batch-normalization-in-tensorflow.html). That post provided the idea of - and some of the code for - plotting the differences in accuracy during training, along with the idea for comparing multiple networks using the same initial weights.
# ## Code to support testing
#
# The following two functions support the demos we run in the notebook.
#
# The first function, `plot_training_accuracies`, simply plots the values found in the `training_accuracies` lists of the `NeuralNet` objects passed to it. If you look at the `train` function in `NeuralNet`, you'll see it that while it's training the network, it periodically measures validation accuracy and stores the results in that list. It does that just to support these plots.
#
# The second function, `train_and_test`, creates two neural nets - one with and one without batch normalization. It then trains them both and tests them, calling `plot_training_accuracies` to plot how their accuracies changed over the course of training. The really imporant thing about this function is that it initializes the starting weights for the networks _outside_ of the networks and then passes them in. This lets it train both networks from the exact same starting weights, which eliminates performance differences that might result from (un)lucky initial weights.
# +
def plot_training_accuracies(*args, **kwargs):
"""
Displays a plot of the accuracies calculated during training to demonstrate
how many iterations it took for the model(s) to converge.
:param args: One or more NeuralNet objects
You can supply any number of NeuralNet objects as unnamed arguments
and this will display their training accuracies. Be sure to call `train`
the NeuralNets before calling this function.
:param kwargs:
You can supply any named parameters here, but `batches_per_sample` is the only
one we look for. It should match the `batches_per_sample` value you passed
to the `train` function.
"""
fig, ax = plt.subplots()
batches_per_sample = kwargs['batches_per_sample']
for nn in args:
ax.plot(range(0,len(nn.training_accuracies)*batches_per_sample,batches_per_sample),
nn.training_accuracies, label=nn.name)
ax.set_xlabel('Training steps')
ax.set_ylabel('Accuracy')
ax.set_title('Validation Accuracy During Training')
ax.legend(loc=4)
ax.set_ylim([0,1])
plt.yticks(np.arange(0, 1.1, 0.1))
plt.grid(True)
plt.show()
def train_and_test(use_bad_weights, learning_rate, activation_fn, training_batches=50000, batches_per_sample=500):
"""
Creates two networks, one with and one without batch normalization, then trains them
with identical starting weights, layers, batches, etc. Finally tests and plots their accuracies.
:param use_bad_weights: bool
If True, initialize the weights of both networks to wildly inappropriate weights;
if False, use reasonable starting weights.
:param learning_rate: float
Learning rate used during gradient descent.
:param activation_fn: Callable
The function used for the output of each hidden layer. The network will use the same
activation function on every hidden layer and no activate function on the output layer.
e.g. Pass tf.nn.relu to use ReLU activations on your hidden layers.
:param training_batches: (default 50000)
Number of batches to train.
:param batches_per_sample: (default 500)
How many batches to train before sampling the validation accuracy.
"""
# Use identical starting weights for each network to eliminate differences in
# weight initialization as a cause for differences seen in training performance
#
# Note: The networks will use these weights to define the number of and shapes of
# its layers. The original batch normalization paper used 3 hidden layers
# with 100 nodes in each, followed by a 10 node output layer. These values
# build such a network, but feel free to experiment with different choices.
# However, the input size should always be 784 and the final output should be 10.
if use_bad_weights:
# These weights should be horrible because they have such a large standard deviation
weights = [np.random.normal(size=(784,100), scale=5.0).astype(np.float32),
np.random.normal(size=(100,100), scale=5.0).astype(np.float32),
np.random.normal(size=(100,100), scale=5.0).astype(np.float32),
np.random.normal(size=(100,10), scale=5.0).astype(np.float32)
]
else:
# These weights should be good because they have such a small standard deviation
weights = [np.random.normal(size=(784,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,10), scale=0.05).astype(np.float32)
]
# Just to make sure the TensorFlow's default graph is empty before we start another
# test, because we don't bother using different graphs or scoping and naming
# elements carefully in this sample code.
tf.reset_default_graph()
# build two versions of same network, 1 without and 1 with batch normalization
nn = NeuralNet(weights, activation_fn, False)
bn = NeuralNet(weights, activation_fn, True)
# train and test the two models
with tf.Session() as sess:
tf.global_variables_initializer().run()
nn.train(sess, learning_rate, training_batches, batches_per_sample)
bn.train(sess, learning_rate, training_batches, batches_per_sample)
nn.test(sess)
bn.test(sess)
# Display a graph of how validation accuracies changed during training
# so we can compare how the models trained and when they converged
plot_training_accuracies(nn, bn, batches_per_sample=batches_per_sample)
# -
# ## Comparisons between identical networks, with and without batch normalization
#
# The next series of cells train networks with various settings to show the differences with and without batch normalization. They are meant to clearly demonstrate the effects of batch normalization. We include a deeper discussion of batch normalization later in the notebook.
# **The following creates two networks using a ReLU activation function, a learning rate of 0.01, and reasonable starting weights.**
train_and_test(False, 0.01, tf.nn.relu)
# As expected, both networks train well and eventually reach similar test accuracies. However, notice that the model with batch normalization converges slightly faster than the other network, reaching accuracies over 90% almost immediately and nearing its max acuracy in 10 or 15 thousand iterations. The other network takes about 3 thousand iterations to reach 90% and doesn't near its best accuracy until 30 thousand or more iterations.
#
# If you look at the raw speed, you can see that without batch normalization we were computing over 1100 batches per second, whereas with batch normalization that goes down to just over 500. However, batch normalization allows us to perform fewer iterations and converge in less time over all. (We only trained for 50 thousand batches here so we could plot the comparison.)
# **The following creates two networks with the same hyperparameters used in the previous example, but only trains for 2000 iterations.**
train_and_test(False, 0.01, tf.nn.relu, 2000, 50)
# As you can see, using batch normalization produces a model with over 95% accuracy in only 2000 batches, and it was above 90% at somewhere around 500 batches. Without batch normalization, the model takes 1750 iterations just to hit 80% – the network with batch normalization hits that mark after around 200 iterations! (Note: if you run the code yourself, you'll see slightly different results each time because the starting weights - while the same for each model - are different for each run.)
#
# In the above example, you should also notice that the networks trained fewer batches per second then what you saw in the previous example. That's because much of the time we're tracking is actually spent periodically performing inference to collect data for the plots. In this example we perform that inference every 50 batches instead of every 500, so generating the plot for this example requires 10 times the overhead for the same 2000 iterations.
# **The following creates two networks using a sigmoid activation function, a learning rate of 0.01, and reasonable starting weights.**
train_and_test(False, 0.01, tf.nn.sigmoid)
# With the number of layers we're using and this small learning rate, using a sigmoid activation function takes a long time to start learning. It eventually starts making progress, but it took over 45 thousand batches just to get over 80% accuracy. Using batch normalization gets to 90% in around one thousand batches.
# **The following creates two networks using a ReLU activation function, a learning rate of 1, and reasonable starting weights.**
train_and_test(False, 1, tf.nn.relu)
# Now we're using ReLUs again, but with a larger learning rate. The plot shows how training started out pretty normally, with the network with batch normalization starting out faster than the other. But the higher learning rate bounces the accuracy around a bit more, and at some point the accuracy in the network without batch normalization just completely crashes. It's likely that too many ReLUs died off at this point because of the high learning rate.
#
# The next cell shows the same test again. The network with batch normalization performs the same way, and the other suffers from the same problem again, but it manages to train longer before it happens.
train_and_test(False, 1, tf.nn.relu)
# In both of the previous examples, the network with batch normalization manages to gets over 98% accuracy, and get near that result almost immediately. The higher learning rate allows the network to train extremely fast.
# **The following creates two networks using a sigmoid activation function, a learning rate of 1, and reasonable starting weights.**
train_and_test(False, 1, tf.nn.sigmoid)
# In this example, we switched to a sigmoid activation function. It appears to handle the higher learning rate well, with both networks achieving high accuracy.
#
# The cell below shows a similar pair of networks trained for only 2000 iterations.
train_and_test(False, 1, tf.nn.sigmoid, 2000, 50)
# As you can see, even though these parameters work well for both networks, the one with batch normalization gets over 90% in 400 or so batches, whereas the other takes over 1700. When training larger networks, these sorts of differences become more pronounced.
# **The following creates two networks using a ReLU activation function, a learning rate of 2, and reasonable starting weights.**
train_and_test(False, 2, tf.nn.relu)
# With this very large learning rate, the network with batch normalization trains fine and almost immediately manages 98% accuracy. However, the network without normalization doesn't learn at all.
# **The following creates two networks using a sigmoid activation function, a learning rate of 2, and reasonable starting weights.**
train_and_test(False, 2, tf.nn.sigmoid)
# Once again, using a sigmoid activation function with the larger learning rate works well both with and without batch normalization.
#
# However, look at the plot below where we train models with the same parameters but only 2000 iterations. As usual, batch normalization lets it train faster.
train_and_test(False, 2, tf.nn.sigmoid, 2000, 50)
# In the rest of the examples, we use really bad starting weights. That is, normally we would use very small values close to zero. However, in these examples we choose random values with a standard deviation of 5. If you were really training a neural network, you would **not** want to do this. But these examples demonstrate how batch normalization makes your network much more resilient.
# **The following creates two networks using a ReLU activation function, a learning rate of 0.01, and bad starting weights.**
train_and_test(True, 0.01, tf.nn.relu)
# As the plot shows, without batch normalization the network never learns anything at all. But with batch normalization, it actually learns pretty well and gets to almost 80% accuracy. The starting weights obviously hurt the network, but you can see how well batch normalization does in overcoming them.
# **The following creates two networks using a sigmoid activation function, a learning rate of 0.01, and bad starting weights.**
train_and_test(True, 0.01, tf.nn.sigmoid)
# Using a sigmoid activation function works better than the ReLU in the previous example, but without batch normalization it would take a tremendously long time to train the network, if it ever trained at all.
# **The following creates two networks using a ReLU activation function, a learning rate of 1, and bad starting weights.**<a id="successful_example_lr_1"></a>
train_and_test(True, 1, tf.nn.relu)
# The higher learning rate used here allows the network with batch normalization to surpass 90% in about 30 thousand batches. The network without it never gets anywhere.
# **The following creates two networks using a sigmoid activation function, a learning rate of 1, and bad starting weights.**
train_and_test(True, 1, tf.nn.sigmoid)
# Using sigmoid works better than ReLUs for this higher learning rate. However, you can see that without batch normalization, the network takes a long time tro train, bounces around a lot, and spends a long time stuck at 90%. The network with batch normalization trains much more quickly, seems to be more stable, and achieves a higher accuracy.
# **The following creates two networks using a ReLU activation function, a learning rate of 2, and bad starting weights.**<a id="successful_example_lr_2"></a>
train_and_test(True, 2, tf.nn.relu)
# We've already seen that ReLUs do not do as well as sigmoids with higher learning rates, and here we are using an extremely high rate. As expected, without batch normalization the network doesn't learn at all. But with batch normalization, it eventually achieves 90% accuracy. Notice, though, how its accuracy bounces around wildly during training - that's because the learning rate is really much too high, so the fact that this worked at all is a bit of luck.
# **The following creates two networks using a sigmoid activation function, a learning rate of 2, and bad starting weights.**
train_and_test(True, 2, tf.nn.sigmoid)
# In this case, the network with batch normalization trained faster and reached a higher accuracy. Meanwhile, the high learning rate makes the network without normalization bounce around erratically and have trouble getting past 90%.
# ### Full Disclosure: Batch Normalization Doesn't Fix Everything
#
# Batch normalization isn't magic and it doesn't work every time. Weights are still randomly initialized and batches are chosen at random during training, so you never know exactly how training will go. Even for these tests, where we use the same initial weights for both networks, we still get _different_ weights each time we run.
#
# This section includes two examples that show runs when batch normalization did not help at all.
#
# **The following creates two networks using a ReLU activation function, a learning rate of 1, and bad starting weights.**
train_and_test(True, 1, tf.nn.relu)
# When we used these same parameters [earlier](#successful_example_lr_1), we saw the network with batch normalization reach 92% validation accuracy. This time we used different starting weights, initialized using the same standard deviation as before, and the network doesn't learn at all. (Remember, an accuracy around 10% is what the network gets if it just guesses the same value all the time.)
#
# **The following creates two networks using a ReLU activation function, a learning rate of 2, and bad starting weights.**
train_and_test(True, 2, tf.nn.relu)
# When we trained with these parameters and batch normalization [earlier](#successful_example_lr_2), we reached 90% validation accuracy. However, this time the network _almost_ starts to make some progress in the beginning, but it quickly breaks down and stops learning.
#
# **Note:** Both of the above examples use *extremely* bad starting weights, along with learning rates that are too high. While we've shown batch normalization _can_ overcome bad values, we don't mean to encourage actually using them. The examples in this notebook are meant to show that batch normalization can help your networks train better. But these last two examples should remind you that you still want to try to use good network design choices and reasonable starting weights. It should also remind you that the results of each attempt to train a network are a bit random, even when using otherwise identical architectures.
# # Batch Normalization: A Detailed Look<a id='implementation_2'></a>
# The layer created by `tf.layers.batch_normalization` handles all the details of implementing batch normalization. Many students will be fine just using that and won't care about what's happening at the lower levels. However, some students may want to explore the details, so here is a short explanation of what's really happening, starting with the equations you're likely to come across if you ever read about batch normalization.
# In order to normalize the values, we first need to find the average value for the batch. If you look at the code, you can see that this is not the average value of the batch _inputs_, but the average value coming _out_ of any particular layer before we pass it through its non-linear activation function and then feed it as an input to the _next_ layer.
#
# We represent the average as $\mu_B$, which is simply the sum of all of the values $x_i$ divided by the number of values, $m$
#
# $$
# \mu_B \leftarrow \frac{1}{m}\sum_{i=1}^m x_i
# $$
#
# We then need to calculate the variance, or mean squared deviation, represented as $\sigma_{B}^{2}$. If you aren't familiar with statistics, that simply means for each value $x_i$, we subtract the average value (calculated earlier as $\mu_B$), which gives us what's called the "deviation" for that value. We square the result to get the squared deviation. Sum up the results of doing that for each of the values, then divide by the number of values, again $m$, to get the average, or mean, squared deviation.
#
# $$
# \sigma_{B}^{2} \leftarrow \frac{1}{m}\sum_{i=1}^m (x_i - \mu_B)^2
# $$
#
# Once we have the mean and variance, we can use them to normalize the values with the following equation. For each value, it subtracts the mean and divides by the (almost) standard deviation. (You've probably heard of standard deviation many times, but if you have not studied statistics you might not know that the standard deviation is actually the square root of the mean squared deviation.)
#
# $$
# \hat{x_i} \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_{B}^{2} + \epsilon}}
# $$
#
# Above, we said "(almost) standard deviation". That's because the real standard deviation for the batch is calculated by $\sqrt{\sigma_{B}^{2}}$, but the above formula adds the term epsilon, $\epsilon$, before taking the square root. The epsilon can be any small, positive constant - in our code we use the value `0.001`. It is there partially to make sure we don't try to divide by zero, but it also acts to increase the variance slightly for each batch.
#
# Why increase the variance? Statistically, this makes sense because even though we are normalizing one batch at a time, we are also trying to estimate the population distribution – the total training set, which itself an estimate of the larger population of inputs your network wants to handle. The variance of a population is higher than the variance for any sample taken from that population, so increasing the variance a little bit for each batch helps take that into account.
#
# At this point, we have a normalized value, represented as $\hat{x_i}$. But rather than use it directly, we multiply it by a gamma value, $\gamma$, and then add a beta value, $\beta$. Both $\gamma$ and $\beta$ are learnable parameters of the network and serve to scale and shift the normalized value, respectively. Because they are learnable just like weights, they give your network some extra knobs to tweak during training to help it learn the function it is trying to approximate.
#
# $$
# y_i \leftarrow \gamma \hat{x_i} + \beta
# $$
#
# We now have the final batch-normalized output of our layer, which we would then pass to a non-linear activation function like sigmoid, tanh, ReLU, Leaky ReLU, etc. In the original batch normalization paper (linked in the beginning of this notebook), they mention that there might be cases when you'd want to perform the batch normalization _after_ the non-linearity instead of before, but it is difficult to find any uses like that in practice.
#
# In `NeuralNet`'s implementation of `fully_connected`, all of this math is hidden inside the following line, where `linear_output` serves as the $x_i$ from the equations:
# ```python
# batch_normalized_output = tf.layers.batch_normalization(linear_output, training=self.is_training)
# ```
# The next section shows you how to implement the math directly.
# ### Batch normalization without the `tf.layers` package
#
# Our implementation of batch normalization in `NeuralNet` uses the high-level abstraction [tf.layers.batch_normalization](https://www.tensorflow.org/api_docs/python/tf/layers/batch_normalization), found in TensorFlow's [`tf.layers`](https://www.tensorflow.org/api_docs/python/tf/layers) package.
#
# However, if you would like to implement batch normalization at a lower level, the following code shows you how.
# It uses [tf.nn.batch_normalization](https://www.tensorflow.org/api_docs/python/tf/nn/batch_normalization) from TensorFlow's [neural net (nn)](https://www.tensorflow.org/api_docs/python/tf/nn) package.
#
# **1)** You can replace the `fully_connected` function in the `NeuralNet` class with the below code and everything in `NeuralNet` will still work like it did before.
def fully_connected(self, layer_in, initial_weights, activation_fn=None):
"""
Creates a standard, fully connected layer. Its number of inputs and outputs will be
defined by the shape of `initial_weights`, and its starting weight values will be
taken directly from that same parameter. If `self.use_batch_norm` is True, this
layer will include batch normalization, otherwise it will not.
:param layer_in: Tensor
The Tensor that feeds into this layer. It's either the input to the network or the output
of a previous layer.
:param initial_weights: NumPy array or Tensor
Initial values for this layer's weights. The shape defines the number of nodes in the layer.
e.g. Passing in 3 matrix of shape (784, 256) would create a layer with 784 inputs and 256
outputs.
:param activation_fn: Callable or None (default None)
The non-linearity used for the output of the layer. If None, this layer will not include
batch normalization, regardless of the value of `self.use_batch_norm`.
e.g. Pass tf.nn.relu to use ReLU activations on your hidden layers.
"""
if self.use_batch_norm and activation_fn:
# Batch normalization uses weights as usual, but does NOT add a bias term. This is because
# its calculations include gamma and beta variables that make the bias term unnecessary.
weights = tf.Variable(initial_weights)
linear_output = tf.matmul(layer_in, weights)
num_out_nodes = initial_weights.shape[-1]
# Batch normalization adds additional trainable variables:
# gamma (for scaling) and beta (for shifting).
gamma = tf.Variable(tf.ones([num_out_nodes]))
beta = tf.Variable(tf.zeros([num_out_nodes]))
# These variables will store the mean and variance for this layer over the entire training set,
# which we assume represents the general population distribution.
# By setting `trainable=False`, we tell TensorFlow not to modify these variables during
# back propagation. Instead, we will assign values to these variables ourselves.
pop_mean = tf.Variable(tf.zeros([num_out_nodes]), trainable=False)
pop_variance = tf.Variable(tf.ones([num_out_nodes]), trainable=False)
# Batch normalization requires a small constant epsilon, used to ensure we don't divide by zero.
# This is the default value TensorFlow uses.
epsilon = 1e-3
def batch_norm_training():
# Calculate the mean and variance for the data coming out of this layer's linear-combination step.
# The [0] defines an array of axes to calculate over.
batch_mean, batch_variance = tf.nn.moments(linear_output, [0])
# Calculate a moving average of the training data's mean and variance while training.
# These will be used during inference.
# Decay should be some number less than 1. tf.layers.batch_normalization uses the parameter
# "momentum" to accomplish this and defaults it to 0.99
decay = 0.99
train_mean = tf.assign(pop_mean, pop_mean * decay + batch_mean * (1 - decay))
train_variance = tf.assign(pop_variance, pop_variance * decay + batch_variance * (1 - decay))
# The 'tf.control_dependencies' context tells TensorFlow it must calculate 'train_mean'
# and 'train_variance' before it calculates the 'tf.nn.batch_normalization' layer.
# This is necessary because the those two operations are not actually in the graph
# connecting the linear_output and batch_normalization layers,
# so TensorFlow would otherwise just skip them.
with tf.control_dependencies([train_mean, train_variance]):
return tf.nn.batch_normalization(linear_output, batch_mean, batch_variance, beta, gamma, epsilon)
def batch_norm_inference():
# During inference, use the our estimated population mean and variance to normalize the layer
return tf.nn.batch_normalization(linear_output, pop_mean, pop_variance, beta, gamma, epsilon)
# Use `tf.cond` as a sort of if-check. When self.is_training is True, TensorFlow will execute
# the operation returned from `batch_norm_training`; otherwise it will execute the graph
# operation returned from `batch_norm_inference`.
batch_normalized_output = tf.cond(self.is_training, batch_norm_training, batch_norm_inference)
# Pass the batch-normalized layer output through the activation function.
# The literature states there may be cases where you want to perform the batch normalization *after*
# the activation function, but it is difficult to find any uses of that in practice.
return activation_fn(batch_normalized_output)
else:
# When not using batch normalization, create a standard layer that multiplies
# the inputs and weights, adds a bias, and optionally passes the result
# through an activation function.
weights = tf.Variable(initial_weights)
biases = tf.Variable(tf.zeros([initial_weights.shape[-1]]))
linear_output = tf.add(tf.matmul(layer_in, weights), biases)
return linear_output if not activation_fn else activation_fn(linear_output)
# This version of `fully_connected` is much longer than the original, but once again has extensive comments to help you understand it. Here are some important points:
#
# 1. It explicitly creates variables to store gamma, beta, and the population mean and variance. These were all handled for us in the previous version of the function.
# 2. It initializes gamma to one and beta to zero, so they start out having no effect in this calculation: $y_i \leftarrow \gamma \hat{x_i} + \beta$. However, during training the network learns the best values for these variables using back propagation, just like networks normally do with weights.
# 3. Unlike gamma and beta, the variables for population mean and variance are marked as untrainable. That tells TensorFlow not to modify them during back propagation. Instead, the lines that call `tf.assign` are used to update these variables directly.
# 4. TensorFlow won't automatically run the `tf.assign` operations during training because it only evaluates operations that are required based on the connections it finds in the graph. To get around that, we add this line: `with tf.control_dependencies([train_mean, train_variance]):` before we run the normalization operation. This tells TensorFlow it needs to run those operations before running anything inside the `with` block.
# 5. The actual normalization math is still mostly hidden from us, this time using [`tf.nn.batch_normalization`](https://www.tensorflow.org/api_docs/python/tf/nn/batch_normalization).
# 5. `tf.nn.batch_normalization` does not have a `training` parameter like `tf.layers.batch_normalization` did. However, we still need to handle training and inference differently, so we run different code in each case using the [`tf.cond`](https://www.tensorflow.org/api_docs/python/tf/cond) operation.
# 6. We use the [`tf.nn.moments`](https://www.tensorflow.org/api_docs/python/tf/nn/moments) function to calculate the batch mean and variance.
# **2)** The current version of the `train` function in `NeuralNet` will work fine with this new version of `fully_connected`. However, it uses these lines to ensure population statistics are updated when using batch normalization:
# ```python
# if self.use_batch_norm:
# with tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):
# train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
# else:
# train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
# ```
# Our new version of `fully_connected` handles updating the population statistics directly. That means you can also simplify your code by replacing the above `if`/`else` condition with just this line:
# ```python
# train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(cross_entropy)
# ```
# **3)** And just in case you want to implement every detail from scratch, you can replace this line in `batch_norm_training`:
#
# ```python
# return tf.nn.batch_normalization(linear_output, batch_mean, batch_variance, beta, gamma, epsilon)
# ```
# with these lines:
# ```python
# normalized_linear_output = (linear_output - batch_mean) / tf.sqrt(batch_variance + epsilon)
# return gamma * normalized_linear_output + beta
# ```
# And replace this line in `batch_norm_inference`:
# ```python
# return tf.nn.batch_normalization(linear_output, pop_mean, pop_variance, beta, gamma, epsilon)
# ```
# with these lines:
# ```python
# normalized_linear_output = (linear_output - pop_mean) / tf.sqrt(pop_variance + epsilon)
# return gamma * normalized_linear_output + beta
# ```
#
# As you can see in each of the above substitutions, the two lines of replacement code simply implement the following two equations directly. The first line calculates the following equation, with `linear_output` representing $x_i$ and `normalized_linear_output` representing $\hat{x_i}$:
#
# $$
# \hat{x_i} \leftarrow \frac{x_i - \mu_B}{\sqrt{\sigma_{B}^{2} + \epsilon}}
# $$
#
# And the second line is a direct translation of the following equation:
#
# $$
# y_i \leftarrow \gamma \hat{x_i} + \beta
# $$
#
# We still use the `tf.nn.moments` operation to implement the other two equations from earlier – the ones that calculate the batch mean and variance used in the normalization step. If you really wanted to do everything from scratch, you could replace that line, too, but we'll leave that to you.
#
# ## Why the difference between training and inference?
#
# In the original function that uses `tf.layers.batch_normalization`, we tell the layer whether or not the network is training by passing a value for its `training` parameter, like so:
# ```python
# batch_normalized_output = tf.layers.batch_normalization(linear_output, training=self.is_training)
# ```
# And that forces us to provide a value for `self.is_training` in our `feed_dict`, like we do in this example from `NeuralNet`'s `train` function:
# ```python
# session.run(train_step, feed_dict={self.input_layer: batch_xs,
# labels: batch_ys,
# self.is_training: True})
# ```
# If you looked at the [low level implementation](#low_level_code), you probably noticed that, just like with `tf.layers.batch_normalization`, we need to do slightly different things during training and inference. But why is that?
#
# First, let's look at what happens when we don't. The following function is similar to `train_and_test` from earlier, but this time we are only testing one network and instead of plotting its accuracy, we perform 200 predictions on test inputs, 1 input at at time. We can use the `test_training_accuracy` parameter to test the network in training or inference modes (the equivalent of passing `True` or `False` to the `feed_dict` for `is_training`).
def batch_norm_test(test_training_accuracy):
"""
:param test_training_accuracy: bool
If True, perform inference with batch normalization using batch mean and variance;
if False, perform inference with batch normalization using estimated population mean and variance.
"""
weights = [np.random.normal(size=(784,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,100), scale=0.05).astype(np.float32),
np.random.normal(size=(100,10), scale=0.05).astype(np.float32)
]
tf.reset_default_graph()
# Train the model
bn = NeuralNet(weights, tf.nn.relu, True)
# First train the network
with tf.Session() as sess:
tf.global_variables_initializer().run()
bn.train(sess, 0.01, 2000, 2000)
bn.test(sess, test_training_accuracy=test_training_accuracy, include_individual_predictions=True)
# In the following cell, we pass `True` for `test_training_accuracy`, which performs the same batch normalization that we normally perform **during training**.
batch_norm_test(True)
# As you can see, the network guessed the same value every time! But why? Because during training, a network with batch normalization adjusts the values at each layer based on the mean and variance **of that batch**. The "batches" we are using for these predictions have a single input each time, so their values _are_ the means, and their variances will always be 0. That means the network will normalize the values at any layer to zero. (Review the equations from before to see why a value that is equal to the mean would always normalize to zero.) So we end up with the same result for every input we give the network, because its the value the network produces when it applies its learned weights to zeros at every layer.
#
# **Note:** If you re-run that cell, you might get a different value from what we showed. That's because the specific weights the network learns will be different every time. But whatever value it is, it should be the same for all 200 predictions.
#
# To overcome this problem, the network does not just normalize the batch at each layer. It also maintains an estimate of the mean and variance for the entire population. So when we perform inference, instead of letting it "normalize" all the values using their own means and variance, it uses the estimates of the population mean and variance that it calculated while training.
#
# So in the following example, we pass `False` for `test_training_accuracy`, which tells the network that we it want to perform inference with the population statistics it calculates during training.
batch_norm_test(False)
# As you can see, now that we're using the estimated population mean and variance, we get a 97% accuracy. That means it guessed correctly on 194 of the 200 samples – not too bad for something that trained in under 4 seconds. :)
#
# # Considerations for other network types
#
# This notebook demonstrates batch normalization in a standard neural network with fully connected layers. You can also use batch normalization in other types of networks, but there are some special considerations.
#
# ### ConvNets
#
# Convolution layers consist of multiple feature maps. (Remember, the depth of a convolutional layer refers to its number of feature maps.) And the weights for each feature map are shared across all the inputs that feed into the layer. Because of these differences, batch normalizaing convolutional layers requires batch/population mean and variance per feature map rather than per node in the layer.
#
# When using `tf.layers.batch_normalization`, be sure to pay attention to the order of your convolutional dimensions.
# Specifically, you may want to set a different value for the `axis` parameter if your layers have their channels first instead of last.
#
# In our low-level implementations, we used the following line to calculate the batch mean and variance:
# ```python
# batch_mean, batch_variance = tf.nn.moments(linear_output, [0])
# ```
# If we were dealing with a convolutional layer, we would calculate the mean and variance with a line like this instead:
# ```python
# batch_mean, batch_variance = tf.nn.moments(conv_layer, [0,1,2], keep_dims=False)
# ```
# The second parameter, `[0,1,2]`, tells TensorFlow to calculate the batch mean and variance over each feature map. (The three axes are the batch, height, and width.) And setting `keep_dims` to `False` tells `tf.nn.moments` not to return values with the same size as the inputs. Specifically, it ensures we get one mean/variance pair per feature map.
#
# ### RNNs
#
# Batch normalization can work with recurrent neural networks, too, as shown in the 2016 paper [Recurrent Batch Normalization](https://arxiv.org/abs/1603.09025). It's a bit more work to implement, but basically involves calculating the means and variances per time step instead of per layer. You can find an example where someone extended `tf.nn.rnn_cell.RNNCell` to include batch normalization in [this GitHub repo](https://gist.github.com/spitis/27ab7d2a30bbaf5ef431b4a02194ac60).
|
batch-norm/Batch_Normalization_Lesson.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda env:pyiron_38]
# language: python
# name: conda-env-pyiron_38-py
# ---
# # Continuum mechanics -- crack tip stress
#
# In this lesson we will look at the stress distribution around a crack tip. Here we switch from atomistic simulations to continuum mechanics with the finite element method (FEM) using the [FEniCS code](https://fenicsproject.org) under the hood.
#
# We won't spend very much time on the mathematics for FEM, but will examine some of the common input parameters and their effect.
#
# For physics, we will examine three fracture modes for a simple triangular crack in a cubic sample. This is shown schematically below courtesy of wikipedia for a rectangular prism:
#
# 
# # Setup
# %matplotlib notebook
from pyiron_base import Project
import pyiron_continuum
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
pr = Project('fenics_linear_elasticity')
pr.remove_jobs_silently(recursive=True)
# # FEM basics
#
# FEM is an approach for solving partial differential equations (PDEs) numerically by discretizing them with a mesh and using the calculus of variations.
#
# The key physical concepts which specify the problem are the equation being solved (obviously), the spatial domain on which this equation is being solved, and the boundary conditions on that domain. The last of these is typically broken down into two varieties: "Dirichlet" boundary conditions, which specify the value of the field being solved for, and "Neumann" boundary conditions, which specify the gradient of that field dotted with the domain normal vector.
#
# Some of the important numerical concepts are the mesh generation (we will look in a bit of detail at the effect of mesh density) and the element order, which controls how the fields are interpolated within the individual elements (which we will touch on only briefly).
#
# There is much, much more depth on both the mathematical and numeric sides of FEM, but it is not my core area of research and from here on we will restrict ourselves to a concrete example.
# ## Linear Elasticity
#
# The static solution to linear elasticity can be summarized with three equations:
#
# 1. $\nabla \cdot \sigma = -f$
# 2. $\sigma = \lambda~\mathrm{tr}(\epsilon) \mathrm{I} + 2 \mu \epsilon$
# 3. $\epsilon = \frac{1}{2}\left(\nabla u + (\nabla u)^\mathrm{T} \right)$
#
# Where the derivatives of the stress tensor, $\sigma$ balance out body forces on the sample, $f$. The stress tensor is shown here using Lame's constants $\lambda$ and $\mu$ -- which we can also describe in terms of very familair bulk ($K$) and shear ($G$) moduli as $\lambda = K - (2 G / 3)$ and $\mu = G$ -- and the symmeterized strain rate tensor, $\epsilon$, which in turn is constructed from gradients of the displacement field $u$.
#
# With FEM we convert this the so-called weak form which contains integrals and a test function `v`. In this form, we solve
#
# $\int_\Omega \sigma(u):\epsilon(v) dx = \int_\Omega f \cdot v dx + \int_{\partial \Omega_T} T \cdot v ds$
#
# Where $\Omega$ is the domain of our sample and $\partial \Omega_T$ is its boundaries subject to the traction $T$ (remaining boundaries are subject to Dirichlet conditions where the solution is given directly), and $:$ is a tensor contraction.
#
# For the problems we look at here both $f$ and $T$ will be strictly zero, i.e. we have a linear elastic material subject to boundaries which are either displacement controlled or free to relax with no external forces on them. So the physcis of our solution (displacement and strain) is controlled by our material properties ($K$ and $G$ moduli), the geometry of our sample, and how we control its deformation with Dirichlet boundary conditions.
# # Geometry
#
# We'll create our sample by making a box, then subtracting out a triangular crack from this domain. The code to do this is nicely wrapped up in the function below, `set_domain_to_cracked_box`. The important thing for us is that we can easily play around with the crack length, width, and depth (in the x-, y-, z-directions of our box, respectively).
def set_domain_to_cracked_box(job, crack_length=1.0, crack_width=0.1, crack_depth=0.5):
"""
Sets the job's domain to a unit box with a triangular crack tip in it. The crack starts at the
z=0 plane running along the x-axis.
The domain is initially a box, then we subtract out a triangular wedge made from three tets.
The mesh generation is not perfect and there can be small defects right at the crack tip.
Args:
job (Fenics): The job whose domain to set.
crack_length (float): How long the crack is. (Default is 1, run the entire length of the box.)
crack_width (float): How wide the mouth of the crack is. (Default is 0.1.)
crack_depth (float): How deep the crack is. (Default is 0.5, reach to the center of the box.
"""
bulk = job.create.domain.box()
p1 = (0.5 * (1 - crack_length), 0.5 * (1 - crack_width), 0.)
p2 = (0.5 * (1 - crack_length), 0.5 * (1 + crack_width), 0.)
p3 = (0.5 * (1 + crack_length), 0.5 * (1 + crack_width), 0.)
p4 = (0.5 * (1 + crack_length), 0.5 * (1 - crack_width), 0.)
p5 = (0.5 * (1 - crack_length), 0.5, crack_depth)
p6 = (0.5 * (1 + crack_length), 0.5, crack_depth)
crack1 = job.create.domain.tetrahedron(p1, p2, p3, p5)
# crack2 = job.create.domain.tetrahedron(p1, p2, p3, p6)
# crack3 = job.create.domain.tetrahedron(p1, p2, p4, p5)
# crack4 = job.create.domain.tetrahedron(p1, p2, p4, p6)
# crack5 = job.create.domain.tetrahedron(p1, p2, p5, p6)
# crack6 = job.create.domain.tetrahedron(p1, p3, p4, p5)
crack7 = job.create.domain.tetrahedron(p1, p3, p4, p6)
crack8 = job.create.domain.tetrahedron(p1, p3, p5, p6)
# crack9 = job.create.domain.tetrahedron(p2, p3, p4, p5)
# crack10 = job.create.domain.tetrahedron(p2, p3, p4, p6)
# crack11 = job.create.domain.tetrahedron(p3, p4, p5, p6)
job.domain = bulk - crack1 - crack7 - crack8
# Let's create a new FEniCS FEM job and examine the behaviour of this function. In addition to the geometry, we will also increase the mesh density from its very low default value of `2`.
job = pr.create.job.FenicsLinearElastic('fem')
set_domain_to_cracked_box(job)
job.input.mesh_resolution = 10
# Now let's visualize the mesh
job.mesh
# ## Exercise 1
#
# Play around with the `crack_length`, `crack_width`, and `crack_depth` arguments until you comfortably understand the effect they have on the sample geometry. Then increase the `input.mesh_resolution` and note its impact on both the overall meshing, and especially on the numeric artefacts right at the tip.
#
# Note: After calling `set_domain_to_cracked_box` again and/or changing the `job.input.mesh_resolution`, you will need to call `job.generate_mesh()` to update the mesh to use the new parameters.
# # Solving for displacement and stress
#
# Let's solve the displacement and von Mises stress for mode 1: openening. This calculation will serve as an example of how the syntax works for the other calculations we'll perform.
# ## Running the calculation
#
# First, we'll instantiate the job and set the material properties, for which we'll use experimental values for Al reported [on wikipedia](https://en.wikipedia.org/wiki/Aluminium) in GPa.
mode1 = pr.create.job.FenicsLinearElastic('mode1', delete_existing_job=True)
K_Al, G_Al = 76, 26
mode1.input.bulk_modulus = K_Al
mode1.input.shear_modulus = G_Al
# Next, we'll apply a technical setting: switch the solver from its default value of direct solution to an iterative solver. This allows us to increase the mesh density to larger values without running out of memory. If you want to know more details about FEM solvers, you can read about them [here](https://www.simscale.com/blog/2016/08/how-to-choose-solvers-for-fem/). For our purposes it's sufficient to know that we're switching over to an iterative solver.
mode1.input.solver_parameters = {
'linear_solver': 'gmres',
'preconditioner': 'ilu'
}
# After this, we'll construct our geometry. We saw above how the constructor works, but we also want to be able to find nodes that belong to the boundaries so we can apply boundary conditions.
mode1.input.mesh_resolution = 30
set_domain_to_cracked_box(mode1)
# FEniCS, which pyiron is using under the hood, does this with a special python function that takes two arguments: the position of the node, `x`, which is three-dimensional for us, and a boolean array `on_boundary` which FEniCS uses internally to keep track of which nodes are on *any* boundary.
#
# For our boundary conditions, we'll hold the end of the sample opposite the crack fixed, and then displace the face of the sample where the crack starts according to which deformation mode we want. For this, we'll need functions to find the face where the crack *starts* and *ends*, as well as functions to see if we have the *top* half of the face above the crack or the *bottom* half of the face below it.
#
# Using `set_domain_to_cracked_box`, our crack penetrates along the z-axis runs the length of the x-axis, i.e. whether we're above or below it is determined by our y-position. Thus, our logical conditions will use `x[2]` (z) and `x[1]` (y).
# +
def near_start(x, on_boundary):
return job.fenics.near(x[2], 0.)
def near_end(x, on_boundary):
return job.fenics.near(x[2], 1.)
def top_half(x, on_boundary):
return on_boundary and x[1] > 0.5 and near_start(x, on_boundary)
def bottom_half(x, on_boundary):
return on_boundary and x[1] < 0.5 and near_start(x, on_boundary)
# -
# Our actual boundary conditions will be "Dirichlet" (i.e. displacement) conditions on these faces. To communicate these to FEniCS we use special data types called `Constant` (for things that don't change, obviously) and `Expression` (in case we have something with variables). Here let's just apply a static strain using `Constant`.
#
# Activating mode 1, we'll move the top half up a bit and the bottom half down a bit in the y-direction:
strain = 0.01
top_bc = mode1.create.bc.dirichlet(mode1.Constant((0, strain, 0)), top_half)
bottom_bc = mode1.create.bc.dirichlet(mode1.Constant((0, -strain, 0)), bottom_half)
rigid_bc = mode1.create.bc.dirichlet(mode1.Constant((0, 0, 0)), near_end)
# These boundary conditions (BCs) get applied to the job as a list.
mode1.BC = [rigid_bc, top_bc, bottom_bc]
# Now all that's left to do is run our job.
#
# Note: FEniCS funcitonality in pyiron is still experimental, so unlike other jobs which get automatically saved and can be re-loaded later, these jobs exist only in the notebook. Thankfully for us, this problem does not use very much CPU time, so we can always simply re-run the calculations without too much headache.
mode1.run()
# ## Analyzing run
#
# The main output from this run is the displacement field (i.e. the `solution`) and the von Mises stress, which is a scalar field value we post-process from the solution and indicates where plastic activity is most likely to start: $\sigma_M = \sqrt{\frac{3}{2}s : s}$, where $s = \sigma - \frac{1}{3}\mathrm{tr}(\sigma)\mathrm{I}$ is the deviatoric strain.
#
# Let's start by looking at a 3D plot of this stress:
mode1.plot.stress3d();
# Reassuringly, there is a line of high-stress dots along the very tip of the crack, as we would expect. Otherwise most of the stress seems to be focused in the half of the sample containing the crack.
#
# 3D plots are useful, but sometimes it is more effective to look at some 2D projection. We also have helper functions to do this, which project all the results onto a single plane. Since we'd like to isolate the crack tip, it's helpful to project on the x-axis onto the yz-plane so that we're looking down the length of the crack.
mode1.plot.stress2d(projection_axis=0);
# Oh no! Where did our crack go?
#
# Actually, it is still there -- this is just a simple interpolating colourmap, so along the crack where we have no data the plot is simply interpolating. This is actually visible: if you look carfully you will see that there is a triangle with its base on the horizontal axis that has horizontal striated colour bands where the interpolation is happening from one side of the open crack to the other.
#
# As with the 3D plot, but a bit easier to see now, the stress is indeed focused at the tip of the crack. It's so focused that this bright spot actually washes out information about the rest of the stress distribution. We can get around this by using a logarithmic scaling for our colours:
mode1.plot.stress2d(projection_axis=0, lognorm=True);
# Finally, we might also be interested in the raw numeric values -- like what is the maximum nodal stress value? These nodal values are stored in the output:
print("Max nodal stress = {}".format(mode1.output.von_Mises[-1].max()))
# ### Thinking Deeper
#
# Which mode do you expect will have the largest maximum stress, which the smallest, and why?
# *Your thoughts here*
# ### Exercise
#
# Let's get some data to test your hypothesis! Run the same calculation for the other two modes; examine the stress plots and directly compare the maximum stresses. Does the data support your hypothesis, or illuminate something new?
#
# Hint: We only need to change the displacements in our Dirichlet boundary conditions.
# +
# Your code here
# -
# # Quasistatic strain profiles
#
# You may have noticed that just like atomistic output we looked at the output with a `[-1]`, i.e. `job.output.von_Mises[-1]`. That's because just like the atomistic data we can look at a time series of results.
#
# In this case, it's fairly easy to set up an experiment studying the stress as a function of increasing strain in the quasistatic limit (i.e. ignoring any sort of momentum effects, etc.). The key difference will be that our boundary conditions are now a time (`t`) dependent `Expression` instead of a `Constant`.
mode1t = pr.create.job.FenicsLinearElastic('mode1t', delete_existing_job=True)
mode1t.input.bulk_modulus = K_Al
mode1t.input.shear_modulus = G_Al
mode1t.input.solver_parameters = {
'linear_solver': 'gmres',
'preconditioner': 'ilu'
}
mode1t.input.mesh_resolution = 30
set_domain_to_cracked_box(mode1t)
# +
strain_step = 0.005
dirichlet_top = mode1t.Expression(('0', 'a * t', '0'), degree=2, a=strain_step, t=0)
dirichlet_bot = mode1t.Expression(('0', '-a * t', '0'), degree=2, a=strain_step, t=0)
top_bc = mode1t.create.bc.dirichlet(dirichlet_top, top_half)
bottom_bc = mode1t.create.bc.dirichlet(dirichlet_bot, bottom_half)
rigid_bc = mode1t.create.bc.dirichlet(mode1t.Constant((0, 0, 0)), near_end)
mode1t.BC = [rigid_bc, top_bc, bottom_bc]
# -
# Lastly, we need to let the job know which expressions are time-dependent so it can update their `t` parameter, and tell it how many steps to run for:
mode1t.time_dependent_expressions.append(dirichlet_top)
mode1t.time_dependent_expressions.append(dirichlet_bot)
mode1t.input.n_steps = 10
mode1t.run()
# As before we can plot the output, but we can also choose which timestep to look at by setting the `frame` argument. Note how the top end of the stress plot is narrower and narrower compared to the bottom part as we apply more and more strain!
mode1t.plot.stress2d(frame=-1, projection_axis=0, lognorm=True);
# We can also examine the peak stress as a function of strain:
fig, ax = plt.subplots() # A little bit of overhead because we're using interactive plots in this notebook
peak_stress_mode1t = np.array(mode1t.output.von_Mises).max(axis=1)
ax.scatter(strain_step * np.arange(len(peak_stress_mode1t)), peak_stress_mode1t)
ax.set_xlabel('Strain')
ax.set_ylabel('Peak stress');
# ## Exercise
#
# What do the stress strain profiles look like for the other two deformation modes?
# +
# Your code here
# -
# # Numerics
#
# At the heart of FEM is a spatial discretization of our PDE, thus the mesh density for this discretization is a critical feature. Let's examine how our solution changes as a function of our numeric paramters.
#
# Since changing the mesh density means the number and position of the nodes, we can't simply compare the output nodal positions. However, the stored solution at the end of the run can be evaluated at points other than just the mesh nodes by using the function defined below like `evaluate_solution(job.solution)`
# +
spacing = np.linspace(0, 1, num=50)
x, y, z = np.meshgrid(spacing, spacing, spacing)
grid_points = np.vstack((x.flatten(), y.flatten(), z.flatten())).T
def evaluate_solution(solution, points=grid_points):
values = []
for p in points:
try:
values.append(solution(p))
except RuntimeError:
# There is no solution where we cut out the crack
pass
return np.array(values)
# -
# ## Exercise
#
# For a variety of mesh values, e.g. `[20, 30, 40, 50, 60]`, look at the root mean square difference of the solution on our uniform grid -- how does this converge as a function of the `input.mesh_resolution`? Use only your favourite deformation mode for this exercise, and a strain of 1%.
#
# Note: we can't exploit the time-dependent expression here to do multiple mesh densities in a single calculation. Just make a regular for-loop and run multiple jobs.
#
# Hint: You can get the magnitude of the difference between two arrays (of the same shape) very quickly using `np.linalg.norm(array1 - array2)`.
# +
# Your code here
# -
# ## Exercise
#
# So far we have been using the default value for `input.element_order` -- 1. That means that values are linearly interpolated throughout each individual finite element formed by our mesh.
#
# Increase this value from 1 to 2, so that values are quadratically interpolated, and repeat the above exercise.
# +
# Your code here
# -
# ## Thinking deeper
#
# Consider the relationship between mesh resolution and element order, their relative accuracy, and expense? What guidelines can we think of for when to use each setting?
# # Physics
#
# Finally, let's experiment with a couple of the actual material system parameters.
# ## Exercise
#
# Increase the crack width smoothly from 0.1 of the sample width to 0.25. What is the effect on the maximum stress value? Does this agree with our textbook knowledge?
# +
# Your code here
# -
# ## Exercise
#
# Suppose that Al had the same bulk modulus, but double the shear modulus. What effect do you expect this to have on the maximum stresses across the different deformation modes? Repeat the quasistatic strain exercise for all three modes with `job.input.shear_modulus = 2 * G_Al` and compare these results to the original results. We'll keep $\lambda$ the same, as given below by modifying the bulk modulus.
# +
# Your code here
# -
|
notebooks/fenics_linear_elasticity_exercises.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from sklearn.datasets import fetch_20newsgroups
import matplotlib as mpl
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import re
import string
from nltk import word_tokenize
from nltk.corpus import stopwords
from nltk.stem import WordNetLemmatizer
from sklearn.feature_extraction.text import TfidfVectorizer
from collections import Counter
from pylab import *
import nltk
import warnings
warnings.filterwarnings('ignore')
stop_words = stopwords.words('english')
stop_words = stop_words + list(string.printable)
lemmatizer = WordNetLemmatizer()
categories= ['misc.forsale', 'sci.electronics', 'talk.religion.misc']
news_data = fetch_20newsgroups(subset='train', categories=categories, shuffle=True, random_state=42, download_if_missing=True)
news_data_df = pd.DataFrame({'text' : news_data['data'], 'category': news_data.target})
news_data_df.head()
news_data_df['cleaned_text'] = news_data_df['text'].apply(\
lambda x : ' '.join([lemmatizer.lemmatize(word.lower()) \
for word in word_tokenize(re.sub(r'([^\s\w]|_)+', ' ', str(x))) if word.lower() not in stop_words]))
tfidf_model = TfidfVectorizer(max_features=20)
tfidf_df = pd.DataFrame(tfidf_model.fit_transform(news_data_df['cleaned_text']).todense())
tfidf_df.columns = sorted(tfidf_model.vocabulary_)
tfidf_df.head()
from sklearn.decomposition import PCA
pca = PCA(2)
pca.fit(tfidf_df)
reduced_tfidf = pca.transform(tfidf_df)
reduced_tfidf
scatter = plt.scatter(reduced_tfidf[:, 0], reduced_tfidf[:, 1], c=news_data_df['category'], cmap='gray')
plt.xlabel('dimension_1')
plt.ylabel('dimension_2')
plt.legend(handles=scatter.legend_elements()[0], labels=categories, loc='lower left')
plt.title('Representation of NEWS documents in 2D')
plt.show()
|
Chapter03/Exercise 3.12.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.10 64-bit (''pytorch'': conda)'
# name: python3
# ---
import torch
print("PyTorch has version {}".format(torch.__version__))
# +
# Helper function for visualization.
# %matplotlib inline
import torch
import networkx as nx
import matplotlib.pyplot as plt
# Visualization function for NX graph or PyTorch tensor
def visualize(h, color, epoch=None, loss=None):
plt.figure(figsize=(7,7))
plt.xticks([])
plt.yticks([])
if torch.is_tensor(h):
h = h.detach().cpu().numpy()
plt.scatter(h[:, 0], h[:, 1], s=140, c=color, cmap="Set2")
if epoch is not None and loss is not None:
plt.xlabel(f'Epoch: {epoch}, Loss: {loss.item():.4f}', fontsize=16)
else:
nx.draw_networkx(G, pos=nx.spring_layout(G, seed=42), with_labels=False,
node_color=color, cmap="Set2")
plt.show()
# -
|
Test/pytorchGeo.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] colab_type="text" id="t09eeeR5prIJ"
# ##### Copyright 2018 The TensorFlow Authors.
# + cellView="form" colab={} colab_type="code" id="GCCk8_dHpuNf"
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
# + [markdown] colab_type="text" id="xh8WkEwWpnm7"
# # 자동 미분과 그래디언트 테이프
# + [markdown] colab_type="text" id="idv0bPeCp325"
# <table class="tfo-notebook-buttons" align="left">
# <td>
# <a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/ko/r1/tutorials/eager/automatic_differentiation.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" />구글 코랩(Colab)에서 실행하기</a>
# </td>
# <td>
# <a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/ko/r1/tutorials/eager/automatic_differentiation.ipynb"><img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />깃허브(GitHub) 소스 보기</a>
# </td>
# </table>
# + [markdown] colab_type="text" id="Q9_NaXPWxEd8"
# Note: 이 문서는 텐서플로 커뮤니티에서 번역했습니다. 커뮤니티 번역 활동의 특성상 정확한 번역과 최신 내용을 반영하기 위해 노력함에도
# 불구하고 [공식 영문 문서](https://www.tensorflow.org/?hl=en)의 내용과 일치하지 않을 수 있습니다.
# 이 번역에 개선할 부분이 있다면
# [tensorflow/docs](https://github.com/tensorflow/docs) 깃헙 저장소로 풀 리퀘스트를 보내주시기 바랍니다.
# 문서 번역이나 리뷰에 참여하려면
# [<EMAIL>](https://groups.google.com/a/tensorflow.org/forum/#!forum/docs-ko)로
# 메일을 보내주시기 바랍니다.
# + [markdown] colab_type="text" id="vDJ4XzMqodTy"
# 이전 튜토리얼에서는 텐서(tensor)와 텐서의 연산에 대해서 알아보았습니다. 이번 튜토리얼에서는 머신러닝 모델을 최적화할 수 있는 주요 기술 중 하나인 [자동 미분(automatic differentiation)](https://en.wikipedia.org/wiki/Automatic_differentiation)에 대해 알아보겠습니다.
# + [markdown] colab_type="text" id="GQJysDM__Qb0"
# ## 설정
#
# + colab={} colab_type="code" id="OiMPZStlibBv"
import tensorflow.compat.v1 as tf
# + [markdown] colab_type="text" id="1CLWJl0QliB0"
# ## 그래디언트 테이프
#
# 텐서플로는 자동 미분(주어진 입력 변수에 대한 연산의 그래디언트(gradient)를 계산하는 것)을 위한 [tf.GradientTape](https://www.tensorflow.org/api_docs/python/tf/GradientTape) API를 제공합니다. `tf.GradientTape`는 안에서 실행된 모든 연산을 테이프(tape)에 "기록"합니다. 그리고 [후진 방식 자동 미분(reverse mode differentiation)](https://en.wikipedia.org/wiki/Automatic_differentiation)을 사용하여 각각의 기록된 연산과 관련된 그래디언트와 테이프를 사용하여 기록된 연산의 그래디언트를 계산합니다.
#
# 예를 들면:
# + colab={} colab_type="code" id="bAFeIE8EuVIq"
x = tf.ones((2, 2))
with tf.GradientTape() as t:
t.watch(x)
y = tf.reduce_sum(x)
z = tf.multiply(y, y)
# 입력 텐서 x에 대한 z의 도함수
dz_dx = t.gradient(z, x)
for i in [0, 1]:
for j in [0, 1]:
assert dz_dx[i][j].numpy() == 8.0
# + [markdown] colab_type="text" id="N4VlqKFzzGaC"
# 또한 `tf.GradientTape` 컨텍스트 안에서 기록되는 동안 계산된 중간 값에 대한 그래디언트도 구할 수 있습니다.
# + colab={} colab_type="code" id="7XaPRAwUyYms"
x = tf.ones((2, 2))
with tf.GradientTape() as t:
t.watch(x)
y = tf.reduce_sum(x)
z = tf.multiply(y, y)
# 테이프 사용하여 중간 값 y에 대한 도함수를 계산합니다.
dz_dy = t.gradient(z, y)
assert dz_dy.numpy() == 8.0
# + [markdown] colab_type="text" id="ISkXuY7YzIcS"
# 기본적으로 GradientTape.gradient() 메서드가 호출되면 GradientTape에 포함된 리소스가 해제됩니다. 동일한 연산 대해 여러 그래디언트를 계산하려면, `지속성있는(persistent)` 그래디언트 테이프를 생성하면 됩니다. 이 그래디언트 테이프는 `gradient()` 메서드의 다중 호출을 허용합니다. 테이프 객체가 쓰레기 수집(garbage collection)될때 리소스는 해체됩니다.
# 예를 들면 다음과 같습니다:
# + colab={} colab_type="code" id="zZaCm3-9zVCi"
x = tf.constant(3.0)
with tf.GradientTape(persistent=True) as t:
t.watch(x)
y = x * x
z = y * y
dz_dx = t.gradient(z, x) # 108.0 (4*x^3 at x = 3)
dy_dx = t.gradient(y, x) # 6.0
del t # 테이프에 대한 참조를 삭제합니다.
# + [markdown] colab_type="text" id="6kADybtQzYj4"
# ### 제어 흐름 기록
#
# 연산이 실행되는 순서대로 테이프에 기록되기 때문에, 파이썬 제어 흐름(예를 들어 `if` `while`, `for`문 같은)이 자연스럽게 처리됩니다.
# + colab={} colab_type="code" id="9FViq92UX7P8"
def f(x, y):
output = 1.0
for i in range(y):
if i > 1 and i < 5:
output = tf.multiply(output, x)
return output
def grad(x, y):
with tf.GradientTape() as t:
t.watch(x)
out = f(x, y)
return t.gradient(out, x)
x = tf.convert_to_tensor(2.0)
assert grad(x, 6).numpy() == 12.0
assert grad(x, 5).numpy() == 12.0
assert grad(x, 4).numpy() == 4.0
# + [markdown] colab_type="text" id="DK05KXrAAld3"
# ### 고계도(Higher-order) 그래디언트
#
# `GradientTape` 컨텍스트 매니저안에 있는 연산들은 자동미분을 위해 기록됩니다. 만약 그래디언트가 컨텍스트 안에서 계산되면 그 그래디언트 연산 또한 기록되어집니다. 그 결과 똑같은 API가 고계도 그래디언트에서도 잘 작동합니다. 예를 들면:
# + colab={} colab_type="code" id="cPQgthZ7ugRJ"
x = tf.Variable(1.0) # 1.0으로 초기화된 텐서플로 변수를 생성합니다.
with tf.GradientTape() as t:
with tf.GradientTape() as t2:
y = x * x * x
# t 컨텍스트 매니저 안의 그래디언트를 계산합니다.
# 이것은 또한 그래디언트 연산 자체도 미분가능하다는것을 의미합니다.
dy_dx = t2.gradient(y, x)
d2y_dx2 = t.gradient(dy_dx, x)
assert dy_dx.numpy() == 3.0
assert d2y_dx2.numpy() == 6.0
# + [markdown] colab_type="text" id="4U1KKzUpNl58"
# ## 다음 단계
#
# 이번 튜토리얼에서는 텐서플로에서 그래디언트 계산법을 다루었습니다. 이를 통해 신경망(neural network)을 구축하고 훈련시키는데 필요한 많은 기본 요소를 배웠습니다.
|
site/ko/r1/tutorials/eager/automatic_differentiation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
import model
from datetime import datetime
from datetime import timedelta
sns.set()
df = pd.read_csv('/home/husein/space/Stock-Prediction-Comparison/dataset/GOOG-year.csv')
date_ori = pd.to_datetime(df.iloc[:, 0]).tolist()
df.head()
minmax = MinMaxScaler().fit(df.iloc[:, 1:].astype('float32'))
df_log = minmax.transform(df.iloc[:, 1:].astype('float32'))
df_log = pd.DataFrame(df_log)
df_log.head()
num_layers = 1
size_layer = 128
timestamp = 5
epoch = 500
dropout_rate = 0.7
future_day = 50
class Model:
def __init__(self, learning_rate, num_layers, size, size_layer, output_size, seq_len,
forget_bias = 0.1):
def lstm_cell(size_layer):
return tf.nn.rnn_cell.LSTMCell(size_layer, state_is_tuple = False)
def global_pooling(x, func):
batch_size = tf.shape(self.X)[0]
num_units = x.get_shape().as_list()[-1]
x = func(x, x.get_shape().as_list()[1], 1)
x = tf.reshape(x, [batch_size, num_units])
return x
rnn_cells = tf.nn.rnn_cell.MultiRNNCell([lstm_cell(size_layer) for _ in range(num_layers)], state_is_tuple = False)
self.X = tf.placeholder(tf.float32, (None, None, size))
self.Y = tf.placeholder(tf.float32, (None, output_size))
drop = tf.contrib.rnn.DropoutWrapper(rnn_cells, output_keep_prob = forget_bias)
self.hidden_layer = tf.placeholder(tf.float32, (None, num_layers * 2 * size_layer))
self.outputs, self.last_state = tf.nn.dynamic_rnn(drop, self.X, initial_state = self.hidden_layer, dtype = tf.float32)
self.outputs = self.outputs[:,:,0]
x = self.X
masks = tf.sign(self.outputs)
batch_size = tf.shape(self.X)[0]
align = tf.matmul(self.X, tf.transpose(self.X, [0,2,1]))
paddings = tf.fill(tf.shape(align), float('-inf'))
k_masks = tf.tile(tf.expand_dims(masks, 1), [1, seq_len, 1])
align = tf.where(tf.equal(k_masks, 0), paddings, align)
align = tf.nn.tanh(align)
q_masks = tf.to_float(masks)
q_masks = tf.tile(tf.expand_dims(q_masks, -1), [1, 1, seq_len])
align *= q_masks
x = tf.matmul(align, x)
g_max = global_pooling(x, tf.layers.max_pooling1d)
g_avg = global_pooling(x, tf.layers.average_pooling1d)
x = tf.concat([g_max, g_avg], -1)
rnn_W = tf.Variable(tf.random_normal((seq_len, output_size)))
rnn_B = tf.Variable(tf.random_normal([output_size]))
self.logits = tf.matmul(self.outputs, rnn_W) + rnn_B
self.cost = tf.reduce_mean(tf.square(self.Y - self.logits))
self.optimizer = tf.train.AdamOptimizer(learning_rate).minimize(self.cost)
tf.reset_default_graph()
modelnn = Model(0.01, num_layers, df_log.shape[1], size_layer, df_log.shape[1], timestamp, dropout_rate)
sess = tf.InteractiveSession()
sess.run(tf.global_variables_initializer())
for i in range(epoch):
init_value = np.zeros((1, num_layers * 2 * size_layer))
total_loss = 0
for k in range(0, (df_log.shape[0] // timestamp) * timestamp, timestamp):
batch_x = np.expand_dims(df_log.iloc[k: k + timestamp, :].values, axis = 0)
batch_y = df_log.iloc[k + 1: k + timestamp + 1, :].values
last_state, _, loss = sess.run([modelnn.last_state,
modelnn.optimizer,
modelnn.cost], feed_dict={modelnn.X: batch_x,
modelnn.Y: batch_y,
modelnn.hidden_layer: init_value})
loss = np.mean(loss)
init_value = last_state
total_loss += loss
total_loss /= (df_log.shape[0] // timestamp)
if (i + 1) % 100 == 0:
print('epoch:', i + 1, 'avg loss:', total_loss)
# +
output_predict = np.zeros((df_log.shape[0] + future_day, df_log.shape[1]))
output_predict[0, :] = df_log.iloc[0, :]
upper_b = (df_log.shape[0] // timestamp) * timestamp
init_value = np.zeros((1, num_layers * 2 * size_layer))
for k in range(0, (df_log.shape[0] // timestamp) * timestamp, timestamp):
try:
out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[k: k + timestamp, :], axis = 0),
modelnn.hidden_layer: init_value})
output_predict[k + 1: k + timestamp + 1, :] = out_logits
except:
out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[-timestamp:, :], axis = 0),
modelnn.hidden_layer: init_value})
output_predict[df_log.shape[0]-timestamp:df_log.shape[0],:] = out_logits
init_value = last_state
df_log.loc[df_log.shape[0]] = out_logits[-1, :]
date_ori.append(date_ori[-1]+timedelta(days=1))
# -
for i in range(future_day - 1):
out_logits, last_state = sess.run([modelnn.logits, modelnn.last_state], feed_dict = {modelnn.X:np.expand_dims(df_log.iloc[-timestamp:, :], axis = 0),
modelnn.hidden_layer: init_value})
init_value = last_state
output_predict[df_log.shape[0], :] = out_logits[-1, :]
df_log.loc[df_log.shape[0]] = out_logits[-1, :]
date_ori.append(date_ori[-1]+timedelta(days=1))
df_log = minmax.inverse_transform(output_predict)
date_ori=pd.Series(date_ori).dt.strftime(date_format='%Y-%m-%d').tolist()
current_palette = sns.color_palette("Paired", 12)
fig = plt.figure(figsize = (15,10))
ax = plt.subplot(111)
x_range_original = np.arange(df.shape[0])
x_range_future = np.arange(df_log.shape[0])
ax.plot(x_range_original, df.iloc[:, 1], label = 'true Open', color = current_palette[0])
ax.plot(x_range_future, df_log[:, 0], label = 'predict Open', color = current_palette[1])
ax.plot(x_range_original, df.iloc[:, 2], label = 'true High', color = current_palette[2])
ax.plot(x_range_future, df_log[:, 1], label = 'predict High', color = current_palette[3])
ax.plot(x_range_original, df.iloc[:, 3], label = 'true Low', color = current_palette[4])
ax.plot(x_range_future, df_log[:, 2], label = 'predict Low', color = current_palette[5])
ax.plot(x_range_original, df.iloc[:, 4], label = 'true Close', color = current_palette[6])
ax.plot(x_range_future, df_log[:, 3], label = 'predict Close', color = current_palette[7])
ax.plot(x_range_original, df.iloc[:, 5], label = 'true Adj Close', color = current_palette[8])
ax.plot(x_range_future, df_log[:, 4], label = 'predict Adj Close', color = current_palette[9])
box = ax.get_position()
ax.set_position([box.x0, box.y0 + box.height * 0.1, box.width, box.height * 0.9])
ax.legend(loc = 'upper center', bbox_to_anchor= (0.5, -0.05), fancybox = True, shadow = True, ncol = 5)
plt.title('overlap stock market')
plt.xticks(x_range_future[::30], date_ori[::30])
plt.show()
fig = plt.figure(figsize = (20,8))
plt.subplot(1, 2, 1)
plt.plot(x_range_original, df.iloc[:, 1], label = 'true Open', color = current_palette[0])
plt.plot(x_range_original, df.iloc[:, 2], label = 'true High', color = current_palette[2])
plt.plot(x_range_original, df.iloc[:, 3], label = 'true Low', color = current_palette[4])
plt.plot(x_range_original, df.iloc[:, 4], label = 'true Close', color = current_palette[6])
plt.plot(x_range_original, df.iloc[:, 5], label = 'true Adj Close', color = current_palette[8])
plt.xticks(x_range_original[::60], df.iloc[:, 0].tolist()[::60])
plt.legend()
plt.title('true market')
plt.subplot(1, 2, 2)
plt.plot(x_range_future, df_log[:, 0], label = 'predict Open', color = current_palette[1])
plt.plot(x_range_future, df_log[:, 1], label = 'predict High', color = current_palette[3])
plt.plot(x_range_future, df_log[:, 2], label = 'predict Low', color = current_palette[5])
plt.plot(x_range_future, df_log[:, 3], label = 'predict Close', color = current_palette[7])
plt.plot(x_range_future, df_log[:, 4], label = 'predict Adj Close', color = current_palette[9])
plt.xticks(x_range_future[::60], date_ori[::60])
plt.legend()
plt.title('predict market')
plt.show()
fig = plt.figure(figsize = (15,10))
ax = plt.subplot(111)
ax.plot(x_range_original, df.iloc[:, -1], label = 'true Volume')
ax.plot(x_range_future, df_log[:, -1], label = 'predict Volume')
box = ax.get_position()
ax.set_position([box.x0, box.y0 + box.height * 0.1, box.width, box.height * 0.9])
ax.legend(loc = 'upper center', bbox_to_anchor= (0.5, -0.05), fancybox = True, shadow = True, ncol = 5)
plt.xticks(x_range_future[::30], date_ori[::30])
plt.title('overlap market volume')
plt.show()
fig = plt.figure(figsize = (20,8))
plt.subplot(1, 2, 1)
plt.plot(x_range_original, df.iloc[:, -1], label = 'true Volume')
plt.xticks(x_range_original[::60], df.iloc[:, 0].tolist()[::60])
plt.legend()
plt.title('true market volume')
plt.subplot(1, 2, 2)
plt.plot(x_range_future, df_log[:, -1], label = 'predict Volume')
plt.xticks(x_range_future[::60], date_ori[::60])
plt.legend()
plt.title('predict market volume')
plt.show()
|
deep-learning/18.lstm-attention-scaleddot.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # WeatherPy
# ----
#
# ### Analysis
# * As expected, the weather becomes significantly warmer as one approaches the equator (0 Deg. Latitude). More interestingly, however, is the fact that the southern hemisphere tends to be warmer this time of year than the northern hemisphere. This may be due to the tilt of the earth.
# * There is no strong relationship between latitude and cloudiness. However, it is interesting to see that a strong band of cities sits at 0, 80, and 100% cloudiness.
# * There is no strong relationship between latitude and wind speed. However, in northern hemispheres there is a flurry of cities with over 20 mph of wind.
#
# ---
#
# #### Note
# * Instructions have been included for each segment. You do not have to follow them exactly, but they are included to help you think through the steps.
# +
#Dependencies
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import requests
import time
import random
import datetime
import seaborn as sns
from pprint import pprint
#Import API Keys
from api_keys import api_key
# Import citipy to determine city based on latitude and longitude
from citipy import citipy
# -
# Range of latitudes and longitudes
lat_range = (-90, 90)
lng_range = (-180, 180)
# ## Generate Cities List
# +
# List for holding lat_lngs and cities
lat_lngs = []
cities = []
lat_lng_list = []
# Create a set of random lat and lng combinations
lats = np.random.uniform(low=-90.000, high=90.000, size=2000)
lngs = np.random.uniform(low=-180.000, high=180.000, size=2000)
lat_lngs = zip(lats, lngs)
# Identify nearest city for each lat, lng combination
for lat_lng in lat_lngs:
city = citipy.nearest_city(lat_lng[0], lat_lng[1]).city_name
# If the city is unique, then add it to a our cities list
if city not in cities:
cities.append(city)
lat_lng_list.append(lat_lng)
# Print the city count to confirm sufficient count
len(cities)
# +
#Create dataframe with list of cities
df = pd.DataFrame(cities)
df = df.rename(columns={0: 'city'})
#Add lat and lngs to dataframe, create separate columns for lats and longs
df['lat_lngs'] = lat_lng_list
df['lat'] = df.lat_lngs.map(lambda x: str(x[0]))
df['long'] = df.lat_lngs.map(lambda x: str(x[1]))
df.head()
# -
# ### Perform API Calls
# * Perform a weather check on each city using a series of successive API calls.
# * Include a print log of each city as it'sbeing processed (with the city number and city name).
#
# +
api_key = '<KEY>' #deactivated for security and publication
#Create columns for data to be collecting from the API
df['temp'] = ""
df['max_temp'] = ""
df['humidity'] = ""
df['wind_speed'] = ""
df['clouds'] = ""
#Iterate over each row as index pairs
#Include a print log of each city as it'sbeing processed (with the city number and city name)
for index, row in df.iterrows():
city = row['city']
print(f"Processing Record {index + 1} | {city}")
city = city.replace(" ", "&")
url = "http://api.openweathermap.org/data/2.5/weather?units=Imperial&q=" + city + "&APPID=" + api_key
print(url)
weather = requests.get(url).json()
try:
df.loc[index, 'temp'] = weather['main']['temp']
df.loc[index, 'max_temp'] = weather['main']['temp_max']
df.loc[index, 'humidity'] = weather['main']['humidity']
df.loc[index, 'wind_speed'] = weather['wind']['speed']
df.loc[index, 'clouds'] = weather['clouds']['all']
except:
df.loc[index, 'temp'] = 'city not found'
df.loc[index, 'humidity'] = 'city not found'
df.loc[index, 'wind_speed'] = 'city not found'
df.loc[index, 'clouds'] = 'city not found'
time.sleep(.50)
print("----------------------")
print("Data Retrieval Complete")
print("-----------------------")
# -
# ### Convert Raw Data to DataFrame
# * Export the city data into a .csv.
# * Display the DataFrame
# +
#Remove cities that could not be found from the dataframe
df = df[df.temp != 'city not found']
#Check that there are still 500+ records
len(df)
# -
#Convert lat from string to float object
df.lat = df.lat.astype(float)
df.head()
#Export dataframe to CSV
df.to_csv("cities.csv", encoding="utf-8", index=False)
df.head()
# ### Plotting the Data
# * Use proper labeling of the plots using plot titles (including date of analysis) and axes labels.
# * Save the plotted figures as .pngs.
# #### Latitude vs. Temperature Plot
# +
#Pull in today's date for graphs
date = datetime.date.today()
date = time.strftime("%m/%d/%Y")
sns.set()
plt.figure(figsize=(10,8))
plt.scatter(df['lat'], df['temp'])
plt.title(f"City Latitude vs. Temperature {date}", fontsize="18")
plt.xlabel("Latitude", fontsize="14")
plt.ylabel("Temperature (F)", fontsize="14")
plt.ylim(0, 120)
plt.savefig("Temperature.png")
plt.show()
#Trend #1 - The temperature is warmer in the Northern Hemisphere
# -
# #### Latitude vs. Humidity Plot
# +
plt.figure(figsize=(10,8))
plt.scatter(df['lat'], df['humidity'])
plt.title(f"City Latitude vs. Humidity {date}", fontsize="18")
plt.xlabel("Latitude", fontsize="14")
plt.ylabel("Humidity (%)", fontsize="14")
plt.ylim(0,120)
plt.savefig("Humidity.png")
plt.show()
#Trend #2 - Latitude does not appear to impact humidity
# -
# #### Latitude vs. Cloudiness Plot
# +
plt.figure(figsize=(10,8))
plt.scatter(df['lat'], df['clouds'])
plt.title(f"City Latitude vs.Cloudiness {date}", fontsize="18")
plt.xlabel("Latitude", fontsize="14")
plt.ylabel("Wind Speed (mph)", fontsize="14")
plt.ylim(-20, 120)
plt.savefig("Cloudiness.png")
plt.show()
#Trend #2 - Latitude does not appear to impact cloudiness
# -
# #### Latitude vs. Wind Speed Plot
# +
plt.figure(figsize=(10,8))
plt.scatter(df['lat'], df['wind_speed'])
plt.title(f"City Latitude vs. Wind Speed {date}", fontsize="18")
plt.xlabel("Latitude", fontsize="14")
plt.ylabel("Wind Speed (mph)", fontsize="14")
plt.ylim(-5,45)
plt.savefig("Wind_Speed.png")
plt.show()
#Trend #2 - Latitude does not appear to greatly impact wind speed
# -
|
API Homework/WeatherPy.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # Practice Problems
# ### Lecture 5
# Answer each number in a separate cell
#
# Rename this notebook with your last name and the lecture
#
# ex. Cych_B_05
#
# Turn-in this notebook on Canvas.
# 1. Doc string
# - Create a function **greeting( )**. Include a doc string that explains what the function does
# - In the body, use the command **print ('Hi there')**
# - print out the docstring with **help(greeting)**
# 2. Functions
# - create a function called **circleArea( )** . The function should take a radius as an argument and return the area of a circle with that radius ($A=\pi r^2$). Include a doc string (as ALWAYS).
# - call the function and print out the result
# - Create a function called **add_em_up( )** that takes an unspecified number of input floating point or integer arguments and returns their sum.
# - Call the function with different numbers of arguments and print the sum.
# 3. Modules
# - Create a module **myMath.py** by copying both functions **add\_em\_up(\*args)** and **circleArea(r)** in a cell
# - rename the two functions **add** and **area**
# - save the module by using the __%%writefile__ magic command and specifying the file name as **myMath.py**.
# - import the **myMath.py** module into your Jupyter notebook and call each function in the module
# 4. Local variables
# - define a variable **myName** with your name
# - define a function **greeting( )** that sets myName to "<NAME>". The function should return the string "Hello" and the variable **myName**
# - print **myName**
# - call the function **greeting( )** and print the output
# - print **myName** again
# - Has the value of **myName** changed after calling the function **greeting( )**?
# 5. Global variables
# - define a variable **name** with your name
# - define a function **greet( )** that sets the global variable **name** to "<NAME>". The function should return "Hello" and the variable **name**
# - print **name**
# - call the function **greet( )** and print the output
# - print **name**
# - Has the value of **name** changed after calling the function **greet( )**?
|
Practice_Problems/.ipynb_checkpoints/Lecture_05_Practice_Problems-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
#import needed libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import math
import seaborn as sns
import statistics as stats
import pylab
from scipy.signal import find_peaks
pvt = pd.read_csv("PVT.csv")
pvt = pvt.rename(index = str, columns={"Joy":"<NAME>", "Other Joy":"<NAME>"})
survey_qs = pd.read_csv("Cognitive_Fatigue_Data.csv")
survey_qs.insert(1, "Gender", ['F', 'F', 'F', 'M', 'F', 'F', 'M', 'F', 'M', 'M', 'M', 'M', 'M', 'M', 'F', 'M', 'F', 'M', 'M', 'M', 'M', 'M','M',], True)
pulse = pd.read_csv("Pulse/ShreyaJainHeartbeat.csv", skiprows = 6, names = ['Time', 'mV'])
# +
# Determining who is fatigued and who isn't based on Reaction Time
# -
pvt.describe()
survey_qs
pvt = pvt[pvt>100000]
pvt_mean = pvt.mean()
pvt_mean
median_pvt = stats.median(pvt_mean)
#pvt_mean = pvt.mean()
#pvt_mean
median_pvt
fatigued = pvt_mean[pvt_mean>median_pvt]
fatigued
not_fatigued = pvt_mean[pvt_mean<=median_pvt]
not_fatigued
plt.hist(pvt_mean, bins=6) # bins = number of bars in the histogram
plt.title("Histogram of Medlytics Class Reactions")
label = pvt_mean > median_pvt # false = not fatigued, true = fatigued
label
# +
# identify columns by what type of data they hold -- first numeric columns
numeric_columns = list(["Income", "Alcohol", "Cholesterol", "Age"])
# categorical columns are everything else
categorical_columns = list(set(mydat.columns) - set(numeric_columns))
# convert numeric columns from strings to numbers
mydat[numeric_columns] = mydat[numeric_columns].apply(pd.to_numeric)
# -
pulse.head(10)
plt.plot(pulse['mV'])
pylab.xlim(0,501) # this is the first 10 seconds
plt.show()
# +
from scipy.misc import electrocardiogram
# x = electrocardiogram()[0:501]
peaks, _ = find_peaks(pulse['mV'])
plt.plot(pulse['mV'])
plt.plot(peaks, pulse['mV'][peaks], "x")
plt.plot(np.zeros_like(pulse['mV']), "--", color="gray")
pylab.xlim(0,501)
plt.show()
# -
fs = 50
peaks, _ = find_peaks(pulse['mV'], distance=fs*40/60)
np.diff(peaks)
plt.plot(pulse['mV'])
plt.plot(peaks, pulse['mV'][peaks], "x")
pylab.xlim(0,501)
plt.show()
peaks[peaks<501].shape[0]*6
# gets number of beats per min by multiplying the number of heartbeats in first 10 seconds by 6
def get_heartrate(name):
pulse = pd.read_csv("Pulse/"+name+"Heartbeat.csv", skiprows = 6, names = ['Time', 'mV'])
peaks, _ = find_peaks(pulse['mV'], distance=fs*40/60)
# np.diff(peaks)
result = peaks[peaks<501].shape[0]*6
return result
names = ['AnnaHe','ElaineChu','MarielaNazarioCastro','HarrisBubalo','OdessaThompson','ShreyaJain','VarunNair','JoyLiu','VishalKumar','ShuenWu','GovindChada','SuatMartin','DavidDelValle','YerielMaldonado','JoyLim','EdwardYan','CarolZhang','VineetChinthakindi','PratikBharadwaj','SharvilTrifale','AlexYu','EstebanCintron','AadiDass-Vattam']
heart_rates = pd.DataFrame(index=np.arange(1),columns = names)
for i in range(len(names)):
heart_rates.iloc[0,i]=get_heartrate(names[i])
heart_rates
# gets number of beats per min by dividing the number of heartbeats in full 2 min by 2
def get_heartrate_avg(name):
pulse = pd.read_csv("Pulse/"+name+"Heartbeat.csv", skiprows = 6, names = ['Time', 'mV'])
peaks, _ = find_peaks(pulse['mV'], distance=fs*40/60)
# np.diff(peaks)
result = peaks.shape[0]/2
return result
get_heartrate_avg('OdessaThompson')
avg_heart_rates = pd.DataFrame(index=np.arange(1),columns = names)
for i in range(len(names)):
avg_heart_rates.iloc[0,i]=get_heartrate_avg(names[i])
avg_heart_rates
get_heartrate_avg('ShreyaJain')
# +
# SPEECH ANALYSIS
# -
# import libraries
import parselmouth as pm
import os
import numpy as np
import matplotlib.pyplot as plt
# importing data
Shreya = pm.Sound("Speech/ShreyaJain.wav")
# getting intensity, pitch, formant
hInt = Shreya.to_intensity()
hPit = Shreya.to_pitch()
hForm = Shreya.to_formant_burg()
intensities = []
for val in hInt.t_grid():
intensities.append(hInt.get_value(val))
plt.plot(intensities[:100])
formants = [[],[],[]]
for val in hForm.t_grid():
formants[0].append(hForm.get_value_at_time(1,val))
formants[1].append(hForm.get_value_at_time(2,val))
formants[2].append(hForm.get_value_at_time(3,val))
plt.plot(formants[0][0:100]) # 3 formants are 3 most significant components of voice
plt.plot(formants[1][0:100]) # this is like dimensionality reduction for sound
plt.plot(formants[2][0:100])
pitches = []
sum_pitches = 0
hPit.t_grid()
for val in hPit.t_grid():
pitches.append(hPit.get_value_at_time(val))
#plt.plot(pitches[:100])
#hPit.get_value_at_time(hPit.t_grid[0])
pitches = np.array(pitches)
np.nanstd(pitches) # standard deviation, range
Harris = pm.Sound("Speech/AnnaHe.wav")
hInt = Harris.to_intensity()
hPit = Harris.to_pitch()
hForm = Harris.to_formant_burg()
pitches = []
sum_pitches = 0
hPit.t_grid()
for val in hPit.t_grid():
pitches.append(hPit.get_value_at_time(val))
pitches = np.array(pitches)
np.nanstd(pitches) # standard deviation, range
names = ['AnnaHe','ElaineChu','MarielaNazarioCastro','HarrisBubalo','OdessaThompson','ShreyaJain','VarunNair','JoyLiu','VishalKumar','ShuenWu','GovindChada','SuatMartin','DavidDelValle','YerielMaldonado','JoyLim','EdwardYan','CarolZhang','VineetChinthakindi','PratikBharadwaj','SharvilTrifale','AlexYu','EstebanCintron','AadiDass-Vattam']
std_pitches = []
def get_pitch_std(name):
speech = pm.Sound("Speech/"+ name + ".wav")
hInt = speech.to_intensity()
hPit = speech.to_pitch()
hForm = speech.to_formant_burg()
pitches = []
hPit.t_grid()
for val in hPit.t_grid():
pitches.append(hPit.get_value_at_time(val))
pitches = np.array(pitches)
return np.nanstd(pitches)
for name in names:
std_pitches.append(get_pitch_std(name))
survey_qs.insert(1,"Pitch STD",std_pitches)
survey_qs
all_pulses =[]
for i in range(len(names)):
all_pulses.append(get_heartrate_avg(names[i]))
all_pulses
survey_qs.insert(1,"Pulse",all_pulses)
survey_qs
final_dat = survey_qs[['Name','Pulse','Pitch STD','Gender','sleep','fatigue scale','exercise(min)','eating scale','stress scale']]
final_dat
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
fulldata
fulldata=fulldata>median_pvt
fatigueness=fatigued.append(not_fatigued)
fatigueness=fatigueness>median_pvt
# +
#final_dat = final_dat.drop('IsFatigued',axis=1)
# -
label
# +
#final_dat.insert(1,'IsFatigued',fatigueness)
# +
#final_dat = final_dat.insert(1, 'rt', pvt_mean)
# -
is_fatigued = pd.Series(pvt_mean>median_pvt)
label
final_dat.insert(1,'Label',[True,True,False,False,False,False,False,True,True,False,False,True,True,True,True,False,False,False,True,True,True,False,False])
# +
#final_dat.loc[4,'Name']='Odessa'
# -
final_dat = final_dat.drop(['LLAABBEELL', 'label'], axis=1)
final_dat
# +
# normalizing data
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
final_dat = final_dat.replace(to_replace = 'F',value=1)
final_dat = final_dat.replace(to_replace='M',value=0)
final_dat
# -
final_dat = final_dat.drop('nPitch STD',axis=1)
final_dat
# +
# Write your code here
data_train, data_val = train_test_split(final_dat, test_size = 0.20, random_state = 1, stratify = final_dat['Label'])
y_train = data_train['Label']
y_val = data_val['Label']
# only features
# X_train = data_train[["Pulse", "Pitch STD", "sleep", "fatigue scale"]]
# X_val = data_val[["Pulse", "Pitch STD", "sleep", "fatigue scale"]]
X_train = data_train[["fatigue scale"]]
X_val = data_val[["fatigue scale"]]
X_train.head()
# +
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import cross_validate
from sklearn.metrics import recall_score
from sklearn.model_selection import cross_val_score
clf = DecisionTreeClassifier()
results = cross_val_score(clf,X_train, y_train,cv=5)
results
# +
#from sklearn.linear_model import LogisticRegression
#logreg = LogisticRegression()
results = clf.fit(X_train, y_train)
# +
from sklearn.metrics import auc
# apply the model to test data
y_val_predict = clf.predict(X_val)
y_val_proba = clf.predict_proba(X_val)
print(y_val[:5],y_val_predict[:5])
from sklearn import metrics
from sklearn.metrics import confusion_matrix
#extract fpr and tpr to plot ROC curve and calculate AUC (Note: fpr-false positive rate and tpr -true positive rate)
fpr, tpr, threshold = metrics.roc_curve(y_val, y_val_proba[:,1])
# This is exctly the first metric you'll be evaluated on!
# Note: this will only work on the binary case -- you'll need a different method to do multi-class case
def cm_metric(y_true,y_prob):
# predict the class with the greatest probability
y_pred = [np.argmax(y) for y in y_prob]
# calculate the confusion matrix
cm = confusion_matrix(y_true, y_val_predict)
cm_norm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
return sum(sum(np.multiply(cm_norm,np.array([[1, -2], [-2, 1]]))))
cm_metric(y_val,y_val_proba)
# Calculate the area under the ROC curve
roc_auc = metrics.auc(fpr, tpr)
print('AUC: ',roc_auc)
import matplotlib.pyplot as plt
plt.title('Receiver Operating Characteristic')
plt.plot(fpr, tpr, 'b', label = 'AUC = %0.3f' % roc_auc)
plt.legend(loc = 'lower right')
plt.plot([0, 1], [0, 1],'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('True Positive Rate')
plt.xlabel('False Positive Rate')
plt.show()
# -
|
.ipynb_checkpoints/Analysis-checkpoint.ipynb
|
// -*- coding: utf-8 -*-
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # Software Development 1
// ---
// Topics for today will include:
// - Polling The Class
// - GitHub
// - Command Line
// - Square One: Printing Things Out
// - Square Two: Taking Things In
// - Reviewing Counting in Binary and Binary Math
// - Values and Data Types
// - Variables
// - Primitive Data Types
// - Reference Data Types
// - Arrays
// - Arithmetic
// ## Square One: Printing Things Out
// So we're going to start with the simple stuff. In programming we need a way to see what the computer is telling us. We can do this with a print statement. This is a little more complex in Java. We can do this a few ways. Printing things out in Java is more similar to the Python Logger. Meaning we have several options when it comes to printing things out.
//
// We're telling the `System` that we need to do something. We have a couple different streams that we can write to. Then there are two options from there.
//
// | Print Stream | Print Types |
// |--------------|-------------|
// | out | print |
// | err | println |
System.out.print("Hello" + "\n");
System.out.println("World");
System.err.print("Hello");
System.err.println("Hello");
// ## Square Two: Taking Things In
// Just like we can send things out we can also take things in. Java have 3 streams that we usually interact with. In, Err, and Out. We did Out and Err. This is a good teaching moment for somethings that will happen in Jupyter Notebooks in this class. This is valid code but isn't going to do anything right now. We'll come back to this later!
Scanner input = new Scanner(System.in);
// ## Reviewing Counting in Binary and Binary Math
//
// So before we do anything we need to sorta understand the math the computer might possibly hide from us. To do this we need to be able to get numbers into a form that we can understand. That typically being decimal. So we're going to break down the positional based math for converting to decimal.
//
// What is 1001 in Binary? What base is binary in? What is a base?
//
// ### Decimal
// [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] Decimal is Base 10
// Decimal is important to us because, well this is how we count. For all of our lives we've counted in decimal. So how do we do that actually?
//
// Let's say we have the value 4896 in Decimal, how is this mathematically broken down?
//
// How do numbers work? When we count to 10 what happens?
// 9 + 1
//
// If we have the number 10 how is it actually broken down?
// Looking at 10 if we go from right to left we do the following:
//
// 10 ^ 0 = 1 This is the math in the ones column, whenever a number is in the ones column it's using this as a base.
// 0 * 1 = 0 Multiplying by the value for the ones column
//
// Same as above for the 10's column
// 10 ^ 1 = 10
// 10 * 1 = 10
//
// Then we add it all together
// 0 + 10 = 10
//
// 10
//
// So for our original value 4896 this breaks down like this.
// | Thousands | Hundreds | Tens | Ones |
// |-----------|----------|--------|--------|
// | 10^3 | 10^2 | 10^1 | 10^0 |
// | 4 | 8 | 9 | 6 |
// | 1000 * 4 | 100 * 8 | 9 * 10 | 1 * 6 |
//
// **4000 + 800 + 90 + 6 = 4896**
//
//
// ### Hexidecimal
// [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F] Hexadecimal is Base 16
// Hexadecimal is interesting. We added letters to essentially gain access to more numbers. Why would we wanna do that. What's the purpose. Why is base 16 so special?
//
// Since it's important to our computers somehow we also need to be able to deal with Hexadecimal. Now this isn't any different than decimal. We just have more digits to work with.
//
// BE
//
// Working from right to left we break it down the same as above. Just with a higher range.
// E
// 16 ^ 0 = 1
// 1 * E(14) = 14
//
// B
// 16 ^ 1 = 16
// 16 * B(11) = 176
//
// 176 + 14 = 190
//
// Let's say we have the value DEAD in Hexadecimal. It would break down like this.
//
// | Four Thousand Ninety Sixths | Two Fifty Sixths | Sixteenths | Ones |
// |-----------------------------|------------------|------------|-----------|
// | 16^3 | 16^2 | 16^1 | 16^0 |
// | D | E | A | D |
// | 4096 * D | 256 * E | 16 * A | 1 * D |
//
// **53248 + 3584 + 160 + 13 = 57005**
//
// ### Octal
// [0, 1, 2, 3, 4, 5, 6, 7] Octal is Base 8
// Octal I'm not gonna lie to you I rarely see personally. To my knowledge it's good for converting Binary numbers to Octal. From my research (I read a bunch of articles for a couple hours.) Processing architectures used to be 12/24/36 bit. Nowadays they're 16/32/64 bit. Apparently Octal was very useful in the 12/24/36 stack, however it's abysmal in the 16/32/64 stack. Nonetheless we need to know how to deal with it. Luckily it's the same as above 😂
//
// For example if we have the number 76, working from right to left:
// 76
//
// 6
// 8 ^ 0 = 1
// 1 * 6 = 6
//
// 7
// 8 ^ 1 = 8
// 8 * 7 = 56
//
// 56 + 6 = 62
//
// Let's say we have the value 2410 in Octal
//
// | Five Hundred Twelfths | Sixty Fourths | Eights | Ones |
// |------------------------|---------------|--------|---------|
// | 8^3 | 8^2 | 8^1 | 8^0 |
// | 2 | 4 | 1 | 0 |
// | 512 * 2 | 64 * 4 | 8 * 1 | 1 * 0 |
//
// **1024 + 256 + 8 + 0 = 1288**
//
// ### Binary
// [0, 1] Binary is Base 2
// Finally we have most common base in early computing. If you want to get into lower level computing you're gonna see binary a fair amount. This is because to gain access to the speed that lower level computing comes with it's very important to understand exactly how the instructions are interaction with each other and making the most out of every bit. On the topic of the word bit. Bits and bytes are often represented with binary.
//
// Let's say we have the value 1011 in Binary
//
// 1001 1111
//
// Working from right to left we can do the following.
//
// 1
// 2 ^ 0 = 1
// 1 * 1 = 1
//
// 1
// 2 ^ 1 = 2
// 1 * 1 = 2
//
// 1
// 2 ^ 2 = 4
// 1 * 1 = 4
//
// 1
// 2 ^ 3 = 8
// 1 * 1 = 8
//
// 1
// 2 ^ 4 = 16
// 1 * 1 = 16
//
// 0
// 2 ^ 5 = 32
// 1 * 0 = 0
//
// 0
// 2 ^ 6 = 64
// 1 * 0 = 0
//
// 1
// 2 ^ 7 = 128
// 1 * 1 = 128
//
// 128 + 0 + 0 + 16 + 8 + 4 + 2 + 1 = 159
//
// | Hundred and Twenty Eights | Sixty Fourths | Thirty Seconds | Sixteenths | Eighths | Fours | Twos | Ones |
// |---------------------------|---------------|-----------------|-------------|---------|-------|-------|-------|
// | 2^7 | 2^6 | 2^3 | 2^4 | 2^3 | 2^2 | 2^1 | 2^0 |
// | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
// | 8 * 1 | 4 * 0 | 2 * 0 | 1 * 1 | 8 * 1 | 4 * 1 | 2 * 1 | 1 * 1 |
//
//
//
// 1111 1111 = 255
// 1 0000 0000 = 256
//
// ### Two's Complement
// So we're probably wondering why did we end with binary? It probably would have been the easiest? Well that's right but it also the one that's got some quirks to it. So far we've talked about getting numbers into decimal. That's great and all but we're finishing with the base of all computing, and that's because we need to start to look a little more into it. This whole time we've been talking about numbers we've only been talking about positive numbers. Now for the others this isn't as important. For binary since this is what every thing at the end of the day is going to be read as by the computer, we need to be able to represent everything in binary.
//
// Two's Complement is going to give us access to negative numbers. So we're essentially going to split our number range in half.
//
// Let's say that we have the number 80.
//
// 80
// 0101 0000 We turn our number into a binary value.
// 1010 1111 We flip the bits.
// 1011 0000 Finally we add one and then the resulting number is our two's complement.
//
// 1 0 1 1 0 0 0 0
// (-128 + 0 + 32 + 16 + 0 + 0 + 0 + 0 = -80)
//
// 0 - 255
//
//
// 8 bits worth of numbers. -128 - 127
//
// ### How Do We Get Numbers Into The Various Bases?
// So we've talked about getting numbers into decimal but how do we go the other way? Well similar to getting it into decimal using the one method once we under it we can do the same with this. Basically we're going to divide by the base that we want to go to. It's that simple with a few extra steps.
//
// Let's look at the hex example from above. We turned the base 16 Hex value DEAD into 57005. Let's look at how to turn it back.
//
// For this we're going to take 57005 and divide it by the desired end base. The nuance here is that we want the remainder. The remainder will be the number to go into the far right column. We're going to build from right to left. After we get the remainder. We divide the quotient by the base again (our divisor) our quotient becomes our new dividend value.
//
// 57005 / 16 = 3562 r 13
// 13 = D
//
// 3562 / 16 = 222 r 10
// 10 = A
//
// 222 / 16 = 13 r 14
// 14 = E
//
// 13 (Since 13 isn't greater than our base we can stop here.)
// 13 = D
//
// Now we can reassemble from the bottom up and get DEAD.
//
// We can do the same with the others too. The base just changes. Here's Octal.
//
// 57005 / 8 = 7125 r 5
// 5
//
// 7125 / 8 = 890 r 5
// 5
//
// 890 / 8 = 111 r 2
// 2
//
// 111 / 8 = 13 r 7
// 7
//
// 13 / 8 = 1 r 5
// 5
//
// 1 (Since 1 isn't greater than our base we can stop here.)
// 1
//
// Now we can reassemble from the bottom up and get 157255.
//
// Here's Binary
//
// 57005 / 2 = 28502 r 1
// 1
//
// 28502 / 2 = 14251 r 0
// 0
//
// 14251 / 2 = 7125 r 1
// 1
//
// 7125 / 2 = 3562 r 1
// 1
//
// 3562 / 2 = 1781 r 0
// 0
//
// 1781 / 2 = 890 r 1
// 1
//
// 890 / 2 = 445 r 0
// 0
//
// 445 / 2 = 222 r 1
// 1
//
// 222 / 2 = 111 r 0
// 0
//
// 111 / 2 = 55 r 1
// 1
//
// 55 / 2 = 27 r 1
// 1
//
// 27 / 2 = 13 r 1
// 1
//
// 13 / 2 = 6 r 1
// 1
//
// 6 / 2 = 3 r 0
// 0
//
// 3 / 2 = 1 r 1
// 1
//
// 1 (Since 1 isn't greater than our base we can stop here.)
// 1
//
// Now we can reassemble from the bottom up and get 1101 1110 1010 1101
//
// With all of that we get the same number in 4 different bases.
//
// 57005 in Decimal (Base 10)
// DEAD in Hexadecimal (Base 16)
// 157255 in Octal (Base 8)
// 1101 1110 1010 1101 in Binary (Base 2)
//
//
//
//
// ## Values and Data Types
// ---
// In Java unlike Python we have to declare our types when we're making a variable. So before we can even declare variables we need to look into data types. I mentioned that we're going to have to start paying attention to things like memory and choosing the right ways to do things. Now in the next sections when I refer to the space that things take it's in representation. Meaning that the value is represented with the memory described. Making the entity exist may take more memory than described. This will make more sense as we go on.
//
//
// ### Variables
// Variables in Java aren't any different then they were in Python. We do have syntactical differences in the way that we declare them. Now depending on whether it's a primitive type or a relative type some of the verbiage changes. More on the differences between the types in a second.
// +
// This won't run!
// Primitive Types
<DataType> VariableName = The Thing;
// Relative Types (varies)
<DataType> VariableName = new <DataType>(The Thing);
// -
// ### Primitive Data Types
// **The types below aren't capitalized because if used in code they need to be lowercase to be recognized*
//
// | Type | Values/Example | Notes |
// |------|----------------|-------|
// | boolean | False or True | This in memory is allocated with a bit. If you think about it a bit can be either 0 or 1. That is eerily similar to False and True huh? When we use a Boolean this is the idea for the value. This isn't saying that we only use a bit, size for booleans aren't precisely defined, but that the value can be represented with a bit. |
// | byte | From -2⁷ through 2⁷-1 | This in memory is allocated with a byte or 8 bits. This is going to be the entry level for getting an integer. This isn't used as often as typically you'd use int or float. |
// | short | From -2¹⁵ through 2¹⁵-1 | This in memory is allocated with 2 bytes or 16 bits. This is the tier after byte and allows you to have a larger range of integers. This isn't used as often as typically you'd use int or float |
// | int | From -2³¹ through 2³¹-1, 10, -94 | This in memory is allocated with 4 bytes or 32 bits. This is typically the default that you'd see when you need a number in Java. |
// | long | From -2⁶³ through 2⁶³-1, 1234L, - 5678L | This in memory is allocated with 8 bytes or 64 bits. This is the backup for int in a way. If you overflow with int you need a long. This isn't used as often as typically you'd use int or float. This will sometimes be represented with an L at the end of the number. |
// | float | 0.123123 | This in memory is allocated with 4 bytes or 32 bits. For this getting the ranges for this and double is not really needed because the number is very large. Since float and double are decimals we're not really looking at range in the same way that we are for regular signed integers. We're more so looking at the level of accuracy that the value is going to. (ex 0.125 is more accurate than 0.12) |
// | double | 0.123123 | This in memory is allocated with 8 bytes or 64 bits. This is basically the same as above and allows for a larger range of numbers. |
// | char | 'a', '\u0061' | This in memory is allocated with 2 bytes or 16 bits. This can store any unicode character. |
// +
// Bit representation. Can either be 0 or 1. Otherwise known as true or false.
boolean is_smart = true;
// 0111 1111 = 127 This holds 128 positions
// 1111 1111 = -128
// 1000 0000 = 128, This is 128 in binary
// Byte representation. Is 8 bits all together. Is a number type. Byte can hold from -128 - 127
byte example_byte = 127;
// 0111 1111 1111 1111 = 32,767 This holds 32,768 positions
// 1111 1111 1111 1111 = -32,768
// 1000 0000 1000 0000 = 65,536, This is 65,536 in binary
// Short representation. Is 16 bits all together. Is a number type. Short can hold from -32,768 - 32,767
short age_as_short = 32767;
// 0111 1111 1111 1111 1111 1111 1111 1111 = 2,147,483,647 This holds 2,147,483,648 positions
// 1111 1111 1111 1111 1111 1111 1111 1111 = -2,147,483,648
// 1000 0000 0000 0000 0000 0000 0000 0000 = 4,294,967,296, This is 4,294,967,296 in binary
// Int representation. Is 32 bits all together. Is a number type. Int can hold from -2,147,483,648 - 2,147,483,647
int age = 2147483647;
// 0111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 = 9.223372036854775e18 This holds x positions
// 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 1111 = -9.223372036854776e18
// 1000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 = 1.844674407370955e19, This is 1.844674407370955e19 in binary
// Long representation. Is 64 bits all together. Is a number type. Long can hold from -2,147,483,648 - 2,147,483,647
long age_as_long = 16L;
float gpa = 0.0f;
double gpa_as_long = 3.9;
char letter = 'c';
System.out.println(example_byte);
// -
// ### Reference Data Types
// Reference types are interesting and well named! \**hint hint*\* They don't store their variables directly. Instead it stores the address where the values are being held. This just boils down to being an **OBJECT!** over being directly accessible. This is usually an Array, a Class, or an Interface.
//
// To discuss and demonstrate this further we're going to look at the Person example in the QuickDemos folder.
// ## Arithmetic
// This is another thing that at the ground level is the same as Python. No need to overcomplicate it.
System.out.println(2 + 2);
System.out.println(3 - 2);
System.out.println(4 / 2);
System.out.println(5 * 5);
System.out.println(10 % 3);
System.out.println(Math.pow(3,3));
|
JupyterNotebooks/Lessons/Lesson 2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import numpy.linalg as npl
import numpy.fft as npf
from scipy.ndimage import gaussian_filter
import matplotlib.pyplot as plt
# +
#Import 2D delta map
#fname1 = '../data/tidal/0.043delta.dat_bicubic_LOS_cone1'
#npix=7745
fname1 = '../data/0.043proj_half_finer_xy_b.dat'
npix=12288
# open the binary map, and skip over the 4-byte header:
with open(fname1, 'rb') as f1:
data_bin = np.fromfile(f1, dtype=np.float32, offset=4)
den_map = np.reshape(np.float32(data_bin), [npix, npix])
# +
# Adapted from <NAME>'s public 3D-version on github, with his permission.
# Smoothing size to be specified in Mpc/h, and set to True or False as follow:
# Do not smooth if the "smoothing" variable is set to 0 or to a negative value
# box and pixel_size and in Mpc/h
def compute_tidal_tensor(dens, smoothing, pixel_size,box):
"""
Computes the projected tidal tensor given a 2D density field
Pixel size and smoothing scale in h^{-1} Mpc
"""
nx = dens.shape[0]
#dfilter = True
norm = nx * nx
print('pixel scale = %3.3f'%pixel_size)
k = npf.fftfreq(nx, d=box/nx)[np.mgrid[0:nx,0:nx]]
tidal_tensor = np.zeros((nx,nx,2,2),dtype=np.float32)
if (smoothing>0):
sigma = smoothing/pixel_size
print('filtering, sigma=%3.3f'%sigma)
G = gaussian_filter(dens,sigma,mode='wrap')
else:
print('not filtering')
G = dens + 1
fft_dens = npf.fftn(G) / norm # 2D (512 x 512) grid ; each cell is a k mode
# Compute the elements of the tensor
for i in range(2):
for j in range(2):
#Skip this element, since j_ij is symmetric under i <-> j
#Will copy instead the results from the [1,0] elements
if (j>i):
print('Not computing', i,j,', will use symmetry properties instead')
continue
else:
print('Launching computation for s_ij with i,j=', i,j)
# k[i], k[j] are 2D matrices
temp = fft_dens * k[i]*k[j]/(k[0]**2 + k[1]**2)
# subtract off the trace...
if (i==j):
temp -= 1./2 * fft_dens
temp[0,0] = 0
tidal_tensor[:,:,i,j] = npf.ifftn(temp).real * norm /nx
# Apply symmetry:
tidal_tensor[:,:,0,1] = tidal_tensor[:,:,1,0]
return tidal_tensor
# +
# Launch the tidalator_2D, assign to variable "s"
# specify density map, smoothing, pixel_size, simulation box size
# No smoothing if the "smoothing" variable to 0.0 or to a negative value
# For SLICS and cosmo-SLICS, box side is 505 Mpc/h, maps have 12288 pixels on the side;
# Pixel scale is 505 Mpc/h / 12288 pixels = 0.041097 Mpc/h on the side
s = compute_tidal_tensor(den_map,smoothing=5.25, pixel_size=0.041097,box=505)
#s = compute_tidal_tensor(den_map,smoothing=0.0, pixel_size=0.041097,box=505)
# -
print("s_ij min,max:", np.min(s[:,:,:,:]), np.max(s[:,:,:,:]))
# +
fig11 = plt.figure(figsize=(16, 16), constrained_layout=False)
# gridspec inside gridspec
outer_grid = fig11.add_gridspec(3, 2, wspace=0.0, hspace=0.0)
ax = fig11.add_subplot(2,2,1)
ax.imshow(np.log(den_map),vmin=2, vmax=7)
ax.set_xticks([])
ax.set_yticks([])
fig11.add_subplot(ax)
ax = fig11.add_subplot(2,2,2)
ax.imshow(s[:,:,0,0],vmin=-0.01, vmax=0.01)
ax.set_xticks([])
ax.set_yticks([])
fig11.add_subplot(ax)
ax = fig11.add_subplot(2,2,3)
ax.imshow(s[:,:,1,1],vmin=-0.01, vmax=0.01)
ax.set_xticks([])
ax.set_yticks([])
fig11.add_subplot(ax)
ax = fig11.add_subplot(2,2,4)
ax.imshow(s[:,:,1,0],vmin=-0.01, vmax=0.01)
ax.set_xticks([])
ax.set_yticks([])
fig11.add_subplot(ax)
#all_axes = fig11.get_axes()
plt.show()
#fig11.savefig("../Plots/0.043tidal.pdf")
fig11.savefig("../Plots/0.043tidal_smoothing_5.25.pdf")
# -
#np.save('0.043Sij_not_smoothed.npy',s)
np.save('0.043Sij_smoothed5.25.npy',s)
|
2D/tools/Tidalator_2D.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ### 資料準備
from keras.utils import np_utils
import numpy as np
np.random.seed(10)
from keras.datasets import mnist
(x_train_image,y_train_label),(x_test_image,y_test_label)=mnist.load_data()
x_train_image.shape
y_train_label.shape
x_train=x_train_image.reshape(60000,784).astype('float32')
x_test=x_test_image.reshape(10000,784).astype('float32')
#標準化
x_train_normalize=x_train/255
x_test_normalize=x_test/255
y_train_OneHot=np_utils.to_categorical(y_train_label)
y_test_OneHot=np_utils.to_categorical(y_test_label)
# ### 建立模型
from keras.models import Sequential
from keras.layers import Dense
# #### 建立Sequential模型
model=Sequential()
# #### 建立輸入層和隱藏層
model.add(Dense(units=256, #定義隱藏藏個數256
input_dim=784, #設定輸入層神經元個數為784
kernel_initializer='normal', #使用normal dist. 常態分佈的亂數,初始化weight和bias
activation='relu')) #定義激活函數為relu
# h1=relu(X*W1+b1)
# #### 建立輸出層
model.add(Dense(units=10,
kernel_initializer='normal',
activation='softmax'))
# y=softmax(h1*W2+b2)
print(model.summary())
# 784*256+256=200960
#
# 256*10+10=2570
# ### 進行訓練
# #### 在模型訓練前,要先使用complie對模型進行設定
model.compile(loss='categorical_crossentropy',
optimizer='adam',metrics=['accuracy'])
# ### 開始訓練
train_history=model.fit(x=x_train_normalize,
y=y_train_OneHot,
validation_split=0.2,
epochs=15,
batch_size=200,
verbose=2)
# ### 顯示訓練過程
import matplotlib.pyplot as plt
def show_train_history(train_history,train,validation):
plt.plot(train_history.history[train])
plt.plot(train_history.history[validation])
plt.title('Train History')
plt.ylabel(train)
plt.xlabel('Epoch')
plt.legend(['train','validation'],loc='upper left')
plt.show()
show_train_history(train_history,'acc','val_acc')
show_train_history(train_history,'loss','val_loss')
# ### Training data的score
result=model.evaluate(x_train_normalize,y_train_OneHot)
print('Train Accuracy=',result[1])
# ### Training data的 loss
result=model.evaluate(x_train_normalize,y_train_OneHot)
print('Train Accuracy=',result[0])
# ### 執行預測
prediction=model.predict_classes(x_test_normalize)
prediction
import matplotlib.pyplot as plt
def plot_images_labels_prediction(images,labels,prediction,idx,num=10):
fig=plt.gcf()
fig.set_size_inches(12,14)
if num>25:num=25
for i in range(0,num):
ax=plt.subplot(5,5,1+i)
ax.imshow(images[idx],cmap='binary')
title='label='+str(labels[idx])
if len(prediction)>0:
title+=',predict='+str(prediction[idx])
ax.set_title(title,fontsize=10)
ax.set_xticks([]);ax.set_yticks([])
idx+=1
plt.show()
plot_images_labels_prediction(x_test_image,y_test_label,prediction,idx=340)
# ### 顯示混淆矩陣
import pandas as pd
pd.crosstab(y_test_label,prediction,
rownames=['label'],colnames=['predict'])
data=pd.DataFrame({'label':y_test_label,'predict':prediction})
data.head()
data[(data.label==5)&(data.predict==3)]
plot_images_labels_prediction(x_test_image,y_test_label,prediction,idx=1393,num=1)
|
12_Deep_Learning/Keras/Keras v2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## **TAREA NUMERO 3**
# ### **<NAME> 161003640**
# ### **<NAME> 161003611**
# Para el desarrollo de la practica, inicialmente es necesario el uso de la librerias numpy (para el desarrollo matematico) y matplotlib para graficar las funciones
#
# %matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from numpy import sin
from numpy import cos
from numpy import exp
# definimos las funcines para trabajar minimizando tiempo de ejecucion
def funcion1(x):
return (3*x)-sin(x)-exp(x)
def funcion2(x):
return 5/(((x-(1/x))**0.5))
def funcion3(x):
return (4*(x**4))+(9*(x**3))-(5*(x**2))+(9*x)-9
def funcion4(x):
return exp(x)+(x**0.5)-2
def funcion5(x):
return (2*(x**3)-(x**2)-(8*x)+4)
def funcion6(x):
return 1/((x-2)((x**2)+(3*x)+1))
def funcion7(x):
return exp((x**3)+2(x**2)+x+1)
def funcion8(x):
return log(x)+(1/(((x**2)-5)(x-2)))
def funcion10(x):
return 4*(cos(log(x)))
def funcion11(x):
return (x+2)/(5(x**2)+(12*x)+4)
def funcion12(x):
return 4(x**2)+(4*x)+17
def funcion13(x):
return (cos(x)+x)/(sin(x)+exp(tan(x)))
# se procede a agregar la tolerancia y los puntos para esta tolerancia. nuestra tolerancia será 0.001
puntos = int(round(1/0.001))
print("ingrese el numero de la funcion a evaluar")
opcion= input()
opcion = int (opcion)
x = np.linspace(2, 5, puntos)
if(opcion==1):
y = funcion1(x)
elif(opcion==2):
y = funcion2(x)
elif(opcion==3):
y = funcion3(x)
elif(opcion==4):
y = funcion4(x)
elif(opcion==5):
y = funcion5(x)
elif(opcion==6):
y = funcion6(x)
elif(opcion==7):
y = funcion7(x)
elif(opcion==8):
y = funcion8(x)
elif(opcion==9):
y = funcion9(x)
elif(opcion==10):
y = funcion10(x)
elif(opcion==11):
y = funcion11(x)
elif(opcion==12):
y = funcion12(x)
elif(opcion==13):
y = funcion13(x)
plt.plot(x, y, lw=2)
plt.grid(True, linestyle='-.')
# ### hallando las raices de la funcion
# funcion 1
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion1(c) == 0:
break
elif funcion1(a)*funcion1(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 2
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion2(c) == 0:
break
elif funcion2(a)*funcion2(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 3
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion3(c) == 0:
break
elif funcion3(a)*funcion3(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 4
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion4(c) == 0:
break
elif funcion4(a)*funcion4(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 5
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion5(c) == 0:
break
elif funcion5(a)*funcion5(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 6
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion6(c) == 0:
break
elif funcion6(a)*funcion6(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 7
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion7(c) == 0:
break
elif funcion7(a)*funcion7(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 8
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion8(c) == 0:
break
elif funcion8(a)*funcion8(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 9
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion1(c) == 0:
break
elif funcion9(a)*funcion9(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 10
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion10(c) == 0:
break
elif funcion10(a)*funcion10(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 11
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion11(c) == 0:
break
elif funcion11(a)*funcion11(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 12
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion12(c) == 0:
break
elif funcion12(a)*funcion12(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
# funcion 13
a=(float(input("ingrese el numero menor del intervalo ")))
b=(float(input("ingrese el numero mayor del intervalo ")))
c=(a+b)/2
while (b-a)/2 > 0.001:
if funcion13(c) == 0:
break
elif funcion13(a)*funcion13(c) < 0:
b = c
else:
a = c
c = (a + b) / 2
print("la raiz en el intervalo es:",c)
|
tarea3/tarea3-03.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
#Question1 using Decorator
def dec_fib(num):
def fibonacci(n):
if n<=0:
print("Incorrect Input")
elif n==1:
return 0
elif n==2:
return 1
else:
return fibonacci(n-1)+fibonacci(n-2)
return num(n)
return fibonacci
# -
@dec_fib
def fib(n):
print("The Fibonacci number is ",n)
fib(1)
fib(2)
fib(-1)
fib(10)
# +
#Question2 file and exceptions
file = open("assignment.txt","r")
file.write("Its the second problem")
file.close()
# -
try:
file = open("assignment.txt","r")
file.write("Its the second problem that's creating problem but I'll make it run any way")
file.close()
print("Success")
except Exception as e:
print(e)
finally:
print("Its the second problem that's creating problem but I'll make it run any way")
|
Assignment Day 8.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **This notebook is an exercise in the [Data Visualization](https://www.kaggle.com/learn/data-visualization) course. You can reference the tutorial at [this link](https://www.kaggle.com/alexisbcook/line-charts).**
#
# ---
#
# In this exercise, you will use your new knowledge to propose a solution to a real-world scenario. To succeed, you will need to import data into Python, answer questions using the data, and generate **line charts** to understand patterns in the data.
#
# ## Scenario
#
# You have recently been hired to manage the museums in the City of Los Angeles. Your first project focuses on the four museums pictured in the images below.
#
# 
#
# You will leverage data from the Los Angeles [Data Portal](https://data.lacity.org/) that tracks monthly visitors to each museum.
#
# 
#
# ## Setup
#
# Run the next cell to import and configure the Python libraries that you need to complete the exercise.
import pandas as pd
pd.plotting.register_matplotlib_converters()
import matplotlib.pyplot as plt
# %matplotlib inline
import seaborn as sns
print("Setup Complete")
# The questions below will give you feedback on your work. Run the following cell to set up the feedback system.
# Set up code checking
import os
if not os.path.exists("../input/museum_visitors.csv"):
os.symlink("../input/data-for-datavis/museum_visitors.csv", "../input/museum_visitors.csv")
from learntools.core import binder
binder.bind(globals())
from learntools.data_viz_to_coder.ex2 import *
print("Setup Complete")
# ## Step 1: Load the data
#
# Your first assignment is to read the LA Museum Visitors data file into `museum_data`. Note that:
# - The filepath to the dataset is stored as `museum_filepath`. Please **do not** change the provided value of the filepath.
# - The name of the column to use as row labels is `"Date"`. (This can be seen in cell A1 when the file is opened in Excel.)
#
# To help with this, you may find it useful to revisit some relevant code from the tutorial, which we have pasted below:
#
# ```python
# # Path of the file to read
# spotify_filepath = "../input/spotify.csv"
#
# # Read the file into a variable spotify_data
# spotify_data = pd.read_csv(spotify_filepath, index_col="Date", parse_dates=True)
# ```
#
# The code you need to write now looks very similar!
# +
# Path of the file to read
museum_filepath = "../input/museum_visitors.csv"
# Fill in the line below to read the file into a variable museum_data
museum_data = pd.read_csv("../input/museum_visitors.csv",index_col="Date",parse_dates=True)
# Run the line below with no changes to check that you've loaded the data correctly
step_1.check()
# +
# Uncomment the line below to receive a hint
#step_1.hint()
# Uncomment the line below to see the solution
#step_1.solution()
# -
museum_data.columns
# ## Step 2: Review the data
#
# Use a Python command to print the last 5 rows of the data.
# Print the last five rows of the data
museum_data.tail(5) # Your code here
# The last row (for `2018-11-01`) tracks the number of visitors to each museum in November 2018, the next-to-last row (for `2018-10-01`) tracks the number of visitors to each museum in October 2018, _and so on_.
#
# Use the last 5 rows of the data to answer the questions below.
# +
# Fill in the line below: How many visitors did the Chinese American Museum
# receive in July 2018?
ca_museum_jul18 = 2620
# Fill in the line below: In October 2018, how many more visitors did Avila
# Adobe receive than the Firehouse Museum?
avila_oct18 = 19280-4622
# Check your answers
step_2.check()
# +
# Lines below will give you a hint or solution code
#step_2.hint()
#step_2.solution()
# -
# ## Step 3: Convince the museum board
#
# The Firehouse Museum claims they ran an event in 2014 that brought an incredible number of visitors, and that they should get extra budget to run a similar event again. The other museums think these types of events aren't that important, and budgets should be split purely based on recent visitors on an average day.
#
# To show the museum board how the event compared to regular traffic at each museum, create a line chart that shows how the number of visitors to each museum evolved over time. Your figure should have four lines (one for each museum).
#
# > **(Optional) Note**: If you have some prior experience with plotting figures in Python, you might be familiar with the `plt.show()` command. If you decide to use this command, please place it **after** the line of code that checks your answer (in this case, place it after `step_3.check()` below) -- otherwise, the checking code will return an error!
# +
# Line chart showing the number of visitors to each museum over time
sns.lineplot(data=museum_data) # Your code here
# Check your answer
step_3.check()
# +
# Lines below will give you a hint or solution code
#step_3.hint()
#step_3.solution_plot()
# -
# ## Step 4: Assess seasonality
#
# When meeting with the employees at Avila Adobe, you hear that one major pain point is that the number of museum visitors varies greatly with the seasons, with low seasons (when the employees are perfectly staffed and happy) and also high seasons (when the employees are understaffed and stressed). You realize that if you can predict these high and low seasons, you can plan ahead to hire some additional seasonal employees to help out with the extra work.
#
# #### Part A
# Create a line chart that shows how the number of visitors to Avila Adobe has evolved over time. (_If your code returns an error, the first thing that you should check is that you've spelled the name of the column correctly! You must write the name of the column exactly as it appears in the dataset._)
# +
# Line plot showing the number of visitors to Avila Adobe over time
plt.figure(figsize=(14,6))
sns.lineplot(data=museum_data['Avila Adobe'], label="Avila Adobe") # Your code here
# Check your answer
step_4.a.check()
# +
# Lines below will give you a hint or solution code
#step_4.a.hint()
#step_4.a.solution_plot()
# -
# #### Part B
#
# Does Avila Adobe get more visitors:
# - in September-February (in LA, the fall and winter months), or
# - in March-August (in LA, the spring and summer)?
#
# Using this information, when should the museum staff additional seasonal employees?
# +
#step_4.b.hint()
# -
# Check your answer (Run this code cell to receive credit!)
step_4.b.solution()
# # Keep going
#
# Move on to learn about **[bar charts and heatmaps](https://www.kaggle.com/alexisbcook/bar-charts-and-heatmaps)** with a new dataset!
# ---
#
#
#
#
# *Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161291) to chat with other Learners.*
|
Data Visualization/exercise-2-line-charts-preet-mehta.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/diem-ai/topic-modeling/blob/master/model_preparation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="f28PG4o7x4SB" colab_type="text"
# #### This note book will clean data and create bag of word and tf-idf sparse matrix and save them with help of Pickle. They will be used again when we build LDA and LSA model.
# + [markdown] id="sC9PMZHNeVTx" colab_type="text"
# #### Google Colab Setup
# + id="Olt7Xq5byPKU" colab_type="code" outputId="2be8142c-8b71-45be-9064-d6dbdaf52361" colab={"base_uri": "https://localhost:8080/", "height": 34}
from google.colab import drive
# This will prompt for authorization.
# authorization code: 4/OwErfUj6QceGXhIGx_RWv0MKclb9rilw8UsJnZqFbSez-QS8zQ399JU
drive.mount('/content/drive')
# + id="q-X20vwCyxDa" colab_type="code" outputId="fd006cb3-5628-435e-932a-d8fe329b76ed" colab={"base_uri": "https://localhost:8080/", "height": 213}
# !pip install PyDrive
from pydrive.auth import GoogleAuth
from pydrive.drive import GoogleDrive
from google.colab import auth
from oauth2client.client import GoogleCredentials
auth.authenticate_user()
gauth = GoogleAuth()
gauth.credentials = GoogleCredentials.get_application_default()
drive = GoogleDrive(gauth)
# + id="aiERuDAhef71" colab_type="code" colab={}
#import accessory_functions.py from Colab
#https://drive.google.com/open?id=1S7URZIBq4zMh5QWv0qXPHv4ixhgHWN_y
my_module = drive.CreateFile({'id':'1S7URZIBq4zMh5QWv0qXPHv4ixhgHWN_y'})
my_module.GetContentFile('accessory_functions.py')
# + [markdown] id="IqAGU-zax4SE" colab_type="text"
# #### Import libraries
# + id="YXVkDzd8x4SG" colab_type="code" outputId="be910cff-7eab-4bf1-ebce-ba585bb72676" colab={"base_uri": "https://localhost:8080/", "height": 157}
import numpy as np
import string
import pandas as pd
import nltk
from nltk.stem import WordNetLemmatizer, SnowballStemmer
from nltk.stem.porter import *
nltk.download('wordnet')
nltk.download('stopwords')
from nltk.corpus import stopwords, wordnet
from nltk.tokenize import word_tokenize
nltk.download('averaged_perceptron_tagger')
import gensim
from gensim.utils import simple_preprocess
import gensim.corpora as corpora
import pickle
from wordcloud import WordCloud
# Plotting tools
import matplotlib.pyplot as plt
# %matplotlib inline
# Make all my plots 538 Style
plt.style.use('fivethirtyeight')
import warnings
warnings.simplefilter('ignore')
from accessory_functions import preprocess_series_text
from accessory_functions import write_pickle_file
# + [markdown] id="-japK8GCUDwR" colab_type="text"
# <p> Data Path </p>
# + id="Ys_ThbPcULFn" colab_type="code" colab={}
datapath = '/content/drive/My Drive/data/'
# + id="fafPRjT9x4SW" colab_type="code" colab={}
data = pd.read_csv(datapath + 'breakingnews.csv')
data.head(2)
# + id="7soRO8Byx4Sv" colab_type="code" colab={}
data_text = data[['headline_text']]
data_text['index'] = data_text.index
documents = data_text
# + [markdown] id="nSF22i0Ix4S3" colab_type="text"
# ##### cleaning data and save it
# + id="yUWPftAIx4TE" colab_type="code" colab={}
processed_docs = preprocess_series_text(documents['headline_text'])
# + [markdown] id="HRO2xCacvwpG" colab_type="text"
#
# + id="R-IG7oaQvv7v" colab_type="code" colab={}
plt.figure(figsize=(15, 15))
wordcloud = WordCloud(
background_color='white'
# max_words=200,
,max_font_size=20
, scale=2) # chosen at random by flipping a coin; it was heads)
wordcloud.generate(str(processed_docs))
plt.imshow(wordcloud, interpolation="bilinear")
plt.axis("off")
plt.show()
# + [markdown] id="cHe0MTHHyNnd" colab_type="text"
# <p> From the visualization, we can guess the topics should be about Donald Trump, Uber, Bank, Tesla, minister. We will check it out in another notebook. Now we save the processed_docs oject for latter use</p>
# + id="Hbo1KRhgyxo5" colab_type="code" colab={}
processed_docs = processed_docs.values.tolist()
write_pickle_file(processed_docs, datapath + 'processed_docs.pkl')
# + [markdown] id="g9R9QuxNx4TN" colab_type="text"
# <p> Create gensim dictionary from processed_docs</p>
# + id="3ii1EdPEx4TQ" colab_type="code" colab={}
# filter out the less common words
# Keep tokens which are contained in at least 15 documents
# Keep tokens which are contained in no more than 50% documents
# Keep only the first 10000 most frequent tokens
#dictionary.filter_extremes(no_below=15, no_above=0.5, keep_n=10000)
dictionary = corpora.Dictionary(processed_docs)
print("1st word in dictionary: {}".format(dictionary[0]))
print("1OOth word in dictionary: {}".format(dictionary[100]))
# + [markdown] id="_D_jUBoUk_uw" colab_type="text"
# <p>Convert processed_docs into bad of word (bow) using dictionary </p>
# <p> It is a list of word id and theirs frequencies </p>
# + id="kGEaKO4pkiJK" colab_type="code" colab={}
bow = [dictionary.doc2bow(doc) for doc in processed_docs]
# + [markdown] id="yS8UxuZCmslK" colab_type="text"
# <p>View the first document in bow and using dictionary to see which words and their frequency</p>
# + id="-1YoTWCWotDQ" colab_type="code" colab={}
doc = bow[1]
[(dictionary[id], freq) for id, freq in doc]
# + [markdown] id="Zf7V4Dfesvge" colab_type="text"
# <p> Save bag-of_word </p>
# + id="Vj6MM8XUskmt" colab_type="code" colab={}
write_pickle_file(bow, datapath+'bow.pkl')
"""
for id, freq in doc:
print("{} : {}".format(dictionary[id], freq))
"""
# + [markdown] id="A0VAQXA3tPAQ" colab_type="text"
# <p>We build Tf-Idf, a simple transformation which takes documents represented as bag-of-words counts and applies a weighting which discounts common terms or equivalently, promotes rare terms </p>
# <p> Then, save tfidf for using later</p>
# + id="cqJe11DBtjWk" colab_type="code" colab={}
tfidf_model = gensim.models.TfidfModel(bow)
tfidf = tfidf_model[bow]
write_pickle_file(tfidf, datapath + "tfidf.pkl")
# + id="EUS4cxaOt4MR" colab_type="code" colab={}
doc = tfidf[1]
[(dictionary[id], freq) for id, freq in doc]
# + [markdown] id="LCCYBWC01Obf" colab_type="text"
# <p>Finally, save gensim dictionary object</p>
# + id="ZgzTZi6m1W8h" colab_type="code" colab={}
write_pickle_file(dictionary, datapath + 'dictionary.pkl')
|
model_preparation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import numpy as np
import matplotlib.pyplot as plt
from SVM import SVM
N = 500
X_1_pos = np.random.rand(N) * 4 * np.pi
X_2_pos = np.sin(X_1_pos) + np.random.normal(0, 0.4, N)
X_pos = np.array([[x_1, x_2, 1] for x_1, x_2 in zip(X_1_pos, X_2_pos)])
plt.scatter(X_1_pos, X_2_pos, c='b')
X_1_neg = np.random.rand(N) * 4 * np.pi
X_2_neg = np.sin(X_1_neg) + np.random.normal(0, 0.4, N) - 1
X_neg = np.array([[x_1, x_2, -1] for x_1, x_2 in zip(X_1_neg, X_2_neg)])
plt.scatter(X_1_neg, X_2_neg, c='r')
plt.show()
X = np.vstack([X_pos, X_neg])
np.random.shuffle(X)
y = X[:, 2]
X = X[:, :2]
model = SVM()
model.fit(X, y)
model.elapsed_time
y_pred = model.predict(X)
model.score(y, y_pred)
model2 = SVM(kernel='sigmoid')
model2.fit(X, y)
y_pred = model2.predict(X)
model2.score(y, y_pred)
model2.elapsed_time
model3 = SVM(kernel='linear')
model3.fit(X,y)
y_pred = model3.predict(X)
model3.score(y, y_pred)
model3.elapsed_time
import train
train.main()
X, y = train.linear_data(500)
plt.scatter(X[y==1][:, 0], X[y==1][:, 1], c='b')
plt.scatter(X[y==-1][:, 0], X[y==-1][:, 1], c='r')
plt.plot(X_lin, y_lin)
plt.show()
X_lin = np.linspace(-3, 3)
y_lin = -(rbf_model.w[0] * X_lin + rbf_model.b) / rbf_model.w[1]
import pandas as pd
kernels = ['RBF', 'Sigmoid', 'Linear']
df = pd.DataFrame(index=[50, 100, 500, 1000, 5000, 10000], columns=kernels)
df.loc[50, 'RBF'] = 1
print(df)
from SVM import SVM
rbf_model = SVM()
rbf_model.fit(X, y)
|
.ipynb_checkpoints/Untitled-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] slideshow={"slide_type": "-"}
# # How to download data from the ORFEUS Data Center using WebDC3 #
# WebDC3 interface can be used to easily download data from the EIDA Federation. It can be found using following link:
#
# [http://orfeus-eu.org/webdc3](http://orfeus-eu.org/webdc3)
#
# Please keep in mind to connect to the WebDC3 using **HTTP** protocol. Some of the underlying services operate exclusively via HTTP. Modern browsers will block HTTPS to HTTP traffic.
# + [markdown] slideshow={"slide_type": "-"}
# 
# **Fig.1 - WebDC3 landing page**
# -
# # Explore events tab:
#
# Let's go to the "Explore events" tab and find all Groningen events stored in the KNMI event catalogue filtered using following griteria:
#
# - Magnitude: >= 2.5
# - Timespan: from 2020-01-01 till 2020-06-01
# - Area: limited by a bounding box defined using following coordinates:
# - 53°N <= latitude <= 53.5°N
# - 6°E <= longitude <= 7°E
#
# After pressing the "Search" button, we can see that one event has been found - Zijldijk earthquake with origin time 2020-05-02 03:13:15, depth 3.0 km and magnitude 2.5.
#
# ℹ️ Please note:
#
# - There are multiple event catalogues available in the WebDC3 portal provided by:
# - [GFZ](http://geofon.gfz-potsdam.de/)
# - [EMSC](http://www.emsc-csem.org/)
# - [USGS](http://earthquake.usgs.gov/)
# - [INGV](http://www.ingv.it/)
# - [ETH](http://seismo.ethz.ch/en/home/)
# - User can provide own list of events by selecting "User Supplied" button
# 
# **Fig.2 - Event search**
# # Explore stations tab
#
# For given event, let's find all NL stations located in the initially defined area:
#
# - Network type: Public permanent network
# - Network code: NL (1993) Netherlands Seismic and Acoustic Network
# - Stations: by Region, bounding box defined in previous step
# - Streams: by Code, all streams selected
#
# After clicking on the "Search" button, all stations meeting the above criteria will be added and presented on the map.
#
# ℹ️ Please note:
#
# - Networks can be filtered using network start and end date
# - Various network types can be selected using the "Network Type" dropdown menu:
# - All nets
# - Virtual nets
# - All permanent nets
# - All temporary nets
# - All public nets
# - All non-public nets
# - Public permanent nets
# - Public temporary nets
# - Non-public permanent nets
# - Non-public temporary nets
# - Stations can be also selected by station code or event distance and azimuth
# - Streams can be also selected by sampling using target sampling rate and following options:
# - Very broad band
# - Broad band
# - Very broad band and broad band
# - Broad band / strong motion
# - Short period
# - Strong motion
# - Ocean bottom seismometer
# 
# **Fig.3 - Station search**
# # Submit request tab (waveforms)
#
# Let's now download all waveforms available from selected stations, starting 2 minutes before and ending 10 minutes after event origin time:
#
# - Time window selection: Relative Mode
# - Start: Origin Time: 2
# - End: Origin Time: 10
# - Request Type: Waveform (Mini-SEED)
#
# ℹ️ Please note:
#
# - NL network data is publicly available and does not require authentication.
# - Start and end time can be set using reference to the event origin time or P/S wave arrival
# - When no event is selected, waveforms can be downloaded in Absolute Mode by providing explicit start and end timestamps
# - To download restricted data, user needs to provide an authentication token using EIDA Authentication System ([https://geofon.gfz-potsdam.de/eas/](https://geofon.gfz-potsdam.de/eas/))
# 
# **Fig.4 - Waveform request**
# # Download data tab (waveforms)
#
# After clicking the "Submit" button, download process will be initiated. When data is downloaded, it can be saved using "Save" button to local machine.
# 
# **Fig.5 - Waveform download progress bar**
# ## Browsing the waveforms using ObsPy
#
# Due to repository limitations, this example is based on 1 station (NO.BGAR) extracted from the downloaded package.
# +
from obspy import read
# Load example mseed file
st = read("data/NL.BGAR.mseed")
# Print statistics
print(st[0].stats)
# Plot the waveform
st[0].plot()
# -
# # Submit request tab (metadata)
#
# In previous step we have downloaded the raw waveforms. In order to obtain the instrumentation metadata, we need to go back to the "Submit request" tab and adjust our request criteria:
#
# - Request Type: Metadata (StationXML)
# - Metadata level: Channel
#
# ℹ️ Please note:
#
# - Station metadata can be also requested on 3 different levels:
# - Station level
# - Channel level
# - Response level
# - Station metadata can be requested in text format
# 
# **Fig.6 - Metadata request**
# # Download data tab (metadata)
#
# After clicking the "Submit" button, metadata download will be initiated. "Save" button will be enabled upon completion of the download process.
# 
# **Fig.7 - Metadata download progress bar**
# ## Browsing the metadata using ObsPy
#
# Due to repository limitations, this example is based on 1 station (NO.BGAR) extracted from the downloaded package.
# +
from obspy import read_inventory
# Load example inventory file
inv = read_inventory("data/NL.BGAR.xml")
# Print its contents
print(inv)
# -
# ℹ️ Please note that metadata can be easily viewed using a web browser or a text editor:
#
# 
# **Fig.8 - Metadata viewed in Google Chrome web browser**
# ***
# Author: <NAME> (KNMI)
|
notebooks/webdc3/EPOS-NL WebDC3 Tutorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 基本程序设计
# - 一切代码输入,请使用英文输入法
# ## 编写一个简单的程序
# - 圆公式面积: area = radius \* radius \* 3.1415
# ### 在Python里面不需要定义数据的类型
# ## 控制台的读取与输入
# - input 输入进去的是字符串
# - eval
# - 在jupyter用shift + tab 键可以跳出解释文档
# ## 变量命名的规范
# - 由字母、数字、下划线构成
# - 不能以数字开头 \*
# - 标识符不能是关键词(实际上是可以强制改变的,但是对于代码规范而言是极其不适合)
# - 可以是任意长度
# - 驼峰式命名
# ## 变量、赋值语句和赋值表达式
# - 变量: 通俗理解为可以变化的量
# - x = 2 \* x + 1 在数学中是一个方程,而在语言中它是一个表达式
# - test = test + 1 \* 变量在赋值之前必须有值
# ## 同时赋值
# var1, var2,var3... = exp1,exp2,exp3...
# ## 定义常量
# - 常量:表示一种定值标识符,适合于多次使用的场景。比如PI
# - 注意:在其他低级语言中如果定义了常量,那么,该常量是不可以被改变的,但是在Python中一切皆对象,常量也是可以被改变的
# ## 数值数据类型和运算符
# - 在Python中有两种数值类型(int 和 float)适用于加减乘除、模、幂次
# <img src = "../Photo/01.jpg"></img>
# ## 运算符 /、//、**
# ## 运算符 %
# ## EP:
# - 25/4 多少,如果要将其转变为整数该怎么改写
# - 输入一个数字判断是奇数还是偶数
# - 进阶: 输入一个秒数,写一个程序将其转换成分和秒:例如500秒等于8分20秒
# - 进阶: 如果今天是星期六,那么10天以后是星期几? 提示:每个星期的第0天是星期天
# ## 科学计数法
# - 1.234e+2
# - 1.234e-2
# ## 计算表达式和运算优先级
# <img src = "../Photo/02.png"></img>
# <img src = "../Photo/03.png"></img>
# ## 增强型赋值运算
# <img src = "../Photo/04.png"></img>
# ## 类型转换
# - float -> int
# - 四舍五入 round
# ## EP:
# - 如果一个年营业税为0.06%,那么对于197.55e+2的年收入,需要交税为多少?(结果保留2为小数)
# - 必须使用科学计数法
# # Project
# - 用Python写一个贷款计算器程序:输入的是月供(monthlyPayment) 输出的是总还款数(totalpayment)
# 
# # Homework
# - 1
# <img src="../Photo/06.png"></img>
celsius = int(input('Enter a degree in Celsius:'))
fahrenheit = (9 / 5.0) * celsius + 32
print('{} Celsius is {} Fahrenheit'.format(celsius,fahrenheit))
# - 2
# <img src="../Photo/07.png"></img>
import math
radius,length=map(float,input('Enter the radius and length of a cylinder:').split())
area = radius * radius * math.pi
volume = area * length
print('The area is {}'.format('%.4f' % area))
print('The volume is {}'.format('%.1f' % volume))
# - 3
# <img src="../Photo/08.png"></img>
feet = float(input('Enter a value for feet:'))
meters = feet * 0.305
print('{} feet is {} meters'.format(feet,meters))
# - 4
# <img src="../Photo/10.png"></img>
M = float(input('Enter the amount of water in kilograms:'))
initialTemperature = float(input('Enter the initial temperature:'))
finalTemperature = float(input('Enter the final temperature:'))
Q = M * (finalTemperature - initialTemperature) * 4184
print('The energy needed is {}'.format(Q))
# - 5
# <img src="../Photo/11.png"></img>
balance,interest = map(float,input('Enter balance and interest rate (e.g.,3 for 3%):').split())
L = balance * (interest / 1200)
print('The interest is {}'.format('%.5f' % L))
# - 6
# <img src="../Photo/12.png"></img>
v0,v1,t= map(float,input('Enter v0,v1,and t:').split())
a = (v1 - v0)/t
print('The average accelration is {}'.format('%.4f' % a))
# - 7 进阶
# <img src="../Photo/13.png"></img>
amount = int(input('Enter the monthly saving amount:'))
count=0
for i in range(6):
account_six = (amount + count) * (1 + 0.00417)
count = account_six
print('After the sixth mount,the account value is {}'.format('%.2f' % count ))
# - 8 进阶
# <img src="../Photo/14.png"></img>
number = int(input('Enter a number between 0 and 1000:'))
sum = (number % 10) + ((number // 10) % 10) + (number // 100)
print('The sum of the digits is {}'.format(sum))
|
7.16.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [py3]
# language: python
# name: Python [py3]
# ---
# # Poker hands
# <p>In the card game poker, a hand consists of five cards and are ranked, from lowest to highest, in the following way:</p>
# <ul><li><b>High Card</b>: Highest value card.</li>
# <li><b>One Pair</b>: Two cards of the same value.</li>
# <li><b>Two Pairs</b>: Two different pairs.</li>
# <li><b>Three of a Kind</b>: Three cards of the same value.</li>
# <li><b>Straight</b>: All cards are consecutive values.</li>
# <li><b>Flush</b>: All cards of the same suit.</li>
# <li><b>Full House</b>: Three of a kind and a pair.</li>
# <li><b>Four of a Kind</b>: Four cards of the same value.</li>
# <li><b>Straight Flush</b>: All cards are consecutive values of same suit.</li>
# <li><b>Royal Flush</b>: Ten, Jack, Queen, King, Ace, in same suit.</li>
# </ul><p>The cards are valued in the order:<br>2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.</p>
# <p>If two players have the same ranked hands then the rank made up of the highest value wins; for example, a pair of eights beats a pair of fives (see example 1 below). But if two ranks tie, for example, both players have a pair of queens, then highest cards in each hand are compared (see example 4 below); if the highest cards tie then the next highest cards are compared, and so on.</p>
# <p>Consider the following five hands dealt to two players:</p>
# <div style="text-align:center;">
# <table><tbody><tr><td><b>Hand</b></td><td> </td><td><b>Player 1</b></td><td> </td><td><b>Player 2</b></td><td> </td><td><b>Winner</b></td>
# </tr><tr><td style="vertical-align:top;"><b>1</b></td><td> </td><td>5H 5C 6S 7S KD<br><div class="note">Pair of Fives</div></td><td> </td><td>2C 3S 8S 8D TD<br><div class="note">Pair of Eights</div></td><td> </td><td style="vertical-align:top;">Player 2</td>
# </tr><tr><td style="vertical-align:top;"><b>2</b></td><td> </td><td>5D 8C 9S JS AC<br><div class="note">Highest card Ace</div></td><td> </td><td>2C 5C 7D 8S QH<br><div class="note">Highest card Queen</div></td><td> </td><td style="vertical-align:top;">Player 1</td>
# </tr><tr><td style="vertical-align:top;"><b>3</b></td><td> </td><td>2D 9C AS AH AC<br><div class="note">Three Aces</div></td><td> </td><td>3D 6D 7D TD QD<br><div class="note">Flush with Diamonds</div></td><td> </td><td style="vertical-align:top;">Player 2</td>
# </tr><tr><td style="vertical-align:top;"><b>4</b></td><td> </td><td>4D 6S 9H QH QC<br><div class="note">Pair of Queens<br>Highest card Nine</div></td><td> </td><td>3D 6D 7H QD QS<br><div class="note">Pair of Queens<br>Highest card Seven</div></td><td> </td><td style="vertical-align:top;">Player 1</td>
# </tr><tr><td style="vertical-align:top;"><b>5</b></td><td> </td><td>2H 2D 4C 4D 4S<br><div class="note">Full House<br>With Three Fours</div></td><td> </td><td>3C 3D 3S 9S 9D<br><div class="note">Full House<br>with Three Threes</div></td><td> </td><td style="vertical-align:top;">Player 1</td>
# </tr></tbody></table></div>
# <p>The file, <a href="https://projecteuler.net/project/resources/p054_poker.txt">poker.txt</a>, contains one-thousand random hands dealt to two players. Each line of the file contains ten cards (separated by a single space): the first five are Player 1's cards and the last five are Player 2's cards. You can assume that all hands are valid (no invalid characters or repeated cards), each player's hand is in no specific order, and in each hand there is a clear winner.</p>
# <p>How many hands does Player 1 win?</p>
# ---
# ### Idea
# Quite direct solution. Just be patient.
#
# From highest to lowest, check if a certain rank pattern exists in player's hand cards.
# ---
from urllib.request import urlopen
from collections import Counter
with urlopen('https://projecteuler.net/project/resources/p054_poker.txt') as f:
resp = f.read().decode('utf-8')
def transform_value(v):
if '2' <= v <= '9':
return int(v)
else:
if v == 'T':
return 10
elif v == 'J':
return 11
elif v == 'Q':
return 12
elif v == 'K':
return 13
elif v == 'A':
return 14
else:
raise ValueError('Wrong representation')
[transform_value(v) for v in list(map(str, range(2, 10))) + ['T', 'J', 'Q', 'K', 'A']]
def transform_hand(hand):
values = list(map(transform_value, [c[0] for c in hand]))
suits = [c[1] for c in hand]
return sorted(zip(values, suits))
transform_hand(['5H', '5C', '6S', '7S', 'KD'])
def split_hand(hand):
cards = hand.split(' ')
p1, p2 = cards[:5], cards[-5:]
return transform_hand(p1), transform_hand(p2)
split_hand('5H 5C 6S 7S KD 2C 3S 8S 8D TD')
def generate_hand(text):
hands = text.splitlines()
for hand in hands:
yield split_hand(hand)
def get_royal_flush(hand):
if hand[0][0] == 10 and hand[-1][0] == 14 and \
len([c[0] for c in hand]) == len(set([c[0] for c in hand])) and \
len(set([c[1] for c in hand])) == 1:
return 'BOOM'
else:
return None
get_royal_flush([(10, 'C'), (11, 'C'), (12, 'C'), (13, 'C'), (14, 'C')])
get_royal_flush([(10, 'C'), (11, 'C'), (12, 'C'), (12, 'C'), (14, 'C')])
def get_straight_flush(hand):
if len([c[0] for c in hand]) == len(set([c[0] for c in hand])) and \
hand[-1][0] - hand[0][0] == 4 and \
len(set([c[1] for c in hand])) == 1:
return hand[0][0]
else:
return None
get_straight_flush([(2, 'C'), (3, 'C'), (4, 'C'), (5, 'C'), (6, 'C')])
get_straight_flush([(2, 'C'), (3, 'C'), (4, 'C'), (5, 'C'), (10, 'C')])
def get_a_kind(hand):
c = Counter([c[0] for c in hand])
vk = [(v, k) for k, v in c.items()]
return sorted(vk, reverse=True)
get_a_kind([(2, 'C'), (2, 'H'), (2, 'S'), (3, 'C'), (4, 'C')])
get_a_kind([(2, 'C'), (2, 'H'), (2, 'S'), (3, 'C'), (3, 'H')])
get_a_kind([(2, 'C'), (2, 'H'), (3, 'S'), (3, 'C'), (4, 'C')])
get_a_kind([(2, 'C'), (2, 'H'), (5, 'S'), (3, 'C'), (4, 'C')])
get_a_kind([(2, 'C'), (10, 'H'), (11, 'S'), (3, 'C'), (4, 'C')])
def get_four_of_a_kind(hand):
h = get_a_kind(hand)
if h[0][0] == 4:
return h
else:
return None
def get_full_house(hand):
h = get_a_kind(hand)
if h[0][0] == 3 and h[1][0] == 2:
return h
else:
return None
def get_flush(hand):
h = get_a_kind(hand)
if len(set([c[1] for c in hand])) == 1:
return h
else:
return None
def get_straight(hand):
if len([c[0] for c in hand]) == len(set([c[0] for c in hand])) and \
hand[-1][0] - hand[0][0] == 4:
return hand[0][0]
else:
return None
def get_three_of_a_kind(hand):
h = get_a_kind(hand)
if h[0][0] == 3:
return h
else:
return None
def get_two_pairs(hand):
h = get_a_kind(hand)
if h[0][0] == 2 and h[1][0] == 2:
return h
else:
return None
def get_others(hand):
return get_a_kind(hand)
check_ranks = [get_royal_flush, get_straight_flush, get_four_of_a_kind,
get_full_house, get_flush, get_straight,
get_three_of_a_kind, get_two_pairs, get_others]
def solve():
p1_win_cnt = 0
p2_win_cnt = 0
for p1, p2 in generate_hand(resp):
p1_result = [rank(p1) for rank in check_ranks]
p2_result = [rank(p2) for rank in check_ranks]
for r1, r2 in zip(p1_result, p2_result):
if r1 is None and r2 is None:
continue
elif r1 and r2 is None:
p1_win_cnt += 1
elif r2 and r1 is None:
p2_win_cnt += 1
elif r1 > r2:
p1_win_cnt += 1
elif r2 > r1:
p2_win_cnt += 1
else:
raise ValueError('A tie occurs')
break
assert p1_win_cnt + p2_win_cnt == 1000
return p1_win_cnt
solve()
|
51-75/p54.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.0.0
# language: julia
# name: julia-1.0
# ---
# # Playing with matrices
# (and if you get the subliminal message about abstractions, we'll be thrilled!)
# Julia is a dynamic language. You don't need type declarations, and can change variable types dynamically and interactively.
#
# For working with simple numbers, arrays, and strings, its syntax is *superficially* similar to Matlab, Python, and other popular languages.
#
# In order to execute the `In` cells, select the cell and press `Shift-Enter`, or press the `Play` button above. To run the entire notebook, navigate to the `Cell` menu and then `Run All`.
# # We tell beginners, you don't need types!
typeof(1.0)
typeof(1)
S = "Hello Julia Class"
typeof(S)
# Exercise fix my spelling in the cell above
S
# # Now forget all that (for now): Julia is not so different from your favorite dynamic language
1 + 1 # shift + enter to run
A = rand(5, 5)
using LinearAlgebra # A LinearAlgebra standard package contains structured matrices
A = SymTridiagonal(rand(6), rand(5))
b = rand(6)
A \ b
A = fill(3.15, 5, 5) # Fill a 5x5 array with 3.15's
# # Let's create some addition tables
# First let's use a nested for loop to fill in a matrix that's initially zero:
# +
A = zeros(5, 5)
for i in 1:5
for j in 1:5
A[i, j] = i+j # Square brackets for indices. Also: indices start at 1, not 0.
end
end
A
# -
# We can abbreviate this using a double `for` loop:
# +
for i in 1:5, j in 1:5
A[i, j] = i+j # Square brackets for indices. Also: indices start at 1, not 0.
end
A
# -
# The Julia way would be to use a so-called **array comprehension**:
[i+j for i in 1:5, j in 1:5]
# Equivalently,
[i+j for i = 1:5, j = 1:5]
# **Explore**: What does the following do?
[i for i in (1:7).^2]
# What happens when we remove the dot syntax?
[i for i in (1:7)^2]
[i^2 for i in 1:7]
# **Explore**: What does the following do?
sort(unique(x^2 + y^2 for x in 1:5, y in 1:5)) # The inner parentheses define a **generator**
# Suppose we want to see $n \times n$ multiplication tables for $n=1,2,3,4,5$:
for n in 1:5
display([i*j for i=1:n, j=1:n])
end
# # `Interact.jl` is a Julia *package* for interacting with data
# It's way more fun to **interact** with our data.
# We install the `Interact.jl` package as follows; this needs to be executed only once for any given Julia installation:
# +
# using Pkg; Pkg.add("Interact")
# -
# Now we load the package with the following `using` command, in each Julia session:
using Interact
# The package contains a `@manipulate` macro, that is wrapped around a `for` loop:
@manipulate for n in 1:1000
n
end
@manipulate for n in 1:20
[i*j for i in 1:n, j in 1:n]
end
# We use a double `for` loop to get a double slider!
@manipulate for n in 3:10, i in 1:9
A = fill(0, n, n)
A[1:3, 1:3] .= i # fill a sub-block
A
end
# # Functions
# Julia is built around functions: all "commands" or "operations" in Julia are functions:
# +
# verbose form:
function f(x)
x^2
end
# one-line form:
f2(x) = x^2
# anonymous form:
f3 = x -> x^2;
# -
f(10)
# Functions just work, as long as they make sense:
# The square of a matrix is unambiguously defined
f(rand(3, 3))
# What the 'square of a vector' means is ambiguous
f(rand(3))
# In the definition below, `a` and `power` are optional arguments to `f`, supplied with default values.
function f(x, a=1, power=2)
a*x^power
end
# `a` defaults to 1 and `power` to 2
f(7)
# The first optional argument passed is assigned to the local variable `a`
# `power` defaults to 2
f(10, 3)
f(10, 3, 3)
# Let's define a function to insert a block in a matrix:
function insert_block(A, i, j, what=7)
B = A[:,:] # B is a copy of A
B[i:i+2, j:j+2] = fill(what, 3, 3)
return B # the `return` keyword is optional
end
A = fill(0, 9, 9)
insert_block(A, 3, 5) # this returns the new matrix
A = fill(0, 9, 9)
insert_block(A, 3, 5, 2) # Use 2 instead of 7
# We can move the block around:
# +
A = fill(0, 10, 10)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j)
end
# -
# # Strings
# Julia can manipulate strings easily:
S = "Hello"
replace(S, "H" => "J")
a = 3
string(S, " ", S, " ", "Julia; a = ", a) # build a string by concatenating things
# More about strings: <a href="http://docs.julialang.org/en/stable/manual/strings/"> Julia Doc on Strings </a>
# Functions in Julia try to be **generic**, i.e. to work with as many kinds of object as possible:
A = fill("Julia", 5, 5)
# Julia allows us to display objects in different ways. For example, the following code displays a matrix of strings
# in the notebook using an HTML representation:
function Base.show(io::IO, ::MIME"text/html", M::Matrix{T}) where {T<:String}
max_length = maximum(length.(M))
dv="<div style='display:flex;flex-direction:row'>"
print(io, dv*join([join("<div style='width:40px; text-align:center'>".*M[i,:].*"</div>", " ") for i in 1:size(M, 1)]
, "</div>$dv")*"</div>")
end
A
# +
# Remember this ????
A = fill(0, 10, 10)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i,j)
end
# -
# Let's use the **same code**, but now with strings:
# +
A = fill("Julia", 10, 10)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i,j, "[FUN]")
end
# -
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j, "π")
end
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j, "♡")
end
airplane = "✈"
alien = "👽"
rand([airplane, alien], 5, 5)
# +
A = fill(airplane, 9, 9)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j, alien)
end
# -
# # Colors
# The `Colors` package provides objects representing colours:
# using Pkg; Pkg.add("Colors")
using Colors
distinguishable_colors(12)
@manipulate for n in 1:80
distinguishable_colors(n)
end
colors = distinguishable_colors(100)
# +
# Remember this ????
A = fill(0, 10, 10)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j)
end
# -
# What happens if we use colors instead?
# +
A = fill(colors[1], 10, 10)
n = size(A, 1)
@manipulate for i in 1:n-2, j in 1:n-2
insert_block(A, i, j, colors[4])
end
# +
# Exercise: Create Tetris Pieces, have them fall from the top
|
introductory-tutorials/intro-to-julia/Working with matrices.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Car damage detection using FRCNN
# +
import os
import glob
import pandas as pd
import argparse
import xml.etree.ElementTree as ET
import pandas as pd
import matplotlib.pyplot as plt
# %matplotlib inline
from matplotlib import patches
# -
# covert Xml file to csv file
# +
# Function that will extract column data for our CSV file as pandas DataFrame
def xml_to_csv(path):
xml_list = []
for xml_file in glob.glob('/home/unni/Car damage detection/blood/keras-frcnn/train_images/*.xml'):
tree = ET.parse(xml_file)
root = tree.getroot()
for member in root.findall('object'):
try:
value = (root.find('filename').text,
int(root.find('size')[0].text),
int(root.find('size')[1].text),
member[0].text,
int(member[4][0].text),
int(member[4][1].text),
int(member[4][2].text),
int(member[4][3].text)
)
xml_list.append(value)
except:
pass
column_name = ['image_names', 'width', 'height', 'cell_type', 'xmin', 'ymin', 'xmax', 'ymax']
xml_df = pd.DataFrame(xml_list, columns=column_name)
return xml_df
# apply the function to convert all XML files in images/ folder into labels.csv
train = xml_to_csv('/home/unni/Car damage detection/blood/keras-frcnn/')
# -
# save csv file in hardisk
train.to_csv(('/home/unni/Car damage detection/blood/keras-frcnn/train.csv'), index=None)
# Display 1st five entries
train
# Display a sample image
# reading single image using imread function of matplotlib
image = plt.imread('/home/unni/Car damage detection/blood/keras-frcnn/train_images/BloodImage_00174.jpg')
plt.imshow(image)
# Number of unique training images
train['image_names'].nunique()
# Number of classes
train['cell_type'].value_counts()
# Display the image with bounding box and the labelled classes
# +
fig = plt.figure()
#add axes to the image
ax = fig.add_axes([0,0,1,1])
# read and plot the image
image = plt.imread('/home/unni/Car damage detection/blood/keras-frcnn/train_images/BloodImage_00174.jpg')
plt.imshow(image)
# iterating over the image for different objects
for _,row in train[train.image_names == "BloodImage_00174.jpg"].iterrows():
xmin = row.xmin
xmax = row.xmax
ymin = row.ymin
ymax = row.ymax
width = xmax - xmin
height = ymax - ymin
# assign different color to different classes of objects
if row.cell_type == 'RBC':
edgecolor = 'r'
ax.annotate('RBC', xy=(xmax-40,ymin+20))
elif row.cell_type == 'WBC':
edgecolor = 'b'
ax.annotate('WBC', xy=(xmax-40,ymin+20))
elif row.cell_type == 'Platelets':
edgecolor = 'g'
ax.annotate('Platelets', xy=(xmax-40,ymin+20))
# add bounding boxes to the image
rect = patches.Rectangle((xmin,ymin), width, height, edgecolor = edgecolor, facecolor = 'none')
ax.add_patch(rect)
# -
data = pd.DataFrame()
data['format'] = train['image_names']
#print(data['format'])
# as the images are in train_images folder, add train_images before the image name
for i in range(data.shape[0]):
data['format'][i] = 'train_images/' + data['format'][i]
#print(data['format'][i])
# add xmin, ymin, xmax, ymax and class as per the format required
for i in range(data.shape[0]):
data['format'][i] = data['format'][i] + ',' + str(train['xmin'][i]) + ',' + str(train['ymin'][i]) + ',' + str(train['xmax'][i]) + ',' + str(train['ymax'][i]) + ',' + train['cell_type'][i]
#print(data['format'][i])
data.to_csv('/home/unni/Car damage detection/blood/keras-frcnn/annotate.txt', header=None, index=None, sep=' ')
# pip install tensorflow==1.13.1
# pip install keras==2.1.6
# +
import h5py
f = h5py.File("/home/unni/my_project_work/car-damage-detection-using-CNN-master/car- damage data/car_damage_raw/keras-frcnn/model_frcnn.hdf5")
list(f)
# -
# !python train_frcnn.py -o simple -p annotate.txt
# !python test_frcnn.py -p test_images
|
Blood_cell.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.3.1
# language: julia
# name: julia-1.3
# ---
push!(LOAD_PATH, pwd())
using DHC_2DUtils
using Profile
using BenchmarkTools
using FFTW
using HDF5
using Test
using SparseArrays
using Statistics
using Plots
using LinearAlgebra
using Measures
using Plots
using MLDatasets
using ImageCore
using Colors
using AbstractFFTs
using Interpolations
using DSP
using StatsBase
using Images
using Distributed
using ProgressMeter
train_x, train_y = CIFAR10.traindata();
test_x, test_y = CIFAR10.testdata();
function color_convert(array, color1, color2)
chan_img = channelview(array)
cv = colorview(color1, StackedView(array[:,:,1],array[:,:,2],array[:,:,3]))
y_im = color2.(cv)
channels = permutedims(channelview(float.(y_im)),(2,3,1))
return channels
end
addprocs(30)
@everywhere begin
push!(LOAD_PATH, pwd())
using DHC_2DUtils
using Profile
using BenchmarkTools
using FFTW
using Test
using SparseArrays
using Statistics
using Plots
using LinearAlgebra
using Measures
using Plots
using MLDatasets
using ImageCore
using Colors
using AbstractFFTs
using Interpolations
using DSP
using StatsBase
using Distributed
using Images
using ProgressMeter
# filter bank
filter_hash = fink_filter_hash(1, 8, nx=128, pc=1, wd=2)
function wind_2d(nx)
dx = nx/2-1
filter = zeros(Float64, nx, nx)
A = DSP.tukey(nx, 0.3)
itp = extrapolate(interpolate(A,BSpline(Linear())),0)
@inbounds for x = 1:nx
sx = x-dx-1 # define sx,sy so that no fftshift() needed
for y = 1:nx
sy = y-dx-1
r = sqrt.((sx).^2 + (sy).^2) + nx/2
filter[x,y] = itp(r)
end
end
return filter
end
function wind_2d_RGB(nx)
dx = nx/2-1
filter = zeros(Float64, nx, nx)
A = DSP.tukey(nx, 0.3)
itp = extrapolate(interpolate(A,BSpline(Linear())),0)
@inbounds for x = 1:nx
sx = x-dx-1 # define sx,sy so that no fftshift() needed
for y = 1:nx
sy = y-dx-1
r = sqrt.((sx).^2 + (sy).^2) + nx/2
filter[x,y] = itp(r)
end
end
return reshape(filter,nx,nx,1)
end
function cifar_pad_RGB(im; θ=0.0)
imbig = convert(Array{Float64,3},imresize(im,(64,64,3)))
datad_w = fweights(wind_2d(64));
mu_imbig = zeros(1,1,3)
for chan = 1:3
mu_imbig[chan] = mean(imbig[:,:,chan],datad_w)
end
imbig .-= mu_imbig
imbig .*= wind_2d_RGB(64)
impad = zeros(Float64,128,128,3)
impad[96:-1:33,33:96,:] = imbig
if θ != 0.0
imrot = imrotate(impad, θ, axes(impad), Cubic(Throw(OnGrid())))
imrot[findall(imrot .!= imrot)] .= 0.0
return imrot .+ mu_imbig
end
return impad.+ mu_imbig
end
function cifar_DHC(x)
image = cifar_pad_RGB(x[:,:,:], θ=0.0)
WST = DHC_compute_RGB(image, filter_hash)
return WST
end
end
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,LCHuv)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,LCHuv)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_LCHuv.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,XYZ)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,XYZ)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_XYZ.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,xyY)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,xyY)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_xyY.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,LMS)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,LMS)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_LMS.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,DIN99)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,DIN99)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_DIN99.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,DIN99d)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,DIN99d)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_DIN99d.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,DIN99o)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,DIN99o)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_DIN99o.h5"
h5write(filename, "main/test_labels", test_y, deflate=3)
h5write(filename, "main/train_labels", train_y, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_train)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/train_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/train_data_iso", cifar_DHC_out_iso, deflate=3)
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# +
train_x_ycbcr = zeros(size(train_x))
for i=1:size(train_x)[4]
train_x_ycbcr[:,:,:,i] = color_convert(train_x[:,:,:,i],RGB,LCHab)
end
test_x_ycbcr = zeros(size(test_x))
for i=1:size(test_x)[4]
test_x_ycbcr[:,:,:,i] = color_convert(test_x[:,:,:,i],RGB,LCHab)
end
lst_train = Array{Any}(undef, 0)
for i = 1:size(train_x_ycbcr)[4]
push!(lst_train,train_x_ycbcr[:,:,:,i])
end
lst_test = Array{Any}(undef, 0)
for i = 1:size(test_x_ycbcr)[4]
push!(lst_test,test_x_ycbcr[:,:,:,i])
end
filename = "cifar10_LCHab.h5"
cifar_DHC_out = @showprogress pmap(cifar_DHC, lst_test)
cifar_DHC_out = hcat(cifar_DHC_out...)
h5write(filename, "main/test_data", cifar_DHC_out, deflate=3)
cifar_DHC_out_iso = transformMaker(cifar_DHC_out',filter_hash["S1_iso_mat"],filter_hash["S2_iso_mat"],Nc=3)
h5write(filename, "main/test_data_iso", cifar_DHC_out_iso, deflate=3)
# -
|
from_cannon/2021_03_16/2021_03_16-Copy2.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Course Description
# A picture can tell a thousand words - but only if you use the right picture! This course teaches you the fundamentals of data visualization with Google Sheets. You'll learn how to create common chart types like bar charts, histograms, and scatter charts, as well as more advanced types, such as sparkline and candlestick charts. You will look at how to prepare your data and use Data Validation and VLookup formulas to target specific data to chart. You'll learn how to use Conditional Formatting to apply a format to a cell or a range of cells based on certain criteria, and finally, how to create a dashboard showing plots and data together. Along the way, you'll use data from the Olympics, sharks attacks, and Marine Technology from the ASX.
#
# ### Business Intelligence and Using Dashboards
# Learn about business intelligence and dashboards for analyzing information in todays data-driven world. Create a basic dashboard and master setting up your data to get the most out of it.
#
# ### Using data validation controls to pick from a list
# In the dashboard example, you are going to pick sequential numbers from a list to show countries meal rankings.
# INSTRUCTIONS
# Change the rank using the drop-down menu, so that the ranks are displayed in order for countries 1 through 5.
#
# See chapter1_1
# ### Using conditional formatting on a dashboard
# Conditional formatting is another functionality that completed dashboards can contain that allows users to modify the visual display on the dashboard. Here, you will explore the conditional formatting on the same dashboard for the 2016 Olympic Games in Brazil.
# INSTRUCTIONS
# Highlight Gold, Silver, and Bronze figures and change the Conditional Formatting rule to Greater than or equal to number to 25.
#
# HINT
# The Gold, Silver, and Bronze figures are in F3:H12.
# Conditional formatting is found by selecting Format then Conditional formatting.
# ### Creating a column chart from your data
# In the dataset you'll find the medal statistics by country from the 2016 Olympic Games held in Brazil in order of ranking. Let's use the data to create a column chart to show the medal tallies of the first 3 ranked countries.
#
# INSTRUCTIONS
# Highlight Gold, Silver, and Bronze medal stats for the first three ranked countries, create a column chart and move it to the right of the data.
#
# See chapter1_2
#
# Need select both data and the country names to the left. May edit the type of chart as the default type might not be the column chart.
# ### Setting up your worksheet with formulas of reference
# In this next task, you will showcase only the data you want to chart using formulas of reference to extract the top 3 countries medal tallies from the dataset and show them in the Dashboard.
# INSTRUCTIONS
# Create a formula of reference in cell A1 that shows the contents of A1 in the dataset.
# Copy the calculation down and across the sheet to show all data for the first 3 ranked countries.
# Make sure column B is wide enough to see the entire country name.
#
# See chapter1_3
#
# =Olympics!A1 Write this in sheet 1 and they drag both vertically and horizontally. Note Olympics is the name of another sheet.
# ### Charting the medal statistics
# Now that you have only the data you want to chart in this task you will create a column chart and display it underneath your extracted data.
# INSTRUCTIONS
# Create a column chart showing the country, Gold, Silver, and Bronze stats.
# Position the chart underneath the data.
#
# Just plot the data in the selected data in previous cell.
# ### Getting started
# Setting up your data in the correct way in the beginning will save you lots of time and effort later on. Here, you will set up your data so you have an efficient spreadsheet to work with as you create your dashboard.
# INSTRUCTIONS
# Remove all rows from the dataset that are empty.
#
# You can select multiple rows at once by holding down the Ctrl or command key.
# ### Format dates and numbers
# To make your data clear at a glance, in this task you will apply a little bit of formatting to your data.
# INSTRUCTIONS
# Format the date so that it shows the day, month in full and year and widen the column so you can see it all.
# Ensure all numbers have 2 decimal places.
#
# HINT
# To format the date go to Format then Number. Then choose ....
# To increase decimals, use the toolbar icon. Select all the data values, and then click the relevant icon in toolbar.
# ## Efficient Column Charts
#
# Create and format a column chart to showcase data and learn a few smart tricks along the way. Look at using named ranges to refer to cells in your worksheet, making them user-friendly and easy to work with.
#
#
# ### Creating a column chart for your dashboard
# In this chapter, you will start to put together your own dashboard.
#
# Your first step is to create a basic column chart showing fatalities, injured, and uninjured statistics for the states of Australia over the last 100 years.
#
# INSTRUCTIONS
# In A1 use a formula that refers to the heading on your dataset.
# Select the State column and the Fatal, Injured, and Uninjured statistics, and create a chart.
# Change the chart to a column chart.
#
# See chapter1_4
# Use the following to refer to the 'Shark Attacks' sheet and the range A1:E1. Note the ! sign.
# ='Shark Attacks'!A1:E1
# ### Format chart, axis titles and series
# Your next task is to apply some basic formatting to the same chart to jazz it up a bit and make it a bit more pleasing to the readers eye.
# INSTRUCTIONS
# Alter the Title of your chart to Fatal, Injured and Uninjured Statistics make the color black and bold it.
# Change the series colors to Fatal - red, Injured - blue, Uninjured - green.
#
# In chart editor -> customize -> Select the drop down arrow next to All series and select each series in turn to change the color.
# ### Removing a series
# Taking things a little further, in the next task you will manipulate the look of your chart a bit more and remove the Uninjured statistical data.
# INSTRUCTIONS
# Remove the Uninjured series from your chart.
#
# HINT
# On the setup tab, click the 3 dots to the right of the series you wish to remove to see this option.
# See chapter1_5
# ### Changing the plotted range
# Its just as easy to change a range as it is to delete it. For this task, have a go at changing the range of your chart so it now only showcases the top 3 States Fatal satistics.
# INSTRUCTIONS
# Change the range of your chart so you are plotting only the fatalites from the 3 states with the highest numbers and change the chart title to Top 3 States Number of Fatalities.
#
# Don't forget you can select the range to be charted, or you can type it out.
# ### Using named ranges
# In this task you are going find an existing range and insert a blank row within the range.
# INSTRUCTIONS
# '- Select Data in the menu then Named ranges and click on the SharkStats Named range to see the highlighted range.
#
# Insert a blank row after row 1.
#
# Did you notice that even though you inserted the blank row, your Named range didn't change? We have just looked at the basic named range in this course, but there are many other types you can use with your data, Remember that named ranges cannot contain spaces, however you can use an underscore to separate words.
# ### Summing using a Named range
# In this task you will remove a blank row and use a Named range in a formula.
# INSTRUCTIONS
# Remove the blank row you inserted in the last exercise.
# In B10 use the named range Total in-lieu of cell references to sum the totals in C10 :E10.
# Remember that if you create a named range in a sheet, it will still be be viewable and usable in the Named range menu on any sheet within your workbook.
#
# =sum(Total) Total is just the equivalent of range c10:E10
# ### Averaging using a Named range
# In this task you will use a named range within a formula to find an average.
# INSTRUCTIONS
# In C11 use the named range Fatalities in-lieu of cell references to average the number of Fatalities.
#
# =average(Fatalities)
# ## Dashboard Controls
# A dashboard is like a control panel. Look at ways to allow a user to use this control panel to get different results from your dashboard.
# ### Setting up your data
# In this task, you are going to use data from the ASX for a Company that sells shark repellent systems and prepare it for charting. The first step is to tidy up and format the data.
# INSTRUCTIONS
# Remove the blank row and standardize your decimal places.
# Ensure the current date has is has the same format as the dates in column.
#
# See chapter1_6
# ### Format numbers within your dataset
# In your next task you will edit the numbers in your dataset so that they are all formatted the same way.
# INSTRUCTIONS
# Format the numbers in the Volume column so that they all include commas to label thousands.
#
# also See chapter1_6
#
# ### Creating and testing the data validation
# With your data optimized and your named ranges set up, in this task you will set up a data validation to allow a user to select a date from a list.
# INSTRUCTIONS
# Enter in the heading SM8 Smart Marine Systems ASX in A15.
# Starting in A16, enter in the column headings Date, Open, High, Low and Close.
# Create a data validation using the named range Dates in A17:26. **Click Data -> Data validation -> cell range is A17:26 -> another range choose the named range 'Dates'**
# Ensure the following text is available for those who need help: Select a date from the list to see Opening and Closing prices.
# ### Adding the calculation
# Your next task is to select the dates you want and then add in a Vlookup calculation to look at the date selected and find an exact match for the Open, High, Low, and Close Data from your dataset.
# INSTRUCTIONS
# Choose the following dates from the list starting in A17: 09-19-17, 09-20,17, 09-25-17, 09-27-17, 09-29-17, 10-04-17, 10-05-17, 10-06-17, 10-09-17, 10-10-17.
# In cell B17 enter in a Vlookup to look for the date in your dataset and show the corresponding Open data, copy the formula down your table.
# Complete Vlookup formulas in C17, D17 and E17 to look for the figures in the dataset that correspond to the column headings, copy the calcuations down.
#
# see chapter1_7
# ### Chart titles, axis, font, gridlines
# Now that you have created a line chart, you will want to format it to make it more pleasing to the eye and professional.
# INSTRUCTIONS
# Change your chart title to Open vs Close.
# Add a title to your vertical axis $AUD.
#
#
# ### Other formatting options
# Its the little things like legend placement and font sizes that give your charts a bit of polish. In this task you will finish off formatting your chart to ensure maximum efficiency.
# INSTRUCTIONS
# Put your Legend Inside the chart area and change the size to 10px.
# ## Other Charts for Your Dashboard
#
# A picture paints a thousand words. Look at what types of charts to use in what situation to showcase your data.
# ### Inserting the Vlookup
# We want to create a histogram to show the distribution of volumes. You will need to start by getting the Volume data you want to show on the dashboard.
# INSTRUCTIONS
# In F16, type in the heading Volume.
# In the cell directly underneath, create a vlookup to look at the date in column A and return the Volume against that date from the ASXTable.
# Copy the calculation down the dataset.
#
# see chapter1_8
#
# ### Creating a histogram on the dashboard
# Let's get more practice with creating histograms. You will show the volumes of stocks from SM8 Smart Marine Systems. Your data will be plotted at intervals.
# INSTRUCTIONS
# Select the Volume data and create a histogram chart.
# Drag and size your chart underneath your data so it fits nicely in your dashboard.
# ### Formatting your histogram
# Formatting your histogram works similarly to the way it does in all charts. Your task is to format your chart by putting some of your previous skills into practice.
# INSTRUCTIONS
# Give your chart the title Share Volumes and change the color of the series to dark green 2.
# Move the legend to the bottom.
# Include item dividers on your chart.
# ### Changing your dates to text
# Your task is to format your dates as plain text so the user can plot a candlestick chart to show data from the Open, Close, High and Low prices. You will do this in the inserted column, using a formula.
# INSTRUCTIONS
# In B16 type in the heading "Plain Dates".
# Enter a formula in B17 that will show the date as plain text and copy the formula down your dataset.
# Remove the dates that have popped up on your line chart.
#
# see chapter1_9
#
# ### Creating the candlestick for the dashboard
# Now that you have your dates sorted, your next task is to create a candlestick chart on the dashboard to show the Open, High, Low and Close stats over a 10 day period.
# INSTRUCTIONS
# Select the data from Plain Dates to Close and create a candlestick chart.
# Size the candlestick chart appropriately on your dashboard, to the right of the histogram.
# ### Formatting the Candlestick
# As with any other chart, once your candlestick chart is created, you should spend some time formatting it.
# INSTRUCTIONS
# Change the Chart title to Price Movement.
# Make the chart title text black, size 18 font, and bold.
#
# see chapter1_10
# ### Creating a scatter chart
# For the purpose of this exercise, you will create a scatter chart to show the trend of Injuries in relation to the number of reported cases of shark attacks. You will take your data from the Shark Attacks Last 100 Yrs dataset.
# INSTRUCTIONS
# Highlight the State, # Cases and Injured stats and create a scatter chart.
# Paste the chart onto your dashboard, and size it to the right of the Fatalities column chart.
# ### Formatting your scatter chart
# Once your chart is created, as with the other charts on your dashboard, you need to format it and smarten it up.
# INSTRUCTIONS
# Title your chart Cases vs Injuries, and make the font black, size 18, and bold.
# Move your legend to the inside of your chart.
# Change the color of the Cases series to black.
#
# see chapter1_11
# ### Sparklines
# In this task you will create a sparkline chart within a cell. You will add a line sparkline for the open/close data using the ASX Dataset.
# INSTRUCTIONS
# Move your histogram chart down so you can see row 27 and type in the word Trend in A27. use =sparkline(C17:C26)
# In C27, enter a formula that will place a line sparkline in this cell and copy it to E27 and F27
#
# see chapter1_12 However, not shown the sparkline in the EXCEL. It is shown in Google sheets.
# ### Changing the color of your sparkline
# In this task we will jazz up the sparklines a bit and change by changing the formula to include the color to red to make them stand out.
# INSTRUCTIONS
# In the blank cell at the end of the High data entries, insert a formula to create a red sparkline.
# =sparkline(D17:D26,{"color","red"})
# ### The column sparkline
# For the next task you will create a column sparkline to show the Volume of shares for the 10 dates selected via the drop-down arrows.
# INSTRUCTIONS
# In the blank cell at the end of the Volume data insert a formula to create a column sparkline.
# Change the color of the column sparkline to blue.
#
# =SPARKLINE(G17:G26,{"charttype","column"})
# ## Conditional Formatting
#
# Learn how to use rules based on criteria you set to format certain cells on your dashboard. See the formatting change as the values in the cells change.
#
#
# ### Creating a simple rule to highlight cells
# In this task you will create a conditional formatting rule, that will color cells yellow, if the Volume of shares from the SM8 Smart Marine Systems ASX is over 60,000
# INSTRUCTIONS
# Highlight the volume data and create a rule that will format cells yellow if the value in them is greater than 60,000.
# ### Highlighting cells between a range
# In this next task you will create a rule that will highlight cells in the Close column if they fall between a certain range.
# INSTRUCTIONS
# Highlight the Close data and create a rule that formats the font color of cells blue that have a value of between 0.040 and 0.050.
# ### Using a custom formula to highlight a row
# In this task, rather than just highlighting cells, you will highlight any rows of your data that show the Volume data as being less than 3,000.
# INSTRUCTIONS
# Highlight all the data and create a conditional format rule that relies on a formula to highlight a whole row when the value in the Volumes column is less than 3,000.
# Make the font color red and bold and italicize it.
# ### Highlighting duplicates
# For this task, have a go at creating a formula that will highlight the duplicates in the Low data.
# INSTRUCTIONS
# Highlight the Low data and enter in a formula that highlights duplicated cells in red.
#
# I did this before.
# ### Using wildcard characters to highlight dates
# In this task, you will create a formula using wildcard characters to highlight any dates that are in 2018.
# INSTRUCTIONS
# Highlight the dates and, using wildcard characters, set a rule that colors the cell background of any date in 2018 pale green.
# The wildcard character you need to use is a question mark.
#
# Not shown in EXCEL.
# ### Change a condition in a format
# Now, you will amend a rule by changing the values of the condition.
# INSTRUCTIONS
# Change the values of the Value is between rule to between 0.050 and 0.060.
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
#
|
dataManipulation/spreadsheets/Part V-- Visualization in spread sheets/visualization in spread sheets.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernel_info:
# name: python3
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Homework 7
#
# ## APMTH 207: Stochastic Methods for Data Analysis, Inference and Optimization
#
# **Due Date: ** Friday, March 23rd, 2018 at 11:00am
#
# **Instructions:**
#
# - Upload your final answers as a Jupyter notebook containing all work to Canvas.
#
# - Structure your notebook and your work to maximize readability.
# ## Problem 1: Gibbs Sampling On A Bivariate Normal
#
# Let $\mathbf{X}$ be a random variable taking values in $\mathbb{R}^2$. That is, $\mathbf{X}$ is a 2-dimensional vector. Suppose that $\mathbf{X}$ is normally distributed as follows
# $$
# \mathbf{X} \sim \mathcal{N} \left(
# \left[
# \begin{array}{c}
# 1 \\
# 2 \\
# \end{array}
# \right],
# \left[
# \begin{array}{ccc}
# 4 & 1.2 \\
# 1.2 & 4 \\
# \end{array}
# \right] \right).
# $$
# That is, the pdf of the distribution of $\mathbf{X}$ is
# $$
# f_{\mathbf{X}}(\mathbf{x}) = \frac{1}{2\pi\sqrt{\vert \Sigma\vert }}\mathrm{exp}\left\{ - \frac{1}{2} (\mathbf{x} - \mu)^\top \Sigma^{-1} (\mathbf{x} - \mu)\right\}
# $$
# where $\mu = \left[
# \begin{array}{c}
# 1 \\
# 2 \\
# \end{array}
# \right]$, $\Sigma = \left[
# \begin{array}{ccc}
# 4 & 1.2 \\
# 1.2 & 4 \\
# \end{array}
# \right]$, and $\vert \cdot\vert $ is the matrix determinant operator.
#
# In the following, we will denote the random variable corresponding to the first component of $\mathbf{X}$ by $X_1$ and the second component by $X_2$.
#
# * Write a Gibbs sampler for this distribution by sampling sequentially from the two conditional distributions $f_{X_1\vert X_2}, f_{X_2\vert X_1}$.
# * Choose a thinning parameter, burn-in factor and total number of iterations that allow you to take 10000 non-autocorrelated draws.
# * You must justify your choice of parameters.
# ***
# +
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
import pymc3 as pm
from pymc3 import traceplot
from pymc3 import autocorrplot
from pymc3 import gelman_rubin
from pymc3 import geweke
from pymc3 import forestplot
# -
# #### Question 1.1
# Lets define all the variables we plan to use:
#
# mu1 = 1
#
# mu2 = 2
#
# sigmax1 = 2
#
# sigmax2 = 2
#
# $rho*sigmax1*sigmax2$ = 1.2
#
# rho = 1.2/4 = 0.3
#
# The conditionals depend on these variables (https://en.wikipedia.org/wiki/Normal_distribution) s.t.:
#
# $$ X1|X2=x2 \sim N(\mu_{x1} + (\sigma_{x1}/\sigma_{x2})*\rho*(x_2-\mu_2), (1-\rho^2)\sigma_{x1}^2) $$
#
# $$ X2|X1=x1 \sim N(\mu_{x2} + (\sigma_{x2}/\sigma_{x1})*\rho*(x_1-\mu_1), (1-\rho^2)\sigma_{x2}^2) $$
#
# +
#gibbs sampler variables
N = 10000
x1all=np.zeros(N+1)
x2all=np.zeros(N+1)
#Initialize x1 and x2
x1all[0]=1.
x2all[0]=2.
sigmax1 = 2.
sigmax2 = 2.
rho = 0.3
mux1 = 1.
mux2 = 2.
sig = lambda p,sval: np.sqrt((1-p**2)*sval**2)
mu = lambda me1,me2,z,i: me1 + 1*rho*(z[i]-me2)
for i in range(1,N,2):
sig_x1 = sig(rho,sigmax1)
mu_x1 = mu(mux1,mux2,x2all,i-1)
x1all[i] = np.random.normal(mu_x1, sig_x1)
x2all[i] = x2all[i-1]
sig_x2 = sig(rho,sigmax2)
mu_x2 = mu(mux2,mux1,x1all, i)
x2all[i+1] = np.random.normal(mu_x2, sig_x2)
x1all[i+1] = x1all[i]
# -
# Trace plot gives a sense of the autocorrelation. We can plot this for both the variables.
fig,ax = plt.subplots(1,2,figsize=(10,5));
ax[0].plot(x1all,alpha=.3);
ax[0].set_title('x1 traceplot');
ax[1].plot(x2all,alpha=.3);
ax[1].set_title('x2 traceplot');
# We can also plot the marginals
#
fig,ax = plt.subplots(1,2,figsize=(10,5));
ax[0].hist(x1all,bins=50,density=True,alpha=.3);
ax[0].set_title('x1 marginal');
ax[1].hist(x2all,bins=50,density=True,alpha=.3);
ax[1].set_title('x2 marginal');
# +
#movements
from scipy.stats import multivariate_normal
def f(x,y):
return multivariate_normal.pdf([x,y],mean=[mux1,mux2],cov = [[sigmax1**2,1.2],[1.2,sigmax2**2]])
xx=np.linspace(-7,7,300)
yy=np.linspace(-5,7,300)
zz = []
xg,yg = np.meshgrid(xx,yy)
for i in range(len(xx)):
for j in range(len(yy)):
zz.append(f(xx[i],yy[j]))
zz = np.array(zz)
zz = zz.reshape(xg.shape).T
plt.figure()
plt.contour(xg,yg,zz, alpha=0.6)
plt.scatter(x1all,x2all, alpha=0.1, c='b', s=5)
plt.xlabel('x1')
plt.ylabel('x2')
plt.title('Contour plot with samples')
# -
def corrplot(trace,ax, maxlags=50):
ax.acorr(trace-np.mean(trace), normed=True, maxlags=maxlags);
ax.set_xlim([0, maxlags])
fig,ax = plt.subplots(1,2,figsize=(10,5))
corrplot(x1all[N//10:],ax[0])
corrplot(x2all[N//10:],ax[1])
ax[0].set_title('Correlation of X1')
ax[1].set_title('Correlation of X2')
# #### Question 1.2
# So we can see that there is some correlation even after burnin. We can obviously use some thinning. One way to test for the best number of effective samples is to use the function presented in lab.
def effectiveSampleSize(data, stepSize = 1):
samples = len(data)
assert len(data) > 1,"no stats for short sequences"
maxLag = min(samples//3, 1000)
gammaStat = [0,]*maxLag
#varGammaStat = [0,]*maxLag
varStat = 0.0;
if type(data) != np.ndarray:
data = np.array(data)
normalizedData = data - data.mean()
for lag in range(maxLag):
v1 = normalizedData[:samples-lag]
v2 = normalizedData[lag:]
v = v1 * v2
gammaStat[lag] = sum(v) / len(v)
#varGammaStat[lag] = sum(v*v) / len(v)
#varGammaStat[lag] -= gammaStat[0] ** 2
# print lag, gammaStat[lag], varGammaStat[lag]
if lag == 0:
varStat = gammaStat[0]
elif lag % 2 == 0:
s = gammaStat[lag-1] + gammaStat[lag]
if s > 0:
varStat += 2.0*s
else:
break
# standard error of mean
# stdErrorOfMean = Math.sqrt(varStat/samples);
# auto correlation time
act = stepSize * varStat / gammaStat[0]
# effective sample size
ess = (stepSize * samples) / act
return ess
#make sampler a function (gibbs sampler)
def gibbs(nsamps):
N = nsamps
x1all=np.zeros(N+1)
x2all=np.zeros(N+1)
#Initialize x1 and x2
x1all[0]=1.
x2all[0]=2.
sigmax1 = 2.
sigmax2 = 2.
rho = 0.3
mux1 = 1.
mux2 = 2.
sig = lambda p,sval: np.sqrt((1-p**2)*sval**2)
mu = lambda me1,me2,z,i: me1 + 1*rho*(z[i]-me2)
for i in range(1,N,2):
sig_x1 = sig(rho,sigmax1)
mu_x1 = mu(mux1,mux2,x2all,i-1)
x1all[i] = np.random.normal(mu_x1, sig_x1)
x2all[i] = x2all[i-1]
sig_x2 = sig(rho,sigmax2)
mu_x2 = mu(mux2,mux1,x1all, i)
x2all[i+1] = np.random.normal(mu_x2, sig_x2)
x1all[i+1] = x1all[i]
return x1all,x2all
# One way to quickly determine the best thinning and burnin parameters is to loop over a range of them and determine the effective sample size. Once we have this, we can look at autocorrelation plots.
import pandas as pd
df = pd.DataFrame(columns=['initial # of samples','thinning rate','burnin','effective_x1','effective_x2'])
nsamps = [12000,15000,20000,25000]
thinningr = [2,5,10]
burnin = [1000,2500,5000]
for ns in range(len(nsamps)):
for tr in range(len(thinningr)):
for b in range(len(burnin)):
x1,x2 = gibbs(nsamps[ns])
xtmp1 = x1[burnin[b]::thinningr[tr]]
xtmp2 = x2[burnin[b]::thinningr[tr]]
esx = effectiveSampleSize(xtmp1)
esy = effectiveSampleSize(xtmp2)
df.loc[len(df)]=[nsamps[ns],thinningr[tr],burnin[b],esx,esy]
# print('initial samples = ' + str(nsamps[ns]) +',thinning = '+str(thinningr[tr])+',burnin = '+str(burnin[b]),',effective samples x1 = ' +str(esx),',effective samples x2 = ' +str(esy))
df
# From the results above, row 27 suggests that we get effective sample sizes of 10,000 when we use an initial sample size of 25,000 with a thinning rate of 2 and a burnin of 1000.
# We can look at the autocorrelation plots of these particular parameters to make sure.
x1,x2 = gibbs(25000)
xtmp1 = x1[1000::2]
xtmp2 = x2[1000::2]
fig,ax = plt.subplots(1,2,figsize=(10,5))
corrplot(xtmp1,ax[0])
corrplot(xtmp2,ax[1])
ax[0].set_title('Correlation of X1')
ax[1].set_title('Correlation of X2')
# Now we are confident that our samples are not autocorrelated.
# ## Problem 2: Rubber Chickens Bawk Bawk!
# In the competitive rubber chicken retail market, the success of a company is built on satisfying the exacting standards of a consumer base with refined and discriminating taste. In particular, customer product reviews are all important. But how should we judge the quality of a product based on customer reviews?
#
# On Amazon, the first customer review statistic displayed for a product is the ***average rating***. The following are the main product pages for two competing rubber chicken products, manufactured by Lotus World and Toysmith respectively:
#
#
# Lotus World | Toysmith
# - | -
#  | 
#
# Clicking on the 'customer review' link on the product pages takes us to a detailed break-down of the reviews. In particular, we can now see the number of times a product is rated a given rating (between 1 and 5 stars).
#
# Lotus World | Toysmith
# - | -
#  | 
#
# (The images above are also included on canvas in case you are offline, see below)
#
# In the following, we will ask you to compare these two products using the various rating statistics. **Larger versions of the images are available in the data set accompanying this notebook**.
#
# Suppose that for each product, we can model the probability of the value each new rating as the following vector:
# $$
# \theta = [\theta_1, \theta_2, \theta_3, \theta_4, \theta_5]
# $$
# where $\theta_i$ is the probability that a given customer will give the product $i$ number of stars.
#
#
# ### Part A: Inference
#
# 1. Suppose you are told that customer opinions are very polarized in the retail world of rubber chickens, that is, most reviews will be 5 stars or 1 stars (with little middle ground). Choose an appropriate Dirichlet prior for $\theta$. Recall that the Dirichlet pdf is given by:
# $$
# f_{\Theta}(\theta) = \frac{1}{B(\alpha)} \prod_{i=1}^k \theta_i^{\alpha_i - 1}, \quad B(\alpha) = \frac{\prod_{i=1}^k\Gamma(\alpha_i)}{\Gamma\left(\sum_{i=1}^k\alpha_i\right)},
# $$
# where $\theta_i \in (0, 1)$ and $\sum_{i=1}^k \theta_i = 1$, $\alpha_i > 0 $ for $i = 1, \ldots, k$.
#
# 2. Write an expression for the posterior pdf, using a using a multinomial model for observed ratings. Recall that the multinomial pdf is given by:
# $$
# f_{\mathbf{X}\vert \Theta}(\mathbf{x}) = \frac{n!}{x_1! \ldots x_k!} \theta_1^{x_1} \ldots \theta_k^{x_k}
# $$
# where $n$ is the total number of trials, $\theta_i$ is the probability of event $i$ and $\sum_i \theta_i = 1$, and $x_i$ is count of outcome $i$ and $\sum_i x_i = n$.
#
# **Note:** The data you will need in order to define the likelihood function should be read off the image files included in the dataset.
#
#
# 3. Sample 1,000 values of $\theta$ from the *posterior distribution*.
#
# 4. Sample 1,000 values of $x$ from the *posterior predictive distribution*.
#
#
# ### Part B: Ranking
#
# 1. Name at least two major potential problems with using only the average customer ratings to compare products.
#
# (**Hint:** if product 1 has a higher average rating than product 2, can we conclude that product 1 is better liked? If product 1 and product 2 have the same average rating, can we conclude that they are equally good?)
#
#
# 2. Using the samples from your *posterior distribution*, determine which rubber chicken product is superior. Justify your conclusion with sample statistics.
#
# 3. Using the samples from your *posterior predictive distribution*, determine which rubber chicken product is superior. Justify your conclusion with sample statistics.
#
# 4. Finally, which rubber chicken product is superior?
#
# (**Note:** we're not looking for "the correct answer" here, any sound decision based on a statistically correct interpretation of your model will be fine)
# ****
# Answers
#
# #### Part A
#
# 1.Since the customers are polarized between 1 and 5, we need to simply set larger alphas at these two end points. The other values can be set to the same value since we don't have any prior knowledge about them.
#
# As such I choose $$ \alpha = [2,1,1,1,2] $$
#
# 2.Since we are given a multinomial for our likelihood, we have dirichlet-multinomial conjugacy. As such, the posterior distribution is:
#
# $$ P(\theta|X) = \prod_{j=1}^{5}p_j^{\alpha_j-1 + \sum_{y}y_i^j} $$
#
#
# ### Note: model 1 is Lotus World and model 2 is toysmith
with pm.Model() as model1:
theta_prior = pm.Dirichlet('theta_prior',a=np.array([10,1,1,1,10]))#parameter's prior
likelihood = pm.Multinomial('likelihood', p=theta_prior, n=162,observed=np.array([10,6,10,28,108]))#likelihood
stepper = pm.NUTS()
tracemodel1=pm.sample(10000, step=stepper,start=[{'theta_prior':np.array([0.4,0.1,0.1,0.1,0.3])},{'theta_prior':np.array([0.3,0.1,0.2,0.1,0.3])}])
with pm.Model() as model2:
theta_prior = pm.Dirichlet('theta_prior',a=np.array([10,1,1,1,10]))#parameter's prior
likelihood = pm.Multinomial('likelihood', p=theta_prior, n=410,observed=np.array([57,33,29,45,246]))#likelihood
stepper=pm.NUTS()
tracemodel2=pm.sample(10000, step=stepper,start=[{'theta_prior':np.array([0.4,0.1,0.1,0.1,0.3])},{'theta_prior':np.array([0.3,0.1,0.2,0.1,0.3])}])
# With 10000 samples in each, I use a burnin of 2000 and a thinning rate of 8 to get our 1000 samples.
# Model 1 Traceplot
burnin = 2000
thin = 8
traceplot(tracemodel1[burnin::thin])
# Model 2 Traceplot
traceplot(tracemodel2[burnin::thin])
# Now, we can use these samples to get the posterior predictive!
postpred_m1 = pm.sample_ppc(tracemodel1[burnin::thin], 1000, model1)
postpred_m2 = pm.sample_ppc(tracemodel2[burnin::thin], 1000, model2)
model1.observed_RVs
# #### Part B
#
# ##### Question 1
# One problem with using the average customer rating is skewness. For example, if the average of 1 product is higher, this may be because there are numerous outliers pulling the score up and vice-versa for a product that is lower. Another problem is sample size. For example, one rubber duck company could be relatively new in the market with only a few reviews and an average rating comparable to an item that has been on the market for years. As a consequence, we could jump to say they are the same quality however, it is very likely that the older company has better industry knowledge and a wider product offering. Also, I wanted to add that often times there are fake reviews which can skew the ratings too.
#
# ##### Question 2
#
# We can look at the posterior distribution samples of theta which capture the probabilities of getting a particular rating given the data. If we look at the MAP of each of the theta_i's we can get a sense of the mode value of each probability and hence a better sense of which duck company receives higher probabilities of 4's and 5's with the data present.
# Distribution of ratings probabilities for model 1
import seaborn as sns
for i in range(5):
sns.kdeplot(tracemodel1['theta_prior'][:,i])
# Distribution of ratings probabilities for model 2
import seaborn as sns
for i in range(5):
sns.kdeplot(tracemodel2['theta_prior'][:,i])
# From the figures above we can see the probabilities of ratings 5 through 1, 5 being in blue. One potential metric is to simply compare the mean of the distribution of probabilities with a rating of 5.
print('mean of model 1 theta_5 = %s' %np.mean(tracemodel1['theta_prior'][:,4]))
print('std = %s' %np.std(tracemodel1['theta_prior'][:,4]))
print('mean of model 2 theta_5= %s' %np.mean(tracemodel2['theta_prior'][:,4]))
print('std = %s' %np.std(tracemodel2['theta_prior'][:,4]))
# From this one can conclude that duck company 1 is better since the probability of receiving a 5 given it's data is higher than that of company 2. However, this does not account for other ratings and is only 1 metric. Another metric could be to multiply the means of each theta distribution by their respective rating. This way, we can weight the importance of a 5 rating.
# ##### Weighting of Company 1 and Company 2 mean probabiities with highest scores being most important.
np.sum(np.mean(tracemodel1['theta_prior'][:,:],axis=0)*[1,2,3,4,5])
np.sum(np.mean(tracemodel2['theta_prior'][:,:],axis=0)*[1,2,3,4,5])
# Using the weighted metric, we still get company 1 being better. We can also do the opposite weighting in which a 1 star is given the most weight.
# ##### Weighting of Company 1 and Company 2 mean probabiities with lowest scores being most important.
np.sum(np.mean(tracemodel1['theta_prior'][:,:],axis=0)*[5,4,3,2,1])
np.sum(np.mean(tracemodel2['theta_prior'][:,:],axis=0)*[5,4,3,2,1])
# Here again, we see that even though we weight the lower ratings higher, company 1 has a lower score which indicates its low ratings aren't as bad as company 2.
# ##### Question 3
# We can do something similar to the above case except using the samples from the posterior predictive.
#
sns.kdeplot(postpred_m1['likelihood'][:,4])
print('mean = %s' %np.mean(postpred_m1['likelihood'][:,4]))
print('std = %s' %np.std(postpred_m1['likelihood'][:,4]))
print('probability of 5 star rating = %s' %(103.4/162))
pm.hpd(postpred_m1['likelihood'])
print('width of hpd for 5star rating = %s' %(119-88))
sns.kdeplot(postpred_m2['likelihood'][:,4])
print('mean = %s' %np.mean(postpred_m2['likelihood'][:,4]))
print('std = %s' %np.std(postpred_m2['likelihood'][:,4]))
print('probability of 5 star rating = %s' %(241.98/410))
pm.hpd(postpred_m2['likelihood'])
print('width of hpd for 5star rating = %s' %(268-216))
# From the metrics above we can see that company 1 is better because it has a higher probability of getting a 5 star on average and its hpd credible interval at this rating is lower than that of company 1 meaning we are much more certain about its value (note that this hpd changes with the number of datapoints so it could be that at some point we can make the hpds similar, however, in this case company 2 already has more datapoints and still maintains a higher hpd width).
# ##### Question 4
# I would buy from company 1(lotus world).
# ## Problem 3: Implementing Rat Tumors in pymc3
#
# (it may help to see the bioassay lab to see how to structure pymc3 code, and also the examples from lecture).
#
# Let us try to do full Bayesian inference with PyMC3 for the rat tumor example that we have solved using explicit Gibbs sampling in lab7. Remember that the goal is to estimate $\theta_i$, the probability of developing a tumor in a population of female rats that have not received treatement.
#
# The posterior for the 70 experiments may be written thus:
#
# $$p( \{\theta_i\}, \alpha, \beta \vert Y, \{n_i\}) \propto p(\alpha, \beta) \prod_{i=1}^{70} Beta(\theta_i, \alpha, \beta) \prod_{i=1}^{70} Binom(n_i, y_i, \theta_i)$$
#
# Use uniform priors on $[0,1]$ on the alternative variables $\mu$ (the mean of the beta distribution) and $\nu$:
#
# $$\mu = \frac{\alpha}{\alpha+\beta}, \nu = (\alpha+\beta)^{-1/2}$$
#
# You may then write $\alpha$ and $\beta$ as deterministics which depend on $\mu$ and $\nu$.
#
# Here is the data:
tumordata="""0 20
0 20
0 20
0 20
0 20
0 20
0 20
0 19
0 19
0 19
0 19
0 18
0 18
0 17
1 20
1 20
1 20
1 20
1 19
1 19
1 18
1 18
3 27
2 25
2 24
2 23
2 20
2 20
2 20
2 20
2 20
2 20
1 10
5 49
2 19
5 46
2 17
7 49
7 47
3 20
3 20
2 13
9 48
10 50
4 20
4 20
4 20
4 20
4 20
4 20
4 20
10 48
4 19
4 19
4 19
5 22
11 46
12 49
5 20
5 20
6 23
5 19
6 22
6 20
6 20
6 20
16 52
15 46
15 47
9 24
"""
tumortuples=[e.strip().split() for e in tumordata.split("\n")]
tumory=np.array([np.int(e[0].strip()) for e in tumortuples if len(e) > 0])
tumorn=np.array([np.int(e[1].strip()) for e in tumortuples if len(e) > 0])
tumory, tumorn
# Some manipulations to determine alpha and beta in terms of alternative variables.
# $$\alpha\mu + \beta \mu = a $$
# $$ a = -\beta \mu/(\mu-1) $$
# $$ v^2 = 1/(\alpha+\beta) $$
# $$ \alpha+\beta = 1/v^2 $$
# $$ \alpha = -\beta +1/v^2 $$
# $$-\beta + 1/v^2 = -\beta \mu/(\mu-1) $$
# $$ \beta(1-\mu/(\mu-1))=1/v^2 $$
# $$ \beta=1/(v^2(1-\mu/(\mu-1))) $$
#
#
#
#
# $$\alpha = 1/v^2 - \beta $$
with pm.Model() as ratumor:
#parent stochastic hyper-priors
mu = pm.Uniform('mu',lower=0.0,upper=1.0)
nu = pm.Uniform('nu',lower=0.0,upper=1.0)
#dependent children
beta = pm.Deterministic('beta',var=(1-mu)/nu**2)
alpha =pm.Deterministic('alpha',var=mu/(nu**2))
#specify 70 dimensions and 70 theta's
theta = pm.Beta('theta',alpha = alpha, beta = beta,shape=70)
likelihood = pm.Binomial('likelihood', p=theta,n=tumorn,observed=tumory)#likelihood
with ratumor:
# instantiate sampler
step = pm.NUTS()
# draw 2000 posterior samples
rat_trace = pm.sample(10000, step=step,start=[{'mu':np.random.uniform(0,1),'nu':np.random.uniform(0,1)},{'mu':np.random.uniform(0,1),'nu':np.random.uniform(0,1)}])
# ### Part A: Report at least the following diagostics on your samples
#
# 1. Autocorrelation (correlation dying by lag 20 is fine)
# 2. Parameter trace correlation after burnin
# 3. Gewecke
# 4. Gelman-Rubin
# 5. $n_{eff}$ (Number of Effective Samples)
# plotting the trace here just to get a sense of convergence at a higher level
pm.plots.traceplot(rat_trace,varnames =['alpha','beta']);
# 1. Autocorrelation after burnin of 2000 seems really good!
autocorrplot(rat_trace[2000:],max_lag=20,varnames =['alpha','beta']);
# \2. alpha beta correlation appears to be quite high
df = pm.trace_to_dataframe(rat_trace[2000:])
df.corr()[['beta','alpha']]
# 3.
z = geweke(rat_trace[2000:], intervals=15)
plt.scatter(*z[0]['alpha'].T,c='g',alpha=0.2)
plt.scatter(*z[0]['beta'].T,c='b',alpha=.3)
plt.hlines([-1,1], 0, 4000, linestyles='dotted')
plt.xlim(0, 4000)
# \4. Gelman Rubin numbers for alpha and beta are basically 1 which is good!
with ratumor:
step = pm.NUTS()
rat_trace1 = pm.sample(10000, njobs=4, step=step, start=[{'mu':np.random.uniform(0,1)}, {'mu':np.random.uniform(0,1)}, {'mu':np.random.uniform(0,1)}, {'mu':np.random.uniform(0,1)}])
gelman_rubin(rat_trace1[2000:],varnames =['alpha','beta'])
forestplot(rat_trace1,varnames =['alpha','beta'])
# 5. From the 10,000 samples we see that roughly 25% are effective. This number is quite low indicating the need for some more initial samples as well as thinning and burnin.From the autocorrelation plots we can see that both these will help since by 20lags the correlation is very low. Note: I did not run the sampler again to get a higher number of effective samples because it runs relatively slowly.
pm.effective_n(rat_trace,varnames=['alpha','beta'])
# ### Part B: Posterior predictive check
#
# Recall from lab notes that in a hierarchical model there are two kinds of posterior predictions that are useful. (1) The distribution of future observations $y_i^*$ given a $\theta_i$, and (2) The distribution of observations $y_j^*$ drawn from a future $\theta_j$ drawn from the super-population (i.e. using the Beta on the estimated hyper parameters).
#
# 1. Carry out posterior predictive checks by using `sample_ppc` to generate posterior-predictives for all 70 experiments. This generates predictives of the first type above.
#
# 2. Plot histograms for these predictives with the actual value shown as a red-dot against the histogram (as in the coal disasters model in lecture 14). Is the data consistent with the predictive?
# 1.
postpred_rat = pm.sample_ppc(rat_trace[2000:], 1000, ratumor)
fig, axes = plt.subplots(1, 4, figsize=(12, 6))
print(axes.shape)
for i in range(30,34):
axes[i-30].hist(postpred_rat['likelihood'][:,i], bins=10)
axes[i-30].plot(tumory[i],1,'ro')
# ### Part C: Shrinkage
#
# 1. Plot the posterior median of the death rate parameters $\theta_1, \theta_2, ...\theta_{70}$ against the observed death rates ($y_i/n_i$)
#
# 2. Explain the shrinkage by comparing against a 45 degree line as done in the lab.
# +
percentiles=np.percentile(rat_trace['theta'][2000:], [2.5,50.0, 97.5], axis=0)
lowerthetas, medianthetas, upperthetas=percentiles
elowertheta = medianthetas - lowerthetas
euppertheta = upperthetas - medianthetas
# medians = np.median(rat_trace['theta'][2000:],axis=0)
drates = tumory/tumorn
plt.errorbar(drates,medianthetas, yerr=[lowerthetas,upperthetas], fmt='o', alpha=0.5)
plt.plot([0,0.5],[0,0.5],'k-')
plt.xlabel("observed rates")
plt.ylabel("posterior median of rate parameters")
plt.xlim(-0.1,0.5)
# -
# We can see that by reducing the parameters we get some skew!
# ### PART D: Experiment 71
#
# Consider an additional experiment -- experiment 71 -- in which 4 out of 14 rats died.
#
# 1. Calculate the marginal posterior of $\theta_{71}$, the "new" experiment,
#
# 2. Find the $y_{71}^*$ posterior predictive for that experiment.
#
# **HINT: ** The critical thing to notice is that the posterior including the 71st experiment factorizes:
#
# $$p(\theta_{71}, \theta_{1..70}, \alpha, \beta \vert D) \propto p(y_{71} \vert n_{71}, \theta_{71} ) p(\theta_{71} \vert \alpha, \beta) p(\theta_{1..70}, \alpha, \beta \vert D)$$
#
# Then we simply marginalize over everything to get the $\theta_{71}$ posterior:
#
# $$p(\theta_{71} \vert \theta_{1..70}, \alpha, \beta, D) = \int d\alpha \,d\beta \,d\theta_{1..70} \,p(\theta_{71}, \theta_{1..70}, \alpha, \beta \vert D)$$
#
# $$= \int d\alpha \,d\beta Beta(\alpha+y_{71}, \beta + n_{71} - y_{71}) \int_{\theta_{1..70}} \,d\theta_{1..70} \,p(\theta_{1..70}, \alpha, \beta \vert D)$$
#
# The $y_{71}^*$ posterior predictive can be found in the usual way.
import scipy as sp
import seaborn as sns
post71=sp.stats.beta.rvs(rat_trace['alpha']+4,rat_trace['beta']+10)
sns.kdeplot(post71)
plt.xlabel('theta_71')
plt.ylabel(r'p($\theta_{71}$ $\vert$ everything)');
y71 = sp.stats.binom.rvs(n=14,p=post71)
sns.distplot(y71)
plt.xlabel('y_71')
plt.ylabel(r'p(y_{71} $\vert$ everything)');
np.mean(y71)
|
AM207_HW7_2018.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import cv2
import numpy as np
import matplotlib.pyplot as plt
from minimum_spanning_tree_kruskal import GraphUndirectedWeighted
from minimum_spanning_tree_prim import PrimMST
from minimum_spanning_tree_kruskal import KruskalMST
# +
# Load sample image
'''
imsample = np.array([[0, 0, 1, 0, 0],
[0, 1, 4, 1, 0],
[1, 4, 6, 4, 1],
[0, 1, 4, 1, 0],
[0, 0, 1, 0, 0]])
'''
imsample = cv2.imread("./cameraman.png")[..., 0].astype(np.float32)
imsample = (imsample - imsample.min())/(imsample.max() - imsample.min())
imsample = imsample[251:271, 251:271]
# Build undirected/weighted image graph
graph = GraphUndirectedWeighted(imsample)(output="graph")
conns = GraphUndirectedWeighted(imsample)(output="connection")
# Print results
#for k, v in graph.items():
# print("Node => [%d]"%k, v)
#for node in nodes:
# print("SortedWeighted Nodes", node)
# -
def drawMSF(x, leaves):
# Get input shape
height, width = x.shape
# Gray-scale
gray = 255*(x - x.min())/(x.max() - x.min())
# Define plot components
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(6, 6))
visited = list()
# Plot MSF
axes.imshow(gray, cmap="Greys")
for leaf in leaves:
# Mark leaf node
xa, ya = leaf.index//width, leaf.index%width
axes.scatter(ya, xa, color="Blue", s=20, marker="s")
while leaf.parent:
# Mark branch node
a, b = leaf.parent.index, leaf.index
if (a, b) in visited or (b, a) in visited:
continue
else:
visited.append((a, b))
visited.append((b, a))
xa, ya = a//width, a%width
xb, yb = b//width, b%width
axes.scatter(ya, xa, color="Red", s=20)
axes.arrow(ya, xa, yb-ya, xb-xa,
color="lime",
head_width=.05,
head_length=.1)
# Mark root node
if leaf.parent == None:
axes.scatter(ya, xa, color="Green", s=20, marker="D")
# Upstream
leaf = leaf.parent
# +
# Find minimum spanning tree with Prim's algorithm
leaves = PrimMST(graph)
# Draw MSF
drawMSF(imsample, leaves)
# +
# Find minimum spanning tree with Kruskal's algorithm
leaves = KruskalMST(graph, conns)
# Draw MSF
drawMSF(imsample, leaves)
|
scratchs/example_minimum_spanning_tree.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# ---
# Set the Datalake Access Key configuration
spark.conf.set(
"fs.azure.account.key.cryptoanalyticslake.dfs.core.windows.net",
dbutils.secrets.get(scope="key-vault-secret-scope",key="cryptoanalyticslake-access-key"))
# +
# Set Day Month Year
from datetime import datetime
today = datetime.utcnow()
year = today.year
month = today.month
day = today.day
# +
# Recursive data load for all files from a day from every partition in the Event Hub Namespace
sourcefolderpath = f"abfss://crypto-bronze@cryptoanalyticslake.dfs.core.windows.net/quotes-by-day-manual-partition/{year}/{month:0>2d}/{day:0>2d}"
print(sourcefolderpath)
df = spark.read.option("recursiveFileLookup","true").parquet(sourcefolderpath)
# -
display(df)
# Define the input and output formats and paths and the table name.
write_format = 'delta'
save_path = 'abfss://delta-table@cryptoanalyticslake.dfs.core.windows.net/unmanaged/quotes'
database_name = 'lake_unmanaged'
table_name = f'{database_name}.crypto_quotes'
# +
# Write the data to its target.
df.write \
.format(write_format) \
.save(save_path)
spark.sql("CREATE DATABASE " + database_name)
# Create the table.
spark.sql("CREATE TABLE " + table_name + " USING DELTA LOCATION '" + save_path + "'")
# -
display(spark.sql("SELECT * FROM " + table_name))
|
notebooks/deltalake/unmanaged-table/create-unmanaged-table-in-lake.ipynb
|
# -*- coding: utf-8 -*-
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .jl
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Julia 1.5.1
# language: julia
# name: julia-1.5
# ---
using Plots
# This notebook will cover two straightforward algorithms for approximately minimizing one-dimensional functions: *grid search* and *random search*. Both are used extensively in, for example, machine learning to find optimal hyperparameters. These two algorithms are ideal to get acquainted with the basics of Julia!
#
# # Grid search
#
# To minimize a one-dimensional function $f(x)$ using grid search in the interval $[a, b]$, we search the interval over $n$ equally-spaced steps and take value that results in the lowest objective value. The larger $n$, the more function evaluations and the better quality the solution will be. Even though grid search being ubiquitously used in machine learning, it is a biased method and often does not yield as good results as the random search. In some cases, it makes sense to search on a logarithmic scale as opposed to a linear scale.
#
# Grid search can easily be extended to higher dimensions by extending the grid $a_i\le x_i \le b_j$, hence providing upper and lower bounds for every dimension. This approach is also called a *full factorial sampling*. Due to the curse of dimensionality, one has to perform exponentially more function evaluations to cover the search space.
#
# # Random search
#
# To minimize a one-dimensional function $f(x)$ using random search, we generate $n$ random values of $x$ in the interval $[a, b]$ and take the one with the lowest objective value. Clever algorithms use other samplings than uniform, driving the search towards particular regions of the search space. Random search can easily be extended to higher dimensions.
#
# # Exercises
#
# We will explore both methods using the [Ackley alpine function](https://en.wikipedia.org/wiki/Ackley_function). We will search between the interval $[-π, π]$. The true minimizer is $x^\star=0$
# +
using STMO.TestFuns: ackley
ackley(1.0) # scalar version
ackley([1.0, -1.0]) # optional 2D version
plot(ackley, -pi, pi, label="Ackley")
# -
# **Assignments**
# 1. Complete the code `grid_search` and use it to minimize the Ackley function using 10 and 50 function evaluations. (hint: use `:` to generate a grid, e.g. `0:0.1:10`)
# 2. Complete the code `random_search` and use it to minimize the Ackley function using 50 function evaluations. (hint `rand()` generates an uniform random number in $[0,1]$.
# 3. Compare the solutions.
# 4. Compare their running time using the `@time` macro.
# 5. Plot the quality of your solution using the two algorithms as a function of the number of evaluations (use $n=10, 50, 100, 500, 1000, 5000$ or so).
# 6. (optional programming exercise) Extend the functions so that you can perform a higher-dimensional search. E.g., `grid_search(Ackley, (-pi, pi), (-pi, pi))` would search in two dimensions.
# 7. (optional exercise) Use dispatch such that there are two versions for grid search, i.e., `grid_search(f, (a, b); n=10)` works as before, but the second method `grid_search(f, grid::Vector)` recognizes that the grid is already given.
#
# Can you see why I suggested the interval $[-π, π]$? I have been sneaky in question 5...
"""
grid_search(f, (a, b); n=10)
Performs a grid search in [`a`, `b`] on `f` with a grid of size `n`.
Returns the best found value of `x`.
"""
function grid_search(f, (a, b); n=10)
@assert a < b "Not a valid interval!"
ybest = Inf
xbest = 0.0
for x in range(a,b,length=n) # you can do it!
y = f(x)
if y < ybest
ybest = y
xbest = x
end
end
return(xbest,ybest)
end
@time xbest,ybest=grid_search(ackley, (-10, 10); n=100)
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest])
"""
random_search(f, (a, b); n=10)
Performs a random search in [`a`, `b`] on `f` using `n` samples.
Returns the best found value of `x`.
"""
function random_search(f, (a, b); n=10)
@assert a < b "Not a valid interval!"
ybest = Inf # I believe in you!
xbest = 0.0
for i in range(1, stop = n)
xrandom = rand(a:b)
yrandom = f(xrandom)
if yrandom < ybest
ybest = yrandom
xbest = xrandom
end
end
return(xbest,ybest)
end
@time xbest,ybest=random_search(ackley, (-10, 10); n=100)
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest])
# +
c = [10,50,100,500,1000,5000]
xbest_random = zeros(length(c))
ybest_random = zeros(length(c))
xbest_grid = zeros(length(c))
ybest_grid = zeros(length(c))
count = 1
for i in c
xbest,ybest = random_search(ackley, (-pi, pi); n=i)
xbest_random[count] = xbest
ybest_random[count] = ybest
xbest2,ybest2 = grid_search(ackley, (-pi, pi); n=i)
xbest_grid[count] = xbest2
ybest_grid[count] = ybest2
count = count + 1
end
return(xbest_random,ybest_random,xbest_grid,ybest_grid)
# -
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest_grid])
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest_random])
# +
c = [10,50,100,500,1000,5000]
xbest_random = zeros(length(c))
ybest_random = zeros(length(c))
xbest_grid = zeros(length(c))
ybest_grid = zeros(length(c))
count = 1
for i in c
xbest,ybest = random_search(ackley, (-10, 10); n=i)
xbest_random[count] = xbest
ybest_random[count] = ybest
xbest2,ybest2 = grid_search(ackley, (-10, 10); n=i)
xbest_grid[count] = xbest2
ybest_grid[count] = ybest2
count = count + 1
end
return(xbest_random,ybest_random,xbest_grid,ybest_grid)
# -
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest_random])
plot(ackley, -pi, pi, label="Ackley")
vline!([xbest_grid])
# # questions for Michiel
# -interval important?
# -sneaky?
|
chapters/00.Introduction/simple_search.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# + [markdown] papermill={"duration": 0.017728, "end_time": "2022-03-17T04:43:20.631944", "exception": false, "start_time": "2022-03-17T04:43:20.614216", "status": "completed"} tags=[]
# # Transfer Learning Template
# + papermill={"duration": 0.922857, "end_time": "2022-03-17T04:43:21.567178", "exception": false, "start_time": "2022-03-17T04:43:20.644321", "status": "completed"} tags=[]
# %load_ext autoreload
# %autoreload 2
# %matplotlib inline
import os, json, sys, time, random
import numpy as np
import torch
from torch.optim import Adam
from easydict import EasyDict
import matplotlib.pyplot as plt
from steves_models.steves_ptn import Steves_Prototypical_Network
from steves_utils.lazy_iterable_wrapper import Lazy_Iterable_Wrapper
from steves_utils.iterable_aggregator import Iterable_Aggregator
from steves_utils.ptn_train_eval_test_jig import PTN_Train_Eval_Test_Jig
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.torch_utils import get_dataset_metrics, ptn_confusion_by_domain_over_dataloader
from steves_utils.utils_v2 import (per_domain_accuracy_from_confusion, get_datasets_base_path)
from steves_utils.PTN.utils import independent_accuracy_assesment
from torch.utils.data import DataLoader
from steves_utils.stratified_dataset.episodic_accessor import Episodic_Accessor_Factory
from steves_utils.ptn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.transforms import get_chained_transform
# + [markdown] papermill={"duration": 0.012702, "end_time": "2022-03-17T04:43:21.592825", "exception": false, "start_time": "2022-03-17T04:43:21.580123", "status": "completed"} tags=[]
# # Allowed Parameters
# These are allowed parameters, not defaults
# Each of these values need to be present in the injected parameters (the notebook will raise an exception if they are not present)
#
# Papermill uses the cell tag "parameters" to inject the real parameters below this cell.
# Enable tags to see what I mean
# + papermill={"duration": 0.025602, "end_time": "2022-03-17T04:43:21.630990", "exception": false, "start_time": "2022-03-17T04:43:21.605388", "status": "completed"} tags=[]
required_parameters = {
"experiment_name",
"lr",
"device",
"seed",
"dataset_seed",
"n_shot",
"n_query",
"n_way",
"train_k_factor",
"val_k_factor",
"test_k_factor",
"n_epoch",
"patience",
"criteria_for_best",
"x_net",
"datasets",
"torch_default_dtype",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
}
# + papermill={"duration": 0.030918, "end_time": "2022-03-17T04:43:21.676465", "exception": false, "start_time": "2022-03-17T04:43:21.645547", "status": "completed"} tags=["parameters"]
from steves_utils.CORES.utils import (
ALL_NODES,
ALL_NODES_MINIMUM_1000_EXAMPLES,
ALL_DAYS
)
from steves_utils.ORACLE.utils_v2 import (
ALL_DISTANCES_FEET_NARROWED,
ALL_RUNS,
ALL_SERIAL_NUMBERS,
)
standalone_parameters = {}
standalone_parameters["experiment_name"] = "STANDALONE PTN"
standalone_parameters["lr"] = 0.001
standalone_parameters["device"] = "cuda"
standalone_parameters["seed"] = 1337
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["n_way"] = 8
standalone_parameters["n_shot"] = 3
standalone_parameters["n_query"] = 2
standalone_parameters["train_k_factor"] = 1
standalone_parameters["val_k_factor"] = 2
standalone_parameters["test_k_factor"] = 2
standalone_parameters["n_epoch"] = 50
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "source_loss"
standalone_parameters["datasets"] = [
{
"labels": ALL_SERIAL_NUMBERS,
"domains": ALL_DISTANCES_FEET_NARROWED,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl"),
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag", "minus_two"],
"episode_transforms": [],
"domain_prefix": "ORACLE_"
},
{
"labels": ALL_NODES,
"domains": ALL_DAYS,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
"source_or_target_dataset": "target",
"x_transforms": ["unit_power", "times_zero"],
"episode_transforms": [],
"domain_prefix": "CORES_"
}
]
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
]
# Parameters relevant to results
# These parameters will basically never need to change
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# + papermill={"duration": 0.040211, "end_time": "2022-03-17T04:43:21.736028", "exception": false, "start_time": "2022-03-17T04:43:21.695817", "status": "completed"} tags=["injected-parameters"]
# Parameters
parameters = {
"experiment_name": "cores+wisig -> oracle.run1.framed",
"device": "cuda",
"lr": 0.001,
"seed": 1337,
"dataset_seed": 1337,
"n_shot": 3,
"n_query": 2,
"train_k_factor": 3,
"val_k_factor": 2,
"test_k_factor": 2,
"torch_default_dtype": "torch.float32",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_loss",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"n_way": 16,
"datasets": [
{
"labels": [
"1-10.",
"1-11.",
"1-15.",
"1-16.",
"1-17.",
"1-18.",
"1-19.",
"10-4.",
"10-7.",
"11-1.",
"11-14.",
"11-17.",
"11-20.",
"11-7.",
"13-20.",
"13-8.",
"14-10.",
"14-11.",
"14-14.",
"14-7.",
"15-1.",
"15-20.",
"16-1.",
"16-16.",
"17-10.",
"17-11.",
"17-2.",
"19-1.",
"19-16.",
"19-19.",
"19-20.",
"19-3.",
"2-10.",
"2-11.",
"2-17.",
"2-18.",
"2-20.",
"2-3.",
"2-4.",
"2-5.",
"2-6.",
"2-7.",
"2-8.",
"3-13.",
"3-18.",
"3-3.",
"4-1.",
"4-10.",
"4-11.",
"4-19.",
"5-5.",
"6-15.",
"7-10.",
"7-14.",
"8-18.",
"8-20.",
"8-3.",
"8-8.",
],
"domains": [1, 2, 3, 4, 5],
"num_examples_per_domain_per_label": 100,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/cores.stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": ["unit_power"],
"episode_transforms": [],
"domain_prefix": "C_A_",
},
{
"labels": [
"1-10",
"1-12",
"1-14",
"1-16",
"1-18",
"1-19",
"1-8",
"10-11",
"10-17",
"10-4",
"10-7",
"11-1",
"11-10",
"11-19",
"11-20",
"11-4",
"11-7",
"12-19",
"12-20",
"12-7",
"13-14",
"13-18",
"13-19",
"13-20",
"13-3",
"13-7",
"14-10",
"14-11",
"14-12",
"14-13",
"14-14",
"14-19",
"14-20",
"14-7",
"14-8",
"14-9",
"15-1",
"15-19",
"15-6",
"16-1",
"16-16",
"16-19",
"16-20",
"17-10",
"17-11",
"18-1",
"18-10",
"18-11",
"18-12",
"18-13",
"18-14",
"18-15",
"18-16",
"18-17",
"18-19",
"18-2",
"18-20",
"18-4",
"18-5",
"18-7",
"18-8",
"18-9",
"19-1",
"19-10",
"19-11",
"19-12",
"19-13",
"19-14",
"19-15",
"19-19",
"19-2",
"19-20",
"19-3",
"19-4",
"19-6",
"19-7",
"19-8",
"19-9",
"2-1",
"2-13",
"2-15",
"2-3",
"2-4",
"2-5",
"2-6",
"2-7",
"2-8",
"20-1",
"20-12",
"20-14",
"20-15",
"20-16",
"20-18",
"20-19",
"20-20",
"20-3",
"20-4",
"20-5",
"20-7",
"20-8",
"3-1",
"3-13",
"3-18",
"3-2",
"3-8",
"4-1",
"4-10",
"4-11",
"5-1",
"5-5",
"6-1",
"6-15",
"6-6",
"7-10",
"7-11",
"7-12",
"7-13",
"7-14",
"7-7",
"7-8",
"7-9",
"8-1",
"8-13",
"8-14",
"8-18",
"8-20",
"8-3",
"8-8",
"9-1",
"9-7",
],
"domains": [1, 2, 3, 4],
"num_examples_per_domain_per_label": 100,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/wisig.node3-19.stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": ["unit_power"],
"episode_transforms": [],
"domain_prefix": "W_A_",
},
{
"labels": [
"3123D52",
"3123D65",
"3123D79",
"3123D80",
"3123D54",
"3123D70",
"3123D7B",
"3123D89",
"3123D58",
"3123D76",
"3123D7D",
"3123EFE",
"3123D64",
"3123D78",
"3123D7E",
"3124E4A",
],
"domains": [32, 38, 8, 44, 14, 50, 20, 26],
"num_examples_per_domain_per_label": 2000,
"pickle_path": "/mnt/wd500GB/CSC500/csc500-main/datasets/oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl",
"source_or_target_dataset": "target",
"x_transforms": ["unit_power"],
"episode_transforms": [],
"domain_prefix": "ORACLE.run1_",
},
],
}
# + papermill={"duration": 0.031725, "end_time": "2022-03-17T04:43:21.785934", "exception": false, "start_time": "2022-03-17T04:43:21.754209", "status": "completed"} tags=[]
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
# + papermill={"duration": 0.03002, "end_time": "2022-03-17T04:43:21.834364", "exception": false, "start_time": "2022-03-17T04:43:21.804344", "status": "completed"} tags=[]
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
# + papermill={"duration": 0.030362, "end_time": "2022-03-17T04:43:21.881130", "exception": false, "start_time": "2022-03-17T04:43:21.850768", "status": "completed"} tags=[]
###########################################
# The stratified datasets honor this
###########################################
torch.set_default_dtype(eval(p.torch_default_dtype))
# + papermill={"duration": 0.054109, "end_time": "2022-03-17T04:43:21.953070", "exception": false, "start_time": "2022-03-17T04:43:21.898961", "status": "completed"} tags=[]
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
###################################
x_net = build_sequential(p.x_net)
# + papermill={"duration": 0.030615, "end_time": "2022-03-17T04:43:22.001699", "exception": false, "start_time": "2022-03-17T04:43:21.971084", "status": "completed"} tags=[]
start_time_secs = time.time()
# + papermill={"duration": 0.025541, "end_time": "2022-03-17T04:43:22.044917", "exception": false, "start_time": "2022-03-17T04:43:22.019376", "status": "completed"} tags=[]
p.domains_source = []
p.domains_target = []
train_original_source = []
val_original_source = []
test_original_source = []
train_original_target = []
val_original_target = []
test_original_target = []
# + papermill={"duration": 0.029146, "end_time": "2022-03-17T04:43:22.089526", "exception": false, "start_time": "2022-03-17T04:43:22.060380", "status": "completed"} tags=[]
# global_x_transform_func = lambda x: normalize(x.to(torch.get_default_dtype()), "unit_power") # unit_power, unit_mag
# global_x_transform_func = lambda x: normalize(x, "unit_power") # unit_power, unit_mag
# + papermill={"duration": 0.03084, "end_time": "2022-03-17T04:43:22.138603", "exception": false, "start_time": "2022-03-17T04:43:22.107763", "status": "completed"} tags=[]
def add_dataset(
labels,
domains,
pickle_path,
x_transforms,
episode_transforms,
domain_prefix,
num_examples_per_domain_per_label,
source_or_target_dataset:str,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
):
if x_transforms == []: x_transform = None
else: x_transform = get_chained_transform(x_transforms)
if episode_transforms == []: episode_transform = None
else: raise Exception("episode_transforms not implemented")
episode_transform = lambda tup, _prefix=domain_prefix: (_prefix + str(tup[0]), tup[1])
eaf = Episodic_Accessor_Factory(
labels=labels,
domains=domains,
num_examples_per_domain_per_label=num_examples_per_domain_per_label,
iterator_seed=iterator_seed,
dataset_seed=dataset_seed,
n_shot=n_shot,
n_way=n_way,
n_query=n_query,
train_val_test_k_factors=train_val_test_k_factors,
pickle_path=pickle_path,
x_transform_func=x_transform,
)
train, val, test = eaf.get_train(), eaf.get_val(), eaf.get_test()
train = Lazy_Iterable_Wrapper(train, episode_transform)
val = Lazy_Iterable_Wrapper(val, episode_transform)
test = Lazy_Iterable_Wrapper(test, episode_transform)
if source_or_target_dataset=="source":
train_original_source.append(train)
val_original_source.append(val)
test_original_source.append(test)
p.domains_source.extend(
[domain_prefix + str(u) for u in domains]
)
elif source_or_target_dataset=="target":
train_original_target.append(train)
val_original_target.append(val)
test_original_target.append(test)
p.domains_target.extend(
[domain_prefix + str(u) for u in domains]
)
else:
raise Exception(f"invalid source_or_target_dataset: {source_or_target_dataset}")
# + papermill={"duration": 20.675766, "end_time": "2022-03-17T04:43:42.832029", "exception": false, "start_time": "2022-03-17T04:43:22.156263", "status": "completed"} tags=[]
for ds in p.datasets:
add_dataset(**ds)
# + papermill={"duration": 0.030866, "end_time": "2022-03-17T04:43:42.881904", "exception": false, "start_time": "2022-03-17T04:43:42.851038", "status": "completed"} tags=[]
# from steves_utils.CORES.utils import (
# ALL_NODES,
# ALL_NODES_MINIMUM_1000_EXAMPLES,
# ALL_DAYS
# )
# add_dataset(
# labels=ALL_NODES,
# domains = ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"cores_{u}"
# )
# + papermill={"duration": 0.03015, "end_time": "2022-03-17T04:43:42.929521", "exception": false, "start_time": "2022-03-17T04:43:42.899371", "status": "completed"} tags=[]
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle1_{u}"
# )
# + papermill={"duration": 0.024826, "end_time": "2022-03-17T04:43:42.972708", "exception": false, "start_time": "2022-03-17T04:43:42.947882", "status": "completed"} tags=[]
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62,56}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle2_{u}"
# )
# + papermill={"duration": 0.02464, "end_time": "2022-03-17T04:43:43.015606", "exception": false, "start_time": "2022-03-17T04:43:42.990966", "status": "completed"} tags=[]
# add_dataset(
# labels=list(range(19)),
# domains = [0,1,2],
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "metehan.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"met_{u}"
# )
# + papermill={"duration": 0.03076, "end_time": "2022-03-17T04:43:43.065231", "exception": false, "start_time": "2022-03-17T04:43:43.034471", "status": "completed"} tags=[]
# # from steves_utils.wisig.utils import (
# # ALL_NODES_MINIMUM_100_EXAMPLES,
# # ALL_NODES_MINIMUM_500_EXAMPLES,
# # ALL_NODES_MINIMUM_1000_EXAMPLES,
# # ALL_DAYS
# # )
# import steves_utils.wisig.utils as wisig
# add_dataset(
# labels=wisig.ALL_NODES_MINIMUM_100_EXAMPLES,
# domains = wisig.ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "wisig.node3-19.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"wisig_{u}"
# )
# + papermill={"duration": 0.027835, "end_time": "2022-03-17T04:43:43.111223", "exception": false, "start_time": "2022-03-17T04:43:43.083388", "status": "completed"} tags=[]
###################################
# Build the dataset
###################################
train_original_source = Iterable_Aggregator(train_original_source, p.seed)
val_original_source = Iterable_Aggregator(val_original_source, p.seed)
test_original_source = Iterable_Aggregator(test_original_source, p.seed)
train_original_target = Iterable_Aggregator(train_original_target, p.seed)
val_original_target = Iterable_Aggregator(val_original_target, p.seed)
test_original_target = Iterable_Aggregator(test_original_target, p.seed)
# For CNN We only use X and Y. And we only train on the source.
# Properly form the data using a transform lambda and Lazy_Iterable_Wrapper. Finally wrap them in a dataloader
transform_lambda = lambda ex: ex[1] # Original is (<domain>, <episode>) so we strip down to episode only
train_processed_source = Lazy_Iterable_Wrapper(train_original_source, transform_lambda)
val_processed_source = Lazy_Iterable_Wrapper(val_original_source, transform_lambda)
test_processed_source = Lazy_Iterable_Wrapper(test_original_source, transform_lambda)
train_processed_target = Lazy_Iterable_Wrapper(train_original_target, transform_lambda)
val_processed_target = Lazy_Iterable_Wrapper(val_original_target, transform_lambda)
test_processed_target = Lazy_Iterable_Wrapper(test_original_target, transform_lambda)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
# + papermill={"duration": 4.837198, "end_time": "2022-03-17T04:43:47.964355", "exception": false, "start_time": "2022-03-17T04:43:43.127157", "status": "completed"} tags=[]
from steves_utils.transforms import get_average_magnitude, get_average_power
print(set([u for u,_ in val_original_source]))
print(set([u for u,_ in val_original_target]))
s_x, s_y, q_x, q_y, _ = next(iter(train_processed_source))
print(s_x)
# for ds in [
# train_processed_source,
# val_processed_source,
# test_processed_source,
# train_processed_target,
# val_processed_target,
# test_processed_target
# ]:
# for s_x, s_y, q_x, q_y, _ in ds:
# for X in (s_x, q_x):
# for x in X:
# assert np.isclose(get_average_magnitude(x.numpy()), 1.0)
# assert np.isclose(get_average_power(x.numpy()), 1.0)
# + papermill={"duration": 0.075913, "end_time": "2022-03-17T04:43:48.061207", "exception": false, "start_time": "2022-03-17T04:43:47.985294", "status": "completed"} tags=[]
###################################
# Build the model
###################################
model = Steves_Prototypical_Network(x_net, device=p.device, x_shape=(2,256))
optimizer = Adam(params=model.parameters(), lr=p.lr)
# + papermill={"duration": 373.997064, "end_time": "2022-03-17T04:50:02.077566", "exception": false, "start_time": "2022-03-17T04:43:48.080502", "status": "completed"} tags=[]
###################################
# train
###################################
jig = PTN_Train_Eval_Test_Jig(model, p.BEST_MODEL_PATH, p.device)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
patience=p.patience,
optimizer=optimizer,
criteria_for_best=p.criteria_for_best,
)
# + papermill={"duration": 0.047469, "end_time": "2022-03-17T04:50:02.155667", "exception": false, "start_time": "2022-03-17T04:50:02.108198", "status": "completed"} tags=[]
total_experiment_time_secs = time.time() - start_time_secs
# + papermill={"duration": 64.638673, "end_time": "2022-03-17T04:51:06.824168", "exception": false, "start_time": "2022-03-17T04:50:02.185495", "status": "completed"} tags=[]
###################################
# Evaluate the model
###################################
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = Iterable_Aggregator((datasets.source.original.val,datasets.target.original.val))
confusion = ptn_confusion_by_domain_over_dataloader(model, p.device, val_dl)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
experiment = {
"experiment_name": p.experiment_name,
"parameters": dict(p),
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "ptn"),
}
# + papermill={"duration": 0.154339, "end_time": "2022-03-17T04:51:07.009662", "exception": false, "start_time": "2022-03-17T04:51:06.855323", "status": "completed"} tags=[]
ax = get_loss_curve(experiment)
plt.show()
# + papermill={"duration": 0.174827, "end_time": "2022-03-17T04:51:07.216143", "exception": false, "start_time": "2022-03-17T04:51:07.041316", "status": "completed"} tags=[]
get_results_table(experiment)
# + papermill={"duration": 0.18546, "end_time": "2022-03-17T04:51:07.430782", "exception": false, "start_time": "2022-03-17T04:51:07.245322", "status": "completed"} tags=[]
get_domain_accuracies(experiment)
# + papermill={"duration": 0.048418, "end_time": "2022-03-17T04:51:07.514735", "exception": false, "start_time": "2022-03-17T04:51:07.466317", "status": "completed"} tags=[]
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
# + papermill={"duration": 0.049137, "end_time": "2022-03-17T04:51:07.598342", "exception": false, "start_time": "2022-03-17T04:51:07.549205", "status": "completed"} tags=["experiment_json"]
json.dumps(experiment)
|
experiments/tl_2/cores_wisig-oracle.run1.framed/trials/0/trial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
# %matplotlib inline
def getdata(dens):
# To read the csv of the large input size cases.
df = pd.read_csv(f"Durations ((250, 3500, 50 then 100), {dens}, 999) (1).csv", usecols = ['nfverts', 'e_duration', 'b_duration', 'f_duration'])
# Conversion from nanoseconds to seconds
df['e_duration'] *= 10**(-9)
df['b_duration'] *= 10**(-9)
df['f_duration'] *= 10**(-9)
return df
def getdata2(dens):
# To read the csv of the low input size cases.
df = pd.read_csv(f"Durations ((10, 200, 10), {dens}, 999) (1).csv", usecols = ['nfverts', 'l_duration','e_duration', 'b_duration', 'f_duration'])
# Conversion from nanoseconds to seconds
df['l_duration'] *= 10**(-9)
df['e_duration'] *= 10**(-9)
df['b_duration'] *= 10**(-9)
df['f_duration'] *= 10**(-9)
return df
def make_graph(ax, df, lazy_included = True, title = "", add_legend = False):
#plt.title("Performance Comparison of Prim's Algorithm using Different Priority Queues")
#if lazy_included: plt.plot(df.nfverts, df.l_duration, label = "lazy naive", color = 'green')
#plt.plot(df.nfverts, df.e_duration, label = "eager naive", color = 'red')
#plt.plot(df.nfverts, df.b_duration, label = "binary heap", color = 'orange')
#plt.plot(df.nfverts, df.f_duration, label = "fib heap", color = 'blue')
ax.set_title(title, fontsize = 'x-large')
if lazy_included:
ax.plot(df.nfverts, df.l_duration, label = "lazy naive", color = 'green')
ax.plot(df.nfverts, df.e_duration, label = "eager naive", color = 'red')
ax.plot(df.nfverts, df.b_duration, label = "binary heap", color = 'orange')
ax.plot(df.nfverts, df.f_duration, label = "fib heap", color = 'blue')
#ax = plt.gca()
#ax.yaxis.offsetText.set_visible(False)
if add_legend: ax.legend(loc = 'upper left')
#plt.show()
# dataframes for large input size case
df1 = getdata(1)
df2 = getdata(2)
df3 = getdata(3)
# dataframes for low input size case
small1 = getdata2(1)
small2 = getdata2(2)
small3 = getdata2(3)
# +
# Plotting large input size case
fig, axs = plt.subplots(nrows = 1, ncols = 3, figsize = (18, 4), sharey = True)
plt.subplots_adjust(top = 0.80)
fig.suptitle("Comparing Eager Naive, Binary Heap and Fib Heap for Large Input Sizes", fontsize = 'x-large', y = 0.95)
fig.text(0.5, 0.01, 'No. of Vertices', ha='center', fontsize = 'x-large')
fig.text(0.10, 0.47, 'Time Taken in Seconds', va='center', rotation='vertical', fontsize = 'x-large')
make_graph(axs[0], df1, False, "Medium Density", add_legend = True)
make_graph(axs[1], df2, False, "High Density")
make_graph(axs[2], df3, False, "Complete")
plt.figtext(0.8, 0, "Note: Tests were taken in steps of 50, then 100.", ha="center", fontsize=10, \
bbox={"alpha":0.5, "pad":5})
plt.show()
fig.savefig('Comparing Eager Naive, Binary Heap and Fib Heap for Large Input Sizes - Second Attempt.png', bbox_inches = 'tight')
# +
# Plotting low input size cases considering lazy naive
fig, axs = plt.subplots(nrows = 1, ncols = 3, figsize = (18, 4), sharey = True)
plt.subplots_adjust(top = 0.80)
fig.suptitle("Comparing Lazy Naive, Eager Naive, Binary Heap and Fib Heap for Low Input Sizes", fontsize = 'x-large', y = 0.95)
fig.text(0.5, 0.01, 'No. of Vertices', ha='center', fontsize = 'x-large')
fig.text(0.10, 0.47, 'Time Taken in Seconds', va='center', rotation='vertical', fontsize = 'x-large')
make_graph(axs[0], small1, True, "Medium Density", add_legend = True)
make_graph(axs[1], small2, True, "High Density")
make_graph(axs[2], small3, True, "Complete")
plt.figtext(0.82, 0, "Note: Tests were taken in steps of 10.", ha="center", fontsize=10, \
bbox={"alpha":0.5, "pad":5})
plt.show()
fig.savefig('Comparing Lazy Naive, Eager Naive, Binary Heap and Fib Heap for Low Input Sizes - Second Attempt.png', bbox_inches = 'tight')
# +
# Plotting low input size cases ignoring lazy naive
fig, axs = plt.subplots(nrows = 1, ncols = 3, figsize = (18, 4), sharey = True)
plt.subplots_adjust(top = 0.80)
fig.suptitle("Comparing Eager Naive, Binary Heap and Fib Heap for Low Input Sizes", fontsize = 'x-large', y = 0.95)
fig.text(0.5, 0.01, 'No. of Vertices', ha='center', fontsize = 'x-large')
fig.text(0.09, 0.47, 'Time Taken in Seconds', va='center', rotation='vertical', fontsize = 'x-large')
make_graph(axs[0], small1, False, "Medium Density", add_legend = True)
make_graph(axs[1], small2, False, "High Density")
make_graph(axs[2], small3, False, "Complete")
plt.figtext(0.82, 0, "Note: Tests were taken in steps of 10.", ha="center", fontsize=10, \
bbox={"alpha":0.5, "pad":5})
plt.show()
fig.savefig('Comparing Eager Naive, Binary Heap and Fib Heap for Low Input Sizes- Second Attempt.png', bbox_inches = 'tight')
# +
# Plotting low input size cases considering lazy naive
fig, axs = plt.subplots(nrows = 1, ncols = 3, figsize = (18, 4), sharey = True)
plt.subplots_adjust(top = 0.80)
fig.suptitle("Comparing Lazy Naive, Eager Naive, Binary Heap and Fib Heap for Low Input Sizes", fontsize = 'x-large', y = 0.95)
fig.text(0.5, 0.01, 'No. of Vertices', ha='center', fontsize = 'x-large')
fig.text(0.085, 0.47, 'Time Taken in Seconds', va='center', rotation='vertical', fontsize = 'x-large')
make_graph(axs[0], small1, True, "Medium Density", add_legend = True)
make_graph(axs[1], small2, True, "High Density")
make_graph(axs[2], small3, True, "Complete")
max_ebf_time = lambda df: max(df[['e_duration', 'b_duration', 'f_duration']].max())
overall_max_ebf_time = max(max_ebf_time(df) for df in [small1, small3, small3])
ylimit = overall_max_ebf_time * 1.1
plt.gca().set_ylim([0, ylimit])
plt.figtext(0.82, 0, "Note: Tests were taken in steps of 10.", ha="center", fontsize=10, \
bbox={"alpha":0.5, "pad":5})
plt.show()
fig.savefig('Comparing Lazy Naive, Eager Naive, Binary Heap and Fib Heap for Low Input Sizes - Second Attempt; Different Format.png', bbox_inches = 'tight')
# -
|
Tests/Performance Comparison Plotter.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# name: python3
# ---
# + [markdown] id="view-in-github" colab_type="text"
# <a href="https://colab.research.google.com/github/btahir/Twitter-Pulse-Checker/blob/master/Twitter_Pulse_Checker.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# + [markdown] id="xNdTFUOmBWM0" colab_type="text"
# # Twitter Pulse Checker
# + [markdown] id="7x39hXNFaJ4Q" colab_type="text"
# 
# + [markdown] id="VDNM2RrQBapg" colab_type="text"
# This is a quick and dirty way to get a sense of what's trending on Twitter related to a particular Topic. For my use case, I am focusing on the city of Seattle but you can easily apply this to any topic.
#
# **Use the GPU for this notebook to speed things up:** select the menu option "Runtime" -> "Change runtime type", select "Hardware Accelerator" -> "GPU" and click "SAVE".
#
# The code in this notebook does the following things:
#
#
# * Scrapes Tweets related to the Topic you are interested in.
# * Extracts relevant Tags from the text (NER: Named Entity Recognition).
# * Does Sentiment Analysis on those Tweets.
# * Provides some visualizations in an interactive format to get a 'pulse' of what's happening.
#
# We use Tweepy to scrape Twitter data and Flair to do NER / Sentiment Analysis. We use Seaborn for visualizations and all of this is possible because of the wonderful, free and fast (with GPU) Google Colab.
#
# **A bit about NER (Named Entity Recognition)**
#
# This is the process of extracting labels form text.
#
# So, take an example sentence: '<NAME> to Washington'. NER will allow us to extract labels such as Person for '<NAME>' and Location for 'Washington (state)'. It is one of the most common and useful applications in NLP and, using it, we can extract labels from Tweets and do analysis on them.
#
# **A bit about Sentiment Analysis**
#
# Most commonly, this is the process of getting a sense of whether some text is Positive or Negative. More generally, you can apply it to any label of your choosing (Spam/No Spam etc.).
#
# So, 'I hated this movie' would be classified as a negative statement but 'I loved this movie' would be classified as positive. Again - it is a very useful application as it allows us to get a sense of people's opinions about something (Twitter topics, Movie reviews etc).
#
# To learn more about these applications, check out the Flair Github homepage and Tutorials: https://github.com/zalandoresearch/flair
#
#
# Note: You will need Twitter API keys (and of course a Twitter account) to make this work. You can get those by signing up here: https://developer.twitter.com/en/apps
# + [markdown] id="7f9m2ucbDH8a" colab_type="text"
# To get up and running, we need to import a bunch of stuff and install Flair. Run through the next 3 cells.
# + id="TGc4FbSqCJDg" colab_type="code" colab={}
# import lots of stuff
import sys
import os
import re
import tweepy
from tweepy import OAuthHandler
from textblob import TextBlob
import numpy as np
import pandas as pd
from datetime import datetime, timedelta
from IPython.display import clear_output
from tqdm import tqdm
import matplotlib.pyplot as plt
import seaborn as sns
% matplotlib inline
from os import path
from PIL import Image
from wordcloud import WordCloud, STOPWORDS
# + id="2YaIwapFC7Yi" colab_type="code" colab={}
# install Flair
# !pip install flair
clear_output()
# + id="CN7bPwceC77g" colab_type="code" colab={}
# import Flair stuff
from flair.data import Sentence
from flair.models import SequenceTagger
tagger = SequenceTagger.load('ner')
clear_output()
# + id="LhUwHI1zDDs_" colab_type="code" colab={}
#import Flair Classifier
from flair.models import TextClassifier
classifier = TextClassifier.load('en-sentiment')
clear_output()
# + [markdown] id="LPfBYe-zqxme" colab_type="text"
# ### Authenticate with Twitter API
# + id="D82o9BhxA0tq" colab_type="code" cellView="form" colab={}
#@title Enter Twitter Credentials
TWITTER_KEY = '' #@param {type:"string"}
TWITTER_SECRET_KEY = '' #@param {type:"string"}
# + id="MOxCv5dKBkVz" colab_type="code" colab={}
# Authenticate
auth = tweepy.AppAuthHandler(TWITTER_KEY, TWITTER_SECRET_KEY)
api = tweepy.API(auth, wait_on_rate_limit=True,
wait_on_rate_limit_notify=True)
if (not api):
print ("Can't Authenticate")
sys.exit(-1)
# + [markdown] id="_0rweWLHXo1v" colab_type="text"
# ###Lets start scraping!
# + [markdown] id="T8oyLAkVYp4k" colab_type="text"
# The Twitter scrape code here was taken from: https://bhaskarvk.github.io/2015/01/how-to-use-twitters-search-rest-api-most-effectively.
#
# My thanks to the author.
#
# We need to provide a Search term and a Max Tweet count. Twitter lets you to request 45,000 tweets every 15 minutes so setting something below that works.
# + id="As_PRtb-Bklo" colab_type="code" colab={}
#@title Twitter Search API Inputs
#@markdown ### Enter Search Query:
searchQuery = 'Seattle' #@param {type:"string"}
#@markdown ### Enter Max Tweets To Scrape:
#@markdown #### The Twitter API Rate Limit (currently) is 45,000 tweets every 15 minutes.
maxTweets = 1000 #@param {type:"slider", min:0, max:45000, step:100}
Filter_Retweets = True #@param {type:"boolean"}
tweetsPerQry = 100 # this is the max the API permits
tweet_lst = []
if Filter_Retweets:
searchQuery = searchQuery + ' -filter:retweets' # to exclude retweets
# If results from a specific ID onwards are reqd, set since_id to that ID.
# else default to no lower limit, go as far back as API allows
sinceId = None
# If results only below a specific ID are, set max_id to that ID.
# else default to no upper limit, start from the most recent tweet matching the search query.
max_id = -10000000000
tweetCount = 0
print("Downloading max {0} tweets".format(maxTweets))
while tweetCount < maxTweets:
try:
if (max_id <= 0):
if (not sinceId):
new_tweets = api.search(q=searchQuery, count=tweetsPerQry, lang="en")
else:
new_tweets = api.search(q=searchQuery, count=tweetsPerQry,
lang="en", since_id=sinceId)
else:
if (not sinceId):
new_tweets = api.search(q=searchQuery, count=tweetsPerQry,
lang="en", max_id=str(max_id - 1))
else:
new_tweets = api.search(q=searchQuery, count=tweetsPerQry,
lang="en", max_id=str(max_id - 1),
since_id=sinceId)
if not new_tweets:
print("No more tweets found")
break
for tweet in new_tweets:
if hasattr(tweet, 'reply_count'):
reply_count = tweet.reply_count
else:
reply_count = 0
if hasattr(tweet, 'retweeted'):
retweeted = tweet.retweeted
else:
retweeted = "NA"
# fixup search query to get topic
topic = searchQuery[:searchQuery.find('-')].capitalize().strip()
# fixup date
tweetDate = tweet.created_at.date()
tweet_lst.append([tweetDate, topic,
tweet.id, tweet.user.screen_name, tweet.user.name, tweet.text, tweet.favorite_count,
reply_count, tweet.retweet_count, retweeted])
tweetCount += len(new_tweets)
print("Downloaded {0} tweets".format(tweetCount))
max_id = new_tweets[-1].id
except tweepy.TweepError as e:
# Just exit if any error
print("some error : " + str(e))
break
clear_output()
print("Downloaded {0} tweets".format(tweetCount))
# + [markdown] id="UVsHZlEroRQY" colab_type="text"
# ##Data Sciencing
# + [markdown] id="CC0Lz66Jn48L" colab_type="text"
# Let's load the tweet data into a Pandas Dataframe so we can do Data Science to it.
#
# The data is also saved down in a tweets.csv file in case you want to download it.
# + id="Bu7qN8q6Bkn9" colab_type="code" outputId="e548591b-3cb2-4ece-f8f6-cae988462158" colab={"base_uri": "https://localhost:8080/", "height": 289}
pd.set_option('display.max_colwidth', -1)
# load it into a pandas dataframe
tweet_df = pd.DataFrame(tweet_lst, columns=['tweet_dt', 'topic', 'id', 'username', 'name', 'tweet', 'like_count', 'reply_count', 'retweet_count', 'retweeted'])
tweet_df.to_csv('tweets.csv')
tweet_df.head()
# + [markdown] id="9lJ8UlW3ZIsH" colab_type="text"
# Unfortunately Twitter does not let you filter by date when you request tweets. However, we can do this at this stage. I have set it up to pull yesterday + todays Tweets by default.
# + id="pf_cZXTHBkqC" colab_type="code" outputId="669fec29-ba09-4efb-fc88-c103837d3f23" colab={"base_uri": "https://localhost:8080/", "height": 34}
#@title Filter By Date Range
today = datetime.now().date()
yesterday = today - timedelta(1)
start_dt = '' #@param {type:"date"}
end_dt = '' #@param {type:"date"}
if start_dt == '':
start_dt = yesterday
else:
start_dt = datetime.strptime(start_dt, '%Y-%m-%d').date()
if end_dt == '':
end_dt = today
else:
end_dt = datetime.strptime(end_dt, '%Y-%m-%d').date()
tweet_df = tweet_df[(tweet_df['tweet_dt'] >= start_dt)
& (tweet_df['tweet_dt'] <= end_dt)]
tweet_df.shape
# + [markdown] id="fC-cQNXwafbt" colab_type="text"
# ## NER and Sentiment Analysis
#
# Now let's do some NER / Sentiment Analysis. We will use the Flair library: https://github.com/zalandoresearch/flair
#
# ###NER
#
# Previosuly, we extracted, and then appended the Tags as separate rows in our dataframe. This helps us later on to Group by Tags.
#
# We also create a new 'Hashtag' Tag as Flair does not recognize it and it's a big one in this context.
#
# ### Sentiment Analysis
#
# We use the Flair Classifier to get Polarity and Result and add those fields to our dataframe.
#
# **Warning:** This can be slow if you have lots of tweets.
# + id="AOKbfZlzBksW" colab_type="code" colab={}
# predict NER
nerlst = []
for index, row in tqdm(tweet_df.iterrows(), total=tweet_df.shape[0]):
cleanedTweet = row['tweet'].replace("#", "")
sentence = Sentence(cleanedTweet, use_tokenizer=True)
# predict NER tags
tagger.predict(sentence)
# get ner
ners = sentence.to_dict(tag_type='ner')['entities']
# predict sentiment
classifier.predict(sentence)
label = sentence.labels[0]
response = {'result': label.value, 'polarity':label.score}
# get hashtags
hashtags = re.findall(r'#\w+', row['tweet'])
if len(hashtags) >= 1:
for hashtag in hashtags:
ners.append({ 'type': 'Hashtag', 'text': hashtag })
for ner in ners:
adj_polarity = response['polarity']
if response['result'] == 'NEGATIVE':
adj_polarity = response['polarity'] * -1
nerlst.append([ row['tweet_dt'], row['topic'], row['id'], row['username'],
row['name'], row['tweet'], ner['type'], ner['text'], response['result'],
response['polarity'], adj_polarity, row['like_count'], row['reply_count'],
row['retweet_count'] ])
clear_output()
# + id="VfZVjXldBkuc" colab_type="code" outputId="0ca77d2c-68d3-4168-fd6e-fb5d41dba993" colab={"base_uri": "https://localhost:8080/", "height": 510}
df_ner = pd.DataFrame(nerlst, columns=['tweet_dt', 'topic', 'id', 'username', 'name', 'tweet', 'tag_type', 'tag', 'sentiment', 'polarity',
'adj_polarity','like_count', 'reply_count', 'retweet_count'])
df_ner.head()
# + [markdown] id="ETnIczIIyN_B" colab_type="text"
# Let's filter out obvious tags like #Seattle that would show up for this search. You can comment this portion out or use different Tags for your list.
# + id="tzwXUKUwBkzM" colab_type="code" cellView="both" colab={}
# filter out obvious tags
banned_words = ['Seattle', 'WA', '#Seattle', '#seattle', 'Washington', 'SEATTLE', 'WASHINGTON',
'seattle', 'Seattle WA', 'seattle wa','Seattle, WA', 'Seattle WA USA',
'Seattle, Washington', 'Seattle Washington', 'Wa', 'wa', '#Wa',
'#wa', '#washington', '#Washington', '#WA', '#PNW', '#pnw', '#northwest']
df_ner = df_ner[~df_ner['tag'].isin(banned_words)]
# + [markdown] id="ajYB9VAC4-Ca" colab_type="text"
# Calculate Frequency, Likes, Replies, Retweets and Average Polarity per Tag.
# + id="xA3E8UTwBkw6" colab_type="code" outputId="4361bf18-cad1-4980-82af-b2b3ee5f66a3" colab={"base_uri": "https://localhost:8080/", "height": 204}
ner_groups = df_ner.groupby(['tag', 'tag_type']).agg({'tag': "count", 'adj_polarity': "mean",
'like_count': 'sum', 'reply_count': 'sum',
'retweet_count': 'sum'})
ner_groups = ner_groups.rename(columns={
"tag": "Frequency",
"adj_polarity": "Avg_Polarity",
"like_count": "Total_Likes",
"reply_count": "Total_Replies",
"retweet_count": "Total_Retweets"
})
ner_groups = ner_groups.sort_values(['Frequency'], ascending=False)
ner_groups = ner_groups.reset_index()
ner_groups.head()
# + [markdown] id="inLWlkSh8IW_" colab_type="text"
# Create an overall Sentiment column based on the Average Polarity of the Tag.
# + id="MeBq0NeO5H3P" colab_type="code" outputId="f6e4943c-9d8c-4a60-832f-4bcd5f8189f1" colab={"base_uri": "https://localhost:8080/", "height": 204}
ner_groups['Sentiment'] = np.where(ner_groups['Avg_Polarity']>=0, 'POSITIVE', 'NEGATIVE')
ner_groups.head()
# + [markdown] id="jLzD6bwyauz9" colab_type="text"
# ## Visualize!
# + [markdown] id="bbhxVDawfaEQ" colab_type="text"
# We can get some bar plots for the Tags based on the following metrics:
#
#
#
# * Most Popular Tweets
# * Most Liked Tweets
# * Most Replied Tweets
# * Most Retweeted Tweets
#
# By default, we do the analysis on all the Tags but we can also filter by Tag by checking the Filter_TAG box.
# This way we can further drill down into the metrics for Hashtags, Persons, Locations & Organizations.
#
# We cut the plots by Sentiment i.e. the color of the bars tells us if the overall Sentiment was Positive or Negative.
#
# + id="D6lMQm32Bk1f" colab_type="code" outputId="56f95c05-d925-4d31-b85d-0a470641c536" colab={"base_uri": "https://localhost:8080/", "height": 644}
#@title Visualize Top TAGs
Filter_TAG = False #@param {type:"boolean"}
TAG = 'Person' #@param ["Hashtag", "Person", "Location", "Organization"]
#@markdown ###Pick how many tags to display per chart:
Top_N = 10 #@param {type:"integer"}
# get TAG value
if TAG != 'Hashtag':
TAG = TAG[:3].upper()
if Filter_TAG:
filtered_group = ner_groups[(ner_groups['tag_type'] == TAG)]
else:
filtered_group = ner_groups
# plot the figures
fig = plt.figure(figsize=(20, 16))
fig.subplots_adjust(hspace=0.2, wspace=0.5)
ax1 = fig.add_subplot(321)
sns.barplot(x="Frequency", y="tag", data=filtered_group[:Top_N], hue="Sentiment")
ax2 = fig.add_subplot(322)
filtered_group = filtered_group.sort_values(['Total_Likes'], ascending=False)
sns.barplot(x="Total_Likes", y="tag", data=filtered_group[:Top_N], hue="Sentiment")
ax3 = fig.add_subplot(323)
filtered_group = filtered_group.sort_values(['Total_Replies'], ascending=False)
sns.barplot(x="Total_Replies", y="tag", data=filtered_group[:Top_N], hue="Sentiment")
ax4 = fig.add_subplot(324)
filtered_group = filtered_group.sort_values(['Total_Retweets'], ascending=False)
sns.barplot(x="Total_Retweets", y="tag", data=filtered_group[:Top_N], hue="Sentiment")
ax1.title.set_text('Most Popular')
ax2.title.set_text('Most Liked')
ax3.title.set_text('Most Replied')
ax4.title.set_text('Most Retweeted')
ax1.set_ylabel('')
ax1.set_xlabel('')
ax2.set_ylabel('')
ax2.set_xlabel('')
ax3.set_ylabel('')
ax3.set_xlabel('')
ax4.set_ylabel('')
ax4.set_xlabel('')
# + [markdown] id="BybFabE9QyUv" colab_type="text"
# ###Get the Average Polarity Distribution.
# + id="LRdgAEbsDLyc" colab_type="code" outputId="cc6bb6c6-0609-45d0-bbe1-7067ed09551d" colab={"base_uri": "https://localhost:8080/", "height": 409}
fig = plt.figure(figsize=(12, 6))
sns.distplot(filtered_group['Avg_Polarity'], hist=False, kde_kws={"shade": True})
# + [markdown] id="ipaVFUOPiJrk" colab_type="text"
# ## Word Cloud
#
# Let's build a Word Cloud based on these metrics.
#
# Since I am interested in Seattle, I am going to use overlay the Seattle city skyline view over my Word Cloud.
# You can change this by selecting a different Mask option from the drop down.
#
# Images for Masks can be found at:
#
# http://clipart-library.com/clipart/2099977.htm
#
# https://needpix.com
# + id="rfYNVV1upjbL" colab_type="code" colab={}
# download mask images
# !wget http://clipart-library.com/img/2099977.jpg -O seattle.jpg
# !wget https://storage.needpix.com/rsynced_images/trotting-horse-silhouette.jpg -O horse.jpg
# !wget https://storage.needpix.com/rsynced_images/black-balloon.jpg -O balloon.jpg
clear_output()
# + id="timxX2vKBk3-" colab_type="code" outputId="ee7c4c13-60ae-47ad-bbfc-235a03378329" colab={"base_uri": "https://localhost:8080/", "height": 652}
#@title Build Word Cloud For Top TAGs
Metric = 'Most Popular' #@param ["Most Popular", "Most Liked", "Most Replied", "Most Retweeted"]
#@markdown
Filter_TAG = False #@param {type:"boolean"}
##@markdown
TAG = 'Location' #@param ["Hashtag", "Person", "Location", "Organization"]
Mask = 'Seattle' #@param ["Rectangle", "Seattle", "Balloon", "Horse"]
# get correct Metric value
if Metric == 'Most Popular':
Metric = 'Frequency'
elif Metric == 'Most Liked':
Metric = 'Total_Likes'
elif Metric == 'Most Replied':
Metric = 'Total_Replies'
elif Metric == 'Most Retweeted':
Metric = 'Total_Retweets'
# get TAG value
if TAG != 'Hashtag':
TAG = TAG[:3].upper()
if Filter_TAG:
filtered_group = ner_groups[(ner_groups['tag_type'] == TAG)]
else:
filtered_group = ner_groups
countDict = {}
for index, row in filtered_group.iterrows():
if row[Metric] == 0:
row[Metric] = 1
countDict.update( {row['tag'] : row[Metric]} )
if Mask == 'Seattle':
Mask = np.array(Image.open("seattle.jpg"))
elif Mask == 'Rectangle':
Mask = np.array(Image.new('RGB', (800,600), (0, 0, 0)))
elif Mask == 'Horse':
Mask = np.array(Image.open("horse.png"))
elif Mask == 'Balloon':
Mask = np.array(Image.open("balloon.jpg"))
clear_output()
# Generate Word Cloud
wordcloud = WordCloud(
max_words=100,
# max_font_size=50,
height=300,
width=800,
background_color = 'white',
mask=Mask,
contour_width=1,
contour_color='steelblue',
stopwords = STOPWORDS).generate_from_frequencies(countDict)
fig = plt.figure(
figsize = (18, 18),
)
plt.imshow(wordcloud, interpolation = 'bilinear')
plt.axis('off')
plt.tight_layout(pad=0)
plt.show()
# + id="LS9tvmFIjUC9" colab_type="code" colab={}
|
Twitter_Pulse_Checker.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %%writefile ReflexAgentEvalUtil.py
import util
def reflexAgentEval(reflexAgent, currentGameState, action):
# Useful information you can extract from a GameState (pacman.py)
successorGameState = currentGameState.generatePacmanSuccessor(action)
newPos = successorGameState.getPacmanPosition()
newFood = successorGameState.getFood()
newGhostStates = successorGameState.getGhostStates()
newScaredTimes = [ghostState.scaredTimer for ghostState in newGhostStates]
if successorGameState.isWin():
return float("inf")
for ghostState in newGhostStates:
if util.manhattanDistance(ghostState.getPosition(), newPos) < 2 and ghostState.scaredTimer < 3:
return float("-inf")
foodDist = []
for food in list(newFood.asList()):
foodDist.append(util.manhattanDistance(food, newPos))
foodSuccessor = 0
if (currentGameState.getNumFood() > successorGameState.getNumFood()):
foodSuccessor = 300
return successorGameState.getScore() - 5 * min(foodDist) + foodSuccessor
import os
os._exit(0)
# %cd Pacman
# %run pacman.py -p ReflexAgent
# %run pacman.py -p ReflexAgent -l trickyClassic
# %run pacman.py -g RandomGhost
# %run pacman.py -g DirectionalGhost
# %run pacman.py -p ReflexAgent -q -n 5 -k 3 -f --timeout 5
import os
os._exit(0)
# %cd Pacman
# %run pacman.py -p AlphaBetaAgent -f
# +
# %%writefile AlphaBetaAgentUtil.py
from util import manhattanDistance
from game import Directions
from MinimaxAgentEvalUtil import minimaxAgentEval
def alphaBetaAgentAction(agent, gameState):
maxValue = float("-inf")
alpha = float("-inf")
beta = float("inf")
maxAction = Directions.STOP
for action in gameState.getLegalActions(0):
nextState = gameState.generateSuccessor(0, action)
nextValue = getValue(agent, nextState, 0, 1, alpha, beta)
if nextValue > maxValue:
maxValue = nextValue
maxAction = action
alpha = max(alpha, maxValue)
return maxAction
def getValue(agent, gameState, currentDepth, agentIndex, alpha, beta):
if currentDepth == agent.depth or gameState.isWin() or gameState.isLose():
return minimaxAgentEval(gameState)
elif agentIndex == 0:
return maxValue(agent, gameState,currentDepth,alpha,beta)
else:
return minValue(agent, gameState,currentDepth,agentIndex,alpha,beta)
def maxValue(agent, gameState, currentDepth, alpha, beta):
maxValue = float("-inf")
for action in gameState.getLegalActions(0):
maxValue = max(maxValue, getValue(agent, gameState.generateSuccessor(0, action), currentDepth, 1, alpha, beta))
if maxValue > beta:
return maxValue
alpha = max(alpha, maxValue)
return maxValue
def minValue(agent, gameState, currentDepth, agentIndex, alpha, beta):
minValue = float("inf")
for action in gameState.getLegalActions(agentIndex):
if agentIndex == gameState.getNumAgents()-1:
minValue = min(minValue, getValue(agent, gameState.generateSuccessor(agentIndex, action), currentDepth+1, 0, alpha, beta))
else:
minValue = min(minValue, getValue(agent, gameState.generateSuccessor(agentIndex, action), currentDepth, agentIndex+1, alpha, beta))
if minValue < alpha:
return minValue
beta = min(beta, minValue)
return minValue
# -
import os
os._exit(0)
# %cd Pacman
# %run pacman.py -p AlphaBetaAgent -f -n 10 -q -g DirectionalGhost
|
MinMax/MiniMax-2/Minimax part 2 - pacman.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Intent Classification
# ## Clinc 150 Dataset from UCI
# [An evaluation datset for intent classification and out-of-scope prediction.](https://archive.ics.uci.edu/ml/datasets/CLINC150)
#
# **Citation**
# * <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, <NAME>, and <NAME>. 2019. An evaluation dataset for intent classification and out-of-scope prediction. In Proceedings of EMNLP-IJCNLP
# ### import dependencies
import os
import json
import pickle
import numpy as np
from sklearn.svm import SVC
from sklearn.preprocessing import LabelEncoder
import nltk
from nltk.stem.porter import PorterStemmer
from nltk.tokenize import word_tokenize, RegexpTokenizer
from nltk.corpus import stopwords
stop_words = stopwords.words('english')
tokenizer = RegexpTokenizer(r'\w+')
stemmer = PorterStemmer()
# ### Load data
path = '../data/clinc150_uci/data_full.json'
with open(path) as file:
data = json.load(file)
data.keys()
# #### Collect texts and labels
train_texts = []
train_labels = []
val_texts = []
val_labels = []
test_texts = []
test_labels = []
# collect texts and labels in train and oos_train set
for item in data['train']:
train_texts.append(item[0])
train_labels.append(item[-1])
# collect texts and labels in oos-train set
for item in data['oos_train']:
train_texts.append(item[0])
train_labels.append(item[-1])
# collect texts and labels in val and oos_val set
for item in data['val']:
val_texts.append(item[0])
val_labels.append(item[-1])
# collect texts and labels in oos-train set
for item in data['oos_val']:
val_texts.append(item[0])
val_labels.append(item[-1])
# collect texts and labels in test and oos_test set
for item in data['test']:
test_texts.append(item[0])
test_labels.append(item[-1])
# collect texts and labels in oos-train set
for item in data['oos_test']:
test_texts.append(item[0])
test_labels.append(item[-1])
# collect unique labels
label_set = list(set(train_labels + val_labels + test_labels))
label_set
len(label_set)
# ### Label Preprocessing
# +
# encode categories
# initializer label encoder
le = LabelEncoder()
le.fit(label_set)
# encode labels
train_y = le.transform(train_labels)
val_y = le.transform(val_labels)
test_y = le.transform(test_labels)
# -
# ### Approach 1: TF-IDF Feature Extraction
# #### Term-Frequency & Inverse-Document-Frequency
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vectorizer = TfidfVectorizer(tokenizer = tokenizer.tokenize, analyzer = 'word', stop_words = 'english').fit(train_texts + val_texts + test_texts)
len(tfidf_vectorizer.vocabulary_)
train_X = tfidf_vectorizer.transform(train_texts)
val_X = tfidf_vectorizer.transform(val_texts)
test_X = tfidf_vectorizer.transform(test_texts)
print(train_X.shape)
# #### Training models
# ##### SVM
# initializer SVM classifier
svm = SVC(C = 2, class_weight = 'balanced', kernel = 'rbf', random_state = 97, gamma = 'scale')
# training SVM
svm.fit(train_X, train_y)
svm.score(train_X, train_y)
svm.score(val_X, val_y)
svm.score(test_X, test_y)
# ##### MLP
from sklearn.neural_network import MLPClassifier
classifier = MLPClassifier(hidden_layer_sizes = (256, 151), activation = 'relu', solver = 'sgd',
batch_size = 32, shuffle = True, random_state = 97, learning_rate = 'adaptive',
verbose = True, early_stopping = True)
classifier.fit(train_X, train_y)
classifier.score(val_X, val_y)
# ##### AdaBoost Classifier
from sklearn.ensemble import GradientBoostingClassifier
# initializer Gradient Boosting Classifier
gb_classifier = GradientBoostingClassifier(learning_rate = 0.01, n_iter_no_change = 10, verbose = 1)
# train gb_classifier
gb_classifier.fit(train_X, train_y)
gb_classifier.score(val_X, val_y)
gb_classifier.score(test_X, test_y)
# ### Save model and intent list
# save model
filename = '../intent_classifier.sav'
pickle.dump(svm, open(filename, 'wb'))
# +
# append new_line character
labels = [label+ '\n' for label in label_set]
labels[-1] = labels[-1].strip('\n')
# save intent list
with open('../intent_list.txt', 'w') as file:
file.writelines(labels)
# save vocabs
with open('../vocabs.pickle', 'wb') as file:
vocabs = tfidf_vectorizer.vocabulary_
pickle.dump(vocabs, file)
# save vectorizer
with open('../tfidf_vectorizer.pickle', 'wb') as file:
pickle.dump(tfidf_vectorizer, file)
# -
|
notebooks/Intent_classifier.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 3. Linear Models for Regression
import torch
torch.__version__
import numpy as np
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt
# %matplotlib inline
np.random.seed(1234)
def create_toy_data(func, sample_size, std, domain=[0, 1]):
x = np.linspace(domain[0], domain[1], sample_size)
np.random.shuffle(x)
t = func(x) + np.random.normal(scale=std, size=x.shape)
return x, t
# ## 3.1 Linear Basis Function Models
from sklearn.preprocessing import PolynomialFeatures
from scipy.stats import norm
# +
def guassian_transform(x, means, std):
X = np.zeros((len(x), len(means)))
for i, mean in enumerate(means):
X[:, i] = norm(mean, std).pdf(x)
return X
def sigmoid_transform(x, means, coef):
X = np.zeros((len(x), len(means)))
for i, mean in enumerate(means):
X[:, i] = np.tanh((x - mean) * coef * 0.5) * 0.5 + 0.5
return X
# -
x = np.linspace(-1, 1, 100)
num_features = 11
means = np.linspace(-1, 1, num_features)
X_polynomial = PolynomialFeatures(num_features).fit_transform(x[:, None])
X_gaussian = guassian_transform(x, means, std=0.1);
X_sigmoid = sigmoid_transform(x, means, coef=10)
plt.figure(figsize=(20, 5))
for i, X in enumerate([X_polynomial, X_gaussian, X_sigmoid]):
print(X.shape)
plt.subplot(1, 3, i + 1)
for j in range(5):
plt.plot(x, X[:, j], label=f"{j}")
plt.legend()
# ### 3.1.1 Maximum likelihood and least squares
# +
def sinusoidal(x):
return np.sin(2 * np.pi * x)
x_train, y_train = create_toy_data(sinusoidal, 10, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = sinusoidal(x_test)
# -
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
# +
# Pick one of the three features below
num_features = 11
means = np.linspace(0, 1, num_features)
poly = PolynomialFeatures(num_features)
X_train = poly.fit_transform(x_train[:,None])
X_test = poly.fit_transform(x_test[:,None])
# X_train = guassian_transform(x_train, means, std=0.1)
# X_test = guassian_transform(x_test, means, std=0.1)
# X_train = sigmoid_transform(x_train, means=np.linspace(0, 1, 8), coef=10)
model = LinearRegression()
model.fit(X_train, y_train)
y = model.predict(X_test)
y_std = y.std()
# -
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, label="$\sin(2\pi x)$")
plt.plot(x_test, y, label="prediction")
plt.fill_between(
x_test, y - y_std, y + y_std,
color="orange", alpha=0.5, label="std.")
plt.title(f"test loss is {mean_squared_error(y, y_test):.2f}")
plt.legend()
plt.show()
# ### 3.1.4 Regularized least squares and Gaussian prior
# Let us assume that the outputs are linearly related to the inputs via $\beta$ and that the data are corrupted by some noise $\epsilon$:
# $$y_{n}=\beta x_{n}+\epsilon$$
# where $\beta$ is Gaussian noise with mean $0$ and variance $\sigma^2$. The likelihood is
# $$\prod_{n=1}^{N} \mathcal{N}\left(y_{n} | \beta x_{n}, \sigma^{2}\right),$$
# suppose $\beta$ is Gaussian $\mathcal{N}\left(\beta | 0, \lambda^{-1}\right)$, where $\lambda > 0$. Then we get
# $$\prod_{n=1}^{N} \mathcal{N}\left(y_{n} | \beta x_{n}, \sigma^{2}\right) \mathcal{N}\left(\beta | 0, \lambda^{-1}\right).$$
# $\lambda^{-1}=\sigma_\beta^2$. If $\lambda\to 0$, then $\beta$ will have so much space to learn. Otherwise if $\lambda\to\infty$, then $\beta$ will be constant. We take the logarithm of this formula and drop the constant
# \begin{align*}
# \arg\max_\beta \log(\beta|x,y) &= \arg\max_\beta \log(x,y|\beta)+\log(\beta) \\
# &=\arg\max_\beta -\frac{N}{2} \ln (2 \pi)-\frac{N}{2} \ln \left(\sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{j=1}^{N}\left(y_{j}-\beta x_j\right)^{2} -\frac{N}{2} \ln (2 \pi)-\frac{N}{2} \ln \left(\lambda^{-1}\right)-\frac{\lambda}{2} \sum_{j=1}^{N}\left(\beta-0\right)^{2}\\
# &=\arg\max_\beta -\frac{1}{2 \sigma^{2}} \sum_{j=1}^{N}\left(y_{j}-\beta x_j\right)^{2}-\frac{\lambda N \beta^2}{2}+ \text{const}
# \end{align*}
# which is just L2 regularization
# $$\min \left(\|\mathrm{Y}-\mathrm{X}(\beta)\|_{2}^{2}+\lambda\|\beta\|_{2}^{2}\right)$$
from sklearn.linear_model import Ridge
# +
model = Ridge(alpha=1e-3)
model.fit(X_train, y_train)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, label="$\sin(2\pi x)$")
plt.plot(x_test, y, label="prediction")
plt.title(f"loss is {mean_squared_error(y, y_test):.2f}")
plt.legend()
plt.show()
# -
# ### 3.1.5 L1 regularization and Laplacian prior
# The Laplace distribution is
# $$\text {Laplace}(\mu, b)=\frac{1}{2 b} e^{-\frac{|x-\mu|}{b}}$$
# +
from scipy.stats import laplace
x = np.linspace(-1, 1, 1000)
for scale in [0.1, 0.3, 0.5, 1]:
y = laplace.pdf(x, loc=0, scale=scale)
plt.plot(x, y, label=f"scale={scale}")
plt.legend()
# -
# Laplacian prior $\beta \sim \text { Laplace }(0, b)$,
# \begin{align*}
# \arg \max _{\beta} -\frac{1}{2 \sigma^{2}} \sum_{j=1}^{N}\left(y_{j}-\beta x_{j}\right)^{2} + \log \prod_{j=0}^{N} \frac{1}{2 b} e^{-\frac{\left|\beta_{j}\right|}{2 b}} &= \arg \max _{\beta}-\frac{1}{2 \sigma^{2}} \sum_{j=1}^{N}\left(y_{j}-\beta x_{j}\right)^{2}+ \sum_{j=1}^{N} \left(-\log 2b -\frac{\left|\beta_{j}\right|}{2 b}\right)\\
# &=\arg \min_{\beta}\frac{1}{2 \sigma^{2}} \sum_{j=1}^{N}\left(y_{j}-\beta x_{j}\right)^{2}+ \sum_{j=1}^{N} \left(\log 2b +\frac{\left|\beta_{j}\right|}{2 b}\right)\\
# &=\arg \min _{\beta} \sum_{j=1}^{N}\left(y_{j}-\beta x_{j}\right)^{2}+\lambda\sum_{j=1}^{N}\left|\beta_{j}\right|
# \end{align*}
# +
from sklearn.linear_model import Lasso
model = Lasso(alpha=1e-2)
model.fit(X_train, y_train)
y = model.predict(X_test)
plt.scatter(x_train, y_train, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(x_test, y_test, label="$\sin(2\pi x)$")
plt.plot(x_test, y, label="prediction")
plt.title(f"loss is {mean_squared_error(y, y_test):.2f}")
plt.legend()
# -
model.coef_
# The Lasso regression will zeroing out many coefficient but ridge will only shrink each coefficient
# $$\beta_0=\|(1,0)\|_{1}=1<\left\|\left(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)\right\|_{1}=\sqrt{2}<\beta_1$$
# ## 3.2 The Bias-Variance Decomposition
# Let $f(x)$ be the real function and $\hat{f}(x)$ be the learned function, the error rate is
# \begin{aligned}
# \operatorname{Err}(x) &=(E[\hat{f}(x)]-f(x))^{2}+E\left[(\hat{f}(x)-E[\hat{f}(x)])^{2}\right]+\sigma_{e}^{2}\\
# &=\text { Bias }^{2}+\text { Variance }+\text { Irreducible Error }
# \end{aligned}
means = np.linspace(0, 1, 24)
feature = PolynomialFeatures(24)
# feature = GaussianFeature(np.linspace(0, 1, 24), 0.1)
# feature = SigmoidalFeature(np.linspace(0, 1, 24), 10)
for alpha in [0, 1e-3, 1e-1, 100]:
y_list = []
plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
for i in range(100):
x_train, y_train = create_toy_data(sinusoidal, sample_size=25, std=0.25)
X_train = feature.fit_transform(x_train[:, None])
X_test = feature.fit_transform(x_test[:, None])
model = Ridge(alpha)
model.fit(X_train, y_train)
y = model.predict(X_test)
y_list.append(y)
if i < 20: plt.plot(x_test, y, c="orange")
plt.ylim(-1.5, 1.5)
y_list = np.array(y_list)
y_mean = y_list.mean(axis=0)
plt.title(f"bias is {np.mean(np.square(y_mean-y_test)):.3f}, variance is {np.mean(np.square(y_list-y_mean)):.3f}")
plt.subplot(1, 2, 2)
plt.plot(x_test, y_test)
plt.plot(x_test, y_mean)
plt.ylim(-1.5, 1.5)
plt.show()
# ## 3.3 Bayesian Linear Regression
#
# BayesianRidge estimates a probabilistic model of the regression problem as described above. The prior for the coefficient $w$ is given by a spherical Gaussian:
# \begin{align*}
# p(w | \lambda)&=\mathcal{N}\left(w | 0, \lambda^{-1} \mathbf{I}_{p}\right)\\
# p(y | X, w, \alpha)&=\mathcal{N}(y | X w, \alpha)
# \end{align*}
# The priors over $\lambda$ and $\alpha$ are chosen to be gamma distributions.
# ### 3.3.1 Parameter distribution
from sklearn.linear_model import BayesianRidge
# +
def linear(x):
return -0.3 + 0.5 * x
x_train, y_train = create_toy_data(linear, 100, 0.1, [-1, 1])
x = np.linspace(-1, 1, 100)
w0, w1 = np.meshgrid(
np.linspace(-1, 1, 100),
np.linspace(-1, 1, 100))
w = np.array([w0, w1]).transpose(1, 2, 0)
print(w.shape)
# -
feature = PolynomialFeatures(degree=1)
X_train = feature.fit_transform(x_train[:,None])
X = feature.fit_transform(x[:,None])
print(X.shape)
model = BayesianRidge(lambda_2=1., alpha_2=100.)
for begin, end in [[0, 2], [2, 4], [4, 6], [6, 8], [8, 20], [20, 100]]:
model.fit(X_train[begin: end], y_train[begin: end])
plt.subplot(1, 2, 1)
plt.scatter(-0.3, 0.5, s=200, marker="x")
plt.contour(w0, w1, multivariate_normal.pdf(w, mean=[model.intercept_, model.coef_[1]], cov=model.sigma_))
plt.gca().set_aspect('equal')
plt.title("prior/posterior")
print(model.coef_, model.intercept_)
print(1/model.alpha_, 1/model.lambda_)
plt.subplot(1, 2, 2)
plt.scatter(x_train[:end], y_train[:end], s=20, facecolor="none", edgecolor="steelblue", lw=1)
plt.plot(x, model.predict(X), c="orange")
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.gca().set_aspect('equal', adjustable='box')
plt.show()
# ### 3.3.2 Predictive distribution
# +
x_train, y_train = create_toy_data(sinusoidal, 100, 0.25)
x_test = np.linspace(0, 1, 100)
y_test = sinusoidal(x_test)
mean, std = np.linspace(0, 1, 9), 0.1
X_train = guassian_transform(x_train, mean, std)
X_test = guassian_transform(x_test, mean, std)
# -
model = BayesianRidge(lambda_2=1e-3, alpha_2=2.)
for begin, end in [[0, 1], [1, 2], [2, 4], [4, 8], [8, 25], [25, 100]]:
model.fit(X_train[begin: end], y_train[begin: end])
y, y_std = model.predict(X_test, return_std=True)
plt.scatter(x_train[:end], y_train[:end], s=20, facecolor="none", edgecolor="steelblue", lw=2)
plt.plot(x_test, y_test)
plt.plot(x_test, y)
plt.fill_between(x_test, y - y_std, y + y_std, color="orange", alpha=0.5)
plt.xlim(0, 1)
plt.ylim(-2, 2)
plt.show()
# ## 3.5 The Evidence Approximation
# +
def cubic(x):
return x * (x - 5) * (x + 5)
x_train, y_train = create_toy_data(cubic, 30, 10, [-5, 5])
x_test = np.linspace(-5, 5, 100)
evidences = []
models = []
for i in range(8):
feature = PolynomialFeatures(degree=i)
X_train = feature.fit_transform(x_train)
model = EmpiricalBayesRegression(alpha=100., beta=100.)
model.fit(X_train, y_train, max_iter=100)
evidences.append(model.log_evidence(X_train, y_train))
models.append(model)
degree = np.nanargmax(evidences)
regression = models[degree]
X_test = PolynomialFeature(degree=int(degree)).transform(x_test)
y, y_std = regression.predict(X_test, return_std=True)
plt.scatter(x_train, y_train, s=50, facecolor="none", edgecolor="steelblue", label="observation")
plt.plot(x_test, cubic(x_test), label="x(x-5)(x+5)")
plt.plot(x_test, y, label="prediction")
plt.fill_between(x_test, y - y_std, y + y_std, alpha=0.5, label="std", color="orange")
plt.legend()
plt.show()
plt.plot(evidences)
plt.title("Model evidence")
plt.xlabel("degree")
plt.ylabel("log evidence")
plt.show()
# -
|
notebooks/ch03_Linear_Models_for_Regression-Copy1.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # SVI Part IV: Tips and Tricks
#
# The three SVI tutorials leading up to this one ([Part I](http://pyro.ai/examples/svi_part_i.html), [Part II](http://pyro.ai/examples/svi_part_ii.html), & [Part III](http://pyro.ai/examples/svi_part_iii.html)) go through
# the various steps involved in using Pyro to do variational
# inference.
# Along the way we defined models and guides (i.e. variational distributions),
# setup variational objectives (in particular [ELBOs](https://docs.pyro.ai/en/dev/inference_algos.html?highlight=elbo#module-pyro.infer.elbo)),
# and constructed optimizers ([pyro.optim](http://docs.pyro.ai/en/dev/optimization.html)).
# The effect of all this machinery is to cast Bayesian inference as a *stochastic optimization problem*.
#
# This is all very useful, but in order to arrive at our ultimate goal—learning model parameters, inferring approximate posteriors, making predictions with the posterior predictive distribution, etc.—we need to successfully solve this optimization problem.
# Depending on the details of the particular problem—for example the dimensionality of the latent space, whether we have discrete latent variables, and so on—this can be easy or hard.
# In this tutorial we cover a few tips and tricks we expect to be generally useful for users doing variational inference in Pyro. *ELBO not converging!? Running into NaNs!?* Look below for possible solutions!
#
# #### Pyro Forum
#
# If you’re still having trouble with optimization after reading this tutorial, please don’t hesitate to ask a question on our [forum](https://forum.pyro.ai/)!
# ### 1. Start with a small learning rate
#
# While large learning rates might be appropriate for some problems, it's usually good practice to start with small learning rates like $10^{-3}$
# or $10^{-4}$:
# ```python
# optimizer = pyro.optim.Adam({"lr": 0.001})
# ```
# This is because ELBO gradients are *stochastic*, and potentially high variance, so large learning rates can quickly lead to regions of model/guide parameter space that are numerically unstable or otherwise undesirable.
#
# You can try a larger learning rate once you have achieved stable
# ELBO optimization using a smaller learning rate.
# This is often a good idea because excessively small learning rates can lead to poor optimization.
# In particular small learning rates can lead to getting stuck in poor local optima of the ELBO.
# ### 2. Use Adam or ClippedAdam by default
#
# Use [Adam](http://docs.pyro.ai/en/stable/optimization.html?highlight=clippedadam#pyro.optim.pytorch_optimizers.Adam)
# or [ClippedAdam](http://docs.pyro.ai/en/stable/optimization.html?highlight=clippedadam#pyro.optim.optim.ClippedAdam) by default when doing Stochastic Variational Inference. Note that `ClippedAdam` is just a convenient extension of `Adam` that provides built-in support for learning rate decay and gradient clipping.
#
# The basic reason these optimization algorithms often do well in the context of variational inference is that the smoothing they provide via per-parameter momentum is often essential when the optimization problem is very stochastic. Note that in SVI stochasticity can come from sampling latent variables, from subsampling data, or from both.
#
# In addition to tuning the learning rate in some cases it may be necessary to also tune the pair of `betas` hyperparameters that controls the momentum used by `Adam`. In particular for very stochastic models it may make sense to use higher values of $\beta_1$:
#
# ```python
# betas = (0.95, 0.999)
# ```
# instead of
# ```python
# betas = (0.90, 0.999)
# ```
# ### 3. Consider using a decaying learning rate
#
# While a moderately large learning rate can be useful at the beginning of optimization when you're far from the optimum and want to take large gradient steps, it's often useful to have a smaller learning rate later on so that you don't bounce around the optimum excessively without converging.
# One way to do this is to use the learning rate schedulers [provided](http://docs.pyro.ai/en/stable/optimization.html?highlight=scheduler#pyro.optim.lr_scheduler.PyroLRScheduler) by Pyro. For example usage see the code snippet [here](https://github.com/pyro-ppl/pyro/blob/a106882e8ffbfe6ac96f19aef9a218026482ed51/examples/scanvi/scanvi.py#L265).
# Another convenient way to do this is to use the [ClippedAdam](http://docs.pyro.ai/en/stable/optimization.html?highlight=clippedadam#pyro.optim.optim.ClippedAdam) optimizer that has built-in support for learning rate decay via the `lrd` argument:
#
# ```python
# num_steps = 1000
# initial_lr = 0.001
# gamma = 0.1 # final learning rate will be gamma * initial_lr
# lrd = gamma ** (1 / num_steps)
# optim = pyro.optim.ClippedAdam({'lr': initial_lr, 'lrd': lrd})
# ```
# ### 4. Make sure your model and guide distributions have the same support
#
# Suppose you have a distribution in your `model` with constrained support, e.g. a LogNormal distribution, which has support on the positive real axis:
# ```python
# def model():
# pyro.sample("x", dist.LogNormal(0.0, 1.0))
# ```
# Then you need to ensure that the accompanying `sample` site in the `guide` has the same support:
# ```python
# def good_guide():
# loc = pyro.param("loc", torch.tensor(0.0))
# pyro.sample("x", dist.LogNormal(loc, 1.0))
# ```
# If you fail to do this and use for example the following inadmissable guide:
# ```python
# def bad_guide():
# loc = pyro.param("loc", torch.tensor(0.0))
# # Normal may sample x < 0
# pyro.sample("x", dist.Normal(loc, 1.0))
# ```
# you will likely run into NaNs very quickly.
# This is because the `log_prob` of a LogNormal distribution evaluated at a sample `x` that satisfies `x<0` is undefined, and the `bad_guide` is likely to produce such samples.
#
# ### 5. Constrain parameters that need to be constrained
# In a similar vein, you need to make sure that the parameters used to instantiate distributions are valid; otherwise you will quickly run into NaNs.
# For example the `scale` parameter of a Normal distribution needs to be positive. Thus the following `bad_guide` is problematic:
# ```python
# def bad_guide():
# scale = pyro.sample("scale", torch.tensor(1.0))
# pyro.sample("x", dist.Normal(0.0, scale))
# ```
# while the following `good_guide` correctly uses a constraint to ensure positivity:
# ```python
# from pyro.distributions import constraints
#
# def good_guide():
# scale = pyro.sample("scale", torch.tensor(0.05),
# constraint=constraints.positive)
# pyro.sample("x", dist.Normal(0.0, scale))
# ```
# ### 6. If you are having trouble constructing a custom guide, use an AutoGuide
#
# In order for a model/guide pair to lead to stable optimization a number of conditions need to be satisfied, some of which we have covered above.
# Sometimes it can be difficult to diagnose the reason for numerical instability or poor convergence.
# Among other reasons this is because the fundamental issue could arise in a number of different places: in the model, in the guide, or in the choice of optimization algorithm or hyperparameters.
#
# Sometimes the problem is actually in your model even though you think it's in the guide.
# Conversely, sometimes the problem is in your guide even though you think it's in the model or somewhere else.
# For these reasons it can be helpful to reduce the number of moving parts while you try to identify the underyling issue.
# One convenient way to do this is to replace your custom guide with a [pyro.infer.AutoGuide](http://docs.pyro.ai/en/stable/infer.autoguide.html#module-pyro.infer.autoguide).
#
# For example, if all the latent variables in your model are continuous, you can try a [pyro.infer.AutoNormal](http://docs.pyro.ai/en/stable/infer.autoguide.html#autonormal) guide.
# Alternatively, you can use MAP inference instead of full-blown variational inference. See the [MLE/MAP](http://pyro.ai/examples/mle_map.html) tutorial for further details. Once you have MAP inference working, there's good reason to believe that your model is setup correctly (at least as far as basic numerical stability is concerned).
# If you're interested in obtaining approximate posterior distributions, you can now follow-up with full-blown SVI. Indeed a natural order of operations might use the following sequence of increasingly flexible autoguides:
#
# [AutoDelta](http://docs.pyro.ai/en/stable/infer.autoguide.html#autodelta) → [AutoNormal](http://docs.pyro.ai/en/stable/infer.autoguide.html#autonormal) → [AutoLowRankMultivariateNormal](http://docs.pyro.ai/en/stable/infer.autoguide.html#autolowrankmultivariatenormal)
#
# If you find that you want a more flexible guide or that you want to take more control over how exactly the guide is defined, at this juncture you can proceed to build a custom guide.
# One way to go about doing this is to leverage [easy guides](http://pyro.ai/examples/easyguide.html), which strike a balance between the control of a fully custom guide and the automation of an autoguide.
#
# Also note that autoguides offer several initialization strategies and it may be necessary in some cases to experiment with these in order to get good optimization performance.
# One way to control initialization behavior is using the `init_loc_fn`.
# For example usage of `init_loc_fn`, including example usage for the easy guide API, see [here](https://github.com/pyro-ppl/pyro/blob/a106882e8ffbfe6ac96f19aef9a218026482ed51/examples/sparse_gamma_def.py#L202).
# ### 7. Parameter initialization matters: initialize guide distributions to have low variance
#
# Initialization in optimization problems can make all the difference between finding a good solution and failing catastrophically.
# It is difficult to come up with a comprehensive set of good practices for initialization, as good initialization schemes are often very problem dependent.
# In the context of Stochastic Variational Inference it is generally a good idea to initialize your guide distributions so that they have **low variance**.
# This is because the ELBO gradients you use to optimize the ELBO are stochastic.
# If the ELBO gradients you get at the beginning of ELBO optimization exhibit high variance, you may be led into numerically unstable or otherwise undesirable regions of parameter space.
# One way to guard against this potential hazard is to pay close attention to parameters in your guide that control variance.
# For example we would generally expect this to be a reasonably initialized guide:
# ```python
# from pyro.distributions import constraints
#
# def good_guide():
# scale = pyro.sample("scale", torch.tensor(0.05),
# constraint=constraints.positive)
# pyro.sample("x", dist.Normal(0.0, scale))
# ```
# while the following high-variance guide is very likely to lead to problems:
# ```python
# def bad_guide():
# scale = pyro.sample("scale", torch.tensor(12345.6),
# constraint=constraints.positive)
# pyro.sample("x", dist.Normal(0.0, scale))
# ```
#
# Note that the initial variance of autoguides can be controlled with the `init_scale` argument, see e.g. [here](http://docs.pyro.ai/en/stable/infer.autoguide.html?highlight=init_scale#autonormal) for `AutoNormal`.
# ### 8. Explore trade-offs controlled by `num_particles`, mini-batch size, etc.
#
# Optimization can be difficult if your ELBO exhibits large variance.
# One way you can try to mitigate this issue is to increase the number of particles used to compute each stochastic ELBO estimate:
#
# ```python
# elbo = pyro.infer.Trace_ELBO(num_particles=10,
# vectorize_particles=True)
# ```
# (Note that to use `vectorized_particles=True` you need to ensure your model and guide are properly vectorized; see the [tensor shapes tutorial](http://pyro.ai/examples/tensor_shapes.html) for best practices.)
# This results in lower variance gradients at the cost of more compute.
# If you are doing data subsampling, the mini-batch size offers a similar trade-off: larger mini-batch sizes reduce the variance at the cost of more compute.
# Although what's best is problem dependent, it's usually worth taking more gradient steps with fewer particles than fewer gradient steps with more particles.
# An important caveat to this is when you're running on a GPU, in which case (at least for some models) the cost of increasing `num_particles` or your mini-batch size may be sublinear, in which case increasing `num_particles` is likely more attractive.
#
# ### 9. Use `TraceMeanField_ELBO` if applicable
#
# The basic `ELBO` implementation in Pyro, [Trace_ELBO](http://docs.pyro.ai/en/stable/inference_algos.html?highlight=tracemeanfield#pyro.infer.trace_elbo.Trace_ELBO), uses stochastic samples to estimate the KL divergence term.
# When analytic KL diverences are available, you may be able to lower ELBO variance by using analytic KL divergences instead. This functionality is provided by [TraceMeanField_ELBO](http://docs.pyro.ai/en/stable/inference_algos.html?highlight=tracemeanfield#pyro.infer.trace_elbo.Trace_ELBO).
# ### 10. Consider normalizing your ELBO
#
# By default Pyro computes a un-normalized ELBO, i.e. it computes the quantity that is a lower bound to the log evidence computed on the full set of data that is being conditioned on.
# For large datasets this can be a number of large magnitude.
# Since computers use finite precision (e.g. 32-bit floats) to do arithmetic, large numbers can be problematic for numerical stability, since they can lead to loss of precision, under/overflow, etc.
# For this reason it can be helpful in many cases to normalize your ELBO so that it is roughly order one.
# This can also be helpful for getting a rough feeling for how good your ELBO numbers are.
# For example if we have $N$ datapoints of dimension $D$ (e.g. $N$ real-valued vectors of dimension $D$) then we generally expect a reasonably well optimized ELBO to be order $N \times D$.
# Thus if we renormalize our ELBO by a factor of $N \times D$ we expect an ELBO of order one.
# While this is just a rough rule-of-thumb, if we use this kind of normalization and obtain ELBO values like $-123.4$ or $1234.5$ then something is probably wrong: perhaps our model is terribly mis-specified; perhaps our initialization is catastrophically bad, etc.
# For details on how you can scale your ELBO by a normalization constant see [this tutorial](http://pyro.ai/examples/custom_objectives.html#Example:-Scaling-the-Loss).
# ### 11. Pay attention to scales
#
# Scales of numbers matter.
# They matter for at least two important reasons:
# i) scales can make or break a particular initialization scheme;
# ii) as discussed in the previous section, scales can have an impact on numerical precision and stability.
#
# To make this concrete suppose you are doing linear regression, i.e.
# you're learning a linear map of the form $Y = W @ X$. Often the data comes with particular units.
# For example some of the components of the covariate $X$ may be in units of dollars (e.g. house prices), while others may be in units of density (e.g. residents per square mile).
# Perhaps the the first covariate has typical values like $10^5$, while the second covariate has typical values like $10^2$.
# You should always pay attention when you encounter numbers that range across many orders of magnitude.
# In many cases it makes sense to normalize things so that they are order unity.
# For example you might measure house prices in units of $100,000.
#
# These sorts of data transformations can have a number of benefits for downstream modeling and inference.
# For example if you've normalized all of your covariates appropriately, it may be reasonable to set a simple
# isotropic prior on your weights
#
# ```python
# pyro.sample("W", dist.Normal(torch.zeros(2), torch.ones(2)))
# ```
# instead of having to specify different prior covariances for different covariates
# ```python
# prior_scale = torch.tensor([1.0e-5, 1.0e-2])
# pyro.sample("W", dist.Normal(torch.zeros(2), prior_scale))
# ```
# There are other benefits too.
# It now becomes easier to initialize appropriate parameters for your guide.
# It is also now much more likely that the default initializations used by a [pyro.infer.AutoGuide](http://docs.pyro.ai/en/stable/infer.autoguide.html#module-pyro.infer.autoguide) will work for your problem.
# ### 12. Keep validation enabled
#
# By default Pyro enables validation logic that can be helpful in debugging models and guides.
# For example, validation logic will inform you when distribution parameters become invalid.
# Unless you have good reason to do otherwise, keep the validation logic enabled.
# Once you're satisfied with a model and inference procedure, you may wish to disable validation using [pyro.enable_validation](http://docs.pyro.ai/en/stable/primitives.html?highlight=enable_validation#pyro.primitives.enable_validation).
#
# Similarly in the context of `ELBOs` it is a good idea to set
# ```python
# strict_enumeration_warning=True
# ```
# when you are enumerating discrete latent variables.
# ### 13. Tensor shape errors
#
# If you're running into tensor shape errors please make sure you have carefully read the [corresponding tutorial](http://pyro.ai/examples/tensor_shapes.html).
# ### 14. Enumerate discrete latent variables if possible
#
# If your model contains discrete latent variables it may make sense to enumerate them out exactly, since this can significantly reduce ELBO variance.
# For more discussion see the [corresponding tutorial](http://pyro.ai/examples/enumeration.html).
# ### 15. Some complex models can benefit from KL annealing
#
# The particular form of the ELBO encodes a trade-off between model fit via the expected log likelihood term and a prior regularization term via the KL divergence.
# In some cases the KL divergence can act as a barrier that makes it difficult to find good optima.
# In these cases it can help to anneal the relevant strength of the KL divergence term during optimization. For further discussion see the [deep markov model tutorial](http://pyro.ai/examples/dmm.html#The-Black-Magic-of-Optimization).
#
#
#
#
# ### 16. Consider clipping gradients or constraining parameters defensively
#
# Certain parameters in your model or guide may control distribution parameters that can be sensitive to numerical issues.
# For example, the `concentration` and `rate` parameters that defines a [Gamma](http://docs.pyro.ai/en/stable/distributions.html#gamma) distribution may exhibit such sensitivity.
# In these cases it may make sense to clip gradients or constrain parameters defensively.
# See [this code snippet](https://github.com/pyro-ppl/pyro/blob/dev/examples/sparse_gamma_def.py#L135) for an example of gradient clipping.
# For a simple example of "defensive" parameter constraints consider the `concentration` parameter of a `Gamma` distribution.
# This parameter must be positive: `concentration` > 0.
# If we want to ensure that `concentration` stays away from zero we can use a `param` statement with an appropriate constraint:
#
# ```python
# from pyro.distributions import constraints
#
# concentration = pyro.param("concentration", torch.tensor(0.5),
# constraints.greater_than(0.001))
# ```
# These kinds of tricks can help ensure that your models and guides stay away from numerically dangerous parts of parameter space.
|
tutorial/source/svi_part_iv.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Load Ni-Mo data
# +
from pymatgen import Structure
from monty.serialization import loadfn
data = loadfn('data.json')
train_structures = [d['structure'] for d in data]
train_energies = [d['outputs']['energy'] for d in data]
train_forces = [d['outputs']['forces'] for d in data]
vasp_stress_order = ['xx', 'yy', 'zz', 'xy', 'yz', 'xz']
snap_stress_order = ['xx', 'yy', 'zz', 'yz', 'xz', 'xy']
train_stresses = []
for d in data:
virial_stress = d['outputs']['stress']
train_stresses.append([virial_stress[vasp_stress_order.index(n)] * 0.1 for n in snap_stress_order]) # convert kbar to GPa
# -
# # Setup the initial weights for training (If not, the weights for energy, force, and stress will be both equal to 1)
# +
import numpy as np
from maml.utils import pool_from, convert_docs
train_pool = pool_from(train_structures, train_energies, train_forces, train_stresses)
_, df = convert_docs(train_pool, include_stress=True)
weights = np.ones(len(df['dtype']), )
# set the weights for energy equal to 100
weights[df['dtype'] == 'energy'] = 100
weights[df['dtype'] == 'force'] = 1
weights[df['dtype'] == 'stress'] = 0.01
# -
# # Set up the SNAP and train
# +
from maml.base import SKLModel
from maml.describers import BispectrumCoefficients
from sklearn.linear_model import LinearRegression
from maml.apps.pes import SNAPotential
element_profile = {'Mo': {'r': 5.0, 'w': 1}, 'Ni': {'r': 5.0, 'w': 1}}
describer = BispectrumCoefficients(rcutfac=0.5, twojmax=6, element_profile=element_profile,
quadratic=True, pot_fit=True, include_stress=True)
model = SKLModel(describer=describer, model=LinearRegression())
qsnap = SNAPotential(model=model)
qsnap.train(train_structures, train_energies, train_forces, train_stresses, include_stress=True, sample_weight=weights)
# -
# # Predict the energies, forces, stresses of training data
df_orig, df_predict = qsnap.evaluate(test_structures=train_structures,
test_energies=train_energies,
test_forces=train_forces,
test_stresses=train_stresses,
include_stress=True)
# # Lattice constants, Elastic constant
# +
from maml.apps.pes import ElasticConstant
Ni_ec_calculator = ElasticConstant(ff_settings=qsnap, lattice='fcc', alat=3.51, atom_type='Ni')
Ni_C11, Ni_C12, Ni_C44, _ = Ni_ec_calculator.calculate()
print('Ni', ' C11: ', Ni_C11, 'C12: ', Ni_C12, 'C44: ', Ni_C44)
# -
Mo_ec_calculator = ElasticConstant(ff_settings=qsnap, lattice='bcc', alat=3.17, atom_type='Mo')
Mo_C11, Mo_C12, Mo_C44, _ = Mo_ec_calculator.calculate()
print('Mo', ' C11: ', Mo_C11, 'C12: ', Mo_C12, 'C44: ', Mo_C44)
|
notebooks/pes/qsnap/example_with_stress.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import pandas as pd
from scrapenhl2.scrape import autoupdate, schedules, team_info, players
from scrapenhl2.manipulate import manipulate as manip
# -
# The purpose of this script is to get game-by-game 5v5 toi counts by player and team for every game since 2012-13. We can get this information from the 5v5 player log easily.
# Update data
# autoupdate.autoupdate() # Comment in if needed, and loop if needed
# manip.get_5v5_player_log(2017, force_create) # Comment in if needed, and loop if needed
log = pd.concat([manip.get_5v5_player_log(season).assign(Season=season) for season in range(2012, 2018)])
sch = pd.concat([schedules.get_season_schedule(season).assign(Season=season) for season in range(2012, 2018)])
log.head()
# All we need to do is:
# - Sum TOION and TOIOFF, and take distinct values to get team counts
# - Take TOION for individual counts
# +
# Teams
teamtoi = log.assign(TOI=log.TOION + log.TOIOFF) \
[['Season', 'Game', 'TOI']] \
.groupby(['Season', 'Game'], as_index=False) \
.max() # take max to avoid floating point errors that may fell drop_duplicates
teamtoi = sch[['Season', 'Game', 'Home', 'Road']] \
.melt(id_vars=['Season', 'Game'], var_name='HR', value_name='TeamID') \
.merge(teamtoi, how='inner', on=['Season', 'Game']) \
.drop_duplicates()
# Make names into str, and convert TOI from hours to minutes
teamtoi.loc[:, 'Team'] = teamtoi.TeamID.apply(lambda x: team_info.team_as_str(x))
teamtoi.loc[:, 'TOI(min)'] = teamtoi.TOI * 60
teamtoi = teamtoi.drop(['TeamID', 'TOI'], axis=1)
teamtoi.head()
# +
# Individuals
indivtoi = log[['Season', 'Game', 'PlayerID', 'TOION', 'TeamID']]
# IDs to names and TOI from hours to minutes
indivtoi.loc[:, 'Player'] = players.playerlst_as_str(indivtoi.PlayerID.values)
indivtoi.loc[:, 'Team'] = indivtoi.TeamID.apply(lambda x: team_info.team_as_str(x))
indivtoi.loc[:, 'TOI(min)'] = indivtoi.TOION * 60
indivtoi = indivtoi.drop(['TeamID', 'TOION', 'PlayerID'], axis=1)
indivtoi.head()
# -
# Write to file
teamtoi.to_csv('/Users/muneebalam/Desktop/teamtoi.csv')
indivtoi.to_csv('/Users/muneebalam/Desktop/indivtoi.csv')
|
examples/5v5 TOI for teams and players/5v5 TOI for teams and players.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # PEL218 - Atividade 1
# Processamento de Linguagem Narual (Prof. <NAME>)
#
# <NAME> (RA 120122-7)
# ## Atividade
# Implementar o HMM
# * Objetivo: classificar Part-Of-Speech (V, N, P, DT, etc...)
# * Treinar na base Folha 95 (pode ser parcial)
# * Testar a classificação na base Folha 94 (pode ser parcial)
# * Fazer um relatório com experimentos:
# * Precisão / Revocação / Assertividade
# * Discussão dos Resultados
# ## Resolução
# Foi escolhida a linguagem *Python* versão 3.8.5. Os arquivos folha95 foram usados para treinamento e os folha94 para teste.
# +
import collections
import math
import re
import numpy as np
import matplotlib.pyplot as plt
# -
folha95_filepath = 'CHAVEFolha/cg.Folha.1995'
folha94_filepath = 'CHAVEFolha/cg.Folha.1994.reduced'
# ### Funções para ler, preparar e tokenizar os documentos:
#
# `read_sentence:` lê o conteudo da tag `<s></s>` na forma de *generator*
#
# `tokenize:` tokenização de palavras na forma de *generator* incluindo seu rótulo
def read_sentences(filepath):
# Controls the position in the state machine
with open(filepath, 'r', encoding='iso-8859-1') as file:
sentence = []
waiting_start = True
for line in file:
if waiting_start:
if '<s>' in line:
waiting_start = False
else:
if '</s>' in line:
if len(sentence) > 1:
# Sentences should have at least 2 elements to be considered valid
yield sentence
# Reset search
waiting_start = True
sentence = []
else:
# Consume the line greedly
sentence.append(line)
def tokenize(sentence, add_tag_cfg=True):
re_word = re.compile(r'^(.+?)(?:\s|\t|$)')
re_tag = re.compile(r'\s([A-Z]+)\s')
tokens = []
for line in sentence:
# Word is the first part. Strip and convert to lower
word = re_word.search(line).group(1).lower()
if add_tag_cfg:
maybe_tag = re_tag.search(line)
tag = maybe_tag.group(1) if maybe_tag else 'INVTAG'
tag_adj = '<<' + tag + '>>'
tokens.append((word, tag_adj))
else:
tokens.append(word)
return tokens
# ### Análise das bases de dados
def words_tags_counter(filepath):
words = collections.Counter()
tags = collections.Counter()
for sentence in read_sentences(filepath):
tokens = tokenize(sentence)
words.update([token[0] for token in tokens])
tags.update([token[1] for token in tokens])
return words, tags
dict_95, tags_95 = words_tags_counter(folha95_filepath)
dict_94, tags_94 = words_tags_counter(folha94_filepath)
n_sentences_95 = sum([1 for _ in read_sentences(folha95_filepath)])
n_sentences_94 = sum([1 for _ in read_sentences(folha94_filepath)])
# +
print('\nQuantidade de rótulos da Folha94 em relação a Folha95: {:.4f}%'.format(sum(dict_94.values()) / sum(dict_95.values()) * 100))
print('Quantidade de sentenças da Folha94 em relação a Folha95: {:.4f}%'.format(n_sentences_94 / n_sentences_95 * 100))
print('\nFolha95')
print('\tQuantide de exemplos:', sum(dict_95.values()))
print('\tQuantide de sentenças:', n_sentences_95)
print('\tTamanho do dicionário:', len(dict_95))
print('\tQuantidade de rótulos:', len(tags_95))
print('\t10 palavras mais frequêntes:', dict_95.most_common(10))
print('\tRótulos e sua frequência:', tags_95.most_common())
print('\nFolha94')
print('\tQuantide de exemplos:', sum(dict_94.values()))
print('\tQuantide de sentenças:', n_sentences_94)
print('\tTamanho do dicionário:', len(dict_94))
print('\tQuantidade de rótulos:', len(tags_94))
print('\t10 palavras mais frequêntes:', dict_94.most_common(10))
print('\tRótulos e sua frequência:', tags_94.most_common())
# -
# Ambas bases possuem distribuições similares, porém a base de treino, a folha 95, possui 2 rótulos a mais do que a outra base sendo elas $IND$ e $S$. Porém, as 10 palavras e símbolos mais utilizas são os mesmos contendo pontuação e *stopwords*. Tais palavras e símbolos são importantes para o modelo atual já que pretendemos aprender a rotular todas as instâncias disponíveis.
# +
freq_dict_95 = freq = sorted(list(dict_95.values()), reverse=True)
freq_tags_95 = freq = sorted(list(tags_95.values()), reverse=True)
freq_dict_94 = freq = sorted(list(dict_94.values()), reverse=True)
freq_tags_94 = freq = sorted(list(tags_94.values()), reverse=True)
plt.subplots(2, 2, figsize=(15,15))
plt.subplot(2, 2, 1)
plt.plot(freq_dict_95)
plt.title('Frequência das palavras - Folha95 (Train)')
plt.xscale('log')
plt.yscale('log')
plt.subplot(2, 2, 2)
plt.plot(freq_tags_95)
plt.title('Frequência das tags - Folha95 (Train)')
plt.subplot(2, 2, 3)
plt.plot(freq_dict_94)
plt.title('Frequência das palavras - Folha94 (Test)')
plt.xscale('log')
plt.yscale('log')
plt.subplot(2, 2, 4)
plt.plot(freq_tags_94)
plt.title('Frequência das tags - Folha94 (Test)')
# -
# O gráfico mais a esquerda representa a frequência das palavras e seu decaimento. É possível reparar que a frequência das palavras diminui de forma logarítmica, tal efeito é semelhante a *Lei de Zipf ([link](https://pt.wikipedia.org/wiki/Lei_de_Zipf)), com ressalvas para as extremidades. Já os gráficos mais a direita representam a frequência dos rótulos e seu decaimento, nesse caso o decaimento não é exponêncial e sim linear nos rótulos mais utilizados. Ambas bases de dados possuem distribuições similares já que os gráficos da parte superior são parecidos com os gráficos da parte inferior.
# ### Modelo escondido de Markov
def train(sentences):
counters = collections.Counter()
words = set()
tags = set()
for sentence in sentences:
last_word = None
last_tag = None
for token in tokenize(sentence):
word = token[0]
tag = token[1]
# Probability of each tag
counters[tag] += 1
# Emission counters
counters[(tag, word)] += 1
last_word = word
# Transitional counter
if last_tag:
counters[(last_tag, tag)] += 1
last_tag = tag
# Update the sets
tags.add(tag)
words.add(word)
# Return a model. The model is the counters and the tags and the dictionary
return counters, words, tags
def predict(sentence, model):
# Use Viterbi dynamic programming
# viterbi table
m = collections.defaultdict(float)
paths = collections.defaultdict(None)
# Model unpacking
counters, words, tags = model
tokens = tokenize(sentence, add_tag_cfg=False)
n_tokens = len(tokens)
# Initial probability of each tag
p_tag = {tag: counters[tag]/n_tokens for tag in tags}
w_0 = tokens[0]
for tag in tags:
# Construct the viterbi table for t_0
m[(tag, 0)] = p_tag[tag] * counters[(tag, w_0)] / counters[tag]
# Calculate the viterbi for each time
for t, w in enumerate(tokens):
if t == 0:
continue
for to_tag in tags:
m[(to_tag, t)] = -1
for from_tag in tags:
tmp = m[(from_tag, t-1)] \
* counters[(from_tag, to_tag)] / counters[from_tag] \
* counters[(to_tag, w)] / counters[to_tag]
if tmp > m[(to_tag, t)]:
m[(to_tag, t)] = tmp
paths[(to_tag, t)] = from_tag
# Build up output
last = {tag: paths[(tag, n_tokens - 1)] for tag in tags}
last = max(last, key=lambda x: last[x])
out = [last]
for t in range(n_tokens - 1, 0, -1):
out.append(paths[(last, t)])
last = paths[(last, t)]
# return the predicitons os each elements of the sentence
return list(reversed(out))
# O cálculo das métricas é feita através de 3 funções, a primeira é a inicializaçao, após a acumulação e depois o cálculo das medidas. Essa divisão é necessária para que seja possível fazer predições de longas sequências de texto sem ter a necessidade de armazenas todo o resultado em memória.
# +
def score_init(model):
# Create the confusion matrix
_, _, tags = model
n_tags = len(tags)
matrix = np.zeros((n_tags, n_tags))
tags_idx = {tag: idx for idx, tag in enumerate(tags)}
return tags, tags_idx, matrix,
def score_acc(labeled_predictions, score_model):
tags, tags_idx, matrix = score_model
for prediction, actual in labeled_predictions:
actual_idx = tags_idx[actual]
prediction_idx = tags_idx[prediction]
matrix[actual_idx][prediction_idx] += 1
return tags, tags_idx, matrix
def score_calc(score_model):
tags, tags_idx, matrix = score_model
# Sum the matrix in both directions (row-wise and column-wise)
matrix_sum_axis_0 = matrix.sum(axis=0)
matrix_sum_axis_1 = matrix.sum(axis=1)
f1_func = lambda precision, recall: (2 * precision * recall) / (precision + recall)
score = {}
# Calculate the score for each label
for tag in tags:
idx = tags_idx[tag]
accuracy = matrix[idx][idx] / np.sum(matrix[idx])
precision = matrix[idx][idx] / matrix_sum_axis_1[idx]
recall = matrix[idx][idx] / matrix_sum_axis_0[idx]
f1 = f1_func(precision, recall)
score[tag] = {
'accuracy': accuracy,
'precision': precision,
'recall': recall,
'f1': f1
}
# Micro averaging
micro_avg_precision = matrix.trace() / sum(matrix_sum_axis_1)
micro_avg_recall = matrix.trace() / sum(matrix_sum_axis_0)
micro_avg_f1 = f1_func(micro_avg_precision, micro_avg_recall)
score['micro-avg'] = {
'precision': micro_avg_precision,
'recall': micro_avg_recall,
'f1': micro_avg_f1
}
# Macro averaging
macro_avg_precision = np.mean([score[label]['precision']
for label in score.keys()])
macro_avg_recall = np.mean([score[label]['recall']
for label in score.keys()])
macro_avg_f1 = f1_func(macro_avg_precision, macro_avg_recall)
score['macro-avg'] = {
'precision': macro_avg_precision,
'recall': macro_avg_recall,
'f1': macro_avg_f1
}
# Return both score (per label, micro and macro) and the confusion matrix
return score, matrix, tags_idx,
# -
# O experimento é realizado utilizando a base de dados `Folha95` e uma amostra das primeiras 1 milhão de linhas da `Folha94` para validação e cálculo de métricas.
# Train the HMM model
model = train(read_sentences(folha95_filepath))
# +
# Validate the model using Folha94
score_model = score_init(model)
#sentences = [next(read_sentences(folha95_filepath))]
#for sentence in sentences:
for sentence in read_sentences(folha94_filepath):
prediction = predict(sentence, model)
# Create a labeled prediction
tokens = tokenize(sentence)
labeled_predictions = []
for token, pred_tag in zip(tokens, prediction):
actual = token[1]
labeled_predictions.append((pred_tag, actual))
# Acumulate the score
score_model = score_acc(labeled_predictions, score_model)
# Calculate the score
score_result, matrix, tags_idx = score_calc(score_model)
# +
micro_f1 = score_result['micro-avg']['f1']
print('Experimento:')
print('\tMicro-averaging f1={:.4f}\n'.format(micro_f1))
# Sort the tags by f1
scored_tags = sorted(tags_idx.keys(),
key=lambda x: score_result[x]['f1']
if not math.isnan(score_result[x]['f1'])
else 0.0,
reverse=True)
for tag in scored_tags:
score = score_result[tag]
accuracy = score['accuracy']
precision = score['precision']
recall = score['recall']
f1 = score['f1']
print('\tRótulo {}: acurácia={:.4f}, precisão={:.4f}, revocação={:.4f}, f1={:.4f}'.format(tag, accuracy, precision, recall, f1))
# -
# ### Análise
#
# O experimento sobre modelo escondido de *Markov* foi realizado utilizando a base de dados `Folha95` como entrada e uma amostra da primeira 1 milhão de linhas da base de dados `Folha94` para avaliação. As bases foram divididas em sentenças delimitadas pelos símbolos $<s>$ e $</s>$; sendo que, somente sentenças maiores do que 1 unidade foram consideradas, já que o modelo necessita de ao menos 1 probabilidade de transição que é composta por no mínimo 2 variáveis.
#
# A necessidade da sub-utilização da base de dados de avaliação é devido ao modelo de predição utilizar o algorítmo de `viterbi` que possui complexidade computacional de $O(N^2T)$, sem considerar a operação $argmax$, tornado o estudo computacionalmente denso.
#
# O rótulo de cada símbolo foi extraído das bases de dados através da utilização de expressão regular buscando a primeira ocorrência de uma sequência de letras maiúsculas separadas por caracteres de espaço (como tabulação, quebra de linha e espaços).
#
# Foi identificado na base de dados `Folha95` 2 rótulos adicionais a versão completa da base `Folha94`, sendo eles `<<S>>` e `<<IND>>`, cada qual com apenas 1 ocorrência, sendo o primeiro proveniente da linha `outros [outro] <-sam> <fmc> IND VFIN @FMV` e o segundo da linha `\t [] <-sam> S ACC`. Tal diferença não causa alterações significativas no resultado do experimento.
#
# Os rótulos `<<PP>>`, `<<F>>`, `<<M>>`, `<<IND>>` e `<<S>>` não foram encontradas na versão reduzida da base de dados de validaçao; e as duas últimas não encontrada na versão completa como explicado no parágrafo anterior; e portanto seu desempenho é representado como `nan` na listagem acima. Dessa lista de rótulos, apenas `<<PP>>` apareceu 4 vezes na base de testes, enquanto todos os outros apareceram apenas 1 vez, indicando sua baixa utilização nessa base de dados. Exemplos de linhas são: `em=frente [em=frente] PP @AS<`, `pra- [=para+a] <hyfen> PRP_DET F S ` e `outro [outro] <-sam> M `.
# Os 3 rótulos com maior desempenho f1 foram `<<V>>`, `<<ADV>>`, `<<N>>`, sendo eles verbos, advérbios e substantivos, sendo que todos esses símbolos estão nos 10 mais frequêntes rótulos da base de treinamento.
#
# Os 3 rótulos com pior desempenho f1 foram `<<ALT>>`, `<<EC>>` e `<<IN>>`, sendo eles formas alternativas, prefixos e interjeicões ou representações diferentes do esperado. A última categoria tende a necessitar de uma análise semântica para identificar representaçõs diferentes do esperado e portanto modelos probabilísticos direcionados para análise sintática possuem desempenho baixa; formas alternativas possui um baixo desempenho porque seu rótulo verdadeiro é diferente desse (devido ao desempenho ruim do tokenizador) e assim sue correlação de emissão e transição é baixa. O rótulo `EC` utilizado em palavras como `pré-`, `semi-` e `ultra-` possui revocaçao alta e precisão baixa, indicando uma grande quantidade de falso-positivos.
#
# Destaca-se também o rótul
#
# A medida f1 *micro-averaging* foi utilizada devido ao não aparecimento de certas classes na base de treinamento. Seu desempenho ficou em 0.7268 favorecendo as classes mais frequêntes, como os 3 rótulos de maior desempenho, já que eles estão nas 5 classes mais utilizadas.
|
PEL218_processamento_de_linguagem_natural/ex5_hidden_markov_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + _cell_guid="b1076dfc-b9ad-4769-8c92-a6c4dae69d19" _uuid="8f2839f25d086af736a60e9eeb907d3b93b6e0e5"
# This Python 3 environment comes with many helpful analytics libraries installed
# It is defined by the kaggle/python docker image: https://github.com/kaggle/docker-python
# For example, here's several helpful packages to load in
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import keras
from keras.layers import Dense, Flatten, BatchNormalization, Activation, Dropout
from keras.layers.convolutional import Conv2D, MaxPooling2D
from keras.models import Sequential
from keras.optimizers import RMSprop
from keras.preprocessing.image import ImageDataGenerator
from keras.callbacks import ReduceLROnPlateau
from sklearn.model_selection import train_test_split
from keras.models import model_from_json
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import cv2
# Input data files are available in the "../input/" directory.
# For example, running this (by clicking run or pressing Shift+Enter) will list the files in the input directory
import os
print(os.listdir("input"))
# Any results you write to the current directory are saved as output.
# + _cell_guid="79c7e3d0-c299-4dcb-8224-4455121ee9b0" _uuid="d629ff2d2480ee46fbb7e2d37f6b5fab8052498a"
test = pd.read_csv('input/test/test.csv')
# -
def plot_pupils(image, left_x, left_y, right_x, right_y):
plt.figure()
plt.imshow(image,cmap='gray')
plt.scatter(left_x, left_y, s=5, c='red', marker='o')
plt.scatter(right_x, right_y, s=5, c='red', marker='o')
plt.show()
# + _uuid="d85087cd6b4e42e7fbf6d49e1994a05ca0c5b849"
ntest = test.shape[0]
image = []
for i in range (0,ntest):
img = test['Image'][i].split(' ')
img = [0 if x =='' else x for x in img]
image.append(img)
image_list = np.array(image,dtype = 'float')
test_data = image_list.reshape(-1,96,96,1)
test_data = test_data/255
# -
test_data[0,:,:,0]
test_data[0,:,:,0].shape
img_test = cv2.imread('yuri_phone.jpg',0)/255
img_test
img_test.shape
dim = (96, 96)
resized = cv2.resize(img_test, dim, interpolation = cv2.INTER_AREA)
resized.shape
# load json and create model
json_file = open('model.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
model = model_from_json(loaded_model_json)
# load weights into new model
model.load_weights("model_weights.h5")
print("Loaded model from disk")
image1 = []
image1.append(resized)
image_list1 = np.array(image1,dtype = 'float')
test_data1 = image_list1.reshape(-1,96,96,1)
def transform_to_model(image):
imgage = image/255
dim = (96, 96)
resized = cv2.resize(imgage, dim, interpolation = cv2.INTER_AREA)
image1 = []
image1.append(resized)
image_list1 = np.array(image1,dtype = 'float')
test_data1 = image_list1.reshape(-1,96,96,1)
return test_data1
y_pred1 = model.predict(test_data1)
plt.imshow(resized,cmap='gray')
plot_pupils(test_data1[0,:,:,0],y_pred1[0,0], y_pred1[0,1],y_pred1[0,2], y_pred1[0,3])
plt.imshow(img_test,cmap='gray')
img_test = cv2.imread('../from_drop_box/<NAME> PD.jpg',0)
# +
#img_test = cv2.imread('yuri_phone.jpg',0)
# -
test_data1 = transform_to_model(img_test)
y_pred1 = model.predict(test_data1)
plot_pupils(test_data1[0,:,:,0],y_pred1[0,0], y_pred1[0,1],y_pred1[0,2], y_pred1[0,3])
img_test.shape
# load json and create model
json_file = open('model.json', 'r')
loaded_model_json = json_file.read()
json_file.close()
model = model_from_json(loaded_model_json)
# load weights into new model
model.load_weights("model_weights.h5")
print("Loaded model from disk")
# + _uuid="548c2060dabed0a895b4b4b6dcc9366ee6cd9a1b"
#predicting test_data
y_pred = model.predict(test_data)
# -
y_pred[0,:]
for i in range(10):
plot_pupils(test_data[i,:,:,0],y_pred[i,0], y_pred[i,1],y_pred[i,2], y_pred[i,3])
|
Run_Inference_on_DK_test_set.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
from mobilechelonian import Turtle
t = Turtle()
t.speed(3)
t.backward(100)
for loop in range(5) :
t.forward(200)
t.right(144)
t = Turtle()
t.speed(10)
t.backward(100)
for i in range(20) :
t.forward(200)
t.right(162)
t = Turtle()
t.speed(10)
t.backward(100)
for i in range(10) :
t.circle(30)
t.right(36)
|
_notebooks/tracés turtle.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Day 14: Docking Data
# As your ferry approaches the sea port, the captain asks for your help again. The computer system that runs this port isn't compatible with the docking program on the ferry, so the docking parameters aren't being correctly initialized in the docking program's memory.
#
# After a brief inspection, you discover that the sea port's computer system uses a strange bitmask system in its initialization program. Although you don't have the correct decoder chip handy, you can emulate it in software!
#
# The initialization program (your puzzle input) can either update the bitmask or write a value to memory. Values and memory addresses are both 36-bit unsigned integers. For example, ignoring bitmasks for a moment, a line like mem[8] = 11 would write the value 11 to memory address 8.
#
# The bitmask is always given as a string of 36 bits, written with the most significant bit (representing 2^35) on the left and the least significant bit (2^0, that is, the 1s bit) on the right. The current bitmask is applied to values immediately before they are written to memory: a 0 or 1 overwrites the corresponding bit in the value, while an X leaves the bit in the value unchanged.
#
# For example, consider the following program:
# ```
# mask = XXXXXXXXXXXXXXXXXXXXXXXXXXXXX1XXXX0X
# mem[8] = 11
# mem[7] = 101
# mem[8] = 0
# ```
# This program starts by specifying a bitmask (mask = ....). The mask it specifies will overwrite two bits in every written value: the 2s bit is overwritten with 0, and the 64s bit is overwritten with 1.
#
# The program then attempts to write the value 11 to memory address 8. By expanding everything out to individual bits, the mask is applied as follows:
# ```
# value: 000000000000000000000000000000001011 (decimal 11)
# mask: XXXXXXXXXXXXXXXXXXXXXXXXXXXXX1XXXX0X
# result: 000000000000000000000000000001001001 (decimal 73)
# ```
# So, because of the mask, the value 73 is written to memory address 8 instead. Then, the program tries to write 101 to address 7:
# ```
# value: 000000000000000000000000000001100101 (decimal 101)
# mask: XXXXXXXXXXXXXXXXXXXXXXXXXXXXX1XXXX0X
# result: 000000000000000000000000000001100101 (decimal 101)
# ```
# This time, the mask has no effect, as the bits it overwrote were already the values the mask tried to set. Finally, the program tries to write 0 to address 8:
# ```
# value: 000000000000000000000000000000000000 (decimal 0)
# mask: XXXXXXXXXXXXXXXXXXXXXXXXXXXXX1XXXX0X
# result: 000000000000000000000000000001000000 (decimal 64)
# ```
# 64 is written to address 8 instead, overwriting the value that was there previously.
#
# To initialize your ferry's docking program, you need the sum of all values left in memory after the initialization program completes. (The entire 36-bit address space begins initialized to the value 0 at every address.) In the above example, only two values in memory are not zero - 101 (at address 7) and 64 (at address 8) - producing a sum of 165.
#
# Execute the initialization program. What is the sum of all values left in memory after it completes?
with open("input.txt","r") as f:
input_data = f.read().split("\n")
def transfer(number, mask):
number_bin = bin(number)[2:]
number_bin = ["0"] * (len(mask) - len(number_bin)) + list(number_bin)
for i, x in enumerate(mask):
if x != "X":
number_bin[i] = x
number_bin_str = ""
for x in number_bin:
number_bin_str = number_bin_str + x
return int(number_bin_str, 2)
def sum_value(input_data):
result = dict()
for row in input_data:
if row.startswith("mask"):
mask = row.split(" = ")[1]
else:
mem, number = row.split(" = ")
mem_int = int(mem[4:-1])
new_number = transfer(int(number), mask)
result[mem_int] = new_number
return sum(list(result.values()))
sum_value(input_data)
# # Part Two
# For some reason, the sea port's computer system still can't communicate with your ferry's docking program. It must be using version 2 of the decoder chip!
#
# A version 2 decoder chip doesn't modify the values being written at all. Instead, it acts as a memory address decoder. Immediately before a value is written to memory, each bit in the bitmask modifies the corresponding bit of the destination memory address in the following way:
#
# * If the bitmask bit is 0, the corresponding memory address bit is unchanged.
# * If the bitmask bit is 1, the corresponding memory address bit is overwritten with 1.
# * If the bitmask bit is X, the corresponding memory address bit is floating.
# A floating bit is not connected to anything and instead fluctuates unpredictably. In practice, this means the floating bits will take on all possible values, potentially causing many memory addresses to be written all at once!
#
# For example, consider the following program:
# ```
# mask = 000000000000000000000000000000X1001X
# mem[42] = 100
# mask = 00000000000000000000000000000000X0XX
# mem[26] = 1
# ```
# When this program goes to write to memory address 42, it first applies the bitmask:
# ```
# address: 000000000000000000000000000000101010 (decimal 42)
# mask: 000000000000000000000000000000X1001X
# result: 000000000000000000000000000000X1101X
# ```
# After applying the mask, four bits are overwritten, three of which are different, and two of which are floating. Floating bits take on every possible combination of values; with two floating bits, four actual memory addresses are written:
# ```
# 000000000000000000000000000000011010 (decimal 26)
# 000000000000000000000000000000011011 (decimal 27)
# 000000000000000000000000000000111010 (decimal 58)
# 000000000000000000000000000000111011 (decimal 59)
# ```
# Next, the program is about to write to memory address 26 with a different bitmask:
# ```
# address: 000000000000000000000000000000011010 (decimal 26)
# mask: 00000000000000000000000000000000X0XX
# result: 00000000000000000000000000000001X0XX
# ```
# This results in an address with three floating bits, causing writes to eight memory addresses:
# ```
# 000000000000000000000000000000010000 (decimal 16)
# 000000000000000000000000000000010001 (decimal 17)
# 000000000000000000000000000000010010 (decimal 18)
# 000000000000000000000000000000010011 (decimal 19)
# 000000000000000000000000000000011000 (decimal 24)
# 000000000000000000000000000000011001 (decimal 25)
# 000000000000000000000000000000011010 (decimal 26)
# 000000000000000000000000000000011011 (decimal 27)
# ```
# The entire 36-bit address space still begins initialized to the value 0 at every address, and you still need the sum of all values left in memory at the end of the program. In this example, the sum is 208.
#
# Execute the initialization program using an emulator for a version 2 decoder chip. What is the sum of all values left in memory after it completes?
#
#
def transferX(number_bin):
if "X" not in number_bin:
return [number_bin]
for i in range(len(number_bin)):
if number_bin[i] == "X":
bin1 = number_bin.copy()
bin1[i] = "1"
bin2 = number_bin.copy()
bin2[i] = "0"
return transferX(bin1)+transferX(bin2)
def transfer_2(number, mask):
number_bin = bin(number)[2:]
number_bin = ["0"] * (len(mask) - len(number_bin)) + list(number_bin)
for i, x in enumerate(mask):
if x == "1":
number_bin[i] = "1"
if x == "X":
number_bin[i] = "X"
all_number_bin = transferX(number_bin)
result = []
for x in all_number_bin:
bin_x = ""
for b in x:
bin_x = bin_x + b
result.append(int(bin_x,2))
return result
def sum_value_2(input_data):
result = dict()
for row in input_data:
if row.startswith("mask"):
mask = row.split(" = ")[1]
else:
mem, number = row.split(" = ")
mem_int = int(mem[4:-1])
mem_list = transfer_2(mem_int, mask)
for x in mem_list:
result[x] = int(number)
return sum(list(result.values()))
sum_value_2(input_data)
|
2020/Day14/Day14.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
import sys
sys.path.append('/mdml_analysis/lib/python3.5/site-packages')
# +
# %matplotlib inline
# for output setting
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
import matplotlib.pyplot as plt
import seaborn as sns; sns.set(rc={'figure.figsize':(15,15)})
import numpy as np
import pandas as pd
import seaborn
from sqlalchemy import create_engine
from sklearn.preprocessing import MinMaxScaler
engine = create_engine('postgresql://postgres:mimic@127.0.0.1:5432/mimic')
# -
def daily_qsofa_analysis():
sql = """
SELECT st0.*
, ROUND(st0.qsofa_more_than_2_cnt * 100.0 / cnt, 2) AS qsofa_ratio
, (max_date_id - min_date_id) AS diff_date
, (CASE WHEN qsofa_more_than_2_cnt = 0 THEN -1 ELSE (min_qsofa_date_id - min_date_id) END) AS diff_qsofa_date
, (CASE WHEN st1.is_death = 'true' THEN 1 ELSE 0 END) AS death_flag
, CASE WHEN is_death = 'true' AND (max_date_id - min_date_id) = 0 THEN 100.00
WHEN is_death = 'true' AND (max_date_id - min_date_id) > 0 THEN ROUND(1 * 100.0 / (max_date_id - min_date_id), 2)
ELSE 0
END AS death_ratio
FROM (
SELECT subject_id
, COUNT(1) AS cnt
, MIN(qsofa_score) AS min_qsofa
, MAX(qsofa_score) AS max_qsofa
, ROUND(AVG(qsofa_score), 2) AS avg_qsofa
, SUM( CASE WHEN qsofa_score = 0 THEN 1 ELSE 0 END) AS qsofa_0_cnt
, SUM( CASE WHEN qsofa_score = 1 THEN 1 ELSE 0 END) AS qsofa_1_cnt
, SUM( CASE WHEN qsofa_score = 2 THEN 1 ELSE 0 END) AS qsofa_2_cnt
, SUM( CASE WHEN qsofa_score = 3 THEN 1 ELSE 0 END) AS qsofa_3_cnt
, SUM( CASE WHEN qsofa_score >= 2 THEN 1 ELSE 0 END) AS qsofa_more_than_2_cnt
, MIN(date_id) AS min_date_id
, MAX(date_id) AS max_date_id
, MIN(CASE WHEN qsofa_score >= 2 THEN date_id ELSE NULL END) AS min_qsofa_date_id
FROM daily_qsofa
GROUP BY subject_id
) st0
LEFT OUTER JOIN detailed_patients st1
ON (st0.subject_id = st1.subject_id)
;
"""
return pd.read_sql(sql, engine)
df = daily_qsofa_analysis()
df.head()
df.set_index(['subject_id'], inplace=True)
df.head()
num_cols = list(df.select_dtypes(exclude=['object']).columns)
num_cols
corr = df[num_cols].corr()
mask = np.zeros_like(corr, dtype=np.bool)
mask[np.triu_indices_from(mask)] = True
f, ax = plt.subplots(figsize=(70, 40))
cmap = seaborn.diverging_palette(220, 10, as_cmap=True)
# Draw the heatmap with the mask and correct aspect ratio
seaborn.heatmap(corr, mask=mask, cmap=cmap, vmax=.3, center=0, square=True, linewidths=.5, cbar_kws={"shrink": .5})
corr['death_flag'].sort_values()
corr['death_ratio'].sort_values()
|
notebook/daily_qsofa_death_correlation.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# This notebook was prepared by [<NAME>](https://github.com/donnemartin). Source and license info is on [GitHub](https://github.com/donnemartin/interactive-coding-challenges).
# # Challenge Notebook
# ## Problem: Flip one bit from 0 to 1 to maximize the longest sequence of 1s.
#
# * [Constraints](#Constraints)
# * [Test Cases](#Test-Cases)
# * [Algorithm](#Algorithm)
# * [Code](#Code)
# * [Unit Test](#Unit-Test)
# * [Solution Notebook](#Solution-Notebook)
# ## Constraints
#
# * Is the input an int, base 2?
# * Yes
# * Can we assume the input is a 32 bit number?
# * Yes
# * Do we have to validate the length of the input?
# * No
# * Is the output an int?
# * Yes
# * Can we assume the inputs are valid?
# * No
# * Can we assume we are using a positive number since Python doesn't have an >>> operator?
# * Yes
# * Can we assume this fits memory?
# * Yes
# ## Test Cases
#
# * None -> Exception
# * All 1's -> Count of 1s
# * All 0's -> 1
# * General case
# * 0000 1111 1101 1101 1111 0011 1111 0000 -> 10 (ten)
# ## Algorithm
#
# Refer to the [Solution Notebook](). If you are stuck and need a hint, the solution notebook's algorithm discussion might be a good place to start.
# ## Code
class Bits(object):
def flip_bit(self, num):
# TODO: Implement me
pass
# ## Unit Test
# **The following unit test is expected to fail until you solve the challenge.**
# +
# # %load test_flip_bit.py
import unittest
class TestBits(unittest.TestCase):
def test_flip_bit(self):
bits = Bits()
self.assertRaises(TypeError, bits.flip_bit, None)
self.assertEqual(bits.flip_bit(0), 1)
self.assertEqual(bits.flip_bit(-1), bits.MAX_BITS)
num = int('00001111110111011110001111110000', base=2)
expected = 10
self.assertEqual(bits.flip_bit(num), expected)
num = int('00000100111011101111100011111011', base=2)
expected = 9
self.assertEqual(bits.flip_bit(num), expected)
num = int('00010011101110111110001111101111', base=2)
expected = 10
self.assertEqual(bits.flip_bit(num), expected)
print('Success: test_print_binary')
def main():
test = TestBits()
test.test_flip_bit()
if __name__ == '__main__':
main()
# -
# ## Solution Notebook
#
# Review the [Solution Notebook]() for a discussion on algorithms and code solutions.
|
bit_manipulation/flip_bit/flip_bit_challenge.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # 1. Paper and Group Details
#
# **Paper Title:** Duplex Generative Adversarial Network for Unsupervised Domain Adaptation - CVPR 2018
#
# **Authors:** <NAME>, <NAME>, <NAME>, <NAME>
#
# **Link:** http://openaccess.thecvf.com/content_cvpr_2018/papers/Hu_Duplex_Generative_Adversarial_CVPR_2018_paper.pdf
#
# **Group Members:** <NAME>, <NAME>
#
# Contact Information can be found in the README.
# **Reviewers:** <NAME>, <NAME>
# # 2. Goals
#
# Our results can be compared with the original results at the last section of the notebook.
#
# ## 2.1. Quantitative Results
#
# We planned to meet the classification accuracy of the architecture mentioned in Table 1, 2nd row from the bottom, 3rd column from the left (92.46%), where the model was trained on SVHN dataset with labels + unlabeled MNIST dataset, and tested against the MNIST dataset (SVHN -> MNIST) to show the domain adaptation quality. We plan to reproduce similar results with digits 0-4 to cut down on dataset size.
#
# ## 2.2. Qualitative Results
#
# We planned to reproduce Figure 4, where the model and the training is the same as the quantitative results, however this time SVHN images are fed into the network to generate images similar to the ones in MNIST, where digit category is preserved (for digits 0-4)
# # 3. Paper Summary
#
# ## 3.1 Problem Statement
#
# As models scale up, collecting new training data to train models becomes more and more expensive. Transfer learning is a remedy technique to this complication where the model exploits its experience gained from training for other tasks that are similar to the one at hand.
#
# DupGAN mainly tackles the issue of **unsupervised domain adaptation**, a subset of Transfer Learning in which there are two domains that share categories but have different data distrubutions. **The ground truth labels are only available for one of the domains** (the source domain), therefore the model is expected to utilize the sample-label relation of this domain to unsupervisedly classify the samples of the other domain (the target domain).
#
# In our reproduction we will treat these domains as follows:
# - Source domain training data: SVHN train set digit images + labels for digits 0-4
# - Target domain training data: MNIST train set digit images for digits 0-4
# - Target domain test data (for classification): MNIST test set digit images for digits 0-4
#
# ## 3.2 Definitions and Model Architecture Overview
# Let the source domain training data be denoted as $S = \{(x^s_i, y^s_i)\}^n_{i=1}$ with source images $X^s = \{x^s_i\}^n_{i=1}$ and labels $Y^s = \{y^s_i\}^n_{i=1}$. Each $y^s \in Y^s$ correspond to a label in the set $B = \{b_0,\ b_1...b_c\}$ with cardinality $c$. Let the target domain training data be denoted as $X^t = \{x^t_i\}^m_{i=1}$. **Note that there is no $Y^t$.**
#
# DupGAN attempts to better the classification quality by training for category preserving domain translation as well as classification. To that end, a hybrid autoencoder GAN architecture where the generator $G$ with two outputs is put against two discriminators $D^s, D^t$ for the source and the target domains respectively:
#
# <img src="images/architecture.png" />
# <center>Figure 1: Overview of DupGAN Architecture</center>
#
# The encoder $E$ at the beginning compresses the images (without any regard to type of domain) into encodings which should be ideally independent of the domain:
#
# \begin{align}
# Z^s &= \{z^s \mid E(x^s) = z^s,\ x^s \in X^s \} \\
# Z^t &= \{z^t \mid E(x^t) = z^t,\ x^t \in X^t \} \\
# Z &= Z^s \cup Z^t
# \end{align}
#
# $G$ takes this encoding as well as a domain code $a$ as input, where $a \in \{s, t \}$ indicates the domain type of the image that should be generated. In the end, the following 4 modes of $G$ are integral during training, for $z^s \in Z^s$ and $z^t \in Z^t$:
#
# - source to source, $X^{ss} = \{x^{ss} \mid G(z^s,s) = x^{ss},\ z^s \in Z^s \}$
# - target to target, $X^{tt} = \{x^{tt} \mid G(z^t,t) = x^{tt},\ z^t \in Z^t \}$
# - source to target, $X^{ss} = \{x^{st} \mid G(z^s,t) = x^{st},\ z^s \in Z^s \}$
# - target to source, $X^{ss} = \{x^{ts} \mid G(z^s,s) = x^{ts},\ z^t \in Z^t \}$
#
# The first two are used for assessing reconstruction quality to ensure $E$ and $G$ work properly as an autoencoder. The other two are to deceive $D^s, D^t$ for GAN training.
#
# Other than telling real images apart from the real ones, the discriminators also categorize the images in the correct labels. To that end, the discriminators categorize images in bins $B' = \{b_0,\ b_1...b_{c+1}\}$ of cardinality $c+1$ with some probabilities $p^s_l, p^t_l$, where first $c$ bins correspond to the labels and the last bin $b_{c+1}$ is reserved for fake images.
#
# \begin{align}
# p^{s}_l &= D^s(x,l) & l \in B',\ x \in X^{s} \cup X^{ts} \\
# p^{t}_l &= D^t(x,l) & l \in B',\ x \in X^{t} \cup X^{st}
# \end{align}
#
# Lastly, there is a classifier $C$ on top of the encodings. It sorts images from both domains into $L$ with some probability $p^c_l$:
#
# \begin{align}
# p^c_l &= C(z,l) & l \in B,\ z \in Z
# \end{align}
#
# It might seem redundant since the $D^s, D^t$ are also doing classification, but the classifier is necessary for the target domain at the pretraining stage. The purpose of $C$ will become clear in the further sections.
# ## 3.3. Training Details and Objective Functions for the Modules
#
# ### 3.3.1. Pseudolabels for Target Domain
#
# In the following sections, the objective function formulations for the models require labels for both domains. **Since the ground truth labels are missing for the target domain, they are compansated with pseudolabels generated from the classifier $C$**. The high confidence target dataset with supervised labels is defined as follows:
#
# \begin{align}
# T &= \{ (x^t,y^{t}) \mid C(E(x^t),y^{t}) > p_{thres},\ x^t \in X^t,\ y^{t} \in B \}
# \end{align}
#
# with $X^{t'}$ and $Y^{t'}$ as data and the labels of this constructed dataset. After pretraining (explained below), $T$ replaces $X^{t}$.
#
# $p_{thres}$ is a model hyperparameter (we picked it as 0.99 in our experiments). Note that **$T$ may change at every training step since $C$ might classify the target domain data in a different way. Therefore $T$ is renewed at every epoch of the training step.**
#
# To increase the chances of pseudolabels being accurate, $E$ and $C$ are pretrained solely with $S$ before core DupGAN training loop.
# ### 3.3.2. Generator Related Losses
#
# The generator $G$ has two purposes:
# - Act as an autoencoder with the Encoder $E$, and reconstruct the original image from the encoding:
#
# \begin{align}
# L_{recon}(E,G) &= \sum_{x^s \in X^s}||x^s - G(E(x^s),s)|| + \sum_{x^t in X^t}||x^t - G(E(x^t),t)|| \\
# &= \sum_{x^s \in X^s}||x^s - x^{ss})|| + \sum_{x^t \in X^t}||x^t - x^{tt}||
# \end{align}
#
# - Decieve the discriminators with fake images generated from the other domain:
#
# \begin{align}
# L_{deceive}(E,G) &= \sum_{{(x^s,y^s)} \in S}H_{B'}(D^t(G(E(x^s),t),y^s))+\sum_{{(x^t,y^t)} \in T} H_{B'}(D^s(G(E(x^t),s),y^t)) \\
# &= \sum_{{(x^s,y^s)} \in S}H_{B'}(D^t(x^{st},y^s))+\sum_{{(x^t,y^t)} \in T} H_{B'}(D^s(x^{ts},y^t))
# \end{align}
# with $H_{B'}(\cdot,\cdot)$ as cross-entropy loss along $B'$. **The labels from the other domains are also used to make the discriminator classify the counterfeit images in the correct category other than not being fake.** This forces the generator to preserve the category when translating images. Also note that **$y^t$ are generated with the classifier $C$ since no ground truth is available** for target domain labels.
#
# In the end, the total generator related loss becomes:
#
# \begin{align}
# L_{gen}(E,G) &= \alpha L_{recon} + L_{deceive}
# \end{align}
#
# where $\alpha$ is a model hyperparameter (we picked it as 40.0).
#
# ### 3.3.3. Discriminator Related Losses
#
# The discriminators are not joint in DupGAN. $D^s$ and $D^t$ discriminate source and target images from counterfeit ones generated from the other domain. Both employ the cross-entropy discriminator loss in the original GAN.
# - Discriminator $D^s$ has the following loss:
# \begin{align}
# L_{D^s} &= \sum_{{(x^s,y^s)} \in S}H_{B'}(D^t(x^s,y^s))+\sum_{{x^t} \in X^t} H_{B'}(G(E(x^t),s),b_{c+1})) \\
# &= \sum_{{(x^s,y^s)} \in S}H_{B'}(D^t(x^s,y^s))+\sum_{{x^t} \in X^t} H_{B'}(D(x^{ts},b_{c+1}))
# \end{align}
# with $b_{c+1}$ representing the fake category.
#
# - Discriminator $D^t$ is similar, **but pseudolabels are used instead of ground truth**:
#
# \begin{align}
# L_{D^t} &= \sum_{{(x^t,y^t)} \in T}H_{B'}(D^t(x^t,y^t))+\sum_{{x^s} \in X^s} H_{B'}(G(E(x^s),t),b_{c+1})) \\
# &= \sum_{{(x^t,y^t)} \in T}H_{B'}(D^t(x^t,y^t))+\sum_{{x^s} \in X^s} H_{B'}(D(x^{st},b_{c+1}))
# \end{align}
#
# The total discriminator loss is the sum of these losses:
#
# \begin{align}
# L_{disc}(D^s,D^t) &= L_{D^s} + L_{D^t}
# \end{align}
#
# ### 3.3.4. Classifier Related Losses
#
# The training for classifier $C$ continues even after pretraining step:
#
# \begin{align}
# L_{cl}(C,E) &= \sum_{(x, y) \in S \cup T}H_{B}(C(E(x),y))
# \end{align}
#
# **During pretraining, $T = \emptyset$. After the pretraining ends, $T$ is recalculated at the beginning of every epoch.**
#
# ### 3.3.5. Total Loss and the Training Loop
#
# Total loss is as follows:
#
# \begin{align}
# L &= \beta L_{cl} + L_{gen} + L_{disc}
# \end{align}
#
# with $\beta$ as model hyperparameter (we picked it as 40.0).
#
# The training loop is similar to the one in the original GAN, but with the addition of pretraining part and the pseudolabel calculation step:
# <br>
# <br>
#
# <center>Algorithm 1: DupGAN Training Loop.</center>
# <hr style="border:2px solid gray"> </hr>
#
# **input**: Source domain $S$.and target domain $X^t$ <br>
# **output**: Model weights $W_E,\ W_G,\ W_C,\ W_{D^s},\ W_{D^t}$
#
# 1: Pretrain $E$ and $C$ with $S$ by backpropping on $L_{cl}$ until convergence: <br>
# $W_E \leftarrow W_E - \eta\frac{\delta L_{cl}}{\delta W_E}$ <br>
# $W_C \leftarrow W_C - \eta\frac{\delta L_{cl}}{\delta W_C}$
#
# 2: **until** convergence, **do** <br>
#
#  2.1: Calculate $T$.
#
#  2.2: Backprop on discriminator losses: <br>
#  $W_{D^s} \leftarrow W_{D^s} - \eta\frac{\delta L_{D^s}}{\delta W_{D^s}}$ <br>
#  $W_{D^t} \leftarrow W_{D^t} - \eta\frac{\delta L_{D^t}}{\delta W_{D^t}}$
#
#  2.2: Backprop on generator and classifier losses: <br>
#  $W_{G} \leftarrow W_{G} - \eta\frac{\delta L_{gen}}{\delta W_G}$ <br>
#  $W_{C} \leftarrow W_{C} - \eta\frac{\delta L_{cl}}{\delta W_C}$ <br>
#  $W_{E} \leftarrow W_{E} - \eta\frac{\delta (L_{cl}+L_{gen}}{\delta W_E}
#
# 3: **return** $W_E,\ W_G,\ W_C,\ W_{D^s},\ W_{D^t}$
#
#
#
# <hr style="border:2px solid gray"> </hr>
# # 4. Implementation
#
# ## 4.1 Implementation Difficulties and Differences from the Paper Specifications
#
# Main difficulty we faced was that the architecture of the network was not presented in the original DUPGAN paper. It was described as "similar" to an architecture from an another paper named Unsupervised Image-to-Image Translation Networks (https://arxiv.org/pdf/1703.00848.pdf). Upon investigating this paper, we noticed that DUPGAN and UNIT had some differences regarding main architecture design (such as UNIT learning an actual probability distrubution which was used to sample the latent representation and DUPGAN outputting the latent vectors directly), which forced us to make some minor changes that we thought to be successful. Because of these assumptions and trials we consider this to be the reason of our accuracy result being different from our initial goal. These differences are listed below.
#
# - In UNIT paper, for SVHN -> MNIST change, authors used the extra training set and test set. The original MNIST images were gray-scale. But in UNIT paper they are converted to RGB images and performed a data augmentation where they also used the inversions of the original MNIST images for training. We did not follow this augmentation method and used all images as they were.
#
# - Classifier C in the original DUPGAN paper was not specified, and did not exist at all in UNIT. So we picked it as a fully connected layer on top of the encoder followed by a LeakyRELU layer, as it was the simplest choice.
#
# - Regarding the encoder implementation UNIT paper has 1024 channels (neurons since inputs/outputs are 1x1) but those are mu,sigmas that represent a 512x1 latent vector. However DUPGAN does not do any sampling, so 512 channels suffice. We also removed the extra fully connected layer that expands to 1024 nodes owing to this.
#
# - Learning rates are changed for experimental purposes
#
# - Highly confident labels are gathered at each epoch rather than each batch. Since GAN training is already unstable, we wanted to make sure we gathered a statistically more meaningful percentage and overcame the batch size being too small (64) to sample properly.
#
# - Hyperparameters $\alpha$ and $\beta$ of the model are different from the ones specified in the paper.
# ## 4.2 Implementation Overview
#
# Hyperparameters and Other Settings are listed here. You may want to change the device field if no gpu support is available.
# +
import torch
import os
from train import EncoderClassifierTrainer, GeneratorDiscriminatorTrainer
from utils import mnist_dataset, svhn_dataset, generic_dataloader
from notebook_utils import *
class Params:
#change to cpu if gpu is not available
device = 'cuda'
datasets_root = os.path.join('datasets', '')
ckpt_root = os.path.join('ckpts', '')
# location of pre-trained encoder_classifier file
encoder_classifier_ckpt_file = 'ckpts/encoder_classifier_16.tar'
# prepended to each saved checkpoint file name for encoder_classifier
encoder_classifier_experiment_name = 'encoder_classifier_notebook'
# location of pre-trained generator_discriminator file
generator_discriminator_ckpt_file = 'ckpts/generator_discriminator_99.tar'
# prepended to each saved checkpoint file name for generator_discriminator
generator_discriminator_experiment_name = 'encoder_classifier_notebook'
# dupgan specific params
dupgan_alpha = 40.0 #different from the specified value in the paper
dupgan_beta = 40.0
encoder_classifier_confidence_threshold = 0.99
# optimizer params
encoder_classifier_adam_lr = 0.0002
generator_adam_lr = 0.00002
discriminator_adam_lr = 0.00001
encoder_classifier_adam_beta1 = 0.5
encoder_classifier_adam_beta2 = 0.999
generator_adam_beta1 = 0.5
generator_adam_beta2 = 0.999
discriminator_adam_beta1 = 0.5
discriminator_adam_beta2 = 0.999
# other training params
batch_size = 64
encoder_classifier_num_epochs = 30
generator_discriminator_num_epochs = 100
# other non-training params
demo = True #demo mode, training outputs are more frequent
params = Params()
# -
# dataloading, missing datasets are automatically downloaded
svhn_trainsplit = svhn_dataset(params.datasets_root, "train")
svhn_testsplit = svhn_dataset(params.datasets_root, "test")
mnist_testsplit = mnist_dataset(params.datasets_root, False)
mnist_trainsplit = mnist_dataset(params.datasets_root, True)
# The Encoder - Classifier architecture is as follows. It has 2 outputs, an encoding of the input and a confidence vector from this encoding for digit classification.
encoder_classifier_trainer = EncoderClassifierTrainer(params.device, params,
svhn_trainsplit, svhn_testsplit, mnist_trainsplit, mnist_testsplit,
ckpt_root=params.ckpt_root)
print(encoder_classifier_trainer.encoder_classifier)
# Pretraining is straightforward, the model is trained only with respect to the labels from the same domain (in our case SVHN digit images and digit labels) at this stage. Here is the training procedure for one batch:
def encoder_classifier_notebook_train_one_batch(self, batch):
inputs, labels = batch
inputs = inputs.to(self.device)
labels = labels.to(self.device)
self.optimizer.zero_grad()
# output is a 1x5 vector of confidences for digits [0-4] (not normalized)
classifier_out, _ = self.encoder_classifier(inputs)
# criterion is cross-entropy loss against labels on top of a softmax layer
loss = self.criterion(classifier_out, labels)
loss.backward()
#optimizer is ADAM
self.optimizer.step()
# The training procedure finds context as follows. The model is saved and evaluated after every epoch in the code below, but you are free to modify it to your liking.
# +
def encoder_classifier_notebook_train_model(self):
self.encoder_classifier.train()
#initial self.epoch value is taken from saved checkpoint, it is -1 for a brand new model.
for self.epoch in range(self.epoch+1, params.encoder_classifier_num_epochs):
for batch in self.svhn_trainsplit_loader:
encoder_classifier_notebook_train_one_batch(self, batch)
if params.demo:
encoder_classifier_notebook_evaluator_evaluate_and_print(self)
encoder_classifier_notebook_evaluator_evaluate_and_print(self)
#saved every epoch under ckpt_root
self.save()
try:
encoder_classifier_notebook_evaluator_reset()
encoder_classifier_notebook_train_model(encoder_classifier_trainer)
except KeyboardInterrupt:
pass
# -
# The "pretrained" model for pretraining can be loaded with the snippet below. You can also load the model you have trained above by changing the path.
#encoder_classifier_trainer.load("absolute path to model.tar that you may have
# trained above and would like to continue training")
encoder_classifier_notebook_load_and_print_params(encoder_classifier_trainer, params.encoder_classifier_ckpt_file)
# Here are the classification results for the pretrained model. About 79% of the MNIST dataset is confidently classified with the classifier pretrained only with SVHN dataset.
encoder_classifier_notebook_evaluator_reset()
encoder_classifier_notebook_evaluator_evaluate_and_print(encoder_classifier_trainer)
# The pretrained Encoder - Classifier is later embedded to the actual GAN architecture below. Here is the Generator architecture. Notice the extra 513th dimension in the first layer accounting for the domain code that the generator takes as an extra input.
encoder_classifier = encoder_classifier_trainer.encoder_classifier
encoder_classifier_optimizer = encoder_classifier_trainer.optimizer
generator_discriminator_trainer = GeneratorDiscriminatorTrainer(params.device, params,
encoder_classifier,
encoder_classifier_optimizer,
svhn_trainsplit,
svhn_testsplit, mnist_trainsplit, mnist_testsplit,
experiment_name=params.generator_discriminator_experiment_name,
ckpt_root=params.ckpt_root)
print(generator_discriminator_trainer.generator)
# The architecture of the Discriminators (they are identical):
print(generator_discriminator_trainer.discriminator_svhn)
# The training procedure for the discriminators is as follows for a pair of batches from both domains. Note that the labels for the MNIST batches are not coming from the dataset, but the Encoder - Classifier of the model itself.
def discriminator_mnist_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch):
svhn_inputs, _ = svhn_batch # don't care about svhn labels here
mnist_hc_inputs, mnist_hc_labels = mnist_hc_batch
# mnist_hc_labels are high confidence digit labels obtained from the classifier, not ground truth
# a utility method to zero all grads in all models
self.zero_grad()
# generate fake mnist images from encodings of svhn images
_, svhn_latent_out = self.encoder_classifier(svhn_inputs)
svhn_to_fake_mnist = self.generator(svhn_latent_out, 1)
# discriminator output is a 1x6 (not 1x5!) vector of confidences for digits [0-4] and fake (not normalized)
# fake image confidences, discriminator has less loss if the 6th item is large
svhn_to_fake_mnist_discriminator_out = self.discriminator_mnist(svhn_to_fake_mnist)
# real image confidences, discriminator has less loss if item matching the high conf. classifier label is large
real_mnist_discriminator_out = self.discriminator_mnist(mnist_hc_inputs)
# criterion is cross-entropy loss against labels on top of a softmax layer
# fake image loss is against fake labels (label "5")
discriminator_mnist_fake_loss = self.discriminator_mnist_criterion(svhn_to_fake_mnist_discriminator_out,
self.fake_label_pool[:svhn_to_fake_mnist_discriminator_out.shape[0]])
# real image loss is against high confidence classifier labels
discriminator_mnist_real_loss = self.discriminator_mnist_criterion(real_mnist_discriminator_out,
mnist_hc_labels)
# total loss
discriminator_mnist_loss = discriminator_mnist_fake_loss + discriminator_mnist_real_loss
discriminator_mnist_loss.backward()
self.discriminator_mnist_optimizer.step()
# The discriminator training procedure for SVHN dataset, where we have the ground truth, is very similar to the discriminator of MNIST. Only this time actual ground truth is available for calculating the loss on real SVHN images.
def discriminator_svhn_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch):
svhn_inputs, svhn_labels = svhn_batch # we have the ground truth digit labels for svhn in training
mnist_hc_inputs, _ = mnist_hc_batch # don't care about mnist labels here
self.zero_grad()
# generate fake svhn images from encodings of mnist images
_, mnist_hc_latent_out = self.encoder_classifier(mnist_hc_inputs)
mnist_to_fake_svhn = self.generator(mnist_hc_latent_out, 0)
# discriminator output is a 1x6 (not 1x5!) vector of confidences for digits [0-4] and fake (not normalized)
# fake image confidences, discriminator has less loss if the 6th item is large
mnist_to_fake_svhn_discriminator_out = self.discriminator_svhn(mnist_to_fake_svhn)
# real image confidences, discriminator has less loss if item matching the ground truth svhn label is large
real_svhn_discriminator_out = self.discriminator_svhn(svhn_inputs)
# criterion is cross-entropy loss against labels on top of a softmax layer
# fake image loss is against fake labels (label "5"), optimizer pulls discriminator towards guessing correctly
discriminator_svhn_fake_loss = self.discriminator_svhn_criterion(mnist_to_fake_svhn_discriminator_out,
self.fake_label_pool[:mnist_to_fake_svhn_discriminator_out.shape[0]])
# real image loss is against ground truth svhn labels, optimizer pulls discriminator towards guessing correctly
discriminator_svhn_real_loss = self.discriminator_svhn_criterion(real_svhn_discriminator_out,
svhn_labels)
# total loss
discriminator_svhn_loss = discriminator_svhn_fake_loss + discriminator_svhn_real_loss
discriminator_svhn_loss.backward()
self.discriminator_svhn_optimizer.step()
# Generator and the encoder - classifier are trained with the following procedure. The generator has two losses, the first one is for deceiving the discriminators and the second one the reconstruction loss for the reconstructed encodings (the reconstructions do not change domain).
def generator_classifier_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch):
svhn_inputs, svhn_labels = svhn_batch # we have the ground truth digit labels for svhn in training
mnist_hc_inputs, mnist_hc_labels = mnist_hc_batch
# mnist_hc_labels are high confidence digit labels obtained from the classifier, not ground truth
self.zero_grad()
# generate fake images (from the other domain) and reconstructed images (from the same domain)
# from the encodings
# classifier confidences will be used for classifier training
mnist_hc_classifier_out, mnist_hc_latent_out = self.encoder_classifier(mnist_hc_inputs)
svhn_classifier_out, svhn_latent_out = self.encoder_classifier(svhn_inputs)
svhn_to_fake_svhn = self.generator(svhn_latent_out, 0)
svhn_to_fake_mnist = self.generator(svhn_latent_out, 1)
mnist_to_fake_svhn = self.generator(mnist_hc_latent_out, 0)
mnist_to_fake_mnist = self.generator(mnist_hc_latent_out, 1)
# 1-) Generator Training
# 1-a) Generator Deception Losses
# discriminator output is a 1x6 (not 1x5!) vector of confidences for digits [0-4] and fake (not normalized)
svhn_to_fake_mnist_discriminator_out = self.discriminator_mnist(svhn_to_fake_mnist)
mnist_to_fake_svhn_discriminator_out = self.discriminator_svhn(mnist_to_fake_svhn)
# deception criterion is cross-entropy loss against labels on top of a softmax layer
# fake mnist image losses are against ground truth svhn labels
# optimizer pulls generator towards making discriminator categorize fake mnist images incorrectly
# in the corresponding ground truth svhn labels
deceive_discriminator_mnist_loss = self.generator_deception_criterion(
svhn_to_fake_mnist_discriminator_out, svhn_labels)
# fake svhn image losses are against mnist high conf. classifier labels (not ground truth)
# optimizer pulls generator towards making discriminator categorize fake svhn images incorrectly
# in the corresponding mnist high conf. classifier labels (not ground truth)
deceive_discriminator_svhn_loss = self.generator_deception_criterion(
mnist_to_fake_svhn_discriminator_out, mnist_hc_labels)
# total deception loss
deception_loss = deceive_discriminator_mnist_loss + deceive_discriminator_svhn_loss
# 1-b) Generator Reconstruction Losses
# reconstructed images should look like the original images, reconstruction criterion is
# L2 loss between original and reconstructed images - no label information used
reconstruction_mnist_loss = self.generator_reconstruction_criterion(mnist_to_fake_mnist,
mnist_hc_inputs)
reconstruction_svhn_loss = self.generator_reconstruction_criterion(svhn_to_fake_svhn,
svhn_inputs)
# total reconstruction loss
reconstruction_loss = reconstruction_mnist_loss+reconstruction_svhn_loss
# total generator loss, there is a reconstruction loss scaling parameter alpha specified in the paper
generator_loss = deception_loss + self.dupgan_alpha*reconstruction_loss
# 2-) Classifier Training
# criterion is cross-entropy loss against labels from own domain, same as pretraining, only difference is
# mnist high confidence images also contribute to the loss with mnist high confidence labels (not ground truth)
mnist_classification_loss = self.encoder_classifier_criterion(mnist_hc_classifier_out, mnist_hc_labels)
svhn_classification_loss = self.encoder_classifier_criterion(svhn_classifier_out, svhn_labels)
# total classification loss, there is a scaling parameter beta specified in the paper
classification_loss = self.dupgan_beta*(mnist_classification_loss + svhn_classification_loss)
generator_ec_loss = generator_loss + classification_loss
generator_ec_loss.backward()
self.generator_optimizer.step()
self.encoder_classifier_optimizer.step()
# The 3 procedures collect in the following main training loop. At the beginning of each epoch, the filtered collection of MNIST images with high classification confidence are renewed. The model is saved and evaluated at every epoch. You can change the frequency of these to your liking by playing with the code below.
# +
def generator_discriminator_notebook_train_models(self):
for self.epoch in range(self.epoch+1, params.generator_discriminator_num_epochs):
# at the beginning every epoch review images in the mnist train split and collect the ones
# that the classifier has high confidence in categorization
# train the models with inferred label - high confidence mnist image pairs
# as if the inferred labels are ground truth
mnist_hc_dataset, pseudolabels = self.get_high_confidence_mnist_dataset_with_pseudolabels()
mnist_hc_loader = generic_dataloader(self.device, mnist_hc_dataset, shuffle=True,
batch_size=self.batch_size)
# since mnist is smaller than svhn, have to use iterators to jointly train
mnist_ind = 0
mnist_iterator = iter(mnist_hc_loader)
for svhn_batch in self.svhn_trainsplit_loader:
# hack to skip 1 sample batches since they give an error with batchnorm
# device compatibility code, etc.
while True:
if mnist_ind >= len(mnist_iterator):
mnist_iterator = iter(mnist_hc_loader)
mnist_ind = 0
mnist_hc_inputs, *_, mnist_hc_indices = next(mnist_iterator)
mnist_ind += 1
if mnist_hc_inputs.shape[0] > 1:
break
mnist_hc_inputs = mnist_hc_inputs.to(self.device)
mnist_hc_labels = pseudolabels[mnist_hc_indices].to(self.device)
svhn_inputs, svhn_labels = svhn_batch
svhn_inputs = svhn_inputs.to(self.device)
svhn_labels = svhn_labels.to(self.device)
#meat of the training code
mnist_hc_batch = (mnist_hc_inputs, mnist_hc_labels)
svhn_batch = (svhn_inputs, svhn_labels)
discriminator_mnist_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch)
discriminator_svhn_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch)
generator_classifier_notebook_train_one_batch(self, svhn_batch, mnist_hc_batch)
#this is here just to show results fast during a demo
if params.demo:
generator_discriminator_notebook_evaluator_evaluate_and_print(self, mnist_hc_loader, pseudolabels)
#saved every epoch under ckpt_root
generator_discriminator_notebook_evaluator_evaluate_and_print(self, mnist_hc_loader, pseudolabels)
self.save()
try:
generator_discriminator_notebook_evaluator_reset()
generator_discriminator_notebook_train_models(generator_discriminator_trainer)
except KeyboardInterrupt:
pass
# -
# The best model we obtained from our experiments can be loaded with the snippet below. Important hyper-parameters are also listed.
generator_discriminator_notebook_load_and_print_params(generator_discriminator_trainer,params.generator_discriminator_ckpt_file)
# # 5. Final Results
#
# Here are our promised goal results for the project. **The paper reports 92.46% accuracy for the classifier, (we had 87.21%).** The image translation results of the paper can be compared with ours below:
#
# <img src="images/translation.png" />
# <center>Figure 2: Image Translation Results of DupGAN Paper</center>
# <img src="images/translation_repr.png"/>
# <center>Figure 3: Our Image Translation Results</center>
generator_discriminator_notebook_evaluator_evaluate_goals_and_print(generator_discriminator_trainer)
|
main.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
#
# + [markdown] tags=[]
# # MCIS6273 Data Mining (Prof. Maull) / Fall 2021 / HW1
#
# **This assignment is worth up to 20 POINTS to your grade total if you complete it on time.**
#
# | Points <br/>Possible | Due Date | Time Commitment <br/>(estimated) |
# |:---------------:|:--------:|:---------------:|
# | 20 | Monday, Sep 20 @ Midnight | _up to_ 20 hours |
#
#
# * **GRADING:** Grading will be aligned with the completeness of the objectives.
#
# * **INDEPENDENT WORK:** Copying, cheating, plagiarism and academic dishonesty _are not tolerated_ by University or course policy. Please see the syllabus for the full departmental and University statement on the academic code of honor.
#
# ## OBJECTIVES
# * Explore the statistical properties of images and build a cloudiness detector
#
# * Gain more practice with the Exploratory Data Analysis (EDA) and statistical functions in Pandas using WWII enlistment data
#
# ## WHAT TO TURN IN
# You are being encouraged to turn the assignment in using the provided
# Jupyter Notebook. To do so, make a directory in your Lab environment called
# `homework/hw1`. Put all of your files in that directory.
#
# Then zip that directory,
# rename it with your name as the first part of the filename (e.g. `maull_hw1_files.tar.gz`), then
# download it to your local machine, then upload the `.tar.gz` to Blackboard.
#
# If you do not know how to do this, please ask, or visit one of the many tutorials out there
# on the basics of using in Linux.
#
# If you choose not to use the provided notebook, you will still need to turn in a
# `.ipynb` Jupyter Notebook and corresponding files according to the instructions in
# this homework.
# + [markdown] tags=[]
# ## ASSIGNMENT TASKS
# ### (50%) Explore the statistical properties of images and build a cloudiness detector
#
# We take for granted our biological capabilities of vision
# and perception. Indeed, human vision, while not the most
# precise or even most capable of Earth species is quite good
# and when paired with the perceptual capabilities of our brain,
# is an incredible mechanism.
#
# The perception and understanding of the words on the screen or
# page you read this assignment right now, is indeed a feat of
# great coordination, between your eyes, brain and the connective
# tissues of the nervous system.
#
# Machine vision, on the other hand, is not an easy task. Vigorous
# research over the last 40 years is now bearing fruit, upon which
# self-driving cars
# and intelligent object detectors are being integrated into
# our daily lives, in some cases when we are least aware of it and
# in others where we might not like them to be (i.e. facial recognition
# in retail contexts).
#
# As we move into statistical skill building in the data mining
# context, images offer a rich area to explore, and we will
# do so in this part of the assignment by building a rudimentary
# "cloudiness detector".
#
# You know that determining whether it is a cloudy, partly or sunny
# day is largely a trivial task, even for the young ones among us --
# most children can accurately determine whether it is sunny by age
# 3, but this task, as you will see, may not be so easy for our
# digital machines.
#
# This part of the assignment will invoke a few new tools,
#
# * we will use [numpy](https://numpy.org/) to manipulate data arrays easily and transform them;
# * we will use [pandas](https://pandas.pydata.org/) to convert numpy data arrays back and forth and provide a richer representation of the data, as well as
# invoke some of the built-in statistical and graphing tools;
# * we will use [matplotlib](https://matplotlib.org/) to manipulate images and image data.
#
#
# ### Image representation
# As you likely already know images are represented in a computer
# as an $n \times m$ array (matrix) consisting of a monochromatic, greyscale
# or color representation. Each value in the array represents
# a _pixel_. Consider the $10 \times 10$ color RGB image, where
# each entry in the matrix is represented as a 3-tuple RGB
# value where each value in the tuple is in the range $0 - 255$. Here
# is a concrete example:
#
# $$
# I_{m,n} =
# \begin{pmatrix}
# (215,191,136) & \cdots & (232,94,254) \\
# (151,195,183) & \cdots & (210,36,220) \\
# (141,225,155) & \cdots & (48,31,65) \\
# \vdots & \ddots & \vdots \\
# (210,23,125) & \cdots & (151,54,128) \\
# (84,165,239) & \cdots & (46,176,84) \\
# \end{pmatrix}
# $$
#
# You will see this as an $n \times m \times 3$ array.
# Put a thumbtack in this representation as it will be used
# heavily in this part of the assignment.
#
# ## Tools you'll need
# You will need to load and display images in this
# assignment.
#
#
# ### `matplotlib.image.mpimg.imread()`
# To load an image, you can use the [`matplotlib.image.mpimg.imread()`](https://matplotlib.org/stable/api/image_api.html?highlight=imread#matplotlib.image.imread) function
# which will load the image into a numpy array as represented above.
#
# ### `matplotlib.pyplot.imshow()`
# To display an image in your notebook, simply write:
#
# ```
# # load an image using imread()
# rgb_img = matplotlib.image.mpimg.imread()
#
# # show the image in the notebook
# matplotlib.pyplot.imshow(rgb_img)
# ```
#
# ### `matplotlib.colors.rgb_to_hsv()`
# While working in RGB color space can be useful, there is another
# color space that affords us some advantages to quickly get at
# some of the image properties we're most interested in for
# analysis. The [`matplotlib.colors.rgb_to_hsv()`](https://matplotlib.org/stable/api/_as_gen/matplotlib.colors.rgb_to_hsv.html) function will
# convert our RGB image into an HSV equivalent. HSV stands for
# Hue, Saturation, Value and it allows us to more easily identify
# colors and their intensities in an image. You can read more
# about that in these links :
#
# * Stack Exchange: [Why do we use the HSV colour space so often in vision and image processing?](https://dsp.stackexchange.com/questions/2687/why-do-we-use-the-hsv-colour-space-so-often-in-vision-and-image-processing)
# * Hue, Value, Saturation at [leighcotnoir.com](http://learn.leighcotnoir.com/artspeak/elements-color/hue-value-saturation/)
# * What are Color Models? at [wigglepixel.nl](https://www.wigglepixel.nl/en/blog/what-are-color-models/)
#
# Here is an example:
# ```
# rgb_img = matplotlib.image.mpimg.imread()
#
# # convert to an hsv representation
# rgb_hsv = matplotlib.colors.rgb_to_hsv(rgb_img / 255.)
#
# # important, don't forget the division by 255 to normalize all the values!!!
#
# ```
#
# ### `numpy.compress()` and `flatten()`
# In one part of the assignment you will be asked to convert
# the HSV image to a Pandas DataFrame. Doing this can be
# done a number of ways, but one thing you will note is the
# array of the image is 3 dimensions -- that is it has
# a width, height and an HSV representation of the pixel
# which is itself a tuple of 3 values (H,S,V).
#
# See information about [`compress()`](https://numpy.org/doc/stable/reference/generated/numpy.compress.html),
# and information about [`flatten()`](https://numpy.org/doc/stable/reference/generated/numpy.ndarray.flatten.html), which are
# just one way to help you get the array reformed to
# fit into the DataFrame in the tasks below.
#
# ### `DataFrame.T`
# Transposing a DataFrame is equivalent to a vector transpose.
#
# Consider the column vector :
#
# $$
# V = \begin{bmatrix}
# 1 \\
# 3 \\
# 6 \\
# 5 \\
# 9
# \end{bmatrix}
# $$
#
# The transpose $V^T$ is a row vector:
#
# $$
# V^T = \begin{bmatrix}
# 1 & 3 & 6 & 5 & 9
# \end{bmatrix}
# $$
#
# So if you have a DataFrame:
# ```python
# df = pd.DataFrame([1, 3, 6, 5, 9],
# columns=['values']
# ```
#
# which gives:
#
# \begin{center}
# \begin{tabular}{lr}
# \toprule
# {} & values \\
# \midrule
# 0 & 1 \\
# 1 & 3 \\
# 2 & 6 \\
# 3 & 5 \\
# 4 & 9 \\
# \bottomrule
# \end{tabular}
# \end{center}
#
# then the transpose
# ```python
# df.T
# ```
# will give:
#
# \begin{center}
# \begin{tabular}{lrrrrr}
# \toprule
# {} & 0 & 1 & 2 & 3 & 4 \\
# \midrule
# values & 1 & 3 & 6 & 5 & 9 \\
# \bottomrule
# \end{tabular}
# \end{center}
#
# ## Naïve Cloudiness Detection
# Building a real cloud object detector is out of the scope
# of this assignment, but we can actually build a pretty good one on
# statistically analyzing the image, and looking for the blue
# in the sky. When you think of it, cloudiness is just a
# ratio of the blueness to non-blueness in the sky. We might
# also need to add some caveats to this detector -- namely, it
# isn't very good at detection if there are other things in
# the image besides clouds (e.g. mountains, cars, etc.). So
# we'll assume that the images we'll analyze with it will all be
# images of the sky (camera pointed up) and not images of lanscapes
# with sky or other types of objects with sky in them.
#
# Looking at it mathematically, if we count all the blue
# pixels in the image and assume the non-blue (non-sky) pixels
# are clouds, we might come rather close to accomplishing
# what we want. So if $p_{all}$ are all the pixels in
# the image and $p_{blue}$ are all the blue pixels
# in our image then $p_{not\_blue} = p_{all} - p_{not\_blue}$,
# then cloudiness is given by
#
# $$
# C(p) = 1 - \frac{p_{blue}}{p_{all}}
# $$
#
# that is to say, the cloudiness is what's left of the pixels which
# are not blue. This number will, of course, be between 0 and 1
# and thus can be interpreted as a percentage "cloudiness", where
# 0 is a clear sky, and 1 is a fully cloudy sky.
#
# Using this simple insight will allow you to develop the detector.
#
# You may structure your code however you like, but one hint
# you might consider is to build a function that takes an
# image file name and performs the necessary transforms to
# return cloudiness.
#
# § Load image #1 (`img01.jpg`) into a variable and display it. Convert
# the image to HSV using the method described above and display the HSV version.
# -
import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from sklearn.preprocessing import MinMaxScaler
rgb_img = mpimg.imread('/home/jovyan/mcis6273_f21_datamining/homework/hw1/images/img01.jpg')
rgb_hsv = matplotlib.colors.rgb_to_hsv(rgb_img/255)
matplotlib.pyplot.imshow(rgb_hsv)
# § Using the HSV image data (converted from RGB), make a Pandas DataFrame
# which looks something like this when your done:
#
# \begin{center}
# \begin{tabular}{lrrr}
# \toprule
# {} & H & S & V \\
# \midrule
# 0 & 205.479452 & 0.618644 & 0.925490 \\
# 1 & 205.479452 & 0.613445 & 0.933333 \\
# 2 & 205.479452 & 0.610879 & 0.937255 \\
# 3 & 205.352113 & 0.617391 & 0.901961 \\
# 4 & 205.957447 & 0.646789 & 0.854902 \\
# $\cdots$ & $\cdots$ & $\cdots$ & $\cdots$ \\
# 85905 & 206.582278 & 0.316000 & 0.980392 \\
# 85906 & 206.582278 & 0.322449 & 0.960784 \\
# 85907 & 204.761905 & 0.272727 & 0.905882 \\
# 85908 & 204.761905 & 0.268085 & 0.921569 \\
# 85909 & 204.761905 & 0.294393 & 0.839216 \\
# \bottomrule
# \end{tabular}
# \end{center}
#
#
# NOTES: (a) Notice the H, S and V are the columnar values! (b) The H value may need to be rescaled by 360 if
# the native value coming from the transform has been normalized to between 0 and 1.
colorArray = np.array(rgb_hsv)
compress_array = np.compress([True, False, False], colorArray, axis=1)
df = pd.DataFrame(compress_array.reshape(-1, 3), columns=['H','S','V'])
df["H"] = 360 * df["H"]
print (df)
# § Use the `DataFrame.hist()` method to produce a histogram
# of the H, S and V values for `img01.jpg`. Make sure the histograms
# are in your notebook and answer the following questions:
hist = df['H'].hist()
plt.title('Histogram of H value')
##plt.savefig("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_H_img01.jpg", bbox_inches='tight', dpi=100)
plt.show ("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_H_img01.jpg")
hist = df['S'].hist()
plt.title('Histogram of S value')
##plt.savefig("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_S_img01.jpg", bbox_inches='tight', dpi=100)
plt.show ("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_S_img01.jpg")
hist = df['V'].hist()
plt.title('Histogram of V value')
##plt.savefig("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_V_img01.jpg", bbox_inches='tight', dpi=100)
plt.show ("/home/jovyan/mcis6273_f21_datamining/homework/hw1/hist_V_img01.jpg")
# * What do you observe about the H values in the histogram?(HINT: you might want to look at the dominant color type in an HSV tool online)
# **Answer:** </br>
# H values describe the color portion of the image with values ranging from 0 to 360. In the histogram, the H value falls predominantly around 195 to 207 which is the color code of **Cyan**.
#
# * What is interesting about the S values in contrast to H (ignore the axis scale in your answer)?</br>
# **Answer**</br>
# S or Saturation value describes the amount of gray added in a particular color. Full saturation refers to the dominance of hue in the color. At maximum saturation, the color is almost like the hue and contains no gray whereas at the minimum, the color contains the maximum amount of gray.
# § Use the `DataFrame.describe()` method to produce the
# descriptive statistics for the HSV data for `img07.jpg`.
rgb_img07 = mpimg.imread('/home/jovyan/mcis6273_f21_datamining/homework/hw1/images/img07.jpg')
rgb_hsv07 = matplotlib.colors.rgb_to_hsv(rgb_img07/255)
colorArray07 = np.array(rgb_hsv07)
compress_array07 = np.compress([True, False, False], colorArray07, axis=1)
df_img07 = pd.DataFrame(compress_array07.reshape(-1, 3), columns=['H','S','V'])
df_img07["H"] = 360 * df_img07["H"]
df_img07.describe()
# Answer the following:
#
# * What is the mean and median H?</br>
# **Answer:**</br>
# Mean = 214.805013</br>
# Median = 214.878049
#
# * What about max and min for H?</br>
# **Answer:** </br>
# Min = 206.929134</br>
# Max = 227.116564
# * What can you say about the standard deviation and how
# it relates to the values between the 25% and 75%-tile?</br>
# **Answer:**</br>
# Standard Deviation describes how the values of a dataframe deviates from an average value or mean. Here in this case, the standard deviation of H is 4.861296. This means **most of the values of H lies around 214.805013(Mean) (plus or minus) 4.861296(SD)**.</br> The 50% (percentile) is considered the median or the middle value of the sorted dataframe. 25 percentile represents that 25% of the values are less than 210.059761 (as in this case) and 75 percentile represents that 75% of the values are below 219.185550. </br>
# **The value in between 25% tile and 75% tile provides the information about the values that are closer to the median, which is approximately similar to the first standard deviation derived by adding/subtracting standard deviation to the mean value.**</br>
#
# * Assuming a normal distribution, what is the expected
# H range for the 1st standard deviation?</br>
# **Answer:**</br>
# 1st Standard deviation range = (Mean + Standard deviation) to (Mean - Standard deviation)
# = (214.805013 + 4.861296) to (214.805013 - 4.861296)
# = 219.666309 to 209.943717
#
# § Use the `DataFrame.describe()` and `DataFrame.join()` to
# compare the descriptive statistics of `img01.jpg` and
# `img07.jpg` side by side in a single table.
df_desc = df.describe()
df_img07_desc = df_img07.describe()
df_desc.join(df_img07_desc, lsuffix='_img01', rsuffix='_img07')
# * What general observation can you make about these images?
# * When looking at the standard deviation and quartiles,
# what would you say about cloudiness?
#
#
# § Write a function `pct_cloudy()` which takes three
# parameters `filename`, `h_range` and `s_range`.
# Where `h_range` and `s_range` take a tuple
# of with (min, max) which give the min and
# max range for the H and S parameters.
#
# A call might look like `pct_cloud("img01.jpg",
# (200, 210), (.1, .2))`.
#
# Your function will return the percent cloudy
# as discussed above in the summary for this part.
def pct_cloud(filename, h_range, s_range):
rgb_img_cl = mpimg.imread(filename)
rgb_hsv_cl = matplotlib.colors.rgb_to_hsv(rgb_img_cl/255)
colorArray_img = np.array(rgb_hsv_cl)
compress_array_img = np.compress([True, False, False], colorArray_img, axis=1)
df_img = pd.DataFrame(compress_array_img.reshape(-1,3), columns=['H','S','V'])
df_img["H"] = 360 * df_img["H"]
p_all = df_img["H"].sum()
p_blue = df_img.loc[df_img["H"].between (*h_range) & df_img["S"].between (*s_range), "H"].sum()
cloudiness = 1-(p_blue/p_all)
return cloudiness
pct_cloud("/home/jovyan/mcis6273_f21_datamining/homework/hw1/images/img01.jpg",(180,240),(0.25,1))
# * Use the following values for `h_range` and `s_range`
# and build a table with the percent cloudy for each **of the 10
# files in the `data/` folder** in the Github repo for this assignment.
#
# ```python
# h_range = (180,240)
# s_range = (.25,1.0)
# ```
df_cloudiness = pd.DataFrame(columns = ['Image', 'Percent_Cloudy'])
for i in range(1,10):
pd.set_option("precision", 10)
cloudiness = pct_cloud("/home/jovyan/mcis6273_f21_datamining/homework/hw1/images/img0"+str(i)+".jpg",(180,240),(0.25,1))
df_cloudiness = df_cloudiness.append ({"Image":"img0"+str(i)+".jpg" ,"Percent_Cloudy":cloudiness}, ignore_index = True)
df_cloudiness = df_cloudiness.append ({"Image":"img10.jpg" ,"Percent_Cloudy":(pct_cloud("/home/jovyan/mcis6273_f21_datamining/homework/hw1/images/img10.jpg",(180,240),(0.25,1)))}, ignore_index = True)
print(df_cloudiness)
# * Using the values given, do you feel the percent cloudiness
# is accurate?
# * Explain why these values make sense (you will need to go
# back to the HSV color wheel to answer this)?
# * Drawing from evidence in the sample files, give a concrete reason
# why the statistical details of the sample files support
# this range.
#
#
#
# ### (50%) Gain more practice with the Exploratory Data Analysis (EDA) and statistical functions in Pandas using WWII enlistment data
#
# No matter your position favorable, unfavorable or indifferent, the
# military generates a lot of data, most of which ordinary citizens
# will never see. One especially interest data that is often released
# to the public are enlistment records, or the basic information about
# those who enlisted into armed services.
#
# The dataset we will explore in this part is from the 9 million
# or so records from World War II of the enlisted men and women
# of the US armed services from 1938 to 1946. In these records
# are a treasure trove of information, including names, ages
# height, weight, race, marital status, education status
# and other vital information of the enlisted.
#
# As a side note, this data was originally capture onto punch cards
# (yes, the same type of punch cards that were used to program
# the first digital computers) and subsequently converted to
# digital form and accessioned into the US National Archives.
#
# Some background on the data can be found from this source link:
#
# * Electronic Army Serial Number Merged File, ca. 1938 - 1946 [https://catalog.archives.gov/id/1263923](https://catalog.archives.gov/id/1263923)
#
# The file we will be working with is a fixed width file (FWF) meaning
# that the number of characters per line is the same and
# that ranges of columns indicate the data in the field.
#
# For example, if you look at page 44 in the [file](https://catalog.archives.gov/OpaAPI/media/1263923/content/arcmedia/electronic-records/rg-064/asnf/100.1ND_NC.pdf?download=false)
# you will notice that the layout of the file is given to you. So
# for example, columns 9-32 are the full name of the enlisted
# while columns 67-68 give the enlisted's year of birth. You will realize
# this can be an efficient way to encode data when you have limited
# storage or memory resources, though the necessary mapping of fields
# to their meaning cannot be lost, or the file may be difficult (or impossible) to
# interpret later. Luckily such mappings exist for this important
# dataset.
#
# An example of FWF data is given below (the first two rows were added to show the column numbers:
#
# ```
# 1 2 3 4 5 6 7 8
# 012345678901234567890123456789012345678901234567890123456789012345678901234567890
# 17006058HANSON LU<NAME> 770197745090840PVT 8FA 30 9 07718109996671451 02382.95
# 36427840<NAME> 611436167260942PVT 8BI 00 5 06102127368671357 10815.143
# 32853721LUSKY CHARLES R 230652390220343PVT 8NO 02 5 02324144331661277 05742.238
# ```
#
# For this assignment we're going to analyze some of the demographic data
# including age, race, marital status and weight data. We
# will also take a look at the enlistment dates and see if
# the data match up with what was going on during that time in US history.
#
# I have prepared a random sample of the data (around 900K records)
# since the full 9M records will put undue stress on the Hub
# and such a sample is a good enough representation of the data. In doing
# so, I have removed missing lines from the file, but that
# is the extent of any filtering that was peformed.
#
# This file can be found on Github in the same folder
# as the [`hw1.ipynb`](https://github.com/kmsaumcis/mcis6273_f21_datamining/blob/main/homework/hw1/hw1.ipynb). You will use it to answer all questions
# in this part of the assignment.
#
# ## Tools you'll need
# You will need to load the fixed width file (FWF) in this
# assignment.
# ### `pandas.read_fwf()`
# Use the [`read_fwf()`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.read_fwf.html) method to load the fixed width file.
namelist = ['Serial_number','Name','Res_State','Res_County','Place_of_Enlistment','Date_of_Enlistment','Grade_Alpha','Grade_Code','Branch_Alpha','Branch_Code','Term_or_enlistment','Longevity','Source','Nativity','Year_of_Birth','Race','Education','civ_Occupation','Marital_Status','Height','Weight','Component','Card_Number']
colspecs=[(0, 8), (8, 32), (32, 34),(34, 37), (37, 41), (41, 47),(47,51),(51,52), (52,55),(55,57),(58,59),(59,62),(62,63),(63,65),(65,67),(67,68),(68,69),(69,72),(72,73),(73,75),(75,78),(78,79),(79,80)]
pd.set_option('display.max_columns', None)
df_fwf = pd.read_fwf('/home/jovyan/mcis6273_f21_datamining/homework/hw1/asnef_900k_records.fin.dat',colspecs =colspecs,names =namelist, header = None)
df_fwf
# I have made a method for doing this which reduces the amount
# of time for you to figure out which columns apply
# to which fields -- this required me to use the
# reference documents from the 1940s, which was tedious,
# but thankfully such documentation existed even if
# it was a scan of a typewritten source!
#
# ### `Series.value_counts()` and `Series.sort_values()`
# Both of these will be useful in getting the values
# sorted for the questions below. Study both of these methods carefully.
#
# ### Data Cleaning Hints
# The data set you will be using is not perfect as it was machine
# translated and there are known issues in it. For example,
# you may get information that may be out of specification,
# for example, height is in inches, but if you look into it,
# height data does have errors, as does weight (i.e. weights
# less than 100, heights greater than 90). Just remember data cleaning
# is an important necessary step before proceeding.
#
# § On September 16, 1940, The Selective Training and
# Service Act of 1940 was signed into law by President
# <NAME>, which was the country's first peacetime
# draft designed to conscript troops in the event of war.
# The timing of the Act was unique, since the US did not
# enter World War II (WWII) until December 1941, but it
# nonetheless required
# all male US citizens ages 21 to 35 to register for the draft
# from which names were drawn through a lottery system. Those
# called to duty were to serve in the military
# for one year. From 1940 to 1947 nearly 10.1 million men and women
# were inducted under the Act, the majority of which
# served in WWII stateside or abroad.ASDAS
#
# To warm up, we will take the enlistment column `enlistment_date`
# and plot the data from our sample file.
#
# * Generate a bar plot of the enlistment numbers from 1939 to 1946.
# The $x$-axis will contain the year (in ascending order) and the $y$-axis the
# number enlisted.
df_fwf["enlst_dt"] = abs(df_fwf['Date_of_Enlistment'])%100 +1900
df_enlst_dt = pd.DataFrame(df_fwf[(df_fwf["enlst_dt"]>=1939) & (df_fwf["enlst_dt"]<=1946)])
s = pd.Series(df_enlst_dt["enlst_dt"]).value_counts().sort_index()
s.plot(kind = 'bar')
# * Does the sample data support the claim that the Act increased enlistment
# during WWII?
#
# * What was the peak year of enlistment? Is this supported by the
# entry of the US into WWII in December 1941. Explain why or why not.
#
# * What is the median age of those enlisted? You may need to clean
# the data since there are unusual `birth_year` values that must be removed.
df_fwf["Age"] = abs(df_fwf['Date_of_Enlistment'])%100 - abs(df_fwf['Year_of_Birth'])
df_clean = pd.DataFrame(df_fwf[(df_fwf["Age"]>=18) & (df_fwf["Age"]<50)]) #Cleaning up negative values for age and considering only above 18 till 50
df_clean["Age"].describe()
# § During WWII large numbers of African-Americans entered the
# armed services, eventhough the US was still largely segregated
# and the armed services maintained separate forces until after
# WWII.
#
# * What was the percentage of African-Americans enlisted in 1941, 1942
# and 1943?
df_total = pd.DataFrame(df_clean[(df_clean["enlst_dt"]>=1941) & (df_clean["enlst_dt"]<=1943)])
df_AA = pd.DataFrame(df_clean[(df_clean["enlst_dt"]>=1941) & (df_clean["enlst_dt"]<=1943) & (df_clean["Race"] == '2') ])
Percent_AA = (pd.Series(df_AA["Name"]).count()/pd.Series(df_total["Name"]).count())*100
Percent_AA
# * The percentage of African Americans in
# the general population was 9.8% in the 1940 census.
# Compare that with the percentage enlisted
# from 1941-43. How do these percentages compare?
# <span style="color:blue">**Answer:**</br>
# The percentage percentage of African Americans enlisted from 1941-43 is 10.36%. The percentage of African Americans in the general population was 9.8% during 1940. This means, much of all African Americans entered the armed services inspite of the segregation.</span>
# * Where were the top 5 states of residence (`res_state`) that African-Americans
# enlisted from? You will need to look at this file: [https://catalog.archives.gov/OpaAPI/media/1263923/content/arcmedia/electronic-records/rg-064/asnf/100.1CL_SD.pdf?download=false](https://catalog.archives.gov/OpaAPI/media/1263923/content/arcmedia/electronic-records/rg-064/asnf/100.1CL_SD.pdf?download=false) and on page 3
# reference the state codes to determine the states. You might first
# want to group the state codes first, then sort, take the top 5,
# then match the code to the state -- this method will
# certainly save time.
df_state_code = pd.read_csv('/home/jovyan/mcis6273_f21_datamining/homework/hw1/state_codes.csv').rename(columns={'code':'Res_State'}).astype(str)
df_AA_all = pd.DataFrame(df_clean[(df_clean["Race"] == '2') ])
df_AA_all["State"] = pd.merge(df_AA_all, df_state_code, how='left',
left_on='Res_State', right_on='Res_State')["state"]
s_state = pd.Series(df_AA_all['State']).value_counts()
s_state.head()
# <span style="color:blue">**Answer**:</br>
# The top 5 states of residence that African-Americans enlisted from are Missisipi, Georgia, Texas, Alabama, New York.</span>
# § Age and marital status are vital bits of information which
# are tracked elsewhere (e.g. the Census), but the WWII military
# enlistment data provides an ample (and unique) subset of the
# population to determine marital and age characterstics of
# US citizens. It should be noted that this data does include
# women, since for the first time in US military history, women
# served in an offical capacity with their own
# branches of service: Women's Army Auxiliary Corps (WAC), Women
# Airforce Service Pilots (WASP) and the Women Accepted for
# Volunteer Emergency Services (WAVES).
#
# For the sake of trying to understand marital status, we
# will use the `component` field to restrict to _men_ and
# _women's_ marital status. When the `component` is 7
# it refers to enlisted men. You can find the complete reference
# for these values on page 306 in [this document](https://catalog.archives.gov/OpaAPI/media/1263923/content/arcmedia/electronic-records/rg-064/asnf/100.1CL_SD.pdf?download=false).
# You will want to use `branch_alpha=="WAC"` to filter for women, indicating
# the Women's Army Auxiliary Corps.
#
# Use the data to answer the following questions:
#
# * What percentage of the enlisted where older than 30? You may
# need to filter the data to eliminate spurious data -- there are
# some values which are not correct!
df_Age_gt_30 = pd.DataFrame(df_clean[df_clean["Age"]>30])
Percent_Age_gt30 = (pd.Series(df_Age_gt_30["Age"]).count()/pd.Series(df_clean["Age"]).count())*100
Percent_Age_gt30
# * What are the percentages of single (without depedents) and married men enlisted? The `marital_status` field will be `6` for
# _single (without dependents)_ and `1` for _married_.
df_Men_Enlst = pd.DataFrame(df_clean[df_clean["Component"]==7])
df_Men_Single = pd.DataFrame(df_Men_Enlst[df_Men_Enlst["Marital_Status"]==6])
df_Men_Married = pd.DataFrame(df_Men_Enlst[df_Men_Enlst["Marital_Status"]==1])
percent_Single = (df_Men_Single.shape[0]/df_Men_Enlst.shape[0])*100
Percent_Married = (df_Men_Married.shape[0]/df_Men_Enlst.shape[0])*100
print ("Percentage of single (Without Dependents) : " + str(percent_Single) +'\n'+ "Percentage of Married : " + str(Percent_Married))
# * What is the median age of a single man?
df_Men_Single["Age"].describe()
# * What are the percentages of married women in the WAC?
#
df_Women = pd.DataFrame(df_clean[df_clean["Branch_Alpha"]=="WAC"])
df_Women_Married = pd.DataFrame(df_Women[df_Women["Marital_Status"]==1])
Percent_Women_Married = (df_Women_Married.shape[0]/df_Women.shape[0])*100
Percent_Women_Married
# § Education of service personnel varied quite a bit, and some
# claim that less educated people are more eager to accept
# entry into the service, especially when skilled labor
# is associated with education level. The draft was presumed
# to be random -- no one was to receive a preference into the service.
# Furthermore, more education is often associated with a
# deeper understanding of the social, economic and political impacts
# of war, and often those with college and graduate degrees would refuse
# to enter the service as _conscientious objectors_.
#
# Interestingly, the Selective Service Act of 1940 did provision for
# _conscientious objectors_ -- those who for religious or
# philosophical reasons did not want to take up arms and
# be confronted with having to kill another human being. Such
# people were still
# forced into service (or jailed if they refused), but
# they were given non-combat duty
# and often were not eligible for veterans benefits once discharged.
#
# In the 1940 census the percent of the population age 25 and older
# with [a college degree (or higher)](https://www.census.gov/data/tables/time-series/demo/educational-attainment/cps-historical-time-series.html) was around 4.6% for all
# races and all genders. The GI Bill was a benefit given to veterans
# to encourage [pursuing and competing a college degree](https://clear.dol.gov/Study/Going-war-and-going-college-Did-World-War-II-and-GI-Bill-increase-educational-attainment-0),
# which contributed to the general rise of college degrees through the 50s and 60s.
#
#
#
# We will answer the following questions using the educational
# attainment data in the `education` field of the data.
#
# The information on which fields map to which education level
# are on page 305 of [this document](https://catalog.archives.gov/OpaAPI/media/1263923/content/arcmedia/electronic-records/rg-064/asnf/100.1CL_SD.pdf?download=false).
# HINT: 4 years of college is code `8` and 4 years of high school
# (grade 9 through 12) is code `4`.
#
# * What percentage of the enlisted people 25 or older in this data
# held college degrees (4 years of college)?
df_Above25 = pd.DataFrame(df_clean[(df_clean["Age"] >=25)])
df_College = pd.DataFrame(df_Above25[df_Above25["Education"]=='8'])
Percent_College_Above25 = (df_College.shape[0]/df_Above25.shape[0])*100
Percent_College_Above25
# * How does that compare to the national average from the Census
# data discussed above? Does this support the claim that the
# draft was disproportionated favorable to the college educated
# during WWII? Why or why not?
# * What percentage only had grammar school (code `0`) education -- you
# can use all ages?
df_grammar = pd.DataFrame(df_clean[df_clean["Education"]=='0'])
Percent_grammar = (df_grammar.shape[0]/df_clean.shape[0])*100
Percent_grammar
# § These last questions will deal with perhaps the dirtiest part of the dataset and will truly be exploratory, but we may be able to get at some interesting relationships while reserving strong judgement.
# Most of the people enlisted represented average healthy adults in the general population, but also those enlisted must adhere to basic physical standards as set by the service. This remains true today (though the standards have changed over time) since basic physical conditioning and evaluation is required to enter the service, so that serious medical conditions do not present issues for basic perfomance of combat duties. We are going to find out what the weight characteristics are of those entering the service in WWII.
#
# * Clean the data, and restrict values only to those that make sense -- for example, no one born before 1890 (age 50) and born after 1923 (age 18).
df_clean
# * What is the median weight of those age 19-23? Compare the median weight in 19-23 to the mean for the same age range. What are the differences? How does the standard deviation help interpret answer?
df_Age_19_23 = pd.DataFrame(df_clean[(df_clean["Age"] >=19) & (df_clean["Age"] <=23) & (df_clean["Weight"] >50)])
df_Age_19_23["Weight"].describe()
# * Plot a line plot of age to median weight and weight standard deviation. Age will be on the $x$-axis, weight on the left $y$-axis and weight standard deviation on the right $y$-axis? Your plot will have two lines -- one with the standard deviation, the other with the weight.
df_new = df_Age_19_23.groupby("Age").agg([np.median, np.std])["Weight"]
print (df_new)
fig,ax = plt.subplots()
# make a plot
#ax.plot(df_new.Age, df_new.mean, color="red")
ax2=ax.twinx()
df_new["median"].plot(ax=ax, style='b-', ylabel= "Median Weight")
ax2.set_ylabel('SD Weight')
df_new["std"].plot(ax=ax2, style='r-', label = 'SD_Weight', secondary_y=True )
plt.show()
|
homework/hw1/.ipynb_checkpoints/hw1-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# **K Nearest Neighbors**
#
# # 1 Load Data
import numpy as np
from data_util import load_CIFAR10
X_train, y_train, X_test, y_test = load_CIFAR10()
print('train data shape:', X_train.shape)
print('train label shape:', y_train.shape)
print('test data shape:', X_test.shape)
print('test label shape:', y_test.shape)
# ## 1.1 display the images
import matplotlib.pyplot as plt
# %matplotlib inline
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
num_class = len(classes)
sample_per_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, sample_per_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_class +y+1
plt.subplot(sample_per_class, num_class, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i==0:
plt.title(cls)
plt.show()
# # 2 subsample and reshape the data
# +
# Subsample the data for more efficient code execution in this exercise
num_training = 5000
mask = range(num_training)
X_train = X_train[mask]
y_train = y_train[mask]
num_test = 500
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
# -
# Reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print(X_train.shape, X_test.shape)
# # 3 Train the data
from KNearestNeighbor import KNearestNeighbor
knn = KNearestNeighbor(k=1)
knn.fit(X_train, y_train)
pred = knn.predict(X_test)
print('accuary is ',(pred==y_test).sum()/y_test.shape)
# choose k equals 5
knn = KNearestNeighbor(k=5)
knn.fit(X_train, y_train)
pred = knn.predict(X_test)
print('accuary is:',(pred==y_test).sum()/len(y_test))
# # 4 cross-validation
# +
num_folds = 5
k_choices = [1, 3, 5, 8, 10]
X_train_folds = []
y_train_folds = []
y_train_ = y_train.reshape(-1, 1)
X_train_folds , y_train_folds = np.array_split(X_train, 5), np.array_split(y_train_, 5)
k_to_accuracies = {}
for k_ in k_choices:
k_to_accuracies.setdefault(k_, [])
for i in range(num_folds):
X_val_train = np.vstack(X_train_folds[0:i] + X_train_folds[i+1:])
y_val_train = np.vstack(y_train_folds[0:i] + y_train_folds[i+1:])
y_val_train = y_val_train[:,0]
for k_ in k_choices:
knn = KNearestNeighbor(k=k_)
knn.fit(X_val_train, y_val_train)
y_val_pred = knn.predict(X_train_folds[i])
num_correct =(y_val_pred == y_train_folds).sum()
accuracy = float(num_correct) / len(y_val_pred)
k_to_accuracies[k_] = k_to_accuracies[k_] + [accuracy]
for k in sorted(k_to_accuracies):
for accuracy in k_to_accuracies[k]:
print ('k = %d, accuracy = %f' % (k, accuracy))
# -
|
assignment1/Knn.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # Data set analyse
# > First analyses on an unknown dataset and data visualization
# - toc: true
# - badges: false
# - comments: true
# - author: <NAME>
# - categories: [Panda, Seaborn]
# # Auto-scrolling
# To disable auto-scrolling, execute this javascript in a notebook cell before other cells are executed ['source stackoverflow'](https://stackoverflow.com/questions/36757301/disable-ipython-notebook-autoscrolling)
# + language="javascript"
# IPython.OutputArea.prototype._should_scroll = function(lines) {
# return false;
# }
# -
# # Imports
import pandas as pd
import seaborn as sns
myDataFrame = pd.read_csv("../../scikit-learn-mooc/datasets/penguins_classification.csv")
# # First analysis
print(f"The dataset contains {myDataFrame.shape[0]} samples and "
f"{myDataFrame.shape[1]} columns")
myDataFrame.columns
myDataFrame.head()
# ## Which column is our target to predict?
target_column = 'Species'
myDataFrame[target_column].value_counts()
# ## Separation between numerical and categorical columns
# ### Type of the objects
myDataFrame.dtypes
myDataFrame.dtypes.unique()
# ### We sort the variable names according to their type
# +
numerical_columns = ['Culmen Length (mm)', 'Culmen Depth (mm)']
categorical_columns = []
all_columns = numerical_columns + categorical_columns + [target_column]
myDataFrame = myDataFrame[all_columns]
myDataFrame.columns
# -
# ## To look at the amplitude and distribution of the data
# >Note: the "_" is to store a variable that we will not reuse
myDataFrame[numerical_columns].describe()
_ = myDataFrame.hist(figsize=(10, 5))
# ### Same with seaborn
# [`seaborn.pairplot`](https://seaborn.pydata.org/generated/seaborn.pairplot.html)
_ = sns.pairplot(myDataFrame)
# ## To detect link between the features and the target column
_ = sns.pairplot(myDataFrame, height=4, hue=target_column, corner=True)
# ### Idem but with circle of "same" data
g = sns.pairplot(myDataFrame, height=4, hue=target_column, corner=True)
g.map_lower(sns.kdeplot, levels=3, color=".2");
# ## Crosstab
# Useful to detect columns containing the same information in two different forms (thus correlated). If this is the case, one of the columns is excluded.
#
# Here, we don't see this kind of link
pd.crosstab(index=myDataFrame[numerical_columns[0]],
columns=myDataFrame[numerical_columns[1]])
|
_notebooks/2021-05-20-DataAnalyse.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] tags=["remove_cell"]
# # Solving Satisfiability Problems using Grover’s Algorithm
# -
# In this section, we demonstrate how to solve satisfiability problems using the implementation of Grover's algorithm in Qiskit Aqua.
# + [markdown] tags=["contents"]
# ## Contents
#
# 1. [Introduction](#introduction)
# 2. [3-Satisfiability Problem](#3satproblem)
# 3. [Qiskit Implementation](#implementation)
# 4. [Problems](#problems)
# 5. [References](#references)
# -
# ## 1. Introduction <a id='introduction'></a>
#
# Grover's algorithm for unstructured search was introduced in an [earlier section](https://qiskit.org/textbook/ch-algorithms/grover.html), with an example and implementation using Qiskit Terra. We saw that Grover search is a quantum algorithm that can be used to search for solutions to unstructured problems quadratically faster than its classical counterparts. Here, we are going to illustrate the use of Grover's algorithm to solve a particular combinatorial Boolean satisfiability problem.
#
# In computer science, the Boolean satisfiability problem is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. This can be seen as a search problem, where the solution is the assignment where the Boolean formula is satisfied.
#
# For _unstructured_ search problems, Grover’s algorithm is optimal with its run time of $O(\sqrt{N}) = O(2^{n/2}) = O(1.414^n)$[2]. In this chapter, we will look at solving a specific Boolean satisfiability problem (3-Satisfiability) using Grover’s algorithm, with the aforementioned run time of $O(1.414^n)$. Interestingly, at the time of writing, the best-known classical algorithm for 3-Satisfiability has an upper-bound of $O(1.307^n)$[3]. You may have heard that Grover’s algorithm can be used to speed up solutions to NP-complete problems, but these NP-complete problems do actually contain structure[4] and we can sometimes do better than the $O(1.414^n)$ of Grover’s algorithm.
#
# While it doesn’t make sense to use Grover’s algorithm on 3-sat problems, the techniques here can be applied to the more general case (k-SAT, discussed in the next section) for which Grover’s algorithm can outperform the best classical algorithm. Additionally, the techniques in Grover’s algorithm can theoretically be combined with the techniques used in the classical algorithms to gain an even better run time than either individually.
# ## 2. 3-Satisfiability Problem <a id='3satproblem'></a>
#
# The 3-Satisfiability (3SAT) Problem is best explained with the following concrete problem. Let us consider a Boolean function $f$ with three Boolean variables $v_1,v_2,v_3$ as below:
#
#
#
# $$f(v_1,v_2,v_3) = (\neg v_1 \vee \neg v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee v_3) \wedge (v_1 \vee v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee \neg v_3) \wedge (\neg v_1 \vee v_2 \vee v_3)$$
#
#
#
# In the above function, the terms on the right-hand side equation which are inside $()$ are called clauses; this function has 5 clauses. In a k-SAT problem, each clause has exactly k literals; our problem is a 3-SAT problem, so each clause has exactly three literals. For instance, the first clause has $\neg v_1$, $\neg v_2$ and $\neg v_3$ as its literals. The symbol $\neg$ is the Boolean NOT that negates (or, flips) the value of its succeeding literal. The symbols $\vee$ and $\wedge$ are, respectively, the Boolean OR and AND. The Boolean $f$ is satisfiable if there is an assignment of $v_1, v_2, v_3$ that evaluates to $f(v_1, v_2, v_3) = 1$ (that is, $f$ evaluates to True).
#
# A naive way to find such an assignment is by trying every possible combinations of input values of $f$. Below is the table obtained from trying all possible combinations of $v_1, v_2, v_3$. For ease of explanation, we interchangeably use $0$ and False, as well as $1$ and True.
#
# |$v_1$ | $v_2$ | $v_3$ | $f$ | Comment |
# |------|-------|-------|-----|---------|
# | 0 | 0 | 0 | 1 | **Solution** |
# | 0 | 0 | 1 | 0 | Not a solution because $f$ is False |
# | 0 | 1 | 0 | 0 | Not a solution because $f$ is False |
# | 0 | 1 | 1 | 0 | Not a solution because $f$ is False |
# | 1 | 0 | 0 | 0 | Not a solution because $f$ is False |
# | 1 | 0 | 1 | 1 | **Solution** |
# | 1 | 1 | 0 | 1 | **Solution** |
# | 1 | 1 | 1 | 0 | Not a solution because $f$ is False |
#
# From the table above, we can see that this 3-SAT problem instance has three satisfying solutions: $(v_1, v_2, v_3) = (T, F, T)$ or $(F, F, F)$ or $(T, T, F)$.
#
# In general, the Boolean function $f$ can have many clauses and more Boolean variables. Note that 3SAT problems can be always written in what is known as conjunctive normal form (CNF), that is, a conjunction of one or more clauses, where a clause is a disjunction of three literals; otherwise put, it is an AND of 3 ORs.
# ## 3. Qiskit Implementation <a id='implementation'></a>
#
# Let's now use Qiskit Aqua to solve the example 3SAT problem:
#
#
# $$f(v_1,v_2,v_3) = (\neg v_1 \vee \neg v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee v_3) \wedge (v_1 \vee v_2 \vee \neg v_3) \wedge (v_1 \vee \neg v_2 \vee \neg v_3) \wedge (\neg v_1 \vee v_2 \vee v_3)$$
#
#
#
# First we need to understand the input [DIMACS CNF](http://www.satcompetition.org/2009/format-benchmarks2009.html) format that Qiskit Aqua uses for such problem, which looks like the following for the problem:
#
# ~~~
# c example DIMACS CNF 3-SAT
# p cnf 3 5
# -1 -2 -3 0
# 1 -2 3 0
# 1 2 -3 0
# 1 -2 -3 0
# -1 2 3 0
# ~~~
#
# - Lines that start with `c` are comments
# - eg. `c example DIMACS CNF 3-SAT`
# - The first non-comment line needs to be of the form `p cnf nbvar nbclauses`, where
# - `cnf` indicates that the input is in CNF format
# - `nbvar` is the exact number of variables appearing in the file
# - `nbclauses` is the exact number of clauses contained in the file
# - eg. `p cnf 3 5`
# - Then there is a line for each clause, where
# - each clause is a sequence of distinct non-null numbers between `-nbvar` and `nbvar` ending with `0` on the same line
# - it cannot contain the opposite literals i and -i simultaneously
# - positive numbers denote the corresponding variables
# - negative numbers denote the negations of the corresponding variables
# - eg. `-1 2 3 0` corresponds to the clause $\neg v_1 \vee v_2 \vee v_3$
#
# Similarly the solutions to the problem $(v_1, v_2, v_3) = (T, F, T)$ or $(F, F, F)$ or $(T, T, F)$ can be written as `1 -2 3`, or `-1 -2 -3`, or `1 2 -3`.
#
# With this example problem input, we create the corresponding oracle for our Grover search. In particular, we use the LogicalExpressionOracle component provided by Aqua, which supports parsing DIMACS CNF format strings and constructing the corresponding oracle circuit.
import numpy as np
from qiskit import BasicAer
from qiskit.visualization import plot_histogram
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import Grover
from qiskit.aqua.components.oracles import LogicalExpressionOracle, TruthTableOracle
input_3sat = '''
c example DIMACS-CNF 3-SAT
p cnf 3 5
-1 -2 -3 0
1 -2 3 0
1 2 -3 0
1 -2 -3 0
-1 2 3 0
'''
oracle = LogicalExpressionOracle(input_3sat)
# The `oracle` can now be used to create an Grover instance:
# # 27/01/2022
grover = Grover(oracle)
# We can then configure a simulator backend and run the Grover instance to get the assignment result:
backend = BasicAer.get_backend('qasm_simulator')
quantum_instance = QuantumInstance(backend, shots=1024)
result = grover.run(quantum_instance)
print(result['assignment'])
# As seen above, a satisfying solution to the specified 3-SAT problem is obtained. And it is indeed one of the three satisfying solutions.
#
# Since we used a simulator backend, the complete measurement result is also returned, as shown in the plot below, where it can be seen that the binary strings `000`, `011`, and `101` (note the bit order in each string), corresponding to the three satisfying solutions all have high probabilities associated with them.
plot_histogram(result['measurement'])
# We have seen that the simulator can find the solutions to the example problem. We would like to see what happens if we use the real quantum devices that have noise and imperfect gates.
#
# However, due to the restriction on the length of strings that can be sent over the network to the real devices (there are more than sixty thousands characters of QASM of the circuit), at the moment the above circuit cannot be run on real device backends. We can see the compiled QASM on real-device `ibmq_16_melbourne` backend as follows:
# + tags=["uses-hardware"]
# Load our saved IBMQ accounts and get the ibmq_16_melbourne backend
from qiskit import IBMQ
IBMQ.load_account()
provider = IBMQ.get_provider(hub='ibm-q')
backend = provider.get_backend('ibmq_16_melbourne')
# + tags=["uses-hardware"]
from qiskit.compiler import transpile
# transpile the circuit for ibmq_16_melbourne
grover_compiled = transpile(result['circuit'], backend=backend, optimization_level=3)
print('gates = ', grover_compiled.count_ops())
print('depth = ', grover_compiled.depth())
# -
# The number of gates needed is far above the limits regarding decoherence time of the current near-term quantum computers. It is a challenge to design a quantum circuit for Grover search to solve satisfiability and other optimization problems.
# ## 4. Problems <a id='problems'></a>
#
# 1. Use Qiskit Aqua to solve the following 3SAT problem: $f(x_1, x_2, x_3) = (x_1 \vee x_2 \vee \neg x_3) \wedge (\neg x_1 \vee \neg x_2 \vee \neg x_3) \wedge (\neg x_1 \vee x_2 \vee x_3)$. Are the results what you expect?
#
# ## 5. References <a id='references'></a>
#
# 1. <NAME> (2017), _"An Introduction to Quantum Computing, Without the Physics",_ [arXiv:1708.03684 ](https://arxiv.org/abs/1708.03684)
#
# 2. <NAME> (1997) _"Grover’s quantum searching algorithm is optimal",_ [arXiv:quant-ph/9711070](https://arxiv.org/pdf/quant-ph/9711070.pdf)
#
# 3. <NAME>, <NAME>, <NAME>, <NAME>, _"Faster k-SAT algorithms using biased-PPSZ",_ [https://dl.acm.org/doi/10.1145/3313276.3316359](https://dl.acm.org/doi/10.1145/3313276.3316359)
#
# 4. <NAME>, <NAME>, <NAME>, _"Nested quantum search and NP-complete problems",_ [arXiv:quant-ph/9806078](https://arxiv.org/pdf/quant-ph/9806078.pdf)
import qiskit
qiskit.__qiskit_version__
|
notebooks/ch-applications/satisfiability-grover.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# ### Functions
# #### Function basic syntax
# +
import pandas as pd
data = pd.read_csv("../python learning/car data.csv")
def func1():
print(data.head())
def func2():
print("The dataset shape is",data.shape)
def func3():
print(data.isnull().sum())
func3()
func2()
func1()
# -
def func():
x = data.isnull().sum().mean()
if x > 0.50:
print("colums greater than 0.50 percent are",x)
elif x < 0.50:
print("colums less than 0.50 percent are",x)
else:
print("not found")
func()
# +
def func():
print('hello world')
func()
# -
# #### Passing arguments to function
# +
def func(a,b): # a and b are arguments
c = a+b
print(c)
func(10,20)
# +
def func(a=20,b=30):
if b>a:
print("b is greater")
else:
print("b is less")
func()
# -
# #### Keyword Arguments
# +
def func(firstname, lastname): ## firstname and lastname are keyword arguments
print('First name is :', firstname)
print('last name is :', lastname)
func(firstname='tulasiram', lastname='ponaganti')
# -
# Variable-length arguments
# In Python, we can pass a variable number of arguments to a function using special symbols. There are two special symbols:
#
# *args (Non-Keyword Arguments)
# **kwargs (Keyword Arguments)
def func(*argv):
for arg in argv:
print(arg)
''' Here i passed three arguments'''
func('tulasi','ram','ponaganti')
def func(*argv):
for arg in argv:
arg+=1
print(arg)
''' Here i passed three arguments'''
func(1,2,3)
# +
def myFun(**kwargs):
for key, value in kwargs.items():
print("%s == %s" % (key, value))
# Driver code
myFun(first='tulasi', mid='ram', last='ponaganti')
# -
# #### using a doc string
def myFun(**kwargs):
'''Function to explain doc string'''
for key, value in kwargs.items():
print("%s == %s" % (key, value))
print(myFun.__doc__) ## doc string syntax
# Driver code
myFun(first='tulasi', mid='ram', last='ponaganti')
# ### using return in a function
def sumFunc(a,b,c):
'''Function passed with arguments and returned sum of arguments'''
return a+b+c
print(sumFunc.__doc__)
sumFunc(10,20,30)
# When we pass a reference and change the received reference to something else, the connection between the passed and received parameter is broken. For example, consider the below program.
#
# intilaise as global and local variable to overcome this
#
# +
def func(list):
list = [1,2,3]
list2 = [4,5,6]
func(list2)
print(list2)
# -
# #### Nested Functions
def f1():
s = "tulasi ram"
def f2():
print(s)
f2()
f1()
def func1():
i=0
def func2():
for i in range(10):
def func3():
print(i*i)
func3()
func2()
func1()
# We have anonymous functions lambda, filter, reduce, map which are explained in part-04
# using yield in functions
#
# Every normal function will become generator function when we use yield inside function. yied will produce sequence of values.
#
# check the below examples
# +
def nextSquare():
i = 1
# An Infinite loop to generate squares
while True:
yield i*i
i += 1 # Next execution resumes
# from this point
# Driver code to test above generator
# function
for num in nextSquare():
if num > 100:
break
print(num)
# +
# Use of yield
def printResult(list) :
for i in list:
if i == 20:
yield i
# initializing string
list = [10,20,20,30,20,20,20,20]
ans = 0
print ("The number of '20s' in word is : ", end=" ")
for j in printResult(list):
ans = ans + 1
print(j)
# +
class MyFirstClass():
#Class Attributes
var = 10
firstObject = MyFirstClass()
print(firstObject) #Printing object's memory hex
print(firstObject.var) #Accessing Class Attributes
secondObject = MyFirstClass()
print(secondObject)
print(secondObject.var)
# +
class Vehicle():
#Class Methods/ Attributes
#Here self is passed as an argument because instance is passed as first argument
def type(self): #Without self it throws an error
print('I have a car')
car = Vehicle()
car.type()
# -
|
05...learn_python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext watermark
# %watermark -v -n -m -p numpy,scipy,sklearn,pandas
import sys
import os
PROJ_ROOT = os.path.abspath(os.path.join(os.pardir))
sys.path.append(os.path.join(PROJ_ROOT, "src"))
#from models.decision_tree import DecisionTree
import pandas as pd
import numpy as np
df1 = pd.read_excel(os.path.join(PROJ_ROOT, "data","processed","validate_data.xlsx"),index_col =0)
header = df1.columns.values.tolist()
labels = df1.iloc[:,-1]
# +
predictions = [13, 11, 12, 11, 13, 12, 10, 10, 12, 11, 16, 13, 9, 11, 12, 12, 13, 13, 12, 11, 13, 13, 11, 10, 11, 10, 10, 11, 12, 14, 13, 12, 13, 13, 12, 11, 13, 13, 13, 14, 10, 14, 14, 12, 14, 13, 17, 13, 10, 11, 13, 11, 16, 10, 12, 10, 11, 11, 13, 13, 10, 13, 13, 11, 13, 13, 16, 13, 13, 14, 12, 12, 11, 13, 12, 12, 10, 12, 10, 13, 10, 10, 11, 13, 11, 12, 10, 13, 13, 13, 13, 11, 10, 14, 10, 10, 11, 13, 10, 11, 13, 13, 12, 13, 14, 13, 16, 16, 13, 12, 15, 13, 12, 13, 10, 10, 10, 12, 14, 11, 13, 10, 11, 13, 11, 13, 10, 10, 13]
TSS = np.sum((np.array(labels) - np.array(labels).mean())** 2)
ESS = np.sum((np.array(predictions) - np.array(labels).mean()) ** 2)
ESS/TSS
# +
#from models.utils import class_counts,is_numeric,partition,gini,gini_impurity,unique_vals,class_counts
#from models.decision_tree import DecisionTree,DecisionTree,Leaf,Question
# -
training_data = [
['Green', 3, 'Apple'],
['Yellow', 3, 'Apple'],
['Red', 1, 'Grape'],
['Red', 1, 'Grape'],
['Yellow', 3, 'Lemon'],
]
training_data1 = [
['Yellow', 3, 'Apple'],
['Yellow', 3, 'Apple'],
['Yellow', 3, 'Apple'],
['Red', 1, 'Grape'],
['Yellow', 3, 'Lemon'],
]
header = ["color", "diameter", "label"]
gini(training_data1)
entropy(training_data1)
# +
import os
import pickle
from random import sample
from math import sqrt,ceil
import pandas as pd
def unique_vals(rows, col):
"""Find the unique values for a column in a dataset."""
return set([row[col] for row in rows])
def class_counts(rows):
"""Counts the number of each type of example in a dataset."""
counts = {} # a dictionary of label -> count.
for row in rows:
# in our dataset format, the label is always the last column
label = row[-1]
if label not in counts:
counts[label] = 0
counts[label] += 1
#return: {'Apple': 2, 'Grape': 2, 'Lemon': 1}
return counts
def is_numeric(value):
"""Test if a value is numeric."""
return isinstance(value, (int,float))
def partition(rows, question):
"""Partitions a dataset.
For each row in the dataset, check if it matches the question. If
so, add it to 'true rows', otherwise, add it to 'false rows'.
"""
true_rows, false_rows = [], []
for row in rows:
if question.match(row):
true_rows.append(row)
else:
false_rows.append(row)
return true_rows, false_rows
########################## decision tree metrics #############################
def gini(rows):
"""Calculate the Gini Impurity for a list of rows.
p_x = probabilities of find element of "x" class
"""
classes_count = class_counts(rows)
impurity = 1
for x in classes_count:
p_x = classes_count[x] / float(len(rows))
impurity -= p_x**2
return impurity
def entropy(rows):
"""
Calculate the entropy of a dataset.
p_x = probabilities of find element of "x" class
"""
classes_count = class_counts(rows)
entropy = 0
for x in classes_count:
p_x = classes_count[x] / float(len(rows))
entropy-=p_x*np.log2(p_x)
return entropy
def gini_impurity(left, right, current_uncertainty):
"""Gini impurity.
The uncertainty of the starting node, minus the weighted impurity of
two child nodes.
"""
p = float(len(left)) / (len(left) + len(right))
return current_uncertainty - p * gini(left) - (1 - p) * gini(right)
def info_gain(rows,current_entropy):
"""
… information gain, is simply the expected reduction in entropy
caused by partitioning the examples according to this attribute.
Entropy(Dataset)
– Count(Group1) / Count(Dataset) * Entropy(Group1)
+ Count(Group2) / Count(Dataset) * Entropy(Group2)
"""
p = float(len(left)) / (len(left) + len(right))
return current_entropy - p * entropy(left) + (1 - p) * entropy(right)
##############################################################################
# -
|
notebooks/.ipynb_checkpoints/Untitled-checkpoint.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# ## Analysis of cognitive atlas terms in openneuro metadata
#
# Using data generated by find_cogat_matches.py, saved to ../data/openneuro/cogatlas_matches.json
import pandas as pd
import json
from collections import defaultdict
import matplotlib.pyplot as plt
from wordcloud import WordCloud
with open('../data/openneuro/cogatlas_matches.json') as f:
cogatlas_matches = json.load(f)
# +
# get matches for each class of terms
def split_matches_by_type(allmatches):
match_dict = {}
for ds, matches in allmatches.items():
for match in matches:
matchtype, term = match[1], match[0]
if matchtype not in match_dict:
match_dict[matchtype] = defaultdict(lambda: [])
match_dict[matchtype][ds].append(term)
return(match_dict)
matches_by_type = split_matches_by_type(cogatlas_matches)
# +
# summarize concept terms
def get_terms_df(term_dict):
# return long df with terms for each dataset
allterms = []
for k, terms in term_dict.items():
# note: remove repetitions of a term within a dataset
for term in list(set(terms)):
allterms.append([k, term])
return(pd.DataFrame(allterms, columns=['ds', 'terms']))
concept_df = get_terms_df(matches_by_type['concept'])
concept_df.head()
# -
concept_df.terms.value_counts()
# ## word cloud for concepts
# +
# drop these terms because they are generally not being used as cognitive concepts in this context
stopterms = ['fixation', 'activation']
concept_text = ' '.join([i.replace(' ', '_') for i in concept_df.terms if i not in stopterms])
wc = WordCloud(background_color="white",
repeat=False, relative_scaling=.5,
width=800, height=600)
wc.generate(concept_text)
plt.axis("off")
plt.imshow(wc, interpolation="bilinear")
plt.tight_layout()
plt.savefig('../figures/wordcloud_concept.png')
plt.show()
# -
# ## word cloud for tasks
# +
task_df = get_terms_df(matches_by_type['task'])
stopterms = ['criteria task']
def cleanup_text(t):
bespoke_replacements = {' ': '_',
'-': '_',
'_task': '',
'_test': '',
'_fmri_paradigm': ''}
for orig, repl in bespoke_replacements.items():
t = t.replace(orig, repl)
return(t)
task_text = ' '.join([cleanup_text(i) for i in task_df.terms if i not in stopterms])
wc = WordCloud(background_color="white",
repeat=False, relative_scaling=0,
width=800, height=600)
wc.generate(task_text)
plt.axis("off")
plt.imshow(wc, interpolation="bilinear")
plt.tight_layout()
plt.savefig('../figures/wordcloud_task.png')
plt.show()
# -
# ## word cloud for disorders
# +
disorder_df = get_terms_df(matches_by_type['disorder'])
stopterms = []
disorder_text = ' '.join([i.replace(' ', '_').replace('-', '_') for i in disorder_df.terms if i not in stopterms])
wc = WordCloud(background_color="white",
repeat=False, relative_scaling=0,
width=800, height=400)
wc.generate(disorder_text)
plt.savefig('../figures/wordcloud_disorder.png')
plt.axis("off")
plt.imshow(wc, interpolation="bilinear")
plt.show()
# -
|
metadata_analyses/CogAtlasTerms.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# %load_ext autoreload
# %autoreload
import logging
from ssd.config.defaults import cfg
from ssd.utils.logger import setup_logger
from test import evaluation
# +
config_file = "configs/vgg_ssd300_voc0712_tdt4265_server.yaml"
ckpt = None # The path to the checkpoint for test, default is the latest checkpoint
cfg.merge_from_file(config_file)
cfg.freeze()
logger = setup_logger("SSD", cfg.OUTPUT_DIR)
logger.info("Loaded configuration file {}".format(config_file))
with open(config_file, "r") as cf:
config_str = "\n" + cf.read()
logger.info(config_str)
logger.info("Running with config:\n{}".format(cfg))
# -
evaluation(cfg, ckpt=ckpt)
|
test.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.9.5 64-bit (''base'': conda)'
# name: python3
# ---
# ---
# author: <NAME> (<EMAIL>)
# ---
#
# The R programming language comes with many free datasets built in. To make these
# same datasets available to Python programmers as well, you can install and import
# the `rdatasets` package.
#
# First, ensure that you have it installed, by running `pip install rdatasets` or
# `conda install rdatasets` from your command line. Then you can get access to many
# datasets as follows:
from rdatasets import data
df = data( 'iris' ) # Load the famous Fisher's irises dataset
df.head()
# But what datasets are available? There are many! You can find a full list in the package itself.
from rdatasets import summary
summary()
|
database/tasks/How to quickly load some sample data/Python.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] heading_collapsed=true
# # Import
# + hidden=true
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib.colors import ListedColormap
# + hidden=true
import warnings
warnings.filterwarnings("ignore")
# + hidden=true
def visualize(X_set, y_set):
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('black', 'white')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'blue'))(i), label = j)
plt.title('Classifier (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
# + [markdown] heading_collapsed=true
# # Preparing Data
# + hidden=true
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
y = dataset.iloc[:, 4].values
# + hidden=true
dataset
# + hidden=true
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)
# + hidden=true
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# -
# # Training the classifier
from sklearn.naive_bayes import GaussianNB
classifier = GaussianNB()
classifier.fit(X_train,y_train)
y_pred = classifier.predict(X_test)
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)
cm
visualize(X_train,y_train)
visualize(X_test,y_test)
|
Implementations/Part 3 - Classification/Naive_Bayes/Naive Bayes Algorithm.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# +
import requests
url = 'http://falcon:8000/bdr'
lines = open('test-small.json').read().split("\n")
for data in lines:
# COMPLETE POST REQUEST TO SEND JSON TO SERVER
print(response)
# -
|
data/user-simulator.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python [conda root]
# language: python
# name: conda-root-py
# ---
#comments in Python
'''multiple lines of comments are being shown here'''
# # Important
# this is a markdown and not a code window
#
2+3+5
66-3-(-4)
32*3
2**3
2^3
43/3
43//3
43%3
import math as mt
mt.exp(2)
mt.log(10)
mt.exp(1)
mt.log(8,2)
mt.sqrt(1000)
import numpy as np
np.std([23,45,67,78])
dir(mt)
type(1)
type("Ajay")
type([23,45,67])
a=[23,45,67]
len(a)
np.std(a)
np.var(a)
123456789123456789*9999999999999999
# +
# np.random??
# -
from random import randrange,randint
print(randint(0,90))
randrange(1000)
for x in range(0,10):
print(randrange(10000000000000000))
def mynewfunction(x,y):
taxes=((x-1000000)*0.35+100000-min(y,100000))
print(taxes)
mynewfunction(2200000,300000)
import os as os
# +
# os??
# -
for x in range(0,30,6):
print(x)
def mynewfunction(x,y):
z=x**3+3*x*y+20*y
print(z)
for x in range(0,30,6):
mynewfunction(x,10)
|
my+first+class+in+python.ipynb
|
// ---
// jupyter:
// jupytext:
// text_representation:
// extension: .java
// format_name: light
// format_version: '1.5'
// jupytext_version: 1.14.4
// kernelspec:
// display_name: Java
// language: java
// name: java
// ---
// # Train your first model
//
// This is the second of our [beginner tutorial series](https://github.com/awslabs/djl/tree/master/jupyter/tutorial) that will take you through creating, training, and running inference on a neural network. In this tutorial, you will learn how to train an image classification model that can recognize handwritten digits.
//
// ## Preparation
//
// This tutorial requires the installation of the Java Jupyter Kernel. To install the kernel, see the [Jupyter README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
// +
// Add the snapshot repository to get the DJL snapshot artifacts
// // %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
// Add the maven dependencies
// %maven ai.djl:api:0.6.0
// %maven ai.djl:basicdataset:0.6.0
// %maven ai.djl:model-zoo:0.6.0
// %maven ai.djl.mxnet:mxnet-engine:0.6.0
// %maven org.slf4j:slf4j-api:1.7.26
// %maven org.slf4j:slf4j-simple:1.7.26
// %maven net.java.dev.jna:jna:5.3.0
// See https://github.com/awslabs/djl/blob/master/mxnet/mxnet-engine/README.md
// for more MXNet library selection options
// %maven ai.djl.mxnet:mxnet-native-auto:1.7.0-b
// +
import java.nio.file.*;
import ai.djl.*;
import ai.djl.basicdataset.*;
import ai.djl.ndarray.types.*;
import ai.djl.training.*;
import ai.djl.training.dataset.*;
import ai.djl.training.initializer.*;
import ai.djl.training.loss.*;
import ai.djl.training.listener.*;
import ai.djl.training.evaluator.*;
import ai.djl.training.optimizer.*;
import ai.djl.training.util.*;
import ai.djl.basicmodelzoo.cv.classification.*;
import ai.djl.basicmodelzoo.basic.*;
// -
// # Step 1: Prepare MNIST dataset for training
//
// When training a deep learning network, it is important to first understand the dataset.
//
// ## Dataset
//
// A [Dataset](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/dataset/Dataset.html) is a collection of sample input/output pairs for the function represented by your neural network. Each single input/output is represented by a [Record](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/dataset/Record.html). Each record could have multiple arrays of inputs or outputs such as an image question and answer dataset where the input is both an image and a question about the image while the output is the answer to the question.
//
// Because data learning is highly parallelizable, training is often done not with a single record at a time but a [Batch](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/dataset/Batch.html) of records at a time. This can lead to significant performance gains, especially when working with images.
//
// ### MNIST
//
// The dataset we will be using is [MNIST](https://en.wikipedia.org/wiki/MNIST_database), a database of handwritten digits. Each image contains a black and white digit from 0-9 in a 28x28 image. It is commonly used when getting started with deep learning because it is small and fast to train.
//
// 
//
// Once you understand your dataset, you should create an implementation of the [Dataset class](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/dataset/Dataset.html). In this case, we provide the MNIST dataset built-in to make it easy for you to use it.
//
// ## Sampler
//
// Then, we must decide the parameters for loading data from the dataset. The only parameter we need for MNIST is the choice of [Sampler](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/dataset/Sampler.html). The sampler decides which and how many element from datasets are part of each batch when iterating through it. We will have it randomly shuffle the elements for the batch and use a batchSize of 32. The batchSize is usually the largest power of 2 that fits within memory.
int batchSize = 32;
Mnist mnist = Mnist.builder().setSampling(batchSize, true).build();
mnist.prepare(new ProgressBar());
// # Step 2: Create your Model
//
// A [Model](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/Model.html) contains a neural network [Block](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/nn/Block.html) along with additional artifacts used for the training process. It possesses additional information about the inputs, outputs, shapes, and data types you will use. Generally, you will use Model once you have fully completed your Block.
//
// In this tutorial, we will use the built-in Multilayer Perceptron Block from the Model Zoo. To learn more, see the previous tutorial: [Create Your First Network](01_create_your_first_network.ipynb).
//
// Because images in the MNIST dataset are 28x28 grayscale images, we will create an MLP block with 28 x 28 input. The output will be 10 because there are 10 possible classes (0 to 9) each image could be. For the hidden layers, we have chosen `new int[] {128, 64}` by experimenting with different values.
Model model = Model.newInstance("mlp");
model.setBlock(new Mlp(28 * 28, 10, new int[] {128, 64}));
// # Step 3: Create a Trainer
//
// Now, you can create a [`Trainer`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/Trainer.html) to train your model. The trainer is the main class to orchestrate the training process. Usually, they will be opened using a try-with-resources and closed after training is over.
//
// The trainer takes an existing model and attempts to optimize the parameters inside the model's Block to best match the dataset. Most optimization is based upon [Stochastic Gradient Descent](https://en.wikipedia.org/wiki/Stochastic_gradient_descent) (SGD).
//
// ## Step 3.1: Setup your training configurations
//
// Before you create your trainer, we we will need a [training configuration](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/DefaultTrainingConfig.html) that describes how to train your model.
//
// The following are a few common items you may need to configure your training:
// * **REQUIRED** [`Loss`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/loss/Loss.html) function: A loss function is used to measure how well our model matches the dataset. Because the lower value of the function is better, it's called the "loss" function. The Loss is the only required argument to the model
// * [`Evaluator`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/evaluator/Evaluator.html) function: An evaluator function is also used to measure how well our model matches the dataset. Unlike the loss, they are only there for people to look at and are not used for optimizing the model. Since many losses are not as intuitive, adding other evaluators such as Accuracy can help to understand how your model is doing. If you know of any useful evaluators, we recommend adding them.
// * batch size: To take the advantage of the natural parallelism, you usually train models with batches of input data items rather than a single item at a time. This should match the batch size provided in the model",
// * [`Device`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/Device.html): The device is what hardware should be used to train your model on. Typically, this is either CPU or GPU. DJL can automatically detect whether a GPU is available. If GPUs are available, it will run on a single GPU by default. If you need to train with multiple GPUs, you need to set devices as : `config.setDevices(Devices.getDevices(maxNumberOfGPUs))`.
// * [`Initializer`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/initializer/Initializer.html): An `Initializer` is used to set the initial values of the model's parameters before training. This can usually be left as the default initializer.
// * [`Optimizer`](https://javadoc.io/static/ai.djl/api/0.6.0/index.html?ai/djl/training/optimizer/Optimizer.html): The optimizer is the code that updates the model parameters to minimize the loss function. There are a variety of optimizers, most of which offer improvements upon the basic SGD. When just starting, you can use the default optimizer. Later on, Customizing the optimizer can result in faster training.
// +
DefaultTrainingConfig config = new DefaultTrainingConfig(Loss.softmaxCrossEntropyLoss())
//softmaxCrossEntropyLoss is a standard loss for classification problems
.addEvaluator(new Accuracy()) // Use accuracy so we humans can understand how accurate the model is
.addTrainingListeners(TrainingListener.Defaults.logging());
// Now that we have our training configuration, we should create a new trainer for our model
Trainer trainer = model.newTrainer(config);
// -
// # Step 5: Initialize Training
//
// Before training your model, you have to initialize all of the parameters with default values. You can use the trainer for this initialization by passing in the input shape.
//
// * The first axis of the input shape is the batch size. This won't impact the parameter initialization, so you can use 1 here.
// * The second axis of the input shape of the MLP - the number of pixels in the input image.
trainer.initialize(new Shape(1, 28 * 28));
// # Step 6: Train your model
//
// Now, we can train the model.
// +
// Deep learning is typically trained in epochs where each epoch trains the model on each item in the dataset once.
int epoch = 2;
for (int i = 0; i < epoch; ++i) {
int index = 0;
// We iterate through the dataset once during this epoch
for (Batch batch : trainer.iterateDataset(mnist)) {
// During trainBatch, we update the loss and evaluators with the results for the training batch.
EasyTrain.trainBatch(trainer, batch);
// Now, we update the model parameters based on the results of the latest trainBatch
trainer.step();
// We must make sure to close the batch to ensure all the memory associated with the batch is cleared quickly.
// If the memory isn't closed after each batch, you will very quickly run out of memory on your GPU
batch.close();
}
// reset training and validation evaluators at end of epoch
trainer.notifyListeners(listener -> listener.onEpoch(trainer));
}
// -
// # Step 7: Save your model
//
// Once your model is trained, you should save it so that it can be reloaded later. You can also add metadata to it such as training accuracy, number of epochs trained, etc that can be used when loading the model or when examining it.
// +
Path modelDir = Paths.get("build/mlp");
Files.createDirectories(modelDir);
model.setProperty("Epoch", String.valueOf(epoch));
model.save(modelDir, "mlp");
model
// -
// # Summary
//
// Now, you've successfully trained a model that can recognize handwritten digits. You'll learn how to apply this model in the next chapter: [Run image classification with your model](03_image_classification_with_your_model.ipynb).
//
// You can find the complete source code for this tutorial in the [examples project](https://github.com/awslabs/djl/blob/master/examples/src/main/java/ai/djl/examples/training/TrainMnist.java).
|
jupyter/tutorial/02_train_your_first_model.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# # `datasets.protein_dataset`
# +
# # %load ../../HPA-competition-solutions/bestfitting/src/datasets/protein_dataset.py
# +
#default_exp datasets.protein_dataset
# +
#export
import os
from pathlib import Path
import numpy as np
import cv2
from torch.utils.data.dataset import Dataset
from kgl_humanprotein.utils.common_util import *
import pandas as pd
from kgl_humanprotein.config.config import *
from kgl_humanprotein.datasets.tool import *
from kgl_humanprotein.utils.augment_util import *
from PIL import Image
import re
# +
#export
class ProteinDataset(Dataset):
def __init__(self,
dir_train_cells,
split_file,
img_size=512,
transform=None,
return_label=True,
is_trainset=True,
in_channels=4,
crop_size=0,
random_crop=False,
):
self.dir_train_cells = Path(dir_train_cells)
self.is_trainset = is_trainset
self.img_size = img_size
self.return_label = return_label
self.in_channels = in_channels
self.transform = transform
self.crop_size = crop_size
self.random_crop = random_crop
data_type = 'train' if is_trainset else 'test'
split_df = pd.read_feather(split_file)
if EXTERNAL not in split_df.columns:
split_df[EXTERNAL] = False
self.split_df = split_df
if is_trainset:
self.labels = self.split_df[LABEL_NAME_LIST].values.astype(int)
assert self.labels.shape == (len(self.split_df), len(LABEL_NAMES))
self.is_external = self.split_df[EXTERNAL].values
self.img_ids = self.split_df[ID].values
self.num = len(self.img_ids)
def read_crop_img(self, img):
random_crop_size = int(np.random.uniform(self.crop_size, self.img_size))
x = int(np.random.uniform(0, self.img_size - random_crop_size))
y = int(np.random.uniform(0, self.img_size - random_crop_size))
crop_img = img[x:x + random_crop_size, y:y + random_crop_size]
return crop_img
def read_rgby(self, img_dir, img_id, index):
if self.is_external[index]:
img_is_external = True
else:
img_is_external = False
suffix = '.jpg' if img_is_external else '.png'
if self.in_channels == 3:
colors = ['red', 'green', 'blue']
else:
colors = ['red', 'green', 'blue', 'yellow']
flags = cv2.IMREAD_GRAYSCALE
fns = [opj(img_dir, img_id + '_' + color + suffix) for color in colors]
for fn in fns:
assert os.path.exists(fn), f'Cannot find {fn}'
img = [cv2.imread(opj(img_dir, img_id + '_' + color + suffix), flags)
for color in colors]
img = np.stack(img, axis=-1)
if self.random_crop and self.crop_size > 0:
img = self.read_crop_img(img)
return img
def __getitem__(self, index):
row = self.split_df.iloc[index]
isubset = row['subset']
img_id = row['Id']
img_dir = (self.dir_train_cells / f'humanpro-train-cells-subset{isubset}'
/ f'humanpro_train_cells_subset{isubset}' / 'train' / f'images_{self.img_size}')
image = self.read_rgby(img_dir, img_id, index)
if image[0] is None:
print(img_dir, img_id)
h, w = image.shape[:2]
if self.crop_size > 0:
if self.crop_size != h or self.crop_size != w:
image = cv2.resize(image, (self.crop_size, self.crop_size), interpolation=cv2.INTER_LINEAR)
else:
if self.img_size != h or self.img_size != w:
image = cv2.resize(image, (self.img_size, self.img_size), interpolation=cv2.INTER_LINEAR)
if self.transform is not None:
image = self.transform(image)
image = image / 255.0
image = image_to_tensor(image)
if self.return_label:
label = self.labels[index]
return image, label, index
else:
return image, index
def __len__(self):
return self.num
# +
#export
class ProteinTestDataset(Dataset):
def __init__(self, images, img_size=512, transform=None,
crop_size=0, random_crop=False):
self.images = images
self.img_size = img_size
self.transform = transform
self.crop_size = crop_size
self.random_crop = random_crop
self.num = len(self.images)
def read_crop_img(self, img):
random_crop_size = int(np.random.uniform(self.crop_size, self.img_size))
x = int(np.random.uniform(0, self.img_size - random_crop_size))
y = int(np.random.uniform(0, self.img_size - random_crop_size))
crop_img = img[x:x + random_crop_size, y:y + random_crop_size]
return crop_img
def read_rgby(self, index):
img = self.images[index]
if self.random_crop and self.crop_size > 0:
img = self.read_crop_img(img)
return img
def __getitem__(self, index):
image = self.read_rgby(index)
h, w = image.shape[:2]
if self.crop_size > 0:
if self.crop_size != h or self.crop_size != w:
image = cv2.resize(image, (self.crop_size, self.crop_size), interpolation=cv2.INTER_LINEAR)
else:
if self.img_size != h or self.img_size != w:
image = cv2.resize(image, (self.img_size, self.img_size), interpolation=cv2.INTER_LINEAR)
if self.transform is not None:
image = self.transform(image)
image = image / 255.0
image = image_to_tensor(image)
return image, index
def __len__(self):
return self.num
# -
|
nbs/03_datasets.protein_dataset.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3.5
# language: python
# name: python3
# ---
# # Transfer Learning
# A Convolutional Neural Network (CNN) for image classification is made up of multiple layers that extract features, such as edges, corners, etc; and then use a final fully-connected layer to classify objects based on these features. You can visualize this like this:
#
# <table>
# <tr><td rowspan=2 style='border: 1px solid black;'>⇒</td><td style='border: 1px solid black;'>Convolutional Layer</td><td style='border: 1px solid black;'>Pooling Layer</td><td style='border: 1px solid black;'>Convolutional Layer</td><td style='border: 1px solid black;'>Pooling Layer</td><td style='border: 1px solid black;'>Fully Connected Layer</td><td rowspan=2 style='border: 1px solid black;'>⇒</td></tr>
# <tr><td colspan=4 style='border: 1px solid black; text-align:center;'>Feature Extraction</td><td style='border: 1px solid black; text-align:center;'>Classification</td></tr>
# </table>
#
# *Transfer Learning* is a technique where you can take an existing trained model and re-use its feature extraction layers, replacing its final classification layer with a fully-connected layer trained on your own custom images. With this technique, your model benefits from the feature extraction training that was performed on the base model (which may have been based on a larger training dataset than you have access to) to build a classification model for your own specific set of object classes.
#
# How does this help? Well, think of it this way. Suppose you take a professional tennis player and a complete beginner, and try to teach them both how to play raquetball. It's reasonable to assume that the professional tennis player will be easier to train, because many of the underlying skills involved in raquetball are already learned. Similarly, a pre-trained CNN model may be easier to train to classify specific set of objects because it's already learned how to identify the features of common objects, such as edges and corners.
#
# In this notebook, we'll see how to implement transfer learning for a classification model.
#
# ## Functions to generate some image data
# First, we'll create some functions to generate our image data. In reality, we'd use images of real objects; but we'll just generate a small number of images of basic geometric shapes.
# +
# function to generate an image of random size and color
def create_image (size, shape):
from random import randint
import numpy as np
from PIL import Image, ImageDraw
xy1 = randint(10,40)
xy2 = randint(60,100)
col = (randint(0,200), randint(0,200), randint(0,200))
img = Image.new("RGB", size, (255, 255, 255))
draw = ImageDraw.Draw(img)
if shape == 'circle':
draw.ellipse([(xy1,xy1), (xy2,xy2)], fill=col)
elif shape == 'square':
draw.rectangle([(xy1,xy1), (xy2,xy2)], fill=col)
else: # triangle
draw.polygon([(xy1,xy1), (xy2,xy2), (xy2,xy1)], fill=col)
del draw
return np.array(img)
# function to create a dataset of images
def generate_image_data (classes, size, cases, img_dir):
import os, shutil
from PIL import Image
if os.path.exists(img_dir):
replace_folder = input("Image folder already exists. Enter Y to replace it (this can take a while!). \n")
if replace_folder == "Y":
print("Deleting old images...")
shutil.rmtree(img_dir)
else:
return # Quit - no need to replace existing images
os.makedirs(img_dir)
print("Generating new images...")
i = 0
while(i < (cases - 1) / len(classes)):
if (i%25 == 0):
print("Progress:{:.0%}".format((i*len(classes))/cases))
i += 1
for classname in classes:
img = Image.fromarray(create_image(size, classname))
saveFolder = os.path.join(img_dir,classname)
if not os.path.exists(saveFolder):
os.makedirs(saveFolder)
imgFileName = os.path.join(saveFolder, classname + str(i) + '.jpg')
try:
img.save(imgFileName)
except:
try:
# Retry (resource constraints in Azure notebooks can cause occassional disk access errors)
img.save(imgFileName)
except:
# We gave it a shot - time to move on with our lives
print("Error saving image", imgFileName)
# Our classes will be circles, squares, and triangles
classnames = ['circle', 'square', 'triangle']
# All images will be 128x128 pixels
img_size = (128,128)
# We'll store the images in a folder named 'shapes'
folder_name = 'shapes'
# Generate 1200 random images.
generate_image_data(classnames, img_size, 1200, folder_name)
print("Image files ready in %s folder!" % folder_name)
# -
# ### Setting up the Frameworks
# Now that we have our data, we're ready to build a CNN. The first step is to import and configure the frameworks we want to use.
# +
import sys
# ! {sys.executable} -m pip install --upgrade keras
import tensorflow, keras
print('TensorFlow version:',tensorflow.__version__)
print('Keras version:',keras.__version__)
from keras import backend as K
# -
# ### Preparing the Data
# Before we can train the model, we need to prepare the data.
# +
from keras.preprocessing.image import ImageDataGenerator
data_folder = 'shapes'
# Our source images are 128x128, but the base model we're going to use was trained with 224x224 images
pretrained_size = (224,224)
batch_size = 15
print("Getting Data...")
datagen = ImageDataGenerator(rescale=1./255, # normalize pixel values
validation_split=0.3) # hold back 30% of the images for validation
print("Preparing training dataset...")
train_generator = datagen.flow_from_directory(
data_folder,
target_size=pretrained_size,
batch_size=batch_size,
class_mode='categorical',
subset='training') # set as training data
print("Preparing validation dataset...")
validation_generator = datagen.flow_from_directory(
data_folder,
target_size=pretrained_size,
batch_size=batch_size,
class_mode='categorical',
subset='validation') # set as validation data
classes = sorted(train_generator.class_indices.keys())
print("class names: ", classes)
# -
# ### Downloading a trained model to use as a base
# The VGG16 model is an image classifier that was trained on the ImageNet dataset - a huge dataset containing thousands of images of many kinds of object. We'll download the trained model, excluding its top layer, and set its input shape to match our image data.
#
# *Note: The **keras.applications** namespace includes multiple base models, some which may perform better for your dataset than others. I've chosen this model because it's fairly lightweight within the limited resources of the Azure Notebooks environment.*
from keras import applications
#Load the base model, not including its final connected layer, and set the input shape to match our images
base_model = keras.applications.vgg16.VGG16(weights='imagenet', include_top=False, input_shape=train_generator.image_shape)
# ### Freeze the already trained layers and add a custom output layer for our classes
# The existing feature extraction layers are already trained, so we just need to add a couple of layers so that the model output is the predictions for our classes.
# +
from keras import Model
from keras.layers import Flatten, Dense
from keras import optimizers
# Freeze the already-trained layers in the base model
for layer in base_model.layers:
layer.trainable = False
# Create layers for classification of our images
x = base_model.output
x = Flatten()(x)
prediction_layer = Dense(len(classes), activation='softmax')(x)
model = Model(inputs=base_model.input, outputs=prediction_layer)
# Compile the model
opt = optimizers.Adam(lr=0.001)
model.compile(loss='categorical_crossentropy',
optimizer=opt,
metrics=['accuracy'])
# Now print the full model, which will include the layers of the base model plus the dense layer we added
print(model.summary())
# -
# ### Training the Model
# With the layers of the CNN defined, we're ready to train the top layer using our image data. This will take a considerable amount of time on a CPU depending on the complexity of the base model.
# Train the model over 2 epochs using 15-image batches and using the validation holdout dataset for validation
num_epochs = 2
history = model.fit_generator(
train_generator,
steps_per_epoch = train_generator.samples // batch_size,
validation_data = validation_generator,
validation_steps = validation_generator.samples // batch_size,
epochs = num_epochs)
# ### View the Loss History
# We tracked average training and validation loss for each epoch. We can plot these to see where the levels of loss converged, and to detect *over-fitting* (which is indicated by a continued drop in training loss after validation loss has levelled out or started to increase.
# +
# %matplotlib inline
from matplotlib import pyplot as plt
epoch_nums = range(1,num_epochs+1)
training_loss = history.history["loss"]
validation_loss = history.history["val_loss"]
plt.plot(epoch_nums, training_loss)
plt.plot(epoch_nums, validation_loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['training', 'validation'], loc='upper right')
plt.show()
# -
# ### Using the Trained Model
# Now that we've trained the model, we can use it to predict the class of an image.
# +
def predict_image(classifier, image_array):
import numpy as np
# We need to format the input to match the training data
# The generator loaded the values as floating point numbers
# and normalized the pixel values, so...
imgfeatures = image_array.astype('float32')
imgfeatures /= 255
# These are the classes our model can predict
classnames = ['circle', 'square', 'triangle']
# Predict the class of each input image
predictions = classifier.predict(imgfeatures)
predicted_classes = []
for prediction in predictions:
# The prediction for each image is the probability for each class, e.g. [0.8, 0.1, 0.2]
# So get the index of the highest probability
class_idx = np.argmax(prediction)
# And append the corresponding class name to the results
predicted_classes.append(classnames[int(class_idx)])
# Return the predictions as a JSON
return predicted_classes
from random import randint
from PIL import Image
import numpy as np
# %matplotlib inline
# Create a random test image
img = create_image ((224,224), classes[randint(0, len(classes)-1)])
plt.imshow(img)
# Create an array of (1) images to match the expected input format
img_array = img.reshape(1, img.shape[0], img.shape[1], img.shape[2])
# get the predicted clases
predicted_classes = predict_image(model, img_array)
# Display the prediction for the first image (we only submitted one!)
print(predicted_classes[0])
# -
# ## Learning More
# * [Tensorflow Documentation](https://www.tensorflow.org/get_started/premade_estimators)
# * [Keras Documentation](https://keras.io/)
|
OCPOpenHack/Azure_Deep_Learning/notebooks/04 - Transfer Learning (Keras).ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3 (ipykernel)
# language: python
# name: python3
# ---
# # T007 · Ligand-based screening: machine learning
#
# Authors:
#
# * <NAME>, CADD seminar 2018, Charité/FU Berlin
# * <NAME>, CADD seminar 2018, Charité/FU Berlin
# * <NAME>, 2019-2020, [Volkamer lab](https://volkamerlab.org)
# * <NAME>, 2019-2020, [Volkamer lab](https://volkamerlab.org)
# __Talktorial T007__: This talktorial is part of the TeachOpenCADD pipeline described in the [first TeachOpenCADD paper](https://jcheminf.biomedcentral.com/articles/10.1186/s13321-019-0351-x), comprising of talktorials T001-T010.
# ## Aim of this talktorial
#
# Due to larger available data sources, machine learning (ML) gained momentum in drug discovery and especially in ligand-based virtual screening. In this talktorial, we learn how to use different supervised ML algorithms to predict the activity of novel compounds against our target of interest (EGFR).
# ### Contents in _Theory_
#
# * Data preparation: Molecule encoding
# * Machine learning (ML)
# * Supervised learning
# * Model validation and evaluation
# * Validation strategy: K-fold cross-validation
# * Performance measures
# ### Contents in _Practical_
#
# * Load compound and activity data
# * Data preparation
# * Data labeling
# * Molecule encoding
# * Machine learning
# * Helper functions
# * Random forest classifier
# * Support vector classifier
# * Neural network classifier
# * Cross-validation
# ### References
#
# * "Fingerprints in the RDKit" [slides](https://www.rdkit.org/UGM/2012/Landrum_RDKit_UGM.Fingerprints.Final.pptx.pdf), <NAME>, RDKit UGM 2012
# * Extended-connectivity fingerprints (ECFPs): Rogers, David, and <NAME>. "Extended-connectivity fingerprints." [_Journal of chemical information and modeling_ 50.5 (2010): 742-754.](https://doi.org/10.1021/ci100050t)
# * Machine learning (ML):
# * Random forest (RF): <NAME>. "Random Forests". [_Machine Learning_ **45**, 5–32 (2001).](https://link.springer.com/article/10.1023%2FA%3A1010933404324)
# * Support vector machines (SVM): <NAME>., <NAME>. "Support-vector networks". [_Machine Learning_ **20**, 273–297 (1995).](https://link.springer.com/article/10.1007%2FBF00994018)
# * Artificial neural networks (ANN): <NAME>, Marcel, and <NAME>. "Artificial neural networks as models of neural information processing." [_Frontiers in Computational Neuroscience_ 11 (2017): 114.](https://doi.org/10.3389/fncom.2017.00114)
# * Performance:
# * Sensitivity and specificity ([Wikipedia](https://en.wikipedia.org/wiki/Sensitivity_and_specificity))
# * ROC curve and AUC ([Wikipedia](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve))
# * See also [github notebook by <NAME>](https://github.com/Team-SKI/Publications/tree/master/Profiling_prediction_of_kinase_inhibitors) from [*J. Med. Chem.*, 2017, 60, 474−485](https://pubs.acs.org/doi/10.1021/acs.jmedchem.6b01611)
# * Activity cutoff $pIC_{50} = 6.3$ used in this talktorial
# * Profiling Prediction of Kinase Inhibitors: Toward the Virtual Assay [<i>J. Med. Chem.</i> (2017), <b>60</b>, 474-485](https://doi.org/10.1021/acs.jmedchem.6b01611)
# * Notebook accompanying the publication mentioned before: [Notebook](https://github.com/Team-SKI/Publications/blob/master/Profiling_prediction_of_kinase_inhibitors/Build_ABL1_model.ipynb)
# ## Theory
#
# To successfully apply ML, we need a large data set of molecules, a molecular encoding, a label per molecule in the data set, and a ML algorithm to train a model. Then, we can make predictions for new molecules.
#
# 
#
# _Figure 1_: Machine learning overview: Molecular encoding, label, ML algorithm, prediction. Figure by <NAME>.
# ### Data preparation: Molecule encoding
#
# For ML, molecules need to be converted into a list of features. Often molecular fingerprints are used as representation.
#
# The fingerprints used in this talktorial as implemented in RDKit (more info can be found in a [presentation by <NAME>](https://www.rdkit.org/UGM/2012/Landrum_RDKit_UGM.Fingerprints.Final.pptx.pdf)) are:
#
# * **maccs**: 'MACCS keys are 166 bit structural key descriptors in which each bit is associated with a SMARTS pattern.' (see OpenEye's `MACCS` [docs](https://docs.eyesopen.com/toolkits/python/graphsimtk/fingerprint.html#maccs))
# * **Morgan fingerprints** (and **ECFP**): 'Extended-Connectivity Fingerprints (ECFPs) are circular topological fingerprints designed for molecular characterization, similarity searching, and structure-activity modeling.' (see ChemAxon's `ECFP` [docs](https://docs.chemaxon.com/display/docs/Extended+Connectivity+Fingerprint+ECFP)) The original implementation of the ECFPs was done in Pipeline Pilot which is not open-source. Instead we use the implementation from RDKit which is called Morgan fingerprint. The two most important parameters of these fingerprints are the radius and fingerprint length. The first specifies the radius of circular neighborhoods considered for each atom. Here two radii are considered: 2 and 3. The length parameter specifies the length to which the bit string representation is hashed. The default length is 2048.
# ### Machine learning (ML)
#
# ML can be applied for (text adapted from [scikit-learn page](http://scikit-learn.org/stable/)):
#
# * **Classification (supervised)**: Identify which category an object belongs to (e.g. : Nearest neighbors, Naive Bayes, RF, SVM, ...)
# * Regression: Prediction of a continuous-values attribute associated with an object
# * Clustering (unsupervised): Automated grouping of similar objects into sets (see also **Talktorial T005**)
# #### Supervised learning
#
# A learning algorithm creates rules by finding patterns in the training data.
# * **Random Forest (RF)**: Ensemble of decision trees. A single decision tree splits the features of the input vector in a way that maximizes an objective function. In the random forest algorithm, the trees that are grown are de-correlated because the choice of features for the splits are chosen randomly.
# * **Support Vector Machines (SVMs)**: SVMs can efficiently perform a non-linear classification using what is called the kernel trick, implicitly mapping their inputs into high-dimensional feature spaces. The classifier is based on the idea of maximizing the margin as the objective function.
# * **Artificial neural networks (ANNs)**: An ANN is based on a collection of connected units or nodes called artificial neurons which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal from one artificial neuron to another. An artificial neuron that receives a signal can process it and then signal additional artificial neurons connected to it.
#
#
# 
#
# _Figure 2_: Example of a neural network with one hidden layer. Figure taken from [Wikipedia](https://en.wikipedia.org/wiki/Artificial_neural_network).
# ### Model validation and evaluation
# #### Validation strategy: K-fold cross validation
#
# * This model validation technique splits the dataset in two groups in an iterative manner:
# * Training data set: Considered as the known dataset on which the model is trained
# * Test dataset: Unknown dataset on which the model is then tested
# * Process is repeated k-times
# * The goal is to test the ability of the model to predict data which it has never seen before in order to flag problems known as over-fitting and to assess the generalization ability of the model.
# #### Performance measures
#
# * **Sensitivity**, also true positive rate
# * TPR = TP/(FN + TP)
# * _Intuitively_: Out of all actual positives, how many were predicted as positive?
# * **Specificity**, also true negative rate
# * TNR = TN/(FP + TN)
# * _Intuitively_: Out of all actual negatives, how many were predicted as negative?
# * **Accuracy**, also the trueness
# * ACC = (TP + TN)/(TP + TN + FP + FN)
# * _Intuitively_: Proportion of correct predictions.
# * **ROC-curve**, receiver operating characteristic curve
# * A graphical plot that illustrates the diagnostic ability of our classifier
# * Plots the sensitivity against the specificity
# * **AUC**, the area under the ROC curve (AUC):
# * Describes the probability that a classifier will rank a randomly chosen positive instance higher than a negative one
# * Values between 0 and 1, the higher the better
# | What the model predicts | True active | True inactive |
# |---|---|---|
# | active | True Positive (TP) | False Positive (FP) |
# | inactive | False Negative (FN) | True Negative (TN) |
# ## Practical
# +
from pathlib import Path
from warnings import filterwarnings
import time
import pandas as pd
import numpy as np
from sklearn import svm, metrics, clone
from sklearn.ensemble import RandomForestClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import KFold, train_test_split
from sklearn.metrics import auc, accuracy_score, recall_score
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt
from rdkit import Chem
from rdkit.Chem import MACCSkeys
from rdkit.Chem.AllChem import GetMorganFingerprintAsBitVect
from teachopencadd.utils import seed_everything
# Silence some expected warnings
filterwarnings("ignore")
# Fix seed for reproducible results
SEED = 22
seed_everything(SEED)
# -
# Set path to this notebook
HERE = Path(_dh[-1])
DATA = HERE / "data"
# ### Load compound and activity data
#
# Let's start by loading our data, which focuses on the Epidermal growth factor receptor (EGFR) kinase. The *csv* file from **Talktorial T002** is loaded into a dataframe with the important columns:
#
# * CHEMBL-ID
# * SMILES string of the corresponding compound
# * Measured affinity: pIC50
# +
# Read data from previous talktorials
chembl_df = pd.read_csv(
HERE / "../T002_compound_adme/data/EGFR_compounds_lipinski.csv",
index_col=0,
)
# Look at head
print("Shape of dataframe : ", chembl_df.shape)
chembl_df.head()
# NBVAL_CHECK_OUTPUT
# -
# Keep only the columns we want
chembl_df = chembl_df[["molecule_chembl_id", "smiles", "pIC50"]]
chembl_df.head()
# NBVAL_CHECK_OUTPUT
# ### Data preparation
# #### Data labeling
# We need to classify each compound as active or inactive. Therefore, we use the pIC50 value.
#
# * pIC50 = -log10(IC50)
# * IC50 describes the amount of substance needed to inhibit, _in vitro_, a process by 50% .
# * A common cut-off value to discretize pIC50 data is 6.3, which we will use for our experiment (refer to [<i>J. Med. Chem.</i> (2017), <b>60</b>, 474-485](https://doi.org/10.1021/acs.jmedchem.6b01611) and the corresponding
# [notebook](https://github.com/Team-SKI/Publications/blob/master/Profiling_prediction_of_kinase_inhibitors/Build_ABL1_model.ipynb))
# * Note that there are several other suggestions for an activity cut-off ranging from an pIC50 value of 5 to 7 in the literature or even to define an exclusion range when not to take data points.
# +
# Add column for activity
chembl_df["active"] = np.zeros(len(chembl_df))
# Mark every molecule as active with an pIC50 of >= 6.3, 0 otherwise
chembl_df.loc[chembl_df[chembl_df.pIC50 >= 6.3].index, "active"] = 1.0
# NBVAL_CHECK_OUTPUT
print("Number of active compounds:", int(chembl_df.active.sum()))
print("Number of inactive compounds:", len(chembl_df) - int(chembl_df.active.sum()))
# -
chembl_df.head()
# NBVAL_CHECK_OUTPUT
# #### Molecule encoding
#
# Now we define a function `smiles_to_fp` to generate fingerprints from SMILES.
# For now, we incorporated the choice between the following fingerprints:
#
# * maccs
# * morgan2 and morgan3
def smiles_to_fp(smiles, method="maccs", n_bits=2048):
"""
Encode a molecule from a SMILES string into a fingerprint.
Parameters
----------
smiles : str
The SMILES string defining the molecule.
method : str
The type of fingerprint to use. Default is MACCS keys.
n_bits : int
The length of the fingerprint.
Returns
-------
array
The fingerprint array.
"""
# convert smiles to RDKit mol object
mol = Chem.MolFromSmiles(smiles)
if method == "maccs":
return np.array(MACCSkeys.GenMACCSKeys(mol))
if method == "morgan2":
return np.array(GetMorganFingerprintAsBitVect(mol, 2, nBits=n_bits))
if method == "morgan3":
return np.array(GetMorganFingerprintAsBitVect(mol, 3, nBits=n_bits))
else:
# NBVAL_CHECK_OUTPUT
print(f"Warning: Wrong method specified: {method}. Default will be used instead.")
return np.array(MACCSkeys.GenMACCSKeys(mol))
compound_df = chembl_df.copy()
# Add column for fingerprint
compound_df["fp"] = compound_df["smiles"].apply(smiles_to_fp)
compound_df.head(3)
# NBVAL_CHECK_OUTPUT
# ### Machine Learning (ML)
#
# In the following, we will try several ML approaches to classify our molecules. We will use:
#
# * Random Forest (RF)
# * Support Vector Machine (SVM)
# * Artificial Neural Network (ANN)
#
# Additionally, we will comment on the results.
#
# The goal is to test the ability of the model to predict data which it has never seen before in order to flag problems known as over fitting and to assess the generalization ability of the model.
#
# We start by defining a function `model_training_and_validation` which fits a model on a random train-test split of the data and returns measures such as accuracy, sensitivity, specificity and AUC evaluated on the test set. We also plot the ROC curves using `plot_roc_curves_for_models`.
#
# We then define a function named `crossvalidation` which executes a cross validation procedure and prints the statistics of the results over the folds.
# #### Helper functions
# Helper function to plot customized ROC curves. Code inspired by [stackoverflow](https://stackoverflow.com/questions/42894871/how-to-plot-multiple-roc-curves-in-one-plot-with-legend-and-auc-scores-in-python).
def plot_roc_curves_for_models(models, test_x, test_y, save_png=False):
"""
Helper function to plot customized roc curve.
Parameters
----------
models: dict
Dictionary of pretrained machine learning models.
test_x: list
Molecular fingerprints for test set.
test_y: list
Associated activity labels for test set.
save_png: bool
Save image to disk (default = False)
Returns
-------
fig:
Figure.
"""
fig, ax = plt.subplots()
# Below for loop iterates through your models list
for model in models:
# Select the model
ml_model = model["model"]
# Prediction probability on test set
test_prob = ml_model.predict_proba(test_x)[:, 1]
# Prediction class on test set
test_pred = ml_model.predict(test_x)
# Compute False postive rate and True positive rate
fpr, tpr, thresholds = metrics.roc_curve(test_y, test_prob)
# Calculate Area under the curve to display on the plot
auc = roc_auc_score(test_y, test_prob)
# Plot the computed values
ax.plot(fpr, tpr, label=(f"{model['label']} AUC area = {auc:.2f}"))
# Custom settings for the plot
ax.plot([0, 1], [0, 1], "r--")
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
ax.set_title("Receiver Operating Characteristic")
ax.legend(loc="lower right")
# Save plot
if save_png:
fig.savefig(f"{DATA}/roc_auc", dpi=300, bbox_inches="tight", transparent=True)
return fig
# Helper function to calculate model performance.
def model_performance(ml_model, test_x, test_y, verbose=True):
"""
Helper function to calculate model performance
Parameters
----------
ml_model: sklearn model object
The machine learning model to train.
test_x: list
Molecular fingerprints for test set.
test_y: list
Associated activity labels for test set.
verbose: bool
Print performance measure (default = True)
Returns
-------
tuple:
Accuracy, sensitivity, specificity, auc on test set.
"""
# Prediction probability on test set
test_prob = ml_model.predict_proba(test_x)[:, 1]
# Prediction class on test set
test_pred = ml_model.predict(test_x)
# Performance of model on test set
accuracy = accuracy_score(test_y, test_pred)
sens = recall_score(test_y, test_pred)
spec = recall_score(test_y, test_pred, pos_label=0)
auc = roc_auc_score(test_y, test_prob)
if verbose:
# Print performance results
# NBVAL_CHECK_OUTPUT print(f"Accuracy: {accuracy:.2}")
print(f"Sensitivity: {sens:.2f}")
print(f"Specificity: {spec:.2f}")
print(f"AUC: {auc:.2f}")
return accuracy, sens, spec, auc
# Helper function to fit a machine learning model on a random train-test split of the data and return the performance measures.
def model_training_and_validation(ml_model, name, splits, verbose=True):
"""
Fit a machine learning model on a random train-test split of the data
and return the performance measures.
Parameters
----------
ml_model: sklearn model object
The machine learning model to train.
name: str
Name of machine learning algorithm: RF, SVM, ANN
splits: list
List of desciptor and label data: train_x, test_x, train_y, test_y.
verbose: bool
Print performance info (default = True)
Returns
-------
tuple:
Accuracy, sensitivity, specificity, auc on test set.
"""
train_x, test_x, train_y, test_y = splits
# Fit the model
ml_model.fit(train_x, train_y)
# Calculate model performance results
accuracy, sens, spec, auc = model_performance(ml_model, test_x, test_y, verbose)
return accuracy, sens, spec, auc
# **Preprocessing**: Split the data (will be reused for the other models)
# +
fingerprint_to_model = compound_df.fp.tolist()
label_to_model = compound_df.active.tolist()
# Split data randomly in train and test set
# note that we use test/train_x for the respective fingerprint splits
# and test/train_y for the respective label splits
(
static_train_x,
static_test_x,
static_train_y,
static_test_y,
) = train_test_split(fingerprint_to_model, label_to_model, test_size=0.2, random_state=SEED)
splits = [static_train_x, static_test_x, static_train_y, static_test_y]
# NBVAL_CHECK_OUTPUT
print("Training data size:", len(static_train_x))
print("Test data size:", len(static_test_x))
# -
# #### Random forest classifier
#
# We start with a random forest classifier, where we first set the parameters.
# We train the model on a random train-test split and plot the results.
# Set model parameter for random forest
param = {
"n_estimators": 100, # number of trees to grows
"criterion": "entropy", # cost function to be optimized for a split
}
model_RF = RandomForestClassifier(**param)
# Fit model on single split
performance_measures = model_training_and_validation(model_RF, "RF", splits)
# Initialize the list that stores all models. First one is RF.
models = [{"label": "Model_RF", "model": model_RF}]
# Plot roc curve
plot_roc_curves_for_models(models, static_test_x, static_test_y);
# #### Support vector classifier
# Here we train a SVM with a radial-basis function kernel (also: squared-exponential kernel).
# For more information, see [sklearn RBF kernel](http://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.kernels.RBF.html).
# +
# Specify model
model_SVM = svm.SVC(kernel="rbf", C=1, gamma=0.1, probability=True)
# Fit model on single split
performance_measures = model_training_and_validation(model_SVM, "SVM", splits)
# + tags=["nbsphinx-thumbnail"]
# Append SVM model
models.append({"label": "Model_SVM", "model": model_SVM})
# Plot roc curve
plot_roc_curves_for_models(models, static_test_x, static_test_y);
# -
# #### Neural network classifier
# The last approach we try here is a neural network model. We train an MLPClassifier (Multi-layer Perceptron classifier) with 3 layers, each with 5 neurons. As before, we do the crossvalidation procedure and plot the results. For more information on MLP, see [sklearn MLPClassifier](http://scikit-learn.org/stable/modules/generated/sklearn.neural_network.MLPClassifier.html).
# +
# Specify model
model_ANN = MLPClassifier(hidden_layer_sizes=(5, 3), random_state=SEED)
# Fit model on single split
performance_measures = model_training_and_validation(model_ANN, "ANN", splits)
# -
# Append ANN model
models.append({"label": "Model_ANN", "model": model_ANN})
# Plot roc curve
plot_roc_curves_for_models(models, static_test_x, static_test_y, True);
# Our models show very good values for all measured values (see AUCs) and thus seem to be predictive.
# #### Cross-validation
#
# Next, we will perform cross-validation experiments with the three different models.
# Therefore, we define a helper function for machine learning model training and validation in a cross-validation loop.
def crossvalidation(ml_model, df, n_folds=5, verbose=False):
"""
Machine learning model training and validation in a cross-validation loop.
Parameters
----------
ml_model: sklearn model object
The machine learning model to train.
df: pd.DataFrame
Data set with SMILES and their associated activity labels.
n_folds: int, optional
Number of folds for cross-validation.
verbose: bool, optional
Performance measures are printed.
Returns
-------
None
"""
t0 = time.time()
# Shuffle the indices for the k-fold cross-validation
kf = KFold(n_splits=n_folds, shuffle=True, random_state=SEED)
# Results for each of the cross-validation folds
acc_per_fold = []
sens_per_fold = []
spec_per_fold = []
auc_per_fold = []
# Loop over the folds
for train_index, test_index in kf.split(df):
# clone model -- we want a fresh copy per fold!
fold_model = clone(ml_model)
# Training
# Convert the fingerprint and the label to a list
train_x = df.iloc[train_index].fp.tolist()
train_y = df.iloc[train_index].active.tolist()
# Fit the model
fold_model.fit(train_x, train_y)
# Testing
# Convert the fingerprint and the label to a list
test_x = df.iloc[test_index].fp.tolist()
test_y = df.iloc[test_index].active.tolist()
# Performance for each fold
accuracy, sens, spec, auc = model_performance(fold_model, test_x, test_y, verbose)
# Save results
acc_per_fold.append(accuracy)
sens_per_fold.append(sens)
spec_per_fold.append(spec)
auc_per_fold.append(auc)
# Print statistics of results
print(
f"Mean accuracy: {np.mean(acc_per_fold):.2f} \t"
f"and std : {np.std(acc_per_fold):.2f} \n"
f"Mean sensitivity: {np.mean(sens_per_fold):.2f} \t"
f"and std : {np.std(sens_per_fold):.2f} \n"
f"Mean specificity: {np.mean(spec_per_fold):.2f} \t"
f"and std : {np.std(spec_per_fold):.2f} \n"
f"Mean AUC: {np.mean(auc_per_fold):.2f} \t"
f"and std : {np.std(auc_per_fold):.2f} \n"
f"Time taken : {time.time() - t0:.2f}s\n"
)
return acc_per_fold, sens_per_fold, spec_per_fold, auc_per_fold
# **Cross-validation**
#
# We now apply cross-validation and show the statistics for all three ML models. In real world conditions, cross-validation usually applies 5 or more folds, but for the sake of performance we will reduce it to 3. You can change the value of `N_FOLDS` in this cell below.
N_FOLDS = 3
# _Note_: Next cell takes long to execute
for model in models:
print("\n======= ")
print(f"{model['label']}")
crossvalidation(model["model"], compound_df, n_folds=N_FOLDS)
# We look at the cross-validation performance for molecules encoded using Morgan fingerprint and not MACCS keys.
# Reset data frame
compound_df = chembl_df.copy()
# Use Morgan fingerprint with radius 3
compound_df["fp"] = compound_df["smiles"].apply(smiles_to_fp, args=("morgan3",))
compound_df.head(3)
# NBVAL_CHECK_OUTPUT
# _Note_: Next cell takes long to execute
for model in models:
if model["label"] == "Model_SVM":
# SVM is super slow with long fingerprints
# and will have a performance similar to RF
# We can skip it in this test, but if you want
# to run it, feel free to replace `continue` with `pass`
continue
print("\n=======")
print(model["label"])
crossvalidation(model["model"], compound_df, n_folds=N_FOLDS)
# ## Discussion
#
# * Which model performed best on our data set and why?
# * All three models perform (very) well on our dataset. The best models are the random forest and support vector machine models which showed a mean AUC of about 90%. Our neural network showed slightly lower results.
# * There might be several reasons that random forest and support vector machine models performed best. Our dataset might be easily separable in active/inactive with some simple tree-like decisions or with the radial basis function, respectively. Thus, there is not such a complex pattern in the fingerprints to do this classification.
# * A cause for the slightly poorer performance of the ANN could be that there was simply too few data to train the model on.
# * Additionally, it is always advisable to have another external validation set for model evaluation.
# * Was MACCS the right choice?
# * Obviously, MACCS was good to start training and validating models to see if a classification is possible.
# * However, MACCS keys are rather short (166 bit) compared to others (2048 bit), as for example Morgan fingerprint. As shown in the last simulation, having longer fingerprint helps the learning process. All tested models performed slightly better using Morgan fingerprints (see mean AUC increase).
#
#
# ### Where can we go from here?
#
# * We successfully trained several models.
# * The next step could be to use these models to do a classification with an unknown screening dataset to predict novel potential EGFR inhibitors.
# * An example for a large screening data set is e.g. [MolPort](https://www.molport.com/shop/database-download) with over 7 million compounds.
# * Our models could be used to rank the MolPort compounds and then further study those with the highest predicted probability of being active.
# * For such an application, see also the [TDT Tutorial](https://github.com/sriniker/TDT-tutorial-2014) developed by <NAME> and <NAME>, where they trained a fusion model to screen [eMolecules](https://www.emolecules.com/) for new anti-malaria drugs.
# ## Quiz
#
# * How can you apply ML for virtual screening?
# * Which machine learning algorithms do you know?
# * What are necessary prerequisites to successfully apply ML?
|
teachopencadd/talktorials/T007_compound_activity_machine_learning/talktorial.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: 'Python 3.7.3 64-bit (''base'': conda)'
# language: python
# name: python37364bitbasecondac1e1af396773407484830c731e4132c7
# ---
# # Chapter 12. Advanced pandas
#
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
# # 12.1 Categorical Data
#
# > <NAME>. Python for Data Analysis (p. 545). O'Reilly Media. Kindle Edition.
values = pd.Series(['apple','orange','apple','apple']*2)
values
values.unique()
values.nunique()
values.value_counts()
# ## Dimension Tables
values = pd.Series([0,1,0,0,]*2)
dim=pd.Series(['apple','orange'])
values
dim
dim.take(values)
# Return the elements in the given *positional* indices along an axis.
np.random.seed(14)
fruits = ['apple', 'orange', 'apple', 'apple'] * 2
N = len(fruits)
df = pd.DataFrame({'fruit': fruits, 'basket_id': np.arange(N),
'count': np.random.randint( 3, 15, size = N),
'weight': np.random.uniform( 0, 4, size = N)},
columns =['basket_id', 'fruit', 'count', 'weight'])
df
fruit_cat=df['fruit'].astype('category')
fruit_cat
c=fruit_cat.values
type(c)
fruit_cat.values.categories
fruit_cat.values.codes
df.info()
df['fruit']=df['fruit'].astype('category')
df
df.info()
my_categories = pd.Categorical(['foo', 'bar', 'baz', 'foo', 'bar'])
my_categories
categories = pd.Categorical(['foo', 'bar', 'baz'])
codes = [0, 1, 2, 0, 0, 1]
my_cats_2 = pd.Categorical.from_codes(codes,categories)
my_cats_2
ordered_cats = pd.Categorical.from_codes(codes,categories,ordered=True)
ordered_cats
# ## converting to ordered
my_cats_2.as_ordered()
# # Computations with Categoricals
#
np.random.seed(12345)
draws = np.random.randn(1000)
draws[:5]
bins = pd.qcut( draws, 4)
bins
# Using labels
bins = pd.qcut( draws, 4,labels=['Q1','Q2','Q3','Q4'])
bins
bins.categories
bins.codes[:10]
bins = pd.Series( bins, name ='quartile')
results = (pd.Series(draws).groupby(bins).agg(['count', 'min', 'max']).reset_index())
results
pd.Series(draws)
N= 10000000
draws=pd.Series(np.random.randn(N))
labels=pd.Series(['foo','bar','baz','qux']*(N//4))
labels
categories=labels.astype('category')
labels.memory_usage(),categories.memory_usage()
# +
# conversion is one time cost
# %time _ = labels.astype('category')
# +
s = pd.Series(['a', 'b', 'c', 'd'] * 2)
cat_s=s.astype('category')
cat_s
# -
cat_s.cat.codes
cat_s.cat.categories
actual_categories = ['a', 'b', 'c', 'd', 'e']
cat_s2 = cat_s.cat.set_categories(actual_categories)
cat_s2
cat_s.value_counts(),cat_s2.value_counts()
cat_s.value_counts(normalize=True),cat_s2.value_counts(normalize=True)
cat_s3 = cat_s[cat_s.isin(['a', 'b'])]
cat_s3
cat_s3.cat.remove_unused_categories()
# # Creating dummy variables for modeling
cat_s = pd.Series(['a', 'b', 'c', 'd'] * 2, dtype ='category')
pd.get_dummies(cat_s)
# # pandas groupby print_groups_head
def print_grp_head(df_grp_by):
for key,grp in df_grp_by:
print(key,' -> ')
print(grp.head())
df = pd.DataFrame({'key': ['a', 'b', 'c'] * 4,'value': np.arange(12.)})
df.head()
print_grp_head(df.groupby('key'))
g = df.groupby('key').value
g
print_grp_head(g)
g.mean()
g.transform(lambda x: x.mean()) # x is groupby series group
g.transform('mean')
g.transform( lambda x: x * 2)
g.transform( lambda x: x.rank(ascending=False))
def normalize(x):
'x: group of groupby obeject'
return (x - x.mean()) / x.std()
g.transform(normalize)
g.apply(normalize)
# %time g.transform('mean')
# %time g.apply(lambda x: x.mean())
normalized = (df['value'] - g.transform('mean')) / g.transform('std')
normalized
# # Grouped Time Resampling
N=15
times = pd.date_range('2017-05-20 00:00', freq ='1min', periods = N)
df = pd.DataFrame({'time': times, 'value': np.arange(N)})
df.head()
df.set_index('time').resample('5min').count()
df2 = pd.DataFrame({'time': times.repeat(3),
'key': np.tile(['a', 'b', 'c'], N),
'value': np.arange( N * 3.)})
df2[:7]
df2.shape
time_key = pd.Grouper(freq='5min')
time_key
resampled=(df2.set_index('time').groupby(['key',time_key])).sum()
resampled
resampled.reset_index()
# # 12.3 Techniques for Method Chaining
# ## The pipe Method
#
# <NAME>. Python for Data Analysis (p. 569). O'Reilly Media. Kindle Edition.
df2.head(10)
def group_demean( df, by, cols):
result = df.copy()
g = df.groupby(by)
for c in cols:
result[c] = df[c] - g[c].transform('mean')
return result
result = (df2.pipe(group_demean, ['key'], ['value']))
result
|
JupyterCode/pandas_scripts_PDA_CH_12.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# + [markdown] hide_input=false
# # Задание 1.1 - Метод К-ближайших соседей (K-neariest neighbor classifier)
#
# В первом задании вы реализуете один из простейших алгоритмов машинного обучения - классификатор на основе метода K-ближайших соседей.
# Мы применим его к задачам
# - бинарной классификации (то есть, только двум классам)
# - многоклассовой классификации (то есть, нескольким классам)
#
# Так как методу необходим гиперпараметр (hyperparameter) - количество соседей, мы выберем его на основе кросс-валидации (cross-validation).
#
# Наша основная задача - научиться пользоваться numpy и представлять вычисления в векторном виде, а также ознакомиться с основными метриками, важными для задачи классификации.
#
# Перед выполнением задания:
# - запустите файл `download_data.sh`, чтобы скачать данные, которые мы будем использовать для тренировки
# - установите все необходимые библиотеки, запустив `pip install -r requirements.txt` (если раньше не работали с `pip`, вам сюда - https://pip.pypa.io/en/stable/quickstart/)
#
# Если вы раньше не работали с numpy, вам может помочь tutorial. Например этот:
# http://cs231n.github.io/python-numpy-tutorial/
# + hide_input=false
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline
# %load_ext autoreload
# %autoreload 2
# + hide_input=false
from dataset import load_svhn
from knn import KNN
from metrics import binary_classification_metrics, multiclass_accuracy
# + [markdown] hide_input=true
# # Загрузим и визуализируем данные
#
# В задании уже дана функция `load_svhn`, загружающая данные с диска. Она возвращает данные для тренировки и для тестирования как numpy arrays.
#
# Мы будем использовать цифры из датасета Street View House Numbers (SVHN, http://ufldl.stanford.edu/housenumbers/), чтобы решать задачу хоть сколько-нибудь сложнее MNIST.
# -
train_X, train_y, test_X, test_y = load_svhn("data", max_train=1000, max_test=100)
samples_per_class = 5 # Number of samples per class to visualize
plot_index = 1
for example_index in range(samples_per_class):
for class_index in range(10):
plt.subplot(5, 10, plot_index)
image = train_X[train_y == class_index][example_index]
plt.imshow(image.astype(np.uint8))
plt.axis('off')
plot_index += 1
# # Сначала реализуем KNN для бинарной классификации
#
# В качестве задачи бинарной классификации мы натренируем модель, которая будет отличать цифру 0 от цифры 9.
# +
# First, let's prepare the labels and the source data
# Only select 0s and 9s
binary_train_mask = (train_y == 0) | (train_y == 9)
binary_train_X = train_X[binary_train_mask]
binary_train_y = train_y[binary_train_mask] == 0
binary_test_mask = (test_y == 0) | (test_y == 9)
binary_test_X = test_X[binary_test_mask]
binary_test_y = test_y[binary_test_mask] == 0
# Reshape to 1-dimensional array [num_samples, 32*32*3]
binary_train_X = binary_train_X.reshape(binary_train_X.shape[0], -1)
binary_test_X = binary_test_X.reshape(binary_test_X.shape[0], -1)
# -
# Create the classifier and call fit to train the model
# KNN just remembers all the data
knn_classifier = KNN(k=1)
knn_classifier.fit(binary_train_X, binary_train_y)
# ## Пришло время написать код!
#
# Последовательно реализуйте функции `compute_distances_two_loops`, `compute_distances_one_loop` и `compute_distances_no_loops`
# в файле `knn.py`.
#
# Эти функции строят массив расстояний между всеми векторами в тестовом наборе и в тренировочном наборе.
# В результате они должны построить массив размера `(num_test, num_train)`, где координата `[i][j]` соотвествует расстоянию между i-м вектором в test (`test[i]`) и j-м вектором в train (`train[j]`).
#
# **Обратите внимание** Для простоты реализации мы будем использовать в качестве расстояния меру L1 (ее еще называют [Manhattan distance](https://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D1%81%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D0%B5_%D0%B3%D0%BE%D1%80%D0%BE%D0%B4%D1%81%D0%BA%D0%B8%D1%85_%D0%BA%D0%B2%D0%B0%D1%80%D1%82%D0%B0%D0%BB%D0%BE%D0%B2)).
#
# 
# TODO: implement compute_distances_two_loops in knn.py
dists = knn_classifier.compute_distances_two_loops(binary_test_X)
print(dists[0])
assert np.isclose(dists[0, 10], np.sum(np.abs(binary_test_X[0] - binary_train_X[10])))
# TODO: implement compute_distances_one_loop in knn.py
dists = knn_classifier.compute_distances_one_loop(binary_test_X)
print(dists[0])
assert np.isclose(dists[0, 10], np.sum(np.abs(binary_test_X[0] - binary_train_X[10])))
# TODO: implement compute_distances_no_loops in knn.py
dists = knn_classifier.compute_distances_no_loops(binary_test_X)
print(dists[0])
assert np.isclose(dists[0, 10], np.sum(np.abs(binary_test_X[0] - binary_train_X[10])))
# Lets look at the performance difference
# %timeit knn_classifier.compute_distances_two_loops(binary_test_X)
# %timeit knn_classifier.compute_distances_one_loop(binary_test_X)
# %timeit knn_classifier.compute_distances_no_loops(binary_test_X)
# TODO: implement predict_labels_binary in knn.py
prediction = knn_classifier.predict(binary_test_X)
prediction, binary_test_y
# TODO: implement binary_classification_metrics in metrics.py
precision, recall, f1, accuracy = binary_classification_metrics(prediction, binary_test_y)
print("KNN with k = %s" % knn_classifier.k)
print("Accuracy: %4.2f, Precision: %4.2f, Recall: %4.2f, F1: %4.2f" % (accuracy, precision, recall, f1))
# +
# Let's put everything together and run KNN with k=3 and see how we do
knn_classifier_3 = KNN(k=3)
knn_classifier_3.fit(binary_train_X, binary_train_y)
prediction = knn_classifier_3.predict(binary_test_X)
precision, recall, f1, accuracy = binary_classification_metrics(prediction, binary_test_y)
print("KNN with k = %s" % knn_classifier_3.k)
print("Accuracy: %4.2f, Precision: %4.2f, Recall: %4.2f, F1: %4.2f" % (accuracy, precision, recall, f1))
# -
# # Кросс-валидация (cross-validation)
#
# Попробуем найти лучшее значение параметра k для алгоритма KNN!
#
# Для этого мы воспользуемся k-fold cross-validation (https://en.wikipedia.org/wiki/Cross-validation_(statistics)#k-fold_cross-validation). Мы разделим тренировочные данные на 5 фолдов (folds), и по очереди будем использовать каждый из них в качестве проверочных данных (validation data), а остальные -- в качестве тренировочных (training data).
#
# В качестве финальной оценки эффективности k мы усредним значения F1 score на всех фолдах.
# После этого мы просто выберем значение k с лучшим значением метрики.
#
# *Бонус*: есть ли другие варианты агрегировать F1 score по всем фолдам? Напишите плюсы и минусы в клетке ниже.
# +
# Find the best k using cross-validation based on F1 score
num_folds = 5
# TODO: split the training data in 5 folds and store them in train_folds_X/train_folds_y
train_folds_X = np.array_split(binary_train_X, num_folds)
train_folds_y = np.array_split(binary_train_y, num_folds)
k_choices = [1, 2, 3, 5, 8, 10, 15, 20, 25, 50]
k_to_f1 = {} # dict mapping k values to mean F1 scores (int -> float)
for k in k_choices:
# TODO: perform cross-validation
# Go through every fold and use it for testing and all other folds for training
# Perform training and produce F1 score metric on the validation dataset
# Average F1 from all the folds and write it into k_to_f1
k_to_f1[k] = 0.0
for f in range(num_folds):
fold_binary_train_X = np.concatenate([fold for idx, fold in enumerate(train_folds_X) if idx != f], 0)
fold_binary_train_y = np.concatenate([fold for idx, fold in enumerate(train_folds_y) if idx != f], 0)
fold_binary_val_X = train_folds_X[f]
fold_binary_val_y = train_folds_y[f]
knn_classifier_k = KNN(k=k)
knn_classifier_k.fit(fold_binary_train_X, fold_binary_train_y)
prediction = knn_classifier_k.predict(fold_binary_val_X)
precision, recall, f1, accuracy = binary_classification_metrics(prediction, fold_binary_val_y)
k_to_f1[k] += f1
k_to_f1[k] = k_to_f1[k] / num_folds
for k in sorted(k_to_f1):
print('k = %d, f1 = %f' % (k, k_to_f1[k]))
print("Max f1 = %f with k = %d" % (k_to_f1[max(k_to_f1, key=k_to_f1.get)], max(k_to_f1, key=k_to_f1.get)))
# -
# ### Проверим, как хорошо работает лучшее значение k на тестовых данных (test data)
# +
# TODO Set the best k to the best value found by cross-validation
best_k = 3
best_knn_classifier = KNN(k=best_k)
best_knn_classifier.fit(binary_train_X, binary_train_y)
prediction = best_knn_classifier.predict(binary_test_X)
precision, recall, f1, accuracy = binary_classification_metrics(prediction, binary_test_y)
print("Best KNN with k = %s" % best_k)
print("Accuracy: %4.2f, Precision: %4.2f, Recall: %4.2f, F1: %4.2f" % (accuracy, precision, recall, f1))
# -
# # Многоклассовая классификация (multi-class classification)
#
# Переходим к следующему этапу - классификации на каждую цифру.
# +
# Now let's use all 10 classes
train_X = train_X.reshape(train_X.shape[0], -1)
test_X = test_X.reshape(test_X.shape[0], -1)
knn_classifier = KNN(k=3)
knn_classifier.fit(train_X, train_y)
# -
# TODO: Implement predict_labels_multiclass
predict = knn_classifier.predict(test_X)
# TODO: Implement multiclass_accuracy
accuracy = multiclass_accuracy(predict, test_y)
print("Accuracy: %4.2f" % accuracy)
# Снова кросс-валидация. Теперь нашей основной метрикой стала точность (accuracy), и ее мы тоже будем усреднять по всем фолдам.
# +
# Find the best k using cross-validation based on accuracy
num_folds = 5
# TODO: split the training data in 5 folds and store them in train_folds_X/train_folds_y
train_folds_X = np.array_split(train_X, num_folds)
train_folds_y = np.array_split(train_y, num_folds)
k_choices = [1, 2, 3, 5, 8, 10, 15, 20, 25, 50]
k_to_accuracy = {}
for k in k_choices:
# TODO: perform cross-validation
# Go through every fold and use it for testing and all other folds for validation
# Perform training and produce accuracy metric on the validation dataset
# Average accuracy from all the folds and write it into k_to_accuracy
k_to_accuracy[k] = 0.0
for f in range(num_folds):
fold_train_X = np.concatenate([fold for idx, fold in enumerate(train_folds_X) if idx != f], 0)
fold_train_y = np.concatenate([fold for idx, fold in enumerate(train_folds_y) if idx != f], 0)
fold_val_X = train_folds_X[f]
fold_val_y = train_folds_y[f]
knn_classifier_k = KNN(k=k)
knn_classifier_k.fit(fold_train_X, fold_train_y)
prediction = knn_classifier_k.predict(fold_val_X)
accuracy = multiclass_accuracy(prediction, fold_val_y)
k_to_accuracy[k] += accuracy
k_to_accuracy[k] = k_to_accuracy[k] / num_folds
for k in sorted(k_to_accuracy):
print('k = %d, accuracy = %f' % (k, k_to_accuracy[k]))
print("Max accuarcy = %f with k = %d" % (k_to_accuracy[max(k_to_accuracy, key=k_to_accuracy.get)], max(k_to_accuracy, key=k_to_accuracy.get)))
# -
# ### Финальный тест - классификация на 10 классов на тестовой выборке (test data)
#
# Если все реализовано правильно, вы должны увидеть точность не менее **0.2**.
# +
# TODO Set the best k as a best from computed
best_k = 5
best_knn_classifier = KNN(k=best_k)
best_knn_classifier.fit(train_X, train_y)
prediction = best_knn_classifier.predict(test_X)
# Accuracy should be around 20%!
accuracy = multiclass_accuracy(prediction, test_y)
print("Accuracy: %4.2f" % accuracy)
|
assignments/assignment1/KNN.ipynb
|
# ---
# jupyter:
# jupytext:
# text_representation:
# extension: .py
# format_name: light
# format_version: '1.5'
# jupytext_version: 1.14.4
# kernelspec:
# display_name: Python 3
# language: python
# name: python3
# ---
# Importing the libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, confusion_matrix
from sklearn.model_selection import cross_val_score
# %matplotlib inline
# Importing the dataset
dataset = pd.read_csv('Social_Network_Ads.csv')
dataset
X = dataset.iloc[:, 2:4].values
y = dataset.iloc[:, -1].values
print(X.shape)
print(y.shape)
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.25, random_state=42)
print(X_train.shape)
print(y_train.shape)
print(X_test.shape)
print(y_test.shape)
# Feature Scaling
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
sc.fit_transform(X_train)
sc.transform(X_test)
# +
# Fitting Random Forest Classification to the Training set
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators=10,
criterion='entropy',
max_depth=10,
#min_samples_split=2,
#min_samples_leaf=1,
#min_weight_fraction_leaf=0.0,
#max_features='auto',
max_leaf_nodes=8,
#min_impurity_decrease=0.0,
#min_impurity_split=None,
#bootstrap=True,
#oob_score=False,
n_jobs=-1,
random_state=42,
verbose=1)
clf.fit(X_train, y_train)
pred = clf.predict(X_test)
print(confusion_matrix(y_test, pred))
print(accuracy_score(y_test, pred))
cross_val = cross_val_score(clf, X, y, cv=10, scoring='accuracy').mean()
# -
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
est = RandomForestClassifier(n_jobs=-1)
params = {'n_estimators':range(0,550,50),
'criterion':['entropy','gini'],
'max_depth': range(0,20,4),
#min_samples_split=2,
'min_samples_leaf': range(1,4),
#min_weight_fraction_leaf=0.0,
'max_features':range(1,3),
'max_leaf_nodes':range(8,40,8),
#min_impurity_decrease=0.0,
#min_impurity_split=None,
'bootstrap':[True, False],
#oob_score=False,
}
def hypertuning_rfclf(classifier, params, iterations, dataset_X, dataset_y):
rdSearch = RandomizedSearchCV(classifier,
params,
n_jobs=-1,
n_iter=iterations,
cv=9)
rdSearch.fit(dataset_X, dataset_y)
best_params = rdSearch.best_params_
best_score = rdSearch.best_score_
return best_params, best_score
rf_params, rf_ht_score = hypertuning_rfclf(est, params, 40, X, y)
rf_params
rf_ht_score
# +
# now that we've been provided with the best values, we create the classifier
# again with these values and make a prediction after fine-tuning the hyper-parameters
classifier = RandomForestClassifier(
n_estimators=500,
criterion='entropy',
max_depth=12,
min_samples_leaf=1,
max_features=2,
max_leaf_nodes=8,
bootstrap=True,
n_jobs=-1,
random_state=42,
)
classifier.fit(X_train, y_train)
pred_new = classifier.predict(X_test)
print(confusion_matrix(y_test, pred_new))
print(accuracy_score(y_test, pred_new))
# -
cross_val = cross_val_score(clf, X, y, cv=10, scoring='accuracy').mean()
|
Randomized_Search_CV/Randomized_Search_CV_with_Random_Forest.ipynb
|